2.1 Coupled Lagrangian-Eulerian

To accurately predict fluidic deformation, CLE, an advanced FEA formulation, was applied. In CLE, the mesh can deform to track the boundaries of a material using the Lagrangian formulation but is periodically rezoned to the ambient Eulerian mesh that may contain multiple materials in a single cell. By combining the advantages of both Lagrangian and Eulerian formulations, a material calculation is conducted until the mesh is distorted (Eulerian), then the distorted mesh is smoothed out by rezoning algorithm (Lagrangian).

The CLE was initially proposed by Noh⁽Reference Noh¹⁵⁾ and Trulio⁽Reference Trulio¹⁶⁾ and has since been implemented by researchers including Hughes et al.⁽Reference Hughes, Liu and Zimmermann¹⁷⁾ in 1981 and more contemporary research programs, the latest being 2014⁽Reference Karimi, Navidbakhsh, Razaghi and Haghpanahi¹⁸⁾. To conserve mass, momentum and energy, an advection algorithm is required to periodically rezone the Lagrangian domain. For this study, a second-order monotone upwind discretisation, known as Van Leer mesh advection⁽Reference Van Leer¹⁹⁾, is used to rezone the mesh. Using the rezoning algorithm to periodically morph the distorted mesh, conservations of mass and momentum in the Lagrangian domain are ensured⁽Reference Dukowicz and Kodis²⁰⁾. The conservation equations for mass, momentum and energy in CLE form can be written as:

Mass:

(1) $$\begin{equation} {\left.\frac{\partial\rho }{\partial t}\right|}_{ref}+\left(v_m-\hat{v}\right)\cdot \nabla\left(\rho \right)=-\rho \nabla\cdot v \label{eqn1} \end{equation}$$

Momentum:

(2) $$\begin{equation} \rho \left({\left.\frac{\partial v}{\partial t}\right|}_{ref}+\left(\left(v_m-\hat{v}\right)\cdot \nabla\right)v\right)=\nabla\cdot \sigma +\rho \vec{f} \label{eqn2} \end{equation}$$

Total Energy:

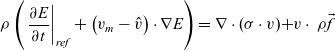(3) $$\begin{equation} \rho \left({\left.\frac{\partial E}{\partial t}\right|}_{ref}+\left(v_m-\hat{v}\right)\cdot \nabla E\right)=\nabla\cdot {\rm (}\sigma \cdot v{\rm )+}v\cdot ~\rho \vec{f} \label{eqn3} \end{equation}$$

where $$$\sigma $$$ is the Cauchy stress tensor, E is the total energy and f is the body force. The right-hand side of the equation is the Eulerian formulation, while the arbitrary motion of the CLE mesh is only reflected in the left-hand side. Subscript ref is the reference domain, $v_m$ is the material velocity inside of CLE mesh and $\hat{v}$ is the CLE mesh grid velocity.

2.2 Fluid body modelling

Conventional FEA material definitions are not suitable for predicting fluidic deformation because the fluidic motion encompasses shear stresses driven by viscous effects. Therefore, the CLE formulation requires appropriate material definitions and a corresponding equation of state (EOS).

2.2.1 Material model for water

For the presented work, a Newtonian viscous fluid model is defined to calculate deviatoric stress based on the strain rate of the continuum. The deviatoric stress $({\sigma {\rm '}}_{xy})$ of this material model is:

(4) $$\begin{equation} {\sigma {\rm '}}_{xy}=2\mu \cdot {\dot{\varepsilon }}_{xy}\label{eqn4}\end{equation}$$

where $\mu$ is the dynamic viscosity, and ${\dot{\varepsilon }}_{xy}$ is the strain rate tensor. To constitute a complete stress tensor to represent the total stress within the fluid continuum, the hydrostatic pressure (p) is calculated using an EOS. For the hydrostatic pressure (p) in tensor form, the hydrostatic pressure (p) is multiplied by Kronecker delta $({\delta }_{xy})$ and added to the previously defined deviatoric stress $({\sigma {\rm '}}_{xy})$ . The total stress $({\sigma }_{xy})$ at a given state can be calculated using:

(5) $$\begin{equation} {\sigma }_{xy}={\sigma {\rm '}}_{xy}+p\cdot {\delta }_{xy} \label{eqn5} \end{equation}$$

2.2.2 EOS for water material

Using the state variables, the EOS calculates a constitutive mathematical relationship of a homogeneous material. For this study, the Mie-Gruneisen (M-G) EOS is used to estimate the dynamic response of fluids under high-velocity impact scenarios⁽Reference Hallquist¹²⁾:

(6) $$\begin{equation} p=\frac{C^{{\rm 2}}{\rho }_0\eta \left[{\rm 1+}\left(1-\frac{{\gamma }_0}{{\rm 2}}\right)\eta -\frac{a}{{\rm 2}}{\eta }^{{\rm 2}}\right]}{\left[1-\left(S_{{\rm 1}}-{\rm 1}\right)\eta -S_{{\rm 2}}\frac{{\eta }^{{\rm 2}}}{\eta {\rm +1\ }}-S_{{\rm 3}}\frac{{\eta }^{{\rm 3}}}{{\left(\eta {\rm +1}\right)}^{{\rm 2}}}\right]}+\left({\gamma }_0+a\eta \right)IE \label{eqn6} \end{equation}$$

where $\eta$ is the relative density ratio $(\eta ={\rho }/{{\rho }_0}-{\rm 1})$ , C is the speed of sound of the material, $S_{1-3}$ are the empirical Hugoniot slope constants for the pressure-volume relationship, ${\gamma }_0$ is the Gruneisen gamma, a is the first-order dimensionless empirical volume correction factor and IE is the internal energy. Several researchers have proposed to use the M-G EOS and various material constants to govern the water behaviour in FEA. Therefore, a set of material constants was selected based on the work done by Shin et al.⁽Reference Shin, Lee, Lam and Yeo²¹⁾. The EOS and material parameters for water are shown in Table 1.

Table 1 Input parameters for water ⁽Reference Shin, Lee, Lam and Yeo²¹⁾

By using the CLE formulations and the fluidic modelling strategy (Eulerian), the FEA solver can predict non-linear fluidic motions. Coupled with the solid (Lagrangian) objects using penalty-based contact, FSI systems can be effectively simulated.

3.1 Virtual fuselage section

Due to the considerable lack of publicly available information regarding contemporary aircraft fuselage structures, the current study resorts to developing and using the Boeing 737 section model, partly constructed based on the only existing references on an unrestricted physical trial. The virtual fuselage section used was previously developed and validated for hard-surface drop tests⁽Reference Song, Horton, Perino, Thurber and Bayandor⁸⁾ by being thoroughly compared with the experiment reported by Jackson et al.⁽Reference Jackson and Fasanella³⁾. The constructed section is shown in Fig. 2.

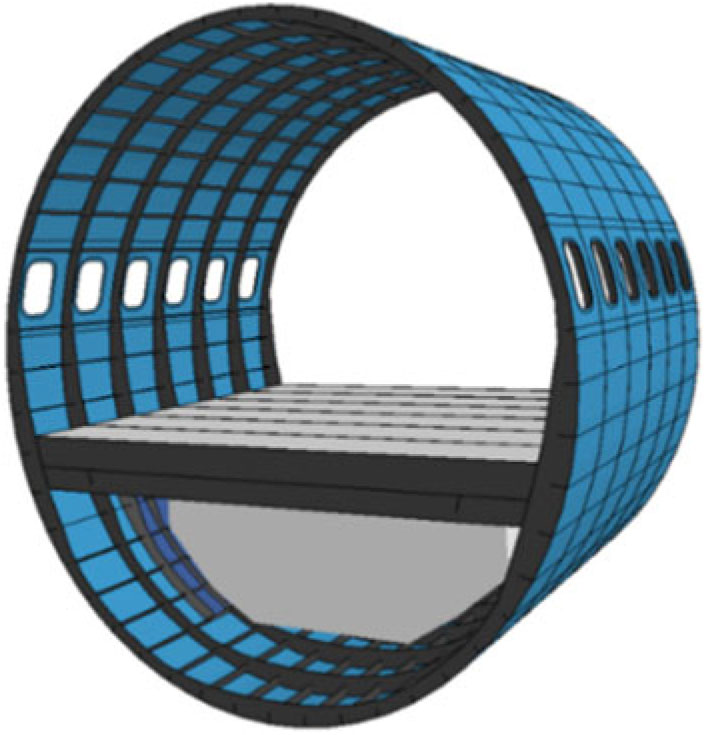
Figure 2. B-737 fuselage section model.

Perfect bonding assumption is applied to the entire fuselage section, except for the cargo door section. In that case, instead of a perfect attachment, the structural connection consists of hinge structures and locks on the cargo door. All components in the fuselage section are assumed to be aluminium alloys, based on an earlier work⁽Reference Jackson and Fasanella³⁾, with an appropriate failure strain. The corresponding properties are listed in Table 2. The plastic failure strain is assumed to account for material aging-effect due to cyclic loading.

Table 2 Material definitions for aluminium alloys used in the simulation

The fuselage section is 4.09 m in height, 3.76 m in width and 3.05 m in length. Both a single cargo door and fuel tank are explicitly modelled in order to replicate the structural discontinuities. The overall mass of the fuselage section is 3,909 kg, which is close to the reported value of 3,977 kg. The fuel tank is 168 kg, suspended from the passenger floor by two longitudinal fuel rails.

The fuel mass inside the tank is represented by evenly distributed nodal mass over the entire mesh of the fuel tank, emulating the total tank mass of 1,694 kg. To account for auxiliary mass such as dummies, seats and other instrumentation used in the test, the overall mass of the passenger floor in the model is defined as 1,640 kg, also uniformly applied over the passenger floor and exactly matching the reported experimental mass. The impact velocity of the model is selected as 9.14 m/s, which matches the velocity reported from the experiment⁽Reference Jackson and Fasanella³⁾. In addition, to ensure realistic impact kinematics, gravity is also applied over the entire domain. Instead of attaching each individual component by tie-contact or failure-enabled connection, this macroscale study assumes perfect bonding between components.

3.2 Verification of computational fluid modelling

The fluid modelling verification was conducted by simulating shear-driven flow over a square cavity. The problem is a well-known fluid mechanics benchmark that has been used in many previous studies to evaluate different fluid modelling methods. Once the model was successfully developed using CLE and SPH, the results computed based on each monolithic solver were compared against the existing literature⁽Reference Ghia, Ghia and Shin²²⁾ as well as Computational Fluid Dynamics (CFD) results using FLUENT⁽Reference Horton, Song, Feaster and Bayandor¹¹⁾.

As shown in Fig. 3(a), the simulated cavity flow is set up for Re = 3,200, using the advanced finite element formulations (CLE and SPH) with $256\times256$ grid resolution. The fluid deformation using FEA solver predicts a primary vortex at the centre of the cavity. However, the secondary vortical structures at each corner are only successfully predicted using CLE and not shown in the results using SPH formulation.

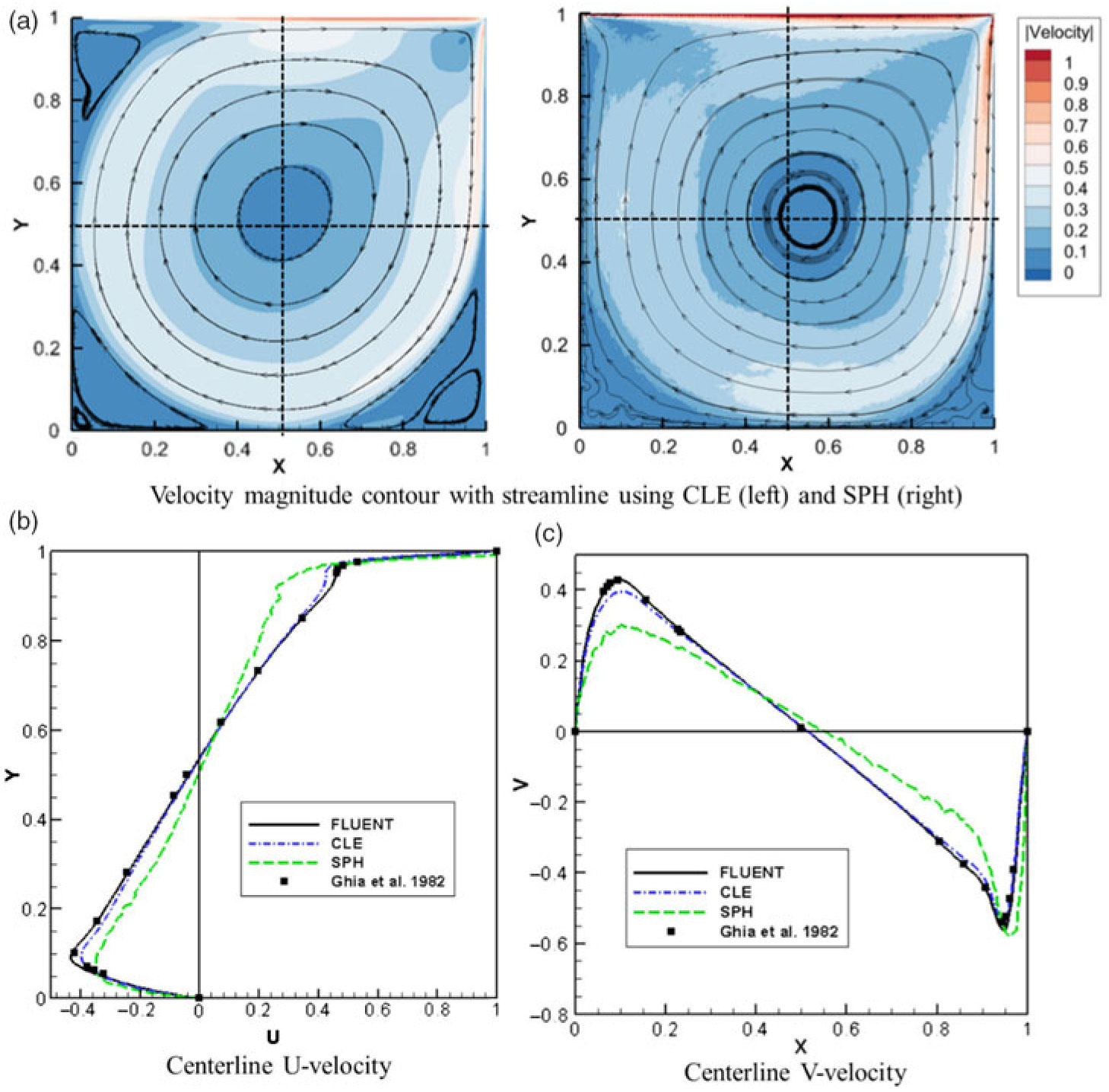
Figure 3. Streamline of the cavity for both CLE and SPH (a) with U velocity (b) and V velocity (c) along the cavity centre with various computational methods (Re=3,200) ⁽Reference Ghia, Ghia and Shin²²⁾.

Further results are depicted in Figs. 3(b) and 3(c). The plots show U and V velocities at the centre of the cavity along the vertical and horizontal direction, respectively. The velocity plots show the quantitative accuracy of the fluid approximation using CLE and SPH by comparing the reported data from the preceding work⁽Reference Ghia, Ghia and Shin²²⁾ and CFD results⁽Reference Horton, Song, Feaster and Bayandor¹¹⁾. As indicated by the velocity results in each direction, the computational accuracy of CLE is superior to that of the SPH formulation with several orders of magnitude less computational effort. The modelling approach and assessment analysis developed for this study are thoroughly discussed in Ref. (bib11).

4.1 Validation of FSI modelling strategy using wedge drop tests

To optimise the computational time and quality of the results, multiple mesh densities are examined to represent the body of water. The optimal mesh density is then selected by conducting the grid convergence index (GCI) study⁽Reference Celik, Ghia, Roache, Freitas, Coleman and Raad²³⁾.

The numerical simulations are based on the experiments conducted by Zhao et al.⁽Reference Zhao, Faltinsen and Aarsnes.¹⁴⁾. The wedge used for the experiment has a mass of 241 kg with a length of 1 m and a $30^{\circ}$ deadrise angle. For the computational work, the thickness of the water and wedge is set as 0.2 m, which corresponds to the reported instrumented length in the experiment. Gravity is applied over the entire domain, and the wedge material is defined as rigid.

In order to reproduce the experiment numerically, a proper mesh resolution is required for both the surrounding water and the wedge. Figure 4 shows the force responses of the wedge drop simulation with three different mesh resolutions, including one that demonstrates the effect that an improper mesh size has on the wedge drop results. As shown in Fig. 4, one of the highest mesh resolution cases suffers from a contact issue when the discrepancy in the mesh resolution between the water and wedge becomes significant. In this example, a single wedge (Lagrangian) element is assigned to contact with approximately six CLE elements.

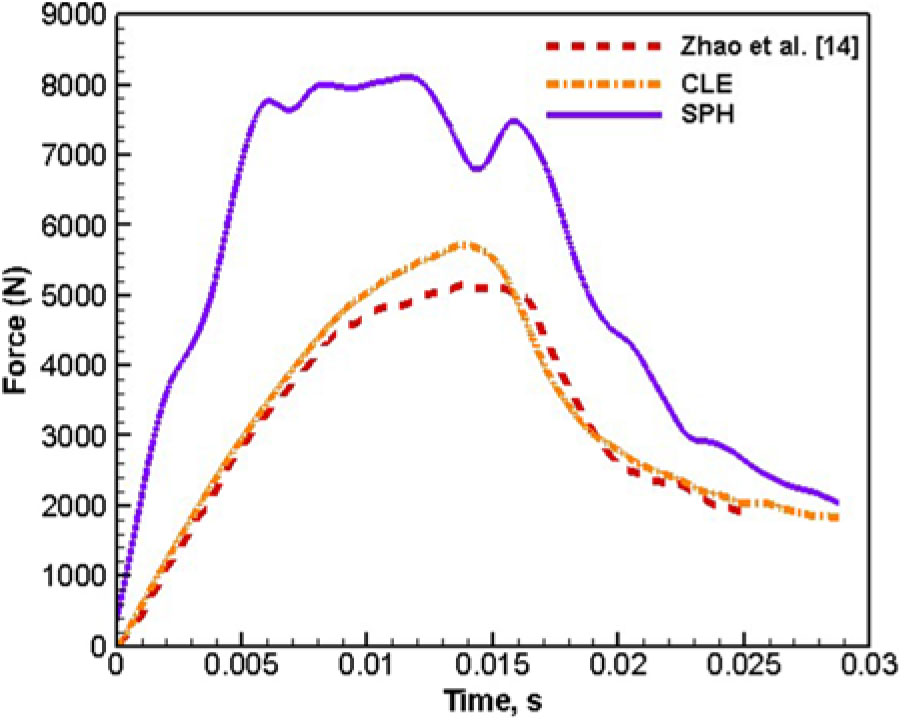
Figure 4. Force-time response between wedge and water using CLE.

To alleviate the computational error, the mesh size for the wedge is refined to a single Lagrangian element contacting with two CLE elements at the highest mesh resolution. Also, three coupling points are distributed over each Lagrangian segments to properly establish the penalty-based contact.

The same wedge model with higher mesh resolution is subsequently used in the other simulations to conduct the GCI study to assess the mesh dependence of the interactive analysis between the fluid and structure. Table 3 tabulates the result of the GCI study for the wedge drop simulation. The GCI reported in this table is calculated by averaging the GCI values at each time step. The averaged GCI between the coarse and medium mesh resolutions is 4.76%, while the medium to highest mesh resolutions shows a GCI of 2.82%. Considering the amount of computational time for each mesh density and their relative accuracy, the medium mesh resolution is selected for further simulations.

Table 3 Result of GCI study

SPH elements are also exploited in modelling the FSI event and compared with CLE results. To develop an equivalent simulation using SPH, the same number of SPH particles are assigned as the number of nodes used for the CLE medium mesh resolution to describe the water domain. To validate, the equivalent force-time response is used as a benchmark from the work done by Zhao et al.⁽Reference Zhao, Faltinsen and Aarsnes.¹⁴⁾, as shown in Fig. 5. CLE produces a much more accurate result than that of the SPH formulations. Additionally, SPH requires approximately six times higher computational effort than CLE. Thus, further simulations are conducted using CLE formulation.

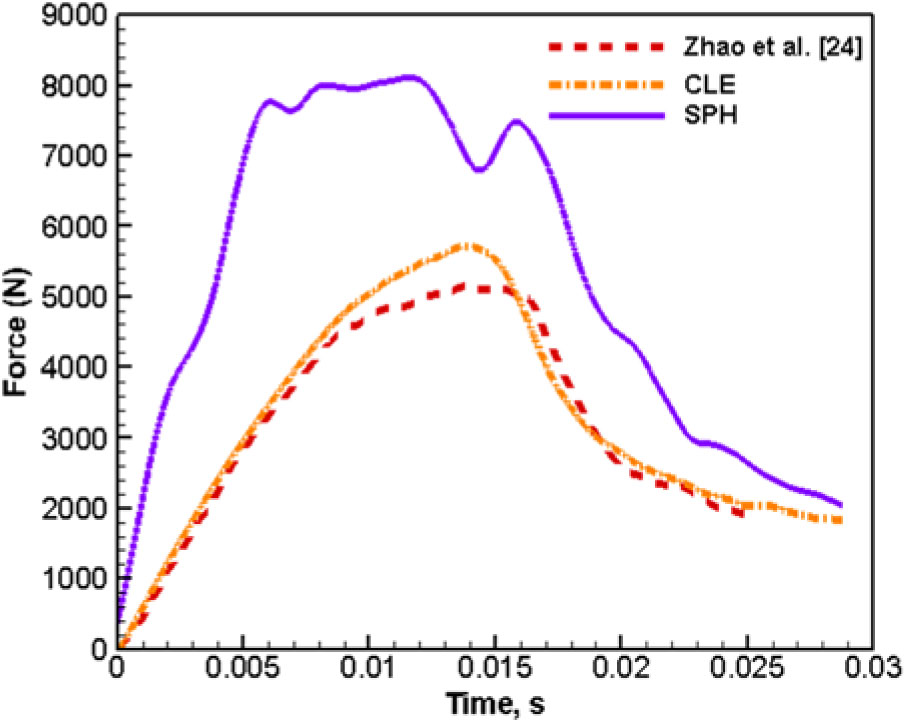
Figure 5. Force-time response of the wedge drop experiment and simulations using two different element formulations.

Given the absence of qualitative results in Ref. (14), a qualitative validation is attempted by comparing the simulations results to the work carried out by Shah⁽Reference Alexander, Carey, DiNardo, Gill, Gonzalez, Harry, Isidro, Judge, Puckett, Schoepfer, Song, Tilghman, Siddens, Satterwhite and Bayandor¹³⁾. For an FSI event, high-speed footage offers one of the most important observations, since the impulse and g-loading signature do not describe the entire dynamic response of the interactive bi-phase system.

Figure 6 shows the comparison between the experiment and the numerical simulation of the equivalent test conducted by Shah⁽Reference Alexander, Carey, DiNardo, Gill, Gonzalez, Harry, Isidro, Judge, Puckett, Schoepfer, Song, Tilghman, Siddens, Satterwhite and Bayandor¹³⁾. The deadrise angle for this particular experiment was reported as $30^{\circ}$ with an impact speed of 1.046 m/s and a mass of 1.639 kg. Further details of the experimental setup are described in Ref. (13).

Figure 6. Qualitative comparison between experiment⁽Reference Alexander, Carey, DiNardo, Gill, Gonzalez, Harry, Isidro, Judge, Puckett, Schoepfer, Song, Tilghman, Siddens, Satterwhite and Bayandor¹³⁾ and simulation.

To reduce the computational effort, the simulation uses plane symmetricity for both front and back face of the mesh. During the initial impact (0.01 s), an impinged jet flow is observed in the experiment at the interface between the free water surface and the wedge. A similar interaction is also predicted by the computational model. The thickness of the impinged flow in the computational work is significantly greater than that of the jet shown in the experiment. In the experiment, water was observed to breach the slight gap between the wedge and wall of the test section. Despite this, the comparisons between the simulation and test demonstrate a reasonable qualitative agreement. The free surface elevation during the impact remains similar between the test and analysis throughout the wedge descent window.

The disparities observed in the computational results are mostly caused by inadequate mesh resolution over the fluid domain. The CLE formulation represents the fluid body within the mesh by using volume fractions. In other words, the fluidic deformation can be more accurately presented with higher mesh density. However, the medium mesh resolution is necessary for CLE to make multiple simulations feasible.

4.2 Comprehensive analysis of fuselage section drop into water

The aforementioned fuselage model used for this study is developed based on an existing experiment⁽Reference Jackson and Fasanella³⁾, with an accompanying validation thoroughly described in a preceding work by Song et al.⁽Reference Song, Horton, Perino, Thurber and Bayandor⁸⁾. To conduct a comprehensive analysis, the FSI methodology is combined with the validated fuselage section model. Two other possible emergency landing surface candidates (soil and rigid ground) are included for comparison, with the g-loading response of the passenger floor as the common metric.

Figure 7 shows the sequential images of the water ditching simulation with the verified virtual fuselage section at 9.1 m/s impact speed. Figure 7(a) shows the initial impact, where jet flows begin to appear and interact with the fuselage. The fuselage continues to descend until 0.4 s, as shown in Fig. 7(b). At this point, the vertical motion of the fuselage is almost ceased due to the buoyancy effect. Despite gravity acting over the entire domain, the buoyancy forces stop the fuselage from uninterrupted sinking.

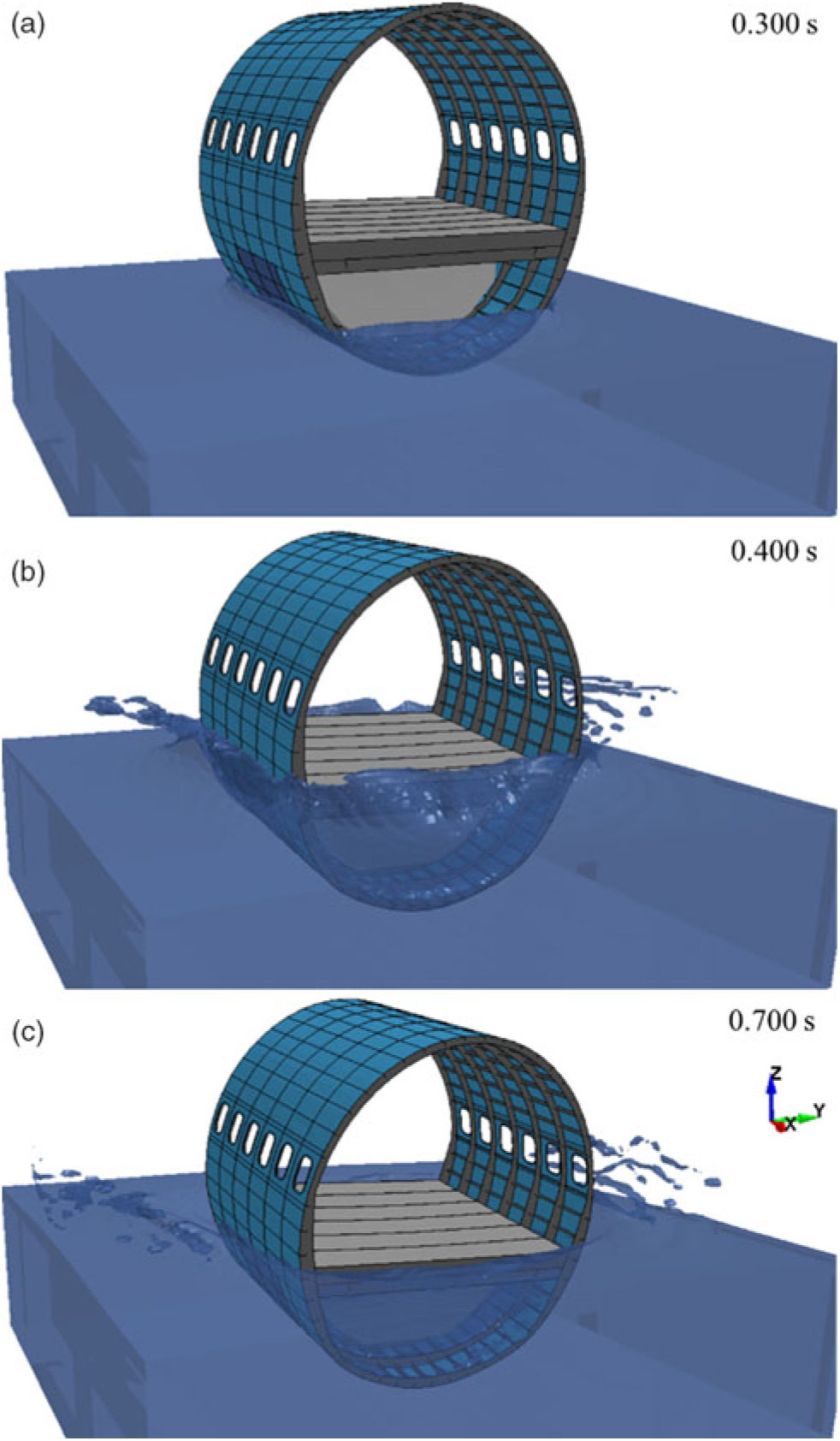
Figure 7. Fuselage section submerging into the water after impacting at 9.1 m/s.

Soon after the descending motion is stopped, shown in Fig. 7(c), the fuselage section starts rising (+Z-dir). Meanwhile, the structure tilts along its Y-axis (backward) due to the asymmetric weight distribution resulted from the location of the suspension points of the fuel tank. The section then resumes sinking as the water rushes through its front and back openings.

Figure 8 shows the computationally simulated g-loading time-history measured on the passenger floor near the cargo door for each of the landing surfaces, and Fig. 9 shows the sequential images of the stress response of fuselage section impacting at 9.1 m/s. Other than the impact surfaces, the contact conditions remain identical.

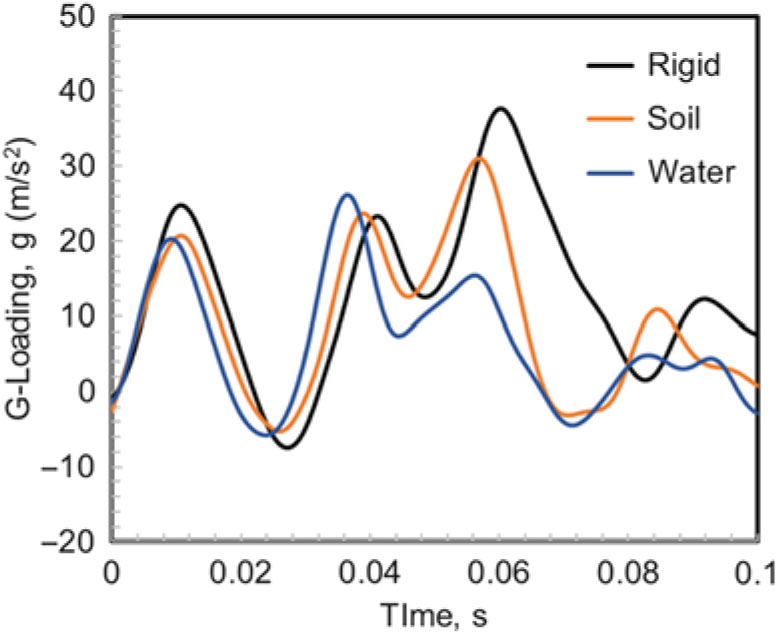
Figure 8. Comparison of g-loading on the passenger floor for three different crash-landing surfaces (9.1 m/s impact velocity).

At the moment of impact (0.01 s), the passenger floor rapidly decelerates as shown in Fig. 8. A large magnitude of stress is induced at the bottom of the fuselage section and transferred through the structure towards the passenger floor as shown in Fig. 9(a). The bottom of the fuel tank suspended from the passenger floor then comes into contact with the bottom of the fuselage section $(\sim 0.03\ \text{s})$ , as depicted in Fig. 9(b). Figure 9(c) highlights the moment when the top of the fuel tank, crushed by and moving in unison with the bottom of the fuselage, comes into contact with the passenger floor. The uneven stress distribution over the XY plane is due to the fuselage asymmetry resulting from the inclusion of the cargo door on the starboard side of the structure, which should not carry any shear loading. As a result, the exerted loading needs to be redistributed and carried mostly by the structure surrounding the door. This causes excess asymmetric loading on the starboard side of the structure (referring to its coordinate system, Fig. 9 depicts the back of the fuselage with the starboard side appearing on the left side of the figures).

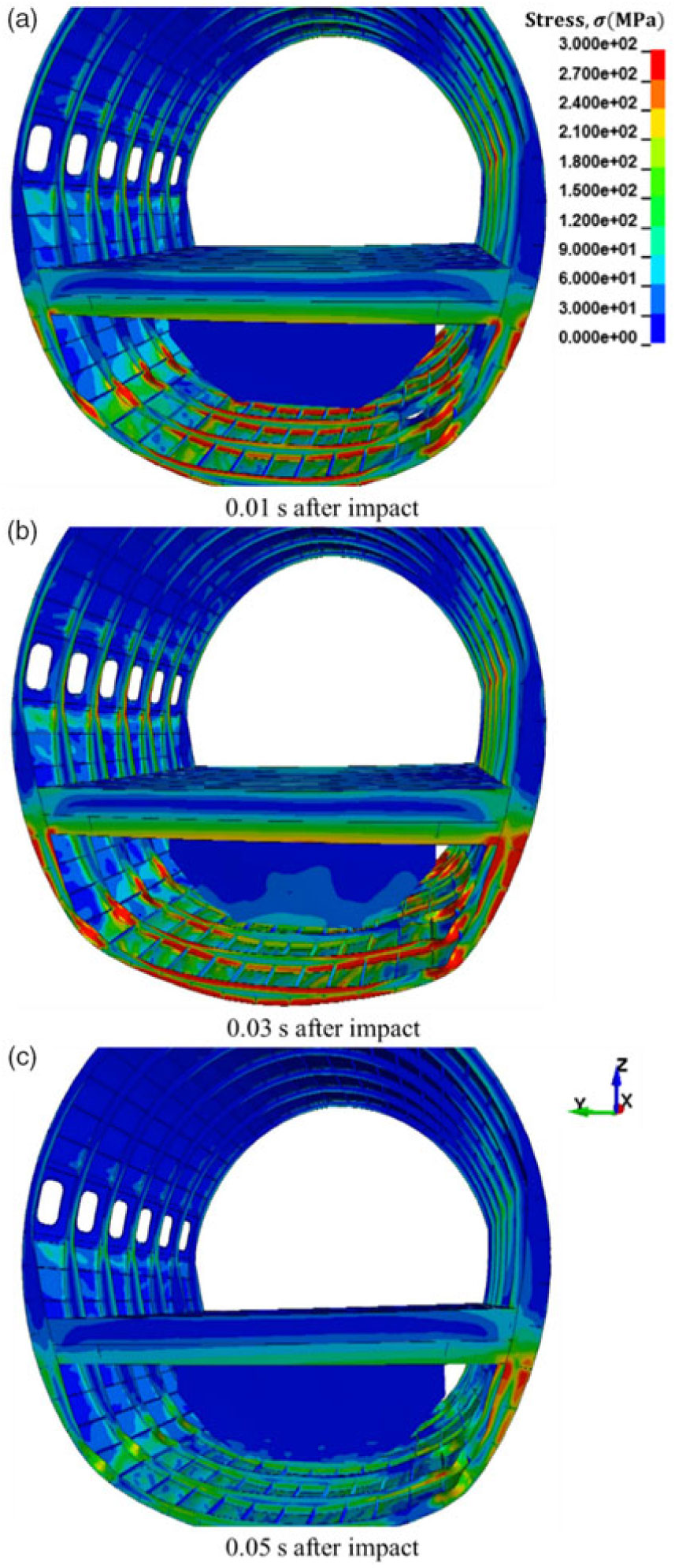
Figure 9. Sequential images of deforming fuselage section during water impact (9.1 m/s).

The corresponding g-loading is plotted in Fig. 8. The main reason why the tertiary peak loading is slightly higher in rigid terrain impact than the other soft-impact conditions is the non-deformability of the rigid ground. The dissipation of kinetic energy is strongly tied to the structural deformation. In the rigid ground impact case, the fuselage structure is allowed to deform more extensively as the impact proceeds, which contributes to higher deceleration. The structural deformation in the water impact case is, however, not as severe. Therefore, the second impact (between the bottom of the fuel tank and the fuselage) in the case of water ditching occurs earlier than that of the other two scenarios. The advanced timing of the second peak in this event can be observed in Fig. 8.

As depicted, the g-loading transferred to the passenger floor at this instance $(\sim 0.03\ \text{to}\ 0.04\ \text{s})$ is slightly higher than that of the rigid ground. In other words, the g-loading based on the second impact peak gradually increases inversely with the stiffness of the impact surface. This is since the kinetic energy absorbing mechanisms embedded in the fuselage structures perform less effectively when coming into contact with softer terrains.

Finally, as the impact progresses, the maximum g-loading occurs at the third point of contact $(\sim 0.06\ \text{to}\ 0.07\ \text{s})$ , as shown in Fig. 8. As discussed, this is the moment when the fuel tank suspension rail buckles and the fuel tank collides with the passenger floor in both impact scenarios onto rigid and soil terrains. Unlike the other two cases, the passenger floor does not severely contact with the fuel tank suspended underneath the passenger floor during water ditching.

Given the distinct differences seen in the failure mechanisms of a sample fuselage section when coming into contact with soft terrains, in particular water, a closer assessment of the applicability of the sequential damage triggers used in the design of the future aircraft structures during gears up, soft emergency landing will be imperative.