Hostname: page-component-cb9f654ff-hn9fh Total loading time: 0 Render date: 2025-08-10T13:13:50.607Z Has data issue: false hasContentIssue false
  • English
  • Français

A bialgebra theory of Gel’fand-Dorfman algebras with applications to Lie conformal bialgebras

Part of: Quantum field theory; related classical field theories Lie algebras and Lie superalgebras General nonassociative rings Other nonassociative rings and algebras

Published online by Cambridge University Press:  11 July 2025

Yanyong Hong Open the ORCID record for Yanyong Hong [Opens in a new window] ,
Chengming Bai Open the ORCID record for Chengming Bai [Opens in a new window]  and
Li Guo Open the ORCID record for Li Guo [Opens in a new window]
Yanyong Hong
Affiliation:
School of Mathematics, https://ror.org/014v1mr15 Hangzhou Normal University , Hangzhou 311121, PR China e-mail: yyhong@hznu.edu.cn
Chengming Bai
Affiliation:
Chern Institute of Mathematics & LPMC, https://ror.org/01y1kjr75 Nankai University , Tianjin 300071, PR China e-mail: baicm@nankai.edu.cn
Li Guo*
Affiliation:
Department of Mathematics and Computer Science, https://ror.org/05vt9qd57 Rutgers University , Newark, NJ 07102, United States
*
e-mail: liguo@rutgers.edu
Get access Rights & Permissions [Opens in a new window]

Abstract

Gel’fand–Dorfman algebras (GD algebras) give a natural construction of Lie conformal algebras and are in turn characterized by this construction. In this article, we define the Gel’fand–Dorfman bialgebra (GD bialgebra) and enrich the above construction to a construction of Lie conformal bialgebras by GD bialgebras. As a special case, Novikov bialgebras yield Lie conformal bialgebras. We further introduce the notion of the Gel’fand–Dorfman Yang–Baxter equation (GDYBE), whose skew-symmetric solutions produce GD bialgebras. Moreover, the notions of 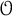$\mathcal {O}$-operators on GD algebras and pre-Gel’fand–Dorfman algebras (pre-GD algebras) are introduced to provide skew-symmetric solutions of the GDYBE. The relationships between these notions for GD algebras and the corresponding ones for Lie conformal algebras are given. In particular, there is a natural construction of Lie conformal bialgebras from pre-GD algebras. Finally, GD bialgebras are characterized by certain matched pairs and Manin triples of GD algebras.

Keywords

Gel’fand–Dorfman algebraGel’fand–Dorfman bialgebraNovikov bialgebraYang–Baxter equationLie conformal bialgebra

MSC classification

Primary: 17A30: Algebras satisfying other identities 17B62: Lie bialgebras; Lie coalgebras 17B69: Vertex operators; vertex operator algebras and related structures 17D25: Lie-admissible algebras
Secondary: 81T40: Two-dimensional field theories, conformal field theories, etc.

Information

Type
Article
Information
Canadian Journal of Mathematics , First View , pp. 1 - 33
Check for updates
Copyright
© The Author(s), 2025. Published by Cambridge University Press on behalf of Canadian Mathematical Society

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Article purchase

Temporarily unavailable

References

Bai, C., A unified algebraic approach to the classical Yang-Baxter equation . J. Phys. A: Math. Theor. 40(2007), 11073–11082.Google Scholar
Bai, C., Bellier, O., Guo, L., and Ni, X., Splitting of operations, Manin products, and Rota-Baxter operators . Int. Math. Res. Not. 3(2013), 485–524.Google Scholar
Bai, C., Li, H., and Pei, Y., ${\phi}_{\epsilon }$ -coordinated modules for vertex algebras . J. Algebra 246(2015), 211–242.Google Scholar
Bai, C. and Meng, D., The classification of Novikov algebras in low dimensions . J. Phys. A: Math. Theor. 34(2001), 1581–1594.Google Scholar
Bakalov, B., D’Andrea, A., and Kac, V., Theory of finite pseudoalgebras . Adv. Math. 162(2001), 1–140.Google Scholar
Bakalov, B. and Kac, V., Field algebras . Int. Math. Res. Not. 3(2003), 123–159.Google Scholar
Bakalov, B., Kac, V., and Voronov, A., Cohomology of conformal algebras . Commun. Math. Phys. 200(1999), 561–598.Google Scholar
Balinsky, A. and Novikov, S., Poisson brackets of hydrodynamic type, Frobenius algebras and Lie algebras . Sov. Math. Dokl. 32(1985), 228–231.Google Scholar
Barakat, A., De sole, A., and Kac, V., Poisson vertex algebras in the theory of Hamiltonian equations . Japan. J. Math. 4(2009), 141–252.Google Scholar
Boyallian, C., Kac, V., and Liberati, J., On the classification of subalgebras of $Cen{d}_N$ and $g{c}_N$ . J. Algebra 260(2003), 32–63.Google Scholar
Chari, V. and Pressley, A., A guide to quantum groups. Cambridge University Press, Cambridge, 1994.Google Scholar
Drinfeld, V., Halmiltonian structure on the Lie groups, Lie bialgebras and the geometric sense of the classical Yang-Baxter equations . Sov. Math. Dokl. 27(1983), 68–71.Google Scholar
Gel’fand, I. and Dorfman, I., Hamiltonian operators and algebraic structures related to them . Funct. Anal. Appl. 13(1979), 248–262.Google Scholar
Gel’fand, I. and Dorfman, I., Hamiltonian operators and infinite dimensional Lie algebras . Funct. Anal. Appl. 15(1981), 173–187.Google Scholar
Gerstenhaber, M., The cohomology structure of an associative ring . Ann. Math. 78(1963), 267–288.Google Scholar
Ginzburg, V. and Kapranov, M., Koszul duality for operads . Duke Math. J. 6(1994), 203–272.Google Scholar
Hong, Y., Extending structures and classifying complements for left-symmetric algebras . Results Math. 74(2019), Paper No. 32. 24pp.Google Scholar
Hong, Y. and Bai, C., Conformal classical Yang-Baxter equation, $S$ -equation and $\mathcal{O}$ -operators . Lett. Math. Phys. 110(2020), 885–909.Google Scholar
Hong, Y. and Bai, C., On antisymmetric infinitesimal conformal bialgebras . J. Algebra 586(2021), 325–356.Google Scholar
Hong, Y., Bai, C., and Guo, L., Infinite-dimensional Lie bialgebras via affinization of Novikov bialgebras and Koszul duality . Commun. Math. Phys. 401(2023), 2011–2049.Google Scholar
Hong, Y., Bai, C., and Guo, L., Deformation families of Novikov bialgebras via differential antisymmetric infinitesimal bialgebras. Preprint. arXiv: 2402.16155.Google Scholar
Hong, Y. and Li, F., On left-symmetric conformal bialgebras . J. Algebra Appl. 14(2015), 1450079.Google Scholar
Hong, Y. and Li, F., Left-symmetric conformal algebras and vertex algebras . J. Pure Appl. Algebra 219(2015), 3543–3567.Google Scholar
Kac, V., Vertex algebras for beginners. 2nd ed., American Mathematical Society, Providence, RI, 1998.Google Scholar
Kac, V., The idea of locality . In: Doebner, H.-D. et al. (eds.), Physical applications and mathematical aspects of geometry, groups and algebras, World Scientific Publishing, Singapore, 1997, pp. 16–32.Google Scholar
Kolesnikov, P., Mashurov, F., and Sartayev, B., On pre-Novikov algebras and derivied Zinbiel variety,. SIGMA. Symmetry, Integr. Geom. Methods Appl. 20(2024), 17, 15 pp.Google Scholar
Kolesnikov, P., Sartayev, B., and Orazgaliev, A., Gel’fand-Dorfman algebras, derived identities, and the Manin product of operads . J. Algebra 539(2019), 260–284.Google Scholar
Koszul, J., Domaines bornés homogénes et orbites de transformations affines . Bull. Soc. Math. France 89(1961), 515–533.Google Scholar
Kozybaev, D., Umirbaev, U., and Zhelyabin, V., Some examples of nonassociative coalgebras and supercoalgebras . Linear Algebra Appl. 643(2022), 235–257.Google Scholar
Kupershmidt, B., What a classical r-matrix really is . J. Nonlinear Math. Phys. 6(1999), 448–488.Google Scholar
Liberati, J., On conformal bialgebras . J. Algebra 319(2008), 2295–2318.Google Scholar
Loday, J., Cup product for Leibniz cohomology and dual Leibniz algebras . Math. Scand. 77(1995), 189–196.Google Scholar
Majid, S., Matched pairs of Lie groups associated to solutions of the Yang-Baxter equations . Pacific J. Math. 141(1990), 311–332.Google Scholar
Osborn, J., Modules for Novikov algebras . Contemp. Math. 184(1995), 327–327.Google Scholar
Osborn, J. and Zel’manov, E., Nonassociative algebras related to Hamiltonian operators in the formal calculus of variations . J. Pure. Appl. Algebra 101(1995), 335–352.Google Scholar
Sartayev, B., Some generalizations of the variety of transposed Poisson algebras . Commun. Math. 32(2024), 55–62.Google Scholar
Vinberg, E., Convex homogeneous cones . Trans. Mosc. Math. Soc. 12(1963), 340–403.Google Scholar
Wen, J. and Hong, Y., Extending structures for Gel’fand-Dorfman bialgebras . Acta. Math. Sin. 40(2024), 619–638.Google Scholar
Xu, X., Quadratic conformal superalgebras . J. Algebra 231(2000), 1–38.Google Scholar
Xu, Z. and Hong, Y., One-dimensional central extensions and simplicities of a class of left-symmetric conformal algebras . J. Algebra Appl. (2024). https://doi.org/10.1142/S0219498826501215.Google Scholar