1 Introduction
Let
![]() $\mathcal {A}_{g}$
be the moduli space of principally polarized abelian varieties over
$\mathcal {A}_{g}$
be the moduli space of principally polarized abelian varieties over
![]() $\bar {\mathbb {F}}_{p}$
. There are two interesting stratifications of this moduli space. The first one is the Newton stratification that stratifies the space according to the Newton polygons of the abelian varieties. The other one is the Ekedahl–Oort stratification that stratifies the space according to the isomorphism classes of the p-torsion subgroups of the abelian varieties. One of the most interesting strata in the Newton stratification is the basic stratum or the supersingular stratum. It is a classical question how the Ekedahl–Oort stratification interacts with the Newton stratification. In particular, one can ask how the Ekedahl–Oort stratification meets the basic Newton stratum. This question was answered by Harashita [Reference HarashitaHar10] where he showed that certain unions of the supersingular Ekedahl–Oort strata are isomorphic to Deligne–Lusztig varieties. This result was refined by Hoeve [Reference HoeveHoe10] where he showed that each individual supersingular Ekedahl–Oort stratum is isomorphic to a fine Deligne–Lusztig variety. For general Shimura varieties that have good integral model and stratification theory, one can still formulate the same questions. Vollaard and Wedhorn [Reference VollaardVo10, Reference Vollaard and WedhornVW11] studied the case of unitary Shimura varieties of signature
$\bar {\mathbb {F}}_{p}$
. There are two interesting stratifications of this moduli space. The first one is the Newton stratification that stratifies the space according to the Newton polygons of the abelian varieties. The other one is the Ekedahl–Oort stratification that stratifies the space according to the isomorphism classes of the p-torsion subgroups of the abelian varieties. One of the most interesting strata in the Newton stratification is the basic stratum or the supersingular stratum. It is a classical question how the Ekedahl–Oort stratification interacts with the Newton stratification. In particular, one can ask how the Ekedahl–Oort stratification meets the basic Newton stratum. This question was answered by Harashita [Reference HarashitaHar10] where he showed that certain unions of the supersingular Ekedahl–Oort strata are isomorphic to Deligne–Lusztig varieties. This result was refined by Hoeve [Reference HoeveHoe10] where he showed that each individual supersingular Ekedahl–Oort stratum is isomorphic to a fine Deligne–Lusztig variety. For general Shimura varieties that have good integral model and stratification theory, one can still formulate the same questions. Vollaard and Wedhorn [Reference VollaardVo10, Reference Vollaard and WedhornVW11] studied the case of unitary Shimura varieties of signature
![]() $(1, n-1)$
at an inert prime and answered this question. Note that in this case, the basic Newton stratum is very special in the sense that it can be covered entirely by Ekedahl–Oort strata, and again each Ekedahl–Oort stratum is a union of Deligne–Lusztig varieties. Those Shimura varieties that satisfy the similar special properties have been classified by the work of Görtz, He, and Nie; see [Reference Görtz and HeGH15, Reference Görtz, He and NieGHN19]. They named these special Shimura varieties the fully Hodge-Newton decomposable Shimura varieties. In fact, they not only treated the case of Ekedahl–Oort stratifications on Shimura varieties with good reductions but also the general cases of Shimura varieties with parahoric level structures. Note in the case of Shimura varieties with parahoric level structures, one has to replace the Ekedahl–Oort strata by the so-called EKOR (Ekedahl–Oort–Kottwitz–Rapoport) strata. This notion was introduced by He and Rapoport in [Reference He and RapoportHR17] where they axiomatized the theory of stratifications on general Shimura varieties with parahoric level structures. This notion interpolates the Ekedahl–Oort stratification and the so-called Kottwitz–Rapoport stratification. The EKOR strata have been studied extensively in the recent preprint [Reference Shen, Yu and ZhangSYZ19] in the cases of Hodge type and abelian type Shimura varieties. The Kottwitz-Rapoport stratification was first studied by Ngô and Genestier in the case of Siegel modular varieties with Iwahori level structure, [Reference Genestier and NgôGN02]. It can be considered as a stratification by singularities as the semisimple traces of Frobenius on the nearby cycle sheaf is constant on each stratum. In [Reference Görtz and YuGY10, Reference Görtz and YuGY12], Görtz and Yu studied those Kottwitz–Rapoport strata contained in the basic Newton strata on the Siegel modular varieties with Iwahori level structures. They showed again that those Kottwitz–Rapoport strata can be described as a union of Deligne–Lusztig varieties. Finally, we remark that the appearances of Deligne–Lusztig varieties in the basic Newton strata are not only beautiful in their own right but are also important in arithmetic applications. Notably, they play an important role in the study of arithmetic fundamental lemma [Reference Rapoport, Terstiege and ZhangRTZ13, Reference He, Li and ZhuHLZ19], and they are also crucial in establishing geometric versions of Jacquet–Langlands correspondence [Reference Helm, Tian and XiaoHTX17].
$(1, n-1)$
at an inert prime and answered this question. Note that in this case, the basic Newton stratum is very special in the sense that it can be covered entirely by Ekedahl–Oort strata, and again each Ekedahl–Oort stratum is a union of Deligne–Lusztig varieties. Those Shimura varieties that satisfy the similar special properties have been classified by the work of Görtz, He, and Nie; see [Reference Görtz and HeGH15, Reference Görtz, He and NieGHN19]. They named these special Shimura varieties the fully Hodge-Newton decomposable Shimura varieties. In fact, they not only treated the case of Ekedahl–Oort stratifications on Shimura varieties with good reductions but also the general cases of Shimura varieties with parahoric level structures. Note in the case of Shimura varieties with parahoric level structures, one has to replace the Ekedahl–Oort strata by the so-called EKOR (Ekedahl–Oort–Kottwitz–Rapoport) strata. This notion was introduced by He and Rapoport in [Reference He and RapoportHR17] where they axiomatized the theory of stratifications on general Shimura varieties with parahoric level structures. This notion interpolates the Ekedahl–Oort stratification and the so-called Kottwitz–Rapoport stratification. The EKOR strata have been studied extensively in the recent preprint [Reference Shen, Yu and ZhangSYZ19] in the cases of Hodge type and abelian type Shimura varieties. The Kottwitz-Rapoport stratification was first studied by Ngô and Genestier in the case of Siegel modular varieties with Iwahori level structure, [Reference Genestier and NgôGN02]. It can be considered as a stratification by singularities as the semisimple traces of Frobenius on the nearby cycle sheaf is constant on each stratum. In [Reference Görtz and YuGY10, Reference Görtz and YuGY12], Görtz and Yu studied those Kottwitz–Rapoport strata contained in the basic Newton strata on the Siegel modular varieties with Iwahori level structures. They showed again that those Kottwitz–Rapoport strata can be described as a union of Deligne–Lusztig varieties. Finally, we remark that the appearances of Deligne–Lusztig varieties in the basic Newton strata are not only beautiful in their own right but are also important in arithmetic applications. Notably, they play an important role in the study of arithmetic fundamental lemma [Reference Rapoport, Terstiege and ZhangRTZ13, Reference He, Li and ZhuHLZ19], and they are also crucial in establishing geometric versions of Jacquet–Langlands correspondence [Reference Helm, Tian and XiaoHTX17].
The first aim of this note is to present a result that generalizes the aforementioned results of Görtz and Yu as well as the results of Harashita and Hoeve. We formulate their results in the setting of Shimura varieties that satisfy the He–Rapoport axiom. Here, we only state an informal version, and the details can found in the proof of Theorem 5.7.
Theorem 1.1 Every EKOR stratum that is contained in the basic Newton stratum can be written as a disjoint union of classical Deligne–Lusztig varieties up to perfection.
Although this theorem is new, it can be deduced from [Reference Görtz and HeGH15, Reference Görtz, He and NieGHN19] without much difficulty. The salient feature of the above theorem is that once the group theoretic data giving rise to the Shimura varieties and their stratifications are at hand, the descriptions of the basic EKOR strata can be made explicit without reference to the Shimura varieties themselves up to perfection. This is especially valuable when the Shimura variety does not admit a good moduli interpretation. We make the above descriptions of the EKOR strata explicit in the case of Siegel modular varieties both in the case of hyperspecial level and in the case of Iwahori level. In particular, this allows us to compare the descriptions of the basic EKOR strata by Görtz–He–Nie with those obtained by Görtz–Yu and by Harashita and Hoeve. Here, we content ourselves with comparing these results up to passing to the perfection in the sense explained in [Reference Xiao and ZhuXZ17, Appendix A].
Theorem 1.2 The descriptions of the basic EKOR strata of Görtz–He–Nie for Siegel modular varieties agree with:
-
(i) the descriptions of Görtz–Yu for the basic KR strata;
-
(ii) the decriptions of Hoeve for the basic Ekedahl–Oort strata;
after passing to the perfection.
The descriptions of the KR strata for Siegel modular varieties with Iwahori level will be discussed in Section 5.2 and the proof of (i) of the theorem above can be found in Theorem 6.4. The descriptions of the Ekedahl–Oort strata for the Siegel modular varieties with hyperspecial level will be discussed in Section 5.3, and (ii) is proved in Theorem 6.8.
2 Preliminaries
2.1 The Iwahori–Weyl Group
Let p be an odd prime. Let F be a non-archimedean local field with valuation ring
![]() $\mathcal {O}_{F}$
and residue field k containing
$\mathcal {O}_{F}$
and residue field k containing
![]() $\mathbb {F}_{p}$
. We denote by
$\mathbb {F}_{p}$
. We denote by
![]() $\breve {F}$
the completion of the maximal unramified extension of F inside a fixed algebraic closure
$\breve {F}$
the completion of the maximal unramified extension of F inside a fixed algebraic closure
![]() $\bar {F}$
with
$\bar {F}$
with
![]() $\breve {\mathcal {O}}_{F}$
the valuation ring and
$\breve {\mathcal {O}}_{F}$
the valuation ring and
![]() $\mathbb {F}$
its residue field. Let
$\mathbb {F}$
its residue field. Let
![]() $\sigma $
be the Frobenius automorphism acting on
$\sigma $
be the Frobenius automorphism acting on
![]() $\mathbb {F},$
and we use the same symbol for its lift on
$\mathbb {F},$
and we use the same symbol for its lift on
![]() $\breve {F}$
. We set
$\breve {F}$
. We set
![]() $\Gamma =\mathrm {Gal}(\bar {F}/F)$
and
$\Gamma =\mathrm {Gal}(\bar {F}/F)$
and
![]() $\Gamma _{0}=\mathrm {Gal}(\bar {F}/\breve {F}),$
which we identify with the inertia group of F.
$\Gamma _{0}=\mathrm {Gal}(\bar {F}/\breve {F}),$
which we identify with the inertia group of F.
Let G be a connected reductive group over F. We write
![]() $\breve {G}$
for its base change to
$\breve {G}$
for its base change to
![]() $\breve {F,}$
which is quasi-split. We choose a maximal
$\breve {F,}$
which is quasi-split. We choose a maximal
![]() $\breve {F}$
-split torus S that contains a maximal F-split torus of
$\breve {F}$
-split torus S that contains a maximal F-split torus of
![]() $G,$
and we denote its centralizer by T. Since
$G,$
and we denote its centralizer by T. Since
![]() $\breve {G}$
is quasi-split, T is a maximal torus of G. Let
$\breve {G}$
is quasi-split, T is a maximal torus of G. Let
![]() $N_{T}$
be the normalizer of T in G. Then we define the finite Weyl group W by
$N_{T}$
be the normalizer of T in G. Then we define the finite Weyl group W by
![]() $W=N_{T}(\breve {F})/T(\breve {F})$
with its natural action by
$W=N_{T}(\breve {F})/T(\breve {F})$
with its natural action by
![]() $\sigma $
. The Iwahori–Weyl group is defined similarly by
$\sigma $
. The Iwahori–Weyl group is defined similarly by
where
![]() $T(\breve {F})_{1}$
is the unique parahoric subgroup of
$T(\breve {F})_{1}$
is the unique parahoric subgroup of
![]() ${T}(\breve {F})$
. The torus S defines an apartment
${T}(\breve {F})$
. The torus S defines an apartment
![]() $\mathfrak {A}$
in the Bruhat–Tits building of
$\mathfrak {A}$
in the Bruhat–Tits building of
![]() ${G}$
over
${G}$
over
![]() $\breve {F}$
. Its underlying affine space is given by
$\breve {F}$
. Its underlying affine space is given by
![]() $V=X_{*}(T)_{\Gamma _{0}}\otimes _{\mathbb {Z}} \mathbb {R}$
and
$V=X_{*}(T)_{\Gamma _{0}}\otimes _{\mathbb {Z}} \mathbb {R}$
and
![]() $\widetilde {W}$
acts on it by affine transformations. The action
$\widetilde {W}$
acts on it by affine transformations. The action
![]() $\sigma $
on
$\sigma $
on
![]() $\breve {T}$
induces an action on
$\breve {T}$
induces an action on
![]() $V,$
and we choose a
$V,$
and we choose a
![]() $\sigma $
-invariant alcove
$\sigma $
-invariant alcove
![]() $\mathfrak {a}$
that we will refer to as the base alcove. The stabilizer in
$\mathfrak {a}$
that we will refer to as the base alcove. The stabilizer in
![]() $\breve {G}$
of the base alcove
$\breve {G}$
of the base alcove
![]() $\mathfrak {a}$
is the Iwahori subgroup
$\mathfrak {a}$
is the Iwahori subgroup
![]() $\breve {I}$
in
$\breve {I}$
in
![]() ${G}(\breve {F})$
corresponding to
${G}(\breve {F})$
corresponding to
![]() $\mathfrak {a}$
. We denote by
$\mathfrak {a}$
. We denote by
![]() $V_{+}$
the closure of the dominant Weyl chamber in V. We also fix a special vertex in the closure of
$V_{+}$
the closure of the dominant Weyl chamber in V. We also fix a special vertex in the closure of
![]() $\mathfrak {a}$
that is invariant under the Frobenius of the unique quasi-split inner form of G. These choices give us a splitting of the Iwahori–Weyl group
$\mathfrak {a}$
that is invariant under the Frobenius of the unique quasi-split inner form of G. These choices give us a splitting of the Iwahori–Weyl group
 $$\begin{align*}\widetilde{W}=X_{*}(T)_{\Gamma_{0}}\rtimes W. \end{align*}$$
$$\begin{align*}\widetilde{W}=X_{*}(T)_{\Gamma_{0}}\rtimes W. \end{align*}$$
When there is no possibility of confusion, we will use the same symbol w to denote an element in
![]() $\widetilde {W}$
and its lift in
$\widetilde {W}$
and its lift in
![]() $N_{T}(\breve {F})$
. For an element
$N_{T}(\breve {F})$
. For an element
![]() $\lambda \in X_{*}(T)_{\Gamma _{0}}$
, we will write
$\lambda \in X_{*}(T)_{\Gamma _{0}}$
, we will write
![]() $t^{\lambda }$
when we consider
$t^{\lambda }$
when we consider
![]() $\lambda $
as element of
$\lambda $
as element of
![]() $\widetilde {W}$
. The stabilizer of
$\widetilde {W}$
. The stabilizer of
![]() $\mathfrak {a}$
in
$\mathfrak {a}$
in
![]() $\widetilde {W}$
will be denoted by
$\widetilde {W}$
will be denoted by
![]() $\Omega ,$
and we have a decomposition
$\Omega ,$
and we have a decomposition
![]() $\widetilde {W}=W_{a}\rtimes \Omega $
where
$\widetilde {W}=W_{a}\rtimes \Omega $
where
![]() $W_{a}$
is the affine Weyl group of G. This is the same as the Iwahori–Weyl group of the simply connected cover of the derived group of G. Thus, we have
$W_{a}$
is the affine Weyl group of G. This is the same as the Iwahori–Weyl group of the simply connected cover of the derived group of G. Thus, we have
where
![]() $T_{sc}$
is the simply connected cover of the image of T in the derived group. Note that
$T_{sc}$
is the simply connected cover of the image of T in the derived group. Note that
![]() $X_{*}(T_{sc})$
is the coroot lattice, and therefore the quotient
$X_{*}(T_{sc})$
is the coroot lattice, and therefore the quotient
![]() $X_{*}(T)/X_{*}(T_{sc})$
is by definition the fundamental group
$X_{*}(T)/X_{*}(T_{sc})$
is by definition the fundamental group
![]() $\pi _{1}(G)$
of G. We then arrive at the following relationship between the Iwahori–Weyl group and the affine Weyl group
$\pi _{1}(G)$
of G. We then arrive at the following relationship between the Iwahori–Weyl group and the affine Weyl group
 $$\begin{align*}\widetilde{W}=W_{a}\rtimes \pi_{1}(G)_{\Gamma_{0}}. \end{align*}$$
$$\begin{align*}\widetilde{W}=W_{a}\rtimes \pi_{1}(G)_{\Gamma_{0}}. \end{align*}$$
And we can identify
![]() $\Omega $
with
$\Omega $
with
![]() $\pi _{1}(G)_{\Gamma _{0}}$
. We also obtain in this way a map
$\pi _{1}(G)_{\Gamma _{0}}$
. We also obtain in this way a map
 $$ \begin{align} \kappa_{\widetilde{W}}: \widetilde{W}\longrightarrow \pi_{1}(G)_{\Gamma} \end{align} $$
$$ \begin{align} \kappa_{\widetilde{W}}: \widetilde{W}\longrightarrow \pi_{1}(G)_{\Gamma} \end{align} $$
by further projecting the natural map
 $\widetilde {W}\rightarrow \pi _{1}(G)_{\Gamma _{0}}$
to
$\widetilde {W}\rightarrow \pi _{1}(G)_{\Gamma _{0}}$
to
![]() $\pi _{1}(G)_{\Gamma }$
. The group
$\pi _{1}(G)_{\Gamma }$
. The group
![]() $W_{a}$
is a Coxeter group, and we denote by
$W_{a}$
is a Coxeter group, and we denote by
![]() $\widetilde {\mathbb {S}}$
the set of simple reflections in
$\widetilde {\mathbb {S}}$
the set of simple reflections in
![]() $W_{a}$
. One has a Bruhat order on it and a well-defined length function on
$W_{a}$
. One has a Bruhat order on it and a well-defined length function on
![]() $W_{a}$
. We extend them to
$W_{a}$
. We extend them to
![]() $\widetilde {W}$
in the usual way: if
$\widetilde {W}$
in the usual way: if
![]() $w=w_{0}\tau \in W_{a}\rtimes \pi _{1}(G)_{\Gamma _{0}}$
with
$w=w_{0}\tau \in W_{a}\rtimes \pi _{1}(G)_{\Gamma _{0}}$
with
![]() $w_{0}\in W_{a}$
and
$w_{0}\in W_{a}$
and
![]() $\tau \in \pi _{1}(G)_{\Gamma _{0}}$
, then we define
$\tau \in \pi _{1}(G)_{\Gamma _{0}}$
, then we define
![]() $l(w)=l(w_{0}),$
and we write
$l(w)=l(w_{0}),$
and we write
![]() $w_{1}\tau _{1}\leq w_{2}\tau _{2}$
if and only if
$w_{1}\tau _{1}\leq w_{2}\tau _{2}$
if and only if
![]() $\tau _{1}=\tau _{2}$
and
$\tau _{1}=\tau _{2}$
and
![]() $w_{1}\leq w_{2}$
.
$w_{1}\leq w_{2}$
.
Let
![]() $K\subset \widetilde {\mathbb {S}}$
be a subset of the set of simple reflections. We denote by
$K\subset \widetilde {\mathbb {S}}$
be a subset of the set of simple reflections. We denote by
![]() $W_{K}$
be the subgroup of
$W_{K}$
be the subgroup of
![]() $\widetilde {W}$
generated by the simple reflections in K and denote by
$\widetilde {W}$
generated by the simple reflections in K and denote by
![]() $^{K}\widetilde {W}$
the set of minimal length representatives in the cosets of
$^{K}\widetilde {W}$
the set of minimal length representatives in the cosets of
![]() $W_{K}\backslash \widetilde {W}$
.
$W_{K}\backslash \widetilde {W}$
.
2.2
 $ \boldsymbol{\sigma} $
-conjugacy Classes
$ \boldsymbol{\sigma} $
-conjugacy Classes
We let
![]() $B(G)$
be the set of
$B(G)$
be the set of
![]() $\sigma $
-conjugacy classes of
$\sigma $
-conjugacy classes of
![]() $G(\breve {F})$
. Then we have the Newton map
$G(\breve {F})$
. Then we have the Newton map
 $$\begin{align*}\nu_{G}: B(G)\longrightarrow \big((X_{*}(T)_{\Gamma_{0}, \mathbb{Q}})^{+}\big)^{\langle\sigma\rangle}, \end{align*}$$
$$\begin{align*}\nu_{G}: B(G)\longrightarrow \big((X_{*}(T)_{\Gamma_{0}, \mathbb{Q}})^{+}\big)^{\langle\sigma\rangle}, \end{align*}$$
where
 $X_{*}(T)^{+}_{\Gamma _{0}, \mathbb {Q}}=X_{*}(T)_{\Gamma _{0}, \mathbb {Q}}\cap V_{+}$
. And the Kottwitz map
$X_{*}(T)^{+}_{\Gamma _{0}, \mathbb {Q}}=X_{*}(T)_{\Gamma _{0}, \mathbb {Q}}\cap V_{+}$
. And the Kottwitz map
For a review of the definitions of these maps, we refer the reader to [Reference Rapoport and RichartzRR96, Reference Rapoport and ViehmannRV14]; we only remark that
![]() $\nu _{G}$
should be considered as the group theoretic incarnation of the notion of Newton polygons and
$\nu _{G}$
should be considered as the group theoretic incarnation of the notion of Newton polygons and
![]() $\kappa _{G}$
encodes the end point of the Newton polygon. The joint map
$\kappa _{G}$
encodes the end point of the Newton polygon. The joint map
 $$\begin{align*}\nu_{G}\times \kappa_{G}: B(G)\longrightarrow \big((X_{*}(T)_{\Gamma_{0}, \mathbb{Q}})^{+}\big)^{\langle\sigma\rangle}\times\pi_{1}(G)_{\Gamma} \end{align*}$$
$$\begin{align*}\nu_{G}\times \kappa_{G}: B(G)\longrightarrow \big((X_{*}(T)_{\Gamma_{0}, \mathbb{Q}})^{+}\big)^{\langle\sigma\rangle}\times\pi_{1}(G)_{\Gamma} \end{align*}$$
is, in fact, injective. The set
![]() $B(G)$
is equipped with a partial order: we write
$B(G)$
is equipped with a partial order: we write
![]() $[b]\leq [b^{\prime }] $
for
$[b]\leq [b^{\prime }] $
for
![]() $[b], [b^{\prime }]\in B(G)$
if
$[b], [b^{\prime }]\in B(G)$
if
![]() $\kappa _{G}([b])=\kappa _{G}([b^{\prime }])$
and
$\kappa _{G}([b])=\kappa _{G}([b^{\prime }])$
and
![]() $\nu _{G}([b])\leq \nu _{G}([b^{\prime }])$
. Here,
$\nu _{G}([b])\leq \nu _{G}([b^{\prime }])$
. Here,
![]() $\nu _{G}([b])\leq \nu _{G}([b^{\prime }])$
if
$\nu _{G}([b])\leq \nu _{G}([b^{\prime }])$
if
![]() $\nu _{G}([b])-\nu _{G}([b^{\prime }])$
is non-negative
$\nu _{G}([b])-\nu _{G}([b^{\prime }])$
is non-negative
![]() $\mathbb {Q}$
-sum of positive coroot.
$\mathbb {Q}$
-sum of positive coroot.
Let
![]() $\{\mu \}$
be a conjugacy class of cocharacters over
$\{\mu \}$
be a conjugacy class of cocharacters over
![]() $\bar {F}$
of G. An element
$\bar {F}$
of G. An element
![]() $[b]\in B(G)$
is called acceptable for
$[b]\in B(G)$
is called acceptable for
![]() $\{\mu \}$
if
$\{\mu \}$
if
![]() $\nu ([b])\leq \bar {\mu }$
where
$\nu ([b])\leq \bar {\mu }$
where
 $\bar {\mu }=[\Gamma : \Gamma _{\mu }]^{-1}\sum _{\gamma \in \Gamma /\Gamma _{\mu }}\gamma (\mu )$
is the Galois average of
$\bar {\mu }=[\Gamma : \Gamma _{\mu }]^{-1}\sum _{\gamma \in \Gamma /\Gamma _{\mu }}\gamma (\mu )$
is the Galois average of
![]() $\mu $
that we define to be the unique dominant element in
$\mu $
that we define to be the unique dominant element in
![]() $\{\mu \}$
with
$\{\mu \}$
with
![]() $\Gamma _{\mu }$
its stabilizer in
$\Gamma _{\mu }$
its stabilizer in
![]() $\Gamma $
. An acceptable element
$\Gamma $
. An acceptable element
![]() $[b]$
is said be neutral if
$[b]$
is said be neutral if
![]() $\kappa ([b])=\mu ^{\natural }$
with
$\kappa ([b])=\mu ^{\natural }$
with
![]() $\mu ^{\natural }$
the common image of
$\mu ^{\natural }$
the common image of
![]() $\{\mu \}$
in
$\{\mu \}$
in
![]() $\pi _{1}(G)_{\Gamma }$
; see [Reference RapoportRap05, Lemma 3.1]. We define the set of neutral acceptable elements with respect to
$\pi _{1}(G)_{\Gamma }$
; see [Reference RapoportRap05, Lemma 3.1]. We define the set of neutral acceptable elements with respect to
![]() $\{\mu \}$
in
$\{\mu \}$
in
![]() $B(G)$
by
$B(G)$
by
 $$ \begin{align} B(G, \{\mu\})=\big\{[b]\in B(G): \kappa([b])=\mu^{\natural}, \nu([b])\leq \overline{\mu}\big\}. \end{align} $$
$$ \begin{align} B(G, \{\mu\})=\big\{[b]\in B(G): \kappa([b])=\mu^{\natural}, \nu([b])\leq \overline{\mu}\big\}. \end{align} $$
This is, in fact, a finite set and inherits a partial order from that of
![]() $B(G)$
and the unique minimal class is called the basic class. We denote by
$B(G)$
and the unique minimal class is called the basic class. We denote by
the unique element of
![]() $\widetilde {W}$
of length
$\widetilde {W}$
of length
![]() $0$
mapping to
$0$
mapping to
![]() $\mu ^{\natural }\in \pi _{1}(G)_{\Gamma _{0}}$
and its
$\mu ^{\natural }\in \pi _{1}(G)_{\Gamma _{0}}$
and its
![]() $\sigma $
-conjugacy class is the basic class defined above. For
$\sigma $
-conjugacy class is the basic class defined above. For
![]() $w\in \widetilde {W}$
, we consider
$w\in \widetilde {W}$
, we consider
![]() $w\sigma $
to be an element in
$w\sigma $
to be an element in
 $\widetilde {W}\rtimes \langle \sigma \rangle $
. There exist n such that
$\widetilde {W}\rtimes \langle \sigma \rangle $
. There exist n such that
![]() $(w\sigma )^{n}=t^{\lambda }$
for an element
$(w\sigma )^{n}=t^{\lambda }$
for an element
![]() $\lambda \in X_{*}(T)_{\Gamma _{0}}$
. Then the Newton vector
$\lambda \in X_{*}(T)_{\Gamma _{0}}$
. Then the Newton vector
![]() $\bar {\nu }_{w}$
of w is defined to be the unique dominant element in the W-orbit of
$\bar {\nu }_{w}$
of w is defined to be the unique dominant element in the W-orbit of
![]() $\lambda /n\in X_{*}(T)_{\Gamma _{0}, \mathbb {Q}}$
. An element
$\lambda /n\in X_{*}(T)_{\Gamma _{0}, \mathbb {Q}}$
. An element
![]() $w\in \widetilde {W}$
is called
$w\in \widetilde {W}$
is called
![]() $\sigma $
-straight if
$\sigma $
-straight if
![]() $l((w\sigma )^{m})=ml(w)$
for all
$l((w\sigma )^{m})=ml(w)$
for all
![]() $m\in \mathbb {N}$
where we extend the length function
$m\in \mathbb {N}$
where we extend the length function
![]() $l(\cdot )$
to
$l(\cdot )$
to
 $\widetilde {W}\rtimes \langle \sigma \rangle $
by requiring that
$\widetilde {W}\rtimes \langle \sigma \rangle $
by requiring that
![]() $l(\sigma )=0$
. We denote by
$l(\sigma )=0$
. We denote by
![]() $B(\widetilde {W})_{\sigma }$
the set of
$B(\widetilde {W})_{\sigma }$
the set of
![]() $\sigma $
-conjugacy classes in
$\sigma $
-conjugacy classes in
![]() $\widetilde {W,}$
and we say that a
$\widetilde {W,}$
and we say that a
![]() $\sigma $
-conjugacy class is straight if it contains a
$\sigma $
-conjugacy class is straight if it contains a
![]() $\sigma $
-straight element. We denote by
$\sigma $
-straight element. We denote by
![]() $B(\widetilde {W})_{\sigma -\mathrm {str}}$
the set of straight
$B(\widetilde {W})_{\sigma -\mathrm {str}}$
the set of straight
![]() $\sigma $
-conjugacy classes of
$\sigma $
-conjugacy classes of
![]() $\widetilde {W}$
. This set is closely related to the Kottwitz set
$\widetilde {W}$
. This set is closely related to the Kottwitz set
![]() $B(G)$
; in fact, we have the following theorem.
$B(G)$
; in fact, we have the following theorem.
Theorem 2.1 ([Reference HeHe14, Theorem 3.3])
The map
![]() $\Psi : B(\widetilde {W})_{\sigma -\mathrm {str}}\rightarrow B(G)$
induced by the inclusion of
$\Psi : B(\widetilde {W})_{\sigma -\mathrm {str}}\rightarrow B(G)$
induced by the inclusion of
![]() $N_{T}(\breve {F})\subset G(\breve {F})$
is a bijection.
$N_{T}(\breve {F})\subset G(\breve {F})$
is a bijection.
We finally remark that the set
![]() $B(G, \{\mu \})$
should be thought of as the collection of Newton polygons that satisfy the Mazur’s inequality and is the index set of the Newton stratification of Shimura varieties.
$B(G, \{\mu \})$
should be thought of as the collection of Newton polygons that satisfy the Mazur’s inequality and is the index set of the Newton stratification of Shimura varieties.
2.3 The Admissible Set
Consider again a conjugacy class
![]() $\{\mu \}$
of G over
$\{\mu \}$
of G over
![]() $\bar {F}$
. Recall that we have fixed a dominant representative
$\bar {F}$
. Recall that we have fixed a dominant representative
![]() $\mu \in \{\mu \}$
and we use the same notation for its image in
$\mu \in \{\mu \}$
and we use the same notation for its image in
![]() $X_{*}(T)_{\Gamma _{0}}$
. The admissible set for
$X_{*}(T)_{\Gamma _{0}}$
. The admissible set for
![]() $\{\mu \}$
is defined by
$\{\mu \}$
is defined by
 $$\begin{align*}\mathrm{Adm(\{\mu\})}=\{x\in\widetilde{W}: x\leq t^{w(\mu)}\text{ for some finite Weyl group element } w\}. \end{align*}$$
$$\begin{align*}\mathrm{Adm(\{\mu\})}=\{x\in\widetilde{W}: x\leq t^{w(\mu)}\text{ for some finite Weyl group element } w\}. \end{align*}$$
From the definition, we immediately obtain
![]() $ \operatorname {\mathrm {Adm}}(\{\mu \})\subset W_{a}\tau $
. Suppose
$ \operatorname {\mathrm {Adm}}(\{\mu \})\subset W_{a}\tau $
. Suppose
![]() $K\subset \widetilde {\mathbb {S}}$
is a
$K\subset \widetilde {\mathbb {S}}$
is a
![]() $\sigma $
-invariant subset. We set
$\sigma $
-invariant subset. We set
 $$ \begin{align*} \mathrm{Adm}^{K}(\{\mu\})&=W_{K}\mathrm{Adm}(\{\mu\})W_{K}\subset \widetilde{W};\\ \mathrm{Adm}(\{\mu\})_{K}&=W_{K}\backslash\mathrm{Adm}^{K}(\{\mu\})/W_{K}\subset W_{K}\backslash \widetilde{W}/W_{K}.\end{align*} $$
$$ \begin{align*} \mathrm{Adm}^{K}(\{\mu\})&=W_{K}\mathrm{Adm}(\{\mu\})W_{K}\subset \widetilde{W};\\ \mathrm{Adm}(\{\mu\})_{K}&=W_{K}\backslash\mathrm{Adm}^{K}(\{\mu\})/W_{K}\subset W_{K}\backslash \widetilde{W}/W_{K}.\end{align*} $$
Let
![]() $ \operatorname {\mathrm {Adm}}(\{\mu \})_{\mathrm {str}}$
be set of the
$ \operatorname {\mathrm {Adm}}(\{\mu \})_{\mathrm {str}}$
be set of the
![]() $\sigma $
-straight elements in
$\sigma $
-straight elements in
![]() $ \operatorname {\mathrm {Adm}}(\{\mu \})$
and let
$ \operatorname {\mathrm {Adm}}(\{\mu \})$
and let
 $B(\widetilde {W}, \{\mu \})_{\mathrm {str}}$
be the image of it in
$B(\widetilde {W}, \{\mu \})_{\mathrm {str}}$
be the image of it in
![]() $B(\widetilde {W})$
. The following theorem refines the previous Theorem 2.1.
$B(\widetilde {W})$
. The following theorem refines the previous Theorem 2.1.
Theorem 2.2 The map
![]() $\Psi $
restricts to a bijection between
$\Psi $
restricts to a bijection between
 $B(\widetilde {W}, \{\mu \})_{\mathrm {str}}$
and
$B(\widetilde {W}, \{\mu \})_{\mathrm {str}}$
and
![]() $B(G, \{\mu \})$
.
$B(G, \{\mu \})$
.
3 EKOR Stratifications of Shimura Varieties
3.1 Shimura Varieties
Let
![]() $({\mathbf {{G}}}, \{h\})$
be a Shimura datum, let
$({\mathbf {{G}}}, \{h\})$
be a Shimura datum, let
![]() ${\mathbf {{K}}}={\mathbf {{K}}}^{p}{\mathbf {{K}}}_{p}$
be an open compact subgroup of
${\mathbf {{K}}}={\mathbf {{K}}}^{p}{\mathbf {{K}}}_{p}$
be an open compact subgroup of
![]() ${\mathbf {{G}}}(\mathbb {A}_{f})$
with
${\mathbf {{G}}}(\mathbb {A}_{f})$
with
![]() ${\mathbf {{K}}}^{p}$
sufficiently small, and let
${\mathbf {{K}}}^{p}$
sufficiently small, and let
![]() ${\mathbf {{K}}}_{p}$
be a standard parahoric subgroup
${\mathbf {{K}}}_{p}$
be a standard parahoric subgroup
![]() $G(\mathbb {Q}_{p})$
with
$G(\mathbb {Q}_{p})$
with
![]() $G={\mathbf {{G}}}_{\mathbb {Q}_{p}}$
containing a fixed Iwahori subgroup I of
$G={\mathbf {{G}}}_{\mathbb {Q}_{p}}$
containing a fixed Iwahori subgroup I of
![]() $G(\mathbb {Q}_{p})$
. Let
$G(\mathbb {Q}_{p})$
. Let
![]() $\mathrm {Sh}_{{\mathbf {{K}}}}=\mathrm {Sh}({\mathbf {{G}}}, \{h\})_{{\mathbf {{K}}}}$
be the corresponding Shimura variety defined over a reflex field
$\mathrm {Sh}_{{\mathbf {{K}}}}=\mathrm {Sh}({\mathbf {{G}}}, \{h\})_{{\mathbf {{K}}}}$
be the corresponding Shimura variety defined over a reflex field
![]() ${\mathbf {{E}}}$
. We denote by E the completion of
${\mathbf {{E}}}$
. We denote by E the completion of
![]() ${\mathbf { E}}$
at a place
${\mathbf { E}}$
at a place
![]() ${\mathbf { p}}$
above p and let
${\mathbf { p}}$
above p and let
![]() $\mathcal {O}_{E}$
be its valuation ring. Let
$\mathcal {O}_{E}$
be its valuation ring. Let
![]() $k_{E}$
be the residue field of E. We assume that there exits a suitable integral model
$k_{E}$
be the residue field of E. We assume that there exits a suitable integral model
![]() $\mathcal {S}h_{{\mathbf {{K}}}}$
of
$\mathcal {S}h_{{\mathbf {{K}}}}$
of
![]() $\mathrm {Sh}_{{\mathbf {{K}}}}$
over
$\mathrm {Sh}_{{\mathbf {{K}}}}$
over
![]() $\mathcal {O}_{E}$
. Let
$\mathcal {O}_{E}$
. Let
![]() $Sh_{K}$
be the special fiber of
$Sh_{K}$
be the special fiber of
![]() $\mathcal {S}h_{{\mathbf {{K}}}}$
over
$\mathcal {S}h_{{\mathbf {{K}}}}$
over
![]() $k_{E}$
. The Shimura datum
$k_{E}$
. The Shimura datum
![]() $({\mathbf {{G}}}, \{h\})$
gives a conjugacy class of cocharacters
$({\mathbf {{G}}}, \{h\})$
gives a conjugacy class of cocharacters
![]() $\{\mu \}$
of G defined over E. Let
$\{\mu \}$
of G defined over E. Let
![]() $\breve {K}$
be the parahoric subgroup of
$\breve {K}$
be the parahoric subgroup of
 ${G}(\breve {\mathbb {Q}}_{p})$
corresponding to
${G}(\breve {\mathbb {Q}}_{p})$
corresponding to
![]() ${\mathbf {{K}}}_{p}$
. Let
${\mathbf {{K}}}_{p}$
. Let
![]() $\mathcal {G}_{K}$
be the Bruhat–Tits group scheme over
$\mathcal {G}_{K}$
be the Bruhat–Tits group scheme over
![]() $\mathbb {Z}_{p}$
correponding to
$\mathbb {Z}_{p}$
correponding to
![]() ${\mathbf {{K}}}_{p},$
and we set
${\mathbf {{K}}}_{p},$
and we set
![]() $\mathcal {G}_{K, k_{E}}=\mathcal {G}_{K}\otimes _{\mathbb {Z}_{p}} k_{E}$
. We write
$\mathcal {G}_{K, k_{E}}=\mathcal {G}_{K}\otimes _{\mathbb {Z}_{p}} k_{E}$
. We write
 $G(\breve {\mathbb {Q}}_{p})/\breve {K}_{\sigma }$
for the
$G(\breve {\mathbb {Q}}_{p})/\breve {K}_{\sigma }$
for the
![]() $\sigma $
-conjugacy class of
$\sigma $
-conjugacy class of
 $G(\breve {\mathbb {Q}}_{p})$
by
$G(\breve {\mathbb {Q}}_{p})$
by
![]() $\breve {K}$
. In particular, we have
$\breve {K}$
. In particular, we have
 $B(G)=G(\breve {\mathbb {Q}}_{p})/G(\breve {\mathbb {Q}}_{p})_{\sigma }$
.
$B(G)=G(\breve {\mathbb {Q}}_{p})/G(\breve {\mathbb {Q}}_{p})_{\sigma }$
.
3.2 Stratifications for Shimura Varieties
We assume that
![]() $Sh_{K}$
satisfies the axioms of He-Rapoport in [Reference He and RapoportHR17]. We will not recall these axioms individually; instead, we record the following commutative diagram whose existence follows from the axioms of He and Rapoport.
$Sh_{K}$
satisfies the axioms of He-Rapoport in [Reference He and RapoportHR17]. We will not recall these axioms individually; instead, we record the following commutative diagram whose existence follows from the axioms of He and Rapoport.
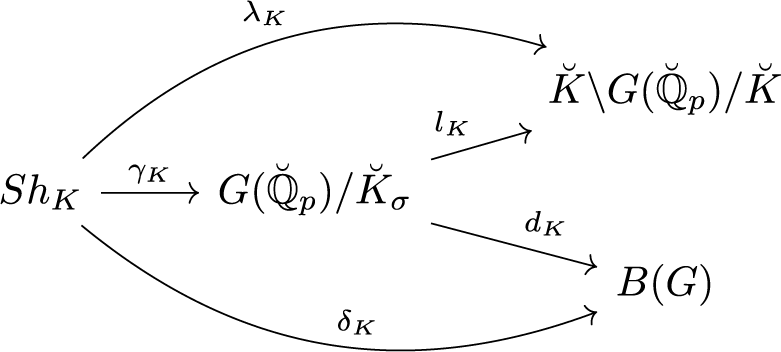
Theorem 3.1 ([Reference He and RapoportHR17])
We have
-
(i)
 $\mathrm {Im}(\lambda _{K})\subset \mathrm {Adm}(\{\mu \})_{K}$
;
$\mathrm {Im}(\lambda _{K})\subset \mathrm {Adm}(\{\mu \})_{K}$
; -
(ii)
 $\mathrm {Im}(\delta _{K})\subset B(G, \{\mu \})$
;
$\mathrm {Im}(\delta _{K})\subset B(G, \{\mu \})$
; -
(iii)
 $\mathrm {Im}(\gamma _{K})=\bigsqcup _{w\in \mathrm {Adm}(\{\mu \})_{K}}\breve {K}w\breve {K}/K_{\sigma }$
.
$\mathrm {Im}(\gamma _{K})=\bigsqcup _{w\in \mathrm {Adm}(\{\mu \})_{K}}\breve {K}w\breve {K}/K_{\sigma }$
.
We remark that (i) was proved in [Reference He and RapoportHR17, Proposition 3.13 (i)]. The map
![]() $\lambda _{K}$
is related to the map from
$\lambda _{K}$
is related to the map from
![]() $Sh_{K}$
to the stack
$Sh_{K}$
to the stack
![]() $[M^{\mathrm {loc}}_{K}/\mathcal {G}_{K, k_{E}}]$
where
$[M^{\mathrm {loc}}_{K}/\mathcal {G}_{K, k_{E}}]$
where
![]() $M^{\mathrm {loc}}_{K}$
is the special fiber of the local model of
$M^{\mathrm {loc}}_{K}$
is the special fiber of the local model of
![]() $Sh_{K}$
. In many cases, one can embed this special fiber in an affine flag variety that can be decomposed into Schubert cells that are indexed by
$Sh_{K}$
. In many cases, one can embed this special fiber in an affine flag variety that can be decomposed into Schubert cells that are indexed by
 $\breve {K}\backslash G(\breve {\mathbb {Q}}_{p})/\breve {K}$
, [Reference GörtzGor01, Reference GörtzGor03]. It is expected that the set
$\breve {K}\backslash G(\breve {\mathbb {Q}}_{p})/\breve {K}$
, [Reference GörtzGor01, Reference GörtzGor03]. It is expected that the set
![]() $\mathrm {Adm}(\{\mu \})_{K}$
is precisely the index set for those cells that could “see” the Shimura variety
$\mathrm {Adm}(\{\mu \})_{K}$
is precisely the index set for those cells that could “see” the Shimura variety
![]() $Sh_{K}$
. Therefore, we define the Kottwitz–Rapoport stratum associated with
$Sh_{K}$
. Therefore, we define the Kottwitz–Rapoport stratum associated with
![]() $w\in \operatorname {\mathrm {Adm}}(\{\mu \})_{K}$
by
$w\in \operatorname {\mathrm {Adm}}(\{\mu \})_{K}$
by
This is a locally closed subvariety of
![]() $Sh_{K}$
.
$Sh_{K}$
.
Next, (ii) is proved in [Reference He and RapoportHR17, Proposition 3.13 (ii)]. The map
![]() $\delta _{K}$
is related to the Newton stratification, and
$\delta _{K}$
is related to the Newton stratification, and
![]() $B(G, \{\mu \})$
is the natural index set of the Newton stratification. We define the Newton stratum associated with an element
$B(G, \{\mu \})$
is the natural index set of the Newton stratification. We define the Newton stratum associated with an element
![]() $[b]\in B(G, \{\mu \})$
by
$[b]\in B(G, \{\mu \})$
by
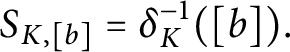 $$ \begin{align} S_{K,[b]}=\delta^{-1}_{K}([b]). \end{align} $$
$$ \begin{align} S_{K,[b]}=\delta^{-1}_{K}([b]). \end{align} $$
This is a locally closed subvariety of
![]() $Sh_{K}$
.
$Sh_{K}$
.
Finally, (iii) is proved in [Reference He and RapoportHR17, Corollary 4.2]. Let
![]() $\breve {K}_{1}$
be the pro-unipotent radical of
$\breve {K}_{1}$
be the pro-unipotent radical of
![]() $\breve {K}$
. Then we have the following inclusions:
$\breve {K}$
. Then we have the following inclusions:
We consider the following composition of two maps
 $$\begin{align*}\nu_{K}: Sh_{K}\longrightarrow G(\breve{\mathbb{Q}}_{p})/\breve{K}_{\sigma}\longrightarrow G(\breve{\mathbb{Q}}_{p})/\breve{K}_{\sigma}(\breve{K}_{1}\times \breve{K}_{1}), \end{align*}$$
$$\begin{align*}\nu_{K}: Sh_{K}\longrightarrow G(\breve{\mathbb{Q}}_{p})/\breve{K}_{\sigma}\longrightarrow G(\breve{\mathbb{Q}}_{p})/\breve{K}_{\sigma}(\breve{K}_{1}\times \breve{K}_{1}), \end{align*}$$
where the first one is the map
![]() $\gamma _{K}$
and the second map is the natural projection map. We will need the following decomposition theorem of the group
$\gamma _{K}$
and the second map is the natural projection map. We will need the following decomposition theorem of the group
 $G(\breve {\mathbb {Q}}_{p})$
.
$G(\breve {\mathbb {Q}}_{p})$
.
Theorem 3.2 ([Reference He and RapoportHR17, Theorem 6.1])
Let K be a parahoric subgroup. Then
 $$\begin{align*}G(\breve{\mathbb{Q}}_{p})=\bigsqcup_{x\in ^{K}\widetilde{W}}\breve{K}_{\sigma}(\breve{K}_{1}x\breve{K}_{1})=\bigsqcup_{x\in ^{K}\widetilde{W}}\breve{K}_{\sigma}(\breve{I}x\breve{I}). \end{align*}$$
$$\begin{align*}G(\breve{\mathbb{Q}}_{p})=\bigsqcup_{x\in ^{K}\widetilde{W}}\breve{K}_{\sigma}(\breve{K}_{1}x\breve{K}_{1})=\bigsqcup_{x\in ^{K}\widetilde{W}}\breve{K}_{\sigma}(\breve{I}x\breve{I}). \end{align*}$$
Combing the previous theorems, we obtain the following lemma.
 $$\begin{align*}\mathrm{Im}(\nu_{K})\subset \bigsqcup_{w\in\operatorname{\mathrm{Adm}}(\{\mu\})^{K}\cap {^{K}\widetilde{W}}} \breve{K}_{\sigma}(\breve{K}_{1}w\breve{K}_{1})/\breve{K}_{\sigma}(\breve{K}_{1}\times \breve{K}_{1}). \end{align*}$$
$$\begin{align*}\mathrm{Im}(\nu_{K})\subset \bigsqcup_{w\in\operatorname{\mathrm{Adm}}(\{\mu\})^{K}\cap {^{K}\widetilde{W}}} \breve{K}_{\sigma}(\breve{K}_{1}w\breve{K}_{1})/\breve{K}_{\sigma}(\breve{K}_{1}\times \breve{K}_{1}). \end{align*}$$
In fact, we have the following fact [Reference HeHe16, Theorem 6.1]:
 $$ \begin{align} \operatorname{\mathrm{Adm}}(\{\mu\})\cap {^{K}\widetilde{W}}=\operatorname{\mathrm{Adm}}(\{\mu\})^{K}\cap {^{K}\widetilde{W}}. \end{align} $$
$$ \begin{align} \operatorname{\mathrm{Adm}}(\{\mu\})\cap {^{K}\widetilde{W}}=\operatorname{\mathrm{Adm}}(\{\mu\})^{K}\cap {^{K}\widetilde{W}}. \end{align} $$
For an element
 $w\in \operatorname {\mathrm {Adm}}(\{\mu \})\cap {^{K}\widetilde {W}}$
, we define the EKOR stratum of
$w\in \operatorname {\mathrm {Adm}}(\{\mu \})\cap {^{K}\widetilde {W}}$
, we define the EKOR stratum of
![]() $Sh_{K}$
by the following subset:
$Sh_{K}$
by the following subset:
Notice that if
![]() ${K}={I}$
is the Iwahori subgroup, then
${K}={I}$
is the Iwahori subgroup, then
 $ \operatorname {\mathrm {Adm}}(\{\mu \})\cap {^{K}\widetilde {W}}= \operatorname {\mathrm {Adm}}(\{\mu \})$
and
$ \operatorname {\mathrm {Adm}}(\{\mu \})\cap {^{K}\widetilde {W}}= \operatorname {\mathrm {Adm}}(\{\mu \})$
and
On the other hand, suppose G is unramified over
![]() $\mathbb {Q}_{p},$
and we let
$\mathbb {Q}_{p},$
and we let
![]() $K=G(\mathbb {Z}_{p})$
be the
$K=G(\mathbb {Z}_{p})$
be the
![]() $\mathbb {Z}_{p}$
of a reductive model of G. Then consider the following set [Reference ViehmannVie14]:
$\mathbb {Z}_{p}$
of a reductive model of G. Then consider the following set [Reference ViehmannVie14]:
 $$ \begin{align} \mathcal{T}=\big\{(w, \mu)\in W\times X_{*}(T)^{+}: w\in {^{\mu}W}\big\}. \end{align} $$
$$ \begin{align} \mathcal{T}=\big\{(w, \mu)\in W\times X_{*}(T)^{+}: w\in {^{\mu}W}\big\}. \end{align} $$
Here,
![]() $^{\mu }W$
means the set of minimal length representatives in the coset space
$^{\mu }W$
means the set of minimal length representatives in the coset space
![]() $W_{\mu }\backslash W$
with
$W_{\mu }\backslash W$
with
![]() $W_{\mu }$
the parabolic subgroup determined by
$W_{\mu }$
the parabolic subgroup determined by
![]() $\mu $
.
$\mu $
.
Example 3.4 Suppose
![]() $G=\mathrm {GSp}_{2g}$
and
$G=\mathrm {GSp}_{2g}$
and
![]() $\mu =(1^{(g)}, 0^{(g)})$
with respect to the standard embedding of G into
$\mu =(1^{(g)}, 0^{(g)})$
with respect to the standard embedding of G into
![]() $\mathrm {GL}_{n}$
. Then
$\mathrm {GL}_{n}$
. Then
![]() $W_{\mu }=W_{J}$
with
$W_{\mu }=W_{J}$
with
![]() $J=\{s_{1}, \cdots , s_{g}\}-\{s_{g}\}$
. One can even identify
$J=\{s_{1}, \cdots , s_{g}\}-\{s_{g}\}$
. One can even identify
![]() $W_{\mu }$
with
$W_{\mu }$
with
![]() $S_{g}$
the symmetric group with g letters. Then
$S_{g}$
the symmetric group with g letters. Then
![]() $^{\mu }W$
is exactly the index set for the Ekedhal–Oort stratification on
$^{\mu }W$
is exactly the index set for the Ekedhal–Oort stratification on
![]() $\mathcal {A}_{g}$
the moduli space of principal polarized abelian schemes of dimension g. The strata classify the isomorphism classes of the p-torsion subgroups of the abelian schemes on
$\mathcal {A}_{g}$
the moduli space of principal polarized abelian schemes of dimension g. The strata classify the isomorphism classes of the p-torsion subgroups of the abelian schemes on
![]() $\mathcal {A}_{g}$
.
$\mathcal {A}_{g}$
.
The main result of [Reference ViehmannVie14] gives us a bijection between
![]() $\mathcal {T}$
and the set of
$\mathcal {T}$
and the set of
![]() $\sigma $
-
$\sigma $
-
![]() $\breve {K}$
-conjugacy classes of
$\breve {K}$
-conjugacy classes of
 $\breve {K}_{1}\backslash G(\breve {\mathbb {Q}}_{p})/\breve {K}_{1}$
, and we denote this bijection by
$\breve {K}_{1}\backslash G(\breve {\mathbb {Q}}_{p})/\breve {K}_{1}$
, and we denote this bijection by
 $$ \begin{align} tr: G(\breve{\mathbb{Q}}_{p})/\breve{K}_{\sigma}(\breve{K}_{1}\times \breve{K}_{1})\longrightarrow \mathcal{T}. \end{align} $$
$$ \begin{align} tr: G(\breve{\mathbb{Q}}_{p})/\breve{K}_{\sigma}(\breve{K}_{1}\times \breve{K}_{1})\longrightarrow \mathcal{T}. \end{align} $$
Now consider the map
![]() $\nu _{K}$
in this setting, as we have known the image is contained in
$\nu _{K}$
in this setting, as we have known the image is contained in
 $$ \begin{align} \bigsqcup_{w\in\operatorname{\mathrm{Adm}}(\{\mu\})^{K}\cap {^{K}\widetilde{W}}} \breve{K}_{\sigma}(\breve{K}_{1}w\breve{K}_{1})/\breve{K}_{\sigma}(\breve{K}_{1}\times \breve{K}_{1})\end{align} $$
$$ \begin{align} \bigsqcup_{w\in\operatorname{\mathrm{Adm}}(\{\mu\})^{K}\cap {^{K}\widetilde{W}}} \breve{K}_{\sigma}(\breve{K}_{1}w\breve{K}_{1})/\breve{K}_{\sigma}(\breve{K}_{1}\times \breve{K}_{1})\end{align} $$
and by the definition of
![]() $ \operatorname {\mathrm {Adm}}(\{\mu \})^{K}$
the restriction of
$ \operatorname {\mathrm {Adm}}(\{\mu \})^{K}$
the restriction of
![]() $tr$
to
$tr$
to
 $$\begin{align*}\bigsqcup_{w\in\operatorname{\mathrm{Adm}}(\{\mu\})^{K}\cap {^{K}\widetilde{W}}} \breve{K}_{\sigma}(\breve{K}_{1}w\breve{K}_{1})/\breve{K}_{\sigma}(\breve{K}_{1}\times \breve{K}_{1})\end{align*}$$
$$\begin{align*}\bigsqcup_{w\in\operatorname{\mathrm{Adm}}(\{\mu\})^{K}\cap {^{K}\widetilde{W}}} \breve{K}_{\sigma}(\breve{K}_{1}w\breve{K}_{1})/\breve{K}_{\sigma}(\breve{K}_{1}\times \breve{K}_{1})\end{align*}$$
is mapped to
![]() $^{\mu }W$
. Therefore, in this case, we call the EKOR stratum indexed by w simply the Ekedahl–Oort stratum (EO stratum) indexed by
$^{\mu }W$
. Therefore, in this case, we call the EKOR stratum indexed by w simply the Ekedahl–Oort stratum (EO stratum) indexed by
![]() $w,$
and we will write
$w,$
and we will write
From the above discussions, we see that the EKOR stratification indeed interpolates the KR stratification and the Ekedahl–Oort stratification.
4 Affine Deligne–Lusztig Varieties
4.1 Deligne–Lusztig Varieties
Before we discuss affine Deligne–Lusztig varieties, we first introduce classical Deligne–Lusztig varieties. In this subsection, we will abuse notation and denote by G a connected reductive algebraic group over
![]() $\mathbb {F}$
that is an algebraic closure of a finite field
$\mathbb {F}$
that is an algebraic closure of a finite field
![]() $\mathbb {F}_{q}$
with q a power of p. Let B be a Borel subgroup of G over
$\mathbb {F}_{q}$
with q a power of p. Let B be a Borel subgroup of G over
![]() $\mathbb {F}_{q}$
with a Levi decomposition
$\mathbb {F}_{q}$
with a Levi decomposition
![]() $B=TU$
that is defined over
$B=TU$
that is defined over
![]() $\mathbb {F}_{q}$
. Let
$\mathbb {F}_{q}$
. Let
![]() $W=N_{T}(\mathbb {F})/T(\mathbb {F})$
be the associated Weyl group with an action of
$W=N_{T}(\mathbb {F})/T(\mathbb {F})$
be the associated Weyl group with an action of
![]() $\sigma $
. We denote by
$\sigma $
. We denote by
![]() $\mathbb {S}$
the set of simple reflections generating W. Let
$\mathbb {S}$
the set of simple reflections generating W. Let
![]() $w\in W$
and we denote by
$w\in W$
and we denote by
![]() $\mathrm {supp}(w)$
the support of
$\mathrm {supp}(w)$
the support of
![]() $w,$
which is the set of simple reflections that occur in some reduced expression of w. An element
$w,$
which is the set of simple reflections that occur in some reduced expression of w. An element
![]() $w\in W$
is called a
$w\in W$
is called a
![]() $\sigma $
-Coxeter element if w is a product of simple reflections, each of which belongs to a unique
$\sigma $
-Coxeter element if w is a product of simple reflections, each of which belongs to a unique
![]() $\sigma $
-orbit of
$\sigma $
-orbit of
![]() $\mathbb {S}$
.
$\mathbb {S}$
.
Recall we have the Bruhat decomposition
 $$\begin{align*}G=\bigsqcup_{w\in W}BwB. \end{align*}$$
$$\begin{align*}G=\bigsqcup_{w\in W}BwB. \end{align*}$$
Then the Deligne–Lusztig variety associated with
![]() $w\in W$
is defined to be
$w\in W$
is defined to be
 $$\begin{align*}Y(w)=\big\{gB\in G/B: g^{-1}\sigma(g)\in BwB/B\big\}. \end{align*}$$
$$\begin{align*}Y(w)=\big\{gB\in G/B: g^{-1}\sigma(g)\in BwB/B\big\}. \end{align*}$$
Here,
![]() $\sigma $
is the Frobenius acting on G and
$\sigma $
is the Frobenius acting on G and
![]() $X(w)$
is considered as a locally closed subvariety of the flag variety
$X(w)$
is considered as a locally closed subvariety of the flag variety
![]() $G/B$
.
$G/B$
.
Let
![]() $J\subset \mathbb {S}$
. Let
$J\subset \mathbb {S}$
. Let
![]() $W_{J}$
be the corresponding parabolic subgroup of W and
$W_{J}$
be the corresponding parabolic subgroup of W and
![]() $P_{J}$
be corresponding parabolic subgroup of G. Recall that
$P_{J}$
be corresponding parabolic subgroup of G. Recall that
![]() ${^{J}W}$
is the set of minimal length representatives of
${^{J}W}$
is the set of minimal length representatives of
![]() $W_{J}\backslash W$
. For any
$W_{J}\backslash W$
. For any
![]() $w\in {^{J}W}$
, we set
$w\in {^{J}W}$
, we set
 $$\begin{align*}Y_{J}(w)= \big\{gP_{J}: g^{-1}\sigma(g)\in {P_{J}}_{\sigma}(BwB)\big\}. \end{align*}$$
$$\begin{align*}Y_{J}(w)= \big\{gP_{J}: g^{-1}\sigma(g)\in {P_{J}}_{\sigma}(BwB)\big\}. \end{align*}$$
This is called the fine Deligne–Lusztig variety.
4.2 Affine Deligne–Lusztig Varities
Now we move back to the set-up in Section 2.1. In particular, we assume for simplicity that G is a connected reductive group over
![]() $\mathbb {Q}_{p}$
. Let
$\mathbb {Q}_{p}$
. Let
 $b\in G(\breve {\mathbb {Q}}_{p})$
be a representative of the
$b\in G(\breve {\mathbb {Q}}_{p})$
be a representative of the
![]() $\sigma $
-conjugacy class
$\sigma $
-conjugacy class
![]() $[b]$
. Let
$[b]$
. Let
![]() $K\subset \widetilde {\mathbb {S}}$
and
$K\subset \widetilde {\mathbb {S}}$
and
![]() $\breve {K}\subset G(\breve {\mathbb {Q}})$
be the corresponding parahoric subgroup. Then the affine Deligne Lusztig variety is given by the set
$\breve {K}\subset G(\breve {\mathbb {Q}})$
be the corresponding parahoric subgroup. Then the affine Deligne Lusztig variety is given by the set
 $$\begin{align*}X_{w}(b)_{K}=\big\{g\breve{K}: g^{-1}b\sigma(g)\in \breve{K}w\breve{K}\big\}. \end{align*}$$
$$\begin{align*}X_{w}(b)_{K}=\big\{g\breve{K}: g^{-1}b\sigma(g)\in \breve{K}w\breve{K}\big\}. \end{align*}$$
This a locally closed subscheme of the p-adic partial affine flag variety
 $G(\breve {\mathbb {Q}}_{p})/\breve {K}$
, [Reference Bhatt and ScholzeBS17, Reference ZhuZhu17]. Note that the
$G(\breve {\mathbb {Q}}_{p})/\breve {K}$
, [Reference Bhatt and ScholzeBS17, Reference ZhuZhu17]. Note that the
![]() $\sigma $
-centralizer group
$\sigma $
-centralizer group
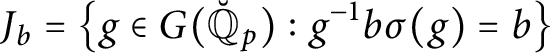 $$ \begin{align} J_{b}=\big\{g\in G(\breve{\mathbb{Q}}_{p}): g^{-1}b\sigma(g)=b\big\} \end{align} $$
$$ \begin{align} J_{b}=\big\{g\in G(\breve{\mathbb{Q}}_{p}): g^{-1}b\sigma(g)=b\big\} \end{align} $$
acts naturally on
![]() $X_{w}(b)_{K}$
.
$X_{w}(b)_{K}$
.
It is natural to consider the following variant of the above set that we will call the generalized affine Deligne–Lusztig variety
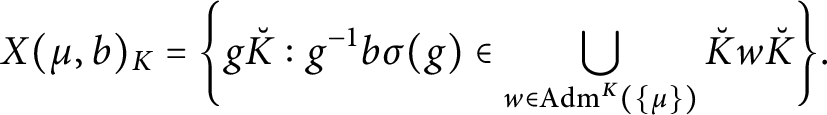 $$\begin{align*}X(\mu, b)_{K}=\bigg\{g\breve{K}: g^{-1}b\sigma(g)\in \bigcup_{w\in \operatorname{\mathrm{Adm}}^{K}(\{\mu\})}\breve{K}w\breve{K} \bigg\}. \end{align*}$$
$$\begin{align*}X(\mu, b)_{K}=\bigg\{g\breve{K}: g^{-1}b\sigma(g)\in \bigcup_{w\in \operatorname{\mathrm{Adm}}^{K}(\{\mu\})}\breve{K}w\breve{K} \bigg\}. \end{align*}$$
It is obvious that we have a natural decomposition
 $$ \begin{align} X(\mu, b)_{K}=\bigcup_{w\in \operatorname{\mathrm{Adm}}^{K}(\{\mu\})} X_{w}(b)_{K}. \end{align} $$
$$ \begin{align} X(\mu, b)_{K}=\bigcup_{w\in \operatorname{\mathrm{Adm}}^{K}(\{\mu\})} X_{w}(b)_{K}. \end{align} $$
We also need the notion of a fine Deligne–Lusztig variety. Let
![]() $w\in {^{K}\widetilde {W}}$
, and we define
$w\in {^{K}\widetilde {W}}$
, and we define
The decomposition in (4.2) can be made finer as in [Reference Görtz and HeGH15, 3.4], and we have
 $$\begin{align*}X(\mu, b)_{K}=\bigsqcup_{w\in {^{K}\widetilde{W}}\cap\operatorname{\mathrm{Adm}}^{K}(\{\mu\})} X_{K, w}(b). \end{align*}$$
$$\begin{align*}X(\mu, b)_{K}=\bigsqcup_{w\in {^{K}\widetilde{W}}\cap\operatorname{\mathrm{Adm}}^{K}(\{\mu\})} X_{K, w}(b). \end{align*}$$
In light of the EKOR stratifications of the Shimura varieties introduced in (3.4) and the relation between the generalized affine Deligne–Lusztig variety and the Rapoport–Zink space that we will discuss later. We will refer to this decomposition of the generalized Deligne–Lusztig variety as the EKOR stratification of
![]() $X(\mu , b)_{K}$
. The affine Deligne–Lusztig variety shows up in the stratification of Shimura varieties in the following explicit way [Reference Görtz, He and NieGHN19, 6.2]. We will restrict the map
$X(\mu , b)_{K}$
. The affine Deligne–Lusztig variety shows up in the stratification of Shimura varieties in the following explicit way [Reference Görtz, He and NieGHN19, 6.2]. We will restrict the map
![]() $\gamma _{K}$
to the Newton stratum
$\gamma _{K}$
to the Newton stratum
 $S_{K,[b]}=\delta ^{-1}_{K}([b])$
and obtain
$S_{K,[b]}=\delta ^{-1}_{K}([b])$
and obtain
 $$ \begin{align} \gamma_{K}(S_{k,[b]})=d^{-1}_{K}([b])\cap l^{-1}_{K}(\operatorname{\mathrm{Adm}}^{K}(\{\mu\}))=J_{b}\backslash X(\mu, b)_{K}. \end{align} $$
$$ \begin{align} \gamma_{K}(S_{k,[b]})=d^{-1}_{K}([b])\cap l^{-1}_{K}(\operatorname{\mathrm{Adm}}^{K}(\{\mu\}))=J_{b}\backslash X(\mu, b)_{K}. \end{align} $$
5 The Basic EKOR Strata
5.1 Basic Newton Stratum
Recall the Langlands–Rapoport conjecture [Reference Langlands and RapoportLR87, Reference RapoportRap05] asserts the following decomposition of the point of
![]() $Sh_{K}$
valued in
$Sh_{K}$
valued in
![]() $\mathbb {F}:$
$\mathbb {F}:$
 $$ \begin{align} \bigsqcup_{\phi}I_{\phi}(\mathbb{Q})\backslash X_{p}(\phi)\times X^{p}(\phi)/K^{p} \xrightarrow{\cong} Sh_{K}(\mathbb{F}). \end{align} $$
$$ \begin{align} \bigsqcup_{\phi}I_{\phi}(\mathbb{Q})\backslash X_{p}(\phi)\times X^{p}(\phi)/K^{p} \xrightarrow{\cong} Sh_{K}(\mathbb{F}). \end{align} $$
We will not recall the general form for this conjecture. But if the Shimura variety is a moduli space of abelian varieties, then
![]() $\phi $
is supposed to run through the isogeny classes on the moduli space. The space
$\phi $
is supposed to run through the isogeny classes on the moduli space. The space
![]() $X_{p}(\phi )$
is supposed to correspond to the part coming from the p-power isogenies, and
$X_{p}(\phi )$
is supposed to correspond to the part coming from the p-power isogenies, and
![]() $X^{p}(\phi )$
should correspond to the prime to p-part of the isogenies. In this case,
$X^{p}(\phi )$
should correspond to the prime to p-part of the isogenies. In this case,
![]() $I_{\phi }$
is the algebraic group over
$I_{\phi }$
is the algebraic group over
![]() $\mathbb {Q}$
corresponding to the automorphism group of an abelian variety in the isogeny class. Furthermore,
$\mathbb {Q}$
corresponding to the automorphism group of an abelian variety in the isogeny class. Furthermore,
![]() $X_{p}(\phi )$
should be given by a suitable affine Deligne–Lusztig variety. Recall that we have a fixed element
$X_{p}(\phi )$
should be given by a suitable affine Deligne–Lusztig variety. Recall that we have a fixed element
![]() $\tau $
in the basic class in
$\tau $
in the basic class in
![]() $B(G, \mu )$
. We now consider the associated basic Newton stratum
$B(G, \mu )$
. We now consider the associated basic Newton stratum
![]() $S_{K, [\tau ]}$
. In light of the above discussion on the Langlands–Rapoport conjecture, we postulate the following axioms in this note. For a scheme X, we will write
$S_{K, [\tau ]}$
. In light of the above discussion on the Langlands–Rapoport conjecture, we postulate the following axioms in this note. For a scheme X, we will write
![]() $X^{\mathrm {pf}}$
as the perfection of X in the sense explained in [Reference Xiao and ZhuXZ17, Definition A.1.7]
$X^{\mathrm {pf}}$
as the perfection of X in the sense explained in [Reference Xiao and ZhuXZ17, Definition A.1.7]
Axiom 5.1 The basic Newton stratum is uniformized by the affine Deligne–Lusztig variety under a uniformization map
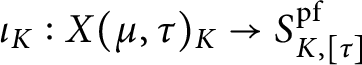 $$ \begin{align} \iota_{K}: X(\mu, \tau)_{K}\rightarrow S^{\mathrm{pf}}_{K, [\tau]} \end{align} $$
$$ \begin{align} \iota_{K}: X(\mu, \tau)_{K}\rightarrow S^{\mathrm{pf}}_{K, [\tau]} \end{align} $$
which induces an isomorphism of the form
 $$ \begin{align} I_{\tau}(\mathbb{Q})\backslash X(\mu, \tau)_{K}\times X^{p}(\tau)/K^{p}\xrightarrow{\cong} S^{\mathrm{pf}}_{K, [\tau]} \end{align} $$
$$ \begin{align} I_{\tau}(\mathbb{Q})\backslash X(\mu, \tau)_{K}\times X^{p}(\tau)/K^{p}\xrightarrow{\cong} S^{\mathrm{pf}}_{K, [\tau]} \end{align} $$
where
![]() $X^{p}(\tau )$
is a
$X^{p}(\tau )$
is a
 $G(\mathbb {A}^{p}_{f})$
-torsor and
$G(\mathbb {A}^{p}_{f})$
-torsor and
![]() $I_{\tau }$
is an algebraic group over
$I_{\tau }$
is an algebraic group over
![]() $\mathbb {Q}$
that acts on
$\mathbb {Q}$
that acts on
![]() $X(\mu , \tau )_{K}$
through a map
$X(\mu , \tau )_{K}$
through a map
![]() $I_{\tau }(\mathbb {Q})\rightarrow J_{\tau }(\mathbb {Q}_{p})$
. In addition, we require that the composite of the map
$I_{\tau }(\mathbb {Q})\rightarrow J_{\tau }(\mathbb {Q}_{p})$
. In addition, we require that the composite of the map
 $$\begin{align*}\gamma_{K}\circ\iota_{K}: X(\mu, \tau)_{K}\longrightarrow S^{\mathrm{pf}}_{K,[\tau]}\longrightarrow J_{\tau}\backslash X(\mu, \tau)_{K} \end{align*}$$
$$\begin{align*}\gamma_{K}\circ\iota_{K}: X(\mu, \tau)_{K}\longrightarrow S^{\mathrm{pf}}_{K,[\tau]}\longrightarrow J_{\tau}\backslash X(\mu, \tau)_{K} \end{align*}$$
be the natural map.
In the case for the Hodge type Shimura varieties, the uniformization map is constructed in [Reference KisinKis17] in the unramified case and in [Reference ZhouZhou19] for the parahoric case. Sometimes, this uniformization can also be obtained by using the “Rapoport–Zink” uniformization
 $$\begin{align*}\mathcal{M}(G, \mu, \tau)^{\mathrm{pf}}_{K}\cong X(\mu, \tau)_{K}, \end{align*}$$
$$\begin{align*}\mathcal{M}(G, \mu, \tau)^{\mathrm{pf}}_{K}\cong X(\mu, \tau)_{K}, \end{align*}$$
where
 $\mathcal {M}(G, \mu , b)^{\mathrm {pf}}_{K}$
is the perfection of a Rapoport–Zink space. See [Reference Hamacher and KimHK17] for the construction of the Rapoport–Zink spaces of Hodge type with parahoric level structures and the uniformization of the basic loci of Hodge-type Shimura varieties using these Rapoport–Zink spaces.
$\mathcal {M}(G, \mu , b)^{\mathrm {pf}}_{K}$
is the perfection of a Rapoport–Zink space. See [Reference Hamacher and KimHK17] for the construction of the Rapoport–Zink spaces of Hodge type with parahoric level structures and the uniformization of the basic loci of Hodge-type Shimura varieties using these Rapoport–Zink spaces.
5.2 The Basic EKOR Stratum
From here on, we will be concerned with the basic EKOR strata. In other words, we will be concerned with those
 $w\in \operatorname {\mathrm {Adm}}(\{\mu \})\cap {^{K}\widetilde {W}}$
such that
$w\in \operatorname {\mathrm {Adm}}(\{\mu \})\cap {^{K}\widetilde {W}}$
such that
For
![]() $w\in W_{a}$
, we denote by
$w\in W_{a}$
, we denote by
![]() $\mathrm {supp}(w)$
the support of w, the set of
$\mathrm {supp}(w)$
the support of w, the set of
![]() $s_{i}\in \widetilde {\mathbb {S}}$
that appears in some reduced expression of w. We also define
$s_{i}\in \widetilde {\mathbb {S}}$
that appears in some reduced expression of w. We also define
 $$\begin{align*}\mathrm{supp}_{\sigma}(w\tau)=\bigcup_{n\in \mathbb{Z}} (\tau\sigma)^{n}(\mathrm{supp}(w)). \end{align*}$$
$$\begin{align*}\mathrm{supp}_{\sigma}(w\tau)=\bigcup_{n\in \mathbb{Z}} (\tau\sigma)^{n}(\mathrm{supp}(w)). \end{align*}$$
We have the following numerical criterion to characterize the basic EKOR strata.
Proposition 5.2 ([Reference Görtz, He and NieGHN19, Proposition 5.6])
Let
 $w\in \operatorname {\mathrm {Adm}}(\{\mu \})\cap {^{K}\widetilde {W}}$
; then
$w\in \operatorname {\mathrm {Adm}}(\{\mu \})\cap {^{K}\widetilde {W}}$
; then
![]() $EKOR_{K, w}\subset S_{K,[\tau ]}$
if and only if
$EKOR_{K, w}\subset S_{K,[\tau ]}$
if and only if
![]() $W_{\mathrm {supp}_{\sigma }(w)}$
is finite.
$W_{\mathrm {supp}_{\sigma }(w)}$
is finite.
Proof Note that
![]() $EKOR_{K, w}\subset S_{K,[\tau ]}$
if and only if
$EKOR_{K, w}\subset S_{K,[\tau ]}$
if and only if
![]() $\breve {K}_{\sigma }(\breve {I}w\breve {I})\subset [\tau ]$
. By [Reference Görtz, He and NieGHN19, Proposition 5.6], this happens if and only if
$\breve {K}_{\sigma }(\breve {I}w\breve {I})\subset [\tau ]$
. By [Reference Görtz, He and NieGHN19, Proposition 5.6], this happens if and only if
![]() $W_{\mathrm {supp}_{\sigma }(w)}$
is finite and
$W_{\mathrm {supp}_{\sigma }(w)}$
is finite and
![]() $\kappa _{\widetilde {W}}(w)=\kappa _{G}(\tau )$
. Since
$\kappa _{\widetilde {W}}(w)=\kappa _{G}(\tau )$
. Since
![]() $w\in \operatorname {\mathrm {Adm}}(\{\mu \})$
, it follows that
$w\in \operatorname {\mathrm {Adm}}(\{\mu \})$
, it follows that
![]() $w\leq t^{w_{0}(\mu )}$
for some finite Weyl group element
$w\leq t^{w_{0}(\mu )}$
for some finite Weyl group element
![]() $w_{0}$
and
$w_{0}$
and
 $\kappa _{\widetilde {W}}(w)=\kappa _{\widetilde {W}}(t^{w_{0}(\mu )})=\kappa _{\widetilde {W}}(w_{0}t^{\mu }w^{-1}_{0})=\kappa _{G}(\tau )$
. ▪
$\kappa _{\widetilde {W}}(w)=\kappa _{\widetilde {W}}(t^{w_{0}(\mu )})=\kappa _{\widetilde {W}}(w_{0}t^{\mu }w^{-1}_{0})=\kappa _{G}(\tau )$
. ▪
Let
![]() $w\in \widetilde {W}$
and
$w\in \widetilde {W}$
and
![]() $K\subset \widetilde {\mathbb {S}}$
. We write
$K\subset \widetilde {\mathbb {S}}$
. We write
![]() $\mathrm {Ad}(w)\sigma (K)=K$
if for any
$\mathrm {Ad}(w)\sigma (K)=K$
if for any
![]() $s_{k}\in K,$
there exists
$s_{k}\in K,$
there exists
![]() $s_{k^{\prime }}\in K$
with
$s_{k^{\prime }}\in K$
with
![]() $w\sigma (s_{k})w^{-1}=s_{k^{\prime }}$
. The set of
$w\sigma (s_{k})w^{-1}=s_{k^{\prime }}$
. The set of
![]() $\{K^{\prime }\subset K: \mathrm {Ad}(w)\sigma (K^{\prime })\subset K^{\prime }\}$
contains a unique maximal element [Reference Görtz and HeGH15, 3.1], which we denote by
$\{K^{\prime }\subset K: \mathrm {Ad}(w)\sigma (K^{\prime })\subset K^{\prime }\}$
contains a unique maximal element [Reference Görtz and HeGH15, 3.1], which we denote by
Proposition 5.3 ([Reference Görtz, He and NieGHN19, Proposition 5.7])
Let K be a
![]() $\sigma $
-invariant subset of
$\sigma $
-invariant subset of
![]() $\widetilde {\mathbb {S}}$
and
$\widetilde {\mathbb {S}}$
and
![]() $w\in {^{K}\widetilde {W}}$
. If
$w\in {^{K}\widetilde {W}}$
. If
![]() $W_{\mathrm {supp}_{\sigma }(w)}$
is finite, then
$W_{\mathrm {supp}_{\sigma }(w)}$
is finite, then
![]() $W_{\mathrm {supp}_{\sigma }(w)\cup I(K, w, \sigma )}$
is also finite.
$W_{\mathrm {supp}_{\sigma }(w)\cup I(K, w, \sigma )}$
is also finite.
Let
 $w\in \operatorname {\mathrm {Adm}}(\{\mu \})\cap {^{K}\widetilde {W}}$
be an element such that
$w\in \operatorname {\mathrm {Adm}}(\{\mu \})\cap {^{K}\widetilde {W}}$
be an element such that
![]() $\mathrm {supp}_{\sigma }(w)$
is finite. Then (the perfections of )
$\mathrm {supp}_{\sigma }(w)$
is finite. Then (the perfections of )
![]() $EKOR_{K, w},$
and the basic Newton stratum
$EKOR_{K, w},$
and the basic Newton stratum
![]() $S_{K, [\tau ]}$
fits in the following diagram under the uniformization map introduced in (5.3):
$S_{K, [\tau ]}$
fits in the following diagram under the uniformization map introduced in (5.3):

Corollary 5.4 Let
 $w\in \operatorname {\mathrm {Adm}}(\{\mu \})\cap {^{K}\widetilde {W}}$
. The basic EKOR stratum
$w\in \operatorname {\mathrm {Adm}}(\{\mu \})\cap {^{K}\widetilde {W}}$
. The basic EKOR stratum
![]() $EKOR_{K, w}$
can be uniformized by the fine Deligne–Lusztig variety
$EKOR_{K, w}$
can be uniformized by the fine Deligne–Lusztig variety
![]() $X_{K, w}(\tau )$
in the sense of Axiom 5.1 that is the following isomorphism
$X_{K, w}(\tau )$
in the sense of Axiom 5.1 that is the following isomorphism
 $$\begin{align*}I_{\tau}(\mathbb{Q})\backslash X_{K, w}(\tau)\times X^{p}(\tau)/K^{p}\xrightarrow{\cong} EKOR^{\mathrm{pf}}_{K, w}. \end{align*}$$
$$\begin{align*}I_{\tau}(\mathbb{Q})\backslash X_{K, w}(\tau)\times X^{p}(\tau)/K^{p}\xrightarrow{\cong} EKOR^{\mathrm{pf}}_{K, w}. \end{align*}$$
Using the above corollary, we can restrict our attention to the fine affine Deligne–Lusztig variety
![]() $X_{K, w}(\tau )$
in order to study the basic EKOR stratum
$X_{K, w}(\tau )$
in order to study the basic EKOR stratum
![]() $EKOR_{K, w}$
. We recall the following results of Görtz and He [Reference Görtz and HeGH15, Proposition 4.1.1, Theorem 4.1.2] concerning the decompositions of fine affine Deligne–Lusztig varieties into fine Deligne–Lusztig varieties. Note that when passing to the double quotient in Corollary 5.4, each Deligne–Lusztig variety is mapped isomorphically to its image.
$EKOR_{K, w}$
. We recall the following results of Görtz and He [Reference Görtz and HeGH15, Proposition 4.1.1, Theorem 4.1.2] concerning the decompositions of fine affine Deligne–Lusztig varieties into fine Deligne–Lusztig varieties. Note that when passing to the double quotient in Corollary 5.4, each Deligne–Lusztig variety is mapped isomorphically to its image.
Theorem 5.5 ([Reference Görtz and HeGH15, Theorem 4.1.1])
For
![]() $J\subset \widetilde {\mathbb {S}}$
and
$J\subset \widetilde {\mathbb {S}}$
and
![]() $w\in {^{J}\widetilde {W}}$
,
$w\in {^{J}\widetilde {W}}$
,
 $$\begin{align*}X_{J, w}(b)=\{g\breve{K}_{I(J, w, \sigma)}: g^{-1}b\sigma(g)\in \breve{K}_{I(J, w, \sigma)}w\breve{K}_{\sigma(I(J, w, \sigma))}\}. \end{align*}$$
$$\begin{align*}X_{J, w}(b)=\{g\breve{K}_{I(J, w, \sigma)}: g^{-1}b\sigma(g)\in \breve{K}_{I(J, w, \sigma)}w\breve{K}_{\sigma(I(J, w, \sigma))}\}. \end{align*}$$
Proposition 5.6 ([Reference Görtz and HeGH15, Proposition 4.1.2])
Let
![]() $J\subset \widetilde {\mathbb {S}}$
and
$J\subset \widetilde {\mathbb {S}}$
and
![]() $w\in {^{J}\widetilde {W}^{\sigma (J)}}\cap W_{a}\tau $
such that
$w\in {^{J}\widetilde {W}^{\sigma (J)}}\cap W_{a}\tau $
such that
![]() $Ad(w)\sigma (J)\subset J$
. If
$Ad(w)\sigma (J)\subset J$
. If
![]() $W_{\mathrm {supp}_{\sigma }(w)\cup J}$
is finite, then
$W_{\mathrm {supp}_{\sigma }(w)\cup J}$
is finite, then
 $$\begin{align*}\{g \breve{K}_{J}: g^{-1}\tau\sigma(g)\in \breve{K}_{J}w\breve{K}_{\sigma(J)}\}=\bigsqcup_{i\in J_{\tau}/J_{\tau}\cap \breve{K}_{\mathrm{supp}_{\sigma}(w)\cup J}}iY_{J}(w), \end{align*}$$
$$\begin{align*}\{g \breve{K}_{J}: g^{-1}\tau\sigma(g)\in \breve{K}_{J}w\breve{K}_{\sigma(J)}\}=\bigsqcup_{i\in J_{\tau}/J_{\tau}\cap \breve{K}_{\mathrm{supp}_{\sigma}(w)\cup J}}iY_{J}(w), \end{align*}$$
where
 $Y_{J}(w)=\{g\breve {K}_{J}\in \breve {K}_{\mathrm {supp}_{\sigma }(w)\cup J}/\breve {K}_{J}: g^{-1}\tau \sigma (g)\in \breve {K}_{J}w\breve {K}_{\sigma (J)}\}$
is a classical Deligne–Lusztig variety.
$Y_{J}(w)=\{g\breve {K}_{J}\in \breve {K}_{\mathrm {supp}_{\sigma }(w)\cup J}/\breve {K}_{J}: g^{-1}\tau \sigma (g)\in \breve {K}_{J}w\breve {K}_{\sigma (J)}\}$
is a classical Deligne–Lusztig variety.
Theorem 5.7 Every basic EKOR stratum on
![]() $Sh_{K}$
can be written as a disjoint union of classical Deligne–Lusztig varieties up to perfection.
$Sh_{K}$
can be written as a disjoint union of classical Deligne–Lusztig varieties up to perfection.
Proof By Theorem 5.5,
 $$\begin{align*}X_{K, w}(\tau)=\{g\breve{K}_{I(K, w, \sigma)}: g^{-1}\tau\sigma(g)\in \breve{K}_{I(K, w, \sigma)}w\breve{K}_{\sigma(I(K, w, \sigma))}\}, \end{align*}$$
$$\begin{align*}X_{K, w}(\tau)=\{g\breve{K}_{I(K, w, \sigma)}: g^{-1}\tau\sigma(g)\in \breve{K}_{I(K, w, \sigma)}w\breve{K}_{\sigma(I(K, w, \sigma))}\}, \end{align*}$$
where
![]() $I(K,w, \sigma )$
is defined as in (5.4) and, in particular,
$I(K,w, \sigma )$
is defined as in (5.4) and, in particular,
![]() $Ad(w)\sigma (I(K,w, \sigma ))\subset I(K,w, \sigma )$
. It follows from Proposition 5.6 that we have
$Ad(w)\sigma (I(K,w, \sigma ))\subset I(K,w, \sigma )$
. It follows from Proposition 5.6 that we have
 $$ \begin{align*} X_{K, w}(\tau)&= \{g\breve{K}_{I(K, w, \sigma)}: g^{-1}\tau\sigma(g)\in \breve{K}_{I(K, w, \sigma)}w\breve{K}_{\sigma(I(K, w, \sigma))}\} \\ & = \bigsqcup_{i\in J_{\tau}/J_{\tau}\cap \breve{K}_{\mathrm{supp}_{\sigma}(w)\cup I(K, w, \sigma)}}iY_{I(K, w, \sigma)}(w).\hfill\blacksquare \end{align*} $$
$$ \begin{align*} X_{K, w}(\tau)&= \{g\breve{K}_{I(K, w, \sigma)}: g^{-1}\tau\sigma(g)\in \breve{K}_{I(K, w, \sigma)}w\breve{K}_{\sigma(I(K, w, \sigma))}\} \\ & = \bigsqcup_{i\in J_{\tau}/J_{\tau}\cap \breve{K}_{\mathrm{supp}_{\sigma}(w)\cup I(K, w, \sigma)}}iY_{I(K, w, \sigma)}(w).\hfill\blacksquare \end{align*} $$
Remark 5.8 In the case where w is a
![]() $\sigma $
-Coxeter element in the finite group
$\sigma $
-Coxeter element in the finite group
![]() $W_{\mathrm {supp}_{\sigma }(w)}$
, the Deligne–Lusztig variety
$W_{\mathrm {supp}_{\sigma }(w)}$
, the Deligne–Lusztig variety
![]() $Y_{I(K, w, \sigma )}(w)$
is isomorphic to the following fine Deligne–Lusztig variety by [Reference Görtz and HeGH15, Corollary 4.6.2]:
$Y_{I(K, w, \sigma )}(w)$
is isomorphic to the following fine Deligne–Lusztig variety by [Reference Görtz and HeGH15, Corollary 4.6.2]:
 $$ \begin{align*} Y_{I(K, w, \sigma)}(w) & = \{g \breve{K}_{\mathrm{supp}_{\sigma}(w)\cap K} \in \breve{K}_{\mathrm{supp}_{\sigma}(w)}/\breve{K}_{\mathrm{supp}_{\sigma}(w)\cap K}: g^{-1}\tau\sigma(g) \\ & \quad \in {\breve{K}_{\mathrm{supp}_{\sigma}(w)\cap K \sigma}}\breve{I}w\breve{I} \}, \end{align*} $$
$$ \begin{align*} Y_{I(K, w, \sigma)}(w) & = \{g \breve{K}_{\mathrm{supp}_{\sigma}(w)\cap K} \in \breve{K}_{\mathrm{supp}_{\sigma}(w)}/\breve{K}_{\mathrm{supp}_{\sigma}(w)\cap K}: g^{-1}\tau\sigma(g) \\ & \quad \in {\breve{K}_{\mathrm{supp}_{\sigma}(w)\cap K \sigma}}\breve{I}w\breve{I} \}, \end{align*} $$
and
![]() $Y_{I(K, w, \sigma )}(w)$
is in turn isomorphic to the classical Deligne–Lusztig variety
$Y_{I(K, w, \sigma )}(w)$
is in turn isomorphic to the classical Deligne–Lusztig variety
 $$\begin{align*}\{g\breve{I}\in \breve{K}_{\mathrm{supp}_{\sigma}(w)}/\breve{I}: g^{-1}\tau\sigma(g)\in \breve{I}w\breve{I}\}. \end{align*}$$
$$\begin{align*}\{g\breve{I}\in \breve{K}_{\mathrm{supp}_{\sigma}(w)}/\breve{I}: g^{-1}\tau\sigma(g)\in \breve{I}w\breve{I}\}. \end{align*}$$
6 Basic EKOR Strata on Siegel Modular Varieties
6.1 Siegel Modular Varieties
We first review the Siegel moduli spaces of abelian varieties with parahoric level structures. The algebraic group associated with this Shimura variety is
![]() $G=\mathrm {GSp}_{2g}$
, the group of symplectic similitudes. We consider the dominant miniscule coweight
$G=\mathrm {GSp}_{2g}$
, the group of symplectic similitudes. We consider the dominant miniscule coweight
![]() $\mu =(1^{(g)}, 0^{(g)})$
as in Example 3.4. The finite Weyl group
$\mu =(1^{(g)}, 0^{(g)})$
as in Example 3.4. The finite Weyl group
![]() $W_{g}$
is generated by the simple reflections given by
$W_{g}$
is generated by the simple reflections given by
The cocharacter group of G with respect to the diagonal torus can be identified with
 $$\begin{align*}X_{*}(T)=\{(x_{1}, \dots, x_{2g})\in \mathbb{Z}^{2g}:x_{1}+x_{2g}=x_{2}+x_{2g-1}=\cdots=x_{g}+x_{g+1}\}. \end{align*}$$
$$\begin{align*}X_{*}(T)=\{(x_{1}, \dots, x_{2g})\in \mathbb{Z}^{2g}:x_{1}+x_{2g}=x_{2}+x_{2g-1}=\cdots=x_{g}+x_{g+1}\}. \end{align*}$$
The set of simple reflections
![]() $\widetilde {\mathbb {S}}$
in the affine Weyl group is
$\widetilde {\mathbb {S}}$
in the affine Weyl group is
![]() $\{s_{0}, s_{1}, \dots , s_{g}\}$
with
$\{s_{0}, s_{1}, \dots , s_{g}\}$
with
We will use the notation
![]() $I:=\{0, 1, 2, \cdots , g\}$
as the index set as well as the notation for the Iwahori subgroup. Consider
$I:=\{0, 1, 2, \cdots , g\}$
as the index set as well as the notation for the Iwahori subgroup. Consider
 $$\begin{align*}\tau= ((0^{(g)}, 1^{(g)}), (1,g+1)(2, g+2)\cdots(g, 2g)) \end{align*}$$
$$\begin{align*}\tau= ((0^{(g)}, 1^{(g)}), (1,g+1)(2, g+2)\cdots(g, 2g)) \end{align*}$$
the unique element of length
![]() $0$
in
$0$
in
![]() $ \operatorname {\mathrm {Adm}}({\{\mu \}})$
. Note that the class
$ \operatorname {\mathrm {Adm}}({\{\mu \}})$
. Note that the class
![]() $[\tau ]$
gives the unique basic class in
$[\tau ]$
gives the unique basic class in
![]() $B(G, \mu )$
.
$B(G, \mu )$
.
Let
![]() $J\subset I$
be given by
$J\subset I$
be given by
![]() $\{j_{0}<j_{1}<\cdots < j_{r}\}$
. The moduli space
$\{j_{0}<j_{1}<\cdots < j_{r}\}$
. The moduli space
![]() $\mathcal {A}_{J}$
over
$\mathcal {A}_{J}$
over
![]() $\mathbb {F}_{p}$
with parahoric level structure of type J parametrizes chains of g-dimensional polarized abelian varieties
$\mathbb {F}_{p}$
with parahoric level structure of type J parametrizes chains of g-dimensional polarized abelian varieties
 $$\begin{align*}(A_{j_{0}}\xrightarrow{\alpha} A_{j_{1}}\xrightarrow{\alpha}\cdots \xrightarrow{\alpha} A_{j_{r}}, \eta), \end{align*}$$
$$\begin{align*}(A_{j_{0}}\xrightarrow{\alpha} A_{j_{1}}\xrightarrow{\alpha}\cdots \xrightarrow{\alpha} A_{j_{r}}, \eta), \end{align*}$$
where
-
(a)
 $A_{j_{i}}$
is a g-dimensional abelian variety and
$A_{j_{i}}$
is a g-dimensional abelian variety and
 $\lambda _{j_{i}}$
a polarization of degree
$\lambda _{j_{i}}$
a polarization of degree
 $p^{2(g-j_{i})}$
whose kernel is contained in
$p^{2(g-j_{i})}$
whose kernel is contained in
 $A_{j_{i}}[p]$
;
$A_{j_{i}}[p]$
; -
(b)
 $\alpha $
is an isogeny that pulls back
$\alpha $
is an isogeny that pulls back
 $\lambda _{j_{i+1}}$
to
$\lambda _{j_{i+1}}$
to
 $\lambda _{j_{i}}$
;
$\lambda _{j_{i}}$
; -
(c)
 $\eta $
is a symplectic level N structure with
$\eta $
is a symplectic level N structure with
 $N\geq 3$
coprime to p with a fixed primitive N-th root of unity.
$N\geq 3$
coprime to p with a fixed primitive N-th root of unity.
Given a chain
![]() $(A_{j_{i}}, \eta )_{j_{i}\in J}$
, we can extend the index set J to
$(A_{j_{i}}, \eta )_{j_{i}\in J}$
, we can extend the index set J to
![]() $J\cup \{2g-j_{i}: j_{i}\in J\}$
by duality:
$J\cup \{2g-j_{i}: j_{i}\in J\}$
by duality:
 $$\begin{align*}A_{j_{0}}\longrightarrow A_{j_{1}}\longrightarrow\cdots \longrightarrow A_{j_{r}} \longrightarrow A_{2g-j_{r}}:=A^{\vee}_{j_{r}}\longrightarrow \cdots \longrightarrow A_{2g-j_{0}}:=A^{\vee}_{j_{0}}. \end{align*}$$
$$\begin{align*}A_{j_{0}}\longrightarrow A_{j_{1}}\longrightarrow\cdots \longrightarrow A_{j_{r}} \longrightarrow A_{2g-j_{r}}:=A^{\vee}_{j_{r}}\longrightarrow \cdots \longrightarrow A_{2g-j_{0}}:=A^{\vee}_{j_{0}}. \end{align*}$$
When
![]() $J=I$
, this recovers the Siegel moduli space with Iwahori level structure
$J=I$
, this recovers the Siegel moduli space with Iwahori level structure
![]() $\mathcal {A}_{I}$
. When
$\mathcal {A}_{I}$
. When
![]() $J=\{0\}$
,
$J=\{0\}$
,
![]() $\mathcal {A}_{J}$
is the classical moduli space
$\mathcal {A}_{J}$
is the classical moduli space
![]() $\mathcal {A}_{g}$
of principally polarized g-dimensional abelian varieties. For simplicity, we will concentrate on these two cases in the sequel.
$\mathcal {A}_{g}$
of principally polarized g-dimensional abelian varieties. For simplicity, we will concentrate on these two cases in the sequel.
6.2 Basic KR Stratum
On
![]() $\mathcal {A}_{I}$
, the relative position of
$\mathcal {A}_{I}$
, the relative position of
![]() $\mathrm {H}_{1}^{\mathrm {dR}}(A_{i})$
and
$\mathrm {H}_{1}^{\mathrm {dR}}(A_{i})$
and
![]() $\omega _{A^{\vee }_{i}}$
gives a well-defined element
$\omega _{A^{\vee }_{i}}$
gives a well-defined element
![]() $w\in \operatorname {\mathrm {Adm}}(\{\mu \})$
, see [Reference Görtz and YuGY12, 3.1]. The resulting map
$w\in \operatorname {\mathrm {Adm}}(\{\mu \})$
, see [Reference Görtz and YuGY12, 3.1]. The resulting map
gives the KR stratification for
![]() $\mathcal {A}_{I}$
. For
$\mathcal {A}_{I}$
. For
![]() $w\in \operatorname {\mathrm {Adm}}(\{\mu \})$
, we will denote the corresponding KR stratum by
$w\in \operatorname {\mathrm {Adm}}(\{\mu \})$
, we will denote the corresponding KR stratum by
![]() $\mathcal {A}_{I, w}$
. The local Dynkin diagram of type
$\mathcal {A}_{I, w}$
. The local Dynkin diagram of type
![]() $\widetilde {C}_{g}$
is given by
$\widetilde {C}_{g}$
is given by

 $\widetilde {\mathbb {S}}-\{c, g-c\}$
.
$\widetilde {\mathbb {S}}-\{c, g-c\}$
.
Proposition 6.1 Let
![]() $w\in \operatorname {\mathrm {Adm}}(\{\mu \})$
. The Weyl group
$w\in \operatorname {\mathrm {Adm}}(\{\mu \})$
. The Weyl group
![]() $W_{\mathrm {supp}_{\sigma }(w)}$
is finite if and only if
$W_{\mathrm {supp}_{\sigma }(w)}$
is finite if and only if
![]() $w\in W_{\{c, g-c\}}\tau $
for some
$w\in W_{\{c, g-c\}}\tau $
for some
![]() $c\leq g/2$
.
$c\leq g/2$
.
Proof One direction is clear; that is, if
![]() $w\in W_{\{c, g-c\}}\tau $
, then
$w\in W_{\{c, g-c\}}\tau $
, then
![]() $W_{\mathrm {supp}_{\sigma }(w)}$
is obviously finite. On the other hand, if
$W_{\mathrm {supp}_{\sigma }(w)}$
is obviously finite. On the other hand, if
![]() $W_{\mathrm {supp}_{\sigma }(w)}$
is finite, then there is some
$W_{\mathrm {supp}_{\sigma }(w)}$
is finite, then there is some
![]() $s_{c}$
that is not in
$s_{c}$
that is not in
![]() $\mathrm {supp}_{\sigma }(w)$
. It follows then that
$\mathrm {supp}_{\sigma }(w)$
. It follows then that
![]() $s_{g-c}\not \in \mathrm {supp}(w\tau ^{-1})$
. Therefore,
$s_{g-c}\not \in \mathrm {supp}(w\tau ^{-1})$
. Therefore,
![]() $w\in W_{\{c, g-c\}}\tau $
. ▪
$w\in W_{\{c, g-c\}}\tau $
. ▪
In [Reference Görtz and YuGY10], the authors call a KR stratum
![]() $\mathcal {A}_{I, w}$
superspecial if there is an
$\mathcal {A}_{I, w}$
superspecial if there is an
![]() $0\leq c\leq [g/2]$
such that for all
$0\leq c\leq [g/2]$
such that for all
![]() $(A_{j}, \eta )_{j\in I}\in \mathcal {A}_{I,w}$
, the abelian varieties
$(A_{j}, \eta )_{j\in I}\in \mathcal {A}_{I,w}$
, the abelian varieties
![]() $A_{c}$
and
$A_{c}$
and
![]() $A_{g-c}$
are superspecial and that the isogeny
$A_{g-c}$
are superspecial and that the isogeny
![]() $A_{c}\rightarrow A^{\vee }_{g-c}$
is the Frobenius map. By [Reference Görtz and YuGY10, Proposition 4.4], the KR stratum
$A_{c}\rightarrow A^{\vee }_{g-c}$
is the Frobenius map. By [Reference Görtz and YuGY10, Proposition 4.4], the KR stratum
![]() $\mathcal {A}_{I,w}$
associated with w is superspecial if and only if
$\mathcal {A}_{I,w}$
associated with w is superspecial if and only if
![]() $w\in W_{\{c, g-c\}}\tau $
for some
$w\in W_{\{c, g-c\}}\tau $
for some
![]() $0\leq c\leq [g/2]$
. Therefore, we have recovered the following theorem of Görtz and Yu.
$0\leq c\leq [g/2]$
. Therefore, we have recovered the following theorem of Görtz and Yu.
Theorem 6.2 ([Reference Görtz and YuGY10, Theorem 1.4])
All basic KR strata are superspecial.
Next we explain how to describe the basic KR stratum
![]() $\mathcal {A}_{I, w}$
in terms of a disjoint union of Deligne–Lusztig varieties as in Theorem 5.7. Note that the axioms of He-Rapoport is verified in [Reference He and RapoportHR17, §7] and Axiom 5.3 is verified using Rapoport–Zink uniformization [Reference Rapoport and ZinkRZ96, Theorem 6.1]. Therefore, Corollary 5.4 takes the following form:
$\mathcal {A}_{I, w}$
in terms of a disjoint union of Deligne–Lusztig varieties as in Theorem 5.7. Note that the axioms of He-Rapoport is verified in [Reference He and RapoportHR17, §7] and Axiom 5.3 is verified using Rapoport–Zink uniformization [Reference Rapoport and ZinkRZ96, Theorem 6.1]. Therefore, Corollary 5.4 takes the following form:
 $$\begin{align*}I_{\tau}(\mathbb{Q})\backslash X_{I, w}(\tau)\times G(\mathbb{A}^{p}_{f})/K^{p}\xrightarrow{\cong} \mathcal{A}^{\mathrm{pf}}_{I, w}, \end{align*}$$
$$\begin{align*}I_{\tau}(\mathbb{Q})\backslash X_{I, w}(\tau)\times G(\mathbb{A}^{p}_{f})/K^{p}\xrightarrow{\cong} \mathcal{A}^{\mathrm{pf}}_{I, w}, \end{align*}$$
where
![]() $I_{\tau }$
is an inner form of
$I_{\tau }$
is an inner form of
![]() $\mathrm {GSp}_{2g}$
and
$\mathrm {GSp}_{2g}$
and
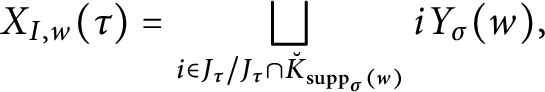 $$\begin{align*}X_{I, w}(\tau)=\bigsqcup_{i\in J_{\tau}/J_{\tau}\cap \breve{K}_{\mathrm{supp}_{\sigma}(w)}}iY_{\sigma}(w), \end{align*}$$
$$\begin{align*}X_{I, w}(\tau)=\bigsqcup_{i\in J_{\tau}/J_{\tau}\cap \breve{K}_{\mathrm{supp}_{\sigma}(w)}}iY_{\sigma}(w), \end{align*}$$
where
 $Y_{\sigma }(w)=\{g\breve {I}\in \breve {K}_{\mathrm {supp}_{\sigma }(w)}/\breve {I}: g^{-1}\tau \sigma (g)\in \breve {I}w\breve {I}\}.$
$Y_{\sigma }(w)=\{g\breve {I}\in \breve {K}_{\mathrm {supp}_{\sigma }(w)}/\breve {I}: g^{-1}\tau \sigma (g)\in \breve {I}w\breve {I}\}.$
Let
![]() $J\subset I$
be a
$J\subset I$
be a
![]() $\tau \sigma $
-stable subset. We make the following manipulation, since
$\tau \sigma $
-stable subset. We make the following manipulation, since
![]() $\mathrm {supp}_{\sigma }(w)\subset J,$
$\mathrm {supp}_{\sigma }(w)\subset J,$
 $$ \begin{align*} X_{I, w}(\tau)&=\bigsqcup_{i\in J_{\tau}/J_{\tau}\cap \breve{K}_{\mathrm{supp}_{\sigma}(w)}}iY_{\sigma}(w)\\ &=\bigsqcup_{i\in J_{\tau}/J_{\tau}\cap \breve{K}_{J}}i \bigsqcup_{j\in J_{\tau}\cap \breve{K}_{J}/J_{\tau}\cap \breve{K}_{\mathrm{supp}_{\sigma}(w)}}jY_{\sigma}(w)\\ &=\bigsqcup_{i\in J_{\tau}/J_{\tau}\cap \breve{K}_{J}}i Y(J, w), \end{align*} $$
$$ \begin{align*} X_{I, w}(\tau)&=\bigsqcup_{i\in J_{\tau}/J_{\tau}\cap \breve{K}_{\mathrm{supp}_{\sigma}(w)}}iY_{\sigma}(w)\\ &=\bigsqcup_{i\in J_{\tau}/J_{\tau}\cap \breve{K}_{J}}i \bigsqcup_{j\in J_{\tau}\cap \breve{K}_{J}/J_{\tau}\cap \breve{K}_{\mathrm{supp}_{\sigma}(w)}}jY_{\sigma}(w)\\ &=\bigsqcup_{i\in J_{\tau}/J_{\tau}\cap \breve{K}_{J}}i Y(J, w), \end{align*} $$
where
![]() $Y(J, w)=\{g\breve {I}\in \breve {K}_{J}/\breve {I}: g^{-1}\tau \sigma (g)\in \breve {I}w\breve {I}\}$
. Consider the stratum
$Y(J, w)=\{g\breve {I}\in \breve {K}_{J}/\breve {I}: g^{-1}\tau \sigma (g)\in \breve {I}w\breve {I}\}$
. Consider the stratum
![]() $\mathcal {A}_{J, \tau }$
on
$\mathcal {A}_{J, \tau }$
on
![]() $\mathcal {A}_{J}$
. This is a finite set of points known as the minimal EKOR stratum. In fact, we have the following lemma.
$\mathcal {A}_{J}$
. This is a finite set of points known as the minimal EKOR stratum. In fact, we have the following lemma.
Lemma 6.3 We have the following.
-
(i) The scheme
 $\mathcal {A}_{J, \tau }$
consists of a finite set of points.
$\mathcal {A}_{J, \tau }$
consists of a finite set of points. -
(ii) There is an isomorphism
 $\mathcal {A}_{J, \tau }\cong I_{\tau }(\mathbb {Q})\backslash (J_{\tau }/J_{\tau }\cap \breve {K}_{J})\times G(\mathbb {A}^{p}_{f})/K^{p}. $
$\mathcal {A}_{J, \tau }\cong I_{\tau }(\mathbb {Q})\backslash (J_{\tau }/J_{\tau }\cap \breve {K}_{J})\times G(\mathbb {A}^{p}_{f})/K^{p}. $
Proof By Corollary 5.4, we have
 $$\begin{align*}I_{\tau}(\mathbb{Q})\backslash X_{K_{J}, \tau}(\tau)\times G(\mathbb{A}^{p}_{f})/K^{p}\xrightarrow{\cong} A^{\mathrm{pf}}_{J, \tau}.\end{align*}$$
$$\begin{align*}I_{\tau}(\mathbb{Q})\backslash X_{K_{J}, \tau}(\tau)\times G(\mathbb{A}^{p}_{f})/K^{p}\xrightarrow{\cong} A^{\mathrm{pf}}_{J, \tau}.\end{align*}$$
Then we need to show that
 $(J_{\tau }/J_{\tau }\cap \breve {K}_{J})\cong X_{K_{J}, \tau }(\tau )$
as
$(J_{\tau }/J_{\tau }\cap \breve {K}_{J})\cong X_{K_{J}, \tau }(\tau )$
as
 $I_{\tau }(\mathbb {Q})\backslash (J_{\tau }/J_{\tau }\cap \breve {K}_{J})\times G(\mathbb {A}^{p}_{f})/K^{p}$
is well known to be a finite set. In the case where
$I_{\tau }(\mathbb {Q})\backslash (J_{\tau }/J_{\tau }\cap \breve {K}_{J})\times G(\mathbb {A}^{p}_{f})/K^{p}$
is well known to be a finite set. In the case where
![]() $\breve {K}_{J}=\breve {I}$
, this is shown in [Reference Görtz and HeGH15, Theorem 2.1.1]. The general case can be deduced from this by using the fact that
$\breve {K}_{J}=\breve {I}$
, this is shown in [Reference Görtz and HeGH15, Theorem 2.1.1]. The general case can be deduced from this by using the fact that
![]() $\mathcal {A}_{I, \tau }\rightarrow \mathcal {A}_{J, \tau }$
is finite étale as shown in [Reference Shen, Yu and ZhangSYZ19]; see also [Reference Görtz and YuGY10, Proposition 6.1].
$\mathcal {A}_{I, \tau }\rightarrow \mathcal {A}_{J, \tau }$
is finite étale as shown in [Reference Shen, Yu and ZhangSYZ19]; see also [Reference Görtz and YuGY10, Proposition 6.1].
▪
Theorem 6.4 The basic KR stratum
 $\mathcal {A}^{\mathrm {pf}}_{I, w}$
is isomorphic to
$\mathcal {A}^{\mathrm {pf}}_{I, w}$
is isomorphic to
![]() $\mathcal {A}_{J, \tau }\times Y(J, w)$
.
$\mathcal {A}_{J, \tau }\times Y(J, w)$
.
Proof This follows by summarizing the above discussions. ▪
Comparing this theorem with [Reference Görtz and YuGY10, Corollary 6.5] shows that the description of the basic KR stratum in Theorem 5.7 agrees with the description by Görtz and Yu in [Reference Görtz and YuGY10, Corollary 6.5]. Note that contravariant Dieudonné module is used in [Reference Görtz and YuGY10] and we are using covariant Dieudonné module here. This explains why we have
![]() $Y_{J}(w)$
instead of
$Y_{J}(w)$
instead of
![]() $X(w^{-1})$
in [Reference Görtz and YuGY10, Corollary 6.5].
$X(w^{-1})$
in [Reference Görtz and YuGY10, Corollary 6.5].
6.3 Basic EO Stratum
Consider the isomorphism class of the p-torsion subgroup
![]() $A[p]$
together with its additional structures coming from a point
$A[p]$
together with its additional structures coming from a point
![]() $(A, \eta )$
on
$(A, \eta )$
on
![]() $\mathcal {A}_{\{0\}}=\mathcal {A}_{g}$
. After passing to its Dieudonné module, we have a map
$\mathcal {A}_{\{0\}}=\mathcal {A}_{g}$
. After passing to its Dieudonné module, we have a map
 $$ \begin{align} \nu_{K}: \mathcal{A}_{g}(\mathbb{F})\longrightarrow G(\breve{\mathbb{Q}}_{p})/\breve{K}_{\sigma}(\breve{K}_{1}\times \breve{K}_{1}). \end{align} $$
$$ \begin{align} \nu_{K}: \mathcal{A}_{g}(\mathbb{F})\longrightarrow G(\breve{\mathbb{Q}}_{p})/\breve{K}_{\sigma}(\breve{K}_{1}\times \breve{K}_{1}). \end{align} $$
Let
![]() $^{g}W$
be the set of minimal length representatives of
$^{g}W$
be the set of minimal length representatives of
![]() $S_{g}\backslash W_{g}$
. As explained in Example 3.4, the image of the map (6.1) can be identified with
$S_{g}\backslash W_{g}$
. As explained in Example 3.4, the image of the map (6.1) can be identified with
![]() $^{g}W\subset W_{g}$
. Let
$^{g}W\subset W_{g}$
. Let
![]() $c\leq g$
, the finite Weyl group
$c\leq g$
, the finite Weyl group
![]() $W_{c}$
of
$W_{c}$
of
![]() $\mathrm {Sp}_{2c}$
can be viewed as a subgroup of
$\mathrm {Sp}_{2c}$
can be viewed as a subgroup of
![]() $W_{g}$
naturally and we define
$W_{g}$
naturally and we define
![]() ${^{c}W}$
exactly the same way as in the case for
${^{c}W}$
exactly the same way as in the case for
![]() ${^{g}W}$
. Explicitly, the reflection
${^{g}W}$
. Explicitly, the reflection
![]() $s_{c+1-i}$
in
$s_{c+1-i}$
in
![]() $W_{c}$
will be mapped to
$W_{c}$
will be mapped to
![]() $s_{g+1-i}$
as a reflection in
$s_{g+1-i}$
as a reflection in
![]() $W_{g}$
. We have the following criterion for identifying the basic EO stratum. Let
$W_{g}$
. We have the following criterion for identifying the basic EO stratum. Let
![]() $K=\widetilde {\mathbb {S}}-\{s_{0}\},$
which corresponds to the hyperspecial subgroup of
$K=\widetilde {\mathbb {S}}-\{s_{0}\},$
which corresponds to the hyperspecial subgroup of
![]() $G(\mathbb {Q}_{p})$
.
$G(\mathbb {Q}_{p})$
.
Proposition 6.5 Let
![]() $w\in ^{g}W$
. Then the EO stratum
$w\in ^{g}W$
. Then the EO stratum
![]() $\mathcal {A}_{g, w}$
is basic if and only if
$\mathcal {A}_{g, w}$
is basic if and only if
![]() $w\in {^{c}W}$
for some
$w\in {^{c}W}$
for some
![]() $c\leq g/2$
.
$c\leq g/2$
.
Proof By Proposition 6.1,
![]() $EO_{K,w}$
is basic if and only if
$EO_{K,w}$
is basic if and only if
![]() $w\in W_{\{c, g-c\}}\tau $
considered as an element in
$w\in W_{\{c, g-c\}}\tau $
considered as an element in
![]() $^{K}\widetilde {W}$
. Since
$^{K}\widetilde {W}$
. Since
by [Reference Görtz and HoeveGH12, Lemma 3.8],
![]() $EO_{K, w}$
is basic if and only if
$EO_{K, w}$
is basic if and only if
![]() $w\in {^{c}W}$
as an element in
$w\in {^{c}W}$
as an element in
![]() ${^{g}W}$
.▪
${^{g}W}$
.▪
This proposition rediscovers [Reference HarashitaHar10, Remark 2.5.7], and we now explain how to describe those basic EO strata as disjoint unions of Deligne–Lusztig varieties. Again Corollary 5.4 takes the following form
 $$\begin{align*}I_{\tau}(\mathbb{Q})\backslash X_{K, w}(\tau)\times G(\mathbb{A}^{p}_{f})/K^{p}\xrightarrow{\cong} \mathcal{A}^{\mathrm{pf}}_{g, w}, \end{align*}$$
$$\begin{align*}I_{\tau}(\mathbb{Q})\backslash X_{K, w}(\tau)\times G(\mathbb{A}^{p}_{f})/K^{p}\xrightarrow{\cong} \mathcal{A}^{\mathrm{pf}}_{g, w}, \end{align*}$$
and by the proof of Theorem 5.7,
 $$\begin{align*}X_{K,w}(\tau)=\bigsqcup_{i\in J_{\tau}/J_{\tau}\cap \breve{K}_{\mathrm{supp}_{\sigma}(w)\cup I(K, w, \sigma)}}iY_{I(K, w, \sigma)}(w) \end{align*}$$
$$\begin{align*}X_{K,w}(\tau)=\bigsqcup_{i\in J_{\tau}/J_{\tau}\cap \breve{K}_{\mathrm{supp}_{\sigma}(w)\cup I(K, w, \sigma)}}iY_{I(K, w, \sigma)}(w) \end{align*}$$
where
 $$ \begin{align*} Y_{I(K, w, \sigma)}(w)&=\{g\breve{K}_{I(K, w, \sigma)}\in \breve{K}_{\mathrm{supp}_{\sigma}(w)\cup I(K, w, \sigma)}/\breve{K}_{I(K, w, \sigma)}: g^{-1}\tau\sigma(g)\\ & \quad \in \breve{K}_{I(K, w, \sigma)}w\breve{K}_{\sigma(I(K, w, \sigma))}\}\\ &=\{g \breve{K}_{\mathrm{supp}_{\sigma}(w)\cap K} \in \breve{K}_{\mathrm{supp}_{\sigma}(w)}/\breve{K}_{\mathrm{supp}_{\sigma}(w)\cap K}: g^{-1}\tau\sigma(g)\\ & \quad \in {\breve{K}_{\mathrm{supp}_{\sigma}(w)\cap K \sigma}}\breve{I}w\breve{I} \}. \end{align*} $$
$$ \begin{align*} Y_{I(K, w, \sigma)}(w)&=\{g\breve{K}_{I(K, w, \sigma)}\in \breve{K}_{\mathrm{supp}_{\sigma}(w)\cup I(K, w, \sigma)}/\breve{K}_{I(K, w, \sigma)}: g^{-1}\tau\sigma(g)\\ & \quad \in \breve{K}_{I(K, w, \sigma)}w\breve{K}_{\sigma(I(K, w, \sigma))}\}\\ &=\{g \breve{K}_{\mathrm{supp}_{\sigma}(w)\cap K} \in \breve{K}_{\mathrm{supp}_{\sigma}(w)}/\breve{K}_{\mathrm{supp}_{\sigma}(w)\cap K}: g^{-1}\tau\sigma(g)\\ & \quad \in {\breve{K}_{\mathrm{supp}_{\sigma}(w)\cap K \sigma}}\breve{I}w\breve{I} \}. \end{align*} $$
Lemma 6.6 Suppose that
![]() $w\in {^{c}W}$
and
$w\in {^{c}W}$
and
![]() $w\not \in {^{c-1}W}$
; then
$w\not \in {^{c-1}W}$
; then
Proof By the proof of [Reference HoeveHoe10, Lemma 7.1] (see also [Reference Görtz and HoeveGH12, Lemma 3.8]) the set of simple reflections in a reduced expression of w is equal to
![]() $\{s_{i}, s_{i+1}, \cdots , s_{g-1}, s_{g}\}$
with
$\{s_{i}, s_{i+1}, \cdots , s_{g-1}, s_{g}\}$
with
![]() $i>g-c$
. Since
$i>g-c$
. Since
![]() $w\not \in {^{c-1}W}$
,
$w\not \in {^{c-1}W}$
,
![]() $i=g-c+1$
. Then by definition, we have
$i=g-c+1$
. Then by definition, we have
Note the proof of the above lemma shows that those
![]() $w\in {^{c}W}$
and
$w\in {^{c}W}$
and
![]() $w\not \in {^{c-1}W}$
are in fact
$w\not \in {^{c-1}W}$
are in fact
![]() $\sigma $
-Coxeter elements in
$\sigma $
-Coxeter elements in
![]() $W_{\mathrm {supp}_{\sigma }(w)}$
. Therefore, we obtain the following lemma.
$W_{\mathrm {supp}_{\sigma }(w)}$
. Therefore, we obtain the following lemma.
Lemma 6.7 The set
![]() $I(K, w, \sigma )$
is equal to
$I(K, w, \sigma )$
is equal to
![]() $\{s_{c+1}, \cdots , s_{g-c-1}\}$
.
$\{s_{c+1}, \cdots , s_{g-c-1}\}$
.
Proof By [Reference Görtz and HeGH15, Lemma 4.6.1],
![]() $I(K, w, \sigma )$
is exactly the set of simple reflections that commute with
$I(K, w, \sigma )$
is exactly the set of simple reflections that commute with
The result is then clear. ▪
For
![]() $I(K, w, \sigma )=\{s_{c+1}, \dots , s_{g-c-1}\}$
, we denote by
$I(K, w, \sigma )=\{s_{c+1}, \dots , s_{g-c-1}\}$
, we denote by
![]() $Y_{c}(w)$
the fine Deligne–Lusztig variety given by
$Y_{c}(w)$
the fine Deligne–Lusztig variety given by
 $$ \begin{align*} Y_{I(K, w, \sigma)}(w) &= \{g \breve{K}_{\mathrm{supp}_{\sigma}(w)\cap K} \in \breve{K}_{\mathrm{supp}_{\sigma}(w)}/\breve{K}_{\mathrm{supp}_{\sigma}(w)\cap K}: g^{-1}\tau\sigma(g)\\ &\quad \in {\breve{K}_{\mathrm{supp}_{\sigma}(w)\cap K \sigma}}\breve{I}w\breve{I} \}. \end{align*} $$
$$ \begin{align*} Y_{I(K, w, \sigma)}(w) &= \{g \breve{K}_{\mathrm{supp}_{\sigma}(w)\cap K} \in \breve{K}_{\mathrm{supp}_{\sigma}(w)}/\breve{K}_{\mathrm{supp}_{\sigma}(w)\cap K}: g^{-1}\tau\sigma(g)\\ &\quad \in {\breve{K}_{\mathrm{supp}_{\sigma}(w)\cap K \sigma}}\breve{I}w\breve{I} \}. \end{align*} $$
Since
![]() $K=\widetilde {S}-\{s_{0}\}$
,
$K=\widetilde {S}-\{s_{0}\}$
,
![]() $K\cap \mathrm {supp}_{\sigma }(w)=\{s_{1}, \dots , s_{c-1}\}\cup \{s_{g-c+1}, \dots , s_{g}\}$
. It follows that
$K\cap \mathrm {supp}_{\sigma }(w)=\{s_{1}, \dots , s_{c-1}\}\cup \{s_{g-c+1}, \dots , s_{g}\}$
. It follows that
![]() $Y_{c}(w)$
is exactly the fine Deligne–Lusztig variety denoted by
$Y_{c}(w)$
is exactly the fine Deligne–Lusztig variety denoted by
![]() $X_{c(w)}\{\tau (w)\}$
in [Reference HoeveHoe10, Theorem 1.2].
$X_{c(w)}\{\tau (w)\}$
in [Reference HoeveHoe10, Theorem 1.2].
Theorem 6.8 For
![]() $w\in {^{c}W}$
and
$w\in {^{c}W}$
and
![]() $w\not \in {^{c-1}W}$
, the basic EO stratum
$w\not \in {^{c-1}W}$
, the basic EO stratum
 $\mathcal {A}^{\mathrm {pf}}_{g, w}$
is isomorphic to
$\mathcal {A}^{\mathrm {pf}}_{g, w}$
is isomorphic to
![]() $\mathcal {A}_{\{c, g-c\}, \tau }\times Y_{c}(w).$
$\mathcal {A}_{\{c, g-c\}, \tau }\times Y_{c}(w).$
Proof We know that
 $$\begin{align*}I_{\tau}(\mathbb{Q})\backslash X_{K, w}(\tau)\times G(\mathbb{A}^{p}_{f})/K^{p}\xrightarrow{\cong} \mathcal{A}^{\mathrm{pf}}_{g, w} \end{align*}$$
$$\begin{align*}I_{\tau}(\mathbb{Q})\backslash X_{K, w}(\tau)\times G(\mathbb{A}^{p}_{f})/K^{p}\xrightarrow{\cong} \mathcal{A}^{\mathrm{pf}}_{g, w} \end{align*}$$
and
 $$\begin{align*}X_{K,w}(\tau)=\bigsqcup_{i\in J_{\tau}/J_{\tau}\cap \breve{K}_{\mathrm{supp}_{\sigma}(w)\cup I(K, w, \sigma)}}iY_{c}(w). \end{align*}$$
$$\begin{align*}X_{K,w}(\tau)=\bigsqcup_{i\in J_{\tau}/J_{\tau}\cap \breve{K}_{\mathrm{supp}_{\sigma}(w)\cup I(K, w, \sigma)}}iY_{c}(w). \end{align*}$$
Notice that
 $\mathrm {supp}_{\sigma }(w)\cup I(K, w, \sigma )=\widetilde {\mathbb {S}}-\{c, g-c\}$
by Lemmas 6.6 and 6.7. The result follows from the fact that
$\mathrm {supp}_{\sigma }(w)\cup I(K, w, \sigma )=\widetilde {\mathbb {S}}-\{c, g-c\}$
by Lemmas 6.6 and 6.7. The result follows from the fact that
 $$\begin{align*}I_{\tau}(\mathbb{Q})\backslash J_{\tau}/J_{\tau}\cap \breve{K}_{\widetilde{\mathbb{S}}-\{c, g-c\}}\times G(\mathbb{A}^{p}_{f})/K^{p}. \end{align*}$$
$$\begin{align*}I_{\tau}(\mathbb{Q})\backslash J_{\tau}/J_{\tau}\cap \breve{K}_{\widetilde{\mathbb{S}}-\{c, g-c\}}\times G(\mathbb{A}^{p}_{f})/K^{p}. \end{align*}$$
is isomorphic to
![]() $\mathcal {A}_{\{c, g-c\}, \tau }$
as shown in Lemma 6.3. ▪
$\mathcal {A}_{\{c, g-c\}, \tau }$
as shown in Lemma 6.3. ▪
This shows that the description of Görtz–He–Nie in Theorem 5.7 for the basic EO stratum agrees with the description of Hoeve as in [Reference HoeveHoe10, Theorem 1.2]. Moreover, let
 $J=\widetilde {\mathbb {S}}-\{c, g-c\}$
in Theorem 6.4 and let
$J=\widetilde {\mathbb {S}}-\{c, g-c\}$
in Theorem 6.4 and let
![]() $w\in {^{c}W}$
as in Theorem 6.8. Then we easily obtain the following commutative diagram combining Theorems 6.4 and 6.8
$w\in {^{c}W}$
as in Theorem 6.8. Then we easily obtain the following commutative diagram combining Theorems 6.4 and 6.8

Acknowledgment
This work was completed when the author was a postdoctoral fellow at McGill university, and he would like to thank Henri Darmon and Pengfei Guan for their generous support. We sincerely thank the referee for all the comments and corrections made to this note.




