Hostname: page-component-cb9f654ff-mwwwr Total loading time: 0 Render date: 2025-08-22T00:10:36.989Z Has data issue: false hasContentIssue false
  • English
  • Français

On weaving Hilbert space frames and Riesz bases

Part of: Nontrigonometric harmonic analysis General theory of linear operators Topological linear spaces and related structures

Published online by Cambridge University Press:  22 July 2025

Animesh Bhandari Open the ORCID record for Animesh Bhandari [Opens in a new window]
Animesh Bhandari*
Affiliation:
Department of Mathematics, https://ror.org/013vs5h31 SRM University, AP - Andhra Pradesh , Neeru Konda, Mangalagiri, Amaravati, Andhra Pradesh - 522240, India
*
e-mail: bhandari.animesh@gmail.com animesh.b@srmap.edu.in
Get access Rights & Permissions [Opens in a new window]

Abstract

Two frames 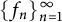$\{f_n\}_{n =1}^{\infty }$ and $\{g_n\}_{n =1}^{\infty }$ in a separable Hilbert space ${\mathcal H}$ are said to be weaving frames, if for every 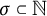$\sigma \subset \mathbb N$, 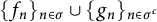$\{f_n\}_{n\in \sigma } \cup \{g_n\}_{n\in \sigma ^c}$ is a frame for ${\mathcal H}$. Weaving frames are proved to be very useful in many areas, such as, distributed processing, wireless sensor networks, packet encoding, and many more. Inspired by the work of Bemrose et al. [2], this paper delves into the properties and characterizations of weaving frames and weaving Riesz bases.

Keywords

FrameBesselian frameweaving frames

MSC classification

Primary: 42C15: General harmonic expansions, frames
Secondary: 46A32: Spaces of linear operators; topological tensor products; approximation properties 47A05: General (adjoints, conjugates, products, inverses, domains, ranges, etc.)

Information

Type
Article
Information
Canadian Mathematical Bulletin , First View , pp. 1 - 10
Check for updates
Copyright
© The Author(s), 2025. Published by Cambridge University Press on behalf of Canadian Mathematical Society

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Article purchase

Temporarily unavailable

References

Arefijamaal, A. and Zekaee, E., Image processing by alternate dual Gabor frames . Bull. Iran. Math. Soc. 42(2016), 1305–1314.Google Scholar
Bemrose, T., Casazza, P. G., Gröchenig, K., Lammers, M. C., and Lynch, R. G., Weaving frames . Oper. Matr. 10(2016), 1093–1116.Google Scholar
Bhandari, A. and Mukherjee, S., Atomic subspaces for operators . Indian J. Pure Appl. Math. 51(2020), 1039–1052.Google Scholar
Casazza, P. G., Freeman, D., and Lynch, R. G., Weaving Schauder frames . J. Approx. Theory 211(2016), 42–60.Google Scholar
Casazza, P. G. and Kutyniok, G., Finite frames: Theory and applications, Applied and Numerical Harmonic Analysis, Birkhäuser, Boston, MA, 2012.Google Scholar
Casazza, P. G. and Kutyniok, G., Frames of subspaces . Contemp. Math. 345(2014), 87–114.Google Scholar
Casazza, P. G., Kutyniok, G., and Li, S., Fusion frames and distributed processing . Appl. Comput. Harmon. Anal. 25(2008), 114–132.Google Scholar
Casazza, P. G., Kutyniok, G., Li, S., and Rozell, C. J., Modeling sensor networks with fusion frames . In: Proc. SPIE, vol. 6701, Wavelets XII, 67011M (20 September 2007); San Diego, California, 2007. https://doi.org/10.1117/12.730719.Google Scholar
Christensen, O., An introduction to frames and Riesz bases, Birkhäuser, Boston, MA, 2003.Google Scholar
Daubechies, I., Grossmann, A., and Meyer, Y., Painless non orthogonal expansions . J. Math. Phys. 27(1986), 1271–1283.Google Scholar
Deepshikha, and Vashisht, L. K., Weaving $K$ -frames in Hilbert spaces. Results Math. 73(2018), 81.Google Scholar
Duffin, R. and Schaeffer, A. C., A class of non harmonic Fourier series . Trans. Amer. Math. Soc. 72(1952), 341–366.Google Scholar
Dunford, N. and Schwartz, J., Linear operators, I, Interscience, New York, NY, 1963.Google Scholar
Ferreira, P., Mathematics for multimedia signal processing II: discrete finite frames and signal reconstruction, Signal Processing for Multimedia, Byrnes, J. S. (ed.), 1999, 35–54.Google Scholar
Gǎvruţa, L., Frames for operators . Appl. Comput. Harmon. Anal. 32(2012), 139–144.Google Scholar
Gröchenig, K., Foundations of time-frequency analysis, Birkhäuser, New York, NY, 2001.Google Scholar
Gumber, A. and Shukla, N. K., Uncertainty principle corresponding to an orthonormal wavelet system . Appl. Anal. 97(2018), 486–498.Google Scholar
Han, D. and Larson, D. R., Frames, bases and group representations, Memoirs of the American Mathematical Society, 147(2000), 94 pp.Google Scholar
Holub, J. R., Pre-frame operators, Besselian frames, and near-Riesz BASES in Hilbert spaces . Proc. Amer. Math. Soc. 122(1994), 779–785.Google Scholar
Retherford, J. and Holub, J., The stability of bases in Banach and Hilbert spaces . J. Reine Angew. Math. 246(1994), 136–146.Google Scholar
Schatten, J., Norm ideals of completely continuous operators, Springer-Verlag, Berlin, 1970.Google Scholar
Singer, I., Bases in Banach spaces, I, Springer-Verlag, Berlin, 1970.Google Scholar
Sun, W., $G$ -frames and $G$ -Riesz bases . J. Math. Anal. Appl. 322(2006), 437–452.Google Scholar
Verma, G., Vashisht, L. K., and Singh, M., On excess of retro Banach frames . J. Contemp. Math. Anal. (Armenian Acad. Sci.) 54(2019), 143–146.Google Scholar
Xu, Y. and Leng, J., New inequalities for weaving frames in Hilbert spaces . J. Inequal. Appl. 188(2021), 15 pp.Google Scholar