Tom Dishion, a pioneer in prevention science, was one of the first to recognize the importance of adapting interventions to the needs of individual families. With colleagues Elizabeth Stormshak and Kathryn Kavanaugh, Tom developed the Family Check-up, a highly adaptive prevention program for reducing developmental risk for later problem behavior and psychopathology (Dishion & Kavanagh, Reference Dishion and Kavanagh2003; Dishion & Stormshak, Reference Dishion and Stormshak2007). The Family Check-up begins by assessing a number of empirically derived risk and protective conditions to determine whether and how a family would benefit from a set of interventions tailored to their specific circumstances. Most other prevention programs developed during this period were either “one-size-fits-all” or indicated prevention programs, targeted for specific subgroups of children or families thought to be at risk. Prevention scientists have recently begun to catch up to Tom's vision, focusing on how existing prevention programs might build in program adaptations for specific children or families, as a means of increasing program efficacy. These include adaptive interventions that can be tested through novel experimental methods, such as sequential, multiple assignment, randomized trial (SMART) designs (August, Piehler, & Bloomquist, Reference August, Piehler and Bloomquist2016).
As a means of identifying populations or contexts that could benefit from adaptation, one promising initiative involves studying whether baseline levels of intervention targets, the factors thought to increase or protect against future risk for disorder, moderate the effect of preventive interventions on those targets and on distal outcomes. Initial work on such baseline target moderation assumed a compensatory model, conjecturing that those participants who entered a program with low levels of a protective target or high levels of a risk target would benefit most from the intervention. More recent work suggests that baseline target moderation analyses may detect other patterns of influence, including iatrogenic effects, and there is little work as yet on how and when to use findings of baseline target moderation to adapt prevention programming.
This paper addresses these two issues. We begin by summarizing the baseline target moderation (BTM) model and its extension in the baseline target moderated mediation (BTMM) model, within the context of causal inference. We then discuss several potential patterns of moderation, including compensatory effects; “rich-get-richer” effects (where benefits are found only for those who already have high levels of some protective factor); crossover effects (where some participants benefit, while other participants may be harmed by the intervention); and fully iatrogenic effects (where intervention effects are increasingly negative as levels of baseline protective factors vary). We illustrate each pattern with findings from recent prevention trials that have employed BTM or BTMM modeling. We then turn to the question of when BTMM effects are strong enough to warrant revision of existing prevention programs. Combining epidemiologic concepts of absolute risk reduction or increase with the BTMM framework, we construct models for each pattern of moderation. Using Monte Carlo methods, we simulate effect strength curves for each pattern and describe how these effect curves can inform decisions about next generation prevention programs and when those interventions need to consider adaptive strategies of the sort pioneered by Dishion and his colleagues. We end by discussing possible implications for the types of adaptations to consider in the face of BTMM effects.
Causal Inference and the Invariance Assumption
Rigorous tests of prevention trials require that we meet a series of assumptions for valid causal inference. We assume at least some understanding of the developmental mechanisms that increase risk for future behavioral or psychological disorders as well as some knowledge of mechanisms that can protect against such risk (Coie et al., Reference Coie, Watt, West, Hawkins, Asarnow, Markman and Long1993). These risk and protective mechanisms are assumed to be causal in that they exert an influence on whether or not disorders are more likely to occur in the future. These are represented by path b in Figure 1a.

Figure 1. Simple mediation and baseline target moderated mediation models.
MacKinnon (Reference MacKinnon2008) has referred to this set of mechanisms as the etiologic model that guides intervention development. We also assume that our interventions are designed to alter at least some of those mechanisms. As such, they are the targets of our intervention. The causal effect of intervention on these targets is represented by path a in Figure 1a. Taken together, these two assumptions imply that the effectiveness of an intervention for reducing risk for later disorder is indirect; they operate through changing more proximal targets, and altering these targets in turn leads to a later effect. It is also possible that our intervention changes other risk and protective mechanisms that we had not considered as targets. Such causal influences are represented by path c′ in Figure 1a. This is often referred to as the direct effect, although in prevention science it almost always reflects influences that operate through unknown or unmeasured mediating mechanisms.
We also assume that the three paths in Figure 1a are causally invariant (Howe, Reference Howe2019b). That is, they hold for all populations and all contexts within the range of application of our intervention theory. This assumption is necessary for inferring cause from any randomized intervention trial. Such trials assign individuals or families to intervention or control conditions, assuming homogeneity. That is, all participants assigned to a condition will have equivalent responses to that condition, regardless of condition assigned. When this assumption holds, we can estimate single effect parameters (such as a difference in means or a regression coefficient) for the sample as a whole as a means of characterizing each of the paths in Figure 1a.
Most prevention scientists would agree that the causal invariance assumption is violated to some degree in most prevention trials. Some youth are more likely to benefit than others are, and it is even possible that some youth will be at greater risk after participating in the intervention. Tom Dishion was again at the forefront in recognizing and studying iatrogenic effects in group-based preventive interventions for high-risk youth based on his studies of deviant peer affiliation (Dishion, McCord, & Poulin, Reference Dishion, McCord and Poulin1999; Dishion, Poulin, & Burraston, Reference Dishion, Poulin and Burraston2001). The net effect of a prevention program, averaged over all participants, may be positive while hiding considerable heterogeneity of effect, both positive and negative.
Figure 1b extends the basic mediation model to include baseline target moderation such that the d path reflects the strength of effect heterogeneity within the effect of intervention on change in the target. This leads to varying influences on the outcome through the mediating path b. It is also possible that baseline target levels will moderate the direct path c′ from intervention to change in outcome. The strength of this effect heterogeneity is indicated by the f path. Although not hypothesized by most prevention theories, such moderation may occur if the influence of the intervention on other unmeasured mediators varies across the baseline target level. It may be necessary to include the f path in order to control for more complex patterns of moderated mediational confounding.
It is also possible that outcomes vary directly as a function of the baseline target level. This is often implicitly assumed in prevention theories, given that intervention targets are chosen because of evidence that they are associated with distal outcomes. The extended model includes two paths that would carry this information: the direct path g from baseline target level to change in outcome, and the mediated path e, which reflects the association of baseline target level with change in outcome through its direct association with change in the target. These paths become important when we wish to estimate the strength of the intervention effect using standard indices that assess differences in risk between experimental and control groups, as they reflect the case where risk rates in the untreated control group are not stable, but vary over baseline target levels.
Baseline Target Moderation
Quantitative methods, such as regression mixture modeling (Van Horn et al., Reference Van Horn, Jaki, Masyn, Howe, Feaster, Lamont and Kim2015), are available for detecting violations of causal invariance even when we have no idea what causes it. However, these methods require large sample sizes, and they can be very sensitive to distributional assumptions. Also, they are easily biased (George et al., Reference George, Yang, Van Horn, Smith, Jaki, Feaster and Howe2013; Kim et al., Reference Kim, Lamont, Jaki, Feaster, Howe and Van Horn2016). As a common alternative, investigators may explore potential sources of heterogeneity through interaction designs that test whether observed variables interact with a treatment to predict differential responses. Such exploratory work is important but often atheoretical, attending to easily measured “usual suspects” such as gender, age, race, or ethnicity.
Howe (Reference Howe2019b) has suggested that theoretically derived hypotheses about the sources of effect heterogeneity may prove more fruitful, and this points to the etiologic model of a preventive intervention as an important source of such hypotheses. Intervention targets derived from the etiologic model include specific risk and protective mechanisms, and youth or families enrolled in prevention trials always vary at baseline on these mechanisms. For example, the Familias Unidas program, a family-focused intervention designed to reduce risk for future substance use and problem behavior in Latino youth, targets family communication patterns (Prado et al., Reference Prado, Pantin, Briones, Schwartz, Feaster, Huang and Szapocznik2007). Families entering the program vary substantially in their communication skills, with some families communicating well, and others poorly. The etiologic model of this program predicts that improvement in family communication will reduce risk for future youth problem behavior, and this implies that families with poor communication may benefit more than families who already communicate well. We refer to this as a compensatory model. In more formal terms, it predicts that levels of the family communication target, measured at baseline, would interact with intervention condition such that the effect of intervention, as mediated through changes in family communication, would be stronger for those with lower baseline levels, and weaker for those with higher baseline levels.
Under this general hypothesis, baseline target moderation (BTM) would occur for both change in target and change in outcome under the assumption that the former mediates the intervention effect on the latter, as illustrated in Figure 2a. This reflects a more complex hypothesis of baseline target moderated mediation (BTMM). Perrino et al. (Reference Perrino, Pantin, Prado, Huang, Brincks, Howe and Brown2014) provide an example, combining data from three randomized trials of the Familias Unidas program. They found that baseline target levels of family communication moderated the effect of the intervention on both changes in family communication and reduced risk for youth internalizing. They also found that changes in communication mediated the moderated effect on the distal outcome.
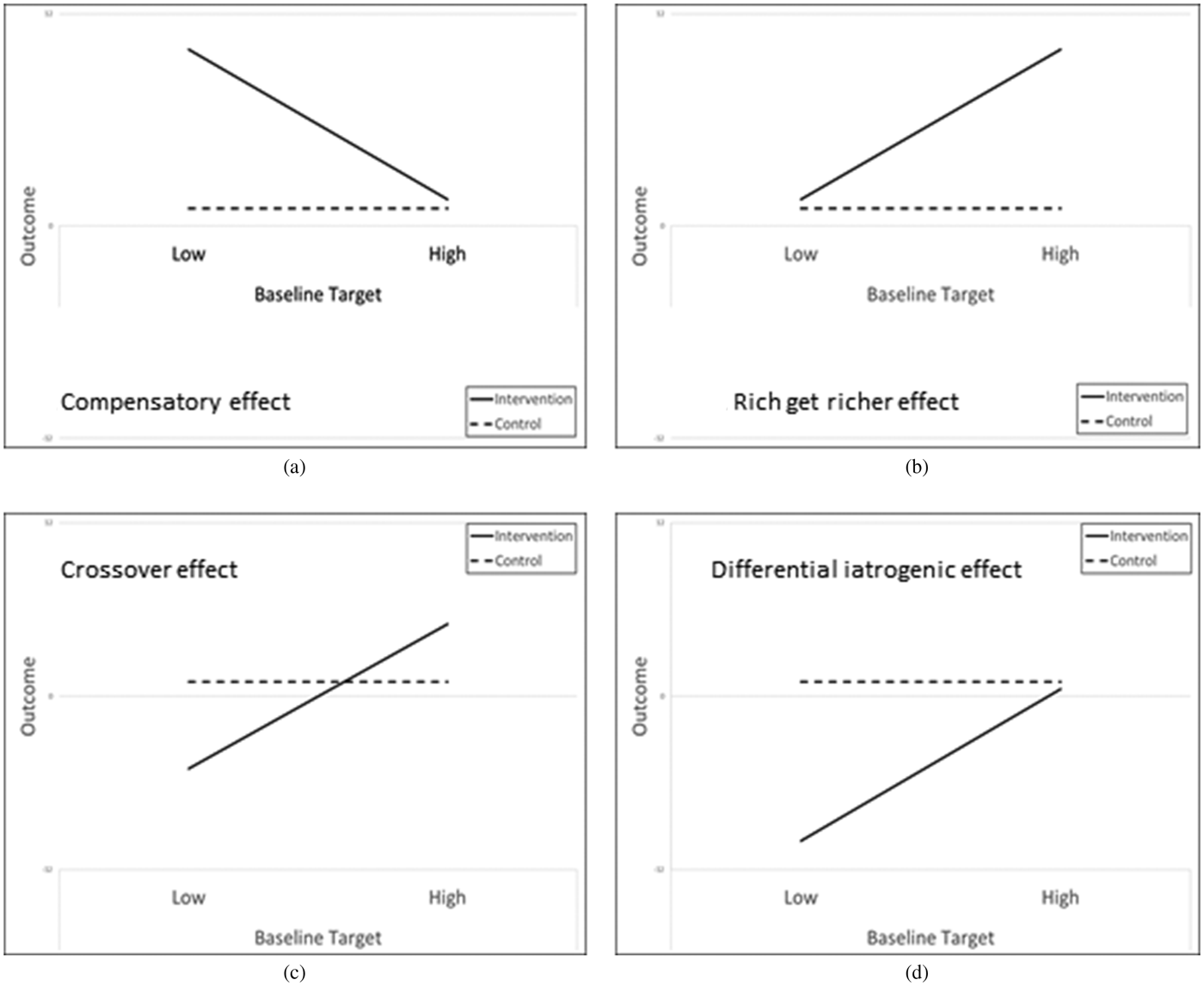
Figure 2. Various forms of baseline target moderation (higher outcome levels reflect better outcomes).
A randomized intervention trial design that allows for complete testing of BTMM requires that we assess target levels at baseline and after the intervention and distal outcomes at subsequent follow-up. Other designs can provide partial evidence. Microtrials (Howe, Beach, & Brody, Reference Howe, Beach and Brody2010; Howe & Ridenour, Reference Howe, Ridenour, Sloboda, Petras, Hingson and Robertson2019) can incorporate baseline target moderators in testing whether the effects of intervention components on specific targets vary by baseline target level. Full scale prevention trials can test baseline target moderation of outcome effects even when target change is not assessed, although such tests provide weaker evidence relevant for adaptation, as they do not clarify whether these effects are carried by changes in that target.
Beyond Compensatory Effects
Compensatory effects emphasize preventive effects through addressing deficiencies in protective factors. Figure 2a provides one simulated outcome of a compensatory effect, where preventive effects occur only for those having initially lower levels of a protective factor. However, other effects are possible, and they have been reported in recent studies. Significant BTM can also reflect rich-get-richer effects. As illustrated in Figure 2b, this occurs when youth or families who enter the program with higher levels of the protective factor show a stronger preventive effect than those at lower levels. Gonzales et al. (Reference Gonzales, Dumka, Millsap, Gottschall, McClain, Wong and Kim2012) tested BTMM effects in their trial of the Bridges/Puentes program designed to reduce risk for a range of substance use, mental health, and school outcomes in Mexican American youth through targeting a number of parenting behaviors. They found a number of BTMM effects, and while most fit a compensatory pattern, effects on father monitoring followed a rich-get-richer pattern, where those fathers initially higher in monitoring showed greater improvement in monitoring, and this mediated an effect on later reports of youth externalizing.
A more complex form of this effect has been reported in studies of education programs. Referred to as the crossover or MatthewFootnote 1 effect, youth with higher baseline levels show faster skill development, while youth with lower baseline levels show slower skill development after intervention (Luyten & ten Bruggencate, Reference Luyten and ten Bruggencate2011). This reflects another possibility: preventive interventions may have a positive effect on some and a negative effect on others. For example, Howe (Reference Howe2019a) found evidence for a crossover effect in a randomized trial of an intervention to reduce future depression in couples experiencing recent job loss through targeting couple communication skills. Partners in couples with high initial levels of communication showed decreases in depressive symptoms at one year following intervention compared with controls, while those with low initial levels maintained or increased levels of depressive symptoms. A simulated example of such an effect is illustrated in Figure 2c.
Finally, BTMM effects may also detect differential iatrogenic influences. For example, Prado and Pantin (Reference Prado and Pantin2011) found that an intervention for Latino youth encouraging parents to communicate with youth about the risks of tobacco use was associated with more tobacco use in adolescents who reported poor communication with their parents, low parental involvement and support, and less family cohesion. Figure 2d illustrates this pattern.
When Do BTMM Findings Call for Adaptation?
Although attention to BTM and BTMM has increased in prevention trials research, there is little discussion as yet on the practical implications of those findings for program adaptation. The need for adaptation becomes more compelling when BTMM designs provide stronger evidence for inferring causal effect and when the strength of intervention effect passes practical thresholds for salutary or iatrogenic effects.
Confidence in Causal Inference
Etiologic models entail a set of causal hypotheses concerning the effect of preventive interventions on specific targets and of target change on future outcomes. Haack (Reference Haack2003) notes that causal inference in the social sciences is not an all-or-nothing proposition. We build confidence in the warrant of causal hypotheses by amassing empirical evidence across many studies and research designs, and our confidence increases in proportion to the rigor of our methods. Pearl (Reference Pearl2009), Rubin (Reference Rubin1974), and others have developed a counterfactual framework that is useful for evaluating whether specific methods increase confidence through reducing the likelihood of confounding. We can apply these to identify a range of designs that provide increasingly stringent tests of causal inference for BTMM.
Full randomization to preventive intervention or control conditions greatly increases (but does not fully guarantee) confidence that the intervention has a causal effect on changing target mechanisms (the a path in Figure 1) by reducing or eliminating unobserved confounding. Although randomized trials are the gold standard, well-designed quasi-experimental studies or observational studies that use propensity score matching can also provide relevant evidence, albeit with less confidence.
To test the BTMM model, these designs need to include careful assessment of baseline target levels and subsequent change in those targets. Weak assessments increase measurement error, reducing sensitivity to detecting moderation. In addition, because baseline target levels are observed rather than randomly assigned, moderational confounding can occur (Howe, Reference Howe2019b). That is, baseline target levels may be shaped by other unobserved factors which are the true moderators of the intervention effect. Measurement and inclusion of plausible confounders as alternate moderators, either directly or through propensity score matching (Green & Stuart, Reference Green and Stuart2014) can increase confidence that baseline targets are the true moderators of an effect.
The BTMM model also hypothesizes that changes in risk or protective mechanisms have an influence on future risk for distal health outcomes (the b path in Figure 1). Random assignment to intervention condition does not control for potential confounding of this path (Pearl, Reference Pearl2012). Careful application of mediation modeling (MacKinnon, Reference MacKinnon2008) that includes both indirect and direct paths (ab and c′ in Figure 1) can help to rule out mediational confounding (Howe, Reiss, & Yuh, Reference Howe, Reiss and Yuh2002), which occurs when the intervention has an effect on unobserved mechanisms that in turn shape both the observed targets and the distal outcome. Unobserved historical confounds that shape both target and outcome can be ruled out through judicious use of lagged change-to-change models (Howe, Reference Howe2019b). These require measurement of change in targets that precedes measured change in distal health outcomes. And, as with moderational confounds, observed covariates that are plausible confounds of the b path can be used as statistical controls. All of these model-based methods increase confidence that plausible confounds are not biasing findings, but they are unlikely to completely rule out the effects of other unobserved confounders. Sensitivity analyses can prove useful in studying how strong such confounds would need to be to account for positive findings (Imai, Keele, & Tingley, Reference Imai, Keele and Tingley2010; VanderWeele, Reference VanderWeele2015).
Practical Thresholds for Preventive Intervention Effect
Findings of statistically significant BTMM effects in trials using rigorous methods to support causal inference suggest that program adaptations to prevention programs may be important, but by themselves do not clarify whether the effects are strong enough to make a practical difference. To do this, we need to establish benchmarks for meaningful preventive effects. Such benchmarks reflect judgments based on value judgements concerning what constitutes a significant disruption of health.
Prevention scientists have focused on three types of thresholds when evaluating preventive effects: diagnosable disorders, midpoint targets, and specific risk or protective targets defined by the etiologic model. Diagnosable disorders are defined as being either present or absent, based on established diagnostic criteria. These criteria may reflect clear discontinuities, such as the presence or absence of HIV infection, but they may also be defined by practical thresholds along a symptom continuum, as with major depressive disorder.
Elevated but subthreshold symptoms are often considered clinically important as well (Gotlib, Lewinsohn, & Seeley, Reference Gotlib, Lewinsohn and Seeley1995). In treatment research, this may lead to distinctions of complete remission (all symptoms have resolved) or partial remission (symptoms are no longer above threshold for diagnosable disorder, but are still present). For prevention trials, the utility of these distinctions will depend in part on whether the intervention is considered universal, selective, or indicated based on the needs of relevant populations. Universal and selective interventions target populations that are not yet showing elevated symptoms, and they would need to develop threshold criteria for what constitutes meaningful elevation in the subclinical range. Indicated interventions target those who are already showing increased but subclinical symptoms; here we may be interested in both prevention thresholds (such as elevation to the diagnosable range) and treatment thresholds (reduction to complete symptom resolution).
Many prevention trials are designed to prevent disorder in the long run through changing more proximal midpoint targets. Dietary interventions to reduce risk of heart disease may assess relative increases in blood pressure as a midpoint target because epidemiologic research demonstrates that elevated blood pressure increases risk of future heart disease. Midpoint targets are more justified when there is strong evidence that the target is causal. Findings that high blood pressure increases inflammation in the circulatory system provide such evidence in the case of heart disease.
Studies of developmental cascades, especially those that test such cascades following preventive intervention, provide similar evidence for behavioral and psychological disorders. As an example, Perrino et al. (Reference Perrino, Brincks, Howe, Brown, Prado, Pantin and Brown2016), in a selective trial of the Familias Unidas intervention for eighth grade students, found that lower levels of externalizing behavior at 18 months after intervention were associated with reduced risk for depressive symptoms at 30 months and mediated the effect of the intervention on depression. Midpoint targets are often defined on a continuum, and establishing prevention thresholds requires that we attend to the strength of attributable risk. We may define the prevention threshold as lower when the midpoint target is very strongly associated with future disorder or higher when the midpoint target has weak attributable risk.
We may also define prevention thresholds for the risk or protective mechanisms directly targeted by an intervention. As with midpoint targets, practical thresholds for such mechanisms need to take into account the strength of attributable risk (or attributable protection), based on findings concerning the association of these mechanisms with the disorders of interest (the b path in Figure 1) as well as evidence that these factors are causal. Again, prevention trials that assess mediation can provide some of the strongest evidence here. The Perrino et al. (Reference Perrino, Brincks, Howe, Brown, Prado, Pantin and Brown2016) trial of Familias Unidas also found that changes in family communication, a primary target of the intervention, mediated the effect of the intervention on externalizing and on subsequent depression.
Indexing preventive thresholds
Thresholds defined by diagnosis, levels of midpoint targets, or RPM targets help us define an index of meaningful preventive effect when we apply them to outcomes from a controlled trial of a preventive intervention. We can use them to define outcome in binary terms, such as whether or not a child goes on to develop a diagnosable condition or exceeds the threshold on a midpoint target or on a targeted risk or protective mechanism. Once we have established a binary outcome, we can specify baseline target moderated mediation models, as illustrated in Figure 1b, and estimate all relevant paths. In the examples we provide here, variables for baseline target level and change in target are continuous, so model estimation of the a, d, and e paths would use linear regression, while model estimation of the b, c′, f, and g paths would use logistic regression. The strength of the moderated indirect path (ab moderated by d) would therefore estimate how the effect of the intervention, mediated through change in the target, varies across the baseline target level. These path estimates can then be used to estimate rates of outcome events (above the prevention threshold) for the intervention group (the experimental event rate, or EER), and compare them with estimated rates for the control group (the control event rate, or CER).
Epidemiologists have developed both absolute and relative indices of intervention effects based on the CER and the EER. Absolute risk reduction (ARR) is defined as the difference in these event rates (CER - EER). In the simulated data for the example illustrated in Figure 3 and discussed in more detail later, 19.4% of control group children later exceeded the preventive threshold, while 17.8% of those in the intervention condition did, resulting in an ARR of 1.6%. The inverse of ARR is defined as the number needed to treat (NNT), or the number needed to harm (NNH) if the ARR is negative. NNT reflects the number of cases (children, adolescents, or families) that would need to participate in the preventive intervention in order to reduce the number of cases exceeding the preventive threshold by one when compared with the rates found in the control group. The number needed to harm (NNH) indexes iatrogenic effect, and it is defined as the number of cases needed to participate in the intervention that increase the number of cases exceeding our preventive threshold by one. Lower NNT rates reflect a stronger preventive effect, lower NNH rates reflect a stronger iatrogenic effect. In our example, the NNT equals 1/.016, or 63. Note that the lowest possible NNT for this study would reflect complete prevention of all cases: ARR would be 19%, and NNT would be 1/.19 or 5.2.
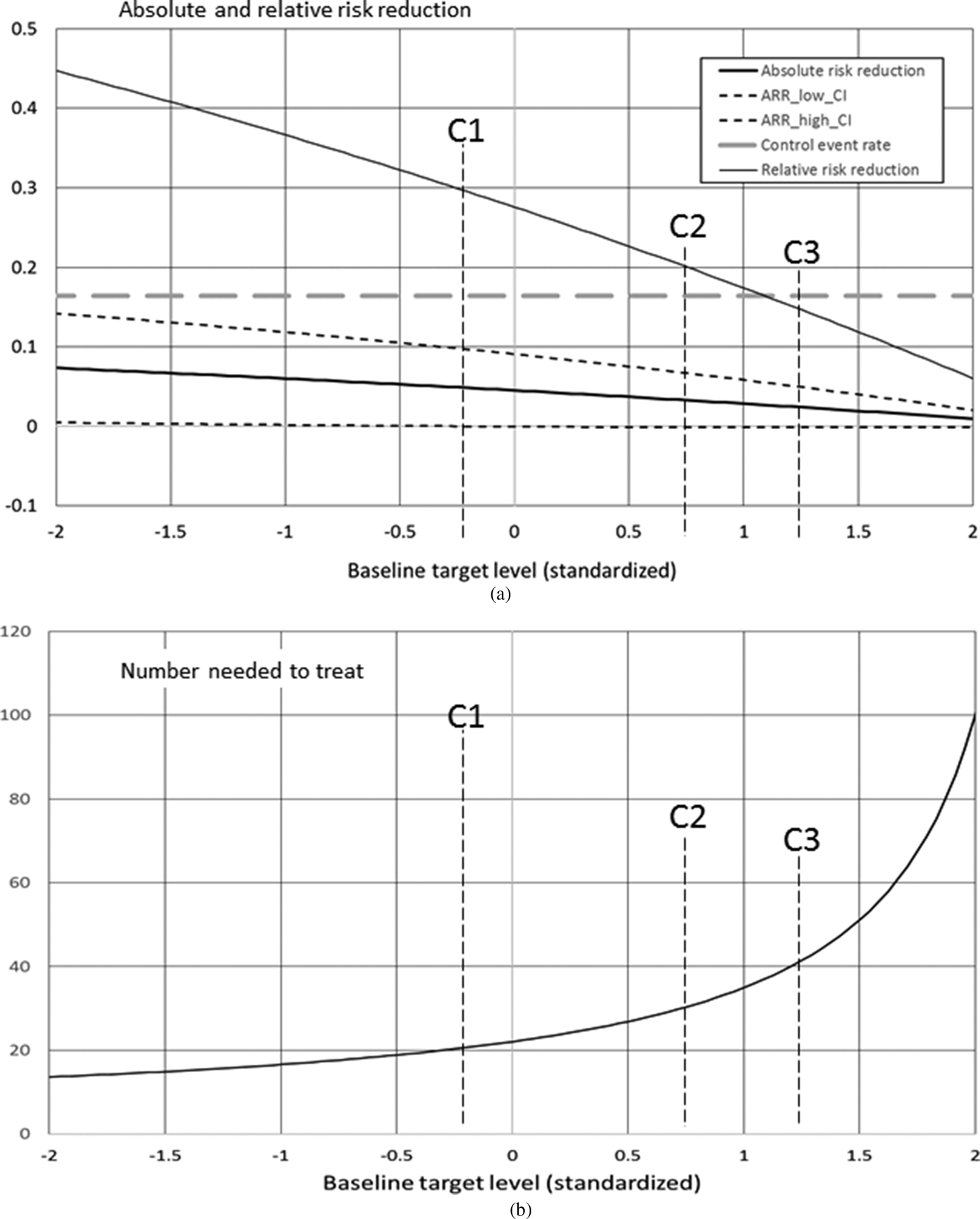
Figure 3. Effect indicatiors for compensatory effect with stable control event rate.
Number needed to treat and NNH have been used in clinical treatment trials for some time, and NNT is increasingly applied in evaluating prevention trials. Rohde, Brière, and Stice (Reference Rohde, Brière and Stice2018) combined data from four indicated prevention programs to reduce risk of depression in late adolescence, reporting NNT rates of 10 to 21 for major depressive disorder assessed from 6 months to 2 years later. D'Amico et al. (Reference D'Amico, Tucker, Miles, Zhou, Shih and Green2012), in a cluster-randomized trial of an after-school intervention to reduce risk for substance use in adolescents, reported an NNT rate of 14.8 for lifetime onset of alcohol use measured 7 months after the intervention. We were unable to find any reports of NNH analyses in prevention trials; it appears to be most common in studying side effects in medication treatment trials.
We can also consider effects relative to incidence in the untreated population. Relative risk reduction (RRR) is defined as the percentage reduction in this incidence, usually measured by the frequency of cases in the control group (CER). The RRR is defined as ARR/CER. In our example, RRR is equal to 0.016/0.19, or 8%, indicating that the intervention reduced the incidence of children's exceeding the prevention threshold by this amount.
Although these indices have usually been calculated for total intervention effects, they can also be used for indirect effects that operate through change in specific targets. In Figure 1a, the indirect effect path is estimated as a times b, reflecting some proportion of the total effect, which also includes the remainder of effect through c′. In certain cases this proportionality does not hold, as when the mediating path is salutary but the direct path is iatrogenic. But in all cases the indirect path can be used to estimate effect size indices that carry information about the strength of intervention effect as mediated through changing that target. This is the approach we take in the remainder of this report.
These indices are point estimates, and they will therefore have confidence intervals (or credible intervals from Bayesian analysis) that define a range of plausible values. When calculated for an individual trial, they must be interpreted in terms of the specific trial sample, conditions, and period of follow-up (McAlister, Reference McAlister2008). Prevalence rates for emotional or behavioral conditions often grow over developmental time, so AAR, NNT, and RRR may change for later follow-ups. These indices also reflect the difference in outcomes between the specific experimental and control conditions employed in our study. When active control conditions (such as those involving placebos) are used, they will reflect relative differences in the effect of the two conditions rather than the effect of the intervention compared with those in a population receiving no intervention.
Effects under baseline target moderation
Point estimates of these indices are single values based on the entire sample; they assume causal invariance (Howe, Reference Howe2019b). That assumption is violated when baseline target moderation is present. In this case effect size estimates will not be constant for the sample, but will vary across levels of the baseline target. For example, if we find compensatory effects, NNT will be lower for those children or families who come into the trial with lower levels of the protective target (requiring fewer cases to achieve preventive effect) and higher for those with higher baseline levels (requiring more cases to achieve preventive effect). These indices therefore take on a range of values for each point along the continuum of the baseline target value.
Here we focus on baseline target moderation of the effect of intervention on change in outcome as mediated through change in target. In this case, the range of values for ARR, RR, or NNT reflect different indirect effect sizes, under the assumption that the association of change in target and change in outcome is constant (the b path in Figure 1b). The d path in Figure 1b reflects this moderation. It indicates that the value of the a path will vary over the baseline target such that the indirect path (ab) will also change in value. Estimates of these risk indices therefore need to take into account all three of these paths, resulting in a curve of values over the baseline target levels. This is illustrated in Figures 3 and 4, based on simulated data for a compensatory effect, described in more detail later. If we establish a practical threshold for any of these indices, we can then identify baseline target levels for the children or families whose indices are higher than that threshold and who might benefit from program adaptation.

Figure 4. Effect indicatiors for compensatory effect with variable control event rate.
All three indices also take into account both the strength of intervention effect and the population risk in the absence of the intervention as indexed by CER. In standard calculations, CER is assumed to be constant for the untreated population. When BTMM is present, intervention effects will vary over baseline target levels. However, the CER may also vary by baseline target. The etiologic model of many preventive interventions would suggest this; for example, those in the untreated control group who enter the study with higher levels of a protective target should have lower risk for future health problems compared with those who enter with lower levels. We therefore need to test whether CER is associated with baseline target levels, and if we find evidence for this association, we need to take that into account when calculating effect size values as they vary over baseline target levels. And, as with standard estimates, we need to take sampling error into account. If these indices vary across baseline target levels, the set of plausible values at each point on that continuum (as defined by confidence or credible intervals) will also vary.
Selecting Cut Points for Adaptation Based on Effect Size Indices
Absolute risk reduction, NNT, and RRR provide different information about the intervention effects operating through a specific target, requiring that we decide what to privilege in selecting baseline target ranges where adaptation would prove useful. This will also depend on the pattern of baseline target moderation of an intervention effect and whether the CER is constant across the sample or varies by baseline target level. To illustrate, we constructed simulated datasets reflecting various patterns of baseline target mediated moderation, using Monte Carlo procedures in MPLUS version 8.1 (Muthén & Muthén, Reference Muthén and Muthén1998–2017). Details of these simulations can be found in supplementary materials. We used the model in Figure 1b as the population model and set model parameters for the a, b, and d paths to reflect each of the four types of baseline target moderation (compensatory, rich-get-richer, crossover, and iatrogenic), constraining the other paths to zero to simplify the examples. We also simulated two versions for each type of moderation, with the g path set to zero or to a moderate value. This allowed us to compare effects when the control event rate was stable and when it varied over baseline target levels. We then used MPLUS to estimate model parameters for the full BTMM model in Figure 1b for each of these eight simulated datasets. These parameters allowed us to calculate point estimates for these indirect effect indices along with their 95% confidence intervals for each value of the baseline target level.
Compensatory effects
Figure 3 illustrates findings from simulated data involving a compensatory effect, with intervention effects on target change (path a) stronger at lower levels of baseline target (in this case a protective factor) and weaker for those who begin with higher levels (moderator path d). The control event rate is unrelated to baseline target levels (paths e, f, and g set to zero) and is constant over the range. The association of change in target to change in outcome is set to be moderate (path b), reflecting the mediated effect of intervention through this target.
Figure 3 illustrates three possible cut points for adaptation. The first cut point (C1) is at the baseline target level, where the lowest plausible value of ARR (based on its 95% confidence interval) falls below zero. All participants with baseline target levels above this would be at increasing risk for iatrogenic effects, as negative values of ARR (which reflect absolute risk increase) now fall within the plausible range. For these data, the cut point is at .16 standard deviations below the mean of the baseline target.
We might also wish to select the point at which the preventive effect falls below some predetermined level, based on the point estimate of RRR. C2 indicates this cut point for a value of 20%, reflecting the point at which reductions in risk are at or less than 20% of the risk for the control group. This corresponds to a baseline target value of .75, or three-quarters of a standard deviation above the mean. As a third option, we can use NNT estimates. In our example, the lowest NNT of 13.6 occurs for those with the lowest baseline target levels. If we select a cut point (C3) at NNT of 40, this would correspond to a baseline target level of 1.2 standard deviations above the mean. Above this point it would require 40 or more participants in the intervention to reduce by one the number of people prevented from surpassing the preventive threshold.
Each of these cut points suggests that participants with higher baseline target levels are not benefiting as much from the intervention because they are not experiencing as much change in this intervention target. And because their risk is just as great (CER is the same for everyone), adapting the intervention so that it has a stronger effect on the target for these participants would be warranted.
We note that C2 and C3 are illustrative rather than recommended. Investigators may select other values based on practical considerations. For example, cost-benefit analyses using information about the economic costs of intervention and economic savings from preventing a case may provide important benchmarks for determining NNT levels where costs no longer outweigh benefits (Crowley et al., Reference Crowley, Dodge, Barnett, Corso, Duffy, Graham and Plotnick2018).
The picture can change when population risk varies with baseline target levels. Figure 4 graphs the effect indices for a simulated dataset where CER is associated with baseline target levels. The parameters for the simulated data are identical to those in the prior example with one exception: the CER varies by baseline target (path g is set to a moderate value), becoming smaller at higher baseline target levels, ranging from 28% at the lowest levels to 20% at the highest. The C1 cut point is no longer useful, as the lower confidence bound for ARR is below zero across the entire range of baseline target values. The C2 cut point based on RRR is nominally at 1.13 standard deviations above the mean, but it may be less useful here, as the risk denominator changes over baseline target levels. The C3 cut point, based on an NNT of 40, now occurs at 1.71 standard deviations above the baseline target mean, where few data points occur. Even though baseline target moderated mediation is present here, there is less support for meaningful cut points for adaptation.
This illustrates the importance of testing all parameters in model 1b and including information about variation in control event rates when present. Compensatory effects may also be more likely to involve variation in CER in that those participants with more of a targeted protective factor may be less likely to need the intervention because they are at lower risk to begin with. If this is the case, then program adaptation will be less useful. Such findings may instead call for implementing the prevention program more selectively, based on an assessment of baseline target levels.
Rich-get-richer effects
We also estimated risk reduction indices for BTMM models that involve rich-get-richer effects with stable CER (Figure SM1 in Supplementary Material). The pattern is similar to the compensatory effect, but in the opposite direction. Participants with high baseline target levels (more of the protective factor) show a more positive effect on preventing outcomes as mediated through changes in that target, while those with lower levels show less effect. Cut points chosen based on ARR, RRR, or NNT would indicate that those below the cut point would benefit from program adaptations that increase effect on this target.
When rich-get-richer effects are present but those with lower baseline target levels have higher population risk (CER varies), the picture can again change substantially. In our simulated data example, C1 is not possible as all lower confidence bounds are below zero. C2 for 20% relative risk reduction occurs at 0.4 standard deviations above the mean, but C3 is not possible because NNT never falls below 47 (Figure SM2 in Supplementary Material). The C2 cut point might suggest the need for program adaptation for those lower on baseline target levels, although the support for this is weaker than that in the prior example.
Crossover and iatrogenic effects
Crossover effects involve estimates of both risk reduction and risk increase (Figures SM3 and SM4 in the Supplementary Material). Those with lower baseline target levels show iatrogenic effects, while those with higher levels show preventive effects. The intervention decreases the targeted protective factor in the former, but increases it in the latter. Based on our simulated data example, the point estimates for ARR and RRR reflect iatrogenic effects below the baseline target mean, but the lower confidence interval continues to include negative values until .84 standard deviations above the mean, suggesting this as a C1 cut point. These findings would provide strong support for adapting the program for those below this point so as to eliminate iatrogenic effects. Relative risk reduction never reaches 20%, while NNT reaches 40 at 1.64 standard deviations above the mean, suggesting that even those above the baseline target mean might benefit from program adaptation, given weak effects in this region.
Adding variation in CER across the baseline target amplifies both the iatrogenic and salutary effects somewhat, although the lower confidence bound for ARR is always below zero, suggesting that iatrogenic effects cannot be ruled out at any level of baseline target (Figure SM4 in Supplementary Material). Neither C2 nor C3 cut points are available here, as relative risk reduction never reaches 20% and NNT never drops below 58.
Iatrogenic effects might be present across the entire range of baseline target levels, even though they vary in strength (Figure SM5 in the supplementary materials). This can occur if the intervention decreases the targeted protective factor (or increases some risk factor) for all participants, but does so more strongly for those with lower baseline target levels. This would provide strong evidence for major program changes for all participants. In our simulated data, this was true when CER was stable (Figure SM6 in the supplementary materials). When CER varied, however, ARR became positive across the entire range, although very weak (1% at the highest point), with the lower confidence bound always below zero. This is also reflected in NNT values that are never below 98.
Summary
These examples highlight the wide range of possible BTMM patterns, and they clarify that risk reduction or increase will depend on the nature and strength of all associations in the complete BTMM model. The four types of patterns illustrated here can provide general guidance in thinking about program adaptation, but cut points will always depend on the specific pattern of results for each application. For example, our simulations set simple treatment effects (path c′) to zero, and they did not include models where a portion of the association between baseline target levels and outcomes is mediated by change in targets (path e). Nonzero parameters for either of these may change the estimates of risk reduction, alter their confidence intervals, or even change the general pattern from one form to another.
What Can BTMM Findings Tell Us About How to Adapt?
Findings for BTMM may also help us consider how an intervention needs to be adapted. Rich-get-richer effects suggest that those with lower baseline target levels may not have foundational skills that are necessary precursors to benefiting from intervention programs. Adaptations that add training for these precursors may enhance intervention effectiveness for those who lack them. For example, Teisl, Wyman, Cross, West, and Sworts (Reference Teisl, Wyman, Cross, West and Sworts2012) conducted a microtrial to test whether preliminary verbal skills training would enhance readiness for an emotion regulation intervention with young children, finding that verbal skills training increased the effectiveness of the emotion regulation program on declarative knowledge of emotions, but only for those children who came to the program with deficiencies in verbal skills.
Differential iatrogenic and crossover effects suggest that intervention components directed at a specific target are activating responses that increase risk. Two likely mechanisms are reactance and stimulation of unresolved conflict. Reactance occurs when a person believes their freedom or control is threatened and acts in opposition to the source of that threat (Rosenberg & Siegel, Reference Rosenberg and Siegel2018). For example, in a microtrial of one session from a substance abuse prevention program, Fishbein et al. (Reference Fishbein, Hyde, Eldreth, Paschall, Hubal, Das and Yung2006) found that those adolescents with problematic conduct behavior became less likely to employ socially competent behavior after participating in the intervention compared with those without these behavior problems, who increased their social competence. This is consistent with a reactance mechanism given that conduct disordered children are more sensitive to perceived threats to their autonomy. Program adaptations that increase sense of control, such as social justice interventions (Ginwright & Cammarota, Reference Ginwright and Cammarota2002), might help to reduce such reactions and increase program effectiveness for children who are becoming more aggressive.
Preventive interventions that work with families or couples may also have components that stimulate conflictual interactions. If families do not have the skills for resolving such conflict, this could also result in iatrogenic or crossover effects when family communication is an intervention target. This may account for the iatrogenic findings reported by Prado and Pantin (Reference Prado and Pantin2011), indicating that those adolescents reporting the poorest family communication increased smoking rates following a program encouraging discussions with parents about the cardiovascular risks of tobacco use. Findings of more positive outcomes with interventions that include more extensive training in communication skills suggest these may be important adaptations for eliminating such effects in these families (Pantin et al., Reference Pantin, Prado, Lopez, Huang, Tapia, Schwartz and Branchini2009).
Conclusions and Future Directions
Exploring baseline target levels as moderators of preventive intervention effects, particularly as mediated through specific target change, holds promise as a basis for determining when and how interventions might be adapted to increase their effectiveness. Longstanding criticisms of statistical significance as a weak benchmark for meaningful treatment effects led to the development and application of risk indices, such as absolute risk reduction and number needed to treat, and these are increasingly used to summarize preventive effects. The strategy presented here provides a means of converting results from BTMM analyses into practical indices of risk reduction or increase for moderated indirect effects based on theoretically derived intervention targets. It asks interventionists to make informed judgements about preventive thresholds and meaningful effect sizes and to use these to determine whether some participants would benefit from adapted interventions. The necessity and nature of those adaptations will depend on the type of BTMM effects found as well as the strength of both mediation and moderation effects. It will also depend on whether the control event rate in the untreated group is constant, or varies over baseline target levels.
This framework has implications for the next generation of prevention trials. In particular it calls for more consistent and rigorous assessment of intervention targets, both at baseline and at follow-up. It also calls for longitudinal follow-ups that can detect important variation in more distal health outcomes, allowing for full tests of BTMM. These methods may also be fruitfully extended in studying and improving program effectiveness in existing prevention services. Most program evaluation research has focused on studying outcomes, but evaluations could easily incorporate the assessment of key targets at baseline and follow-up. Although randomized control designs provide the strongest evidence for causal inference, BTMM models can also be applied to nonrandomized studies that measure variation in exposure to services as the intervention variable.
The strategies illustrated here also have limitations that need to be addressed in future research. Our simulation models assumed that intervention effects were mediated entirely through change in a single target. This is an unreasonable assumption for most preventive interventions, where a target carries only some proportion of the preventive effect. Strong moderation of an intervention effect on a weak target may have little practical effect on more distal health outcomes.
Most preventive interventions target a number of risk and protective mechanisms. For example, Gonzales et al. (Reference Gonzales, Dumka, Millsap, Gottschall, McClain, Wong and Kim2012) studied 13 targets of their Bridges/Puentes program for Mexican American adolescents and their families, including several different parenting behaviors, youth coping skills, and school engagement. They found mediation effects for nine of the targets, and the effect of the intervention on target change was moderated by baseline levels for several of them. Strategies for addressing the effect sizes of multiple targets in considering adaptation have yet to be worked out. Targets are often strongly correlated, suggesting that latent factors or latent classes may prove useful as a means of combining several targets. More complex effects are also possible. For example, Gonzales et al. (Reference Gonzales, Dumka, Millsap, Gottschall, McClain, Wong and Kim2012) found evidence for compensatory effects for some targets, but rich-get-richer effects for at least one other. And if some targets have compensatory effects while others have differential iatrogenic effects, we may need to include both in the BTMM model because of suppression effects (MacKinnon, Krull, & Lockwood, Reference MacKinnon, Krull and Lockwood2000). More work is needed to understand how best to include multiple targets when evaluating risk reduction or increase and the need for program adaptation.
Our simulations also followed the most common analytic models in considering only linear models (or log linear models for binary outcomes). But moderator effects could also be nonlinear across the range of baseline target levels. Threshold effects are possible, such that moderation occurs only for some part of that range. For example, compensatory effects of family communication training may be less important when families already communicate relatively well, if not at the highest levels. In colloquial terms, good-enough parenting may be just as effective as stellar parenting for preventing some developmental problems (Fisher, Rahman, Cabral de Mello, Chandra, & Herrman, Reference Fisher, Rahman, Cabral de Mello, Chandra, Herrman, Tyano, Keren, Herrman and Cox2010). Methods are available for detecting nonlinear moderation (Knafl et al., Reference Knafl, Barakat, Hanlon, Hardie, Knafl, Li and Deatrick2017), but we have been unable to find any applications to BTMM models as yet.
Baseline target moderated mediation analyses of simulated data also employed standard frequentist methods. When data are available from multiple trials (or from developmental studies of risk and protective mechanisms used as targets), Bayesian methods (Wagenmakers, Morey, & Lee, Reference Wagenmakers, Morey and Lee2016) may be preferable as a means of incorporating prior information for more precise estimates of risk reduction or increase curves. This may be particularly useful when using information about uncertainty, such as confidence or credible intervals, to identify cut points based on the range of plausible values.
In addition, BTMM models attend only to the targets we observe. Preventive interventions may have an effect on distal outcomes through changing other unobserved or unknown mechanisms. If these effects are invariant across our sample, they will be accurately characterized by the direct effect in this model (path c′ in Figure 1). This would be the case for “sleeper” effects, which are not detected through tests of observed mediators (paths a and b). When such effects are found, they call for greater attention to other etiologic pathways in future studies.
In summary, findings from baseline target moderated mediation can guide considerations of when to adapt a preventive intervention as well as the form that adaptation might take. Evidence of iatrogenic effects for some participants would point toward more selective application of existing interventions and more work on adaptations that mitigate such effects. Greater attention to the targets of our preventive efforts, and to the possibility that different children and families are best served by interventions sensitive to their needs, moves us closer to Tom Dishion's vision of tailored interventions that informed his groundbreaking work with the Family Check-up.
Acknowledgment
I wish to acknowledge the support of Getachew Dagne from the University of South Florida, who provided guidance on the simulation modeling that was used in this study.
Supplementary Material
The supplementary material for this article can be found at https://doi.org/10.1017/S0954579419001044





