1. Introduction
In this paper, we consider the continuous random energy model (CREM) introduced by Bovier and Kurkova in [Reference Bovier and Kurkova3] based on previous work by Derrida and Spohn [Reference Derrida and Spohn5]. The model is defined as follows. Let
![]() $N\in\mathbb{N}$
. Denote by
$N\in\mathbb{N}$
. Denote by
![]() $\mathbb{T}_N$
the binary tree with depth N. Given
$\mathbb{T}_N$
the binary tree with depth N. Given
![]() $u\in\mathbb{T}_N$
, we denote by
$u\in\mathbb{T}_N$
, we denote by
![]() $|u|$
the depth of u, and we write
$|u|$
the depth of u, and we write
![]() $w\leq u$
if w is an ancestor of u. For all
$w\leq u$
if w is an ancestor of u. For all
![]() $u,v\in\mathbb{T}_N$
, let
$u,v\in\mathbb{T}_N$
, let
![]() $u\wedge v$
be the most recent common ancestor of u and v. The CREM is a centered Gaussian process
$u\wedge v$
be the most recent common ancestor of u and v. The CREM is a centered Gaussian process
![]() $(X_u)_{u\in\mathbb{T}_N}$
indexed by the binary tree
$(X_u)_{u\in\mathbb{T}_N}$
indexed by the binary tree
![]() $\mathbb{T}_N$
of depth N with covariance function
$\mathbb{T}_N$
of depth N with covariance function
To study the CREM, one of the key quantities is the partition function defined as
In this paper, we study the negative moments of the partition function, which gives us information on the small values of the partition function. This type of study was conducted in the context of other related models such as homogeneous branching random walks, multiplicative cascades, or Gaussian multiplicative chaos, and came with the name of negative moments, left-tail behavior, small deviations of the partition function. We give a survey of these results in Section 1.2.
1.1. Main result
For this paper, we require that the function A satisfies the following assumption.
Assumption 1.1. We suppose that A is a non-decreasing function defined on the interval [0, 1] such that
![]() $A(0)=0$
and
$A(0)=0$
and
![]() $A(1)=1$
. Let
$A(1)=1$
. Let
![]() $\hat{A}$
be the concave hull of A, and we denote by
$\hat{A}$
be the concave hull of A, and we denote by
![]() $\hat{A}'$
the right derivative of
$\hat{A}'$
the right derivative of
![]() $\hat{A}$
. Throughout this paper, we assume the following regularity conditions.
$\hat{A}$
. Throughout this paper, we assume the following regularity conditions.
-
(i) The function A is differentiable in a neighborhood of 0, i.e. there is an
 $x_0\in (0,1]$
such that A is differentiable on the interval
$x_0\in (0,1]$
such that A is differentiable on the interval
 $(0,x_0)$
. Furthermore, we assume that A has a finite right derivative at 0.
$(0,x_0)$
. Furthermore, we assume that A has a finite right derivative at 0. -
(ii) There exists
 $\alpha\in (0,1)$
such that the derivative of A is locally Hölder continuous with exponent
$\alpha\in (0,1)$
such that the derivative of A is locally Hölder continuous with exponent
 $\alpha$
in a neighborhood of 0, i.e. there exists
$\alpha$
in a neighborhood of 0, i.e. there exists
 $x_1\in (0,1]$
such that
$x_1\in (0,1]$
such that  \begin{align*}\sup\limits_{x,y\in [0,x_1],\,x\neq y} \frac{|A'(x)-A'(y)|}{{|x-y|}^\alpha} < \infty.\end{align*}
\begin{align*}\sup\limits_{x,y\in [0,x_1],\,x\neq y} \frac{|A'(x)-A'(y)|}{{|x-y|}^\alpha} < \infty.\end{align*}
-
(iii) The right derivative of
 $\hat{A}$
at
$\hat{A}$
at
 $x=0$
is finite, i.e.
$x=0$
is finite, i.e.
 $\hat{A}'(0) < \infty$
.
$\hat{A}'(0) < \infty$
.
Remark 1.1. Points (i)–(iii) are technical conditions that are required in the moment estimates perform in Sections 2.2 and 2.3 so that the estimates only depend on
![]() $\hat{A}'(0)$
.
$\hat{A}'(0)$
.
The free energy of the CREM is defined as
![]() $F_\beta \,:\!=\, \lim_{N\rightarrow\infty}\mathbb{E}[\log Z_{\beta,N}]\mathbb{N}$
, and admits an explicit expression: for all
$F_\beta \,:\!=\, \lim_{N\rightarrow\infty}\mathbb{E}[\log Z_{\beta,N}]\mathbb{N}$
, and admits an explicit expression: for all
![]() $\beta\geq 0$
,
$\beta\geq 0$
,
 \begin{equation} F_\beta = \int_0^1 f\big(\beta\sqrt{\hat{A}'(t)}\big) \mathrm{d}{t}, \quad \text{where} \quad f(x) \,:\!=\, \begin{cases} \displaystyle \frac{x^2}{2} + \log 2, & x< \sqrt{2\log 2}, \\[6pt] \sqrt{2\log 2}x, & x\geq \sqrt{2\log 2}. \end{cases}\end{equation}
\begin{equation} F_\beta = \int_0^1 f\big(\beta\sqrt{\hat{A}'(t)}\big) \mathrm{d}{t}, \quad \text{where} \quad f(x) \,:\!=\, \begin{cases} \displaystyle \frac{x^2}{2} + \log 2, & x< \sqrt{2\log 2}, \\[6pt] \sqrt{2\log 2}x, & x\geq \sqrt{2\log 2}. \end{cases}\end{equation}
This formula was proved in [Reference Bovier and Kurkova3, Theorem 3.3], based on a Gaussian comparison lemma [Reference Bovier and Kurkova3, Lemma 3.2] and previous work in [Reference Capocaccia, Cassandro and Picco4]. While [Reference Bovier and Kurkova3] assumed the function A to be piecewise smooth (line 4 after [Reference Bovier and Kurkova3, (1.2)]) to simplify the article, the proof of [Reference Bovier and Kurkova3, Theorem 3.3] does not use this regularity assumption and the proof also holds for the class of functions that are non-decreasing on the interval [0, 1] such that
![]() $A(0)=0$
and
$A(0)=0$
and
![]() $A(1)=1$
.
$A(1)=1$
.
The same paper also showed that the maximum of the CREM satisfies
Combining this with (1.1) indicates that there exists
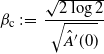 \begin{equation} \beta_\mathrm{c} \,:\!=\, \frac{\sqrt{2\log2}}{\sqrt{\hat{A}'(0)}} \end{equation}
\begin{equation} \beta_\mathrm{c} \,:\!=\, \frac{\sqrt{2\log2}}{\sqrt{\hat{A}'(0)}} \end{equation}
such that the following phase transition occurs. (i) For all
![]() $\beta< \beta_\mathrm{c}$
, the main contribution to the partition function comes from an exponential number of particles. (ii) For all
$\beta< \beta_\mathrm{c}$
, the main contribution to the partition function comes from an exponential number of particles. (ii) For all
![]() $\beta>\beta_\mathrm{c}$
, the maximum starts to contribute significantly to the partition function. The quantity
$\beta>\beta_\mathrm{c}$
, the maximum starts to contribute significantly to the partition function. The quantity
![]() $\beta_\mathrm{c}$
is sometimes referred to as the static critical inverse temperature of the CREM. In the following, we refer to the subcritical regime
$\beta_\mathrm{c}$
is sometimes referred to as the static critical inverse temperature of the CREM. In the following, we refer to the subcritical regime
![]() $\beta<\beta_\mathrm{c}$
as the high-temperature regime.
$\beta<\beta_\mathrm{c}$
as the high-temperature regime.
Our goal is to study the negative moments of the partition function
![]() $Z_{\beta,N}$
in the high-temperature regime, and we obtain the following result.
$Z_{\beta,N}$
in the high-temperature regime, and we obtain the following result.
Theorem 1.1. Suppose Assumption 1.1 is true. Let
![]() $\beta<\beta_\mathrm{c}$
. For all
$\beta<\beta_\mathrm{c}$
. For all
![]() $s>0$
, there exist
$s>0$
, there exist
![]() $N_0 = N_0(A,\beta,s)\in\mathbb{N}$
and a constant
$N_0 = N_0(A,\beta,s)\in\mathbb{N}$
and a constant
![]() $C=C(A,\beta,s)$
, independent of N, such that, for all
$C=C(A,\beta,s)$
, independent of N, such that, for all
![]() $N\geq N_0$
,
$N\geq N_0$
,
![]() $\mathbb{E}[(Z_{\beta,N})^{-s}] \leq C\mathbb{E}[Z_{\beta,N}]^{-s}$
.
$\mathbb{E}[(Z_{\beta,N})^{-s}] \leq C\mathbb{E}[Z_{\beta,N}]^{-s}$
.
Remark 1.2. For all
![]() $\beta>0$
,
$\beta>0$
,
![]() $N\in\mathbb{N}$
, and
$N\in\mathbb{N}$
, and
![]() $s>0$
, we have the trivial lower bound provided by the Jensen inequality and the convexity of
$s>0$
, we have the trivial lower bound provided by the Jensen inequality and the convexity of
![]() $x\mapsto x^{-s}$
:
$x\mapsto x^{-s}$
:
![]() $\mathbb{E}[(Z_{\beta,N})^{-s}] \geq \mathbb{E}[Z_{\beta,N}]^{-s}$
. Combining this with Theorem 1.1, we see that, for all
$\mathbb{E}[(Z_{\beta,N})^{-s}] \geq \mathbb{E}[Z_{\beta,N}]^{-s}$
. Combining this with Theorem 1.1, we see that, for all
![]() $\beta<\beta_\mathrm{c}$
in the high-temperature regime and for all
$\beta<\beta_\mathrm{c}$
in the high-temperature regime and for all
![]() $s>0$
,
$s>0$
,
![]() $\mathbb{E}[(Z_{\beta,N})^{-s}]$
is comparable with
$\mathbb{E}[(Z_{\beta,N})^{-s}]$
is comparable with
![]() $\mathbb{E}[Z_{\beta,N}]^{-s}$
.
$\mathbb{E}[Z_{\beta,N}]^{-s}$
.
1.2. Related models
For the (homogeneous) branching random walk, the typical approach is not to study the partition function directly but to consider the additive martingale
![]() $W_{\beta,N}=Z_{\beta,N}/\mathbb{E}[Z_{\beta,N}]$
, which converges to a pointwise limit
$W_{\beta,N}=Z_{\beta,N}/\mathbb{E}[Z_{\beta,N}]$
, which converges to a pointwise limit
![]() $W_{\beta,\infty}$
. A standard method to establish that
$W_{\beta,\infty}$
. A standard method to establish that
![]() $W_{\beta,\infty}$
has negative moments involves the following observation. Suppose that Y
′, Y
′′, W
′, and W
′′ are independent random variables such that Y
′ and Y
′′ share the law of the increment of the branching random walk, and each of W
′ and W
′′ follows the same distribution as
$W_{\beta,\infty}$
has negative moments involves the following observation. Suppose that Y
′, Y
′′, W
′, and W
′′ are independent random variables such that Y
′ and Y
′′ share the law of the increment of the branching random walk, and each of W
′ and W
′′ follows the same distribution as
![]() $W_{\beta,\infty}$
. Then, the limit of the additive martingale
$W_{\beta,\infty}$
. Then, the limit of the additive martingale
![]() $W_{\beta,\infty}$
satisfies the following fixed point equation in distribution:
$W_{\beta,\infty}$
satisfies the following fixed point equation in distribution:
This is a special case of the so-called smoothing transform, which has been studied extensively in the literature. In the context of multiplicative cascades, which is an equivalent model of the branching random walk, [Reference Molchan12] showed that if
![]() $\mathbb{E}[(Y')^{-s}]<\infty$
for some
$\mathbb{E}[(Y')^{-s}]<\infty$
for some
![]() $s>0$
, then
$s>0$
, then
![]() $\mathbb{E}[(W_{\beta,\infty})^{-s}]<\infty$
. This result was subsequently extended in [Reference Liu10, Reference Liu11]. More recently, [Reference Hu9] studied the small deviation of the maximum of the branching random walk based on the latter result. On the other hand, [Reference Nikula13] provided small deviations for lognormal multiplicative cascades, thereby refining the result in [Reference Molchan12].
$\mathbb{E}[(W_{\beta,\infty})^{-s}]<\infty$
. This result was subsequently extended in [Reference Liu10, Reference Liu11]. More recently, [Reference Hu9] studied the small deviation of the maximum of the branching random walk based on the latter result. On the other hand, [Reference Nikula13] provided small deviations for lognormal multiplicative cascades, thereby refining the result in [Reference Molchan12].
In the context of Gaussian multiplicative chaos (GMC), [Reference Garban, Holden, Sepúlveda and Sun8] showed that given a subcritical GMC measure with mild conditions on the base measure, the total mass of this GMC measure has negative moments of all orders. This expanded on the findings of [Reference Duplantier and Sheffield6, Reference Remy14, Reference Robert and Vargas15], with the base measure taken as the Lebesgue measure restricted to some open set, where these works were interested in quantifying the left-tail behavior of the total mass of the GMC near 0. A final remark is that the proof of [Reference Robert and Vargas15, Theorem 3.6], which concerned the negative moment of the total mass of the GMC, was referred to [Reference Barral and Mandelbrot1], which studied a log-Poisson cascade.
1.3. Proof strategy
For the CREM in general,
![]() $W_{\beta,N}$
is not a martingale, so there is no obvious way to show that
$W_{\beta,N}$
is not a martingale, so there is no obvious way to show that
![]() $W_{\beta,\infty}$
exists. To prove Theorem 1.1, we adapt the proof of [Reference Benjamini and Schramm2, Lemma A.3], which studied the multiplicative cascade.
$W_{\beta,\infty}$
exists. To prove Theorem 1.1, we adapt the proof of [Reference Benjamini and Schramm2, Lemma A.3], which studied the multiplicative cascade.
While that argument also involved the smoothing transform, it can be adjusted for a general CREM. In particular, we show that for all
![]() $s>0$
, there exist two positive sequences
$s>0$
, there exist two positive sequences
![]() $\varepsilon_k$
and
$\varepsilon_k$
and
![]() $\eta_k$
that both decay double exponentially to 0 as
$\eta_k$
that both decay double exponentially to 0 as
![]() $k\rightarrow\infty$
such that, for N sufficiently large,
$k\rightarrow\infty$
such that, for N sufficiently large,
and that for all
![]() $k\in[\![ 1, C'\log N]\!]$
, where
$k\in[\![ 1, C'\log N]\!]$
, where
![]() $C'>0$
, there exist
$C'>0$
, there exist
![]() $C=C(A,\beta,s)>0$
and
$C=C(A,\beta,s)>0$
and
![]() $c=c(A,\beta,s)>0$
such that
$c=c(A,\beta,s)>0$
such that
The proof of (1.4) and (1.5) is by establishing an initial left-tail estimate, and then using the branching property to bootstrap the estimate.
2. Initial estimate for the left tail of the partition function
The main goal of this section is to estimate the left tail of
![]() $Z_{\beta,N}$
. The main idea is to adapt (1.3) to the inhomogeneous setting via a recursive argument of
$Z_{\beta,N}$
. The main idea is to adapt (1.3) to the inhomogeneous setting via a recursive argument of
![]() $Z_{\beta,N}$
that we will explain immediately with the following notation.
$Z_{\beta,N}$
that we will explain immediately with the following notation.
We denote by
![]() $[\![ m_1,m_2]\!]$
$[\![ m_1,m_2]\!]$
![]() $\{m_1,m_1+1,\ldots,m_2-1,m_2\}$
for two integers
$\{m_1,m_1+1,\ldots,m_2-1,m_2\}$
for two integers
![]() $m-1<m_2$
. Fix
$m-1<m_2$
. Fix
![]() $k\in[\![ 0,N]\!]$
. Define
$k\in[\![ 0,N]\!]$
. Define
![]() $(X^{(k)}_u)_{|u|=N-k}$
to be the centered Gaussian process with covariance function
$(X^{(k)}_u)_{|u|=N-k}$
to be the centered Gaussian process with covariance function
We also introduce the corresponding partition function,
![]() $Z^{(k)}_{\beta,N-k} = \sum_{|u|=N-k} {\mathrm{e}}^{\beta X^{(k)}_u}$
. By the covariance function of
$Z^{(k)}_{\beta,N-k} = \sum_{|u|=N-k} {\mathrm{e}}^{\beta X^{(k)}_u}$
. By the covariance function of
![]() $(X^{(k)}_u)_{|u|=N-k}$
and the definition of
$(X^{(k)}_u)_{|u|=N-k}$
and the definition of
![]() $Z^{(k)}_{\beta,N-k}$
, we obtain
$Z^{(k)}_{\beta,N-k}$
, we obtain
With this notation,
![]() $Z_{\beta,N}$
admits the one-step decomposition
$Z_{\beta,N}$
admits the one-step decomposition
![]() $Z_{\beta,N} = \sum_{|u|=1}{\mathrm{e}}^{\beta X_u}Z^{u}_{\beta,N-1}$
, where
$Z_{\beta,N} = \sum_{|u|=1}{\mathrm{e}}^{\beta X_u}Z^{u}_{\beta,N-1}$
, where
![]() $\big(Z^{u}_{\beta,N}\big)_{|u|}$
are independent and have the same distribution as
$\big(Z^{u}_{\beta,N}\big)_{|u|}$
are independent and have the same distribution as
![]() $Z^{(1)}_{\beta,N-1}$
. Then, the task of controlling the left tail of
$Z^{(1)}_{\beta,N-1}$
. Then, the task of controlling the left tail of
![]() $Z_{\beta,N}$
can be reduced to controlling
$Z_{\beta,N}$
can be reduced to controlling
![]() $Z^{(1)}_{\beta,N-1}$
and
$Z^{(1)}_{\beta,N-1}$
and
![]() ${\mathrm{e}}^{X_u}$
for
${\mathrm{e}}^{X_u}$
for
![]() $|u|=1$
. Then, we decompose
$|u|=1$
. Then, we decompose
![]() $Z^{(1)}_{\beta,N-1}$
in the same manner. We call this procedure the bootstrap argument, which will be made precise in Section 3. The point is that for the bootstrap argument to work, it requires an initial bound, independent of N large and k small, for the left tail of the partition function
$Z^{(1)}_{\beta,N-1}$
in the same manner. We call this procedure the bootstrap argument, which will be made precise in Section 3. The point is that for the bootstrap argument to work, it requires an initial bound, independent of N large and k small, for the left tail of the partition function
![]() $Z^{(k)}_{\beta,N-k}$
in the high-temperature regime. This bound is provided in the following result.
$Z^{(k)}_{\beta,N-k}$
in the high-temperature regime. This bound is provided in the following result.
Proposition 2.1. Let
![]() $\beta<\beta_\mathrm{c}$
. Let
$\beta<\beta_\mathrm{c}$
. Let
![]() $K=\lfloor 2\log_\gamma N \rfloor$
, where
$K=\lfloor 2\log_\gamma N \rfloor$
, where
![]() $\gamma\in (11/10,2)$
. Then there exist
$\gamma\in (11/10,2)$
. Then there exist
![]() $N_0=N_0(A,\beta)\in\mathbb{N}$
and a constant
$N_0=N_0(A,\beta)\in\mathbb{N}$
and a constant
![]() $\eta_0 = \eta_0(A,\beta) < 1$
such that, for all
$\eta_0 = \eta_0(A,\beta) < 1$
such that, for all
![]() $N\geq N_0$
and
$N\geq N_0$
and
![]() $k\in [\![ 0,K]\!]$
,
$k\in [\![ 0,K]\!]$
,
![]() $\mathbb{P}\big(Z^{(k)}_{\beta,N-k} \leq \frac{1}{2}\mathbb{E}\big[Z^{(k)}_{\beta,N-k}\big]\big) \leq \eta_0$
, where the expectation of
$\mathbb{P}\big(Z^{(k)}_{\beta,N-k} \leq \frac{1}{2}\mathbb{E}\big[Z^{(k)}_{\beta,N-k}\big]\big) \leq \eta_0$
, where the expectation of
![]() $Z^{(k)}_{\beta,N-k}$
is given in (2.1).
$Z^{(k)}_{\beta,N-k}$
is given in (2.1).
To prove Proposition 2.1, we might want to apply the Paley–Zygmund type argument directly to
![]() $Z^{(k)}_{\beta,N-k}$
. This, however, will not provide the desired result for the whole high-temperature regime due to the correlation of the model. Happily, this can be resolved by introducing a good truncated partition function, which is defined as follows. For all
$Z^{(k)}_{\beta,N-k}$
. This, however, will not provide the desired result for the whole high-temperature regime due to the correlation of the model. Happily, this can be resolved by introducing a good truncated partition function, which is defined as follows. For all
![]() $|u|=N$
,
$|u|=N$
,
![]() $k\in[\![ 0,N]\!]$
,
$k\in[\![ 0,N]\!]$
,
![]() $a>0$
, and
$a>0$
, and
![]() $b>0$
, define the truncating set
$b>0$
, define the truncating set
 \begin{align*} G_{u,k} \,:\!=\, \big\{\text{for all}\ n\in[\![ 1,N-k]\!] \mid\, & X_w^{(k)} \leq \beta\cdot N\cdot\big(A\big(\tfrac{n+k}{N}\big) - A\big(\tfrac{k}{N}\big)\big) + a\cdot n + b, \\ & \rm{where}\,\textit{w}\, \rm{is \,an\, ancestor\, of \,}\textit{u}\, \rm{with}\, |w|=n \big\}.\end{align*}
\begin{align*} G_{u,k} \,:\!=\, \big\{\text{for all}\ n\in[\![ 1,N-k]\!] \mid\, & X_w^{(k)} \leq \beta\cdot N\cdot\big(A\big(\tfrac{n+k}{N}\big) - A\big(\tfrac{k}{N}\big)\big) + a\cdot n + b, \\ & \rm{where}\,\textit{w}\, \rm{is \,an\, ancestor\, of \,}\textit{u}\, \rm{with}\, |w|=n \big\}.\end{align*}
Define the truncated partition function
![]() $Z^{(k),\leq}_{\beta,N-k} \,:\!=\, \sum_{|u|=N-k}{\mathrm{e}}^{\beta X^{(k)}_u} \boldsymbol{1}_{G_{u,k}}$
. In Section 2.3, we will prove that the truncated partition has matching squared first moment and second moment. Once we have these two estimates, by passing to a Paley–Zygmund type argument, we can estimate the left tail of the untruncated partition function.
$Z^{(k),\leq}_{\beta,N-k} \,:\!=\, \sum_{|u|=N-k}{\mathrm{e}}^{\beta X^{(k)}_u} \boldsymbol{1}_{G_{u,k}}$
. In Section 2.3, we will prove that the truncated partition has matching squared first moment and second moment. Once we have these two estimates, by passing to a Paley–Zygmund type argument, we can estimate the left tail of the untruncated partition function.
2.1. Many-to-one and many-to-two
To perform the first and second moment estimates, we state and prove the following many-to-one/two lemmas.
Lemma 2.1. (Many-to-one.) Define
![]() $\big(X^{(k)}_n\big)_{n\in [\![ 0,N-k]\!]}$
to be a non-homogeneous random walk such that, for all
$\big(X^{(k)}_n\big)_{n\in [\![ 0,N-k]\!]}$
to be a non-homogeneous random walk such that, for all
![]() $n\in [\![ 0,N-k-1]\!]$
, the increment
$n\in [\![ 0,N-k-1]\!]$
, the increment
![]() $X^{(k)}_{n+1}-X^{(k)}_n$
is distributed as a centered Gaussian random variable with variance
$X^{(k)}_{n+1}-X^{(k)}_n$
is distributed as a centered Gaussian random variable with variance
![]() $N(A((n+1)/N)-A(n/N))$
. Let
$N(A((n+1)/N)-A(n/N))$
. Let
Then
![]() $\mathbb{E}\big[Z^{(k),\leq}_{\beta,N-k}\big] = 2^{N-k}\mathbb{E}\big[{\mathrm{e}}^{\beta X_{N-k}^{(k)}}\boldsymbol{1}_{G_{k}}\big]$
.
$\mathbb{E}\big[Z^{(k),\leq}_{\beta,N-k}\big] = 2^{N-k}\mathbb{E}\big[{\mathrm{e}}^{\beta X_{N-k}^{(k)}}\boldsymbol{1}_{G_{k}}\big]$
.
Proof. By the linearity of expectation, we have
![]() $\mathbb{E}\big[Z^{(k),\leq}_{\beta,N-k}\big] = \sum_{|u|=N-k}\mathbb{E}\big[{\mathrm{e}}^{\beta X_{u}^{(k)}}\boldsymbol{1}_{G_{u,k}}\big]$
. On the other hand, for each u with
$\mathbb{E}\big[Z^{(k),\leq}_{\beta,N-k}\big] = \sum_{|u|=N-k}\mathbb{E}\big[{\mathrm{e}}^{\beta X_{u}^{(k)}}\boldsymbol{1}_{G_{u,k}}\big]$
. On the other hand, for each u with
![]() $|u|=N-k$
, the path
$|u|=N-k$
, the path
![]() $\big(X_{w}^{(k)}\big)_{w\leq u}$
has the same distribution as
$\big(X_{w}^{(k)}\big)_{w\leq u}$
has the same distribution as
![]() $\big(X^{(k)}_n\big)_{n\in[\![ 0,N-k]\!]}$
, and the proof follows.
$\big(X^{(k)}_n\big)_{n\in[\![ 0,N-k]\!]}$
, and the proof follows.
Lemma 2.2. (Many-to-two.) Define non-homogeneous random walks
![]() $\big(X^{(k)}_{\ell,n}\big)_{n\in[\![ 0,N-k]\!]}$
and
$\big(X^{(k)}_{\ell,n}\big)_{n\in[\![ 0,N-k]\!]}$
and
![]() $\big(\tilde{X}^{(k)}_{\ell,n}\big)_{n\in[\![ 0,N-k]\!]}$
to be such that:
$\big(\tilde{X}^{(k)}_{\ell,n}\big)_{n\in[\![ 0,N-k]\!]}$
to be such that:
-
• for all
 $n\in[\![ 0,N-k-1]\!]$
, the increments
$n\in[\![ 0,N-k-1]\!]$
, the increments
 $X^{(k)}_{\ell,n+1}-X^{(k)}_{\ell,n}$
and
$X^{(k)}_{\ell,n+1}-X^{(k)}_{\ell,n}$
and
 $\tilde{X}^{(k)}_{\ell,n+1}-\tilde{X}^{(k)}_{\ell,n}$
are both distributed as a centered Gaussian random variable with variance
$\tilde{X}^{(k)}_{\ell,n+1}-\tilde{X}^{(k)}_{\ell,n}$
are both distributed as a centered Gaussian random variable with variance
 $N(A((n+1)/N)-A(n/N))$
;
$N(A((n+1)/N)-A(n/N))$
; -
•
 $X^{(k)}_{\ell,n}=\tilde{X}^{(k)}_{\ell,n}$
for all
$X^{(k)}_{\ell,n}=\tilde{X}^{(k)}_{\ell,n}$
for all
 $n\in[\![ 0,\ell]\!]$
; and
$n\in[\![ 0,\ell]\!]$
; and -
•
 $\big(X^{(k)}_{\ell,\ell+m}-X^{(k)}_{\ell,\ell}\big)_{m\in[\![ 0,N-k-\ell]\!]}$
and
$\big(X^{(k)}_{\ell,\ell+m}-X^{(k)}_{\ell,\ell}\big)_{m\in[\![ 0,N-k-\ell]\!]}$
and
 $\big(\tilde{X}^{(k)}_{\ell,\ell+m}-\tilde{X}^{(k)}_{\ell,\ell}\big)_{m\in[\![ 0,N-k-\ell]\!]}$
are independent.
$\big(\tilde{X}^{(k)}_{\ell,\ell+m}-\tilde{X}^{(k)}_{\ell,\ell}\big)_{m\in[\![ 0,N-k-\ell]\!]}$
are independent.
Let
 \begin{align*} G_{\ell,k} & = \bigg\{\textit{for all}\ n\in[\![ 1,N-k]\!] \colon X_{\ell,n}^{(k)} \leq \beta\cdot N\cdot\bigg(A\bigg(\frac{n+k}{N}\bigg) - A\bigg(\frac{k}{N}\bigg)\bigg) + a\cdot n + b \bigg\}, \\ \tilde{G}_{\ell,k} & = \bigg\{\textit{for all}\ n\in[\![ 1,N-k]\!] \colon \tilde{X}_{\ell,n}^{(k)} \leq \beta\cdot N\cdot\bigg(A\bigg(\frac{n+k}{N}\bigg) - A\bigg(\frac{k}{N}\bigg)\bigg) + a\cdot n + b \bigg\}. \end{align*}
\begin{align*} G_{\ell,k} & = \bigg\{\textit{for all}\ n\in[\![ 1,N-k]\!] \colon X_{\ell,n}^{(k)} \leq \beta\cdot N\cdot\bigg(A\bigg(\frac{n+k}{N}\bigg) - A\bigg(\frac{k}{N}\bigg)\bigg) + a\cdot n + b \bigg\}, \\ \tilde{G}_{\ell,k} & = \bigg\{\textit{for all}\ n\in[\![ 1,N-k]\!] \colon \tilde{X}_{\ell,n}^{(k)} \leq \beta\cdot N\cdot\bigg(A\bigg(\frac{n+k}{N}\bigg) - A\bigg(\frac{k}{N}\bigg)\bigg) + a\cdot n + b \bigg\}. \end{align*}
Then
 \begin{equation*} \mathbb{E}\big[\big(Z^{(k),\leq}_{\beta,N-k}\big)^2\big] = 2^{N-k}\mathbb{E}\big[{\mathrm{e}}^{\beta X_{N-k}^{(k)}}\boldsymbol{1}_{G_{k}}\big] + \sum_{\ell=0}^{N-k-1}2^{2(N-k)-\ell-1}\mathbb{E}\Big[{\mathrm{e}}^{\beta\left(X^{(k)}_{\ell,N-k}+\tilde{X}_{\ell,N-k}^{(k)}\right)} \boldsymbol{1}_{G_{\ell,k}\cap \tilde{G}_{\ell,k}}\Big]. \end{equation*}
\begin{equation*} \mathbb{E}\big[\big(Z^{(k),\leq}_{\beta,N-k}\big)^2\big] = 2^{N-k}\mathbb{E}\big[{\mathrm{e}}^{\beta X_{N-k}^{(k)}}\boldsymbol{1}_{G_{k}}\big] + \sum_{\ell=0}^{N-k-1}2^{2(N-k)-\ell-1}\mathbb{E}\Big[{\mathrm{e}}^{\beta\left(X^{(k)}_{\ell,N-k}+\tilde{X}_{\ell,N-k}^{(k)}\right)} \boldsymbol{1}_{G_{\ell,k}\cap \tilde{G}_{\ell,k}}\Big]. \end{equation*}
Proof. By the linearity of expectation, we have the decomposition
 \begin{align} \mathbb{E}\big[\big(Z^{(k),\leq}_{\beta,N-k}\big)^2\big] & = \sum_{|u|=|w|=N-k}\mathbb{E}\Big[{\mathrm{e}}^{\beta\left(X^{(k)}_{u}+X_{w}^{(k)}\right)} \boldsymbol{1}_{G_{u}\cap \tilde{G}_{w}}\Big] \nonumber \\ & = \sum_{\ell=0}^{N-k}\,\sum_{\substack{|u|=|w|=N-k,\\|{u\wedge w}|=\ell}} \mathbb{E}\Big[{\mathrm{e}}^{\beta\left(X^{(k)}_{u}+X_{w}^{(k)}\right)}\boldsymbol{1}_{G_{u}\cap G_{w}}\Big]. \end{align}
\begin{align} \mathbb{E}\big[\big(Z^{(k),\leq}_{\beta,N-k}\big)^2\big] & = \sum_{|u|=|w|=N-k}\mathbb{E}\Big[{\mathrm{e}}^{\beta\left(X^{(k)}_{u}+X_{w}^{(k)}\right)} \boldsymbol{1}_{G_{u}\cap \tilde{G}_{w}}\Big] \nonumber \\ & = \sum_{\ell=0}^{N-k}\,\sum_{\substack{|u|=|w|=N-k,\\|{u\wedge w}|=\ell}} \mathbb{E}\Big[{\mathrm{e}}^{\beta\left(X^{(k)}_{u}+X_{w}^{(k)}\right)}\boldsymbol{1}_{G_{u}\cap G_{w}}\Big]. \end{align}
For all
![]() $\ell\in[\![ 0,N-k-1]\!]$
, we have
$\ell\in[\![ 0,N-k-1]\!]$
, we have
![]() $\big(X^{(k)}_{u_1},X^{(k)}_{u_2}\big)_{u_1\leq u,w\leq u_2} \stackrel{(\mathrm{d})}{=} \big(X^{(k)}_{\ell,n_1},\tilde{X}^{(k)}_{\ell,n_2}\big)_{n_1,n_2\in [\![ 0,N-k]\!]}$
, and for
$\big(X^{(k)}_{u_1},X^{(k)}_{u_2}\big)_{u_1\leq u,w\leq u_2} \stackrel{(\mathrm{d})}{=} \big(X^{(k)}_{\ell,n_1},\tilde{X}^{(k)}_{\ell,n_2}\big)_{n_1,n_2\in [\![ 0,N-k]\!]}$
, and for
![]() $\ell= N-k$
,
$\ell= N-k$
,
![]() $\big(X^{(k)}_{u_1}\big)_{u_1\leq w} = \big(X^{(k)}_{u_2}\big)_{u_2\leq w} \stackrel{(\mathrm{d})}{=} \big(X^{(k)}_n\big)_{n\in [\![ 0,N-k]\!]}$
, where
$\big(X^{(k)}_{u_1}\big)_{u_1\leq w} = \big(X^{(k)}_{u_2}\big)_{u_2\leq w} \stackrel{(\mathrm{d})}{=} \big(X^{(k)}_n\big)_{n\in [\![ 0,N-k]\!]}$
, where
![]() $\big(X^{(k)}_n\big)_{n\in [\![ 0,N-k]\!]}$
was introduced in Lemma 2.1. On the other hand, the number of pairs (u, w) with
$\big(X^{(k)}_n\big)_{n\in [\![ 0,N-k]\!]}$
was introduced in Lemma 2.1. On the other hand, the number of pairs (u, w) with
![]() $|u|=|w|=N-k$
and
$|u|=|w|=N-k$
and
![]() $|{u\wedge w}|=\ell$
is given by
$|{u\wedge w}|=\ell$
is given by
 \begin{equation*} \begin{cases} 2^{2(N-k)-\ell-1}, & \ell\in[\![ 0,N-k-1]\!], \\ 2^{N-k}, & \ell=N-k. \end{cases} \end{equation*}
\begin{equation*} \begin{cases} 2^{2(N-k)-\ell-1}, & \ell\in[\![ 0,N-k-1]\!], \\ 2^{N-k}, & \ell=N-k. \end{cases} \end{equation*}
Therefore, (2.2) yields
 \begin{equation*} \mathbb{E}\big[\big(Z^{(k),\leq}_{\beta,N-k}\big)^2\big] = 2^{N-k}\mathbb{E}\big[{\mathrm{e}}^{\beta X_{N-k}^{(k)}} \boldsymbol{1}_{G_{k}}\big] + \sum_{\ell=0}^{N-k-1}2^{2(N-k)-\ell-1}\mathbb{E}\Big[{\mathrm{e}}^{\beta\left(X^{(k)}_{\ell,N-k}+\tilde{X}_{\ell,N-k}^{(k)}\right)} \boldsymbol{1}_{G_{\ell,k}\cap \tilde{G}_{\ell,k}}\Big], \end{equation*}
\begin{equation*} \mathbb{E}\big[\big(Z^{(k),\leq}_{\beta,N-k}\big)^2\big] = 2^{N-k}\mathbb{E}\big[{\mathrm{e}}^{\beta X_{N-k}^{(k)}} \boldsymbol{1}_{G_{k}}\big] + \sum_{\ell=0}^{N-k-1}2^{2(N-k)-\ell-1}\mathbb{E}\Big[{\mathrm{e}}^{\beta\left(X^{(k)}_{\ell,N-k}+\tilde{X}_{\ell,N-k}^{(k)}\right)} \boldsymbol{1}_{G_{\ell,k}\cap \tilde{G}_{\ell,k}}\Big], \end{equation*}
and the proof is completed.
2.2. Two useful lemmas for the moment estimates
The following lemma estimates the difference between A(y) and A(z) when y and z are close to 0.
Lemma 2.3. For all
![]() $y,z\in [0,x_1]$
, where
$y,z\in [0,x_1]$
, where
![]() $x_1$
is given in Assumption 1.1(ii), there exists a constant
$x_1$
is given in Assumption 1.1(ii), there exists a constant
![]() $C=C(A,x_1)>0$
such that
$C=C(A,x_1)>0$
such that
![]() $|{A\left(y\right) - A\left( z\right)}| \leq \hat{A}'(0) |{y-z}| + Cy^\alpha|{y-z}| + C{|y-z|}^{1+\alpha}$
, where
$|{A\left(y\right) - A\left( z\right)}| \leq \hat{A}'(0) |{y-z}| + Cy^\alpha|{y-z}| + C{|y-z|}^{1+\alpha}$
, where
![]() $\alpha$
appeared in Assumption 1.1(ii).
$\alpha$
appeared in Assumption 1.1(ii).
Proof. Fix
![]() $y,z\in [0,x_1]$
, where
$y,z\in [0,x_1]$
, where
![]() $x_1$
is given in Assumption 1.1(ii). Then, by applying the first-order Taylor expansion of A at y with Lagrange remainder, we have
$x_1$
is given in Assumption 1.1(ii). Then, by applying the first-order Taylor expansion of A at y with Lagrange remainder, we have
where
![]() $\xi$
is between z and y. Then, the triangle inequality and the fact that A is non-decreasing yield
$\xi$
is between z and y. Then, the triangle inequality and the fact that A is non-decreasing yield
By the local Hölder continuity of A in a neighborhood around 0 provided by Assumption 1.1, there exists
![]() $C=C(A,x_1)>0$
such that
$C=C(A,x_1)>0$
such that
Similarly, by the local Hölder continuity of A in a neighborhood around 0 provided by Assumption 1.1, we have
where C is the same constant as in (2.4). Combining (2.3)–(2.5), we conclude that
and this completes the proof.
We now state and prove the following exponential tilting formula that we apply later.
Lemma 2.4. (Exponential tilting.) Fix
![]() $m\in\mathbb{N}$
. Let
$m\in\mathbb{N}$
. Let
![]() $(Y_n)_{n\in[\![ 1,m]\!]}$
be a collection of independent centered Gaussian variables with variance
$(Y_n)_{n\in[\![ 1,m]\!]}$
be a collection of independent centered Gaussian variables with variance
![]() $\sigma_n^2 > 0$
. For all
$\sigma_n^2 > 0$
. For all
![]() $n\in[\![ 1,m]\!]$
, define
$n\in[\![ 1,m]\!]$
, define
![]() $S_n = Y_1+\cdots +Y_n$
. Let
$S_n = Y_1+\cdots +Y_n$
. Let
![]() $g\colon[\![ 1,m]\!]\rightarrow\mathbb{R}$
be a function, and
$g\colon[\![ 1,m]\!]\rightarrow\mathbb{R}$
be a function, and
![]() $G_n = \{\textit{for all}\ \ell\in[\![ 1,n]\!]\colon S_\ell \leq g(\ell)\}$
,
$G_n = \{\textit{for all}\ \ell\in[\![ 1,n]\!]\colon S_\ell \leq g(\ell)\}$
,
![]() $n\in[\![ 1,m]\!]$
. Then, for all
$n\in[\![ 1,m]\!]$
. Then, for all
![]() $\beta\in\mathbb{R}$
,
$\beta\in\mathbb{R}$
,
![]() $\mathbb{E}\big[{\mathrm{e}}^{\beta S_n}\boldsymbol{1}_{G_n}\big] = \mathbb{E}\big[{\mathrm{e}}^{\beta S_n}\big] \mathbb{P}\big(\textit{for all}\ \ell\in[\![ 1,n]\!]\colon S_\ell \leq g(\ell)-\beta \sum_{r=1}^\ell \sigma_r^2\big)$
.
$\mathbb{E}\big[{\mathrm{e}}^{\beta S_n}\boldsymbol{1}_{G_n}\big] = \mathbb{E}\big[{\mathrm{e}}^{\beta S_n}\big] \mathbb{P}\big(\textit{for all}\ \ell\in[\![ 1,n]\!]\colon S_\ell \leq g(\ell)-\beta \sum_{r=1}^\ell \sigma_r^2\big)$
.
Proof. Fix
![]() $n\in\mathbb{N}$
. Firstly, from the independence of
$n\in\mathbb{N}$
. Firstly, from the independence of
![]() $\{Y_i\}_{i=1}^n$
we have
$\{Y_i\}_{i=1}^n$
we have
Next, for all
![]() $x_1,\ldots,x_n\in\mathbb{R}$
, we define
$x_1,\ldots,x_n\in\mathbb{R}$
, we define
Then,
 \begin{align*} \mathbb{E}\big[{\mathrm{e}}^{\beta S_n}\boldsymbol{1}_{G_n}\big] & = \frac{1}{\prod_{i=1}^n \sqrt{2\pi \sigma_i^2}\,} \int_{\mathbb{R}^n}{\mathrm{e}}^{\beta\sum_{i=1}^n x_i} \boldsymbol{1}_{G_n(x_1,\ldots,x_n)} \exp\bigg(-\sum_{i=1}^n \frac{x^2_i}{2\sigma_i^2}\bigg) \mathrm{d}{x_1}\cdots\mathrm{d}{x_n} \\ & = \exp\bigg(\frac{\beta^2}{2}\sum_{i=1}^n \sigma_i^2\bigg) \\ & \quad \times \frac{1}{\prod_{i=1}^n\sqrt{2\pi \sigma_i^2}\,} \int_{\mathbb{R}^n}\boldsymbol{1}_{G_n(x_1,\ldots,x_n)} \exp\bigg(-\sum_{i=1}^n \frac{(x_i-\beta\sigma_i^2)^2}{2\sigma_i^2}\bigg) \mathrm{d}{x_1}\cdots\mathrm{d}{x_n} \\ & = \exp\bigg(\frac{\beta^2}{2}\sum_{i=1}^n \sigma_i^2\bigg) \frac{1}{\prod_{i=1}^n \sqrt{2\pi \sigma_i^2}\,} \int_{\mathbb{R}^n} \boldsymbol{1}_{\tilde{G}_n(y_1,\ldots,y_n)} \exp\bigg(\!-\sum_{i=1}^n \frac{y_i^2}{2\sigma_i^2}\bigg) \mathrm{d}{y_1}\cdots\mathrm{d}{y_n} \\ & = \mathbb{E}\big[{\mathrm{e}}^{\beta S_n}\big] \mathbb{P}\Bigg(\text{for all}\ \ell\in[\![ 1,n]\!] \colon S_\ell \leq g(\ell)-\beta \sum_{r=1}^\ell \sigma_r^2\Bigg), \end{align*}
\begin{align*} \mathbb{E}\big[{\mathrm{e}}^{\beta S_n}\boldsymbol{1}_{G_n}\big] & = \frac{1}{\prod_{i=1}^n \sqrt{2\pi \sigma_i^2}\,} \int_{\mathbb{R}^n}{\mathrm{e}}^{\beta\sum_{i=1}^n x_i} \boldsymbol{1}_{G_n(x_1,\ldots,x_n)} \exp\bigg(-\sum_{i=1}^n \frac{x^2_i}{2\sigma_i^2}\bigg) \mathrm{d}{x_1}\cdots\mathrm{d}{x_n} \\ & = \exp\bigg(\frac{\beta^2}{2}\sum_{i=1}^n \sigma_i^2\bigg) \\ & \quad \times \frac{1}{\prod_{i=1}^n\sqrt{2\pi \sigma_i^2}\,} \int_{\mathbb{R}^n}\boldsymbol{1}_{G_n(x_1,\ldots,x_n)} \exp\bigg(-\sum_{i=1}^n \frac{(x_i-\beta\sigma_i^2)^2}{2\sigma_i^2}\bigg) \mathrm{d}{x_1}\cdots\mathrm{d}{x_n} \\ & = \exp\bigg(\frac{\beta^2}{2}\sum_{i=1}^n \sigma_i^2\bigg) \frac{1}{\prod_{i=1}^n \sqrt{2\pi \sigma_i^2}\,} \int_{\mathbb{R}^n} \boldsymbol{1}_{\tilde{G}_n(y_1,\ldots,y_n)} \exp\bigg(\!-\sum_{i=1}^n \frac{y_i^2}{2\sigma_i^2}\bigg) \mathrm{d}{y_1}\cdots\mathrm{d}{y_n} \\ & = \mathbb{E}\big[{\mathrm{e}}^{\beta S_n}\big] \mathbb{P}\Bigg(\text{for all}\ \ell\in[\![ 1,n]\!] \colon S_\ell \leq g(\ell)-\beta \sum_{r=1}^\ell \sigma_r^2\Bigg), \end{align*}
where the second to last line follows from the change of variables
![]() $y_i=x_i - \beta \sigma_i^2$
,
$y_i=x_i - \beta \sigma_i^2$
,
![]() $i=1,\ldots,n$
, and the last line follows from (2.6).
$i=1,\ldots,n$
, and the last line follows from (2.6).
2.3. Moment estimates of the truncated partition function
We now proceed with the first moment estimate.
Lemma 2.5. (First moment estimate.) For all
![]() $a>0$
and
$a>0$
and
there exists
![]() $N_0=N_0(A,\beta,a,b)\in\mathbb{N}$
such that, for all
$N_0=N_0(A,\beta,a,b)\in\mathbb{N}$
such that, for all
![]() $N\geq N_0$
and
$N\geq N_0$
and
![]() $k\in[\![ 0,K]\!]$
where
$k\in[\![ 0,K]\!]$
where
![]() $K=\lfloor 2\log_\gamma N \rfloor$
with
$K=\lfloor 2\log_\gamma N \rfloor$
with
![]() $\gamma\in(11/10,2)$
,
$\gamma\in(11/10,2)$
,
![]() $\mathbb{E}\big[Z_{\beta,N-k}^{(k),\leq}\big] \geq \frac{7}{10}\mathbb{E}\big[Z_{\beta,N-k}^{(k)}\big]$
.
$\mathbb{E}\big[Z_{\beta,N-k}^{(k),\leq}\big] \geq \frac{7}{10}\mathbb{E}\big[Z_{\beta,N-k}^{(k)}\big]$
.
Proof. By Lemma 2.1, we have
![]() $\mathbb{E}\big[Z^{(k),\leq}_{\beta,N-k}\big] = 2^{N-k}\mathbb{E}\big[e^{\beta X^{(k)}_{N-k}} \boldsymbol{1}_{G_{N-k}}\big]$
. By Lemma 2.4, we have
$\mathbb{E}\big[Z^{(k),\leq}_{\beta,N-k}\big] = 2^{N-k}\mathbb{E}\big[e^{\beta X^{(k)}_{N-k}} \boldsymbol{1}_{G_{N-k}}\big]$
. By Lemma 2.4, we have
 \begin{multline} \mathbb{E}\big[e^{\beta X^{(k)}_{N-k}} \boldsymbol{1}_{G_{N-k}}\big] \\ = \exp\bigg(\frac{\beta^2 N}{2}\bigg(1-A\bigg(\frac{k}{N}\bigg)\bigg)\bigg) \cdot \mathbb{P}\big(\text{for all}\ n\in[\![ 1,N-k]\!]\colon X^{(k)}_{N-k}(n)\leq a\cdot n + b \big). \end{multline}
\begin{multline} \mathbb{E}\big[e^{\beta X^{(k)}_{N-k}} \boldsymbol{1}_{G_{N-k}}\big] \\ = \exp\bigg(\frac{\beta^2 N}{2}\bigg(1-A\bigg(\frac{k}{N}\bigg)\bigg)\bigg) \cdot \mathbb{P}\big(\text{for all}\ n\in[\![ 1,N-k]\!]\colon X^{(k)}_{N-k}(n)\leq a\cdot n + b \big). \end{multline}
We want to give a lower bound for the probability in (2.7). The union bound and the Chernoff bound yield
 \begin{align} & \mathbb{P}\big(\text{there exists}\ n\in[\![ 1,N-k]\!] \colon X^{(k)}_{N-k}(n) > a\cdot n + b\big) \nonumber \\ & \qquad \leq \sum_{n=1}^{N-k}\mathbb{P}\big(X^{(k)}_{N-k}(n)> a\cdot n + b \big) \leq \sum_{n=1}^{N-k}\exp\bigg({-}\frac{(a\cdot n+b)^2}{2N\cdot (A(({n+k})/{N})-A({k}/{N}))}\bigg). \end{align}
\begin{align} & \mathbb{P}\big(\text{there exists}\ n\in[\![ 1,N-k]\!] \colon X^{(k)}_{N-k}(n) > a\cdot n + b\big) \nonumber \\ & \qquad \leq \sum_{n=1}^{N-k}\mathbb{P}\big(X^{(k)}_{N-k}(n)> a\cdot n + b \big) \leq \sum_{n=1}^{N-k}\exp\bigg({-}\frac{(a\cdot n+b)^2}{2N\cdot (A(({n+k})/{N})-A({k}/{N}))}\bigg). \end{align}
We separate (2.8) into two terms:
 \begin{align} (2.8) & = \sum_{n=1}^{K}\exp\bigg({-}\frac{(a\cdot n+b)^2}{2N\cdot(A(({n+k})/{N})-A({k}/{N}))}\bigg) \nonumber \\ & \quad + \sum_{n=K+1}^{N-k}\exp\bigg({-}\frac{(a\cdot n+b)^2}{2N\cdot(A(({n+k})/{N})-A({k}/{N}))}\bigg). \end{align}
\begin{align} (2.8) & = \sum_{n=1}^{K}\exp\bigg({-}\frac{(a\cdot n+b)^2}{2N\cdot(A(({n+k})/{N})-A({k}/{N}))}\bigg) \nonumber \\ & \quad + \sum_{n=K+1}^{N-k}\exp\bigg({-}\frac{(a\cdot n+b)^2}{2N\cdot(A(({n+k})/{N})-A({k}/{N}))}\bigg). \end{align}
We start by bounding the first term of (2.9). Take
![]() $N_1\in\mathbb{N}$
such that
$N_1\in\mathbb{N}$
such that
![]() $2K/N\leq x_1$
for all
$2K/N\leq x_1$
for all
![]() $N\geq N_1$
. Then, by Lemma 2.3, for all
$N\geq N_1$
. Then, by Lemma 2.3, for all
![]() $n\in [\![ 1,K]\!]$
, we have
$n\in [\![ 1,K]\!]$
, we have
 \begin{align} N\cdot \bigg(A\bigg(\frac{n+k}{N}\bigg)-A\bigg(\frac{k}{N}\bigg)\bigg) & \leq \hat{A}'(0)n + C\frac{n(n+k)^\alpha}{N} + C\frac{n^{1+\alpha}}{N^\alpha} \nonumber \\ & \leq \hat{A}'(0)n + C\frac{K(2K)^\alpha}{N} + C\frac{K^{1+\alpha}}{N^{\alpha}} \end{align}
\begin{align} N\cdot \bigg(A\bigg(\frac{n+k}{N}\bigg)-A\bigg(\frac{k}{N}\bigg)\bigg) & \leq \hat{A}'(0)n + C\frac{n(n+k)^\alpha}{N} + C\frac{n^{1+\alpha}}{N^\alpha} \nonumber \\ & \leq \hat{A}'(0)n + C\frac{K(2K)^\alpha}{N} + C\frac{K^{1+\alpha}}{N^{\alpha}} \end{align}
where h(N) is defined as
(2.10) follows by the assumption that
![]() $n\leq K$
and
$n\leq K$
and
![]() $k\leq K$
, and (2.12) follows from the fact that
$k\leq K$
, and (2.12) follows from the fact that
![]() $n\geq 1$
and
$n\geq 1$
and
![]() $h(N)\geq 0$
.
$h(N)\geq 0$
.
By (2.12) and the fact that
![]() $(an+b)^2 \geq a^2n^2 + 2abn$
for all
$(an+b)^2 \geq a^2n^2 + 2abn$
for all
![]() $a,b,n>0$
, the first term of (2.9) is bounded from above by
$a,b,n>0$
, the first term of (2.9) is bounded from above by
 \begin{align} & \sum_{n=1}^{K}\exp\bigg({-}\frac{(a\cdot n+b)^2}{2N\cdot(A(({n+k})/{N})-A({k}/{N}))}\bigg) \nonumber \\ & \qquad \leq \sum_{n=1}^{K}\exp\bigg({-}\frac{a^2 n^2 + 2abn}{2(\hat{A}'(0) + h(N))n}\bigg) \nonumber \\ & \qquad = \exp\bigg(-\frac{ab}{\hat{A}'(0)+h(N)}\bigg)\sum_{n=1}^{K} \exp\bigg(-\frac{a^2n}{2(\hat{A}'(0)+h(N))}\bigg). \end{align}
\begin{align} & \sum_{n=1}^{K}\exp\bigg({-}\frac{(a\cdot n+b)^2}{2N\cdot(A(({n+k})/{N})-A({k}/{N}))}\bigg) \nonumber \\ & \qquad \leq \sum_{n=1}^{K}\exp\bigg({-}\frac{a^2 n^2 + 2abn}{2(\hat{A}'(0) + h(N))n}\bigg) \nonumber \\ & \qquad = \exp\bigg(-\frac{ab}{\hat{A}'(0)+h(N)}\bigg)\sum_{n=1}^{K} \exp\bigg(-\frac{a^2n}{2(\hat{A}'(0)+h(N))}\bigg). \end{align}
The summation in (2.14) is bounded from above by
 \begin{align*} \sum_{n=1}^{K}\exp\bigg(-\frac{a^2n}{2(\hat{A}'(0)+h(N))}\bigg) & \leq \sum_{n=1}^{\infty}\exp\bigg(-\frac{a^2n}{2(\hat{A}'(0)+h(N))}\bigg) \\ & \leq \frac{\exp\big(\!-{a^2}/({2(\hat{A}'(0)+h(N))})\big)}{1-\exp\big(\!-{a^2}/({2(\hat{A}'(0)+h(N))})\big)}. \end{align*}
\begin{align*} \sum_{n=1}^{K}\exp\bigg(-\frac{a^2n}{2(\hat{A}'(0)+h(N))}\bigg) & \leq \sum_{n=1}^{\infty}\exp\bigg(-\frac{a^2n}{2(\hat{A}'(0)+h(N))}\bigg) \\ & \leq \frac{\exp\big(\!-{a^2}/({2(\hat{A}'(0)+h(N))})\big)}{1-\exp\big(\!-{a^2}/({2(\hat{A}'(0)+h(N))})\big)}. \end{align*}
This and (2.14) yield
 \begin{multline} \sum_{n=1}^{K}\exp\bigg({-}\frac{(a\cdot n+b)^2}{2N\cdot(A(({n+k})/{N})-A({k}/{N}))}\bigg) \\ \leq \exp\bigg(-\frac{ab}{\hat{A}'(0)+h(N)}\bigg) \frac{\exp\big(-{a^2}/({2(\hat{A}'(0)+h(N))})\big)}{1-\exp\big(-{a^2}/({2(\hat{A}'(0)+h(N))})\big)}. \end{multline}
\begin{multline} \sum_{n=1}^{K}\exp\bigg({-}\frac{(a\cdot n+b)^2}{2N\cdot(A(({n+k})/{N})-A({k}/{N}))}\bigg) \\ \leq \exp\bigg(-\frac{ab}{\hat{A}'(0)+h(N)}\bigg) \frac{\exp\big(-{a^2}/({2(\hat{A}'(0)+h(N))})\big)}{1-\exp\big(-{a^2}/({2(\hat{A}'(0)+h(N))})\big)}. \end{multline}
Since
![]() $h(N)\rightarrow 0$
as
$h(N)\rightarrow 0$
as
![]() $N\rightarrow\infty$
, by the choice of parameters a and b we have
$N\rightarrow\infty$
, by the choice of parameters a and b we have
 \begin{multline*} \limsup_{N\rightarrow\infty}\frac{\exp\big(-{a^2}/({2(\hat{A}'(0)+h(N))})\big)}{1-\exp\big(-{a^2}/({2(\hat{A}'(0)+h(N))})\big)} \exp\bigg(-\frac{ab}{\hat{A}'(0)+h(N)}\bigg) \\ = \frac{{\mathrm{e}}^{-a^2/(2\hat{A}'(0))}}{1-{\mathrm{e}}^{-a^2/(2\hat{A}'(0))}}{\mathrm{e}}^{-ab/\hat{A}'(0)} \leq \frac{1}{10}. \end{multline*}
\begin{multline*} \limsup_{N\rightarrow\infty}\frac{\exp\big(-{a^2}/({2(\hat{A}'(0)+h(N))})\big)}{1-\exp\big(-{a^2}/({2(\hat{A}'(0)+h(N))})\big)} \exp\bigg(-\frac{ab}{\hat{A}'(0)+h(N)}\bigg) \\ = \frac{{\mathrm{e}}^{-a^2/(2\hat{A}'(0))}}{1-{\mathrm{e}}^{-a^2/(2\hat{A}'(0))}}{\mathrm{e}}^{-ab/\hat{A}'(0)} \leq \frac{1}{10}. \end{multline*}
Combining this with (2.15), there exists
![]() $N_2=N_2(A,\beta)\in\mathbb{N}$
such that, for all
$N_2=N_2(A,\beta)\in\mathbb{N}$
such that, for all
![]() $N\in N_2$
, the first term of (2.9) is bounded from above by
$N\in N_2$
, the first term of (2.9) is bounded from above by
 \begin{equation} \sum_{n=1}^{K}\exp\bigg({-}\frac{(a\cdot n+b)^2}{2N\cdot(A(({n+k})/{N})-A({k}/{N}))}\bigg) \leq \frac{2}{10}. \end{equation}
\begin{equation} \sum_{n=1}^{K}\exp\bigg({-}\frac{(a\cdot n+b)^2}{2N\cdot(A(({n+k})/{N})-A({k}/{N}))}\bigg) \leq \frac{2}{10}. \end{equation}
It remains to bound the second term of (2.9). By Assumption 1.1, we know that
![]() $A(x)\geq 0$
for all
$A(x)\geq 0$
for all
![]() $x\in [0, 1]$
and
$x\in [0, 1]$
and
![]() $A(x)\leq \hat{A}(0)x$
for all
$A(x)\leq \hat{A}(0)x$
for all
![]() $x\in [0, 1]$
. Thus,
$x\in [0, 1]$
. Thus,
For
![]() $n\geq K+1$
and
$n\geq K+1$
and
![]() $k\leq K$
, we have
$k\leq K$
, we have
![]() $1+{k}/{n} \leq 1+{K}/({K+1}) \leq 2$
. Combining this with (2.17) then yields, for
$1+{k}/{n} \leq 1+{K}/({K+1}) \leq 2$
. Combining this with (2.17) then yields, for
![]() $n\geq K+1$
and
$n\geq K+1$
and
![]() $k\leq K$
,
$k\leq K$
,
Using this and the fact that
![]() $(an+b)^2 \geq a^2 n^2$
for all
$(an+b)^2 \geq a^2 n^2$
for all
![]() $a,b,n>0$
,
$a,b,n>0$
,
 \begin{align*} & \sum_{n=K+1}^{N-k}\exp\bigg({-}\frac{(a n+b)^2}{2N\cdot(A(({n+k})/{N})-A({k}/{N}))}\bigg) \\ & \qquad\qquad \leq \sum_{n=K+1}^{N-k}\exp\bigg({-}\frac{a^2n^2}{4\hat{A}(0) n}\bigg) \\ & \qquad\qquad = \sum_{n=K+1}^{N-k}\exp\bigg({-}\frac{a^2}{4\hat{A}'(0)}n\bigg) \\ & \qquad\qquad \leq \sum_{n=K+1}^{\infty}\exp\bigg({-}\frac{a^2}{4\hat{A}'(0)}n\bigg) \\ & \qquad\qquad \leq \exp\bigg(-\frac{a^2}{4\hat{A}'(0)}(K+1)\bigg) \frac{1}{1-\exp(\!-{a^2}/({4\hat{A}'(0)}))}. \end{align*}
\begin{align*} & \sum_{n=K+1}^{N-k}\exp\bigg({-}\frac{(a n+b)^2}{2N\cdot(A(({n+k})/{N})-A({k}/{N}))}\bigg) \\ & \qquad\qquad \leq \sum_{n=K+1}^{N-k}\exp\bigg({-}\frac{a^2n^2}{4\hat{A}(0) n}\bigg) \\ & \qquad\qquad = \sum_{n=K+1}^{N-k}\exp\bigg({-}\frac{a^2}{4\hat{A}'(0)}n\bigg) \\ & \qquad\qquad \leq \sum_{n=K+1}^{\infty}\exp\bigg({-}\frac{a^2}{4\hat{A}'(0)}n\bigg) \\ & \qquad\qquad \leq \exp\bigg(-\frac{a^2}{4\hat{A}'(0)}(K+1)\bigg) \frac{1}{1-\exp(\!-{a^2}/({4\hat{A}'(0)}))}. \end{align*}
By our choice of K, the lim sup of this expression equals 0 as
![]() $N\rightarrow\infty$
. In particular, there exists
$N\rightarrow\infty$
. In particular, there exists
![]() $N_3=N_3(A,\beta)$
such that, for all
$N_3=N_3(A,\beta)$
such that, for all
![]() $N\geq N_2$
,
$N\geq N_2$
,
 \begin{equation} \sum_{n=K+1}^{N-k}\exp\bigg({-}\frac{(a\cdot n+b)^2}{2N\cdot(A(({n+k})/{N})-A({k}/{N}))}\bigg) \leq \frac{1}{10}. \end{equation}
\begin{equation} \sum_{n=K+1}^{N-k}\exp\bigg({-}\frac{(a\cdot n+b)^2}{2N\cdot(A(({n+k})/{N})-A({k}/{N}))}\bigg) \leq \frac{1}{10}. \end{equation}
Let
![]() $N_0\,:\!=\, \max\{N_1,N_2,N_3\}$
. Combining (2.9), (2.16), and (2.18), for all
$N_0\,:\!=\, \max\{N_1,N_2,N_3\}$
. Combining (2.9), (2.16), and (2.18), for all
![]() $N\geq N_0$
and for all
$N\geq N_0$
and for all
![]() $k\in[\![ 0,K]\!]$
,
$k\in[\![ 0,K]\!]$
,
Combining (2.1), (2.7), (2.7), and (2.19), we conclude that, for all
![]() $N\geq N_0$
and for all
$N\geq N_0$
and for all
![]() $k\in[\![ 0,K]\!]$
,
$k\in[\![ 0,K]\!]$
,
where the equality follows from (2.1).
It remains to provide a second moment estimate of the truncated partition function.
Lemma 2.6. (Second moment estimate.) Let
![]() $\beta<\beta_\mathrm{c}$
. For all
$\beta<\beta_\mathrm{c}$
. For all
![]() $a\in\big(0,({\log 2})/{\beta}-\frac{1}{2}\beta\hat{A}'(0)\big)$
and
$a\in\big(0,({\log 2})/{\beta}-\frac{1}{2}\beta\hat{A}'(0)\big)$
and
![]() $b>0$
, there exist
$b>0$
, there exist
![]() $N_0=N_0(A,\beta)\in\mathbb{N}$
and
$N_0=N_0(A,\beta)\in\mathbb{N}$
and
![]() $C=C(A,\beta)>0$
such that, for all
$C=C(A,\beta)>0$
such that, for all
![]() $N\geq N_0$
and
$N\geq N_0$
and
![]() $k\in[\![ 0,K ]\!]$
, where
$k\in[\![ 0,K ]\!]$
, where
![]() $K=\lfloor 2\log_\gamma N\rfloor$
with
$K=\lfloor 2\log_\gamma N\rfloor$
with
![]() $\gamma\in(11/10,2)$
,
$\gamma\in(11/10,2)$
,
![]() $\mathbb{E}\big[\big(Z^{(k),\leq}_{\beta,N-k}\big)^2\big] \leq C\mathbb{E}\big[Z^{(k)}_{\beta,N-k}\big]^2$
.
$\mathbb{E}\big[\big(Z^{(k),\leq}_{\beta,N-k}\big)^2\big] \leq C\mathbb{E}\big[Z^{(k)}_{\beta,N-k}\big]^2$
.
Proof. Fix
![]() $\beta<\beta_\mathrm{c}$
and
$\beta<\beta_\mathrm{c}$
and
![]() $a\in\big(0,({\log 2})/{\beta}-\frac{1}{2}\beta\hat{A}'(0)\big)$
. Define
$a\in\big(0,({\log 2})/{\beta}-\frac{1}{2}\beta\hat{A}'(0)\big)$
. Define
where the positivity follows from the definition of
![]() $\beta_\mathrm{c}$
in (1.2).
$\beta_\mathrm{c}$
in (1.2).
By Lemma 2.2, we have
 \begin{align} \mathbb{E}\big[\big(Z^{(k),\leq}_{\beta,N-k}\big)^2\big] & = 2^{N-k}\mathbb{E}\big[{\mathrm{e}}^{2\beta X_{N-k}^{(k)}}\boldsymbol{1}_{G_{k}}\big] \nonumber \\ & \quad + \sum_{\ell=0}^{N-k-1}2^{2(N-k)-\ell-1}\mathbb{E}\Big[{\mathrm{e}}^{\beta\left(X^{(k)}_{\ell,N-k}+\tilde{X}_{\ell,N-k}^{(k)}\right)} \boldsymbol{1}_{G_{\ell,k}\cap \tilde{G}_{\ell,k}}\Big]. \end{align}
\begin{align} \mathbb{E}\big[\big(Z^{(k),\leq}_{\beta,N-k}\big)^2\big] & = 2^{N-k}\mathbb{E}\big[{\mathrm{e}}^{2\beta X_{N-k}^{(k)}}\boldsymbol{1}_{G_{k}}\big] \nonumber \\ & \quad + \sum_{\ell=0}^{N-k-1}2^{2(N-k)-\ell-1}\mathbb{E}\Big[{\mathrm{e}}^{\beta\left(X^{(k)}_{\ell,N-k}+\tilde{X}_{\ell,N-k}^{(k)}\right)} \boldsymbol{1}_{G_{\ell,k}\cap \tilde{G}_{\ell,k}}\Big]. \end{align}
We now want to estimate the expectations in (2.20). For all
![]() $\ell\in[\![ 1,N]\!]$
and
$\ell\in[\![ 1,N]\!]$
and
![]() $n\in[\![ 1, N-\ell]\!]$
, define
$n\in[\![ 1, N-\ell]\!]$
, define
Then, we see that the expectation in the first term of (2.20) is bounded from above by
Fix
![]() $\ell\in[\![ 0,N-k-1]\!]$
. We have
$\ell\in[\![ 0,N-k-1]\!]$
. We have
Then, we have
where (2.22) follows from (2.21), and both (2.23) and (2.24) from Lemma 2.2.
For
![]() $\ell\in[\![ 0,N-k]\!]$
, Lemma 2.4 yields
$\ell\in[\![ 0,N-k]\!]$
, Lemma 2.4 yields
 \begin{align} \mathbb{E}\Big[{\mathrm{e}}^{2\beta X_{\ell}^{(k)}} \boldsymbol{1}_{H_{\ell}^{(k)}}\Big] & = \exp\bigg(2\beta^2 N \bigg(A\bigg(\frac{\ell+k}{N}\bigg)-A\bigg(\frac{k}{N}\bigg)\bigg)\bigg) \nonumber \\ & \quad \times \mathbb{P}\bigg(X_{\ell}^{(k)} \leq -\beta N\bigg(A\bigg(\frac{k+\ell}{N}\bigg)-A\bigg(\frac{k}{N}\bigg)\bigg) + a \ell + b\bigg). \end{align}
\begin{align} \mathbb{E}\Big[{\mathrm{e}}^{2\beta X_{\ell}^{(k)}} \boldsymbol{1}_{H_{\ell}^{(k)}}\Big] & = \exp\bigg(2\beta^2 N \bigg(A\bigg(\frac{\ell+k}{N}\bigg)-A\bigg(\frac{k}{N}\bigg)\bigg)\bigg) \nonumber \\ & \quad \times \mathbb{P}\bigg(X_{\ell}^{(k)} \leq -\beta N\bigg(A\bigg(\frac{k+\ell}{N}\bigg)-A\bigg(\frac{k}{N}\bigg)\bigg) + a \ell + b\bigg). \end{align}
We distinguish the following two cases.
Case 1:
![]() $-\beta N(A(({\ell+k})/{N})-A({k}/{N})) + a \ell + b\geq 0$
. In this case, by bounding the probability in (2.26) by 1, we obtain
$-\beta N(A(({\ell+k})/{N})-A({k}/{N})) + a \ell + b\geq 0$
. In this case, by bounding the probability in (2.26) by 1, we obtain
 \begin{align*} (2.26) & \leq \exp\bigg(2\beta^2N\bigg(A\bigg(\frac{\ell+k}{N}\bigg)-A\bigg(\frac{k}{N}\bigg)\bigg)\bigg) \\ & \leq \exp\bigg(\beta^2N\bigg(A\bigg(\frac{\ell+k}{N}\bigg)-A\bigg(\frac{k}{N}\bigg)\bigg)\bigg)\exp\!(\beta(a\ell+b)). \end{align*}
\begin{align*} (2.26) & \leq \exp\bigg(2\beta^2N\bigg(A\bigg(\frac{\ell+k}{N}\bigg)-A\bigg(\frac{k}{N}\bigg)\bigg)\bigg) \\ & \leq \exp\bigg(\beta^2N\bigg(A\bigg(\frac{\ell+k}{N}\bigg)-A\bigg(\frac{k}{N}\bigg)\bigg)\bigg)\exp\!(\beta(a\ell+b)). \end{align*}
Case 2:
![]() $-\beta N(A(({\ell+k})/{N})-A({k}/{N})) + a \ell + b<0$
. In this case, the Chernoff bound yields
$-\beta N(A(({\ell+k})/{N})-A({k}/{N})) + a \ell + b<0$
. In this case, the Chernoff bound yields
 \begin{align} (2.27) & \leq \exp\bigg(2\beta^2N\bigg(A\bigg(\frac{\ell+k}{N}\bigg)-A\bigg(\frac{k}{N}\bigg)\bigg)\bigg) \nonumber \\ & \quad \times \exp\bigg(-\frac{(\beta N(A(({\ell+k})/{N})-A({k}/{N})) - (a \ell+b))^2} {2N(A(({\ell+k})/{N})-A({k}/{N}))}\bigg). \end{align}
\begin{align} (2.27) & \leq \exp\bigg(2\beta^2N\bigg(A\bigg(\frac{\ell+k}{N}\bigg)-A\bigg(\frac{k}{N}\bigg)\bigg)\bigg) \nonumber \\ & \quad \times \exp\bigg(-\frac{(\beta N(A(({\ell+k})/{N})-A({k}/{N})) - (a \ell+b))^2} {2N(A(({\ell+k})/{N})-A({k}/{N}))}\bigg). \end{align}
By the fact that
 \begin{multline*} \bigg(\beta N\bigg(A\bigg(\frac{\ell+k}{N}\bigg)-A\bigg(\frac{k}{N}\bigg)\bigg) - (a \ell+b)\bigg)^2 \\ \geq \beta^2N^2\bigg(A\bigg(\frac{\ell+k}{N}\bigg)-A\bigg(\frac{k}{N}\bigg)\bigg)^2 - 2\beta N\bigg(A\bigg(\frac{\ell+k}{N}\bigg)-A\bigg(\frac{k}{N}\bigg)\bigg)(a\ell+b), \end{multline*}
\begin{multline*} \bigg(\beta N\bigg(A\bigg(\frac{\ell+k}{N}\bigg)-A\bigg(\frac{k}{N}\bigg)\bigg) - (a \ell+b)\bigg)^2 \\ \geq \beta^2N^2\bigg(A\bigg(\frac{\ell+k}{N}\bigg)-A\bigg(\frac{k}{N}\bigg)\bigg)^2 - 2\beta N\bigg(A\bigg(\frac{\ell+k}{N}\bigg)-A\bigg(\frac{k}{N}\bigg)\bigg)(a\ell+b), \end{multline*}
(2.27) yields the bound
From the case study above, we conclude that
Applying the bounds in (2.25) and (2.28) to (2.20), we obtain
 \begin{align} & \mathbb{E}\big[\big(Z^{(k),\leq}_{\beta,N-k}\big)^2\big] \nonumber \\ & \leq 2^{N-k}\exp\bigg(\frac{3}{2}\beta^2N\bigg(A\bigg(\frac{1}{N}\bigg)-A\bigg(\frac{k}{N}\bigg)\bigg)\bigg) \exp\!(\beta(a(N-k) + b)) \nonumber \\ & \quad + \sum_{\ell=0}^{N-k-1}2^{2(N-k)-\ell-1}\exp\bigg(\frac{3}{2}\beta^2N \bigg(A\bigg(\frac{\ell+k}{N}\bigg)-A\bigg(\frac{k}{N}\bigg)\bigg)\bigg)\exp\!(\beta(a\ell + b)) \nonumber \\ & \quad \times \exp\bigg(\beta^2N\bigg(1-A\bigg(\frac{\ell+k}{N}\bigg)\bigg)\bigg) \nonumber \\ & \leq 2^{2(N-k)}\exp\bigg(\beta^2N\bigg(1-A\bigg(\frac{k}{N}\bigg)\bigg)\bigg) \nonumber \\ & \quad \times \sum_{\ell=0}^{N-k}2^{-\ell} \exp\bigg(\frac{1}{2}\beta^2N\bigg(A\bigg(\frac{\ell+k}{N}\bigg)-A\bigg(\frac{k}{N}\bigg)\bigg)\bigg) \exp\!(\beta(a\ell + b)) \end{align}
\begin{align} & \mathbb{E}\big[\big(Z^{(k),\leq}_{\beta,N-k}\big)^2\big] \nonumber \\ & \leq 2^{N-k}\exp\bigg(\frac{3}{2}\beta^2N\bigg(A\bigg(\frac{1}{N}\bigg)-A\bigg(\frac{k}{N}\bigg)\bigg)\bigg) \exp\!(\beta(a(N-k) + b)) \nonumber \\ & \quad + \sum_{\ell=0}^{N-k-1}2^{2(N-k)-\ell-1}\exp\bigg(\frac{3}{2}\beta^2N \bigg(A\bigg(\frac{\ell+k}{N}\bigg)-A\bigg(\frac{k}{N}\bigg)\bigg)\bigg)\exp\!(\beta(a\ell + b)) \nonumber \\ & \quad \times \exp\bigg(\beta^2N\bigg(1-A\bigg(\frac{\ell+k}{N}\bigg)\bigg)\bigg) \nonumber \\ & \leq 2^{2(N-k)}\exp\bigg(\beta^2N\bigg(1-A\bigg(\frac{k}{N}\bigg)\bigg)\bigg) \nonumber \\ & \quad \times \sum_{\ell=0}^{N-k}2^{-\ell} \exp\bigg(\frac{1}{2}\beta^2N\bigg(A\bigg(\frac{\ell+k}{N}\bigg)-A\bigg(\frac{k}{N}\bigg)\bigg)\bigg) \exp\!(\beta(a\ell + b)) \end{align}
 \begin{align} = \mathbb{E}\big[Z_{\beta,N-k}^{(k)}\big]^2\sum_{\ell=0}^{N-k} 2^{-\ell} \exp\bigg(\frac{1}{2}\beta^2N\bigg(A\bigg(\frac{\ell+k}{N}\bigg)-A\bigg(\frac{k}{N}\bigg)\bigg)\bigg) \exp\!(\beta (a\ell + b)),\end{align}
\begin{align} = \mathbb{E}\big[Z_{\beta,N-k}^{(k)}\big]^2\sum_{\ell=0}^{N-k} 2^{-\ell} \exp\bigg(\frac{1}{2}\beta^2N\bigg(A\bigg(\frac{\ell+k}{N}\bigg)-A\bigg(\frac{k}{N}\bigg)\bigg)\bigg) \exp\!(\beta (a\ell + b)),\end{align}
where (2.29) follows from (2.1) and the fact that
![]() $2^{-\ell-1}\leq 2^{-\ell}$
for any integer
$2^{-\ell-1}\leq 2^{-\ell}$
for any integer
![]() $\ell$
. Now, we decompose the summation in (2.30) into
$\ell$
. Now, we decompose the summation in (2.30) into
 \begin{align} & \sum_{\ell=0}^{N-k}2^{-\ell} \exp\bigg(\frac{1}{2}\beta^2N\bigg(A\bigg(\frac{\ell+k}{N}\bigg)-A\bigg(\frac{k}{N}\bigg)\bigg)\bigg) \exp\!(\beta(a\ell + b)) \nonumber \\ & = \sum_{\ell=0}^{K_1}2^{-\ell} \exp\bigg(\frac{1}{2}\beta^2N\bigg(A\bigg(\frac{\ell+k}{N}\bigg)-A\bigg(\frac{k}{N}\bigg)\bigg)\bigg) \exp\!(\beta(a\ell + b)) \nonumber \\ & \quad + \sum_{\ell=K_1+1}^{N-k}2^{-\ell} \exp\bigg(\frac{1}{2}\beta^2N\bigg(A\bigg(\frac{\ell+k}{N}\bigg)-A\bigg(\frac{k}{N}\bigg)\bigg)\bigg) \exp\!(\beta(a\ell + b)), \end{align}
\begin{align} & \sum_{\ell=0}^{N-k}2^{-\ell} \exp\bigg(\frac{1}{2}\beta^2N\bigg(A\bigg(\frac{\ell+k}{N}\bigg)-A\bigg(\frac{k}{N}\bigg)\bigg)\bigg) \exp\!(\beta(a\ell + b)) \nonumber \\ & = \sum_{\ell=0}^{K_1}2^{-\ell} \exp\bigg(\frac{1}{2}\beta^2N\bigg(A\bigg(\frac{\ell+k}{N}\bigg)-A\bigg(\frac{k}{N}\bigg)\bigg)\bigg) \exp\!(\beta(a\ell + b)) \nonumber \\ & \quad + \sum_{\ell=K_1+1}^{N-k}2^{-\ell} \exp\bigg(\frac{1}{2}\beta^2N\bigg(A\bigg(\frac{\ell+k}{N}\bigg)-A\bigg(\frac{k}{N}\bigg)\bigg)\bigg) \exp\!(\beta(a\ell + b)), \end{align}
where
![]() $K_1=K^2$
. We start by bounding the first term in (2.31). Take
$K_1=K^2$
. We start by bounding the first term in (2.31). Take
![]() $N_1$
such that
$N_1$
such that
![]() $(K_1+K)/N\leq x_1$
for all
$(K_1+K)/N\leq x_1$
for all
![]() $N\geq N_1$
. Following the same derivation as for (2.11), for all
$N\geq N_1$
. Following the same derivation as for (2.11), for all
![]() $N\geq N_1$
,
$N\geq N_1$
,
![]() $k\in[\![ 1,K]\!]$
, and
$k\in[\![ 1,K]\!]$
, and
![]() $\ell\in[\![ 0,K_1]\!]$
, we have
$\ell\in[\![ 0,K_1]\!]$
, we have
where h(N) is defined in (2.13). Applying this then yields
 \begin{align} \text{first term in (2.31)} & \leq \exp\!(h(N)+\beta b)\sum_{\ell=0}^{K_1}\exp\bigg(\!-\bigg(\log 2-\frac{\beta^2}{2}\hat{A}(0)-\beta a\bigg)\ell\bigg) \nonumber \\ & = \exp\!(h(N)+\beta b)\sum_{\ell=0}^{K_1} \exp\!(\!-c\ell) \nonumber \\ & \leq \exp\!(h(N)+\beta b)\sum_{\ell=0}^{\infty} \exp\!(\!-c\ell) = \exp\!(h(N)+\beta b) \frac{1}{1-{\mathrm{e}}^{-c}}. \end{align}
\begin{align} \text{first term in (2.31)} & \leq \exp\!(h(N)+\beta b)\sum_{\ell=0}^{K_1}\exp\bigg(\!-\bigg(\log 2-\frac{\beta^2}{2}\hat{A}(0)-\beta a\bigg)\ell\bigg) \nonumber \\ & = \exp\!(h(N)+\beta b)\sum_{\ell=0}^{K_1} \exp\!(\!-c\ell) \nonumber \\ & \leq \exp\!(h(N)+\beta b)\sum_{\ell=0}^{\infty} \exp\!(\!-c\ell) = \exp\!(h(N)+\beta b) \frac{1}{1-{\mathrm{e}}^{-c}}. \end{align}
It remains to bound the second term in (2.31). As in (2.17), Assumption 1.1 implies that
![]() $A(x)\geq 0$
for all
$A(x)\geq 0$
for all
![]() $x\in [0, 1]$
, and
$x\in [0, 1]$
, and
![]() $A(x)\leq \hat{A}(0)x$
for all
$A(x)\leq \hat{A}(0)x$
for all
![]() $x\in [0, 1]$
, so
$x\in [0, 1]$
, so
where the second inequality is by the assumption that
![]() $k\leq K$
. Thus,
$k\leq K$
. Thus,
 \begin{align} \text{second term in (2.31)} & \leq \exp(\hat{A}'(0)K+\beta b) \sum_{\ell=K_1+1}^{N-k}\exp\bigg(\!-\bigg(\log 2 - \frac{\beta^2}{2}\hat{A}'(0)-\beta a\bigg)\ell\bigg) \nonumber \\ & = \exp(\hat{A}'(0)K+\beta b)\sum_{\ell=K_1+1}^{N-k}\exp\!(\!-c\ell) \nonumber \\ & \leq \exp(\hat{A}'(0)K+\beta b)\sum_{\ell=K_1+1}^{\infty}\exp\!(\!-c\ell) \nonumber \\ & = \exp(\hat{A}'(0)K+\beta b)\frac{{\mathrm{e}}^{-c(K_1+1)}}{1-{\mathrm{e}}^{-c}} = \exp\!(\!-L(N)+\beta b)\frac{{\mathrm{e}}^{-c}}{1-{\mathrm{e}}^{-c}}, \end{align}
\begin{align} \text{second term in (2.31)} & \leq \exp(\hat{A}'(0)K+\beta b) \sum_{\ell=K_1+1}^{N-k}\exp\bigg(\!-\bigg(\log 2 - \frac{\beta^2}{2}\hat{A}'(0)-\beta a\bigg)\ell\bigg) \nonumber \\ & = \exp(\hat{A}'(0)K+\beta b)\sum_{\ell=K_1+1}^{N-k}\exp\!(\!-c\ell) \nonumber \\ & \leq \exp(\hat{A}'(0)K+\beta b)\sum_{\ell=K_1+1}^{\infty}\exp\!(\!-c\ell) \nonumber \\ & = \exp(\hat{A}'(0)K+\beta b)\frac{{\mathrm{e}}^{-c(K_1+1)}}{1-{\mathrm{e}}^{-c}} = \exp\!(\!-L(N)+\beta b)\frac{{\mathrm{e}}^{-c}}{1-{\mathrm{e}}^{-c}}, \end{align}
where
![]() $L(N) = c K_1 - \hat{A}'(0)K = c K^2 - \hat{A}'(0)K$
. Combining (2.31), (2.32), and (2.33), we derive that
$L(N) = c K_1 - \hat{A}'(0)K = c K^2 - \hat{A}'(0)K$
. Combining (2.31), (2.32), and (2.33), we derive that
 \begin{multline} \sum_{\ell=0}^{N-k} 2^{-\ell} \exp\bigg(\frac{1}{2}\beta^2N\bigg(A\bigg(\frac{\ell+k}{N}\bigg)-A\bigg(\frac{k}{N}\bigg)\bigg)\bigg) \exp\!(\beta (a \ell + b)) \\ \leq \exp\!(h(N)+\beta b)\frac{1}{1-{\mathrm{e}}^{-c}} + \exp\!(\!-L(N)+\beta b)\frac{{\mathrm{e}}^{-c}}{1-{\mathrm{e}}^{-c}}. \end{multline}
\begin{multline} \sum_{\ell=0}^{N-k} 2^{-\ell} \exp\bigg(\frac{1}{2}\beta^2N\bigg(A\bigg(\frac{\ell+k}{N}\bigg)-A\bigg(\frac{k}{N}\bigg)\bigg)\bigg) \exp\!(\beta (a \ell + b)) \\ \leq \exp\!(h(N)+\beta b)\frac{1}{1-{\mathrm{e}}^{-c}} + \exp\!(\!-L(N)+\beta b)\frac{{\mathrm{e}}^{-c}}{1-{\mathrm{e}}^{-c}}. \end{multline}
Note that
![]() $h(N)\rightarrow 0$
and
$h(N)\rightarrow 0$
and
![]() $L(N)\rightarrow\infty$
as
$L(N)\rightarrow\infty$
as
![]() $N\rightarrow\infty$
, so there exists
$N\rightarrow\infty$
, so there exists
![]() $N_2$
such that
$N_2$
such that
![]() $h(N)\leq 1$
and
$h(N)\leq 1$
and
![]() $L(N)\geq 1$
for all
$L(N)\geq 1$
for all
![]() $N\geq N_2$
. Take
$N\geq N_2$
. Take
![]() $N_0=\max\{N_1,N_2\}$
. For all
$N_0=\max\{N_1,N_2\}$
. For all
![]() $N\geq N_0$
, we conclude from (2.30) and (2.34) that
$N\geq N_0$
, we conclude from (2.30) and (2.34) that
![]() $\mathbb{E}\big[\big(Z^{(k),\leq}_{\beta,N-k}\big)^2\big] \leq C\mathbb{E}\big[Z^{(k)}_{\beta,N-k}\big]^2$
, where
$\mathbb{E}\big[\big(Z^{(k),\leq}_{\beta,N-k}\big)^2\big] \leq C\mathbb{E}\big[Z^{(k)}_{\beta,N-k}\big]^2$
, where
![]() $C = C(A,\beta) = \exp(1+\beta b)/({1-{\mathrm{e}}^{-c}}) + \exp\!(\!-1+\beta b){{\mathrm{e}}^{-c}}/({1-{\mathrm{e}}^{-c}})$
.
$C = C(A,\beta) = \exp(1+\beta b)/({1-{\mathrm{e}}^{-c}}) + \exp\!(\!-1+\beta b){{\mathrm{e}}^{-c}}/({1-{\mathrm{e}}^{-c}})$
.
2.4. Proof of Proposition 2.1
We are now ready to prove Proposition 2.1.
Proof of Proposition
2.1. Fix
![]() $\beta<\beta_\mathrm{c}$
. By Lemmas 2.5 and 2.6, if we choose
$\beta<\beta_\mathrm{c}$
. By Lemmas 2.5 and 2.6, if we choose
then there exist
![]() $N_1=N_1(A,\beta)\in\mathbb{N}$
,
$N_1=N_1(A,\beta)\in\mathbb{N}$
,
![]() $N_2=N_2(A,\beta)\in\mathbb{N}$
, and
$N_2=N_2(A,\beta)\in\mathbb{N}$
, and
![]() $C=C(A,\beta)>0$
such that, for all
$C=C(A,\beta)>0$
such that, for all
![]() $N\geq N_1$
and
$N\geq N_1$
and
![]() $k\in[\![ 0,K]\!]$
,
$k\in[\![ 0,K]\!]$
,
and for all
![]() $N\geq N_2$
and
$N\geq N_2$
and
![]() $k\in[\![ 0,K]\!]$
,
$k\in[\![ 0,K]\!]$
,
Now, since
![]() $Z^{(k),\leq}_{\beta,N-k} \leq Z^{(k)}_{\beta,N-k}$
, we have
$Z^{(k),\leq}_{\beta,N-k} \leq Z^{(k)}_{\beta,N-k}$
, we have
On the other hand, by the Cauchy–Schwarz inequality, we have
 \begin{align} & \mathbb{E}\big[Z^{(k),\leq}_{\beta,N-k}\big] \nonumber \\ & \qquad = \mathbb{E}\bigg[Z^{(k),\leq}_{\beta,N-k} \boldsymbol{1}\bigg\{Z^{(k),\leq}_{\beta,N-k} > \frac{1}{2}\mathbb{E}\big[Z^{(k)}_{\beta,N-k}\big]\bigg\}\bigg] + \underbrace{\mathbb{E}\bigg[Z^{(k),\leq}_{\beta,N-k}\boldsymbol{1}\bigg\{Z^{(k),\leq}_{\beta,N-k} \leq \frac{1}{2}\mathbb{E}\big[Z^{(k)}_{\beta,N-k}\big]\bigg\}\bigg]}_{\leq\frac{1}{2}\mathbb{E}\left[Z^{(k)}_{\beta,N-k}\right]} \nonumber \\ & \qquad \leq \mathbb{E}\big[\big(Z^{(k),\leq}_{\beta,N-k}\big)^2\big]^{1/2} \mathbb{P}\bigg(Z^{(k),\leq}_{\beta,N-k} > \frac{1}{2}\mathbb{E}\big[Z^{(k)}_{\beta,N-k}\big]\bigg)^{1/2} + \frac{1}{2}\mathbb{E}\big[Z^{(k)}_{\beta,N-k}\big]. \end{align}
\begin{align} & \mathbb{E}\big[Z^{(k),\leq}_{\beta,N-k}\big] \nonumber \\ & \qquad = \mathbb{E}\bigg[Z^{(k),\leq}_{\beta,N-k} \boldsymbol{1}\bigg\{Z^{(k),\leq}_{\beta,N-k} > \frac{1}{2}\mathbb{E}\big[Z^{(k)}_{\beta,N-k}\big]\bigg\}\bigg] + \underbrace{\mathbb{E}\bigg[Z^{(k),\leq}_{\beta,N-k}\boldsymbol{1}\bigg\{Z^{(k),\leq}_{\beta,N-k} \leq \frac{1}{2}\mathbb{E}\big[Z^{(k)}_{\beta,N-k}\big]\bigg\}\bigg]}_{\leq\frac{1}{2}\mathbb{E}\left[Z^{(k)}_{\beta,N-k}\right]} \nonumber \\ & \qquad \leq \mathbb{E}\big[\big(Z^{(k),\leq}_{\beta,N-k}\big)^2\big]^{1/2} \mathbb{P}\bigg(Z^{(k),\leq}_{\beta,N-k} > \frac{1}{2}\mathbb{E}\big[Z^{(k)}_{\beta,N-k}\big]\bigg)^{1/2} + \frac{1}{2}\mathbb{E}\big[Z^{(k)}_{\beta,N-k}\big]. \end{align}
Let
![]() $N_0 = N_0(A,\beta) \,:\!=\, \max\{N_1,N_2\}$
. Combining (2.35), (2.36), and (2.38), we derive that, for all
$N_0 = N_0(A,\beta) \,:\!=\, \max\{N_1,N_2\}$
. Combining (2.35), (2.36), and (2.38), we derive that, for all
![]() $N\geq N_0$
and
$N\geq N_0$
and
![]() $k\in[\![ 0,K]\!]$
,
$k\in[\![ 0,K]\!]$
,
 \begin{equation} \mathbb{P}\bigg(Z^{(k),\leq}_{\beta,N-k}\geq\frac{1}{2}\mathbb{E}\big[Z^{(k)}_{\beta,N-k}\big]\bigg)^{1/2} \geq \frac{\mathbb{E}\big[Z^{(k),\leq}_{\beta,N-k}\big]-\frac{1}{2}\mathbb{E}\big[Z^{(k)}_{\beta,N-k}\big]} {\mathbb{E}\big[\big(Z^{(k),\leq}_{\beta,N-k}\big)^2\big]^{1/2}} \geq \frac{2}{10\sqrt{C}\,}. \end{equation}
\begin{equation} \mathbb{P}\bigg(Z^{(k),\leq}_{\beta,N-k}\geq\frac{1}{2}\mathbb{E}\big[Z^{(k)}_{\beta,N-k}\big]\bigg)^{1/2} \geq \frac{\mathbb{E}\big[Z^{(k),\leq}_{\beta,N-k}\big]-\frac{1}{2}\mathbb{E}\big[Z^{(k)}_{\beta,N-k}\big]} {\mathbb{E}\big[\big(Z^{(k),\leq}_{\beta,N-k}\big)^2\big]^{1/2}} \geq \frac{2}{10\sqrt{C}\,}. \end{equation}
Combining (2.37) and (2.39), we conclude that, for all
![]() $N\geq N_0$
and
$N\geq N_0$
and
![]() $k\in[\![ 0,K]\!]$
,
$k\in[\![ 0,K]\!]$
,
 \begin{align*} \mathbb{P}\bigg(Z^{(k)}_{\beta,N-k} \leq \frac{1}{2}\mathbb{E}\big[Z^{(k)}_{\beta,N-k}\big]\bigg) & = 1 - \mathbb{P}\bigg(Z^{(k)}_{\beta,N-k} > \frac{1}{2}\mathbb{E}\big[Z^{(k)}_{\beta,N-k}\big]\bigg) \\ & \leq 1 - \mathbb{P}\bigg(Z^{(k),\leq}_{\beta,N-k} > \frac{1}{2}\mathbb{E}\big[Z^{(k)}_{\beta,N-k}\big]\bigg) \leq 1- \frac{4}{100C}. \end{align*}
\begin{align*} \mathbb{P}\bigg(Z^{(k)}_{\beta,N-k} \leq \frac{1}{2}\mathbb{E}\big[Z^{(k)}_{\beta,N-k}\big]\bigg) & = 1 - \mathbb{P}\bigg(Z^{(k)}_{\beta,N-k} > \frac{1}{2}\mathbb{E}\big[Z^{(k)}_{\beta,N-k}\big]\bigg) \\ & \leq 1 - \mathbb{P}\bigg(Z^{(k),\leq}_{\beta,N-k} > \frac{1}{2}\mathbb{E}\big[Z^{(k)}_{\beta,N-k}\big]\bigg) \leq 1- \frac{4}{100C}. \end{align*}
By taking
![]() $\eta_0 = \eta_0(A,\beta) = 1-{4}/{100 C}$
, the proof is completed.
$\eta_0 = \eta_0(A,\beta) = 1-{4}/{100 C}$
, the proof is completed.
3. Left tail estimates via a bootstrap argument
The main goal of this section is to provide a finer estimate of the left tail of
![]() $Z_{\beta,N}$
than the one provided by Proposition 2.1. Namely, we want to construct two sequences that satisfy (1.5), and this is manifested in the following proposition.
$Z_{\beta,N}$
than the one provided by Proposition 2.1. Namely, we want to construct two sequences that satisfy (1.5), and this is manifested in the following proposition.
Proposition 3.1. Let
![]() $K=\lfloor 2 \log_\gamma N \rfloor$
with
$K=\lfloor 2 \log_\gamma N \rfloor$
with
![]() $\gamma\in (11/10,2)$
. Then, there exist
$\gamma\in (11/10,2)$
. Then, there exist
![]() $N_0=N_0(A,\beta)\in\mathbb{N}$
and two sequences
$N_0=N_0(A,\beta)\in\mathbb{N}$
and two sequences
![]() $(\eta_k)_{k=0}^K$
and
$(\eta_k)_{k=0}^K$
and
![]() $(\varepsilon_k)_{k=0}^K$
such that
$(\varepsilon_k)_{k=0}^K$
such that
-
(i) for all
 $N\geq N_0$
and
$N\geq N_0$
and
 $k\in [\![ 0,K ]\!]$
,
$k\in [\![ 0,K ]\!]$
,
 $\mathbb{P}(Z_{\beta,N} \leq \varepsilon_k \mathbb{E}[Z_{\beta,N}]) \leq \eta_k$
;
$\mathbb{P}(Z_{\beta,N} \leq \varepsilon_k \mathbb{E}[Z_{\beta,N}]) \leq \eta_k$
; -
(ii) for all
 $s>0$
, there exists a constant
$s>0$
, there exists a constant
 $C=C(A,\beta,s)>0$
, independent of K, such that
$C=C(A,\beta,s)>0$
, independent of K, such that
 $\sum_{r=0}^{K-1} (\varepsilon_{r+1})^{-s} \eta_r \leq C$
.
$\sum_{r=0}^{K-1} (\varepsilon_{r+1})^{-s} \eta_r \leq C$
.
The proof of Proposition 3.1 requires the following two lemmas. For all
![]() $k\in[\![ 0,N-1]\!]$
, define
$k\in[\![ 0,N-1]\!]$
, define
![]() $M^{(k)}_{\beta,1} = {{\mathrm{e}}^{\beta X^{(k)}_{1}}}/{\mathbb{E}\big[Z^{(k)}_{\beta,1}\big]}$
, where
$M^{(k)}_{\beta,1} = {{\mathrm{e}}^{\beta X^{(k)}_{1}}}/{\mathbb{E}\big[Z^{(k)}_{\beta,1}\big]}$
, where
![]() $X^{(k)}_1$
is defined in Lemma 2.1. The first lemma states a bootstrap inequality.
$X^{(k)}_1$
is defined in Lemma 2.1. The first lemma states a bootstrap inequality.
Lemma 3.1. For all
![]() $c>0$
,
$c>0$
,
![]() $\delta>0$
,
$\delta>0$
,
![]() $N\in\mathbb{N}$
, and
$N\in\mathbb{N}$
, and
![]() $k\in [\![ 0,N-1]\!]$
,
$k\in [\![ 0,N-1]\!]$
,
Proof. Fix
![]() $N\in\mathbb{N}$
. For every
$N\in\mathbb{N}$
. For every
![]() $c>0$
,
$c>0$
,
![]() $\delta>0$
, and
$\delta>0$
, and
![]() $k\in [\![ 0,N-1]\!]$
, we have
$k\in [\![ 0,N-1]\!]$
, we have
 \begin{align} \mathbb{P}\big(Z^{(k)}_{\beta,N-k} \leq c\delta\cdot\mathbb{E}\big[Z^{(k)}_{\beta,N-k}\big]\big) & = \mathbb{P}\Bigg(\sum_{|u|=1}M_{\beta,u}^{(k)}\cdot Z^{(k),u}_{\beta,N-k-1} \leq c\delta\cdot\mathbb{E}\big[Z^{(k+1)}_{\beta,N-k-1}\big]\Bigg) \nonumber \\ & \leq \mathbb{P}\big(\text{for all}\ |u|=1\colon M_{\beta,u}^{(k)}\cdot Z^{(k),u}_{\beta,N-k-1} \leq c\delta\cdot\mathbb{E}\big[Z^{(k+1)}_{\beta,N-k-1}\big]\big) \nonumber \\ & = \mathbb{P}\big(M_{\beta,1}^{(k)}\cdot Z^{(k+1)}_{\beta,N-k-1} \leq c\delta\cdot\mathbb{E}\big[Z^{(k+1)}_{\beta,N-k-1}\big]\big)^2 \nonumber\\ & \leq \big[\mathbb{P}\big(Z^{(k+1)}_{\beta,N-k-1} \leq c\cdot\mathbb{E}\big[Z^{(k+1)}_{\beta,N-k-1}\big]\big) + \mathbb{P}\big(M_{\beta,1}^{(k)} \leq \delta\big) \big]^2, \end{align}
\begin{align} \mathbb{P}\big(Z^{(k)}_{\beta,N-k} \leq c\delta\cdot\mathbb{E}\big[Z^{(k)}_{\beta,N-k}\big]\big) & = \mathbb{P}\Bigg(\sum_{|u|=1}M_{\beta,u}^{(k)}\cdot Z^{(k),u}_{\beta,N-k-1} \leq c\delta\cdot\mathbb{E}\big[Z^{(k+1)}_{\beta,N-k-1}\big]\Bigg) \nonumber \\ & \leq \mathbb{P}\big(\text{for all}\ |u|=1\colon M_{\beta,u}^{(k)}\cdot Z^{(k),u}_{\beta,N-k-1} \leq c\delta\cdot\mathbb{E}\big[Z^{(k+1)}_{\beta,N-k-1}\big]\big) \nonumber \\ & = \mathbb{P}\big(M_{\beta,1}^{(k)}\cdot Z^{(k+1)}_{\beta,N-k-1} \leq c\delta\cdot\mathbb{E}\big[Z^{(k+1)}_{\beta,N-k-1}\big]\big)^2 \nonumber\\ & \leq \big[\mathbb{P}\big(Z^{(k+1)}_{\beta,N-k-1} \leq c\cdot\mathbb{E}\big[Z^{(k+1)}_{\beta,N-k-1}\big]\big) + \mathbb{P}\big(M_{\beta,1}^{(k)} \leq \delta\big) \big]^2, \end{align}
where (3.1) follows from independence.
The next lemma provides a uniform estimate for the left tail of
![]() $M_{\beta,1}^{(k)}$
when k is small compared to N.
$M_{\beta,1}^{(k)}$
when k is small compared to N.
Lemma 3.2. Let
![]() $N\in\mathbb{N}$
and
$N\in\mathbb{N}$
and
![]() $K=\lfloor 2 \log_\gamma N \rfloor$
with
$K=\lfloor 2 \log_\gamma N \rfloor$
with
![]() $\gamma\in(11/10,2)$
. For all
$\gamma\in(11/10,2)$
. For all
![]() $\beta>0$
,
$\beta>0$
,
![]() $k\in[\![ 0, K]\!]$
, and
$k\in[\![ 0, K]\!]$
, and
![]() $s>0$
, there exist
$s>0$
, there exist
![]() $N_0=N(A,\beta,s)\in\mathbb{N}$
and a constant
$N_0=N(A,\beta,s)\in\mathbb{N}$
and a constant
![]() $C=C(A,\beta,s)\geq 1$
, independent of N, such that, for all
$C=C(A,\beta,s)\geq 1$
, independent of N, such that, for all
![]() $N\geq N_0$
,
$N\geq N_0$
,
![]() $\mathbb{E}\big[(M^{(k)}_{\beta,1})^{-s}\big] \leq C$
. In particular, by Markov’s inequality this implies that, for all
$\mathbb{E}\big[(M^{(k)}_{\beta,1})^{-s}\big] \leq C$
. In particular, by Markov’s inequality this implies that, for all
![]() $\delta>0$
and all
$\delta>0$
and all
![]() $N\geq N_0$
,
$N\geq N_0$
,
![]() $\mathbb{P}\big(M^{(k)}_{\beta,1} \leq \delta\big) \leq C \cdot \delta^s$
.
$\mathbb{P}\big(M^{(k)}_{\beta,1} \leq \delta\big) \leq C \cdot \delta^s$
.
Proof. Let
![]() $k\in[\![ 0,K]\!]$
. By Lemma 2.3, there exist
$k\in[\![ 0,K]\!]$
. By Lemma 2.3, there exist
![]() $N_1=N_1(A,\beta)\in\mathbb{N}$
and
$N_1=N_1(A,\beta)\in\mathbb{N}$
and
![]() $C_1>0$
such that, for all
$C_1>0$
such that, for all
![]() $N\geq N_1$
,
$N\geq N_1$
,
Since
![]() $\limsup_{N\rightarrow\infty}C_1({(K+1)^\alpha+1})/{N^\alpha} = 0$
, in particular, there exists
$\limsup_{N\rightarrow\infty}C_1({(K+1)^\alpha+1})/{N^\alpha} = 0$
, in particular, there exists
![]() $N_2=N_2(A,\beta)\in\mathbb{N}$
such that, for all
$N_2=N_2(A,\beta)\in\mathbb{N}$
such that, for all
![]() $N\geq N_2$
,
$N\geq N_2$
,
Let
![]() $N_0\,:\!=\, \max\{N_1,N_2\}$
and
$N_0\,:\!=\, \max\{N_1,N_2\}$
and
Note that this constant is greater than or equal to 1 since
![]() ${\beta^2 s^2}(\hat{A}'(0)+1)/{2}$
, s, and
${\beta^2 s^2}(\hat{A}'(0)+1)/{2}$
, s, and
![]() ${\beta^2 s}(\hat{A}'(0)+1)/{2}$
are non-negative. For all
${\beta^2 s}(\hat{A}'(0)+1)/{2}$
are non-negative. For all
![]() $N\geq N_0$
, we conclude that
$N\geq N_0$
, we conclude that
 \begin{align*} & \mathbb{E}\big[(M^{(k)}_{\beta,1})^{-s}\big] \\ & \quad = \mathbb{E}\big[{\mathrm{e}}^{-\beta s X^{(k)}_{1}}\big] \cdot \mathbb{E}\big[Z^{(k)}_{\beta,1}\big]^s \\ & \quad = \exp\bigg(\frac{\beta^2s^2}{2}N\bigg(A\bigg(\frac{k+1}{N}\bigg)-A\bigg(\frac{k}{N}\bigg)\bigg)\bigg) \cdot 2^s\exp\bigg(\frac{\beta^2s}{2}N\bigg(A\bigg(\frac{k+1}{N}\bigg)-A\bigg(\frac{k}{N}\bigg)\bigg)\bigg) \\ & \quad \leq \exp\bigg(\frac{\beta^2 s^2}{2}(\hat{A}'(0)+1)\bigg) \cdot 2^s \exp\bigg(\frac{\beta^2 s}{2}(\hat{A}'(0)+1)\bigg) = C, \end{align*}
\begin{align*} & \mathbb{E}\big[(M^{(k)}_{\beta,1})^{-s}\big] \\ & \quad = \mathbb{E}\big[{\mathrm{e}}^{-\beta s X^{(k)}_{1}}\big] \cdot \mathbb{E}\big[Z^{(k)}_{\beta,1}\big]^s \\ & \quad = \exp\bigg(\frac{\beta^2s^2}{2}N\bigg(A\bigg(\frac{k+1}{N}\bigg)-A\bigg(\frac{k}{N}\bigg)\bigg)\bigg) \cdot 2^s\exp\bigg(\frac{\beta^2s}{2}N\bigg(A\bigg(\frac{k+1}{N}\bigg)-A\bigg(\frac{k}{N}\bigg)\bigg)\bigg) \\ & \quad \leq \exp\bigg(\frac{\beta^2 s^2}{2}(\hat{A}'(0)+1)\bigg) \cdot 2^s \exp\bigg(\frac{\beta^2 s}{2}(\hat{A}'(0)+1)\bigg) = C, \end{align*}
and this completes the proof.
We now turn to the proof of Proposition 3.1.
Proof of Proposition
3.1. Fix
![]() $\gamma \in (11/10,2)$
and
$\gamma \in (11/10,2)$
and
![]() $s>0$
. Let
$s>0$
. Let
![]() $\eta_0=\eta(A,\beta)<1$
be the same as in Proposition 2.1, and for all
$\eta_0=\eta(A,\beta)<1$
be the same as in Proposition 2.1, and for all
![]() $k\in[\![ 1,K]\!]$
define
$k\in[\![ 1,K]\!]$
define
![]() $\eta_k = (\eta_0)^{\gamma^k}$
. Let
$\eta_k = (\eta_0)^{\gamma^k}$
. Let
![]() $\varepsilon_0=\frac{1}{2}$
. With
$\varepsilon_0=\frac{1}{2}$
. With
![]() $C=C(A,\beta,10s)\geq 1$
being the same constant that appeared in Lemma 3.2, for all
$C=C(A,\beta,10s)\geq 1$
being the same constant that appeared in Lemma 3.2, for all
![]() $k\in[\![ 1,K]\!]$
define
$k\in[\![ 1,K]\!]$
define
![]() $\varepsilon_k$
such that
$\varepsilon_k$
such that
 \begin{equation*} (\varepsilon_k)^s = \frac{1}{2^s}\frac{1}{C^k}\prod_{n=0}^{k-1}\big((\eta_n)^{\gamma/2}-\eta_n\big)^{1/10}. \end{equation*}
\begin{equation*} (\varepsilon_k)^s = \frac{1}{2^s}\frac{1}{C^k}\prod_{n=0}^{k-1}\big((\eta_n)^{\gamma/2}-\eta_n\big)^{1/10}. \end{equation*}
We first claim that, for all
![]() $k\in[\![ 0,K]\!]$
,
$k\in[\![ 0,K]\!]$
,
![]() $\ell\in[\![ 0,K-k]\!]$
, and
$\ell\in[\![ 0,K-k]\!]$
, and
![]() $N\geq N_0$
, where
$N\geq N_0$
, where
![]() $N_0=N_0(A,\beta)$
appeared in the statement of Proposition 2.1,
$N_0=N_0(A,\beta)$
appeared in the statement of Proposition 2.1,
Note that (3.2) implies Proposition 3.1(i) by taking
![]() $\ell=0$
.
$\ell=0$
.
We prove (3.2) by induction on k. The case where
![]() $k=0$
follows from Proposition 2.1. Suppose that (3.2) is true for
$k=0$
follows from Proposition 2.1. Suppose that (3.2) is true for
![]() $k\in[\![ 0,K-1]\!]$
. As
$k\in[\![ 0,K-1]\!]$
. As
![]() $\varepsilon_{k+1} = \varepsilon_{k}\big(\big(\eta_{k}^{\gamma/2}-\eta_{k}\big)/C\big)^{{1}/{10s}}$
, applying Lemma 3.1 with
$\varepsilon_{k+1} = \varepsilon_{k}\big(\big(\eta_{k}^{\gamma/2}-\eta_{k}\big)/C\big)^{{1}/{10s}}$
, applying Lemma 3.1 with
![]() $c=\varepsilon_{k}$
and
$c=\varepsilon_{k}$
and
![]() $\delta=\big(\big(\eta_{k}^{\gamma/2}-\eta_{k}\big)/C\big)^{{1}/{10s}}$
yields that, for all
$\delta=\big(\big(\eta_{k}^{\gamma/2}-\eta_{k}\big)/C\big)^{{1}/{10s}}$
yields that, for all
![]() $\ell\in[\![ 0,K-k-1]\!]$
and
$\ell\in[\![ 0,K-k-1]\!]$
and
![]() $N\geq N_0$
,
$N\geq N_0$
,
 \begin{align*} & \mathbb{P}\big(Z_{\beta,N-\ell}^{(\ell)}\leq\varepsilon_{k+1}\mathbb{E}\big[Z_{\beta,N-\ell}^{(\ell)}\big]\big) \\ & \qquad = \mathbb{P}\bigg(Z_{\beta,N-\ell}^{(\ell)} \leq \varepsilon_{k}\cdot\bigg(\frac{1}{C}\big(\eta_{k}^{\gamma/2}-\eta_{k}\big)\bigg)^{1/s} \mathbb{E}\big[Z_{\beta,N-\ell}^{(\ell)}\big]\bigg) \\ & \qquad \leq \bigg(\mathbb{P}\big(Z_{\beta,N-\ell-1}^{(\ell+1)} \leq \varepsilon_{k}\mathbb{E}\big[Z_{\beta,N-\ell-1}^{(\ell+1)}\big]\big) + \mathbb{P}\bigg(M_{\beta,1}^{(\ell)} \leq \bigg(\frac{1}{C}\big(\eta_{k}^{\gamma/2}-\eta_{k}\big)\bigg)^{{1}/{10s}}\bigg)\bigg)^2 \\ & \qquad \leq \big(\eta_{k}+\eta_{k}^{\gamma/2}-\eta_{k}\big)^2 = (\eta_{k})^{\gamma} = \eta_{k+1}, \end{align*}
\begin{align*} & \mathbb{P}\big(Z_{\beta,N-\ell}^{(\ell)}\leq\varepsilon_{k+1}\mathbb{E}\big[Z_{\beta,N-\ell}^{(\ell)}\big]\big) \\ & \qquad = \mathbb{P}\bigg(Z_{\beta,N-\ell}^{(\ell)} \leq \varepsilon_{k}\cdot\bigg(\frac{1}{C}\big(\eta_{k}^{\gamma/2}-\eta_{k}\big)\bigg)^{1/s} \mathbb{E}\big[Z_{\beta,N-\ell}^{(\ell)}\big]\bigg) \\ & \qquad \leq \bigg(\mathbb{P}\big(Z_{\beta,N-\ell-1}^{(\ell+1)} \leq \varepsilon_{k}\mathbb{E}\big[Z_{\beta,N-\ell-1}^{(\ell+1)}\big]\big) + \mathbb{P}\bigg(M_{\beta,1}^{(\ell)} \leq \bigg(\frac{1}{C}\big(\eta_{k}^{\gamma/2}-\eta_{k}\big)\bigg)^{{1}/{10s}}\bigg)\bigg)^2 \\ & \qquad \leq \big(\eta_{k}+\eta_{k}^{\gamma/2}-\eta_{k}\big)^2 = (\eta_{k})^{\gamma} = \eta_{k+1}, \end{align*}
where the last inequality follows from the induction hypothesis and Lemma 3.2. Thus, by induction, (3.2) holds for all
![]() $k\in[\![ 0,K]\!]$
.
$k\in[\![ 0,K]\!]$
.
It remains to show that, for all
![]() $s>0$
,
$s>0$
,
![]() $\sum_{k=0}^K(\varepsilon_{k+1})^{-s}\eta_{k}$
is uniformly bounded in K. For all
$\sum_{k=0}^K(\varepsilon_{k+1})^{-s}\eta_{k}$
is uniformly bounded in K. For all
![]() $k\in[\![ 0,K]\!]$
,
$k\in[\![ 0,K]\!]$
,
 \begin{align} (\varepsilon_{k+1})^{-s} & = 2^{s}C^{k+1}\prod_{n=0}^k\big(\eta_n^{\gamma/2}-\eta_n\big)^{-1/10} \nonumber \\ & = 2^{s}C^{k+1}\prod_{n=0}^k\eta_n^{-\gamma/20}\big(1-\eta_n^{1-\gamma/2}\big)^{-(k+1)/10} \nonumber \\ & \leq 2^{s}C^{k+1}\big(1-\eta_0^{1-\gamma/2}\big)^{-1/10}\prod_{n=0}^k \eta_n^{-\gamma/20} \end{align}
\begin{align} (\varepsilon_{k+1})^{-s} & = 2^{s}C^{k+1}\prod_{n=0}^k\big(\eta_n^{\gamma/2}-\eta_n\big)^{-1/10} \nonumber \\ & = 2^{s}C^{k+1}\prod_{n=0}^k\eta_n^{-\gamma/20}\big(1-\eta_n^{1-\gamma/2}\big)^{-(k+1)/10} \nonumber \\ & \leq 2^{s}C^{k+1}\big(1-\eta_0^{1-\gamma/2}\big)^{-1/10}\prod_{n=0}^k \eta_n^{-\gamma/20} \end{align}
 \begin{align} & = 2^{s}C^{k+1}\big(1-\eta_0^{1-\gamma/2}\big)^{-(k+1)/10}\eta_0^{-({\gamma}/{20})(({\gamma^{k+1}-1})/({\gamma-1}))} \nonumber \\ & = C_1 C^{k+1}\big(1-\eta_0^{1-\gamma/2}\big)^{-(k+1)/10}\eta_0^{-{\gamma^2\gamma^k}/{20(\gamma-1)}}, \end{align}
\begin{align} & = 2^{s}C^{k+1}\big(1-\eta_0^{1-\gamma/2}\big)^{-(k+1)/10}\eta_0^{-({\gamma}/{20})(({\gamma^{k+1}-1})/({\gamma-1}))} \nonumber \\ & = C_1 C^{k+1}\big(1-\eta_0^{1-\gamma/2}\big)^{-(k+1)/10}\eta_0^{-{\gamma^2\gamma^k}/{20(\gamma-1)}}, \end{align}
where
![]() $C_1=C_1(s,\eta_0,\gamma)=2^{s}\eta_0^{{\gamma}/{20(\gamma-1)}}$
, and (3.3) follows from the definition of
$C_1=C_1(s,\eta_0,\gamma)=2^{s}\eta_0^{{\gamma}/{20(\gamma-1)}}$
, and (3.3) follows from the definition of
![]() $\eta_n$
and the fact that
$\eta_n$
and the fact that
![]() $(\eta_k)$
is a decreasing sequence, which implies in particular that
$(\eta_k)$
is a decreasing sequence, which implies in particular that
![]() $\eta_k\leq \eta_0$
for all
$\eta_k\leq \eta_0$
for all
![]() $k\in[\![ 0,K]\!]$
. Applying (3.4),
$k\in[\![ 0,K]\!]$
. Applying (3.4),
 \begin{align} \sum_{k=0}^{K-1} (\varepsilon_{k+1})^{-s}\eta_{k} & \leq C_1\sum_{k=0}^{K-1}C^{k+1}\big(1-\eta_0^{1-\gamma/2}\big)^{-(k+1)/10} \eta_0^{-{\gamma^2\gamma^k}/{20(\gamma-1)}} \eta_k \nonumber \\ & = C_1\sum_{k=0}^{K-1}C^{k+1}\big(1-\eta_0^{1-\gamma/2}\big)^{-(k+1)/10} \eta_0^{(1-{\gamma^2}/{20(\gamma-1)})\gamma^k} \end{align}
\begin{align} \sum_{k=0}^{K-1} (\varepsilon_{k+1})^{-s}\eta_{k} & \leq C_1\sum_{k=0}^{K-1}C^{k+1}\big(1-\eta_0^{1-\gamma/2}\big)^{-(k+1)/10} \eta_0^{-{\gamma^2\gamma^k}/{20(\gamma-1)}} \eta_k \nonumber \\ & = C_1\sum_{k=0}^{K-1}C^{k+1}\big(1-\eta_0^{1-\gamma/2}\big)^{-(k+1)/10} \eta_0^{(1-{\gamma^2}/{20(\gamma-1)})\gamma^k} \end{align}
 \begin{align} & \leq C_1\sum_{k=0}^{\infty}C^{k+1}\big(1-\eta_0^{1-\gamma/2}\big)^{-(k+1)/10} \eta_0^{(1-{\gamma^2}/{20(\gamma-1)})\gamma^k} \nonumber \\ & \leq C_1\sum_{k=0}^\infty\exp\bigg(\!\!\log\bigg(\!\frac{C}{\big(1-\eta_0^{1-\gamma/2}\big)^{1/10}}\bigg)(k+1) + \bigg(\!1-\frac{\gamma^2}{20(\gamma-1)}\bigg)(\!\log\eta_0)\gamma^k\!\bigg),\end{align}
\begin{align} & \leq C_1\sum_{k=0}^{\infty}C^{k+1}\big(1-\eta_0^{1-\gamma/2}\big)^{-(k+1)/10} \eta_0^{(1-{\gamma^2}/{20(\gamma-1)})\gamma^k} \nonumber \\ & \leq C_1\sum_{k=0}^\infty\exp\bigg(\!\!\log\bigg(\!\frac{C}{\big(1-\eta_0^{1-\gamma/2}\big)^{1/10}}\bigg)(k+1) + \bigg(\!1-\frac{\gamma^2}{20(\gamma-1)}\bigg)(\!\log\eta_0)\gamma^k\!\bigg),\end{align}
where (3.5) follows from the definition of
![]() $\eta_k$
. Since
$\eta_k$
. Since
![]() $\gamma\in(11/10,2)$
and
$\gamma\in(11/10,2)$
and
![]() $\eta_0 < 1$
,
$\eta_0 < 1$
,
![]() $1-{\gamma^2}/{20(\gamma-1)}>0$
and
$1-{\gamma^2}/{20(\gamma-1)}>0$
and
![]() $\log \eta_0 < 1$
. Therefore, (3.6) depends only on s,
$\log \eta_0 < 1$
. Therefore, (3.6) depends only on s,
![]() $\gamma\in(11/10,2)$
, and
$\gamma\in(11/10,2)$
, and
![]() $\eta_0=\eta_0(A,\beta)$
, and we conclude that
$\eta_0=\eta_0(A,\beta)$
, and we conclude that
![]() $\sum_{k=0}^K (\varepsilon_{k+1})^{-s}\eta_{k}$
is bounded from above by a constant
$\sum_{k=0}^K (\varepsilon_{k+1})^{-s}\eta_{k}$
is bounded from above by a constant
![]() $C_2=C_2(A,\beta,s)>0$
, as desired.
$C_2=C_2(A,\beta,s)>0$
, as desired.
4. Proof of Theorem 1.1
Proof. Suppose that
![]() $\beta<\beta_\mathrm{c}$
. Let
$\beta<\beta_\mathrm{c}$
. Let
![]() $N\in\mathbb{N}$
. Fix
$N\in\mathbb{N}$
. Fix
![]() $K=\lfloor 2 \log_\gamma N \rfloor$
and
$K=\lfloor 2 \log_\gamma N \rfloor$
and
![]() $s>0$
. Also, we define
$s>0$
. Also, we define
![]() $W_{\beta,N}\,:\!=\, Z_{\beta,N}/\mathbb{E}[Z_{\beta,N}]$
. It suffices to prove that there exists a constant
$W_{\beta,N}\,:\!=\, Z_{\beta,N}/\mathbb{E}[Z_{\beta,N}]$
. It suffices to prove that there exists a constant
![]() $C=C(A,\beta,s)>0$
such that
$C=C(A,\beta,s)>0$
such that
![]() $\mathbb{E}[(W_{\beta,N})^{-s}] \leq C$
. We have
$\mathbb{E}[(W_{\beta,N})^{-s}] \leq C$
. We have
 \begin{align} & \mathbb{E}[(W_{\beta,N})^{-s}] \nonumber \\ & \quad \leq \varepsilon_0^{-s}\mathbb{P}(W_{\beta,N}>\varepsilon_0) + \sum_{k=0}^{K-1}(\varepsilon_{k+1})^{-s}\cdot\mathbb{P}(\varepsilon_{k+1} \leq W_{\beta,N}\leq \varepsilon_k) + \mathbb{E}[(W_{\beta,N})^{-s}\boldsymbol{1}_{W_{\beta,N}\leq \varepsilon_K}] \nonumber \\ & \quad \leq 2^s + \sum_{n=0}^{K-1}(\varepsilon_{k+1})^{-s}\cdot\mathbb{P}(W_{\beta,N}\leq \varepsilon_k) + \mathbb{E}[(W_{\beta,N})^{-s}\boldsymbol{1}_{W_{\beta,N}\leq \varepsilon_K}]. \end{align}
\begin{align} & \mathbb{E}[(W_{\beta,N})^{-s}] \nonumber \\ & \quad \leq \varepsilon_0^{-s}\mathbb{P}(W_{\beta,N}>\varepsilon_0) + \sum_{k=0}^{K-1}(\varepsilon_{k+1})^{-s}\cdot\mathbb{P}(\varepsilon_{k+1} \leq W_{\beta,N}\leq \varepsilon_k) + \mathbb{E}[(W_{\beta,N})^{-s}\boldsymbol{1}_{W_{\beta,N}\leq \varepsilon_K}] \nonumber \\ & \quad \leq 2^s + \sum_{n=0}^{K-1}(\varepsilon_{k+1})^{-s}\cdot\mathbb{P}(W_{\beta,N}\leq \varepsilon_k) + \mathbb{E}[(W_{\beta,N})^{-s}\boldsymbol{1}_{W_{\beta,N}\leq \varepsilon_K}]. \end{align}
By Proposition 3.1, there exist
![]() $N_1=N(A,\beta,s)\in\mathbb{N}$
and
$N_1=N(A,\beta,s)\in\mathbb{N}$
and
![]() $C_1=C_1(A,\beta,s)>0$
such that, for all
$C_1=C_1(A,\beta,s)>0$
such that, for all
![]() $N\geq N_1$
, the second term of (4.1) is bounded by
$N\geq N_1$
, the second term of (4.1) is bounded by
![]() $C_1$
. Thus, it remains to bound the third term of (4.1).
$C_1$
. Thus, it remains to bound the third term of (4.1).
For all
![]() $|u|=N$
,
$|u|=N$
,
![]() $Z_{\beta,N} \geq {\mathrm{e}}^{\beta X_u}$
. Fix a vertex u with
$Z_{\beta,N} \geq {\mathrm{e}}^{\beta X_u}$
. Fix a vertex u with
![]() $|u|=N$
. By the previous inequality and Lemma 2.4, the second term of (4.1) is bounded from above by
$|u|=N$
. By the previous inequality and Lemma 2.4, the second term of (4.1) is bounded from above by
 \begin{align} \mathbb{E}[(W_{\beta,N})^{-s}\boldsymbol{1}_{W_{\beta,N}\leq \varepsilon_K}] & \leq \mathbb{E}[Z_{\beta,N}]^{s} \cdot \mathbb{E}\big[({\mathrm{e}}^{\beta X_u})^{-s}\boldsymbol{1}_{{\mathrm{e}}^{\beta X_u} \leq \varepsilon_K\mathbb{E}[Z_{\beta,N}]}\big] \nonumber \\ & = \mathbb{E}[Z_{\beta,N}]^{s} \cdot \mathbb{E}\big[{\mathrm{e}}^{-\beta s X_u}\boldsymbol{1}_{X_u\leq(\log\varepsilon_K+\log\mathbb{E}[Z_{\beta,N}])/{\beta}}\big] \nonumber \\ & = \mathbb{E}[Z_{\beta,N}]^{s} \mathbb{E}\big[e^{-\beta sX_u}\boldsymbol{1}_{X_u\leq(\log\varepsilon_K+N\log 2+N{\beta^2}/{2})/{\beta}}\big] \nonumber \\ & = \exp\bigg(\frac{\beta^2sN}{2}\bigg) \mathbb{E}\big[{\mathrm{e}}^{-\beta sX_u}\boldsymbol{1}_{X_u\leq(\log\varepsilon_K+N\log 2+N{\beta^2}/{2})/{\beta}}\big]. \end{align}
\begin{align} \mathbb{E}[(W_{\beta,N})^{-s}\boldsymbol{1}_{W_{\beta,N}\leq \varepsilon_K}] & \leq \mathbb{E}[Z_{\beta,N}]^{s} \cdot \mathbb{E}\big[({\mathrm{e}}^{\beta X_u})^{-s}\boldsymbol{1}_{{\mathrm{e}}^{\beta X_u} \leq \varepsilon_K\mathbb{E}[Z_{\beta,N}]}\big] \nonumber \\ & = \mathbb{E}[Z_{\beta,N}]^{s} \cdot \mathbb{E}\big[{\mathrm{e}}^{-\beta s X_u}\boldsymbol{1}_{X_u\leq(\log\varepsilon_K+\log\mathbb{E}[Z_{\beta,N}])/{\beta}}\big] \nonumber \\ & = \mathbb{E}[Z_{\beta,N}]^{s} \mathbb{E}\big[e^{-\beta sX_u}\boldsymbol{1}_{X_u\leq(\log\varepsilon_K+N\log 2+N{\beta^2}/{2})/{\beta}}\big] \nonumber \\ & = \exp\bigg(\frac{\beta^2sN}{2}\bigg) \mathbb{E}\big[{\mathrm{e}}^{-\beta sX_u}\boldsymbol{1}_{X_u\leq(\log\varepsilon_K+N\log 2+N{\beta^2}/{2})/{\beta}}\big]. \end{align}
Note that
![]() $X_u$
appearing in the expectation of (4.2) is distributed as a centered Gaussian variable with variance N, so the second expectation of (4.2) can be rewritten as
$X_u$
appearing in the expectation of (4.2) is distributed as a centered Gaussian variable with variance N, so the second expectation of (4.2) can be rewritten as
 \begin{align} & \mathbb{E}\big[{\mathrm{e}}^{-\beta sX_u}\boldsymbol{1}_{X_u\leq(\log\varepsilon_K+N\log 2+N{\beta^2}/{2})/{\beta}}\big] \nonumber \\ & = \frac{1}{\sqrt{2\pi N}\,}\int_{-\infty}^{(\log\varepsilon_K+N\log 2+N{\beta^2}/{2})/{\beta}} {\mathrm{e}}^{-\beta sx}{\mathrm{e}}^{-{x^2}/{2N}}\,\mathrm{d}{x} \nonumber \\ & = {\mathrm{e}}^{{\beta^2s^2}N/{2}}\frac{1}{\sqrt{2\pi N}\,}\int_{-\infty}^{(\log\varepsilon_K+N\log 2+N{\beta^2}/{2})/{\beta}} {\mathrm{e}}^{-{(x+\beta s N)^2}/{2N}}\,\mathrm{d}{x} \nonumber \\ & = {\mathrm{e}}^{{\beta^2s^2}N/{2}}\frac{1}{\sqrt{2\pi N}\,}\int_{-(\log\varepsilon_K+N\log 2+N{\beta^2}/{2}+N\beta s)/{\beta\sqrt{N}}}^\infty {\mathrm{e}}^{-{y^2}/{2}}\,\mathrm{d}{y} \end{align}
\begin{align} & \mathbb{E}\big[{\mathrm{e}}^{-\beta sX_u}\boldsymbol{1}_{X_u\leq(\log\varepsilon_K+N\log 2+N{\beta^2}/{2})/{\beta}}\big] \nonumber \\ & = \frac{1}{\sqrt{2\pi N}\,}\int_{-\infty}^{(\log\varepsilon_K+N\log 2+N{\beta^2}/{2})/{\beta}} {\mathrm{e}}^{-\beta sx}{\mathrm{e}}^{-{x^2}/{2N}}\,\mathrm{d}{x} \nonumber \\ & = {\mathrm{e}}^{{\beta^2s^2}N/{2}}\frac{1}{\sqrt{2\pi N}\,}\int_{-\infty}^{(\log\varepsilon_K+N\log 2+N{\beta^2}/{2})/{\beta}} {\mathrm{e}}^{-{(x+\beta s N)^2}/{2N}}\,\mathrm{d}{x} \nonumber \\ & = {\mathrm{e}}^{{\beta^2s^2}N/{2}}\frac{1}{\sqrt{2\pi N}\,}\int_{-(\log\varepsilon_K+N\log 2+N{\beta^2}/{2}+N\beta s)/{\beta\sqrt{N}}}^\infty {\mathrm{e}}^{-{y^2}/{2}}\,\mathrm{d}{y} \end{align}
where (4.3) follows from the change of variables
![]() $y=(x+\beta s)/\sqrt{N}$
and r(N) in (4.4) is defined as
$y=(x+\beta s)/\sqrt{N}$
and r(N) in (4.4) is defined as
![]() $r(N)=-(\log \varepsilon_K + N\log 2 + N{\beta^2}/{2}+N \beta s)/{\beta\sqrt{N}}$
.
$r(N)=-(\log \varepsilon_K + N\log 2 + N{\beta^2}/{2}+N \beta s)/{\beta\sqrt{N}}$
.
Recalling the definition of
![]() $(\varepsilon_k)_{k=0}^K$
in the proof of Proposition 3.1, we have
$(\varepsilon_k)_{k=0}^K$
in the proof of Proposition 3.1, we have
 \begin{align} \varepsilon_K = \frac{1}{2}\frac{1}{C^K}\prod_{n=0}^{K-1}\big((\eta_n)^{\gamma/2}-\eta_n\big)^{1/(10s)} \leq \prod_{n=0}^{K-1}\eta_n^{\gamma/(20s)} = \prod_{n=0}^{K-1}\eta_0^{\gamma^{n+1}/(20s)}, \end{align}
\begin{align} \varepsilon_K = \frac{1}{2}\frac{1}{C^K}\prod_{n=0}^{K-1}\big((\eta_n)^{\gamma/2}-\eta_n\big)^{1/(10s)} \leq \prod_{n=0}^{K-1}\eta_n^{\gamma/(20s)} = \prod_{n=0}^{K-1}\eta_0^{\gamma^{n+1}/(20s)}, \end{align}
where the inequality follows from the fact that
![]() $\gamma/2\geq 1$
,
$\gamma/2\geq 1$
,
![]() $C\geq 1$
, and
$C\geq 1$
, and
![]() $\eta_n\geq 0$
for all
$\eta_n\geq 0$
for all
![]() $n\in[\![ 0,K-1]\!]$
. Recall that
$n\in[\![ 0,K-1]\!]$
. Recall that
![]() $K=\lfloor 2\log_\gamma N \rfloor$
, so
$K=\lfloor 2\log_\gamma N \rfloor$
, so
This and (4.5) imply that
 \begin{align*} r(N) & \geq -\frac{1}{\beta\sqrt{N}\,}\bigg(\frac{\gamma}{20(\gamma-1)s}(\log\eta_0)N^2 + N\log 2 + N\frac{\beta^2}{2}+N \beta s\bigg) \\ & = c_1N^{3/2} - \bigg(\frac{\log 2}{\beta} + \frac{\beta}{2} + s\bigg) N^{1/2}, \end{align*}
\begin{align*} r(N) & \geq -\frac{1}{\beta\sqrt{N}\,}\bigg(\frac{\gamma}{20(\gamma-1)s}(\log\eta_0)N^2 + N\log 2 + N\frac{\beta^2}{2}+N \beta s\bigg) \\ & = c_1N^{3/2} - \bigg(\frac{\log 2}{\beta} + \frac{\beta}{2} + s\bigg) N^{1/2}, \end{align*}
and since
![]() $\eta_0<1$
, we have
$\eta_0<1$
, we have
Therefore, there exists
![]() $N_2=N_2(A,\beta,s)$
such that, for all
$N_2=N_2(A,\beta,s)$
such that, for all
![]() $N\geq N_2$
,
$N\geq N_2$
,
![]() $r(N) \geq {c_1}N^{3/2}/{2}$
, and this implies that for
$r(N) \geq {c_1}N^{3/2}/{2}$
, and this implies that for
![]() $N\geq N_2$
we have
$N\geq N_2$
we have
where the second inequality follows from a standard estimate for Gaussian tails (see, e.g., [Reference Durrett7, Theorem 1.2.6]). Combining (4.2), (4.4), and (4.6), we see that
 \begin{multline*} \limsup_{N\rightarrow\infty}\mathbb{E}[(W_{\beta,N})^{-s}\boldsymbol{1}_{W_{\beta,N}}] \\ \leq \limsup_{N\rightarrow\infty}\bigg({\mathrm{e}}^{{\beta^2sN}/{2}}\cdot{\mathrm{e}}^{{\beta^2s^2}N/{2}}\frac{1}{\sqrt{2\pi N}\,} \cdot \frac{1}{(c_1/2) N^{3/2}}{\mathrm{e}}^{-{c_1^2N^3}/{8}}\bigg) = 0. \end{multline*}
\begin{multline*} \limsup_{N\rightarrow\infty}\mathbb{E}[(W_{\beta,N})^{-s}\boldsymbol{1}_{W_{\beta,N}}] \\ \leq \limsup_{N\rightarrow\infty}\bigg({\mathrm{e}}^{{\beta^2sN}/{2}}\cdot{\mathrm{e}}^{{\beta^2s^2}N/{2}}\frac{1}{\sqrt{2\pi N}\,} \cdot \frac{1}{(c_1/2) N^{3/2}}{\mathrm{e}}^{-{c_1^2N^3}/{8}}\bigg) = 0. \end{multline*}
From this and (4.1), we conclude that there exists
![]() $N_0 = N_0(A,\beta,s)\geq \max\{N_1,N_2\}$
such that, for
$N_0 = N_0(A,\beta,s)\geq \max\{N_1,N_2\}$
such that, for
![]() $N\geq N_0$
,
$N\geq N_0$
,
![]() $\mathbb{E}[(W_{\beta,N})^{-s}]\leq 2^s + C_1 + 1$
. By taking
$\mathbb{E}[(W_{\beta,N})^{-s}]\leq 2^s + C_1 + 1$
. By taking
![]() $C = 2^s + C_1+1$
, the proof is completed.
$C = 2^s + C_1+1$
, the proof is completed.
Acknowledgements
I would like to thank Pascal Maillard for his guidance throughout the whole project and Michel Pain for his comments on the early draft of the paper. I also appreciate the constructive suggestions from an anonymous referee, which have substantially improved the quality of the paper.
Funding information
There are no funding bodies to thank relating to the creation of this article.
Competing interests
There were no competing interests to declare that arose during the preparation or publication process of this article.