1 Introduction
The noise generated by aerodynamic bodies in fluid flow has motivated significant research for decades, ranging from simple analytical models for flat plates in uniform flow with unsteady perturbations (Amiet Reference Amiet1975) to high-fidelity numerical models that predict the noise generated by turbulent interactions with realistic thick aerofoils (Lockard & Morris Reference Lockard and Morris1998; Allampalli et al. Reference Allampalli, Hixon, Nallasamy and Sawyer2009; Gill, Zhang, & Joseph Reference Gill, Zhang and Joseph2013; Kim & Haeri Reference Kim and Haeri2015). A particularly important and unavoidable source of aerofoil noise is so-called trailing-edge noise which is generated by turbulence in the boundary layer scattering off the sharp trailing edge of an aerofoil. The analytic work of Howe (Reference Howe1998) presents a simplified picture of a line vortex interacting with the trailing edge of a semi-infinite flat plate and predicts the effects of a rigid trailing-edge condition on the acoustic scattering. With this boundary condition being key to the total level of far-field noise generated by turbulence–edge interaction, it is clear why the next steps into the investigation of reducing trailing-edge noise were to consider adapted trailing-edge designs, for example a serrated edge (Lyu et al. Reference Lyu, Azarpeyvand and Sinayoko2016; Oerlemans Reference Oerlemans2016), a rough surface canopy (Clark et al. Reference Clark, Daly, Devenport, Alexander, Peake, Jaworski and Glegg2016) or a porous and/or flexible edge (Jaworski & Peake Reference Jaworski and Peake2013; Geyer & Sarradj Reference Geyer and Sarradj2014; Schlanderer & Sandberg Reference Schlanderer and Sandberg2016). These adapted designs are inspired by the silent flight of owls, first discussed by Graham (Reference Graham1934), and now with increasing pressure on the aviation industry to reduce aircraft noise (European Commission 2011) are of great interest worldwide.
In order to understand and quickly predict any noise-reduction capabilities of adapted trailing-edge designs we turn to analytic solutions to elucidate the physics of the fluid–structure interactions. Recently Jaworski & Peake (Reference Jaworski and Peake2013) used the Wiener–Hopf technique to obtain an analytic solution capable of predicting the far-field trailing-edge noise from a semi-infinite poroelastic plate in uniform flow of characteristic Mach number
$M<1$
. It is shown that, whilst a rigid impermeable edge has a far-field acoustic power scaling of
$M^{5}$
(Ffowcs Williams & Hall Reference Ffowcs Williams and Hall1970), scalings of
$M^{6}$
and
$M^{7}$
can be achieved with suitable tuning of the porosity and elasticity of the edge. A further key insight is that porosity is seen to dominate low-frequency noise reduction, whilst elasticity affects high-frequency noise. The work of Jaworski & Peake (Reference Jaworski and Peake2013) has recently been extended to consider the effects of a finite leading edge (Cavalieri et al.
Reference Cavalieri, Wolf and Jaworski2016) although in this case the full plate is poroelastic. Practical application of trailing-edge adaptations would be restricted to short extensions to minimise adverse aerodynamic effects, therefore it is sensible to assume the turbulent boundary layer would encounter both rigid and porous sections of a plate. For this reason in this paper we investigate the noise generated by a gust convecting over a semi-infinite rigid plate with finite porous extension. To do so we use the Wiener–Hopf technique.
The Wiener–Hopf technique (Noble Reference Noble1958) affords itself to the scattering of sound by edges since these are problems with mixed boundary conditions: a velocity condition on the plate
$y=0,x<0$
and a pressure continuity condition behind the plate
$y=0,x>0$
. With two mixed boundary conditions like these, one constructs a one-dimensional (or scalar) Wiener–Hopf problem requiring the multiplicative factorisation of a scalar kernel function,
$K(\unicode[STIX]{x1D6FC})$
, into two parts that are analytic in the upper and lower halves of the complex
$\unicode[STIX]{x1D6FC}$
-plane, i.e.
$K(\unicode[STIX]{x1D6FC})=K_{+}(\unicode[STIX]{x1D6FC})K_{-}(\unicode[STIX]{x1D6FC})$
, where
$\pm$
denotes analyticity in the upper/lower half-plane respectively. Analytic factorisations are tractable in some cases, such as the Sommerfeld diffraction problem (Crighton et al.
Reference Crighton, Dowling, Williams, Heckl and Leppington1996), however in more complicated situations such as the poroelastic plate of (Jaworski & Peake Reference Jaworski and Peake2013) closed-form factorisation can only be found in certain asymptotic limits, and otherwise have to be computed numerically.
In more complicated scattering problems with more than two mixed boundary conditions, such as a finite elastic strip (Scott Reference Scott1992), or a perforated plate (Abrahams Reference Abrahams1999), one is faced with a matrix kernel to factorise. The general question of constructive matrix Wiener–Hopf factorisation is open (Lawrie & Abrahams Reference Lawrie and Abrahams2007; Rogosin & Mishuris Reference Rogosin and Mishuris2016). In this paper we are concerned with a class of Wiener–Hopf equations with triangular matrix functions containing exponential factors. More precisely finding functions
$\unicode[STIX]{x1D6F7}_{-}^{(0)}(\unicode[STIX]{x1D6FC})$
,
$\unicode[STIX]{x1D6F7}_{-}^{(L)}(\unicode[STIX]{x1D6FC})$
,
$\unicode[STIX]{x1D6F9}_{+}^{(0)}(\unicode[STIX]{x1D6FC})$
and
$\unicode[STIX]{x1D6F9}_{+}^{(L)}(\unicode[STIX]{x1D6FC})$
analytic in respective half-planes, satisfying the relationship
$$\begin{eqnarray}\left(\begin{array}{@{}c@{}}\unicode[STIX]{x1D6F7}_{-}^{(0)}(\unicode[STIX]{x1D6FC})\\ \unicode[STIX]{x1D6F7}_{-}^{(L)}(\unicode[STIX]{x1D6FC})\end{array}\right)=\left(\begin{array}{@{}cc@{}}A(\unicode[STIX]{x1D6FC}) & B(\unicode[STIX]{x1D6FC})\text{e}^{\text{i}\unicode[STIX]{x1D6FC}L}\\ C(\unicode[STIX]{x1D6FC})\text{e}^{-\text{i}\unicode[STIX]{x1D6FC}L} & 0\end{array}\right)\left(\begin{array}{@{}c@{}}\unicode[STIX]{x1D6F9}_{+}^{(0)}(\unicode[STIX]{x1D6FC})\\ \unicode[STIX]{x1D6F9}_{+}^{(L)}(\unicode[STIX]{x1D6FC})\end{array}\right)+\left(\begin{array}{@{}c@{}}f_{1}(\unicode[STIX]{x1D6FC})\\ f_{2}(\unicode[STIX]{x1D6FC})\end{array}\right),\end{eqnarray}$$
on the real line. The remaining functions
$A(\unicode[STIX]{x1D6FC})$
,
$B(\unicode[STIX]{x1D6FC})$
,
$C(\unicode[STIX]{x1D6FC})$
and
$f_{1,2}(\unicode[STIX]{x1D6FC})$
are known and
$L$
is a positive constant. Many problems have a Wiener–Hopf equation of this type (Aktosun, Klaus & van der Mee Reference Aktosun, Klaus and van der Mee1992; Antipov Reference Antipov2015) or could be reduced to such an equation by performing matrix manipulations. Presently, no complete solution of (1.1) is known. We note that there is an additional difficulty in finding a factorisation of the matrix in (1.1) because of the presence of analytic functions
$\text{e}^{\text{i}\unicode[STIX]{x1D6FC}L}$
and
$\text{e}^{-\text{i}\unicode[STIX]{x1D6FC}L}$
which have exponential growth in one of the half-planes.
In the literature concerning applications of the Wiener–Hopf technique, one of the most widely used methods is the so-called ‘pole removal’ or ‘singularities matching’ method (Noble Reference Noble1958, §§ 4.4, 5.3); (Daniele & Zich Reference Daniele and Zich2014, § 4.4.2). It has a severe limitation that certain functions have to be rational or meromorphic. One way to extend the use of this method is by employing a rational approximation (Abrahams Reference Abrahams2000; Kisil Reference Kisil2013), which was successfully used in Abrahams (Reference Abrahams1996), Abrahams et al. (Reference Abrahams, Davis and Llewellyn Smith2008), Veitch & Peake (Reference Veitch and Peake2008). However, even with this extension the class of functions which can be solved is rather limited. In Ayton (Reference Ayton2016) scattering by a finite flat plate with a poroelastic extension is considered yielding a 3
$\times$
3 Wiener–Hopf matrix system. The far-field acoustics are obtained by employing rational approximations, however this approach cannot be used to determine mid- or near-field results accurately since the functions involved are not meromorphic and cannot be accurately represented by rational functions everywhere. Additionally, the results were most accurate in Ayton (Reference Ayton2016) when considering high-frequency interactions. In this paper we propose a different extension to the pole removal technique for functions that have arbitrary singularities. This new method is suitable for accurately predicting the scattered field everywhere, and is not restrictive on frequency. This new method could also be extended to higher-dimensional matrices, however in this paper we shall specifically only consider 2
$\times$
2 matrices.
The proposed procedure is related to Schwarzschild’s series. In the original paper (Schwarzschild Reference Schwarzschild1901) Schwarzschild studied diffraction of a normal incidence plane wave by a slit of finite length in a perfectly conducting screen. This was achieved by considering the diffractions from each half-plane as a sequence of excitations from the other. This was later extended to near-normal incidence in Karp & Russek (Reference Karp and Russek1956) and to all angles in Grinberg (Reference Grinberg1957), Millar (Reference Millar1958). Schwarzschild’s series relates to a more general framework of the geometric theory of diffraction (Keller Reference Keller1962) and the physical theory of diffraction, see Ufimtsev, Terzuoli & Moore (Reference Ufimtsev, Terzuoli and Moore2003, § 8.7.3). What is common between all those approaches and the one proposed in this paper is the idea of solving parts of the problem and then bringing the parts together in an iterative manner. Recently, Schwarzschild’s series was used in Roger & Moreau (Reference Roger and Moreau2005), Lyu et al. (Reference Lyu, Azarpeyvand and Sinayoko2016) but only to obtain the scattered pressure on the surface of the flat plate, and the far-field sound was obtained using the surface pressure integral based on the theories of Kirchhoff and Curle.
The proposed procedure in this paper could be summarised as follows (see § 3 for details):
-
(i) a partial factorisation with exponential factors in the desired half-planes;
-
(ii) additive splitting of some terms;
-
(iii) application of Liouville’s theorem;
-
(iv) iterative procedure to determine the remaining unknowns.
Importantly, this method is entirely algorithmic and bypasses the need to construct a multiplicative matrix factorisation. Theoretical aspects of this method were addressed in Kisil (Reference Kisil2017). We validate the method by considering the two-dimensional Wiener–Hopf problem of the scattering of a sound wave by a finite impermeable plate, which has a known solution (McLachlan Reference McLachlan1964). We then use the method to investigate the generation of sound by a gust convecting in uniform flow over a semi-infinite impermeable plate with a finite porous extension. We use these results to investigate the effects of a impermeable–permeable junction on the results predicted by Jaworski & Peake (Reference Jaworski and Peake2013).
We present full details for the derivation of the porous extension problem in § 2, followed by the iterative Wiener–Hopf method in § 3. In § 4 we briefly discuss the appropriate formulation of the finite plate problem. In § 5.1 we present results validating the new Wiener–Hopf factorisation method by comparing our finite plate results to the known solution, then in § 5.2 we present results for the gust interacting with a porous extension and the effects of an impermeable–permeable junction on the noise-reduction predictions of Jaworski & Peake (Reference Jaworski and Peake2013). Finally we discuss our conclusions in § 6.
2 Formulation of the problem
Figure 1. Diagram of the model problem: a semi-infinite rigid plate lies in
$y=0$
,
$x<0$
, and a finite porous plate lies in
$y=0$
,
$0<x<L$
. An unsteady perturbation,
$\unicode[STIX]{x1D719}_{i}$
, convects with the mean flow in the positive
$x$
direction.
In order to investigate the effect of a finite porous edge on trailing-edge noise, we consider the generation of noise by a convective gust with velocity potential
$\unicode[STIX]{x1D719}_{i}(x,y)\text{e}^{\text{i}k_{3}z-\text{i}\unicode[STIX]{x1D714}t}$
interacting with a semi-infinite impermeable plate,
$x\in (-\infty ,0),y=0$
, with a porous edge,
$x\in (0,L),y=0$
, such that the impermeable–permeable junction is at
$x,y=0$
, as illustrated in figure 1. The steady background mean flow is parallel to the plate in the positive
$x$
-direction and has Mach number
$M$
. The matrix Wiener–Hopf problem is obtained by considering the Fourier transform of appropriate boundary conditions with respect to the ends of the porous plate at
$x=0$
and
$x=L$
.
We introduce a scattered velocity potential of the form
$$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D719}_{1}(x,y)\text{e}^{\text{i}k_{3}z-\text{i}\unicode[STIX]{x1D714}t}, & & \displaystyle\end{eqnarray}$$
and in what follows, the time factor
$\text{e}^{-\text{i}\unicode[STIX]{x1D714}t}$
will be omitted and we shall neglect the
$z$
-dependence (
$k_{3}=0$
).
The velocity potential
$\unicode[STIX]{x1D719}_{i}$
associated with a gust incident at angle
$\unicode[STIX]{x1D703}_{i}$
to the
$x$
axis with wavenumber
$k_{0}$
is
$$\begin{eqnarray}\unicode[STIX]{x1D719}_{i}=\exp (\text{i}k_{0}x\cos \unicode[STIX]{x1D703}_{i}-\text{i}k_{0}y\sin \unicode[STIX]{x1D703}_{i}).\end{eqnarray}$$
The governing convective Helmholtz equation is
$$\begin{eqnarray}(1-M^{2})\frac{\unicode[STIX]{x2202}^{2}\unicode[STIX]{x1D719}_{1}}{\unicode[STIX]{x2202}x^{2}}+\frac{\unicode[STIX]{x2202}^{2}\unicode[STIX]{x1D719}_{1}}{\unicode[STIX]{x2202}y^{2}}-2\text{i}\frac{\unicode[STIX]{x1D714}}{c_{0}}M\frac{\unicode[STIX]{x2202}\unicode[STIX]{x1D719}_{1}}{\unicode[STIX]{x2202}x}+\frac{\unicode[STIX]{x1D714}^{2}}{c_{0}^{2}}\unicode[STIX]{x1D719}_{1}=0,\end{eqnarray}$$
with
$\unicode[STIX]{x1D714}=k_{0}\cos \unicode[STIX]{x1D703}_{i}Mc_{0}$
and where
$c_{0}$
is the speed of sound.
We apply a convective transform,
$$\begin{eqnarray}\unicode[STIX]{x1D719}_{1}=\unicode[STIX]{x1D719}\text{e}^{\text{i}k_{0}\cos \unicode[STIX]{x1D703}_{i}M^{2}x/\unicode[STIX]{x1D6FD}^{2}},\end{eqnarray}$$
where
$\unicode[STIX]{x1D6FD}^{2}=1-M^{2}$
, and the Prandtl–Glauert transformation (
$y\rightarrow \unicode[STIX]{x1D6FD}y$
) to reduce the governing equation to
$$\begin{eqnarray}\displaystyle \left(\frac{\unicode[STIX]{x2202}}{\unicode[STIX]{x2202}x^{2}}+\frac{\unicode[STIX]{x2202}}{\unicode[STIX]{x2202}y^{2}}+w^{2}\right)\unicode[STIX]{x1D719}=0, & & \displaystyle\end{eqnarray}$$
where
$w=\unicode[STIX]{x1D6FF}M$
, with
$\unicode[STIX]{x1D6FF}=k_{0}\cos \unicode[STIX]{x1D703}_{i}/\unicode[STIX]{x1D6FD}^{2}$
. Full details of the convective transform and Prandtl–Glauert scaling can be found in Tsai (Reference Tsai1992).
The boundary conditions on the impermeable and permeable sections are
$$\begin{eqnarray}\displaystyle & \displaystyle \frac{\unicode[STIX]{x2202}\unicode[STIX]{x1D719}(x,y)}{\unicode[STIX]{x2202}y}+\frac{\unicode[STIX]{x2202}\unicode[STIX]{x1D719}_{i}(x,y)}{\unicode[STIX]{x2202}y}=0,\quad y=0,~-\infty <x<0, & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle \frac{\unicode[STIX]{x2202}\unicode[STIX]{x1D719}(x,y)}{\unicode[STIX]{x2202}y}+\frac{\unicode[STIX]{x2202}\unicode[STIX]{x1D719}_{i}(x,y)}{\unicode[STIX]{x2202}y}=\frac{\unicode[STIX]{x1D707}}{2}\unicode[STIX]{x1D6E5}(\unicode[STIX]{x1D719}(x,0)+\unicode[STIX]{x1D719}_{i}(x,0)),\quad y=0,~0<x<L, & \displaystyle\end{eqnarray}$$
respectively, where
$\unicode[STIX]{x1D6E5}$
stands for the jump across
$y=0+$
and
$y=0-$
, and
$\unicode[STIX]{x1D707}$
is the porosity parameter (
$\unicode[STIX]{x1D707}=\unicode[STIX]{x1D6FC}_{H}K_{R}/(\unicode[STIX]{x03C0}R^{2}\unicode[STIX]{x1D6FD})$
) for a porous plate with evenly spaced circular apertures of radius
$R$
, Rayleigh conductivity of
$K_{R}=2R$
and fractional open area
$\unicode[STIX]{x1D6FC}_{H}$
(see Howe Reference Howe1998). The conditions on the permeable section are equivalent to impedance boundary conditions. We require the length scale of the incident disturbance to be larger than the aperture radius,
$k_{0}R\ll 1$
, and the fractional open area to be small,
$\unicode[STIX]{x1D6FC}_{H}^{2}\ll 1$
, so that the porous boundary condition provides a first-order correction accounting for the perforations in the plate. We shall focus on small
$\unicode[STIX]{x1D707}$
values as this will be beneficial later to ensure rapid convergence of the iterative method. For comparison, the range of corresponding
$\unicode[STIX]{x1D707}$
values investigated by Jaworski & Peake (Reference Jaworski and Peake2013) in connection to the silent flight of owl is
$\unicode[STIX]{x1D707}\in [10^{-9},12.24]$
.
We require
$$\begin{eqnarray}\unicode[STIX]{x1D719}(x,0)+\unicode[STIX]{x1D719}_{i}(x,0)=0,\quad x>L,\end{eqnarray}$$
to ensure continuity of pressure downstream of the plate. Also
$\unicode[STIX]{x2202}\unicode[STIX]{x1D719}(x,y)/\unicode[STIX]{x2202}y$
(which will be denoted by
$\unicode[STIX]{x1D719}^{\prime }(x,y)$
) must be continuous across
$y=0$
$$\begin{eqnarray}\frac{\unicode[STIX]{x2202}\unicode[STIX]{x1D719}(x,0+)}{\unicode[STIX]{x2202}y}=\frac{\unicode[STIX]{x2202}\unicode[STIX]{x1D719}(x,0-)}{\unicode[STIX]{x2202}y},\quad y=0.\end{eqnarray}$$
The solution,
$\unicode[STIX]{x1D719}$
, is required to satisfy the Sommerfeld radiation condition for outgoing waves at infinity,
$$\begin{eqnarray}r^{-1/2}\left(\frac{\unicode[STIX]{x2202}\unicode[STIX]{x1D719}}{\unicode[STIX]{x2202}r}-\text{i}k_{0}\unicode[STIX]{x1D719}\right)\rightarrow 0,\quad \text{where }r=\sqrt{x^{2}+y^{2}},\end{eqnarray}$$
and the edge conditions are taken as in Noble (Reference Noble1958, § 2.1) to achieve the least singular solutions.
$$\begin{eqnarray}\displaystyle & \displaystyle \unicode[STIX]{x1D719}(x,0)\rightarrow c_{1},\quad \text{as }x\rightarrow 0-, & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle \unicode[STIX]{x1D719}(x,0)\rightarrow c_{2},\quad \text{as }x\rightarrow L-, & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle \frac{\unicode[STIX]{x2202}\unicode[STIX]{x1D719}(x,0)}{\unicode[STIX]{x2202}y}\rightarrow c_{3}x^{-1/2},\quad \text{as }x\rightarrow 0+, & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle \frac{\unicode[STIX]{x2202}\unicode[STIX]{x1D719}(x,0)}{\unicode[STIX]{x2202}y}\rightarrow c_{4}x^{-1/2},\quad \text{as }x\rightarrow L+, & \displaystyle\end{eqnarray}$$
$c_{i}$
are constants. The two conditions at
$L$
impose the unsteady Kutta conditions, see Ayton, Gill & Peake (Reference Ayton, Gill and Peake2016) for more details.
2.1 Reduction to Wiener–Hopf equation
The next step is to write down the relationship between different half-range Fourier transforms by using the boundary conditions. These relations can be combined to form a matrix Wiener–Hopf equation.
We define the half-range and full-range Fourier transforms with respect to
$x=0$
by
$$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D6F7}(\unicode[STIX]{x1D6FC},y) & = & \displaystyle \int _{-\infty }^{0}\unicode[STIX]{x1D719}(\unicode[STIX]{x1D709},y)\text{e}^{\text{i}\unicode[STIX]{x1D6FC}\unicode[STIX]{x1D709}}\,\text{d}\unicode[STIX]{x1D709}+\int _{0}^{\infty }\unicode[STIX]{x1D719}(\unicode[STIX]{x1D709},y)\text{e}^{\text{i}\unicode[STIX]{x1D6FC}\unicode[STIX]{x1D709}}\,\text{d}\unicode[STIX]{x1D709},\nonumber\\ \displaystyle & = & \displaystyle \unicode[STIX]{x1D6F7}_{-}^{(0)}(\unicode[STIX]{x1D6FC},y)+\unicode[STIX]{x1D6F7}_{+}^{(0)}(\unicode[STIX]{x1D6FC},y),\end{eqnarray}$$
and the Fourier transforms with respect to the point
$x=L$
by
$$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D6F7}^{(L)}(\unicode[STIX]{x1D6FC},y) & = & \displaystyle \int _{-\infty }^{L}\unicode[STIX]{x1D719}(\unicode[STIX]{x1D709},y)\text{e}^{\text{i}\unicode[STIX]{x1D6FC}(\unicode[STIX]{x1D709}-L)}\,\text{d}\unicode[STIX]{x1D709}+\int _{L}^{\infty }\unicode[STIX]{x1D719}(\unicode[STIX]{x1D709},y)\text{e}^{\text{i}\unicode[STIX]{x1D6FC}(\unicode[STIX]{x1D709}-L)}\,\text{d}\unicode[STIX]{x1D709},\nonumber\\ \displaystyle & = & \displaystyle \unicode[STIX]{x1D6F7}_{-}^{(L)}(\unicode[STIX]{x1D6FC},y)+\unicode[STIX]{x1D6F7}_{+}^{(L)}(\unicode[STIX]{x1D6FC},y).\end{eqnarray}$$
At the end of the analysis the inverse Fourier transforms are applied. The relation between the transforms is
$$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D6F7}^{(L)}(\unicode[STIX]{x1D6FC},y)=\unicode[STIX]{x1D6F7}(\unicode[STIX]{x1D6FC},y)\text{e}^{-\text{i}\unicode[STIX]{x1D6FC}L}. & & \displaystyle\end{eqnarray}$$
We can also define the transform of the finite interval only
$$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D6F7}_{1}(\unicode[STIX]{x1D6FC},y)=\int _{0}^{L}\unicode[STIX]{x1D719}(\unicode[STIX]{x1D709},y)\text{e}^{\text{i}\unicode[STIX]{x1D6FC}\unicode[STIX]{x1D709}}\,\text{d}\unicode[STIX]{x1D709}, & & \displaystyle\end{eqnarray}$$
and note that
$$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D6F7}_{1}(\unicode[STIX]{x1D6FC},y)=\text{e}^{\text{i}\unicode[STIX]{x1D6FC}L}\unicode[STIX]{x1D6F7}_{-}^{(L)}(\unicode[STIX]{x1D6FC},y)-\unicode[STIX]{x1D6F7}_{-}^{(0)}(\unicode[STIX]{x1D6FC},y). & & \displaystyle\end{eqnarray}$$
Now transforming the boundary conditions for the rigid plate, equation (2.6), we obtain
$$\begin{eqnarray}\unicode[STIX]{x1D6F7}_{-}^{\prime (0)}(\unicode[STIX]{x1D6FC},0)=-\unicode[STIX]{x1D6F7}_{i-}^{\prime (0)}(\unicode[STIX]{x1D6FC},0).\end{eqnarray}$$
From the condition on the porous plate, (2.7),
$$\begin{eqnarray}\unicode[STIX]{x1D6F7}_{1}^{\prime }(\unicode[STIX]{x1D6FC},0)+\unicode[STIX]{x1D6F7}_{i1}^{\prime }(\unicode[STIX]{x1D6FC},0)=\unicode[STIX]{x1D707}\unicode[STIX]{x1D6F7}_{1}(\unicode[STIX]{x1D6FC},0),\end{eqnarray}$$
where we use
$\unicode[STIX]{x1D6F7}_{1}(\unicode[STIX]{x1D6FC},0+)=-\unicode[STIX]{x1D6F7}_{1}(\unicode[STIX]{x1D6FC},0-)$
. Finally from (2.8) we obtain
$$\begin{eqnarray}\unicode[STIX]{x1D6F7}_{+}^{(L)}(\unicode[STIX]{x1D6FC},0)=0.\end{eqnarray}$$
The solution to the governing equation can be written as
$$\begin{eqnarray}\unicode[STIX]{x1D6F7}(\unicode[STIX]{x1D6FC},y)=\text{sgn}(y)A(\unicode[STIX]{x1D6FC})\text{e}^{-\unicode[STIX]{x1D6FE}|y|},\end{eqnarray}$$
where
$\unicode[STIX]{x1D6FE}(\unicode[STIX]{x1D6FC})=\sqrt{\unicode[STIX]{x1D6FC}^{2}-w^{2}}$
(where the branch cuts are chosen in the standard way, see Noble (Reference Noble1958, p. 9). The Wiener–Hopf equations are now obtained from the following relationships
$$\begin{eqnarray}\displaystyle & \displaystyle \unicode[STIX]{x1D6F7}_{-}^{\prime (0)}+\unicode[STIX]{x1D6F7}_{1}^{\prime }+\text{e}^{\text{i}\unicode[STIX]{x1D6FC}L}\unicode[STIX]{x1D6F7}_{+}^{\prime (L)}=-\unicode[STIX]{x1D6FE}\text{e}^{\text{i}\unicode[STIX]{x1D6FC}L}(\unicode[STIX]{x1D6F7}_{+}^{(L)}+\unicode[STIX]{x1D6F7}_{-}^{(L)}), & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle \unicode[STIX]{x1D6F7}_{-}^{\prime (0)}+\unicode[STIX]{x1D6F7}_{+}^{\prime (0)}=-\unicode[STIX]{x1D6FE}\text{e}^{\text{i}\unicode[STIX]{x1D6FC}L}(\unicode[STIX]{x1D6F7}_{+}^{(L)}+\unicode[STIX]{x1D6F7}_{-}^{(L)}), & \displaystyle\end{eqnarray}$$
by substituting the known transforms (2.17), (2.18) and (2.19), and using the relationship
$\unicode[STIX]{x1D6F7}^{\prime }(\unicode[STIX]{x1D6FC},y)=-\unicode[STIX]{x1D6FE}\unicode[STIX]{x1D6F7}(\unicode[STIX]{x1D6FC},y)$
. The Wiener–Hopf equations can now finally be written (by substituting an expression for
$\unicode[STIX]{x1D6F7}_{-}^{(L)}$
from (2.21) to (2.22)) as:
$$\begin{eqnarray}\left(\begin{array}{@{}c@{}}\unicode[STIX]{x1D6F7}_{-}^{(0)}(\unicode[STIX]{x1D6FC})\\ \unicode[STIX]{x1D6F7}_{-}^{(L)}(\unicode[STIX]{x1D6FC})\end{array}\right)=-\left(\begin{array}{@{}cc@{}}\displaystyle \frac{1}{\unicode[STIX]{x1D6FE}(\unicode[STIX]{x1D6FC})}-P & P\text{e}^{\text{i}\unicode[STIX]{x1D6FC}L}\\ \displaystyle \frac{1}{\unicode[STIX]{x1D6FE}(\unicode[STIX]{x1D6FC})}\text{e}^{-\text{i}\unicode[STIX]{x1D6FC}L} & 0\end{array}\right)\left(\begin{array}{@{}c@{}}\unicode[STIX]{x1D6F7}_{+}^{\prime (0)}(\unicode[STIX]{x1D6FC})\\ \unicode[STIX]{x1D6F7}_{+}^{\prime (L)}(\unicode[STIX]{x1D6FC})\end{array}\right)-\left(\begin{array}{@{}c@{}}f_{1}(\unicode[STIX]{x1D6FC})\\ f_{2}(\unicode[STIX]{x1D6FC})\end{array}\right),\end{eqnarray}$$
where
$P=-1/\unicode[STIX]{x1D707}$
. The forcing provided by the gust is
$$\begin{eqnarray}f_{1}=\frac{k_{0}\sin \unicode[STIX]{x1D703}_{i}}{\unicode[STIX]{x1D6FE}(\unicode[STIX]{x1D6FC})(\unicode[STIX]{x1D6FC}+\unicode[STIX]{x1D6FF})}+\frac{k_{0}\sin \unicode[STIX]{x1D703}_{i}}{(\unicode[STIX]{x1D6FC}+\unicode[STIX]{x1D6FF})}(-P+P\text{e}^{\text{i}(\unicode[STIX]{x1D6FC}+\unicode[STIX]{x1D6FF})L})+\frac{1}{\text{i}(\unicode[STIX]{x1D6FC}+\unicode[STIX]{x1D6FF})}\text{e}^{\text{i}(\unicode[STIX]{x1D6FC}+\unicode[STIX]{x1D6FF})L},\end{eqnarray}$$
and
$$\begin{eqnarray}f_{2}=\frac{k_{0}\sin \unicode[STIX]{x1D703}_{i}}{\unicode[STIX]{x1D6FE}(\unicode[STIX]{x1D6FC})(\unicode[STIX]{x1D6FC}+\unicode[STIX]{x1D6FF})}\text{e}^{-\text{i}\unicode[STIX]{x1D6FC}L}+\frac{1}{\text{i}(\unicode[STIX]{x1D6FC}+\unicode[STIX]{x1D6FF})}\text{e}^{\text{i}\unicode[STIX]{x1D6FF}L}.\end{eqnarray}$$
We note that on the left-hand side of (2.23) the unknown functions are minus half-transforms,
$\unicode[STIX]{x1D6F7}_{-}^{(0)}(\unicode[STIX]{x1D6FC})$
and
$\unicode[STIX]{x1D6F7}_{-}^{(L)}(\unicode[STIX]{x1D6FC})$
, and on the right are the derivatives of the plus half-transforms,
$\unicode[STIX]{x1D6F7}_{+}^{\prime (0)}(\unicode[STIX]{x1D6FC})$
and
$\unicode[STIX]{x1D6F7}_{+}^{\prime (L)}(\unicode[STIX]{x1D6FC})$
.
The behaviour of various transforms at infinity is determined by the edge conditions (2.11). We have
$\unicode[STIX]{x1D6F7}_{-}^{(0)}(\unicode[STIX]{x1D6FC})\rightarrow \unicode[STIX]{x1D6FC}^{-1}$
and
$\unicode[STIX]{x1D6F7}_{-}^{(L)}(\unicode[STIX]{x1D6FC})\rightarrow \unicode[STIX]{x1D6FC}^{-1}$
as
$\unicode[STIX]{x1D6FC}\rightarrow \infty$
in the lower half-plane, and
$\unicode[STIX]{x1D6F7}_{+}^{\prime (0)}(\unicode[STIX]{x1D6FC})\rightarrow \unicode[STIX]{x1D6FC}^{-1/2}$
and
$\unicode[STIX]{x1D6F7}_{+}^{\prime (L)}(\unicode[STIX]{x1D6FC})\rightarrow \unicode[STIX]{x1D6FC}^{-1/2}$
as
$\unicode[STIX]{x1D6FC}\rightarrow \infty$
in the upper half-plane.
2.2 Far-field acoustic directivity
Supposing we can solve (2.23) for the unknown
$\unicode[STIX]{x1D6F7}$
terms, we can determine the full acoustic solution, equation (2.20), which can be written as
$$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D6F7}(\unicode[STIX]{x1D6FC},y)=\unicode[STIX]{x1D6F7}_{-}^{(L)}(\unicode[STIX]{x1D6FC},0)\text{sgn}(y)\text{e}^{-\unicode[STIX]{x1D6FE}|y|}. & & \displaystyle\end{eqnarray}$$
This can be inverted to obtain the velocity potential
$$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D719}(x,y)=\frac{\text{sgn}(y)}{2\unicode[STIX]{x03C0}}\int _{-\infty }^{\infty }\unicode[STIX]{x1D6F7}_{-}^{(L)}(\unicode[STIX]{x1D6FC},0)\text{e}^{-\text{i}\unicode[STIX]{x1D6FC}x-\unicode[STIX]{x1D6FE}|y|}\,\text{d}\unicode[STIX]{x1D6FC}, & & \displaystyle\end{eqnarray}$$
which for
$x,y\rightarrow \infty$
can be approximated by the method of steepest descents to yield
$$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D719}(r,\unicode[STIX]{x1D703})\sim \frac{\sqrt{w}\text{e}^{-\unicode[STIX]{x03C0}\text{i}/4}}{\sqrt{2\unicode[STIX]{x03C0}}}\unicode[STIX]{x1D6F7}_{-}^{(L)}(-w\cos \unicode[STIX]{x1D703},0)\sin \unicode[STIX]{x1D703}\frac{\text{e}^{\text{i}wr}}{\sqrt{r}}, & & \displaystyle\end{eqnarray}$$
where
$(r,\unicode[STIX]{x1D703})$
are polar coordinates measured from the rigid–porous junction,
$x=y=0$
. The far-field directivity,
$D(\unicode[STIX]{x1D703})$
, is then defined via
$$\begin{eqnarray}\unicode[STIX]{x1D719}(r,\unicode[STIX]{x1D703})\sim D(\unicode[STIX]{x1D703})\frac{\text{e}^{\text{i}wr}}{\sqrt{r}},\quad r\rightarrow \infty .\end{eqnarray}$$
3 Approximate Wiener–Hopf factorisation
We look for an approximate matrix factorisation of (2.23). We will be using the standard results in the theory of scalar Wiener–Hopf factorisation, and in what follows a superscript/subscript
$+$
(or
$-$
) indicates that the function is analytic in the upper (lower) half-plane. Functions without the superscript/subscript are known. A convention is introduced here to distinguish the additive and the multiplicative factorisation by using a superscript and subscript notation (e.g.
$K(\unicode[STIX]{x1D6FC})=K^{-}(\unicode[STIX]{x1D6FC})+K^{+}(\unicode[STIX]{x1D6FC})$
for additive Wiener–Hopf splitting and
$K(\unicode[STIX]{x1D6FC})=K_{-}(\unicode[STIX]{x1D6FC})K_{+}(\unicode[STIX]{x1D6FC})$
for multiplicative factorisation). For more details on the scalar factorisation see Noble (Reference Noble1958), Daniele & Zich (Reference Daniele and Zich2014).
The most characteristic aspect of the Wiener–Hopf method is the application of Liouville’s theorem in order to obtain two separate connected equations from one equation. In order for Liouville’s theorem to be used two conditions have to be satisfied: the analyticity and (at most) polynomial growth at infinity. These two conditions will be treated here in turn. First, a partial factorisation is considered that has the exponential functions in the right place (in the half-planes where they decay exponentially) and some of the required analyticity. To do so we premultiply (2.23) by a suitably chosen matrix yielding
$$\begin{eqnarray}\displaystyle & & \displaystyle \left(\begin{array}{@{}cc@{}}\displaystyle \frac{-\text{e}^{-\text{i}\unicode[STIX]{x1D6FC}L}}{P_{-}} & \displaystyle \frac{1-\unicode[STIX]{x1D6FE}P}{P_{-}}\\ \displaystyle \frac{1}{P_{-}} & 0\end{array}\right)\left(\begin{array}{@{}c@{}}\unicode[STIX]{x1D6F7}_{-}^{(0)}\\ \unicode[STIX]{x1D6F7}_{-}^{(L)}\end{array}\right)\nonumber\\ \displaystyle & & \displaystyle \quad =-\left(\begin{array}{@{}cc@{}}0 & -P_{+}\\ \displaystyle \frac{P_{+}}{\unicode[STIX]{x1D6FE}P}-P_{+} & P_{+}\text{e}^{\text{i}\unicode[STIX]{x1D6FC}L}\end{array}\right)\left(\begin{array}{@{}c@{}}\unicode[STIX]{x1D6F7}_{+}^{\prime (0)}\\ \unicode[STIX]{x1D6F7}_{+}^{\prime (L)}\end{array}\right)+\left(\begin{array}{@{}c@{}}f_{3}\\ f_{4}\end{array}\right),\end{eqnarray}$$
or re-arranged
$$\begin{eqnarray}\displaystyle & & \displaystyle \left(\begin{array}{@{}cc@{}}\displaystyle \frac{-\text{e}^{-\text{i}\unicode[STIX]{x1D6FC}L}}{P_{-}} & \displaystyle \frac{1}{P_{-}}\\ \displaystyle \frac{1}{P_{-}} & 0\end{array}\right)\left(\begin{array}{@{}c@{}}\unicode[STIX]{x1D6F7}_{-}^{(0)}\\ \unicode[STIX]{x1D6F7}_{-}^{(L)}\end{array}\right)+\left(\begin{array}{@{}c@{}}-\unicode[STIX]{x1D6FE}P_{+}\unicode[STIX]{x1D6F7}_{-}^{(L)}\\ \displaystyle \frac{1}{\unicode[STIX]{x1D6FE}P_{-}}\unicode[STIX]{x1D6F7}_{+}^{\prime (0)}\end{array}\right)\nonumber\\ \displaystyle & & \displaystyle \quad =-\left(\begin{array}{@{}cc@{}}0 & -P_{+}\\ -P_{+} & P_{+}\text{e}^{\text{i}\unicode[STIX]{x1D6FC}L}\end{array}\right)\left(\begin{array}{@{}c@{}}\unicode[STIX]{x1D6F7}_{+}^{\prime (0)}\\ \unicode[STIX]{x1D6F7}_{+}^{\prime (L)}\end{array}\right)+\left(\begin{array}{@{}c@{}}f_{3}\\ f_{4}\end{array}\right),\end{eqnarray}$$
where
$f_{4}=-f_{1}/P_{-}$
(with
$f_{1}$
given by (2.24)) and
$f_{3}$
defined as
$$\begin{eqnarray}\displaystyle f_{3}=\frac{k_{0}\sin \unicode[STIX]{x1D703}_{i}\text{e}^{-\text{i}\unicode[STIX]{x1D6FC}L}P_{+}}{(\unicode[STIX]{x1D6FC}+\unicode[STIX]{x1D6FF})}[2\text{e}^{\text{i}(\unicode[STIX]{x1D6FC}+\unicode[STIX]{x1D6FF})L}]+\frac{1}{\text{i}(\unicode[STIX]{x1D6FC}+\unicode[STIX]{x1D6FF})}\text{e}^{\text{i}\unicode[STIX]{x1D6FF}L}\unicode[STIX]{x1D6FE}P_{+}. & & \displaystyle\end{eqnarray}$$
Even though our example problem of a finite porous section has
$P=\text{const.}$
, this method extends to
$P(\unicode[STIX]{x1D6FC})$
with at most polynomial growth at infinity, for example in the case of an elastic edge
$P(\unicode[STIX]{x1D6FC})$
would be a polynomial of degree
$4$
. Therefore we include the relevant details of the factorisation in the more general case, which is suitable for tackling any matrix of the form (1.1).
The next step is to perform some additive splittings:
$$\begin{eqnarray}\displaystyle & \displaystyle \unicode[STIX]{x1D6FE}P_{+}\unicode[STIX]{x1D6F7}_{-}^{(L)}=(\unicode[STIX]{x1D6FE}P_{+}\unicode[STIX]{x1D6F7}_{-}^{(L)})^{-}+(\unicode[STIX]{x1D6FE}P_{+}\unicode[STIX]{x1D6F7}_{-}^{(L)})^{+}, & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle \frac{1}{\unicode[STIX]{x1D6FE}P_{-}}\unicode[STIX]{x1D6F7}_{+}^{\prime (0)}=\left(\frac{1}{\unicode[STIX]{x1D6FE}P_{-}}\unicode[STIX]{x1D6F7}_{+}^{\prime (0)}\right)^{-}+\left(\frac{1}{\unicode[STIX]{x1D6FE}P_{-}}\unicode[STIX]{x1D6F7}_{+}^{\prime (0)}\right)^{+}. & \displaystyle\end{eqnarray}$$
Note that we cannot calculate these directly since
$\unicode[STIX]{x1D6F7}_{-}^{(L)}$
and
$\unicode[STIX]{x1D6F7}_{+}^{\prime (0)}$
are unknown. An approximation for the splittings will be found later. Note the similarities with the ‘pole removal’ or ‘singularities matching’ (Noble Reference Noble1958, §§ 4.4, 5.3) Daniele & Zich (Reference Daniele and Zich2014, § 4.4.2) where one of
$()^{-}$
or
$()^{+}$
would be an infinite sum of unknown coefficients. Those unknown coefficients are determined later in an approximate fashion.
We would like to note that (2.23) cannot be fully solved by first performing rational approximation and then using the ‘pole removal’ method. The reason is that a rational approximation of
$\unicode[STIX]{x1D6FE}$
or
$1/\unicode[STIX]{x1D6FE}$
which is accurate on the whole real line is not possible. This is due to the fact that
$\unicode[STIX]{x1D6FE}\rightarrow |\unicode[STIX]{x1D6FC}|$
as
$|\unicode[STIX]{x1D6FC}|\rightarrow \infty$
and no rational function has this property. It is on the other hand possible to obtain good rational approximation on an interval of the real line and this in turn could be used to obtain the far-field solution using the steepest descent method. So in this case the proposed method is the only way of fully extending the ‘pole removal’ technique.
Now Liouville’s theorem can be applied because the exponential functions are in the correct place and all the functions have the desired analyticity. Thus, we can apply the Wiener–Hopf procedure as usual and the four equations become
$$\begin{eqnarray}\displaystyle & \displaystyle \frac{-\text{e}^{-\text{i}\unicode[STIX]{x1D6FC}L}}{P_{-}}\unicode[STIX]{x1D6F7}_{-}^{(0)}+\frac{1}{P_{-}}\unicode[STIX]{x1D6F7}_{-}^{(L)}-(\unicode[STIX]{x1D6FE}P_{+}\unicode[STIX]{x1D6F7}_{-}^{(L)})^{-}-f_{3}^{-}=0, & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle P_{+}\unicode[STIX]{x1D6F7}_{+}^{\prime (L)}+(\unicode[STIX]{x1D6FE}P_{+}\unicode[STIX]{x1D6F7}_{-}^{(L)})^{+}+f_{3}^{+}=0, & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle \frac{1}{P_{-}}\unicode[STIX]{x1D6F7}_{-}^{(0)}+\left(\frac{1}{\unicode[STIX]{x1D6FE}P_{-}}\unicode[STIX]{x1D6F7}_{+}^{\prime (0)}\right)^{-}-f_{4}^{-}=C, & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle P_{+}\unicode[STIX]{x1D6F7}_{+}^{\prime (0)}-P_{+}\text{e}^{\text{i}\unicode[STIX]{x1D6FC}L}\unicode[STIX]{x1D6F7}_{+}^{\prime (L)}-\left(\frac{1}{\unicode[STIX]{x1D6FE}P_{-}}\unicode[STIX]{x1D6F7}_{+}^{\prime (0)}\right)^{+}+f_{4}^{+}=C, & \displaystyle\end{eqnarray}$$
where
$C$
is a constant. It turns out that this constant plays no role, as is discussed at the end of § 4.1, so can be taken to be zero. The four equations can be rearranged (and their order changed):
$$\begin{eqnarray}\displaystyle & \displaystyle \unicode[STIX]{x1D6F7}_{-}^{(L)}=P_{-}((\unicode[STIX]{x1D6FE}P_{+}\unicode[STIX]{x1D6F7}_{-}^{(L)})^{-}+f_{3}^{-})+\text{e}^{-\text{i}\unicode[STIX]{x1D6FC}L}\unicode[STIX]{x1D6F7}_{-}^{(0)}, & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle \unicode[STIX]{x1D6F7}_{+}^{\prime (L)}=\frac{1}{P_{+}}(-(\unicode[STIX]{x1D6FE}P_{+}\unicode[STIX]{x1D6F7}_{-}^{(L)})^{+}-f_{3}^{+}), & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle \unicode[STIX]{x1D6F7}_{+}^{\prime (0)}=\frac{1}{P_{+}}\left(\left(\frac{1}{\unicode[STIX]{x1D6FE}P_{-}}\unicode[STIX]{x1D6F7}_{+}^{\prime (0)}\right)^{+}-f_{4}^{+}\right)+\text{e}^{\text{i}\unicode[STIX]{x1D6FC}L}\unicode[STIX]{x1D6F7}_{+}^{\prime (L)}. & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle \unicode[STIX]{x1D6F7}_{-}^{(0)}=P_{-}\left(-\left(\frac{1}{\unicode[STIX]{x1D6FE}P_{-}}\unicode[STIX]{x1D6F7}_{+}^{\prime (0)}\right)^{-}+f_{4}^{-}\right). & \displaystyle\end{eqnarray}$$
When the equations are written in this form it is clear that if
$\unicode[STIX]{x1D6F7}_{-}^{(L)}$
is known then it could be used to calculate
$\unicode[STIX]{x1D6F7}_{+}^{\prime (L)}$
from (3.11) and this, in turn, produces
$\unicode[STIX]{x1D6F7}_{+}^{\prime (0)}$
by looking at (3.12) followed by the calculation of
$\unicode[STIX]{x1D6F7}_{-}^{(0)}$
in (3.13) and then it loops round. This observation will form the basis of the iterative procedure. So far the solution is exact but in order to make progress an approximation is needed.
In order to solve approximately we will describe an iterative procedure and denote the
$n$
th iteration by
$\unicode[STIX]{x1D6F7}_{-}^{(L)n}$
. The equation (3.10) is going to be approximated by neglecting the
$\text{e}^{-\text{i}\unicode[STIX]{x1D6FC}L}\unicode[STIX]{x1D6F7}_{-}^{(0)}$
term (which as we will see later is small in many cases) i.e.
$$\begin{eqnarray}\unicode[STIX]{x1D6F7}_{-}^{(L)1}=P_{-}((\unicode[STIX]{x1D6FE}P_{+}\unicode[STIX]{x1D6F7}_{-}^{(L)1})^{-}+f_{3}^{-}),\end{eqnarray}$$
which corresponds to only considering the junction at
$x=L$
. In other words we are considering the problem of scattering from a semi-infinite porous plane. Note that
$\unicode[STIX]{x1D6F7}_{-}^{(L)1}$
is an approximation to
$\unicode[STIX]{x1D6F7}_{-}^{(L)}$
but importantly
$\unicode[STIX]{x1D6F7}_{-}^{(L)1}$
has the same analyticity properties as
$\unicode[STIX]{x1D6F7}_{-}^{(L)}$
. The above equation (3.14) can be rearranged as a scalar Wiener–Hopf equation in the following manner,
$$\begin{eqnarray}\left(\frac{1-\unicode[STIX]{x1D6FE}P}{P_{-}}\unicode[STIX]{x1D6F7}_{-}^{(L)1}\right)^{-}=f_{3}^{-}.\end{eqnarray}$$
We introduce an unknown function
$D_{+}$
defined by
$$\begin{eqnarray}\left(\frac{1-\unicode[STIX]{x1D6FE}P}{P_{-}}\unicode[STIX]{x1D6F7}_{-}^{(L)1}\right)^{+}=D^{+},\end{eqnarray}$$
then adding together yields
$$\begin{eqnarray}\frac{1-\unicode[STIX]{x1D6FE}P}{P_{-}}\unicode[STIX]{x1D6F7}_{-}^{(L)1}=D^{+}+f_{3}^{-},\end{eqnarray}$$
which is a Wiener–Hopf equation, with solution
$$\begin{eqnarray}\unicode[STIX]{x1D6F7}_{-}^{(L)1}=\frac{P_{-}}{(1-\unicode[STIX]{x1D6FE}P)_{-}}\left(\left(\frac{f_{3}^{-}}{(1-\unicode[STIX]{x1D6FE}P)_{+}}\right)^{-}\right).\end{eqnarray}$$
Also we are able to compute
$(\unicode[STIX]{x1D6FE}P_{+}\unicode[STIX]{x1D6F7}_{-}^{(L)1})^{+}$
(which we need in (3.11)) by considering
$D^{+}$
. Note that
$$\begin{eqnarray}D^{+}=\left(\frac{1-\unicode[STIX]{x1D6FE}P}{P_{-}}\unicode[STIX]{x1D6F7}_{-}^{(L)1}\right)^{+}=-(\unicode[STIX]{x1D6FE}P_{+}\unicode[STIX]{x1D6F7}_{-}^{(L)1})^{+},\end{eqnarray}$$
and solving the Wiener–Hopf equation (3.17) for
$D^{+}$
gives
$$\begin{eqnarray}D^{+}=(1-\unicode[STIX]{x1D6FE}P)_{+}\left(-\left(\frac{f_{3}^{-}}{(1-\unicode[STIX]{x1D6FE}P)_{+}}\right)^{+}\right).\end{eqnarray}$$
So we are solving this Wiener–Hopf matrix factorisation by first considering the scalar equation which arises from one of the junctions (
$x=L$
) in the boundary conditions. So now using (3.11) we easily obtain an expression for
$\unicode[STIX]{x1D6F7}_{+}^{\prime (L)1}$
. This in turn is used in (3.12) to reduce the solution for
$\unicode[STIX]{x1D6F7}_{+}^{\prime (0)1}$
to a scalar Wiener–Hopf problem in the same fashion as (3.14). This is now coupling junction at
$x=L$
with the junction at
$x=0$
, and gives
$$\begin{eqnarray}\unicode[STIX]{x1D6F7}_{+}^{\prime (0)1}=\frac{\unicode[STIX]{x1D6FE}_{+}}{(\unicode[STIX]{x1D6FE}P-1)_{+}}\left(\left(\frac{(-f_{4}^{+}+P_{+}\text{e}^{\text{i}\unicode[STIX]{x1D6FC}L}\unicode[STIX]{x1D6F7}_{+}^{\prime (L)1})P_{-}\unicode[STIX]{x1D6FE}_{-}}{(\unicode[STIX]{x1D6FE}P-1)_{-}}\right)^{+}\right).\end{eqnarray}$$
An expression for
$\unicode[STIX]{x1D6F7}_{-}^{(0)1}$
can in turn be obtained from (3.13). In order to simplify again note that
$$\begin{eqnarray}\left(\frac{1}{\unicode[STIX]{x1D6FE}P_{-}}\unicode[STIX]{x1D6F7}_{+}^{\prime (0)1}\right)^{-}=\frac{(\unicode[STIX]{x1D6FE}P-1)_{-}}{P_{-}\unicode[STIX]{x1D6FE}_{-}}\left(-\left(\frac{(-f_{4}^{+}+P_{+}\text{e}^{\text{i}\unicode[STIX]{x1D6FC}L}\unicode[STIX]{x1D6F7}_{+}^{\prime (L)1})P_{-}\unicode[STIX]{x1D6FE}_{-}}{(\unicode[STIX]{x1D6FE}P-1)_{-}}\right)^{-}\right).\end{eqnarray}$$
Once
$\unicode[STIX]{x1D6F7}_{-}^{(0)1}$
is computed this can be looped round to calculate
$\unicode[STIX]{x1D6F7}_{-}^{(L)2}$
from using the full equations (3.10) and (3.13). As the loops are performed the coupling between the junction
$x=L$
and
$x=0$
is successively corrected and
$\unicode[STIX]{x1D6F7}_{+}^{\prime (0)n}$
approaches the correct solution. As it is shown in the next sections, in practice in most case the convergence is very fast and the desired accuracy is achieved for
$n=2$
or
$n=3$
.
The formula, after some computation, for the iterations would be
$$\begin{eqnarray}\unicode[STIX]{x1D6F7}_{+}^{\prime (0)n}=\frac{-1}{(K_{3})_{+}}\left(\frac{f_{4}^{+}+\text{e}^{\text{i}\unicode[STIX]{x1D6FC}L}((\unicode[STIX]{x1D6FE}P_{+}\unicode[STIX]{x1D6F7}_{-}^{(L)n-1})^{+}+f_{3}^{+})}{(K_{3})_{-}}\right)^{+},\end{eqnarray}$$
where
$K_{3}=(\unicode[STIX]{x1D6FE}P-1)/\unicode[STIX]{x1D6FE}P_{-}$
and also
$$\begin{eqnarray}\unicode[STIX]{x1D6F7}_{-}^{(L)n}=\frac{1}{(K_{1})_{-}}\left(\frac{f_{3}^{-}+\text{e}^{-\text{i}\unicode[STIX]{x1D6FC}L}\left(-\left(\displaystyle \frac{1}{\unicode[STIX]{x1D6FE}P_{-}}\unicode[STIX]{x1D6F7}_{+}^{\prime (0)n}\right)^{-}+f_{4}^{-}\right)}{(K_{1})_{+}}\right)^{-},\end{eqnarray}$$
with
$K_{1}=(\unicode[STIX]{x1D6FE}P-1)/P_{-}$
.
3.1 Convergence
The convergence of the proposed procedure was considered in Kisil (Reference Kisil2017). It gave some of the sufficient conditions for convergence but not the necessary conditions. In this paper the class of matrix (1.1) is more general than is considered in that paper. Two main differences are that: we have no common strip of analyticity in (1.1) and
$A$
,
$B$
and
$C$
do not belong to the classes described in Kisil (Reference Kisil2017). With respect to the later, on the application of Liouville’s theorem the entire functions are constant rather than zero, this is discussed in § 4.1.
In the case when
$k_{0}$
has a small imaginary part the convergence analysis follows almost unchanged as in Kisil (Reference Kisil2017). This gives that convergence occurs for large enough
$|k_{0}|$
, and is faster the larger
$|k_{0}|$
is. We found that the procedure converges fast, for a large range of parameters, even without ‘the strip of analyticity’, in other words, we have taken
$k_{0}$
without an imaginary part. This is unlike other methods such as the rational approximation and ‘pole removal’ methods that rely on taking non-zero imaginary part in
$k_{0}$
. In this paper we also found that the results converge faster for large
$|k_{0}|$
(which is equivalent to larger
$L$
) as was found in Kisil (Reference Kisil2017).
Note that the issue of convergence and the issue of having a good first approximation (3.14) are quite different. It is very possible to have a very bad first approximation which converges fast to the correct solution (see figure 5 in Kisil (Reference Kisil2017)). On the other hand, it is also possible to have a situation where no matter how close to the exact solution is to the initial guess (as long as it is not exactly the solution) each iteration will make the solution only further away from the exact solution, so it diverges. Of course in the case where there is convergence picking a better first guess means that the error in the iterations is smaller and so fewer iterations are needed. A better first guess can be achieved sometimes by first considering (3.12) rather than (3.10) (and neglecting the exponential term) or by keeping some of the exponential terms e.g.
$\text{e}^{-\text{i}\unicode[STIX]{x1D6FC}L}P_{-}f_{4}^{-}$
in (3.10).
For the acoustic problems considered here we have found that the second and the third iteration were very close together, in almost all cases. This means that
$\unicode[STIX]{x1D6F7}_{-}^{(L)3}$
and
$\unicode[STIX]{x1D6F7}_{+}^{\prime (0)3}$
satisfy (2.23) almost exactly and hence are very close to the exact solution. In summary, although we could not guarantee a priori that the method would converge for (2.23), once it is found to converge we can deduce that it is close to the correct solution.
4 A finite plate
4.1 Wiener–Hopf formulation
As a way of verifying the procedure in the previous section we consider a simpler problem to which an exact solution can be constructed using Mathieu functions in the limit of zero porosity. Even for this simple problem the resulting Wiener–Hopf matrix equation cannot be solved exactly.
We look at the situation where the semi-infinite rigid plate is not present, only the finite porous plate. We also suppose there is no background flow, and the incident perturbation is given by
$$\begin{eqnarray}\unicode[STIX]{x1D719}_{i}=\exp (-\text{i}k_{0}x\cos \unicode[STIX]{x1D703}_{i}-\text{i}k_{0}y\sin \unicode[STIX]{x1D703}_{i}-\text{i}k_{0}ct).\end{eqnarray}$$
The governing equation for the scattered field is
$$\begin{eqnarray}\displaystyle \left(\frac{\unicode[STIX]{x2202}}{\unicode[STIX]{x2202}x^{2}}+\frac{\unicode[STIX]{x2202}}{\unicode[STIX]{x2202}y^{2}}+k_{0}^{2}\right)\unicode[STIX]{x1D719}=0. & & \displaystyle\end{eqnarray}$$
The boundary condition required on the plate transforms to
$$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D6F7}_{1}^{\prime }(\unicode[STIX]{x1D6FC},0)=\unicode[STIX]{x1D707}\unicode[STIX]{x1D6F7}_{1}(\unicode[STIX]{x1D6FC},0)-\frac{k_{0}\sin \unicode[STIX]{x1D703}_{i}}{\unicode[STIX]{x1D6FC}-k_{0}\cos \unicode[STIX]{x1D703}_{i}}(\text{e}^{\text{i}(\unicode[STIX]{x1D6FC}-k_{0}\cos \unicode[STIX]{x1D703}_{i})L}-1), & & \displaystyle\end{eqnarray}$$
and since there is no plate for
$x<0$
and
$x>L$
we require
$$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D6F7}_{+}^{(L)}(\unicode[STIX]{x1D6FC},0)=0=\unicode[STIX]{x1D6F7}_{-}^{(0)}(\unicode[STIX]{x1D6FC},0). & & \displaystyle\end{eqnarray}$$
Now the Wiener–Hopf equations arise from the following
$$\begin{eqnarray}\displaystyle & \displaystyle \unicode[STIX]{x1D6F7}_{+}^{\prime (0)}+\unicode[STIX]{x1D6F7}_{1}^{\prime }+\text{e}^{\text{i}\unicode[STIX]{x1D6FC}L}\unicode[STIX]{x1D6F7}_{-}^{\prime (L)}=-\unicode[STIX]{x1D6FE}\text{e}^{\text{i}\unicode[STIX]{x1D6FC}L}(\unicode[STIX]{x1D6F7}_{+}^{(L)}+\unicode[STIX]{x1D6F7}_{-}^{(L)}), & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle \unicode[STIX]{x1D6F7}_{-}^{(0)}+\unicode[STIX]{x1D6F7}_{+}^{(0)}=\text{e}^{\text{i}\unicode[STIX]{x1D6FC}L}(\unicode[STIX]{x1D6F7}_{+}^{(L)}+\unicode[STIX]{x1D6F7}_{-}^{(L)}), & \displaystyle\end{eqnarray}$$
giving
$$\begin{eqnarray}\displaystyle \left(\begin{array}{@{}c@{}}\unicode[STIX]{x1D6F7}_{-}^{\prime (0)}(\unicode[STIX]{x1D6FC})\\ \unicode[STIX]{x1D6F7}_{-}^{(L)}(\unicode[STIX]{x1D6FC})\end{array}\right)=-\left(\begin{array}{@{}cc@{}}-\displaystyle \frac{1}{P}+\unicode[STIX]{x1D6FE}(\unicode[STIX]{x1D6FC}) & \text{e}^{\text{i}\unicode[STIX]{x1D6FC}L}\\ -\text{e}^{-\text{i}\unicode[STIX]{x1D6FC}L} & 0\end{array}\right)\left(\begin{array}{@{}c@{}}\unicode[STIX]{x1D6F7}_{+}^{(0)}(\unicode[STIX]{x1D6FC})\\ \unicode[STIX]{x1D6F7}_{+}^{\prime (L)}(\unicode[STIX]{x1D6FC})\end{array}\right)+\left(\begin{array}{@{}c@{}}g_{1}(\unicode[STIX]{x1D6FC})\\ 0\end{array}\right), & & \displaystyle\end{eqnarray}$$
with
$$\begin{eqnarray}\displaystyle g_{1}(\unicode[STIX]{x1D6FC})=\frac{k_{0}\sin \unicode[STIX]{x1D703}_{i}}{\unicode[STIX]{x1D6FC}-k_{0}\cos \unicode[STIX]{x1D703}_{i}}(\text{e}^{\text{i}(\unicode[STIX]{x1D6FC}-k_{0}\cos \unicode[STIX]{x1D703}_{i})L}-1). & & \displaystyle\end{eqnarray}$$
Again we need to know the growth at infinity of
$\unicode[STIX]{x1D6F7}_{-}^{\prime (0)}(\unicode[STIX]{x1D6FC})$
,
$\unicode[STIX]{x1D6F7}_{-}^{(L)}(\unicode[STIX]{x1D6FC})$
,
$\unicode[STIX]{x1D6F7}_{+}^{(0)}(\unicode[STIX]{x1D6FC})$
and
$\unicode[STIX]{x1D6F7}_{+}^{\prime (L)}(\unicode[STIX]{x1D6FC})$
in the relevant half-planes. We have
$\unicode[STIX]{x1D6F7}_{-}^{\prime (0)}(\unicode[STIX]{x1D6FC})\rightarrow \unicode[STIX]{x1D6FC}^{-1/2}$
and
$\unicode[STIX]{x1D6F7}_{-}^{(L)}(\unicode[STIX]{x1D6FC})\rightarrow \unicode[STIX]{x1D6FC}^{-1}$
as
$\unicode[STIX]{x1D6FC}\rightarrow \infty$
in the lower half-plane and
$\unicode[STIX]{x1D6F7}_{+}^{(0)}(\unicode[STIX]{x1D6FC})\rightarrow \unicode[STIX]{x1D6FC}^{-1}$
and
$\unicode[STIX]{x1D6F7}_{+}^{\prime (L)}(\unicode[STIX]{x1D6FC})\rightarrow \unicode[STIX]{x1D6FC}^{-1/2}$
as
$\unicode[STIX]{x1D6FC}\rightarrow \infty$
in the upper half-plane.
For a finite impermeable plate we can set
$\unicode[STIX]{x1D707}=0$
(equivalently
$P\rightarrow -\infty$
). In this case an exact solution for the scattering of a plane wave by a plate can be found in terms of Mathieu functions (discussed in the following subsection).
The equation has the same structure as before and is solved using the same method which we will not repeat here but simply state the relevant formula. The four equations this time are
$$\begin{eqnarray}\displaystyle & \displaystyle -\text{e}^{-\text{i}\unicode[STIX]{x1D6FC}L}\unicode[STIX]{x1D6F7}_{-}^{\prime (0)}-\unicode[STIX]{x1D6FE}^{-}\unicode[STIX]{x1D6F7}_{-}^{(L)}-(\unicode[STIX]{x1D6FE}^{+}\unicode[STIX]{x1D6F7}_{-}^{(L)})^{-}-g_{2}^{-}=C_{1}, & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle \unicode[STIX]{x1D6F7}_{+}^{\prime (L)}+(\unicode[STIX]{x1D6FE}^{+}\unicode[STIX]{x1D6F7}_{-}^{(L)})^{+}+g_{2}^{+}=C_{1}, & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle \unicode[STIX]{x1D6F7}_{-}^{\prime (0)}+(\unicode[STIX]{x1D6FE}^{-}\unicode[STIX]{x1D6F7}_{+}^{(0)})^{-}-g_{1}^{-}=C_{2}, & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle -\unicode[STIX]{x1D6FE}^{+}\unicode[STIX]{x1D6F7}_{+}^{(0)}-\text{e}^{\text{i}\unicode[STIX]{x1D6FC}L}\unicode[STIX]{x1D6F7}_{+}^{\prime (L)}-(\unicode[STIX]{x1D6FE}^{-}\unicode[STIX]{x1D6F7}_{+}^{(0)})^{+}+g_{1}^{+}=C_{2}, & \displaystyle\end{eqnarray}$$
where
$g_{2}=-\text{e}^{-\text{i}\unicode[STIX]{x1D6FC}L}g_{1}$
. For the initial step we have
$$\begin{eqnarray}\unicode[STIX]{x1D6F7}_{-}^{(L)1}=\frac{-1}{(\unicode[STIX]{x1D6FE})_{-}}\left(\frac{g_{4}^{-}}{(\unicode[STIX]{x1D6FE})_{+}}\right)^{-},\end{eqnarray}$$
where we defined
$g_{4}^{-}=g_{2}^{-}+C_{1}$
,
$g_{4}^{+}=g_{2}^{+}-C_{1}$
and
$g_{3}^{-}=g_{1}+C_{2}$
,
$g_{3}^{+}=g_{1}^{+}-C_{2}$
. The iterative solution is obtained
$$\begin{eqnarray}\unicode[STIX]{x1D6F7}_{-}^{(L)n}=\frac{-1}{(\unicode[STIX]{x1D6FE})_{-}}\left(\frac{g_{4}^{-}+\text{e}^{-\text{i}\unicode[STIX]{x1D6FC}L}((\unicode[STIX]{x1D6FE}\unicode[STIX]{x1D6F7}_{+}^{(0)n})^{-}+g_{3}^{-})}{(\unicode[STIX]{x1D6FE})_{+}}\right)^{-},\end{eqnarray}$$
and
$$\begin{eqnarray}\unicode[STIX]{x1D6F7}_{+}^{(0)n}=\frac{1}{(\unicode[STIX]{x1D6FE})_{+}}\left(\frac{g_{3}^{+}+\text{e}^{\text{i}\unicode[STIX]{x1D6FC}L}(-(\unicode[STIX]{x1D6FE}\unicode[STIX]{x1D6F7}_{-}^{(L)n-1})^{+}+g_{4}^{+})}{(\unicode[STIX]{x1D6FE})_{-}}\right)^{+}.\end{eqnarray}$$
We notice from the formulation above that the constants
$C_{1,2}$
cancel at each stage. For example,
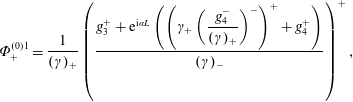$$\begin{eqnarray}\unicode[STIX]{x1D6F7}_{+}^{(0)1}=\frac{1}{(\unicode[STIX]{x1D6FE})_{+}}\left(\frac{g_{3}^{+}+\text{e}^{\text{i}\unicode[STIX]{x1D6FC}L}\left(\left(\unicode[STIX]{x1D6FE}_{+}\left(\displaystyle \frac{g_{4}^{-}}{(\unicode[STIX]{x1D6FE})_{+}}\right)^{-}\right)^{+}+g_{4}^{+}\right)}{(\unicode[STIX]{x1D6FE})_{-}}\right)^{+},\end{eqnarray}$$
where
$$\begin{eqnarray}\displaystyle \left(\unicode[STIX]{x1D6FE}_{+}\left(\frac{g_{4}^{-}}{(\unicode[STIX]{x1D6FE})_{+}}\right)^{-}\right)^{+}=\left(\unicode[STIX]{x1D6FE}_{+}\frac{g_{4}^{-}}{(\unicode[STIX]{x1D6FE})_{+}}-\unicode[STIX]{x1D6FE}_{+}\left(\frac{g_{4}^{-}}{(\unicode[STIX]{x1D6FE})_{+}}\right)^{+}\right)^{+}=-\unicode[STIX]{x1D6FE}_{+}\left(\frac{g_{4}^{-}}{(\unicode[STIX]{x1D6FE})_{+}}\right)^{+}. & & \displaystyle\end{eqnarray}$$
Considering only the terms in (4.16) that contain constants
$C_{1,2}$
we find
$$\begin{eqnarray}\frac{1}{(\unicode[STIX]{x1D6FE})_{+}}\left(\frac{-C_{2}-\text{e}^{\text{i}\unicode[STIX]{x1D6FC}L}\left(\unicode[STIX]{x1D6FE}_{+}\left(\displaystyle \frac{C_{1}}{\unicode[STIX]{x1D6FE}_{+}}\right)^{+}-C_{1}\right)}{\unicode[STIX]{x1D6FE}_{-}}\right)^{+}=0,\end{eqnarray}$$
hence neither
$C_{1}$
nor
$C_{2}$
contribute towards the calculation of
$\unicode[STIX]{x1D6F7}_{+}^{(0)1}$
. A similar calculation shows neither contribute to
$\unicode[STIX]{x1D6F7}_{-}^{(L)2}$
, and so on for all iterative steps.
4.2 Exact solution
An exact solution of acoustic scattering by a finite rigid plate currently cannot be obtained using a Wiener–Hopf formulation but it is possible using other methods. It is achieved by considering the Helmholtz equation in an elliptic coordinate system (McLachlan Reference McLachlan1964). The advantage of this coordinate transformation is that the boundary condition on a finite-range interval, i.e. a degenerate ellipse, maps to a full-range elliptic coordinate interval.
Here we present the exact solution without derivation (which can be found in McLachlan (Reference McLachlan1964)). To transform from Cartesian coordinates to elliptic coordinates we use the formula
$$\begin{eqnarray}x=\frac{d}{2}\cosh \unicode[STIX]{x1D709}\cos \unicode[STIX]{x1D702},\quad y=\frac{d}{2}\sinh \unicode[STIX]{x1D709}\sin \unicode[STIX]{x1D702},\end{eqnarray}$$
where
$d$
is the focal distance of the ellipses.
We first need to introduce the even and odd angular Mathieu functions, which are denoted by
$$\begin{eqnarray}\displaystyle H_{m}(\unicode[STIX]{x1D702};q)=\left\{\begin{array}{@{}ll@{}}ce_{m}(\unicode[STIX]{x1D702};q),\quad & m=0,1,2\ldots ,\\ se_{m}(\unicode[STIX]{x1D702};q),\quad & m=1,2,3\ldots .\end{array}\right. & & \displaystyle\end{eqnarray}$$
The even and odd radial Mathieu functions of first and second order are denoted by
$$\begin{eqnarray}\displaystyle G_{m}(\unicode[STIX]{x1D709};q)=\left\{\begin{array}{@{}ll@{}}Je_{m}(\unicode[STIX]{x1D709};q),Jo_{m}(\unicode[STIX]{x1D709};q),\quad & \text{first kind},\\ Ne_{m}(\unicode[STIX]{x1D709};q),No_{m}(\unicode[STIX]{x1D709};q),\quad & \text{second kind},\end{array}\right. & & \displaystyle\end{eqnarray}$$
and finally the Mathieu–Hankel function is given by
$$\begin{eqnarray}Ho_{m}^{(1)}(\unicode[STIX]{x1D709};q)=Jo_{m}(\unicode[STIX]{x1D709};q)+\text{i}No_{m}(\unicode[STIX]{x1D709};q).\end{eqnarray}$$
The scattered acoustic field can be thus expressed as in McLachlan (Reference McLachlan1964, 19.14)
$$\begin{eqnarray}\mathop{\sum }_{r=0}^{\infty }S_{r}Ho_{r}(\unicode[STIX]{x1D709})se_{r}(\unicode[STIX]{x1D702}),\end{eqnarray}$$
where the coefficients
$S_{r}$
are found to be
$$\begin{eqnarray}S_{n}=-\text{i}^{n}\sqrt{8\unicode[STIX]{x03C0}}se_{n}(\unicode[STIX]{x1D6FC})\frac{Jo_{n}^{\prime }(0)}{Ho_{n}^{\prime }(0)}.\end{eqnarray}$$
This solution is valid everywhere. In order to calculate the far-field numerically an asymptotic formula is used for
$Ho_{r}(\unicode[STIX]{x1D709})$
. We shall refer to this solution as the ‘Mathieu solution’.
5 Results
Here we investigate the effects of a finite porous extension on the generation of noise by of a gust convecting past a trailing edge by implementing the new Wiener–Hopf factorisation procedure as outlined in the preceding sections. First we illustrate the convergence of the new factorisation method by considering the scattering of a plane sound wave by a finite rigid plate in zero mean flow, for which the solution is known.
5.1 Validation of the iterative method
We begin by illustrating our new iterative factorisation method by considering the scattering of a plane sound wave of frequency
$k_{0}$
and incidence angle
$\unicode[STIX]{x1D703}_{i}$
by a finite impermeable plate of length
$2$
as discussed in § 4. The iterative procedure converges quickly when the initially neglected term,
$\text{e}^{-\text{i}\unicode[STIX]{x1D6FC}L}\unicode[STIX]{x1D6F7}_{-}^{(0)}$
is much smaller than the terms initially retained (Kisil Reference Kisil2017). It is known from Ayton & Peake (Reference Ayton and Peake2013) that for high-frequency finite plate acoustic interactions, the dominant contribution to the scattered field can be calculated from only one edge (as if the plate were semi-infinite). The correction term due to the rescattering of this acoustic field by the second edge is
$O(k_{0}^{-1/2})$
smaller, except at shallow angles directly upstream and downstream where the two fields are formally of the same magnitude to enforce the edge continuity conditions. Subsequent correction terms continue to be
$O(k_{0}^{-1/2})$
smaller than the last term calculated.
Figure 2. Far-field scattered acoustic directivity generated by a plane sound wave incident at
$45^{\circ }$
from the far field of varying frequencies
$k_{0}$
scattering off a finite impermeable plate of length
$2$
. Solutions obtained from the first and second iterative steps are plotted against the Mathieu solution.
With this in mind we consider the scattering of plane waves of frequencies
$k_{0}=1,6,10,16$
. In figure 2 we show the truncated Mathieu solutions against the first and second iterative solutions for the far-field acoustic directivity for a sound wave with incident angle
$\unicode[STIX]{x1D703}_{i}=\unicode[STIX]{x03C0}/4$
. For
$k_{0}=1$
we do not expect convergence of the result, as the initially neglected term is not small. Indeed in figure 2(a) we see the first and second iterative solutions vary greatly, however they give us some insight into how the iterative procedure works: the initial solution neglects one scattering edge (at
$x=0$
), thus we see a semi-infinite style directivity pattern which is zero at
$\unicode[STIX]{x1D703}=0$
but non-zero at
$\unicode[STIX]{x1D703}=\unicode[STIX]{x03C0}$
. The second iteration introduces a correction for the
$x=0$
edge, thus forcing the pressure to be zero at
$\unicode[STIX]{x1D703}=\unicode[STIX]{x03C0}$
, but as the iterative procedure is not complete we no longer have zero pressure at
$\unicode[STIX]{x1D703}=0$
. Even after 5 iterations we found that the solution had not converged for
$k_{0}=1$
, thus we believe in this case the iterative procedure is simply not appropriate.
For frequencies
$k_{0}=6,10,16$
there is good agreement between the iterative solution and the Mathieu solution after just 2 iterations, with better agreement for the higher frequencies (as expected). The key differences between the first and second iterative solutions follow similar reasoning to
$k_{0}=1$
, with the first iterative solutions having significant errors for
$\unicode[STIX]{x1D703}=\unicode[STIX]{x03C0}$
which are quickly corrected by the time of the second iteration. We note however that the first iteration does not resemble high-frequency single-edge scattering (i.e. a semi-infinite plate result) as it includes oscillations which arise from leading- and trailing-edge interaction. These are present in the first iterative solution because the forcing,
$f_{3,4}$
, used in the initial steps come from finite plate forcing, not semi-infinite plate forcing, thus includes some interacting leading- and trailing-edge terms.
5.2 Semi-infinite impermeable plate with finite porous extension
5.2.1 Comparison to Ayton (Reference Ayton2016)
Here we compare results for our semi-infinite partially porous plate to the sound scattering results for a finite partially porous plate given by Ayton (Reference Ayton2016). Ayton (Reference Ayton2016) uses a pole removal technique to obtain the far-field acoustic directivity due to a sound wave scattering off a flat plate that consists of a finite impermeable rigid section and a finite poroelastic section (which for the purposes of this section we consider to be only porous). For our new iterative method we require a multiplicative factorisation of
$(\unicode[STIX]{x1D6FE}P-1)$
, equivalently,
$\unicode[STIX]{x1D707}+\unicode[STIX]{x1D6FE}$
, where the constant porosity parameter,
$\unicode[STIX]{x1D707}$
, is small. We can therefore use the asymptotic factorisation from Crighton & Leppington (Reference Crighton and Leppington1970);
$$\begin{eqnarray}(\unicode[STIX]{x1D707}+\unicode[STIX]{x1D6FE}(\unicode[STIX]{x1D6FC}))_{\pm }=\unicode[STIX]{x1D6FE}_{\pm }(\unicode[STIX]{x1D6FC})\left(1+\frac{\unicode[STIX]{x1D707}}{\unicode[STIX]{x03C0}\unicode[STIX]{x1D6FE}(\unicode[STIX]{x1D6FC})}\cos ^{-1}\left(\pm \frac{\unicode[STIX]{x1D6FC}}{k_{0}}\right)+o(\unicode[STIX]{x1D707})\right),\end{eqnarray}$$
and neglect the
$o(\unicode[STIX]{x1D707})$
contribution. This factorisation is obtained by supposing
$(\unicode[STIX]{x1D707}+\unicode[STIX]{x1D6FE})_{\pm }=\unicode[STIX]{x1D6FE}_{\pm }+\unicode[STIX]{x1D707}G_{\pm }+o(\unicode[STIX]{x1D707}^{2})$
, and using the known additive factorisation
$\unicode[STIX]{x1D6FE}=\unicode[STIX]{x1D6FE}^{+}+\unicode[STIX]{x1D6FE}^{-}$
from Noble (Reference Noble1958, p. 21) to solve for
$G_{\pm }$
.
For investigation of
$\unicode[STIX]{x1D707}=O(1)$
a numerical factorisation of
$\unicode[STIX]{x1D707}+\unicode[STIX]{x1D6FE}$
could be performed similar to that used in Jaworski & Peake (Reference Jaworski and Peake2013). Note the pole removal method does not rely on an asymptotic factorisation thus can investigate plates with higher porosity distributions.
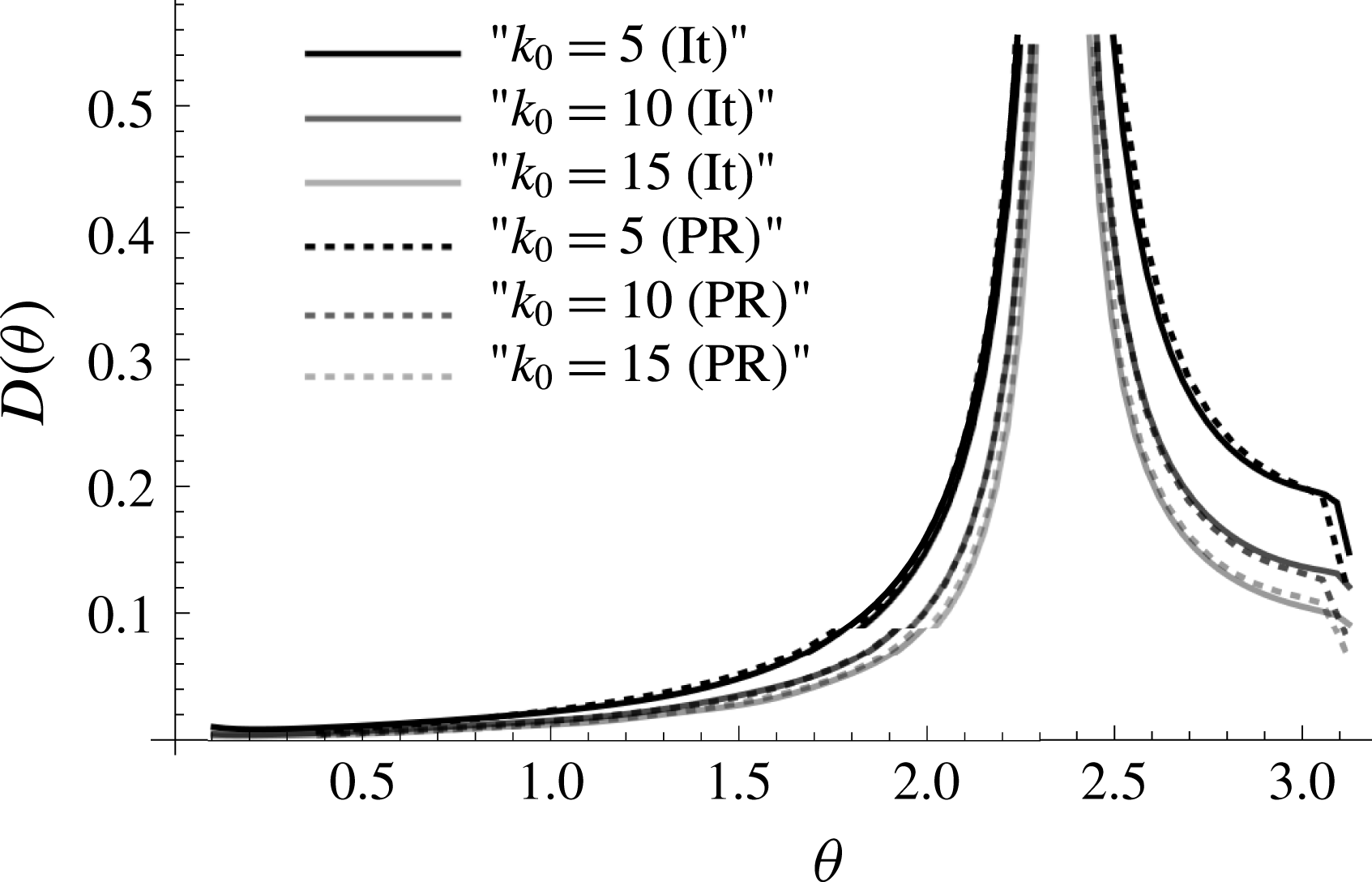
Figure 3. Comparison of far-field directivity calculated using the iterative method (It) or pole removal method (PR) for an incident sound wave with frequency
$k_{0}$
impinging on a semi-infinite flat plate with porous section of length
$L=1$
,
$\unicode[STIX]{x1D707}=0.1$
.
First we consider a direct comparison of the two methods by applying the pole removal technique to the semi-infinite partially porous plate. In figure 3 we see good agreement between the two methods for mid and high frequencies. The results are heavily dominated by the Fresnel zone at the angle of reflection of the incident sound wave,
$\unicode[STIX]{x1D703}=3\unicode[STIX]{x03C0}/4$
and uniformly valid expansions for the far-field directivity are required to deal with the pole singularity at this angle. Note that the pole removal method of Ayton (Reference Ayton2016) was seen only to be accurate at high frequencies and does not have a formal error bound to an exact solution, whilst our new iterative method is proved to converge to the exact solution (Kisil Reference Kisil2017) thus is able to present results to within a specified error bound. Further, the pole removal method can only recover the far-field acoustic field and not the mid or near field. A benefit of the new method in this paper is that we can not only consider a wider range of frequencies, but we can also obtain the scattered field at any point in the domain, thus can use near-field results from a far-field incident sound wave to obtain an acoustic amplification factor for far-field scattering from a near-field source by reciprocity (Jaworski & Peake Reference Jaworski and Peake2013). We shall comment on this amplification factor shortly. The main advantage of the pole removal method over the iterative approach is that it is easy to adapt for use on any size matrix Wiener–Hopf problem (Ayton (Reference Ayton2016) considers a 3
$\times$
3 matrix problem), whilst the iterative method would be more complicated to adapt to higher dimensions, and likely require stricter conditions to be placed on the parameters used to ensure convergence.
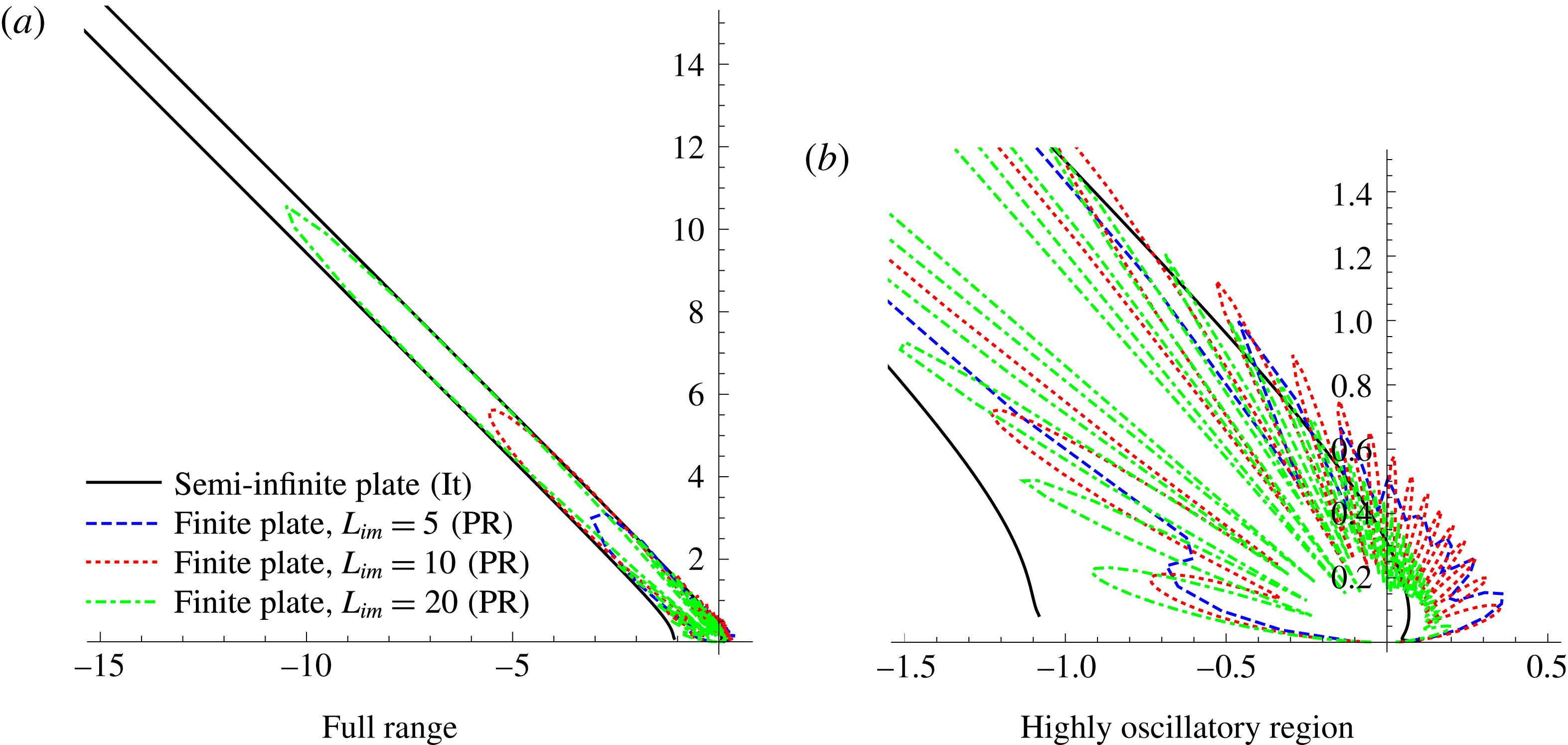
Figure 4. Comparison of far-field directivity calculated using the iterative method (It) for a semi-infinite plate to the directivity from a finite plate calculated using the pole removal method (PR). Both have porous lengths of
$L=1$
, sound wave frequency
$k_{0}=5$
incident from angle
$\unicode[STIX]{x03C0}/4$
and porosity
$\unicode[STIX]{x1D707}=0.1$
. The finite impermeable plate length,
$L_{im}$
, is allowed to vary.
By including the finite leading edge we see it have a big effect on the overall directivity in figure 4 for the scattering of a sound wave. In particular the Fresnel regions at the angle of direct reflection of the incident wave (thereby indicated by the largest lobes) are significantly altered by the extra leading-edge scattered field. Uniformly valid expansions for the far-field directivity are now not required, as the combination of the Fresnel regions from the leading and trailing edges regularise one another, resulting in the pole at
$\unicode[STIX]{x1D703}=3\unicode[STIX]{x03C0}/4$
becoming a removable singularity. As such, the leading-edge field significantly reduces the overall impact of the trailing-edge Fresnel region on the far-field noise. As the length of the impermeable section is increased, the amplitude of the Fresnel region increases, and the modulation of the directivity increases. We also observe that the finite leading edge reduces the scattered field directly upstream for any plate length, illustrating that the leading-edge field is formally the same magnitude as the trailing-edge field close to the downstream direction (as discussed in § 5.1).
For sound scattering we therefore note that there is a great influence of a finite leading edge on the overall predictions of the far-field noise as both leading and trailing-edge scattered fields particularly in the Fresnel regions since both the leading and trailing edge directly scatter the sound wave at angle
$\unicode[STIX]{x1D703}=3\unicode[STIX]{x03C0}/4$
. However, we are not concerned by this influence for predicting trailing-edge noise as our convective gust model supposes the incident field does not interact with the leading edge directly. And, of course, for a convective gust there are no Fresnel regions thus no regularisation of the far-field directivity is required.
5.2.2 Trailing-edge noise
Now that we have validated our new approach, we consider the original problem of a convective boundary layer gust interacting with the semi-infinite partially porous plate. In all results in this section we shall take
$\unicode[STIX]{x1D703}_{i}=\unicode[STIX]{x03C0}/4$
, and
$L=1$
.
We begin by illustrating the convergence of the iterative procedure in figure 5 which shows the far-field acoustic directivity for different
$k_{0}$
and
$\unicode[STIX]{x1D707}$
values. After 2 iterations the solution is indistinguishable from the third iteration in each case with differences of less than
$10^{-5}$
between the two solutions. The convergence of the iterative method is fast in this case for low frequency (compared to the finite plate case where the condition of high frequency ensured quick convergence), since we restrict attention to low porosity, and therefore by considering the scalings of terms in the initial equation, (3.10), in terms of porosity,
$\unicode[STIX]{x1D707}\ll 1$
or equivalently
$|P|\gg 1$
, we see the initially neglected term,
$\unicode[STIX]{x1D6F7}_{-}^{(0)}\text{e}^{-\text{i}\unicode[STIX]{x1D6FC}L}$
, is smaller than those retained. We illustrate the relative size of the neglected terms in figure 6 to verify it is indeed formally smaller than the initially retained terms, thus we expect (and see) quick convergence of the iterative method. For lower values of
$\unicode[STIX]{x1D707}$
and lower frequencies
$k_{0}$
the relative size of the neglected term is much smaller than at higher values of
$\unicode[STIX]{x1D707}$
and
$k_{0}$
, however in these cases the neglected term is still formally smaller and therefore the iterative procedure converges.
From hereon our results are given as the second iterative solution.
Figure 5. Far-field acoustic directivity generated by a convective gust in mean flow
$M=0.6$
of varying frequencies
$k_{0}$
interacting with a semi-infinite impermeable plate with an attached finite porous plate of unit length and porosity parameter
$\unicode[STIX]{x1D707}$
. First, second and third iterative solutions are presented.
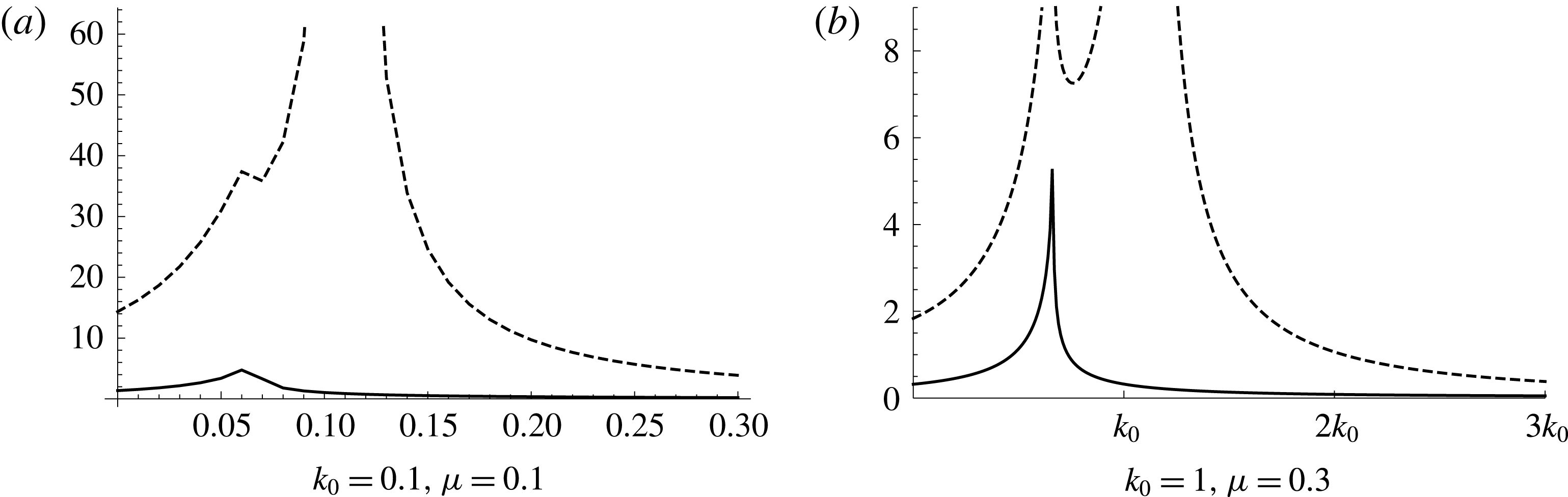
Figure 6. Absolute value of the two terms on the right-hand side of (3.10) as calculated after one complete iterative loop. First term is the dashed line, second term (which is initially neglected) is the solid line.
Figure 7 shows the effects of altering the porosity parameter
$\unicode[STIX]{x1D707}$
on the far-field acoustic directivity for gusts of different frequencies,
$k_{0}$
. We see that the reduction of far-field acoustic pressure achievable by an increasingly porous plate is lessened as the incident frequency increases, as expected from the results of Jaworski & Peake (Reference Jaworski and Peake2013). However, at high frequency the directivity pattern, although not significantly reduced in magnitude, significantly changes in overall shape.
For low frequencies, the acoustic directivity behaves as a single source from just the trailing edge,
$x=L$
, (driven by a pressure jump across the trailing edge) therefore increasing porosity behaves in an identical manner to that seen for the scattering of a near-field trailing-edge source by a finite porous plate investigated in Cavalieri et al. (Reference Cavalieri, Wolf and Jaworski2016, figure 7a). At higher frequencies, the source is no longer compact therefore there is notable interaction from scattering by the trailing edge,
$x=L$
, and the impermeable–permeable junction,
$x=0$
. This secondary acoustic field, emanating from the permeable–impermeable junction, is expected to be weaker than the secondary source in Cavalieri et al. (Reference Cavalieri, Wolf and Jaworski2016), the (finite) leading-edge field. We see from figure 7 that at high frequency
$k_{0}=2$
, increasing porosity rotates the directivity away from the upstream direction without drastically altering the overall magnitude compared to the rigid plate. This effect is different to the effects of the finite leading edge seen in Cavalieri et al. (Reference Cavalieri, Wolf and Jaworski2016, figure 7b) (reduction of overall magnitude and oscillations).
Figure 7. Far-field acoustic directivity generated by gusts of varying frequencies
$k_{0}$
interacting with a semi-infinite impermeable plate with an attached finite porous plate of unit length and porosity parameter
$\unicode[STIX]{x1D707}$
, in mean flow
$M=0.6$
.
We can consider the effect of the secondary acoustic field emanating from permeable–impermeable junction by considering the correction term between the first iterative solution and the converged iterative solution (which for the cases we consider here is the second iterative solution), since the first solution accounts for the edge at
$x=L$
and successive solutions correct for the edge at
$x=0$
. Figure 5 shows the far-field directivities calculated by the first and second iterative solutions; for low frequencies this correction rescales the overall pressure almost uniformly over all
$\unicode[STIX]{x1D703}$
directions. This indicates the source at
$x=0$
behaves in an identical but weaker manner to the source at
$x=L$
, i.e. is dipole-like. For
$k_{0}=2$
,
$\unicode[STIX]{x1D707}=0.3$
we see a significant change in directivity between the first and second iterative solutions, therefore the permeable–impermeable junction is no longer behaving in an identical manner to the trailing edge. The trailing edge (first solution) directs noise strongly at some angle
$\unicode[STIX]{x03C0}/2<\unicode[STIX]{x1D717}<\unicode[STIX]{x03C0}$
as expected for edge interaction in subsonic flow with high Mach number,
$M=0.6$
. The permeable–impermeable junction (correction to the first solution) instead seems to direct noise predominantly at some angle
$\unicode[STIX]{x1D717}^{\prime }<\unicode[STIX]{x1D717}$
.
In figure 8 we investigate the far-field directivity generated by the difference between the first and second iterative solutions for high-frequency interactions with
$M=0.6$
, and indeed see that for higher frequencies the impermeable–permeable correction term has a significantly different directivity pattern that is directed away from the main region of pressure for the trailing-edge term. We also see that whilst increasing porosity reduces the magnitude of the trailing-edge term, it increases the magnitude of the correction term, therefore when the two terms are combined there is little difference in the overall magnitude of the acoustic pressure in figure 7(d). The directivity pattern generated by the correction term is significantly different to the
$\sin \unicode[STIX]{x1D703}/2$
directivity expected from a finite leading edge.
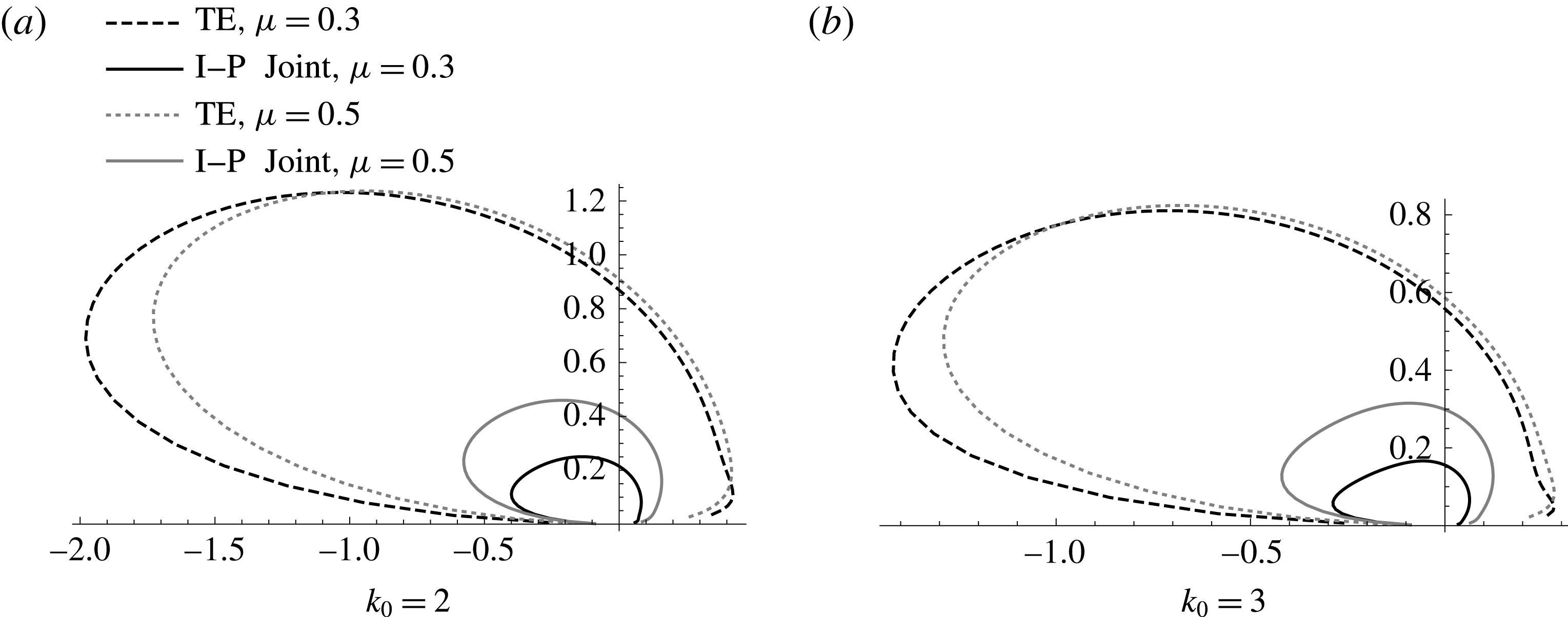
Figure 8. Absolute value of the difference between the first and second iterative solutions (I–P Junction), compared to the first iterative solution (TE) for
$M=0.6$
.
Finally we can investigate the acoustic amplification factor,
$B$
due to a near-field acoustic source; by considering the near-field scattering of a far-field incident sound wave we can invoke reciprocity to obtain the far-field acoustic amplification due to a near-field quadrupole source. The amplification factor is defined in Jaworski & Peake (Reference Jaworski and Peake2013) as
$B=|\tilde{B}|k_{0}^{-2}$
, where
$$\begin{eqnarray}\frac{\unicode[STIX]{x2202}\unicode[STIX]{x1D6F7}_{+}}{\unicode[STIX]{x2202}y}(\unicode[STIX]{x1D6FC},0)\sim \tilde{B}\unicode[STIX]{x1D6FC}^{-1/2}\quad \text{as }|\unicode[STIX]{x1D6FC}|\rightarrow \infty .\end{eqnarray}$$
It is seen in Jaworski & Peake (Reference Jaworski and Peake2013) that for a low porosity edge with
$\unicode[STIX]{x1D6FC}_{H}=0.0014$
(equivalent to
$\unicode[STIX]{x1D707}=0.034$
) the amplification factor as a function of frequency has a gradient of
$-1$
for low frequency, and a gradient of
$-1.5$
for high frequency (which is also the gradient found for a rigid edge). We recover these limits for low porosities in figure 9 as expected since the near-field quadrupole primarily only interacts with the porous section of the plate, thus this can be well approximated by the semi-infinite porous plate.
These results further validate our new approach, however considering a near-field trailing-edge source does not suitably investigate the effects of an impermeable–permeable junction lying within the turbulent boundary layer – this paper has focussed on a convective gust over both the impermeable and permeable sections of the plate to enable turbulence to interact with both the junction and the trailing edge.
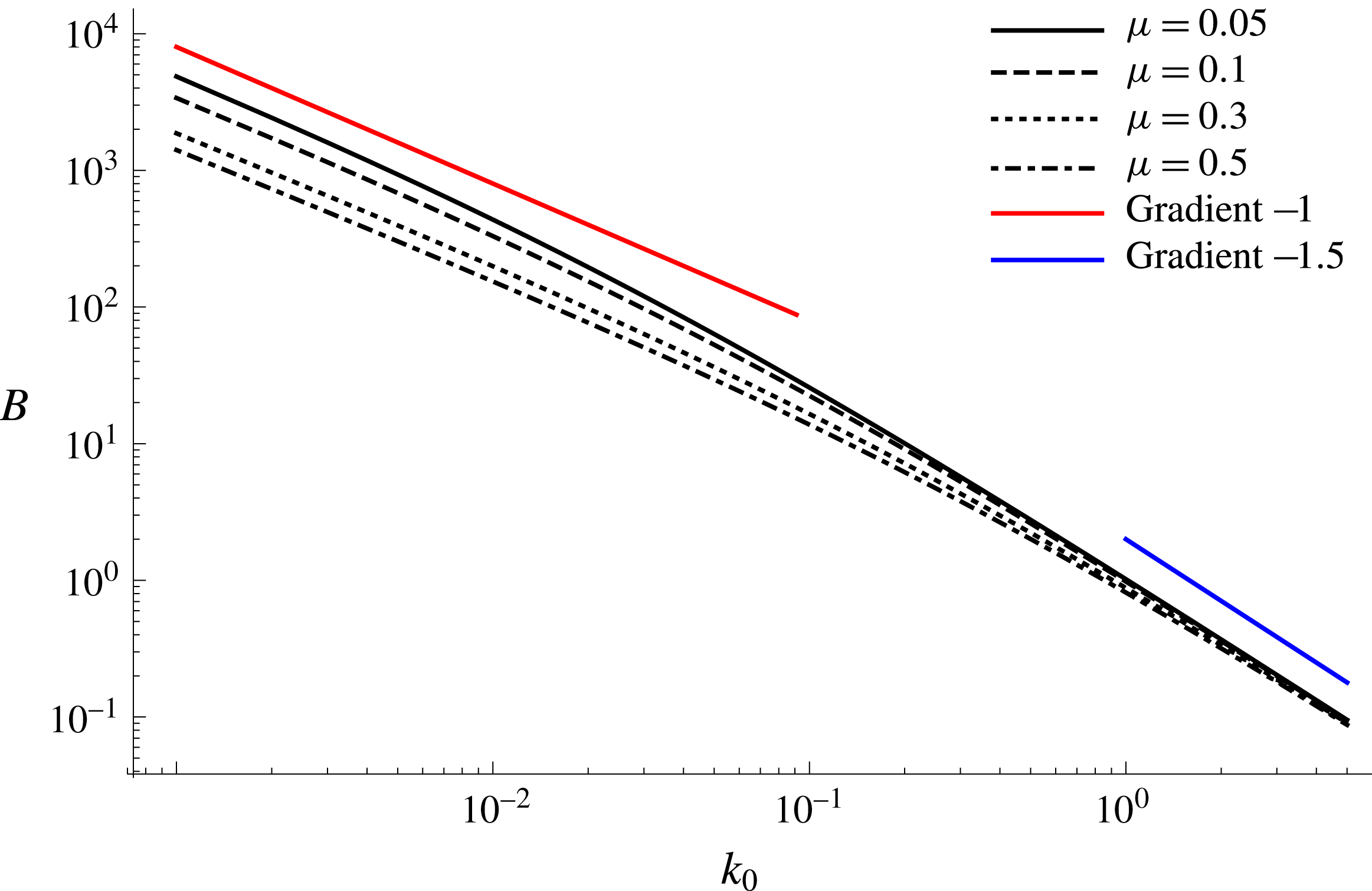
Figure 9. Amplification factor,
$B$
, as a function of frequency
$k_{0}$
for a range of partially porous plates.
In this section we have determined that at low frequencies the impermeable–permeable junction seems not to greatly affect the noise generated in the far field by near-field turbulence, and thus the predictions by Jaworski & Peake (Reference Jaworski and Peake2013) using a semi-infinite permeable plate are accurate even if the plate were only partially porous. However, for higher-frequency turbulence, the impermeable–permeable junction has a greater effect on the far-field directivity pattern, thus we expect that for high frequencies the predictions of Jaworski & Peake (Reference Jaworski and Peake2013) may not be sufficiently accurate to present the full picture of a partially porous aerofoil. Thus we investigate the effects of the impermeable–permeable junction on specifically high-frequency interactions in the following section.
5.3 Effects of porosity on high-frequency turbulence
It is known that trailing-edge noise dominates overall aerofoil noise for high-frequency interactions, whilst at mid- to low-frequency interactions leading-edge noise dominates (Chaitanya et al.
Reference Chaitanya, Gill, Narayanan, Joseph, Vanderwel, Zhang and Ganapathisubramani2015). A proposed parameter indicating where trailing-edge noise becomes dominant is
$\unicode[STIX]{x1D714}^{\ast }t/U^{\ast }>1$
, where
$\unicode[STIX]{x1D714}^{\ast }$
is dimensionalised frequency,
$t$
is the ratio of aerofoil thickness to chord length and
$U^{\ast }$
is dimensionalised mean flow velocity. Thus if we wish to investigate the effects of porosity on total aerofoil noise generation, we must consider a high-frequency regime where trailing-edge noise plays a key part. Despite previous studies indicating that porosity only has an effect at low frequencies (Jaworski & Peake Reference Jaworski and Peake2013) we have seen in the previous section that a partially porous semi-infinite plate behaves differently to a fully rigid (or indeed fully porous) semi-infinite plate, due to the interaction between the impermeable–permeable junction and the trailing-edge tip itself. This interaction is influential at high frequencies because the wavelength of the gust is much shorter than the distance between the two points, and is clearly not modelled in Jaworski & Peake’s (Reference Jaworski and Peake2013) work for a fully porous plate.
Figure 10 shows the difference in
$\text{d}\text{B}$
of the sound power predicted from a fully porous plate to that predicted from our partially porous plate, namely
$$\begin{eqnarray}\unicode[STIX]{x0394}P(k_{0})=10\log _{10}\left[\frac{\displaystyle \int _{0}^{\unicode[STIX]{x03C0}}|D_{fully}(\unicode[STIX]{x1D703})|^{2}\,\text{d}\unicode[STIX]{x1D703}}{\displaystyle \int _{0}^{\unicode[STIX]{x03C0}}|D_{partial}(\unicode[STIX]{x1D703})|^{2}\,\text{d}\unicode[STIX]{x1D703}}\right],\end{eqnarray}$$
where
$D_{partial}(\unicode[STIX]{x1D703})$
is the directivity predicted for our partially porous plate, equation (2.29), and
$D_{fully}(\unicode[STIX]{x1D703})$
is the corresponding directivity predicted if the plate were fully porous.
Figure 10.
$\unicode[STIX]{x0394}P(k_{0})$
for semi-infinite partially porous plates with varying porosity parameter,
$\unicode[STIX]{x1D707}$
.
We see for all mid to high frequencies and all porosity parameters the relative difference is always negative. We therefore assess that the effect of the permeable–impermeable joint is to slightly increase the total noise generated at the trailing edge in comparison to either a fully rigid or fully porous plate (since at high frequencies these two predictions are identical). This increase is minor (approximately 1–2 dB) in comparison to the decreases in noise seen at low frequencies. The increase is greatest for higher porosity plates since there is a bigger difference in the two scattering points thus a greater interaction effect of the two fields. The difference in sound oscillates with frequency
$k_{0}$
since an interference between the trailing edge and the impermeable–permeable junction can be constructive or destructive. Our prediction of an increase in noise for a partially porous plate is in agreement with the experimental findings of Geyer & Sarradj (Reference Geyer and Sarradj2014), although they speculated that their observed high-frequency noise increase for partially porous aerofoil (compared to fully impermeable aerofoils) was due to increased surface roughness noise. As our model does not allow for roughness noise, we propose a combination of increased roughness noise, and interference effects between the impermeable–permeable junction and trailing edge can lead to an increase of noise at high frequencies when an aerofoil is partially porous.
Using the results of figure 10 we can estimate the interaction effect of the impermeable–permeable junction to be of the form
$1+\unicode[STIX]{x1D707}\text{e}^{\text{i}M^{2}Lk_{0}}$
, where the
$1$
denotes the scattering from the porous trailing-edge tip, and
$\unicode[STIX]{x1D707}\text{e}^{\text{i}M^{2}Lk_{0}}$
is the interference caused by the impermeable–permeable junction, which sensibly tends to zero as the plate becomes fully rigid. In figure 11 we plot this interaction function (shifted to align with figure 10) across the same range of frequencies as used figure 10, and see good relative agreement between results. This implies that the overall radiation is generated by two fields; a trailing-edge field and an impermeable–permeable junction field which interfere when summed in the far field.
One would perhaps expect as
$k_{0}\rightarrow \infty$
the interaction effect to significantly decay as the interference should scale inversely with
$k_{0}$
and therefore the partially porous plate to behave identically to the fully porous plate. We do not see this in our integrated results because the two acoustic fields directly upstream (
$\unicode[STIX]{x1D703}=\unicode[STIX]{x03C0}$
) are of the same magnitude thus any constructive or destructive interference here will always have a notable effect on the total sound. We illustrate this feature, in the extreme cases of
$k_{0}=100,110$
, in figure 12; we clearly see for the majority of the far field the acoustic directivities are in very good agreement, however as we approach the downstream direction, the interference leads to a large different between the directivities.
Figure 11. Interference function,
$1+\unicode[STIX]{x1D707}\text{e}^{\text{i}M^{2}L(k_{0}+3)}$
, for various
$\unicode[STIX]{x1D707}$
with fixed
$L=1$
.
Figure 12. Far-field directivity for partially porous plate with
$\unicode[STIX]{x1D707}=0.1$
,
$L=1$
,
$M=0.6$
compared to a fully rigid plate,
$\unicode[STIX]{x1D707}=0$
.
6 Conclusions
This paper investigates the interaction of a convective gust with a partially porous semi-infinite plate in uniform steady flow. We find, in agreement with previous work, that porous trailing-edge adaptations can significantly reduce low-frequency interaction noise. New insight into the effects of the impermeable–permeable junction have been found as we see increasing porosity has the capability to rotate the far-field directivity away from the upstream region for mid-frequency interactions due to interference between acoustic fields from the permeable–impermeable junction, and the trailing-edge tip itself. Whilst a porous trailing-edge adaptation does not significantly reduce far-field mid-frequency trailing-edge noise it could prove useful for controlling the predominant direction of noise propagation. Further, at high-frequencies the interference of the impermeable–permeable junction has been seen to increase the total far-field noise slightly when compared to a fully rigid plate in agreement with experimental findings of Geyer & Sarradj (Reference Geyer and Sarradj2014).
Elasticity has not been included in this problem as the interaction between the mean flow and the elastic plate would cause significant complications to the analysis. An approach involving matched asymptotic expansions, similar to Abrahams (Reference Abrahams1983), and the Wiener–Hopf technique could be used to tackle the elasticity problem in the future. We have also restricted the porosity of the extension to satisfy
$\unicode[STIX]{x1D707}\ll 1$
to allow both an asymptotic factorisation of the kernel function,
$\unicode[STIX]{x1D707}+\unicode[STIX]{x1D6FE}$
, and to ensure rapid convergence of the iterative solution. This restriction only discounts a small range of values investigated by Jaworski & Peake (Reference Jaworski and Peake2013). Currently the iterative procedure using an asymptotic factorisation of
$\unicode[STIX]{x1D707}+\unicode[STIX]{x1D6FE}$
, implemented in Mathematica on a standard 4-core desktop computer, calculates the third iteration for the results presented in under 60 seconds.
This paper also presents the application of a new way of solving Wiener–Hopf equations of (1.1). We present a constructive iterating method of approximate solution of the Wiener–Hopf matrix problem. This is an innovative way which allows us to consider the two scalar equations corresponding to the transition points separately and then couple them in an iterative manner. This paper provided some examples of how the procedure could be numerically implemented in acoustics. Both problems considered cannot be solved using standard Wiener–Hopf techniques. The solution of finite rigid plate problem is obtained using a different method (Mathieu functions) and is presented in order to validate the proposed method. They were found to be in good agreement. It is found that for the two acoustic problems which were considered the convergence is very fast and only two or three iterations are required. We have also included an illustration of when the method is not expected to converge see figure 5(a). This is due to the fact that the neglected terms were not small. We believe this method to be more versatile and more accurate than the pole removal method used in Ayton (Reference Ayton2016), as the iterative method can allow the solution to be found anywhere in the scattering domain (not just the far field), and is proven to formally converge to an exact solution, thus allowing us to determine accurate error bounds.
We expect the proposed method to find applications in a variety of fields. Many problems could be reduced to Wiener–Hopf equations of the type of (1.1). The matrix is typical for problems which have two changes in the boundary conditions. This method could also be applied to a wider class of Wiener–Hopf systems than (1.1), in particular Wiener–Hopf matrix need not be triangular.
Acknowledgements
The authors are very grateful to Professor N. Peake for suggesting this problem and useful discussions along the way. A.K. acknowledges support from Sultan Qaboos Research Fellowship at Corpus Christi College at University of Cambridge. L.J.A. acknowledges support from a Research Fellowship at Sidney Sussex College.
