1 Introduction
Microstructures and nanostructures can be manufactured by depositing particles on a solid surface (Vogel et al. Reference Vogel, Retsch, Fustin, del Campo and Jonas2015). The simplest way to deposit nanoparticles on a substrate is by using controlled evaporation of droplets (Kim et al. Reference Kim, Li, Lee and Cho2011). By exploiting the capillary force of water, combined with controlled evaporation, a vertical deposition method has also been developed (Armstrong et al. Reference Armstrong, Khunsin, Osiak, Blömker, Torres and O’Dwyer2014). However, due to the number of parameters to be controlled in evaporation methods, external forces have been used for controlling deposition patterns, such as electrostatic deposition (Zhang et al. Reference Zhang, Zhang, Zhu, Li, Zhang, Wang and Yang2010) and electrophoretic deposition (Huang et al. Reference Huang, Zhou, Fu, Li, Wang, Zhao, Yang, Xie and Li2007). The requirements on hydrophilic or hydrophobic properties of substrates used in direct deposition are considered as being high.
Particle deposition by drying or evaporation has been in vogue for some time. The coffee-ring effect (Deegan et al. Reference Deegan, Bakajin, Dupont, Huber, Nagel and Witten1997; Deegan Reference Deegan2000) and related theoretical studies on deposition pattern and control have attracted a great deal of attention in this field. The competition between pinning and dewetting (Deegan Reference Deegan2000) along with the deposition of colloidal particles in droplets (Fischer Reference Fischer2002) have been reported. Flow fields in droplets under slow evaporation have been solved numerically and lubrication theory has been used for different contact angles (Hu & Larson Reference Hu and Larson2005a ,Reference Hu and Larson b ). The exact analytical solution for Stokes flow in both inviscid and viscous droplets due to evaporation has also been provided by Masoud & Felske (Reference Masoud and Felske2009a ,Reference Masoud and Felske b ) who evaluated the stream function and velocities for normal velocity boundary conditions at the free surface in toroidal coordinates. In addition to evaporation, surface tension also affects the flow (Scriven & Sternling Reference Scriven and Sternling1964) especially in creeping flow (Jeong & Moffatt Reference Jeong and Moffatt1992). Surface tension-induced circulation has also been studied by evaluating solutal Marangoni flow with different solutes (Marin et al. Reference Marin, Liepelt, Rossi and Kähler2016; Diddens et al. Reference Diddens, Tan, Lv, Versluis, Kuerten, Zhang and Lohse2017) and by evaluating thermal Marangoni flow experimentally and analytically in spherical drop or spherical cap (Ristenpart et al. Reference Ristenpart, Kim, Domingues, Wan and Stone2007; Tam et al. Reference Tam, von Arnim, McKinley and Hosoi2009). In Stokes flows, corner vortices called the Moffatt eddies (Moffatt Reference Moffatt1964; Shtern Reference Shtern2018) may appear in succession at a fixed geometric ratio in size and intensity (Shankar Reference Shankar1993; Biswas & Kalita Reference Biswas and Kalita2018).
Not all direct deposition methods can be arbitrarily applied to any particle which might have unique physical and chemical properties. In order to deposit particles, UV light (365 nm wavelength) may need be passed through the droplet made of photosensitive solution using a novel evaporative optical Marangoni convection (Anyfantakis & Baigl Reference Anyfantakis and Baigl2014; Varanakkottu et al. Reference Varanakkottu, Anyfantakis, Morel, Rudiuk and Baigl2015; Anyfantakis et al. Reference Anyfantakis, Varanakkottu, Rudiuk, Morel and Baigl2017). AzoTAB is a type of photosensitive surfactant having two isomers, trans-azoTAB and cis-azoTAB (Brown, Butts & Eastoe Reference Brown, Butts and Eastoe2013). Transition of trans-azoTAB to cis-azoTAB under UV light increases the surface tension of the solution (Chevallier et al. Reference Chevallier, Mamane, Stone, Tribet, Lequeux and Monteux2011). Despite the preponderance of research in particle deposition, no analytical work has been done in an attempt to understand the precise control of deposition using a laser as the source to deposit particles. The optical Marangoni flow method is robust, has the ability to assemble various particles in photosensitive surfactant solutions on different substrates and has shown promise in different fields.
This work provides a theoretical framework in toroidal coordinates following Masoud & Felske (Reference Masoud and Felske2009b ) to understand the Marangoni flow patterns in photosensitive droplets for tangential stress as the boundary condition at the free surface of the droplet. This boundary condition arises due to surface tension gradients induced by different UV light intensity patterns. The analytical solution identifies the primary circulation regions and downward dividing streamline locations where the suspended particles are likely to agglomerate. The relationship between the location of particle deposition and the location of UV beam is provided as a guidance for precise control of deposition.
2 Model development and solutions
2.1 The model and a general solution
The geometry of a droplet is a spherical cap on a substrate, which can be described in toroidal coordinates with toroid, spherical cap angle and azimuthal angle (
$\unicode[STIX]{x1D6FC},\;\unicode[STIX]{x1D6FD},\;\unicode[STIX]{x1D719}$
). By taking
$\unicode[STIX]{x1D6FC}=\unicode[STIX]{x1D702}$
,
$\unicode[STIX]{x1D6FD}=\unicode[STIX]{x03C0}-\unicode[STIX]{x1D703}$
and
$\unicode[STIX]{x1D719}=\unicode[STIX]{x1D6F9}$
, where
$\unicode[STIX]{x1D702}$
,
$\unicode[STIX]{x1D703}$
and
$\unicode[STIX]{x1D6F9}$
are defined in (Moon & Spencer Reference Moon and Spencer1971) for toroidal coordinates, the Cartesian coordinates (
$x,\;y,\;z$
) can be related to the toroidal coordinates by the following expressions
$$\begin{eqnarray}\displaystyle x={\displaystyle \frac{R\sinh \unicode[STIX]{x1D6FC}\cos \unicode[STIX]{x1D719}}{\cosh \unicode[STIX]{x1D6FC}+\cos \unicode[STIX]{x1D6FD}}},\quad y={\displaystyle \frac{R\sinh \unicode[STIX]{x1D6FC}\sin \unicode[STIX]{x1D719}}{\cosh \unicode[STIX]{x1D6FC}+\cos \unicode[STIX]{x1D6FD}}},\quad z={\displaystyle \frac{R\sin \unicode[STIX]{x1D6FD}}{\cosh \unicode[STIX]{x1D6FC}+\cos \unicode[STIX]{x1D6FD}}}, & & \displaystyle\end{eqnarray}$$
where
$\unicode[STIX]{x1D6FC}\in [0,\infty ),\unicode[STIX]{x1D6FD}\in [0,\unicode[STIX]{x03C0}/2]$
and
$\unicode[STIX]{x1D719}\in [0,2\unicode[STIX]{x03C0})$
, and
$R$
is the radius of the spherical cap on the substrate surface. The metric coefficients are
$$\begin{eqnarray}\displaystyle h_{\unicode[STIX]{x1D6FC}}=h_{\unicode[STIX]{x1D6FD}}={\displaystyle \frac{R}{\cosh \unicode[STIX]{x1D6FC}+\cos \unicode[STIX]{x1D6FD}}},\quad h_{\unicode[STIX]{x1D719}}={\displaystyle \frac{R\sinh \unicode[STIX]{x1D6FC}}{\cosh \unicode[STIX]{x1D6FC}+\cos \unicode[STIX]{x1D6FD}}}. & & \displaystyle\end{eqnarray}$$
Figure 1 is a view of two vertical planes of the toroidal coordinate system, showing the spherical cap of dimension
$r^{\ast }\in [0,1]$
and
$z^{\ast }\in [0,1]$
with the dimensionless radius
$r^{\ast }$
and height
$z^{\ast }$
defined as
$$\begin{eqnarray}\displaystyle r^{\ast }={\displaystyle \frac{\sqrt{x^{2}+y^{2}}}{R}},\quad z^{\ast }={\displaystyle \frac{z}{R}}. & & \displaystyle\end{eqnarray}$$
The UV light is incident on the surface of the droplet, which creates a surface tension gradient on the surface and drives the Marangoni flow inside the droplet. Shown in figure 2 are the different surface tension profiles corresponding linearly to UV laser profiles with peaks moving from the middle of the droplet to the edge, with or without O-masks. These beams are either Gaussian spot or ring. Based on these laser patterns, the surface tension profiles of azoTAB droplets are written as (Chevallier et al. Reference Chevallier, Mamane, Stone, Tribet, Lequeux and Monteux2011):
(1) Constant surface tension ring (CSTR) produced by an annular beam of constant intensity distribution
$$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D70E}(r^{\ast })-\unicode[STIX]{x1D70E}_{0}=\unicode[STIX]{x0394}\unicode[STIX]{x1D70E}[H(r^{\ast }-p_{1}^{\ast })-H(r^{\ast }-p_{2}^{\ast })], & & \displaystyle\end{eqnarray}$$
where
$H$
is the Heaviside function defined by
$$\begin{eqnarray}\displaystyle H(r\ast )=\left\{\begin{array}{@{}ll@{}}0\quad & \quad r^{\ast }<0\\ 1\quad & \quad r^{\ast }>0.\end{array}\right. & & \displaystyle\end{eqnarray}$$
(2) Gaussian surface tension spot (GSTS) or Gaussian surface tension ring (GSTR) produced by an annular beam of Gaussian intensity distribution (Zeng, Latham & Kar Reference Zeng, Latham and Kar2006)
$$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D70E}(r^{\ast })-\unicode[STIX]{x1D70E}_{0}=\unicode[STIX]{x0394}\unicode[STIX]{x1D70E}\exp [-a(r^{\ast }-p^{\ast })^{2}], & & \displaystyle\end{eqnarray}$$
where
$\unicode[STIX]{x1D70E}_{0}$
is the surface tension of droplets with trans-azoTAB, and
$\unicode[STIX]{x0394}\unicode[STIX]{x1D70E}$
is the increase of surface tension under UV light. Here
$r^{\ast }$
,
$p_{1}^{\ast }$
,
$p_{2}^{\ast }$
and
$p^{\ast }$
are all dimensionless horizontal distances away from droplet centre. For case 1, from
$p_{1}^{\ast }$
to
$p_{2}^{\ast }$
, surface tension is higher than in other parts of the droplet. For cases 2 and 3,
$p^{\ast }$
represents the location of maximum surface tension. ‘
$a$
’ is related to the dimensionless beam width
$w^{\ast }$
by
$w^{\ast }=2\sqrt{2/a}$
. In case 2,
$a=2$
represents Gaussian surface tension spot produced by overlapped Gaussian intensity distribution of an annular beam of small average radius. In case 3,
$a=1000$
represents a Gaussian surface tension ring produced by an annular beam of Gaussian intensity distribution (figure 2).
Figure 1. Illustration of toroidal coordinates for a spherical cap on a substrate.
Figure 2. Sketch of surface tension profiles. (a) Case 1: Constant Surface Tension Ring (CSTR) with
$p_{1}^{\ast }=0.33$
and
$p_{2}^{\ast }=0.45$
. (b) Case 2: Gaussian Surface Tension Spot (GSTS) with
$p^{\ast }=0.5$
and
$a=2$
for a beam width
$w^{\ast }=2$
to study the effect of broad illumination. (c) Case 3: Gaussian Surface Tension Ring (GSTR) with
$p^{\ast }=0.5$
and
$a=1000$
for a beam width
$w^{\ast }=0.089$
to study the effect of narrow illumination.
The characteristic velocity in the drop due to surface tension gradient can be expressed as
$$\begin{eqnarray}\displaystyle V_{0}={\displaystyle \frac{\unicode[STIX]{x0394}\unicode[STIX]{x1D70E}}{\unicode[STIX]{x1D707}}}, & & \displaystyle\end{eqnarray}$$
where
$\unicode[STIX]{x1D707}$
is the dynamic viscosity of the solution. In ambient conditions, the characteristic velocity in the drop due to evaporation scales is (Gelderblom, Bloemen & Snoeijer Reference Gelderblom, Bloemen and Snoeijer2012)
$$\begin{eqnarray}\displaystyle V_{e}(r^{\ast })\sim A(\unicode[STIX]{x1D6FD}_{c}){\displaystyle \frac{\unicode[STIX]{x1D70C}_{g}D(Y_{s}-Y_{\infty })}{\unicode[STIX]{x1D70C}R}}(1-r^{\ast })^{\unicode[STIX]{x1D706}(\unicode[STIX]{x1D6FD}_{c})-1}, & & \displaystyle\end{eqnarray}$$
where
$\unicode[STIX]{x1D70C}$
is the density of the solution and
$\unicode[STIX]{x1D70C}_{g}$
is the vapour density;
$D$
is the coefficient of binary diffusion of the vapour in the gas phase;
$Y_{s}$
and
$Y_{\infty }$
are the vapour mass fractions near the drop surface and far-field, respectively; and
$R$
is the radius of the drop. Here
$\unicode[STIX]{x1D6FD}_{c}$
denotes the droplet contact angle and
$\unicode[STIX]{x1D706}(\unicode[STIX]{x1D6FD}_{c})=\unicode[STIX]{x03C0}/(2\unicode[STIX]{x03C0}-2\unicode[STIX]{x1D6FD}_{c})$
(Deegan et al.
Reference Deegan, Bakajin, Dupont, Huber, Nagel and Witten1997).
$A(\unicode[STIX]{x1D6FD}_{c})\sim 1$
for large
$\unicode[STIX]{x1D6FD}_{c}$
in the current study. The characteristic velocity may be much larger at
$r^{\ast }\rightarrow 1$
(i.e.
$r^{\ast }>0.99$
).
For droplets of 10 mM azoTAB solution and
${\sim}$
3 mm radius under controlled evaporation for
$22.5\pm 1~^{\circ }\text{C}$
and relative humidity of
$45\pm 10\,\%$
(Lee, Smith & Hatton Reference Lee, Smith and Hatton2004; Varanakkottu et al.
Reference Varanakkottu, Anyfantakis, Morel, Rudiuk and Baigl2015),
$V_{0}\sim 1\;\text{mm}~\text{s}^{-1}$
and
$V_{e}\sim 10^{-4}~\text{mm}~\text{s}^{-1}$
from (2.7) and (2.8), respectively, and
$V_{e}<V_{0}\times 10^{-3}$
for
$r^{\ast }<0.99$
. Since
$V_{e}\ll V_{0}$
for the majority of the droplet, except near the contact line, evaporation is neglected in this study. For
$Re\sim 2\times 10^{-4}$
, the problem is governed by the Stokes flow. The continuity and vorticity equations for Stokes flow are
$$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D735}\boldsymbol{\cdot }\boldsymbol{V}=0, & & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D6FB}^{2}\unicode[STIX]{x1D74E}=0. & & \displaystyle\end{eqnarray}$$
The continuity equation in toroidal coordinates can be written as
$$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D735}\boldsymbol{\cdot }\boldsymbol{V} & = & \displaystyle {\displaystyle \frac{1}{h_{\unicode[STIX]{x1D6FC}}h_{\unicode[STIX]{x1D6FD}}h_{\unicode[STIX]{x1D719}}}}\left[{\displaystyle \frac{\unicode[STIX]{x2202}}{\unicode[STIX]{x2202}\unicode[STIX]{x1D6FC}}}(h_{\unicode[STIX]{x1D6FD}}h_{\unicode[STIX]{x1D719}}V_{\unicode[STIX]{x1D6FC}})+{\displaystyle \frac{\unicode[STIX]{x2202}}{\unicode[STIX]{x2202}\unicode[STIX]{x1D6FD}}}(h_{\unicode[STIX]{x1D6FC}}h_{\unicode[STIX]{x1D719}}V_{\unicode[STIX]{x1D6FD}})\right]\nonumber\\ \displaystyle & = & \displaystyle {\displaystyle \frac{(\cosh \unicode[STIX]{x1D6FC}+\cos \unicode[STIX]{x1D6FD})^{2}}{R\sinh \unicode[STIX]{x1D6FC}}}\left\{{\displaystyle \frac{\unicode[STIX]{x2202}}{\unicode[STIX]{x2202}\unicode[STIX]{x1D6FC}}}\left[{\displaystyle \frac{V_{\unicode[STIX]{x1D6FC}}\sinh \unicode[STIX]{x1D6FC}}{(\cosh \unicode[STIX]{x1D6FC}+\cos \unicode[STIX]{x1D6FD})^{2}}}\right]+{\displaystyle \frac{\unicode[STIX]{x2202}}{\unicode[STIX]{x2202}\unicode[STIX]{x1D6FD}}}\left[{\displaystyle \frac{V_{\unicode[STIX]{x1D6FD}}\sinh \unicode[STIX]{x1D6FC}}{(\cosh \unicode[STIX]{x1D6FC}+\cos \unicode[STIX]{x1D6FD})^{2}}}\right]\!\right\},\nonumber\\ \displaystyle & & \displaystyle\end{eqnarray}$$
where
$$\begin{eqnarray}\displaystyle V_{\unicode[STIX]{x1D6FC}}={\displaystyle \frac{1}{h_{\unicode[STIX]{x1D719}}h_{\unicode[STIX]{x1D6FD}}}}{\displaystyle \frac{\unicode[STIX]{x2202}\unicode[STIX]{x1D713}}{\unicode[STIX]{x2202}\unicode[STIX]{x1D6FD}}}={\displaystyle \frac{(\cosh \unicode[STIX]{x1D6FC}+\cos \unicode[STIX]{x1D6FD})^{2}}{R^{2}\sinh \unicode[STIX]{x1D6FC}}}{\displaystyle \frac{\unicode[STIX]{x2202}\unicode[STIX]{x1D713}}{\unicode[STIX]{x2202}\unicode[STIX]{x1D6FD}}}, & & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle V_{\unicode[STIX]{x1D6FD}}=-{\displaystyle \frac{1}{h_{\unicode[STIX]{x1D719}}h_{\unicode[STIX]{x1D6FC}}}}{\displaystyle \frac{\unicode[STIX]{x2202}\unicode[STIX]{x1D713}}{\unicode[STIX]{x2202}\unicode[STIX]{x1D6FC}}}=-{\displaystyle \frac{(\cosh \unicode[STIX]{x1D6FC}+\cos \unicode[STIX]{x1D6FD})^{2}}{R^{2}\sinh \unicode[STIX]{x1D6FC}}}{\displaystyle \frac{\unicode[STIX]{x2202}\unicode[STIX]{x1D713}}{\unicode[STIX]{x2202}\unicode[STIX]{x1D6FC}}}. & & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D74E}=\unicode[STIX]{x1D735}\times \boldsymbol{V}=\hat{\boldsymbol{e}}_{\unicode[STIX]{x1D719}}{\displaystyle \frac{1}{h_{\unicode[STIX]{x1D719}}}}E^{2}\unicode[STIX]{x1D713}, & & \displaystyle\end{eqnarray}$$
where
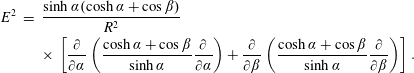$$\begin{eqnarray}\displaystyle E^{2} & = & \displaystyle {\displaystyle \frac{\sinh \unicode[STIX]{x1D6FC}(\cosh \unicode[STIX]{x1D6FC}+\cos \unicode[STIX]{x1D6FD})}{R^{2}}}\nonumber\\ \displaystyle & & \displaystyle \times \,\left[{\displaystyle \frac{\unicode[STIX]{x2202}}{\unicode[STIX]{x2202}\unicode[STIX]{x1D6FC}}}\left({\displaystyle \frac{\cosh \unicode[STIX]{x1D6FC}+\cos \unicode[STIX]{x1D6FD}}{\sinh \unicode[STIX]{x1D6FC}}}{\displaystyle \frac{\unicode[STIX]{x2202}}{\unicode[STIX]{x2202}\unicode[STIX]{x1D6FC}}}\right)+{\displaystyle \frac{\unicode[STIX]{x2202}}{\unicode[STIX]{x2202}\unicode[STIX]{x1D6FD}}}\left({\displaystyle \frac{\cosh \unicode[STIX]{x1D6FC}+\cos \unicode[STIX]{x1D6FD}}{\sinh \unicode[STIX]{x1D6FC}}}{\displaystyle \frac{\unicode[STIX]{x2202}}{\unicode[STIX]{x2202}\unicode[STIX]{x1D6FD}}}\right)\right].\end{eqnarray}$$
The vorticity equation in toroidal coordinates can be expressed in terms of
$\unicode[STIX]{x1D713}$
as
$$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D6FB}^{2}\unicode[STIX]{x1D74E}=\unicode[STIX]{x1D735}(\unicode[STIX]{x1D735}\boldsymbol{\cdot }\unicode[STIX]{x1D74E})-\unicode[STIX]{x1D735}\times (\unicode[STIX]{x1D735}\times \unicode[STIX]{x1D74E})=-\unicode[STIX]{x1D735}\times (\unicode[STIX]{x1D735}\times \unicode[STIX]{x1D74E})=-\hat{\boldsymbol{e}}_{\unicode[STIX]{x1D719}}{\displaystyle \frac{1}{h_{\unicode[STIX]{x1D719}}}}E^{2}(E^{2}\unicode[STIX]{x1D713}). & & \displaystyle\end{eqnarray}$$
Thus the governing equation for stream function corresponding to the vorticity equation in toroidal coordinates is
$$\begin{eqnarray}\displaystyle E^{4}\unicode[STIX]{x1D713}=0. & & \displaystyle\end{eqnarray}$$
The general solution for (2.16) in toroidal coordinates has been given in several studies (El-Kareh & Secomb Reference El-Kareh and Secomb1996; Masoud & Felske Reference Masoud and Felske2009b
). To deal with non-homogeneous boundary conditions in the
$\unicode[STIX]{x1D6FC}$
-direction, Masoud & Felske (Reference Masoud and Felske2009b
) proposed a general solution with Gegenbauer functions serving as eigenfunctions in
$\unicode[STIX]{x1D6FC}$
-direction, which is given below:
$$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D713}(\unicode[STIX]{x1D6FC},\unicode[STIX]{x1D6FD}) & = & \displaystyle (\cosh \unicode[STIX]{x1D6FC}+\cos \unicode[STIX]{x1D6FD})^{-3/2}\int _{0}^{\infty }[A(\unicode[STIX]{x1D70F})C_{1/2+\text{i}\unicode[STIX]{x1D70F}}^{-1/2}(\cosh \unicode[STIX]{x1D6FC})+B(\unicode[STIX]{x1D70F}){C^{\ast }}_{1/2+\text{i}\unicode[STIX]{x1D70F}}^{-1/2}(\cosh \unicode[STIX]{x1D6FC})]\nonumber\\ \displaystyle & & \displaystyle \times \,\big\{\!\!\sinh \unicode[STIX]{x1D70F}\unicode[STIX]{x1D6FD}\big[C(\unicode[STIX]{x1D70F})\sin \unicode[STIX]{x1D6FD}+D(\unicode[STIX]{x1D70F})\cos \unicode[STIX]{x1D6FD}\big]\nonumber\\ \displaystyle & & \displaystyle +\,\cosh \unicode[STIX]{x1D70F}\unicode[STIX]{x1D6FD}\big[E(\unicode[STIX]{x1D70F})\sin \unicode[STIX]{x1D6FD}+F(\unicode[STIX]{x1D70F})\cos \unicode[STIX]{x1D6FD}\big]\!\big\}\,\text{d}\unicode[STIX]{x1D70F},\end{eqnarray}$$
where
$C_{1/2+\text{i}\unicode[STIX]{x1D70F}}^{-1/2}(\cosh \unicode[STIX]{x1D6FC})$
and
${C^{\ast }}_{1/2+\text{i}\unicode[STIX]{x1D70F}}^{-1/2}(\cosh \unicode[STIX]{x1D6FC})$
are the first and second kind Gegenbauer functions, respectively, of degree
$-1/2$
and complex order
$1/2+\text{i}\unicode[STIX]{x1D70F}$
with
$\text{i}$
as the imaginary unit (Happel & Brenner Reference Happel and Brenner2012).
2.2 Boundary conditions and solution
The boundary conditions for the stream function are obtained from the velocity boundary conditions. Normal to the rotation axis of symmetry, velocity is zero, i.e.
$\boldsymbol{V}\boldsymbol{\cdot }\hat{\boldsymbol{e}}_{\unicode[STIX]{x1D6FC}}(0,\unicode[STIX]{x1D6FD})=V_{\unicode[STIX]{x1D6FC}}(0,\unicode[STIX]{x1D6FD})=0$
. On the substrate, the no slip boundary condition is
$\boldsymbol{V}(\unicode[STIX]{x1D6FC},0)=\mathbf{0}$
, i.e.
$V_{\unicode[STIX]{x1D6FC}}(\unicode[STIX]{x1D6FC},0)=0$
and
$V_{\unicode[STIX]{x1D6FD}}(\unicode[STIX]{x1D6FC},0)=0$
. Defining the value of
$\unicode[STIX]{x1D6FD}$
at the surface to be
$\unicode[STIX]{x1D6FD}_{c}$
, which is the contact angle,
$\boldsymbol{V}\boldsymbol{\cdot }\hat{\boldsymbol{e}}_{\unicode[STIX]{x1D6FD}}(\unicode[STIX]{x1D6FC},\unicode[STIX]{x1D6FD}_{c})=V_{\unicode[STIX]{x1D6FD}}(\unicode[STIX]{x1D6FC},\unicode[STIX]{x1D6FD}_{c})=0$
is assumed on the droplet surface. In the tangential direction of the droplet surface, surface tension and shear stress are balanced and, hence,
$(\bar{\bar{\unicode[STIX]{x1D749}}}\boldsymbol{\cdot }\hat{\boldsymbol{n}})\boldsymbol{\cdot }\hat{\boldsymbol{t}}=(\unicode[STIX]{x1D735}\unicode[STIX]{x1D70E})\boldsymbol{\cdot }\hat{\boldsymbol{t}}$
, or
$\unicode[STIX]{x1D70F}_{\unicode[STIX]{x1D6FC}\unicode[STIX]{x1D6FD}}=1/h_{\unicode[STIX]{x1D6FC}}\unicode[STIX]{x2202}\unicode[STIX]{x1D70E}/\unicode[STIX]{x2202}\unicode[STIX]{x1D6FC}|_{\unicode[STIX]{x1D6FD}_{c}}$
. Where
$\bar{\bar{\unicode[STIX]{x1D749}}}$
is the stress tensor,
$\hat{\boldsymbol{n}}$
and
$\hat{\boldsymbol{t}}$
are the unit outward normal vector and unit tangential vector to the droplet surface, respectively. The tangential stress can be generated by laser illumination on the droplet surface utilizing the concentration-dependent and temperature-dependent surface tension to induce Marangoni convection in the droplet. The flow pattern can be modified by changing the surface tension gradient on the free surface of sessile drop and the gradient, in turn, can be altered by modulating the laser intensity distribution. This study explores a mechanism for generating streamlines on-demand for affecting the agglomeration of particles on the surface of a substrate.
Applying (2.12a ) and (2.12b ), boundary conditions of velocities normal to the boundaries are converted as follows:
$$\begin{eqnarray}\displaystyle & \displaystyle V_{\unicode[STIX]{x1D6FC}}(0,\unicode[STIX]{x1D6FD})=0\qquad \Longrightarrow \qquad \left.{\displaystyle \frac{\unicode[STIX]{x2202}\unicode[STIX]{x1D713}}{\unicode[STIX]{x2202}\unicode[STIX]{x1D6FD}}}\right|_{\unicode[STIX]{x1D6FC}=0}=0\qquad \Longrightarrow \qquad \unicode[STIX]{x1D713}(0,\unicode[STIX]{x1D6FD})=C_{1}, & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle V_{\unicode[STIX]{x1D6FD}}(\unicode[STIX]{x1D6FC},0)=0\qquad \Longrightarrow \qquad \left.{\displaystyle \frac{\unicode[STIX]{x2202}\unicode[STIX]{x1D713}}{\unicode[STIX]{x2202}\unicode[STIX]{x1D6FC}}}\right|_{\unicode[STIX]{x1D6FD}=0}=0\qquad \Longrightarrow \qquad \unicode[STIX]{x1D713}(\unicode[STIX]{x1D6FC},0)=C_{2}, & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle V_{\unicode[STIX]{x1D6FD}}(\unicode[STIX]{x1D6FC},\unicode[STIX]{x1D6FD}_{c})=0\qquad \Longrightarrow \qquad \left.{\displaystyle \frac{\unicode[STIX]{x2202}\unicode[STIX]{x1D713}}{\unicode[STIX]{x2202}\unicode[STIX]{x1D6FC}}}\right|_{\unicode[STIX]{x1D6FD}=\unicode[STIX]{x1D6FD}_{c}}=0\qquad \Longrightarrow \qquad \unicode[STIX]{x1D713}(\unicode[STIX]{x1D6FC},\unicode[STIX]{x1D6FD}_{c})=C_{3}. & \displaystyle\end{eqnarray}$$
Since streamlines
$\unicode[STIX]{x1D713}(0,\unicode[STIX]{x1D6FD})$
connects with
$\unicode[STIX]{x1D713}(\unicode[STIX]{x1D6FC},0)$
at point
$(0,0)$
and
$\unicode[STIX]{x1D713}(\unicode[STIX]{x1D6FC},\unicode[STIX]{x1D6FD}_{c})$
at point
$(0,\unicode[STIX]{x1D6FD}_{c})$
, we have that
$C_{1}$
,
$C_{2}$
and
$C_{3}$
are equal and set to
$0$
. Thus,
$$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D713}(0,\unicode[STIX]{x1D6FD})=0, & & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D713}(\unicode[STIX]{x1D6FC},0)=0, & & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D713}(\unicode[STIX]{x1D6FC},\unicode[STIX]{x1D6FD}_{c})=0. & & \displaystyle\end{eqnarray}$$
The boundary condition
$V_{\unicode[STIX]{x1D6FC}}(\unicode[STIX]{x1D6FC},0)=0$
becomes
$$\begin{eqnarray}\displaystyle V_{\unicode[STIX]{x1D6FC}}(\unicode[STIX]{x1D6FC},0)=0\Longrightarrow {\displaystyle \frac{\unicode[STIX]{x2202}\unicode[STIX]{x1D713}}{\unicode[STIX]{x2202}\unicode[STIX]{x1D6FD}}}\Big|_{\unicode[STIX]{x1D6FD}=0}=0. & & \displaystyle\end{eqnarray}$$
Invoking the shear stress in toroidal coordinates (Moon & Spencer Reference Moon and Spencer1971),
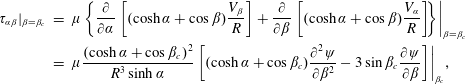$$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D70F}_{\unicode[STIX]{x1D6FC}\unicode[STIX]{x1D6FD}}|_{\unicode[STIX]{x1D6FD}=\unicode[STIX]{x1D6FD}_{c}} & = & \displaystyle \unicode[STIX]{x1D707}\left\{{\displaystyle \frac{\unicode[STIX]{x2202}}{\unicode[STIX]{x2202}\unicode[STIX]{x1D6FC}}}\left[(\cosh \unicode[STIX]{x1D6FC}+\cos \unicode[STIX]{x1D6FD}){\displaystyle \frac{V_{\unicode[STIX]{x1D6FD}}}{R}}\right]+\frac{\unicode[STIX]{x2202}}{\unicode[STIX]{x2202}\unicode[STIX]{x1D6FD}}\left[(\cosh \unicode[STIX]{x1D6FC}+\cos \unicode[STIX]{x1D6FD}){\displaystyle \frac{V_{\unicode[STIX]{x1D6FC}}}{R}}\right]\!\right\}\!\bigg|_{\unicode[STIX]{x1D6FD}=\unicode[STIX]{x1D6FD}_{c}}\nonumber\\ \displaystyle & = & \displaystyle \unicode[STIX]{x1D707}{\displaystyle \frac{(\cosh \unicode[STIX]{x1D6FC}+\cos \unicode[STIX]{x1D6FD}_{c})^{2}}{R^{3}\sinh \unicode[STIX]{x1D6FC}}}\left[(\cosh \unicode[STIX]{x1D6FC}+\cos \unicode[STIX]{x1D6FD}_{c}){\displaystyle \frac{\unicode[STIX]{x2202}^{2}\unicode[STIX]{x1D713}}{\unicode[STIX]{x2202}\unicode[STIX]{x1D6FD}^{2}}}-3\sin \unicode[STIX]{x1D6FD}_{c}{\displaystyle \frac{\unicode[STIX]{x2202}\unicode[STIX]{x1D713}}{\unicode[STIX]{x2202}\unicode[STIX]{x1D6FD}}}\right]\!\bigg|_{\unicode[STIX]{x1D6FD}_{c}},\end{eqnarray}$$
the boundary condition
$\unicode[STIX]{x1D70F}_{\unicode[STIX]{x1D6FC}\unicode[STIX]{x1D6FD}}=1/h_{\unicode[STIX]{x1D6FC}}\unicode[STIX]{x2202}\unicode[STIX]{x1D70E}/\unicode[STIX]{x2202}\unicode[STIX]{x1D6FC}|_{\unicode[STIX]{x1D6FD}_{c}}$
can be written as
$$\begin{eqnarray}\displaystyle {\displaystyle \frac{(\cosh \unicode[STIX]{x1D6FC}+\cos \unicode[STIX]{x1D6FD}_{c})}{R^{2}\sinh \unicode[STIX]{x1D6FC}}}\left[(\cosh \unicode[STIX]{x1D6FC}+\cos \unicode[STIX]{x1D6FD}_{c})\left.{\displaystyle \frac{\unicode[STIX]{x2202}^{2}\unicode[STIX]{x1D713}}{\unicode[STIX]{x2202}\unicode[STIX]{x1D6FD}^{2}}}-3\sin \unicode[STIX]{x1D6FD}_{c}{\displaystyle \frac{\unicode[STIX]{x2202}\unicode[STIX]{x1D713}}{\unicode[STIX]{x2202}\unicode[STIX]{x1D6FD}}}\right]\right|_{\unicode[STIX]{x1D6FD}_{c}}=\left.{\displaystyle \frac{1}{\unicode[STIX]{x1D707}}}{\displaystyle \frac{\unicode[STIX]{x2202}\unicode[STIX]{x1D70E}}{\unicode[STIX]{x2202}\unicode[STIX]{x1D6FC}}}\right|_{\unicode[STIX]{x1D6FD}_{c}}. & & \displaystyle\end{eqnarray}$$
The other three boundary conditions are non-singular boundary conditions at the axis of symmetry as well as at the contact line. The velocities are finite
$$\begin{eqnarray}\displaystyle V_{\unicode[STIX]{x1D6FD}}(0,\unicode[STIX]{x1D6FD})=\text{finite},\quad V_{\unicode[STIX]{x1D6FC}}(\unicode[STIX]{x1D6FC}\rightarrow \infty ,\unicode[STIX]{x1D6FD})=\text{finite},\quad V_{\unicode[STIX]{x1D6FD}}(\unicode[STIX]{x1D6FC}\rightarrow \infty ,\unicode[STIX]{x1D6FD})=\text{finite},\qquad \quad & & \displaystyle\end{eqnarray}$$
therefore
$$\begin{eqnarray}\displaystyle \left.{\displaystyle \frac{(\cosh \unicode[STIX]{x1D6FC}+\cos \unicode[STIX]{x1D6FD})^{2}}{R^{2}\sinh \unicode[STIX]{x1D6FC}}}{\displaystyle \frac{\unicode[STIX]{x2202}\unicode[STIX]{x1D713}}{\unicode[STIX]{x2202}\unicode[STIX]{x1D6FC}}}\right|_{\unicode[STIX]{x1D6FC}=0}=\text{finite}, & & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \left.{\displaystyle \frac{(\cosh \unicode[STIX]{x1D6FC}+\cos \unicode[STIX]{x1D6FD})^{2}}{R^{2}\sinh \unicode[STIX]{x1D6FC}}}{\displaystyle \frac{\unicode[STIX]{x2202}\unicode[STIX]{x1D713}}{\unicode[STIX]{x2202}\unicode[STIX]{x1D6FD}}}\right|_{\unicode[STIX]{x1D6FC}\rightarrow \infty }=\text{finite}, & & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \left.{\displaystyle \frac{(\cosh \unicode[STIX]{x1D6FC}+\cos \unicode[STIX]{x1D6FD})^{2}}{R^{2}\sinh \unicode[STIX]{x1D6FC}}}{\displaystyle \frac{\unicode[STIX]{x2202}\unicode[STIX]{x1D713}}{\unicode[STIX]{x2202}\unicode[STIX]{x1D6FC}}}\right|_{\unicode[STIX]{x1D6FC}\rightarrow \infty }=\text{finite}. & & \displaystyle\end{eqnarray}$$
Applying boundary conditions (2.21) in (2.17),
$B(\unicode[STIX]{x1D70F})=0$
for
${C^{\ast }}_{1/2+\text{i}\unicode[STIX]{x1D70F}}^{-1/2}(\cosh \unicode[STIX]{x1D6FC})|_{\unicode[STIX]{x1D6FC}=0}\neq 0$
(Masoud & Felske Reference Masoud and Felske2009a
). It also follows from (2.22) that
$F(\unicode[STIX]{x1D70F})=0$
. Then from (2.24),
$$\begin{eqnarray}\displaystyle E(\unicode[STIX]{x1D70F})=-\unicode[STIX]{x1D70F}D(\unicode[STIX]{x1D70F}). & & \displaystyle\end{eqnarray}$$
Inserting the above results into (2.17), the stream function becomes
$$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D713}(\unicode[STIX]{x1D6FC},\unicode[STIX]{x1D6FD})=(\cosh \unicode[STIX]{x1D6FC}+\cos \unicode[STIX]{x1D6FD})^{-3/2}\int _{0}^{\infty }K(\unicode[STIX]{x1D6FD},\unicode[STIX]{x1D70F})C_{1/2+\text{i}\unicode[STIX]{x1D70F}}^{-1/2}(\cosh \unicode[STIX]{x1D6FC})\,\text{d}\unicode[STIX]{x1D70F}, & & \displaystyle\end{eqnarray}$$
where
$$\begin{eqnarray}\displaystyle K(\unicode[STIX]{x1D6FD},\unicode[STIX]{x1D70F})=k_{1}(\unicode[STIX]{x1D70F})\sin \unicode[STIX]{x1D6FD}\sinh (\unicode[STIX]{x1D70F}\unicode[STIX]{x1D6FD})+k_{2}(\unicode[STIX]{x1D70F})\big[\cos \unicode[STIX]{x1D6FD}\sinh (\unicode[STIX]{x1D70F}\unicode[STIX]{x1D6FD})-\unicode[STIX]{x1D70F}\sin \unicode[STIX]{x1D6FD}\cosh (\unicode[STIX]{x1D70F}\unicode[STIX]{x1D6FD})\big].\qquad & & \displaystyle\end{eqnarray}$$
Non-singular boundary conditions, equations (2.28), can be checked by asymptotic analysis. Note that (Happel & Brenner Reference Happel and Brenner2012)
$$\begin{eqnarray}\displaystyle {\displaystyle \frac{(\cosh \unicode[STIX]{x1D6FC}+\cos \unicode[STIX]{x1D6FD})^{2}}{R^{2}\sinh \unicode[STIX]{x1D6FC}}}{\displaystyle \frac{\unicode[STIX]{x2202}\unicode[STIX]{x1D713}}{\unicode[STIX]{x2202}\unicode[STIX]{x1D6FC}}} & = & \displaystyle -{\displaystyle \frac{3(\cosh \unicode[STIX]{x1D6FC}+\cos \unicode[STIX]{x1D6FD})^{-1/2}}{2R^{2}}}\int _{0}^{\infty }K(\unicode[STIX]{x1D6FD},\unicode[STIX]{x1D70F})C_{1/2+\text{i}\unicode[STIX]{x1D70F}}^{-1/2}(\cosh \unicode[STIX]{x1D6FC})\,\text{d}\unicode[STIX]{x1D70F}\nonumber\\ \displaystyle & & \displaystyle -\,{\displaystyle \frac{(\cosh \unicode[STIX]{x1D6FC}+\cos \unicode[STIX]{x1D6FD})^{1/2}}{R^{2}}}\int _{0}^{\infty }K(\unicode[STIX]{x1D6FD},\unicode[STIX]{x1D70F})P_{-1/2+\text{i}\unicode[STIX]{x1D70F}}(\cosh \unicode[STIX]{x1D6FC})\,\text{d}\unicode[STIX]{x1D70F}\nonumber\\ \displaystyle & & \displaystyle\end{eqnarray}$$
and
$$\begin{eqnarray}\displaystyle {\displaystyle \frac{(\cosh \unicode[STIX]{x1D6FC}+\cos \unicode[STIX]{x1D6FD})^{2}}{R^{2}\sinh \unicode[STIX]{x1D6FC}}}{\displaystyle \frac{\unicode[STIX]{x2202}\unicode[STIX]{x1D713}}{\unicode[STIX]{x2202}\unicode[STIX]{x1D6FD}}} & = & \displaystyle -{\displaystyle \frac{3(\cosh \unicode[STIX]{x1D6FC}+\cos \unicode[STIX]{x1D6FD})^{-1/2}\sin \unicode[STIX]{x1D6FD}}{2R^{2}\sinh \unicode[STIX]{x1D6FC}}}\int _{0}^{\infty }K(\unicode[STIX]{x1D6FD},\unicode[STIX]{x1D70F})C_{1/2+\text{i}\unicode[STIX]{x1D70F}}^{-1/2}(\cosh \unicode[STIX]{x1D6FC})\,\text{d}\unicode[STIX]{x1D70F}\nonumber\\ \displaystyle & & \displaystyle +\,{\displaystyle \frac{(\cosh \unicode[STIX]{x1D6FC}+\cos \unicode[STIX]{x1D6FD})^{1/2}}{R^{2}\sinh \unicode[STIX]{x1D6FC}}}\int _{0}^{\infty }{\displaystyle \frac{\unicode[STIX]{x2202}K}{\unicode[STIX]{x2202}\unicode[STIX]{x1D6FD}}}C_{1/2+\text{i}\unicode[STIX]{x1D70F}}^{-1/2}(\cosh \unicode[STIX]{x1D6FC})\,\text{d}\unicode[STIX]{x1D70F}.\end{eqnarray}$$
With
$C_{1/2+\text{i}\unicode[STIX]{x1D70F}}^{-1/2}(\cosh \unicode[STIX]{x1D6FC})\sim O(\cosh ^{1/2}\unicode[STIX]{x1D6FC})$
and
$P_{-1/2+\text{i}\unicode[STIX]{x1D70F}}(\cosh \unicode[STIX]{x1D6FC})\sim O(\cosh ^{-1/2}\unicode[STIX]{x1D6FC})$
when
$\unicode[STIX]{x1D6FC}\rightarrow \infty$
(Silverman et al.
Reference Silverman1972), equations (2.28a–c
) are satisfied automatically.
By applying (2.23), the relationship of
$k_{1}(\unicode[STIX]{x1D70F})$
and
$k_{2}(\unicode[STIX]{x1D70F})$
can be shown as
$$\begin{eqnarray}\displaystyle k_{2}(\unicode[STIX]{x1D70F})=-k_{1}(\unicode[STIX]{x1D70F}){\displaystyle \frac{\sin \unicode[STIX]{x1D6FD}_{c}\sinh (\unicode[STIX]{x1D70F}\unicode[STIX]{x1D6FD}_{c})}{\cos \unicode[STIX]{x1D6FD}_{c}\sinh (\unicode[STIX]{x1D70F}\unicode[STIX]{x1D6FD}_{c})-\unicode[STIX]{x1D70F}\sin \unicode[STIX]{x1D6FD}_{c}\cosh (\unicode[STIX]{x1D70F}\unicode[STIX]{x1D6FD}_{c})}}. & & \displaystyle\end{eqnarray}$$
Next, by substituting the integral transfer relationship (Masoud & Felske Reference Masoud and Felske2009a ) in (2.30)
$$\begin{eqnarray}\displaystyle K(\unicode[STIX]{x1D6FD},\unicode[STIX]{x1D70F})=\unicode[STIX]{x1D70F}\left(\unicode[STIX]{x1D70F}^{2}+{\displaystyle \frac{1}{4}}\right)\tanh (\unicode[STIX]{x03C0}\unicode[STIX]{x1D70F})\int _{0}^{\infty }{\displaystyle \frac{\unicode[STIX]{x1D713}(\unicode[STIX]{x1D6FC},\unicode[STIX]{x1D6FD})(\cosh \unicode[STIX]{x1D6FC}+\cos \unicode[STIX]{x1D6FD})^{3/2}}{\sinh \unicode[STIX]{x1D6FC}}}C_{1/2+\text{i}\unicode[STIX]{x1D70F}}^{-1/2}(\cosh \unicode[STIX]{x1D6FC})\,\text{d}\unicode[STIX]{x1D6FC}. & & \displaystyle \nonumber\\ \displaystyle & & \displaystyle\end{eqnarray}$$
Applying the operator
$\unicode[STIX]{x2202}^{2}/\unicode[STIX]{x2202}\unicode[STIX]{x1D6FD}^{2}$
on both sides of (2.35) at
$\unicode[STIX]{x1D6FD}=\unicode[STIX]{x1D6FD}_{c}$
$$\begin{eqnarray}\displaystyle \left.{\displaystyle \frac{\unicode[STIX]{x2202}^{2}K}{\unicode[STIX]{x2202}\unicode[STIX]{x1D6FD}^{2}}}\right|_{\unicode[STIX]{x1D6FD}_{c}} & = & \displaystyle \unicode[STIX]{x1D70F}\left(\unicode[STIX]{x1D70F}^{2}+{\displaystyle \frac{1}{4}}\right)\tanh (\unicode[STIX]{x03C0}\unicode[STIX]{x1D70F})\nonumber\\ \displaystyle & & \displaystyle \times \,\int _{0}^{\infty }{\displaystyle \frac{\unicode[STIX]{x2202}^{2}}{\unicode[STIX]{x2202}\unicode[STIX]{x1D6FD}^{2}}}[\unicode[STIX]{x1D713}(\unicode[STIX]{x1D6FC},\unicode[STIX]{x1D6FD})(\cosh \unicode[STIX]{x1D6FC}+\cos \unicode[STIX]{x1D6FD})^{3/2}]\bigg|_{\unicode[STIX]{x1D6FD}_{c}}{\displaystyle \frac{C_{1/2+\text{i}\unicode[STIX]{x1D70F}}^{-1/2}(\cosh \unicode[STIX]{x1D6FC})}{\sinh \unicode[STIX]{x1D6FC}}}\,\text{d}\unicode[STIX]{x1D6FC}.\end{eqnarray}$$
By invoking (2.23) and the last boundary condition, (2.26),
$\unicode[STIX]{x2202}^{2}/\unicode[STIX]{x2202}\unicode[STIX]{x1D6FD}^{2}\big[\unicode[STIX]{x1D713}(\unicode[STIX]{x1D6FC},\unicode[STIX]{x1D6FD})(\cosh \unicode[STIX]{x1D6FC}+\cos \unicode[STIX]{x1D6FD})^{3/2}\big]\big|_{\unicode[STIX]{x1D6FD}_{c}}$
can be simplified as
$$\begin{eqnarray}\displaystyle & & \displaystyle \left.{\displaystyle \frac{\unicode[STIX]{x2202}^{2}}{\unicode[STIX]{x2202}\unicode[STIX]{x1D6FD}^{2}}}[\unicode[STIX]{x1D713}(\unicode[STIX]{x1D6FC},\unicode[STIX]{x1D6FD})(\cosh \unicode[STIX]{x1D6FC}+\cos \unicode[STIX]{x1D6FD})^{3/2}]\right|_{\unicode[STIX]{x1D6FD}_{c}}\nonumber\\ \displaystyle & & \displaystyle \quad =(\cosh \unicode[STIX]{x1D6FC}+\cos \unicode[STIX]{x1D6FD})^{1/2}\left[(\cosh \unicode[STIX]{x1D6FC}+\cos \unicode[STIX]{x1D6FD}){\displaystyle \frac{\unicode[STIX]{x2202}^{2}\unicode[STIX]{x1D713}}{\unicode[STIX]{x2202}\unicode[STIX]{x1D6FD}^{2}}}-3\sin \unicode[STIX]{x1D6FD}\left.{\displaystyle \frac{\unicode[STIX]{x2202}\unicode[STIX]{x1D713}}{\unicode[STIX]{x2202}\unicode[STIX]{x1D6FD}}}\right]\!\right|_{\unicode[STIX]{x1D6FD}_{c}}\nonumber\\ \displaystyle & & \displaystyle \quad =\left.R^{2}\sinh \unicode[STIX]{x1D6FC}(\cosh \unicode[STIX]{x1D6FC}+\cos \unicode[STIX]{x1D6FD}_{c})^{-1/2}\frac{\unicode[STIX]{x2202}\unicode[STIX]{x1D70E}}{\unicode[STIX]{x1D707}\unicode[STIX]{x2202}\unicode[STIX]{x1D6FC}}\right|_{\unicode[STIX]{x1D6FD}_{c}}.\end{eqnarray}$$
By inserting (2.37) and (2.34) into (2.36) for
$\unicode[STIX]{x1D6FD}=\unicode[STIX]{x1D6FD}_{c}$
, we can solve for
$k_{1}(\unicode[STIX]{x1D70F})$
with
$$\begin{eqnarray}\displaystyle k_{1}(\unicode[STIX]{x1D70F})={\displaystyle \frac{N_{1}N_{2}}{M_{1}+M_{2}M_{3}}}, & & \displaystyle\end{eqnarray}$$
where
$$\begin{eqnarray}\displaystyle & \displaystyle N_{1}=\unicode[STIX]{x1D70F}\left(\unicode[STIX]{x1D70F}^{2}+{\textstyle \frac{1}{4}}\right)\tanh (\unicode[STIX]{x03C0}\unicode[STIX]{x1D70F}), & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle N_{2}=\int _{0}^{\infty }R^{2}(\cosh \unicode[STIX]{x1D6FC}^{\prime }+\cos \unicode[STIX]{x1D6FD}_{c})^{-1/2}\left.{\displaystyle \frac{\unicode[STIX]{x2202}\unicode[STIX]{x1D70E}}{\unicode[STIX]{x1D707}\unicode[STIX]{x2202}\unicode[STIX]{x1D6FC}^{\prime }}}\right|_{\unicode[STIX]{x1D6FD}_{c}}C_{1/2+\text{i}\unicode[STIX]{x1D70F}}^{-1/2}(\cosh \unicode[STIX]{x1D6FC}^{\prime })\,\text{d}\unicode[STIX]{x1D6FC}^{\prime }, & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle M_{1}=2\unicode[STIX]{x1D70F}\cos \unicode[STIX]{x1D6FD}_{c}\cosh (\unicode[STIX]{x1D70F}\unicode[STIX]{x1D6FD}_{c})+(\unicode[STIX]{x1D70F}^{2}-1)\sin \unicode[STIX]{x1D6FD}_{c}\sinh (\unicode[STIX]{x1D70F}\unicode[STIX]{x1D6FD}_{c}), & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle M_{2}=(\unicode[STIX]{x1D70F}^{2}+1)\cos \unicode[STIX]{x1D6FD}_{c}\sinh (\unicode[STIX]{x1D70F}\unicode[STIX]{x1D6FD}_{c})+(\unicode[STIX]{x1D70F}+\unicode[STIX]{x1D70F}^{3})\sin \unicode[STIX]{x1D6FD}_{c}\cosh (\unicode[STIX]{x1D70F}\unicode[STIX]{x1D6FD}_{c}), & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle M_{3}={\displaystyle \frac{\sin \unicode[STIX]{x1D6FD}_{c}\sinh (\unicode[STIX]{x1D70F}\unicode[STIX]{x1D6FD}_{c})}{\cos \unicode[STIX]{x1D6FD}_{c}\sinh (\unicode[STIX]{x1D70F}\unicode[STIX]{x1D6FD}_{c})-\unicode[STIX]{x1D70F}\sin \unicode[STIX]{x1D6FD}_{c}\cosh (\unicode[STIX]{x1D70F}\unicode[STIX]{x1D6FD}_{c})}}. & \displaystyle\end{eqnarray}$$
Nondimentionalizing
$\unicode[STIX]{x1D713}(\unicode[STIX]{x1D6FC},\unicode[STIX]{x1D6FD})$
by
$\unicode[STIX]{x1D713}_{0}=R^{2}\unicode[STIX]{x0394}\unicode[STIX]{x1D70E}/\unicode[STIX]{x1D707}$
$$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D713}^{\ast }(\unicode[STIX]{x1D6FC},\unicode[STIX]{x1D6FD})={\displaystyle \frac{\unicode[STIX]{x1D713}}{\unicode[STIX]{x1D713}_{0}}}=(\cosh \unicode[STIX]{x1D6FC}+\cos \unicode[STIX]{x1D6FD})^{-3/2}\int _{0}^{\infty }K^{\ast }(\unicode[STIX]{x1D6FD},\unicode[STIX]{x1D70F})C_{1/2+\text{i}\unicode[STIX]{x1D70F}}^{-1/2}(\cosh \unicode[STIX]{x1D6FC})\,\text{d}\unicode[STIX]{x1D70F}, & & \displaystyle\end{eqnarray}$$
with
$$\begin{eqnarray}\displaystyle K^{\ast }(\unicode[STIX]{x1D6FD},\unicode[STIX]{x1D70F}) & = & \displaystyle \Bigg[\sin \unicode[STIX]{x1D6FD}\sinh (\unicode[STIX]{x1D70F}\unicode[STIX]{x1D6FD})-\sin \unicode[STIX]{x1D6FD}_{c}\sinh (\unicode[STIX]{x1D70F}\unicode[STIX]{x1D6FD}_{c})\nonumber\\ \displaystyle & & \displaystyle \times \,{\displaystyle \frac{\cos \unicode[STIX]{x1D6FD}\sinh (\unicode[STIX]{x1D70F}\unicode[STIX]{x1D6FD})-\unicode[STIX]{x1D70F}\sin \unicode[STIX]{x1D6FD}\cosh (\unicode[STIX]{x1D70F}\unicode[STIX]{x1D6FD})}{\cos \unicode[STIX]{x1D6FD}_{c}\sinh (\unicode[STIX]{x1D70F}\unicode[STIX]{x1D6FD}_{c})-\unicode[STIX]{x1D70F}\sin \unicode[STIX]{x1D6FD}_{c}\cosh (\unicode[STIX]{x1D70F}\unicode[STIX]{x1D6FD}_{c})}}\Bigg]k_{1}^{\ast }(\unicode[STIX]{x1D70F}),\end{eqnarray}$$
where the expression for
$k_{1}^{\ast }(\unicode[STIX]{x1D70F})$
is the same as
$k_{1}(\unicode[STIX]{x1D70F})$
with
$N_{2}$
replaced by
$N_{2}^{\ast }$
, and
$$\begin{eqnarray}\displaystyle N_{2}^{\ast }=\int _{0}^{\infty }(\cosh \unicode[STIX]{x1D6FC}^{\prime }+\cos \unicode[STIX]{x1D6FD}_{c})^{-1/2}\left.{\displaystyle \frac{1}{\unicode[STIX]{x0394}\unicode[STIX]{x1D70E}}}{\displaystyle \frac{\unicode[STIX]{x2202}\unicode[STIX]{x1D70E}}{\unicode[STIX]{x2202}\unicode[STIX]{x1D6FC}^{\prime }}}\right|_{\unicode[STIX]{x1D6FD}_{c}}C_{1/2+\text{i}\unicode[STIX]{x1D70F}}^{-1/2}(\cosh \unicode[STIX]{x1D6FC}^{\prime })\,\text{d}\unicode[STIX]{x1D6FC}^{\prime }. & & \displaystyle\end{eqnarray}$$
One of the advantages of developing an analytical solution is that one can predict the effect of different surface tension distributions in toroidal coordinates. The effect of light illumination on the stream function appears in (2.42) through the surface tension profiles given in (2.4) and (2.6). The solution can be used to find the number of vortices and dividing streamlines that allow unique deposition patterns for the specified surface tension profile. It is also possible to find the solution in isolated areas, such as near the contact line or the substrate.
For the Heaviside step function in (2.4), surface tension gradient
$\unicode[STIX]{x2202}\unicode[STIX]{x1D70E}/\unicode[STIX]{x2202}\unicode[STIX]{x1D6FC}$
becomes the Dirac delta function and therefore
$N_{2}^{\ast }$
can be written as
$$\begin{eqnarray}\displaystyle N_{2}^{\ast }=(\cosh \unicode[STIX]{x1D6FC}_{1}+\cos \unicode[STIX]{x1D6FD}_{c})^{-1/2}C_{1/2+\text{i}\unicode[STIX]{x1D70F}}^{-1/2}(\cosh \unicode[STIX]{x1D6FC}_{1})-(\cosh \unicode[STIX]{x1D6FC}_{2}+\cos \unicode[STIX]{x1D6FD}_{c})^{-1/2}C_{1/2+\text{i}\unicode[STIX]{x1D70F}}^{-1/2}(\cosh \unicode[STIX]{x1D6FC}_{2}), & & \displaystyle \nonumber\\ \displaystyle & & \displaystyle\end{eqnarray}$$
where
$\unicode[STIX]{x1D6FC}_{1}$
and
$\unicode[STIX]{x1D6FC}_{2}$
are the toroids of the points at
$r^{\ast }=p_{1}^{\ast }$
and
$r^{\ast }=p_{2}^{\ast }$
, respectively, on the droplet surface where
$\unicode[STIX]{x1D6FD}=\unicode[STIX]{x1D6FD}_{c}$
. Using (2.1) and (2.3),
$\unicode[STIX]{x1D6FC}_{1}$
and
$\unicode[STIX]{x1D6FC}_{2}$
are obtained as
$$\begin{eqnarray}\displaystyle \cosh \unicode[STIX]{x1D6FC}_{1}={\displaystyle \frac{\cos \unicode[STIX]{x1D6FD}_{c}+\sqrt{\cos ^{2}\unicode[STIX]{x1D6FD}_{c}+({p_{1}^{\ast }}^{-2}-1)(\cos ^{2}\unicode[STIX]{x1D6FD}_{c}+{p_{1}^{\ast }}^{-2})}}{{p_{1}^{\ast }}^{-2}-1}}, & & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \cosh \unicode[STIX]{x1D6FC}_{2}={\displaystyle \frac{\cos \unicode[STIX]{x1D6FD}_{c}+\sqrt{\cos ^{2}\unicode[STIX]{x1D6FD}_{c}+({p_{2}^{\ast }}^{-2}-1)(\cos ^{2}\unicode[STIX]{x1D6FD}_{c}+{p_{2}^{\ast }}^{-2})}}{{p_{2}^{\ast }}^{-2}-1}}. & & \displaystyle\end{eqnarray}$$
In (2.40),
$\unicode[STIX]{x1D6FC}$
varies up to
$\infty$
since the physical dimension of the droplet,
$r^{\ast }$
, which varies from 0 to 1, is transformed by the toroid
$\unicode[STIX]{x1D6FC}$
to an infinite range of
$\unicode[STIX]{x1D6FC}\in [1,\infty )$
in toroidal coordinates. However,
$\unicode[STIX]{x1D6FC}=6$
corresponds to
$r^{\ast }=0.995$
which approximates the position of the contact line with a high degree of accuracy, therefore
$\unicode[STIX]{x1D6FC}$
is taken to be six for calculating the stream function near the contact line. In (2.42), the integration represents the effect of the boundary condition, i.e. the surface tension gradient for all possible values of the toroid
$\unicode[STIX]{x1D6FC}^{\prime }$
extending up to
$\infty$
as the upper limit of integration, but the maximum value of
$\unicode[STIX]{x1D6FC}^{\prime }$
can be taken as six since it corresponds to
$r^{\ast }=0.995$
.
For the Gaussian surface tension profile in (2.6), (2.42) is evaluated numerically by approximating the infinite upper limit of the integration to a finite value
$\unicode[STIX]{x1D6FC}_{max}^{\prime }=6$
. Here (2.42) is integrated numerically using the Trapezoidal rule for each value of
$\unicode[STIX]{x1D70F}$
and
$\unicode[STIX]{x1D6FD}_{c}$
by taking the interval of numerical integration
$\unicode[STIX]{x0394}\unicode[STIX]{x1D6FC}^{\prime }=0.01$
and 0.001 for the cases in figures 2(b) and 2(c), respectively, and the resulting
$N_{2}^{\ast }$
is substituted in (2.40). Generally, the results of the integration oscillate due to Gibbs’ phenomenon when the infinite upper limit of integration is replaced with finite values and the integration represents the solution of a physical problem involving a discontinuity such as a discontinuous boundary condition. In the present case, the integrand decays rapidly due to the exponential term in the Gaussian profile. Therefore, the result of (2.42) is expected to be free of Gibbs’ oscillation.
Using (2.40), the dimensionless stream function
$\unicode[STIX]{x1D713}^{\ast }$
is calculated by approximating the infinite upper limit to a finite value
$\unicode[STIX]{x1D70F}_{max}$
. Due to this approximation, the stream function would also exhibit Gibbs’ oscillation as in the case of (2.42). For example, spurious vortices were observed in the droplet when
$\unicode[STIX]{x1D70F}_{max}=50$
for case 3 in figure 2(c) (Gaussian Surface Tension Ring) and these spurious vortices disappear for sufficiently large values of
$\unicode[STIX]{x1D70F}_{max}$
. Therefore
$\unicode[STIX]{x1D713}^{\ast }$
has been determined by taking
$\unicode[STIX]{x1D70F}_{max}$
as 900, 50 and 200 for cases 1, 2 and 3, respectively, and the numerical integration interval
$\unicode[STIX]{x0394}\unicode[STIX]{x1D70F}$
as 0.1 for all cases. Identical flow patterns were observed for higher values of
$\unicode[STIX]{x1D70F}_{max}$
and lower values of
$\unicode[STIX]{x0394}\unicode[STIX]{x1D70F}$
.
Here
$\unicode[STIX]{x1D70F}_{max}$
is very high for case 1 because of the sharp discontinuity in the surface tension profile represented by the Heaviside function (2.4). On the other hand,
$\unicode[STIX]{x1D70F}_{max}$
is fairly low for case 2 since a broad Gaussian function (2.6) with a value of
$a=2$
represents the surface tension profile as a slowly varying slope. In case 3, however,
$\unicode[STIX]{x1D70F}_{max}$
is higher than in case 2 since a narrow Gaussian function (2.6) represents the surface tension profile with a steeper slope than in case 2. The value of
$\unicode[STIX]{x0394}\unicode[STIX]{x1D70F}$
depends upon the periodicity of the Gegenbauer function
$C_{1/2+\text{i}\unicode[STIX]{x1D70F}}^{-1/2}(\cosh \unicode[STIX]{x1D6FC})$
with respect to
$\unicode[STIX]{x1D70F}$
for a fixed value of
$\unicode[STIX]{x1D6FC}$
, and this function oscillates rapidly with short periodicity for large values of
$\unicode[STIX]{x1D6FC}$
(El-Kareh & Secomb Reference El-Kareh and Secomb1996). In the present study, the shortest periodicity was found to be
$1.1$
for
$\unicode[STIX]{x1D6FC}=6$
, and the value of
$\unicode[STIX]{x0394}\unicode[STIX]{x1D70F}=0.1$
corresponds to taking 11 points within one period of the oscillation. In (2.40), the above-mentioned values of
$\unicode[STIX]{x1D70F}_{max}$
and
$\unicode[STIX]{x0394}\unicode[STIX]{x1D70F}$
yield convergent solutions in most of the droplet volume except near the free surface where the integrand decays very slowly and Gibbs’ oscillation may exist.
3 Results
In this section, flow patterns inside the droplet of azoTAB solution are evaluated for different UV light patterns as well as for different contact angles. First, two experimental cases are used to validate the current analytical results and then the formation of vortices are analysed by varying the profiles of light illumination on the droplet.
Figure 3. Stream function and deposition prediction for Constant Surface Tension Ring with
$p_{1}^{\ast }=0.33$
,
$p_{2}^{\ast }=0.45$
and
$\unicode[STIX]{x1D6FD}_{c}=0.21\unicode[STIX]{x03C0}$
. Particles are gathered by the contour-rotating circulations and deposited on the substrate by the downward dividing streamline, forming a ring. A few particles are trapped near the contact line due to the Moffatt eddies.
Figure 4. Comparison of the particle deposition patterns in the experiments (Varanakkottu et al.
Reference Varanakkottu, Anyfantakis, Morel, Rudiuk and Baigl2015) and analytical solutions for droplets under UV light. Reprinted with permission from (Varanakkottu et al.
Reference Varanakkottu, Anyfantakis, Morel, Rudiuk and Baigl2015). Copyright (2016) American Chemical Society. (a,b) Stream functions and depositions of carboxylate polystyrene particles on the substrate by UV light of a ring shape for contact angle
$\unicode[STIX]{x1D6FD}_{c}=0.21\unicode[STIX]{x03C0}$
and
$\unicode[STIX]{x1D6FD}_{c}=\unicode[STIX]{x03C0}/9$
respectively. (c) Comparison of particle deposition between the analytical solution and in experiments by UV light of a ring shape. (d,e) Stream functions and cationic particle depositions on the substrate with UV beam at drop centre for contact angle
$\unicode[STIX]{x1D6FD}_{c}=0.21\unicode[STIX]{x03C0}$
and
$\unicode[STIX]{x1D6FD}_{c}=\unicode[STIX]{x03C0}/9$
, respectively. (f) Comparison of particle deposition between the analytical solution and in experiments by UV light at drop centre.
3.1 Experimental Validation
Experiment 1: In this experiment, a spherical cap droplet of radius 3 mm and contact angle
$0.21\unicode[STIX]{x03C0}$
with 10 mM azoTAB concentration undergoes Marangoni convection due to UV light illumination through a transparent ring in a mask. The inner and outer radii of the transparent ring are 1.0 and 1.35 mm, respectively (Varanakkottu et al.
Reference Varanakkottu, Anyfantakis, Morel, Rudiuk and Baigl2015). At the end of the experiment, the carboxylate polystyrene particles are deposited on the substrate as a ring of radius 1.13 mm with a width of 0.27 mm. A supporting video is given in their paper where the deposition occurs in half the time (25 min) compared to evaporation (50 min).
This experimental condition is simulated by considering a spherical cap droplet of contact angle
$0.21\unicode[STIX]{x03C0}$
and a Constant Surface Tension Ring (case 1 in figure 2
a) of dimensionless inner and outer radii
$p_{1}^{\ast }=0.33$
and
$p_{2}^{\ast }=0.45$
, respectively, corresponding to the radii of the UV illumination through the transparent ring of the mask. The analytical solution for the stream function under this condition is presented in figure 3, showing two counter-rotating eddies of almost equal strength around
$r^{\ast }=0.35$
. The majority of the particles are expected to be gathered by the counter-rotating eddies and follow the downward dividing streamline between the eddies,
$\unicode[STIX]{x1D713}^{\ast }=0$
, to deposit on the substrate. The locus of the contact point between the downward dividing streamline and the substrate forms a ring around the axis of symmetry.
In figure 4, the contact angles in the droplet are changed from
$0.21\unicode[STIX]{x03C0}$
to
$\unicode[STIX]{x03C0}/9$
to simulate the changes in the droplet height due to evaporation during the deposition. This reduction in height is accounted for by varying the contact angle. By calculating the stream functions of series of contact angle from
$0.21\unicode[STIX]{x03C0}$
to
$\unicode[STIX]{x03C0}/9$
, the changes in the position of intersection between the downward streamline and substrate, defined as deposition position
$D^{\ast }$
, can be tracked.
$D^{\ast }$
shifts toward the contact line from
$D^{\ast }=0.33$
to 0.37 for the contact angles decreasing from
$0.21\unicode[STIX]{x03C0}$
to
$\unicode[STIX]{x03C0}/9$
(figures 4
a and 4
b). Therefore, the deposited particles are expected to form a deposition ring of finite width during the period of deposition when the contact angle changes in the above-mentioned range. The current analysis predicts the location of the particle deposition given by the dimensionless radius of the centre line of the deposition ring, 0.35, i.e. 1.05 mm, which matches very well with the experimental result. The dimensionless width of the deposition ring is found to be 0.04, i.e. 0.12 mm, which also appears to be well-predicted within experimental uncertainty and the striations on the ring as shown in figure 4(c). The other eddies appearing in figures 3 and 4 are discussed at the end of this section.
Experiment 2: A spherical cap droplet of radius 2.3 mm and contact angle
$0.21\unicode[STIX]{x03C0}$
with 10 mM azoTAB concentration undergoes Marangoni convection due to UV light located above the droplet centre with a beam width of
$165~\unicode[STIX]{x03BC}\text{m}$
(Varanakkottu et al.
Reference Varanakkottu, Anyfantakis, Morel, Rudiuk and Baigl2015). At the end of the experiment cationic particles deposit on the substrate as a dot at the droplet centre.
In the corresponding analytical solution, shown in figure 4(d), a constant surface tension spot of dimensionless width
$w^{\ast }=0.072$
located at the droplet centre is used to simulate the laser spot size and location in the experiment. This analysis is also performed for decreasing contact angles from
$0.21\unicode[STIX]{x03C0}$
to
$\unicode[STIX]{x03C0}/9$
(figures 4
d and 4
f) as done in figures 4(a) and 4(b). The deposition region
$D^{\ast }$
remains zero for contact angle decreasing from
$0.21\unicode[STIX]{x03C0}$
to
$\unicode[STIX]{x03C0}/9$
indicating that particles are expected to deposit on the substrate as a dot at the droplet centre. Thus, the predicted deposition locations from the analytical solutions agree with both available experimental results.
Shown in both figures 3 and 4, the primary circulations appear near where the surface tension is high and undergoes a toroidal rotation while a series of weak vortices, which are Moffatt eddies, forms near the contact line.
3.2 Marangoni convection patterns for different surface tension profiles:
After validating the analytical solution for case 1, the effects of light modulation by varying
$p^{\ast }$
and
$a$
for cases 2 and 3 are evaluated. The resulting flow patterns due to different surface tension profiles are expected to agglomerate the particles to certain selected regions on the substrate.
Figure 5. Contour of dimensionless stream function for case 2 with
$a=2$
. The geometry of the droplet is
$R=1~\text{mm}$
, contact angle
$\unicode[STIX]{x1D6FD}_{c}=\unicode[STIX]{x03C0}/6$
. The arrow indicates the peak intensity position of the laser incident on the droplet. The azoTAB concentration is
$10\,\text{mM}$
. (a) Position of the peak is
$p^{\ast }=0$
. A large toroidal circulation (counter-clockwise on paper) is formed. (b) At
$p^{\ast }=0.195$
, a new counter-rotating toroidal circulation is formed at the top centre. (c) At
$p^{\ast }=0.6$
, this counter-rotating circulation near the centre grows, and the original circulation (counter-clockwise on paper) diminishes in size. (d) At the droplet edge, the stronger counter-rotating circulation completely takes over the droplet.
(1) Effect of broad Gaussian illumination: This effect is examined for Gaussian Surface Tension Spot using (2.6) (case 2 in figure 2
b), varying
$p^{\ast }$
and constant
$a$
.
$R=1~\text{mm}$
; contact angle
$\unicode[STIX]{x1D6FD}_{c}=\unicode[STIX]{x03C0}/6$
; azoTAB concentration
$=10~\text{mM}$
;
$a=2$
;
$\unicode[STIX]{x1D70E}_{0}=43~\text{mN}~\text{m}^{-1}$
;
$\unicode[STIX]{x0394}\unicode[STIX]{x1D70E}=5~\text{mN}~\text{m}^{-1}$
. By varying
$p^{\ast }$
from
$0$
to
$1$
, the flow pattern in the droplet changes from a toroidal circulation (appears as counter-clockwise circulation in figure 5
a) to a clockwise toroidal cell near the top of the droplet (figure 5
b), growing to a larger volume (figure 5
c) and eventually to a single clockwise cell (figure 5
d). This type of modulation in the circulation pattern, which has not been observed or reported previously, provides the requisite Marangoni circulation to obtain various deposition patterns on demand.
For the same case as in figure 5, a flow regime map is developed to understand various circulation patterns for different values of the Gaussian beam position
$p^{\ast }$
and the droplet contact angle
$\unicode[STIX]{x1D6FD}_{c}$
. When the peak of the beam is shifted from the centre of the droplet to its edge, i.e.
$p^{\ast }$
is varied from 0 to 1, the orientation of circulation changes as a function of
$\unicode[STIX]{x1D6FD}_{c}$
. A large single counter-clockwise circulation appears when
$p^{\ast }$
is less than certain values depending on
$\unicode[STIX]{x1D6FD}_{c}$
and the boundary of this phenomenon is shown in figure 6(a). Above this boundary, i.e. when the peak of the beam is in the mid-section of the droplet, both counter-clockwise and clockwise circulations appear in the droplet. As
$p^{\ast }$
increases, however, the size and strength of the counter-clockwise circulation decreases while the clockwise circulation becomes larger and stronger. When the peak of the beam is shifted at the edge of the droplet, i.e.
$p^{\ast }=1$
, a large single clockwise circulation dominates the Marangoni convection.
Figure 6(b) shows the particle deposition position
$D^{\ast }$
as a function of
$p^{\ast }$
. For
$\unicode[STIX]{x1D6FD}_{c}=\unicode[STIX]{x03C0}/6$
as an example, deposition occurs at the droplet centre as
$D^{\ast }$
remains zero for
$p^{\ast }\leqslant 0.19$
; then for a small shift in the beam peak, i.e. from
$p^{\ast }=0.19$
to
$0.23$
,
$D^{\ast }$
rapidly shifts to
$0.15$
and from this point on until the beam reaches the droplet edge the profile stays linear. This is seen for all cases, however for smaller
$\unicode[STIX]{x1D6FD}_{c}$
, a smaller beam shift is needed to start a clockwise toroidal circulation and to achieve the rapidly and linearly increasing region of
$D^{\ast }$
.
Figure 6. (a) Single counter-clockwise circulation region, twin circulation region and single clockwise circulation line determined by surface tension peak
$p^{\ast }$
and contact angle
$\unicode[STIX]{x1D6FD}_{c}$
for case 2 with
$a=2$
. (b) Relationship of deposition region
$D^{\ast }$
and surface tension peak
$p^{\ast }$
for case 2 with
$a=2$
.
(2) Effect of narrow Gaussian illumination: For Gaussian Surface Tension Ring using (2.4) (case 3 in figure 2
c), the effect of narrow illumination is evaluated by changing the beam position
$p^{\ast }$
and constant
$a$
.
$R=1~\text{mm}$
; contact angle
$\unicode[STIX]{x1D6FD}_{c}=\unicode[STIX]{x03C0}/6$
; azoTAB concentration
$=10~\text{mM}$
;
$a=1000$
;
$\unicode[STIX]{x1D70E}_{0}=43~\text{mN}~\text{m}^{-1}$
;
$\unicode[STIX]{x0394}\unicode[STIX]{x1D70E}=5~\text{mN}~\text{m}^{-1}$
. Figure 7 shows two cases of stream function under (2.4), with
$a=1000$
, beam peak at
$p^{\ast }=0$
(figure 7
a) and
$p^{\ast }=0.5$
(figure 7
b). The effect of narrow Gaussian Surface Tension Ring on the flow patterns is similar to that of Constant Surface Tension Ring (figure 3 and figure 4) in generating the primary circulations near the beam peak with Moffatt eddies occurring away from the beam peak.
Figure 7. Contour of dimensionless stream function by narrow illuminations for case 3 with contact angle
$\unicode[STIX]{x1D6FD}_{c}=\unicode[STIX]{x03C0}/6$
,
$a=1000$
: (a) Surface tension peak is set as
$p^{\ast }=0$
. (b) Surface tension peak is set as
$p^{\ast }=0.5$
.
4 Conclusion
An analytical solution is developed to determine the stream function in sessile azoTAB droplets for different surface tension gradients produced by different intensity distributions of UV light. The downward dividing streamline is expected to deposit the particles on the substrate. The solution to a biharmonic stream function equation has yielded multiple cells. The downward dividing streamlines are expected to deposit particles as dots at the droplet centre or as rings around the axisymmetric axis. These dots and rings predict the experimental results very well. The effect of broad UV illumination on the position of the downward dividing streamline (i.e. possible position of particle agglomeration) is studied using Gaussian Surface Tension Spot by varying the position of the peak intensity
$p^{\ast }$
and the contact angle
$\unicode[STIX]{x1D6FD}_{c}$
of droplets. The resultant flow regime map reveals that the circulations change from counter-clockwise at
$p^{\ast }<0.15$
to clockwise at
$p^{\ast }=1$
for the contact angle of
$\unicode[STIX]{x1D6FD}_{c}=\unicode[STIX]{x03C0}/6$
. The values of
$p^{\ast }$
affect the size and number of circulations. The effect of contact angle is also studied and a single counter-clockwise circulation is found to occur below certain critical values of
$p^{\ast }$
, both counter-clockwise and clockwise circulations occur above these critical values leading to a single clockwise circulation at
$p^{\ast }=1$
. Narrow Gaussian UV light illumination at the droplet centre produces localized primary circulation centred at the droplet centre along with weaker secondary circulations called Moffatt eddies. A similar effect is also observed when the illumination is centred half way from the droplet centre producing a narrow Gaussian surface tension ring.
Acknowledgements
This work was partially supported by the National Science Foundation, CMMI, MME (1563448).
