2. Basic framework and dataset

2.1. Basic framework

As shown in Table 1, our investigation pools 17,136 observations at the individual level from four experiments that are part of the same project and model charitable giving as individual contributions to N threshold public goods indexed $n \in\{1,...,N\}$. This framework aims to reproduce fundraising scenarios where multiple charities indistinguishable from each other compete for limited donor contributions. Therefore, not only do participants have to contribute enough to achieve the threshold, but they also need to choose where to direct their contributions, thereby facing an increased risk of miscoordination.

Table 1 Included studies

For each study the columns report number of treatments, number of observations, number of subjects, relative frequencies for gender, number of groups, and country where the experiment takes place.

In each of these studies, J participants are divided into unchanging 4-person groups, whose members are indexed $j \in\{1,...,4\}$ and play the game throughout 12 sequential rounds. In every round, each of the subjects is endowed with $y_j \gt 0$ tokens and is asked to independently split the initial endowment between a private account and N collective accounts (i.e., public goods), with $c_j \in [0, y_j]$ being the total contributions made by subject j to the collective accounts. The private account pays an individual profit of 2 points per token assigned, whereas each of the collective accounts potentially benefits the whole group and returns no points, if the tokens therein do not reach the threshold τ. Otherwise, each group member earns one point for every token therein (regardless of who contributes) plus a bonus $b_{j,n}$ that captures efficiency and makes all the collective accounts payoff-dominant as compared with the private account. Unless noted otherwise, (i) the individual endowment is the same across subjects, (ii) the threshold τ is set to 60% of the sum of individual endowments, and (iii) the bonus $b_{j,n}$ is the same for every player j and every public good n. These conditions imply that, while each group can fund at most one public good at its threshold, player j is unable to do it unilaterally and unwilling to contribute to a collective account unless she expects others to contribute to the same public good.Footnote ²

Let $C_n = \sum_{j=1}^{4} c_{j,n}$ and $c_{j,n} \geq 0$ indicate the group contributions to collective account n and the contributions made by subject j to collective account n, respectively. As a result, the individual benefit $B_{j,n}$ associated with each public good n is as follows:

\begin{equation*} B_{j,n} (C_n) = \begin{cases} 0 & \text{when} \quad C_n \lt \tau \\ C_n + b_{j,n} & \text{when} \quad C_n \geq \tau \\ \end{cases} \end{equation*}

whereas the payoff u_j earned by player j in each round amounts to:

\begin{equation*} u_j (c_j) = 2 \left(y_j - \sum_{n=1}^{N} c_{j,n}\right) + \sum_{n=1}^{N} B_{j,n} (C_n) \end{equation*}

At the end of each round, players are informed of the group contributions received by each collective account.

3. Analysis and results

Distinguishing between two levels of analysis, Table 2 summarizes the three outcome variables and highlights that the average Coordination (M = 0.564), Rel_contributions (M = 0.532), and Rel_earnings (M = 2.839) in the single-public-good scenario are higher than those in the presence of multiple collective accounts (M = 0.487, M = 0.478, and M = 2.565, respectively).Footnote ⁴

Table 2 Summary statistics

The group-level columns report absolute (relative) frequencies and means for Coordination, whereas the individual-level columns report absolute (relative) frequencies, means for Rel_contributions and Rel_earnings. Multiple_PG is a dummy that equals 1 if more than one collective account is available. Delegation is a dummy that takes value 1 if the game features the delegation phase.

LOWESS smoothers in Figure 1 indicate that, interestingly, while donations follow a similar declining trend in both settings, differences emerge when it comes to successful coordination and resulting earnings. On the one hand, decreasing contributions are associated with lower coordination rates and earnings when only one collective account is available, reflecting common findings from the single-public-good literature. On the other hand, in the presence of multiple public goods we observe an inverted U-shaped trend in coordination rates and individual earnings that suggests learning as a potential coordination device.

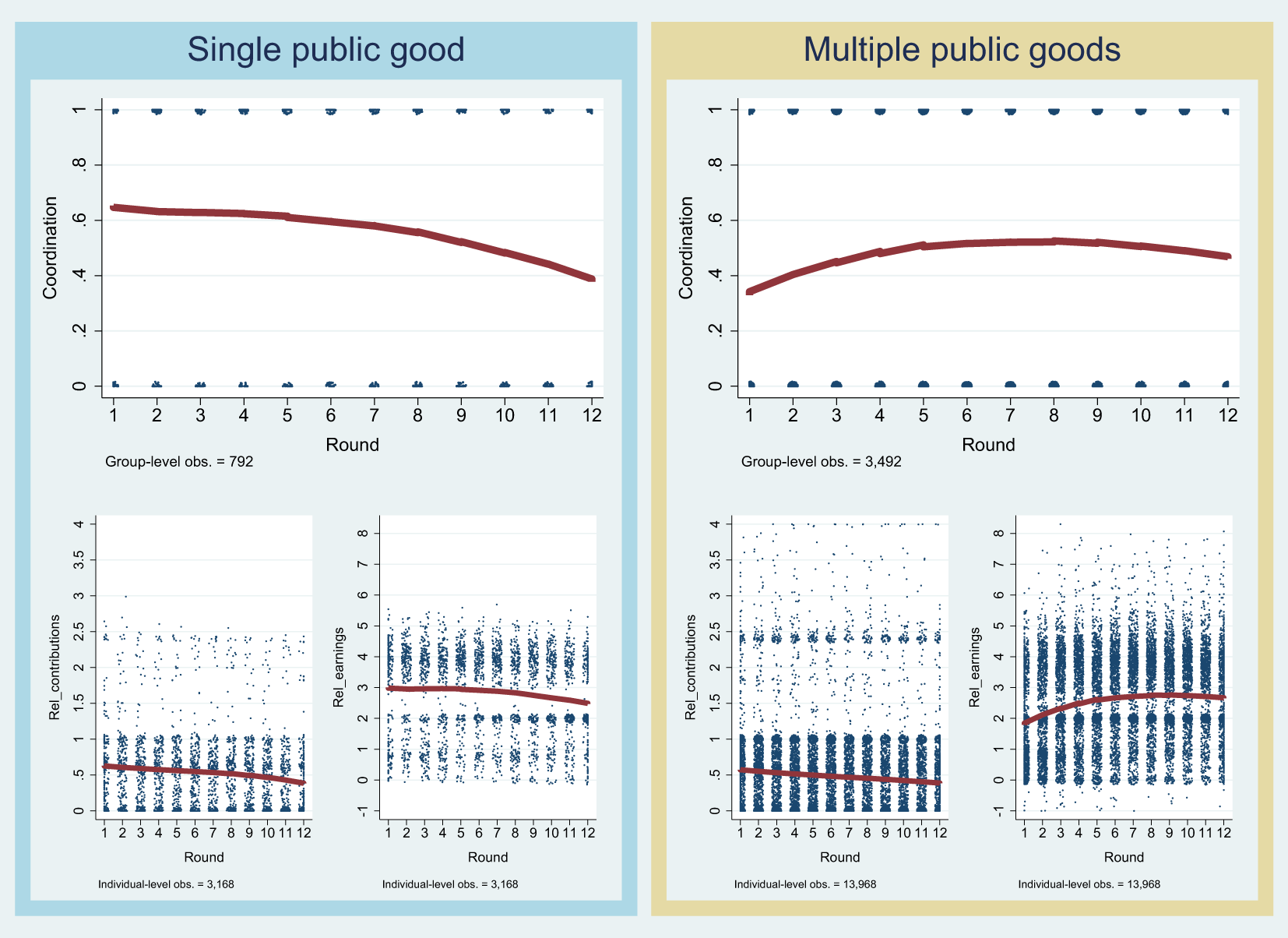
Fig. 1 Time trends of coordination, contributions, and earnings

As to the other variables categorized as coordination devices in Table 2, one preliminary remark is that 1PG_ME (M = 0.806) and R_signal (M = 0.753) on average perform better than 1PG_LE (M = 0.375) and Delegation (M = 0.429). Figure A2 in Appendix A provides a few additional insights. First, the presence of a single less efficient public good is arguably not even perceived as a coordination device, since the threshold is never achieved in round 1 and repeated interactions are necessary to develop coordination in this condition. Second, the performance of the random signal visibly deteriorates in case every player can afford to fund one collective account by herself. Third, delegation is increasingly effective as the intermediaries face more restrictions on the destination of the transferred resources, but performs poorly in case the delegates are to bear sunk costs.

To examine statistical significance of these initial insights, in Table 3 we perform multilevel regression models with clustering at both the group and individual level. Following best practices (Borenstein et al., Reference Borenstein, Hedges, Higgins and Rothstein2009), we include study dummies as covariates to preserve the identity of each study and capture the effect of variables (e.g., cross-cultural differences, online vs lab experiments, exchange rate) that are not coded due to insufficient variation and multicollinearity issues.

Table 3 Multilevel regression models

(1): marginal effects from multilevel probit (MP) model, with standard errors clustered at the group level in parentheses. (2): coefficient estimates from multilevel one-limit tobit (M1LT) model, with lower limit 0 and standard errors clustered at both the group and the individual level in parentheses. (3): coefficient estimates from multilevel two-limit tobit (M2LT) model, with lower limit 0, upper limit 1, and standard errors clustered at both the group and the individual level in parentheses. The latter model includes only observations from non-delegates and treatments implementing delegation. (4) coefficient estimates from multilevel mixed-effects (MME) model, with standard errors clustered at both the group and the individual level in parentheses. The label “Other controls” includes Dominated_PG, No_constraint, Low_overheads, Reshuffling, Het_endow, Het_pref, and the interaction term between the latter two variables.

*** p-value < 0.01.

** p-value < 0.05.

* p-value < 0.10.

Column (1) implements a multilevel probit model to evaluate the relative performance of coordination devices while controlling for confounders. First and foremost, the availability of a single contribution option increases the probability of successful coordination by 33.4% (p = 0.003) as compared with the case of four equally efficient public goods, revealing the negative effect of multiplicity on coordination. In addition, Figure 2 shows that the marginal effects of all the round dummies (except for Round 12 with p = 0.084) are positive and significant at the 1% level, highlighting the role of learning in facilitating convergence of donations to the same collective account. There is also evidence for the inverted U-shaped relationship between learning and coordination if we replace the round dummies in model (1) with a linear time Trend and its square, whose effects are significantly positive and negative, respectively (p < 0.001 in both cases). By using the delta method (Moffatt, Reference Moffatt2015) we estimate the number of interactions maximizing the probability of coordination to be 5.818, that is, approximately half of the duration of the experimental session. Another highly powerful coordination device turns out to be the presence of a single more efficient public good, which increases the probability of successful provision by 29.0% (p = 0.010). Delegation significantly promotes the chances of coordination (+21.7% and +17.2%) only if a destination rule formally requires the intermediary to pass 80% or the totality of the transfers along to the collective accounts (p = 0.020 and p = 0.008, respectively). Indeed, in the absence of a destination rule delegation can even hamper coordination (p = 0.042). Other potential coordination devices such as 1PG_LE and R_signal do not accomplish the goal. Linear restriction tests show that the marginal effects of the effective coordination devices do not significantly differ from each other, nor do they differ from the marginal effect of Single_PG. In sum, the effective coordination devices are able to offset the perils of the multiple-public-good framework represented by miscoordination.

Fig. 2 Comparing marginal effects

Column (2) analyzes donations through a multilevel one-limit tobit model.Footnote ⁵ We find that, in addition to solving the coordination dilemma, the availability of a single public good also boosts contributions (p = 0.041). In other words, the multiple-public-good environment is associated not only with increased risk of miscoordination, but also with lower contributions. Moreover, the effective coordination devices do not leverage greater contributions to solve the coordination dilemma. Rather, they work in spite of the negative donation trend (p < 0.001), and delegation can even decrease contributions if the destination rule is absent (p < 0.001) or equal to 20% (p = 0.021). Risk tolerance increases overall donations (p < 0.001) and women contribute significantly more than men (p = 0.001). To further explore the mechanics of delegation, in column (3) we include only observations from non-delegates and treatments implementing delegation, and we estimate a multilevel two-limit tobit model with Rel_transfers as dependent variable, namely, the individual amount of tokens transferred to the delegate divided by the initial endowment. The negative significant coefficient of the covariate Single_PG (p = 0.031) points out that delegation becomes a less and less popular fundraising channel as the risk of miscoordination decreases. Its use follows the same declining trend as direct contributions (p < 0.001). In the presence of the two most restrictive destination rules (i.e., 80% and 100%) non-delegates anticipate a minor risk of expropriation by the intermediary, thus raising transfers by 34.6% and 42.8% of their initial endowment, respectively (p < 0.001 in both cases). On the contrary, overheads appear to have the opposite effect (p < 0.001). Also, risk-lover donors appear more willing to bear the risk of expropriation and transfer tokens to the delegate (p = 0.026). In any case, the most interesting result of model (3) is that women delegate less than men (p = 0.011), preferring direct contributions.Footnote ⁶ Column (4) investigates the implications for the individual earnings by means of a multilevel mixed-effects model. Since the collective accounts are payoff-dominant, in general it is unsurprising that greater chances to successfully fund a public good correspond to higher individual earnings. We indeed observe that the effective coordination devices generate higher individual profits. In addition, it turns out that being risk-lover does not pay off (p < 0.001), leading to significantly waste monetary resources.

To sum up, Table A4 in Appendix A shows how these results accomplish the two goals of our meta-study.

4. Discussion and conclusions

Meta-analyzing individual participant data, we find that competition between public goods implies massive coordination problems that on average originate from fewer contributions and result in lower earnings. This general result adds to a host of recent studies that inquire whether competing charities are substitutes for each other (Filiz-Ozbay & Uler, Reference Filiz-Ozbay and Uler2019; Krieg & Samek, Reference Krieg and Samek2017; Meer, Reference Meer2017; Reinstein, Reference Reinstein2011; Schmitz, Reference Schmitz2021). A possible explanation is that players are fully rational and accordingly anticipate the increased risk of miscoordination, thereby reducing their donations. Indeed, subjects’ risk tolerance is positively associated with their contributions, as risk-lovers are more willing to bear the increased risk of miscoordination typical of this framework. In the presence of multiple public goods, one of the effective coordination devices turns out to be the existence of a single contribution option that is more profitable than the alternatives. This outcome tallies with a line of research showing that, when it comes to equilibrium selection in games, groups tend to focus on the payoff-dominant option even when the latter does not correspond to the risk-dominance prediction (Février & Linnemer, Reference Février and Linnemer2006; Gold & Colman, Reference Gold and Colman2020; Harsanyi & Selten, Reference Harsanyi and Selten1988; Schmidt et al., Reference Schmidt, Shupp, Walker and Ostrom2003). Consequently, competing charities should seek to stand out on their merits by improving features that might be valued by donors, such as transparency and alignment between donors’ expectations and charities’ actions. Moreover, we observe an inverted U-shaped trend in the successful provision of public goods, offering evidence for learning as a coordination device peculiar to the multiple-public-good framework. This may stem from the combination of an initial learning phase required by the complexity of the framework and, once coordination is achieved, a decline in contributions similar to that one typically observed in the single-public-good literature (Chaudhuri, Reference Chaudhuri2011; Croson & Marks, Reference Croson and Marks2000; Gächter & Thöni, Reference Gächter and Thöni2005; Marini et al., Reference Marini, García-Gallego and Corazzini2020). We also come to the conclusion that the effective coordination devices do not leverage greater contributions to solve the coordination dilemma, but they do generate higher earnings. Conversely, risk tolerance does not pay off and decreases individual earnings. Finally, in line with studies showing its effectiveness in comparable settings (Butera & Houser, Reference Butera and Houser2018; Fernández Domingos et al., Reference Fernández Domingos, Terrucha, Suchon, Grujić, Burguillo, Santos and Lenaerts2022; Hamman et al., Reference Hamman, Weber and Woon2011; Kocher et al., Reference Kocher, Tan and Yu2018), delegation proves to be a sound device for reducing the risk of miscoordination as long as the delegate is formally obliged to pass along a high enough percentage of the transferred resources. Women delegate less than men, thereby preferring direct contributions. This interesting result is consistent with recent meta-analytic evidence of gender differences in trust games, where men are found to be more trusting than women (Van Den Akker et al., Reference Van Den Akker, van Assen, Van Vugt and Wicherts2020). Indeed, in our framework the act of delegating involves an element of trust and the willigness to be vulnerable to the intermediary’s adverse behavior. Given that this finding emerges while risk attitude is kept constant, we propose an alternative explanation: although delegation can be viewed as both agentic and communal, women tend to associate it with agency and negative emotions more than do men, shying away from gender-role incongruent behaviors (Akinola et al., Reference Akinola, Martin and Phillips2018). If that were the case, reframing delegation as communal would be a sound intervention to promote greater uptake of this coordination device on the part of women. Even so, we also emphasize that subjects are less willing to transfer funds when the delegate is to incur administrative and fundraising costs tied to the function of intermediation, consistent with an extensive body of research documenting donors’ overhead aversion (Bowman, Reference Bowman2006; Gneezy et al., Reference Gneezy, Keenan and Gneezy2014; Meer, Reference Meer2014; Portillo & Stinn, Reference Portillo and Stinn2018). To fully exploit the advantages of delegation, it would therefore be advisable for intermediaries to use initial donations from major contributors for covering overhead costs, in such a way as to subsequently offer prospective donors an overhead-free donation opportunity (Gneezy et al., Reference Gneezy, Keenan and Gneezy2014).

In conclusion, we believe that further research should clarify the reasons behind overhead aversion, at the same time testing sustainable solutions. Academic efforts could also be directed toward the temporal dimension, to study whether sequential giving can act as a coordination device, as well as to investigate how donors use past contributions to develop coordination in the following interactions. We warmly support broader use of single-project meta-analyses within the experimental community, given their clear benefits for summarizing and extending the project results. Last but not least, we encourage scholars to delve into cross-national differences in charitable giving, considering the insufficient variation in our dataset (only two countries involved) and the well-established role played by cultural factors and economic development in this respect (Cai et al., Reference Cai, Caskey, Cowen, Murtazashvili, Murtazashvili and Salahodjaev2022; Kemmelmeier et al., Reference Kemmelmeier, Jambor and Letner2006).