Hostname: page-component-cb9f654ff-mwwwr Total loading time: 0 Render date: 2025-08-17T21:10:16.303Z Has data issue: false hasContentIssue false
  • English
  • Français

CATEGORICAL PROOF OF HOLOMORPHIC ATIYAH–BOTT FORMULA

Part of: General theory of categories and functors Homological algebra Algebraic geometry: Foundations

Published online by Cambridge University Press:  20 December 2018

Grigory Kondyrev  and
Artem Prikhodko
Grigory Kondyrev
Affiliation:
National Research University Higher School of Economics, Russian Federation (gkondyrev@gmail.com)
Artem Prikhodko
Affiliation:
National Research University Higher School of Economics, Russian Federation, Center for Advanced Studies, Skoltech, Moscow, Russian Federation (artem.n.prihodko@gmail.com)
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Given a $2$-commutative diagram

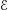in a symmetric monoidal $(\infty ,2)$-category $\mathscr{E}$ where $X,Y\in \mathscr{E}$ are dualizable objects and $\unicode[STIX]{x1D711}$ admits a right adjoint we construct a natural morphism $\mathsf{Tr}_{\mathscr{E}}(F_{X})\xrightarrow[{}]{~~~~~}\mathsf{Tr}_{\mathscr{E}}(F_{Y})$between the traces of $F_{X}$ and $F_{Y}$, respectively. We then apply this formalism to the case when $\mathscr{E}$ is the $(\infty ,2)$-category of $k$-linear presentable categories which in combination of various calculations in the setting of derived algebraic geometry gives a categorical proof of the classical Atiyah–Bott formula (also known as the Holomorphic Lefschetz fixed point formula).

Keywords

tracesfixed-points formulas2-categories

MSC classification

Primary: 14A99: None of the above, but in this section 18A99: None of the above, but in this section
Secondary: 18G99: None of the above, but in this section

Information

Type
Research Article
Information
Journal of the Institute of Mathematics of Jussieu , Volume 19 , Issue 5 , September 2020 , pp. 1739 - 1763
Check for updates
Copyright
© Cambridge University Press 2018

References

Atiyah, M. F. and Bott, R, A Lefschetz fixed point formula for elliptic complexes I, Ann. of Math. (2) 86(2) (1967), 374–407.Google Scholar
Atiyah, M. F. and Bott, R., A Lefschetz fixed point formula for elliptic complexes II. Applications, Ann. of Math. (2) 88(3) (1968), 451–491.Google Scholar
Ben-Zvi, D., Francis, J. and Nadler, D., Integral transforms and Drinfeld centers in derived algebraic geometry, J. Amer. Math. Soc. 23(4) (2010), 909–966.Google Scholar
Ben-Zvi, D. and Nadler, D., Nonlinear traces, Preprint, 2013, available at arXiv:1305.7175v3.Google Scholar
Gaitsgory, D. and Rozenblyum, N., A study in derived algebraic geometry, available at http://www.math.harvard.edu/∼gaitsgde/GL/.Google Scholar
Lefschetz, S., Intersections and transformations of complexes and manifolds, Trans. Amer. Math. Soc. 28 (1926), 1–49.Google Scholar
Lurie, J., Higher algebra, available at http://www.math.harvard.edu/∼lurie/papers/HA.pdf.Google Scholar