Hostname: page-component-cb9f654ff-5kfdg Total loading time: 0 Render date: 2025-08-16T08:51:40.121Z Has data issue: false hasContentIssue false
  • English
  • Français

Loewy series of parabolically induced $G_1T$ -Verma modules

Part of: Linear algebraic groups and related topics

Published online by Cambridge University Press:  28 March 2014

Abe Noriyuki  and
Kaneda Masaharu
Abe Noriyuki
Affiliation:
Hokkaido University, Creative Research Institution (CRIS), Japan(abenori@math.sci.hokudai.ac.jp)
Kaneda Masaharu
Affiliation:
Osaka City University, Department of Mathematics, Japan(kaneda@sci.osaka-cu.ac.jp)
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

We show that the modules for the Frobenius kernel of a reductive algebraic group over an algebraically closed field of positive characteristic 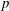$p$ induced from the 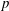$p$ -regular blocks of its parabolic subgroups can be 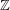$\mathbb{Z}$ -graded. In particular, we obtain that the modules induced from the simple modules of 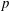$p$ -regular highest weights are rigid and determine their Loewy series, assuming the Lusztig conjecture on the irreducible characters for the reductive algebraic groups, which is now a theorem for large 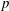$p$ . We say that a module is rigid if and only if it admits a unique filtration of minimal length with each subquotient semisimple, in which case the filtration is called the Loewy series.

Keywords

Loewy seriesparabolic inductiongraded inductionrigidityFrobenius kernel

MSC classification

Secondary: 20G05: Representation theory

Information

Type
Research Article
Information
Journal of the Institute of Mathematics of Jussieu , Volume 14 , Issue 1 , January 2015 , pp. 185 - 220
Copyright
© Cambridge University Press 2014 

References

Andersen, H. H., Jantzen, J. C. and Soergel, W., Representations of quantum groups at a $p$ -th root of unity and of semisimple groups in characteristic $p$ : independence of $p$ , Astérisque 220 (1994), (SMF).Google Scholar
Andersen, H. H. and Kaneda, M., Loewy series of modules for the first Frobenius kernel in a reductive algebraic group, Proc. LMS 59(3) (1989), 74–98.Google Scholar
Atiyah, M. and Macdonald, I. G., Introduction to Commutative Algebra. (Addison-Wesley, Reading, 1969).Google Scholar
Beilinson, A., Ginzburg, D. and Soergel, W., Koszul duality patterns in representation theory, J. Am. Math. Soc. 9(2) (1996), 473–527.Google Scholar
Fiebig, P., Sheaves on affine Schubert varieties, modular representations and Lusztig’s conjecture, J. Am. Math. Soc. 24 (2011), 133–181.Google Scholar
Hashimoto, Y., Kaneda, M. and Rumynin, D., On localization of $\bar{D}$ -modules, in Representations of Algebraic Groups, Quantum Groups, and Lie Algebras, Contemp. Math., Volume volume 413, pp. 43–62. (2006).Google Scholar
Jantzen, J. C., Representations of Algebraic Groups. (American Math. Soc., 2003).Google Scholar
Kaneda, M. and Ye, J. -C., Some observations on Karoubian complete strongly exceptional posets on the projective homogeneous varieties, arXiv:0911.2568v2 [math.RT].Google Scholar
Kaneda, M., The structure of Humphreys–Verma modules for projective spaces, J. Algebra 322 (2009), 237–244.Google Scholar
Kaneda, M., Homomorphisms between neighbouring $G_1T$ -Verma modules, Contemp. Math. 565 (2012), 105–113.Google Scholar
Kashiwara, M. and Tanisaki, T., Kazhdan–Lusztig conjecture for symmetrizable Kac–Moody Lie algebras with negative level II. Nonintegral case, Duke Math. J. 84 (1996), 771–813.CrossRefGoogle Scholar
Kato, S., On the Kazhdan–Lusztig polynomials for affine Weyl groups, Adv. Math. 55 (1995), 103–130.Google Scholar
Kazhdan, D. and Lusztig, G., Tensor structures arising from affine Lie algebras I, II, J. Am. Math. Soc. 6 (1993), 905–1011 ; Tensor structures arising from affine Lie algebras III, IV. J. Am. Math. Soc. 7, (1994) 335–453.Google Scholar
Lusztig, G., Hecke algebras and Jantzen’s generic decomposition patterns, Adv. Math. 37 (1980), 121–164.Google Scholar
Lusztig, G., Monodromic systems on affine flag manifolds, Proc. R. Soc. Lond. A 445 (1994), 231–246 ; Errata, 450, (1995) 731–732.Google Scholar
Matsumura, H., Commutative ring theory. (Cambridge Univ. Press, Cambridge, 1990).Google Scholar