Hostname: page-component-cb9f654ff-hqlzj Total loading time: 0 Render date: 2025-08-18T11:13:49.647Z Has data issue: false hasContentIssue false
  • English
  • Français

A different approach to unbounded operator algebras

Published online by Cambridge University Press:  24 October 2008

M. A. Hennings
M. A. Hennings
Affiliation:
Sidney Sussex College, Cambridge CB2 3HU
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

When considering *-algebras of unbounded operators, the usual approach is perhaps the one to be expected. One starts with a Hilbert space , and then defines a common dense domain X associated with some *-algebra 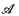of unbounded operators on . The algebra 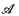is then used to define a locally convex topology (the graph topology) on X, with respect to which the inner product on X is continuous, and this in turn defines a variety of topologies on 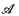, which are then studied.

Information

Type
Research Article
Information
Mathematical Proceedings of the Cambridge Philosophical Society , Volume 106 , Issue 1 , July 1989 , pp. 125 - 141
Copyright
Copyright © Cambridge Philosophical Society 1989

References

REFERENCES

[1]Dubinsky, E.. The Structure of Nuclear Fréchet Space. Lecture Notes in Math. vol. 720 (Springer-Verlag, 1979).CrossRefGoogle Scholar
[2]Hussain, T.. Multiplicative Functionals on Topological Algebras. Research Notes in Math. no. 85 (Pitman, 1983).Google Scholar
[3]Jarchow, H.. Locally Convex Spaces (Teubner-Verlag, 1981).CrossRefGoogle Scholar
[4]Lassner, G.. Topological algebras of operators. Rep. Math. Phys. 3 (1972), 279–293.CrossRefGoogle Scholar
[5]Lassner, G.. The β-topology on operator algebras. Colloq. Internal. CNRS 274 (1981), 249–260.Google Scholar
[6]Lassner, G. and Timmermann, W.. Classification of domains of operator algebras. Rep. Math. Phys. 9 (1976), 205–217.CrossRefGoogle Scholar
[7]Lassner, G. and Lassner, G. A.. On the continuity of entropy. Rep. Math. Phys. 15 (1979). 41–46.CrossRefGoogle Scholar
[8]Perez-Carreras, and Bonet, J.. Barreled Locally Convex Spaces. North-Holland Mathematical Studies no. 131 (North-Holland, 1987).Google Scholar
[9]Pietsch, A.. Nuclear Locally Convex Spaces. Ergebnisse der Mathematik und ihrer Grenzgebiete no. 66 (Springer-Verlag, 1972).Google Scholar
[10]Reed, M. and Simon, B.. Methods of Modern Mathematical Physics. I. Functional Analysis (Academic Press, 1972).Google Scholar
[11]Schaefer, H. H.. Topological Vector Spaces. Graduate Texts in Math. no. 3 (Springer-Verlag, 1970).Google Scholar
[12]Schmüdgen, K.. On trace representation of linear functional on unbounded operator algebras. Comm. Math. Phys. 63 (1978), 113–130.CrossRefGoogle Scholar
[13]Schmüdgen, K.. On topologisation of unbounded operator algebras. Rep. Math. Phys. 17 (1980), 359–371.CrossRefGoogle Scholar
[14]Schmüdgen, K.. Graded and filtrated topological *-algebras; the closure of the opositive cone. Rev. Roumaine Math. Pures Appl. (to appear).Google Scholar
[15]Trèves, F.. Topological Vector Spaces, Distributions and Kernels (Academic Press. 1967).Google Scholar