Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Wang, Xiao-Tian
Liang, Xiang-Qian
and
Zhang, Yu-Lin
2003.
On harmonic typically real mappings.
Journal of Mathematical Analysis and Applications,
Vol. 277,
Issue. 2,
p.
533.
Duren, Peter
2004.
Harmonic Mappings in the Plane.
Bshouty, D.
Lyzzaik, A.
and
Weitsman, A.
2007.
Uniqueness of harmonic mappings with Blaschke dilatations.
The Journal of Geometric Analysis,
Vol. 17,
Issue. 1,
p.
41.
Bshouty, Daoud
Lyzzaik, Abdallah
and
Weitsman, Allen
2008.
On the Boundary Behaviour of Univalent Harmonic Mappings onto Convex Domains.
Computational Methods and Function Theory,
Vol. 8,
Issue. 1,
p.
261.
Bshouty, Daoud
and
Lyzzaik, Abdallah
2008.
Uniqueness of Harmonic Mappings into Strictly Starlike Domains.
Computational Methods and Function Theory,
Vol. 8,
Issue. 2,
p.
433.
Dorff, Michael
Nowak, Maria
and
Szapiel, Wojciech
2012.
Typically real harmonic functions.
Rocky Mountain Journal of Mathematics,
Vol. 42,
Issue. 2,
Bshouty, Daoud
and
Lyzzaik, Abdallah
2014.
Current Topics in Pure and Computational Complex Analysis.
p.
1.
PONNUSAMY, SAMINATHAN
and
QIAO, JINJING
2015.
CLASSIFICATION OF UNIVALENT HARMONIC MAPPINGS ON THE UNIT DISK WITH HALF-INTEGER COEFFICIENTS.
Journal of the Australian Mathematical Society,
Vol. 98,
Issue. 2,
p.
257.
Bagapsh, A. O.
2019.
On the Geometric Properties of the Poisson Kernel for the Lamé Equation.
Computational Mathematics and Mathematical Physics,
Vol. 59,
Issue. 12,
p.
2124.
Garg, Raj K.
Dorff, Michael
and
Jahangiri, Jay M.
2022.
Directional Convexity of Convolutions of Harmonic Functions with Certain Dilatations.
Computational Methods and Function Theory,
Vol. 22,
Issue. 3,
p.
519.
Long, Bo-Yong
and
Wang, Qi-Han
2022.
Some coefficient estimates on real kernel 𝛼-harmonic mappings.
Proceedings of the American Mathematical Society,
Vol. 150,
Issue. 4,
p.
1529.


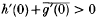 and is not typically real. Furthermore, we give a geometric characterization for univalent, harmonic and typically real mappings.
and is not typically real. Furthermore, we give a geometric characterization for univalent, harmonic and typically real mappings.