The first factor of the class number of a cyclotomic number field can be obtainable by the analytic class number formula and there are some tables which show the decompositions of the first factors into primes. But, using just the analytic formula, we cannot tell what kinds of primes will appear as the factors of the class number of a given cyclotomic number field, except for those of the genus number, or the irregular primes. It is significant to find in advance the prime factors, particularly those prime to the degree of the field. For instance, in the table of the first factors we can pick out some pairs (l, p) of two odd primes l and p such that the class number of each lpth cyclotomic number field is divisible by l even if p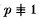 1 (mod l). If p ≡ (mod l) for l ≥ 5 or p ≡ 1 (mod 32) for l = 3, then it is easy from the outset to achieve our intention of finding the factor l using the genus number formula. Otherwise it seems to be difficult. We wish to make it clear algebraically why the class number has the prime factor l.