Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Nashed, M.Z.
and
Rall, L.B.
1976.
Generalized Inverses and Applications.
p.
771.
Guyker, James
1978.
A structure theorem for operators with closed range.
Bulletin of the Australian Mathematical Society,
Vol. 18,
Issue. 2,
p.
169.
Bagheri-Bardi, G.A.
Elyaspour, A.
and
Esslamzadeh, G.H.
2019.
The role of algebraic structure in the invariant subspace theory.
Linear Algebra and its Applications,
Vol. 583,
Issue. ,
p.
102.

 denote a Hilbert space (real or complex), with inner product (|). In order to present our notation, we recall that if
denote a Hilbert space (real or complex), with inner product (|). In order to present our notation, we recall that if  is a vector subspace of
is a vector subspace of 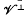 ,
, 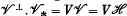 is the
is the 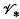 and final domain
and final domain 