Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Fulton, William
and
Laksov, Dan
1977.
Real and complex singularities, Oslo 1976.
p.
171.
Kleiman, Steven L.
1977.
Real and complex singularities, Oslo 1976.
p.
297.
Fulton, William
and
MacPherson, Robert
1977.
Real and complex singularities, Oslo 1976.
p.
179.
Laksov, Dan
1978.
Residual intersections and Todds formula for the double locus of a morphism.
Acta Mathematica,
Vol. 140,
Issue. 0,
p.
75.
Ionescu, Paltin
1984.
Algebraic Geometry Bucharest 1982.
Vol. 1056,
Issue. ,
p.
142.
Alzati, A.
1986.
3-scroll immersi inG(1,4).
ANNALI DELL UNIVERSITA DI FERRARA,
Vol. 32,
Issue. 1,
p.
45.
Pan, Ivan
and
Russo, Francesco
2005.
Cremona transformations and special double structures.
manuscripta mathematica,
Vol. 117,
Issue. 4,
p.
491.
Pasquotto, Federica
2005.
Symplectic geography in dimension 8..
manuscripta mathematica,
Vol. 116,
Issue. 3,
p.
341.
Grivaux, Julien
2010.
Chern classes in Deligne cohomology for coherent analytic sheaves.
Mathematische Annalen,
Vol. 347,
Issue. 2,
p.
249.
Hanamura, Masaki
2011.
Blow-ups and mixed motives.
Tohoku Mathematical Journal,
Vol. 63,
Issue. 4,
Aprodu, Marian
and
Toma, Matei
2014.
Boundedness for Some Rationally Connected Threefolds in ℙ6.
Communications in Algebra,
Vol. 42,
Issue. 9,
p.
3876.
Glazebrook, James F.
and
Verjovsky, Alberto
2019.
Homology theory formulas for generalized Riemann–Hurwitz and generalized monoidal transformations.
Boletín de la Sociedad Matemática Mexicana,
Vol. 25,
Issue. 2,
p.
427.
Catanese, Fabrizio
and
Oguiso, Keiji
2020.
The double point formula with isolated singularities and canonical embeddings.
Journal of the London Mathematical Society,
Vol. 102,
Issue. 3,
p.
1337.
Miranda-Neto, Cleto B
2021.
Pullback of the Normal Module of Ideals with Low Codimension.
The Quarterly Journal of Mathematics,
Vol. 72,
Issue. 4,
p.
1147.
Rampazzo, Marco
2021.
Equivalences between Calabi–Yau manifolds and roofs of projective bundles.
Kapustka, Michał
and
Rampazzo, Marco
2022.
Mukai duality via roofs of projective bundles.
Bulletin of the London Mathematical Society,
Vol. 54,
Issue. 2,
p.
694.
Berget, Andrew
Eur, Christopher
Spink, Hunter
and
Tseng, Dennis
2023.
Tautological classes of matroids.
Inventiones mathematicae,
Vol. 233,
Issue. 2,
p.
951.


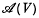 will be the Chow ring of rational equivalence classes of cycles of
will be the Chow ring of rational equivalence classes of cycles of 

