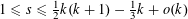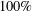1 Introduction
Our focus in this paper is the Vinogradov system of Diophantine equations. When
![]() $k$
and
$k$
and
![]() $s$
are natural numbers, and
$s$
are natural numbers, and
![]() $X$
is a large real number, denote by
$X$
is a large real number, denote by
![]() $J_{s,k}(X)$
the number of integral solutions of the system
$J_{s,k}(X)$
the number of integral solutions of the system
 $$\begin{eqnarray}x_{1}^{j}+\cdots +x_{s}^{j}=y_{1}^{j}+\cdots +y_{s}^{j}\quad (1\leqslant j\leqslant k),\end{eqnarray}$$
$$\begin{eqnarray}x_{1}^{j}+\cdots +x_{s}^{j}=y_{1}^{j}+\cdots +y_{s}^{j}\quad (1\leqslant j\leqslant k),\end{eqnarray}$$
with
 $1\leqslant x_{i},y_{i}\leqslant X$
$1\leqslant x_{i},y_{i}\leqslant X$
 $(1\leqslant i\leqslant s)$
. Bounds for
$(1\leqslant i\leqslant s)$
. Bounds for
![]() $J_{s,k}(X)$
are linked via orthogonality to mean value estimates for exponential sums and hence feature prominently in the analysis of problems spanning the analytic theory of numbers. Thus, for example, the strongest available conclusions concerning the validity of the asymptotic formula in Waring’s problem, the zero-free region for the Riemann zeta function and the distribution modulo
$J_{s,k}(X)$
are linked via orthogonality to mean value estimates for exponential sums and hence feature prominently in the analysis of problems spanning the analytic theory of numbers. Thus, for example, the strongest available conclusions concerning the validity of the asymptotic formula in Waring’s problem, the zero-free region for the Riemann zeta function and the distribution modulo
![]() $1$
of polynomial sequences all depend on bounds for
$1$
of polynomial sequences all depend on bounds for
![]() $J_{s,k}(X)$
. We refer the reader to the comprehensive sources due to Arkhipov et al [Reference Arkhipov, Chubarikov and Karatsuba1] and Vinogradov [Reference Vinogradov11] for discussion of the many applications of such estimates, collectively described as instances of Vinogradov’s mean value theorem. A more recent tour of the subject is described in [Reference Wooley18]. By considering mean values of an associated exponential sum, it follows that the validity of the strongly diagonal estimate
$J_{s,k}(X)$
. We refer the reader to the comprehensive sources due to Arkhipov et al [Reference Arkhipov, Chubarikov and Karatsuba1] and Vinogradov [Reference Vinogradov11] for discussion of the many applications of such estimates, collectively described as instances of Vinogradov’s mean value theorem. A more recent tour of the subject is described in [Reference Wooley18]. By considering mean values of an associated exponential sum, it follows that the validity of the strongly diagonal estimate
 $$\begin{eqnarray}J_{s,k}(X)\ll X^{s+\unicode[STIX]{x1D700}},\end{eqnarray}$$
$$\begin{eqnarray}J_{s,k}(X)\ll X^{s+\unicode[STIX]{x1D700}},\end{eqnarray}$$
for
 $1\leqslant s\leqslant \frac{1}{2}k(k+1)$
, would imply the main conjecture in Vinogradov’s mean value theorem, which asserts that for each
$1\leqslant s\leqslant \frac{1}{2}k(k+1)$
, would imply the main conjecture in Vinogradov’s mean value theorem, which asserts that for each
![]() $\unicode[STIX]{x1D700}>0$
, one has
$\unicode[STIX]{x1D700}>0$
, one has
 $$\begin{eqnarray}J_{s,k}(X)\ll X^{\unicode[STIX]{x1D700}}(X^{s}+X^{2s-k(k+1)/2}).\end{eqnarray}$$
$$\begin{eqnarray}J_{s,k}(X)\ll X^{\unicode[STIX]{x1D700}}(X^{s}+X^{2s-k(k+1)/2}).\end{eqnarray}$$
Here and throughout this paper, the implicit constants associated with Vinogradov’s notation
![]() $\ll$
and
$\ll$
and
![]() $\gg$
may depend on
$\gg$
may depend on
![]() $s$
,
$s$
,
![]() $k$
and
$k$
and
![]() $\unicode[STIX]{x1D700}$
.
$\unicode[STIX]{x1D700}$
.
For almost all of the eighty year history of the subject, an estimate of the strength of (1.3) has seemed a very remote prospect indeed, for until only a year before this paper was written, the bound (1.2) was known to hold only for
 $s\leqslant k+1$
(see [Reference Hua8, Lemma 5.4]). By enhancing the efficient congruencing method introduced in [Reference Wooley15], recent work of the author joint with Ford [Reference Ford and Wooley4] has established the estimate (1.2) for
$s\leqslant k+1$
(see [Reference Hua8, Lemma 5.4]). By enhancing the efficient congruencing method introduced in [Reference Wooley15], recent work of the author joint with Ford [Reference Ford and Wooley4] has established the estimate (1.2) for
 $s\leqslant \frac{1}{4}(k+1)^{2}$
, amounting to half of the range
$s\leqslant \frac{1}{4}(k+1)^{2}$
, amounting to half of the range
 $s\leqslant \frac{1}{2}k(k+1)$
in which diagonal behaviour dominates (1.3). Our goal in this paper is to adapt the multigrade efficient congruencing method detailed in our very recent work [Reference Wooley19] so as to obtain strongly diagonal estimates of the shape (1.2). It transpires that when
$s\leqslant \frac{1}{2}k(k+1)$
in which diagonal behaviour dominates (1.3). Our goal in this paper is to adapt the multigrade efficient congruencing method detailed in our very recent work [Reference Wooley19] so as to obtain strongly diagonal estimates of the shape (1.2). It transpires that when
![]() $k$
is large, we are able to establish the validity of the conjectured estimate (1.2) for almost all
$k$
is large, we are able to establish the validity of the conjectured estimate (1.2) for almost all
![]() $s$
in the critical interval
$s$
in the critical interval
 $1\leqslant s\leqslant \frac{1}{2}k(k+1)$
or, as one might say, a proportion asymptotically approaching
$1\leqslant s\leqslant \frac{1}{2}k(k+1)$
or, as one might say, a proportion asymptotically approaching
![]() $100\%$
of the critical interval. We consequently find ourselves within a whisker of the proof of the main conjecture (1.3), a situation hitherto unprecedented in the analysis of mean value estimates for exponential sums of large degree.
$100\%$
of the critical interval. We consequently find ourselves within a whisker of the proof of the main conjecture (1.3), a situation hitherto unprecedented in the analysis of mean value estimates for exponential sums of large degree.
The most precise form of our new estimate may be found in Theorem 2.1 below. For the present, we restrict ourselves to a conclusion relatively simple to state that is indicative of what may now be achieved.
Theorem 1.1. Let
![]() $k$
be a natural number with
$k$
be a natural number with
![]() $k\geqslant 7$
, put
$k\geqslant 7$
, put
 $r=k-\lceil 2\sqrt{k}\rceil +2$
and suppose that
$r=k-\lceil 2\sqrt{k}\rceil +2$
and suppose that
![]() $s$
is an integer satisfying
$s$
is an integer satisfying
 $$\begin{eqnarray}1\leqslant s\leqslant kr-\frac{1}{2}r(r-1)-\mathop{\sum }_{m=1}^{r-1}\frac{m(r-m)}{s-r-m}.\end{eqnarray}$$
$$\begin{eqnarray}1\leqslant s\leqslant kr-\frac{1}{2}r(r-1)-\mathop{\sum }_{m=1}^{r-1}\frac{m(r-m)}{s-r-m}.\end{eqnarray}$$
Then, for each
![]() $\unicode[STIX]{x1D700}>0$
, one has
$\unicode[STIX]{x1D700}>0$
, one has
 $J_{s,k}(X)\ll X^{s+\unicode[STIX]{x1D700}}$
.
$J_{s,k}(X)\ll X^{s+\unicode[STIX]{x1D700}}$
.
A modicum of computation reveals that when
![]() $k$
is large, this estimate confirms the main conjecture (1.3) for almost all of the critical interval of exponents
$k$
is large, this estimate confirms the main conjecture (1.3) for almost all of the critical interval of exponents
 $1\leqslant s\leqslant {\textstyle \frac{1}{2}}k(k+1)$
.
$1\leqslant s\leqslant {\textstyle \frac{1}{2}}k(k+1)$
.
Corollary 1.2. When
![]() $s$
and
$s$
and
![]() $k$
are natural numbers with
$k$
are natural numbers with
![]() $k\geqslant 7$
and
$k\geqslant 7$
and
 $$\begin{eqnarray}1\leqslant s\leqslant {\textstyle \frac{1}{2}}k(k+1)-{\textstyle \frac{7}{3}}k,\end{eqnarray}$$
$$\begin{eqnarray}1\leqslant s\leqslant {\textstyle \frac{1}{2}}k(k+1)-{\textstyle \frac{7}{3}}k,\end{eqnarray}$$
then, for each
![]() $\unicode[STIX]{x1D700}>0$
, one has
$\unicode[STIX]{x1D700}>0$
, one has
 $J_{s,k}(X)\ll X^{s+\unicode[STIX]{x1D700}}$
.
$J_{s,k}(X)\ll X^{s+\unicode[STIX]{x1D700}}$
.
As we have already noted, a conclusion analogous to Theorem 1.1 is made available in [Reference Ford and Wooley4, Theorem 1.1] in the more limited range
 $1\leqslant s\leqslant \frac{1}{4}(k+1)^{2}$
. Earlier conclusions were limited to the much shorter interval
$1\leqslant s\leqslant \frac{1}{4}(k+1)^{2}$
. Earlier conclusions were limited to the much shorter interval
 $1\leqslant s\leqslant k+1$
(see [Reference Vaughan and Wooley10] for a particularly precise statement in this situation). In view of the lower bound
$1\leqslant s\leqslant k+1$
(see [Reference Vaughan and Wooley10] for a particularly precise statement in this situation). In view of the lower bound
 $$\begin{eqnarray}J_{s,k}(X)\gg X^{s}+X^{2s-k(k+1)/2},\end{eqnarray}$$
$$\begin{eqnarray}J_{s,k}(X)\gg X^{s}+X^{2s-k(k+1)/2},\end{eqnarray}$$
that arises by considering the diagonal solutions of (1.1) with
![]() $\mathbf{x}=\mathbf{y}$
, together with a lower bound for the product of local densities (see [Reference Vaughan9, equation (7.4)]), one sees that the conclusion of Theorem 1.1 cannot hold when
$\mathbf{x}=\mathbf{y}$
, together with a lower bound for the product of local densities (see [Reference Vaughan9, equation (7.4)]), one sees that the conclusion of Theorem 1.1 cannot hold when
 $s>{\textstyle \frac{1}{2}}k(k+1)$
.
$s>{\textstyle \frac{1}{2}}k(k+1)$
.
The gap between our new result and a complete proof of the main conjecture (1.3) stands at
![]() ${\textstyle \frac{7}{3}}k$
variables, amounting to a proportion
${\textstyle \frac{7}{3}}k$
variables, amounting to a proportion
![]() $O(1/k)$
of the length of the critical interval
$O(1/k)$
of the length of the critical interval
 $1\leqslant s\leqslant \frac{1}{2}k(k+1)$
. In a certain sense, therefore, our conclusion establishes the main conjecture in 100% of the critical interval as
$1\leqslant s\leqslant \frac{1}{2}k(k+1)$
. In a certain sense, therefore, our conclusion establishes the main conjecture in 100% of the critical interval as
![]() $k\rightarrow \infty$
, justifying the assertion concluding our opening paragraph. In §11, we describe some modifications to our basic strategy which offer some improvement in the conclusion of Corollary 1.2 towards the main conjecture (1.3). We have opted for a relatively concise account of this improvement, since the details of the associated argument are of sufficient complexity that the key elements of our basic strategy would be obscured were we to make this account the main focus of our exposition.
$k\rightarrow \infty$
, justifying the assertion concluding our opening paragraph. In §11, we describe some modifications to our basic strategy which offer some improvement in the conclusion of Corollary 1.2 towards the main conjecture (1.3). We have opted for a relatively concise account of this improvement, since the details of the associated argument are of sufficient complexity that the key elements of our basic strategy would be obscured were we to make this account the main focus of our exposition.
Theorem 1.3. When
![]() $k$
is a sufficiently large natural number and
$k$
is a sufficiently large natural number and
![]() $s$
is an integer satisfying
$s$
is an integer satisfying
 $$\begin{eqnarray}1\leqslant s\leqslant {\textstyle \frac{1}{2}}k(k+1)-{\textstyle \frac{1}{3}}k-8k^{2/3},\end{eqnarray}$$
$$\begin{eqnarray}1\leqslant s\leqslant {\textstyle \frac{1}{2}}k(k+1)-{\textstyle \frac{1}{3}}k-8k^{2/3},\end{eqnarray}$$
then, for each
![]() $\unicode[STIX]{x1D700}>0$
, one has
$\unicode[STIX]{x1D700}>0$
, one has
 $J_{s,k}(X)\ll X^{s+\unicode[STIX]{x1D700}}$
.
$J_{s,k}(X)\ll X^{s+\unicode[STIX]{x1D700}}$
.
Our methods are applicable not only for large values of
![]() $k$
. By taking
$k$
. By taking
 $r=k-\lceil 2\sqrt{k}\rceil +2$
in Theorem 2.1 below, one may establish an improvement on the conclusion of [Reference Ford and Wooley4, Theorem 1.1]. We note here that the latter delivers the bound
$r=k-\lceil 2\sqrt{k}\rceil +2$
in Theorem 2.1 below, one may establish an improvement on the conclusion of [Reference Ford and Wooley4, Theorem 1.1]. We note here that the latter delivers the bound
 $J_{s,k}(X)\ll X^{s+\unicode[STIX]{x1D700}}$
for
$J_{s,k}(X)\ll X^{s+\unicode[STIX]{x1D700}}$
for
 $1\leqslant s\leqslant \frac{1}{4}(k+1)^{2}$
.
$1\leqslant s\leqslant \frac{1}{4}(k+1)^{2}$
.
Theorem 1.4. Define the number
![]() $D(k)$
as in Table 1. Then, whenever
$D(k)$
as in Table 1. Then, whenever
![]() $k\geqslant 4$
and
$k\geqslant 4$
and
 $1\leqslant s\leqslant D(k)$
, one has
$1\leqslant s\leqslant D(k)$
, one has
 $J_{s,k}(X)\ll X^{s+\unicode[STIX]{x1D700}}$
.
$J_{s,k}(X)\ll X^{s+\unicode[STIX]{x1D700}}$
.
Table 1 Values for
![]() $D(k)$
described in Theorem 1.4.
$D(k)$
described in Theorem 1.4.

One may enquire concerning the impact of our methods in the case
![]() $k=3$
. Here, although the methods of this paper do not apply directly, a careful variant of our ideas proves surprisingly successful. This is a matter which we address elsewhere (see [Reference Wooley20]).
$k=3$
. Here, although the methods of this paper do not apply directly, a careful variant of our ideas proves surprisingly successful. This is a matter which we address elsewhere (see [Reference Wooley20]).
A trivial consequence of the estimate supplied by Theorems 1.1 and 1.3 provides a new upper bound for
![]() $J_{s,k}(X)$
at the critical value
$J_{s,k}(X)$
at the critical value
 $s=\frac{1}{2}k(k+1)$
.
$s=\frac{1}{2}k(k+1)$
.
Theorem 1.5. Suppose that
![]() $k$
is a large natural number. Then
$k$
is a large natural number. Then
 $$\begin{eqnarray}J_{(1/2)k(k+1),k}(X)\ll X^{k(k+1)/2+\unicode[STIX]{x1D6E5}},\end{eqnarray}$$
$$\begin{eqnarray}J_{(1/2)k(k+1),k}(X)\ll X^{k(k+1)/2+\unicode[STIX]{x1D6E5}},\end{eqnarray}$$
where
 $\unicode[STIX]{x1D6E5}=({\textstyle \frac{1}{3}}+o(1))k$
.
$\unicode[STIX]{x1D6E5}=({\textstyle \frac{1}{3}}+o(1))k$
.
As remarked in the discussion following the statement of [Reference Ford and Wooley4, Theorem 1.2], the work of that paper shows that a conclusion analogous to Theorem 1.5 holds with
 $\unicode[STIX]{x1D6E5}=(\frac{3}{2}-\sqrt{2})k^{2}+O(k)$
. Our new result for the first time in the subject obtains a conclusion in which
$\unicode[STIX]{x1D6E5}=(\frac{3}{2}-\sqrt{2})k^{2}+O(k)$
. Our new result for the first time in the subject obtains a conclusion in which
 $\unicode[STIX]{x1D6E5}=o(k^{2})$
. Indeed, one now has a good asymptotic approximation to the main conjecture (1.3) for all
$\unicode[STIX]{x1D6E5}=o(k^{2})$
. Indeed, one now has a good asymptotic approximation to the main conjecture (1.3) for all
![]() $s$
, since we have
$s$
, since we have
 $$\begin{eqnarray}J_{s,k}(X)\ll X^{\unicode[STIX]{x1D6E5}_{s,k}}(X^{s}+X^{2s-k(k+1)/2}),\end{eqnarray}$$
$$\begin{eqnarray}J_{s,k}(X)\ll X^{\unicode[STIX]{x1D6E5}_{s,k}}(X^{s}+X^{2s-k(k+1)/2}),\end{eqnarray}$$
with
 $\unicode[STIX]{x1D6E5}_{s,k}=O(k)$
for all
$\unicode[STIX]{x1D6E5}_{s,k}=O(k)$
for all
![]() $s$
.
$s$
.
We are also able to obtain a very slight improvement in our previous bound for the the number of variables required to establish the anticipated asymptotic formula in Waring’s problem, at least, when
![]() $k$
is sufficiently large. We refer the reader to Theorem 12.2 for an account of this new bound, and to Theorem 12.1 for some consequences of Theorem 1.3 in the context of Tarry’s problem. The latter is worth highlighting already. When
$k$
is sufficiently large. We refer the reader to Theorem 12.2 for an account of this new bound, and to Theorem 12.1 for some consequences of Theorem 1.3 in the context of Tarry’s problem. The latter is worth highlighting already. When
![]() $h$
,
$h$
,
![]() $k$
and
$k$
and
![]() $s$
are positive integers with
$s$
are positive integers with
![]() $h\geqslant 2$
, consider the Diophantine system
$h\geqslant 2$
, consider the Diophantine system
 $$\begin{eqnarray}\mathop{\sum }_{i=1}^{s}x_{i1}^{j}=\mathop{\sum }_{i=1}^{s}x_{i2}^{j}=\cdots =\mathop{\sum }_{i=1}^{s}x_{ih}^{j}\quad (1\leqslant j\leqslant k).\end{eqnarray}$$
$$\begin{eqnarray}\mathop{\sum }_{i=1}^{s}x_{i1}^{j}=\mathop{\sum }_{i=1}^{s}x_{i2}^{j}=\cdots =\mathop{\sum }_{i=1}^{s}x_{ih}^{j}\quad (1\leqslant j\leqslant k).\end{eqnarray}$$
Let
![]() $W(k,h)$
denote the least natural number
$W(k,h)$
denote the least natural number
![]() $s$
having the property that the simultaneous equations (1.5) possess an integral solution
$s$
having the property that the simultaneous equations (1.5) possess an integral solution
![]() $\mathbf{x}$
with
$\mathbf{x}$
with
 $$\begin{eqnarray}\mathop{\sum }_{i=1}^{s}x_{iu}^{k+1}\neq \mathop{\sum }_{i=1}^{s}x_{iv}^{k+1}\quad (1\leqslant u<v\leqslant h).\end{eqnarray}$$
$$\begin{eqnarray}\mathop{\sum }_{i=1}^{s}x_{iu}^{k+1}\neq \mathop{\sum }_{i=1}^{s}x_{iv}^{k+1}\quad (1\leqslant u<v\leqslant h).\end{eqnarray}$$
Also, let
![]() $P(k,h)$
denote the least natural number
$P(k,h)$
denote the least natural number
![]() $s$
having the property that the simultaneous equations (1.5) possess an integral solution
$s$
having the property that the simultaneous equations (1.5) possess an integral solution
![]() $\mathbf{x}$
with
$\mathbf{x}$
with
 $$\begin{eqnarray}\{x_{1u},\ldots ,x_{su}\}\neq \{x_{1v},\ldots ,x_{sv}\}\quad (1\leqslant u<v\leqslant h).\end{eqnarray}$$
$$\begin{eqnarray}\{x_{1u},\ldots ,x_{su}\}\neq \{x_{1v},\ldots ,x_{sv}\}\quad (1\leqslant u<v\leqslant h).\end{eqnarray}$$
It is trivial that
 $P(k,h)\leqslant W(k,h)$
, and relatively straightforward to establish that when
$P(k,h)\leqslant W(k,h)$
, and relatively straightforward to establish that when
![]() $h$
and
$h$
and
![]() $k$
are natural numbers with
$k$
are natural numbers with
![]() $h\geqslant 2$
, then
$h\geqslant 2$
, then
 $P(k,h)\leqslant {\textstyle \frac{1}{2}}k(k+1)+1$
(see Hardy and Wright [Reference Hardy and Wright5, Theorem 409]). The corresponding bound for the more difficult quantity
$P(k,h)\leqslant {\textstyle \frac{1}{2}}k(k+1)+1$
(see Hardy and Wright [Reference Hardy and Wright5, Theorem 409]). The corresponding bound for the more difficult quantity
![]() $W(k,h)$
has, however, hitherto remained far beyond reach. By applying Theorem 1.5, we are now able to show in Theorem 12.1 that when
$W(k,h)$
has, however, hitherto remained far beyond reach. By applying Theorem 1.5, we are now able to show in Theorem 12.1 that when
![]() $h$
and
$h$
and
![]() $k$
are natural numbers with
$k$
are natural numbers with
![]() $h\geqslant 2$
and
$h\geqslant 2$
and
![]() $k$
sufficiently large, then one has
$k$
sufficiently large, then one has
 $W(k,h)\leqslant {\textstyle \frac{1}{2}}k(k+1)+1$
. As noted earlier, other applications of Vinogradov’s mean value theorem can be found in the classical literature on the subject, such as [Reference Arkhipov, Chubarikov and Karatsuba1, Reference Vinogradov11, Reference Wooley12].
$W(k,h)\leqslant {\textstyle \frac{1}{2}}k(k+1)+1$
. As noted earlier, other applications of Vinogradov’s mean value theorem can be found in the classical literature on the subject, such as [Reference Arkhipov, Chubarikov and Karatsuba1, Reference Vinogradov11, Reference Wooley12].
We have written elsewhere concerning the basic strategy underlying efficient congruencing; a sketch of the basic ideas can be found in [Reference Wooley15, §2]. The multigrade efficient congruencing method seeks to more fully extract the information available from congruences of different levels. We direct the reader to [Reference Wooley19] for an introduction to such ideas. Perhaps it is worth noting that the main challenge in the present adaptation of multigrade efficient congruencing is that no loss of more than a constant factor can be tolerated in the basic congruencing steps. This task is complicated as we progress through the iteration, stepping from congruences modulo
![]() $p^{a}$
to congruences modulo
$p^{a}$
to congruences modulo
![]() $p^{b}$
, since the ratio
$p^{b}$
, since the ratio
![]() $b/a$
can vary widely according to which of the several possible moduli dominate proceedings at each stage of the iteration. Finally, we remark that although one can envision further improvement in the range of
$b/a$
can vary widely according to which of the several possible moduli dominate proceedings at each stage of the iteration. Finally, we remark that although one can envision further improvement in the range of
![]() $s$
accommodated by Theorem 1.3, it would seem that a new idea is required to replace the defect
$s$
accommodated by Theorem 1.3, it would seem that a new idea is required to replace the defect
![]() ${\textstyle \frac{1}{3}}k$
by a quantity
${\textstyle \frac{1}{3}}k$
by a quantity
![]() $ck$
with
$ck$
with
![]() $c<{\textstyle \frac{1}{3}}$
. The term
$c<{\textstyle \frac{1}{3}}$
. The term
![]() ${\textstyle \frac{1}{3}}k$
seems to be an unavoidable consequence of the application of Hölder’s inequality underlying Lemmas 7.1 and 11.3 that teases apart the information available from congruences of different levels.
${\textstyle \frac{1}{3}}k$
seems to be an unavoidable consequence of the application of Hölder’s inequality underlying Lemmas 7.1 and 11.3 that teases apart the information available from congruences of different levels.
Recent developments (added 29th May 2016)
The area of research focusing on Vinogradov’s mean value theorem and its hinterland has recently undergone a burst of activity, with rapid progress from several quarters. On the one hand, the author [Reference Wooley20] has applied the methods of this paper to establish the cubic case of the main conjecture in full. On the other hand, very recent work of Bourgain et al [Reference Bourgain, Demeter and Guth2] extended the range
 $$\begin{eqnarray}1\leqslant s\leqslant {\textstyle \frac{1}{2}}k(k+1)-{\textstyle \frac{1}{3}}k-8k^{2/3},\end{eqnarray}$$
$$\begin{eqnarray}1\leqslant s\leqslant {\textstyle \frac{1}{2}}k(k+1)-{\textstyle \frac{1}{3}}k-8k^{2/3},\end{eqnarray}$$
in which our Theorem 1.3 applies, to the full critical range
 $1\leqslant s\leqslant {\textstyle \frac{1}{2}}k(k+1)$
, thereby confirming the main conjecture in full. The latter work [Reference Bourgain, Demeter and Guth2] was submitted to the arXiv on 14th December 2015, the most recent (third) revision having been submitted on 1st April 2016. This paper is in all essential mathematical respects identical with a version predating the work of Bourgain et al, and was submitted to the arXiv on 13th January 2014. However, its appearance in print has been delayed by forces beyond the author’s control.
$1\leqslant s\leqslant {\textstyle \frac{1}{2}}k(k+1)$
, thereby confirming the main conjecture in full. The latter work [Reference Bourgain, Demeter and Guth2] was submitted to the arXiv on 14th December 2015, the most recent (third) revision having been submitted on 1st April 2016. This paper is in all essential mathematical respects identical with a version predating the work of Bourgain et al, and was submitted to the arXiv on 13th January 2014. However, its appearance in print has been delayed by forces beyond the author’s control.
The methods of this paper may be seen as a
![]() $p$
-adic version of the method underlying [Reference Bourgain, Demeter and Guth2], the latter being more akin to Vinogradov’s use of real short intervals dating from the 1930s. Two comments are in order here. First, the
$p$
-adic version of the method underlying [Reference Bourgain, Demeter and Guth2], the latter being more akin to Vinogradov’s use of real short intervals dating from the 1930s. Two comments are in order here. First, the
![]() $p$
-adic methods of the present work continue to represent a useful alternative to those of [Reference Bourgain, Demeter and Guth2], since they are easily adapted to other number-theoretic situations, such as those relevant to number fields and function fields. Second, it seems now very likely that the methods of the present paper, in combination with subsequent developments, will also establish the main conjecture in full, in all the settings just outlined as well as in the real setting explored in [Reference Bourgain, Demeter and Guth2]. It seems reasonable to speculate that methods of the widest applicability will incorporate elements of both approaches.
$p$
-adic methods of the present work continue to represent a useful alternative to those of [Reference Bourgain, Demeter and Guth2], since they are easily adapted to other number-theoretic situations, such as those relevant to number fields and function fields. Second, it seems now very likely that the methods of the present paper, in combination with subsequent developments, will also establish the main conjecture in full, in all the settings just outlined as well as in the real setting explored in [Reference Bourgain, Demeter and Guth2]. It seems reasonable to speculate that methods of the widest applicability will incorporate elements of both approaches.
2 The basic infrastructure
We begin our discussion of the proof of Theorem 1.1 by describing the components and basic notation that we subsequently assemble into the apparatus required for the multigrade efficient congruencing method. This is very similar to that introduced in our recent work [Reference Wooley19], and resembles the infrastructure of our earliest work on efficient congruencing [Reference Wooley15]. The reader might wonder whether some kind of universal account could be given that would encompass all possibilities. For the present such a goal seems premature, since innovations are the rule for such a rapidly evolving circle of ideas. Instead, novel consequences of the method seem to require careful arrangement of parameters together with a significant measure of artistry.
We establish Theorem 1.1 as a consequence of a theorem that in many circumstances is somewhat sharper, though more complicated to state.
Theorem 2.1. Suppose that
![]() $s$
,
$s$
,
![]() $k$
and
$k$
and
![]() $r$
are natural numbers with
$r$
are natural numbers with
![]() $k\geqslant 4$
,
$k\geqslant 4$
,
 $$\begin{eqnarray}2\leqslant r\leqslant k-\lceil 2\sqrt{k}\rceil +2\quad \text{and}\quad \max \{2r-1,{\textstyle \frac{1}{2}}r(r-1)+\unicode[STIX]{x1D6E5}\}\leqslant s<s_{1},\end{eqnarray}$$
$$\begin{eqnarray}2\leqslant r\leqslant k-\lceil 2\sqrt{k}\rceil +2\quad \text{and}\quad \max \{2r-1,{\textstyle \frac{1}{2}}r(r-1)+\unicode[STIX]{x1D6E5}\}\leqslant s<s_{1},\end{eqnarray}$$
where
 $$\begin{eqnarray}s_{1}=\frac{1}{2}\biggl(kr-\frac{1}{2}r(r-1)-\unicode[STIX]{x1D6E5}\biggr)\biggl(1+\sqrt{1-\frac{4r(r(r-1)/2+\unicode[STIX]{x1D6E5})}{(kr-r(r-1)/2-\unicode[STIX]{x1D6E5})^{2}}}\biggr)\end{eqnarray}$$
$$\begin{eqnarray}s_{1}=\frac{1}{2}\biggl(kr-\frac{1}{2}r(r-1)-\unicode[STIX]{x1D6E5}\biggr)\biggl(1+\sqrt{1-\frac{4r(r(r-1)/2+\unicode[STIX]{x1D6E5})}{(kr-r(r-1)/2-\unicode[STIX]{x1D6E5})^{2}}}\biggr)\end{eqnarray}$$
and
 $$\begin{eqnarray}\unicode[STIX]{x1D6E5}=\mathop{\sum }_{m=1}^{r-1}\frac{m(r-m)}{s-m}.\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D6E5}=\mathop{\sum }_{m=1}^{r-1}\frac{m(r-m)}{s-m}.\end{eqnarray}$$
Then, for each
![]() $\unicode[STIX]{x1D700}>0$
, one has
$\unicode[STIX]{x1D700}>0$
, one has
 $J_{s+r}(X)\ll X^{s+r+\unicode[STIX]{x1D700}}$
.
$J_{s+r}(X)\ll X^{s+r+\unicode[STIX]{x1D700}}$
.
We consider
![]() $k$
to be fixed, and abbreviate
$k$
to be fixed, and abbreviate
![]() $J_{s,k}(X)$
to
$J_{s,k}(X)$
to
![]() $J_{s}(X)$
without further comment. Let
$J_{s}(X)$
without further comment. Let
![]() $s\in \mathbb{N}$
be arbitrary, and define
$s\in \mathbb{N}$
be arbitrary, and define
![]() $\unicode[STIX]{x1D706}_{s}^{\ast }\in \mathbb{R}$
by means of the relation
$\unicode[STIX]{x1D706}_{s}^{\ast }\in \mathbb{R}$
by means of the relation
 $$\begin{eqnarray}\unicode[STIX]{x1D706}_{s}^{\ast }=\underset{X\rightarrow \infty }{\lim \sup }\frac{\log J_{s}(X)}{\log X}.\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D706}_{s}^{\ast }=\underset{X\rightarrow \infty }{\lim \sup }\frac{\log J_{s}(X)}{\log X}.\end{eqnarray}$$
Thus, for each
![]() $\unicode[STIX]{x1D700}>0$
, and any
$\unicode[STIX]{x1D700}>0$
, and any
![]() $X\in \mathbb{R}$
sufficiently large in terms of
$X\in \mathbb{R}$
sufficiently large in terms of
![]() $s$
,
$s$
,
![]() $k$
and
$k$
and
![]() $\unicode[STIX]{x1D700}$
, one has
$\unicode[STIX]{x1D700}$
, one has
 $J_{s}(X)\ll X^{\unicode[STIX]{x1D706}_{s}^{\ast }+\unicode[STIX]{x1D700}}$
. Note that the lower bound (1.4) combines with a trivial estimate for
$J_{s}(X)\ll X^{\unicode[STIX]{x1D706}_{s}^{\ast }+\unicode[STIX]{x1D700}}$
. Note that the lower bound (1.4) combines with a trivial estimate for
![]() $J_{s}(X)$
to show that
$J_{s}(X)$
to show that
 $s\leqslant \unicode[STIX]{x1D706}_{s}^{\ast }\leqslant 2s$
, whilst the conjectured upper bound (1.2) implies that
$s\leqslant \unicode[STIX]{x1D706}_{s}^{\ast }\leqslant 2s$
, whilst the conjectured upper bound (1.2) implies that
![]() $\unicode[STIX]{x1D706}_{s}^{\ast }=s$
for
$\unicode[STIX]{x1D706}_{s}^{\ast }=s$
for
 $s\leqslant \frac{1}{2}k(k+1)$
.
$s\leqslant \frac{1}{2}k(k+1)$
.
Next, we recall some standard notational conventions. The letters
![]() $s$
and
$s$
and
![]() $k$
denote natural numbers with
$k$
denote natural numbers with
![]() $k\geqslant 3$
, and
$k\geqslant 3$
, and
![]() $\unicode[STIX]{x1D700}$
denotes a sufficiently small positive number. Our basic parameter is
$\unicode[STIX]{x1D700}$
denotes a sufficiently small positive number. Our basic parameter is
![]() $X$
, a large real number depending at most on
$X$
, a large real number depending at most on
![]() $k$
,
$k$
,
![]() $s$
and
$s$
and
![]() $\unicode[STIX]{x1D700}$
, unless otherwise indicated. Whenever
$\unicode[STIX]{x1D700}$
, unless otherwise indicated. Whenever
![]() $\unicode[STIX]{x1D700}$
appears in a statement, we assert that the statement holds for each
$\unicode[STIX]{x1D700}$
appears in a statement, we assert that the statement holds for each
![]() $\unicode[STIX]{x1D700}>0$
. As usual, we write
$\unicode[STIX]{x1D700}>0$
. As usual, we write
![]() $\lfloor \unicode[STIX]{x1D713}\rfloor$
to denote the largest integer no larger than
$\lfloor \unicode[STIX]{x1D713}\rfloor$
to denote the largest integer no larger than
![]() $\unicode[STIX]{x1D713}$
, and
$\unicode[STIX]{x1D713}$
, and
![]() $\lceil \unicode[STIX]{x1D713}\rceil$
to denote the least integer no smaller than
$\lceil \unicode[STIX]{x1D713}\rceil$
to denote the least integer no smaller than
![]() $\unicode[STIX]{x1D713}$
. We make sweeping use of vector notation. Thus, with
$\unicode[STIX]{x1D713}$
. We make sweeping use of vector notation. Thus, with
![]() $t$
implied from the environment at hand, we write
$t$
implied from the environment at hand, we write
 $\mathbf{z}\equiv \mathbf{w}~(\text{mod}~p)$
to denote that
$\mathbf{z}\equiv \mathbf{w}~(\text{mod}~p)$
to denote that
 $z_{i}\equiv w_{i}~(\text{mod}~p)$
$z_{i}\equiv w_{i}~(\text{mod}~p)$
 $(1\leqslant i\leqslant t)$
, or
$(1\leqslant i\leqslant t)$
, or
 $\mathbf{z}\equiv \unicode[STIX]{x1D709}~(\text{mod}~p)$
to denote that
$\mathbf{z}\equiv \unicode[STIX]{x1D709}~(\text{mod}~p)$
to denote that
 $z_{i}\equiv \unicode[STIX]{x1D709}~(\text{mod}~p)$
$z_{i}\equiv \unicode[STIX]{x1D709}~(\text{mod}~p)$
 $(1\leqslant i\leqslant t)$
, or
$(1\leqslant i\leqslant t)$
, or
 $[\mathbf{z}~(\text{mod}~q)]$
to denote the
$[\mathbf{z}~(\text{mod}~q)]$
to denote the
![]() $t$
-tuple
$t$
-tuple
 $(\unicode[STIX]{x1D701}_{1},\ldots ,\unicode[STIX]{x1D701}_{t})$
, where for
$(\unicode[STIX]{x1D701}_{1},\ldots ,\unicode[STIX]{x1D701}_{t})$
, where for
 $1\leqslant i\leqslant t$
one has
$1\leqslant i\leqslant t$
one has
 $1\leqslant \unicode[STIX]{x1D701}_{i}\leqslant q$
and
$1\leqslant \unicode[STIX]{x1D701}_{i}\leqslant q$
and
 $z_{i}\equiv \unicode[STIX]{x1D701}_{i}~(\text{mod}~q)$
. Finally, we employ the convention that whenever
$z_{i}\equiv \unicode[STIX]{x1D701}_{i}~(\text{mod}~q)$
. Finally, we employ the convention that whenever
 $G: [0,1)^{k}\rightarrow \mathbb{C}$
is integrable, then
$G: [0,1)^{k}\rightarrow \mathbb{C}$
is integrable, then
 $$\begin{eqnarray}\oint G(\unicode[STIX]{x1D736})\,d\unicode[STIX]{x1D736}=\int _{[0,1 )^{k}}G(\unicode[STIX]{x1D736})\,d\unicode[STIX]{x1D736}.\end{eqnarray}$$
$$\begin{eqnarray}\oint G(\unicode[STIX]{x1D736})\,d\unicode[STIX]{x1D736}=\int _{[0,1 )^{k}}G(\unicode[STIX]{x1D736})\,d\unicode[STIX]{x1D736}.\end{eqnarray}$$
Thus, on writing
 $$\begin{eqnarray}f_{k}(\unicode[STIX]{x1D736};X)=\mathop{\sum }_{1\leqslant x\leqslant X}e(\unicode[STIX]{x1D6FC}_{1}x+\unicode[STIX]{x1D6FC}_{2}x^{2}+\cdots +\unicode[STIX]{x1D6FC}_{k}x^{k}),\end{eqnarray}$$
$$\begin{eqnarray}f_{k}(\unicode[STIX]{x1D736};X)=\mathop{\sum }_{1\leqslant x\leqslant X}e(\unicode[STIX]{x1D6FC}_{1}x+\unicode[STIX]{x1D6FC}_{2}x^{2}+\cdots +\unicode[STIX]{x1D6FC}_{k}x^{k}),\end{eqnarray}$$
where as usual
![]() $e(z)$
denotes
$e(z)$
denotes
![]() $\text{e}^{2\unicode[STIX]{x1D70B}\text{i}z}$
, it follows from orthogonality that
$\text{e}^{2\unicode[STIX]{x1D70B}\text{i}z}$
, it follows from orthogonality that
 $$\begin{eqnarray}J_{t}(X)=\oint |f_{k}(\unicode[STIX]{x1D736};X)|^{2t}\,d\unicode[STIX]{x1D736}\quad (t\in \mathbb{N}).\end{eqnarray}$$
$$\begin{eqnarray}J_{t}(X)=\oint |f_{k}(\unicode[STIX]{x1D736};X)|^{2t}\,d\unicode[STIX]{x1D736}\quad (t\in \mathbb{N}).\end{eqnarray}$$
We next introduce the parameters which define the iterative method that is the central concern of this paper. We suppose throughout that
![]() $k\geqslant 4$
, and put
$k\geqslant 4$
, and put
 $$\begin{eqnarray}r_{0}=k-\lceil 2\sqrt{k}\rceil +2.\end{eqnarray}$$
$$\begin{eqnarray}r_{0}=k-\lceil 2\sqrt{k}\rceil +2.\end{eqnarray}$$
We take
![]() $r$
to be an integral parameter satisfying
$r$
to be an integral parameter satisfying
 $1\leqslant r\leqslant r_{0}$
, and we consider a natural number
$1\leqslant r\leqslant r_{0}$
, and we consider a natural number
![]() $s$
with
$s$
with
 $k+1\leqslant s\leqslant {\textstyle \frac{1}{2}}k(k+1)$
. We then define
$k+1\leqslant s\leqslant {\textstyle \frac{1}{2}}k(k+1)$
. We then define
 $\unicode[STIX]{x1D6E5}=\unicode[STIX]{x1D6E5}(r,s)$
by taking
$\unicode[STIX]{x1D6E5}=\unicode[STIX]{x1D6E5}(r,s)$
by taking
 $$\begin{eqnarray}\unicode[STIX]{x1D6E5}=\mathop{\sum }_{m=1}^{r-1}\frac{m(r-m)}{s-m}\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D6E5}=\mathop{\sum }_{m=1}^{r-1}\frac{m(r-m)}{s-m}\end{eqnarray}$$
and suppose in what follows that
 $$\begin{eqnarray}s\geqslant \max \{2r-1,{\textstyle \frac{1}{2}}r(r-1)+\unicode[STIX]{x1D6E5}\}.\end{eqnarray}$$
$$\begin{eqnarray}s\geqslant \max \{2r-1,{\textstyle \frac{1}{2}}r(r-1)+\unicode[STIX]{x1D6E5}\}.\end{eqnarray}$$
Next, we put
 $$\begin{eqnarray}\mathfrak{a}=kr-{\textstyle \frac{1}{2}}r(r-1)-\unicode[STIX]{x1D6E5}\quad \text{and}\quad \mathfrak{b}=r({\textstyle \frac{1}{2}}r(r-1)+\unicode[STIX]{x1D6E5}),\end{eqnarray}$$
$$\begin{eqnarray}\mathfrak{a}=kr-{\textstyle \frac{1}{2}}r(r-1)-\unicode[STIX]{x1D6E5}\quad \text{and}\quad \mathfrak{b}=r({\textstyle \frac{1}{2}}r(r-1)+\unicode[STIX]{x1D6E5}),\end{eqnarray}$$
and then define
 $$\begin{eqnarray}\unicode[STIX]{x1D703}_{+}={\textstyle \frac{1}{2}}(\mathfrak{a}+\sqrt{\mathfrak{a}^{2}-4\mathfrak{b}})\quad \text{and}\quad \unicode[STIX]{x1D703}_{-}={\textstyle \frac{1}{2}}(\mathfrak{a}-\sqrt{\mathfrak{a}^{2}-4\mathfrak{b}}).\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D703}_{+}={\textstyle \frac{1}{2}}(\mathfrak{a}+\sqrt{\mathfrak{a}^{2}-4\mathfrak{b}})\quad \text{and}\quad \unicode[STIX]{x1D703}_{-}={\textstyle \frac{1}{2}}(\mathfrak{a}-\sqrt{\mathfrak{a}^{2}-4\mathfrak{b}}).\end{eqnarray}$$
We will suppose throughout that
![]() $s<\unicode[STIX]{x1D703}_{+}$
. Here, some explanation may defuse confusion that may arise from the implicit dependence of
$s<\unicode[STIX]{x1D703}_{+}$
. Here, some explanation may defuse confusion that may arise from the implicit dependence of
![]() $\unicode[STIX]{x1D703}_{+}$
on
$\unicode[STIX]{x1D703}_{+}$
on
![]() $s$
. In practice, the definition (2.3) ensures that
$s$
. In practice, the definition (2.3) ensures that
![]() $\unicode[STIX]{x1D6E5}$
is no larger than about
$\unicode[STIX]{x1D6E5}$
is no larger than about
![]() ${\textstyle \frac{1}{3}}k$
, and hence one finds from (2.6) that
${\textstyle \frac{1}{3}}k$
, and hence one finds from (2.6) that
![]() $\unicode[STIX]{x1D703}_{+}$
is roughly
$\unicode[STIX]{x1D703}_{+}$
is roughly
 $$\begin{eqnarray}kr-{\textstyle \frac{1}{2}}r(r+1)-\unicode[STIX]{x1D6E5}>{\textstyle \frac{1}{2}}r(r-1)+\unicode[STIX]{x1D6E5}.\end{eqnarray}$$
$$\begin{eqnarray}kr-{\textstyle \frac{1}{2}}r(r+1)-\unicode[STIX]{x1D6E5}>{\textstyle \frac{1}{2}}r(r-1)+\unicode[STIX]{x1D6E5}.\end{eqnarray}$$
The condition
![]() $s<\unicode[STIX]{x1D703}_{+}$
is consequently easily verified, since there are relatively few values of
$s<\unicode[STIX]{x1D703}_{+}$
is consequently easily verified, since there are relatively few values of
![]() $s$
to check, and in particular none exceeding
$s$
to check, and in particular none exceeding
 ${\textstyle \frac{1}{2}}k(k+1)$
. Likewise, the condition (2.4) is also easily verified for the values of
${\textstyle \frac{1}{2}}k(k+1)$
. Likewise, the condition (2.4) is also easily verified for the values of
![]() $s$
open to discussion.
$s$
open to discussion.
Our goal is to establish that
 $\unicode[STIX]{x1D706}_{s+r}^{\ast }=s+r$
. Having established the latter, one finds by applying Hölder’s inequality to the right-hand side of (2.1) that whenever
$\unicode[STIX]{x1D706}_{s+r}^{\ast }=s+r$
. Having established the latter, one finds by applying Hölder’s inequality to the right-hand side of (2.1) that whenever
 $1\leqslant t\leqslant s+r$
, one has
$1\leqslant t\leqslant s+r$
, one has
 $$\begin{eqnarray}J_{t}(X)\leqslant \biggl(\oint |f_{k}(\unicode[STIX]{x1D736};X)|^{2s+2r}\,d\unicode[STIX]{x1D736}\biggr)^{t/(s+r)}\ll X^{t+\unicode[STIX]{x1D700}},\end{eqnarray}$$
$$\begin{eqnarray}J_{t}(X)\leqslant \biggl(\oint |f_{k}(\unicode[STIX]{x1D736};X)|^{2s+2r}\,d\unicode[STIX]{x1D736}\biggr)^{t/(s+r)}\ll X^{t+\unicode[STIX]{x1D700}},\end{eqnarray}$$
whence
![]() $\unicode[STIX]{x1D706}_{t}^{\ast }=t$
. Thus, it is clear that the main conclusions of this paper follow by focusing on
$\unicode[STIX]{x1D706}_{t}^{\ast }=t$
. Thus, it is clear that the main conclusions of this paper follow by focusing on
![]() $\unicode[STIX]{x1D706}_{s+r}^{\ast }$
. Henceforth, for brevity we write
$\unicode[STIX]{x1D706}_{s+r}^{\ast }$
. Henceforth, for brevity we write
 $\unicode[STIX]{x1D706}=\unicode[STIX]{x1D706}_{s+r}^{\ast }$
.
$\unicode[STIX]{x1D706}=\unicode[STIX]{x1D706}_{s+r}^{\ast }$
.
Let
![]() $R$
be a natural number sufficiently large in terms of
$R$
be a natural number sufficiently large in terms of
![]() $s$
and
$s$
and
![]() $k$
. Specifically, we choose
$k$
. Specifically, we choose
![]() $R$
as follows. From (2.5) and (2.6), one finds that
$R$
as follows. From (2.5) and (2.6), one finds that
 $\unicode[STIX]{x1D703}_{+}\unicode[STIX]{x1D703}_{-}=\mathfrak{b}$
, and so the hypothesis
$\unicode[STIX]{x1D703}_{+}\unicode[STIX]{x1D703}_{-}=\mathfrak{b}$
, and so the hypothesis
![]() $s<\unicode[STIX]{x1D703}_{+}$
ensures that
$s<\unicode[STIX]{x1D703}_{+}$
ensures that
 $$\begin{eqnarray}\unicode[STIX]{x1D703}_{-}=\mathfrak{b}/\unicode[STIX]{x1D703}_{+}<\mathfrak{b}/s\leqslant \mathfrak{b}/({\textstyle \frac{1}{2}}r(r-1)+\unicode[STIX]{x1D6E5})=r.\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D703}_{-}=\mathfrak{b}/\unicode[STIX]{x1D703}_{+}<\mathfrak{b}/s\leqslant \mathfrak{b}/({\textstyle \frac{1}{2}}r(r-1)+\unicode[STIX]{x1D6E5})=r.\end{eqnarray}$$
Observe next that
![]() $\unicode[STIX]{x1D703}_{+}>\unicode[STIX]{x1D703}_{-}$
, so that on writing
$\unicode[STIX]{x1D703}_{+}>\unicode[STIX]{x1D703}_{-}$
, so that on writing
 $\unicode[STIX]{x1D70F}=\unicode[STIX]{x1D703}_{+}/\unicode[STIX]{x1D703}_{-}$
, one finds that
$\unicode[STIX]{x1D70F}=\unicode[STIX]{x1D703}_{+}/\unicode[STIX]{x1D703}_{-}$
, one finds that
 $$\begin{eqnarray}\displaystyle \frac{1}{\unicode[STIX]{x1D703}_{-}^{R}}\biggl(\frac{\unicode[STIX]{x1D703}_{+}^{R+1}-\unicode[STIX]{x1D703}_{-}^{R+1}}{\unicode[STIX]{x1D703}_{+}-\unicode[STIX]{x1D703}_{-}}-\frac{\unicode[STIX]{x1D703}_{+}\unicode[STIX]{x1D703}_{-}}{r\sqrt{k}}\biggl(\frac{\unicode[STIX]{x1D703}_{+}^{R}-\unicode[STIX]{x1D703}_{-}^{R}}{\unicode[STIX]{x1D703}_{+}-\unicode[STIX]{x1D703}_{-}}\biggr)\biggr) & = & \displaystyle \frac{\unicode[STIX]{x1D70F}^{R+1}-1}{\unicode[STIX]{x1D70F}-1}-\frac{\unicode[STIX]{x1D70F}\unicode[STIX]{x1D703}_{-}}{r\sqrt{k}}\biggl(\frac{\unicode[STIX]{x1D70F}^{R}-1}{\unicode[STIX]{x1D70F}-1}\biggr)\nonumber\\ \displaystyle & {>} & \displaystyle \biggl(1-\frac{1}{\sqrt{k}}\biggr)\biggl(\frac{\unicode[STIX]{x1D70F}^{R+1}-1}{\unicode[STIX]{x1D70F}-1}\biggr)\nonumber\\ \displaystyle & {>} & \displaystyle (1-1/\sqrt{k})\unicode[STIX]{x1D70F}^{R}.\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \frac{1}{\unicode[STIX]{x1D703}_{-}^{R}}\biggl(\frac{\unicode[STIX]{x1D703}_{+}^{R+1}-\unicode[STIX]{x1D703}_{-}^{R+1}}{\unicode[STIX]{x1D703}_{+}-\unicode[STIX]{x1D703}_{-}}-\frac{\unicode[STIX]{x1D703}_{+}\unicode[STIX]{x1D703}_{-}}{r\sqrt{k}}\biggl(\frac{\unicode[STIX]{x1D703}_{+}^{R}-\unicode[STIX]{x1D703}_{-}^{R}}{\unicode[STIX]{x1D703}_{+}-\unicode[STIX]{x1D703}_{-}}\biggr)\biggr) & = & \displaystyle \frac{\unicode[STIX]{x1D70F}^{R+1}-1}{\unicode[STIX]{x1D70F}-1}-\frac{\unicode[STIX]{x1D70F}\unicode[STIX]{x1D703}_{-}}{r\sqrt{k}}\biggl(\frac{\unicode[STIX]{x1D70F}^{R}-1}{\unicode[STIX]{x1D70F}-1}\biggr)\nonumber\\ \displaystyle & {>} & \displaystyle \biggl(1-\frac{1}{\sqrt{k}}\biggr)\biggl(\frac{\unicode[STIX]{x1D70F}^{R+1}-1}{\unicode[STIX]{x1D70F}-1}\biggr)\nonumber\\ \displaystyle & {>} & \displaystyle (1-1/\sqrt{k})\unicode[STIX]{x1D70F}^{R}.\nonumber\end{eqnarray}$$
Hence, we obtain the upper bound
 $$\begin{eqnarray}(1-1/\sqrt{k})\unicode[STIX]{x1D703}_{+}^{R}<\frac{\unicode[STIX]{x1D703}_{+}^{R+1}-\unicode[STIX]{x1D703}_{-}^{R+1}}{\unicode[STIX]{x1D703}_{+}-\unicode[STIX]{x1D703}_{-}}-\frac{\unicode[STIX]{x1D703}_{+}\unicode[STIX]{x1D703}_{-}}{r\sqrt{k}}\biggl(\frac{\unicode[STIX]{x1D703}_{+}^{R}-\unicode[STIX]{x1D703}_{-}^{R}}{\unicode[STIX]{x1D703}_{+}-\unicode[STIX]{x1D703}_{-}}\biggr).\end{eqnarray}$$
$$\begin{eqnarray}(1-1/\sqrt{k})\unicode[STIX]{x1D703}_{+}^{R}<\frac{\unicode[STIX]{x1D703}_{+}^{R+1}-\unicode[STIX]{x1D703}_{-}^{R+1}}{\unicode[STIX]{x1D703}_{+}-\unicode[STIX]{x1D703}_{-}}-\frac{\unicode[STIX]{x1D703}_{+}\unicode[STIX]{x1D703}_{-}}{r\sqrt{k}}\biggl(\frac{\unicode[STIX]{x1D703}_{+}^{R}-\unicode[STIX]{x1D703}_{-}^{R}}{\unicode[STIX]{x1D703}_{+}-\unicode[STIX]{x1D703}_{-}}\biggr).\end{eqnarray}$$
Recall again our assumption that
![]() $s<\unicode[STIX]{x1D703}_{+}$
, and put
$s<\unicode[STIX]{x1D703}_{+}$
, and put
 $\unicode[STIX]{x1D708}=\unicode[STIX]{x1D703}_{+}-s>0$
. Then we have
$\unicode[STIX]{x1D708}=\unicode[STIX]{x1D703}_{+}-s>0$
. Then we have
 $$\begin{eqnarray}s^{n}=\unicode[STIX]{x1D703}_{+}^{n}(1-\unicode[STIX]{x1D708}/\unicode[STIX]{x1D703}_{+})^{n}\leqslant \unicode[STIX]{x1D703}_{+}^{n}\text{e}^{-\unicode[STIX]{x1D708}n/\unicode[STIX]{x1D703}_{+}}.\end{eqnarray}$$
$$\begin{eqnarray}s^{n}=\unicode[STIX]{x1D703}_{+}^{n}(1-\unicode[STIX]{x1D708}/\unicode[STIX]{x1D703}_{+})^{n}\leqslant \unicode[STIX]{x1D703}_{+}^{n}\text{e}^{-\unicode[STIX]{x1D708}n/\unicode[STIX]{x1D703}_{+}}.\end{eqnarray}$$
Consequently, if we take
 $R=\lceil W\unicode[STIX]{x1D703}_{+}/\unicode[STIX]{x1D708}\rceil$
, with
$R=\lceil W\unicode[STIX]{x1D703}_{+}/\unicode[STIX]{x1D708}\rceil$
, with
![]() $W$
a large enough integer, then we ensure that
$W$
a large enough integer, then we ensure that
 $$\begin{eqnarray}s^{R}\leqslant \text{e}^{-W}\unicode[STIX]{x1D703}_{+}^{R}<(1-1/\sqrt{k})\unicode[STIX]{x1D703}_{+}^{R},\end{eqnarray}$$
$$\begin{eqnarray}s^{R}\leqslant \text{e}^{-W}\unicode[STIX]{x1D703}_{+}^{R}<(1-1/\sqrt{k})\unicode[STIX]{x1D703}_{+}^{R},\end{eqnarray}$$
whence
 $$\begin{eqnarray}s^{R}<\frac{\unicode[STIX]{x1D703}_{+}^{R+1}-\unicode[STIX]{x1D703}_{-}^{R+1}}{\unicode[STIX]{x1D703}_{+}-\unicode[STIX]{x1D703}_{-}}-\frac{\unicode[STIX]{x1D703}_{+}\unicode[STIX]{x1D703}_{-}}{r\sqrt{k}}\biggl(\frac{\unicode[STIX]{x1D703}_{+}^{R}-\unicode[STIX]{x1D703}_{-}^{R}}{\unicode[STIX]{x1D703}_{+}-\unicode[STIX]{x1D703}_{-}}\biggr).\end{eqnarray}$$
$$\begin{eqnarray}s^{R}<\frac{\unicode[STIX]{x1D703}_{+}^{R+1}-\unicode[STIX]{x1D703}_{-}^{R+1}}{\unicode[STIX]{x1D703}_{+}-\unicode[STIX]{x1D703}_{-}}-\frac{\unicode[STIX]{x1D703}_{+}\unicode[STIX]{x1D703}_{-}}{r\sqrt{k}}\biggl(\frac{\unicode[STIX]{x1D703}_{+}^{R}-\unicode[STIX]{x1D703}_{-}^{R}}{\unicode[STIX]{x1D703}_{+}-\unicode[STIX]{x1D703}_{-}}\biggr).\end{eqnarray}$$
The significance of this condition will become apparent in due course (see equation (8.1) below, and the ensuing discussion).
Having fixed
![]() $R$
satisfying these conditions, we take
$R$
satisfying these conditions, we take
![]() $N$
to be a natural number sufficiently large in terms of
$N$
to be a natural number sufficiently large in terms of
![]() $s$
,
$s$
,
![]() $k$
and
$k$
and
![]() $R$
, and then put
$R$
, and then put
 $$\begin{eqnarray}\displaystyle & B=Nk^{N},\qquad \unicode[STIX]{x1D703}=(17N^{2}(s+k))^{-3RN},\qquad \unicode[STIX]{x1D6FF}=(1000N^{4}(s+k))^{-3RN}\unicode[STIX]{x1D703}. & \displaystyle \nonumber\\ \displaystyle & & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & B=Nk^{N},\qquad \unicode[STIX]{x1D703}=(17N^{2}(s+k))^{-3RN},\qquad \unicode[STIX]{x1D6FF}=(1000N^{4}(s+k))^{-3RN}\unicode[STIX]{x1D703}. & \displaystyle \nonumber\\ \displaystyle & & \displaystyle\end{eqnarray}$$
In view of the definition of
![]() $\unicode[STIX]{x1D706}$
, there exists a sequence of natural numbers
$\unicode[STIX]{x1D706}$
, there exists a sequence of natural numbers
![]() $(X_{l})_{l=1}^{\infty }$
, tending to infinity, with the property that
$(X_{l})_{l=1}^{\infty }$
, tending to infinity, with the property that
 $J_{s+r}(X_{l})>X_{l}^{\unicode[STIX]{x1D706}-\unicode[STIX]{x1D6FF}}$
$J_{s+r}(X_{l})>X_{l}^{\unicode[STIX]{x1D706}-\unicode[STIX]{x1D6FF}}$
![]() $(l\in \mathbb{N})$
. Also, provided that
$(l\in \mathbb{N})$
. Also, provided that
![]() $X_{l}$
is sufficiently large, one has the corresponding upper bound
$X_{l}$
is sufficiently large, one has the corresponding upper bound
 $J_{s+r}(Y)<Y^{\unicode[STIX]{x1D706}+\unicode[STIX]{x1D6FF}}$
for
$J_{s+r}(Y)<Y^{\unicode[STIX]{x1D706}+\unicode[STIX]{x1D6FF}}$
for
 $Y\geqslant X_{l}^{1/2}$
. We consider a fixed element
$Y\geqslant X_{l}^{1/2}$
. We consider a fixed element
![]() $X=X_{l}$
of the sequence
$X=X_{l}$
of the sequence
![]() $(X_{l})_{l=1}^{\infty }$
, which we may assume to be sufficiently large in terms of
$(X_{l})_{l=1}^{\infty }$
, which we may assume to be sufficiently large in terms of
![]() $s$
,
$s$
,
![]() $k$
and
$k$
and
![]() $N$
. We put
$N$
. We put
 $M=X^{\unicode[STIX]{x1D703}}$
, and note from (2.8) that
$M=X^{\unicode[STIX]{x1D703}}$
, and note from (2.8) that
 $X^{\unicode[STIX]{x1D6FF}}<M^{1/N}$
. Throughout, implicit constants may depend on
$X^{\unicode[STIX]{x1D6FF}}<M^{1/N}$
. Throughout, implicit constants may depend on
![]() $s$
,
$s$
,
![]() $k$
,
$k$
,
![]() $N$
, and also on
$N$
, and also on
![]() $\unicode[STIX]{x1D700}$
in view of our earlier convention, but not on any other variable.
$\unicode[STIX]{x1D700}$
in view of our earlier convention, but not on any other variable.
We next introduce the cast of exponential sums and mean values appearing in our arguments. Let
![]() $p$
be a prime number with
$p$
be a prime number with
 $M<p\leqslant 2M$
to be fixed in due course. When
$M<p\leqslant 2M$
to be fixed in due course. When
![]() $c$
and
$c$
and
![]() $\unicode[STIX]{x1D709}$
are non-negative integers, and
$\unicode[STIX]{x1D709}$
are non-negative integers, and
 $\unicode[STIX]{x1D736}\in [0,1)^{k}$
, we define
$\unicode[STIX]{x1D736}\in [0,1)^{k}$
, we define
 $$\begin{eqnarray}\mathfrak{f}_{c}(\unicode[STIX]{x1D736};\unicode[STIX]{x1D709})=\mathop{\sum }_{\substack{ 1\leqslant x\leqslant X \\ x\equiv \unicode[STIX]{x1D709}~(\text{mod}~p^{c})}}e(\unicode[STIX]{x1D6FC}_{1}x+\unicode[STIX]{x1D6FC}_{2}x^{2}+\cdots +\unicode[STIX]{x1D6FC}_{k}x^{k}).\end{eqnarray}$$
$$\begin{eqnarray}\mathfrak{f}_{c}(\unicode[STIX]{x1D736};\unicode[STIX]{x1D709})=\mathop{\sum }_{\substack{ 1\leqslant x\leqslant X \\ x\equiv \unicode[STIX]{x1D709}~(\text{mod}~p^{c})}}e(\unicode[STIX]{x1D6FC}_{1}x+\unicode[STIX]{x1D6FC}_{2}x^{2}+\cdots +\unicode[STIX]{x1D6FC}_{k}x^{k}).\end{eqnarray}$$
When
 $1\leqslant m\leqslant k-1$
, denote by
$1\leqslant m\leqslant k-1$
, denote by
![]() $\unicode[STIX]{x1D6EF}_{c}^{m}(\unicode[STIX]{x1D709})$
the set of integral
$\unicode[STIX]{x1D6EF}_{c}^{m}(\unicode[STIX]{x1D709})$
the set of integral
![]() $m$
-tuples
$m$
-tuples
 $(\unicode[STIX]{x1D709}_{1},\ldots ,\unicode[STIX]{x1D709}_{m})$
, with
$(\unicode[STIX]{x1D709}_{1},\ldots ,\unicode[STIX]{x1D709}_{m})$
, with
 $1\leqslant \unicode[STIX]{x1D743}\leqslant p^{c+1}$
and
$1\leqslant \unicode[STIX]{x1D743}\leqslant p^{c+1}$
and
 $\unicode[STIX]{x1D743}\equiv \unicode[STIX]{x1D709}~(\text{mod}~p^{c})$
, and satisfying the property that
$\unicode[STIX]{x1D743}\equiv \unicode[STIX]{x1D709}~(\text{mod}~p^{c})$
, and satisfying the property that
 $\unicode[STIX]{x1D709}_{i}\not \equiv \unicode[STIX]{x1D709}_{j}~(\text{mod}~p^{c+1})$
for
$\unicode[STIX]{x1D709}_{i}\not \equiv \unicode[STIX]{x1D709}_{j}~(\text{mod}~p^{c+1})$
for
![]() $i\neq j$
. We then put
$i\neq j$
. We then put
 $$\begin{eqnarray}\mathfrak{F}_{c}^{m}(\unicode[STIX]{x1D736};\unicode[STIX]{x1D709})=\mathop{\sum }_{\unicode[STIX]{x1D743}\in \unicode[STIX]{x1D6EF}_{c}^{m}(\unicode[STIX]{x1D709})}\mathop{\prod }_{i=1}^{m}\mathfrak{f}_{c+1}(\unicode[STIX]{x1D736};\unicode[STIX]{x1D709}_{i}).\end{eqnarray}$$
$$\begin{eqnarray}\mathfrak{F}_{c}^{m}(\unicode[STIX]{x1D736};\unicode[STIX]{x1D709})=\mathop{\sum }_{\unicode[STIX]{x1D743}\in \unicode[STIX]{x1D6EF}_{c}^{m}(\unicode[STIX]{x1D709})}\mathop{\prod }_{i=1}^{m}\mathfrak{f}_{c+1}(\unicode[STIX]{x1D736};\unicode[STIX]{x1D709}_{i}).\end{eqnarray}$$
When
![]() $a$
and
$a$
and
![]() $b$
are positive integers, we define
$b$
are positive integers, we define
 $$\begin{eqnarray}\displaystyle I_{a,b}^{m,r}(X;\unicode[STIX]{x1D709},\unicode[STIX]{x1D702}) & = & \displaystyle \oint |\mathop{\mathfrak{F}}_{a}^{m}(\unicode[STIX]{x1D736};\unicode[STIX]{x1D709})^{2}\mathfrak{f}_{b}(\unicode[STIX]{x1D736};\unicode[STIX]{x1D702})^{2s+2r-2m}|\,d\unicode[STIX]{x1D736},\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle I_{a,b}^{m,r}(X;\unicode[STIX]{x1D709},\unicode[STIX]{x1D702}) & = & \displaystyle \oint |\mathop{\mathfrak{F}}_{a}^{m}(\unicode[STIX]{x1D736};\unicode[STIX]{x1D709})^{2}\mathfrak{f}_{b}(\unicode[STIX]{x1D736};\unicode[STIX]{x1D702})^{2s+2r-2m}|\,d\unicode[STIX]{x1D736},\end{eqnarray}$$
 $$\begin{eqnarray}\displaystyle K_{a,b}^{m,r}(X;\unicode[STIX]{x1D709},\unicode[STIX]{x1D702}) & = & \displaystyle \oint |\mathop{\mathfrak{F}}_{a}^{m}(\unicode[STIX]{x1D736};\unicode[STIX]{x1D709})^{2}\mathfrak{F}_{b}^{r}(\unicode[STIX]{x1D736};\unicode[STIX]{x1D702})^{2}\mathfrak{f}_{b}(\unicode[STIX]{x1D736};\unicode[STIX]{x1D702})^{2s-2m}|\,d\unicode[STIX]{x1D736}.\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle K_{a,b}^{m,r}(X;\unicode[STIX]{x1D709},\unicode[STIX]{x1D702}) & = & \displaystyle \oint |\mathop{\mathfrak{F}}_{a}^{m}(\unicode[STIX]{x1D736};\unicode[STIX]{x1D709})^{2}\mathfrak{F}_{b}^{r}(\unicode[STIX]{x1D736};\unicode[STIX]{x1D702})^{2}\mathfrak{f}_{b}(\unicode[STIX]{x1D736};\unicode[STIX]{x1D702})^{2s-2m}|\,d\unicode[STIX]{x1D736}.\end{eqnarray}$$
This notation extends to the case
![]() $m=0$
, of course, by simply interpreting the exponential sum
$m=0$
, of course, by simply interpreting the exponential sum
 $\mathfrak{F}_{c}^{0}(\unicode[STIX]{x1D736};\unicode[STIX]{x1D709})$
to be
$\mathfrak{F}_{c}^{0}(\unicode[STIX]{x1D736};\unicode[STIX]{x1D709})$
to be
![]() $1$
.
$1$
.
Note that, by orthogonality, the mean value
 $I_{a,b}^{m,r}(X;\unicode[STIX]{x1D709},\unicode[STIX]{x1D702})$
counts the number of integral solutions of the system
$I_{a,b}^{m,r}(X;\unicode[STIX]{x1D709},\unicode[STIX]{x1D702})$
counts the number of integral solutions of the system
 $$\begin{eqnarray}\mathop{\sum }_{i=1}^{m}(x_{i}^{j}-y_{i}^{j})=\mathop{\sum }_{l=1}^{s+r-m}(v_{l}^{j}-w_{l}^{j})\quad (1\leqslant j\leqslant k),\end{eqnarray}$$
$$\begin{eqnarray}\mathop{\sum }_{i=1}^{m}(x_{i}^{j}-y_{i}^{j})=\mathop{\sum }_{l=1}^{s+r-m}(v_{l}^{j}-w_{l}^{j})\quad (1\leqslant j\leqslant k),\end{eqnarray}$$
with
 $1\leqslant \mathbf{x},\mathbf{y},\mathbf{v},\mathbf{w}\leqslant X$
,
$1\leqslant \mathbf{x},\mathbf{y},\mathbf{v},\mathbf{w}\leqslant X$
,
 $\mathbf{v}\equiv \mathbf{w}\equiv \unicode[STIX]{x1D702}~(\text{mod}~p^{b})$
and
$\mathbf{v}\equiv \mathbf{w}\equiv \unicode[STIX]{x1D702}~(\text{mod}~p^{b})$
and
 $\mathbf{x},\mathbf{y}\in \unicode[STIX]{x1D6EF}_{a}^{m}(\unicode[STIX]{x1D709})~(\text{mod}~p^{a+1})$
. Similarly, the mean value
$\mathbf{x},\mathbf{y}\in \unicode[STIX]{x1D6EF}_{a}^{m}(\unicode[STIX]{x1D709})~(\text{mod}~p^{a+1})$
. Similarly, the mean value
 $K_{a,b}^{m,r}(X;\unicode[STIX]{x1D709},\unicode[STIX]{x1D702})$
counts the number of solutions of
$K_{a,b}^{m,r}(X;\unicode[STIX]{x1D709},\unicode[STIX]{x1D702})$
counts the number of solutions of
 $$\begin{eqnarray}\mathop{\sum }_{i=1}^{m}(x_{i}^{j}-y_{i}^{j})=\mathop{\sum }_{l=1}^{r}(u_{l}^{j}-v_{l}^{j})+\mathop{\sum }_{n=1}^{s-m}(w_{n}^{j}-z_{n}^{j})\quad (1\leqslant j\leqslant k),\end{eqnarray}$$
$$\begin{eqnarray}\mathop{\sum }_{i=1}^{m}(x_{i}^{j}-y_{i}^{j})=\mathop{\sum }_{l=1}^{r}(u_{l}^{j}-v_{l}^{j})+\mathop{\sum }_{n=1}^{s-m}(w_{n}^{j}-z_{n}^{j})\quad (1\leqslant j\leqslant k),\end{eqnarray}$$
with
 $1\leqslant \mathbf{x},\mathbf{y},\mathbf{u},\mathbf{v},\mathbf{w},\mathbf{z}\leqslant X$
, and satisfying
$1\leqslant \mathbf{x},\mathbf{y},\mathbf{u},\mathbf{v},\mathbf{w},\mathbf{z}\leqslant X$
, and satisfying
 $\mathbf{w}\equiv \mathbf{z}\equiv \unicode[STIX]{x1D702}~(\text{mod}~p^{b})$
,
$\mathbf{w}\equiv \mathbf{z}\equiv \unicode[STIX]{x1D702}~(\text{mod}~p^{b})$
,
 $$\begin{eqnarray}\mathbf{x},\mathbf{y}\in \unicode[STIX]{x1D6EF}_{a}^{m}(\unicode[STIX]{x1D709})~(\text{mod}~p^{a+1})\quad \text{and}\quad \mathbf{u},\mathbf{v}\in \unicode[STIX]{x1D6EF}_{b}^{r}(\unicode[STIX]{x1D702})~(\text{mod}~p^{b+1}).\end{eqnarray}$$
$$\begin{eqnarray}\mathbf{x},\mathbf{y}\in \unicode[STIX]{x1D6EF}_{a}^{m}(\unicode[STIX]{x1D709})~(\text{mod}~p^{a+1})\quad \text{and}\quad \mathbf{u},\mathbf{v}\in \unicode[STIX]{x1D6EF}_{b}^{r}(\unicode[STIX]{x1D702})~(\text{mod}~p^{b+1}).\end{eqnarray}$$
Given any one such solution of the system (2.14), an application of the binomial theorem shows that
![]() $\mathbf{x}-\unicode[STIX]{x1D702}$
,
$\mathbf{x}-\unicode[STIX]{x1D702}$
,
![]() $\mathbf{y}-\unicode[STIX]{x1D702}$
,
$\mathbf{y}-\unicode[STIX]{x1D702}$
,
![]() $\mathbf{u}-\unicode[STIX]{x1D702}$
,
$\mathbf{u}-\unicode[STIX]{x1D702}$
,
![]() $\mathbf{v}-\unicode[STIX]{x1D702}$
,
$\mathbf{v}-\unicode[STIX]{x1D702}$
,
![]() $\mathbf{w}-\unicode[STIX]{x1D702}$
,
$\mathbf{w}-\unicode[STIX]{x1D702}$
,
![]() $\mathbf{z}-\unicode[STIX]{x1D702}$
is also a solution. Since in any solution counted by
$\mathbf{z}-\unicode[STIX]{x1D702}$
is also a solution. Since in any solution counted by
 $K_{a,b}^{m,r}(X;\unicode[STIX]{x1D709},\unicode[STIX]{x1D702})$
, one has
$K_{a,b}^{m,r}(X;\unicode[STIX]{x1D709},\unicode[STIX]{x1D702})$
, one has
 $\mathbf{u}\equiv \mathbf{v}\equiv \unicode[STIX]{x1D702}~(\text{mod}~p^{b})$
and
$\mathbf{u}\equiv \mathbf{v}\equiv \unicode[STIX]{x1D702}~(\text{mod}~p^{b})$
and
 $\mathbf{w}\equiv \mathbf{z}\equiv \unicode[STIX]{x1D702}~(\text{mod}~p^{b})$
, we deduce that
$\mathbf{w}\equiv \mathbf{z}\equiv \unicode[STIX]{x1D702}~(\text{mod}~p^{b})$
, we deduce that
 $$\begin{eqnarray}\mathop{\sum }_{i=1}^{m}(x_{i}-\unicode[STIX]{x1D702})^{j}\equiv \mathop{\sum }_{i=1}^{m}(y_{i}-\unicode[STIX]{x1D702})^{j}~(\text{mod}~p^{jb})\quad (1\leqslant j\leqslant k).\end{eqnarray}$$
$$\begin{eqnarray}\mathop{\sum }_{i=1}^{m}(x_{i}-\unicode[STIX]{x1D702})^{j}\equiv \mathop{\sum }_{i=1}^{m}(y_{i}-\unicode[STIX]{x1D702})^{j}~(\text{mod}~p^{jb})\quad (1\leqslant j\leqslant k).\end{eqnarray}$$
We put
 $$\begin{eqnarray}\displaystyle I_{a,b}^{m,r}(X) & = & \displaystyle \max _{1\leqslant \unicode[STIX]{x1D709}\leqslant p^{a}}\max _{\substack{ 1\leqslant \unicode[STIX]{x1D702}\leqslant p^{b} \\ \unicode[STIX]{x1D702}\not \equiv \unicode[STIX]{x1D709}~(\text{mod}~p)}}I_{a,b}^{m,r}(X;\unicode[STIX]{x1D709},\unicode[STIX]{x1D702}),\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle I_{a,b}^{m,r}(X) & = & \displaystyle \max _{1\leqslant \unicode[STIX]{x1D709}\leqslant p^{a}}\max _{\substack{ 1\leqslant \unicode[STIX]{x1D702}\leqslant p^{b} \\ \unicode[STIX]{x1D702}\not \equiv \unicode[STIX]{x1D709}~(\text{mod}~p)}}I_{a,b}^{m,r}(X;\unicode[STIX]{x1D709},\unicode[STIX]{x1D702}),\end{eqnarray}$$
 $$\begin{eqnarray}\displaystyle K_{a,b}^{m,r}(X) & = & \displaystyle \max _{1\leqslant \unicode[STIX]{x1D709}\leqslant p^{a}}\max _{\substack{ 1\leqslant \unicode[STIX]{x1D702}\leqslant p^{b} \\ \unicode[STIX]{x1D702}\not \equiv \unicode[STIX]{x1D709}~(\text{mod}~p)}}K_{a,b}^{m,r}(X;\unicode[STIX]{x1D709},\unicode[STIX]{x1D702}).\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle K_{a,b}^{m,r}(X) & = & \displaystyle \max _{1\leqslant \unicode[STIX]{x1D709}\leqslant p^{a}}\max _{\substack{ 1\leqslant \unicode[STIX]{x1D702}\leqslant p^{b} \\ \unicode[STIX]{x1D702}\not \equiv \unicode[STIX]{x1D709}~(\text{mod}~p)}}K_{a,b}^{m,r}(X;\unicode[STIX]{x1D709},\unicode[STIX]{x1D702}).\end{eqnarray}$$
The implicit dependence on
![]() $p$
in the above notation will be rendered irrelevant in §5, since we fix the choice of this prime following the proof of Lemma 5.1.
$p$
in the above notation will be rendered irrelevant in §5, since we fix the choice of this prime following the proof of Lemma 5.1.
We must align the definition of
 $K_{0,b}^{m,r}(X)$
with the conditioning idea. When
$K_{0,b}^{m,r}(X)$
with the conditioning idea. When
![]() $\boldsymbol{\unicode[STIX]{x1D701}}$
is a tuple of integers, we denote by
$\boldsymbol{\unicode[STIX]{x1D701}}$
is a tuple of integers, we denote by
![]() $\unicode[STIX]{x1D6EF}^{m}(\boldsymbol{\unicode[STIX]{x1D701}})$
the set of
$\unicode[STIX]{x1D6EF}^{m}(\boldsymbol{\unicode[STIX]{x1D701}})$
the set of
![]() $m$
-tuples
$m$
-tuples
 $(\unicode[STIX]{x1D709}_{1},\ldots ,\unicode[STIX]{x1D709}_{m})\in \unicode[STIX]{x1D6EF}_{0}^{m}(0)$
such that
$(\unicode[STIX]{x1D709}_{1},\ldots ,\unicode[STIX]{x1D709}_{m})\in \unicode[STIX]{x1D6EF}_{0}^{m}(0)$
such that
 $\unicode[STIX]{x1D709}_{i}\not \equiv \unicode[STIX]{x1D701}_{j}~(\text{mod}~p)$
for all
$\unicode[STIX]{x1D709}_{i}\not \equiv \unicode[STIX]{x1D701}_{j}~(\text{mod}~p)$
for all
![]() $i$
and
$i$
and
![]() $j$
. Recalling (2.9), we put
$j$
. Recalling (2.9), we put
 $$\begin{eqnarray}\mathfrak{F}^{m}(\unicode[STIX]{x1D736};\boldsymbol{\unicode[STIX]{x1D701}})=\mathop{\sum }_{\unicode[STIX]{x1D743}\in \unicode[STIX]{x1D6EF}^{m}(\boldsymbol{\unicode[STIX]{x1D701}})}\mathop{\prod }_{i=1}^{m}\mathfrak{f}_{1}(\unicode[STIX]{x1D736};\unicode[STIX]{x1D709}_{i})\end{eqnarray}$$
$$\begin{eqnarray}\mathfrak{F}^{m}(\unicode[STIX]{x1D736};\boldsymbol{\unicode[STIX]{x1D701}})=\mathop{\sum }_{\unicode[STIX]{x1D743}\in \unicode[STIX]{x1D6EF}^{m}(\boldsymbol{\unicode[STIX]{x1D701}})}\mathop{\prod }_{i=1}^{m}\mathfrak{f}_{1}(\unicode[STIX]{x1D736};\unicode[STIX]{x1D709}_{i})\end{eqnarray}$$
and then define
 $$\begin{eqnarray}\displaystyle \widetilde{I}_{c}^{m,r}(X;\unicode[STIX]{x1D702}) & = & \displaystyle \oint |\mathfrak{F}^{m}(\unicode[STIX]{x1D736};\unicode[STIX]{x1D702})^{2}\mathfrak{f}_{c}(\unicode[STIX]{x1D736};\unicode[STIX]{x1D702})^{2s+2r-2m}|\,d\unicode[STIX]{x1D736},\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \widetilde{I}_{c}^{m,r}(X;\unicode[STIX]{x1D702}) & = & \displaystyle \oint |\mathfrak{F}^{m}(\unicode[STIX]{x1D736};\unicode[STIX]{x1D702})^{2}\mathfrak{f}_{c}(\unicode[STIX]{x1D736};\unicode[STIX]{x1D702})^{2s+2r-2m}|\,d\unicode[STIX]{x1D736},\end{eqnarray}$$
 $$\begin{eqnarray}\displaystyle \widetilde{K}_{c}^{m,r}(X;\unicode[STIX]{x1D702}) & = & \displaystyle \oint |\mathfrak{F}^{m}(\unicode[STIX]{x1D736};\unicode[STIX]{x1D702})^{2}\mathfrak{F}_{c}^{r}(\unicode[STIX]{x1D736};\unicode[STIX]{x1D702})^{2}\mathfrak{f}_{c}(\unicode[STIX]{x1D736};\unicode[STIX]{x1D702})^{2s-2m}|\,d\unicode[STIX]{x1D736},\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \widetilde{K}_{c}^{m,r}(X;\unicode[STIX]{x1D702}) & = & \displaystyle \oint |\mathfrak{F}^{m}(\unicode[STIX]{x1D736};\unicode[STIX]{x1D702})^{2}\mathfrak{F}_{c}^{r}(\unicode[STIX]{x1D736};\unicode[STIX]{x1D702})^{2}\mathfrak{f}_{c}(\unicode[STIX]{x1D736};\unicode[STIX]{x1D702})^{2s-2m}|\,d\unicode[STIX]{x1D736},\end{eqnarray}$$
 $$\begin{eqnarray}\displaystyle K_{0,c}^{m,r}(X) & = & \displaystyle \max _{1\leqslant \unicode[STIX]{x1D702}\leqslant p^{c}}\widetilde{K}_{c}^{m,r}(X;\unicode[STIX]{x1D702}).\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle K_{0,c}^{m,r}(X) & = & \displaystyle \max _{1\leqslant \unicode[STIX]{x1D702}\leqslant p^{c}}\widetilde{K}_{c}^{m,r}(X;\unicode[STIX]{x1D702}).\end{eqnarray}$$
As in our earlier work, we make use of an operator that makes transparent the relationship between mean values and their anticipated magnitudes. For the purposes at hand, it is useful to reconfigure this normalization so as to make visible the deviation in a mean value from strongly diagonal behaviour. Thus, in the present circumstances, we adopt the convention that
 $$\begin{eqnarray}\displaystyle \unicode[STIX]{x27E6}J_{s+r}(X)\unicode[STIX]{x27E7} & = & \displaystyle J_{s+r}(X)/X^{s+r},\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \unicode[STIX]{x27E6}J_{s+r}(X)\unicode[STIX]{x27E7} & = & \displaystyle J_{s+r}(X)/X^{s+r},\end{eqnarray}$$
 $$\begin{eqnarray}\displaystyle \unicode[STIX]{x27E6}I_{a,b}^{m,r}(X)\unicode[STIX]{x27E7} & = & \displaystyle \frac{I_{a,b}^{m,r}(X)}{(X/M^{a})^{m}(X/M^{b})^{s+r-m}},\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \unicode[STIX]{x27E6}I_{a,b}^{m,r}(X)\unicode[STIX]{x27E7} & = & \displaystyle \frac{I_{a,b}^{m,r}(X)}{(X/M^{a})^{m}(X/M^{b})^{s+r-m}},\end{eqnarray}$$
 $$\begin{eqnarray}\displaystyle \unicode[STIX]{x27E6}K_{a,b}^{m,r}(X)\unicode[STIX]{x27E7} & = & \displaystyle \frac{K_{a,b}^{m,r}(X)}{(X/M^{a})^{m}(X/M^{b})^{s+r-m}}.\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \unicode[STIX]{x27E6}K_{a,b}^{m,r}(X)\unicode[STIX]{x27E7} & = & \displaystyle \frac{K_{a,b}^{m,r}(X)}{(X/M^{a})^{m}(X/M^{b})^{s+r-m}}.\end{eqnarray}$$
Using this notation, our earlier bounds for
![]() $J_{s+r}(X)$
may be rewritten in the form
$J_{s+r}(X)$
may be rewritten in the form
 $$\begin{eqnarray}\unicode[STIX]{x27E6}J_{s+r}(X)\unicode[STIX]{x27E7}>X^{\unicode[STIX]{x1D6EC}-\unicode[STIX]{x1D6FF}}\quad \text{and}\quad \unicode[STIX]{x27E6}J_{s+r}(Y)\unicode[STIX]{x27E7}<Y^{\unicode[STIX]{x1D6EC}+\unicode[STIX]{x1D6FF}}\quad (Y\geqslant X^{1/2}),\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x27E6}J_{s+r}(X)\unicode[STIX]{x27E7}>X^{\unicode[STIX]{x1D6EC}-\unicode[STIX]{x1D6FF}}\quad \text{and}\quad \unicode[STIX]{x27E6}J_{s+r}(Y)\unicode[STIX]{x27E7}<Y^{\unicode[STIX]{x1D6EC}+\unicode[STIX]{x1D6FF}}\quad (Y\geqslant X^{1/2}),\end{eqnarray}$$
where
![]() $\unicode[STIX]{x1D6EC}$
is defined by
$\unicode[STIX]{x1D6EC}$
is defined by
 $\unicode[STIX]{x1D6EC}=\unicode[STIX]{x1D706}-(s+r)$
.
$\unicode[STIX]{x1D6EC}=\unicode[STIX]{x1D706}-(s+r)$
.
Finally, we recall two simple estimates associated with the system (1.1).
Lemma 2.2. Suppose that
![]() $c$
is a non-negative integer with
$c$
is a non-negative integer with
![]() $c\unicode[STIX]{x1D703}\leqslant 1$
. Then, for each natural number
$c\unicode[STIX]{x1D703}\leqslant 1$
. Then, for each natural number
![]() $u$
, one has
$u$
, one has
 $$\begin{eqnarray}\max _{1\leqslant \unicode[STIX]{x1D709}\leqslant p^{c}}\oint |\mathfrak{f}_{c}(\unicode[STIX]{x1D736};\unicode[STIX]{x1D709})|^{2u}\,d\unicode[STIX]{x1D736}\ll _{u}J_{u}(X/M^{c}).\end{eqnarray}$$
$$\begin{eqnarray}\max _{1\leqslant \unicode[STIX]{x1D709}\leqslant p^{c}}\oint |\mathfrak{f}_{c}(\unicode[STIX]{x1D736};\unicode[STIX]{x1D709})|^{2u}\,d\unicode[STIX]{x1D736}\ll _{u}J_{u}(X/M^{c}).\end{eqnarray}$$
Proof. This is [Reference Wooley15, Lemma 3.1]. ◻
Lemma 2.3. Suppose that
![]() $c$
and
$c$
and
![]() $d$
are non-negative integers with
$d$
are non-negative integers with
![]() $c\leqslant \unicode[STIX]{x1D703}^{-1}$
and
$c\leqslant \unicode[STIX]{x1D703}^{-1}$
and
![]() $d\leqslant \unicode[STIX]{x1D703}^{-1}$
. Then, whenever
$d\leqslant \unicode[STIX]{x1D703}^{-1}$
. Then, whenever
 $u,v\in \mathbb{N}$
and
$u,v\in \mathbb{N}$
and
 $\unicode[STIX]{x1D709},\unicode[STIX]{x1D701}\in \mathbb{Z}$
, one has
$\unicode[STIX]{x1D709},\unicode[STIX]{x1D701}\in \mathbb{Z}$
, one has
 $$\begin{eqnarray}\oint |\mathfrak{f}_{c}(\unicode[STIX]{x1D736};\unicode[STIX]{x1D709})^{2u}\mathfrak{f}_{d}(\unicode[STIX]{x1D736};\unicode[STIX]{x1D701})^{2v}|\,d\unicode[STIX]{x1D736}\ll _{u,v}(J_{u+v}(X/M^{c}))^{u/(u+v)}(J_{u+v}(X/M^{d}))^{v/(u+v)}.\end{eqnarray}$$
$$\begin{eqnarray}\oint |\mathfrak{f}_{c}(\unicode[STIX]{x1D736};\unicode[STIX]{x1D709})^{2u}\mathfrak{f}_{d}(\unicode[STIX]{x1D736};\unicode[STIX]{x1D701})^{2v}|\,d\unicode[STIX]{x1D736}\ll _{u,v}(J_{u+v}(X/M^{c}))^{u/(u+v)}(J_{u+v}(X/M^{d}))^{v/(u+v)}.\end{eqnarray}$$
Proof. This is [Reference Ford and Wooley4, Corollary 2.2]. ◻
3 Auxiliary systems of congruences
Our goal of establishing strongly diagonal behaviour dictates that we must establish essentially diagonal behaviour for the solutions of auxiliary congruences central to our methods. Complicating our discussion in present circumstances is the potential for the ratio
![]() $b/a$
to be small, for in earlier work [Reference Ford and Wooley4, Reference Wooley17] this was assumed to be at least
$b/a$
to be small, for in earlier work [Reference Ford and Wooley4, Reference Wooley17] this was assumed to be at least
 $\frac{1}{2}(k-1)$
or thereabouts. We begin by adjusting our notation to accommodate the demands of this paper. When
$\frac{1}{2}(k-1)$
or thereabouts. We begin by adjusting our notation to accommodate the demands of this paper. When
![]() $a$
and
$a$
and
![]() $b$
are integers with
$b$
are integers with
 $1\leqslant a<b$
, we write
$1\leqslant a<b$
, we write
 ${\mathcal{B}}_{a,b}^{n}(\mathbf{m};\unicode[STIX]{x1D709},\unicode[STIX]{x1D702})$
for the set of solutions of the system of congruences
${\mathcal{B}}_{a,b}^{n}(\mathbf{m};\unicode[STIX]{x1D709},\unicode[STIX]{x1D702})$
for the set of solutions of the system of congruences
 $$\begin{eqnarray}\mathop{\sum }_{i=1}^{n}(z_{i}-\unicode[STIX]{x1D702})^{j}\equiv m_{j}~(\text{mod}~p^{jb})\quad (1\leqslant j\leqslant k),\end{eqnarray}$$
$$\begin{eqnarray}\mathop{\sum }_{i=1}^{n}(z_{i}-\unicode[STIX]{x1D702})^{j}\equiv m_{j}~(\text{mod}~p^{jb})\quad (1\leqslant j\leqslant k),\end{eqnarray}$$
with
 $1\leqslant \mathbf{z}\leqslant p^{kb}$
and
$1\leqslant \mathbf{z}\leqslant p^{kb}$
and
 $\mathbf{z}\equiv \unicode[STIX]{x1D743}~(\text{mod}~p^{a+1})$
for some
$\mathbf{z}\equiv \unicode[STIX]{x1D743}~(\text{mod}~p^{a+1})$
for some
 $\unicode[STIX]{x1D743}\in \unicode[STIX]{x1D6EF}_{a}^{n}(\unicode[STIX]{x1D709})$
. We define an equivalence relation
$\unicode[STIX]{x1D743}\in \unicode[STIX]{x1D6EF}_{a}^{n}(\unicode[STIX]{x1D709})$
. We define an equivalence relation
![]() ${\mathcal{R}}(\unicode[STIX]{x1D706})$
on integral
${\mathcal{R}}(\unicode[STIX]{x1D706})$
on integral
![]() $n$
-tuples by declaring
$n$
-tuples by declaring
![]() $\mathbf{x}$
and
$\mathbf{x}$
and
![]() $\mathbf{y}$
to be
$\mathbf{y}$
to be
![]() ${\mathcal{R}}(\unicode[STIX]{x1D706})$
-equivalent when
${\mathcal{R}}(\unicode[STIX]{x1D706})$
-equivalent when
 $\mathbf{x}\equiv \mathbf{y}~(\text{mod}~p^{\unicode[STIX]{x1D706}})$
. When
$\mathbf{x}\equiv \mathbf{y}~(\text{mod}~p^{\unicode[STIX]{x1D706}})$
. When
![]() $hb\in \mathbb{N}$
, we then write
$hb\in \mathbb{N}$
, we then write
 ${\mathcal{C}}_{a,b}^{n,h}(\mathbf{m};\unicode[STIX]{x1D709},\unicode[STIX]{x1D702})$
for the set of
${\mathcal{C}}_{a,b}^{n,h}(\mathbf{m};\unicode[STIX]{x1D709},\unicode[STIX]{x1D702})$
for the set of
![]() ${\mathcal{R}}(hb)$
-equivalence classes of
${\mathcal{R}}(hb)$
-equivalence classes of
 ${\mathcal{B}}_{a,b}^{n}(\mathbf{m};\unicode[STIX]{x1D709},\unicode[STIX]{x1D702})$
, and we define
${\mathcal{B}}_{a,b}^{n}(\mathbf{m};\unicode[STIX]{x1D709},\unicode[STIX]{x1D702})$
, and we define
![]() $B_{a,b}^{n,h}(p)$
by putting
$B_{a,b}^{n,h}(p)$
by putting
 $$\begin{eqnarray}B_{a,b}^{n,h}(p)=\max _{1\leqslant \unicode[STIX]{x1D709}\leqslant p^{a}}\max _{\substack{ 1\leqslant \unicode[STIX]{x1D702}\leqslant p^{b} \\ \unicode[STIX]{x1D702}\not \equiv \unicode[STIX]{x1D709}~(\text{mod}~p)}}\max _{1\leqslant \mathbf{m}\leqslant p^{kb}}\text{card}({\mathcal{C}}_{a,b}^{n,h}(\mathbf{m};\unicode[STIX]{x1D709},\unicode[STIX]{x1D702})).\end{eqnarray}$$
$$\begin{eqnarray}B_{a,b}^{n,h}(p)=\max _{1\leqslant \unicode[STIX]{x1D709}\leqslant p^{a}}\max _{\substack{ 1\leqslant \unicode[STIX]{x1D702}\leqslant p^{b} \\ \unicode[STIX]{x1D702}\not \equiv \unicode[STIX]{x1D709}~(\text{mod}~p)}}\max _{1\leqslant \mathbf{m}\leqslant p^{kb}}\text{card}({\mathcal{C}}_{a,b}^{n,h}(\mathbf{m};\unicode[STIX]{x1D709},\unicode[STIX]{x1D702})).\end{eqnarray}$$
When
![]() $a=0$
we modify these definitions, so that
$a=0$
we modify these definitions, so that
 ${\mathcal{B}}_{0,b}^{n}(\mathbf{m};\unicode[STIX]{x1D709},\unicode[STIX]{x1D702})$
denotes the set of solutions of the system of congruences (3.1) with
${\mathcal{B}}_{0,b}^{n}(\mathbf{m};\unicode[STIX]{x1D709},\unicode[STIX]{x1D702})$
denotes the set of solutions of the system of congruences (3.1) with
 $1\leqslant \mathbf{z}\leqslant p^{kb}$
and
$1\leqslant \mathbf{z}\leqslant p^{kb}$
and
 $\mathbf{z}\equiv \unicode[STIX]{x1D743}~(\text{mod}~p)$
for some
$\mathbf{z}\equiv \unicode[STIX]{x1D743}~(\text{mod}~p)$
for some
 $\unicode[STIX]{x1D743}\in \unicode[STIX]{x1D6EF}_{0}^{n}(\unicode[STIX]{x1D709})$
, and for which in addition
$\unicode[STIX]{x1D743}\in \unicode[STIX]{x1D6EF}_{0}^{n}(\unicode[STIX]{x1D709})$
, and for which in addition
 $\mathbf{z}\not \equiv \unicode[STIX]{x1D702}~(\text{mod}~p)$
. As in the situation in which one has
$\mathbf{z}\not \equiv \unicode[STIX]{x1D702}~(\text{mod}~p)$
. As in the situation in which one has
![]() $a\geqslant 1$
, when
$a\geqslant 1$
, when
![]() $hb\in \mathbb{N}$
, we write
$hb\in \mathbb{N}$
, we write
 ${\mathcal{C}}_{0,b}^{n,h}(\mathbf{m};\unicode[STIX]{x1D709},\unicode[STIX]{x1D702})$
for the set of
${\mathcal{C}}_{0,b}^{n,h}(\mathbf{m};\unicode[STIX]{x1D709},\unicode[STIX]{x1D702})$
for the set of
![]() ${\mathcal{R}}(hb)$
-equivalence classes of
${\mathcal{R}}(hb)$
-equivalence classes of
 ${\mathcal{B}}_{0,b}^{n}(\mathbf{m};\unicode[STIX]{x1D709},\unicode[STIX]{x1D702})$
, but we define
${\mathcal{B}}_{0,b}^{n}(\mathbf{m};\unicode[STIX]{x1D709},\unicode[STIX]{x1D702})$
, but we define
![]() $B_{0,b}^{n,h}(p)$
by putting
$B_{0,b}^{n,h}(p)$
by putting
 $$\begin{eqnarray}B_{0,b}^{n,h}(p)=\max _{1\leqslant \unicode[STIX]{x1D702}\leqslant p^{b}}\max _{1\leqslant \mathbf{m}\leqslant p^{kb}}\text{card}({\mathcal{C}}_{0,b}^{n,h}(\mathbf{m};0,\unicode[STIX]{x1D702})).\end{eqnarray}$$
$$\begin{eqnarray}B_{0,b}^{n,h}(p)=\max _{1\leqslant \unicode[STIX]{x1D702}\leqslant p^{b}}\max _{1\leqslant \mathbf{m}\leqslant p^{kb}}\text{card}({\mathcal{C}}_{0,b}^{n,h}(\mathbf{m};0,\unicode[STIX]{x1D702})).\end{eqnarray}$$
We observe that the definition of
![]() $B_{a,b}^{n,h}(p)$
ensures that whenever
$B_{a,b}^{n,h}(p)$
ensures that whenever
 $0<h^{\prime }\leqslant h$
and both
$0<h^{\prime }\leqslant h$
and both
![]() $hb$
and
$hb$
and
![]() $h^{\prime }b$
are natural numbers, one has
$h^{\prime }b$
are natural numbers, one has
 $$\begin{eqnarray}B_{a,b}^{n,h^{\prime }}(p)\leqslant B_{a,b}^{n,h}(p).\end{eqnarray}$$
$$\begin{eqnarray}B_{a,b}^{n,h^{\prime }}(p)\leqslant B_{a,b}^{n,h}(p).\end{eqnarray}$$
Readers might wonder concerning the wisdom of permitting in
![]() $B_{a,b}^{n,h}(p)$
the parameter
$B_{a,b}^{n,h}(p)$
the parameter
![]() $h$
to be a rational number with
$h$
to be a rational number with
![]() $hb\in \mathbb{N}$
. We remark that this somewhat strange notational device is designed to facilitate ease of comparison with the earlier work [Reference Ford and Wooley4, Reference Wooley17, Reference Wooley19]. Since the role of the parameter
$hb\in \mathbb{N}$
. We remark that this somewhat strange notational device is designed to facilitate ease of comparison with the earlier work [Reference Ford and Wooley4, Reference Wooley17, Reference Wooley19]. Since the role of the parameter
![]() $h$
is simply that of indicating certain congruence relations modulo
$h$
is simply that of indicating certain congruence relations modulo
![]() $p^{hb}$
, the reader may take comfort from our imposition of the condition
$p^{hb}$
, the reader may take comfort from our imposition of the condition
![]() $hb\in \mathbb{N}$
.
$hb\in \mathbb{N}$
.
Lemma 3.1. Let
![]() $m$
be an integer with
$m$
be an integer with
 $0\leqslant m\leqslant k-1$
, and suppose that
$0\leqslant m\leqslant k-1$
, and suppose that
![]() $a$
and
$a$
and
![]() $b$
are integers with
$b$
are integers with
 $0\leqslant a<b$
and
$0\leqslant a<b$
and
 $(k-m)b\geqslant (m+1)a$
. Suppose in addition that
$(k-m)b\geqslant (m+1)a$
. Suppose in addition that
![]() $h$
is a natural number with
$h$
is a natural number with
 $a\leqslant h\leqslant (k-m)b-ma$
. Then one has
$a\leqslant h\leqslant (k-m)b-ma$
. Then one has
 $$\begin{eqnarray}B_{a,b}^{m+1,h/b}(p)\leqslant k!.\end{eqnarray}$$
$$\begin{eqnarray}B_{a,b}^{m+1,h/b}(p)\leqslant k!.\end{eqnarray}$$
Proof. We are able to follow the arguments of the proofs of [Reference Wooley17, Lemma 3.5] and [Reference Ford and Wooley4, Lemma 3.3], with some modifications. For the sake of transparency of exposition, we provide an essentially complete account. We begin by considering the situation with
![]() $a\geqslant 1$
, the alterations required when
$a\geqslant 1$
, the alterations required when
![]() $a=0$
being easily accommodated within our basic argument. Consider fixed natural numbers
$a=0$
being easily accommodated within our basic argument. Consider fixed natural numbers
![]() $a$
and
$a$
and
![]() $b$
with
$b$
with
 $1\leqslant a<b$
and
$1\leqslant a<b$
and
 $(k-m)b\geqslant (m+1)a$
, and fixed integers
$(k-m)b\geqslant (m+1)a$
, and fixed integers
![]() $\unicode[STIX]{x1D709}$
and
$\unicode[STIX]{x1D709}$
and
![]() $\unicode[STIX]{x1D702}$
with
$\unicode[STIX]{x1D702}$
with
 $1\leqslant \unicode[STIX]{x1D709}\leqslant p^{a}$
,
$1\leqslant \unicode[STIX]{x1D709}\leqslant p^{a}$
,
 $1\leqslant \unicode[STIX]{x1D702}\leqslant p^{b}$
and
$1\leqslant \unicode[STIX]{x1D702}\leqslant p^{b}$
and
 $\unicode[STIX]{x1D702}\not \equiv \unicode[STIX]{x1D709}~(\text{mod}~p)$
. Note that in view of the relation (3.4), the conclusion of the lemma follows in general if we can establish it when
$\unicode[STIX]{x1D702}\not \equiv \unicode[STIX]{x1D709}~(\text{mod}~p)$
. Note that in view of the relation (3.4), the conclusion of the lemma follows in general if we can establish it when
 $h=(k-m)b-ma$
. We henceforth assume that the latter is the case. We then denote by
$h=(k-m)b-ma$
. We henceforth assume that the latter is the case. We then denote by
![]() ${\mathcal{D}}_{1}(\mathbf{n})$
the set of
${\mathcal{D}}_{1}(\mathbf{n})$
the set of
![]() ${\mathcal{R}}(h)$
-equivalence classes of solutions of the system of congruences
${\mathcal{R}}(h)$
-equivalence classes of solutions of the system of congruences
 $$\begin{eqnarray}\mathop{\sum }_{i=1}^{m+1}(z_{i}-\unicode[STIX]{x1D702})^{j}\equiv n_{j}~(\text{mod}~p^{(k-m)b})\quad (k-m\leqslant j\leqslant k),\end{eqnarray}$$
$$\begin{eqnarray}\mathop{\sum }_{i=1}^{m+1}(z_{i}-\unicode[STIX]{x1D702})^{j}\equiv n_{j}~(\text{mod}~p^{(k-m)b})\quad (k-m\leqslant j\leqslant k),\end{eqnarray}$$
with
 $1\leqslant \mathbf{z}\leqslant p^{kb}$
and
$1\leqslant \mathbf{z}\leqslant p^{kb}$
and
 $\mathbf{z}\equiv \unicode[STIX]{x1D743}~(\text{mod}~p^{a+1})$
for some
$\mathbf{z}\equiv \unicode[STIX]{x1D743}~(\text{mod}~p^{a+1})$
for some
 $\unicode[STIX]{x1D743}\in \unicode[STIX]{x1D6EF}_{a}^{m+1}(\unicode[STIX]{x1D709})$
. To any solution
$\unicode[STIX]{x1D743}\in \unicode[STIX]{x1D6EF}_{a}^{m+1}(\unicode[STIX]{x1D709})$
. To any solution
![]() $\mathbf{z}$
of (3.1) there corresponds a unique
$\mathbf{z}$
of (3.1) there corresponds a unique
![]() $(m+1)$
-tuple
$(m+1)$
-tuple
 $(n_{k-m},\ldots ,n_{k})$
, satisfying
$(n_{k-m},\ldots ,n_{k})$
, satisfying
 $1\leqslant \mathbf{n}\leqslant p^{(k-m)b}$
, for which (3.5) holds and
$1\leqslant \mathbf{n}\leqslant p^{(k-m)b}$
, for which (3.5) holds and
 $$\begin{eqnarray}n_{j}\equiv m_{j}~(\text{mod}~p^{(k-m)b})\quad (k-m\leqslant j\leqslant k).\end{eqnarray}$$
$$\begin{eqnarray}n_{j}\equiv m_{j}~(\text{mod}~p^{(k-m)b})\quad (k-m\leqslant j\leqslant k).\end{eqnarray}$$
Since
 $h/b\leqslant k-m$
, we therefore infer that
$h/b\leqslant k-m$
, we therefore infer that
 $$\begin{eqnarray}\text{card}({\mathcal{C}}_{a,b}^{m+1,h/b}(\mathbf{m};\unicode[STIX]{x1D709},\unicode[STIX]{x1D702}))\leqslant \max _{1\leqslant \mathbf{n}\leqslant p^{(k-m)b}}\text{card}({\mathcal{D}}_{1}(\mathbf{n})).\end{eqnarray}$$
$$\begin{eqnarray}\text{card}({\mathcal{C}}_{a,b}^{m+1,h/b}(\mathbf{m};\unicode[STIX]{x1D709},\unicode[STIX]{x1D702}))\leqslant \max _{1\leqslant \mathbf{n}\leqslant p^{(k-m)b}}\text{card}({\mathcal{D}}_{1}(\mathbf{n})).\end{eqnarray}$$
We fix any choice of
![]() $\mathbf{n}$
for which the maximum is achieved in (3.6). There is plainly no loss of generality in supposing that
$\mathbf{n}$
for which the maximum is achieved in (3.6). There is plainly no loss of generality in supposing that
![]() ${\mathcal{D}}_{1}(\mathbf{n})$
is non-empty. Observe that for any solution
${\mathcal{D}}_{1}(\mathbf{n})$
is non-empty. Observe that for any solution
![]() $\mathbf{z}^{\prime }$
of (3.5) there is an
$\mathbf{z}^{\prime }$
of (3.5) there is an
 ${\mathcal{R}}(k-m)$
-equivalent solution
${\mathcal{R}}(k-m)$
-equivalent solution
![]() $\mathbf{z}$
satisfying
$\mathbf{z}$
satisfying
 $1\leqslant \mathbf{z}\leqslant p^{(k-m)b}$
. Rewriting each variable
$1\leqslant \mathbf{z}\leqslant p^{(k-m)b}$
. Rewriting each variable
![]() $z_{i}$
in (3.5) in the shape
$z_{i}$
in (3.5) in the shape
 $z_{i}=p^{a}y_{i}+\unicode[STIX]{x1D709}$
, we infer from the hypothesis that
$z_{i}=p^{a}y_{i}+\unicode[STIX]{x1D709}$
, we infer from the hypothesis that
 $\mathbf{z}\equiv \unicode[STIX]{x1D743}~(\text{mod}~p^{a+1})$
for some
$\mathbf{z}\equiv \unicode[STIX]{x1D743}~(\text{mod}~p^{a+1})$
for some
 $\unicode[STIX]{x1D743}\in \unicode[STIX]{x1D6EF}_{a}^{m+1}(\unicode[STIX]{x1D709})$
that the
$\unicode[STIX]{x1D743}\in \unicode[STIX]{x1D6EF}_{a}^{m+1}(\unicode[STIX]{x1D709})$
that the
![]() $(m+1)$
-tuple
$(m+1)$
-tuple
![]() $\mathbf{y}$
necessarily satisfies
$\mathbf{y}$
necessarily satisfies
 $$\begin{eqnarray}y_{i}\not \equiv y_{l}~(\text{mod}~p)\quad (1\leqslant i<l\leqslant m+1).\end{eqnarray}$$
$$\begin{eqnarray}y_{i}\not \equiv y_{l}~(\text{mod}~p)\quad (1\leqslant i<l\leqslant m+1).\end{eqnarray}$$
Write
 $\unicode[STIX]{x1D701}=\unicode[STIX]{x1D709}-\unicode[STIX]{x1D702}$
, and note that the constraint
$\unicode[STIX]{x1D701}=\unicode[STIX]{x1D709}-\unicode[STIX]{x1D702}$
, and note that the constraint
 $\unicode[STIX]{x1D702}\not \equiv \unicode[STIX]{x1D709}~(\text{mod}~p)$
ensures that
$\unicode[STIX]{x1D702}\not \equiv \unicode[STIX]{x1D709}~(\text{mod}~p)$
ensures that
![]() $p\nmid \unicode[STIX]{x1D701}$
. We denote the multiplicative inverse of
$p\nmid \unicode[STIX]{x1D701}$
. We denote the multiplicative inverse of
![]() $\unicode[STIX]{x1D701}$
modulo
$\unicode[STIX]{x1D701}$
modulo
![]() $p^{(k-m)b}$
by
$p^{(k-m)b}$
by
![]() $\unicode[STIX]{x1D701}^{-1}$
. Then we deduce from (3.5) that
$\unicode[STIX]{x1D701}^{-1}$
. Then we deduce from (3.5) that
 $\text{card}({\mathcal{D}}_{1}(\mathbf{n}))$
is bounded above by the number of
$\text{card}({\mathcal{D}}_{1}(\mathbf{n}))$
is bounded above by the number of
 ${\mathcal{R}}(h-a)$
-equivalence classes of solutions of the system of congruences
${\mathcal{R}}(h-a)$
-equivalence classes of solutions of the system of congruences
 $$\begin{eqnarray}\mathop{\sum }_{i=1}^{m+1}(p^{a}y_{i}\unicode[STIX]{x1D701}^{-1}+1)^{j}\equiv n_{j}(\unicode[STIX]{x1D701}^{-1})^{j}~(\text{mod}~p^{(k-m)b})\quad (k-m\leqslant j\leqslant k),\end{eqnarray}$$
$$\begin{eqnarray}\mathop{\sum }_{i=1}^{m+1}(p^{a}y_{i}\unicode[STIX]{x1D701}^{-1}+1)^{j}\equiv n_{j}(\unicode[STIX]{x1D701}^{-1})^{j}~(\text{mod}~p^{(k-m)b})\quad (k-m\leqslant j\leqslant k),\end{eqnarray}$$
with
 $1\leqslant \mathbf{y}\leqslant p^{(k-m)b-a}$
satisfying (3.7). Let
$1\leqslant \mathbf{y}\leqslant p^{(k-m)b-a}$
satisfying (3.7). Let
![]() $\mathbf{y}=\mathbf{w}$
be any solution of the system (3.8). Then we find that all other solutions
$\mathbf{y}=\mathbf{w}$
be any solution of the system (3.8). Then we find that all other solutions
![]() $\mathbf{y}$
satisfy the system
$\mathbf{y}$
satisfy the system
 $$\begin{eqnarray}\mathop{\sum }_{i=1}^{m+1}((p^{a}y_{i}\unicode[STIX]{x1D701}^{-1}+1)^{j}-(p^{a}w_{i}\unicode[STIX]{x1D701}^{-1}+1)^{j})\equiv 0~(\text{mod}~p^{(k-m)b})\quad (k-m\leqslant j\leqslant k).\end{eqnarray}$$
$$\begin{eqnarray}\mathop{\sum }_{i=1}^{m+1}((p^{a}y_{i}\unicode[STIX]{x1D701}^{-1}+1)^{j}-(p^{a}w_{i}\unicode[STIX]{x1D701}^{-1}+1)^{j})\equiv 0~(\text{mod}~p^{(k-m)b})\quad (k-m\leqslant j\leqslant k).\end{eqnarray}$$
We next apply [Reference Wooley17, Lemma 3.2], just as in the arguments of the proofs of [Reference Wooley17, Lemmas 3.3 to 3.6]. Consider an index
![]() $j$
with
$j$
with
 $k-m\leqslant j\leqslant k$
, and apply the latter lemma with
$k-m\leqslant j\leqslant k$
, and apply the latter lemma with
 $\unicode[STIX]{x1D6FC}=k-m-1$
and
$\unicode[STIX]{x1D6FC}=k-m-1$
and
 $\unicode[STIX]{x1D6FD}=j-k+m+1$
. We find that there exist integers
$\unicode[STIX]{x1D6FD}=j-k+m+1$
. We find that there exist integers
![]() $c_{j,l}$
$c_{j,l}$
 $(k-m-1\leqslant l\leqslant j)$
and
$(k-m-1\leqslant l\leqslant j)$
and
![]() $d_{j,u}$
$d_{j,u}$
 $(j-k+m+1\leqslant u\leqslant j)$
, bounded in terms of
$(j-k+m+1\leqslant u\leqslant j)$
, bounded in terms of
![]() $k$
, and with
$k$
, and with
 $d_{j,j-k+m+1}\neq 0$
, for which one has the polynomial identity
$d_{j,j-k+m+1}\neq 0$
, for which one has the polynomial identity
 $$\begin{eqnarray}c_{j,k-m-1}+\mathop{\sum }_{l=k-m}^{j}c_{j,l}(x+1)^{l}=\mathop{\sum }_{u=j-k+m+1}^{j}d_{j,u}x^{u}.\end{eqnarray}$$
$$\begin{eqnarray}c_{j,k-m-1}+\mathop{\sum }_{l=k-m}^{j}c_{j,l}(x+1)^{l}=\mathop{\sum }_{u=j-k+m+1}^{j}d_{j,u}x^{u}.\end{eqnarray}$$
Since we may assume
![]() $p$
to be large, we may suppose that
$p$
to be large, we may suppose that
 $p\nmid d_{j,j-k+m+1}$
. Thus, multiplying (3.10) through by the multiplicative inverse of
$p\nmid d_{j,j-k+m+1}$
. Thus, multiplying (3.10) through by the multiplicative inverse of
 $d_{j,j-k+m+1}$
modulo
$d_{j,j-k+m+1}$
modulo
![]() $p^{(k-m)b}$
, we see that there is no loss in supposing that
$p^{(k-m)b}$
, we see that there is no loss in supposing that
 $$\begin{eqnarray}d_{j,j-k+m+1}\equiv 1~(\text{mod}~p^{(k-m)b}).\end{eqnarray}$$
$$\begin{eqnarray}d_{j,j-k+m+1}\equiv 1~(\text{mod}~p^{(k-m)b}).\end{eqnarray}$$
Consequently, by taking suitable linear combinations of the congruences comprising (3.9), we discern that any solution of this system satisfies
 $$\begin{eqnarray}(\unicode[STIX]{x1D701}^{-1}p^{a})^{j-k+m+1}\mathop{\sum }_{i=1}^{m+1}(\unicode[STIX]{x1D713}_{j}(y_{i})-\unicode[STIX]{x1D713}_{j}(w_{i}))\equiv 0~(\text{mod}~p^{(k-m)b})\quad (k-m\leqslant j\leqslant k),\end{eqnarray}$$
$$\begin{eqnarray}(\unicode[STIX]{x1D701}^{-1}p^{a})^{j-k+m+1}\mathop{\sum }_{i=1}^{m+1}(\unicode[STIX]{x1D713}_{j}(y_{i})-\unicode[STIX]{x1D713}_{j}(w_{i}))\equiv 0~(\text{mod}~p^{(k-m)b})\quad (k-m\leqslant j\leqslant k),\end{eqnarray}$$
in which
 $$\begin{eqnarray}\unicode[STIX]{x1D713}_{j}(z)=z^{j-k+m+1}+\mathop{\sum }_{u=j-k+m+2}^{j}d_{j,u}(\unicode[STIX]{x1D701}^{-1}p^{a})^{u-j+k-m-1}z^{u}.\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D713}_{j}(z)=z^{j-k+m+1}+\mathop{\sum }_{u=j-k+m+2}^{j}d_{j,u}(\unicode[STIX]{x1D701}^{-1}p^{a})^{u-j+k-m-1}z^{u}.\end{eqnarray}$$
Note here that
 $$\begin{eqnarray}\unicode[STIX]{x1D713}_{j}(z)\equiv z^{j-k+m+1}~(\text{mod}~p).\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D713}_{j}(z)\equiv z^{j-k+m+1}~(\text{mod}~p).\end{eqnarray}$$
Denote by
![]() ${\mathcal{D}}_{2}(\mathbf{u})$
the set of
${\mathcal{D}}_{2}(\mathbf{u})$
the set of
 ${\mathcal{R}}(h-a)$
-equivalence classes of solutions of the system of congruences
${\mathcal{R}}(h-a)$
-equivalence classes of solutions of the system of congruences
 $$\begin{eqnarray}\mathop{\sum }_{i=1}^{m+1}\unicode[STIX]{x1D713}_{j}(y_{i})\equiv u_{j}~(\text{mod}~p^{(k-m)b-(j-k+m+1)a})\quad (k-m\leqslant j\leqslant k),\end{eqnarray}$$
$$\begin{eqnarray}\mathop{\sum }_{i=1}^{m+1}\unicode[STIX]{x1D713}_{j}(y_{i})\equiv u_{j}~(\text{mod}~p^{(k-m)b-(j-k+m+1)a})\quad (k-m\leqslant j\leqslant k),\end{eqnarray}$$
with
 $1\leqslant \mathbf{y}\leqslant p^{(k-m)b-a}$
satisfying (3.7). Then we have shown thus far that
$1\leqslant \mathbf{y}\leqslant p^{(k-m)b-a}$
satisfying (3.7). Then we have shown thus far that
 $$\begin{eqnarray}\text{card}({\mathcal{D}}_{1}(\mathbf{n}))\leqslant \max _{1\leqslant \mathbf{u}\leqslant p^{(k-m)b}}\text{card}({\mathcal{D}}_{2}(\mathbf{u})).\end{eqnarray}$$
$$\begin{eqnarray}\text{card}({\mathcal{D}}_{1}(\mathbf{n}))\leqslant \max _{1\leqslant \mathbf{u}\leqslant p^{(k-m)b}}\text{card}({\mathcal{D}}_{2}(\mathbf{u})).\end{eqnarray}$$
Let
![]() ${\mathcal{D}}_{3}(\mathbf{v})$
denote the set of solutions of the congruence
${\mathcal{D}}_{3}(\mathbf{v})$
denote the set of solutions of the congruence
 $$\begin{eqnarray}\mathop{\sum }_{i=1}^{m+1}\unicode[STIX]{x1D713}_{j}(y_{i})\equiv v_{j}~(\text{mod}~p^{h-a})\quad (k-m\leqslant j\leqslant k),\end{eqnarray}$$
$$\begin{eqnarray}\mathop{\sum }_{i=1}^{m+1}\unicode[STIX]{x1D713}_{j}(y_{i})\equiv v_{j}~(\text{mod}~p^{h-a})\quad (k-m\leqslant j\leqslant k),\end{eqnarray}$$
with
 $1\leqslant \mathbf{y}\leqslant p^{h-a}$
satisfying (3.7). For
$1\leqslant \mathbf{y}\leqslant p^{h-a}$
satisfying (3.7). For
 $k-m\leqslant j\leqslant k$
, we have
$k-m\leqslant j\leqslant k$
, we have
 $$\begin{eqnarray}(k-m)b-(j-k+m+1)a\geqslant (k-m)b-(m+1)a=h-a.\end{eqnarray}$$
$$\begin{eqnarray}(k-m)b-(j-k+m+1)a\geqslant (k-m)b-(m+1)a=h-a.\end{eqnarray}$$
Then we arrive at the upper bound
 $$\begin{eqnarray}\text{card}({\mathcal{D}}_{2}(\mathbf{u}))\leqslant \max _{1\leqslant \mathbf{v}\leqslant p^{h-a}}\text{card}({\mathcal{D}}_{3}(\mathbf{v})).\end{eqnarray}$$
$$\begin{eqnarray}\text{card}({\mathcal{D}}_{2}(\mathbf{u}))\leqslant \max _{1\leqslant \mathbf{v}\leqslant p^{h-a}}\text{card}({\mathcal{D}}_{3}(\mathbf{v})).\end{eqnarray}$$
By combining (3.6), (3.12) and (3.13), we discern at this point that
 $$\begin{eqnarray}\text{card}({\mathcal{C}}_{a,b}^{m+1,h/b}(\mathbf{m};\unicode[STIX]{x1D709},\unicode[STIX]{x1D702}))\leqslant \max _{1\leqslant \mathbf{v}\leqslant p^{h-a}}\text{card}({\mathcal{D}}_{3}(\mathbf{v})).\end{eqnarray}$$
$$\begin{eqnarray}\text{card}({\mathcal{C}}_{a,b}^{m+1,h/b}(\mathbf{m};\unicode[STIX]{x1D709},\unicode[STIX]{x1D702}))\leqslant \max _{1\leqslant \mathbf{v}\leqslant p^{h-a}}\text{card}({\mathcal{D}}_{3}(\mathbf{v})).\end{eqnarray}$$
Define the determinant
 $$\begin{eqnarray}J(\unicode[STIX]{x1D74D};\mathbf{x})=\det (\unicode[STIX]{x1D713}_{k-m+l-1}^{\prime }(x_{i}))_{1\leqslant i,l\leqslant m+1}.\end{eqnarray}$$
$$\begin{eqnarray}J(\unicode[STIX]{x1D74D};\mathbf{x})=\det (\unicode[STIX]{x1D713}_{k-m+l-1}^{\prime }(x_{i}))_{1\leqslant i,l\leqslant m+1}.\end{eqnarray}$$
In view of (3.11), one has
 $\unicode[STIX]{x1D713}_{k-m+l-1}^{\prime }(y_{i})\equiv ly_{i}^{l-1}~(\text{mod}~p)$
. It follows from (3.7) that
$\unicode[STIX]{x1D713}_{k-m+l-1}^{\prime }(y_{i})\equiv ly_{i}^{l-1}~(\text{mod}~p)$
. It follows from (3.7) that
 $$\begin{eqnarray}\det (y_{i}^{l-1})_{1\leqslant i,l\leqslant m+1}=\mathop{\prod }_{1\leqslant i<u\leqslant m+1}(y_{i}-y_{u})\not \equiv 0~(\text{mod}~p),\end{eqnarray}$$
$$\begin{eqnarray}\det (y_{i}^{l-1})_{1\leqslant i,l\leqslant m+1}=\mathop{\prod }_{1\leqslant i<u\leqslant m+1}(y_{i}-y_{u})\not \equiv 0~(\text{mod}~p),\end{eqnarray}$$
so that, since
![]() $p>k$
, we have
$p>k$
, we have
 $(J(\unicode[STIX]{x1D74D};\mathbf{y}),p)=1$
. We therefore deduce from [Reference Wooley13, Theorem 1], just as in the corresponding argument of the proof of [Reference Wooley17, Lemma 3.3] following [Reference Wooley17, equation (3.17)], that
$(J(\unicode[STIX]{x1D74D};\mathbf{y}),p)=1$
. We therefore deduce from [Reference Wooley13, Theorem 1], just as in the corresponding argument of the proof of [Reference Wooley17, Lemma 3.3] following [Reference Wooley17, equation (3.17)], that
 $$\begin{eqnarray}\text{card}({\mathcal{D}}_{3}(\mathbf{v}))\leqslant (k-m)(k-m+1)\cdots k\leqslant k!\end{eqnarray}$$
$$\begin{eqnarray}\text{card}({\mathcal{D}}_{3}(\mathbf{v}))\leqslant (k-m)(k-m+1)\cdots k\leqslant k!\end{eqnarray}$$
and thus the conclusion of the lemma when
![]() $a\geqslant 1$
follows at once from (3.2) and (3.14).
$a\geqslant 1$
follows at once from (3.2) and (3.14).
When
![]() $a=0$
, we must apply some minor modifications to the above argument. In this case, we denote by
$a=0$
, we must apply some minor modifications to the above argument. In this case, we denote by
 ${\mathcal{D}}_{1}(\mathbf{n};\unicode[STIX]{x1D702})$
the set of
${\mathcal{D}}_{1}(\mathbf{n};\unicode[STIX]{x1D702})$
the set of
![]() ${\mathcal{R}}(h)$
-equivalence classes of solutions of the system of congruences (3.5) with
${\mathcal{R}}(h)$
-equivalence classes of solutions of the system of congruences (3.5) with
 $1\leqslant \mathbf{z}\leqslant p^{kb}$
and
$1\leqslant \mathbf{z}\leqslant p^{kb}$
and
 $\mathbf{z}\equiv \unicode[STIX]{x1D743}~(\text{mod}~p)$
for some
$\mathbf{z}\equiv \unicode[STIX]{x1D743}~(\text{mod}~p)$
for some
 $\unicode[STIX]{x1D743}\in \unicode[STIX]{x1D6EF}_{0}^{m+1}(0)$
, and for which in addition
$\unicode[STIX]{x1D743}\in \unicode[STIX]{x1D6EF}_{0}^{m+1}(0)$
, and for which in addition
 $z_{i}\not \equiv \unicode[STIX]{x1D702}~(\text{mod}~p)$
for
$z_{i}\not \equiv \unicode[STIX]{x1D702}~(\text{mod}~p)$
for
 $1\leqslant i\leqslant m+1$
. Then, as in the opening paragraph of our proof, it follows from (3.1) that
$1\leqslant i\leqslant m+1$
. Then, as in the opening paragraph of our proof, it follows from (3.1) that
 $$\begin{eqnarray}\text{card}({\mathcal{C}}_{0,b}^{m+1,h/b}(\mathbf{m};0,\unicode[STIX]{x1D702}))\leqslant \max _{1\leqslant \mathbf{n}\leqslant p^{(k-m)b}}\text{card}({\mathcal{D}}_{1}(\mathbf{n};\unicode[STIX]{x1D702})).\end{eqnarray}$$
$$\begin{eqnarray}\text{card}({\mathcal{C}}_{0,b}^{m+1,h/b}(\mathbf{m};0,\unicode[STIX]{x1D702}))\leqslant \max _{1\leqslant \mathbf{n}\leqslant p^{(k-m)b}}\text{card}({\mathcal{D}}_{1}(\mathbf{n};\unicode[STIX]{x1D702})).\end{eqnarray}$$
But
 $\text{card}({\mathcal{D}}_{1}(\mathbf{n};\unicode[STIX]{x1D702}))=\text{card}({\mathcal{D}}_{1}(\mathbf{n};0))$
, and
$\text{card}({\mathcal{D}}_{1}(\mathbf{n};\unicode[STIX]{x1D702}))=\text{card}({\mathcal{D}}_{1}(\mathbf{n};0))$
, and
 $\text{card}({\mathcal{D}}_{1}(\mathbf{n};0))$
counts the solutions of the system of congruences
$\text{card}({\mathcal{D}}_{1}(\mathbf{n};0))$
counts the solutions of the system of congruences
 $$\begin{eqnarray}\mathop{\sum }_{i=1}^{m+1}y_{i}^{j}\equiv n_{j}~(\text{mod}~p^{(k-m)b})\quad (k-m\leqslant j\leqslant k),\end{eqnarray}$$
$$\begin{eqnarray}\mathop{\sum }_{i=1}^{m+1}y_{i}^{j}\equiv n_{j}~(\text{mod}~p^{(k-m)b})\quad (k-m\leqslant j\leqslant k),\end{eqnarray}$$
with
 $1\leqslant \mathbf{y}\leqslant p^{(k-m)b}$
satisfying (3.7), and in addition
$1\leqslant \mathbf{y}\leqslant p^{(k-m)b}$
satisfying (3.7), and in addition
![]() $p\nmid y_{i}$
$p\nmid y_{i}$
 $(1\leqslant i\leqslant m+1)$
. Write
$(1\leqslant i\leqslant m+1)$
. Write
 $$\begin{eqnarray}J(\mathbf{y})=\det ((k-m+j-1)y_{i}^{k-m+j-2})_{1\leqslant i,j\leqslant m+1}.\end{eqnarray}$$
$$\begin{eqnarray}J(\mathbf{y})=\det ((k-m+j-1)y_{i}^{k-m+j-2})_{1\leqslant i,j\leqslant m+1}.\end{eqnarray}$$
Then, since
![]() $p>k$
, we have
$p>k$
, we have
 $$\begin{eqnarray}J(\mathbf{y})=\frac{k!}{(k-m-1)!}(y_{1}\cdots y_{m+1})^{k-m-1}\mathop{\prod }_{1\leqslant i<j\leqslant m+1}(y_{i}-y_{j})\not \equiv 0~(\text{mod}~p).\end{eqnarray}$$
$$\begin{eqnarray}J(\mathbf{y})=\frac{k!}{(k-m-1)!}(y_{1}\cdots y_{m+1})^{k-m-1}\mathop{\prod }_{1\leqslant i<j\leqslant m+1}(y_{i}-y_{j})\not \equiv 0~(\text{mod}~p).\end{eqnarray}$$
We therefore conclude from [Reference Wooley13, Theorem 1] that
 $$\begin{eqnarray}\text{card}({\mathcal{D}}_{1}(\mathbf{n};0))\leqslant (k-m)(k-m+1)\cdots k\leqslant k!.\end{eqnarray}$$
$$\begin{eqnarray}\text{card}({\mathcal{D}}_{1}(\mathbf{n};0))\leqslant (k-m)(k-m+1)\cdots k\leqslant k!.\end{eqnarray}$$
In view of (3.3), the conclusion of the lemma therefore follows from (3.15) when
![]() $a=0$
. This completes our account of the proof of the lemma.◻
$a=0$
. This completes our account of the proof of the lemma.◻
4 The conditioning process
The mean value
 $K_{a,b}^{m,r}(X;\unicode[STIX]{x1D709},\unicode[STIX]{x1D702})$
differs only slightly from the special case
$K_{a,b}^{m,r}(X;\unicode[STIX]{x1D709},\unicode[STIX]{x1D702})$
differs only slightly from the special case
 $K_{a,b}^{k-1,k-1}(X;\unicode[STIX]{x1D709},\unicode[STIX]{x1D702})$
considered in [Reference Wooley19], and thus our treatment of the conditioning process may be swiftly executed.
$K_{a,b}^{k-1,k-1}(X;\unicode[STIX]{x1D709},\unicode[STIX]{x1D702})$
considered in [Reference Wooley19], and thus our treatment of the conditioning process may be swiftly executed.
Lemma 4.1. Let
![]() $a$
and
$a$
and
![]() $b$
be integers with
$b$
be integers with
 $b>a\geqslant 1$
. Then, whenever
$b>a\geqslant 1$
. Then, whenever
 $s\geqslant 2r-1$
, one has
$s\geqslant 2r-1$
, one has
 $$\begin{eqnarray}I_{a,b}^{r,r}(X)\ll K_{a,b}^{r,r}(X)+M^{2s/3}I_{a,b+1}^{r,r}(X).\end{eqnarray}$$
$$\begin{eqnarray}I_{a,b}^{r,r}(X)\ll K_{a,b}^{r,r}(X)+M^{2s/3}I_{a,b+1}^{r,r}(X).\end{eqnarray}$$
Proof. Our argument follows the proof of [Reference Wooley19, Lemma 4.1] with minor adjustments. Consider fixed integers
![]() $\unicode[STIX]{x1D709}$
and
$\unicode[STIX]{x1D709}$
and
![]() $\unicode[STIX]{x1D702}$
with
$\unicode[STIX]{x1D702}$
with
 $\unicode[STIX]{x1D702}\not \equiv \unicode[STIX]{x1D709}~(\text{mod}~p)$
. Let
$\unicode[STIX]{x1D702}\not \equiv \unicode[STIX]{x1D709}~(\text{mod}~p)$
. Let
![]() $T_{1}$
denote the number of integral solutions
$T_{1}$
denote the number of integral solutions
![]() $\mathbf{x}$
,
$\mathbf{x}$
,
![]() $\mathbf{y}$
,
$\mathbf{y}$
,
![]() $\mathbf{v}$
,
$\mathbf{v}$
,
![]() $\mathbf{w}$
of the system (2.13) counted by
$\mathbf{w}$
of the system (2.13) counted by
 $I_{a,b}^{r,r}(X;\unicode[STIX]{x1D709},\unicode[STIX]{x1D702})$
in which
$I_{a,b}^{r,r}(X;\unicode[STIX]{x1D709},\unicode[STIX]{x1D702})$
in which
 $v_{1},\ldots ,v_{s}$
together occupy at least
$v_{1},\ldots ,v_{s}$
together occupy at least
![]() $r$
distinct residue classes modulo
$r$
distinct residue classes modulo
![]() $p^{b+1}$
, and let
$p^{b+1}$
, and let
![]() $T_{2}$
denote the corresponding number of solutions in which these integers together occupy at most
$T_{2}$
denote the corresponding number of solutions in which these integers together occupy at most
![]() $r-1$
distinct residue classes modulo
$r-1$
distinct residue classes modulo
![]() $p^{b+1}$
. Then
$p^{b+1}$
. Then
 $$\begin{eqnarray}I_{a,b}^{r,r}(X;\unicode[STIX]{x1D709},\unicode[STIX]{x1D702})=T_{1}+T_{2}.\end{eqnarray}$$
$$\begin{eqnarray}I_{a,b}^{r,r}(X;\unicode[STIX]{x1D709},\unicode[STIX]{x1D702})=T_{1}+T_{2}.\end{eqnarray}$$
From (2.10) to (2.12), orthogonality and Schwarz’s inequality, one has
 $$\begin{eqnarray}\displaystyle T_{1} & {\leqslant} & \displaystyle \binom{s}{r}\oint |\mathop{\mathfrak{F}}_{a}^{r}(\unicode[STIX]{x1D736};\unicode[STIX]{x1D709})|^{2}\mathfrak{F}_{b}^{r}(\unicode[STIX]{x1D736};\unicode[STIX]{x1D702})\mathfrak{f}_{b}(\unicode[STIX]{x1D736};\unicode[STIX]{x1D702})^{s-r}\mathfrak{f}_{b}(-\unicode[STIX]{x1D736};\unicode[STIX]{x1D702})^{s}\,d\unicode[STIX]{x1D736}\nonumber\\ \displaystyle & \ll & \displaystyle (K_{a,b}^{r,r}(X;\unicode[STIX]{x1D709},\unicode[STIX]{x1D702}))^{1/2}(I_{a,b}^{r,r}(X;\unicode[STIX]{x1D709},\unicode[STIX]{x1D702}))^{1/2}.\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle T_{1} & {\leqslant} & \displaystyle \binom{s}{r}\oint |\mathop{\mathfrak{F}}_{a}^{r}(\unicode[STIX]{x1D736};\unicode[STIX]{x1D709})|^{2}\mathfrak{F}_{b}^{r}(\unicode[STIX]{x1D736};\unicode[STIX]{x1D702})\mathfrak{f}_{b}(\unicode[STIX]{x1D736};\unicode[STIX]{x1D702})^{s-r}\mathfrak{f}_{b}(-\unicode[STIX]{x1D736};\unicode[STIX]{x1D702})^{s}\,d\unicode[STIX]{x1D736}\nonumber\\ \displaystyle & \ll & \displaystyle (K_{a,b}^{r,r}(X;\unicode[STIX]{x1D709},\unicode[STIX]{x1D702}))^{1/2}(I_{a,b}^{r,r}(X;\unicode[STIX]{x1D709},\unicode[STIX]{x1D702}))^{1/2}.\end{eqnarray}$$
In order to treat
![]() $T_{2}$
, we observe first that the hypothesis
$T_{2}$
, we observe first that the hypothesis
 $s\geqslant 2r-1$
ensures that there is an integer
$s\geqslant 2r-1$
ensures that there is an integer
 $\unicode[STIX]{x1D701}\equiv \unicode[STIX]{x1D702}~(\text{mod}~p^{b})$
having the property that three at least of the variables
$\unicode[STIX]{x1D701}\equiv \unicode[STIX]{x1D702}~(\text{mod}~p^{b})$
having the property that three at least of the variables
 $v_{1},\ldots ,v_{s}$
are congruent to
$v_{1},\ldots ,v_{s}$
are congruent to
![]() $\unicode[STIX]{x1D701}$
modulo
$\unicode[STIX]{x1D701}$
modulo
![]() $p^{b+1}$
. Hence, recalling the definitions (2.10) and (2.11), one finds from orthogonality and Hölder’s inequality that
$p^{b+1}$
. Hence, recalling the definitions (2.10) and (2.11), one finds from orthogonality and Hölder’s inequality that
 $$\begin{eqnarray}\displaystyle T_{2} & {\leqslant} & \displaystyle \binom{s}{3}\mathop{\sum }_{\substack{ 1\leqslant \unicode[STIX]{x1D701}\leqslant p^{b+1} \\ \unicode[STIX]{x1D701}\equiv \unicode[STIX]{x1D702}~(\text{mod}~p^{b})}}\oint |\mathop{\mathfrak{F}}_{a}^{r}(\unicode[STIX]{x1D736};\unicode[STIX]{x1D709})|^{2}\mathfrak{f}_{b+1}(\unicode[STIX]{x1D736};\unicode[STIX]{x1D701})^{3}\mathfrak{f}_{b}(\unicode[STIX]{x1D736};\unicode[STIX]{x1D702})^{s-3}\mathfrak{f}_{b}(-\unicode[STIX]{x1D736};\unicode[STIX]{x1D702})^{s}\,d\unicode[STIX]{x1D736}\nonumber\\ \displaystyle & \ll & \displaystyle M\max _{\substack{ 1\leqslant \unicode[STIX]{x1D701}\leqslant p^{b+1} \\ \unicode[STIX]{x1D701}\equiv \unicode[STIX]{x1D702}~(\text{mod}~p^{b})}}(I_{a,b}^{r,r}(X;\unicode[STIX]{x1D709},\unicode[STIX]{x1D702}))^{1-3/(2s)}(I_{a,b+1}^{r,r}(X;\unicode[STIX]{x1D709},\unicode[STIX]{x1D701}))^{3/(2s)}.\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle T_{2} & {\leqslant} & \displaystyle \binom{s}{3}\mathop{\sum }_{\substack{ 1\leqslant \unicode[STIX]{x1D701}\leqslant p^{b+1} \\ \unicode[STIX]{x1D701}\equiv \unicode[STIX]{x1D702}~(\text{mod}~p^{b})}}\oint |\mathop{\mathfrak{F}}_{a}^{r}(\unicode[STIX]{x1D736};\unicode[STIX]{x1D709})|^{2}\mathfrak{f}_{b+1}(\unicode[STIX]{x1D736};\unicode[STIX]{x1D701})^{3}\mathfrak{f}_{b}(\unicode[STIX]{x1D736};\unicode[STIX]{x1D702})^{s-3}\mathfrak{f}_{b}(-\unicode[STIX]{x1D736};\unicode[STIX]{x1D702})^{s}\,d\unicode[STIX]{x1D736}\nonumber\\ \displaystyle & \ll & \displaystyle M\max _{\substack{ 1\leqslant \unicode[STIX]{x1D701}\leqslant p^{b+1} \\ \unicode[STIX]{x1D701}\equiv \unicode[STIX]{x1D702}~(\text{mod}~p^{b})}}(I_{a,b}^{r,r}(X;\unicode[STIX]{x1D709},\unicode[STIX]{x1D702}))^{1-3/(2s)}(I_{a,b+1}^{r,r}(X;\unicode[STIX]{x1D709},\unicode[STIX]{x1D701}))^{3/(2s)}.\end{eqnarray}$$
By substituting (4.2) and (4.3) into (4.1), and recalling (2.16) and (2.17), we therefore conclude that
 $$\begin{eqnarray}I_{a,b}^{r,r}(X)\ll (K_{a,b}^{r,r}(X))^{1/2}(I_{a,b}^{r,r}(X))^{1/2}+M(I_{a,b}^{r,r}(X))^{1-3/(2s)}(I_{a,b+1}^{r,r}(X))^{3/(2s)},\end{eqnarray}$$
$$\begin{eqnarray}I_{a,b}^{r,r}(X)\ll (K_{a,b}^{r,r}(X))^{1/2}(I_{a,b}^{r,r}(X))^{1/2}+M(I_{a,b}^{r,r}(X))^{1-3/(2s)}(I_{a,b+1}^{r,r}(X))^{3/(2s)},\end{eqnarray}$$
whence
 $$\begin{eqnarray}I_{a,b}^{r,r}(X)\ll K_{a,b}^{r,r}(X)+M^{2s/3}I_{a,b+1}^{r,r}(X).\end{eqnarray}$$
$$\begin{eqnarray}I_{a,b}^{r,r}(X)\ll K_{a,b}^{r,r}(X)+M^{2s/3}I_{a,b+1}^{r,r}(X).\end{eqnarray}$$
This completes the proof of the lemma. ◻
Repeated application of Lemma 4.1 combines with a trivial bound for the mean value
 $K_{a,b+H}^{r,r}(X)$
to deliver the basic conditioning lemma of this section.
$K_{a,b+H}^{r,r}(X)$
to deliver the basic conditioning lemma of this section.
Lemma 4.2. Let
![]() $a$
and
$a$
and
![]() $b$
be integers with
$b$
be integers with
 $1\leqslant a<b$
, and let
$1\leqslant a<b$
, and let
![]() $H$
be any integer with
$H$
be any integer with
![]() $H\geqslant 15$
. Suppose that
$H\geqslant 15$
. Suppose that
 $b+H\leqslant (2\unicode[STIX]{x1D703})^{-1}$
. Then there exists an integer
$b+H\leqslant (2\unicode[STIX]{x1D703})^{-1}$
. Then there exists an integer
![]() $h$
with
$h$
with
 $0\leqslant h<H$
having the property that
$0\leqslant h<H$
having the property that
 $$\begin{eqnarray}I_{a,b}^{r,r}(X)\ll (M^{h})^{2s/3}K_{a,b+h}^{r,r}(X)+(M^{H})^{-s/4}(X/M^{b})^{s}(X/M^{a})^{\unicode[STIX]{x1D706}-s}.\end{eqnarray}$$
$$\begin{eqnarray}I_{a,b}^{r,r}(X)\ll (M^{h})^{2s/3}K_{a,b+h}^{r,r}(X)+(M^{H})^{-s/4}(X/M^{b})^{s}(X/M^{a})^{\unicode[STIX]{x1D706}-s}.\end{eqnarray}$$
Proof. Repeated application of Lemma 4.1 yields the upper bound
 $$\begin{eqnarray}I_{a,b}^{r,r}(X)\ll \mathop{\sum }_{h=0}^{H-1}(M^{h})^{2s/3}K_{a,b+h}^{r,r}(X)+(M^{H})^{2s/3}I_{a,b+H}^{r,r}(X).\end{eqnarray}$$
$$\begin{eqnarray}I_{a,b}^{r,r}(X)\ll \mathop{\sum }_{h=0}^{H-1}(M^{h})^{2s/3}K_{a,b+h}^{r,r}(X)+(M^{H})^{2s/3}I_{a,b+H}^{r,r}(X).\end{eqnarray}$$
On considering the underlying Diophantine systems, it follows from Lemma 2.3 that for each
![]() $\unicode[STIX]{x1D709}$
and
$\unicode[STIX]{x1D709}$
and
![]() $\unicode[STIX]{x1D702}$
, one has
$\unicode[STIX]{x1D702}$
, one has
 $$\begin{eqnarray}\displaystyle I_{a,b+H}^{r,r}(X;\unicode[STIX]{x1D709},\unicode[STIX]{x1D702}) & {\leqslant} & \displaystyle \oint |\mathfrak{f}_{a}(\unicode[STIX]{x1D736};\unicode[STIX]{x1D709})^{2r}\mathfrak{f}_{b+H}(\unicode[STIX]{x1D736};\unicode[STIX]{x1D702})^{2s}|\,d\unicode[STIX]{x1D736}\nonumber\\ \displaystyle & \ll & \displaystyle (J_{s+r}(X/M^{a}))^{r/(s+r)}(J_{s+r}(X/M^{b+H}))^{s/(s+r)}.\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle I_{a,b+H}^{r,r}(X;\unicode[STIX]{x1D709},\unicode[STIX]{x1D702}) & {\leqslant} & \displaystyle \oint |\mathfrak{f}_{a}(\unicode[STIX]{x1D736};\unicode[STIX]{x1D709})^{2r}\mathfrak{f}_{b+H}(\unicode[STIX]{x1D736};\unicode[STIX]{x1D702})^{2s}|\,d\unicode[STIX]{x1D736}\nonumber\\ \displaystyle & \ll & \displaystyle (J_{s+r}(X/M^{a}))^{r/(s+r)}(J_{s+r}(X/M^{b+H}))^{s/(s+r)}.\nonumber\end{eqnarray}$$
Since
 $M^{b+H}=(X^{\unicode[STIX]{x1D703}})^{b+H}\leqslant X^{1/2}$
, we deduce from (2.16) and (2.24) that
$M^{b+H}=(X^{\unicode[STIX]{x1D703}})^{b+H}\leqslant X^{1/2}$
, we deduce from (2.16) and (2.24) that
 $$\begin{eqnarray}\displaystyle (M^{H})^{2s/3}I_{a,b+H}^{r,r}(X) & \ll & \displaystyle X^{\unicode[STIX]{x1D6FF}}((X/M^{a})^{r/(s+r)}(X/M^{b+H})^{s/(s+r)})^{\unicode[STIX]{x1D706}}(M^{H})^{2s/3}\nonumber\\ \displaystyle & = & \displaystyle X^{\unicode[STIX]{x1D6FF}}(X/M^{b})^{s}(X/M^{a})^{\unicode[STIX]{x1D706}-s}M^{\unicode[STIX]{x1D6FA}},\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle (M^{H})^{2s/3}I_{a,b+H}^{r,r}(X) & \ll & \displaystyle X^{\unicode[STIX]{x1D6FF}}((X/M^{a})^{r/(s+r)}(X/M^{b+H})^{s/(s+r)})^{\unicode[STIX]{x1D706}}(M^{H})^{2s/3}\nonumber\\ \displaystyle & = & \displaystyle X^{\unicode[STIX]{x1D6FF}}(X/M^{b})^{s}(X/M^{a})^{\unicode[STIX]{x1D706}-s}M^{\unicode[STIX]{x1D6FA}},\nonumber\end{eqnarray}$$
where
 $$\begin{eqnarray}\unicode[STIX]{x1D6FA}=\unicode[STIX]{x1D706}\biggl(a-\frac{ar}{s+r}-\frac{bs}{s+r}\biggr)+s(b-a)+Hs\biggl(\frac{2}{3}-\frac{\unicode[STIX]{x1D706}}{s+r}\biggr).\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D6FA}=\unicode[STIX]{x1D706}\biggl(a-\frac{ar}{s+r}-\frac{bs}{s+r}\biggr)+s(b-a)+Hs\biggl(\frac{2}{3}-\frac{\unicode[STIX]{x1D706}}{s+r}\biggr).\end{eqnarray}$$
Since
 $\unicode[STIX]{x1D706}\geqslant s+r$
, the lower bound
$\unicode[STIX]{x1D706}\geqslant s+r$
, the lower bound
![]() $b>a$
leads to the estimate
$b>a$
leads to the estimate
 $$\begin{eqnarray}\unicode[STIX]{x1D6FA}\leqslant -s(b-a)\frac{\unicode[STIX]{x1D706}}{s+r}+s(b-a)-\frac{1}{3}Hs\leqslant -\frac{1}{3}Hs.\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D6FA}\leqslant -s(b-a)\frac{\unicode[STIX]{x1D706}}{s+r}+s(b-a)-\frac{1}{3}Hs\leqslant -\frac{1}{3}Hs.\end{eqnarray}$$
This completes the proof of the lemma, since with
![]() $H\geqslant 15$
one has
$H\geqslant 15$
one has
 $$\begin{eqnarray}X^{\unicode[STIX]{x1D6FF}}M^{-Hs/3}\ll M^{-Hs/4}.\end{eqnarray}$$
$$\begin{eqnarray}X^{\unicode[STIX]{x1D6FF}}M^{-Hs/3}\ll M^{-Hs/4}.\end{eqnarray}$$
◻
5 The precongruencing step
The alteration of the definition of
 $K_{a,b}^{m,r}(X)$
relative to our earlier treatments does not prevent previous precongruencing arguments from applying, mutatis mutandis. However, we seek to ensure that our initial value of
$K_{a,b}^{m,r}(X)$
relative to our earlier treatments does not prevent previous precongruencing arguments from applying, mutatis mutandis. However, we seek to ensure that our initial value of
![]() $b$
is very large, so that subsequent iterations work efficiently. For this reason, the argument of the proof of [Reference Ford and Wooley4, Lemma 6.1] must be modified in several ways that demand a fairly complete account of the proof. We recall the definition (2.8) of
$b$
is very large, so that subsequent iterations work efficiently. For this reason, the argument of the proof of [Reference Ford and Wooley4, Lemma 6.1] must be modified in several ways that demand a fairly complete account of the proof. We recall the definition (2.8) of
![]() $B$
.
$B$
.
Lemma 5.1. There exist a prime number
![]() $p$
, with
$p$
, with
 $M<p\leqslant 2M$
, and an integer
$M<p\leqslant 2M$
, and an integer
![]() $h$
, with
$h$
, with
 $0\leqslant h\leqslant 4B$
, for which one has
$0\leqslant h\leqslant 4B$
, for which one has
 $$\begin{eqnarray}J_{s+r}(X)\ll M^{2sB+2sh/3}K_{0,B+h}^{r,r}(X).\end{eqnarray}$$
$$\begin{eqnarray}J_{s+r}(X)\ll M^{2sB+2sh/3}K_{0,B+h}^{r,r}(X).\end{eqnarray}$$
Proof. The mean value
![]() $J_{s+r}(X)$
counts the number of integral solutions of the system
$J_{s+r}(X)$
counts the number of integral solutions of the system
 $$\begin{eqnarray}\mathop{\sum }_{i=1}^{s+r}(x_{i}^{j}-y_{i}^{j})=0\quad (1\leqslant j\leqslant k),\end{eqnarray}$$
$$\begin{eqnarray}\mathop{\sum }_{i=1}^{s+r}(x_{i}^{j}-y_{i}^{j})=0\quad (1\leqslant j\leqslant k),\end{eqnarray}$$
with
 $1\leqslant \mathbf{x},\mathbf{y}\leqslant X$
. Let
$1\leqslant \mathbf{x},\mathbf{y}\leqslant X$
. Let
![]() ${\mathcal{P}}$
denote a set of
${\mathcal{P}}$
denote a set of
 $\lceil (s+r)^{2}\unicode[STIX]{x1D703}^{-1}\rceil$
prime numbers lying in
$\lceil (s+r)^{2}\unicode[STIX]{x1D703}^{-1}\rceil$
prime numbers lying in
 $(M,2M]$
. That such a set exists is a consequence of the prime number theorem. The argument of the proof of [Reference Ford and Wooley4, Lemma 6.1] leading to equation (6.2) of that paper shows that for some
$(M,2M]$
. That such a set exists is a consequence of the prime number theorem. The argument of the proof of [Reference Ford and Wooley4, Lemma 6.1] leading to equation (6.2) of that paper shows that for some
![]() $p\in {\mathcal{P}}$
, one has
$p\in {\mathcal{P}}$
, one has
 $J_{s+r}(X)\ll T(p)$
, where
$J_{s+r}(X)\ll T(p)$
, where
![]() $T(p)$
denotes the number of solutions of the system (5.1) counted by
$T(p)$
denotes the number of solutions of the system (5.1) counted by
![]() $J_{s+r}(X)$
in which
$J_{s+r}(X)$
in which
 $x_{1},\ldots ,x_{s+r}$
are distinct modulo
$x_{1},\ldots ,x_{s+r}$
are distinct modulo
![]() $p$
, and likewise
$p$
, and likewise
 $y_{1},\ldots ,y_{s+r}$
are distinct modulo
$y_{1},\ldots ,y_{s+r}$
are distinct modulo
![]() $p$
.
$p$
.
We now examine the residue classes modulo
![]() $p^{B}$
of a given solution
$p^{B}$
of a given solution
![]() $\mathbf{x},\mathbf{y}$
counted by
$\mathbf{x},\mathbf{y}$
counted by
![]() $T(p)$
. Let
$T(p)$
. Let
![]() $\unicode[STIX]{x1D6C8}$
and
$\unicode[STIX]{x1D6C8}$
and
![]() $\boldsymbol{\unicode[STIX]{x1D701}}$
be
$\boldsymbol{\unicode[STIX]{x1D701}}$
be
![]() $s$
-tuples with
$s$
-tuples with
 $1\leqslant \unicode[STIX]{x1D6C8},\boldsymbol{\unicode[STIX]{x1D701}}\leqslant p^{B}$
satisfying the condition that for
$1\leqslant \unicode[STIX]{x1D6C8},\boldsymbol{\unicode[STIX]{x1D701}}\leqslant p^{B}$
satisfying the condition that for
 $1\leqslant i\leqslant s$
, one has
$1\leqslant i\leqslant s$
, one has
 $x_{i}\equiv \unicode[STIX]{x1D702}_{i}~(\text{mod}~p^{B})$
and
$x_{i}\equiv \unicode[STIX]{x1D702}_{i}~(\text{mod}~p^{B})$
and
 $y_{i}\equiv \unicode[STIX]{x1D701}_{i}~(\text{mod}~p^{B})$
. Recall the notation introduced prior to (2.18). Then, since
$y_{i}\equiv \unicode[STIX]{x1D701}_{i}~(\text{mod}~p^{B})$
. Recall the notation introduced prior to (2.18). Then, since
 $x_{1},\ldots ,x_{s+r}$
are distinct modulo
$x_{1},\ldots ,x_{s+r}$
are distinct modulo
![]() $p$
, it follows that
$p$
, it follows that
 $(x_{s+1},\ldots ,x_{s+r})\in \unicode[STIX]{x1D6EF}^{r}(\unicode[STIX]{x1D6C8})$
, and likewise one finds that
$(x_{s+1},\ldots ,x_{s+r})\in \unicode[STIX]{x1D6EF}^{r}(\unicode[STIX]{x1D6C8})$
, and likewise one finds that
 $(y_{s+1},\ldots ,y_{s+r})\in \unicode[STIX]{x1D6EF}^{r}(\boldsymbol{\unicode[STIX]{x1D701}})$
. Then, on considering the underlying Diophantine systems, one finds that
$(y_{s+1},\ldots ,y_{s+r})\in \unicode[STIX]{x1D6EF}^{r}(\boldsymbol{\unicode[STIX]{x1D701}})$
. Then, on considering the underlying Diophantine systems, one finds that
 $$\begin{eqnarray}T(p)\leqslant \mathop{\sum }_{1\leqslant \unicode[STIX]{x1D6C8},\boldsymbol{\unicode[STIX]{x1D701}}\leqslant p^{B}}\oint \biggl(\mathop{\prod }_{i=1}^{s}\mathfrak{f}_{B}(\unicode[STIX]{x1D736};\unicode[STIX]{x1D702}_{i})\mathfrak{f}_{B}(-\unicode[STIX]{x1D736};\unicode[STIX]{x1D701}_{i})\biggr)\mathfrak{F}^{r}(\unicode[STIX]{x1D736};\unicode[STIX]{x1D6C8})\mathfrak{F}^{r}(-\unicode[STIX]{x1D736};\boldsymbol{\unicode[STIX]{x1D701}})\,d\unicode[STIX]{x1D736}.\end{eqnarray}$$
$$\begin{eqnarray}T(p)\leqslant \mathop{\sum }_{1\leqslant \unicode[STIX]{x1D6C8},\boldsymbol{\unicode[STIX]{x1D701}}\leqslant p^{B}}\oint \biggl(\mathop{\prod }_{i=1}^{s}\mathfrak{f}_{B}(\unicode[STIX]{x1D736};\unicode[STIX]{x1D702}_{i})\mathfrak{f}_{B}(-\unicode[STIX]{x1D736};\unicode[STIX]{x1D701}_{i})\biggr)\mathfrak{F}^{r}(\unicode[STIX]{x1D736};\unicode[STIX]{x1D6C8})\mathfrak{F}^{r}(-\unicode[STIX]{x1D736};\boldsymbol{\unicode[STIX]{x1D701}})\,d\unicode[STIX]{x1D736}.\end{eqnarray}$$
Write
 $$\begin{eqnarray}{\mathcal{J}}(\unicode[STIX]{x1D73D},\unicode[STIX]{x1D713})=\oint |\mathfrak{F}^{r}(\unicode[STIX]{x1D736};\unicode[STIX]{x1D73D})^{2}\mathfrak{f}_{B}(\unicode[STIX]{x1D736};\unicode[STIX]{x1D713})^{2s}|\,d\unicode[STIX]{x1D736}.\end{eqnarray}$$
$$\begin{eqnarray}{\mathcal{J}}(\unicode[STIX]{x1D73D},\unicode[STIX]{x1D713})=\oint |\mathfrak{F}^{r}(\unicode[STIX]{x1D736};\unicode[STIX]{x1D73D})^{2}\mathfrak{f}_{B}(\unicode[STIX]{x1D736};\unicode[STIX]{x1D713})^{2s}|\,d\unicode[STIX]{x1D736}.\end{eqnarray}$$
Then, by applying Hölder’s inequality, and again considering the underlying Diophantine systems, we discern that
 $$\begin{eqnarray}\displaystyle T(p) & {\leqslant} & \displaystyle \mathop{\sum }_{1\leqslant \unicode[STIX]{x1D6C8},\boldsymbol{\unicode[STIX]{x1D701}}\leqslant p^{B}}\mathop{\prod }_{i=1}^{s}({\mathcal{J}}(\unicode[STIX]{x1D6C8},\unicode[STIX]{x1D702}_{i}){\mathcal{J}}(\boldsymbol{\unicode[STIX]{x1D701}},\unicode[STIX]{x1D701}_{i}))^{1/(2s)}\nonumber\\ \displaystyle & {\leqslant} & \displaystyle \mathop{\sum }_{1\leqslant \unicode[STIX]{x1D6C8},\boldsymbol{\unicode[STIX]{x1D701}}\leqslant p^{B}}\mathop{\prod }_{i=1}^{s}({\mathcal{J}}(\unicode[STIX]{x1D702}_{i},\unicode[STIX]{x1D702}_{i}){\mathcal{J}}(\unicode[STIX]{x1D701}_{i},\unicode[STIX]{x1D701}_{i}))^{1/(2s)}.\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle T(p) & {\leqslant} & \displaystyle \mathop{\sum }_{1\leqslant \unicode[STIX]{x1D6C8},\boldsymbol{\unicode[STIX]{x1D701}}\leqslant p^{B}}\mathop{\prod }_{i=1}^{s}({\mathcal{J}}(\unicode[STIX]{x1D6C8},\unicode[STIX]{x1D702}_{i}){\mathcal{J}}(\boldsymbol{\unicode[STIX]{x1D701}},\unicode[STIX]{x1D701}_{i}))^{1/(2s)}\nonumber\\ \displaystyle & {\leqslant} & \displaystyle \mathop{\sum }_{1\leqslant \unicode[STIX]{x1D6C8},\boldsymbol{\unicode[STIX]{x1D701}}\leqslant p^{B}}\mathop{\prod }_{i=1}^{s}({\mathcal{J}}(\unicode[STIX]{x1D702}_{i},\unicode[STIX]{x1D702}_{i}){\mathcal{J}}(\unicode[STIX]{x1D701}_{i},\unicode[STIX]{x1D701}_{i}))^{1/(2s)}.\nonumber\end{eqnarray}$$
Hence, on recalling the definition (2.18), we obtain the upper bound
 $$\begin{eqnarray}\displaystyle T(p) & {\leqslant} & \displaystyle p^{2sB}\max _{1\leqslant \unicode[STIX]{x1D702}\leqslant p^{B}}\oint |\mathfrak{F}^{r}(\unicode[STIX]{x1D736};\unicode[STIX]{x1D702})^{2}\mathfrak{f}_{B}(\unicode[STIX]{x1D736};\unicode[STIX]{x1D702})^{2s}|\,d\unicode[STIX]{x1D736}\nonumber\\ \displaystyle & = & \displaystyle p^{2sB}\max _{1\leqslant \unicode[STIX]{x1D702}\leqslant p^{B}}\widetilde{I}_{B}^{r,r}(X;\unicode[STIX]{x1D702}).\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle T(p) & {\leqslant} & \displaystyle p^{2sB}\max _{1\leqslant \unicode[STIX]{x1D702}\leqslant p^{B}}\oint |\mathfrak{F}^{r}(\unicode[STIX]{x1D736};\unicode[STIX]{x1D702})^{2}\mathfrak{f}_{B}(\unicode[STIX]{x1D736};\unicode[STIX]{x1D702})^{2s}|\,d\unicode[STIX]{x1D736}\nonumber\\ \displaystyle & = & \displaystyle p^{2sB}\max _{1\leqslant \unicode[STIX]{x1D702}\leqslant p^{B}}\widetilde{I}_{B}^{r,r}(X;\unicode[STIX]{x1D702}).\end{eqnarray}$$
By modifying the argument of the proof of [Reference Ford and Wooley4, Lemma 6.1] leading from equation (6.3) to equation (6.6) of that paper, along the lines easily surmised from our proof of Lemma 4.1 above, one finds that
 $$\begin{eqnarray}\widetilde{I}_{c}^{r,r}(X;\unicode[STIX]{x1D702})\ll \widetilde{K}_{c}^{r,r}(X;\unicode[STIX]{x1D702})+M^{2s/3}\max _{1\leqslant \unicode[STIX]{x1D701}\leqslant p^{c+1}}\widetilde{I}_{c+1}^{r,r}(X;\unicode[STIX]{x1D701}).\end{eqnarray}$$
$$\begin{eqnarray}\widetilde{I}_{c}^{r,r}(X;\unicode[STIX]{x1D702})\ll \widetilde{K}_{c}^{r,r}(X;\unicode[STIX]{x1D702})+M^{2s/3}\max _{1\leqslant \unicode[STIX]{x1D701}\leqslant p^{c+1}}\widetilde{I}_{c+1}^{r,r}(X;\unicode[STIX]{x1D701}).\end{eqnarray}$$
Iterating (5.3) in order to bound
 $\widetilde{I}_{B}^{r,r}(X;\unicode[STIX]{x1D702})$
, just as in the argument concluding the proof of [Reference Ford and Wooley4, Lemma 6.1] (and see also (4.4) above), we discern from (5.2) that
$\widetilde{I}_{B}^{r,r}(X;\unicode[STIX]{x1D702})$
, just as in the argument concluding the proof of [Reference Ford and Wooley4, Lemma 6.1] (and see also (4.4) above), we discern from (5.2) that
 $$\begin{eqnarray}\displaystyle J_{s+r}(X) & \ll & \displaystyle M^{2sB}\max _{0\leqslant h\leqslant 4B}(M^{h})^{2s/3}K_{0,B+h}^{r,r}(X)\nonumber\\ \displaystyle & & \displaystyle +\,M^{2sB+8sB/3}\max _{1\leqslant \unicode[STIX]{x1D701}\leqslant p^{5B+1}}\widetilde{I}_{5B+1}^{r,r}(X;\unicode[STIX]{x1D701}).\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle J_{s+r}(X) & \ll & \displaystyle M^{2sB}\max _{0\leqslant h\leqslant 4B}(M^{h})^{2s/3}K_{0,B+h}^{r,r}(X)\nonumber\\ \displaystyle & & \displaystyle +\,M^{2sB+8sB/3}\max _{1\leqslant \unicode[STIX]{x1D701}\leqslant p^{5B+1}}\widetilde{I}_{5B+1}^{r,r}(X;\unicode[STIX]{x1D701}).\end{eqnarray}$$
By considering the underlying Diophantine systems, we deduce from Lemma 2.3 that
 $$\begin{eqnarray}\widetilde{I}_{5B+1}^{r,r}(X;\unicode[STIX]{x1D701})\ll (J_{s+r}(X))^{r/(s+r)}(J_{s+r}(X/M^{5B+1}))^{s/(s+r)}.\end{eqnarray}$$
$$\begin{eqnarray}\widetilde{I}_{5B+1}^{r,r}(X;\unicode[STIX]{x1D701})\ll (J_{s+r}(X))^{r/(s+r)}(J_{s+r}(X/M^{5B+1}))^{s/(s+r)}.\end{eqnarray}$$
In this way, we find from (5.4) either that
 $$\begin{eqnarray}J_{s+r}(X)\ll M^{2sB+2sh/3}K_{0,B+h}^{r,r}(X)\end{eqnarray}$$
$$\begin{eqnarray}J_{s+r}(X)\ll M^{2sB+2sh/3}K_{0,B+h}^{r,r}(X)\end{eqnarray}$$
for some index
![]() $h$
with
$h$
with
 $0\leqslant h\leqslant 4B$
, so that the conclusion of the lemma holds, or else that
$0\leqslant h\leqslant 4B$
, so that the conclusion of the lemma holds, or else that
 $$\begin{eqnarray}J_{s+r}(X)\ll M^{14sB/3}(J_{s+r}(X))^{r/(s+r)}(J_{s+r}(X/M^{5B+1}))^{s/(s+r)}.\end{eqnarray}$$
$$\begin{eqnarray}J_{s+r}(X)\ll M^{14sB/3}(J_{s+r}(X))^{r/(s+r)}(J_{s+r}(X/M^{5B+1}))^{s/(s+r)}.\end{eqnarray}$$
In the latter case, since
 $\unicode[STIX]{x1D706}\geqslant s+r$
, we obtain the upper bound
$\unicode[STIX]{x1D706}\geqslant s+r$
, we obtain the upper bound
 $$\begin{eqnarray}\displaystyle J_{s+r}(X) & \ll & \displaystyle M^{14(s+r)B/3}J_{s+r}(X/M^{5B+1})\nonumber\\ \displaystyle & \ll & \displaystyle M^{14(s+r)B/3}(X/M^{5B+1})^{\unicode[STIX]{x1D706}+\unicode[STIX]{x1D6FF}}\nonumber\\ \displaystyle & \ll & \displaystyle X^{\unicode[STIX]{x1D706}+\unicode[STIX]{x1D6FF}}M^{-(s+r)B/3}.\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle J_{s+r}(X) & \ll & \displaystyle M^{14(s+r)B/3}J_{s+r}(X/M^{5B+1})\nonumber\\ \displaystyle & \ll & \displaystyle M^{14(s+r)B/3}(X/M^{5B+1})^{\unicode[STIX]{x1D706}+\unicode[STIX]{x1D6FF}}\nonumber\\ \displaystyle & \ll & \displaystyle X^{\unicode[STIX]{x1D706}+\unicode[STIX]{x1D6FF}}M^{-(s+r)B/3}.\nonumber\end{eqnarray}$$
Invoking the definition (2.8) of
![]() $\unicode[STIX]{x1D6FF}$
, we find that
$\unicode[STIX]{x1D6FF}$
, we find that
 $J_{s+r}(X)\ll X^{\unicode[STIX]{x1D706}-2\unicode[STIX]{x1D6FF}}$
, contradicting the lower bound (2.24) if
$J_{s+r}(X)\ll X^{\unicode[STIX]{x1D706}-2\unicode[STIX]{x1D6FF}}$
, contradicting the lower bound (2.24) if
![]() $X=X_{l}$
is large enough. We are therefore forced to accept the former upper bound (5.5), and hence the proof of the lemma is completed by reference to (2.20).◻
$X=X_{l}$
is large enough. We are therefore forced to accept the former upper bound (5.5), and hence the proof of the lemma is completed by reference to (2.20).◻
At this point, we fix the prime number
![]() $p$
, once and for all, in accordance with Lemma 5.1.
$p$
, once and for all, in accordance with Lemma 5.1.
6 The efficient congruencing step
Our strategy for executing the efficient congruencing process is based on that in our recent work [Reference Wooley19, §6], though in present circumstances only one phase is required, relating
 $K_{a,b}^{m+1,r}(X)$
to
$K_{a,b}^{m+1,r}(X)$
to
 $K_{a,b}^{m,r}(X)$
and
$K_{a,b}^{m,r}(X)$
and
![]() $I_{b,b^{\prime }}^{r,r}(X)$
, for a suitable value of
$I_{b,b^{\prime }}^{r,r}(X)$
, for a suitable value of
![]() $b^{\prime }$
. We begin our discussion of the efficient congruencing process with some additional notation. We define the generating function
$b^{\prime }$
. We begin our discussion of the efficient congruencing process with some additional notation. We define the generating function
 $$\begin{eqnarray}\mathfrak{H}_{c,d}^{m}(\unicode[STIX]{x1D736};\unicode[STIX]{x1D709})=\mathop{\sum }_{\unicode[STIX]{x1D743}\in \unicode[STIX]{x1D6EF}_{c}^{m}(\unicode[STIX]{x1D709})}\mathop{\sum }_{\substack{ 1\leqslant \boldsymbol{\unicode[STIX]{x1D701}}\leqslant p^{d} \\ \boldsymbol{\unicode[STIX]{x1D701}}\equiv \unicode[STIX]{x1D743}~(\text{mod}~p^{c+1})}}\mathop{\prod }_{i=1}^{m}|\mathfrak{f}_{d}(\unicode[STIX]{x1D736};\unicode[STIX]{x1D701}_{i})|^{2},\end{eqnarray}$$
$$\begin{eqnarray}\mathfrak{H}_{c,d}^{m}(\unicode[STIX]{x1D736};\unicode[STIX]{x1D709})=\mathop{\sum }_{\unicode[STIX]{x1D743}\in \unicode[STIX]{x1D6EF}_{c}^{m}(\unicode[STIX]{x1D709})}\mathop{\sum }_{\substack{ 1\leqslant \boldsymbol{\unicode[STIX]{x1D701}}\leqslant p^{d} \\ \boldsymbol{\unicode[STIX]{x1D701}}\equiv \unicode[STIX]{x1D743}~(\text{mod}~p^{c+1})}}\mathop{\prod }_{i=1}^{m}|\mathfrak{f}_{d}(\unicode[STIX]{x1D736};\unicode[STIX]{x1D701}_{i})|^{2},\end{eqnarray}$$
in which we adopt the natural convention that
 $\mathfrak{H}_{c,d}^{0}(\unicode[STIX]{x1D736};\unicode[STIX]{x1D709})=1$
. It is useful for future reference to record the consequence of Hölder’s inequality given in [Reference Wooley19, equation (6.2)], namely that whenever
$\mathfrak{H}_{c,d}^{0}(\unicode[STIX]{x1D736};\unicode[STIX]{x1D709})=1$
. It is useful for future reference to record the consequence of Hölder’s inequality given in [Reference Wooley19, equation (6.2)], namely that whenever
![]() $\unicode[STIX]{x1D714}$
is a real number with
$\unicode[STIX]{x1D714}$
is a real number with
![]() $m\unicode[STIX]{x1D714}\geqslant 1$
, then
$m\unicode[STIX]{x1D714}\geqslant 1$
, then
 $$\begin{eqnarray}\mathfrak{H}_{c,d}^{m}(\unicode[STIX]{x1D736};\unicode[STIX]{x1D709})^{\unicode[STIX]{x1D714}}\leqslant (p^{d-c})^{m\unicode[STIX]{x1D714}-1}\mathop{\sum }_{\substack{ 1\leqslant \unicode[STIX]{x1D701}\leqslant p^{d} \\ \unicode[STIX]{x1D701}\equiv \unicode[STIX]{x1D709}~(\text{mod}~p^{c})}}|\mathfrak{f}_{d}(\unicode[STIX]{x1D736};\unicode[STIX]{x1D701})|^{2m\unicode[STIX]{x1D714}}.\end{eqnarray}$$
$$\begin{eqnarray}\mathfrak{H}_{c,d}^{m}(\unicode[STIX]{x1D736};\unicode[STIX]{x1D709})^{\unicode[STIX]{x1D714}}\leqslant (p^{d-c})^{m\unicode[STIX]{x1D714}-1}\mathop{\sum }_{\substack{ 1\leqslant \unicode[STIX]{x1D701}\leqslant p^{d} \\ \unicode[STIX]{x1D701}\equiv \unicode[STIX]{x1D709}~(\text{mod}~p^{c})}}|\mathfrak{f}_{d}(\unicode[STIX]{x1D736};\unicode[STIX]{x1D701})|^{2m\unicode[STIX]{x1D714}}.\end{eqnarray}$$
Lemma 6.1. Let
![]() $m$
be an integer with
$m$
be an integer with
 $0\leqslant m\leqslant r-1$
. Suppose that
$0\leqslant m\leqslant r-1$
. Suppose that
![]() $a$
and
$a$
and
![]() $b$
are integers with
$b$
are integers with
 $0\leqslant a<b\leqslant \unicode[STIX]{x1D703}^{-1}$
and
$0\leqslant a<b\leqslant \unicode[STIX]{x1D703}^{-1}$
and
 $(k-m)b\geqslant (m+1)a$
, and suppose further that
$(k-m)b\geqslant (m+1)a$
, and suppose further that
 $a\leqslant b/\sqrt{k}$
. Then, whenever
$a\leqslant b/\sqrt{k}$
. Then, whenever
![]() $b^{\prime }$
is an integer with
$b^{\prime }$
is an integer with
 $a\leqslant b^{\prime }\leqslant (k-m)b-ma$
, one has
$a\leqslant b^{\prime }\leqslant (k-m)b-ma$
, one has
 $$\begin{eqnarray}K_{a,b}^{m+1,r}(X)\ll ((M^{b^{\prime }-a})^{s}I_{b,b^{\prime }}^{r,r}(X))^{1/(s-m)}(K_{a,b}^{m,r}(X))^{(s-m-1)/(s-m)}.\end{eqnarray}$$
$$\begin{eqnarray}K_{a,b}^{m+1,r}(X)\ll ((M^{b^{\prime }-a})^{s}I_{b,b^{\prime }}^{r,r}(X))^{1/(s-m)}(K_{a,b}^{m,r}(X))^{(s-m-1)/(s-m)}.\end{eqnarray}$$
Proof. We first consider the situation in which
![]() $a\geqslant 1$
. The argument associated with the case
$a\geqslant 1$
. The argument associated with the case
![]() $a=0$
is very similar, and so we are able to appeal later to a highly abbreviated argument for this case in order to complete the proof of the lemma. Consider fixed integers
$a=0$
is very similar, and so we are able to appeal later to a highly abbreviated argument for this case in order to complete the proof of the lemma. Consider fixed integers
![]() $\unicode[STIX]{x1D709}$
and
$\unicode[STIX]{x1D709}$
and
![]() $\unicode[STIX]{x1D702}$
with
$\unicode[STIX]{x1D702}$
with
 $$\begin{eqnarray}1\leqslant \unicode[STIX]{x1D709}\leqslant p^{a},\quad 1\leqslant \unicode[STIX]{x1D702}\leqslant p^{b}\quad \text{and}\quad \unicode[STIX]{x1D702}\not \equiv \unicode[STIX]{x1D709}~(\text{mod}~p).\end{eqnarray}$$
$$\begin{eqnarray}1\leqslant \unicode[STIX]{x1D709}\leqslant p^{a},\quad 1\leqslant \unicode[STIX]{x1D702}\leqslant p^{b}\quad \text{and}\quad \unicode[STIX]{x1D702}\not \equiv \unicode[STIX]{x1D709}~(\text{mod}~p).\end{eqnarray}$$
The quantity
 $K_{a,b}^{m+1,r}(X;\unicode[STIX]{x1D709},\unicode[STIX]{x1D702})$
counts the number of integral solutions of the system (2.14) with
$K_{a,b}^{m+1,r}(X;\unicode[STIX]{x1D709},\unicode[STIX]{x1D702})$
counts the number of integral solutions of the system (2.14) with
![]() $m$
replaced by
$m$
replaced by
![]() $m+1$
, subject to the attendant conditions on
$m+1$
, subject to the attendant conditions on
![]() $\mathbf{x}$
,
$\mathbf{x}$
,
![]() $\mathbf{y}$
,
$\mathbf{y}$
,
![]() $\mathbf{u}$
,
$\mathbf{u}$
,
![]() $\mathbf{v}$
,
$\mathbf{v}$
,
![]() $\mathbf{w}$
,
$\mathbf{w}$
,
![]() $\mathbf{z}$
. Given such a solution of the system (2.14), the discussion leading to (2.15) shows that
$\mathbf{z}$
. Given such a solution of the system (2.14), the discussion leading to (2.15) shows that
 $$\begin{eqnarray}\mathop{\sum }_{i=1}^{m+1}(x_{i}-\unicode[STIX]{x1D702})^{j}\equiv \mathop{\sum }_{i=1}^{m+1}(y_{i}-\unicode[STIX]{x1D702})^{j}~(\text{mod}~p^{jb})\quad (1\leqslant j\leqslant k).\end{eqnarray}$$
$$\begin{eqnarray}\mathop{\sum }_{i=1}^{m+1}(x_{i}-\unicode[STIX]{x1D702})^{j}\equiv \mathop{\sum }_{i=1}^{m+1}(y_{i}-\unicode[STIX]{x1D702})^{j}~(\text{mod}~p^{jb})\quad (1\leqslant j\leqslant k).\end{eqnarray}$$
In the notation introduced in §3, it follows that for some
![]() $k$
-tuple of integers
$k$
-tuple of integers
![]() $\mathbf{m}$
, both
$\mathbf{m}$
, both
 $[\mathbf{x}~(\text{mod}~p^{kb})]$
and
$[\mathbf{x}~(\text{mod}~p^{kb})]$
and
 $[\mathbf{y}~(\text{mod}~p^{kb})]$
lie in
$[\mathbf{y}~(\text{mod}~p^{kb})]$
lie in
 ${\mathcal{B}}_{a,b}^{m+1}(\mathbf{m};\unicode[STIX]{x1D709},\unicode[STIX]{x1D702})$
. Write
${\mathcal{B}}_{a,b}^{m+1}(\mathbf{m};\unicode[STIX]{x1D709},\unicode[STIX]{x1D702})$
. Write
 $$\begin{eqnarray}\mathfrak{G}_{a,b}(\unicode[STIX]{x1D736};\mathbf{m})=\mathop{\sum }_{\unicode[STIX]{x1D73D}\in {\mathcal{B}}_{a,b}^{m+1}(\mathbf{m};\unicode[STIX]{x1D709},\unicode[STIX]{x1D702})}\mathop{\prod }_{i=1}^{m+1}\mathfrak{f}_{kb}(\unicode[STIX]{x1D736};\unicode[STIX]{x1D703}_{i}).\end{eqnarray}$$
$$\begin{eqnarray}\mathfrak{G}_{a,b}(\unicode[STIX]{x1D736};\mathbf{m})=\mathop{\sum }_{\unicode[STIX]{x1D73D}\in {\mathcal{B}}_{a,b}^{m+1}(\mathbf{m};\unicode[STIX]{x1D709},\unicode[STIX]{x1D702})}\mathop{\prod }_{i=1}^{m+1}\mathfrak{f}_{kb}(\unicode[STIX]{x1D736};\unicode[STIX]{x1D703}_{i}).\end{eqnarray}$$
Then, on considering the underlying Diophantine systems, we see from (2.12) and (6.4) that
 $$\begin{eqnarray}K_{a,b}^{m+1,r}(X;\unicode[STIX]{x1D709},\unicode[STIX]{x1D702})=\mathop{\sum }_{m_{1}=1}^{p^{b}}\cdots \mathop{\sum }_{m_{k}=1}^{p^{kb}}\oint |\mathfrak{G}_{a,b}(\unicode[STIX]{x1D736};\mathbf{m})^{2}\mathfrak{F}_{m}^{\ast }(\unicode[STIX]{x1D736})^{2}|\,d\unicode[STIX]{x1D736},\end{eqnarray}$$
$$\begin{eqnarray}K_{a,b}^{m+1,r}(X;\unicode[STIX]{x1D709},\unicode[STIX]{x1D702})=\mathop{\sum }_{m_{1}=1}^{p^{b}}\cdots \mathop{\sum }_{m_{k}=1}^{p^{kb}}\oint |\mathfrak{G}_{a,b}(\unicode[STIX]{x1D736};\mathbf{m})^{2}\mathfrak{F}_{m}^{\ast }(\unicode[STIX]{x1D736})^{2}|\,d\unicode[STIX]{x1D736},\end{eqnarray}$$
where we write
 $$\begin{eqnarray}\mathfrak{F}_{m}^{\ast }(\unicode[STIX]{x1D736})=\mathfrak{F}_{b}^{r}(\unicode[STIX]{x1D736};\unicode[STIX]{x1D702})\mathfrak{f}_{b}(\unicode[STIX]{x1D736};\unicode[STIX]{x1D702})^{s-m-1}.\end{eqnarray}$$
$$\begin{eqnarray}\mathfrak{F}_{m}^{\ast }(\unicode[STIX]{x1D736})=\mathfrak{F}_{b}^{r}(\unicode[STIX]{x1D736};\unicode[STIX]{x1D702})\mathfrak{f}_{b}(\unicode[STIX]{x1D736};\unicode[STIX]{x1D702})^{s-m-1}.\end{eqnarray}$$
We now partition the vectors in each set
 ${\mathcal{B}}_{a,b}^{m+1}(\mathbf{m};\unicode[STIX]{x1D709},\unicode[STIX]{x1D702})$
into equivalence classes modulo
${\mathcal{B}}_{a,b}^{m+1}(\mathbf{m};\unicode[STIX]{x1D709},\unicode[STIX]{x1D702})$
into equivalence classes modulo
![]() $p^{b^{\prime }}$
as in §3. Write
$p^{b^{\prime }}$
as in §3. Write
 ${\mathcal{C}}(\mathbf{m})={\mathcal{C}}_{a,b}^{m+1,b^{\prime }/b}(\mathbf{m};\unicode[STIX]{x1D709},\unicode[STIX]{x1D702})$
. An application of Cauchy’s inequality leads via (3.2) and Lemma 3.1 to the bound
${\mathcal{C}}(\mathbf{m})={\mathcal{C}}_{a,b}^{m+1,b^{\prime }/b}(\mathbf{m};\unicode[STIX]{x1D709},\unicode[STIX]{x1D702})$
. An application of Cauchy’s inequality leads via (3.2) and Lemma 3.1 to the bound
 $$\begin{eqnarray}\displaystyle |\mathfrak{G}_{a,b}(\unicode[STIX]{x1D736};\mathbf{m})|^{2} & = & \displaystyle \biggl|\mathop{\sum }_{\mathfrak{C}\in {\mathcal{C}}(\mathbf{m})}\mathop{\sum }_{\unicode[STIX]{x1D73D}\in \mathfrak{C}}\mathop{\prod }_{i=1}^{m+1}\mathfrak{f}_{kb}(\unicode[STIX]{x1D736};\unicode[STIX]{x1D703}_{i})\biggr|^{2}\nonumber\\ \displaystyle & {\leqslant} & \displaystyle \text{card}({\mathcal{C}}(\mathbf{m}))\mathop{\sum }_{\mathfrak{C}\in {\mathcal{C}}(\mathbf{m})}\biggl|\mathop{\sum }_{\unicode[STIX]{x1D73D}\in \mathfrak{C}}\mathop{\prod }_{i=1}^{m+1}\mathfrak{f}_{kb}(\unicode[STIX]{x1D736};\unicode[STIX]{x1D703}_{i})\biggr|^{2}\nonumber\\ \displaystyle & {\leqslant} & \displaystyle k!\mathop{\sum }_{\mathfrak{C}\in {\mathcal{C}}(\mathbf{m})}\biggl|\mathop{\sum }_{\unicode[STIX]{x1D73D}\in \mathfrak{C}}\mathop{\prod }_{i=1}^{m+1}\mathfrak{f}_{kb}(\unicode[STIX]{x1D736};\unicode[STIX]{x1D703}_{i})\biggr|^{2}.\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle |\mathfrak{G}_{a,b}(\unicode[STIX]{x1D736};\mathbf{m})|^{2} & = & \displaystyle \biggl|\mathop{\sum }_{\mathfrak{C}\in {\mathcal{C}}(\mathbf{m})}\mathop{\sum }_{\unicode[STIX]{x1D73D}\in \mathfrak{C}}\mathop{\prod }_{i=1}^{m+1}\mathfrak{f}_{kb}(\unicode[STIX]{x1D736};\unicode[STIX]{x1D703}_{i})\biggr|^{2}\nonumber\\ \displaystyle & {\leqslant} & \displaystyle \text{card}({\mathcal{C}}(\mathbf{m}))\mathop{\sum }_{\mathfrak{C}\in {\mathcal{C}}(\mathbf{m})}\biggl|\mathop{\sum }_{\unicode[STIX]{x1D73D}\in \mathfrak{C}}\mathop{\prod }_{i=1}^{m+1}\mathfrak{f}_{kb}(\unicode[STIX]{x1D736};\unicode[STIX]{x1D703}_{i})\biggr|^{2}\nonumber\\ \displaystyle & {\leqslant} & \displaystyle k!\mathop{\sum }_{\mathfrak{C}\in {\mathcal{C}}(\mathbf{m})}\biggl|\mathop{\sum }_{\unicode[STIX]{x1D73D}\in \mathfrak{C}}\mathop{\prod }_{i=1}^{m+1}\mathfrak{f}_{kb}(\unicode[STIX]{x1D736};\unicode[STIX]{x1D703}_{i})\biggr|^{2}.\nonumber\end{eqnarray}$$
It may be helpful to note here that since
 $b^{\prime }/b\leqslant k-m-ma/b$
, then in view of the relation (3.2), it follows from Lemma 3.1 that
$b^{\prime }/b\leqslant k-m-ma/b$
, then in view of the relation (3.2), it follows from Lemma 3.1 that
 $$\begin{eqnarray}\text{card}({\mathcal{C}}(\mathbf{m}))=B_{a,b}^{m+1,b^{\prime }/b}(p)\leqslant k!.\end{eqnarray}$$
$$\begin{eqnarray}\text{card}({\mathcal{C}}(\mathbf{m}))=B_{a,b}^{m+1,b^{\prime }/b}(p)\leqslant k!.\end{eqnarray}$$
Hence,
 $$\begin{eqnarray}K_{a,b}^{m+1,r}(X;\unicode[STIX]{x1D709},\unicode[STIX]{x1D702})\ll \mathop{\sum }_{\mathbf{m}}\mathop{\sum }_{\mathfrak{C}\in {\mathcal{C}}(\mathbf{m})}\oint \biggl|\mathop{\mathfrak{F}}_{m}^{\ast }(\unicode[STIX]{x1D6FC})\mathop{\sum }_{\unicode[STIX]{x1D73D}\in \mathfrak{C}}\mathop{\prod }_{i=1}^{m+1}\mathfrak{f}_{kb}(\unicode[STIX]{x1D736};\unicode[STIX]{x1D703}_{i})\biggr|^{2}\,d\unicode[STIX]{x1D736}.\end{eqnarray}$$
$$\begin{eqnarray}K_{a,b}^{m+1,r}(X;\unicode[STIX]{x1D709},\unicode[STIX]{x1D702})\ll \mathop{\sum }_{\mathbf{m}}\mathop{\sum }_{\mathfrak{C}\in {\mathcal{C}}(\mathbf{m})}\oint \biggl|\mathop{\mathfrak{F}}_{m}^{\ast }(\unicode[STIX]{x1D6FC})\mathop{\sum }_{\unicode[STIX]{x1D73D}\in \mathfrak{C}}\mathop{\prod }_{i=1}^{m+1}\mathfrak{f}_{kb}(\unicode[STIX]{x1D736};\unicode[STIX]{x1D703}_{i})\biggr|^{2}\,d\unicode[STIX]{x1D736}.\end{eqnarray}$$
For each
![]() $k$
-tuple
$k$
-tuple
![]() $\mathbf{m}$
and equivalence class
$\mathbf{m}$
and equivalence class
![]() $\mathfrak{C}$
, the integral above counts solutions of (2.14) with the additional constraint that both
$\mathfrak{C}$
, the integral above counts solutions of (2.14) with the additional constraint that both
 $[\mathbf{x}~(\text{mod}~p^{kb})]$
and
$[\mathbf{x}~(\text{mod}~p^{kb})]$
and
 $[\mathbf{y}~(\text{mod}~p^{kb})]$
lie in
$[\mathbf{y}~(\text{mod}~p^{kb})]$
lie in
![]() $\mathfrak{C}$
. In particular, one has
$\mathfrak{C}$
. In particular, one has
 $\mathbf{x}\equiv \mathbf{y}~(\text{mod}~p^{b^{\prime }})$
. Moreover, the sets
$\mathbf{x}\equiv \mathbf{y}~(\text{mod}~p^{b^{\prime }})$
. Moreover, the sets
 ${\mathcal{B}}_{a,b}^{m+1}(\mathbf{m};\unicode[STIX]{x1D709},\unicode[STIX]{x1D702})$
are disjoint for distinct
${\mathcal{B}}_{a,b}^{m+1}(\mathbf{m};\unicode[STIX]{x1D709},\unicode[STIX]{x1D702})$
are disjoint for distinct
![]() $k$
-tuples
$k$
-tuples
![]() $\mathbf{m}$
with
$\mathbf{m}$
with
 $1\leqslant m_{j}\leqslant p^{jb}$
$1\leqslant m_{j}\leqslant p^{jb}$
 $(1\leqslant j\leqslant k)$
, so to each pair
$(1\leqslant j\leqslant k)$
, so to each pair
![]() $(\mathbf{x},\mathbf{y})$
there corresponds at most one pair
$(\mathbf{x},\mathbf{y})$
there corresponds at most one pair
![]() $(\mathbf{m},\mathfrak{C})$
. Thus, we deduce that
$(\mathbf{m},\mathfrak{C})$
. Thus, we deduce that
 $$\begin{eqnarray}K_{a,b}^{m+1,r}(X;\unicode[STIX]{x1D709},\unicode[STIX]{x1D702})\ll H^{\dagger }(X;\unicode[STIX]{x1D709},\unicode[STIX]{x1D702}),\end{eqnarray}$$
$$\begin{eqnarray}K_{a,b}^{m+1,r}(X;\unicode[STIX]{x1D709},\unicode[STIX]{x1D702})\ll H^{\dagger }(X;\unicode[STIX]{x1D709},\unicode[STIX]{x1D702}),\end{eqnarray}$$
where
 $H^{\dagger }(X;\unicode[STIX]{x1D709},\unicode[STIX]{x1D702})$
denotes the number of solutions of (2.14) subject to the additional condition
$H^{\dagger }(X;\unicode[STIX]{x1D709},\unicode[STIX]{x1D702})$
denotes the number of solutions of (2.14) subject to the additional condition
 $\mathbf{x}\equiv \mathbf{y}~(\text{mod}~p^{b^{\prime }})$
. Hence, on considering the underlying Diophantine systems and recalling (6.1), we discern that
$\mathbf{x}\equiv \mathbf{y}~(\text{mod}~p^{b^{\prime }})$
. Hence, on considering the underlying Diophantine systems and recalling (6.1), we discern that
 $$\begin{eqnarray}K_{a,b}^{m+1,r}(X;\unicode[STIX]{x1D709},\unicode[STIX]{x1D702})\ll \oint \mathop{\mathfrak{H}}_{a,b^{\prime }}^{m+1}(\unicode[STIX]{x1D736};\unicode[STIX]{x1D709})|\mathfrak{F}_{m}^{\ast }(\unicode[STIX]{x1D736})|^{2}\,d\unicode[STIX]{x1D736}.\end{eqnarray}$$
$$\begin{eqnarray}K_{a,b}^{m+1,r}(X;\unicode[STIX]{x1D709},\unicode[STIX]{x1D702})\ll \oint \mathop{\mathfrak{H}}_{a,b^{\prime }}^{m+1}(\unicode[STIX]{x1D736};\unicode[STIX]{x1D709})|\mathfrak{F}_{m}^{\ast }(\unicode[STIX]{x1D736})|^{2}\,d\unicode[STIX]{x1D736}.\end{eqnarray}$$
An inspection of the definition of
![]() $\unicode[STIX]{x1D6EF}_{a}^{m}(\unicode[STIX]{x1D709})$
in the preamble to (2.10) reveals on this occasion that when
$\unicode[STIX]{x1D6EF}_{a}^{m}(\unicode[STIX]{x1D709})$
in the preamble to (2.10) reveals on this occasion that when
 $\unicode[STIX]{x1D743}\in \unicode[STIX]{x1D6EF}_{a}^{m+1}(\unicode[STIX]{x1D709})$
, then
$\unicode[STIX]{x1D743}\in \unicode[STIX]{x1D6EF}_{a}^{m+1}(\unicode[STIX]{x1D709})$
, then
 $$\begin{eqnarray}(\unicode[STIX]{x1D709}_{1},\ldots ,\unicode[STIX]{x1D709}_{m})\in \unicode[STIX]{x1D6EF}_{a}^{m}(\unicode[STIX]{x1D709})\quad \text{and}\quad (\unicode[STIX]{x1D709}_{m+1})\in \unicode[STIX]{x1D6EF}_{a}^{1}(\unicode[STIX]{x1D709}).\end{eqnarray}$$
$$\begin{eqnarray}(\unicode[STIX]{x1D709}_{1},\ldots ,\unicode[STIX]{x1D709}_{m})\in \unicode[STIX]{x1D6EF}_{a}^{m}(\unicode[STIX]{x1D709})\quad \text{and}\quad (\unicode[STIX]{x1D709}_{m+1})\in \unicode[STIX]{x1D6EF}_{a}^{1}(\unicode[STIX]{x1D709}).\end{eqnarray}$$
Then a further consideration of the underlying Diophantine systems leads from (6.6) via (6.1) to the upper bound
 $$\begin{eqnarray}K_{a,b}^{m+1,r}(X;\unicode[STIX]{x1D709},\unicode[STIX]{x1D702})\ll \oint \mathop{\mathfrak{H}}_{a,b^{\prime }}^{m}(\unicode[STIX]{x1D736};\unicode[STIX]{x1D709})\mathfrak{H}_{a,b^{\prime }}^{1}(\unicode[STIX]{x1D736};\unicode[STIX]{x1D709})|\mathfrak{F}_{m}^{\ast }(\unicode[STIX]{x1D736})|^{2}\,d\unicode[STIX]{x1D736}.\end{eqnarray}$$
$$\begin{eqnarray}K_{a,b}^{m+1,r}(X;\unicode[STIX]{x1D709},\unicode[STIX]{x1D702})\ll \oint \mathop{\mathfrak{H}}_{a,b^{\prime }}^{m}(\unicode[STIX]{x1D736};\unicode[STIX]{x1D709})\mathfrak{H}_{a,b^{\prime }}^{1}(\unicode[STIX]{x1D736};\unicode[STIX]{x1D709})|\mathfrak{F}_{m}^{\ast }(\unicode[STIX]{x1D736})|^{2}\,d\unicode[STIX]{x1D736}.\end{eqnarray}$$
By applying Hölder’s inequality to the integral on the right-hand side of this relation, bearing in mind the definition (6.5), we obtain the bound
 $$\begin{eqnarray}K_{a,b}^{m+1,r}(X;\unicode[STIX]{x1D709},\unicode[STIX]{x1D702})\ll U_{1}^{\unicode[STIX]{x1D714}_{1}}U_{2}^{\unicode[STIX]{x1D714}_{2}}U_{3}^{\unicode[STIX]{x1D714}_{3}},\end{eqnarray}$$
$$\begin{eqnarray}K_{a,b}^{m+1,r}(X;\unicode[STIX]{x1D709},\unicode[STIX]{x1D702})\ll U_{1}^{\unicode[STIX]{x1D714}_{1}}U_{2}^{\unicode[STIX]{x1D714}_{2}}U_{3}^{\unicode[STIX]{x1D714}_{3}},\end{eqnarray}$$
where
 $$\begin{eqnarray}\unicode[STIX]{x1D714}_{1}=\frac{s-m-1}{s-m},\qquad \unicode[STIX]{x1D714}_{2}=\frac{1}{s},\qquad \unicode[STIX]{x1D714}_{3}=\frac{m}{s(s-m)}\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D714}_{1}=\frac{s-m-1}{s-m},\qquad \unicode[STIX]{x1D714}_{2}=\frac{1}{s},\qquad \unicode[STIX]{x1D714}_{3}=\frac{m}{s(s-m)}\end{eqnarray}$$
and
 $$\begin{eqnarray}\displaystyle & \displaystyle U_{1}=\oint \mathop{\mathfrak{H}}_{a,b^{\prime }}^{m}(\unicode[STIX]{x1D736};\unicode[STIX]{x1D709})|\mathfrak{F}_{b}^{r}(\unicode[STIX]{x1D736};\unicode[STIX]{x1D702})^{2}\mathfrak{f}_{b}(\unicode[STIX]{x1D736};\unicode[STIX]{x1D702})^{2s-2m}|\,d\unicode[STIX]{x1D736}, & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle U_{1}=\oint \mathop{\mathfrak{H}}_{a,b^{\prime }}^{m}(\unicode[STIX]{x1D736};\unicode[STIX]{x1D709})|\mathfrak{F}_{b}^{r}(\unicode[STIX]{x1D736};\unicode[STIX]{x1D702})^{2}\mathfrak{f}_{b}(\unicode[STIX]{x1D736};\unicode[STIX]{x1D702})^{2s-2m}|\,d\unicode[STIX]{x1D736}, & \displaystyle\end{eqnarray}$$
 $$\begin{eqnarray}\displaystyle & \displaystyle U_{2}=\oint |\mathop{\mathfrak{F}}_{b}^{r}(\unicode[STIX]{x1D736};\unicode[STIX]{x1D702})|^{2}\mathfrak{H}_{a,b^{\prime }}^{1}(\unicode[STIX]{x1D736};\unicode[STIX]{x1D709})^{s}\,d\unicode[STIX]{x1D736}, & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle U_{2}=\oint |\mathop{\mathfrak{F}}_{b}^{r}(\unicode[STIX]{x1D736};\unicode[STIX]{x1D702})|^{2}\mathfrak{H}_{a,b^{\prime }}^{1}(\unicode[STIX]{x1D736};\unicode[STIX]{x1D709})^{s}\,d\unicode[STIX]{x1D736}, & \displaystyle\end{eqnarray}$$
 $$\begin{eqnarray}\displaystyle & \displaystyle U_{3}=\oint |\mathop{\mathfrak{F}}_{b}^{r}(\unicode[STIX]{x1D736};\unicode[STIX]{x1D702})|^{2}\mathfrak{H}_{a,b^{\prime }}^{m}(\unicode[STIX]{x1D736};\unicode[STIX]{x1D709})^{s/m}\,d\unicode[STIX]{x1D736}. & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle U_{3}=\oint |\mathop{\mathfrak{F}}_{b}^{r}(\unicode[STIX]{x1D736};\unicode[STIX]{x1D702})|^{2}\mathfrak{H}_{a,b^{\prime }}^{m}(\unicode[STIX]{x1D736};\unicode[STIX]{x1D709})^{s/m}\,d\unicode[STIX]{x1D736}. & \displaystyle\end{eqnarray}$$
We now relate the mean values
![]() $U_{i}$
to those introduced in §2. Observe first that a consideration of the underlying Diophantine systems leads from (6.9) via (6.1) and (2.10) to the upper bound
$U_{i}$
to those introduced in §2. Observe first that a consideration of the underlying Diophantine systems leads from (6.9) via (6.1) and (2.10) to the upper bound
 $$\begin{eqnarray}U_{1}\leqslant \oint |\mathop{\mathfrak{F}}_{a}^{m}(\unicode[STIX]{x1D736};\unicode[STIX]{x1D709})^{2}\mathfrak{F}_{b}^{r}(\unicode[STIX]{x1D736};\unicode[STIX]{x1D702})^{2}\mathfrak{f}_{b}(\unicode[STIX]{x1D736};\unicode[STIX]{x1D702})^{2s-2m}|\,d\unicode[STIX]{x1D736}.\end{eqnarray}$$
$$\begin{eqnarray}U_{1}\leqslant \oint |\mathop{\mathfrak{F}}_{a}^{m}(\unicode[STIX]{x1D736};\unicode[STIX]{x1D709})^{2}\mathfrak{F}_{b}^{r}(\unicode[STIX]{x1D736};\unicode[STIX]{x1D702})^{2}\mathfrak{f}_{b}(\unicode[STIX]{x1D736};\unicode[STIX]{x1D702})^{2s-2m}|\,d\unicode[STIX]{x1D736}.\end{eqnarray}$$
On recalling (2.12) and (2.17), we thus deduce that
 $$\begin{eqnarray}U_{1}\leqslant K_{a,b}^{m,r}(X).\end{eqnarray}$$
$$\begin{eqnarray}U_{1}\leqslant K_{a,b}^{m,r}(X).\end{eqnarray}$$
Next, by employing (6.2) within (6.10) and (6.11), we find that
 $$\begin{eqnarray}U_{2}+U_{3}\ll (M^{b^{\prime }-a})^{s}\max _{\substack{ 1\leqslant \unicode[STIX]{x1D701}\leqslant p^{b^{\prime }} \\ \unicode[STIX]{x1D701}\equiv \unicode[STIX]{x1D709}~(\text{mod}~p^{a})}}\oint |\mathop{\mathfrak{F}}_{b}^{r}(\unicode[STIX]{x1D736};\unicode[STIX]{x1D702})^{2}\mathfrak{f}_{b^{\prime }}(\unicode[STIX]{x1D736};\unicode[STIX]{x1D701})^{2s}|\,d\unicode[STIX]{x1D736}.\end{eqnarray}$$
$$\begin{eqnarray}U_{2}+U_{3}\ll (M^{b^{\prime }-a})^{s}\max _{\substack{ 1\leqslant \unicode[STIX]{x1D701}\leqslant p^{b^{\prime }} \\ \unicode[STIX]{x1D701}\equiv \unicode[STIX]{x1D709}~(\text{mod}~p^{a})}}\oint |\mathop{\mathfrak{F}}_{b}^{r}(\unicode[STIX]{x1D736};\unicode[STIX]{x1D702})^{2}\mathfrak{f}_{b^{\prime }}(\unicode[STIX]{x1D736};\unicode[STIX]{x1D701})^{2s}|\,d\unicode[STIX]{x1D736}.\end{eqnarray}$$
Notice here that since the condition (6.3) implies that
 $\unicode[STIX]{x1D702}\not \equiv \unicode[STIX]{x1D709}~(\text{mod}~p)$
, and we have
$\unicode[STIX]{x1D702}\not \equiv \unicode[STIX]{x1D709}~(\text{mod}~p)$
, and we have
 $\unicode[STIX]{x1D701}\equiv \unicode[STIX]{x1D709}~(\text{mod}~p^{a})$
with
$\unicode[STIX]{x1D701}\equiv \unicode[STIX]{x1D709}~(\text{mod}~p^{a})$
with
![]() $a\geqslant 1$
, then once more one has
$a\geqslant 1$
, then once more one has
 $\unicode[STIX]{x1D701}\not \equiv \unicode[STIX]{x1D702}~(\text{mod}~p)$
. In this way we deduce from (2.11) and (2.16) that
$\unicode[STIX]{x1D701}\not \equiv \unicode[STIX]{x1D702}~(\text{mod}~p)$
. In this way we deduce from (2.11) and (2.16) that
 $$\begin{eqnarray}U_{2}+U_{3}\ll (M^{b^{\prime }-a})^{s}I_{b,b^{\prime }}^{r,r}(X).\end{eqnarray}$$
$$\begin{eqnarray}U_{2}+U_{3}\ll (M^{b^{\prime }-a})^{s}I_{b,b^{\prime }}^{r,r}(X).\end{eqnarray}$$
By substituting (6.12) and (6.13) into the relation
 $$\begin{eqnarray}K_{a,b}^{m+1,r}(X;\unicode[STIX]{x1D709},\unicode[STIX]{x1D702})\ll U_{1}^{\unicode[STIX]{x1D714}_{1}}(U_{2}+U_{3})^{1-\unicode[STIX]{x1D714}_{1}},\end{eqnarray}$$
$$\begin{eqnarray}K_{a,b}^{m+1,r}(X;\unicode[STIX]{x1D709},\unicode[STIX]{x1D702})\ll U_{1}^{\unicode[STIX]{x1D714}_{1}}(U_{2}+U_{3})^{1-\unicode[STIX]{x1D714}_{1}},\end{eqnarray}$$
that is immediate from (6.7), and then recalling (6.8) and (2.17), the conclusion of the lemma follows when
![]() $a\geqslant 1$
. When
$a\geqslant 1$
. When
![]() $a=0$
, we must modify this argument slightly. In this case, from (2.19) and (2.20), we find that
$a=0$
, we must modify this argument slightly. In this case, from (2.19) and (2.20), we find that
 $$\begin{eqnarray}K_{0,b}^{m+1,r}(X)=\max _{1\leqslant \unicode[STIX]{x1D702}\leqslant p^{b}}\oint |\mathfrak{F}^{m+1}(\unicode[STIX]{x1D736};\unicode[STIX]{x1D702})^{2}\mathfrak{F}_{b}^{r}(\unicode[STIX]{x1D736};\unicode[STIX]{x1D702})^{2}\mathfrak{f}_{b}(\unicode[STIX]{x1D736};\unicode[STIX]{x1D702})^{2s-2m-2}|\,d\unicode[STIX]{x1D736}.\end{eqnarray}$$
$$\begin{eqnarray}K_{0,b}^{m+1,r}(X)=\max _{1\leqslant \unicode[STIX]{x1D702}\leqslant p^{b}}\oint |\mathfrak{F}^{m+1}(\unicode[STIX]{x1D736};\unicode[STIX]{x1D702})^{2}\mathfrak{F}_{b}^{r}(\unicode[STIX]{x1D736};\unicode[STIX]{x1D702})^{2}\mathfrak{f}_{b}(\unicode[STIX]{x1D736};\unicode[STIX]{x1D702})^{2s-2m-2}|\,d\unicode[STIX]{x1D736}.\end{eqnarray}$$
The desired conclusion follows in this instance by pursuing the proof given above in the case
![]() $a\geqslant 1$
, noting that the definition of
$a\geqslant 1$
, noting that the definition of
 $\mathfrak{F}^{m+1}(\unicode[STIX]{x1D736};\unicode[STIX]{x1D702})$
ensures that the variables resulting from the congruencing argument avoid the congruence class
$\mathfrak{F}^{m+1}(\unicode[STIX]{x1D736};\unicode[STIX]{x1D702})$
ensures that the variables resulting from the congruencing argument avoid the congruence class
![]() $\unicode[STIX]{x1D702}$
modulo
$\unicode[STIX]{x1D702}$
modulo
![]() $p$
. This completes our account of the proof of the lemma.◻
$p$
. This completes our account of the proof of the lemma.◻
We note that in our application of Lemma 6.1, we restrict to situations with
 $0\leqslant m\leqslant r-1$
. Thus, since
$0\leqslant m\leqslant r-1$
. Thus, since
![]() $r\leqslant r_{0}$
, it follows from (2.2) that the hypothesis
$r\leqslant r_{0}$
, it follows from (2.2) that the hypothesis
 $a\leqslant b/\sqrt{k}$
ensures that
$a\leqslant b/\sqrt{k}$
ensures that
 $$\begin{eqnarray}k-m-ma/b\geqslant k-(k-2\sqrt{k}+1)-(k-2\sqrt{k}+1)/\sqrt{k}>\sqrt{k}.\end{eqnarray}$$
$$\begin{eqnarray}k-m-ma/b\geqslant k-(k-2\sqrt{k}+1)-(k-2\sqrt{k}+1)/\sqrt{k}>\sqrt{k}.\end{eqnarray}$$
Since
![]() $b$
is large, we are therefore at liberty to apply Lemma 6.1 with a choice for
$b$
is large, we are therefore at liberty to apply Lemma 6.1 with a choice for
![]() $b^{\prime }$
satisfying the condition
$b^{\prime }$
satisfying the condition
 $b/b^{\prime }<1/\sqrt{k}$
, thereby preparing appropriately for subsequent applications of Lemma 6.1.
$b/b^{\prime }<1/\sqrt{k}$
, thereby preparing appropriately for subsequent applications of Lemma 6.1.
7 The multigrade combination
We next combine the estimates supplied by Lemma 6.1 so as to bound
![]() $K_{a,b}^{r,r}(X)$
in terms of the mean values
$K_{a,b}^{r,r}(X)$
in terms of the mean values
 $I_{b,k_{m}b}^{r,r}(X)$
$I_{b,k_{m}b}^{r,r}(X)$
 $(0\leqslant m\leqslant r-1)$
, in which the integers
$(0\leqslant m\leqslant r-1)$
, in which the integers
![]() $k_{m}$
satisfy
$k_{m}$
satisfy
 $k_{m}\leqslant k-m-\lceil m/\sqrt{k}\rceil$
. Before announcing our basic asymptotic estimate, we define the exponents
$k_{m}\leqslant k-m-\lceil m/\sqrt{k}\rceil$
. Before announcing our basic asymptotic estimate, we define the exponents
 $$\begin{eqnarray}s_{m}=s-m\quad \text{and}\quad \unicode[STIX]{x1D719}_{m}=(s-r)/(s_{m}s_{m+1})\quad (0\leqslant m\leqslant r-1).\end{eqnarray}$$
$$\begin{eqnarray}s_{m}=s-m\quad \text{and}\quad \unicode[STIX]{x1D719}_{m}=(s-r)/(s_{m}s_{m+1})\quad (0\leqslant m\leqslant r-1).\end{eqnarray}$$
In addition, we write
 $$\begin{eqnarray}\unicode[STIX]{x1D719}^{\ast }=(s-r)/s,\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D719}^{\ast }=(s-r)/s,\end{eqnarray}$$
so that
 $$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D719}^{\ast }+\mathop{\sum }_{m=0}^{r-1}\unicode[STIX]{x1D719}_{m} & = & \displaystyle \frac{s-r}{s}+(s-r)\mathop{\sum }_{m=0}^{r-1}(s_{m+1}^{-1}-s_{m}^{-1})\nonumber\\ \displaystyle & = & \displaystyle \frac{s-r}{s}+(s-r)\biggl(\frac{1}{s-r}-\frac{1}{s}\biggr)=1.\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D719}^{\ast }+\mathop{\sum }_{m=0}^{r-1}\unicode[STIX]{x1D719}_{m} & = & \displaystyle \frac{s-r}{s}+(s-r)\mathop{\sum }_{m=0}^{r-1}(s_{m+1}^{-1}-s_{m}^{-1})\nonumber\\ \displaystyle & = & \displaystyle \frac{s-r}{s}+(s-r)\biggl(\frac{1}{s-r}-\frac{1}{s}\biggr)=1.\end{eqnarray}$$
Lemma 7.1. Suppose that
![]() $a$
and
$a$
and
![]() $b$
are integers with
$b$
are integers with
 $0\leqslant a<b\leqslant \unicode[STIX]{x1D703}^{-1}$
and
$0\leqslant a<b\leqslant \unicode[STIX]{x1D703}^{-1}$
and
 $(k-r+1)b\geqslant ra$
, and suppose further that
$(k-r+1)b\geqslant ra$
, and suppose further that
 $a\leqslant b/\sqrt{k}$
. Then, whenever
$a\leqslant b/\sqrt{k}$
. Then, whenever
![]() $a^{\prime }$
is an integer with
$a^{\prime }$
is an integer with
![]() $a^{\prime }\geqslant a$
for which
$a^{\prime }\geqslant a$
for which
 $(k-r+1)b\geqslant ra^{\prime }$
, one has
$(k-r+1)b\geqslant ra^{\prime }$
, one has
 $$\begin{eqnarray}K_{a,b}^{r,r}(X)\ll (J_{s+r}(X/M^{b}))^{\unicode[STIX]{x1D719}^{\ast }}\mathop{\prod }_{m=0}^{r-1}((M^{b_{m}-a})^{s}I_{b,b_{m}}^{r,r}(X))^{\unicode[STIX]{x1D719}_{m}},\end{eqnarray}$$
$$\begin{eqnarray}K_{a,b}^{r,r}(X)\ll (J_{s+r}(X/M^{b}))^{\unicode[STIX]{x1D719}^{\ast }}\mathop{\prod }_{m=0}^{r-1}((M^{b_{m}-a})^{s}I_{b,b_{m}}^{r,r}(X))^{\unicode[STIX]{x1D719}_{m}},\end{eqnarray}$$
where we write
 $b_{m}=(k-m)b-ma^{\prime }$
.
$b_{m}=(k-m)b-ma^{\prime }$
.
Proof. We prove by backwards induction that for
 $0\leqslant l\leqslant r-1$
, one has
$0\leqslant l\leqslant r-1$
, one has
 $$\begin{eqnarray}K_{a,b}^{r,r}(X)\ll (K_{a,b}^{l,r}(X))^{\unicode[STIX]{x1D719}_{l}^{\ast }}\mathop{\prod }_{m=l}^{r-1}((M^{b_{m}-a})^{s}I_{b,b_{m}}^{r,r}(X))^{\unicode[STIX]{x1D719}_{m}},\end{eqnarray}$$
$$\begin{eqnarray}K_{a,b}^{r,r}(X)\ll (K_{a,b}^{l,r}(X))^{\unicode[STIX]{x1D719}_{l}^{\ast }}\mathop{\prod }_{m=l}^{r-1}((M^{b_{m}-a})^{s}I_{b,b_{m}}^{r,r}(X))^{\unicode[STIX]{x1D719}_{m}},\end{eqnarray}$$
where
 $$\begin{eqnarray}\unicode[STIX]{x1D719}_{l}^{\ast }=(s-r)/(s-l).\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D719}_{l}^{\ast }=(s-r)/(s-l).\end{eqnarray}$$
The conclusion of the lemma follows from the case
![]() $l=0$
of (7.4), on noting that Lemma 2.2 delivers the estimate
$l=0$
of (7.4), on noting that Lemma 2.2 delivers the estimate
 $K_{a,b}^{0,r}(X)\ll J_{s+r}(X/M^{b})$
.
$K_{a,b}^{0,r}(X)\ll J_{s+r}(X/M^{b})$
.
We observe first that the inductive hypothesis (7.4) holds when
 $l=r-1$
, as a consequence of the case
$l=r-1$
, as a consequence of the case
 $m=r-1$
of Lemma 6.1 and the definitions (7.1) and (7.2). Suppose then that
$m=r-1$
of Lemma 6.1 and the definitions (7.1) and (7.2). Suppose then that
![]() $J$
is a non-negative integer not exceeding
$J$
is a non-negative integer not exceeding
![]() $r-2$
, and that the inductive hypothesis (7.4) holds for
$r-2$
, and that the inductive hypothesis (7.4) holds for
 $J<l\leqslant r-1$
. An application of Lemma 6.1 yields the estimate
$J<l\leqslant r-1$
. An application of Lemma 6.1 yields the estimate
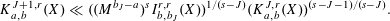 $$\begin{eqnarray}K_{a,b}^{J+1,r}(X)\ll ((M^{b_{J}-a})^{s}I_{b,b_{J}}^{r,r}(X))^{1/(s-J)}(K_{a,b}^{J,r}(X))^{(s-J-1)/(s-J)}.\end{eqnarray}$$
$$\begin{eqnarray}K_{a,b}^{J+1,r}(X)\ll ((M^{b_{J}-a})^{s}I_{b,b_{J}}^{r,r}(X))^{1/(s-J)}(K_{a,b}^{J,r}(X))^{(s-J-1)/(s-J)}.\end{eqnarray}$$
On substituting this bound into the estimate (7.4) with
 $l=J+1$
, one obtains the new upper bound
$l=J+1$
, one obtains the new upper bound
 $$\begin{eqnarray}K_{a,b}^{r,r}(X)\ll (K_{a,b}^{J,r}(X))^{\unicode[STIX]{x1D719}_{J}^{\ast }}\mathop{\prod }_{m=J}^{r-1}((M^{b_{m}-a})^{s}I_{b,b_{m}}^{r,r}(X))^{\unicode[STIX]{x1D719}_{m}}\end{eqnarray}$$
$$\begin{eqnarray}K_{a,b}^{r,r}(X)\ll (K_{a,b}^{J,r}(X))^{\unicode[STIX]{x1D719}_{J}^{\ast }}\mathop{\prod }_{m=J}^{r-1}((M^{b_{m}-a})^{s}I_{b,b_{m}}^{r,r}(X))^{\unicode[STIX]{x1D719}_{m}}\end{eqnarray}$$
and thus the inductive hypothesis holds with
![]() $l=J$
. This completes the inductive step, so in view of our earlier remarks, the conclusion of the lemma now follows.◻
$l=J$
. This completes the inductive step, so in view of our earlier remarks, the conclusion of the lemma now follows.◻
We next convert Lemma 7.1 into a more portable form by making use of the anticipated magnitude operator
![]() $\unicode[STIX]{x27E6}\,\cdot \,\unicode[STIX]{x27E7}$
introduced in (2.21) to (2.23).
$\unicode[STIX]{x27E6}\,\cdot \,\unicode[STIX]{x27E7}$
introduced in (2.21) to (2.23).
Lemma 7.2. Suppose that
![]() $a$
and
$a$
and
![]() $b$
are integers with
$b$
are integers with
 $0\leqslant a<b\leqslant \unicode[STIX]{x1D703}^{-1}$
and
$0\leqslant a<b\leqslant \unicode[STIX]{x1D703}^{-1}$
and
 $(k-r+1)b\geqslant ra$
, and suppose further that
$(k-r+1)b\geqslant ra$
, and suppose further that
 $a\leqslant b/\sqrt{k}$
. Then, whenever
$a\leqslant b/\sqrt{k}$
. Then, whenever
![]() $a^{\prime }$
is an integer with
$a^{\prime }$
is an integer with
![]() $a^{\prime }\geqslant a$
for which
$a^{\prime }\geqslant a$
for which
 $(k-r+1)b\geqslant ra^{\prime }$
, one has
$(k-r+1)b\geqslant ra^{\prime }$
, one has
 $$\begin{eqnarray}\unicode[STIX]{x27E6}K_{a,b}^{r,r}(X)\unicode[STIX]{x27E7}\ll ((X/M^{b})^{\unicode[STIX]{x1D6EC}+\unicode[STIX]{x1D6FF}})^{\unicode[STIX]{x1D719}^{\ast }}\mathop{\prod }_{m=0}^{r-1}\unicode[STIX]{x27E6}I_{b,b_{m}}^{r,r}(X)\unicode[STIX]{x27E7}^{\unicode[STIX]{x1D719}_{m}},\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x27E6}K_{a,b}^{r,r}(X)\unicode[STIX]{x27E7}\ll ((X/M^{b})^{\unicode[STIX]{x1D6EC}+\unicode[STIX]{x1D6FF}})^{\unicode[STIX]{x1D719}^{\ast }}\mathop{\prod }_{m=0}^{r-1}\unicode[STIX]{x27E6}I_{b,b_{m}}^{r,r}(X)\unicode[STIX]{x27E7}^{\unicode[STIX]{x1D719}_{m}},\end{eqnarray}$$
where
 $b_{m}=(k-m)b-ma^{\prime }$
.
$b_{m}=(k-m)b-ma^{\prime }$
.
Proof. We find from Lemma 7.1 in combination with (2.23) that
 $$\begin{eqnarray}\unicode[STIX]{x27E6}K_{a,b}^{r,r}(X)\unicode[STIX]{x27E7}\ll M^{\unicode[STIX]{x1D707}^{\ast }b+\unicode[STIX]{x1D708}^{\ast }a}((X/M^{b})^{\unicode[STIX]{x1D6EC}+\unicode[STIX]{x1D6FF}})^{\unicode[STIX]{x1D719}^{\ast }}\mathop{\prod }_{m=0}^{r}\unicode[STIX]{x27E6}I_{b,b_{m}}^{r,r}(X)\unicode[STIX]{x27E7}^{\unicode[STIX]{x1D719}_{m}},\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x27E6}K_{a,b}^{r,r}(X)\unicode[STIX]{x27E7}\ll M^{\unicode[STIX]{x1D707}^{\ast }b+\unicode[STIX]{x1D708}^{\ast }a}((X/M^{b})^{\unicode[STIX]{x1D6EC}+\unicode[STIX]{x1D6FF}})^{\unicode[STIX]{x1D719}^{\ast }}\mathop{\prod }_{m=0}^{r}\unicode[STIX]{x27E6}I_{b,b_{m}}^{r,r}(X)\unicode[STIX]{x27E7}^{\unicode[STIX]{x1D719}_{m}},\end{eqnarray}$$
where
 $$\begin{eqnarray}\unicode[STIX]{x1D707}^{\ast }=s-\unicode[STIX]{x1D719}^{\ast }(s+r)-r\mathop{\sum }_{m=0}^{r-1}\unicode[STIX]{x1D719}_{m}\quad \text{and}\quad \unicode[STIX]{x1D708}^{\ast }=r-s\mathop{\sum }_{m=0}^{r-1}\unicode[STIX]{x1D719}_{m}.\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D707}^{\ast }=s-\unicode[STIX]{x1D719}^{\ast }(s+r)-r\mathop{\sum }_{m=0}^{r-1}\unicode[STIX]{x1D719}_{m}\quad \text{and}\quad \unicode[STIX]{x1D708}^{\ast }=r-s\mathop{\sum }_{m=0}^{r-1}\unicode[STIX]{x1D719}_{m}.\end{eqnarray}$$
On recalling (7.2) and (7.3), a modicum of computation confirms that
 $$\begin{eqnarray}\unicode[STIX]{x1D707}^{\ast }=s-\unicode[STIX]{x1D719}^{\ast }(s+r)-r(1-\unicode[STIX]{x1D719}^{\ast })=0\quad \text{and}\quad \unicode[STIX]{x1D708}^{\ast }=r-s(1-\unicode[STIX]{x1D719}^{\ast })=0.\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D707}^{\ast }=s-\unicode[STIX]{x1D719}^{\ast }(s+r)-r(1-\unicode[STIX]{x1D719}^{\ast })=0\quad \text{and}\quad \unicode[STIX]{x1D708}^{\ast }=r-s(1-\unicode[STIX]{x1D719}^{\ast })=0.\end{eqnarray}$$
The conclusion of the lemma is therefore immediate from (7.5). ◻
We next turn to the task of establishing a multistep multigrade combination. Here, in order to keep complications under control, we discard some information not essential to our ultimate iterative process. We begin by introducing some additional notation. We recall that
![]() $R$
is a positive integer sufficiently large in terms of
$R$
is a positive integer sufficiently large in terms of
![]() $s$
and
$s$
and
![]() $k$
. We consider
$k$
. We consider
![]() $R$
-tuples of integers
$R$
-tuples of integers
 $(m_{1},\ldots ,m_{R})\in [0,r-1]^{R}$
, to each of which we associate an
$(m_{1},\ldots ,m_{R})\in [0,r-1]^{R}$
, to each of which we associate an
![]() $R$
-tuple of integers
$R$
-tuple of integers
 $\mathbf{h}(\mathbf{m})=(h_{1}(\mathbf{m}),\ldots ,h_{R}(\mathbf{m}))\in [0,\infty )^{R}$
. The integral tuples
$\mathbf{h}(\mathbf{m})=(h_{1}(\mathbf{m}),\ldots ,h_{R}(\mathbf{m}))\in [0,\infty )^{R}$
. The integral tuples
![]() $\mathbf{h}(\mathbf{m})$
will be fixed as the iteration proceeds, with
$\mathbf{h}(\mathbf{m})$
will be fixed as the iteration proceeds, with
![]() $h_{n}(\mathbf{m})$
depending at most on the first
$h_{n}(\mathbf{m})$
depending at most on the first
![]() $n$
coordinates of
$n$
coordinates of
 $(m_{1},\ldots ,m_{R})$
. We may abuse notation in some circumstances by writing
$(m_{1},\ldots ,m_{R})$
. We may abuse notation in some circumstances by writing
 $h_{n}(\mathbf{m},m_{n})$
or
$h_{n}(\mathbf{m},m_{n})$
or
 $h_{n}(m_{1},\ldots ,m_{n-1},m_{n})$
in place of
$h_{n}(m_{1},\ldots ,m_{n-1},m_{n})$
in place of
 $h_{n}(m_{1},\ldots ,m_{R})$
, reflecting the latter implicit dependence. We suppose that a (large) positive integer
$h_{n}(m_{1},\ldots ,m_{R})$
, reflecting the latter implicit dependence. We suppose that a (large) positive integer
![]() $b$
has already been fixed. We then define the sequences
$b$
has already been fixed. We then define the sequences
 $(a_{n})=(a_{n}(\mathbf{m};\mathbf{h}))$
and
$(a_{n})=(a_{n}(\mathbf{m};\mathbf{h}))$
and
 $(b_{n})=(b_{n}(\mathbf{m};\mathbf{h}))$
by putting
$(b_{n})=(b_{n}(\mathbf{m};\mathbf{h}))$
by putting
 $$\begin{eqnarray}a_{0}=\lfloor b/\sqrt{k}\rfloor \quad \text{and}\quad b_{0}=b,\end{eqnarray}$$
$$\begin{eqnarray}a_{0}=\lfloor b/\sqrt{k}\rfloor \quad \text{and}\quad b_{0}=b,\end{eqnarray}$$
and then applying the iterative relations
 $$\begin{eqnarray}a_{n}=b_{n-1}\quad \text{and}\quad b_{n}=(k-m_{n})b_{n-1}-m_{n}a_{n-1}+h_{n}(\mathbf{m})\quad (1\leqslant n\leqslant R).\end{eqnarray}$$
$$\begin{eqnarray}a_{n}=b_{n-1}\quad \text{and}\quad b_{n}=(k-m_{n})b_{n-1}-m_{n}a_{n-1}+h_{n}(\mathbf{m})\quad (1\leqslant n\leqslant R).\end{eqnarray}$$
Finally, we define the quantity
 $\unicode[STIX]{x1D6E9}_{n}(\mathbf{m};\mathbf{h})$
for
$\unicode[STIX]{x1D6E9}_{n}(\mathbf{m};\mathbf{h})$
for
 $0\leqslant n\leqslant R$
by putting
$0\leqslant n\leqslant R$
by putting
 $$\begin{eqnarray}\unicode[STIX]{x1D6E9}_{n}(\mathbf{m};\mathbf{h})=(X/M^{b})^{-\unicode[STIX]{x1D6EC}-\unicode[STIX]{x1D6FF}}\unicode[STIX]{x27E6}K_{a_{n},b_{n}}^{r,r}(X)\unicode[STIX]{x27E7}+M^{-3sk^{R}b}.\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D6E9}_{n}(\mathbf{m};\mathbf{h})=(X/M^{b})^{-\unicode[STIX]{x1D6EC}-\unicode[STIX]{x1D6FF}}\unicode[STIX]{x27E6}K_{a_{n},b_{n}}^{r,r}(X)\unicode[STIX]{x27E7}+M^{-3sk^{R}b}.\end{eqnarray}$$
Lemma 7.3. Suppose that
![]() $a$
and
$a$
and
![]() $b$
are integers with
$b$
are integers with
 $0\leqslant a<b\leqslant (16Rk^{2R}\unicode[STIX]{x1D703})^{-1}$
and
$0\leqslant a<b\leqslant (16Rk^{2R}\unicode[STIX]{x1D703})^{-1}$
and
 $(k-r+1)b\geqslant ra$
, and suppose further that
$(k-r+1)b\geqslant ra$
, and suppose further that
 $a\leqslant b/\sqrt{k}$
. Then there exists a choice for
$a\leqslant b/\sqrt{k}$
. Then there exists a choice for
 $\mathbf{h}(\mathbf{m})\in [0,\infty )^{R}$
, satisfying the condition that
$\mathbf{h}(\mathbf{m})\in [0,\infty )^{R}$
, satisfying the condition that
 $0\leqslant h_{n}(\mathbf{m})\leqslant 15k^{R}b$
$0\leqslant h_{n}(\mathbf{m})\leqslant 15k^{R}b$
 $(1\leqslant n\leqslant R)$
, and for which one has
$(1\leqslant n\leqslant R)$
, and for which one has
 $$\begin{eqnarray}(X/M^{b})^{-\unicode[STIX]{x1D6EC}-\unicode[STIX]{x1D6FF}}\unicode[STIX]{x27E6}K_{a,b}^{r,r}(X)\unicode[STIX]{x27E7}\ll \mathop{\prod }_{\mathbf{m}\in [0,r-1]^{R}}\unicode[STIX]{x1D6E9}_{R}(\mathbf{m};\mathbf{h})^{\unicode[STIX]{x1D719}_{m_{1}}\cdots \unicode[STIX]{x1D719}_{m_{R}}}.\end{eqnarray}$$
$$\begin{eqnarray}(X/M^{b})^{-\unicode[STIX]{x1D6EC}-\unicode[STIX]{x1D6FF}}\unicode[STIX]{x27E6}K_{a,b}^{r,r}(X)\unicode[STIX]{x27E7}\ll \mathop{\prod }_{\mathbf{m}\in [0,r-1]^{R}}\unicode[STIX]{x1D6E9}_{R}(\mathbf{m};\mathbf{h})^{\unicode[STIX]{x1D719}_{m_{1}}\cdots \unicode[STIX]{x1D719}_{m_{R}}}.\end{eqnarray}$$
Proof. We prove by induction on
![]() $l$
that when
$l$
that when
 $1\leqslant l\leqslant R$
, one has the upper bound
$1\leqslant l\leqslant R$
, one has the upper bound
 $$\begin{eqnarray}(X/M^{b})^{-\unicode[STIX]{x1D6EC}-\unicode[STIX]{x1D6FF}}\unicode[STIX]{x27E6}K_{a,b}^{r,r}(X)\unicode[STIX]{x27E7}\ll \mathop{\prod }_{\mathbf{m}\in [0,r-1]^{l}}\unicode[STIX]{x1D6E9}_{l}(\mathbf{m};\mathbf{h})^{\unicode[STIX]{x1D719}_{m_{1}}\cdots \unicode[STIX]{x1D719}_{m_{l}}}.\end{eqnarray}$$
$$\begin{eqnarray}(X/M^{b})^{-\unicode[STIX]{x1D6EC}-\unicode[STIX]{x1D6FF}}\unicode[STIX]{x27E6}K_{a,b}^{r,r}(X)\unicode[STIX]{x27E7}\ll \mathop{\prod }_{\mathbf{m}\in [0,r-1]^{l}}\unicode[STIX]{x1D6E9}_{l}(\mathbf{m};\mathbf{h})^{\unicode[STIX]{x1D719}_{m_{1}}\cdots \unicode[STIX]{x1D719}_{m_{l}}}.\end{eqnarray}$$
We observe first that, as a consequence of (7.3) and Lemma 7.2, one has
 $$\begin{eqnarray}(X/M^{b})^{-\unicode[STIX]{x1D6EC}-\unicode[STIX]{x1D6FF}}\unicode[STIX]{x27E6}K_{a,b}^{r,r}(X)\unicode[STIX]{x27E7}\ll \mathop{\prod }_{m=0}^{r-1}((X/M^{b})^{-\unicode[STIX]{x1D6EC}-\unicode[STIX]{x1D6FF}}\unicode[STIX]{x27E6}I_{b,b_{m}^{\ast }}^{r,r}(X)\unicode[STIX]{x27E7})^{\unicode[STIX]{x1D719}_{m}},\end{eqnarray}$$
$$\begin{eqnarray}(X/M^{b})^{-\unicode[STIX]{x1D6EC}-\unicode[STIX]{x1D6FF}}\unicode[STIX]{x27E6}K_{a,b}^{r,r}(X)\unicode[STIX]{x27E7}\ll \mathop{\prod }_{m=0}^{r-1}((X/M^{b})^{-\unicode[STIX]{x1D6EC}-\unicode[STIX]{x1D6FF}}\unicode[STIX]{x27E6}I_{b,b_{m}^{\ast }}^{r,r}(X)\unicode[STIX]{x27E7})^{\unicode[STIX]{x1D719}_{m}},\end{eqnarray}$$
where
 $$\begin{eqnarray}b_{m}^{\ast }=(k-m)b-m\lfloor b/\sqrt{k}\rfloor .\end{eqnarray}$$
$$\begin{eqnarray}b_{m}^{\ast }=(k-m)b-m\lfloor b/\sqrt{k}\rfloor .\end{eqnarray}$$
Moreover, it follows from Lemma 4.2 that for each
![]() $m$
with
$m$
with
 $0\leqslant m\leqslant r-1$
, there exists an integer
$0\leqslant m\leqslant r-1$
, there exists an integer
 $h=h(m)$
, with
$h=h(m)$
, with
 $0\leqslant h\leqslant 15k^{R}b$
, having the property that
$0\leqslant h\leqslant 15k^{R}b$
, having the property that
 $$\begin{eqnarray}I_{b,b_{m}^{\ast }}^{r,r}(X)\ll (M^{h})^{2s/3}K_{b,b_{m}^{\ast }+h}^{r,r}(X)+(M^{15k^{R}b})^{-s/4}(X/M^{b_{m}^{\ast }})^{s}(X/M^{b})^{\unicode[STIX]{x1D706}-s},\end{eqnarray}$$
$$\begin{eqnarray}I_{b,b_{m}^{\ast }}^{r,r}(X)\ll (M^{h})^{2s/3}K_{b,b_{m}^{\ast }+h}^{r,r}(X)+(M^{15k^{R}b})^{-s/4}(X/M^{b_{m}^{\ast }})^{s}(X/M^{b})^{\unicode[STIX]{x1D706}-s},\end{eqnarray}$$
whence from (2.22) and (2.23) we discern that
 $$\begin{eqnarray}\unicode[STIX]{x27E6}I_{b,b_{m}^{\ast }}^{r,r}(X)\unicode[STIX]{x27E7}\ll M^{-hs/3}\unicode[STIX]{x27E6}K_{b,b_{1}}^{r,r}(X)\unicode[STIX]{x27E7}+M^{-3sk^{R}b}(X/M^{b})^{\unicode[STIX]{x1D6EC}+\unicode[STIX]{x1D6FF}},\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x27E6}I_{b,b_{m}^{\ast }}^{r,r}(X)\unicode[STIX]{x27E7}\ll M^{-hs/3}\unicode[STIX]{x27E6}K_{b,b_{1}}^{r,r}(X)\unicode[STIX]{x27E7}+M^{-3sk^{R}b}(X/M^{b})^{\unicode[STIX]{x1D6EC}+\unicode[STIX]{x1D6FF}},\end{eqnarray}$$
where
 $$\begin{eqnarray}b_{1}=(k-m)b_{0}-ma_{0}+h(m).\end{eqnarray}$$
$$\begin{eqnarray}b_{1}=(k-m)b_{0}-ma_{0}+h(m).\end{eqnarray}$$
The inductive hypothesis (7.9) therefore follows in the case
![]() $R=1$
by substituting (7.11) into (7.10). Notice here that we have discarded the factor
$R=1$
by substituting (7.11) into (7.10). Notice here that we have discarded the factor
![]() $M^{-hs/3}$
from (7.11), since at this stage of our argument it serves only as an unwelcome complication.
$M^{-hs/3}$
from (7.11), since at this stage of our argument it serves only as an unwelcome complication.
Suppose next that the inductive hypothesis (7.9) holds for
 $1\leqslant l<L$
, with some integer
$1\leqslant l<L$
, with some integer
![]() $L$
satisfying
$L$
satisfying
![]() $L\leqslant R$
. Consider the quantity
$L\leqslant R$
. Consider the quantity
 $\unicode[STIX]{x1D6E9}_{L-1}(\mathbf{m};\mathbf{h})$
for a given tuple
$\unicode[STIX]{x1D6E9}_{L-1}(\mathbf{m};\mathbf{h})$
for a given tuple
 $\mathbf{m}\in [0,r-1]^{L-1}$
and a fixed tuple
$\mathbf{m}\in [0,r-1]^{L-1}$
and a fixed tuple
 $\mathbf{h}=\mathbf{h}(\mathbf{m})$
. We distinguish two possibilities. If it is the case that
$\mathbf{h}=\mathbf{h}(\mathbf{m})$
. We distinguish two possibilities. If it is the case that
 $$\begin{eqnarray}\unicode[STIX]{x1D6E9}_{L-1}(\mathbf{m};\mathbf{h})\ll M^{-3sk^{R}b},\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D6E9}_{L-1}(\mathbf{m};\mathbf{h})\ll M^{-3sk^{R}b},\end{eqnarray}$$
then from (7.3) one finds that
 $$\begin{eqnarray}\unicode[STIX]{x1D6E9}_{L-1}(\mathbf{m};\mathbf{h})\ll \biggl(\mathop{\prod }_{m_{L}=0}^{r-1}(M^{-3sk^{R}b})^{\unicode[STIX]{x1D719}_{m_{L}}}\biggr)^{s/r},\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D6E9}_{L-1}(\mathbf{m};\mathbf{h})\ll \biggl(\mathop{\prod }_{m_{L}=0}^{r-1}(M^{-3sk^{R}b})^{\unicode[STIX]{x1D719}_{m_{L}}}\biggr)^{s/r},\end{eqnarray}$$
so that
 $$\begin{eqnarray}\unicode[STIX]{x1D6E9}_{L-1}(\mathbf{m};\mathbf{h})\ll \mathop{\prod }_{m_{L}=0}^{r-1}(M^{-3sk^{R}b})^{\unicode[STIX]{x1D719}_{m_{L}}}\ll \mathop{\prod }_{m_{L}=0}^{r-1}\unicode[STIX]{x1D6E9}_{L}(\mathbf{m},m_{L};\mathbf{h},0)^{\unicode[STIX]{x1D719}_{m_{L}}}.\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D6E9}_{L-1}(\mathbf{m};\mathbf{h})\ll \mathop{\prod }_{m_{L}=0}^{r-1}(M^{-3sk^{R}b})^{\unicode[STIX]{x1D719}_{m_{L}}}\ll \mathop{\prod }_{m_{L}=0}^{r-1}\unicode[STIX]{x1D6E9}_{L}(\mathbf{m},m_{L};\mathbf{h},0)^{\unicode[STIX]{x1D719}_{m_{L}}}.\end{eqnarray}$$
When
 $$\begin{eqnarray}\unicode[STIX]{x1D6E9}_{L-1}(\mathbf{m};\mathbf{h})\ll (X/M^{b})^{-\unicode[STIX]{x1D6EC}-\unicode[STIX]{x1D6FF}}\unicode[STIX]{x27E6}K_{a_{L-1},b_{L-1}}^{r,r}(X)\unicode[STIX]{x27E7},\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D6E9}_{L-1}(\mathbf{m};\mathbf{h})\ll (X/M^{b})^{-\unicode[STIX]{x1D6EC}-\unicode[STIX]{x1D6FF}}\unicode[STIX]{x27E6}K_{a_{L-1},b_{L-1}}^{r,r}(X)\unicode[STIX]{x27E7},\end{eqnarray}$$
meanwhile, we apply Lemma 7.2 to obtain the bound
 $$\begin{eqnarray}\unicode[STIX]{x1D6E9}_{L-1}(\mathbf{m};\mathbf{h})\ll \biggl(\frac{X}{M^{b}}\biggr)^{-\unicode[STIX]{x1D6EC}-\unicode[STIX]{x1D6FF}}\biggl(\frac{X}{M^{b_{L-1}}}\biggr)^{(\unicode[STIX]{x1D6EC}+\unicode[STIX]{x1D6FF})(1-r/s)}\mathop{\prod }_{m_{L}=0}^{r-1}\unicode[STIX]{x27E6}I_{b_{L-1},b_{m_{L}}^{\ast }}^{r,r}(X)\unicode[STIX]{x27E7}^{\unicode[STIX]{x1D719}_{m_{L}}},\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D6E9}_{L-1}(\mathbf{m};\mathbf{h})\ll \biggl(\frac{X}{M^{b}}\biggr)^{-\unicode[STIX]{x1D6EC}-\unicode[STIX]{x1D6FF}}\biggl(\frac{X}{M^{b_{L-1}}}\biggr)^{(\unicode[STIX]{x1D6EC}+\unicode[STIX]{x1D6FF})(1-r/s)}\mathop{\prod }_{m_{L}=0}^{r-1}\unicode[STIX]{x27E6}I_{b_{L-1},b_{m_{L}}^{\ast }}^{r,r}(X)\unicode[STIX]{x27E7}^{\unicode[STIX]{x1D719}_{m_{L}}},\end{eqnarray}$$
where
 $$\begin{eqnarray}b_{m_{L}}^{\ast }=(k-m_{L})b_{L-1}-ma_{L-1}.\end{eqnarray}$$
$$\begin{eqnarray}b_{m_{L}}^{\ast }=(k-m_{L})b_{L-1}-ma_{L-1}.\end{eqnarray}$$
Two observations here serve to confirm that Lemma 7.2 is applicable. First, the hypothesis
 $b\leqslant (16Rk^{2R}\unicode[STIX]{x1D703})^{-1}$
ensures that
$b\leqslant (16Rk^{2R}\unicode[STIX]{x1D703})^{-1}$
ensures that
 $b_{L-1}\leqslant \unicode[STIX]{x1D703}^{-1}$
. Second, just as in the discussion concluding §6, an inductive argument shows that
$b_{L-1}\leqslant \unicode[STIX]{x1D703}^{-1}$
. Second, just as in the discussion concluding §6, an inductive argument shows that
 $a_{n}\leqslant b_{n}/\sqrt{k}$
for each
$a_{n}\leqslant b_{n}/\sqrt{k}$
for each
![]() $n$
, for the hypothesis
$n$
, for the hypothesis
 $1\leqslant r\leqslant r_{0}=k-\lceil 2\sqrt{k}\rceil +2$
ensures that whenever
$1\leqslant r\leqslant r_{0}=k-\lceil 2\sqrt{k}\rceil +2$
ensures that whenever
 $a_{n-1}\leqslant b_{n-1}/\sqrt{k}$
, then
$a_{n-1}\leqslant b_{n-1}/\sqrt{k}$
, then
 $$\begin{eqnarray}k-m_{n}-m_{n}a_{n-1}/b_{n-1}\geqslant k-(k-2\sqrt{k}+1)-(k-2\sqrt{k}+1)/\sqrt{k}>\sqrt{k},\end{eqnarray}$$
$$\begin{eqnarray}k-m_{n}-m_{n}a_{n-1}/b_{n-1}\geqslant k-(k-2\sqrt{k}+1)-(k-2\sqrt{k}+1)/\sqrt{k}>\sqrt{k},\end{eqnarray}$$
whence
 $b_{n}>\sqrt{k}b_{n-1}=\sqrt{k}a_{n}$
. The claimed relation therefore follows by induction from (7.6), and in particular one obtains
$b_{n}>\sqrt{k}b_{n-1}=\sqrt{k}a_{n}$
. The claimed relation therefore follows by induction from (7.6), and in particular one obtains
 $$\begin{eqnarray}(k-r+1)b_{L-1}-ra_{L-1}\geqslant b_{L-1}(k-(k-2\sqrt{k}+1)-(k-2\sqrt{k}+1)/\sqrt{k})>0.\end{eqnarray}$$
$$\begin{eqnarray}(k-r+1)b_{L-1}-ra_{L-1}\geqslant b_{L-1}(k-(k-2\sqrt{k}+1)-(k-2\sqrt{k}+1)/\sqrt{k})>0.\end{eqnarray}$$
The applicability of Lemma 7.2 now confirmed, we again invoke Lemma 4.2, finding that for each integer
![]() $m_{L}$
with
$m_{L}$
with
 $0\leqslant m_{L}\leqslant r-1$
, there exists an integer
$0\leqslant m_{L}\leqslant r-1$
, there exists an integer
 $h_{L}=h_{L}(\mathbf{m},m_{L})$
, with
$h_{L}=h_{L}(\mathbf{m},m_{L})$
, with
 $0\leqslant h_{L}\leqslant 15k^{R}b$
, having the property that
$0\leqslant h_{L}\leqslant 15k^{R}b$
, having the property that
 $$\begin{eqnarray}\unicode[STIX]{x27E6}I_{b_{L-1},b_{m_{L}}^{\ast }}^{r,r}(X)\unicode[STIX]{x27E7}\ll M^{-h_{L}s/3}\unicode[STIX]{x27E6}K_{b_{L-1},b_{L}}^{r,r}(X)\unicode[STIX]{x27E7}+M^{-3sk^{R}b}(X/M^{b_{L-1}})^{\unicode[STIX]{x1D6EC}+\unicode[STIX]{x1D6FF}}.\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x27E6}I_{b_{L-1},b_{m_{L}}^{\ast }}^{r,r}(X)\unicode[STIX]{x27E7}\ll M^{-h_{L}s/3}\unicode[STIX]{x27E6}K_{b_{L-1},b_{L}}^{r,r}(X)\unicode[STIX]{x27E7}+M^{-3sk^{R}b}(X/M^{b_{L-1}})^{\unicode[STIX]{x1D6EC}+\unicode[STIX]{x1D6FF}}.\end{eqnarray}$$
Thus, we deduce that
 $$\begin{eqnarray}\displaystyle (X/M^{b})^{-\unicode[STIX]{x1D6EC}-\unicode[STIX]{x1D6FF}}\unicode[STIX]{x27E6}I_{b_{L-1},b_{m_{L}}^{\ast }}^{r,r}(X)\unicode[STIX]{x27E7} & \ll & \displaystyle (X/M^{b})^{-\unicode[STIX]{x1D6EC}-\unicode[STIX]{x1D6FF}}\unicode[STIX]{x27E6}K_{a_{L},b_{L}}^{r,r}(X)\unicode[STIX]{x27E7}+M^{-3sk^{R}b}\nonumber\\ \displaystyle & \ll & \displaystyle \unicode[STIX]{x1D6E9}_{L}(\mathbf{m},m_{L};\mathbf{h},h_{L}).\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle (X/M^{b})^{-\unicode[STIX]{x1D6EC}-\unicode[STIX]{x1D6FF}}\unicode[STIX]{x27E6}I_{b_{L-1},b_{m_{L}}^{\ast }}^{r,r}(X)\unicode[STIX]{x27E7} & \ll & \displaystyle (X/M^{b})^{-\unicode[STIX]{x1D6EC}-\unicode[STIX]{x1D6FF}}\unicode[STIX]{x27E6}K_{a_{L},b_{L}}^{r,r}(X)\unicode[STIX]{x27E7}+M^{-3sk^{R}b}\nonumber\\ \displaystyle & \ll & \displaystyle \unicode[STIX]{x1D6E9}_{L}(\mathbf{m},m_{L};\mathbf{h},h_{L}).\nonumber\end{eqnarray}$$
On substituting this estimate into (7.13), we deduce from (7.3) that
 $$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D6E9}_{L-1}(\mathbf{m};\mathbf{h}) & \ll & \displaystyle (M^{b-b_{L-1}})^{(1-r/s)(\unicode[STIX]{x1D6EC}+\unicode[STIX]{x1D6FF})}\mathop{\prod }_{m_{L}=0}^{r-1}\unicode[STIX]{x1D6E9}_{L}(\mathbf{m},m_{L};\mathbf{h},h_{L})^{\unicode[STIX]{x1D719}_{m_{L}}}\nonumber\\ \displaystyle & \ll & \displaystyle \mathop{\prod }_{m_{L}=0}^{r-1}\unicode[STIX]{x1D6E9}_{L}(\mathbf{m},m_{L};\mathbf{h},h_{L})^{\unicode[STIX]{x1D719}_{m_{L}}}.\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D6E9}_{L-1}(\mathbf{m};\mathbf{h}) & \ll & \displaystyle (M^{b-b_{L-1}})^{(1-r/s)(\unicode[STIX]{x1D6EC}+\unicode[STIX]{x1D6FF})}\mathop{\prod }_{m_{L}=0}^{r-1}\unicode[STIX]{x1D6E9}_{L}(\mathbf{m},m_{L};\mathbf{h},h_{L})^{\unicode[STIX]{x1D719}_{m_{L}}}\nonumber\\ \displaystyle & \ll & \displaystyle \mathop{\prod }_{m_{L}=0}^{r-1}\unicode[STIX]{x1D6E9}_{L}(\mathbf{m},m_{L};\mathbf{h},h_{L})^{\unicode[STIX]{x1D719}_{m_{L}}}.\end{eqnarray}$$
Applying this estimate in combination with (7.12) within the case
 $l=L-1$
of the inductive hypothesis (7.9), we conclude that for some choice of the integer
$l=L-1$
of the inductive hypothesis (7.9), we conclude that for some choice of the integer
 $h_{L}=h_{L}(\mathbf{m})$
, one has the upper bound
$h_{L}=h_{L}(\mathbf{m})$
, one has the upper bound
 $$\begin{eqnarray}(X/M^{b})^{-\unicode[STIX]{x1D6EC}-\unicode[STIX]{x1D6FF}}\unicode[STIX]{x27E6}K_{a,b}(X)\unicode[STIX]{x27E7}\ll \mathop{\prod }_{\mathbf{m}\in [0,r-1]^{L-1}}\mathop{\prod }_{m_{L}=0}^{r-1}\unicode[STIX]{x1D6E9}_{L}(\mathbf{m},m_{L};\mathbf{h},h_{L})^{\unicode[STIX]{x1D719}_{m_{1}}\cdots \unicode[STIX]{x1D719}_{m_{L}}}.\end{eqnarray}$$
$$\begin{eqnarray}(X/M^{b})^{-\unicode[STIX]{x1D6EC}-\unicode[STIX]{x1D6FF}}\unicode[STIX]{x27E6}K_{a,b}(X)\unicode[STIX]{x27E7}\ll \mathop{\prod }_{\mathbf{m}\in [0,r-1]^{L-1}}\mathop{\prod }_{m_{L}=0}^{r-1}\unicode[STIX]{x1D6E9}_{L}(\mathbf{m},m_{L};\mathbf{h},h_{L})^{\unicode[STIX]{x1D719}_{m_{1}}\cdots \unicode[STIX]{x1D719}_{m_{L}}}.\end{eqnarray}$$
This confirms the inductive hypothesis (7.9) for
![]() $l=L$
, and thus the conclusion of the lemma follows by induction.◻
$l=L$
, and thus the conclusion of the lemma follows by induction.◻
We remark that in obtaining the estimate (7.14), we made use of the trivial lower bound
 $b_{L-1}\geqslant b$
. By discarding the power
$b_{L-1}\geqslant b$
. By discarding the power
 $M^{b-b_{L-1}}$
at this point, we are throwing away potentially useful information. However, it transpires that the weak information made available by the factor
$M^{b-b_{L-1}}$
at this point, we are throwing away potentially useful information. However, it transpires that the weak information made available by the factor
![]() $M^{b}$
in the conclusion of Lemma 7.3 already suffices for our purposes in the main iteration.
$M^{b}$
in the conclusion of Lemma 7.3 already suffices for our purposes in the main iteration.
8 The latent monograde process
Our objective in this section is to convert the block estimate encoded in Lemma 7.3 into a single monograde estimate that can be incorporated into our iterative method. We begin by recalling an elementary lemma from our previous work [Reference Wooley19].
Lemma 8.1. Suppose that
 $z_{0},\ldots ,z_{l}\in \mathbb{C}$
, and that
$z_{0},\ldots ,z_{l}\in \mathbb{C}$
, and that
![]() $\unicode[STIX]{x1D6FD}_{i}$
and
$\unicode[STIX]{x1D6FD}_{i}$
and
![]() $\unicode[STIX]{x1D6FE}_{i}$
are positive real numbers for
$\unicode[STIX]{x1D6FE}_{i}$
are positive real numbers for
 $0\leqslant i\leqslant l$
. Put
$0\leqslant i\leqslant l$
. Put
 $\unicode[STIX]{x1D6FA}=\unicode[STIX]{x1D6FD}_{0}\unicode[STIX]{x1D6FE}_{0}+\cdots +\unicode[STIX]{x1D6FD}_{l}\unicode[STIX]{x1D6FE}_{l}$
. Then one has
$\unicode[STIX]{x1D6FA}=\unicode[STIX]{x1D6FD}_{0}\unicode[STIX]{x1D6FE}_{0}+\cdots +\unicode[STIX]{x1D6FD}_{l}\unicode[STIX]{x1D6FE}_{l}$
. Then one has
 $$\begin{eqnarray}|z_{0}^{\unicode[STIX]{x1D6FD}_{0}}\cdots z_{l}^{\unicode[STIX]{x1D6FD}_{l}}|\leqslant \mathop{\sum }_{i=0}^{l}|z_{i}|^{\unicode[STIX]{x1D6FA}/\unicode[STIX]{x1D6FE}_{i}}.\end{eqnarray}$$
$$\begin{eqnarray}|z_{0}^{\unicode[STIX]{x1D6FD}_{0}}\cdots z_{l}^{\unicode[STIX]{x1D6FD}_{l}}|\leqslant \mathop{\sum }_{i=0}^{l}|z_{i}|^{\unicode[STIX]{x1D6FA}/\unicode[STIX]{x1D6FE}_{i}}.\end{eqnarray}$$
Proof. This is [Reference Wooley19, Lemma 8.1]. ◻
Before proceeding further, we introduce some additional notation. Define the positive number
![]() $s_{0}$
by means of the relation
$s_{0}$
by means of the relation
 $$\begin{eqnarray}s_{0}^{R}=\frac{\unicode[STIX]{x1D703}_{+}^{R+1}-\unicode[STIX]{x1D703}_{-}^{R+1}}{\unicode[STIX]{x1D703}_{+}-\unicode[STIX]{x1D703}_{-}}-\frac{\unicode[STIX]{x1D703}_{+}\unicode[STIX]{x1D703}_{-}}{r\sqrt{k}}\biggl(\frac{\unicode[STIX]{x1D703}_{+}^{R}-\unicode[STIX]{x1D703}_{-}^{R}}{\unicode[STIX]{x1D703}_{+}-\unicode[STIX]{x1D703}_{-}}\biggr),\end{eqnarray}$$
$$\begin{eqnarray}s_{0}^{R}=\frac{\unicode[STIX]{x1D703}_{+}^{R+1}-\unicode[STIX]{x1D703}_{-}^{R+1}}{\unicode[STIX]{x1D703}_{+}-\unicode[STIX]{x1D703}_{-}}-\frac{\unicode[STIX]{x1D703}_{+}\unicode[STIX]{x1D703}_{-}}{r\sqrt{k}}\biggl(\frac{\unicode[STIX]{x1D703}_{+}^{R}-\unicode[STIX]{x1D703}_{-}^{R}}{\unicode[STIX]{x1D703}_{+}-\unicode[STIX]{x1D703}_{-}}\biggr),\end{eqnarray}$$
in which
![]() $\unicode[STIX]{x1D703}_{\pm }$
are defined as in (2.6). We recall that, in view of (2.7), one has
$\unicode[STIX]{x1D703}_{\pm }$
are defined as in (2.6). We recall that, in view of (2.7), one has
![]() $s<s_{0}$
. Next, casting an eye towards the iterative relations (7.6) and (7.7), we define new sequences
$s<s_{0}$
. Next, casting an eye towards the iterative relations (7.6) and (7.7), we define new sequences
 $(\tilde{a}_{n})=(\tilde{a}_{n}(\mathbf{m}))$
and
$(\tilde{a}_{n})=(\tilde{a}_{n}(\mathbf{m}))$
and
 $(\tilde{b}_{n})=(\tilde{b}_{n}(\mathbf{m}))$
by means of the relations
$(\tilde{b}_{n})=(\tilde{b}_{n}(\mathbf{m}))$
by means of the relations
 $$\begin{eqnarray}\tilde{a}_{0}=1/\sqrt{k}\quad \text{and}\quad \tilde{b}_{0}=1,\end{eqnarray}$$
$$\begin{eqnarray}\tilde{a}_{0}=1/\sqrt{k}\quad \text{and}\quad \tilde{b}_{0}=1,\end{eqnarray}$$
and
 $$\begin{eqnarray}\tilde{a}_{n}=\tilde{b}_{n-1}\quad \text{and}\quad \tilde{b}_{n}=(k-m_{n})\tilde{b}_{n-1}-m_{n}\tilde{a}_{n-1}\quad (1\leqslant n\leqslant R).\end{eqnarray}$$
$$\begin{eqnarray}\tilde{a}_{n}=\tilde{b}_{n-1}\quad \text{and}\quad \tilde{b}_{n}=(k-m_{n})\tilde{b}_{n-1}-m_{n}\tilde{a}_{n-1}\quad (1\leqslant n\leqslant R).\end{eqnarray}$$
We then define
 $$\begin{eqnarray}k_{\mathbf{m}}=\tilde{b}_{R}(\mathbf{m})\quad \text{and}\quad \unicode[STIX]{x1D70C}_{\mathbf{m}}=\tilde{b}_{R}(\mathbf{m})(s/s_{0})^{R}\quad \text{for}~\mathbf{m}\in [0,r-1]^{R}.\end{eqnarray}$$
$$\begin{eqnarray}k_{\mathbf{m}}=\tilde{b}_{R}(\mathbf{m})\quad \text{and}\quad \unicode[STIX]{x1D70C}_{\mathbf{m}}=\tilde{b}_{R}(\mathbf{m})(s/s_{0})^{R}\quad \text{for}~\mathbf{m}\in [0,r-1]^{R}.\end{eqnarray}$$
The motivation for defining the sequences
![]() $(\tilde{a}_{n})$
and
$(\tilde{a}_{n})$
and
![]() $(\tilde{b}_{n})$
is to provide a base pair of sequences corresponding to the simplified situation in which
$(\tilde{b}_{n})$
is to provide a base pair of sequences corresponding to the simplified situation in which
 $h_{n}(\mathbf{m})=0$
for all
$h_{n}(\mathbf{m})=0$
for all
![]() $n$
and
$n$
and
![]() $\mathbf{m}$
. It transpires that the corresponding sequences
$\mathbf{m}$
. It transpires that the corresponding sequences
![]() $(a_{n})$
and
$(a_{n})$
and
![]() $(b_{n})$
, equipped with potentially positive values of
$(b_{n})$
, equipped with potentially positive values of
![]() $h_{n}(\mathbf{m})$
, may be bounded below by the sequences
$h_{n}(\mathbf{m})$
, may be bounded below by the sequences
![]() $(\tilde{a}_{n})$
and
$(\tilde{a}_{n})$
and
![]() $(\tilde{b}_{n})$
, although this turns out to be less simple to establish than might be supposed.
$(\tilde{b}_{n})$
, although this turns out to be less simple to establish than might be supposed.
Lemma 8.2. Suppose that
![]() $\unicode[STIX]{x1D6EC}\geqslant 0$
, let
$\unicode[STIX]{x1D6EC}\geqslant 0$
, let
![]() $a$
and
$a$
and
![]() $b$
be integers with
$b$
be integers with
 $$\begin{eqnarray}0\leqslant a<b\leqslant (20Rk^{2R}\unicode[STIX]{x1D703})^{-1}\quad \text{and}\quad (k-r+1)b\geqslant ra,\end{eqnarray}$$
$$\begin{eqnarray}0\leqslant a<b\leqslant (20Rk^{2R}\unicode[STIX]{x1D703})^{-1}\quad \text{and}\quad (k-r+1)b\geqslant ra,\end{eqnarray}$$
and suppose further that
 $a\leqslant b/\sqrt{k}$
. Suppose in addition that there are real numbers
$a\leqslant b/\sqrt{k}$
. Suppose in addition that there are real numbers
![]() $\unicode[STIX]{x1D713}$
,
$\unicode[STIX]{x1D713}$
,
![]() $c$
and
$c$
and
![]() $\unicode[STIX]{x1D6FE}$
, with
$\unicode[STIX]{x1D6FE}$
, with
 $$\begin{eqnarray}0\leqslant c\leqslant (2\unicode[STIX]{x1D6FF})^{-1}\unicode[STIX]{x1D703},\qquad \unicode[STIX]{x1D6FE}\geqslant -sb\quad \text{and}\quad \unicode[STIX]{x1D713}\geqslant 0,\end{eqnarray}$$
$$\begin{eqnarray}0\leqslant c\leqslant (2\unicode[STIX]{x1D6FF})^{-1}\unicode[STIX]{x1D703},\qquad \unicode[STIX]{x1D6FE}\geqslant -sb\quad \text{and}\quad \unicode[STIX]{x1D713}\geqslant 0,\end{eqnarray}$$
such that
 $$\begin{eqnarray}X^{\unicode[STIX]{x1D6EC}}M^{\unicode[STIX]{x1D6EC}\unicode[STIX]{x1D713}}\ll X^{c\unicode[STIX]{x1D6FF}}M^{-\unicode[STIX]{x1D6FE}}\unicode[STIX]{x27E6}K_{a,b}^{r,r}(X)\unicode[STIX]{x27E7}.\end{eqnarray}$$
$$\begin{eqnarray}X^{\unicode[STIX]{x1D6EC}}M^{\unicode[STIX]{x1D6EC}\unicode[STIX]{x1D713}}\ll X^{c\unicode[STIX]{x1D6FF}}M^{-\unicode[STIX]{x1D6FE}}\unicode[STIX]{x27E6}K_{a,b}^{r,r}(X)\unicode[STIX]{x27E7}.\end{eqnarray}$$
Then, for some
 $\mathbf{m}\in [0,r-1]^{R}$
, there are a real number
$\mathbf{m}\in [0,r-1]^{R}$
, there are a real number
![]() $h$
with
$h$
with
 $0\leqslant h\leqslant 16k^{2R}b$
, and positive integers
$0\leqslant h\leqslant 16k^{2R}b$
, and positive integers
![]() $a^{\prime }$
and
$a^{\prime }$
and
![]() $b^{\prime }$
with
$b^{\prime }$
with
 $a^{\prime }\leqslant b^{\prime }/\sqrt{k}$
, such that
$a^{\prime }\leqslant b^{\prime }/\sqrt{k}$
, such that
 $$\begin{eqnarray}X^{\unicode[STIX]{x1D6EC}}M^{\unicode[STIX]{x1D6EC}\unicode[STIX]{x1D713}^{\prime }}\ll X^{c^{\prime }\unicode[STIX]{x1D6FF}}M^{-\unicode[STIX]{x1D6FE}^{\prime }}\unicode[STIX]{x27E6}K_{a^{\prime },b^{\prime }}^{r,r}(X)\unicode[STIX]{x27E7},\end{eqnarray}$$
$$\begin{eqnarray}X^{\unicode[STIX]{x1D6EC}}M^{\unicode[STIX]{x1D6EC}\unicode[STIX]{x1D713}^{\prime }}\ll X^{c^{\prime }\unicode[STIX]{x1D6FF}}M^{-\unicode[STIX]{x1D6FE}^{\prime }}\unicode[STIX]{x27E6}K_{a^{\prime },b^{\prime }}^{r,r}(X)\unicode[STIX]{x27E7},\end{eqnarray}$$
where
![]() $\unicode[STIX]{x1D713}^{\prime }$
,
$\unicode[STIX]{x1D713}^{\prime }$
,
![]() $c^{\prime }$
,
$c^{\prime }$
,
![]() $\unicode[STIX]{x1D6FE}^{\prime }$
and
$\unicode[STIX]{x1D6FE}^{\prime }$
and
![]() $b^{\prime }$
are real numbers satisfying the conditions
$b^{\prime }$
are real numbers satisfying the conditions
 $$\begin{eqnarray}\displaystyle & \displaystyle \unicode[STIX]{x1D713}^{\prime }=\unicode[STIX]{x1D70C}_{\mathbf{m}}(\unicode[STIX]{x1D713}+(1-r/s)b),\qquad c^{\prime }=\unicode[STIX]{x1D70C}_{\mathbf{m}}(c+1),\qquad & \displaystyle \nonumber\\ \displaystyle & \displaystyle \unicode[STIX]{x1D6FE}^{\prime }=\unicode[STIX]{x1D70C}_{\mathbf{m}}\unicode[STIX]{x1D6FE},\qquad b^{\prime }=k_{\mathbf{m}}b+h. & \displaystyle \nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle \unicode[STIX]{x1D713}^{\prime }=\unicode[STIX]{x1D70C}_{\mathbf{m}}(\unicode[STIX]{x1D713}+(1-r/s)b),\qquad c^{\prime }=\unicode[STIX]{x1D70C}_{\mathbf{m}}(c+1),\qquad & \displaystyle \nonumber\\ \displaystyle & \displaystyle \unicode[STIX]{x1D6FE}^{\prime }=\unicode[STIX]{x1D70C}_{\mathbf{m}}\unicode[STIX]{x1D6FE},\qquad b^{\prime }=k_{\mathbf{m}}b+h. & \displaystyle \nonumber\end{eqnarray}$$
Moreover, the real number
![]() $k_{\mathbf{m}}$
satisfies
$k_{\mathbf{m}}$
satisfies
 $2^{R}\leqslant k_{\mathbf{m}}\leqslant k^{R}$
.
$2^{R}\leqslant k_{\mathbf{m}}\leqslant k^{R}$
.
Proof. We deduce from the postulated bound (8.5) and Lemma 7.3 that there exists a choice of the tuple
 $\mathbf{h}=\mathbf{h}(\mathbf{m})$
, with
$\mathbf{h}=\mathbf{h}(\mathbf{m})$
, with
 $0\leqslant h_{n}(\mathbf{m})\leqslant 15k^{R}b$
$0\leqslant h_{n}(\mathbf{m})\leqslant 15k^{R}b$
 $(1\leqslant n\leqslant R)$
, such that
$(1\leqslant n\leqslant R)$
, such that
 $$\begin{eqnarray}X^{\unicode[STIX]{x1D6EC}}M^{\unicode[STIX]{x1D6EC}\unicode[STIX]{x1D713}}\ll X^{(c+1)\unicode[STIX]{x1D6FF}}M^{-\unicode[STIX]{x1D6FE}}(X/M^{b})^{\unicode[STIX]{x1D6EC}}\mathop{\prod }_{\mathbf{m}\in [0,r-1]^{R}}\unicode[STIX]{x1D6E9}_{R}(\mathbf{m};\mathbf{h})^{\unicode[STIX]{x1D719}_{m_{1}}\cdots \unicode[STIX]{x1D719}_{m_{R}}}.\end{eqnarray}$$
$$\begin{eqnarray}X^{\unicode[STIX]{x1D6EC}}M^{\unicode[STIX]{x1D6EC}\unicode[STIX]{x1D713}}\ll X^{(c+1)\unicode[STIX]{x1D6FF}}M^{-\unicode[STIX]{x1D6FE}}(X/M^{b})^{\unicode[STIX]{x1D6EC}}\mathop{\prod }_{\mathbf{m}\in [0,r-1]^{R}}\unicode[STIX]{x1D6E9}_{R}(\mathbf{m};\mathbf{h})^{\unicode[STIX]{x1D719}_{m_{1}}\cdots \unicode[STIX]{x1D719}_{m_{R}}}.\end{eqnarray}$$
Consequently, one has
 $$\begin{eqnarray}\mathop{\prod }_{\mathbf{m}\in [0,r-1]^{R}}\unicode[STIX]{x1D6E9}_{R}(\mathbf{m};\mathbf{h})^{\unicode[STIX]{x1D719}_{m_{1}}\cdots \unicode[STIX]{x1D719}_{m_{R}}}\gg X^{-(c+1)\unicode[STIX]{x1D6FF}}M^{\unicode[STIX]{x1D6EC}(\unicode[STIX]{x1D713}+b)+\unicode[STIX]{x1D6FE}}.\end{eqnarray}$$
$$\begin{eqnarray}\mathop{\prod }_{\mathbf{m}\in [0,r-1]^{R}}\unicode[STIX]{x1D6E9}_{R}(\mathbf{m};\mathbf{h})^{\unicode[STIX]{x1D719}_{m_{1}}\cdots \unicode[STIX]{x1D719}_{m_{R}}}\gg X^{-(c+1)\unicode[STIX]{x1D6FF}}M^{\unicode[STIX]{x1D6EC}(\unicode[STIX]{x1D713}+b)+\unicode[STIX]{x1D6FE}}.\end{eqnarray}$$
Note that, in view of (7.3), one has
 $$\begin{eqnarray}\mathop{\sum }_{m=0}^{r-1}\unicode[STIX]{x1D719}_{m}=r/s,\end{eqnarray}$$
$$\begin{eqnarray}\mathop{\sum }_{m=0}^{r-1}\unicode[STIX]{x1D719}_{m}=r/s,\end{eqnarray}$$
so that
 $$\begin{eqnarray}\mathop{\sum }_{\mathbf{m}\in [0,r-1]^{R}}\unicode[STIX]{x1D719}_{m_{1}}\cdots \unicode[STIX]{x1D719}_{m_{R}}=(r/s)^{R}\leqslant r/s.\end{eqnarray}$$
$$\begin{eqnarray}\mathop{\sum }_{\mathbf{m}\in [0,r-1]^{R}}\unicode[STIX]{x1D719}_{m_{1}}\cdots \unicode[STIX]{x1D719}_{m_{R}}=(r/s)^{R}\leqslant r/s.\end{eqnarray}$$
Then we deduce from the definition (7.8) of
 $\unicode[STIX]{x1D6E9}_{n}(\mathbf{m};\mathbf{h})$
that
$\unicode[STIX]{x1D6E9}_{n}(\mathbf{m};\mathbf{h})$
that
 $$\begin{eqnarray}\displaystyle & & \displaystyle \mathop{\prod }_{\mathbf{m}\in [0,r-1]^{R}}(X^{-\unicode[STIX]{x1D6EC}}\unicode[STIX]{x27E6}K_{a_{R},b_{R}}^{r,r}(X)\unicode[STIX]{x27E7}+M^{-3sk^{R}b})^{\unicode[STIX]{x1D719}_{m_{1}}\cdots \unicode[STIX]{x1D719}_{m_{R}}}\nonumber\\ \displaystyle & & \displaystyle \quad \gg X^{-(c+1)\unicode[STIX]{x1D6FF}}M^{\unicode[STIX]{x1D6EC}(\unicode[STIX]{x1D713}+(1-r/s)b)+\unicode[STIX]{x1D6FE}}.\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle \mathop{\prod }_{\mathbf{m}\in [0,r-1]^{R}}(X^{-\unicode[STIX]{x1D6EC}}\unicode[STIX]{x27E6}K_{a_{R},b_{R}}^{r,r}(X)\unicode[STIX]{x27E7}+M^{-3sk^{R}b})^{\unicode[STIX]{x1D719}_{m_{1}}\cdots \unicode[STIX]{x1D719}_{m_{R}}}\nonumber\\ \displaystyle & & \displaystyle \quad \gg X^{-(c+1)\unicode[STIX]{x1D6FF}}M^{\unicode[STIX]{x1D6EC}(\unicode[STIX]{x1D713}+(1-r/s)b)+\unicode[STIX]{x1D6FE}}.\end{eqnarray}$$
In preparation for our application of Lemma 8.1, we examine the exponents
 $\unicode[STIX]{x1D719}_{m_{1}}\cdots \unicode[STIX]{x1D719}_{m_{R}}$
occurring in the lower bound (8.8). Our plan is to apply Lemma 8.1 with exponents given by
$\unicode[STIX]{x1D719}_{m_{1}}\cdots \unicode[STIX]{x1D719}_{m_{R}}$
occurring in the lower bound (8.8). Our plan is to apply Lemma 8.1 with exponents given by
 $$\begin{eqnarray}\unicode[STIX]{x1D6FD}_{\mathbf{m}}^{(n)}=\unicode[STIX]{x1D719}_{m_{1}}\cdots \unicode[STIX]{x1D719}_{m_{n}}\quad \text{and}\quad \unicode[STIX]{x1D6FE}_{\mathbf{m}}^{(n)}=\tilde{b}_{n}(\mathbf{m})\quad (\mathbf{m}\in [0,r-1]^{n}),\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D6FD}_{\mathbf{m}}^{(n)}=\unicode[STIX]{x1D719}_{m_{1}}\cdots \unicode[STIX]{x1D719}_{m_{n}}\quad \text{and}\quad \unicode[STIX]{x1D6FE}_{\mathbf{m}}^{(n)}=\tilde{b}_{n}(\mathbf{m})\quad (\mathbf{m}\in [0,r-1]^{n}),\end{eqnarray}$$
in the natural sense. In order to analyze the quantity
![]() $\unicode[STIX]{x1D6FA}$
that will emerge from the application of this lemma, we define
$\unicode[STIX]{x1D6FA}$
that will emerge from the application of this lemma, we define
 $$\begin{eqnarray}B_{n}=\mathop{\sum }_{\mathbf{m}\in [0,r-1]^{n}}\unicode[STIX]{x1D6FD}_{\mathbf{m}}^{(n)}\tilde{b}_{n}(\mathbf{m})\quad \text{and}\quad A_{n}=\mathop{\sum }_{\mathbf{m}\in [0,r-1]^{n}}\unicode[STIX]{x1D6FD}_{\mathbf{m}}^{(n)}\tilde{a}_{n}(\mathbf{m}),\end{eqnarray}$$
$$\begin{eqnarray}B_{n}=\mathop{\sum }_{\mathbf{m}\in [0,r-1]^{n}}\unicode[STIX]{x1D6FD}_{\mathbf{m}}^{(n)}\tilde{b}_{n}(\mathbf{m})\quad \text{and}\quad A_{n}=\mathop{\sum }_{\mathbf{m}\in [0,r-1]^{n}}\unicode[STIX]{x1D6FD}_{\mathbf{m}}^{(n)}\tilde{a}_{n}(\mathbf{m}),\end{eqnarray}$$
and then put
![]() $\unicode[STIX]{x1D6FA}=B_{R}$
. From the iterative formulae (8.2) and (8.3), we obtain for
$\unicode[STIX]{x1D6FA}=B_{R}$
. From the iterative formulae (8.2) and (8.3), we obtain for
![]() $n\geqslant 1$
the relations
$n\geqslant 1$
the relations
 $$\begin{eqnarray}\displaystyle B_{n+1} & = & \displaystyle \mathop{\sum }_{m_{n+1}=0}^{r-1}~\mathop{\sum }_{\mathbf{m}\in [0,r-1]^{n}}((k-m_{n+1})\tilde{b}_{n}(\mathbf{m})-m_{n+1}\tilde{a}_{n}(\mathbf{m}))\unicode[STIX]{x1D719}_{m_{1}}\cdots \unicode[STIX]{x1D719}_{m_{n+1}}\nonumber\\ \displaystyle & = & \displaystyle B_{n}\mathop{\sum }_{m=0}^{r-1}(k-m)\unicode[STIX]{x1D719}_{m}-A_{n}\mathop{\sum }_{m=0}^{r-1}m\unicode[STIX]{x1D719}_{m}\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle B_{n+1} & = & \displaystyle \mathop{\sum }_{m_{n+1}=0}^{r-1}~\mathop{\sum }_{\mathbf{m}\in [0,r-1]^{n}}((k-m_{n+1})\tilde{b}_{n}(\mathbf{m})-m_{n+1}\tilde{a}_{n}(\mathbf{m}))\unicode[STIX]{x1D719}_{m_{1}}\cdots \unicode[STIX]{x1D719}_{m_{n+1}}\nonumber\\ \displaystyle & = & \displaystyle B_{n}\mathop{\sum }_{m=0}^{r-1}(k-m)\unicode[STIX]{x1D719}_{m}-A_{n}\mathop{\sum }_{m=0}^{r-1}m\unicode[STIX]{x1D719}_{m}\end{eqnarray}$$
and
 $$\begin{eqnarray}A_{n+1}=\mathop{\sum }_{m_{n+1}=0}^{r-1}\mathop{\sum }_{\mathbf{m}\in [0,r-1]^{n}}\tilde{b}_{n}(\mathbf{m})\unicode[STIX]{x1D719}_{m_{1}}\cdots \unicode[STIX]{x1D719}_{m_{n+1}}=B_{n}\mathop{\sum }_{m=0}^{r-1}\unicode[STIX]{x1D719}_{m}.\end{eqnarray}$$
$$\begin{eqnarray}A_{n+1}=\mathop{\sum }_{m_{n+1}=0}^{r-1}\mathop{\sum }_{\mathbf{m}\in [0,r-1]^{n}}\tilde{b}_{n}(\mathbf{m})\unicode[STIX]{x1D719}_{m_{1}}\cdots \unicode[STIX]{x1D719}_{m_{n+1}}=B_{n}\mathop{\sum }_{m=0}^{r-1}\unicode[STIX]{x1D719}_{m}.\end{eqnarray}$$
We observe that from (7.1), one has
 $$\begin{eqnarray}\mathop{\sum }_{m=0}^{r-1}(k-m)\unicode[STIX]{x1D719}_{m}=\mathop{\sum }_{m=0}^{r-1}\frac{(k-m)(s-r)}{(s-m)(s-m-1)}.\end{eqnarray}$$
$$\begin{eqnarray}\mathop{\sum }_{m=0}^{r-1}(k-m)\unicode[STIX]{x1D719}_{m}=\mathop{\sum }_{m=0}^{r-1}\frac{(k-m)(s-r)}{(s-m)(s-m-1)}.\end{eqnarray}$$
The summands on the right-hand side here may be rewritten in the shape
 $$\begin{eqnarray}\frac{(r-m)(k-m)}{s-m}-\frac{(r-m-1)(k-m-1)}{s-m-1}-\frac{r-m-1}{s-m-1}.\end{eqnarray}$$
$$\begin{eqnarray}\frac{(r-m)(k-m)}{s-m}-\frac{(r-m-1)(k-m-1)}{s-m-1}-\frac{r-m-1}{s-m-1}.\end{eqnarray}$$
Hence, we obtain
 $$\begin{eqnarray}s\mathop{\sum }_{m=0}^{r-1}(k-m)\unicode[STIX]{x1D719}_{m}=kr-s\mathop{\sum }_{l=1}^{r}\frac{r-l}{s-l}=kr-\frac{1}{2}r(r-1)-\unicode[STIX]{x1D6E5},\end{eqnarray}$$
$$\begin{eqnarray}s\mathop{\sum }_{m=0}^{r-1}(k-m)\unicode[STIX]{x1D719}_{m}=kr-s\mathop{\sum }_{l=1}^{r}\frac{r-l}{s-l}=kr-\frac{1}{2}r(r-1)-\unicode[STIX]{x1D6E5},\end{eqnarray}$$
in which
![]() $\unicode[STIX]{x1D6E5}$
is defined via (2.3). In addition, one has
$\unicode[STIX]{x1D6E5}$
is defined via (2.3). In addition, one has
 $$\begin{eqnarray}\displaystyle s\mathop{\sum }_{m=0}^{r-1}m\unicode[STIX]{x1D719}_{m} & = & \displaystyle sk\mathop{\sum }_{m=0}^{r-1}\unicode[STIX]{x1D719}_{m}-s\mathop{\sum }_{m=0}^{r-1}(k-m)\unicode[STIX]{x1D719}_{m}\nonumber\\ \displaystyle & = & \displaystyle kr-\biggl(kr-\frac{1}{2}r(r-1)-\unicode[STIX]{x1D6E5}\biggr)\nonumber\\ \displaystyle & = & \displaystyle \frac{1}{2}r(r-1)+\unicode[STIX]{x1D6E5}.\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle s\mathop{\sum }_{m=0}^{r-1}m\unicode[STIX]{x1D719}_{m} & = & \displaystyle sk\mathop{\sum }_{m=0}^{r-1}\unicode[STIX]{x1D719}_{m}-s\mathop{\sum }_{m=0}^{r-1}(k-m)\unicode[STIX]{x1D719}_{m}\nonumber\\ \displaystyle & = & \displaystyle kr-\biggl(kr-\frac{1}{2}r(r-1)-\unicode[STIX]{x1D6E5}\biggr)\nonumber\\ \displaystyle & = & \displaystyle \frac{1}{2}r(r-1)+\unicode[STIX]{x1D6E5}.\nonumber\end{eqnarray}$$
Utilizing the formulae just obtained, we conclude from (8.9) that for
![]() $n\geqslant 1$
, one has
$n\geqslant 1$
, one has
 $$\begin{eqnarray}sB_{n+1}=(kr-{\textstyle \frac{1}{2}}r(r-1)-\unicode[STIX]{x1D6E5})B_{n}-({\textstyle \frac{1}{2}}r(r-1)+\unicode[STIX]{x1D6E5})A_{n},\end{eqnarray}$$
$$\begin{eqnarray}sB_{n+1}=(kr-{\textstyle \frac{1}{2}}r(r-1)-\unicode[STIX]{x1D6E5})B_{n}-({\textstyle \frac{1}{2}}r(r-1)+\unicode[STIX]{x1D6E5})A_{n},\end{eqnarray}$$
while from (8.7) and (8.10), one sees that
 $$\begin{eqnarray}sA_{n+1}=rB_{n}.\end{eqnarray}$$
$$\begin{eqnarray}sA_{n+1}=rB_{n}.\end{eqnarray}$$
Then, on recalling (2.5), we arrive at the iterative relation
 $$\begin{eqnarray}s^{2}B_{n+2}-s\mathfrak{a}B_{n+1}+\mathfrak{b}B_{n}=0\quad (n\geqslant 1).\end{eqnarray}$$
$$\begin{eqnarray}s^{2}B_{n+2}-s\mathfrak{a}B_{n+1}+\mathfrak{b}B_{n}=0\quad (n\geqslant 1).\end{eqnarray}$$
In addition, also from (2.5) and (8.2), one has the initial data
 $$\begin{eqnarray}sB_{1}=s\mathop{\sum }_{m=0}^{r-1}((k-m)\tilde{b}_{0}-m\tilde{a}_{0})\unicode[STIX]{x1D719}_{m}=\mathfrak{a}-\mathfrak{b}/(r\sqrt{k})\end{eqnarray}$$
$$\begin{eqnarray}sB_{1}=s\mathop{\sum }_{m=0}^{r-1}((k-m)\tilde{b}_{0}-m\tilde{a}_{0})\unicode[STIX]{x1D719}_{m}=\mathfrak{a}-\mathfrak{b}/(r\sqrt{k})\end{eqnarray}$$
and, from (8.2) and (8.7), one finds that
 $$\begin{eqnarray}sA_{1}=s\mathop{\sum }_{m=0}^{r-1}\tilde{b}_{0}\unicode[STIX]{x1D719}_{m}=r.\end{eqnarray}$$
$$\begin{eqnarray}sA_{1}=s\mathop{\sum }_{m=0}^{r-1}\tilde{b}_{0}\unicode[STIX]{x1D719}_{m}=r.\end{eqnarray}$$
Thus, we see also that
 $$\begin{eqnarray}\displaystyle s^{2}B_{2} & = & \displaystyle s^{2}\mathop{\sum }_{m=0}^{r-1}((k-m)B_{1}-mA_{1})\unicode[STIX]{x1D719}_{m}=s(\mathfrak{a}B_{1}-\mathfrak{b}A_{1}/r)\nonumber\\ \displaystyle & = & \displaystyle \mathfrak{a}(\mathfrak{a}-\mathfrak{b}/(r\sqrt{k}))-\mathfrak{b}.\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle s^{2}B_{2} & = & \displaystyle s^{2}\mathop{\sum }_{m=0}^{r-1}((k-m)B_{1}-mA_{1})\unicode[STIX]{x1D719}_{m}=s(\mathfrak{a}B_{1}-\mathfrak{b}A_{1}/r)\nonumber\\ \displaystyle & = & \displaystyle \mathfrak{a}(\mathfrak{a}-\mathfrak{b}/(r\sqrt{k}))-\mathfrak{b}.\end{eqnarray}$$
On recalling (2.6), one finds that the recurrence formula (8.11) has a solution of the shape
 $$\begin{eqnarray}s^{n}B_{n}=\unicode[STIX]{x1D70E}_{+}\unicode[STIX]{x1D703}_{+}^{n}+\unicode[STIX]{x1D70E}_{-}\unicode[STIX]{x1D703}_{-}^{n}\quad (n\geqslant 1),\end{eqnarray}$$
$$\begin{eqnarray}s^{n}B_{n}=\unicode[STIX]{x1D70E}_{+}\unicode[STIX]{x1D703}_{+}^{n}+\unicode[STIX]{x1D70E}_{-}\unicode[STIX]{x1D703}_{-}^{n}\quad (n\geqslant 1),\end{eqnarray}$$
where, in view of (8.12) and (8.13), one has
 $$\begin{eqnarray}\unicode[STIX]{x1D70E}_{+}\unicode[STIX]{x1D703}_{+}+\unicode[STIX]{x1D70E}_{-}\unicode[STIX]{x1D703}_{-}=sB_{1}=\mathfrak{a}-\mathfrak{b}/(r\sqrt{k})\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D70E}_{+}\unicode[STIX]{x1D703}_{+}+\unicode[STIX]{x1D70E}_{-}\unicode[STIX]{x1D703}_{-}=sB_{1}=\mathfrak{a}-\mathfrak{b}/(r\sqrt{k})\end{eqnarray}$$
and
 $$\begin{eqnarray}\unicode[STIX]{x1D70E}_{+}\unicode[STIX]{x1D703}_{+}^{2}+\unicode[STIX]{x1D70E}_{-}\unicode[STIX]{x1D703}_{-}^{2}=s^{2}B_{2}=\mathfrak{a}(\mathfrak{a}-\mathfrak{b}/(r\sqrt{k}))-\mathfrak{b}.\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D70E}_{+}\unicode[STIX]{x1D703}_{+}^{2}+\unicode[STIX]{x1D70E}_{-}\unicode[STIX]{x1D703}_{-}^{2}=s^{2}B_{2}=\mathfrak{a}(\mathfrak{a}-\mathfrak{b}/(r\sqrt{k}))-\mathfrak{b}.\end{eqnarray}$$
Since
 $\mathfrak{a}=\unicode[STIX]{x1D703}_{+}+\unicode[STIX]{x1D703}_{-}$
and
$\mathfrak{a}=\unicode[STIX]{x1D703}_{+}+\unicode[STIX]{x1D703}_{-}$
and
 $\mathfrak{b}=\unicode[STIX]{x1D703}_{+}\unicode[STIX]{x1D703}_{-}$
, we therefore deduce that
$\mathfrak{b}=\unicode[STIX]{x1D703}_{+}\unicode[STIX]{x1D703}_{-}$
, we therefore deduce that
 $$\begin{eqnarray}s^{n}B_{n}=\frac{\unicode[STIX]{x1D703}_{+}^{n+1}-\unicode[STIX]{x1D703}_{-}^{n+1}}{\unicode[STIX]{x1D703}_{+}-\unicode[STIX]{x1D703}_{-}}-\frac{\unicode[STIX]{x1D703}_{+}\unicode[STIX]{x1D703}_{-}}{r\sqrt{k}}\biggl(\frac{\unicode[STIX]{x1D703}_{+}^{n}-\unicode[STIX]{x1D703}_{-}^{n}}{\unicode[STIX]{x1D703}_{+}-\unicode[STIX]{x1D703}_{-}}\biggr).\end{eqnarray}$$
$$\begin{eqnarray}s^{n}B_{n}=\frac{\unicode[STIX]{x1D703}_{+}^{n+1}-\unicode[STIX]{x1D703}_{-}^{n+1}}{\unicode[STIX]{x1D703}_{+}-\unicode[STIX]{x1D703}_{-}}-\frac{\unicode[STIX]{x1D703}_{+}\unicode[STIX]{x1D703}_{-}}{r\sqrt{k}}\biggl(\frac{\unicode[STIX]{x1D703}_{+}^{n}-\unicode[STIX]{x1D703}_{-}^{n}}{\unicode[STIX]{x1D703}_{+}-\unicode[STIX]{x1D703}_{-}}\biggr).\end{eqnarray}$$
In particular, on recalling (8.1), we find that
 $s^{R}B_{R}=s_{0}^{R}$
, so that
$s^{R}B_{R}=s_{0}^{R}$
, so that
 $$\begin{eqnarray}B_{R}=(s_{0}/s)^{R}.\end{eqnarray}$$
$$\begin{eqnarray}B_{R}=(s_{0}/s)^{R}.\end{eqnarray}$$
Also, therefore, it follows from (2.7) that
![]() $s<s_{0}$
and hence also that
$s<s_{0}$
and hence also that
![]() $B_{R}>1$
.
$B_{R}>1$
.
Returning now to the application of Lemma 8.1, we note first that
![]() $\unicode[STIX]{x1D6FA}=B_{R}$
and hence (8.8) yields the relation
$\unicode[STIX]{x1D6FA}=B_{R}$
and hence (8.8) yields the relation
 $$\begin{eqnarray}\displaystyle & & \displaystyle \mathop{\sum }_{\mathbf{m}\in [0,r-1]^{R}}(X^{-\unicode[STIX]{x1D6EC}}\unicode[STIX]{x27E6}K_{a_{R},b_{R}}^{r,r}(X)\unicode[STIX]{x27E7}+M^{-3sk^{R}b})^{B_{R}/\tilde{b}_{R}(\mathbf{m})}\nonumber\\ \displaystyle & & \displaystyle \quad \gg X^{-(c+1)\unicode[STIX]{x1D6FF}}M^{\unicode[STIX]{x1D6EC}(\unicode[STIX]{x1D713}+(1-r/s)b)+\unicode[STIX]{x1D6FE}}.\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle \mathop{\sum }_{\mathbf{m}\in [0,r-1]^{R}}(X^{-\unicode[STIX]{x1D6EC}}\unicode[STIX]{x27E6}K_{a_{R},b_{R}}^{r,r}(X)\unicode[STIX]{x27E7}+M^{-3sk^{R}b})^{B_{R}/\tilde{b}_{R}(\mathbf{m})}\nonumber\\ \displaystyle & & \displaystyle \quad \gg X^{-(c+1)\unicode[STIX]{x1D6FF}}M^{\unicode[STIX]{x1D6EC}(\unicode[STIX]{x1D713}+(1-r/s)b)+\unicode[STIX]{x1D6FE}}.\nonumber\end{eqnarray}$$
But, in view of (8.4) and (8.14), one has
 $\tilde{b}_{R}(\mathbf{m})/B_{R}=\unicode[STIX]{x1D70C}_{\mathbf{m}}$
, and thus we find that for some tuple
$\tilde{b}_{R}(\mathbf{m})/B_{R}=\unicode[STIX]{x1D70C}_{\mathbf{m}}$
, and thus we find that for some tuple
 $\mathbf{m}\in [0,r-1]^{R}$
, one has
$\mathbf{m}\in [0,r-1]^{R}$
, one has
 $$\begin{eqnarray}X^{-\unicode[STIX]{x1D6EC}}\unicode[STIX]{x27E6}K_{a_{R},b_{R}}^{r,r}(X)\unicode[STIX]{x27E7}+M^{-3sk^{R}b}\gg X^{-\unicode[STIX]{x1D70C}_{\mathbf{m}}(c+1)\unicode[STIX]{x1D6FF}}M^{\unicode[STIX]{x1D6EC}\unicode[STIX]{x1D70C}_{\mathbf{m}}(\unicode[STIX]{x1D713}+(1-r/s)b)+\unicode[STIX]{x1D70C}_{\mathbf{m}}\unicode[STIX]{x1D6FE}},\end{eqnarray}$$
$$\begin{eqnarray}X^{-\unicode[STIX]{x1D6EC}}\unicode[STIX]{x27E6}K_{a_{R},b_{R}}^{r,r}(X)\unicode[STIX]{x27E7}+M^{-3sk^{R}b}\gg X^{-\unicode[STIX]{x1D70C}_{\mathbf{m}}(c+1)\unicode[STIX]{x1D6FF}}M^{\unicode[STIX]{x1D6EC}\unicode[STIX]{x1D70C}_{\mathbf{m}}(\unicode[STIX]{x1D713}+(1-r/s)b)+\unicode[STIX]{x1D70C}_{\mathbf{m}}\unicode[STIX]{x1D6FE}},\end{eqnarray}$$
whence
 $$\begin{eqnarray}X^{-\unicode[STIX]{x1D6EC}}\unicode[STIX]{x27E6}K_{a_{R},b_{R}}^{r,r}(X)\unicode[STIX]{x27E7}+M^{-3sk^{R}b}\gg X^{-c^{\prime }\unicode[STIX]{x1D6FF}}M^{\unicode[STIX]{x1D6EC}\unicode[STIX]{x1D713}^{\prime }+\unicode[STIX]{x1D6FE}^{\prime }}.\end{eqnarray}$$
$$\begin{eqnarray}X^{-\unicode[STIX]{x1D6EC}}\unicode[STIX]{x27E6}K_{a_{R},b_{R}}^{r,r}(X)\unicode[STIX]{x27E7}+M^{-3sk^{R}b}\gg X^{-c^{\prime }\unicode[STIX]{x1D6FF}}M^{\unicode[STIX]{x1D6EC}\unicode[STIX]{x1D713}^{\prime }+\unicode[STIX]{x1D6FE}^{\prime }}.\end{eqnarray}$$
Two further issues remain to be resolved, the first being the removal of the term
 $M^{-3sk^{R}b}$
on the left-hand side of (8.15). We observe that the relations (8.3) ensure that
$M^{-3sk^{R}b}$
on the left-hand side of (8.15). We observe that the relations (8.3) ensure that
 $\tilde{b}_{R}(\mathbf{m})\leqslant k^{R}$
, and hence (8.4) reveals that
$\tilde{b}_{R}(\mathbf{m})\leqslant k^{R}$
, and hence (8.4) reveals that
 $\unicode[STIX]{x1D70C}_{\mathbf{m}}<\tilde{b}_{R}(\mathbf{m})\leqslant k^{R}$
. Our hypothesis on
$\unicode[STIX]{x1D70C}_{\mathbf{m}}<\tilde{b}_{R}(\mathbf{m})\leqslant k^{R}$
. Our hypothesis on
![]() $c$
therefore ensures that
$c$
therefore ensures that
 $$\begin{eqnarray}c^{\prime }\unicode[STIX]{x1D6FF}\leqslant k^{R}(c+1)\unicode[STIX]{x1D6FF}\leqslant k^{R}({\textstyle \frac{1}{2}}\unicode[STIX]{x1D703}+\unicode[STIX]{x1D6FF})\leqslant k^{R}\unicode[STIX]{x1D703},\end{eqnarray}$$
$$\begin{eqnarray}c^{\prime }\unicode[STIX]{x1D6FF}\leqslant k^{R}(c+1)\unicode[STIX]{x1D6FF}\leqslant k^{R}({\textstyle \frac{1}{2}}\unicode[STIX]{x1D703}+\unicode[STIX]{x1D6FF})\leqslant k^{R}\unicode[STIX]{x1D703},\end{eqnarray}$$
so that
 $$\begin{eqnarray}X^{-c^{\prime }\unicode[STIX]{x1D6FF}}M^{\unicode[STIX]{x1D6EC}\unicode[STIX]{x1D713}^{\prime }+\unicode[STIX]{x1D6FE}^{\prime }}\geqslant M^{-k^{R}+\unicode[STIX]{x1D70C}_{\boldsymbol{ m}}\unicode[STIX]{x1D6FE}}>M^{-k^{R}-sk^{R}b}.\end{eqnarray}$$
$$\begin{eqnarray}X^{-c^{\prime }\unicode[STIX]{x1D6FF}}M^{\unicode[STIX]{x1D6EC}\unicode[STIX]{x1D713}^{\prime }+\unicode[STIX]{x1D6FE}^{\prime }}\geqslant M^{-k^{R}+\unicode[STIX]{x1D70C}_{\boldsymbol{ m}}\unicode[STIX]{x1D6FE}}>M^{-k^{R}-sk^{R}b}.\end{eqnarray}$$
Since
 $$\begin{eqnarray}M^{-3sk^{R}b}\leqslant M^{-2sk^{R}-sk^{R}b},\end{eqnarray}$$
$$\begin{eqnarray}M^{-3sk^{R}b}\leqslant M^{-2sk^{R}-sk^{R}b},\end{eqnarray}$$
it follows from (8.15) that
 $$\begin{eqnarray}X^{-\unicode[STIX]{x1D6EC}}\unicode[STIX]{x27E6}K_{a_{R},b_{R}}^{r,r}(X)\unicode[STIX]{x27E7}\gg X^{-c^{\prime }\unicode[STIX]{x1D6FF}}M^{\unicode[STIX]{x1D6EC}\unicode[STIX]{x1D713}^{\prime }+\unicode[STIX]{x1D6FE}^{\prime }}.\end{eqnarray}$$
$$\begin{eqnarray}X^{-\unicode[STIX]{x1D6EC}}\unicode[STIX]{x27E6}K_{a_{R},b_{R}}^{r,r}(X)\unicode[STIX]{x27E7}\gg X^{-c^{\prime }\unicode[STIX]{x1D6FF}}M^{\unicode[STIX]{x1D6EC}\unicode[STIX]{x1D713}^{\prime }+\unicode[STIX]{x1D6FE}^{\prime }}.\end{eqnarray}$$
Our final task consists of extracting appropriate constraints on the parameters
![]() $a_{R}$
and
$a_{R}$
and
![]() $b_{R}$
. We note first that from (7.6), one has
$b_{R}$
. We note first that from (7.6), one has
 $a_{0}=\lfloor b/\sqrt{k}\rfloor \leqslant b/\sqrt{k}$
, so that on writing
$a_{0}=\lfloor b/\sqrt{k}\rfloor \leqslant b/\sqrt{k}$
, so that on writing
 $$\begin{eqnarray}h_{1}^{\ast }(\mathbf{m})=h_{1}(\mathbf{m})+m_{1}(b/\sqrt{k}-a_{0})\end{eqnarray}$$
$$\begin{eqnarray}h_{1}^{\ast }(\mathbf{m})=h_{1}(\mathbf{m})+m_{1}(b/\sqrt{k}-a_{0})\end{eqnarray}$$
and
 $$\begin{eqnarray}h_{n}^{\ast }(\mathbf{m})=h_{n}(\mathbf{m})\quad (n>1),\end{eqnarray}$$
$$\begin{eqnarray}h_{n}^{\ast }(\mathbf{m})=h_{n}(\mathbf{m})\quad (n>1),\end{eqnarray}$$
we have
 $$\begin{eqnarray}h_{1}^{\ast }(\mathbf{m})\leqslant h_{1}(\mathbf{m})+m_{1}\leqslant h_{1}(\mathbf{m})+k<16k^{R}b\end{eqnarray}$$
$$\begin{eqnarray}h_{1}^{\ast }(\mathbf{m})\leqslant h_{1}(\mathbf{m})+m_{1}\leqslant h_{1}(\mathbf{m})+k<16k^{R}b\end{eqnarray}$$
and
 $$\begin{eqnarray}h_{n}^{\ast }(\mathbf{m})=h_{n}(\mathbf{m})\leqslant 16k^{R}b\quad (n>1).\end{eqnarray}$$
$$\begin{eqnarray}h_{n}^{\ast }(\mathbf{m})=h_{n}(\mathbf{m})\leqslant 16k^{R}b\quad (n>1).\end{eqnarray}$$
Define the sequences
 $(a_{n}^{\ast })=(a_{n}^{\ast }(\mathbf{m};\mathbf{h}))$
and
$(a_{n}^{\ast })=(a_{n}^{\ast }(\mathbf{m};\mathbf{h}))$
and
 $(b_{n}^{\ast })=(b_{n}^{\ast }(\mathbf{m};\mathbf{h}))$
by means of the relations
$(b_{n}^{\ast })=(b_{n}^{\ast }(\mathbf{m};\mathbf{h}))$
by means of the relations
 $$\begin{eqnarray}a_{n}^{\ast }=b_{n-1}^{\ast }\quad \text{and}\quad b_{n}^{\ast }=(k-m_{n})b_{n-1}^{\ast }-m_{n}a_{n-1}^{\ast }+h_{n}^{\ast }(\mathbf{m})\quad (1\leqslant n\leqslant R),\end{eqnarray}$$
$$\begin{eqnarray}a_{n}^{\ast }=b_{n-1}^{\ast }\quad \text{and}\quad b_{n}^{\ast }=(k-m_{n})b_{n-1}^{\ast }-m_{n}a_{n-1}^{\ast }+h_{n}^{\ast }(\mathbf{m})\quad (1\leqslant n\leqslant R),\end{eqnarray}$$
where
 $$\begin{eqnarray}a_{0}^{\ast }=b/\sqrt{k}\quad \text{and}\quad b_{0}^{\ast }=b.\end{eqnarray}$$
$$\begin{eqnarray}a_{0}^{\ast }=b/\sqrt{k}\quad \text{and}\quad b_{0}^{\ast }=b.\end{eqnarray}$$
Then a comparison with (7.6) and (7.7) reveals that
![]() $a_{n}^{\ast }=a_{n}$
and
$a_{n}^{\ast }=a_{n}$
and
![]() $b_{n}^{\ast }=b_{n}$
for
$b_{n}^{\ast }=b_{n}$
for
![]() $n\geqslant 1$
. Moreover, it is apparent from (8.2) and (8.3) that
$n\geqslant 1$
. Moreover, it is apparent from (8.2) and (8.3) that
 $\tilde{a}_{n}b=a_{n}^{\ast }(\mathbf{m};\mathbf{0})$
and
$\tilde{a}_{n}b=a_{n}^{\ast }(\mathbf{m};\mathbf{0})$
and
 $\tilde{b}_{n}b=b_{n}^{\ast }(\mathbf{m};\mathbf{0})$
for
$\tilde{b}_{n}b=b_{n}^{\ast }(\mathbf{m};\mathbf{0})$
for
![]() $n\geqslant 0$
. We claim that for
$n\geqslant 0$
. We claim that for
![]() $n\geqslant 0$
, one has
$n\geqslant 0$
, one has
 $$\begin{eqnarray}b_{n}^{\ast }(\mathbf{m};\mathbf{0})\leqslant b_{n}^{\ast }(\mathbf{m};\mathbf{h})\leqslant b_{n}^{\ast }(\mathbf{m};\mathbf{0})+16k^{R+n}b.\end{eqnarray}$$
$$\begin{eqnarray}b_{n}^{\ast }(\mathbf{m};\mathbf{0})\leqslant b_{n}^{\ast }(\mathbf{m};\mathbf{h})\leqslant b_{n}^{\ast }(\mathbf{m};\mathbf{0})+16k^{R+n}b.\end{eqnarray}$$
The validity of these inequalities for
![]() $n=0$
is immediate from the definition of
$n=0$
is immediate from the definition of
 $b_{n}^{\ast }(\mathbf{m};\mathbf{h})$
. We use an inductive argument to establish (8.17) for
$b_{n}^{\ast }(\mathbf{m};\mathbf{h})$
. We use an inductive argument to establish (8.17) for
![]() $n\geqslant 1$
, though this requires some discussion.
$n\geqslant 1$
, though this requires some discussion.
Observe first that, by linearity, the recurrence sequence
 $b_{n}^{\ast }(\mathbf{m};\mathbf{h})$
is given by the formula
$b_{n}^{\ast }(\mathbf{m};\mathbf{h})$
is given by the formula
 $$\begin{eqnarray}b_{n}^{\ast }(\mathbf{m};\mathbf{h})=b_{n}^{\ast }(\mathbf{m};\mathbf{0})+\mathop{\sum }_{l=1}^{R}c_{n,l}(\mathbf{m};\mathbf{h})\quad (0\leqslant n\leqslant R),\end{eqnarray}$$
$$\begin{eqnarray}b_{n}^{\ast }(\mathbf{m};\mathbf{h})=b_{n}^{\ast }(\mathbf{m};\mathbf{0})+\mathop{\sum }_{l=1}^{R}c_{n,l}(\mathbf{m};\mathbf{h})\quad (0\leqslant n\leqslant R),\end{eqnarray}$$
in which
 $c_{n,l}(\mathbf{m};\mathbf{h})$
is determined by the relations
$c_{n,l}(\mathbf{m};\mathbf{h})$
is determined by the relations
 $$\begin{eqnarray}c_{l,l}(\mathbf{m};\mathbf{h})=h_{l}^{\ast }(\mathbf{m})\quad \text{and}\quad c_{n,l}(\mathbf{m};\mathbf{h})=0\quad (n<l),\end{eqnarray}$$
$$\begin{eqnarray}c_{l,l}(\mathbf{m};\mathbf{h})=h_{l}^{\ast }(\mathbf{m})\quad \text{and}\quad c_{n,l}(\mathbf{m};\mathbf{h})=0\quad (n<l),\end{eqnarray}$$
with
 $$\begin{eqnarray}c_{n+1,l}(\mathbf{m};\mathbf{h})=(k-m_{n+1})c_{n,l}(\mathbf{m};\mathbf{h})-m_{n+1}c_{n-1,l}(\mathbf{m};\mathbf{h})\quad (n\geqslant l).\end{eqnarray}$$
$$\begin{eqnarray}c_{n+1,l}(\mathbf{m};\mathbf{h})=(k-m_{n+1})c_{n,l}(\mathbf{m};\mathbf{h})-m_{n+1}c_{n-1,l}(\mathbf{m};\mathbf{h})\quad (n\geqslant l).\end{eqnarray}$$
We recall our assumption that
 $r\leqslant k-\lceil 2\sqrt{k}\rceil +2$
, which ensures that
$r\leqslant k-\lceil 2\sqrt{k}\rceil +2$
, which ensures that
 $$\begin{eqnarray}m_{n+1}\leqslant r-1\leqslant k-\lceil 2\sqrt{k}\rceil +1.\end{eqnarray}$$
$$\begin{eqnarray}m_{n+1}\leqslant r-1\leqslant k-\lceil 2\sqrt{k}\rceil +1.\end{eqnarray}$$
In view of this upper bound, we are able to prove by induction that
 $$\begin{eqnarray}c_{n+1,l}(\mathbf{m};\mathbf{h})>\sqrt{k}c_{n,l}(\mathbf{m};\mathbf{h})\end{eqnarray}$$
$$\begin{eqnarray}c_{n+1,l}(\mathbf{m};\mathbf{h})>\sqrt{k}c_{n,l}(\mathbf{m};\mathbf{h})\end{eqnarray}$$
for each integer
![]() $n$
with
$n$
with
 $n\geqslant l-1$
. In order to confirm this assertion, note first that such is the case when
$n\geqslant l-1$
. In order to confirm this assertion, note first that such is the case when
 $n=l-1$
. Granted that
$n=l-1$
. Granted that
 $c_{n,l}(\mathbf{m};\mathbf{h})>\sqrt{k}c_{n-1,l}(\mathbf{m};\mathbf{h})$
, meanwhile, one deduces from (8.19) that when
$c_{n,l}(\mathbf{m};\mathbf{h})>\sqrt{k}c_{n-1,l}(\mathbf{m};\mathbf{h})$
, meanwhile, one deduces from (8.19) that when
 $n\geqslant l-1$
, one has
$n\geqslant l-1$
, one has
 $$\begin{eqnarray}\displaystyle c_{n+1,l}(\mathbf{m};\mathbf{h}) & {\geqslant} & \displaystyle (\lceil 2\sqrt{k}\rceil -1)c_{n,l}(\mathbf{m};\mathbf{h})-(k-\lceil 2\sqrt{k}\rceil +1)c_{n,l}(\mathbf{m};\mathbf{h})/\sqrt{k}\nonumber\\ \displaystyle & {\geqslant} & \displaystyle ((2\sqrt{k}-1)-(\sqrt{k}-2+1/\sqrt{k}))c_{n,l}(\mathbf{m};\mathbf{h})\nonumber\\ \displaystyle & {>} & \displaystyle \sqrt{k}c_{n,l}(\mathbf{m};\mathbf{h}),\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle c_{n+1,l}(\mathbf{m};\mathbf{h}) & {\geqslant} & \displaystyle (\lceil 2\sqrt{k}\rceil -1)c_{n,l}(\mathbf{m};\mathbf{h})-(k-\lceil 2\sqrt{k}\rceil +1)c_{n,l}(\mathbf{m};\mathbf{h})/\sqrt{k}\nonumber\\ \displaystyle & {\geqslant} & \displaystyle ((2\sqrt{k}-1)-(\sqrt{k}-2+1/\sqrt{k}))c_{n,l}(\mathbf{m};\mathbf{h})\nonumber\\ \displaystyle & {>} & \displaystyle \sqrt{k}c_{n,l}(\mathbf{m};\mathbf{h}),\end{eqnarray}$$
establishing this inductive hypothesis. Thus, in particular, one arrives at the lower bound
 $c_{n,l}(\mathbf{m};\mathbf{h})\geqslant 0$
for all
$c_{n,l}(\mathbf{m};\mathbf{h})\geqslant 0$
for all
![]() $n$
. On substituting this conclusion into (8.18), we deduce that
$n$
. On substituting this conclusion into (8.18), we deduce that
 $b_{n}^{\ast }(\mathbf{m};\mathbf{h})\geqslant b_{n}^{\ast }(\mathbf{m};\mathbf{0})$
for every
$b_{n}^{\ast }(\mathbf{m};\mathbf{h})\geqslant b_{n}^{\ast }(\mathbf{m};\mathbf{0})$
for every
![]() $n$
, confirming the first of the inequalities in (8.17).
$n$
, confirming the first of the inequalities in (8.17).
Next, making use of the lower bound
 $c_{n,l}(\mathbf{m};\mathbf{h})\geqslant 0$
, just obtained, within (8.19), we find that
$c_{n,l}(\mathbf{m};\mathbf{h})\geqslant 0$
, just obtained, within (8.19), we find that
 $$\begin{eqnarray}c_{n+1,l}(\mathbf{m};\mathbf{h})\leqslant kc_{n,l}(\mathbf{m};\mathbf{h})\quad (n\geqslant l),\end{eqnarray}$$
$$\begin{eqnarray}c_{n+1,l}(\mathbf{m};\mathbf{h})\leqslant kc_{n,l}(\mathbf{m};\mathbf{h})\quad (n\geqslant l),\end{eqnarray}$$
so that
 $$\begin{eqnarray}c_{n,l}(\mathbf{m};\mathbf{h})\leqslant k^{n-l}h_{l}^{\ast }(\mathbf{m})\quad (n\geqslant l).\end{eqnarray}$$
$$\begin{eqnarray}c_{n,l}(\mathbf{m};\mathbf{h})\leqslant k^{n-l}h_{l}^{\ast }(\mathbf{m})\quad (n\geqslant l).\end{eqnarray}$$
We therefore deduce from (8.18) and the bound
 $h_{n}^{\ast }(\mathbf{m})\leqslant 16k^{R}b$
that
$h_{n}^{\ast }(\mathbf{m})\leqslant 16k^{R}b$
that
 $$\begin{eqnarray}b_{n}^{\ast }(\mathbf{m};\mathbf{h})\leqslant b_{n}^{\ast }(\mathbf{m};\mathbf{0})+16k^{R}b\mathop{\sum }_{l=1}^{n}k^{n-l}\leqslant b_{n}^{\ast }(\mathbf{m};\mathbf{0})+16k^{R+n}b.\end{eqnarray}$$
$$\begin{eqnarray}b_{n}^{\ast }(\mathbf{m};\mathbf{h})\leqslant b_{n}^{\ast }(\mathbf{m};\mathbf{0})+16k^{R}b\mathop{\sum }_{l=1}^{n}k^{n-l}\leqslant b_{n}^{\ast }(\mathbf{m};\mathbf{0})+16k^{R+n}b.\end{eqnarray}$$
This confirms the second of the inequalities in (8.17).
We now make use of the inequalities (8.17). Observe first that in view of (8.4), one has
 $$\begin{eqnarray}b_{R}=b_{R}^{\ast }(\mathbf{m};\mathbf{h})\leqslant b_{R}^{\ast }(\mathbf{m};\mathbf{0})+16k^{2R}b=\tilde{b}_{R}(\mathbf{m})b+16k^{2R}b=k_{\boldsymbol{ m}}b+16k^{2R}b.\end{eqnarray}$$
$$\begin{eqnarray}b_{R}=b_{R}^{\ast }(\mathbf{m};\mathbf{h})\leqslant b_{R}^{\ast }(\mathbf{m};\mathbf{0})+16k^{2R}b=\tilde{b}_{R}(\mathbf{m})b+16k^{2R}b=k_{\boldsymbol{ m}}b+16k^{2R}b.\end{eqnarray}$$
In addition, one has
 $$\begin{eqnarray}b_{R}=b_{R}^{\ast }(\mathbf{m};\mathbf{h})\geqslant b_{R}^{\ast }(\mathbf{m};\mathbf{0})=\tilde{b}_{R}(\mathbf{m})b=k_{\mathbf{m}}b.\end{eqnarray}$$
$$\begin{eqnarray}b_{R}=b_{R}^{\ast }(\mathbf{m};\mathbf{h})\geqslant b_{R}^{\ast }(\mathbf{m};\mathbf{0})=\tilde{b}_{R}(\mathbf{m})b=k_{\mathbf{m}}b.\end{eqnarray}$$
Thus, there exists an integer
![]() $h_{\mathbf{m}}$
, with
$h_{\mathbf{m}}$
, with
 $0\leqslant h_{\mathbf{m}}\leqslant 16k^{2R}b$
, for which one has
$0\leqslant h_{\mathbf{m}}\leqslant 16k^{2R}b$
, for which one has
 $b_{R}=k_{\mathbf{m}}b+h_{\mathbf{m}}$
.
$b_{R}=k_{\mathbf{m}}b+h_{\mathbf{m}}$
.
The argument confirming (8.21) shows also that for each
![]() $n\geqslant 0$
, one has
$n\geqslant 0$
, one has
 $$\begin{eqnarray}b_{n+1}^{\ast }(\mathbf{m};\mathbf{0})>\sqrt{k}b_{n}^{\ast }(\mathbf{m};\mathbf{0}).\end{eqnarray}$$
$$\begin{eqnarray}b_{n+1}^{\ast }(\mathbf{m};\mathbf{0})>\sqrt{k}b_{n}^{\ast }(\mathbf{m};\mathbf{0}).\end{eqnarray}$$
Then it follows from (8.18) and (8.20) that
 $$\begin{eqnarray}b_{R}^{\ast }(\mathbf{m};\mathbf{h})>\sqrt{k}b_{R-1}^{\ast }(\mathbf{m};\mathbf{h}),\end{eqnarray}$$
$$\begin{eqnarray}b_{R}^{\ast }(\mathbf{m};\mathbf{h})>\sqrt{k}b_{R-1}^{\ast }(\mathbf{m};\mathbf{h}),\end{eqnarray}$$
whence
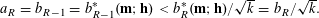 $$\begin{eqnarray}a_{R}=b_{R-1}=b_{R-1}^{\ast }(\mathbf{m};\mathbf{h})<b_{R}^{\ast }(\mathbf{m};\mathbf{h})/\sqrt{k}=b_{R}/\sqrt{k}.\end{eqnarray}$$
$$\begin{eqnarray}a_{R}=b_{R-1}=b_{R-1}^{\ast }(\mathbf{m};\mathbf{h})<b_{R}^{\ast }(\mathbf{m};\mathbf{h})/\sqrt{k}=b_{R}/\sqrt{k}.\end{eqnarray}$$
Then we deduce from (8.16) that there exist integers
![]() $b^{\prime }=b_{R}$
,
$b^{\prime }=b_{R}$
,
![]() $a^{\prime }=a_{R}$
and
$a^{\prime }=a_{R}$
and
![]() $h=h_{\mathbf{m}}$
satisfying the conditions
$h=h_{\mathbf{m}}$
satisfying the conditions
 $$\begin{eqnarray}0\leqslant h_{\mathbf{m}}\leqslant 16k^{2R}b,\qquad b^{\prime }=k_{\boldsymbol{ m}}b+h\qquad \text{and}\qquad a^{\prime }\leqslant b^{\prime }/\sqrt{k},\end{eqnarray}$$
$$\begin{eqnarray}0\leqslant h_{\mathbf{m}}\leqslant 16k^{2R}b,\qquad b^{\prime }=k_{\boldsymbol{ m}}b+h\qquad \text{and}\qquad a^{\prime }\leqslant b^{\prime }/\sqrt{k},\end{eqnarray}$$
and for which
 $$\begin{eqnarray}X^{-\unicode[STIX]{x1D6EC}}\unicode[STIX]{x27E6}K_{a^{\prime },b^{\prime }}^{r,r}(X)\unicode[STIX]{x27E7}\gg X^{-c^{\prime }\unicode[STIX]{x1D6FF}}M^{\unicode[STIX]{x1D6EC}\unicode[STIX]{x1D713}^{\prime }+\unicode[STIX]{x1D6FE}^{\prime }}.\end{eqnarray}$$
$$\begin{eqnarray}X^{-\unicode[STIX]{x1D6EC}}\unicode[STIX]{x27E6}K_{a^{\prime },b^{\prime }}^{r,r}(X)\unicode[STIX]{x27E7}\gg X^{-c^{\prime }\unicode[STIX]{x1D6FF}}M^{\unicode[STIX]{x1D6EC}\unicode[STIX]{x1D713}^{\prime }+\unicode[STIX]{x1D6FE}^{\prime }}.\end{eqnarray}$$
The desired conclusion (8.6) now follows, with all the associated conditions.
It now remains only to confirm the bounds on
![]() $k_{\mathbf{m}}$
asserted in the final line of the statement of the lemma. For this, we note that by applying (8.22) in an inductive argument, one obtains from (8.4) the lower bound
$k_{\mathbf{m}}$
asserted in the final line of the statement of the lemma. For this, we note that by applying (8.22) in an inductive argument, one obtains from (8.4) the lower bound
 $$\begin{eqnarray}k_{\mathbf{m}}=\tilde{b}_{R}(\mathbf{m})=b_{R}^{\ast }(\mathbf{m};\mathbf{0})/b\geqslant (\sqrt{k})^{R}b_{0}^{\ast }(\mathbf{m};\mathbf{0})/b\geqslant 2^{R}.\end{eqnarray}$$
$$\begin{eqnarray}k_{\mathbf{m}}=\tilde{b}_{R}(\mathbf{m})=b_{R}^{\ast }(\mathbf{m};\mathbf{0})/b\geqslant (\sqrt{k})^{R}b_{0}^{\ast }(\mathbf{m};\mathbf{0})/b\geqslant 2^{R}.\end{eqnarray}$$
Likewise, though more directly, one has
 $$\begin{eqnarray}k_{\mathbf{m}}=\tilde{b}_{R}(\mathbf{m})=b_{R}^{\ast }(\mathbf{m};\mathbf{0})/b\leqslant k^{R}b_{0}^{\ast }(\mathbf{m};\mathbf{0})/b=k^{R}.\end{eqnarray}$$
$$\begin{eqnarray}k_{\mathbf{m}}=\tilde{b}_{R}(\mathbf{m})=b_{R}^{\ast }(\mathbf{m};\mathbf{0})/b\leqslant k^{R}b_{0}^{\ast }(\mathbf{m};\mathbf{0})/b=k^{R}.\end{eqnarray}$$
Thus,
 $2^{R}\leqslant k_{\mathbf{m}}\leqslant k^{R}$
, and the proof of the lemma is complete.◻
$2^{R}\leqslant k_{\mathbf{m}}\leqslant k^{R}$
, and the proof of the lemma is complete.◻
9 The iterative process
We begin with a crude estimate of use at the conclusion of our argument.
Lemma 9.1. Suppose that
![]() $a$
and
$a$
and
![]() $b$
are integers with
$b$
are integers with
 $0\leqslant a<b\leqslant (2\unicode[STIX]{x1D703})^{-1}$
. Then, provided that
$0\leqslant a<b\leqslant (2\unicode[STIX]{x1D703})^{-1}$
. Then, provided that
![]() $\unicode[STIX]{x1D6EC}\geqslant 0$
, one has
$\unicode[STIX]{x1D6EC}\geqslant 0$
, one has
 $$\begin{eqnarray}\unicode[STIX]{x27E6}K_{a,b}^{r,r}(X)\unicode[STIX]{x27E7}\ll X^{\unicode[STIX]{x1D6EC}+\unicode[STIX]{x1D6FF}}.\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x27E6}K_{a,b}^{r,r}(X)\unicode[STIX]{x27E7}\ll X^{\unicode[STIX]{x1D6EC}+\unicode[STIX]{x1D6FF}}.\end{eqnarray}$$
Proof. On considering the underlying Diophantine equations, we deduce from Lemma 2.3 that
 $$\begin{eqnarray}K_{a,b}^{r,r}(X)\ll (J_{s+r}(X/M^{a}))^{r/(s+r)}(J_{s+r}(X/M^{b}))^{s/(s+r)},\end{eqnarray}$$
$$\begin{eqnarray}K_{a,b}^{r,r}(X)\ll (J_{s+r}(X/M^{a}))^{r/(s+r)}(J_{s+r}(X/M^{b}))^{s/(s+r)},\end{eqnarray}$$
whence
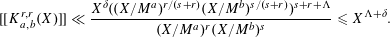 $$\begin{eqnarray}\unicode[STIX]{x27E6}K_{a,b}^{r,r}(X)\unicode[STIX]{x27E7}\ll \frac{X^{\unicode[STIX]{x1D6FF}}((X/M^{a})^{r/(s+r)}(X/M^{b})^{s/(s+r)})^{s+r+\unicode[STIX]{x1D6EC}}}{(X/M^{a})^{r}(X/M^{b})^{s}}\leqslant X^{\unicode[STIX]{x1D6EC}+\unicode[STIX]{x1D6FF}}.\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x27E6}K_{a,b}^{r,r}(X)\unicode[STIX]{x27E7}\ll \frac{X^{\unicode[STIX]{x1D6FF}}((X/M^{a})^{r/(s+r)}(X/M^{b})^{s/(s+r)})^{s+r+\unicode[STIX]{x1D6EC}}}{(X/M^{a})^{r}(X/M^{b})^{s}}\leqslant X^{\unicode[STIX]{x1D6EC}+\unicode[STIX]{x1D6FF}}.\end{eqnarray}$$
This completes the proof of the lemma. ◻
We now come to the main event.
The Proof of Theorem 2.1.
We prove that when
![]() $s$
is the largest integer smaller than
$s$
is the largest integer smaller than
![]() $s_{1}$
, then one has
$s_{1}$
, then one has
![]() $\unicode[STIX]{x1D6EC}\leqslant 0$
, for in such circumstances the conclusion of the lemma follows at once from (2.24). By reference to (2.5) and (2.6), we find that
$\unicode[STIX]{x1D6EC}\leqslant 0$
, for in such circumstances the conclusion of the lemma follows at once from (2.24). By reference to (2.5) and (2.6), we find that
 $s<s_{1}=\unicode[STIX]{x1D703}_{+}$
. Thus, since
$s<s_{1}=\unicode[STIX]{x1D703}_{+}$
. Thus, since
![]() $R$
has been chosen sufficiently large in terms of
$R$
has been chosen sufficiently large in terms of
![]() $s$
,
$s$
,
![]() $k$
and
$k$
and
![]() $\unicode[STIX]{x1D703}_{+}$
, the hypothesis
$\unicode[STIX]{x1D703}_{+}$
, the hypothesis
![]() $s<s_{1}$
ensures that
$s<s_{1}$
ensures that
![]() $s<s_{0}$
, where
$s<s_{0}$
, where
![]() $s_{0}$
is defined by means of (8.1). Assume then that
$s_{0}$
is defined by means of (8.1). Assume then that
![]() $\unicode[STIX]{x1D6EC}\geqslant 0$
, for otherwise there is nothing to prove. We begin by noting that as a consequence of Lemma 5.1, one finds from (2.21) and (2.23) that there exists an integer
$\unicode[STIX]{x1D6EC}\geqslant 0$
, for otherwise there is nothing to prove. We begin by noting that as a consequence of Lemma 5.1, one finds from (2.21) and (2.23) that there exists an integer
![]() $h_{-1}$
with
$h_{-1}$
with
 $0\leqslant h_{-1}\leqslant 4B$
such that
$0\leqslant h_{-1}\leqslant 4B$
such that
 $$\begin{eqnarray}\unicode[STIX]{x27E6}J_{s+r}(X)\unicode[STIX]{x27E7}\ll M^{Bs-sh_{-1}/3}\unicode[STIX]{x27E6}K_{0,B+h_{-1}}^{r,r}(X)\unicode[STIX]{x27E7}.\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x27E6}J_{s+r}(X)\unicode[STIX]{x27E7}\ll M^{Bs-sh_{-1}/3}\unicode[STIX]{x27E6}K_{0,B+h_{-1}}^{r,r}(X)\unicode[STIX]{x27E7}.\end{eqnarray}$$
We therefore deduce from (2.24) that
 $$\begin{eqnarray}X^{\unicode[STIX]{x1D6EC}}\ll X^{\unicode[STIX]{x1D6FF}}\unicode[STIX]{x27E6}J_{s+r}(X)\unicode[STIX]{x27E7}\ll X^{\unicode[STIX]{x1D6FF}}M^{Bs-sh_{-1}/3}\unicode[STIX]{x27E6}K_{0,B+h_{-1}}^{r,r}(X)\unicode[STIX]{x27E7}.\end{eqnarray}$$
$$\begin{eqnarray}X^{\unicode[STIX]{x1D6EC}}\ll X^{\unicode[STIX]{x1D6FF}}\unicode[STIX]{x27E6}J_{s+r}(X)\unicode[STIX]{x27E7}\ll X^{\unicode[STIX]{x1D6FF}}M^{Bs-sh_{-1}/3}\unicode[STIX]{x27E6}K_{0,B+h_{-1}}^{r,r}(X)\unicode[STIX]{x27E7}.\end{eqnarray}$$
Next, we define sequences
![]() $(\unicode[STIX]{x1D705}_{n})$
,
$(\unicode[STIX]{x1D705}_{n})$
,
![]() $(h_{n})$
,
$(h_{n})$
,
![]() $(a_{n})$
,
$(a_{n})$
,
![]() $(b_{n})$
,
$(b_{n})$
,
![]() $(c_{n})$
,
$(c_{n})$
,
![]() $(\unicode[STIX]{x1D713}_{n})$
and
$(\unicode[STIX]{x1D713}_{n})$
and
![]() $(\unicode[STIX]{x1D6FE}_{n})$
, for
$(\unicode[STIX]{x1D6FE}_{n})$
, for
 $0\leqslant n\leqslant N$
, in such a way that
$0\leqslant n\leqslant N$
, in such a way that
 $$\begin{eqnarray}2^{R}\leqslant \unicode[STIX]{x1D705}_{n-1}\leqslant k^{R},\qquad 0\leqslant h_{n-1}\leqslant \max \{16k^{2R}b_{n-1},4B\}\end{eqnarray}$$
$$\begin{eqnarray}2^{R}\leqslant \unicode[STIX]{x1D705}_{n-1}\leqslant k^{R},\qquad 0\leqslant h_{n-1}\leqslant \max \{16k^{2R}b_{n-1},4B\}\end{eqnarray}$$
and
 $$\begin{eqnarray}X^{\unicode[STIX]{x1D6EC}}M^{\unicode[STIX]{x1D6EC}\unicode[STIX]{x1D713}_{n}}\ll X^{c_{n}\unicode[STIX]{x1D6FF}}M^{-\unicode[STIX]{x1D6FE}_{n}}\unicode[STIX]{x27E6}K_{a_{n},b_{n}}^{r,r}(X)\unicode[STIX]{x27E7}.\end{eqnarray}$$
$$\begin{eqnarray}X^{\unicode[STIX]{x1D6EC}}M^{\unicode[STIX]{x1D6EC}\unicode[STIX]{x1D713}_{n}}\ll X^{c_{n}\unicode[STIX]{x1D6FF}}M^{-\unicode[STIX]{x1D6FE}_{n}}\unicode[STIX]{x27E6}K_{a_{n},b_{n}}^{r,r}(X)\unicode[STIX]{x27E7}.\end{eqnarray}$$
We note here that the sequences
![]() $(a_{n})$
and
$(a_{n})$
and
![]() $(b_{n})$
are not directly related to our earlier use of these letters. Given a fixed choice for the sequences
$(b_{n})$
are not directly related to our earlier use of these letters. Given a fixed choice for the sequences
![]() $(a_{n})$
,
$(a_{n})$
,
![]() $(\unicode[STIX]{x1D705}_{n})$
and
$(\unicode[STIX]{x1D705}_{n})$
and
![]() $(h_{n})$
, the remaining sequences are defined by means of the relations
$(h_{n})$
, the remaining sequences are defined by means of the relations
 $$\begin{eqnarray}\displaystyle b_{n+1} & = & \displaystyle \unicode[STIX]{x1D705}_{n}b_{n}+h_{n},\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle b_{n+1} & = & \displaystyle \unicode[STIX]{x1D705}_{n}b_{n}+h_{n},\end{eqnarray}$$
 $$\begin{eqnarray}\displaystyle c_{n+1} & = & \displaystyle (s/s_{0})^{R}\unicode[STIX]{x1D705}_{n}(c_{n}+1),\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle c_{n+1} & = & \displaystyle (s/s_{0})^{R}\unicode[STIX]{x1D705}_{n}(c_{n}+1),\end{eqnarray}$$
 $$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D713}_{n+1} & = & \displaystyle (s/s_{0})^{R}\unicode[STIX]{x1D705}_{n}(\unicode[STIX]{x1D713}_{n}+(1-r/s)b_{n}),\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D713}_{n+1} & = & \displaystyle (s/s_{0})^{R}\unicode[STIX]{x1D705}_{n}(\unicode[STIX]{x1D713}_{n}+(1-r/s)b_{n}),\end{eqnarray}$$
 $$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D6FE}_{n+1} & = & \displaystyle (s/s_{0})^{R}\unicode[STIX]{x1D705}_{n}\unicode[STIX]{x1D6FE}_{n}.\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D6FE}_{n+1} & = & \displaystyle (s/s_{0})^{R}\unicode[STIX]{x1D705}_{n}\unicode[STIX]{x1D6FE}_{n}.\end{eqnarray}$$
We put
 $$\begin{eqnarray}\displaystyle & \displaystyle \unicode[STIX]{x1D705}_{-1}=k^{R},\qquad b_{-1}=0,\qquad a_{0}=0,\qquad b_{0}=B+h_{-1}, & \displaystyle \nonumber\\ \displaystyle & \displaystyle \unicode[STIX]{x1D713}_{0}=0,\qquad c_{0}=1,\qquad \unicode[STIX]{x1D6FE}_{0}={\textstyle \frac{1}{3}}sh_{-1}-Bs, & \displaystyle \nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle \unicode[STIX]{x1D705}_{-1}=k^{R},\qquad b_{-1}=0,\qquad a_{0}=0,\qquad b_{0}=B+h_{-1}, & \displaystyle \nonumber\\ \displaystyle & \displaystyle \unicode[STIX]{x1D713}_{0}=0,\qquad c_{0}=1,\qquad \unicode[STIX]{x1D6FE}_{0}={\textstyle \frac{1}{3}}sh_{-1}-Bs, & \displaystyle \nonumber\end{eqnarray}$$
so that both (9.2) and (9.3) hold with
![]() $n=0$
as a consequence of our initial choice of
$n=0$
as a consequence of our initial choice of
![]() $\unicode[STIX]{x1D705}_{-1}$
and
$\unicode[STIX]{x1D705}_{-1}$
and
![]() $b_{-1}$
, together with (9.1). We prove by induction that for each non-negative integer
$b_{-1}$
, together with (9.1). We prove by induction that for each non-negative integer
![]() $n$
with
$n$
with
![]() $n<N$
, the sequences
$n<N$
, the sequences
 $(a_{m})_{m=0}^{n}$
,
$(a_{m})_{m=0}^{n}$
,
 $(\unicode[STIX]{x1D705}_{m})_{m=0}^{n}$
and
$(\unicode[STIX]{x1D705}_{m})_{m=0}^{n}$
and
 $(h_{m})_{m=-1}^{n}$
may be chosen in such a way that
$(h_{m})_{m=-1}^{n}$
may be chosen in such a way that
 $$\begin{eqnarray}\displaystyle & \displaystyle 1\leqslant b_{n}\leqslant (20Rk^{2R}\unicode[STIX]{x1D703})^{-1},\quad \unicode[STIX]{x1D713}_{n}\geqslant 0,\quad \unicode[STIX]{x1D6FE}_{n}\geqslant -sb_{n},\quad 0\leqslant c_{n}\leqslant (2\unicode[STIX]{x1D6FF})^{-1}\unicode[STIX]{x1D703},\quad \quad & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle 1\leqslant b_{n}\leqslant (20Rk^{2R}\unicode[STIX]{x1D703})^{-1},\quad \unicode[STIX]{x1D713}_{n}\geqslant 0,\quad \unicode[STIX]{x1D6FE}_{n}\geqslant -sb_{n},\quad 0\leqslant c_{n}\leqslant (2\unicode[STIX]{x1D6FF})^{-1}\unicode[STIX]{x1D703},\quad \quad & \displaystyle\end{eqnarray}$$
 $$\begin{eqnarray}\displaystyle & \displaystyle 0\leqslant a_{n}\leqslant b_{n}/\sqrt{k},\qquad (k-r+1)b_{n}\geqslant ra_{n}, & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle 0\leqslant a_{n}\leqslant b_{n}/\sqrt{k},\qquad (k-r+1)b_{n}\geqslant ra_{n}, & \displaystyle\end{eqnarray}$$
and so that (9.2) and (9.3) both hold with
![]() $n$
replaced by
$n$
replaced by
![]() $n+1$
.
$n+1$
.
Let
 $0\leqslant n<N$
, and suppose that (9.2) and (9.3) both hold for the index
$0\leqslant n<N$
, and suppose that (9.2) and (9.3) both hold for the index
![]() $n$
. We have already shown such to be the case for
$n$
. We have already shown such to be the case for
![]() $n=0$
. From (9.2) and (9.4), we find that
$n=0$
. From (9.2) and (9.4), we find that
 $b_{n}\leqslant 5(17k^{2R})^{n}B$
, whence, by invoking (2.8), we find that for
$b_{n}\leqslant 5(17k^{2R})^{n}B$
, whence, by invoking (2.8), we find that for
 $0\leqslant n\leqslant N$
, one has
$0\leqslant n\leqslant N$
, one has
 $$\begin{eqnarray}b_{n}\leqslant (20Rk^{2R}\unicode[STIX]{x1D703})^{-1}.\end{eqnarray}$$
$$\begin{eqnarray}b_{n}\leqslant (20Rk^{2R}\unicode[STIX]{x1D703})^{-1}.\end{eqnarray}$$
It is apparent from (9.5) and (9.6) that
![]() $c_{n}$
and
$c_{n}$
and
![]() $\unicode[STIX]{x1D713}_{n}$
are non-negative for all
$\unicode[STIX]{x1D713}_{n}$
are non-negative for all
![]() $n$
. Observe also that since
$n$
. Observe also that since
![]() $s\leqslant s_{0}$
and
$s\leqslant s_{0}$
and
 $\unicode[STIX]{x1D705}_{m}\leqslant k^{R}$
, then by iterating (9.5) we obtain the bound
$\unicode[STIX]{x1D705}_{m}\leqslant k^{R}$
, then by iterating (9.5) we obtain the bound
 $$\begin{eqnarray}c_{n}\leqslant k^{Rn}+k^{R}\biggl(\frac{k^{Rn}-1}{k^{R}-1}\biggr)\leqslant 3k^{Rn}\quad (n\geqslant 0),\end{eqnarray}$$
$$\begin{eqnarray}c_{n}\leqslant k^{Rn}+k^{R}\biggl(\frac{k^{Rn}-1}{k^{R}-1}\biggr)\leqslant 3k^{Rn}\quad (n\geqslant 0),\end{eqnarray}$$
and by reference to (2.8) we see that
 $c_{n}\leqslant (2\unicode[STIX]{x1D6FF})^{-1}\unicode[STIX]{x1D703}$
for
$c_{n}\leqslant (2\unicode[STIX]{x1D6FF})^{-1}\unicode[STIX]{x1D703}$
for
 $0\leqslant n<N$
.
$0\leqslant n<N$
.
In order to bound
![]() $\unicode[STIX]{x1D6FE}_{n}$
, we recall that
$\unicode[STIX]{x1D6FE}_{n}$
, we recall that
![]() $s\leqslant s_{0}$
and iterate the relation (9.7) to deduce that
$s\leqslant s_{0}$
and iterate the relation (9.7) to deduce that
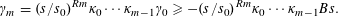 $$\begin{eqnarray}\unicode[STIX]{x1D6FE}_{m}=(s/s_{0})^{Rm}\unicode[STIX]{x1D705}_{0}\cdots \unicode[STIX]{x1D705}_{m-1}\unicode[STIX]{x1D6FE}_{0}\geqslant -(s/s_{0})^{Rm}\unicode[STIX]{x1D705}_{0}\cdots \unicode[STIX]{x1D705}_{m-1}Bs.\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D6FE}_{m}=(s/s_{0})^{Rm}\unicode[STIX]{x1D705}_{0}\cdots \unicode[STIX]{x1D705}_{m-1}\unicode[STIX]{x1D6FE}_{0}\geqslant -(s/s_{0})^{Rm}\unicode[STIX]{x1D705}_{0}\cdots \unicode[STIX]{x1D705}_{m-1}Bs.\end{eqnarray}$$
In addition, we find from (9.4) that for
![]() $m\geqslant 0$
one has
$m\geqslant 0$
one has
 $b_{m+1}\geqslant \unicode[STIX]{x1D705}_{m}b_{m}$
, so that an inductive argument yields the lower bound
$b_{m+1}\geqslant \unicode[STIX]{x1D705}_{m}b_{m}$
, so that an inductive argument yields the lower bound
 $$\begin{eqnarray}b_{m}\geqslant \unicode[STIX]{x1D705}_{0}\cdots \unicode[STIX]{x1D705}_{m-1}b_{0}\geqslant \unicode[STIX]{x1D705}_{0}\cdots \unicode[STIX]{x1D705}_{m-1}B.\end{eqnarray}$$
$$\begin{eqnarray}b_{m}\geqslant \unicode[STIX]{x1D705}_{0}\cdots \unicode[STIX]{x1D705}_{m-1}b_{0}\geqslant \unicode[STIX]{x1D705}_{0}\cdots \unicode[STIX]{x1D705}_{m-1}B.\end{eqnarray}$$
Hence, we deduce from (9.11) that
 $$\begin{eqnarray}\unicode[STIX]{x1D6FE}_{m}\geqslant -(s/s_{0})^{Rm}sb_{m}>-sb_{m}.\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D6FE}_{m}\geqslant -(s/s_{0})^{Rm}sb_{m}>-sb_{m}.\end{eqnarray}$$
Assembling this conclusion together with those of the previous paragraph, we have shown that (9.8) holds for
 $0\leqslant n\leqslant N$
.
$0\leqslant n\leqslant N$
.
At this point in the argument, we may suppose that (9.3), (9.8) and (9.9) hold for the index
![]() $n$
. An application of Lemma 8.2 therefore reveals that there exist real numbers
$n$
. An application of Lemma 8.2 therefore reveals that there exist real numbers
![]() $\unicode[STIX]{x1D705}_{n}$
and
$\unicode[STIX]{x1D705}_{n}$
and
![]() $h_{n}$
satisfying the constraints implied by (9.2) with
$h_{n}$
satisfying the constraints implied by (9.2) with
![]() $n$
replaced by
$n$
replaced by
![]() $n+1$
, for which the upper bound (9.3) holds for some
$n+1$
, for which the upper bound (9.3) holds for some
![]() $a_{n}$
with
$a_{n}$
with
 $0\leqslant a_{n}\leqslant b_{n}/\sqrt{k}$
, also with
$0\leqslant a_{n}\leqslant b_{n}/\sqrt{k}$
, also with
![]() $n$
replaced by
$n$
replaced by
![]() $n+1$
. Our hypothesis on
$n+1$
. Our hypothesis on
![]() $r$
, moreover, ensures that
$r$
, moreover, ensures that
 $(k-r+1)b_{n+1}\geqslant ra_{n+1}$
. Hence (9.9) holds also with
$(k-r+1)b_{n+1}\geqslant ra_{n+1}$
. Hence (9.9) holds also with
![]() $n$
replaced by
$n$
replaced by
![]() $n+1$
. This completes the inductive step, so that in particular the upper bound (9.3) holds for
$n+1$
. This completes the inductive step, so that in particular the upper bound (9.3) holds for
 $0\leqslant n\leqslant N$
.
$0\leqslant n\leqslant N$
.
We now exploit the bound just established. Since we have the upper bound
 $b_{N}\leqslant 5(17k^{2R})^{N}B\leqslant (2\unicode[STIX]{x1D703})^{-1}$
, it is a consequence of Lemma 9.1 that
$b_{N}\leqslant 5(17k^{2R})^{N}B\leqslant (2\unicode[STIX]{x1D703})^{-1}$
, it is a consequence of Lemma 9.1 that
 $$\begin{eqnarray}\unicode[STIX]{x27E6}K_{a_{N},b_{N}}^{r,r}(X)\unicode[STIX]{x27E7}\ll X^{\unicode[STIX]{x1D6EC}+\unicode[STIX]{x1D6FF}}.\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x27E6}K_{a_{N},b_{N}}^{r,r}(X)\unicode[STIX]{x27E7}\ll X^{\unicode[STIX]{x1D6EC}+\unicode[STIX]{x1D6FF}}.\end{eqnarray}$$
By combining this with (9.3) and (9.11), we obtain the bound
 $$\begin{eqnarray}X^{\unicode[STIX]{x1D6EC}}M^{\unicode[STIX]{x1D6EC}\unicode[STIX]{x1D713}_{N}}\ll X^{\unicode[STIX]{x1D6EC}+(c_{N}+1)\unicode[STIX]{x1D6FF}}M^{\unicode[STIX]{x1D705}_{0}\cdots \unicode[STIX]{x1D705}_{N-1}Bs(s/s_{0})^{RN}}.\end{eqnarray}$$
$$\begin{eqnarray}X^{\unicode[STIX]{x1D6EC}}M^{\unicode[STIX]{x1D6EC}\unicode[STIX]{x1D713}_{N}}\ll X^{\unicode[STIX]{x1D6EC}+(c_{N}+1)\unicode[STIX]{x1D6FF}}M^{\unicode[STIX]{x1D705}_{0}\cdots \unicode[STIX]{x1D705}_{N-1}Bs(s/s_{0})^{RN}}.\end{eqnarray}$$
Meanwhile, an application of (9.10) in combination with (2.8) shows that
 $X^{(c_{N}+1)\unicode[STIX]{x1D6FF}}<M$
. We therefore deduce from (9.12) that
$X^{(c_{N}+1)\unicode[STIX]{x1D6FF}}<M$
. We therefore deduce from (9.12) that
 $$\begin{eqnarray}\unicode[STIX]{x1D6EC}\unicode[STIX]{x1D713}_{N}\leqslant (s/s_{0})^{RN}\unicode[STIX]{x1D705}_{0}\cdots \unicode[STIX]{x1D705}_{N-1}Bs+1.\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D6EC}\unicode[STIX]{x1D713}_{N}\leqslant (s/s_{0})^{RN}\unicode[STIX]{x1D705}_{0}\cdots \unicode[STIX]{x1D705}_{N-1}Bs+1.\end{eqnarray}$$
Notice here that
![]() $\unicode[STIX]{x1D705}_{n}\geqslant 2^{R}$
and
$\unicode[STIX]{x1D705}_{n}\geqslant 2^{R}$
and
 $$\begin{eqnarray}s/s_{0}\geqslant (s_{1}-1)/s_{0}\geqslant 1-2/s_{0}>{\textstyle \frac{1}{2}}.\end{eqnarray}$$
$$\begin{eqnarray}s/s_{0}\geqslant (s_{1}-1)/s_{0}\geqslant 1-2/s_{0}>{\textstyle \frac{1}{2}}.\end{eqnarray}$$
Hence,
 $$\begin{eqnarray}1<(s/s_{0})^{RN}\unicode[STIX]{x1D705}_{0}\cdots \unicode[STIX]{x1D705}_{N-1}Bs,\end{eqnarray}$$
$$\begin{eqnarray}1<(s/s_{0})^{RN}\unicode[STIX]{x1D705}_{0}\cdots \unicode[STIX]{x1D705}_{N-1}Bs,\end{eqnarray}$$
so that
 $$\begin{eqnarray}\unicode[STIX]{x1D6EC}\unicode[STIX]{x1D713}_{N}\leqslant 2(s/s_{0})^{RN}\unicode[STIX]{x1D705}_{0}\cdots \unicode[STIX]{x1D705}_{N-1}Bs.\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D6EC}\unicode[STIX]{x1D713}_{N}\leqslant 2(s/s_{0})^{RN}\unicode[STIX]{x1D705}_{0}\cdots \unicode[STIX]{x1D705}_{N-1}Bs.\end{eqnarray}$$
A further application of the lower bound
 $b_{n}\geqslant \unicode[STIX]{x1D705}_{0}\cdots \unicode[STIX]{x1D705}_{n-1}B$
leads from (9.6) and the bound
$b_{n}\geqslant \unicode[STIX]{x1D705}_{0}\cdots \unicode[STIX]{x1D705}_{n-1}B$
leads from (9.6) and the bound
![]() $s\leqslant s_{0}$
to the relation
$s\leqslant s_{0}$
to the relation
 $$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D713}_{n+1} & = & \displaystyle (s/s_{0})^{R}(\unicode[STIX]{x1D705}_{n}\unicode[STIX]{x1D713}_{n}+\unicode[STIX]{x1D705}_{n}(1-r/s)b_{n})\nonumber\\ \displaystyle & {\geqslant} & \displaystyle (s/s_{0})^{R}\unicode[STIX]{x1D705}_{n}\unicode[STIX]{x1D713}_{n}+(s/s_{0})^{R}\unicode[STIX]{x1D705}_{n}(1-r/s)\unicode[STIX]{x1D705}_{0}\cdots \unicode[STIX]{x1D705}_{n-1}B\nonumber\\ \displaystyle & {\geqslant} & \displaystyle (s/s_{0})^{R}\unicode[STIX]{x1D705}_{n}\unicode[STIX]{x1D713}_{n}+(s/s_{0})^{R(n+1)}(1-r/s)\unicode[STIX]{x1D705}_{0}\cdots \unicode[STIX]{x1D705}_{n}B.\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D713}_{n+1} & = & \displaystyle (s/s_{0})^{R}(\unicode[STIX]{x1D705}_{n}\unicode[STIX]{x1D713}_{n}+\unicode[STIX]{x1D705}_{n}(1-r/s)b_{n})\nonumber\\ \displaystyle & {\geqslant} & \displaystyle (s/s_{0})^{R}\unicode[STIX]{x1D705}_{n}\unicode[STIX]{x1D713}_{n}+(s/s_{0})^{R}\unicode[STIX]{x1D705}_{n}(1-r/s)\unicode[STIX]{x1D705}_{0}\cdots \unicode[STIX]{x1D705}_{n-1}B\nonumber\\ \displaystyle & {\geqslant} & \displaystyle (s/s_{0})^{R}\unicode[STIX]{x1D705}_{n}\unicode[STIX]{x1D713}_{n}+(s/s_{0})^{R(n+1)}(1-r/s)\unicode[STIX]{x1D705}_{0}\cdots \unicode[STIX]{x1D705}_{n}B.\nonumber\end{eqnarray}$$
An inductive argument therefore delivers the lower bound
 $$\begin{eqnarray}\unicode[STIX]{x1D713}_{N}\geqslant N(1-r/s)(s/s_{0})^{RN}\unicode[STIX]{x1D705}_{0}\cdots \unicode[STIX]{x1D705}_{N-1}B.\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D713}_{N}\geqslant N(1-r/s)(s/s_{0})^{RN}\unicode[STIX]{x1D705}_{0}\cdots \unicode[STIX]{x1D705}_{N-1}B.\end{eqnarray}$$
Thus, we deduce from (9.13) that
 $$\begin{eqnarray}\unicode[STIX]{x1D6EC}\leqslant \frac{2(s/s_{0})^{RN}\unicode[STIX]{x1D705}_{0}\cdots \unicode[STIX]{x1D705}_{N-1}Bs}{N(1-r/s)(s/s_{0})^{RN}\unicode[STIX]{x1D705}_{0}\cdots \unicode[STIX]{x1D705}_{N-1}B}=\frac{2s(1-r/s)^{-1}}{N}.\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D6EC}\leqslant \frac{2(s/s_{0})^{RN}\unicode[STIX]{x1D705}_{0}\cdots \unicode[STIX]{x1D705}_{N-1}Bs}{N(1-r/s)(s/s_{0})^{RN}\unicode[STIX]{x1D705}_{0}\cdots \unicode[STIX]{x1D705}_{N-1}B}=\frac{2s(1-r/s)^{-1}}{N}.\end{eqnarray}$$
Since we are at liberty to take
![]() $N$
as large as we please in terms of
$N$
as large as we please in terms of
![]() $s$
and
$s$
and
![]() $k$
, we are forced to conclude that
$k$
, we are forced to conclude that
![]() $\unicode[STIX]{x1D6EC}\leqslant 0$
. In view of our opening discussion, this completes the proof of the theorem.◻
$\unicode[STIX]{x1D6EC}\leqslant 0$
. In view of our opening discussion, this completes the proof of the theorem.◻
10 Strongly diagonal behaviour
We are now equipped to establish Theorem 1.1 and its corollary. Let
![]() $k$
be an integer with
$k$
be an integer with
![]() $k\geqslant 7$
, put
$k\geqslant 7$
, put
 $r=k-\lceil 2\sqrt{k}\rceil +2$
and suppose that
$r=k-\lceil 2\sqrt{k}\rceil +2$
and suppose that
![]() $s$
is a natural number with
$s$
is a natural number with
 $s\geqslant {\textstyle \frac{1}{4}}(k+1)^{2}$
. We note that [Reference Ford and Wooley4, Theorem 1.1] demonstrates that whenever
$s\geqslant {\textstyle \frac{1}{4}}(k+1)^{2}$
. We note that [Reference Ford and Wooley4, Theorem 1.1] demonstrates that whenever
 $1\leqslant s\leqslant {\textstyle \frac{1}{4}}(k+1)^{2}$
, then one has
$1\leqslant s\leqslant {\textstyle \frac{1}{4}}(k+1)^{2}$
, then one has
 $J_{s,k}(X)\ll X^{s+\unicode[STIX]{x1D700}}$
, and so we are certainly at liberty to assume that
$J_{s,k}(X)\ll X^{s+\unicode[STIX]{x1D700}}$
, and so we are certainly at liberty to assume that
 $s>{\textstyle \frac{1}{4}}(k+1)^{2}$
. Write
$s>{\textstyle \frac{1}{4}}(k+1)^{2}$
. Write
 $$\begin{eqnarray}\unicode[STIX]{x1D6E5}=\mathop{\sum }_{m=1}^{r-1}\frac{m(r-m)}{s-m-r},\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D6E5}=\mathop{\sum }_{m=1}^{r-1}\frac{m(r-m)}{s-m-r},\end{eqnarray}$$
and define
![]() $s_{1}$
as in the statement of Theorem 2.1. We aim to show that the real number
$s_{1}$
as in the statement of Theorem 2.1. We aim to show that the real number
 $$\begin{eqnarray}t_{0}=kr-{\textstyle \frac{1}{2}}r(r+1)-\unicode[STIX]{x1D6E5}\end{eqnarray}$$
$$\begin{eqnarray}t_{0}=kr-{\textstyle \frac{1}{2}}r(r+1)-\unicode[STIX]{x1D6E5}\end{eqnarray}$$
satisfies the bounds
 $$\begin{eqnarray}\max \{2r-1,\lceil {\textstyle \frac{1}{2}}r(r-1)+\unicode[STIX]{x1D6E5}\rceil \}\leqslant t_{0}\leqslant s_{1}.\end{eqnarray}$$
$$\begin{eqnarray}\max \{2r-1,\lceil {\textstyle \frac{1}{2}}r(r-1)+\unicode[STIX]{x1D6E5}\rceil \}\leqslant t_{0}\leqslant s_{1}.\end{eqnarray}$$
If these bounds be confirmed, then it follows from Theorem 2.1 that whenever
 $$\begin{eqnarray}1\leqslant s\leqslant t_{0}+r=kr-{\textstyle \frac{1}{2}}r(r-1)-\unicode[STIX]{x1D6E5},\end{eqnarray}$$
$$\begin{eqnarray}1\leqslant s\leqslant t_{0}+r=kr-{\textstyle \frac{1}{2}}r(r-1)-\unicode[STIX]{x1D6E5},\end{eqnarray}$$
then
 $J_{s,k}(X)\ll X^{s+\unicode[STIX]{x1D700}}$
, and the conclusion of Theorem 1.1 follows.
$J_{s,k}(X)\ll X^{s+\unicode[STIX]{x1D700}}$
, and the conclusion of Theorem 1.1 follows.
We observe in our first step that, in view of the lower bound
 $s>{\textstyle \frac{1}{4}}(k+1)^{2}$
and our hypothesis
$s>{\textstyle \frac{1}{4}}(k+1)^{2}$
and our hypothesis
![]() $k\geqslant 7$
, one has
$k\geqslant 7$
, one has
 $$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D6E5} & {\leqslant} & \displaystyle \mathop{\sum }_{m=1}^{k-5}\frac{m(k-4-m)}{s-k+4-m}\leqslant \mathop{\sum }_{m=1}^{k-5}\frac{m(k-4-m)}{(k^{2}-6k+37)/4}\nonumber\\ \displaystyle & = & \displaystyle \frac{2(k-3)(k-4)(k-5)}{3(k^{2}-6k+37)}<\frac{2}{3}(k-6).\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D6E5} & {\leqslant} & \displaystyle \mathop{\sum }_{m=1}^{k-5}\frac{m(k-4-m)}{s-k+4-m}\leqslant \mathop{\sum }_{m=1}^{k-5}\frac{m(k-4-m)}{(k^{2}-6k+37)/4}\nonumber\\ \displaystyle & = & \displaystyle \frac{2(k-3)(k-4)(k-5)}{3(k^{2}-6k+37)}<\frac{2}{3}(k-6).\nonumber\end{eqnarray}$$
Next, one finds that
![]() $t_{0}\leqslant s_{1}$
provided only that
$t_{0}\leqslant s_{1}$
provided only that
 $$\begin{eqnarray}(kr-{\textstyle \frac{1}{2}}r(r-1)-\unicode[STIX]{x1D6E5}-2r)^{2}\leqslant (kr-{\textstyle \frac{1}{2}}r(r-1)-\unicode[STIX]{x1D6E5})^{2}-4r({\textstyle \frac{1}{2}}r(r-1)+\unicode[STIX]{x1D6E5}),\end{eqnarray}$$
$$\begin{eqnarray}(kr-{\textstyle \frac{1}{2}}r(r-1)-\unicode[STIX]{x1D6E5}-2r)^{2}\leqslant (kr-{\textstyle \frac{1}{2}}r(r-1)-\unicode[STIX]{x1D6E5})^{2}-4r({\textstyle \frac{1}{2}}r(r-1)+\unicode[STIX]{x1D6E5}),\end{eqnarray}$$
an inequality that is satisfied provided that
 $$\begin{eqnarray}4r(kr-{\textstyle \frac{1}{2}}r(r-1)-\unicode[STIX]{x1D6E5})-4r^{2}\geqslant 4r({\textstyle \frac{1}{2}}r(r-1)+\unicode[STIX]{x1D6E5}).\end{eqnarray}$$
$$\begin{eqnarray}4r(kr-{\textstyle \frac{1}{2}}r(r-1)-\unicode[STIX]{x1D6E5})-4r^{2}\geqslant 4r({\textstyle \frac{1}{2}}r(r-1)+\unicode[STIX]{x1D6E5}).\end{eqnarray}$$
This last inequality amounts to the constraint
 $kr-r(r-1)-r\geqslant 2\unicode[STIX]{x1D6E5}$
. We therefore conclude that
$kr-r(r-1)-r\geqslant 2\unicode[STIX]{x1D6E5}$
. We therefore conclude that
![]() $t_{0}\leqslant s_{1}$
whenever
$t_{0}\leqslant s_{1}$
whenever
 $r(k-r)\geqslant {\textstyle \frac{4}{3}}(k-6)$
. But when
$r(k-r)\geqslant {\textstyle \frac{4}{3}}(k-6)$
. But when
![]() $k\geqslant 7$
, it is easily verified that
$k\geqslant 7$
, it is easily verified that
 $$\begin{eqnarray}r(k-r)\geqslant (k-\lceil 2\sqrt{k}\rceil +2)(\lceil 2\sqrt{k}\rceil -2)\geqslant {\textstyle \frac{4}{3}}(k-6)+1\end{eqnarray}$$
$$\begin{eqnarray}r(k-r)\geqslant (k-\lceil 2\sqrt{k}\rceil +2)(\lceil 2\sqrt{k}\rceil -2)\geqslant {\textstyle \frac{4}{3}}(k-6)+1\end{eqnarray}$$
and hence we confirm that
![]() $t_{0}\leqslant s_{1}$
, as desired.
$t_{0}\leqslant s_{1}$
, as desired.
Meanwhile, the bound
 $\unicode[STIX]{x1D6E5}<{\textstyle \frac{2}{3}}(k-6)$
ensures that
$\unicode[STIX]{x1D6E5}<{\textstyle \frac{2}{3}}(k-6)$
ensures that
 $$\begin{eqnarray}\displaystyle kr-{\textstyle \frac{1}{2}}r(r+1)-\unicode[STIX]{x1D6E5} & {\geqslant} & \displaystyle (k-r)r+({\textstyle \frac{1}{2}}r(r-1)+\unicode[STIX]{x1D6E5})-2\unicode[STIX]{x1D6E5}\nonumber\\ \displaystyle & {>} & \displaystyle {\textstyle \frac{1}{2}}r(r-1)+\unicode[STIX]{x1D6E5}+(r(k-r)-{\textstyle \frac{4}{3}}(k-6))\nonumber\\ \displaystyle & {\geqslant} & \displaystyle {\textstyle \frac{1}{2}}r(r-1)+\unicode[STIX]{x1D6E5}+1.\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle kr-{\textstyle \frac{1}{2}}r(r+1)-\unicode[STIX]{x1D6E5} & {\geqslant} & \displaystyle (k-r)r+({\textstyle \frac{1}{2}}r(r-1)+\unicode[STIX]{x1D6E5})-2\unicode[STIX]{x1D6E5}\nonumber\\ \displaystyle & {>} & \displaystyle {\textstyle \frac{1}{2}}r(r-1)+\unicode[STIX]{x1D6E5}+(r(k-r)-{\textstyle \frac{4}{3}}(k-6))\nonumber\\ \displaystyle & {\geqslant} & \displaystyle {\textstyle \frac{1}{2}}r(r-1)+\unicode[STIX]{x1D6E5}+1.\nonumber\end{eqnarray}$$
Since
![]() $k\geqslant 7$
, moreover, one has
$k\geqslant 7$
, moreover, one has
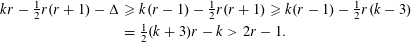 $$\begin{eqnarray}\displaystyle kr-{\textstyle \frac{1}{2}}r(r+1)-\unicode[STIX]{x1D6E5} & {\geqslant} & \displaystyle k(r-1)-{\textstyle \frac{1}{2}}r(r+1)\geqslant k(r-1)-{\textstyle \frac{1}{2}}r(k-3)\nonumber\\ \displaystyle & = & \displaystyle {\textstyle \frac{1}{2}}(k+3)r-k>2r-1.\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle kr-{\textstyle \frac{1}{2}}r(r+1)-\unicode[STIX]{x1D6E5} & {\geqslant} & \displaystyle k(r-1)-{\textstyle \frac{1}{2}}r(r+1)\geqslant k(r-1)-{\textstyle \frac{1}{2}}r(k-3)\nonumber\\ \displaystyle & = & \displaystyle {\textstyle \frac{1}{2}}(k+3)r-k>2r-1.\nonumber\end{eqnarray}$$
Then we have
 $t_{0}\geqslant \max \{2r-1,\lceil {\textstyle \frac{1}{2}}r(r-1)+\unicode[STIX]{x1D6E5}\rceil \}$
, confirming the final claimed bound. In view of our earlier discussion, the proof of Theorem 1.1 is complete.
$t_{0}\geqslant \max \{2r-1,\lceil {\textstyle \frac{1}{2}}r(r-1)+\unicode[STIX]{x1D6E5}\rceil \}$
, confirming the final claimed bound. In view of our earlier discussion, the proof of Theorem 1.1 is complete.
We turn now to the proof of Corollary 1.2. We suppose again that
![]() $k\geqslant 7$
, and we put
$k\geqslant 7$
, and we put
 $$\begin{eqnarray}s={\textstyle \frac{1}{2}}k(k+1)-\lceil {\textstyle \frac{7}{3}}k\rceil .\end{eqnarray}$$
$$\begin{eqnarray}s={\textstyle \frac{1}{2}}k(k+1)-\lceil {\textstyle \frac{7}{3}}k\rceil .\end{eqnarray}$$
Again defining
![]() $\unicode[STIX]{x1D6E5}$
as in (10.1), in which
$\unicode[STIX]{x1D6E5}$
as in (10.1), in which
 $r=k-\lceil 2\sqrt{k}\rceil +2$
, we find that
$r=k-\lceil 2\sqrt{k}\rceil +2$
, we find that
 $$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D6E5} & {\leqslant} & \displaystyle \mathop{\sum }_{m=1}^{k-5}\frac{m(k-4-m)}{k(k+1)/2-(k-4)-(7k/3+2/3)-m}\nonumber\\ \displaystyle & {\leqslant} & \displaystyle \frac{(k-3)(k-4)(k-5)}{3k^{2}-23k+50}<\frac{1}{3}k.\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D6E5} & {\leqslant} & \displaystyle \mathop{\sum }_{m=1}^{k-5}\frac{m(k-4-m)}{k(k+1)/2-(k-4)-(7k/3+2/3)-m}\nonumber\\ \displaystyle & {\leqslant} & \displaystyle \frac{(k-3)(k-4)(k-5)}{3k^{2}-23k+50}<\frac{1}{3}k.\nonumber\end{eqnarray}$$
Hence, we deduce that
 $$\begin{eqnarray}\displaystyle & & \displaystyle kr-{\textstyle \frac{1}{2}}r(r-1)-\unicode[STIX]{x1D6E5}\nonumber\\ \displaystyle & & \displaystyle \quad >k(k-\lceil 2\sqrt{k}\rceil +2)-{\textstyle \frac{1}{2}}(k-\lceil 2\sqrt{k}\rceil +2)(k-\lceil 2\sqrt{k}\rceil +1)-{\textstyle \frac{1}{3}}k\nonumber\\ \displaystyle & & \displaystyle \quad ={\textstyle \frac{1}{2}}k(k+1)-{\textstyle \frac{1}{2}}(\lceil 2\sqrt{k}\rceil -1)(\lceil 2\sqrt{k}\rceil -2)-{\textstyle \frac{1}{3}}k\nonumber\\ \displaystyle & & \displaystyle \quad \geqslant {\textstyle \frac{1}{2}}k(k+1)-\sqrt{k}(2\sqrt{k}-1)-{\textstyle \frac{1}{3}}k>s.\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle kr-{\textstyle \frac{1}{2}}r(r-1)-\unicode[STIX]{x1D6E5}\nonumber\\ \displaystyle & & \displaystyle \quad >k(k-\lceil 2\sqrt{k}\rceil +2)-{\textstyle \frac{1}{2}}(k-\lceil 2\sqrt{k}\rceil +2)(k-\lceil 2\sqrt{k}\rceil +1)-{\textstyle \frac{1}{3}}k\nonumber\\ \displaystyle & & \displaystyle \quad ={\textstyle \frac{1}{2}}k(k+1)-{\textstyle \frac{1}{2}}(\lceil 2\sqrt{k}\rceil -1)(\lceil 2\sqrt{k}\rceil -2)-{\textstyle \frac{1}{3}}k\nonumber\\ \displaystyle & & \displaystyle \quad \geqslant {\textstyle \frac{1}{2}}k(k+1)-\sqrt{k}(2\sqrt{k}-1)-{\textstyle \frac{1}{3}}k>s.\nonumber\end{eqnarray}$$
We therefore deduce from Theorem 1.1 that since
 $$\begin{eqnarray}s<kr-\frac{1}{2}r(r-1)-\mathop{\sum }_{m=1}^{r-1}\frac{m(r-m)}{s-r-m},\end{eqnarray}$$
$$\begin{eqnarray}s<kr-\frac{1}{2}r(r-1)-\mathop{\sum }_{m=1}^{r-1}\frac{m(r-m)}{s-r-m},\end{eqnarray}$$
then
 $J_{s,k}(X)\ll X^{s+\unicode[STIX]{x1D700}}$
. This completes the proof of the corollary.
$J_{s,k}(X)\ll X^{s+\unicode[STIX]{x1D700}}$
. This completes the proof of the corollary.
11 A refinement of the core iteration
Our goal in this section is to outline an extension of our basic method that permits, for large exponents
![]() $k$
, the refinement of Corollary 1.2 to deliver Theorem 1.3. The details of this extension are complicated enough that we aim for a somewhat abbreviated account, exploiting the discussion of §§2–10 so as to provide an outline.
$k$
, the refinement of Corollary 1.2 to deliver Theorem 1.3. The details of this extension are complicated enough that we aim for a somewhat abbreviated account, exploiting the discussion of §§2–10 so as to provide an outline.
In §2, we fixed
![]() $r$
to be a parameter satisfying
$r$
to be a parameter satisfying
 $1\leqslant r\leqslant k-\lceil 2\sqrt{k}\rceil +2$
in order to ensure that, as the iteration bounding
$1\leqslant r\leqslant k-\lceil 2\sqrt{k}\rceil +2$
in order to ensure that, as the iteration bounding
![]() $K_{a,b}^{r,r}(X)$
in terms of related mean values
$K_{a,b}^{r,r}(X)$
in terms of related mean values
 $K_{a^{\prime },b^{\prime }}^{r,r}(X)$
proceeds, the exponents
$K_{a^{\prime },b^{\prime }}^{r,r}(X)$
proceeds, the exponents
![]() $a^{\prime }$
and
$a^{\prime }$
and
![]() $b^{\prime }$
satisfy the condition
$b^{\prime }$
satisfy the condition
 $a^{\prime }\leqslant b^{\prime }/\sqrt{k}$
. The point of the latter constraint, in fact, is to ensure that the iteration tree of mean values does not encounter a situation in which
$a^{\prime }\leqslant b^{\prime }/\sqrt{k}$
. The point of the latter constraint, in fact, is to ensure that the iteration tree of mean values does not encounter a situation in which
![]() $b^{\prime }<a^{\prime }$
, which would be fatal for the method. By relaxing this condition, but pruning the iteration tree, we permit the possibility that
$b^{\prime }<a^{\prime }$
, which would be fatal for the method. By relaxing this condition, but pruning the iteration tree, we permit the possibility that
![]() $a^{\prime }$
may be much closer to
$a^{\prime }$
may be much closer to
![]() $b^{\prime }$
in size, with the exponent mean
$b^{\prime }$
in size, with the exponent mean
![]() $s_{0}$
increased so that it becomes closer to
$s_{0}$
increased so that it becomes closer to
 ${\textstyle \frac{1}{2}}k(k+1)$
.
${\textstyle \frac{1}{2}}k(k+1)$
.
Let
 $l=\lceil k^{1/3}\rceil$
and put
$l=\lceil k^{1/3}\rceil$
and put
 $r=k-l$
. We take
$r=k-l$
. We take
![]() $s$
to be a natural number satisfying
$s$
to be a natural number satisfying
 $$\begin{eqnarray}{\textstyle \frac{1}{2}}k(k+1)-3k\leqslant s+r\leqslant {\textstyle \frac{1}{2}}k(k+1)-{\textstyle \frac{1}{3}}k-8k^{2/3}.\end{eqnarray}$$
$$\begin{eqnarray}{\textstyle \frac{1}{2}}k(k+1)-3k\leqslant s+r\leqslant {\textstyle \frac{1}{2}}k(k+1)-{\textstyle \frac{1}{3}}k-8k^{2/3}.\end{eqnarray}$$
We take
![]() $R$
and
$R$
and
![]() $N$
to be natural numbers sufficiently large in terms of
$N$
to be natural numbers sufficiently large in terms of
![]() $s$
and
$s$
and
![]() $k$
in the same manner as in §2, and define
$k$
in the same manner as in §2, and define
![]() $B$
,
$B$
,
![]() $\unicode[STIX]{x1D703}$
and
$\unicode[STIX]{x1D703}$
and
![]() $\unicode[STIX]{x1D6FF}$
as in (2.8). Other aspects of our initial set-up follow those of §2, mutatis mutandis. Lemma 6.1 remains valid provided that
$\unicode[STIX]{x1D6FF}$
as in (2.8). Other aspects of our initial set-up follow those of §2, mutatis mutandis. Lemma 6.1 remains valid provided that
 $(k-m)b\geqslant (m+1)a$
. If instead one has
$(k-m)b\geqslant (m+1)a$
. If instead one has
 $(k-m)b<(m+1)a$
, then one may make use of an alternative inequality based on the application of Hölder’s inequality.
$(k-m)b<(m+1)a$
, then one may make use of an alternative inequality based on the application of Hölder’s inequality.
Lemma 11.1. Let
![]() $m$
be an integer with
$m$
be an integer with
 $0\leqslant m\leqslant r-1$
. Suppose that
$0\leqslant m\leqslant r-1$
. Suppose that
![]() $a$
and
$a$
and
![]() $b$
are integers with
$b$
are integers with
 $0\leqslant a<b\leqslant \unicode[STIX]{x1D703}^{-1}$
. Then one has
$0\leqslant a<b\leqslant \unicode[STIX]{x1D703}^{-1}$
. Then one has
 $$\begin{eqnarray}K_{a,b}^{m+1,r}(X)\ll (J_{s+r}(X/M^{a}))^{\unicode[STIX]{x1D714}_{1}}(J_{s+r}(X/M^{b}))^{\unicode[STIX]{x1D714}_{2}}(K_{a,b}^{m,r}(X))^{\unicode[STIX]{x1D714}_{3}},\end{eqnarray}$$
$$\begin{eqnarray}K_{a,b}^{m+1,r}(X)\ll (J_{s+r}(X/M^{a}))^{\unicode[STIX]{x1D714}_{1}}(J_{s+r}(X/M^{b}))^{\unicode[STIX]{x1D714}_{2}}(K_{a,b}^{m,r}(X))^{\unicode[STIX]{x1D714}_{3}},\end{eqnarray}$$
where
 $$\begin{eqnarray}\unicode[STIX]{x1D714}_{1}=\frac{s}{(s+r)(s-m)},\qquad \unicode[STIX]{x1D714}_{2}=\frac{r}{(s+r)(s-m)}\qquad \text{and}\qquad \unicode[STIX]{x1D714}_{3}=\frac{s\,-\,m\,-\,1}{s\,-\,m}.\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D714}_{1}=\frac{s}{(s+r)(s-m)},\qquad \unicode[STIX]{x1D714}_{2}=\frac{r}{(s+r)(s-m)}\qquad \text{and}\qquad \unicode[STIX]{x1D714}_{3}=\frac{s\,-\,m\,-\,1}{s\,-\,m}.\end{eqnarray}$$
Proof. On considering the underlying Diophantine systems, it follows from (2.12) and (2.14) that for some integers
![]() $\unicode[STIX]{x1D709}$
and
$\unicode[STIX]{x1D709}$
and
![]() $\unicode[STIX]{x1D702}$
, one has
$\unicode[STIX]{x1D702}$
, one has
 $$\begin{eqnarray}K_{a,b}^{m+1,r}(X)\leqslant \oint |\mathop{\mathfrak{F}}_{a}^{m}(\unicode[STIX]{x1D736};\unicode[STIX]{x1D709})^{2}\mathfrak{f}_{a}(\unicode[STIX]{x1D736};\unicode[STIX]{x1D709})^{2}\mathfrak{F}_{b}^{r}(\unicode[STIX]{x1D736};\unicode[STIX]{x1D702})^{2}\mathfrak{f}_{b}(\unicode[STIX]{x1D736};\unicode[STIX]{x1D702})^{2s-2m-2}|\,d\unicode[STIX]{x1D736}.\end{eqnarray}$$
$$\begin{eqnarray}K_{a,b}^{m+1,r}(X)\leqslant \oint |\mathop{\mathfrak{F}}_{a}^{m}(\unicode[STIX]{x1D736};\unicode[STIX]{x1D709})^{2}\mathfrak{f}_{a}(\unicode[STIX]{x1D736};\unicode[STIX]{x1D709})^{2}\mathfrak{F}_{b}^{r}(\unicode[STIX]{x1D736};\unicode[STIX]{x1D702})^{2}\mathfrak{f}_{b}(\unicode[STIX]{x1D736};\unicode[STIX]{x1D702})^{2s-2m-2}|\,d\unicode[STIX]{x1D736}.\end{eqnarray}$$
Then, by Hölder’s inequality, we obtain
 $$\begin{eqnarray}K_{a,b}^{m+1,r}(X)\leqslant I_{1}^{\unicode[STIX]{x1D713}_{1}}I_{2}^{\unicode[STIX]{x1D713}_{2}}I_{3}^{\unicode[STIX]{x1D713}_{3}}I_{4}^{\unicode[STIX]{x1D713}_{4}}I_{5}^{\unicode[STIX]{x1D713}_{5}},\end{eqnarray}$$
$$\begin{eqnarray}K_{a,b}^{m+1,r}(X)\leqslant I_{1}^{\unicode[STIX]{x1D713}_{1}}I_{2}^{\unicode[STIX]{x1D713}_{2}}I_{3}^{\unicode[STIX]{x1D713}_{3}}I_{4}^{\unicode[STIX]{x1D713}_{4}}I_{5}^{\unicode[STIX]{x1D713}_{5}},\end{eqnarray}$$
where
 $$\begin{eqnarray}\displaystyle & \displaystyle I_{1}=\oint |\mathop{\mathfrak{F}}_{a}^{m}(\unicode[STIX]{x1D736};\unicode[STIX]{x1D709})^{4}\mathfrak{f}_{a}(\unicode[STIX]{x1D736};\unicode[STIX]{x1D709})^{2s+2r-4m}|\,d\unicode[STIX]{x1D736}, & \displaystyle \nonumber\\ \displaystyle & \displaystyle I_{2}=\oint |\mathfrak{f}_{a}(\unicode[STIX]{x1D736};\unicode[STIX]{x1D709})|^{2s+2r}\,d\unicode[STIX]{x1D736},\qquad I_{3}=\oint |\mathfrak{f}_{b}(\unicode[STIX]{x1D736};\unicode[STIX]{x1D702})|^{2s+2r}\,d\unicode[STIX]{x1D736}, & \displaystyle \nonumber\\ \displaystyle & \displaystyle I_{4}=\oint |\mathop{\mathfrak{F}}_{a}^{m}(\unicode[STIX]{x1D736};\unicode[STIX]{x1D709})^{2}\mathfrak{F}_{b}^{r}(\unicode[STIX]{x1D736};\unicode[STIX]{x1D702})^{2}\mathfrak{f}_{b}(\unicode[STIX]{x1D736};\unicode[STIX]{x1D702})^{2s-2m}|\,d\unicode[STIX]{x1D736}, & \displaystyle \nonumber\\ \displaystyle & \displaystyle I_{5}=\oint |\mathop{\mathfrak{F}}_{a}^{m}(\unicode[STIX]{x1D736};\unicode[STIX]{x1D709})^{2}\mathfrak{F}_{b}^{r}(\unicode[STIX]{x1D736};\unicode[STIX]{x1D702})^{4}\mathfrak{f}_{b}(\unicode[STIX]{x1D736};\unicode[STIX]{x1D702})^{2s-2r-2m}|\,d\unicode[STIX]{x1D736}, & \displaystyle \nonumber\\ \displaystyle & \displaystyle \unicode[STIX]{x1D713}_{1}=\frac{1}{2s-2m},\qquad \unicode[STIX]{x1D713}_{2}=\frac{s-r}{(s+r)(2s-2m)},\qquad \unicode[STIX]{x1D713}_{3}=\unicode[STIX]{x1D714}_{2}, & \displaystyle \nonumber\\ \displaystyle & \displaystyle \unicode[STIX]{x1D713}_{4}=\frac{s-m-2}{s-m}\quad \text{and}\quad \unicode[STIX]{x1D713}_{5}=\frac{1}{s-m}. & \displaystyle \nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle I_{1}=\oint |\mathop{\mathfrak{F}}_{a}^{m}(\unicode[STIX]{x1D736};\unicode[STIX]{x1D709})^{4}\mathfrak{f}_{a}(\unicode[STIX]{x1D736};\unicode[STIX]{x1D709})^{2s+2r-4m}|\,d\unicode[STIX]{x1D736}, & \displaystyle \nonumber\\ \displaystyle & \displaystyle I_{2}=\oint |\mathfrak{f}_{a}(\unicode[STIX]{x1D736};\unicode[STIX]{x1D709})|^{2s+2r}\,d\unicode[STIX]{x1D736},\qquad I_{3}=\oint |\mathfrak{f}_{b}(\unicode[STIX]{x1D736};\unicode[STIX]{x1D702})|^{2s+2r}\,d\unicode[STIX]{x1D736}, & \displaystyle \nonumber\\ \displaystyle & \displaystyle I_{4}=\oint |\mathop{\mathfrak{F}}_{a}^{m}(\unicode[STIX]{x1D736};\unicode[STIX]{x1D709})^{2}\mathfrak{F}_{b}^{r}(\unicode[STIX]{x1D736};\unicode[STIX]{x1D702})^{2}\mathfrak{f}_{b}(\unicode[STIX]{x1D736};\unicode[STIX]{x1D702})^{2s-2m}|\,d\unicode[STIX]{x1D736}, & \displaystyle \nonumber\\ \displaystyle & \displaystyle I_{5}=\oint |\mathop{\mathfrak{F}}_{a}^{m}(\unicode[STIX]{x1D736};\unicode[STIX]{x1D709})^{2}\mathfrak{F}_{b}^{r}(\unicode[STIX]{x1D736};\unicode[STIX]{x1D702})^{4}\mathfrak{f}_{b}(\unicode[STIX]{x1D736};\unicode[STIX]{x1D702})^{2s-2r-2m}|\,d\unicode[STIX]{x1D736}, & \displaystyle \nonumber\\ \displaystyle & \displaystyle \unicode[STIX]{x1D713}_{1}=\frac{1}{2s-2m},\qquad \unicode[STIX]{x1D713}_{2}=\frac{s-r}{(s+r)(2s-2m)},\qquad \unicode[STIX]{x1D713}_{3}=\unicode[STIX]{x1D714}_{2}, & \displaystyle \nonumber\\ \displaystyle & \displaystyle \unicode[STIX]{x1D713}_{4}=\frac{s-m-2}{s-m}\quad \text{and}\quad \unicode[STIX]{x1D713}_{5}=\frac{1}{s-m}. & \displaystyle \nonumber\end{eqnarray}$$
A further consideration of the underlying Diophantine systems reveals that
![]() $I_{1}\leqslant I_{2}$
and
$I_{1}\leqslant I_{2}$
and
![]() $I_{5}\leqslant I_{4}$
, and thus it follows from Lemma 2.2 and (2.12) that
$I_{5}\leqslant I_{4}$
, and thus it follows from Lemma 2.2 and (2.12) that
 $$\begin{eqnarray}K_{a,b}^{m+1,r}(X)\ll (J_{s+r}(X/M^{a}))^{\unicode[STIX]{x1D713}_{1}+\unicode[STIX]{x1D713}_{2}}(J_{s+r}(X/M^{b}))^{\unicode[STIX]{x1D714}_{2}}(K_{a,b}^{m,r}(X))^{\unicode[STIX]{x1D713}_{4}+\unicode[STIX]{x1D713}_{5}}.\end{eqnarray}$$
$$\begin{eqnarray}K_{a,b}^{m+1,r}(X)\ll (J_{s+r}(X/M^{a}))^{\unicode[STIX]{x1D713}_{1}+\unicode[STIX]{x1D713}_{2}}(J_{s+r}(X/M^{b}))^{\unicode[STIX]{x1D714}_{2}}(K_{a,b}^{m,r}(X))^{\unicode[STIX]{x1D713}_{4}+\unicode[STIX]{x1D713}_{5}}.\end{eqnarray}$$
The conclusion of the lemma follows at once. ◻
Our substitute for Lemma 7.2 must offer a surrogate for the upper bound supplied by Lemma 6.1 in those circumstances wherein
![]() $m$
and
$m$
and
![]() $a$
are both large. In this context, we introduce the parameter
$a$
are both large. In this context, we introduce the parameter
 $u=u(a,b)$
defined by
$u=u(a,b)$
defined by
 $$\begin{eqnarray}u(a,b)=rb/(a+b).\end{eqnarray}$$
$$\begin{eqnarray}u(a,b)=rb/(a+b).\end{eqnarray}$$
Notice that when
 $0\leqslant m\leqslant u-1$
, one then has
$0\leqslant m\leqslant u-1$
, one then has
 $$\begin{eqnarray}(k-m)b-ma>(k-r)b=lb.\end{eqnarray}$$
$$\begin{eqnarray}(k-m)b-ma>(k-r)b=lb.\end{eqnarray}$$
We recall also the definitions of
![]() $\unicode[STIX]{x1D719}_{m}$
and
$\unicode[STIX]{x1D719}_{m}$
and
![]() $\unicode[STIX]{x1D719}^{\ast }$
from (7.1) and (7.2), and also write
$\unicode[STIX]{x1D719}^{\ast }$
from (7.1) and (7.2), and also write
 $$\begin{eqnarray}\unicode[STIX]{x1D711}_{0}=\frac{s(r-u)}{(s+r)(s-u)}\quad \text{and}\quad \unicode[STIX]{x1D711}_{1}=\frac{r(r-u)}{(s+r)(s-u)}.\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D711}_{0}=\frac{s(r-u)}{(s+r)(s-u)}\quad \text{and}\quad \unicode[STIX]{x1D711}_{1}=\frac{r(r-u)}{(s+r)(s-u)}.\end{eqnarray}$$
Lemma 11.2. Suppose that
![]() $a$
and
$a$
and
![]() $b$
are integers with
$b$
are integers with
 $0\leqslant a<b\leqslant \unicode[STIX]{x1D703}^{-1}$
, and define
$0\leqslant a<b\leqslant \unicode[STIX]{x1D703}^{-1}$
, and define
![]() $u(a,b)$
by means of (11.1). Then, whenever
$u(a,b)$
by means of (11.1). Then, whenever
![]() $a^{\prime }$
is an integer with
$a^{\prime }$
is an integer with
![]() $a^{\prime }\geqslant a$
for which
$a^{\prime }\geqslant a$
for which
 $(k-r+1)b\geqslant ra^{\prime }$
, and
$(k-r+1)b\geqslant ra^{\prime }$
, and
![]() $u$
is an integer with
$u$
is an integer with
 $0\leqslant u\leqslant u(a,b)$
, one has
$0\leqslant u\leqslant u(a,b)$
, one has
 $$\begin{eqnarray}\unicode[STIX]{x27E6}K_{a,b}^{r,r}(X)\unicode[STIX]{x27E7}\ll ((X/M^{a})^{\unicode[STIX]{x1D711}_{0}}(X/M^{b})^{\unicode[STIX]{x1D719}^{\ast }+\unicode[STIX]{x1D711}_{1}})^{\unicode[STIX]{x1D6EC}+\unicode[STIX]{x1D6FF}}\mathop{\prod }_{m=0}^{u-1}\unicode[STIX]{x27E6}I_{b,b_{m}}^{r,r}(X)\unicode[STIX]{x27E7}^{\unicode[STIX]{x1D719}_{m}},\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x27E6}K_{a,b}^{r,r}(X)\unicode[STIX]{x27E7}\ll ((X/M^{a})^{\unicode[STIX]{x1D711}_{0}}(X/M^{b})^{\unicode[STIX]{x1D719}^{\ast }+\unicode[STIX]{x1D711}_{1}})^{\unicode[STIX]{x1D6EC}+\unicode[STIX]{x1D6FF}}\mathop{\prod }_{m=0}^{u-1}\unicode[STIX]{x27E6}I_{b,b_{m}}^{r,r}(X)\unicode[STIX]{x27E7}^{\unicode[STIX]{x1D719}_{m}},\end{eqnarray}$$
where we write
 $b_{m}=(k-m)b-ma^{\prime }$
.
$b_{m}=(k-m)b-ma^{\prime }$
.
Proof. By following the argument of the proof of Lemma 7.1, though substituting Lemma 11.1 in place of Lemma 6.1 when
 $u\leqslant m\leqslant r-1$
, we deduce that
$u\leqslant m\leqslant r-1$
, we deduce that
 $$\begin{eqnarray}\displaystyle K_{a,b}^{r,r}(X) & \ll & \displaystyle (J_{s+r}(X/M^{b}))^{\unicode[STIX]{x1D719}^{\ast }}(J_{s+r}(X/M^{a}))^{\unicode[STIX]{x1D711}_{0}}(J_{s+r}(X/M^{b}))^{\unicode[STIX]{x1D711}_{1}}\nonumber\\ \displaystyle & & \displaystyle \,\times \mathop{\prod }_{m=0}^{u-1}((M^{b_{m}-a})^{s}I_{b,b_{m}}^{r,r}(X))^{\unicode[STIX]{x1D719}_{m}}.\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle K_{a,b}^{r,r}(X) & \ll & \displaystyle (J_{s+r}(X/M^{b}))^{\unicode[STIX]{x1D719}^{\ast }}(J_{s+r}(X/M^{a}))^{\unicode[STIX]{x1D711}_{0}}(J_{s+r}(X/M^{b}))^{\unicode[STIX]{x1D711}_{1}}\nonumber\\ \displaystyle & & \displaystyle \,\times \mathop{\prod }_{m=0}^{u-1}((M^{b_{m}-a})^{s}I_{b,b_{m}}^{r,r}(X))^{\unicode[STIX]{x1D719}_{m}}.\nonumber\end{eqnarray}$$
It may be useful here to note that
 $$\begin{eqnarray}\mathop{\sum }_{m=u}^{r-1}\unicode[STIX]{x1D719}_{m}=(s-r)\mathop{\sum }_{m=u}^{r-1}(s_{m+1}^{-1}-s_{m}^{-1})=(s-r)\biggl(\frac{1}{s-r}-\frac{1}{s-u}\biggr)=\frac{r-u}{s-u}.\end{eqnarray}$$
$$\begin{eqnarray}\mathop{\sum }_{m=u}^{r-1}\unicode[STIX]{x1D719}_{m}=(s-r)\mathop{\sum }_{m=u}^{r-1}(s_{m+1}^{-1}-s_{m}^{-1})=(s-r)\biggl(\frac{1}{s-r}-\frac{1}{s-u}\biggr)=\frac{r-u}{s-u}.\end{eqnarray}$$
Thus, on recalling the definitions (2.21) to (2.23), we obtain the conclusion of the lemma, just as in the argument delivering Lemma 7.2. ◻
We next combine iterated applications of Lemma 11.2 so as to engineer a block multigrade process analogous to that delivered by Lemma 7.3. Before announcing the lemma that summarizes this process, we pause to modify the notation of §7. We consider
![]() $R$
-tuples
$R$
-tuples
![]() $\mathbf{h}$
just as in the preamble to Lemma 7.3. The sequences
$\mathbf{h}$
just as in the preamble to Lemma 7.3. The sequences
 $(a_{n})=(a_{n}(\mathbf{m};\mathbf{h}))$
and
$(a_{n})=(a_{n}(\mathbf{m};\mathbf{h}))$
and
 $(b_{n})=(b_{n}(\mathbf{m};\mathbf{h}))$
are now defined by putting
$(b_{n})=(b_{n}(\mathbf{m};\mathbf{h}))$
are now defined by putting
 $$\begin{eqnarray}a_{0}=\lfloor b/l\rfloor \quad \text{and}\quad b_{0}=b\end{eqnarray}$$
$$\begin{eqnarray}a_{0}=\lfloor b/l\rfloor \quad \text{and}\quad b_{0}=b\end{eqnarray}$$
and then applying the iterative relations (7.7). We then define
 $u_{n}(\mathbf{m};\mathbf{h})$
by putting
$u_{n}(\mathbf{m};\mathbf{h})$
by putting
 $$\begin{eqnarray}u_{n}(\mathbf{m};\mathbf{h})=rb_{n-1}/(a_{n-1}+b_{n-1}).\end{eqnarray}$$
$$\begin{eqnarray}u_{n}(\mathbf{m};\mathbf{h})=rb_{n-1}/(a_{n-1}+b_{n-1}).\end{eqnarray}$$
We emphasize here that, since
![]() $a_{n-1}$
and
$a_{n-1}$
and
![]() $b_{n-1}$
depend at most on the first
$b_{n-1}$
depend at most on the first
![]() $n-1$
coordinates of
$n-1$
coordinates of
![]() $\mathbf{m}$
and
$\mathbf{m}$
and
![]() $\mathbf{h}$
, then the same holds for
$\mathbf{h}$
, then the same holds for
 $u_{n}(\mathbf{m};\mathbf{h})$
. We use the notation
$u_{n}(\mathbf{m};\mathbf{h})$
. We use the notation
 $$\begin{eqnarray}\mathop{\prod }_{\mathbf{0}\leqslant \mathbf{m}\leqslant \mathbf{u}-1}\end{eqnarray}$$
$$\begin{eqnarray}\mathop{\prod }_{\mathbf{0}\leqslant \mathbf{m}\leqslant \mathbf{u}-1}\end{eqnarray}$$
as shorthand for the ordered product
 $$\begin{eqnarray}\mathop{\prod }_{0\leqslant m_{1}\leqslant u_{1}-1}\mathop{\prod }_{0\leqslant m_{2}\leqslant u_{2}-1}\cdots \mathop{\prod }_{0\leqslant m_{R}\leqslant u_{R}-1}.\end{eqnarray}$$
$$\begin{eqnarray}\mathop{\prod }_{0\leqslant m_{1}\leqslant u_{1}-1}\mathop{\prod }_{0\leqslant m_{2}\leqslant u_{2}-1}\cdots \mathop{\prod }_{0\leqslant m_{R}\leqslant u_{R}-1}.\end{eqnarray}$$
Finally, we redefine the quantity
 $\unicode[STIX]{x1D6E9}_{n}(\mathbf{m};\mathbf{h})$
for
$\unicode[STIX]{x1D6E9}_{n}(\mathbf{m};\mathbf{h})$
for
 $0\leqslant n\leqslant R$
by putting
$0\leqslant n\leqslant R$
by putting
 $$\begin{eqnarray}\unicode[STIX]{x1D6E9}_{n}(\mathbf{m};\mathbf{h})=(X/M^{b/2})^{-\unicode[STIX]{x1D6EC}-\unicode[STIX]{x1D6FF}}\unicode[STIX]{x27E6}K_{a_{n},b_{n}}^{r,r}(X)\unicode[STIX]{x27E7}+M^{-3sk^{R}b}.\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D6E9}_{n}(\mathbf{m};\mathbf{h})=(X/M^{b/2})^{-\unicode[STIX]{x1D6EC}-\unicode[STIX]{x1D6FF}}\unicode[STIX]{x27E6}K_{a_{n},b_{n}}^{r,r}(X)\unicode[STIX]{x27E7}+M^{-3sk^{R}b}.\end{eqnarray}$$
Lemma 11.3. Suppose that
![]() $a$
and
$a$
and
![]() $b$
are integers with
$b$
are integers with
 $$\begin{eqnarray}0\leqslant a<b\leqslant (16Rk^{2R}\unicode[STIX]{x1D703})^{-1},\end{eqnarray}$$
$$\begin{eqnarray}0\leqslant a<b\leqslant (16Rk^{2R}\unicode[STIX]{x1D703})^{-1},\end{eqnarray}$$
and suppose further that
![]() $a\leqslant b/l$
. Suppose also that
$a\leqslant b/l$
. Suppose also that
 $u_{1},\ldots ,u_{R}$
are integers with
$u_{1},\ldots ,u_{R}$
are integers with
 $0\leqslant u_{i}\leqslant u_{i}(\mathbf{m};\mathbf{h})$
$0\leqslant u_{i}\leqslant u_{i}(\mathbf{m};\mathbf{h})$
 $(1\leqslant i\leqslant R)$
. Then there exists a choice for
$(1\leqslant i\leqslant R)$
. Then there exists a choice for
 $\mathbf{h}(\mathbf{m})\in [0,\infty )^{R}$
, satisfying the condition that
$\mathbf{h}(\mathbf{m})\in [0,\infty )^{R}$
, satisfying the condition that
 $0\leqslant h_{n}(\mathbf{m})\leqslant 15k^{R}b$
$0\leqslant h_{n}(\mathbf{m})\leqslant 15k^{R}b$
 $(1\leqslant n\leqslant R)$
, and for which one has
$(1\leqslant n\leqslant R)$
, and for which one has
 $$\begin{eqnarray}(X/M^{b/2})^{-\unicode[STIX]{x1D6EC}-\unicode[STIX]{x1D6FF}}\unicode[STIX]{x27E6}K_{a,b}^{r,r}(X)\unicode[STIX]{x27E7}\ll \mathop{\prod }_{\mathbf{0}\leqslant \mathbf{m}\leqslant \mathbf{u}-1}\unicode[STIX]{x1D6E9}_{R}(\mathbf{m};\mathbf{h})^{\unicode[STIX]{x1D719}_{m_{1}}\cdots \unicode[STIX]{x1D719}_{m_{R}}}.\end{eqnarray}$$
$$\begin{eqnarray}(X/M^{b/2})^{-\unicode[STIX]{x1D6EC}-\unicode[STIX]{x1D6FF}}\unicode[STIX]{x27E6}K_{a,b}^{r,r}(X)\unicode[STIX]{x27E7}\ll \mathop{\prod }_{\mathbf{0}\leqslant \mathbf{m}\leqslant \mathbf{u}-1}\unicode[STIX]{x1D6E9}_{R}(\mathbf{m};\mathbf{h})^{\unicode[STIX]{x1D719}_{m_{1}}\cdots \unicode[STIX]{x1D719}_{m_{R}}}.\end{eqnarray}$$
Proof. One may follow the inductive strategy adopted in the proof of Lemma 7.3. The key difference in the present setting is that Lemma 11.2 contains additional factors in the estimate made available for
 $\unicode[STIX]{x27E6}K_{a,b}^{r,r}(X)\unicode[STIX]{x27E7}$
. However, it follows from Lemma 11.2 that whenever
$\unicode[STIX]{x27E6}K_{a,b}^{r,r}(X)\unicode[STIX]{x27E7}$
. However, it follows from Lemma 11.2 that whenever
 $u\leqslant u(a,b)$
, then
$u\leqslant u(a,b)$
, then
 $$\begin{eqnarray}(X/M^{b/2})^{-\unicode[STIX]{x1D6EC}-\unicode[STIX]{x1D6FF}}\unicode[STIX]{x27E6}K_{a,b}^{r,r}(X)\unicode[STIX]{x27E7}\ll (M^{(\unicode[STIX]{x1D6EC}+\unicode[STIX]{x1D6FF})b})^{\unicode[STIX]{x1D6FA}}\mathop{\prod }_{m=0}^{u-1}((X/M^{b/2})^{-\unicode[STIX]{x1D6EC}-\unicode[STIX]{x1D6FF}}\unicode[STIX]{x27E6}I_{b,b_{m}}^{r,r}(X)\unicode[STIX]{x27E7})^{\unicode[STIX]{x1D719}_{m}},\end{eqnarray}$$
$$\begin{eqnarray}(X/M^{b/2})^{-\unicode[STIX]{x1D6EC}-\unicode[STIX]{x1D6FF}}\unicode[STIX]{x27E6}K_{a,b}^{r,r}(X)\unicode[STIX]{x27E7}\ll (M^{(\unicode[STIX]{x1D6EC}+\unicode[STIX]{x1D6FF})b})^{\unicode[STIX]{x1D6FA}}\mathop{\prod }_{m=0}^{u-1}((X/M^{b/2})^{-\unicode[STIX]{x1D6EC}-\unicode[STIX]{x1D6FF}}\unicode[STIX]{x27E6}I_{b,b_{m}}^{r,r}(X)\unicode[STIX]{x27E7})^{\unicode[STIX]{x1D719}_{m}},\end{eqnarray}$$
where
 $$\begin{eqnarray}\unicode[STIX]{x1D6FA}=\frac{1}{2}-\frac{1}{2}\mathop{\sum }_{m=0}^{u-1}\unicode[STIX]{x1D719}_{m}-(\unicode[STIX]{x1D719}^{\ast }+\unicode[STIX]{x1D711}_{1}).\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D6FA}=\frac{1}{2}-\frac{1}{2}\mathop{\sum }_{m=0}^{u-1}\unicode[STIX]{x1D719}_{m}-(\unicode[STIX]{x1D719}^{\ast }+\unicode[STIX]{x1D711}_{1}).\end{eqnarray}$$
But we have
 $$\begin{eqnarray}\mathop{\sum }_{m=0}^{u-1}\unicode[STIX]{x1D719}_{m}=(s-r)\mathop{\sum }_{m=0}^{u-1}\biggl(\frac{1}{s-m-1}-\frac{1}{s-m}\biggr)=\frac{u(s-r)}{s(s-u)}\end{eqnarray}$$
$$\begin{eqnarray}\mathop{\sum }_{m=0}^{u-1}\unicode[STIX]{x1D719}_{m}=(s-r)\mathop{\sum }_{m=0}^{u-1}\biggl(\frac{1}{s-m-1}-\frac{1}{s-m}\biggr)=\frac{u(s-r)}{s(s-u)}\end{eqnarray}$$
and hence
 $2s(s-u)(s+r)\unicode[STIX]{x1D6FA}$
is equal to
$2s(s-u)(s+r)\unicode[STIX]{x1D6FA}$
is equal to
 $$\begin{eqnarray}\displaystyle & & \displaystyle -s(s+r)(s-u)-u(s-r)(s+r)+2r(s-u)(s+r)-2r(r-u)s\nonumber\\ \displaystyle & & \displaystyle \qquad =-s^{3}+rs^{2}+urs-ur^{2}=-(s-r)(s^{2}-ur).\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle -s(s+r)(s-u)-u(s-r)(s+r)+2r(s-u)(s+r)-2r(r-u)s\nonumber\\ \displaystyle & & \displaystyle \qquad =-s^{3}+rs^{2}+urs-ur^{2}=-(s-r)(s^{2}-ur).\nonumber\end{eqnarray}$$
Since we may suppose that
![]() $s>r$
,
$s>r$
,
![]() $s>u$
and
$s>u$
and
![]() $s^{2}>ur$
, we find that
$s^{2}>ur$
, we find that
![]() $\unicode[STIX]{x1D6FA}<0$
and hence
$\unicode[STIX]{x1D6FA}<0$
and hence
 $$\begin{eqnarray}(X/M^{b/2})^{-\unicode[STIX]{x1D6EC}-\unicode[STIX]{x1D6FF}}\unicode[STIX]{x27E6}K_{a,b}^{r,r}(X)\unicode[STIX]{x27E7}\ll \mathop{\prod }_{m=0}^{u-1}((X/M^{b/2})^{-\unicode[STIX]{x1D6EC}-\unicode[STIX]{x1D6FF}}\unicode[STIX]{x27E6}I_{b,b_{m}}^{r,r}(X)\unicode[STIX]{x27E7})^{\unicode[STIX]{x1D719}_{m}}.\end{eqnarray}$$
$$\begin{eqnarray}(X/M^{b/2})^{-\unicode[STIX]{x1D6EC}-\unicode[STIX]{x1D6FF}}\unicode[STIX]{x27E6}K_{a,b}^{r,r}(X)\unicode[STIX]{x27E7}\ll \mathop{\prod }_{m=0}^{u-1}((X/M^{b/2})^{-\unicode[STIX]{x1D6EC}-\unicode[STIX]{x1D6FF}}\unicode[STIX]{x27E6}I_{b,b_{m}}^{r,r}(X)\unicode[STIX]{x27E7})^{\unicode[STIX]{x1D719}_{m}}.\end{eqnarray}$$
This relation serves as a substitute for Lemma 7.2 in the proof of Lemma 7.3, the proof of which now applies without serious modification. This completes our account of the proof of Lemma 11.3. ◻
We must now grapple with the somewhat daunting task of developing an analogue of Lemma 8.2 in the current setting. We now define the sequences
 $(\tilde{a}_{n})=(\tilde{a}_{n}(\mathbf{m}))$
and
$(\tilde{a}_{n})=(\tilde{a}_{n}(\mathbf{m}))$
and
 $(\tilde{b}_{n})=(\tilde{b}_{n}(\mathbf{m}))$
by putting
$(\tilde{b}_{n})=(\tilde{b}_{n}(\mathbf{m}))$
by putting
 $$\begin{eqnarray}\tilde{a}_{0}=1/l\quad \text{and}\quad \tilde{b}_{0}=1,\end{eqnarray}$$
$$\begin{eqnarray}\tilde{a}_{0}=1/l\quad \text{and}\quad \tilde{b}_{0}=1,\end{eqnarray}$$
and then applying the relations (8.3). We define the parameters
 $\tilde{u} _{i}=\tilde{u} _{i}(\mathbf{m})$
and
$\tilde{u} _{i}=\tilde{u} _{i}(\mathbf{m})$
and
 $\tilde{v}_{i}=\tilde{v}_{i}(\mathbf{m})$
for
$\tilde{v}_{i}=\tilde{v}_{i}(\mathbf{m})$
for
 $1\leqslant i\leqslant R$
by putting
$1\leqslant i\leqslant R$
by putting
 $$\begin{eqnarray}\tilde{u} _{i}(\mathbf{m})=r\tilde{b}_{i-1}/(\tilde{a}_{i-1}+\tilde{b}_{i-1})\quad \text{and}\quad \tilde{v}_{i}(\mathbf{m})=\lfloor \tilde{u} _{i}(\mathbf{m})\rfloor .\end{eqnarray}$$
$$\begin{eqnarray}\tilde{u} _{i}(\mathbf{m})=r\tilde{b}_{i-1}/(\tilde{a}_{i-1}+\tilde{b}_{i-1})\quad \text{and}\quad \tilde{v}_{i}(\mathbf{m})=\lfloor \tilde{u} _{i}(\mathbf{m})\rfloor .\end{eqnarray}$$
Next, we define the positive real number
![]() $s_{0}$
by means of the relation
$s_{0}$
by means of the relation
 $$\begin{eqnarray}s_{0}^{R}=s^{R}\mathop{\sum }_{m_{1}=0}^{\tilde{v}_{1}-1}\mathop{\sum }_{m_{2}=0}^{\tilde{v}_{2}-1}\cdots \mathop{\sum }_{m_{R}=0}^{\tilde{v}_{R}-1}\unicode[STIX]{x1D719}_{m_{1}}\unicode[STIX]{x1D719}_{m_{2}}\cdots \unicode[STIX]{x1D719}_{m_{R}}\tilde{b}_{R}(\mathbf{m}),\end{eqnarray}$$
$$\begin{eqnarray}s_{0}^{R}=s^{R}\mathop{\sum }_{m_{1}=0}^{\tilde{v}_{1}-1}\mathop{\sum }_{m_{2}=0}^{\tilde{v}_{2}-1}\cdots \mathop{\sum }_{m_{R}=0}^{\tilde{v}_{R}-1}\unicode[STIX]{x1D719}_{m_{1}}\unicode[STIX]{x1D719}_{m_{2}}\cdots \unicode[STIX]{x1D719}_{m_{R}}\tilde{b}_{R}(\mathbf{m}),\end{eqnarray}$$
and then put
 $$\begin{eqnarray}k_{\mathbf{m}}=\tilde{b}_{R}(\mathbf{m})\quad \text{and}\quad \unicode[STIX]{x1D70C}_{\mathbf{m}}=\tilde{b}_{R}(\mathbf{m})(s/s_{0})^{R}\quad (\mathbf{m}\in [0,r-1]^{R}).\end{eqnarray}$$
$$\begin{eqnarray}k_{\mathbf{m}}=\tilde{b}_{R}(\mathbf{m})\quad \text{and}\quad \unicode[STIX]{x1D70C}_{\mathbf{m}}=\tilde{b}_{R}(\mathbf{m})(s/s_{0})^{R}\quad (\mathbf{m}\in [0,r-1]^{R}).\end{eqnarray}$$
We note here that the values of
![]() $k_{\mathbf{m}}$
and
$k_{\mathbf{m}}$
and
![]() $\unicode[STIX]{x1D70C}_{\mathbf{m}}$
are not relevant when
$\unicode[STIX]{x1D70C}_{\mathbf{m}}$
are not relevant when
![]() $\mathbf{m}$
does not satisfy the condition
$\mathbf{m}$
does not satisfy the condition
 $0\leqslant m_{i}\leqslant \tilde{v}_{i}-1$
$0\leqslant m_{i}\leqslant \tilde{v}_{i}-1$
 $(1\leqslant i\leqslant R)$
, and so we are indifferent to the values stemming from (11.6) in such circumstances.
$(1\leqslant i\leqslant R)$
, and so we are indifferent to the values stemming from (11.6) in such circumstances.
Before proceeding further, we pause to relate
![]() $u_{i}$
and
$u_{i}$
and
![]() $\tilde{u} _{i}$
.
$\tilde{u} _{i}$
.
Lemma 11.4. Suppose that
![]() $a\leqslant b/l$
and
$a\leqslant b/l$
and
 $0\leqslant h_{n}(\mathbf{m})\leqslant 16k^{R}b$
$0\leqslant h_{n}(\mathbf{m})\leqslant 16k^{R}b$
 $(1\leqslant n\leqslant R)$
. Then one has
$(1\leqslant n\leqslant R)$
. Then one has
 $0\leqslant \tilde{u} _{n}(\mathbf{m})\leqslant u_{n}(\mathbf{m};\mathbf{h})$
$0\leqslant \tilde{u} _{n}(\mathbf{m})\leqslant u_{n}(\mathbf{m};\mathbf{h})$
 $(1\leqslant n\leqslant R)$
.
$(1\leqslant n\leqslant R)$
.
Proof. We prove the asserted inequalities by induction, beginning with the case
![]() $n=1$
. From (11.4), we find on the one hand that
$n=1$
. From (11.4), we find on the one hand that
 $$\begin{eqnarray}\tilde{u} _{1}=r\tilde{b}_{0}/(\tilde{a}_{0}+\tilde{b}_{0})=r/(1+1/l),\end{eqnarray}$$
$$\begin{eqnarray}\tilde{u} _{1}=r\tilde{b}_{0}/(\tilde{a}_{0}+\tilde{b}_{0})=r/(1+1/l),\end{eqnarray}$$
whilst, on the other, from (11.2), one has
 $$\begin{eqnarray}u_{1}=rb_{0}/(a_{0}+b_{0})=r/(1+a_{0}/b)\geqslant r(1+1/l).\end{eqnarray}$$
$$\begin{eqnarray}u_{1}=rb_{0}/(a_{0}+b_{0})=r/(1+a_{0}/b)\geqslant r(1+1/l).\end{eqnarray}$$
Thus
![]() $\tilde{u} _{1}\leqslant u_{1}$
, confirming the inductive hypothesis when
$\tilde{u} _{1}\leqslant u_{1}$
, confirming the inductive hypothesis when
![]() $n=1$
. Suppose next that
$n=1$
. Suppose next that
![]() $n\geqslant 1$
and
$n\geqslant 1$
and
![]() $\tilde{u} _{n}\leqslant u_{n}$
. One has
$\tilde{u} _{n}\leqslant u_{n}$
. One has
 $$\begin{eqnarray}\frac{b_{n+1}}{a_{n+1}+b_{n+1}}\geqslant \frac{\tilde{b}_{n+1}}{\tilde{a}_{n+1}+\tilde{b}_{n+1}}\end{eqnarray}$$
$$\begin{eqnarray}\frac{b_{n+1}}{a_{n+1}+b_{n+1}}\geqslant \frac{\tilde{b}_{n+1}}{\tilde{a}_{n+1}+\tilde{b}_{n+1}}\end{eqnarray}$$
if and only if
 $b_{n+1}/a_{n+1}\geqslant \tilde{b}_{n+1}/\tilde{a}_{n+1}$
, which is to say that
$b_{n+1}/a_{n+1}\geqslant \tilde{b}_{n+1}/\tilde{a}_{n+1}$
, which is to say that
 $$\begin{eqnarray}((k-m_{n+1})b_{n}-m_{n+1}a_{n}+h_{n+1})/b_{n}\geqslant ((k-m_{n+1})\tilde{b}_{n}-m_{n+1}\tilde{a}_{n})/\tilde{b}_{n}.\end{eqnarray}$$
$$\begin{eqnarray}((k-m_{n+1})b_{n}-m_{n+1}a_{n}+h_{n+1})/b_{n}\geqslant ((k-m_{n+1})\tilde{b}_{n}-m_{n+1}\tilde{a}_{n})/\tilde{b}_{n}.\end{eqnarray}$$
This lower bound is satisfied if and only if
 $m_{n+1}\tilde{a}_{n}/\tilde{b}_{n}\geqslant (m_{n+1}a_{n}-h_{n+1})/b_{n}$
. The latter is automatically satisfied when either
$m_{n+1}\tilde{a}_{n}/\tilde{b}_{n}\geqslant (m_{n+1}a_{n}-h_{n+1})/b_{n}$
. The latter is automatically satisfied when either
 $m_{n+1}=0$
or
$m_{n+1}=0$
or
 $h_{n+1}\geqslant m_{n+1}a_{n}$
, and otherwise it is equivalent to the upper bound
$h_{n+1}\geqslant m_{n+1}a_{n}$
, and otherwise it is equivalent to the upper bound
 $$\begin{eqnarray}\frac{\tilde{b}_{n}}{\tilde{a}_{n}+\tilde{b}_{n}}\leqslant \frac{b_{n}}{a_{n}+b_{n}-h_{n+1}/m_{n+1}}.\end{eqnarray}$$
$$\begin{eqnarray}\frac{\tilde{b}_{n}}{\tilde{a}_{n}+\tilde{b}_{n}}\leqslant \frac{b_{n}}{a_{n}+b_{n}-h_{n+1}/m_{n+1}}.\end{eqnarray}$$
However, when
 $m_{n+1}>0$
, in view of our hypothesis
$m_{n+1}>0$
, in view of our hypothesis
![]() $\tilde{u} _{n}\leqslant u_{n}$
, one has
$\tilde{u} _{n}\leqslant u_{n}$
, one has
 $$\begin{eqnarray}\frac{\tilde{b}_{n}}{\tilde{a}_{n}+\tilde{b}_{n}}\leqslant \frac{b_{n}}{a_{n}+b_{n}}\leqslant \frac{b_{n}}{a_{n}+b_{n}-h_{n+1}/m_{n+1}}.\end{eqnarray}$$
$$\begin{eqnarray}\frac{\tilde{b}_{n}}{\tilde{a}_{n}+\tilde{b}_{n}}\leqslant \frac{b_{n}}{a_{n}+b_{n}}\leqslant \frac{b_{n}}{a_{n}+b_{n}-h_{n+1}/m_{n+1}}.\end{eqnarray}$$
Thus, we conclude from (11.2), (11.4) and (11.7) that
 $\tilde{u} _{n+1}\leqslant u_{n+1}$
. This confirms the inductive hypothesis and hence we deduce that
$\tilde{u} _{n+1}\leqslant u_{n+1}$
. This confirms the inductive hypothesis and hence we deduce that
 $0\leqslant \tilde{u} _{n}\leqslant u_{n}$
for
$0\leqslant \tilde{u} _{n}\leqslant u_{n}$
for
 $1\leqslant n\leqslant R$
, as claimed.◻
$1\leqslant n\leqslant R$
, as claimed.◻
We next introduce some additional quantities of use in our ultimate application of Lemma 8.1. Define the exponents
![]() $\unicode[STIX]{x1D6FD}_{\mathbf{m}}^{(l)}$
and
$\unicode[STIX]{x1D6FD}_{\mathbf{m}}^{(l)}$
and
![]() $\unicode[STIX]{x1D6FE}_{\mathbf{m}}^{(l)}$
just as in the discussion following (8.8) above. We now put
$\unicode[STIX]{x1D6FE}_{\mathbf{m}}^{(l)}$
just as in the discussion following (8.8) above. We now put
 $$\begin{eqnarray}B_{n}=\mathop{\sum }_{m_{1}=0}^{\tilde{v}_{1}-1}\cdots \mathop{\sum }_{m_{n}=0}^{\tilde{v}_{n}-1}\unicode[STIX]{x1D6FD}_{\mathbf{m}}^{(n)}\tilde{b}_{n}(\mathbf{m})\quad \text{and}\quad A_{n}=\mathop{\sum }_{m_{1}=0}^{\tilde{v}_{1}-1}\cdots \mathop{\sum }_{m_{n}=0}^{\tilde{v}_{n}-1}\unicode[STIX]{x1D6FD}_{\mathbf{m}}^{(n)}\tilde{a}_{n}(\mathbf{m}).\end{eqnarray}$$
$$\begin{eqnarray}B_{n}=\mathop{\sum }_{m_{1}=0}^{\tilde{v}_{1}-1}\cdots \mathop{\sum }_{m_{n}=0}^{\tilde{v}_{n}-1}\unicode[STIX]{x1D6FD}_{\mathbf{m}}^{(n)}\tilde{b}_{n}(\mathbf{m})\quad \text{and}\quad A_{n}=\mathop{\sum }_{m_{1}=0}^{\tilde{v}_{1}-1}\cdots \mathop{\sum }_{m_{n}=0}^{\tilde{v}_{n}-1}\unicode[STIX]{x1D6FD}_{\mathbf{m}}^{(n)}\tilde{a}_{n}(\mathbf{m}).\end{eqnarray}$$
In order to understand these sequences, we introduce some auxiliary sequences
![]() $\tilde{A}_{n}$
and
$\tilde{A}_{n}$
and
![]() $\tilde{B}_{n}$
as follows. We put
$\tilde{B}_{n}$
as follows. We put
 $$\begin{eqnarray}\mathfrak{a}={\textstyle \frac{1}{2}}k(k+1)-{\textstyle \frac{1}{3}}k-3k^{2/3}\quad \text{and}\quad \mathfrak{b}={\textstyle \frac{1}{2}}k(k-1)+3k^{5/3}.\end{eqnarray}$$
$$\begin{eqnarray}\mathfrak{a}={\textstyle \frac{1}{2}}k(k+1)-{\textstyle \frac{1}{3}}k-3k^{2/3}\quad \text{and}\quad \mathfrak{b}={\textstyle \frac{1}{2}}k(k-1)+3k^{5/3}.\end{eqnarray}$$
The sequence
![]() $\tilde{B}_{n}$
is then defined for
$\tilde{B}_{n}$
is then defined for
![]() $n\geqslant 1$
by means of the relations
$n\geqslant 1$
by means of the relations
 $$\begin{eqnarray}s\tilde{B}_{1}=\mathfrak{a}-\mathfrak{b}/l,\qquad s^{2}\tilde{B}_{2}=\mathfrak{a}(\mathfrak{a}-\mathfrak{b}/l)-r\mathfrak{b}\end{eqnarray}$$
$$\begin{eqnarray}s\tilde{B}_{1}=\mathfrak{a}-\mathfrak{b}/l,\qquad s^{2}\tilde{B}_{2}=\mathfrak{a}(\mathfrak{a}-\mathfrak{b}/l)-r\mathfrak{b}\end{eqnarray}$$
and
 $$\begin{eqnarray}s^{2}\tilde{B}_{n+2}=s\mathfrak{a}\tilde{B}_{n+1}-r\mathfrak{b}\tilde{B}_{n}\quad (n\geqslant 1).\end{eqnarray}$$
$$\begin{eqnarray}s^{2}\tilde{B}_{n+2}=s\mathfrak{a}\tilde{B}_{n+1}-r\mathfrak{b}\tilde{B}_{n}\quad (n\geqslant 1).\end{eqnarray}$$
Finally, we put
 $$\begin{eqnarray}\unicode[STIX]{x1D703}_{\pm }={\textstyle \frac{1}{2}}(\mathfrak{a}\pm \sqrt{\mathfrak{a}^{2}-4r\mathfrak{b}}).\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D703}_{\pm }={\textstyle \frac{1}{2}}(\mathfrak{a}\pm \sqrt{\mathfrak{a}^{2}-4r\mathfrak{b}}).\end{eqnarray}$$
Lemma 11.5. When
![]() $n\geqslant 1$
, one has
$n\geqslant 1$
, one has
 $B_{n}\geqslant \tilde{B}_{n}$
. In particular, one has the lower bound
$B_{n}\geqslant \tilde{B}_{n}$
. In particular, one has the lower bound
 $B_{R}\geqslant \tilde{B}_{R}$
and hence
$B_{R}\geqslant \tilde{B}_{R}$
and hence
 $$\begin{eqnarray}s_{0}^{R}\geqslant \frac{\unicode[STIX]{x1D703}_{+}^{R+1}-\unicode[STIX]{x1D703}_{-}^{R+1}}{\unicode[STIX]{x1D703}_{+}-\unicode[STIX]{x1D703}_{-}}-\frac{\unicode[STIX]{x1D703}_{+}\unicode[STIX]{x1D703}_{-}}{lr}\biggl(\frac{\unicode[STIX]{x1D703}_{+}^{R}-\unicode[STIX]{x1D703}_{-}^{R}}{\unicode[STIX]{x1D703}_{+}-\unicode[STIX]{x1D703}_{-}}\biggr).\end{eqnarray}$$
$$\begin{eqnarray}s_{0}^{R}\geqslant \frac{\unicode[STIX]{x1D703}_{+}^{R+1}-\unicode[STIX]{x1D703}_{-}^{R+1}}{\unicode[STIX]{x1D703}_{+}-\unicode[STIX]{x1D703}_{-}}-\frac{\unicode[STIX]{x1D703}_{+}\unicode[STIX]{x1D703}_{-}}{lr}\biggl(\frac{\unicode[STIX]{x1D703}_{+}^{R}-\unicode[STIX]{x1D703}_{-}^{R}}{\unicode[STIX]{x1D703}_{+}-\unicode[STIX]{x1D703}_{-}}\biggr).\end{eqnarray}$$
Proof. We have
 $$\begin{eqnarray}B_{n+1}=\mathop{\sum }_{m_{1}=0}^{\tilde{v}_{1}-1}\cdots \mathop{\sum }_{m_{n}=0}^{\tilde{v}_{n}-1}\unicode[STIX]{x1D6FD}_{\mathbf{m}}^{(n)}\mathop{\sum }_{m_{n+1}=0}^{\tilde{v}_{n+1}-1}\unicode[STIX]{x1D719}_{m_{n+1}}\tilde{b}_{n+1}(\mathbf{m}).\end{eqnarray}$$
$$\begin{eqnarray}B_{n+1}=\mathop{\sum }_{m_{1}=0}^{\tilde{v}_{1}-1}\cdots \mathop{\sum }_{m_{n}=0}^{\tilde{v}_{n}-1}\unicode[STIX]{x1D6FD}_{\mathbf{m}}^{(n)}\mathop{\sum }_{m_{n+1}=0}^{\tilde{v}_{n+1}-1}\unicode[STIX]{x1D719}_{m_{n+1}}\tilde{b}_{n+1}(\mathbf{m}).\end{eqnarray}$$
The innermost sum here is
 $$\begin{eqnarray}\mathop{\sum }_{m_{n+1}=0}^{\tilde{v}_{n+1}-1}\unicode[STIX]{x1D719}_{m_{n+1}}\tilde{b}_{n+1}(\mathbf{m})=\mathfrak{B}(\tilde{v}_{n+1})\tilde{b}_{n}(\mathbf{m})-\mathfrak{A}(\tilde{v}_{n+1})\tilde{a}_{n}(\mathbf{m}),\end{eqnarray}$$
$$\begin{eqnarray}\mathop{\sum }_{m_{n+1}=0}^{\tilde{v}_{n+1}-1}\unicode[STIX]{x1D719}_{m_{n+1}}\tilde{b}_{n+1}(\mathbf{m})=\mathfrak{B}(\tilde{v}_{n+1})\tilde{b}_{n}(\mathbf{m})-\mathfrak{A}(\tilde{v}_{n+1})\tilde{a}_{n}(\mathbf{m}),\end{eqnarray}$$
where
 $$\begin{eqnarray}\mathfrak{B}(u)=\mathop{\sum }_{m=0}^{u-1}(k-m)\unicode[STIX]{x1D719}_{m}\quad \text{and}\quad \mathfrak{A}(u)=\mathop{\sum }_{m=0}^{u-1}m\unicode[STIX]{x1D719}_{m}.\end{eqnarray}$$
$$\begin{eqnarray}\mathfrak{B}(u)=\mathop{\sum }_{m=0}^{u-1}(k-m)\unicode[STIX]{x1D719}_{m}\quad \text{and}\quad \mathfrak{A}(u)=\mathop{\sum }_{m=0}^{u-1}m\unicode[STIX]{x1D719}_{m}.\end{eqnarray}$$
We observe that when
![]() $u$
is a positive integer, one has
$u$
is a positive integer, one has
 $$\begin{eqnarray}\displaystyle \mathfrak{B}(u) & = & \displaystyle \mathop{\sum }_{m=0}^{u-1}\frac{(k-m)(s-r)}{(s-m)(s-m-1)}\nonumber\\ \displaystyle & = & \displaystyle \mathop{\sum }_{m=0}^{u-1}\biggl(\frac{(r-m)(k-m)}{s-m}-\frac{(r-m-1)(k-m-1)}{s-m-1}-\frac{r-m-1}{s-m-1}\biggr),\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \mathfrak{B}(u) & = & \displaystyle \mathop{\sum }_{m=0}^{u-1}\frac{(k-m)(s-r)}{(s-m)(s-m-1)}\nonumber\\ \displaystyle & = & \displaystyle \mathop{\sum }_{m=0}^{u-1}\biggl(\frac{(r-m)(k-m)}{s-m}-\frac{(r-m-1)(k-m-1)}{s-m-1}-\frac{r-m-1}{s-m-1}\biggr),\nonumber\end{eqnarray}$$
whence
 $$\begin{eqnarray}\displaystyle s\mathfrak{B}(u) & = & \displaystyle kr-\frac{s(r-u)(k-u)}{s-u}-s\mathop{\sum }_{m=1}^{u}\frac{r-m}{s-m}\nonumber\\ \displaystyle & = & \displaystyle u(k+r-u)-\frac{u(r-u)(k-u)}{s-u}-\frac{1}{2}r(r-1)\nonumber\\ \displaystyle & & \displaystyle +\,\frac{1}{2}(r-u-1)(r-u)-\mathop{\sum }_{m=1}^{u}\frac{m(r-m)}{s-m}.\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle s\mathfrak{B}(u) & = & \displaystyle kr-\frac{s(r-u)(k-u)}{s-u}-s\mathop{\sum }_{m=1}^{u}\frac{r-m}{s-m}\nonumber\\ \displaystyle & = & \displaystyle u(k+r-u)-\frac{u(r-u)(k-u)}{s-u}-\frac{1}{2}r(r-1)\nonumber\\ \displaystyle & & \displaystyle +\,\frac{1}{2}(r-u-1)(r-u)-\mathop{\sum }_{m=1}^{u}\frac{m(r-m)}{s-m}.\nonumber\end{eqnarray}$$
Thus, we conclude that
 $$\begin{eqnarray}s\mathfrak{B}(u)=ku-\frac{1}{2}u(u-1)-\frac{u(r-u)(k-u)}{s-u}-\mathop{\sum }_{m=1}^{u}\frac{m(r-m)}{s-m}.\end{eqnarray}$$
$$\begin{eqnarray}s\mathfrak{B}(u)=ku-\frac{1}{2}u(u-1)-\frac{u(r-u)(k-u)}{s-u}-\mathop{\sum }_{m=1}^{u}\frac{m(r-m)}{s-m}.\end{eqnarray}$$
One finds in like manner that
 $$\begin{eqnarray}\displaystyle s\mathfrak{A}(u) & = & \displaystyle sk\mathop{\sum }_{m=0}^{u-1}\unicode[STIX]{x1D719}_{m}-s\mathop{\sum }_{m=0}^{u-1}(k-m)\unicode[STIX]{x1D719}_{m}\nonumber\\ \displaystyle & = & \displaystyle \frac{ku(s-r)}{s-u}-\biggl(ku-\frac{1}{2}u(u-1)-\frac{u(r-u)(k-u)}{s-u}\nonumber\\ \displaystyle & & \displaystyle -\,\mathop{\sum }_{m=1}^{u}\frac{m(r-m)}{s-m}\biggr)\nonumber\\ \displaystyle & = & \displaystyle \frac{1}{2}u(u-1)-\frac{u^{2}(r-u)}{s-u}+\mathop{\sum }_{m=1}^{u}\frac{m(r-m)}{s-m}.\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle s\mathfrak{A}(u) & = & \displaystyle sk\mathop{\sum }_{m=0}^{u-1}\unicode[STIX]{x1D719}_{m}-s\mathop{\sum }_{m=0}^{u-1}(k-m)\unicode[STIX]{x1D719}_{m}\nonumber\\ \displaystyle & = & \displaystyle \frac{ku(s-r)}{s-u}-\biggl(ku-\frac{1}{2}u(u-1)-\frac{u(r-u)(k-u)}{s-u}\nonumber\\ \displaystyle & & \displaystyle -\,\mathop{\sum }_{m=1}^{u}\frac{m(r-m)}{s-m}\biggr)\nonumber\\ \displaystyle & = & \displaystyle \frac{1}{2}u(u-1)-\frac{u^{2}(r-u)}{s-u}+\mathop{\sum }_{m=1}^{u}\frac{m(r-m)}{s-m}.\end{eqnarray}$$
Write
 $$\begin{eqnarray}v=\tilde{v}_{n+1},\qquad h=r-v=k-l-v\quad \text{and}\quad \widetilde{\unicode[STIX]{x1D6E5}}=\mathop{\sum }_{m=1}^{v}\frac{m(r-m)}{s-m}.\end{eqnarray}$$
$$\begin{eqnarray}v=\tilde{v}_{n+1},\qquad h=r-v=k-l-v\quad \text{and}\quad \widetilde{\unicode[STIX]{x1D6E5}}=\mathop{\sum }_{m=1}^{v}\frac{m(r-m)}{s-m}.\end{eqnarray}$$
Then we see from (11.15) that
![]() $s\mathfrak{B}(v)$
is equal to
$s\mathfrak{B}(v)$
is equal to
 $$\begin{eqnarray}\displaystyle & & \displaystyle k(k-l-h)-\frac{1}{2}(k-l-h)(k-l-h-1)-\frac{h(l+h)(k-l-h)}{s-k+l+h}-\widetilde{\unicode[STIX]{x1D6E5}}\nonumber\\ \displaystyle & & \displaystyle \quad =\frac{1}{2}k(k+1)-\frac{1}{2}(l+h)(l+h+1)-\frac{h(l+h)(k-l-h)}{s-k+l+h}-\widetilde{\unicode[STIX]{x1D6E5}}.\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle k(k-l-h)-\frac{1}{2}(k-l-h)(k-l-h-1)-\frac{h(l+h)(k-l-h)}{s-k+l+h}-\widetilde{\unicode[STIX]{x1D6E5}}\nonumber\\ \displaystyle & & \displaystyle \quad =\frac{1}{2}k(k+1)-\frac{1}{2}(l+h)(l+h+1)-\frac{h(l+h)(k-l-h)}{s-k+l+h}-\widetilde{\unicode[STIX]{x1D6E5}}.\nonumber\end{eqnarray}$$
Also, from (11.16), we find that
![]() $s\mathfrak{A}(v)$
is equal to
$s\mathfrak{A}(v)$
is equal to
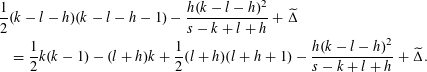 $$\begin{eqnarray}\displaystyle & & \displaystyle \frac{1}{2}(k-l-h)(k-l-h-1)-\frac{h(k-l-h)^{2}}{s-k+l+h}+\widetilde{\unicode[STIX]{x1D6E5}}\nonumber\\ \displaystyle & & \displaystyle \quad =\frac{1}{2}k(k-1)-(l+h)k+\frac{1}{2}(l+h)(l+h+1)-\frac{h(k-l-h)^{2}}{s-k+l+h}+\widetilde{\unicode[STIX]{x1D6E5}}.\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle \frac{1}{2}(k-l-h)(k-l-h-1)-\frac{h(k-l-h)^{2}}{s-k+l+h}+\widetilde{\unicode[STIX]{x1D6E5}}\nonumber\\ \displaystyle & & \displaystyle \quad =\frac{1}{2}k(k-1)-(l+h)k+\frac{1}{2}(l+h)(l+h+1)-\frac{h(k-l-h)^{2}}{s-k+l+h}+\widetilde{\unicode[STIX]{x1D6E5}}.\nonumber\end{eqnarray}$$
On substituting these formulae into (11.14), we find that
 $$\begin{eqnarray}s\mathop{\sum }_{m_{n+1}=0}^{\tilde{v}_{n+1}-1}\unicode[STIX]{x1D719}_{m_{n+1}}\tilde{b}_{n+1}(\mathbf{m})=\mathfrak{a}_{0}\tilde{b}_{n}(\mathbf{m})-\mathfrak{b}_{0}\tilde{a}_{n}(\mathbf{m})-\unicode[STIX]{x1D6F6},\end{eqnarray}$$
$$\begin{eqnarray}s\mathop{\sum }_{m_{n+1}=0}^{\tilde{v}_{n+1}-1}\unicode[STIX]{x1D719}_{m_{n+1}}\tilde{b}_{n+1}(\mathbf{m})=\mathfrak{a}_{0}\tilde{b}_{n}(\mathbf{m})-\mathfrak{b}_{0}\tilde{a}_{n}(\mathbf{m})-\unicode[STIX]{x1D6F6},\end{eqnarray}$$
where
 $$\begin{eqnarray}\displaystyle \mathfrak{a}_{0} & = & \displaystyle {\textstyle \frac{1}{2}}k(k+1)-{\textstyle \frac{1}{2}}l(l+1)-\widetilde{\unicode[STIX]{x1D6E5}},\nonumber\\ \displaystyle \mathfrak{b}_{0} & = & \displaystyle {\textstyle \frac{1}{2}}k(k-1)-lk+{\textstyle \frac{1}{2}}l(l+1)+\widetilde{\unicode[STIX]{x1D6E5}}\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \mathfrak{a}_{0} & = & \displaystyle {\textstyle \frac{1}{2}}k(k+1)-{\textstyle \frac{1}{2}}l(l+1)-\widetilde{\unicode[STIX]{x1D6E5}},\nonumber\\ \displaystyle \mathfrak{b}_{0} & = & \displaystyle {\textstyle \frac{1}{2}}k(k-1)-lk+{\textstyle \frac{1}{2}}l(l+1)+\widetilde{\unicode[STIX]{x1D6E5}}\nonumber\end{eqnarray}$$
and
 $$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D6F6} & = & \displaystyle \biggl(lh+\frac{1}{2}h(h+1)\biggr)(\tilde{a}_{n}+\tilde{b}_{n})+\frac{h(l+h)(k-l-h)}{s-k+l+h}\tilde{b}_{n}\nonumber\\ \displaystyle & & \displaystyle -\,\biggl(hk+\frac{h(k-l-h)^{2}}{s-k+l+h}\biggr)\tilde{a}_{n}.\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D6F6} & = & \displaystyle \biggl(lh+\frac{1}{2}h(h+1)\biggr)(\tilde{a}_{n}+\tilde{b}_{n})+\frac{h(l+h)(k-l-h)}{s-k+l+h}\tilde{b}_{n}\nonumber\\ \displaystyle & & \displaystyle -\,\biggl(hk+\frac{h(k-l-h)^{2}}{s-k+l+h}\biggr)\tilde{a}_{n}.\end{eqnarray}$$
We next seek to estimate the expression
![]() $\unicode[STIX]{x1D6F6}$
, this requiring us to obtain an upper bound for
$\unicode[STIX]{x1D6F6}$
, this requiring us to obtain an upper bound for
![]() $h$
. We begin with a proof that
$h$
. We begin with a proof that
 $\tilde{v}_{n}(\mathbf{m})\geqslant k(1-2/l)$
for
$\tilde{v}_{n}(\mathbf{m})\geqslant k(1-2/l)$
for
 $1\leqslant n\leqslant R$
. Note first that, since we assume
$1\leqslant n\leqslant R$
. Note first that, since we assume
![]() $k$
to be sufficiently large and
$k$
to be sufficiently large and
 $l=\lceil k^{1/3}\rceil$
, one finds from (11.4) that
$l=\lceil k^{1/3}\rceil$
, one finds from (11.4) that
 $$\begin{eqnarray}\tilde{u} _{1}=r\tilde{b}_{0}/(\tilde{a}_{0}+\tilde{b}_{0})=(k-l)/(1+1/l)>k-2k/l+1.\end{eqnarray}$$
$$\begin{eqnarray}\tilde{u} _{1}=r\tilde{b}_{0}/(\tilde{a}_{0}+\tilde{b}_{0})=(k-l)/(1+1/l)>k-2k/l+1.\end{eqnarray}$$
Meanwhile, when
![]() $n\geqslant 1$
, the condition
$n\geqslant 1$
, the condition
 $$\begin{eqnarray}m_{n}\leqslant \tilde{v}_{n}\leqslant \tilde{u} _{n}=r\tilde{b}_{n-1}/(\tilde{a}_{n-1}+\tilde{b}_{n-1})\end{eqnarray}$$
$$\begin{eqnarray}m_{n}\leqslant \tilde{v}_{n}\leqslant \tilde{u} _{n}=r\tilde{b}_{n-1}/(\tilde{a}_{n-1}+\tilde{b}_{n-1})\end{eqnarray}$$
that follows from (11.4) ensures that
 $$\begin{eqnarray}\tilde{b}_{n}=k\tilde{b}_{n-1}-m_{n}(\tilde{a}_{n-1}+\tilde{b}_{n-1})\geqslant (k-r)\tilde{b}_{n-1}=l\tilde{b}_{n-1},\end{eqnarray}$$
$$\begin{eqnarray}\tilde{b}_{n}=k\tilde{b}_{n-1}-m_{n}(\tilde{a}_{n-1}+\tilde{b}_{n-1})\geqslant (k-r)\tilde{b}_{n-1}=l\tilde{b}_{n-1},\end{eqnarray}$$
whence
 $$\begin{eqnarray}\tilde{u} _{n+1}=r\tilde{b}_{n}/(\tilde{a}_{n}+\tilde{b}_{n})=r/(1+\tilde{b}_{n-1}/\tilde{b}_{n})\geqslant r/(1+1/l)>k-2k/l+1.\end{eqnarray}$$
$$\begin{eqnarray}\tilde{u} _{n+1}=r\tilde{b}_{n}/(\tilde{a}_{n}+\tilde{b}_{n})=r/(1+\tilde{b}_{n-1}/\tilde{b}_{n})\geqslant r/(1+1/l)>k-2k/l+1.\end{eqnarray}$$
We therefore deduce that
 $\tilde{v}_{n}\geqslant k(1-2/l)$
for
$\tilde{v}_{n}\geqslant k(1-2/l)$
for
![]() $n\geqslant 1$
, as we had claimed. It follows, in particular, that
$n\geqslant 1$
, as we had claimed. It follows, in particular, that
 $$\begin{eqnarray}h=k-l-v\leqslant k-l-k(1-2/l)\leqslant 2k/l\leqslant 2k^{2/3}.\end{eqnarray}$$
$$\begin{eqnarray}h=k-l-v\leqslant k-l-k(1-2/l)\leqslant 2k/l\leqslant 2k^{2/3}.\end{eqnarray}$$
We use this opportunity also to recall the bounds
 $s\geqslant {\textstyle \frac{1}{2}}k(k+1)-4k$
and
$s\geqslant {\textstyle \frac{1}{2}}k(k+1)-4k$
and
 $l\leqslant k^{1/3}+1$
.
$l\leqslant k^{1/3}+1$
.
Before exploiting the crude bound for
![]() $h$
just obtained, we make use of the more opaque though stronger bound
$h$
just obtained, we make use of the more opaque though stronger bound
 $$\begin{eqnarray}h=r-\lfloor r\tilde{b}_{n}/(\tilde{a}_{n}+\tilde{b}_{n})\rfloor \leqslant r\tilde{a}_{n}/(\tilde{a}_{n}+\tilde{b}_{n})+1.\end{eqnarray}$$
$$\begin{eqnarray}h=r-\lfloor r\tilde{b}_{n}/(\tilde{a}_{n}+\tilde{b}_{n})\rfloor \leqslant r\tilde{a}_{n}/(\tilde{a}_{n}+\tilde{b}_{n})+1.\end{eqnarray}$$
On substituting these bounds into (11.18), we see that
 $$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D6F6} & {\leqslant} & \displaystyle (l+{\textstyle \frac{1}{2}}(h+1))r\tilde{a}_{n}+(l+{\textstyle \frac{1}{2}}(h+1))(\tilde{a}_{n}+\tilde{b}_{n})+9k^{1/3}\tilde{b}_{n}\nonumber\\ \displaystyle & {\leqslant} & \displaystyle 2k^{5/3}\tilde{a}_{n}+2k^{2/3}\tilde{b}_{n}.\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D6F6} & {\leqslant} & \displaystyle (l+{\textstyle \frac{1}{2}}(h+1))r\tilde{a}_{n}+(l+{\textstyle \frac{1}{2}}(h+1))(\tilde{a}_{n}+\tilde{b}_{n})+9k^{1/3}\tilde{b}_{n}\nonumber\\ \displaystyle & {\leqslant} & \displaystyle 2k^{5/3}\tilde{a}_{n}+2k^{2/3}\tilde{b}_{n}.\nonumber\end{eqnarray}$$
Finally, we observe that
 $$\begin{eqnarray}\widetilde{\unicode[STIX]{x1D6E5}}\leqslant \mathop{\sum }_{m=1}^{k-4}\frac{m(k-3-m)}{s-k+4}\leqslant \frac{(k-2)(k-3)(k-4)/6}{k(k+1)/2-5k+4}<\frac{1}{3}k+1.\end{eqnarray}$$
$$\begin{eqnarray}\widetilde{\unicode[STIX]{x1D6E5}}\leqslant \mathop{\sum }_{m=1}^{k-4}\frac{m(k-3-m)}{s-k+4}\leqslant \frac{(k-2)(k-3)(k-4)/6}{k(k+1)/2-5k+4}<\frac{1}{3}k+1.\end{eqnarray}$$
By combining these estimates with (11.17), we arrive at the relation
 $$\begin{eqnarray}\displaystyle s\mathop{\sum }_{m_{n+1}=0}^{\tilde{v}_{n+1}-1}\unicode[STIX]{x1D719}_{m_{n+1}}\tilde{b}_{n+1}(\mathbf{m}) & {\geqslant} & \displaystyle \biggl(\frac{1}{2}k(k+1)-\frac{1}{3}k-3k^{2/3}\biggr)\tilde{b}_{n}(\mathbf{m})\nonumber\\ \displaystyle & & \displaystyle -\,\biggl(\frac{1}{2}k(k-1)+3k^{5/3}\biggr)\tilde{a}_{n}(\mathbf{m})\nonumber\\ \displaystyle & = & \displaystyle \mathfrak{a}\tilde{b}_{n}(\mathbf{m})-\mathfrak{b}\tilde{a}_{n}(\mathbf{m}).\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle s\mathop{\sum }_{m_{n+1}=0}^{\tilde{v}_{n+1}-1}\unicode[STIX]{x1D719}_{m_{n+1}}\tilde{b}_{n+1}(\mathbf{m}) & {\geqslant} & \displaystyle \biggl(\frac{1}{2}k(k+1)-\frac{1}{3}k-3k^{2/3}\biggr)\tilde{b}_{n}(\mathbf{m})\nonumber\\ \displaystyle & & \displaystyle -\,\biggl(\frac{1}{2}k(k-1)+3k^{5/3}\biggr)\tilde{a}_{n}(\mathbf{m})\nonumber\\ \displaystyle & = & \displaystyle \mathfrak{a}\tilde{b}_{n}(\mathbf{m})-\mathfrak{b}\tilde{a}_{n}(\mathbf{m}).\nonumber\end{eqnarray}$$
Then we deduce from (11.13) that
 $$\begin{eqnarray}sB_{n+1}\geqslant \mathfrak{a}B_{n}-\mathfrak{b}A_{n}\quad (n\geqslant 1).\end{eqnarray}$$
$$\begin{eqnarray}sB_{n+1}\geqslant \mathfrak{a}B_{n}-\mathfrak{b}A_{n}\quad (n\geqslant 1).\end{eqnarray}$$
On the other hand, we have
 $$\begin{eqnarray}\displaystyle s\mathop{\sum }_{m_{n+1}=0}^{\tilde{v}_{n+1}-1}\unicode[STIX]{x1D719}_{m_{n+1}}\tilde{a}_{n+1}(\mathbf{m}) & = & \displaystyle s\tilde{b}_{n}(\mathbf{m})\mathop{\sum }_{m=0}^{\tilde{v}_{n+1}-1}\unicode[STIX]{x1D719}_{m}\nonumber\\ \displaystyle & = & \displaystyle \tilde{b}_{n}(\mathbf{m})\frac{\tilde{v}_{n+1}(s-r)}{s-\tilde{v}_{n+1}}\leqslant r\tilde{b}_{n}(\mathbf{m}),\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle s\mathop{\sum }_{m_{n+1}=0}^{\tilde{v}_{n+1}-1}\unicode[STIX]{x1D719}_{m_{n+1}}\tilde{a}_{n+1}(\mathbf{m}) & = & \displaystyle s\tilde{b}_{n}(\mathbf{m})\mathop{\sum }_{m=0}^{\tilde{v}_{n+1}-1}\unicode[STIX]{x1D719}_{m}\nonumber\\ \displaystyle & = & \displaystyle \tilde{b}_{n}(\mathbf{m})\frac{\tilde{v}_{n+1}(s-r)}{s-\tilde{v}_{n+1}}\leqslant r\tilde{b}_{n}(\mathbf{m}),\nonumber\end{eqnarray}$$
whence
 $$\begin{eqnarray}sA_{n+1}\leqslant rB_{n}\quad (n\geqslant 1).\end{eqnarray}$$
$$\begin{eqnarray}sA_{n+1}\leqslant rB_{n}\quad (n\geqslant 1).\end{eqnarray}$$
By combining (11.19) and (11.20), we conclude at this point that
 $$\begin{eqnarray}s^{2}B_{n+2}\geqslant s\mathfrak{a}B_{n+1}-r\mathfrak{b}B_{n}\quad (n\geqslant 1).\end{eqnarray}$$
$$\begin{eqnarray}s^{2}B_{n+2}\geqslant s\mathfrak{a}B_{n+1}-r\mathfrak{b}B_{n}\quad (n\geqslant 1).\end{eqnarray}$$
In addition, we have the initial data
 $$\begin{eqnarray}sB_{1}\geqslant \mathfrak{a}\tilde{b}_{0}-\mathfrak{b}\tilde{a}_{0}=\mathfrak{a}-\mathfrak{b}/l\quad \text{and}\quad sA_{1}\leqslant r\tilde{b}_{0}=r\end{eqnarray}$$
$$\begin{eqnarray}sB_{1}\geqslant \mathfrak{a}\tilde{b}_{0}-\mathfrak{b}\tilde{a}_{0}=\mathfrak{a}-\mathfrak{b}/l\quad \text{and}\quad sA_{1}\leqslant r\tilde{b}_{0}=r\end{eqnarray}$$
and hence
 $$\begin{eqnarray}s^{2}B_{2}\geqslant s\mathfrak{a}B_{1}-s\mathfrak{b}A_{1}\geqslant \mathfrak{a}(\mathfrak{a}-\mathfrak{b}/l)-\mathfrak{b}r.\end{eqnarray}$$
$$\begin{eqnarray}s^{2}B_{2}\geqslant s\mathfrak{a}B_{1}-s\mathfrak{b}A_{1}\geqslant \mathfrak{a}(\mathfrak{a}-\mathfrak{b}/l)-\mathfrak{b}r.\end{eqnarray}$$
Our goal is now to extract from the recurrence inequality (11.21) a lower bound for
![]() $B_{n}$
. Were we to be presented with an equation, this would be straightforward, but in present circumstances we must work less directly by relating
$B_{n}$
. Were we to be presented with an equation, this would be straightforward, but in present circumstances we must work less directly by relating
![]() $B_{n}$
to
$B_{n}$
to
![]() $\tilde{B}_{n}$
. By reference to (11.11), we see that
$\tilde{B}_{n}$
. By reference to (11.11), we see that
![]() $\tilde{B}_{n}$
satisfies a recurrence equation related to the inequality (11.19).
$\tilde{B}_{n}$
satisfies a recurrence equation related to the inequality (11.19).
Our first observation is that the recurrence formula (11.11) has a solution of the shape
 $$\begin{eqnarray}s^{n}\tilde{B}_{n}=\unicode[STIX]{x1D70E}_{+}\unicode[STIX]{x1D703}_{+}^{n}+\unicode[STIX]{x1D70E}_{-}\unicode[STIX]{x1D703}_{-}^{n}\quad (n\geqslant 1),\end{eqnarray}$$
$$\begin{eqnarray}s^{n}\tilde{B}_{n}=\unicode[STIX]{x1D70E}_{+}\unicode[STIX]{x1D703}_{+}^{n}+\unicode[STIX]{x1D70E}_{-}\unicode[STIX]{x1D703}_{-}^{n}\quad (n\geqslant 1),\end{eqnarray}$$
where
 $$\begin{eqnarray}\unicode[STIX]{x1D70E}_{+}\unicode[STIX]{x1D703}_{+}+\unicode[STIX]{x1D70E}_{-}\unicode[STIX]{x1D703}_{-}=s\tilde{B}_{1}=\mathfrak{a}-\mathfrak{b}/l\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D70E}_{+}\unicode[STIX]{x1D703}_{+}+\unicode[STIX]{x1D70E}_{-}\unicode[STIX]{x1D703}_{-}=s\tilde{B}_{1}=\mathfrak{a}-\mathfrak{b}/l\end{eqnarray}$$
and
 $$\begin{eqnarray}\unicode[STIX]{x1D70E}_{+}\unicode[STIX]{x1D703}_{+}^{2}+\unicode[STIX]{x1D70E}_{-}\unicode[STIX]{x1D703}_{-}^{2}=s^{2}\tilde{B}_{2}=\mathfrak{a}(\mathfrak{a}-\mathfrak{b}/l)-\mathfrak{b}r.\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D70E}_{+}\unicode[STIX]{x1D703}_{+}^{2}+\unicode[STIX]{x1D70E}_{-}\unicode[STIX]{x1D703}_{-}^{2}=s^{2}\tilde{B}_{2}=\mathfrak{a}(\mathfrak{a}-\mathfrak{b}/l)-\mathfrak{b}r.\end{eqnarray}$$
Then we deduce that
 $$\begin{eqnarray}s^{n}\tilde{B}_{n}=\frac{\unicode[STIX]{x1D703}_{+}^{n+1}-\unicode[STIX]{x1D703}_{-}^{n+1}}{\unicode[STIX]{x1D703}_{+}-\unicode[STIX]{x1D703}_{-}}-\frac{\unicode[STIX]{x1D703}_{+}\unicode[STIX]{x1D703}_{-}}{lr}\biggl(\frac{\unicode[STIX]{x1D703}_{+}^{n}-\unicode[STIX]{x1D703}_{-}^{n}}{\unicode[STIX]{x1D703}_{+}-\unicode[STIX]{x1D703}_{-}}\biggr).\end{eqnarray}$$
$$\begin{eqnarray}s^{n}\tilde{B}_{n}=\frac{\unicode[STIX]{x1D703}_{+}^{n+1}-\unicode[STIX]{x1D703}_{-}^{n+1}}{\unicode[STIX]{x1D703}_{+}-\unicode[STIX]{x1D703}_{-}}-\frac{\unicode[STIX]{x1D703}_{+}\unicode[STIX]{x1D703}_{-}}{lr}\biggl(\frac{\unicode[STIX]{x1D703}_{+}^{n}-\unicode[STIX]{x1D703}_{-}^{n}}{\unicode[STIX]{x1D703}_{+}-\unicode[STIX]{x1D703}_{-}}\biggr).\end{eqnarray}$$
Note that since
![]() $k$
is large, it follows from (11.9) and (11.12) that
$k$
is large, it follows from (11.9) and (11.12) that
 $$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D703}_{+} & = & \displaystyle {\textstyle \frac{1}{2}}k(k+1)-{\textstyle \frac{1}{3}}k-3k^{2/3}-\mathfrak{b}r/\mathfrak{a}+O((\mathfrak{b}r)^{2}/\mathfrak{a}^{3})\nonumber\\ \displaystyle & {\geqslant} & \displaystyle {\textstyle \frac{1}{2}}k(k-1)-{\textstyle \frac{1}{3}}k-7k^{2/3}\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D703}_{+} & = & \displaystyle {\textstyle \frac{1}{2}}k(k+1)-{\textstyle \frac{1}{3}}k-3k^{2/3}-\mathfrak{b}r/\mathfrak{a}+O((\mathfrak{b}r)^{2}/\mathfrak{a}^{3})\nonumber\\ \displaystyle & {\geqslant} & \displaystyle {\textstyle \frac{1}{2}}k(k-1)-{\textstyle \frac{1}{3}}k-7k^{2/3}\end{eqnarray}$$
and
 $$\begin{eqnarray}\unicode[STIX]{x1D703}_{-}\leqslant \mathfrak{b}r/\mathfrak{a}+O((\mathfrak{b}r)^{2}/\mathfrak{a}^{3})\leqslant k+7k^{2/3}.\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D703}_{-}\leqslant \mathfrak{b}r/\mathfrak{a}+O((\mathfrak{b}r)^{2}/\mathfrak{a}^{3})\leqslant k+7k^{2/3}.\end{eqnarray}$$
Thus, in particular, we deduce from (11.22) that
![]() $\tilde{B}_{n}$
is positive for every natural number
$\tilde{B}_{n}$
is positive for every natural number
![]() $n$
.
$n$
.
We now reinterpret the recurrence inequality (11.21) as a recurrence equation with variable shifts. Let
![]() $(g_{n})$
be a sequence of positive real numbers. Then, for an appropriate choice of this sequence
$(g_{n})$
be a sequence of positive real numbers. Then, for an appropriate choice of this sequence
![]() $(g_{n})$
, the recurrence sequence
$(g_{n})$
, the recurrence sequence
![]() $B_{n}$
may be interpreted as the solution of the new recurrence sequence
$B_{n}$
may be interpreted as the solution of the new recurrence sequence
 $$\begin{eqnarray}s^{2}B_{n+2}=s\mathfrak{a}B_{n+1}-r\mathfrak{b}B_{n}+g_{n}\quad (n\geqslant 1),\end{eqnarray}$$
$$\begin{eqnarray}s^{2}B_{n+2}=s\mathfrak{a}B_{n+1}-r\mathfrak{b}B_{n}+g_{n}\quad (n\geqslant 1),\end{eqnarray}$$
with the initial data
 $$\begin{eqnarray}sB_{1}=\mathfrak{a}-\mathfrak{b}/l+g_{1}\quad \text{and}\quad s^{2}B_{2}=\mathfrak{a}(\mathfrak{a}-\mathfrak{b}/l+g_{1})-\mathfrak{b}r+g_{2}.\end{eqnarray}$$
$$\begin{eqnarray}sB_{1}=\mathfrak{a}-\mathfrak{b}/l+g_{1}\quad \text{and}\quad s^{2}B_{2}=\mathfrak{a}(\mathfrak{a}-\mathfrak{b}/l+g_{1})-\mathfrak{b}r+g_{2}.\end{eqnarray}$$
Define the real numbers
![]() $\tilde{g}_{n}$
by means of the relation
$\tilde{g}_{n}$
by means of the relation
 $$\begin{eqnarray}\tilde{g}_{n}=s^{n}(B_{n}-\tilde{B}_{n}).\end{eqnarray}$$
$$\begin{eqnarray}\tilde{g}_{n}=s^{n}(B_{n}-\tilde{B}_{n}).\end{eqnarray}$$
Thus, in particular, it follows from (11.10) and (11.25) that
 $$\begin{eqnarray}\tilde{g}_{1}=g_{1}\quad \text{and}\quad \tilde{g}_{2}=\mathfrak{a}g_{1}+g_{2}\end{eqnarray}$$
$$\begin{eqnarray}\tilde{g}_{1}=g_{1}\quad \text{and}\quad \tilde{g}_{2}=\mathfrak{a}g_{1}+g_{2}\end{eqnarray}$$
and from (11.11) and (11.24) that
 $$\begin{eqnarray}\tilde{g}_{n+2}=\mathfrak{a}\tilde{g}_{n+1}-r\mathfrak{b}\tilde{g}_{n}+g_{n}\quad (n\geqslant 1).\end{eqnarray}$$
$$\begin{eqnarray}\tilde{g}_{n+2}=\mathfrak{a}\tilde{g}_{n+1}-r\mathfrak{b}\tilde{g}_{n}+g_{n}\quad (n\geqslant 1).\end{eqnarray}$$
We claim that
![]() $\tilde{g}_{n}\geqslant 0$
, whence also
$\tilde{g}_{n}\geqslant 0$
, whence also
 $B_{n}\geqslant \tilde{B}_{n}$
, for each natural number
$B_{n}\geqslant \tilde{B}_{n}$
, for each natural number
![]() $n$
.
$n$
.
In order to verify the last claim, we prove by induction that for each natural number
![]() $n$
, one has
$n$
, one has
 $$\begin{eqnarray}\tilde{g}_{n+1}\geqslant s\tilde{g}_{n}\tilde{B}_{n+1}/\tilde{B}_{n}.\end{eqnarray}$$
$$\begin{eqnarray}\tilde{g}_{n+1}\geqslant s\tilde{g}_{n}\tilde{B}_{n+1}/\tilde{B}_{n}.\end{eqnarray}$$
We first confirm this inductive hypothesis for
![]() $n=1$
. Here we note that when
$n=1$
. Here we note that when
 $\tilde{g}_{1}=g_{1}=0$
, then the trivial lower bound
$\tilde{g}_{1}=g_{1}=0$
, then the trivial lower bound
 $\tilde{g}_{2}=g_{2}\geqslant 0$
that follows from (11.27) suffices to confirm (11.29). When
$\tilde{g}_{2}=g_{2}\geqslant 0$
that follows from (11.27) suffices to confirm (11.29). When
![]() $g_{1}\neq 0$
, meanwhile, we find from (11.10) and (11.27) that
$g_{1}\neq 0$
, meanwhile, we find from (11.10) and (11.27) that
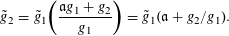 $$\begin{eqnarray}\tilde{g}_{2}=\tilde{g}_{1}\biggl(\frac{\mathfrak{a}g_{1}+g_{2}}{g_{1}}\biggr)=\tilde{g}_{1}(\mathfrak{a}+g_{2}/g_{1}).\end{eqnarray}$$
$$\begin{eqnarray}\tilde{g}_{2}=\tilde{g}_{1}\biggl(\frac{\mathfrak{a}g_{1}+g_{2}}{g_{1}}\biggr)=\tilde{g}_{1}(\mathfrak{a}+g_{2}/g_{1}).\end{eqnarray}$$
The positivity of
![]() $g_{1}$
,
$g_{1}$
,
![]() $g_{2}$
and
$g_{2}$
and
 $$\begin{eqnarray}\mathfrak{a}-\mathfrak{b}/l={\textstyle \frac{1}{2}}k(k+1)+O(k^{5/3})\end{eqnarray}$$
$$\begin{eqnarray}\mathfrak{a}-\mathfrak{b}/l={\textstyle \frac{1}{2}}k(k+1)+O(k^{5/3})\end{eqnarray}$$
consequently ensures that
 $$\begin{eqnarray}\tilde{g}_{2}\geqslant \tilde{g}_{1}\mathfrak{a}\geqslant \tilde{g}_{1}\biggl(\frac{\mathfrak{a}(\mathfrak{a}-\mathfrak{b}/l)-\mathfrak{b}r}{\mathfrak{a}-\mathfrak{b}/l}\biggr)=s\tilde{g}_{1}\tilde{B}_{2}/\tilde{B}_{1}.\end{eqnarray}$$
$$\begin{eqnarray}\tilde{g}_{2}\geqslant \tilde{g}_{1}\mathfrak{a}\geqslant \tilde{g}_{1}\biggl(\frac{\mathfrak{a}(\mathfrak{a}-\mathfrak{b}/l)-\mathfrak{b}r}{\mathfrak{a}-\mathfrak{b}/l}\biggr)=s\tilde{g}_{1}\tilde{B}_{2}/\tilde{B}_{1}.\end{eqnarray}$$
This confirms the inductive hypothesis when
![]() $n=1$
.
$n=1$
.
Suppose next that
![]() $n\geqslant 2$
and
$n\geqslant 2$
and
 $$\begin{eqnarray}\tilde{g}_{n}\geqslant s\tilde{g}_{n-1}\tilde{B}_{n}/\tilde{B}_{n-1}.\end{eqnarray}$$
$$\begin{eqnarray}\tilde{g}_{n}\geqslant s\tilde{g}_{n-1}\tilde{B}_{n}/\tilde{B}_{n-1}.\end{eqnarray}$$
Then, on making use of (11.11) and (11.28), one deduces that
 $$\begin{eqnarray}\displaystyle \tilde{g}_{n+1}-s\tilde{g}_{n}\tilde{B}_{n+1}/\tilde{B}_{n} & = & \displaystyle (\mathfrak{a}\tilde{g}_{n}-r\mathfrak{b}\tilde{g}_{n-1}+g_{n-1})-\tilde{g}_{n}(\mathfrak{a}\tilde{B}_{n}-s^{-1}r\mathfrak{b}\tilde{B}_{n-1})/\tilde{B}_{n}\nonumber\\ \displaystyle & {\geqslant} & \displaystyle (s^{-1}r\mathfrak{b}\tilde{B}_{n-1}/\tilde{B}_{n})(\tilde{g}_{n}-s\tilde{g}_{n-1}\tilde{B}_{n}/\tilde{B}_{n-1})\geqslant 0.\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \tilde{g}_{n+1}-s\tilde{g}_{n}\tilde{B}_{n+1}/\tilde{B}_{n} & = & \displaystyle (\mathfrak{a}\tilde{g}_{n}-r\mathfrak{b}\tilde{g}_{n-1}+g_{n-1})-\tilde{g}_{n}(\mathfrak{a}\tilde{B}_{n}-s^{-1}r\mathfrak{b}\tilde{B}_{n-1})/\tilde{B}_{n}\nonumber\\ \displaystyle & {\geqslant} & \displaystyle (s^{-1}r\mathfrak{b}\tilde{B}_{n-1}/\tilde{B}_{n})(\tilde{g}_{n}-s\tilde{g}_{n-1}\tilde{B}_{n}/\tilde{B}_{n-1})\geqslant 0.\nonumber\end{eqnarray}$$
This confirms the inductive hypothesis with
![]() $n+1$
in place of
$n+1$
in place of
![]() $n$
, and so by applying induction we deduce that (11.29) holds for every natural number
$n$
, and so by applying induction we deduce that (11.29) holds for every natural number
![]() $n$
. A particular consequence of the lower bound (11.29) is that
$n$
. A particular consequence of the lower bound (11.29) is that
![]() $\tilde{g}_{n}\geqslant 0$
for every natural number
$\tilde{g}_{n}\geqslant 0$
for every natural number
![]() $n$
. Finally, we conclude from (11.26) that
$n$
. Finally, we conclude from (11.26) that
 $B_{n}\geqslant \tilde{B}_{n}$
for every natural number
$B_{n}\geqslant \tilde{B}_{n}$
for every natural number
![]() $n$
.
$n$
.
In order to complete the proof of the lemma, we note first from (11.5) and (11.8) that
 $s_{0}^{R}=s^{R}B_{R}$
. Since
$s_{0}^{R}=s^{R}B_{R}$
. Since
 $B_{R}\geqslant \tilde{B}_{R}$
, the final conclusion of the lemma follows from (11.22).◻
$B_{R}\geqslant \tilde{B}_{R}$
, the final conclusion of the lemma follows from (11.22).◻
We next turn to the problem of controlling the behaviour of
![]() $a_{R}$
and
$a_{R}$
and
![]() $b_{R}$
.
$b_{R}$
.
Lemma 11.6. Suppose that the tuples
![]() $\mathbf{m}$
and
$\mathbf{m}$
and
![]() $\mathbf{h}(\mathbf{m})$
satisfy the conditions
$\mathbf{h}(\mathbf{m})$
satisfy the conditions
 $$\begin{eqnarray}1\leqslant m_{n}\leqslant \tilde{u} _{n}(\mathbf{m})-1\quad \text{and}\quad 0\leqslant h_{n}(\mathbf{m})\leqslant 15k^{R}b\quad (1\leqslant n\leqslant R).\end{eqnarray}$$
$$\begin{eqnarray}1\leqslant m_{n}\leqslant \tilde{u} _{n}(\mathbf{m})-1\quad \text{and}\quad 0\leqslant h_{n}(\mathbf{m})\leqslant 15k^{R}b\quad (1\leqslant n\leqslant R).\end{eqnarray}$$
Then one has
 $$\begin{eqnarray}k_{\mathbf{m}}b\leqslant b_{R}(\mathbf{m};\mathbf{h})\leqslant k_{\mathbf{m}}b+16k^{2R}b\end{eqnarray}$$
$$\begin{eqnarray}k_{\mathbf{m}}b\leqslant b_{R}(\mathbf{m};\mathbf{h})\leqslant k_{\mathbf{m}}b+16k^{2R}b\end{eqnarray}$$
and furthermore
 $$\begin{eqnarray}a_{R}(\mathbf{m};\mathbf{h})\leqslant b_{R}(\mathbf{m};\mathbf{h})/l.\end{eqnarray}$$
$$\begin{eqnarray}a_{R}(\mathbf{m};\mathbf{h})\leqslant b_{R}(\mathbf{m};\mathbf{h})/l.\end{eqnarray}$$
Proof. We again make use of auxiliary recurrence sequences in order to disentangle information on recurrence inequalities. Write
 $$\begin{eqnarray}h_{1}^{\ast }(\mathbf{m})=h_{1}(\mathbf{m})+m_{1}(b/l-a_{0})\end{eqnarray}$$
$$\begin{eqnarray}h_{1}^{\ast }(\mathbf{m})=h_{1}(\mathbf{m})+m_{1}(b/l-a_{0})\end{eqnarray}$$
and
 $$\begin{eqnarray}h_{n}^{\ast }(\mathbf{m})=h_{n}(\mathbf{m})\quad (n>1).\end{eqnarray}$$
$$\begin{eqnarray}h_{n}^{\ast }(\mathbf{m})=h_{n}(\mathbf{m})\quad (n>1).\end{eqnarray}$$
Then we find that
 $$\begin{eqnarray}h_{1}^{\ast }(\mathbf{m})\leqslant h_{1}(\mathbf{m})+m_{1}\leqslant h_{1}(\mathbf{m})+k<16k^{R}b\end{eqnarray}$$
$$\begin{eqnarray}h_{1}^{\ast }(\mathbf{m})\leqslant h_{1}(\mathbf{m})+m_{1}\leqslant h_{1}(\mathbf{m})+k<16k^{R}b\end{eqnarray}$$
and
 $$\begin{eqnarray}h_{n}^{\ast }(\mathbf{m})=h_{n}(\mathbf{m})\leqslant 15k^{R}b\quad (n>1).\end{eqnarray}$$
$$\begin{eqnarray}h_{n}^{\ast }(\mathbf{m})=h_{n}(\mathbf{m})\leqslant 15k^{R}b\quad (n>1).\end{eqnarray}$$
We define the sequences
 $(a_{n}^{\ast })=(a_{n}^{\ast }(\mathbf{m};\mathbf{h}))$
and
$(a_{n}^{\ast })=(a_{n}^{\ast }(\mathbf{m};\mathbf{h}))$
and
 $(b_{n}^{\ast })=(b_{n}^{\ast }(\mathbf{m};\mathbf{h}))$
by means of the relations
$(b_{n}^{\ast })=(b_{n}^{\ast }(\mathbf{m};\mathbf{h}))$
by means of the relations
 $$\begin{eqnarray}a_{0}^{\ast }=b/l\quad \text{and}\quad b_{0}^{\ast }=b,\end{eqnarray}$$
$$\begin{eqnarray}a_{0}^{\ast }=b/l\quad \text{and}\quad b_{0}^{\ast }=b,\end{eqnarray}$$
and
 $$\begin{eqnarray}a_{n}^{\ast }=b_{n-1}^{\ast }\quad \text{and}\quad b_{n}^{\ast }=(k-m_{n})b_{n-1}^{\ast }-m_{n}a_{n-1}^{\ast }+h_{n}^{\ast }(\mathbf{m})\quad (1\leqslant n\leqslant R).\end{eqnarray}$$
$$\begin{eqnarray}a_{n}^{\ast }=b_{n-1}^{\ast }\quad \text{and}\quad b_{n}^{\ast }=(k-m_{n})b_{n-1}^{\ast }-m_{n}a_{n-1}^{\ast }+h_{n}^{\ast }(\mathbf{m})\quad (1\leqslant n\leqslant R).\end{eqnarray}$$
It follows that
![]() $a_{n}=a_{n}^{\ast }$
and
$a_{n}=a_{n}^{\ast }$
and
![]() $b_{n}=b_{n}^{\ast }$
for
$b_{n}=b_{n}^{\ast }$
for
![]() $n\geqslant 1$
. We next put
$n\geqslant 1$
. We next put
 $$\begin{eqnarray}g_{n}^{\ast }=b_{n}^{\ast }-\tilde{b}_{n}b\quad (n\geqslant 0)\end{eqnarray}$$
$$\begin{eqnarray}g_{n}^{\ast }=b_{n}^{\ast }-\tilde{b}_{n}b\quad (n\geqslant 0)\end{eqnarray}$$
and we seek to show in the first instance that
![]() $g_{n}^{\ast }\geqslant 0$
for each
$g_{n}^{\ast }\geqslant 0$
for each
![]() $n$
. This of course implies in particular that
$n$
. This of course implies in particular that
 $b_{R}^{\ast }\geqslant \tilde{b}_{R}b=k_{\mathbf{m}}b$
.
$b_{R}^{\ast }\geqslant \tilde{b}_{R}b=k_{\mathbf{m}}b$
.
We prove that
![]() $g_{n}^{\ast }\geqslant 0$
for each
$g_{n}^{\ast }\geqslant 0$
for each
![]() $n$
by induction. Observe first that by applying (11.30) in combination with the recurrence relations for
$n$
by induction. Observe first that by applying (11.30) in combination with the recurrence relations for
![]() $\tilde{a}_{n}$
,
$\tilde{a}_{n}$
,
![]() $\tilde{b}_{n}$
,
$\tilde{b}_{n}$
,
![]() $a_{n}^{\ast }$
,
$a_{n}^{\ast }$
,
![]() $b_{n}^{\ast }$
, we obtain
$b_{n}^{\ast }$
, we obtain
 $$\begin{eqnarray}\displaystyle g_{0}^{\ast }\tilde{b}_{1}-\tilde{b}_{0}g_{1}^{\ast } & = & \displaystyle \,(b_{0}^{\ast }-\tilde{b}_{0}b)((k-m_{1})\tilde{b}_{0}-m_{1}\tilde{a}_{0})\nonumber\\ \displaystyle & & \displaystyle -\,\tilde{b}_{0}((k-m_{1})(b_{0}^{\ast }-\tilde{b}_{0}b)-m_{1}(a_{0}^{\ast }-\tilde{a}_{0}b)+h_{1}^{\ast }),\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle g_{0}^{\ast }\tilde{b}_{1}-\tilde{b}_{0}g_{1}^{\ast } & = & \displaystyle \,(b_{0}^{\ast }-\tilde{b}_{0}b)((k-m_{1})\tilde{b}_{0}-m_{1}\tilde{a}_{0})\nonumber\\ \displaystyle & & \displaystyle -\,\tilde{b}_{0}((k-m_{1})(b_{0}^{\ast }-\tilde{b}_{0}b)-m_{1}(a_{0}^{\ast }-\tilde{a}_{0}b)+h_{1}^{\ast }),\nonumber\end{eqnarray}$$
whence
 $g_{0}^{\ast }\tilde{b}_{1}-\tilde{b}_{0}g_{1}^{\ast }=-h_{1}^{\ast }\leqslant 0$
. Moreover, if we assume that
$g_{0}^{\ast }\tilde{b}_{1}-\tilde{b}_{0}g_{1}^{\ast }=-h_{1}^{\ast }\leqslant 0$
. Moreover, if we assume that
 $$\begin{eqnarray}g_{n-1}^{\ast }\tilde{b}_{n}-\tilde{b}_{n-1}g_{n}^{\ast }\leqslant 0,\end{eqnarray}$$
$$\begin{eqnarray}g_{n-1}^{\ast }\tilde{b}_{n}-\tilde{b}_{n-1}g_{n}^{\ast }\leqslant 0,\end{eqnarray}$$
then we find in like manner that
 $$\begin{eqnarray}\displaystyle g_{n}^{\ast }\tilde{b}_{n+1}-\tilde{b}_{n}g_{n+1}^{\ast } & = & \displaystyle (b_{n}^{\ast }-\tilde{b}_{n}b)((k-m_{n+1})\tilde{b}_{n}-m_{n+1}\tilde{a}_{n})\nonumber\\ \displaystyle & & \displaystyle -\,\tilde{b}_{n}((k-m_{n+1})(b_{n}^{\ast }-\tilde{b}_{n}b)-m_{n+1}(a_{n}^{\ast }-\tilde{a}_{n}b)+h_{n+1}^{\ast }).\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle g_{n}^{\ast }\tilde{b}_{n+1}-\tilde{b}_{n}g_{n+1}^{\ast } & = & \displaystyle (b_{n}^{\ast }-\tilde{b}_{n}b)((k-m_{n+1})\tilde{b}_{n}-m_{n+1}\tilde{a}_{n})\nonumber\\ \displaystyle & & \displaystyle -\,\tilde{b}_{n}((k-m_{n+1})(b_{n}^{\ast }-\tilde{b}_{n}b)-m_{n+1}(a_{n}^{\ast }-\tilde{a}_{n}b)+h_{n+1}^{\ast }).\nonumber\end{eqnarray}$$
Thus, we obtain the bound
 $$\begin{eqnarray}\displaystyle g_{n}^{\ast }\tilde{b}_{n+1}-\tilde{b}_{n}g_{n+1}^{\ast } & {\leqslant} & \displaystyle m_{n+1}(a_{n}^{\ast }\tilde{b}_{n}-b_{n}^{\ast }\tilde{a}_{n})\nonumber\\ \displaystyle & = & \displaystyle m_{n+1}((g_{n-1}^{\ast }+\tilde{b}_{n-1}b)\tilde{b}_{n}-(g_{n}^{\ast }+\tilde{b}_{n}b)\tilde{b}_{n-1})\nonumber\\ \displaystyle & = & \displaystyle m_{n+1}(g_{n-1}^{\ast }\tilde{b}_{n}-g_{n}^{\ast }\tilde{b}_{n-1}).\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle g_{n}^{\ast }\tilde{b}_{n+1}-\tilde{b}_{n}g_{n+1}^{\ast } & {\leqslant} & \displaystyle m_{n+1}(a_{n}^{\ast }\tilde{b}_{n}-b_{n}^{\ast }\tilde{a}_{n})\nonumber\\ \displaystyle & = & \displaystyle m_{n+1}((g_{n-1}^{\ast }+\tilde{b}_{n-1}b)\tilde{b}_{n}-(g_{n}^{\ast }+\tilde{b}_{n}b)\tilde{b}_{n-1})\nonumber\\ \displaystyle & = & \displaystyle m_{n+1}(g_{n-1}^{\ast }\tilde{b}_{n}-g_{n}^{\ast }\tilde{b}_{n-1}).\nonumber\end{eqnarray}$$
We thus conclude from (11.31) that
 $g_{n}^{\ast }\tilde{b}_{n+1}-\tilde{b}_{n}g_{n+1}^{\ast }\leqslant 0$
, thereby confirming the inductive hypothesis (11.31) with
$g_{n}^{\ast }\tilde{b}_{n+1}-\tilde{b}_{n}g_{n+1}^{\ast }\leqslant 0$
, thereby confirming the inductive hypothesis (11.31) with
![]() $n+1$
in place of
$n+1$
in place of
![]() $n$
. We therefore deduce by induction that
$n$
. We therefore deduce by induction that
 $g_{n-1}^{\ast }\tilde{b}_{n}\leqslant \tilde{b}_{n-1}g_{n}^{\ast }$
for every
$g_{n-1}^{\ast }\tilde{b}_{n}\leqslant \tilde{b}_{n-1}g_{n}^{\ast }$
for every
![]() $n$
, whence
$n$
, whence
 $$\begin{eqnarray}g_{n}^{\ast }\geqslant g_{n-1}^{\ast }\tilde{b}_{n}/\tilde{b}_{n-1}\geqslant 0\quad (n\geqslant 1).\end{eqnarray}$$
$$\begin{eqnarray}g_{n}^{\ast }\geqslant g_{n-1}^{\ast }\tilde{b}_{n}/\tilde{b}_{n-1}\geqslant 0\quad (n\geqslant 1).\end{eqnarray}$$
In this way, we therefore conclude that
 $b_{R}=b_{R}^{\ast }\geqslant \tilde{b}_{R}b=k_{\mathbf{m}}b$
, as desired.
$b_{R}=b_{R}^{\ast }\geqslant \tilde{b}_{R}b=k_{\mathbf{m}}b$
, as desired.
Having confirmed the lower bound on
 $b_{R}(\mathbf{m};\mathbf{h})$
claimed in the statement of the lemma, we turn our attention next to the upper bound. Observe that the recurrence relations for
$b_{R}(\mathbf{m};\mathbf{h})$
claimed in the statement of the lemma, we turn our attention next to the upper bound. Observe that the recurrence relations for
![]() $\tilde{a}_{n}$
,
$\tilde{a}_{n}$
,
![]() $\tilde{b}_{n}$
,
$\tilde{b}_{n}$
,
![]() $a_{n}^{\ast }$
,
$a_{n}^{\ast }$
,
![]() $b_{n}^{\ast }$
lead us from (11.30) to the relations
$b_{n}^{\ast }$
lead us from (11.30) to the relations
 $$\begin{eqnarray}\displaystyle g_{1}^{\ast } & = & \displaystyle (k-m_{1})(b_{0}^{\ast }-\tilde{b}_{0}b)-m_{1}(a_{0}^{\ast }-\tilde{a}_{0}b)+h_{1}^{\ast }(\mathbf{m})\nonumber\\ \displaystyle & = & \displaystyle h_{1}^{\ast }(\mathbf{m})\leqslant 15k^{R}b\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle g_{1}^{\ast } & = & \displaystyle (k-m_{1})(b_{0}^{\ast }-\tilde{b}_{0}b)-m_{1}(a_{0}^{\ast }-\tilde{a}_{0}b)+h_{1}^{\ast }(\mathbf{m})\nonumber\\ \displaystyle & = & \displaystyle h_{1}^{\ast }(\mathbf{m})\leqslant 15k^{R}b\nonumber\end{eqnarray}$$
and
 $$\begin{eqnarray}g_{n}^{\ast }=(k-m_{n})g_{n-1}^{\ast }-m_{n}g_{n-2}^{\ast }+h_{n}^{\ast }(\mathbf{m})\quad (n\geqslant 2).\end{eqnarray}$$
$$\begin{eqnarray}g_{n}^{\ast }=(k-m_{n})g_{n-1}^{\ast }-m_{n}g_{n-2}^{\ast }+h_{n}^{\ast }(\mathbf{m})\quad (n\geqslant 2).\end{eqnarray}$$
In particular, we have the trivial upper bound
 $$\begin{eqnarray}g_{n}^{\ast }\leqslant kg_{n-1}^{\ast }+15k^{R}b\quad (n\geqslant 2)\end{eqnarray}$$
$$\begin{eqnarray}g_{n}^{\ast }\leqslant kg_{n-1}^{\ast }+15k^{R}b\quad (n\geqslant 2)\end{eqnarray}$$
and so we deduce by induction that
 $$\begin{eqnarray}g_{n}^{\ast }\leqslant 15k^{R}b(1+k+\cdots +k^{n-1})\leqslant 16k^{R+n}b.\end{eqnarray}$$
$$\begin{eqnarray}g_{n}^{\ast }\leqslant 15k^{R}b(1+k+\cdots +k^{n-1})\leqslant 16k^{R+n}b.\end{eqnarray}$$
Hence, on recalling (11.30) once again, we obtain the bound
 $$\begin{eqnarray}b_{R}^{\ast }\leqslant \tilde{b}_{R}b+16k^{2R}b=k_{\boldsymbol{ m}}b+16k^{2R}b.\end{eqnarray}$$
$$\begin{eqnarray}b_{R}^{\ast }\leqslant \tilde{b}_{R}b+16k^{2R}b=k_{\boldsymbol{ m}}b+16k^{2R}b.\end{eqnarray}$$
Collecting together the conclusions of the last two paragraphs, we find that
 $$\begin{eqnarray}k_{\mathbf{m}}b\leqslant b_{R}(\mathbf{m};\mathbf{h})\leqslant k_{\mathbf{m}}b+16k^{2R}b,\end{eqnarray}$$
$$\begin{eqnarray}k_{\mathbf{m}}b\leqslant b_{R}(\mathbf{m};\mathbf{h})\leqslant k_{\mathbf{m}}b+16k^{2R}b,\end{eqnarray}$$
thereby confirming the first assertion of the lemma. It remains now only to bound
![]() $a_{R}$
in terms of
$a_{R}$
in terms of
![]() $b_{R}$
. To this end, we observe that for each
$b_{R}$
. To this end, we observe that for each
![]() $n\geqslant 0$
, it follows from (11.4) and our hypothesis
$n\geqslant 0$
, it follows from (11.4) and our hypothesis
 $m_{n+1}\leqslant \tilde{u} _{n}(\mathbf{m})-1$
that
$m_{n+1}\leqslant \tilde{u} _{n}(\mathbf{m})-1$
that
 $m_{n+1}\leqslant r\tilde{b}_{n}/(\tilde{a}_{n}+\tilde{b}_{n})$
and hence
$m_{n+1}\leqslant r\tilde{b}_{n}/(\tilde{a}_{n}+\tilde{b}_{n})$
and hence
 $$\begin{eqnarray}\tilde{b}_{n+1}=(k-m_{n+1})\tilde{b}_{n}-m_{n+1}\tilde{a}_{n}\geqslant (k-r)\tilde{b}_{n}=l\tilde{b}_{n}.\end{eqnarray}$$
$$\begin{eqnarray}\tilde{b}_{n+1}=(k-m_{n+1})\tilde{b}_{n}-m_{n+1}\tilde{a}_{n}\geqslant (k-r)\tilde{b}_{n}=l\tilde{b}_{n}.\end{eqnarray}$$
We therefore deduce from (11.32) that
 $g_{n+1}^{\ast }\geqslant lg_{n}^{\ast }$
for
$g_{n+1}^{\ast }\geqslant lg_{n}^{\ast }$
for
![]() $n\geqslant 0$
. Consequently, recalling again the relation (11.30), we see that
$n\geqslant 0$
. Consequently, recalling again the relation (11.30), we see that
 $$\begin{eqnarray}b_{R}=b_{R}^{\ast }=\tilde{b}_{R}b+g_{R}^{\ast }\geqslant l(\tilde{b}_{R-1}b+g_{R-1}^{\ast })=lb_{R-1}^{\ast }=la_{R}.\end{eqnarray}$$
$$\begin{eqnarray}b_{R}=b_{R}^{\ast }=\tilde{b}_{R}b+g_{R}^{\ast }\geqslant l(\tilde{b}_{R-1}b+g_{R-1}^{\ast })=lb_{R-1}^{\ast }=la_{R}.\end{eqnarray}$$
We have therefore shown that
 $a_{R}\leqslant b_{R}/l$
, as desired. This completes the proof of the lemma.◻
$a_{R}\leqslant b_{R}/l$
, as desired. This completes the proof of the lemma.◻
Before initiating our discussion of the next lemma, we observe that in view of (11.23) and our hypotheses concerning
![]() $s$
, one has
$s$
, one has
 $$\begin{eqnarray}\unicode[STIX]{x1D703}_{+}+r\geqslant {\textstyle \frac{1}{2}}k(k-1)-{\textstyle \frac{1}{3}}k-7k^{2/3}+(k-l)>s+r.\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D703}_{+}+r\geqslant {\textstyle \frac{1}{2}}k(k-1)-{\textstyle \frac{1}{3}}k-7k^{2/3}+(k-l)>s+r.\end{eqnarray}$$
Then it follows that, provided
![]() $R$
is sufficiently large in terms of
$R$
is sufficiently large in terms of
![]() $s$
and
$s$
and
![]() $k$
, one has
$k$
, one has
![]() $s<\unicode[STIX]{x1D703}_{+}$
, and so we deduce from Lemma 11.5 that
$s<\unicode[STIX]{x1D703}_{+}$
, and so we deduce from Lemma 11.5 that
Lemma 11.7. Suppose that
![]() $\unicode[STIX]{x1D6EC}\geqslant 0$
, let
$\unicode[STIX]{x1D6EC}\geqslant 0$
, let
![]() $a$
and
$a$
and
![]() $b$
be integers with
$b$
be integers with
 $0\leqslant a<b\leqslant (20Rk^{2R}\unicode[STIX]{x1D703})^{-1}$
and suppose further that
$0\leqslant a<b\leqslant (20Rk^{2R}\unicode[STIX]{x1D703})^{-1}$
and suppose further that
![]() $a\leqslant b/l$
. Suppose in addition that there are real numbers
$a\leqslant b/l$
. Suppose in addition that there are real numbers
![]() $\unicode[STIX]{x1D713}$
,
$\unicode[STIX]{x1D713}$
,
![]() $c$
and
$c$
and
![]() $\unicode[STIX]{x1D6FE}$
, with
$\unicode[STIX]{x1D6FE}$
, with
 $$\begin{eqnarray}0\leqslant c\leqslant (2\unicode[STIX]{x1D6FF})^{-1}\unicode[STIX]{x1D703},\qquad \unicode[STIX]{x1D6FE}\geqslant -sb\qquad \text{and}\qquad \unicode[STIX]{x1D713}\geqslant 0,\end{eqnarray}$$
$$\begin{eqnarray}0\leqslant c\leqslant (2\unicode[STIX]{x1D6FF})^{-1}\unicode[STIX]{x1D703},\qquad \unicode[STIX]{x1D6FE}\geqslant -sb\qquad \text{and}\qquad \unicode[STIX]{x1D713}\geqslant 0,\end{eqnarray}$$
such that
 $$\begin{eqnarray}X^{\unicode[STIX]{x1D6EC}}M^{\unicode[STIX]{x1D6EC}\unicode[STIX]{x1D713}}\ll X^{c\unicode[STIX]{x1D6FF}}M^{-\unicode[STIX]{x1D6FE}}\unicode[STIX]{x27E6}K_{a,b}^{r,r}(X)\unicode[STIX]{x27E7}.\end{eqnarray}$$
$$\begin{eqnarray}X^{\unicode[STIX]{x1D6EC}}M^{\unicode[STIX]{x1D6EC}\unicode[STIX]{x1D713}}\ll X^{c\unicode[STIX]{x1D6FF}}M^{-\unicode[STIX]{x1D6FE}}\unicode[STIX]{x27E6}K_{a,b}^{r,r}(X)\unicode[STIX]{x27E7}.\end{eqnarray}$$
Then, for some
 $\mathbf{m}\in [0,r-1]^{R}$
, there are a real number
$\mathbf{m}\in [0,r-1]^{R}$
, there are a real number
![]() $h$
with
$h$
with
 $0\leqslant h\leqslant 16k^{2R}b$
and positive integers
$0\leqslant h\leqslant 16k^{2R}b$
and positive integers
![]() $a^{\prime }$
and
$a^{\prime }$
and
![]() $b^{\prime }$
with
$b^{\prime }$
with
 $a^{\prime }\leqslant b^{\prime }/l$
, such that
$a^{\prime }\leqslant b^{\prime }/l$
, such that
 $$\begin{eqnarray}X^{\unicode[STIX]{x1D6EC}}M^{\unicode[STIX]{x1D6EC}\unicode[STIX]{x1D713}^{\prime }}\ll X^{c^{\prime }\unicode[STIX]{x1D6FF}}M^{-\unicode[STIX]{x1D6FE}^{\prime }}\unicode[STIX]{x27E6}K_{a^{\prime },b^{\prime }}^{r,r}(X)\unicode[STIX]{x27E7},\end{eqnarray}$$
$$\begin{eqnarray}X^{\unicode[STIX]{x1D6EC}}M^{\unicode[STIX]{x1D6EC}\unicode[STIX]{x1D713}^{\prime }}\ll X^{c^{\prime }\unicode[STIX]{x1D6FF}}M^{-\unicode[STIX]{x1D6FE}^{\prime }}\unicode[STIX]{x27E6}K_{a^{\prime },b^{\prime }}^{r,r}(X)\unicode[STIX]{x27E7},\end{eqnarray}$$
where
![]() $\unicode[STIX]{x1D713}^{\prime }$
,
$\unicode[STIX]{x1D713}^{\prime }$
,
![]() $c^{\prime }$
,
$c^{\prime }$
,
![]() $\unicode[STIX]{x1D6FE}^{\prime }$
and
$\unicode[STIX]{x1D6FE}^{\prime }$
and
![]() $b^{\prime }$
are real numbers satisfying the conditions
$b^{\prime }$
are real numbers satisfying the conditions
 $$\begin{eqnarray}\unicode[STIX]{x1D713}^{\prime }=\unicode[STIX]{x1D70C}_{\boldsymbol{ m}}(\unicode[STIX]{x1D713}+({\textstyle \frac{1}{2}}-r/s)b),\qquad \!c^{\prime }=\unicode[STIX]{x1D70C}_{\boldsymbol{ m}}(c+1),\qquad \!\unicode[STIX]{x1D6FE}^{\prime }=\unicode[STIX]{x1D70C}_{\boldsymbol{ m}}\unicode[STIX]{x1D6FE},\qquad \!b^{\prime }=k_{\boldsymbol{ m}}b+h.\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D713}^{\prime }=\unicode[STIX]{x1D70C}_{\boldsymbol{ m}}(\unicode[STIX]{x1D713}+({\textstyle \frac{1}{2}}-r/s)b),\qquad \!c^{\prime }=\unicode[STIX]{x1D70C}_{\boldsymbol{ m}}(c+1),\qquad \!\unicode[STIX]{x1D6FE}^{\prime }=\unicode[STIX]{x1D70C}_{\boldsymbol{ m}}\unicode[STIX]{x1D6FE},\qquad \!b^{\prime }=k_{\boldsymbol{ m}}b+h.\end{eqnarray}$$
Moreover, the real number
![]() $k_{\mathbf{m}}$
satisfies
$k_{\mathbf{m}}$
satisfies
 $2^{R}\leqslant k_{\mathbf{m}}\leqslant k^{R}$
.
$2^{R}\leqslant k_{\mathbf{m}}\leqslant k^{R}$
.
Proof. We deduce from the postulated bound (11.34), together with Lemmas 11.3 and 11.4, that there exists a choice
 $\mathbf{h}=\mathbf{h}(\mathbf{m})$
of tuples, with
$\mathbf{h}=\mathbf{h}(\mathbf{m})$
of tuples, with
 $$\begin{eqnarray}0\leqslant h_{n}(\mathbf{m})\leqslant 15k^{R}b\quad (1\leqslant n\leqslant R),\end{eqnarray}$$
$$\begin{eqnarray}0\leqslant h_{n}(\mathbf{m})\leqslant 15k^{R}b\quad (1\leqslant n\leqslant R),\end{eqnarray}$$
such that
 $$\begin{eqnarray}X^{\unicode[STIX]{x1D6EC}}M^{\unicode[STIX]{x1D6EC}\unicode[STIX]{x1D713}}\ll X^{(c+1)\unicode[STIX]{x1D6FF}}M^{-\unicode[STIX]{x1D6FE}}(X/M^{b/2})^{\unicode[STIX]{x1D6EC}}\mathop{\prod }_{\mathbf{0}\leqslant \mathbf{m}\leqslant \tilde{\mathbf{u}}-1}\unicode[STIX]{x1D6E9}_{R}(\mathbf{m};\mathbf{h})^{\unicode[STIX]{x1D719}_{m_{1}}\cdots \unicode[STIX]{x1D719}_{m_{R}}}.\end{eqnarray}$$
$$\begin{eqnarray}X^{\unicode[STIX]{x1D6EC}}M^{\unicode[STIX]{x1D6EC}\unicode[STIX]{x1D713}}\ll X^{(c+1)\unicode[STIX]{x1D6FF}}M^{-\unicode[STIX]{x1D6FE}}(X/M^{b/2})^{\unicode[STIX]{x1D6EC}}\mathop{\prod }_{\mathbf{0}\leqslant \mathbf{m}\leqslant \tilde{\mathbf{u}}-1}\unicode[STIX]{x1D6E9}_{R}(\mathbf{m};\mathbf{h})^{\unicode[STIX]{x1D719}_{m_{1}}\cdots \unicode[STIX]{x1D719}_{m_{R}}}.\end{eqnarray}$$
Consequently, one has
 $$\begin{eqnarray}\mathop{\prod }_{\mathbf{0}\leqslant \mathbf{m}\leqslant \tilde{\mathbf{u}}-1}\unicode[STIX]{x1D6E9}_{R}(\mathbf{m};\mathbf{h})^{\unicode[STIX]{x1D719}_{m_{1}}\cdots \unicode[STIX]{x1D719}_{m_{R}}}\gg X^{-(c+1)\unicode[STIX]{x1D6FF}}M^{\unicode[STIX]{x1D6EC}(\unicode[STIX]{x1D713}+b/2)+\unicode[STIX]{x1D6FE}}.\end{eqnarray}$$
$$\begin{eqnarray}\mathop{\prod }_{\mathbf{0}\leqslant \mathbf{m}\leqslant \tilde{\mathbf{u}}-1}\unicode[STIX]{x1D6E9}_{R}(\mathbf{m};\mathbf{h})^{\unicode[STIX]{x1D719}_{m_{1}}\cdots \unicode[STIX]{x1D719}_{m_{R}}}\gg X^{-(c+1)\unicode[STIX]{x1D6FF}}M^{\unicode[STIX]{x1D6EC}(\unicode[STIX]{x1D713}+b/2)+\unicode[STIX]{x1D6FE}}.\end{eqnarray}$$
Note that from (7.1) one has
 $$\begin{eqnarray}\mathop{\sum }_{m=0}^{v-1}\unicode[STIX]{x1D719}_{m}=\frac{v(s-r)}{s(s-v)}\leqslant \frac{r}{s},\end{eqnarray}$$
$$\begin{eqnarray}\mathop{\sum }_{m=0}^{v-1}\unicode[STIX]{x1D719}_{m}=\frac{v(s-r)}{s(s-v)}\leqslant \frac{r}{s},\end{eqnarray}$$
so that
 $$\begin{eqnarray}\mathop{\sum }_{m_{1}=0}^{\tilde{v}_{1}-1}\cdots \mathop{\sum }_{m_{R}=0}^{\tilde{v}_{R}-1}\unicode[STIX]{x1D719}_{m_{1}}\cdots \unicode[STIX]{x1D719}_{m_{R}}\leqslant (r/s)^{R}\leqslant r/s.\end{eqnarray}$$
$$\begin{eqnarray}\mathop{\sum }_{m_{1}=0}^{\tilde{v}_{1}-1}\cdots \mathop{\sum }_{m_{R}=0}^{\tilde{v}_{R}-1}\unicode[STIX]{x1D719}_{m_{1}}\cdots \unicode[STIX]{x1D719}_{m_{R}}\leqslant (r/s)^{R}\leqslant r/s.\end{eqnarray}$$
Then we deduce from the definition (11.3) of
 $\unicode[STIX]{x1D6E9}_{n}(\mathbf{m};\mathbf{h})$
that
$\unicode[STIX]{x1D6E9}_{n}(\mathbf{m};\mathbf{h})$
that
 $$\begin{eqnarray}\displaystyle & & \displaystyle \mathop{\prod }_{\mathbf{0}\leqslant \mathbf{m}\leqslant \tilde{\mathbf{u}}-1}(X^{-\unicode[STIX]{x1D6EC}}\unicode[STIX]{x27E6}K_{a_{R},b_{R}}^{r,r}(X)\unicode[STIX]{x27E7}+M^{-3sk^{R}b})^{\unicode[STIX]{x1D719}_{m_{1}}\cdots \unicode[STIX]{x1D719}_{m_{R}}}\nonumber\\ \displaystyle & & \displaystyle \qquad \gg X^{-(c+1)\unicode[STIX]{x1D6FF}}M^{\unicode[STIX]{x1D6EC}(\unicode[STIX]{x1D713}+(1/2-r/s)b)+\unicode[STIX]{x1D6FE}}.\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle \mathop{\prod }_{\mathbf{0}\leqslant \mathbf{m}\leqslant \tilde{\mathbf{u}}-1}(X^{-\unicode[STIX]{x1D6EC}}\unicode[STIX]{x27E6}K_{a_{R},b_{R}}^{r,r}(X)\unicode[STIX]{x27E7}+M^{-3sk^{R}b})^{\unicode[STIX]{x1D719}_{m_{1}}\cdots \unicode[STIX]{x1D719}_{m_{R}}}\nonumber\\ \displaystyle & & \displaystyle \qquad \gg X^{-(c+1)\unicode[STIX]{x1D6FF}}M^{\unicode[STIX]{x1D6EC}(\unicode[STIX]{x1D713}+(1/2-r/s)b)+\unicode[STIX]{x1D6FE}}.\end{eqnarray}$$
Put
 $$\begin{eqnarray}\unicode[STIX]{x1D6FA}=B_{R}=\mathop{\sum }_{m_{1}=0}^{\tilde{v}_{1}-1}\cdots \mathop{\sum }_{m_{R}=0}^{\tilde{v}_{R}-1}\unicode[STIX]{x1D6FD}_{\mathbf{m}}^{(R)}\tilde{b}_{R}(\mathbf{m}),\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D6FA}=B_{R}=\mathop{\sum }_{m_{1}=0}^{\tilde{v}_{1}-1}\cdots \mathop{\sum }_{m_{R}=0}^{\tilde{v}_{R}-1}\unicode[STIX]{x1D6FD}_{\mathbf{m}}^{(R)}\tilde{b}_{R}(\mathbf{m}),\end{eqnarray}$$
so that in view of Lemma 11.5 one has
![]() $\unicode[STIX]{x1D6FA}\geqslant \tilde{B}_{R}$
. Then an application of Lemma 8.1 to (11.36) yields the relation
$\unicode[STIX]{x1D6FA}\geqslant \tilde{B}_{R}$
. Then an application of Lemma 8.1 to (11.36) yields the relation
 $$\begin{eqnarray}\displaystyle & & \displaystyle \mathop{\sum }_{m_{1}=0}^{\tilde{v}_{1}-1}\cdots \mathop{\sum }_{m_{R}=0}^{\tilde{v}_{R}-1}(X^{-\unicode[STIX]{x1D6EC}}\unicode[STIX]{x27E6}K_{a_{R},b_{R}}^{r,r}(X)\unicode[STIX]{x27E7}+M^{-3sk^{R}b})^{\unicode[STIX]{x1D6FA}/\tilde{b}_{R}(\mathbf{m})}\nonumber\\ \displaystyle & & \displaystyle \quad \gg X^{-(c+1)\unicode[STIX]{x1D6FF}}M^{\unicode[STIX]{x1D6EC}(\unicode[STIX]{x1D713}+(1/2-r/s)b)+\unicode[STIX]{x1D6FE}}.\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle \mathop{\sum }_{m_{1}=0}^{\tilde{v}_{1}-1}\cdots \mathop{\sum }_{m_{R}=0}^{\tilde{v}_{R}-1}(X^{-\unicode[STIX]{x1D6EC}}\unicode[STIX]{x27E6}K_{a_{R},b_{R}}^{r,r}(X)\unicode[STIX]{x27E7}+M^{-3sk^{R}b})^{\unicode[STIX]{x1D6FA}/\tilde{b}_{R}(\mathbf{m})}\nonumber\\ \displaystyle & & \displaystyle \quad \gg X^{-(c+1)\unicode[STIX]{x1D6FF}}M^{\unicode[STIX]{x1D6EC}(\unicode[STIX]{x1D713}+(1/2-r/s)b)+\unicode[STIX]{x1D6FE}}.\nonumber\end{eqnarray}$$
We see from (11.5) and (11.37) that
 $\unicode[STIX]{x1D6FA}=(s_{0}/s)^{R}$
, and so it follows from (11.6) that
$\unicode[STIX]{x1D6FA}=(s_{0}/s)^{R}$
, and so it follows from (11.6) that
 $\unicode[STIX]{x1D6FA}/\tilde{b}_{R}(\mathbf{m})=1/\unicode[STIX]{x1D70C}_{\mathbf{m}}$
. Thus, we conclude that for some
$\unicode[STIX]{x1D6FA}/\tilde{b}_{R}(\mathbf{m})=1/\unicode[STIX]{x1D70C}_{\mathbf{m}}$
. Thus, we conclude that for some
![]() $R$
-tuple
$R$
-tuple
![]() $\mathbf{m}$
, one has
$\mathbf{m}$
, one has
 $$\begin{eqnarray}\displaystyle X^{-\unicode[STIX]{x1D6EC}}\unicode[STIX]{x27E6}K_{a_{R},b_{R}}^{r,r}(X)\unicode[STIX]{x27E7}+M^{-3sk^{R}b} & \gg & \displaystyle X^{-\unicode[STIX]{x1D70C}_{\mathbf{m}}(c+1)\unicode[STIX]{x1D6FF}}M^{\unicode[STIX]{x1D6EC}\unicode[STIX]{x1D70C}_{\mathbf{m}}(\unicode[STIX]{x1D713}+(1/2-r/s)b)+\unicode[STIX]{x1D70C}_{\mathbf{m}}\unicode[STIX]{x1D6FE}}\nonumber\\ \displaystyle & \gg & \displaystyle X^{-c^{\prime }\unicode[STIX]{x1D6FF}}M^{\unicode[STIX]{x1D6EC}\unicode[STIX]{x1D713}^{\prime }+\unicode[STIX]{x1D6FE}^{\prime }}.\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle X^{-\unicode[STIX]{x1D6EC}}\unicode[STIX]{x27E6}K_{a_{R},b_{R}}^{r,r}(X)\unicode[STIX]{x27E7}+M^{-3sk^{R}b} & \gg & \displaystyle X^{-\unicode[STIX]{x1D70C}_{\mathbf{m}}(c+1)\unicode[STIX]{x1D6FF}}M^{\unicode[STIX]{x1D6EC}\unicode[STIX]{x1D70C}_{\mathbf{m}}(\unicode[STIX]{x1D713}+(1/2-r/s)b)+\unicode[STIX]{x1D70C}_{\mathbf{m}}\unicode[STIX]{x1D6FE}}\nonumber\\ \displaystyle & \gg & \displaystyle X^{-c^{\prime }\unicode[STIX]{x1D6FF}}M^{\unicode[STIX]{x1D6EC}\unicode[STIX]{x1D713}^{\prime }+\unicode[STIX]{x1D6FE}^{\prime }}.\end{eqnarray}$$
We must again handle the removal of the term
 $M^{-3sk^{R}b}$
on the left-hand side of (11.38). We note that, just as in the concluding paragraph of the proof of Lemma 11.6, one has
$M^{-3sk^{R}b}$
on the left-hand side of (11.38). We note that, just as in the concluding paragraph of the proof of Lemma 11.6, one has
 $\tilde{b}_{n+1}\geqslant l\tilde{b}_{n}$
$\tilde{b}_{n+1}\geqslant l\tilde{b}_{n}$
![]() $(n\geqslant 0)$
and hence
$(n\geqslant 0)$
and hence
 $\tilde{b}_{n}(\mathbf{m})\geqslant 0$
. Hence, a direct induction leads from (8.3) to the upper bound
$\tilde{b}_{n}(\mathbf{m})\geqslant 0$
. Hence, a direct induction leads from (8.3) to the upper bound
 $\tilde{b}_{R}(\mathbf{m})\leqslant k^{R}$
, and we find by means of (11.6) and (11.33) that
$\tilde{b}_{R}(\mathbf{m})\leqslant k^{R}$
, and we find by means of (11.6) and (11.33) that
 $$\begin{eqnarray}\unicode[STIX]{x1D70C}_{\mathbf{m}}=\tilde{b}_{R}(\mathbf{m})(s/s_{0})^{R}<\tilde{b}_{R}(\mathbf{m})\leqslant k^{R}.\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D70C}_{\mathbf{m}}=\tilde{b}_{R}(\mathbf{m})(s/s_{0})^{R}<\tilde{b}_{R}(\mathbf{m})\leqslant k^{R}.\end{eqnarray}$$
We may therefore follow the analysis leading to (8.16), mutatis mutandis, to conclude as before that
 $$\begin{eqnarray}X^{-\unicode[STIX]{x1D6EC}}\unicode[STIX]{x27E6}K_{a_{R},b_{R}}^{r,r}(X)\unicode[STIX]{x27E7}\gg X^{-c^{\prime }\unicode[STIX]{x1D6FF}}M^{\unicode[STIX]{x1D6EC}\unicode[STIX]{x1D713}^{\prime }+\unicode[STIX]{x1D6FE}^{\prime }}.\end{eqnarray}$$
$$\begin{eqnarray}X^{-\unicode[STIX]{x1D6EC}}\unicode[STIX]{x27E6}K_{a_{R},b_{R}}^{r,r}(X)\unicode[STIX]{x27E7}\gg X^{-c^{\prime }\unicode[STIX]{x1D6FF}}M^{\unicode[STIX]{x1D6EC}\unicode[STIX]{x1D713}^{\prime }+\unicode[STIX]{x1D6FE}^{\prime }}.\end{eqnarray}$$
We find from Lemma 11.6 that one has
 $a_{R}\leqslant b_{R}/l$
, and that
$a_{R}\leqslant b_{R}/l$
, and that
 $$\begin{eqnarray}k_{\mathbf{m}}b\leqslant b_{R}\leqslant k_{\mathbf{m}}b+16k^{2R}b.\end{eqnarray}$$
$$\begin{eqnarray}k_{\mathbf{m}}b\leqslant b_{R}\leqslant k_{\mathbf{m}}b+16k^{2R}b.\end{eqnarray}$$
Then we conclude that there exist integers
![]() $b^{\prime }=b_{R}$
,
$b^{\prime }=b_{R}$
,
![]() $a^{\prime }=a_{R}$
and
$a^{\prime }=a_{R}$
and
![]() $h$
satisfying the conditions
$h$
satisfying the conditions
 $$\begin{eqnarray}0\leqslant h\leqslant 16k^{2R}b,\qquad b^{\prime }=k_{\boldsymbol{ m}}b+h\qquad \text{and}\qquad a^{\prime }\leqslant b^{\prime }/l,\end{eqnarray}$$
$$\begin{eqnarray}0\leqslant h\leqslant 16k^{2R}b,\qquad b^{\prime }=k_{\boldsymbol{ m}}b+h\qquad \text{and}\qquad a^{\prime }\leqslant b^{\prime }/l,\end{eqnarray}$$
for which
 $$\begin{eqnarray}X^{-\unicode[STIX]{x1D6EC}}\unicode[STIX]{x27E6}K_{a^{\prime },b^{\prime }}^{r,r}(X)\unicode[STIX]{x27E7}\gg X^{-c^{\prime }\unicode[STIX]{x1D6FF}}M^{\unicode[STIX]{x1D6EC}\unicode[STIX]{x1D713}^{\prime }+\unicode[STIX]{x1D6FE}^{\prime }}.\end{eqnarray}$$
$$\begin{eqnarray}X^{-\unicode[STIX]{x1D6EC}}\unicode[STIX]{x27E6}K_{a^{\prime },b^{\prime }}^{r,r}(X)\unicode[STIX]{x27E7}\gg X^{-c^{\prime }\unicode[STIX]{x1D6FF}}M^{\unicode[STIX]{x1D6EC}\unicode[STIX]{x1D713}^{\prime }+\unicode[STIX]{x1D6FE}^{\prime }}.\end{eqnarray}$$
The desired conclusion (11.35) follows at once, together with its associated conditions.
The only task that remains is to confirm the bounds
 $2^{R}\leqslant k_{\mathbf{m}}\leqslant k^{R}$
. On the one hand, just as in the proof of Lemma 11.6, one has
$2^{R}\leqslant k_{\mathbf{m}}\leqslant k^{R}$
. On the one hand, just as in the proof of Lemma 11.6, one has
 $\tilde{b}_{n+1}\geqslant l\tilde{b}_{n}$
for each
$\tilde{b}_{n+1}\geqslant l\tilde{b}_{n}$
for each
![]() $n\geqslant 0$
. Then an inductive argument confirms that
$n\geqslant 0$
. Then an inductive argument confirms that
 $k_{\mathbf{m}}=\tilde{b}_{R}\geqslant l^{R}\tilde{b}_{0}\geqslant 2^{R}$
. On the other hand, we have already shown that
$k_{\mathbf{m}}=\tilde{b}_{R}\geqslant l^{R}\tilde{b}_{0}\geqslant 2^{R}$
. On the other hand, we have already shown that
 $\tilde{b}_{R}\leqslant k^{R}$
and thus
$\tilde{b}_{R}\leqslant k^{R}$
and thus
 $k_{\mathbf{m}}=\tilde{b}_{R}\leqslant k^{R}$
. This completes the proof of the lemma.◻
$k_{\mathbf{m}}=\tilde{b}_{R}\leqslant k^{R}$
. This completes the proof of the lemma.◻
We now employ the conclusion of the last lemma to bound
![]() $J_{s+r}(X)$
.
$J_{s+r}(X)$
.
Theorem 11.8. Suppose that
![]() $s$
,
$s$
,
![]() $k$
and
$k$
and
![]() $r$
are natural numbers with
$r$
are natural numbers with
![]() $k$
sufficiently large,
$k$
sufficiently large,
 $r=k-\lceil k^{1/3}\rceil$
and
$r=k-\lceil k^{1/3}\rceil$
and
 $1\leqslant s\leqslant s_{1}$
, where
$1\leqslant s\leqslant s_{1}$
, where
 $$\begin{eqnarray}\displaystyle s_{1} & = & \displaystyle \frac{1}{2}\biggl(\frac{1}{2}k(k+1)-\frac{1}{3}k-3k^{2/3}\biggr)\nonumber\\ \displaystyle & & \displaystyle \times \,\biggl(1+\sqrt{1-\frac{4r(k(k-1)/2+3k^{5/3})}{(k(k+1)/2-k/3-3k^{2/3})^{2}}}\biggr).\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle s_{1} & = & \displaystyle \frac{1}{2}\biggl(\frac{1}{2}k(k+1)-\frac{1}{3}k-3k^{2/3}\biggr)\nonumber\\ \displaystyle & & \displaystyle \times \,\biggl(1+\sqrt{1-\frac{4r(k(k-1)/2+3k^{5/3})}{(k(k+1)/2-k/3-3k^{2/3})^{2}}}\biggr).\nonumber\end{eqnarray}$$
Then, for each
![]() $\unicode[STIX]{x1D700}>0$
, one has
$\unicode[STIX]{x1D700}>0$
, one has
 $J_{s+r}(X)\ll X^{s+r+\unicode[STIX]{x1D700}}$
.
$J_{s+r}(X)\ll X^{s+r+\unicode[STIX]{x1D700}}$
.
Proof. Defining
![]() $s_{0}$
via (11.5) as in the preamble to Lemma 11.4, one finds that there are no serious modifications required in order to apply the argument of the proof of Theorem 2.1 to pass from Lemma 11.7 to the conclusion of the theorem, but with
$s_{0}$
via (11.5) as in the preamble to Lemma 11.4, one finds that there are no serious modifications required in order to apply the argument of the proof of Theorem 2.1 to pass from Lemma 11.7 to the conclusion of the theorem, but with
![]() $s_{0}$
in place of
$s_{0}$
in place of
![]() $s_{1}=\unicode[STIX]{x1D703}_{+}$
. The argument leading to (11.33) shows, however, that whenever
$s_{1}=\unicode[STIX]{x1D703}_{+}$
. The argument leading to (11.33) shows, however, that whenever
![]() $s<s_{1}$
, one has also that
$s<s_{1}$
, one has also that
![]() $s<s_{0}$
. The conclusion of the theorem is now immediate.◻
$s<s_{0}$
. The conclusion of the theorem is now immediate.◻
In order to establish Theorem 1.3, we have only to note that, on recalling (11.23), one finds that
 $$\begin{eqnarray}\displaystyle s_{1}+r & = & \displaystyle \unicode[STIX]{x1D703}_{+}+k-l\geqslant {\textstyle \frac{1}{2}}k(k-1)-{\textstyle \frac{1}{3}}k-7k^{2/3}+(k-k^{1/3})\nonumber\\ \displaystyle & {\geqslant} & \displaystyle {\textstyle \frac{1}{2}}k(k+1)-{\textstyle \frac{1}{3}}k-8k^{2/3}.\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle s_{1}+r & = & \displaystyle \unicode[STIX]{x1D703}_{+}+k-l\geqslant {\textstyle \frac{1}{2}}k(k-1)-{\textstyle \frac{1}{3}}k-7k^{2/3}+(k-k^{1/3})\nonumber\\ \displaystyle & {\geqslant} & \displaystyle {\textstyle \frac{1}{2}}k(k+1)-{\textstyle \frac{1}{3}}k-8k^{2/3}.\nonumber\end{eqnarray}$$
Thus, whenever
 $$\begin{eqnarray}1\leqslant s\leqslant {\textstyle \frac{1}{2}}k(k+1)-{\textstyle \frac{1}{3}}k-8k^{2/3},\end{eqnarray}$$
$$\begin{eqnarray}1\leqslant s\leqslant {\textstyle \frac{1}{2}}k(k+1)-{\textstyle \frac{1}{3}}k-8k^{2/3},\end{eqnarray}$$
one has
 $J_{s,k}(X)\ll X^{s+\unicode[STIX]{x1D700}}$
.
$J_{s,k}(X)\ll X^{s+\unicode[STIX]{x1D700}}$
.
12 Some consequences of Theorem 1.3
We finish this paper by turning our attention to a few consequences of the asymptotically sharpest of our conclusions, namely Theorem 1.3. We begin by proving Theorem 1.5. Suppose that
![]() $k$
is a sufficiently large natural number and put
$k$
is a sufficiently large natural number and put
 $$\begin{eqnarray}\mathfrak{s}=\lfloor {\textstyle \frac{1}{2}}k(k+1)-{\textstyle \frac{1}{3}}k-8k^{2/3}\rfloor .\end{eqnarray}$$
$$\begin{eqnarray}\mathfrak{s}=\lfloor {\textstyle \frac{1}{2}}k(k+1)-{\textstyle \frac{1}{3}}k-8k^{2/3}\rfloor .\end{eqnarray}$$
In addition, take
 $s={\textstyle \frac{1}{2}}k(k+1)$
and put
$s={\textstyle \frac{1}{2}}k(k+1)$
and put
 $\unicode[STIX]{x1D6E5}=s-\mathfrak{s}$
. Then we find that
$\unicode[STIX]{x1D6E5}=s-\mathfrak{s}$
. Then we find that
 $$\begin{eqnarray}\unicode[STIX]{x1D6E5}\leqslant {\textstyle \frac{1}{3}}k+8k^{2/3}+1.\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D6E5}\leqslant {\textstyle \frac{1}{3}}k+8k^{2/3}+1.\end{eqnarray}$$
Consequently, on making use of the trivial estimate
 $f_{k}(\unicode[STIX]{x1D736};X)=O(X)$
, we deduce from (2.1) in combination with Theorem 1.3 that
$f_{k}(\unicode[STIX]{x1D736};X)=O(X)$
, we deduce from (2.1) in combination with Theorem 1.3 that
 $$\begin{eqnarray}\displaystyle J_{s,k}(X) & = & \displaystyle \oint |f_{k}(\unicode[STIX]{x1D736};X)|^{2\mathfrak{s}+2\unicode[STIX]{x1D6E5}}\,d\unicode[STIX]{x1D736}\ll X^{2\unicode[STIX]{x1D6E5}}\oint |f_{k}(\unicode[STIX]{x1D736};X)|^{2\mathfrak{s}}\,d\unicode[STIX]{x1D736}\nonumber\\ \displaystyle & \ll & \displaystyle X^{2\unicode[STIX]{x1D6E5}}J_{\mathfrak{s},k}(X)\ll X^{\mathfrak{s}+2\unicode[STIX]{x1D6E5}+\unicode[STIX]{x1D700}}\ll X^{s+\unicode[STIX]{x1D6E5}+\unicode[STIX]{x1D700}}.\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle J_{s,k}(X) & = & \displaystyle \oint |f_{k}(\unicode[STIX]{x1D736};X)|^{2\mathfrak{s}+2\unicode[STIX]{x1D6E5}}\,d\unicode[STIX]{x1D736}\ll X^{2\unicode[STIX]{x1D6E5}}\oint |f_{k}(\unicode[STIX]{x1D736};X)|^{2\mathfrak{s}}\,d\unicode[STIX]{x1D736}\nonumber\\ \displaystyle & \ll & \displaystyle X^{2\unicode[STIX]{x1D6E5}}J_{\mathfrak{s},k}(X)\ll X^{\mathfrak{s}+2\unicode[STIX]{x1D6E5}+\unicode[STIX]{x1D700}}\ll X^{s+\unicode[STIX]{x1D6E5}+\unicode[STIX]{x1D700}}.\nonumber\end{eqnarray}$$
The conclusion of Theorem 1.5 is now immediate.
We next point out an application of Theorem 1.3 to Tarry’s problem. Recall the definition of the natural number
![]() $W(k,h)$
associated with the system of equations (1.5).
$W(k,h)$
associated with the system of equations (1.5).
Theorem 12.1. When
![]() $h$
and
$h$
and
![]() $k$
are natural numbers with
$k$
are natural numbers with
![]() $h\geqslant 2$
and
$h\geqslant 2$
and
![]() $k$
sufficiently large, one has
$k$
sufficiently large, one has
 $W(k,h)\leqslant {\textstyle \frac{1}{2}}k(k+1)+1$
.
$W(k,h)\leqslant {\textstyle \frac{1}{2}}k(k+1)+1$
.
Proof. The argument of the proof of [Reference Wooley15, Theorem 1.3] shows that
 $W(k,h)\leqslant s$
whenever one can establish the estimate
$W(k,h)\leqslant s$
whenever one can establish the estimate
 $$\begin{eqnarray}J_{s,k+1}(X)=o(X^{2s-k(k+1)/2}).\end{eqnarray}$$
$$\begin{eqnarray}J_{s,k+1}(X)=o(X^{2s-k(k+1)/2}).\end{eqnarray}$$
But, as a consequence of Theorem 1.3, when
![]() $k$
is sufficiently large and
$k$
is sufficiently large and
 $$\begin{eqnarray}1\leqslant s\leqslant {\textstyle \frac{1}{2}}(k+1)(k+2)-{\textstyle \frac{1}{3}}(k+1)-8(k+1)^{2/3},\end{eqnarray}$$
$$\begin{eqnarray}1\leqslant s\leqslant {\textstyle \frac{1}{2}}(k+1)(k+2)-{\textstyle \frac{1}{3}}(k+1)-8(k+1)^{2/3},\end{eqnarray}$$
one has
 $J_{s,k+1}(X)\ll X^{s+\unicode[STIX]{x1D700}}$
. Observe, however, that
$J_{s,k+1}(X)\ll X^{s+\unicode[STIX]{x1D700}}$
. Observe, however, that
 $X^{s+\unicode[STIX]{x1D700}}=o(X^{2s-k(k+1)/2})$
provided only that
$X^{s+\unicode[STIX]{x1D700}}=o(X^{2s-k(k+1)/2})$
provided only that
 $s<2s-{\textstyle \frac{1}{2}}k(k+1)$
, which is to say that
$s<2s-{\textstyle \frac{1}{2}}k(k+1)$
, which is to say that
 $s\geqslant {\textstyle \frac{1}{2}}k(k+1)+1$
. Moreover, when
$s\geqslant {\textstyle \frac{1}{2}}k(k+1)+1$
. Moreover, when
![]() $k$
is sufficiently large, one finds that the value
$k$
is sufficiently large, one finds that the value
 $s={\textstyle \frac{1}{2}}k(k+1)+1$
satisfies the condition (12.2) and thus we have
$s={\textstyle \frac{1}{2}}k(k+1)+1$
satisfies the condition (12.2) and thus we have
 $W(k,h)\leqslant {\textstyle \frac{1}{2}}k(k+1)+1$
. This completes the proof of the theorem.◻
$W(k,h)\leqslant {\textstyle \frac{1}{2}}k(k+1)+1$
. This completes the proof of the theorem.◻
The problem of estimating
![]() $W(k,h)$
has been investigated extensively by Wright and Hua (see [Reference Hua6], [Reference Hua7] and [Reference Wright21]). Hua was able to show that
$W(k,h)$
has been investigated extensively by Wright and Hua (see [Reference Hua6], [Reference Hua7] and [Reference Wright21]). Hua was able to show that
 $W(k,h)\leqslant k^{2}(\log k+O(1))$
. This bound was improved in [Reference Wooley15, Theorem 1.3] by means of the efficient congruencing method, delivering the upper bound
$W(k,h)\leqslant k^{2}(\log k+O(1))$
. This bound was improved in [Reference Wooley15, Theorem 1.3] by means of the efficient congruencing method, delivering the upper bound
 $W(k,h)\leqslant k^{2}+k-2$
. In our most recent work on multigrade efficient congruencing, this bound was further improved in [Reference Wooley19, Theorem 12.1] to obtain
$W(k,h)\leqslant k^{2}+k-2$
. In our most recent work on multigrade efficient congruencing, this bound was further improved in [Reference Wooley19, Theorem 12.1] to obtain
 $W(k,h)\leqslant {\textstyle \frac{5}{8}}(k+1)^{2}$
for
$W(k,h)\leqslant {\textstyle \frac{5}{8}}(k+1)^{2}$
for
![]() $k\geqslant 3$
. The bound recorded in Theorem 12.1 above achieves the limit of the methods currently employed in which an elementary application of Vinogradov’s mean value theorem is applied, as described in [Reference Wooley14] and enhanced in [Reference Wooley19, §12]. As far as the author is aware, there is no lower bound available on
$k\geqslant 3$
. The bound recorded in Theorem 12.1 above achieves the limit of the methods currently employed in which an elementary application of Vinogradov’s mean value theorem is applied, as described in [Reference Wooley14] and enhanced in [Reference Wooley19, §12]. As far as the author is aware, there is no lower bound available on
![]() $W(k,h)$
superior to
$W(k,h)$
superior to
 $W(k,h)\geqslant k+1$
. There consequently remains a substantial gap between our upper and lower bounds in Tarry’s problem.
$W(k,h)\geqslant k+1$
. There consequently remains a substantial gap between our upper and lower bounds in Tarry’s problem.
Finally, we explore the consequences of Theorem 1.3 in the context of Waring’s problem. When
![]() $s$
and
$s$
and
![]() $k$
are natural numbers, let
$k$
are natural numbers, let
![]() $R_{s,k}(n)$
denote the number of representations of the natural number
$R_{s,k}(n)$
denote the number of representations of the natural number
![]() $n$
as the sum of
$n$
as the sum of
![]() $s$
$s$
![]() $k$
th powers of positive integers. A formal application of the circle method suggests that for
$k$
th powers of positive integers. A formal application of the circle method suggests that for
![]() $k\geqslant 3$
and
$k\geqslant 3$
and
 $s\geqslant k+1$
, one should have
$s\geqslant k+1$
, one should have
 $$\begin{eqnarray}R_{s,k}(n)=\frac{\unicode[STIX]{x1D6E4}(1+1/k)^{s}}{\unicode[STIX]{x1D6E4}(s/k)}\mathfrak{S}_{s,k}(n)n^{s/k-1}+o(n^{s/k-1}),\end{eqnarray}$$
$$\begin{eqnarray}R_{s,k}(n)=\frac{\unicode[STIX]{x1D6E4}(1+1/k)^{s}}{\unicode[STIX]{x1D6E4}(s/k)}\mathfrak{S}_{s,k}(n)n^{s/k-1}+o(n^{s/k-1}),\end{eqnarray}$$
where
 $$\begin{eqnarray}\mathfrak{S}_{s,k}(n)=\mathop{\sum }_{q=1}^{\infty }\mathop{\sum }_{\substack{ a=1 \\ (a,q)=1}}^{q}\biggl(q^{-1}\mathop{\sum }_{r=1}^{q}e(ar^{k}/q)\biggr)^{s}e(-na/q).\end{eqnarray}$$
$$\begin{eqnarray}\mathfrak{S}_{s,k}(n)=\mathop{\sum }_{q=1}^{\infty }\mathop{\sum }_{\substack{ a=1 \\ (a,q)=1}}^{q}\biggl(q^{-1}\mathop{\sum }_{r=1}^{q}e(ar^{k}/q)\biggr)^{s}e(-na/q).\end{eqnarray}$$
With suitable congruence conditions imposed on
![]() $n$
, one has
$n$
, one has
 $1\ll \mathfrak{S}_{s,k}(n)\ll n^{\unicode[STIX]{x1D700}}$
, so that the conjectured relation (12.3) constitutes an honest asymptotic formula. Let
$1\ll \mathfrak{S}_{s,k}(n)\ll n^{\unicode[STIX]{x1D700}}$
, so that the conjectured relation (12.3) constitutes an honest asymptotic formula. Let
![]() $\widetilde{G}(k)$
denote the least integer
$\widetilde{G}(k)$
denote the least integer
![]() $t$
with the property that, for all
$t$
with the property that, for all
![]() $s\geqslant t$
, and all sufficiently large natural numbers
$s\geqslant t$
, and all sufficiently large natural numbers
![]() $n$
, one has the asymptotic formula (12.3). By combining the conclusion of Theorem 1.3 with our recent work concerning the asymptotic formula in Waring’s problem [Reference Wooley16], and the enhancement [Reference Ford and Wooley4, Theorem 8.5] of Ford’s work [Reference Ford3], we are able to derive new upper bounds for
$n$
, one has the asymptotic formula (12.3). By combining the conclusion of Theorem 1.3 with our recent work concerning the asymptotic formula in Waring’s problem [Reference Wooley16], and the enhancement [Reference Ford and Wooley4, Theorem 8.5] of Ford’s work [Reference Ford3], we are able to derive new upper bounds for
![]() $\widetilde{G}(k)$
when
$\widetilde{G}(k)$
when
![]() $k$
is sufficiently large.
$k$
is sufficiently large.
Theorem 12.2. Let
![]() $\unicode[STIX]{x1D709}$
denote the real root of the polynomial
$\unicode[STIX]{x1D709}$
denote the real root of the polynomial
 $6\unicode[STIX]{x1D709}^{3}+3\unicode[STIX]{x1D709}^{2}-1$
and put
$6\unicode[STIX]{x1D709}^{3}+3\unicode[STIX]{x1D709}^{2}-1$
and put
 $C=(5+6\unicode[STIX]{x1D709}-3\unicode[STIX]{x1D709}^{2})/(2+6\unicode[STIX]{x1D709})$
, so that
$C=(5+6\unicode[STIX]{x1D709}-3\unicode[STIX]{x1D709}^{2})/(2+6\unicode[STIX]{x1D709})$
, so that
 $$\begin{eqnarray}\unicode[STIX]{x1D709}=0.424\,574\ldots \quad \text{and}\quad C=1.540\,789\ldots .\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D709}=0.424\,574\ldots \quad \text{and}\quad C=1.540\,789\ldots .\end{eqnarray}$$
Then, for large values of
![]() $k$
, one has
$k$
, one has
 $\widetilde{G}(k)<Ck^{2}+O(k^{5/3})$
.
$\widetilde{G}(k)<Ck^{2}+O(k^{5/3})$
.
For comparison, in [Reference Wooley19, Theorem 1.3], we derived an analogous bound in which
![]() $C$
is replaced by the slightly larger number
$C$
is replaced by the slightly larger number
 $1.542\,749\ldots .$
$1.542\,749\ldots .$
The Proof of Theorem 12.2.
In general, we write
![]() $\unicode[STIX]{x1D6E5}_{s,k}$
for the least real number with the property that, for all
$\unicode[STIX]{x1D6E5}_{s,k}$
for the least real number with the property that, for all
![]() $\unicode[STIX]{x1D700}>0$
, one has
$\unicode[STIX]{x1D700}>0$
, one has
 $$\begin{eqnarray}J_{s,k}(X)\ll X^{2s-k(k+1)/2+\unicode[STIX]{x1D6E5}_{s,k}+\unicode[STIX]{x1D700}}.\end{eqnarray}$$
$$\begin{eqnarray}J_{s,k}(X)\ll X^{2s-k(k+1)/2+\unicode[STIX]{x1D6E5}_{s,k}+\unicode[STIX]{x1D700}}.\end{eqnarray}$$
Then it follows from [Reference Wooley19, Lemma 10.7] that one has
 $\widetilde{G}(k)\leqslant \lfloor u_{1}(k)\rfloor +1$
, where
$\widetilde{G}(k)\leqslant \lfloor u_{1}(k)\rfloor +1$
, where
 $$\begin{eqnarray}u_{1}(k)=\min _{\substack{ 1\leqslant t\leqslant k^{2}-k+1 \\ \unicode[STIX]{x1D6E5}_{t,k}<1}}\underset{2v+w(w-1)<2t}{\min _{1\leqslant w\leqslant k-1}\min _{v\geqslant 1}}\,u_{0}(k,t,v,w)\end{eqnarray}$$
$$\begin{eqnarray}u_{1}(k)=\min _{\substack{ 1\leqslant t\leqslant k^{2}-k+1 \\ \unicode[STIX]{x1D6E5}_{t,k}<1}}\underset{2v+w(w-1)<2t}{\min _{1\leqslant w\leqslant k-1}\min _{v\geqslant 1}}\,u_{0}(k,t,v,w)\end{eqnarray}$$
and
 $$\begin{eqnarray}u_{0}(k,t,v,w)=2t-\frac{(1-\unicode[STIX]{x1D6E5}_{t,k})(2t-2v-w(w-1))}{1-\unicode[STIX]{x1D6E5}_{t,k}+\unicode[STIX]{x1D6E5}_{v,k}/w}.\end{eqnarray}$$
$$\begin{eqnarray}u_{0}(k,t,v,w)=2t-\frac{(1-\unicode[STIX]{x1D6E5}_{t,k})(2t-2v-w(w-1))}{1-\unicode[STIX]{x1D6E5}_{t,k}+\unicode[STIX]{x1D6E5}_{v,k}/w}.\end{eqnarray}$$
Suppose that
![]() $k$
is a large natural number and let
$k$
is a large natural number and let
![]() $\unicode[STIX]{x1D6FD}$
be a positive parameter to be determined in due course. We take
$\unicode[STIX]{x1D6FD}$
be a positive parameter to be determined in due course. We take
 $$\begin{eqnarray}w=\lfloor \unicode[STIX]{x1D6FD}k\rfloor \quad \text{and}\quad v={\textstyle \frac{1}{2}}k(k+1).\end{eqnarray}$$
$$\begin{eqnarray}w=\lfloor \unicode[STIX]{x1D6FD}k\rfloor \quad \text{and}\quad v={\textstyle \frac{1}{2}}k(k+1).\end{eqnarray}$$
Then it follows from Theorem 1.3, just as in the discussion leading to (12.1), that the exponent
![]() $\unicode[STIX]{x1D6E5}_{v,k}$
is permissible, where
$\unicode[STIX]{x1D6E5}_{v,k}$
is permissible, where
 $$\begin{eqnarray}\unicode[STIX]{x1D6E5}_{v,k}\leqslant {\textstyle \frac{1}{3}}k+8k^{2/3}+1.\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D6E5}_{v,k}\leqslant {\textstyle \frac{1}{3}}k+8k^{2/3}+1.\end{eqnarray}$$
Also, by taking
 $t=k^{2}-k+1$
, one sees from [Reference Wooley19, Corollary 1.2] that
$t=k^{2}-k+1$
, one sees from [Reference Wooley19, Corollary 1.2] that
 $\unicode[STIX]{x1D6E5}_{t,k}=0$
. Then we deduce that
$\unicode[STIX]{x1D6E5}_{t,k}=0$
. Then we deduce that
 $$\begin{eqnarray}u_{1}(k)\leqslant 2(k^{2}-k+1)-\frac{2k^{2}-k(k+1)-(\unicode[STIX]{x1D6FD}k)^{2}+O(k)}{1+k/(3\unicode[STIX]{x1D6FD}k)+O(k^{-1/3})}.\end{eqnarray}$$
$$\begin{eqnarray}u_{1}(k)\leqslant 2(k^{2}-k+1)-\frac{2k^{2}-k(k+1)-(\unicode[STIX]{x1D6FD}k)^{2}+O(k)}{1+k/(3\unicode[STIX]{x1D6FD}k)+O(k^{-1/3})}.\end{eqnarray}$$
It follows that
 $$\begin{eqnarray}\displaystyle u_{1}(k)/(2k^{2}) & {\leqslant} & \displaystyle 1-\frac{\unicode[STIX]{x1D6FD}(1-\unicode[STIX]{x1D6FD}^{2})/2}{\unicode[STIX]{x1D6FD}+1/3}+O(k^{-1/3})\nonumber\\ \displaystyle & = & \displaystyle \frac{3\unicode[STIX]{x1D6FD}^{3}+3\unicode[STIX]{x1D6FD}+2}{6\unicode[STIX]{x1D6FD}+2}+O(k^{-1/3}).\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle u_{1}(k)/(2k^{2}) & {\leqslant} & \displaystyle 1-\frac{\unicode[STIX]{x1D6FD}(1-\unicode[STIX]{x1D6FD}^{2})/2}{\unicode[STIX]{x1D6FD}+1/3}+O(k^{-1/3})\nonumber\\ \displaystyle & = & \displaystyle \frac{3\unicode[STIX]{x1D6FD}^{3}+3\unicode[STIX]{x1D6FD}+2}{6\unicode[STIX]{x1D6FD}+2}+O(k^{-1/3}).\nonumber\end{eqnarray}$$
A modest computation confirms that the optimal choice for the parameter
![]() $\unicode[STIX]{x1D6FD}$
is
$\unicode[STIX]{x1D6FD}$
is
![]() $\unicode[STIX]{x1D709}$
, where
$\unicode[STIX]{x1D709}$
, where
![]() $\unicode[STIX]{x1D709}$
is the real root of the polynomial equation
$\unicode[STIX]{x1D709}$
is the real root of the polynomial equation
 $6\unicode[STIX]{x1D709}^{3}+3\unicode[STIX]{x1D709}^{2}-1=0$
. With this choice for
$6\unicode[STIX]{x1D709}^{3}+3\unicode[STIX]{x1D709}^{2}-1=0$
. With this choice for
![]() $\unicode[STIX]{x1D6FD}$
, one finds that
$\unicode[STIX]{x1D6FD}$
, one finds that
 $$\begin{eqnarray}u_{1}(k)\leqslant \biggl(\frac{5+6\unicode[STIX]{x1D709}-3\unicode[STIX]{x1D709}^{2}}{2+6\unicode[STIX]{x1D709}}\biggr)k^{2}+O(k^{5/3}).\end{eqnarray}$$
$$\begin{eqnarray}u_{1}(k)\leqslant \biggl(\frac{5+6\unicode[STIX]{x1D709}-3\unicode[STIX]{x1D709}^{2}}{2+6\unicode[STIX]{x1D709}}\biggr)k^{2}+O(k^{5/3}).\end{eqnarray}$$
The conclusion of Theorem 12.2 is now immediate. ◻