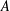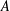1 Introduction and main results
It is well known that a line segment can be continuously moved in a planar set of arbitrarily small area such that it returns to its starting position, with its direction reversed. This fact was first proved by Besicovitch as a solution to the classical Kakeya problem [Reference Besicovitch1].
We may ask if there are other sets in the plane having a similar property. We shall say that a planar set
![]() $A$
has the Kakeya property (property (K) for short) if there exist two different positions of
$A$
has the Kakeya property (property (K) for short) if there exist two different positions of
![]() $A$
such that one can move
$A$
such that one can move
![]() $A$
continuously from the first position to the second such that the set of points touched by the moving set has an arbitrarily small area. Obviously, every line segment has property (K). More generally, if
$A$
continuously from the first position to the second such that the set of points touched by the moving set has an arbitrarily small area. Obviously, every line segment has property (K). More generally, if
![]() $A$
is a null set, and
$A$
is a null set, and
![]() $A$
is the union of parallel lines, then
$A$
is the union of parallel lines, then
![]() $A$
has property (K). Indeed, sliding
$A$
has property (K). Indeed, sliding
![]() $A$
in the direction of the lines we only cover a set of measure zero. Similarly, if
$A$
in the direction of the lines we only cover a set of measure zero. Similarly, if
![]() $A$
is a null set, and
$A$
is a null set, and
![]() $A$
is the union of concentric circles, then
$A$
is the union of concentric circles, then
![]() $A$
has property (K), as rotating
$A$
has property (K), as rotating
![]() $A$
about the centre of the circles we only cover a set of measure zero. We shall say that a set
$A$
about the centre of the circles we only cover a set of measure zero. We shall say that a set
![]() $A\subset \mathbb{R}^{2}$
is a trivial (K)-set if
$A\subset \mathbb{R}^{2}$
is a trivial (K)-set if
![]() $A$
can be covered by a null set which is either the union of parallel lines or the union of concentric circles. Our aim is to prove that if
$A$
can be covered by a null set which is either the union of parallel lines or the union of concentric circles. Our aim is to prove that if
![]() $A$
is closed and has the Kakeya property, then the union of the non-trivial connected components of
$A$
is closed and has the Kakeya property, then the union of the non-trivial connected components of
![]() $A$
is trivial.
$A$
is trivial.
Besicovitch’s construction used the ‘Pál joins’ in order to shift the line segment to an arbitrary parallel position using an arbitrarily small area. (There are solutions to the Kakeya problem without using Pál joins; see e.g. [Reference Cunningham3–Reference Davies5].) Using the Pál joins and Besicovitch’s theorem, it is clear that every line segment can be moved to arrive at any prescribed position within a set of arbitrarily small area.
We shall say that a planar set
![]() $A$
has the strong Kakeya property (property
$A$
has the strong Kakeya property (property
![]() $(\text{K}^{\text{s}})$
for short) if, for every prescribed position,
$(\text{K}^{\text{s}})$
for short) if, for every prescribed position,
![]() $A$
can be continuously moved within a set of arbitrarily small area to the prescribed final position.
$A$
can be continuously moved within a set of arbitrarily small area to the prescribed final position.
The question of whether or not circular arcs have property
![]() $(\text{K}^{\text{s}})$
was asked by Cunningham (see [Reference Cunningham4, p. 591]). It is proved in [Reference Chang and Csörnyei2, Reference Héra and Laczkovich6] that the answer is affirmative, at least for circular arcs of angle short enough. In this note we shall prove that every connected closed set with property
$(\text{K}^{\text{s}})$
was asked by Cunningham (see [Reference Cunningham4, p. 591]). It is proved in [Reference Chang and Csörnyei2, Reference Héra and Laczkovich6] that the answer is affirmative, at least for circular arcs of angle short enough. In this note we shall prove that every connected closed set with property
![]() $(\text{K}^{\text{s}})$
is a line segment or a circular arc.
$(\text{K}^{\text{s}})$
is a line segment or a circular arc.
Now we formulate these notions and results precisely. A rigid motion is an isometry of the plane preserving orientation; that is, a translation or a rotation. We denote the identity map by
![]() $j$
. We identify the plane with the complex plane
$j$
. We identify the plane with the complex plane
![]() $\mathbb{C}$
, and put
$\mathbb{C}$
, and put
![]() $S^{1}=\{x\in \mathbb{C}:|x|=1\}$
. Then every rigid motion is a function of the form
$S^{1}=\{x\in \mathbb{C}:|x|=1\}$
. Then every rigid motion is a function of the form
![]() $x\mapsto ux+c$
, where
$x\mapsto ux+c$
, where
![]() $u,c\in \mathbb{C}$
and
$u,c\in \mathbb{C}$
and
![]() $u\in S^{1}$
. By a continuous movement
$u\in S^{1}$
. By a continuous movement
![]() $M$
we mean a map
$M$
we mean a map
![]() $t\mapsto M_{t}$
$t\mapsto M_{t}$
![]() $(t\in [0,1])$
such that
$(t\in [0,1])$
such that
![]() $M_{t}$
is a rigid motion for every
$M_{t}$
is a rigid motion for every
![]() $t\in [0,1]$
, the map
$t\in [0,1]$
, the map
![]() $(t,x)\mapsto M_{t}(x)$
is continuous on
$(t,x)\mapsto M_{t}(x)$
is continuous on
![]() $[0,1]\times \mathbb{R}^{2}$
and
$[0,1]\times \mathbb{R}^{2}$
and
![]() $M_{0}=j$
. If
$M_{0}=j$
. If
![]() $M$
is a continuous movement, then the set of points touched by a moving set
$M$
is a continuous movement, then the set of points touched by a moving set
![]() $A$
is
$A$
is
The two-dimensional Lebesgue measure of the set
![]() $A\subset \mathbb{R}^{2}$
is denoted by
$A\subset \mathbb{R}^{2}$
is denoted by
![]() $\unicode[STIX]{x1D706}(A)$
.
$\unicode[STIX]{x1D706}(A)$
.
The set
![]() $A$
has property (K) if there is a rigid motion
$A$
has property (K) if there is a rigid motion
![]() $\unicode[STIX]{x1D6FC}\neq j$
such that for every
$\unicode[STIX]{x1D6FC}\neq j$
such that for every
![]() $\unicode[STIX]{x1D700}>0$
there exists a continuous movement
$\unicode[STIX]{x1D700}>0$
there exists a continuous movement
![]() $M$
such that
$M$
such that
![]() $M_{1}=\unicode[STIX]{x1D6FC}$
and
$M_{1}=\unicode[STIX]{x1D6FC}$
and
![]() $\unicode[STIX]{x1D706}(W_{M}(A))<\unicode[STIX]{x1D700}$
. The set
$\unicode[STIX]{x1D706}(W_{M}(A))<\unicode[STIX]{x1D700}$
. The set
![]() $A$
has property
$A$
has property
![]() $(\text{K}^{\text{s}})$
if for every rigid motion
$(\text{K}^{\text{s}})$
if for every rigid motion
![]() $\unicode[STIX]{x1D6FC}$
and for every
$\unicode[STIX]{x1D6FC}$
and for every
![]() $\unicode[STIX]{x1D700}>0$
there exists a continuous movement
$\unicode[STIX]{x1D700}>0$
there exists a continuous movement
![]() $M$
such that
$M$
such that
![]() $M_{1}=\unicode[STIX]{x1D6FC}$
and
$M_{1}=\unicode[STIX]{x1D6FC}$
and
![]() $\unicode[STIX]{x1D706}(W_{M}(A))<\unicode[STIX]{x1D700}$
. By a non-trivial connected component of a set
$\unicode[STIX]{x1D706}(W_{M}(A))<\unicode[STIX]{x1D700}$
. By a non-trivial connected component of a set
![]() $A$
we mean a connected component of
$A$
we mean a connected component of
![]() $A$
having at least two points. Our main results are the following.
$A$
having at least two points. Our main results are the following.
Theorem 1.1. Let
![]() $A\subset \mathbb{R}^{2}$
be a closed set having property
$A\subset \mathbb{R}^{2}$
be a closed set having property
![]() $(\text{K})$
. Then the union of the non-trivial connected components of
$(\text{K})$
. Then the union of the non-trivial connected components of
![]() $A$
is a trivial
$A$
is a trivial
![]() $\text{(K)}$
-set. If
$\text{(K)}$
-set. If
![]() $A$
is non-empty, closed, connected and has property
$A$
is non-empty, closed, connected and has property
![]() $\text{(K)}$
, then
$\text{(K)}$
, then
![]() $A$
is a line segment, a half line, a line, a circular arc, a circle or a singleton.
$A$
is a line segment, a half line, a line, a circular arc, a circle or a singleton.
Theorem 1.2. If
![]() $A\subset \mathbb{R}^{2}$
is a non-empty closed and connected set having property
$A\subset \mathbb{R}^{2}$
is a non-empty closed and connected set having property
![]() $(\text{K}^{\text{s}})$
, then
$(\text{K}^{\text{s}})$
, then
![]() $A$
is a line segment, a circular arc or a singleton.
$A$
is a line segment, a circular arc or a singleton.
It is easy to see that full circles do not have property
![]() $(\text{K}^{\text{s}})$
. Indeed, moving a circle
$(\text{K}^{\text{s}})$
. Indeed, moving a circle
![]() $C$
to a circle disjoint from
$C$
to a circle disjoint from
![]() $C$
, the moving circle must touch every point inside
$C$
, the moving circle must touch every point inside
![]() $C$
. Since every circle has property (K), we can see that properties (K) and
$C$
. Since every circle has property (K), we can see that properties (K) and
![]() $(\text{K}^{\text{s}})$
are not equivalent. As we mentioned earlier, all circular arcs of angle short enough have property
$(\text{K}^{\text{s}})$
are not equivalent. As we mentioned earlier, all circular arcs of angle short enough have property
![]() $(\text{K}^{\text{s}})$
. It is not clear, however, whether or not all circular arcs other than the full circles have property
$(\text{K}^{\text{s}})$
. It is not clear, however, whether or not all circular arcs other than the full circles have property
![]() $(\text{K}^{\text{s}})$
, while, obviously, they have property (K).
$(\text{K}^{\text{s}})$
, while, obviously, they have property (K).
It is easy to see that every set of Hausdorff dimension less than 1 has property
![]() $(\text{K}^{\text{s}})$
. We show that there are compact sets with property
$(\text{K}^{\text{s}})$
. We show that there are compact sets with property
![]() $(\text{K}^{\text{s}})$
having Hausdorff dimension 2. Let
$(\text{K}^{\text{s}})$
having Hausdorff dimension 2. Let
![]() $E\subset [1,2]$
and
$E\subset [1,2]$
and
![]() $F\subset [0,1/2]$
be compact sets of linear measure zero and of Hausdorff dimension 1. We put
$F\subset [0,1/2]$
be compact sets of linear measure zero and of Hausdorff dimension 1. We put
It is easy to check that
![]() $A$
is a bi-Lipschitz image of
$A$
is a bi-Lipschitz image of
![]() $E\times F$
, and thus
$E\times F$
, and thus
![]() $A$
has Hausdorff dimension
$A$
has Hausdorff dimension
![]() $2$
. We prove that
$2$
. We prove that
![]() $A$
has property
$A$
has property
![]() $(\text{K}^{\text{s}})$
. Let
$(\text{K}^{\text{s}})$
. Let
![]() $\unicode[STIX]{x1D6FC}(x)=ux+c$
be a rigid motion, where
$\unicode[STIX]{x1D6FC}(x)=ux+c$
be a rigid motion, where
![]() $|u|=1$
. Let
$|u|=1$
. Let
![]() $c=r\cdot v$
, where
$c=r\cdot v$
, where
![]() $r\geqslant 0$
and
$r\geqslant 0$
and
![]() $|v|=1$
. Then the following continuous movement brings
$|v|=1$
. Then the following continuous movement brings
![]() $A$
onto
$A$
onto
![]() $\unicode[STIX]{x1D6FC}(A)$
. First we rotate
$\unicode[STIX]{x1D6FC}(A)$
. First we rotate
![]() $A$
about the origin to obtain
$A$
about the origin to obtain
![]() $v\cdot A$
, then we translate
$v\cdot A$
, then we translate
![]() $v\cdot A$
by the vector
$v\cdot A$
by the vector
![]() $c$
to obtain
$c$
to obtain
![]() $v\cdot A+c$
and then we rotate
$v\cdot A+c$
and then we rotate
![]() $v\cdot A+c$
about the point
$v\cdot A+c$
about the point
![]() $c$
to obtain
$c$
to obtain
![]() $u\cdot A+c=\unicode[STIX]{x1D6FC}(A)$
. If
$u\cdot A+c=\unicode[STIX]{x1D6FC}(A)$
. If
![]() $B=\{(x,y):\sqrt{x^{2}+y^{2}}\in E\}$
, then the set of points touched by this continuous movement is a subset of
$B=\{(x,y):\sqrt{x^{2}+y^{2}}\in E\}$
, then the set of points touched by this continuous movement is a subset of
This is a set of plane measure zero, showing that
![]() $A$
has property
$A$
has property
![]() $(\text{K}^{\text{s}})$
.
$(\text{K}^{\text{s}})$
.
We note that the union of finitely many parallel segments has property
![]() $(\text{K}^{\text{s}})$
; this was proved by Davies in [Reference Davies5, Theorem 3]. It is not clear if the union of finitely many concentric circular arcs can have property
$(\text{K}^{\text{s}})$
; this was proved by Davies in [Reference Davies5, Theorem 3]. It is not clear if the union of finitely many concentric circular arcs can have property
![]() $(\text{K}^{\text{s}})$
.
$(\text{K}^{\text{s}})$
.
Remark 1.3. There are compact subsets of the plane having property
![]() $\text{(K)}$
without being trivial
$\text{(K)}$
without being trivial
![]() $\text{(K)}$
-sets.
$\text{(K)}$
-sets.
We sketch the construction of a totally disconnected compact set
![]() $A$
having property
$A$
having property
![]() $\text{(K)}$
such that
$\text{(K)}$
such that
![]() $A$
has orthogonal projection of positive linear measure in every direction
$A$
has orthogonal projection of positive linear measure in every direction
![]() $e\in S^{1}$
, and the distance set
$e\in S^{1}$
, and the distance set
has positive linear measure for all
![]() $p\in \mathbb{R}^{2}$
. This easily implies that
$p\in \mathbb{R}^{2}$
. This easily implies that
![]() $A$
is not trivial. The construction is based on the so-called “Venetian blind” construction. Using this method, Talagrand proved in [Reference Talagrand8] that for every upper semi-continuous function
$A$
is not trivial. The construction is based on the so-called “Venetian blind” construction. Using this method, Talagrand proved in [Reference Talagrand8] that for every upper semi-continuous function
![]() $f$
on
$f$
on
![]() $S^{1}$
there exists a compact set
$S^{1}$
there exists a compact set
![]() $K\subset \mathbb{R}^{2}$
such that the measure of the projection of
$K\subset \mathbb{R}^{2}$
such that the measure of the projection of
![]() $K$
in the direction
$K$
in the direction
![]() $e$
is
$e$
is
![]() $f(e)$
for every
$f(e)$
for every
![]() $e\in S^{1}$
. We say that a rectangle
$e\in S^{1}$
. We say that a rectangle
![]() $R$
is in the direction
$R$
is in the direction
![]() $e$
if the longer side of
$e$
if the longer side of
![]() $R$
is of direction
$R$
is of direction
![]() $e$
.
$e$
.
We fix a direction
![]() $e$
and choose a convergent sequence of distinct directions
$e$
and choose a convergent sequence of distinct directions
![]() $e_{n}\rightarrow e$
. We shall construct a decreasing sequence of compact sets
$e_{n}\rightarrow e$
. We shall construct a decreasing sequence of compact sets
![]() $K_{n}$
such that
$K_{n}$
such that
![]() $K_{n}$
is the union of finitely many narrow rectangles in the direction
$K_{n}$
is the union of finitely many narrow rectangles in the direction
![]() $e_{n}$
for every
$e_{n}$
for every
![]() $n$
. Let
$n$
. Let
![]() $K_{1}$
be a closed rectangle in the direction
$K_{1}$
be a closed rectangle in the direction
![]() $e_{1}$
of width less than
$e_{1}$
of width less than
![]() $1$
. Then the measure of the projection of
$1$
. Then the measure of the projection of
![]() $K_{1}$
in the direction
$K_{1}$
in the direction
![]() $e_{1}$
is less than
$e_{1}$
is less than
![]() $1$
, and the measure of the distance set
$1$
, and the measure of the distance set
![]() $D(K_{1};p)$
is positive for all
$D(K_{1};p)$
is positive for all
![]() $p\in \mathbb{R}^{2}$
. In the
$p\in \mathbb{R}^{2}$
. In the
![]() $(n+1)\text{th}$
step we replace each member of the finite system of closed rectangles whose union is
$(n+1)\text{th}$
step we replace each member of the finite system of closed rectangles whose union is
![]() $K_{n}$
by a finite union of closed rectangles such that the new rectangles have direction
$K_{n}$
by a finite union of closed rectangles such that the new rectangles have direction
![]() $e_{n+1}$
, and the union of these
$e_{n+1}$
, and the union of these
![]() $(n+1)\text{th}$
-generation rectangles,
$(n+1)\text{th}$
-generation rectangles,
![]() $K_{n+1}$
, is a subset of
$K_{n+1}$
, is a subset of
![]() $K_{n}$
. Moreover, by choosing these rectangles appropriately, the measure of the projection of
$K_{n}$
. Moreover, by choosing these rectangles appropriately, the measure of the projection of
![]() $K_{n+1}$
in the direction
$K_{n+1}$
in the direction
![]() $e_{n+1}$
will be less than
$e_{n+1}$
will be less than
![]() $1/(n+1)$
, and the measure of the projection of
$1/(n+1)$
, and the measure of the projection of
![]() $K_{n+1}$
in directions
$K_{n+1}$
in directions
![]() $e_{1},\ldots ,e_{n}$
will be only slightly smaller than that of the projection of
$e_{1},\ldots ,e_{n}$
will be only slightly smaller than that of the projection of
![]() $K_{n}$
in directions
$K_{n}$
in directions
![]() $e_{1},\ldots ,e_{n}$
, respectively. If we choose the new rectangles originating from a fixed previous rectangle to be close enough to each other, we can achieve that the set
$e_{1},\ldots ,e_{n}$
, respectively. If we choose the new rectangles originating from a fixed previous rectangle to be close enough to each other, we can achieve that the set
![]() $D(K_{n+1};p)$
is only slightly smaller than
$D(K_{n+1};p)$
is only slightly smaller than
![]() $D(K_{n};p)$
for all
$D(K_{n};p)$
for all
![]() $p\in \mathbb{R}^{2}$
,
$p\in \mathbb{R}^{2}$
,
![]() $|p|\leqslant n$
. We set
$|p|\leqslant n$
. We set
![]() $K=\bigcap _{n=1}^{\infty }K_{n}$
. We may also ensure that the projection of
$K=\bigcap _{n=1}^{\infty }K_{n}$
. We may also ensure that the projection of
![]() $K$
has positive linear measure in all directions (see [Reference Talagrand8]). The set
$K$
has positive linear measure in all directions (see [Reference Talagrand8]). The set
![]() $D(K;p)$
has positive measure for all
$D(K;p)$
has positive measure for all
![]() $p\in \mathbb{R}^{2}$
. Indeed, for every
$p\in \mathbb{R}^{2}$
. Indeed, for every
![]() $p$
there is an
$p$
there is an
![]() $n$
such that
$n$
such that
![]() $|p|\leqslant n$
and, then, for all
$|p|\leqslant n$
and, then, for all
![]() $m\geqslant n$
we have
$m\geqslant n$
we have
![]() $\unicode[STIX]{x1D706}_{1}(D(K_{m};p))\geqslant \unicode[STIX]{x1D706}_{1}(D(K_{n};p))/2$
and thus
$\unicode[STIX]{x1D706}_{1}(D(K_{m};p))\geqslant \unicode[STIX]{x1D706}_{1}(D(K_{n};p))/2$
and thus
![]() $\unicode[STIX]{x1D706}_{1}(D(K;p))\geqslant \unicode[STIX]{x1D706}_{1}(D(K_{n};p))/2>0$
. It is easy to see that
$\unicode[STIX]{x1D706}_{1}(D(K;p))\geqslant \unicode[STIX]{x1D706}_{1}(D(K_{n};p))/2>0$
. It is easy to see that
![]() $K$
has property
$K$
has property
![]() $(\text{K})$
. Indeed, if
$(\text{K})$
. Indeed, if
![]() $\unicode[STIX]{x1D6FC}$
is a translation by a vector of direction
$\unicode[STIX]{x1D6FC}$
is a translation by a vector of direction
![]() $e$
and length
$e$
and length
![]() $R>0$
, then
$R>0$
, then
![]() $K$
can be moved continuously to
$K$
can be moved continuously to
![]() $\unicode[STIX]{x1D6FC}(K)$
within a set of arbitrarily small area. Then
$\unicode[STIX]{x1D6FC}(K)$
within a set of arbitrarily small area. Then
![]() $K$
has the desired properties, and the proof is finished.
$K$
has the desired properties, and the proof is finished.
2 Some auxiliary results and the proofs of Theorems 1.1 and 1.2
In this section we formulate some auxiliary results needed for the proofs of Theorems 1.1 and 1.2.
The translation by the vector
![]() $c$
will be denoted by
$c$
will be denoted by
![]() $T_{c}$
. Thus,
$T_{c}$
. Thus,
![]() $T_{c}(x)=x+c$
for every
$T_{c}(x)=x+c$
for every
![]() $x\in \mathbb{C}$
. The rotation about the point
$x\in \mathbb{C}$
. The rotation about the point
![]() $c$
by angle
$c$
by angle
![]() $\unicode[STIX]{x1D719}$
is denoted by
$\unicode[STIX]{x1D719}$
is denoted by
![]() $R_{c,\unicode[STIX]{x1D719}}$
. Thus,
$R_{c,\unicode[STIX]{x1D719}}$
. Thus,
![]() $R_{c,\unicode[STIX]{x1D719}}(x)=\text{e}^{\text{i}\unicode[STIX]{x1D719}}(x-c)+c$
for every
$R_{c,\unicode[STIX]{x1D719}}(x)=\text{e}^{\text{i}\unicode[STIX]{x1D719}}(x-c)+c$
for every
![]() $x\in \mathbb{C}$
. If
$x\in \mathbb{C}$
. If
![]() $\unicode[STIX]{x1D6FC}$
is a rigid motion and
$\unicode[STIX]{x1D6FC}$
is a rigid motion and
![]() $\unicode[STIX]{x1D6FC}^{2}\neq j$
, then we define the elementary movement
$\unicode[STIX]{x1D6FC}^{2}\neq j$
, then we define the elementary movement
![]() $E^{\unicode[STIX]{x1D6FC}}$
determined by
$E^{\unicode[STIX]{x1D6FC}}$
determined by
![]() $\unicode[STIX]{x1D6FC}$
as follows. If
$\unicode[STIX]{x1D6FC}$
as follows. If
![]() $\unicode[STIX]{x1D6FC}=T_{c}$
, then we put
$\unicode[STIX]{x1D6FC}=T_{c}$
, then we put
![]() $E_{t}^{\unicode[STIX]{x1D6FC}}=T_{tc}$
for every
$E_{t}^{\unicode[STIX]{x1D6FC}}=T_{tc}$
for every
![]() $t\in [0,1]$
. If
$t\in [0,1]$
. If
![]() $\unicode[STIX]{x1D6FC}=R_{a,\unicode[STIX]{x1D719}}$
, then the condition
$\unicode[STIX]{x1D6FC}=R_{a,\unicode[STIX]{x1D719}}$
, then the condition
![]() $\unicode[STIX]{x1D6FC}^{2}\neq j$
implies that
$\unicode[STIX]{x1D6FC}^{2}\neq j$
implies that
![]() $\unicode[STIX]{x1D719}\not \equiv \unicode[STIX]{x1D70B}$
(mod
$\unicode[STIX]{x1D719}\not \equiv \unicode[STIX]{x1D70B}$
(mod
![]() $2\unicode[STIX]{x1D70B}$
). Therefore, we may assume that
$2\unicode[STIX]{x1D70B}$
). Therefore, we may assume that
![]() $|\unicode[STIX]{x1D719}|<\unicode[STIX]{x1D70B}$
. Then we define
$|\unicode[STIX]{x1D719}|<\unicode[STIX]{x1D70B}$
. Then we define
![]() $E_{t}^{\unicode[STIX]{x1D6FC}}=R_{a,t\unicode[STIX]{x1D719}}$
for every
$E_{t}^{\unicode[STIX]{x1D6FC}}=R_{a,t\unicode[STIX]{x1D719}}$
for every
![]() $t\in [0,1]$
.
$t\in [0,1]$
.
The inverse of the rigid motion
![]() $\unicode[STIX]{x1D6FC}$
is denoted by
$\unicode[STIX]{x1D6FC}$
is denoted by
![]() $\unicode[STIX]{x1D6FC}^{-1}$
. It is clear that if
$\unicode[STIX]{x1D6FC}^{-1}$
. It is clear that if
![]() $M$
is a continuous movement, then so is
$M$
is a continuous movement, then so is
![]() $M^{-1}$
, where we put
$M^{-1}$
, where we put
![]() $M_{t}^{-1}=(M_{t})^{-1}$
$M_{t}^{-1}=(M_{t})^{-1}$
![]() $(t\in [0,1])$
. The
$(t\in [0,1])$
. The
![]() $\unicode[STIX]{x1D700}$
-neighbourhood of a set
$\unicode[STIX]{x1D700}$
-neighbourhood of a set
![]() $E\subset \mathbb{R}^{2}$
is defined by
$E\subset \mathbb{R}^{2}$
is defined by
We denote by
![]() $L$
the space of functions
$L$
the space of functions
![]() $x\mapsto ux+v$
$x\mapsto ux+v$
![]() $(x\in \mathbb{C})$
, where
$(x\in \mathbb{C})$
, where
![]() $u,v\in \mathbb{C}$
. Clearly,
$u,v\in \mathbb{C}$
. Clearly,
![]() $L$
is a linear space over
$L$
is a linear space over
![]() $\mathbb{C}$
with pointwise addition and multiplication by constants. We endow
$\mathbb{C}$
with pointwise addition and multiplication by constants. We endow
![]() $L$
with the norm
$L$
with the norm
![]() $\Vert f\Vert =|u|+|v|$
. It is easy to check that
$\Vert f\Vert =|u|+|v|$
. It is easy to check that
![]() $\Vert f\Vert =\sup \{|f(x)|:x\in \mathbb{C},|x|\leqslant 1\}$
for every
$\Vert f\Vert =\sup \{|f(x)|:x\in \mathbb{C},|x|\leqslant 1\}$
for every
![]() $f\in L$
, and thus
$f\in L$
, and thus
![]() $\Vert \cdot \Vert$
is indeed a norm.
$\Vert \cdot \Vert$
is indeed a norm.
It is also easy to check that if
![]() $f_{1}(x)=u_{1}x+v_{1}$
and
$f_{1}(x)=u_{1}x+v_{1}$
and
![]() $f_{2}(x)=u_{2}x+v_{2}$
are rigid motions, then
$f_{2}(x)=u_{2}x+v_{2}$
are rigid motions, then
Lemma 2.1. If
![]() $A\subset \mathbb{R}^{2}$
has property
$A\subset \mathbb{R}^{2}$
has property
![]() $(\text{K})$
, then there exists a rigid motion
$(\text{K})$
, then there exists a rigid motion
![]() $\unicode[STIX]{x1D6FC}$
such that
$\unicode[STIX]{x1D6FC}$
such that
![]() $\unicode[STIX]{x1D6FC}^{2}\neq j$
, and the following condition is satisfied. For every
$\unicode[STIX]{x1D6FC}^{2}\neq j$
, and the following condition is satisfied. For every
![]() $\unicode[STIX]{x1D700}>0$
there is a continuous movement
$\unicode[STIX]{x1D700}>0$
there is a continuous movement
![]() $M$
such that
$M$
such that
![]() $M_{1}=\unicode[STIX]{x1D6FC}$
,
$M_{1}=\unicode[STIX]{x1D6FC}$
,
![]() $\unicode[STIX]{x1D706}(W_{M}(A))<\unicode[STIX]{x1D700}$
and
$\unicode[STIX]{x1D706}(W_{M}(A))<\unicode[STIX]{x1D700}$
and
![]() $\Vert M_{t}-E_{t}^{\unicode[STIX]{x1D6FC}}\Vert <~\unicode[STIX]{x1D700}$
for every
$\Vert M_{t}-E_{t}^{\unicode[STIX]{x1D6FC}}\Vert <~\unicode[STIX]{x1D700}$
for every
![]() $t\in [0,1]$
.
$t\in [0,1]$
.
By a continuum we mean a compact connected set. The set
![]() $A\subset \mathbb{R}^{2}$
is said to be irreducible between the distinct points
$A\subset \mathbb{R}^{2}$
is said to be irreducible between the distinct points
![]() $a$
and
$a$
and
![]() $b$
provided that
$b$
provided that
![]() $A$
is connected,
$A$
is connected,
![]() $a,b\in A$
and these two points cannot be joined by any closed, connected, proper subset of
$a,b\in A$
and these two points cannot be joined by any closed, connected, proper subset of
![]() $A$
. We shall need the following topological lemma on irreducible continuums.
$A$
. We shall need the following topological lemma on irreducible continuums.
Lemma 2.2. Let
![]() $A\subset \mathbb{R}^{2}$
be a continuum which is irreducible between the distinct points
$A\subset \mathbb{R}^{2}$
be a continuum which is irreducible between the distinct points
![]() $a$
and
$a$
and
![]() $b$
, and suppose that
$b$
, and suppose that
![]() $\mathbb{R}^{2}\setminus A$
is connected. Let
$\mathbb{R}^{2}\setminus A$
is connected. Let
![]() $D$
be an open disc not containing the points
$D$
be an open disc not containing the points
![]() $a$
and
$a$
and
![]() $b$
. Then every neighbourhood of every point of
$b$
. Then every neighbourhood of every point of
![]() $A\cap D$
intersects at least two of the connected components of
$A\cap D$
intersects at least two of the connected components of
![]() $D\setminus A$
.
$D\setminus A$
.
The proofs of Lemmas 2.1 and 2.2 will be given in the next two sections.
Lemma 2.3. Let
![]() $A\subset D\subset \mathbb{R}^{2}$
be arbitrary and
$A\subset D\subset \mathbb{R}^{2}$
be arbitrary and
![]() $G\subset D\setminus A$
. Suppose that
$G\subset D\setminus A$
. Suppose that
![]() $M$
is a continuous movement,
$M$
is a continuous movement,
![]() $t\in [0,1]$
and
$t\in [0,1]$
and
![]() $M_{s}^{-1}(x)\in D$
for every
$M_{s}^{-1}(x)\in D$
for every
![]() $s\in [0,t]$
and
$s\in [0,t]$
and
![]() $x\in G$
. If
$x\in G$
. If
![]() $G$
and
$G$
and
![]() $M_{t}^{-1}(G)$
are subsets of distinct connected components of
$M_{t}^{-1}(G)$
are subsets of distinct connected components of
![]() $D\setminus A$
, then
$D\setminus A$
, then
![]() $G\subset W_{M}(A)$
.
$G\subset W_{M}(A)$
.
Proof. Let
![]() $u\in G$
be arbitrary. Clearly, the map
$u\in G$
be arbitrary. Clearly, the map
![]() $\unicode[STIX]{x1D6FE}:[0,t]\rightarrow D$
defined by
$\unicode[STIX]{x1D6FE}:[0,t]\rightarrow D$
defined by
![]() $\unicode[STIX]{x1D6FE}(s)=M_{s}^{-1}(u)$
$\unicode[STIX]{x1D6FE}(s)=M_{s}^{-1}(u)$
![]() $(s\in [0,t])$
is a continuous curve. Now
$(s\in [0,t])$
is a continuous curve. Now
![]() $\unicode[STIX]{x1D6FE}(0)=u\in G$
and
$\unicode[STIX]{x1D6FE}(0)=u\in G$
and
![]() $\unicode[STIX]{x1D6FE}(t)=M_{t}^{-1}(u)\in M_{t}^{-1}(G)$
. Since
$\unicode[STIX]{x1D6FE}(t)=M_{t}^{-1}(u)\in M_{t}^{-1}(G)$
. Since
![]() $G$
and
$G$
and
![]() $M_{t}^{-1}(G)$
are subsets of distinct connected components of
$M_{t}^{-1}(G)$
are subsets of distinct connected components of
![]() $D\setminus A$
and
$D\setminus A$
and
![]() $\unicode[STIX]{x1D6FE}([0,t])\subset D$
, it follows that there exists an
$\unicode[STIX]{x1D6FE}([0,t])\subset D$
, it follows that there exists an
![]() $s\in [0,t]$
such that
$s\in [0,t]$
such that
![]() $\unicode[STIX]{x1D6FE}(s)\in A$
. If
$\unicode[STIX]{x1D6FE}(s)\in A$
. If
![]() $\unicode[STIX]{x1D6FE}(s)=a$
, then
$\unicode[STIX]{x1D6FE}(s)=a$
, then
![]() $M_{s}^{-1}(u)=a$
and
$M_{s}^{-1}(u)=a$
and
![]() $u=M_{s}(a)\in M_{s}(A)\subset W_{M}(A)$
. This is true for every
$u=M_{s}(a)\in M_{s}(A)\subset W_{M}(A)$
. This is true for every
![]() $u\in G$
, and thus
$u\in G$
, and thus
![]() $G\subset W_{M}(A)$
.◻
$G\subset W_{M}(A)$
.◻
Proof of Theorem 1.1.
(Subject to Lemmas 2.1 and 2.2.) We denote by
![]() $B(x,r)$
the open disc with centre
$B(x,r)$
the open disc with centre
![]() $x$
and radius
$x$
and radius
![]() $r$
. Let
$r$
. Let
![]() $A\subset \mathbb{R}^{2}$
be a closed set having property (K). By Lemma 2.1, there exists a rigid motion
$A\subset \mathbb{R}^{2}$
be a closed set having property (K). By Lemma 2.1, there exists a rigid motion
![]() $\unicode[STIX]{x1D6FC}$
satisfying the conditions of Lemma 2.1. Let
$\unicode[STIX]{x1D6FC}$
satisfying the conditions of Lemma 2.1. Let
![]() $A^{\prime }$
denote the union of all non-trivial components of
$A^{\prime }$
denote the union of all non-trivial components of
![]() $A$
. Since
$A$
. Since
![]() $A^{\prime }\subset A$
and
$A^{\prime }\subset A$
and
![]() $A$
has property (K), we have
$A$
has property (K), we have
![]() $\unicode[STIX]{x1D706}(A)=0$
and
$\unicode[STIX]{x1D706}(A)=0$
and
![]() $\unicode[STIX]{x1D706}(A^{\prime })=0$
. We shall prove that if
$\unicode[STIX]{x1D706}(A^{\prime })=0$
. We shall prove that if
![]() $\unicode[STIX]{x1D6FC}$
is a translation by the vector
$\unicode[STIX]{x1D6FC}$
is a translation by the vector
![]() $v\neq 0$
, then every non-trivial connected component of
$v\neq 0$
, then every non-trivial connected component of
![]() $A$
is covered by a line parallel to
$A$
is covered by a line parallel to
![]() $v$
, and if
$v$
, and if
![]() $\unicode[STIX]{x1D6FC}$
is a rotation about the point
$\unicode[STIX]{x1D6FC}$
is a rotation about the point
![]() $c$
, then every non-trivial connected component of
$c$
, then every non-trivial connected component of
![]() $A$
is covered by a circle of centre
$A$
is covered by a circle of centre
![]() $c$
. Clearly, since
$c$
. Clearly, since
![]() $A^{\prime }$
has measure zero, it therefore cannot meet positively many parallel lines in positive length and, similarly, it cannot meet positively many concentric circles in positive length. Therefore, indeed
$A^{\prime }$
has measure zero, it therefore cannot meet positively many parallel lines in positive length and, similarly, it cannot meet positively many concentric circles in positive length. Therefore, indeed
![]() $A^{\prime }$
is a trivial (K)-set.
$A^{\prime }$
is a trivial (K)-set.
We shall only prove the statement when
![]() $\unicode[STIX]{x1D6FC}$
is a rotation; the case when
$\unicode[STIX]{x1D6FC}$
is a rotation; the case when
![]() $\unicode[STIX]{x1D6FC}$
is a translation can be treated similarly.
$\unicode[STIX]{x1D6FC}$
is a translation can be treated similarly.
Let
![]() $\unicode[STIX]{x1D6FC}$
be a rotation. We may assume that the centre of rotation is the origin. Let
$\unicode[STIX]{x1D6FC}$
be a rotation. We may assume that the centre of rotation is the origin. Let
![]() $A_{1}$
be a connected component of
$A_{1}$
be a connected component of
![]() $A$
. We have to prove that
$A$
. We have to prove that
![]() $A_{1}$
is covered by a circle of centre
$A_{1}$
is covered by a circle of centre
![]() $0$
. Suppose that this is not true. Then the set
$0$
. Suppose that this is not true. Then the set
![]() $\unicode[STIX]{x1D6E4}=\{|x|:x\in A_{1}\}$
is a non-degenerate interval. Let
$\unicode[STIX]{x1D6E4}=\{|x|:x\in A_{1}\}$
is a non-degenerate interval. Let
![]() $r_{1},r_{2}\in \unicode[STIX]{x1D6E4}$
be such that
$r_{1},r_{2}\in \unicode[STIX]{x1D6E4}$
be such that
![]() $0<r_{1}<r_{2}$
. We may assume that
$0<r_{1}<r_{2}$
. We may assume that
![]() $r_{2}<1$
, since otherwise we replace
$r_{2}<1$
, since otherwise we replace
![]() $A$
by a suitable similar copy.
$A$
by a suitable similar copy.
Let
![]() $U$
denote the annulus
$U$
denote the annulus
![]() $\{x:r_{1}<|x|<r_{2}\}\subset B(0,1)$
. The set
$\{x:r_{1}<|x|<r_{2}\}\subset B(0,1)$
. The set
![]() $A_{1}$
contains an irreducible (that is, minimal) connected closed subset
$A_{1}$
contains an irreducible (that is, minimal) connected closed subset
![]() $C$
such that it intersects both of the circles
$C$
such that it intersects both of the circles
![]() $|x|=r_{1}$
and
$|x|=r_{1}$
and
![]() $|x|=r_{2}$
. (The existence of such a set follows from [Reference Kuratowski7, Theorem 2, §42, IV, p. 54].)Footnote
1
Then
$|x|=r_{2}$
. (The existence of such a set follows from [Reference Kuratowski7, Theorem 2, §42, IV, p. 54].)Footnote
1
Then
![]() $C$
is contained in
$C$
is contained in
![]() $\text{cl}\,U$
. Indeed, every connected component of
$\text{cl}\,U$
. Indeed, every connected component of
![]() $C\cap \text{cl}\,U$
is a quasi-component of
$C\cap \text{cl}\,U$
is a quasi-component of
![]() $C\cap \text{cl}\,U$
by [Reference Kuratowski7, Theorem 2, §47, II, p. 169]. Using this fact, one can prove that there is a connected component
$C\cap \text{cl}\,U$
by [Reference Kuratowski7, Theorem 2, §47, II, p. 169]. Using this fact, one can prove that there is a connected component
![]() $C_{1}$
of
$C_{1}$
of
![]() $C\cap \text{cl}\,U$
which intersects the circles
$C\cap \text{cl}\,U$
which intersects the circles
![]() $|x|=r_{1}$
and
$|x|=r_{1}$
and
![]() $|x|=r_{2}$
. Thus, by the minimality of
$|x|=r_{2}$
. Thus, by the minimality of
![]() $C$
, we have
$C$
, we have
![]() $C_{1}=C$
and
$C_{1}=C$
and
![]() $C\subset \text{cl}\,U$
.
$C\subset \text{cl}\,U$
.
Let
![]() $C^{\ast }$
denote the set of points
$C^{\ast }$
denote the set of points
![]() $p\in C\cap U$
with the following property: if
$p\in C\cap U$
with the following property: if
![]() $B(p,r)\subset U$
, then every neighbourhood of
$B(p,r)\subset U$
, then every neighbourhood of
![]() $p$
intersects at least two connected components of
$p$
intersects at least two connected components of
![]() $B(p,r)\setminus C$
. First we prove that if
$B(p,r)\setminus C$
. First we prove that if
![]() $p\in C^{\ast }$
, then
$p\in C^{\ast }$
, then
![]() $C$
contains a subarc of the circle
$C$
contains a subarc of the circle
![]() $\{x:|x|=|p|\}$
.
$\{x:|x|=|p|\}$
.
Let
![]() $p\in C^{\ast }$
, and fix an
$p\in C^{\ast }$
, and fix an
![]() $r>0$
with
$r>0$
with
![]() $B(p,r)\subset U$
. Put
$B(p,r)\subset U$
. Put
![]() $D=B(p,r)$
. There is a
$D=B(p,r)$
. There is a
![]() $0<t_{0}\leqslant 1$
such that the arc
$0<t_{0}\leqslant 1$
such that the arc
![]() $I=\{E_{t}^{\unicode[STIX]{x1D6FC}^{-1}}(p):t\in [0,t_{0}]\}$
is in
$I=\{E_{t}^{\unicode[STIX]{x1D6FC}^{-1}}(p):t\in [0,t_{0}]\}$
is in
![]() $D$
. We prove that
$D$
. We prove that
![]() $I\subset C$
. Suppose that this is not true. Then there is a
$I\subset C$
. Suppose that this is not true. Then there is a
![]() $0<t_{1}\leqslant t_{0}$
such that
$0<t_{1}\leqslant t_{0}$
such that
![]() $q=E_{t_{1}}^{\unicode[STIX]{x1D6FC}^{-1}}(p)\in D\setminus C$
. Let
$q=E_{t_{1}}^{\unicode[STIX]{x1D6FC}^{-1}}(p)\in D\setminus C$
. Let
![]() $\unicode[STIX]{x1D6FF}>0$
be such that
$\unicode[STIX]{x1D6FF}>0$
be such that
![]() $B(q,\unicode[STIX]{x1D6FF})\subset D\setminus C$
. Since
$B(q,\unicode[STIX]{x1D6FF})\subset D\setminus C$
. Since
![]() $p\in C^{\ast }$
, the neighbourhood
$p\in C^{\ast }$
, the neighbourhood
![]() $B(p,\unicode[STIX]{x1D6FF})$
intersects at least two connected components of
$B(p,\unicode[STIX]{x1D6FF})$
intersects at least two connected components of
![]() $D\setminus C$
. Since
$D\setminus C$
. Since
![]() $B(q,\unicode[STIX]{x1D6FF})$
belongs to a connected component of
$B(q,\unicode[STIX]{x1D6FF})$
belongs to a connected component of
![]() $D\setminus C$
, there is an open disc
$D\setminus C$
, there is an open disc
![]() $G$
such that
$G$
such that
![]() $\text{cl}\,G\subset B(p,\unicode[STIX]{x1D6FF})\setminus C$
, and
$\text{cl}\,G\subset B(p,\unicode[STIX]{x1D6FF})\setminus C$
, and
![]() $G$
and
$G$
and
![]() $B(q,\unicode[STIX]{x1D6FF})$
belong to distinct connected components of
$B(q,\unicode[STIX]{x1D6FF})$
belong to distinct connected components of
![]() $D\setminus C$
.
$D\setminus C$
.
Since
![]() $\unicode[STIX]{x1D6FC}$
satisfies the conditions of Lemma 2.1, it follows that for every
$\unicode[STIX]{x1D6FC}$
satisfies the conditions of Lemma 2.1, it follows that for every
![]() $\unicode[STIX]{x1D700}>0$
there is a continuous movement
$\unicode[STIX]{x1D700}>0$
there is a continuous movement
![]() $M$
such that
$M$
such that
![]() $\unicode[STIX]{x1D706}(W_{M}(A))<\unicode[STIX]{x1D700}$
and
$\unicode[STIX]{x1D706}(W_{M}(A))<\unicode[STIX]{x1D700}$
and
![]() $\Vert M_{s}-E_{s}^{\unicode[STIX]{x1D6FC}}\Vert <\unicode[STIX]{x1D700}$
for every
$\Vert M_{s}-E_{s}^{\unicode[STIX]{x1D6FC}}\Vert <\unicode[STIX]{x1D700}$
for every
![]() $s\in [0,t_{1}]$
. Therefore, applying (1) with
$s\in [0,t_{1}]$
. Therefore, applying (1) with
![]() $f_{1}=M_{s}$
and
$f_{1}=M_{s}$
and
![]() $f_{2}=\unicode[STIX]{x1D6FC}$
, we obtain
$f_{2}=\unicode[STIX]{x1D6FC}$
, we obtain
![]() $\Vert M_{s}^{-1}-E_{s}^{\unicode[STIX]{x1D6FC}^{-1}}\Vert <\unicode[STIX]{x1D700}$
for every
$\Vert M_{s}^{-1}-E_{s}^{\unicode[STIX]{x1D6FC}^{-1}}\Vert <\unicode[STIX]{x1D700}$
for every
![]() $s\in [0,t_{1}]$
. (Note that we have
$s\in [0,t_{1}]$
. (Note that we have
![]() $v_{2}=0$
in this case.) Since
$v_{2}=0$
in this case.) Since
![]() $G\subset U\subset B(0,1)$
, we obtain
$G\subset U\subset B(0,1)$
, we obtain
for all
![]() $x\in G$
and
$x\in G$
and
![]() $s\in [0,t_{1}]$
. It is clear that if
$s\in [0,t_{1}]$
. It is clear that if
![]() $\unicode[STIX]{x1D700}$
is small enough, then
$\unicode[STIX]{x1D700}$
is small enough, then
![]() $M_{s}^{-1}(G)\subset U(E_{s}^{\unicode[STIX]{x1D6FC}^{-1}}(G),\unicode[STIX]{x1D700})\subset D$
for every
$M_{s}^{-1}(G)\subset U(E_{s}^{\unicode[STIX]{x1D6FC}^{-1}}(G),\unicode[STIX]{x1D700})\subset D$
for every
![]() $s\in [0,t_{1}]$
. Also, we have
$s\in [0,t_{1}]$
. Also, we have
![]() $E_{t_{1}}^{\unicode[STIX]{x1D6FC}^{-1}}(p)=q$
. Since
$E_{t_{1}}^{\unicode[STIX]{x1D6FC}^{-1}}(p)=q$
. Since
![]() $E_{t_{1}}^{\unicode[STIX]{x1D6FC}^{-1}}$
is a rigid motion,
$E_{t_{1}}^{\unicode[STIX]{x1D6FC}^{-1}}$
is a rigid motion,
![]() $\text{cl}\,E_{t_{1}}^{\unicode[STIX]{x1D6FC}^{-1}}(G)\subset B(q,\unicode[STIX]{x1D6FF})$
. Therefore, for small
$\text{cl}\,E_{t_{1}}^{\unicode[STIX]{x1D6FC}^{-1}}(G)\subset B(q,\unicode[STIX]{x1D6FF})$
. Therefore, for small
![]() $\unicode[STIX]{x1D700}$
, we have
$\unicode[STIX]{x1D700}$
, we have
![]() $M_{t_{1}}^{-1}(G)\subset B(q,\unicode[STIX]{x1D6FF})$
. Thus, by Lemma 2.3, we have
$M_{t_{1}}^{-1}(G)\subset B(q,\unicode[STIX]{x1D6FF})$
. Thus, by Lemma 2.3, we have
![]() $G\subset W_{M}(C)$
. Thus,
$G\subset W_{M}(C)$
. Thus,
![]() $\unicode[STIX]{x1D706}(G)\leqslant \unicode[STIX]{x1D706}(W_{M}(C))$
. Since
$\unicode[STIX]{x1D706}(G)\leqslant \unicode[STIX]{x1D706}(W_{M}(C))$
. Since
![]() $\unicode[STIX]{x1D706}(W_{M}(C))<\unicode[STIX]{x1D700}$
, this is impossible if
$\unicode[STIX]{x1D706}(W_{M}(C))<\unicode[STIX]{x1D700}$
, this is impossible if
![]() $\unicode[STIX]{x1D700}<\unicode[STIX]{x1D706}(G)$
. This contradiction shows that
$\unicode[STIX]{x1D700}<\unicode[STIX]{x1D706}(G)$
. This contradiction shows that
![]() $I\subset C$
as we stated.
$I\subset C$
as we stated.
There are points
![]() $a,b\in C$
such that
$a,b\in C$
such that
![]() $|a|=r_{1}$
and
$|a|=r_{1}$
and
![]() $|b|=r_{2}$
. It is clear that
$|b|=r_{2}$
. It is clear that
![]() $C$
is irreducible between
$C$
is irreducible between
![]() $a$
and
$a$
and
![]() $b$
. Suppose that
$b$
. Suppose that
![]() $\mathbb{R}^{2}\setminus C$
is connected. Then, by Lemma 2.2, we have
$\mathbb{R}^{2}\setminus C$
is connected. Then, by Lemma 2.2, we have
![]() $C^{\ast }=C\cap U$
. Then, by what we proved above, every point of
$C^{\ast }=C\cap U$
. Then, by what we proved above, every point of
![]() $C\cap U$
is covered by a circular arc of centre
$C\cap U$
is covered by a circular arc of centre
![]() $0$
belonging to
$0$
belonging to
![]() $C$
. Since
$C$
. Since
![]() $C$
is connected, this implies that for every
$C$
is connected, this implies that for every
![]() $r_{1}<r<r_{2}$
, the circle
$r_{1}<r<r_{2}$
, the circle
![]() $|x|=r$
contains an arc belonging to
$|x|=r$
contains an arc belonging to
![]() $C$
. This, however, is impossible, since
$C$
. This, however, is impossible, since
![]() $\unicode[STIX]{x1D706}(C)=0$
.
$\unicode[STIX]{x1D706}(C)=0$
.
Therefore, the set
![]() $\mathbb{R}^{2}\setminus C$
cannot be connected. Let
$\mathbb{R}^{2}\setminus C$
cannot be connected. Let
![]() $V$
be a bounded connected component of
$V$
be a bounded connected component of
![]() $\mathbb{R}^{2}\setminus C$
. Clearly, we have
$\mathbb{R}^{2}\setminus C$
. Clearly, we have
![]() $V\subset B(0,r_{2})$
. We show that
$V\subset B(0,r_{2})$
. We show that
![]() $C$
contains a full circle of centre
$C$
contains a full circle of centre
![]() $0$
. This is clear if
$0$
. This is clear if
![]() $V=B(0,r_{1})$
since, in that case,
$V=B(0,r_{1})$
since, in that case,
![]() $\unicode[STIX]{x2202}V$
is a circle and is contained in
$\unicode[STIX]{x2202}V$
is a circle and is contained in
![]() $C$
. So, we may assume that
$C$
. So, we may assume that
![]() $V\neq B(0,r_{1})$
. Then
$V\neq B(0,r_{1})$
. Then
![]() $V\cap U\neq \emptyset$
. We prove that
$V\cap U\neq \emptyset$
. We prove that
![]() $\text{cl}\,V$
is an annulus of centre
$\text{cl}\,V$
is an annulus of centre
![]() $0$
. Suppose that this is not true. Then there are points
$0$
. Suppose that this is not true. Then there are points
![]() $x_{1}\in \text{cl}\,V$
and
$x_{1}\in \text{cl}\,V$
and
![]() $x_{2}\notin \text{cl}\,V$
such that
$x_{2}\notin \text{cl}\,V$
such that
![]() $|x_{1}|=|x_{2}|$
. Then
$|x_{1}|=|x_{2}|$
. Then
![]() $B(x_{2},\unicode[STIX]{x1D700})\cap V=\emptyset$
for
$B(x_{2},\unicode[STIX]{x1D700})\cap V=\emptyset$
for
![]() $\unicode[STIX]{x1D700}$
small enough. Since
$\unicode[STIX]{x1D700}$
small enough. Since
![]() $B(x_{1},\unicode[STIX]{x1D700})\cap V\neq \emptyset$
and
$B(x_{1},\unicode[STIX]{x1D700})\cap V\neq \emptyset$
and
![]() $C$
is nowhere dense, it is clear that there are points
$C$
is nowhere dense, it is clear that there are points
![]() $y_{1}\in V$
and
$y_{1}\in V$
and
![]() $y_{2}\in B(x_{2},\unicode[STIX]{x1D700})$
such that
$y_{2}\in B(x_{2},\unicode[STIX]{x1D700})$
such that
![]() $|y_{1}|=|y_{2}|$
. Then
$|y_{1}|=|y_{2}|$
. Then
![]() $y_{2}$
belongs to a connected component of
$y_{2}$
belongs to a connected component of
![]() $\mathbb{R}^{2}\setminus C$
different from
$\mathbb{R}^{2}\setminus C$
different from
![]() $V$
.
$V$
.
This easily implies that there is an
![]() $\unicode[STIX]{x1D702}>0$
such that for every
$\unicode[STIX]{x1D702}>0$
such that for every
![]() $|y_{1}|-\unicode[STIX]{x1D702}<r<|y_{1}|$
, there is a point
$|y_{1}|-\unicode[STIX]{x1D702}<r<|y_{1}|$
, there is a point
![]() $p\in \unicode[STIX]{x2202}(\text{cl}\,V)$
with
$p\in \unicode[STIX]{x2202}(\text{cl}\,V)$
with
![]() $|p|=r$
. It is easy to see that if
$|p|=r$
. It is easy to see that if
![]() $p\in U\cap \unicode[STIX]{x2202}(\text{cl}\,V)$
, then
$p\in U\cap \unicode[STIX]{x2202}(\text{cl}\,V)$
, then
![]() $p\in C^{\ast }$
. Indeed, let
$p\in C^{\ast }$
. Indeed, let
![]() $D$
be an open disc such that
$D$
be an open disc such that
![]() $p\in D\subset U$
. Then
$p\in D\subset U$
. Then
![]() $D$
intersects
$D$
intersects
![]() $V$
, and thus it intersects at least two connected components of
$V$
, and thus it intersects at least two connected components of
![]() $U\setminus C$
, since otherwise
$U\setminus C$
, since otherwise
![]() $D$
would be a subset of
$D$
would be a subset of
![]() $\text{cl}\,V$
, contradicting
$\text{cl}\,V$
, contradicting
![]() $p\in \unicode[STIX]{x2202}(\text{cl}\,V)$
. This is true for every disc
$p\in \unicode[STIX]{x2202}(\text{cl}\,V)$
. This is true for every disc
![]() $B(p,\unicode[STIX]{x1D6FF})\subset D$
as well, and thus
$B(p,\unicode[STIX]{x1D6FF})\subset D$
as well, and thus
![]() $B(p,\unicode[STIX]{x1D6FF})$
intersects at least two connected components of
$B(p,\unicode[STIX]{x1D6FF})$
intersects at least two connected components of
![]() $D\setminus C$
, proving that
$D\setminus C$
, proving that
![]() $p\in C^{\ast }$
. As we saw above, this implies that for every
$p\in C^{\ast }$
. As we saw above, this implies that for every
![]() $|y_{1}|-\unicode[STIX]{x1D702}<r<|y_{1}|$
,
$|y_{1}|-\unicode[STIX]{x1D702}<r<|y_{1}|$
,
![]() $C$
contains a subarc of the circle
$C$
contains a subarc of the circle
![]() $|x|=r$
. This, however, contradicts the fact that
$|x|=r$
. This, however, contradicts the fact that
![]() $C$
is of measure zero.
$C$
is of measure zero.
Therefore, the set
![]() $\text{cl}\,V$
must be an annulus. Since
$\text{cl}\,V$
must be an annulus. Since
![]() $\unicode[STIX]{x2202}(\text{cl}\,V)\subset \unicode[STIX]{x2202}V\subset C$
, it follows that
$\unicode[STIX]{x2202}(\text{cl}\,V)\subset \unicode[STIX]{x2202}V\subset C$
, it follows that
![]() $C\cap \text{cl}\,U$
contains a full circle of centre
$C\cap \text{cl}\,U$
contains a full circle of centre
![]() $0$
.
$0$
.
We proved that
![]() $A_{1}\cap \{x:r_{1}<|x|<r_{2}\}$
contains a full circle of centre
$A_{1}\cap \{x:r_{1}<|x|<r_{2}\}$
contains a full circle of centre
![]() $0$
for every
$0$
for every
![]() $r_{1},r_{2}\in \unicode[STIX]{x1D6E4}$
with
$r_{1},r_{2}\in \unicode[STIX]{x1D6E4}$
with
![]() $r_{1}<r_{2}<1$
. Thus,
$r_{1}<r_{2}<1$
. Thus,
![]() $A_{1}$
contains a dense subset of
$A_{1}$
contains a dense subset of
![]() $\{x:|x|\in \unicode[STIX]{x1D6E4}\}\cap B(0,1)$
. Since
$\{x:|x|\in \unicode[STIX]{x1D6E4}\}\cap B(0,1)$
. Since
![]() $A_{1}$
is closed, we find that
$A_{1}$
is closed, we find that
![]() $A_{1}$
must contain the whole set
$A_{1}$
must contain the whole set
![]() $\{x:|x|\in \unicode[STIX]{x1D6E4}\}\cap B(0,1)$
, which is clearly impossible. Thus, Theorem 1.1 is proved.◻
$\{x:|x|\in \unicode[STIX]{x1D6E4}\}\cap B(0,1)$
, which is clearly impossible. Thus, Theorem 1.1 is proved.◻
In order to prove Theorem 1.2, we only have to show that halflines and full circles do not have property
![]() $(\text{K}^{\text{s}})$
. We already saw this for circles. The case of halflines is also clear, as a horizontal halfline cannot be moved continuously to a vertical halfline touching only a finite area.
$(\text{K}^{\text{s}})$
. We already saw this for circles. The case of halflines is also clear, as a horizontal halfline cannot be moved continuously to a vertical halfline touching only a finite area.
3 Proof of Lemma 2.1
Let
![]() $\unicode[STIX]{x1D6FC}$
be a rigid motion and
$\unicode[STIX]{x1D6FC}$
be a rigid motion and
![]() $\unicode[STIX]{x1D6FC}(x)=ux+a$
, where
$\unicode[STIX]{x1D6FC}(x)=ux+a$
, where
![]() $|u|=1$
. Let
$|u|=1$
. Let
![]() $\unicode[STIX]{x1D6FC}^{n}$
denote the
$\unicode[STIX]{x1D6FC}^{n}$
denote the
![]() $n\text{th}$
iterate of
$n\text{th}$
iterate of
![]() $\unicode[STIX]{x1D6FC}$
. We would like to compare the distances
$\unicode[STIX]{x1D6FC}$
. We would like to compare the distances
![]() $\Vert \unicode[STIX]{x1D6FC}^{n}-j\Vert$
and
$\Vert \unicode[STIX]{x1D6FC}^{n}-j\Vert$
and
![]() $\Vert \unicode[STIX]{x1D6FC}-j\Vert$
.
$\Vert \unicode[STIX]{x1D6FC}-j\Vert$
.
It is easy to check that if
![]() $\unicode[STIX]{x1D6FC}(x)=ux+a$
, where
$\unicode[STIX]{x1D6FC}(x)=ux+a$
, where
![]() $|u|=1$
, then
$|u|=1$
, then
![]() $\unicode[STIX]{x1D6FC}^{n}(x)=u^{n}x+(1+u+\cdots +u^{n-1})a$
, and thus
$\unicode[STIX]{x1D6FC}^{n}(x)=u^{n}x+(1+u+\cdots +u^{n-1})a$
, and thus
 $$\begin{eqnarray}\displaystyle \Vert \unicode[STIX]{x1D6FC}^{n}-j\Vert & = & \displaystyle |u^{n}-1|+|1+u+\cdots +u^{n-1}|\cdot |a|\nonumber\\ \displaystyle & = & \displaystyle |1+u+\cdots +u^{n-1}|\cdot (|u-1|+|a|)\nonumber\\ \displaystyle & = & \displaystyle |1+u+\cdots +u^{n-1}|\cdot \Vert \unicode[STIX]{x1D6FC}-j\Vert .\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \Vert \unicode[STIX]{x1D6FC}^{n}-j\Vert & = & \displaystyle |u^{n}-1|+|1+u+\cdots +u^{n-1}|\cdot |a|\nonumber\\ \displaystyle & = & \displaystyle |1+u+\cdots +u^{n-1}|\cdot (|u-1|+|a|)\nonumber\\ \displaystyle & = & \displaystyle |1+u+\cdots +u^{n-1}|\cdot \Vert \unicode[STIX]{x1D6FC}-j\Vert .\end{eqnarray}$$
Since
![]() $|u|=1$
, it follows from (2) that
$|u|=1$
, it follows from (2) that
![]() $\Vert \unicode[STIX]{x1D6FC}^{n}-j\Vert \leqslant n\cdot \Vert \unicode[STIX]{x1D6FC}-j\Vert$
for every
$\Vert \unicode[STIX]{x1D6FC}^{n}-j\Vert \leqslant n\cdot \Vert \unicode[STIX]{x1D6FC}-j\Vert$
for every
![]() $\unicode[STIX]{x1D6FC}$
. Now we show that if
$\unicode[STIX]{x1D6FC}$
. Now we show that if
![]() $|u-1|\leqslant 1/n$
, then
$|u-1|\leqslant 1/n$
, then
Since
![]() $|u^{i}-u^{i-1}|=|u-1|$
for every
$|u^{i}-u^{i-1}|=|u-1|$
for every
![]() $i=1,2,\ldots$
, we obtain
$i=1,2,\ldots$
, we obtain
![]() $|u^{k}-1|\leqslant k\cdot |u-1|$
for every
$|u^{k}-1|\leqslant k\cdot |u-1|$
for every
![]() $k=1,2,\ldots \,$
. Then, assuming that
$k=1,2,\ldots \,$
. Then, assuming that
![]() $|u-1|\leqslant 1/n$
, we find that
$|u-1|\leqslant 1/n$
, we find that
Thus,
![]() $|1+u+\cdots +u^{n-1}|\geqslant n/2$
, and then (2) gives (3).
$|1+u+\cdots +u^{n-1}|\geqslant n/2$
, and then (2) gives (3).
It is clear that if
![]() $\unicode[STIX]{x1D6FC}$
is a translation or a rotation of angle
$\unicode[STIX]{x1D6FC}$
is a translation or a rotation of angle
![]() $\unicode[STIX]{x1D719}$
with
$\unicode[STIX]{x1D719}$
with
![]() $|\unicode[STIX]{x1D719}|<\unicode[STIX]{x1D70B}/n$
, then
$|\unicode[STIX]{x1D719}|<\unicode[STIX]{x1D70B}/n$
, then
We shall also need the following estimate.
Lemma 3.1. Let
![]() $\unicode[STIX]{x1D6FC}$
be a rigid motion. If
$\unicode[STIX]{x1D6FC}$
be a rigid motion. If
![]() $\unicode[STIX]{x1D6FC}^{2}\neq j$
, then, for every
$\unicode[STIX]{x1D6FC}^{2}\neq j$
, then, for every
![]() $t_{1},t_{2}\in [0,1]$
and
$t_{1},t_{2}\in [0,1]$
and
![]() $|x|\leqslant 1$
, we have
$|x|\leqslant 1$
, we have
Proof. If
![]() $\unicode[STIX]{x1D6FC}=T_{c}$
, then
$\unicode[STIX]{x1D6FC}=T_{c}$
, then
from which (5) is clear.
Now let
![]() $\unicode[STIX]{x1D6FC}=R_{c,\unicode[STIX]{x1D719}}$
,
$\unicode[STIX]{x1D6FC}=R_{c,\unicode[STIX]{x1D719}}$
,
![]() $R_{c,\unicode[STIX]{x1D719}}(x)=\text{e}^{\text{i}\unicode[STIX]{x1D719}}(x-c)+c=\text{e}^{\text{i}\unicode[STIX]{x1D719}}x+c(1-\text{e}^{\text{i}\unicode[STIX]{x1D719}})$
, where
$R_{c,\unicode[STIX]{x1D719}}(x)=\text{e}^{\text{i}\unicode[STIX]{x1D719}}(x-c)+c=\text{e}^{\text{i}\unicode[STIX]{x1D719}}x+c(1-\text{e}^{\text{i}\unicode[STIX]{x1D719}})$
, where
![]() $|\unicode[STIX]{x1D719}|<\unicode[STIX]{x1D70B}$
. Then
$|\unicode[STIX]{x1D719}|<\unicode[STIX]{x1D70B}$
. Then
Let
![]() $S$
denote the circle having centre
$S$
denote the circle having centre
![]() $c$
and radius
$c$
and radius
![]() $|x-c|$
. Then
$|x-c|$
. Then
![]() $E_{t_{1}}^{\unicode[STIX]{x1D6FC}}(x)$
and
$E_{t_{1}}^{\unicode[STIX]{x1D6FC}}(x)$
and
![]() $E_{t_{2}}^{\unicode[STIX]{x1D6FC}}(x)$
are the end points of a subarc of
$E_{t_{2}}^{\unicode[STIX]{x1D6FC}}(x)$
are the end points of a subarc of
![]() $S$
of angle
$S$
of angle
![]() $t_{1}\unicode[STIX]{x1D719}-t_{2}\unicode[STIX]{x1D719}$
. Therefore, assuming that
$t_{1}\unicode[STIX]{x1D719}-t_{2}\unicode[STIX]{x1D719}$
. Therefore, assuming that
![]() $|x|\leqslant 1$
and putting
$|x|\leqslant 1$
and putting
![]() $h=|t_{1}-t_{2}|$
, we have
$h=|t_{1}-t_{2}|$
, we have
Since
![]() $\sin x\geqslant (2/\unicode[STIX]{x1D70B})\cdot x$
for every
$\sin x\geqslant (2/\unicode[STIX]{x1D70B})\cdot x$
for every
![]() $x\in [0,\unicode[STIX]{x1D70B}/2]$
, we have
$x\in [0,\unicode[STIX]{x1D70B}/2]$
, we have
![]() $|\text{sin}(\unicode[STIX]{x1D719}/2)|\geqslant |\unicode[STIX]{x1D719}/\unicode[STIX]{x1D70B}|$
by
$|\text{sin}(\unicode[STIX]{x1D719}/2)|\geqslant |\unicode[STIX]{x1D719}/\unicode[STIX]{x1D70B}|$
by
![]() $|\unicode[STIX]{x1D719}/2|<\unicode[STIX]{x1D70B}/2$
. Thus, by (6), we get
$|\unicode[STIX]{x1D719}/2|<\unicode[STIX]{x1D70B}/2$
. Thus, by (6), we get
 $$\begin{eqnarray}\displaystyle |E_{t_{1}}^{\unicode[STIX]{x1D6FC}}(x)-E_{t_{2}}^{\unicode[STIX]{x1D6FC}}(x)| & {\leqslant} & \displaystyle h\cdot \unicode[STIX]{x1D70B}\cdot |\text{sin}(\unicode[STIX]{x1D719}/2)|\cdot (1+|c|)\nonumber\\ \displaystyle & = & \displaystyle h\cdot (\unicode[STIX]{x1D70B}/2)\cdot 2|\text{sin}(\unicode[STIX]{x1D719}/2)|\cdot (1+|c|)\nonumber\\ \displaystyle & = & \displaystyle h\cdot (\unicode[STIX]{x1D70B}/2)\cdot 2|\text{sin}(\unicode[STIX]{x1D719}/2)|\cdot |c|+h\cdot (\unicode[STIX]{x1D70B}/2)\cdot 2|\text{sin}(\unicode[STIX]{x1D719}/2)|\nonumber\\ \displaystyle & {\leqslant} & \displaystyle h\cdot (\unicode[STIX]{x1D70B}/2)\cdot 2|\text{sin}(\unicode[STIX]{x1D719}/2)|\cdot |c|+h\cdot (\unicode[STIX]{x1D70B}/2)\cdot 2\nonumber\\ \displaystyle & = & \displaystyle h\cdot (\unicode[STIX]{x1D70B}/2)(\Vert \unicode[STIX]{x1D6FC}\Vert +1)\leqslant 2h(\Vert \unicode[STIX]{x1D6FC}\Vert +1),\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle |E_{t_{1}}^{\unicode[STIX]{x1D6FC}}(x)-E_{t_{2}}^{\unicode[STIX]{x1D6FC}}(x)| & {\leqslant} & \displaystyle h\cdot \unicode[STIX]{x1D70B}\cdot |\text{sin}(\unicode[STIX]{x1D719}/2)|\cdot (1+|c|)\nonumber\\ \displaystyle & = & \displaystyle h\cdot (\unicode[STIX]{x1D70B}/2)\cdot 2|\text{sin}(\unicode[STIX]{x1D719}/2)|\cdot (1+|c|)\nonumber\\ \displaystyle & = & \displaystyle h\cdot (\unicode[STIX]{x1D70B}/2)\cdot 2|\text{sin}(\unicode[STIX]{x1D719}/2)|\cdot |c|+h\cdot (\unicode[STIX]{x1D70B}/2)\cdot 2|\text{sin}(\unicode[STIX]{x1D719}/2)|\nonumber\\ \displaystyle & {\leqslant} & \displaystyle h\cdot (\unicode[STIX]{x1D70B}/2)\cdot 2|\text{sin}(\unicode[STIX]{x1D719}/2)|\cdot |c|+h\cdot (\unicode[STIX]{x1D70B}/2)\cdot 2\nonumber\\ \displaystyle & = & \displaystyle h\cdot (\unicode[STIX]{x1D70B}/2)(\Vert \unicode[STIX]{x1D6FC}\Vert +1)\leqslant 2h(\Vert \unicode[STIX]{x1D6FC}\Vert +1),\nonumber\end{eqnarray}$$
proving (5). ◻
Lemma 3.2. Let
![]() $\unicode[STIX]{x1D6FC}_{n}(x)=u_{n}x+v_{n}$
$\unicode[STIX]{x1D6FC}_{n}(x)=u_{n}x+v_{n}$
![]() $(n=1,2,\ldots )$
and
$(n=1,2,\ldots )$
and
![]() $\unicode[STIX]{x1D6FC}(x)=ux+v$
be rigid motions, where
$\unicode[STIX]{x1D6FC}(x)=ux+v$
be rigid motions, where
![]() $u_{n}\rightarrow u$
and
$u_{n}\rightarrow u$
and
![]() $v_{n}\rightarrow v$
as
$v_{n}\rightarrow v$
as
![]() $n\rightarrow \infty$
. Suppose that
$n\rightarrow \infty$
. Suppose that
![]() $\unicode[STIX]{x1D6FC}^{2}\neq j$
. Then we have
$\unicode[STIX]{x1D6FC}^{2}\neq j$
. Then we have
![]() $E_{t}^{\unicode[STIX]{x1D6FC}_{n}}(x)\rightarrow E_{t}^{\unicode[STIX]{x1D6FC}}(x)$
uniformly on the set
$E_{t}^{\unicode[STIX]{x1D6FC}_{n}}(x)\rightarrow E_{t}^{\unicode[STIX]{x1D6FC}}(x)$
uniformly on the set
![]() $\{(t,x):t\in [0,1],|x|\leqslant 1\}$
.
$\{(t,x):t\in [0,1],|x|\leqslant 1\}$
.
In order to prove the lemma, one has to distinguish between the cases
![]() $u=1$
and
$u=1$
and
![]() $u\neq 1$
. In both cases the proof is an easy computation; we leave the details to the reader.
$u\neq 1$
. In both cases the proof is an easy computation; we leave the details to the reader.
Now we turn to the proof of Lemma 2.1. Since
![]() $A\subset \mathbb{R}^{2}$
has property (K), there is a rigid motion
$A\subset \mathbb{R}^{2}$
has property (K), there is a rigid motion
![]() $\unicode[STIX]{x1D6FD}\neq j$
such that for every
$\unicode[STIX]{x1D6FD}\neq j$
such that for every
![]() $\unicode[STIX]{x1D700}>0$
there exists a continuous movement
$\unicode[STIX]{x1D700}>0$
there exists a continuous movement
![]() $M$
with
$M$
with
![]() $M_{1}=\unicode[STIX]{x1D6FD}$
and
$M_{1}=\unicode[STIX]{x1D6FD}$
and
![]() $\unicode[STIX]{x1D706}(W_{M}(A))<\unicode[STIX]{x1D700}$
. Let
$\unicode[STIX]{x1D706}(W_{M}(A))<\unicode[STIX]{x1D700}$
. Let
![]() $\unicode[STIX]{x1D6FD}(x)=v_{0}x+b_{0}$
, where
$\unicode[STIX]{x1D6FD}(x)=v_{0}x+b_{0}$
, where
![]() $|v_{0}|=1$
. We put
$|v_{0}|=1$
. We put
![]() $\unicode[STIX]{x1D702}=\min (|v_{0}-1|+|b_{0}|,1)$
. Since
$\unicode[STIX]{x1D702}=\min (|v_{0}-1|+|b_{0}|,1)$
. Since
![]() $\unicode[STIX]{x1D6FD}\neq j$
, we have
$\unicode[STIX]{x1D6FD}\neq j$
, we have
![]() $\unicode[STIX]{x1D702}>0$
.
$\unicode[STIX]{x1D702}>0$
.
We choose, for every
![]() $n$
, a continuous movement
$n$
, a continuous movement
![]() $M^{n}$
such that
$M^{n}$
such that
![]() $M_{1}^{n}=\unicode[STIX]{x1D6FD}$
and
$M_{1}^{n}=\unicode[STIX]{x1D6FD}$
and
![]() $\unicode[STIX]{x1D706}(W_{M^{n}}(A))<1/n^{2}$
. Let
$\unicode[STIX]{x1D706}(W_{M^{n}}(A))<1/n^{2}$
. Let
![]() $M_{t}^{n}(x)=v_{n}(t)x+b_{n}(t)$
for every
$M_{t}^{n}(x)=v_{n}(t)x+b_{n}(t)$
for every
![]() $x\in \mathbb{C}$
and
$x\in \mathbb{C}$
and
![]() $t\in [0,1]$
, where
$t\in [0,1]$
, where
![]() $|v_{n}|=1$
. Since the maps
$|v_{n}|=1$
. Since the maps
![]() $t\mapsto v_{n}(t)$
,
$t\mapsto v_{n}(t)$
,
![]() $t\mapsto b_{n}(t)$
are continuous and
$t\mapsto b_{n}(t)$
are continuous and
![]() $v_{n}(1)=v_{0},~b_{n}(1)=b_{0}$
, there is a
$v_{n}(1)=v_{0},~b_{n}(1)=b_{0}$
, there is a
![]() $0<t_{n}\leqslant 1$
such that
$0<t_{n}\leqslant 1$
such that
![]() $|v_{n}(t_{n})-1|+|b_{n}(t_{n})|=\unicode[STIX]{x1D702}/n$
, and
$|v_{n}(t_{n})-1|+|b_{n}(t_{n})|=\unicode[STIX]{x1D702}/n$
, and
![]() $|v_{n}(t)-1|+|b_{n}(t)|<\unicode[STIX]{x1D702}/n$
for every
$|v_{n}(t)-1|+|b_{n}(t)|<\unicode[STIX]{x1D702}/n$
for every
![]() $t\in [0,t_{n} )$
. Replacing
$t\in [0,t_{n} )$
. Replacing
![]() $M^{n}$
by
$M^{n}$
by
![]() $M^{n}\circ \unicode[STIX]{x1D713}$
, where
$M^{n}\circ \unicode[STIX]{x1D713}$
, where
![]() $\unicode[STIX]{x1D713}$
is a suitable homeomorphism of
$\unicode[STIX]{x1D713}$
is a suitable homeomorphism of
![]() $[0,1]$
onto itself, we may assume that
$[0,1]$
onto itself, we may assume that
![]() $t_{n}=1/n$
.
$t_{n}=1/n$
.
We put
![]() $\unicode[STIX]{x1D6FD}_{n}=M_{1/n}^{n}$
and
$\unicode[STIX]{x1D6FD}_{n}=M_{1/n}^{n}$
and
![]() $\unicode[STIX]{x1D6FC}_{n}=\unicode[STIX]{x1D6FD}_{n}^{n}$
. Then
$\unicode[STIX]{x1D6FC}_{n}=\unicode[STIX]{x1D6FD}_{n}^{n}$
. Then
![]() $\Vert \unicode[STIX]{x1D6FD}_{n}-j\Vert =\unicode[STIX]{x1D702}/n$
and
$\Vert \unicode[STIX]{x1D6FD}_{n}-j\Vert =\unicode[STIX]{x1D702}/n$
and
![]() $\unicode[STIX]{x1D702}/2\leqslant \Vert \unicode[STIX]{x1D6FC}_{n}-j\Vert \leqslant \unicode[STIX]{x1D702}$
by (3). Let
$\unicode[STIX]{x1D702}/2\leqslant \Vert \unicode[STIX]{x1D6FC}_{n}-j\Vert \leqslant \unicode[STIX]{x1D702}$
by (3). Let
![]() $\unicode[STIX]{x1D6FC}_{n}(x)=u_{n}x+a_{n}$
, where
$\unicode[STIX]{x1D6FC}_{n}(x)=u_{n}x+a_{n}$
, where
![]() $|u_{n}|=1$
. Since
$|u_{n}|=1$
. Since
![]() $\unicode[STIX]{x1D702}/2\leqslant |u_{n}-1|+|a_{n}|\leqslant \unicode[STIX]{x1D702}$
for every
$\unicode[STIX]{x1D702}/2\leqslant |u_{n}-1|+|a_{n}|\leqslant \unicode[STIX]{x1D702}$
for every
![]() $n$
, the sequences
$n$
, the sequences
![]() $(u_{n})$
and
$(u_{n})$
and
![]() $(a_{n})$
have convergent subsequences. Turning to a suitable subsequence, we may assume that the sequences
$(a_{n})$
have convergent subsequences. Turning to a suitable subsequence, we may assume that the sequences
![]() $(u_{n})$
and
$(u_{n})$
and
![]() $(a_{n})$
converge. Let
$(a_{n})$
converge. Let
![]() $u_{n}\rightarrow u$
and
$u_{n}\rightarrow u$
and
![]() $a_{n}\rightarrow a$
. Then
$a_{n}\rightarrow a$
. Then
![]() $|u|=1$
, and thus
$|u|=1$
, and thus
![]() $\unicode[STIX]{x1D6FC}(x)=ux+a$
defines a rigid motion. Our aim is to show that
$\unicode[STIX]{x1D6FC}(x)=ux+a$
defines a rigid motion. Our aim is to show that
![]() $\unicode[STIX]{x1D6FC}$
satisfies the requirements. Since
$\unicode[STIX]{x1D6FC}$
satisfies the requirements. Since
![]() $\Vert \unicode[STIX]{x1D6FC}-j\Vert =|u-1|+|a|\geqslant \unicode[STIX]{x1D702}/2>0$
, we can see that
$\Vert \unicode[STIX]{x1D6FC}-j\Vert =|u-1|+|a|\geqslant \unicode[STIX]{x1D702}/2>0$
, we can see that
![]() $\unicode[STIX]{x1D6FC}\neq j$
. Also, by
$\unicode[STIX]{x1D6FC}\neq j$
. Also, by
![]() $\Vert \unicode[STIX]{x1D6FC}-j\Vert \leqslant \unicode[STIX]{x1D702}\leqslant 1$
, we have
$\Vert \unicode[STIX]{x1D6FC}-j\Vert \leqslant \unicode[STIX]{x1D702}\leqslant 1$
, we have
![]() $\unicode[STIX]{x1D6FC}^{2}\neq j$
. Indeed,
$\unicode[STIX]{x1D6FC}^{2}\neq j$
. Indeed,
![]() $\unicode[STIX]{x1D6FC}^{2}=j$
would imply that
$\unicode[STIX]{x1D6FC}^{2}=j$
would imply that
![]() $u=-1$
and
$u=-1$
and
![]() $\Vert \unicode[STIX]{x1D6FC}-j\Vert \geqslant 2$
.
$\Vert \unicode[STIX]{x1D6FC}-j\Vert \geqslant 2$
.
We define the continuous movement
![]() $F^{n}$
as follows: we replace the movement
$F^{n}$
as follows: we replace the movement
![]() $E_{t}^{\unicode[STIX]{x1D6FC}_{n}}$
between the moments
$E_{t}^{\unicode[STIX]{x1D6FC}_{n}}$
between the moments
![]() $t=(i-1)/n$
and
$t=(i-1)/n$
and
![]() $t=i/n$
by suitable copies of the movement
$t=i/n$
by suitable copies of the movement
![]() $M_{t}$
$M_{t}$
![]() $(t\in [0,1/n])$
. More precisely, we put
$(t\in [0,1/n])$
. More precisely, we put
for
![]() $t\in [(i-1)/n,i/n]$
and
$t\in [(i-1)/n,i/n]$
and
![]() $i=1,\ldots ,n$
. Since
$i=1,\ldots ,n$
. Since
![]() $M_{0}^{n}=j$
and
$M_{0}^{n}=j$
and
![]() $M_{1/n}^{n}=\unicode[STIX]{x1D6FD}_{n}$
, it follows that
$M_{1/n}^{n}=\unicode[STIX]{x1D6FD}_{n}$
, it follows that
![]() $\unicode[STIX]{x1D6FD}_{n}^{i-1}\circ M_{1/n}^{n}=\unicode[STIX]{x1D6FD}_{n}^{i}\circ M_{0}^{n}$
, and thus the definition makes sense. This also proves that
$\unicode[STIX]{x1D6FD}_{n}^{i-1}\circ M_{1/n}^{n}=\unicode[STIX]{x1D6FD}_{n}^{i}\circ M_{0}^{n}$
, and thus the definition makes sense. This also proves that
![]() $F^{n}$
is a continuous movement. Let
$F^{n}$
is a continuous movement. Let
![]() $W=\{M_{t}^{n}(x):x\in A,t\in [0,\,1/n]\}$
. Since
$W=\{M_{t}^{n}(x):x\in A,t\in [0,\,1/n]\}$
. Since
![]() $W\subset W_{M}(A)$
, we have
$W\subset W_{M}(A)$
, we have
![]() $\unicode[STIX]{x1D706}(W)<1/n^{2}$
. Also,
$\unicode[STIX]{x1D706}(W)<1/n^{2}$
. Also,
![]() $W_{F^{n}}(A)$
is the union of
$W_{F^{n}}(A)$
is the union of
![]() $n$
congruent copies of
$n$
congruent copies of
![]() $W$
; therefore, we have
$W$
; therefore, we have
![]() $\unicode[STIX]{x1D706}(W_{F^{n}}(A))<1/n$
.
$\unicode[STIX]{x1D706}(W_{F^{n}}(A))<1/n$
.
Next we show that for every
![]() $x\in \mathbb{C}$
,
$x\in \mathbb{C}$
,
![]() $|x|\leqslant 1$
and
$|x|\leqslant 1$
and
![]() $t\in [0,1]$
, we have
$t\in [0,1]$
, we have
If
![]() $t\in [0,1/n]$
, then
$t\in [0,1/n]$
, then
![]() $|v_{n}(t)-1|+|b_{n}(t)|\leqslant \unicode[STIX]{x1D702}/n\leqslant 1/n$
, and thus
$|v_{n}(t)-1|+|b_{n}(t)|\leqslant \unicode[STIX]{x1D702}/n\leqslant 1/n$
, and thus
for every
![]() $x\in \mathbb{C}$
. Let
$x\in \mathbb{C}$
. Let
![]() $1\leqslant i\leqslant n$
and
$1\leqslant i\leqslant n$
and
![]() $t\in [(i-1)/n,i/n]$
be given. Then we have
$t\in [(i-1)/n,i/n]$
be given. Then we have
where we used the fact that
![]() $\unicode[STIX]{x1D6FD}_{n}^{i-1}$
is an isometry. On the other hand, by Lemma 3.1 and (4), we have
$\unicode[STIX]{x1D6FD}_{n}^{i-1}$
is an isometry. On the other hand, by Lemma 3.1 and (4), we have
Note that
![]() $\Vert \unicode[STIX]{x1D6FD}_{n}-j\Vert =\unicode[STIX]{x1D702}/n<1/n$
implies that either
$\Vert \unicode[STIX]{x1D6FD}_{n}-j\Vert =\unicode[STIX]{x1D702}/n<1/n$
implies that either
![]() $\unicode[STIX]{x1D6FD}_{n}$
is a translation or it is a rotation by an angle
$\unicode[STIX]{x1D6FD}_{n}$
is a translation or it is a rotation by an angle
![]() $\unicode[STIX]{x1D719}$
with
$\unicode[STIX]{x1D719}$
with
![]() $\unicode[STIX]{x1D719}|<\unicode[STIX]{x1D70B}/n$
, and thus (4) can be applied. Then, comparing with (8), we have (7). Since
$\unicode[STIX]{x1D719}|<\unicode[STIX]{x1D70B}/n$
, and thus (4) can be applied. Then, comparing with (8), we have (7). Since
![]() $u_{n}\rightarrow u$
and
$u_{n}\rightarrow u$
and
![]() $a_{n}\rightarrow a$
, it follows from Lemma 3.2 that
$a_{n}\rightarrow a$
, it follows from Lemma 3.2 that
![]() $E_{t}^{\unicode[STIX]{x1D6FC}_{n}}(x)\rightarrow E_{t}^{\unicode[STIX]{x1D6FC}}(x)$
uniformly on the set
$E_{t}^{\unicode[STIX]{x1D6FC}_{n}}(x)\rightarrow E_{t}^{\unicode[STIX]{x1D6FC}}(x)$
uniformly on the set
![]() $\{(t,x):t\in [0,1],|x|\leqslant 1\}$
. Let
$\{(t,x):t\in [0,1],|x|\leqslant 1\}$
. Let
![]() $\unicode[STIX]{x1D700}>0$
be given. Then we can choose an
$\unicode[STIX]{x1D700}>0$
be given. Then we can choose an
![]() $n$
such that
$n$
such that
![]() $8/n<\unicode[STIX]{x1D700}/2$
and
$8/n<\unicode[STIX]{x1D700}/2$
and
for every
![]() $t\in [0,1]$
and
$t\in [0,1]$
and
![]() $|x|\leqslant 1$
. Then, by (7), we find that
$|x|\leqslant 1$
. Then, by (7), we find that
![]() $|F_{t}^{n}(x)-E_{t}^{\unicode[STIX]{x1D6FC}}(x)|<\unicode[STIX]{x1D700}$
for every
$|F_{t}^{n}(x)-E_{t}^{\unicode[STIX]{x1D6FC}}(x)|<\unicode[STIX]{x1D700}$
for every
![]() $t\in [0,1]$
and
$t\in [0,1]$
and
![]() $|x|\leqslant 1$
. Thus,
$|x|\leqslant 1$
. Thus,
![]() $\Vert F_{t}^{n}-E_{t}^{\unicode[STIX]{x1D6FC}}\Vert <\unicode[STIX]{x1D700}$
for every
$\Vert F_{t}^{n}-E_{t}^{\unicode[STIX]{x1D6FC}}\Vert <\unicode[STIX]{x1D700}$
for every
![]() $t\in [0,1]$
. Since
$t\in [0,1]$
. Since
![]() $\unicode[STIX]{x1D706}(W_{F^{n}}(A))<1/n<\unicode[STIX]{x1D700}$
, this completes the proof.◻
$\unicode[STIX]{x1D706}(W_{F^{n}}(A))<1/n<\unicode[STIX]{x1D700}$
, this completes the proof.◻
4 Proof of Lemma 2.2
If
![]() $\unicode[STIX]{x1D6FE}:[a,b]\rightarrow \mathbb{C}$
is a continuous curve and
$\unicode[STIX]{x1D6FE}:[a,b]\rightarrow \mathbb{C}$
is a continuous curve and
![]() $p\in \mathbb{C}\setminus \unicode[STIX]{x1D6FE}([a,b])$
, then we denote by
$p\in \mathbb{C}\setminus \unicode[STIX]{x1D6FE}([a,b])$
, then we denote by
![]() $w(\unicode[STIX]{x1D6FE};p)$
the increment of the argument of
$w(\unicode[STIX]{x1D6FE};p)$
the increment of the argument of
![]() $\unicode[STIX]{x1D6FE}(t)-p$
, as
$\unicode[STIX]{x1D6FE}(t)-p$
, as
![]() $t$
goes from
$t$
goes from
![]() $a$
to
$a$
to
![]() $b$
. More precisely, if
$b$
. More precisely, if
![]() $\unicode[STIX]{x1D719}:[a,b]\rightarrow \mathbb{R}$
is a continuous function such that
$\unicode[STIX]{x1D719}:[a,b]\rightarrow \mathbb{R}$
is a continuous function such that
![]() $\unicode[STIX]{x1D719}(t)$
is one of the arguments of
$\unicode[STIX]{x1D719}(t)$
is one of the arguments of
![]() $\unicode[STIX]{x1D6FE}(t)-p$
for every
$\unicode[STIX]{x1D6FE}(t)-p$
for every
![]() $t\in [a,b]$
, then we put
$t\in [a,b]$
, then we put
![]() $w(\unicode[STIX]{x1D6FE};p)=\unicode[STIX]{x1D719}(b)-\unicode[STIX]{x1D719}(a)$
. It is easy to see that
$w(\unicode[STIX]{x1D6FE};p)=\unicode[STIX]{x1D719}(b)-\unicode[STIX]{x1D719}(a)$
. It is easy to see that
![]() $w(\unicode[STIX]{x1D6FE};p)$
does not depend on the choice of the continuous function
$w(\unicode[STIX]{x1D6FE};p)$
does not depend on the choice of the continuous function
![]() $\unicode[STIX]{x1D719}$
. If
$\unicode[STIX]{x1D719}$
. If
![]() $\unicode[STIX]{x1D6FE}$
is a closed curve, then
$\unicode[STIX]{x1D6FE}$
is a closed curve, then
![]() $w(\unicode[STIX]{x1D6FE};p)/(2\unicode[STIX]{x1D70B})$
is the winding number of
$w(\unicode[STIX]{x1D6FE};p)/(2\unicode[STIX]{x1D70B})$
is the winding number of
![]() $\unicode[STIX]{x1D6FE}$
with respect to the point
$\unicode[STIX]{x1D6FE}$
with respect to the point
![]() $p$
.
$p$
.
Let
![]() $p$
be an arbitrary element of
$p$
be an arbitrary element of
![]() $A\cap D$
, and let
$A\cap D$
, and let
![]() $U\subset D$
be an open disc of centre
$U\subset D$
be an open disc of centre
![]() $p$
. We prove that
$p$
. We prove that
![]() $\text{cl}\,U$
intersects at least two connected components of
$\text{cl}\,U$
intersects at least two connected components of
![]() $D\setminus A$
.
$D\setminus A$
.
Since
![]() $A$
is irreducible between the points
$A$
is irreducible between the points
![]() $a,b\in A\setminus U$
, it follows that
$a,b\in A\setminus U$
, it follows that
![]() $A\setminus U$
is not connected; moreover,
$A\setminus U$
is not connected; moreover,
![]() $a$
and
$a$
and
![]() $b$
belong to different connected components of
$b$
belong to different connected components of
![]() $A\setminus U$
. Let
$A\setminus U$
. Let
![]() $C_{b}$
denote the connected component of
$C_{b}$
denote the connected component of
![]() $A\setminus U$
containing the point
$A\setminus U$
containing the point
![]() $b$
.
$b$
.
By [Reference Kuratowski7, Theorem 2, §47, II, p. 169],
![]() $C_{b}$
is a quasi-component of
$C_{b}$
is a quasi-component of
![]() $A\setminus U$
; that is,
$A\setminus U$
; that is,
![]() $C_{b}$
is the intersection of all (relative) clopen subsets of
$C_{b}$
is the intersection of all (relative) clopen subsets of
![]() $A\setminus U$
containing
$A\setminus U$
containing
![]() $b$
. Since
$b$
. Since
![]() $a\notin C_{b}$
, there is a relative clopen set
$a\notin C_{b}$
, there is a relative clopen set
![]() $G\subset A\setminus U$
such that
$G\subset A\setminus U$
such that
![]() $C_{b}\subset G$
and
$C_{b}\subset G$
and
![]() $a\notin G$
. Then
$a\notin G$
. Then
![]() $(A\setminus U)\setminus G$
and
$(A\setminus U)\setminus G$
and
![]() $G$
are disjoint compact sets.
$G$
are disjoint compact sets.
Since
![]() $A$
is irreducible between
$A$
is irreducible between
![]() $a$
and
$a$
and
![]() $b$
, it follows that
$b$
, it follows that
![]() $A$
is nowhere dense. Indeed, it is clear that otherwise it would contain proper subcontinuums containing
$A$
is nowhere dense. Indeed, it is clear that otherwise it would contain proper subcontinuums containing
![]() $a$
and
$a$
and
![]() $b$
.
$b$
.
By assumption, the set
![]() $\mathbb{R}^{2}\setminus A$
is connected. This implies that
$\mathbb{R}^{2}\setminus A$
is connected. This implies that
![]() $\mathbb{R}^{2}\setminus C$
is connected for every
$\mathbb{R}^{2}\setminus C$
is connected for every
![]() $C\subset A$
. Indeed,
$C\subset A$
. Indeed,
![]() $\mathbb{R}^{2}\setminus C$
contains the connected set
$\mathbb{R}^{2}\setminus C$
contains the connected set
![]() $\mathbb{R}^{2}\setminus A$
, and is contained in its closure, so must be connected itself. Thus,
$\mathbb{R}^{2}\setminus A$
, and is contained in its closure, so must be connected itself. Thus,
![]() $(A\setminus U)\setminus G$
and
$(A\setminus U)\setminus G$
and
![]() $G$
are disjoint compact sets such that they do not cut the plane. Indeed,
$G$
are disjoint compact sets such that they do not cut the plane. Indeed,
![]() $\mathbb{R}^{2}\setminus (A\setminus U)$
and
$\mathbb{R}^{2}\setminus (A\setminus U)$
and
![]() $\mathbb{R}^{2}\setminus G$
are semicontinuums, being connected open sets.
$\mathbb{R}^{2}\setminus G$
are semicontinuums, being connected open sets.
Therefore, by [Reference Kuratowski7, Theorem 9, §61, II, p. 514],
![]() $(A\setminus U)\setminus G$
and
$(A\setminus U)\setminus G$
and
![]() $G$
can be separated by a simple closed curve. Let
$G$
can be separated by a simple closed curve. Let
![]() $J$
be a simple closed curve separating them. Then
$J$
be a simple closed curve separating them. Then
![]() $J\cap (A\setminus U)=\emptyset$
and
$J\cap (A\setminus U)=\emptyset$
and
![]() $J$
separates
$J$
separates
![]() $a$
and
$a$
and
![]() $b$
. By symmetry, we may assume that
$b$
. By symmetry, we may assume that
![]() $a\in \text{Int}\,J$
and
$a\in \text{Int}\,J$
and
![]() $b\in \text{Ext}\,J$
.
$b\in \text{Ext}\,J$
.
If
![]() $J\subset D$
, then
$J\subset D$
, then
![]() $\text{Int}\,J\subset D$
and
$\text{Int}\,J\subset D$
and
![]() $a\notin \text{Int}\,J$
, which is impossible. Therefore,
$a\notin \text{Int}\,J$
, which is impossible. Therefore,
![]() $J$
is not covered by
$J$
is not covered by
![]() $D$
, and we can pick a point
$D$
, and we can pick a point
![]() $a_{0}\in J\setminus D$
.
$a_{0}\in J\setminus D$
.
Since
![]() $A$
is connected and contains the points
$A$
is connected and contains the points
![]() $a,b$
,
$a,b$
,
![]() $A$
must intersect
$A$
must intersect
![]() $J$
. Now we have
$J$
. Now we have
![]() $J\cap (A\setminus U)=\emptyset$
, and thus
$J\cap (A\setminus U)=\emptyset$
, and thus
![]() $J\cap U\neq \emptyset$
. Since
$J\cap U\neq \emptyset$
. Since
![]() $a_{0}\notin U$
, it follows that
$a_{0}\notin U$
, it follows that
![]() $J\cap \unicode[STIX]{x2202}U\neq \emptyset$
.
$J\cap \unicode[STIX]{x2202}U\neq \emptyset$
.
Let
![]() $J$
be the range of the continuous map
$J$
be the range of the continuous map
![]() $\unicode[STIX]{x1D6FE}:[0,1]\rightarrow \mathbb{R}^{2}$
, where
$\unicode[STIX]{x1D6FE}:[0,1]\rightarrow \mathbb{R}^{2}$
, where
![]() $\unicode[STIX]{x1D6FE}(0)=\unicode[STIX]{x1D6FE}(1)\in \unicode[STIX]{x2202}U$
, and
$\unicode[STIX]{x1D6FE}(0)=\unicode[STIX]{x1D6FE}(1)\in \unicode[STIX]{x2202}U$
, and
![]() $\unicode[STIX]{x1D6FE}$
is injective on
$\unicode[STIX]{x1D6FE}$
is injective on
![]() $[\!0,1\!)$
. The set
$[\!0,1\!)$
. The set
![]() $F=\unicode[STIX]{x1D6FE}^{-1}(\unicode[STIX]{x2202}U)$
is a closed subset of
$F=\unicode[STIX]{x1D6FE}^{-1}(\unicode[STIX]{x2202}U)$
is a closed subset of
![]() $[0,1]$
such that
$[0,1]$
such that
![]() $0,1\in F$
. If
$0,1\in F$
. If
![]() $(x,y)$
is a connected component of
$(x,y)$
is a connected component of
![]() $[0,1]\setminus F$
, then
$[0,1]\setminus F$
, then
![]() $\unicode[STIX]{x1D6FE}((x,y))\cap \unicode[STIX]{x2202}U=\emptyset$
, and thus
$\unicode[STIX]{x1D6FE}((x,y))\cap \unicode[STIX]{x2202}U=\emptyset$
, and thus
![]() $\unicode[STIX]{x1D6FE}((x,y))$
is covered by one of
$\unicode[STIX]{x1D6FE}((x,y))$
is covered by one of
![]() $U$
and
$U$
and
![]() $\text{ext}\,U$
. By the uniform continuity of
$\text{ext}\,U$
. By the uniform continuity of
![]() $\unicode[STIX]{x1D6FE}$
, there exists a
$\unicode[STIX]{x1D6FE}$
, there exists a
![]() $\unicode[STIX]{x1D6FF}>0$
such that whenever
$\unicode[STIX]{x1D6FF}>0$
such that whenever
![]() $x,y\in F$
and
$x,y\in F$
and
![]() $|x-y|<\unicode[STIX]{x1D6FF}$
, then
$|x-y|<\unicode[STIX]{x1D6FF}$
, then
![]() $\unicode[STIX]{x1D6FE}((x,y))\subset D$
. This easily implies that there is a partition
$\unicode[STIX]{x1D6FE}((x,y))\subset D$
. This easily implies that there is a partition
![]() $0=t_{0}<t_{1}<\cdots <t_{n}=1$
such that
$0=t_{0}<t_{1}<\cdots <t_{n}=1$
such that
![]() $t_{0},\ldots ,t_{n}\in F$
and, for every
$t_{0},\ldots ,t_{n}\in F$
and, for every
![]() $i=1,\ldots ,n$
, either
$i=1,\ldots ,n$
, either
![]() $\unicode[STIX]{x1D6FE}((t_{i-1},t_{i}))\subset D$
or
$\unicode[STIX]{x1D6FE}((t_{i-1},t_{i}))\subset D$
or
![]() $\unicode[STIX]{x1D6FE}((t_{i-1},t_{i}))\cap \text{cl}\,U=\emptyset$
.
$\unicode[STIX]{x1D6FE}((t_{i-1},t_{i}))\cap \text{cl}\,U=\emptyset$
.
Let
![]() $J_{i}=\unicode[STIX]{x1D6FE}([t_{i-1},t_{i}])$
for every
$J_{i}=\unicode[STIX]{x1D6FE}([t_{i-1},t_{i}])$
for every
![]() $i=1,\ldots ,n$
. If
$i=1,\ldots ,n$
. If
![]() $L_{i}$
denotes the subarc of the circle
$L_{i}$
denotes the subarc of the circle
![]() $\unicode[STIX]{x2202}U$
with end points
$\unicode[STIX]{x2202}U$
with end points
![]() $\unicode[STIX]{x1D6FE}(t_{i})$
and
$\unicode[STIX]{x1D6FE}(t_{i})$
and
![]() $\unicode[STIX]{x1D6FE}(t_{i-1})$
in this order, then
$\unicode[STIX]{x1D6FE}(t_{i-1})$
in this order, then
![]() $J_{i}\cup L_{i}$
is a closed curve for every
$J_{i}\cup L_{i}$
is a closed curve for every
![]() $i=1,\ldots ,n$
. Since the points
$i=1,\ldots ,n$
. Since the points
![]() $a$
and
$a$
and
![]() $b$
are outside the closed disc
$b$
are outside the closed disc
![]() $\text{cl}\,U$
, we have
$\text{cl}\,U$
, we have
Thus,
and
Therefore, we can choose an index
![]() $i$
such that
$i$
such that
![]() $w(J_{i}\cup L_{i};a)\neq w(J_{i}\cup L_{i};b)$
.
$w(J_{i}\cup L_{i};a)\neq w(J_{i}\cup L_{i};b)$
.
We prove that
![]() $\unicode[STIX]{x1D6FE}(t_{i-1})$
and
$\unicode[STIX]{x1D6FE}(t_{i-1})$
and
![]() $\unicode[STIX]{x1D6FE}(t_{i})$
belong to different connected components of
$\unicode[STIX]{x1D6FE}(t_{i})$
belong to different connected components of
![]() $D\setminus A$
. Since
$D\setminus A$
. Since
![]() $\unicode[STIX]{x1D6FE}(t_{i-1})$
,
$\unicode[STIX]{x1D6FE}(t_{i-1})$
,
![]() $\unicode[STIX]{x1D6FE}(t_{i})\in \text{cl}\,U$
, this will prove the statement of the lemma.
$\unicode[STIX]{x1D6FE}(t_{i})\in \text{cl}\,U$
, this will prove the statement of the lemma.
Suppose that
![]() $\unicode[STIX]{x1D6FE}(t_{i-1})$
and
$\unicode[STIX]{x1D6FE}(t_{i-1})$
and
![]() $\unicode[STIX]{x1D6FE}(t_{i})$
belong to the same connected component of
$\unicode[STIX]{x1D6FE}(t_{i})$
belong to the same connected component of
![]() $D\setminus A$
. Then there is an arc
$D\setminus A$
. Then there is an arc
![]() $L\subset D\setminus A$
with end points
$L\subset D\setminus A$
with end points
![]() $\unicode[STIX]{x1D6FE}(t_{i-1})$
and
$\unicode[STIX]{x1D6FE}(t_{i-1})$
and
![]() $\unicode[STIX]{x1D6FE}(t_{i})$
.
$\unicode[STIX]{x1D6FE}(t_{i})$
.
We have
![]() $w(L_{i}\cup L;a)=w(L_{i}\cup L;b)=0$
, since the closed curve
$w(L_{i}\cup L;a)=w(L_{i}\cup L;b)=0$
, since the closed curve
![]() $L_{i}\cup L$
is in
$L_{i}\cup L$
is in
![]() $D$
, while
$D$
, while
![]() $a$
and
$a$
and
![]() $b$
are not in
$b$
are not in
![]() $D$
. Therefore, we have
$D$
. Therefore, we have
![]() $w(L_{i};a)=-w(L;a)=w(\overline{L};a)$
and
$w(L_{i};a)=-w(L;a)=w(\overline{L};a)$
and
![]() $w(L_{i};b)=-w(L;b)=w(\overline{L};b)$
, where
$w(L_{i};b)=-w(L;b)=w(\overline{L};b)$
, where
![]() $\overline{L}$
is obtained from
$\overline{L}$
is obtained from
![]() $L$
by changing its direction. Then we have
$L$
by changing its direction. Then we have
 $$\begin{eqnarray}\displaystyle w(J_{i}\cup \overline{L};a)-w(J_{i}\cup \overline{L};b) & = & \displaystyle w(J_{i};a)-w(L;a)-w(J_{i};b)+w(L;b)\nonumber\\ \displaystyle & = & \displaystyle w(J_{i};a)+w(L_{i};a)-w(J_{i};b)-w(L_{i};b)\nonumber\\ \displaystyle & = & \displaystyle w(J_{i}\cup L_{i};b)-w(J_{i}\cup L_{i};a)\neq 0.\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle w(J_{i}\cup \overline{L};a)-w(J_{i}\cup \overline{L};b) & = & \displaystyle w(J_{i};a)-w(L;a)-w(J_{i};b)+w(L;b)\nonumber\\ \displaystyle & = & \displaystyle w(J_{i};a)+w(L_{i};a)-w(J_{i};b)-w(L_{i};b)\nonumber\\ \displaystyle & = & \displaystyle w(J_{i}\cup L_{i};b)-w(J_{i}\cup L_{i};a)\neq 0.\nonumber\end{eqnarray}$$
Consequently,
![]() $a$
and
$a$
and
![]() $b$
belong to different connected components of the open set
$b$
belong to different connected components of the open set
![]() $\mathbb{R}^{2}\setminus (J_{i}\cup \overline{L})$
. This, however, is impossible, as
$\mathbb{R}^{2}\setminus (J_{i}\cup \overline{L})$
. This, however, is impossible, as
![]() $a,b\in A$
,
$a,b\in A$
,
![]() $(J_{i}\cup \overline{L})\cap A=\emptyset$
and
$(J_{i}\cup \overline{L})\cap A=\emptyset$
and
![]() $A$
is connected.◻
$A$
is connected.◻