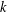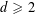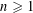1 Introduction
In this paper we consider power-free values of polynomials
$F(x_{1},\ldots ,x_{n})$
with integer coefficients and degree
$d\geqslant 2$
. Put
$$\begin{eqnarray}\displaystyle N_{F,k}(B) & = & \displaystyle \#\{(x_{1},\ldots ,x_{n})\in \mathbb{Z}^{n}:|x_{i}|\leqslant B\nonumber\\ \displaystyle & & \displaystyle \quad \text{for }i=1,\ldots ,n,F(x_{1},\ldots ,x_{n})\text{ is }k\text{-free}\}.\end{eqnarray}$$
Our goal is to show that
$N_{F,k}(B)$
satisfies an asymptotic formula provided that
$F$
is not always divisible by
$p^{k}$
for a fixed prime
$p$
and
$k$
is suitably large compared to
$d$
.
The case
$k=d-1$
is of particular interest. In the case of polynomials in a single variable, the first to establish the infinitude of
$N_{F,d-1}(B)$
was Erdős [Reference Erdős5]. His argument did not establish an asymptotic formula for
$N_{F,d-1}(B)$
; this had to wait until Hooley [Reference Hooley10]. In the two-variable case, the asymptotic formula for
$N_{F,d-1}(B)$
was only established by Hooley [Reference Hooley12] in the case when
$F$
splits into linear factors over some finite extension of
$\mathbb{Q}$
. In this paper we provide an asymptotic formula for
$N_{F,d-1}(B)$
for any number of variables
$n\geqslant 1$
and any square-free polynomial
$F$
with degree
$d\geqslant 5$
.
For general
$k$
and
$n=1$
, various authors have worked on the problem of estimating
$N_{F,k}(B)$
. The record is a theorem of Browning [Reference Browning4], which asserts that the expected asymptotic formula for
$N_{F,k}(B)$
holds when
$k\geqslant (3d+1)/4$
. The main point of our paper is to reduce the problem for general
$n$
to the setting of Browning’s theorem.
In the case of multiple variables, most of the work has been done in the case of binary forms only. The asymptotic formula for
$N_{F,k}(B)$
for binary forms
$F$
was established for
$k\geqslant (d-1)/2$
by Greaves [Reference Greaves7],
$k>(2\sqrt{2}-1)d/4$
by Filaseta [Reference Filaseta6],
$k>7d/16$
by Browning [Reference Browning4], and
$k>7d/18$
by Xiao [Reference Xiao17]. For polynomials of more variables, Bhargava handled square-free values for discriminants of representations of some prehomogeneous vector spaces in [Reference Bhargava1] and Bhargava et al handled the case of discriminants of polynomials in [Reference Bhargava, Shankar and Wang3]. Xiao handled the case of square-free values of decomposable forms in [Reference Xiao18]. In fact, he obtained an asymptotic relation for
$N_{F,2}(B)$
when
$F$
is decomposable whenever
$d\leqslant 2n+2$
.
For inhomogeneous polynomials of two variables the works of Hooley [Reference Hooley11] and Browning [Reference Browning4] provided lower bounds for the number of
$k$
-free values and Hooley [Reference Hooley12] managed to provide an asymptotic formula in certain cases. There are also several specific inhomogeneous polynomials of more variables whose power-free values were estimated asymptotically; see e.g. [Reference Lapkova13, Reference Le Boudec14]. We should mention that Poonen [Reference Poonen15] showed that the number of square-free values of multivariable polynomials
$F$
has a positive density, assuming the abc-conjecture; however, the considered density is differently defined than the one arising when we evaluate asymptotically (1.1).
The main result in this paper is the following theorem, which asserts that an asymptotic relation for
$N_{F,k}(B)$
holds whenever
$k\geqslant (3d+1)/4$
for any
$n\geqslant 1$
and assuming only a necessary condition on the divisibility of the square-free polynomial
$F$
. Observe that the lower bound for
$k$
is the same as in Browning’s theorem in [Reference Browning4].
Theorem 1.1. Let
$k\geqslant 2$
be a positive integer and let
$F$
be a square-free polynomial with integer coefficients and degree
$d\geqslant 2$
in
$n$
variables, such that for all primes
$p$
, there exists an integer
$n$
-tuple
$(m_{1},\ldots ,m_{n})$
such that
$p^{k}\nmid F(m_{1},\ldots ,m_{n})$
. Then there exists a positive number
$C_{F,k}$
such that the asymptotic relation
$$\begin{eqnarray}N_{F,k}(B)\sim C_{F,k}B^{n}\end{eqnarray}$$
holds whenever
$k\geqslant (3d+1)/4$
.
Here the constant term is given by the limit of an absolutely convergent infinite product
$$\begin{eqnarray}C_{F,k}=\mathop{\prod }_{p}\biggl(1-\frac{\unicode[STIX]{x1D70C}_{F}(p^{k})}{p^{kn}}\biggr),\end{eqnarray}$$
where
$$\begin{eqnarray}\unicode[STIX]{x1D70C}_{F}(m)=\#\{(s_{1},\ldots ,s_{n})\in (\mathbb{Z}/m\mathbb{Z})^{n}:F(s_{1},\ldots ,s_{n})\equiv 0~(\text{mod}~m)\}.\end{eqnarray}$$
Under our assumptions
$C_{F,k}$
is positive. (The convergence is a well-known fact when
$n=1$
and follows from Lemma 2.1 for
$n\geqslant 2$
.) In particular, whenever
$d\geqslant 5$
, the quantity
$N_{F,d-1}(B)$
will satisfy the expected asymptotic formula.
Following Browning [Reference Browning4], we can also handle the case when we restrict the inputs to be primes. This extends an Erdős conjecture for
$(d-1)$
-free values of one-variable polynomials at prime arguments to multivariable polynomials with
$d\geqslant 5$
. We thus obtain the following theorem.
Theorem 1.2. Let
$k\geqslant 2$
be a positive integer and let
$F$
be a square-free polynomial with integer coefficients and degree
$d\geqslant 2$
in
$n$
variables, such that for all primes
$p$
, there exists an integer
$n$
-tuple
$(m_{1},\ldots ,m_{n})$
such that
$p^{k}\nmid F(m_{1},\ldots ,m_{n})$
. Put
$$\begin{eqnarray}\displaystyle {\mathcal{N}}_{F,k}(B) & = & \displaystyle \#\{(p_{1},\ldots ,p_{n})\in \mathbb{Z}^{n}:|p_{i}|\leqslant B\nonumber\\ \displaystyle & & \displaystyle \quad ~\text{for }1\leqslant i\leqslant n,F(p_{1},\ldots ,p_{n})\text{ is }k\text{-free}\},\nonumber\end{eqnarray}$$
where
$p_{i}$
is prime for
$1\leqslant i\leqslant n$
. Then there exists a positive number
$C_{F,k}^{\prime }$
such that the asymptotic relation
$$\begin{eqnarray}{\mathcal{N}}_{F,k}(B)\sim C_{F,k}^{\prime }\frac{B^{n}}{(\log B)^{n}}\end{eqnarray}$$
holds whenever
$k\geqslant (3d+1)/4$
.
Here we have
$$\begin{eqnarray}C_{F,k}^{\prime }=\mathop{\prod }_{p}\biggl(1-\frac{\unicode[STIX]{x1D70C}_{F}^{\ast }(p^{k})}{\unicode[STIX]{x1D719}(p^{k})^{n}}\biggr),\end{eqnarray}$$
where
$$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D70C}_{F}^{\ast }(m) & = & \displaystyle \#\{\mathbf{s}\in \mathbb{Z}^{n}:|s_{i}|\leqslant m-1,\text{ for }1\leqslant i\leqslant n,\nonumber\\ \displaystyle & & \displaystyle \quad \gcd (s_{i},s_{j})=1\text{ for all }i<j,F(\mathbf{s})\equiv 0~(\text{mod}~m)\}\end{eqnarray}$$
and
$C_{F,k}^{\prime }$
is again positive under our assumptions.
The proof of Theorems 1.1 and 1.2 will largely rely on the affine determinant method of Heath-Brown [Reference Heath-Brown9], which is the same tool used by Browning in [Reference Browning4]. The main innovation in this paper is using sieve methods to handle medium-sized primes which contribute to
$N_{F,k}(B)$
and
${\mathcal{N}}_{F,k}(B)$
.
2 Preliminaries: the simple and Ekedahl sieves
2.1 Counting
$k$
-free values over integer inputs
We shall find quantities
$N_{1}(B)$
,
$N_{2}(B)$
,
$N_{3}(B)$
such that
$$\begin{eqnarray}N_{1}(B)-N_{2}(B)-N_{3}(B)\leqslant N_{F,k}(B)\leqslant N_{1}(B)\end{eqnarray}$$
and for which
$N_{2}(B),N_{3}(B)=o(B^{n})$
. This is similar to the simple sieve technique of Hooley.
Let
$\unicode[STIX]{x1D709}_{1}=(1/nk)\log B$
and
$\unicode[STIX]{x1D709}_{2}=B(\log B)^{1/2}$
and put
$$\begin{eqnarray}\displaystyle N_{1}(B)=N_{1,k}(B) & = & \displaystyle \#\{(x_{1},\ldots ,x_{n})\in \mathbb{Z}^{n}:|x_{i}|\leqslant B,\nonumber\\ \displaystyle & & \displaystyle \quad p^{k}\mid F(x_{1},\ldots ,x_{n})\Rightarrow p>\unicode[STIX]{x1D709}_{1}\},\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle N_{2}(B)=N_{2,k}(B) & = & \displaystyle \#\{(x_{1},\ldots ,x_{n})\in \mathbb{Z}^{n}:|x_{i}|\leqslant B,\nonumber\\ \displaystyle & & \displaystyle \quad p^{k}\mid F(x_{1},\ldots ,x_{n})\Rightarrow p>\unicode[STIX]{x1D709}_{1},\nonumber\\ \displaystyle & & \displaystyle \quad \exists \unicode[STIX]{x1D709}_{1}<p\leqslant \unicode[STIX]{x1D709}_{2}\text{ s.t. }p^{2}\mid F(x_{1},\ldots ,x_{n})\},\end{eqnarray}$$
and
$$\begin{eqnarray}\displaystyle N_{3}(B)=N_{3,k}(B) & = & \displaystyle \#\{(x_{1},\ldots ,x_{n})\in \mathbb{Z}^{n}:|x_{i}|\leqslant B,\nonumber\\ \displaystyle & & \displaystyle \quad p^{k}\mid F(x_{1},\ldots ,x_{n})\Rightarrow p>\unicode[STIX]{x1D709}_{1},\nonumber\\ \displaystyle & & \displaystyle \quad p^{2}\nmid F(x_{1},\ldots ,x_{n})\text{ for }\unicode[STIX]{x1D709}_{1}<p\leqslant \unicode[STIX]{x1D709}_{2},\nonumber\\ \displaystyle & & \displaystyle \quad \exists p>\unicode[STIX]{x1D709}_{2}\text{ s.t. }p^{k}\mid F(x_{1},\ldots ,x_{n})\}.\end{eqnarray}$$
Then it is clear that (2.1) holds.
We first show that
$N_{1}(X)$
gives us a term with the expected order of magnitude. We require an estimate for
$\unicode[STIX]{x1D70C}_{F}(p^{k})$
given by the following lemma.
Lemma 2.1. Let
$F$
be a square-free polynomial in
$n$
variables with integer coefficients and such that for all primes
$p$
,
$p^{k}$
does not divide
$F$
identically. Then for any
$k\geqslant 2$
we have
$\unicode[STIX]{x1D70C}_{F}(p^{k})=O_{F}(p^{nk-2})$
.
Proof. For a positive integer
$m$
, let
$S_{m}(F)$
denote the set of points (over
$\mathbb{C}$
, say) of
$F$
which have multiplicity
$m$
. It is clear that
$m\leqslant \deg F$
. By our hypothesis on
$F$
it follows that for
$m\geqslant 2$
,
$S_{m}(F)$
is not Zariski dense in the variety
$X_{F}:F=0$
and hence as a subvariety of
$X_{F}$
it has codimension at least one. For all but finitely many primes
$p$
, we have that any smooth point
$\mathbf{x}\in X_{F}\cap \mathbb{Z}^{n}$
over
$\mathbb{C}$
reduces to a smooth point over
$\mathbb{F}_{p}$
; moreover, it follows from standard arguments that smooth points over
$\mathbb{F}_{p}$
contribute at most
$Cp^{n(k-1)}$
to
$\unicode[STIX]{x1D70C}_{F}(p^{k})$
.
We now estimate the contribution from
$S_{m}(F)$
for
$m\geqslant 2$
. For any such point
$\mathbf{x}_{0}\in X_{F}\cap \mathbb{Z}^{n}$
, we can take a Taylor expansion around
$\mathbf{x}_{0}$
and see that
$p^{k}\mid F(\mathbf{x})$
whenever
$\mathbf{x}\equiv \mathbf{x}_{0}\hspace{0.6em}({\rm mod}\hspace{0.2em}p^{\lceil k/m\rceil })$
. Thus, working over
$(\mathbb{Z}/p^{k}\mathbb{Z})^{n}$
and taking
$e=\lceil k/m\rceil$
, we see that each
$\mathbf{x}_{0}\hspace{0.6em}({\rm mod}\hspace{0.2em}p^{e})$
which is the reduction of a point in
$S_{m}(F)$
mod
$p^{e}$
contributes
$O(p^{(k-e)n})=O(p^{kn-en})$
to
$\unicode[STIX]{x1D70C}_{F}(p^{k})$
.
Now, the number of such points mod
$p^{e}$
can be counted as follows. First begin with the set
$S_{m}(F)(p)$
, the set of points of
$X_{F}\hspace{0.6em}({\rm mod}\hspace{0.2em}p)$
which has multiplicity
$m$
. There are
$O(p^{n-2})$
such points, since
$S_{m}(F)(p)$
has codimension one in
$X_{F}$
by hypothesis. For each such point there are at most
$O(p^{(e-1)n})$
points in
$(\mathbb{Z}/p^{e}\mathbb{Z})^{n}$
which lie above it. Thus, there are
$O(p^{(e-1)n+n-2})$
such points. Thus, there are
$$\begin{eqnarray}O(p^{kn-en+(e-1)n+n-2})=O(p^{kn-2})\end{eqnarray}$$
such points, as desired.◻
Now put
$$\begin{eqnarray}N(B;h)=\#\{\mathbf{x}\in \mathbb{Z}^{n}:|x_{i}|\leqslant B,h^{k}\mid F(x_{1},\ldots ,x_{n})\}.\end{eqnarray}$$
By standard properties of the Möbius function
$\unicode[STIX]{x1D707}$
, we then see that
$$\begin{eqnarray}\displaystyle N_{1}(B) & = & \displaystyle \mathop{\sum }_{\substack{ h\in \mathbb{N} \\ p\mid h\Rightarrow p\leqslant \unicode[STIX]{x1D709}_{1}}}\unicode[STIX]{x1D707}(h)N(B;h)\nonumber\\ \displaystyle & = & \displaystyle \mathop{\sum }_{\substack{ h\in \mathbb{N} \\ p\mid h\Rightarrow p\leqslant \unicode[STIX]{x1D709}_{1}}}\unicode[STIX]{x1D707}(h)\unicode[STIX]{x1D70C}_{F}(h^{k})\bigg\{\frac{B^{n}}{h^{nk}}+O\biggl(\frac{B^{n-1}}{h^{k(n-1)}}+1\biggr)\bigg\}.\end{eqnarray}$$
Since the summand vanishes when
$h$
is not square-free, we may assume that
$h$
is in fact square-free. Hence,
$$\begin{eqnarray}h\leqslant \mathop{\prod }_{p\leqslant \unicode[STIX]{x1D709}_{1}}p=\exp \biggl(\mathop{\sum }_{p\leqslant \unicode[STIX]{x1D709}_{1}}\log p\biggr)\leqslant e^{2\unicode[STIX]{x1D709}_{1}}.\end{eqnarray}$$
By Lemma 2.1, we then see that
$$\begin{eqnarray}N_{1}(B)=B^{n}\mathop{\prod }_{p\leqslant \unicode[STIX]{x1D709}_{1}}\biggl(1-\frac{\unicode[STIX]{x1D70C}_{F}(p^{k})}{p^{nk}}\biggr)+O\biggl(\mathop{\sum }_{h\leqslant e^{2\unicode[STIX]{x1D709}_{1}}}h^{kn-2+\unicode[STIX]{x1D700}}(B^{n-1}h^{-k(n-1)}+1)\biggr).\end{eqnarray}$$
The big-
$O$
term can be evaluated to be
$$\begin{eqnarray}O_{\unicode[STIX]{x1D700}}(B^{\unicode[STIX]{x1D700}}(B^{n-1+(k-1)/nk}+B^{(kn-1)/nk}))\end{eqnarray}$$
and we see that this is
$O(B^{n-\unicode[STIX]{x1D6FF}})$
for some
$\unicode[STIX]{x1D6FF}>0$
. Thus, we have
$$\begin{eqnarray}N_{1}(B)=C_{F,k}B^{n}+O(B^{n}\unicode[STIX]{x1D709}_{1}^{-1})+O(B^{n-\unicode[STIX]{x1D6FF}}).\end{eqnarray}$$
Next we give an estimate for
$N_{2}(B)$
.
Lemma 2.2. Let
$N_{2}(B)$
be as in (2.3). Then
$$\begin{eqnarray}N_{2}(B)=O_{d}\biggl(\frac{B^{n}}{\unicode[STIX]{x1D709}_{1}}+\frac{B^{n-1}\unicode[STIX]{x1D709}_{2}}{\log \unicode[STIX]{x1D709}_{2}}\biggr).\end{eqnarray}$$
To prove this lemma, we will need the following result due to Ekedahl; the formulation below is due to Bhargava and Shankar [Reference Bhargava and Shankar2].
Lemma 2.3 (Ekedahl).
Let
${\mathcal{B}}$
be a compact region in
$\mathbb{R}^{n}$
with positive measure and let
$Y$
be any closed subscheme of
$\mathbb{A}_{\mathbb{Z}}^{n}$
of co-dimension
$k\geqslant 2$
. Let
$r$
and
$M$
be positive real numbers. Then we have
$$\begin{eqnarray}\displaystyle & & \displaystyle \#\{v\in r{\mathcal{B}}\cap \mathbb{Z}^{n}:v~(\text{mod}~p)\in Y(\mathbb{F}_{p})\text{ for some }p>M\}\nonumber\\ \displaystyle & & \displaystyle \qquad =O\biggl(\frac{r^{n}}{M^{k-1}\log M}+r^{n-k+1}\biggr).\nonumber\end{eqnarray}$$
Proof of Lemma 2.2.
We fix the variables
$\mathbf{x}=(x_{2},\ldots ,x_{n})$
and, for each such choice, we put
$$\begin{eqnarray}F_{\mathbf{x}}(x)=F(x,x_{2},\ldots ,x_{n}).\end{eqnarray}$$
Define the function, for a polynomial
$f$
in a single variable
$x$
, by
$$\begin{eqnarray}\unicode[STIX]{x1D70C}_{f}(m)=\#\{s\in \mathbb{Z}/m\mathbb{Z}:f(s)\equiv 0~(\text{mod}~m)\}.\end{eqnarray}$$
It is clear from the Chinese remainder theorem that
$\unicode[STIX]{x1D70C}_{f}$
is multiplicative. Observe that
$\unicode[STIX]{x1D70C}_{f}(p)\leqslant d$
if
$p$
does not divide all coefficients of
$f$
and in this case the bound is independent of
$p$
. Moreover, if
$p\nmid \unicode[STIX]{x1D6E5}(f)$
, then for any positive integer
$k$
we have
$\unicode[STIX]{x1D70C}_{f}(p^{k})\leqslant d$
. We now use Lemma 2.3 as follows. Let
$G(x_{1},\ldots ,x_{n})=(\unicode[STIX]{x2202}F/\unicode[STIX]{x2202}x_{1})(x_{1},\ldots ,x_{n})$
. Define the variety
$V_{F,G}$
to be
$$\begin{eqnarray}V_{F,G}=\{(x_{1},\ldots ,x_{n})\in \mathbb{C}^{n}:F(x_{1},\ldots ,x_{n})=G(x_{1},\ldots ,x_{n})=0\}.\end{eqnarray}$$
Observe that
$V_{F,G}$
is of co-dimension two and is defined over
$\mathbb{Z}$
. Put
$$\begin{eqnarray}{\mathcal{N}}_{p}^{\ast }(B)=\{(x_{1},\ldots ,x_{n})\in \mathbb{Z}^{n}:|x_{i}|\leqslant B,(x_{1},\ldots ,x_{n})~(\text{mod}~p)\in V_{F,G}(\mathbb{F}_{p})\}.\end{eqnarray}$$
It follows from Lemma 2.3 that
$$\begin{eqnarray}\#\mathop{\bigcup }_{p>\unicode[STIX]{x1D709}_{1}}{\mathcal{N}}_{p}^{\ast }(B)=O\biggl(\frac{B^{n}}{\unicode[STIX]{x1D709}_{1}\log \unicode[STIX]{x1D709}_{1}}+B^{n-1}\biggr),\end{eqnarray}$$
which is an acceptable error term.
Now put
$$\begin{eqnarray}N_{p}^{\dagger }(B)=\#\{(x_{1},\ldots ,x_{n})\,\in \,\mathbb{Z}^{n}:|x_{i}|\,\leqslant \,B,p^{2}\,\mid \,F(x_{1},\ldots ,x_{n}),p\nmid G(x_{1},\ldots ,x_{n})\}.\end{eqnarray}$$
It then follows that
$$\begin{eqnarray}N_{2}(B)\leqslant \mathop{\sum }_{\unicode[STIX]{x1D709}_{1}<p\leqslant \unicode[STIX]{x1D709}_{2}}N_{p}^{\dagger }(B)+\mathop{\sum }_{\unicode[STIX]{x1D709}_{1}<p\leqslant \unicode[STIX]{x1D709}_{2}}N_{p}^{\ast }(B)\end{eqnarray}$$
and, since we have already estimated the second sum, it suffices to estimate the former. For fixed
$(x_{2},\ldots ,x_{n})$
, the solutions to
$f(x)=F(x,x_{2},\ldots ,x_{n})\equiv 0\hspace{0.6em}({\rm mod}\hspace{0.2em}p^{2})$
contributing to
$N_{p}^{\dagger }(B)$
must satisfy
$p\nmid \unicode[STIX]{x1D6E5}(f)$
; in particular, the number of solutions in
$\mathbb{Z}/p^{2}\mathbb{Z}$
is at most
$d$
. We then have that
$$\begin{eqnarray}\mathop{\sum }_{\unicode[STIX]{x1D709}_{1}<p\leqslant \unicode[STIX]{x1D709}_{2}}N_{p}^{\dagger }(B)=O_{d}\biggl(B^{n-1}\mathop{\sum }_{\unicode[STIX]{x1D709}_{1}<p\leqslant \unicode[STIX]{x1D709}_{2}}\biggl(\frac{B}{p^{2}}+1\biggr)\biggr)=O_{d}\biggl(\frac{B^{n}}{\unicode[STIX]{x1D709}_{1}}+\frac{B^{n-1}\unicode[STIX]{x1D709}_{2}}{\log \unicode[STIX]{x1D709}_{2}}\biggr).\square\end{eqnarray}$$
2.2 Counting
$k$
-free values over prime inputs
We shall seek an analogue to (2.1) for the case of prime inputs. Put
${\mathcal{N}}_{1}(B)$
,
${\mathcal{N}}_{2}(B)$
,
${\mathcal{N}}_{3}(B)$
for the analogues to (2.2), (2.3), (2.4) in the case of prime inputs. We begin with an estimate for
${\mathcal{N}}_{1}(B)$
. Since we are interested in prime inputs, we should modify the function
$\unicode[STIX]{x1D70C}_{F}(m)$
. In particular, the only way for
$\mathbf{m}$
with all prime coordinates to have two coordinates to share a common factor is if they are equal and thus
$\mathbf{m}$
lies on one of the hyperplanes in
$\mathbb{R}^{n}$
defined by
$x_{i}=x_{j}$
for some
$i<j$
. These points are negligible in the box
$[-B,B]^{n}\cap \mathbb{Z}^{n}$
, so we may assume that
$\gcd (m_{i},m_{j})=1$
for all
$i<j$
and consider the modified quantity (1.2).
It is immediate that
$\unicode[STIX]{x1D70C}_{F}^{\ast }(p^{k})=O_{d,n}(p^{kn-2})$
. Moreover, the number of possible elements in
$(\mathbb{Z}/p^{k}\mathbb{Z})^{n}$
such that no coordinate is divisible by
$p$
is
$\unicode[STIX]{x1D719}(p^{k})^{n}=(p^{k}-p^{k-1})^{n}$
. Similar to (2.5), we find that
$$\begin{eqnarray}\displaystyle {\mathcal{N}}_{1}(B) & = & \displaystyle \mathop{\sum }_{\substack{ p\in \mathbb{N} \\ p\mid h\Rightarrow p>\unicode[STIX]{x1D709}_{1}^{\prime }}}\unicode[STIX]{x1D707}(h)\unicode[STIX]{x1D70C}_{F}^{\ast }(p^{k})(\frac{B^{n}}{\unicode[STIX]{x1D719}(p^{k})^{n}(\log B)^{n}}\nonumber\\ \displaystyle & & \displaystyle +\,O_{c}\biggl(\frac{B^{n}}{\unicode[STIX]{x1D719}(p^{k})^{n-1}(\log B)^{n-1}\exp (c\sqrt{\log B})}\biggr))\nonumber\end{eqnarray}$$
by the Siegel–Walfisz theorem. We thus find that
$$\begin{eqnarray}{\mathcal{N}}_{1}(B)=\frac{B^{n}}{(\log B)^{n}}\mathop{\prod }_{p\leqslant \unicode[STIX]{x1D709}_{1}^{\prime }}\biggl(1-\frac{\unicode[STIX]{x1D70C}_{F}^{\ast }(p^{k})}{\unicode[STIX]{x1D719}(p^{k})^{n}}\biggr)+O_{c}\biggl(\frac{B^{n}(\unicode[STIX]{x1D709}_{1}^{\prime })^{nk}}{(\log B)^{n-1}\exp (c\sqrt{\log B})}\biggr).\end{eqnarray}$$
Since
$\exp (c\sqrt{\log B})$
is eventually larger than any power of
$\log B$
, we may take
$\unicode[STIX]{x1D709}_{1}^{\prime }=(\log B)^{n^{2}k^{2}}$
, say. We then see that
${\mathcal{N}}_{1}(B)$
approximates our main term, bearing in mind that in a similar way we have
$C_{F,k}^{\prime }>0$
. Now the proof of the analogue of Lemma 2.2 for
${\mathcal{N}}_{2}(B)$
carries through as before, with
$\unicode[STIX]{x1D709}_{1}$
replaced with
$\unicode[STIX]{x1D709}_{1}^{\prime }$
and
$\unicode[STIX]{x1D709}_{2}$
replaced with
$B\exp (-c\sqrt{\log B})$
. The remaining quantity
${\mathcal{N}}_{3}(B)$
will be estimated by the upper bound of
$N_{3}(B)$
, which is obtained at the end of the paper in §3.1.
In the next section, we shall derive a version of the global determinant method which applies to affine varieties, refining Heath-Brown’s Theorem 15 in [Reference Heath-Brown9]. It is well known that the global determinant method produces estimates which are uniform in the coefficients of the polynomials involved and produces power-saving error terms. Thus, the proofs of Theorems 1.1 and 1.2 in the case
$d>4$
can be carried out simultaneously.
3 Global affine determinant method
In [Reference Heath-Brown8], Heath-Brown introduced a novel technique which is widely applicable to the subject of counting rational points on algebraic varieties, which is now known as the
$p$
-adic determinant method. It is a generalization of the original determinant method of Bombieri and Pila, which is based on real analytic arguments. This was later refined by Salberger in [Reference Salberger16]. Salberger named his refinement the global determinant method, in reference to the fact that it uses multiple primes simultaneously.
In [Reference Heath-Brown9], Heath-Brown gave a different refinement of his
$p$
-adic determinant method in [Reference Heath-Brown8]. Originally the
$p$
-adic determinant method could only treat projective hypersurfaces, but in [Reference Heath-Brown9] Heath-Brown showed that an analogous version exists for affine varieties. Browning combined Salberger’s global determinant method with the affine method of Heath-Brown for surfaces in [Reference Browning4], in application to power-free values of polynomials in one or two variables.
We now give a complete statement of the global determinant method in the affine setting, recovering the generality given by Salberger in [Reference Salberger16] and Xiao in [Reference Xiao17] (in the setting of weighted projective spaces).
For positive numbers
$B_{1},\ldots ,B_{n}$
all exceeding one, put
$$\begin{eqnarray}S(F;B_{1},\ldots ,B_{n})=\{\mathbf{x}\in \mathbb{Z}^{n}:|x_{i}|\leqslant B_{i},F(\mathbf{x})=0\}.\end{eqnarray}$$
Put
$X$
for the hypersurface in
$\mathbb{A}^{n}$
defined by
$F$
. For a prime
$p$
and a point
$P\in X(\mathbb{F}_{p})$
, put
$$\begin{eqnarray}S_{p}(F;B_{1},\ldots ,B_{n};P)=\{\mathbf{x}\in S(F;B_{1},\ldots ,B_{n}):\mathbf{x}\equiv P~(\text{mod}~p)\}.\end{eqnarray}$$
For a vector of non-negative integers
$\mathbf{e}=(e_{1},\ldots ,e_{n})$
, put
$\mathbf{x}^{\mathbf{e}}=x_{1}^{e_{1}}\cdots x_{n}^{e_{n}}$
. Let
${\mathcal{E}}$
be a finite set of vectors in
$\mathbb{Z}^{n}$
with non-negative entries. Put
$s_{P}=\#S_{p}(F;\mathbf{B};P)$
and
$E=\#{\mathcal{E}}$
. Consider the
$s_{P}\times E$
matrix
${\mathcal{M}}$
whose
$(ij)$
th entry is the
$i$
th monomial in
${\mathcal{E}}$
evaluated at the
$j$
th element of
$S_{p}(F;\mathbf{x};P)$
.
We pick the same exponent set
${\mathcal{E}}$
as Heath-Brown in [Reference Heath-Brown9]. In particular, write
$$\begin{eqnarray}F(x_{1},\ldots ,x_{n})=\mathop{\sum }_{\mathbf{f}}a_{\mathbf{f}}\mathbf{x}^{\mathbf{f}}\end{eqnarray}$$
and let
${\mathcal{P}}(F)$
be the Newton polyhedron of
$F$
. Put
$$\begin{eqnarray}T=\max _{\mathbf{f}\in {\mathcal{P}}(F)}\mathbf{B}^{\mathbf{f}},\end{eqnarray}$$
where
$\mathbf{B}=(B_{1},\ldots ,B_{n})$
is a vector in
$\mathbb{R}^{n}$
with
$B_{i}\geqslant 1$
for
$1\leqslant i\leqslant n$
. Then there is at least one element
$\mathbf{m}\in {\mathcal{P}}(F)$
such that
$T=\mathbf{B}^{\mathbf{m}}$
. We pick a parameter
$\unicode[STIX]{x1D706}>0$
and put
${\mathcal{Y}}=\unicode[STIX]{x1D706}\log T$
. We then define our exponent set
${\mathcal{E}}$
to be
$$\begin{eqnarray}{\mathcal{E}}=\bigg\{\!\mathbf{e}\in \mathbb{Z}^{n}:e_{i}\geqslant 0\text{ for }1\leqslant i\leqslant n,\!\mathop{\sum }_{i=1}^{n}e_{i}\log B_{i}\leqslant {\mathcal{Y}},e_{i}<m_{i}\text{ for at least one }i\!\bigg\}.\end{eqnarray}$$
We shall abuse notation and also refer to
${\mathcal{E}}$
as a set of monomials. It was shown by Heath-Brown in [Reference Heath-Brown9] that all non-trivial linear combinations of monomials whose exponent vectors lie in
${\mathcal{E}}$
lead to a polynomial which is not divisible by
$F$
.
Put
$$\begin{eqnarray}W=\exp \biggl(\biggl(\frac{\mathop{\prod }_{1\leqslant i\leqslant n}\log B_{i}}{\log T}\biggr)^{1/(n-1)}\biggr).\end{eqnarray}$$
We can now state the main result of this section, which is the global determinant method analogue of Heath-Brown’s Theorem 15 in [Reference Heath-Brown9].
Theorem 3.1. Let
$\mathbf{B}=(B_{1},\ldots ,B_{n})\in \mathbb{R}^{n}$
be a vector of positive numbers of size at least
$1$
. Let
$X$
be a hypersurface defined over
$\mathbb{Z}$
in
$\mathbb{A}^{n}$
which is irreducible over
$\mathbb{Q}$
and defined by an irreducible polynomial
$F$
. Let
${\mathcal{U}}$
be a finite set of primes and put
$$\begin{eqnarray}{\mathcal{Q}}=\mathop{\prod }_{p\in {\mathcal{U}}}p.\end{eqnarray}$$
For each prime
$p\in {\mathcal{U}}$
, let
$P_{p}$
be a non-singular point in
$X(\mathbb{F}_{p})$
and put
$$\begin{eqnarray}\mathbf{U}=\{P_{p}:p\in {\mathcal{U}}\}.\end{eqnarray}$$
Let
${\mathcal{E}}$
be as given in (3.1). Then:
(a) let
$\unicode[STIX]{x1D700}>0$
. If then there is a hypersurface$$\begin{eqnarray}WT^{\unicode[STIX]{x1D700}}<{\mathcal{Q}}\leqslant WT^{2\unicode[STIX]{x1D700}},\end{eqnarray}$$
$Y(\mathbf{U})$
containing
$S(F;\mathbf{B};\mathbf{U})$
, not containing
$X$
and defined by a primitive polynomial
$G$
, whose degree is
$O_{d,n,\unicode[STIX]{x1D700}}(1)$
and whose height is at most
$O_{d,n,\unicode[STIX]{x1D700}}(\log T)$
;(b) if
$X$
is geometrically integral, then there exists a hypersurface
$Y(\mathbf{U})$
containing
$S(F;\mathbf{B},\mathbf{U})$
, not containing
$X$
and defined by a primitive polynomial
$G$
, whose degree satisfies $$\begin{eqnarray}\deg G=O_{d,n}((1+{\mathcal{Q}}^{-1}W)\log T{\mathcal{Q}}).\end{eqnarray}$$
Theorem 3.1 can be proved using the same arguments as in [Reference Salberger16] or [Reference Xiao17]. The key insight is that the proofs in [Reference Salberger16] and [Reference Xiao17] producing large divisors of the discriminants essentially reduce to the affine case, so they remain valid if one starts with the affine case.
We will now need the following lemma, which is a consequence of Theorem 3.1, and was stated without proof in [Reference Browning4].
Lemma 3.2. Let
$X$
be a geometrically integral affine surface of degree
$d$
in
$\mathbb{A}^{3}$
defined by an integral polynomial
$F$
and let
$\mathbf{B}=(B_{1},B_{2},B_{3})$
be a vector of positive numbers exceeding one. Then for any
$\unicode[STIX]{x1D700}>0$
there exists a collection of integral polynomials
$\unicode[STIX]{x1D6E4}$
, defined over
$\mathbb{Z}$
, such that:
(a)
$\#\unicode[STIX]{x1D6E4}=O_{d,\unicode[STIX]{x1D700}}(W^{1+\unicode[STIX]{x1D700}});$
(b) each polynomial
$G\in \unicode[STIX]{x1D6E4}$
is co-prime with
$F$
;(c) the number of points in
$X(\mathbb{Z};\mathbf{B})$
not lying on
$\{G=0\},G\in \unicode[STIX]{x1D6E4}$
is at most
$O_{d,\unicode[STIX]{x1D700}}(W^{2+\unicode[STIX]{x1D700}})$
; and(d) each polynomial
$G\in \unicode[STIX]{x1D6E4}$
has degree
$O_{d,\unicode[STIX]{x1D700}}(1)$
.
Proof. The proof given here follows the proofs of Lemma 2.8 in [Reference Salberger16] and Theorem 1.1 in [Reference Xiao17]. By Theorem 3.1, there exists an affine surface
$Y_{0}$
, defined over
$\mathbb{Z}$
, which contains
$X(\mathbb{Z};\mathbf{B})$
but does not contain
$X$
as a component, which is defined by a polynomial
$G_{0}$
of degree
$O_{d}(W^{1+\unicode[STIX]{x1D700}})$
.
Let
$p_{1}<\cdots <p_{t+1}$
be the sequence of increasing consecutive primes satisfying
$p_{1}>\log (B_{1}B_{2}B_{3})$
and
$$\begin{eqnarray}p_{1}\cdots p_{t}\leqslant WT^{\unicode[STIX]{x1D700}}<p_{1}\cdots p_{t+1}.\end{eqnarray}$$
Write
$$\begin{eqnarray}Q_{t}=\mathop{\prod }_{i=1}^{t+1}p_{i}.\end{eqnarray}$$
Then, following the arguments in [Reference Xiao17], we see that
$Q_{t}=O(W^{1+\unicode[STIX]{x1D700}}\log W)$
.
We now begin constructing the set of polynomials
$\unicode[STIX]{x1D6E4}$
. By Theorem 3.1, for each point
$P_{p_{1}}\in X(\mathbb{F}_{p_{1}})$
, there exists a surface
$Y(P_{p_{1}})$
containing
$X(\mathbb{Z};\mathbf{B};P_{p_{1}})$
but which does not contain
$X$
as a component of degree
$$\begin{eqnarray}O_{d}((1+p_{1}^{-1}W)\log W).\end{eqnarray}$$
The surface
$Y(P_{p_{1}})$
is defined by a polynomial
$G_{P_{p_{1}}}$
with integer coefficients. Put
$\unicode[STIX]{x1D6E4}(P_{p_{1}})$
for the set of irreducible factors
$g$
of
$G_{P_{p_{1}}}$
for which the intersection of
$\{g=0\}\cap X$
contains a curve which lies in the intersection
$Y_{0}\cap X$
. Now put
$\unicode[STIX]{x1D6E4}^{(1)}=\bigcup _{P_{p_{1}}\in X(\mathbb{F}_{p_{1}})}\unicode[STIX]{x1D6E4}(P_{p_{1}})$
. Note that
$\#\unicode[STIX]{x1D6E4}^{(1)}$
is bounded by the number of components of
$Y_{0}\cap X$
, which is bounded by
$O_{d}(W^{1+\unicode[STIX]{x1D700}})$
by Bézout’s theorem. Moreover, since for each
$g\in \unicode[STIX]{x1D6E4}^{(1)}$
there is a divisor of
$G_{P_{p_{1}}}$
for some
$P_{p_{1}}\in X(\mathbb{F}_{p_{1}})$
, its degree is at most
$O_{d}((1+p_{1}^{-1}W)\log W)$
.
Likewise, for any points
$P_{1}\in X(\mathbb{F}_{p_{1}})$
and
$P_{2}\in X(\mathbb{F}_{p_{2}})$
, there exists a polynomial
$G_{P_{1},P_{2}}$
defining a surface
$Y(P_{1},P_{2})$
of degree
$O_{d,\unicode[STIX]{x1D700}}((1+(p_{1}p_{2})^{-1}W)\log W)$
which contains
$X(\mathbb{Z};\mathbf{B};P_{1},P_{2})$
. Now put
$\unicode[STIX]{x1D6E4}^{(2)}$
for the collection of polynomials
$g$
dividing
$G_{P_{1},P_{2}}$
for some
$P_{1}\in X(\mathbb{F}_{p_{1}}),P_{2}\in X(\mathbb{F}_{p_{2}})$
and such that
$\{g=0\}\cap X$
contains a curve which is also contained in
$Y_{0}\cap X$
. Again, we see that
$$\begin{eqnarray}\deg g=O_{d,\unicode[STIX]{x1D700}}((1+(p_{1}p_{2})^{-1}W)\log W)\end{eqnarray}$$
and
$$\begin{eqnarray}\#\unicode[STIX]{x1D6E4}^{(2)}=O_{d,\unicode[STIX]{x1D700}}(W^{1+\unicode[STIX]{x1D700}}).\end{eqnarray}$$
We continue this process until we reach
$t+1$
and set
$\unicode[STIX]{x1D6E4}=\unicode[STIX]{x1D6E4}^{(t+1)}$
. We then see that
$$\begin{eqnarray}\#\unicode[STIX]{x1D6E4}=O_{d,\unicode[STIX]{x1D700}}(W^{1+\unicode[STIX]{x1D700}})\end{eqnarray}$$
and, for each
$g\in \unicode[STIX]{x1D6E4}$
, we have
$$\begin{eqnarray}\deg g=O_{d,\unicode[STIX]{x1D700}}(1)\end{eqnarray}$$
by part (a) of Theorem 3.1.
The points which lie on the complement
${\mathcal{Z}}$
of the union of the integral points on the surfaces defined by polynomials in
$\unicode[STIX]{x1D6E4}$
in
$X(\mathbb{Z};\mathbf{B})$
can be estimated as follows. If
$\mathbf{x}\in {\mathcal{Z}}$
, then there exists
$0\leqslant j\leqslant t+1$
such that the irreducible component of
$Y(P_{1},\ldots ,P_{j})$
containing
$\mathbf{x}$
and the irreducible component of
$Y(P_{1},\ldots ,P_{j+1})$
containing
$\mathbf{x}$
differ. Then
$\mathbf{x}$
lies on a zero-dimensional scheme defined by
$F,g_{1},g_{2}$
, where
$g_{1},g_{2}$
are distinct polynomials such that
$g_{1}\mid G(P_{1},\ldots ,P_{j})$
and
$g_{2}\mid G(P_{1},\ldots ,P_{j+1})$
. Thus, the number of such
$\mathbf{x}$
is bounded by
$$\begin{eqnarray}O_{d}((1+(p_{1}\cdots p_{j})^{-1}W)\log W)((1+(p_{1}\cdots p_{j+1})^{-1}W)\log W)\end{eqnarray}$$
by Bézout’s theorem. Since
$t=O_{d}((\log T)/\text{log}\log T)$
, it follows that
$$\begin{eqnarray}\#{\mathcal{Z}}=O_{d,\unicode[STIX]{x1D700}}(W^{2+\unicode[STIX]{x1D700}}),\end{eqnarray}$$
as desired.◻
The next lemma, given as Lemma 2 in [Reference Browning4], then follows.
Lemma 3.3. Let
$f(x)$
be a polynomial of degree
$d$
with integer coefficients and let
$B_{1},B_{2},B_{3}$
be positive real numbers. Put
$M(f;\mathbf{B})$
for the number of integer solutions to the equation
$$\begin{eqnarray}f(x)=yz^{k}\end{eqnarray}$$
satisfying
$$\begin{eqnarray}B_{1}/2\leqslant x<B_{1},\qquad B_{2}/2\leqslant y<B_{2},\qquad B_{3}/2\leqslant z<B_{3}.\end{eqnarray}$$
Then
$$\begin{eqnarray}M(f;\mathbf{B})=O_{d,\unicode[STIX]{x1D700},k}((B_{1}B_{2}B_{3})^{\unicode[STIX]{x1D700}}W(W+B_{1}B_{3}^{-k}+B_{3}^{1/d})).\end{eqnarray}$$
We remark that in [Reference Browning4], Browning had required that
$f$
be irreducible, but this is not a necessary assumption. Indeed, the surface defined by
$f(x)=yz^{k}$
is geometrically integral whenever
$f$
is not identically zero; therefore, the machinery established by Salberger in [Reference Salberger16] will be applicable.
We may now finalize the proofs of Theorems 1.1 and 1.2 when
$d\geqslant 5$
.
3.1 Estimate of
$N_{3}(B)$
Following the strategy of Browning in [Reference Browning4], we may fix
$n-1$
variables, say
$x_{2},\ldots ,x_{n}$
, and reduce the problem to the single-variable case. For a positive number
$H$
, put
$$\begin{eqnarray}R(F;B,H)=\#\{\mathbf{x}\in \mathbb{Z}^{n}:|x_{i}|\leqslant B,y\ll B^{d}/H^{k},H/2\leqslant z<H,F(\mathbf{x})=yz^{k}\}.\end{eqnarray}$$
We then see, by dyadic summation, that
$$\begin{eqnarray}N_{3}(B)\ll (\log B)\sup _{\unicode[STIX]{x1D709}_{2}<H\ll B^{d/k}}R(F;B,H).\end{eqnarray}$$
Put
$F_{\mathbf{m}}(x)=F(x,m_{2},\ldots ,m_{n})$
, where
$\mathbf{m}=(m_{2},\ldots ,m_{n})$
. Then
$$\begin{eqnarray}R(F;B,H)\leqslant \mathop{\sum }_{|m_{2}|,\ldots ,|m_{n}|\leqslant B}R(F_{\mathbf{m}};B,H).\end{eqnarray}$$
Put
$H=B^{\unicode[STIX]{x1D702}}$
and
$e=\deg F_{\mathbf{m}}(x)$
. We can assume that the
$x_{1}^{d}$
coefficient in
$F$
is non-zero after applying a unimodular transformation to the variables. Then we see from (3.2) and our hypothesis that
$$\begin{eqnarray}W=\exp \left(\sqrt{\frac{(\log B)\unicode[STIX]{x1D702}(\log B)(d\log B-\unicode[STIX]{x1D702}k\log B)}{d\log B}}\right)=B^{\sqrt{\unicode[STIX]{x1D702}(1-k\unicode[STIX]{x1D702}/d)}}.\end{eqnarray}$$
We need to ensure that
$F(x_{1},\mathbf{n})$
is non-singular as a polynomial in a single variable. Let
$\unicode[STIX]{x1D6E5}(x_{2},\ldots ,x_{n})$
be the discriminant of
$F(x_{1},\ldots ,x_{n})$
, where we view the
$x_{2},\ldots ,x_{n}$
as coefficients of
$F(x_{1},\mathbf{x})$
. Then
$F(x_{1},\mathbf{m})$
is singular if and only if
$\unicode[STIX]{x1D6E5}(m_{2},\ldots ,m_{n})=0$
. Thus, we may apply Ekedahl’s sieve to conclude that such tuples are negligible.
We then apply Lemma 3.3 to see that
$$\begin{eqnarray}R(F_{\mathbf{m}};B,H)\ll \biggl(BH\frac{B^{d}}{H^{k}}\biggr)^{\unicode[STIX]{x1D700}}B^{\sqrt{\unicode[STIX]{x1D702}(1-k\unicode[STIX]{x1D702}/d)}}(B^{\sqrt{\unicode[STIX]{x1D702}(1-k\unicode[STIX]{x1D702}/d)}}+B^{1-k\unicode[STIX]{x1D702}}+B^{\unicode[STIX]{x1D702}/d}).\end{eqnarray}$$
We note that for any
$v>0$
, the quadratic function
$$\begin{eqnarray}y=x(1-vx)\end{eqnarray}$$
is concave down and decreasing on the positive real line. Therefore, the maximum value for the term
$\sqrt{\unicode[STIX]{x1D702}(1-k\unicode[STIX]{x1D702}/d)}$
is achieved when
$\unicode[STIX]{x1D702}$
is minimum. Since
$H\gg \unicode[STIX]{x1D709}_{2}$
, it follows that
$\unicode[STIX]{x1D702}\geqslant 1$
, so the maximum occurs when
$\unicode[STIX]{x1D702}=1$
. Thus, the maximum value is
$$\begin{eqnarray}\sqrt{1-k/d}.\end{eqnarray}$$
Note that
$$\begin{eqnarray}\sqrt{1-\frac{k}{d}}>1-k\quad \text{and}\quad \sqrt{1-\frac{k}{d}}>\frac{1}{d}.\end{eqnarray}$$
It thus follows that
$$\begin{eqnarray}N_{3}(B)=O_{d,n,\unicode[STIX]{x1D700}}(B^{n-1+2\sqrt{\unicode[STIX]{x1D702}(1-k\unicode[STIX]{x1D702}/d)}+\unicode[STIX]{x1D700}}).\end{eqnarray}$$
We want to have
$N_{3}(B)=O(B^{n-\unicode[STIX]{x1D716}})$
, so that to prove both Theorems 1.1 and 1.2, we shall simply insist that
$$\begin{eqnarray}2\sqrt{1-k/d}<1,\end{eqnarray}$$
which is equivalent to
$k>3d/4$
. This finishes the proofs.
Acknowledgements
We would like to thank the referee for her/his very careful reading and pointing out several issues which were addressed in the current version. K. Lapkova is supported by a Hertha Firnberg grant (T846-N35) of the Austrian Science Fund (FWF).
