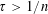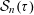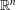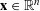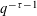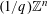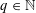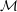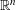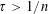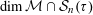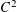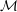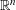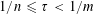1 Introduction
Throughout
$\unicode[STIX]{x1D713}:\mathbb{N}\rightarrow \mathbb{R}^{+}$
will denote a monotonic function that will be referred to as an approximating function,
$n\in \mathbb{N}$
and
${\mathcal{S}}_{n}(\unicode[STIX]{x1D713})$
will be the set of
$\unicode[STIX]{x1D713}$
-approximable points
$\mathbf{y}\in \mathbb{R}^{n}$
, that is points
$\mathbf{y}=(y_{1},\ldots ,y_{n})$
$\in \mathbb{R}^{n}$
such that
$$\begin{eqnarray}\max _{1\leqslant i\leqslant n}|qy_{i}-p|<\unicode[STIX]{x1D713}(q)\end{eqnarray}$$
holds for infinitely many integer vectors
$(\mathbf{p},q)=(p_{1},\ldots ,p_{n},q)\in \mathbb{Z}^{n}\times \mathbb{N}$
. Thus the point
$\mathbf{y}$
lies within distance
$\unicode[STIX]{x1D713}(q)/q$
(in the supremum norm) from the lattice
$(1/q)\mathbb{Z}^{n}$
for infinitely many
$q\in \mathbb{N}$
.
If
$\unicode[STIX]{x1D713}(q)=q^{-\unicode[STIX]{x1D70F}}$
for some
$\unicode[STIX]{x1D70F}>0$
, then we write
${\mathcal{S}}_{n}(\unicode[STIX]{x1D70F})$
for
${\mathcal{S}}_{n}(\unicode[STIX]{x1D713})$
and say that
$\mathbf{y}\in {\mathcal{S}}_{n}(\unicode[STIX]{x1D70F})$
is
$\unicode[STIX]{x1D70F}$
-approximable. The classical theorem of Dirichlet states that for any
$\mathbf{y}\in \mathbb{R}^{n}$
, there exist infinitely many
$(\mathbf{p},q)=(p_{1},\ldots ,p_{n},q)\in \mathbb{Z}^{n}\times \mathbb{N}$
such that
$$\begin{eqnarray}\max _{1\leqslant i\leqslant n}|qy_{i}-p_{i}|<q^{-1/n}\quad (1\leqslant i\leqslant n).\end{eqnarray}$$
Hence,
$$\begin{eqnarray}{\mathcal{S}}_{n}(\unicode[STIX]{x1D70F})=\mathbb{R}^{n}\quad \text{for any }\unicode[STIX]{x1D70F}\leqslant \frac{1}{n}.\end{eqnarray}$$
In turn, a rather simple consequence of the Borel–Cantelli lemma from probability theory is that
${\mathcal{S}}_{n}(\unicode[STIX]{x1D713})$
is null (that is of
$n$
-dimensional Lebesgue measure zero) whenever
$\sum _{q=1}^{\infty }\unicode[STIX]{x1D713}^{n}(q)<\infty$
. Thus, for any
$\unicode[STIX]{x1D70F}>1/n$
almost every point
$\mathbf{y}\in \mathbb{R}^{n}$
is not
$\unicode[STIX]{x1D70F}$
-approximable. However, Khintchine’s theorem [Reference Khintchine21] tells us that the set
${\mathcal{S}}_{n}(\unicode[STIX]{x1D713})$
is full (that is its complement is of Lebesgue measure zero) whenever
$\sum _{q=1}^{\infty }\unicode[STIX]{x1D713}^{n}(q)=\infty$
. In order to quantify the size of
${\mathcal{S}}_{n}(\unicode[STIX]{x1D713})$
when it is null, Jarník [Reference Jarník20] and Besicovitch [Reference Besicovitch15] pioneered the use of Hausdorff measures and dimension. Throughout,
$\dim X$
will denote the Hausdorff dimension of a subset
$X$
of
$\mathbb{R}^{n}$
and
${\mathcal{H}}^{s}(X)$
the
$s$
-dimensional Hausdorff measure (see §2 for the definition and further details). The modern version of the classical Jarník–Besicovitch theorem (see [Reference Beresnevich, Bernik, Dodson, Velani, William, Gowers, Halberstam, Schmidt and Vaughan2, Reference Beresnevich, Dickinson and Velani3]) states that for any approximating function
$\unicode[STIX]{x1D713}$
$$\begin{eqnarray}\dim {\mathcal{S}}_{n}(\unicode[STIX]{x1D713})=\min \biggl\{n,\frac{n+1}{\unicode[STIX]{x1D70F}_{\unicode[STIX]{x1D713}}^{\ast }+1}\biggr\}\quad \text{where }\unicode[STIX]{x1D70F}_{\unicode[STIX]{x1D713}}^{\ast }:=\liminf _{q\rightarrow \infty }\frac{-\text{log}\,\unicode[STIX]{x1D713}(q)}{\log q}.\end{eqnarray}$$
In other words, the “modern theorem” relates the Hausdorff dimension of
${\mathcal{S}}_{n}(\unicode[STIX]{x1D713})$
to the lower order at infinity of
$1/\unicode[STIX]{x1D713}$
and up to a certain degree allows us to discriminate between
$\unicode[STIX]{x1D713}$
-approximable sets of Lebesgue measure zero. The classical Jarník–Besicovitch theorem corresponds to (1.3) with
${\mathcal{S}}_{n}(\unicode[STIX]{x1D713})$
replaced by
${\mathcal{S}}_{n}(\unicode[STIX]{x1D70F})$
and so by definition
$\unicode[STIX]{x1D70F}_{\unicode[STIX]{x1D713}}^{\ast }=\unicode[STIX]{x1D70F}$
. A more delicate measurement of the “size” of
${\mathcal{S}}_{n}(\unicode[STIX]{x1D713})$
is obtained by expressing the size in terms of Hausdorff measures
${\mathcal{H}}^{s}$
. With respect to such measures, the modern version of Jarník theorem (see [Reference Beresnevich, Bernik, Dodson, Velani, William, Gowers, Halberstam, Schmidt and Vaughan2] or [Reference Beresnevich, Dickinson and Velani3]) states that for any
$s\in (0,n)$
and any approximating function
$\unicode[STIX]{x1D713}$
$$\begin{eqnarray}{\mathcal{H}}^{s}({\mathcal{S}}_{n}(\unicode[STIX]{x1D713}))=\left\{\begin{array}{@{}ll@{}}0 & \text{if}\;\displaystyle \mathop{\sum }_{q=1}^{\infty }q^{n-s}\unicode[STIX]{x1D713}^{s}(q)<\infty ,\\ \infty & \text{if}\;\displaystyle \mathop{\sum }_{q=1}^{\infty }q^{n-s}\unicode[STIX]{x1D713}^{s}(q)=\infty .\end{array}\right.\end{eqnarray}$$
This statement is a natural generalization of Khintchine’s theorem (a Lebesgue measure statement) to Hausdorff measures and it is easily verified that it implies (1.3). It is worth pointing out that there is an even more general version of (1.4) that makes use of more general Hausdorff measures, see [Reference Beresnevich, Bernik, Dodson, Velani, William, Gowers, Halberstam, Schmidt and Vaughan2, Reference Beresnevich, Dickinson and Velani3, Reference Beresnevich and Velani9, Reference Dickinson and Velani17]. Within this paper we restrict ourselves to the case of
$s$
-dimensional Hausdorff measures. For background and further details regarding the classical theory of metric Diophantine approximation with an emphasis on the statements described above see [Reference Beresnevich, Ramírez, Velani, Badziahin, Gorodnik and Peyerimhoff5, Reference Beresnevich and Velani12].
When the coordinates of the approximated point
$\mathbf{y}\in \mathbb{R}^{n}$
are confined by functional relations, we fall into the theory of Diophantine approximation on manifolds. In short, given a manifold
${\mathcal{M}}$
of
$\mathbb{R}^{n}$
the aim is to establish analogues of the fundamental theorems of Khintchine, Jarník–Besicovitch and Jarník, and thereby provide a complete measure theoretic description of the sets
${\mathcal{S}}_{n}(\unicode[STIX]{x1D713})\,\cap \,{\mathcal{M}}$
. The fact that the points
$\mathbf{y}\in \mathbb{R}^{n}$
of interest are of dependent variables, which reflects the fact that
$\mathbf{y}\in {\mathcal{M}}$
, introduces major difficulties in attempting to describe the measure theoretic structure of
${\mathcal{S}}_{n}(\unicode[STIX]{x1D713})\cap {\mathcal{M}}$
.
A differentiable manifold
${\mathcal{M}}$
of
$\mathbb{R}^{n}$
is called extremal if for any
$\unicode[STIX]{x1D70F}>1/n$
almost every
$\mathbf{y}\in {\mathcal{M}}$
(in the sense of the induced Lebesgue measure on
${\mathcal{M}}$
) is not
$\unicode[STIX]{x1D70F}$
-approximable [Reference Bernik and Dodson14]. Thus,
${\mathcal{M}}=\mathbb{R}^{n}$
is extremal. In 1998 Kleinbock and Margulis [Reference Kleinbock and Margulis23] proved Sprindžuk’s conjecture; namely that any non-degenerate submanifold of
$\mathbb{R}^{n}$
is extremal. Essentially, these are smooth submanifolds of
$\mathbb{R}^{n}$
which are sufficiently curved so as to deviate from any hyperplane. Any real, connected analytic manifold not contained in any hyperplane of
$\mathbb{R}^{n}$
is non-degenerate. The extremality result of [Reference Kleinbock and Margulis23] has subsequently been extended to include various degenerate manifolds and more generally subsets of
$\mathbb{R}^{n}$
that support so called friendly measures, see [Reference Kleinbock22, Reference Kleinbock, Lindenstrauss and Weiss24, Reference Pollington and Velani25] and references within. Indeed, over the last decade or so, the theory of Diophantine approximation on manifolds has developed at some considerable pace with the catalyst being the pioneering work of Kleinbock and Margulis. For details of this and an overview of the current state of the more subtle Khintchine and Jarník type results for
${\mathcal{S}}_{n}(\unicode[STIX]{x1D713})\cap {\mathcal{M}}$
see [Reference Beresnevich, Ramírez, Velani, Badziahin, Gorodnik and Peyerimhoff5, §6] and references within.
The main goal of this paper is to establish Jarník–Besicovitch type results for manifolds. In other words, we are interested in the Hausdorff dimension of
${\mathcal{S}}_{n}(\unicode[STIX]{x1D70F})\cap {\mathcal{M}}$
for
$\unicode[STIX]{x1D70F}>1/n$
. Note that in view of (1.2), for
$\unicode[STIX]{x1D70F}\leqslant 1/n$
we always have that
${\mathcal{S}}_{n}(\unicode[STIX]{x1D70F})\cap {\mathcal{M}}={\mathcal{M}}$
and so there is nothing more to say. Throughout, let
$m$
denote the codimension of the differentiable submanifold
${\mathcal{M}}$
of
$\mathbb{R}^{n}$
. Then, heuristic considerations quickly lead to the following formula:
$$\begin{eqnarray}\dim {\mathcal{S}}_{n}(\unicode[STIX]{x1D70F})\cap {\mathcal{M}}=\frac{n+1}{\unicode[STIX]{x1D70F}+1}-m.\end{eqnarray}$$
In the case
${\mathcal{M}}=\mathbb{R}^{n}$
(so that
$m=0$
) the above formula coincides with (1.3) and holds for all
$\unicode[STIX]{x1D70F}\geqslant 1/n$
. Indeed, it corresponds to the classical Jarník–Besicovitch theorem. For non-degenerate curves in
$\mathbb{R}^{2}$
, as a result of various works [Reference Beresnevich, Dickinson and Velani4, Reference Beresnevich and Zorin13, Reference Huang19, Reference Vaughan and Velani30], we know that (1.5) holds for all
$\unicode[STIX]{x1D70F}\in [{\textstyle \frac{1}{2}},1)$
. For completeness it is worth pointing out that non-degenerate planar curves are characterised by being
$C^{2}$
and having non-zero curvature.
Beyond planar curves, for analytic non-degenerate manifolds
${\mathcal{M}}$
in
$\mathbb{R}^{n}$
the lower bound associated with (1.5) is established in [Reference Beresnevich1] and holds for
$\unicode[STIX]{x1D70F}\in [1/n,1/m)$
. The analytic condition is removed in the case of curves and manifolds that can be “fibred” into non-degenerate curves [Reference Beresnevich, Vaughan, Velani and Zorin8]. The latter includes
$C^{\infty }$
non-degenerate submanifolds of
$\mathbb{R}^{n}$
which are not necessarily analytic. The complementary upper bound associated with (1.5) has been established [Reference Beresnevich, Vaughan, Velani and Zorin7, Reference Simmons29] under additional geometric restrictions on
${\mathcal{M}}$
and a more limited range of
$\unicode[STIX]{x1D70F}$
. The difficulty in obtaining upper bounds lies in the notoriously difficult problem of bounding the number of rational points lying near the manifold of interest. For a discussion of this including the heuristics see [Reference Beresnevich, Ramírez, Velani, Badziahin, Gorodnik and Peyerimhoff5, §6.1.3].
We emphasize that all the lower bound dimension results mentioned in the above discussion are actually derived from corresponding stronger divergent Jarník-type results for
${\mathcal{H}}^{s}({\mathcal{S}}_{n}(\unicode[STIX]{x1D713})\cap {\mathcal{M}})$
. The main substance of this paper is the introduction of a new approach, based on the Mass Transference Principle of [Reference Beresnevich and Velani9], that is primarily geared towards establishing dimension statements. As a consequence we are able to prove the following general result, not just for non-degenerate manifolds but for any
$C^{2}$
submanifold of
$\mathbb{R}^{n}$
. Furthermore, the proof is significantly easier than those based on establishing a divergent Jarník-type result.
Theorem 1. Let
${\mathcal{M}}$
be any
$C^{2}$
submanifold of
$\mathbb{R}^{n}$
of codimension
$m$
and let
$$\begin{eqnarray}\frac{1}{n}\leqslant \unicode[STIX]{x1D70F}<\frac{1}{m}.\end{eqnarray}$$
Then
$$\begin{eqnarray}\dim {\mathcal{S}}_{n}(\unicode[STIX]{x1D70F})\cap {\mathcal{M}}\geqslant s:=\frac{n+1}{\unicode[STIX]{x1D70F}+1}-m.\end{eqnarray}$$
Furthermore,
$$\begin{eqnarray}{\mathcal{H}}^{s}({\mathcal{S}}_{n}(\unicode[STIX]{x1D70F})\cap {\mathcal{M}})={\mathcal{H}}^{s}({\mathcal{M}}).\end{eqnarray}$$
Before we state the more general result for the Hausdorff dimension of
${\mathcal{S}}_{n}(\unicode[STIX]{x1D713})\cap {\mathcal{M}}$
with
$\unicode[STIX]{x1D713}$
not necessarily of the form
$\unicode[STIX]{x1D713}(q):=q^{-\unicode[STIX]{x1D70F}}$
, we introduce the Mass Transference Principle and give a “simple” proof of Theorem 1 in the special case that
${\mathcal{M}}$
is an affine coordinate plane. This will bring to the forefront the main ingredients of the new approach developed in this paper. It is worth mentioning that for such planes (which are clearly degenerate) Khintchine-type results have recently been established [Reference Ramírez26, Reference Ramŕez, Simmons and Süess27]—see also [Reference Beresnevich, Ramírez, Velani, Badziahin, Gorodnik and Peyerimhoff5, §4.4].
2 Introducing the main ingredients
First some notation. Throughout,
$\mathbb{R}^{k}$
will be regarded as a metric space with distance induced by any fixed norm (not necessarily Euclidean) and
$B(\mathbf{x},r)$
will denote a ball centred at
$\mathbf{x}\in \mathbb{R}^{k}$
of radius
$r>0$
. Given a ball
$B=B(\mathbf{x},r)$
and a positive real number
$\unicode[STIX]{x1D706}$
, we denote by
$\unicode[STIX]{x1D706}B$
the ball
$B$
scaled by the factor
$\unicode[STIX]{x1D706}$
; i.e.
$\unicode[STIX]{x1D706}B(\mathbf{x},r):=B(\mathbf{x},\unicode[STIX]{x1D706}r)$
. Also, given
$s>0$
and a ball
$B=B(\mathbf{x},r)$
in
$\mathbb{R}^{k}$
, we define another ball
$$\begin{eqnarray}B^{s}:=B(\mathbf{x},r^{s/k}).\end{eqnarray}$$
Note that trivially
$B^{k}=B$
.
Suppose
$F$
is a subset of
$\mathbb{R}^{k}$
. Given a ball
$B$
in
$\mathbb{R}^{k}$
, let
$\text{diam}(B)$
denote the diameter of
$B$
. For
$\unicode[STIX]{x1D70C}>0$
, a countable collection
$\{B_{i}\}$
of balls in
$\mathbb{R}^{k}$
with
$\text{diam}(B_{i})\leqslant \unicode[STIX]{x1D70C}$
for each
$i$
such that
$F\subset \bigcup _{i}B_{i}$
is called a
$\unicode[STIX]{x1D70C}$
-cover for
$F$
. Given a real number
$s\geqslant 0$
, the Hausdorff
$s$
-measure of
$F$
is given by
$$\begin{eqnarray}{\mathcal{H}}^{s}(F):=\lim _{\unicode[STIX]{x1D70C}\rightarrow 0}\inf \mathop{\sum }_{i}\operatorname{diam}(B_{i})^{s},\end{eqnarray}$$
where the infimum is taken over all
$\unicode[STIX]{x1D70C}$
-covers of
$F$
. When
$s$
is an integer,
${\mathcal{H}}^{s}$
is a constant multiple of
$s$
-dimensional Lebesgue measure. The Hausdorff dimension of
$F$
is defined by
$$\begin{eqnarray}\dim F:=\inf \{s:{\mathcal{H}}^{s}(F)=0\}.\end{eqnarray}$$
Further details regarding Hausdorff measure and dimension can be found in [Reference Falconer18].
Observe that the set
${\mathcal{S}}_{n}(\unicode[STIX]{x1D713})$
of
$\unicode[STIX]{x1D713}$
-well approximable points in
$\mathbb{R}^{n}$
is the
$\limsup$
of the sequence of hypercubes in
$\mathbb{R}^{n}$
defined by (1.1). Recall that, by definition, given a sequence of sets
$(S_{i})_{i\in I}$
indexed by a countable set
$I$
, then
$$\begin{eqnarray}\limsup S_{i}:=\{\mathbf{x}\in S_{i}:\text{for infinitely many }i\in I\}.\end{eqnarray}$$
The following transference theorem concerning
$\limsup$
sets is the key to establishing the results of this paper.
Theorem 2 (Mass Transference Principle).
Let
${\mathcal{U}}$
be an open subset of
$\mathbb{R}^{k}$
. Let
$\{B_{i}\}_{i\in \mathbb{N}}$
be a sequence of balls in
$\mathbb{R}^{k}$
centred in
${\mathcal{U}}$
with
$\text{diam}(B_{i})\rightarrow 0$
as
$i\rightarrow \infty$
. Let
$s>0$
and suppose that for any ball
$B$
in
${\mathcal{U}}$
$$\begin{eqnarray}{\mathcal{H}}^{k}\Bigl(B\cap \limsup _{i\rightarrow \infty }B_{i}^{s}\Bigr)={\mathcal{H}}^{k}(B).\end{eqnarray}$$
Then, for any ball
$B$
in
${\mathcal{U}}$
$$\begin{eqnarray}{\mathcal{H}}^{s}\Bigl(B\cap \limsup _{i\rightarrow \infty }B_{i}^{k}\Bigr)={\mathcal{H}}^{s}(B).\end{eqnarray}$$
The above version of the Mass Transference Principle is easily deduced from the original statement appearing as [Reference Beresnevich and Velani9, Theorem 2].
Armed with the Mass Transference Principle it is easy to deduce the Jarník–Besicovitch theorem directly from Dirichlet’s theorem. For reasons that will soon become apparent we provide the details. To begin with, observe that
$\mathbf{y}=(y_{1},\ldots ,y_{n})\in {\mathcal{S}}_{n}(\unicode[STIX]{x1D70F})$
if and only if
$$\begin{eqnarray}\mathbf{y}\in B_{\mathbf{p},q}:=\biggl\{\mathbf{x}=(x_{1},\ldots ,x_{n})\in \mathbb{R}^{n}:\max _{1\leqslant i\leqslant n}\biggl|x_{i}-\frac{p_{i}}{q}\biggr|<q^{-\unicode[STIX]{x1D70F}-1}\biggr\}\end{eqnarray}$$
for infinitely many
$q\in \mathbb{N}$
and
$\mathbf{p}=(p_{1},\ldots ,p_{n})\in \mathbb{Z}^{n}$
; that is
$$\begin{eqnarray}{\mathcal{S}}_{n}(\unicode[STIX]{x1D70F})=\limsup _{q\rightarrow \infty }B_{\mathbf{p},q}.\end{eqnarray}$$
Next, in view of Dirichlet’s theorem we have that
$$\begin{eqnarray}\limsup _{q\rightarrow \infty }B_{\mathbf{p},q}^{s}=\mathbb{R}^{n}\quad \text{where}\;s:=\frac{n+1}{\unicode[STIX]{x1D70F}+1}\end{eqnarray}$$
and the ball
$B_{\mathbf{p},q}^{s}$
associated with
$B_{\mathbf{p},q}$
is defined via (2.1) with
$k=n$
. Thus, for any ball
$B$
in
$\mathbb{R}^{n}$
it trivially follows that
$$\begin{eqnarray}{\mathcal{H}}^{n}\Bigl(B\cap \limsup _{q\rightarrow \infty }B_{\mathbf{p},q}^{s}\Bigr)={\mathcal{H}}^{n}(B).\end{eqnarray}$$
In turn, for any
$\unicode[STIX]{x1D70F}>1/n$
(so that
$s<n$
) the Mass Transference Principle implies that
$$\begin{eqnarray}{\mathcal{H}}^{s}({\mathcal{S}}_{n}(\unicode[STIX]{x1D70F}))={\mathcal{H}}^{s}(\mathbb{R}^{n})=\infty .\end{eqnarray}$$
Hence, by the definition of Hausdorff dimension,
$\dim {\mathcal{S}}_{n}(\unicode[STIX]{x1D70F})\geqslant s$
. This is the hard part in establishing the Jarník–Besicovitch theorem. The complementary upper bound is straightforward—see for example [Reference Beresnevich, Ramírez, Velani, Badziahin, Gorodnik and Peyerimhoff5, §2]. Observe that we have proved more than the Jarník–Besicovitch theorem alone. We have shown that the Hausdorff
$s$
-measure of
${\mathcal{S}}_{n}(\unicode[STIX]{x1D70F})$
at the critical exponent is infinite.
We shall now see that to establish Theorem 1 in the case of affine coordinate planes is essentially as easy as the proof of the Jarník–Besicovitch theorem just given. To the best of our knowledge, even this restricted version of Theorem 1 is new and can be thought of as the “fibred” version of the classical Jarník–Besicovitch theorem.
Corollary 1. Let
$n>m\geqslant 1$
be integers and
$d:=n-m$
. Let
$\unicode[STIX]{x1D70F}$
satisfy (1.6) and given
$\boldsymbol{\unicode[STIX]{x1D6FD}}=(\unicode[STIX]{x1D6FD}_{1},\ldots ,\unicode[STIX]{x1D6FD}_{m})\in \mathbb{R}^{m}$
, let
$$\begin{eqnarray}\unicode[STIX]{x1D6F1}_{\boldsymbol{\unicode[STIX]{x1D6FD}}}:=\{(\unicode[STIX]{x1D6FC}_{1},\ldots ,\unicode[STIX]{x1D6FC}_{d},\unicode[STIX]{x1D6FD}_{1},\ldots ,\unicode[STIX]{x1D6FD}_{m}):\boldsymbol{\unicode[STIX]{x1D6FC}}=(\unicode[STIX]{x1D6FC}_{1},\ldots ,\unicode[STIX]{x1D6FC}_{d})\in \mathbb{R}^{d}\}\subset \mathbb{R}^{n}.\end{eqnarray}$$
Then
$$\begin{eqnarray}\dim {\mathcal{S}}_{n}(\unicode[STIX]{x1D70F})\cap \unicode[STIX]{x1D6F1}_{\boldsymbol{\unicode[STIX]{x1D6FD}}}\geqslant s:=\frac{n+1}{\unicode[STIX]{x1D70F}+1}-m.\end{eqnarray}$$
Furthermore,
$$\begin{eqnarray}{\mathcal{H}}^{s}({\mathcal{S}}_{n}(\unicode[STIX]{x1D70F})\cap \unicode[STIX]{x1D6F1}_{\boldsymbol{\unicode[STIX]{x1D6FD}}})={\mathcal{H}}^{s}(\unicode[STIX]{x1D6F1}_{\boldsymbol{\unicode[STIX]{x1D6FD}}}).\end{eqnarray}$$
Proof. There is nothing to prove in the case
$\unicode[STIX]{x1D70F}=1/n$
since by Dirichlet’s theorem,
${\mathcal{S}}_{n}(1/n)=\mathbb{R}^{n}$
. Hence, we will assume that
$1/n<\unicode[STIX]{x1D70F}<1/m$
and so by definition
$s<d$
. Hence, it follows that
$$\begin{eqnarray}{\mathcal{H}}^{s}(\unicode[STIX]{x1D6F1}_{\boldsymbol{\unicode[STIX]{x1D6FD}}})=\infty .\end{eqnarray}$$
Next, given
$\unicode[STIX]{x1D70F}$
and
$\boldsymbol{\unicode[STIX]{x1D6FD}}\in \mathbb{R}^{m}$
let
$$\begin{eqnarray}B(\boldsymbol{\unicode[STIX]{x1D6FD}};\unicode[STIX]{x1D70F}):=\Bigl\{q\in \mathbb{N}:\max _{1\leqslant i\leqslant m}\Vert q\unicode[STIX]{x1D6FD}_{i}\Vert <q^{-\unicode[STIX]{x1D70F}}\Bigr\},\end{eqnarray}$$
where
$\Vert \cdot \Vert$
stands for distance from the nearest integer. Also, given a set
$X\subseteq \mathbb{R}^{n}$
let
$\unicode[STIX]{x1D70B}_{d}(X)$
denote the orthogonal projection of
$X$
onto the first
$d$
coordinates of
$\mathbb{R}^{n}$
. Then, it is easily verified that
$\boldsymbol{\unicode[STIX]{x1D6FC}}\in \unicode[STIX]{x1D70B}_{d}({\mathcal{S}}_{n}(\unicode[STIX]{x1D70F})\cap \unicode[STIX]{x1D6F1}_{\boldsymbol{\unicode[STIX]{x1D6FD}}})$
if and only if
$$\begin{eqnarray}\boldsymbol{\unicode[STIX]{x1D6FC}}\in B_{\mathbf{p},q}:=\biggl\{\mathbf{x}=(x_{1},\ldots ,x_{d})\in \mathbb{R}^{d}:\max _{1\leqslant i\leqslant d}\biggl|x_{i}-\frac{p_{i}}{q}\biggr|<q^{-\unicode[STIX]{x1D70F}-1}\biggr\}\end{eqnarray}$$
for infinitely many integers
$q\in B(\boldsymbol{\unicode[STIX]{x1D6FD}};\unicode[STIX]{x1D70F})$
and
$\mathbf{p}=(p_{1},\ldots ,p_{n})\in \mathbb{Z}^{n}$
; that is
$$\begin{eqnarray}\unicode[STIX]{x1D70B}_{d}({\mathcal{S}}_{n}(\unicode[STIX]{x1D70F})\cap \unicode[STIX]{x1D6F1}_{\boldsymbol{\unicode[STIX]{x1D6FD}}}):=\limsup _{q\rightarrow \infty ,\,q\in B(\boldsymbol{\unicode[STIX]{x1D6FD}};\unicode[STIX]{x1D70F})}B_{\mathbf{p},q}.\end{eqnarray}$$
The projection map
$\unicode[STIX]{x1D70B}_{d}$
is bi-Lipschitz and thus the measure part (2.6) of the corollary follows on showing that
$$\begin{eqnarray}{\mathcal{H}}^{s}(\unicode[STIX]{x1D70B}_{d}({\mathcal{S}}_{n}(\unicode[STIX]{x1D70F})\cap \unicode[STIX]{x1D6F1}_{\boldsymbol{\unicode[STIX]{x1D6FD}}}))=\infty .\end{eqnarray}$$
The dimension part (2.5) of the corollary follows directly from (2.6) and the definition of Hausdorff dimension. This completes the proof of Corollary 1 modulo (2.9).
We now establish (2.9). Define
$\unicode[STIX]{x1D702}$
to be the real number such that
$$\begin{eqnarray}d\unicode[STIX]{x1D702}+m\unicode[STIX]{x1D70F}=1.\end{eqnarray}$$
It is easily seen that
$0<\unicode[STIX]{x1D702}<\unicode[STIX]{x1D70F}$
. By Minkowski’s theorem for systems of linear forms [Reference Schmidt28], for any
$\boldsymbol{\unicode[STIX]{x1D6FC}}\in \mathbb{R}^{d}$
and for any integer
$Q\geqslant 1$
there exists
$(p_{1},\ldots ,p_{n},q)$
$\in \mathbb{Z}^{n+1}\setminus \{\mathbf{0}\}$
such that
$$\begin{eqnarray}\left\{\begin{array}{@{}ll@{}}|q\unicode[STIX]{x1D6FC}_{i}-p_{i}|<Q^{-\unicode[STIX]{x1D702}} & (1\leqslant i\leqslant d),\\ |q\unicode[STIX]{x1D6FD}_{j}-p_{d+j}|<Q^{-\unicode[STIX]{x1D70F}} & (1\leqslant j\leqslant m),\\ |q|\leqslant Q. & \end{array}\right.\end{eqnarray}$$
Since both
$\unicode[STIX]{x1D702}$
and
$\unicode[STIX]{x1D70F}$
are positive, we have that
$Q^{-\unicode[STIX]{x1D702}}\leqslant 1$
,
$Q^{-\unicode[STIX]{x1D70F}}\leqslant 1$
and we necessarily have that
$q\neq 0$
. Furthermore, without loss of generality, we can assume that
$q>0$
. Assume that
$\unicode[STIX]{x1D6FC}_{1}$
is irrational. Then, since
$\unicode[STIX]{x1D702}>0$
, there must be infinitely many different
$q\in \mathbb{N}$
amongst the solutions
$(p_{1},\ldots ,p_{n},q)$
to (2.11) taken over all
$Q>1$
. Indeed, if the same
$q$
repeatedly occurred in the first inequality, the left-hand side would be a fixed positive constant for this
$q$
. However, the right-hand side of the first inequality tends to zero as
$Q$
increases and we obtain a contradiction for
$Q$
large. Therefore, the system of inequalities
$$\begin{eqnarray}\left\{\begin{array}{@{}ll@{}}|q\unicode[STIX]{x1D6FC}_{i}-p_{i}|<q^{-\unicode[STIX]{x1D702}} & (1\leqslant i\leqslant d),\\ |q\unicode[STIX]{x1D6FD}_{j}-p_{d+j}|<q^{-\unicode[STIX]{x1D70F}} & (1\leqslant j\leqslant m)\end{array}\right.\end{eqnarray}$$
is satisfied for infinitely many different
$q\in \mathbb{N}$
and
$(p_{1},\ldots ,p_{n})\in \mathbb{Z}^{n}$
. This means that
$$\begin{eqnarray}\limsup _{q\rightarrow \infty ,\,q\in B(\boldsymbol{\unicode[STIX]{x1D6FD}};\unicode[STIX]{x1D70F})}B_{\mathbf{p},q}^{s}\supseteq \mathbb{R}^{d}\setminus \mathbb{Q}^{d},\end{eqnarray}$$
where
$$\begin{eqnarray}s:=\frac{(\unicode[STIX]{x1D702}+1)d}{\unicode[STIX]{x1D70F}+1}\;\stackrel{\text{(2.10)}}{=}\;\frac{n+1}{\unicode[STIX]{x1D70F}+1}-m\end{eqnarray}$$
and the ball
$B_{\mathbf{p},q}^{s}$
associated with
$B_{\mathbf{p},q}$
is defined via (2.1) with
$k=d$
. Thus, for any ball
$B$
in
$\mathbb{R}^{d}$
it trivially follows that
$$\begin{eqnarray}{\mathcal{H}}^{d}\Bigl(B\cap \limsup _{q\rightarrow \infty ,q\in B(\boldsymbol{\unicode[STIX]{x1D6FD}};\unicode[STIX]{x1D70F})}B_{\mathbf{p},q}^{s}\Bigr)={\mathcal{H}}^{d}(B).\end{eqnarray}$$
Now
$s<d$
and so, by the Mass Transference Principle, we conclude that for any ball
$B$
in
$\mathbb{R}^{d}$
$$\begin{eqnarray}{\mathcal{H}}^{s}\biggl(B\cap \limsup _{q\rightarrow \infty ,q\in B(\boldsymbol{\unicode[STIX]{x1D6FD}};\unicode[STIX]{x1D70F})}B_{\mathbf{p},q}\biggr)={\mathcal{H}}^{s}(B)=\infty .\end{eqnarray}$$
This together with (2.8) implies (2.9) and thereby completes the proof of the corollary. ◻
Remark 1. When it comes to establishing Theorem 1 (or rather Theorem 3 below) for arbitrary submanifolds
${\mathcal{M}}$
of
$\mathbb{R}^{n}$
, it will be apparent that the role of the affine coordinate plane
$\unicode[STIX]{x1D6F1}_{\boldsymbol{\unicode[STIX]{x1D6FD}}}$
in the above proof will be played by tangent planes to
${\mathcal{M}}$
and the set
$B(\boldsymbol{\unicode[STIX]{x1D6FD}};\unicode[STIX]{x1D70F})$
will correspond to rational points lying close to
${\mathcal{M}}$
.
3 The general case
The following is a version of Theorem 1 for general approximating functions
$\unicode[STIX]{x1D713}$
.
Theorem 3. Let
${\mathcal{M}}$
be any
$C^{2}$
submanifold of
$\mathbb{R}^{n}$
of codimension
$m$
and let
$\unicode[STIX]{x1D713}:\mathbb{N}\rightarrow \mathbb{R}^{+}$
be any monotonic function such that
$$\begin{eqnarray}\limsup _{Q\rightarrow \infty }Q^{1/m}\unicode[STIX]{x1D713}(Q)=\infty .\end{eqnarray}$$
Suppose that for some
$\unicode[STIX]{x1D70F}$
with
$1/n\leqslant \unicode[STIX]{x1D70F}\leqslant 1/m$
we have that
$$\begin{eqnarray}\inf _{Q\in \mathbb{N}}Q^{\unicode[STIX]{x1D70F}}\unicode[STIX]{x1D713}(Q)>0.\end{eqnarray}$$
Then
$$\begin{eqnarray}\dim {\mathcal{S}}_{n}(\unicode[STIX]{x1D713})\cap {\mathcal{M}}\geqslant s:=\frac{n+1}{\unicode[STIX]{x1D70F}+1}-m.\end{eqnarray}$$
Furthermore,
$$\begin{eqnarray}{\mathcal{H}}^{s}({\mathcal{S}}_{n}(\unicode[STIX]{x1D713})\cap {\mathcal{M}})={\mathcal{H}}^{s}({\mathcal{M}}).\end{eqnarray}$$
Observe that any approximating function
$\unicode[STIX]{x1D713}$
given by
$\unicode[STIX]{x1D713}(q)=q^{-\unicode[STIX]{x1D70F}}$
with
$1/n\leqslant \unicode[STIX]{x1D70F}<1/m$
satisfies conditions (3.1) and (3.2). Thus, Theorem 1 is a simple consequence of Theorem 3. The following is another consequence of Theorem 3 expressed in terms of the upper order at infinity of
$1/\unicode[STIX]{x1D713}$
defined by
$$\begin{eqnarray}\hat{\unicode[STIX]{x1D70F}}_{\unicode[STIX]{x1D713}}:=\limsup _{Q\rightarrow \infty }\frac{-\text{log}\,\unicode[STIX]{x1D713}(Q)}{\log Q}.\end{eqnarray}$$
Corollary 2. Let
${\mathcal{M}}$
be any
$C^{2}$
submanifold of
$\mathbb{R}^{n}$
of codimension
$m$
and let
$\unicode[STIX]{x1D713}:\mathbb{N}\rightarrow \mathbb{R}^{+}$
be any monotonic function satisfying (3.1) and
$$\begin{eqnarray}\inf _{Q\in \mathbb{N}}Q^{1/m}\unicode[STIX]{x1D713}(Q)>0.\end{eqnarray}$$
Suppose that
$\hat{\unicode[STIX]{x1D70F}}_{\unicode[STIX]{x1D713}}\geqslant 1/n$
. Then
$$\begin{eqnarray}\dim {\mathcal{S}}_{n}(\unicode[STIX]{x1D713})\cap {\mathcal{M}}\geqslant \frac{n+1}{\hat{\unicode[STIX]{x1D70F}}_{\unicode[STIX]{x1D713}}+1}-m.\end{eqnarray}$$
Proof. Note that, by (3.5),
$\hat{\unicode[STIX]{x1D70F}}_{\unicode[STIX]{x1D713}}\leqslant 1/m$
. First assume that
$\hat{\unicode[STIX]{x1D70F}}_{\unicode[STIX]{x1D713}}=1/m$
. Let
$\unicode[STIX]{x1D70F}=\unicode[STIX]{x1D70F}_{\unicode[STIX]{x1D713}}$
. Then (3.2) becomes identical to (3.5) and Theorem 3 is applicable. In this case (3.6) coincides with (3.3).
Now assume that
$1/n\leqslant \hat{\unicode[STIX]{x1D70F}}_{\unicode[STIX]{x1D713}}<1/m$
and fix any
$\unicode[STIX]{x1D70F}$
such that
$\hat{\unicode[STIX]{x1D70F}}_{\unicode[STIX]{x1D713}}<\unicode[STIX]{x1D70F}<1/m$
. It readily follows from the definition of
$\hat{\unicode[STIX]{x1D70F}}_{\unicode[STIX]{x1D713}}$
that for all sufficiently large
$q$
we have that
$$\begin{eqnarray}\frac{-\text{log}\,\unicode[STIX]{x1D713}(q)}{\log q}<\unicode[STIX]{x1D70F},\end{eqnarray}$$
or equivalently
$\unicode[STIX]{x1D713}(q)>q^{-\unicode[STIX]{x1D70F}}$
for all sufficiently large
$q$
. This implies the validity of (3.2) and thus Theorem 3 is applicable. In turn, since
$\unicode[STIX]{x1D70F}$
can be taken to be arbitrarily close to
$\hat{\unicode[STIX]{x1D70F}}_{\unicode[STIX]{x1D713}}$
the desired lower bound (3.6) then follows from (3.3).◻
Remark 2. In the case
$\hat{\unicode[STIX]{x1D70F}}_{\unicode[STIX]{x1D713}}$
is strictly bigger than the lower order at infinity of
$1/\unicode[STIX]{x1D713}$
, that is
$$\begin{eqnarray}\unicode[STIX]{x1D70F}_{\unicode[STIX]{x1D713}}^{\ast }:=\liminf _{Q\rightarrow \infty }\frac{-\text{log}\,\unicode[STIX]{x1D713}(Q)}{\log Q},\end{eqnarray}$$
(3.6) is not always sharp. For example, this is the case for non-degenerate submanifolds of
$\mathbb{R}^{n}$
[Reference Beresnevich1], where the lower bound is shown to be
$$\begin{eqnarray}\dim {\mathcal{S}}_{n}(\unicode[STIX]{x1D713})\cap {\mathcal{M}}\geqslant \frac{n+1}{\unicode[STIX]{x1D70F}_{\unicode[STIX]{x1D713}}^{\ast }+1}-m.\end{eqnarray}$$
Remark 3. Observe that if
$\unicode[STIX]{x1D70F}<1/m$
, then condition (3.2) implies (3.1). In the case
$\unicode[STIX]{x1D70F}=1/m$
condition (3.2) implies that
$$\begin{eqnarray}\limsup _{Q\rightarrow \infty }Q^{1/m}\unicode[STIX]{x1D713}(Q)>0.\end{eqnarray}$$
However, this alone is not sufficient. To see this, consider the plane
$\unicode[STIX]{x1D6F1}_{\boldsymbol{\unicode[STIX]{x1D6FD}}}$
given by (2.4) with
$\boldsymbol{\unicode[STIX]{x1D6FD}}$
being any badly approximable point in
$\mathbb{R}^{m}$
. This means that there exists a constant
$c_{0}>0$
such that
$$\begin{eqnarray}c_{0}:=\inf _{q\in \mathbb{N}}q^{1/m}\max _{1\leqslant j\leqslant m}\Vert q\unicode[STIX]{x1D6FD}_{j}\Vert >0.\end{eqnarray}$$
Let
$$\begin{eqnarray}\unicode[STIX]{x1D713}(q)=c_{0}q^{-1/m}.\end{eqnarray}$$
Clearly condition (3.8) is satisfied. Indeed, the corresponding limit exists and is strictly positive and finite and thus
$\unicode[STIX]{x1D70F}_{\unicode[STIX]{x1D713}}=1/m$
. However, by our choice of
$\boldsymbol{\unicode[STIX]{x1D6FD}}$
and
$\unicode[STIX]{x1D713}$
, we have that
$$\begin{eqnarray}\unicode[STIX]{x1D6F1}_{\boldsymbol{\unicode[STIX]{x1D6FD}}}\cap {\mathcal{S}}_{n}(\unicode[STIX]{x1D713})=\emptyset ,\end{eqnarray}$$
and hence the conclusions of either the theorem or corollary are not valid.
Remark 4. Despite the above remark, it should be noted that imposing additional “curvature” or Diophantine conditions on
${\mathcal{M}}$
may help in extending the range of
$\unicode[STIX]{x1D713}$
for which (3.6) holds. For instance, it follows from [Reference Beresnevich1, Theorem 7.2] that for non-degenerate analytic curves (3.7) holds if
$1/n\leqslant \unicode[STIX]{x1D70F}_{\unicode[STIX]{x1D713}}^{\ast }<3/(2n-1)$
.
4 A Dirichlet type theorem for rational approximations to manifolds
Let
${\mathcal{M}}$
be any
$C^{2}$
submanifold of
$\mathbb{R}^{n}$
of codimension
$m$
and let
$d:=n-m$
denote the dimension of
${\mathcal{M}}$
. Without loss of generality, we will assume that
${\mathcal{M}}$
is given by a Monge parametrisation, that is
$$\begin{eqnarray}{\mathcal{M}}:=\{(\boldsymbol{\unicode[STIX]{x1D6FC}},\mathbf{f}(\boldsymbol{\unicode[STIX]{x1D6FC}}))\in \mathbb{R}^{n}:\boldsymbol{\unicode[STIX]{x1D6FC}}=(\unicode[STIX]{x1D6FC}_{1},\ldots ,\unicode[STIX]{x1D6FC}_{d})\in {\mathcal{U}}\},\end{eqnarray}$$
where
${\mathcal{U}}$
is an open subset of
$\mathbb{R}^{d}$
and where
$\mathbf{f}=(f_{1},\ldots ,f_{m})$
is defined and twice continuously differentiable on
${\mathcal{U}}$
. We furthermore assume without loss of generality that
$$\begin{eqnarray}D:=\max _{\substack{ 1\leqslant j\leqslant m \\ 1\leqslant i\leqslant d}}\,\sup _{\boldsymbol{\unicode[STIX]{x1D6FC}}\in {\mathcal{U}}}\biggl|\frac{\unicode[STIX]{x2202}f_{j}}{\unicode[STIX]{x2202}\unicode[STIX]{x1D6FC}_{i}}(\boldsymbol{\unicode[STIX]{x1D6FC}})\biggr|<\infty\end{eqnarray}$$
and
$$\begin{eqnarray}C:=\max _{\substack{ 1\leqslant j\leqslant m \\ 1\leqslant i,k\leqslant d}}\,\sup _{\boldsymbol{\unicode[STIX]{x1D6FC}}\in {\mathcal{U}}}\biggl|\frac{\unicode[STIX]{x2202}^{2}f_{j}}{\unicode[STIX]{x2202}\unicode[STIX]{x1D6FC}_{i}\unicode[STIX]{x2202}\unicode[STIX]{x1D6FC}_{k}}(\boldsymbol{\unicode[STIX]{x1D6FC}})\biggr|<\infty .\end{eqnarray}$$
The following result can be viewed as an analogue of Dirichlet’s theorem for manifolds
${\mathcal{M}}\subset \mathbb{R}^{n}$
. In short, the points of interest are restricted to
${\mathcal{M}}$
and given an approximating function
$\unicode[STIX]{x1D713}$
, the rational points
$\mathbf{p}/q\in \mathbb{Q}^{n}$
lie within some
$\unicode[STIX]{x1D713}$
-neighbourhood of
${\mathcal{M}}$
.
Theorem 4. Let
${\mathcal{M}}$
be as above and let
$\unicode[STIX]{x1D713}:\mathbb{N}\rightarrow (0,1]$
be any monotonic function satisfying (3.1) and
$$\begin{eqnarray}\inf _{Q\in \mathbb{N}}Q\unicode[STIX]{x1D713}(Q)>0.\end{eqnarray}$$
Then for any
$\boldsymbol{\unicode[STIX]{x1D6FC}}=(\unicode[STIX]{x1D6FC}_{1},\ldots ,\unicode[STIX]{x1D6FC}_{d})\in {\mathcal{U}}$
there is an infinite subset
${\mathcal{Q}}\subset \mathbb{N}$
such that for any
$Q\in {\mathcal{Q}}$
there exists
$(p_{1},\ldots ,p_{n},q)\in \mathbb{Z}^{n+1}$
with
$1\leqslant q\leqslant Q$
and
$(p_{1}/q,\ldots ,p_{d}/q)\in {\mathcal{U}}$
such that
$$\begin{eqnarray}\biggl|\unicode[STIX]{x1D6FC}_{i}-\frac{p_{i}}{q}\biggr|<\frac{2^{m/d}}{q(Q\unicode[STIX]{x1D713}(Q)^{m})^{1/d}}\quad \text{for}\;1\leqslant i\leqslant d\end{eqnarray}$$
and
$$\begin{eqnarray}\biggl|f_{j}\biggl(\frac{p_{1}}{q},\ldots ,\frac{p_{d}}{q}\biggr)-\frac{p_{d+j}}{q}\biggr|<\frac{\unicode[STIX]{x1D713}(q)}{q}\quad \text{for}\;1\leqslant j\leqslant m.\end{eqnarray}$$
Proof. Define the following functions of
$\boldsymbol{\unicode[STIX]{x1D6FC}}\in {\mathcal{U}}$
$$\begin{eqnarray}g_{j}:=f_{j}-\mathop{\sum }_{i=1}^{d}\unicode[STIX]{x1D6FC}_{i}\frac{\unicode[STIX]{x2202}f_{j}}{\unicode[STIX]{x2202}\unicode[STIX]{x1D6FC}_{i}}\quad (1\leqslant j\leqslant m)\end{eqnarray}$$
and consider the system of inequalities
$$\begin{eqnarray}\displaystyle \biggl|qg_{j}(\boldsymbol{\unicode[STIX]{x1D6FC}})+\mathop{\sum }_{i=1}^{d}p_{i}\frac{\unicode[STIX]{x2202}f_{j}}{\unicode[STIX]{x2202}\unicode[STIX]{x1D6FC}_{i}}(\boldsymbol{\unicode[STIX]{x1D6FC}})-p_{d+j}\biggr|<\frac{1}{2}\unicode[STIX]{x1D713}(Q)\quad (1\leqslant j\leqslant m) & & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle |q\unicode[STIX]{x1D6FC}_{i}-p_{i}|<(2^{-m}Q\unicode[STIX]{x1D713}(Q)^{m})^{-1/d}\quad (1\leqslant i\leqslant d) & & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle |q|\leqslant Q. & & \displaystyle\end{eqnarray}$$
On the left-hand side of this system of inequalities we have
$(m+d+1)$
linear forms that correspond to the
$(m+d+1)$
rows of the matrix
$$\begin{eqnarray}G=G(\boldsymbol{\unicode[STIX]{x1D6FC}}):=\left(\begin{array}{@{}cccccccc@{}}g_{1} & \displaystyle \frac{\unicode[STIX]{x2202}f_{1}}{\unicode[STIX]{x2202}\unicode[STIX]{x1D6FC}_{1}} & \cdots \, & \displaystyle \frac{\unicode[STIX]{x2202}f_{1}}{\unicode[STIX]{x2202}\unicode[STIX]{x1D6FC}_{d}} & -1 & 0 & \cdots \, & 0\\ \vdots & \vdots & \ddots & \vdots & \vdots & & \ddots & \vdots \\ g_{m} & \displaystyle \frac{\unicode[STIX]{x2202}f_{m}}{\unicode[STIX]{x2202}\unicode[STIX]{x1D6FC}_{1}} & \cdots \, & \displaystyle \frac{\unicode[STIX]{x2202}f_{m}}{\unicode[STIX]{x2202}\unicode[STIX]{x1D6FC}_{d}} & 0 & 0 & \cdots \, & -1\\ \unicode[STIX]{x1D6FC}_{1} & -1 & \cdots \, & 0 & 0 & 0 & \cdots \, & 0\\ \vdots & \vdots & \ddots & \vdots & \vdots & \vdots & & \vdots \\ \unicode[STIX]{x1D6FC}_{d} & 0 & \cdots \, & -1 & 0 & 0 & \cdots \, & 0\\ 1 & 0 & \cdots \, & 0 & 0 & 0 & \cdots \, & 0\end{array}\right).\end{eqnarray}$$
The determinant of
$G$
is easily seen to be
$\pm 1$
, while the product of the quantities on the right-hand side of the system of inequalities (4.8)–(4.10) is
$1$
. Therefore, by Minkowski’s theorem for systems of linear forms, there exists a non-zero solution
$(p_{1},\ldots ,p_{n},q)\in \mathbb{Z}^{n+1}$
to the system of inequalities (4.8)–(4.10). Without loss of generality, we will assume that
$q\geqslant 0$
. In other words, inequality (4.10) reads
$$\begin{eqnarray}0\leqslant q\leqslant Q.\end{eqnarray}$$
From now on we fix
$\boldsymbol{\unicode[STIX]{x1D6FC}}\in {\mathcal{U}}$
and let
$$\begin{eqnarray}B:=\inf _{Q\in \mathbb{N}}Q\unicode[STIX]{x1D713}(Q)\stackrel{\text{(4.4)}}{{>}}0.\end{eqnarray}$$
Furthermore, since
${\mathcal{U}}$
is open there exists a ball
$B(\boldsymbol{\unicode[STIX]{x1D6FC}},r)$
centred at
$\boldsymbol{\unicode[STIX]{x1D6FC}}$
of radius
$r$
which is contained in
${\mathcal{U}}$
. Define
$$\begin{eqnarray}{\mathcal{Q}}:=\biggl\{Q\in \mathbb{N}:(2^{-m}Q\unicode[STIX]{x1D713}(Q)^{m})^{-1/d}<\min \biggl\{1,r,\biggl(\frac{B}{Cd^{2}}\biggr)^{1/2}\biggr\}\biggr\},\end{eqnarray}$$
where
$C$
is given by (4.3). Then, by (3.1),
${\mathcal{Q}}$
is an infinite subset of
$\mathbb{N}$
.
The upshot of the above is that the proof of Theorem 4 is reduced to showing that for any
$Q\in {\mathcal{Q}}$
the solution
$(p_{1},\ldots ,p_{n},q)$
to the system of inequalities (4.8), (4.9) and (4.11) arising from Minkowski’s theorem is in fact a solution to the system of inequalities associated with Theorem 4. With this in mind, we first show that we can take
$q\geqslant 1$
in (4.11). Indeed, suppose
$q$
vanishes. Then, by (4.12), we have that
$(2^{-m}Q\unicode[STIX]{x1D713}(Q)^{m})^{-d}<1$
. Hence, inequalities (4.9) imply that
$|p_{i}|<1$
for each
$1\leqslant i\leqslant d$
, and as
$p_{i}\in \mathbb{Z}$
we must therefore have
$p_{i}=0$
for
$1\leqslant i\leqslant d$
. This together with (4.8) implies that
$|p_{d+j}|<\unicode[STIX]{x1D713}(Q)<1$
and so, by the same reasoning,
$|p_{d+j}|=0$
for
$1\leqslant j\leqslant m$
. Hence
$(p_{1},\ldots ,p_{n},q)=\mathbf{0}$
, contradicting the fact that the solution guaranteed by Minkowski’s theorem is non-zero. Thus,
$q\geqslant 1$
as claimed. In turn, on dividing (4.9) by
$q$
, we obtain (4.5) and by the definition of
${\mathcal{Q}}$
the associated rational point
$\mathbf{p}/q:=(p_{1}/q,\ldots ,p_{d}/q)\in B(\boldsymbol{\unicode[STIX]{x1D6FC}},r)\subset {\mathcal{U}}$
.
It remains to show that (4.6) is satisfied. By Taylor’s formula, for each
$1\leqslant j\leqslant m$
, we have that
$$\begin{eqnarray}f_{j}\biggl(\frac{\mathbf{p}}{q}\biggr)=f_{j}(\boldsymbol{\unicode[STIX]{x1D6FC}})+\mathop{\sum }_{n=1}^{d}\unicode[STIX]{x1D6FC}_{i}\frac{\unicode[STIX]{x2202}f_{j}}{\unicode[STIX]{x2202}\unicode[STIX]{x1D6FC}_{i}}(\boldsymbol{\unicode[STIX]{x1D6FC}})\biggl(\frac{p_{i}}{q}-\unicode[STIX]{x1D6FC}_{i}\biggr)+R_{j}(\boldsymbol{\unicode[STIX]{x1D6FC}},\tilde{\boldsymbol{\unicode[STIX]{x1D6FC}}})\end{eqnarray}$$
for some
$\tilde{\boldsymbol{\unicode[STIX]{x1D6FC}}}$
(depending on
$\boldsymbol{\unicode[STIX]{x1D6FC}}$
and
$\mathbf{p}/q$
) which lies on the line joining
$\boldsymbol{\unicode[STIX]{x1D6FC}}$
and
$\mathbf{p}/q$
, where
$$\begin{eqnarray}R_{j}(\boldsymbol{\unicode[STIX]{x1D6FC}},\tilde{\boldsymbol{\unicode[STIX]{x1D6FC}}}):=\frac{1}{2}\mathop{\sum }_{i=1}^{d}\mathop{\sum }_{k=1}^{d}\frac{\unicode[STIX]{x2202}^{2}f_{j}}{\unicode[STIX]{x2202}\unicode[STIX]{x1D6FC}_{i}\unicode[STIX]{x2202}\unicode[STIX]{x1D6FC}_{k}}(\tilde{\boldsymbol{\unicode[STIX]{x1D6FC}}})\biggl(\frac{p_{i}}{q}-\unicode[STIX]{x1D6FC}_{i}\biggr)\biggl(\frac{p_{k}}{q}-\unicode[STIX]{x1D6FC}_{k}\biggr).\end{eqnarray}$$
In particular, since
$\mathbf{p}/q\in B(\boldsymbol{\unicode[STIX]{x1D6FC}},r)$
and a ball is a convex set,
$\tilde{\boldsymbol{\unicode[STIX]{x1D6FC}}}\in B(\boldsymbol{\unicode[STIX]{x1D6FC}},r)\subset {\mathcal{U}}$
and so
$R_{j}(\boldsymbol{\unicode[STIX]{x1D6FC}},\tilde{\boldsymbol{\unicode[STIX]{x1D6FC}}})$
is well defined. Using (4.14), we now rewrite the left-hand side of (4.8) in the following way:
$$\begin{eqnarray}\displaystyle & & \displaystyle \biggl|qg_{j}(\boldsymbol{\unicode[STIX]{x1D6FC}})+\mathop{\sum }_{i=1}^{d}p_{i}\frac{\unicode[STIX]{x2202}f_{j}}{\unicode[STIX]{x2202}\unicode[STIX]{x1D6FC}_{i}}(\boldsymbol{\unicode[STIX]{x1D6FC}})-p_{d+j}\biggr|\nonumber\\ \displaystyle & & \displaystyle \quad =\biggl|q\biggl(f_{j}(\boldsymbol{\unicode[STIX]{x1D6FC}})-\mathop{\sum }_{i=1}^{d}\unicode[STIX]{x1D6FC}_{i}\frac{\unicode[STIX]{x2202}f_{j}}{\unicode[STIX]{x2202}\unicode[STIX]{x1D6FC}_{i}}(\boldsymbol{\unicode[STIX]{x1D6FC}})\biggr)+\mathop{\sum }_{i=1}^{d}p_{i}\frac{\unicode[STIX]{x2202}f_{j}}{\unicode[STIX]{x2202}\unicode[STIX]{x1D6FC}_{i}}(\boldsymbol{\unicode[STIX]{x1D6FC}})-p_{d+j}\biggr|\nonumber\\ \displaystyle & & \displaystyle \quad =\biggl|qf_{j}(\boldsymbol{\unicode[STIX]{x1D6FC}})+\mathop{\sum }_{i=1}^{d}(p_{i}-q\unicode[STIX]{x1D6FC}_{i})\frac{\unicode[STIX]{x2202}f_{j}}{\unicode[STIX]{x2202}\unicode[STIX]{x1D6FC}_{i}}(\boldsymbol{\unicode[STIX]{x1D6FC}})-p_{d+j}\biggr|\nonumber\\ \displaystyle & & \displaystyle \quad =\biggl|q\biggl(f_{j}\biggl(\frac{\mathbf{p}}{q}\biggr)-\mathop{\sum }_{n=1}^{d}\unicode[STIX]{x1D6FC}_{i}\frac{\unicode[STIX]{x2202}f_{j}}{\unicode[STIX]{x2202}\unicode[STIX]{x1D6FC}_{i}}(\boldsymbol{\unicode[STIX]{x1D6FC}})\biggl(\frac{p_{i}}{q}-\unicode[STIX]{x1D6FC}_{i}\biggr)-R_{j}(\boldsymbol{\unicode[STIX]{x1D6FC}},\tilde{\boldsymbol{\unicode[STIX]{x1D6FC}}})\biggr)\nonumber\\ \displaystyle & & \displaystyle \qquad +\,\mathop{\sum }_{i=1}^{d}(p_{i}-q\unicode[STIX]{x1D6FC}_{i})\frac{\unicode[STIX]{x2202}f_{j}}{\unicode[STIX]{x2202}\unicode[STIX]{x1D6FC}_{i}}(\boldsymbol{\unicode[STIX]{x1D6FC}})-p_{d+j}\biggr|\nonumber\\ \displaystyle & & \displaystyle \quad =\biggl|qf_{j}\biggl(\frac{\mathbf{p}}{q}\biggr)-p_{d+j}-qR_{j}(\boldsymbol{\unicode[STIX]{x1D6FC}},\tilde{\boldsymbol{\unicode[STIX]{x1D6FC}}})\biggr|.\end{eqnarray}$$
Suppose for the moment that
$$\begin{eqnarray}|qR_{j}(\boldsymbol{\unicode[STIX]{x1D6FC}},\tilde{\boldsymbol{\unicode[STIX]{x1D6FC}}})|<\frac{\unicode[STIX]{x1D713}(q)}{2}.\end{eqnarray}$$
Then together with (4.8) and (4.15), we obtain that
$$\begin{eqnarray}\displaystyle \biggl|qf_{j}\biggl(\frac{\mathbf{p}}{q}\biggr)-p_{d+j}\biggr| & {\leqslant} & \displaystyle \biggl|qf_{j}\biggl(\frac{\mathbf{p}}{q}\biggr)-p_{d+j}-qR_{j}(\boldsymbol{\unicode[STIX]{x1D6FC}},\tilde{\boldsymbol{\unicode[STIX]{x1D6FC}}})\biggr|+|qR_{j}(\boldsymbol{\unicode[STIX]{x1D6FC}},\tilde{\boldsymbol{\unicode[STIX]{x1D6FC}}})|\nonumber\\ \displaystyle & {<} & \displaystyle \frac{\unicode[STIX]{x1D713}(Q)}{2}+\frac{\unicode[STIX]{x1D713}(q)}{2},\end{eqnarray}$$
and so, by the monotonicity of
$\unicode[STIX]{x1D713}$
, we conclude that
$$\begin{eqnarray}\biggl|qf_{j}\biggl(\frac{\mathbf{p}}{q}\biggr)-p_{d+j}\biggr|<\unicode[STIX]{x1D713}(q).\end{eqnarray}$$
This implies (4.6) and thereby completes the proof of Theorem 4 modulo the truth of (4.16).
In order to establish (4.16), we use (4.3) and (4.5) to obtain that
$$\begin{eqnarray}\displaystyle |qR_{j}(\boldsymbol{\unicode[STIX]{x1D6FC}},\tilde{\boldsymbol{\unicode[STIX]{x1D6FC}}})| & = & \displaystyle \biggl|\frac{q}{2}\mathop{\sum }_{i=1}^{d}\mathop{\sum }_{k=1}^{d}\frac{\unicode[STIX]{x2202}^{2}f_{j}}{\unicode[STIX]{x2202}\unicode[STIX]{x1D6FC}_{i}\unicode[STIX]{x2202}\unicode[STIX]{x1D6FC}_{k}}(\tilde{\boldsymbol{\unicode[STIX]{x1D6FC}}})\biggl(\frac{p_{i}}{q}-\unicode[STIX]{x1D6FC}_{i}\biggr)\biggl(\frac{p_{k}}{q}-\unicode[STIX]{x1D6FC}_{k}\biggr)\biggr|\nonumber\\ \displaystyle & {<} & \displaystyle \frac{Cqd^{2}}{2}\biggl(\frac{2^{m/d}}{q(Q\unicode[STIX]{x1D713}(Q)^{m})^{1/d}}\biggr)^{2}.\nonumber\end{eqnarray}$$
Thus (4.16) follows if
$$\begin{eqnarray}\frac{Cqd^{2}}{2}\biggl(\frac{2^{m/d}}{q(Q\unicode[STIX]{x1D713}(Q)^{m})^{1/d}}\biggr)^{2}<\frac{\unicode[STIX]{x1D713}(q)}{2}.\end{eqnarray}$$
The latter is true if and only if
$$\begin{eqnarray}2^{2m/d}Cd^{2}<q\unicode[STIX]{x1D713}(q)(Q\unicode[STIX]{x1D713}(Q)^{m})^{2/d}\end{eqnarray}$$
and, in view of the definition of
$B$
, is implied by the inequality
$$\begin{eqnarray}2^{2m/d}Cd^{2}<B(Q\unicode[STIX]{x1D713}(Q)^{m})^{2/d}.\end{eqnarray}$$
The latter however is true for any
$Q\in {\mathcal{Q}}$
—see (4.12). Therefore (4.19) and consequently (4.18) are satisfied. This establishes (4.16) as desired.◻
The following “infinitely often” consequence of Dirichlet’s theorem for manifolds will be the key to establishing Theorem 3.
Corollary 3. Let
${\mathcal{M}}$
and
$\unicode[STIX]{x1D713}$
be as in Theorem 4. Furthermore, let
$\unicode[STIX]{x1D70F}\leqslant 1/m$
and suppose there exists a constant
$\unicode[STIX]{x1D705}>0$
such that
$$\begin{eqnarray}\unicode[STIX]{x1D705}\leqslant Q^{\unicode[STIX]{x1D70F}}\unicode[STIX]{x1D713}(Q)\end{eqnarray}$$
for infinitely many
$Q\in \mathbb{N}$
. Then, for any
$\boldsymbol{\unicode[STIX]{x1D6FC}}\in {\mathcal{U}}\setminus \mathbb{Q}^{d}$
there exist infinitely many different vectors
$(p_{1},\ldots ,p_{n},q)\in \mathbb{Z}^{n}\times \mathbb{N}$
with
$(p_{1}/q,\ldots ,p_{n}/q)\in {\mathcal{U}}$
satisfying the system of inequalities (4.6) and
$$\begin{eqnarray}\biggl|\unicode[STIX]{x1D6FC}_{i}-\frac{p_{i}}{q}\biggr|<\biggl(\frac{2}{\unicode[STIX]{x1D705}}\biggr)^{m/d}q^{-1-(1-\unicode[STIX]{x1D70F}m)/d}\quad \text{for}\;1\leqslant i\leqslant d.\end{eqnarray}$$
Proof. Fix any
$\boldsymbol{\unicode[STIX]{x1D6FC}}\in {\mathcal{U}}$
and let
${\mathcal{Q}}$
be given by (4.12). Then, as was shown in the proof of Theorem 4, for any
$Q\in {\mathcal{Q}}$
there exists
$(p_{1},\ldots ,p_{n},q)\in \mathbb{Z}^{n}\times \mathbb{N}$
with
$q\leqslant Q$
,
$(p_{1}/q,\ldots ,p_{n}/q)\in {\mathcal{U}}$
and such that (4.5) and (4.6) hold. Let
$S$
be the set of
$Q\in \mathbb{N}$
satisfying (4.20). By the conditions of the corollary,
$S$
is infinite. Clearly
$Q\unicode[STIX]{x1D713}(Q)^{m}\geqslant Q^{1-m\unicode[STIX]{x1D70F}}\unicode[STIX]{x1D705}$
for
$Q\in S$
. Hence,
$Q\unicode[STIX]{x1D713}(Q)^{m}$
is unbounded on
$S$
if
$\unicode[STIX]{x1D70F}<1/m$
. By (3.1),
$Q\unicode[STIX]{x1D713}(Q)^{m}$
is unbounded on
$S$
in the case
$\unicode[STIX]{x1D70F}=1/m$
as well. Choose, as we may, any strictly increasing sequence
$(Q_{i})_{i\in \mathbb{N}}$
of numbers from
$S$
such that
$\lim _{i\rightarrow \infty }Q_{i}\unicode[STIX]{x1D713}(Q_{i})^{m}$
. By the definition (4.12) of
${\mathcal{Q}}$
, there is a sufficiently large
$i_{0}$
such that
$Q_{i}\in {\mathcal{Q}}$
for all
$i\geqslant i_{0}$
. Define
${\mathcal{Q}}^{\ast }=\{Q_{i}:i\geqslant i_{0}\}$
. Then, by construction, (4.20) holds for any
$Q\in {\mathcal{Q}}^{\ast }$
and
$$\begin{eqnarray}\sup _{Q\in {\mathcal{Q}}^{\ast }}Q\unicode[STIX]{x1D713}(Q)^{m}=\infty .\end{eqnarray}$$
By (4.5) and (4.20), we have that for any
$Q\in {\mathcal{Q}}^{\ast }$
the associated solution
$(p_{1},\ldots ,p_{n},q)\in \mathbb{Z}^{n}\times \mathbb{N}$
satisfies
$$\begin{eqnarray}\displaystyle \biggl|\unicode[STIX]{x1D6FC}_{i}-\frac{p_{i}}{q}\biggr| & {<} & \displaystyle \frac{2^{m/d}}{q(Q\unicode[STIX]{x1D713}(Q)^{m})^{1/d}}\leqslant \frac{2^{m/d}}{q(Q\unicode[STIX]{x1D705}^{m}Q^{-\unicode[STIX]{x1D70F}m})^{1/d}}\nonumber\\ \displaystyle & = & \displaystyle \biggl(\frac{2}{\unicode[STIX]{x1D705}}\biggr)^{m/d}\frac{1}{qQ^{(1-\unicode[STIX]{x1D70F}m)/d}}\leqslant \biggl(\frac{2}{\unicode[STIX]{x1D705}}\biggr)^{m/d}\frac{1}{q\cdot q^{(1-\unicode[STIX]{x1D70F}m)/d}}\quad \text{for}\;1\leqslant i\leqslant d.\nonumber\end{eqnarray}$$
This is exactly (4.21) as desired. To complete the proof it suffices to show that there are infinitely many different
$q$
among the solutions
$(p_{1},\ldots ,p_{n},q)$
as
$Q$
runs through
${\mathcal{Q}}^{\ast }$
. With this in mind, suppose on the contrary that there are only finitely many such
$q$
and let
$A$
be the corresponding set. As
$\boldsymbol{\unicode[STIX]{x1D6FC}}\in {\mathcal{U}}\setminus \mathbb{Q}^{d}$
, there exists some
$1\leqslant i\leqslant d$
for which
$\unicode[STIX]{x1D6FC}_{i}\not \in \mathbb{Q}$
. Hence, there exists some
$\unicode[STIX]{x1D6FF}_{0}>0$
such that
$$\begin{eqnarray}\unicode[STIX]{x1D6FF}_{0}\leqslant \min _{\substack{ q\in A \\ p_{i}\in \mathbb{Z}}}|q\unicode[STIX]{x1D6FC}_{i}-p_{i}|.\end{eqnarray}$$
Together with (4.5), it follows that
$$\begin{eqnarray}\unicode[STIX]{x1D6FF}_{0}\leqslant |q\unicode[STIX]{x1D6FC}_{i}-p_{i}|\leqslant \frac{2^{m/d}}{(Q\unicode[STIX]{x1D713}(Q)^{m})^{1/d}}.\end{eqnarray}$$
This contradicts (4.22) and thereby completes the proof of the corollary. ◻
5 Proof of the main theorem
Let
$\unicode[STIX]{x1D713}$
be as in Theorem 3 and let
$\unicode[STIX]{x1D705}$
denote the infimum defined by (3.2). We can assume without loss of generality that
$\unicode[STIX]{x1D713}:\mathbb{N}\rightarrow (0,1]$
. Indeed, if this was not the case we define the auxiliary function
$\tilde{\unicode[STIX]{x1D713}}:q\rightarrow \tilde{\unicode[STIX]{x1D713}}(q):=\min \{1,\unicode[STIX]{x1D713}(q)\}$
and since
${\mathcal{S}}_{n}(\tilde{\unicode[STIX]{x1D713}})\subseteq {\mathcal{S}}_{n}(\unicode[STIX]{x1D713})$
, it suffices to prove the theorem with
$\unicode[STIX]{x1D713}$
replaced by
$\tilde{\unicode[STIX]{x1D713}}$
.
The following lemma from [Reference Beresnevich and Velani11] will be required during the course of the proof of the theorem.
Lemma 1. Let
$\{B_{i}\}$
be a sequence of balls in
$\mathbb{R}^{k}$
with
$|B_{i}|\rightarrow 0$
as
$i\rightarrow \infty$
. Let
$\{U_{i}\}$
be a sequence of Lebesgue measurable sets such that
$U_{i}\subset B_{i}$
for all
$i$
. Assume that for some
$c>0$
,
$|U_{i}|\geqslant c|B_{i}|$
for all
$i$
. Then the sets
${\mathcal{C}}:=\limsup _{i\rightarrow \infty }U_{i}$
and
${\mathcal{B}}:=\limsup _{i\rightarrow \infty }B_{i}$
have the same Lebesgue measure.
Without loss of generality, we assume that
${\mathcal{M}}$
is given (4.1). Now, given
$\mathbf{f}$
and
$\unicode[STIX]{x1D713}$
let
$$\begin{eqnarray}B(\mathbf{f},\unicode[STIX]{x1D713}):=\{(\mathbf{p},q)\in \mathbb{Z}^{n}\times \mathbb{N}:(p_{1}/q,\ldots ,p_{d}/q)\in {\mathcal{U}}~\text{and (4.6) holds}\}.\end{eqnarray}$$
In view of Corollary 3, we have that for almost every
$\boldsymbol{\unicode[STIX]{x1D6FC}}\in {\mathcal{U}}$
(in fact all irrational
$\boldsymbol{\unicode[STIX]{x1D6FC}}\in {\mathcal{U}}$
) there are infinitely many different vectors
$(\mathbf{p},q)\in B(\mathbf{f},\unicode[STIX]{x1D713})$
satisfying (4.21). Then, for any fixed
$\unicode[STIX]{x1D6FF}>0$
, it follows via Lemma 1 that for almost every
$\boldsymbol{\unicode[STIX]{x1D6FC}}\in {\mathcal{U}}$
there are infinitely many different vectors
$(\mathbf{p},q)\in B(\mathbf{f},\unicode[STIX]{x1D713})$
satisfying
$$\begin{eqnarray}\biggl|\unicode[STIX]{x1D6FC}_{i}-\frac{p_{i}}{q}\biggr|<\unicode[STIX]{x1D6FF}q^{-1-\unicode[STIX]{x1D702}}\quad \text{for}\;1\leqslant i\leqslant d,\end{eqnarray}$$
where
$\unicode[STIX]{x1D702}$
is as in (2.10).
Next, for
$(\mathbf{p},q)\in B(\mathbf{f},\unicode[STIX]{x1D713})$
consider the ball
$$\begin{eqnarray}B_{\mathbf{p},q}=\biggl\{\mathbf{x}=(x_{1},\ldots ,x_{d})\in \mathbb{R}^{d}:\max _{1\leqslant i\leqslant d}\biggl|x_{i}-\frac{p_{i}}{q}\biggr|<\unicode[STIX]{x1D6FF}^{d/s}q^{-\unicode[STIX]{x1D70F}-1}\biggr\},\end{eqnarray}$$
where
$s$
is given by (3.3). The previous statement concerning (5.2) implies that for any ball
$B$
in
${\mathcal{U}}\subset \mathbb{R}^{d}$
we have that
$$\begin{eqnarray}{\mathcal{H}}^{d}\biggl(B\cap \limsup _{(\mathbf{p},q)\in B(\mathbf{f},\unicode[STIX]{x1D713})}B_{\mathbf{p},q}^{s}\biggr)={\mathcal{H}}^{d}(B),\end{eqnarray}$$
where the ball
$B_{\mathbf{p},q}^{s}$
associated with
$B_{\mathbf{p},q}$
is defined via (2.1) with
$k=d$
. Let
$$\begin{eqnarray}W:=\limsup _{(\mathbf{p},q)\in B(\mathbf{f},\unicode[STIX]{x1D713})}B_{\mathbf{p},q}.\end{eqnarray}$$
Then, by the Mass Transference Principle, for any ball
$B$
in
${\mathcal{U}}$
it trivially follows that
$$\begin{eqnarray}{\mathcal{H}}^{s}(B\cap W)={\mathcal{H}}^{s}(B).\end{eqnarray}$$
Now let
$\boldsymbol{\unicode[STIX]{x1D6FC}}\in B_{\mathbf{p},q}$
for some
$(\mathbf{p},q)\in B(\mathbf{f},\unicode[STIX]{x1D713})$
. Then on using the triangle inequality and the Mean Value Theorem, for each
$1\leqslant j\leqslant m$
and some
$\mathbf{c}\in {\mathcal{U}}$
, it follows that
$$\begin{eqnarray}\displaystyle \biggl|f_{j}(\boldsymbol{\unicode[STIX]{x1D6FC}})-\frac{p_{d+j}}{q}\biggr| & {\leqslant} & \displaystyle \biggl|f_{j}(\boldsymbol{\unicode[STIX]{x1D6FC}})-f_{j}\biggl(\frac{\mathbf{p}}{q}\biggr)\biggr|+\biggl|f_{j}\biggl(\frac{\mathbf{p}}{q}\biggr)-\frac{p_{d+j}}{q}\biggr|\nonumber\\ \displaystyle & = & \displaystyle \biggl|\unicode[STIX]{x1D6FB}f_{j}(\mathbf{c})\cdot \biggl(\boldsymbol{\unicode[STIX]{x1D6FC}}-\frac{\mathbf{p}}{q}\biggr)\biggr|+\biggl|f_{j}\biggl(\frac{\mathbf{p}}{q}\biggr)-\frac{p_{d+j}}{q}\biggr|\nonumber\\ \displaystyle & \;\stackrel{\text{(4.2) and (4.6)}}{{\leqslant}}\; & \displaystyle dD\max _{1\leqslant i\leqslant d}\biggl|\unicode[STIX]{x1D6FC}_{i}-\frac{p_{i}}{q}\biggr|+\frac{\unicode[STIX]{x1D713}(q)}{q}\nonumber\\ \displaystyle & \stackrel{\text{(5.3)}}{{\leqslant}} & \displaystyle \unicode[STIX]{x1D6FF}^{d/s}dDq^{-1-\unicode[STIX]{x1D70F}}+\frac{\unicode[STIX]{x1D713}(q)}{q}\nonumber\\ \displaystyle & {\leqslant} & \displaystyle \unicode[STIX]{x1D6FF}^{d/s}dD\unicode[STIX]{x1D705}^{-1}\frac{\unicode[STIX]{x1D713}(q)}{q}+\frac{\unicode[STIX]{x1D713}(q)}{q}\leqslant \frac{2\unicode[STIX]{x1D713}(q)}{q}\nonumber\end{eqnarray}$$
provided
$\unicode[STIX]{x1D6FF}>0$
is sufficiently small. In view of (3.2), we can also ensure that
$\unicode[STIX]{x1D6FF}$
is small enough so that
$$\begin{eqnarray}B_{\mathbf{p},q}\subset \biggl\{\mathbf{x}=(x_{1},\ldots ,x_{d})\in \mathbb{R}^{d}:\max _{1\leqslant i\leqslant d}\biggl|x_{i}-\frac{p_{i}}{q}\biggr|<\frac{\unicode[STIX]{x1D713}(q)}{q}\biggr\}.\end{eqnarray}$$
Hence, in view of the definition of
$W$
, it follows that
$$\begin{eqnarray}W\subset \unicode[STIX]{x1D70B}_{d}({\mathcal{S}}_{n}(2\unicode[STIX]{x1D713})\cap {\mathcal{M}}).\end{eqnarray}$$
The projection map
$\unicode[STIX]{x1D70B}_{d}$
is bi-Lipschitz and thus it follows from (5.4) that
$$\begin{eqnarray}{\mathcal{H}}^{s}({\mathcal{S}}_{n}(2\unicode[STIX]{x1D713})\cap {\mathcal{M}})={\mathcal{H}}^{s}({\mathcal{M}}).\end{eqnarray}$$
Using (5.5) with
$\frac{1}{2}\unicode[STIX]{x1D713}$
(instead of
$\unicode[STIX]{x1D713}$
) implies the measure part (3.4) of the theorem. The dimension part (3.3) of the theorem follows directly from (3.4) and the definition of Hausdorff dimension. This completes the proof of Theorem 3.
6 Concluding comments
The new approach developed in this paper is simple and easy to apply. It is based on first establishing an appropriate Dirichlet-type result (assuming it does not already exist) and then applying the Mass Transference Principle. Within the context of Diophantine approximation on manifolds, our approach enables us to establish lower bound dimension results for any
$C^{2}$
submanifold of
$\mathbb{R}^{n}$
. This is well beyond the class of non-degenerate manifolds for which general results are perceived to hold. However, there is a cost. The new approach does not allow us to obtain the stronger divergent Jarník-type results for
${\mathcal{H}}^{s}({\mathcal{S}}_{n}(\unicode[STIX]{x1D713})\cap {\mathcal{M}})$
. For this we require the significantly more sophisticated “ubiquity” approach developed in [Reference Beresnevich, Dickinson and Velani4].
We end the paper with several natural problems that explore the scope of the new approach.
Problem 1. Within the context of Corollary 2, the new approach as implemented requires the existence of the order
$\unicode[STIX]{x1D70F}_{\unicode[STIX]{x1D713}}$
at infinity of
$1/\unicode[STIX]{x1D713}$
. It is not immediately clear whether or not it is possible to get away with the weaker notion of the lower order at infinity of
$1/\unicode[STIX]{x1D713}$
as in the modern version of the classical Jarník–Besicovitch theorem—see (1.3).
Problem 2. Within the context of Theorem 1, it would be interesting to know if the range of
$\unicode[STIX]{x1D70F}$
given by (1.6) can be extended to a larger range by imposing additional “mild” constraints on the
$C^{2}$
submanifolds of
$\mathbb{R}^{n}$
.
Problem 3. We suspect that the new approach can successfully be applied to problems within the setup of weighted approximations on manifolds. More precisely, it should be possible to give a simpler proof of the lower bound statement appearing in [Reference Beresnevich and Velani10, Theorem 4] and, at the same time, broaden the class of planar curves under consideration.
Problem 4. It would be highly desirable to be able to apply the new approach to inhomogeneous problems. The goal would be to obtain inhomogeneous Jarník–Besicovitch type results for manifolds. This seems to be a much harder task than the previous “weighted” problem. In the first instance it might be useful to consider the case of planar curves and see if the new approach can be utilised to give a simpler proof of the lower bound statement appearing in [Reference Beresnevich, Vaughan and Velani6, Corollary 1].
Problem 5. In this paper we have completely restricted our attention to simultaneous approximation. In [Reference Dickinson and Dodson16], Dickinson and Dodson consider the problem of establishing a Jarník–Besicovitch type result for dual approximation on manifolds. In short, they prove a lower bound statement [Reference Dickinson and Dodson16, Theorem 2] that is valid for any extremal manifold. We suspect that the new approach can be applied to problems within the dual setup. Indeed, it may be possible to show that [Reference Dickinson and Dodson16, Theorem 2] is in fact valid well beyond the class of extremal manifolds, possibly to all
$C^{2}$
submanifolds of
$\mathbb{R}^{n}$
.
Acknowledgements
The authors are grateful to the anonymous reviewer of the paper for their valuable suggestions. SV would like to thank Sharifa Ansari for relieving him of excruciating pain. Her attitude and generosity in a world full of immoral and selfish money grabbers has been most refreshing and humbling. Her actions have been a timely reminder that there is always hope for humanity—even after the political disasters of 2016!
