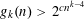1 Introduction
Given a finite point set
$P$
in
$d$
-dimensional Euclidean space
$\mathbb{R}^{d}$
, we say that
$P$
is in general position if no
$d+1$
members lie on a common hyperplane. Let
$ES_{d}(n)$
denote the minimum integer
$N$
, such that any set of
$N$
points in
$\mathbb{R}^{d}$
in general position contains
$n$
members in convex position, that is,
$n$
points that form the vertex set of a convex polytope. In their classic 1935 paper, Erdős and Szekeres [Reference Erdős and Szekeres1] proved that in the plane,
$ES_{2}(n)\leqslant 4^{n}$
. In 1960 [Reference Erdős and Szekeres2], they showed that
$ES_{2}(n)\geqslant 2^{n-2}+1$
and conjectured this to be sharp for every integer
$n\geqslant 3$
. Their conjecture has been verified for
$n\leqslant 6$
[Reference Erdős and Szekeres1, Reference Szekeres and Peters7], and determining the exact value of
$ES_{2}(n)$
for
$n\geqslant 7$
is one of the longest-standing open problems in Ramsey theory/discrete geometry. Recently [Reference Suk8], the second author asymptotically verified the Erdős–Szekeres conjecture by showing that
$ES_{2}(n)=2^{n+o(n)}$
.
In higher dimensions,
$d\geqslant 3$
, much less is known about
$ES_{d}(n)$
. In [Reference Károlyi3], Károlyi showed that projections into lower-dimensional spaces can be used to bound these functions, since most generic projections preserve general position, and the preimage of a set in convex position must itself be in convex position. Hence,
$ES_{d}(n)\leqslant ES_{2}(n)=2^{n+o(n)}$
. However, the best known lower bound for
$ES_{d}(n)$
is only of the order of
$2^{cn^{1/(d-1)}}$
, due to Károlyi and Valtr [Reference Károlyi and Valtr4]. An old conjecture of Füredi (see [Reference Matoušek5, Ch. 3]) says that this lower bound is essentially the truth.
Conjecture 1.1. For
$d\geqslant 3$
,
$ES_{d}(n)=2^{\unicode[STIX]{x1D6E9}(n^{1/(d-1)})}$
.
It was observed by Motzkin [Reference Motzkin6] that any set of
$d+3$
points in
$\mathbb{R}^{d}$
in general position contains either 0, 2, or 4
$(d+2)$
-tuples not in convex position. By defining a hypergraph
$H$
whose vertices are
$N$
points in
$\mathbb{R}^{d}$
in general position, and edges are
$(d+2)$
-tuples not in convex position, then every set of
$d+3$
vertices induces 0, 2, or 4 edges. Moreover, by Carathéodory’s theorem (see [Reference Matoušek5, Theorem 1.2.3]), an independent set in
$H$
would correspond to a set of points in convex position. This leads us to the following combinatorial parameter.
Let
$g_{k}(n)$
be the minimum integer
$N$
such that any
$k$
-uniform hypergraph on
$N$
vertices with the property that every set of
$k+1$
vertices induces 0, 2, or 4 edges, contains an independent set of size
$n$
. For
$k\geqslant 5$
, the geometric construction of Károlyi and Valtr [Reference Károlyi and Valtr4] mentioned earlier implies that
$$\begin{eqnarray}g_{k}(n)\geqslant ES_{k-2}(n)\geqslant 2^{cn^{1/(k-3)}},\end{eqnarray}$$
where
$c=c(k)$
. One might be tempted to prove Conjecture 1.1 by establishing a similar upper bound for
$g_{k}(n)$
. However, our main result shows that this is not possible.
Theorem 1.2. For each
$k\geqslant 5$
there exists
$c=c(k)>0$
such that for any
$n\geqslant k$
we have
$g_{k}(n)>2^{cn^{k-4}}$
.
In the other direction, we can bound
$g_{k}(n)$
from above as follows. For
$n\geqslant k\geqslant 5$
and
$t<k$
, let
$h_{k}(t,n)$
be the minimum integer
$N$
such that any
$k$
-uniform hypergraph on
$N$
vertices with the property that any set of
$k+1$
vertices induces at most
$t$
edges, contains an independent set of size
$n$
. In a forthcoming paper, the authors prove the following.
Theorem 1.3. For
$k\geqslant 5$
and
$t<k$
, there is a positive constant
$c^{\prime }=c^{\prime }(k,t)$
such that
$$\begin{eqnarray}h_{k}(t,n)\leqslant \operatorname{twr}_{t}(c^{\prime }n^{k-t}\log n),\end{eqnarray}$$
where
$\operatorname{twr}$
is defined recursively as
$\operatorname{twr}_{1}(x)=x$
and
$\operatorname{twr}_{i+1}(x)=2^{\operatorname{twr}_{i}(x)}$
.
Hence, we have the following corollary.
Corollary 1.4. For
$k\geqslant 5$
, there is a constant
$c^{\prime }=c^{\prime }(k)$
such that
$$\begin{eqnarray}g_{k}(n)\leqslant h_{k}(4,n)\leqslant 2^{2^{2^{c^{\prime }n^{k-4}\log n}}}.\end{eqnarray}$$
It is an interesting open problem to improve either the upper or lower bounds for
$g_{k}(n)$
.
Problem 1.5. Determine the tower growth rate for
$g_{k}(n)$
.
Actually, this Ramsey function can be generalized further as follows: for every
$S\subset \{0,1,\ldots ,k\}$
, define
$g_{k}(n,S)$
to be the minimum integer
$N$
such that any
$N$
-vertex
$k$
-uniform hypergraph with the property that every set of
$k+1$
vertices induces
$s$
edges for some
$s\in S$
, contains an independent set of size
$n$
. General results for
$g_{k}(n,S)$
may shed light on classical Ramsey problems, but it appears difficult to determine even the tower height for any nontrivial cases.
2 Proof of Theorem 1.2
Let
$k\geqslant 5$
and
$N=2^{cn^{k-4}}$
where
$c=c_{k}>0$
is sufficiently small to be chosen later. We are to produce a
$k$
-uniform hypergraph
$H$
on
$N$
vertices with
$\unicode[STIX]{x1D6FC}(H)<n$
and every
$k+1$
vertices of
$H$
span 0, 2, or 4 edges. Let
$\unicode[STIX]{x1D719}:\binom{[N]}{k-3}\rightarrow \binom{[k-1]}{2}$
be a random
$\binom{k-1}{2}$
-coloring, where each color appears on each
$(k-3)$
-tuple independently with probability
$1/\binom{k-1}{2}$
. For
$f=(v_{1},\ldots ,v_{k-1})\in \binom{[N]}{k-1}$
, where
$v_{1}<v_{2}<\cdots <v_{k-1}$
, define the function
$\unicode[STIX]{x1D712}_{f}:\binom{f}{k-3}\rightarrow \binom{[k-1]}{2}$
as follows: for all
$\{i,j\}\in \binom{[k-1]}{2}$
, let
$$\begin{eqnarray}\unicode[STIX]{x1D712}_{f}(f\setminus \{v_{i},v_{j}\})=\{i,j\}.\end{eqnarray}$$
We define the
$(k-1)$
-uniform hypergraph
$G$
, whose vertex set is
$[N]$
, such that
$$\begin{eqnarray}G\,=\,G_{\unicode[STIX]{x1D719}}\,:=\,\bigg\{\!f\,\in \,\binom{[N]}{k-1}\,:\,\unicode[STIX]{x1D719}(f\setminus \{u,v\})\,=\,\unicode[STIX]{x1D712}_{f}(f\setminus \{u,v\})\text{ for all }\{u,v\}\,\in \,\binom{f}{2}\!\bigg\}.\end{eqnarray}$$
For example, if
$k=4$
(which is excluded for the theorem but we allow it to illustrate this construction) then
$\unicode[STIX]{x1D719}:[N]\rightarrow \{12,13,23\}$
and for
$f=(v_{1},v_{2},v_{3})$
, where
$v_{1}<v_{2}<v_{3}$
, we have
$f\in G$
if and only if
$\unicode[STIX]{x1D719}(v_{1})=23,\unicode[STIX]{x1D719}(v_{2})=13$
, and
$\unicode[STIX]{x1D719}(v_{3})=12$
.
Given a subset
$S\subset [N]$
, let
$G[S]$
be the subhypergraph of
$G$
induced by the vertex set
$S$
. Finally, we define the
$k$
-uniform hypergraph
$H$
, whose vertex set is
$[N]$
, such that
$$\begin{eqnarray}H=H_{\unicode[STIX]{x1D719}}:=\bigg\{e\in \binom{[N]}{k}:|G[e]|\text{is odd}\bigg\}.\end{eqnarray}$$
Claim 2.1.
$|H[S]|$
is even for every
$S\in \binom{[N]}{k+1}$
.
Proof. Let
$S\in \binom{[N]}{k+1}$
and suppose for contradiction that
$|H[S]|$
is odd. Then
$$\begin{eqnarray}2|G[S]|=\!\mathop{\sum }_{f\in G[S]}2=\!\mathop{\sum }_{f\in G[S]}\mathop{\sum }_{\substack{ e\in \binom{S}{k} \\ e\supset f}}1=\!\mathop{\sum }_{e\in \binom{S}{k}}|G[e]|=\!\mathop{\sum }_{e\not \in H[S]}|G[e]|+\mathop{\sum }_{e\in H[S]}|G[e]|.\end{eqnarray}$$
The first sum on the right-hand side above is even by definition of
$H$
and the second sum is odd by definition of
$H$
and the assumption that
$|H[S]|$
is odd. This contradiction completes the proof.◻
Claim 2.2.
$|G[e]|\leqslant 2$
for every
$e\in \binom{[N]}{k}$
.
Proof. For sake of contradiction, suppose that for
$e=(v_{1},\ldots ,v_{k})$
, where
$v_{1}<\cdots <v_{k}$
, we have
$|G[e]|\geqslant 3$
. Let
$e_{p}=e\setminus \{v_{p}\}$
for
$p\in [k]$
and suppose that
$e_{i},e_{j},e_{l}\in G$
with
$i<j<l$
. In what follows, we will find a set
$S$
of size
$k-3$
, where
$S\subset e_{i}$
and
$S\subset e_{l}$
, such that
$\unicode[STIX]{x1D712}_{e_{i}}(S)\neq \unicode[STIX]{x1D712}_{e_{l}}(S)$
. This will give us our contradiction since
$e_{i},e_{l}\in G$
implies that
$\unicode[STIX]{x1D712}_{e_{i}}(S)=\unicode[STIX]{x1D719}(S)=\unicode[STIX]{x1D712}_{e_{l}}(S)$
.
Let
$Y=e\setminus \{v_{i},v_{j},v_{l}\}$
and
$Y^{\prime }=Y\setminus \{\min Y\}$
. Let us first assume that
$i>1$
so that
$\min Y=v_{1}$
. In this case,
$$\begin{eqnarray}\unicode[STIX]{x1D712}_{e_{i}}(Y^{\prime }\cup \{v_{j}\})=\{1,l-1\},\end{eqnarray}$$
since we obtain
$Y^{\prime }\cup \{v_{j}\}$
from
$e_{i}$
by removing
$\min Y$
and
$v_{l}$
which are the first and
$(l-1)$
st elements of
$e_{i}$
. Similarly,
$$\begin{eqnarray}\unicode[STIX]{x1D712}_{e_{l}}(Y^{\prime }\cup \{v_{j}\})=\{1,i\},\end{eqnarray}$$
since we obtain
$Y^{\prime }\cup \{v_{j}\}$
from
$e_{l}$
by removing
$\min Y$
and
$v_{i}$
which are the first and
$i$
th elements of
$e_{l}$
. Because
$l>i+1$
, we conclude that
$\unicode[STIX]{x1D712}_{e_{i}}(Y^{\prime }\cup \{v_{j}\})\neq \unicode[STIX]{x1D712}_{e_{l}}(Y^{\prime }\cup \{v_{j}\})$
as desired.
Next, we assume that
$i=1$
and
$\min Y=v_{q}$
where
$q>1$
. In this case,
$$\begin{eqnarray}\unicode[STIX]{x1D712}_{e_{i}}(Y^{\prime }\cup \{v_{j}\})=\{q-1,l-1\},\end{eqnarray}$$
since we obtain
$Y^{\prime }\cup \{v_{j}\}$
from
$e_{i}$
by removing
$v_{q}$
and
$v_{l}$
which are the
$(q-1)$
st and
$(l-1)$
st elements of
$e_{i}$
. Similarly,
$$\begin{eqnarray}\unicode[STIX]{x1D712}_{e_{l}}(Y^{\prime }\cup \{v_{j}\})=\{1,q^{\prime }\}\quad \text{where }q^{\prime }=q\text{ if }q<l\text{ and }q^{\prime }=q-1\text{ if }q>l,\end{eqnarray}$$
since we obtain
$Y^{\prime }\cup \{v_{j}\}$
from
$e_{l}$
by removing
$v_{i}=v_{1}$
and
$v_{q}$
which are the first and
$q^{\prime }$
th elements of
$e_{l}$
. If
$q\neq 2$
, then we immediately obtain
$\unicode[STIX]{x1D712}_{e_{i}}(Y^{\prime }\cup \{v_{j}\})\neq \unicode[STIX]{x1D712}_{e_{l}}(Y^{\prime }\cup \{v_{j}\})$
as desired. On the other hand, if
$q=2$
, then
$q^{\prime }=q=2$
as well and
$l\geqslant 4$
, so
$l-1\neq q^{\prime }$
and again
$$\begin{eqnarray}\unicode[STIX]{x1D712}_{e_{i}}(Y^{\prime }\cup \{v_{j}\})=\{q-1,l-1\}\neq \{1,q^{\prime }\}=\unicode[STIX]{x1D712}_{e_{l}}(Y^{\prime }\cup \{v_{j}\}).\end{eqnarray}$$
This completes the proof of the claim. ◻
Let
$T_{3}$
be the
$(k-1)$
-uniform hypergraph with vertex set
$S$
with
$|S|=k+1$
and three edges
$e_{1},e_{2},e_{3}$
such that there are three pairwise disjoint pairs
$p_{1},p_{2},p_{3}\in \binom{S}{2}$
with
$p_{i}=\{v_{i},v_{i}^{\prime }\}$
and
$e_{i}=S\setminus p_{i}$
for
$i\in \{1,2,3\}$
.
Claim 2.3.
$T_{3}\not \subset G$
.
Proof. Suppose for a contradiction that there is a subset
$S\subset [N]$
of size
$k+1$
such that
$T_{3}\subset G[S]$
. Using the notation above, assume without loss of generality that
$v_{1}=\min \cup _{i}p_{i}$
and
$v_{2}=\min (p_{2}\cup p_{3})$
. Let
$Y=S\setminus (p_{1}\cup p_{3})$
and note that
$Y\in \binom{e_{1}\cap e_{3}}{k-3}$
. Let
$Y_{1}\subset Y$
be the set of elements in
$Y$
that are smaller than
$v_{1}$
, so we have the ordering
$$\begin{eqnarray}Y_{1}<v_{1}<v_{2}<\{v_{3},v_{3}^{\prime }\}.\end{eqnarray}$$
Now,
$\unicode[STIX]{x1D712}_{e_{1}}(Y)$
is the pair of positions of
$v_{3}$
and
$v_{3}^{\prime }$
in
$e_{1}$
. Both of these positions are at least
$|Y_{1}|+2$
as
$Y_{1}\cup \{v_{2}\}$
lies before
$p_{3}$
. On the other hand, the smallest element of
$\unicode[STIX]{x1D712}_{e_{3}}(Y)$
is
$|Y_{1}|+1$
which is the position of
$v_{1}$
in
$e_{3}$
. This shows that
$\unicode[STIX]{x1D712}_{e_{1}}(Y)\neq \unicode[STIX]{x1D712}_{e_{3}}(Y)$
, which is a contradiction as both must be equal to
$\unicode[STIX]{x1D719}(Y)$
as
$e_{1},e_{3}\subset G$
.◻
We now show that every
$(k+1)$
-set
$S\subset [N]$
spans
$0,2$
or
$4$
edges of
$H$
. By Claim 2.1,
$|H[S]|$
is even. Let
$G^{\prime }$
be the graph with vertex set
$S$
and edge set
$\{S\setminus f:f\in G[S]\}$
. So there is a one-to-one correspondence between
$G[S]$
and
$G^{\prime }$
via the map
$f\rightarrow S\setminus f$
. If
$G^{\prime }$
has a vertex
$x$
of degree at least three, then
$|G[S\setminus \{x\}]|\geqslant 3$
which contradicts Claim 2.2. Therefore
$G^{\prime }$
consists of disjoint paths, cycles, and isolated vertices. This implies that a
$k$
-set
$A\subset S$
is an edge in
$H$
exactly when
$S\setminus A$
is a vertex of degree one in
$G^{\prime }$
. Next, observe that Claim 2.3 implies that
$G^{\prime }$
does not contain a matching of size three, for the complementary sets of this matching yield a copy of
$T_{3}\subset G$
. Hence, the number of degree-one vertices in
$G^{\prime }$
is 0, 2, or 4, and therefore
$|H[S]|\in \{0,2,4\}$
for all
$S\in \binom{[N]}{k+1}$
.
Let us now argue that
$\unicode[STIX]{x1D6FC}(H)<n$
, which is a straightforward application of the probabilistic method. Indeed, we will show that this happens with positive probability and conclude that an
$H$
with this property exists. For a given
$k$
-set, the probability that it is an edge of
$H$
is
$p>0$
, where
$p$
depends only on
$k$
. Consequently, the probability that
$H$
has an independent set of size
$n$
is at most
$$\begin{eqnarray}\binom{N}{n}(1-p)^{c^{\prime }n^{k-3}}\end{eqnarray}$$
for some
$c^{\prime }>0$
. Note that the exponent
$k-3$
above is obtained by taking a partial Steiner
$(n,k,k-3)$
system
$S$
within a potential independent set of size
$n$
and observing that we have independence within the edges of
$S$
. A short calculation shows that this probability is less than 1 as long as
$c$
is sufficiently small. This completes the proof of Theorem 1.2.◻
Acknowledgement
We thank the referee for helpful comments.
