Hostname: page-component-cb9f654ff-hn9fh Total loading time: 0 Render date: 2025-08-12T22:51:51.120Z Has data issue: false hasContentIssue false
  • English
  • Français

On Hayman's alternative

Part of: Entire and meromorphic functions, and related topics

Published online by Cambridge University Press:  26 February 2010

J. K. Langley
J. K. Langley
Affiliation:
Department of Pure Mathematics, University of St. Andrews, St. Andrews, Fife, Scotland.

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Suppose that f(z) is non-constant and meromorphic in the plane and that, for some k≥= 1, a0(z),…, ak(z) are meromorphic in the plane with

for j' = 0,…, k. Here, using standard notation from [3], S(r,f) denotes any quantity satisfying S(r,f) = o(T(r,f)) as r→ ∞, possibly outside a set of finite linear measure. Then, setting

we have ([3, p. 57])

Theorem A. Suppose that f(z) is non-constant and meromorphic in the plane, and thatψ (z) given by (1.2) and (1.1) and is non-constant. Then

where N0(r, l/ψ') counts only zeros of ψ' which are not zeros of ψ − 1, and the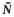counting functions count points without regard to multiplicity.

MSC classification

Secondary: 30D35: Distribution of values, Nevanlinna theory

Information

Type
Research Article
Information
Mathematika , Volume 32 , Issue 1 , June 1985 , pp. 139 - 146
Copyright
Copyright © University College London 1985

References

1.Frank, G. and Mues, E.. Differentialpolynome (Oberwolfach, 1979).Google Scholar
2.Hayman, W. K.. Picard values of meromorphic functions and their derivatives. Ann. of Math., 70 (1959), 9–42.Google Scholar
3.Hayman, W. K.. Meromorphic Functions (Oxford, 1964).Google Scholar
4.Ince, E. L.. Ordinary Differential Equations (Dover, 1926).Google Scholar
5.Langley, J. K.. On differential polynomials and results of Hayman and Doeringer. Math. Zeit., 187 (1984), 1–11.CrossRefGoogle Scholar