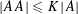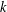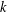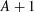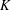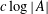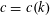1 Introduction
Let
![]() $A$
be a finite set of integers. The sum set and product set of
$A$
be a finite set of integers. The sum set and product set of
![]() $A$
are defined respectively as
$A$
are defined respectively as
The sum–product problem is concerned with showing that one of these sets is always large. It was conjectured by Erdős and Szemerédi [Reference Erdős and Szemerédi7] that, for all
![]() $\unicode[STIX]{x1D716}>0$
and any finite
$\unicode[STIX]{x1D716}>0$
and any finite
![]() $A\subset \mathbb{Z}$
,
$A\subset \mathbb{Z}$
,
where
![]() $c(\unicode[STIX]{x1D716})>0$
is an absolute constant. The same conjecture can also be made over the reals, and indeed other fields. The Erdős–Szemerédi conjecture remains open, and it appears to be a deep problem. Konyagin and Shkredov [Reference Konyagin and Shkredov13] proved that (1) holds with
$c(\unicode[STIX]{x1D716})>0$
is an absolute constant. The same conjecture can also be made over the reals, and indeed other fields. The Erdős–Szemerédi conjecture remains open, and it appears to be a deep problem. Konyagin and Shkredov [Reference Konyagin and Shkredov13] proved that (1) holds with
![]() $\unicode[STIX]{x1D716}<2/3$
, and the current best bound, due to Shakan [Reference Shakan14], has
$\unicode[STIX]{x1D716}<2/3$
, and the current best bound, due to Shakan [Reference Shakan14], has
![]() $\unicode[STIX]{x1D716}\leqslant 2/3-5/5277+o(1)$
. These bounds hold over real numbers, and their proofs are geometric in nature.
$\unicode[STIX]{x1D716}\leqslant 2/3-5/5277+o(1)$
. These bounds hold over real numbers, and their proofs are geometric in nature.
A similar question can also be considered with more variables. The
![]() $k$
-fold sumset and
$k$
-fold sumset and
![]() $k$
-fold product set of
$k$
-fold product set of
![]() $A\subset \mathbb{Z}$
are defined respectively as
$A\subset \mathbb{Z}$
are defined respectively as
Erdős and Szemerédi also made the even more general conjecture that, for all
![]() $\unicode[STIX]{x1D716}>0$
and any finite
$\unicode[STIX]{x1D716}>0$
and any finite
![]() $A\subset \mathbb{Z}$
,
$A\subset \mathbb{Z}$
,
Given the state of progress with the
![]() $k=2$
version of this conjecture, it is not surprising that the more general conjecture is also wide open. However, over the rationals, a series of remarkable results concerning unlimited growth does exist. The first of these results is the following theorem of Chang [Reference Chang5].
$k=2$
version of this conjecture, it is not surprising that the more general conjecture is also wide open. However, over the rationals, a series of remarkable results concerning unlimited growth does exist. The first of these results is the following theorem of Chang [Reference Chang5].
Theorem 1.1. Let
![]() $A\subset \mathbb{Q}$
be a finite set with
$A\subset \mathbb{Q}$
be a finite set with
![]() $|AA|\leqslant K|A|$
and let
$|AA|\leqslant K|A|$
and let
![]() $k\geqslant 2$
be an integer. Then
$k\geqslant 2$
be an integer. Then
The results proved in [Reference Chang5] were actually somewhat more general. It was established that
where
![]() $E_{k}^{+}(A)$
is the
$E_{k}^{+}(A)$
is the
![]() $k$
-fold additive energy, which is defined as the quantity
$k$
-fold additive energy, which is defined as the quantity
Note that the trivial solutions with
![]() $a_{1}=a_{k+1},\ldots ,a_{k}=a_{2k}$
ensure that
$a_{1}=a_{k+1},\ldots ,a_{k}=a_{2k}$
ensure that
![]() $E_{K}^{+}(A)\geqslant |A|^{k}$
and so (4) is a factor of
$E_{K}^{+}(A)\geqslant |A|^{k}$
and so (4) is a factor of
![]() $(Ck^{2})^{kK}$
away from being optimal. Inequality (3) follows from (4) after an application of the Cauchy–Schwarz inequality.
$(Ck^{2})^{kK}$
away from being optimal. Inequality (3) follows from (4) after an application of the Cauchy–Schwarz inequality.
Giving a result with even more generality, Chang in fact proved a version of (4) with weighted energy. See the forthcoming §3 for a discussion on energy and weighted energy featuring the relevant definitions.
In the statement of Theorem 1.1, we think of
![]() $k$
as a fixed constant. The theorem then gives a very strong lower bound for the size of
$k$
as a fixed constant. The theorem then gives a very strong lower bound for the size of
![]() $kA$
when
$kA$
when
![]() $K$
is significantly smaller than
$K$
is significantly smaller than
![]() $\log |A|$
. However, if we push to the range
$\log |A|$
. However, if we push to the range
![]() $K=|A|^{\unicode[STIX]{x1D716}}$
for some positive
$K=|A|^{\unicode[STIX]{x1D716}}$
for some positive
![]() $\unicode[STIX]{x1D716}$
, then Theorem 1.1 gives only a trivial bound.
$\unicode[STIX]{x1D716}$
, then Theorem 1.1 gives only a trivial bound.
In a follow-up paper of Bourgain and Chang [Reference Bourgain and Chang4], this method was used as a foundation and developed considerably in order to prove the following result.
Theorem 1.2. Let
![]() $k\geqslant 2$
be a fixed integer. Given
$k\geqslant 2$
be a fixed integer. Given
![]() $\unicode[STIX]{x1D6FE}>0$
, there is a constant
$\unicode[STIX]{x1D6FE}>0$
, there is a constant
![]() $\unicode[STIX]{x1D6EC}=\unicode[STIX]{x1D6EC}(\unicode[STIX]{x1D6FE},k)$
such that for all finite sets
$\unicode[STIX]{x1D6EC}=\unicode[STIX]{x1D6EC}(\unicode[STIX]{x1D6FE},k)$
such that for all finite sets
![]() $A\subset \mathbb{Q}$
with
$A\subset \mathbb{Q}$
with
![]() $|AA|\leqslant K|A|$
,
$|AA|\leqslant K|A|$
,
In particular, this now gives an excellent lower bound for
![]() $|kA|$
when
$|kA|$
when
![]() $K=|A|^{\unicode[STIX]{x1D716}}$
, for some small but positive
$K=|A|^{\unicode[STIX]{x1D716}}$
, for some small but positive
![]() $\unicode[STIX]{x1D716}$
.
$\unicode[STIX]{x1D716}$
.
Once again, a more general version of Theorem 1.2 was actually proved in [Reference Bourgain and Chang4], giving an upper bound for the weighted energy of
![]() $A$
. This level of generality was important for establishing the main result of [Reference Bourgain and Chang4], which was the following result on unbounded growth of sums or products.
$A$
. This level of generality was important for establishing the main result of [Reference Bourgain and Chang4], which was the following result on unbounded growth of sums or products.
Theorem 1.3. For all
![]() $b\geqslant 0$
, there is an integer
$b\geqslant 0$
, there is an integer
![]() $k=k(b)$
such that for all
$k=k(b)$
such that for all
![]() $A\subset \mathbb{Q}$
with
$A\subset \mathbb{Q}$
with
![]() $|A|\geqslant 2$
,
$|A|\geqslant 2$
,
See Zhelezov [Reference Zhelezov17] for an exposition of the work of [Reference Chang5] and [Reference Bourgain and Chang4].
In this paper, we consider an alternative formulation of the sum–product problem with products and products of shifts. Given an arbitrary
![]() $A\subset \mathbb{R}$
, sum–product heuristics lead one to believe that
$A\subset \mathbb{R}$
, sum–product heuristics lead one to believe that
![]() $\max \{|AA|,|(A+1)(A+1)|\}$
is large. Roughly speaking, this is an assertion that if
$\max \{|AA|,|(A+1)(A+1)|\}$
is large. Roughly speaking, this is an assertion that if
![]() $A$
is multiplicatively structured then an additive shift will disturb this structure. A similar problem was considered in the finite field setting by Bourgain [Reference Bourgain3], and it was established by Garaev and Shen [Reference Garaev and Shen10] that for any finite
$A$
is multiplicatively structured then an additive shift will disturb this structure. A similar problem was considered in the finite field setting by Bourgain [Reference Bourgain3], and it was established by Garaev and Shen [Reference Garaev and Shen10] that for any finite
![]() $A\subset \mathbb{R}$
,
$A\subset \mathbb{R}$
,
where
![]() $c>0$
is an absolute constant. See also Jones–Roche-Newton [Reference Jones and Roche-Newton12] for a slightly improved exponent. In principle, the value of
$c>0$
is an absolute constant. See also Jones–Roche-Newton [Reference Jones and Roche-Newton12] for a slightly improved exponent. In principle, the value of
![]() $1$
for the shift is not important, and a shift by any non-zero
$1$
for the shift is not important, and a shift by any non-zero
![]() $x$
should give the same outcome. Indeed, the proof of (5) works in exactly the same way if
$x$
should give the same outcome. Indeed, the proof of (5) works in exactly the same way if
![]() $1$
is replaced with any
$1$
is replaced with any
![]() $x\neq 0$
.
$x\neq 0$
.
It seems plausible that the numerology of the Erdős–Szemerédi conjecture holds for this problem too. That is, we expect that
![]() $\max \{|A^{k}|,|(A+1)^{k}|\}$
should be close to
$\max \{|A^{k}|,|(A+1)^{k}|\}$
should be close to
![]() $|A|^{k}$
. The main result of this paper proves a result in this direction, although under the stronger assumption that
$|A|^{k}$
. The main result of this paper proves a result in this direction, although under the stronger assumption that
![]() $A$
has small multiplicative doubling.
$A$
has small multiplicative doubling.
Theorem 1.4. Let
![]() $A\subset \mathbb{Q}$
be finite and suppose that
$A\subset \mathbb{Q}$
be finite and suppose that
![]() $|AA|=K|A|$
. Then, for any
$|AA|=K|A|$
. Then, for any
![]() $k\geqslant 2$
,
$k\geqslant 2$
,
This is an analogue of Theorem 1.1 above, and gives an essentially optimal lower bound for
![]() $|(A+1)^{k}|$
in the case when
$|(A+1)^{k}|$
in the case when
![]() $K<c\log |A|$
. Again, we actually prove a more general result with energies and weights. See Theorem 6.1 for the full statement.
$K<c\log |A|$
. Again, we actually prove a more general result with energies and weights. See Theorem 6.1 for the full statement.
Note that, since this theorem holds for any set of rationals, it follows that the shift value
![]() $1$
can be replaced by any rational
$1$
can be replaced by any rational
![]() $\unicode[STIX]{x1D706}\neq 0$
. Indeed, if
$\unicode[STIX]{x1D706}\neq 0$
. Indeed, if
![]() $|AA|=K|A|$
then also
$|AA|=K|A|$
then also
![]() $|(A/\unicode[STIX]{x1D706})(A/\unicode[STIX]{x1D706})|=K|A|$
for any rational
$|(A/\unicode[STIX]{x1D706})(A/\unicode[STIX]{x1D706})|=K|A|$
for any rational
![]() $\unicode[STIX]{x1D706}$
. We can therefore apply Theorem 1.4 to the set
$\unicode[STIX]{x1D706}$
. We can therefore apply Theorem 1.4 to the set
![]() $A/\unicode[STIX]{x1D706}$
and conclude that
$A/\unicode[STIX]{x1D706}$
and conclude that
It seems that an analogue of Theorem 1.3 for products and products of shifts would have several interesting consequences in additive number theory. The authors consider this problem in the article [Reference Hanson, Roche-Newton and Zhelezov11]. The extension to the regime
![]() $K=|A|^{\unicode[STIX]{x1D700}}$
with for small
$K=|A|^{\unicode[STIX]{x1D700}}$
with for small
![]() $\unicode[STIX]{x1D700}>0$
is technical and builds of the ideas in this article.
$\unicode[STIX]{x1D700}>0$
is technical and builds of the ideas in this article.
As stated, a naive version of Theorem 1.4 can be derived using a quantitative version the Subspace Theorem [Reference Evertse, Schlickewei and Schmidt9] similarly to [Reference Chang6]. The resulting bound will be of the form
One of the improvements in this direction is that Theorem 1.4 in its most general form, discussed in Remark 6.3, holds under a strictly weaker hypothesis than what is needed to apply the Subspace theorem.
Next, apart from relying on a very hard result [Reference Evertse, Schlickewei and Schmidt9], another disadvantage of using the Subspace Theorem is that the dependence
![]() $c(k)$
turns out to be triply exponential in
$c(k)$
turns out to be triply exponential in
![]() $k$
(comparing to almost linear in our case). Indeed, the number of terms after expanding the brackets in
$k$
(comparing to almost linear in our case). Indeed, the number of terms after expanding the brackets in
![]() $(A+1)^{k}$
grows exponentially in
$(A+1)^{k}$
grows exponentially in
![]() $k$
, while the state-of-the-art quantitative bound for the Subspace Theorem is doubly exponential in the number of variables; see [Reference Chang6, Reference Amoroso and Viada1] for further details.
$k$
, while the state-of-the-art quantitative bound for the Subspace Theorem is doubly exponential in the number of variables; see [Reference Chang6, Reference Amoroso and Viada1] for further details.
On the other hand, the dependence
![]() $c(k)$
may be important for applications. For example, in the regime
$c(k)$
may be important for applications. For example, in the regime
![]() $K=O(1)$
of a multiplicatively structured set
$K=O(1)$
of a multiplicatively structured set
![]() $A$
, Theorem 1.4 tells us that the iterated shifted products
$A$
, Theorem 1.4 tells us that the iterated shifted products
![]() $(A+1)^{(k)}$
have maximal growth up to
$(A+1)^{(k)}$
have maximal growth up to
![]() $k\approx \log |A|$
, rapidly expanding to a set of size at least
$k\approx \log |A|$
, rapidly expanding to a set of size at least
![]() $\exp (\unicode[STIX]{x1D6FA}(\log ^{2}|A|))$
. Such a long-range expansion does not seem to follow from the Subspace Theorem due to the poor dependence on
$\exp (\unicode[STIX]{x1D6FA}(\log ^{2}|A|))$
. Such a long-range expansion does not seem to follow from the Subspace Theorem due to the poor dependence on
![]() $k$
.
$k$
.
Finally, in the following application to
![]() $S$
-unit equations it is crucial that
$S$
-unit equations it is crucial that
![]() $c(k)$
is almost linear.
$c(k)$
is almost linear.
Corollary 1.5. Let
![]() $q_{1},\ldots ,q_{r}$
be rational integers,
$q_{1},\ldots ,q_{r}$
be rational integers,
![]() $I$
an integer interval of length
$I$
an integer interval of length
![]() $H$
and
$H$
and
![]() $S$
a set of numbers of the form
$S$
a set of numbers of the form
such that
![]() $\unicode[STIX]{x1D6FC}_{i}\in I$
. Then for any rational
$\unicode[STIX]{x1D6FC}_{i}\in I$
. Then for any rational
![]() $c_{1},c_{2}\neq 0$
, the number of solutions
$c_{1},c_{2}\neq 0$
, the number of solutions
![]() $(s_{1},s_{2})\in S\times S$
to
$(s_{1},s_{2})\in S\times S$
to
is bounded by
![]() $(\log H)^{Cr}$
with some absolute effective constant
$(\log H)^{Cr}$
with some absolute effective constant
![]() $C>0$
.
$C>0$
.
Corollary 1.5 gives near-optimal bounds (see [Reference Evertse, Győry, Stewart and Tijdeman8]) when
![]() $H=O(1)$
and can be used to estimate the number of solutions with small relative height (e.g., replace [Reference Beukers and Schlickewei2, Lemma 2.4]). In particular, one can combine Corollary 1.5 with the elementary Thue’s polynomial method as in [Reference Beukers and Schlickewei2] and recover a universal bound
$H=O(1)$
and can be used to estimate the number of solutions with small relative height (e.g., replace [Reference Beukers and Schlickewei2, Lemma 2.4]). In particular, one can combine Corollary 1.5 with the elementary Thue’s polynomial method as in [Reference Beukers and Schlickewei2] and recover a universal bound
![]() $\exp (O(r))$
for the number of rational solutions to an
$\exp (O(r))$
for the number of rational solutions to an
![]() $S$
-unit equation in two variables. Such a bound is comparable to the result of Beukers and Schlikewei [Reference Beukers and Schlickewei2]
$S$
-unit equation in two variables. Such a bound is comparable to the result of Beukers and Schlikewei [Reference Beukers and Schlickewei2]
but with a substantially different and elementary proof. We prove Corollary 1.5 in §7.
1.1 Outline of the proof
Our proof strategy is based on the ideas that Chang used to prove Theorem 1.1. Chang’s strategy begins by using Freiman’s Lemma to show that the elements of a set
![]() $A$
with
$A$
with
![]() $|AA|=K|A|$
are determined by the powers of a set
$|AA|=K|A|$
are determined by the powers of a set
![]() $\{p_{1},\ldots ,p_{K}\}$
of
$\{p_{1},\ldots ,p_{K}\}$
of
![]() $K$
primes. The aim is to use this information to bound the number of solutions to
$K$
primes. The aim is to use this information to bound the number of solutions to
such that
![]() $a_{1},\ldots ,a_{2k}\in A$
. The problem of bounding the number of solutions to (6) is converted into the problem of bounding certain trigonometric sums. The proof then proceeds by induction on
$a_{1},\ldots ,a_{2k}\in A$
. The problem of bounding the number of solutions to (6) is converted into the problem of bounding certain trigonometric sums. The proof then proceeds by induction on
![]() $K$
. If
$K$
. If
![]() $K=1$
then it follows that some power of the determining prime
$K=1$
then it follows that some power of the determining prime
![]() $p$
must occur more than once in (6). Using this and an application of Hölder’s inequality establishes the base case, and closing the induction is then fairly straightforward.
$p$
must occur more than once in (6). Using this and an application of Hölder’s inequality establishes the base case, and closing the induction is then fairly straightforward.
We imitate this argument, with the role of trigonometric sums played instead by Dirichlet polynomials, since we are now bounding the number of solutions to the multiplicative equation
When
![]() $A$
is a set of integers things go through rather smoothly. However, the statement of Theorem 1.4 is not so satisfying in this case, since the lack of dilation invariance in our problem restricts the value of the additive shift we can take. The case when
$A$
is a set of integers things go through rather smoothly. However, the statement of Theorem 1.4 is not so satisfying in this case, since the lack of dilation invariance in our problem restricts the value of the additive shift we can take. The case when
![]() $A$
consists of rational numbers, and in particular when the powers of our determining prime may be negative, does not yield to this method immediately, and the major challenge we faced was to tackle this case.
$A$
consists of rational numbers, and in particular when the powers of our determining prime may be negative, does not yield to this method immediately, and the major challenge we faced was to tackle this case.
To explain how we overcome this hurdle, let us begin with the base case
![]() $K=1$
. We can control the number of solutions to (7) by those solutions consisting only of positive powers of
$K=1$
. We can control the number of solutions to (7) by those solutions consisting only of positive powers of
![]() $p$
and those consisting of only negative powers. We can then bound those solutions coming from the first case by treating them as integers. However, we cannot yet say anything about the solutions coming from negative powers of
$p$
and those consisting of only negative powers. We can then bound those solutions coming from the first case by treating them as integers. However, we cannot yet say anything about the solutions coming from negative powers of
![]() $p$
. We thus get a base case with two separate terms, and this blows up into a rather complicated statement after the induction process. However, once we apply a little extra information coming from Freiman’s Lemma, we are able to bound these terms with only negative powers, and after some tricky calculations the desired result follows.
$p$
. We thus get a base case with two separate terms, and this blows up into a rather complicated statement after the induction process. However, once we apply a little extra information coming from Freiman’s Lemma, we are able to bound these terms with only negative powers, and after some tricky calculations the desired result follows.
Note that, for the case
![]() $k=2$
of Theorem 1.1, and indeed also that of Theorem 1.2, things are somewhat easier, as the whole proof can be carried out in the “physical space”, without the need for trigonometric sums. See [Reference Zhelezov17] for the details of the modifications to the argument. A similar situation arises here, as the case
$k=2$
of Theorem 1.1, and indeed also that of Theorem 1.2, things are somewhat easier, as the whole proof can be carried out in the “physical space”, without the need for trigonometric sums. See [Reference Zhelezov17] for the details of the modifications to the argument. A similar situation arises here, as the case
![]() $k=2$
of Theorem 1.4 can be proven without using Dirichlet polynomials. However, when
$k=2$
of Theorem 1.4 can be proven without using Dirichlet polynomials. However, when
![]() $k=2$
, a better version of Theorem 1.4 is available, even over
$k=2$
, a better version of Theorem 1.4 is available, even over
![]() $\mathbb{R}$
; see Shkredov [Reference Shkredov15, Theorem 12].
$\mathbb{R}$
; see Shkredov [Reference Shkredov15, Theorem 12].
1.2 Notation
For two integers
![]() $a,b$
we write, as usual,
$a,b$
we write, as usual,
![]() $(a,b)=1$
if
$(a,b)=1$
if
![]() $a$
and
$a$
and
![]() $b$
are coprime. Similarly for
$b$
are coprime. Similarly for
![]() $a,b\in \mathbb{Q}$
we say that
$a,b\in \mathbb{Q}$
we say that
![]() $a$
and
$a$
and
![]() $b$
are coprime if, after writing
$b$
are coprime if, after writing
![]() $a=n_{a}/d_{a}$
and
$a=n_{a}/d_{a}$
and
![]() $b=n_{b}/d_{b}$
as reduced fractions, there is no prime which appears in both
$b=n_{b}/d_{b}$
as reduced fractions, there is no prime which appears in both
![]() $a$
and
$a$
and
![]() $b$
. That is,
$b$
. That is,
![]() $(n_{a},n_{b})=(n_{a},d_{b})=(d_{a},n_{b})=(d_{a},d_{b})=1$
.
$(n_{a},n_{b})=(n_{a},d_{b})=(d_{a},n_{b})=(d_{a},d_{b})=1$
.
We write
![]() $\mathbb{Z}_{{\geqslant}0}$
for the set of all non-negative integers, and
$\mathbb{Z}_{{\geqslant}0}$
for the set of all non-negative integers, and
![]() $\mathbb{Z}_{-}$
for the set of all negative integers.
$\mathbb{Z}_{-}$
for the set of all negative integers.
2 Background on Dirichlet Polynomials
Let
![]() $(w_{n})_{n=1}^{N}$
be a finite sequence of non-negative reals. The associated Dirichlet polynomial is
$(w_{n})_{n=1}^{N}$
be a finite sequence of non-negative reals. The associated Dirichlet polynomial is
which is a function of a complex variable
![]() $s$
. These polynomials are not periodic in
$s$
. These polynomials are not periodic in
![]() $T$
, but still satisfy similar properties to those of trigonometric polynomials when integrated over a long interval.
$T$
, but still satisfy similar properties to those of trigonometric polynomials when integrated over a long interval.
Lemma 2.1. For any
![]() $m,n\in \mathbb{Q}$
we have
$m,n\in \mathbb{Q}$
we have
Consequently, for
![]() $k\geqslant 1$
, we have
$k\geqslant 1$
, we have
where the implied constants in
![]() $o_{T\rightarrow \infty }(1)$
depend on the sequence
$o_{T\rightarrow \infty }(1)$
depend on the sequence
![]() $w_{n}$
.
$w_{n}$
.
We will be interested in the following sorts of Dirichlet polynomials, and only interested at purely imaginary values. For
![]() $p$
a prime and a rational number
$p$
a prime and a rational number
![]() $x$
, let
$x$
, let
![]() $v_{p}(x)$
denote the
$v_{p}(x)$
denote the
![]() $p$
-adic valuation of
$p$
-adic valuation of
![]() $x$
, that is, the power of
$x$
, that is, the power of
![]() $p$
when
$p$
when
![]() $x$
is expressed in its reduced form as a product of primes:
$x$
is expressed in its reduced form as a product of primes:
For any
![]() $u\in \mathbb{Q}$
, write
$u\in \mathbb{Q}$
, write
![]() ${\mathcal{F}}_{p,j,u}$
for the set of those Dirichlet polynomials of the form
${\mathcal{F}}_{p,j,u}$
for the set of those Dirichlet polynomials of the form
3 Weighted multiplicative energy
A key notion in this paper is that of the multiplicative energy of order
![]() $k$
of a set
$k$
of a set
![]() $A$
, which is defined as
$A$
, which is defined as
where
![]() $\unicode[STIX]{x1D6E4}_{k,A}(n)=|\{(a_{1},\ldots ,a_{k})\in A^{k}:a_{1}\cdots a_{k}=n\}$
. Alternatively, this is the number of solutions to the equation
$\unicode[STIX]{x1D6E4}_{k,A}(n)=|\{(a_{1},\ldots ,a_{k})\in A^{k}:a_{1}\cdots a_{k}=n\}$
. Alternatively, this is the number of solutions to the equation
Good upper bounds for
![]() $E_{k}(A)$
lead to good lower bounds for
$E_{k}(A)$
lead to good lower bounds for
![]() $|A^{k}|$
, because of the following inequality which is a standard application of the Cauchy–Schwarz inequality:
$|A^{k}|$
, because of the following inequality which is a standard application of the Cauchy–Schwarz inequality:
It turns out that a certain weighted version of
![]() $E_{k}(A)$
is more robust for applications. Let
$E_{k}(A)$
is more robust for applications. Let
![]() $A$
be a finite set of size
$A$
be a finite set of size
![]() $N$
with elements
$N$
with elements
![]() $a_{1},\ldots ,a_{N}$
(the actual ordering is not important). Next, let
$a_{1},\ldots ,a_{N}$
(the actual ordering is not important). Next, let
![]() $w=\{w_{1},\ldots ,w_{N}\}$
be a set of non-negative real numbers. One can think of
$w=\{w_{1},\ldots ,w_{N}\}$
be a set of non-negative real numbers. One can think of
![]() $w_{i}$
as the weight attached to the element
$w_{i}$
as the weight attached to the element
![]() $a_{i}$
. Then define the multiplicative energy of order
$a_{i}$
. Then define the multiplicative energy of order
![]() $k$
with weights
$k$
with weights
![]() $w_{i}$
as
$w_{i}$
as
where the summation is taken over all
![]() $2k$
-tuples
$2k$
-tuples
![]() $(i_{1},\ldots ,i_{2k})$
such that
$(i_{1},\ldots ,i_{2k})$
such that
In particular, the following result, which is a corollary of Lemma 2.1, gives a connection between Dirichlet polynomials defined in §2 and the weighted multiplicative energy of
![]() $A$
.
$A$
.
Corollary 3.1. Let
![]() $A$
be a finite set of rationals and let
$A$
be a finite set of rationals and let
![]() $w=\{w_{a}:a\in A\}$
be a set of weights on
$w=\{w_{a}:a\in A\}$
be a set of weights on
![]() $A$
. Then
$A$
. Then
Finally, define
![]() $\unicode[STIX]{x1D6EC}_{k}(A)$
as
$\unicode[STIX]{x1D6EC}_{k}(A)$
as
where the maximum is taken over all weights
![]() $w$
such that
$w$
such that
It is well-defined by compactness.
An attentive reader will notice that our definition of
![]() $\unicode[STIX]{x1D6EC}_{k}$
is a straightforward “multiplicative” adaptation of the
$\unicode[STIX]{x1D6EC}_{k}$
is a straightforward “multiplicative” adaptation of the
![]() $\unicode[STIX]{x1D6EC}$
-constants widely used in harmonic analysis.
$\unicode[STIX]{x1D6EC}$
-constants widely used in harmonic analysis.
The use of
![]() $\unicode[STIX]{x1D6EC}$
-constants for sum–product type problems was pioneered by Chang and Bourgain (see [Reference Chang5], [Reference Bourgain and Chang4] and references therein). The present note is largely based on the ideas of [Reference Chang5]. In particular, §4 is an adaptation of the technique used in [Reference Chang5] to the multiplicative setting.
$\unicode[STIX]{x1D6EC}$
-constants for sum–product type problems was pioneered by Chang and Bourgain (see [Reference Chang5], [Reference Bourgain and Chang4] and references therein). The present note is largely based on the ideas of [Reference Chang5]. In particular, §4 is an adaptation of the technique used in [Reference Chang5] to the multiplicative setting.
Now we record some properties of
![]() $\unicode[STIX]{x1D6EC}_{k}(A)$
in order to justify such a quantity. Let
$\unicode[STIX]{x1D6EC}_{k}(A)$
in order to justify such a quantity. Let
![]() $\Vert \cdot \Vert _{2k}$
be the standard norm in
$\Vert \cdot \Vert _{2k}$
be the standard norm in
![]() $L_{2k}[0,T]$
, normalized such that
$L_{2k}[0,T]$
, normalized such that
![]() $\Vert 1\Vert _{2k}=1$
. So,
$\Vert 1\Vert _{2k}=1$
. So,
Lemma 3.2. Let
![]() $A$
be a finite set with some non-negative real numbers
$A$
be a finite set with some non-negative real numbers
![]() $w_{a}$
assigned to each element
$w_{a}$
assigned to each element
![]() $a\in A$
. Then
$a\in A$
. Then
Proof. If
![]() $\sum _{a\in A}w_{a}^{2}=0$
the claim of the lemma is trivial. Otherwise, define new weights
$\sum _{a\in A}w_{a}^{2}=0$
the claim of the lemma is trivial. Otherwise, define new weights
which satisfy (8). It thus suffices to show that
which is a straightforward consequence of our definition of
![]() $\unicode[STIX]{x1D6EC}_{k}(A)$
and Lemma 2.1.◻
$\unicode[STIX]{x1D6EC}_{k}(A)$
and Lemma 2.1.◻
A crucial corollary is the following stability property of
![]() $\unicode[STIX]{x1D6EC}_{k}$
which does not seem to be available when one works with multiplicative energies.
$\unicode[STIX]{x1D6EC}_{k}$
which does not seem to be available when one works with multiplicative energies.
Corollary 3.3. Let
![]() $A^{\prime }\subset A$
. Then
$A^{\prime }\subset A$
. Then
In particular,
Proof. Apply Lemma 3.2 with
![]() $w_{a}=1$
if
$w_{a}=1$
if
![]() $a\in A^{\prime }$
and
$a\in A^{\prime }$
and
![]() $w_{a}=0$
otherwise.◻
$w_{a}=0$
otherwise.◻
4 The integer case
In this section we restrict ourselves to the integer case and prove the following bound.
Theorem 4.1. Let
![]() $A$
be a sufficiently large but finite set of positive integers, with the property that
$A$
be a sufficiently large but finite set of positive integers, with the property that
![]() $|AA|\leqslant K|A|$
for some integer
$|AA|\leqslant K|A|$
for some integer
![]() $K$
. Then, for any
$K$
. Then, for any
![]() $u$
coprime with the elements of
$u$
coprime with the elements of
![]() $A$
, we have
$A$
, we have
In particular,
The following is analogous to Chang [Reference Chang5, Proposition 6]. Here, we have an extra restriction that we are dealing only with positive powers of a given prime
![]() $p$
. This makes things rather simpler for us, and we can follow the strategy of Chang, making the appropriate minor alterations.
$p$
. This makes things rather simpler for us, and we can follow the strategy of Chang, making the appropriate minor alterations.
Lemma 4.2. Let
![]() $p$
be a prime and let
$p$
be a prime and let
![]() ${\mathcal{J}}$
be a set of positive integers. Let
${\mathcal{J}}$
be a set of positive integers. Let
![]() $u\in \mathbb{Z}$
such that
$u\in \mathbb{Z}$
such that
![]() $(p,u)=1$
. Suppose
$(p,u)=1$
. Suppose
![]() $f_{j}\in {\mathcal{F}}_{p,j,u}$
for
$f_{j}\in {\mathcal{F}}_{p,j,u}$
for
![]() $j\in {\mathcal{J}}$
. Then for
$j\in {\mathcal{J}}$
. Then for
![]() $k\geqslant 1$
,
$k\geqslant 1$
,
Proof. Expanding the
![]() $k$
th power of the left-hand side of (12) gives
$k$
th power of the left-hand side of (12) gives
For fixed
![]() $j_{1},\ldots ,j_{2k}$
, the quantity
$j_{1},\ldots ,j_{2k}$
, the quantity
gives a weighted count of the number of solutions to equations of the form
with each of the
![]() $m_{i}\in \mathbb{Q}$
coprime to
$m_{i}\in \mathbb{Q}$
coprime to
![]() $p$
. We claim that there are no solutions to (14) if all of the
$p$
. We claim that there are no solutions to (14) if all of the
![]() $j_{i}$
are distinct. Indeed, suppose that all of these powers are distinct, and in particular there is a unique smallest power, say
$j_{i}$
are distinct. Indeed, suppose that all of these powers are distinct, and in particular there is a unique smallest power, say
![]() $j_{1}<j_{2},j_{3},\ldots ,j_{2k}$
. Then we get (expanding the brackets, subtracting
$j_{1}<j_{2},j_{3},\ldots ,j_{2k}$
. Then we get (expanding the brackets, subtracting
![]() $u^{k}$
from both sides, and multiplying out all denominators of the
$u^{k}$
from both sides, and multiplying out all denominators of the
![]() $m_{i}$
) an equation
$m_{i}$
) an equation
for some integers
![]() $M,N_{1}$
and
$M,N_{1}$
and
![]() $N_{2}$
, such that
$N_{2}$
, such that
![]() $(M,p)=1$
. This is a contradiction, since the right-hand side is divisible by
$(M,p)=1$
. This is a contradiction, since the right-hand side is divisible by
![]() $p^{j_{1}+1}$
and the left-hand side is not. Therefore, there are no contributions to (13) coming from those terms where all of the
$p^{j_{1}+1}$
and the left-hand side is not. Therefore, there are no contributions to (13) coming from those terms where all of the
![]() $j_{i}$
are distinct.
$j_{i}$
are distinct.
It remains to consider the cases where two or more of the powers
![]() $j_{1},\ldots ,j_{2k}$
are the same. There are three kinds of ways in which this can happen:
$j_{1},\ldots ,j_{2k}$
are the same. There are three kinds of ways in which this can happen:
(1)
 $j_{i}=j_{i}^{\prime }$
with
$j_{i}=j_{i}^{\prime }$
with
 $1\leqslant i\leqslant k$
and
$1\leqslant i\leqslant k$
and
 $k+1\leqslant i^{\prime }\leqslant 2k$
(there are
$k+1\leqslant i^{\prime }\leqslant 2k$
(there are
 $k^{2}$
possible positions for such a pair
$k^{2}$
possible positions for such a pair
 $(i,i^{\prime })$
);
$(i,i^{\prime })$
);(2)
 $j_{i}=j_{i}^{\prime }$
with
$j_{i}=j_{i}^{\prime }$
with
 $1\leqslant i,i^{\prime }\leqslant k$
(there are
$1\leqslant i,i^{\prime }\leqslant k$
(there are
 $\binom{k}{2}$
possible positions for such a pair
$\binom{k}{2}$
possible positions for such a pair
 $(i,i^{\prime })$
);
$(i,i^{\prime })$
);(3)
 $j_{i}=j_{i}^{\prime }$
with
$j_{i}=j_{i}^{\prime }$
with
 $k+1\leqslant i,i^{\prime }\leqslant 2k$
(there are
$k+1\leqslant i,i^{\prime }\leqslant 2k$
(there are
 $\binom{k}{2}$
possible positions for such a pair
$\binom{k}{2}$
possible positions for such a pair
 $(i,i^{\prime })$
).
$(i,i^{\prime })$
).
Suppose we are in situation (1) above. Specifically, suppose that
![]() $j_{1}=j_{2k}$
. The other
$j_{1}=j_{2k}$
. The other
![]() $k^{2}-1$
cases can be dealt with by the same argument. Then these terms in (13) can be rewritten as
$k^{2}-1$
cases can be dealt with by the same argument. Then these terms in (13) can be rewritten as
 $$\begin{eqnarray}\displaystyle & & \displaystyle \mathop{\sum }_{j_{1}}\lim _{T\rightarrow \infty }\frac{1}{T}\int _{0}^{T}f_{j_{1}}(t)\overline{f_{j_{1}}(t)}\mathop{\sum }_{j_{2},\ldots ,j_{2k-1}}f_{j_{2}}(t)\cdots f_{j_{k}}(t)\overline{f_{j_{k+1}}(t)}\cdots \overline{f_{j_{2k-1}}(t)}\,dt\nonumber\\ \displaystyle & & \displaystyle \quad =\mathop{\sum }_{j}\lim _{T\rightarrow \infty }\frac{1}{T}\int _{0}^{T}|f_{j}(t)|^{2}\biggl|\mathop{\sum }_{j}f_{j}(t)\biggr|^{2(k-1)}\,dt.\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle \mathop{\sum }_{j_{1}}\lim _{T\rightarrow \infty }\frac{1}{T}\int _{0}^{T}f_{j_{1}}(t)\overline{f_{j_{1}}(t)}\mathop{\sum }_{j_{2},\ldots ,j_{2k-1}}f_{j_{2}}(t)\cdots f_{j_{k}}(t)\overline{f_{j_{k+1}}(t)}\cdots \overline{f_{j_{2k-1}}(t)}\,dt\nonumber\\ \displaystyle & & \displaystyle \quad =\mathop{\sum }_{j}\lim _{T\rightarrow \infty }\frac{1}{T}\int _{0}^{T}|f_{j}(t)|^{2}\biggl|\mathop{\sum }_{j}f_{j}(t)\biggr|^{2(k-1)}\,dt.\nonumber\end{eqnarray}$$
Suppose we are in situation (2). Specifically, suppose that
![]() $j_{1}=j_{2}$
. The other
$j_{1}=j_{2}$
. The other
![]() $\binom{k}{2}$
cases can be dealt with by the same argument. Then these terms in (13) can be rewritten as
$\binom{k}{2}$
cases can be dealt with by the same argument. Then these terms in (13) can be rewritten as
 $$\begin{eqnarray}\displaystyle & & \displaystyle \mathop{\sum }_{j_{1}}\lim _{T\rightarrow \infty }\frac{1}{T}\int _{0}^{T}f_{j_{1}}^{2}(t)\mathop{\sum }_{j_{3},\ldots ,j_{2k}}f_{j_{3}}(t)\cdots f_{j_{k}}(t)\overline{f_{j_{k+1}}(t)}\cdots \overline{f_{j_{2k}}(t)}\,dt\nonumber\\ \displaystyle & & \displaystyle \quad \leqslant \mathop{\sum }_{j}\lim _{T\rightarrow \infty }\frac{1}{T}\int _{0}^{T}|f_{j}(t)|^{2}\biggl|\mathop{\sum }_{j}f_{j}(t)\biggr|^{k-2}\biggl|\mathop{\sum }_{j}\overline{f_{j}(t)}\biggr|^{k}\,dt\nonumber\\ \displaystyle & & \displaystyle \quad =\mathop{\sum }_{j}\lim _{T\rightarrow \infty }\frac{1}{T}\int _{0}^{T}|f_{j}(t)|^{2}\biggl|\mathop{\sum }_{j}f_{j}(t)\biggr|^{2(k-1)}\,dt.\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle \mathop{\sum }_{j_{1}}\lim _{T\rightarrow \infty }\frac{1}{T}\int _{0}^{T}f_{j_{1}}^{2}(t)\mathop{\sum }_{j_{3},\ldots ,j_{2k}}f_{j_{3}}(t)\cdots f_{j_{k}}(t)\overline{f_{j_{k+1}}(t)}\cdots \overline{f_{j_{2k}}(t)}\,dt\nonumber\\ \displaystyle & & \displaystyle \quad \leqslant \mathop{\sum }_{j}\lim _{T\rightarrow \infty }\frac{1}{T}\int _{0}^{T}|f_{j}(t)|^{2}\biggl|\mathop{\sum }_{j}f_{j}(t)\biggr|^{k-2}\biggl|\mathop{\sum }_{j}\overline{f_{j}(t)}\biggr|^{k}\,dt\nonumber\\ \displaystyle & & \displaystyle \quad =\mathop{\sum }_{j}\lim _{T\rightarrow \infty }\frac{1}{T}\int _{0}^{T}|f_{j}(t)|^{2}\biggl|\mathop{\sum }_{j}f_{j}(t)\biggr|^{2(k-1)}\,dt.\nonumber\end{eqnarray}$$
The same argument also works in case (3). Returning to (13), we then have
 $$\begin{eqnarray}\displaystyle & & \displaystyle \lim _{T\rightarrow \infty }\biggl(\frac{1}{T}\int _{0}^{T}\biggl|\mathop{\sum }_{j}f_{j}(t)\biggr|^{2k}\,dt\biggr)\nonumber\\ \displaystyle & & \displaystyle \qquad \times \mathop{\sum }_{j_{1},\ldots ,j_{2k}}\lim _{T\rightarrow \infty }\frac{1}{T}\int _{0}^{T}f_{j_{1}}(t)\cdots f_{j_{k}}(t)\overline{f_{j_{k+1}}(t)}\cdots \overline{f_{j_{2k}}(t)}\,dt\nonumber\\ \displaystyle & & \displaystyle \quad \leqslant \biggl(k^{2}+2\binom{k}{2}\biggr)\mathop{\sum }_{j}\lim _{T\rightarrow \infty }\frac{1}{T}\int _{0}^{T}|f_{j}(t)|^{2}\biggl|\mathop{\sum }_{j}f_{j}(t)\biggr|^{2(k-1)}dt\nonumber\\ \displaystyle & & \displaystyle \quad \leqslant 2k^{2}\mathop{\sum }_{j}\lim _{T\rightarrow \infty }\frac{1}{T}\int _{0}^{T}|f_{j}(t)|^{2}\biggl|\mathop{\sum }_{j}f_{j}(t)\biggr|^{2(k-1)}\,dt.\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle \lim _{T\rightarrow \infty }\biggl(\frac{1}{T}\int _{0}^{T}\biggl|\mathop{\sum }_{j}f_{j}(t)\biggr|^{2k}\,dt\biggr)\nonumber\\ \displaystyle & & \displaystyle \qquad \times \mathop{\sum }_{j_{1},\ldots ,j_{2k}}\lim _{T\rightarrow \infty }\frac{1}{T}\int _{0}^{T}f_{j_{1}}(t)\cdots f_{j_{k}}(t)\overline{f_{j_{k+1}}(t)}\cdots \overline{f_{j_{2k}}(t)}\,dt\nonumber\\ \displaystyle & & \displaystyle \quad \leqslant \biggl(k^{2}+2\binom{k}{2}\biggr)\mathop{\sum }_{j}\lim _{T\rightarrow \infty }\frac{1}{T}\int _{0}^{T}|f_{j}(t)|^{2}\biggl|\mathop{\sum }_{j}f_{j}(t)\biggr|^{2(k-1)}dt\nonumber\\ \displaystyle & & \displaystyle \quad \leqslant 2k^{2}\mathop{\sum }_{j}\lim _{T\rightarrow \infty }\frac{1}{T}\int _{0}^{T}|f_{j}(t)|^{2}\biggl|\mathop{\sum }_{j}f_{j}(t)\biggr|^{2(k-1)}\,dt.\nonumber\end{eqnarray}$$
Here we have used the fact that the weights are positive and real, which allows us to overcount solutions which may occur in more than one of the three cases above. Finally, an application of Hölder’s inequality gives
 $$\begin{eqnarray}\displaystyle & & \displaystyle \lim _{T\rightarrow \infty }\biggl(\frac{1}{T}\int _{0}^{T}\biggl|\mathop{\sum }_{j}f_{j}(t)\biggr|^{2k}\,dt\biggr)\nonumber\\ \displaystyle & & \displaystyle \quad \leqslant 2k^{2}\mathop{\sum }_{j}\lim _{T\rightarrow \infty }\biggl(\frac{1}{T}\int _{0}^{T}|f_{j}(t)|^{2k}\,dt\biggr)^{1/k}\biggl(\frac{1}{T}\int _{0}^{T}\biggl|\mathop{\sum }_{j}f_{j}(t)\biggr|^{2k}\,dt\biggr)^{1-1/k}.\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle \lim _{T\rightarrow \infty }\biggl(\frac{1}{T}\int _{0}^{T}\biggl|\mathop{\sum }_{j}f_{j}(t)\biggr|^{2k}\,dt\biggr)\nonumber\\ \displaystyle & & \displaystyle \quad \leqslant 2k^{2}\mathop{\sum }_{j}\lim _{T\rightarrow \infty }\biggl(\frac{1}{T}\int _{0}^{T}|f_{j}(t)|^{2k}\,dt\biggr)^{1/k}\biggl(\frac{1}{T}\int _{0}^{T}\biggl|\mathop{\sum }_{j}f_{j}(t)\biggr|^{2k}\,dt\biggr)^{1-1/k}.\nonumber\end{eqnarray}$$
A rearrangement of this inequality completes the proof. ◻
Using an inductive argument, we can extend this result to handle generalized geometric progressions. To that end, for a vector
![]() $\boldsymbol{p}=(p_{1},\ldots ,p_{t})$
of prime numbers and a vector
$\boldsymbol{p}=(p_{1},\ldots ,p_{t})$
of prime numbers and a vector
![]() $\boldsymbol{j}=(j_{1},\ldots ,j_{t})$
of non-negative integers, let
$\boldsymbol{j}=(j_{1},\ldots ,j_{t})$
of non-negative integers, let
![]() ${\mathcal{F}}_{\boldsymbol{p},\,\boldsymbol{j},u}$
be the set of Dirichlet polynomials of the form
${\mathcal{F}}_{\boldsymbol{p},\,\boldsymbol{j},u}$
be the set of Dirichlet polynomials of the form
Lemma 4.3. Let
![]() $\boldsymbol{p}=(p_{1},\ldots ,p_{K})$
be a vector of prime numbers and let
$\boldsymbol{p}=(p_{1},\ldots ,p_{K})$
be a vector of prime numbers and let
![]() ${\mathcal{J}}$
be a set of vectors with non-negative entries. Let
${\mathcal{J}}$
be a set of vectors with non-negative entries. Let
![]() $u\in \mathbb{Z}$
such that
$u\in \mathbb{Z}$
such that
![]() $(u,p_{1}\cdots p_{K})=1$
. Suppose
$(u,p_{1}\cdots p_{K})=1$
. Suppose
![]() $f_{\boldsymbol{j}}\in {\mathcal{F}}_{\boldsymbol{p},\,\boldsymbol{j},u}$
for
$f_{\boldsymbol{j}}\in {\mathcal{F}}_{\boldsymbol{p},\,\boldsymbol{j},u}$
for
![]() $\boldsymbol{j}\in {\mathcal{J}}$
. Then for
$\boldsymbol{j}\in {\mathcal{J}}$
. Then for
![]() $k\geqslant 1$
, we have
$k\geqslant 1$
, we have
Proof. We establish the convention that
![]() $f_{\boldsymbol{j}}$
is identically zero for all
$f_{\boldsymbol{j}}$
is identically zero for all
![]() $\boldsymbol{j}\notin {\mathcal{J}}$
. Therefore, we can complete the sum in (16), and the aim is to prove that
$\boldsymbol{j}\notin {\mathcal{J}}$
. Therefore, we can complete the sum in (16), and the aim is to prove that
 $$\begin{eqnarray}\displaystyle & & \displaystyle \lim _{T\rightarrow \infty }\biggl(\frac{1}{T}\int _{0}^{T}\biggl|\mathop{\sum }_{\boldsymbol{ j}\in \mathbb{Z}_{{\geqslant}0}^{K}}f_{\boldsymbol{j}}(t)\biggr|^{2k}\,dt\biggr)^{1/k}\nonumber\\ \displaystyle & & \displaystyle \quad \leqslant (2k^{2})^{K}\mathop{\sum }_{\boldsymbol{j}\in \mathbb{Z}_{{\geqslant}0}^{K}}\lim _{T\rightarrow \infty }\biggl(\frac{1}{T}\int _{0}^{T}|f_{\boldsymbol{ j}}(t)|^{2k}\,dt\biggr)^{1/k}.\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle \lim _{T\rightarrow \infty }\biggl(\frac{1}{T}\int _{0}^{T}\biggl|\mathop{\sum }_{\boldsymbol{ j}\in \mathbb{Z}_{{\geqslant}0}^{K}}f_{\boldsymbol{j}}(t)\biggr|^{2k}\,dt\biggr)^{1/k}\nonumber\\ \displaystyle & & \displaystyle \quad \leqslant (2k^{2})^{K}\mathop{\sum }_{\boldsymbol{j}\in \mathbb{Z}_{{\geqslant}0}^{K}}\lim _{T\rightarrow \infty }\biggl(\frac{1}{T}\int _{0}^{T}|f_{\boldsymbol{ j}}(t)|^{2k}\,dt\biggr)^{1/k}.\nonumber\end{eqnarray}$$
We proceed by induction on
![]() $K$
, the base case
$K$
, the base case
![]() $K=1$
being given by Lemma 4.2. Then
$K=1$
being given by Lemma 4.2. Then
 $$\begin{eqnarray}\displaystyle & & \displaystyle \lim _{T\rightarrow \infty }\biggl(\frac{1}{T}\int _{0}^{T}\biggl|\mathop{\sum }_{\boldsymbol{ j}\in \mathbb{Z}_{{\geqslant}0}^{K}}f_{\boldsymbol{j}}(t)\biggr|^{2k}\,dt\biggr)^{1/k}\nonumber\\ \displaystyle & & \displaystyle \quad =\lim _{T\rightarrow \infty }\biggl(\frac{1}{T}\int _{0}^{T}\biggl|\mathop{\sum }_{j_{K}\in \mathbb{Z}_{{\geqslant}0}}\biggl(\mathop{\sum }_{\boldsymbol{j}^{\prime }\in \mathbb{Z}_{{\geqslant}0}^{K-1}}f_{\boldsymbol{j}^{\prime },j_{K}}(t)\biggr)\biggr|^{2k}\,dt\biggr)^{1/k}\nonumber\\ \displaystyle & & \displaystyle \quad \leqslant 2k^{2}\mathop{\sum }_{j_{K}\in \mathbb{Z}_{{\geqslant}0}}\lim _{T\rightarrow \infty }\biggl(\frac{1}{T}\int _{0}^{T}\biggl|\mathop{\sum }_{\boldsymbol{ j}^{\prime }\in \mathbb{Z}_{{\geqslant}0}^{K-1}}f_{\boldsymbol{j}^{\prime },j_{K}}(t)\biggr|^{2k}\,dt\biggr)^{1/k}\nonumber\\ \displaystyle & & \displaystyle \quad \leqslant 2k^{2}\mathop{\sum }_{j_{K}\in \mathbb{Z}_{{\geqslant}0}}(2k^{2})^{K-1}\mathop{\sum }_{\boldsymbol{j}^{\prime }\in \mathbb{Z}_{{\geqslant}0}^{K-1}}\lim _{T\rightarrow \infty }\biggl(\frac{1}{T}\int _{0}^{T}|f_{\boldsymbol{ j}^{\prime },j_{K}}(t)|^{2k}\,dt\biggr)^{1/k}\nonumber\\ \displaystyle & & \displaystyle \quad =(2k^{2})^{K}\mathop{\sum }_{\boldsymbol{j}\in \mathbb{Z}_{{\geqslant}0}^{K}}\lim _{T\rightarrow \infty }\biggl(\frac{1}{T}\int _{0}^{T}|f_{\boldsymbol{ j}}(t)|^{2k}\,dt\biggr)^{1/k}.\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle \lim _{T\rightarrow \infty }\biggl(\frac{1}{T}\int _{0}^{T}\biggl|\mathop{\sum }_{\boldsymbol{ j}\in \mathbb{Z}_{{\geqslant}0}^{K}}f_{\boldsymbol{j}}(t)\biggr|^{2k}\,dt\biggr)^{1/k}\nonumber\\ \displaystyle & & \displaystyle \quad =\lim _{T\rightarrow \infty }\biggl(\frac{1}{T}\int _{0}^{T}\biggl|\mathop{\sum }_{j_{K}\in \mathbb{Z}_{{\geqslant}0}}\biggl(\mathop{\sum }_{\boldsymbol{j}^{\prime }\in \mathbb{Z}_{{\geqslant}0}^{K-1}}f_{\boldsymbol{j}^{\prime },j_{K}}(t)\biggr)\biggr|^{2k}\,dt\biggr)^{1/k}\nonumber\\ \displaystyle & & \displaystyle \quad \leqslant 2k^{2}\mathop{\sum }_{j_{K}\in \mathbb{Z}_{{\geqslant}0}}\lim _{T\rightarrow \infty }\biggl(\frac{1}{T}\int _{0}^{T}\biggl|\mathop{\sum }_{\boldsymbol{ j}^{\prime }\in \mathbb{Z}_{{\geqslant}0}^{K-1}}f_{\boldsymbol{j}^{\prime },j_{K}}(t)\biggr|^{2k}\,dt\biggr)^{1/k}\nonumber\\ \displaystyle & & \displaystyle \quad \leqslant 2k^{2}\mathop{\sum }_{j_{K}\in \mathbb{Z}_{{\geqslant}0}}(2k^{2})^{K-1}\mathop{\sum }_{\boldsymbol{j}^{\prime }\in \mathbb{Z}_{{\geqslant}0}^{K-1}}\lim _{T\rightarrow \infty }\biggl(\frac{1}{T}\int _{0}^{T}|f_{\boldsymbol{ j}^{\prime },j_{K}}(t)|^{2k}\,dt\biggr)^{1/k}\nonumber\\ \displaystyle & & \displaystyle \quad =(2k^{2})^{K}\mathop{\sum }_{\boldsymbol{j}\in \mathbb{Z}_{{\geqslant}0}^{K}}\lim _{T\rightarrow \infty }\biggl(\frac{1}{T}\int _{0}^{T}|f_{\boldsymbol{ j}}(t)|^{2k}\,dt\biggr)^{1/k}.\nonumber\end{eqnarray}$$
The first inequality above follows from an application of Lemma 4.2, using the fact that
The second inequality follows from the induction hypothesis. ◻
We are now in a strong position to establish results on the physical side, starting with the following lemma.
Lemma 4.4. Let
![]() $\boldsymbol{p}=(p_{1},\ldots ,p_{K})$
be a vector of prime numbers and let
$\boldsymbol{p}=(p_{1},\ldots ,p_{K})$
be a vector of prime numbers and let
![]() ${\mathcal{J}}\subset \mathbb{Z}^{K}$
be a set of vectors with non-negative entries. Let
${\mathcal{J}}\subset \mathbb{Z}^{K}$
be a set of vectors with non-negative entries. Let
![]() $u\in \mathbb{Z}$
such that
$u\in \mathbb{Z}$
such that
![]() $(u,p_{1}\ldots p_{K})=1$
. Suppose that
$(u,p_{1}\ldots p_{K})=1$
. Suppose that
with each
![]() $x(\boldsymbol{j})\in \mathbb{Q}$
coprime to
$x(\boldsymbol{j})\in \mathbb{Q}$
coprime to
![]() $p_{1}\cdots p_{K}$
. Then
$p_{1}\cdots p_{K}$
. Then
Proof. For each
![]() $\boldsymbol{j}=(j_{1},\ldots ,j_{K})\in {\mathcal{J}}$
, define
$\boldsymbol{j}=(j_{1},\ldots ,j_{K})\in {\mathcal{J}}$
, define
![]() $a_{\boldsymbol{j}}=p_{1}^{j_{1}}\ldots p_{K}^{j_{K}}x(\boldsymbol{j})$
, so that
$a_{\boldsymbol{j}}=p_{1}^{j_{1}}\ldots p_{K}^{j_{K}}x(\boldsymbol{j})$
, so that
![]() $A=\{a_{\boldsymbol{j}}:\boldsymbol{j}\in {\mathcal{J}}\}$
. Define
$A=\{a_{\boldsymbol{j}}:\boldsymbol{j}\in {\mathcal{J}}\}$
. Define
![]() $f_{\boldsymbol{j}}(t)=w_{\boldsymbol{j}}(a_{\boldsymbol{j}}+u)^{it}$
for some weights
$f_{\boldsymbol{j}}(t)=w_{\boldsymbol{j}}(a_{\boldsymbol{j}}+u)^{it}$
for some weights
![]() $w=\{w_{\boldsymbol{j}}:\boldsymbol{j}\in {\mathcal{J}}\}$
satisfying
$w=\{w_{\boldsymbol{j}}:\boldsymbol{j}\in {\mathcal{J}}\}$
satisfying
Note that
![]() $f_{\boldsymbol{j}}(t)\in {\mathcal{F}}_{\boldsymbol{p},\,\boldsymbol{j},u}$
, because of the divisibility conditions in the statement of the lemma. Note also that
$f_{\boldsymbol{j}}(t)\in {\mathcal{F}}_{\boldsymbol{p},\,\boldsymbol{j},u}$
, because of the divisibility conditions in the statement of the lemma. Note also that
Using this, as well as Lemma 4.3 and Corollary 3.1, we conclude that
 $$\begin{eqnarray}\displaystyle E_{k,w}(A+u)^{1/k} & = & \displaystyle \lim _{T\rightarrow \infty }\biggl(\frac{1}{T}\int _{0}^{T}\biggl|\mathop{\sum }_{\boldsymbol{ j}\in {\mathcal{J}}}w_{\boldsymbol{j}}(a_{\boldsymbol{j}}+u)^{it}\biggr|^{2k}\,dt\biggr)^{1/k}\nonumber\\ \displaystyle & = & \displaystyle \lim _{T\rightarrow \infty }\biggl(\frac{1}{T}\int _{0}^{T}\biggl|\mathop{\sum }_{\boldsymbol{ j}\in {\mathcal{J}}}f_{\boldsymbol{j}}(t)\biggr|^{2k}\,dt\biggr)^{1/k}\nonumber\\ \displaystyle & {\leqslant} & \displaystyle (2k^{2})^{K}\mathop{\sum }_{\boldsymbol{j}\in {\mathcal{J}}}\lim _{T\rightarrow \infty }\biggl(\frac{1}{T}\int _{0}^{T}|f_{\boldsymbol{ j}}(t)|^{2k}\,dt\biggr)^{1/k}\nonumber\\ \displaystyle & = & \displaystyle (2k^{2})^{K}.\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle E_{k,w}(A+u)^{1/k} & = & \displaystyle \lim _{T\rightarrow \infty }\biggl(\frac{1}{T}\int _{0}^{T}\biggl|\mathop{\sum }_{\boldsymbol{ j}\in {\mathcal{J}}}w_{\boldsymbol{j}}(a_{\boldsymbol{j}}+u)^{it}\biggr|^{2k}\,dt\biggr)^{1/k}\nonumber\\ \displaystyle & = & \displaystyle \lim _{T\rightarrow \infty }\biggl(\frac{1}{T}\int _{0}^{T}\biggl|\mathop{\sum }_{\boldsymbol{ j}\in {\mathcal{J}}}f_{\boldsymbol{j}}(t)\biggr|^{2k}\,dt\biggr)^{1/k}\nonumber\\ \displaystyle & {\leqslant} & \displaystyle (2k^{2})^{K}\mathop{\sum }_{\boldsymbol{j}\in {\mathcal{J}}}\lim _{T\rightarrow \infty }\biggl(\frac{1}{T}\int _{0}^{T}|f_{\boldsymbol{ j}}(t)|^{2k}\,dt\biggr)^{1/k}\nonumber\\ \displaystyle & = & \displaystyle (2k^{2})^{K}.\nonumber\end{eqnarray}$$
Since the bound above does not depend on the weights, we are done. ◻
Before completing the proof of Theorem 4.1, we need the following more or less obvious lemma.
Lemma 4.5. Let
![]() $L$
be an affine subspace of
$L$
be an affine subspace of
![]() $\mathbb{F}^{l}$
of dimension
$\mathbb{F}^{l}$
of dimension
![]() $d$
. Then, after relabeling the coordinates if necessary,
$d$
. Then, after relabeling the coordinates if necessary,
![]() $L$
has the form
$L$
has the form
where each of the functions
![]() $f_{i}$
are polynomials of degree at most
$f_{i}$
are polynomials of degree at most
![]() $1$
in variables
$1$
in variables
![]() $x_{1},\ldots ,x_{d}$
.
$x_{1},\ldots ,x_{d}$
.
In particular, there are
![]() $d$
coordinate projections
$d$
coordinate projections
![]() $\unicode[STIX]{x1D70B}_{1},\ldots ,\unicode[STIX]{x1D70B}_{d}$
such that the map
$\unicode[STIX]{x1D70B}_{1},\ldots ,\unicode[STIX]{x1D70B}_{d}$
such that the map
![]() $\unicode[STIX]{x1D70B}:\mathbb{F}^{l}\rightarrow \mathbb{F}^{d}$
given by
$\unicode[STIX]{x1D70B}:\mathbb{F}^{l}\rightarrow \mathbb{F}^{d}$
given by
![]() $\unicode[STIX]{x1D70B}(\boldsymbol{v})=(\unicode[STIX]{x1D70B}_{1}(\boldsymbol{v}),\ldots ,\unicode[STIX]{x1D70B}_{d}(\boldsymbol{v}))$
is injective on
$\unicode[STIX]{x1D70B}(\boldsymbol{v})=(\unicode[STIX]{x1D70B}_{1}(\boldsymbol{v}),\ldots ,\unicode[STIX]{x1D70B}_{d}(\boldsymbol{v}))$
is injective on
![]() $L$
.
$L$
.
Proof. By shifting if necessary, we may assume
![]() $L$
is a linear subspace without loss of generality. Let
$L$
is a linear subspace without loss of generality. Let
![]() $v_{1},\ldots ,v_{d}$
be
$v_{1},\ldots ,v_{d}$
be
![]() $d$
linearly independent vectors in
$d$
linearly independent vectors in
![]() $L$
which we place as rows in a matrix
$L$
which we place as rows in a matrix
![]() $M$
of dimension
$M$
of dimension
![]() $d\times l$
and rank
$d\times l$
and rank
![]() $d$
. Performing row reduction on
$d$
. Performing row reduction on
![]() $M$
and permuting columns if necessary, we get a matrix
$M$
and permuting columns if necessary, we get a matrix
![]() $M^{\prime }$
in a row echelon form. Since the rank of
$M^{\prime }$
in a row echelon form. Since the rank of
![]() $M^{\prime }$
is
$M^{\prime }$
is
![]() $d$
, the left-most minor of
$d$
, the left-most minor of
![]() $M^{\prime }$
is a
$M^{\prime }$
is a
![]() $d\times d$
identity matrix. The rows of
$d\times d$
identity matrix. The rows of
![]() $M^{\prime }$
span
$M^{\prime }$
span
![]() $L$
, and this is exactly the claim of the lemma.◻
$L$
, and this is exactly the claim of the lemma.◻
Let
![]() $A$
be a set of positive integers and let
$A$
be a set of positive integers and let
![]() ${\mathcal{P}}=\{p_{1},\ldots ,p_{t}\}$
be the set of primes dividing any element of
${\mathcal{P}}=\{p_{1},\ldots ,p_{t}\}$
be the set of primes dividing any element of
![]() $A$
. Abusing notation slightly, we define a map
$A$
. Abusing notation slightly, we define a map
![]() ${\mathcal{P}}:A\rightarrow \mathbb{Z}^{t}$
where
${\mathcal{P}}:A\rightarrow \mathbb{Z}^{t}$
where
![]() ${\mathcal{P}}(a)=(v_{p_{1}}(a),\ldots ,v_{p_{t}}(a))$
. Denoting by
${\mathcal{P}}(a)=(v_{p_{1}}(a),\ldots ,v_{p_{t}}(a))$
. Denoting by
![]() ${\mathcal{P}}(X)$
the image of a set
${\mathcal{P}}(X)$
the image of a set
![]() $X$
under
$X$
under
![]() ${\mathcal{P}}$
, observe that
${\mathcal{P}}$
, observe that
![]() ${\mathcal{P}}(AA)={\mathcal{P}}(A)+{\mathcal{P}}(A)$
. We define the multiplicative dimension of
${\mathcal{P}}(AA)={\mathcal{P}}(A)+{\mathcal{P}}(A)$
. We define the multiplicative dimension of
![]() $A$
to be the least dimension of an affine space
$A$
to be the least dimension of an affine space
![]() $L$
containing
$L$
containing
![]() ${\mathcal{P}}(A)$
.
${\mathcal{P}}(A)$
.
Theorem 4.6 (Freiman’s Lemma (see [Reference Tao and Vu16, Lemma 5.13])).
Let
![]() $A\subset \mathbb{R}^{m}$
be a finite set not contained in a proper affine subspace. Then
$A\subset \mathbb{R}^{m}$
be a finite set not contained in a proper affine subspace. Then
Theorem 4.1 now becomes a simple corollary.
Proof (of Theorem 4.1).
It follows from Freiman’s Lemma that if
![]() $|AA|\leqslant K|A|$
with
$|AA|\leqslant K|A|$
with
![]() $|A|$
sufficiently large, then
$|A|$
sufficiently large, then
![]() $A$
has multiplicative dimension at most
$A$
has multiplicative dimension at most
![]() $K$
. Thus, there is an affine subspace of
$K$
. Thus, there is an affine subspace of
![]() $\mathbb{R}^{t}$
containing
$\mathbb{R}^{t}$
containing
![]() ${\mathcal{P}}(A)$
and of dimension at most
${\mathcal{P}}(A)$
and of dimension at most
![]() $K$
. Permuting the coordinates if necessary, it follows from an application of Lemma 4.5 that each
$K$
. Permuting the coordinates if necessary, it follows from an application of Lemma 4.5 that each
![]() $a\in A$
can be written as
$a\in A$
can be written as
![]() $a=p_{1}^{v_{p_{1}}(a)}\cdots p_{K}^{v_{p_{K}}(a)}n_{a}$
where
$a=p_{1}^{v_{p_{1}}(a)}\cdots p_{K}^{v_{p_{K}}(a)}n_{a}$
where
![]() $n_{a}$
is not divisible by any
$n_{a}$
is not divisible by any
![]() $p_{i}$
with
$p_{i}$
with
![]() $1\leqslant i\leqslant K$
and the vector
$1\leqslant i\leqslant K$
and the vector
![]() $(v_{p_{1}}(a),\ldots ,v_{p_{K}}(a))$
is unique to
$(v_{p_{1}}(a),\ldots ,v_{p_{K}}(a))$
is unique to
![]() $a$
. This is precisely the situation of Lemma 4.4. This proves (10).
$a$
. This is precisely the situation of Lemma 4.4. This proves (10).
From the Cauchy–Schwarz inequality and Corollary 3.3
whence
5 The rational case—the main lemma
In this section, we begin to deal with the rational case, which is rather more complicated. The first aim is prove an analogue of Lemma 4.3. We begin to tackle this by proving the following lemma which helps us to decompose
![]() ${\mathcal{J}}$
suitably.
${\mathcal{J}}$
suitably.
Lemma 5.1. Let
![]() ${\mathcal{J}}\subset \mathbb{Z}^{K}$
and decompose it as
${\mathcal{J}}\subset \mathbb{Z}^{K}$
and decompose it as
![]() ${\mathcal{J}}={\mathcal{J}}_{1}\cup \cdots \cup {\mathcal{J}}_{N}$
. Let
${\mathcal{J}}={\mathcal{J}}_{1}\cup \cdots \cup {\mathcal{J}}_{N}$
. Let
![]() $\boldsymbol{p}=(p_{1},\ldots ,p_{K})$
be a vector of prime numbers and for each
$\boldsymbol{p}=(p_{1},\ldots ,p_{K})$
be a vector of prime numbers and for each
![]() $\boldsymbol{j}\in {\mathcal{J}}$
let
$\boldsymbol{j}\in {\mathcal{J}}$
let
![]() $f_{\boldsymbol{j}}\in {\mathcal{F}}_{\boldsymbol{j},\boldsymbol{p},1}$
. Then
$f_{\boldsymbol{j}}\in {\mathcal{F}}_{\boldsymbol{j},\boldsymbol{p},1}$
. Then
Proof. It suffices to prove the inequality for all sufficiently large
![]() $T$
, which we assume fixed for now. Then
$T$
, which we assume fixed for now. Then
by the triangle inequality. By the Cauchy–Schwarz inequality, (18) is bounded by
Letting
![]() $T\rightarrow \infty$
we get the claim of the lemma.◻
$T\rightarrow \infty$
we get the claim of the lemma.◻
We need to introduce some notation which will be convenient for the forthcoming statement and its proof. Let
![]() $S\subset [K]$
for a fixed positive integer
$S\subset [K]$
for a fixed positive integer
![]() $K$
. For a set
$K$
. For a set
![]() ${\mathcal{J}}\subset \mathbb{Z}^{K}$
, we write
${\mathcal{J}}\subset \mathbb{Z}^{K}$
, we write
![]() ${\mathcal{J}}_{S}\subset {\mathcal{J}}$
for the set of all vectors in
${\mathcal{J}}_{S}\subset {\mathcal{J}}$
for the set of all vectors in
![]() ${\mathcal{J}}$
whose non-negative entries lie exclusively in the positions corresponding to elements of
${\mathcal{J}}$
whose non-negative entries lie exclusively in the positions corresponding to elements of
![]() $S$
. We will let
$S$
. We will let
![]() $\unicode[STIX]{x1D70B}_{S}$
denote the projection onto the coordinates from
$\unicode[STIX]{x1D70B}_{S}$
denote the projection onto the coordinates from
![]() $S$
. Suppose
$S$
. Suppose
![]() $\boldsymbol{j}_{S}\in \unicode[STIX]{x1D70B}_{S}({\mathcal{J}})$
, then we define
$\boldsymbol{j}_{S}\in \unicode[STIX]{x1D70B}_{S}({\mathcal{J}})$
, then we define
Theorem 5.2. Let
![]() $\boldsymbol{p}=(p_{1},\ldots ,p_{K})$
be a vector of prime numbers and let
$\boldsymbol{p}=(p_{1},\ldots ,p_{K})$
be a vector of prime numbers and let
![]() ${\mathcal{J}}\subset \mathbb{Z}^{K}$
be a finite set of vectors. Suppose
${\mathcal{J}}\subset \mathbb{Z}^{K}$
be a finite set of vectors. Suppose
![]() $f_{\boldsymbol{j}}\in {\mathcal{F}}_{\boldsymbol{p},\,\boldsymbol{j},1}$
for
$f_{\boldsymbol{j}}\in {\mathcal{F}}_{\boldsymbol{p},\,\boldsymbol{j},1}$
for
![]() $\boldsymbol{j}\in {\mathcal{J}}$
. Then for
$\boldsymbol{j}\in {\mathcal{J}}$
. Then for
![]() $k\geqslant 1$
, we have
$k\geqslant 1$
, we have
 $$\begin{eqnarray}\displaystyle & & \displaystyle \lim _{T\rightarrow \infty }\biggl(\frac{1}{T}\int _{0}^{T}\biggl|\mathop{\sum }_{\boldsymbol{ j}\in {\mathcal{J}}}f_{\boldsymbol{j}}(t)\biggr|^{2k}\,dt\biggr)^{1/k}\nonumber\\ \displaystyle & & \displaystyle \quad \leqslant (4k^{2})^{K}\mathop{\sum }_{S\subset \{1,\ldots ,K\}}\mathop{\sum }_{\boldsymbol{j}_{S}\in \unicode[STIX]{x1D70B}_{S}({\mathcal{J}}_{S})}\lim _{T\rightarrow \infty }\biggl(\frac{1}{T}\int _{0}^{T}\biggl|\mathop{\sum }_{\boldsymbol{ j}\in {\mathcal{J}}_{S}(\boldsymbol{j}_{S})}f_{\boldsymbol{j}}(t)\biggr|^{2k}\,dt\biggr)^{1/k}.\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle \lim _{T\rightarrow \infty }\biggl(\frac{1}{T}\int _{0}^{T}\biggl|\mathop{\sum }_{\boldsymbol{ j}\in {\mathcal{J}}}f_{\boldsymbol{j}}(t)\biggr|^{2k}\,dt\biggr)^{1/k}\nonumber\\ \displaystyle & & \displaystyle \quad \leqslant (4k^{2})^{K}\mathop{\sum }_{S\subset \{1,\ldots ,K\}}\mathop{\sum }_{\boldsymbol{j}_{S}\in \unicode[STIX]{x1D70B}_{S}({\mathcal{J}}_{S})}\lim _{T\rightarrow \infty }\biggl(\frac{1}{T}\int _{0}^{T}\biggl|\mathop{\sum }_{\boldsymbol{ j}\in {\mathcal{J}}_{S}(\boldsymbol{j}_{S})}f_{\boldsymbol{j}}(t)\biggr|^{2k}\,dt\biggr)^{1/k}.\nonumber\end{eqnarray}$$
Proof. First we partition
By Lemma 5.1, we have
 $$\begin{eqnarray}\displaystyle & & \displaystyle \lim _{T\rightarrow \infty }\biggl(\frac{1}{T}\int _{0}^{T}\biggl|\mathop{\sum }_{\boldsymbol{ j}\in {\mathcal{J}}}f_{\boldsymbol{j}}(t)\biggr|^{2k}\,dt\biggr)^{1/k}\nonumber\\ \displaystyle & & \displaystyle \quad \leqslant 2^{K}\mathop{\sum }_{S\subseteq \{1,\ldots ,K\}}\lim _{T\rightarrow \infty }\biggl(\frac{1}{T}\int _{0}^{T}\biggl|\mathop{\sum }_{\boldsymbol{ j}\in {\mathcal{J}}_{S}}f_{\boldsymbol{j}}(t)\biggr|^{2k}\,dt\biggr)^{1/k}.\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle \lim _{T\rightarrow \infty }\biggl(\frac{1}{T}\int _{0}^{T}\biggl|\mathop{\sum }_{\boldsymbol{ j}\in {\mathcal{J}}}f_{\boldsymbol{j}}(t)\biggr|^{2k}\,dt\biggr)^{1/k}\nonumber\\ \displaystyle & & \displaystyle \quad \leqslant 2^{K}\mathop{\sum }_{S\subseteq \{1,\ldots ,K\}}\lim _{T\rightarrow \infty }\biggl(\frac{1}{T}\int _{0}^{T}\biggl|\mathop{\sum }_{\boldsymbol{ j}\in {\mathcal{J}}_{S}}f_{\boldsymbol{j}}(t)\biggr|^{2k}\,dt\biggr)^{1/k}.\nonumber\end{eqnarray}$$
Now consider the set
![]() $\unicode[STIX]{x1D70B}_{S}({\mathcal{J}}_{S})$
which consists of vectors in
$\unicode[STIX]{x1D70B}_{S}({\mathcal{J}}_{S})$
which consists of vectors in
![]() $\mathbb{Z}^{|S|}$
, each with non-negative entries. Thus, applying Lemma 4.3 to these, we get
$\mathbb{Z}^{|S|}$
, each with non-negative entries. Thus, applying Lemma 4.3 to these, we get
 $$\begin{eqnarray}\displaystyle & & \displaystyle \lim _{T\rightarrow \infty }\biggl(\frac{1}{T}\int _{0}^{T}\biggl|\mathop{\sum }_{\boldsymbol{ j}\in {\mathcal{J}}_{S}}f_{\boldsymbol{j}}(t)\biggr|^{2k}\,dt\biggr)^{1/k}\nonumber\\ \displaystyle & & \displaystyle \quad \leqslant (2k^{2})^{|S|}\mathop{\sum }_{\boldsymbol{j}_{S}\in \unicode[STIX]{x1D70B}_{S}({\mathcal{J}}_{S})}\lim _{T\rightarrow \infty }\biggl(\frac{1}{T}\int _{0}^{T}\biggl|\mathop{\sum }_{\boldsymbol{ j}\in {\mathcal{J}}_{S}(\boldsymbol{j}_{S})}f_{\boldsymbol{j}}(t)\biggr|^{2k}\,dt\biggr)^{1/k}\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle \lim _{T\rightarrow \infty }\biggl(\frac{1}{T}\int _{0}^{T}\biggl|\mathop{\sum }_{\boldsymbol{ j}\in {\mathcal{J}}_{S}}f_{\boldsymbol{j}}(t)\biggr|^{2k}\,dt\biggr)^{1/k}\nonumber\\ \displaystyle & & \displaystyle \quad \leqslant (2k^{2})^{|S|}\mathop{\sum }_{\boldsymbol{j}_{S}\in \unicode[STIX]{x1D70B}_{S}({\mathcal{J}}_{S})}\lim _{T\rightarrow \infty }\biggl(\frac{1}{T}\int _{0}^{T}\biggl|\mathop{\sum }_{\boldsymbol{ j}\in {\mathcal{J}}_{S}(\boldsymbol{j}_{S})}f_{\boldsymbol{j}}(t)\biggr|^{2k}\,dt\biggr)^{1/k}\nonumber\end{eqnarray}$$
and the theorem follows. ◻
6 The rational case—concluding the proof
This section is devoted to proving the main result of this paper, which we now state in full.
Theorem 6.1. Let
![]() $A\subset \mathbb{Q}$
be a finite set, with the property that
$A\subset \mathbb{Q}$
be a finite set, with the property that
![]() $|AA|\leqslant K|A|$
for some integer
$|AA|\leqslant K|A|$
for some integer
![]() $K$
. Then we have
$K$
. Then we have
In particular, by Corollary 3.3
Proof. Suppose that
![]() $A\subset \mathbb{Q}$
and
$A\subset \mathbb{Q}$
and
![]() $|AA|\leqslant K|A|$
and let
$|AA|\leqslant K|A|$
and let
![]() $\unicode[STIX]{x1D6F1}=\{p_{1},\ldots ,p_{l}\}$
be the set of all primes that appear in the prime decomposition of the elements of
$\unicode[STIX]{x1D6F1}=\{p_{1},\ldots ,p_{l}\}$
be the set of all primes that appear in the prime decomposition of the elements of
![]() $A$
. So, each element
$A$
. So, each element
![]() $a\in A$
can be expressed uniquely as
$a\in A$
can be expressed uniquely as
![]() $a=p_{1}^{v_{p_{1}}(a)}\cdots p_{l}^{v_{p_{l}}(a)}$
. We have no control over the size of
$a=p_{1}^{v_{p_{1}}(a)}\cdots p_{l}^{v_{p_{l}}(a)}$
. We have no control over the size of
![]() $\unicode[STIX]{x1D6F1}$
, but we do know that
$\unicode[STIX]{x1D6F1}$
, but we do know that
![]() $\unicode[STIX]{x1D6F1}$
is finite.
$\unicode[STIX]{x1D6F1}$
is finite.
As in the proof of Theorem 4.1, we also let
![]() ${\mathcal{P}}:A\rightarrow \mathbb{Z}^{n}$
denote the prime evaluation map defined by
${\mathcal{P}}:A\rightarrow \mathbb{Z}^{n}$
denote the prime evaluation map defined by
![]() ${\mathcal{P}}(p_{1}^{v_{p_{1}}}(a)\cdots p_{n}^{v_{p_{t}}}(a))=(v_{p_{1}}(a),\ldots ,v_{p_{t}}(a))$
and note that
${\mathcal{P}}(p_{1}^{v_{p_{1}}}(a)\cdots p_{n}^{v_{p_{t}}}(a))=(v_{p_{1}}(a),\ldots ,v_{p_{t}}(a))$
and note that
![]() $|{\mathcal{P}}(A)+{\mathcal{P}}(A)|=|AA|$
.
$|{\mathcal{P}}(A)+{\mathcal{P}}(A)|=|AA|$
.
By Freiman’s Lemma
![]() ${\mathcal{P}}(A)$
has affine dimension at most
${\mathcal{P}}(A)$
has affine dimension at most
![]() $K$
. Then, by Lemma 4.5, we have that
$K$
. Then, by Lemma 4.5, we have that
where
![]() $\unicode[STIX]{x1D70B}$
in the projection from
$\unicode[STIX]{x1D70B}$
in the projection from
![]() $\mathbb{R}^{l}$
to the first
$\mathbb{R}^{l}$
to the first
![]() $K$
coordinates, and each
$K$
coordinates, and each
![]() $f_{i}$
is either constant, or linear in variables
$f_{i}$
is either constant, or linear in variables
![]() $j_{1},\ldots ,j_{K}$
.
$j_{1},\ldots ,j_{K}$
.
We then apply the inverse map
![]() ${\mathcal{P}}^{-1}$
and see that
${\mathcal{P}}^{-1}$
and see that
![]() $A$
has the form
$A$
has the form
where
![]() $x(j_{1},\ldots ,j_{K})=p_{K+1}^{f_{K+1}(j_{1},\ldots ,j_{K})}\cdots p_{l}^{f_{l}(j_{1},\ldots ,j_{K})}$
. Note that
$x(j_{1},\ldots ,j_{K})=p_{K+1}^{f_{K+1}(j_{1},\ldots ,j_{K})}\cdots p_{l}^{f_{l}(j_{1},\ldots ,j_{K})}$
. Note that
![]() $x$
is coprime to
$x$
is coprime to
![]() $p_{1}\cdots p_{K}$
. Let
$p_{1}\cdots p_{K}$
. Let
![]() ${\mathcal{J}}=\unicode[STIX]{x1D70B}({\mathcal{P}}(A))$
and for
${\mathcal{J}}=\unicode[STIX]{x1D70B}({\mathcal{P}}(A))$
and for
![]() $\boldsymbol{j}=(j_{1},\ldots ,j_{K})\in {\mathcal{J}}$
, let
$\boldsymbol{j}=(j_{1},\ldots ,j_{K})\in {\mathcal{J}}$
, let
Now suppose
![]() $w$
is any weight function defined on
$w$
is any weight function defined on
![]() $A+1$
and we consider
$A+1$
and we consider
 $$\begin{eqnarray}\displaystyle \mathop{\sum }_{a\in A}w_{a+1}(a+1)^{it} & = & \displaystyle \mathop{\sum }_{\boldsymbol{j}\in {\mathcal{J}}}w_{a_{\boldsymbol{j}}+1}(a_{\boldsymbol{j}}+1)^{it}\nonumber\\ \displaystyle & = & \displaystyle \mathop{\sum }_{S\subset \{1,\ldots ,K\}}\mathop{\sum }_{\boldsymbol{j}_{S}\in \unicode[STIX]{x1D70B}_{S}({\mathcal{J}}_{S})}~\mathop{\sum }_{\boldsymbol{j}\in {\mathcal{J}}_{S}(\boldsymbol{j}_{S})}w_{a_{\boldsymbol{j}}+1}(a_{\boldsymbol{j}}+1)^{it}.\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \mathop{\sum }_{a\in A}w_{a+1}(a+1)^{it} & = & \displaystyle \mathop{\sum }_{\boldsymbol{j}\in {\mathcal{J}}}w_{a_{\boldsymbol{j}}+1}(a_{\boldsymbol{j}}+1)^{it}\nonumber\\ \displaystyle & = & \displaystyle \mathop{\sum }_{S\subset \{1,\ldots ,K\}}\mathop{\sum }_{\boldsymbol{j}_{S}\in \unicode[STIX]{x1D70B}_{S}({\mathcal{J}}_{S})}~\mathop{\sum }_{\boldsymbol{j}\in {\mathcal{J}}_{S}(\boldsymbol{j}_{S})}w_{a_{\boldsymbol{j}}+1}(a_{\boldsymbol{j}}+1)^{it}.\nonumber\end{eqnarray}$$
By Theorem 5.2,
 $$\begin{eqnarray}\displaystyle & & \displaystyle \lim _{T\rightarrow \infty }\biggl(\frac{1}{T}\int _{0}^{T}\biggl|\mathop{\sum }_{a\in A}w_{a+1}(a+1)^{it}\biggr|^{2k}\,dt\biggr)^{1/k}\nonumber\\ \displaystyle & & \displaystyle \quad \leqslant (4k^{2})^{K}\mathop{\sum }_{S\subset \{1,\ldots ,K\}}\mathop{\sum }_{\boldsymbol{j}_{S}\in \unicode[STIX]{x1D70B}_{S}({\mathcal{J}}_{S})}\lim _{T\rightarrow \infty }\biggl(\frac{1}{T}\int _{0}^{T}\biggl|\mathop{\sum }_{\boldsymbol{ j}\in {\mathcal{J}}_{S}(\boldsymbol{j}_{S})}w_{a_{\boldsymbol{j}}+1}(a_{\boldsymbol{j}}+1)^{it}\biggr|^{2k}\,dt\biggr)^{1/k}.\nonumber\\ \displaystyle & & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle \lim _{T\rightarrow \infty }\biggl(\frac{1}{T}\int _{0}^{T}\biggl|\mathop{\sum }_{a\in A}w_{a+1}(a+1)^{it}\biggr|^{2k}\,dt\biggr)^{1/k}\nonumber\\ \displaystyle & & \displaystyle \quad \leqslant (4k^{2})^{K}\mathop{\sum }_{S\subset \{1,\ldots ,K\}}\mathop{\sum }_{\boldsymbol{j}_{S}\in \unicode[STIX]{x1D70B}_{S}({\mathcal{J}}_{S})}\lim _{T\rightarrow \infty }\biggl(\frac{1}{T}\int _{0}^{T}\biggl|\mathop{\sum }_{\boldsymbol{ j}\in {\mathcal{J}}_{S}(\boldsymbol{j}_{S})}w_{a_{\boldsymbol{j}}+1}(a_{\boldsymbol{j}}+1)^{it}\biggr|^{2k}\,dt\biggr)^{1/k}.\nonumber\\ \displaystyle & & \displaystyle\end{eqnarray}$$
If we define
and
![]() $w_{S,\,\boldsymbol{j}_{S}}$
to be the weights
$w_{S,\,\boldsymbol{j}_{S}}$
to be the weights
![]() $w$
restricted to
$w$
restricted to
![]() $A_{S,\,\boldsymbol{j}_{S}}+1$
then the innermost quantity above is
$A_{S,\,\boldsymbol{j}_{S}}+1$
then the innermost quantity above is
This energy is a weighted count of solutions to the equation
Define
![]() $\boldsymbol{l}_{S}$
to be the
$\boldsymbol{l}_{S}$
to be the
![]() $K$
-dimensional vector obtained from
$K$
-dimensional vector obtained from
![]() $\boldsymbol{j}_{S}$
by adding zero entries to those positions not corresponding to
$\boldsymbol{j}_{S}$
by adding zero entries to those positions not corresponding to
![]() $S$
. We can then write
$S$
. We can then write
![]() $\boldsymbol{j}\in {\mathcal{J}}_{S}(\boldsymbol{j}_{S})$
as
$\boldsymbol{j}\in {\mathcal{J}}_{S}(\boldsymbol{j}_{S})$
as
![]() $\boldsymbol{l}_{S}+\boldsymbol{j}^{\prime }$
where
$\boldsymbol{l}_{S}+\boldsymbol{j}^{\prime }$
where
![]() $\boldsymbol{j}^{\prime }$
has negative entries on coordinates from
$\boldsymbol{j}^{\prime }$
has negative entries on coordinates from
![]() $S^{\prime }=\{1,\ldots ,K\}\setminus S$
and zeros on coordinates in
$S^{\prime }=\{1,\ldots ,K\}\setminus S$
and zeros on coordinates in
![]() $S$
. We let
$S$
. We let
![]() $\boldsymbol{p}_{S}$
denote the vector of primes with indices from
$\boldsymbol{p}_{S}$
denote the vector of primes with indices from
![]() $S$
and
$S$
and
![]() $\boldsymbol{q}$
denote the vector of primes with indices from
$\boldsymbol{q}$
denote the vector of primes with indices from
![]() $S^{\prime }$
. Finally, if we use the notation
$S^{\prime }$
. Finally, if we use the notation
![]() $\boldsymbol{z}^{\boldsymbol{m}}=z_{1}^{m_{1}}\cdots z_{K}^{m_{K}}$
, then for
$\boldsymbol{z}^{\boldsymbol{m}}=z_{1}^{m_{1}}\cdots z_{K}^{m_{K}}$
, then for
![]() $\boldsymbol{j}_{i}=\boldsymbol{l}_{S}+\boldsymbol{j}_{i}^{\prime }$
we have
$\boldsymbol{j}_{i}=\boldsymbol{l}_{S}+\boldsymbol{j}_{i}^{\prime }$
we have
Now we claim the following.
Claim 6.2. If (23) holds then
and
In particular
Proof of claim.
We begin with (24). We have
The non-zero entries of
![]() $-\boldsymbol{j}_{i}^{\prime }$
are positive and correspond to indices in
$-\boldsymbol{j}_{i}^{\prime }$
are positive and correspond to indices in
![]() $S^{\prime }$
. Furthermore
$S^{\prime }$
. Furthermore
![]() $\boldsymbol{p}_{S}^{\boldsymbol{l}_{S}}x(\boldsymbol{j}_{i})$
is coprime to
$\boldsymbol{p}_{S}^{\boldsymbol{l}_{S}}x(\boldsymbol{j}_{i})$
is coprime to
![]() $p_{t}$
for any
$p_{t}$
for any
![]() $t\in S^{\prime }$
. Thus
$t\in S^{\prime }$
. Thus
and from this (24) follows.
Next, we recall that
![]() $x(\boldsymbol{j}_{i})$
is of the form
$x(\boldsymbol{j}_{i})$
is of the form
![]() $p_{K+1}^{f_{K+1}(\boldsymbol{j}_{i})}\cdots p_{l}^{f_{l}(\boldsymbol{j}_{i})}$
for primes
$p_{K+1}^{f_{K+1}(\boldsymbol{j}_{i})}\cdots p_{l}^{f_{l}(\boldsymbol{j}_{i})}$
for primes
![]() $p_{K+1},\ldots ,p_{l}$
and functions
$p_{K+1},\ldots ,p_{l}$
and functions
![]() $f_{i}$
which are linear or constant. Thus
$f_{i}$
which are linear or constant. Thus
and
for any
![]() $t\in \{K+1,\ldots ,l\}$
. Writing
$t\in \{K+1,\ldots ,l\}$
. Writing
![]() $f_{t}=H_{t}+c_{t}$
for a linear form
$f_{t}=H_{t}+c_{t}$
for a linear form
![]() $H_{t}$
and a constant
$H_{t}$
and a constant
![]() $c_{t}$
we see
$c_{t}$
we see
and
In view of the first part of the claim and the fact that
![]() $\boldsymbol{j}_{i}=\boldsymbol{l}_{S}\oplus \boldsymbol{j}_{i}^{\prime }$
, we have
$\boldsymbol{j}_{i}=\boldsymbol{l}_{S}\oplus \boldsymbol{j}_{i}^{\prime }$
, we have
and (25) follows. ◻
Having established this claim, we can multiply both sides of (23) by
to get the equation
Counting such equations with the same weights, we are now evaluating
Crucially, the powers of primes indexed by
![]() $S^{\prime }$
are now all positive in the above quantity, and we can apply Lemma 4.3. The above is thus at most
$S^{\prime }$
are now all positive in the above quantity, and we can apply Lemma 4.3. The above is thus at most
 $$\begin{eqnarray}\displaystyle & & \displaystyle (2k^{2})^{K-|S|}\mathop{\sum }_{\boldsymbol{j}\in {\mathcal{J}}_{S}(\boldsymbol{j}_{S})}\lim _{T\rightarrow \infty }\biggl(\frac{1}{T}\int _{0}^{T}|w_{a_{\boldsymbol{j}}+1}(a_{\boldsymbol{j}}^{-1}+1)^{it}|^{2k}\,dt\biggr)^{1/k}\nonumber\\ \displaystyle & & \displaystyle \quad \leqslant (2k^{2})^{K}\mathop{\sum }_{\boldsymbol{j}\in {\mathcal{J}}_{S}(\boldsymbol{j}_{S})}|w_{a_{\boldsymbol{j}}+1}|^{2}.\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle (2k^{2})^{K-|S|}\mathop{\sum }_{\boldsymbol{j}\in {\mathcal{J}}_{S}(\boldsymbol{j}_{S})}\lim _{T\rightarrow \infty }\biggl(\frac{1}{T}\int _{0}^{T}|w_{a_{\boldsymbol{j}}+1}(a_{\boldsymbol{j}}^{-1}+1)^{it}|^{2k}\,dt\biggr)^{1/k}\nonumber\\ \displaystyle & & \displaystyle \quad \leqslant (2k^{2})^{K}\mathop{\sum }_{\boldsymbol{j}\in {\mathcal{J}}_{S}(\boldsymbol{j}_{S})}|w_{a_{\boldsymbol{j}}+1}|^{2}.\nonumber\end{eqnarray}$$
Inserting this into (22), we conclude that
 $$\begin{eqnarray}\displaystyle & & \displaystyle \lim _{T\rightarrow \infty }\biggl(\frac{1}{T}\int _{0}^{T}\biggl|\mathop{\sum }_{a\in A}w_{a+1}(a+1)^{it}\biggr|^{2k}\,dt\biggr)^{1/k}\nonumber\\ \displaystyle & & \displaystyle \quad \leqslant (4k^{2})^{K}\mathop{\sum }_{S\subset \{1,\ldots ,K\}}\mathop{\sum }_{\boldsymbol{j}_{S}\in \unicode[STIX]{x1D70B}_{S}({\mathcal{J}}_{S})}(2k^{2})^{K}\mathop{\sum }_{\boldsymbol{j}\in {\mathcal{J}}_{S}(\boldsymbol{j}_{S})}|w_{a_{\boldsymbol{j}}+1}|^{2}\nonumber\\ \displaystyle & & \displaystyle \quad =(8k^{4})^{K}\mathop{\sum }_{\boldsymbol{j}\in {\mathcal{J}}}|w_{a_{\boldsymbol{j}}+1}|^{2}.\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle \lim _{T\rightarrow \infty }\biggl(\frac{1}{T}\int _{0}^{T}\biggl|\mathop{\sum }_{a\in A}w_{a+1}(a+1)^{it}\biggr|^{2k}\,dt\biggr)^{1/k}\nonumber\\ \displaystyle & & \displaystyle \quad \leqslant (4k^{2})^{K}\mathop{\sum }_{S\subset \{1,\ldots ,K\}}\mathop{\sum }_{\boldsymbol{j}_{S}\in \unicode[STIX]{x1D70B}_{S}({\mathcal{J}}_{S})}(2k^{2})^{K}\mathop{\sum }_{\boldsymbol{j}\in {\mathcal{J}}_{S}(\boldsymbol{j}_{S})}|w_{a_{\boldsymbol{j}}+1}|^{2}\nonumber\\ \displaystyle & & \displaystyle \quad =(8k^{4})^{K}\mathop{\sum }_{\boldsymbol{j}\in {\mathcal{J}}}|w_{a_{\boldsymbol{j}}+1}|^{2}.\nonumber\end{eqnarray}$$
Since the inequality above is true for any set of weights on
![]() $A+1$
, (20) then follows from the definition of
$A+1$
, (20) then follows from the definition of
![]() $\unicode[STIX]{x1D6EC}_{k}(A+1)$
.
$\unicode[STIX]{x1D6EC}_{k}(A+1)$
.
To prove (21), we apply the Cauchy–Schwarz inequality and Corollary 3.3, just as we did in the conclusion of the proof of Theorem 4.1. This yields
 $$\begin{eqnarray}\displaystyle |A|^{2k} & {\leqslant} & \displaystyle E_{k}(A+1)|(A+1)^{(k)}|\nonumber\\ \displaystyle & {\leqslant} & \displaystyle \unicode[STIX]{x1D6EC}_{k}^{k}(A+1)|A|^{k}|(A+1)^{(k)}|\nonumber\\ \displaystyle & {\leqslant} & \displaystyle (8k^{4})^{k}K|A|^{k}|(A+1)^{(k)}|,\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle |A|^{2k} & {\leqslant} & \displaystyle E_{k}(A+1)|(A+1)^{(k)}|\nonumber\\ \displaystyle & {\leqslant} & \displaystyle \unicode[STIX]{x1D6EC}_{k}^{k}(A+1)|A|^{k}|(A+1)^{(k)}|\nonumber\\ \displaystyle & {\leqslant} & \displaystyle (8k^{4})^{k}K|A|^{k}|(A+1)^{(k)}|,\nonumber\end{eqnarray}$$
and a rearrangement of this inequality completes the proof of (21). ◻
Remark 6.3. A closer inspection of the proof shows that Theorem 6.1 holds under the following weaker condition: there are
![]() $K$
primes
$K$
primes
![]() $p_{1},\ldots ,p_{K}$
such that the map
$p_{1},\ldots ,p_{K}$
such that the map
is injective on
![]() $A$
.
$A$
.
7 Proof of Corollary 1.5
Recall the statement of Corollary 1.5.
Corollary.
Let
![]() $q_{1},\ldots ,q_{r}$
be rationals,
$q_{1},\ldots ,q_{r}$
be rationals,
![]() $I$
an integer interval of length
$I$
an integer interval of length
![]() $H$
and
$H$
and
![]() $S$
be a set of rational numbers of the form
$S$
be a set of rational numbers of the form
such that
![]() $\unicode[STIX]{x1D6FC}_{i}\in I$
. Then for any rational
$\unicode[STIX]{x1D6FC}_{i}\in I$
. Then for any rational
![]() $c_{1},c_{2}\neq 0$
the number of solutions
$c_{1},c_{2}\neq 0$
the number of solutions
![]() $(s_{1},s_{2})\in S\times S$
to
$(s_{1},s_{2})\in S\times S$
to
is bounded by
![]() $(\log H)^{Cr}$
with some absolute effective constant
$(\log H)^{Cr}$
with some absolute effective constant
![]() $C>0$
.
$C>0$
.
Proof. We may assume without loss of generality that none of
![]() $q_{i},i=1,\ldots ,r$
divide
$q_{i},i=1,\ldots ,r$
divide
![]() $c_{1}$
or
$c_{1}$
or
![]() $c_{2}$
. Let
$c_{2}$
. Let
![]() $S_{1}$
be the set of
$S_{1}$
be the set of
![]() $s_{1}\in S$
such that
$s_{1}\in S$
such that
![]() $(s_{1},s_{2})$
is a solution to (26) for some
$(s_{1},s_{2})$
is a solution to (26) for some
![]() $s_{2}\in S$
. By the hypothesis
$s_{2}\in S$
. By the hypothesis
![]() $S_{1}$
is contained in the generalized geometric progression
$S_{1}$
is contained in the generalized geometric progression
By Lemma 4.5, there exists a set of primes
![]() $p_{1},\ldots ,p_{r}$
such that each element in
$p_{1},\ldots ,p_{r}$
such that each element in
![]() $x\in c_{1}S_{1}$
is uniquely defined by the powers of
$x\in c_{1}S_{1}$
is uniquely defined by the powers of
![]() $p_{1},\ldots ,p_{r}$
in the prime decomposition of
$p_{1},\ldots ,p_{r}$
in the prime decomposition of
![]() $x$
. Thus, we can apply the argument of Theorem 6.1 with
$x$
. Thus, we can apply the argument of Theorem 6.1 with
![]() $K=r$
(see Remark 6.3) and then Corollary 3.3 for
$K=r$
(see Remark 6.3) and then Corollary 3.3 for
![]() $c_{1}S_{1}$
and write
$c_{1}S_{1}$
and write
On the other hand, the shifted set
![]() $c_{1}S_{1}-1$
is contained in
$c_{1}S_{1}-1$
is contained in
![]() $-c_{2}G$
, so
$-c_{2}G$
, so
Applying Cauchy–Schwarz to (27) and combining with (28) we have
so
Taking
we get
for some absolute
![]() $C^{\prime }>0$
.◻
$C^{\prime }>0$
.◻
Acknowledgements
Oliver Roche-Newton was partially supported by the Austrian Science Fund FWF Projects F5509 and P 30405-N32. Dmitrii Zhelezov was partially supported by the Knuth and Alice Wallenberg Foundation Program for Mathematics 2017.
We thank Brendan Murphy and Endre Szemerédi for helpful conversations. We also thank the anonymous referee for several helpful comments and corrections.