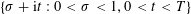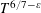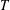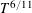1 Introduction
Let
$K$
be a quadratic extension of the rationals with discriminant
$D$
and let
$\unicode[STIX]{x1D701}_{K}(s)$
be the Dedekind zeta-function of
$K$
. It is well known that all the non-real zeros of
$\unicode[STIX]{x1D701}_{K}(s)$
are in the critical strip
$\mathscr{R}=\{s\in \mathbb{C}:0<\text{Re}(s)<1\}$
, and that the number of such zeros with imaginary part between
$0$
and
$T$
is asymptotically
$\unicode[STIX]{x1D70B}^{-1}T\log T$
.
In this paper, we investigate the simple zeros of
$\unicode[STIX]{x1D701}_{K}(s)$
in the strip
$\mathscr{R}$
. Prior to the 1970s, it was not even known that the Riemann zeta-function
$\unicode[STIX]{x1D701}(s)$
has infinitely many complex simple zeros, although Selberg [Reference Selberg17] established in 1942 that a positive proportion of complex zeros of
$\unicode[STIX]{x1D701}(s)$
are of odd order and lie on the critical line. In 1972, Montgomery [Reference Montgomery14] showed that at least
$2/3$
of complex zeros of
$\unicode[STIX]{x1D701}(s)$
are simple provided that the Riemann hypothesis is true. For the improvement on the proportion
$2/3$
, we may refer to [Reference Bui and Heath-Brown4, Reference Cheer and Goldston6, Reference Conrey, Ghsoh and Gonek9, Reference Montgomery15]. In 1974, Levinson [Reference Levinson13] proved that at least
$1/3$
of complex zeros of
$\unicode[STIX]{x1D701}(s)$
lie on the critical line. Heath-Brown and Selberg independently observed that Levinson’s work actually implied that at least
$1/3$
of complex zeros of
$\unicode[STIX]{x1D701}(s)$
are simple and on the critical line (see [Reference Heath-Brown11]). The proportion
$1/3$
has been refined in a series of works in [Reference Bui, Conrey and Young3, Reference Conrey5, Reference Feng10, Reference Wu19]. In particular, it was proved very recently in [Reference Pratt, Robles, Zaharescu and Zeindler16] and [Reference Wu19] that at least
$40.74\%$
of complex zeros of
$\unicode[STIX]{x1D701}(s)$
are simple and on the critical line.
Levinson’s method is the only known method to date that gives unconditional results on the number of simple zeros of Dirichlet series on the critical line, and it does not work for simple zeros of
$\unicode[STIX]{x1D701}_{K}(s)$
. In 1986, Conrey et al [Reference Conrey, Ghsoh and Gonek7] developed a new method to deal with simple zeros of
$\unicode[STIX]{x1D701}_{K}(s)$
in the critical strip
$\mathscr{R}$
. Let
$\mathscr{R}_{T}$
be the rectangle
$$\begin{eqnarray}\displaystyle \mathscr{R}_{T}=\{s=\unicode[STIX]{x1D70E}+\text{i}t:0<\unicode[STIX]{x1D70E}<1,0<t<T\}. & & \displaystyle\end{eqnarray}$$
We introduce the number of simple zeros of
$\unicode[STIX]{x1D701}_{K}$
in the rectangle
$\mathscr{R}_{T}$
as follows:
$$\begin{eqnarray}\displaystyle N_{K}^{\prime }(T)=\#\{\unicode[STIX]{x1D70C}_{K}\in \mathscr{R}_{T}:\unicode[STIX]{x1D70C}_{K}\text{ is a simple zero of }\unicode[STIX]{x1D701}_{K}\}. & & \displaystyle\end{eqnarray}$$
Conrey et al [Reference Conrey, Ghsoh and Gonek7] established the following remarkable result.
Theorem 1 (Conrey–Ghosh–Gonek).
One has
$N_{K}^{\prime }(T)\gg T^{6/11}$
if
$T$
is sufficiently large.
Indeed, they established the following slightly stronger result:
$$\begin{eqnarray}\displaystyle N_{K}^{\prime }(T)\gg T^{\unicode[STIX]{x1D703}-\unicode[STIX]{x1D700}} & & \displaystyle\end{eqnarray}$$
for sufficiently large
$T$
, where
$$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D703}=\frac{\sqrt{1+16c+16c^{2}}-1-4c}{4c} & & \displaystyle\end{eqnarray}$$
and the constant
$c$
is any non-negative number such that
$$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D701}({\textstyle \frac{1}{2}}+\text{i}t)\ll (1+|t|)^{c+\unicode[STIX]{x1D700}}. & & \displaystyle\end{eqnarray}$$
By taking
$c=9/56$
due to Bombieri and Iwaniec [Reference Bombieri and Iwaniec1], Conrey et al actually obtained from inequality (1.3) and equality (1.4) that
$N_{K}^{\prime }(T)\gg T^{\unicode[STIX]{x1D703}-\unicode[STIX]{x1D700}}$
with
$\unicode[STIX]{x1D703}=54949\ldots .$
Note that
$6/11=0.54545\ldots .$
Invoking the recent record
$c=13/84$
by Bourgain [Reference Bourgain2], we obtain from equality (1.4) that
$\unicode[STIX]{x1D703}=0.55810\ldots .$
Subject to the Lindelöf hypothesis, which asserts that inequality (1.5) is valid with
$c=0$
, we conclude from inequality (1.3) and equality (1.4) that
$N_{K}^{\prime }(T)\gg T^{1-\unicode[STIX]{x1D700}}$
. In the follow-up work [Reference Conrey, Ghsoh and Gonek8], it was proved that the Riemann hypothesis implies that a positive proportion (at least
$1/54$
) of the zeros of
$\unicode[STIX]{x1D701}_{K}(s)$
are simple.
In this paper, we shall push the method in [Reference Conrey, Ghsoh and Gonek7] further and refine Theorem 1 as follows.
Theorem 2. Let
$\unicode[STIX]{x1D700}>0$
be an arbitrarily small number. Then we have
$N_{K}^{\prime }(T)\gg T^{6/7-\unicode[STIX]{x1D700}}$
if
$T$
is sufficiently large.
We also provide a conditional result on the lower bound
$N_{K}^{\prime }(T)\gg T^{1-\unicode[STIX]{x1D700}}$
. In order to state the conditional result precisely, we shall introduce the
$k$
th moment hypothesis and the density hypothesis, respectively. The first one is on the
$k$
th moment of Dirichlet
$L$
-functions (and the Riemann zeta-function). Suppose that
$k$
is a positive integer.
kth moment Hypothesis. Let
$q\geqslant 1$
be a given integer, and let
$\unicode[STIX]{x1D712}$
be a real primitive character to the modulus
$q$
. Let
$T\geqslant 1$
. Then for any
$\unicode[STIX]{x1D700}>0$
, one has
$$\begin{eqnarray}\displaystyle \int _{1}^{T}\biggl|L\biggl(\frac{1}{2}+\text{i}t,\unicode[STIX]{x1D712}\biggr)\biggr|^{k}\ll _{q}T^{1+\unicode[STIX]{x1D700}}. & & \displaystyle\end{eqnarray}$$
Note that when
$q=1$
,
$L(s,\unicode[STIX]{x1D712})$
is reduced to the Riemann zeta-function. It is well known that the
$k$
th moment hypothesis for all
$k\in \mathbb{Z}^{+}$
is equivalent to the Lindelöf hypothesis. For
$1/2\leqslant \unicode[STIX]{x1D70E}\leqslant 1$
, let
$N(\unicode[STIX]{x1D70E},T)$
denote the number of zeros
$\unicode[STIX]{x1D70C}=\unicode[STIX]{x1D6FD}+\text{i}\unicode[STIX]{x1D6FE}$
of
$\unicode[STIX]{x1D701}(s)$
for which
$\unicode[STIX]{x1D6FD}\geqslant \unicode[STIX]{x1D70E}$
and
$|\unicode[STIX]{x1D6FE}|\leqslant T$
. The next important conjecture is the density hypothesis.
Density Hypothesis. Let
$1/2\leqslant \unicode[STIX]{x1D70E}\leqslant 1$
. For any
$\unicode[STIX]{x1D700}>0$
, one has
$$\begin{eqnarray}\displaystyle N(\unicode[STIX]{x1D70E},T)\ll T^{2-2\unicode[STIX]{x1D70E}+\unicode[STIX]{x1D700}}. & & \displaystyle\end{eqnarray}$$
With the above notation, we now introduce our second result.
Theorem 3. Let
$\unicode[STIX]{x1D700}>0$
be an arbitrarily small number, and let
$T$
be sufficiently large. We have
$N_{K}^{\prime }(T)\gg T^{1-\unicode[STIX]{x1D700}}$
if either the
$k$
th moment hypothesis is true with
$k=8$
for both
$\unicode[STIX]{x1D701}(s)$
and
$L(s,\unicode[STIX]{x1D712})$
in equation (2.3) or the density hypothesis is true.
In §2, we review some known results. We prepare some mean value estimates in §3, and then we consider a summation over zeros of the Riemann zeta-function restricted in a narrow strip in §4. The main theorems will be proved in the last section.
2 Notation and standard results
As usual, we use
$\unicode[STIX]{x1D700}$
to denote an arbitrarily small positive constant that may vary from statement to statement. We assume
$T>1$
is sufficiently large. For a finite set
$A$
, we use
$\#A$
to denote the cardinality of
$A$
.
The Riemann zeta-function is given by
$$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D701}(s)=\mathop{\sum }_{n=1}^{\infty }n^{-s}\quad (\unicode[STIX]{x1D70E}>1), & & \displaystyle\end{eqnarray}$$
and the Dirichlet
$L$
-function for the character
$\unicode[STIX]{x1D712}$
is defined as
$$\begin{eqnarray}\displaystyle L(s,\unicode[STIX]{x1D712})=\mathop{\sum }_{n=1}^{\infty }\unicode[STIX]{x1D712}(n)n^{-s}\quad (\unicode[STIX]{x1D70E}>1). & & \displaystyle\end{eqnarray}$$
Throughout this paper, the letter
$\unicode[STIX]{x1D70C}=\unicode[STIX]{x1D6FD}+\text{i}\unicode[STIX]{x1D6FE}$
(with
$\unicode[STIX]{x1D6FD},\unicode[STIX]{x1D6FE}\in \mathbb{R}$
) will denote the zero of the Riemann zeta-function
$\unicode[STIX]{x1D701}(s)$
. Recall that
$\unicode[STIX]{x1D701}_{K}(s)$
is the Dedekind zeta-function of a quadratic number field
$K$
. It is well known that
$$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D701}_{K}(s)=\unicode[STIX]{x1D701}(s)L(s,\unicode[STIX]{x1D712}), & & \displaystyle\end{eqnarray}$$
where
$\unicode[STIX]{x1D712}$
is the Kronecker symbol
$(D|\cdot )$
. The Kronecker symbol
$\unicode[STIX]{x1D712}$
is a real primitive character to the modulus
$q=|D|$
. We shall adopt the standard notation
$\ll$
,
$\gg$
and
$O$
, while the implied constants may depend on
$K$
(and
$q$
).
The Riemann zeta-function satisfies the functional equation
$$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D701}(1-s)=X(1-s)\unicode[STIX]{x1D701}(s) & & \displaystyle\end{eqnarray}$$
with
$$\begin{eqnarray}\displaystyle X(1-s)=2(2\unicode[STIX]{x1D70B})^{-s}\unicode[STIX]{x1D6E4}(s)\cos \frac{\unicode[STIX]{x1D70B}s}{2}, & & \displaystyle \nonumber\end{eqnarray}$$
and the Dirichlet
$L$
-function satisfies
$$\begin{eqnarray}\displaystyle L(1-s,\unicode[STIX]{x1D712})=X(1-s,\unicode[STIX]{x1D712})L(s,\unicode[STIX]{x1D712}) & & \displaystyle\end{eqnarray}$$
with
$$\begin{eqnarray}\displaystyle X(1-s,\unicode[STIX]{x1D712})=\frac{q^{s}}{\unicode[STIX]{x1D70F}(\unicode[STIX]{x1D712})}(2\unicode[STIX]{x1D70B})^{-s}\unicode[STIX]{x1D6E4}(s)(\text{e}^{\unicode[STIX]{x1D70B}\text{i}s/2}+\unicode[STIX]{x1D712}(-1)\text{e}^{-\unicode[STIX]{x1D70B}\text{i}s/2}), & & \displaystyle \nonumber\end{eqnarray}$$
where
$\unicode[STIX]{x1D70F}(\unicode[STIX]{x1D712})$
denotes the Gauss sum
$$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D70F}(\unicode[STIX]{x1D712})=\mathop{\sum }_{a=1}^{q}\unicode[STIX]{x1D712}(a)\text{e}^{2\unicode[STIX]{x1D70B}\text{i}a/q}. & & \displaystyle \nonumber\end{eqnarray}$$
The following estimates are standard (one may refer to Titchmarsh [Reference Titchmarsh18], for example):
$$\begin{eqnarray}\displaystyle X(1-s),~X(1-s,\unicode[STIX]{x1D712})\ll t^{\unicode[STIX]{x1D70E}-1/2}\quad (t>1,\unicode[STIX]{x1D70E}<2). & & \displaystyle\end{eqnarray}$$
By the functional equation (2.5) and the inequality (2.6), for
$\unicode[STIX]{x1D70C}\in \mathscr{R}_{T}$
,
$$\begin{eqnarray}\displaystyle |L(1-\unicode[STIX]{x1D70C},\unicode[STIX]{x1D712})|\ll T^{\unicode[STIX]{x1D6FD}-1/2}|L(\unicode[STIX]{x1D70C},\unicode[STIX]{x1D712})|. & & \displaystyle\end{eqnarray}$$
Also, by differentiating the functional equation (2.4), we have
$$\begin{eqnarray}\displaystyle -\unicode[STIX]{x1D701}^{\prime }(1-s)=X(1-s)\unicode[STIX]{x1D701}^{\prime }(s)-X^{\prime }(1-s)\unicode[STIX]{x1D701}(s), & & \displaystyle \nonumber\end{eqnarray}$$
which implies
$$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D701}^{\prime }(1-\unicode[STIX]{x1D70C})=-X(1-\unicode[STIX]{x1D70C})\unicode[STIX]{x1D701}^{\prime }(\unicode[STIX]{x1D70C}), & & \displaystyle \nonumber\end{eqnarray}$$
where as pointed out before,
$\unicode[STIX]{x1D70C}=\unicode[STIX]{x1D6FD}+\text{i}\unicode[STIX]{x1D6FE}$
is a zero of
$\unicode[STIX]{x1D701}(s)$
. Then by (2.6), for
$\unicode[STIX]{x1D70C}\in \mathscr{R}_{T}$
, we have
$$\begin{eqnarray}\displaystyle |\unicode[STIX]{x1D701}^{\prime }(1-\unicode[STIX]{x1D70C})|\ll T^{\unicode[STIX]{x1D6FD}-1/2}|\unicode[STIX]{x1D701}^{\prime }(\unicode[STIX]{x1D70C})|. & & \displaystyle\end{eqnarray}$$
Although the density hypothesis is still open, the following density estimate due to Ingham is well known.
Lemma 1. One has
$$\begin{eqnarray}\displaystyle N(\unicode[STIX]{x1D70E},T)\ll _{\unicode[STIX]{x1D700}}T^{(3/(2-\unicode[STIX]{x1D70E}))(1-\unicode[STIX]{x1D70E})+\unicode[STIX]{x1D700}}\quad (\unicode[STIX]{x1D70E}\geqslant 1/2). & & \displaystyle\end{eqnarray}$$
Proof. This is [Reference Titchmarsh18, Theorem 9.19(B)]. ◻
3 Mean value results
In this section, we prepare some mean value results on the Riemann zeta-function
$\unicode[STIX]{x1D701}(s)$
and the Dirichlet
$L$
-function
$L(s,\unicode[STIX]{x1D712})$
.
Lemma 2 [Reference Ivić12, Theorem 8.4].
Let
$1/2\leqslant \unicode[STIX]{x1D70E}\leqslant 1$
. Suppose that
$m(\unicode[STIX]{x1D70E})=4/(3-4\unicode[STIX]{x1D70E})$
for
$1/2\leqslant \unicode[STIX]{x1D70E}\leqslant 5/8$
and
$m(\unicode[STIX]{x1D70E})=8$
for
$5/8\leqslant \unicode[STIX]{x1D70E}\leqslant 1$
. Then we have
$$\begin{eqnarray}\displaystyle \int _{1}^{T}|\unicode[STIX]{x1D701}(\unicode[STIX]{x1D70E}+\text{i}t)|^{m(\unicode[STIX]{x1D70E})}\,dt\ll T^{1+\unicode[STIX]{x1D700}} & & \displaystyle\end{eqnarray}$$
and
$$\begin{eqnarray}\displaystyle \int _{1}^{T}|L(\unicode[STIX]{x1D70E}+\text{i}t,\unicode[STIX]{x1D712})|^{m(\unicode[STIX]{x1D70E})}\,dt\ll T^{1+\unicode[STIX]{x1D700}}. & & \displaystyle\end{eqnarray}$$
Proof. The inequality (3.1) follows from [Reference Ivić12, Theorem 8.4], and the inequality (3.2) for
$L(s,\unicode[STIX]{x1D712})$
can be established similarly.◻
Theorem 8.4 [Reference Ivić12] of Ivić provides stronger mean value estimate when
$5/8\leqslant \unicode[STIX]{x1D70E}\leqslant 1$
, however it leads to no further improvement in this paper.
Lemma 3. Let
$m>1$
and let
$\mathscr{R}_{T}$
be the rectangle defined by equality (1.1). Suppose
$1/2\leqslant \unicode[STIX]{x1D70E}\leqslant 1$
and
$\unicode[STIX]{x1D6E5}=(\log T)^{-1}$
. Then
$$\begin{eqnarray}\displaystyle \mathop{\sum }_{\substack{ \unicode[STIX]{x1D70C}\in \mathscr{R}_{T} \\ \unicode[STIX]{x1D6FD}\geqslant \unicode[STIX]{x1D70E}}}|\unicode[STIX]{x1D701}^{\prime }(\unicode[STIX]{x1D70C})|^{m}\ll T^{\unicode[STIX]{x1D700}}\int _{\unicode[STIX]{x1D70E}-2\unicode[STIX]{x1D6E5}}^{1+2\unicode[STIX]{x1D6E5}}\int _{1}^{T+1}|\unicode[STIX]{x1D701}(\unicode[STIX]{x1D6FF}+\text{i}t)|^{m}\,dt\,d\unicode[STIX]{x1D6FF}+O(1) & & \displaystyle\end{eqnarray}$$
and
$$\begin{eqnarray}\displaystyle \mathop{\sum }_{\substack{ \unicode[STIX]{x1D70C}\in \mathscr{R}_{T} \\ \unicode[STIX]{x1D6FD}\geqslant \unicode[STIX]{x1D70E}}}|L(\unicode[STIX]{x1D70C},\unicode[STIX]{x1D712})|^{m}\ll T^{\unicode[STIX]{x1D700}}\int _{\unicode[STIX]{x1D70E}-2\unicode[STIX]{x1D6E5}}^{1+2\unicode[STIX]{x1D6E5}}\int _{1}^{T+1}|L(\unicode[STIX]{x1D6FF}+\text{i}t,\unicode[STIX]{x1D712})|^{m}\,dt\,d\unicode[STIX]{x1D6FF}+O(1).\quad & & \displaystyle\end{eqnarray}$$
Proof. The number of zeros
$\unicode[STIX]{x1D70C}\in \mathscr{R}_{T}$
with
$\unicode[STIX]{x1D6FE}\leqslant 2$
is finite. Therefore, it suffices to consider the contribution from
$\unicode[STIX]{x1D6FE}>2$
. By the residue theorem,
$$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D701}^{\prime }(\unicode[STIX]{x1D70C})=\frac{1}{\unicode[STIX]{x1D6E5}}\int _{\unicode[STIX]{x1D6E5}}^{2\unicode[STIX]{x1D6E5}}\frac{1}{2\unicode[STIX]{x1D70B}\text{i}}\int _{|s-\unicode[STIX]{x1D70C}|=\unicode[STIX]{x1D6FF}}\frac{\unicode[STIX]{x1D701}(s)}{(s-\unicode[STIX]{x1D70C})^{2}}\,ds\,d\unicode[STIX]{x1D6FF}, & & \displaystyle \nonumber\end{eqnarray}$$
and it follows that
$$\begin{eqnarray}\displaystyle |\unicode[STIX]{x1D701}^{\prime }(\unicode[STIX]{x1D70C})|\ll \unicode[STIX]{x1D6E5}^{-3}\int _{\unicode[STIX]{x1D70E}-2\unicode[STIX]{x1D6E5}}^{1+2\unicode[STIX]{x1D6E5}}\int _{\unicode[STIX]{x1D6FE}-2\unicode[STIX]{x1D6E5}}^{\unicode[STIX]{x1D6FE}+2\unicode[STIX]{x1D6E5}}|\unicode[STIX]{x1D701}(\unicode[STIX]{x1D6FF}+\text{i}t)|\,dt\,d\unicode[STIX]{x1D6FF}. & & \displaystyle \nonumber\end{eqnarray}$$
By Hölder’s inequality, we have
$$\begin{eqnarray}\displaystyle |\unicode[STIX]{x1D701}^{\prime }(\unicode[STIX]{x1D70C})|^{m}\ll \unicode[STIX]{x1D6E5}^{-2m-1}\int _{\unicode[STIX]{x1D70E}-2\unicode[STIX]{x1D6E5}}^{1+2\unicode[STIX]{x1D6E5}}\int _{\unicode[STIX]{x1D6FE}-2\unicode[STIX]{x1D6E5}}^{\unicode[STIX]{x1D6FE}+2\unicode[STIX]{x1D6E5}}|\unicode[STIX]{x1D701}(\unicode[STIX]{x1D6FF}+\text{i}t)|^{m}\,dt\,d\unicode[STIX]{x1D6FF}. & & \displaystyle \nonumber\end{eqnarray}$$
Since the number of
$\unicode[STIX]{x1D70C}\in \mathscr{R}_{T}$
in a square of side length
$1$
is
$\ll \log T$
, we have
$$\begin{eqnarray}\displaystyle \mathop{\sum }_{\substack{ \unicode[STIX]{x1D70C}\in \mathscr{R}_{T} \\ \unicode[STIX]{x1D6FD}\geqslant \unicode[STIX]{x1D70E}}}|\unicode[STIX]{x1D701}^{\prime }(\unicode[STIX]{x1D70C})|^{m}\ll (\log T)^{2m+2}\int _{\unicode[STIX]{x1D70E}-2\unicode[STIX]{x1D6E5}}^{1+2\unicode[STIX]{x1D6E5}}\int _{1}^{T+1}|\unicode[STIX]{x1D701}(\unicode[STIX]{x1D6FF}+\text{i}t)|^{m}\,dt\,d\unicode[STIX]{x1D6FF}+O(1). & & \displaystyle \nonumber\end{eqnarray}$$
We finally conclude that
$$\begin{eqnarray}\displaystyle \mathop{\sum }_{\substack{ \unicode[STIX]{x1D70C}\in \mathscr{R}_{T} \\ \unicode[STIX]{x1D6FD}\geqslant \unicode[STIX]{x1D70E}}}|\unicode[STIX]{x1D701}^{\prime }(\unicode[STIX]{x1D70C})|^{m}\ll T^{\unicode[STIX]{x1D700}}\int _{\unicode[STIX]{x1D70E}-2\unicode[STIX]{x1D6E5}}^{1+2\unicode[STIX]{x1D6E5}}\int _{1}^{T+1}|\unicode[STIX]{x1D701}(\unicode[STIX]{x1D6FF}+\text{i}t)|^{m}\,dt\,d\unicode[STIX]{x1D6FF}+O(1). & & \displaystyle \nonumber\end{eqnarray}$$
The inequality (3.4) can be established in a similar way. We complete the proof. ◻
Lemma 4. Let
$1/2\leqslant \unicode[STIX]{x1D70E}\leqslant 1$
. Let
$m(\unicode[STIX]{x1D70E})$
be defined as in Lemma 2. Suppose that
$1<m\leqslant m(\unicode[STIX]{x1D70E})$
. Then we have
$$\begin{eqnarray}\displaystyle \mathop{\sum }_{\substack{ \unicode[STIX]{x1D70C}\in \mathscr{R}_{T} \\ \unicode[STIX]{x1D6FD}\geqslant \unicode[STIX]{x1D70E}}}|\unicode[STIX]{x1D701}^{\prime }(\unicode[STIX]{x1D70C})|^{m}\ll T^{1+\unicode[STIX]{x1D700}}\quad \text{and}\quad \mathop{\sum }_{\substack{ \unicode[STIX]{x1D70C}\in \mathscr{R}_{T} \\ \unicode[STIX]{x1D6FD}\geqslant \unicode[STIX]{x1D70E}}}|L(\unicode[STIX]{x1D70C},\unicode[STIX]{x1D712})|^{m}\ll T^{1+\unicode[STIX]{x1D700}}. & & \displaystyle\end{eqnarray}$$
4 A summation restricted in a narrow strip
Due to the factorization (2.3), we have
$$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D701}_{K}^{\prime }(s)=\unicode[STIX]{x1D701}^{\prime }(s)L(s,\unicode[STIX]{x1D712})+\unicode[STIX]{x1D701}(s)L^{\prime }(s,\unicode[STIX]{x1D712}). & & \displaystyle \nonumber\end{eqnarray}$$
Therefore,
$\unicode[STIX]{x1D70C}$
is a simple zero of
$\unicode[STIX]{x1D701}_{K}$
if and only if
$$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D701}^{\prime }(\unicode[STIX]{x1D70C})L(\unicode[STIX]{x1D70C},\unicode[STIX]{x1D712})\neq 0. & & \displaystyle\end{eqnarray}$$
In [Reference Conrey, Ghsoh and Gonek7], Conrey et al investigated the summation
$$\begin{eqnarray}\displaystyle {\mathcal{S}}(T)=\mathop{\sum }_{\unicode[STIX]{x1D70C}\in \mathscr{R}_{T}}\unicode[STIX]{x1D701}^{\prime }(\unicode[STIX]{x1D70C})L(1-\unicode[STIX]{x1D70C},\unicode[STIX]{x1D712}), & & \displaystyle\end{eqnarray}$$
and they found an asymptotic formula as follows.
Lemma 5. One has
$$\begin{eqnarray}\displaystyle {\mathcal{S}}(T)=L(1,\unicode[STIX]{x1D712})\frac{T}{4\unicode[STIX]{x1D70B}}\log ^{2}T+O(T\log T). & & \displaystyle\end{eqnarray}$$
Proof. This is formula (18) of Conrey et al in [Reference Conrey, Ghsoh and Gonek7]. ◻
For
$1/2\leqslant \unicode[STIX]{x1D706}\leqslant 1$
, we introduce
$$\begin{eqnarray}\displaystyle {\mathcal{S}}(T;\unicode[STIX]{x1D706})=\mathop{\sum }_{\substack{ \unicode[STIX]{x1D70C}\in \mathscr{R}_{T} \\ 1-\unicode[STIX]{x1D706}\leqslant \unicode[STIX]{x1D6FD}\leqslant \unicode[STIX]{x1D706}}}\unicode[STIX]{x1D701}^{\prime }(\unicode[STIX]{x1D70C})L(1-\unicode[STIX]{x1D70C},\unicode[STIX]{x1D712}), & & \displaystyle\end{eqnarray}$$
where the summation is taken over
$\unicode[STIX]{x1D70C}$
in the narrow strip
$1-\unicode[STIX]{x1D706}\leqslant \unicode[STIX]{x1D6FD}\leqslant \unicode[STIX]{x1D706}$
. Note that
${\mathcal{S}}(T)={\mathcal{S}}(T;1)$
, and we define
$$\begin{eqnarray}\displaystyle {\mathcal{E}}(T;\unicode[STIX]{x1D706})={\mathcal{S}}(T)-{\mathcal{S}}(T;\unicode[STIX]{x1D706}). & & \displaystyle\end{eqnarray}$$
We have
$$\begin{eqnarray}\displaystyle {\mathcal{E}}(T;\unicode[STIX]{x1D706})=\mathop{\sum }_{\substack{ \unicode[STIX]{x1D70C}\in \mathscr{R}_{T} \\ 0\leqslant \unicode[STIX]{x1D6FD}<1-\unicode[STIX]{x1D706}\;\text{or}\;\unicode[STIX]{x1D706}<\unicode[STIX]{x1D6FD}\leqslant 1}}\unicode[STIX]{x1D701}^{\prime }(\unicode[STIX]{x1D70C})L(1-\unicode[STIX]{x1D70C},\unicode[STIX]{x1D712}), & & \displaystyle \nonumber\end{eqnarray}$$
and it follows from inequalities (2.7) and (2.8) that
$$\begin{eqnarray}\displaystyle {\mathcal{E}}(T;\unicode[STIX]{x1D706})\ll \unicode[STIX]{x1D6EF}(T;\unicode[STIX]{x1D706}), & & \displaystyle\end{eqnarray}$$
where
$$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D6EF}(T;\unicode[STIX]{x1D706})=\mathop{\sum }_{\substack{ \unicode[STIX]{x1D70C}\in \mathscr{R}_{T} \\ \unicode[STIX]{x1D6FD}\geqslant \unicode[STIX]{x1D706}}}T^{\unicode[STIX]{x1D6FD}-1/2}|\unicode[STIX]{x1D701}^{\prime }(\unicode[STIX]{x1D70C})L(\unicode[STIX]{x1D70C},\unicode[STIX]{x1D712})|. & & \displaystyle \nonumber\end{eqnarray}$$
Using Stieltjes’ integration, we have
$$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D6EF}(T;\unicode[STIX]{x1D706}) & = & \displaystyle \int _{\unicode[STIX]{x1D706}}^{1}T^{\unicode[STIX]{x1D70E}-1/2}\,d\biggl(\mathop{\sum }_{\substack{ \unicode[STIX]{x1D70C}\in \mathscr{R}_{T} \\ \unicode[STIX]{x1D6FD}\geqslant \unicode[STIX]{x1D70E}}}|\unicode[STIX]{x1D701}^{\prime }(\unicode[STIX]{x1D70C})L(\unicode[STIX]{x1D70C},\unicode[STIX]{x1D712})|\biggr)\nonumber\\ \displaystyle & {\leqslant} & \displaystyle \sup _{\unicode[STIX]{x1D706}\leqslant \unicode[STIX]{x1D70E}\leqslant 1}T^{\unicode[STIX]{x1D70E}-1/2}\mathop{\sum }_{\substack{ \unicode[STIX]{x1D70C}\in \mathscr{R}_{T} \\ \unicode[STIX]{x1D6FD}\geqslant \unicode[STIX]{x1D70E}}}|\unicode[STIX]{x1D701}^{\prime }(\unicode[STIX]{x1D70C})L(\unicode[STIX]{x1D70C},\unicode[STIX]{x1D712})|.\end{eqnarray}$$
We first prove a lower bound for
${\mathcal{S}}(T;\unicode[STIX]{x1D706})$
with
$\unicode[STIX]{x1D706}>3/5$
.
Lemma 6. For any constant
$\unicode[STIX]{x1D706}>3/5~(\text{independent of }T)$
, we have
$$\begin{eqnarray}\displaystyle |{\mathcal{S}}(T;\unicode[STIX]{x1D706})|\gg T\log ^{2}T. & & \displaystyle\end{eqnarray}$$
Proof. By Hölder’s inequality, we have
$$\begin{eqnarray}\displaystyle & & \displaystyle \mathop{\sum }_{\substack{ \unicode[STIX]{x1D70C}\in \mathscr{R}_{T} \\ \unicode[STIX]{x1D6FD}\geqslant \unicode[STIX]{x1D70E}}}|\unicode[STIX]{x1D701}^{\prime }(\unicode[STIX]{x1D70C})L(\unicode[STIX]{x1D70C},\unicode[STIX]{x1D712})|\nonumber\\ \displaystyle & & \displaystyle \qquad \leqslant N(\unicode[STIX]{x1D70E},T)^{7/10}\biggl(\mathop{\sum }_{\substack{ \unicode[STIX]{x1D70C}\in \mathscr{R}_{T} \\ \unicode[STIX]{x1D6FD}\geqslant \unicode[STIX]{x1D70E}}}|\unicode[STIX]{x1D701}^{\prime }(\unicode[STIX]{x1D70C})|^{20/3}\biggr)^{3/20}\biggl(\mathop{\sum }_{\substack{ \unicode[STIX]{x1D70C}\in \mathscr{R}_{T} \\ \unicode[STIX]{x1D6FD}\geqslant \unicode[STIX]{x1D70E}}}|L(\unicode[STIX]{x1D70C},\unicode[STIX]{x1D712})|^{20/3}\biggr)^{3/20}.\qquad\end{eqnarray}$$
Recalling the function
$m(\unicode[STIX]{x1D70E})$
defined in Lemma 2, we note that
$m(3/5)=20/3$
. By Lemma 4, for
$\unicode[STIX]{x1D70E}\geqslant 3/5$
, we have
$$\begin{eqnarray}\displaystyle \mathop{\sum }_{\substack{ \unicode[STIX]{x1D70C}\in \mathscr{R}_{T} \\ \unicode[STIX]{x1D6FD}\geqslant \unicode[STIX]{x1D70E}}}|\unicode[STIX]{x1D701}^{\prime }(\unicode[STIX]{x1D70C})|^{20/3}\ll T^{1+\unicode[STIX]{x1D700}}\quad \text{and}\quad \mathop{\sum }_{\substack{ \unicode[STIX]{x1D70C}\in \mathscr{R}_{T} \\ \unicode[STIX]{x1D6FD}\geqslant \unicode[STIX]{x1D70E}}}|L(\unicode[STIX]{x1D70C},\unicode[STIX]{x1D712})|^{20/3}\ll T^{1+\unicode[STIX]{x1D700}}. & & \displaystyle\end{eqnarray}$$
We conclude from inequalities (4.9), (4.10) and Lemma 1 that
$$\begin{eqnarray}\displaystyle \mathop{\sum }_{\substack{ \unicode[STIX]{x1D70C}\in \mathscr{R}_{T} \\ \unicode[STIX]{x1D6FD}\geqslant \unicode[STIX]{x1D70E}}}|\unicode[STIX]{x1D701}^{\prime }(\unicode[STIX]{x1D70C})L(\unicode[STIX]{x1D70C},\unicode[STIX]{x1D712})|\leqslant T^{(21/10(2-\unicode[STIX]{x1D70E}))(1-\unicode[STIX]{x1D70E})+3/10+\unicode[STIX]{x1D700}}\quad \text{for }\unicode[STIX]{x1D70E}\geqslant 3/5.\quad & & \displaystyle\end{eqnarray}$$
Inserting inequality (4.11) into equality (4.7), we obtain
$$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D6EF}(T;\unicode[STIX]{x1D706})\ll \sup _{\unicode[STIX]{x1D706}\leqslant \unicode[STIX]{x1D70E}\leqslant 1}T^{\unicode[STIX]{x1D70E}-1/2+(21/10(2-\unicode[STIX]{x1D70E}))(1-\unicode[STIX]{x1D70E})+3/10+\unicode[STIX]{x1D700}}\quad \text{for }\unicode[STIX]{x1D706}\geqslant 3/5. & & \displaystyle \nonumber\end{eqnarray}$$
A simple verification reveals that
$$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D6EF}(T;\unicode[STIX]{x1D706})\ll T^{1-(1/10(2-\unicode[STIX]{x1D706}))(5\unicode[STIX]{x1D706}-3)(2\unicode[STIX]{x1D706}-1)+\unicode[STIX]{x1D700}}\quad \text{for }\unicode[STIX]{x1D706}\geqslant 3/5, & & \displaystyle\end{eqnarray}$$
which implies
$\unicode[STIX]{x1D6EF}(T;\unicode[STIX]{x1D706})=o(T)$
for any constant
$\unicode[STIX]{x1D706}>3/5$
. Then we deduce from equality (4.5) and inequality (4.6) that
$$\begin{eqnarray}\displaystyle {\mathcal{S}}(T;\unicode[STIX]{x1D706})={\mathcal{S}}(T)+o(T). & & \displaystyle\end{eqnarray}$$
Now inequality (4.8) follows from equality (4.13) and Lemma 5. ◻
Essentially, the argument in the proof of Lemma 6 also yields the following conditional result.
Lemma 7. For any constant
$\unicode[STIX]{x1D706}>1/2$
, we have
$$\begin{eqnarray}\displaystyle |{\mathcal{S}}(T;\unicode[STIX]{x1D706})|\gg T\log ^{2}T & & \displaystyle \nonumber\end{eqnarray}$$
provided that either the
$k$
th moment hypothesis is valid for
$k=8$
or the density hypothesis is true.
Proof. In order to apply the
$8$
th moment hypothesis, instead of inequality (4.9), we work with
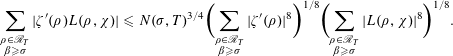$$\begin{eqnarray}\displaystyle \mathop{\sum }_{\substack{ \unicode[STIX]{x1D70C}\in \mathscr{R}_{T} \\ \unicode[STIX]{x1D6FD}\geqslant \unicode[STIX]{x1D70E}}}|\unicode[STIX]{x1D701}^{\prime }(\unicode[STIX]{x1D70C})L(\unicode[STIX]{x1D70C},\unicode[STIX]{x1D712})|\leqslant N(\unicode[STIX]{x1D70E},T)^{3/4}\biggl(\mathop{\sum }_{\substack{ \unicode[STIX]{x1D70C}\in \mathscr{R}_{T} \\ \unicode[STIX]{x1D6FD}\geqslant \unicode[STIX]{x1D70E}}}|\unicode[STIX]{x1D701}^{\prime }(\unicode[STIX]{x1D70C})|^{8}\biggr)^{1/8}\biggl(\mathop{\sum }_{\substack{ \unicode[STIX]{x1D70C}\in \mathscr{R}_{T} \\ \unicode[STIX]{x1D6FD}\geqslant \unicode[STIX]{x1D70E}}}|L(\unicode[STIX]{x1D70C},\unicode[STIX]{x1D712})|^{8}\biggr)^{1/8}. & & \displaystyle \nonumber\\ \displaystyle & & \displaystyle\end{eqnarray}$$
The argument leading to inequality (4.12) in combination with inequality (4.14) will also imply
$$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D6EF}(T;\unicode[STIX]{x1D706})\ll T^{1-(1/(2-\unicode[STIX]{x1D706}))(\unicode[STIX]{x1D706}-1/2)^{2}+\unicode[STIX]{x1D700}}\quad \text{for }\unicode[STIX]{x1D706}\geqslant 1/2 & & \displaystyle\end{eqnarray}$$
subject to the truth of the
$k$
th moment hypothesis with
$k=8$
. Note that inequality (4.15) gives
$\unicode[STIX]{x1D6EF}(T;\unicode[STIX]{x1D706})=o(T)$
for any constant
$\unicode[STIX]{x1D706}>1/2$
, and the desired lower bound for
$S(T;\unicode[STIX]{x1D706})$
now follows.
For
$1/2\leqslant \unicode[STIX]{x1D70E}\leqslant 5/8$
, we deduce that
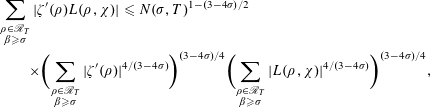$$\begin{eqnarray}\displaystyle & & \displaystyle \mathop{\sum }_{\substack{ \unicode[STIX]{x1D70C}\in \mathscr{R}_{T} \\ \unicode[STIX]{x1D6FD}\geqslant \unicode[STIX]{x1D70E}}}|\unicode[STIX]{x1D701}^{\prime }(\unicode[STIX]{x1D70C})L(\unicode[STIX]{x1D70C},\unicode[STIX]{x1D712})|\leqslant N(\unicode[STIX]{x1D70E},T)^{1-(3-4\unicode[STIX]{x1D70E})/2}\nonumber\\ \displaystyle & & \displaystyle \qquad \times \biggl(\mathop{\sum }_{\substack{ \unicode[STIX]{x1D70C}\in \mathscr{R}_{T} \\ \unicode[STIX]{x1D6FD}\geqslant \unicode[STIX]{x1D70E}}}|\unicode[STIX]{x1D701}^{\prime }(\unicode[STIX]{x1D70C})|^{4/(3-4\unicode[STIX]{x1D70E})}\biggr)^{(3-4\unicode[STIX]{x1D70E})/4}\biggl(\mathop{\sum }_{\substack{ \unicode[STIX]{x1D70C}\in \mathscr{R}_{T} \\ \unicode[STIX]{x1D6FD}\geqslant \unicode[STIX]{x1D70E}}}|L(\unicode[STIX]{x1D70C},\unicode[STIX]{x1D712})|^{4/(3-4\unicode[STIX]{x1D70E})}\biggr)^{(3-4\unicode[STIX]{x1D70E})/4},\nonumber\end{eqnarray}$$
and then by Lemma 4
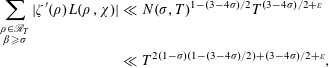$$\begin{eqnarray}\displaystyle \mathop{\sum }_{\substack{ \unicode[STIX]{x1D70C}\in \mathscr{R}_{T} \\ \unicode[STIX]{x1D6FD}\geqslant \unicode[STIX]{x1D70E}}}|\unicode[STIX]{x1D701}^{\prime }(\unicode[STIX]{x1D70C})L(\unicode[STIX]{x1D70C},\unicode[STIX]{x1D712})| & \ll & \displaystyle N(\unicode[STIX]{x1D70E},T)^{1-(3-4\unicode[STIX]{x1D70E})/2}T^{(3-4\unicode[STIX]{x1D70E})/2+\unicode[STIX]{x1D700}}\nonumber\\ \displaystyle & \ll & \displaystyle T^{2(1-\unicode[STIX]{x1D70E})(1-(3-4\unicode[STIX]{x1D70E})/2)+(3-4\unicode[STIX]{x1D70E})/2+\unicode[STIX]{x1D700}},\nonumber\end{eqnarray}$$
where the last inequality above is subject to the truth of inequality (1.7). Inserting the above inequality into inequality (4.7), we finally obtain
$$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D6EF}(T;\unicode[STIX]{x1D706})\ll T^{1-4(\unicode[STIX]{x1D706}-1/2)^{2}+\unicode[STIX]{x1D700}}\quad \text{for }\unicode[STIX]{x1D706}\geqslant 1/2 & & \displaystyle\end{eqnarray}$$
subject to the density hypothesis. Therefore, the desired lower bound for
$S(T;\unicode[STIX]{x1D706})$
now follows again. We complete the proof.◻
5 The proof of theorems
We define
$$\begin{eqnarray}\displaystyle N_{K}^{\prime }(T;\unicode[STIX]{x1D706})=\#\{\unicode[STIX]{x1D70C}=\unicode[STIX]{x1D6FD}+\text{i}\unicode[STIX]{x1D6FE}\in \mathscr{R}_{T}:\unicode[STIX]{x1D70C}\text{ is a simple zero of }\unicode[STIX]{x1D701}_{K}\text{ and }1/2\leqslant \unicode[STIX]{x1D6FD}\leqslant \unicode[STIX]{x1D706}\}, & & \displaystyle \nonumber\\ \displaystyle & & \displaystyle\end{eqnarray}$$
which counts the number of simple zeros of
$\unicode[STIX]{x1D701}_{K}(s)$
in a narrow strip. We have the following lower bound for
$N_{K}^{\prime }(T;\unicode[STIX]{x1D706})$
.
Lemma 8. Let
$1/2\leqslant \unicode[STIX]{x1D706}\leqslant 5/8$
. Suppose that
$|{\mathcal{S}}(T;\unicode[STIX]{x1D706})|\gg T$
. Then we have
$$\begin{eqnarray}\displaystyle N_{K}^{\prime }(T;\unicode[STIX]{x1D706})\gg T^{2\unicode[STIX]{x1D706}/(4\unicode[STIX]{x1D706}-1)-\unicode[STIX]{x1D700}}. & & \displaystyle\end{eqnarray}$$
Proof. For
$1/2\leqslant \unicode[STIX]{x1D706}\leqslant 5/8$
, it follows from inequalities (2.7) and (2.8) that
$$\begin{eqnarray}\displaystyle {\mathcal{S}}(T;\unicode[STIX]{x1D706})\ll {\mathcal{S}}^{+}(T;\unicode[STIX]{x1D706}), & & \displaystyle \nonumber\end{eqnarray}$$
where
$$\begin{eqnarray}\displaystyle {\mathcal{S}}^{+}(T;\unicode[STIX]{x1D706})=\mathop{\sum }_{\substack{ \unicode[STIX]{x1D70C}\in \mathscr{R}_{T} \\ 1/2\leqslant \unicode[STIX]{x1D6FD}\leqslant \unicode[STIX]{x1D706}}}T^{\unicode[STIX]{x1D6FD}-1/2}|\unicode[STIX]{x1D701}^{\prime }(\unicode[STIX]{x1D70C})L(\unicode[STIX]{x1D70C},\unicode[STIX]{x1D712})|. & & \displaystyle \nonumber\end{eqnarray}$$
Applying Stieltjes’ integration and Hölder’s inequality, we deduce that
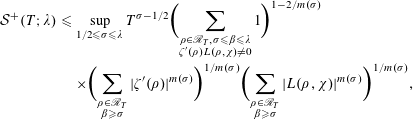$$\begin{eqnarray}\displaystyle {\mathcal{S}}^{+}(T;\unicode[STIX]{x1D706}) & {\leqslant} & \displaystyle \sup _{1/2\leqslant \unicode[STIX]{x1D70E}\leqslant \unicode[STIX]{x1D706}}T^{\unicode[STIX]{x1D70E}-1/2}\biggl(\mathop{\sum }_{\substack{ \unicode[STIX]{x1D70C}\in \mathscr{R}_{T},\unicode[STIX]{x1D70E}\leqslant \unicode[STIX]{x1D6FD}\leqslant \unicode[STIX]{x1D706} \\ \unicode[STIX]{x1D701}^{\prime }(\unicode[STIX]{x1D70C})L(\unicode[STIX]{x1D70C},\unicode[STIX]{x1D712})\neq 0}}1\biggr)^{1-2/m(\unicode[STIX]{x1D70E})}\nonumber\\ \displaystyle & & \displaystyle \times \biggl(\mathop{\sum }_{\substack{ \unicode[STIX]{x1D70C}\in \mathscr{R}_{T} \\ \unicode[STIX]{x1D6FD}\geqslant \unicode[STIX]{x1D70E}}}|\unicode[STIX]{x1D701}^{\prime }(\unicode[STIX]{x1D70C})|^{m(\unicode[STIX]{x1D70E})}\biggr)^{1/m(\unicode[STIX]{x1D70E})}\biggl(\mathop{\sum }_{\substack{ \unicode[STIX]{x1D70C}\in \mathscr{R}_{T} \\ \unicode[STIX]{x1D6FD}\geqslant \unicode[STIX]{x1D70E}}}|L(\unicode[STIX]{x1D70C},\unicode[STIX]{x1D712})|^{m(\unicode[STIX]{x1D70E})}\biggr)^{1/m(\unicode[STIX]{x1D70E})},\nonumber\end{eqnarray}$$
where
$m(\unicode[STIX]{x1D70E})$
is given in Lemma 2. Then by Lemma 4,
$$\begin{eqnarray}\displaystyle {\mathcal{S}}^{+}(T;\unicode[STIX]{x1D706})\leqslant \sup _{1/2\leqslant \unicode[STIX]{x1D70E}\leqslant \unicode[STIX]{x1D706}}T^{\unicode[STIX]{x1D70E}-1/2+2/m(\unicode[STIX]{x1D70E})+\unicode[STIX]{x1D700}}\biggl(\mathop{\sum }_{\substack{ \unicode[STIX]{x1D70C}\in \mathscr{R}_{T},\unicode[STIX]{x1D70E}\leqslant \unicode[STIX]{x1D6FD}\leqslant \unicode[STIX]{x1D706} \\ \unicode[STIX]{x1D701}^{\prime }(\unicode[STIX]{x1D70C})L(\unicode[STIX]{x1D70C},\unicode[STIX]{x1D712})\neq 0}}1\biggr)^{1-2/m(\unicode[STIX]{x1D70E})}. & & \displaystyle\end{eqnarray}$$
On recalling the definition of
$N_{K}^{\prime }(T;\unicode[STIX]{x1D706})$
in equality (5.1) and the argument around inequality (4.1), we conclude that
$$\begin{eqnarray}\displaystyle \mathop{\sum }_{\substack{ \unicode[STIX]{x1D70C}\in \mathscr{R}_{T},\unicode[STIX]{x1D70E}\leqslant \unicode[STIX]{x1D6FD}\leqslant \unicode[STIX]{x1D706} \\ \unicode[STIX]{x1D701}^{\prime }(\unicode[STIX]{x1D70C})L(\unicode[STIX]{x1D70C},\unicode[STIX]{x1D712})\neq 0}}1\leqslant N_{K}^{\prime }(T;\unicode[STIX]{x1D706}). & & \displaystyle\end{eqnarray}$$
From inequalities (5.3) and (5.4), we have
$$\begin{eqnarray}\displaystyle {\mathcal{S}}^{+}(T;\unicode[STIX]{x1D706})\leqslant \sup _{1/2\leqslant \unicode[STIX]{x1D70E}\leqslant \unicode[STIX]{x1D706}}T^{\unicode[STIX]{x1D70E}-1/2+2/m(\unicode[STIX]{x1D70E})+\unicode[STIX]{x1D700}}N_{K}^{\prime }(T;\unicode[STIX]{x1D706})^{1-2/m(\unicode[STIX]{x1D70E})}. & & \displaystyle \nonumber\end{eqnarray}$$
Invoking the condition
${\mathcal{S}}^{+}(T;\unicode[STIX]{x1D706})\gg T$
, we obtain
$$\begin{eqnarray}\displaystyle T\ll \sup _{1/2\leqslant \unicode[STIX]{x1D70E}\leqslant \unicode[STIX]{x1D706}}T^{\unicode[STIX]{x1D70E}-1/2+2/m(\unicode[STIX]{x1D70E})+\unicode[STIX]{x1D700}}N_{K}^{\prime }(T;\unicode[STIX]{x1D706})^{1-2/m(\unicode[STIX]{x1D70E})}. & & \displaystyle\end{eqnarray}$$
The left-hand side of inequality (5.5) is continuous on
$\unicode[STIX]{x1D70E}$
, and thus there exists
$\frac{1}{2}\leqslant \unicode[STIX]{x1D70E}\leqslant \unicode[STIX]{x1D706}$
such that
$$\begin{eqnarray}\displaystyle T\ll T^{\unicode[STIX]{x1D70E}-1/2+2/m(\unicode[STIX]{x1D70E})+\unicode[STIX]{x1D700}}N_{K}^{\prime }(T;\unicode[STIX]{x1D706})^{1-2/m(\unicode[STIX]{x1D70E})}. & & \displaystyle \nonumber\end{eqnarray}$$
Now we obtain
$$\begin{eqnarray}\displaystyle N_{K}^{\prime }(T;\unicode[STIX]{x1D706})\gg T^{2\unicode[STIX]{x1D70E}/(4\unicode[STIX]{x1D70E}-1)-\unicode[STIX]{x1D700}} & & \displaystyle \nonumber\end{eqnarray}$$
for some
$\frac{1}{2}\leqslant \unicode[STIX]{x1D70E}\leqslant \unicode[STIX]{x1D706}$
. Since
$2\unicode[STIX]{x1D70E}/(4\unicode[STIX]{x1D70E}-1)$
is decreasing when
$\frac{1}{2}\leqslant \unicode[STIX]{x1D70E}\leqslant \unicode[STIX]{x1D706}$
, we finally arrive at
$$\begin{eqnarray}\displaystyle N_{K}^{\prime }(T;\unicode[STIX]{x1D706})\gg T^{2\unicode[STIX]{x1D706}/(4\unicode[STIX]{x1D706}-1)-\unicode[STIX]{x1D700}}. & & \displaystyle \nonumber\end{eqnarray}$$
This completes the proof. ◻
Proof of Theorems 1.2 and 1.3.
Let
$\unicode[STIX]{x1D6FF}>0$
be any small constant (independent of
$T$
). We take
$\unicode[STIX]{x1D706}=3/5+\unicode[STIX]{x1D6FF}$
in the proof of Theorem 1.2 and
$\unicode[STIX]{x1D706}=1/2+\unicode[STIX]{x1D6FF}$
in the proof of Theorem 1.3. By Lemma 6 and Lemma 7, respectively, we have in both cases that
$$\begin{eqnarray}|{\mathcal{S}}(T;\unicode[STIX]{x1D706})|\gg T\log ^{2}T.\end{eqnarray}$$
It now follows from Lemma 8 that
$$\begin{eqnarray}\displaystyle N_{K}^{\prime }(T;\unicode[STIX]{x1D706})\gg T^{2\unicode[STIX]{x1D706}/(4\unicode[STIX]{x1D706}-1)-\unicode[STIX]{x1D700}}, & & \displaystyle\end{eqnarray}$$
where
$N_{K}^{\prime }(T;\unicode[STIX]{x1D706})$
is defined in equality (5.1). Note that when
$\unicode[STIX]{x1D706}=3/5+\unicode[STIX]{x1D6FF}$
, the estimate (5.6) asserts that
$$\begin{eqnarray}\displaystyle N_{K}^{\prime }(T;\unicode[STIX]{x1D706})\gg T^{(6+2\unicode[STIX]{x1D6FF})/(7+4\unicode[STIX]{x1D6FF})-\unicode[STIX]{x1D700}}. & & \displaystyle \nonumber\end{eqnarray}$$
In particular,
$$\begin{eqnarray}\displaystyle N_{K}^{\prime }(T)\gg T^{(6+2\unicode[STIX]{x1D6FF})/(7+4\unicode[STIX]{x1D6FF})-\unicode[STIX]{x1D700}}. & & \displaystyle \nonumber\end{eqnarray}$$
This confirms Theorem 1.2 since the constant
$\unicode[STIX]{x1D6FF}>0$
can be arbitrarily small. Similarly, when
$\unicode[STIX]{x1D706}=1/2+\unicode[STIX]{x1D6FF}$
, the inequality (5.6) gives
$$\begin{eqnarray}\displaystyle N_{K}^{\prime }(T;\unicode[STIX]{x1D706})\gg T^{(1+2\unicode[STIX]{x1D6FF})/(1+4\unicode[STIX]{x1D6FF})-\unicode[STIX]{x1D700}}, & & \displaystyle \nonumber\end{eqnarray}$$
and we complete the proof of Theorem 1.3. ◻
Acknowledgements
This work is supported by the National Natural Science Foundation of China (Grant No. 11871187 and 11401154). Wu is also supported by the Fundamental Research Funds for the Central Universities.
