1 Introduction
For any integer
$q$
, we denote by
$X_{q}$
the group of multiplicative characters modulo
$q$
. We denote by
$X_{q}^{+}$
the subgroup of
$X_{q}$
consisting of primitive even characters
$\unicode[STIX]{x1D712}$
(those satisfying
$\unicode[STIX]{x1D712}(-1)=1$
) and by
$X_{q}^{-}$
the subset of
$X_{q}$
consisting of primitive odd characters
$\unicode[STIX]{x1D712}$
(those satisfying
$\unicode[STIX]{x1D712}(-1)=-1$
). Furthermore, we use
$X_{q}^{\ast }$
to denote the set of primitive characters modulo
$q$
.
This paper is divided into two parts. Firstly, we study shifted moments of Dirichlet
$L$
-functions and, secondly, we apply this to obtain upper bounds on moments of theta functions.
A standard problem in analytic number theory is the study of moments of the Riemann zeta function or, more generally,
$L$
-functions on the critical line. For instance, it is conjectured (see [Reference Conrey and Farmer6], [Reference Conrey, Farmer, Keating, Rubinstein and Snaith7] or [Reference Murty and Murty17, Ch. 5]) that the moments at the central point satisfy the asymptotic formulas
$$\begin{eqnarray}M_{2k}(q)=\mathop{\sum }_{\unicode[STIX]{x1D712}\in X_{q}^{\ast }}|L(1/2,\unicode[STIX]{x1D712})|^{2k}\sim C_{k}q\log ^{k^{2}}q,\quad C_{k}>0.\end{eqnarray}$$
Even though the asymptotic formulas are not known for
$k\geqslant 3$
, lower bounds of the expected order of magnitude
$$\begin{eqnarray}\mathop{\sum }_{\unicode[STIX]{x1D712}\in X_{q}^{\ast }}|L(1/2,\unicode[STIX]{x1D712})|^{2k}\gg q\log ^{k^{2}}q\end{eqnarray}$$
have been given by Rudnick and Soundararajan [Reference Rudnick and Soundararajan18] for
$q$
prime. Assuming the generalized Riemann hypothesis (GRH), Soundararajan mentioned in [Reference Soundararajan21] that we could derive the upper bound
$M_{2k}(q)\ll q\log ^{k^{2}+\unicode[STIX]{x1D716}}q$
(indeed, it follows from the work of Sono [Reference Sono20]). We can generalize, in some way, these moments using shifts and consider
$$\begin{eqnarray}\mathop{\sum }_{\unicode[STIX]{x1D712}\in X_{q}^{\ast }}L\biggl(\frac{1}{2}+\text{i}t_{1},\unicode[STIX]{x1D712}\biggr)\cdots L\biggl(\frac{1}{2}+\text{i}t_{2k},\unicode[STIX]{x1D712}\biggr),\end{eqnarray}$$
where
$(t_{1},\ldots ,t_{2k})$
is a sequence of real numbers. If the
$t_{i}$
are reasonably small, an asymptotic formula is expected for (1.2) (see, for instance, [Reference Conrey, Farmer, Keating, Rubinstein and Snaith7] for a survey about shifted moments in families of
$L$
-functions). Although, we cannot prove such a general result even assuming the GRH, we are able to give a conditional upper bound of nearly the conjectured order of magnitude.
Theorem 1.1. Assume that the Dirichlet
$L$
-functions modulo
$q$
satisfy the GRH. Suppose that
$q$
is large and the
$2k$
-tuple
$t=(t_{1},\ldots ,t_{2k})$
is such that
$t_{i}\ll \log q$
. Then, for all
$\unicode[STIX]{x1D716}>0$
, there exists the uniform bound
$$\begin{eqnarray}\mathop{\sum }_{\unicode[STIX]{x1D712}\in X_{q}^{\ast }}\biggl|L\biggl(\frac{1}{2}+\text{i}t_{1},\unicode[STIX]{x1D712}\biggr)\cdots L\biggl(\frac{1}{2}+\text{i}t_{2k},\unicode[STIX]{x1D712}\biggr)\biggr|\ll _{\unicode[STIX]{x1D716}}\unicode[STIX]{x1D719}(q)(\log q)^{k/2+\unicode[STIX]{x1D716}}\mathop{\prod }_{i<j}E_{i,j},\end{eqnarray}$$
where
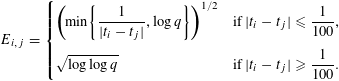$$\begin{eqnarray}E_{i,j}=\left\{\begin{array}{@{}ll@{}}\displaystyle \biggl(\min \biggl\{\frac{1}{|t_{i}-t_{j}|},\log q\biggr\}\biggr)^{1/2}\quad & \displaystyle \text{if }|t_{i}-t_{j}|\leqslant \frac{1}{100},\\ \displaystyle \sqrt{\log \log q}\quad & \displaystyle \text{if }|t_{i}-t_{j}|\geqslant \frac{1}{100}.\end{array}\right.\end{eqnarray}$$
This can be related to the main result of [Reference Chandee3] and reflects the fact that
$L(\frac{1}{2}+\text{i}t_{i},\unicode[STIX]{x1D712})$
and
$L(\frac{1}{2}+\text{i}t_{j},\unicode[STIX]{x1D712})$
are essentially correlated when
$|t_{i}-t_{j}|\approx 1/\text{log}\,q$
and are “independent” as long as
$|t_{i}-t_{j}|$
is significantly larger than
$\log q$
.
For real
$x>0$
and
$\unicode[STIX]{x1D702}\in \{0,1\}$
we set
$$\begin{eqnarray}\unicode[STIX]{x1D703}(\unicode[STIX]{x1D702},x,\unicode[STIX]{x1D712})=\mathop{\sum }_{n=1}^{\infty }\unicode[STIX]{x1D712}(n)n^{\unicode[STIX]{x1D702}}\text{e}^{-\unicode[STIX]{x1D70B}n^{2}x/q},\quad \unicode[STIX]{x1D712}\in X_{q}.\end{eqnarray}$$
We note that, if we set
$\unicode[STIX]{x1D702}_{\unicode[STIX]{x1D712}}=1$
if
$\unicode[STIX]{x1D712}$
is odd and
$\unicode[STIX]{x1D702}_{\unicode[STIX]{x1D712}}=0$
otherwise, then
$$\begin{eqnarray}\unicode[STIX]{x1D703}_{q}(\unicode[STIX]{x1D702}_{\unicode[STIX]{x1D712}},x,\unicode[STIX]{x1D712})=\unicode[STIX]{x1D703}_{q}(x,\unicode[STIX]{x1D712})\end{eqnarray}$$
is the classical theta-function of the character
$\unicode[STIX]{x1D712}$
(see [Reference Davenport8] for a background and basic properties). We can express these values using Mellin transforms of
$L$
-functions which makes the use of our result about moments of shifted
$L$
-functions very appropriate.
When computing the root number of
$\unicode[STIX]{x1D712}$
appearing in the functional equation of the associated Dirichlet
$L$
-function, the question of whether
$\unicode[STIX]{x1D703}_{q}(1,\unicode[STIX]{x1D712})\neq 0$
appears naturally (see [Reference Louboutin13] for details). Numerical computations led to the conjecture that it never happens if
$\unicode[STIX]{x1D712}$
is primitive (see [Reference Cohen and Zagier5] for a counterexample with
$\unicode[STIX]{x1D712}$
imprimitive). In order to investigate the non-vanishing of theta functions at their central point, the study of moments has been initiated in [Reference Louboutin and Munsch14–Reference Munsch and Shparlinski16]. For
$k$
a positive integer, let us define
$$\begin{eqnarray}S_{2k}^{+}(q)=\mathop{\sum }_{\unicode[STIX]{x1D712}\in X_{q}^{+}\backslash \unicode[STIX]{x1D712}_{0}}|\unicode[STIX]{x1D703}(1,\unicode[STIX]{x1D712})|^{2k}\quad \text{and}\quad S_{2k}^{-}(q)=\mathop{\sum }_{\unicode[STIX]{x1D712}\in X_{q}^{-}}|\unicode[STIX]{x1D703}(1,\unicode[STIX]{x1D712})|^{2k}.\end{eqnarray}$$
It is conjectured in [Reference Munsch and Shparlinski16], based on numerical computation and some theoretical support, that
$$\begin{eqnarray}\begin{array}{@{}c@{}}S_{2k}^{+}(q)\sim a_{k}\unicode[STIX]{x1D719}(q)q^{k/2}(\log q)^{(k-1)^{2}},\\ S_{2k}^{-}(q)\sim b_{k}\unicode[STIX]{x1D719}(q)q^{3k/2}(\log q)^{(k-1)^{2}},\end{array}\end{eqnarray}$$
for some positive constants
$a_{k}$
and
$b_{k}$
, depending only on
$k$
. Recently, a lower bound of expected order for
$S_{2k}^{+}(q)$
and
$S_{2k}^{-}(q)$
has been proved unconditionally in [Reference Munsch and Shparlinski16]. In the second part of the paper, we will derive upper bounds giving good support towards Conjecture (1.3).
Precisely, we prove the following theorem.
Theorem 1.2. Assume the GRH for all Dirichlet
$L$
-functions modulo
$q$
. Let
$k\geqslant 1$
be a positive integer. Then, for all
$\unicode[STIX]{x1D716}>0$
,
$$\begin{eqnarray}S_{2k}^{+}(q)\ll \unicode[STIX]{x1D719}(q)q^{k/2}(\log q)^{(k-1)^{2}+\unicode[STIX]{x1D716}}\quad \text{and}\quad S_{2k}^{-}(q)\ll \unicode[STIX]{x1D719}(q)q^{3k/2}(\log q)^{(k-1)^{2}+\unicode[STIX]{x1D716}},\end{eqnarray}$$
where the implied constants depend on
$k$
and
$\unicode[STIX]{x1D716}$
.
This can be related to recent results of [Reference Harper, Nikeghbali and Radziwill11] (see also [Reference Heap and Lindqvist12]), where the authors obtain the asymptotic behaviour of a Steinhaus random multiplicative function (basically a multiplicative random variable whose values at prime integers are uniformly distributed on the unit circle). This can be viewed as a random model for
$\unicode[STIX]{x1D703}_{q}(x,\unicode[STIX]{x1D712})$
. In fact, the rapidly decaying factor
$\text{e}^{-\unicode[STIX]{x1D70B}n^{2}/q}$
is mostly equivalent to restricting the sum over integers
$n\leqslant n_{0}(q)$
for some
$n_{0}(q)\approx \sqrt{q}$
and the averaging behavior of
$\unicode[STIX]{x1D712}(n)$
with
$n\ll q^{1/2}$
is essentially similar to that of a Steinhaus random multiplicative function. Hence, these results are a good support for Conjecture (1.3). Upper bounds of Theorem 1.2 together with lower bounds obtained in [Reference Munsch and Shparlinski16, Theorem 1.1] confirm this heuristic.
The method of the proof of Theorem 1.2 relies on the bound obtained for moments of shifted
$L$
-functions.
2 Moments of shifted
$L$
-functions
In this section, we mostly adapt results and ideas of [Reference Soundararajan21] to our situation. These techniques build on ideas of Selberg on the distribution of
$|\text{log}\,\unicode[STIX]{x1D701}(1/2+\text{i}t)|$
(see [Reference Selberg19]). The starting point is the equality
$$\begin{eqnarray}\displaystyle \int _{T}^{2T}|\unicode[STIX]{x1D701}(1/2+\text{i}t)|^{2k}\,dt & = & \displaystyle -\int _{-\infty }^{+\infty }\text{e}^{2kV}d\text{ meas}(S(T,V))\nonumber\\ \displaystyle & = & \displaystyle 2k\int _{-\infty }^{+\infty }\text{e}^{2kV}\text{meas}(S(T,V))\,dV,\nonumber\end{eqnarray}$$
where
$S(T,V)=\{t\in [T,2T]\,:\,\!\log |\unicode[STIX]{x1D701}(1/2+\text{i}t)|\geqslant V\}$
. From this, an upper bound for the moment can be directly deduced from the upper bound of
$\text{meas }(S(T,V))$
. In our case, we have to study the frequency (in terms of characters) of large values of
$L$
-functions. Thus, we will proceed in the same way by estimating the measure of
$$\begin{eqnarray}\displaystyle S_{t}(q,V) & = & \displaystyle \{\!\unicode[STIX]{x1D712}(\text{mod}\,q),\unicode[STIX]{x1D712}^{2}\neq \unicode[STIX]{x1D712}_{0}:\log |L({\textstyle \frac{1}{2}}+\text{i}t_{1},\unicode[STIX]{x1D712})|+\cdots \nonumber\\ \displaystyle & & \displaystyle +\,\log |L({\textstyle \frac{1}{2}}+\text{i}t_{2k},\unicode[STIX]{x1D712})|\geqslant V\!\}\nonumber\end{eqnarray}$$
for
$V>0$
and a
$2k$
-tuple
$t=(t_{1},\ldots ,t_{2k})$
. Most of the work involves keeping the dependence both in terms of the modulus
$q$
and the height of the shifts. If the shifts are not too large, we are able to obtain a quasi-optimal upper bound under the GRH. This result will be sufficient for our application to moments of theta functions. It should be noticed that the recent method of Harper (see [Reference Harper10]) may be used to remove the
$\unicode[STIX]{x1D716}$
factor in Theorem 1.1.
Now set
$N_{t}(q,V)=\#S_{t}(q,V)$
. We can express the shifted moments of
$L$
-functions as
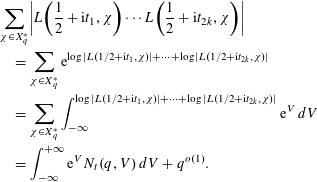$$\begin{eqnarray}\displaystyle & & \displaystyle \mathop{\sum }_{\unicode[STIX]{x1D712}\in X_{q}^{\ast }}\biggl|L\biggl(\frac{1}{2}+\text{i}t_{1},\unicode[STIX]{x1D712}\biggr)\cdots L\biggl(\frac{1}{2}+\text{i}t_{2k},\unicode[STIX]{x1D712}\biggr)\biggr|\nonumber\\ \displaystyle & & \displaystyle \quad =\mathop{\sum }_{\unicode[STIX]{x1D712}\in X_{q}^{\ast }}\text{e}^{\log |L(1/2+\text{i}t_{1},\unicode[STIX]{x1D712})|+\cdots +\log |L(1/2+\text{i}t_{2k},\unicode[STIX]{x1D712})|}\nonumber\\ \displaystyle & & \displaystyle \quad =\mathop{\sum }_{\unicode[STIX]{x1D712}\in X_{q}^{\ast }}\int _{-\infty }^{\log |L(1/2+\text{i}t_{1},\unicode[STIX]{x1D712})|+\cdots +\log |L(1/2+\text{i}t_{2k},\unicode[STIX]{x1D712})|}\text{e}^{V}\,dV\nonumber\\ \displaystyle & & \displaystyle \quad =\int _{-\infty }^{+\infty }\text{e}^{V}N_{t}(q,V)\,dV+q^{o(1)}.\end{eqnarray}$$
The error term comes from the contribution of quadratic characters which can easily be bounded, using Corollary 2.4, by
$$\begin{eqnarray}O\biggl(\int _{-\infty }^{4ck(\log q/\text{log}\,\log q)}\text{e}^{V}\,dV\biggr)\ll q^{o(1)}.\end{eqnarray}$$
Hence, the problem of estimating the moments boils down to getting precise bounds for
$N_{t}(q,V)$
. In order to do that, we define the quantity
$$\begin{eqnarray}W=2k\log \log q+2\mathop{\sum }_{\substack{ i,j \\ i<j}}F_{i,j},\end{eqnarray}$$
where
$$\begin{eqnarray}F_{i,j}=\left\{\begin{array}{@{}ll@{}}\displaystyle \log \biggl(\min \biggl\{\frac{1}{|t_{i}-t_{j}|},\log q\biggr\}\biggr)\quad & \displaystyle \text{if }|t_{i}-t_{j}|\leqslant \frac{1}{100},\\ \displaystyle \log \log \log q\quad & \displaystyle \text{if }|t_{i}-t_{j}|\geqslant \frac{1}{100}.\end{array}\right.\end{eqnarray}$$
We will prove the following theorem which estimates the measure of
$S_{t}(q,V)$
for large
$q$
and all
$V$
.
Theorem 2.1. Assume that the Dirichlet
$L$
-functions modulo
$q$
satisfy the GRH. Suppose that
$|t|\leqslant T\leqslant \log ^{A}q$
, where
$A>0$
and
$V$
is a large real number. If
$4\sqrt{\log \log q}\leqslant V\leqslant W$
, then
$$\begin{eqnarray}N_{t}(q,V)\ll \unicode[STIX]{x1D719}(q)\frac{V}{\sqrt{W}}\exp \biggl(-\frac{V^{2}}{W}\biggl(1-\frac{18k}{5\log W}\biggr)^{2}\biggr).\end{eqnarray}$$
If
$W<V<(1/4k)W\log W$
, then
$$\begin{eqnarray}N_{t}(q,V)\ll \unicode[STIX]{x1D719}(q)\frac{V}{\sqrt{W}}\exp \biggl(-\frac{V^{2}}{W}\biggl(1-\frac{18kV}{5W\log W}\biggr)^{2}\biggr).\end{eqnarray}$$
If
$(1/4k)W\log W<V$
, then
$$\begin{eqnarray}N_{t}(q,V)\ll \unicode[STIX]{x1D719}(q)\exp \biggl(-\frac{V}{801k}\log V\biggr).\end{eqnarray}$$
Proof of Theorem 1.1.
Inserting the bounds of Theorem 2.1 in equation (2.1) gives the upper bound in Theorem 1.1. Precisely, it is appropriate for this computation to use Theorem 2.1 in the weakest form
$$\begin{eqnarray}\displaystyle & \displaystyle N_{t}(q,V)\ll \unicode[STIX]{x1D719}(q)(\log q)^{o(1)}\exp (-V^{2}/W)\quad \text{for }3\leqslant V\leqslant 200W, & \displaystyle \nonumber\\ \displaystyle & \displaystyle N_{t}(q,V)\ll \unicode[STIX]{x1D719}(q)(\log q)^{o(1)}\exp (-2V)\quad \text{for }V>200W. & \displaystyle \nonumber\end{eqnarray}$$
This allows us to bound the moments by
$\unicode[STIX]{x1D719}(q)(\log q)^{o(1)}\text{e}^{W/4}$
which concludes the proof.◻
2.1 Preliminary results
In this subsection, we regroup all the technical results that we will use in the proof of Theorem 2.1. These are mainly the Lemmas of [Reference Soundararajan21] that have been suitably adapted to our case. In the subsequent work, we will always write
$s=\unicode[STIX]{x1D70E}+\text{i}t$
for a complex number
$s$
. We write
$\log ^{+}(x):=\max (\log x,0)$
.
Lemma 2.2. Unconditionally, for any
$s$
not coinciding with
$1$
,
$0$
or a zero of
$L(s,\unicode[STIX]{x1D712})$
, and for any
$x\geqslant 2$
$$\begin{eqnarray}\displaystyle -\!\frac{L^{\prime }}{L}(s,\unicode[STIX]{x1D712}) & = & \displaystyle \mathop{\sum }_{n\leqslant x}\frac{\unicode[STIX]{x1D712}(n)\unicode[STIX]{x1D6EC}(n)}{n^{s}}\frac{\log (x/n)}{\log x}+\frac{1}{\log x}\biggl(\frac{L^{\prime }}{L}(s,\unicode[STIX]{x1D712})\biggr)^{\prime }\nonumber\\ \displaystyle & & \displaystyle +\,\frac{1}{\log x}\mathop{\sum }_{\unicode[STIX]{x1D70C}\neq 0,1}\frac{x^{\unicode[STIX]{x1D70C}-s}}{(\unicode[STIX]{x1D70C}-s)^{2}}\nonumber\\ \displaystyle & & \displaystyle +\,\frac{1}{\log x}\mathop{\sum }_{n=0}^{\infty }\frac{x^{-2n-a-s}}{(2n+a+s)^{2}}.\nonumber\end{eqnarray}$$
Proof. This is Lemma 2.4 of [Reference Chandee1] with
$a(n)=\unicode[STIX]{x1D712}(n)\unicode[STIX]{x1D6EC}(n)$
,
$d=1$
and
$k(j)=a$
(here
$a=0$
or
$1$
is the number given by
$\unicode[STIX]{x1D712}(-1)=(-1)^{a}$
).◻
Proposition 2.3. Assume the GRH for all Dirichlet L-functions of modulus
$q$
. Let
$T$
be a parameter and let
$x\geqslant 2$
. Let
$\unicode[STIX]{x1D706}_{0}=0.56\ldots$
denote the unique positive real number satisfying
$\text{e}^{-\unicode[STIX]{x1D706}_{0}}=\unicode[STIX]{x1D706}_{0}$
. For all
$\unicode[STIX]{x1D706}\geqslant \unicode[STIX]{x1D706}_{0}$
, the estimate
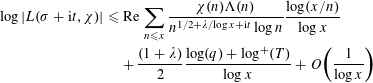$$\begin{eqnarray}\displaystyle \log |L(\unicode[STIX]{x1D70E}+\text{i}t,\unicode[STIX]{x1D712})| & {\leqslant} & \displaystyle \text{Re}\,\mathop{\sum }_{n\leqslant x}\frac{\unicode[STIX]{x1D712}(n)\unicode[STIX]{x1D6EC}(n)}{n^{1/2+\unicode[STIX]{x1D706}/\text{log}\,x+\text{i}t}\log n}\frac{\log (x/n)}{\log x}\nonumber\\ \displaystyle & & \displaystyle +\,\frac{(1+\unicode[STIX]{x1D706})}{2}\frac{\log (q)+\log ^{+}(T)}{\log x}+O\biggl(\frac{1}{\log x}\biggr)\nonumber\end{eqnarray}$$
holds uniformly for
$|t|\leqslant T$
and
$1/2\leqslant \unicode[STIX]{x1D70E}\leqslant \unicode[STIX]{x1D70E}_{0}=1/2+\unicode[STIX]{x1D706}/\text{log}\,x$
.
Proof. Let
$a=0$
or
$1$
be again the number given by
$\unicode[STIX]{x1D712}(-1)=(-1)^{a}$
. Letting
$\unicode[STIX]{x1D70C}=1/2+i\unicode[STIX]{x1D6FE}$
run over the non-trivial zeros of
$L(s,\unicode[STIX]{x1D712})$
, we define
$$\begin{eqnarray}F_{\unicode[STIX]{x1D712}}(s)=\text{Re }\mathop{\sum }_{\unicode[STIX]{x1D70C}}\frac{1}{s-\unicode[STIX]{x1D70C}}=\mathop{\sum }_{\unicode[STIX]{x1D70C}}\frac{\unicode[STIX]{x1D70E}-1/2}{(\unicode[STIX]{x1D70E}-1/2)^{2}+(t-\unicode[STIX]{x1D6FE})^{2}}.\end{eqnarray}$$
Obviously,
$F_{\unicode[STIX]{x1D712}}(s)$
is non-negative in the half-plane
$\unicode[STIX]{x1D70E}\geqslant 1/2$
. By Hadamard’s factorization (see [Reference Davenport8, Ch. 12, equation (17)]),
$$\begin{eqnarray}\frac{L^{\prime }(s,\unicode[STIX]{x1D712})}{L(s,\unicode[STIX]{x1D712})}=-\frac{1}{2}\log \frac{q}{\unicode[STIX]{x1D70B}}-\frac{1}{2}\frac{\unicode[STIX]{x1D6E4}^{\prime }}{\unicode[STIX]{x1D6E4}}\biggl(\frac{s+a}{2}\biggr)+B(\unicode[STIX]{x1D712})+\mathop{\sum }_{\unicode[STIX]{x1D70C}}\biggl(\frac{1}{s-\unicode[STIX]{x1D70C}}+\frac{1}{\unicode[STIX]{x1D70C}}\biggr).\end{eqnarray}$$
Here,
$B(\unicode[STIX]{x1D712})$
is a constant depending only on
$\unicode[STIX]{x1D712}$
, whose real part is given by
$$\begin{eqnarray}\text{Re}(B(\unicode[STIX]{x1D712}))=-\mathop{\sum }_{\unicode[STIX]{x1D70C}}\frac{1}{\unicode[STIX]{x1D70C}}.\end{eqnarray}$$
By taking the real parts of both sides of (2.2), an application of Stirling’s formula yields
$$\begin{eqnarray}-\text{Re}\,\frac{L^{\prime }(s,\unicode[STIX]{x1D712})}{L(s,\unicode[STIX]{x1D712})}=\frac{\log (q)+\log ^{+}(t)}{2}-F_{\unicode[STIX]{x1D712}}(s)+O(1)\leqslant \frac{\log (q)+\log ^{+}(T)}{2}+O(1),\end{eqnarray}$$
where we used the positivity of
$F_{\unicode[STIX]{x1D712}}(s)$
in that region. Integrating (2.3) as
$\unicode[STIX]{x1D70E}=\text{Re}\,(s)$
varies from
$\unicode[STIX]{x1D70E}$
to
$\unicode[STIX]{x1D70E}_{0}~({>}1/2)$
and setting
$s_{0}=\unicode[STIX]{x1D70E}_{0}+\text{i}t$
, we obtain
$$\begin{eqnarray}\log |L(s,\unicode[STIX]{x1D712})|-\log |L(s_{0},\unicode[STIX]{x1D712})|\leqslant \biggl(\frac{\log (q)+\log ^{+}(T)}{2}+O(1)\biggr)(\unicode[STIX]{x1D70E}_{0}-\unicode[STIX]{x1D70E}).\end{eqnarray}$$
On the other hand, using Lemma 2.2, we get
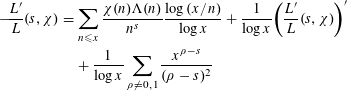$$\begin{eqnarray}\displaystyle -\!\frac{L^{\prime }}{L}(s,\unicode[STIX]{x1D712}) & = & \displaystyle \mathop{\sum }_{n\leqslant x}\frac{\unicode[STIX]{x1D712}(n)\unicode[STIX]{x1D6EC}(n)}{n^{s}}\frac{\log (x/n)}{\log x}+\frac{1}{\log x}\biggl(\frac{L^{\prime }}{L}(s,\unicode[STIX]{x1D712})\biggr)^{\prime }\nonumber\\ \displaystyle & & \displaystyle +\,\frac{1}{\log x}\mathop{\sum }_{\unicode[STIX]{x1D70C}\neq 0,1}\frac{x^{\unicode[STIX]{x1D70C}-s}}{(\unicode[STIX]{x1D70C}-s)^{2}}\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle +\,\frac{1}{\log x}\mathop{\sum }_{n=0}^{\infty }\frac{x^{-2n-a-s}}{(2n+a+s)^{2}}\end{eqnarray}$$
for any
$s$
not coinciding with a zero of
$L(s,\unicode[STIX]{x1D712})$
and for any
$x\geqslant 2$
. Taking
$s=\unicode[STIX]{x1D70E}+\text{i}t$
, integrating (2.5) over
$\unicode[STIX]{x1D70E}$
from
$\unicode[STIX]{x1D70E}_{0}$
to
$\infty$
and extracting the real parts, we obtain, for
$x\geqslant 2$
,
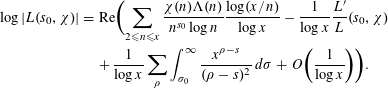$$\begin{eqnarray}\displaystyle \log |L(s_{0},\unicode[STIX]{x1D712})| & = & \displaystyle \text{Re}\biggl(\mathop{\sum }_{2\leqslant n\leqslant x}\frac{\unicode[STIX]{x1D712}(n)\unicode[STIX]{x1D6EC}(n)}{n^{s_{0}}\log n}\frac{\log (x/n)}{\log x}-\frac{1}{\log x}\frac{L^{\prime }}{L}(s_{0},\unicode[STIX]{x1D712})\nonumber\\ \displaystyle & & \displaystyle +\,\frac{1}{\log x}\mathop{\sum }_{\unicode[STIX]{x1D70C}}\int _{\unicode[STIX]{x1D70E}_{0}}^{\infty }\frac{x^{\unicode[STIX]{x1D70C}-s}}{(\unicode[STIX]{x1D70C}-s)^{2}}\,d\unicode[STIX]{x1D70E}+O\biggl(\frac{1}{\log x}\biggr)\biggr).\end{eqnarray}$$
The integral in (2.7) is bounded as
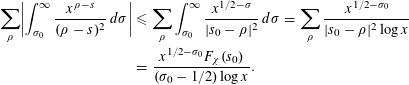$$\begin{eqnarray}\displaystyle \mathop{\sum }_{\unicode[STIX]{x1D70C}}\biggl|\int _{\unicode[STIX]{x1D70E}_{0}}^{\infty }\frac{x^{\unicode[STIX]{x1D70C}-s}}{(\unicode[STIX]{x1D70C}-s)^{2}}\,d\unicode[STIX]{x1D70E}\biggr| & {\leqslant} & \displaystyle \mathop{\sum }_{\unicode[STIX]{x1D70C}}\int _{\unicode[STIX]{x1D70E}_{0}}^{\infty }\frac{x^{1/2-\unicode[STIX]{x1D70E}}}{|s_{0}-\unicode[STIX]{x1D70C}|^{2}}\,d\unicode[STIX]{x1D70E}=\mathop{\sum }_{\unicode[STIX]{x1D70C}}\frac{x^{1/2-\unicode[STIX]{x1D70E}_{0}}}{|s_{0}-\unicode[STIX]{x1D70C}|^{2}\log x}\nonumber\\ \displaystyle & = & \displaystyle \frac{x^{1/2-\unicode[STIX]{x1D70E}_{0}}F_{\unicode[STIX]{x1D712}}(s_{0})}{(\unicode[STIX]{x1D70E}_{0}-1/2)\log x}.\nonumber\end{eqnarray}$$
Thus, using (2.3), we deduce that, for
$x\geqslant 2$
,
$$\begin{eqnarray}\displaystyle \log |L(s_{0},\unicode[STIX]{x1D712})| & {\leqslant} & \displaystyle \text{Re}\,\mathop{\sum }_{2\leqslant n\leqslant x}\frac{\unicode[STIX]{x1D712}(n)\unicode[STIX]{x1D6EC}(n)}{n^{s_{0}}\log n}\frac{\log (x/n)}{\log x}\nonumber\\ \displaystyle & & \displaystyle +\,\frac{\log (q)+\log ^{+}(t)}{2\log x}-\frac{F_{\unicode[STIX]{x1D712}}(s_{0})}{\log x}+\frac{x^{1/2-\unicode[STIX]{x1D70E}_{0}}}{\log ^{2}x}\frac{F_{\unicode[STIX]{x1D712}}(s_{0})}{(\unicode[STIX]{x1D70E}_{0}-1/2)}\nonumber\\ \displaystyle & & \displaystyle +\,O\biggl(\frac{1}{\log x}\biggr).\end{eqnarray}$$
Hence, combining (2.4) together with (2.8), the inequality
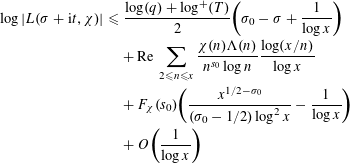$$\begin{eqnarray}\displaystyle \log |L(\unicode[STIX]{x1D70E}+\text{i}t,\unicode[STIX]{x1D712})| & {\leqslant} & \displaystyle \frac{\log (q)+\log ^{+}(T)}{2}\biggl(\unicode[STIX]{x1D70E}_{0}-\unicode[STIX]{x1D70E}+\frac{1}{\log x}\biggr)\nonumber\\ \displaystyle & & \displaystyle +\,\text{Re }\mathop{\sum }_{2\leqslant n\leqslant x}\frac{\unicode[STIX]{x1D712}(n)\unicode[STIX]{x1D6EC}(n)}{n^{s_{0}}\log n}\frac{\log (x/n)}{\log x}\nonumber\\ \displaystyle & & \displaystyle +\,F_{\unicode[STIX]{x1D712}}(s_{0})\biggl(\frac{x^{1/2-\unicode[STIX]{x1D70E}_{0}}}{(\unicode[STIX]{x1D70E}_{0}-1/2)\log ^{2}x}-\frac{1}{\log x}\biggr)\nonumber\\ \displaystyle & & \displaystyle +\,O\biggl(\frac{1}{\log x}\biggr)\end{eqnarray}$$
holds for
$x\geqslant 2$
and uniformly for
$1/2\leqslant \unicode[STIX]{x1D70E}\leqslant \unicode[STIX]{x1D70E}_{0}\leqslant 3/2$
,
$|t|\leqslant T$
. We choose
$\unicode[STIX]{x1D70E}_{0}=\frac{1}{2}+\unicode[STIX]{x1D706}/\text{log}\,x$
, where
$\unicode[STIX]{x1D706}\geqslant \unicode[STIX]{x1D706}_{0}$
. This restriction on
$\unicode[STIX]{x1D706}$
ensures that the term involving
$F_{\unicode[STIX]{x1D712}}(s_{0})$
in (2.9) makes a negative contribution and may therefore be omitted. The proposition follows easily.◻
Corollary 2.4. Let
$\unicode[STIX]{x1D712}$
be a primitive character modulo
$q$
and assume the GRH for
$L(s,\unicode[STIX]{x1D712})$
. Then, if
$q$
is large enough, there exists an absolute constant
$c>0$
such that
$$\begin{eqnarray}\biggl|L\biggl(\frac{1}{2}+\text{i}t,\unicode[STIX]{x1D712}\biggr)\biggr|\ll \exp \biggl(c\frac{\log q+\log ^{+}t}{\log \log q}\biggr).\end{eqnarray}$$
Proof. This follows directly from the above proposition by setting
$x=\log ^{2-\unicode[STIX]{x1D716}}q$
.◻
Remark 2.5. This inequality is less precise than [Reference Chandee1, Corollary 1.2] or [Reference Chandee and Soundararajan4, §4] when
$qt$
is large. Nevertheless, this covers the case when
$t$
is relatively small compared with
$q$
which is suitable for our applications.
Our proof of Theorem 1.1 rests upon our main Proposition 2.3. We begin by showing that the sum over prime powers appearing in that proposition may, in fact, be restricted over primes.
Lemma 2.6. Assume that the Dirichlet
$L$
-functions modulo
$q$
satisfy the GRH. Let
$t\leqslant \log ^{A}q$
with
$A>0$
,
$x\geqslant 2$
and
$\unicode[STIX]{x1D70E}\geqslant \frac{1}{2}$
. Then, if
$\unicode[STIX]{x1D712}$
is a Dirichlet character modulo
$q$
such that
$\unicode[STIX]{x1D712}^{2}\neq \unicode[STIX]{x1D712}_{0}$
,
$$\begin{eqnarray}\biggl|\mathop{\sum }_{\substack{ n\leqslant x \\ n\neq p}}\frac{\unicode[STIX]{x1D712}(n)\unicode[STIX]{x1D6EC}(n)}{n^{\unicode[STIX]{x1D70E}+\text{i}t}\log n}\frac{\log (x/n)}{\log x}\biggr|\ll \log \log \log q+O(1).\end{eqnarray}$$
Proof. Clearly, the contribution coming from the prime powers
$p^{k}$
with
$k\geqslant 3$
is
$\ll 1$
. It remains to handle the terms
$n=p^{2}$
. Hence, we have to bound
$$\begin{eqnarray}\mathop{\sum }_{p\leqslant \sqrt{x}}\frac{\unicode[STIX]{x1D712}^{2}(p)}{p^{2\unicode[STIX]{x1D70E}+2\text{i}t}}\frac{\log (\sqrt{x}/p)}{\log \sqrt{x}}.\end{eqnarray}$$
We split this sum into ranges
$2\leqslant p\leqslant \log ^{8+4A+\unicode[STIX]{x1D716}}q$
and
$\log ^{8+4A+\unicode[STIX]{x1D716}}q\leqslant p\leqslant \sqrt{x}$
. Then the first sum is easily bounded by
$\sum _{p\leqslant \log ^{8+4A+\unicode[STIX]{x1D716}}q}1/p\ll \log \log \log q$
.
To treat the second sum, let us recall (see, for instance, [Reference Davenport8, p. 125]) that under the GRH, the estimate
$$\begin{eqnarray}\mathop{\sum }_{n\leqslant x}\unicode[STIX]{x1D712}(n)\unicode[STIX]{x1D6EC}(n)\ll x^{1/2}\log ^{2}(qx)\end{eqnarray}$$
holds for
$x\geqslant 2$
and
$\unicode[STIX]{x1D712}$
is a non-trivial character. By partial summation, we can deduce that
$$\begin{eqnarray}\mathop{\sum }_{p\leqslant x}\frac{\unicode[STIX]{x1D712}(p)\log p}{p^{2\text{i}t}}\ll |t|x^{1/2}\log ^{2}(qx).\end{eqnarray}$$
Thus, again by partial summation, we derive (using our restriction on
$t$
and the fact that
$\unicode[STIX]{x1D712}^{2}$
is non-trivial) that the sum over primes
${\geqslant}\log ^{8+4A+\unicode[STIX]{x1D716}}q$
is
$O(1)$
, which concludes the proof.◻
Proposition 2.3 together with Lemma 2.6 give directly the following corollary.
Corollary 2.7. For a Dirichlet character
$\unicode[STIX]{x1D712}$
modulo
$q$
such that
$\unicode[STIX]{x1D712}^{2}\neq \unicode[STIX]{x1D712}_{0}$
, the inequality
$$\begin{eqnarray}\displaystyle \log |L(\unicode[STIX]{x1D70E}+\text{i}t,\unicode[STIX]{x1D712})| & {\leqslant} & \displaystyle \text{Re}\,\mathop{\sum }_{p\leqslant x}\frac{\unicode[STIX]{x1D712}(p)}{p^{\unicode[STIX]{x1D70E}+\unicode[STIX]{x1D706}/\text{log}\,x+\text{i}t}}\frac{\log (x/p)}{\log x}\nonumber\\ \displaystyle & & \displaystyle +\,\frac{(1+\unicode[STIX]{x1D706})}{2}\frac{\log q+\log ^{+}T}{\log x}+O(\log \log \log q)\nonumber\end{eqnarray}$$
holds uniformly for
$|t|\leqslant T<\log ^{A}q$
and
$1/2\leqslant \unicode[STIX]{x1D70E}\leqslant 1/2+\unicode[STIX]{x1D706}/\text{log}\,x$
.
The next result was proved by Sono [Reference Sono20, Lemma 4.3] and is a
$q$
-analogue of [Reference Soundararajan21, Lemma 3].
Lemma 2.8. Suppose that
$x\geqslant 2$
and
$k$
is an integer such that
$x^{k}<q$
. Then, for any
$t\in \mathbb{R}$
and any complex numbers
$a(p)$
,
$$\begin{eqnarray}\mathop{\sum }_{\unicode[STIX]{x1D712}\in X_{q}}\biggl|\mathop{\sum }_{p\leqslant x}\frac{\unicode[STIX]{x1D712}(p)a(p)}{p^{1/2+\text{i}t}}\biggr|^{2k}\leqslant \unicode[STIX]{x1D719}(q)k!\biggl(\mathop{\sum }_{p\leqslant x}\frac{|a(p)|^{2}}{p}\biggr)^{k}.\end{eqnarray}$$
Hence, there exist positive constants
$c_{\unicode[STIX]{x1D712}}$
such that
$\sum _{\unicode[STIX]{x1D712}\,\text{mod}\,q}c_{\unicode[STIX]{x1D712}}=\unicode[STIX]{x1D719}(q)$
and the following inequality holds: that is,
$$\begin{eqnarray}\biggl|\mathop{\sum }_{p\leqslant x}\frac{\unicode[STIX]{x1D712}(p)a(p)}{p^{1/2+\text{i}t}}\biggr|^{2k}\leqslant c_{\unicode[STIX]{x1D712}}k!\biggl(\mathop{\sum }_{p\leqslant x}\frac{|a(p)|^{2}}{p}\biggr)^{k}.\end{eqnarray}$$
We will need the following adaptation of [Reference Chandee3, Lemma 3.5].
Lemma 2.9.
$$\begin{eqnarray}\mathop{\sum }_{p\leqslant z}\frac{\cos (a\log p)}{p}\leqslant \left\{\begin{array}{@{}ll@{}}\displaystyle \log \biggl(\min \biggl\{\frac{1}{|a|},\log z\biggr\}\biggr)+O(1)\quad & \displaystyle \text{if }|a|\leqslant \frac{1}{100},\\ \displaystyle \log \log (2+|a|)+O(1)\quad & \displaystyle \text{if }|a|\geqslant \frac{1}{100}.\end{array}\right.\end{eqnarray}$$
Proof. If
$|a|\leqslant 1/\text{log}\,z$
, the proof follows from Mertens’ theorem. Otherwise, it is exactly the inequality (2.1.6), [Reference Granville and Soundararajan9, p. 57] (written with
$\Re (p^{ia})$
instead of
$\cos (a\log p)$
).◻
2.2 Proof of Theorem 2.1
First, remark that if
$-\infty \leqslant V\leqslant 4\sqrt{\log \log q}$
, then, trivially,
$$\begin{eqnarray}\int _{-\infty }^{+\infty }\text{e}^{V}N_{t}(q,V)\,dV\leqslant \unicode[STIX]{x1D719}(q)\text{e}^{4\sqrt{\log \log q}}=o(\unicode[STIX]{x1D719}(q)\log q).\end{eqnarray}$$
In view of Corollary 2.4, we can assume that
$$\begin{eqnarray}4\sqrt{\log \log q}\leqslant V\leqslant 4ck\frac{\log q}{\log \log q}\end{eqnarray}$$
using the fact that
$t_{0}=\max (t_{i},i=1,\ldots ,2k)\leqslant \log ^{A}q.$
It remains to estimate
$N_{t}(q,V)$
for large
$q$
with an explicit dependence on
$t_{0}$
. Choosing
$\unicode[STIX]{x1D706}=0.6$
in Corollary 2.7 and if
$\unicode[STIX]{x1D712}^{2}\neq \unicode[STIX]{x1D712}_{0}$
, we obtain
$$\begin{eqnarray}\displaystyle & & \displaystyle \log \biggl|L\biggl(\frac{1}{2}+\text{i}t_{1},\unicode[STIX]{x1D712}\biggr)\biggr|+\cdots +\log \biggl|L\biggl(\frac{1}{2}+\text{i}t_{2k},\unicode[STIX]{x1D712}\biggr)\biggr|\nonumber\\ \displaystyle & & \displaystyle \quad \leqslant \text{Re}\biggl(\mathop{\sum }_{p\leqslant x}\frac{\unicode[STIX]{x1D712}(p)p^{-\text{i}t_{1}}}{p^{1/2+0.6/\text{log}\,x}}\frac{\log (x/p)}{\log x}+\cdots +\frac{\unicode[STIX]{x1D712}(p)p^{-\text{i}t_{2k}}}{p^{1/2+0.6/\text{log}\,x}}\frac{\log (x/p)}{\log x}\biggr)\nonumber\\ \displaystyle & & \displaystyle \qquad +\,\frac{8k}{5}\frac{\log q+\log ^{+}T}{\log x}+O(\log \log \log q).\nonumber\end{eqnarray}$$
Following [Reference Chandee3] and [Reference Soundararajan21], we define the quantity
$A$
as
$$\begin{eqnarray}A=\left\{\begin{array}{@{}ll@{}}\displaystyle \frac{\log W}{2}\quad & \displaystyle \text{if }4\sqrt{\log \log q}\leqslant V\leqslant W,\\ \displaystyle \frac{W\log W}{2V}\quad & \displaystyle \text{if }W\leqslant V\leqslant \frac{1}{4k}W\log W,\\ \displaystyle 2k\quad & \displaystyle \text{if }V>\frac{1}{4k}W\log W.\end{array}\right.\end{eqnarray}$$
Let
$x=(q\max (T,1))^{A/V}$
and
$z=x^{1/\text{log}\,\log q}$
. From the previous bounds,
$$\begin{eqnarray}\displaystyle & & \displaystyle \log \biggl|L\biggl(\frac{1}{2}+\text{i}t_{1},\unicode[STIX]{x1D712}\biggr)\biggr|+\cdots +\log \biggl|L\biggl(\frac{1}{2}+\text{i}t_{2k},\unicode[STIX]{x1D712}\biggr)\biggr|\nonumber\\ \displaystyle & & \displaystyle \quad \leqslant S_{1}(\unicode[STIX]{x1D712})+S_{2}(\unicode[STIX]{x1D712})+\frac{8k}{5}\frac{\log q+\log ^{+}T}{\log x}+O(\log \log \log q),\nonumber\end{eqnarray}$$
where
$$\begin{eqnarray}S_{1}(\unicode[STIX]{x1D712})=\biggl|\mathop{\sum }_{p\leqslant z}\frac{\unicode[STIX]{x1D712}(p)(p^{-\text{i}t_{1}}+\cdots +p^{-\text{i}t_{2k}})}{p^{1/2+0.6/\text{log}\,x}}\frac{\log (x/p)}{\log x}\biggr|\end{eqnarray}$$
and
$$\begin{eqnarray}S_{2}(\unicode[STIX]{x1D712})=\biggl|\mathop{\sum }_{z<p\leqslant x}\frac{\unicode[STIX]{x1D712}(p)(p^{-\text{i}t_{1}}+\cdots +p^{-\text{i}t_{2k}})}{p^{1/2+0.6/\text{log}\,x}}\frac{\log (x/p)}{\log x}\biggr|.\end{eqnarray}$$
It remains to study how often with respect to characters these quantities could be large. Firstly, if
$\unicode[STIX]{x1D712}\in S_{t}(q,V)$
, it must be thatFootnote
1
$$\begin{eqnarray}S_{1}(\unicode[STIX]{x1D712})\geqslant V_{1}:=V\biggl(1-\frac{9k}{5A}\biggr)\quad \text{or}\quad S_{2}(\unicode[STIX]{x1D712})\geqslant V_{2}:=\frac{kV}{5A}.\end{eqnarray}$$
Let
$N_{i}(q)=\#S_{i}(q):=\{\unicode[STIX]{x1D712}(\text{mod}\,q),\unicode[STIX]{x1D712}^{2}\neq \unicode[STIX]{x1D712}_{0}:S_{i}(\unicode[STIX]{x1D712})\geqslant V_{i}\}$
for
$i=1,2$
. We want to find upper bounds for
$N_{i}(q)$
with a certain uniformity in
$t$
Footnote
2
. By Lemma 2.8, we see that, for any natural number
$l\leqslant \frac{3}{4}V/A$
Footnote
3
,
$$\begin{eqnarray}|S_{2}(\unicode[STIX]{x1D712})|^{2l}\leqslant c_{\unicode[STIX]{x1D712}}l!\biggl(\mathop{\sum }_{z<p\leqslant x}\frac{4k^{2}}{p}\biggr)^{l}\ll c_{\unicode[STIX]{x1D712}}(4lk^{2}(\log \log \log q+O(1)))^{l}.\end{eqnarray}$$
Choosing
$l=\lfloor 3V/4A\rfloor$
and observing that
$$\begin{eqnarray}\mathop{\sum }_{\unicode[STIX]{x1D712}\in S_{2}(q)}|S_{2}(\unicode[STIX]{x1D712})|^{2l}\geqslant N_{2}(q)V_{2}^{2l},\end{eqnarray}$$
we derive
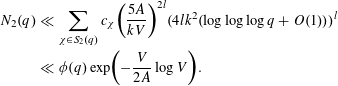$$\begin{eqnarray}\displaystyle N_{2}(q) & \ll & \displaystyle \mathop{\sum }_{\unicode[STIX]{x1D712}\in S_{2}(q)}c_{\unicode[STIX]{x1D712}}\biggl(\frac{5A}{kV}\biggr)^{2l}(4lk^{2}(\log \log \log q+O(1)))^{l}\nonumber\\ \displaystyle & \ll & \displaystyle \unicode[STIX]{x1D719}(q)\exp \biggl(-\frac{V}{2A}\log V\biggr).\nonumber\end{eqnarray}$$
It remains to find an upper bound for
$N_{1}(q)$
. By Lemma 2.8, for any
$l<\log q/\text{log}\,z$
,
$$\begin{eqnarray}\displaystyle |S_{1}(\unicode[STIX]{x1D712})|^{2l} & {\leqslant} & \displaystyle c_{\unicode[STIX]{x1D712}}l!\biggl(\mathop{\sum }_{p\leqslant z}\frac{|p^{-\text{i}t_{1}}+\cdots +p^{-\text{i}t_{2k}}|^{2}}{p}\biggr)^{l}\nonumber\\ \displaystyle & \ll & \displaystyle c_{\unicode[STIX]{x1D712}}l!\biggl(\mathop{\sum }_{p\leqslant z}\frac{2k+2\mathop{\sum }_{i<j}\cos ((t_{i}-t_{j})\log p)}{p}\biggr)^{l}\nonumber\\ \displaystyle & \ll & \displaystyle c_{\unicode[STIX]{x1D712}}l!\biggl(2k\log \log z+2\mathop{\sum }_{\substack{ i,j \\ i<j}}F_{i,j}\biggr)^{l}\nonumber\\ \displaystyle & \ll & \displaystyle c_{\unicode[STIX]{x1D712}}l!\,W^{l}\ll c_{\unicode[STIX]{x1D712}}\sqrt{l}\biggl(\frac{lW}{e}\biggr)^{l},\nonumber\end{eqnarray}$$
where we applied Lemma 2.9 and used Stirling’s formula together with the fact that
$z<q$
.
Remark 2.10. If
$|t_{i}-t_{j}|\geqslant \frac{1}{100}$
, by hypothesis, this quantity is at most
$2\log ^{A}q$
. Hence, the second case of Lemma 2.9 implies that the sum over primes is
$\ll \log \log \log q$
.
Proceeding as in (2.11) for
$N_{2}$
, we deduce that
$$\begin{eqnarray}N_{1}(q)\ll V_{1}^{-2l}\mathop{\sum }_{\unicode[STIX]{x1D712}\in S_{1}(q)}|S_{1}(\unicode[STIX]{x1D712})|^{2l}\ll \unicode[STIX]{x1D719}(q)\sqrt{l}\biggl(l\frac{W}{eV_{1}^{2}}\biggr)^{l}.\end{eqnarray}$$
When
$V\leqslant W^{2}/4k^{3}$
, we choose
$l=\lfloor V_{1}^{2}/W\rfloor$
and, when
$V>W^{2}/4k^{3}$
, we choose
$l=\lfloor 8V\rfloor$
. We easily verify, using the definition of
$A$
, that the condition
$l<\log q/\text{log}\,z$
Footnote
1
holds in both cases. Finally we get
$$\begin{eqnarray}N_{1}(q)\ll \unicode[STIX]{x1D719}(q)\frac{V}{\sqrt{W}}\exp \biggl(-\frac{V_{1}^{2}}{W}\biggr)+\unicode[STIX]{x1D719}(q)\exp (-3V\log V).\end{eqnarray}$$
Using our bounds on
$N_{1}(q)$
and
$N_{2}(q)$
in (2.1), elementary computations lead to the proof of Theorem 2.1.
3 Application to upper bounds for moments of theta functions
In this section, we will prove Theorem 1.2 in the case of even characters. The proof for odd characters follows exactly the same lines. The method is as follows. We express theta values as Mellin transform of
$L$
-functions and then we use our previous result about moments of shifted
$L$
-functions.
For every even primitive character
$\unicode[STIX]{x1D712}$
modulo
$q$
, recall the relation for
$c>1/2$
$$\begin{eqnarray}\unicode[STIX]{x1D703}(1,\unicode[STIX]{x1D712})=\int _{c-i\infty }^{c+\infty }L(2s,\unicode[STIX]{x1D712})\biggl(\frac{q}{2\unicode[STIX]{x1D70B}}\biggr)^{s}\unicode[STIX]{x1D6E4}(2s)\,ds.\end{eqnarray}$$
Shifting the line of integration to
$\Re (s)=1/4$
and using the decay of
$\unicode[STIX]{x1D6E4}(s)$
in vertical strips, we end up with
$$\begin{eqnarray}\unicode[STIX]{x1D703}(1,\unicode[STIX]{x1D712})=\biggl(\frac{q}{\unicode[STIX]{x1D70B}}\biggr)^{1/4}\int _{-\infty }^{\infty }L\biggl(\frac{1}{2}+2\text{i}t,\unicode[STIX]{x1D712}\biggr)\biggl(\frac{q}{\unicode[STIX]{x1D70B}}\biggr)^{2\text{i}t}\unicode[STIX]{x1D6E4}\biggl(\frac{1}{2}+2\text{i}t\biggr)\,dt.\end{eqnarray}$$
We express the moments as
$$\begin{eqnarray}\displaystyle & & \displaystyle \mathop{\sum }_{\unicode[STIX]{x1D712}\in X_{q}^{+}\backslash \unicode[STIX]{x1D712}_{0}}|\unicode[STIX]{x1D703}(1,\unicode[STIX]{x1D712})|^{2k}=\biggl(\frac{q}{\unicode[STIX]{x1D70B}}\biggr)^{k/2}\nonumber\\ \displaystyle & & \displaystyle \qquad \times \mathop{\sum }_{\unicode[STIX]{x1D712}\in X_{q}^{+}\backslash \unicode[STIX]{x1D712}_{0}}\biggl|\int _{-\infty }^{\infty }L\biggl(\frac{1}{2}+2\text{i}t,\unicode[STIX]{x1D712}\biggr)\biggl(\frac{q}{\unicode[STIX]{x1D70B}}\biggr)^{2\text{i}t}\unicode[STIX]{x1D6E4}\biggl(\frac{1}{2}+2\text{i}t\biggr)\,dt\biggr|^{2k}.\end{eqnarray}$$
Hence, the problem boils down to getting a bound of size
$\log ^{(k-1)^{2}+\unicode[STIX]{x1D716}}q$
for the
$2k$
-fold integral. In the following, we can sum over
$X_{q}^{\ast }$
without substantial loss.
3.1 Truncating the integrals
The strategy is the following. We will cut up to a certain reasonable height, for instance
$\log ^{\unicode[STIX]{x1D716}}q$
. Precisely, using the decay of
$\unicode[STIX]{x1D6E4}(\frac{1}{2}+2\text{i}t)$
, we bound the tail.
Lemma 3.1. Fix
$\unicode[STIX]{x1D716}>0$
. There exists an absolute constant
$c$
such that
$$\begin{eqnarray}\displaystyle & & \displaystyle \mathop{\sum }_{\unicode[STIX]{x1D712}\in X_{q}^{\ast }}\biggl|\int _{-\infty }^{\infty }L\biggl(\frac{1}{2}+2\text{i}t,\unicode[STIX]{x1D712}\biggr)\biggl(\frac{q}{\unicode[STIX]{x1D70B}}\biggr)^{2\text{i}t}\unicode[STIX]{x1D6E4}\biggl(\frac{1}{2}+2\text{i}t\biggr)\unicode[STIX]{x1D7D9}_{|t|\geqslant \log ^{\unicode[STIX]{x1D716}}(q)}(t)\,dt\biggr|^{2k}\nonumber\\ \displaystyle & & \displaystyle \quad \ll \unicode[STIX]{x1D719}(q)\text{e}^{-c\log ^{\unicode[STIX]{x1D716}}q}.\nonumber\end{eqnarray}$$
Proof. Using the Hölder inequality with parameters
$1/2k+(2k-1)/2k=1$
, the problem reduces to finding the bound of
$$\begin{eqnarray}\displaystyle & & \displaystyle \mathop{\sum }_{\unicode[STIX]{x1D712}\in X_{q}^{\ast }}\biggl(\int _{|t|\geqslant \log ^{\unicode[STIX]{x1D716}}q}\biggl|L\biggl(\frac{1}{2}+2\text{i}t,\unicode[STIX]{x1D712}\biggr)\biggr|^{2k}\biggl|\unicode[STIX]{x1D6E4}\biggl(\frac{1}{2}+2\text{i}t\biggr)\biggr|\,dt\biggr)\nonumber\\ \displaystyle & & \displaystyle \qquad \times \biggl(\int _{|t|\geqslant \log ^{\unicode[STIX]{x1D716}}q}\biggl|\unicode[STIX]{x1D6E4}\biggl(\frac{1}{2}+2\text{i}t\biggr)\biggr|\,dt\biggr)^{2k-1}.\nonumber\end{eqnarray}$$
We decompose dyadically the range of integration in the left-hand side and use the convergence of the right-hand side to end up with
$$\begin{eqnarray}\mathop{\sum }_{n\geqslant \log ^{\unicode[STIX]{x1D716}}q}\mathop{\sum }_{\unicode[STIX]{x1D712}\in X_{q}^{\ast }}\int _{n}^{2n}\biggl|L\biggl(\frac{1}{2}+2\text{i}t,\unicode[STIX]{x1D712}\biggr)\biggr|^{2k}\biggl|\unicode[STIX]{x1D6E4}\biggl(\frac{1}{2}+2\text{i}t\biggr)\biggr|\,dt.\end{eqnarray}$$
Using Stirling’s formula and [Reference Chandee and Li2, Proposition 2.9]Footnote
1
, we get, for
$c_{1}>0$
, an absolute constant
$$\begin{eqnarray}\displaystyle & & \displaystyle \mathop{\sum }_{n\geqslant \log ^{\unicode[STIX]{x1D716}}q}\mathop{\sum }_{\unicode[STIX]{x1D712}\in X_{q}^{\ast }}\int _{n}^{2n}\biggl|L\biggl(\frac{1}{2}+2\text{i}t,\unicode[STIX]{x1D712}\biggr)\biggr|^{2k}\biggl|\unicode[STIX]{x1D6E4}\biggl(\frac{1}{2}+2\text{i}t\biggr)\biggr|\,dt\nonumber\\ \displaystyle & & \displaystyle \quad \ll \mathop{\sum }_{n\geqslant \log ^{\unicode[STIX]{x1D716}}q}\text{e}^{-c_{1}n}\mathop{\sum }_{\unicode[STIX]{x1D712}\in X_{q}^{\ast }}\int _{n}^{2n}\biggl|L\biggl(\frac{1}{2}+2\text{i}t,\unicode[STIX]{x1D712}\biggr)\biggr|^{2k}\,dt\nonumber\\ \displaystyle & & \displaystyle \quad \ll \unicode[STIX]{x1D719}(q)(\log q)^{k^{2}+\unicode[STIX]{x1D716}}\mathop{\sum }_{n\geqslant \log ^{\unicode[STIX]{x1D716}}q}\text{e}^{-c_{1}n}n(\log n)^{k^{2}+\unicode[STIX]{x1D716}}\ll \unicode[STIX]{x1D719}(q)\text{e}^{-c\log ^{\unicode[STIX]{x1D716}}q}.\Box \nonumber\end{eqnarray}$$
3.2 Bound for the hypercube integral
It remains to bound optimally the integral on the
$2k$
-hypercube
${\mathcal{H}}$
of size
$\log ^{\unicode[STIX]{x1D716}}q$
. First, observing that
$\unicode[STIX]{x1D6E4}(\frac{1}{2}+2\text{i}t)$
is bounded on
${\mathcal{H}}$
and expanding the integral in (3.1), we get
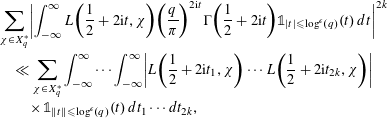$$\begin{eqnarray}\displaystyle & & \displaystyle \mathop{\sum }_{\unicode[STIX]{x1D712}\in X_{q}^{\ast }}\biggl|\int _{-\infty }^{\infty }L\biggl(\frac{1}{2}+2\text{i}t,\unicode[STIX]{x1D712}\biggr)\biggl(\frac{q}{\unicode[STIX]{x1D70B}}\biggr)^{2\text{i}t}\unicode[STIX]{x1D6E4}\biggl(\frac{1}{2}+2\text{i}t\biggr)\unicode[STIX]{x1D7D9}_{|t|\leqslant \log ^{\unicode[STIX]{x1D716}}(q)}(t)\,dt\biggr|^{2k}\nonumber\\ \displaystyle & & \displaystyle \quad \ll \mathop{\sum }_{\unicode[STIX]{x1D712}\in X_{q}^{\ast }}\int _{-\infty }^{\infty }\cdots \int _{-\infty }^{\infty }\biggl|L\biggl(\frac{1}{2}+2\text{i}t_{1},\unicode[STIX]{x1D712}\biggr)\cdots L\biggl(\frac{1}{2}+2\text{i}t_{2k},\unicode[STIX]{x1D712}\biggr)\biggr|\nonumber\\ \displaystyle & & \displaystyle \qquad \times \,\unicode[STIX]{x1D7D9}_{\Vert t\Vert \leqslant \log ^{\unicode[STIX]{x1D716}}(q)}(t)\,dt_{1}\cdots dt_{2k},\end{eqnarray}$$
where
$\Vert t\Vert =\max _{i=1,\ldots ,2k}|t_{i}|$
. We will use Theorem 2.1 to handle that integral. In order to do this, we have to control how close the shifts
$t_{i}$
are to each other.
By a permutation change of the variables, we can assume that
$t_{1}\leqslant t_{2}\leqslant \cdots \leqslant t_{2k}$
. Indeed, the integral on
${\mathcal{H}}$
is equal to
$(2k)!$
times the integral with that additional restriction.
For every
$2k$
-tuple
$\overline{t}=(t_{1},\ldots ,t_{2k})$
, we define a
$(2k-1)$
-tuple
$\overline{j}=(j_{1},\ldots ,j_{2k-1})$
, where
$j_{i}=\min \{i+1\leqslant j\leqslant 2k,|t_{i}-t_{j}|>1/\text{log}\,q\}$
. If, for some
$i$
, no such
$j$
exists, we set
$j_{i}=2k+1$
. In the following, we will say that
$\overline{t}=(t_{1},\ldots ,t_{2k})$
is of type
$\overline{j}$
. Let us give few remarks about that definition. First of all, we have to think about
$j_{i}$
as the first occurrence of a shift lying far from
$t_{i}$
. Furthermore, notice that
$2\leqslant j_{1}\leqslant j_{2}\leqslant \cdots \leqslant j_{2k-1}\leqslant 2k+1$
and that we can split the domain of integration
${\mathcal{H}}$
into a disjoint union
${\mathcal{H}}=\cup {\mathcal{H}}_{\overline{j}}$
of
$2k$
-tuples
$\overline{t}=(t_{1},\ldots ,t_{2k})$
, where
$\overline{t}$
is of type
$\overline{j}$
. Hence, proving Theorem 1.2 reduces to finding the bound of the contribution of the integral over
$\overline{t}$
of type
$\overline{j}$
for all possible choices of
$\overline{j}$
.
The strategy is to apply the Theorem 1.1 in an appropriate way to obtain the expected bound. Using Theorem 1.1, we get that the contribution in (3.2) of
$\overline{t}$
of type
$\overline{j}$
is bounded by
$$\begin{eqnarray}\unicode[STIX]{x1D719}(q)(\log q)^{k/2+\unicode[STIX]{x1D716}}\int \cdots \int _{{\mathcal{H}}_{\overline{j}}}\left(\mathop{\prod }_{i<j}E_{i,j}\right)\,dt_{1}\cdots dt_{2k},\end{eqnarray}$$
where
$E_{i,j}$
is defined in Theorem 1.1. For every
$i=1,2,\ldots ,2k-1$
, we will essentially bound
$\prod _{j=i+1}^{2k}E_{i,j}$
in two different ways, depending on whether the variable
$t_{i}$
possesses a close shift or not.
$\bullet$
Case 1: Close shifts.
If
$t_{i}$
admits a close shift, then
$j_{i}>i+1$
. Using the first case of Theorem 1.1, we have the trivial bound
$$\begin{eqnarray}\biggl|\mathop{\prod }_{j=i+1}^{2k}E_{i,j}\biggr|\leqslant (\log q)^{2k-i/2}.\end{eqnarray}$$
$\bullet$
Case 2: Isolated shifts.
For those indices
$i$
,
$t_{i}$
does not admit a close shift, which means that
$j_{i}=i+1$
. We remark that
$1/|t_{i}-t_{j}|\leqslant 1/|t_{i}-t_{j_{i}}|$
for
$j\geqslant j_{i}$
since we have
$t_{1}\leqslant t_{2}\leqslant \cdots \leqslant t_{2k}$
. Hence, using again both cases of Theorem 1.1, we derive the bound
$$\begin{eqnarray}\biggl|\mathop{\prod }_{j=i+1}^{2k}E_{i,j}\biggr|\leqslant \frac{1}{|t_{i}-t_{i+1}|^{(2k-i)/2}}(\log \log q)^{(2k-i)/2}.\end{eqnarray}$$
To deal with the integral in (3.3), we can make the linear change of variables
$$\begin{eqnarray}u_{i}=\left\{\begin{array}{@{}ll@{}}t_{i}-t_{i+1}\quad & \text{if }i\leqslant 2k-1,\\ t_{2k}\quad & \text{if }i=2k.\end{array}\right.\end{eqnarray}$$
Thus, as the determinant of the Jacobian is equal to one, the integral in (3.3) becomes
$$\begin{eqnarray}\displaystyle & & \displaystyle (\log \log q)^{k(2k-1)}\mathop{\prod }_{\substack{ i=1 \\ i\mid j_{i}\neq i+1}}^{2k-1}(\log q)^{(2k-i)/2}\nonumber\\ \displaystyle & & \displaystyle \qquad \times \int \cdots \int _{{\mathcal{D}}_{\overline{j}}}\mathop{\prod }_{\substack{ i=1 \\ i\mid j_{i}=i+1}}^{2k-1}\frac{1}{|u_{i}|^{(2k-i)/2}}\,du_{1}\cdots du_{2k},\end{eqnarray}$$
where the domain
${\mathcal{D}}_{\overline{j}}$
is included in
$$\begin{eqnarray}\mathop{\prod }_{i\mid j_{i}\neq i+1} ]-1/\text{log}\,q,0]\mathop{\prod }_{i\mid j_{i}=i+1} ]-\log ^{\unicode[STIX]{x1D716}}q,-1/\text{log}\,q].\end{eqnarray}$$
For those
$i$
such that
$j_{i}\neq i+1$
, we bound the integral over
$u_{i}$
by the length of the interval of integration
$1/\text{log}\,q$
. For the other indices, we integrate explicitly on
$]-\text{log}^{\unicode[STIX]{x1D716}}\,q,-1/\text{log}\,q\!]$
. In order to obtain the expected bound, we need to “save” a logarithm for each integration
$du_{i}$
for
$i=1\cdots 2k-1$
. An additional problem arises when the variable does not admit a close shift and we integrate
$u_{2k-1}^{-1/2}$
. Let us first treat the easiest case.
$\spadesuit$
Subcase 1:
$j_{2k-1}\neq 2k$
.
In this case, all the exponents in the denominator of the integral in (3.7) are greater than one. Therefore, we obtain after explicit integration that (3.7) is bounded by
$$\begin{eqnarray}(\log \log q)^{k(2k-1)}\mathop{\prod }_{i|j_{i}\neq i+1}\frac{(\log q)^{(2k-i)/2}}{\log q}\mathop{\prod }_{\substack{ i=1 \\ i|j_{i}=i+1}}^{2k-1}\frac{(\log q)^{(2k-i)/2}}{\log q}\log \log q,\end{eqnarray}$$
where the factor
$\log \log q$
comes from the possible integration of
$1/u$
when
$i=2k-2$
. Hence, (3.3) is bounded by
$$\begin{eqnarray}\unicode[STIX]{x1D719}(q)(\log q)^{f(k)+2k^{2}\unicode[STIX]{x1D716}},\end{eqnarray}$$
where
$$\begin{eqnarray}\displaystyle f(k) & = & \displaystyle \frac{k}{2}+\frac{1}{2}\mathop{\sum }_{i=1}^{2k-1}(2k-i-2)\nonumber\\ \displaystyle & = & \displaystyle \frac{k}{2}+\frac{1}{2}\mathop{\sum }_{i=-1}^{2k-3}i\nonumber\\ \displaystyle & = & \displaystyle \frac{k}{2}+\frac{(2k-3)(2k-2)}{4}-\frac{1}{2}\nonumber\\ \displaystyle & = & \displaystyle (k-1)^{2},\nonumber\end{eqnarray}$$
which proves Theorem 1.2 in this case.
$\spadesuit$
Subcase 2:
$j_{2k-1}=2k$
.
The only remaining problem arises when
$t_{2k-1}$
does not have a close shift. In this case, an explicit integration in (3.7) is not sufficient to save
$\log q$
after integration, but only saves
$\log ^{1/2}q$
. We are going to split the proof in two subcases depending on whether
$t_{1}$
admits a close shift or not.
$\clubsuit$
Subsubcase 1:
$j_{1}\neq 2$
.
We will use exactly the same bounds as before, except for
$i=1$
. The trivial inequality
$|t_{1}-t_{2k}|^{-1/2}\leqslant |t_{2k-1}-t_{2k}|^{-1/2}$
together with the simple observation that
$|t_{2k-1}-t_{2k}|$
is large (by hypothesis
$j_{2k-1}=2k$
) implies the bound
$$\begin{eqnarray}\mathop{\prod }_{j>1}E_{1,j}\leqslant (\log q)^{(2k-2)/2}\frac{\log \log q}{|t_{2k-1}-t_{2k}|^{1/2}}.\end{eqnarray}$$
Doing the same change of variables as before in (3.6) and using (3.9), we end up with the bound
$$\begin{eqnarray}\displaystyle & & \displaystyle (\log \log q)^{k(2k-1)}(\log q)^{(2k-2)/2}\mathop{\prod }_{\substack{ i=2 \\ i|j_{i}\neq i+1}}^{2k-2}(\log q)^{(2k-i)/2}\nonumber\\ \displaystyle & & \displaystyle \qquad \times \int \cdots \int _{{\mathcal{D}}_{\overline{j}}}\mathop{\prod }_{\substack{ 2=1 \\ i|j_{i}=i+1}}^{2k-2}\frac{1}{|u_{i}|^{(2k-i)/2}}\frac{1}{|u_{2k-1}|}\,du_{1}\cdots du_{2k}.\nonumber\end{eqnarray}$$
A slight modification of the computation following (3.8) enables us to obtain the expected bound
$(\log q)^{(k-1)^{2}+\unicode[STIX]{x1D716}}$
.
$\clubsuit$
Subsubcase 2:
$j_{1}=2$
.
We proceed as in the previous subsubcase with the following bound (the
$\log \log$
factor coming from the possible case where the shifts are far away from each other)
$$\begin{eqnarray}\displaystyle \mathop{\prod }_{j>1}E_{1,j} & \ll & \displaystyle \frac{(\log \log q)^{(2k-1)/2}}{\mathop{\prod }_{j=2}^{2k}|t_{1}-t_{j}|^{1/2}}\leqslant \frac{(\log \log q)^{(2k-1)/2}}{|t_{1}-t_{2}|^{(2k-2)/2}}\frac{1}{|t_{1}-t_{2k}|^{1/2}}\nonumber\\ \displaystyle & {\leqslant} & \displaystyle \frac{(\log \log q)^{(2k-1)/2}}{|t_{1}-t_{2}|^{(2k-2)/2}}\frac{1}{|t_{2k-1}-t_{2k}|^{1/2}}.\nonumber\end{eqnarray}$$
Doing the same change of variables as before in (3.6), we end up with the same integral as in the previous subsubcase. Hence a similar computation works and this concludes the proof of Theorem 1.2.
Acknowledgements
The author is grateful to Dimitri Dias and Igor E. Shparlinski for very helpful discussions, to the reviewer for the careful reading and the useful comments and to Maksym Radziwill for pointing out reference [Reference Chandee3].
The author is supported by the Austrian Science Fund (FWF), START-project Y-901 “Probabilistic methods in analysis and number theory” headed by Christoph Aistleitner.
