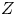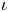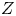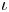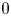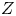1. Introduction
Given a smooth projective variety $X$![]() over $\mathbb {C}$
over $\mathbb {C}$![]() , let $A^{i}(X):=CH^{i}(X)_{\mathbb {Q}}$
, let $A^{i}(X):=CH^{i}(X)_{\mathbb {Q}}$![]() denote the Chow groups of $X$
denote the Chow groups of $X$![]() (i.e. the groups of codimension $i$
(i.e. the groups of codimension $i$![]() algebraic cycles on $X$
algebraic cycles on $X$![]() with $\mathbb {Q}$
with $\mathbb {Q}$![]() -coefficients, modulo rational equivalence).
-coefficients, modulo rational equivalence).
In this article, we consider the Chow ring of Lehn–Lehn–Sorger–van Straten (=LLSS) eightfolds. These eightfolds (defined in terms of twisted cubic curves contained in a given cubic fourfold $Y$![]() ) form a $20$
) form a $20$![]() -dimensional locally complete family of hyperkähler varieties, deformation equivalent to the Hilbert scheme of points on a K3 surface [Reference Addington and Lehn2, Reference Lehn36, Reference Lehn, Lehn, Sorger and van Straten38]. One notable feature of the construction is that any LLSS eightfold admits an anti-symplectic involution $\iota$
-dimensional locally complete family of hyperkähler varieties, deformation equivalent to the Hilbert scheme of points on a K3 surface [Reference Addington and Lehn2, Reference Lehn36, Reference Lehn, Lehn, Sorger and van Straten38]. One notable feature of the construction is that any LLSS eightfold admits an anti-symplectic involution $\iota$![]() [Reference Lehn37].
[Reference Lehn37].
Our main result gives an explicit formula for the action of $\iota$![]() on the Chow group of $0$
on the Chow group of $0$![]() -cycles for certain LLSS eightfolds:
-cycles for certain LLSS eightfolds:
Theorem =Theorem 3.11
Let $Z=Z(Y)$![]() be an LLSS eightfold$,$
be an LLSS eightfold$,$![]() and let $\iota \in \operatorname {Aut}(Z)$
and let $\iota \in \operatorname {Aut}(Z)$![]() be the anti-symplectic involution. Assume $Z$
be the anti-symplectic involution. Assume $Z$![]() is birational to a Hilbert scheme $Z^{\prime }=S^{[4]}$
is birational to a Hilbert scheme $Z^{\prime }=S^{[4]}$![]() where $S$
where $S$![]() is a K3 surface. Then the action of $\iota$
is a K3 surface. Then the action of $\iota$![]() on $A^{8}(Z^{\prime })$
on $A^{8}(Z^{\prime })$![]() is given by
is given by

$($![]() Here$,$
Here$,$![]() $x,y,z,t\in S$
$x,y,z,t\in S$![]() and $o\in A^{2}(S)$
and $o\in A^{2}(S)$![]() denotes the distinguished $0$
denotes the distinguished $0$![]() -cycle of [Reference Beauville and Voisin7].)
-cycle of [Reference Beauville and Voisin7].)
This theorem applies to a countably infinite number of divisors in the moduli space of LLSS eightfolds (the condition on $Z$![]() is equivalent to asking that the cubic fourfold $Y$
is equivalent to asking that the cubic fourfold $Y$![]() has discriminant of the form $(6n^{2}-6n+2)/a^{2}$
has discriminant of the form $(6n^{2}-6n+2)/a^{2}$![]() for some $n,a\in \mathbb {Z}$
for some $n,a\in \mathbb {Z}$![]() [Reference Li, Pertusi and Zhao39, Proposition 5.3]. In particular, Theorem 3.11 applies to Pfaffian cubics).
[Reference Li, Pertusi and Zhao39, Proposition 5.3]. In particular, Theorem 3.11 applies to Pfaffian cubics).
The statement of Theorem 3.11 is similar to a statement for double EPW sextics proven in [Reference Laterveer and Vial33, Theorem 2] and answers a question raised there [Reference Laterveer and Vial33, Introduction].
The proof of Theorem 3.11 consists of a two-step argument. First, we prove that for any LLSS eightfold $Z$![]() (not necessarily birational to a Hilbert scheme), there is equality
(not necessarily birational to a Hilbert scheme), there is equality
where $S^\textrm {mob}_\ast$![]() is related to Voisin's orbit filtration on zero-cycles [Reference Voisin59], cf. Definition 2.9. (As explained in Remark 2.10, one expects that the piece $S^\textrm {mob}_3 A^{8}(Z)\cap A^{8}_\textrm {hom}(Z)$
is related to Voisin's orbit filtration on zero-cycles [Reference Voisin59], cf. Definition 2.9. (As explained in Remark 2.10, one expects that the piece $S^\textrm {mob}_3 A^{8}(Z)\cap A^{8}_\textrm {hom}(Z)$![]() is related, via the Bloch–Beilinson conjectures, to $H^{2,0}(Z)$
is related, via the Bloch–Beilinson conjectures, to $H^{2,0}(Z)$![]() . Since $\iota$
. Since $\iota$![]() acts as $-\operatorname {id}$
acts as $-\operatorname {id}$![]() on $H^{2,0}(Z)$
on $H^{2,0}(Z)$![]() , equality (1) is in keeping with this expectation.) Next, we restrict attention to LLSS eightfolds birational to a Hilbert scheme $Z^{\prime }$
, equality (1) is in keeping with this expectation.) Next, we restrict attention to LLSS eightfolds birational to a Hilbert scheme $Z^{\prime }$![]() . In this case, Vial [Reference Vial54] has constructed a multiplicative Chow–Künneth decomposition, giving a bigrading on the Chow ring $A^{\ast }_{(\ast )}(Z^{\prime })$
. In this case, Vial [Reference Vial54] has constructed a multiplicative Chow–Künneth decomposition, giving a bigrading on the Chow ring $A^{\ast }_{(\ast )}(Z^{\prime })$![]() such that the piece $S^\textrm {mob}_3 A^{8}(Z)\cap A^{8}_\textrm {hom}(Z^{\prime })$
such that the piece $S^\textrm {mob}_3 A^{8}(Z)\cap A^{8}_\textrm {hom}(Z^{\prime })$![]() is exactly $A^{8}_{(2)}(Z^{\prime })$
is exactly $A^{8}_{(2)}(Z^{\prime })$![]() . Exploiting the good formal properties of this bigrading, one can deduce Theorem 3.11 from equality (1).
. Exploiting the good formal properties of this bigrading, one can deduce Theorem 3.11 from equality (1).
Theorem 3.11 admits a reformulation that does not mention LLSS eightfolds:
Theorem =Theorem 3.12
Let $X=S^{[4]}$![]() be a Hilbert scheme$,$
be a Hilbert scheme$,$![]() where $S$
where $S$![]() is a K3 surface of Picard number 1 and degree $d$
is a K3 surface of Picard number 1 and degree $d$![]() such that $d>2$
such that $d>2$![]() and $d= (6n^{2}-6n+2)/a^{2}$
and $d= (6n^{2}-6n+2)/a^{2}$![]() for some $n,a\in \mathbb {Z}$
for some $n,a\in \mathbb {Z}$![]() . Then $\operatorname {Bir}(X)=\mathbb {Z}/2\mathbb {Z}$
. Then $\operatorname {Bir}(X)=\mathbb {Z}/2\mathbb {Z}$![]() and the non-trivial element $\iota \in \operatorname {Bir}(X)$
and the non-trivial element $\iota \in \operatorname {Bir}(X)$![]() acts on $A^{8}(X)$
acts on $A^{8}(X)$![]() as in Theorem 3.11.
as in Theorem 3.11.
As another consequence of Theorem 3.11, we can show that the Chow ring of the quotient of the involution behaves somewhat like the Chow ring of Calabi–Yau varieties:
Corollary =Corollary 3.13
Let $Z$![]() be an LLSS eightfold birational to a Hilbert scheme $Z^{\prime }=S^{[4]}$
be an LLSS eightfold birational to a Hilbert scheme $Z^{\prime }=S^{[4]}$![]() where $S$
where $S$![]() is a K3 surface. Let $X:=Z/\langle \iota \rangle$
is a K3 surface. Let $X:=Z/\langle \iota \rangle$![]() be the quotient under the anti-symplectic involution $\iota \in \operatorname {Aut}(Z)$
be the quotient under the anti-symplectic involution $\iota \in \operatorname {Aut}(Z)$![]() . Then
. Then
where $h\in A^{1}(X)$![]() is an ample divisor.
is an ample divisor.
Corollary 3.13 is expected to be true for all LLSS eightfolds, and not merely those birational to a Hilbert scheme. Since for a general LLSS eightfold, we do not know how to construct a multiplicative Chow–Künneth decomposition, this expectation seems difficult to prove.
Conventions In this article, the word variety will refer to a reduced irreducible scheme of finite type over $\mathbb {C}$![]() . A subvariety is a $($
. A subvariety is a $($![]() possibly reducible$)$
possibly reducible$)$![]() reduced subscheme which is equidimensional.
reduced subscheme which is equidimensional.
All Chow groups will be with rational coefficients$:$![]() we will denote by $A_j(X)$
we will denote by $A_j(X)$![]() the Chow group of $j$
the Chow group of $j$![]() -dimensional cycles on $X$
-dimensional cycles on $X$![]() with $\mathbb {Q}$
with $\mathbb {Q}$![]() -coefficients$;$
-coefficients$;$![]() for $X$
for $X$![]() smooth of dimension $n,$
smooth of dimension $n,$![]() the notations $A_j(X)$
the notations $A_j(X)$![]() and $A^{n-j}(X)$
and $A^{n-j}(X)$![]() are used interchangeably.
are used interchangeably.
The notations $A^{j}_\textrm {hom}(X),$![]() $A^{j}_{AJ}(X)$
$A^{j}_{AJ}(X)$![]() will be used to indicate the subgroups of homologically trivial$,$
will be used to indicate the subgroups of homologically trivial$,$![]() respectively$,$
respectively$,$![]() Abel–Jacobi trivial cycles. For a morphism $f\colon X\to Y,$
Abel–Jacobi trivial cycles. For a morphism $f\colon X\to Y,$![]() we will write $\Gamma _f\in A_\ast (X\times Y)$
we will write $\Gamma _f\in A_\ast (X\times Y)$![]() for the graph of $f$
for the graph of $f$![]() . The contravariant category of Chow motives $($
. The contravariant category of Chow motives $($![]() i.e.$,$
i.e.$,$![]() pure motives with respect to rational equivalence as in [Reference Murre, Nagel and Peters42, Reference Scholl48]) will be denoted $\mathcal {M}_\textrm {rat}$
pure motives with respect to rational equivalence as in [Reference Murre, Nagel and Peters42, Reference Scholl48]) will be denoted $\mathcal {M}_\textrm {rat}$![]() .
.
We will write $H^{j}(X)$![]() to indicate singular cohomology $H^{j}(X, \mathbb {Q})$
to indicate singular cohomology $H^{j}(X, \mathbb {Q})$![]() .
.
Given an automorphism $\sigma \in \operatorname {Aut}(X),$![]() we will write $A^{j}(X)^{\sigma }$
we will write $A^{j}(X)^{\sigma }$![]() $($
$($![]() and $H^{j}(X)^{\sigma })$
and $H^{j}(X)^{\sigma })$![]() for the subgroup of $A^{j}(X)$
for the subgroup of $A^{j}(X)$![]() $($
$($![]() respectively $H^{j}(X))$
respectively $H^{j}(X))$![]() invariant under $\sigma$
invariant under $\sigma$![]() .
.
2. Preliminaries
2.1. Quotient varieties
Definition 2.1 A projective quotient variety is a variety
where $Z$![]() is a smooth projective variety and $G\subset \hbox {Aut}(Z)$
is a smooth projective variety and $G\subset \hbox {Aut}(Z)$![]() is a finite group.
is a finite group.
Proposition 2.2 Fulton [Reference Fulton22]
Let $X$![]() be a projective quotient variety of dimension $n$
be a projective quotient variety of dimension $n$![]() . Let $A^{\ast }(X)$
. Let $A^{\ast }(X)$![]() denote the operational Chow cohomology ring. The natural map
denote the operational Chow cohomology ring. The natural map
is an isomorphism for all $i$![]() .
.
Proof. This is [Reference Fulton22, Example 17.4.10].
Remark 2.3 It follows from Proposition 2.2 that the formalism of correspondences goes through unchanged for projective quotient varieties $($![]() this is also noted in [Reference Fulton22, Example 16.1.13]). We may thus consider motives $(X,p,0)\in \mathcal {M}_\textrm {rat},$
this is also noted in [Reference Fulton22, Example 16.1.13]). We may thus consider motives $(X,p,0)\in \mathcal {M}_\textrm {rat},$![]() where $X$
where $X$![]() is a projective quotient variety and $p\in A^{n}(X\times X)$
is a projective quotient variety and $p\in A^{n}(X\times X)$![]() is a projector. For a projective quotient variety $X=Z/G,$
is a projector. For a projective quotient variety $X=Z/G,$![]() one readily proves $($
one readily proves $($![]() using Manin's identity principle$)$
using Manin's identity principle$)$![]() that there is an isomorphism
that there is an isomorphism
where $\Delta _G$![]() denotes the idempotent $({1}/{\vert G\vert }){\sum \nolimits _{g\in G}}\Gamma _g$
denotes the idempotent $({1}/{\vert G\vert }){\sum \nolimits _{g\in G}}\Gamma _g$![]() .
.
2.2. LLSS eightfolds
In this subsection, we briefly recall the construction of the Lehn–Lehn–Sorger–van Straten eightfold (see [Reference Lehn, Lehn, Sorger and van Straten38] for additional details). Let $Y \subset \mathbb {P}^{5}$![]() be a smooth cubic fourfold which does not contain a plane. Twisted cubic curves on $Y$
be a smooth cubic fourfold which does not contain a plane. Twisted cubic curves on $Y$![]() belong to an irreducible component $M_3(Y)$
belong to an irreducible component $M_3(Y)$![]() of the Hilbert scheme $\textrm {Hilb}^{3m+1}(Y)$
of the Hilbert scheme $\textrm {Hilb}^{3m+1}(Y)$![]() ; in particular, $M_3(Y)$
; in particular, $M_3(Y)$![]() is a ten-dimensional smooth projective variety and it is referred to as the Hilbert scheme of generalized twisted cubics on $Y$
is a ten-dimensional smooth projective variety and it is referred to as the Hilbert scheme of generalized twisted cubics on $Y$![]() . There exists a hyperkähler eightfold $Z = Z(Y)$
. There exists a hyperkähler eightfold $Z = Z(Y)$![]() and a morphism $u: M_3(Y) \to Z$
and a morphism $u: M_3(Y) \to Z$![]() which factorizes as $u = \Phi \circ a$
which factorizes as $u = \Phi \circ a$![]() , where $a: M_3(Y) \to Z'$
, where $a: M_3(Y) \to Z'$![]() is a $\mathbb {P}^{2}$
is a $\mathbb {P}^{2}$![]() -bundle and $\Phi : Z' \to Z$
-bundle and $\Phi : Z' \to Z$![]() is the blow-up of the image of a Lagrangian embedding $j: Y\hookrightarrow Z$
is the blow-up of the image of a Lagrangian embedding $j: Y\hookrightarrow Z$![]() . By [Reference Addington and Lehn2] (or alternatively [Reference Lehn36], or [Reference Kollár, Laza, Saccà and Voisin27, Section 5.4]), the manifold $Z$
. By [Reference Addington and Lehn2] (or alternatively [Reference Lehn36], or [Reference Kollár, Laza, Saccà and Voisin27, Section 5.4]), the manifold $Z$![]() is of $K3^{[4]}$
is of $K3^{[4]}$![]() -type.
-type.
For a point $j(y) \in j(Y) \subset Z$![]() , a curve $C \in u^{-1}(j(y))$
, a curve $C \in u^{-1}(j(y))$![]() is a singular cubic (with an embedded point in $y$
is a singular cubic (with an embedded point in $y$![]() ), cut out on $Y$
), cut out on $Y$![]() by a plane tangent to $Y$
by a plane tangent to $Y$![]() in $y$
in $y$![]() . In particular, $u^{-1}(j(Y)) \subset M_3(Y)$
. In particular, $u^{-1}(j(Y)) \subset M_3(Y)$![]() is the locus of non-Cohen–Macaulay curves on $Y$
is the locus of non-Cohen–Macaulay curves on $Y$![]() . If instead we consider an element $C \in M_3(Y)$
. If instead we consider an element $C \in M_3(Y)$![]() such that $u(C) \notin j(Y)$
such that $u(C) \notin j(Y)$![]() , let $\Gamma _C := \langle C \rangle \cong \mathbb {P}^{3}$
, let $\Gamma _C := \langle C \rangle \cong \mathbb {P}^{3}$![]() be the convex hull of the curve $C$
be the convex hull of the curve $C$![]() in $\mathbb {P}^{5}$
in $\mathbb {P}^{5}$![]() . Then, the fibre $u^{-1}(u(C))$
. Then, the fibre $u^{-1}(u(C))$![]() is one of the $72$
is one of the $72$![]() distinct linear systems of aCM twisted cubics on the smooth integral cubic surface $S_C := \Gamma _C \cap Y$
distinct linear systems of aCM twisted cubics on the smooth integral cubic surface $S_C := \Gamma _C \cap Y$![]() (cf. [Reference Buckley and Košir11]). This two-dimensional family of curves, whose general element is smooth, is determined by the choice of a linear determinantal representation $[A]$
(cf. [Reference Buckley and Košir11]). This two-dimensional family of curves, whose general element is smooth, is determined by the choice of a linear determinantal representation $[A]$![]() of the surface $S_C$
of the surface $S_C$![]() (see [Reference Dolgachev17, Chapter 9]). This means that $A$
(see [Reference Dolgachev17, Chapter 9]). This means that $A$![]() is a $3 \times 3$
is a $3 \times 3$![]() -matrix with entries in $H^{0}(\mathcal {O}_{\Gamma _C}(1))$
-matrix with entries in $H^{0}(\mathcal {O}_{\Gamma _C}(1))$![]() and such that $\det (A) = 0$
and such that $\det (A) = 0$![]() is an equation for $S_C$
is an equation for $S_C$![]() in $\Gamma _C$
in $\Gamma _C$![]() . The orbit $[A]$
. The orbit $[A]$![]() is taken with respect to the action of $(\textrm {GL}_3(\mathbb {C}) \times \textrm {GL}_3(\mathbb { C}))/\Delta$
is taken with respect to the action of $(\textrm {GL}_3(\mathbb {C}) \times \textrm {GL}_3(\mathbb { C}))/\Delta$![]() , where $\Delta = \{ (tI_3,tI_3) \mid t \in \mathbb {C}^{*}\}$
, where $\Delta = \{ (tI_3,tI_3) \mid t \in \mathbb {C}^{*}\}$![]() . Moreover, any curve $C' \in u^{-1}(u(C))$
. Moreover, any curve $C' \in u^{-1}(u(C))$![]() is such that $I_{C'/S_C}$
is such that $I_{C'/S_C}$![]() is generated by the three minors of a $3 \times 2$
is generated by the three minors of a $3 \times 2$![]() -matrix $A_{0}$
-matrix $A_{0}$![]() of rank two, whose columns are in the $\mathbb {C}$
of rank two, whose columns are in the $\mathbb {C}$![]() -linear span of the columns of $A$
-linear span of the columns of $A$![]() .
.
2.3. Voisin's rational map and the involution $\iota$
Proposition 2.4 Voisin [Reference Voisin59]
Let $Y\subset \mathbb {P}^{5}$![]() be a smooth cubic fourfold not containing a plane. Let $F=F(Y)$
be a smooth cubic fourfold not containing a plane. Let $F=F(Y)$![]() be the Fano variety of lines and let $Z=Z(Y)$
be the Fano variety of lines and let $Z=Z(Y)$![]() be the LLSS eightfold of $Y$
be the LLSS eightfold of $Y$![]() . There exists a degree $6$
. There exists a degree $6$![]() dominant rational map
dominant rational map
Moreover, let $\omega _F, \omega _Z$![]() denote the symplectic forms of $F,$
denote the symplectic forms of $F,$![]() respectively $Z$
respectively $Z$![]() . Then we have
. Then we have
$($![]() where $p_j$
where $p_j$![]() denotes projection on the $j$
denotes projection on the $j$![]() th factor$)$
th factor$)$![]() .
.
Proof. This is [Reference Voisin59, Proposition 4.8]. Let us briefly recall the geometric construction of the rational map $\psi$![]() . Let $(l,l') \in F \times F$
. Let $(l,l') \in F \times F$![]() be a generic point, so that the two lines $l, l'$
be a generic point, so that the two lines $l, l'$![]() on $Y$
on $Y$![]() span a three-dimensional linear space in $\mathbb {P}^{5}$
span a three-dimensional linear space in $\mathbb {P}^{5}$![]() . For any point $x \in l$
. For any point $x \in l$![]() , the plane $\langle x, l'\rangle$
, the plane $\langle x, l'\rangle$![]() intersects the smooth cubic surface $S = \langle l, l' \rangle \cap Y$
intersects the smooth cubic surface $S = \langle l, l' \rangle \cap Y$![]() along the union of $l'$
along the union of $l'$![]() and a residual conic $Q'_x$
and a residual conic $Q'_x$![]() , which passes through $x$
, which passes through $x$![]() . Then, $\psi (l,l') \in Z$
. Then, $\psi (l,l') \in Z$![]() is the point corresponding to the two-dimensional linear system of twisted cubics on $S$
is the point corresponding to the two-dimensional linear system of twisted cubics on $S$![]() linearly equivalent to the rational curve $l \cup _x Q'_x$
linearly equivalent to the rational curve $l \cup _x Q'_x$![]() (this linear system actually contains the $\mathbb {P}^{1}$
(this linear system actually contains the $\mathbb {P}^{1}$![]() of curves $\{ l \cup _x Q'_x \mid x \in l\}$
of curves $\{ l \cup _x Q'_x \mid x \in l\}$![]() ).
).
Remark 2.5 The indeterminacy locus of the rational map $\psi$![]() is the codimension $2$
is the codimension $2$![]() locus $I\subset F\times F$
locus $I\subset F\times F$![]() of intersecting lines $($
of intersecting lines $($![]() see [Reference Muratore40, Theorem 1.2]). As proven in [Reference Chen15, Theorem 1.1], the indeterminacy of the rational map $\psi$
see [Reference Muratore40, Theorem 1.2]). As proven in [Reference Chen15, Theorem 1.1], the indeterminacy of the rational map $\psi$![]() is resolved by a blow-up with centre $I\subset F\times F$
is resolved by a blow-up with centre $I\subset F\times F$![]() .
.
Remark 2.6 As is known from unpublished work of Lehn$,$![]() Lehn$,$
Lehn$,$![]() Sorger and van Straten$,$
Sorger and van Straten$,$![]() the LLSS eightfold $Z$
the LLSS eightfold $Z$![]() is equipped with a biholomorphic anti-symplectic involution $\iota \in \operatorname {Aut}(Z)$
is equipped with a biholomorphic anti-symplectic involution $\iota \in \operatorname {Aut}(Z)$![]() $($
$($![]() cf. [Reference Lehn35, Reference Lehn37]) which is induced$,$
cf. [Reference Lehn35, Reference Lehn37]) which is induced$,$![]() via the rational map $\psi : F \times F \dashrightarrow Z,$
via the rational map $\psi : F \times F \dashrightarrow Z,$![]() by the involution of $F \times F$
by the involution of $F \times F$![]() exchanging the two factors. Indeed$,$
exchanging the two factors. Indeed$,$![]() by [Reference Lahoz, Lehn, Macrì and Stellari28, Remark 3.8], the involution $\iota$
by [Reference Lahoz, Lehn, Macrì and Stellari28, Remark 3.8], the involution $\iota$![]() acts on the subset $Z \setminus j(Y)$
acts on the subset $Z \setminus j(Y)$![]() as follows. A point $p \in Z \setminus j(Y)$
as follows. A point $p \in Z \setminus j(Y)$![]() corresponds to a linear determinantal representation $[A]$
corresponds to a linear determinantal representation $[A]$![]() of a smooth cubic surface $S = Y \cap \mathbb {P}^{3},$
of a smooth cubic surface $S = Y \cap \mathbb {P}^{3},$![]() or equivalently to a six of lines $(e_1, \ldots , e_6)$
or equivalently to a six of lines $(e_1, \ldots , e_6)$![]() on $S$
on $S$![]() $($
$($![]() see [Reference Dolgachev17, Section 9.1.2, Reference Buckley and Košir11]). Then, $\iota (p)$
see [Reference Dolgachev17, Section 9.1.2, Reference Buckley and Košir11]). Then, $\iota (p)$![]() is the point of $Z \setminus j(Y)$
is the point of $Z \setminus j(Y)$![]() associated with the $($
associated with the $($![]() unique$)$
unique$)$![]() six $(e'_1, \ldots , e'_6)$
six $(e'_1, \ldots , e'_6)$![]() on the same surface $S$
on the same surface $S$![]() which forms a double-six together with $(e_1, \ldots , e_6)$
which forms a double-six together with $(e_1, \ldots , e_6)$![]() . In terms of linear determinantal representations$,$
. In terms of linear determinantal representations$,$![]() $\iota (p)$
$\iota (p)$![]() corresponds to the transposed representation $[A^{t}]$
corresponds to the transposed representation $[A^{t}]$![]() of the surface $S$
of the surface $S$![]() by [Reference Buckley and Košir11, Proposition 3.2]. It can be checked that$,$
by [Reference Buckley and Košir11, Proposition 3.2]. It can be checked that$,$![]() if $C$
if $C$![]() is a twisted cubic curve on $S$
is a twisted cubic curve on $S$![]() in the linear system parametrized by the point $p,$
in the linear system parametrized by the point $p,$![]() then$,$
then$,$![]() for any quadric $\mathcal {Q} \subset \langle C \rangle$
for any quadric $\mathcal {Q} \subset \langle C \rangle$![]() containing $C,$
containing $C,$![]() the residual intersection $C'$
the residual intersection $C'$![]() of $S$
of $S$![]() with $\mathcal {Q}$
with $\mathcal {Q}$![]() belongs to the fibre $u^{-1}(\iota (p))$
belongs to the fibre $u^{-1}(\iota (p))$![]() (see for instance [Reference Debarre16, Footnote 47]). By the geometric description of the rational map $\psi ,$
(see for instance [Reference Debarre16, Footnote 47]). By the geometric description of the rational map $\psi ,$![]() we conclude that $\iota (\psi (l,l')) = \psi (l',l):$
we conclude that $\iota (\psi (l,l')) = \psi (l',l):$![]() in fact$,$
in fact$,$![]() for $x \in l$
for $x \in l$![]() and $x' \in l',$
and $x' \in l',$![]() the reducible quadric $\mathcal {Q} = \langle x, l'\rangle \cup \langle x', l \rangle$
the reducible quadric $\mathcal {Q} = \langle x, l'\rangle \cup \langle x', l \rangle$![]() intersects the surface $S$
intersects the surface $S$![]() along the union of $l \cup _x Q'_x$
along the union of $l \cup _x Q'_x$![]() and $l' \cup _{x'} Q_{x'}$
and $l' \cup _{x'} Q_{x'}$![]() .
.
2.4. Voisin's orbit filtration
Definition 2.7 Voisin [Reference Voisin59]
Let $X$![]() be a variety of dimension $n$
be a variety of dimension $n$![]() . One defines $S_j X\subset X$
. One defines $S_j X\subset X$![]() as the set of points whose orbit under rational equivalence has dimension $\ge j$
as the set of points whose orbit under rational equivalence has dimension $\ge j$![]() . The descending filtration $S_\ast$
. The descending filtration $S_\ast$![]() on $A^{n}(X)$
on $A^{n}(X)$![]() is defined by letting $S_j A^{n}(X)$
is defined by letting $S_j A^{n}(X)$![]() be the subgroup generated by points $x\in S_j X$
be the subgroup generated by points $x\in S_j X$![]() .
.
Remark 2.8 Let $X$![]() be a hyperkähler variety. As explained in [Reference Voisin59], the expectation is that the filtration $S_\ast$
be a hyperkähler variety. As explained in [Reference Voisin59], the expectation is that the filtration $S_\ast$![]() is opposite to the $($
is opposite to the $($![]() conjectural$)$
conjectural$)$![]() Bloch–Beilinson filtration$,$
Bloch–Beilinson filtration$,$![]() and thus provides a splitting of the Bloch–Beilinson filtration on $A^{n}(X)$
and thus provides a splitting of the Bloch–Beilinson filtration on $A^{n}(X)$![]() $($
$($![]() this is motivated by Beauville's famous speculations in [Reference Beauville4]). This splitting should be ‘natural’, in the sense that it can be defined by correspondences and that it induces a bigrading on the Chow ring of $X$
this is motivated by Beauville's famous speculations in [Reference Beauville4]). This splitting should be ‘natural’, in the sense that it can be defined by correspondences and that it induces a bigrading on the Chow ring of $X$![]() .
.
Definition 2.9 Let $Z$![]() be an LLSS eightfold$,$
be an LLSS eightfold$,$![]() and let $D\subset Z$
and let $D\subset Z$![]() be the uniruled divisor obtained by resolving the indeterminacy locus of the rational map $\psi$
be the uniruled divisor obtained by resolving the indeterminacy locus of the rational map $\psi$![]() of Proposition 2.4. One defines $S_j^\textrm {mob} A^{8}(Z)$
of Proposition 2.4. One defines $S_j^\textrm {mob} A^{8}(Z)$![]() to be the subgroup generated by points in $S_j (Z\setminus D)$
to be the subgroup generated by points in $S_j (Z\setminus D)$![]() .
.
Remark 2.10 There is an inclusion
which possibly is an equality $($![]() this is true when $Z$
this is true when $Z$![]() is birational to a Hilbert scheme of points on a K3 surface$,$
is birational to a Hilbert scheme of points on a K3 surface$,$![]() cf. the proof of Lemma 3.10$)$
cf. the proof of Lemma 3.10$)$![]() . As explained in [Reference Voisin59], the piece $S_3 A^{8}(Z)\cap A^{8}_\textrm {hom}(Z)$
. As explained in [Reference Voisin59], the piece $S_3 A^{8}(Z)\cap A^{8}_\textrm {hom}(Z)$![]() is supposed to be isomorphic to the graded $\hbox {Gr}_{F_{BB}}^{2} A^{8}(Z),$
is supposed to be isomorphic to the graded $\hbox {Gr}_{F_{BB}}^{2} A^{8}(Z),$![]() where $F^{\ast }_{BB}$
where $F^{\ast }_{BB}$![]() is the $($
is the $($![]() conjectural$)$
conjectural$)$![]() Bloch–Beilinson filtration. On the other hand$,$
Bloch–Beilinson filtration. On the other hand$,$![]() the graded $\hbox {Gr}_{F_{BB}}^{2} A^{8}(Z)$
the graded $\hbox {Gr}_{F_{BB}}^{2} A^{8}(Z)$![]() should be defined by the projector $\pi ^{14}_Z$
should be defined by the projector $\pi ^{14}_Z$![]() of some Chow–Künneth decomposition for $Z$
of some Chow–Künneth decomposition for $Z$![]() . In particular$,$
. In particular$,$![]() the expectation is that $S_3^\textrm {mob} A^{8}(Z)$
the expectation is that $S_3^\textrm {mob} A^{8}(Z)$![]() is somehow related to ($H^{14}(Z$
is somehow related to ($H^{14}(Z$![]() ) and hence) $H^{2,0}(Z)$
) and hence) $H^{2,0}(Z)$![]() .
.
2.5. MCK decomposition
Definition 2.11 Murre [Reference Murre41]
Let $X$![]() be a smooth projective variety of dimension $n$
be a smooth projective variety of dimension $n$![]() . We say that $X$
. We say that $X$![]() has a CK decomposition if there exists a decomposition of the diagonal
has a CK decomposition if there exists a decomposition of the diagonal
such that the $\pi _i$![]() are mutually orthogonal idempotents and $(\pi _i)_\ast H^{\ast }(X)= H^{i}(X)$
are mutually orthogonal idempotents and $(\pi _i)_\ast H^{\ast }(X)= H^{i}(X)$![]() .
.
$($![]() NB$:$
NB$:$![]() ‘CK decomposition’ is shorthand for ‘Chow–Künneth decomposition’.)
‘CK decomposition’ is shorthand for ‘Chow–Künneth decomposition’.)
Remark 2.12 The existence of a CK decomposition for any smooth projective variety is part of Murre’s conjectures [Reference Jannsen25, Reference Murre41].
Definition 2.13 Shen–Vial [Reference Shen and Vial49]
Let $X$![]() be a smooth projective variety of dimension $n$
be a smooth projective variety of dimension $n$![]() . Let $\Delta _X^{sm}\in A^{2n}(X\times X\times X)$
. Let $\Delta _X^{sm}\in A^{2n}(X\times X\times X)$![]() be the class of the small diagonal
be the class of the small diagonal
An MCK decomposition is a CK decomposition $\{\pi ^{X}_i\}$![]() of $X$
of $X$![]() that is multiplicative $,$
that is multiplicative $,$![]() i.e. it satisfies
i.e. it satisfies
$($![]() NB$:$
NB$:$![]() ‘MCK decomposition’ is shorthand for ‘multiplicative Chow–Künneth decomposition’.)
‘MCK decomposition’ is shorthand for ‘multiplicative Chow–Künneth decomposition’.)
A weak MCK decomposition is a CK decomposition $\{\pi ^{X}_i\}$![]() of $X$
of $X$![]() that satisfies
that satisfies
Remark 2.14 The small diagonal $($![]() seen as a correspondence from $X\times X$
seen as a correspondence from $X\times X$![]() to $X)$
to $X)$![]() induces the multiplication morphism
induces the multiplication morphism
Suppose $X$![]() has a CK decomposition
has a CK decomposition

By definition$,$![]() this decomposition is multiplicative if for any $i,j$
this decomposition is multiplicative if for any $i,j$![]() the composition
the composition
factors through $h^{i+j}(X)$![]() .
.
If $X$![]() has a weak MCK decomposition$,$
has a weak MCK decomposition$,$![]() then setting
then setting
one obtains a bigraded ring structure on the Chow ring$:$![]() that is$,$
that is$,$![]() the intersection product sends $A^{i}_{(j)}(X)\otimes A^{i^{\prime }}_{(j^{\prime })}(X)$
the intersection product sends $A^{i}_{(j)}(X)\otimes A^{i^{\prime }}_{(j^{\prime })}(X)$![]() to $A^{i+i^{\prime }}_{(j+j^{\prime })}(X)$
to $A^{i+i^{\prime }}_{(j+j^{\prime })}(X)$![]() .
.
It is expected that for any $X$![]() with a weak MCK decomposition$,$
with a weak MCK decomposition$,$![]() one has
one has
this is related to Murre's conjectures B and D that have been formulated for any CK decomposition [Reference Murre41].
The property of having an MCK decomposition is severely restrictive and is closely related to Beauville’s ‘(weak) splitting property’ [Reference Beauville4]. For more ample discussion$,$![]() and examples of varieties with an MCK decomposition, we refer to [Reference Shen and Vial49, Section 8], as well as [Reference Fu, Tian and Vial21, Reference Laterveer and Vial32, Reference Shen and Vial50, Reference Vial54].
and examples of varieties with an MCK decomposition, we refer to [Reference Shen and Vial49, Section 8], as well as [Reference Fu, Tian and Vial21, Reference Laterveer and Vial32, Reference Shen and Vial50, Reference Vial54].
In what follows, we will make use of the following:
Theorem 2.15 Vial [Reference Vial54]
Let $X$![]() be a Hilbert scheme $S^{[m]},$
be a Hilbert scheme $S^{[m]},$![]() where $S$
where $S$![]() is a $K3$
is a $K3$![]() surface. Then $X$
surface. Then $X$![]() has an MCK decomposition. Let $A^{\ast }_{(\ast )}(X)$
has an MCK decomposition. Let $A^{\ast }_{(\ast )}(X)$![]() denote the resulting bigrading. One has
denote the resulting bigrading. One has

where $S_\ast$![]() is Voisin’s orbit filtration $($
is Voisin’s orbit filtration $($![]() Definition 2.7).
Definition 2.7).
The pieces $A^{2m}_{(\ast )}(X)$![]() can be described as follows$:$
can be described as follows$:$![]() $A^{2m}_{(0)}(X)$
$A^{2m}_{(0)}(X)$![]() is generated by $[o,o,\ldots ,o]$
is generated by $[o,o,\ldots ,o]$![]() $($
$($![]() where $o\in A^{2}(S)$
where $o\in A^{2}(S)$![]() is the distinguished $0$
is the distinguished $0$![]() -cycle of [Reference Beauville and Voisin7]). $A^{2m}_{(2)}(X)$
-cycle of [Reference Beauville and Voisin7]). $A^{2m}_{(2)}(X)$![]() is generated by expressions
is generated by expressions
$($![]() where $x,y$
where $x,y$![]() range over all points of $S)$
range over all points of $S)$![]() . $A^{2m}_{(4)}(X)$
. $A^{2m}_{(4)}(X)$![]() is generated by expressions
is generated by expressions
$A^{2m}_{(6)}(X)$![]() is generated by expressions
is generated by expressions
$($![]() And so on$\ldots )$
And so on$\ldots )$![]()
Proof. The MCK decomposition is constructed in [Reference Vial54, Theorem 1] (an alternative construction is given in [Reference Negut, Oberdieck and Yin43]). The compatibility with Voisin's filtration $S_\ast$![]() is stated in [Reference Voisin59, End of Section 4.1]. The formulae for the generators follow from [Reference Voisin59, Theorem 2.5], where it is proven that the filtration $S_\ast$
is stated in [Reference Voisin59, End of Section 4.1]. The formulae for the generators follow from [Reference Voisin59, Theorem 2.5], where it is proven that the filtration $S_\ast$![]() coincides with the filtration $N_\ast$
coincides with the filtration $N_\ast$![]() defined in [Reference Voisin59, Proposition 2.2].
defined in [Reference Voisin59, Proposition 2.2].
(The $m=2$![]() case also follows from [Reference Shen and Vial49].)
case also follows from [Reference Shen and Vial49].)
2.6. Multiplicative behaviour of the Chow ring of $S^{[m]}$
Let $X$![]() be a Hilbert scheme of points on a K3 surface. The following proposition shows that the Chow group of $0$
be a Hilbert scheme of points on a K3 surface. The following proposition shows that the Chow group of $0$![]() -cycles on $X$
-cycles on $X$![]() is completely determined by the piece $A^{2}_{(2)}(X)$
is completely determined by the piece $A^{2}_{(2)}(X)$![]() . (This can be interpreted as a motivic manifestation of the fact that $H^{\ast }(X,\mathcal {O}_X)$
. (This can be interpreted as a motivic manifestation of the fact that $H^{\ast }(X,\mathcal {O}_X)$![]() is determined by $H^{2}(X,\mathcal {O}_X)$
is determined by $H^{2}(X,\mathcal {O}_X)$![]() , since $A^{2}_{(2)}(X)$
, since $A^{2}_{(2)}(X)$![]() is defined by the projector $\pi ^{2}_X$
is defined by the projector $\pi ^{2}_X$![]() ).
).
Proposition 2.16 Let $X$![]() be a Hilbert scheme $X=S^{[m]}$
be a Hilbert scheme $X=S^{[m]}$![]() where $S$
where $S$![]() is a K3 surface$,$
is a K3 surface$,$![]() and let $A^{\ast }_{(\ast )}(X)$
and let $A^{\ast }_{(\ast )}(X)$![]() refer to the bigrading of Theorem 2.15.
refer to the bigrading of Theorem 2.15.
(i) For any $j\ge 1,$
 intersection product induces surjections
\[ A^{2}_{(2)}(X)^{{\otimes} j} \twoheadrightarrow A^{2j}_{(2j)}(X). \]
intersection product induces surjections
\[ A^{2}_{(2)}(X)^{{\otimes} j} \twoheadrightarrow A^{2j}_{(2j)}(X). \]
(ii) Let $h\in A^{1}(X)$
 be a big divisor. For any $j\ge 0$
be a big divisor. For any $j\ge 0$ there are isomorphisms
\[{\cdot} h^{2m-j}\colon A^{j}_{(j)}(X) \xrightarrow{\cong} A^{2m}_{(j)}(X). \]
there are isomorphisms
\[{\cdot} h^{2m-j}\colon A^{j}_{(j)}(X) \xrightarrow{\cong} A^{2m}_{(j)}(X). \]
Proof. (i) Let us just treat the case $j=2$![]() (the other cases are only notationally more complicated). Let us write $A^{\ast }(S^{m})^{\mathfrak S_m}$
(the other cases are only notationally more complicated). Let us write $A^{\ast }(S^{m})^{\mathfrak S_m}$![]() for the $\mathfrak S_m$
for the $\mathfrak S_m$![]() -invariant part, where the symmetric group on $m$
-invariant part, where the symmetric group on $m$![]() elements $\mathfrak S_m$
elements $\mathfrak S_m$![]() acts on $S^{m}$
acts on $S^{m}$![]() by permutation of the factors. We need to show that the map induced by intersection product
by permutation of the factors. We need to show that the map induced by intersection product
is surjective. By definition, an element $a$![]() on the right-hand side is a symmetric cycle of the form
on the right-hand side is a symmetric cycle of the form
(where $d\in A^{4}(S^{m})$![]() ). That is,
). That is,
where $a_1, a_2\in A^{2}(S)$![]() are degree zero $0$
are degree zero $0$![]() -cycles.
-cycles.
Let us define

We have that
is a non-zero multiple of $a$![]() , and so we have proven surjectivity.
, and so we have proven surjectivity.
(ii) Again, one reduces to the Cartesian product $S^{m}$![]() . That is, one considers
. That is, one considers

where $f$![]() is the Hilbert–Chow morphism and $p$
is the Hilbert–Chow morphism and $p$![]() is the quotient morphism.
is the quotient morphism.
There is a commutative diagram

in which composition of two vertical arrows on the left respectively on the right is an isomorphism (NB: the commutativity of the upper square follows from the projection formula).
Thus, it will suffice to prove that for a big $\mathfrak S_m$![]() -invariant divisor $h$
-invariant divisor $h$![]() on $S^{m}$
on $S^{m}$![]() , there are isomorphisms
, there are isomorphisms
The case $j=2$![]() is proven in [Reference Laterveer31, Theorem 3.1]; the general case is only notationally more complicated.
is proven in [Reference Laterveer31, Theorem 3.1]; the general case is only notationally more complicated.
Remark 2.17 The $m=2$![]() case of Proposition 2.16 is already proven in [Reference Shen and Vial49].
case of Proposition 2.16 is already proven in [Reference Shen and Vial49].
2.7. Birational hyperkähler varieties
Theorem 2.18 Rieß [Reference Rieß47]
Let $\phi \colon X\dashrightarrow X^{\prime }$![]() be a birational map between two hyperKähler varieties of dimension $n$
be a birational map between two hyperKähler varieties of dimension $n$![]() .
.
(i) There exists a correspondence $R_\phi \in A^{n}(X\times X^{\prime })$
 such that
\[ (R_\phi)_\ast \colon A^{{\ast}}(X) \to A^{{\ast}}(X^{\prime}) \]is a graded ring isomorphism.
such that
\[ (R_\phi)_\ast \colon A^{{\ast}}(X) \to A^{{\ast}}(X^{\prime}) \]is a graded ring isomorphism.
(ii) For any $j,$
 there is equality
\[ (R_\phi)_\ast c_j(X)= c_j(X^{\prime})\quad \hbox{ in}\ A^{j}(X^{\prime}). \]
there is equality
\[ (R_\phi)_\ast c_j(X)= c_j(X^{\prime})\quad \hbox{ in}\ A^{j}(X^{\prime}). \]
(iii) There is equality
\[ (\Gamma_R)_\ast=(\bar{\Gamma}_\phi)_\ast\colon A^{j}(X) \to A^{j}(X^{\prime})\quad \hbox{for}\ j=0,1,\ n-1, n \]$($
 where $\bar {\Gamma }_\phi$
where $\bar {\Gamma }_\phi$ denotes the closure of the graph of $\phi )$
denotes the closure of the graph of $\phi )$ .
.
Proof. Item (i) is [Reference Rieß47, Theorem 3.2], while item (ii) is [Reference Rieß47, Lemma 4.4].
In a nutshell, the construction of the correspondence $R_\phi$![]() is as follows: [Reference Rieß47, Section 2] provides a diagram
is as follows: [Reference Rieß47, Section 2] provides a diagram

where $\mathcal {X}, \mathcal {X}^{\prime }$![]() are algebraic spaces over a quasi-projective curve $C$
are algebraic spaces over a quasi-projective curve $C$![]() such that the fibres $\mathcal {X}_0, \mathcal {X}^{\prime }_0$
such that the fibres $\mathcal {X}_0, \mathcal {X}^{\prime }_0$![]() are isomorphic to $X$
are isomorphic to $X$![]() respectively $X^{\prime }$
respectively $X^{\prime }$![]() , and where $\Psi \colon \mathcal {X} \dashrightarrow \mathcal {X}^{\prime }$
, and where $\Psi \colon \mathcal {X} \dashrightarrow \mathcal {X}^{\prime }$![]() is a birational map inducing an isomorphism $\mathcal {X}_{C\setminus 0}\cong \mathcal {X}^{\prime }_{C\setminus 0}$
is a birational map inducing an isomorphism $\mathcal {X}_{C\setminus 0}\cong \mathcal {X}^{\prime }_{C\setminus 0}$![]() and whose restriction $\Psi \vert _{\mathcal {X}_0}$
and whose restriction $\Psi \vert _{\mathcal {X}_0}$![]() coincides with $\phi$
coincides with $\phi$![]() . The correspondence $R_\phi$
. The correspondence $R_\phi$![]() is then defined as the specialization (in the sense of [Reference Fulton22], extended to algebraic spaces) of the graphs of the isomorphisms $\mathcal {X}_c\cong \mathcal {X}^{\prime }_c$
is then defined as the specialization (in the sense of [Reference Fulton22], extended to algebraic spaces) of the graphs of the isomorphisms $\mathcal {X}_c\cong \mathcal {X}^{\prime }_c$![]() , $c\not =0$
, $c\not =0$![]() .
.
Point (iii) is not stated explicitly in [Reference Rieß47], and can be seen as follows. Let $U\subset X$![]() be the locus on which $\phi$
be the locus on which $\phi$![]() induces an isomorphism. The complement $T:=X\setminus U$
induces an isomorphism. The complement $T:=X\setminus U$![]() has codimension $\ge 2$
has codimension $\ge 2$![]() . Using complete intersections of hypersurfaces, one can find a closed subset $\mathcal {T}\subset \mathcal {X}$
. Using complete intersections of hypersurfaces, one can find a closed subset $\mathcal {T}\subset \mathcal {X}$![]() of codimension $2$
of codimension $2$![]() such that $\mathcal {T}_0$
such that $\mathcal {T}_0$![]() contains $T$
contains $T$![]() , i.e. $\Psi$
, i.e. $\Psi$![]() restricts to an isomorphism on $V:=\mathcal {X}_0\setminus \mathcal {T}_0$
restricts to an isomorphism on $V:=\mathcal {X}_0\setminus \mathcal {T}_0$![]() . Since specialization commutes with pullback, the restriction of $R_\phi$
. Since specialization commutes with pullback, the restriction of $R_\phi$![]() to $V\times X^{\prime }$
to $V\times X^{\prime }$![]() is the specialization of the graphs of the morphisms $\mathcal {X}_c\setminus \mathcal {T}_c\to \mathcal {X}^{\prime }_c$
is the specialization of the graphs of the morphisms $\mathcal {X}_c\setminus \mathcal {T}_c\to \mathcal {X}^{\prime }_c$![]() , $c\not =0$
, $c\not =0$![]() to $V\times X^{\prime }$
to $V\times X^{\prime }$![]() , which is exactly the graph of the morphism $\phi \vert _V$
, which is exactly the graph of the morphism $\phi \vert _V$![]() , i.e.
, i.e.
It follows that one has
where $\gamma$![]() is some cycle supported on $\mathcal {T}_0\times X^{\prime }$
is some cycle supported on $\mathcal {T}_0\times X^{\prime }$![]() . This proves point $(iii)$
. This proves point $(iii)$![]() : $0$
: $0$![]() -cycles and $1$
-cycles and $1$![]() -cycles on $X$
-cycles on $X$![]() can be moved to be disjoint of $\mathcal {T}_0$
can be moved to be disjoint of $\mathcal {T}_0$![]() , and so $\gamma _\ast$
, and so $\gamma _\ast$![]() acts as zero on $A^{j}(X)$
acts as zero on $A^{j}(X)$![]() for $j\ge n-1$
for $j\ge n-1$![]() . Likewise, $\gamma ^{\ast }$
. Likewise, $\gamma ^{\ast }$![]() acts as zero on $A^{j}(X^{\prime })$
acts as zero on $A^{j}(X^{\prime })$![]() for $j\le 1$
for $j\le 1$![]() for dimension reasons, and so (by inverting the roles of $X$
for dimension reasons, and so (by inverting the roles of $X$![]() and $X^{\prime }$
and $X^{\prime }$![]() ) statement $(iii)$
) statement $(iii)$![]() is proven.
is proven.
Remark 2.19 As observed in [Reference Vial54, Introduction], the correspondence $R_\phi$![]() of Theorem 2.18 actually induces an isomorphism of Chow motives as $\mathbb {Q}$
of Theorem 2.18 actually induces an isomorphism of Chow motives as $\mathbb {Q}$![]() -algebra objects. This implies that the property ‘having a MCK decomposition’ is birationally invariant among hyperkähler varieties.
-algebra objects. This implies that the property ‘having a MCK decomposition’ is birationally invariant among hyperkähler varieties.
2.8. The Franchetta property
An important role in this paper is played by the Franchetta property. In a nutshell, a family of varieties has the Franchetta property if algebraic cycles that exist for all members of the family are well behaved. This is relevant here, because the graph of the anti-symplectic involution of an LLSS eightfold is such a cycle: it exists for all members of the locally complete family of LLSS eightfolds.
Definition 2.21 Let $\mathcal {X}\to B$![]() be some family of smooth projective varieties $X_b,$
be some family of smooth projective varieties $X_b,$![]() $b\in B$
$b\in B$![]() . We say that $\mathcal {X}\to B$
. We say that $\mathcal {X}\to B$![]() has the Franchetta property if for any $a\in A^{i}( \mathcal {X})$
has the Franchetta property if for any $a\in A^{i}( \mathcal {X})$![]() and for any $b\in B,$
and for any $b\in B,$![]() there is equivalence
there is equivalence
This property is studied in [Reference O'Grady44, Reference Pavic, Shen and Yin46] for the universal family of $K3$![]() surfaces of low genus. This is extended to certain families of hyperkähler varieties in [Reference Fu, Laterveer and Vial18, Reference Fu, Laterveer and Vial20].
surfaces of low genus. This is extended to certain families of hyperkähler varieties in [Reference Fu, Laterveer and Vial18, Reference Fu, Laterveer and Vial20].
Proposition 2.22 Let $\mathcal {Y}\to B$![]() denote the universal family of smooth cubic fourfolds$,$
denote the universal family of smooth cubic fourfolds$,$![]() where $B$
where $B$![]() is a Zariski open in $\mathbb {P}^{55}$
is a Zariski open in $\mathbb {P}^{55}$![]() . The Franchetta property holds for
. The Franchetta property holds for
Proof. Let $\Gamma \in A^{4}(\mathcal {Y}\times _B \mathcal {Y})$![]() be a correspondence that is homologically trivial when restricted to the very general fibre. According to [Reference Voisin58, Proposition 1.6] (cf. also [Reference Laterveer, Nagel and Peters34, Proposition 5.1], where the precise form of Voisin's argument applied here is detailed), there exists a cycle $\gamma \in A^{4}(\mathbb {P}^{5}\times \mathbb {P}^{5})$
be a correspondence that is homologically trivial when restricted to the very general fibre. According to [Reference Voisin58, Proposition 1.6] (cf. also [Reference Laterveer, Nagel and Peters34, Proposition 5.1], where the precise form of Voisin's argument applied here is detailed), there exists a cycle $\gamma \in A^{4}(\mathbb {P}^{5}\times \mathbb {P}^{5})$![]() such that
such that
The cycle $\gamma$![]() is of the form $\sum \nolimits _{j=0}^{4} c_j h^{j}\times h^{4-j}$
is of the form $\sum \nolimits _{j=0}^{4} c_j h^{j}\times h^{4-j}$![]() , where $h\in A^{1}(\mathbb {P}^{5})$
, where $h\in A^{1}(\mathbb {P}^{5})$![]() is a hyperplane section and $c_j\in \mathbb {Q}$
is a hyperplane section and $c_j\in \mathbb {Q}$![]() . The assumptions imply that $\gamma \vert _b$
. The assumptions imply that $\gamma \vert _b$![]() is homologically trivial for $b\in B$
is homologically trivial for $b\in B$![]() very general. Since the summands $(h^{j}\times h^{4-j})\vert _b$
very general. Since the summands $(h^{j}\times h^{4-j})\vert _b$![]() live in different summands of the Künneth decomposition of $H^{8}(Y_b\times Y_b)$
live in different summands of the Künneth decomposition of $H^{8}(Y_b\times Y_b)$![]() , each $c_j (h^{j}\times h^{4-j})\vert _b$
, each $c_j (h^{j}\times h^{4-j})\vert _b$![]() must be homologically trivial, which is only possible when $c_j=0$
must be homologically trivial, which is only possible when $c_j=0$![]() , and so $\gamma =0$
, and so $\gamma =0$![]() .
.
Remark 2.23 Using the Franchetta property for $\mathcal {F}\times _B \mathcal {F}$![]() $($
$($![]() where $\mathcal {F}$
where $\mathcal {F}$![]() is the universal Fano variety of lines in a cubic fourfold$)$
is the universal Fano variety of lines in a cubic fourfold$)$![]() [Reference Fu, Laterveer and Vial18], it is possible to prove that $\mathcal {Y}\times _B \mathcal {Y}\to B$
[Reference Fu, Laterveer and Vial18], it is possible to prove that $\mathcal {Y}\times _B \mathcal {Y}\to B$![]() $($
$($![]() and also $\mathcal {Y}^{(2)}\times _B \mathcal {Y}^{(2)}\to B)$
and also $\mathcal {Y}^{(2)}\times _B \mathcal {Y}^{(2)}\to B)$![]() has the Franchetta property in all codimensions. We will not need this generality here.
has the Franchetta property in all codimensions. We will not need this generality here.
2.9. The transcendental motive of a cubic fourfold
Proposition 2.24 Bolognesi and Pedrini [Reference Bolognesi and Pedrini10]
Let $Y\subset \mathbb {P}^{5}$![]() be a smooth cubic fourfold. There exists a Chow motive $t(Y)\in \mathcal {M}_\textrm {rat},$
be a smooth cubic fourfold. There exists a Chow motive $t(Y)\in \mathcal {M}_\textrm {rat},$![]() with the property that
with the property that

$($![]() where $H^{4}_{tr}(Y)$
where $H^{4}_{tr}(Y)$![]() denotes the orthogonal complement of the algebraic classes with respect to cup-product$)$
denotes the orthogonal complement of the algebraic classes with respect to cup-product$)$![]() .
.
Proof. The construction, which is a variant of the construction of the transcendental motive of a surface [Reference Kahn, Murre and Pedrini26], is done in [Reference Bolognesi and Pedrini10, Section 2]. Alternatively, one can use the projectors on the algebraic part of cohomology constructed for any variety satisfying the standard conjectures in [Reference Vial53].
3. Main results
For any LLSS eightfold $Z$![]() , we construct (Theorem 3.1) a Chow motive $t(Z)$
, we construct (Theorem 3.1) a Chow motive $t(Z)$![]() which is responsible for one piece of Voisin's orbit filtration on the Chow group of zero-cycles, i.e. the motive $t(Z)$
which is responsible for one piece of Voisin's orbit filtration on the Chow group of zero-cycles, i.e. the motive $t(Z)$![]() determines $S_3^\textrm {mob} A^{8}(Z)\cap A^{8}_\textrm {hom}(Z)$
determines $S_3^\textrm {mob} A^{8}(Z)\cap A^{8}_\textrm {hom}(Z)$![]() . Using this construction, we can show (Theorem 3.7) that the anti-symplectic involution $\iota$
. Using this construction, we can show (Theorem 3.7) that the anti-symplectic involution $\iota$![]() acts as $-\operatorname {id}$
acts as $-\operatorname {id}$![]() on this piece $S_3^\textrm {mob} A^{8}(Z)\cap A^{8}_\textrm {hom}(Z)$
on this piece $S_3^\textrm {mob} A^{8}(Z)\cap A^{8}_\textrm {hom}(Z)$![]() . Next, we restrict to LLSS eightfolds birational to Hilbert schemes, where we have an MCK decomposition. Using the good properties of the MCK decomposition, we deduce (Theorems 3.9 and 3.11) that the involution $\iota$
. Next, we restrict to LLSS eightfolds birational to Hilbert schemes, where we have an MCK decomposition. Using the good properties of the MCK decomposition, we deduce (Theorems 3.9 and 3.11) that the involution $\iota$![]() acts on zero-cycles in the expected way.
acts on zero-cycles in the expected way.
3.1. An isomorphism of motives
Theorem 3.1 Let $Z=Z(Y)$![]() be an LLSS eightfold$,$
be an LLSS eightfold$,$![]() where $Y\subset \mathbb {P}^{5}$
where $Y\subset \mathbb {P}^{5}$![]() is any smooth cubic not containing a plane. There exists a motive $t(Z)\in \mathcal {M}_\textrm {rat}$
is any smooth cubic not containing a plane. There exists a motive $t(Z)\in \mathcal {M}_\textrm {rat}$![]() with the property that
with the property that
There is an isomorphism of motives
inducing$,$![]() in particular$,$
in particular$,$![]() an isomorphism of $\mathbb {Q}$
an isomorphism of $\mathbb {Q}$![]() -vector spaces
-vector spaces
Proof. Let us write $F:=F(Y)$![]() for the Fano variety of lines, and $P\in A^{3}(F\times Y)$
for the Fano variety of lines, and $P\in A^{3}(F\times Y)$![]() for the universal line. We define a correspondence
for the universal line. We define a correspondence
where $\psi \colon F\times F\dashrightarrow Z$![]() is Voisin's rational map, and $p_j\colon F\times F\to F$
is Voisin's rational map, and $p_j\colon F\times F\to F$![]() is projection to the $j$
is projection to the $j$![]() th factor. The correspondence $Q$
th factor. The correspondence $Q$![]() has the following property:
has the following property:
Claim 3.2 Let $h\in A^{1}(Z)$![]() be the polarization. There exists a constant $c_h\in \mathbb {Q}^{\ast }$
be the polarization. There exists a constant $c_h\in \mathbb {Q}^{\ast }$![]() such that
such that
$($![]() Here $\Gamma _{h^{6}}:=\Gamma _\tau \circ {}^{t} \Gamma _\tau \in A^{14}(Z\times Z),$
Here $\Gamma _{h^{6}}:=\Gamma _\tau \circ {}^{t} \Gamma _\tau \in A^{14}(Z\times Z),$![]() where $\tau \colon {S}\to Z$
where $\tau \colon {S}\to Z$![]() is the inclusion of a smooth complete intersection surface $S\subset Z$
is the inclusion of a smooth complete intersection surface $S\subset Z$![]() cut out by $h.)$
cut out by $h.)$![]()
In particular$,$![]() the composition
the composition
is the identity.
Admitting the claim, the theorem is readily proven: one defines the motive $t(Z)$![]() by the projector
by the projector
The claim implies that $\pi ^{tr}_Z$![]() is idempotent, and that
is idempotent, and that
is an isomorphism, with inverse
The isomorphism of motives $t(Z)\cong t(Y)(-5)$![]() implies that $A^{\ast }(t(Z))=A^{3}(t(Z))$
implies that $A^{\ast }(t(Z))=A^{3}(t(Z))$![]() . To determine $A^{3}(t(Z))$
. To determine $A^{3}(t(Z))$![]() , we use the relation with the Fano variety of lines $F:=F(Y)$
, we use the relation with the Fano variety of lines $F:=F(Y)$![]() via Voisin's rational map $\psi$
via Voisin's rational map $\psi$![]() . Indeed, by construction we have
. Indeed, by construction we have
Now, there are equalities

Here, the first equality is by definition of $Q$![]() . The second equality is the fact that $P^{\ast } A^{3}_\textrm {hom}(Y)=A^{2}_{(2)}(F)$
. The second equality is the fact that $P^{\ast } A^{3}_\textrm {hom}(Y)=A^{2}_{(2)}(F)$![]() (indeed, $A^{2}_{(2)}(F)=P^{\ast } P_\ast A^{4}_\textrm {hom}(F)$
(indeed, $A^{2}_{(2)}(F)=P^{\ast } P_\ast A^{4}_\textrm {hom}(F)$![]() [Reference Shen and Vial49, Proof of Proposition 21.10], and $P_\ast A^{4}_\textrm {hom}(F)=A^{3}_\textrm {hom}(Y)$
[Reference Shen and Vial49, Proof of Proposition 21.10], and $P_\ast A^{4}_\textrm {hom}(F)=A^{3}_\textrm {hom}(Y)$![]() , since $A^{3}(Y)$
, since $A^{3}(Y)$![]() is generated by lines [Reference Paranjape45]). For the third equality, one observes that $H^{1}(F,\mathbb {Q})=0$
is generated by lines [Reference Paranjape45]). For the third equality, one observes that $H^{1}(F,\mathbb {Q})=0$![]() and so the big line bundle $\psi ^{\ast }(h)\in A^{1}(F\times F)$
and so the big line bundle $\psi ^{\ast }(h)\in A^{1}(F\times F)$![]() can be written $\psi ^{\ast }(h)=(p_1)^{\ast }(\ell _1)+(p_2)^{\ast }(\ell _2)$
can be written $\psi ^{\ast }(h)=(p_1)^{\ast }(\ell _1)+(p_2)^{\ast }(\ell _2)$![]() with $\ell _j\in A^{1}(F)$
with $\ell _j\in A^{1}(F)$![]() big and universally defined. Since the very general $F$
big and universally defined. Since the very general $F$![]() has Picard number 1, the $\ell _j$
has Picard number 1, the $\ell _j$![]() must be non-zero multiples of the polarization class of $F$
must be non-zero multiples of the polarization class of $F$![]() . Hence, one has isomorphisms $A^{2}_{(2)}(F)\xrightarrow {\cdot \ell _j^{2}} A^{4}_{(2)}(F)$
. Hence, one has isomorphisms $A^{2}_{(2)}(F)\xrightarrow {\cdot \ell _j^{2}} A^{4}_{(2)}(F)$![]() [Reference Shen and Vial49, Proposition 22.2] and surjections
[Reference Shen and Vial49, Proposition 22.2] and surjections
(hard Lefschetz), which proves the third equality. The fourth equality is an application of [Reference Voisin59, Proposition 4.5]. For the last equality, one notes that $S_1 A^{4}(F)$![]() is generated by points lying on a uniruled divisor, and $S_2 A^{4}(F)$
is generated by points lying on a uniruled divisor, and $S_2 A^{4}(F)$![]() is generated by points on the constant cycle surfaces constructed by Voisin [Reference Voisin59, Proposition 4.4]; since one can find a uniruled divisor $D$
is generated by points on the constant cycle surfaces constructed by Voisin [Reference Voisin59, Proposition 4.4]; since one can find a uniruled divisor $D$![]() and a constant cycle surface $S$
and a constant cycle surface $S$![]() such that $D\times S$
such that $D\times S$![]() is in general position with respect to the indeterminacy locus of $\psi$
is in general position with respect to the indeterminacy locus of $\psi$![]() , this gives the last equality.
, this gives the last equality.
Altogether, this proves that
It only remains to prove Claim 3.2, i.e. we need to prove the vanishing
Let $\pi ^\textrm {prim}_Y\in A^{4}(Y\times Y)$![]() be the projector defined as
be the projector defined as

Since $H^{2,2}(Y,\mathbb {Q})$![]() is one-dimensional for a very general cubic $Y$
is one-dimensional for a very general cubic $Y$![]() , there is equality $\pi ^{tr}_Y=\pi ^\textrm {prim}_Y$
, there is equality $\pi ^{tr}_Y=\pi ^\textrm {prim}_Y$![]() for very general $Y$
for very general $Y$![]() . Since $(Y,\pi _Y^{tr},0)$
. Since $(Y,\pi _Y^{tr},0)$![]() is a submotive of $(Y,\pi _Y^\textrm {prim},0)$
is a submotive of $(Y,\pi _Y^\textrm {prim},0)$![]() , it suffices to prove the vanishing
, it suffices to prove the vanishing
for all smooth cubic fourfolds $Y$![]() . But this cycle is universally defined (i.e., it is the restriction of a cycle in $A^{4}(\mathcal {Y}\times _B \mathcal {Y})$
. But this cycle is universally defined (i.e., it is the restriction of a cycle in $A^{4}(\mathcal {Y}\times _B \mathcal {Y})$![]() , where $\mathcal {Y}\to B$
, where $\mathcal {Y}\to B$![]() is the universal family of cubic fourfolds as in Proposition 2.22). Hence, thanks to the Franchetta property (Proposition 2.22) one is reduced to showing the vanishing
is the universal family of cubic fourfolds as in Proposition 2.22). Hence, thanks to the Franchetta property (Proposition 2.22) one is reduced to showing the vanishing
for the very general cubic $Y$![]() .
.
To prove the vanishing (3), we proceed as follows:
Lemma 3.3 Let $Y\subset \mathbb {P}^{5}$![]() be any smooth cubic. There exists a non-zero constant ${ c_h}$
be any smooth cubic. There exists a non-zero constant ${ c_h}$![]() such that
such that
Proof. Since $H^{4}_{tr}(Y)$![]() is the smallest Hodge structure for which the complexification contains $H^{3,1}(Y)\cong \mathbb {C}$
is the smallest Hodge structure for which the complexification contains $H^{3,1}(Y)\cong \mathbb {C}$![]() , it suffices to prove there is a non-zero constant ${ c_h}$
, it suffices to prove there is a non-zero constant ${ c_h}$![]() such that
such that
By definition of $Q$![]() , it suffices to prove there is a non-zero constant $c_h$
, it suffices to prove there is a non-zero constant $c_h$![]() making the following diagram commute:
making the following diagram commute:

(Here $h_F\in A^{1}(F)$![]() denotes a polarization,)
denotes a polarization,)
The left square of this diagram is well known to be commutative (essentially this is the Abel–Jacobi isomorphism established in [Reference Beauville and Donagi6]). To see that the right-hand square of this diagram commutes, we observe that thanks to Proposition 2.4, we have a relation $\widetilde {\psi }^{\ast }(\omega _Z)=\widetilde {p_1}^{\ast }(\omega _F)-\widetilde {p_2}^{\ast }(\omega _F)$![]() . This implies that the top horizontal line is an isomorphism: more precisely, the composition $\psi _\ast (p_1^{\ast } -p_2^{\ast })$
. This implies that the top horizontal line is an isomorphism: more precisely, the composition $\psi _\ast (p_1^{\ast } -p_2^{\ast })$![]() sends $\omega _F$
sends $\omega _F$![]() to $6\omega _Z\in H^{2,0}(Z)$
to $6\omega _Z\in H^{2,0}(Z)$![]() . Let $\omega _Z^{\vee }\in H^{6,8}(Z)$
. Let $\omega _Z^{\vee }\in H^{6,8}(Z)$![]() be the class dual to $\omega _Z$
be the class dual to $\omega _Z$![]() under cup product, and let $\bar {\omega }_Z^{\vee }\in H^{8,6}(Z)$
under cup product, and let $\bar {\omega }_Z^{\vee }\in H^{8,6}(Z)$![]() be its complex conjugate. By hard Lefschetz, we know that $\omega _Z\cdot h^{6}\in H^{8,6}(Z)$
be its complex conjugate. By hard Lefschetz, we know that $\omega _Z\cdot h^{6}\in H^{8,6}(Z)$![]() is a rational multiple of the class $\bar {\omega }_Z^{\vee }$
is a rational multiple of the class $\bar {\omega }_Z^{\vee }$![]() . By duality, the composition $((p_1)_\ast -(p_2)_\ast ) \psi ^{\ast }$
. By duality, the composition $((p_1)_\ast -(p_2)_\ast ) \psi ^{\ast }$![]() sends $\omega _Z^{\vee }\in H^{6,8}(Z)$
sends $\omega _Z^{\vee }\in H^{6,8}(Z)$![]() to ${1\over 6}\omega _F^{\vee }\in H^{0,2}(F)$
to ${1\over 6}\omega _F^{\vee }\in H^{0,2}(F)$![]() , and so $\bar {\omega }_Z^{\vee }\in H^{6,8}(Z)$
, and so $\bar {\omega }_Z^{\vee }\in H^{6,8}(Z)$![]() is sent to ${1\over 6}\bar {\omega }_F^{\vee }\in H^{0,2}(F)$
is sent to ${1\over 6}\bar {\omega }_F^{\vee }\in H^{0,2}(F)$![]() . Using hard Lefschetz on $F$
. Using hard Lefschetz on $F$![]() , we can rescale $h_F$
, we can rescale $h_F$![]() by some rational multiple to make the right-hand square commutative. This proves Lemma 3.3.
by some rational multiple to make the right-hand square commutative. This proves Lemma 3.3.
Lemma 3.3 implies that one can write
where $\gamma$![]() is a completely decomposed cycle, i.e. a cycle supported on a finite union of subvarieties $V_i\times W_i\subset Y\times Y$
is a completely decomposed cycle, i.e. a cycle supported on a finite union of subvarieties $V_i\times W_i\subset Y\times Y$![]() , with $\dim V_i+\dim W_i=4$
, with $\dim V_i+\dim W_i=4$![]() . Since the composition of the completely decomposed cycle $\gamma$
. Since the composition of the completely decomposed cycle $\gamma$![]() with $\pi ^\textrm {prim}_Y$
with $\pi ^\textrm {prim}_Y$![]() is zero (for any smooth cubic $Y$
is zero (for any smooth cubic $Y$![]() ), this implies the necessary vanishing (3), and so the theorem is proven.
), this implies the necessary vanishing (3), and so the theorem is proven.
Remark 3.4 For cyclic cubic fourfolds $($![]() i.e. cubic fourfolds of the form $f(x_0,\ldots ,x_4)+ x_5^{3}=0),$
i.e. cubic fourfolds of the form $f(x_0,\ldots ,x_4)+ x_5^{3}=0),$![]() a statement similar to Theorem 3.1 was proven in [Reference Camere, Cattaneo and Laterveer13, Proposition 3.7].
a statement similar to Theorem 3.1 was proven in [Reference Camere, Cattaneo and Laterveer13, Proposition 3.7].
We also define the corresponding piece in the codimension $2$![]() Chow group of $Z$
Chow group of $Z$![]() :
:
Definition 3.5 For any LLSS eightfold $Z,$![]() let
let
$($![]() where $Q$
where $Q$![]() is as in (2)).
is as in (2)).
The piece $A^{2}_{[2]}(Z)$![]() is likely to coincide with $A^{2}_\textrm {hom}(Z)$
is likely to coincide with $A^{2}_\textrm {hom}(Z)$![]() , although this seems hard to prove (just as it is hard to prove that the inclusion $A^{2}_{(2)}(F(Y))\subset A^{2}_\textrm {hom}(F(Y))$
, although this seems hard to prove (just as it is hard to prove that the inclusion $A^{2}_{(2)}(F(Y))\subset A^{2}_\textrm {hom}(F(Y))$![]() is an equality, cf. [Reference Shen and Vial49]).
is an equality, cf. [Reference Shen and Vial49]).
Proposition 3.6 Let $Y\subset \mathbb {P}^{5}$![]() be a smooth cubic not containing a plane$,$
be a smooth cubic not containing a plane$,$![]() and let $F:=F(Y)$
and let $F:=F(Y)$![]() and $Z:=Z(Y)$
and $Z:=Z(Y)$![]() be the Fano variety of lines$,$
be the Fano variety of lines$,$![]() respectively the associated LLSS eightfold.
respectively the associated LLSS eightfold.
(i) The projector ${}^{t} \pi ^{tr}_Z\in A^{8}(Z\times Z)$
 has the property that
\[ ({}^{t} \pi^{tr}_Z)_\ast A^{{\ast}}(Z) = A^{2}_{[2]}(Z). \]
has the property that
\[ ({}^{t} \pi^{tr}_Z)_\ast A^{{\ast}}(Z) = A^{2}_{[2]}(Z). \]
(ii) There is an isomorphism
\[{\cdot} h^{6}\colon A^{2}_{[2]}(Z) \xrightarrow{\cong} S_3^\textrm{mob} A^{8}(Z)\cap A^{8}_\textrm{hom}(Z) \]$($
 In particular$,$
In particular$,$ there is a correspondence-induced isomorphism $A^{2}_{[2]}(Z)\cong A^{3}_\textrm {hom}(Y)).$
there is a correspondence-induced isomorphism $A^{2}_{[2]}(Z)\cong A^{3}_\textrm {hom}(Y)).$
Proof. (i) Claim 3.2 guarantees that
is idempotent, and that
is an isomorphism, with inverse $c_h {}^{t} Q\circ \Gamma _{h^{6}}$![]() . It follows that
. It follows that
and
(ii) This is immediate from the proof of Theorem 3.1, where it is shown that
3.2. The anti-symplectic involution and $0$ -cycles
-cycles
Theorem 3.7 Let $Z=Z(Y)$![]() be an LLSS eightfold$,$
be an LLSS eightfold$,$![]() where $Y\subset \mathbb {P}^{5}$
where $Y\subset \mathbb {P}^{5}$![]() is any smooth cubic not containing a plane. Let $\iota \in \operatorname {Aut}(Z)$
is any smooth cubic not containing a plane. Let $\iota \in \operatorname {Aut}(Z)$![]() be the anti-symplectic involution; Then
be the anti-symplectic involution; Then

Proof. Let $F=F(Y)$![]() be the Fano variety of lines in $Y$
be the Fano variety of lines in $Y$![]() . Via Voisin's rational map, one sees as in [Reference Voisin59] that $S_4A^{8}_{}(Z)$
. Via Voisin's rational map, one sees as in [Reference Voisin59] that $S_4A^{8}_{}(Z)$![]() is one-dimensional with generator $\psi _\ast (o_F\times o_F)$
is one-dimensional with generator $\psi _\ast (o_F\times o_F)$![]() , where $o_F\in A^{4}_{(0)}(F)=S_2 A^{4}(F)$
, where $o_F\in A^{4}_{(0)}(F)=S_2 A^{4}(F)$![]() is the distinguished zero-cycle of [Reference Shen and Vial49]. There is a commutative diagram
is the distinguished zero-cycle of [Reference Shen and Vial49]. There is a commutative diagram

where $\iota _F$![]() is the map exchanging the two factors [Reference Camere, Cattaneo and Laterveer13, Remark 2.19]. Since $o_F\times o_F$
is the map exchanging the two factors [Reference Camere, Cattaneo and Laterveer13, Remark 2.19]. Since $o_F\times o_F$![]() is invariant under $\iota _F$
is invariant under $\iota _F$![]() , it follows that $\iota$
, it follows that $\iota$![]() acts as the identity on $S_4 A^{8}_{}(Z)$
acts as the identity on $S_4 A^{8}_{}(Z)$![]() .
.
To prove the statement for $S_3^\textrm {mob} A^{8}(Z)\cap A^{8}_\textrm {hom}(Z)$![]() , let us first ensure that $\iota _\ast$
, let us first ensure that $\iota _\ast$![]() preserves this subgroup:
preserves this subgroup:
Lemma 3.8 We have
Proof. Clearly, the involution $\iota$![]() preserves $S_\ast$
preserves $S_\ast$![]() and preserves homological triviality. To see that $\iota$
and preserves homological triviality. To see that $\iota$![]() also preserves $S_\ast ^\textrm {mob}$
also preserves $S_\ast ^\textrm {mob}$![]() , let $x\in Z$
, let $x\in Z$![]() be a point outside the uniruled divisor $D$
be a point outside the uniruled divisor $D$![]() and having a $j$
and having a $j$![]() -dimensional orbit. The inverse image $\psi ^{-1}(x)\subset F\times F$
-dimensional orbit. The inverse image $\psi ^{-1}(x)\subset F\times F$![]() consists of points outside the indeterminacy locus $I$
consists of points outside the indeterminacy locus $I$![]() of $\psi$
of $\psi$![]() . Let $i\in \operatorname {Aut}(F\times F)$
. Let $i\in \operatorname {Aut}(F\times F)$![]() be the map exchanging the two factors. Since $I$
be the map exchanging the two factors. Since $I$![]() is symmetric, $i_\ast (\psi ^{-1}(x))$
is symmetric, $i_\ast (\psi ^{-1}(x))$![]() is disjoint from $I$
is disjoint from $I$![]() , and so $\iota (x)$
, and so $\iota (x)$![]() , which is equal to the support of $\psi _\ast i_\ast (\psi ^{-1}(x))$
, which is equal to the support of $\psi _\ast i_\ast (\psi ^{-1}(x))$![]() (Remark 2.6) lies outside of $D$
(Remark 2.6) lies outside of $D$![]() , i.e. $\iota _\ast (x)\in S_j^\textrm {mob} A^{8}(Z)$
, i.e. $\iota _\ast (x)\in S_j^\textrm {mob} A^{8}(Z)$![]() .
.
Next, we use the fact that

(where $Q$![]() is the correspondence of (2), and $\pi ^{tr}_Y$
is the correspondence of (2), and $\pi ^{tr}_Y$![]() is the projector on $H^{4}_{tr}(Y)$
is the projector on $H^{4}_{tr}(Y)$![]() as in Proposition 2.24). The involution $\iota$
as in Proposition 2.24). The involution $\iota$![]() , being anti-symplectic, acts as $-\operatorname {id}$
, being anti-symplectic, acts as $-\operatorname {id}$![]() on $H^{2}_{tr}(Z) = (Q\circ \pi ^{tr}_Y)_\ast H^{4}(Y)$
on $H^{2}_{tr}(Z) = (Q\circ \pi ^{tr}_Y)_\ast H^{4}(Y)$![]() , and so
, and so
(where $c_h\in \mathbb {Q}^{\ast }$![]() and $h$
and $h$![]() are as in Claim 3.2).
are as in Claim 3.2).
Let us now consider things family-wise. As in Proposition 2.22, let $\mathcal {Y}\to B$![]() and $\mathcal {Z}\to B$
and $\mathcal {Z}\to B$![]() denote the universal family of smooth cubic fourfolds not containing a plane, respectively LLSS eightfolds. Let $Q\in A^{3}(\mathcal {Y}\times _B \mathcal {Z})$
denote the universal family of smooth cubic fourfolds not containing a plane, respectively LLSS eightfolds. Let $Q\in A^{3}(\mathcal {Y}\times _B \mathcal {Z})$![]() be the relative correspondence as in the proof of Claim 3.2, and let $\Gamma _{h^{6}}\in A^{14}(\mathcal {Z}\times _B \mathcal {Z})$
be the relative correspondence as in the proof of Claim 3.2, and let $\Gamma _{h^{6}}\in A^{14}(\mathcal {Z}\times _B \mathcal {Z})$![]() be the relative correspondence induced by some ample element $h\in A^{1}(\mathcal {Z})$
be the relative correspondence induced by some ample element $h\in A^{1}(\mathcal {Z})$![]() . Let $h_\mathcal {Y}\in A^{1}(\mathcal {Y})$
. Let $h_\mathcal {Y}\in A^{1}(\mathcal {Y})$![]() be a relative hyperplane section. The correspondence
be a relative hyperplane section. The correspondence

is such that $\pi ^\textrm {prim}_\mathcal {Y}\vert _b=\pi ^{tr}_{Y_b}$![]() for $b\in B$
for $b\in B$![]() very general, and
very general, and
It follows from the above considerations that the relative correspondence
is homologically trivial when restricted to the very general fibre. But then, the Franchetta property (Proposition 2.22) ensures that this relative correspondence is fibrewise zero, i.e.
Composing on both sides with $Q\vert _b$![]() on the right and with $(c_h \Gamma _{h^{6}}\circ Q\circ \pi ^\textrm {prim}_\mathcal {Y})\vert _b$
on the right and with $(c_h \Gamma _{h^{6}}\circ Q\circ \pi ^\textrm {prim}_\mathcal {Y})\vert _b$![]() on the left, it follows that
on the left, it follows that

for all $b\in B$![]() . Applying this equality of correspondences to $A^{8}_\textrm {hom}(Z_b)$
. Applying this equality of correspondences to $A^{8}_\textrm {hom}(Z_b)$![]() , and using (4), we obtain the equality of actions
, and using (4), we obtain the equality of actions
where $\pi ^{tr}_{Z_b}:=c_h \Gamma _{h_b^{6}}\circ Q_b\circ \pi ^{tr}_{Y_b}\circ {}^{t} Q_b$![]() is the projector on $S_3^\textrm {mob}\cap A^{8}_\textrm {hom}(Z_b)$
is the projector on $S_3^\textrm {mob}\cap A^{8}_\textrm {hom}(Z_b)$![]() as in Theorem 3.1. Combined with Lemma 3.8, this means that
as in Theorem 3.1. Combined with Lemma 3.8, this means that
and so the theorem is proven.
Theorem 3.9 Let $Z$![]() be an LLSS eightfold birational to a Hilbert scheme $Z^{\prime }=S^{[4]}$
be an LLSS eightfold birational to a Hilbert scheme $Z^{\prime }=S^{[4]}$![]() where $S$
where $S$![]() is a K3 surface. Let $\iota ^{\prime }\in \operatorname {Bir}(Z^{\prime })$
is a K3 surface. Let $\iota ^{\prime }\in \operatorname {Bir}(Z^{\prime })$![]() be the map induced by $\iota \in \operatorname {Aut}(Z)$
be the map induced by $\iota \in \operatorname {Aut}(Z)$![]() . Then
. Then

$($![]() Here the bigrading refers to the MCK decomposition of [Reference Vial54].)
Here the bigrading refers to the MCK decomposition of [Reference Vial54].)
Proof. The Hilbert scheme $Z^{\prime }$![]() has an MCK decomposition [Reference Vial54], and the induced decomposition of $A^{8}(Z^{\prime })$
has an MCK decomposition [Reference Vial54], and the induced decomposition of $A^{8}(Z^{\prime })$![]() is compatible with Voisin's orbit filtration $S_\ast$
is compatible with Voisin's orbit filtration $S_\ast$![]() , in the sense that
, in the sense that

[Reference Voisin59, End of section 4.1].
Using Rieß’ work (Theorem 2.18), the MCK decomposition of $Z^{\prime }$![]() induces an MCK decomposition for $Z$
induces an MCK decomposition for $Z$![]() , and there exists a correspondence $R_\phi \in A^{8}(Z^{\prime }\times Z)$
, and there exists a correspondence $R_\phi \in A^{8}(Z^{\prime }\times Z)$![]() inducing an isomorphism of bigraded rings $A^{\ast }_{(\ast )}(Z^{\prime })\cong A^{\ast }_{(\ast )}(Z)$
inducing an isomorphism of bigraded rings $A^{\ast }_{(\ast )}(Z^{\prime })\cong A^{\ast }_{(\ast )}(Z)$![]() . In order to prove Theorem 3.9, we want to relate the orbit filtration $S_\ast$
. In order to prove Theorem 3.9, we want to relate the orbit filtration $S_\ast$![]() on $A^{8}(Z)$
on $A^{8}(Z)$![]() with the ‘motivic’ decomposition $A^{8}_{(\ast )}(Z)$
with the ‘motivic’ decomposition $A^{8}_{(\ast )}(Z)$![]() . This is the content of the following lemma.
. This is the content of the following lemma.
Lemma 3.10 Let $Z$![]() be as in Theorem 3.9, and let $A^{\ast }_{(\ast )}(Z)$
be as in Theorem 3.9, and let $A^{\ast }_{(\ast )}(Z)$![]() refer to the bigrading induced by the bigrading on $A^{\ast }(Z^{\prime })$
refer to the bigrading induced by the bigrading on $A^{\ast }(Z^{\prime })$![]() . There is an inclusion
. There is an inclusion
Proof. Let $\phi \colon Z^{\prime }\dashrightarrow Z$![]() denote the birational map. By virtue of Rieß’ work (Theorem 2.18), there is equality
denote the birational map. By virtue of Rieß’ work (Theorem 2.18), there is equality
Thanks to equality (5), it follows there is an inclusion
Let $I\subset Z^{\prime }$![]() denote the indeterminacy locus of the map $\phi$
denote the indeterminacy locus of the map $\phi$![]() , and let $D^{\prime }\subset Z^{\prime }$
, and let $D^{\prime }\subset Z^{\prime }$![]() denote the strict transform of the uniruled divisor $D\subset Z$
denote the strict transform of the uniruled divisor $D\subset Z$![]() coming from the rational map $\psi$
coming from the rational map $\psi$![]() . For any point $z\in Z^{\prime }$
. For any point $z\in Z^{\prime }$![]() , the maximal-dimensional components of the orbit under rational equivalence $O_z$
, the maximal-dimensional components of the orbit under rational equivalence $O_z$![]() are Zariski dense in $Z^{\prime }$
are Zariski dense in $Z^{\prime }$![]() ([Reference Voisin57, Lemma 3.5], cf. also [Reference Shen, Yin and Zhao51, Proof of Theorem 0.5] where this precise statement is obtained). Hence, the orbit of any point in $Z^{\prime }$
([Reference Voisin57, Lemma 3.5], cf. also [Reference Shen, Yin and Zhao51, Proof of Theorem 0.5] where this precise statement is obtained). Hence, the orbit of any point in $Z^{\prime }$![]() has a maximal-dimensional irreducible component not contained in $I\cup D^{\prime }$
has a maximal-dimensional irreducible component not contained in $I\cup D^{\prime }$![]() , and hence
, and hence
Combining (6) and (7), one obtains
Since clearly $A^{8}_{(2)}(Z)\subset A^{8}_\textrm {hom}(Z)$![]() , this proves the lemma.
, this proves the lemma.
Theorem 3.7, combined with Lemma 3.10, implies that
There is a commutative diagram

(To check commutativity of this diagram, we note that (thanks to the moving lemma) any $0$![]() -cycle $b\in A^{8}(Z^{\prime })$
-cycle $b\in A^{8}(Z^{\prime })$![]() can be represented by a cycle $\beta$
can be represented by a cycle $\beta$![]() supported on an open $U^{\prime }$
supported on an open $U^{\prime }$![]() such that the birational map $\phi \colon Z^{\prime }\dashrightarrow Z$
such that the birational map $\phi \colon Z^{\prime }\dashrightarrow Z$![]() restricts to an isomorphism $\phi \vert _{U^{\prime }}\colon U^{\prime }\cong U$
restricts to an isomorphism $\phi \vert _{U^{\prime }}\colon U^{\prime }\cong U$![]() and $U\subset Z$
and $U\subset Z$![]() is $\iota$
is $\iota$![]() -stable. As $(R_\phi )_\ast$
-stable. As $(R_\phi )_\ast$![]() and $(\bar {\Gamma }_\phi )_\ast$
and $(\bar {\Gamma }_\phi )_\ast$![]() coincide on $0$
coincide on $0$![]() -cycles (Theorem 2.18), the image $(R_\phi )_\ast (b)\in A^{8}(Z)$
-cycles (Theorem 2.18), the image $(R_\phi )_\ast (b)\in A^{8}(Z)$![]() is represented by the cycle $(\phi \vert _{U^{\prime }})_\ast (\beta )$
is represented by the cycle $(\phi \vert _{U^{\prime }})_\ast (\beta )$![]() with support on $U$
with support on $U$![]() . This shows commutativity of the diagram.)
. This shows commutativity of the diagram.)
This commutative diagram, plus the fact that $\iota$![]() acts as the identity on $S_4 A^{8}(Z)=A^{8}_{(0)}(Z)$
acts as the identity on $S_4 A^{8}(Z)=A^{8}_{(0)}(Z)$![]() (Theorem 3.7), proves the $j=0$
(Theorem 3.7), proves the $j=0$![]() case of the theorem. Moreover, the commutative diagram, plus equality (8), gives
case of the theorem. Moreover, the commutative diagram, plus equality (8), gives
which is the $j=2$![]() case of the theorem.
case of the theorem.
Taking a $\iota$![]() -invariant ample divisor $h\in A^{1}(Z)$
-invariant ample divisor $h\in A^{1}(Z)$![]() and invoking the isomorphism
and invoking the isomorphism
(Remark 2.20), it follows from (8) that also
The intersection product induces surjections
(Remark 2.20). Since intersection product and $\iota ^{\ast }$![]() commute, equality (12) thus implies that
commute, equality (12) thus implies that
Taking once again a $\iota$![]() -invariant ample divisor $h\in A^{1}(Z)$
-invariant ample divisor $h\in A^{1}(Z)$![]() , and invoking the isomorphism
, and invoking the isomorphism
(Remark 2.20), it follows that
Combining (13) with the commutative diagram (9), we find that
The theorem is now proven.
3.3. A reformulation
We can reformulate Theorem 3.9 into a simpler statement, that does not mention MCK decompositions or bigradings on the Chow ring:
Theorem 3.11 Let $Z$![]() be an LLSS eightfold birational to a Hilbert scheme $Z^{\prime }=S^{[4]}$
be an LLSS eightfold birational to a Hilbert scheme $Z^{\prime }=S^{[4]}$![]() where $S$
where $S$![]() is a K3 surface. Let $\iota ^{\prime }\in \operatorname {Bir}(Z^{\prime })$
is a K3 surface. Let $\iota ^{\prime }\in \operatorname {Bir}(Z^{\prime })$![]() be the map induced by $\iota \in \operatorname {Aut}(Z)$
be the map induced by $\iota \in \operatorname {Aut}(Z)$![]() . Then
. Then

$($![]() Here$,$
Here$,$![]() $x,y,z,t\in S$
$x,y,z,t\in S$![]() and $o\in A^{2}(S)$
and $o\in A^{2}(S)$![]() denotes the distinguished $0$
denotes the distinguished $0$![]() -cycle.$)$
-cycle.$)$![]()
Proof. This is a translation of Theorem 3.9, using the generators for the various pieces $A^{8}_{(j)}(Z^{\prime })$![]() given in Theorem 2.15. We know that $\iota ^{\prime }$
given in Theorem 2.15. We know that $\iota ^{\prime }$![]() preserves these pieces (Theorem 3.9), and so one can check the formula of Theorem 3.11 piece by piece. This is a direct computation. For example, Theorem 2.15 says that $A^{8}_{(8)}(Z^{\prime })$
preserves these pieces (Theorem 3.9), and so one can check the formula of Theorem 3.11 piece by piece. This is a direct computation. For example, Theorem 2.15 says that $A^{8}_{(8)}(Z^{\prime })$![]() is generated by expressions of the form
is generated by expressions of the form

and the formula of Theorem 3.11 leaves expressions of this form invariant, which is in agreement with the fact that $\iota ^{\prime }$![]() is the identity on $A^{8}_{(8)}(Z^{\prime })$
is the identity on $A^{8}_{(8)}(Z^{\prime })$![]() (Theorem 3.9). The verification of the action of $\iota ^{\prime }$
(Theorem 3.9). The verification of the action of $\iota ^{\prime }$![]() on $A^{8}_{(j)}(Z^{\prime })$
on $A^{8}_{(j)}(Z^{\prime })$![]() , $j<8$
, $j<8$![]() is similar (but easier).
is similar (but easier).
3.4. Another reformulation
Theorem 3.9 also admits a reformulation that does not mention LLSS eightfolds:
Theorem 3.12 Let $S$![]() be a K3 surface of Picard number 1 and degree $d$
be a K3 surface of Picard number 1 and degree $d$![]() satisfying $d>2$
satisfying $d>2$![]() and $d= (6n^{2}-6n+2)/a^{2}$
and $d= (6n^{2}-6n+2)/a^{2}$![]() for some $n,a\in \mathbb {Z}$
for some $n,a\in \mathbb {Z}$![]() . Let $X=S^{[4]}$
. Let $X=S^{[4]}$![]() be the Hilbert scheme. Then $\operatorname {Bir}(X)=\mathbb {Z}/2\mathbb {Z}$
be the Hilbert scheme. Then $\operatorname {Bir}(X)=\mathbb {Z}/2\mathbb {Z}$![]() and the non-trivial element $\iota \in \operatorname {Bir}(X)$
and the non-trivial element $\iota \in \operatorname {Bir}(X)$![]() acts on $A^{8}(X)$
acts on $A^{8}(X)$![]() as in Theorem 3.11.
as in Theorem 3.11.
Proof. Given a K3 surface $S$![]() of Picard number 1 and degree $d>2$
of Picard number 1 and degree $d>2$![]() , the Hilbert scheme $X=S^{[4]}$
, the Hilbert scheme $X=S^{[4]}$![]() has $\operatorname {Bir}(X)$
has $\operatorname {Bir}(X)$![]() a group of order $1$
a group of order $1$![]() or $2$
or $2$![]() [Reference Debarre16, Section 4.3.1]. On the other hand, the condition $d= (6n^{2}-6n+2)/a^{2}$
[Reference Debarre16, Section 4.3.1]. On the other hand, the condition $d= (6n^{2}-6n+2)/a^{2}$![]() for some $n,a\in \mathbb {Z}$
for some $n,a\in \mathbb {Z}$![]() implies (and actually is equivalent to the fact) that $X$
implies (and actually is equivalent to the fact) that $X$![]() is birational to an LLSS eightfold [Reference Li, Pertusi and Zhao39, Proposition 5.3], and so $\operatorname {Bir}(X)$
is birational to an LLSS eightfold [Reference Li, Pertusi and Zhao39, Proposition 5.3], and so $\operatorname {Bir}(X)$![]() is non-trivial. It follows that $X$
is non-trivial. It follows that $X$![]() as in the theorem must have $\operatorname {Bir}(X)=\mathbb {Z}/2\mathbb {Z}$
as in the theorem must have $\operatorname {Bir}(X)=\mathbb {Z}/2\mathbb {Z}$![]() , and the non-trivial element $\iota \in \operatorname {Bir}(X)$
, and the non-trivial element $\iota \in \operatorname {Bir}(X)$![]() acts on $A^{8}(X)$
acts on $A^{8}(X)$![]() as in Theorem 3.11.
as in Theorem 3.11.
3.5. A consequence
Corollary 3.13 Let $Z$![]() be an LLSS eightfold birational to a Hilbert scheme $Z^{\prime }=S^{[4]}$
be an LLSS eightfold birational to a Hilbert scheme $Z^{\prime }=S^{[4]}$![]() where $S$
where $S$![]() is a K3 surface. Let $X:=Z/\langle \iota \rangle$
is a K3 surface. Let $X:=Z/\langle \iota \rangle$![]() be the quotient under the anti-symplectic involution $\iota \in \operatorname {Aut}(Z)$
be the quotient under the anti-symplectic involution $\iota \in \operatorname {Aut}(Z)$![]() . Then
. Then
where $h\in A^{1}(X)$![]() is an ample divisor.
is an ample divisor.
Proof. Recall that $X$![]() is a quotient variety, and so the Chow groups with $\mathbb {Q}$
is a quotient variety, and so the Chow groups with $\mathbb {Q}$![]() -coefficients of $X$
-coefficients of $X$![]() have a ring structure (cf. § 2.1).
have a ring structure (cf. § 2.1).
As noted before, the birationality $Z\to Z^{\prime }$![]() induces an isomorphism of bigraded rings $A^{\ast }_{(\ast )}(Z)\cong A^{\ast }_{(\ast )}(Z^{\prime })$
induces an isomorphism of bigraded rings $A^{\ast }_{(\ast )}(Z)\cong A^{\ast }_{(\ast )}(Z^{\prime })$![]() (Theorem 2.18). We have seen (equality (12)) that $\iota$
(Theorem 2.18). We have seen (equality (12)) that $\iota$![]() acts as $-\operatorname {id}$
acts as $-\operatorname {id}$![]() on $A^{2}_{(2)}(Z)$
on $A^{2}_{(2)}(Z)$![]() , and so
, and so
Similar reasoning also shows that
Indeed, let $b\in A^{2}(Z)^{\iota }$![]() , and let $h\in A^{1}(Z)$
, and let $h\in A^{1}(Z)$![]() be once again a $g$
be once again a $g$![]() -invariant ample class. Then $b\cdot h^{6}\in A^{8}(Z)^{ \iota }$
-invariant ample class. Then $b\cdot h^{6}\in A^{8}(Z)^{ \iota }$![]() and so (in view of Theorem 3.9) we know that $b\cdot h^{6}\in A^{8}_{(0)}(Z)$
and so (in view of Theorem 3.9) we know that $b\cdot h^{6}\in A^{8}_{(0)}(Z)$![]() . Writing the decomposition $b=b_0+b_2$
. Writing the decomposition $b=b_0+b_2$![]() , where $b_j\in A^{2}_{(j)}(Z)$
, where $b_j\in A^{2}_{(j)}(Z)$![]() , and invoking the hard Lefschetz type isomorphism (11), we see that $b_2=0$
, and invoking the hard Lefschetz type isomorphism (11), we see that $b_2=0$![]() .
.
The corollary is now readily proven. For instance, the image of the intersection map
is contained in

On the other hand, the image is obviously $\iota$![]() -invariant, and so
-invariant, and so

(where the second inclusion is equality (13)). It follows that
Acknowledgements
Thanks to the referee for many insightful comments. Thanks to Christian Lehn, who very patiently explained details of the involution $\iota$![]() on a crowded train [Reference Lehn35]. I am also very grateful to Chiara Camere, Alberto Cattaneo, Lie Fu, Laura Pertusi, Ulrike Rieß and Charles Vial for various inspiring exchanges. Supported by ANR grant ANR-20-CE40-0023.
on a crowded train [Reference Lehn35]. I am also very grateful to Chiara Camere, Alberto Cattaneo, Lie Fu, Laura Pertusi, Ulrike Rieß and Charles Vial for various inspiring exchanges. Supported by ANR grant ANR-20-CE40-0023.