No CrossRef data available.
Article contents
Concentration and oscillation analysis of positive solutions to semilinear elliptic equations with exponential growth in a disc. II
Published online by Cambridge University Press: 31 July 2025
Abstract
This paper is the latter part of a series of our studies on the concentration and oscillation analysis of semilinear elliptic equations with exponential growth 
$e^{u^p}$. In the first one [17], we completed the concentration analysis of blow-up positive solutions in the supercritical case p > 2 via a scaling approach. As a result, we detected infinite sequences of concentrating parts with precise quantification. In the present paper, we proceed to our second aim, the oscillation analysis. Especially, we deduce an infinite oscillation estimate directly from the previous infinite concentration ones. This allows us to investigate intersection properties between blow-up solutions and singular functions. Consequently, we show that the intersection number between blow-up and singular solutions diverges to infinity. This leads to a proof of infinite oscillations of bifurcation diagrams, which ensures the existence of infinitely many solutions. Finally, we also remark on infinite concentration and oscillation phenomena in the limit cases 
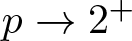$p\to2^+$ and 
$p\to \infty$.
Keywords
MSC classification
Primary:
35B32: Bifurcation
Information
- Type
- Research Article
- Information
- Copyright
- © The Author(s), 2025. Published by Cambridge University Press on behalf of The Royal Society of Edinburgh
References
Adimurthi, K. A. and Giacomoni, J.. Uniqueness of positive solutions of a n-Laplace equation in a ball in 
$\mathbb{R}^n$ with exponential nonlinearity. J. Differential Equations. 260 (2016), 7739–7799.10.1016/j.jde.2016.02.002CrossRefGoogle Scholar
$\mathbb{R}^n$ with exponential nonlinearity. J. Differential Equations. 260 (2016), 7739–7799.10.1016/j.jde.2016.02.002CrossRefGoogle ScholarAtkinson, F. V. and Peletier, L. A.. Ground states and Dirichlet problems for
$-\Delta u=f(u)$ in
$\mathbb{R}^2$. Arch. Rational Mech. Anal. 96 (1986), 103–127.10.1007/BF00279955CrossRefGoogle Scholar
$-\Delta u=f(u)$ in 
$\mathbb{R}^2$. Arch. Rational Mech. Anal. 96 (1986), 103–127.10.1007/BF00279955CrossRefGoogle ScholarDruet, O.. Multibumps analysis in dimention 2: quantification of blow-up levels. Duke Math. J. 132 (2006), 217–269.10.1215/S0012-7094-06-13222-2CrossRefGoogle Scholar
Druet, O. and , P. D. T. Multi-bump analysis for Trudinger-Moser nonlinearities. I. Quantification and location of concentration points. J. Eur. Math. Soc. 22 (2020), 4025–4096.10.4171/jems/1002CrossRefGoogle Scholar
Fujishima, Y., Ioku, N., Ruf, B. and Terraneo, E.. Singular solutions of semilinear elliptic equations with exponential nonlinearities in 2-dimensions. J. Funct. Anal. 289 (2025), .10.1016/j.jfa.2025.110922CrossRefGoogle Scholar
Ghergu, M., Giacomoni, J. and Prashanth, S. and , S. Radial singular solutions for the N-Laplace equation with exponential nonlinearities. J. Math. Anal. Appl. 475 (2019), 668–685.10.1016/j.jmaa.2019.02.062CrossRefGoogle Scholar
Gidas, B., Ni, W. M. and Nirenberg, L.. Symmetry and related properties via the maximum principle. Comm. Math. Phys. 68 (1979), 209–243.10.1007/BF01221125CrossRefGoogle Scholar
Ioku, N., Ruf, B. and Terraneo, E.. Non-uniqueness for a critical heat equation in two dimensions with singular data. Ann. Inst. H. Poincaré C Anal. Non LinéAire. 36 (2019), 2027–2051.10.1016/j.anihpc.2019.07.004CrossRefGoogle Scholar
Kikuchi, H. and Wei, J.. A bifurcation diagram of solutions to an elliptic equation with exponential nonlinearity in higher dimensions. Proc. Roy. Soc. Edinburgh Sect. A. 148 (2018), 101–122.10.1017/S0308210517000154CrossRefGoogle Scholar
Korman, P.. Solution curves for semilinear equations on a ball. Proc. Amer. Math. Soc. 125 (1997), 1997–2005.10.1090/S0002-9939-97-04119-1CrossRefGoogle Scholar
Kumagai, K.. Bifurcation diagrams of semilinear elliptic equations for supercritical nonlinearities in two dimensions. NoDEA Nonlinear Differential Equations Appl. 32 (2025), .10.1007/s00030-025-01043-9CrossRefGoogle Scholar
McLeod, B. and McLeod, K.. The critical Sobolev exponent in two dimensions. Proc. Roy. Soc. Edinburgh Sect. A. 109 (1988), 1–15.10.1017/S0308210500026640CrossRefGoogle Scholar
Miyamoto, Y.. Structure of the positive solutions for supercritical elliptic equations in a ball. J. Math. Pures Appl. 102 (2014), 672–701.10.1016/j.matpur.2014.02.002CrossRefGoogle Scholar
Miyamoto, Y.. Classification of bifurcation diagrams for elliptic equations with exponential growth in a ball. Ann. Mat. Pura Appl. 94 (2015), 931–952.10.1007/s10231-014-0404-8CrossRefGoogle Scholar
Miyamoto, Y. and Naito, Y.. Singular solutions for semilinear elliptic equations with general supercritical growth. Ann. Mat. Pura Appl. 202 (2023), 341–366.10.1007/s10231-022-01244-4CrossRefGoogle Scholar
Nabana, E. and de Thélin, F.. On the uniqueness of positive solutions for quasilinear elliptic equations. Nonlinear Anal. 31 (1998), 413–430.10.1016/S0362-546X(96)00318-5CrossRefGoogle Scholar
Naimen, D.. Concentration and oscillation analysis of positive solutions to semilinear elliptic equations with exponential growth in a disc. I. Sections 1,2,3, and 4. (arXiv:2404.01634).Google Scholar