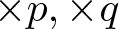1. Introduction
A self-similar higher rank graph ![]() $(G, \Lambda)$ is a pair, which consists of a group G and a higher rank graph Λ such that G acts on Λ from the left and Λ ‘acts’ on G from the right, where these two actions are compatible in an appropriate way. After [Reference Duwenig, Gillaspy, Norton, Reznikoff and Wright22, Reference Li and Yang38], self-similar higher rank graphs and their C*-algebras
$(G, \Lambda)$ is a pair, which consists of a group G and a higher rank graph Λ such that G acts on Λ from the left and Λ ‘acts’ on G from the right, where these two actions are compatible in an appropriate way. After [Reference Duwenig, Gillaspy, Norton, Reznikoff and Wright22, Reference Li and Yang38], self-similar higher rank graphs and their C*-algebras ![]() ${\mathcal{O}}_{G, \Lambda}$ have been systematically studied in [Reference Li33–Reference Li and Yang35]. In particular, in [Reference Li33], when Λ is strongly connected, we find a canonical Cartan subalgebra of
${\mathcal{O}}_{G, \Lambda}$ have been systematically studied in [Reference Li33–Reference Li and Yang35]. In particular, in [Reference Li33], when Λ is strongly connected, we find a canonical Cartan subalgebra of ![]() ${\mathcal{O}}_{G, \Lambda}$ en route to the study of the Kubo-Martin-Schwinger (KMS) states of
${\mathcal{O}}_{G, \Lambda}$ en route to the study of the Kubo-Martin-Schwinger (KMS) states of ![]() ${\mathcal{O}}_{G, \Lambda}$. However, to achieve this, Λ is required to be locally faithful. The local faithfulness is a key property to obtain the main results in [Reference Li33]. Roughly speaking, it guarantees that one could define a periodicity group in a way very similar to higher rank graphs in [Reference Davidson, Power and Yang17, Reference Davidson and Yang18]. It turns out that the local faithfulness condition blocks a lot of interesting examples. This provides our starting point of this paper—to explore non-locally faithful self-similar higher rank graphs and their C*-algebras. During the exploration, we found that a particular non-locally faithful class is closely related to Baumslag–Solitar (BS) semigroups. Due to the higher rank feature, we call such self-similar higher rank graphs higher rank BS semigroups. One extreme case of higher rank BS semigroups is about products of odometers [Reference Laca, Raeburn, Ramagge and Whittaker32], while the other extreme case is surprisingly related to Furstenberg’s
${\mathcal{O}}_{G, \Lambda}$. However, to achieve this, Λ is required to be locally faithful. The local faithfulness is a key property to obtain the main results in [Reference Li33]. Roughly speaking, it guarantees that one could define a periodicity group in a way very similar to higher rank graphs in [Reference Davidson, Power and Yang17, Reference Davidson and Yang18]. It turns out that the local faithfulness condition blocks a lot of interesting examples. This provides our starting point of this paper—to explore non-locally faithful self-similar higher rank graphs and their C*-algebras. During the exploration, we found that a particular non-locally faithful class is closely related to Baumslag–Solitar (BS) semigroups. Due to the higher rank feature, we call such self-similar higher rank graphs higher rank BS semigroups. One extreme case of higher rank BS semigroups is about products of odometers [Reference Laca, Raeburn, Ramagge and Whittaker32], while the other extreme case is surprisingly related to Furstenberg’s ![]() $\times p, \times q$ conjecture.
$\times p, \times q$ conjecture.
With semigroups mentioned, there is no surprise that Λ is assumed to be single-vertex in this paper. Taking rank 1 (i.e., classical) BS semigroups into consideration, we also consider ![]() $G={\mathbb{Z}}$ only. For single-vertex higher rank graphs, they have been systematically studied in the literature. To name just a few, see, for instance, [Reference Davidson15, Reference Davidson, Power and Yang16, Reference Serre46, Reference Spielberg47]. Those graphs seem very special but exhibit a lot of interesting properties. Surprisingly, they are also shown to interact intimately with the Yang–Baxter equation [Reference Yang49]. For BS semigroups, they have been attracting increasing attention in Operator Algebras recently. See [Reference an Huef, Laca, Raeburn and Sims2, Reference Brown, Nagy, Reznikoff, Sims and Williams7, Reference Chen and Li12, Reference Kumjian and Pask30, Reference Laca and Raeburn31, Reference Rudolph44] and the references therein. Those semigroups provide, on one hand, a class of nice examples for some properties [Reference Chen and Li12, Reference Kumjian and Pask30, Reference Rudolph44], and on the other hand, some counter-examples for other properties [Reference an Huef, Laca, Raeburn and Sims2, Reference Brown, Nagy, Reznikoff, Sims and Williams7]. Our main purpose in this paper is to mingle single-vertex higher rank graphs and BS semigroups.
$G={\mathbb{Z}}$ only. For single-vertex higher rank graphs, they have been systematically studied in the literature. To name just a few, see, for instance, [Reference Davidson15, Reference Davidson, Power and Yang16, Reference Serre46, Reference Spielberg47]. Those graphs seem very special but exhibit a lot of interesting properties. Surprisingly, they are also shown to interact intimately with the Yang–Baxter equation [Reference Yang49]. For BS semigroups, they have been attracting increasing attention in Operator Algebras recently. See [Reference an Huef, Laca, Raeburn and Sims2, Reference Brown, Nagy, Reznikoff, Sims and Williams7, Reference Chen and Li12, Reference Kumjian and Pask30, Reference Laca and Raeburn31, Reference Rudolph44] and the references therein. Those semigroups provide, on one hand, a class of nice examples for some properties [Reference Chen and Li12, Reference Kumjian and Pask30, Reference Rudolph44], and on the other hand, some counter-examples for other properties [Reference an Huef, Laca, Raeburn and Sims2, Reference Brown, Nagy, Reznikoff, Sims and Williams7]. Our main purpose in this paper is to mingle single-vertex higher rank graphs and BS semigroups.
The paper is structured as follows. In § 2, some necessary preliminaries are provided. Although most of them are known, § 2.4 is new, where we introduce a notion of semigroups from self-similar actions. Those semigroups are different from self-similar semigroups/monoids in [Reference Barlak, Omland and Stammeier4] and the references therein (remark 2.10). Since the rank 1 case is studied in a more general setting, we focus on this case in § 3. Even in this case, it includes generalized Baumslag–Solitar (GBS) semigroups, and BS semigroups as well, as examples. We study the periodicity of the associated self-similar graph and obtain a canonical Cartan subalgebra of its C*-algebra (propositions 3.22 and 3.23). The simplicity of the C*-algebra is characterized in terms of the relation between the number of edges and the restriction map; and when it is Kirchberg is also described (theorem 3.20). We turn to higher rank cases in § 4. We first propose a notion of higher rank BS semigroups (definition 4.2). We briefly discuss how higher rank BS semigroups are related to Furstenberg’s ![]() $\times p, \times q$ conjecture in § 4.2. We then focus on two extreme classes. The first extreme class is about products of odometers studied in [Reference Laca, Raeburn, Ramagge and Whittaker32]; but here, we investigate the associated von Neumann algebra: Its factoriality is characterized and its type is also determined (theorem 4.13). The second extreme class seems trivial at first sight but turns out to be intriguing. We exhibit a canonical Cartan in this case, which is generally a proper subalgebra of the cycline algebra (theorem 4.22). We close with computing the spectrum of the fixed point algebra of its gauge action. We hope that we could push Furstenberg’s
$\times p, \times q$ conjecture in § 4.2. We then focus on two extreme classes. The first extreme class is about products of odometers studied in [Reference Laca, Raeburn, Ramagge and Whittaker32]; but here, we investigate the associated von Neumann algebra: Its factoriality is characterized and its type is also determined (theorem 4.13). The second extreme class seems trivial at first sight but turns out to be intriguing. We exhibit a canonical Cartan in this case, which is generally a proper subalgebra of the cycline algebra (theorem 4.22). We close with computing the spectrum of the fixed point algebra of its gauge action. We hope that we could push Furstenberg’s ![]() $\times p, \times q$ conjecture further in this vein in our future studies.
$\times p, \times q$ conjecture further in this vein in our future studies.
Notation and conventions
Given ![]() $1\le n\in {\mathbb{N}}$, let
$1\le n\in {\mathbb{N}}$, let ![]() $[n]:=\{0, 1, \ldots, n-1\}$. For
$[n]:=\{0, 1, \ldots, n-1\}$. For ![]() $1\le \mathsf k\in {\mathbb{N}}$, let
$1\le \mathsf k\in {\mathbb{N}}$, let ![]() $\mathbb{1}_{\mathsf k}:=(1,\ldots, 1)\in {\mathbb{N}}^{\mathsf{k}}$.
$\mathbb{1}_{\mathsf k}:=(1,\ldots, 1)\in {\mathbb{N}}^{\mathsf{k}}$.
We use the multi-index notation: For ![]() $\mathbf{q}=(q_1,\ldots, q_{\mathsf k})$ and
$\mathbf{q}=(q_1,\ldots, q_{\mathsf k})$ and ![]() $\mathbf{p}=(p_1,\ldots, p_\mathsf{k})$ in
$\mathbf{p}=(p_1,\ldots, p_\mathsf{k})$ in ![]() ${\mathbb{Z}}^{\mathsf k}$ with all
${\mathbb{Z}}^{\mathsf k}$ with all ![]() $p_i\ne 0$, let
$p_i\ne 0$, let  $\mathbf{p}^{\mathbf q}:=\prod_{i=1}^{\mathsf k} p_i^{q_i}$.
$\mathbf{p}^{\mathbf q}:=\prod_{i=1}^{\mathsf k} p_i^{q_i}$.
For convenience, sometimes we also let ![]() ${\mathbb{Z}}=\langle a\rangle$, which is written multiplicatively.
${\mathbb{Z}}=\langle a\rangle$, which is written multiplicatively.
As with most literatures in Operator Algebras, all semigroups in this paper are assumed to be monoids, unless otherwise specified.
2. Preliminaries
2.1. Single-vertex rank  $\mathsf k$ graphs
$\mathsf k$ graphs
A countable small category Λ is called a rank ![]() $\mathsf k$ graph (or
$\mathsf k$ graph (or ![]() $\mathsf k$-graph) if there exists a functor
$\mathsf k$-graph) if there exists a functor ![]() $d:\Lambda \to \mathbb{N}^{\mathsf k}$ satisfying the following unique factorization property: For
$d:\Lambda \to \mathbb{N}^{\mathsf k}$ satisfying the following unique factorization property: For ![]() $\mu\in\Lambda, {\mathbf{n}}, {\mathbf{m}} \in \mathbb{N}^k$ with
$\mu\in\Lambda, {\mathbf{n}}, {\mathbf{m}} \in \mathbb{N}^k$ with ![]() $d(\mu)={\mathbf{n}}+{\mathbf{m}}$, there exist unique
$d(\mu)={\mathbf{n}}+{\mathbf{m}}$, there exist unique ![]() $\beta\in d^{-1}({\mathbf{n}})$ and
$\beta\in d^{-1}({\mathbf{n}})$ and ![]() $\alpha\in d^{-1}({\mathbf{m}}) $ such that
$\alpha\in d^{-1}({\mathbf{m}}) $ such that ![]() $\mu=\beta\alpha$. A functor
$\mu=\beta\alpha$. A functor ![]() $f:\Lambda_1 \to \Lambda_2$ is called a graph morphism if
$f:\Lambda_1 \to \Lambda_2$ is called a graph morphism if ![]() $d_2 \circ f=d_1$.
$d_2 \circ f=d_1$.
Let Λ be a ![]() $\mathsf{k}$-graph and
$\mathsf{k}$-graph and ![]() ${\mathbf{n}}\in {\mathbb{N}}^k$. Set
${\mathbf{n}}\in {\mathbb{N}}^k$. Set ![]() $\Lambda^{\mathbf{n}}:=d^{-1}({\mathbf{n}})$. For
$\Lambda^{\mathbf{n}}:=d^{-1}({\mathbf{n}})$. For ![]() $\mu\in \Lambda$, we write
$\mu\in \Lambda$, we write ![]() $s(\mu)$ and
$s(\mu)$ and ![]() $r(\mu)$ for the source and range of µ, respectively. Then Λ is said to be row-finite if
$r(\mu)$ for the source and range of µ, respectively. Then Λ is said to be row-finite if ![]() $\vert v\Lambda^{{\mathbf{n}}}\vert \lt \infty$ for all
$\vert v\Lambda^{{\mathbf{n}}}\vert \lt \infty$ for all ![]() $v \in \Lambda^0$ and
$v \in \Lambda^0$ and ![]() ${\mathbf{n}} \in \mathbb{N}^{\mathsf k}$; and source-free if
${\mathbf{n}} \in \mathbb{N}^{\mathsf k}$; and source-free if ![]() $v\Lambda^{{\mathbf{n}}} \neq \varnothing$ for all
$v\Lambda^{{\mathbf{n}}} \neq \varnothing$ for all ![]() $v \in \Lambda^0$ and
$v \in \Lambda^0$ and ![]() ${\mathbf{n}} \in \mathbb{N}^{\mathsf k}$. For more information about
${\mathbf{n}} \in \mathbb{N}^{\mathsf k}$. For more information about ![]() $\mathsf k$-graphs, refer to [Reference Katsura29]. In this paper, all
$\mathsf k$-graphs, refer to [Reference Katsura29]. In this paper, all ![]() $\mathsf k$-graphs are assumed to be row-finite and source-free. Actually, we focus on a special class of rank
$\mathsf k$-graphs are assumed to be row-finite and source-free. Actually, we focus on a special class of rank ![]() $\mathsf k$ graphs—single-vertex rank
$\mathsf k$ graphs—single-vertex rank ![]() $\mathsf k$ graphs.
$\mathsf k$ graphs.
Single-vertex ![]() $\mathsf k$-graphs, at first sight, seem to be a very special class of
$\mathsf k$-graphs, at first sight, seem to be a very special class of ![]() $\mathsf k$-graphs. It turns out that they are a rather intriguing class to study. They have been systematically studied in the literature, e.g., [Reference Davidson15–Reference Davidson and Yang18]. There are close connections with the well-known Yang–Baxter equation [Reference Yang49].
$\mathsf k$-graphs. It turns out that they are a rather intriguing class to study. They have been systematically studied in the literature, e.g., [Reference Davidson15–Reference Davidson and Yang18]. There are close connections with the well-known Yang–Baxter equation [Reference Yang49].
Let ![]() $\{\epsilon_1,\ldots, \epsilon_{\mathsf{k}}\}$ be the standard basis of
$\{\epsilon_1,\ldots, \epsilon_{\mathsf{k}}\}$ be the standard basis of ![]() ${\mathbb{N}}^{\mathsf{k}}$, and Λ be a single-vertex rank
${\mathbb{N}}^{\mathsf{k}}$, and Λ be a single-vertex rank ![]() $\mathsf{k}$ graph. For
$\mathsf{k}$ graph. For ![]() $1\le i\le \mathsf{k}$, write
$1\le i\le \mathsf{k}$, write ![]() $
\Lambda^{\epsilon_i}:=\{{\mathbf{x}}^i_{\mathfrak{s}}:{\mathfrak{s}}\in[n_i]\},
$ where
$
\Lambda^{\epsilon_i}:=\{{\mathbf{x}}^i_{\mathfrak{s}}:{\mathfrak{s}}\in[n_i]\},
$ where ![]() $n_i=|\Lambda^{\epsilon_i}|$. It follows from the factorization property of Λ that, for
$n_i=|\Lambda^{\epsilon_i}|$. It follows from the factorization property of Λ that, for ![]() $1\le i \lt j\le \mathsf{k}$, there is a permutation
$1\le i \lt j\le \mathsf{k}$, there is a permutation ![]() $\theta_{ij}\in S_{n_i\times n_j}$ satisfying the following θ-commutation relations
$\theta_{ij}\in S_{n_i\times n_j}$ satisfying the following θ-commutation relations
 \begin{align*}
{\mathbf{x}}^i_{\mathfrak{s}} {\mathbf{x}}^j_{\mathfrak{t}} = {\mathbf{x}}^j_{{\mathfrak{t}}'} {\mathbf{x}}^i_{{\mathfrak{s}}'}
\quad\text{if}\quad
\theta_{ij}({\mathfrak{s}},{\mathfrak{t}}) = ({\mathfrak{s}}',{\mathfrak{t}}').
\end{align*}
\begin{align*}
{\mathbf{x}}^i_{\mathfrak{s}} {\mathbf{x}}^j_{\mathfrak{t}} = {\mathbf{x}}^j_{{\mathfrak{t}}'} {\mathbf{x}}^i_{{\mathfrak{s}}'}
\quad\text{if}\quad
\theta_{ij}({\mathfrak{s}},{\mathfrak{t}}) = ({\mathfrak{s}}',{\mathfrak{t}}').
\end{align*} To emphasize θ-commutation relations involved, this single-vertex ![]() $\mathsf k$-graph Λ is denoted as
$\mathsf k$-graph Λ is denoted as ![]() $\Lambda_\theta$ in this paper. So
$\Lambda_\theta$ in this paper. So ![]() $\Lambda_\theta$ is the following (unital) semigroup
$\Lambda_\theta$ is the following (unital) semigroup
 \begin{align*}
\Lambda_\theta=\big\langle {\mathbf{x}}_{\mathfrak{s}}^i: {\mathfrak{s}}\in [n_i],\, 1\le i\le \mathsf{k};\, {\mathbf{x}}^i_{\mathfrak{s}} {\mathbf{x}}^j_{\mathfrak{t}} = {\mathbf{x}}^j_{{\mathfrak{t}}'} {\mathbf{x}}^i_{{\mathfrak{s}}'}
\text{ whenever }
\theta_{ij}({\mathfrak{s}},{\mathfrak{t}}) = ({\mathfrak{s}}',{\mathfrak{t}}') \big\rangle^+,
\end{align*}
\begin{align*}
\Lambda_\theta=\big\langle {\mathbf{x}}_{\mathfrak{s}}^i: {\mathfrak{s}}\in [n_i],\, 1\le i\le \mathsf{k};\, {\mathbf{x}}^i_{\mathfrak{s}} {\mathbf{x}}^j_{\mathfrak{t}} = {\mathbf{x}}^j_{{\mathfrak{t}}'} {\mathbf{x}}^i_{{\mathfrak{s}}'}
\text{ whenever }
\theta_{ij}({\mathfrak{s}},{\mathfrak{t}}) = ({\mathfrak{s}}',{\mathfrak{t}}') \big\rangle^+,
\end{align*}which is also occasionally written as
 \begin{align*}
\Lambda_\theta=\big\langle {\mathbf{x}}_{\mathfrak{s}}^i: {\mathfrak{s}}\in [n_i],\ 1\le i\le \mathsf{k}; \, \theta_{ij}, \, 1\le i \lt j\le \mathsf{k} \big\rangle^+.
\end{align*}
\begin{align*}
\Lambda_\theta=\big\langle {\mathbf{x}}_{\mathfrak{s}}^i: {\mathfrak{s}}\in [n_i],\ 1\le i\le \mathsf{k}; \, \theta_{ij}, \, 1\le i \lt j\le \mathsf{k} \big\rangle^+.
\end{align*} One should notice that ![]() $\Lambda_\theta$ has the cancellation property due to the unique factorization property. It follows from the θ-commutation relations that every element
$\Lambda_\theta$ has the cancellation property due to the unique factorization property. It follows from the θ-commutation relations that every element ![]() $w\in \Lambda_\theta$ has the normal form
$w\in \Lambda_\theta$ has the normal form  $
w={\mathbf{x}}_{u_1}^1\cdots {\mathbf{x}}_{u_{\mathsf{k}}}^{\mathsf{k}}
$ for some
$
w={\mathbf{x}}_{u_1}^1\cdots {\mathbf{x}}_{u_{\mathsf{k}}}^{\mathsf{k}}
$ for some  ${\mathbf{x}}_{u_i}^i\in\Lambda_\theta^{\epsilon_i{\mathbb{N}}}$ (
${\mathbf{x}}_{u_i}^i\in\Lambda_\theta^{\epsilon_i{\mathbb{N}}}$ (![]() $1\le i\le \mathsf{k}$). Here we use the multi-index notation:
$1\le i\le \mathsf{k}$). Here we use the multi-index notation: ![]() ${\mathbf{x}}^i_{u_i}={\mathbf{x}}^i_{{\mathfrak{s}}_1}\cdots {\mathbf{x}}^i_{{\mathfrak{s}}_n}$ if
${\mathbf{x}}^i_{u_i}={\mathbf{x}}^i_{{\mathfrak{s}}_1}\cdots {\mathbf{x}}^i_{{\mathfrak{s}}_n}$ if ![]() $u_i={\mathfrak{s}}_1\cdots{\mathfrak{s}}_n$ with all
$u_i={\mathfrak{s}}_1\cdots{\mathfrak{s}}_n$ with all ![]() ${\mathfrak{s}}_i$’s in
${\mathfrak{s}}_i$’s in ![]() $[n_i]$.
$[n_i]$.
For ![]() $\mathsf{k}=2$, every permutation
$\mathsf{k}=2$, every permutation ![]() $\theta\in S_{n_1\times n_2}$ determines a single-vertex rank 2 graph. But for
$\theta\in S_{n_1\times n_2}$ determines a single-vertex rank 2 graph. But for ![]() $\mathsf{k}\ge 3$,
$\mathsf{k}\ge 3$, ![]() $\theta=\{\theta_{ij}:1\le i \lt j\le \mathsf{k}\}$ determines a rank
$\theta=\{\theta_{ij}:1\le i \lt j\le \mathsf{k}\}$ determines a rank ![]() $\mathsf k$ graph if and only if it satisfies a cubic condition (see, e.g., [Reference Davidson and Yang18, Reference Exel and Pardo23] for its definition). This cubic condition exactly provides interplay between
$\mathsf k$ graph if and only if it satisfies a cubic condition (see, e.g., [Reference Davidson and Yang18, Reference Exel and Pardo23] for its definition). This cubic condition exactly provides interplay between ![]() $\mathsf k$-graphs and the Yang–Baxter equation [Reference Yang49].
$\mathsf k$-graphs and the Yang–Baxter equation [Reference Yang49].
Here are some examples of single-vertex ![]() $\mathsf k$-graphs which will be used later.
$\mathsf k$-graphs which will be used later.
Example 2.1. (Trivial permutation)
For ![]() $1\le i \lt j\le \mathsf{k}$, let θij be the trivial permutation:
$1\le i \lt j\le \mathsf{k}$, let θij be the trivial permutation: ![]() $\theta_{ij}(s,t) = (s,t)$ for all
$\theta_{ij}(s,t) = (s,t)$ for all ![]() $s\in [n_i]$ and
$s\in [n_i]$ and ![]() $t\in [n_j]$. Then clearly
$t\in [n_j]$. Then clearly ![]() $\Lambda_\theta$ is a
$\Lambda_\theta$ is a ![]() $\mathsf{k}$-graph for all
$\mathsf{k}$-graph for all ![]() $\mathsf{k}\ge 1$, which is written as
$\mathsf{k}\ge 1$, which is written as ![]() $\Lambda_{\operatorname{id}}$.
$\Lambda_{\operatorname{id}}$.
Example 2.2. (Division permutation)
Let θij be defined by ![]() $\theta_{ij}(s,t) = (s',t')$, where
$\theta_{ij}(s,t) = (s',t')$, where ![]() $s'\in [n_i]$ and
$s'\in [n_i]$ and ![]() $t'\in [n_j]$ are the unique integers such that
$t'\in [n_j]$ are the unique integers such that ![]() $s + tn_i = t' + s'n_j$. One can check that this determines a
$s + tn_i = t' + s'n_j$. One can check that this determines a ![]() $\mathsf{k}$-graph for any
$\mathsf{k}$-graph for any ![]() $\mathsf{k}\ge 1$ (see, e.g., [Reference Laca, Raeburn, Ramagge and Whittaker32]), denoted as
$\mathsf{k}\ge 1$ (see, e.g., [Reference Laca, Raeburn, Ramagge and Whittaker32]), denoted as ![]() $\Lambda_{\mathsf{d}}$.
$\Lambda_{\mathsf{d}}$.
In particular, if ![]() $n_i=n$ for all
$n_i=n$ for all ![]() $1\le i\le \mathsf{k}$, then θ coincides with the flip commutation relation:
$1\le i\le \mathsf{k}$, then θ coincides with the flip commutation relation: ![]() $\theta_{ij}(s,t) = (t,s)$.
$\theta_{ij}(s,t) = (t,s)$.
Example 2.3. (‘Trivial’ case)
Let ![]() $n_i=1$ for all
$n_i=1$ for all ![]() $1\le i\le \mathsf{k}$. Then θij has to be the trivial commutation relation, which is the same as the division commutation relation. This is a special case of both examples 2.1 and 2.2.
$1\le i\le \mathsf{k}$. Then θij has to be the trivial commutation relation, which is the same as the division commutation relation. This is a special case of both examples 2.1 and 2.2.
Very surprisingly, this case is not trivial at all when it is equipped with self-similar actions! It is extremely interesting and related to Furstenberg’s ![]() $\times p, \times q$ conjecture. See § 4.2 below.
$\times p, \times q$ conjecture. See § 4.2 below.
2.2. Self-similar single-vertex  $\mathsf k$-graph C*-algebras
$\mathsf k$-graph C*-algebras
To unify the treatments of [Reference Johnson27] and [Reference Li and Yang38, Reference Murphy40], self-similar graphs and their C*-algebras naturally arise in [Reference Duwenig, Gillaspy, Norton, Reznikoff and Wright22] and are well studied there. Later, they are generalized to higher rank cases in [Reference Li and Yang34] and are further studied in [Reference Li33, Reference Li and Yang35].
Since this paper mainly focuses on single-vertex ![]() $\mathsf k$-graphs, we adapt the notions of [Reference Li33, Reference Li and Yang34] to our setting and simplify them accordingly.
$\mathsf k$-graphs, we adapt the notions of [Reference Li33, Reference Li and Yang34] to our setting and simplify them accordingly.
Let ![]() $\Lambda_\theta$ be a single-vertex
$\Lambda_\theta$ be a single-vertex ![]() $\mathsf k$-graph. A bijection
$\mathsf k$-graph. A bijection ![]() $\pi:\Lambda_\theta \to \Lambda_\theta$ is called an automorphism of
$\pi:\Lambda_\theta \to \Lambda_\theta$ is called an automorphism of ![]() $\Lambda_\theta$ if π preserves the degree map d. In general, an automorphism on
$\Lambda_\theta$ if π preserves the degree map d. In general, an automorphism on ![]() $\Lambda_\theta$ is not necessarily a semigroup automorphism on
$\Lambda_\theta$ is not necessarily a semigroup automorphism on ![]() $\Lambda_\theta$, as a semigroup. Denote by
$\Lambda_\theta$, as a semigroup. Denote by ![]() $\operatorname{Aut}(\Lambda_\theta)$ the automorphism group of Λ.
$\operatorname{Aut}(\Lambda_\theta)$ the automorphism group of Λ.
Let G be a (discrete countable) group. We say that G acts on ![]() $\Lambda_\theta$ if there is a group homomorphism φ from G to
$\Lambda_\theta$ if there is a group homomorphism φ from G to ![]() $\operatorname{Aut}(\Lambda_\theta)$. For
$\operatorname{Aut}(\Lambda_\theta)$. For ![]() $g\in G$ and
$g\in G$ and ![]() $\mu\in\Lambda_\theta$, we often simply write
$\mu\in\Lambda_\theta$, we often simply write ![]() $\varphi_g(\mu)$ as
$\varphi_g(\mu)$ as ![]() $g\cdot \mu$.
$g\cdot \mu$.
Definition 2.4. ([Reference Li33, Definition 3.2])
Let ![]() $\Lambda_\theta$ be a single-vertex
$\Lambda_\theta$ be a single-vertex ![]() $\mathsf k$-graph, G be a group acting on
$\mathsf k$-graph, G be a group acting on ![]() $\Lambda_\theta$, and
$\Lambda_\theta$, and ![]() $G\times \Lambda_\theta \to G$,
$G\times \Lambda_\theta \to G$, ![]() $(g,\mu)\mapsto g|_\mu$ be a given map. Then we call
$(g,\mu)\mapsto g|_\mu$ be a given map. Then we call ![]() $(G,\Lambda_\theta)$ a self-similar
$(G,\Lambda_\theta)$ a self-similar ![]() $\mathsf k$-graph if the following properties hold true:
$\mathsf k$-graph if the following properties hold true:
(i)
 $g\cdot (\mu\nu)=(g \cdot \mu)(g \vert_\mu \cdot \nu)$ for all
$g\cdot (\mu\nu)=(g \cdot \mu)(g \vert_\mu \cdot \nu)$ for all  $g \in G,\mu,\nu \in \Lambda_\theta$;
$g \in G,\mu,\nu \in \Lambda_\theta$;(ii)
 $g \vert_v =g$ for all
$g \vert_v =g$ for all  $g \in G,v \in \Lambda_\theta^0$;
$g \in G,v \in \Lambda_\theta^0$;(iii)
 $g \vert_{\mu\nu}=g \vert_\mu \vert_\nu$ for all
$g \vert_{\mu\nu}=g \vert_\mu \vert_\nu$ for all  $g \in G,\mu,\nu \in \Lambda_\theta$;
$g \in G,\mu,\nu \in \Lambda_\theta$;(iv)
 $1_G \vert_{\mu}=1_G$ for all
$1_G \vert_{\mu}=1_G$ for all  $\mu \in \Lambda_\theta$;
$\mu \in \Lambda_\theta$;(v)
 $(gh)\vert_\mu=g \vert_{h \cdot \mu} h \vert_\mu$ for all
$(gh)\vert_\mu=g \vert_{h \cdot \mu} h \vert_\mu$ for all  $g,h \in G,\mu \in \Lambda_\theta$.
$g,h \in G,\mu \in \Lambda_\theta$.
In this case, we also say that ![]() $\Lambda_\theta$ is a self-similar
$\Lambda_\theta$ is a self-similar ![]() $\mathsf k$-graph over G, and that G acts on
$\mathsf k$-graph over G, and that G acts on ![]() $\Lambda_\theta$ self-similarly.
$\Lambda_\theta$ self-similarly.
Definition 2.5. A self-similar ![]() $\mathsf k$-graph
$\mathsf k$-graph ![]() $(G,\Lambda_\theta)$ is said to be pseudo-free if
$(G,\Lambda_\theta)$ is said to be pseudo-free if ![]() $g \cdot \mu=\mu$ and
$g \cdot \mu=\mu$ and ![]() $g \vert_\mu=1_G $ implies
$g \vert_\mu=1_G $ implies ![]() $g=1_G$ for all
$g=1_G$ for all ![]() $g\in G$ and
$g\in G$ and ![]() $\mu\in \Lambda_\theta$.
$\mu\in \Lambda_\theta$.
Definition 2.6. ([Reference Li33, Definition 3.8])
Let ![]() $(G,\Lambda_\theta)$ be a self-similar
$(G,\Lambda_\theta)$ be a self-similar ![]() $\mathsf k$-graph. The self-similar
$\mathsf k$-graph. The self-similar ![]() $\mathsf k$-graph C*-algebra
$\mathsf k$-graph C*-algebra ![]() $\mathcal{O}_{G,\Lambda_\theta}$ is defined to be the universal unital C*-algebra generated by a family of unitaries
$\mathcal{O}_{G,\Lambda_\theta}$ is defined to be the universal unital C*-algebra generated by a family of unitaries ![]() $\{u_g\}_{g \in G}$ and a family of isometries
$\{u_g\}_{g \in G}$ and a family of isometries ![]() $\{s_\mu: \mu\in \Lambda_\theta\}$ satisfying
$\{s_\mu: \mu\in \Lambda_\theta\}$ satisfying
(i)
 $u_{gh}=u_g u_h$ for all
$u_{gh}=u_g u_h$ for all  $g, \ h \in G$;
$g, \ h \in G$;(ii)
 $s_\mu s_\nu=s_{\mu\nu}$ for all
$s_\mu s_\nu=s_{\mu\nu}$ for all  $\mu,\ \nu\in \Lambda_\theta$;
$\mu,\ \nu\in \Lambda_\theta$;(iii)
 $\sum\limits_{\mu\in \Lambda_\theta^{\mathbf{n}}} s_\mu s_\mu^*=I$ for all
$\sum\limits_{\mu\in \Lambda_\theta^{\mathbf{n}}} s_\mu s_\mu^*=I$ for all  ${\mathbf{n}}\in {\mathbb{N}}^{\mathsf k}$;
${\mathbf{n}}\in {\mathbb{N}}^{\mathsf k}$;(iv)
 $u_g s_\mu=s_{g \cdot \mu} u_{g \vert_\mu}$ for all
$u_g s_\mu=s_{g \cdot \mu} u_{g \vert_\mu}$ for all  $g \in G$ and
$g \in G$ and  $\mu \in \Lambda_\theta$.
$\mu \in \Lambda_\theta$.
Let us record the following result [Reference Li and Yang34, Propositions 3.12 and 5.10], which will be used later without mentioning.
Proposition 2.7. Let ![]() $(G,\Lambda_\theta)$ be a self-similar
$(G,\Lambda_\theta)$ be a self-similar ![]() $\mathsf k$-graph. Then
$\mathsf k$-graph. Then
(i) the linear span of
 $\{s_\mu u_g s_\nu^*: \mu, \nu \in \Lambda_\theta, g \in G\}$ is a dense
$\{s_\mu u_g s_\nu^*: \mu, \nu \in \Lambda_\theta, g \in G\}$ is a dense  $*$-subalgebra of
$*$-subalgebra of  $\mathcal{O}_{G,\Lambda_\theta}$;
$\mathcal{O}_{G,\Lambda_\theta}$;(ii) The
 $\mathsf k$-graph C*-algebra
$\mathsf k$-graph C*-algebra  ${\mathcal{O}}_{\Lambda_\theta}$ naturally embeds into
${\mathcal{O}}_{\Lambda_\theta}$ naturally embeds into  ${\mathcal{O}}_{G,\Lambda_\theta}$;
${\mathcal{O}}_{G,\Lambda_\theta}$;(iii) G and
 $\mathrm{C}^*(G)$ embed into
$\mathrm{C}^*(G)$ embed into  ${\mathcal{O}}_{G, \Lambda_\theta}$, provided that
${\mathcal{O}}_{G, \Lambda_\theta}$, provided that  $(G, \Lambda_\theta)$ is pseudo-free and G is amenable.
$(G, \Lambda_\theta)$ is pseudo-free and G is amenable.
As in [Reference Li and Yang34], let γ be the gauge action of ![]() ${\mathbb{T}}^{\mathsf k}$ on
${\mathbb{T}}^{\mathsf k}$ on ![]() ${\mathcal{O}}_{{\mathbb{Z}}, \Lambda_\theta}$:
${\mathcal{O}}_{{\mathbb{Z}}, \Lambda_\theta}$:
 \begin{equation*}
\gamma_{\mathbf{t}}(s_\mu u_g s_\nu^*)={\mathbf{t}}^{d(\mu)-d(\nu)}s_\mu u_g s_\nu^*
\end{equation*}
\begin{equation*}
\gamma_{\mathbf{t}}(s_\mu u_g s_\nu^*)={\mathbf{t}}^{d(\mu)-d(\nu)}s_\mu u_g s_\nu^*
\end{equation*} for all ![]() $\mu, \nu \in \Lambda_\theta$,
$\mu, \nu \in \Lambda_\theta$, ![]() $g\in {\mathbb{Z}}$, and
$g\in {\mathbb{Z}}$, and ![]() ${\mathbf{t}}\in {\mathbb{T}}^{\mathsf{k}}$. The fixed point algebra,
${\mathbf{t}}\in {\mathbb{T}}^{\mathsf{k}}$. The fixed point algebra,  ${\mathcal{O}}_{{\mathbb{Z}}, \Lambda_\theta}^\gamma$, of γ is generated by the standard generators
${\mathcal{O}}_{{\mathbb{Z}}, \Lambda_\theta}^\gamma$, of γ is generated by the standard generators ![]() $s_\mu u_g s_\nu^*$ with
$s_\mu u_g s_\nu^*$ with ![]() $d(\mu)=d(\nu)$. We often write
$d(\mu)=d(\nu)$. We often write ![]() ${\mathcal{F}}$ to stand for
${\mathcal{F}}$ to stand for  ${\mathcal{O}}_{{\mathbb{Z}}, \Lambda_\theta}^\gamma$. More generally, for
${\mathcal{O}}_{{\mathbb{Z}}, \Lambda_\theta}^\gamma$. More generally, for ![]() ${\mathbf{n}}\in {\mathbb{N}}^{\mathsf k}$, we define a mapping on
${\mathbf{n}}\in {\mathbb{N}}^{\mathsf k}$, we define a mapping on ![]() ${\mathcal{O}}_{{\mathbb{Z}},\Lambda_\theta}$ by
${\mathcal{O}}_{{\mathbb{Z}},\Lambda_\theta}$ by
 \begin{equation*}
\Phi_{\mathbf{n}}(x) = \int_{{\mathbb{T}}^{\mathsf k}} {\mathbf{t}}^{-{\mathbf{n}}}\gamma_{\mathbf{t}}(x)d{\mathbf{t}} \text{ for all }x \in {\mathcal{O}}_{{\mathbb{Z}},\Lambda_\theta}.
\end{equation*}
\begin{equation*}
\Phi_{\mathbf{n}}(x) = \int_{{\mathbb{T}}^{\mathsf k}} {\mathbf{t}}^{-{\mathbf{n}}}\gamma_{\mathbf{t}}(x)d{\mathbf{t}} \text{ for all }x \in {\mathcal{O}}_{{\mathbb{Z}},\Lambda_\theta}.
\end{equation*} Note that for ![]() $\mu,\nu \in \Lambda_\theta$,
$\mu,\nu \in \Lambda_\theta$, ![]() $g \in G$ we have
$g \in G$ we have
 \begin{equation*}
\Phi_{\mathbf{n}}(s_\mu u_g s_\nu^*) =
\begin{cases}
s_\mu u_g s_\nu^* & \text{if } d(\mu)-d(\nu) = {\mathbf{n}}, \\
0 & \text{otherwise.}
\end{cases}
\end{equation*}
\begin{equation*}
\Phi_{\mathbf{n}}(s_\mu u_g s_\nu^*) =
\begin{cases}
s_\mu u_g s_\nu^* & \text{if } d(\mu)-d(\nu) = {\mathbf{n}}, \\
0 & \text{otherwise.}
\end{cases}
\end{equation*} In particular,  ${\mathcal{O}}_{{\mathbb{Z}}, \Lambda_\theta}^\gamma=\operatorname{Ran}\Phi_{\mathbf 0}$. Also
${\mathcal{O}}_{{\mathbb{Z}}, \Lambda_\theta}^\gamma=\operatorname{Ran}\Phi_{\mathbf 0}$. Also ![]() $\Phi_{\mathbf 0}$ is a faithful conditional expectation from
$\Phi_{\mathbf 0}$ is a faithful conditional expectation from ![]() ${\mathcal{O}}_{{\mathbb{Z}},\Lambda_\theta}$ onto
${\mathcal{O}}_{{\mathbb{Z}},\Lambda_\theta}$ onto  ${\mathcal{O}}_{{\mathbb{Z}}, \Lambda_\theta}^\gamma$.
${\mathcal{O}}_{{\mathbb{Z}}, \Lambda_\theta}^\gamma$.
We end this subsection by briefly recalling the periodicity of ![]() $(G, \Lambda_\theta)$. Let
$(G, \Lambda_\theta)$. Let ![]() $(G,\Lambda_\theta)$ be a self-similar
$(G,\Lambda_\theta)$ be a self-similar ![]() $\mathsf k$-graph. For
$\mathsf k$-graph. For ![]() $\mu,\nu \in \Lambda_\theta, g \in G$, the triple
$\mu,\nu \in \Lambda_\theta, g \in G$, the triple ![]() $(\mu,g,\nu)$ is called cycline if
$(\mu,g,\nu)$ is called cycline if ![]() $\mu(g \cdot x)=\nu x$ for all
$\mu(g \cdot x)=\nu x$ for all ![]() $x \in s(\nu)\Lambda^\infty$. Clearly, every triple
$x \in s(\nu)\Lambda^\infty$. Clearly, every triple ![]() $(\mu, 1_G, \mu)$
$(\mu, 1_G, \mu)$ ![]() $(\mu \in \Lambda)$ is cycline. Those cycline triples are said to be trivial. An infinite path
$(\mu \in \Lambda)$ is cycline. Those cycline triples are said to be trivial. An infinite path ![]() $x \in \Lambda_\theta^\infty$ is said to be G-aperiodic if, for
$x \in \Lambda_\theta^\infty$ is said to be G-aperiodic if, for ![]() $g \in G, \mathbf p, \mathbf q \in \mathbb{N}^{\mathsf k}$ with
$g \in G, \mathbf p, \mathbf q \in \mathbb{N}^{\mathsf k}$ with ![]() $g \neq 1_G$ or
$g \neq 1_G$ or ![]() $\mathbf p \neq \mathbf q$, we have
$\mathbf p \neq \mathbf q$, we have ![]() $\sigma^{\mathbf p}(x) \neq g \cdot \sigma^{\mathbf q}(x)$; otherwise, x is called G-periodic.
$\sigma^{\mathbf p}(x) \neq g \cdot \sigma^{\mathbf q}(x)$; otherwise, x is called G-periodic. ![]() $(G,\Lambda_\theta)$ is said to be aperiodic if there exists a G-aperiodic path
$(G,\Lambda_\theta)$ is said to be aperiodic if there exists a G-aperiodic path ![]() $x\in \Lambda_\theta^\infty$; and periodic otherwise.
$x\in \Lambda_\theta^\infty$; and periodic otherwise.
Theorem 2.8. (Li-Yang [Reference Li33])
![]() $(G,\Lambda_\theta)$ is aperiodic
$(G,\Lambda_\theta)$ is aperiodic ![]() $\iff$ all cycline triples are trivial.
$\iff$ all cycline triples are trivial.
2.3. Right LCM semigroup C*-algebras and their boundary quotient C*-algebras
Let us recall some basics about right LCM semigroups and their C*-algebras from [Reference Brownlowe, Larsen, Ramagge and Stammeier8]. Let P be a discrete left-cancellative semigroup. We say P is a right LCM semigroup if any two elements ![]() $x,y\in P$ with a right common multiple have a right least common multiple
$x,y\in P$ with a right common multiple have a right least common multiple ![]() $z\in P$. Equivalently, P is right LCM if, for any
$z\in P$. Equivalently, P is right LCM if, for any ![]() $x,y\in P$, the intersection
$x,y\in P$, the intersection ![]() $xP\cap yP$ is either empty or equal to zP for some
$xP\cap yP$ is either empty or equal to zP for some ![]() $z\in P$.
$z\in P$.
For a right LCM semigroup P, its C*-algebra ![]() $\mathrm{C}^*(P)$ defined in [Reference Li and Yang36] can be greatly simplified as follows:
$\mathrm{C}^*(P)$ defined in [Reference Li and Yang36] can be greatly simplified as follows: ![]() $\mathrm{C}^*(P)$ is the universal C*-algebra generated by isometries
$\mathrm{C}^*(P)$ is the universal C*-algebra generated by isometries ![]() $\{v_p: p\in P\}$ and projections
$\{v_p: p\in P\}$ and projections ![]() $\{e_{pP}: p\in P\}$ satisfying
$\{e_{pP}: p\in P\}$ satisfying
for all ![]() $p, q\in P$.
$p, q\in P$.
Recall that a subset ![]() $F\subseteq P$ is called a foundation set if it is finite and for each
$F\subseteq P$ is called a foundation set if it is finite and for each ![]() $p \in P$, there exists
$p \in P$, there exists ![]() $q\in F$ such that
$q\in F$ such that ![]() $pP \cap qP\ne \varnothing$. Then the boundary quotient
$pP \cap qP\ne \varnothing$. Then the boundary quotient ![]() ${\mathcal{Q}}(P)$ of
${\mathcal{Q}}(P)$ of ![]() $\mathrm{C}^*(P)$ is the universal C*-algebra generated by isometries
$\mathrm{C}^*(P)$ is the universal C*-algebra generated by isometries ![]() $\{v_p: p\in P\}$ and projections
$\{v_p: p\in P\}$ and projections ![]() $\{e_{pP}: p\in P\}$ satisfying the relations in (1) and
$\{e_{pP}: p\in P\}$ satisfying the relations in (1) and
 \begin{equation*}
\prod_{p\in F}(1-e_{pP})=0 \text{ for every foundation set}\ F\subseteq P.
\end{equation*}
\begin{equation*}
\prod_{p\in F}(1-e_{pP})=0 \text{ for every foundation set}\ F\subseteq P.
\end{equation*}2.4. Semigroups from self-similar actions
Let ![]() $\Lambda_\theta$ be a single-vertex
$\Lambda_\theta$ be a single-vertex ![]() $\mathsf{k}$-graph. By
$\mathsf{k}$-graph. By ![]() $\Lambda^\epsilon$, we denote the set of all edges of
$\Lambda^\epsilon$, we denote the set of all edges of ![]() $\Lambda_\theta$:
$\Lambda_\theta$:  $\Lambda^\epsilon=\bigcup_{i=1}^{\mathsf{k}}\{e\in \Lambda: d(e)=\epsilon_i\}$. Suppose that
$\Lambda^\epsilon=\bigcup_{i=1}^{\mathsf{k}}\{e\in \Lambda: d(e)=\epsilon_i\}$. Suppose that ![]() ${\mathbb{Z}}=\langle a \rangle$ acts on
${\mathbb{Z}}=\langle a \rangle$ acts on ![]() $\Lambda_\theta$ self-similarly. Then one can naturally associate a semigroup to the self-similar
$\Lambda_\theta$ self-similarly. Then one can naturally associate a semigroup to the self-similar ![]() $\mathsf k$-graph
$\mathsf k$-graph ![]() $({\mathbb{Z}}, \Lambda_\theta)$ as follows:
$({\mathbb{Z}}, \Lambda_\theta)$ as follows:
 \begin{align}
\mathsf{S}_{{\mathbb{N}}, \Lambda_\theta}
:=\left\langle a, e:
\begin{array}{ll}
a e=a\cdot e a|_{e} &\text{if}\ e\in \Lambda_\theta^\epsilon\ \text{and}\ a|_e\ge 0, \\
a e (a|_{e})^{-1}=a\cdot e &\text{if}\ e\in \Lambda_\theta^\epsilon\ \text{and}\ a|_e \lt 0,
\end{array}
\; e\in\Lambda_\theta^\epsilon
\right\rangle^+.
\end{align}
\begin{align}
\mathsf{S}_{{\mathbb{N}}, \Lambda_\theta}
:=\left\langle a, e:
\begin{array}{ll}
a e=a\cdot e a|_{e} &\text{if}\ e\in \Lambda_\theta^\epsilon\ \text{and}\ a|_e\ge 0, \\
a e (a|_{e})^{-1}=a\cdot e &\text{if}\ e\in \Lambda_\theta^\epsilon\ \text{and}\ a|_e \lt 0,
\end{array}
\; e\in\Lambda_\theta^\epsilon
\right\rangle^+.
\end{align}This is the semigroup we focus on in this paper. Because of its importance, it deserves a name.
Definition 2.9. The semigroup ![]() $\mathsf{S}_{{\mathbb{N}}, \Lambda_\theta}$ defined in (2) is called the semigroup of the self-similar
$\mathsf{S}_{{\mathbb{N}}, \Lambda_\theta}$ defined in (2) is called the semigroup of the self-similar ![]() $\mathsf k$-graph
$\mathsf k$-graph ![]() $({\mathbb{Z}}, \Lambda_\theta)$.
$({\mathbb{Z}}, \Lambda_\theta)$.
Here are another semigroup and a group which are closely related to the semigroup ![]() $\mathsf{S}_{{\mathbb{N}}, \Lambda_\theta}$:
$\mathsf{S}_{{\mathbb{N}}, \Lambda_\theta}$:
 \begin{align*}
\mathsf{S}_{{\mathbb{Z}}, \Lambda_\theta}
&:=\langle a, a^{-1}, e: a e=a\cdot e a|_e, \, e\in \Lambda_\theta^\epsilon \rangle^+,\\
\mathsf{G}_{{\mathbb{Z}}, \Lambda_\theta}
&:=\langle a, e: a e=a\cdot e a|_e, \, e\in \Lambda_\theta^\epsilon \rangle.
\end{align*}
\begin{align*}
\mathsf{S}_{{\mathbb{Z}}, \Lambda_\theta}
&:=\langle a, a^{-1}, e: a e=a\cdot e a|_e, \, e\in \Lambda_\theta^\epsilon \rangle^+,\\
\mathsf{G}_{{\mathbb{Z}}, \Lambda_\theta}
&:=\langle a, e: a e=a\cdot e a|_e, \, e\in \Lambda_\theta^\epsilon \rangle.
\end{align*}Remark 2.10. Some remarks are in order.
(i) We should mention that
 ${\mathbb{N}}$ used in
${\mathbb{N}}$ used in  $\mathsf{S}_{{\mathbb{N}}, \Lambda_\theta}$ emphasizes that only non-negative integers from
$\mathsf{S}_{{\mathbb{N}}, \Lambda_\theta}$ emphasizes that only non-negative integers from  ${\mathbb{Z}}$ are involved, although the self-similar graph
${\mathbb{Z}}$ are involved, although the self-similar graph  $({\mathbb{Z}}, \Lambda_\theta)$ is considered.
$({\mathbb{Z}}, \Lambda_\theta)$ is considered.(ii) We have intended to call
 $\mathsf{S}_{{\mathbb{N}}, \Lambda_\theta}$ the self-similar monoid/semigroup of
$\mathsf{S}_{{\mathbb{N}}, \Lambda_\theta}$ the self-similar monoid/semigroup of  $({\mathbb{Z}}, \Lambda_\theta)$. But the term ‘self-similar monoids/semigroups’ is already used in the literature for a very different meaning (see, e.g., [Reference Barlak, Omland and Stammeier4]) and is similar to the notion of groups over self-similar
$({\mathbb{Z}}, \Lambda_\theta)$. But the term ‘self-similar monoids/semigroups’ is already used in the literature for a very different meaning (see, e.g., [Reference Barlak, Omland and Stammeier4]) and is similar to the notion of groups over self-similar  $\mathsf{k}$-graphs given in [Reference Li33].
$\mathsf{k}$-graphs given in [Reference Li33].(iii) At first glance, it seems that the semigroup
 $\mathsf{S}_{{\mathbb{N}}, \Lambda_\theta}$ has been considered in [Reference Laca, Raeburn, Ramagge and Whittaker32, Section 3]. But one should notice that it is required that the restriction map is surjective in [Reference Laca, Raeburn, Ramagge and Whittaker32]. This is a rather strong condition. Most semigroups
$\mathsf{S}_{{\mathbb{N}}, \Lambda_\theta}$ has been considered in [Reference Laca, Raeburn, Ramagge and Whittaker32, Section 3]. But one should notice that it is required that the restriction map is surjective in [Reference Laca, Raeburn, Ramagge and Whittaker32]. This is a rather strong condition. Most semigroups  $\mathsf{S}_{{\mathbb{N}}, \Lambda_\theta}$ studied in this paper are not covered there.
$\mathsf{S}_{{\mathbb{N}}, \Lambda_\theta}$ studied in this paper are not covered there.
3. Rank 1 case: more than GBS semigroups
For ![]() $1\le n\in {\mathbb{N}}$, let
$1\le n\in {\mathbb{N}}$, let ![]() $\mathsf{E}_n$ denote the single-vertex (directed) graph with n edges. Suppose that
$\mathsf{E}_n$ denote the single-vertex (directed) graph with n edges. Suppose that ![]() $({\mathbb{Z}}, \mathsf E_n)$ is a self-similar graph. Assume that the action of
$({\mathbb{Z}}, \mathsf E_n)$ is a self-similar graph. Assume that the action of ![]() ${\mathbb{Z}}$ on the edge set
${\mathbb{Z}}$ on the edge set ![]() $\mathsf{E}_n^1$ has κ orbits
$\mathsf{E}_n^1$ has κ orbits  ${\mathcal{E}}_i:=\{e_s^i: a\cdot e_s^i = e_{s+1\!\!\mod n_i}^i, s\in [n_i]\}$ for each
${\mathcal{E}}_i:=\{e_s^i: a\cdot e_s^i = e_{s+1\!\!\mod n_i}^i, s\in [n_i]\}$ for each ![]() $1\le i\le \kappa$. Thus
$1\le i\le \kappa$. Thus
 \begin{equation*}
n=\sum_{i=1}^\kappa n_i \quad\text{and}\quad \mathsf{E}_n^1=\bigsqcup_{i=1}^\kappa {\mathcal{E}}_i.
\end{equation*}
\begin{equation*}
n=\sum_{i=1}^\kappa n_i \quad\text{and}\quad \mathsf{E}_n^1=\bigsqcup_{i=1}^\kappa {\mathcal{E}}_i.
\end{equation*} For ![]() $1\le i\le \kappa$, let
$1\le i\le \kappa$, let
 \begin{equation*}
m_i:=\sum_{s\in [n_i]} a|_{e_s^i} \quad \text{and}\quad m:=\sum\limits_{i=1}^\kappa m_i.
\end{equation*}
\begin{equation*}
m_i:=\sum_{s\in [n_i]} a|_{e_s^i} \quad \text{and}\quad m:=\sum\limits_{i=1}^\kappa m_i.
\end{equation*} Clearly the self-similar action of ![]() $({\mathbb{Z}}, \mathsf{E}_n)$ induces a self-similar graph
$({\mathbb{Z}}, \mathsf{E}_n)$ induces a self-similar graph ![]() $({\mathbb{Z}}, \mathsf{E}_{n_i})$ for each
$({\mathbb{Z}}, \mathsf{E}_{n_i})$ for each ![]() $1\le i\le \kappa$. Conversely, if there is a self-similar action
$1\le i\le \kappa$. Conversely, if there is a self-similar action ![]() ${\mathbb{Z}}$ on each
${\mathbb{Z}}$ on each ![]() $\mathsf{E}_{n_i}$, then these κ self-similar graphs
$\mathsf{E}_{n_i}$, then these κ self-similar graphs ![]() $({\mathbb{Z}}, \mathsf{E}_{n_i})$ determine a self-similar graph
$({\mathbb{Z}}, \mathsf{E}_{n_i})$ determine a self-similar graph ![]() $({\mathbb{Z}}, \mathsf{E}_n)$.
$({\mathbb{Z}}, \mathsf{E}_n)$.
So, in the rank 1 case, one can rewrite
 \begin{align*}
\mathsf{S}_{{\mathbb{N}}, \mathsf{E}_n}
:=\left \langle a, e\in \mathsf{E}_n^1: \!\!
\begin{array}{ll}
a e=a\cdot e a|_{e} & \text{if }a|_e\ge 0\\
a e (a|_{e})^{-1}=a\cdot e & \text{if }a|_e \lt 0
\end{array}
\right\rangle^+.
\end{align*}
\begin{align*}
\mathsf{S}_{{\mathbb{N}}, \mathsf{E}_n}
:=\left \langle a, e\in \mathsf{E}_n^1: \!\!
\begin{array}{ll}
a e=a\cdot e a|_{e} & \text{if }a|_e\ge 0\\
a e (a|_{e})^{-1}=a\cdot e & \text{if }a|_e \lt 0
\end{array}
\right\rangle^+.
\end{align*} Before going further, we should mention that [Reference Li and Yang38] also deals with the rank 1 case. But there, in terms of our terminology, the action of ![]() ${\mathbb{Z}}$ on the infinite path space
${\mathbb{Z}}$ on the infinite path space ![]() $\mathsf E_n^\infty$ is assumed to be faithful. This in particular implies that the self-similar graph
$\mathsf E_n^\infty$ is assumed to be faithful. This in particular implies that the self-similar graph ![]() $({\mathbb{Z}}, \mathsf E_n)$ is aperiodic. Thus this eliminates all interesting (periodic) self-similar graphs (cf. propositions 3.18, 3.22, 3.23, and theorem 3.20).
$({\mathbb{Z}}, \mathsf E_n)$ is aperiodic. Thus this eliminates all interesting (periodic) self-similar graphs (cf. propositions 3.18, 3.22, 3.23, and theorem 3.20).
Throughout this section, we assume that
This condition assures that the self-similar graph ![]() $({\mathbb{Z}}, \mathsf E_n)$ is pseudo-free (lemma 3.11), which is required in [Reference Duwenig, Gillaspy, Norton, Reznikoff and Wright22, Reference Li33, Reference Li and Yang34].
$({\mathbb{Z}}, \mathsf E_n)$ is pseudo-free (lemma 3.11), which is required in [Reference Duwenig, Gillaspy, Norton, Reznikoff and Wright22, Reference Li33, Reference Li and Yang34].
Remark 3.1. It is worth mentioning that, under the assumptions (†), ![]() $\mathsf{S}_{{\mathbb{N}}, \mathsf{E}_n}$ is embedded into the group
$\mathsf{S}_{{\mathbb{N}}, \mathsf{E}_n}$ is embedded into the group ![]() $\mathsf{G}_{{\mathbb{Z}}, \mathsf{E}_n}$ [Reference Adjan1].
$\mathsf{G}_{{\mathbb{Z}}, \mathsf{E}_n}$ [Reference Adjan1].
A special class of self-similar graphs is worth mentioning for later use.
Example 3.2. ((n, m)-odometer  $\mathsf E(n,m)$)
$\mathsf E(n,m)$)
For ![]() $1\le n\in {\mathbb{N}}$ and
$1\le n\in {\mathbb{N}}$ and ![]() $0\ne m \in {\mathbb{Z}}$, an (n, m)-odometer is a self-similar graph
$0\ne m \in {\mathbb{Z}}$, an (n, m)-odometer is a self-similar graph ![]() $({\mathbb{Z}}, \mathsf{E}_n)$ with the action and restriction given by
$({\mathbb{Z}}, \mathsf{E}_n)$ with the action and restriction given by
 \begin{align*}
a\cdot e_s &=
\begin{cases}
e_{s+1} & \text{if } 0\le s \lt n-1, \\
e_0 & \text{if } s=n-1;
\end{cases}\\
a|_{e_s} &=
\begin{cases}
0 &\text{if } 0\le s \lt n-1 , \\
a^{m} & \text{if } s=n-1.
\end{cases}
\end{align*}
\begin{align*}
a\cdot e_s &=
\begin{cases}
e_{s+1} & \text{if } 0\le s \lt n-1, \\
e_0 & \text{if } s=n-1;
\end{cases}\\
a|_{e_s} &=
\begin{cases}
0 &\text{if } 0\le s \lt n-1 , \\
a^{m} & \text{if } s=n-1.
\end{cases}
\end{align*} The (n, m)-odometer is denoted as ![]() $\mathsf E(n,m)$. The case of m = 1 yields the classical odometers which have been extensively studied in the literature (see, e.g., [Reference Li39] and the references therein).
$\mathsf E(n,m)$. The case of m = 1 yields the classical odometers which have been extensively studied in the literature (see, e.g., [Reference Li39] and the references therein).
In the sequel, we provide two examples of important semigroups which can be realized as semigroups of self-similar graphs.
Example 3.3. (BS semigroups)
For ![]() $1\le n\in {\mathbb{N}}$ and
$1\le n\in {\mathbb{N}}$ and ![]() $0\ne m \in {\mathbb{Z}}$, the (BS) semigroup is
$0\ne m \in {\mathbb{Z}}$, the (BS) semigroup is
 \begin{align*}
\operatorname{BS}^+(n, m)
:=\left\langle a, b\mid\!\!
\begin{array}{ll}
a^n b=b a^{m} &\text{if}\ m \gt 0 \\
a^{n} b a^{-m}=b &\text{if}\ m \lt 0
\end{array}
\right\rangle^+.
\end{align*}
\begin{align*}
\operatorname{BS}^+(n, m)
:=\left\langle a, b\mid\!\!
\begin{array}{ll}
a^n b=b a^{m} &\text{if}\ m \gt 0 \\
a^{n} b a^{-m}=b &\text{if}\ m \lt 0
\end{array}
\right\rangle^+.
\end{align*} The semigroup ![]() $\operatorname{BS}^+(n, m)$ can be realized as the semigroup of an (n, m)-odometer.
$\operatorname{BS}^+(n, m)$ can be realized as the semigroup of an (n, m)-odometer.
From now on, we use the semigroups ![]() $\operatorname{BS}^+(n,m)$ and (n, m)-odometer interchangeably.
$\operatorname{BS}^+(n,m)$ and (n, m)-odometer interchangeably.
Example 3.4. (GBS semigroups)
As the name indicates, this example generalizes BS semigroups in example 3.3. Let ![]() $1\le \kappa\in {\mathbb{N}} \cup\{\infty\}$. For
$1\le \kappa\in {\mathbb{N}} \cup\{\infty\}$. For ![]() $1\le n_i\in {\mathbb{N}}$ and
$1\le n_i\in {\mathbb{N}}$ and ![]() $0\ne m_i\in {\mathbb{Z}}$ (
$0\ne m_i\in {\mathbb{Z}}$ (![]() $1\le i\le \kappa$), the GBS semigroup is
$1\le i\le \kappa$), the GBS semigroup is
 \begin{align*}
\operatorname{GBS}_\kappa^+(n_i, m_i)
:=\left\langle a, b_i\mid \!\!
\begin{array}{ll}
a^{n_i} b_i=b_i a^{m_i} &\text{if}\ m_i \gt 0, \\
a^{n_i} b_i a^{-m_i}=b_i &\text{if}\ m_i \lt 0,
\end{array}
\ 1\le i\le \kappa\right\rangle^+.
\end{align*}
\begin{align*}
\operatorname{GBS}_\kappa^+(n_i, m_i)
:=\left\langle a, b_i\mid \!\!
\begin{array}{ll}
a^{n_i} b_i=b_i a^{m_i} &\text{if}\ m_i \gt 0, \\
a^{n_i} b_i a^{-m_i}=b_i &\text{if}\ m_i \lt 0,
\end{array}
\ 1\le i\le \kappa\right\rangle^+.
\end{align*} The GBS semigroup ![]() $\operatorname{GBS}_k^+(n_i, m_i)$ can also be realized as the semigroup of a self-similar graph as follows. Let
$\operatorname{GBS}_k^+(n_i, m_i)$ can also be realized as the semigroup of a self-similar graph as follows. Let ![]() $\mathsf{E}$ be the single-vertex directed graph with the edge set
$\mathsf{E}$ be the single-vertex directed graph with the edge set ![]() $\{e^i_s: 1\le i\le \kappa, s\in [n_i]\}$. To each
$\{e^i_s: 1\le i\le \kappa, s\in [n_i]\}$. To each ![]() $1\le i\le \kappa$, we associate an
$1\le i\le \kappa$, we associate an ![]() $(n_i, m_i)$-odometer. Then
$(n_i, m_i)$-odometer. Then ![]() $\operatorname{GBS}_\kappa^+(n_i, m_i)\cong \textsf{S}_{{\mathbb{N}}, \mathsf{E}}$.
$\operatorname{GBS}_\kappa^+(n_i, m_i)\cong \textsf{S}_{{\mathbb{N}}, \mathsf{E}}$.
Therefore, semigroups of self-similar graphs encompass GBS semigroups.
Remark 3.5. In this remark, let us mention some connections with the literature.
(i) BS semigroups usually provide a nice class of examples or counter-examples for some properties (e.g., [Reference an Huef, Laca, Raeburn and Sims2, Reference Brown, Nagy, Reznikoff, Sims and Williams7]). They have been attracting a lot of operator algebraists’ attention recently. For instance, in [Reference Rudolph44], the boundary quotient of the semigroup C*-algebra
 $\operatorname{BS}^+(n,m)$ is first investigated via the C*-algebra for a category of paths. In [Reference Chen and Li12], the KMS states of the semigroup C*-algebra of quasi-lattice ordered BS semigroups are studied. This is generalized to all BS semigroups later in [Reference Brown, Nagy, Reznikoff, Sims and Williams7].
$\operatorname{BS}^+(n,m)$ is first investigated via the C*-algebra for a category of paths. In [Reference Chen and Li12], the KMS states of the semigroup C*-algebra of quasi-lattice ordered BS semigroups are studied. This is generalized to all BS semigroups later in [Reference Brown, Nagy, Reznikoff, Sims and Williams7].(ii) Very recently, in [Reference Carlsen, Ruiz, Sims and Tomforde11] Chen–Li study the C*-algebras for a class of semigroups, which are graphs of semigroups which are constructed very similarly to graphs of groups in [Reference Nekrashevych43]. There is some intersection: For instance, their semigroups encompass GBS semigroups. However, theirs do not include all semigroups
 $\mathsf{S}_{{\mathbb{Z}}, \Lambda_\theta}$. Most importantly, theirs do not include any ‘genuine’ higher rank BS semigroups studied in § 4 below.
$\mathsf{S}_{{\mathbb{Z}}, \Lambda_\theta}$. Most importantly, theirs do not include any ‘genuine’ higher rank BS semigroups studied in § 4 below.
3.1. Some basic properties
The two lemmas below will be used frequently. One can prove the first one by simple calculations, and the second one by applying remark 3.1. Their proofs are omitted here.
Lemma 3.6. Let ![]() $({\mathbb{Z}}, \mathsf{E}_n)$ be a self-similar graph. Then, for
$({\mathbb{Z}}, \mathsf{E}_n)$ be a self-similar graph. Then, for ![]() $\ell\in {\mathbb{Z}}$,
$\ell\in {\mathbb{Z}}$, ![]() $1\le i\le \kappa$, and
$1\le i\le \kappa$, and ![]() $p\in [n_i]$, one has
$p\in [n_i]$, one has
(i)
 $a^{\ell n_i+ p}\cdot{e_s^i}=e_{(s+p)\!\!\mod\! n_i}^i$;
$a^{\ell n_i+ p}\cdot{e_s^i}=e_{(s+p)\!\!\mod\! n_i}^i$;(ii)
 $
a^{\ell n_i+ p}|_{e_s^i}=
\begin{cases}
a^{\ell m_i} &\text{if}\ p=0,\\
a^{\ell m_i} \prod_{q=0}^{p-1} a|_{e_{(s+q)\!\!\mod\! n_i}^i} & \text{if}\ 0 \lt p \lt n_i-1.
\end{cases}
$
$
a^{\ell n_i+ p}|_{e_s^i}=
\begin{cases}
a^{\ell m_i} &\text{if}\ p=0,\\
a^{\ell m_i} \prod_{q=0}^{p-1} a|_{e_{(s+q)\!\!\mod\! n_i}^i} & \text{if}\ 0 \lt p \lt n_i-1.
\end{cases}
$
Lemma 3.7. Every element ![]() $x\in \mathsf{S}_{{\mathbb{N}}, \mathsf{E}_n}$ has a unique representation
$x\in \mathsf{S}_{{\mathbb{N}}, \mathsf{E}_n}$ has a unique representation ![]() $x= e_\mu a^\ell$ for some
$x= e_\mu a^\ell$ for some ![]() $\mu \in \mathsf{E}_n^*$ and
$\mu \in \mathsf{E}_n^*$ and ![]() $\ell\in {\mathbb{Z}}$.
$\ell\in {\mathbb{Z}}$.
Proposition 3.8. ![]() $\mathsf{S}_{{\mathbb{N}}, \mathsf{E}_n}$ is right LCM.
$\mathsf{S}_{{\mathbb{N}}, \mathsf{E}_n}$ is right LCM.
Proof. Consider ![]() $e_\mu a^k$ and
$e_\mu a^k$ and ![]() $e_\nu a^\ell$ in
$e_\nu a^\ell$ in ![]() $\mathsf{S}_{{\mathbb{N}}, \mathsf{E}_n}$. It is not hard to see that they have a right common upper bound if, and only if either
$\mathsf{S}_{{\mathbb{N}}, \mathsf{E}_n}$. It is not hard to see that they have a right common upper bound if, and only if either ![]() $e_\mu = e_\nu e_{\tilde \mu}$ for some
$e_\mu = e_\nu e_{\tilde \mu}$ for some ![]() $e_{\tilde \mu}\in \mathsf E_n^*$ or
$e_{\tilde \mu}\in \mathsf E_n^*$ or ![]() $e_\nu = e_\mu e_{\tilde \nu}$ for some
$e_\nu = e_\mu e_{\tilde \nu}$ for some ![]() $e_{\tilde \nu}\in \mathsf E_n^*$. WLOG we assume that
$e_{\tilde \nu}\in \mathsf E_n^*$. WLOG we assume that ![]() $e_\nu = e_\mu e_{\tilde \nu}$ for some
$e_\nu = e_\mu e_{\tilde \nu}$ for some ![]() $e_{\tilde \nu}\in \mathsf E_n^*$. Let
$e_{\tilde \nu}\in \mathsf E_n^*$. Let ![]() $e_\alpha:=a^{-k}\cdot e_{\tilde \nu}$. Then one can show the following: If
$e_\alpha:=a^{-k}\cdot e_{\tilde \nu}$. Then one can show the following: If ![]() $a^\ell \ge a^k|_{e_\alpha}$ (resp.
$a^\ell \ge a^k|_{e_\alpha}$ (resp. ![]() $a^\ell \lt a^k|_{e_\alpha}$), then
$a^\ell \lt a^k|_{e_\alpha}$), then ![]() $e_\nu a^\ell$ (reps.
$e_\nu a^\ell$ (reps. ![]() $e_\nu a^k|_{e_\alpha}$) is a least right common upper bound of
$e_\nu a^k|_{e_\alpha}$) is a least right common upper bound of ![]() $e_\mu a^k$ and
$e_\mu a^k$ and ![]() $e_\nu a^\ell$ (in
$e_\nu a^\ell$ (in ![]() $\mathsf{S}_{{\mathbb{N}}, \mathsf{E}_n}$).\hfill▪
$\mathsf{S}_{{\mathbb{N}}, \mathsf{E}_n}$).\hfill▪
Remark 3.9. If ![]() $a|_e\ge 0$ for all
$a|_e\ge 0$ for all ![]() $e\in \mathsf{E}_n$, then
$e\in \mathsf{E}_n$, then ![]() $\mathsf{S}_{{\mathbb{N}}, \mathsf{E}_n}$ is a Zappa–Szép product of the semigroups
$\mathsf{S}_{{\mathbb{N}}, \mathsf{E}_n}$ is a Zappa–Szép product of the semigroups ![]() ${\mathbb{N}}$ and
${\mathbb{N}}$ and ![]() $\mathbb{F}_n^+$ [Reference Brownlowe, Larsen, Ramagge and Stammeier8].
$\mathbb{F}_n^+$ [Reference Brownlowe, Larsen, Ramagge and Stammeier8].
Since ![]() $\mathsf{S}_{{\mathbb{N}}, \mathsf{E}_n}$ is right LCM, from § 2.3 and the analysis above, one has the following
$\mathsf{S}_{{\mathbb{N}}, \mathsf{E}_n}$ is right LCM, from § 2.3 and the analysis above, one has the following
Corollary 3.10. ![]() $
{\mathcal{Q}}(\mathsf{S}_{{\mathbb{N}}, \mathsf{E}_n})\cong{\mathcal{O}}_{{\mathbb{Z}}, \mathsf{E}_n}\cong {\mathcal{Q}}(\mathsf{S}_{{\mathbb{Z}}, \mathsf{E}_n}).
$
$
{\mathcal{Q}}(\mathsf{S}_{{\mathbb{N}}, \mathsf{E}_n})\cong{\mathcal{O}}_{{\mathbb{Z}}, \mathsf{E}_n}\cong {\mathcal{Q}}(\mathsf{S}_{{\mathbb{Z}}, \mathsf{E}_n}).
$
Proof. By proposition 3.8, the sets ![]() $\{a\}$ and
$\{a\}$ and ![]() $\{e_i: i\in [n]\}$ are foundation sets of
$\{e_i: i\in [n]\}$ are foundation sets of ![]() $\mathsf{S}_{{\mathbb{N}}, \mathsf{E}_n}$. Then the map
$\mathsf{S}_{{\mathbb{N}}, \mathsf{E}_n}$. Then the map
 \begin{equation*}
{\mathcal{Q}}(\mathsf{S}_{{\mathbb{N}}, \mathsf{E}_n})\to{\mathcal{O}}_{{\mathbb{Z}}, \mathsf{E}_n},\ v_{e_\mu a^\ell} \mapsto s_{e_\mu} u_{a^\ell},\
e_{e_\mu a^\ell\mathsf{S}_{{\mathbb{N}}, \mathsf{E}_n}}\mapsto s_{e_\mu} s_{e_\mu}^*
\end{equation*}
\begin{equation*}
{\mathcal{Q}}(\mathsf{S}_{{\mathbb{N}}, \mathsf{E}_n})\to{\mathcal{O}}_{{\mathbb{Z}}, \mathsf{E}_n},\ v_{e_\mu a^\ell} \mapsto s_{e_\mu} u_{a^\ell},\
e_{e_\mu a^\ell\mathsf{S}_{{\mathbb{N}}, \mathsf{E}_n}}\mapsto s_{e_\mu} s_{e_\mu}^*
\end{equation*} yields an isomorphism. The proof of ![]() ${\mathcal{Q}}(\mathsf S_{{\mathbb{Z}}, \mathsf E_n})\cong{\mathcal{O}}_{{\mathbb{Z}}, \mathsf{E}_n}$ is even simpler.\hfill▪
${\mathcal{Q}}(\mathsf S_{{\mathbb{Z}}, \mathsf E_n})\cong{\mathcal{O}}_{{\mathbb{Z}}, \mathsf{E}_n}$ is even simpler.\hfill▪
3.2. Pseudo-freeness of  $({\mathbb{Z}}, \mathsf{E}_n)$
$({\mathbb{Z}}, \mathsf{E}_n)$
Let ![]() $({\mathbb{Z}}, \mathsf{E}_n)$ be a self-similar graph satisfying our standing assumption †.
$({\mathbb{Z}}, \mathsf{E}_n)$ be a self-similar graph satisfying our standing assumption †.
Lemma 3.11. The self-similar graph ![]() $({\mathbb{Z}}, \mathsf{E}_n)$ is pseudo-free.
$({\mathbb{Z}}, \mathsf{E}_n)$ is pseudo-free.
Proof. This follows from lemma 3.6. In fact, suppose that ![]() $g\cdot \mu=\mu$ and
$g\cdot \mu=\mu$ and ![]() $g|_\mu=0$. If
$g|_\mu=0$. If ![]() $|\mu|=1$, it then follows from lemma 3.6 and the assumption (
$|\mu|=1$, it then follows from lemma 3.6 and the assumption (![]() $\dagger$) that g = 0. Now suppose that
$\dagger$) that g = 0. Now suppose that ![]() $g\cdot \mu=\mu$ and
$g\cdot \mu=\mu$ and ![]() $g|_\mu=0$ with
$g|_\mu=0$ with ![]() $|\mu|=k$ imply g = 0. Let
$|\mu|=k$ imply g = 0. Let ![]() $g\cdot(\mu e_s^i)=\mu e_s^i$ and
$g\cdot(\mu e_s^i)=\mu e_s^i$ and ![]() $g|_{\mu e_s^i}=0$ for some edge
$g|_{\mu e_s^i}=0$ for some edge ![]() $e_s^i$ in the i-th orbit. Then
$e_s^i$ in the i-th orbit. Then ![]() $g\cdot \mu g|_\mu\cdot e_s^i=\mu e_s^i\implies g\cdot \mu=\mu$ and
$g\cdot \mu g|_\mu\cdot e_s^i=\mu e_s^i\implies g\cdot \mu=\mu$ and ![]() $g|_\mu\cdot e_s^i=e_s^i$. So the latter implies
$g|_\mu\cdot e_s^i=e_s^i$. So the latter implies ![]() $g|_\mu=a^{\ell n_i}$ for some
$g|_\mu=a^{\ell n_i}$ for some ![]() $\ell\in{\mathbb{Z}}$. But also
$\ell\in{\mathbb{Z}}$. But also ![]() $g|_{\mu e_s^i}=0$ implies that
$g|_{\mu e_s^i}=0$ implies that  $0=g|_\mu|_{e_s^i}=a^{\ell n_i}|_{e_s^i}=a^{\ell m_i}$. Hence
$0=g|_\mu|_{e_s^i}=a^{\ell n_i}|_{e_s^i}=a^{\ell m_i}$. Hence ![]() $\ell=0$ as
$\ell=0$ as ![]() $m_i\ne 0$. Therefore,
$m_i\ne 0$. Therefore, ![]() $g\cdot \mu=\mu$ and
$g\cdot \mu=\mu$ and ![]() $g|_\mu=0$. By our inductive assumption, we have g = 0. This proves the pseudo-freeness of
$g|_\mu=0$. By our inductive assumption, we have g = 0. This proves the pseudo-freeness of ![]() $({\mathbb{Z}}, \mathsf{E}_n)$.\hfill▪
$({\mathbb{Z}}, \mathsf{E}_n)$.\hfill▪
Remark 3.12. Lemma 3.11 is no longer true if ![]() $m_i=0$ for some
$m_i=0$ for some ![]() $1\le i\le \kappa$. For example, consider the self-similar graph
$1\le i\le \kappa$. For example, consider the self-similar graph ![]() $({\mathbb{Z}}, \textsf{E}_2)$ with
$({\mathbb{Z}}, \textsf{E}_2)$ with ![]() $ae_1=e_2a$ and
$ae_1=e_2a$ and ![]() $ae_2=e_1a^{-1}$. Then
$ae_2=e_1a^{-1}$. Then ![]() $a^2e_i=e_i$ for
$a^2e_i=e_i$ for ![]() $i=1,2$, and
$i=1,2$, and ![]() $a^2|_{e_i}=0$. Clearly, this self-similar graph
$a^2|_{e_i}=0$. Clearly, this self-similar graph ![]() $({\mathbb{Z}}, \mathsf{E}_2)$ is not pseudo-free.
$({\mathbb{Z}}, \mathsf{E}_2)$ is not pseudo-free.
3.3. The periodicity of  $({\mathbb{Z}}, \mathsf{E}_n)$
$({\mathbb{Z}}, \mathsf{E}_n)$
In this subsection, we study the periodicity of self-similar graphs ![]() $({\mathbb{Z}}, \mathsf{E}_n)$ in detail. We first analyze the case when κ = 1, and then use it to study the general case.
$({\mathbb{Z}}, \mathsf{E}_n)$ in detail. We first analyze the case when κ = 1, and then use it to study the general case.
Recall that κ is the number of orbits of ![]() ${\mathbb{Z}}$ on
${\mathbb{Z}}$ on ![]() $\mathsf{E}_n$.
$\mathsf{E}_n$.
3.3.1. The case of κ = 1
Proposition 3.13. If κ = 1, then ![]() $({\mathbb{Z}}, \mathsf{E}_n)$ is periodic if and only if
$({\mathbb{Z}}, \mathsf{E}_n)$ is periodic if and only if ![]() $n\!\mid\! m$.
$n\!\mid\! m$.
Proof. Suppose that ![]() $m=n\ell$ for some
$m=n\ell$ for some ![]() $\ell \in {\mathbb{Z}}$. Let
$\ell \in {\mathbb{Z}}$. Let ![]() $x=e_{i_1}e_{i_2}\cdots\in \mathsf{E}_n^\infty$ be an infinite path. Repeatedly applying lemma 3.6 gives
$x=e_{i_1}e_{i_2}\cdots\in \mathsf{E}_n^\infty$ be an infinite path. Repeatedly applying lemma 3.6 gives
 \begin{equation*}
a^{nk}\cdot x=a^{nk}\cdot e_{i_1} a^{n k}|_{e_{i_1}}\cdot (e_{i_2}\cdots)=e_{i_1} a^{n\ell k}\cdot(e_{i_2}\cdots)=\cdots=x \quad\text{for all}\quad k\in {\mathbb{Z}}.
\end{equation*}
\begin{equation*}
a^{nk}\cdot x=a^{nk}\cdot e_{i_1} a^{n k}|_{e_{i_1}}\cdot (e_{i_2}\cdots)=e_{i_1} a^{n\ell k}\cdot(e_{i_2}\cdots)=\cdots=x \quad\text{for all}\quad k\in {\mathbb{Z}}.
\end{equation*} This shows that every infinite path ![]() $x\in \mathsf{E}_n^\infty$ is
$x\in \mathsf{E}_n^\infty$ is ![]() ${\mathbb{Z}}$-periodic in the sense of [Reference Li and Yang34]. So
${\mathbb{Z}}$-periodic in the sense of [Reference Li and Yang34]. So ![]() $({\mathbb{Z}}, \mathsf{E}_n)$ is periodic.
$({\mathbb{Z}}, \mathsf{E}_n)$ is periodic.
It remains to show that if ![]() $n\nmid m$ then
$n\nmid m$ then ![]() $({\mathbb{Z}},\mathsf{E}_n)$ is aperiodic. To the contrary, assume that
$({\mathbb{Z}},\mathsf{E}_n)$ is aperiodic. To the contrary, assume that ![]() $({\mathbb{Z}}, \mathsf{E}_n)$ is periodic. It follows from [Reference Li33, Theorem 3.7]
$({\mathbb{Z}}, \mathsf{E}_n)$ is periodic. It follows from [Reference Li33, Theorem 3.7] ![]() $({\mathbb{Z}}, \mathsf{E}_n)$ has a non-trivial cycline triple
$({\mathbb{Z}}, \mathsf{E}_n)$ has a non-trivial cycline triple ![]() $(\mu, g, \nu)$. That is,
$(\mu, g, \nu)$. That is, ![]() $\mu g\cdot x=\nu x$ for all
$\mu g\cdot x=\nu x$ for all ![]() $x\in \mathsf{E}_n^\infty$ with
$x\in \mathsf{E}_n^\infty$ with ![]() $g\ne 0$ or
$g\ne 0$ or ![]() $\mu\ne \nu$.
$\mu\ne \nu$.
Case (a): ![]() $|\mu| \lt |\nu|$. Then there is a unique
$|\mu| \lt |\nu|$. Then there is a unique ![]() $\nu'\in \mathsf{E}_n^*\setminus \mathsf{E}_n^0$ such that
$\nu'\in \mathsf{E}_n^*\setminus \mathsf{E}_n^0$ such that ![]() $\nu=\mu\nu'$. Thus
$\nu=\mu\nu'$. Thus ![]() $g\cdot x=\nu'x$ and so
$g\cdot x=\nu'x$ and so ![]() $g\cdot x(0, |\nu'|)=\nu'$ for all
$g\cdot x(0, |\nu'|)=\nu'$ for all ![]() $x\in \mathsf{E}_n^\infty$. This is impossible by noticing that n has to be greater than 1.
$x\in \mathsf{E}_n^\infty$. This is impossible by noticing that n has to be greater than 1.
Case (b): ![]() $|\mu| \gt |\nu|$. Since
$|\mu| \gt |\nu|$. Since ![]() $x\in \mathsf{E}_n^\infty$ is arbitrary, we replace x with
$x\in \mathsf{E}_n^\infty$ is arbitrary, we replace x with ![]() $g^{-1}\cdot x$ and then apply case (a).
$g^{-1}\cdot x$ and then apply case (a).
Case (c): ![]() $|\mu|=|\nu|$. Then
$|\mu|=|\nu|$. Then ![]() $\mu=\nu$ and
$\mu=\nu$ and ![]() $g\cdot x=x$ for all
$g\cdot x=x$ for all ![]() $x\in \mathsf{E}_n^\infty$. Let
$x\in \mathsf{E}_n^\infty$. Let ![]() $d:=\gcd(m,n) \gt 0$. Write
$d:=\gcd(m,n) \gt 0$. Write ![]() $m=dm_0$ and
$m=dm_0$ and ![]() $n=dn_0$. Since
$n=dn_0$. Since ![]() $n\nmid m$, we have
$n\nmid m$, we have ![]() $n_0\nmid m_0$. Write
$n_0\nmid m_0$. Write ![]() $x=e_{i_1}e_{i_2}\cdots$ with
$x=e_{i_1}e_{i_2}\cdots$ with ![]() $i_j\in [n]$. Then
$i_j\in [n]$. Then
Hence there is a sequence ![]() $\{k_i\}_{i\ge 1}\subseteq {\mathbb{Z}}$ of (non-zero) integers such that
$\{k_i\}_{i\ge 1}\subseteq {\mathbb{Z}}$ of (non-zero) integers such that
So
imply
Thus one has that ![]() $m_0^p k_1 = n_0^p k_{p+1}$ for all
$m_0^p k_1 = n_0^p k_{p+1}$ for all ![]() $p\ge 1$. In particular
$p\ge 1$. In particular ![]() $n_0^p\!\mid\! k_1$ for all
$n_0^p\!\mid\! k_1$ for all ![]() $p\ge 1$ as
$p\ge 1$ as ![]() $\gcd(m_0, n_0)=1$. But
$\gcd(m_0, n_0)=1$. But ![]() $n\!\nmid\! m$ implies
$n\!\nmid\! m$ implies ![]() $n_0 \gt 1$. So
$n_0 \gt 1$. So ![]() $k_1=0$ and hence g = 0. Then
$k_1=0$ and hence g = 0. Then ![]() $(\mu, g, \nu)=(\mu, 0, \mu)$ is a trivial cycline triple. This is a contradiction.\hfill▪
$(\mu, g, \nu)=(\mu, 0, \mu)$ is a trivial cycline triple. This is a contradiction.\hfill▪
Remark 3.14. Let ![]() $(G, \Lambda)$ be a self-similar
$(G, \Lambda)$ be a self-similar ![]() $\mathsf{k}$-graph. As mentioned in [Reference Li and Yang34], it is easy to see that if Λ is periodic, then
$\mathsf{k}$-graph. As mentioned in [Reference Li and Yang34], it is easy to see that if Λ is periodic, then ![]() $(G, \Lambda)$ is periodic. But the converse is not true. Here is a class of counter-examples: It is well-known that
$(G, \Lambda)$ is periodic. But the converse is not true. Here is a class of counter-examples: It is well-known that ![]() $\mathsf{E}_n$ is aperiodic if n > 1. But proposition 3.13 shows that
$\mathsf{E}_n$ is aperiodic if n > 1. But proposition 3.13 shows that ![]() $({\mathbb{Z}}, \mathsf{E}_n)$ is periodic whenever
$({\mathbb{Z}}, \mathsf{E}_n)$ is periodic whenever ![]() $n\!\mid\! m$. Therefore, the periodicity of
$n\!\mid\! m$. Therefore, the periodicity of ![]() $(G, \Lambda)$ is more complicated than that of the ambient graph Λ.
$(G, \Lambda)$ is more complicated than that of the ambient graph Λ.
We now determine all cycline triples of ![]() $({\mathbb{Z}}, \mathsf{E}_n)$ when κ = 1. Notice that all cycline triples are trivial if
$({\mathbb{Z}}, \mathsf{E}_n)$ when κ = 1. Notice that all cycline triples are trivial if ![]() $({\mathbb{Z}}, \mathsf{E}_n)$ is aperiodic by theorem 2.8. Hence it suffices to consider periodic self-similar graphs
$({\mathbb{Z}}, \mathsf{E}_n)$ is aperiodic by theorem 2.8. Hence it suffices to consider periodic self-similar graphs ![]() $({\mathbb{Z}}, \mathsf{E}_n)$.
$({\mathbb{Z}}, \mathsf{E}_n)$.
When n = 1, there is a unique infinite path. So the following is straightforward.
Lemma 3.15. If n = 1, then every triple ![]() $(\mu, a^\ell, \nu)$ is cycline.
$(\mu, a^\ell, \nu)$ is cycline.
Proposition 3.16. Suppose that κ = 1, n > 1, and ![]() $({\mathbb{Z}}, \mathsf{E}_n)$ is periodic. Then
$({\mathbb{Z}}, \mathsf{E}_n)$ is periodic. Then ![]() $(\mu, g, \nu)$ is cycline if and only if
$(\mu, g, \nu)$ is cycline if and only if ![]() $\mu=\nu$ and
$\mu=\nu$ and ![]() $g=a^{\ell n}$ for some
$g=a^{\ell n}$ for some ![]() $\ell \in {\mathbb{Z}}$.
$\ell \in {\mathbb{Z}}$.
Proof. ‘If’ part is clear. For the ‘Only if’ part, assume that ![]() $(\mu, g, \nu)$ is cycline. Then
$(\mu, g, \nu)$ is cycline. Then
If ![]() $|\mu|=|\nu|$, then
$|\mu|=|\nu|$, then ![]() $\mu=\nu$ and
$\mu=\nu$ and ![]() $g\cdot x=x$ for all
$g\cdot x=x$ for all ![]() $x\in \mathsf{E}_n^\infty$. As in the proof of proposition 3.13, one can see that
$x\in \mathsf{E}_n^\infty$. As in the proof of proposition 3.13, one can see that ![]() $g=a^{\ell n}$ for some
$g=a^{\ell n}$ for some ![]() $\ell\in {\mathbb{Z}}$.
$\ell\in {\mathbb{Z}}$.
If ![]() $|\mu|\ne |\nu|$, WLOG,
$|\mu|\ne |\nu|$, WLOG, ![]() $|\nu| \gt |\mu|$. Then
$|\nu| \gt |\mu|$. Then ![]() $\nu=\mu\nu'$ for some
$\nu=\mu\nu'$ for some ![]() $\nu'\in \mathsf{E}_n^*\setminus\mathsf{E}_n^0$ and
$\nu'\in \mathsf{E}_n^*\setminus\mathsf{E}_n^0$ and ![]() $g\cdot x= \nu' x$. This is impossible as n > 1.\hfill▪
$g\cdot x= \nu' x$. This is impossible as n > 1.\hfill▪
Combining [Reference Li and Yang34, Theorem 6.6, Theorem 6.13] with corollary 3.10 yields
Theorem 3.17. ![]() ${\mathcal{Q}}(\mathsf{S}_{{\mathbb{N}}, \mathsf{E}_n})$ with κ = 1 satisfies UCT. It is simple iff
${\mathcal{Q}}(\mathsf{S}_{{\mathbb{N}}, \mathsf{E}_n})$ with κ = 1 satisfies UCT. It is simple iff ![]() $n\!\nmid\! m$. So it is a Kirchberg algebra iff
$n\!\nmid\! m$. So it is a Kirchberg algebra iff ![]() $n\!\nmid\! m$.
$n\!\nmid\! m$.
3.3.2. The general case
For the general ![]() $\kappa\ge 1$, we begin with a relation between the periodicity of
$\kappa\ge 1$, we begin with a relation between the periodicity of ![]() $({\mathbb{Z}}, \mathsf{E}_n)$ and that of its restrictions on orbits.
$({\mathbb{Z}}, \mathsf{E}_n)$ and that of its restrictions on orbits.
For simplification, let ![]() $\mathfrak N:=\operatorname{lcm}(n_i:1\le i\le \kappa)$.
$\mathfrak N:=\operatorname{lcm}(n_i:1\le i\le \kappa)$.
Proposition 3.18. ![]() $({\mathbb{Z}}, \mathsf{E}_n)$ is periodic, if and only if the restriction
$({\mathbb{Z}}, \mathsf{E}_n)$ is periodic, if and only if the restriction ![]() $({\mathbb{Z}}, \mathsf{E}_{n_i})$ is periodic for each
$({\mathbb{Z}}, \mathsf{E}_{n_i})$ is periodic for each ![]() $1\le i\le \kappa$, if and only if
$1\le i\le \kappa$, if and only if ![]() $n_i\!\mid\! m_i$ for every
$n_i\!\mid\! m_i$ for every ![]() $1\le i\le \kappa$.
$1\le i\le \kappa$.
Proof. If there is ![]() $1\le i\le \kappa$ such that
$1\le i\le \kappa$ such that ![]() $n_i\!\nmid\! m_i$, then
$n_i\!\nmid\! m_i$, then ![]() $({\mathbb{Z}}, \mathsf{E}_{n_i})$ is aperiodic by proposition 3.16. Then clearly
$({\mathbb{Z}}, \mathsf{E}_{n_i})$ is aperiodic by proposition 3.16. Then clearly ![]() $({\mathbb{Z}}, \mathsf{E}_{n})$ is aperiodic.
$({\mathbb{Z}}, \mathsf{E}_{n})$ is aperiodic.
Now let us assume that ![]() $n_i\!\mid\! m_i$ for all
$n_i\!\mid\! m_i$ for all ![]() $1\le i\le \kappa$. Say
$1\le i\le \kappa$. Say ![]() $m_i=n_i \widetilde{m}_i$ with
$m_i=n_i \widetilde{m}_i$ with ![]() $0\ne \widetilde m_i\in{\mathbb{Z}}$ for
$0\ne \widetilde m_i\in{\mathbb{Z}}$ for ![]() $1\le i\le \kappa$. Then
$1\le i\le \kappa$. Then
 \begin{equation*}
a^{\mathfrak N} \, e_{s_1}^{i_1}\cdots e_{s_p}^{i_p}=e_{s_1}^{i_1}\cdots e_{s_p}^{i_p} \, a^{\mathfrak N\, \widetilde m_{i_1}\cdots\widetilde m_{i_p}}.
\end{equation*}
\begin{equation*}
a^{\mathfrak N} \, e_{s_1}^{i_1}\cdots e_{s_p}^{i_p}=e_{s_1}^{i_1}\cdots e_{s_p}^{i_p} \, a^{\mathfrak N\, \widetilde m_{i_1}\cdots\widetilde m_{i_p}}.
\end{equation*} Thus one can check that for arbitrary ![]() $x\in \mathsf{E}_n^\infty$ one has
$x\in \mathsf{E}_n^\infty$ one has ![]() $a^{\mathfrak N} \cdot x= x$. Therefore, every infinite path x is
$a^{\mathfrak N} \cdot x= x$. Therefore, every infinite path x is ![]() ${\mathbb{Z}}$-periodic, and so
${\mathbb{Z}}$-periodic, and so ![]() $({\mathbb{Z}}, \mathsf{E}_n)$ is periodic.
$({\mathbb{Z}}, \mathsf{E}_n)$ is periodic.
We now determine all cycline triples. If n = 1, this is provided in lemma 3.15.
Proposition 3.19. If ![]() $({\mathbb{Z}}, \mathsf{E}_n)$ is periodic with n > 1, then
$({\mathbb{Z}}, \mathsf{E}_n)$ is periodic with n > 1, then ![]() $(\mu, g, \nu)$ is cycline if and only if
$(\mu, g, \nu)$ is cycline if and only if ![]() $\mu=\nu$ and
$\mu=\nu$ and ![]() $g=a^{\ell \mathfrak N}$ for some
$g=a^{\ell \mathfrak N}$ for some ![]() $\ell \in {\mathbb{Z}}$.
$\ell \in {\mathbb{Z}}$.
Proof. ‘If’ part is clear. For the ‘Only if’ part, assume that ![]() $(\mu, g, \nu)$ is cycline. Then
$(\mu, g, \nu)$ is cycline. Then
If ![]() $|\mu|=|\nu|$, then
$|\mu|=|\nu|$, then ![]() $\mu=\nu$ and
$\mu=\nu$ and ![]() $g\cdot x=x$ for all
$g\cdot x=x$ for all ![]() $x\in \mathsf{E}_n^\infty$. It is now not hard to see that
$x\in \mathsf{E}_n^\infty$. It is now not hard to see that ![]() $g=a^{\ell \mathfrak N}$ for some
$g=a^{\ell \mathfrak N}$ for some ![]() $\ell\in {\mathbb{Z}}$.
$\ell\in {\mathbb{Z}}$.
If ![]() $|\mu|\ne |\nu|$, WLOG,
$|\mu|\ne |\nu|$, WLOG, ![]() $|\nu| \gt |\mu|$. Then
$|\nu| \gt |\mu|$. Then ![]() $\nu=\mu\nu'$ for some
$\nu=\mu\nu'$ for some ![]() $\nu'\in \mathsf{E}_n^*\setminus\mathsf{E}_n^0$ and
$\nu'\in \mathsf{E}_n^*\setminus\mathsf{E}_n^0$ and ![]() $g\cdot x= \nu' x$. This is impossible as n > 1.\hfill▪
$g\cdot x= \nu' x$. This is impossible as n > 1.\hfill▪
Combining [Reference Li and Yang34, Theorem 6.6, Theorem 6.13] with corollary 3.10 yields
Theorem 3.20. ![]() ${\mathcal{O}}_{{\mathbb{Z}}, \mathsf{E}_n}$ satisfies UCT. It is simple iff
${\mathcal{O}}_{{\mathbb{Z}}, \mathsf{E}_n}$ satisfies UCT. It is simple iff ![]() $n_i\!\nmid\! m_i$ for some
$n_i\!\nmid\! m_i$ for some ![]() $1\le i\le \kappa$. So it is a Kirchberg algebra iff
$1\le i\le \kappa$. So it is a Kirchberg algebra iff ![]() $n_i\!\nmid \! m_i$ for some
$n_i\!\nmid \! m_i$ for some ![]() $1\le i\le \kappa$.
$1\le i\le \kappa$.
Remark 3.21. It is well-known that the roles of n and m in BS groups ![]() $\operatorname{BS}(n,m)$ are symmetric in the sense of
$\operatorname{BS}(n,m)$ are symmetric in the sense of ![]() $\operatorname{BS}(n,m)\cong \operatorname{BS}(m,n)$. So
$\operatorname{BS}(n,m)\cong \operatorname{BS}(m,n)$. So ![]() $\mathrm{C}^*(\operatorname{BS}(n,m))\cong \mathrm{C}^*(\operatorname{BS}(m,n))$. However, the symmetry is lost for BS semigroups. For instance, If
$\mathrm{C}^*(\operatorname{BS}(n,m))\cong \mathrm{C}^*(\operatorname{BS}(m,n))$. However, the symmetry is lost for BS semigroups. For instance, If ![]() $0 \lt n\ne m\in {\mathbb{N}}$ satisfies
$0 \lt n\ne m\in {\mathbb{N}}$ satisfies ![]() $n\!\mid\!m$, then
$n\!\mid\!m$, then ![]() ${\mathcal{Q}}(\operatorname{BS}^+(n,m))$ is not simple while
${\mathcal{Q}}(\operatorname{BS}^+(n,m))$ is not simple while ![]() ${\mathcal{Q}}(\operatorname{BS}^+(m,n))$ is simple.
${\mathcal{Q}}(\operatorname{BS}^+(m,n))$ is simple.
3.4. Cartan subalgebras of  ${\mathcal{O}}_{{\mathbb{Z}}, \mathsf{E}_n}$
${\mathcal{O}}_{{\mathbb{Z}}, \mathsf{E}_n}$
We begin with the definition of Cartan subalgebras. Let ![]() ${\mathcal{B}}$ be an abelian C*-subalgebra of a given C*-algebra
${\mathcal{B}}$ be an abelian C*-subalgebra of a given C*-algebra ![]() ${\mathcal{A}}$.
${\mathcal{A}}$. ![]() ${\mathcal{B}}$ is called a Cartan subalgebra in
${\mathcal{B}}$ is called a Cartan subalgebra in ![]() ${\mathcal{A}}$ if
${\mathcal{A}}$ if
(i)
 ${\mathcal{B}}$ contains an approximate unit in
${\mathcal{B}}$ contains an approximate unit in  ${\mathcal{A}}$;
${\mathcal{A}}$;(ii)
 ${\mathcal{B}}$ is a MASA;
${\mathcal{B}}$ is a MASA;(iii)
 ${\mathcal{B}}$ is regular: the normalizer set
${\mathcal{B}}$ is regular: the normalizer set  $N({\mathcal{B}})=\{x\in {\mathcal{A}}: x{\mathcal{B}} x^*\cup x^*{\mathcal{B}} x\subseteq {\mathcal{B}}\}$ generates
$N({\mathcal{B}})=\{x\in {\mathcal{A}}: x{\mathcal{B}} x^*\cup x^*{\mathcal{B}} x\subseteq {\mathcal{B}}\}$ generates  ${\mathcal{A}}$;
${\mathcal{A}}$;(iv) there is a faithful conditional expectation
 ${\mathcal{E}}$ from
${\mathcal{E}}$ from  ${\mathcal{A}}$ onto
${\mathcal{A}}$ onto  ${\mathcal{B}}$.
${\mathcal{B}}$.
In this subsection, we show that there is a canonical Cartan subalgebra for each ![]() ${\mathcal{O}}_{{\mathbb{Z}}, \mathsf E_n}$. It is closely related to the fixed point algebra
${\mathcal{O}}_{{\mathbb{Z}}, \mathsf E_n}$. It is closely related to the fixed point algebra  ${\mathcal{O}}_{{\mathbb{Z}}, \mathsf{E}_n}^\gamma$ of the gauge action γ. However, there is an essential difference between the cases of n = 1 and n > 1.
${\mathcal{O}}_{{\mathbb{Z}}, \mathsf{E}_n}^\gamma$ of the gauge action γ. However, there is an essential difference between the cases of n = 1 and n > 1.
3.4.1. The case of n = 1
The case of n = 1 is a special case of § 4.4 below with ![]() $\mathsf k=1$ (i.e., rank 1), which does not use any results from this section. So we record the result below just for completeness.
$\mathsf k=1$ (i.e., rank 1), which does not use any results from this section. So we record the result below just for completeness.
In what follows, to simplify our writing, let us set  ${\mathcal{F}}:={\mathcal{O}}_{{\mathbb{Z}}, \mathsf E_n}^\gamma$, and
${\mathcal{F}}:={\mathcal{O}}_{{\mathbb{Z}}, \mathsf E_n}^\gamma$, and ![]() ${\mathcal{F}}'$ to be the (relative) commutant of
${\mathcal{F}}'$ to be the (relative) commutant of ![]() ${\mathcal{F}}$ in
${\mathcal{F}}$ in ![]() ${\mathcal{O}}_{{\mathbb{Z}}, \mathsf E_n}$.
${\mathcal{O}}_{{\mathbb{Z}}, \mathsf E_n}$.
Proposition 3.22. Keep the above notation. Then ![]() ${\mathcal{F}}'=\overline{\operatorname{span}}\{s_{e^p} a^\ell s_{e^q}^*: m^p=m^q, \ell \in {\mathbb{Z}}\}$ and
${\mathcal{F}}'=\overline{\operatorname{span}}\{s_{e^p} a^\ell s_{e^q}^*: m^p=m^q, \ell \in {\mathbb{Z}}\}$ and ![]() ${\mathcal{F}}'$ is a Cartan subalgebra of
${\mathcal{F}}'$ is a Cartan subalgebra of ![]() ${\mathcal{O}}_{{\mathbb{Z}}, \mathsf E_1}$.
${\mathcal{O}}_{{\mathbb{Z}}, \mathsf E_1}$.
It is worth noticing that there are three possible cases for ![]() ${\mathcal{F}}'$:
${\mathcal{F}}'$:
• If m = 1, then
 ${\mathcal{F}}'=\overline{\operatorname{span}}\{s_{e^p} u_{a^\ell} s_{e^q}^*: p,q\in {\mathbb{N}}, \ell \in {\mathbb{Z}}\}={\mathcal{O}}_{{\mathbb{Z}}, \mathsf E_1} \cong {\mathrm{C}}({\mathbb{T}}^2)$.
${\mathcal{F}}'=\overline{\operatorname{span}}\{s_{e^p} u_{a^\ell} s_{e^q}^*: p,q\in {\mathbb{N}}, \ell \in {\mathbb{Z}}\}={\mathcal{O}}_{{\mathbb{Z}}, \mathsf E_1} \cong {\mathrm{C}}({\mathbb{T}}^2)$.• If
 $m=-1$, then
$m=-1$, then  ${\mathcal{F}}'=\overline{\operatorname{span}}\{s_{e^p} u_{a^\ell} s_{e^q}^*: p,q\in {\mathbb{N}} \text{ with }p-q\in 2{\mathbb{Z}}, \ell \in {\mathbb{Z}}\}$.
${\mathcal{F}}'=\overline{\operatorname{span}}\{s_{e^p} u_{a^\ell} s_{e^q}^*: p,q\in {\mathbb{N}} \text{ with }p-q\in 2{\mathbb{Z}}, \ell \in {\mathbb{Z}}\}$.• If
 $m\ne \pm 1$, then
$m\ne \pm 1$, then  ${\mathcal{F}}'={\mathcal{F}}$.
${\mathcal{F}}'={\mathcal{F}}$.
3.4.2. The case of n > 1
Recall that ![]() $\mathfrak N =\operatorname{lcm}(n_i:1\le i\le \kappa)$ and
$\mathfrak N =\operatorname{lcm}(n_i:1\le i\le \kappa)$ and  $n=\sum\limits_{i=1}^\kappa n_i$.
$n=\sum\limits_{i=1}^\kappa n_i$.
Proposition 3.23. If n > 1, then the cycline C*-subalgebra ![]() ${\mathcal{M}}:=\mathrm{C}^*(s_\mu u_{a^{\ell\mathfrak{N}}} s_\mu^*: \mu \in \mathsf{E}_n^*, \ell\in {\mathbb{Z}})$ is a MASA in
${\mathcal{M}}:=\mathrm{C}^*(s_\mu u_{a^{\ell\mathfrak{N}}} s_\mu^*: \mu \in \mathsf{E}_n^*, \ell\in {\mathbb{Z}})$ is a MASA in ![]() ${\mathcal{O}}_{{\mathbb{Z}}, \mathsf{E}_n}$.
${\mathcal{O}}_{{\mathbb{Z}}, \mathsf{E}_n}$.
Proof. We first show that ![]() ${\mathcal{M}}$ is abelian. Compute
${\mathcal{M}}$ is abelian. Compute
 \begin{align*}
&(s_\mu u_{a^{K\mathfrak{N}}}s_\mu^*)(s_\nu u_{a^{L\mathfrak{N}}}s_\nu^*)\\
&=
\begin{cases}
s_\mu u_{a^{(K+L)\mathfrak{N}}}s_\mu^*& \text{if }\mu=\nu,\\
s_\mu u_{a^{K\mathfrak{N}}}s_{\nu'} u_{a^{L\mathfrak{N}}}s_\nu^*=s_\mu s_{\nu'} u_{a^{K\mathfrak{N}}|_{\nu'}}u_{a^{L\mathfrak{N}}}s_\nu^*
=s_\nu u_{a^{K\mathfrak{N}}|_{\nu'}}u_{a^{L\mathfrak{N}}}s_\nu^* & \text{if }\nu=\mu\nu',\\
s_\mu u_{a^{K\mathfrak{N}}}s_{\mu'}^* u_{a^{L\mathfrak{N}}}s_\nu^*=s_\mu u_{a^{K\mathfrak{N}}} u_{(a^{-L{\mathbf{n}}}|_{a^{L\mathfrak{N}}\cdot\mu'})^{-1}}s_{\mu'}^* s_\nu^*
& \text{if }\mu=\nu\mu',\\
=s_\mu u_{a^{K\mathfrak{N}}} u_{a^{L\mathfrak{N}}|_{\mu'}}s_{\mu}^*&\\
0&\text{otherwise}.
\end{cases}
\end{align*}
\begin{align*}
&(s_\mu u_{a^{K\mathfrak{N}}}s_\mu^*)(s_\nu u_{a^{L\mathfrak{N}}}s_\nu^*)\\
&=
\begin{cases}
s_\mu u_{a^{(K+L)\mathfrak{N}}}s_\mu^*& \text{if }\mu=\nu,\\
s_\mu u_{a^{K\mathfrak{N}}}s_{\nu'} u_{a^{L\mathfrak{N}}}s_\nu^*=s_\mu s_{\nu'} u_{a^{K\mathfrak{N}}|_{\nu'}}u_{a^{L\mathfrak{N}}}s_\nu^*
=s_\nu u_{a^{K\mathfrak{N}}|_{\nu'}}u_{a^{L\mathfrak{N}}}s_\nu^* & \text{if }\nu=\mu\nu',\\
s_\mu u_{a^{K\mathfrak{N}}}s_{\mu'}^* u_{a^{L\mathfrak{N}}}s_\nu^*=s_\mu u_{a^{K\mathfrak{N}}} u_{(a^{-L{\mathbf{n}}}|_{a^{L\mathfrak{N}}\cdot\mu'})^{-1}}s_{\mu'}^* s_\nu^*
& \text{if }\mu=\nu\mu',\\
=s_\mu u_{a^{K\mathfrak{N}}} u_{a^{L\mathfrak{N}}|_{\mu'}}s_{\mu}^*&\\
0&\text{otherwise}.
\end{cases}
\end{align*}Similar calculations yield
 \begin{align*}
(s_\nu u_{a^{L\mathfrak{N}}}s_\nu^*)(s_\mu u_{a^{K\mathfrak{N}}}s_\mu^*)
=
\begin{cases}
s_\nu u_{a^{(K+L)\mathfrak{N}}}s_\nu^* &\text{if }\mu=\nu,\\
s_\nu u_{a^{L\mathfrak{N}}} u_{a^{K\mathfrak{N}}|_{\nu'}}s_{\nu}^*& \text{if }\nu=\mu\nu',\\
s_\mu u_{a^{L\mathfrak{N}}|_{\mu'}}u_{a^{K\mathfrak{N}}}s_\mu^*& \text{if }\mu=\nu\mu',\\
0&\text{otherwise}.
\end{cases}
\end{align*}
\begin{align*}
(s_\nu u_{a^{L\mathfrak{N}}}s_\nu^*)(s_\mu u_{a^{K\mathfrak{N}}}s_\mu^*)
=
\begin{cases}
s_\nu u_{a^{(K+L)\mathfrak{N}}}s_\nu^* &\text{if }\mu=\nu,\\
s_\nu u_{a^{L\mathfrak{N}}} u_{a^{K\mathfrak{N}}|_{\nu'}}s_{\nu}^*& \text{if }\nu=\mu\nu',\\
s_\mu u_{a^{L\mathfrak{N}}|_{\mu'}}u_{a^{K\mathfrak{N}}}s_\mu^*& \text{if }\mu=\nu\mu',\\
0&\text{otherwise}.
\end{cases}
\end{align*} Thus ![]() ${\mathcal{M}}$ is abelian.
${\mathcal{M}}$ is abelian.
As in [Reference Li33], let ![]() ${\mathcal{G}}_{{\mathbb{Z}}, \mathsf{E}_n}$ be the groupoid associated with the self-similar graph
${\mathcal{G}}_{{\mathbb{Z}}, \mathsf{E}_n}$ be the groupoid associated with the self-similar graph ![]() $({\mathbb{Z}}, \mathsf{E}_n)$. It follows from [Reference Li33, Lemma 5.2] and proposition 3.19 that
$({\mathbb{Z}}, \mathsf{E}_n)$. It follows from [Reference Li33, Lemma 5.2] and proposition 3.19 that  $\text{Iso}({\mathcal{G}}_{{\mathbb{Z}}, \mathsf{E}_n})^\circ=\bigcup\limits_{\mu\in \mathsf{E}_n^*, \ell\in {\mathbb{Z}}} Z(\mu, a^{\ell\mathfrak{N}}, \mu)$. Also notice that
$\text{Iso}({\mathcal{G}}_{{\mathbb{Z}}, \mathsf{E}_n})^\circ=\bigcup\limits_{\mu\in \mathsf{E}_n^*, \ell\in {\mathbb{Z}}} Z(\mu, a^{\ell\mathfrak{N}}, \mu)$. Also notice that ![]() ${\mathcal{M}}\cong \mathrm{C}^*(\text{Iso}({\mathcal{G}}_{{\mathbb{Z}}, \mathsf{E}_n})^\circ)$. So
${\mathcal{M}}\cong \mathrm{C}^*(\text{Iso}({\mathcal{G}}_{{\mathbb{Z}}, \mathsf{E}_n})^\circ)$. So ![]() $\mathrm{C}^*(\text{Iso}({\mathcal{G}}_{{\mathbb{Z}}, \mathsf{E}_n})^\circ)$ is abelian. Hence, by [Reference Bruce and Scarparo10, Corollary 5.4],
$\mathrm{C}^*(\text{Iso}({\mathcal{G}}_{{\mathbb{Z}}, \mathsf{E}_n})^\circ)$ is abelian. Hence, by [Reference Bruce and Scarparo10, Corollary 5.4], ![]() ${\mathcal{M}}$ is a MASA.
${\mathcal{M}}$ is a MASA.
Remark 3.24. By lemma 3.15, when n = 1, the cycline subalgebra of ![]() ${\mathcal{O}}_{{\mathbb{Z}}, \mathsf{E}_1}$ coincides with
${\mathcal{O}}_{{\mathbb{Z}}, \mathsf{E}_1}$ coincides with ![]() ${\mathcal{O}}_{{\mathbb{Z}}, \mathsf{E}_1}$, which is generally not abelian. So proposition 3.23 does not hold true for n = 1.
${\mathcal{O}}_{{\mathbb{Z}}, \mathsf{E}_1}$, which is generally not abelian. So proposition 3.23 does not hold true for n = 1.
Remark 3.25. Keep the same notation in the proof above. If ![]() $\text{Iso}({\mathcal{G}}_{{\mathbb{Z}}, \mathsf{E}_n})^\circ$ is closed, then applying [Reference Bratteli and Robinson6, Corollary 4.5] one can conclude that
$\text{Iso}({\mathcal{G}}_{{\mathbb{Z}}, \mathsf{E}_n})^\circ$ is closed, then applying [Reference Bratteli and Robinson6, Corollary 4.5] one can conclude that ![]() ${\mathcal{M}}$ is Cartan in
${\mathcal{M}}$ is Cartan in ![]() ${\mathcal{O}}_{{\mathbb{Z}}, \mathsf{E}_n}$. But, unfortunately,
${\mathcal{O}}_{{\mathbb{Z}}, \mathsf{E}_n}$. But, unfortunately, ![]() $\text{Iso}({\mathcal{G}}_{{\mathbb{Z}}, \mathsf{E}_n})^\circ$ needn’t be closed in general.
$\text{Iso}({\mathcal{G}}_{{\mathbb{Z}}, \mathsf{E}_n})^\circ$ needn’t be closed in general.
3.5. Some old examples revisited
Recall the flip (single-vertex) rank 2 graphs
and the square rank 2 graph
Example 3.26. In [Reference Chen and Li12], it is shown that ![]() ${\mathcal{Q}}(\operatorname{BS}^+(n,n))\cong {\mathrm{C}}({\mathbb{T}}) \otimes {\mathcal{O}}_n$. From what we have obtained so far, we can prove this by relating to rank 2 graphs. In fact, we have
${\mathcal{Q}}(\operatorname{BS}^+(n,n))\cong {\mathrm{C}}({\mathbb{T}}) \otimes {\mathcal{O}}_n$. From what we have obtained so far, we can prove this by relating to rank 2 graphs. In fact, we have
 \begin{equation*}
{\mathcal{Q}}(\operatorname{BS}^+(n,n))\cong {\mathrm{C}}({\mathbb{T}}) \otimes {\mathcal{O}}_n\cong {\mathcal{O}}_{\Lambda_{\text{flip}}}.
\end{equation*}
\begin{equation*}
{\mathcal{Q}}(\operatorname{BS}^+(n,n))\cong {\mathrm{C}}({\mathbb{T}}) \otimes {\mathcal{O}}_n\cong {\mathcal{O}}_{\Lambda_{\text{flip}}}.
\end{equation*} To see this, we construct an explicit isomorphism from ![]() ${\mathcal{O}}_{\Lambda_{\text{flip}}}$ onto
${\mathcal{O}}_{\Lambda_{\text{flip}}}$ onto ![]() ${\mathcal{Q}}(\operatorname{BS}^+(n,n))$. Let
${\mathcal{Q}}(\operatorname{BS}^+(n,n))$. Let  $\pi: {\mathcal{O}}_{\Lambda_{\text{flip}}}\to {\mathcal{Q}}(\operatorname{BS}^+(n,n))$ be the homomorphism determined by
$\pi: {\mathcal{O}}_{\Lambda_{\text{flip}}}\to {\mathcal{Q}}(\operatorname{BS}^+(n,n))$ be the homomorphism determined by
It is easy to see that ![]() $E_iF_j=F_iE_j$ as
$E_iF_j=F_iE_j$ as ![]() $u_{a^n}$ is in the center of
$u_{a^n}$ is in the center of ![]() ${\mathcal{Q}}(\operatorname{BS}^+(n,n))$. Also π is surjective as from
${\mathcal{Q}}(\operatorname{BS}^+(n,n))$. Also π is surjective as from ![]() $a e_i=e_{i+1}$
$a e_i=e_{i+1}$ ![]() $(0\le i\le n-2$) and
$(0\le i\le n-2$) and ![]() $a e_{n-1}=e_0 a^n$ one has
$a e_{n-1}=e_0 a^n$ one has
 \begin{align*}
\sum_{i=0}^{n-1}u_a s_{e_i} s_{e_i}^*
&=\sum_{i=0}^{n-2} s_{e_{i+1}} s_{e_i}^* + s_{e_0} u_{a^n} s_{e_{n-1}}^*
=\sum_{i=0}^{n-2} s_{e_{i+1}} s_{e_i}^* + u_{a^n} s_{e_0} s_{e_{n-1}}^*\\
&=\sum_{i=0}^{n-2} s_{e_{i+1}} s_{e_i}^* + F_0 s_{e_{n-1}}^*.
\end{align*}
\begin{align*}
\sum_{i=0}^{n-1}u_a s_{e_i} s_{e_i}^*
&=\sum_{i=0}^{n-2} s_{e_{i+1}} s_{e_i}^* + s_{e_0} u_{a^n} s_{e_{n-1}}^*
=\sum_{i=0}^{n-2} s_{e_{i+1}} s_{e_i}^* + u_{a^n} s_{e_0} s_{e_{n-1}}^*\\
&=\sum_{i=0}^{n-2} s_{e_{i+1}} s_{e_i}^* + F_0 s_{e_{n-1}}^*.
\end{align*} Conversely, define  $\rho: {\mathcal{Q}}(\operatorname{BS}^+(n,n))\to {\mathcal{O}}_{\Lambda_{\text{flip}}}$ by
$\rho: {\mathcal{Q}}(\operatorname{BS}^+(n,n))\to {\mathcal{O}}_{\Lambda_{\text{flip}}}$ by
 \begin{equation*}
s_{e_i}\mapsto s_{{\mathbf{e}}_i}, \ u_a\mapsto \sum_{i=0}^{n-2} s_{{\mathbf{e}}_{i+1}}s_{{\mathbf{e}}_i}^* + s_{{\mathbf{f}}_0} s_{{\mathbf{e}}_{n-1}}^*.
\end{equation*}
\begin{equation*}
s_{e_i}\mapsto s_{{\mathbf{e}}_i}, \ u_a\mapsto \sum_{i=0}^{n-2} s_{{\mathbf{e}}_{i+1}}s_{{\mathbf{e}}_i}^* + s_{{\mathbf{f}}_0} s_{{\mathbf{e}}_{n-1}}^*.
\end{equation*} Then ρ determines a homomorphism. Also one can check that π and ρ are the inverse to each other. Therefore one has  $ {\mathcal{Q}}(\operatorname{BS}^+(n,n))\cong {\mathcal{O}}_{\Lambda_{\text{flip}}}$, which is also isomorphic to
$ {\mathcal{Q}}(\operatorname{BS}^+(n,n))\cong {\mathcal{O}}_{\Lambda_{\text{flip}}}$, which is also isomorphic to ![]() ${\mathrm{C}}({\mathbb{T}}) \otimes {\mathcal{O}}_n$ by [Reference Davidson, Power and Yang17].
${\mathrm{C}}({\mathbb{T}}) \otimes {\mathcal{O}}_n$ by [Reference Davidson, Power and Yang17].
Example 3.27. In this example, through ![]() $\operatorname{BS}^+(2,2)$, we are able to show that
$\operatorname{BS}^+(2,2)$, we are able to show that ![]() ${\mathcal{O}}_{\Lambda_{\text{square}}}\cong {\mathcal{O}}_{\Lambda_{\text{flip}}}$, which seems unclear in [Reference Davidson, Power and Yang17] although both
${\mathcal{O}}_{\Lambda_{\text{square}}}\cong {\mathcal{O}}_{\Lambda_{\text{flip}}}$, which seems unclear in [Reference Davidson, Power and Yang17] although both ![]() ${\mathcal{O}}_{\Lambda_{\text{flip}}}$ and
${\mathcal{O}}_{\Lambda_{\text{flip}}}$ and ![]() ${\mathcal{O}}_{\Lambda_{\text{square}}}$ are well-studied there.
${\mathcal{O}}_{\Lambda_{\text{square}}}$ are well-studied there.
Let ![]() $W:=s_{{\mathbf{e}}_1} s_{{\mathbf{e}}_0}^*+ s_{{\mathbf{f}}_0} s_{{\mathbf{e}}_1}^*$. Then
$W:=s_{{\mathbf{e}}_1} s_{{\mathbf{e}}_0}^*+ s_{{\mathbf{f}}_0} s_{{\mathbf{e}}_1}^*$. Then  $W^2=s_{{\mathbf{f}}_0} s_{{\mathbf{e}}_0}^*+s_{{\mathbf{f}}_1} s_{{\mathbf{e}}_1}^*$. Define
$W^2=s_{{\mathbf{f}}_0} s_{{\mathbf{e}}_0}^*+s_{{\mathbf{f}}_1} s_{{\mathbf{e}}_1}^*$. Define ![]() $\pi: {\mathcal{O}}_{\Lambda_{\text{square}}}\to {\mathcal{O}}_{\Lambda_{\text{flip}}}$ via
$\pi: {\mathcal{O}}_{\Lambda_{\text{square}}}\to {\mathcal{O}}_{\Lambda_{\text{flip}}}$ via
Then one can verify that π is a homomorphism.
Let ![]() $F:=s_{{\mathbf{y}}_1} s_{{\mathbf{x}}_1}^* + s_{{\mathbf{y}}_0} s_{{\mathbf{x}}_0}^*$. Then
$F:=s_{{\mathbf{y}}_1} s_{{\mathbf{x}}_1}^* + s_{{\mathbf{y}}_0} s_{{\mathbf{x}}_0}^*$. Then  $F^2=\sum_{i, j\in [2]} s_{{\mathbf{y}}_i{\mathbf{y}}_j} s_{{\mathbf{x}}_{(i+1)}{\mathbf{x}}_j}^*$. Let
$F^2=\sum_{i, j\in [2]} s_{{\mathbf{y}}_i{\mathbf{y}}_j} s_{{\mathbf{x}}_{(i+1)}{\mathbf{x}}_j}^*$. Let ![]() $\rho: {\mathcal{O}}_{\Lambda_{\text{flip}}}\to {\mathcal{O}}_{\Lambda_{\text{square}}}$ be defined as
$\rho: {\mathcal{O}}_{\Lambda_{\text{flip}}}\to {\mathcal{O}}_{\Lambda_{\text{square}}}$ be defined as
Then ρ is a homomorphism. Moreover, π and ρ are the inverse to each other, and ![]() $\rho(W)=F$ and
$\rho(W)=F$ and ![]() $\pi(F)=W$.
$\pi(F)=W$.
4. Rank  $\mathsf k$ case: more than higher rank BS semigroups
$\mathsf k$ case: more than higher rank BS semigroups
In this section, we first propose a notion of higher rank BS semigroups ![]() $\Lambda_\theta(\mathfrak n, \mathfrak m)$. We then briefly describe how higher rank BS semigroups relate to Furstenberg’s
$\Lambda_\theta(\mathfrak n, \mathfrak m)$. We then briefly describe how higher rank BS semigroups relate to Furstenberg’s ![]() $\times p, \times q$ conjecture. Our main focus here are two cases—
$\times p, \times q$ conjecture. Our main focus here are two cases— ![]() $\Lambda_{\mathsf d}(\mathfrak n, \mathbb{ 1}_{\mathsf k})$ and
$\Lambda_{\mathsf d}(\mathfrak n, \mathbb{ 1}_{\mathsf k})$ and ![]() $\Lambda_{\mathsf d}(\mathbb{ 1}_{\mathsf k}, \mathfrak m)$. For
$\Lambda_{\mathsf d}(\mathbb{ 1}_{\mathsf k}, \mathfrak m)$. For ![]() $\Lambda_{\mathsf d}(\mathfrak n, \mathbb{ 1}_{\mathsf k})$, it is related to products of odometers studied in [Reference Laca, Raeburn, Ramagge and Whittaker32]. Applying some results in [Reference Laca, Raeburn, Ramagge and Whittaker32, Reference Li33], one can easily characterize the simplicity of
$\Lambda_{\mathsf d}(\mathfrak n, \mathbb{ 1}_{\mathsf k})$, it is related to products of odometers studied in [Reference Laca, Raeburn, Ramagge and Whittaker32]. Applying some results in [Reference Laca, Raeburn, Ramagge and Whittaker32, Reference Li33], one can easily characterize the simplicity of ![]() ${\mathcal{O}}_{\Lambda_{\mathsf d}(\mathfrak n, \mathbb{ 1}_{\mathsf k})}$ and see that the cycline subalgebra is Cartan in
${\mathcal{O}}_{\Lambda_{\mathsf d}(\mathfrak n, \mathbb{ 1}_{\mathsf k})}$ and see that the cycline subalgebra is Cartan in ![]() ${\mathcal{O}}_{\Lambda_{\mathsf d}(\mathfrak n, \mathbb{ 1}_{\mathsf k})}$. But, here, we first show the fixed point algebra
${\mathcal{O}}_{\Lambda_{\mathsf d}(\mathfrak n, \mathbb{ 1}_{\mathsf k})}$. But, here, we first show the fixed point algebra ![]() ${\mathcal{F}}$ of the gauge action γ is a Bunce–Deddens algebra, and so
${\mathcal{F}}$ of the gauge action γ is a Bunce–Deddens algebra, and so ![]() ${\mathcal{F}}$ has a unique faithful tracial state τ. Then composing with the conditional expectation Φ from
${\mathcal{F}}$ has a unique faithful tracial state τ. Then composing with the conditional expectation Φ from ![]() ${\mathcal{O}}_{\Lambda_{\mathsf d}(\mathfrak n, \mathbb{ 1}_{\mathsf k})}$ onto
${\mathcal{O}}_{\Lambda_{\mathsf d}(\mathfrak n, \mathbb{ 1}_{\mathsf k})}$ onto ![]() ${\mathcal{F}}$ yields a state
${\mathcal{F}}$ yields a state ![]() $\omega=\tau\circ\Phi$. We then study the associated von Neumann algebra
$\omega=\tau\circ\Phi$. We then study the associated von Neumann algebra ![]() $\pi_\omega({\mathcal{O}}_{\Lambda_{\mathsf d}(\mathfrak n, \mathbb{ 1}_{\mathsf k})})^{\prime\prime}$ in the same vein of [Reference Serre46, Reference Spielberg47]. More precisely, we provide some characterizations of when
$\pi_\omega({\mathcal{O}}_{\Lambda_{\mathsf d}(\mathfrak n, \mathbb{ 1}_{\mathsf k})})^{\prime\prime}$ in the same vein of [Reference Serre46, Reference Spielberg47]. More precisely, we provide some characterizations of when ![]() $\pi_\omega({\mathcal{O}}_{\Lambda_{\mathsf d}(\mathfrak n, \mathbb{ 1}_{\mathsf k})})^{\prime\prime}$ is a factor and further obtain its type. For
$\pi_\omega({\mathcal{O}}_{\Lambda_{\mathsf d}(\mathfrak n, \mathbb{ 1}_{\mathsf k})})^{\prime\prime}$ is a factor and further obtain its type. For ![]() $\Lambda_{\mathsf d}(\mathbb{ 1}_{\mathsf k}, \mathfrak m)$, it is intimately related to Furstenberg’s
$\Lambda_{\mathsf d}(\mathbb{ 1}_{\mathsf k}, \mathfrak m)$, it is intimately related to Furstenberg’s ![]() $\times p, \times q$ conjecture. In this case, we obtain a canonical Cartan for
$\times p, \times q$ conjecture. In this case, we obtain a canonical Cartan for ![]() ${\mathcal{O}}_{\Lambda_{\mathsf d}(\mathbb{ 1}_{\mathsf k}, \mathfrak m)}$, which is generally a proper subalgebra of its cycline subalgebra. We will continue studying
${\mathcal{O}}_{\Lambda_{\mathsf d}(\mathbb{ 1}_{\mathsf k}, \mathfrak m)}$, which is generally a proper subalgebra of its cycline subalgebra. We will continue studying ![]() ${\mathcal{O}}_{\Lambda_{\mathsf d}(\mathbb{ 1}_{\mathsf k}, \mathfrak m)}$ and its relative(s) in a forthcoming paper.
${\mathcal{O}}_{\Lambda_{\mathsf d}(\mathbb{ 1}_{\mathsf k}, \mathfrak m)}$ and its relative(s) in a forthcoming paper.
4.1. Higher rank BS semigroups
Consider ![]() $\mathsf{k}$ given self-similar graphs
$\mathsf{k}$ given self-similar graphs ![]() $({\mathbb{Z}}, \mathsf{E}_{n_i})$ with
$({\mathbb{Z}}, \mathsf{E}_{n_i})$ with ![]() $\mathsf{E}_{n_i}=\{{\mathbf{x}}_{\mathfrak{s}}^i: s\in [n_i]\}$ (
$\mathsf{E}_{n_i}=\{{\mathbf{x}}_{\mathfrak{s}}^i: s\in [n_i]\}$ (![]() $1\le i\le \mathsf k$). Suppose that
$1\le i\le \mathsf k$). Suppose that ![]() ${\mathbf{x}}^i_{\mathfrak{s}}$’s satisfy the commutation relations
${\mathbf{x}}^i_{\mathfrak{s}}$’s satisfy the commutation relations  $\theta_{ij}({\mathbf{x}}_{\mathfrak{s}}^i, {\mathbf{x}}_{\mathfrak{t}}^j)= ({\mathbf{x}}_{{\mathfrak{t}}'}^j , {\mathbf{x}}_{{\mathfrak{s}}'}^i)$ for
$\theta_{ij}({\mathbf{x}}_{\mathfrak{s}}^i, {\mathbf{x}}_{\mathfrak{t}}^j)= ({\mathbf{x}}_{{\mathfrak{t}}'}^j , {\mathbf{x}}_{{\mathfrak{s}}'}^i)$ for ![]() $1 \leq i \lt j \leq \mathsf{k}$. Applying [Reference Laca, Raeburn, Ramagge and Whittaker32, Proposition 4.1], one has
$1 \leq i \lt j \leq \mathsf{k}$. Applying [Reference Laca, Raeburn, Ramagge and Whittaker32, Proposition 4.1], one has
Proposition 4.1. Keep the same notation. The ![]() $\mathsf k$ self-similar graphs
$\mathsf k$ self-similar graphs ![]() $({\mathbb{Z}}, \mathsf{E}_{n_i})$ with the commutation relations θij’s determine a self-similar
$({\mathbb{Z}}, \mathsf{E}_{n_i})$ with the commutation relations θij’s determine a self-similar ![]() $\mathsf k$-graph
$\mathsf k$-graph ![]() $({\mathbb{Z}}, \Lambda_\theta)$ if and only if
$({\mathbb{Z}}, \Lambda_\theta)$ if and only if
 \begin{align}
(a\cdot {\mathbf{x}}_{\mathfrak{s}}^i)(a|_{{\mathbf{x}}_{\mathfrak{s}}^i} \cdot {\mathbf{x}}_{\mathfrak{t}}^j) &= (a \cdot {\mathbf{x}}_{{\mathfrak{t}}'}^j)(a|_{{\mathbf{x}}_{{\mathfrak{t}}'}^j} \cdot {\mathbf{x}}_{{\mathfrak{s}}'}^i)
\end{align}
\begin{align}
(a\cdot {\mathbf{x}}_{\mathfrak{s}}^i)(a|_{{\mathbf{x}}_{\mathfrak{s}}^i} \cdot {\mathbf{x}}_{\mathfrak{t}}^j) &= (a \cdot {\mathbf{x}}_{{\mathfrak{t}}'}^j)(a|_{{\mathbf{x}}_{{\mathfrak{t}}'}^j} \cdot {\mathbf{x}}_{{\mathfrak{s}}'}^i)
\end{align} for all ![]() $1 \leq i \lt j \leq \mathsf{k}$,
$1 \leq i \lt j \leq \mathsf{k}$, ![]() ${\mathfrak{s}}\in [n_i]$,
${\mathfrak{s}}\in [n_i]$, ![]() ${\mathfrak{t}}\in [n_j]$.
${\mathfrak{t}}\in [n_j]$.
Based on example 3.3, it is reasonable to introduce the following notion.
Definition 4.2. A self-similar ![]() $\mathsf k$-graph obtained from
$\mathsf k$-graph obtained from ![]() $(n_i, m_i)$-odometers with the commutation relations θij’s is called a rank
$(n_i, m_i)$-odometers with the commutation relations θij’s is called a rank ![]() $\mathsf k$ BS semigroup, denoted as
$\mathsf k$ BS semigroup, denoted as ![]() $\Lambda_\theta((n_1, \ldots, n_{\mathsf k}), (m_1, \ldots, m_{\mathsf k}))$, or simply
$\Lambda_\theta((n_1, \ldots, n_{\mathsf k}), (m_1, \ldots, m_{\mathsf k}))$, or simply ![]() $\Lambda_\theta(\mathfrak n, \mathfrak m)$ if the context is clear. The ambient
$\Lambda_\theta(\mathfrak n, \mathfrak m)$ if the context is clear. The ambient ![]() $\mathsf k$-graph is still written as
$\mathsf k$-graph is still written as ![]() $\Lambda_\theta$.
$\Lambda_\theta$.
Here are some examples of higher rank BS semigroups.
Example 4.3. A standard product of odometers studied in [Reference Laca, Raeburn, Ramagge and Whittaker32] is a rank ![]() $\mathsf{k}$ BS semigroup induced from
$\mathsf{k}$ BS semigroup induced from ![]() $(n_i, 1)$-odometers
$(n_i, 1)$-odometers ![]() $\mathsf E(n_i, 1)$ (
$\mathsf E(n_i, 1)$ (![]() $1\le i\le \mathsf{k}$) with the division commutation relations (refer to example 2.2 for
$1\le i\le \mathsf{k}$) with the division commutation relations (refer to example 2.2 for ![]() $\mathsf d$). So it is of the form
$\mathsf d$). So it is of the form ![]() $\Lambda_{\mathsf d}(\mathfrak n, \mathbb{ 1}_{\mathsf k})$.
$\Lambda_{\mathsf d}(\mathfrak n, \mathbb{ 1}_{\mathsf k})$.
Example 4.4. Consider ![]() $(n_i, m_i)$-odometers with the trivial permutation θij (
$(n_i, m_i)$-odometers with the trivial permutation θij (![]() $1\le i \lt j\le \mathsf k$) (see example 2.1). Then they induce a rank
$1\le i \lt j\le \mathsf k$) (see example 2.1). Then they induce a rank ![]() $\mathsf k$ BS semigroup if and only if
$\mathsf k$ BS semigroup if and only if ![]() $n_i=1$ for each
$n_i=1$ for each ![]() $1\le i\le \mathsf{k}$. In fact, the condition (4) in proposition 4.1 implies
$1\le i\le \mathsf{k}$. In fact, the condition (4) in proposition 4.1 implies ![]() $n_i = 1$ for all
$n_i = 1$ for all ![]() $1\le i\le \mathsf{k}$. Then the trivial relation is the same as the division commutation relation. The rank
$1\le i\le \mathsf{k}$. Then the trivial relation is the same as the division commutation relation. The rank ![]() $\mathsf{k}$ BS semigroup obtained in this case is of the form
$\mathsf{k}$ BS semigroup obtained in this case is of the form ![]() $\Lambda_{\mathsf d}(\mathbb{ 1}_{\mathsf k}, \mathfrak m)$.
$\Lambda_{\mathsf d}(\mathbb{ 1}_{\mathsf k}, \mathfrak m)$.
Example 4.5. Suppose that ![]() $n_i=n$ for all
$n_i=n$ for all ![]() $1 \le i\le \mathsf{k}$, and that θij is the division permutation. Then one necessarily has
$1 \le i\le \mathsf{k}$, and that θij is the division permutation. Then one necessarily has ![]() $\theta_{ij}(s,t)=(t,s)$. One can check that this yields a rank
$\theta_{ij}(s,t)=(t,s)$. One can check that this yields a rank ![]() $\mathsf{k}$ BS semigroup if and only if either
$\mathsf{k}$ BS semigroup if and only if either ![]() $m_i = m_j$ for all
$m_i = m_j$ for all ![]() $1\le i,j\le \mathsf{k}$, or
$1\le i,j\le \mathsf{k}$, or ![]() $n\!\mid\!m_i$ for all
$n\!\mid\!m_i$ for all ![]() $1\le i\le \mathsf{k}$. These are rank
$1\le i\le \mathsf{k}$. These are rank ![]() $\mathsf{k}$ BS semigroups of the form
$\mathsf{k}$ BS semigroups of the form ![]() $\Lambda_{\mathsf d}((n,\ldots, n), (m, \ldots, m))$, or
$\Lambda_{\mathsf d}((n,\ldots, n), (m, \ldots, m))$, or ![]() $\Lambda_{\mathsf d}((n,\ldots, n), (n\widetilde m_1, \ldots, n \widetilde m_{\mathsf k}))$.
$\Lambda_{\mathsf d}((n,\ldots, n), (n\widetilde m_1, \ldots, n \widetilde m_{\mathsf k}))$.
So the class obtained in example 4.4 is a special case here with n = 1.
In the sequel, we provide some interesting C*-algebras studied in the literature, which can be realized from higher rank BS semigroups.
(1) It is shown in [Reference Laca, Raeburn, Ramagge and Whittaker32] that the Cuntz algebra
 ${\mathcal{Q}}_{\mathbb{N}}$ is isomorphic to the boundary quotient of a semigroup of the form in example 4.3.
${\mathcal{Q}}_{\mathbb{N}}$ is isomorphic to the boundary quotient of a semigroup of the form in example 4.3.(2) For
 $2\le p\in {\mathbb{N}}$, the p-adic C*-algebra
$2\le p\in {\mathbb{N}}$, the p-adic C*-algebra  ${\mathcal{Q}}_p$ can also be recovered from a semigroup of the form in example 4.3 (cf. [Reference Laca, Raeburn, Ramagge and Whittaker32] for p = 2 in terms of standard product of odometers).
${\mathcal{Q}}_p$ can also be recovered from a semigroup of the form in example 4.3 (cf. [Reference Laca, Raeburn, Ramagge and Whittaker32] for p = 2 in terms of standard product of odometers).(3)
 ${\mathcal{Q}}_{\mathbb{N}}$ can be also realized as a boundary quotient of the left ax + b semigroup
${\mathcal{Q}}_{\mathbb{N}}$ can be also realized as a boundary quotient of the left ax + b semigroup  ${\mathbb{N}}\rtimes {\mathbb{N}}^\times$ studied in [Reference Laca and Raeburn31]. The C*-algebra of
${\mathbb{N}}\rtimes {\mathbb{N}}^\times$ studied in [Reference Laca and Raeburn31]. The C*-algebra of  ${\mathbb{N}}\rtimes {\mathbb{N}}^\times$ itself is also related to higher rank BS semigroups.
${\mathbb{N}}\rtimes {\mathbb{N}}^\times$ itself is also related to higher rank BS semigroups.(4) The boundary
 $\partial {\mathcal{T}}({\mathbb{N}}^\times \lt imes {\mathbb{N}})$ of the right ax + b semigroup
$\partial {\mathcal{T}}({\mathbb{N}}^\times \lt imes {\mathbb{N}})$ of the right ax + b semigroup  ${\mathbb{N}}^\times \lt imes {\mathbb{N}}$ is a boundary quotient of a higher-rank BS semigroup of the form given in example 4.4.
${\mathbb{N}}^\times \lt imes {\mathbb{N}}$ is a boundary quotient of a higher-rank BS semigroup of the form given in example 4.4.(5) The C*-algebra
 ${\mathcal{O}}(E_{n,m})$ studied by Katsura in [Reference Katsura28] is isomorphic to
${\mathcal{O}}(E_{n,m})$ studied by Katsura in [Reference Katsura28] is isomorphic to  ${\mathcal{O}}_{\mathsf E(n,m)}$ (see examples 3.2 and 3.3).
${\mathcal{O}}_{\mathsf E(n,m)}$ (see examples 3.2 and 3.3).
Remark 4.6. The C*-algebras of both the left ax + b semigroup ![]() ${\mathbb{N}}\rtimes {\mathbb{N}}^\times$ and the right ax + b semigroup
${\mathbb{N}}\rtimes {\mathbb{N}}^\times$ and the right ax + b semigroup ![]() ${\mathbb{N}}^\times \lt imes {\mathbb{N}}$ are related to higher rank BS semigroups. This will be studied elsewhere.
${\mathbb{N}}^\times \lt imes {\mathbb{N}}$ are related to higher rank BS semigroups. This will be studied elsewhere.
4.2. Relation to Furstenberg’s  $\times p, \times q$ conjecture
$\times p, \times q$ conjecture
We first give a very brief introduction on Furstenberg’s ![]() $\times p, \times q$ conjecture. For all undefined notions or any further information, refer to [Reference Brownlowe, Ramagge, Robertson and Whittaker9, Reference Fowler and Sims24, Reference Furstenberg25, Reference Nekrashevych42].
$\times p, \times q$ conjecture. For all undefined notions or any further information, refer to [Reference Brownlowe, Ramagge, Robertson and Whittaker9, Reference Fowler and Sims24, Reference Furstenberg25, Reference Nekrashevych42].
Let ![]() $2\le p,q\in {\mathbb{N}}$ be multiplicatively independent, i.e.,
$2\le p,q\in {\mathbb{N}}$ be multiplicatively independent, i.e.,  $\frac{\ln p}{\ln q}\not\in {\mathbb{Q}}$. Define
$\frac{\ln p}{\ln q}\not\in {\mathbb{Q}}$. Define ![]() $T_p: {\mathbb{T}}\to {\mathbb{T}}$ by
$T_p: {\mathbb{T}}\to {\mathbb{T}}$ by ![]() $T_p(z)=z^p$ for all
$T_p(z)=z^p$ for all ![]() $z\in {\mathbb{T}}$. Similarly for Tq. A subset of
$z\in {\mathbb{T}}$. Similarly for Tq. A subset of ![]() ${\mathbb{T}}$ is said to be
${\mathbb{T}}$ is said to be ![]() $\times p, \times q$-invariant if it is invariant under both Tp and Tq. Furstenberg classifies all closed
$\times p, \times q$-invariant if it is invariant under both Tp and Tq. Furstenberg classifies all closed ![]() $\times p, \times q$-invariant subsets of
$\times p, \times q$-invariant subsets of ![]() ${\mathbb{T}}$ in [Reference Fowler and Sims24]: Such a subset is either finite or
${\mathbb{T}}$ in [Reference Fowler and Sims24]: Such a subset is either finite or ![]() ${\mathbb{T}}$ itself. Then he conjectures the following:
${\mathbb{T}}$ itself. Then he conjectures the following:
Conjecture (Furstenberg’s ![]() $\times p, \times q$ conjecture). An ergodic
$\times p, \times q$ conjecture). An ergodic ![]() $\times p, \times q$-invariant Borel probability measure of
$\times p, \times q$-invariant Borel probability measure of ![]() ${\mathbb{T}}$ is either finitely supported or the Lebesgue measure.
${\mathbb{T}}$ is either finitely supported or the Lebesgue measure.
According to our best knowledge, this conjecture is still open. The best known result so far is the following theorem, which is proved by Rudolph when p and q are coprime in [Reference Nekrashevych41] and later improved by Johnson in [Reference Huang and Wu26].
Theorem (Rudolph–Johnson). If µ is an ergodic ![]() $\times p, \times q$-invariant measure on
$\times p, \times q$-invariant measure on ![]() ${\mathbb{T}}$, then either both entropies of Tp and Tq with respect to µ are 0, or µ is the Lebesgue measure.
${\mathbb{T}}$, then either both entropies of Tp and Tq with respect to µ are 0, or µ is the Lebesgue measure.
When both entropies of Tp and Tq with respect to µ are 0, Furstenberg’s ![]() $\times p, \times q$ conjecture is reduced to studying the C*-algebra
$\times p, \times q$ conjecture is reduced to studying the C*-algebra ![]() $\mathrm{C}^*(G)$ of the group G, where
$\mathrm{C}^*(G)$ of the group G, where
It turns out that  $\mathrm{C}^*(G)\cong \mathrm{C}^*({\mathbb{Z}}[\frac{1}{pq}])\rtimes {\mathbb{Z}}^2\cong \mathrm{C}^*({\mathbb{Z}}[\frac{1}{pq}]\rtimes {\mathbb{Z}}^2)$. In [Reference Furstenberg25], the representation theory of
$\mathrm{C}^*(G)\cong \mathrm{C}^*({\mathbb{Z}}[\frac{1}{pq}])\rtimes {\mathbb{Z}}^2\cong \mathrm{C}^*({\mathbb{Z}}[\frac{1}{pq}]\rtimes {\mathbb{Z}}^2)$. In [Reference Furstenberg25], the representation theory of  $\mathrm{C}^*({\mathbb{Z}}[\frac{1}{pq}])\rtimes {\mathbb{Z}}^2$ is studied. In particular, the authors focus on which kind of its representations are induced by
$\mathrm{C}^*({\mathbb{Z}}[\frac{1}{pq}])\rtimes {\mathbb{Z}}^2$ is studied. In particular, the authors focus on which kind of its representations are induced by ![]() $\times p, \times q$-invariant measures on
$\times p, \times q$-invariant measures on ![]() ${\mathbb{T}}$. Later, the following equivalence is shown in [Reference Brownlowe, Ramagge, Robertson and Whittaker9]: Furstenberg’s
${\mathbb{T}}$. Later, the following equivalence is shown in [Reference Brownlowe, Ramagge, Robertson and Whittaker9]: Furstenberg’s ![]() $\times p, \times q$ conjecture holds true if and only if the canonical trace is the only faithful extreme tracial state on
$\times p, \times q$ conjecture holds true if and only if the canonical trace is the only faithful extreme tracial state on  $\mathrm{C}^*(G)\cong \mathrm{C}^*({\mathbb{Z}}[\frac{1}{pq}]\rtimes {\mathbb{Z}}^2)$.
$\mathrm{C}^*(G)\cong \mathrm{C}^*({\mathbb{Z}}[\frac{1}{pq}]\rtimes {\mathbb{Z}}^2)$.
Our purpose here is to connect Furstenberg’s conjecture with higher rank BS semigroups. For this, from (5) one has
Let ![]() $\tilde G$ be the group
$\tilde G$ be the group
Thus ![]() $G\cong \tilde G$ and so
$G\cong \tilde G$ and so ![]() $\mathrm{C}^*(G)\cong \mathrm{C}^*(\tilde G)$. The upshot by doing so is
$\mathrm{C}^*(G)\cong \mathrm{C}^*(\tilde G)$. The upshot by doing so is ![]() $\mathrm{C}^*(G)\cong {\mathcal{O}}_{\Lambda_{\mathsf d}((1,1),(p,q))}$.
$\mathrm{C}^*(G)\cong {\mathcal{O}}_{\Lambda_{\mathsf d}((1,1),(p,q))}$.
Now return to (5) again. Let ![]() $G^+$ be the corresponding semigroup
$G^+$ be the corresponding semigroup
Then we claim that ![]() ${\mathcal{Q}}(G^+)\cong {\mathcal{O}}_{\Lambda_{\mathsf d}((p,q),(1,1))}$. In fact, let
${\mathcal{Q}}(G^+)\cong {\mathcal{O}}_{\Lambda_{\mathsf d}((p,q),(1,1))}$. In fact, let ![]() $e_i:=z^i s$ and
$e_i:=z^i s$ and ![]() $f_j:=z^j t$ for
$f_j:=z^j t$ for ![]() $i\in [p]$ and
$i\in [p]$ and ![]() $j\in [q]$. Then
$j\in [q]$. Then ![]() $st=ts\iff e_0 f_0=f_0e_0$. For
$st=ts\iff e_0 f_0=f_0e_0$. For ![]() $k\in [p]$ and
$k\in [p]$ and ![]() $\ell \in [q]$, let
$\ell \in [q]$, let ![]() $k'\in [p]$ and
$k'\in [p]$ and ![]() $\ell'\in [q]$ be the unique ones such that
$\ell'\in [q]$ be the unique ones such that ![]() $k+\ell p= \ell' + k' q$. Then we have
$k+\ell p= \ell' + k' q$. Then we have
 \begin{align*}
e_k f_\ell =z^k s z^\ell t=z^k z^{\ell p} st= z^{\ell'} z^{k' q} ts=z^{\ell'} tz^{k'}s=f_{\ell'} e_{k'}.
\end{align*}
\begin{align*}
e_k f_\ell =z^k s z^\ell t=z^k z^{\ell p} st= z^{\ell'} z^{k' q} ts=z^{\ell'} tz^{k'}s=f_{\ell'} e_{k'}.
\end{align*}Thus there is a homomorphism
 \begin{equation*}
\pi: {\mathcal{O}}_{\Lambda_{\mathsf d}((p,q),(1,1))} = {\mathcal{O}}_{{\mathbb{Z}}, \Lambda_{\mathsf d}} \to {\mathcal{Q}}(G^+),
\ s_{{\mathbf{x}}_i^1}\mapsto v_{e_i},\ s_{{\mathbf{x}}_j^2}\mapsto v_{f_j},\ u_a\mapsto v_z,
\end{equation*}
\begin{equation*}
\pi: {\mathcal{O}}_{\Lambda_{\mathsf d}((p,q),(1,1))} = {\mathcal{O}}_{{\mathbb{Z}}, \Lambda_{\mathsf d}} \to {\mathcal{Q}}(G^+),
\ s_{{\mathbf{x}}_i^1}\mapsto v_{e_i},\ s_{{\mathbf{x}}_j^2}\mapsto v_{f_j},\ u_a\mapsto v_z,
\end{equation*}which is an isomorphism as it has an inverse given by
Hence ![]() ${\mathcal{O}}_{\Lambda_{\mathsf d}((p,q),(1,1))} \cong {\mathcal{Q}}(G^+)$.
${\mathcal{O}}_{\Lambda_{\mathsf d}((p,q),(1,1))} \cong {\mathcal{Q}}(G^+)$.
To sum up, we have shown that
 \begin{align}
\mathrm{C}^*(G)\cong {\mathcal{O}}_{\Lambda_{\mathsf d}((1,1),(p,q))} \text{ and }{\mathcal{Q}}(G^+)\cong {\mathcal{O}}_{\Lambda_{\mathsf d}((p,q),(1,1))}.
\end{align}
\begin{align}
\mathrm{C}^*(G)\cong {\mathcal{O}}_{\Lambda_{\mathsf d}((1,1),(p,q))} \text{ and }{\mathcal{Q}}(G^+)\cong {\mathcal{O}}_{\Lambda_{\mathsf d}((p,q),(1,1))}.
\end{align} Based on the above, in what follows, we focus on two extreme, but rather interesting, classes of higher rank BS semigroups: ![]() $\Lambda_{\mathsf d}(\mathfrak n, \mathbb{ 1}_{\mathsf k})$ with
$\Lambda_{\mathsf d}(\mathfrak n, \mathbb{ 1}_{\mathsf k})$ with ![]() $\mathbb{ 1}_{\mathsf k}\le \mathfrak n\in {\mathbb{N}}^{\mathsf k}$ and
$\mathbb{ 1}_{\mathsf k}\le \mathfrak n\in {\mathbb{N}}^{\mathsf k}$ and ![]() $\Lambda_{\mathsf d}(\mathbb{ 1}_{\mathsf k}, \mathfrak m)$ with
$\Lambda_{\mathsf d}(\mathbb{ 1}_{\mathsf k}, \mathfrak m)$ with ![]() $m_i\ne 0$ for all
$m_i\ne 0$ for all ![]() $1\le i\le \mathsf k$.
$1\le i\le \mathsf k$.
From now on, to unify our notation, the set ![]() $\{0,1\ne p_i \in {\mathbb{Z}}: 1\le i\le \mathsf k\}$ is said to be multiplicatively independent if there is no
$\{0,1\ne p_i \in {\mathbb{Z}}: 1\le i\le \mathsf k\}$ is said to be multiplicatively independent if there is no ![]() $\mathbf 0\ne q\in {\mathbb{Z}}^{\mathsf k}$ such that
$\mathbf 0\ne q\in {\mathbb{Z}}^{\mathsf k}$ such that  $\prod\limits_{i=1}^{\mathsf k} p_i^{q_i}=1$. When all pi’s are also
$\prod\limits_{i=1}^{\mathsf k} p_i^{q_i}=1$. When all pi’s are also ![]() $\ge 1$,
$\ge 1$, ![]() $\{p_i: 1\le i\le \mathsf k\}$ is multiplicatively independent if and only if
$\{p_i: 1\le i\le \mathsf k\}$ is multiplicatively independent if and only if ![]() $\{\ln p_i: 1\le i\le \mathsf k\}$ is rationally independent.
$\{\ln p_i: 1\le i\le \mathsf k\}$ is rationally independent.
4.3. The case of  $\mathfrak m=\mathbb{ 1}_{\mathsf k}$
$\mathfrak m=\mathbb{ 1}_{\mathsf k}$
The C*-algebra of the self-similar ![]() $\mathsf k$-graph
$\mathsf k$-graph ![]() $\Lambda_{\mathsf d} (\mathfrak n, \mathbb{ 1}_{\mathsf k})$ is studied in [Reference Laca, Raeburn, Ramagge and Whittaker32]. It is shown there that
$\Lambda_{\mathsf d} (\mathfrak n, \mathbb{ 1}_{\mathsf k})$ is studied in [Reference Laca, Raeburn, Ramagge and Whittaker32]. It is shown there that ![]() ${\mathcal{O}}_{\Lambda_{\mathsf d}(\mathfrak n, \mathbb{ 1}_{\mathsf k})}$ is simple if and only if
${\mathcal{O}}_{\Lambda_{\mathsf d}(\mathfrak n, \mathbb{ 1}_{\mathsf k})}$ is simple if and only if ![]() $\{n_i: 1\le i\le \mathsf k\}$ is multiplicatively independent, and that its cycline subalgebra is Cartan by [Reference Li33, Theorem 5.6]. In what follows, we identify the center of
$\{n_i: 1\le i\le \mathsf k\}$ is multiplicatively independent, and that its cycline subalgebra is Cartan by [Reference Li33, Theorem 5.6]. In what follows, we identify the center of ![]() ${\mathcal{O}}_{\Lambda_{\mathsf d}(\mathfrak n, \mathbb{ 1}_{\mathsf k})}$, which is overlooked in [Reference Laca, Raeburn, Ramagge and Whittaker32, Reference Li33]. A useful lemma first:
${\mathcal{O}}_{\Lambda_{\mathsf d}(\mathfrak n, \mathbb{ 1}_{\mathsf k})}$, which is overlooked in [Reference Laca, Raeburn, Ramagge and Whittaker32, Reference Li33]. A useful lemma first:
Lemma 4.7. (i) Let ![]() $\mu,\nu\in \Lambda_{\mathsf d}^{\mathbf p}$
$\mu,\nu\in \Lambda_{\mathsf d}^{\mathbf p}$ ![]() $(\mathsf p\in {\mathbb{N}}^{\mathsf k}$) and
$(\mathsf p\in {\mathbb{N}}^{\mathsf k}$) and ![]() $m\in {\mathbb{Z}}$. Then there is
$m\in {\mathbb{Z}}$. Then there is ![]() $\ell\in {\mathbb{Z}}$ such that
$\ell\in {\mathbb{Z}}$ such that ![]() $ \nu a^m = a^\ell \mu$.
$ \nu a^m = a^\ell \mu$.
(ii) ![]() ${\mathcal{O}}_{\Lambda_{\mathsf d}(\mathfrak n, \mathbb{ 1}_{\mathsf k})}=\overline{\operatorname{span}}\{u_{a^m} s_\alpha s_\beta^*: m\in {\mathbb{Z}}, \alpha, \beta\in \Lambda_{\mathsf d}\}$.
${\mathcal{O}}_{\Lambda_{\mathsf d}(\mathfrak n, \mathbb{ 1}_{\mathsf k})}=\overline{\operatorname{span}}\{u_{a^m} s_\alpha s_\beta^*: m\in {\mathbb{Z}}, \alpha, \beta\in \Lambda_{\mathsf d}\}$.
Proof. (i) We first prove the lemma holds true for the classical odometer action ![]() $\mathsf E(n, 1)$. We argue this by induction with respect to the lengths of µ and ν. If
$\mathsf E(n, 1)$. We argue this by induction with respect to the lengths of µ and ν. If ![]() $\mu:=e_i$ and
$\mu:=e_i$ and ![]() $\nu:=e_j$. WLOG we assume that
$\nu:=e_j$. WLOG we assume that ![]() $i\ge j\in [n]$. For any
$i\ge j\in [n]$. For any ![]() $m \in {\mathbb{Z}}$, by lemma 3.6, one can verify that
$m \in {\mathbb{Z}}$, by lemma 3.6, one can verify that ![]() $a^{mn+i-j} \nu = \mu a^m$. Assume that this is true for any
$a^{mn+i-j} \nu = \mu a^m$. Assume that this is true for any ![]() $m\in {\mathbb{Z}}$ and all
$m\in {\mathbb{Z}}$ and all ![]() $\mu, \nu \in \mathsf{E}_n^*$ with
$\mu, \nu \in \mathsf{E}_n^*$ with ![]() $|\mu|=|\nu|\le k$. Now consider
$|\mu|=|\nu|\le k$. Now consider ![]() $e_s \mu$ and
$e_s \mu$ and ![]() $e_t \nu$ with
$e_t \nu$ with ![]() $|\mu|=|\nu|=k$. Let
$|\mu|=|\nu|=k$. Let ![]() $m\in {\mathbb{Z}}$. By our inductive assumption, we have
$m\in {\mathbb{Z}}$. By our inductive assumption, we have ![]() $e_s \mu a^m = e_s a^{\ell'} \nu = a^{\ell} e_t\nu$ for some
$e_s \mu a^m = e_s a^{\ell'} \nu = a^{\ell} e_t\nu$ for some ![]() $\ell', \ell\in {\mathbb{Z}}$. This proves the
$\ell', \ell\in {\mathbb{Z}}$. This proves the ![]() $\mathsf E(n, 1)$ case.
$\mathsf E(n, 1)$ case.
Now return to ![]() $\Lambda_{\mathsf d}$. Let
$\Lambda_{\mathsf d}$. Let ![]() $\mu, \nu\in \Lambda_d$ with
$\mu, \nu\in \Lambda_d$ with ![]() $d(\mu)=d(\nu)=\mathbf p\in {\mathbb{N}}^{\mathsf k}$. Then by the unique factorization property
$d(\mu)=d(\nu)=\mathbf p\in {\mathbb{N}}^{\mathsf k}$. Then by the unique factorization property ![]() $\mu = \mu_1\cdots \mu_{\mathsf k}$ and
$\mu = \mu_1\cdots \mu_{\mathsf k}$ and ![]() $\nu = \nu_1\cdots \nu_{\mathsf k}$ with
$\nu = \nu_1\cdots \nu_{\mathsf k}$ with ![]() $\mu_i, \nu_i \in \Lambda_{\mathsf d}^{p_i \epsilon_i}$ for
$\mu_i, \nu_i \in \Lambda_{\mathsf d}^{p_i \epsilon_i}$ for ![]() $1\le i\le \mathsf k$. Then for any
$1\le i\le \mathsf k$. Then for any ![]() $m\in {\mathbb{Z}}$, apply the above to
$m\in {\mathbb{Z}}$, apply the above to ![]() $\mu_{\mathsf k} a^m$ in
$\mu_{\mathsf k} a^m$ in ![]() $\mathsf E(n_{\mathsf k}, 1)$, there is
$\mathsf E(n_{\mathsf k}, 1)$, there is ![]() $\ell_{\mathsf k}\in {\mathbb{Z}}$ such that
$\ell_{\mathsf k}\in {\mathbb{Z}}$ such that ![]() $\mu a^m = \mu_1\cdots \mu_{\mathsf k -1} a^{\ell_{\mathsf k}} \nu_{\mathsf k}$. Repeatedly using the above gives
$\mu a^m = \mu_1\cdots \mu_{\mathsf k -1} a^{\ell_{\mathsf k}} \nu_{\mathsf k}$. Repeatedly using the above gives ![]() $\mu a^m = a^\ell \nu$ for some
$\mu a^m = a^\ell \nu$ for some ![]() $\ell \in {\mathbb{Z}}$.
$\ell \in {\mathbb{Z}}$.
(ii) This follows from (i) and proposition 2.7 (i).\hfill▪
By [Reference Li33, Theorem 7.5] (or Appendix there), ![]() $\Lambda_{\mathsf d}(\mathfrak n, \mathbb{ 1}_{\mathsf k})$ and
$\Lambda_{\mathsf d}(\mathfrak n, \mathbb{ 1}_{\mathsf k})$ and ![]() $\Lambda_{\mathsf d}$ share the same periodicity
$\Lambda_{\mathsf d}$ share the same periodicity ![]() $\{\mathbf p\in {\mathbb{Z}}^{\mathsf k}: \mathfrak n^{\mathbf p}=1\}$. Thus, for each pair
$\{\mathbf p\in {\mathbb{Z}}^{\mathsf k}: \mathfrak n^{\mathbf p}=1\}$. Thus, for each pair ![]() $(\mathbf p, \mathbf q)\in {\mathbb{N}}^{\mathsf k}\times {\mathbb{N}}^{\mathsf k}$ with
$(\mathbf p, \mathbf q)\in {\mathbb{N}}^{\mathsf k}\times {\mathbb{N}}^{\mathsf k}$ with ![]() $\mathfrak n^{\mathbf p}=\mathfrak n^{\mathbf q}$, there is a bijection
$\mathfrak n^{\mathbf p}=\mathfrak n^{\mathbf q}$, there is a bijection ![]() $\phi_{\mathbf p, \mathbf q}: \Lambda_{\mathsf d}^{\mathbf p} \to \Lambda_{\mathsf d}^{\mathbf q} $ satisfying
$\phi_{\mathbf p, \mathbf q}: \Lambda_{\mathsf d}^{\mathbf p} \to \Lambda_{\mathsf d}^{\mathbf q} $ satisfying
 \begin{align}
\mu \nu = \phi_{\mathbf p, \mathbf q}(\mu) \phi_{\mathbf p, \mathbf q}^{-1}(\nu),\ \phi_{\mathbf p, \mathbf q}^{-1}(\nu)\phi_{\mathbf p, \mathbf q}(\mu)=\nu \mu
\end{align}
\begin{align}
\mu \nu = \phi_{\mathbf p, \mathbf q}(\mu) \phi_{\mathbf p, \mathbf q}^{-1}(\nu),\ \phi_{\mathbf p, \mathbf q}^{-1}(\nu)\phi_{\mathbf p, \mathbf q}(\mu)=\nu \mu
\end{align} for every pair ![]() $(\mu, \nu)\in \Lambda_{\mathsf d}^{\mathbf p}\times \Lambda_{\mathsf d}^{\mathbf q}$ [Reference Davidson and Yang18, Theorem 7.1] (or [Section 5]). Let
$(\mu, \nu)\in \Lambda_{\mathsf d}^{\mathbf p}\times \Lambda_{\mathsf d}^{\mathbf q}$ [Reference Davidson and Yang18, Theorem 7.1] (or [Section 5]). Let
 \begin{equation*}
V_{\mathbf p, \mathbf q}:=\sum_{\mu\in \Lambda_{\mathsf d}^{\mathbf p}} s_\mu s_{\phi_{\mathbf p, \mathbf q}(\mu)}^*.
\end{equation*}
\begin{equation*}
V_{\mathbf p, \mathbf q}:=\sum_{\mu\in \Lambda_{\mathsf d}^{\mathbf p}} s_\mu s_{\phi_{\mathbf p, \mathbf q}(\mu)}^*.
\end{equation*} By [Reference Davidson and Yang18, Theorem 4.9], each ![]() $V_{\mathbf p, \mathbf q}$ is a unitary in
$V_{\mathbf p, \mathbf q}$ is a unitary in ![]() ${\mathcal{O}}_{\Lambda_{\mathsf d}(\mathfrak n, \mathbb{ 1}_{\mathsf k})}$.
${\mathcal{O}}_{\Lambda_{\mathsf d}(\mathfrak n, \mathbb{ 1}_{\mathsf k})}$.
Proposition 4.8. The center of ![]() ${\mathcal{O}}_{\Lambda_{\mathsf d}(\mathfrak n, \mathbb{ 1}_{\mathsf k})}$ is given by
${\mathcal{O}}_{\Lambda_{\mathsf d}(\mathfrak n, \mathbb{ 1}_{\mathsf k})}$ is given by
 \begin{equation*}
{\mathcal{Z}}({\mathcal{O}}_{\Lambda_{\mathsf d}(\mathfrak n, \mathbb{ 1}_{\mathsf k})}) =\mathrm{C}^*(V_{\mathbf p, \mathbf q}: (\mathbf p, \mathbf q)\in {\mathbb{N}}^{\mathsf k}\times {\mathbb{N}}^{\mathsf k},\ \mathfrak n^{\mathbf p}=\mathfrak n^{\mathbf q}).
\end{equation*}
\begin{equation*}
{\mathcal{Z}}({\mathcal{O}}_{\Lambda_{\mathsf d}(\mathfrak n, \mathbb{ 1}_{\mathsf k})}) =\mathrm{C}^*(V_{\mathbf p, \mathbf q}: (\mathbf p, \mathbf q)\in {\mathbb{N}}^{\mathsf k}\times {\mathbb{N}}^{\mathsf k},\ \mathfrak n^{\mathbf p}=\mathfrak n^{\mathbf q}).
\end{equation*} In particular, ![]() ${\mathcal{Z}}({\mathcal{O}}_{\Lambda_{\mathsf d}(\mathfrak n, \mathbb{ 1}_{\mathsf k})})$ is trivial, if and only if
${\mathcal{Z}}({\mathcal{O}}_{\Lambda_{\mathsf d}(\mathfrak n, \mathbb{ 1}_{\mathsf k})})$ is trivial, if and only if ![]() $\{n_i: 1\le i\le \mathsf k\}$ is multiplicatively independent.
$\{n_i: 1\le i\le \mathsf k\}$ is multiplicatively independent.
Proof. Suppose that ![]() $A\in {\mathcal{Z}}({\mathcal{O}}_{\Lambda_{\mathsf d}(\mathfrak n, \mathbb{ 1}_{\mathsf k})})$. Then by proposition 2.7, one has
$A\in {\mathcal{Z}}({\mathcal{O}}_{\Lambda_{\mathsf d}(\mathfrak n, \mathbb{ 1}_{\mathsf k})})$. Then by proposition 2.7, one has ![]() $A\in {\mathcal{Z}}({\mathcal{O}}_{\Lambda_{\mathsf d}})$. But
$A\in {\mathcal{Z}}({\mathcal{O}}_{\Lambda_{\mathsf d}})$. But ![]() ${\mathcal{Z}}({\mathcal{O}}_{\Lambda_{\mathsf d}})=\mathrm{C}^*(V_{\mathbf p, \mathbf q}: (\mathbf p, \mathbf q)\in {\mathbb{N}}^{\mathsf k}\times {\mathbb{N}}^{\mathsf k},\ \mathfrak n^{\mathbf p}=\mathfrak n^{\mathbf q})$ [Reference Davidson and Yang18].
${\mathcal{Z}}({\mathcal{O}}_{\Lambda_{\mathsf d}})=\mathrm{C}^*(V_{\mathbf p, \mathbf q}: (\mathbf p, \mathbf q)\in {\mathbb{N}}^{\mathsf k}\times {\mathbb{N}}^{\mathsf k},\ \mathfrak n^{\mathbf p}=\mathfrak n^{\mathbf q})$ [Reference Davidson and Yang18].
It remains to show that each ![]() $V_{\mathbf p, \mathbf q}$ is indeed in
$V_{\mathbf p, \mathbf q}$ is indeed in ![]() ${\mathcal{Z}}({\mathcal{O}}_{\Lambda_{\mathsf d}(\mathfrak n, \mathbb{ 1}_{\mathsf k})})$. This has been proved in [Reference Davidson and Yang18, Theorem 4.9]. In what follows, we prove this by invoking lemma 4.7.
${\mathcal{Z}}({\mathcal{O}}_{\Lambda_{\mathsf d}(\mathfrak n, \mathbb{ 1}_{\mathsf k})})$. This has been proved in [Reference Davidson and Yang18, Theorem 4.9]. In what follows, we prove this by invoking lemma 4.7.
We first show that ua commutes with ![]() $V_{\mathbf p, \mathbf q}$. Then on one hand, we have
$V_{\mathbf p, \mathbf q}$. Then on one hand, we have
 \begin{align*}
a\cdot (\mu \nu)=a\cdot(\phi_{\mathbf p, \mathbf q}(\mu) \phi_{\mathbf p, \mathbf q}^{-1}(\nu))
\implies a\cdot \mu a|_\mu\cdot \nu = a\cdot \phi_{\mathbf p, \mathbf q}(\mu) a|_{\phi(\mu)}\cdot \phi_{\mathbf p, \mathbf q}^{-1}(\nu).
\end{align*}
\begin{align*}
a\cdot (\mu \nu)=a\cdot(\phi_{\mathbf p, \mathbf q}(\mu) \phi_{\mathbf p, \mathbf q}^{-1}(\nu))
\implies a\cdot \mu a|_\mu\cdot \nu = a\cdot \phi_{\mathbf p, \mathbf q}(\mu) a|_{\phi(\mu)}\cdot \phi_{\mathbf p, \mathbf q}^{-1}(\nu).
\end{align*}On the other hand, we have
 \begin{equation*}
a\cdot \mu a|_\mu\cdot \nu = \phi_{\mathbf p, \mathbf q}(a\cdot \mu) \phi_{\mathbf p, \mathbf q}^{-1}(a|_\mu\cdot \nu).
\end{equation*}
\begin{equation*}
a\cdot \mu a|_\mu\cdot \nu = \phi_{\mathbf p, \mathbf q}(a\cdot \mu) \phi_{\mathbf p, \mathbf q}^{-1}(a|_\mu\cdot \nu).
\end{equation*}Thus
 \begin{align}
& a^{-1}\cdot \phi_{\mathbf p, \mathbf q}(\mu) a^{-1}|_{\phi_{\mathbf p, \mathbf q}(\mu)}\cdot \phi_{\mathbf p, \mathbf q}^{-1}(\nu)
=\phi_{\mathbf p, \mathbf q}(a^{-1}\cdot \mu) \phi_{\mathbf p, \mathbf q}^{-1}(a^{-1}|_\mu\cdot \nu) \nonumber\\
&\implies a^{-1}\cdot \phi_{\mathbf p, \mathbf q}(\mu)
=\phi_{\mathbf p, \mathbf q}(a^{-1}\cdot \mu) \quad \text{and} \quad a^{-1}|_{\phi_{\mathbf p, \mathbf q}(\mu)}\cdot \phi_{\mathbf p, \mathbf q}^{-1}(\nu)=\phi_{\mathbf p, \mathbf q}^{-1}(a^{-1}|_\mu\cdot \nu)
\end{align}
\begin{align}
& a^{-1}\cdot \phi_{\mathbf p, \mathbf q}(\mu) a^{-1}|_{\phi_{\mathbf p, \mathbf q}(\mu)}\cdot \phi_{\mathbf p, \mathbf q}^{-1}(\nu)
=\phi_{\mathbf p, \mathbf q}(a^{-1}\cdot \mu) \phi_{\mathbf p, \mathbf q}^{-1}(a^{-1}|_\mu\cdot \nu) \nonumber\\
&\implies a^{-1}\cdot \phi_{\mathbf p, \mathbf q}(\mu)
=\phi_{\mathbf p, \mathbf q}(a^{-1}\cdot \mu) \quad \text{and} \quad a^{-1}|_{\phi_{\mathbf p, \mathbf q}(\mu)}\cdot \phi_{\mathbf p, \mathbf q}^{-1}(\nu)=\phi_{\mathbf p, \mathbf q}^{-1}(a^{-1}|_\mu\cdot \nu)
\end{align} Then one can easily see ![]() $g\cdot \phi_{\mathbf p, \mathbf q}(\mu) = \phi_{\mathbf p, \mathbf q}(g\cdot \mu)$ for any
$g\cdot \phi_{\mathbf p, \mathbf q}(\mu) = \phi_{\mathbf p, \mathbf q}(g\cdot \mu)$ for any ![]() $g\in {\mathbb{Z}}$. Similarly, one gets from the second identity of (9) that
$g\in {\mathbb{Z}}$. Similarly, one gets from the second identity of (9) that  $g\cdot \phi_{\mathbf p, \mathbf q}^{-1}(\nu) = \phi_{\mathbf p, \mathbf q}^{-1}(g\cdot \nu)$ for any
$g\cdot \phi_{\mathbf p, \mathbf q}^{-1}(\nu) = \phi_{\mathbf p, \mathbf q}^{-1}(g\cdot \nu)$ for any ![]() $g\in {\mathbb{Z}}$. Thus the second identity of (10) yields
$g\in {\mathbb{Z}}$. Thus the second identity of (10) yields  $a^{-1}|_{\phi_{\mathbf p, \mathbf q}(\mu)}=a^{-1}|_\mu$, and so
$a^{-1}|_{\phi_{\mathbf p, \mathbf q}(\mu)}=a^{-1}|_\mu$, and so  $
(a^{-1}|_{\phi_{\mathbf p, \mathbf q}(\mu)})^{-1}=(a^{-1}|_\mu)^{-1}.
$ Therefore
$
(a^{-1}|_{\phi_{\mathbf p, \mathbf q}(\mu)})^{-1}=(a^{-1}|_\mu)^{-1}.
$ Therefore
Now compute
 \begin{align*}
u_a V_{\mathbf p, \mathbf q}&
= \sum_{d(\mu)=\mathbf p} s_{a\cdot \mu}u_{a|_\mu} s_{\phi_{\mathbf p, \mathbf q}(\mu)}^*
= \sum_{d(\mu)=\mathbf p} s_\mu u_{a|_{a^{-1}\cdot \mu}} s_{\phi_{\mathbf p, \mathbf q}(a^{-1}\cdot\mu)}^*\\
&= \sum_{d(\mu)=\mathbf p} s_\mu u_{a|_{a^{-1}\cdot \phi_{\mathbf p, \mathbf q}(\mu)}} s_{a^{-1}\cdot\phi_{\mathbf p, \mathbf q}(\mu)}^* \
(\text{from } (10)\text{and }(11))\\
&= \sum_{d(\mu)=\mathbf p} s_\mu u_{({a^{-1}|_ {\phi_{\mathbf p, \mathbf q}(\mu)})^{-1}}} s_{a^{-1}\cdot\phi_{\mathbf p, \mathbf q}(\mu)}^*
= \left(\sum_{d(\mu)=\mathbf p} s_\mu s_{\phi_{\mathbf p, \mathbf q}(\mu)}^*\right)u_a\\
&= V_{\mathbf p, \mathbf q}\, u_a .
\end{align*}
\begin{align*}
u_a V_{\mathbf p, \mathbf q}&
= \sum_{d(\mu)=\mathbf p} s_{a\cdot \mu}u_{a|_\mu} s_{\phi_{\mathbf p, \mathbf q}(\mu)}^*
= \sum_{d(\mu)=\mathbf p} s_\mu u_{a|_{a^{-1}\cdot \mu}} s_{\phi_{\mathbf p, \mathbf q}(a^{-1}\cdot\mu)}^*\\
&= \sum_{d(\mu)=\mathbf p} s_\mu u_{a|_{a^{-1}\cdot \phi_{\mathbf p, \mathbf q}(\mu)}} s_{a^{-1}\cdot\phi_{\mathbf p, \mathbf q}(\mu)}^* \
(\text{from } (10)\text{and }(11))\\
&= \sum_{d(\mu)=\mathbf p} s_\mu u_{({a^{-1}|_ {\phi_{\mathbf p, \mathbf q}(\mu)})^{-1}}} s_{a^{-1}\cdot\phi_{\mathbf p, \mathbf q}(\mu)}^*
= \left(\sum_{d(\mu)=\mathbf p} s_\mu s_{\phi_{\mathbf p, \mathbf q}(\mu)}^*\right)u_a\\
&= V_{\mathbf p, \mathbf q}\, u_a .
\end{align*}Then
By lemma 4.7 (ii),  $\sum\limits_{d(\mu)=\mathbf p} s_\mu s_{\phi_{\mathbf p, \mathbf q}(\mu)}^*\in {\mathcal{Z}}({\mathcal{O}}_{\Lambda_{\mathsf d}(\mathfrak n, \mathbb{ 1}_{\mathsf k})})$.\hfill▪
$\sum\limits_{d(\mu)=\mathbf p} s_\mu s_{\phi_{\mathbf p, \mathbf q}(\mu)}^*\in {\mathcal{Z}}({\mathcal{O}}_{\Lambda_{\mathsf d}(\mathfrak n, \mathbb{ 1}_{\mathsf k})})$.\hfill▪
For ![]() ${\mathbf{m}}\in {\mathbb{N}}^{\mathsf{k}}$, let
${\mathbf{m}}\in {\mathbb{N}}^{\mathsf{k}}$, let ![]() ${\mathcal{F}}_{{\mathbf{m}}}:=\overline{\operatorname{span}}\{s_\mu a^n s_\nu^*: \mu,\nu\in \Lambda_{(\mathfrak n, \mathbb{ 1}_{\mathsf k})} \text{with } d(\mu)=d(\nu)={\mathbf{m}}, n\in {\mathbb{Z}}\}$, and so
${\mathcal{F}}_{{\mathbf{m}}}:=\overline{\operatorname{span}}\{s_\mu a^n s_\nu^*: \mu,\nu\in \Lambda_{(\mathfrak n, \mathbb{ 1}_{\mathsf k})} \text{with } d(\mu)=d(\nu)={\mathbf{m}}, n\in {\mathbb{Z}}\}$, and so  ${\mathcal{F}}=\overline{\bigcup\limits_{m\in {\mathbb{N}}^{\mathsf{k}}} {\mathcal{F}}_{{\mathbf{m}}}}^{\|\cdot\|}$. Also notice that, due to the Cuntz–Krieger relations, we have
${\mathcal{F}}=\overline{\bigcup\limits_{m\in {\mathbb{N}}^{\mathsf{k}}} {\mathcal{F}}_{{\mathbf{m}}}}^{\|\cdot\|}$. Also notice that, due to the Cuntz–Krieger relations, we have  ${\mathcal{F}}=\lim\limits_{\stackrel{\longrightarrow}{m\in {\mathbb{N}}}}{\mathcal{F}}_{m\mathbb{1}_{\mathsf k}}$.
${\mathcal{F}}=\lim\limits_{\stackrel{\longrightarrow}{m\in {\mathbb{N}}}}{\mathcal{F}}_{m\mathbb{1}_{\mathsf k}}$.
Let  $d:=\prod\limits_{i=1}^{\mathsf{k}}\prod\limits_{p\in {\mathcal{P}}, \, p|n_i} p$, the product of all primes dividing some ni’s.
$d:=\prod\limits_{i=1}^{\mathsf{k}}\prod\limits_{p\in {\mathcal{P}}, \, p|n_i} p$, the product of all primes dividing some ni’s.
Lemma 4.9. ![]() ${\mathcal{F}}$ is a Bunce–Deddens algebra of type
${\mathcal{F}}$ is a Bunce–Deddens algebra of type ![]() $d^\infty$. In particular,
$d^\infty$. In particular, ![]() ${\mathcal{F}}$ has a unique faithful tracial state.
${\mathcal{F}}$ has a unique faithful tracial state.
Proof. The proof below is motivated by the proof of [Reference Li and Yang35, Theorem 3.16].
For ![]() ${\mathbf{m}} \in {\mathbb{N}}^{\mathsf k}$, let
${\mathbf{m}} \in {\mathbb{N}}^{\mathsf k}$, let ![]() $\{e_{\mu,\nu}\}_{\mu,\nu\in \Lambda^{{\mathbf{m}}}_{\mathsf d}}$ be the matrix entries of
$\{e_{\mu,\nu}\}_{\mu,\nu\in \Lambda^{{\mathbf{m}}}_{\mathsf d}}$ be the matrix entries of ![]() $K(\ell^2(\Lambda_{\mathsf d}^{\mathbf{m}})).$ To simplify our notation, let
$K(\ell^2(\Lambda_{\mathsf d}^{\mathbf{m}})).$ To simplify our notation, let ![]() $\{a^n\}_{n\in {\mathbb{Z}}}$ be the generating unitaries of
$\{a^n\}_{n\in {\mathbb{Z}}}$ be the generating unitaries of ![]() $\mathrm{C}^*({\mathbb{Z}})$. Clearly, there is a homomorphism
$\mathrm{C}^*({\mathbb{Z}})$. Clearly, there is a homomorphism
 \begin{equation*}
\rho_1: K(\ell^2(\Lambda_{\mathsf d}^{m\mathbb{1}_{\mathsf k}}))\to {\mathcal{F}}_{m\mathbb{1}_{\mathsf k}},\ e_{\mu,\nu}\mapsto s_\mu s_\nu^*,
\end{equation*}
\begin{equation*}
\rho_1: K(\ell^2(\Lambda_{\mathsf d}^{m\mathbb{1}_{\mathsf k}}))\to {\mathcal{F}}_{m\mathbb{1}_{\mathsf k}},\ e_{\mu,\nu}\mapsto s_\mu s_\nu^*,
\end{equation*}and
 \begin{equation*}
\rho_2:{\mathrm{C}}({\mathbb{T}})\to {\mathcal{F}}_{m\mathbb{1}_{\mathsf k}},\ a^n\mapsto \sum_{\mu\in\Lambda_{\mathsf d}^{m\mathbb{1}_{\mathsf k}}} s_\mu u_{a^n} s_\mu^*.
\end{equation*}
\begin{equation*}
\rho_2:{\mathrm{C}}({\mathbb{T}})\to {\mathcal{F}}_{m\mathbb{1}_{\mathsf k}},\ a^n\mapsto \sum_{\mu\in\Lambda_{\mathsf d}^{m\mathbb{1}_{\mathsf k}}} s_\mu u_{a^n} s_\mu^*.
\end{equation*} Some simple calculations show the images of ρ 1 and ρ 2 commute. By [Reference Li and Yang37, Theorem 6.3.7], there is a homomorphism  $\rho: K(\ell^2(\Lambda_{\mathsf d}^{m\mathbb{1}_{\mathsf k}}))\otimes \mathrm{C}^*({\mathbb{Z}})\to {\mathcal{F}}_{m\mathbb{1}_{\mathsf k}}$ satisfying
$\rho: K(\ell^2(\Lambda_{\mathsf d}^{m\mathbb{1}_{\mathsf k}}))\otimes \mathrm{C}^*({\mathbb{Z}})\to {\mathcal{F}}_{m\mathbb{1}_{\mathsf k}}$ satisfying ![]() $\rho(e_{\mu, \nu}\otimes a^n)= s_\mu u_{a^n} s_\nu^*$. It is not hard to see that ρ is also invertible and so an isomorphism.
$\rho(e_{\mu, \nu}\otimes a^n)= s_\mu u_{a^n} s_\nu^*$. It is not hard to see that ρ is also invertible and so an isomorphism.
Set ![]() $\mu_0:={\mathbf{x}}_0^1\cdots {\mathbf{x}}^{\mathsf k}_0$ and
$\mu_0:={\mathbf{x}}_0^1\cdots {\mathbf{x}}^{\mathsf k}_0$ and  $\mu_{\mathfrak n -\mathbb{1}}:={\mathbf{x}}^1_{n_1-1}\cdots {\mathbf{x}}^{\mathsf k}_{n_{\mathsf k}-1}$. Embed
$\mu_{\mathfrak n -\mathbb{1}}:={\mathbf{x}}^1_{n_1-1}\cdots {\mathbf{x}}^{\mathsf k}_{n_{\mathsf k}-1}$. Embed  $K(\ell^2(\Lambda_{\mathsf d}^{m\mathbb{ 1}_{\mathsf k}}))\otimes \mathrm{C}^*({\mathbb{Z}})$ into
$K(\ell^2(\Lambda_{\mathsf d}^{m\mathbb{ 1}_{\mathsf k}}))\otimes \mathrm{C}^*({\mathbb{Z}})$ into  $K(\ell^2(\Lambda_{\mathsf d}^{(m+1)\mathbb{ 1}_{\mathsf k}}))\otimes \mathrm{C}^*({\mathbb{Z}})$ as follows:
$K(\ell^2(\Lambda_{\mathsf d}^{(m+1)\mathbb{ 1}_{\mathsf k}}))\otimes \mathrm{C}^*({\mathbb{Z}})$ as follows:
 \begin{equation*}
e_{\mu, \nu}\otimes a^n\mapsto \sum\limits_{\alpha\in \Lambda_{\mathsf d}^{\mathbb{1}}}e_{\mu a^n\cdot \alpha, \nu\alpha}\otimes a^n|_\alpha.
\end{equation*}
\begin{equation*}
e_{\mu, \nu}\otimes a^n\mapsto \sum\limits_{\alpha\in \Lambda_{\mathsf d}^{\mathbb{1}}}e_{\mu a^n\cdot \alpha, \nu\alpha}\otimes a^n|_\alpha.
\end{equation*} Notice that ![]() $a|_\alpha=a$ if
$a|_\alpha=a$ if ![]() $\alpha=\mu_{\mathfrak n -\mathbb{1}_{\mathsf k}}$, and
$\alpha=\mu_{\mathfrak n -\mathbb{1}_{\mathsf k}}$, and ![]() $a|_\alpha=0$, otherwise.
$a|_\alpha=0$, otherwise.
Now we have
 \begin{align*}
u_a
&=u_a \sum_{\mu\in\Lambda^{m\mathbb{1}_{\mathsf k}}} s_\mu s_\mu^*
=\sum_{\mu\in\Lambda_{\mathsf d}^{m\mathbb{1}_{\mathsf k}}} s_{a\cdot\mu} u_{a|_\mu} s_\mu^*\\
&=\sum_{\mu\ne \mu_{\mathfrak n-\mathbb{1}_{\mathsf k}}} s_{a\cdot\mu} s_\mu^*+s_{a\cdot\mu_{\mathfrak n-\mathbb{1}_{\mathsf k}}} u_a s_{\mu_{\mathfrak n-\mathbb{1}_{\mathsf k}}}^*\\
&=\sum_{\mu\ne \mu_{\mathfrak n-\mathbb{1}_{\mathsf k}}} s_{a\cdot\mu} s_\mu^*+s_{\mu_0} u_a s_{\mu_{\mathfrak n-\mathbb{1}_{\mathsf k}}}^*.
\end{align*}
\begin{align*}
u_a
&=u_a \sum_{\mu\in\Lambda^{m\mathbb{1}_{\mathsf k}}} s_\mu s_\mu^*
=\sum_{\mu\in\Lambda_{\mathsf d}^{m\mathbb{1}_{\mathsf k}}} s_{a\cdot\mu} u_{a|_\mu} s_\mu^*\\
&=\sum_{\mu\ne \mu_{\mathfrak n-\mathbb{1}_{\mathsf k}}} s_{a\cdot\mu} s_\mu^*+s_{a\cdot\mu_{\mathfrak n-\mathbb{1}_{\mathsf k}}} u_a s_{\mu_{\mathfrak n-\mathbb{1}_{\mathsf k}}}^*\\
&=\sum_{\mu\ne \mu_{\mathfrak n-\mathbb{1}_{\mathsf k}}} s_{a\cdot\mu} s_\mu^*+s_{\mu_0} u_a s_{\mu_{\mathfrak n-\mathbb{1}_{\mathsf k}}}^*.
\end{align*} Therefore ![]() ${\mathcal{F}}$ is isomorphic to a Bunce–Deddens algebra of type of
${\mathcal{F}}$ is isomorphic to a Bunce–Deddens algebra of type of ![]() $d^\infty$, and so it has a unique faithful tracial state [Reference Connes and Marcolli14].\hfill▪
$d^\infty$, and so it has a unique faithful tracial state [Reference Connes and Marcolli14].\hfill▪
Remark 4.10. It is worth mentioning the following: If ![]() $S:=\{n_1,\ldots, n_{\mathsf k}\}\subset {\mathbb{N}}$ is a set of mutually coprime natural numbers, then
$S:=\{n_1,\ldots, n_{\mathsf k}\}\subset {\mathbb{N}}$ is a set of mutually coprime natural numbers, then ![]() ${\mathcal{F}}$ is isomorphic to BS in [Reference an Huef, Nucinkis, Sehnem and Yang3].
${\mathcal{F}}$ is isomorphic to BS in [Reference an Huef, Nucinkis, Sehnem and Yang3].
By lemma 4.9 and [Reference Connes and Marcolli14], ![]() ${\mathcal{F}}$ has a unique faithful tracial state, say τ, given by
${\mathcal{F}}$ has a unique faithful tracial state, say τ, given by
 \begin{equation*}
\tau(s_\mu u_{a^n} s_\mu^*)=\mathfrak n^{-d(\mu)}\delta_{n,0}.
\end{equation*}
\begin{equation*}
\tau(s_\mu u_{a^n} s_\mu^*)=\mathfrak n^{-d(\mu)}\delta_{n,0}.
\end{equation*} Recall that ![]() $\Phi_{\mathbf 0}$ is the faithful conditional expectation from
$\Phi_{\mathbf 0}$ is the faithful conditional expectation from ![]() ${\mathcal{O}}_{\Lambda_{\mathsf d}(\mathfrak n, \mathbb{ 1})}$ onto
${\mathcal{O}}_{\Lambda_{\mathsf d}(\mathfrak n, \mathbb{ 1})}$ onto ![]() ${\mathcal{F}}$ via the gauge action γ (see § 2.2). Then
${\mathcal{F}}$ via the gauge action γ (see § 2.2). Then ![]() $\omega:=\tau\circ \Phi_{\mathbf 0}$ is a state of
$\omega:=\tau\circ \Phi_{\mathbf 0}$ is a state of ![]() ${\mathcal{O}}_{\Lambda_{\mathsf d}(\mathfrak n, \mathbb{ 1}_{\mathsf k})}$.
${\mathcal{O}}_{\Lambda_{\mathsf d}(\mathfrak n, \mathbb{ 1}_{\mathsf k})}$.
We recall the notion of KMS states from [Reference Bartholdi, Grigorchuk and Nekrashevych5] (also see [Reference Clark, an Huef and Raeburn13]) and give some basic properties of KMS states for ![]() ${\mathcal{O}}_{\Lambda_{\mathsf d}(\mathfrak n, \mathbb{ 1}_{\mathsf k})}$.
${\mathcal{O}}_{\Lambda_{\mathsf d}(\mathfrak n, \mathbb{ 1}_{\mathsf k})}$.
Definition 4.11. Let A be a C*-algebra, α be an action of ![]() ${\mathbb{R}}$ on A, and Aa be the set of all analytic elements of A. Let
${\mathbb{R}}$ on A, and Aa be the set of all analytic elements of A. Let ![]() $0 \lt \beta \lt \infty$. A state τ of A is called a KMS
$0 \lt \beta \lt \infty$. A state τ of A is called a KMS ![]() $_\beta$ state of
$_\beta$ state of ![]() $(A,\mathbb{R},\alpha)$ if
$(A,\mathbb{R},\alpha)$ if ![]() $\tau(xy)=\tau(y \alpha_{i\beta}(x))$ for all
$\tau(xy)=\tau(y \alpha_{i\beta}(x))$ for all ![]() $x,y \in A^a$.
$x,y \in A^a$.
Recall the gauge action  $\gamma:{\mathbb{T}}^{\mathsf k} \to \operatorname{Aut}({\mathcal{O}}_{\Lambda_{\mathsf d}(\mathfrak n, \mathbb{ 1}_{\mathsf k})})$:
$\gamma:{\mathbb{T}}^{\mathsf k} \to \operatorname{Aut}({\mathcal{O}}_{\Lambda_{\mathsf d}(\mathfrak n, \mathbb{ 1}_{\mathsf k})})$:
 \begin{equation*}
\gamma_z(s_\mu)=z^{d(\mu)}s_\mu\text{and } \gamma_z(u_g)=u_g\quad\text{for all}\quad z \in {\mathbb{T}}^{\mathsf k}, \mu \in \Lambda,g \in {\mathbb{Z}}.
\end{equation*}
\begin{equation*}
\gamma_z(s_\mu)=z^{d(\mu)}s_\mu\text{and } \gamma_z(u_g)=u_g\quad\text{for all}\quad z \in {\mathbb{T}}^{\mathsf k}, \mu \in \Lambda,g \in {\mathbb{Z}}.
\end{equation*} Let ![]() $\mathsf{r}=(\ln n_1, \ldots, \ln n_{\mathsf k})\in {\mathbb{R}}^{\mathsf k}$. Define a strongly continuous homomorphism
$\mathsf{r}=(\ln n_1, \ldots, \ln n_{\mathsf k})\in {\mathbb{R}}^{\mathsf k}$. Define a strongly continuous homomorphism ![]() $\alpha^{\mathsf{r}}:\mathbb{R} \to \operatorname{Aut}({\mathcal{O}}_{\Lambda_\mathsf d(\mathfrak n,\mathbb{ 1}_{\mathsf k})})$ by
$\alpha^{\mathsf{r}}:\mathbb{R} \to \operatorname{Aut}({\mathcal{O}}_{\Lambda_\mathsf d(\mathfrak n,\mathbb{ 1}_{\mathsf k})})$ by ![]() $\alpha^{\mathsf{r}}_t:=\gamma_{e^{it\mathsf{r}}}$. Notice that, for
$\alpha^{\mathsf{r}}_t:=\gamma_{e^{it\mathsf{r}}}$. Notice that, for ![]() $\mu,\nu \in \Lambda_\mathsf d(\mathfrak n, \mathbb{ 1}_{\mathsf k}), g \in {\mathbb{Z}}$, the function
$\mu,\nu \in \Lambda_\mathsf d(\mathfrak n, \mathbb{ 1}_{\mathsf k}), g \in {\mathbb{Z}}$, the function ![]() $\mathbb{C} \to {\mathcal{O}}_{\Lambda_\mathsf d(\mathfrak n, \mathbb{ 1})}$,
$\mathbb{C} \to {\mathcal{O}}_{\Lambda_\mathsf d(\mathfrak n, \mathbb{ 1})}$,  $\xi \mapsto e^{i \xi \mathsf{r} \cdot (d(\mu)-d(\nu))}s_\mu u_g s_\nu^*$ is an entire function. So
$\xi \mapsto e^{i \xi \mathsf{r} \cdot (d(\mu)-d(\nu))}s_\mu u_g s_\nu^*$ is an entire function. So ![]() $s_\mu u_g s_\nu^*$ is an analytic element. By proposition 2.7, in order to check the KMS
$s_\mu u_g s_\nu^*$ is an analytic element. By proposition 2.7, in order to check the KMS![]() $_\beta$ condition, it is sufficient to check whether it is valid on the set
$_\beta$ condition, it is sufficient to check whether it is valid on the set ![]() $\{s_\mu u_g s_\nu^*:\mu,\nu \in \Lambda_\mathsf d(\mathfrak n, \mathbb{ 1}_{\mathsf k}), g\in {\mathbb{Z}}\}$. In this section, we study basic properties of KMS
$\{s_\mu u_g s_\nu^*:\mu,\nu \in \Lambda_\mathsf d(\mathfrak n, \mathbb{ 1}_{\mathsf k}), g\in {\mathbb{Z}}\}$. In this section, we study basic properties of KMS![]() $_\beta$ states of the one-parameter dynamical system
$_\beta$ states of the one-parameter dynamical system ![]() $(\mathcal{O}_{\Lambda_\mathsf d(\mathfrak n, \mathbb{ 1})},\mathbb{R},\alpha^{\mathsf{r}})$.
$(\mathcal{O}_{\Lambda_\mathsf d(\mathfrak n, \mathbb{ 1})},\mathbb{R},\alpha^{\mathsf{r}})$.
Lemma 4.12. Suppose that ![]() $\{n_i: 1\le i\le \mathsf k\}$ is multiplicatively independent. Then ω is the unique KMS1 state on
$\{n_i: 1\le i\le \mathsf k\}$ is multiplicatively independent. Then ω is the unique KMS1 state on ![]() ${\mathcal{O}}_{\Lambda_\mathsf d(\mathfrak n, \mathbb{ 1}_{\mathsf k})}$.
${\mathcal{O}}_{\Lambda_\mathsf d(\mathfrak n, \mathbb{ 1}_{\mathsf k})}$.
Proof. An easy calculation shows
 \begin{align*}
\omega(s_\mu u_{a^n} s_\nu^*)=\delta_{\mu, \nu} \delta_{n,0} \, \mathfrak n^{-d(\mu)}.
\end{align*}
\begin{align*}
\omega(s_\mu u_{a^n} s_\nu^*)=\delta_{\mu, \nu} \delta_{n,0} \, \mathfrak n^{-d(\mu)}.
\end{align*} By [Reference Li33, Theorems 6.11 and 6.12], ω is the unique KMS1 state of ![]() ${\mathcal{O}}_{\Lambda_\mathsf d(\mathfrak n, \mathbb{ 1})}$ (also see [Reference Li33, Theorem 7.1]).\hfill▪
${\mathcal{O}}_{\Lambda_\mathsf d(\mathfrak n, \mathbb{ 1})}$ (also see [Reference Li33, Theorem 7.1]).\hfill▪
As in [Reference Serre46, Reference Spielberg47], let  $L^2({\mathcal{O}}_{\Lambda_\mathsf d(\mathfrak n, \mathbb{ 1}_{\mathsf k})})$ be the GNS Hilbert space determined by the state ω:
$L^2({\mathcal{O}}_{\Lambda_\mathsf d(\mathfrak n, \mathbb{ 1}_{\mathsf k})})$ be the GNS Hilbert space determined by the state ω: ![]() $\langle A, B\rangle:=\omega(A^*B)$ for all
$\langle A, B\rangle:=\omega(A^*B)$ for all ![]() $A, B\in {\mathcal{O}}_{\Lambda_\mathsf d(\mathfrak n, \mathbb{ 1}_{\mathsf k})}$. For
$A, B\in {\mathcal{O}}_{\Lambda_\mathsf d(\mathfrak n, \mathbb{ 1}_{\mathsf k})}$. For ![]() $A \in {\mathcal{O}}_{\Lambda_\mathsf d(\mathfrak n, \mathbb{ 1}_{\mathsf k})}$, we denote the left action of A by
$A \in {\mathcal{O}}_{\Lambda_\mathsf d(\mathfrak n, \mathbb{ 1}_{\mathsf k})}$, we denote the left action of A by ![]() $\pi (A): \pi(A)B = AB$ for all
$\pi (A): \pi(A)B = AB$ for all ![]() $B \in {\mathcal{O}}_{\Lambda_\mathsf d(\mathfrak n, \mathbb{ 1})}$. Let
$B \in {\mathcal{O}}_{\Lambda_\mathsf d(\mathfrak n, \mathbb{ 1})}$. Let  $ {\mathcal{O}}_{\Lambda_\mathsf d(\mathfrak n, \mathbb{ 1}_{\mathsf k})}^c$ stand for the algebra as the finite linear span of the generators
$ {\mathcal{O}}_{\Lambda_\mathsf d(\mathfrak n, \mathbb{ 1}_{\mathsf k})}^c$ stand for the algebra as the finite linear span of the generators ![]() $s_\mu u_g s_\nu^*$.
$s_\mu u_g s_\nu^*$.
Define
 \begin{align*}
S(A):=A^*,\ F(s_\mu u_{a^n} s_\nu^*):=\mathfrak n^{d(\mu)-d(\nu)} s_\nu u_{a^{-n}} s_\mu^*, \quad\text{for}\quad A\in {\mathcal{O}}_{\Lambda_\mathsf d(\mathfrak n, \mathbb{ 1}_{\mathsf k})}^c.
\end{align*}
\begin{align*}
S(A):=A^*,\ F(s_\mu u_{a^n} s_\nu^*):=\mathfrak n^{d(\mu)-d(\nu)} s_\nu u_{a^{-n}} s_\mu^*, \quad\text{for}\quad A\in {\mathcal{O}}_{\Lambda_\mathsf d(\mathfrak n, \mathbb{ 1}_{\mathsf k})}^c.
\end{align*} Then ![]() $F=S^*$. Also, if
$F=S^*$. Also, if
 \begin{equation*}
J(s_\mu u_{a^n} s_\nu^*):=\mathfrak n^{\frac{d(\mu)-d(\nu)}{2}} s_\nu u_{a^{-n}} s_\mu^*, \
\Delta (s_\mu u_{a^n} s_\nu^*):=\mathfrak n^{d(\nu)-d(\mu)} s_\mu u_{a^n} s_\nu^*,
\end{equation*}
\begin{equation*}
J(s_\mu u_{a^n} s_\nu^*):=\mathfrak n^{\frac{d(\mu)-d(\nu)}{2}} s_\nu u_{a^{-n}} s_\mu^*, \
\Delta (s_\mu u_{a^n} s_\nu^*):=\mathfrak n^{d(\nu)-d(\mu)} s_\mu u_{a^n} s_\nu^*,
\end{equation*}one has
 \begin{equation*}
S=J\Delta^{\frac{1}{2}}=\Delta^{-\frac{1}{2}} J,\ F=J\Delta^{-\frac{1}{2}}= \Delta^{\frac{1}{2}}J.
\end{equation*}
\begin{equation*}
S=J\Delta^{\frac{1}{2}}=\Delta^{-\frac{1}{2}} J,\ F=J\Delta^{-\frac{1}{2}}= \Delta^{\frac{1}{2}}J.
\end{equation*} Let ![]() $\pi_\omega({\mathcal{O}}_{\Lambda_d(\mathfrak n, \mathbb{ 1}_{\mathsf k})})^{\prime\prime}$ be the von Neumann algebra generated by the GNS representation of ω. Then
$\pi_\omega({\mathcal{O}}_{\Lambda_d(\mathfrak n, \mathbb{ 1}_{\mathsf k})})^{\prime\prime}$ be the von Neumann algebra generated by the GNS representation of ω. Then ![]() $\pi_\omega({\mathcal{O}}_{\Lambda_d(\mathfrak n, \mathbb{ 1}_{\mathsf k})})^{\prime\prime}$ coincides with the left von Neumann algebra of
$\pi_\omega({\mathcal{O}}_{\Lambda_d(\mathfrak n, \mathbb{ 1}_{\mathsf k})})^{\prime\prime}$ coincides with the left von Neumann algebra of  $ {\mathcal{O}}_{\Lambda_\mathsf d(\mathfrak n, \mathbb{ 1}_{\mathsf k})}^c$.
$ {\mathcal{O}}_{\Lambda_\mathsf d(\mathfrak n, \mathbb{ 1}_{\mathsf k})}^c$.
The proof of the following theorem can now be easily adapted from [Reference Serre46, Reference Spielberg47] combined with [Reference Laca, Raeburn, Ramagge and Whittaker32, Reference Li33] and is left to the interested reader.
Theorem 4.13. The following statements are equivalent:
(i)
 ${\mathcal{O}}_{\Lambda_\mathsf d(\mathfrak n, \mathbb{ 1}_{\mathsf k})}$ is simple.
${\mathcal{O}}_{\Lambda_\mathsf d(\mathfrak n, \mathbb{ 1}_{\mathsf k})}$ is simple.(ii)
 ${\mathcal{O}}_{\Lambda_{\mathsf d}}$ is simple.
${\mathcal{O}}_{\Lambda_{\mathsf d}}$ is simple.(iii)
 $\{n_i: 1\le i\le \mathsf k\}$ is multiplicatively independent.
$\{n_i: 1\le i\le \mathsf k\}$ is multiplicatively independent.(iv)
 $\Lambda_{\mathsf d}(\mathfrak n, \mathbb{ 1}_{\mathsf k})$ is aperiodic.
$\Lambda_{\mathsf d}(\mathfrak n, \mathbb{ 1}_{\mathsf k})$ is aperiodic.(v) The ambient
 $\mathsf k$-graph
$\mathsf k$-graph  $\Lambda_{\mathsf d}$ is aperiodic.
$\Lambda_{\mathsf d}$ is aperiodic.(vi)
 $\pi_\omega({\mathcal{O}}_{\Lambda_\mathsf d(\mathfrak n, \mathbb{ 1}_{\mathsf k})})^{\prime\prime}$ is a factor.
$\pi_\omega({\mathcal{O}}_{\Lambda_\mathsf d(\mathfrak n, \mathbb{ 1}_{\mathsf k})})^{\prime\prime}$ is a factor.
When ![]() $\pi_\omega({\mathcal{O}}_{\Lambda_\mathsf d(\mathfrak n, \mathbb{ 1}_{\mathsf k})})^{\prime\prime}$ is a factor,
$\pi_\omega({\mathcal{O}}_{\Lambda_\mathsf d(\mathfrak n, \mathbb{ 1}_{\mathsf k})})^{\prime\prime}$ is a factor,
• it is an AFD factor of type III
 $_{\frac{1}{n}}$ if
$_{\frac{1}{n}}$ if  $\mathsf k=1$; and
$\mathsf k=1$; and• it is an AFD factor of type III1 if
 $\mathsf k\ge 2$.
$\mathsf k\ge 2$.
4.4. The case of  $\mathfrak n=\mathbb{ 1}_{\mathsf k}$
$\mathfrak n=\mathbb{ 1}_{\mathsf k}$
Since there is only one edge for each colour i, in order to ease our notation, we write ![]() ${\mathbf{x}}_i$ (instead of the notation
${\mathbf{x}}_i$ (instead of the notation ![]() ${\mathbf{x}}_1^i$ used above) for this unique edge. Thus
${\mathbf{x}}_1^i$ used above) for this unique edge. Thus ![]() ${\mathbf{x}}_i {\mathbf{x}}_j={\mathbf{x}}_j {\mathbf{x}}_i$ for all
${\mathbf{x}}_i {\mathbf{x}}_j={\mathbf{x}}_j {\mathbf{x}}_i$ for all ![]() $1\le i\ne j\le \mathsf k$. Since this is the unique commutation relation on
$1\le i\ne j\le \mathsf k$. Since this is the unique commutation relation on ![]() ${\mathbf{x}}_i$’s, we denote
${\mathbf{x}}_i$’s, we denote ![]() $\Lambda_\mathsf d(\mathbb{ 1}_{\mathsf k}, \mathfrak m)$ simply as
$\Lambda_\mathsf d(\mathbb{ 1}_{\mathsf k}, \mathfrak m)$ simply as ![]() $\Lambda(\mathbb{ 1}_{\mathsf k}, \mathfrak m)$. The ambient
$\Lambda(\mathbb{ 1}_{\mathsf k}, \mathfrak m)$. The ambient ![]() $\mathsf k$-graph is just denoted as
$\mathsf k$-graph is just denoted as ![]() $\Lambda_{\mathbb{ 1}_{\mathsf k}}$.
$\Lambda_{\mathbb{ 1}_{\mathsf k}}$.
We should mention that it seems that the case of ![]() $\mathfrak n=\mathbb{ 1}_{\mathsf k}$ is also studied in [Reference Li33]. However, this is exactly the case which is completely ignored there. This could be due to two reasons: one is that
$\mathfrak n=\mathbb{ 1}_{\mathsf k}$ is also studied in [Reference Li33]. However, this is exactly the case which is completely ignored there. This could be due to two reasons: one is that ![]() $\Lambda_\mathsf d(\mathbb{ 1}_{\mathsf k}, \mathfrak m)$ is clearly not locally faithful, which is the crucial property required in [Reference Li33]; the other is that this case, at first glance, seems too special.
$\Lambda_\mathsf d(\mathbb{ 1}_{\mathsf k}, \mathfrak m)$ is clearly not locally faithful, which is the crucial property required in [Reference Li33]; the other is that this case, at first glance, seems too special.
Observation 4.14. The observations below are obvious and will be used frequently later without any further mention.
(i) For every
 $\mathbf p\in {\mathbb{N}}^k$,
$\mathbf p\in {\mathbb{N}}^k$,  $\Lambda_{\mathbb{ 1}_{\mathsf k}}^{\mathbf p}$ is a singleton:
$\Lambda_{\mathbb{ 1}_{\mathsf k}}^{\mathbf p}$ is a singleton:  $\Lambda_{\mathbb{ 1}_{\mathsf k}}^{\mathbf p}=\{{\mathbf{x}}^{\mathbf p}:={\mathbf{x}}_1^{p_1}\cdots {\mathbf{x}}_{\mathsf k}^{p_{\mathsf k}}\}$. Also, sµ is a unitary for every
$\Lambda_{\mathbb{ 1}_{\mathsf k}}^{\mathbf p}=\{{\mathbf{x}}^{\mathbf p}:={\mathbf{x}}_1^{p_1}\cdots {\mathbf{x}}_{\mathsf k}^{p_{\mathsf k}}\}$. Also, sµ is a unitary for every  $\mu\in\Lambda_{\mathbb{ 1}_{\mathsf k}}$.
$\mu\in\Lambda_{\mathbb{ 1}_{\mathsf k}}$.(ii)
 $\Lambda(\mathbb{ 1}_{\mathsf k},\mathfrak m)$ is pseudo-free. In fact, some computations show
$\Lambda(\mathbb{ 1}_{\mathsf k},\mathfrak m)$ is pseudo-free. In fact, some computations show  $a^n|_\mu=a^{n{\mathfrak m}^{d(\mu)}}$ and so
$a^n|_\mu=a^{n{\mathfrak m}^{d(\mu)}}$ and so  $a^n|_\mu =0\iff n=0$.
$a^n|_\mu =0\iff n=0$.
Our next goal is to show that ![]() $\Lambda_{\mathsf d}(\mathbb{ 1}_{\mathsf k}, \mathfrak m)$ has a canonical Cartan subalgebra. In particular, this canonical Cartan subalgebra is
$\Lambda_{\mathsf d}(\mathbb{ 1}_{\mathsf k}, \mathfrak m)$ has a canonical Cartan subalgebra. In particular, this canonical Cartan subalgebra is ![]() ${\mathcal{F}}$ if
${\mathcal{F}}$ if ![]() $\{|m_i|: 1\le i\le \mathsf k\}$ is multiplicatively independent; it properly contains
$\{|m_i|: 1\le i\le \mathsf k\}$ is multiplicatively independent; it properly contains ![]() ${\mathcal{F}}$, otherwise.
${\mathcal{F}}$, otherwise.
Lemma 4.15. ![]() ${\mathcal{F}}=\overline{\operatorname{span}}\{s_\mu u_{a^\ell} s_\mu^*: \mu \in \Lambda_{\mathbb{ 1}_{\mathsf k}}, \ell\in {\mathbb{Z}}\}=\overline{\operatorname{span}}\{s_\mu^n u_{a^\ell} s_\mu^{-n}: d(\mu)=\mathbb{1}_{\mathsf k}, n\in {\mathbb{N}}, \ell\in {\mathbb{Z}}\}$.
${\mathcal{F}}=\overline{\operatorname{span}}\{s_\mu u_{a^\ell} s_\mu^*: \mu \in \Lambda_{\mathbb{ 1}_{\mathsf k}}, \ell\in {\mathbb{Z}}\}=\overline{\operatorname{span}}\{s_\mu^n u_{a^\ell} s_\mu^{-n}: d(\mu)=\mathbb{1}_{\mathsf k}, n\in {\mathbb{N}}, \ell\in {\mathbb{Z}}\}$.
Proof. It is known and easy to see that ![]() ${\mathcal{F}}=\overline{\operatorname{span}}\{s_\mu u_{a^m} s_\nu^*\mid \mu,\nu\in \Lambda_{\mathbb{ 1}_{\mathsf k}}, d(\mu)=d(\nu), m\in {\mathbb{Z}}\}$. It follows from observation 4.14 that
${\mathcal{F}}=\overline{\operatorname{span}}\{s_\mu u_{a^m} s_\nu^*\mid \mu,\nu\in \Lambda_{\mathbb{ 1}_{\mathsf k}}, d(\mu)=d(\nu), m\in {\mathbb{Z}}\}$. It follows from observation 4.14 that ![]() $d(\mu)=d(\nu)$ forces
$d(\mu)=d(\nu)$ forces ![]() $\mu=\nu$, say equal to
$\mu=\nu$, say equal to ![]() ${\mathbf{x}}^{\mathbf n}$ for some
${\mathbf{x}}^{\mathbf n}$ for some ![]() $\mathbf n\in {\mathbb{N}}^{\mathsf k}$. WLOG, we assume that
$\mathbf n\in {\mathbb{N}}^{\mathsf k}$. WLOG, we assume that ![]() $n_1-n_2=l \ge 0$. Then
$n_1-n_2=l \ge 0$. Then
 \begin{align*}
s_{{\mathbf{x}}^{\mathbf n}} u_{a^m} s_{{\mathbf{x}}^{\mathbf n}}^{-1}
=&s_{{\mathbf{x}}_3^{n_3}\cdots {\mathbf{x}}_{\mathsf k}^{n_{\mathsf k}}} s_{{\mathbf{x}}_1^{n_1}} s_{{\mathbf{x}}_2^{n_2}} u_{a^m} s_{{\mathbf{x}}_2^{n_2}}^{-1} s_{{\mathbf{x}}_1^{n_1}} ^{-1} s_{{\mathbf{x}}_3^{n_3}\cdots {\mathbf{x}}_{\mathsf k}^{n_{\mathsf k}}}^{-1}\\
=&s_{{\mathbf{x}}_3^{n_3}\cdots {\mathbf{x}}_{\mathsf k}^{n_{\mathsf k}}} s_{{\mathbf{x}}_1^{n_1}} s_{{\mathbf{x}}_2^{n_2}} s_{{\mathbf{x}}_2^\ell} u_{a^m|_{{\mathbf{x}}_2^\ell}} s^{-1}_{{\mathbf{x}}_2^\ell} s_{{\mathbf{x}}_3^{n_3}\cdots {\mathbf{x}}_{\mathsf k}^{n_{\mathsf k}}}^{-1} s_{{\mathbf{x}}_2^{n_2}}^{-1} s_{{\mathbf{x}}_1^{n_1}}^{-1}\\
=&s_{{\mathbf{x}}_3^{n_3}\cdots {\mathbf{x}}_{\mathsf k}^{n_{\mathsf k}}} s_{{\mathbf{x}}_1^{n_1}} s_{{\mathbf{x}}_2^{n_1}} u_{a^m|_{{\mathbf{x}}_2^\ell}} s_{{\mathbf{x}}_3^{n_3}\cdots {\mathbf{x}}_{\mathsf k}^{n_{\mathsf k}}}^{-1} s_{{\mathbf{x}}_2^{n_1}}^{-1} s_{{\mathbf{x}}_1^{n_1}}^{-1}.
\end{align*}
\begin{align*}
s_{{\mathbf{x}}^{\mathbf n}} u_{a^m} s_{{\mathbf{x}}^{\mathbf n}}^{-1}
=&s_{{\mathbf{x}}_3^{n_3}\cdots {\mathbf{x}}_{\mathsf k}^{n_{\mathsf k}}} s_{{\mathbf{x}}_1^{n_1}} s_{{\mathbf{x}}_2^{n_2}} u_{a^m} s_{{\mathbf{x}}_2^{n_2}}^{-1} s_{{\mathbf{x}}_1^{n_1}} ^{-1} s_{{\mathbf{x}}_3^{n_3}\cdots {\mathbf{x}}_{\mathsf k}^{n_{\mathsf k}}}^{-1}\\
=&s_{{\mathbf{x}}_3^{n_3}\cdots {\mathbf{x}}_{\mathsf k}^{n_{\mathsf k}}} s_{{\mathbf{x}}_1^{n_1}} s_{{\mathbf{x}}_2^{n_2}} s_{{\mathbf{x}}_2^\ell} u_{a^m|_{{\mathbf{x}}_2^\ell}} s^{-1}_{{\mathbf{x}}_2^\ell} s_{{\mathbf{x}}_3^{n_3}\cdots {\mathbf{x}}_{\mathsf k}^{n_{\mathsf k}}}^{-1} s_{{\mathbf{x}}_2^{n_2}}^{-1} s_{{\mathbf{x}}_1^{n_1}}^{-1}\\
=&s_{{\mathbf{x}}_3^{n_3}\cdots {\mathbf{x}}_{\mathsf k}^{n_{\mathsf k}}} s_{{\mathbf{x}}_1^{n_1}} s_{{\mathbf{x}}_2^{n_1}} u_{a^m|_{{\mathbf{x}}_2^\ell}} s_{{\mathbf{x}}_3^{n_3}\cdots {\mathbf{x}}_{\mathsf k}^{n_{\mathsf k}}}^{-1} s_{{\mathbf{x}}_2^{n_1}}^{-1} s_{{\mathbf{x}}_1^{n_1}}^{-1}.
\end{align*} After repeating this process, all the ![]() ${\mathbf{x}}_i$’s will have the same exponent.\hfill▪
${\mathbf{x}}_i$’s will have the same exponent.\hfill▪
Lemma 4.16. ![]() ${\mathcal{F}}$ is commutative.
${\mathcal{F}}$ is commutative.
Proof. Compute
 \begin{align*}
(s_\mu u_{a^l} s_\mu^*)(s_\nu u_{a^n} s_\nu^*)
&=s_\mu u_{a^l} s_\nu s_\mu^* u_{a^n} s_\nu^*\ (\text{as}\ s_\mu^*s_\nu= s_\nu s_\mu^*)\\
&=s_\mu s_\nu u_{a^l|_{\nu}} (u_{a^{-n}} s_\mu)^* s_\nu^*\ (\text{as}\ a^l\cdot \nu =\nu)\\
&=s_\mu s_\nu u_{a^l|_{\nu}} (u_{a^{-n}}|_{\mu})^{-1} s_\mu^* s_\nu^*\\
&=s_\mu s_\nu u_{a^l|_{\nu}} u_{a^n|_{a^{-n}\cdot \mu}} s_\mu^* s_\nu^*\\
&=s_\mu s_\nu u_{a^l|_{\nu}} u_{a^n|_\mu} s_\mu^* s_\nu^*\ (\text{as}\ a^{-n}\cdot \mu =\mu)\\
&=(s_\nu u_{a^n} s_\nu^*)(s_\mu u_{a^l} s_\mu^*).
\end{align*}
\begin{align*}
(s_\mu u_{a^l} s_\mu^*)(s_\nu u_{a^n} s_\nu^*)
&=s_\mu u_{a^l} s_\nu s_\mu^* u_{a^n} s_\nu^*\ (\text{as}\ s_\mu^*s_\nu= s_\nu s_\mu^*)\\
&=s_\mu s_\nu u_{a^l|_{\nu}} (u_{a^{-n}} s_\mu)^* s_\nu^*\ (\text{as}\ a^l\cdot \nu =\nu)\\
&=s_\mu s_\nu u_{a^l|_{\nu}} (u_{a^{-n}}|_{\mu})^{-1} s_\mu^* s_\nu^*\\
&=s_\mu s_\nu u_{a^l|_{\nu}} u_{a^n|_{a^{-n}\cdot \mu}} s_\mu^* s_\nu^*\\
&=s_\mu s_\nu u_{a^l|_{\nu}} u_{a^n|_\mu} s_\mu^* s_\nu^*\ (\text{as}\ a^{-n}\cdot \mu =\mu)\\
&=(s_\nu u_{a^n} s_\nu^*)(s_\mu u_{a^l} s_\mu^*).
\end{align*} It now follows from lemma 4.15 that ![]() ${\mathcal{F}}$ is commutative.\hfill▪
${\mathcal{F}}$ is commutative.\hfill▪
Lemma 4.17. ![]() ${\mathcal{F}}'=\overline{\operatorname{span}} \{s_\mu u_{a^n} s_{\nu}^*:\mu,\nu\in\Lambda_{\mathbb{ 1}} \text{with } \mathfrak m^{d(\mu)}=\mathfrak m^{d(\nu)},\ n\in {\mathbb{Z}}\}$.
${\mathcal{F}}'=\overline{\operatorname{span}} \{s_\mu u_{a^n} s_{\nu}^*:\mu,\nu\in\Lambda_{\mathbb{ 1}} \text{with } \mathfrak m^{d(\mu)}=\mathfrak m^{d(\nu)},\ n\in {\mathbb{Z}}\}$.
Proof. Similar to [Reference Takeda48], it suffices to show ![]() $x\in \operatorname{Ran} \Phi_{\mathbf p}\cap{\mathcal{F}}'$ has the given form. By the Cuntz–Krieger relation, one could assume that
$x\in \operatorname{Ran} \Phi_{\mathbf p}\cap{\mathcal{F}}'$ has the given form. By the Cuntz–Krieger relation, one could assume that ![]() $x=s_\mu A s_\nu^*$ with
$x=s_\mu A s_\nu^*$ with ![]() $d(\mu)-d(\nu)=\mathbf p$ and
$d(\mu)-d(\nu)=\mathbf p$ and ![]() $A\in \mathrm{C}^*(u_a)$. One could further assume that
$A\in \mathrm{C}^*(u_a)$. One could further assume that ![]() $A=f(u_a)$, where
$A=f(u_a)$, where ![]() $f(z)=\sum_{i=1}^{n} \lambda_{i} z^{M_i}\ne 0$ for some
$f(z)=\sum_{i=1}^{n} \lambda_{i} z^{M_i}\ne 0$ for some ![]() $0\ne \lambda_i\in {\mathbb{C}}$ and
$0\ne \lambda_i\in {\mathbb{C}}$ and ![]() $M_i\in {\mathbb{Z}}$.
$M_i\in {\mathbb{Z}}$.
Also, it is clear that ![]() $s_\mu s_\nu= s_\nu s_\mu$ and
$s_\mu s_\nu= s_\nu s_\mu$ and ![]() $\ s_\mu s_\nu^*= s_\nu^* s_\mu$ for all
$\ s_\mu s_\nu^*= s_\nu^* s_\mu$ for all ![]() $\mu, \nu\in \Lambda_{\mathbb{ 1}_{\mathsf k}}$. Then, for all
$\mu, \nu\in \Lambda_{\mathbb{ 1}_{\mathsf k}}$. Then, for all ![]() $N\in {\mathbb{Z}}$ and
$N\in {\mathbb{Z}}$ and ![]() $\omega\in \Lambda_{\mathbb{ 1}_{\mathsf k}}$, one has
$\omega\in \Lambda_{\mathbb{ 1}_{\mathsf k}}$, one has
 \begin{align*}
&\ s_\mu A s_{\nu}^*s_{\omega}u_{a^N} s_{\omega}^* - s_{\omega} u_{a^N} s_{\omega}^*s_\mu A s_{\nu}^*\\
=& \ s_\mu \left( \sum_{i=1}^{n} \lambda_i u_{a^{M_i}} \right) s_\omega s_{\nu}^* u_{a^N} s_{\omega}^*
- s_{\omega} u_{a^N} s_\mu s_{\omega}^* \left( \sum_{i=1}^{n} \lambda_i u_{a^{M_{i}}} \right) s_{\nu}^* \\
= &\ s_\mu s_\omega \left( \sum_{i=1}^{n} \lambda_{i} u_{a^{M_{i}\mathfrak m^{d(\omega)}}} \right) u_{a^{N\mathfrak m^{d(\nu)}}} s_{\nu}^* s_{\omega}^*
- s_{\omega} s_\mu u_{a^{N{\mathbf{m}}^{d(\mu)}}} \left( \sum_{i=1}^{n} \lambda_{i} u_{a^{M_{i} \mathfrak m^{d(\omega)}}} \right) s_{\omega}^* s_{\nu}^* \\
= &\ s_{\mu}s_{\omega} \left( \sum_{i=1}^{n} \lambda_{i} u_{a^{M_{i}\mathfrak m^{d(\omega)}}} \right) \left(u_{a^{N\mathfrak m^{d(\nu)}}}
- u_{a^{N{\mathfrak m}^{d(\mu)}}}\right) s_{\omega}^* s_{\nu}^*\\
= &\ s_{\mu}s_{\omega} f\big(u_{a^{\mathfrak m^{d(\omega)}}} \big)\left(u_{a^{N\mathfrak m^{d(\nu)}}}
- u_{a^{N{\mathfrak m}^{d(\mu)}}}\right) s_{\omega}^* s_{\nu}^*.
\end{align*}
\begin{align*}
&\ s_\mu A s_{\nu}^*s_{\omega}u_{a^N} s_{\omega}^* - s_{\omega} u_{a^N} s_{\omega}^*s_\mu A s_{\nu}^*\\
=& \ s_\mu \left( \sum_{i=1}^{n} \lambda_i u_{a^{M_i}} \right) s_\omega s_{\nu}^* u_{a^N} s_{\omega}^*
- s_{\omega} u_{a^N} s_\mu s_{\omega}^* \left( \sum_{i=1}^{n} \lambda_i u_{a^{M_{i}}} \right) s_{\nu}^* \\
= &\ s_\mu s_\omega \left( \sum_{i=1}^{n} \lambda_{i} u_{a^{M_{i}\mathfrak m^{d(\omega)}}} \right) u_{a^{N\mathfrak m^{d(\nu)}}} s_{\nu}^* s_{\omega}^*
- s_{\omega} s_\mu u_{a^{N{\mathbf{m}}^{d(\mu)}}} \left( \sum_{i=1}^{n} \lambda_{i} u_{a^{M_{i} \mathfrak m^{d(\omega)}}} \right) s_{\omega}^* s_{\nu}^* \\
= &\ s_{\mu}s_{\omega} \left( \sum_{i=1}^{n} \lambda_{i} u_{a^{M_{i}\mathfrak m^{d(\omega)}}} \right) \left(u_{a^{N\mathfrak m^{d(\nu)}}}
- u_{a^{N{\mathfrak m}^{d(\mu)}}}\right) s_{\omega}^* s_{\nu}^*\\
= &\ s_{\mu}s_{\omega} f\big(u_{a^{\mathfrak m^{d(\omega)}}} \big)\left(u_{a^{N\mathfrak m^{d(\nu)}}}
- u_{a^{N{\mathfrak m}^{d(\mu)}}}\right) s_{\omega}^* s_{\nu}^*.
\end{align*} After identifying ![]() $\mathrm{C}^*(a)$ with
$\mathrm{C}^*(a)$ with ![]() ${\mathrm{C}}({\mathbb{T}})$ (see proposition 2.7), the above is equal to 0 iff
${\mathrm{C}}({\mathbb{T}})$ (see proposition 2.7), the above is equal to 0 iff
 \begin{equation*}
f\big(z^{\mathfrak m^{d(\omega)}} \big)\left(z^{N\mathfrak m^{d(\nu)}}
- z^{N{\mathfrak m}^{d(\mu)}}\right)=0,
\end{equation*}
\begin{equation*}
f\big(z^{\mathfrak m^{d(\omega)}} \big)\left(z^{N\mathfrak m^{d(\nu)}}
- z^{N{\mathfrak m}^{d(\mu)}}\right)=0,
\end{equation*} and therefore, if and only if ![]() $\mathfrak m^{d(\mu)}=\mathfrak m^{d(\nu)}$.\hfill▪
$\mathfrak m^{d(\mu)}=\mathfrak m^{d(\nu)}$.\hfill▪
Lemma 4.18. ![]() ${\mathcal{F}}'$ is a MASA of
${\mathcal{F}}'$ is a MASA of ![]() ${\mathcal{O}}_{\Lambda(\mathbb{ 1}_{\mathsf k}, \mathfrak m)}$.
${\mathcal{O}}_{\Lambda(\mathbb{ 1}_{\mathsf k}, \mathfrak m)}$.
Proof. We first show that ![]() ${\mathcal{F}}'$ is abelian. For this, let
${\mathcal{F}}'$ is abelian. For this, let ![]() $A:=s_\mu u_{a^M} s_{\nu}^*$ and
$A:=s_\mu u_{a^M} s_{\nu}^*$ and ![]() $B:=s_\alpha u_{a^N} s_\beta ^*$ be two standard generators in
$B:=s_\alpha u_{a^N} s_\beta ^*$ be two standard generators in ![]() ${\mathcal{F}}'$. Then
${\mathcal{F}}'$. Then
 \begin{align*}
AB=s_\mu u_{a^M} s_{\nu}^*s_\alpha u_{a^N} s_\beta^*
&=s_\mu u_{a^M} s_\alpha s_{\nu}^* u_{a^N} s_\beta^*
=s_\mu s_\alpha u_{a^{M{\mathbf{n}}^{d(\alpha)}}}u_{a^{N{\mathbf{m}}^{d(\nu)}}} s_{\nu}^*s_\beta^*, \\
BA=s_\alpha u_{a^N} s_\beta^* s_\mu u_{a^M} s_{\nu}^*
&=s_\alpha u_{a^N} s_\mu s_{\beta}^* u_{a^M} s_\nu^*
=s_\mu s_\alpha u_{a^{N{\mathbf{n}}^{d(\mu)}}}u_{a^{M{\mathbf{m}}^{d(\beta)}}} s_{\nu}^*s_\beta^*.
\end{align*}
\begin{align*}
AB=s_\mu u_{a^M} s_{\nu}^*s_\alpha u_{a^N} s_\beta^*
&=s_\mu u_{a^M} s_\alpha s_{\nu}^* u_{a^N} s_\beta^*
=s_\mu s_\alpha u_{a^{M{\mathbf{n}}^{d(\alpha)}}}u_{a^{N{\mathbf{m}}^{d(\nu)}}} s_{\nu}^*s_\beta^*, \\
BA=s_\alpha u_{a^N} s_\beta^* s_\mu u_{a^M} s_{\nu}^*
&=s_\alpha u_{a^N} s_\mu s_{\beta}^* u_{a^M} s_\nu^*
=s_\mu s_\alpha u_{a^{N{\mathbf{n}}^{d(\mu)}}}u_{a^{M{\mathbf{m}}^{d(\beta)}}} s_{\nu}^*s_\beta^*.
\end{align*} But ![]() $\mathfrak m^{d(\mu)}=\mathfrak m^{d(\nu)}$ and
$\mathfrak m^{d(\mu)}=\mathfrak m^{d(\nu)}$ and ![]() $\mathfrak m^{d(\alpha)}=\mathfrak m^{d(\beta)}$ as
$\mathfrak m^{d(\alpha)}=\mathfrak m^{d(\beta)}$ as ![]() $A, B\in {\mathcal{F}}'$. Thus AB = BA and so
$A, B\in {\mathcal{F}}'$. Thus AB = BA and so ![]() ${\mathcal{F}}'$ is abelian.
${\mathcal{F}}'$ is abelian.
Now we show ![]() ${\mathcal{F}}'$ is a MASA. Let
${\mathcal{F}}'$ is a MASA. Let ![]() $s_\alpha u_{a^N} s_{\beta}^*\in {\mathcal{F}}'$ and
$s_\alpha u_{a^N} s_{\beta}^*\in {\mathcal{F}}'$ and ![]() $s_\mu A s_{\nu}^*\in \operatorname{Ran}\Phi_{\mathbf p}\cap {\mathcal{F}}^{\prime\prime}$ with
$s_\mu A s_{\nu}^*\in \operatorname{Ran}\Phi_{\mathbf p}\cap {\mathcal{F}}^{\prime\prime}$ with ![]() $A\in \mathrm{C}^*(u_a)$. Similar to the proof of lemma 4.17, we have for all
$A\in \mathrm{C}^*(u_a)$. Similar to the proof of lemma 4.17, we have for all ![]() $\mu,\nu\in\Lambda_{\mathbb{ 1}_{\mathsf k}}$ and
$\mu,\nu\in\Lambda_{\mathbb{ 1}_{\mathsf k}}$ and ![]() $N\in {\mathbb{Z}}$
$N\in {\mathbb{Z}}$
 \begin{align*}
&\ s_\mu A s_{\nu}^*s_{\alpha} u_{a^N} s_{\beta}^* -s_{\alpha} u_{a^N} s_{\beta}^*s_\mu A s_{\nu}^*\\
=& \ s_\mu \left( \sum_{i=1}^{n} \lambda_{i} u_{a^{M_{i}}} \right) s_\alpha s_{\nu}^* u_{a^N} s_{\beta}^*
- s_{\alpha} u_{a^N} s_\mu s_{\beta}^* \left( \sum_{i=1}^{n} \lambda_{i} u_{a^{M_{i}}} \right) s_{\nu}^* \\
=&\ s_\mu s_\alpha \left( \sum_{i=1}^{n} \lambda_{i} u_{a^{M_{i}\mathfrak m^{d(\alpha)}}} \right) u_{a^{N\mathfrak m^{d(\nu)}}} s_{\nu}^* s_{\beta}^*
- s_{\alpha} s_\mu u_{a^{N\mathfrak m^{d(\mu)}}} \left( \sum_{i=1}^{n} \lambda_{i} u_{a^{M_{i} \mathfrak m^{d(\beta)}}} \right) s_{\beta}^* s_{\nu}^* \\
=&s_{\alpha} s_\mu \left[\left( \sum_{i=1}^{n} \lambda_{i} u_{a^{M_{i}\mathfrak m^{d(\alpha)}}} \right) u_{a^{N{\mathbf{m}}^{d(\nu)}}}
- u_{a^{N\mathfrak m^{d(\mu)}}} \left( \sum_{i=1}^{n} \lambda_{i} u_{a^{M_{i} \mathfrak m^{d(\beta)}}} \right)\right] s_{\beta}^* s_{\nu}^*.
\end{align*}
\begin{align*}
&\ s_\mu A s_{\nu}^*s_{\alpha} u_{a^N} s_{\beta}^* -s_{\alpha} u_{a^N} s_{\beta}^*s_\mu A s_{\nu}^*\\
=& \ s_\mu \left( \sum_{i=1}^{n} \lambda_{i} u_{a^{M_{i}}} \right) s_\alpha s_{\nu}^* u_{a^N} s_{\beta}^*
- s_{\alpha} u_{a^N} s_\mu s_{\beta}^* \left( \sum_{i=1}^{n} \lambda_{i} u_{a^{M_{i}}} \right) s_{\nu}^* \\
=&\ s_\mu s_\alpha \left( \sum_{i=1}^{n} \lambda_{i} u_{a^{M_{i}\mathfrak m^{d(\alpha)}}} \right) u_{a^{N\mathfrak m^{d(\nu)}}} s_{\nu}^* s_{\beta}^*
- s_{\alpha} s_\mu u_{a^{N\mathfrak m^{d(\mu)}}} \left( \sum_{i=1}^{n} \lambda_{i} u_{a^{M_{i} \mathfrak m^{d(\beta)}}} \right) s_{\beta}^* s_{\nu}^* \\
=&s_{\alpha} s_\mu \left[\left( \sum_{i=1}^{n} \lambda_{i} u_{a^{M_{i}\mathfrak m^{d(\alpha)}}} \right) u_{a^{N{\mathbf{m}}^{d(\nu)}}}
- u_{a^{N\mathfrak m^{d(\mu)}}} \left( \sum_{i=1}^{n} \lambda_{i} u_{a^{M_{i} \mathfrak m^{d(\beta)}}} \right)\right] s_{\beta}^* s_{\nu}^*.
\end{align*} Identify ![]() $\mathrm{C}^*(u_a)$ with
$\mathrm{C}^*(u_a)$ with ![]() ${\mathrm{C}}({\mathbb{T}})$ and notice
${\mathrm{C}}({\mathbb{T}})$ and notice ![]() $ m^{d(\alpha)}= m^{d(\beta)}$. Then the above is equal to 0, iff
$ m^{d(\alpha)}= m^{d(\beta)}$. Then the above is equal to 0, iff
 \begin{equation*}
f\big(z^{\mathfrak m^{d(\alpha)}}\big)\left(z^{N\mathfrak m^{d(\nu)}} - z^{N\mathfrak m^{d(\mu)}}\right)=0 \iff \mathfrak m^{d(\mu)}=\mathfrak m^{d(\nu)}.
\end{equation*}
\begin{equation*}
f\big(z^{\mathfrak m^{d(\alpha)}}\big)\left(z^{N\mathfrak m^{d(\nu)}} - z^{N\mathfrak m^{d(\mu)}}\right)=0 \iff \mathfrak m^{d(\mu)}=\mathfrak m^{d(\nu)}.
\end{equation*} Hence ![]() $s_\mu A s_{\nu}^*\in {\mathcal{F}}'$ and therefore
$s_\mu A s_{\nu}^*\in {\mathcal{F}}'$ and therefore ![]() ${\mathcal{F}}'={\mathcal{F}}^{\prime\prime}$.\hfill▪
${\mathcal{F}}'={\mathcal{F}}^{\prime\prime}$.\hfill▪
Now suppose that ![]() $\{|m_i|: 1\le i\le k\}$ is multiplicatively independent. Then
$\{|m_i|: 1\le i\le k\}$ is multiplicatively independent. Then ![]() ${\mathcal{F}}'={\mathcal{F}}$, which is also the diagonal subalgebra of
${\mathcal{F}}'={\mathcal{F}}$, which is also the diagonal subalgebra of ![]() ${\mathcal{O}}_{\Lambda(\mathbb{ 1}_{\mathsf k},\mathfrak m)}$. So there is a conditional expectation Φ from
${\mathcal{O}}_{\Lambda(\mathbb{ 1}_{\mathsf k},\mathfrak m)}$. So there is a conditional expectation Φ from ![]() ${\mathcal{O}}_{\Lambda(\mathbb{ 1}_{\mathsf k},\mathfrak m)}$ onto
${\mathcal{O}}_{\Lambda(\mathbb{ 1}_{\mathsf k},\mathfrak m)}$ onto ![]() ${\mathcal{F}}$. Therefore
${\mathcal{F}}$. Therefore ![]() ${\mathcal{F}}$ is a Cartan subalgebra of
${\mathcal{F}}$ is a Cartan subalgebra of ![]() ${\mathcal{O}}_{\Lambda(\mathbb{ 1}_{\mathsf k},\mathfrak m)}$.
${\mathcal{O}}_{\Lambda(\mathbb{ 1}_{\mathsf k},\mathfrak m)}$.
Corollary 4.19. Suppose that ![]() $\{|m_i|: 1\le i\le \mathsf k\}$ is multiplicatively independent. Then
$\{|m_i|: 1\le i\le \mathsf k\}$ is multiplicatively independent. Then ![]() ${\mathcal{F}}$ is a Cartan subalgebra of
${\mathcal{F}}$ is a Cartan subalgebra of ![]() ${\mathcal{O}}_{\Lambda(\mathbb{ 1},\mathfrak m)}$.
${\mathcal{O}}_{\Lambda(\mathbb{ 1},\mathfrak m)}$.
Suppose that ![]() $m_i \gt 0$
$m_i \gt 0$ ![]() $(1\le i\le \mathsf k$). For convenience, we use the convention: If
$(1\le i\le \mathsf k$). For convenience, we use the convention: If ![]() $a|_\mu=a^n$, then
$a|_\mu=a^n$, then ![]() $t^{\ln a|_\mu}:=t^{\ln n}$. Thus
$t^{\ln a|_\mu}:=t^{\ln n}$. Thus
 \begin{align*}
\ln a|_{\mu\nu}
=\ln \mathfrak m^{d(\mu\nu)}
=\ln \mathfrak m^{d(\mu)}+\ln\mathfrak m^{d(\nu)}=\ln a|_\mu+\ln a|_\nu.
\end{align*}
\begin{align*}
\ln a|_{\mu\nu}
=\ln \mathfrak m^{d(\mu\nu)}
=\ln \mathfrak m^{d(\mu)}+\ln\mathfrak m^{d(\nu)}=\ln a|_\mu+\ln a|_\nu.
\end{align*} Therefore, we obtain action α of ![]() ${\mathbb{T}}$ on
${\mathbb{T}}$ on ![]() ${\mathcal{O}}_{\Lambda(\mathbb{ 1}_{\mathsf k},\mathfrak m)}$ as follows:
${\mathcal{O}}_{\Lambda(\mathbb{ 1}_{\mathsf k},\mathfrak m)}$ as follows:
 \begin{equation*}
\alpha_t(s_\mu)=t^{\ln a|_\mu} s_\mu, \ \alpha_t(u_a)=u_a \text{for all }\mu \in \Lambda_{\mathbb{ 1}_{\mathsf k}}\text{and }t\in {\mathbb{T}}.
\end{equation*}
\begin{equation*}
\alpha_t(s_\mu)=t^{\ln a|_\mu} s_\mu, \ \alpha_t(u_a)=u_a \text{for all }\mu \in \Lambda_{\mathbb{ 1}_{\mathsf k}}\text{and }t\in {\mathbb{T}}.
\end{equation*}Define
 \begin{equation*}
\Psi(x):=\int_{{\mathbb{T}}} \alpha_t(x) d t\quad\text{for all}\quad x\in {\mathcal{O}}_{\Lambda(\mathbb{ 1},\mathfrak m)}.
\end{equation*}
\begin{equation*}
\Psi(x):=\int_{{\mathbb{T}}} \alpha_t(x) d t\quad\text{for all}\quad x\in {\mathcal{O}}_{\Lambda(\mathbb{ 1},\mathfrak m)}.
\end{equation*}Lemma 4.20. Suppose that ![]() $m_i \gt 0$
$m_i \gt 0$ ![]() $(1\le i\le \mathsf k$). Then
$(1\le i\le \mathsf k$). Then ![]() ${\mathcal{F}}'$ is the fixed point algebra of α. Furthermore, Ψ a faithful conditional expectation from
${\mathcal{F}}'$ is the fixed point algebra of α. Furthermore, Ψ a faithful conditional expectation from ![]() ${\mathcal{O}}_{\Lambda(\mathbb{ 1}_{\mathsf k},\mathfrak m)}$ onto
${\mathcal{O}}_{\Lambda(\mathbb{ 1}_{\mathsf k},\mathfrak m)}$ onto ![]() ${\mathcal{F}}'$.
${\mathcal{F}}'$.
Proof. We only need to show the faithfulness of Ψ here, as other parts can be proved similarly to the corresponding parts for ![]() $\Phi_{\mathbf 0}$. Let
$\Phi_{\mathbf 0}$. Let ![]() $\Phi_{\mathbf 0}|_{{\mathcal{F}}'}$ be the restriction of
$\Phi_{\mathbf 0}|_{{\mathcal{F}}'}$ be the restriction of ![]() $\Phi_{\mathbf 0}$ onto
$\Phi_{\mathbf 0}$ onto ![]() ${\mathcal{F}}'$, and Ψ be the expectation induced from α above. Then one can check that
${\mathcal{F}}'$, and Ψ be the expectation induced from α above. Then one can check that ![]() $\Phi_{\mathbf 0}=\Phi|_{{\mathcal{F}}'}\circ \Psi$. The faithfulness of Ψ follows from that of
$\Phi_{\mathbf 0}=\Phi|_{{\mathcal{F}}'}\circ \Psi$. The faithfulness of Ψ follows from that of ![]() $\Phi_{\mathbf 0}$.\hfill▪
$\Phi_{\mathbf 0}$.\hfill▪
Theorem 4.21. Suppose that ![]() $m_i \gt 0$
$m_i \gt 0$ ![]() $(1\le i\le \mathsf k$). Then
$(1\le i\le \mathsf k$). Then ![]() ${\mathcal{F}}'$ is a Cartan subalgebra of
${\mathcal{F}}'$ is a Cartan subalgebra of ![]() ${\mathcal{O}}_{\Lambda(\mathbb{ 1}_{\mathsf k},\mathfrak m)}$.
${\mathcal{O}}_{\Lambda(\mathbb{ 1}_{\mathsf k},\mathfrak m)}$.
Proof. It remains to show that ![]() ${\mathcal{F}}'$ is regular. For this, let
${\mathcal{F}}'$ is regular. For this, let ![]() $A:=s_\mu u_a^M s_{\nu}^*\in {\mathcal{F}}'$ and
$A:=s_\mu u_a^M s_{\nu}^*\in {\mathcal{F}}'$ and  $B:=s_\alpha u_a^N s_\beta ^*\in {\mathcal{O}}_{\Lambda(\mathbb{ 1}_{\mathsf k},\mathfrak m)}$. Then
$B:=s_\alpha u_a^N s_\beta ^*\in {\mathcal{O}}_{\Lambda(\mathbb{ 1}_{\mathsf k},\mathfrak m)}$. Then
 \begin{align*}
B^*AB
&=s_\beta u_{a^{-N}} s_\alpha^* s_\mu u_{a^M} s_{\nu}^*s_\alpha u_{a^N} s_\beta^* \\
&=s_\beta u_{a^{-N}} s_\mu s_\alpha^* u_{a^M} s_\alpha s_{\nu}^* u_{a^N} s_\beta^* \\
&=s_\beta s_\mu u_{a^{-N\mathfrak m^{d(\mu)}}} u_{a^{M\mathfrak m^{d(\alpha)}}} s_\alpha^* s_\alpha s_{\nu}^* u_{a^N} s_\beta^* \\
&=s_\beta s_\mu u_{a^{-N\mathfrak m^{d(\mu)}}} u_{a^{M\mathfrak m^{d(\alpha)}}} u_{a^{N\mathfrak m^{d(\nu)}}} s_{\nu}^* s_\beta^* \\
&=s_\beta s_\mu u_{a^{M\mathfrak m^{d(\alpha)}}} s_\nu^* s_\beta^* \text{(as}\ \mathfrak m^{d(\mu)}=\mathfrak m^{d(\nu)}\text{)}\\
&\in {\mathcal{F}}'.
\end{align*}
\begin{align*}
B^*AB
&=s_\beta u_{a^{-N}} s_\alpha^* s_\mu u_{a^M} s_{\nu}^*s_\alpha u_{a^N} s_\beta^* \\
&=s_\beta u_{a^{-N}} s_\mu s_\alpha^* u_{a^M} s_\alpha s_{\nu}^* u_{a^N} s_\beta^* \\
&=s_\beta s_\mu u_{a^{-N\mathfrak m^{d(\mu)}}} u_{a^{M\mathfrak m^{d(\alpha)}}} s_\alpha^* s_\alpha s_{\nu}^* u_{a^N} s_\beta^* \\
&=s_\beta s_\mu u_{a^{-N\mathfrak m^{d(\mu)}}} u_{a^{M\mathfrak m^{d(\alpha)}}} u_{a^{N\mathfrak m^{d(\nu)}}} s_{\nu}^* s_\beta^* \\
&=s_\beta s_\mu u_{a^{M\mathfrak m^{d(\alpha)}}} s_\nu^* s_\beta^* \text{(as}\ \mathfrak m^{d(\mu)}=\mathfrak m^{d(\nu)}\text{)}\\
&\in {\mathcal{F}}'.
\end{align*} Therefore ![]() ${\mathcal{F}}'$ is regular.
${\mathcal{F}}'$ is regular.
Let G be a discrete (countable) group. A subgroup ![]() $S\subseteq G$ is called immediately centralizing if, for every
$S\subseteq G$ is called immediately centralizing if, for every ![]() $g\in G$, we either have
$g\in G$, we either have ![]() $\{xgx^{-1}: x\in S\}=\{g\}$ or
$\{xgx^{-1}: x\in S\}=\{g\}$ or ![]() $\{xgx^{-1}: x\in S\}$ is infinite. This definition is slightly different from the one used in [Reference Duwenig, Gillaspy, Norton, Reznikoff and Wright22] but mentioned in [Reference Duwenig20] and [Reference Duwenig, Gillaspy and Norton21]. Thanks to Anna Duwenig and Rachael Norton for some discussion.
$\{xgx^{-1}: x\in S\}$ is infinite. This definition is slightly different from the one used in [Reference Duwenig, Gillaspy, Norton, Reznikoff and Wright22] but mentioned in [Reference Duwenig20] and [Reference Duwenig, Gillaspy and Norton21]. Thanks to Anna Duwenig and Rachael Norton for some discussion.
Theorem 4.22. ![]() ${\mathcal{F}}'$ is a Cartan subalgebra of
${\mathcal{F}}'$ is a Cartan subalgebra of ![]() ${\mathcal{O}}_{\Lambda(\mathbb{ 1}_{\mathsf k},\mathfrak m)}$.
${\mathcal{O}}_{\Lambda(\mathbb{ 1}_{\mathsf k},\mathfrak m)}$.
Proof. Let ![]() $G:=\langle a, {\mathbf{x}}_i: a{\mathbf{x}}_i={\mathbf{x}}_i a^{m_i}, 1\le i\le \mathsf k\rangle$. Then it it easy to see that
$G:=\langle a, {\mathbf{x}}_i: a{\mathbf{x}}_i={\mathbf{x}}_i a^{m_i}, 1\le i\le \mathsf k\rangle$. Then it it easy to see that ![]() ${\mathcal{O}}_{\Lambda(\mathbb{ 1}_{\mathsf k},\mathfrak m)}\cong \mathrm{C}^*(G)$ via
${\mathcal{O}}_{\Lambda(\mathbb{ 1}_{\mathsf k},\mathfrak m)}\cong \mathrm{C}^*(G)$ via ![]() $u_a\mapsto a$ and
$u_a\mapsto a$ and ![]() $s_{{\mathbf{x}}_i} \mapsto {\mathbf{x}}_i$. By [Reference Li and Yang34],
$s_{{\mathbf{x}}_i} \mapsto {\mathbf{x}}_i$. By [Reference Li and Yang34], ![]() ${\mathcal{O}}_{\Lambda(\mathbb{ 1}_{\mathsf k},\mathfrak m)}$ is amenable and so is
${\mathcal{O}}_{\Lambda(\mathbb{ 1}_{\mathsf k},\mathfrak m)}$ is amenable and so is ![]() $\mathrm{C}^*(G)$. Thus
$\mathrm{C}^*(G)$. Thus ![]() ${\mathcal{O}}_{\Lambda(\mathbb{ 1}_{\mathsf k},\mathfrak m)}\cong \mathrm{C}^*(G)\cong \mathrm{C}^*_{\text r}(G)$.
${\mathcal{O}}_{\Lambda(\mathbb{ 1}_{\mathsf k},\mathfrak m)}\cong \mathrm{C}^*(G)\cong \mathrm{C}^*_{\text r}(G)$.
Let ![]() $S:=\{\mu a^n \nu^{-1}: \mathfrak m^{d(\mu)}=\mathfrak m^{d(\nu)}, n\in {\mathbb{Z}}\}$. Similar to the proof of theorem 4.21, one can easily show that S is a normal subgroup of G. Also, analogous to the proof of lemma 4.18, one can show that, for
$S:=\{\mu a^n \nu^{-1}: \mathfrak m^{d(\mu)}=\mathfrak m^{d(\nu)}, n\in {\mathbb{Z}}\}$. Similar to the proof of theorem 4.21, one can easily show that S is a normal subgroup of G. Also, analogous to the proof of lemma 4.18, one can show that, for ![]() $\alpha a^k \beta^{-1}\in G$, if the set
$\alpha a^k \beta^{-1}\in G$, if the set ![]() $\{(\mu a^n \nu^{-1})(\alpha a^k \beta^{-1})(\nu a^{-n} \mu^{-1}): \mu, \nu \in \Lambda(\mathbb{ 1}_{\mathsf k},\mathfrak m), n\in {\mathbb{Z}}\}$ is not a singleton, then it has to be infinite. Indeed,
$\{(\mu a^n \nu^{-1})(\alpha a^k \beta^{-1})(\nu a^{-n} \mu^{-1}): \mu, \nu \in \Lambda(\mathbb{ 1}_{\mathsf k},\mathfrak m), n\in {\mathbb{Z}}\}$ is not a singleton, then it has to be infinite. Indeed,
 \begin{align*}
(\mu a^n \nu^{-1})(\alpha a^k \beta^{-1})(\nu a^{-n} \mu^{-1}) &= (\mu' a^{n'} \nu'^{-1})(\alpha a^k \beta^{-1})(\nu' a^{-n'} \mu'^{-1})\\
&\iff n \mathfrak{m}^{d(\mu')}=n' \mathfrak{m}^{d(\mu)}.
\end{align*}
\begin{align*}
(\mu a^n \nu^{-1})(\alpha a^k \beta^{-1})(\nu a^{-n} \mu^{-1}) &= (\mu' a^{n'} \nu'^{-1})(\alpha a^k \beta^{-1})(\nu' a^{-n'} \mu'^{-1})\\
&\iff n \mathfrak{m}^{d(\mu')}=n' \mathfrak{m}^{d(\mu)}.
\end{align*} Hence S is immediately centralizing. By [Reference Duwenig, Gillaspy and Norton21, Theorem 3.1], ![]() $\mathrm{C}^*_{\text r}(S)$ is Cartan in
$\mathrm{C}^*_{\text r}(S)$ is Cartan in ![]() $\mathrm{C}^*_{\text r}(G)$. Therefore
$\mathrm{C}^*_{\text r}(G)$. Therefore ![]() ${\mathcal{F}}'$ is Cartan in
${\mathcal{F}}'$ is Cartan in ![]() ${\mathcal{O}}_{\Lambda(\mathbb{ 1}_{\mathsf k},\mathfrak m)}$.
${\mathcal{O}}_{\Lambda(\mathbb{ 1}_{\mathsf k},\mathfrak m)}$.
Remark 4.23. Notice that, since ![]() $\Lambda_{\mathbb{ 1}_{\mathsf k}}$ has a unique infinite path, every triple
$\Lambda_{\mathbb{ 1}_{\mathsf k}}$ has a unique infinite path, every triple ![]() $(\mu, a^n, \nu)$ is cycline. So the cycline subalgebra of
$(\mu, a^n, \nu)$ is cycline. So the cycline subalgebra of ![]() ${\mathcal{O}}_{\Lambda(\mathbb{ 1}_{\mathsf k},\mathfrak m)}$ coincides with
${\mathcal{O}}_{\Lambda(\mathbb{ 1}_{\mathsf k},\mathfrak m)}$ coincides with ![]() ${\mathcal{O}}_{\Lambda(\mathbb{ 1}_{\mathsf k},\mathfrak m)}$ and does not provide much information of the canonical Cartan subalgebra
${\mathcal{O}}_{\Lambda(\mathbb{ 1}_{\mathsf k},\mathfrak m)}$ and does not provide much information of the canonical Cartan subalgebra ![]() ${\mathcal{F}}'$ in general.
${\mathcal{F}}'$ in general.
4.5. The spectrum of  ${\mathcal{F}}$
${\mathcal{F}}$
We end this paper by computing the spectrum of ![]() ${\mathcal{F}}$ to connect with Furstenberg’s
${\mathcal{F}}$ to connect with Furstenberg’s ![]() $\times p, \times q$ conjecture in the viewpoint of [Reference Brownlowe, Ramagge, Robertson and Whittaker9, Reference Furstenberg25]. Let
$\times p, \times q$ conjecture in the viewpoint of [Reference Brownlowe, Ramagge, Robertson and Whittaker9, Reference Furstenberg25]. Let ![]() $1\le p_1, \ldots, p_n\in {\mathbb{N}}$ and
$1\le p_1, \ldots, p_n\in {\mathbb{N}}$ and
Then the inverse limit
 \begin{equation*}
\varprojlim({\mathbb{T}}, \varphi):=\left\{(x_n)_{n\in {\mathbb{N}}}\in \prod_{n\in {\mathbb{N}}} {\mathbb{T}}: x_n =\varphi(x_{n+1}) \text{for all }n \in {\mathbb{N}}\right\}
\end{equation*}
\begin{equation*}
\varprojlim({\mathbb{T}}, \varphi):=\left\{(x_n)_{n\in {\mathbb{N}}}\in \prod_{n\in {\mathbb{N}}} {\mathbb{T}}: x_n =\varphi(x_{n+1}) \text{for all }n \in {\mathbb{N}}\right\}
\end{equation*} is a solenoid, denoted as ![]() $S_{p_1\cdots p_n}$.
$S_{p_1\cdots p_n}$.
Let ![]() $\mathfrak{e}:={\mathbf{x}}_1\cdots {\mathbf{x}}_{\mathsf k}$, the unique path in
$\mathfrak{e}:={\mathbf{x}}_1\cdots {\mathbf{x}}_{\mathsf k}$, the unique path in ![]() $\Lambda_{\mathbb{ 1}_{\mathsf k}}$ of degree
$\Lambda_{\mathbb{ 1}_{\mathsf k}}$ of degree ![]() $\mathbb{ 1}_{\mathsf k}$. For
$\mathbb{ 1}_{\mathsf k}$. For ![]() $n \in {\mathbb{N}}$, we have
$n \in {\mathbb{N}}$, we have
 \begin{align*}
{\mathcal{F}}_{n\mathbb{ 1}_{\mathsf k}}&= \overline{\text{span}}\{s_{\mathfrak{e}^n} u_{a^m} s_{\mathfrak{e}^n}^* | \ m \in {\mathbb{Z}} \},\\
{\mathcal{F}} &= \overline{\text{span}}\{s_{\mathfrak{e}^n} u_{a^m} s_{\mathfrak{e}^n}^* | \ n \in {\mathbb{N}}, m \in {\mathbb{Z}} \}=\overline{\bigcup_{n\in {\mathbb{N}}}{\mathcal{F}}_{n\mathbb{ 1}_{\mathsf k}}}.
\end{align*}
\begin{align*}
{\mathcal{F}}_{n\mathbb{ 1}_{\mathsf k}}&= \overline{\text{span}}\{s_{\mathfrak{e}^n} u_{a^m} s_{\mathfrak{e}^n}^* | \ m \in {\mathbb{Z}} \},\\
{\mathcal{F}} &= \overline{\text{span}}\{s_{\mathfrak{e}^n} u_{a^m} s_{\mathfrak{e}^n}^* | \ n \in {\mathbb{N}}, m \in {\mathbb{Z}} \}=\overline{\bigcup_{n\in {\mathbb{N}}}{\mathcal{F}}_{n\mathbb{ 1}_{\mathsf k}}}.
\end{align*} Note that for any ![]() $n \in {\mathbb{N}}$,
$n \in {\mathbb{N}}$, ![]() $s_{\mathfrak{e}^n} u_a s_{\mathfrak{e}^n}^*$ is a unitary that generates
$s_{\mathfrak{e}^n} u_a s_{\mathfrak{e}^n}^*$ is a unitary that generates ![]() ${\mathcal{F}}_{n\mathbb{ 1}_{\mathsf k}}$. Then one can see that there is an isomorphism
${\mathcal{F}}_{n\mathbb{ 1}_{\mathsf k}}$. Then one can see that there is an isomorphism ![]() $\psi_n:{\mathcal{F}}_{n\mathbb{ 1}_{\mathsf k}} \to {\mathrm{C}}({\mathbb{T}})$.
$\psi_n:{\mathcal{F}}_{n\mathbb{ 1}_{\mathsf k}} \to {\mathrm{C}}({\mathbb{T}})$.
Let  $\mathfrak M:=\prod_{i=1}^{\mathsf k} m_i$.
$\mathfrak M:=\prod_{i=1}^{\mathsf k} m_i$.
Proposition 4.24. Consider the subalgebras ![]() ${\mathcal{F}}_{n\mathbb{ 1}_{\mathsf k}}$ along with the inclusions
${\mathcal{F}}_{n\mathbb{ 1}_{\mathsf k}}$ along with the inclusions ![]() $\varphi_n: {\mathcal{F}}_{n\mathbb{ 1}_{\mathsf k}} \hookrightarrow {\mathcal{F}}_{(n+1)\mathbb{ 1}_{\mathsf k}}$ given by
$\varphi_n: {\mathcal{F}}_{n\mathbb{ 1}_{\mathsf k}} \hookrightarrow {\mathcal{F}}_{(n+1)\mathbb{ 1}_{\mathsf k}}$ given by ![]() $\varphi_n(s_{\mathfrak{e}^n} u_{a^p} s_{\mathfrak{e}^n}^*) = s_{\mathfrak{e}^{n+1}} u_{a^{p\mathfrak M}} s_{\mathfrak{e}^{n+1}}^*$. Then
$\varphi_n(s_{\mathfrak{e}^n} u_{a^p} s_{\mathfrak{e}^n}^*) = s_{\mathfrak{e}^{n+1}} u_{a^{p\mathfrak M}} s_{\mathfrak{e}^{n+1}}^*$. Then  ${\mathcal{F}} = \varinjlim\limits_{n\to \infty} {\mathcal{F}}_{n\mathbb{ 1}_{\mathsf k}}$, and the spectrum of
${\mathcal{F}} = \varinjlim\limits_{n\to \infty} {\mathcal{F}}_{n\mathbb{ 1}_{\mathsf k}}$, and the spectrum of ![]() ${\mathcal{F}}$ is homeomorphic to
${\mathcal{F}}$ is homeomorphic to ![]() $S_{\mathfrak M}$.
$S_{\mathfrak M}$.
Proof. Notice that
This shows that φn is indeed an inclusion of C*-algebras. Since the union ![]() $\bigcup_{n=0}^{\infty} {\mathcal{F}}_{n\mathbb{ 1}_{\mathsf k}}$ is dense in
$\bigcup_{n=0}^{\infty} {\mathcal{F}}_{n\mathbb{ 1}_{\mathsf k}}$ is dense in ![]() ${\mathcal{F}}$ (actually they are equal), we have that
${\mathcal{F}}$ (actually they are equal), we have that ![]() ${\mathcal{F}}$ is isomorphic to the direct limit of
${\mathcal{F}}$ is isomorphic to the direct limit of ![]() $({\mathcal{F}}_{n\mathbb{ 1}_{\mathsf k}},\varphi_n)$ (see [Reference Li and Yang37, Remark 6.1.3]).
$({\mathcal{F}}_{n\mathbb{ 1}_{\mathsf k}},\varphi_n)$ (see [Reference Li and Yang37, Remark 6.1.3]).
Due to [Reference Scarparo45, Theorem 2], the spectrum of ![]() ${\mathcal{F}}$ is the projective limit of the spectra of the subalgebras
${\mathcal{F}}$ is the projective limit of the spectra of the subalgebras ![]() ${\mathcal{F}}_{n\mathbb{ 1}_{\mathsf k}}$, with the maps
${\mathcal{F}}_{n\mathbb{ 1}_{\mathsf k}}$, with the maps  $\phi_{n+1}:\widehat{{\mathcal{F}}_{(n+1)\mathbb{ 1}_{\mathsf k}}} \rightarrow \widehat{{\mathcal{F}}_{n\mathbb{ 1}_{\mathsf k}}}$ which induce the maps φn. However, we will work with an isomorphic direct system in order to make things more concrete. Observe that we have an isomorphism ψn between
$\phi_{n+1}:\widehat{{\mathcal{F}}_{(n+1)\mathbb{ 1}_{\mathsf k}}} \rightarrow \widehat{{\mathcal{F}}_{n\mathbb{ 1}_{\mathsf k}}}$ which induce the maps φn. However, we will work with an isomorphic direct system in order to make things more concrete. Observe that we have an isomorphism ψn between ![]() ${\mathcal{F}}_{n\mathbb{ 1}_{\mathsf k}}$ and
${\mathcal{F}}_{n\mathbb{ 1}_{\mathsf k}}$ and ![]() ${\mathrm{C}}({\mathbb{T}})$ that sends the element
${\mathrm{C}}({\mathbb{T}})$ that sends the element ![]() $s_{\mathfrak{e}^n} a s_{\mathfrak{e}^n}^* \in {\mathcal{F}}_n$ to the function
$s_{\mathfrak{e}^n} a s_{\mathfrak{e}^n}^* \in {\mathcal{F}}_n$ to the function ![]() $f(z) = z$ in
$f(z) = z$ in ![]() ${\mathrm{C}}({\mathbb{T}})$, which we will just denote by z (note that z is a unitary element that generates
${\mathrm{C}}({\mathbb{T}})$, which we will just denote by z (note that z is a unitary element that generates ![]() ${\mathrm{C}}({\mathbb{T}})$ ). Let
${\mathrm{C}}({\mathbb{T}})$ ). Let ![]() $\varphi'_{n}: {\mathrm{C}}({\mathbb{T}}) \rightarrow {\mathrm{C}}({\mathbb{T}})$ be the map defined by sending the function z to
$\varphi'_{n}: {\mathrm{C}}({\mathbb{T}}) \rightarrow {\mathrm{C}}({\mathbb{T}})$ be the map defined by sending the function z to ![]() $z^{\mathfrak M}$. Then by a direct calculation the following diagram commutes:
$z^{\mathfrak M}$. Then by a direct calculation the following diagram commutes:

By [Reference Scarparo45, Proposition 2], ![]() ${\mathcal{F}}$ is then isomorphic to the direct limit of the system
${\mathcal{F}}$ is then isomorphic to the direct limit of the system ![]() $({\mathrm{C}}({\mathbb{T}}), \varphi'_{n,n+1})$. We now observe that homeomorphism
$({\mathrm{C}}({\mathbb{T}}), \varphi'_{n,n+1})$. We now observe that homeomorphism ![]() $\rho:{\mathbb{T}} \rightarrow {\mathbb{T}}$ defined by
$\rho:{\mathbb{T}} \rightarrow {\mathbb{T}}$ defined by ![]() $\rho(z) = z^{\mathfrak M}$ induces the maps
$\rho(z) = z^{\mathfrak M}$ induces the maps ![]() $\varphi'_n:{\mathrm{C}}({\mathbb{T}})\rightarrow {\mathrm{C}}({\mathbb{T}})$, and so the spectrum
$\varphi'_n:{\mathrm{C}}({\mathbb{T}})\rightarrow {\mathrm{C}}({\mathbb{T}})$, and so the spectrum ![]() ${\mathcal{F}}$ is homeomorphic to the projective limit of
${\mathcal{F}}$ is homeomorphic to the projective limit of
which is precisely ![]() $S_{\mathfrak M}$.\hfill▪
$S_{\mathfrak M}$.\hfill▪
Remark 4.25. One can show that  ${\mathcal{O}}_{\Lambda(\mathbb{ 1}_{\mathsf k},\mathfrak m)}\cong {\mathcal{F}} \lt imes {\mathbb{Z}}^{\mathsf k}\cong {\mathrm{C}}(S_{\mathfrak M}) \lt imes {\mathbb{Z}}^{\mathsf k}$. In fact, the action of
${\mathcal{O}}_{\Lambda(\mathbb{ 1}_{\mathsf k},\mathfrak m)}\cong {\mathcal{F}} \lt imes {\mathbb{Z}}^{\mathsf k}\cong {\mathrm{C}}(S_{\mathfrak M}) \lt imes {\mathbb{Z}}^{\mathsf k}$. In fact, the action of ![]() ${\mathbb{Z}}^{\mathsf k}$ on
${\mathbb{Z}}^{\mathsf k}$ on ![]() ${\mathcal{F}}$ is given by
${\mathcal{F}}$ is given by
where ν is the unique path in ![]() $\Lambda_{\mathbb{ 1}_{\mathsf k}}$ of degree
$\Lambda_{\mathbb{ 1}_{\mathsf k}}$ of degree ![]() $\mathbf n$.
$\mathbf n$.
Acknowledgements
Some results in this paper were presented at COSy 2023 and the workshop ‘Groups and Group Actions’ in Thematic Program on Operator Algebras and Applications in 2023. The second author is very grateful to the organizers for the invitations and providing great opportunities to present our results. Also, thanks go to Boyu Li for some discussion at the early stage of this paper, and the anonymous referee for careful reading.
R.V. was partially supported by Queen Elizabeth II Graduate Scholarship in Science and Technology (QEII-GSST), and D.Y. was partially supported by an NSERC Discovery Grant.