1. ‘Arithmetization’ of Mathematics
Near the end of the nineteenth century, a part of mathematical research was focused on unification: the goal was to find ‘one sort of thing’ that mathematics is (or could be taken to be) about. The stage that most mathematicians agreed to have achieved was the so-called ‘arithmetization’ of mathematics: with some naïve set theory in the background, nearly all mathematical objects could be thought of as objects ‘constructed’ from natural numbers.Reference Ferreirós1
For instance, Cantor provided a definition of real numbers in terms of Cauchy sequences and Dedekind defined real numbers in terms of Dedekind cuts. Let us take a quick look at the constructions before we draw a moral.
A Cauchy sequence of rational numbers is a sequence whose members get arbitrarily close to each other as it proceeds.2 Two Cauchy sequences are equivalent iff the difference between their respective elements tends to zero. Now, take the sets of Cauchy sequences of rational numbers modulo this equivalence. This domain will satisfy the standard axioms of real number theory.3
A Dedekind cut is a pair 
$$\left\langle {A,B} \right\rangle $$
of sets of rational numbers, such that 
$$A,B\, \ne \, \emptyset $$
, A is closed downwards, B is closed upwards and A contains no greatest element. Each cut is uniquely represented by either of its two elements, so it is customary to identify real numbers with non-universal and downward closed sets of rational numbers that contain no greatest elements.
The set of all Dedekind cuts also satisfies the axioms of real number theory.
A few observations are due:
∙ Assuming, as was normal, that rational numbers can be, in an analogous manner, reduced to natural numbers,4 these strategies were taken to provide reductions of real numbers to natural numbers.
∙ Such constructions had two ingredients: natural numbers and a set-theoretic component. After all, Cauchy sequences were sequences, Dedekind cuts were pairs of sets, and integers and rationals were equivalence classes, all of which seem to be set-theoretic items.
∙ Yet, at that stage, there was no axiomatization of set theory and mathematicians just used set-theoretic notions intuitively (one of the reasons why we call such set theory ‘naïve’).
∙ Such reductions were not unique, at all stages of the construction. People didn’t worry about this then, but later on this led some mathematicians and philosophers to believe that mathematical theories are not about some selected objects (like natural numbers) but rather about whole bunches of structures satisfying the same formal constraints.
Thus, to further the ‘arithmetization’ of mathematics, a more precise mathematical theory of sets was needed, telling us exactly which sets exist and what their properties are. This need became even clearer with the arrival of set-theoretic paradoxes.
2. Russell’s Paradox
One of the first and most important attempts at axiomatizing set theory was that of Friedrich Ludwig Gottlob Frege (1848–1925).Reference Beaney5 Frege not only constructed a formal system that constituted the first formulation of second-order logic,6 but also attempted to give an axiomatization of set-theory. This axiomatization would not only provide the arithmetization of mathematics with a precise tool, but also allow one to actually reduce numbers to sets, showing that the essential mathematical component of foundations of mathematics was set-theoretic.7
The reduction of natural numbers to sets within Frege’s framework identified each number n with the extension whose members are all and only those concepts,8 which applied to exactly n objects. (In fact, there is no circularity here: you can define ‘applying to the same number of objects’ without reference to numbers, in terms of there being a 1–1 mapping, and use this notion in further definitions.)
The sole really set-theoretic axiom in Frege’s system was his Basic Law V, which said that the extension of a concept F is identical to the extension of a concept G just in case concepts F and G apply to the same objects:
$$\matrix{ {\left( {{\rm BLV}} \right)} & {\{ x\mid Fx\} =\{ x \mid Gx\} \equiv \forall x\:\:\ (Fx \equiv Gx)} \cr } $$
From (BLV), together with his definition of numbers, Frege managed to derive the so-called Hume’s Principle, which reads ‘the number of Fs is the same as the number of Gs iff F and G are equinumerous’:9
$$({\rm Hume})\quad N(F)=N(G) \equiv F \approx G$$
From (Hume), with his logic in the background, Frege managed to derive the standard axioms of second-order Peano Arithmetic, a fairly standard axiomatization of the natural number arithmetic.
Alas, within this framework a problem arises, observed independently by Zermelo and Russell (and yet, usually called ‘Russell’s paradox’). Once we notice that 
$$\forall x[\phi x \equiv \phi x]$$
is a logical truth for any formula 
$$\phi $$
, (BLV) allows us to derive 
$$\{ x \mid \phi x\} =\{ x \mid \phi x\} $$
, it is only one step to reaching a principle called ‘full comprehension’: 
$$\exists x\ x=\{ x \mid \phi x\} $$
. Roughly speaking, the principle states that for any property there is a set of all and only those objects, which have this property. The set of Fs is supposed to contain as elements all and only those objects that have the property F.
Let us consider a rather unusual property: the property an object x has if it is not its own element (
$$x\,\notin \,x$$
). This property seems to be shared by chairs, human beings and power drills. These are not sets, so they have no elements, and therefore are not their own elements. In contrast, take the set of sets – if there were such a thing, it would be a set and by the same token it should be its own element. The property of not being its own element turns out to be problematic in the company of full comprehension.
If there is such a property, full comprehension entails that the set of objects that are not their own elements exists. Let’s call this set R. Thus, any object belongs to R iff it doesn’t belong to itself:
$$\matrix{ {\left( {{\rm Russell}\ {\rm 1}} \right)} & {x\in R \equiv x\,\notin x} \cr } $$
But extensions are supposed to be objects and therefore by (Russel 1) should apply to them. In particular, it should apply to R as well. R should be its own element just in case it is not its own element:
$$\matrix{ {\left( {{\rm Russell \ 2}} \right)} & {R\in R \equiv R\, \notin R} \cr } $$
which is clearly a contradiction.
The paradox is somewhat analogous to the so-called ‘barber paradox’. Consider a town in which there is a barber who is a man and who who shaves all and only those men in town who do not shave themselves. A short reasoning should lead you to the conclusion that this barber shaves himself if and only if he doesn’t shave himself.
While these paradoxical reasonings seem structurally similar, there is at least one important difference. There is no prima facie intuitive mathematical principle that entails the existence of the aforementioned barber, and so one can easily avoid the latter paradox by concluding that there cannot be such a barber.
Yet, the existence of Russell’s set seems to be entailed by an assumption that many people find intuitive. Thus, avoiding the former paradox by concluding that Russell’s set doesn’t exist requires a bit more work. One should explain why our intuitions about sets went awry when it came to full comprehension and tell us what full comprehension should be replaced with if we want to have a sensible set theory. Obtaining a nice set theory is a slightly more interesting and plausible goal than obtaining a mathematical theory of barberhood.
We’re getting close to the point where Leśniewski kicks in. There is one more piece of the puzzle that we need.
3. Cantor’s Theorem and Paradox
In the 1890s, Georg Cantor (1845–1918) proved a theorem according to which for any set A, its powerset (
$${\cal P}(A)$$
) – that is, the set of all subsets of A – has more elements than A itself.
It is easy to see how this holds for particular finite cases. Take a small set, say 
$$\{ a,b\} $$
. There are more than two subsets of this set: 
$$\emptyset ,\{ a\} ,\{ b\} ,\{ a,b\} $$
. For a full argument for the general claim, see Appendix D.
Now, together with fairly widely accepted assumptions that the set of natural numbers exists and that for any set its powerset exists, Cantor’s theorem has the consequence that there is not one but many (a lot, really) infinite sizes. The smallest infinite set is the set of natural numbers. Take its powerset – you get a set that has more elements, even though the initial set was infinite already. Take the powerset of that set, you get another, yet greater set, and so on.
With naïve, unaxiomatized set theory in the background, Cantor’s theorem also leads to trouble. Naïvely speaking, the set of all sets should exist. Call it 
$${\cal U}$$
. Now consider its powerset, 
$${\cal P}(U)$$
. Each element of 
$${\cal P}(U)$$
is a set. So 
$${\cal P}(U)$$
is a subset of 
$${\cal U}$$
. But subsets don’t have more elements than sets whose subsets they are. So 
$${\cal P}(U)$$
shouldn’t have more elements than 
$${\cal U}$$
itself. Yet, by Cantor’s theorem, it does!
4. Enter Leśniewski
Things have slightly changed by the time Leśniewski (Figure 1) entered the battlefield. On one hand, Cantor’s surprising theories about infinite sets became opposed only by a small group of mathematicians who thought actual infinity cannot exist and tried to do mathematics without it. Most of researchers accepted Cantor’s account of infinity.
Figure 1 Stanisław Leśniewski
On the other hand, the naïve and bold assumption that for each property there is a corresponding set, has been abandoned. Instead, mathematicians (such as Zermelo and Fraenkel) took a more piecemeal approach to set theory, converting paradoxes into non-existence theorems. What remained from full comprehension was ‘the axiom of separation’, which only requires that once the domain you’re looking at is a set, each property determines a subset of that set and existence claims are handled by a variety of other axioms. Such axioms say, for instance, that pairs of objects exist, or that once you have a set of sets, the union of its members exists, or that once you have a set its powerset exists, or that an infinite set exists. This modified set theory has been on the table since the early years of the twentieth century, has been put to many uses, and no one so far has been able to show it is inconsistent.
For Leśniewski there were at least three reasons to worry about this state of affairs:
∙ Instead of simple and intuitive axioms (such as (BLV)), now set theory consisted of a group of separate axioms, which struck the balance between usefulness and inconsistency, but did so without a clear intuitive motivation. It seemed as if the axioms were chosen just so that the paradoxes could be avoided and the essential mathematical strength preserved, in a rather unprincipled manner. In addition, no serious effort was made to explain the initial intuitions leading to paradoxes.10
∙ The logic underlying such systems didn’t satisfy Leśniewski’s own standards of precision and clarity.
∙ The whole story about sets didn’t seem philosophically convincing to Leśniewski, because he was a nominalist. On the standard interpretation, sets are abstract mathematical objects. This means that they are supposed to be atemporal, aspatial and causally inefficacious. For Leśniewski, this hardly made sense. Many times he emphasized that he doesn’t even understand what such objects would be like. He also had an argument against the existence of such objects, but that’s a different story.
Accordingly, he devised his own logic and a theory alternative to set theory, meant to do (more or less) the same job. Actually, historically speaking, it was the other way round. First, in 1914 he used his mereological intuitions to explain away the Russell’s paradox. Then, in 1916 he semi-formally axiomatized his alternative to set theory, underlying his approach to Russell’s paradox. Only later, in the 1920s, did he spend more time thinking about formalization, and he constructed a fully formalized language and logic to underly his approach.
The key difference between set theory and Leśniewski’s Mereology (the name coming from Greek meros, meaning part; in the beginning Leśniewski didn’t use the name but rather explicitly called his theory a ‘theory of sets’) is that while set theory uses sets and elementhood, Mereology used wholes and parthood. While sets were supposed to be abstract objects, mereological wholes were meant to be nominalistically acceptable. When I look at the heap of stones in my garden, the set of these stones is supposed to be an abstract object, while the mereological whole composed of these stones is just a heap of stones.
As for Leśniewski’s logic, he devised two systems: ‘Protothetic’, a generalized version of propositional calculus in which quantification over propositional functions, functions of propositional functions and so on was available, and ‘Ontology’, which was his variant of higher-order logic.
While there are various factors that distinguish Leśniewski’s logical systems from other logical systems, they are rather irrelevant for our current purpose. I will say only a few words about how Leśniewski thought about formal systems in general.
∙ While normally languages of formal systems are abstract sets of formulas, for Leśniewski all that existed was written instructions as to how new inscriptions should be constructed to count as formulas of the language and those inscriptions, which have been already written down.
∙ While normally proofs and theorems of formal systems are taken to exist, no matter whether they’ve been discovered or written down, for Leśniewski only those proofs and theorems exist, which have been written down.
Thus, for Leśniewski the system is a concrete object which changes with time as people write down formulas. They consists only of concrete objects: the inscriptions that someone actually cared to write down following the instructions.
It’s time to look at what Mereology looked like and how Leśniewski used it to approach the Russell’s paradox.
5. Mereology and Russell’s Paradox
For now, let us proceed intuitively and see what would happen, if classes were thought of mereologically. (So, from now on, when we talk about sets and classes, please take those phrases to refer to mereological wholes.) We’ll look at an axiomatization of Mereology in the next section.11
As phrased by Leśniewski, the paradox assumes that one of the following sentences is true:
(Russell 1) The class of classes not subordinated to themselves is subordinated to itself.
(Russell 2) The class of classes not subordinated to themselves is not subordinated to itself.
where by ‘subordinated to’ Leśniewski means ‘being an element of’.
Next, standard paradoxical reasoning indicates that each of the above sentences implies the other, thus yielding a contradiction.
Leśniewski points out that if no object is the class of classes not subordinated to themselves, then both (Russell 1) and (Russell 2) are false, without implying a contradiction. Thus, his goal in handling the paradox is to show, independently of the paradox, that there is no such a class.
To start with, if we think about mereological wholes rather than abstract sets, we need to find a correlate of the elementhood relation. For Leśniewski, it was being an ingredient, where each object is its own ingredient and each part of an object is among its ingredients.12
Now, if being an element is being an ingredient and each object is by definition its own ingredient, each object is its own element. This has two consequences, which are relevant to current considerations.
∙ First, there is no empty class. For a class to be empty, it would have to have no elements. But we know it is impossible, because it is its own element.
∙ Second, there are no things that are not their own elements.
As a consequence, Russell’s set would have to be empty. For it would have to contain things that are not their own elements. But there are no such things. Yet, we already know that the empty set doesn’t exist, and by the same token Russell’s set doesn’t exist either.
So if classes are understood mereologically, we have independent reasons to think that Russell’s set doesn’t exist and if it doesn’t exist, no contradiction arises. So, at least, we have solved one problem: we avoided Russell’s paradox in a principled manner. Do we get a mathematically interesting theory that could do the job that the standard set theory is intended for, though?
6. Axioms of Mereology
Leśniewski provided a few axiomatizations of his Mereology. They are all equivalent and we’ll take a look at the earliest one, coming from 1916. I will just give the content of the axioms and definitions in a rather informal manner.
The 1916 formulation had two axioms not containing defined terms and two axioms that involved previously defined terms.
(Axiom I) If a is a part of b, b is not a part of a.
(Axiom II) If a is a part of b and b is a part of c, then a is a part of c.
For the other two axioms, we need two definitions:
(Definition I) a is an ingredient of b if and only if either a and b are the same object, or a is a part of b.
Two other important definitions are that of a set and that of a class. As it turns out, this has nothing to do with the standard set-theoretic distinction between sets and classes.
(Definition II) An object a is a set of bs if and only if every one of a’s ingredients has an ingredient that is an ingredient of an object that is b.
This sounds a bit convoluted, but the idea is rather simple. For instance, the mereological whole constituted, say, by all people in Canada is a set of people, because every one of its ingredients has an ingredient which is an ingredient of a person (in Canada).
To see why this rather complicated iteration of ‘ingredienthood’ is needed, consider what would happen if the definition required only that every ingredient of a be an ingredient of an object which is b. Then, the mereological whole constituted by all people in Canada (call it CAN) would not be a set of people, because CAN would have ingredients, like the mereological fusion of one person’s leg and another person’s right hand, which would not be ingredients of any particular person.
Also, note that the indefinite article in ‘is a set’ is there not without a purpose. According to this definition, one countable noun may generate quite a few different sets. The intuition here is that every mereological whole constituted by some objects b (i.e. by some objects denoted by the countable noun phrase ‘b’) is a set of b, although choosing different representatives (or groups of representatives) of b we get different mereological wholes.
Take another example: any heap of stones is a set of stones in the sense introduced by Definition II. Therefore, if a names more than one object, the name 
$$set(a)$$
also names more than one object: it names any mereological whole constructed from some objects that fall under a.
Another notion defined by Leśniewski is the one that determines the ‘maximal’ set of objects a, that is the set of all as. This is the notion of a class:
(Definition III) an object a is a class of objects b if and only if every object b is an ingredient of a, and any ingredient of a has an ingredient that is also an ingredient of some object b.
The remaining two axioms employ the notion of a class:
(Axiom III) If there is at least one b, there is a class of bs. (Any non-empty name generates its class.)
(Axiom IV) For any b, there is at most one class of bs. (A name generates at most one class.)
Leśniewski proceeded to prove various theorems in the system. For us, the interesting question is: how much mathematics can be obtained within the system?
7. Mereology and Standard Mathematics
First of all, it is clear that Leśniewski invented Mereology while thinking hard about Russell’s paradox:
I occupied myself zealously with the ‘antinomies’. From the time when in the year 1911 I began an acquaintance with them by meeting with the ‘antinomies’ of Russell related to the ‘class of classes not elements of themselves’, and problems concerning the antinomies were the most demanding subject of my deliberations for over eleven years. (Ref. Reference Leśniewsk13, p. 199)]
Second, it is equally clear that he thought Mereology should play a foundational role in mathematics:
The present work is the first link in an extended series of works, which I intend to publish in the near or distant future, desiring to contribute as much as possible to the justification of modern mathematics ... The arrangement of definitions and truths, which I established in the present work dedicated to the most general problems of the theory of sets, has for me, in comparison to other previously known arrangements of definitions and truths (Zermelo, Russell, etc.) this advantage that it eliminates the ‘antinomies’ of the general theory of sets without narrowing the original domain of Cantor’s term ‘set’... and on the other hand, it does not lead to assertions which are in such startling conflict with intuitions of the ‘commonalty’... (Ref. Reference Leśniewsk14, pp. 129–130)
In the series of papers in which he described various axiomatizations of Mereology Leśniewski also proved numerous theorems that are intended as analogues of certain theorems of set theory, the strongest and the most mathematically interesting of them being an analogue of Cantor’s theorem.
This analogue states that if a name a names more than one object, and the objects it names do not overlap, then there are more sets of as than objects as. So, for instance, if I have five (obviously, non-overlapping) lizards, and I name this little lounge ‘Aldos’,15 then the theorem implies that there are more than five sets of Aldos.
Interestingly, despite containing an analogue of Cantor’s theorem, Mereology proves the existence of the universal class defined as the class of all objects. The mereological analogue of Cantor’s theorem doesn’t apply, because subsets of the universe overlap and so, Cantor’s paradox doesn’t arise.
However, this is as mathematically interesting as it gets. Leśniewski never developed a ‘mereologization of arithmetic in the manner analogous to Frege’s treatment of arithmetic. He did axiomatize an arithmetic in the language of Ontology, but that was a pretty much standard axiomatization with axioms such as ‘one is a natural number’, ‘the successor of a natural number is a natural number’ and so on. No attempt at elimination of numbers in virtue of anything else can be found in Leśniewski’s works.
Mereology was constructed by Leśniewski, as he explicitly stated, to provide an alternative form of the foundation of mathematics. This new system indeed provides an interesting theory of classes, at least in one sense of this word. Unfortunately, neither Leśniewski nor later developments have shown that Mereology actually constitutes a foundation of mathematics in any sense remotely similar to that in which classical set theory does.
It is said that Leśniewski eventually became dissatisfied with Mereology as a system of foundations of mathematics. He did not publish such a comment anywhere, and the information seems to come from secondary sources. For instance, KearnsReference Kearns16 says: ‘Leśniewski did not give up his claims that it [Mereology] is intuitively acceptable, but he did realize that it cannot replace set theory.’
Peter Simons points out:
Leśniewski’s alternative to set theory is based on the (justified) assumption: If you follow me in what you mean by ‘member’ and ‘set’ you will not get into logical trouble. That is true, but the proponents of inconsistent set theory were doing more than trying to stay out of trouble (which is why they got into it in the first place): they were trying to provide a logical foundation for mathematics, some of them with a view to showing at least part of mathematics to be just logic. Leśniewski’s weaker system may, or, more likely, may not be adequate to that purpose.Reference Simons17
There is some work on enriching the framework with elements that would be nominalistically acceptable and which would result in mathematically richer theories (Peter Simons and Rafal Urbaniak, see also HellmanReference Hellman18). But these attempts move forward thanks to serious modifications to the original systems and are still a bit far from being successful.
8. Unexpected Usefulness of Mereology
All this does not mean that Mereology as a separate theory is useless. Quite recently, mereology resurfaced as quite an important tool in various fields.
Some of the applications are in philosophy. Philosophers speak about existence in time, identity in space-time and so on and often employ a mereological framework for their discussions.
Some recent applications are in linguistics,Reference Link19, Reference Champollion20 in natural language processing,Reference Indriunas, Taylor and Raskin21 in the semantics of mass terms.Reference Bunt22
Another sort of use is in AI, where mereological framework is used to encode certain relations in ontological databasesReference Klinov and Mazlack23 or spatial reasoning.Reference Polkowski and Skowron24
Acknowledgement
I would like to express my gratitude to Dagfinn Føllesdal for his comments.
Appendices
A. Axioms of Real Number Theory
A structure 
$$\langle {\Bbb R},{\plus},{\times},\leq \rangle $$
is a real number structure iff it is a complete ordered field. For it to be a field, the following conditions have to be satisfied:
$$\matrix{ {\left( {{\rm Closure}} \right)} \hfill & {\forall x,y\in {\Bbb R} \ \exists z\in {\Bbb R} \ z=x{\plus}y} \hfill \cr {} \hfill & {\forall x,y\in {\Bbb R} \ \exists z\in {\Bbb R} \ z=x{\times}y} \hfill \cr {\left( {{\rm Associativity}} \right)} \hfill & {\forall x,y,z\in {\Bbb R} \ x{\plus}(y{\plus}z)=(x{\plus}y){\plus}z} \hfill \cr {} \hfill & {\forall x,y,z\in {\Bbb R} \ x{\times}(y{\times}z)=(x{\times}y){\times}z} \hfill \cr {\left( {{\rm Commutativity}} \right)} \hfill & {\forall x,y\in {\Bbb R} \ x{\plus}y=y{\plus}x} \hfill \cr {} \hfill & {\forall x,y\in {\Bbb R} \ x{\times}y=y{\times}x} \hfill \cr {\left( {{\rm Identity}} \right)} \hfill & {\exists y\in {\Bbb R} \ \forall x\in {\Bbb R} \ x{\plus}y=x} \hfill \cr {} \hfill & {\exists y\in {\Bbb R} \ \forall x\in {\Bbb R} \ x{\times}y=x} \hfill \cr {\left( {{\rm Inverses}} \right)} \hfill & {\forall x\in {\Bbb R} \ \exists y\in {\Bbb R} \ x{\plus}y=0} \hfill \cr {} \hfill & {\forall x \,\ne \,0\in {\Bbb R} \ \exists y\in {\Bbb R} \ x{\times}y=1} \hfill \cr {\left( {{\rm Distributivity}} \right)} \hfill & {\forall x,y,z\in {\Bbb R} \ x{\times}(y{\plus}z)=(x{\times}y){\plus}(x{\times}z)} \hfill \cr } $$
The first three types of conditions are straightforward. The third type requires the existence of identity elements which are (respectively) called 0 and 1. The next type of conditions requires that addition and multiplication have their inverses. The last requirement is straightforward.
For a field to be ordered, ≤ has to be total order on 
$${\Bbb R}$$
. That is, it has to be reflexive (
$$\forall x\in {\Bbb R} \ x\leq x$$
), antisymmetric (
$$\forall x,y \in mr\ [x \leq y \wedge y \leq x \to x=y]$$
), transitive (
$$\forall x,y,z\in {\Bbb R} \ [x\leq y\wedge y\leq z \to x\leq z]$$
) and total (
$$\forall x,y\in {\Bbb R} \ [x\leq y\vee y \leq x]$$
). Moreover, this order should have the following properties:
$$\eqalignno{ & \matrix{ {\left( {{\rm Preservation}} \right)} & {\forall x,y,z\in {\Bbb R} \ [x\leq y \to x{\plus}z\leq y{\plus}z]} \cr } \cr & \matrix{ {} & {\forall x,y \in {\Bbb R} \ [0\leq x \wedge 0\leq y \to 0\leq x{\times}y]} \cr } $$
For an ordered field to be (Dedekind) complete each non-empty subset of 
$${\Bbb R}$$
which has an upper bound in 
$${\Bbb R}$$
should have a least upper bound.
The requirements described above determine the structure of real numbers up to isomorphism.
B. Construction of Rational Numbers
The construction of real numbers proceeds through integers and rational numbers. One way to go about this is to observe that every integer can be represented by 
$$m{\minus}n$$
for 
$$m,n\in {\Bbb N}$$
. The representation is not unique, but we can identify those results of subtraction that yield the same integers:
$$\matrix{ {\left( {{\rm Difference}} \right)} & {x{\minus}y=x'{\minus}y' \equiv x{\plus}y'=x'{\plus}y} \cr } $$
An integer, on this approach is taken be such an equivalence class of a pair of natural numbers. The set of integers, Z, is identified with the set of all such equivalence classes of pairs of natural numbers. It is countable, because the set of pairs from a countable set is also countable.
Once integers are in place, we move on to rationals. The key observation here is that assuming 
$$y,y'\, \ne\, 0$$
:
$$\matrix{ {\left( {{\rm Ratio}\ {\rm I}} \right)} \ {{x \over y}={{x'} \over {y'}} \equiv x{\times}y'=x'{\times}y} \cr } $$
This, again, introduces an equivalence relation – only this time between pairs of integers whose second elements differ from zero. Thus, the standard move is to identify each rational number with an appropriate equivalence class of such an equivalence relation.
C. Set-theoretic Construction of Natural Numbers
An ordered pair 
$$\langle x,y\rangle $$
is identified with the set 
$$\{ \{ x\} ,\{ x,y\} \} $$
(this is by no means the only way to do this). With this definition, it is possible to prove in standard set theory:
$$\matrix{ {\left( {{\rm Pairs}} \right)} & {\langle x,y\rangle =\langle x',y' \rangle \equiv x=x' \wedge y=y'} \cr } $$
One way to identify natural-number-like objects in set theory is to take:
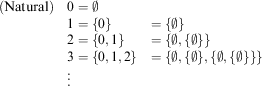$$\matrix{ {\left( {{\rm Natural}} \right)} \hfill & {0=\emptyset } \hfill & {} \hfill \cr {} \hfill & {1=\{ 0\} } \hfill & {=\{ \emptyset \} } \hfill \cr {} \hfill & {2=\{ 0,1\} } \hfill & {=\{ \emptyset ,\{ \emptyset \} \} } \hfill \cr {} \hfill & {3=\{ 0,1,2\} } \hfill & {=\{ \emptyset ,\{ \emptyset \} ,\{ \emptyset ,\{ \emptyset \} \} \} } \hfill \cr {} \hfill & \vdots \hfill & {} \hfill \cr } $$
In general, the successor of a set x is 
$$x{\cup}\{ x\} $$
. A set is called inductive if it contains 
$$\emptyset $$
and is closed under the successor operator. The set of natural numbers is identified with the smallest inductive set. Appropriate definitions of addition and multiplication provide us with a set-theoretic model of natural numbers. (Again, it is by no means the only way to construct a model of natural number arithmetic in set theory.)
D. Cantor’s Theorem and Diagonalization
The proof of a general claim, including infinite cases, requires ingenuity. First, you need to explicate in more detail what you want to prove. To prove that there are more elements of 
$${\cal P}(A)$$
than elements of A, you need to prove that:
∙ There is a 1–1 mapping between A and a subset of
$${\cal P}(A)$$
. This is rather easy: associate each
$$x\in A$$
with
$$\{ x\} \in {\cal P}(A)$$
.∙ For no subset
$A'$
of A there is a 1–1-mapping from
$A'$
to the powerset of A. In fact, it is enough to show that there is no function from A′ onto this powerset (if there is no such a function, there definitely is no 1–1 function). This requires ingenuity.
The proof that there is no such a mapping is a reductio proof and it employs a technique called ‘diagonalization’, which turned out to be very important in twentieth-century logic and mathematics.
For a reductio proof, assume that there is a function with required properties and show that from this assumption a contradiction follows.
So suppose 
$$A' \subseteq A$$
and 
$$f:A'\mapsto_{{onto}} {\cal P}(A)$$
. Now, define 
$${\cal C}$$
to be the set of those elements of A′ that do not belong to sets assigned to them.
$$\matrix{ {\left( {{\rm Def}\ {\rm C}} \right)} & {x\in {\cal C} \equiv x\in A' \wedge x \,\notin\, f(x)} \cr } $$
This means to that to check if some element of 
$A'$
is in 
$${\cal C}$$
, we need to first see which set is 
$$f(x)$$
. Then, we check if x is in that set. If not, we throw it in to 
$${\cal C}$$
. If yes, we don’t.
Now observe that 
$${\cal C}$$
is a subset of 
$A'$
(and by the same token, a subset of A). So, it also belongs to the powerset under consideration. This being the case, it is assigned by f to some element of A′. Call this element c:
$$\matrix{ {\left( {{\rm Cantor} \ {\rm 1}} \right)} & {f(c)={\cal C}} \cr } $$
Now, from (Def C) (and the fact that 
$$c\in A'$$
) it follows:
$$\matrix{ {\left( {{\rm Cantor} \ {\rm 2}} \right)} & {c\in {\cal C} \equiv c\,\notin \,f(c)} \cr } $$
The problem now appears. (Control 1) and (Control 2) together entail the contradictory claim:
$$c\in {\cal C} \equiv c \, \notin\, {\cal C}$$
So the function whose existence we tentatively assumed doesn’t exist, which completes the proof.
Rafal Urbaniak completed his Master’s degree at the University of Gdansk, working on various aspects of definability in higher-order calculi (committee: Professor J. Mrozek and Professor A.W. Mostowski). In 2008 he completed his PhD in Logic and Philosophy of Mathematics at the University of Calgary (working with Professor R. Zach), focusing on the development of Leśniewski foundations of mathematics. Currently, he is a postdoctoral fellow of the Research Foundation Flanders at the Centre for Logic and Philosophy of Science at Ghent University in Belgium and an Assistant Professor at the Department of Philosophy, Sociology and Journalism at the University of Gdansk in Poland. Rafal Urbaniak is mostly interested in applications of formal methods to philosophical problems, such as those related to theories of rationality, belief revision, philosophy of mathematics, time travel, philosophy of mind, theories of conditionals or philosophy of thought experiments. More details and papers are available at http://ugent.academia.edu/RafalUrbaniak
