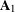1 Introduction
In the late 1980s, Manin and his collaborators [Reference Franke, Manin and Tschinkel22] proposed a precise conjecture predicting, for smooth Fano varieties, the behaviour of the number of rational points of bounded height (with respect to an anticanonical height function) in terms of geometric invariants of the variety. The conjecture was later generalized by Peyre [Reference Peyre26] to “almost Fano” varieties in the sense of [Reference Peyre26, Définition 3.1].
Conjecture 1.1 (Manin, 1989).
Let
$V$
be an “almost Fano” variety in the sense of [Reference Peyre26, Définition 3.1] with
$V(\mathbb{Q})\neq \varnothing$
and let
$H$
be an anticanonical height function on
$V(\mathbb{Q})$
. Then there exist a Zariski open subset
$U$
of
$V$
and a constant
$c_{H,V}$
such that, for
$B\geqslant 1$
,
$$\begin{eqnarray}N_{U,H}(B):=\#\{x\in U(\mathbb{Q})\mid H(x)\leqslant B\}=c_{H,V}B(\log B)^{\unicode[STIX]{x1D70C}-1}(1+o(1)),\end{eqnarray}$$
where
$\unicode[STIX]{x1D70C}=\text{rank}(\text{Pic}(V))$
.
Peyre [Reference Peyre26] and then Batyrev and Tschinkel [Reference Batyrev and Tschinkel2] and Salberger [Reference Salberger28], in a more general setting, also proposed a conjectural expression for the constant
$c_{H,V}$
in terms of geometric invariants of the variety. We do not record this conjecture here in any more details and refer the interested reader to [Reference Peyre27] for example. There are a number of refinements of the Manin–Peyre conjectures and we will focus throughout this paper on the following one [Reference Browning15].
Conjecture 1.2 (Refinement of the Manin–Peyre conjectures).
Let
$V$
be an “almost Fano” variety in the sense of [Reference Peyre26, Définition 3.1] with
$V(\mathbb{Q})\neq \varnothing$
and let
$H$
be an anticanonical height function on
$V(\mathbb{Q})$
. Then there exist a Zariski open subset
$U$
of
$V$
, a polynomial
$P_{U,H}$
of degree
$\unicode[STIX]{x1D70C}$
and
$\unicode[STIX]{x1D6FF}\in ]0,1[$
such that, for
$B\geqslant 1$
$$\begin{eqnarray}N_{U,H}(B)=BP_{U,H}(\log B)+O(B^{1-\unicode[STIX]{x1D6FF}}),\end{eqnarray}$$
where
$\unicode[STIX]{x1D70C}=\text{rank}(\text{Pic}(V))$
and the leading coefficient of
$P_{U,H}$
agrees with Peyre’s prediction.
There has been very little investigation on the lower order coefficients and this seems to be a difficult question, but the examples we study in this paper might be an interesting testing ground.
These two conjectures have been the centre of numerous investigations in the past few years using techniques from harmonic analysis in the case of equivariant compactifications of some algebraic groups (see, for example, [Reference Batyrev and Tschinkel1, Reference Tanimoto and Tschinkel30]) or from analytic number theory and more specifically the circle method in the case where the number of variables is large enough with respect to the degree (see, for example, [Reference Birch5, Reference Browning and Heath-Brown17]). In the remaining cases, the only available method relies on a combination of analytic number theory or geometry of numbers and on a descent on some quasi-versal torsors in the sense of [Reference Colliot-Thélène and Sansuc19]. Most of these investigations (especially in cases relying on a descent) are concerned with surfaces (see, for example, works of Browning, La Bretèche, Derenthal and Peyre [Reference de la Bretèche and Browning12, Reference de la Bretèche, Browning and Peyre13, Reference Browning and Derenthal16]), whereas very little is known in higher dimensions. In particular, there are only very few examples of varieties in higher dimension for which Conjecture 1.2, or even Conjecture 1.1, is known to hold using such a descent argument (see [Reference Blomer, Brüdern and Salberger7, Reference de la Bretèche10, Reference Destagnol21, Reference Schmidt29]). The goal of this paper is to give another such example.
In this paper we shall consider the solutions to the equation
$$\begin{eqnarray}x_{1}y_{2}y_{3}\cdots y_{n}+x_{2}y_{1}y_{3}\cdots y_{n}+\cdots +x_{n}y_{1}y_{2}\cdots y_{n-1}=0.\end{eqnarray}$$
Notice that, upon excluding the points for which
$y_{1}\cdots y_{n}=0$
, one can also rewrite the above equation as a linear equation between fractions
$$\begin{eqnarray}\displaystyle \frac{x_{1}}{y_{1}}+\cdots +\frac{x_{n}}{y_{n}}=0. & & \displaystyle \nonumber\end{eqnarray}$$
We shall focus on the case
$n=3$
in the present paper. The cases
$n\geqslant 4$
will be the subject of future work.
One can view equation (1.1) in three natural ways. First, one can consider the singular projective hypersurface of
$\mathbb{P}^{2n-1}$
with homogeneous coordinates
$[x_{1}:\cdots :x_{n}:y_{1}:\cdots :y_{n}]$
defined by (1.1). This was done in 2014 by Blomer et al, who in [Reference Blomer, Brüdern and Salberger7] proved Conjecture 1.2 for
$n=3$
using a combination of lattice point counting and analytic counting by multiple Mellin integrals. This setting was also studied by the second author [Reference Destagnol21], who, by elementary counting methods, proved Conjecture 1.1 when
$n\geqslant 2$
for the following anticanonical height function:
$$\begin{eqnarray}H([x_{1}:\cdots :x_{n}:y_{1}:\cdots :y_{n}])=\max _{1\leqslant i\leqslant n}\max \{|x_{i}|,|y_{i}|\}^{n}.\end{eqnarray}$$
It is worth noticing that in this case, the varieties under consideration are equivariant compactifications of the algebraic groups
$\mathbb{G}_{a}^{n-1}\times \mathbb{G}_{m}^{n-1}$
. Harmonic analysis techniques might also be able to handle this case and to prove Conjecture 1.2 for every
$n\geqslant 4$
. To our knowledge this has not been done so far, but it would be interesting to compare this approach with a generalization of the methods of [Reference Blomer, Brüdern and Salberger7] or of the present paper.
One can also think of (1.1) as defining the singular biprojective variety
$\widetilde{W}_{n}$
of
$(\mathbb{P}^{n-1})^{2}$
with bihomogeneous coordinates
$[x_{1}:\cdots :x_{n}],[y_{1}:\cdots :y_{n}]$
defined by the equation (1.1). An anticanonical height function is then given by
$$\begin{eqnarray}\widetilde{H}([x_{1}:\cdots :x_{n}],[y_{1}:\cdots :y_{n}])=\max _{1\leqslant i\leqslant n}|x_{i}|^{n-1}\max _{1\leqslant i\leqslant n}|y_{i}|.\end{eqnarray}$$
In this case, the varieties under consideration are not equivariant compactifications, the rank of the Picard group of
$\widetilde{W}_{n}$
is
$2^{n}-n$
and the subset where
$x_{1}\cdots x_{n}y_{1}\cdots y_{n}=0$
is an accumulating subset. In recent work [Reference Blomer, Brüdern and Salberger8], Blomer et al showed that Conjecture 1.1 holds for
$\widetilde{W}_{3}$
using Fourier analysis. Using recent results of the first author [Reference Bettin4], we are able to refine the aforementioned result [Reference Blomer, Brüdern and Salberger8] proving the stronger Conjecture 1.2 for
$\widetilde{W}_{3}$
.
Theorem 1. Let
$\widetilde{U}$
be the Zariski open subset of
$\widetilde{W}_{3}$
given by the condition
$x_{1}x_{2}x_{3}y_{1}y_{2}y_{3}\neq 0$
. There exist
$\unicode[STIX]{x1D709}_{1}>0$
and a polynomial
$P_{1}$
of degree 4 such that
$$\begin{eqnarray}\displaystyle N_{\widetilde{W}_{3},\widetilde{H}}(B) & := & \displaystyle \#\{([x_{1}:x_{2}:x_{3}],[y_{1}:y_{2}:y_{3}])\in \widetilde{U}(\mathbb{Q})\mid \widetilde{H}(\mathbf{x},\mathbf{y})\leqslant B\}\nonumber\\ \displaystyle & = & \displaystyle BP_{1}(\log B)+O(B^{1-\unicode[STIX]{x1D709}_{1}}).\nonumber\end{eqnarray}$$
The leading coefficient of
$P_{1}$
is equal to
$(\mathfrak{S}_{1}\cdot {\mathcal{I}})/144$
, where
$$\begin{eqnarray}\displaystyle \mathfrak{S}_{1} & := & \displaystyle \mathop{\prod }_{p}\biggl(1-\frac{1}{p}\biggr)^{5}\biggl(1+\frac{5}{p}+\frac{5}{p^{2}}+\frac{1}{p^{3}}\biggr),\nonumber\\ \displaystyle {\mathcal{I}} & := & \displaystyle \iint _{[-1,1]^{3}\times [0,1]^{2}}\unicode[STIX]{x1D712}_{[0,1/|z|]}\biggl(\frac{x_{1}}{y_{1}}+\frac{x_{2}}{y_{2}}\biggr)\,dx_{1}\,dx_{2}\,dz\cdot \frac{dy_{1}\,dy_{2}}{y_{1}y_{2}}\nonumber\\ \displaystyle & = & \displaystyle \unicode[STIX]{x1D70B}^{2}+24\log 2-3\nonumber\end{eqnarray}$$
and
$\unicode[STIX]{x1D712}_{X}$
denotes the characteristic function of a set
$X$
.
The work of [Reference Blomer, Brüdern and Salberger8] shows that
$(\mathfrak{S}_{1}\cdot {\mathcal{I}})/144$
coincides with Peyre’s prediction for this variety and so Theorem 1 gives Conjecture 1.2 for
$\widetilde{W}_{3}$
.
Finally, a third interpretation of (1.1) is as the singular subvariety
$\widehat{W}_{n}$
of
$(\mathbb{P}^{1})^{n}$
with multihomogeneous coordinates
$[x_{1}:y_{1}],\ldots ,[x_{n}:y_{n}]$
. The only record of study of an analogous equation is from La Bretèche [Reference de la Bretèche11], but with a non-anticanonical height function. An anticanonical height is given in this setting by
$$\begin{eqnarray}\widehat{H}([x_{1}:y_{1}],\ldots ,[x_{n}:y_{n}])=\mathop{\prod }_{i=1}^{n}\max \{|x_{i}|,|y_{i}|\}.\end{eqnarray}$$
We prove the two following theorems, which, combined, give that Conjecture 1.2 holds for
$\widehat{W}_{3}$
.
Theorem 2. Let
$\widehat{U}$
be the Zariski open subset of
$\widehat{W}_{3}$
defined by the condition
$y_{1}y_{2}y_{3}\neq 0$
. Then there exist
$\unicode[STIX]{x1D709}_{2}>0$
and a polynomial
$P_{2}$
of degree 3 such that
$$\begin{eqnarray}\displaystyle N_{\widehat{W}_{3},\widehat{H}}(B) & := & \displaystyle \#\{([x_{1}:y_{1}],[x_{2}:y_{2}],[x_{3}:y_{3}])\in \widehat{U}(\mathbb{Q})\mid \widehat{H}(\mathbf{x},\mathbf{y})\leqslant B\}\nonumber\\ \displaystyle & = & \displaystyle BP_{2}(\log B)+O(B^{1-\unicode[STIX]{x1D709}_{2}}).\nonumber\end{eqnarray}$$
The leading coefficient of
$P_{2}$
is equal to
$(\mathfrak{S}_{2}\cdot {\mathcal{I}})/144$
, where
${\mathcal{I}}$
is as in Theorem 1 and
$$\begin{eqnarray}\displaystyle \mathfrak{S}_{2}:=\mathop{\prod }_{p}\biggl(1-\frac{1}{p}\biggr)^{4}\biggl(1+\frac{4}{p}+\frac{1}{p^{2}}\biggr). & & \displaystyle \nonumber\end{eqnarray}$$
Theorem 3. The variety
$\widehat{W}_{3}$
is isomorphic to a del Pezzo surface of degree 6 with singularity type
$\mathbf{A}_{1}$
and three lines over
$\mathbb{Q}$
and the leading constant of the polynomial
$P_{2}$
in Theorem 2 agrees with Peyre’s prediction.
We remark that by Theorem 3 and [Reference Loughran25], one has that
$\widehat{W}_{3}$
is an equivariant compactification of
$\mathbb{G}_{a}^{2}$
. In particular, Theorem 2 follows from the more general work of Chambert-Loir and Tschinkel [Reference Chambert-Loir and Tschinkel18].
The purpose of giving a new independent proof of Theorem 2 is double. First, the method presented here uses a descent on the versal torsor and thus it is different from the method in [Reference Chambert-Loir and Tschinkel18], which relies on harmonic analysis techniques and the study of the height zeta function. To our knowledge this is the first time that a full asymptotic with a power-saving error term is obtained on this del Pezzo surface by means of a descent on the versal torsor. The best result using such a method can be found in [Reference Browning15, Ch. 5], where Browning obtained a statement somewhere in between Conjectures 1.1 and 1.2.
Secondly, following the same approach for proving Theorems 1 and 2 allows one to appreciate the difference in the structure of the main terms in these two cases, showing how the extraction of the main term in the first case becomes substantially harder as well as allowing the use of the proof of Theorem 2 as a guide for that of Theorem 1.
Remark.
We prove Theorem 2 for any
$\unicode[STIX]{x1D709}_{2}<0.00228169\ldots \,$
. One can easily give an explicit power saving also in the case of Theorem 1 as well as improving the allowed range for
$\unicode[STIX]{x1D709}_{2}$
, but, in order to simplify the presentation, we choose not to do so, since in any case the values obtained could be greatly improved by tailoring the methods of [Reference Bettin4] to these specific problems.
The proofs of Theorems 1 and 2 roughly proceed as follows. We use the same unique factorization as in recent work of the second author [Reference Destagnol21] to parametrize the counting problem combined with recent work of the first author [Reference Bettin4]. More precisely, by means of a descent on the versal torsor we can transform the problem of counting solutions to (1.1) to that of counting solutions to
$a_{1}x_{1}z_{1}+a_{2}x_{2}z_{3}+a_{3}x_{3}z_{3}=0$
with some coprimality conditions, with certain restraints on the sizes of
$x_{i},z_{j}$
(depending on the height we had originally chosen) and with
$a_{1},a_{2},a_{3}$
that can be thought of being very small. By [Reference Bettin4] (see also [Reference Bettin3]), we have the meromorphic continuation for the “parabolic Eisenstein series”
$$\begin{eqnarray}\displaystyle & \mathop{\sum }_{\substack{ m_{1},m_{2},m_{3}\in \mathbb{Z}_{{>}0} \\ a_{1}m_{1}+a_{2}m_{2}+a_{3}m_{3}=0}}\frac{\unicode[STIX]{x1D70F}_{\unicode[STIX]{x1D6FC}_{1},\unicode[STIX]{x1D6FD}_{1}}(m_{1})\unicode[STIX]{x1D70F}_{\unicode[STIX]{x1D6FC}_{2},\unicode[STIX]{x1D6FD}_{2}}(m_{3})\unicode[STIX]{x1D70F}_{\unicode[STIX]{x1D6FC}_{3},\unicode[STIX]{x1D6FD}_{3}}(m_{3})}{(m_{1}m_{2}m_{3})^{s}}, & \displaystyle \nonumber\\ \displaystyle & \Re (s)>\frac{2}{3}-\min (\Re (\unicode[STIX]{x1D6FC}_{i}),\Re (\unicode[STIX]{x1D6FD}_{i}))\quad \text{for all }i=1,2,3, & \displaystyle \nonumber\end{eqnarray}$$
where
$\unicode[STIX]{x1D70F}_{\unicode[STIX]{x1D6FC}_{i},\unicode[STIX]{x1D6FD}_{i}}(m)=\sum _{d_{1}d_{2}=m}d_{1}^{-\unicode[STIX]{x1D6FC}_{i}}d_{2}^{-\unicode[STIX]{x1D6FD}_{i}}$
for
$(\unicode[STIX]{x1D6FC}_{1},\unicode[STIX]{x1D6FC}_{2},\unicode[STIX]{x1D6FC}_{3}),(\unicode[STIX]{x1D6FD}_{1},\unicode[STIX]{x1D6FD}_{2},\unicode[STIX]{x1D6FD}_{3})\in \mathbb{C}^{3}$
. Using this, we obtain that the counting problem in both cases is given by a certain multiple complex integral of the products of
$\unicode[STIX]{x1D6E4}$
and
$\unicode[STIX]{x1D701}$
functions, up to a power-saving error term. The main part of the paper is then devoted to the use of complex analytic methods to extract the main terms from such integrals. This process is reminiscent of the work [Reference de la Bretèche9] of La Bretèche, where he showed how to deduce asymptotic formulas for generic arithmetic averages from the analytic properties of their associated Dirichlet series. However, his work is not directly applicable to our case. Indeed, in his setting all variables are summed in boxes, whereas in our case the main action happens at complicated hyperbolic spikes. Of course, one could use La Bretèche’s work in combination with some suitable version of the hyperbola method, but in fact this would not simplify substantially the problem and would still eventually require arithmetic and complex-analytic computations essentially equivalent to ours. For this reason, we preferred to approach the relevant sums in a more direct way.
The paper is structured as follows. First, in §2 we reparametrize the solutions to (1.1) using a descent on the versal torsor. In §3 we prove Theorem 3. In §4 we state the main lemma on the parabolic Eisenstein series and a smoothing lemma useful to avoid problems of sharp cut-offs. Then in §§5–7 we prove Theorems 2 and 1 in three steps of increasing difficulties: first Theorem 2 without the aforementioned coprimality conditions, then we include these conditions and finally we prove Theorem 1.
Notation. We use the vector notation
$\boldsymbol{v}=(v_{1},\ldots ,v_{k})$
, where the dimension is clear from the context. Also, given a vector
$\boldsymbol{v}\in \mathbb{C}^{k}$
and
$c\in \mathbb{C}$
, with
$\boldsymbol{v}+c$
we mean
$(v_{1}+c,\ldots ,v_{k}+c)$
. With
$\iint$
we indicate the integration with respect to several variables, whose number is clear from the context. For
$c\in \mathbb{R}$
, with
$\int _{(c)}$
we indicate that the integral is taken along the vertical line from
$c-i\infty$
to
$c+i\infty$
. Also, we indicate with
$c_{z}$
the line of integration corresponding to the variable
$z$
. Given
$a_{1},\ldots ,a_{k}\in \mathbb{Z}$
, we indicate the greatest common divisor (gcd) and the least common multiple of
$a_{1},\ldots ,a_{k}$
by
$(a_{1},\ldots ,a_{k})$
and
$[a_{1},\ldots ,a_{k}]$
, respectively.
We indicate the real and imaginary parts of a complex number
$s\in \mathbb{C}$
by
$\unicode[STIX]{x1D70E}$
and
$t$
, respectively, so that
$s=\unicode[STIX]{x1D70E}+it$
. Also,
$\unicode[STIX]{x1D700}$
will denote an arbitrary small and positive real number, which is assumed to be sufficiently small and upon which all bounds are allowed to depend. Finally, in §7, we denote by
$C_{1},C_{2},C_{3},\ldots \,$
a sequence of fixed positive real numbers.
2 The descent on the versal torsor
For
$n\geqslant 2$
, we let
$N=2^{n}-1$
. For every
$h\in \{1,\ldots ,N\}$
, we denote its binary expansion by
$$\begin{eqnarray}h=\mathop{\sum }_{1\leqslant j\leqslant n}\unicode[STIX]{x1D716}_{j}(h)2^{j-1},\end{eqnarray}$$
with
$\unicode[STIX]{x1D716}_{j}(h)\in \{0,1\}$
. We will let
$s(h)=\sum _{j\geqslant 1}\unicode[STIX]{x1D716}_{j}(h)$
be the sum of the bits of
$h$
. We will say that a integer
$h$
is dominated by
$\ell$
if for every
$j\in \mathbb{N}$
, we have
$\unicode[STIX]{x1D716}_{j}(h)\leqslant \unicode[STIX]{x1D716}_{j}(\ell )$
. We will use the notation
$h\preccurlyeq \ell$
to indicate that
$h$
is dominated by
$\ell$
. We will say that an
$N$
-tuple
$(z_{1},\ldots ,z_{N})$
is reduced if
$\gcd (z_{h},z_{\ell })=1$
when
$h\not \preccurlyeq \ell$
and
$\ell \not \preccurlyeq h$
.
We give the following lemma, which gives a unique factorization for the variables
$y_{i}$
inspired by [Reference de la Bretèche and Tenenbaum14, Reference Hall24] and [Reference de la Bretèche11] and which will be very useful to parametrize rational solutions of (1.1).
Lemma 1 [Reference de la Bretèche11].
There is a one-to-one correspondence between the
$n$
-tuples of non-negative integers
$(y_{i})_{1\leqslant i\leqslant n}$
and the reduced
$N$
-tuples
$(z_{h})_{1\leqslant h\leqslant N}$
of non-negative integers such that
$$\begin{eqnarray}\text{for all }j\in \unicode[STIX]{x27E6}1,n\unicode[STIX]{x27E7},\quad y_{j}=\mathop{\prod }_{1\leqslant h\leqslant N}z_{h}^{\unicode[STIX]{x1D716}_{j}(h)}\quad \text{and}\quad [y_{1},\ldots ,y_{n}]=\mathop{\prod }_{1\leqslant h\leqslant N}z_{h}.\end{eqnarray}$$
2.1 The case of
$\widehat{W}_{n}$
Let
$n\geqslant 2$
. We want to estimate, for
$B\geqslant 1$
, the quantity
$$\begin{eqnarray}N_{\widehat{W}_{n},\widehat{H}}(B):=\#\{([x_{1}:y_{1}],\ldots ,[x_{n}:y_{n}])\in \widehat{U}(\mathbb{Q})\mid \widehat{H}(\mathbf{x},\mathbf{y})\leqslant B\}.\end{eqnarray}$$
Clearly, we have
$$\begin{eqnarray}N_{\widehat{W}_{n},\widehat{H}}(B)=\#\left\{(\mathbf{x},\mathbf{y})\in \mathbb{Z}^{n}\times \mathbb{Z}_{{>}0}^{n}:\begin{array}{@{}l@{}}\widehat{H}(\mathbf{x},\mathbf{y})\leqslant B\\ (\mathbf{x},\mathbf{y})\text{ satisfies (1.1)},\gcd (x_{i},y_{i})=1\end{array}\right\}.\end{eqnarray}$$
Using Lemma 1, the equation (1.1) can be rewritten as
$$\begin{eqnarray}\mathop{\sum }_{j=1}^{n}d_{j}x_{j}=0\quad \text{with}\quad d_{i}=\mathop{\prod }_{1\leqslant h\leqslant N}z_{h}^{1-\unicode[STIX]{x1D716}_{i}(h)}\quad \text{for all }i\in \unicode[STIX]{x27E6}1,n\unicode[STIX]{x27E7}.\end{eqnarray}$$
We then obtain the divisibility relation
$z_{2^{j-1}}\mid x_{j}$
for every
$j\in \{1,\ldots ,n\}$
. Since we have the conditions
$\gcd (x_{j},y_{j})=1$
and
$z_{2^{j-1}}\mid y_{j}$
, we can deduce that for every
$j\in \{1,\ldots ,n\}$
,
$z_{2^{j-1}}=1$
. Finally, we have
$$\begin{eqnarray}N_{\widehat{W}_{n},\widehat{H}}(B)=\#\left\{(\mathbf{x},\mathbf{z})\in \mathbb{Z}^{n}\times \mathbb{Z}_{{>}0}^{N-n}:\begin{array}{@{}l@{}}\displaystyle \mathop{\prod }_{i=1}^{n}\max \!\left\{|x_{i}|,\mathop{\prod }_{1\leqslant h\leqslant N}|z_{h}|^{\unicode[STIX]{x1D716}_{i}(h)}\!\right\}\!\leqslant B\\ \displaystyle (z_{h})_{1\leqslant h\leqslant N}\text{ reduced},\mathop{\sum }_{i=1}^{n}x_{i}d_{i}=0\end{array}\right\}\!.\end{eqnarray}$$
In the case
$n=3$
, renaming for simplicity
$z_{6}$
by
$z_{1}$
,
$z_{5}$
by
$z_{2}$
and
$z_{7}$
by
$z_{4}$
, one gets the following expression for
$N_{\widehat{W}_{3},\widehat{H}}(B)$
:
$$\begin{eqnarray}\displaystyle & & \displaystyle N_{\widehat{W}_{3},\widehat{H}}(B)\nonumber\\ \displaystyle & & \displaystyle \quad =\#\left\{(\mathbf{x},\mathbf{z})\in \mathbb{Z}^{3}\times \mathbb{Z}_{{>}0}^{4}:\right.\nonumber\\ \displaystyle & & \displaystyle \quad \left.\begin{array}{@{}l@{}}\gcd (x_{1},z_{2}z_{3}z_{4})=\gcd (x_{2},z_{1}z_{3}z_{4})=\gcd (x_{3},z_{1}z_{2}z_{4})=1\\ \gcd (z_{1},z_{2})=\gcd (z_{1},z_{3})=\gcd (z_{2},z_{3})=1\\ \max \{|x_{1}|,z_{2}z_{3}z_{4}\}\times \max \{|x_{2}|,z_{1}z_{3}z_{4}\}\times \max \{|x_{3}|,z_{1}z_{2}z_{4}\}\leqslant B\\ x_{1}z_{1}+x_{2}z_{2}+x_{3}z_{3}=0\end{array}\right\}.\qquad\end{eqnarray}$$
As explained in §3, the open subvariety of
$\mathbb{A}^{7}$
given by the equation
$x_{1}z_{1}+x_{2}z_{2}+x_{3}z_{3}=0$
along with the conditions
$$\begin{eqnarray}(x_{1},z_{2}z_{3}z_{4})\neq (0,0),\qquad (x_{2},z_{1}z_{3}z_{4})\neq (0,0),\qquad (x_{3},z_{1}z_{2}z_{4})\neq (0,0)\end{eqnarray}$$
and
$$\begin{eqnarray}(z_{1},z_{2})\neq (0,0),\qquad (z_{1},z_{3})\neq (0,0),\qquad (z_{2},z_{3})\neq (0,0)\end{eqnarray}$$
is the versal torsor of the minimal desingularization of
$\widehat{W}_{3}$
and, hence, through this parametrization, we just performed a descent on the versal torsor of this minimal desingularization of
$\widehat{W}_{3}$
.
2.2 The case of
$\widetilde{W}_{n}$
Let
$n\geqslant 2$
. We now want to estimate, for
$B\geqslant 1$
, the quantity
$$\begin{eqnarray}\displaystyle & & \displaystyle N_{\widetilde{W}_{n},\widetilde{H}}(B)\nonumber\\ \displaystyle & & \displaystyle \quad =\frac{1}{4}\#\left\{(\mathbf{x},\mathbf{y})\in \mathbb{Z}^{n}\times \mathbb{Z}_{\neq 0}^{n}:\begin{array}{@{}l@{}}\widetilde{H}(\mathbf{x},\mathbf{y})\leqslant B\\ (\mathbf{x},\mathbf{y})\text{ satisfy (1.1)}\\ \gcd (x_{1},\ldots ,x_{n})=\gcd (y_{1},\ldots ,y_{n})=1\end{array}\right\}.\nonumber\end{eqnarray}$$
Clearly, we have
$$\begin{eqnarray}\displaystyle & & \displaystyle N_{\widetilde{W}_{n},\widetilde{H}}(B)\nonumber\\ \displaystyle & & \displaystyle \quad =2^{n-2}\#\left\{(\mathbf{x},\mathbf{y})\in \mathbb{Z}^{n}\times \mathbb{Z}_{{>}0}^{n}:\begin{array}{@{}l@{}}\widetilde{H}(\mathbf{x},\mathbf{y})\leqslant B\\ (\mathbf{x},\mathbf{y})\text{ satisfy (1.1)}\\ \gcd (x_{1},\ldots ,x_{n})=\gcd (y_{1},\ldots ,y_{n})=1\end{array}\right\}.\nonumber\end{eqnarray}$$
We can still rewrite the equation (1.1) as (2.1) using Lemma 1, but we can no longer deduce that
$z_{2^{j-1}}=1$
. We only have the divisibility relation
$z_{2^{j-1}}\mid x_{j}$
. However, we have
$z_{N}=1$
.
Finally, one gets
$$\begin{eqnarray}\displaystyle & & \displaystyle N_{\widetilde{W}_{3},\widetilde{H}}(B)\nonumber\\ \displaystyle & & \displaystyle \quad =2\#\left\{(\mathbf{x},\mathbf{z})\in \mathbb{Z}^{n}\times \mathbb{Z}_{{>}0}^{N-1}:\begin{array}{@{}l@{}}\displaystyle \max _{1\leqslant i\leqslant n}|x_{i}|^{n-1}\max _{1\leqslant i\leqslant n}\biggl|\mathop{\prod }_{1\leqslant h\leqslant N-1}z_{h}^{\unicode[STIX]{x1D716}_{i}(h)}\biggr|\leqslant B\\ \displaystyle \mathop{\sum }_{i=1}^{n}x_{i}d_{i}=0\\ \gcd (x_{1},\ldots ,x_{n})=1,(z_{h})_{1\leqslant h\leqslant N-1}\text{ reduced}\end{array}\right\}\nonumber\end{eqnarray}$$
and, particularly, in the case
$n=3$
, we obtain
$$\begin{eqnarray}\displaystyle & & \displaystyle N_{\widetilde{W}_{3},\widetilde{H}}(B)\nonumber\\ \displaystyle & & \displaystyle \quad =2\#\left\{(\mathbf{x},\mathbf{z})\in \mathbb{Z}^{3}\times \mathbb{Z}_{{>}0}^{6}:\begin{array}{@{}l@{}}\displaystyle \max _{1\leqslant i\leqslant 3}|x_{i}|^{2}\max \{z_{1}z_{3}z_{5},z_{2}z_{3}z_{6},z_{4}z_{5}z_{6}\}\leqslant B\\ x_{1}z_{2}z_{4}z_{6}+x_{2}z_{1}z_{4}z_{5}+x_{3}z_{1}z_{2}z_{3}=0\\ \gcd (x_{1},x_{2},x_{3})=1,(z_{h})_{1\leqslant h\leqslant 6}\text{ reduced}\end{array}\right\}\nonumber\\ \displaystyle & & \displaystyle \quad =2\#\left\{(\mathbf{x}^{\prime },\mathbf{z})\in \mathbb{Z}^{3}\times \mathbb{Z}_{{>}0}^{6}:\right.\nonumber\\ \displaystyle & & \displaystyle \quad \left.\begin{array}{@{}l@{}}\displaystyle \max \{z_{1}|x_{1}^{\prime }|,z_{2}|x_{2}^{\prime }|,z_{4}|x_{3}^{\prime }|\}^{2}\max \{z_{1}z_{3}z_{5},z_{2}z_{3}z_{6},z_{4}z_{5}z_{6}\}\leqslant B\\ x_{1}^{\prime }z_{6}+x_{2}^{\prime }z_{5}+x_{3}^{\prime }z_{3}=0\\ \gcd (z_{1}x_{1}^{\prime },z_{2}x_{2}^{\prime },z_{4}x_{3}^{\prime })=1,(z_{h})_{1\leqslant h\leqslant 6}\text{ reduced}\end{array}\right\}.\end{eqnarray}$$
It is easily seen that the coprimality conditions given by
$\gcd (z_{1}x_{1}^{\prime },z_{2}x_{2}^{\prime },z_{4}x_{3}^{\prime })=1$
and
$(z_{h})_{1\leqslant h\leqslant 6}$
reduced are equivalent to
$$\begin{eqnarray}\gcd (x_{1}^{\prime },x_{2}^{\prime },x_{3}^{\prime })=\gcd (x_{1}^{\prime },x_{2}^{\prime },z_{3})=\gcd (x_{1}^{\prime },z_{5},x_{3}^{\prime })=\gcd (z_{6},x_{2}^{\prime },x_{3}^{\prime })=1\end{eqnarray}$$
together with the fact that
$(z_{h})_{1\leqslant h\leqslant 6}$
is reduced. It then follows from [Reference Blomer, Brüdern, Blomer and Mihailescu6] that the open subvariety of
$\mathbb{A}^{9}$
given by the equation
$x_{1}^{\prime }z_{6}+x_{2}^{\prime }z_{5}+x_{3}^{\prime }z_{3}=0$
along with the conditions
$$\begin{eqnarray}\displaystyle & (x_{1}^{\prime },x_{2}^{\prime },x_{3}^{\prime })\neq (0,0,0),\qquad (x_{1}^{\prime },x_{2}^{\prime },z_{3})\neq (0,0,0), & \displaystyle \nonumber\\ \displaystyle & (x_{1}^{\prime },z_{5},x_{3}^{\prime })\neq (0,0,0),\qquad (z_{6},x_{2}^{\prime },x_{3}^{\prime })\neq (0,0,0) & \displaystyle \nonumber\end{eqnarray}$$
and
$$\begin{eqnarray}\displaystyle & (z_{1},z_{2})\neq (0,0),\qquad (z_{1},z_{4})\neq (0,0),\qquad (z_{1},z_{6})\neq (0,0), & \displaystyle \nonumber\\ \displaystyle & (z_{2},z_{4})\neq (0,0),\qquad (z_{2},z_{5})\neq (0,0),\qquad (z_{3},z_{4})\neq (0,0), & \displaystyle \nonumber\\ \displaystyle & (z_{3},z_{5})\neq (0,0),\qquad (z_{3},z_{6})\neq (0,0),\qquad (z_{5},z_{6})\neq (0,0) & \displaystyle \nonumber\end{eqnarray}$$
is the versal torsor of the minimal desingularization of
$\widetilde{W}_{3}$
and, hence, through this parametrization, we just performed a descent on the versal torsor of this minimal desingularization of
$\widetilde{W}_{3}$
.
3 Geometry and the constant in the case
$\mathbb{P}^{1}\times \mathbb{P}^{1}\times \mathbb{P}^{1}$
We give in this section the proof of Theorem 3. For example, [Reference Browning15] yields that the surface
$S\subseteq \mathbb{P}^{6}$
cut out by the following nine quadrics:
$$\begin{eqnarray}\displaystyle X_{1}^{2}-X_{2}X_{4} & = & \displaystyle X_{1}X_{5}-X_{3}X_{4}=X_{1}X_{3}-X_{2}X_{5}=X_{1}X_{6}-X_{3}X_{5}\nonumber\\ \displaystyle & = & \displaystyle X_{2}X_{6}-X_{3}^{2}=X_{4}X_{6}-X_{5}^{2}=X_{1}^{2}-X_{1}X_{4}+X_{5}X_{7}\nonumber\\ \displaystyle & = & \displaystyle X_{1}^{2}-X_{1}X_{2}-X_{3}X_{7}=X_{1}X_{3}-X_{1}X_{5}+X_{6}X_{7}=0\nonumber\end{eqnarray}$$
is a del Pezzo surface of degree 6 of singularity type
$\mathbf{A}_{1}$
with three lines, the lines being given by
$$\begin{eqnarray}X_{1}=X_{2}=X_{3}=X_{5}=X_{6}=0,\qquad X_{1}=X_{3}=X_{4}=X_{5}=X_{6}=0\end{eqnarray}$$
and
$$\begin{eqnarray}X_{3}=X_{5}=X_{6}=X_{1}-X_{4}=X_{1}-X_{2}=0.\end{eqnarray}$$
The maps
$f:\widetilde{W}_{3}\rightarrow S$
given by
$$\begin{eqnarray}\left\{\begin{array}{@{}l@{}}X_{1}=-y_{3}x_{1}x_{2},\\ X_{2}=-x_{1}(x_{2}y_{3}+x_{3}y_{2}),\\ X_{3}=-y_{2}y_{3}x_{1},\\ X_{4}=-x_{2}(x_{1}y_{3}+x_{3}y_{1}),\\ X_{5}=y_{1}y_{3}x_{2},\\ X_{6}=y_{1}y_{2}y_{3},\\ X_{7}=x_{1}x_{2}x_{3}\end{array}\right.\end{eqnarray}$$
and
$g:S\rightarrow \widetilde{W}_{3}$
given by
$$\begin{eqnarray}g([X_{1}:\cdots :X_{7}])=([X_{1}:-X_{5}],[X_{5}:X_{6}],[X_{7}:-X_{1}])\end{eqnarray}$$
are well defined and inverse from each other. Thus,
$\widetilde{W}_{3}\cong S$
and is therefore a del Pezzo surface of degree 6 of singularity type
$\mathbf{A}_{1}$
with three lines, the lines being given by
$y_{i}=y_{j}=0$
for
$1\leqslant i\neq j\leqslant 3$
. As mentioned in the introduction, it follows then from [Reference Loughran25] and from this isomorphism that
$\widehat{W}_{3}$
is an equivariant compactification of
$\mathbb{G}_{a}^{2}$
and Theorem 2 can be derived from the more general work of Chambert-Loir and Tschinkel [Reference Chambert-Loir and Tschinkel18]. However, the method presented here using a descent on the versal torsor is different from the method in [Reference Chambert-Loir and Tschinkel18] and it is always interesting to unravel a different proof.
Let us denote by
$\widetilde{W}_{3}^{\ast }$
the minimal desingularization of
$\widetilde{W}_{3}$
. The fact that the open subvariety
$O\subseteq \mathbb{A}^{7}$
given by
$$\begin{eqnarray}x_{1}z_{1}+x_{2}z_{2}+x_{3}z_{3}=0\end{eqnarray}$$
with the conditions
$$\begin{eqnarray}(x_{1},z_{2}z_{3}z_{4})\neq 0,\qquad (x_{2},z_{1}z_{3}z_{4})\neq 0,\qquad (x_{3},z_{1}z_{2}z_{4})\neq 0\end{eqnarray}$$
and
$$\begin{eqnarray}(z_{1},z_{2})\neq 0,\qquad (z_{1},z_{3})\neq 0,\qquad (z_{2},z_{3})\neq 0\end{eqnarray}$$
is the versal torsor of
$\widetilde{W}_{3}^{\ast }$
is a consequence of work of Derenthal [Reference Derenthal20].
To conclude, let us briefly justify why the leading constant of Theorem 2,
$$\begin{eqnarray}\frac{1}{144}(\unicode[STIX]{x1D70B}^{2}+24\log 2-3)\mathop{\prod }_{p}\biggl(1-\frac{1}{p}\biggr)^{4}\biggl(1+\frac{4}{p}+\frac{1}{p^{2}}\biggr),\end{eqnarray}$$
agrees with Peyre’s prediction.
First of all, the variety
$\widetilde{W}_{3}$
being rational, we know that
$\unicode[STIX]{x1D6FD}(\widetilde{W}_{3}^{\ast })=1$
and work from Derenthal [Reference Derenthal20] immediately yields
$\unicode[STIX]{x1D6FC}(\widetilde{W}_{3}^{\ast })=\frac{1}{144}$
. We now have that
$$\begin{eqnarray}\unicode[STIX]{x1D714}_{H}(\widetilde{W}_{3}^{\ast }(\mathbb{A}_{\mathbb{ Q}}))=\unicode[STIX]{x1D714}_{\infty }\mathop{\prod }_{p}\unicode[STIX]{x1D714}_{p}\end{eqnarray}$$
with
$\unicode[STIX]{x1D714}_{p}$
and
$\unicode[STIX]{x1D714}_{\infty }$
being respectively the
$p$
-adic and archimedean densities. It is now easy to get that
$$\begin{eqnarray}\unicode[STIX]{x1D714}_{p}=\frac{\#O(\mathbb{F}_{p})}{p^{6}}=\biggl(1-\frac{1}{p}\biggr)^{4}\biggl(1+\frac{4}{p}+\frac{1}{p^{2}}\biggr)\end{eqnarray}$$
either by direct computation or by calling upon a more general result of Loughran [Reference Loughran25]. Turning to the archimedean density and reasoning like in [Reference Blomer, Brüdern and Salberger7], one gets that
$\unicode[STIX]{x1D714}_{\infty }$
is given by the archimedean density on the open subset
$y_{1}\neq 0$
,
$y_{2}\neq 0$
and
$y_{3}\neq 0$
of
$\widetilde{W}_{3}$
. This is the affine variety given by the equation
$$\begin{eqnarray}u_{1}+u_{2}+u_{3}=0.\end{eqnarray}$$
Using a Leray form to parametrize in
$u_{3}$
, one finally obtains
$$\begin{eqnarray}\unicode[STIX]{x1D714}_{\infty }=\int _{-\infty }^{+\infty }\int _{-\infty }^{+\infty }\frac{du_{1}\,du_{2}}{\max (|u_{1}|,1)\max (|u_{2}|,1)\max (|u_{1}+u_{2}|,1)}.\end{eqnarray}$$
An easy computation now yields
$$\begin{eqnarray}\int _{-\infty }^{+\infty }\int _{-\infty }^{+\infty }\frac{du_{1}\,du_{2}}{\max (|u_{1}|,1)\max (|u_{2}|,1)\max (|u_{1}+u_{2}|,1)}=\unicode[STIX]{x1D70B}^{2}+24\log 2-3,\end{eqnarray}$$
which finally shows that the conjectural value of Peyre’s constant is
$$\begin{eqnarray}\displaystyle & & \displaystyle \unicode[STIX]{x1D6FC}(\widetilde{W}_{3}^{\ast })\unicode[STIX]{x1D6FD}(\widetilde{W}_{3}^{\ast })\unicode[STIX]{x1D714}_{H}(\widetilde{W}_{3}^{\ast }(\mathbb{A}_{\mathbb{Q}}))\nonumber\\ \displaystyle & & \displaystyle \quad =\frac{1}{144}(\unicode[STIX]{x1D70B}^{2}+24\log 2-3)\mathop{\prod }_{p}\biggl(1-\frac{1}{p}\biggr)^{4}\biggl(1+\frac{4}{p}+\frac{1}{p^{2}}\biggr)\nonumber\end{eqnarray}$$
and hence that the leading constant in Theorem 2 agrees with Peyre’s prediction.
4 The parabolic Eisenstein series and smooth approximations
We quote the following lemma from [Reference Bettin4, Lemma 4 and Remark 2].
Lemma 2. Let
$$\begin{eqnarray}\displaystyle {\mathcal{A}}_{\boldsymbol{a}}(\boldsymbol{\unicode[STIX]{x1D6FC}},\boldsymbol{\unicode[STIX]{x1D6FD}}):=\frac{1}{8}\mathop{\sum }_{\substack{ n_{1},n_{2},n_{3},m_{1},m_{2},m_{3}\in \mathbb{Z}_{\neq 0}, \\ a_{1}n_{1}m_{1}+a_{2}n_{2}m_{2}+a_{3}n_{3}m_{3}=0}}\frac{1}{|n_{1}|^{\unicode[STIX]{x1D6FC}_{1}}|m_{1}|^{\unicode[STIX]{x1D6FD}_{1}}|n_{2}|^{\unicode[STIX]{x1D6FC}_{2}}|m_{2}|^{\unicode[STIX]{x1D6FD}_{2}}|n_{3}|^{\unicode[STIX]{x1D6FC}_{3}}|m_{3}|^{\unicode[STIX]{x1D6FD}_{3}}}, & & \displaystyle \nonumber\\ \displaystyle & & \displaystyle\end{eqnarray}$$
where
$\boldsymbol{a}=(a_{1},a_{2},a_{3})\in \mathbb{Z}_{\neq 0}^{3}$
and
$\boldsymbol{\unicode[STIX]{x1D6FC}}=(\unicode[STIX]{x1D6FC}_{1},\unicode[STIX]{x1D6FC}_{2},\unicode[STIX]{x1D6FC}_{3}),\boldsymbol{\unicode[STIX]{x1D6FD}}=(\unicode[STIX]{x1D6FD}_{1},\unicode[STIX]{x1D6FD}_{2},\unicode[STIX]{x1D6FD}_{3})\in \mathbb{C}^{3}$
are such that
$\Re (\unicode[STIX]{x1D6FC}_{i}),\Re (\unicode[STIX]{x1D6FD}_{i})>1$
for all
$i\in \{1,2,3\}$
. Then
${\mathcal{A}}_{\boldsymbol{a}}(\boldsymbol{\unicode[STIX]{x1D6FC}},\boldsymbol{\unicode[STIX]{x1D6FD}})$
converges absolutely if
$\Re (\unicode[STIX]{x1D6FC}_{i}),\Re (\unicode[STIX]{x1D6FD}_{i})>\frac{2}{3}$
for all
$i\in \{1,2,3\}$
. Moreover, for
$\frac{2}{3}+\unicode[STIX]{x1D700}<\Re (\unicode[STIX]{x1D6FC}_{i}),\Re (\unicode[STIX]{x1D6FD}_{i})\leqslant \frac{11}{12}$
, it satisfies
${\mathcal{A}}_{\boldsymbol{a}}(\boldsymbol{\unicode[STIX]{x1D6FC}},\boldsymbol{\unicode[STIX]{x1D6FD}})\ll 1$
and
$$\begin{eqnarray}\displaystyle {\mathcal{A}}_{\boldsymbol{a}}(\boldsymbol{\unicode[STIX]{x1D6FC}},\boldsymbol{\unicode[STIX]{x1D6FD}})={\mathcal{M}}_{\boldsymbol{a}}(\boldsymbol{\unicode[STIX]{x1D6FC}},\boldsymbol{\unicode[STIX]{x1D6FD}})+{\mathcal{E}}_{\boldsymbol{a}}(\boldsymbol{\unicode[STIX]{x1D6FC}},\boldsymbol{\unicode[STIX]{x1D6FD}}), & & \displaystyle\end{eqnarray}$$
where
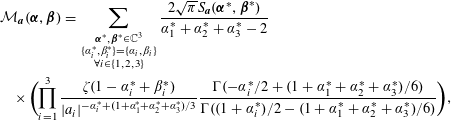$$\begin{eqnarray}\displaystyle & & \displaystyle {\mathcal{M}}_{\boldsymbol{a}}(\boldsymbol{\unicode[STIX]{x1D6FC}},\boldsymbol{\unicode[STIX]{x1D6FD}})=\mathop{\sum }_{\substack{ \boldsymbol{\unicode[STIX]{x1D6FC}}^{\ast },\boldsymbol{\unicode[STIX]{x1D6FD}}^{\ast }\in \mathbb{C}^{3} \\ \{\unicode[STIX]{x1D6FC}_{i}^{\ast },\unicode[STIX]{x1D6FD}_{i}^{\ast }\}=\{\unicode[STIX]{x1D6FC}_{i},\unicode[STIX]{x1D6FD}_{i}\} \\ \forall i\in \{1,2,3\}}}\frac{2\sqrt{\unicode[STIX]{x1D70B}}S_{\boldsymbol{a}}(\boldsymbol{\unicode[STIX]{x1D6FC}}^{\ast },\boldsymbol{\unicode[STIX]{x1D6FD}}^{\ast })}{\unicode[STIX]{x1D6FC}_{1}^{\ast }+\unicode[STIX]{x1D6FC}_{2}^{\ast }+\unicode[STIX]{x1D6FC}_{3}^{\ast }-2}\nonumber\\ \displaystyle & & \displaystyle \quad \times \,\biggl(\mathop{\prod }_{i=1}^{3}\frac{\unicode[STIX]{x1D701}(1-\unicode[STIX]{x1D6FC}_{i}^{\ast }+\unicode[STIX]{x1D6FD}_{i}^{\ast })}{|a_{i}|^{-\unicode[STIX]{x1D6FC}_{i}^{\ast }+(1+\unicode[STIX]{x1D6FC}_{1}^{\ast }+\unicode[STIX]{x1D6FC}_{2}^{\ast }+\unicode[STIX]{x1D6FC}_{3}^{\ast })/3}}\frac{\unicode[STIX]{x1D6E4}(-\unicode[STIX]{x1D6FC}_{i}^{\ast }/2+(1+\unicode[STIX]{x1D6FC}_{1}^{\ast }+\unicode[STIX]{x1D6FC}_{2}^{\ast }+\unicode[STIX]{x1D6FC}_{3}^{\ast })/6)}{\unicode[STIX]{x1D6E4}((1+\unicode[STIX]{x1D6FC}_{i}^{\ast })/2-(1+\unicode[STIX]{x1D6FC}_{1}^{\ast }+\unicode[STIX]{x1D6FC}_{2}^{\ast }+\unicode[STIX]{x1D6FC}_{3}^{\ast })/6)}\biggr),\nonumber\end{eqnarray}$$
with
$$\begin{eqnarray}\displaystyle S_{\boldsymbol{a}}(\boldsymbol{\unicode[STIX]{x1D6FC}}^{\ast },\boldsymbol{\unicode[STIX]{x1D6FD}}^{\ast }):=\mathop{\sum }_{\ell \geqslant 1}\frac{(a_{1},\ell )^{1-\unicode[STIX]{x1D6FC}_{1}^{\ast }+\unicode[STIX]{x1D6FD}_{1}^{\ast }}(a_{2},\ell )^{1-\unicode[STIX]{x1D6FC}_{2}^{\ast }+\unicode[STIX]{x1D6FD}_{2}^{\ast }}(a_{3},\ell )^{1-\unicode[STIX]{x1D6FC}_{3}^{\ast }+\unicode[STIX]{x1D6FD}_{3}^{\ast }}}{\ell ^{3-\mathop{\sum }_{i=1}^{3}(\unicode[STIX]{x1D6FC}_{i}^{\ast }-\unicode[STIX]{x1D6FD}_{i}^{\ast })}}\unicode[STIX]{x1D711}(\ell ) & & \displaystyle \nonumber\end{eqnarray}$$
and where
${\mathcal{E}}_{\boldsymbol{a}}(\boldsymbol{\unicode[STIX]{x1D6FC}},\boldsymbol{\unicode[STIX]{x1D6FD}})$
is a holomorphic function on
$$\begin{eqnarray}\displaystyle & & \displaystyle \unicode[STIX]{x1D6FA}_{\unicode[STIX]{x1D700}}:=\{(\boldsymbol{\unicode[STIX]{x1D6FC}},\boldsymbol{\unicode[STIX]{x1D6FD}})\in \mathbb{C}^{6}\mid \Re (\unicode[STIX]{x1D6FC}_{i}),\Re (\unicode[STIX]{x1D6FD}_{i})\in [{\textstyle \frac{5}{12}}+\unicode[STIX]{x1D700},{\textstyle \frac{11}{12}}-\unicode[STIX]{x1D700}]\nonumber\\ \displaystyle & & \displaystyle \qquad \qquad \forall i\in \{1,2,3\},~\unicode[STIX]{x1D702}<{\textstyle \frac{2}{9}}-\unicode[STIX]{x1D700}\}\end{eqnarray}$$
for all
$\unicode[STIX]{x1D700}>0$
with
$\unicode[STIX]{x1D702}:=\sum _{i=1}^{3}(|\Re (\unicode[STIX]{x1D6FC}_{i})-\frac{2}{3}|+|\Re (\unicode[STIX]{x1D6FD}_{i})-\frac{2}{3}|)$
. Moreover, for
$(\boldsymbol{\unicode[STIX]{x1D6FC}},\boldsymbol{\unicode[STIX]{x1D6FD}})\in \unicode[STIX]{x1D6FA}_{\unicode[STIX]{x1D700}}$
, one has
$$\begin{eqnarray}\displaystyle {\mathcal{E}}_{\boldsymbol{a}}(\boldsymbol{\unicode[STIX]{x1D6FC}},\boldsymbol{\unicode[STIX]{x1D6FD}})\ll \biggl(\!\biggl(\max _{1\leqslant i\leqslant 3}|a_{i}|\biggr)^{14}\biggl(\!1+\max _{1\leqslant i\leqslant 3}(|\Im (\unicode[STIX]{x1D6FC}_{i})|+|\Im (\unicode[STIX]{x1D6FD}_{i})|)\biggr)^{21}\biggr)^{(9\unicode[STIX]{x1D702}+18\unicode[STIX]{x1D700})/(4-9\unicode[STIX]{x1D702})}. & & \displaystyle \nonumber\\ \displaystyle & & \displaystyle\end{eqnarray}$$
Remark.
Note that the sum over
$\boldsymbol{\unicode[STIX]{x1D6FC}}^{\ast },\boldsymbol{\unicode[STIX]{x1D6FD}}^{\ast }\in \mathbb{C}^{3}$
such that
$\{\unicode[STIX]{x1D6FC}_{i}^{\ast },\unicode[STIX]{x1D6FD}_{i}^{\ast }\}=\{\unicode[STIX]{x1D6FC}_{i},\unicode[STIX]{x1D6FD}_{i}\}$
for all
$i\in \{1,2,3\}$
appearing in the definition of the quantity
${\mathcal{M}}_{\boldsymbol{a}}(\boldsymbol{\unicode[STIX]{x1D6FC}},\boldsymbol{\unicode[STIX]{x1D6FD}})$
contains eight terms given by
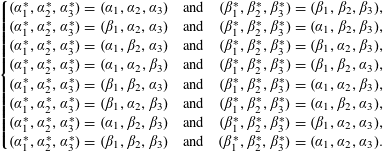$$\begin{eqnarray}\left\{\begin{array}{@{}l@{}}(\unicode[STIX]{x1D6FC}_{1}^{\ast },\unicode[STIX]{x1D6FC}_{2}^{\ast },\unicode[STIX]{x1D6FC}_{3}^{\ast })=(\unicode[STIX]{x1D6FC}_{1},\unicode[STIX]{x1D6FC}_{2},\unicode[STIX]{x1D6FC}_{3})\quad \text{and}\quad (\unicode[STIX]{x1D6FD}_{1}^{\ast },\unicode[STIX]{x1D6FD}_{2}^{\ast },\unicode[STIX]{x1D6FD}_{3}^{\ast })=(\unicode[STIX]{x1D6FD}_{1},\unicode[STIX]{x1D6FD}_{2},\unicode[STIX]{x1D6FD}_{3}),\\ (\unicode[STIX]{x1D6FC}_{1}^{\ast },\unicode[STIX]{x1D6FC}_{2}^{\ast },\unicode[STIX]{x1D6FC}_{3}^{\ast })=(\unicode[STIX]{x1D6FD}_{1},\unicode[STIX]{x1D6FC}_{2},\unicode[STIX]{x1D6FC}_{3})\quad \text{and}\quad (\unicode[STIX]{x1D6FD}_{1}^{\ast },\unicode[STIX]{x1D6FD}_{2}^{\ast },\unicode[STIX]{x1D6FD}_{3}^{\ast })=(\unicode[STIX]{x1D6FC}_{1},\unicode[STIX]{x1D6FD}_{2},\unicode[STIX]{x1D6FD}_{3}),\\ (\unicode[STIX]{x1D6FC}_{1}^{\ast },\unicode[STIX]{x1D6FC}_{2}^{\ast },\unicode[STIX]{x1D6FC}_{3}^{\ast })=(\unicode[STIX]{x1D6FC}_{1},\unicode[STIX]{x1D6FD}_{2},\unicode[STIX]{x1D6FC}_{3})\quad \text{and}\quad (\unicode[STIX]{x1D6FD}_{1}^{\ast },\unicode[STIX]{x1D6FD}_{2}^{\ast },\unicode[STIX]{x1D6FD}_{3}^{\ast })=(\unicode[STIX]{x1D6FD}_{1},\unicode[STIX]{x1D6FC}_{2},\unicode[STIX]{x1D6FD}_{3}),\\ (\unicode[STIX]{x1D6FC}_{1}^{\ast },\unicode[STIX]{x1D6FC}_{2}^{\ast },\unicode[STIX]{x1D6FC}_{3}^{\ast })=(\unicode[STIX]{x1D6FC}_{1},\unicode[STIX]{x1D6FC}_{2},\unicode[STIX]{x1D6FD}_{3})\quad \text{and}\quad (\unicode[STIX]{x1D6FD}_{1}^{\ast },\unicode[STIX]{x1D6FD}_{2}^{\ast },\unicode[STIX]{x1D6FD}_{3}^{\ast })=(\unicode[STIX]{x1D6FD}_{1},\unicode[STIX]{x1D6FD}_{2},\unicode[STIX]{x1D6FC}_{3}),\\ (\unicode[STIX]{x1D6FC}_{1}^{\ast },\unicode[STIX]{x1D6FC}_{2}^{\ast },\unicode[STIX]{x1D6FC}_{3}^{\ast })=(\unicode[STIX]{x1D6FD}_{1},\unicode[STIX]{x1D6FD}_{2},\unicode[STIX]{x1D6FC}_{3})\quad \text{and}\quad (\unicode[STIX]{x1D6FD}_{1}^{\ast },\unicode[STIX]{x1D6FD}_{2}^{\ast },\unicode[STIX]{x1D6FD}_{3}^{\ast })=(\unicode[STIX]{x1D6FC}_{1},\unicode[STIX]{x1D6FC}_{2},\unicode[STIX]{x1D6FD}_{3}),\\ (\unicode[STIX]{x1D6FC}_{1}^{\ast },\unicode[STIX]{x1D6FC}_{2}^{\ast },\unicode[STIX]{x1D6FC}_{3}^{\ast })=(\unicode[STIX]{x1D6FD}_{1},\unicode[STIX]{x1D6FC}_{2},\unicode[STIX]{x1D6FD}_{3})\quad \text{and}\quad (\unicode[STIX]{x1D6FD}_{1}^{\ast },\unicode[STIX]{x1D6FD}_{2}^{\ast },\unicode[STIX]{x1D6FD}_{3}^{\ast })=(\unicode[STIX]{x1D6FC}_{1},\unicode[STIX]{x1D6FD}_{2},\unicode[STIX]{x1D6FC}_{3}),\\ (\unicode[STIX]{x1D6FC}_{1}^{\ast },\unicode[STIX]{x1D6FC}_{2}^{\ast },\unicode[STIX]{x1D6FC}_{3}^{\ast })=(\unicode[STIX]{x1D6FC}_{1},\unicode[STIX]{x1D6FD}_{2},\unicode[STIX]{x1D6FD}_{3})\quad \text{and}\quad (\unicode[STIX]{x1D6FD}_{1}^{\ast },\unicode[STIX]{x1D6FD}_{2}^{\ast },\unicode[STIX]{x1D6FD}_{3}^{\ast })=(\unicode[STIX]{x1D6FD}_{1},\unicode[STIX]{x1D6FC}_{2},\unicode[STIX]{x1D6FC}_{3}),\\ (\unicode[STIX]{x1D6FC}_{1}^{\ast },\unicode[STIX]{x1D6FC}_{2}^{\ast },\unicode[STIX]{x1D6FC}_{3}^{\ast })=(\unicode[STIX]{x1D6FD}_{1},\unicode[STIX]{x1D6FD}_{2},\unicode[STIX]{x1D6FD}_{3})\quad \text{and}\quad (\unicode[STIX]{x1D6FD}_{1}^{\ast },\unicode[STIX]{x1D6FD}_{2}^{\ast },\unicode[STIX]{x1D6FD}_{3}^{\ast })=(\unicode[STIX]{x1D6FC}_{1},\unicode[STIX]{x1D6FC}_{2},\unicode[STIX]{x1D6FC}_{3}).\end{array}\right.\end{eqnarray}$$
Proof. Let
$\boldsymbol{a}=(a_{1},a_{2},a_{3})\in \mathbb{Z}_{\neq 0}^{3}$
and
$\boldsymbol{\unicode[STIX]{x1D6FC}}=(\unicode[STIX]{x1D6FC}_{1},\unicode[STIX]{x1D6FC}_{2},\unicode[STIX]{x1D6FC}_{3}),\boldsymbol{\unicode[STIX]{x1D6FD}}=(\unicode[STIX]{x1D6FD}_{1},\unicode[STIX]{x1D6FD}_{2},\unicode[STIX]{x1D6FD}_{3})\in \mathbb{C}^{3}$
be such that
$\Re (\unicode[STIX]{x1D6FC}_{i}),\Re (\unicode[STIX]{x1D6FD}_{i})>1$
for all
$i\in \{1,2,3\}$
. It is easy to see that
${\mathcal{A}}_{\boldsymbol{a}}(\boldsymbol{\unicode[STIX]{x1D6FC}},\boldsymbol{\unicode[STIX]{x1D6FD}})$
converges absolutely if
$\Re (\unicode[STIX]{x1D6FC}_{i}),\Re (\unicode[STIX]{x1D6FD}_{i})>\frac{2}{3}$
for all
$i\in \{1,2,3\}$
by alluding to inequalities of the form
$x+y\geqslant 2\sqrt{xy}$
for
$x,y\geqslant 0$
.
We also clearly have
$$\begin{eqnarray}{\mathcal{A}}_{\boldsymbol{a}}(\boldsymbol{\unicode[STIX]{x1D6FC}},\boldsymbol{\unicode[STIX]{x1D6FD}})={\mathcal{A}}_{(-\unicode[STIX]{x1D700}_{1}a_{1},\unicode[STIX]{x1D700}_{2}a_{2},\unicode[STIX]{x1D700}_{3}a_{3})}(\boldsymbol{\unicode[STIX]{x1D6FC}},\boldsymbol{\unicode[STIX]{x1D6FD}})={\mathcal{A}}_{\mathbf{a},\boldsymbol{\unicode[STIX]{x1D6FC}}-2/3,\boldsymbol{\unicode[STIX]{x1D6FD}}-2/3}^{\ast }({\textstyle \frac{2}{3}}),\end{eqnarray}$$
with the notation of [Reference Bettin4, §2, (2.7)]. Therefore, [Reference Bettin4, Lemma 4] with
$k=3$
and
$3\unicode[STIX]{x1D700}$
instead of
$\unicode[STIX]{x1D700}$
implies the first part of the lemma, namely that for
$\frac{2}{3}+\unicode[STIX]{x1D700}<\Re (\unicode[STIX]{x1D6FC}_{i}),\Re (\unicode[STIX]{x1D6FD}_{i})\leqslant \frac{11}{12}$
, we have
${\mathcal{A}}_{\boldsymbol{a}}(\boldsymbol{\unicode[STIX]{x1D6FC}},\boldsymbol{\unicode[STIX]{x1D6FD}})\ll 1$
and
$$\begin{eqnarray}\displaystyle {\mathcal{A}}_{\boldsymbol{a}}(\boldsymbol{\unicode[STIX]{x1D6FC}},\boldsymbol{\unicode[STIX]{x1D6FD}})={\mathcal{M}}_{\boldsymbol{a}}(\boldsymbol{\unicode[STIX]{x1D6FC}},\boldsymbol{\unicode[STIX]{x1D6FD}})+{\mathcal{E}}_{\boldsymbol{a}}(\boldsymbol{\unicode[STIX]{x1D6FC}},\boldsymbol{\unicode[STIX]{x1D6FD}}), & & \displaystyle\end{eqnarray}$$
with
${\mathcal{M}}_{\boldsymbol{a}}(\boldsymbol{\unicode[STIX]{x1D6FC}},\boldsymbol{\unicode[STIX]{x1D6FD}})$
being given by the quantity
${\mathcal{M}}_{\mathbf{a},\boldsymbol{\unicode[STIX]{x1D6FC}}-2/3,\boldsymbol{\unicode[STIX]{x1D6FD}}-2/3}^{\ast }(\frac{2}{3})$
in [Reference Bettin4, Remark 2] with
$k=3$
and
${\mathcal{E}}_{\boldsymbol{a}}(\boldsymbol{\unicode[STIX]{x1D6FC}},\boldsymbol{\unicode[STIX]{x1D6FD}})$
being defined by
${\mathcal{A}}_{\boldsymbol{a}}(\boldsymbol{\unicode[STIX]{x1D6FC}},\boldsymbol{\unicode[STIX]{x1D6FD}})-{\mathcal{M}}_{\boldsymbol{a}}(\boldsymbol{\unicode[STIX]{x1D6FC}},\boldsymbol{\unicode[STIX]{x1D6FD}})$
. Now, the expression at the end of [Reference Bettin4, Remark 2] in which one has only one summand corresponding to
${\mathcal{I}}=\{1,2,3\}$
and
${\mathcal{J}}=\emptyset$
in the case
$k=3$
immediately yields the expression of
${\mathcal{M}}_{\boldsymbol{a}}(\boldsymbol{\unicode[STIX]{x1D6FC}},\boldsymbol{\unicode[STIX]{x1D6FD}})$
given in the statement of the lemma.
The final part of the lemma follows from [Reference Bettin4, Theorem 3] for
$k=3$
, with
$3\unicode[STIX]{x1D700}$
instead of
$\unicode[STIX]{x1D700}$
and after noticing that, contrary to [Reference Bettin4], we do not have the fraction
$\frac{3}{2}$
in front of the sum in the definition of
$\unicode[STIX]{x1D702}$
. Hence, in particular,
$\unicode[STIX]{x1D702}$
is given by
$\frac{3}{2}\unicode[STIX]{x1D702}_{\boldsymbol{\unicode[STIX]{x1D6FC}}-2/3,\boldsymbol{\unicode[STIX]{x1D6FD}}-2/3}$
, with the notation of [Reference Bettin4, Theorem 3].◻
Since Lemma 2 constitutes the main tool for our proof of Theorems 1 and 2, we say a few words about its proof. First, one divides the variables
$r_{i}=n_{i}m_{i}$
into various ranges and eliminates the largest one (say
$r_{1}$
) using the linear relation among them. In order to do this, one has to write
$\sum _{n_{1}m_{1}=r_{1}}|n_{1}|^{-\unicode[STIX]{x1D6FC}_{1}}|m_{1}|^{-\unicode[STIX]{x1D6FD}_{1}}$
in an efficient way in terms of the remaining variables. This is done by using (a shifted version of) the identity of Ramanujan for the divisor function
$\unicode[STIX]{x1D70F}$
in terms of Ramanujan sums, in combination with a careful use of Mellin transforms to separate variables in expressions such as
$(r_{2}\pm r_{3})^{s}$
. After the variables are completely separated, one applies Voronoi’s summation formula to the sums over
$r_{2}$
and
$r_{3}$
. The main terms will then give the polar structure, whereas the error term will produce functions which are holomorphic on the stated range.
The following lemma allows us to replace the characteristic function of the interval
$[0,1]$
by a smooth approximation at a cost of a controlled error.
Lemma 3. Let
$f(x)=\text{e}^{-1/(x-x^{2})}$
for
$0<x<1$
and
$f(x)=0$
otherwise. Let
$C:=\int _{0}^{1}f(y)\,dy$
and, for
$0<\unicode[STIX]{x1D6FF}<1/2$
, let
$$\begin{eqnarray}F_{\unicode[STIX]{x1D6FF}}^{\pm }(x):=\frac{1}{\unicode[STIX]{x1D6FF}C}\int _{x}^{+\infty }f\biggl(\frac{y-1+(1\mp 1)\unicode[STIX]{x1D6FF}/2}{\unicode[STIX]{x1D6FF}}\biggr)\,dy,\quad x\in \mathbb{R}^{+}.\end{eqnarray}$$
Then
$F_{\unicode[STIX]{x1D6FF}}^{\pm }\in {\mathcal{C}}^{\infty }(\mathbb{R}^{+})$
,
$F_{\unicode[STIX]{x1D6FF}}^{\pm }(x)=1$
for
$x\leqslant 1-\unicode[STIX]{x1D6FF}$
,
$F_{\unicode[STIX]{x1D6FF}}^{\pm }(x)=0$
for
$x\geqslant 1+\unicode[STIX]{x1D6FF}$
and, for
$x\geqslant 0$
,
$$\begin{eqnarray}0\leqslant F_{\unicode[STIX]{x1D6FF}}^{-}(x)\leqslant \unicode[STIX]{x1D712}_{[0,1]}(x)\leqslant F_{\unicode[STIX]{x1D6FF}}^{+}(x),\end{eqnarray}$$
where
$\unicode[STIX]{x1D712}_{[0,1]}$
is the indicator function of the interval
$[0,1].$
Moreover, the Mellin transform
$\tilde{F}_{\unicode[STIX]{x1D6FF}}^{\pm }(s)$
of
$F_{\unicode[STIX]{x1D6FF}}^{\pm }(x)$
is holomorphic in
$\mathbb{C}\setminus \{0\}$
with a simple pole of residue one at
$s=0$
and for all
$n\geqslant 0$
it satisfies for all
$s\in \mathbb{C}\setminus \{0\}$
,
$$\begin{eqnarray}\displaystyle \tilde{F}_{\unicode[STIX]{x1D6FF}}^{\pm }(s)\ll _{n}\frac{1}{\unicode[STIX]{x1D6FF}^{n}(1+|s|)^{n+1}},\qquad \tilde{F}_{\unicode[STIX]{x1D6FF}}^{\pm }(s)-\frac{1}{s}\ll \min (\unicode[STIX]{x1D6FF},(1+|s|)^{-1}).\quad & & \displaystyle\end{eqnarray}$$
Proof. The statements on
$F_{\unicode[STIX]{x1D6FF}}^{\pm }$
are immediate from the definitions. Moreover, assuming that
$\Re (s)>0$
and integrating by parts, we have
$$\begin{eqnarray}\displaystyle \tilde{F}_{\unicode[STIX]{x1D6FF}}^{\pm }(s) & = & \displaystyle \frac{1}{\unicode[STIX]{x1D6FF}Cs}\int _{0}^{+\infty }x^{s}f\biggl(\frac{x-1+(1\mp 1)\unicode[STIX]{x1D6FF}/2}{\unicode[STIX]{x1D6FF}}\biggr)\,dx\nonumber\\ \displaystyle & = & \displaystyle \frac{1}{sC}\int _{0}^{1}(1+\unicode[STIX]{x1D6FF}x-(1\mp 1)\unicode[STIX]{x1D6FF}/2)^{s}f(x)\,dx,\nonumber\end{eqnarray}$$
the last inequality resulting from a change of variable. This already shows that
$\tilde{F}_{\unicode[STIX]{x1D6FF}}^{\pm }$
is holomorphic in
$\mathbb{C}\setminus \{0\}$
with a simple pole of residue one at
$s=0$
. Integrating by parts
$n$
times then yields
$\tilde{F}_{\unicode[STIX]{x1D6FF}}^{\pm }(s)\ll _{n}\unicode[STIX]{x1D6FF}^{-n}(1+|s|)^{-n-1}$
, which also implies the second bound in (4.6) if
$\unicode[STIX]{x1D6FF}\geqslant 1/|s|$
. Finally, if
$\unicode[STIX]{x1D6FF}<1/|s|$
, we have
$$\begin{eqnarray}\displaystyle \tilde{F}_{\unicode[STIX]{x1D6FF}}^{\pm }(s)-\frac{1}{s}=\frac{1}{sC}\int _{0}^{1}((1+\unicode[STIX]{x1D6FF}x-(1\mp 1)\unicode[STIX]{x1D6FF}/2)^{s}-1)f(x)\,dx\ll \unicode[STIX]{x1D6FF} & & \displaystyle \nonumber\end{eqnarray}$$
since
$(1+x)^{s}=1+O(|sx|)$
for
$|sx|<1$
,
$|x|\leqslant \frac{1}{2}$
.◻
5 Proof of Theorem 2 neglecting the coprimality conditions
By §2.1, we need to count the integer solutions to
$$\begin{eqnarray}\displaystyle x_{1}z_{1}+x_{2}z_{3}+x_{3}z_{3}=0 & & \displaystyle\end{eqnarray}$$
satisfying the inequality
$\max \{|x_{1}|,z_{2}z_{3}z_{4}\}\times \max \{|x_{2}|,z_{1}z_{3}z_{4}\}\times \max \{|x_{3}|,z_{1}z_{2}z_{4}\}\leqslant B$
and the coprimality conditions
$$\begin{eqnarray}\displaystyle \begin{array}{@{}c@{}}\gcd (z_{1},z_{2})=\gcd (z_{1},z_{3})=\gcd (z_{2},z_{3})=1,\\ \gcd (x_{1},z_{2}z_{3}z_{4})=\gcd (x_{2},z_{1}z_{3}z_{4})=\gcd (x_{3},z_{2}z_{3}z_{4})=1,\end{array} & & \displaystyle\end{eqnarray}$$
with
$z_{1},z_{2},z_{3},z_{4}>0$
. The case where
$x_{1}x_{2}x_{3}=0$
can be dealt with easily and we postpone its treatment to §6, so we focus on the case where
$x_{1}x_{2}x_{3}\neq 0$
. We start with the following proposition, which gives an asymptotic formula for the number of solutions to the more general equation
$a_{1}x_{1}z_{1}+a_{2}x_{2}z_{3}+a_{3}x_{3}z_{3}=0$
without imposing any coprimality conditions. These conditions do not factor out immediately at the beginning of the argument, so one cannot deduce Theorem 2 directly from Proposition 1; however, it is instructive to prove this result first, as all the analytic difficulties are exactly the same but the notation and the arithmetic are simplified. In §6 we shall give the proof of Theorem 2 by performing the required arithmetic computations and indicating the minor differences in the analytic argument.
Proposition 1. Let
$B\geqslant 1$
and
$\unicode[STIX]{x1D700}>0$
. Let
$\boldsymbol{a}=(a_{1},a_{2},a_{3})\in \mathbb{Z}_{\neq 0}^{3}$
and
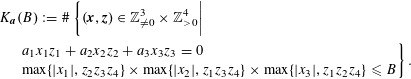$$\begin{eqnarray}\displaystyle & & \displaystyle K_{\boldsymbol{a}}(B):=\#\left.\left\{(\boldsymbol{x},\boldsymbol{z})\in \mathbb{Z}_{\neq 0}^{3}\times \mathbb{Z}_{{>}0}^{4}\right|\right.\nonumber\\ \displaystyle & & \displaystyle \quad \left.\begin{array}{@{}l@{}}a_{1}x_{1}z_{1}+a_{2}x_{2}z_{2}+a_{3}x_{3}z_{3}=0\\ \max \{|x_{1}|,z_{2}z_{3}z_{4}\}\times \max \{|x_{2}|,z_{1}z_{3}z_{4}\}\times \max \{|x_{3}|,z_{1}z_{2}z_{4}\}\leqslant B\end{array}\right\}.\qquad\end{eqnarray}$$
Then there exists a polynomial
$P_{\mathbf{a}}$
of degree
$3$
such that
$$\begin{eqnarray}\displaystyle K_{\boldsymbol{a}}(B):=BP_{\mathbf{a}}(\log B)+O_{\unicode[STIX]{x1D700}}\Bigl(B^{296/297+\unicode[STIX]{x1D700}}\max _{1\leqslant i\leqslant 3}|a_{i}|^{14}\Bigr), & & \displaystyle\end{eqnarray}$$
where the implied constant only depends on
$\unicode[STIX]{x1D700}$
. The coefficients of the polynomial
$P_{\mathbf{a}}$
are
$O(\max _{1\leqslant i\leqslant 3}|a_{i}|^{5})$
and the leading coefficient is
$\frac{1}{144}{\mathcal{I}}_{\boldsymbol{a}}\mathfrak{S}_{\boldsymbol{a}}^{\prime }$
, where
$$\begin{eqnarray}\displaystyle {\mathcal{I}}_{\boldsymbol{a}}:=\iint _{[-1,1]^{3}\times [0,1]^{2}}\unicode[STIX]{x1D712}_{[0,|a_{3}/z|]}\biggl(a_{1}\frac{x_{1}}{y_{1}}+a_{2}\frac{x_{2}}{y_{2}}\biggr)\,dx_{1}\,dx_{2}\,dz\frac{dy_{1}\,dy_{2}}{|a_{3}|y_{1}y_{2}}\quad & & \displaystyle\end{eqnarray}$$
and
$$\begin{eqnarray}\displaystyle \mathfrak{S}_{\boldsymbol{a}}^{\prime }:=\mathop{\sum }_{\ell =1}^{\infty }\frac{(a_{1},\ell )(a_{2},\ell )(a_{3},\ell )\unicode[STIX]{x1D711}(\ell )}{\ell ^{3}}. & & \displaystyle \nonumber\end{eqnarray}$$
Proof. In the set defining
$K_{\boldsymbol{a}}(B)$
we have eight inequalities coming from all the possible values taken by the maxima. In other words, given each subset
$I\subseteq S_{3}:=\{1,2,3\}$
we have the condition
$$\begin{eqnarray}\frac{(z_{1}z_{2}z_{3}z_{4})^{|J|}}{B}\mathop{\prod }_{i\in I}|x_{i}|\mathop{\prod }_{j\in J}z_{j}^{-1}\leqslant 1,\end{eqnarray}$$
where
$J:=S_{3}\setminus I$
. Now, let
$0<\unicode[STIX]{x1D6FF}<\frac{1}{2}$
and
$F_{\unicode[STIX]{x1D6FF}}^{\pm }$
be as in Lemma 3. Then we have
$K_{\boldsymbol{a}}^{-}(B)\leqslant K_{\boldsymbol{a}}(B)\leqslant K_{\boldsymbol{a}}^{+}(B)$
, where
$$\begin{eqnarray}\displaystyle K_{\boldsymbol{a}}^{\pm }(B):=\mathop{\sum }_{\substack{ (\boldsymbol{x},\boldsymbol{z})\in \mathbb{Z}_{\neq 0}^{3}\times \mathbb{Z}_{{>}0}^{4} \\ a_{1}x_{1}z_{1}+a_{2}x_{2}z_{2}+a_{3}x_{3}z_{3}=0}}\mathop{\prod }_{I\subseteq S_{3}}F_{\unicode[STIX]{x1D6FF}}^{\pm }\biggl(\frac{(z_{1}z_{2}z_{3}z_{4})^{|J|}}{B}\mathop{\prod }_{i\in I}|x_{i}|\mathop{\prod }_{j\in J}z_{j}^{-1}\biggr). & & \displaystyle \nonumber\end{eqnarray}$$
Clearly, it is sufficient to show that (5.4) holds for both
$K_{\boldsymbol{a}}^{-}(B)$
and
$K_{\boldsymbol{a}}^{+}(B)$
with the same polynomial
$P$
. We now write each
$F_{\unicode[STIX]{x1D6FF}}^{\pm }$
in terms of its Mellin transform using the variable
$s_{I}$
for the cut-off function corresponding to the set
$I$
. For brevity, we shall often indicate for example with
$s_{123}$
the variable
$s_{\{1,2,3\}}$
and with
$c_{\{1,2,3\}}$
or
$c_{123}$
the corresponding line of integration, and similarly for the other variables. In particular, we will denote by
$s$
the variable
$s_{\emptyset }$
. As lines of integration, we take
$c_{I}=|I|/12+\unicode[STIX]{x1D700}$
for all
$I$
for a fixed
$\unicode[STIX]{x1D700}>0$
small enough. Doing so, we obtain
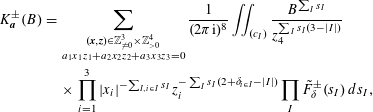$$\begin{eqnarray}\displaystyle K_{\boldsymbol{a}}^{\pm }(B) & = & \displaystyle \mathop{\sum }_{\substack{ (\boldsymbol{x},\boldsymbol{z})\in \mathbb{Z}_{\neq 0}^{3}\times \mathbb{Z}_{{>}0}^{4} \\ a_{1}x_{1}z_{1}+a_{2}x_{2}z_{2}+a_{3}x_{3}z_{3}=0}}\frac{1}{(2\unicode[STIX]{x1D70B}\text{i})^{8}}\iint _{(c_{I})}\frac{B^{\mathop{\sum }_{I}s_{I}}}{z_{4}^{\mathop{\sum }_{I}s_{I}(3-|I|)}}\nonumber\\ \displaystyle & & \displaystyle \times \,\mathop{\prod }_{i=1}^{3}|x_{i}|^{-\!\mathop{\sum }_{I,i\in I}s_{I}}z_{i}^{-\mathop{\sum }_{I}s_{I}(2+\unicode[STIX]{x1D6FF}_{i\in I}-|I|)}\mathop{\prod }_{I}\tilde{F}_{\unicode[STIX]{x1D6FF}}^{\pm }(s_{I})\,ds_{I},\nonumber\end{eqnarray}$$
where
$\unicode[STIX]{x1D6FF}_{i\in I}=1$
if
$i\in I$
and
$\unicode[STIX]{x1D6FF}_{i\in I}=0$
otherwise and where the sums inside the integrals are over
$I\subseteq S_{3}$
. Notice that with this choice we have
$$\begin{eqnarray}\displaystyle & \mathop{\sum }_{I\subseteq S_{3}}c_{I}=1+8\unicode[STIX]{x1D700},\qquad \mathop{\sum }_{\substack{ I\subseteq S_{3} \\ i\in I}}c_{I}=\frac{2}{3}+4\unicode[STIX]{x1D700}, & \displaystyle \nonumber\\ \displaystyle & \mathop{\sum }_{I\subseteq S_{3}}c_{I}(2+\unicode[STIX]{x1D6FF}_{i\in I}-|I|)=\frac{2}{3}+8\unicode[STIX]{x1D700},\qquad \mathop{\sum }_{I\subseteq S_{3}}c_{I}(3-|I|)=1+12\unicode[STIX]{x1D700}. & \displaystyle \nonumber\end{eqnarray}$$
In particular, the above series are absolutely convergent by Lemma 2. Now, write
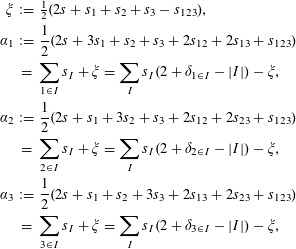$$\begin{eqnarray}\begin{array}{@{}rcl@{}}\displaystyle \unicode[STIX]{x1D709}\,\, & :=\,\, & {\textstyle \frac{1}{2}}(2s+s_{1}+s_{2}+s_{3}-s_{123}),\\ \unicode[STIX]{x1D6FC}_{1}\,\, & :=\,\, & \displaystyle \frac{1}{2}(2s+3s_{1}+s_{2}+s_{3}+2s_{12}+2s_{13}+s_{123})\\ \,\, & =\,\, & \displaystyle \mathop{\sum }_{1\in I}s_{I}+\unicode[STIX]{x1D709}=\mathop{\sum }_{I}s_{I}(2+\unicode[STIX]{x1D6FF}_{1\in I}-|I|)-\unicode[STIX]{x1D709},\\ \unicode[STIX]{x1D6FC}_{2}\,\, & :=\,\, & \displaystyle \frac{1}{2}(2s+s_{1}+3s_{2}+s_{3}+2s_{12}+2s_{23}+s_{123})\\ \,\, & =\,\, & \displaystyle \mathop{\sum }_{2\in I}s_{I}+\unicode[STIX]{x1D709}=\mathop{\sum }_{I}s_{I}(2+\unicode[STIX]{x1D6FF}_{2\in I}-|I|)-\unicode[STIX]{x1D709},\\ \unicode[STIX]{x1D6FC}_{3}\,\, & :=\,\, & \displaystyle \frac{1}{2}(2s+s_{1}+s_{2}+3s_{3}+2s_{13}+2s_{23}+s_{123})\\ \,\, & =\,\, & \displaystyle \mathop{\sum }_{3\in I}s_{I}+\unicode[STIX]{x1D709}=\mathop{\sum }_{I}s_{I}(2+\unicode[STIX]{x1D6FF}_{3\in I}-|I|)-\unicode[STIX]{x1D709},\end{array}\end{eqnarray}$$
where we are neglecting here the dependences on the variables
$s_{I}$
in the notation in order to simplify the exposition. Notice then that
$$\begin{eqnarray}\displaystyle \!\mathop{\sum }_{I\subseteq S_{3}}\!s_{I}=\frac{1}{2}(\unicode[STIX]{x1D6FC}_{1}+\unicode[STIX]{x1D6FC}_{2}+\unicode[STIX]{x1D6FC}_{3}-\unicode[STIX]{x1D709}),\qquad \mathop{\sum }_{I\subseteq S_{3}}\!s_{I}(3-|I|)=\frac{1}{2}(\unicode[STIX]{x1D6FC}_{1}+\unicode[STIX]{x1D6FC}_{2}+\unicode[STIX]{x1D6FC}_{3}+3\unicode[STIX]{x1D709}). & & \displaystyle \nonumber\end{eqnarray}$$
Thus, summing the Dirichlet series, we have
$$\begin{eqnarray}\displaystyle K_{\boldsymbol{a}}^{\pm }(B) & = & \displaystyle \frac{1}{(2\unicode[STIX]{x1D70B}\text{i})^{8}}\iint _{(c_{I})}B^{(1/2)(\unicode[STIX]{x1D6FC}_{1}+\unicode[STIX]{x1D6FC}_{2}+\unicode[STIX]{x1D6FC}_{3}-\unicode[STIX]{x1D709})}\nonumber\\ \displaystyle & & \displaystyle \times \,\unicode[STIX]{x1D701}\biggl(\frac{1}{2}(\unicode[STIX]{x1D6FC}_{1}+\unicode[STIX]{x1D6FC}_{2}+\unicode[STIX]{x1D6FC}_{3}+3\unicode[STIX]{x1D709})\biggr){\mathcal{A}}_{\boldsymbol{a}}(\boldsymbol{\unicode[STIX]{x1D6FC}}-\unicode[STIX]{x1D709},\boldsymbol{\unicode[STIX]{x1D6FC}}+\unicode[STIX]{x1D709})\mathop{\prod }_{I}\tilde{F}_{\unicode[STIX]{x1D6FF}}^{\pm }(s_{I})\,ds_{I},\nonumber\end{eqnarray}$$
with the notation of Lemma 2. By Lemma 2 and using the notation (4.5), we can split
${\mathcal{A}}_{\boldsymbol{a}}(\boldsymbol{\unicode[STIX]{x1D6FC}}-\unicode[STIX]{x1D709},\boldsymbol{\unicode[STIX]{x1D6FC}}+\unicode[STIX]{x1D709})$
into
$$\begin{eqnarray}{\mathcal{A}}_{\boldsymbol{a}}(\boldsymbol{\unicode[STIX]{x1D6FC}}-\unicode[STIX]{x1D709},\boldsymbol{\unicode[STIX]{x1D6FC}}+\unicode[STIX]{x1D709})={\mathcal{M}}_{\boldsymbol{a}}(\boldsymbol{\unicode[STIX]{x1D6FC}}-\unicode[STIX]{x1D709},\boldsymbol{\unicode[STIX]{x1D6FC}}+\unicode[STIX]{x1D709})+{\mathcal{E}}_{\boldsymbol{a}}(\boldsymbol{\unicode[STIX]{x1D6FC}}-\unicode[STIX]{x1D709},\boldsymbol{\unicode[STIX]{x1D6FC}}+\unicode[STIX]{x1D709}),\end{eqnarray}$$
thus obtaining the corresponding decomposition
$K_{\boldsymbol{a}}^{\pm }(B)=M_{\boldsymbol{a}}^{\pm }(B)+E_{\boldsymbol{a}}^{\pm }(B)$
, with
$$\begin{eqnarray}\displaystyle M_{\boldsymbol{a}}^{\pm }(B) & := & \displaystyle \frac{1}{(2\unicode[STIX]{x1D70B}\text{i})^{8}}\iint _{(c_{I})}B^{(1/2)(\unicode[STIX]{x1D6FC}_{1}+\unicode[STIX]{x1D6FC}_{2}+\unicode[STIX]{x1D6FC}_{3}-\unicode[STIX]{x1D709})}\nonumber\\ \displaystyle & & \displaystyle \times \,\unicode[STIX]{x1D701}\biggl(\frac{1}{2}(\unicode[STIX]{x1D6FC}_{1}+\unicode[STIX]{x1D6FC}_{2}+\unicode[STIX]{x1D6FC}_{3}+3\unicode[STIX]{x1D709})\biggr){\mathcal{M}}_{\boldsymbol{a}}(\boldsymbol{\unicode[STIX]{x1D6FC}}-\unicode[STIX]{x1D709},\boldsymbol{\unicode[STIX]{x1D6FC}}+\unicode[STIX]{x1D709})\nonumber\\ \displaystyle & & \displaystyle \times \,\mathop{\prod }_{I}\tilde{F}_{\unicode[STIX]{x1D6FF}}^{\pm }(s_{I})\,ds_{I}\end{eqnarray}$$
and
$$\begin{eqnarray}\displaystyle E_{\boldsymbol{a}}^{\pm }(B) & := & \displaystyle \frac{1}{(2\unicode[STIX]{x1D70B}\text{i})^{8}}\iint _{(c_{I})}B^{(1/2)(\unicode[STIX]{x1D6FC}_{1}+\unicode[STIX]{x1D6FC}_{2}+\unicode[STIX]{x1D6FC}_{3}-\unicode[STIX]{x1D709})}\nonumber\\ \displaystyle & & \displaystyle \times \,\unicode[STIX]{x1D701}\biggl(\frac{1}{2}(\unicode[STIX]{x1D6FC}_{1}+\unicode[STIX]{x1D6FC}_{2}+\unicode[STIX]{x1D6FC}_{3}+3\unicode[STIX]{x1D709})\biggr){\mathcal{E}}_{\boldsymbol{a}}(\boldsymbol{\unicode[STIX]{x1D6FC}}-\unicode[STIX]{x1D709},\boldsymbol{\unicode[STIX]{x1D6FC}}+\unicode[STIX]{x1D709})\mathop{\prod }_{I}\tilde{F}_{\unicode[STIX]{x1D6FF}}^{\pm }(s_{I})\,ds_{I}.\nonumber\end{eqnarray}$$
In the latter integral we move the line of integration
$c_{S_{3}}$
to
$c_{S_{3}}=\frac{1}{4}-\frac{2}{27}+6\unicode[STIX]{x1D700}=\frac{19}{108}+6\unicode[STIX]{x1D700}$
. Notice that by doing so, in the new lines of integration, we have
$\Re (\unicode[STIX]{x1D6FC}_{i}+\unicode[STIX]{x1D709})=\frac{2}{3}+8\unicode[STIX]{x1D700}$
and
$\Re (\unicode[STIX]{x1D6FC}_{i}-\unicode[STIX]{x1D709})=\frac{2}{3}-\frac{2}{27}+9\unicode[STIX]{x1D700}=\frac{16}{27}+9\unicode[STIX]{x1D700}$
for all
$i\in \{1,2,3\}$
. In particular, we have
$\unicode[STIX]{x1D702}=\sum _{i=1}^{3}(|\Re (\unicode[STIX]{x1D6FC}_{i}-\unicode[STIX]{x1D709})-\frac{2}{3}|+|\Re (\unicode[STIX]{x1D6FC}_{i}+\unicode[STIX]{x1D709})-\frac{2}{3}|)=\frac{2}{9}-3\unicode[STIX]{x1D700}$
on the new lines of integration. Moreover, since
$$\begin{eqnarray}\frac{\unicode[STIX]{x1D6FC}_{1}+\unicode[STIX]{x1D6FC}_{2}+\unicode[STIX]{x1D6FC}_{3}+3\unicode[STIX]{x1D709}}{2}=3s+2(s_{1}+s_{2}+s_{3})+s_{12}+s_{13}+s_{23}\end{eqnarray}$$
is independent of
$s_{123}$
, we have
$\Re (\frac{1}{2}(\unicode[STIX]{x1D6FC}_{1}+\unicode[STIX]{x1D6FC}_{2}+\unicode[STIX]{x1D6FC}_{3}+3\unicode[STIX]{x1D709}))=1+12\unicode[STIX]{x1D700}$
on the range
$\frac{19}{108}+6\unicode[STIX]{x1D700}\leqslant c_{S_{3}}\leqslant \frac{1}{4}+\unicode[STIX]{x1D700}$
and hence we stay on the right of the pole of the
$\unicode[STIX]{x1D701}$
-function. By (4.4), we then have for
$\unicode[STIX]{x1D700}$
small enough,
$$\begin{eqnarray}\displaystyle E_{\boldsymbol{a}}^{\pm }(B)\ll A^{14}B^{25/27+13\unicode[STIX]{x1D700}}\iint _{(c_{I})}\Bigl(1+\max _{I}|s_{I}|\Bigr)^{21}\mathop{\prod }_{I}|\tilde{F}_{\unicode[STIX]{x1D6FF}}^{\pm }(s_{I})|\,ds_{I}, & & \displaystyle \nonumber\end{eqnarray}$$
where
$A:=\max _{1\leqslant i\leqslant 3}|a_{i}|$
. Now, we have
$$\begin{eqnarray}\begin{array}{@{}c@{}}\displaystyle \int _{1}^{+\infty }\min \biggl(\frac{1}{x},\frac{1}{\unicode[STIX]{x1D6FF}x^{2}}\biggr)\,dx\ll |\text{log}\,\unicode[STIX]{x1D6FF}|\ll _{\unicode[STIX]{x1D700}}\unicode[STIX]{x1D6FF}^{-\unicode[STIX]{x1D700}},\\ \displaystyle \int _{1}^{+\infty }x^{21}\min \biggl(\frac{1}{x},\frac{1}{\unicode[STIX]{x1D6FF}^{22}x^{23}}\biggr)\,dx\leqslant \int _{1}^{1/\unicode[STIX]{x1D6FF}}x^{20}\,dx+\unicode[STIX]{x1D6FF}^{-22}\int _{1/\unicode[STIX]{x1D6FF}}^{+\infty }x^{-2}\,dx\ll \unicode[STIX]{x1D6FF}^{-21}\end{array}\end{eqnarray}$$
and so, using Lemma 3, we find that
$$\begin{eqnarray}\displaystyle E_{\boldsymbol{a}}^{\pm }(B)\ll A^{14}B^{25/27+13\unicode[STIX]{x1D700}}\unicode[STIX]{x1D6FF}^{-21-\unicode[STIX]{x1D700}}. & & \displaystyle\end{eqnarray}$$
Now, we consider the main term
$M_{\boldsymbol{a}}^{\pm }(B)$
defined in (5.7). We can write
${\mathcal{M}}_{\boldsymbol{a}}(\boldsymbol{\unicode[STIX]{x1D6FC}}-\unicode[STIX]{x1D709},\boldsymbol{\unicode[STIX]{x1D6FC}}+\unicode[STIX]{x1D709})$
as
$$\begin{eqnarray}\displaystyle {\mathcal{M}}_{\boldsymbol{a}}(\boldsymbol{\unicode[STIX]{x1D6FC}}-\unicode[STIX]{x1D709},\boldsymbol{\unicode[STIX]{x1D6FC}}+\unicode[STIX]{x1D709})=\mathop{\sum }_{k=0}^{3}\frac{\unicode[STIX]{x1D701}(1+2\unicode[STIX]{x1D709})^{k}\unicode[STIX]{x1D701}(1-2\unicode[STIX]{x1D709})^{3-k}}{\unicode[STIX]{x1D6FC}_{1}+\unicode[STIX]{x1D6FC}_{2}+\unicode[STIX]{x1D6FC}_{3}+(3-2k)\unicode[STIX]{x1D709}-2}{\mathcal{Q}}_{\boldsymbol{a},k}(\boldsymbol{\unicode[STIX]{x1D6FC}},\unicode[STIX]{x1D709}), & & \displaystyle \nonumber\end{eqnarray}$$
with
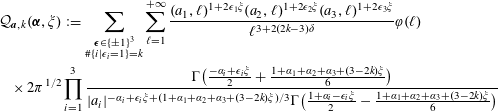$$\begin{eqnarray}\displaystyle & & \displaystyle {\mathcal{Q}}_{\boldsymbol{a},k}(\boldsymbol{\unicode[STIX]{x1D6FC}},\unicode[STIX]{x1D709}):=\mathop{\sum }_{\substack{ \boldsymbol{\unicode[STIX]{x1D716}}\in \{\pm 1\}^{3} \\ \#\{i\mid \unicode[STIX]{x1D716}_{i}=1\}=k}}\mathop{\sum }_{\ell =1}^{+\infty }\frac{(a_{1},\ell )^{1+2\unicode[STIX]{x1D716}_{1}\unicode[STIX]{x1D709}}(a_{2},\ell )^{1+2\unicode[STIX]{x1D716}_{2}\unicode[STIX]{x1D709}}(a_{3},\ell )^{1+2\unicode[STIX]{x1D716}_{3}\unicode[STIX]{x1D709}}}{\ell ^{3+2(2k-3)\unicode[STIX]{x1D6FF}}}\unicode[STIX]{x1D711}(\ell )\nonumber\\ \displaystyle & & \displaystyle \quad \times \,2\unicode[STIX]{x1D70B}^{1/2}\mathop{\prod }_{i=1}^{3}\frac{\unicode[STIX]{x1D6E4}\big(\frac{-\unicode[STIX]{x1D6FC}_{i}+\unicode[STIX]{x1D716}_{i}\unicode[STIX]{x1D709}}{2}+\frac{1+\unicode[STIX]{x1D6FC}_{1}+\unicode[STIX]{x1D6FC}_{2}+\unicode[STIX]{x1D6FC}_{3}+(3-2k)\unicode[STIX]{x1D709}}{6}\big)}{|a_{i}|^{-\unicode[STIX]{x1D6FC}_{i}+\unicode[STIX]{x1D716}_{i}\unicode[STIX]{x1D709}+(1+\unicode[STIX]{x1D6FC}_{1}+\unicode[STIX]{x1D6FC}_{2}+\unicode[STIX]{x1D6FC}_{3}+(3-2k)\unicode[STIX]{x1D709})/3}\unicode[STIX]{x1D6E4}\big(\frac{1+\unicode[STIX]{x1D6FC}_{i}-\unicode[STIX]{x1D716}_{i}\unicode[STIX]{x1D709}}{2}-\frac{1+\unicode[STIX]{x1D6FC}_{1}+\unicode[STIX]{x1D6FC}_{2}+\unicode[STIX]{x1D6FC}_{3}+(3-2k)\unicode[STIX]{x1D709}}{6}\big)}\nonumber\\ \displaystyle & & \displaystyle\end{eqnarray}$$
and where the sum is over
$\boldsymbol{\unicode[STIX]{x1D716}}=(\unicode[STIX]{x1D716}_{1},\unicode[STIX]{x1D716}_{2},\unicode[STIX]{x1D716}_{3})\in \{\pm 1\}^{3}$
. Notice that in the region
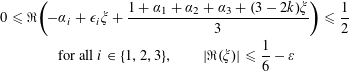$$\begin{eqnarray}\displaystyle & & \displaystyle 0\leqslant \Re \biggl(-\unicode[STIX]{x1D6FC}_{i}+\unicode[STIX]{x1D716}_{i}\unicode[STIX]{x1D709}+\frac{1+\unicode[STIX]{x1D6FC}_{1}+\unicode[STIX]{x1D6FC}_{2}+\unicode[STIX]{x1D6FC}_{3}+(3-2k)\unicode[STIX]{x1D709}}{3}\biggr)\leqslant \frac{1}{2}\nonumber\\ \displaystyle & & \displaystyle \qquad \qquad \text{for all }i\in \{1,2,3\},\qquad |\Re (\unicode[STIX]{x1D709})|\leqslant \frac{1}{6}-\unicode[STIX]{x1D700}\end{eqnarray}$$
we have that
${\mathcal{Q}}_{\boldsymbol{a},k}(\boldsymbol{\unicode[STIX]{x1D6FC}},\unicode[STIX]{x1D709})$
is holomorphic and satisfies
$$\begin{eqnarray}\displaystyle {\mathcal{Q}}_{\boldsymbol{a},k}(\boldsymbol{\unicode[STIX]{x1D6FC}},\unicode[STIX]{x1D709})\ll A^{3+6\Re (\unicode[STIX]{x1D709})} & & \displaystyle\end{eqnarray}$$
uniformly in
$\boldsymbol{a}$
, by the bound
$|(a,\ell )^{s}/\ell ^{s}|\leqslant (|a|/\ell )^{\Re (s)}$
for
$\Re (s)\geqslant 0$
, and since
$$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D6E4}\biggl(\frac{s}{2}\biggr)/\unicode[STIX]{x1D6E4}\biggl(\frac{1-s}{2}\biggr)\ll _{\unicode[STIX]{x1D70E}}(1+|t|)^{\unicode[STIX]{x1D70E}-1/2} & & \displaystyle\end{eqnarray}$$
by Stirling’s formula [Reference Gradshteyn and Ryzhik23, (8.328.1)].
Then we write
$M_{\boldsymbol{a}}^{\pm }(B)=\sum _{k=0}^{3}M_{\boldsymbol{a},k}^{\pm }(B)$
, where
$$\begin{eqnarray}\displaystyle M_{\boldsymbol{a},k}^{\pm }(B) & = & \displaystyle \frac{1}{(2\unicode[STIX]{x1D70B}\text{i})^{8}}\iint _{(c_{I})}B^{(1/2)(\unicode[STIX]{x1D6FC}_{1}+\unicode[STIX]{x1D6FC}_{2}+\unicode[STIX]{x1D6FC}_{3}-\unicode[STIX]{x1D709})}\unicode[STIX]{x1D701}\biggl(\frac{1}{2}(\unicode[STIX]{x1D6FC}_{1}+\unicode[STIX]{x1D6FC}_{2}+\unicode[STIX]{x1D6FC}_{3}+3\unicode[STIX]{x1D709})\biggr)\nonumber\\ \displaystyle & & \displaystyle \times \,\frac{\unicode[STIX]{x1D701}(1+2\unicode[STIX]{x1D709})^{k}\unicode[STIX]{x1D701}(1-2\unicode[STIX]{x1D709})^{3-k}}{\unicode[STIX]{x1D6FC}_{1}+\unicode[STIX]{x1D6FC}_{2}+\unicode[STIX]{x1D6FC}_{3}+(3-2k)\unicode[STIX]{x1D709}-2}\nonumber\\ \displaystyle & & \displaystyle \times \,{\mathcal{Q}}_{\boldsymbol{a},k}(\boldsymbol{\unicode[STIX]{x1D6FC}},\unicode[STIX]{x1D709})\mathop{\prod }_{I}\tilde{F}_{\unicode[STIX]{x1D6FF}}^{\pm }(s_{I})\,ds_{I}\nonumber\end{eqnarray}$$
and with all the lines of integration still at
$c_{I}=|I|/12+\unicode[STIX]{x1D700}$
for all
$I$
. If
$k\in \{0,1\}$
, we move the lines of integration
$c_{S_{3}}$
and
$c_{\emptyset }$
to
$c_{S_{3}}=\frac{1}{4}-\frac{8}{81}+\unicode[STIX]{x1D700}$
and
$c=\frac{2}{81}+\unicode[STIX]{x1D700}$
without passing through any pole. Indeed, by (5.8), we have
$$\begin{eqnarray}1+12\unicode[STIX]{x1D700}\leqslant \Re ({\textstyle \frac{1}{2}}(\unicode[STIX]{x1D6FC}_{1}+\unicode[STIX]{x1D6FC}_{2}+\unicode[STIX]{x1D6FC}_{3}+3\unicode[STIX]{x1D709}))\leqslant {\textstyle \frac{29}{27}}+12\unicode[STIX]{x1D700}\end{eqnarray}$$
and
$\Re (\unicode[STIX]{x1D709})=\Re (s)-\Re (s_{123})/2+\frac{1}{8}+\frac{3}{2}\unicode[STIX]{x1D700}$
satisfies
$\Re (\unicode[STIX]{x1D709})\geqslant 2\unicode[STIX]{x1D700}$
in the range
$\frac{1}{4}+\unicode[STIX]{x1D700}\leqslant c_{S_{3}}\leqslant \frac{49}{324}+\unicode[STIX]{x1D700}$
and
$\unicode[STIX]{x1D700}\leqslant c_{\emptyset }\leqslant \frac{2}{81}+\unicode[STIX]{x1D700}$
. Thus, for
$k\in \{0,1\}$
, we have
$$\begin{eqnarray}\displaystyle M_{\boldsymbol{a},k}^{\pm }(B) & \ll & \displaystyle A^{31/9+12\unicode[STIX]{x1D700}}B^{25/27+8\unicode[STIX]{x1D700}}\iint _{(c_{I})}\Bigl(1+\max _{I}|s_{I}|\Bigr)\mathop{\prod }_{I}|\tilde{F}_{\unicode[STIX]{x1D6FF}}^{\pm }(s_{I})|\,ds_{I}\nonumber\\ \displaystyle & \ll & \displaystyle A^{31/9+12\unicode[STIX]{x1D700}}B^{25/27+8\unicode[STIX]{x1D700}}\unicode[STIX]{x1D6FF}^{-1-\unicode[STIX]{x1D700}}\end{eqnarray}$$
since we are inside the region (5.12) and since
$|\unicode[STIX]{x1D701}(1-2\unicode[STIX]{x1D709})|^{3}\ll 1+|\unicode[STIX]{x1D709}|$
for
$\Re (\unicode[STIX]{x1D709})=\frac{2}{27}+\unicode[STIX]{x1D700}$
by the convexity bound [Reference Titchmarsh32, (5.1.4)].
Now, consider the case
$k\in \{2,3\}$
. In those cases and for
$\unicode[STIX]{x1D700}$
small enough, we move the line of integration
$c_{S_{3}}$
to
$c_{S_{3}}=\frac{19}{108}+\unicode[STIX]{x1D700}$
passing through the pole at
$\unicode[STIX]{x1D6FC}_{1}+\unicode[STIX]{x1D6FC}_{2}+\unicode[STIX]{x1D6FC}_{3}+(3-2k)\unicode[STIX]{x1D709}-2=0$
, namely
$s_{123}=2/k-(1/k)\sum _{I\neq S_{3}}((2-|I|)(3-k)+|I|)s_{I}$
with respect to
$s_{123}$
, but without crossing the poles of the
$\unicode[STIX]{x1D701}$
-functions by (5.8) and since we increased
$\Re (\unicode[STIX]{x1D709})$
from
$2\unicode[STIX]{x1D700}$
to
$\frac{1}{27}+2\unicode[STIX]{x1D700}$
. The contribution of the integral on the new lines of integration is easily seen to be
$O(A^{29/9+12\unicode[STIX]{x1D700}}B^{25/27+8\unicode[STIX]{x1D700}}\unicode[STIX]{x1D6FF}^{-1-\unicode[STIX]{x1D700}})$
and so we are left with examining the contribution of the residue.
First we consider the case
$k=2$
. As mentioned above, with respect to
$s_{123}$
the pole is located at
$s_{123}=1-\sum _{I\neq S_{3}}s_{I}$
. Also, we can replace each
$\tilde{F}_{\unicode[STIX]{x1D6FF}}^{\pm }(s_{I})$
with
$1/s_{I}$
at a cost of committing an error, which, by (4.6) and (5.13) since (5.12) is satisfied, is bounded by
$$\begin{eqnarray}\displaystyle \ll B\max _{I^{\prime }\subseteq S_{3}}\iint _{(c_{I})_{I\neq S_{3}}}A^{3+6\Re (\unicode[STIX]{x1D709})}|\unicode[STIX]{x1D701}(1-2\unicode[STIX]{x1D709})|\min \biggl(\unicode[STIX]{x1D6FF},\frac{1}{|s_{I^{\prime }}|}\biggr)\mathop{\prod }_{I\neq I^{\prime }}\frac{1}{|s_{I}|}\cdot \mathop{\prod }_{I\neq S_{3}}\,ds_{I}, & & \displaystyle \nonumber\end{eqnarray}$$
where
$s_{123}:=1-\sum _{I\neq S_{3}}s_{I}$
. In particular,
$\Re (s_{123})=\frac{1}{4}-7\unicode[STIX]{x1D700}$
. Also,
$\Re (\unicode[STIX]{x1D709})=6\unicode[STIX]{x1D700}$
and so
$|\unicode[STIX]{x1D701}(1-2\unicode[STIX]{x1D709})|\ll |\unicode[STIX]{x1D709}|^{7\unicode[STIX]{x1D700}}$
by the convexity bound [Reference Titchmarsh32, (5.1.4)]. Thus, the above is, for
$I^{\prime }\neq S_{3}$
,
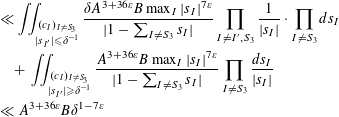$$\begin{eqnarray}\displaystyle & & \displaystyle \ll \iint _{\substack{ (c_{I})_{I\neq S_{3}} \\ |s_{I^{\prime }}|\leqslant \unicode[STIX]{x1D6FF}^{-1}}}\frac{\unicode[STIX]{x1D6FF}A^{3+36\unicode[STIX]{x1D700}}B\max _{I}|s_{I}|^{7\unicode[STIX]{x1D700}}}{|1-\mathop{\sum }_{I\neq S_{3}}s_{I}|}\mathop{\prod }_{I\neq I^{\prime },S_{3}}\frac{1}{|s_{I}|}\cdot \mathop{\prod }_{I\neq S_{3}}ds_{I}\nonumber\\ \displaystyle & & \displaystyle \quad +\,\iint _{\substack{ (c_{I})_{I\neq S_{3}} \\ |s_{I^{\prime }}|\geqslant \unicode[STIX]{x1D6FF}^{-1}}}\frac{A^{3+36\unicode[STIX]{x1D700}}B\max _{I}|s_{I}|^{7\unicode[STIX]{x1D700}}}{|1-\mathop{\sum }_{I\neq S_{3}}s_{I}|}\mathop{\prod }_{I\neq S_{3}}\frac{ds_{I}}{|s_{I}|}\nonumber\\ \displaystyle & & \displaystyle \ll A^{3+36\unicode[STIX]{x1D700}}B\unicode[STIX]{x1D6FF}^{1-7\unicode[STIX]{x1D700}}\end{eqnarray}$$
and a similar argument gives the same bound also for
$I=S_{3}$
. It follows that
$$\begin{eqnarray}M_{\boldsymbol{a},2}^{\pm }(B)=W_{\boldsymbol{ a}}B+O(A^{31/9+12\unicode[STIX]{x1D700}}B^{25/27+8\unicode[STIX]{x1D700}}\unicode[STIX]{x1D6FF}^{-1-\unicode[STIX]{x1D700}}+A^{3+36\unicode[STIX]{x1D700}}B\unicode[STIX]{x1D6FF}^{1-8\unicode[STIX]{x1D700}}),\end{eqnarray}$$
where
$$\begin{eqnarray}\displaystyle W_{\boldsymbol{a}}:=\frac{1}{(2\unicode[STIX]{x1D70B}\text{i})^{7}}\iint _{(c_{I})_{I\neq S_{3}}}\frac{\unicode[STIX]{x1D701}(1+2\unicode[STIX]{x1D709})^{3}\unicode[STIX]{x1D701}(1-2\unicode[STIX]{x1D709})}{2(1-\mathop{\sum }_{I\neq S_{3}}s_{I})}{\mathcal{Q}}_{\boldsymbol{a},2}(\boldsymbol{\unicode[STIX]{x1D6FC}},\unicode[STIX]{x1D709})\mathop{\prod }_{I\neq S_{3}}\frac{ds_{I}}{s_{I}} & & \displaystyle \nonumber\end{eqnarray}$$
and where
$\boldsymbol{\unicode[STIX]{x1D6FC}}$
and
$\unicode[STIX]{x1D709}$
are given by (5.6) with
$s_{123}$
replaced by
$1-\sum _{I\neq S_{3}}s_{I}$
. Notice that by (5.13), we have
$W_{\boldsymbol{a}}\ll A^{5}$
.
Now, let us consider the case
$k=3$
. We proceed as above replacing
$\tilde{F}_{\unicode[STIX]{x1D6FF}}^{\pm }(s_{I})$
by
$s_{I}^{-1}$
for all
$I\neq \emptyset$
. We cannot do the same for
$I=\emptyset$
yet because the pole giving the residue is, for
$\unicode[STIX]{x1D700}$
small enough, at
$s_{123}=\frac{2}{3}-\frac{1}{3}\sum _{I\neq S_{3}}|I|s_{I}$
with respect to
$s_{123}$
, which does not depend on
$s$
and thus the integral with
$\tilde{F}_{\unicode[STIX]{x1D6FF}}^{\pm }(s)$
replaced by
$1/s$
is not absolutely convergent. We arrive at
$$\begin{eqnarray}\displaystyle M_{\boldsymbol{a},3}^{\pm }(B) & = & \displaystyle \frac{1}{(2\unicode[STIX]{x1D70B}\text{i})^{7}}\iint _{(c_{I})_{I\neq S_{3}}}\nonumber\\ \displaystyle & & \displaystyle \times \,B^{1+\unicode[STIX]{x1D709}}\frac{\unicode[STIX]{x1D701}(1+3\unicode[STIX]{x1D709})\unicode[STIX]{x1D701}(1+2\unicode[STIX]{x1D709})^{3}}{2-\mathop{\sum }_{I\neq S_{3}}|I|s_{I}}{\mathcal{Q}}_{\boldsymbol{a},3}(\boldsymbol{\unicode[STIX]{x1D6FC}},\unicode[STIX]{x1D709})s\tilde{F}_{\unicode[STIX]{x1D6FF}}^{\pm }(s)\mathop{\prod }_{I\neq S_{3}}\frac{ds_{I}}{s_{I}}\nonumber\\ \displaystyle & & \displaystyle +\,O(A^{31/9+12\unicode[STIX]{x1D700}}B^{25/27+8\unicode[STIX]{x1D700}}\unicode[STIX]{x1D6FF}^{-1-\unicode[STIX]{x1D700}}+A^{3+36\unicode[STIX]{x1D700}}B^{1+4\unicode[STIX]{x1D700}}\unicode[STIX]{x1D6FF}^{1-8\unicode[STIX]{x1D700}}),\nonumber\end{eqnarray}$$
where the lines of integration are still at
$c_{I}=|I|/12+\unicode[STIX]{x1D700}$
for all
$I\neq S_{3}$
. Next, we move the lines of integration
$c_{I}$
to
$c_{I}=\unicode[STIX]{x1D700}$
for all
$I$
satisfying
$|I|=1$
. This has the effect of moving
$\Re (\unicode[STIX]{x1D709})$
from
$4\unicode[STIX]{x1D700}$
to
$-\frac{1}{6}+4\unicode[STIX]{x1D700}$
and
$\Re (\frac{2}{3}-\frac{1}{3}\sum _{I\neq S_{3}}|I|s_{I})$
from
$\frac{1}{4}-3\unicode[STIX]{x1D700}$
to
$\frac{1}{3}-3\unicode[STIX]{x1D700}$
. In particular, we stay on the right of the poles at
$s_{I}=0$
for all
$I$
and we encounter a quadruple pole at
$s:=\frac{1}{3}-\frac{1}{3}\sum _{I\neq \emptyset ,S_{3}}(3-|I|)s_{I}$
with respect to
$s$
. Note that we have
$\unicode[STIX]{x1D709}=0$
at the quadruple pole. The contribution of the integrals on the new lines of integration is, as in (5.9),
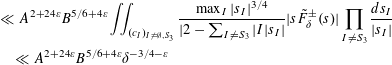$$\begin{eqnarray}\displaystyle & & \displaystyle \ll A^{2+24\unicode[STIX]{x1D700}}B^{5/6+4\unicode[STIX]{x1D700}}\iint _{(c_{I})_{I\neq \emptyset ,S_{3}}}\frac{\max _{I}|s_{I}|^{3/4}}{|2-\mathop{\sum }_{I\neq S_{3}}|I|s_{I}|}|s\tilde{F}_{\unicode[STIX]{x1D6FF}}^{\pm }(s)|\mathop{\prod }_{I\neq S_{3}}\frac{ds_{I}}{|s_{I}|}\nonumber\\ \displaystyle & & \displaystyle \quad \ll A^{2+24\unicode[STIX]{x1D700}}B^{5/6+4\unicode[STIX]{x1D700}}\unicode[STIX]{x1D6FF}^{-3/4-\unicode[STIX]{x1D700}}\nonumber\end{eqnarray}$$
since we are on the region (5.12) and since, by the convexity bound [Reference Titchmarsh32, (5.1.4)],
$|\unicode[STIX]{x1D701}(1+3\unicode[STIX]{x1D709})\unicode[STIX]{x1D701}(1+2\unicode[STIX]{x1D709})|^{3}\ll |\unicode[STIX]{x1D709}|^{3/4}$
for
$\Re (\unicode[STIX]{x1D709})=-\frac{1}{6}\,+\,4\unicode[STIX]{x1D700}$
. As for the residue, we notice that we can replace
$s\tilde{F}_{\unicode[STIX]{x1D6FF}}^{\pm }(s)$
by
$1$
at a cost of an error, which is
$O(\unicode[STIX]{x1D6FF}A^{3+6\unicode[STIX]{x1D700}}B^{1+5\unicode[STIX]{x1D700}})$
. Indeed, we can write the residue as an integral in
$s$
along a circle of radius
$\unicode[STIX]{x1D700}$
around
$\frac{1}{3}-\frac{1}{3}\sum _{I\neq \emptyset ,S_{3}}(3-|I|)s_{I}=O(\unicode[STIX]{x1D700})$
. We then use
$s\tilde{F}_{\unicode[STIX]{x1D6FF}}^{\pm }(s)-1=O(|s|\unicode[STIX]{x1D6FF})$
coming from (4.6) and bound trivially the integrals. Thus, we have
$$\begin{eqnarray}\displaystyle & & \displaystyle M_{\boldsymbol{a},3}^{\pm }(B)\nonumber\\ \displaystyle & & \displaystyle \quad =\frac{1}{(2\unicode[STIX]{x1D70B}\text{i})^{6}}\iint _{(c_{I})_{I\neq S_{3}}}\operatorname{ \ast}Res_{\unicode[STIX]{x1D709}=0}\biggl(B^{1+\unicode[STIX]{x1D709}}\frac{\unicode[STIX]{x1D701}(1+3\unicode[STIX]{x1D709})\unicode[STIX]{x1D701}(1+2\unicode[STIX]{x1D709})^{3}}{3s_{123}s}{\mathcal{Q}}_{\boldsymbol{a},3}(\boldsymbol{\unicode[STIX]{x1D6FC}},\unicode[STIX]{x1D709})\biggr)\mathop{\prod }_{I\neq \emptyset ,S_{3}}\frac{ds_{I}}{s_{I}}\nonumber\\ \displaystyle & & \displaystyle \qquad +\,O(B^{25/27+8\unicode[STIX]{x1D700}}\unicode[STIX]{x1D6FF}^{-1-\unicode[STIX]{x1D700}}+B^{1+5\unicode[STIX]{x1D700}}\unicode[STIX]{x1D6FF}),\nonumber\end{eqnarray}$$
with
$$\begin{eqnarray}s:=\frac{1}{3}-\frac{1}{3}\mathop{\sum }_{I\neq \emptyset ,S_{3}}(3-|I|)s_{I},\qquad s_{123}:=\frac{2}{3}-\frac{1}{3}\mathop{\sum }_{I\neq S_{3}}|I|s_{I},\end{eqnarray}$$
$\boldsymbol{\unicode[STIX]{x1D6FC}}$
being given by (5.6) with
$s_{123}$
and
$s$
replaced by (5.18) and lines of integration which we can take to be
$c_{I}=\frac{1}{12}$
for all
$I\neq S_{3},\emptyset$
. Note that computing the residue in
$\unicode[STIX]{x1D709}$
rather than in
$s$
does not change the result. Computing the residue then gives
$$\begin{eqnarray}M_{\boldsymbol{a},3}^{\pm }(B)=BP_{\boldsymbol{ a}}(\log B)+O(A^{31/9+12\unicode[STIX]{x1D700}}B^{25/27+8\unicode[STIX]{x1D700}}\unicode[STIX]{x1D6FF}^{-1-\unicode[STIX]{x1D700}}+A^{3+36\unicode[STIX]{x1D700}}B^{1+5\unicode[STIX]{x1D700}}\unicode[STIX]{x1D6FF}^{1-7\unicode[STIX]{x1D700}}),\end{eqnarray}$$
where
$P_{\boldsymbol{a}}$
is a degree-3 polynomial with leading coefficient
$$\begin{eqnarray}\displaystyle P_{\boldsymbol{a},3}:=\frac{1}{(2\unicode[STIX]{x1D70B}\text{i})^{6}}\iint _{(1/12)}\frac{{\mathcal{Q}}_{\boldsymbol{a},3}(\boldsymbol{\unicode[STIX]{x1D6FC}},0)}{432s_{123}s}\mathop{\prod }_{I\neq \emptyset ,S_{3}}\frac{ds_{I}}{s_{I}} & & \displaystyle\end{eqnarray}$$
with
$s$
and
$s_{123}$
given by (5.18),
$$\begin{eqnarray}\displaystyle \begin{array}{@{}c@{}}\unicode[STIX]{x1D6FC}_{2}={\textstyle \frac{1}{3}}(2+2s_{2}-s_{1}-s_{3}+s_{12}+s_{23}-2s_{13}),\\ \unicode[STIX]{x1D6FC}_{3}={\textstyle \frac{1}{3}}(2+2s_{3}-s_{1}-s_{2}+s_{13}+s_{23}-2s_{12})\end{array} & & \displaystyle\end{eqnarray}$$
and
$\unicode[STIX]{x1D6FC}_{1}=2-\unicode[STIX]{x1D6FC}_{2}-\unicode[STIX]{x1D6FC}_{3}$
, where again we neglect the dependences on
$s_{I}$
for
$I\neq \emptyset ,S_{3}$
in the notation. Note that we will establish later that
$P_{\boldsymbol{a},3}=\frac{1}{144}{\mathcal{I}}_{\boldsymbol{a}}\mathfrak{S}_{\boldsymbol{a}}^{\prime }$
with the notation of Proposition 1 and hence
$P_{\boldsymbol{a},3}\neq 0$
. Also, by (5.13) and the corresponding bound for the derivatives of
${\mathcal{Q}}_{\boldsymbol{a},k}(\boldsymbol{\unicode[STIX]{x1D6FC}},\unicode[STIX]{x1D709})$
with respect to
$\unicode[STIX]{x1D709}$
, we have that the coefficients of
$P_{\boldsymbol{a},3}$
are
$O(A^{5})$
.
Collecting the estimates (5.10), (5.15), (5.17) and (5.19), we have
$$\begin{eqnarray}\displaystyle K_{\boldsymbol{a}}^{\pm }(B) & = & \displaystyle BP_{\boldsymbol{a}}(\log B)+W_{\boldsymbol{a}}B\nonumber\\ \displaystyle & & \displaystyle +\,O(A^{3+36\unicode[STIX]{x1D700}}B^{1+5\unicode[STIX]{x1D700}}\unicode[STIX]{x1D6FF}^{1-7\unicode[STIX]{x1D700}}+A^{14}B^{25/27+13\unicode[STIX]{x1D700}}\unicode[STIX]{x1D6FF}^{-21-\unicode[STIX]{x1D700}})\nonumber\\ \displaystyle & = & \displaystyle BP_{\boldsymbol{a}}(\log B)+W_{\boldsymbol{a}}B+O(A^{14}B^{296/297+14\unicode[STIX]{x1D700}}),\nonumber\end{eqnarray}$$
upon choosing
$\unicode[STIX]{x1D6FF}=B^{-1/297}$
. Thus, it remains to show that
$P_{\boldsymbol{a},3}=\frac{1}{144}{\mathcal{I}}_{\boldsymbol{a}}\mathfrak{S}_{\boldsymbol{a}}^{\prime }$
with the notation of Proposition 1.
First, we notice that, for
$\unicode[STIX]{x1D6FC}_{1}+\unicode[STIX]{x1D6FC}_{2}+\unicode[STIX]{x1D6FC}_{3}=2$
and
$\unicode[STIX]{x1D709}=0$
,
${\mathcal{Q}}_{\boldsymbol{a},3}(\boldsymbol{\unicode[STIX]{x1D6FC}},\unicode[STIX]{x1D709})$
simplifies to
$$\begin{eqnarray}\displaystyle {\mathcal{Q}}_{\boldsymbol{a},3}(\boldsymbol{\unicode[STIX]{x1D6FC}},0)=2\unicode[STIX]{x1D70B}^{1/2}\mathfrak{S}_{\boldsymbol{a}}^{\prime }\mathop{\prod }_{i=1}^{3}\frac{\unicode[STIX]{x1D6E4}((1-\unicode[STIX]{x1D6FC}_{i})/2)}{|a_{i}|^{1-\unicode[STIX]{x1D6FC}_{i}}\unicode[STIX]{x1D6E4}(\unicode[STIX]{x1D6FC}_{i}/2)}. & & \displaystyle \nonumber\end{eqnarray}$$
Next, we use
$\unicode[STIX]{x1D6FC}_{2},\unicode[STIX]{x1D6FC}_{3}$
as new variables, writing
$s_{2}$
and
$s_{3}$
as
$$\begin{eqnarray}s_{2}=-2+2\unicode[STIX]{x1D6FC}_{2}+\unicode[STIX]{x1D6FC}_{3}+s_{1}+s_{13}-s_{23},\qquad s_{3}=-2+2\unicode[STIX]{x1D6FC}_{3}+\unicode[STIX]{x1D6FC}_{2}+s_{1}+s_{12}-s_{23}.\end{eqnarray}$$
Note that with this change of variables, we also have
$$\begin{eqnarray}s_{123}=2-\unicode[STIX]{x1D6FC}_{2}-\unicode[STIX]{x1D6FC}_{3}-s_{1}-s_{12}-s_{13},\qquad s=3-2\unicode[STIX]{x1D6FC}_{2}-2\unicode[STIX]{x1D6FC}_{3}-2s_{1}-s_{12}-s_{13}+s_{23}\end{eqnarray}$$
and recall that
$\unicode[STIX]{x1D6FC}_{1}=2-\unicode[STIX]{x1D6FC}_{2}-\unicode[STIX]{x1D6FC}_{3}$
. The lines of integration for
$\unicode[STIX]{x1D6FC}_{2},\unicode[STIX]{x1D6FC}_{3}$
are at real part equal to
$\frac{2}{3}$
. Since the Jacobian of the above change of variables is equal to
$3$
, we find, with (5.22) and (5.23),
$$\begin{eqnarray}\displaystyle P_{\boldsymbol{a},3} & = & \displaystyle \frac{1}{(2\unicode[STIX]{x1D70B}\text{i})^{2}}\iint _{(2/3)}{\mathcal{Q}}_{\boldsymbol{a},3}(\boldsymbol{\unicode[STIX]{x1D6FC}},0)\frac{1}{(2\unicode[STIX]{x1D70B}\text{i})^{4}}\nonumber\\ \displaystyle & & \displaystyle \times \,\iint _{(1/12)}\frac{ds_{1}\,ds_{12}\,ds_{13}\,ds_{23}}{144s_{123}ss_{2}s_{3}s_{1}s_{12}s_{13}s_{23}}\,d\unicode[STIX]{x1D6FC}_{2}\,d\unicode[STIX]{x1D6FC}_{3}.\nonumber\end{eqnarray}$$
The inner integrals can be evaluated by moving each integral to
$-\infty$
(or, equivalently, to
$+\infty$
), repeatedly applying the residue theorem. For example, one can start by moving
$c_{s_{1}}$
to
$-\infty$
encountering poles at
$s_{1}=0,$
$s_{1}=2-2\unicode[STIX]{x1D6FC}_{2}-\unicode[STIX]{x1D6FC}_{3}-s_{2}-s_{13}+s_{23}$
and
$s_{1}=2-2\unicode[STIX]{x1D6FC}_{3}-\unicode[STIX]{x1D6FC}_{2}-s_{3}-s_{12}+s_{23}$
. Inserting the contribution of the residues and moving the remaining integrals in the same way one finds, after a simple but tedious calculation which can be readily checked using Mathematica, that
$$\begin{eqnarray}\displaystyle P_{\boldsymbol{a},3} & = & \displaystyle \frac{1}{(2\unicode[STIX]{x1D70B}\text{i})^{2}}\iint _{(2/3)}\frac{-{\mathcal{Q}}_{\boldsymbol{a},3}(\boldsymbol{\unicode[STIX]{x1D6FC}},0)}{144\unicode[STIX]{x1D6FC}_{1}\unicode[STIX]{x1D6FC}_{2}\unicode[STIX]{x1D6FC}_{3}(\unicode[STIX]{x1D6FC}_{1}-1)(\unicode[STIX]{x1D6FC}_{2}-1)(\unicode[STIX]{x1D6FC}_{3}-1)}\,d\unicode[STIX]{x1D6FC}_{2}\,d\unicode[STIX]{x1D6FC}_{3}\nonumber\\ \displaystyle & = & \displaystyle \frac{\mathfrak{S}_{\boldsymbol{a}}^{\prime }}{(2\unicode[STIX]{x1D70B}\text{i})^{2}}\iint _{(2/3)}\frac{2\unicode[STIX]{x1D70B}^{1/2}}{144}\mathop{\prod }_{i=1}^{3}\frac{\unicode[STIX]{x1D6E4}((1-\unicode[STIX]{x1D6FC}_{i})/2)}{\unicode[STIX]{x1D6FC}_{i}(1-\unicode[STIX]{x1D6FC}_{i})|a_{i}|^{1-\unicode[STIX]{x1D6FC}_{i}}\unicode[STIX]{x1D6E4}(\unicode[STIX]{x1D6FC}_{i}/2)}\,d\unicode[STIX]{x1D6FC}_{2}\,d\unicode[STIX]{x1D6FC}_{3},\nonumber\end{eqnarray}$$
with
$\unicode[STIX]{x1D6FC}_{1}=2-\unicode[STIX]{x1D6FC}_{2}-\unicode[STIX]{x1D6FC}_{3}$
and the result follows by the following lemma.◻
Lemma 4. For
$\boldsymbol{a}\in \mathbb{Z}_{\neq 0}^{3}$
, we have
$$\begin{eqnarray}\displaystyle {\mathcal{I}}_{\boldsymbol{a}}=\frac{1}{(2\unicode[STIX]{x1D70B}\text{i})^{2}}\iint _{(2/3)}2\unicode[STIX]{x1D70B}^{1/2}\mathop{\prod }_{i=1}^{3}\frac{\unicode[STIX]{x1D6E4}((1-\unicode[STIX]{x1D6FC}_{i})/2)}{\unicode[STIX]{x1D6FC}_{i}(1-\unicode[STIX]{x1D6FC}_{i})|a_{i}|^{1-\unicode[STIX]{x1D6FC}_{i}}\unicode[STIX]{x1D6E4}(\unicode[STIX]{x1D6FC}_{i}/2)}\,d\unicode[STIX]{x1D6FC}_{2}\,d\unicode[STIX]{x1D6FC}_{3},\quad & & \displaystyle\end{eqnarray}$$
where
$\unicode[STIX]{x1D6FC}_{1}:=2-\unicode[STIX]{x1D6FC}_{2}-\unicode[STIX]{x1D6FC}_{3}$
. Moreover,
${\mathcal{I}}_{\mathbf{1}}=\unicode[STIX]{x1D70B}^{2}+24\log 2-3$
.
Proof. For
$\unicode[STIX]{x1D6FC}_{1}+\unicode[STIX]{x1D6FC}_{2}+\unicode[STIX]{x1D6FC}_{3}=2$
, we have the
$\unicode[STIX]{x1D6E4}$
identity (see (2.8) in [Reference Bettin4])
$$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D70B}^{1/2}\mathop{\prod }_{i=1}^{3}\frac{\unicode[STIX]{x1D6E4}((1-\unicode[STIX]{x1D6FC}_{i})/2)}{\unicode[STIX]{x1D6E4}(\unicode[STIX]{x1D6FC}_{i}/2)}=\mathop{\sum }_{i=1}^{3}\frac{\unicode[STIX]{x1D6E4}(1-\unicode[STIX]{x1D6FC}_{1})\unicode[STIX]{x1D6E4}(1-\unicode[STIX]{x1D6FC}_{2})\unicode[STIX]{x1D6E4}(1-\unicode[STIX]{x1D6FC}_{3})}{\unicode[STIX]{x1D6E4}(1-\unicode[STIX]{x1D6FC}_{i})\unicode[STIX]{x1D6E4}(\unicode[STIX]{x1D6FC}_{i})} & & \displaystyle \nonumber\end{eqnarray}$$
and, considering
$\unicode[STIX]{x1D6FC}_{1}=2-\unicode[STIX]{x1D6FC}_{2}-\unicode[STIX]{x1D6FC}_{3}$
as a function of
$\unicode[STIX]{x1D6FC}_{2}$
with
$\unicode[STIX]{x1D6FC}_{3}$
fixed, we have the Mellin transforms [Reference Titchmarsh31, (7.7.9) and (7.7.14–15)] for
$x>0$
,
$$\begin{eqnarray}\displaystyle & & \displaystyle \frac{1}{2\unicode[STIX]{x1D70B}\text{i}}\int _{(c)}\frac{\unicode[STIX]{x1D6E4}(1-\unicode[STIX]{x1D6FC}_{1})\unicode[STIX]{x1D6E4}(1-\unicode[STIX]{x1D6FC}_{2})\unicode[STIX]{x1D6E4}(1-\unicode[STIX]{x1D6FC}_{3})}{\unicode[STIX]{x1D6E4}(1-\unicode[STIX]{x1D6FC}_{i})\unicode[STIX]{x1D6E4}(\unicode[STIX]{x1D6FC}_{i})}x^{\unicode[STIX]{x1D6FC}_{2}-1}\,d\unicode[STIX]{x1D6FC}_{2}\nonumber\\ \displaystyle & & \displaystyle \quad =\left\{\begin{array}{@{}ll@{}}(1-x)^{-\unicode[STIX]{x1D6FC}_{3}}\unicode[STIX]{x1D712}_{[0,1]}(x)\quad & \text{if }i=1,\\ (x-1)^{-\unicode[STIX]{x1D6FC}_{3}}\unicode[STIX]{x1D712}_{[1,\infty )}(x)\quad & \text{if }i=2,\\ (1+x)^{-\unicode[STIX]{x1D6FC}_{3}}\quad & \text{if }i=3,\end{array}\right.\end{eqnarray}$$
for
$c>0$
and
$\Re (\unicode[STIX]{x1D6FC}_{3})<1$
if
$i=1$
,
$\Re (\unicode[STIX]{x1D6FC}_{3})>0$
if
$i=2$
and
$0<c<\Re (\unicode[STIX]{x1D6FC}_{3})$
if
$i=3$
. Also, for
$0<\Re (\unicode[STIX]{x1D6FC}_{2}),\Re (\unicode[STIX]{x1D6FC}_{3})<1$
, we have the identity
$$\begin{eqnarray}\displaystyle & & \displaystyle \int _{[0,1]^{4}}(x_{1}/y_{1})^{1-\unicode[STIX]{x1D6FC}_{2}-\unicode[STIX]{x1D6FC}_{3}}(x_{2}/y_{2})^{\unicode[STIX]{x1D6FC}_{2}-1}(y_{1}y_{2})^{-1}\,dx_{1}\,dx_{2}\,dy_{1}\,dy_{2}\nonumber\\ \displaystyle & & \displaystyle \quad =\frac{1}{\unicode[STIX]{x1D6FC}_{1}(\unicode[STIX]{x1D6FC}_{1}-1)\unicode[STIX]{x1D6FC}_{2}(\unicode[STIX]{x1D6FC}_{2}-1)}.\nonumber\end{eqnarray}$$
It follows that, in the case
$i=1$
,
$$\begin{eqnarray}\displaystyle & & \displaystyle \frac{1}{(2\unicode[STIX]{x1D70B}\text{i})^{2}}\iint _{(2/3)}\frac{\unicode[STIX]{x1D6E4}(1-\unicode[STIX]{x1D6FC}_{2})\unicode[STIX]{x1D6E4}(1-\unicode[STIX]{x1D6FC}_{3})|a_{1}|^{1-\unicode[STIX]{x1D6FC}_{2}-\unicode[STIX]{x1D6FC}_{3}}|a_{2}|^{\unicode[STIX]{x1D6FC}_{2}-1}|a_{3}|^{\unicode[STIX]{x1D6FC}_{3}-1}}{\unicode[STIX]{x1D6FC}_{1}\unicode[STIX]{x1D6FC}_{2}\unicode[STIX]{x1D6FC}_{3}(1-\unicode[STIX]{x1D6FC}_{1})(1-\unicode[STIX]{x1D6FC}_{2})(1-\unicode[STIX]{x1D6FC}_{3})\unicode[STIX]{x1D6E4}(\unicode[STIX]{x1D6FC}_{1})}\,d\unicode[STIX]{x1D6FC}_{2}\,d\unicode[STIX]{x1D6FC}_{3}\nonumber\\ \displaystyle & & \displaystyle \quad =\int _{\substack{ [0,1]^{4} \\ |a_{1}|x_{1}/y_{1}-|a_{2}|x_{2}/y_{2}\geqslant 0}}\frac{1}{2\unicode[STIX]{x1D70B}\text{i}}\nonumber\\ \displaystyle & & \displaystyle \qquad \times \,\int _{(2/3)}\frac{(|a_{1}|x_{1}/y_{1}-|a_{2}|x_{2}/y_{2})^{-\unicode[STIX]{x1D6FC}_{3}}|a_{3}|^{\unicode[STIX]{x1D6FC}_{3}-1}}{\unicode[STIX]{x1D6FC}_{3}(1-\unicode[STIX]{x1D6FC}_{3})}\,d\unicode[STIX]{x1D6FC}_{3}(y_{1}y_{2})^{-1}\,dx_{1}\,dx_{2}\,dy_{1}\,dy_{2}\nonumber\\ \displaystyle & & \displaystyle \quad =\int _{\substack{ [0,1]^{5} \\ 0\leqslant |a_{1}|x_{1}/y_{1}-|a_{2}|x_{2}/y_{2}\leqslant |a_{3}|/z}}(|a_{3}|y_{1}y_{2})^{-1}\,dx_{1}\,dx_{2}\,dy_{1}\,dy_{2}\,dz\nonumber\end{eqnarray}$$
since
$(1/2\unicode[STIX]{x1D70B}\text{i})\int _{(2/3)}x^{-s}(ds/s(s-1))=\int _{0}^{1}\unicode[STIX]{x1D712}_{[0,1/z)}(x)\,dz$
for
$x>0$
. One evaluates similarly the cases arising from
$i\in \{2,3\}$
and (5.24) easily follows.
Finally, in the case where
$\mathbf{a}=(1,1,1)$
, we notice that after using the Gamma identity
$\cos (\unicode[STIX]{x1D70B}s/2)\unicode[STIX]{x1D6E4}(s)=\unicode[STIX]{x1D70B}^{1/2}2^{s-1}\unicode[STIX]{x1D6E4}(s/2)/\unicode[STIX]{x1D6E4}((1-s)/2)$
, which follows from the reflection and duplication formulas for the Gamma function, the integral on the right-hand side of (5.24) reduces to
$$\begin{eqnarray}\displaystyle & & \displaystyle \frac{8}{\unicode[STIX]{x1D70B}}\times \frac{1}{(2\text{i}\unicode[STIX]{x1D70B})^{2}}\iint _{(2/3)}\mathop{\prod }_{i=1}^{3}\frac{\unicode[STIX]{x1D6E4}(1-\unicode[STIX]{x1D6FC}_{i})\cos (\unicode[STIX]{x1D70B}(1-\unicode[STIX]{x1D6FC}_{i})/2)}{\unicode[STIX]{x1D6FC}_{i}(1-\unicode[STIX]{x1D6FC}_{i})}\,d\unicode[STIX]{x1D6FC}_{2}\,d\unicode[STIX]{x1D6FC}_{3}\nonumber\\ \displaystyle & & \displaystyle \quad =\frac{8}{\unicode[STIX]{x1D70B}}\times \frac{1}{(2\text{i}\unicode[STIX]{x1D70B})^{2}}\iint _{(1/3)}\nonumber\\ \displaystyle & & \displaystyle \qquad \times \,\frac{\unicode[STIX]{x1D6E4}(z_{1})\unicode[STIX]{x1D6E4}(z_{2})\unicode[STIX]{x1D6E4}(1-z_{1}-z_{2})\cos (\unicode[STIX]{x1D70B}z_{1}/2)\cos (\unicode[STIX]{x1D70B}z_{2}/2)\cos (\unicode[STIX]{x1D70B}(1-z_{1}-z_{2})/2)}{z_{1}z_{2}(1-z_{1}-z_{2})(1-z_{1})(1-z_{2})(z_{1}+z_{2})}\nonumber\\ \displaystyle & & \displaystyle \qquad \times \,\,dz_{1}\,dz_{2}\nonumber\end{eqnarray}$$
after the change of variables
$z_{1}=\unicode[STIX]{x1D6FC}_{2}$
and
$z_{2}=\unicode[STIX]{x1D6FC}_{3}$
and remembering that
$\unicode[STIX]{x1D6FC}_{1}=2-\unicode[STIX]{x1D6FC}_{2}-\unicode[STIX]{x1D6FC}_{3}$
. The last integral above is computed in [Reference Blomer, Brüdern and Salberger8, Lemma 2.10], where it was shown to be equal to
$\unicode[STIX]{x1D70B}^{2}+24\log 2-3$
by means of a long calculation. One could also give a shorter proof of this identity (still requiring some computations) by writing
$(\unicode[STIX]{x1D6FC}_{1}(\unicode[STIX]{x1D6FC}_{1}-1)\unicode[STIX]{x1D6FC}_{2}(\unicode[STIX]{x1D6FC}_{2}-1))^{-1}$
in terms of its (one-variable) Mellin transform, applying (5.25) and evaluating the resulting integrals.◻
6 Proof of Theorem 2
We now move to the proof of Theorem 2, namely counting points satisfying (5.1) and the coprimality conditions (5.2). First, we give three lemmas which respectively remove the extra coprimality conditions by means of Möbius’ inversion formula, show the convergence of the resulting sums and compute the Euler product arising in the main term.
Lemma 5. Let
$f:\mathbb{R}^{7}\rightarrow \mathbb{C}$
be a function of compact support. Then
$$\begin{eqnarray}\displaystyle & & \displaystyle \sum _{\substack{ (\boldsymbol{x},\boldsymbol{z})\in \mathbb{Z}_{\neq 0}^{3}\times \mathbb{Z}_{{>}0}^{4}}}f(x_{1},z_{1},x_{2},z_{2},x_{3},z_{3},z_{4})\nonumber\\ \displaystyle & & \displaystyle \quad =\mathop{\sum }_{\substack{ \boldsymbol{e},\boldsymbol{\ell }\in \mathbb{N}^{3} \\ \boldsymbol{d}\in \mathbb{N}^{6}}}\unicode[STIX]{x1D707}(\boldsymbol{e},\boldsymbol{d},\boldsymbol{\ell })\mathop{\sum }_{\substack{ (\boldsymbol{x},\boldsymbol{z})\in \mathbb{Z}_{\neq 0}^{3}\times \mathbb{Z}_{{>}0}^{4}}}f(b_{1}x_{1},c_{1}z_{1},b_{2}x_{2},c_{2}z_{2},b_{3}x_{3},c_{3}z_{3},c_{4}z_{4}),\nonumber\end{eqnarray}$$
where here and below
$\sum ^{\prime }$
indicates that the sum is restricted to satisfy the coprimality conditions
$$\begin{eqnarray}\displaystyle & (z_{1},z_{2})=(z_{1},z_{3})=(z_{2},z_{3})=1, & \displaystyle \nonumber\\ \displaystyle & (x_{1},z_{2}z_{3}z_{4})=(x_{2},z_{1}z_{3}z_{4})=(x_{3},z_{1}z_{2}z_{4})=1 & \displaystyle \nonumber\end{eqnarray}$$
and where
$\boldsymbol{e}:=(e_{1},e_{2},e_{3})$
,
$\boldsymbol{d}:=(d_{12},d_{13},d_{21},d_{23},d_{31},d_{32})$
,
$\boldsymbol{\ell }:=(\ell _{12},\ell _{13},\ell _{23})$
,
$$\begin{eqnarray}\displaystyle \begin{array}{@{}c@{}}b_{1}:=[e_{1},d_{12},d_{13}],\qquad b_{2}:=[e_{2},d_{21},d_{23}],\qquad b_{3}:=[e_{3},d_{31},d_{32}],\\ c_{1}:=[d_{21},d_{31},\ell _{12},\ell _{13}],\qquad c_{2}:=[d_{12},d_{32},\ell _{12},\ell _{23}],\\ c_{3}:=[d_{13},d_{23},\ell _{13},\ell _{23}],\qquad c_{4}:=[e_{1},e_{2},e_{3}]\end{array} & & \displaystyle\end{eqnarray}$$
and, with a slight abuse of notation,
$$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D707}(\boldsymbol{e},\boldsymbol{d},\boldsymbol{\ell }):=\unicode[STIX]{x1D707}(\ell _{12})\unicode[STIX]{x1D707}(\ell _{13})\unicode[STIX]{x1D707}(\ell _{23})\mathop{\prod }_{1\leqslant i\leqslant 3}\unicode[STIX]{x1D707}(e_{i})\mathop{\prod }_{\substack{ 1\leqslant i,j\leqslant 3 \\ i\neq j}}\unicode[STIX]{x1D707}(d_{ij}). & & \displaystyle \nonumber\end{eqnarray}$$
Proof. This is just an immediate application of Möbius’ inversion formula. ◻
Lemma 6. With the notation of (6.1) and for real numbers
$u_{1},u_{2},u_{3},w_{1},w_{2},w_{3},w_{4}$
satisfying
$$\begin{eqnarray}\displaystyle \begin{array}{@{}c@{}}u_{i},w_{i},u_{i}+w_{4}-1-\unicode[STIX]{x1D700}\geqslant \unicode[STIX]{x1D705}\quad \text{for all }i\in \{1,2,3\};w_{4}\geqslant 0;\unicode[STIX]{x1D705}\geqslant 0;\\ u_{i}+w_{j}-\unicode[STIX]{x1D705}>1+\unicode[STIX]{x1D700}\quad \text{for all }i,j\in \{1,2,3\},i\neq j;\\ w_{i}+w_{j}-\unicode[STIX]{x1D705}>1+\unicode[STIX]{x1D700}\quad \text{for all }i,j\in \{1,2,3\},i<j;\end{array} & & \displaystyle\end{eqnarray}$$
we have
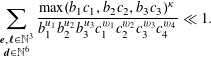$$\begin{eqnarray}\displaystyle \mathop{\sum }_{\substack{ \boldsymbol{e},\boldsymbol{\ell }\in \mathbb{N}^{3} \\ \boldsymbol{d}\in \mathbb{N}^{6}}}\frac{\max (b_{1}c_{1},b_{2}c_{2},b_{3}c_{3})^{\unicode[STIX]{x1D705}}}{b_{1}^{u_{1}}b_{2}^{u_{2}}b_{3}^{u_{3}}c_{1}^{w_{1}}c_{2}^{w_{2}}c_{3}^{w_{3}}c_{4}^{w_{4}}}\ll 1. & & \displaystyle\end{eqnarray}$$
Proof. We have the formal Euler product formula
$$\begin{eqnarray}\displaystyle & & \displaystyle \mathop{\sum }_{\substack{ \boldsymbol{e},\boldsymbol{\ell }\in \mathbb{N}^{3} \\ \boldsymbol{d}\in \mathbb{N}^{6}}}\frac{1}{b_{1}^{u_{1}}b_{2}^{u_{2}}b_{3}^{u_{3}}c_{1}^{w_{1}}c_{2}^{w_{2}}c_{3}^{w_{3}}c_{4}^{w_{4}}}\nonumber\\ \displaystyle & & \displaystyle \quad =\mathop{\prod }_{p}\biggl(\mathop{\sum }_{\boldsymbol{e}^{\prime },\boldsymbol{\ell }^{\prime }\in \mathbb{Z}_{{\geqslant}0}^{3},\boldsymbol{d}^{\prime }\in \mathbb{Z}_{{\geqslant}0}^{6}}p^{-(b_{1}^{\prime }u_{1}+b_{2}^{\prime }u_{2}+b_{3}^{\prime }u_{3}+c_{1}^{\prime }w_{1}+c_{2}^{\prime }w_{2}+c_{3}^{\prime }w_{3}+c_{4}^{\prime }w_{4})}\biggr),\end{eqnarray}$$
where
$$\begin{eqnarray}\displaystyle \begin{array}{@{}c@{}}b_{1}^{\prime }=\max (e_{1}^{\prime },d_{12}^{\prime },d_{13}^{\prime }),\qquad b_{2}^{\prime }=\max (e_{2}^{\prime },d_{21}^{\prime },d_{23}^{\prime }),\\ b_{3}^{\prime }=\max (e_{3}^{\prime },d_{31}^{\prime },d_{32}^{\prime }),\qquad c_{4}^{\prime }=\max (e_{1}^{\prime },e_{2}^{\prime },e_{3}^{\prime }),\\ c_{1}^{\prime }=\max (d_{21}^{\prime },d_{31}^{\prime },\ell _{12}^{\prime },\ell _{13}^{\prime }),\qquad c_{2}^{\prime }=\max (d_{12}^{\prime },d_{32}^{\prime },\ell _{12}^{\prime },\ell _{23}^{\prime }),\\ c_{3}^{\prime }=\max (d_{13}^{\prime },d_{23}^{\prime },\ell _{13}^{\prime },\ell _{23}^{\prime }).\end{array} & & \displaystyle\end{eqnarray}$$
We have that the
$p$
-factor of the Euler product is
$$\begin{eqnarray}\displaystyle 1+O\biggl(\mathop{\sum }_{1\leqslant i\leqslant 3}p^{-(u_{i}+w_{4})}+\mathop{\sum }_{\substack{ 1\leqslant i,j\leqslant 3, \\ i\neq j}}p^{-(u_{i}+w_{j})}+\mathop{\sum }_{1\leqslant i<j\leqslant 3}p^{-(w_{i}+w_{j})}\biggr) & & \displaystyle \nonumber\end{eqnarray}$$
and thus both sides of (6.4) converge whenever each of the exponents above are smaller than
$-1$
.
As for (6.3), we notice that by symmetry it suffices to consider the contribution to the series coming from the terms with
$b_{1}c_{1}\geqslant b_{2}c_{2},b_{3}c_{3}$
. This is less than or equal to the left-hand side of (6.4) with
$(u_{1},w_{1})$
replaced by
$(u_{1}-\unicode[STIX]{x1D705},w_{1}-\unicode[STIX]{x1D705})$
and the lemma follows.◻
Lemma 7. With the notation of (6.1) and for
$\mathbf{a}=(a_{1},a_{2},a_{3})\in \mathbb{Z}_{\neq 0}^{3}$
, let
$$\begin{eqnarray}\displaystyle \mathfrak{S}_{\boldsymbol{a}}^{\ast }:=\mathop{\sum }_{q\geqslant 1}\frac{\unicode[STIX]{x1D711}(q)}{q^{3}}\mathop{\sum }_{\substack{ \boldsymbol{e},\boldsymbol{\ell }\in \mathbb{N}^{3} \\ \boldsymbol{d}\in \mathbb{N}^{6}}}\unicode[STIX]{x1D707}(\mathbf{e},\mathbf{d},\boldsymbol{\ell })\frac{(a_{1}b_{1}c_{1},q)(a_{2}b_{2}c_{2},q)(a_{3}b_{3}c_{3},q)}{b_{1}b_{2}b_{3}c_{1}c_{2}c_{3}c_{4}}. & & \displaystyle\end{eqnarray}$$
Then
$\mathfrak{S}_{(1,1,1)}^{\ast }=\mathfrak{S}_{2}$
with
$\mathfrak{S}_{2}$
as in Theorem 2.
Proof. With the same notation as in (6.5), we have that for
$\boldsymbol{a}=\mathbf{1}$
, the right-hand side of (6.6) is equal to
$$\begin{eqnarray}\displaystyle & & \displaystyle \mathop{\prod }_{p}\biggl(\mathop{\sum }_{\substack{ q^{\prime }\in \mathbb{Z}_{{\geqslant}0},\boldsymbol{d}^{\prime }\in \{0,1\}^{6} \\ \boldsymbol{e}^{\prime },\boldsymbol{\ell }^{\prime }\in \{0,1\}^{3}}}\nonumber\\ \displaystyle & & \displaystyle \quad \times \frac{(p-1)^{\unicode[STIX]{x1D70C}_{q^{\prime }}}(-1)^{e_{1}^{\prime }+e_{2}^{\prime }+e_{3}^{\prime }+d_{12}^{\prime }+d_{13}^{\prime }+d_{21}^{\prime }+d_{23}^{\prime }+d_{31}^{\prime }+d_{32}^{\prime }+\ell _{12}^{\prime }+\ell _{13}^{\prime }+\ell _{23}^{\prime }}}{p^{2q^{\prime }+\unicode[STIX]{x1D70C}_{q^{\prime }}+b_{1}^{\prime }+b_{2}^{\prime }+b_{3}^{\prime }+c_{1}^{\prime }+c_{2}^{\prime }+c_{3}^{\prime }+c_{4}^{\prime }-\min (q^{\prime },b_{1}^{\prime }+c_{1}^{\prime })-\min (q^{\prime },b_{2}^{\prime }+c_{2}^{\prime })-\min (q^{\prime },b_{3}^{\prime }+c_{3}^{\prime })}}\biggr),\nonumber\end{eqnarray}$$
where
$\unicode[STIX]{x1D70C}_{0}=0$
and
$\unicode[STIX]{x1D70C}_{q^{\prime }}=1$
if
$q^{\prime }\geqslant 1$
. As in [Reference Blomer, Brüdern and Salberger8, Lemma 2.7], we observe that the terms with
$q^{\prime }\geqslant 2$
do not contribute. Indeed, if
$q^{\prime }\geqslant 2$
, then
$\min (q^{\prime },b_{i}^{\prime }+c_{i}^{\prime })=b_{i}^{\prime }+c_{i}^{\prime }$
, so that the exponent of
$p$
above is
$2q^{\prime }+c_{4}^{\prime }$
and so it does not depend on
$d_{12}^{\prime }$
. In particular, the contributions of
$d_{12}^{\prime }=0$
and
$d_{12}^{\prime }=1$
cancel out. After restricting the sum over
$q^{\prime }$
to
$q^{\prime }\in \{0,1\}$
, we are just left with performing a finite computation over the
$2^{13}$
possible values of the variables. With the help of mathematical software we then obtain the claimed Euler product formula for
$\mathfrak{S}_{(1,1,1)}^{\ast }$
.◻
We are now ready to prove our Theorem 2.
Proof of Theorem 2.
Let
$K_{\boldsymbol{a}}^{\ast }(B)$
be as in (5.3) but imposing also the coprimality conditions (5.2). In particular, by (2.2), we have
$$\begin{eqnarray}\displaystyle N_{\widehat{W}_{3},\widehat{H}}(B)=K_{(1,1,1)}^{\ast }(B)+N_{\widehat{W}_{3},\widehat{H}}^{\prime }(B), & & \displaystyle\end{eqnarray}$$
where
$N_{\widehat{W}_{3},\widehat{H}}^{\prime }(B)$
counts the number of points in
$\widehat{W}_{3}$
of height less than
$B$
which also satisfy
$x_{1}x_{2}x_{3}=0$
. Now, for
$x_{3}=0$
(and thus
$y_{3}=1$
), then (1.1) reduces to
$x_{1}/y_{1}+x_{2}/y_{2}=0$
. Since we have
$(x_{1},y_{1})=(x_{2},y_{2})=1$
, then
$x_{1}=-x_{2}$
,
$y_{1}=y_{2}$
and thus
$$\begin{eqnarray}\displaystyle N_{\widehat{W}_{3},\widehat{H}}^{\prime }(B)=1+3\mathop{\sum }_{\substack{ x\in \mathbb{Z}_{\neq 0},y\in \mathbb{N},(x,y)=1 \\ |x|,y\leqslant B^{1/2}}}1=\frac{36}{\unicode[STIX]{x1D70B}^{2}}B+O(B^{1/2}\log B). & & \displaystyle\end{eqnarray}$$
In particular, it suffices to prove an asymptotic formula with power-saving error term for
$K_{(1,1,1)}^{\ast }(B)$
. Since it does not introduce any difficulties, in the following we shall compute an asymptotic formula for
$K_{\boldsymbol{a}}^{\ast }(B)$
for all
$\boldsymbol{a}\in \mathbb{Z}_{\neq 0}^{3}$
.
Let
$0<\unicode[STIX]{x1D6FF}<\frac{1}{2}$
. Using the same approach used for Proposition 1 and with the notation of Lemma 5 and of the proof of Proposition 1, we need to compute an asymptotic formula for
$$\begin{eqnarray}\displaystyle K_{\boldsymbol{a}}^{\ast \pm }(B)=\sum _{\substack{ (\boldsymbol{x},\boldsymbol{z})\in \mathbb{Z}_{\neq 0}^{3}\times \mathbb{Z}_{{>}0}^{4} \\ a_{1}x_{1}z_{1}+a_{2}x_{2}z_{2}+a_{3}x_{3}z_{3}=0}}\mathop{\prod }_{I\subseteq S_{3}}F_{\unicode[STIX]{x1D6FF}}^{\pm }\biggl(\frac{(z_{1}z_{2}z_{3}z_{4})^{|J|}}{B}\mathop{\prod }_{i\in I}|x_{i}|\mathop{\prod }_{j\in J}z_{j}^{-1}\biggr). & & \displaystyle \nonumber\end{eqnarray}$$
With the notation of Lemma 5, we can rewrite this as
$$\begin{eqnarray}\displaystyle K_{\boldsymbol{a}}^{\ast \pm }(B) & = & \displaystyle \mathop{\sum }_{\substack{ \boldsymbol{e},\boldsymbol{\ell }\in \mathbb{N}^{3}, \\ \boldsymbol{d}\in \mathbb{N}^{6}}}\unicode[STIX]{x1D707}(\boldsymbol{e},\boldsymbol{d},\boldsymbol{\ell })\mathop{\sum }_{\substack{ (\boldsymbol{x},\boldsymbol{z})\in \mathbb{Z}_{\neq 0}^{3}\times \mathbb{Z}_{{>}0}^{4} \\ a_{1}^{\ast }x_{1}z_{1}+a_{2}^{\ast }x_{2}z_{2}+a_{3}^{\ast }x_{3}z_{3}=0}}\nonumber\\ \displaystyle & & \displaystyle \times \,\mathop{\prod }_{I\subseteq S_{3}}F_{\unicode[STIX]{x1D6FF}}^{\pm }\biggl(\frac{(c_{1}z_{1}c_{2}z_{2}c_{3}z_{3}c_{4}z_{4})^{|J|}}{B}\mathop{\prod }_{i\in I}|b_{i}x_{i}|\mathop{\prod }_{j\in J}(c_{j}z_{j})^{-1}\biggr),\nonumber\end{eqnarray}$$
where
$\boldsymbol{a}^{\ast }:=(a_{1}^{\ast },a_{2}^{\ast },a_{3}^{\ast })=(a_{1}b_{1}c_{1},a_{2}b_{2}c_{2},a_{3}b_{3}c_{3})$
with
$b_{i},c_{i}$
as in (6.1). Thus, proceeding as in Proposition 1 and using the same notation and lines of integration, we find the following expression for
$K_{\boldsymbol{a}}^{\ast \pm }(B)$
:
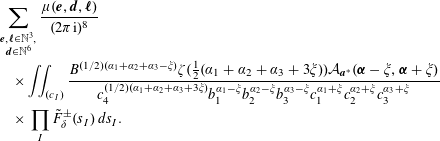$$\begin{eqnarray}\displaystyle & & \displaystyle \mathop{\sum }_{\substack{ \boldsymbol{e},\boldsymbol{\ell }\in \mathbb{N}^{3}, \\ \boldsymbol{d}\in \mathbb{N}^{6}}}\frac{\unicode[STIX]{x1D707}(\boldsymbol{e},\boldsymbol{d},\boldsymbol{\ell })}{(2\unicode[STIX]{x1D70B}\text{i})^{8}}\nonumber\\ \displaystyle & & \displaystyle \quad \times \iint _{(c_{I})}\frac{B^{(1/2)(\unicode[STIX]{x1D6FC}_{1}+\unicode[STIX]{x1D6FC}_{2}+\unicode[STIX]{x1D6FC}_{3}-\unicode[STIX]{x1D709})}\unicode[STIX]{x1D701}({\textstyle \frac{1}{2}}(\unicode[STIX]{x1D6FC}_{1}+\unicode[STIX]{x1D6FC}_{2}+\unicode[STIX]{x1D6FC}_{3}+3\unicode[STIX]{x1D709})){\mathcal{A}}_{\boldsymbol{a}^{\ast }}(\boldsymbol{\unicode[STIX]{x1D6FC}}-\unicode[STIX]{x1D709},\boldsymbol{\unicode[STIX]{x1D6FC}}+\unicode[STIX]{x1D709})}{c_{4}^{(1/2)(\unicode[STIX]{x1D6FC}_{1}+\unicode[STIX]{x1D6FC}_{2}+\unicode[STIX]{x1D6FC}_{3}+3\unicode[STIX]{x1D709})}b_{1}^{\unicode[STIX]{x1D6FC}_{1}-\unicode[STIX]{x1D709}}b_{2}^{\unicode[STIX]{x1D6FC}_{2}-\unicode[STIX]{x1D709}}b_{3}^{\unicode[STIX]{x1D6FC}_{3}-\unicode[STIX]{x1D709}}c_{1}^{\unicode[STIX]{x1D6FC}_{1}+\unicode[STIX]{x1D709}}c_{2}^{\unicode[STIX]{x1D6FC}_{2}+\unicode[STIX]{x1D709}}c_{3}^{\unicode[STIX]{x1D6FC}_{3}+\unicode[STIX]{x1D709}}}\nonumber\\ \displaystyle & & \displaystyle \quad \times \,\mathop{\prod }_{I}\tilde{F}_{\unicode[STIX]{x1D6FF}}^{\pm }(s_{I})\,ds_{I}.\nonumber\end{eqnarray}$$
Notice that by (6.3) with
$\unicode[STIX]{x1D705}=0$
, the outer series converges absolutely. We keep following the same approach as the proof of Proposition 1 splitting
${\mathcal{A}}_{\boldsymbol{a}}$
into
${\mathcal{M}}_{\boldsymbol{a}}+{\mathcal{E}}_{\boldsymbol{a}}$
and thus
$K_{\boldsymbol{a}}^{\ast \pm }(B)$
into
$M_{\boldsymbol{a}}^{\ast \pm }(B)+E_{\boldsymbol{a}}^{\ast \pm }(B)$
. We can treat
$E_{\boldsymbol{a}}^{\ast \pm }(B)$
as above with the only difference that in this case we move
$c_{S_{3}}$
to
$\frac{1}{4}\,-\,2\unicode[STIX]{x1D6FE}\,+\,6\unicode[STIX]{x1D700}$
, where
$\unicode[STIX]{x1D6FE}:=(391-\sqrt{152737})/108$
(this value is the smallest one can take under the condition that the inequalities (6.2) are satisfied). With this choice, (4.4) and (6.3) give the bound
$$\begin{eqnarray}\displaystyle E_{\boldsymbol{a}}^{\ast \pm }(B) & \ll & \displaystyle \mathop{\sum }_{\substack{ \boldsymbol{e},\boldsymbol{\ell }\in \mathbb{N}^{3}, \\ \boldsymbol{d}\in \mathbb{N}^{6}}}\frac{\max (a_{1}b_{1}c_{1},a_{2}b_{2}c_{2},a_{3}b_{3}c_{3})^{378\unicode[STIX]{x1D6FE}/(2-27\unicode[STIX]{x1D6FE})}}{c_{4}^{1+12\unicode[STIX]{x1D700}}(b_{1}b_{2}b_{3})^{2/3-2\unicode[STIX]{x1D6FE}+9\unicode[STIX]{x1D700}}c_{1}^{2/3}c_{2}^{2/3}c_{3}^{2/3}}B^{1-2\unicode[STIX]{x1D6FE}+13\unicode[STIX]{x1D700}}\nonumber\\ \displaystyle & & \displaystyle \times \,\iint _{(c_{I})}\Bigl(1+\max _{I}|s_{I}|\Bigr)^{567\unicode[STIX]{x1D6FE}/(2-27\unicode[STIX]{x1D6FE})}\mathop{\prod }_{I}|\tilde{F}_{\unicode[STIX]{x1D6FF}}^{\pm }(s_{I})|\,ds_{I}\nonumber\\ \displaystyle & \ll _{A} & \displaystyle \,B^{1-2\unicode[STIX]{x1D6FE}+13\unicode[STIX]{x1D700}}\unicode[STIX]{x1D6FF}^{-567\unicode[STIX]{x1D6FE}/(2-27\unicode[STIX]{x1D6FE})-\unicode[STIX]{x1D700}},\nonumber\end{eqnarray}$$
where
$A:=\max _{1\leqslant i\leqslant 3}|a_{i}|$
. As for
$M_{\boldsymbol{a}}^{\ast \pm }(B)$
, we treat it exactly as in Proposition 1, splitting it into
$M_{\boldsymbol{a}}^{\ast \pm }(B)=\sum _{k=0}^{3}E_{\boldsymbol{a},k}^{\ast \pm }(B)$
. As above, we have that
$M_{\boldsymbol{a},0}^{\ast \pm }(B),M_{\boldsymbol{a},1}^{\ast \pm }(B)\ll _{A}B^{25/27+8\unicode[STIX]{x1D700}}\unicode[STIX]{x1D6FF}^{-1-\unicode[STIX]{x1D700}}$
, where the sums in the error terms are immediately seen to be convergent by (5.13) and (6.3). For
$M_{\boldsymbol{a},3}^{\ast \pm }(B)$
, we find similarly as in the proof of Proposition 1,
$$\begin{eqnarray}\displaystyle & & \displaystyle M_{\boldsymbol{a},3}^{\ast \pm }(B)\nonumber\\ \displaystyle & & \displaystyle \quad =\mathop{\sum }_{\substack{ \boldsymbol{e},\boldsymbol{\ell }\in \mathbb{N}^{3}, \\ \boldsymbol{d}\in \mathbb{N}^{6}}}\frac{\unicode[STIX]{x1D707}(\boldsymbol{e},\boldsymbol{d},\boldsymbol{\ell })}{(2\unicode[STIX]{x1D70B}\text{i})^{6}}\nonumber\\ \displaystyle & & \displaystyle \qquad \times \iint _{(c_{I})}\operatorname{ \ast}Res_{\unicode[STIX]{x1D709}=0}\biggl(\frac{B^{1+\unicode[STIX]{x1D709}}\unicode[STIX]{x1D701}(1+3\unicode[STIX]{x1D709})\unicode[STIX]{x1D701}(1+2\unicode[STIX]{x1D709})^{3}{\mathcal{Q}}_{\boldsymbol{a}^{\ast },3}(\boldsymbol{\unicode[STIX]{x1D6FC}},\unicode[STIX]{x1D709})}{3s_{123}sc_{4}^{1+3\unicode[STIX]{x1D709}}b_{1}^{\unicode[STIX]{x1D6FC}_{1}-\unicode[STIX]{x1D709}}b_{2}^{\unicode[STIX]{x1D6FC}_{2}-\unicode[STIX]{x1D709}}b_{3}^{\unicode[STIX]{x1D6FC}_{3}-\unicode[STIX]{x1D709}}c_{1}^{\unicode[STIX]{x1D6FC}_{1}+\unicode[STIX]{x1D709}}c_{2}^{\unicode[STIX]{x1D6FC}_{2}+\unicode[STIX]{x1D709}}c_{3}^{\unicode[STIX]{x1D6FC}_{3}+\unicode[STIX]{x1D709}}}\biggr)\mathop{\prod }_{I\neq \emptyset ,S_{3}}\frac{ds_{I}}{s_{I}}\nonumber\\ \displaystyle & & \displaystyle \qquad +\,O_{A}(B^{25/27+8\unicode[STIX]{x1D700}}\unicode[STIX]{x1D6FF}^{-1-\unicode[STIX]{x1D700}}+B^{1+5\unicode[STIX]{x1D700}}\unicode[STIX]{x1D6FF}^{1-7\unicode[STIX]{x1D700}}),\nonumber\end{eqnarray}$$
with
$s:=\frac{1}{3}-\frac{1}{3}\sum _{I\neq \emptyset ,S_{3}}(3-|I|)s_{I}$
,
$s_{123}:=\frac{2}{3}-\frac{1}{3}\sum _{I\neq S_{3}}|I|s_{I}$
, lines of integration
$c_{I}=\frac{1}{12}$
for all
$I\neq S_{3},\emptyset$
,
${\mathcal{Q}}_{\boldsymbol{a}^{\ast },3}$
as in (5.11) and
$\boldsymbol{\unicode[STIX]{x1D6FC}}$
and
$\unicode[STIX]{x1D709}$
given by (5.6) with
$s_{123}$
and
$s$
replaced by (5.18). Computing the residue then gives
$$\begin{eqnarray}\displaystyle M_{\boldsymbol{a},3}^{\pm }(B)=BP_{\boldsymbol{a}}^{\ast }(\log B)+O_{A}(B^{25/27+8\unicode[STIX]{x1D700}}\unicode[STIX]{x1D6FF}^{-1-\unicode[STIX]{x1D700}}+B^{1+5\unicode[STIX]{x1D700}}\unicode[STIX]{x1D6FF}^{1-7\unicode[STIX]{x1D700}}) & & \displaystyle \nonumber\end{eqnarray}$$
where
$P_{\boldsymbol{a}}^{\ast }$
is a degree
$3$
polynomial with leading constant
$$\begin{eqnarray}\displaystyle P_{\boldsymbol{a},3}^{\ast }:=\mathop{\sum }_{\substack{ \boldsymbol{e},\boldsymbol{\ell }\in \mathbb{N}^{3}, \\ \boldsymbol{d}\in \mathbb{N}^{6}}}\frac{\unicode[STIX]{x1D707}(\boldsymbol{e},\boldsymbol{d},\boldsymbol{\ell })}{(2\unicode[STIX]{x1D70B}\text{i})^{6}}\iint _{(1/12)}\frac{{\mathcal{Q}}_{\boldsymbol{a}^{\ast },3}(\boldsymbol{\unicode[STIX]{x1D6FC}},0)}{432s_{123}sc_{4}b_{1}^{\unicode[STIX]{x1D6FC}_{1}}b_{2}^{\unicode[STIX]{x1D6FC}_{2}}b_{3}^{\unicode[STIX]{x1D6FC}_{3}}c_{1}^{\unicode[STIX]{x1D6FC}_{1}}c_{2}^{\unicode[STIX]{x1D6FC}_{2}}c_{3}^{\unicode[STIX]{x1D6FC}_{3}}}\mathop{\prod }_{I\neq \emptyset ,S_{3}}\frac{ds_{I}}{s_{I}} & & \displaystyle \nonumber\end{eqnarray}$$
and
$\unicode[STIX]{x1D6FC}_{2},\unicode[STIX]{x1D6FC}_{3}$
as in (5.21) and
$\unicode[STIX]{x1D6FC}_{1}=2-\unicode[STIX]{x1D6FC}_{2}-\unicode[STIX]{x1D6FC}_{3}$
. Now,
$$\begin{eqnarray}\displaystyle {\mathcal{Q}}_{\boldsymbol{a}^{\ast },3}(\boldsymbol{\unicode[STIX]{x1D6FC}},0) & = & \displaystyle 2\unicode[STIX]{x1D70B}^{1/2}\mathop{\sum }_{\ell =1}^{\infty }\frac{(a_{1}b_{1}c_{1},\ell )(a_{2}b_{2}c_{2},\ell )(a_{3}b_{3}c_{3},\ell )\unicode[STIX]{x1D711}(\ell )}{\ell ^{3}}\nonumber\\ \displaystyle & & \displaystyle \times \,\mathop{\prod }_{i=1}^{3}\frac{\unicode[STIX]{x1D6E4}((1-\unicode[STIX]{x1D6FC}_{i})/2)}{|a_{i}|^{1-\unicode[STIX]{x1D6FC}_{i}}\unicode[STIX]{x1D6E4}(\unicode[STIX]{x1D6FC}_{i}/2)}\nonumber\end{eqnarray}$$
and hence by the same computation as in Proposition 1, we find that
$P_{\boldsymbol{a},3}^{\ast }=\frac{1}{144}\mathfrak{S}_{\boldsymbol{a}}^{\ast }{\mathcal{I}}_{\boldsymbol{a}}$
with
$\mathfrak{S}_{\boldsymbol{a}}^{\ast }$
as in Lemma 7.
Finally, we treat
$M_{\boldsymbol{a},2}^{\ast \pm }(B)$
exactly as in Proposition 1 and so, collecting the various asymptotics and bounds, we arrive at
$$\begin{eqnarray}\displaystyle K_{\boldsymbol{a}}^{\ast \pm }(B) & = & \displaystyle BP_{\boldsymbol{a}}^{\ast }(\log B)+W_{\boldsymbol{a}}^{\ast }B\nonumber\\ \displaystyle & & \displaystyle +\,O_{A}(B^{1+5\unicode[STIX]{x1D700}}\unicode[STIX]{x1D709}^{1-8\unicode[STIX]{x1D700}}+B^{1-2\unicode[STIX]{x1D6FE}+13\unicode[STIX]{x1D700}}\unicode[STIX]{x1D6FF}^{-567\unicode[STIX]{x1D6FE}/(2-27\unicode[STIX]{x1D6FE})-7\unicode[STIX]{x1D700}})\nonumber\end{eqnarray}$$
for a certain
$W_{\boldsymbol{a}}^{\ast }\in \mathbb{R}$
. Choosing
$\unicode[STIX]{x1D6FF}=B^{-\unicode[STIX]{x1D6FE}(2-27\unicode[STIX]{x1D6FE})/(1+270\unicode[STIX]{x1D6FE})}$
, we obtain
$$\begin{eqnarray}\displaystyle K_{\boldsymbol{a}}^{\ast }(B):=BP_{\boldsymbol{a}}^{\ast }(\log B)^{3}+W_{\boldsymbol{a}}^{\ast }B+O_{A}(B^{1-\unicode[STIX]{x1D6FE}(2-27\unicode[STIX]{x1D6FE})/(1+270\unicode[STIX]{x1D6FE})+13\unicode[STIX]{x1D700}}). & & \displaystyle \nonumber\end{eqnarray}$$
In particular, by (6.7), (6.8) and Lemma 7 and recalling that
$\unicode[STIX]{x1D6FE}=(391-\sqrt{152737})/108$
, we obtain Theorem 2 for all
$\unicode[STIX]{x1D709}_{2}\leqslant (1165-3\sqrt{152737})/3264=0.00228169\ldots .$
◻
7 Proof of Theorem 1
By (2.3) and renaming for simplicity
$z_{6}=d_{1}$
,
$z_{5}=d_{2}$
,
$z_{3}=d_{3}$
and
$z_{4}$
by
$z_{3}$
, we have to count the solutions to
$$\begin{eqnarray}\displaystyle x_{1}d_{1}+x_{2}d_{2}+x_{3}d_{3}=0, & & \displaystyle \nonumber\end{eqnarray}$$
where
$\boldsymbol{x}\in \mathbb{Z}_{\neq 0}^{3},\boldsymbol{d},\boldsymbol{z}\in \mathbb{N}^{3}$
with
$\boldsymbol{x}=(x_{1},x_{2},x_{3}),\boldsymbol{d}=(d_{1},d_{2},d_{3}),\boldsymbol{z}=(z_{1},z_{2},z_{3})$
subject to the coprimality conditions
$$\begin{eqnarray}\displaystyle \begin{array}{@{}c@{}}(d_{i},d_{j})=(z_{i},z_{j})=(d_{k},z_{k})=1\quad \text{for all }i,j,k\in \{1,2,3\},i\neq j,\\ (x_{1},x_{2},x_{3})=(x_{i},x_{j},z_{k})=1\quad \text{for all }i,j,k\text{ such that }\{i,j,k\}=\{1,2,3\}\end{array} & & \displaystyle \nonumber\\ \displaystyle & & \displaystyle\end{eqnarray}$$
and
$$\begin{eqnarray}\displaystyle \max _{1\leqslant i,j\leqslant 3}\left\{|x_{i}z_{i}|^{2}d_{1}d_{2}d_{3}\frac{z_{j}}{d_{j}}\right\}\leqslant B. & & \displaystyle \nonumber\end{eqnarray}$$
Let
$0<\unicode[STIX]{x1D6FF}<\frac{1}{2}$
. This parametrization and (2.3) then imply that we just need to consider
$$\begin{eqnarray}\displaystyle N_{\unicode[STIX]{x1D6FF}}^{\pm }(B):=2\sum _{\substack{ \boldsymbol{x}\in \mathbb{Z}_{\neq 0}^{3},\boldsymbol{d},\boldsymbol{z}\in \mathbb{N}^{3} \\ x_{1}d_{1}+x_{2}d_{2}+x_{3}d_{3}=0}}\mathop{\prod }_{1\leqslant i,j\leqslant 3}F_{\unicode[STIX]{x1D6FF}}^{\pm }\biggl((x_{i}z_{i})^{2}\frac{d_{1}d_{2}d_{3}}{d_{j}}\frac{z_{j}}{B}\biggr), & & \displaystyle\end{eqnarray}$$
where
$\sum ^{\prime }$
indicates the coprimality conditions (7.1) since for all
$\unicode[STIX]{x1D6FF}>0$
we have
$$\begin{eqnarray}\displaystyle N_{\unicode[STIX]{x1D6FF}}^{-}(B)\leqslant N_{\widetilde{W}_{3},\widetilde{H}}(B)\leqslant N_{\unicode[STIX]{x1D6FF}}^{+}(B). & & \displaystyle \nonumber\end{eqnarray}$$
We shall prove that
$$\begin{eqnarray}\displaystyle N_{\unicode[STIX]{x1D6FF}}^{\pm }(B)=BP_{1}(\log B)+O(B^{1+\unicode[STIX]{x1D700}}\unicode[STIX]{x1D6FF}^{1-C\unicode[STIX]{x1D700}}+B^{1-K}\unicode[STIX]{x1D6FF}^{-C}), & & \displaystyle\end{eqnarray}$$
where
$P_{1}$
is a polynomial of degree
$4$
with leading coefficient
$(\mathfrak{S}_{1}\cdot {\mathcal{I}})/144$
with the notation of Theorem 1 and for some
$C,K>0$
and
$\unicode[STIX]{x1D700}>0$
small enough, so that choosing
$\unicode[STIX]{x1D6FF}=B^{-K/(C+1)}$
, we obtain Theorem 1.
7.1 Initial manipulations
We write
$F_{\unicode[STIX]{x1D6FF}}^{\pm }$
in terms of its Mellin transform using the variable
$s_{ij}$
for the cut-off function corresponding to
$(i,j)$
and choosing
$$\begin{eqnarray}\displaystyle c_{s_{1j}}={\textstyle \frac{1}{9}}+\unicode[STIX]{x1D700},\qquad c_{s_{2j}}={\textstyle \frac{1}{9}}+4\unicode[STIX]{x1D700},\qquad c_{s_{3j}}={\textstyle \frac{1}{9}}+6\unicode[STIX]{x1D700} & & \displaystyle \nonumber\end{eqnarray}$$
as lines of integration for all
$j\in \{1,2,3\}$
. We obtain
$$\begin{eqnarray}\displaystyle N_{\unicode[STIX]{x1D6FF}}^{\pm }(B) & = & \displaystyle 2\sum _{\substack{ \boldsymbol{x}\in \mathbb{Z}_{\neq 0}^{3},\boldsymbol{d},\boldsymbol{z}\in \mathbb{N}^{3} \\ x_{1}d_{1}+x_{2}d_{2}+x_{3}d_{3}=0}}\frac{1}{(2\unicode[STIX]{x1D70B}\text{i})^{9}}\nonumber\\ \displaystyle & & \displaystyle \times \,\iint _{(c_{s_{ij}})}\frac{B^{\mathop{\sum }_{i,j}s_{ij}}}{\mathop{\prod }_{k}x_{k}^{2\mathop{\sum }_{j}s_{kj}}d_{k}^{\mathop{\sum }_{i,j\,j\neq k}s_{ij}}z_{k}^{2\mathop{\sum }_{j}s_{kj}+\mathop{\sum }_{i}s_{i,k}}}\mathop{\prod }_{i,j}\tilde{F}_{\unicode[STIX]{x1D6FF}}^{\pm }(s_{ij})\,ds_{ij}\nonumber\\ \displaystyle & = & \displaystyle 2\sum _{\substack{ \boldsymbol{x}\in \mathbb{Z}_{\neq 0}^{3},\boldsymbol{d},\boldsymbol{z}\in \mathbb{N}^{3} \\ x_{1}d_{1}+x_{2}d_{2}+x_{3}d_{3}=0}}\frac{1}{(2\unicode[STIX]{x1D70B}\text{i})^{9}}\nonumber\\ \displaystyle & & \displaystyle \times \,\iint _{(c_{s_{ij}})}\frac{B^{s^{\ast }}}{\mathop{\prod }_{k}x_{k}^{\unicode[STIX]{x1D6FC}_{k}-\unicode[STIX]{x1D709}_{k}}d_{k}^{\unicode[STIX]{x1D6FC}_{k}+\unicode[STIX]{x1D709}_{k}}z_{k}^{s^{\ast }-2\unicode[STIX]{x1D709}_{k}}}\mathop{\prod }_{i,j}\tilde{F}_{\unicode[STIX]{x1D6FF}}^{\pm }(s_{ij}),\,ds_{ij},\nonumber\end{eqnarray}$$
where
$$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D6FC}_{k} & := & \displaystyle \frac{1}{2}\mathop{\sum }_{1\leqslant i,j\leqslant 3}s_{ij}+\mathop{\sum }_{1\leqslant j\leqslant 3}s_{kj}-\frac{1}{2}\mathop{\sum }_{1\leqslant i\leqslant 3}s_{ik},\nonumber\\ \displaystyle \unicode[STIX]{x1D709}_{k} & := & \displaystyle \frac{1}{2}\mathop{\sum }_{\substack{ 1\leqslant i,j\leqslant 3 \\ j\neq k}}s_{ij}-\mathop{\sum }_{1\leqslant j\leqslant 3}s_{kj}\quad \text{for all }k\in \{1,2,3\},\nonumber\\ \displaystyle s^{\ast } & := & \displaystyle \mathop{\sum }_{1\leqslant i,j\leqslant 3}s_{ij},\nonumber\end{eqnarray}$$
so that
$$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D6FC}_{k}-\unicode[STIX]{x1D709}_{k}=2\mathop{\sum }_{1\leqslant j\leqslant 3}s_{kj},\qquad \unicode[STIX]{x1D6FC}_{k}+\unicode[STIX]{x1D709}_{k}=\mathop{\sum }_{\substack{ 1\leqslant i,j\leqslant 3 \\ j\neq k}}s_{ij}. & & \displaystyle \nonumber\end{eqnarray}$$
Note that we have
$$\begin{eqnarray}\unicode[STIX]{x1D709}_{1}+\unicode[STIX]{x1D709}_{2}+\unicode[STIX]{x1D709}_{3}=0,\qquad \unicode[STIX]{x1D6FC}_{1}+\unicode[STIX]{x1D6FC}_{2}+\unicode[STIX]{x1D6FC}_{3}=2s^{\ast }\end{eqnarray}$$
and that, like in the proof of Theorem 2, we are neglecting the dependences of this notation on variables
$s_{ij}$
in order to simplify the exposition. Also, notice that with the above lines of integration, we have
$$\begin{eqnarray}\displaystyle \!\!\!\!\!\!\!\begin{array}{@{}c@{}}\Re (\unicode[STIX]{x1D709}_{1})=8\unicode[STIX]{x1D700},\qquad \Re (\unicode[STIX]{x1D709}_{2})=-\unicode[STIX]{x1D700},\qquad \Re (\unicode[STIX]{x1D709}_{3})=-7\unicode[STIX]{x1D700},\qquad \Re (s^{\ast })=1+33\unicode[STIX]{x1D700},\\ \Re (\unicode[STIX]{x1D6FC}_{1})=\frac{2}{3}+14\unicode[STIX]{x1D700},\qquad \Re (\unicode[STIX]{x1D6FC}_{2})=\frac{2}{3}+23\unicode[STIX]{x1D700},\qquad \Re (\unicode[STIX]{x1D6FC}_{3})=\frac{2}{3}+29\unicode[STIX]{x1D700},\end{array}\quad & & \displaystyle\end{eqnarray}$$
so that in particular the above series are absolutely convergent by Lemma 2.
We make a change of variables, discarding the variables
$s_{11},s_{22},s_{13},s_{23}$
and
$s_{33}$
and introducing the variables
$\unicode[STIX]{x1D6FC}_{1},\unicode[STIX]{x1D6FC}_{2},\unicode[STIX]{x1D709}_{1},\unicode[STIX]{x1D709}_{2}$
and
$s^{\ast }$
. The inverse transformations are
$$\begin{eqnarray}\displaystyle \begin{array}{@{}c@{}}s_{11}=s^{\ast }-\unicode[STIX]{x1D6FC}_{1}-\unicode[STIX]{x1D709}_{1}-s_{21}-s_{31},\qquad s_{22}=s^{\ast }-\unicode[STIX]{x1D6FC}_{2}-\unicode[STIX]{x1D709}_{2}-s_{12}-s_{32},\\ s_{13}=-s^{\ast }+{\textstyle \frac{3}{2}}\unicode[STIX]{x1D6FC}_{1}+{\textstyle \frac{1}{2}}\unicode[STIX]{x1D709}_{1}-s_{12}+s_{21}+s_{31},\\ s_{23}=-s^{\ast }+{\textstyle \frac{3}{2}}\unicode[STIX]{x1D6FC}_{2}+{\textstyle \frac{1}{2}}\unicode[STIX]{x1D709}_{2}+s_{12}-s_{21}+s_{32},\\ s_{33}=s^{\ast }-{\textstyle \frac{1}{2}}(\unicode[STIX]{x1D6FC}_{1}+\unicode[STIX]{x1D6FC}_{2}-\unicode[STIX]{x1D709}_{1}-\unicode[STIX]{x1D709}_{2})-s_{31}-s_{32}\end{array} & & \displaystyle\end{eqnarray}$$
and the Jacobian is equal to
$1$
. In the following, to simplify the exposition, we shall keep using also the older variables (as well as
$\unicode[STIX]{x1D709}_{3}$
and
$\unicode[STIX]{x1D6FC}_{3}$
given by (7.4)), treating them as functions of the new ones.
7.2 Resolving the coprimality conditions
For
$\Re (\unicode[STIX]{x1D6FC}_{k}\pm \unicode[STIX]{x1D709}_{k})\,>\,\frac{2}{3}$
and
$\Re (s^{\ast }-2\unicode[STIX]{x1D709}_{k})\,>\,1$
, using Möbius’ inversion formula to remove the coprimality conditions (7.1) (this is [Reference Blomer, Brüdern and Salberger8, Lemma 2.1]), we obtain
$$\begin{eqnarray}\displaystyle & & \displaystyle \sum _{\substack{ \boldsymbol{x}\in \mathbb{Z}_{\neq 0}^{3},\boldsymbol{d},\boldsymbol{z}\in \mathbb{N}^{3} \\ x_{1}d_{1}+x_{2}d_{2}+x_{3}d_{3}=0}}\mathop{\prod }_{k=1}^{3}\frac{1}{x_{k}^{\unicode[STIX]{x1D6FC}_{k}-\unicode[STIX]{x1D709}_{k}}d_{k}^{\unicode[STIX]{x1D6FC}_{k}+\unicode[STIX]{x1D709}_{k}}z_{k}^{s^{\ast }-2\unicode[STIX]{x1D709}_{k}}}\nonumber\\ \displaystyle & & \displaystyle \quad =\mathop{\sum }_{\substack{ \boldsymbol{b},\boldsymbol{c},\,\boldsymbol{f},\boldsymbol{g}\in \mathbb{N}^{3}, \\ h\in \mathbb{N}}}\mathop{\sum }_{\substack{ \boldsymbol{x}\in \mathbb{Z}_{\neq 0}^{3},\boldsymbol{d},\boldsymbol{z}\in \mathbb{N}^{3} \\ \mathop{\sum }_{k=1}^{3}r_{k}x_{k}d_{k}=0}}\unicode[STIX]{x1D707}(h)\mathop{\prod }_{k=1}^{3}\frac{\unicode[STIX]{x1D707}(b_{k})\unicode[STIX]{x1D707}(c_{k})\unicode[STIX]{x1D707}(f_{k})\unicode[STIX]{x1D707}(g_{k})}{(r_{1,k}x_{k})^{\unicode[STIX]{x1D6FC}_{k}-\unicode[STIX]{x1D709}_{k}}(r_{2,k}d_{k})^{\unicode[STIX]{x1D6FC}_{k}+\unicode[STIX]{x1D709}_{k}}(r_{3,k}z_{k})^{s^{\ast }-2\unicode[STIX]{x1D709}_{k}}}\nonumber\\ \displaystyle & & \displaystyle \quad =\!\mathop{\sum }_{\substack{ \boldsymbol{b},\boldsymbol{c},\,\boldsymbol{f},\boldsymbol{g}\in \mathbb{N}^{3}, \\ h\in \mathbb{N}}}\!\unicode[STIX]{x1D707}(h)\biggl(\mathop{\prod }_{k=1}^{3}\!\frac{\unicode[STIX]{x1D707}(b_{k})\unicode[STIX]{x1D707}(c_{k})\unicode[STIX]{x1D707}(f_{k})\unicode[STIX]{x1D707}(g_{k})}{r_{1,k}^{\unicode[STIX]{x1D6FC}_{k}-\unicode[STIX]{x1D709}_{k}}r_{2,k}^{\unicode[STIX]{x1D6FC}_{k}+\unicode[STIX]{x1D709}_{k}}r_{3,k}^{s^{\ast }-2\unicode[STIX]{x1D709}_{k}}}\unicode[STIX]{x1D701}(s^{\ast }\!-2\unicode[STIX]{x1D709}_{k})\!\!\biggr){\mathcal{A}}_{\boldsymbol{r}}(\boldsymbol{\unicode[STIX]{x1D6FC}}-\boldsymbol{\unicode[STIX]{x1D709}},\boldsymbol{\unicode[STIX]{x1D6FC}}+\boldsymbol{\unicode[STIX]{x1D709}}),\nonumber\\ \displaystyle & & \displaystyle\end{eqnarray}$$
with the notation of Lemma 2 and where for
$\{i,j,k\}=\{1,2,3\}$
, we defined
$$\begin{eqnarray}\displaystyle \begin{array}{@{}c@{}}r_{1,k}:=[g_{i},g_{j},h],\qquad r_{2,k}:=[b_{i},b_{j},f_{k}],\\ r_{3,k}:=[c_{i},c_{j},f_{k},g_{k}],\qquad r_{k}:=r_{1,k}r_{2,k}.\end{array} & & \displaystyle\end{eqnarray}$$
For future use we also observe that for
$\unicode[STIX]{x1D70E}\geqslant \frac{1}{2}+\unicode[STIX]{x1D700}$
with
$\unicode[STIX]{x1D700}>0$
, we have
$$\begin{eqnarray}\displaystyle & & \displaystyle \mathop{\sum }_{\substack{ \boldsymbol{b},\boldsymbol{c},\,\boldsymbol{f},\boldsymbol{g}\in \mathbb{N}^{3}, \\ h\in \mathbb{N}}}\mathop{\prod }_{k=1}^{3}\frac{1}{(r_{1,k}r_{2,k}r_{3,k})^{\unicode[STIX]{x1D70E}}}\nonumber\\ \displaystyle & & \displaystyle \quad =\mathop{\prod }_{p}\biggl(\mathop{\sum }_{\substack{ \boldsymbol{b}^{\prime },\boldsymbol{c}^{\prime },\,\boldsymbol{f}^{\prime },\boldsymbol{g}^{\prime }\in \mathbb{N}^{3}, \\ h^{\prime }\in \mathbb{N}}}p^{-\unicode[STIX]{x1D70E}\mathop{\sum }_{k}(\max (g_{i}^{\prime },g_{j}^{\prime },h^{\prime })+\max (b_{i}^{\prime },b_{j}^{\prime },f_{k}^{\prime })+\max (c_{i}^{\prime },c_{j}^{\prime },f_{k}^{\prime },g_{k}^{\prime }))}\biggr)\nonumber\\ \displaystyle & & \displaystyle \quad =\mathop{\prod }_{p}(1+O(p^{-2\unicode[STIX]{x1D70E}}))\ll 1,\end{eqnarray}$$
where, in the sum over
$k$
in the first line,
$i,j$
are such that
$\{i,j,k\}=\{1,2,3\}$
.
Now, by (7.7), we have
$$\begin{eqnarray}\displaystyle N_{\unicode[STIX]{x1D6FF}}^{\pm }(B) & = & \displaystyle 2\mathop{\sum }_{\substack{ \boldsymbol{b},\boldsymbol{c},\,\boldsymbol{f},\boldsymbol{g}\in \mathbb{N}^{3}, \\ h\in \mathbb{N}}}\frac{\unicode[STIX]{x1D707}(h)}{(2\unicode[STIX]{x1D70B}\text{i})^{9}}\nonumber\\ \displaystyle & & \displaystyle \times \,\iint _{(\cdots \,)}B^{s^{\ast }}\biggl(\mathop{\prod }_{k=1}^{3}\frac{\unicode[STIX]{x1D707}(b_{k})\unicode[STIX]{x1D707}(c_{k})\unicode[STIX]{x1D707}(f_{k})\unicode[STIX]{x1D707}(g_{k})}{r_{1,k}^{\unicode[STIX]{x1D6FC}_{k}-\unicode[STIX]{x1D709}_{k}}r_{2,k}^{\unicode[STIX]{x1D6FC}_{k}+\unicode[STIX]{x1D709}_{k}}r_{3,k}^{s^{\ast }-2\unicode[STIX]{x1D709}_{k}}}\unicode[STIX]{x1D701}(s^{\ast }-2\unicode[STIX]{x1D709}_{k})\biggr)\nonumber\\ \displaystyle & & \displaystyle \times \,{\mathcal{A}}_{\boldsymbol{r}}(\boldsymbol{\unicode[STIX]{x1D6FC}}-\boldsymbol{\unicode[STIX]{x1D709}},\boldsymbol{\unicode[STIX]{x1D6FC}}+\boldsymbol{\unicode[STIX]{x1D709}})\biggl(\mathop{\prod }_{i,j}\tilde{F}_{\unicode[STIX]{x1D6FF}}^{\pm }(s_{ij})\biggr)\,d(\cdots \,),\nonumber\end{eqnarray}$$
where, here and below, we indicate by
$\int _{(\cdots \,)}d(\cdots \,)$
an integral with respect to the variables
$s^{\ast }$
,
$\unicode[STIX]{x1D6FC}_{1}$
,
$\unicode[STIX]{x1D6FC}_{2}$
,
$\unicode[STIX]{x1D6FF}_{1}$
,
$\unicode[STIX]{x1D6FF}_{2}$
and
$s_{12}$
,
$s_{21}$
,
$s_{31}$
,
$s_{32}$
, along the lines of integration previously indicated, with the exclusion of the variables which have been eliminated by the computation of a residue.
7.3 Applying Lemma 2
We write
${\mathcal{A}}_{\boldsymbol{r}}(\boldsymbol{\unicode[STIX]{x1D6FC}}-\boldsymbol{\unicode[STIX]{x1D709}},\boldsymbol{\unicode[STIX]{x1D6FC}}+\boldsymbol{\unicode[STIX]{x1D709}})$
as
${\mathcal{M}}_{\boldsymbol{r}}(\boldsymbol{\unicode[STIX]{x1D6FC}}-\boldsymbol{\unicode[STIX]{x1D709}},\boldsymbol{\unicode[STIX]{x1D6FC}}+\boldsymbol{\unicode[STIX]{x1D709}})+{\mathcal{E}}_{\boldsymbol{r}}(\boldsymbol{\unicode[STIX]{x1D6FC}}-\boldsymbol{\unicode[STIX]{x1D709}},\boldsymbol{\unicode[STIX]{x1D6FC}}+\boldsymbol{\unicode[STIX]{x1D709}})$
and we split accordingly
$N_{\unicode[STIX]{x1D6FF}}^{\pm }(B)$
into
$$\begin{eqnarray}\displaystyle N_{\unicode[STIX]{x1D6FF}}^{\pm }(B)=M_{\unicode[STIX]{x1D6FF}}^{\pm }(B)+E_{\unicode[STIX]{x1D6FF}}^{\pm }(B). & & \displaystyle\end{eqnarray}$$
Differently from the case of Theorem 2, here
$E_{\unicode[STIX]{x1D6FF}}^{\pm }(B)$
also contributes to a main term, of size
$B$
, which can be extracted as follows.
We move the lines of integration
$c_{\unicode[STIX]{x1D709}_{1}}$
,
$c_{\unicode[STIX]{x1D709}_{2}}$
and
$c_{s^{\ast }}$
in the integrals defining
$E_{\unicode[STIX]{x1D6FF}}^{\pm }(B)$
to
$c_{\unicode[STIX]{x1D709}_{1}}=2K$
,
$c_{\unicode[STIX]{x1D709}_{2}}=-K$
and
$c_{s^{\ast }}=1-K$
for some fixed real number
$K>0$
small enough, passing through the simple pole of the integrand at
$s^{\ast }=1+2\unicode[STIX]{x1D709}_{1}$
. If
$K$
is sufficiently small, then we do not pass through any other pole and we stay inside the region (4.3) where
${\mathcal{E}}_{\boldsymbol{r}}$
is holomorphic and where the sums are absolutely convergent. For the integral on the new lines of integration, we use (4.4) and a trivial bound for
$\unicode[STIX]{x1D701}$
and we obtain that, for
$K$
small enough, the integral is bounded by
$$\begin{eqnarray}\displaystyle & & \displaystyle \ll B^{1-K}\mathop{\sum }_{\substack{ \boldsymbol{b},\boldsymbol{c},\,\boldsymbol{f},\boldsymbol{g}\in \mathbb{N}^{3}, \\ h\in \mathbb{N}}}\iint _{(\cdots \,)}\biggl(\mathop{\prod }_{k=1}^{3}\frac{(r_{k}(|s^{\ast }|+|\unicode[STIX]{x1D709}_{k}|)(|\unicode[STIX]{x1D6FC}_{k}|+|\unicode[STIX]{x1D709}_{k}|))^{C_{1}K}}{(r_{1,k}r_{2,k}r_{3,k})^{2/3-K}}\biggr)\nonumber\\ \displaystyle & & \displaystyle \quad \times \biggl|\mathop{\prod }_{i,j}\tilde{F}_{\unicode[STIX]{x1D6FF}}^{\pm }(s_{ij})\biggr|d(\cdots \,)\nonumber\\ \displaystyle & & \displaystyle \ll B^{1-K}\unicode[STIX]{x1D6FF}^{-C_{2}K},\nonumber\end{eqnarray}$$
where the second line is obtained as for (5.10) using (4.6) and (7.9), after reintroducing the original variables
$s_{ij}$
. Also, we recall that, here and below,
$C_{1},C_{2},C_{3},\ldots \,$
will indicate fixed positive real numbers.
Collecting the contribution of the residue, we obtain
$$\begin{eqnarray}\displaystyle E_{\unicode[STIX]{x1D6FF}}^{\pm }(B) & = & \displaystyle 2\mathop{\sum }_{\substack{ \boldsymbol{b},\boldsymbol{c},\,\boldsymbol{f},\boldsymbol{g}\in \mathbb{N}^{3}, \\ h\in \mathbb{N}}}\frac{\unicode[STIX]{x1D707}(h)}{(2\unicode[STIX]{x1D70B}\text{i})^{8}}\iint _{(\cdots \,)}B^{1+2\unicode[STIX]{x1D709}_{1}}\biggl(\mathop{\prod }_{k=1}^{3}\frac{\unicode[STIX]{x1D707}(b_{k})\unicode[STIX]{x1D707}(c_{k})\unicode[STIX]{x1D707}(f_{k})\unicode[STIX]{x1D707}(g_{k})}{r_{1,k}^{\unicode[STIX]{x1D6FC}_{k}-\unicode[STIX]{x1D709}_{k}}r_{2,k}^{\unicode[STIX]{x1D6FC}_{k}+\unicode[STIX]{x1D709}_{k}}r_{3,k}^{1+2\unicode[STIX]{x1D709}_{1}-2\unicode[STIX]{x1D709}_{k}}}\biggr)\nonumber\\ \displaystyle & & \displaystyle \times \,\unicode[STIX]{x1D701}(1+2\unicode[STIX]{x1D709}_{1}-2\unicode[STIX]{x1D709}_{2})\unicode[STIX]{x1D701}(1+4\unicode[STIX]{x1D709}_{1}+2\unicode[STIX]{x1D709}_{2}){\mathcal{E}}_{\boldsymbol{r}}(\boldsymbol{\unicode[STIX]{x1D6FC}}-\boldsymbol{\unicode[STIX]{x1D709}},\boldsymbol{\unicode[STIX]{x1D6FC}}+\boldsymbol{\unicode[STIX]{x1D709}})\nonumber\\ \displaystyle & & \displaystyle \times \,\biggl(\mathop{\prod }_{i,j}\tilde{F}_{\unicode[STIX]{x1D6FF}}^{\pm }(s_{ij})\biggr)\,d(\cdots \,)+O(B^{1-K}\unicode[STIX]{x1D6FF}^{-C_{2}K})\nonumber\end{eqnarray}$$
since
$\unicode[STIX]{x1D709}_{3}=-\unicode[STIX]{x1D709}_{1}-\unicode[STIX]{x1D709}_{2}$
and with the notation (7.6). We then move the line of integration
$c_{\unicode[STIX]{x1D709}_{1}}$
to
$c_{\unicode[STIX]{x1D709}_{1}}=-K/2$
passing through the pole at
$\unicode[STIX]{x1D709}_{1}=-\unicode[STIX]{x1D709}_{2}/2$
. The integral on the new lines of integration can be bounded as above, whereas in the integral coming from the contribution of the residue, we move
$c_{\unicode[STIX]{x1D709}_{2}}$
to
$c_{\unicode[STIX]{x1D709}_{2}}=K$
passing through a simple pole at
$\unicode[STIX]{x1D709}_{2}=0$
(in which case
$\unicode[STIX]{x1D709}_{3}=0$
). Bounding once again the contribution of the integral as above, we arrive at
$$\begin{eqnarray}\displaystyle E_{\unicode[STIX]{x1D6FF}}^{\pm }(B) & = & \displaystyle \frac{B}{6}\mathop{\sum }_{\substack{ \boldsymbol{b},\boldsymbol{c},\,\boldsymbol{f},\boldsymbol{g}\in \mathbb{N}^{3}, \\ h\in \mathbb{N}}}\frac{\unicode[STIX]{x1D707}(h)}{(2\unicode[STIX]{x1D70B}\text{i})^{6}}\iint _{(\cdots \,)}\biggl(\mathop{\prod }_{k=1}^{3}\frac{\unicode[STIX]{x1D707}(b_{k})\unicode[STIX]{x1D707}(c_{k})\unicode[STIX]{x1D707}(f_{k})\unicode[STIX]{x1D707}(g_{k})}{r_{1,k}^{\unicode[STIX]{x1D6FC}_{k}}r_{2,k}^{\unicode[STIX]{x1D6FC}_{k}}r_{3,k}}\biggr)\nonumber\\ \displaystyle & & \displaystyle \times \,{\mathcal{E}}_{\boldsymbol{r}}(\boldsymbol{\unicode[STIX]{x1D6FC}},\boldsymbol{\unicode[STIX]{x1D6FC}})\biggl(\mathop{\prod }_{i,j}\tilde{F}_{\unicode[STIX]{x1D6FF}}^{\pm }(s_{ij})\biggr)\,d(\cdots \,)+O(B^{1-K}\unicode[STIX]{x1D6FF}^{-C_{3}K}).\nonumber\end{eqnarray}$$
The product
$\prod _{i,j}\tilde{F}_{\unicode[STIX]{x1D6FF}}^{\pm }(s_{ij})$
can now be replaced by
$\prod _{i,j}1/s_{ij}$
at a cost of an error which is
$O(B\unicode[STIX]{x1D6FF}^{1-C_{5}\unicode[STIX]{x1D700}})$
. Indeed, by (4.4) and (7.9), we have
$$\begin{eqnarray}\displaystyle & & \displaystyle \mathop{\sum }_{\substack{ \boldsymbol{b},\boldsymbol{c},\,\boldsymbol{f},\boldsymbol{g}\in \mathbb{N}^{3}, \\ h\in \mathbb{N}}}\frac{\unicode[STIX]{x1D707}(h)}{(2\unicode[STIX]{x1D70B}\text{i})^{6}}\iint _{(\cdots \,)}\biggl(\mathop{\prod }_{k=1}^{3}\frac{\unicode[STIX]{x1D707}(b_{k})\unicode[STIX]{x1D707}(c_{k})\unicode[STIX]{x1D707}(f_{k})\unicode[STIX]{x1D707}(g_{k})}{r_{1,k}^{\unicode[STIX]{x1D6FC}_{k}}r_{2,k}^{\unicode[STIX]{x1D6FC}_{k}}r_{3,k}}\biggr){\mathcal{E}}_{\boldsymbol{r}}(\boldsymbol{\unicode[STIX]{x1D6FC}},\boldsymbol{\unicode[STIX]{x1D6FC}})\nonumber\\ \displaystyle & & \displaystyle \qquad \times \,\biggl(\mathop{\prod }_{i,j}\tilde{F}_{\unicode[STIX]{x1D6FF}}^{\pm }(s_{ij})-\frac{1}{s_{ij}}\biggr)\,d(\cdots \,)\nonumber\\ \displaystyle & & \displaystyle \quad \ll \iint _{(\cdots \,)}\biggl(\mathop{\prod }_{i,j}\biggl|\tilde{F}_{\unicode[STIX]{x1D6FF}}^{\pm }(s_{ij})-\frac{1}{s_{ij}}\biggr||s_{ij}|^{C_{4}\unicode[STIX]{x1D700}}\biggr)\,d(\cdots \,)\ll \unicode[STIX]{x1D6FF}^{1-C_{5}\unicode[STIX]{x1D700}},\nonumber\end{eqnarray}$$
by proceeding as in (5.16) after reintroducing six of the variables
$s_{ij}$
(with the remaining three variables kept as functions of those), since we now have the extra relation
$\sum _{1\leqslant i,j\leqslant 3}s_{ij}=s^{\ast }=1$
. Collecting the above computations, we then get
$$\begin{eqnarray}\displaystyle E_{\unicode[STIX]{x1D6FF}}^{\pm }(B)=BP_{0}+O(B\unicode[STIX]{x1D6FF}^{1-C_{5}\unicode[STIX]{x1D700}}+B^{1-K}\unicode[STIX]{x1D6FF}^{-C_{6}K}) & & \displaystyle\end{eqnarray}$$
for some
$P_{0}\in \mathbb{R}$
.
We now move to the analysis of
$M_{\unicode[STIX]{x1D6FF}}^{\pm }(B)$
. Following the definition of
${\mathcal{M}}_{\boldsymbol{r}}$
, we split
$M_{\unicode[STIX]{x1D6FF}}^{\pm }(B)$
in the following way:
$$\begin{eqnarray}\displaystyle M_{\unicode[STIX]{x1D6FF}}^{\pm }(B)=\mathop{\sum }_{\boldsymbol{\unicode[STIX]{x1D716}}\in \{\pm 1\}^{3}}M_{\unicode[STIX]{x1D6FF},\boldsymbol{\unicode[STIX]{x1D716}}}^{\pm }(B), & & \displaystyle\end{eqnarray}$$
where the sum is over
$\boldsymbol{\unicode[STIX]{x1D716}}=(\unicode[STIX]{x1D716}_{1},\unicode[STIX]{x1D716}_{2},\unicode[STIX]{x1D716}_{3})\in \{\pm 1\}^{3}$
and
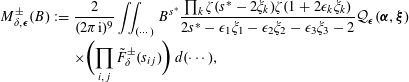$$\begin{eqnarray}\displaystyle M_{\unicode[STIX]{x1D6FF},\boldsymbol{\unicode[STIX]{x1D716}}}^{\pm }(B) & := & \displaystyle \frac{2}{(2\unicode[STIX]{x1D70B}\text{i})^{9}}\iint _{(\cdots \,)}B^{s^{\ast }}\frac{\mathop{\prod }_{k}\unicode[STIX]{x1D701}(s^{\ast }-2\unicode[STIX]{x1D709}_{k})\unicode[STIX]{x1D701}(1+2\unicode[STIX]{x1D716}_{k}\unicode[STIX]{x1D709}_{k})}{2s^{\ast }-\unicode[STIX]{x1D716}_{1}\unicode[STIX]{x1D709}_{1}-\unicode[STIX]{x1D716}_{2}\unicode[STIX]{x1D709}_{2}-\unicode[STIX]{x1D716}_{3}\unicode[STIX]{x1D709}_{3}-2}{\mathcal{Q}}_{\boldsymbol{\unicode[STIX]{x1D716}}}(\boldsymbol{\unicode[STIX]{x1D6FC}},\boldsymbol{\unicode[STIX]{x1D709}})\nonumber\\ \displaystyle & & \displaystyle \times \biggl(\mathop{\prod }_{i,j}\tilde{F}_{\unicode[STIX]{x1D6FF}}^{\pm }(s_{ij})\biggr)\,d(\cdots \,),\end{eqnarray}$$
with lines of integration as given in §7.1 (in particular (7.5) is satisfied) and where
$$\begin{eqnarray}\displaystyle & & \displaystyle {\mathcal{Q}}_{\boldsymbol{\unicode[STIX]{x1D716}}}(\boldsymbol{\unicode[STIX]{x1D6FC}},\boldsymbol{\unicode[STIX]{x1D709}})\nonumber\\ \displaystyle & & \displaystyle \quad :=\mathop{\sum }_{\substack{ \boldsymbol{b},\boldsymbol{c},\,\boldsymbol{f},\boldsymbol{g}\in \mathbb{N}^{3}, \\ h,\ell \in \mathbb{N}}}\unicode[STIX]{x1D707}(h)\biggl(\mathop{\prod }_{k=1}^{3}\frac{\unicode[STIX]{x1D707}(b_{k})\unicode[STIX]{x1D707}(c_{k})\unicode[STIX]{x1D707}(f_{k})\unicode[STIX]{x1D707}(g_{k})}{r_{1,k}^{\unicode[STIX]{x1D6FC}_{k}-\unicode[STIX]{x1D709}_{k}}r_{2,k}^{\unicode[STIX]{x1D6FC}_{k}+\unicode[STIX]{x1D709}_{k}}r_{3,k}^{s^{\ast }-2\unicode[STIX]{x1D709}_{k}}}\biggr)\frac{(r_{1},\ell )^{1+2\unicode[STIX]{x1D716}_{1}\unicode[STIX]{x1D709}_{1}}(r_{2},\ell )^{1+2\unicode[STIX]{x1D716}_{2}\unicode[STIX]{x1D709}_{2}}(r_{3},\ell )^{1+2\unicode[STIX]{x1D716}_{3}\unicode[STIX]{x1D709}_{2}}}{\ell ^{3+2\unicode[STIX]{x1D716}_{1}\unicode[STIX]{x1D709}_{1}+2\unicode[STIX]{x1D716}_{2}\unicode[STIX]{x1D709}_{2}+2\unicode[STIX]{x1D716}_{3}\unicode[STIX]{x1D709}_{3}}}\unicode[STIX]{x1D711}(\ell )\nonumber\\ \displaystyle & & \displaystyle \qquad \times \,2\unicode[STIX]{x1D70B}^{1/2}\mathop{\prod }_{i=1}^{3}\frac{\unicode[STIX]{x1D6E4}\big(\frac{-\unicode[STIX]{x1D6FC}_{i}+\unicode[STIX]{x1D716}_{i}\unicode[STIX]{x1D709}_{i}}{2}+\frac{1+2s^{\ast }-\unicode[STIX]{x1D716}_{1}\unicode[STIX]{x1D709}_{1}-\unicode[STIX]{x1D716}_{2}\unicode[STIX]{x1D709}_{2}-\unicode[STIX]{x1D716}_{3}\unicode[STIX]{x1D709}_{3}}{6}\big)}{r_{i}^{-\unicode[STIX]{x1D6FC}_{i}+\unicode[STIX]{x1D716}_{i}\unicode[STIX]{x1D709}_{i}+(1+2s^{\ast }-\unicode[STIX]{x1D716}_{1}\unicode[STIX]{x1D709}_{1}-\unicode[STIX]{x1D716}_{2}\unicode[STIX]{x1D709}_{2}-\unicode[STIX]{x1D716}_{3}\unicode[STIX]{x1D709}_{3})/3}\unicode[STIX]{x1D6E4}\big(\frac{1+\unicode[STIX]{x1D6FC}_{i}-\unicode[STIX]{x1D716}_{i}\unicode[STIX]{x1D709}_{i}}{2}-\frac{1+2s^{\ast }-\unicode[STIX]{x1D716}_{1}\unicode[STIX]{x1D709}_{1}-\unicode[STIX]{x1D716}_{2}\unicode[STIX]{x1D709}_{2}-\unicode[STIX]{x1D716}_{3}\unicode[STIX]{x1D709}_{3}}{6}\big)},\nonumber\end{eqnarray}$$
where we recall that
$2s^{\ast }=\unicode[STIX]{x1D6FC}_{1}+\unicode[STIX]{x1D6FC}_{2}+\unicode[STIX]{x1D6FC}_{3}$
and the notation (7.6). Notice that by (7.9) and (5.14), we have that
${\mathcal{Q}}_{\boldsymbol{\unicode[STIX]{x1D716}}}(\boldsymbol{\unicode[STIX]{x1D6FC}},\boldsymbol{\unicode[STIX]{x1D709}})$
is holomorphic and bounded for
$$\begin{eqnarray}\displaystyle |\Re (s^{\ast }-1)|,|\Re (\unicode[STIX]{x1D709}_{i})|,|\Re (\unicode[STIX]{x1D6FC}_{i}-{\textstyle \frac{2}{3}})|<20K, & & \displaystyle \nonumber\end{eqnarray}$$
with
$K$
small enough.
Now, we move the lines of integration
$c_{s^{\ast }},c_{\unicode[STIX]{x1D709}_{1}},c_{\unicode[STIX]{x1D709}_{2}}$
in (7.13) to
$c_{s^{\ast }}=1-K$
,
$c_{\unicode[STIX]{x1D709}_{1}}=16K$
,
$c_{\unicode[STIX]{x1D709}_{2}}=-14K$
(so that on the new lines of integration
$\Re (\unicode[STIX]{x1D709}_{3})=-2K$
since
$\unicode[STIX]{x1D709}_{1}+\unicode[STIX]{x1D709}_{2}+\unicode[STIX]{x1D709}_{3}=0$
) passing through simple poles at
$s^{\ast }=1+2\unicode[STIX]{x1D709}_{1}$
and, if
$\boldsymbol{\unicode[STIX]{x1D716}}\neq (-1,1,1)$
,
$(-1,-1,1)$
,
$(-1,1,-1)$
, at
$s^{\ast }=1+\frac{1}{2}(\unicode[STIX]{x1D716}_{1}\unicode[STIX]{x1D709}_{1}+\unicode[STIX]{x1D716}_{2}\unicode[STIX]{x1D709}_{2}+\unicode[STIX]{x1D716}_{3}\unicode[STIX]{x1D709}_{3})$
. Indeed, the denominator has positive real part on the original lines of integration whereas on the new lines of integration it has real part equal to
$2(-K-8\unicode[STIX]{x1D716}_{1}K+7\unicode[STIX]{x1D716}_{2}K+\unicode[STIX]{x1D716}_{3}K)$
, which is negative if and only if
$\unicode[STIX]{x1D716}_{1}=1$
or
$\unicode[STIX]{x1D716}_{1}=\unicode[STIX]{x1D716}_{2}=\unicode[STIX]{x1D716}_{3}=-1$
. Also note that we stay on the same side of the poles of the other
$\unicode[STIX]{x1D701}$
factors. Alluding to (4.6), a trivial bound for
$\unicode[STIX]{x1D701}$
and the fact that
${\mathcal{Q}}_{\boldsymbol{\unicode[STIX]{x1D716}}}$
is bounded, we can use the same argument used several times in §§5–6 in order to bound trivially the contribution of the integral on the new lines of integration, obtaining that its contribution is
$O(B^{1-K/2}\unicode[STIX]{x1D6FF}^{-C_{7}})$
.
It follows that
$$\begin{eqnarray}\displaystyle M_{\boldsymbol{\unicode[STIX]{x1D716}}}^{\pm }(B)=M_{\boldsymbol{\unicode[STIX]{x1D716}},1}^{\pm }(B)+M_{\boldsymbol{\unicode[STIX]{x1D716}},2}^{\pm }(B), & & \displaystyle \nonumber\end{eqnarray}$$
where
$M_{\boldsymbol{\unicode[STIX]{x1D716}},1}^{\pm }$
denotes the contribution of the pole at
$s^{\ast }=1+2\unicode[STIX]{x1D709}_{1}$
and
$M_{\boldsymbol{\unicode[STIX]{x1D716}},2}^{\pm }(B)$
is the contribution of the pole at
$s^{\ast }=1+\frac{1}{2}(\unicode[STIX]{x1D716}_{1}\unicode[STIX]{x1D709}_{1}+\unicode[STIX]{x1D716}_{2}\unicode[STIX]{x1D709}_{2}+\unicode[STIX]{x1D716}_{3}\unicode[STIX]{x1D709}_{3})$
if
$\boldsymbol{\unicode[STIX]{x1D716}}\notin \{(-1,1,1),(-1,-1,1),(-1,1,-1)\}$
and
$M_{\boldsymbol{\unicode[STIX]{x1D716}},2}^{\pm }(B):=0$
otherwise.
7.4 The pole at
$s^{\ast }=1+2\unicode[STIX]{x1D709}_{1}$
when
$\boldsymbol{\unicode[STIX]{x1D716}}\neq (1,-1,1)$
Using the fact that
$\unicode[STIX]{x1D709}_{3}=-\unicode[STIX]{x1D709}_{1}-\unicode[STIX]{x1D709}_{2}$
, we have
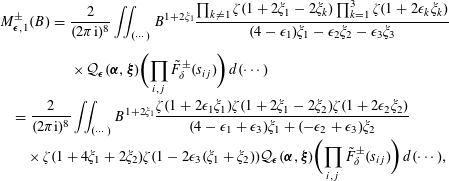$$\begin{eqnarray}\displaystyle & & \displaystyle M_{\boldsymbol{\unicode[STIX]{x1D716}},1}^{\pm }(B)=\frac{2}{(2\unicode[STIX]{x1D70B}\text{i})^{8}}\iint _{(\cdots \,)}B^{1+2\unicode[STIX]{x1D709}_{1}}\frac{\mathop{\prod }_{k\neq 1}\unicode[STIX]{x1D701}(1+2\unicode[STIX]{x1D709}_{1}-2\unicode[STIX]{x1D709}_{k})\mathop{\prod }_{k=1}^{3}\unicode[STIX]{x1D701}(1+2\unicode[STIX]{x1D716}_{k}\unicode[STIX]{x1D709}_{k})}{(4-\unicode[STIX]{x1D716}_{1})\unicode[STIX]{x1D709}_{1}-\unicode[STIX]{x1D716}_{2}\unicode[STIX]{x1D709}_{2}-\unicode[STIX]{x1D716}_{3}\unicode[STIX]{x1D709}_{3}}\nonumber\\ \displaystyle & & \displaystyle \quad \qquad \qquad \times \,{\mathcal{Q}}_{\boldsymbol{\unicode[STIX]{x1D716}}}(\boldsymbol{\unicode[STIX]{x1D6FC}},\boldsymbol{\unicode[STIX]{x1D709}})\biggl(\mathop{\prod }_{i,j}\tilde{F}_{\unicode[STIX]{x1D6FF}}^{\pm }(s_{ij})\biggr)\,d(\cdots \,)\nonumber\\ \displaystyle & & \displaystyle \quad =\frac{2}{(2\unicode[STIX]{x1D70B}\text{i})^{8}}\iint _{(\cdots \,)}B^{1+2\unicode[STIX]{x1D709}_{1}}\frac{\unicode[STIX]{x1D701}(1+2\unicode[STIX]{x1D716}_{1}\unicode[STIX]{x1D709}_{1})\unicode[STIX]{x1D701}(1+2\unicode[STIX]{x1D709}_{1}-2\unicode[STIX]{x1D709}_{2})\unicode[STIX]{x1D701}(1+2\unicode[STIX]{x1D716}_{2}\unicode[STIX]{x1D709}_{2})}{(4-\unicode[STIX]{x1D716}_{1}+\unicode[STIX]{x1D716}_{3})\unicode[STIX]{x1D709}_{1}+(-\unicode[STIX]{x1D716}_{2}+\unicode[STIX]{x1D716}_{3})\unicode[STIX]{x1D709}_{2}}\nonumber\\ \displaystyle & & \displaystyle \qquad \times \,\unicode[STIX]{x1D701}(1+4\unicode[STIX]{x1D709}_{1}+2\unicode[STIX]{x1D709}_{2})\unicode[STIX]{x1D701}(1-2\unicode[STIX]{x1D716}_{3}(\unicode[STIX]{x1D709}_{1}+\unicode[STIX]{x1D709}_{2})){\mathcal{Q}}_{\boldsymbol{\unicode[STIX]{x1D716}}}(\boldsymbol{\unicode[STIX]{x1D6FC}},\boldsymbol{\unicode[STIX]{x1D709}})\biggl(\mathop{\prod }_{i,j}\tilde{F}_{\unicode[STIX]{x1D6FF}}^{\pm }(s_{ij})\biggr)\,d(\cdots \,),\nonumber\\ \displaystyle & & \displaystyle\end{eqnarray}$$
with
$c_{\unicode[STIX]{x1D709}_{1}}=8\unicode[STIX]{x1D700}$
and
$c_{\unicode[STIX]{x1D709}_{2}}=-\unicode[STIX]{x1D700}$
. Notice that for
$\boldsymbol{\unicode[STIX]{x1D716}}=(1,-1,1)$
, one has a double pole when
$4\unicode[STIX]{x1D709}_{1}+2\unicode[STIX]{x1D709}_{2}=0$
, which causes some (mostly notational) issues when moving the lines of integration as we shall do throughout this section. For this reason, we prefer to defer to the next section the treatment of this term.
Next, we move the lines of integration
$c_{\unicode[STIX]{x1D709}_{1}}$
and
$c_{\unicode[STIX]{x1D709}_{2}}$
to
$c_{\unicode[STIX]{x1D709}_{1}}=-K$
and
$c_{\unicode[STIX]{x1D709}_{2}}=-4K$
passing through several poles. As before, the integral on the new lines of integration is
$O(B^{1-K}\unicode[STIX]{x1D6FF}^{-C_{8}})$
. The poles we encounter are the following:
(a) a pole at
$\unicode[STIX]{x1D709}_{1}=0$
which is simple if
$\unicode[STIX]{x1D716}_{2}\neq \unicode[STIX]{x1D716}_{3}$
and is double if
$\unicode[STIX]{x1D716}_{2}=\unicode[STIX]{x1D716}_{3}$
;(b) a simple pole at
$\unicode[STIX]{x1D709}_{1}=-\frac{1}{2}\unicode[STIX]{x1D709}_{2}$
;(c) a simple pole at
$\unicode[STIX]{x1D709}_{1}=-\unicode[STIX]{x1D709}_{2}$
;(d) a simple pole at
$\unicode[STIX]{x1D709}_{1}=-\frac{1}{3}\unicode[STIX]{x1D709}_{2}$
if
$\boldsymbol{\unicode[STIX]{x1D716}}=(-1,-1,1)$
.
We now examine the contribution of the residue of each of these poles.
(a) We write the contribution of the residue at
$\unicode[STIX]{x1D709}_{1}=0$
as a small circuit integral
$$\begin{eqnarray}\displaystyle & & \displaystyle \frac{2B}{(2\unicode[STIX]{x1D70B}\text{i})^{7}}\iint _{(\cdots \,)}\frac{1}{2\unicode[STIX]{x1D70B}\text{i}}\nonumber\\ \displaystyle & & \displaystyle \quad \times \oint _{|\unicode[STIX]{x1D709}_{1}|=\unicode[STIX]{x1D700}/2}\biggl((1+2\unicode[STIX]{x1D709}_{1}\log B)\frac{\unicode[STIX]{x1D701}(1+2\unicode[STIX]{x1D716}_{1}\unicode[STIX]{x1D709}_{1})\unicode[STIX]{x1D701}(1+2\unicode[STIX]{x1D709}_{1}-2\unicode[STIX]{x1D709}_{2})\unicode[STIX]{x1D701}(1+2\unicode[STIX]{x1D716}_{2}\unicode[STIX]{x1D709}_{2})}{(4-\unicode[STIX]{x1D716}_{1}+\unicode[STIX]{x1D716}_{3})\unicode[STIX]{x1D709}_{1}+(-\unicode[STIX]{x1D716}_{2}+\unicode[STIX]{x1D716}_{3})\unicode[STIX]{x1D709}_{2}}\nonumber\\ \displaystyle & & \displaystyle \quad \times \,\unicode[STIX]{x1D701}(1+4\unicode[STIX]{x1D709}_{1}+2\unicode[STIX]{x1D709}_{2})\unicode[STIX]{x1D701}(1\mp _{3}2(\unicode[STIX]{x1D709}_{1}+\unicode[STIX]{x1D709}_{2})){\mathcal{Q}}_{\boldsymbol{\unicode[STIX]{x1D716}}}(\boldsymbol{\unicode[STIX]{x1D6FC}},\boldsymbol{\unicode[STIX]{x1D709}})\biggl(\mathop{\prod }_{i,j}\tilde{F}_{\unicode[STIX]{x1D6FF}}^{\pm }(s_{ij})\biggr)\biggr)\,d(\cdots \,),\nonumber\end{eqnarray}$$
where we can assume that the line of integration
$c_{\unicode[STIX]{x1D709}_{2}}$
is at
$c_{\unicode[STIX]{x1D709}_{2}}=-\unicode[STIX]{x1D700}$
. The next step is to observe that we can replace
$\prod _{i,j}\tilde{F}_{\unicode[STIX]{x1D6FF}}^{\pm }(s_{ij})$
by
$\prod _{i,j}1/s_{ij}$
at a cost of an error which is
$$\begin{eqnarray}\displaystyle O(B^{1+\unicode[STIX]{x1D700}}\unicode[STIX]{x1D6FF}^{1-C_{9}\unicode[STIX]{x1D700}}). & & \displaystyle\end{eqnarray}$$
To show this, we first observe that, by the convexity bound [Reference Titchmarsh32, (5.1.4)], on the lines of integration the integrand is
$$\begin{eqnarray}\displaystyle & & \displaystyle \ll \log B(1+|\unicode[STIX]{x1D709}_{1}|+|\unicode[STIX]{x1D709}_{2}|)^{C_{10}\unicode[STIX]{x1D700}}\mathop{\prod }_{i,j}|\tilde{F}_{\unicode[STIX]{x1D6FF}}^{\pm }(s_{ij})|\nonumber\\ \displaystyle & & \displaystyle \ll \log B\mathop{\prod }_{i,j}|\tilde{F}_{\unicode[STIX]{x1D6FF}}^{\pm }(s_{ij})|(1+|s_{ij}|)^{C_{11}\unicode[STIX]{x1D700}}.\nonumber\end{eqnarray}$$
We go back to using the
$s_{ij}$
as variables (excluding for example the variable
$s_{11}$
because we have a variable fewer) and observe that we have
$s^{\ast }=\sum _{1\leqslant i,j\leqslant 3}s_{ij}=1+2\unicode[STIX]{x1D709}_{1}=1+O(\unicode[STIX]{x1D700})$
and thus
$s_{11}=1-\sum _{(i,j)\neq (1,1)}s_{ij}+O(\unicode[STIX]{x1D700})$
. Thus, proceeding as for (5.16), we can replace
$\prod _{i,j}\tilde{F}_{\unicode[STIX]{x1D6FF}}^{\pm }(s_{ij})$
by
$\prod _{i,j}1/s_{ij}$
at a cost of an error which is bounded by (7.15). In the end, we find that the contribution of the pole at
$\unicode[STIX]{x1D709}_{1}=0$
is
$$\begin{eqnarray}\displaystyle BP_{\boldsymbol{\unicode[STIX]{x1D716}},1,1}(\log B)+O(B^{1+\unicode[STIX]{x1D700}}\unicode[STIX]{x1D6FF}^{1-C_{9}\unicode[STIX]{x1D700}}+B^{1-K}\unicode[STIX]{x1D6FF}^{-C_{8}}), & & \displaystyle \nonumber\end{eqnarray}$$
where
$P_{\boldsymbol{\unicode[STIX]{x1D716}},1,1}$
is a polynomial of degree
$0$
or
$1$
(not depending on the choice of
$\unicode[STIX]{x1D6FF}$
and
$\pm$
in
$N_{\unicode[STIX]{x1D6FF}}^{\pm }(B)$
) obtained by evaluating the above integral with
$\prod _{i,j}1/s_{ij}$
instead of
$\prod _{i,j}\tilde{F}_{\unicode[STIX]{x1D6FF}}^{\pm }(s_{ij})$
.
(b) The contribution of the pole at
$\unicode[STIX]{x1D709}_{1}=-\frac{1}{2}\unicode[STIX]{x1D709}_{2}$
is
$$\begin{eqnarray}\displaystyle & & \displaystyle \frac{-1}{(2\unicode[STIX]{x1D70B}\text{i})^{7}}\iint _{(\cdots \,)}B^{1-\unicode[STIX]{x1D709}_{2}}\frac{\unicode[STIX]{x1D701}(1-\unicode[STIX]{x1D716}_{1}\unicode[STIX]{x1D709}_{2})\unicode[STIX]{x1D701}(1-3\unicode[STIX]{x1D709}_{2})\unicode[STIX]{x1D701}(1+2\unicode[STIX]{x1D716}_{2}\unicode[STIX]{x1D709}_{2})\unicode[STIX]{x1D701}(1-\unicode[STIX]{x1D716}_{3}\unicode[STIX]{x1D709}_{2})}{(4-\unicode[STIX]{x1D716}_{1}+2\unicode[STIX]{x1D716}_{2}-\unicode[STIX]{x1D716}_{3})\unicode[STIX]{x1D709}_{2}}{\mathcal{Q}}_{\boldsymbol{\unicode[STIX]{x1D716}}}(\boldsymbol{\unicode[STIX]{x1D6FC}},\boldsymbol{\unicode[STIX]{x1D709}})\nonumber\\ \displaystyle & & \displaystyle \quad \times \,\biggl(\mathop{\prod }_{i,j}\tilde{F}_{\unicode[STIX]{x1D6FF}}^{\pm }(s_{ij})\biggr)\,d(\cdots \,).\nonumber\end{eqnarray}$$
We move the line of integration
$c_{\unicode[STIX]{x1D709}_{2}}$
to
$c_{\unicode[STIX]{x1D709}_{2}}=K$
passing through a pole at
$\unicode[STIX]{x1D6FF}_{2}=0$
. The contribution of the integral on the new lines of integration is
$O(B^{1-K}\unicode[STIX]{x1D6FF}^{-C_{12}})$
. For the contribution of the residue, we follow the same approach as above writing it as a small circle integral and observing that since again
$s^{\ast }=\sum _{1\leqslant i,j\leqslant 3}s_{ij}=1+2\unicode[STIX]{x1D709}_{1}=1-\unicode[STIX]{x1D709}_{2}=1+O(\unicode[STIX]{x1D700})$
, we can replace
$\prod _{i,j}\tilde{F}_{\unicode[STIX]{x1D6FF}}^{\pm }(s_{ij})$
by
$\prod _{i,j}1/s_{ij}$
at the cost of an error which is
$O(B^{1+\unicode[STIX]{x1D700}}\unicode[STIX]{x1D6FF}^{1-C_{13}\unicode[STIX]{x1D700}})$
. Then, computing the integral, we find that the contribution to (7.14) from the pole at
$\unicode[STIX]{x1D709}_{1}=-\frac{1}{2}\unicode[STIX]{x1D709}_{2}$
is
$$\begin{eqnarray}\displaystyle BP_{\boldsymbol{\unicode[STIX]{x1D716}},1,2}(\log B)+O(B^{1+\unicode[STIX]{x1D700}}\unicode[STIX]{x1D6FF}^{1-C_{13}\unicode[STIX]{x1D700}}+B^{1-K}\unicode[STIX]{x1D6FF}^{-C_{12}}), & & \displaystyle \nonumber\end{eqnarray}$$
where
$P_{\boldsymbol{\unicode[STIX]{x1D716}},1,2}$
is a polynomial of degree
$4$
of leading coefficient
$$\begin{eqnarray}\displaystyle -\frac{\unicode[STIX]{x1D716}_{1}\unicode[STIX]{x1D716}_{2}\unicode[STIX]{x1D716}_{3}}{2\cdot 3\cdot (4-\unicode[STIX]{x1D716}_{1}+2\unicode[STIX]{x1D716}_{2}-\unicode[STIX]{x1D716}_{3})}{\mathcal{J}}, & & \displaystyle \nonumber\end{eqnarray}$$
where
$$\begin{eqnarray}{\mathcal{J}}:=\frac{1}{4!}\frac{1}{(2\unicode[STIX]{x1D70B}\text{i})^{6}}\iint _{(\cdots \,)}{\mathcal{Q}}_{\boldsymbol{\unicode[STIX]{x1D716}}}(\boldsymbol{\unicode[STIX]{x1D6FC}},\mathbf{0})\biggl(\mathop{\prod }_{i,j}\frac{1}{s_{ij}}\biggr)\,d(\cdots \,).\end{eqnarray}$$
It is noteworthy that, since
$\boldsymbol{\unicode[STIX]{x1D709}}=\mathbf{0}$
,
${\mathcal{J}}$
does not depend on
$\boldsymbol{\unicode[STIX]{x1D716}}$
. Moreover, we will see below with (7.17) that
${\mathcal{J}}\neq 0$
.
(c) The contribution of the pole at
$\unicode[STIX]{x1D709}_{1}=-\unicode[STIX]{x1D709}_{2}$
is
$$\begin{eqnarray}\displaystyle & & \displaystyle \frac{\unicode[STIX]{x1D716}_{3}}{(2\unicode[STIX]{x1D70B}\text{i})^{7}}\iint _{(\cdots \,)}B^{1-2\unicode[STIX]{x1D709}_{2}}\frac{\unicode[STIX]{x1D701}(1-2\unicode[STIX]{x1D716}_{1}\unicode[STIX]{x1D709}_{2})\unicode[STIX]{x1D701}(1-4\unicode[STIX]{x1D709}_{2})\unicode[STIX]{x1D701}(1+2\unicode[STIX]{x1D716}_{2}\unicode[STIX]{x1D709}_{2})\unicode[STIX]{x1D701}(1-2\unicode[STIX]{x1D709}_{2})}{(4-\unicode[STIX]{x1D716}_{1}+\unicode[STIX]{x1D716}_{2})\unicode[STIX]{x1D709}_{2}}\nonumber\\ \displaystyle & & \displaystyle \quad \times \,{\mathcal{Q}}_{\boldsymbol{\unicode[STIX]{x1D716}}}(\boldsymbol{\unicode[STIX]{x1D6FC}},(-\unicode[STIX]{x1D709}_{2},\unicode[STIX]{x1D709}_{2},0))\biggl(\mathop{\prod }_{i,j}\tilde{F}_{\unicode[STIX]{x1D6FF}}^{\pm }(s_{ij})\biggr)\,d(\cdots \,)\nonumber\end{eqnarray}$$
and, proceeding as above, we have that this is
$$\begin{eqnarray}\displaystyle BP_{\boldsymbol{\unicode[STIX]{x1D716}},1,3}(\log B)+O(B^{1+\unicode[STIX]{x1D700}}\unicode[STIX]{x1D6FF}^{1-C_{14}\unicode[STIX]{x1D700}}+B^{1-K}\unicode[STIX]{x1D6FF}^{-C_{15}}), & & \displaystyle \nonumber\end{eqnarray}$$
where
$P_{\boldsymbol{\unicode[STIX]{x1D716}},1,3}$
is a polynomial of degree
$4$
of leading coefficient
$$\begin{eqnarray}\displaystyle \frac{\unicode[STIX]{x1D716}_{1}\unicode[STIX]{x1D716}_{2}\unicode[STIX]{x1D716}_{3}}{2\cdot (4-\unicode[STIX]{x1D716}_{1}+\unicode[STIX]{x1D716}_{2})}{\mathcal{J}}, & & \displaystyle \nonumber\end{eqnarray}$$
with the notation (7.16).
(d) The contribution of the pole at
$\unicode[STIX]{x1D709}_{1}=-\frac{1}{3}\unicode[STIX]{x1D709}_{2}$
with
$\boldsymbol{\unicode[STIX]{x1D716}}=(-1,-1,1)$
is
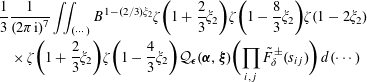$$\begin{eqnarray}\displaystyle & & \displaystyle \frac{1}{3}\frac{1}{(2\unicode[STIX]{x1D70B}\text{i})^{7}}\iint _{(\cdots \,)}B^{1-(2/3)\unicode[STIX]{x1D709}_{2}}\unicode[STIX]{x1D701}\biggl(1+\frac{2}{3}\unicode[STIX]{x1D709}_{2}\biggr)\unicode[STIX]{x1D701}\biggl(1-\frac{8}{3}\unicode[STIX]{x1D709}_{2}\biggr)\unicode[STIX]{x1D701}(1-2\unicode[STIX]{x1D709}_{2})\nonumber\\ \displaystyle & & \displaystyle \quad \times \,\unicode[STIX]{x1D701}\biggl(1+\frac{2}{3}\unicode[STIX]{x1D709}_{2}\biggr)\unicode[STIX]{x1D701}\biggl(1-\frac{4}{3}\unicode[STIX]{x1D709}_{2}\biggr){\mathcal{Q}}_{\boldsymbol{\unicode[STIX]{x1D716}}}(\boldsymbol{\unicode[STIX]{x1D6FC}},\boldsymbol{\unicode[STIX]{x1D709}})\biggl(\mathop{\prod }_{i,j}\tilde{F}_{\unicode[STIX]{x1D6FF}}^{\pm }(s_{ij})\biggr)\,d(\cdots \,)\nonumber\end{eqnarray}$$
and, proceeding as above, we have that this is
$$\begin{eqnarray}\displaystyle BP_{\boldsymbol{\unicode[STIX]{x1D716}},1,4}(\log B)+O(B^{1+\unicode[STIX]{x1D700}}\unicode[STIX]{x1D6FF}^{1-C_{16}\unicode[STIX]{x1D700}}+B^{1-K}\unicode[STIX]{x1D6FF}^{-C_{17}}), & & \displaystyle \nonumber\end{eqnarray}$$
where
$P_{\boldsymbol{\unicode[STIX]{x1D716}},1,4}$
is a polynomial of degree
$4$
of leading coefficient
$$\begin{eqnarray}\displaystyle \frac{1}{2^{4}\cdot 3}{\mathcal{J}}. & & \displaystyle \nonumber\end{eqnarray}$$
Regrouping the above four contributions, we obtain that for
$\boldsymbol{\unicode[STIX]{x1D716}}\neq (1,-1,1)$
, we have
$$\begin{eqnarray}\displaystyle M_{\boldsymbol{a},\boldsymbol{\unicode[STIX]{x1D716}},1}^{\pm }(B)=BP_{\boldsymbol{\unicode[STIX]{x1D716}},1}(\log B)+O(B^{1+\unicode[STIX]{x1D700}}\unicode[STIX]{x1D6FF}^{1-C_{18}\unicode[STIX]{x1D700}}+B^{1-K}\unicode[STIX]{x1D6FF}^{-C_{19}}), & & \displaystyle \nonumber\end{eqnarray}$$
where
$P_{\boldsymbol{\unicode[STIX]{x1D716}},1}$
is a degree-
$4$
polynomial with leading coefficient
$$\begin{eqnarray}\displaystyle {\mathcal{J}}\times \left\{\begin{array}{@{}l@{}}\displaystyle -\frac{\unicode[STIX]{x1D716}_{1}\unicode[STIX]{x1D716}_{2}\unicode[STIX]{x1D716}_{3}}{2\cdot 3\cdot (4-\unicode[STIX]{x1D716}_{1}+2\unicode[STIX]{x1D716}_{2}-\unicode[STIX]{x1D716}_{3})}+\frac{\unicode[STIX]{x1D716}_{1}\unicode[STIX]{x1D716}_{2}\unicode[STIX]{x1D716}_{3}}{2\cdot (4-\unicode[STIX]{x1D716}_{1}+\unicode[STIX]{x1D716}_{2})},\\ \qquad \qquad \text{if }\boldsymbol{\unicode[STIX]{x1D716}}\neq (-1,-1,1),(1,-1,1),\\ \displaystyle \frac{1}{2^{4}}\quad \text{if }\boldsymbol{\unicode[STIX]{x1D716}}=(-1,-1,1),\end{array}\right. & & \displaystyle \nonumber\end{eqnarray}$$
with the notation (7.16).
7.5 The pole at
$s^{\ast }=1+2\unicode[STIX]{x1D709}_{1}$
for
$\boldsymbol{\unicode[STIX]{x1D716}}=(1,-1,1)$
For brevity, in this section we write
$\boldsymbol{\unicode[STIX]{x1D716}}^{\ast }:=(1,-1,1)$
. We have
$$\begin{eqnarray}\displaystyle & & \displaystyle M_{\boldsymbol{\unicode[STIX]{x1D716}}^{\ast },1}^{\pm }(B)=\frac{2}{(2\unicode[STIX]{x1D70B}\text{i})^{8}}\iint _{(\cdots \,)}B^{1+2\unicode[STIX]{x1D709}_{1}}\frac{\unicode[STIX]{x1D701}(1+2\unicode[STIX]{x1D709}_{1})\unicode[STIX]{x1D701}(1+2\unicode[STIX]{x1D709}_{1}-2\unicode[STIX]{x1D709}_{2})\unicode[STIX]{x1D701}(1-2\unicode[STIX]{x1D709}_{2})}{4\unicode[STIX]{x1D709}_{1}+2\unicode[STIX]{x1D709}_{2}}\nonumber\\ \displaystyle & & \displaystyle \quad \times \,\unicode[STIX]{x1D701}(1+4\unicode[STIX]{x1D709}_{1}+2\unicode[STIX]{x1D709}_{2})\unicode[STIX]{x1D701}(1-2(\unicode[STIX]{x1D709}_{1}+\unicode[STIX]{x1D709}_{2})){\mathcal{Q}}_{\boldsymbol{\unicode[STIX]{x1D716}}^{\ast }}(\boldsymbol{\unicode[STIX]{x1D6FC}},\boldsymbol{\unicode[STIX]{x1D709}})\biggl(\mathop{\prod }_{i,j}\tilde{F}_{\unicode[STIX]{x1D6FF}}^{\pm }(s_{ij})\biggr)\,d(\cdots \,).\nonumber\end{eqnarray}$$
Here, we move
$c_{\unicode[STIX]{x1D709}_{2}}$
to
$c_{\unicode[STIX]{x1D709}_{2}}=2K$
, passing through simple poles at
$\unicode[STIX]{x1D709}_{2}=0$
and
$\unicode[STIX]{x1D709}_{2}=\unicode[STIX]{x1D709}_{1}$
. For the integral on the new lines of integration, we move
$c_{\unicode[STIX]{x1D709}_{1}}$
to
$c_{\unicode[STIX]{x1D709}_{1}}=-K/2$
passing through a pole at
$\unicode[STIX]{x1D709}_{1}=0$
. If
$K$
is sufficiently small, the integral on these new lines of integration can then be estimated trivially by
$O(B^{1-K}\unicode[STIX]{x1D6FF}^{-C_{20}})$
. Thus, overall we shall compute the following residues arising for the following poles.
(a) A simple pole at
$\unicode[STIX]{x1D709}_{2}=0$
.(b) A simple pole
$\unicode[STIX]{x1D709}_{2}=\unicode[STIX]{x1D709}_{1}$
.(c) A simple pole at
$\unicode[STIX]{x1D6FF}_{1}=0$
(with
$c_{\unicode[STIX]{x1D709}_{2}}>0$
).
(a) The contribution of the residue at
$\unicode[STIX]{x1D709}_{2}=0$
is
$$\begin{eqnarray}\displaystyle & & \displaystyle \frac{1}{(2\unicode[STIX]{x1D70B}\text{i})^{7}}\iint _{(\cdots \,)}B^{1+2\unicode[STIX]{x1D709}_{1}}\frac{\unicode[STIX]{x1D701}(1+2\unicode[STIX]{x1D709}_{1})^{2}\unicode[STIX]{x1D701}(1+4\unicode[STIX]{x1D709}_{1})\unicode[STIX]{x1D701}(1-2\unicode[STIX]{x1D709}_{1})}{4\unicode[STIX]{x1D709}_{1}}\nonumber\\ \displaystyle & & \displaystyle \quad \times \,{\mathcal{Q}}_{\boldsymbol{\unicode[STIX]{x1D716}}^{\ast }}(\boldsymbol{\unicode[STIX]{x1D6FC}},\boldsymbol{\unicode[STIX]{x1D709}})\biggl(\mathop{\prod }_{i,j}\tilde{F}_{\unicode[STIX]{x1D6FF}}^{\pm }(s_{ij})\biggr)\,d(\cdots \,)\nonumber\end{eqnarray}$$
and, as in the previous section, one sees that this is
$$\begin{eqnarray}BP_{\boldsymbol{\unicode[STIX]{x1D716}}^{\ast },1,4}(\log B)+O(B^{1+\unicode[STIX]{x1D700}}\unicode[STIX]{x1D6FF}^{1-C_{21}\unicode[STIX]{x1D700}}+B^{1-K}\unicode[STIX]{x1D6FF}^{-C_{22}}),\end{eqnarray}$$
with
$P_{\boldsymbol{\unicode[STIX]{x1D716}}^{\ast },4,1}$
of degree
$4$
with leading coefficient
$$\begin{eqnarray}\displaystyle -\frac{1}{2^{3}}{\mathcal{J}}, & & \displaystyle \nonumber\end{eqnarray}$$
with the notation (7.16).
(b) The contribution of the residue at
$\unicode[STIX]{x1D709}_{2}=\unicode[STIX]{x1D709}_{1}$
is
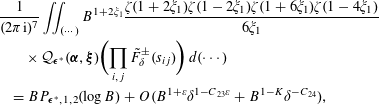$$\begin{eqnarray}\displaystyle & & \displaystyle \frac{1}{(2\unicode[STIX]{x1D70B}\text{i})^{7}}\iint _{(\cdots \,)}B^{1+2\unicode[STIX]{x1D709}_{1}}\frac{\unicode[STIX]{x1D701}(1+2\unicode[STIX]{x1D709}_{1})\unicode[STIX]{x1D701}(1-2\unicode[STIX]{x1D709}_{1})\unicode[STIX]{x1D701}(1+6\unicode[STIX]{x1D709}_{1})\unicode[STIX]{x1D701}(1-4\unicode[STIX]{x1D709}_{1})}{6\unicode[STIX]{x1D709}_{1}}\nonumber\\ \displaystyle & & \displaystyle \qquad \times \,{\mathcal{Q}}_{\boldsymbol{\unicode[STIX]{x1D716}}^{\ast }}(\boldsymbol{\unicode[STIX]{x1D6FC}},\boldsymbol{\unicode[STIX]{x1D709}})\biggl(\mathop{\prod }_{i,j}\tilde{F}_{\unicode[STIX]{x1D6FF}}^{\pm }(s_{ij})\biggr)\,d(\cdots \,)\nonumber\\ \displaystyle & & \displaystyle \quad =BP_{\boldsymbol{\unicode[STIX]{x1D716}}^{\ast },1,2}(\log B)+O(B^{1+\unicode[STIX]{x1D700}}\unicode[STIX]{x1D6FF}^{1-C_{23}\unicode[STIX]{x1D700}}+B^{1-K}\unicode[STIX]{x1D6FF}^{-C_{24}}),\nonumber\end{eqnarray}$$
with
$P_{\unicode[STIX]{x1D716}^{\ast },1,2}$
of degree
$4$
with leading coefficient
$$\begin{eqnarray}\displaystyle \frac{1}{2^{2}\cdot 3^{2}}{\mathcal{J}}. & & \displaystyle \nonumber\end{eqnarray}$$
(c) The contribution of the residue at
$\unicode[STIX]{x1D709}_{1}=0$
is
$$\begin{eqnarray}\displaystyle & & \displaystyle \frac{1}{(2\unicode[STIX]{x1D70B}\text{i})^{7}}\iint _{(\cdots \,)}B\frac{\unicode[STIX]{x1D701}(1-2\unicode[STIX]{x1D709}_{2})^{3}\unicode[STIX]{x1D701}(1+2\unicode[STIX]{x1D709}_{2})}{2\unicode[STIX]{x1D709}_{2}}{\mathcal{Q}}_{\boldsymbol{\unicode[STIX]{x1D716}}^{\ast }}(\boldsymbol{\unicode[STIX]{x1D6FC}},\boldsymbol{\unicode[STIX]{x1D709}})\biggl(\mathop{\prod }_{i,j}\tilde{F}_{\unicode[STIX]{x1D6FF}}^{\pm }(s_{ij})\biggr)\,d(\cdots \,)\nonumber\\ \displaystyle & & \displaystyle \quad =P_{\boldsymbol{\unicode[STIX]{x1D716}}^{\ast },1,3}B+O(B^{1+\unicode[STIX]{x1D700}}\unicode[STIX]{x1D6FF}^{1-C_{25}\unicode[STIX]{x1D700}}+B^{1-K}\unicode[STIX]{x1D6FF}^{-C_{26}}),\nonumber\end{eqnarray}$$
with
$P_{\boldsymbol{\unicode[STIX]{x1D716}}^{\ast },1,3}\in \mathbb{R}$
.
Collecting the various terms, we then find that
$$\begin{eqnarray}\displaystyle M_{\boldsymbol{\unicode[STIX]{x1D716}}^{\ast },1}^{\pm }(B)=BP_{\boldsymbol{\unicode[STIX]{x1D716}}^{\ast },1}(\log B)+O(B^{1+\unicode[STIX]{x1D700}}\unicode[STIX]{x1D6FF}^{1-C_{27}\unicode[STIX]{x1D700}}+B^{1-K}\unicode[STIX]{x1D6FF}^{-C_{28}}), & & \displaystyle \nonumber\end{eqnarray}$$
where
$P_{\boldsymbol{\unicode[STIX]{x1D716}}^{\ast },1}$
is a polynomial of degree
$4$
with leading coefficient
$$\begin{eqnarray}\displaystyle -\frac{7}{2^{3}\cdot 3^{2}}{\mathcal{J}}. & & \displaystyle \nonumber\end{eqnarray}$$
7.6 The pole at
$s^{\ast }=1+\frac{1}{2}(\unicode[STIX]{x1D716}_{1}\unicode[STIX]{x1D709}_{1}+\unicode[STIX]{x1D716}_{2}\unicode[STIX]{x1D709}_{2}+\unicode[STIX]{x1D716}_{3}\unicode[STIX]{x1D709}_{3})$
Recall that
$M_{\boldsymbol{\unicode[STIX]{x1D716}},2}^{\pm }(B):=0$
if
$\boldsymbol{\unicode[STIX]{x1D716}}=(-1,1,1)$
,
$(-1,-1,1)$
,
$(-1,1,-1)$
. In all other cases, we have
$$\begin{eqnarray}\displaystyle M_{\boldsymbol{\unicode[STIX]{x1D716}},2}^{\pm }(B) & = & \displaystyle \frac{1}{(2\unicode[STIX]{x1D70B}\text{i})^{8}}\iint _{(\cdots \,)}B^{1+(1/2)(\unicode[STIX]{x1D716}_{1}\unicode[STIX]{x1D709}_{1}+\unicode[STIX]{x1D716}_{2}\unicode[STIX]{x1D709}_{2}+\unicode[STIX]{x1D716}_{3}\unicode[STIX]{x1D709}_{3})}\nonumber\\ \displaystyle & & \displaystyle \times \,\mathop{\prod }_{k}\unicode[STIX]{x1D701}\biggl(1+\frac{1}{2}(\unicode[STIX]{x1D716}_{1}\unicode[STIX]{x1D709}_{1}+\unicode[STIX]{x1D716}_{2}\unicode[STIX]{x1D709}_{2}+\unicode[STIX]{x1D716}_{3}\unicode[STIX]{x1D709}_{3})-2\unicode[STIX]{x1D709}_{k}\biggr)\unicode[STIX]{x1D701}(1+2\unicode[STIX]{x1D716}_{k}\unicode[STIX]{x1D709}_{k})\nonumber\\ \displaystyle & & \displaystyle \times \,{\mathcal{Q}}_{\boldsymbol{\unicode[STIX]{x1D716}}}(\boldsymbol{\unicode[STIX]{x1D6FC}},\boldsymbol{\unicode[STIX]{x1D709}})\biggl(\mathop{\prod }_{i,j}\tilde{F}_{\unicode[STIX]{x1D6FF}}^{\pm }(s_{ij})\biggr)\,d(\cdots \,).\nonumber\end{eqnarray}$$
If
$\unicode[STIX]{x1D716}_{1}=\unicode[STIX]{x1D716}_{2}=\unicode[STIX]{x1D716}_{3}$
, then the exponent of
$B$
is
$1$
. In particular, since in this case we have the relation
$s^{\ast }=\sum _{i,j}s_{ij}=1$
because
$\unicode[STIX]{x1D709}_{1}+\unicode[STIX]{x1D709}_{2}+\unicode[STIX]{x1D709}_{3}=0$
, we can replace
$\prod _{i,j}\tilde{F}_{\unicode[STIX]{x1D6FF}}^{\pm }(s_{ij})$
by
$\prod _{i,j}s_{ij}^{-1}$
at a cost of an error which is
$O(B^{1+\unicode[STIX]{x1D700}}\unicode[STIX]{x1D6FF}^{1-C_{25}\unicode[STIX]{x1D700}})$
like in §7.3. Thus, for
$\boldsymbol{\unicode[STIX]{x1D716}}=(1,1,1),(-1,-1,-1)$
, we have
$$\begin{eqnarray}\displaystyle M_{\boldsymbol{\unicode[STIX]{x1D716}},2^{\pm }(B)}=P_{\boldsymbol{\unicode[STIX]{x1D716}},2,1}B+O(B^{1+\unicode[STIX]{x1D700}}\unicode[STIX]{x1D6FF}^{1-C_{29}\unicode[STIX]{x1D700}}) & & \displaystyle \nonumber\end{eqnarray}$$
for some
$P_{\boldsymbol{\unicode[STIX]{x1D716}},2,1}\in \mathbb{R}$
.
Therefore, we are left with considering the cases where
$\unicode[STIX]{x1D716}_{r}=-\unicode[STIX]{x1D716}_{k_{1}}=-\unicode[STIX]{x1D716}_{k_{2}}$
, with
$\{r,k_{1},k_{2}\}=\{1,2,3\}$
and
$k_{1}<k_{2}$
. Notice in particular that since
$\unicode[STIX]{x1D709}_{1}+\unicode[STIX]{x1D709}_{2}+\unicode[STIX]{x1D709}_{3}=0$
, then we have
$\unicode[STIX]{x1D716}_{1}\unicode[STIX]{x1D709}_{1}+\unicode[STIX]{x1D716}_{2}\unicode[STIX]{x1D709}_{2}+\unicode[STIX]{x1D716}_{3}\unicode[STIX]{x1D709}_{3}=2\unicode[STIX]{x1D716}_{r}\unicode[STIX]{x1D709}_{r}$
. Thus,
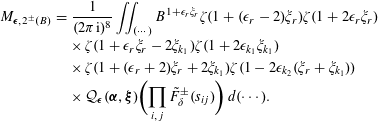$$\begin{eqnarray}\displaystyle M_{\boldsymbol{\unicode[STIX]{x1D716}},2^{\pm }(B)} & = & \displaystyle \frac{1}{(2\unicode[STIX]{x1D70B}\text{i})^{8}}\iint _{(\cdots \,)}B^{1+\unicode[STIX]{x1D716}_{r}\unicode[STIX]{x1D709}_{r}}\unicode[STIX]{x1D701}(1+(\unicode[STIX]{x1D716}_{r}-2)\unicode[STIX]{x1D709}_{r})\unicode[STIX]{x1D701}(1+2\unicode[STIX]{x1D716}_{r}\unicode[STIX]{x1D709}_{r})\nonumber\\ \displaystyle & & \displaystyle \times \,\unicode[STIX]{x1D701}(1+\unicode[STIX]{x1D716}_{r}\unicode[STIX]{x1D709}_{r}-2\unicode[STIX]{x1D709}_{k_{1}})\unicode[STIX]{x1D701}(1+2\unicode[STIX]{x1D716}_{k_{1}}\unicode[STIX]{x1D709}_{k_{1}})\nonumber\\ \displaystyle & & \displaystyle \times \,\unicode[STIX]{x1D701}(1+(\unicode[STIX]{x1D716}_{r}+2)\unicode[STIX]{x1D709}_{r}+2\unicode[STIX]{x1D709}_{k_{1}})\unicode[STIX]{x1D701}(1-2\unicode[STIX]{x1D716}_{k_{2}}(\unicode[STIX]{x1D709}_{r}+\unicode[STIX]{x1D709}_{k_{1}}))\nonumber\\ \displaystyle & & \displaystyle \times \,{\mathcal{Q}}_{\boldsymbol{\unicode[STIX]{x1D716}}}(\boldsymbol{\unicode[STIX]{x1D6FC}},\boldsymbol{\unicode[STIX]{x1D709}})\biggl(\mathop{\prod }_{i,j}\tilde{F}_{\unicode[STIX]{x1D6FF}}^{\pm }(s_{ij})\biggr)\,d(\cdots \,).\nonumber\end{eqnarray}$$
Notice that we made a change of variables (of Jacobian
$\pm 1$
, since
$\unicode[STIX]{x1D709}_{1}\,+\,\unicode[STIX]{x1D709}_{2}\,+\,\unicode[STIX]{x1D709}_{3}=0$
) using
$\unicode[STIX]{x1D709}_{r},\unicode[STIX]{x1D709}_{k_{1}}$
rather than
$\unicode[STIX]{x1D709}_{1},\unicode[STIX]{x1D709}_{2}$
.
Next, we move the lines of integration
$c_{\unicode[STIX]{x1D709}_{r}}$
,
$c_{\unicode[STIX]{x1D709}_{k_{1}}}$
to
$c_{\unicode[STIX]{x1D709}_{r}}=c_{\unicode[STIX]{x1D709}_{k_{1}}}=-\unicode[STIX]{x1D716}_{r}K$
. In doing so, we pass through a double pole at
$\unicode[STIX]{x1D709}_{r}=0$
and, if
$r=1$
, through the simple poles of the
$\unicode[STIX]{x1D701}$
factors on the second line at
$\unicode[STIX]{x1D709}_{1}=-\frac{2}{3}\unicode[STIX]{x1D709}_{2}$
and
$\unicode[STIX]{x1D709}_{1}=-\unicode[STIX]{x1D709}_{2}$
. Thus, as in the previous sections, if
$\boldsymbol{\unicode[STIX]{x1D716}}=(1,-1,1),(1,1,-1)$
, we find that
$$\begin{eqnarray}\displaystyle M_{\boldsymbol{\unicode[STIX]{x1D716}},2^{\pm }(B)}=BP_{\boldsymbol{\unicode[STIX]{x1D716}},2,2}(\log B)+O(B^{1+\unicode[STIX]{x1D700}}\unicode[STIX]{x1D6FF}^{1-C_{30}\unicode[STIX]{x1D700}}+B^{1-K}\unicode[STIX]{x1D6FF}^{-C_{31}}), & & \displaystyle \nonumber\end{eqnarray}$$
with
$P_{\boldsymbol{\unicode[STIX]{x1D716}},2,2}(\log B)$
of degree at most
$1$
and the same holds for the contribution of the pole at
$\unicode[STIX]{x1D709}_{r}=0$
when
$r=1$
. We are therefore left with computing the contributions of the two remaining poles when
$\boldsymbol{\unicode[STIX]{x1D716}}=(1,-1,-1)$
and
$(r,k_{1},k_{2})=(1,2,3)$
. The contribution of the pole at
$\unicode[STIX]{x1D709}_{1}=-\frac{2}{3}\unicode[STIX]{x1D709}_{2}$
is
$$\begin{eqnarray}\displaystyle & & \displaystyle \frac{1}{3}\frac{1}{(2\unicode[STIX]{x1D70B}\text{i})^{7}}\iint _{(\cdots \,)}B^{1-(2/3)\unicode[STIX]{x1D709}_{2}}\unicode[STIX]{x1D701}\biggl(1+\frac{2}{3}\unicode[STIX]{x1D709}_{2}\biggr)^{2}\unicode[STIX]{x1D701}\biggl(1-\frac{4}{3}\unicode[STIX]{x1D709}_{2}\biggr)\nonumber\\ \displaystyle & & \displaystyle \quad \times \,\unicode[STIX]{x1D701}\biggl(1-\frac{8}{3}\unicode[STIX]{x1D709}_{2}\biggr)\unicode[STIX]{x1D701}(1-2\unicode[STIX]{x1D709}_{2}){\mathcal{Q}}_{(1,-1,-1)}(\boldsymbol{\unicode[STIX]{x1D6FC}},\boldsymbol{\unicode[STIX]{x1D709}})\biggl(\mathop{\prod }_{i,j}\tilde{F}_{\unicode[STIX]{x1D6FF}}^{\pm }(s_{ij})\biggr)\,d(\cdots \,)\nonumber\end{eqnarray}$$
and this is
$BP_{(1,-1,-1),2,3}(\log B)+O(B^{1+\unicode[STIX]{x1D700}}\unicode[STIX]{x1D6FF}^{1-C_{31}\unicode[STIX]{x1D700}}+B^{1-K}\unicode[STIX]{x1D6FF}^{-C_{32}})$
with
$P_{(1,-1,-1),2,3}$
a polynomial of degree
$4$
and leading coefficient
$$\begin{eqnarray}\displaystyle \frac{1}{2^{4}\cdot 3}{\mathcal{J}}, & & \displaystyle \nonumber\end{eqnarray}$$
with the notation (7.16).
The contribution of the pole at
$\unicode[STIX]{x1D709}_{1}=-\unicode[STIX]{x1D709}_{2}$
is
$$\begin{eqnarray}\displaystyle & & \displaystyle \frac{1}{2}\frac{1}{(2\unicode[STIX]{x1D70B}\text{i})^{7}}\iint _{(\cdots \,)}B^{1-\unicode[STIX]{x1D709}_{2}}\unicode[STIX]{x1D701}(1+\unicode[STIX]{x1D709}_{2})\unicode[STIX]{x1D701}(1-2\unicode[STIX]{x1D709}_{2})^{2}\unicode[STIX]{x1D701}(1-3\unicode[STIX]{x1D709}_{2})\unicode[STIX]{x1D701}(1-\unicode[STIX]{x1D709}_{2})\nonumber\\ \displaystyle & & \displaystyle \quad \times \,{\mathcal{Q}}_{(1,-1,-1)}(\boldsymbol{\unicode[STIX]{x1D6FC}},\boldsymbol{\unicode[STIX]{x1D709}})\biggl(\mathop{\prod }_{i,j}\tilde{F}_{\unicode[STIX]{x1D6FF}}^{\pm }(s_{ij})\biggr)\,d(\cdots \,).\nonumber\end{eqnarray}$$
And this is
$BP_{(1,-1,-1),2,4}(\log B)+O(B^{1+\unicode[STIX]{x1D700}}\unicode[STIX]{x1D6FF}^{1-C_{33}\unicode[STIX]{x1D700}}+B^{1-K}\unicode[STIX]{x1D6FF}^{-C_{34}})$
with
$P_{(1,-1,-1),2,4}$
of degree
$4$
with leading coefficient
$$\begin{eqnarray}\displaystyle -\frac{1}{2^{3}\cdot 3}{\mathcal{J}}. & & \displaystyle \nonumber\end{eqnarray}$$
Thus, summarizing for all
$\boldsymbol{\unicode[STIX]{x1D716}}\in \{1,-1\}^{3}$
, we have
$$\begin{eqnarray}\displaystyle M_{\boldsymbol{\unicode[STIX]{x1D716}},2}^{\pm }(B)=BP_{\boldsymbol{\unicode[STIX]{x1D716}},2}(\log B)+O(B^{1+\unicode[STIX]{x1D700}}\unicode[STIX]{x1D6FF}^{1-C_{35}\unicode[STIX]{x1D700}}+B^{1-K}\unicode[STIX]{x1D6FF}^{-C_{36}}), & & \displaystyle \nonumber\end{eqnarray}$$
where
$P_{\boldsymbol{\unicode[STIX]{x1D716}},2}$
is a polynomial of degree at most
$1$
unless
$\boldsymbol{\unicode[STIX]{x1D716}}=(1,-1,-1)$
, in which case
$P_{\boldsymbol{\unicode[STIX]{x1D716}},2}$
is of degree
$4$
with leading coefficient
$$\begin{eqnarray}\displaystyle -\frac{1}{2^{4}\cdot 3}{\mathcal{J}}. & & \displaystyle \nonumber\end{eqnarray}$$
7.7 Regrouping the various contributions
By (7.10), (7.11), (7.12) and regrouping the contributions from §§7.4, 7.5 and 7.6, we find that
$$\begin{eqnarray}\displaystyle N_{\unicode[STIX]{x1D6FF}}^{\pm }(B) & = & \displaystyle B\mathop{\sum }_{\boldsymbol{\unicode[STIX]{x1D716}}\in \{1,-1\}^{3}}(P_{\boldsymbol{\unicode[STIX]{x1D716}},1}(\log B)+P_{\boldsymbol{\unicode[STIX]{x1D716}},2}(\log B))\nonumber\\ \displaystyle & & \displaystyle +\,BP_{0}+O(B^{1+\unicode[STIX]{x1D700}}\unicode[STIX]{x1D6FF}^{1-C_{37}\unicode[STIX]{x1D700}}+B^{1-K}\unicode[STIX]{x1D6FF}^{-C_{38}})\nonumber\\ \displaystyle & = & \displaystyle BP_{1}(\log B)+O(B^{1+\unicode[STIX]{x1D700}}\unicode[STIX]{x1D6FF}^{1-C_{37}\unicode[STIX]{x1D700}}+B^{1-K}\unicode[STIX]{x1D6FF}^{-C_{38}}),\nonumber\end{eqnarray}$$
where
$P_{1}$
is a polynomial of degree
$4$
with leading coefficient
$$\begin{eqnarray}\displaystyle & & \displaystyle \biggl(\frac{1}{16}-\frac{7}{72}-\frac{1}{48}+\mathop{\sum }_{\boldsymbol{\unicode[STIX]{x1D716}}\neq (-1,-1,1),(1,-1,1)}\nonumber\\ \displaystyle & & \displaystyle \quad \times \biggl(\frac{\unicode[STIX]{x1D716}_{1}\unicode[STIX]{x1D716}_{2}\unicode[STIX]{x1D716}_{3}}{2\cdot (4-\unicode[STIX]{x1D716}_{1}+\unicode[STIX]{x1D716}_{2})}-\frac{\unicode[STIX]{x1D716}_{1}\unicode[STIX]{x1D716}_{2}\unicode[STIX]{x1D716}_{3}}{2\cdot 3\cdot (4-\unicode[STIX]{x1D716}_{1}+2\unicode[STIX]{x1D716}_{2}-\unicode[STIX]{x1D716}_{3})}\biggr)\biggr){\mathcal{J}}=\frac{1}{48}{\mathcal{J}}.\nonumber\end{eqnarray}$$
The estimate (7.3) and then Theorem 1 then follow by the final next lemma.
Lemma 8. With the notation of Theorem 1 and (7.16), we have
${\mathcal{J}}=\frac{1}{3}{\mathcal{I}}\mathfrak{S}_{1}.$
Proof. First, we observe that for
$s^{\ast }=1$
, we have
$$\begin{eqnarray}\displaystyle {\mathcal{Q}}_{\boldsymbol{\unicode[STIX]{x1D716}}}(\boldsymbol{\unicode[STIX]{x1D6FC}},\mathbf{0}) & = & \displaystyle \mathop{\sum }_{\substack{ \boldsymbol{b},\boldsymbol{c},\,\boldsymbol{f},\boldsymbol{g}\in \mathbb{N}^{3}, \\ h,\ell \in \mathbb{N}}}\unicode[STIX]{x1D707}(h)\biggl(\mathop{\prod }_{k=1}^{3}\frac{\unicode[STIX]{x1D707}(b_{k})\unicode[STIX]{x1D707}(c_{k})\unicode[STIX]{x1D707}(f_{k})\unicode[STIX]{x1D707}(g_{k})}{r_{1,k}r_{2,k}r_{3,k}}\biggr)\nonumber\\ \displaystyle & & \displaystyle \times \,\frac{(r_{1},\ell )(r_{2},\ell )(r_{3},\ell )}{\ell ^{3}}\unicode[STIX]{x1D711}(\ell )\cdot 2\unicode[STIX]{x1D70B}^{1/2}\mathop{\prod }_{i=1}^{3}\frac{\unicode[STIX]{x1D6E4}((1-\unicode[STIX]{x1D6FC}_{i})/2)}{\unicode[STIX]{x1D6E4}(\unicode[STIX]{x1D6FC}_{i}/2)}\nonumber\\ \displaystyle & = & \displaystyle \mathfrak{S}_{1}\cdot 2\unicode[STIX]{x1D70B}^{1/2}\mathop{\prod }_{i=1}^{3}\frac{\unicode[STIX]{x1D6E4}((1-\unicode[STIX]{x1D6FC}_{i})/2)}{\unicode[STIX]{x1D6E4}(\unicode[STIX]{x1D6FC}_{i}/2)},\nonumber\end{eqnarray}$$
where in the second row we computed the Euler product thanks to [Reference Blomer, Brüdern and Salberger8, Lemma 2.7]. Therefore, we have
$$\begin{eqnarray}\displaystyle {\mathcal{J}} & = & \displaystyle \frac{\mathfrak{S}_{1}}{4!(2\unicode[STIX]{x1D70B}\text{i})^{2}}\iint _{(c_{\unicode[STIX]{x1D6FC}_{1}},c_{\unicode[STIX]{x1D6FC}_{2}})}2\unicode[STIX]{x1D70B}^{1/2}\biggl(\mathop{\prod }_{i=1}^{3}\frac{\unicode[STIX]{x1D6E4}((1-\unicode[STIX]{x1D6FC}_{i})/2)}{\unicode[STIX]{x1D6E4}(\unicode[STIX]{x1D6FC}_{i}/2)}\biggr)\nonumber\\ \displaystyle & & \displaystyle \times \frac{1}{(2\unicode[STIX]{x1D70B}\text{i})^{4}}\int _{(c_{s_{12}},c_{s_{31}},c_{s_{32}},c_{s_{21}})}\frac{ds_{12}\,ds_{21}\,ds_{31}\,ds_{32}}{L(\boldsymbol{\unicode[STIX]{x1D6FC}},s_{12},s_{21},s_{31},s_{32})}\,d\unicode[STIX]{x1D6FC}_{1}\,d\unicode[STIX]{x1D6FC}_{2},\nonumber\end{eqnarray}$$
where the lines of integration can be taken at
$c_{s_{ij}}=\frac{1}{9}$
,
$c_{\unicode[STIX]{x1D6FC}_{1}}=c_{\unicode[STIX]{x1D6FC}_{2}}=\frac{2}{3}$
and, by (7.6),
$$\begin{eqnarray}\displaystyle & & \displaystyle L(\boldsymbol{\unicode[STIX]{x1D6FC}},s_{12},s_{21},s_{31},s_{32})=(1-\unicode[STIX]{x1D6FC}_{1}-s_{21}-s_{31})\nonumber\\ \displaystyle & & \displaystyle \quad \times \,(1-\unicode[STIX]{x1D6FC}_{2}-s_{12}-s_{32})(-1+{\textstyle \frac{3}{2}}\unicode[STIX]{x1D6FC}_{1}-s_{12}+s_{21}+s_{31})\nonumber\\ \displaystyle & & \displaystyle \quad \times \,(-1+{\textstyle \frac{3}{2}}\unicode[STIX]{x1D6FC}_{2}+s_{12}-s_{21}+s_{32})(1-{\textstyle \frac{1}{2}}\unicode[STIX]{x1D6FC}_{1}-{\textstyle \frac{1}{2}}\unicode[STIX]{x1D6FC}_{2}-s_{31}-s_{32})s_{12}s_{21}s_{31}s_{32}.\nonumber\end{eqnarray}$$
In the same way as in the end of the proof of Proposition 1, one has that the inner integral over
$s_{12},s_{21},s_{31},s_{32}$
can be evaluated by moving each line of integration to
$-\infty$
and collecting the residues of the poles encountered in the process. After this simple but a bit lengthy calculation, which can be easily performed with the help of Mathematica, one finds that the inner integral is equal to
$8(\unicode[STIX]{x1D6FC}_{1}\unicode[STIX]{x1D6FC}_{2}\unicode[STIX]{x1D6FC}_{3}(1-\unicode[STIX]{x1D6FC}_{1})(1-\unicode[STIX]{x1D6FC}_{2})(1-\unicode[STIX]{x1D6FC}_{3}))^{-1}$
, with
$\unicode[STIX]{x1D6FC}_{3}=2-\unicode[STIX]{x1D6FC}_{1}-\unicode[STIX]{x1D6FC}_{2}$
. Thus, we finally get
$$\begin{eqnarray}{\mathcal{J}}=\frac{\mathfrak{S}_{1}}{3(2\unicode[STIX]{x1D70B}\text{i})^{2}}\iint _{(c_{\unicode[STIX]{x1D6FC}_{1}},c_{\unicode[STIX]{x1D6FC}_{2}})}2\unicode[STIX]{x1D70B}^{1/2}\mathop{\prod }_{i=1}^{3}\frac{\unicode[STIX]{x1D6E4}((1-\unicode[STIX]{x1D6FC}_{i})/2)}{\unicode[STIX]{x1D6FC}_{i}(1-\unicode[STIX]{x1D6FC}_{i})\unicode[STIX]{x1D6E4}(\unicode[STIX]{x1D6FC}_{i}/2)}\,d\unicode[STIX]{x1D6FC}_{2}\,d\unicode[STIX]{x1D6FC}_{3}=\frac{1}{3}\mathfrak{S}_{1}\cdot {\mathcal{I}}\end{eqnarray}$$
by Lemma 4. ◻
Acknowledgements
The authors are grateful to Régis de la Bretèche for helpful conversations and comments, for his supervision of the second author during the end of his PhD research and for inviting the first author to Paris, where this collaboration started. The authors would also like to thank the anonymous referee for a careful reading of this paper. The first author is a member of the INdAM group GNAMPA and is partially supported by PRIN “Number Theory and Arithmetic Geometry”.
