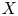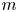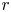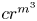1. Introduction
A parameterization of a set $X \subset \operatorname {\mathbb {R}}^{n}$![]() of dimension $m$
of dimension $m$![]() is a finite set of maps $\{f_i: (0,\,1)^{m} \to X \mid i \in \{1,\,\ldots ,\,N\}\}$
is a finite set of maps $\{f_i: (0,\,1)^{m} \to X \mid i \in \{1,\,\ldots ,\,N\}\}$![]() for some $N \in \operatorname {\mathbb {N}}$
for some $N \in \operatorname {\mathbb {N}}$![]() , such that the images of these maps cover $X$
, such that the images of these maps cover $X$![]() . Consider the following question: given any positive integer $r$
. Consider the following question: given any positive integer $r$![]() , can one construct a parameterization of $X$
, can one construct a parameterization of $X$![]() consisting of $r$
consisting of $r$![]() times continuously differentiable maps whose $C^{r}$
times continuously differentiable maps whose $C^{r}$![]() -norm is bounded by $1$
-norm is bounded by $1$![]() , i.e. a $C^{r}$
, i.e. a $C^{r}$![]() -parameterization?
-parameterization?
The interest in this question first arose in 1987 in the study of entropy of dynamical systems in [Reference Yomdin16, Reference Yomdin17]. In these papers, Yomdin sketched a $C^{r}$![]() -parameterization result for semi-algebraic sets. A more refined explanation was given by Gromov in [Reference Gromov7], a complete proof by Burguet in [Reference Burguet3]. In their result, the number of maps of the parameterization is shown to depend on combinatorial data defining $X$
-parameterization result for semi-algebraic sets. A more refined explanation was given by Gromov in [Reference Gromov7], a complete proof by Burguet in [Reference Burguet3]. In their result, the number of maps of the parameterization is shown to depend on combinatorial data defining $X$![]() , i.e. $n$
, i.e. $n$![]() , $m$
, $m$![]() , $r$
, $r$![]() and the complexity $\beta$
and the complexity $\beta$![]() , which is the maximum degree of the equations and inequalities necessary to define $X$
, which is the maximum degree of the equations and inequalities necessary to define $X$![]() . However, there is no explicit formula for the number of maps. Yomdin has written a nice survey on the study of parameterizations in [Reference Yomdin19].
. However, there is no explicit formula for the number of maps. Yomdin has written a nice survey on the study of parameterizations in [Reference Yomdin19].
Using o-minimality, a tool of model theory, Pila and Wilkie showed in 2006 that any bounded definable set in any o-minimal structure (containing the semi-algebraic sets) has a $C^{r}$![]() -parameterization [Reference Pila and Wilkie13]. However, even in the special case that $X$
-parameterization [Reference Pila and Wilkie13]. However, even in the special case that $X$![]() is semi-algebraic, they did not deduce a formula for the number of maps of the parameterization in terms of the complexity of $X$
is semi-algebraic, they did not deduce a formula for the number of maps of the parameterization in terms of the complexity of $X$![]() . The main result of [Reference Pila and Wilkie13] bounds the number of rational points on a definable set $X$
. The main result of [Reference Pila and Wilkie13] bounds the number of rational points on a definable set $X$![]() up to a certain height, known as the counting theorem. To obtain this result, they constructed $C^{r}$
up to a certain height, known as the counting theorem. To obtain this result, they constructed $C^{r}$![]() -parameterizations for arbitrarily large $r$
-parameterizations for arbitrarily large $r$![]() and therefore it is interesting to know how large the parameterization becomes depending on $r$
and therefore it is interesting to know how large the parameterization becomes depending on $r$![]() .
.
The dependence on $r$![]() has recently been investigated in [Reference Binyamini and Novikov1] by Binyamini and Novikov, who construct a $C^{r}$
has recently been investigated in [Reference Binyamini and Novikov1] by Binyamini and Novikov, who construct a $C^{r}$![]() -parameterization consisting of $cr^{m}$
-parameterization consisting of $cr^{m}$![]() maps for subanalytic sets. Here, $c$
maps for subanalytic sets. Here, $c$![]() is a constant that depends on $X$
is a constant that depends on $X$![]() . Moreover, they show that $c$
. Moreover, they show that $c$![]() depends polynomially on the complexity of $X$
depends polynomially on the complexity of $X$![]() , if $X$
, if $X$![]() is semi-algebraic. Around the same time, Cluckers, Pila and Wilkie proved in [Reference Cluckers, Pila and Wilkie4] a $C^{r}$
is semi-algebraic. Around the same time, Cluckers, Pila and Wilkie proved in [Reference Cluckers, Pila and Wilkie4] a $C^{r}$![]() -parameterization result for power-subanalytic sets using $cr^{d}$
-parameterization result for power-subanalytic sets using $cr^{d}$![]() maps, where $c$
maps, where $c$![]() and $d$
and $d$![]() are constants depending on $X$
are constants depending on $X$![]() , and this result is uniform.
, and this result is uniform.
In this paper, we built on the methods of [Reference Cluckers, Pila and Wilkie4] to further refine their result in Theorem 3.12. It is weaker than the result of [Reference Binyamini and Novikov1] for subanalytic sets but holds for the larger class of power-subanalytic sets.
Theorem. If $X \subset [-1,\,1]^{n}$![]() is power-subanalytic of dimension $m \leq n$
is power-subanalytic of dimension $m \leq n$![]() , then for any positive integer $r$
, then for any positive integer $r$![]() there exists a $C^{r}$
there exists a $C^{r}$![]() -parameterization of $X$
-parameterization of $X$![]() consisting of $cr^{m^{3}}$
consisting of $cr^{m^{3}}$![]() maps whose $C^{r}$
maps whose $C^{r}$![]() -norm is bounded by $1$
-norm is bounded by $1$![]() . Moreover, if $X$
. Moreover, if $X$![]() belongs a power-subanalytic family of such sets, the constant $c$
belongs a power-subanalytic family of such sets, the constant $c$![]() holds for all members of the family.
holds for all members of the family.
The theorem above and the results of [Reference Cluckers, Pila and Wilkie4] actually hold for structures $\operatorname {\mathbb {R}}^{K}_\mathcal {F}$![]() , which were studied by Miller in [Reference Miller10]. These structures expand the semi-algebraic sets with restricted analytic functions in a Weierstrass system $\mathcal {F}$
, which were studied by Miller in [Reference Miller10]. These structures expand the semi-algebraic sets with restricted analytic functions in a Weierstrass system $\mathcal {F}$![]() and power maps $x \mapsto x^{\mu }$
and power maps $x \mapsto x^{\mu }$![]() for any $\mu \in K$
for any $\mu \in K$![]() , where $K$
, where $K$![]() is a subfield of the field of exponents of $\mathcal {F}$
is a subfield of the field of exponents of $\mathcal {F}$![]() (see the introduction of § 3 for precise definitions). The structures $\operatorname {\mathbb {R}}$
(see the introduction of § 3 for precise definitions). The structures $\operatorname {\mathbb {R}}$![]() , $\operatorname {\mathbb {R}}_\text {an}$
, $\operatorname {\mathbb {R}}_\text {an}$![]() and $\operatorname {\mathbb {R}}^\text {pow}_\text {an}$
and $\operatorname {\mathbb {R}}^\text {pow}_\text {an}$![]() , corresponding to the semi-algebraic, subanalytic and power-subanalytic sets respectively, are all examples of this class of structures. The main result of [Reference Miller10] is a preparation theorem for functions definable in these structures, which is one of the main ingredients for the proof of the main result.
, corresponding to the semi-algebraic, subanalytic and power-subanalytic sets respectively, are all examples of this class of structures. The main result of [Reference Miller10] is a preparation theorem for functions definable in these structures, which is one of the main ingredients for the proof of the main result.
In 2011, Jones, Miller and Thomas have shown in [Reference Jones, Miller and Thomas8] that any set definable in (any reduct of) $\mathbb {R}_\text {an}$![]() expanding the real field has an $(A,\,0)$
expanding the real field has an $(A,\,0)$![]() -mild parameterization for some $A>0$
-mild parameterization for some $A>0$![]() , i.e. a parameterization consisting of maps that are $(A,\,0)$
, i.e. a parameterization consisting of maps that are $(A,\,0)$![]() -mild. The precise definition of a mild function is given in § 2. Informally, for $C \geq 0$
-mild. The precise definition of a mild function is given in § 2. Informally, for $C \geq 0$![]() , an $(A,\,C)$
, an $(A,\,C)$![]() -mild function is a smooth function with good bounds on the derivatives depending on $A$
-mild function is a smooth function with good bounds on the derivatives depending on $A$![]() and $C$
and $C$![]() . For any integer $r > 0$
. For any integer $r > 0$![]() , these bounds allow us to bound the $C^{r}$
, these bounds allow us to bound the $C^{r}$![]() -norm by $1$
-norm by $1$![]() after a suitable substitution. Since we only control the derivatives up to order $r$
after a suitable substitution. Since we only control the derivatives up to order $r$![]() , their result is stronger. However, by an elementary example of Yomdin [Reference Yomdin18, Proposition 3.3], their result cannot be made uniform. Indeed, the family of hyperbolas $\{ xy = t^{2} \mid (x,\,y) \in (0,\,1)^{2},\, t \in (0,\,1)\}$
, their result is stronger. However, by an elementary example of Yomdin [Reference Yomdin18, Proposition 3.3], their result cannot be made uniform. Indeed, the family of hyperbolas $\{ xy = t^{2} \mid (x,\,y) \in (0,\,1)^{2},\, t \in (0,\,1)\}$![]() does not have a uniform $(A,\,0)$
does not have a uniform $(A,\,0)$![]() -mild parameterization, i.e. the amount of maps will depend on the parameter $t$
-mild parameterization, i.e. the amount of maps will depend on the parameter $t$![]() . Recently, it has been shown in [Reference Van Hille15] that it has a uniform $(A,\,C)$
. Recently, it has been shown in [Reference Van Hille15] that it has a uniform $(A,\,C)$![]() -mild parameterization for all $C>0$
-mild parameterization for all $C>0$![]() .
.
The paper is organized as follows. In § 2, we prove various properties of mild functions using only standard techniques of real analysis. A key result on the composition of these functions, Theorem 2.10, permits us to make all of the results of [Reference Cluckers, Pila and Wilkie4] on mild functions explicit and thus also the constant $d$![]() . This key result is in fact an old result on Gevrey functions [Reference Gevrey6]. We will give the original proof of this result, but in full generality, and reformulate it in terms of mild functions. In § 3, we provide the necessary background in model theory to state the main theorem and we prove the main theorem. Finally, we explain that when $m \geq 2$
. This key result is in fact an old result on Gevrey functions [Reference Gevrey6]. We will give the original proof of this result, but in full generality, and reformulate it in terms of mild functions. In § 3, we provide the necessary background in model theory to state the main theorem and we prove the main theorem. Finally, we explain that when $m \geq 2$![]() , we can in fact obtain a parameterization consisting of $cr^{m^{2}(m-1)}$
, we can in fact obtain a parameterization consisting of $cr^{m^{2}(m-1)}$![]() maps.
maps.
2. Mild functions
Mild functions are a class of $C^{\infty }$![]() -maps introduced by Pila in [Reference Pila11]. The upper bounds on the derivatives of a mild function are very suitable to use the determinant method. This method, which Pila developed with Bombieri [Reference Bombieri and Pila2], is a useful tool in diophantine geometry. For example, the determinant method is used in the proof of the counting theorem in [Reference Pila and Wilkie13].
-maps introduced by Pila in [Reference Pila11]. The upper bounds on the derivatives of a mild function are very suitable to use the determinant method. This method, which Pila developed with Bombieri [Reference Bombieri and Pila2], is a useful tool in diophantine geometry. For example, the determinant method is used in the proof of the counting theorem in [Reference Pila and Wilkie13].
Cluckers, Pila and Wilkie introduced several variants to mild functions in [Reference Cluckers, Pila and Wilkie4]. Since in their result (and our main theorem), they only cared about derivatives up to order $r$![]() , they defined functions that are mild up to order $r$
, they defined functions that are mild up to order $r$![]() . These functions are $C^{r}$
. These functions are $C^{r}$![]() -maps that satisfy the same bounds on the derivatives as mild functions, but up to order $r$
-maps that satisfy the same bounds on the derivatives as mild functions, but up to order $r$![]() . In fact, the maps are actually smooth in their work.
. In fact, the maps are actually smooth in their work.
Since we will encounter many compositions of mild maps, we need a result on compositions of these maps. This result on compositions will allow us to find the amount of maps in § 3. One can think of mild functions as functions of some class indexed by a real number $C \geq 0$![]() . When $C = 0$
. When $C = 0$![]() , these maps are real analytic, when $C= +\infty$
, these maps are real analytic, when $C= +\infty$![]() , they are real smooth. Using the theory of Gevrey functions [Reference Gevrey6], we show that compositions of mild functions of class $C$
, they are real smooth. Using the theory of Gevrey functions [Reference Gevrey6], we show that compositions of mild functions of class $C$![]() are again of class $C$
are again of class $C$![]() .
.
We start with some definitions of multidimensional calculus. Throughout this section, we will work with maps $f = (f_1,\,\ldots ,\,f_n): U \subset \operatorname {\mathbb {R}}^{d} \to \operatorname {\mathbb {R}}^{n}$![]() , where $U$
, where $U$![]() is always assumed to be open in $\operatorname {\mathbb {R}}^{d}$
is always assumed to be open in $\operatorname {\mathbb {R}}^{d}$![]() . We say that $f: U \subset \operatorname {\mathbb {R}}^{d} \to \operatorname {\mathbb {R}}$
. We say that $f: U \subset \operatorname {\mathbb {R}}^{d} \to \operatorname {\mathbb {R}}$![]() is $C^{r}$
is $C^{r}$![]() for a natural number $r$
for a natural number $r$![]() (or $+\infty$
(or $+\infty$![]() ) if $f$
) if $f$![]() is $r$
is $r$![]() times continuously differentiable on $U$
times continuously differentiable on $U$![]() and $f = (f_1,\,\ldots ,\,f_n): U \subset \operatorname {\mathbb {R}}^{d} \to \operatorname {\mathbb {R}}^{n}$
and $f = (f_1,\,\ldots ,\,f_n): U \subset \operatorname {\mathbb {R}}^{d} \to \operatorname {\mathbb {R}}^{n}$![]() is $C^{r}$
is $C^{r}$![]() if $f_1,\,\ldots ,\,f_n$
if $f_1,\,\ldots ,\,f_n$![]() are all $C^{r}$
are all $C^{r}$![]() . For any $i \in \{1,\,\ldots ,\,d\}$
. For any $i \in \{1,\,\ldots ,\,d\}$![]() , denote $(\partial f / \partial x_i) = (\partial f_1 / \partial x_i,\,\ldots ,\, \partial f_n / \partial x_i)$
, denote $(\partial f / \partial x_i) = (\partial f_1 / \partial x_i,\,\ldots ,\, \partial f_n / \partial x_i)$![]() . For any multi-index $\nu = (\nu _1,\,\ldots ,\,\nu _d) \in \operatorname {\mathbb {N}}^{d}$
. For any multi-index $\nu = (\nu _1,\,\ldots ,\,\nu _d) \in \operatorname {\mathbb {N}}^{d}$![]() , map $f: U \to \operatorname {\mathbb {R}}^{n}$
, map $f: U \to \operatorname {\mathbb {R}}^{n}$![]() and $x = (x_1,\,\ldots ,\,x_d) \in U$
and $x = (x_1,\,\ldots ,\,x_d) \in U$![]() we set:
we set:

where by definition $0! = 1$![]() , and $0^{0} = 1$
, and $0^{0} = 1$![]() .
.
Definition 2.1 $C^{r}$![]() -norm
-norm
Suppose that $f: U \subset \operatorname {\mathbb {R}}^{d} \to \operatorname {\mathbb {R}}$![]() is $C^{r}$
is $C^{r}$![]() . Then we define the $C^{r}$
. Then we define the $C^{r}$![]() -norm $|\cdot |_r$
-norm $|\cdot |_r$![]() of $f$
of $f$![]() as follows:
as follows:

Note that $|f|_r$![]() can be $+\infty$
can be $+\infty$![]() . We define the $C^{r}$
. We define the $C^{r}$![]() -norm of a map $f:U \subset \operatorname {\mathbb {R}}^{d} \to \operatorname {\mathbb {R}}^{n}$
-norm of a map $f:U \subset \operatorname {\mathbb {R}}^{d} \to \operatorname {\mathbb {R}}^{n}$![]() to be the maximum of the $C^{r}$
to be the maximum of the $C^{r}$![]() -norms of the component functions $f_1,\,\ldots ,\,f_n$
-norms of the component functions $f_1,\,\ldots ,\,f_n$![]() .
.
This is the norm used in [Reference Binyamini and Novikov1]. In [Reference Cluckers, Pila and Wilkie4], they did not divide by $|\nu |!$![]() . This yields equivalent norms but has an impact on the exponent of $r$
. This yields equivalent norms but has an impact on the exponent of $r$![]() in the main theorem (see Lemma 2.5).
in the main theorem (see Lemma 2.5).
Definition 2.2 (Mild functions) Suppose that $A,\,B>0$![]() , $C \geq 0$
, $C \geq 0$![]() are real numbers and $f: U \subset \operatorname {\mathbb {R}}^{d} \to \operatorname {\mathbb {R}}$
are real numbers and $f: U \subset \operatorname {\mathbb {R}}^{d} \to \operatorname {\mathbb {R}}$![]() . Then $f$
. Then $f$![]() is called $(A,\,B,\,C)$
is called $(A,\,B,\,C)$![]() -mild if it is $C^{\infty }$
-mild if it is $C^{\infty }$![]() and if for all $\nu \in \operatorname {\mathbb {N}}^{d}$
and if for all $\nu \in \operatorname {\mathbb {N}}^{d}$![]() and $x \in U$
and $x \in U$![]() :
:
A map $f: U \subset \operatorname {\mathbb {R}}^{d} \to \operatorname {\mathbb {R}}^{n}$![]() is $(A,\,B,\,C)$
is $(A,\,B,\,C)$![]() -mild if all component functions $f_1,\,\ldots ,\,f_n$
-mild if all component functions $f_1,\,\ldots ,\,f_n$![]() are $(A,\,B,\,C)$
are $(A,\,B,\,C)$![]() -mild. If $B \leq 1$
-mild. If $B \leq 1$![]() , we simply say that $f$
, we simply say that $f$![]() is $(A,\,C)$
is $(A,\,C)$![]() -mild and if we say that $f$
-mild and if we say that $f$![]() is mild, then we mean that $f$
is mild, then we mean that $f$![]() is $(A,\,C)$
is $(A,\,C)$![]() -mild for some $A>0$
-mild for some $A>0$![]() and $C\geq 0$
and $C\geq 0$![]() .
.
This definition is slightly different than the original one by Pila in [Reference Pila11] ([Reference Pila12] for the multivariate case), where the bounds on the derivatives for an $(A,\,C)$![]() -mild function are given by $\nu !(A|\nu |^{C})^{|\nu |}$
-mild function are given by $\nu !(A|\nu |^{C})^{|\nu |}$![]() . Now, due to the following inequalities:
. Now, due to the following inequalities:

(where the number $e$![]() appears as a result of Stirling's formula), one sees that the definitions of $(A,\,C)$
appears as a result of Stirling's formula), one sees that the definitions of $(A,\,C)$![]() -mild coincide in the following way: $f$
-mild coincide in the following way: $f$![]() is $(A_1,\,C)$
is $(A_1,\,C)$![]() -mild for some $A_1>0$
-mild for some $A_1>0$![]() as in our definition if and only if $f$
as in our definition if and only if $f$![]() is $(A_2,\,C)$
is $(A_2,\,C)$![]() -mild for some $A_2 > 0$
-mild for some $A_2 > 0$![]() as in [Reference Pila12]. The reason to adjust the definition is to keep the proof of Theorem 2.10 as simple as possible.
as in [Reference Pila12]. The reason to adjust the definition is to keep the proof of Theorem 2.10 as simple as possible.
Following [Reference Cluckers, Pila and Wilkie4], we will use ‘up to order $r$![]() ’ versions of many definitions and theorems, for example, the following definition.
’ versions of many definitions and theorems, for example, the following definition.
Definition 2.3 (Mild up to order $r$![]() )
)
Suppose that $A,\,B>0$![]() , $C \geq 0$
, $C \geq 0$![]() are real numbers, $r > 0$
are real numbers, $r > 0$![]() an integer or $+\infty$
an integer or $+\infty$![]() and $f: U \subset \operatorname {\mathbb {R}}^{d} \to \operatorname {\mathbb {R}}$
and $f: U \subset \operatorname {\mathbb {R}}^{d} \to \operatorname {\mathbb {R}}$![]() . Then $f$
. Then $f$![]() is called $(A,\,B,\,C)$
is called $(A,\,B,\,C)$![]() -mild up to order $r$
-mild up to order $r$![]() if it is $C^{r}$
if it is $C^{r}$![]() and if for all $\nu \in \operatorname {\mathbb {N}}^{d}$
and if for all $\nu \in \operatorname {\mathbb {N}}^{d}$![]() with $|\nu | \leq r$
with $|\nu | \leq r$![]() and $x \in U$
and $x \in U$![]() :
:
A map $f: U \subset \operatorname {\mathbb {R}}^{d} \to \operatorname {\mathbb {R}}^{n}$![]() is $(A,\,B,\,C)$
is $(A,\,B,\,C)$![]() -mild up to order $r$
-mild up to order $r$![]() if all component functions $f_1,\,\ldots ,\,f_n$
if all component functions $f_1,\,\ldots ,\,f_n$![]() are $(A,\,B,\,C)$
are $(A,\,B,\,C)$![]() -mild up to order $r$
-mild up to order $r$![]() . If $B \leq 1$
. If $B \leq 1$![]() , we simply say that $f$
, we simply say that $f$![]() is $(A,\,C)$
is $(A,\,C)$![]() -mild up to order $r$
-mild up to order $r$![]() and if we say that $f$
and if we say that $f$![]() is mild up to order $r$
is mild up to order $r$![]() , then we mean that $f$
, then we mean that $f$![]() is $(A,\,C)$
is $(A,\,C)$![]() -mild up to order $r$
-mild up to order $r$![]() for some $A>0$
for some $A>0$![]() and $C \geq 0$
and $C \geq 0$![]() .
.
Note $(A,\,B,\,C)$![]() -mild up to order $+\infty$
-mild up to order $+\infty$![]() agrees with $(A,\,B,\,C)$
agrees with $(A,\,B,\,C)$![]() -mild. The following corollary is an immediate consequence of the definitions.
-mild. The following corollary is an immediate consequence of the definitions.
Corollary 2.4 Suppose $f: U \subset \operatorname {\mathbb {R}}^{d} \to \operatorname {\mathbb {R}}^{n}$![]() is $C^{r}$
is $C^{r}$![]() . Then $f$
. Then $f$![]() has $C^{r}$
has $C^{r}$![]() -norm less than or equal to $B$
-norm less than or equal to $B$![]() if and only if $f$
if and only if $f$![]() is $(1,\,B,\,0)$
is $(1,\,B,\,0)$![]() -mild up to order $r$
-mild up to order $r$![]() .
.
For $(A,\,C)$![]() -mild functions up to order $r$
-mild functions up to order $r$![]() , one can bound the $C^{r}$
, one can bound the $C^{r}$![]() -norm by $1$
-norm by $1$![]() with an easy substitution. It will be used to count the numbers of maps in the proof of the main theorem. More precisely, we will construct a parameterization consisting of $(A,\,0)$
with an easy substitution. It will be used to count the numbers of maps in the proof of the main theorem. More precisely, we will construct a parameterization consisting of $(A,\,0)$![]() -mild maps up to order $r$
-mild maps up to order $r$![]() .
.
Lemma 2.5 Suppose that $f: U \subset (0,\,1)^{d} \to [-1,\,1]$![]() is $(A,\,C)$
is $(A,\,C)$![]() -mild up to order $r$
-mild up to order $r$![]() . Let $P = (P_1,\,\ldots ,\,P_d)$
. Let $P = (P_1,\,\ldots ,\,P_d)$![]() be any point in $(0,\,1)^{d}$
be any point in $(0,\,1)^{d}$![]() and consider the map
and consider the map
If $V = \psi ^{-1}(U)$![]() then $(f \circ \psi ): V \to [-1,\,1]$
then $(f \circ \psi ): V \to [-1,\,1]$![]() has $C^{r}$
has $C^{r}$![]() -norm bounded by $1$
-norm bounded by $1$![]() .
.
Proof. This is a direct calculation using the chain rule.
This lemma is nearly identical to [Reference Cluckers, Pila and Wilkie4, Lemma 4.1.3]. The difference is the exponent of $r$![]() , which is $C+1$
, which is $C+1$![]() in [Reference Cluckers, Pila and Wilkie4], because they use the following norm:
in [Reference Cluckers, Pila and Wilkie4], because they use the following norm:

Since this norm is stronger, the number of maps in the $C^{r}$![]() -parameterization is larger.
-parameterization is larger.
We conclude this section with the following class of examples which will show up in § 3. For a proof, we refer to [Reference Krantz and Parks9, Proposition 2.2.10].
Lemma 2.6 Suppose that $f: U \subset \operatorname {\mathbb {R}}^{d} \to \operatorname {\mathbb {R}}$![]() is analytic on an open neighbourhood of the topological closure $\overline {U}$
is analytic on an open neighbourhood of the topological closure $\overline {U}$![]() of $U$
of $U$![]() . Then $f$
. Then $f$![]() is $(A,\,B,\,0)$
is $(A,\,B,\,0)$![]() -mild for some $A,\,B>0$
-mild for some $A,\,B>0$![]() .
.
2.1. Compositions of mild functions
In this section, we show that if $f$![]() and $g$
and $g$![]() are $(A_f,\,B_f,\,C)$
are $(A_f,\,B_f,\,C)$![]() - and $(A_g,\,B_g,\,C)$
- and $(A_g,\,B_g,\,C)$![]() -mild respectively, then the composition $f\circ g$
-mild respectively, then the composition $f\circ g$![]() is $(A,\,B,\,C)$
is $(A,\,B,\,C)$![]() -mild for some explicit $A$
-mild for some explicit $A$![]() and $B$
and $B$![]() . Of course, we will need a multivariate version of a formula for arbitrary derivatives of a composite function. This is known as the Faà di Bruno formula, which has first been proved in [Reference Constantine and Savits5] and we reformulate it here. A proof can also be found in [Reference Krantz and Parks9, Theorem 1.3.2].
. Of course, we will need a multivariate version of a formula for arbitrary derivatives of a composite function. This is known as the Faà di Bruno formula, which has first been proved in [Reference Constantine and Savits5] and we reformulate it here. A proof can also be found in [Reference Krantz and Parks9, Theorem 1.3.2].
Theorem 2.7 Suppose that $n$![]() is a positive integer, $V \subset \operatorname {\mathbb {R}}^{d}$
is a positive integer, $V \subset \operatorname {\mathbb {R}}^{d}$![]() and $U \subset \operatorname {\mathbb {R}}^{e}$
and $U \subset \operatorname {\mathbb {R}}^{e}$![]() are open, $f: V \to \operatorname {\mathbb {R}}$
are open, $f: V \to \operatorname {\mathbb {R}}$![]() , $g: U \to V$
, $g: U \to V$![]() and that $f$
and that $f$![]() and $g$
and $g$![]() are $C^{n}$
are $C^{n}$![]() . For any $x \in U$
. For any $x \in U$![]() and $\nu \in \operatorname {\mathbb {N}}^{e}$
and $\nu \in \operatorname {\mathbb {N}}^{e}$![]() with $|\nu | = n$
with $|\nu | = n$![]() we have that
we have that

where $p_s(\nu ,\,\lambda )$![]() is the set consisting of all $k_1,\,\ldots ,\,k_s \in \operatorname {\mathbb {N}}^{d}$
is the set consisting of all $k_1,\,\ldots ,\,k_s \in \operatorname {\mathbb {N}}^{d}$![]() with $|k_i| > 0$
with $|k_i| > 0$![]() and $l_1,\,\ldots ,\,l_s \in \operatorname {\mathbb {N}}^{e}$
and $l_1,\,\ldots ,\,l_s \in \operatorname {\mathbb {N}}^{e}$![]() with $0 \prec l_1 \prec \ldots \prec l_s$
with $0 \prec l_1 \prec \ldots \prec l_s$![]() such that:
such that:

and

Here $l_i \prec l_{i+1}$![]() means that $|l_i| < |l_{i+1}|$
means that $|l_i| < |l_{i+1}|$![]() or, if $|l_i| = |l_{i+1}|$
or, if $|l_i| = |l_{i+1}|$![]() , then $l_i$
, then $l_i$![]() comes lexicographically before $l_{i+1}$
comes lexicographically before $l_{i+1}$![]() .
.
This formula is the heart of all of the proofs of results on compositions of mild functions that will follow. In [Reference Cluckers, Pila and Wilkie4], Cluckers, Pila and Wilkie use this formula to deduce that the composition of mild functions is mild. However, they show this by roughly estimating the sum and hence they obtain no explicit formulas for $A,\,B$![]() and $C$
and $C$![]() . In his paper [Reference Gevrey6], Gevrey introduces ‘functions of class $\alpha$
. In his paper [Reference Gevrey6], Gevrey introduces ‘functions of class $\alpha$![]() ’ (see below), later known as Gevrey functions, and showed that the functions of class $\alpha$
’ (see below), later known as Gevrey functions, and showed that the functions of class $\alpha$![]() with $\alpha \geq 1$
with $\alpha \geq 1$![]() are closed under composition. In fact, Gevrey proved his result only where one of the functions involved has only one variable. The proof uses the Faà di Bruno formula in an essential way. Even though we refer to a more recent paper for the proof of this formula, the formula was already known for a long time. Because the result on Gevrey functions will immediately yield our result on mild functions and the technique is important for all other proofs, we will give a full proof of Gevrey's theorem for functions in arbitrary many variables, that is, the general version of what he proved.
are closed under composition. In fact, Gevrey proved his result only where one of the functions involved has only one variable. The proof uses the Faà di Bruno formula in an essential way. Even though we refer to a more recent paper for the proof of this formula, the formula was already known for a long time. Because the result on Gevrey functions will immediately yield our result on mild functions and the technique is important for all other proofs, we will give a full proof of Gevrey's theorem for functions in arbitrary many variables, that is, the general version of what he proved.
Definition 2.8 (Gevrey functions) Suppose that $\alpha \geq 0$![]() and $f: U \subset \operatorname {\mathbb {R}}^{d} \to \operatorname {\mathbb {R}}$
and $f: U \subset \operatorname {\mathbb {R}}^{d} \to \operatorname {\mathbb {R}}$![]() . We say that $f$
. We say that $f$![]() is a Gevrey function of class $\alpha$
is a Gevrey function of class $\alpha$![]() if it is $C^{\infty }$
if it is $C^{\infty }$![]() and for all $\nu \in \operatorname {\mathbb {N}}^{d}$
and for all $\nu \in \operatorname {\mathbb {N}}^{d}$![]() and $x \in U$
and $x \in U$![]() we have:
we have:
for some $M,\,R > 0$![]() . A map $f: U \subset \operatorname {\mathbb {R}}^{d} \to \operatorname {\mathbb {R}}^{n}$
. A map $f: U \subset \operatorname {\mathbb {R}}^{d} \to \operatorname {\mathbb {R}}^{n}$![]() is a Gevrey function of class $\alpha$
is a Gevrey function of class $\alpha$![]() if all of its component functions are Gevrey functions of class $\alpha$
if all of its component functions are Gevrey functions of class $\alpha$![]() .
.
The following proposition, together with Theorem 2.10, motivates why we adjusted the definition of a mild function, as we explained below Definition 2.2.
Proposition 2.9 Suppose that $f: U \subset \operatorname {\mathbb {R}}^{d} \to \operatorname {\mathbb {R}}$![]() is $C^{\infty }$
is $C^{\infty }$![]() , then $f$
, then $f$![]() is $(A,\,B,\,C)$
is $(A,\,B,\,C)$![]() -mild for some $A,\,B >0$
-mild for some $A,\,B >0$![]() if and only if it is a Gevrey function of class $C+1$
if and only if it is a Gevrey function of class $C+1$![]() .
.
Proof. If one sets $R = A^{-1/(C+1)}$![]() and $M = B$
and $M = B$![]() , then it follows immediately that the bounds on the derivatives are the same.
, then it follows immediately that the bounds on the derivatives are the same.
Of course, one could define a Gevrey function of class $\alpha$![]() up to order $r$
up to order $r$![]() and the result above has an up to order $r$
and the result above has an up to order $r$![]() version and thus, so do the theorem and the subsequent corollary below.
version and thus, so do the theorem and the subsequent corollary below.
Theorem 2.10 (Gevrey [Reference Gevrey6])
Suppose that $f:V\subset \operatorname {\mathbb {R}}^{d} \to \operatorname {\mathbb {R}}$![]() and $g: U \subset \operatorname {\mathbb {R}}^{e} \to V$
and $g: U \subset \operatorname {\mathbb {R}}^{e} \to V$![]() are Gevrey functions of class $\alpha \geq 1$
are Gevrey functions of class $\alpha \geq 1$![]() , then $f \circ g$
, then $f \circ g$![]() is a Gevrey function of class $\alpha$
is a Gevrey function of class $\alpha$![]() .
.
Proof. The idea of this ingenious proof of Gevrey is as follows. For some specific $F$![]() and $G$
and $G$![]() , we can explicitly compute both sides of the Faà di Bruno formula at some well chosen point since all derivatives of $F \circ G$
, we can explicitly compute both sides of the Faà di Bruno formula at some well chosen point since all derivatives of $F \circ G$![]() will be easy to compute. In turns out that the values of these derivatives at this point are exactly the bounds we have for the derivatives of our given maps $f$
will be easy to compute. In turns out that the values of these derivatives at this point are exactly the bounds we have for the derivatives of our given maps $f$![]() and $g$
and $g$![]() . Now let $x \in U$
. Now let $x \in U$![]() be arbitrary. Using the Faà di Bruno formula and the triangle inequality to bound $|(f \circ g)^{(\nu )}(x)|$
be arbitrary. Using the Faà di Bruno formula and the triangle inequality to bound $|(f \circ g)^{(\nu )}(x)|$![]() , we obtain the same sum of positive terms where the bounds on the derivatives of $f$
, we obtain the same sum of positive terms where the bounds on the derivatives of $f$![]() and $g$
and $g$![]() occur. Moreover, this sum does not depend on $x$
occur. Moreover, this sum does not depend on $x$![]() , since the bounds of a Gevrey function are uniform.
, since the bounds of a Gevrey function are uniform.
To define the maps $F$![]() and $G$
and $G$![]() , we need the constants that bound the derivatives of $f$
, we need the constants that bound the derivatives of $f$![]() and $g$
and $g$![]() . Since they're Gevrey functions of class $\alpha$
. Since they're Gevrey functions of class $\alpha$![]() , we have:
, we have:

and

for $i = 1,\,\ldots ,\,d$![]() . The maps that do the trick are the following $F$
. The maps that do the trick are the following $F$![]() and $G = (G_1,\,\ldots ,\,G_d)$
and $G = (G_1,\,\ldots ,\,G_d)$![]() :
:
and for $i = 1,\,\ldots ,\,d$![]() :
:
We first compute an arbitrary derivative of $G_i$![]() for some $i \in \{1,\,\ldots ,\,d\}$
for some $i \in \{1,\,\ldots ,\,d\}$![]() . Set $S(x) = x_1+\ldots + x_e$
. Set $S(x) = x_1+\ldots + x_e$![]() . Then we have for all $j \in \{1,\,\ldots ,\,e\}$
. Then we have for all $j \in \{1,\,\ldots ,\,e\}$![]() that $(\partial /\partial x_j)(S(x)) = 1$
that $(\partial /\partial x_j)(S(x)) = 1$![]() . Writing $G_i(x) = M_gR_g(R_g-S(x))^{-1}$
. Writing $G_i(x) = M_gR_g(R_g-S(x))^{-1}$![]() we easily obtain that for any $\lambda \in \operatorname {\mathbb {N}}^{e}$
we easily obtain that for any $\lambda \in \operatorname {\mathbb {N}}^{e}$![]() :
:
Hence we get:
Noticing that $G(0) = (M_g,\,\ldots ,\,M_g)$![]() , we see that for all $\lambda \in \operatorname {\mathbb {N}}^{d}$
, we see that for all $\lambda \in \operatorname {\mathbb {N}}^{d}$![]() we obtain similarly:
we obtain similarly:

Next, one checks that:
and that for any $\lambda \in \operatorname {\mathbb {N}}^{e}$![]() with $|\lambda | \geq 1$
with $|\lambda | \geq 1$![]() :
:
Finally, we get that:
with $M = \frac {dM_fM_g}{R_f+dM_g}$![]() and $R = \frac {R_fR_g}{R_f+dM_g}$
and $R = \frac {R_fR_g}{R_f+dM_g}$![]() . Hence if we plug in values as in (2.2) and (2.1) in the sum of Theorem 2.7, then we know that it is equal to (2.3). More precisely, we get the following equalities:
. Hence if we plug in values as in (2.2) and (2.1) in the sum of Theorem 2.7, then we know that it is equal to (2.3). More precisely, we get the following equalities:

Now first suppose $\alpha = 1$![]() . To compute an upper bound on $|(f \circ g)^{(\nu )}(x)|$
. To compute an upper bound on $|(f \circ g)^{(\nu )}(x)|$![]() , use the Faà di Bruno formula, the triangle inequality and finally the bounds on the derivatives of $f$
, use the Faà di Bruno formula, the triangle inequality and finally the bounds on the derivatives of $f$![]() and $g$
and $g$![]() to obtain the sum on the right-hand side of these equations. We now know it equals the desired form on the left-hand side. This finishes the proof if $\alpha = 1$
to obtain the sum on the right-hand side of these equations. We now know it equals the desired form on the left-hand side. This finishes the proof if $\alpha = 1$![]() . If $\alpha > 1$
. If $\alpha > 1$![]() , you additionally use that $r^{\alpha } + s^{\alpha } \leq (r+s)^{\alpha }$
, you additionally use that $r^{\alpha } + s^{\alpha } \leq (r+s)^{\alpha }$![]() $(r,\,s \geq 0)$
$(r,\,s \geq 0)$![]() , which yields the result.
, which yields the result.
Combining this with Proposition 2.9, one deduces from this proof the following result on mild functions.
Corollary 2.11 Suppose that $f: V \subset \operatorname {\mathbb {R}}^{d} \to \operatorname {\mathbb {R}}$![]() is $(A_f,\,B_f,\,C)$
is $(A_f,\,B_f,\,C)$![]() -mild and that $g: U \subset \operatorname {\mathbb {R}}^{e} \to V$
-mild and that $g: U \subset \operatorname {\mathbb {R}}^{e} \to V$![]() is $(A_g,\,B_g,\,C)$
is $(A_g,\,B_g,\,C)$![]() -mild. Then $f\circ g$
-mild. Then $f\circ g$![]() is $(A,\,B,\,C)$
is $(A,\,B,\,C)$![]() -mild where:
-mild where:

In particular, if $f$![]() is $(A_f,\,0)$
is $(A_f,\,0)$![]() -mild and $g$
-mild and $g$![]() is $(A_g,\,0)$
is $(A_g,\,0)$![]() -mild then $f \circ g$
-mild then $f \circ g$![]() is $(A,\,0)$
is $(A,\,0)$![]() -mild with:
-mild with:
2.2. Weakly mild functions and power substitutions
Many nice functions are not mild. For instance, if $f$![]() is analytic on $U$
is analytic on $U$![]() , this still is not sufficient: consider, for example, the function $x \mapsto x^{1/2}$
, this still is not sufficient: consider, for example, the function $x \mapsto x^{1/2}$![]() on $(0,\,1)$
on $(0,\,1)$![]() . So one can not weaken the conditions of Lemma 2.6. Maps of this form will be crucial later on. They are also examples of the next definition, a variant on mild functions that has been introduced by Cluckers, Pila and Wilkie in [Reference Cluckers, Pila and Wilkie4]. By a reparameterization, which we will call a power substitution, we can make these functions mild up to any order if they satisfy an additional condition.
. So one can not weaken the conditions of Lemma 2.6. Maps of this form will be crucial later on. They are also examples of the next definition, a variant on mild functions that has been introduced by Cluckers, Pila and Wilkie in [Reference Cluckers, Pila and Wilkie4]. By a reparameterization, which we will call a power substitution, we can make these functions mild up to any order if they satisfy an additional condition.
Definition 2.12 (Weakly mild functions) Suppose that $A,\,B>0$![]() , $C \geq 0$
, $C \geq 0$![]() are real numbers, $r>0$
are real numbers, $r>0$![]() an integer or $+\infty$
an integer or $+\infty$![]() and $f: U \subset (0,\,1)^{d} \to \operatorname {\mathbb {R}}$
and $f: U \subset (0,\,1)^{d} \to \operatorname {\mathbb {R}}$![]() . Then $f$
. Then $f$![]() is called weakly $(A,\,B,\,C)$
is called weakly $(A,\,B,\,C)$![]() -mild up to order $r$
-mild up to order $r$![]() if it is $C^{r}$
if it is $C^{r}$![]() and if for all $\nu \in \operatorname {\mathbb {N}}^{d}$
and if for all $\nu \in \operatorname {\mathbb {N}}^{d}$![]() with $|\nu | \leq r$
with $|\nu | \leq r$![]() and $x \in U$
and $x \in U$![]() :
:
A map $f = (f_1,\,\ldots ,\,f_n): U \subset (0,\,1)^{d} \to \operatorname {\mathbb {R}}^{n}$![]() is weakly $(A,\,B,\,C)$
is weakly $(A,\,B,\,C)$![]() -mild up to order $r$
-mild up to order $r$![]() if all component functions $f_1,\,\ldots ,\,f_n$
if all component functions $f_1,\,\ldots ,\,f_n$![]() are weakly $(A,\,B,\,C)$
are weakly $(A,\,B,\,C)$![]() -mild up to order $r$
-mild up to order $r$![]() . If $B \leq 1$
. If $B \leq 1$![]() , we simply say that $f$
, we simply say that $f$![]() is weakly $(A,\,C)$
is weakly $(A,\,C)$![]() -mild up to order $r$
-mild up to order $r$![]() and if we say that $f$
and if we say that $f$![]() is weakly mild up to order $r$
is weakly mild up to order $r$![]() , then we mean that $f$
, then we mean that $f$![]() is weakly $(A,\,C)$
is weakly $(A,\,C)$![]() -mild up to order $r$
-mild up to order $r$![]() for some $A>0$
for some $A>0$![]() and $C \geq 0$
and $C \geq 0$![]() . Finally, if $r = +\infty$
. Finally, if $r = +\infty$![]() , we might just say weakly $(A,\,B,\,C)$
, we might just say weakly $(A,\,B,\,C)$![]() -mild or weakly mild.
-mild or weakly mild.
Using the technique of the proof of Theorem 2.10, we can make the result of [Reference Cluckers, Pila and Wilkie4, Proposition 4.1.5] more explicit in the proposition below. In particular, we have an explicit formula for $\tilde {A}$![]() and the constant $C$
and the constant $C$![]() is preserved.
is preserved.
Proposition 2.13 (Power substitution) Let $A \geq 1$![]() , $B>0$
, $B>0$![]() and $C \geq 0$
and $C \geq 0$![]() be real numbers and suppose that $f: U \subset (0,\,1)^{d} \to \operatorname {\mathbb {R}}$
be real numbers and suppose that $f: U \subset (0,\,1)^{d} \to \operatorname {\mathbb {R}}$![]() is a map such that $f$
is a map such that $f$![]() and all first-order derivatives of $f$
and all first-order derivatives of $f$![]() are weakly $(A,\,B,\,C)$
are weakly $(A,\,B,\,C)$![]() -mild. Let $r>0$
-mild. Let $r>0$![]() be an integer and define $\phi : (0,\,1)^{d} \to (0,\,1)^{d}$
be an integer and define $\phi : (0,\,1)^{d} \to (0,\,1)^{d}$![]() by:
by:
with $n_i \geq r$![]() for all $i \in \{1,\,\ldots ,\,d\}$
for all $i \in \{1,\,\ldots ,\,d\}$![]() , and denote $V = \phi ^{-1}(U)$
, and denote $V = \phi ^{-1}(U)$![]() . Then the map $f \circ \phi : V \to \operatorname {\mathbb {R}}$
. Then the map $f \circ \phi : V \to \operatorname {\mathbb {R}}$![]() is $(\tilde {A},\,B,\,C)$
is $(\tilde {A},\,B,\,C)$![]() -mild up to order $r$
-mild up to order $r$![]() with $\tilde {A} = NA(d+1)^{C+1}$
with $\tilde {A} = NA(d+1)^{C+1}$![]() , with $N = \max (n_1,\,\ldots ,\,n_d)$
, with $N = \max (n_1,\,\ldots ,\,n_d)$![]() .
.
Remark If $f$![]() satisfies the conditions above, but with $0< A<1$
satisfies the conditions above, but with $0< A<1$![]() instead, one can apply the proposition after enlarging $A$
instead, one can apply the proposition after enlarging $A$![]() to $1$
to $1$![]() .
.
Proof. We first take a look at the derivatives of $\phi$![]() . Take any component function $\phi _i$
. Take any component function $\phi _i$![]() of $\phi$
of $\phi$![]() . Because it only depends on $x_i$
. Because it only depends on $x_i$![]() , we just have to bound the following derivatives:
, we just have to bound the following derivatives:
Thus, $\phi$![]() is $(N,\,0)$
is $(N,\,0)$![]() -mild. However, we will use the sharper bound (involving the power $n_i-k$
-mild. However, we will use the sharper bound (involving the power $n_i-k$![]() of $x_i$
of $x_i$![]() ) to deal with the derivatives of $f$
) to deal with the derivatives of $f$![]() . By Theorem 2.7 and the triangle inequality, we have for every $x \in V$
. By Theorem 2.7 and the triangle inequality, we have for every $x \in V$![]() that
that

Consider one term in this sum, so we also have a fixed $\lambda \in \operatorname {\mathbb {N}}^{d}$![]() with $1 \leq |\lambda | \leq |\nu |$
with $1 \leq |\lambda | \leq |\nu |$![]() , $s \in \{1,\,\ldots ,\,n\}$
, $s \in \{1,\,\ldots ,\,n\}$![]() and $(k_1,\,\ldots ,\,k_s ,\,l_1,\,\ldots ,\,l_s) \in p_s(\nu ,\,\lambda )$
and $(k_1,\,\ldots ,\,k_s ,\,l_1,\,\ldots ,\,l_s) \in p_s(\nu ,\,\lambda )$![]() . Then, for any $i \in \{1,\,\ldots ,\,d\}$
. Then, for any $i \in \{1,\,\ldots ,\,d\}$![]() and $j \in \{1,\,\ldots ,\,s\}$
and $j \in \{1,\,\ldots ,\,s\}$![]() , we have:
, we have:
and thus the power of $x_i$![]() coming from the product over $j$
coming from the product over $j$![]() is $\sum \nolimits _{j = 1}^{s} (n_i-l_{j,i})k_{j,i}$
is $\sum \nolimits _{j = 1}^{s} (n_i-l_{j,i})k_{j,i}$![]() .
.
We now compute the ‘negative’ contribution to the powers of $x_i$![]() in this term coming from $f^{(\lambda )}(\phi (x))$
in this term coming from $f^{(\lambda )}(\phi (x))$![]() . Write $\lambda = \lambda ' + \beta$
. Write $\lambda = \lambda ' + \beta$![]() for some $\beta \in \operatorname {\mathbb {N}}^{d}$
for some $\beta \in \operatorname {\mathbb {N}}^{d}$![]() with $|\beta | = 1$
with $|\beta | = 1$![]() and let $k \in \{1,\,\ldots ,\,d\}$
and let $k \in \{1,\,\ldots ,\,d\}$![]() be the unique index such that $\beta _{k}=1$
be the unique index such that $\beta _{k}=1$![]() . For any choice of $\beta$
. For any choice of $\beta$![]() , we have the following (thus, we may pick some particular $\beta$
, we have the following (thus, we may pick some particular $\beta$![]() , equivalently, make a choice for $k$
, equivalently, make a choice for $k$![]() , later):
, later):
Hence the power of $x_i$![]() coming from $f^{(\lambda )}(\phi (x))$
coming from $f^{(\lambda )}(\phi (x))$![]() in the term is equal to $-n_i\lambda '_i$
in the term is equal to $-n_i\lambda '_i$![]() . We can now compute the total power of $x_i$
. We can now compute the total power of $x_i$![]() occurring in the term. The total power of $x_i$
occurring in the term. The total power of $x_i$![]() when $i \neq k$
when $i \neq k$![]() is (then $\lambda _i' = \lambda _i$
is (then $\lambda _i' = \lambda _i$![]() ):
):

When $i = k$![]() (then $\lambda '_k = \lambda _k-1$
(then $\lambda '_k = \lambda _k-1$![]() ) one computes in the same way that the power of $x_k$
) one computes in the same way that the power of $x_k$![]() is $n_k - \sum \nolimits _{j = 1}^{s} k_{j,k}l_{j,k}$
is $n_k - \sum \nolimits _{j = 1}^{s} k_{j,k}l_{j,k}$![]() . We now pick $k$
. We now pick $k$![]() such that
such that
Then we have for all $i \in \{1,\,\ldots ,\,d\}$![]() :
:
and we can bound the product of all $x_i$![]() and their powers by:
and their powers by:
since $n_k \geq r$![]() and $|\nu | \leq r$
and $|\nu | \leq r$![]() . So we can bound this term independent of $x$
. So we can bound this term independent of $x$![]() .
.
Putting everything together we obtain that:

This is the same upper bound as the one that one would find for the composition of an $(A,\,B,\,C)$![]() -mild function up to order $r$
-mild function up to order $r$![]() and an $(N,\,1,\,C)$
and an $(N,\,1,\,C)$![]() -mild function up to order $r$
-mild function up to order $r$![]() using Proposition 2.9 and then the proof of Theorem 2.10. Therefore, one can use the formula of Corollary 2.11 to find the expression for $\tilde {A}$
using Proposition 2.9 and then the proof of Theorem 2.10. Therefore, one can use the formula of Corollary 2.11 to find the expression for $\tilde {A}$![]() .
.
The extra condition that all first-order derivatives are weakly mild is crucial and cannot be omitted. For instance, consider again the map $x \mapsto x^{1/2}$![]() . Then we see that by composing with the power map $x \mapsto x^{3}$
. Then we see that by composing with the power map $x \mapsto x^{3}$![]() , we do not obtain a map that is mild up to order $3$
, we do not obtain a map that is mild up to order $3$![]() . Of course, using the power map $x \mapsto x^{2}$
. Of course, using the power map $x \mapsto x^{2}$![]() , it becomes mild (up to order $+\infty$
, it becomes mild (up to order $+\infty$![]() ). This observation will be the key to slightly improve the main theorem in § 3.
). This observation will be the key to slightly improve the main theorem in § 3.
Even though we can say something about the derivatives of a composition of weakly mild functions, it is not necessarily weakly mild. We do have the following result.
Proposition 2.14 Suppose that $f: V \subset \operatorname {\mathbb {R}}^{d} \to \operatorname {\mathbb {R}}$![]() is $(A_f,\,B_f,\,C)$
is $(A_f,\,B_f,\,C)$![]() -mild up to order $r$
-mild up to order $r$![]() and that $g: U \subset (0,\,1)^{e} \to V$
and that $g: U \subset (0,\,1)^{e} \to V$![]() is weakly $(A_g,\,B_g,\,C)$
is weakly $(A_g,\,B_g,\,C)$![]() -mild up to order $r$
-mild up to order $r$![]() . Then $f \circ g$
. Then $f \circ g$![]() is weakly $(A,\,B,\,C)$
is weakly $(A,\,B,\,C)$![]() -mild up to order $r$
-mild up to order $r$![]() , where $A$
, where $A$![]() and $B$
and $B$![]() are as in Corollary 2.11.
are as in Corollary 2.11.
Proof. The strategy of the proof is completely the same as in Proposition 2.13: one just checks that in each term one obtains exactly a factor ${1}/{x^{\nu }}$![]() when bounding $(f \circ g)^{(\nu )}(x)$
when bounding $(f \circ g)^{(\nu )}(x)$![]() using Theorem 2.7.
using Theorem 2.7.
We conclude this section with a result on the product of (weakly) mild functions. In this proposition, one can replace $(0,\,1)^{d}$![]() by $\operatorname {\mathbb {R}}^{d}$
by $\operatorname {\mathbb {R}}^{d}$![]() in the case of mild functions.
in the case of mild functions.
Proposition 2.15 Suppose that $f_1,\,\ldots ,\,f_l: U \subset (0,\,1)^{d} \to \operatorname {\mathbb {R}}$![]() are (weakly) $(A,B,C)$
are (weakly) $(A,B,C)$![]() -mild up to order $r$
-mild up to order $r$![]() for some $A,\,B > 0$
for some $A,\,B > 0$![]() and $C \geq 0$
and $C \geq 0$![]() . Then the product $f_1 \cdots f_l$
. Then the product $f_1 \cdots f_l$![]() is (weakly) $(lA,\,B^{l},\,C)$
is (weakly) $(lA,\,B^{l},\,C)$![]() -mild up to order $r$
-mild up to order $r$![]() .
.
Proof. As in [Reference Pila12, Proposition 2.6], we have that:

where the sum runs over all $\nu _1,\,\ldots ,\,\nu _l \in \operatorname {\mathbb {N}}^{d}$![]() such that $\nu _1+\ldots +\nu _l = \nu$
such that $\nu _1+\ldots +\nu _l = \nu$![]() and $\text {Ch}(\nu _1,\,\ldots ,\,\nu _l)$
and $\text {Ch}(\nu _1,\,\ldots ,\,\nu _l)$![]() is a constant depending on $\nu _1,\,\ldots ,\,\nu _l$
is a constant depending on $\nu _1,\,\ldots ,\,\nu _l$![]() . If $f_1,\,\ldots ,\,f_l$
. If $f_1,\,\ldots ,\,f_l$![]() are $(A,\,B,\,C)$
are $(A,\,B,\,C)$![]() -mild, we find:
-mild, we find:

If $f_1,\,\ldots ,\,f_l$![]() are weakly $(A,\,B,\,C)$
are weakly $(A,\,B,\,C)$![]() -mild, one obtains an extra factor $1/x^{\nu }$
-mild, one obtains an extra factor $1/x^{\nu }$![]() as desired. Finally, in § 3.2 of [Reference Cluckers, Pila and Wilkie4], it is shown that $\sum \nolimits _{\nu _1+\ldots +\nu _l = \nu } \text {Ch}(\nu _1,\,\ldots ,\,\nu _l) \leq l^{|\nu |}$
as desired. Finally, in § 3.2 of [Reference Cluckers, Pila and Wilkie4], it is shown that $\sum \nolimits _{\nu _1+\ldots +\nu _l = \nu } \text {Ch}(\nu _1,\,\ldots ,\,\nu _l) \leq l^{|\nu |}$![]() .
.
3. The $C^{r}$ -parameterization theorem
-parameterization theorem
In this section, we give a precise definition of the structure wherein the family $X_T$![]() , $T \subset \operatorname {\mathbb {R}}^{k}$
, $T \subset \operatorname {\mathbb {R}}^{k}$![]() , of our main theorem should be definable. This structure is o-minimal, a powerful tool of model theory, and thus enables us to use the cell decomposition theorem, see [Reference van den Dries14]. Furthermore, in [Reference Miller10], Miller has shown a preparation theorem for definable functions in this structure. Combining these results, we obtain a very strong parameterization theorem from which we will easily deduce the main theorem with the results of the last section.
, of our main theorem should be definable. This structure is o-minimal, a powerful tool of model theory, and thus enables us to use the cell decomposition theorem, see [Reference van den Dries14]. Furthermore, in [Reference Miller10], Miller has shown a preparation theorem for definable functions in this structure. Combining these results, we obtain a very strong parameterization theorem from which we will easily deduce the main theorem with the results of the last section.
We start with the necessary definitions of model theory and the result of Miller. In his paper definability (in $\operatorname {\mathbb {R}}^{n}$![]() ) is with respect to the following language. Let $\mathcal {L}_{r} = \{+,\,-,\,\cdot, <,\,0,\,1\}$
) is with respect to the following language. Let $\mathcal {L}_{r} = \{+,\,-,\,\cdot, <,\,0,\,1\}$![]() be the language of ordered rings and expand it with a symbol for each of the following functions:
be the language of ordered rings and expand it with a symbol for each of the following functions:

where $f: U \to \operatorname {\mathbb {R}}$![]() is a real analytic function on an open neighbourhood U of $[-1,\,1]^{n}$
is a real analytic function on an open neighbourhood U of $[-1,\,1]^{n}$![]() . Denote this language $\mathcal {L}_\text {an}$
. Denote this language $\mathcal {L}_\text {an}$![]() . If $X$
. If $X$![]() is $\mathcal {L}_\text {an}$
is $\mathcal {L}_\text {an}$![]() -definable in $\operatorname {\mathbb {R}}^{n}$
-definable in $\operatorname {\mathbb {R}}^{n}$![]() , then it is called (globally) subanalytic. Remember that a function is definable if its graph is a definable set. Next, if we expand $\mathcal {L}_\text {an}$
, then it is called (globally) subanalytic. Remember that a function is definable if its graph is a definable set. Next, if we expand $\mathcal {L}_\text {an}$![]() with a symbol for all functions
with a symbol for all functions

for $r \in \operatorname {\mathbb {R}}$![]() , we obtain the language $\mathcal {L}^\text{pow}_\text {an}$
, we obtain the language $\mathcal {L}^\text{pow}_\text {an}$![]() and the corresponding structure $\operatorname {\mathbb {R}}^\text{pow}_\text {an}$
and the corresponding structure $\operatorname {\mathbb {R}}^\text{pow}_\text {an}$![]() . If $X$
. If $X$![]() is $\mathcal {L}_\text {an}^\text{pow}$
is $\mathcal {L}_\text {an}^\text{pow}$![]() -definable in $\operatorname {\mathbb {R}}^{n}$
-definable in $\operatorname {\mathbb {R}}^{n}$![]() , we say that $X$
, we say that $X$![]() is power-subanalytic. In [Reference Miller10], Miller considers the following reducts of $\operatorname {\mathbb {R}}^\text{pow}_\text {an}$
is power-subanalytic. In [Reference Miller10], Miller considers the following reducts of $\operatorname {\mathbb {R}}^\text{pow}_\text {an}$![]() . Let $\mathcal {F}$
. Let $\mathcal {F}$![]() be a Weierstrass system: a collection $\mathcal {F}_n$
be a Weierstrass system: a collection $\mathcal {F}_n$![]() of real analytic functions $\operatorname {\mathbb {R}}^{n} \to \operatorname {\mathbb {R}}$
of real analytic functions $\operatorname {\mathbb {R}}^{n} \to \operatorname {\mathbb {R}}$![]() for each $n \in \operatorname {\mathbb {N}}$
for each $n \in \operatorname {\mathbb {N}}$![]() , containing the polynomials in $n$
, containing the polynomials in $n$![]() variables, for all $n$
variables, for all $n$![]() which is closed under several operations such as the ring operations, composition and Weierstrass preparation (for a precise definition, see [Reference Miller10]). If one adds to the language $\mathcal {L}_r$
which is closed under several operations such as the ring operations, composition and Weierstrass preparation (for a precise definition, see [Reference Miller10]). If one adds to the language $\mathcal {L}_r$![]() symbols for each $\tilde {f}$
symbols for each $\tilde {f}$![]() , where $f \in \mathcal {F}$
, where $f \in \mathcal {F}$![]() , one obtains the language $\mathcal {L}_\mathcal {F}$
, one obtains the language $\mathcal {L}_\mathcal {F}$![]() . For any Weierstrass system $\mathcal {F}$
. For any Weierstrass system $\mathcal {F}$![]() , one can consider its field of exponents:
, one can consider its field of exponents:
(Miller shows in his paper that this is indeed a field.) For the smallest Weierstrass system, this field is $\operatorname {\mathbb {Q}}$![]() and thus any field of exponents $K$
and thus any field of exponents $K$![]() contains $\operatorname {\mathbb {Q}}$
contains $\operatorname {\mathbb {Q}}$![]() . For the largest Weierstrass system, i.e. consisting of all analytic functions, this field is $\operatorname {\mathbb {R}}$
. For the largest Weierstrass system, i.e. consisting of all analytic functions, this field is $\operatorname {\mathbb {R}}$![]() . Denote $\mathcal {L}^{K}_\mathcal {F}$
. Denote $\mathcal {L}^{K}_\mathcal {F}$![]() the language obtained by adding to $\mathcal {L}_\mathcal {F}$
the language obtained by adding to $\mathcal {L}_\mathcal {F}$![]() a symbol for all power maps $x \mapsto x^{r}$
a symbol for all power maps $x \mapsto x^{r}$![]() for $r \in K$
for $r \in K$![]() (as above), where $K$
(as above), where $K$![]() can be any subfield of $\operatorname {\mathbb {R}}$
can be any subfield of $\operatorname {\mathbb {R}}$![]() . From now on, definability is with respect to the language $\mathcal {L}_\mathcal {F}^{K}$
. From now on, definability is with respect to the language $\mathcal {L}_\mathcal {F}^{K}$![]() , where $K$
, where $K$![]() is a subfield of the field of exponents of $\mathcal {F}$
is a subfield of the field of exponents of $\mathcal {F}$![]() . The corresponding structure $\operatorname {\mathbb {R}}_\mathcal {F}^{K}$
. The corresponding structure $\operatorname {\mathbb {R}}_\mathcal {F}^{K}$![]() is o-minimal.
is o-minimal.
Definition 3.1 (Cell) A cell in $\operatorname {\mathbb {R}}^{m}$![]() is a set of the following form:
is a set of the following form:
where $x_{< i} = (x_1,\,\ldots ,\,x_{i-1})$![]() , $\alpha _i$
, $\alpha _i$![]() and $\beta _i$
and $\beta _i$![]() are continuous definable functions, with $\alpha _i < \beta _i$
are continuous definable functions, with $\alpha _i < \beta _i$![]() , and $\Box$
, and $\Box$![]() is ‘no condition’ or the conditions $<$
is ‘no condition’ or the conditions $<$![]() or $=$
or $=$![]() , where $\Box _{i2}$
, where $\Box _{i2}$![]() is $<$
is $<$![]() or no condition if $\Box _{i1}$
or no condition if $\Box _{i1}$![]() is equality. Obviously, a cell is open in $\operatorname {\mathbb {R}}^{m}$
is equality. Obviously, a cell is open in $\operatorname {\mathbb {R}}^{m}$![]() if and only if $\Box _{i1}$
if and only if $\Box _{i1}$![]() is not equality for all $i$
is not equality for all $i$![]() . In that case we call $\alpha _i$
. In that case we call $\alpha _i$![]() and $\beta _i$
and $\beta _i$![]() the walls of $x_i$
the walls of $x_i$![]() .
.
Suppose that $C$![]() is a cell in $\operatorname {\mathbb {R}}^{n}$
is a cell in $\operatorname {\mathbb {R}}^{n}$![]() . Then, up to reordering the variables if necessary, we may suppose that for $i = 1,\,\ldots ,\,m$
. Then, up to reordering the variables if necessary, we may suppose that for $i = 1,\,\ldots ,\,m$![]() ($m \leq n$
($m \leq n$![]() ) the condition $\Box _{i1}$
) the condition $\Box _{i1}$![]() is inequality and for the last $n-m$
is inequality and for the last $n-m$![]() variables $\Box _{i1}$
variables $\Box _{i1}$![]() is equality. In this way, we see that any cell in $\operatorname {\mathbb {R}}^{n}$
is equality. In this way, we see that any cell in $\operatorname {\mathbb {R}}^{n}$![]() corresponds to the graph of a definable function $f:U \subset \operatorname {\mathbb {R}}^{m} \to \operatorname {\mathbb {R}}^{n-m}$
corresponds to the graph of a definable function $f:U \subset \operatorname {\mathbb {R}}^{m} \to \operatorname {\mathbb {R}}^{n-m}$![]() . Combining this with the fact that an open cell in $\operatorname {\mathbb {R}}^{n}$
. Combining this with the fact that an open cell in $\operatorname {\mathbb {R}}^{n}$![]() is definably homeomorphic to $(0,\,1)^{n}$
is definably homeomorphic to $(0,\,1)^{n}$![]() , we get that a cell in $\operatorname {\mathbb {R}}^{n}$
, we get that a cell in $\operatorname {\mathbb {R}}^{n}$![]() is the same as the graph of a definable function $(0,\,1)^{m} \to \operatorname {\mathbb {R}}^{n-m}$
is the same as the graph of a definable function $(0,\,1)^{m} \to \operatorname {\mathbb {R}}^{n-m}$![]() . The number $m$
. The number $m$![]() is the dimension of the cell and thus is nothing more than counting how many times $\Box _{i1}$
is the dimension of the cell and thus is nothing more than counting how many times $\Box _{i1}$![]() is inequality. We will do many manipulations with these functions and thus end up in general with definable maps $U \subset (0,\,1)^{m} \to \operatorname {\mathbb {R}}^{n-m}$
is inequality. We will do many manipulations with these functions and thus end up in general with definable maps $U \subset (0,\,1)^{m} \to \operatorname {\mathbb {R}}^{n-m}$![]() , where $U$
, where $U$![]() is an open cell in $(0,\,1)^{m}$
is an open cell in $(0,\,1)^{m}$![]() . To conclude, because any definable set in an o-minimal structure is a finite union of cells, it suffices to prove the main theorem, where we assume $X_{T}$
. To conclude, because any definable set in an o-minimal structure is a finite union of cells, it suffices to prove the main theorem, where we assume $X_{T}$![]() to be a definable family of $m$
to be a definable family of $m$![]() -dimensional subsets of $[-1,\,1]^{n}$
-dimensional subsets of $[-1,\,1]^{n}$![]() , with $T \subset \operatorname {\mathbb {R}}^{k}$
, with $T \subset \operatorname {\mathbb {R}}^{k}$![]() the set of parameters, in the case that $X_T$
the set of parameters, in the case that $X_T$![]() is the graph of a definable map $f: T \times (0,\,1)^{m} \to [-1,\,1]^{n-m}$
is the graph of a definable map $f: T \times (0,\,1)^{m} \to [-1,\,1]^{n-m}$![]() . (If $X$
. (If $X$![]() does not depend on parameters, $T = \operatorname {\mathbb {R}}^{0}$
does not depend on parameters, $T = \operatorname {\mathbb {R}}^{0}$![]() , which is by definition a set with only one point.) Later on, our map will be of the form $f: C \subset T \times (0,\,1)^{m} \to [-1,\,1]^{n-m}$
, which is by definition a set with only one point.) Later on, our map will be of the form $f: C \subset T \times (0,\,1)^{m} \to [-1,\,1]^{n-m}$![]() , where the fibres $C_t$
, where the fibres $C_t$![]() of $C$
of $C$![]() are open cells in $(0,\,1)^{m}$
are open cells in $(0,\,1)^{m}$![]() for any $t \in T$
for any $t \in T$![]() and we will denote $f_t$
and we will denote $f_t$![]() for the map $C_t \to [-1,\,1]^{n-m}$
for the map $C_t \to [-1,\,1]^{n-m}$![]() given by $x \mapsto f(t,\,x)$
given by $x \mapsto f(t,\,x)$![]() .
.
In this section, $T$![]() is a definable subset of $\operatorname {\mathbb {R}}^{k}$
is a definable subset of $\operatorname {\mathbb {R}}^{k}$![]() and we will often use the following notation. Suppose $U \subset \operatorname {\mathbb {R}}^{m}$
and we will often use the following notation. Suppose $U \subset \operatorname {\mathbb {R}}^{m}$![]() . Then we denote by $\overline {U}$
. Then we denote by $\overline {U}$![]() the topological closure of $U$
the topological closure of $U$![]() in $\mathbb {R}^{m}$
in $\mathbb {R}^{m}$![]() endowed with the standard topology. Furthermore, for any $i \in \{2,\,\ldots ,\,m\}$
endowed with the standard topology. Furthermore, for any $i \in \{2,\,\ldots ,\,m\}$![]() , $\pi _{< i}: T \times \operatorname {\mathbb {R}}^{m} \to T \times \operatorname {\mathbb {R}}^{i-1}$
, $\pi _{< i}: T \times \operatorname {\mathbb {R}}^{m} \to T \times \operatorname {\mathbb {R}}^{i-1}$![]() denotes the map
denotes the map
and $\pi _{<1}(t,\,x) = t$![]() . The following two definitions coincide with [Reference Cluckers, Pila and Wilkie4, Definition 4.4.1].
. The following two definitions coincide with [Reference Cluckers, Pila and Wilkie4, Definition 4.4.1].
Definition 3.2 (Centre of a cell) Suppose that $C$![]() is a cell in $\operatorname {\mathbb {R}}^{m}$
is a cell in $\operatorname {\mathbb {R}}^{m}$![]() . A definable continuous map $\theta : \pi _{< m}(C) \to \operatorname {\mathbb {R}}$
. A definable continuous map $\theta : \pi _{< m}(C) \to \operatorname {\mathbb {R}}$![]() is called a centre for $C$
is called a centre for $C$![]() if its graph and $\overline {C}$
if its graph and $\overline {C}$![]() are disjoint or if its graph is contained in $\overline {C} \setminus C$
are disjoint or if its graph is contained in $\overline {C} \setminus C$![]() , and $\theta$
, and $\theta$![]() is identically zero or $\theta (x_{< m}) \sim x_m$
is identically zero or $\theta (x_{< m}) \sim x_m$![]() for all $x \in C$
for all $x \in C$![]() , that is, there exists some $\epsilon \in (0,\,1)$
, that is, there exists some $\epsilon \in (0,\,1)$![]() such that for all $x \in C$
such that for all $x \in C$![]() :
:
The next definition motivates why $\theta$![]() is called the centre of a cell.
is called the centre of a cell.
Definition 3.3 Prepared with centre A bounded definable function $f: C \to \operatorname {\mathbb {R}}$![]() , where $C$
, where $C$![]() is a cell in $\operatorname {\mathbb {R}}^{m}$
is a cell in $\operatorname {\mathbb {R}}^{m}$![]() , is called prepared with centre $\theta$
, is called prepared with centre $\theta$![]() if $\theta$
if $\theta$![]() is a centre for $C$
is a centre for $C$![]() and $f$
and $f$![]() can be written in the following way:
can be written in the following way:
where $b: C \to \operatorname {\mathbb {R}}^{N}$![]() (for some $N \in \operatorname {\mathbb {N}}$
(for some $N \in \operatorname {\mathbb {N}}$![]() ) is bounded, $b_j$
) is bounded, $b_j$![]() is a component function of $b$
is a component function of $b$![]() and the component functions $b_i$
and the component functions $b_i$![]() , $i \in \{1,\,\ldots ,\,N\}$
, $i \in \{1,\,\ldots ,\,N\}$![]() , of $b$
, of $b$![]() are of the following form:
are of the following form:
with $r_i \in K$![]() and $a_i: \pi _{< m}(C) \to \operatorname {\mathbb {R}}$
and $a_i: \pi _{< m}(C) \to \operatorname {\mathbb {R}}$![]() definable and, finally, $F$
definable and, finally, $F$![]() is a non-vanishing analytic function on an open neighbourhood of $\overline {b(C)}$
is a non-vanishing analytic function on an open neighbourhood of $\overline {b(C)}$![]() . We call $b$
. We call $b$![]() the associated bounded range map of $f$
the associated bounded range map of $f$![]() . A map $f: C \to \operatorname {\mathbb {R}}^{n}$
. A map $f: C \to \operatorname {\mathbb {R}}^{n}$![]() is prepared with centre $\theta$
is prepared with centre $\theta$![]() if all of its component functions are prepared with centre $\theta$
if all of its component functions are prepared with centre $\theta$![]() and moreover have the same bounded range map $b$
and moreover have the same bounded range map $b$![]() .
.
We now state the preparation theorem as in [Reference Cluckers, Pila and Wilkie4, Proposition 4.4.2], which follows from the main theorem of [Reference Miller10, Lemma 3.7 and Lemma 4.4].
Theorem 3.4 Suppose that $f: X \subset \operatorname {\mathbb {R}}^{m} \to \operatorname {\mathbb {R}}^{n}$![]() is a bounded definable map. Then there exists a finite partition of $X$
is a bounded definable map. Then there exists a finite partition of $X$![]() into cells $C_i$
into cells $C_i$![]() with centre $\theta _i$
with centre $\theta _i$![]() such that the restriction $f|_{C_i}$
such that the restriction $f|_{C_i}$![]() of $f$
of $f$![]() to $C_i$
to $C_i$![]() is prepared with centre $\theta _i$
is prepared with centre $\theta _i$![]() .
.
We follow [Reference Cluckers, Pila and Wilkie4, § 4], but in our proofs, we avoid transforming parameters, i.e. we prove everything uniformly. The main reason we do this is to clearly point out that the power substitution in the proof of [Reference Cluckers, Pila and Wilkie4, Theorem 2.1.3] does not require a power substitution in the parameter variables. The idea here is that we stop the inductive proof of [Reference Cluckers, Pila and Wilkie4, Theorem 4.3.1] when we reach the parameter variables (see Theorem 3.11) and then apply a (uniform) power substitution (Theorem 3.10). To achieve this, we slightly adjusted some definitions, namely the notion of an a–b–m function in [Reference Cluckers, Pila and Wilkie4], which is here replaced by ‘prepared in $x$![]() ’ (see below). The main theorem will be deduced from Theorem 3.11. In this theorem, we parameterize $X_T$
’ (see below). The main theorem will be deduced from Theorem 3.11. In this theorem, we parameterize $X_T$![]() with maps that satisfy the conditions of Proposition 2.13. Finally, we conclude by Lemma 2.5.
with maps that satisfy the conditions of Proposition 2.13. Finally, we conclude by Lemma 2.5.
Definition 3.5 Suppose that $C$![]() is a cell in $\operatorname {\mathbb {R}}^{k}\times (0,\,1)^{m}$
is a cell in $\operatorname {\mathbb {R}}^{k}\times (0,\,1)^{m}$![]() and denote an element of $C$
and denote an element of $C$![]() as a tuple $(t,\,x)$
as a tuple $(t,\,x)$![]() . A bounded definable function $f: C \to \operatorname {\mathbb {R}}$
. A bounded definable function $f: C \to \operatorname {\mathbb {R}}$![]() is prepared in $x$
is prepared in $x$![]() if it can be written as:
if it can be written as:
where $b: C \to \operatorname {\mathbb {R}}^{N}$![]() (for some $N \in \operatorname {\mathbb {N}}$
(for some $N \in \operatorname {\mathbb {N}}$![]() ) is bounded, $b_j$
) is bounded, $b_j$![]() is a component function of $b$
is a component function of $b$![]() , any component function $b_i$
, any component function $b_i$![]() , $i \in \{1,\,\ldots ,\,N\}$
, $i \in \{1,\,\ldots ,\,N\}$![]() , of $b$
, of $b$![]() is of the form:
is of the form:

for some definable function $a_i: \pi _{< k+1}(C) \to \operatorname {\mathbb {R}}$![]() , $\mu _i \in K^{m}$
, $\mu _i \in K^{m}$![]() and $F$
and $F$![]() is analytic and non-vanishing on an open neighbourhood of $\overline {b(C)}$
is analytic and non-vanishing on an open neighbourhood of $\overline {b(C)}$![]() . We call $b$
. We call $b$![]() the associated bounded monomial map of $f$
the associated bounded monomial map of $f$![]() . A bounded definable map $f: C \to \operatorname {\mathbb {R}}^{n}$
. A bounded definable map $f: C \to \operatorname {\mathbb {R}}^{n}$![]() is prepared in $x$
is prepared in $x$![]() if all of its component functions are prepared in $x$
if all of its component functions are prepared in $x$![]() and have the same associated bounded monomial map $b$
and have the same associated bounded monomial map $b$![]() .
.
Note that $k$![]() can be zero. In that case, up to a scalar $a$
can be zero. In that case, up to a scalar $a$![]() , the associated bounded monomial map $b$
, the associated bounded monomial map $b$![]() is a monomial and the definition of prepared in $x$
is a monomial and the definition of prepared in $x$![]() coincides with the definition of an analytic-bounded-monomial map of [Reference Cluckers, Pila and Wilkie4]. We now show some properties of these maps that relate to the previous section.
coincides with the definition of an analytic-bounded-monomial map of [Reference Cluckers, Pila and Wilkie4]. We now show some properties of these maps that relate to the previous section.
Lemma 3.6 Let $b: U \subset (0,\,1)^{m} \to \operatorname {\mathbb {R}}$![]() , where $U$
, where $U$![]() is open, be given by $b(x) = ax^{\mu }$
is open, be given by $b(x) = ax^{\mu }$![]() for some $a \in \operatorname {\mathbb {R}}$
for some $a \in \operatorname {\mathbb {R}}$![]() and some $\mu \in \operatorname {\mathbb {R}}^{m}$
and some $\mu \in \operatorname {\mathbb {R}}^{m}$![]() . If $b$
. If $b$![]() is bounded, then $b$
is bounded, then $b$![]() is weakly $(M,\,B,\,0)$
is weakly $(M,\,B,\,0)$![]() -mild, where $M = \max (1,\,|\mu _1|,\,\ldots ,\,|\mu _m|)$
-mild, where $M = \max (1,\,|\mu _1|,\,\ldots ,\,|\mu _m|)$![]() and $B = \sup _U b(x)$
and $B = \sup _U b(x)$![]() .
.
Proof. Clearly, for any $\nu \in \operatorname {\mathbb {N}}^{m}$![]() , by the form of $b$
, by the form of $b$![]() , we have:
, we have:
for some constant $c(\nu ,\,\mu )$![]() depending on $\nu$
depending on $\nu$![]() and $\mu$
and $\mu$![]() , which remains to be bounded as desired. It is easy to see that computing the next order derivative would multiply $c(\nu ,\,\mu )$
, which remains to be bounded as desired. It is easy to see that computing the next order derivative would multiply $c(\nu ,\,\mu )$![]() with a factor that is at most $M + |\nu |$
with a factor that is at most $M + |\nu |$![]() in absolute value. Therefore, we find that:
in absolute value. Therefore, we find that:
Lemma 3.7 Suppose that $f: U \subset T \times (0,\,1)^{m} \to \operatorname {\mathbb {R}}$![]() is prepared in $x$
is prepared in $x$![]() with associated bounded monomial map $b$
with associated bounded monomial map $b$![]() , where for any $t \in T$
, where for any $t \in T$![]() the fibre $U_t$
the fibre $U_t$![]() is open. Then there exist $A,\,B>0$
is open. Then there exist $A,\,B>0$![]() such that for any $t \in T$
such that for any $t \in T$![]() the map $f_t$
the map $f_t$![]() is weakly $(A,\,B,\,0)$
is weakly $(A,\,B,\,0)$![]() -mild. Moreover, if the $C^{1}$
-mild. Moreover, if the $C^{1}$![]() -norm of the associated bounded monomial map $b_t$
-norm of the associated bounded monomial map $b_t$![]() of $f_t$
of $f_t$![]() is bounded independently of $t$
is bounded independently of $t$![]() , then there exist $A,\,B>0$
, then there exist $A,\,B>0$![]() such that for any $\beta \in \operatorname {\mathbb {N}}^{m}$
such that for any $\beta \in \operatorname {\mathbb {N}}^{m}$![]() with $|\beta | \leq 1$
with $|\beta | \leq 1$![]() and $t \in T$
and $t \in T$![]() the map $f^{(\beta )}_t$
the map $f^{(\beta )}_t$![]() is weakly $(A,\,B,\,0)$
is weakly $(A,\,B,\,0)$![]() -mild.
-mild.
Proof. Since $f$![]() is prepared in $x$
is prepared in $x$![]() , we have that $f(t,\,x) = b_j(t,\,x)F(b(t,\,x))$
, we have that $f(t,\,x) = b_j(t,\,x)F(b(t,\,x))$![]() as in Definition 3.5. By Lemma 3.6, there exist $A,\,B>0$
as in Definition 3.5. By Lemma 3.6, there exist $A,\,B>0$![]() , such that for any $t \in T$
, such that for any $t \in T$![]() the map $b_t$
the map $b_t$![]() is weakly $(A,\,B,\,0)$
is weakly $(A,\,B,\,0)$![]() -mild. The constant $A$
-mild. The constant $A$![]() does not depend on $t$
does not depend on $t$![]() and, since $b$
and, since $b$![]() is bounded, we may suppose $B$
is bounded, we may suppose $B$![]() does not depend on $t$
does not depend on $t$![]() . Finally, by Proposition 2.14 and Lemma 2.6, for any $t \in T$
. Finally, by Proposition 2.14 and Lemma 2.6, for any $t \in T$![]() we have that $F \circ b_t$
we have that $F \circ b_t$![]() is weakly $(A,\,B,\,0)$
is weakly $(A,\,B,\,0)$![]() -mild for some $A,\,B > 0$
-mild for some $A,\,B > 0$![]() that do not depend on $t$
that do not depend on $t$![]() and we can conclude by Proposition 2.15 that for any $t \in T$
and we can conclude by Proposition 2.15 that for any $t \in T$![]() , $f_{t}$
, $f_{t}$![]() is weakly $(A,\,B,\,0)$
is weakly $(A,\,B,\,0)$![]() -mild for some $A,\,B>0$
-mild for some $A,\,B>0$![]() that do not depend on $t$
that do not depend on $t$![]() .
.
Now fix any $t \in T$![]() and $1 \leq i \leq m$
and $1 \leq i \leq m$![]() . By the product rule, we have
. By the product rule, we have

Since we can bound the derivatives of $b_t$![]() independently of $t$
independently of $t$![]() , this is for any $t$
, this is for any $t$![]() a sum of weakly $(A,\,B,\,0)$
a sum of weakly $(A,\,B,\,0)$![]() -mild functions for some $A,\,B>0$
-mild functions for some $A,\,B>0$![]() independent of $t$
independent of $t$![]() and thus is also weakly $(A,\,B,\,0)$
and thus is also weakly $(A,\,B,\,0)$![]() -mild (for possibly larger $A>0$
-mild (for possibly larger $A>0$![]() and $B>0$
and $B>0$![]() ).
).
This lemma motivates the following definition.
Definition 3.8 Suppose that $f: U \subset \operatorname {\mathbb {R}}^{k} \times \operatorname {\mathbb {R}}^{m} \to \operatorname {\mathbb {R}}^{n}$![]() is a family of functions. If there exists a $B$
is a family of functions. If there exists a $B$![]() such that for all $t \in \pi _{<1}(U)$
such that for all $t \in \pi _{<1}(U)$![]() and $x \in U_t$
and $x \in U_t$![]() we have that $|f_t(x)|< B$
we have that $|f_t(x)|< B$![]() , we say that $f$
, we say that $f$![]() is bounded in $x$
is bounded in $x$![]() . More generally, if $r$
. More generally, if $r$![]() is a natural number, we say $f$
is a natural number, we say $f$![]() is $C^{r}$
is $C^{r}$![]() -bounded in $x$
-bounded in $x$![]() if there exists a $B$
if there exists a $B$![]() such that for any $t \in \pi _{<1}(U)$
such that for any $t \in \pi _{<1}(U)$![]() the map $f_t$
the map $f_t$![]() is $C^{r}$
is $C^{r}$![]() and for any $x \in U_t$
and for any $x \in U_t$![]() the $C^{r}$
the $C^{r}$![]() -norm of $f_t$
-norm of $f_t$![]() is bounded by $B$
is bounded by $B$![]() .
.
As an example, let $T = (0,\,1)$![]() and consider the family of maps $f_T: (t,\,x) \mapsto t^{2}/x$
and consider the family of maps $f_T: (t,\,x) \mapsto t^{2}/x$![]() on the cell given by
on the cell given by
Then for a fixed $t \in T$![]() , the map $f_t$
, the map $f_t$![]() is in fact mild, but the upper bound depends on $t$
is in fact mild, but the upper bound depends on $t$![]() . However, one sees that $f$
. However, one sees that $f$![]() is $C^{1}$
is $C^{1}$![]() -bounded in $x$
-bounded in $x$![]() .
.
Lemma 3.7 shows that if $f$![]() is prepared in $x$
is prepared in $x$![]() such that its associated bounded monomial map $b$
such that its associated bounded monomial map $b$![]() is $C^{1}$
is $C^{1}$![]() -bounded in $x$
-bounded in $x$![]() , then we can apply Proposition 2.13 to $f$
, then we can apply Proposition 2.13 to $f$![]() . The following result, which we need in the proof of Proposition 3.10, is a more refined version of Proposition 2.13 for the bounded monomial map $b$
. The following result, which we need in the proof of Proposition 3.10, is a more refined version of Proposition 2.13 for the bounded monomial map $b$![]() . The technique of the proof is similar, but will use the particular form of $b$
. The technique of the proof is similar, but will use the particular form of $b$![]() .
.
Proposition 3.9 Let $b: U \subset (0,\,1)^{m} \to \operatorname {\mathbb {R}}$![]() , where $U$
, where $U$![]() is open, be given by $b(x) = ax^{\mu }$
is open, be given by $b(x) = ax^{\mu }$![]() for some $a \in \operatorname {\mathbb {R}}$
for some $a \in \operatorname {\mathbb {R}}$![]() and $\mu \in \operatorname {\mathbb {R}}^{m}$
and $\mu \in \operatorname {\mathbb {R}}^{m}$![]() . Suppose that $b$
. Suppose that $b$![]() is $C^{1}$
is $C^{1}$![]() -bounded. Let $r>0$
-bounded. Let $r>0$![]() be an integer and $\phi : (0,\,1)^{m} \to (0,\,1)^{m}$
be an integer and $\phi : (0,\,1)^{m} \to (0,\,1)^{m}$![]() be the map given by:
be the map given by:
where for all $i \in \{1,\,\ldots ,\,m\}$![]() , we have that $n_i \geq r^{l}$
, we have that $n_i \geq r^{l}$![]() for some integer $l \geq 1$
for some integer $l \geq 1$![]() and set $V = \phi ^{-1}(U)$
and set $V = \phi ^{-1}(U)$![]() . Then $(b \circ \phi )^{1/r^{l-1}}: V \to \operatorname {\mathbb {R}}$
. Then $(b \circ \phi )^{1/r^{l-1}}: V \to \operatorname {\mathbb {R}}$![]() is $(\max (n_{1},\,\ldots ,\,n_{m})A,\,B,\,0)$
is $(\max (n_{1},\,\ldots ,\,n_{m})A,\,B,\,0)$![]() -mild up to order $r$
-mild up to order $r$![]() , for some $A,\,B>0$
, for some $A,\,B>0$![]() depending on $b$
depending on $b$![]() only.
only.
Proof. For simplicity, we assume that $a = 1$![]() . We have that $(b \circ \phi )(x) = x^{N\mu }$
. We have that $(b \circ \phi )(x) = x^{N\mu }$![]() , where $N\mu = (n_i\mu _i)_i$
, where $N\mu = (n_i\mu _i)_i$![]() . We apply Theorem 2.7 to the composition $(b \circ \phi )^{1/r^{l-1}} = b^{1/r^{l-1}} \circ \phi$
. We apply Theorem 2.7 to the composition $(b \circ \phi )^{1/r^{l-1}} = b^{1/r^{l-1}} \circ \phi$![]() to get:
to get:

for any $x \in V$![]() . We again compute the power of $x_i$
. We again compute the power of $x_i$![]() in a fixed term of this sum as in the proof of Proposition 2.13. The product of the $|(\phi ^{(l_j)}(x))^{k_j}|$
in a fixed term of this sum as in the proof of Proposition 2.13. The product of the $|(\phi ^{(l_j)}(x))^{k_j}|$![]() gives a power $\sum \nolimits _{j = 1}^{s} (n_i-l_{j,i})k_{j,i}$
gives a power $\sum \nolimits _{j = 1}^{s} (n_i-l_{j,i})k_{j,i}$![]() . Using the notation of Lemma 3.6, we have that
. Using the notation of Lemma 3.6, we have that
where $N\lambda = (n_i\lambda _i)_i$![]() and $c(\lambda ,\,r^{-(l-1)}\mu )$
and $c(\lambda ,\,r^{-(l-1)}\mu )$![]() is a constant depending on $\lambda ,\,r,\,l$
is a constant depending on $\lambda ,\,r,\,l$![]() and $\mu$
and $\mu$![]() . We have that $x_i^{\sum \nolimits _{j = 1}^{s} ((n_i-l_{j,i})k_{j,i}) - n_i \lambda _i} = x_i^{-\sum \nolimits _{j = 1}^{s} l_{j,i}k_{j,i}}$
. We have that $x_i^{\sum \nolimits _{j = 1}^{s} ((n_i-l_{j,i})k_{j,i}) - n_i \lambda _i} = x_i^{-\sum \nolimits _{j = 1}^{s} l_{j,i}k_{j,i}}$![]() . Let $k \in \{1,\,\ldots ,\,m\}$
. Let $k \in \{1,\,\ldots ,\,m\}$![]() be such that $x_{k} = \min _{i}\{x_{i} \mid \lambda _{i} \neq 0\}$
be such that $x_{k} = \min _{i}\{x_{i} \mid \lambda _{i} \neq 0\}$![]() . We may then assume that $\mu _{k} \neq 0$
. We may then assume that $\mu _{k} \neq 0$![]() for the computations below, since if $\mu _{k} = 0$
for the computations below, since if $\mu _{k} = 0$![]() , the partial derivative of $b^{1/r^{l-1}}$
, the partial derivative of $b^{1/r^{l-1}}$![]() with respect to $\lambda$
with respect to $\lambda$![]() is zero since $\lambda _{k} \neq 0$
is zero since $\lambda _{k} \neq 0$![]() . Then we bound the product over all $x_i$
. Then we bound the product over all $x_i$![]() in terms of $x_k$
in terms of $x_k$![]() :
:

Finally, assume $|\nu | \leq r$![]() . Using that $n_k \geq r^{l}$
. Using that $n_k \geq r^{l}$![]() , we further bound:
, we further bound:

Finally, observe that
which is bounded since $\phi (x) \in U$![]() and $b$
and $b$![]() is $C^{1}$
is $C^{1}$![]() -bounded on $U$
-bounded on $U$![]() . This bound only depends on $b$
. This bound only depends on $b$![]() and the $r^{l-1}$
and the $r^{l-1}$![]() -th root of this bound can be bounded by some constant that only depends on $b$
-th root of this bound can be bounded by some constant that only depends on $b$![]() , not on $r$
, not on $r$![]() or $l$
or $l$![]() . As in the proof of Lemma 3.6, we can bound $|c(\lambda ,\,r^{-(l-1)}\mu )|$
. As in the proof of Lemma 3.6, we can bound $|c(\lambda ,\,r^{-(l-1)}\mu )|$![]() by $M^{|\lambda |}|\lambda |!$
by $M^{|\lambda |}|\lambda |!$![]() , where $M>0$
, where $M>0$![]() can be further bounded to only depend on $b$
can be further bounded to only depend on $b$![]() . One now finishes the proof similarly as the (end of) the proof of Proposition 2.13.
. One now finishes the proof similarly as the (end of) the proof of Proposition 2.13.
The next proposition is one of the two main ingredients for the proof of the main theorem.
Proposition 3.10 Suppose that $f: C \subset T \times (0,\,1)^{m} \to [-1,\,1]$![]() is prepared in $x$
is prepared in $x$![]() such that the associated bounded monomial $b$
such that the associated bounded monomial $b$![]() is $C^{1}$
is $C^{1}$![]() -bounded in $x$
-bounded in $x$![]() . Suppose moreover that for any $t \in T$
. Suppose moreover that for any $t \in T$![]() , the cell $C_t$
, the cell $C_t$![]() is open and that the walls of $C$
is open and that the walls of $C$![]() are also prepared in $x$
are also prepared in $x$![]() with associated bounded monomial maps that are $C^{1}$
with associated bounded monomial maps that are $C^{1}$![]() -bounded in $x$
-bounded in $x$![]() . Let $r>0$
. Let $r>0$![]() be any integer and consider the map $\phi _r: T \times (0,\,1)^{m} \to T \times (0,\,1)^{m}$
be any integer and consider the map $\phi _r: T \times (0,\,1)^{m} \to T \times (0,\,1)^{m}$![]() given by
given by
Then $C_r = \phi _r^{-1}(C)$![]() is a cell and there exists an $A>0$
is a cell and there exists an $A>0$![]() such that for any $t \in T$
such that for any $t \in T$![]() the walls of the open cell $C_{r,t}$
the walls of the open cell $C_{r,t}$![]() of $x_1$
of $x_1$![]() are $(A,\,0)$
are $(A,\,0)$![]() -mild, for $i = 2,\,\ldots ,\,m$
-mild, for $i = 2,\,\ldots ,\,m$![]() , the walls of $x_i$
, the walls of $x_i$![]() are $(r^{m}A,\,0)$
are $(r^{m}A,\,0)$![]() -mild up to order $r$
-mild up to order $r$![]() and $(f \circ \phi _r)_t: C_{r,t} \to [-1,\,1]$
and $(f \circ \phi _r)_t: C_{r,t} \to [-1,\,1]$![]() is $(r^{m}A,\,0)$
is $(r^{m}A,\,0)$![]() -mild up to order $r$
-mild up to order $r$![]() .
.
Proof. Fix some $t \in T$![]() and consider a wall of the cell $C_{t}$
and consider a wall of the cell $C_{t}$![]() , say $\alpha _i$
, say $\alpha _i$![]() of $x_i$
of $x_i$![]() . If $i = 1$
. If $i = 1$![]() , the walls are constant and there is nothing to show, so suppose $i \geq 2$
, the walls are constant and there is nothing to show, so suppose $i \geq 2$![]() . Then $\alpha _i(x_{< i}) = b_{j,t}(x_{< i})F(b_t(x_{< i}))$
. Then $\alpha _i(x_{< i}) = b_{j,t}(x_{< i})F(b_t(x_{< i}))$![]() for some $b$
for some $b$![]() and $F$
and $F$![]() as in Definition 3.5, since $\alpha _i$
as in Definition 3.5, since $\alpha _i$![]() is prepared in $x$
is prepared in $x$![]() . It follows that the corresponding wall of $x_i$
. It follows that the corresponding wall of $x_i$![]() in the cell $C_{r,t}$
in the cell $C_{r,t}$![]() is given by:
is given by:
By a uniform version of Proposition 3.9, we have that the function $\sqrt[r^{m-i+1}]{b_{j,t}(x_1^{r^{m}}, \ldots , x_{i-1}^{r^{m-i+2}})}$![]() is $(r^{m}A_1, B_1, 0)$
is $(r^{m}A_1, B_1, 0)$![]() -mild up to order $r$
-mild up to order $r$![]() for some $A_1,\,B_1 > 0$
for some $A_1,\,B_1 > 0$![]() independent of $t$
independent of $t$![]() and $r$
and $r$![]() . Indeed, $A_{1}$
. Indeed, $A_{1}$![]() does not depend on $t$
does not depend on $t$![]() since it only depends on the exponent of $x$
since it only depends on the exponent of $x$![]() in $b_{j}$
in $b_{j}$![]() , which does not depend on $t$
, which does not depend on $t$![]() by Definition 3.5. To show that $B_{1}$
by Definition 3.5. To show that $B_{1}$![]() does not depend on $t$
does not depend on $t$![]() , one should dismiss the assumption that $a = 1$
, one should dismiss the assumption that $a = 1$![]() in the proof of Proposition 3.9, but can later use that $b_{j}$
in the proof of Proposition 3.9, but can later use that $b_{j}$![]() is $C^{1}$
is $C^{1}$![]() -bounded in $x$
-bounded in $x$![]() to find $B_{1}$
to find $B_{1}$![]() independent of $t$
independent of $t$![]() (and also of $r$
(and also of $r$![]() and $l$
and $l$![]() ).
).
Since $F$![]() is a non-vanishing analytic function on some open neighbourhood of $\operatorname {\text {Im}}(b_t)$
is a non-vanishing analytic function on some open neighbourhood of $\operatorname {\text {Im}}(b_t)$![]() , we may suppose that there is some $S>1$
, we may suppose that there is some $S>1$![]() such that $\operatorname {\text {Im}}(F) \subset (1/S,\,S)$
such that $\operatorname {\text {Im}}(F) \subset (1/S,\,S)$![]() . On this domain, the function $\sqrt [r^{m-i+1}]{}$
. On this domain, the function $\sqrt [r^{m-i+1}]{}$![]() is $(S,\,S,\,0)$
is $(S,\,S,\,0)$![]() -mild. Hence, $\sqrt [r^{m-i+1}]{} \circ F$
-mild. Hence, $\sqrt [r^{m-i+1}]{} \circ F$![]() is an $(A_F,\,B_F,\,0)$
is an $(A_F,\,B_F,\,0)$![]() -mild map for some $A_F,\,B_F>0$
-mild map for some $A_F,\,B_F>0$![]() by Lemma 2.6 and Corollary 2.11, where $A_F$
by Lemma 2.6 and Corollary 2.11, where $A_F$![]() and $B_F$
and $B_F$![]() only depend on $F$
only depend on $F$![]() , not on $t$
, not on $t$![]() or $r$
or $r$![]() . Next, $b_t(x_1^{r^{m}},\,\ldots ,\,x_{i-1}^{r^{m-i+2}})$
. Next, $b_t(x_1^{r^{m}},\,\ldots ,\,x_{i-1}^{r^{m-i+2}})$![]() is $(r^{m}A',\,B',\,0)$
is $(r^{m}A',\,B',\,0)$![]() -mild up to order $r$
-mild up to order $r$![]() by Proposition 2.13 for some $A',\,B' > 0$
by Proposition 2.13 for some $A',\,B' > 0$![]() depending only on $b$
depending only on $b$![]() , not on $t$
, not on $t$![]() or $r$
or $r$![]() . Applying the up to order $r$
. Applying the up to order $r$![]() version of Corollary 2.11, we see that $\sqrt [r^{m-i+1}]{F(b_t(x_1^{r^{m}},\,\ldots ,\,x_{i-1}^{r^{m-i+2}}))}$
version of Corollary 2.11, we see that $\sqrt [r^{m-i+1}]{F(b_t(x_1^{r^{m}},\,\ldots ,\,x_{i-1}^{r^{m-i+2}}))}$![]() is $(r^{m}A_2,\,B_2,\,0)$
is $(r^{m}A_2,\,B_2,\,0)$![]() -mild up to order $r$
-mild up to order $r$![]() for some $A_2,\,B_2 > 0$
for some $A_2,\,B_2 > 0$![]() depending only on $\alpha _i$
depending only on $\alpha _i$![]() , not on $t$
, not on $t$![]() or $r$
or $r$![]() .
.
By Proposition 2.15, we see that $\alpha _{r,t}$![]() is $(r^{m}A,\,B,\,0)$
is $(r^{m}A,\,B,\,0)$![]() -mild up to order $r$
-mild up to order $r$![]() for some $A,\,B > 0$
for some $A,\,B > 0$![]() independent of $t$
independent of $t$![]() and $r$
and $r$![]() . Since $\operatorname {\text {Im}}(\alpha _{r,t}) \subset (0,\,1)$
. Since $\operatorname {\text {Im}}(\alpha _{r,t}) \subset (0,\,1)$![]() , after possibly enlarging $A$
, after possibly enlarging $A$![]() , we can conclude that $\alpha _{r,t}$
, we can conclude that $\alpha _{r,t}$![]() is $(r^{m}A,\,0)$
is $(r^{m}A,\,0)$![]() -mild up to order $r$
-mild up to order $r$![]() for some $A>0$
for some $A>0$![]() independent of $t$
independent of $t$![]() and $r$
and $r$![]() . Finally, by Proposition 2.13 and Lemma 3.7, the function $(f \circ \phi _r)_t$
. Finally, by Proposition 2.13 and Lemma 3.7, the function $(f \circ \phi _r)_t$![]() is $(r^{m}A'',\,B'',\,0)$
is $(r^{m}A'',\,B'',\,0)$![]() -mild up to order $r$
-mild up to order $r$![]() for some $A'',\,B''>0$
for some $A'',\,B''>0$![]() independent of $t$
independent of $t$![]() and $r$
and $r$![]() . Since $|f| \leq 1$
. Since $|f| \leq 1$![]() , after possibly enlarging $A''$
, after possibly enlarging $A''$![]() , we have that $(f \circ \phi _r)_t$
, we have that $(f \circ \phi _r)_t$![]() is $(r^{m}A'',\,0)$
is $(r^{m}A'',\,0)$![]() -mild up to order $r$
-mild up to order $r$![]() . We conclude after redefining $A$
. We conclude after redefining $A$![]() to be the maximum over all $A$
to be the maximum over all $A$![]() corresponding to the mildness of the walls and $A''$
corresponding to the mildness of the walls and $A''$![]() of the mildness of $(f \circ \phi _r)_t$
of the mildness of $(f \circ \phi _r)_t$![]() .
.
We will now show one can obtain the conditions of this proposition. It is a parameterization result, a slight modification of [Reference Cluckers, Pila and Wilkie4, Theorem 4.3.1], that will allow us to easily deduce the main theorem.
Theorem 3.11 Suppose that $X_T$![]() is the graph of a definable function $\varphi : C \subset T \times (0,\,1)^{m} \to [-1,\,1]^{n-m}$
is the graph of a definable function $\varphi : C \subset T \times (0,\,1)^{m} \to [-1,\,1]^{n-m}$![]() , where $C$
, where $C$![]() is open in $T \times (0,\,1)^{m}$
is open in $T \times (0,\,1)^{m}$![]() . Then there exist finitely many definable maps
. Then there exist finitely many definable maps
such that:
1. ${\bigcup} _{l} \text {Im}(f_l) = X_T$
 ,
,2. for each $l$
 , $C_l$
, $C_l$ is an open cell in $T_l \times (0,\,1)^{m}$
is an open cell in $T_l \times (0,\,1)^{m}$ , where $T_l$
, where $T_l$ is a cell contained in $T$
is a cell contained in $T$ ,
,3. for each $l$
 and for any $(t,\,x) \in C_l$
and for any $(t,\,x) \in C_l$ , $f_l(t,\,x) \in X_t$
, $f_l(t,\,x) \in X_t$ , thus $f_l$
, thus $f_l$ is a family of maps $C_{l,t} \to X_t$
is a family of maps $C_{l,t} \to X_t$ with $C_{l,t}$
with $C_{l,t}$ open in $(0,\,1)^{m}$
open in $(0,\,1)^{m}$ ,
,4. each $f_l$
 is prepared in $x$
is prepared in $x$ and the associated bounded monomial map of $f_l$
and the associated bounded monomial map of $f_l$ is $C^{1}$
is $C^{1}$ -bounded in $x$
-bounded in $x$ ,
,5. the walls of all $C_l$
 are prepared in $x$
are prepared in $x$ and their associated bounded monomial maps are $C^{1}$
and their associated bounded monomial maps are $C^{1}$ -bounded in $x$
-bounded in $x$ .
.
Proof. The proof uses induction on $m$![]() . The case $m=0$
. The case $m=0$![]() is trivial. By o-minimality, we may assume that there exist finitely many $f_{l}: C_{l} \subset T \times (0,\,1)^{m} \to X_{T}$
is trivial. By o-minimality, we may assume that there exist finitely many $f_{l}: C_{l} \subset T \times (0,\,1)^{m} \to X_{T}$![]() , satisfying properties $1$
, satisfying properties $1$![]() , $2$
, $2$![]() and $3$
and $3$![]() . For the rest of the proof, we focus on one such map $f_{l}$
. For the rest of the proof, we focus on one such map $f_{l}$![]() . Next, we apply Theorem 3.4 to $f_{l}$
. Next, we apply Theorem 3.4 to $f_{l}$![]() such that we may suppose that $f_{l}$
such that we may suppose that $f_{l}$![]() is prepared on $C_{l}$
is prepared on $C_{l}$![]() with centre $\theta _{l}$
with centre $\theta _{l}$![]() . Note that some of the cells obtained by applying (3.4) might not be open, but then they have lower dimension, therefore can be considered separately and can be ignored by induction. For this reason, whenever we further partition $C_{l}$
. Note that some of the cells obtained by applying (3.4) might not be open, but then they have lower dimension, therefore can be considered separately and can be ignored by induction. For this reason, whenever we further partition $C_{l}$![]() , we always assume the cells are open.
, we always assume the cells are open.
Next, we will show that we may assume $\theta _l = 0$![]() on $C_l$
on $C_l$![]() . Since $x_m \sim \theta _l(x_{< m})$
. Since $x_m \sim \theta _l(x_{< m})$![]() on $C_l$
on $C_l$![]() , there exists some $\epsilon \in (0,\,1)$
, there exists some $\epsilon \in (0,\,1)$![]() such that $\epsilon x_m < \theta _l(t,\,x_{< m}) < (1/\epsilon ) x_m$
such that $\epsilon x_m < \theta _l(t,\,x_{< m}) < (1/\epsilon ) x_m$![]() for all $(t,\,x) \in C_l$
for all $(t,\,x) \in C_l$![]() . Up to finite partitioning, if necessary, we may assume that either $\theta _l(t,\,x_{< m}) > x_m$
. Up to finite partitioning, if necessary, we may assume that either $\theta _l(t,\,x_{< m}) > x_m$![]() for all $(t,\,x) \in C_l$
for all $(t,\,x) \in C_l$![]() or $\theta _l(t,\,x_{< m}) < x_m$
or $\theta _l(t,\,x_{< m}) < x_m$![]() for all $(t,\,x) \in C_l$
for all $(t,\,x) \in C_l$![]() . In the first case, the other is similar, consider the cell
. In the first case, the other is similar, consider the cell
and define $\tilde {f}_l: \tilde {C}_l \to X_{T}$![]() by $\tilde {f}_{l}(t,\,x) = f_l(t,\,x_{< m},\,(({-1})/{\epsilon })x_m+\theta _l(t,\,x_{< m}))$
by $\tilde {f}_{l}(t,\,x) = f_l(t,\,x_{< m},\,(({-1})/{\epsilon })x_m+\theta _l(t,\,x_{< m}))$![]() . Then $\tilde {f}_l$
. Then $\tilde {f}_l$![]() is prepared on $\tilde {C}_l$
is prepared on $\tilde {C}_l$![]() with centre zero. Moreover, properties $1$
with centre zero. Moreover, properties $1$![]() , $2$
, $2$![]() and $3$
and $3$![]() are still satisfied. Thus, from now on, we will assume additionally that $f_l$
are still satisfied. Thus, from now on, we will assume additionally that $f_l$![]() is prepared on $C_l$
is prepared on $C_l$![]() with centre zero.
with centre zero.
Next, we show that, up to finite partitioning, if necessary, the associated bounded range map $b_l = (b_{l,1},\,\ldots ,\,b_{l,N})$![]() of $f_l$
of $f_l$![]() is $C^{1}$
is $C^{1}$![]() and $| \partial b_l / \partial x_m | \leq 1$
and $| \partial b_l / \partial x_m | \leq 1$![]() . That we may suppose that $b_l$
. That we may suppose that $b_l$![]() is $C^{1}$
is $C^{1}$![]() is a classical consequence of the cell decomposition theorem. Up to further partitioning using o-minimality, we may suppose that there exists some $i \in \{1,\,\ldots ,\,N\}$
is a classical consequence of the cell decomposition theorem. Up to further partitioning using o-minimality, we may suppose that there exists some $i \in \{1,\,\ldots ,\,N\}$![]() such that for any other $i' \in \{1,\,\ldots ,\,N\}$
such that for any other $i' \in \{1,\,\ldots ,\,N\}$![]() we have: $|\partial b_{l,i} / \partial x_m | \geq |\partial b_{l,i'} / \partial x_m|$
we have: $|\partial b_{l,i} / \partial x_m | \geq |\partial b_{l,i'} / \partial x_m|$![]() on $C_l$
on $C_l$![]() and that either $|\partial b_{l,i} / \partial x_m | \geq 1$
and that either $|\partial b_{l,i} / \partial x_m | \geq 1$![]() or $|\partial b_{l,i} / \partial x_m | < 1$
or $|\partial b_{l,i} / \partial x_m | < 1$![]() on $C_l$
on $C_l$![]() . The second case is exactly what we want. In the first case, we do a change of variables. To ensure that we recover a map $T \times (0,\,1)^{m} \to [-1,\,1]^{m-n}$
. The second case is exactly what we want. In the first case, we do a change of variables. To ensure that we recover a map $T \times (0,\,1)^{m} \to [-1,\,1]^{m-n}$![]() , we first have to further partition $C_l$
, we first have to further partition $C_l$![]() such that $b_{l,i}$
such that $b_{l,i}$![]() is either identically $-1$
is either identically $-1$![]() ,$0$
,$0$![]() or $1$
or $1$![]() , $b_{l,i} > 0$
, $b_{l,i} > 0$![]() or $b_{l,i} < 0$
or $b_{l,i} < 0$![]() . We only have to consider the last two cases. Suppose we have $b_{l,i} > 0$
. We only have to consider the last two cases. Suppose we have $b_{l,i} > 0$![]() (the case $b_{l,i} < 0$
(the case $b_{l,i} < 0$![]() is similar up to changing a sign). Once more using o-minimality, we may assume that for fixed $(t,\,x_1,\,\ldots ,\,x_{m-1})$
is similar up to changing a sign). Once more using o-minimality, we may assume that for fixed $(t,\,x_1,\,\ldots ,\,x_{m-1})$![]() the map $x_m \mapsto b_{l,i}(t,\,x_1,\,\ldots ,\,x_{m-1},\,x_m)$
the map $x_m \mapsto b_{l,i}(t,\,x_1,\,\ldots ,\,x_{m-1},\,x_m)$![]() is injective and it follows that the map
is injective and it follows that the map
is invertible. Set $\bar {C}_l = \phi (C_l)$![]() and $\bar {f}_l = f_l \circ \phi ^{-1}$
and $\bar {f}_l = f_l \circ \phi ^{-1}$![]() . Then $\bar {C}_l$
. Then $\bar {C}_l$![]() is an open cell in $T \times (0,\,1)^{m}$
is an open cell in $T \times (0,\,1)^{m}$![]() and $\bar {f}_l$
and $\bar {f}_l$![]() satisfies the same properties as $f_l$
satisfies the same properties as $f_l$![]() , in particular, it is prepared in $x_m$
, in particular, it is prepared in $x_m$![]() with bounded range map $\bar {b_l}$
with bounded range map $\bar {b_l}$![]() but moreover $|\partial \bar {b}_{l,i} / \partial x_m | \leq 1$
but moreover $|\partial \bar {b}_{l,i} / \partial x_m | \leq 1$![]() for all component functions $\bar {b}_{l,i}$
for all component functions $\bar {b}_{l,i}$![]() of $\bar {b}_l$
of $\bar {b}_l$![]() (by the chain rule and the choice of $i$
(by the chain rule and the choice of $i$![]() ).
).
So up to now, we may suppose we have finitely many maps $f_l:C_l \to X_T$![]() satisfying the first three properties, that are prepared in $x_m$
satisfying the first three properties, that are prepared in $x_m$![]() and the associated bounded range map $b_l$
and the associated bounded range map $b_l$![]() of $f_l$
of $f_l$![]() is $C^{1}$
is $C^{1}$![]() and $|\partial b_{l,i} / \partial x_m| \leq 1$
and $|\partial b_{l,i} / \partial x_m| \leq 1$![]() . Thus, for any $i \in \{1,\,\ldots ,\,N\}$
. Thus, for any $i \in \{1,\,\ldots ,\,N\}$![]() , the component function $b_{l,i}$
, the component function $b_{l,i}$![]() of $b_l$
of $b_l$![]() is given by:
is given by:
Denote $\alpha _m$![]() for the wall of $C_l$
for the wall of $C_l$![]() bounding the variable $x_m$
bounding the variable $x_m$![]() from below and $\beta _m$
from below and $\beta _m$![]() for the wall of $C_l$
for the wall of $C_l$![]() bounding $x_m$
bounding $x_m$![]() from above. Up to further partitioning, we may suppose $\alpha _m \neq 0$
from above. Up to further partitioning, we may suppose $\alpha _m \neq 0$![]() on $C_l$
on $C_l$![]() and we will also suppose that $r_{l,i} \neq 0$
and we will also suppose that $r_{l,i} \neq 0$![]() for every $i \in \{1,\,\ldots ,\,N\}$
for every $i \in \{1,\,\ldots ,\,N\}$![]() . We will come back to this at the end of the proof. Now consider the following maps:
. We will come back to this at the end of the proof. Now consider the following maps:

and define $h_\beta$![]() and $g_\beta$
and $g_\beta$![]() analogously. Note that $g_{\alpha }$
analogously. Note that $g_{\alpha }$![]() and $g_{\beta }$
and $g_{\beta }$![]() are well defined by our effort to bound $|\partial b_{l,i}/\partial x_{m}|$
are well defined by our effort to bound $|\partial b_{l,i}/\partial x_{m}|$![]() by 1. For any $i \in \{1,\,\ldots ,\,N\}$
by 1. For any $i \in \{1,\,\ldots ,\,N\}$![]() , by the form of $b_{l,i}$
, by the form of $b_{l,i}$![]() , the component functions of $h_{\alpha ,i}$
, the component functions of $h_{\alpha ,i}$![]() and $g_{\alpha ,i}$
and $g_{\alpha ,i}$![]() (similarly for $h_\beta$
(similarly for $h_\beta$![]() and $g_\beta$
and $g_\beta$![]() ) become:
) become:

Now define the map $F: \pi _{< m}(C_l) \to \text {Im}(F)$![]() whose component functions are $\alpha _m,\,\beta _m,\,h_\alpha ,\,h_\beta ,\,g_\alpha$
whose component functions are $\alpha _m,\,\beta _m,\,h_\alpha ,\,h_\beta ,\,g_\alpha$![]() and $g_\beta$
and $g_\beta$![]() . Next, apply the induction hypothesis to the graph of $F$
. Next, apply the induction hypothesis to the graph of $F$![]() . Hence we obtain finitely many maps $\psi _{l,j}:D_{l,j} \to \text {graph}(F)$
. Hence we obtain finitely many maps $\psi _{l,j}:D_{l,j} \to \text {graph}(F)$![]() satisfying all properties of the theorem. In particular, they are prepared in $x_{< m}$
satisfying all properties of the theorem. In particular, they are prepared in $x_{< m}$![]() with associated bounded monomial map $c_{l,j}$
with associated bounded monomial map $c_{l,j}$![]() that is $C^{1}$
that is $C^{1}$![]() -bounded in $x_{< m}$
-bounded in $x_{< m}$![]() . Therefore, by their form, the maps $\psi _{l,j}$
. Therefore, by their form, the maps $\psi _{l,j}$![]() are $C^{1}$
are $C^{1}$![]() -bounded in $x_{< m}$
-bounded in $x_{< m}$![]() . Note that $\psi _{l,j}(t,\,x_{< m})_{< m} \in \pi _{< m}(C_l)$
. Note that $\psi _{l,j}(t,\,x_{< m})_{< m} \in \pi _{< m}(C_l)$![]() and thus, for instance, $\alpha _m(\psi _{l,j}(t,\,x_{< m})_{< m})$
and thus, for instance, $\alpha _m(\psi _{l,j}(t,\,x_{< m})_{< m})$![]() is a component function of $\psi _{l,j}$
is a component function of $\psi _{l,j}$![]() . Now set
. Now set
By construction, these cells have all the properties we want. Finally define $f_{l,j}:C_{l,j} \to X_T$![]() by:
by:
By the form of $f_l$![]() , it remains to show that for any $i \in \{1,\,\ldots ,\,N\}$
, it remains to show that for any $i \in \{1,\,\ldots ,\,N\}$![]() , $b_{l,i}(\psi _{l,j}(t,x_{< m})_{< m},x_m)$
, $b_{l,i}(\psi _{l,j}(t,x_{< m})_{< m},x_m)$![]() is prepared in $x$
is prepared in $x$![]() and is $C^{1}$
and is $C^{1}$![]() -bounded in $x$
-bounded in $x$![]() . Thus, let $b_{l,i}$
. Thus, let $b_{l,i}$![]() be a component function of $b_l$
be a component function of $b_l$![]() and suppose $r_{l,i} < 0$
and suppose $r_{l,i} < 0$![]() (in the case $r_{l,i} > 0$
(in the case $r_{l,i} > 0$![]() , use $\beta$
, use $\beta$![]() instead of $\alpha$
instead of $\alpha$![]() in the calculations). We have that:
in the calculations). We have that:

By the construction, $h_{\alpha ,i}(\psi _{l,j}(t,\,x_{< m})_{< m})$![]() and $\alpha _m(\psi _{l,j}(t,\,x_{< m})_{< m})$
and $\alpha _m(\psi _{l,j}(t,\,x_{< m})_{< m})$![]() are prepared in $x_{< m}$
are prepared in $x_{< m}$![]() with associated bounded monomial map $c_{l,j}$
with associated bounded monomial map $c_{l,j}$![]() that is $C^{1}$
that is $C^{1}$![]() -bounded in $x_{< m}$
-bounded in $x_{< m}$![]() . Therefore, it follows that $b_{l,i}(\psi _{l,j}(t,\,x_{< m})_{< m},\,x_m)$
. Therefore, it follows that $b_{l,i}(\psi _{l,j}(t,\,x_{< m})_{< m},\,x_m)$![]() is prepared in $x$
is prepared in $x$![]() . We now look at the $C^{1}$
. We now look at the $C^{1}$![]() -norm. To simplify notation, denote $y = \psi _{l,j}(t,\,x_{< m})_{< m}$
-norm. To simplify notation, denote $y = \psi _{l,j}(t,\,x_{< m})_{< m}$![]() . Let $s \in \{1,\,\ldots ,\,m-1\}$
. Let $s \in \{1,\,\ldots ,\,m-1\}$![]() , then:
, then:

The first term is bounded in $x$![]() since $h_{\alpha ,i}(y) = h_{\alpha ,i}(\psi _{i,l}(t,\,x_{< m})_{< m})$
since $h_{\alpha ,i}(y) = h_{\alpha ,i}(\psi _{i,l}(t,\,x_{< m})_{< m})$![]() is $C^{1}$
is $C^{1}$![]() -bounded in $x_{< m}$
-bounded in $x_{< m}$![]() (because it is prepared in $x_{< m}$
(because it is prepared in $x_{< m}$![]() , with $C^{1}$
, with $C^{1}$![]() -bounded associated bounded monomial map) and $(x_m/\alpha _m(y))^{r_{l,i}} <1$
-bounded associated bounded monomial map) and $(x_m/\alpha _m(y))^{r_{l,i}} <1$![]() since $x_m > \alpha _m(y)$
since $x_m > \alpha _m(y)$![]() and $r_{l,i} < 0$
and $r_{l,i} < 0$![]() . We further compute the last term:
. We further compute the last term:

Hence we see that also this term is bounded in $x$![]() . Since $(\partial b_l / \partial x_m)$
. Since $(\partial b_l / \partial x_m)$![]() was already bounded, we obtain that $b_{l,i}(\psi _{l,j}(t,\,x_{< m})_{< m},\,x_m)$
was already bounded, we obtain that $b_{l,i}(\psi _{l,j}(t,\,x_{< m})_{< m},\,x_m)$![]() is $C^{1}$
is $C^{1}$![]() -bounded in $x$
-bounded in $x$![]() .
.
To conclude we explain the cases $\alpha _m = 0$![]() and $r_{l,i} = 0$
and $r_{l,i} = 0$![]() . If $\alpha _m = 0$
. If $\alpha _m = 0$![]() , this forces the exponent $r_{l,i}$
, this forces the exponent $r_{l,i}$![]() to be positive or zero since $b_l$
to be positive or zero since $b_l$![]() is bounded. If $r_{l,i} > 0$
is bounded. If $r_{l,i} > 0$![]() , we can just use the maps $h_\beta$
, we can just use the maps $h_\beta$![]() and $g_\beta$
and $g_\beta$![]() as above since $\beta _m > 0$
as above since $\beta _m > 0$![]() . If $r_{l,i} = 0$
. If $r_{l,i} = 0$![]() , one can use the induction hypothesis on $b_{l,i} = a_{l,i}$
, one can use the induction hypothesis on $b_{l,i} = a_{l,i}$![]() immediately.
immediately.
We can now easily prove the main theorem using this parameterization result and Lemma 2.5. It refines the $C^{r}$![]() -parameterization theorem of [Reference Cluckers, Pila and Wilkie4] by making the constant $d$
-parameterization theorem of [Reference Cluckers, Pila and Wilkie4] by making the constant $d$![]() more explicit; we have $d = m^{3}$
more explicit; we have $d = m^{3}$![]() .
.
Theorem 3.12 Suppose that $X_T$![]() is a definable family of $m$
is a definable family of $m$![]() -dimensional subsets in $[-1,\,1]^{n}$
-dimensional subsets in $[-1,\,1]^{n}$![]() . Then there exists a constant $c>0$
. Then there exists a constant $c>0$![]() such that for any integer $r > 0$
such that for any integer $r > 0$![]() and $t \in T$
and $t \in T$![]() there is a collection of finitely many analytic maps
there is a collection of finitely many analytic maps
whose $C^{r}$![]() -norm is bounded by $1$
-norm is bounded by $1$![]() and such that for any $t \in T$
and such that for any $t \in T$![]() the ranges of $f_{r,i,t}$
the ranges of $f_{r,i,t}$![]() , for $i = 1,\,\ldots ,\,cr^{m^{3}}$
, for $i = 1,\,\ldots ,\,cr^{m^{3}}$![]() , cover $X_t$
, cover $X_t$![]() . Moreover, for each $i$
. Moreover, for each $i$![]() and $r$
and $r$![]() , $\{f_{r,i,t} \mid t \in T\}$
, $\{f_{r,i,t} \mid t \in T\}$![]() is a definable family of maps.
is a definable family of maps.
Proof. As we explained below Definition 3.1, we may suppose that $X_T$![]() is the graph of a definable function $T \times (0,\,1)^{m} \to [-1,\,1]^{n-m}$
is the graph of a definable function $T \times (0,\,1)^{m} \to [-1,\,1]^{n-m}$![]() . By the previous result, we obtain finitely many $f: C \to X_T$
. By the previous result, we obtain finitely many $f: C \to X_T$![]() , where $C$
, where $C$![]() is an open cell in $T \times (0,\,1)^{m}$
is an open cell in $T \times (0,\,1)^{m}$![]() . Furthermore, $f$
. Furthermore, $f$![]() is prepared in $x$
is prepared in $x$![]() with associated bounded monomial map $b$
with associated bounded monomial map $b$![]() that is $C^{1}$
that is $C^{1}$![]() -bounded in $x$
-bounded in $x$![]() and also the walls of $C$
and also the walls of $C$![]() are of this form. By Proposition 3.10 using the map
are of this form. By Proposition 3.10 using the map
we get finitely many maps $f_{r}: C_{r} \to X_T$![]() , where $C_{r}$
, where $C_{r}$![]() is open in $T \times (0,\,1)^{m}$
is open in $T \times (0,\,1)^{m}$![]() . Moreover, there is an $A > 0$
. Moreover, there is an $A > 0$![]() such that for any $t \in T$
such that for any $t \in T$![]() , the walls $\alpha _1$
, the walls $\alpha _1$![]() and $\beta _1$
and $\beta _1$![]() of $C_{r,t}$
of $C_{r,t}$![]() of $x_1$
of $x_1$![]() are $(A,\,0)$
are $(A,\,0)$![]() -mild, for $i = 2,\,\ldots ,\,m$
-mild, for $i = 2,\,\ldots ,\,m$![]() , the walls $\alpha _i$
, the walls $\alpha _i$![]() and $\beta _i$
and $\beta _i$![]() of $x_i$
of $x_i$![]() are $(Ar^{m},\,0)$
are $(Ar^{m},\,0)$![]() -mild up to order $r$
-mild up to order $r$![]() and $f_{r,t}: C_{r,t} \to X_t$
and $f_{r,t}: C_{r,t} \to X_t$![]() is $(Ar^{m},\,0)$
is $(Ar^{m},\,0)$![]() -mild up to order $r$
-mild up to order $r$![]() .
.
We now inductively map $T \times (0,\,1)^{m}$![]() on the cell $C_r$
on the cell $C_r$![]() as follows. For $i = 1,\,\ldots ,\,m$
as follows. For $i = 1,\,\ldots ,\,m$![]() , define the map
, define the map
given by:
and let $\varPhi = \varPhi _1 \circ \ldots \circ \varPhi _m: T \times (0,\,1)^{m} \to C_r$![]() . If $i \geq 2$
. If $i \geq 2$![]() , since for any $t \in T$
, since for any $t \in T$![]() , $\alpha _i$
, $\alpha _i$![]() and $\beta _i$
and $\beta _i$![]() are $(Ar^{m},\,0)$
are $(Ar^{m},\,0)$![]() -mild up to order $r$
-mild up to order $r$![]() , there is some $A'>0$
, there is some $A'>0$![]() such that for any $t \in T$
such that for any $t \in T$![]() , the map $\varPhi _{i,t}$
, the map $\varPhi _{i,t}$![]() is $(A'r^{m},\,0)$
is $(A'r^{m},\,0)$![]() -mild up to order $r$
-mild up to order $r$![]() , where $A'>0$
, where $A'>0$![]() is possibly larger than $A$
is possibly larger than $A$![]() due to the product (2.15) and addition of mild functions. If $i = 1$
due to the product (2.15) and addition of mild functions. If $i = 1$![]() , $\varPhi _{1,t}$
, $\varPhi _{1,t}$![]() is $(A',\,0)$
is $(A',\,0)$![]() -mild, for possibly larger $A'$
-mild, for possibly larger $A'$![]() . Thus, we obtain that there is some $A' > 0$
. Thus, we obtain that there is some $A' > 0$![]() , possibly larger than $A'$
, possibly larger than $A'$![]() by Corollary 2.11, such that for any $t \in T$
by Corollary 2.11, such that for any $t \in T$![]() , the map $(f_r \circ \varPhi )_t$
, the map $(f_r \circ \varPhi )_t$![]() is $(A''r^{m^{2}},\,0)$
is $(A''r^{m^{2}},\,0)$![]() -mild up to order $r$
-mild up to order $r$![]() .
.
Finally, by Lemma 2.5, covering the unit cube with cubes of size $1/(A''r^{m^{2}})$![]() , we obtain $cr^{m^{3}}$
, we obtain $cr^{m^{3}}$![]() maps that parametrize $X_T$
maps that parametrize $X_T$![]() with bounded $C^{r}$
with bounded $C^{r}$![]() -norm.
-norm.
Remark The main obstacle to obtain a better result (e.g. $cr^{m}$![]() maps as in [Reference Binyamini and Novikov1]), is the power substitution using $r^{m}$
maps as in [Reference Binyamini and Novikov1]), is the power substitution using $r^{m}$![]() to ensure that the walls of the cell are mild up to order $r$
to ensure that the walls of the cell are mild up to order $r$![]() too. Thus it would be interesting to prove a stronger version of Theorem 3.11 that has better walls.
too. Thus it would be interesting to prove a stronger version of Theorem 3.11 that has better walls.
A small improvement that we show now slightly improves the walls. More precisely, if $m \geq 2$![]() , we will show that we can first improve the walls bounding the variable $x_2$
, we will show that we can first improve the walls bounding the variable $x_2$![]() and use a slightly better power substitution with powers up to $r^{m-1}$
and use a slightly better power substitution with powers up to $r^{m-1}$![]() (instead of $r^{m}$
(instead of $r^{m}$![]() ).
).
Suppose we are given a map as a result of Theorem 3.11, call it $f: C \to X_T$![]() , where $C$
, where $C$![]() is an open cell in $T' \times (0,\,1)^{m}$
is an open cell in $T' \times (0,\,1)^{m}$![]() and $T'$
and $T'$![]() a cell contained in $T$
a cell contained in $T$![]() . Now, since the walls bounding $x_1$
. Now, since the walls bounding $x_1$![]() and $x_2$
and $x_2$![]() are prepared in $x$
are prepared in $x$![]() , the first two inequalities defining $C_{t}$
, the first two inequalities defining $C_{t}$![]() are:
are:
We will now manipulate $f$![]() and $C$
and $C$![]() to ensure that the maps $a_i(t)x_1^{r}$
to ensure that the maps $a_i(t)x_1^{r}$![]() and $b_j(t)x_1^{s}$
and $b_j(t)x_1^{s}$![]() become mild for any $t \in T$
become mild for any $t \in T$![]() , by transforming $r$
, by transforming $r$![]() and $s$
and $s$![]() to natural numbers. If they are already mild, there is no power substitution required for these walls and we can use a better version of Proposition 3.10. Suppose that $r-s \geq 0$
to natural numbers. If they are already mild, there is no power substitution required for these walls and we can use a better version of Proposition 3.10. Suppose that $r-s \geq 0$![]() , the other case is similar. Since $G$
, the other case is similar. Since $G$![]() is analytic and non-vanishing on $\text {Im}(b)$
is analytic and non-vanishing on $\text {Im}(b)$![]() , there exists $S>0$
, there exists $S>0$![]() such that $G(b(t,\,x_1)) \in (1/S,\,S)$
such that $G(b(t,\,x_1)) \in (1/S,\,S)$![]() for all $t$
for all $t$![]() and $x$
and $x$![]() . Equivalently: $G(b(t,\,x_1))/S \in (1/S^{2},\,1)$
. Equivalently: $G(b(t,\,x_1))/S \in (1/S^{2},\,1)$![]() . Now consider the map $\phi$
. Now consider the map $\phi$![]() given by:
given by:
Since $b_j(t)x_1^{s}$![]() is $C^{1}$
is $C^{1}$![]() -bounded in $x_1$
-bounded in $x_1$![]() by assumption, the map $\phi$
by assumption, the map $\phi$![]() is $C^{1}$
is $C^{1}$![]() -bounded in $x$
-bounded in $x$![]() . We see that $\phi ^{-1}(C)$
. We see that $\phi ^{-1}(C)$![]() is a cell where the walls bounding $x_1$
is a cell where the walls bounding $x_1$![]() and $x_2$
and $x_2$![]() are now given by:
are now given by:

By the form of $\phi$![]() , the walls bounding $x_3,\,\ldots ,\,x_m$
, the walls bounding $x_3,\,\ldots ,\,x_m$![]() are still prepared in $x$
are still prepared in $x$![]() and their associated bounded monomial map is $C^{1}$
and their associated bounded monomial map is $C^{1}$![]() -bounded in $x$
-bounded in $x$![]() . If $r-s = 0$
. If $r-s = 0$![]() , the walls are already as desired. Denote by $R$
, the walls are already as desired. Denote by $R$![]() the smallest integer greater than or equal to $r-s$
the smallest integer greater than or equal to $r-s$![]() . We then use the power substitution
. We then use the power substitution
to obtain a cell $\tilde {C}$![]() and a map $\tilde {f}: \tilde {C} \to X_T$
and a map $\tilde {f}: \tilde {C} \to X_T$![]() with the same properties as $f$
with the same properties as $f$![]() , i.e. $\tilde {f}$
, i.e. $\tilde {f}$![]() and all of the walls of $\tilde {C}$
and all of the walls of $\tilde {C}$![]() are prepared in $x$
are prepared in $x$![]() with an associated bounded monomial map that is $C^{1}$
with an associated bounded monomial map that is $C^{1}$![]() -bounded in $x$
-bounded in $x$![]() . The walls of $\tilde {C}$
. The walls of $\tilde {C}$![]() bounding $x_1$
bounding $x_1$![]() and $x_2$
and $x_2$![]() are of the form:
are of the form:

where $N \in \operatorname {\mathbb {N}}$![]() . We now have that for any $t \in T$
. We now have that for any $t \in T$![]() , $\tilde {a}_i(t)x_1^{N}$
, $\tilde {a}_i(t)x_1^{N}$![]() is mild. One now proceeds as in the proof of (3.12) using a slightly modified version of Proposition 3.10, namely with the power substitution
is mild. One now proceeds as in the proof of (3.12) using a slightly modified version of Proposition 3.10, namely with the power substitution
In the proof of Theorem 3.12, we would now have that there is some $A>0$![]() such that for any $t \in T$
such that for any $t \in T$![]() , the walls $\alpha _i$
, the walls $\alpha _i$![]() and $\beta _i$
and $\beta _i$![]() of $x_i$
of $x_i$![]() are $(Ar^{m-1},\,0)$
are $(Ar^{m-1},\,0)$![]() -mild up to order $r$
-mild up to order $r$![]() and $f_{r,t}$
and $f_{r,t}$![]() is $(Ar^{m-1},\,0)$
is $(Ar^{m-1},\,0)$![]() -mild up to order $r$
-mild up to order $r$![]() . It follows that for some possibly larger $A$
. It follows that for some possibly larger $A$![]() and for any $t \in T$
and for any $t \in T$![]() , $(f_r \circ \varPhi )_t$
, $(f_r \circ \varPhi )_t$![]() is $(Ar^{m(m-1)},\,0)$
is $(Ar^{m(m-1)},\,0)$![]() -mild up to order $r$
-mild up to order $r$![]() and thus obtain $cr^{m^{2}(m-1)}$
and thus obtain $cr^{m^{2}(m-1)}$![]() maps as result.
maps as result.
It would be interesting to know if we could also transform the walls of the other variables in this way. However, currently, it is not clear how to achieve this.
Acknowledgements
The author would like to thank the referee for reading the article in great detail and giving numerous helpful comments to improve the presentation. The author is partially supported by KU Leuven grant IF C14/17/083.