1 Introduction
Thanks to its excellent performance at high Mach numbers, the scramjet has become one of the first choices of hypersonic air-breathing propulsion systems. It is well known that detonative combustion has been explored extensively for propulsion applications because of its inherent theoretical advantage (Smirnov & Nikitin Reference Smirnov and Nikitin2014; Smirnov et al.
Reference Smirnov, Betelin, Shagaliev, Nikitin, Belyakov, Deryuguin, Aksenov and Korchazhkin2014, Reference Smirnov, Nikitin, Stamov and Altoukhov2015). Therefore, it is believed that the performance of the scramjet might be improved dramatically if detonation-driven combustion can be fully or even partly realized in the supersonic flow inside the scramjet combustor. Based on this idea, we have conducted a series of numerical simulations (Cai et al.
Reference Cai, Liang, Lin, Deiterding and Liu2014, Reference Cai, Liang, Lin, Deiterding and Zhuang2015a
, Reference Cai, Liang, Deiterding and Lin2016a
,Reference Cai, Liang, Deiterding and Lin
b
) on detonation combustion in supersonic combustible mixtures initiated through shock reflection or Mach reflection (Melguizo-Gavilanes et al.
Reference Melguizo-Gavilanes, Rezaeyan, Tian and Bauwens2011; Bhattacharjee et al.
Reference Bhattacharjee, Lau-Chapdelaine, Maines, Maley and Radulescu2013; Melguizo-Gavilanes & Bauwens Reference Melguizo-Gavilanes and Bauwens2013; Lv & Ihme Reference Lv and Ihme2015; Maley et al.
Reference Maley, Bhattacharjee, Lau-Chapdelaine and Radulescu2015) induced by a hot jet, where the open-source program AMROC (adaptive mesh refinement in object-oriented C
$++$
) (Deiterding Reference Deiterding2003, Reference Deiterding2009, Reference Deiterding2011), based on the structured adaptive mesh refinement (SAMR) approach (Berger Reference Berger1982; Berger & Olier Reference Berger and Olier1984), is adopted to solve the reactive Euler equations with a robust second-order accurate monotone upstream-centred scheme for conservation laws/total variation diminishing scheme (MUSCL-TVD). Even though some non-physical substructures may be generated at high grid resolution, the Euler equations have been widely used in detonation simulations (Gamezo, Desbordes & Oran Reference Gamezo, Desbordes and Oran1999; Radulescu et al.
Reference Radulescu, Sharpe, Law and Lee2007; Kessler, Gamezo & Oran Reference Kessler, Gamezo and Oran2011; Mével et al.
Reference Mével, Davidenko, Lafosse, Chaumeix, Dupré, Paillard and Shepherd2015), and qualitative agreement can be obtained between inviscid solutions and experimental observations, especially for weakly unstable detonations (Bhattacharjee et al.
Reference Bhattacharjee, Lau-Chapdelaine, Maines, Maley and Radulescu2013; Mazaheri et al.
Reference Mazaheri, Mahmoudi, Sabzpooshani and Radulescu2015).
Compared with the Euler equations, solving the Navier–Stokes (NS) equations in detonation simulations is theoretically more reliable for actual applications, and has become a topic of recent research interest. Singh et al. (Reference Singh, Rastigejev, Paolucci and Powers2001) investigated viscous detonations in a hydrogen–oxygen–argon mixture using the method of intrinsic low-dimensional manifolds (ILDM) coupled with a wavelet adaptive multilevel representation (WAMR) spatial discretization technique. They found that the resolution of physical diffusion processes minimizes the effects of potentially reaction-inducing artificial entropy layers associated with numerical diffusion. Gamezo, Khokhlov & Oran (Reference Gamezo, Khokhlov and Oran2001) conducted reactive NS simulations to examine the effects of bifurcated shock structures on shock-flame interactions and deflagration to detonation transition (DDT) in shock-tube experiments. They concluded that the presence of a bifurcated structure leads to an increase in the energy-release rate, the formation of the Mach stems in the middle of the shock tube, and the creation of multiple hot spots behind the Mach stem, which eventually facilitates DDT. Flame acceleration and DDT were simulated using the reactive NS equations with a single-step reaction model by Oran & Gamezo (Reference Oran and Gamezo2007). It is reported that the origin of the turbulence in DDT is the Richtmyer–Meshkov (RM) instability induced by repeated shock-flame interactions, and another source of turbulence on small scales is the Kelvin–Helmholtz (KH) instability that appears to be less important than the RM instability. Using the two-dimensional reactive NS equations with one-step Arrhenius kinetics, Gamezo, Ogawa & Oran (Reference Gamezo, Ogawa and Oran2007, Reference Gamezo, Ogawa and Oran2008) computed the flame acceleration and DDT in channels with obstacles. They reproduced the main regimes of flame propagation observed in experiments and studied flame acceleration and DDT phenomena for different configurations with varied obstacle spacing, illustrating two main effects of obstacle spacing. Using the reactive NS equations and one-step chemistry models with diffusive transport of a stoichiometric mixture, Kessler, Gamezo & Oran (Reference Kessler, Gamezo and Oran2010) carried out extensive two-dimensional and three-dimensional simulations of detonation structures with models of diffusive processes in order to investigate the mechanism of flame acceleration and DDT in large obstructed channels, and found that the utilization of the simple reaction model, which is largely insensitive to small variations in model parameters, can qualitatively and quantitatively match the experiments. The dynamics of a one-dimensional detonation was studied by Romick, Aslam & Powers (Reference Romick, Aslam and Powers2012) using a one-step irreversible Arrhenius kinetics model. They reported that diffusion can affect the behaviour of the system by delaying the onset of instability and strongly influencing the dynamics in the unstable regime, and found that the use of the reactive Euler equations to predict detonation dynamics in the unstable and marginally stable regimes is called into question as the selected reactive and diffusive length scales are representative of real physical systems, concluding that the reactive NS is a more appropriate model in such regimes. Paolucci, Zikoski & Wirasaet (Reference Paolucci, Zikoski and Wirasaet2014a ) and Paolucci, Zikoski & Grenga (Reference Paolucci, Zikoski and Grenga2014b ) employed the wavelet adaptive multiresolution representation (WAMR) method including detailed diffusive transport and chemical kinetics models for both one-dimensional and two-dimensional viscous hydrogen–oxygen–argon detonation simulations. They found that small inhomogeneities in species mass fractions are observed due to multicomponent diffusion. When solving viscous equations, the physical viscosity imposes a small-scale cut-off so that the solution subsequently will not change after sufficient refinement, i.e. when the artificial viscosity becomes much smaller than the physical viscosity. Unsteady dynamics of viscous hydrogen–air detonations were investigated by Romick, Aslam & Powers (Reference Romick, Aslam and Powers2015) using a one-dimensional piston-driven method and several distinct propagation behaviours were predicted: a stable detonation, a high-frequency pulsating detonation, a pulsating detonation with two competing modes, a low-frequency pulsating detonation and a propagating detonation with many active frequencies. It was found that the addition of viscosity shifts the neutral stability boundary by about 2 % with respect to the supporting piston velocity. As the supporting piston velocity is lowered, the intrinsic instability grows in strength, and the effect of viscosity is weakened such that the results are indistinguishable from the inviscid predictions. Goodwin, Houim & Oran (Reference Goodwin, Houim and Oran2016, Reference Goodwin, Houim and Oran2017) studied DDT and the effect of decreasing blockage ratio in small channels with obstacles by solving the multidimensional reactive NS equations with one-step Arrhenius kinetics, mainly presenting two types of simulations: one with DDT occurring in a gradient of reactivity and another, in which DDT arises from energy focusing as shocks converge. Simulations with a detailed hydrogen–oxygen reaction model were performed by Grogan & Ihme (Reference Grogan and Ihme2015) with a second-order accurate NS solver to study weak and strong ignition regimes in a shock-tube system, which indicated that the transition from ignition kernel to detonation is well described by the shock wave amplification by coherent energy release (SWACER) mechanism.
The reviewed previous investigations mainly used the reactive NS simulations with diffusive transport. The emphasis has primarily been on flame acceleration and DDT, and comparisons of inviscid and viscous propagating detonation simulations were not presented. The comparison between inviscid and viscous detonations is an interesting issue. When using shock-capturing methods, e.g. the second-order accurate MUSCL-TVD scheme, it is inevitable that numerical diffusion is introduced. Sharpe (Reference Sharpe2001) showed that the detonation structure solved with the Euler equations is grid resolution dependent and indicated that the results can be improved by solving the NS equations. Owing to the domination of numerical diffusion over physical diffusion at low grid resolution, the results solving the Euler and NS equations are quite similar. However, as the grid resolution increases, numerical diffusion decreases and physical diffusion becomes more important. A comprehensive discussion of this issue is also provided by Samtaney & Pullin (Reference Samtaney and Pullin1996).
Oran et al. (Reference Oran, Weber, Stefaniw, Lefebvre and Anderson1998) conducted a series of detonation simulations using both the Euler and NS equations with a detailed reaction model and observed similar detonation structures. They indicated that the small-scale structures, which are eliminated in the Euler equations, do not have a significant influence on the overall detonation features; however, it should be noted that only the weakly unstable detonation was considered in these simulations. Mazaheri, Mahmoudi & Radulescu (Reference Mazaheri, Mahmoudi and Radulescu2012) suggested that from the comparison using the reactive Euler and NS equations, the diffusion effect plays no role in weakly unstable detonations due to the absence of hydrodynamic instabilities, i.e. the KH and RM instability; however, in highly unstable detonations the diffusion effect behind the detonation fronts can play a significant role in detonation structures due to hydrodynamic instabilities, indicating that the NS equations should be solved especially for highly unstable cases. Furthermore, Mahmoudi et al. (Reference Mahmoudi, Karimi, Deiterding and Emami2014) showed that purely hydrodynamic instabilities alone cannot lead to full consumption of the unburned gases behind the shock front and they pointed out that the effect of vorticity generation and energy dissipation should in addition be considered. Shen & Parsani (Reference Shen and Parsani2017) have demonstrated that for mildly and highly unstable detonations, one-dimensional approaches break down because they cannot take the effects and interactions of multidimensional instabilities into account, while for stable detonations one-dimensional approaches are valid due to the absence of multidimensional instabilities. Oran & Gamezo (Reference Oran and Gamezo2007) noticed that the main detonation features grow at intrinsically the same rate in both the reactive Euler and NS simulations; however, the generation and development of the secondary instability, i.e. the KH instability, is suppressed in the NS simulation. Ziegler et al. (Reference Ziegler, Deiterding, Shepherd and Pullin2011) carried out direct numerical simulations of the multicomponent compressible reactive NS equations to investigate the accurate solution of diffusive processes within reaction zones. It is demonstrated that there is a clear difference between simulations with and without diffusive transport in regions close to shear layers and jetting, and the diffusion dramatically affects the presence of the large-scale structures within the shear layer, which are very prominent features (Liang et al. Reference Liang, Browne, Deiterding and Shepherd2007) in the inviscid detonation.
The numerical investigations mentioned above have contributed significantly to the understanding of inviscid and viscous detonations. However, the diffusion effect resulting from hydrodynamic instabilities is still not well understood in propagating detonations, especially associated with the mixing effect. We recently computed two-dimensional adaptive detonation simulations with a hot jet initiation, using the reactive NS equations and a one-step two-species chemistry model in expanding channels filled with a supersonic hydrogen–oxygen mixture (Cai et al. Reference Cai, Deiterding, Liang and Mahmoudi2017), in which the role of the diffusion effect on the unburned jet resulting from the expansion fan is discussed. It is indicated that the diffusion effect inherent to the NS equations can suppress the small-scale vortices, but it plays an almost negligible role in the evolution of large-scale vortices resulting from both the highly unstable KH instability along the shear layers and the RM instability behind the detonation front. However, a detailed investigation on diffusion and mixing effects is still absent for the hot jet initiation, and the role of diffusion and mixing effects on propagating modes of detonations in supersonic combustible mixtures has not been addressed so far. Therefore, in the present work, utilizing the robust second-order accurate MUSCL-TVD scheme together with the efficient SAMR framework, viscous detonation simulations with a hot jet initiation in supersonic combustible mixtures are performed solving the reactive NS equations with the simple one-step reaction model. Also, the corresponding inviscid detonation simulations are additionally conducted using the reactive Euler equations and the same simplified reaction model for a direct comparison and analysis. It is reported that the detonation evolution in supersonic combustible mixtures is considerably different to that in quiescent combustible mixtures (Cai et al. Reference Cai, Liang, Lin, Deiterding, Qin and Han2015b ; Cai, Liang & Deiterding Reference Cai, Liang and Deiterding2016). Our work is part of ongoing research, aimed at providing information to improve the overall understanding of detonation physics in supersonic combustible mixtures.
The remainder of the paper is organized as follows: the calculation method is presented in § 2, including the governing equations, numerical scheme and calculation set-up. Validation of adaptive mesh refinement, grid resolution effects and evaluation of diffusive scales are discussed in § 3. The hot jet initiation and propagating modes in supersonic combustible mixtures are shown in § 4, in which the diffusion and mixing effects are studied through the inviscid and viscous reactive double Mach reflection (DMR) patterns during the initiation process. By solving the reactive Euler and NS equations, propagating detonation structures and their development under diffusion and mixing effects are analysed. In § 5, the effect of the simple reaction model is discussed, and finally § 6 concludes the paper.
2 Governing equations and numerical methods
2.1 Governing equations
The reactive compressible flows are governed by the Euler and NS equations in combination with the one-step two-species chemistry model (Ziegler et al. Reference Ziegler, Deiterding, Shepherd and Pullin2011). An ideal gas mixture with zero bulk viscosity and mixture averaged transport is assumed. Thermal diffusion due to concentration gradients, external body forces and radiative heat transfer are neglected (Williams Reference Williams1985). The two-dimensional governing equations are expressed as follows:
$$\begin{eqnarray}\displaystyle & \displaystyle \frac{\unicode[STIX]{x2202}U}{\unicode[STIX]{x2202}t}+\frac{\unicode[STIX]{x2202}F_{conv}}{\unicode[STIX]{x2202}x}+\frac{\unicode[STIX]{x2202}H_{conv}}{\unicode[STIX]{x2202}y}=S_{chem}, & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle \frac{\unicode[STIX]{x2202}U}{\unicode[STIX]{x2202}t}+\frac{\unicode[STIX]{x2202}(F_{conv}-F_{diff})}{\unicode[STIX]{x2202}x}+\frac{\unicode[STIX]{x2202}(H_{conv}-H_{diff})}{\unicode[STIX]{x2202}y}=S_{chem}. & \displaystyle\end{eqnarray}$$
Equations (2.1a ) and (2.1b ) are the corresponding reactive Euler and NS equations, respectively, where the vector of state is
$$\begin{eqnarray}U=(\unicode[STIX]{x1D70C},\unicode[STIX]{x1D70C}u,\unicode[STIX]{x1D70C}v,\unicode[STIX]{x1D70C}e,\unicode[STIX]{x1D70C}Y_{1}).\end{eqnarray}$$
Here,
$\unicode[STIX]{x1D70C}$
,
$u$
,
$v$
,
$e$
and
$Y_{1}$
are the total density, the velocity in the
$x$
-direction, the velocity in the
$y$
-direction, the total energy per unit mass and the mass fraction of the reactant, respectively.
The convective and diffusive fluxes are
$$\begin{eqnarray}\displaystyle & \displaystyle F_{conv}=(\unicode[STIX]{x1D70C}u,\unicode[STIX]{x1D70C}u^{2}+p,\unicode[STIX]{x1D70C}uv,\unicode[STIX]{x1D70C}ue+up,\unicode[STIX]{x1D70C}uY_{1}), & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle H_{conv}=(\unicode[STIX]{x1D70C}v,\unicode[STIX]{x1D70C}uv,\unicode[STIX]{x1D70C}v^{2}+p,\unicode[STIX]{x1D70C}ve+vp,\unicode[STIX]{x1D70C}vY_{1}), & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle F_{diff}=\left(0,\unicode[STIX]{x1D70F}_{xx},\unicode[STIX]{x1D70F}_{xy},u\unicode[STIX]{x1D70F}_{xx}+v\unicode[STIX]{x1D70F}_{xy}+k\frac{\unicode[STIX]{x2202}T}{\unicode[STIX]{x2202}x}+\unicode[STIX]{x1D70C}h_{1}D_{1}\frac{\unicode[STIX]{x2202}Y_{1}}{\unicode[STIX]{x2202}x}+\unicode[STIX]{x1D70C}h_{2}D_{2}\frac{\unicode[STIX]{x2202}Y_{2}}{\unicode[STIX]{x2202}x},\unicode[STIX]{x1D70C}D_{1}\frac{\unicode[STIX]{x2202}Y_{1}}{\unicode[STIX]{x2202}x}\right), & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle H_{diff}=\left(0,\unicode[STIX]{x1D70F}_{yx},\unicode[STIX]{x1D70F}_{yy},u\unicode[STIX]{x1D70F}_{yx}+v\unicode[STIX]{x1D70F}_{yy}+k\frac{\unicode[STIX]{x2202}T}{\unicode[STIX]{x2202}y}+\unicode[STIX]{x1D70C}h_{1}D_{1}\frac{\unicode[STIX]{x2202}Y_{1}}{\unicode[STIX]{x2202}y}+\unicode[STIX]{x1D70C}h_{2}D_{2}\frac{\unicode[STIX]{x2202}Y_{2}}{\unicode[STIX]{x2202}x},\unicode[STIX]{x1D70C}D_{1}\frac{\unicode[STIX]{x2202}Y_{1}}{\unicode[STIX]{x2202}y}\right), & \displaystyle\end{eqnarray}$$
and the reactive source term is
$$\begin{eqnarray}S_{chem}=(0,0,0,0,0,{\dot{w}}_{1}).\end{eqnarray}$$
Here
$\unicode[STIX]{x1D749}$
is the stress tensor;
$h_{1}$
and
$h_{2}$
are the enthalpies of the reactant and product, respectively;
${\dot{w}}_{1}$
is the mass production rate of the reactant. Then
$\unicode[STIX]{x1D707}$
,
$k$
,
$D_{1}$
,
$D_{2}$
are the mixture viscosity, the thermal conductivity and the mass diffusivities of the reactant and the product, respectively. Here
$e$
is defined as
$$\begin{eqnarray}e=\frac{p}{\unicode[STIX]{x1D70C}(\unicode[STIX]{x1D6FE}-1)}+\frac{(u^{2}+v^{2})}{2}+Y_{1}q,\end{eqnarray}$$
where
$q$
is the heat release per unit mass. The stresses read
$$\begin{eqnarray}\displaystyle \left.\begin{array}{@{}c@{}}\displaystyle \unicode[STIX]{x1D70F}_{xx}=\unicode[STIX]{x1D707}\left(\frac{4}{3}\frac{\unicode[STIX]{x2202}u}{\unicode[STIX]{x2202}x}-\frac{2}{3}\frac{\unicode[STIX]{x2202}v}{\unicode[STIX]{x2202}y}\right),\\ \displaystyle \unicode[STIX]{x1D70F}_{xy}=\unicode[STIX]{x1D70F}_{yx}=\unicode[STIX]{x1D707}\left(\frac{\unicode[STIX]{x2202}v}{\unicode[STIX]{x2202}x}+\frac{\unicode[STIX]{x2202}u}{\unicode[STIX]{x2202}y}\right)\quad \text{and}\quad \unicode[STIX]{x1D70F}_{yy}=\unicode[STIX]{x1D707}\left(\frac{4}{3}\frac{\unicode[STIX]{x2202}v}{\unicode[STIX]{x2202}y}-\frac{2}{3}\frac{\unicode[STIX]{x2202}u}{\unicode[STIX]{x2202}x}\right).\end{array}\right\} & & \displaystyle\end{eqnarray}$$
Currently, it is very expensive to conduct high-resolution multi-dimensional detonation simulations solving the NS equations with detailed chemistry. The Arrhenius law that relates chemical reaction rates to temperature variation is widely used as the simplest mode for detonation simulations (Oran & Gamezo Reference Oran and Gamezo2007; Kessler et al. Reference Kessler, Gamezo and Oran2010; Goodwin et al. Reference Goodwin, Houim and Oran2016, Reference Goodwin, Houim and Oran2017).
Here the reaction model is selected and fitted to the physical parameters of a
$\text{H}_{2}/\text{O}_{2}$
detonation initially at
$T=300~\text{K}$
and
$P=6.67~\text{kPa}$
, which defines a marginally stable detonation. The Zel’dovich–von Neumann–Döring (ZND) solution calculated with detailed chemistry is used to make an approximate chemistry and transport model. The Arrhenius rate, activation energy, pre-exponential, heat release and specific heat ratio are calculated by matching the Chapman–Jouguet (CJ) speed and the von Neumann pressure at the front of the ZND detonation.
For the two species, the calorically perfect model
$$\begin{eqnarray}\unicode[STIX]{x1D6FE}=\unicode[STIX]{x1D6FE}_{1}=\unicode[STIX]{x1D6FE}_{2},\quad p=\unicode[STIX]{x1D70C}RT,\quad R=R_{1}=R_{2}\end{eqnarray}$$
is used. The mass fraction production rates are given as follows:
$$\begin{eqnarray}{\dot{w}}_{1}=-{\dot{w}}_{2}=\unicode[STIX]{x1D70C}Y_{1}A\exp \left(\frac{E_{a}}{RT}\right).\end{eqnarray}$$
The thermodynamic parameters are shown in table 1 and yield a CJ velocity of
$V_{CJ}=1587.84~\text{m}~\text{s}^{-1}$
. At the end of the ZND reaction zone, the temperature is about 2500 K and the pressure is approximately 101.325 kPa, which gives the following transport parameters for the one-step model:
$T_{ref}=2500~\text{K}$
,
$\unicode[STIX]{x1D707}_{ref}=1.07\times 10^{-4}~\text{Pa}~\text{s}$
,
$k_{ref}=0.148~\text{W}~(\text{m}~\text{K})^{-1}$
,
$D_{1ref}=5.5\times 10^{-4}~\text{m}^{2}~\text{s}^{-1}$
,
$D_{2ref}=6.4\times 10^{-4}~\text{m}^{2}~\text{s}^{-1}$
(Ziegler Reference Ziegler2011; Ziegler et al.
Reference Ziegler, Deiterding, Shepherd and Pullin2011).
Table 1. Thermodynamic parameters of the mixture.
By matching the general trends and values at the end of the ZND reaction zone between the one-step and the detailed reaction model, the viscosity and conductivity are given by the Sutherland model, while the mass diffusion is given by a simple expression which includes the inverse dependence on pressure, i.e.
$$\begin{eqnarray}\frac{u}{u_{ref}}=\left(\frac{T}{T_{ref}}\right)^{5/2},\quad \frac{k}{k_{ref}}=\left(\frac{T}{T_{ref}}\right)^{5/2},\end{eqnarray}$$
$$\begin{eqnarray}\frac{D_{1}}{D_{1ref}}=\left(\frac{T}{T_{ref}}\right)^{5/2}\frac{p_{atm}}{p},\quad \frac{D_{2}}{D_{2ref}}=\left(\frac{T}{T_{ref}}\right)^{5/2}\frac{p_{atm}}{p}.\end{eqnarray}$$
2.2 Numerical scheme
Dimensional splitting is employed for the two-dimensional simulations. For the reactive simulations, a time-splitting method is used due to the large difference in time scales between the fluid dynamics and the reactive source term.
The second-order accurate MUSCL-TVD finite volume method (FVM) is adopted for discretization of the convective part of the NS equations, while the second-order accurate centred difference (CD) scheme is used for the diffusive term. Unlike shock-capturing methods, no numerical viscosity is introduced for schemes based on centred stencils, thus being able to accurately describe the physical diffusion. As for the reactive source term, a semi-implicit, A-stable generalized Runge–Kutta method of fourth order (GRK4A) implemented by Kaps & Rentrop (Reference Kaps and Rentrop1979) is utilized for the integration, avoiding a globally coupled implicit problem.
Additional restrictions are imposed on the time integration by the CD scheme. It is relatively easy to use explicit multi-stage time integration methods for the implementation with SAMR. Because of the stability properties of the explicit integration schemes, the preferred practical methods with the ability of inexpensive time adaptation in SAMR are Runge–Kutta methods. Here, the optimal second-order accurate strong stability preserving (SSP) Runge–Kutta scheme is used with a CFL parameter of 0.98.
2.3 Calculation set-up
Numerical simulations of viscous and inviscid detonations in the supersonic combustible mixture using a hot jet initiation are conducted in a straight channel, as depicted in figure 1. A reflecting boundary with slip wall condition is used on the upper and lower wall, while an inflow set-up is embedded into the lower wall boundary to model the hot jet. The right boundary is given the inflow condition and the left one imposes an ideal outflow condition, implemented by constant value extrapolation of the interior data into the ghost cells.
Figure 1. Schematic of the calculation set-up.
The inflow parameters of the hot jet are set to the ZND state of
$\text{H}_{2}$
and
$\text{O}_{2}$
under the condition of pressure 6.67 kPa and temperature 300 K. The injection velocity is given the sonic speed to make it a chocked hot jet, as shown in table 2.
Table 2. The equilibrium CJ state. Note that the parameters for the species are given as mass fractions.
2.4 Dimensional splitting
It is reported that when considering the reactive source term utilizing the first-order accurate Godunov splitting or the second-order accurate Strang splitting, the difference is marginal (Deiterding Reference Deiterding2003). However, as the difference between Godunov and Strang is a question of how boundary conditions interact with the splitting method, the results could change considerably for problems with very strong boundary dependence. To demonstrate that the difference is in fact small for the configurations in the present work, a small calculation is performed with both the first-order-accurate Godunov splitting and the second-order-accurate Strang splitting.
As shown in figure 2, it can be observed that the overall detonation structures for the two methods are very similar. When using the Strang splitting method, a secondary triple point can be noticed in the detonation front in figure 2(d). After the triple point collision, an additional detached shear layer is therefore generated behind the detonation front and becomes gradually dissipated, as shown in figure 2(e,f). Indicated from the comparison between figures 2(c) and 2(f), it can be concluded that the utilized splitting methods do not play an important role in the overall detonation structure, although an additional secondary triple point is formed in the front.
Figure 2. Detonation propagation using both Godunov and Strang splitting: (a–c) Godunov splitting, (d–f) Strang splitting; (a,d)
$t=325~\unicode[STIX]{x03BC}\text{s}$
, (b,e)
$t=340~\unicode[STIX]{x03BC}\text{s}$
, (c,f)
$t=355~\unicode[STIX]{x03BC}\text{s}$
.
Figure 3 shows the locations of detonation fronts versus time for the two splitting methods. In figure 3(a), the two curves are almost coupled together, although the curve enlargement in figure 3(b) shows slightly staggered positions. Nevertheless, the periods using the two different methods are the same, indicated from figure 3(b).
Based on these results, it is justified to conclude that the difference between the two splitting methods is generally minor. Therefore, the computationally more efficient Godunov splitting is employed for the decoupling of the source term in the following simulations.
3 Results and analysis
As shown in figure 1, the length of the straight channel is
$x_{1}=75~\text{mm}$
and the height is
$y_{1}=25~\text{mm}$
. The distance between the hot jet and the head wall is
$x_{2}=25~\text{mm}$
, and the width of the hot jet is
$x_{3}=4~\text{mm}$
. The initial mesh has
$600\times 200$
cells, giving an initial grid resolution of
$1.25\times 10^{-4}~\text{m}$
in both
$x$
- and
$y$
-directions. All computations used 15 nodes, where every node had 20 cores on a parallel cluster. The processors are Intel E5-2692 (Ivy Bridge) with a clock speed of 2.2 GHz.
3.1 Validation of adaptive mesh refinement
Three different cases of adaptive mesh refinement are conducted to investigate the effect of the SAMR level distribution on detonation evolution. Here, the viscous detonation is chosen for the verification. The detailed information of the adaptive mesh refinement is shown in table 3.
Figure 3. Locations of detonation fronts using the two methods.
Table 3. Mesh refinement parameters.
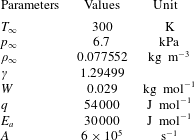
After the injection of the hot jet into the supersonic combustible mixture, a bow shock is first induced and finally a Mach reflection is generated after the bow shock reflection on the upper wall. Figure 4 depicts the typical hot-jet-induced Mach reflection during the initiation process. This kind of reactive Mach reflection is in fact a local Mach detonation due to the tight coupling of the Mach stem and the reaction front following behind (Cai et al. Reference Cai, Liang, Lin, Deiterding and Zhuang2015a ). The overall pattern associated with the primary triple point resulting from the reactive Mach reflection (Mach stem, transverse wave, incident shock, slip line and reaction zone) are qualitatively similar in the three cases with different grid resolutions. Beside the primary triple point, the secondary triple point is also resolved clearly, generating a typical DMR together with the primary Mach reflection. It should be especially noted that these characteristic structures are all captured by the highest refinement levels, indicating that adaptive mesh refinement is established efficiently in the simulations.
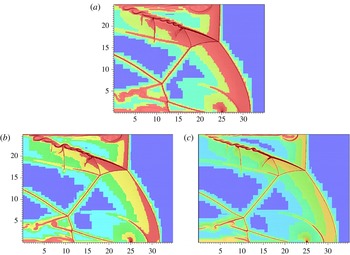
Figure 4. Reactive Mach reflection induced by the hot jet injection for the three different cases given in table 3: (a) Case 1, (b) Case 2, (c) Case 3.
3.2 Effect of grid resolution
It is believed that the influence of diffusion is strongest in shear layers and at unburned pocket boundaries (Mazaheri et al. Reference Mazaheri, Mahmoudi and Radulescu2012). For the inviscid detonation considered here, the diffusion effect is determined by numerical dissipation introduced by the MUSCL-type scheme, which is highly grid-resolution dependent. Therefore, with the increase of grid resolution, the diffusion effect in the inviscid detonation gradually becomes weaker, thus resulting in a decreased suppression of small-scale vortices induced by the secondary instability (i.e. the KH instability). As a result a growing number of small-scale vortices can be observed along the slip lines in figure 5(a–c), which is due to the highly unstable shear layers driven by the KH instability. Note that figure 5(a–c) indicates non-convergence, which is the expected result when the inviscid equations are approximated with a high-resolution scheme at very fine grid resolutions.
In the case of the viscous detonation, physical viscosity reduces the unstable growth. Small-scale vortices along the slip lines are nearly all smeared out and only the large-scale modes of the KH instability remain. When the slip line is fully developed to generate highly unstable shear layers, the large-scale vortices driven by the KH instability are still clearly observed, almost unaltered by diffusion. This is in accordance with the experimental observation of Pintgen et al. (Reference Pintgen, Eckett, Austin and Shepherd2003), which indicates that the large-scale characteristics induced by the KH instability are correctly reproduced. Therefore, the structures in the vicinity of the slip lines in figure 5(d–f) are smoother and more regular than those in the corresponding flow fields in figure 5(a–c). In addition, with the increase of grid resolution, the results in figure 5(d–f) do not differ considerably, indicating a better converging trend of these simulations. In general, figure 5 illustrates that under certain conditions the accurate modelling of physical viscosity can be essential for obtaining reliable high-resolution results when simulating supersonic detonation ignition.
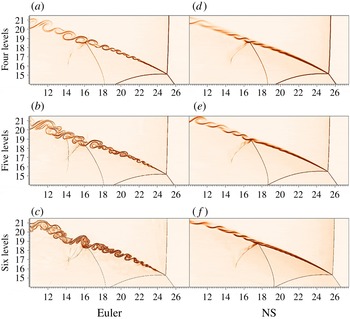
Figure 5. Effect of grid resolution on inviscid and viscous shear layers.
3.3 Diffusive scales
Resolving diffusive processes in viscous detonations properly requires first the estimation of the necessary grid resolution. Table 4 gives the density, temperature and pressure at the top and bottom of the shear layer behind the primary triple point for the three cases. It is shown that these quantities for the three grid resolutions at the same corresponding positions are very close to one another and within a relative error band smaller than 1 %, further indicating that using the NS equations for viscous detonations can provide reliable results.
Table 4. Three quantities behind the primary triple point.
Using the average density (
$0.3754~\text{kg}~\text{m}^{-3}$
), temperature (1871.8 K) and pressure (176.82 kPa) in table 4, the viscosity, mass diffusivity and thermal conductivity are calculated as
$5.19\times 10^{-5}~\text{Pa}~\text{s}$
,
$1.528\times 10^{-4}~\text{m}^{-2}~\text{s}^{-1}$
, and
$7.179\times 10^{-2}~\text{W}~(\text{m}~\text{K})^{-1}$
, respectively. Subsequently, using the time scale at which the shear layer begins to become unstable (approximate
$30~\unicode[STIX]{x03BC}\text{s}$
in figure 4), following Ziegler et al. (Reference Ziegler, Deiterding, Shepherd and Pullin2011), the diffusive scales of viscosity, mass diffusivity and heat conductivity are evaluated as
$6.467\times 10^{-5}~\text{m}$
,
$2.104\times 10^{-4}~\text{m}$
and
$7.711\times 10^{-5}~\text{m}$
, respectively. Among the three diffusive scales, the viscous scale is the smallest one, indicating that the viscous scale is the only limit for a fully resolved simulation. As shown in table 3, the highest grid resolutions for all the three cases are all smaller than the viscous scale, and about 5 to 20 cells are within the smallest viscous scale, suggesting that these diffusive scales are expected to be fully resolved. As a compromise between computational cost and resolved resolution, the five-level mesh refinement is adopted tacitly in the following simulations, unless otherwise mentioned.
4 Hot jet initiation and propagation
Understanding the behaviour of the hot jet initiation and propagating detonation in the supersonic combustible mixture is important for detonation physics and actual applications (Cai et al. Reference Cai, Liang, Lin, Deiterding and Liu2014, Reference Cai, Liang, Lin, Deiterding, Qin and Han2015b ). In this section, the hot jet initiation and propagating detonation are investigated using both the Euler and NS equations. The diffusion and mixing effects are discussed in detail.
4.1 Hot jet initiation
The hot jet initiation process in the supersonic combustible mixture has been fully described in our previous work (Cai et al. Reference Cai, Liang, Lin, Deiterding, Qin and Han2015b ). To obtain an overall understanding of this issue, a brief illustration is first provided here as shown in figure 6, where the hot jet is illustrated using the red arrows.
A bow shock is induced in the channel when the hot jet is injected into the supersonic incoming flow, and subsequently a Mach reflection is formed after the bow shock reflection on the upper wall, as shown in figure 6(a). It has been demonstrated that the Mach stem is in fact a local Mach detonation (Cai et al. Reference Cai, Liang, Deiterding, Che and Lin2016c ), indicating the detonation onset in the supersonic combustible mixture. Due to the formation of the contractive passage generated by the upper wall and the free boundary of the slip line directly behind the triple point, the Mach detonation propagates forward towards the incoming combustible mixture, as shown in figure 6(b). After the triple point reaches the lower wall, the second reflection is produced in figure 6(c) which acts as a strong ignition source for the successful full realization of detonation. As shown in figure 6(d), the detonation propagates forward continuously with the help of the continuous injection of the hot jet, hence resulting in the formation of an overdriven detonation (Liang et al. Reference Liang, Cai, Lin and Deiterding2014).
Figure 6. The hot jet induced detonation initiation: (a)
$t=140~\unicode[STIX]{x03BC}\text{s}$
, (b)
$t=160~\unicode[STIX]{x03BC}\text{s}$
, (c)
$t=190~\unicode[STIX]{x03BC}\text{s}$
, (d)
$t=210~\unicode[STIX]{x03BC}\text{s}$
.
4.1.1 Inviscid and viscous reactive DMRs
Figure 7 shows the enlarged DMRs for both the viscous and inviscid detonations using density isolines and product mass fraction contours. Near the upper wall are the large-scale vortices resulting from the Mach stem bifurcation (Mach & Radulescu Reference Mach and Radulescu2011), which initially undergoes an RM instability involving the baroclinic vorticity production mechanism (Radulescu et al. Reference Radulescu, Sharpe, Lee, Kiyanda, Higgins and Hanson2005). The vortices are detaching from the Mach stem when it gradually becomes normal to the upper wall. Between the slip line behind the primary triple point and the reaction front induced by the bow shock, a large triangular unburned jet is generated behind the shock front. Underneath the unburned jet is the partly unburned reactant behind the bow shock. Besides the primary and secondary triple points and the related structures, an expansion wave is also generated from the interaction between the Mach stem of the secondary Mach reflection and the slip line associated with the highly unstable shear layer. Apparently, the structures of the inviscid and viscous reactive DMR patterns in figure 7 are mostly the same.
Figure 7. Inviscid and viscous reactive DMRs.
However, the main difference occurs within the slip line associated with the highly unstable shear layer resulting from the KH instability and the large-scale vortices behind the primary Mach stem, generated from the Mach stem bifurcation. In the viscous DMR, the slip line directly emitted from the primary triple point is initially very smooth without any vortices, indicating that the KH instability is completely suppressed. The diffusion effect can easily suppress small-scale vortices produced by the KH instability (Gamezo et al.
Reference Gamezo, Khokhlov and Oran2001; Oran & Gamezo Reference Oran and Gamezo2007). In figure 7(a), the instability along the slip line begins to occur at
$x=19~\text{mm}$
and then the vortices gradually grow larger due to the KH instability. In the inviscid DMR, however, the small-scale vortices are generated almost as soon as the slip line emits from the triple point at
$x=23~\text{mm}$
, as shown in figure 7(c). Therefore, the vortices associated with the slip line in the inviscid DMR grow more quickly and reach a larger extent than in the viscous DMR.
In figure 7(b,d), the free boundary separated by the slip line can be observed between the unburned jet and burned product behind the Mach stem. Due to the entrainment effect of the vortices, the unburned reactant in the vicinity of the boundary can be easily consumed through the mixing with the burned product. In figure 7(b), the mass fraction of the product is 20.3 % near the slip line behind the expansion wave, while in figure 7(d) it reaches 22.07 % at approximately the same position, which is 8.72 % higher than that in figure 7(b), indicating that the vortices resulting from the KH instability are beneficial for the consumption of the reactant through the mixing effect. At the same time, it is also suggested that the diffusion effect in the viscous detonation can efficiently suppress the growth of the KH instability, which can decrease the mixing rate and further slow the consumption of the unburned reactant.
4.1.2 Consumption of the partly unburned reactant
As the Mach detonation propagates forward, the triple point moves towards the lower wall with the shear layer following behind. Although a marginally stable detonation is adopted, due to the KH instability the shear layer becomes more unstable and even turbulent when it moves downwards. It is reported that the large-scale vortices in the highly unstable shear layer can induce the formation of turbulent flow and rapid turbulent mixing between the unburned jet and the burned product (Cai et al. Reference Cai, Deiterding, Liang and Mahmoudi2017).
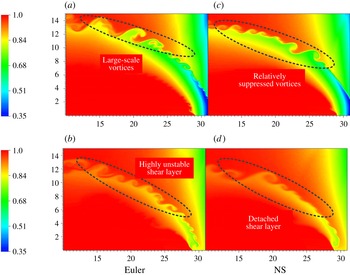
Figure 8. Consumption of the partly unburned reactant: (a)
$t=200~\unicode[STIX]{x03BC}\text{s}$
, (b)
$t=210~\unicode[STIX]{x03BC}\text{s}$
, (c)
$t=190~\unicode[STIX]{x03BC}\text{s}$
, (d)
$t=200~\unicode[STIX]{x03BC}\text{s}$
.
Hence, the unburned triangular jet is quickly consumed because of rapid turbulent mixing, as shown in figure 8(a,c). After the triple point collision on the lower wall, the highly unstable shear layer is detached from the triple point and then is entirely mixed with the partly unburned reactant behind the bow shock depicted in figure 7, which can efficiently accelerate the consumption of the partly unburned reactant. As shown in figure 8(b,d), the mass fraction of the product in the vicinity of the hot jet exit is approximately 85 %, while in figure 8(a,c) it is only about 65 %, suggesting that the mixing effect of the vortices resulting from the highly unstable detached shear layer can accelerate the consumption of the partly unburned reactant.
Figure 9. Maximal mass fraction of the product in the vicinity of the detached shear layers in figure 6(b,d).
Compared with figure 8(a), the vortices in figure 8(c) are relatively smaller due to the suppression of the KH instability resulting from the stronger diffusion effect in the NS solution, thus to some degree lowering the mixing effect on the consumption of the partly unburned reactant. The diffusion effect can increase the reaction rate of the unburned reactant as a result of the heat and mass transport from the neighbouring burned product (Mazaheri et al. Reference Mazaheri, Mahmoudi and Radulescu2012). Figure 9 shows the maximal mass fraction of the product between [12.5, 27.5] mm along the shear layers in the inviscid and viscous detonations. It is found that the mass fraction for the viscous detonation is generally slightly higher than that in the inviscid detonation, indicating that more unburned reactant is consumed in the viscous shear layer.
It should be noted that the burning rate of the reactant, which is represented by the slope of the curve, also shows different characteristics. The burning rate for the viscous detonation is relatively steady, while for the inviscid detonation it shows larger variations. In the viscous shear layer, the vortices are more regular because of the stronger influence of physical viscosity and diffusion. Mixing from vortices plays a role in the consumption of the unburned reactant; however, in the inviscid shear layer, the vortices are more irregular and associated with larger oscillations. As a result of the limited numerical viscosity in the inviscid detonation, artificial mixing has an important influence on the consumption of the unburned reactant. Yet, in the viscous case an increased diffusion, rather than mixing, leads to an ultimately faster consumption of the reactant within the shear layer.
4.2 Propagating detonation
4.2.1 Inviscid detonation
Figure 10 shows the inviscid detonation structure with the continuous injection of the hot jet. Two primary triple points coexist together in all four successive frames.
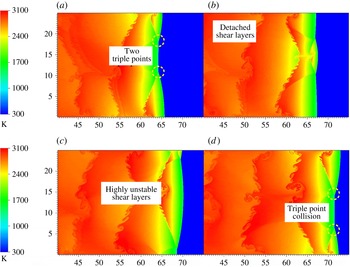
Figure 10. The inviscid detonation structure: (a)
$t=330~\unicode[STIX]{x03BC}\text{s}$
, (b)
$t=340~\unicode[STIX]{x03BC}\text{s}$
, (c)
$t=350~\unicode[STIX]{x03BC}\text{s}$
, (d)
$t=360~\unicode[STIX]{x03BC}\text{s}$
.
In figure 10(a), the two triple points are going to collide with each other, and after the collision in figure 10(b) the shear layers have detached from the triple points. Behind the detonation front, irregular vortices are observed along the detached shear layers. Further away from the detonation front as shown in figure 10(c), the detached shear layers become more unstable, and the small-scale vortices undergo a transition to the large-scale vortices due to hydrodynamic instabilities, thus resulting in the formation of the highly unstable shear layers. Eventually in figure 10(d), the two triple points are going to collide once again. The results in figure 8 illustrate a complete periodic process of the two triple point collisions for the inviscid propagating detonation. It can be calculated that a full period of triple point collisions is approximately
$T_{inv}=30~\unicode[STIX]{x03BC}\text{s}$
and subsequently the transverse wave velocity is obtained as
$v_{T_{inv}}=833~\text{m}~\text{s}^{-1}$
(
$v_{T_{inv}}=Y_{1}/T_{inv}$
).
It has been shown conclusively that particularly small-scale vortices behind the inviscid detonation front are unphysical, lead to non-convergence under high grid resolution and are the result of a lack of viscous damping in the Euler model.
4.2.2 Viscous detonation
Figure 11 shows the structure of the viscous detonation with continuous injection of the hot jet. In all the four successive frames, only one primary triple point can be observed in the detonation front, which is different from the inviscid detonation. Other than the primary triple point, about two secondary triple points can also be observed in the detonation front. It is apparent that diffusion effects in the viscous detonation can alter and partially suppress the oscillating instability at the detonation front, thus generating only one primary triple point at this instant in time. Behind the detonation front, there also exist detached shear layers; however, these shear layers are essentially very smooth without any small-scale vortices generated and only a few large-scale vortices occur in the tails of the shear layers. Unlike that in figure 10, the detached shear layers away from the detonation front are gradually dissipated and even disappear eventually. Due to the diffusion effect of the physical viscosity in the NS equations, the small-scale vortices induced by the KH instability are almost entirely suppressed.
Figure 11 shows roughly one periodic process and the full period of the triple point collision is about
$T_{vis}=28.75~\unicode[STIX]{x03BC}\text{s}$
, 4.17 % lower than the inviscid result. The corresponding transverse velocity is
$v_{T_{vis}}=869~\text{m}~\text{s}^{-1}$
, 4.32 % higher than that of the inviscid one. Lee (Reference Lee1984) pointed out that the transverse wave propagates at about the sound speed of the product. Therefore, it is believed that the temperature behind the viscous detonation is relatively higher than that in the inviscid case, which is due to the exclusive dependence of the sound speed on temperature here, suggesting a faster heat release rate behind the viscous detonation.
Figure 11. The viscous detonation structures: (a)
$t=320~\unicode[STIX]{x03BC}\text{s}$
, (b)
$t=330~\unicode[STIX]{x03BC}\text{s}$
, (c)
$t=340~\unicode[STIX]{x03BC}\text{s}$
, (d)
$t=350~\unicode[STIX]{x03BC}\text{s}$
.
As previously discussed in § 4.1.1, the small-scale vortices induced by the KH instability in the inviscid detonation, instead of the viscous detonation, are beneficial for the mixing between the reactant and product, hence being able to enhance the consumption of the reactant. In the inviscid detonation, more vortices can be observed than in the viscous detonation, indicating that the mixing effect in the inviscid detonation should be stronger than the corresponding viscous one. However, as shown in figure 10, around the highly unstable shear layers the reactant is nearly fully combusted behind the detonation front. Therefore, the mixing effect of the vortices generated from the KH instability does not have any chance to facilitate the reactant consumption due to the absence of the unburned reactant away from the detonation front.
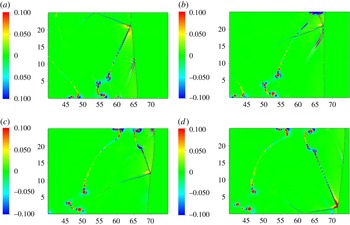
Figure 12. Q-criteria for figure 11: (a)
$t=320~\unicode[STIX]{x03BC}\text{s}$
, (b)
$t=330~\unicode[STIX]{x03BC}\text{s}$
, (c)
$t=340~\unicode[STIX]{x03BC}\text{s}$
, (d)
$t=350~\unicode[STIX]{x03BC}\text{s}$
.
Figure 12 shows the instantaneous Q-criterion, which is the second invariant of the velocity gradient tensor defined as follows:
$$\begin{eqnarray}Q=\frac{\unicode[STIX]{x2202}u}{\unicode[STIX]{x2202}x}\frac{\unicode[STIX]{x2202}v}{\unicode[STIX]{x2202}y}-\frac{\unicode[STIX]{x2202}u}{\unicode[STIX]{x2202}y}\frac{\unicode[STIX]{x2202}v}{\unicode[STIX]{x2202}x}.\end{eqnarray}$$
Note how the vortices mainly occur along the shear layers emitted from the triple point or detached shear layers. Although the Q-criterion is expected to illustrate vertical structures more obviously than figure 11, most of the flow is still laminar. It is apparent that diffusion effects in the viscous detonation can alter and partially suppress the oscillating instability at the detonation front. The small-scale vortices induced by the KH instability are almost entirely suppressed due to the diffusion effect of the physical viscosity in the NS equations. This is the main difference with figure 10 using the inviscid Euler equations and the main reason why few small-scales/vortices are presented and the flow looks laminar in figure 11.
Recent investigations have indicated that although the diffusion effect is important for the evolution of highly unstable detonations (Mahmoudi & Mazaheri Reference Mahmoudi and Mazaheri2011, Reference Mahmoudi and Mazaheri2012, Reference Mahmoudi and Mazaheri2015; Mazaheri et al. Reference Mazaheri, Mahmoudi, Sabzpooshani and Radulescu2015), it does not play any major role in weakly unstable detonations, owing to the absence of hydrodynamic instabilities (the KH instability and RM instability, etc.) (Mahmoudi et al. Reference Mahmoudi, Karimi, Deiterding and Emami2014). However, it is indicated that the diffusion effect in the viscous detonation associated with heat conduction, mass diffusion, etc., can still accelerate the reactant consumption closely behind the detonation front, even for the marginally stable detonation adopted here. In the weakly unstable detonation, the reactant is quickly combusted after crossing the detonation front, without any unburned pocket produced behind the detonation front. Therefore, the mixing effect resulting from the vortices generated from hydrodynamic instabilities does not provide any further support for the consumption of the reactant. Instead of the small-scale or large-scale vortices, only the limited diffusion effect can promote the reaction and subsequent heat release behind the front. For the highly unstable detonation, other than the diffusion effect, the mixing effect enhanced by the small-scale or large-scale vortices is also able to play an important role in the consumption of the unburned pocket away from the detonation front, but on the other hand mixing is also suppressed by the diffusion effect. Therefore, in the highly unstable detonation, it is difficult to clearly distinguish between the diffusion and mixing effects for the reactant consumption. It should be noted that the unburned reactant can also be produced in the weakly unstable detonation under some special conditions, e.g. the structure of the reactive DMR in § 4.1. It is also reported by Cai et al. (Reference Cai, Deiterding, Liang and Mahmoudi2017) that an unburned jet is generated behind the shock front because of the non-uniformity produced by the expansion fan in the expanding channel. Large-scale vortices involved in the highly unstable shear layers dominate the formation of the turbulent flow and the rapid turbulent mixing between the unburned jet and burned product. Maxwell et al. (Reference Maxwell, Bhattacharjee, Lau-Chapdelaine, Falle, Sharpe and Radulescu2017) also showed that for planar detonation propagation in a thin channel, turbulent mixing rates can significantly influence the observed cell patterns and detonation structure. Therefore, to account for diffusion and mixing effects, rather than the commonly known classification of weakly unstable and highly unstable detonations, it should be more appropriate to quantify to what extent the unburned reactant is still present behind the shock front under a specific condition.
4.3 Discussion and analysis
Figure 13 shows the location records of the detonation fronts for both the inviscid and viscous detonations, where the slopes of the curves represent the relative propagation velocities. It can be calculated from figure 13 that the relative propagation velocities for the inviscid and viscous detonations are approximately
$v_{inv}=251.35~\text{m}~\text{s}^{-1}$
and
$v_{vis}=263.95~\text{m}~\text{s}^{-1}$
, respectively. Therefore, the absolute propagation velocities are obtained as
$V_{inv}=1839.19~\text{m}~\text{s}^{-1}$
and
$V_{vis}=1851.79~\text{m}~\text{s}^{-1}$
along with the corresponding overdrive degrees of
$f_{inv}=1.34$
and
$f_{vis}=1.36$
, respectively, indicating that in relative terms the overall strength of the viscous detonation is larger than the inviscid one.
Figure 13. The location records of detonation fronts for both the inviscid and viscous detonations.
In general, an overdriven detonation can generate more transverse waves and subsequently more triple points than the corresponding CJ detonation (Cai et al. Reference Cai, Liang, Lin, Deiterding and Zhuang2015a , Reference Cai, Liang and Deiterding2016), indicating that more triple points might be expected for the detonation with higher overdrive degree. However, as shown in figure 9, the viscous detonation with a larger overdrive degree has only one dominant triple point in the detonation front at this instant in time, while in the inviscid detonation with a lower overdrive degree two triple points of similar strength have already been generated. Clearly, diffusion effects can play a significant role in the suppression of the instability in the detonation front, thus eventually delaying or possibly even preventing the generation of triple point Mach reflection structures in this configuration.
Figure 14. The location records of viscous detonation fronts for three refinement levels.
During the propagation process, for the marginally stable detonation, no unburned pocket is generated far away from the detonation front. Therefore, the mixing effect dominated by the vortices resulting from hydrodynamic instabilities does not provide any help for the consumption of the reactant. As previously discussed, in the viscous detonation the diffusion effect from physical viscosity can enhance the consumption of the unburned reactant closely behind the detonation front, hence accelerating the chemical heat release rate and further resulting in the formation of a stronger detonation eventually. Compared with the viscous detonation, the diffusion effect in the inviscid detonation can only be generated from the limited numerical dissipation at the high grid resolution. Although the mixing effect produced by the vortices is stronger in the inviscid detonation, it does not aid in the reactant consumption, hence resulting in a relatively weaker detonation than in the viscous case. In addition, due to the faster heat release of the viscous detonation, the transverse wave can propagate more rapidly as a result of its dependence on the heat release (Lee Reference Lee2008). It is for this reason that the period of the viscous detonation is lower than that of the inviscid one. Although similar structures using both the Euler and NS equations can be observed, and most of the time the reactive Euler equations used for weakly unstable detonations can give qualitatively correct conclusions, the viscous model should lead to more accurate predictions. It should be noted that in the present work only two-dimensional NS equations are solved; however, turbulent flows are truly three-dimensional. Hence, three-dimensional reactive NS equations are necessary for further viscous detonation simulations.
Figure 14 shows the location records of the viscous propagating detonations at three different grid resolutions. The three curves are overall straight lines, and the slopes are almost the same, indicating that the viscous detonation propagates at almost the same speed for the present grid resolutions. However, it is shown that at the same time the locations of the detonation front vary slightly at different refinement levels. For example, at
$t=300~\unicode[STIX]{x03BC}\text{s}$
, the locations of the detonation front are 58.6 mm for the four-level refinement, 60.3 mm for the five-level refinement and 62.2 mm for the six-level refinement, respectively, indicating that the distance of the front location rises as the grid resolution increases. When increasing the grid resolution, the physical viscosity does not change but the numerical viscosity decreases, resulting in a reduction of the overall viscosity.
During the initiation period, because of the existence of the unburned triangular jet behind the shock front, the whole process evolves more rapidly with increasing grid resolution, which is due to the enhanced consumption of the unburned jet and subsequently faster heat release as a result of the mixing effect. It is also indicated that at this moment, mixing plays an important role in the consumption of the unburned jet. During the later period of detonation propagation, the diffusion effect closely behind the detonation front does not undergo any obvious change, and at the same time the mixing effect does not have any influence on the reactant consumption. As a result, the detonation propagates almost at the same speed during the later process for different grid resolutions. It should be noted that this is qualitatively correct for weakly unstable detonations because of the absence of any unburned reactant behind the detonation front. It can also be speculated that for highly unstable detonations the mixing effect can also play an important role in the consumption of the unburned mixture, suggesting that the detonation would propagate more rapidly when the grid resolution is increased.
5 Effect of chemical kinetics
In the present work, a single-step chemical kinetic has been adopted to study inviscid and viscous detonations in the supersonic combustible mixture. One of the failures of the one-step model is its inability to capture the chain-branching character of the reactions and the corresponding cross-over effect (Varatharajan & Williams Reference Varatharajan and Williams2001). This can provide a change in the shock sensitivity of the reaction rates if the shock strength falls below a critical value. Nonetheless, there are additional issues that make the simulation of gaseous detonations challenging. These include the three-dimensional nature of the coherent structures and turbulent flow in the reaction zone, the challenge of carrying out high-order simulations needed for turbulence modelling and simultaneously capturing shock waves, and finally the storage requirements for detailed chemical reaction mechanisms with 50–500 individual species required for typical hydrocarbon fuels (Shepherd Reference Shepherd2009). Thus, most detonation simulations have been carried out using a simplified chemical kinetic model in either one (Ng & Lee Reference Ng and Lee2003; Watt & Sharpe Reference Watt and Sharpe2005; Ng et al. Reference Ng, Botros, Chao, Yang, Nikiforakis and Lee2006) or two (Arienti & Shepherd Reference Arienti and Shepherd2005; Liang & Bauwens Reference Liang and Bauwens2005) space dimensions. Even with this simple reaction model, the results are in remarkable qualitative agreement with the experimental observations (Radulescu & Maxwell Reference Radulescu and Maxwell2011). A small number of simulations have been carried out with detailed chemical reaction mechanisms for hydrogen–oxygen mixtures in two space dimensions (Hu et al. Reference Hu, Khoo, Zhang and Jiang2004, Reference Hu, Zhang, Khoo and Jiang2005; Taylor et al. Reference Taylor, Kessler, Gamezo and Oran2013; Cai et al. Reference Cai, Liang, Deiterding and Lin2016b ; Gallier et al. Reference Gallier, Le Palud, Pintgen, Mével and Shepherd2017). However, the detonation structures obtained using detailed kinetics for stable detonations are very similar to those by Sharpe (Reference Sharpe2001) with Arrhenius kinetics. Therefore, for many practical situations, an extensive description of the details of the chemical pathways is unnecessary. Instead, it is more important to have an accurate model of the turbulent diffusive flow field coupled to the single step reaction model for the chemical energy release, which models the released energy in the right place in the flow at the right time. Thus, it is essential to first establish that the reaction zone structure can be modelled reliably before trying to simulate detonations with realistic chemistry involving multiple species and reaction length scales. After developing a proper fluid dynamics turbulent diffusive model, using realistic detailed kinetics is useful for more accurate modelling of the reaction zone structure behind the main shock.
6 Conclusion
In an effort to investigate the role of diffusion and mixing effects in detonation initiation and propagation with a hot jet initiation in a supersonic combustible mixture, two-dimensional high-resolution simulations were conducted solving the reactive Euler and NS equations with a simple reaction model using the second-order accurate MUSCL-TVD scheme and the adaptive mesh refinement method. The results are as follows:
-
(1) In the inviscid detonation, the small-scale vortices induced by the KH instability, which are suppressed in the viscous detonation, are beneficial for the mixing between the burned and unburned mixtures, hence being able to enhance the consumption of the reactant. However, the diffusion effect suppresses efficiently the growth of the KH instability, which can decrease the mixing rate and further slow the consumption of the unburned reactant.
-
(2) After the detonation is fully initiated, the mixing effect induced by the vortices does not have any opportunity to facilitate the reactant consumption due to the absence of the unburned reactant away from the detonation front. The diffusion effects associated with heat conduction, mass diffusion, etc., can accelerate the reactant consumption closely behind the detonation front, even for the marginally stable detonation adopted. Therefore, although the mixing effect produced by the vortices is stronger in the inviscid case, the unburned reactant closely behind the detonation front is still consumed more slowly, decreasing the heat release rate and resulting in a relatively weaker detonation than the viscous one.
-
(3) As for the diffusion and mixing effects, rather than the commonly known classification of weakly unstable and highly unstable detonations, it should be more correct to make sure whether the unburned reactant is preserved behind the shock front under a specific condition.
-
(4) At high grid resolutions, the physical viscosity plays a dominant role in the whole diffusion effect. Compared with the inviscid case, the diffusion effects in the viscous detonation can play a more significant role in the suppression of the oscillating instability at the detonation front, thus eventually altering the triple point generation mechanism, even with a larger overdrive degree.
-
(5) Although similar structures using both the Euler and NS equations can be observed, and most of the time the reactive Euler equations used for weakly unstable detonations can give qualitatively correct conclusions, the viscous detonation solved with the NS equations should give more accurate predictions, especially when hydrodynamic instabilities interact with the combustion processes. Considering that the actual turbulent flow is truly three-dimensional, solving three-dimensional reactive NS equations is necessary for further viscous detonation simulations.
Acknowledgements
This work is supported by the National Natural Science Foundation of China (no. 11702323) and the National Foundation of Defense Technology (no. 3101032).
