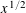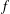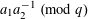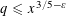1 Introduction
In this paper we prove a Bombieri–Vinogradov type theorem for general multiplicative functions supported on smooth numbers, with a fixed member of the residue class. Given a multiplicative function
$f$
, we define, whenever
$(a,q)=1$
,
$$\begin{eqnarray}\unicode[STIX]{x1D6E5}(f,x;q,a):=\mathop{\sum }_{\substack{ n\leqslant x \\ n\equiv a\;(\text{mod}\;q)}}f(n)-\frac{1}{\unicode[STIX]{x1D711}(q)}\mathop{\sum }_{\substack{ n\leqslant x \\ (n,q)=1}}f(n).\end{eqnarray}$$
We wish to prove that, for an arbitrary fixed
$A>0$
,
$$\begin{eqnarray}\mathop{\sum }_{\substack{ q\sim Q \\ (a,q)=1}}|\unicode[STIX]{x1D6E5}(f,x;q,a)|\ll \frac{x}{(\log x)^{A}}\end{eqnarray}$$
where, here and henceforth, “
$q\sim Q$
” denotes the set of integers
$q$
in the range
$Q<q\leqslant 2Q$
, for as large values of
$Q$
as possible. Let
$$\begin{eqnarray}F(s)=\mathop{\sum }_{n=1}^{\infty }\frac{f(n)}{n^{s}}\quad \text{and}\quad -\frac{F^{\prime }(s)}{F(s)}=\mathop{\sum }_{n=2}^{\infty }\frac{\unicode[STIX]{x1D6EC}_{f}(n)}{n^{s}},\end{eqnarray}$$
for Re
$(s)>1$
. Following [Reference Granville, Harper and Soundararajan5], we restrict attention to the class
${\mathcal{C}}$
of multiplicative functions
$f$
for which
$$\begin{eqnarray}|\unicode[STIX]{x1D6EC}_{f}(n)|\leqslant \unicode[STIX]{x1D6EC}(n)\quad \text{for all}~n\geqslant 1.\end{eqnarray}$$
This includes most
$1$
-bounded multiplicative functions of interest, including all
$1$
-bounded completely multiplicative functions. Two key observations are that if
$f\in {\mathcal{C}}$
then each
$|f(n)|\leqslant 1$
, and if
$f\in {\mathcal{C}}$
and
$F(s)G(s)=1$
then
$g\in {\mathcal{C}}$
.
In [Reference Granville and Shao6] the last two authors showed that there are two different reasons that the sum in (1.1) might be
$\gg x/\!\log x$
. First
$f$
might be a character of small conductor (for example
$f(n)=(n/3)$
), or might “correlate” with such a character; secondly
$f$
might have been selected so that
$f(p)$
works against us for most primes
$p$
in the range
$x/2<p\leqslant x$
. We handled these potential pretentious problems as follows.
To avoid issues with the values
$f(p)$
at the large primes
$p$
we only allow
$f$
to be supported on
$y$
-smooth integersFootnote
1
for
$y=x^{\unicode[STIX]{x1D703}}$
, for some small
$\unicode[STIX]{x1D703}>0$
.
To avoid issues with the function
$f$
correlating with a given character
$\unicode[STIX]{x1D712}$
, note that this happens when
$$\begin{eqnarray}S_{f}(X,\unicode[STIX]{x1D712}):=\mathop{\sum }_{n\leqslant X}f(n)\overline{\unicode[STIX]{x1D712}}(n)\end{eqnarray}$$
is “large” (that is,
$\gg X$
, or
$\gg X/(\log X)^{A}$
) for some
$X$
in the range
$x^{1/2}<X\leqslant x$
, in which case (1.1) might well be false. We can either assume that this is false for all
$\unicode[STIX]{x1D712}$
(which is equivalent to what is known as a “Siegel–Walfisz criterion” in the literature), or we can take account of such
$\unicode[STIX]{x1D712}$
in the “Expected Main Term”. We will begin by doing the latter, and then deduce the former as a corollary.
We start by stating the Siegel–Walfisz criterion:
The Siegel–Walfisz criterion: for any fixed
$A>0$
, we say that
$f$
satisfies the
$A$
-Siegel–Walfisz criterion if for any
$(a,q)=1$
and any
$x\geqslant 2$
we have the bound
$$\begin{eqnarray}|\unicode[STIX]{x1D6E5}(f,x;q,a)|\ll _{A}\frac{1}{(\log x)^{A}}\mathop{\sum }_{n\leqslant x}|f(n)|.\end{eqnarray}$$
We say that
$f$
satisfies the Siegel–Walfisz criterion if it satisfies the
$A$
-Siegel–Walfisz criterion for all
$A>0$
.
For a set of primitive characters
$\unicode[STIX]{x1D6EF}$
, let
$\unicode[STIX]{x1D6EF}_{q}$
be the set of those characters
$(\text{mod}~q)$
which are induced by the characters in
$\unicode[STIX]{x1D6EF}$
. Then denote
$$\begin{eqnarray}\unicode[STIX]{x1D6E5}_{\unicode[STIX]{x1D6EF}}(f,x;q,a):=\mathop{\sum }_{\substack{ n\leqslant x \\ n\equiv a\;(\text{mod}\;q)}}f(n)-\frac{1}{\unicode[STIX]{x1D711}(q)}\mathop{\sum }_{\substack{ \unicode[STIX]{x1D712}\in \unicode[STIX]{x1D6EF}_{q}}}\unicode[STIX]{x1D712}(a)S_{f}(x,\unicode[STIX]{x1D712}).\end{eqnarray}$$
In [Reference Granville and Shao6] we proved the following result.
Theorem 1.1. Fix
$\unicode[STIX]{x1D6FF},B>0$
. Let
$y=x^{\unicode[STIX]{x1D700}}$
for some
$\unicode[STIX]{x1D700}>0$
sufficiently small in terms of
$\unicode[STIX]{x1D6FF}$
. Let
$f\in {\mathcal{C}}$
be a multiplicative function which is only supported on
$y$
-smooth integers. Then there exists a set,
$\unicode[STIX]{x1D6EF}$
, of primitive characters, containing
$\ll (\log x)^{6B+7+o(1)}$
elements, such that for any
$1\leqslant |a|\ll Q\leqslant x^{20/39-\unicode[STIX]{x1D6FF}}$
, we have
$$\begin{eqnarray}\mathop{\sum }_{\substack{ q\sim Q \\ (a,q)=1}}|\unicode[STIX]{x1D6E5}_{\unicode[STIX]{x1D6EF}}(f,x;q,a)|\ll \frac{x}{(\log x)^{B}}.\end{eqnarray}$$
Moreover, if
$f$
satisfies the Siegel–Walfisz criterion then
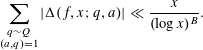$$\begin{eqnarray}\mathop{\sum }_{\substack{ q\sim Q \\ (a,q)=1}}|\unicode[STIX]{x1D6E5}(f,x;q,a)|\ll \frac{x}{(\log x)^{B}}.\end{eqnarray}$$
In this article we develop Theorem 1.1 further, allowing
$Q$
as well as
$y$
to vary over a much wider range, and obtaining upper bounds in terms of (the more appropriate)
$\unicode[STIX]{x1D6F9}(x,y)$
, the number of
$y$
-smooth integers up to
$x$
.
Theorem 1.2. Fix
$\unicode[STIX]{x1D700},A>0$
. Suppose that
$f\in {\mathcal{C}}$
, and is only supported on
$y$
-smooth numbers, where
$$\begin{eqnarray}x^{\unicode[STIX]{x1D6FF}}>y\geqslant \exp \biggl(\frac{5}{2}\cdot \frac{\sqrt{\log x}\log \log x}{\sqrt{\log \log \log x}}\biggr)\end{eqnarray}$$
for some sufficiently small
$\unicode[STIX]{x1D6FF}>0$
. Then there exists a set,
$\unicode[STIX]{x1D6EF}$
, of primitive characters, containing
$\ll (\log x)^{6A+38}$
elements, such that if
$1\leqslant |a_{1}|,|a_{2}|\leqslant x^{\unicode[STIX]{x1D6FF}}$
then
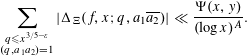$$\begin{eqnarray}\mathop{\sum }_{\substack{ q\leqslant x^{3/5-\unicode[STIX]{x1D700}} \\ (q,a_{1}a_{2})=1}}|\unicode[STIX]{x1D6E5}_{\unicode[STIX]{x1D6EF}}(f,x;q,a_{1}\overline{a_{2}})|\ll \frac{\unicode[STIX]{x1D6F9}(x,y)}{(\log x)^{A}}.\end{eqnarray}$$
Moreover, if
$f$
satisfies the Siegel–Walfisz criterion then
$$\begin{eqnarray}\mathop{\sum }_{\substack{ q\leqslant x^{3/5-\unicode[STIX]{x1D700}} \\ (q,a_{1}a_{2})=1}}|\unicode[STIX]{x1D6E5}(f,x;q,a_{1}\overline{a_{2}})|\ll \frac{\unicode[STIX]{x1D6F9}(x,y)}{(\log x)^{A}}.\end{eqnarray}$$
It would be interesting to extend the range (1.2) in Theorem 1.2 down to any
$y\geqslant (\log x)^{C}$
for some large constant
$C$
. We discuss the main issue that forces us to restrict the range in Theorem 1.2 to
$y>\exp ((\log x)^{1/2+o(1)})$
in Remark 4.3. In our proofs we have used the range
$y\geqslant (\log x)^{C}$
when we can, as an aid to future research on this topic, and to make clear what are the sticking points.
Fouvry and Tenenbaum [Reference Fouvry and Tenenbaum4, Théorème 2] established such a result when
$f$
is the characteristic function of the
$y$
-smooth integers (with
$y<x^{\unicode[STIX]{x1D6FF}}$
) and
$a_{2}=1$
, in the same range
$q\leqslant x^{3/5-\unicode[STIX]{x1D700}}$
, but with the bound
$\ll x/(\log x)^{A}$
. This was improved by Drappeau [Reference Drappeau2] to
$\ll \unicode[STIX]{x1D6F9}(x,y)/(\log x)^{A}$
for
$(\log x)^{C}<y\leqslant x^{\unicode[STIX]{x1D6FF}}$
.
The proof of Theorem 1.2 combines the ideas from our earlier articles [Reference Drappeau2] and [Reference Granville and Shao6]. Perhaps the most innovative feature of this article, given [Reference Drappeau2] and [Reference Granville and Shao6], comes in Theorem 5.1 in which we prove a version of the classical large sieve inequality (towards which Roth’s work [Reference Roth10] played a pivotal role) for (the notably sparse) sequences supported on the
$y$
-smooth numbers, which may be of independent interest.
2 Reduction to a larger set of exceptional moduli
We begin by modifying estimates from [Reference Drappeau2] to prove Theorem 2.1, which is a version of Theorem 1.2 with a far larger exceptional set of characters. This is key to the proof of Theorem 1.2 since we now only need to cope with relatively small moduli. We therefore define
${\mathcal{A}}(D)$
to be the set of all primitive characters of conductor
${\leqslant}D$
.
Theorem 2.1. For fixed
$\unicode[STIX]{x1D700},A>0$
, there exist
$C,\unicode[STIX]{x1D6FF}>0$
such that for any
$y$
in the range
$(\log x)^{C}<y\leqslant x^{\unicode[STIX]{x1D6FF}}$
, and any
$f\in {\mathcal{C}}$
which is only supported on
$y$
-smooth numbers, we have
$$\begin{eqnarray}\mathop{\sum }_{\substack{ q\leqslant x^{3/5-\unicode[STIX]{x1D700}} \\ (q,a_{1}a_{2})=1}}|\unicode[STIX]{x1D6E5}_{{\mathcal{A}}}(f,x;q,a_{1}\overline{a_{2}})|\ll _{A}\frac{\unicode[STIX]{x1D6F9}(x,y)}{(\log x)^{A}},\end{eqnarray}$$
for any integers
$a_{1},a_{2}$
for which
$1\leqslant |a_{1}|,|a_{2}|\leqslant x^{\unicode[STIX]{x1D6FF}}$
, with
${\mathcal{A}}={\mathcal{A}}(D)$
where
$D=(x/\unicode[STIX]{x1D6F9}(x,y))^{2}(\log x)^{2A+20}$
.
We prove this by modifying some of the estimates in [Reference Drappeau2]. For any
$D\geqslant 1$
and integer
$q\geqslant 1$
let
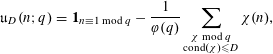$$\begin{eqnarray}\,\mathfrak{u}_{D}(n;q)=\mathbf{1}_{n\equiv 1\;\text{mod}\;q}-\frac{1}{\unicode[STIX]{x1D711}(q)}\mathop{\sum }_{\substack{ \unicode[STIX]{x1D712}\;\text{mod}\;q \\ \text{cond}(\unicode[STIX]{x1D712})\leqslant D}}\unicode[STIX]{x1D712}(n),\end{eqnarray}$$
so that
$$\begin{eqnarray}\unicode[STIX]{x1D6E5}_{{\mathcal{A}}}(f,x;q,a_{1}\overline{a_{2}})=\mathop{\sum }_{n\leqslant x}f(n)\,\mathfrak{u}_{D}(n\overline{a_{1}}a_{2};q).\end{eqnarray}$$
Note that
$\,\mathfrak{u}_{D}(n;q)=0$
unless
$(n,q)=1$
and
$q>D$
, in which case
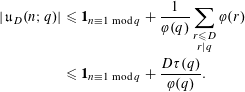$$\begin{eqnarray}\displaystyle |\,\mathfrak{u}_{D}(n;q)| & {\leqslant} & \displaystyle \mathbf{1}_{n\equiv 1\;\text{mod}\;q}+\frac{1}{\unicode[STIX]{x1D711}(q)}\mathop{\sum }_{\substack{ r\leqslant D \\ r|q}}\unicode[STIX]{x1D711}(r)\nonumber\\ \displaystyle & {\leqslant} & \displaystyle \mathbf{1}_{n\equiv 1\;\text{mod}\;q}+\frac{D\unicode[STIX]{x1D70F}(q)}{\unicode[STIX]{x1D711}(q)}.\end{eqnarray}$$
For
$(n,q)=1$
, since
$$\begin{eqnarray}\mathop{\sum }_{\substack{ \unicode[STIX]{x1D712}\;(\text{mod}\;q) \\ \text{cond}(\unicode[STIX]{x1D712})\leqslant D}}\unicode[STIX]{x1D712}(n)=\mathop{\sum }_{\substack{ s\leqslant D \\ s\mid q}}\mathop{\sum }_{\substack{ \unicode[STIX]{x1D713}\;(\text{mod}\;s) \\ \unicode[STIX]{x1D713}\text{ primitive}}}\unicode[STIX]{x1D713}(n)=\mathop{\sum }_{\substack{ s\leqslant D \\ s|q}}\mathop{\sum }_{d|s}\unicode[STIX]{x1D707}(s/d)\unicode[STIX]{x1D711}(d)\mathbf{1}_{d|n-1},\end{eqnarray}$$
by letting
$b=s/d$
we obtain the alternate expression
$$\begin{eqnarray}\,\mathfrak{u}_{D}(n;q)=\boldsymbol{ 1}_{n\equiv 1\;\text{mod}\;q}-\frac{1}{\unicode[STIX]{x1D711}(q)}\mathop{\sum }_{\substack{ d\leqslant D \\ d|(q,n-1)}}\unicode[STIX]{x1D711}(d)\mathop{\sum }_{\substack{ b\leqslant D/d \\ b|q/d}}\unicode[STIX]{x1D707}(b).\end{eqnarray}$$
Theorem 2.1 is an immediate consequence of Theorem 2.2.
Theorem 2.2. For any fixed
$\unicode[STIX]{x1D700}>0$
, there exists
$C,\unicode[STIX]{x1D6FF}>0$
such that whenever
$$\begin{eqnarray}1\leqslant D\leqslant x^{\unicode[STIX]{x1D6FF}},\qquad (\log x)^{C}\leqslant y\leqslant x^{\unicode[STIX]{x1D6FF}},\end{eqnarray}$$
we have, uniformly for
$0<|a_{1}|,|a_{2}|\leqslant x^{\unicode[STIX]{x1D6FF}}$
and
$f\in {\mathcal{C}}$
,
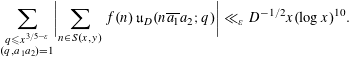$$\begin{eqnarray}\mathop{\sum }_{\substack{ q\leqslant x^{3/5-\unicode[STIX]{x1D700}} \\ (q,a_{1}a_{2})=1}}\biggl|\mathop{\sum }_{n\in S(x,y)}f(n)\,\mathfrak{u}_{D}(n\overline{a_{1}}a_{2};q)\biggr|\ll _{\unicode[STIX]{x1D700}}D^{-1/2}x(\log x)^{10}.\end{eqnarray}$$
To prove Theorem 2.2, we first prove the following generalization of [Reference Drappeau2, Theorem 3], where the bound
$D$
on the conductor is allowed to vary.
Lemma 2.3. Let
$M,N,L,R\geqslant 1$
and
$(\unicode[STIX]{x1D6FC}_{m})$
,
$(\unicode[STIX]{x1D6FD}_{n})$
,
$(\unicode[STIX]{x1D706}_{\ell })$
be three sequences, bounded in modulus by
$1$
, supported on integers inside
$(M,2M]$
,
$(N,2N]$
, and
$(L,2L]$
respectively. Let
$x=MNL$
. For any fixed
$\unicode[STIX]{x1D700}>0$
, there exists
$\unicode[STIX]{x1D6FF}>0$
such that whenever either the conditions (3.1), or the conditions (3.2) of [Reference Drappeau2] are met, we have
$$\begin{eqnarray}\mathop{\sum }_{\substack{ R<r\leqslant 2R \\ (r,a_{1}a_{2})=1}}\biggl|\mathop{\sum }_{m}\mathop{\sum }_{n}\mathop{\sum }_{\ell }\unicode[STIX]{x1D6FC}_{m}\unicode[STIX]{x1D6FD}_{n}\unicode[STIX]{x1D706}_{\ell }\,\mathfrak{u}_{D}(mn\ell \overline{a_{1}}a_{2};q)\biggr|\ll D^{-1/2}x(\log x)^{3}\end{eqnarray}$$
for
$1\leqslant D\leqslant x^{\unicode[STIX]{x1D6FF}}$
.
Theorem 3 of [Reference Drappeau2] is the special case when
$D$
has maximal size,
$D=x^{\unicode[STIX]{x1D6FF}}$
. The conditions (3.1) or (3.2) of [Reference Drappeau2] concern the relative sizes of
$M,N,L$
. They are rather technical, but a critical case when the conditions are met is
$$\begin{eqnarray}R\approx x^{3/5},\qquad M\approx x^{1/5},\qquad N\approx x^{2/5},\qquad L\approx x^{2/5}.\end{eqnarray}$$
Proof. We follow closely the arguments of [Reference Drappeau2]. Roughly speaking, the main point is that reducing the size of
$D$
only reduces the error terms, except in a certain diagonal contribution which yields the dominant error term, and which we analyze more carefully. Proceeding as in [Reference Drappeau2, §3], we reduce to the estimation of
${\mathcal{S}}_{1}-2\,\text{Re}({\mathcal{S}}_{2})+{\mathcal{S}}_{3}$
, where
${\mathcal{S}}_{1}$
is defined in the first display of [Reference Drappeau2, pp. 838],
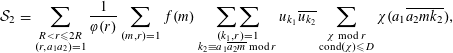$$\begin{eqnarray}{\mathcal{S}}_{2}=\mathop{\sum }_{\substack{ R<r\leqslant 2R \\ (r,a_{1}a_{2})=1}}\frac{1}{\unicode[STIX]{x1D711}(r)}\mathop{\sum }_{(m,r)=1}f(m)\sum _{\substack{ (k_{1},r)=1 \\ k_{2}\equiv a_{1}\overline{a_{2}m}\;\text{mod}\;r}}u_{k_{1}}\overline{u_{k_{2}}}\mathop{\sum }_{\substack{ \unicode[STIX]{x1D712}\;\text{mod}\;r \\ \text{cond}(\unicode[STIX]{x1D712})\leqslant D}}\unicode[STIX]{x1D712}(a_{1}\overline{a_{2}mk_{2}}),\end{eqnarray}$$
and
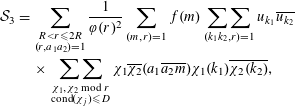$$\begin{eqnarray}\displaystyle {\mathcal{S}}_{3} & = & \displaystyle \mathop{\sum }_{\substack{ R<r\leqslant 2R \\ (r,a_{1}a_{2})=1}}\frac{1}{\unicode[STIX]{x1D711}(r)^{2}}\mathop{\sum }_{(m,r)=1}f(m)\sum _{(k_{1}k_{2},r)=1}u_{k_{1}}\overline{u_{k_{2}}}\nonumber\\ \displaystyle & & \displaystyle \times \,\sum _{\substack{ \unicode[STIX]{x1D712}_{1},\unicode[STIX]{x1D712}_{2}\;\text{mod}\;r \\ \text{cond}(\unicode[STIX]{x1D712}_{j})\leqslant D}}\unicode[STIX]{x1D712}_{1}\overline{\unicode[STIX]{x1D712}_{2}}(a_{1}\overline{a_{2}m})\unicode[STIX]{x1D712}_{1}(k_{1})\overline{\unicode[STIX]{x1D712}_{2}(k_{2})},\nonumber\end{eqnarray}$$
where
$u_{k}=\sum _{k=n\ell }\unicode[STIX]{x1D6FD}_{n}\unicode[STIX]{x1D706}_{\ell }$
, and
$f$
is a smooth function supported inside
$[M/2,3M]$
satisfying
$\Vert f^{(j)}{\Vert _{\infty }\ll }_{j}M^{-j}$
for any
$j\geqslant 0$
.
The quantity
${\mathcal{S}}_{1}$
being the same as in [Reference Drappeau2], we can quote the estimate
$$\begin{eqnarray}{\mathcal{S}}_{1}=\hat{f}(0)X_{1}+O(x^{1-\unicode[STIX]{x1D6FF}}KR^{-1})\end{eqnarray}$$
from [Reference Drappeau2, formula (3.17)], where
$K=NL$
. Here
$\hat{f}(0)=\int _{\mathbb{R}}f$
, and
$X_{1}$
is defined at [Reference Drappeau2, formula (3.12)]. For the estimation of
${\mathcal{S}}_{2}$
and
${\mathcal{S}}_{3}$
, we reproduce [Reference Drappeau2, §§3.2 and 3.3], the only difference being that the set
${\mathcal{X}}=\{\unicode[STIX]{x1D712}\text{primitive}:~\text{cond}(\unicode[STIX]{x1D712})\leqslant x^{\unicode[STIX]{x1D700}}\}$
is replaced with the subset
${\mathcal{X}}=\{\unicode[STIX]{x1D712}\text{primitive}:~\text{cond}(\unicode[STIX]{x1D712})\leqslant D\}$
. We claim that the estimates
$$\begin{eqnarray}{\mathcal{S}}_{j}=\hat{f}(0)X_{j}+O(x^{1-\unicode[STIX]{x1D6FF}}KR^{-1})\end{eqnarray}$$
hold for
$j\in \{2,3\}$
, with
$$\begin{eqnarray}\displaystyle X_{2} & = & \displaystyle \mathop{\sum }_{\substack{ R<r\leqslant 2R \\ (r,a_{1}a_{2})=1}}\frac{1}{r\unicode[STIX]{x1D711}(r)}\sum _{(k_{1}k_{2},r)=1}\mathop{\sum }_{\substack{ \unicode[STIX]{x1D712}\;\text{mod}\;r \\ \text{cond}(\unicode[STIX]{x1D712})\leqslant D}}u_{k_{1}}\overline{u_{k_{2}}}\unicode[STIX]{x1D712}(k_{1}\overline{k_{2}}),\nonumber\\ \displaystyle X_{3} & = & \displaystyle \mathop{\sum }_{\substack{ R<r\leqslant 2R \\ (r,a_{1}a_{2})=1}}\frac{1}{r}\mathop{\sum }_{\substack{ 0<b\leqslant r \\ (b,r)=1}}\biggl|\frac{1}{\unicode[STIX]{x1D711}(r)}\mathop{\sum }_{(k,r)=1}\mathop{\sum }_{\substack{ \unicode[STIX]{x1D712}\;\text{mod}\;r \\ \text{cond}(\unicode[STIX]{x1D712})\leqslant D}}u_{k}\unicode[STIX]{x1D712}(k\overline{b})\biggr|^{2}.\nonumber\end{eqnarray}$$
To see this, we merely note that reducing the cardinality of
${\mathcal{X}}$
, and the bound
$D$
on the conductors, leads to better error terms in the analysis. This is clear from the bound on
$R_{3}$
in [Reference Drappeau2, formula (3.8)], which grows proportionally to
$|{\mathcal{X}}|D^{2}$
, and from the bound on
$\sum _{z\in {\mathcal{Z}}}\unicode[STIX]{x1D706}(z)|G_{2}(z,\unicode[STIX]{x1D709})|$
in [Reference Drappeau2, formula (3.10)], which grows proportionally to
$|{\mathcal{X}}|$
.
Finally we are left with evaluating
$X_{1}-2\,\text{Re}(X_{2})+X_{3}$
, which makes use of the multiplicative large sieve. Proceeding as in [Reference Drappeau2, §3.6], we find
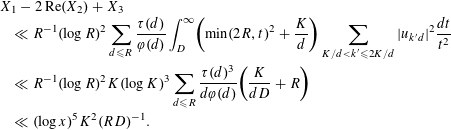$$\begin{eqnarray}\displaystyle & & \displaystyle \displaystyle X_{1}-2\,\text{Re}(X_{2})+X_{3}\nonumber\\ \displaystyle & & \displaystyle \quad \displaystyle \ll R^{-1}(\log R)^{2}\mathop{\sum }_{d\leqslant R}\frac{\unicode[STIX]{x1D70F}(d)}{\unicode[STIX]{x1D711}(d)}\int _{D}^{\infty }\biggl(\min (2R,t)^{2}+\frac{K}{d}\biggr)\mathop{\sum }_{K/d<k^{\prime }\leqslant 2K/d}|u_{k^{\prime }d}|^{2}\frac{dt}{t^{2}}\nonumber\\ \displaystyle & & \displaystyle \quad \displaystyle \ll R^{-1}(\log R)^{2}K(\log K)^{3}\mathop{\sum }_{d\leqslant R}\frac{\unicode[STIX]{x1D70F}(d)^{3}}{d\unicode[STIX]{x1D711}(d)}\biggl(\frac{K}{dD}+R\biggr)\nonumber\\ \displaystyle & & \displaystyle \quad \displaystyle \ll (\log x)^{5}K^{2}(RD)^{-1}.\end{eqnarray}$$
Here we have used the boundFootnote
2
$|u_{k}|\leqslant \unicode[STIX]{x1D70F}(k)$
, and the hypothesis
$R\leqslant x^{-\unicode[STIX]{x1D700}}K\leqslant K/D$
. Following [Reference Drappeau2, formula (3.34)], this leads to the upper bound
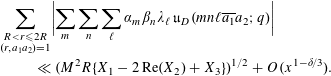$$\begin{eqnarray}\displaystyle & & \displaystyle \displaystyle \mathop{\sum }_{\substack{ R<r\leqslant 2R \\ (r,a_{1}a_{2})=1}}\biggl|\mathop{\sum }_{m}\mathop{\sum }_{n}\mathop{\sum }_{\ell }\unicode[STIX]{x1D6FC}_{m}\unicode[STIX]{x1D6FD}_{n}\unicode[STIX]{x1D706}_{\ell }\,\mathfrak{u}_{D}(mn\ell \overline{a_{1}}a_{2};q)\biggr|\nonumber\\ \displaystyle & & \displaystyle ~\qquad \displaystyle \ll (M^{2}R\{X_{1}-2\,\text{Re}(X_{2})+X_{3}\})^{1/2}+O(x^{1-\unicode[STIX]{x1D6FF}/3}).\nonumber\end{eqnarray}$$
To deduce Theorem 2.2 from Lemma 2.3, we start with the following special case of Theorem 2.2.
Proposition 2.4. Theorem 2.2 holds true for functions
$f$
supported on squarefree integers.
Proof. We extend the arguments of [Reference Drappeau2, pp. 852–853], renaming the variable
$q$
into
$r$
. Suppose first
$R\geqslant x^{4/9}$
. We restrict
$n$
and
$r$
to dyadic intervals
$x<n\leqslant 2x$
and
$R<r\leqslant 2R$
. Choosing the parameters
$(M_{0},N_{0},L_{0})$
as in [Reference Drappeau2, p. 852, last display], we obtain
$$\begin{eqnarray}\displaystyle & & \displaystyle \displaystyle \mathop{\sum }_{\substack{ R<r\leqslant 2R \\ (r,a_{1}a_{2})=1}}\biggl|\mathop{\sum }_{\substack{ x<n\leqslant 2x \\ P^{+}(n)\leqslant y}}f(n)\,\mathfrak{u}_{D}(n\overline{a_{1}}a_{2};r)\biggr|\nonumber\\ \displaystyle & & \displaystyle \quad \displaystyle =\mathop{\sum }_{\substack{ R<r\leqslant 2R \\ (r,a_{1}a_{2})=1}}~\biggl|\mathop{\sum }_{\substack{ L_{0}<\ell \leqslant L_{0}P^{-}(\ell ) \\ P^{+}(\ell )\leqslant y}}~\mathop{\sum }_{\substack{ M_{0}<m\leqslant M_{0}P^{-}(m) \\ P^{+}(m)\leqslant P^{-}(\ell )}}\nonumber\\ \displaystyle & & \displaystyle \qquad \times \,\mathop{\sum }_{\substack{ x<mn\ell \leqslant 2x \\ P^{+}(n)\leqslant P^{-}(m)}}f(mn\ell )\,\mathfrak{u}_{D}(mn\ell \overline{a_{1}}a_{2};r)\biggr|\nonumber\\ \displaystyle & & \displaystyle \quad \displaystyle =\mathop{\sum }_{\substack{ R<r\leqslant 2R \\ (r,a_{1}a_{2})=1}}\biggl|\mathop{\sum }_{\substack{ L_{0}<\ell \leqslant L_{0}P^{-}(\ell ) \\ P^{+}(\ell )\leqslant y}}~\mathop{\sum }_{\substack{ M_{0}<m\leqslant M_{0}P^{-}(m) \\ P^{+}(m)<P^{-}(\ell )}}\nonumber\\ \displaystyle & & \displaystyle \qquad \times \,\mathop{\sum }_{\substack{ x<mn\ell \leqslant 2x \\ P^{+}(n)<P^{-}(m)}}f(m)f(n)f(\ell )\,\mathfrak{u}_{D}(mn\ell \overline{a_{1}}a_{2};r)\biggr|\nonumber\end{eqnarray}$$
where we have used the fact that
$f$
is supported on squarefree integers in the last equality. The rest of the argument consists in cutting the sums over
$(m,n,\ell )$
in dyadic segments, and analytically separating the four conditions
$x<mn\ell \leqslant 2x$
,
$P^{+}(m)<P^{-}(\ell )$
and
$P^{+}(n)<P^{-}(m)$
. The details are identical to the proof of Proposition 2 of [Reference Drappeau2], using our Lemma 2.3 instead of [Reference Drappeau2, Theorem 3]; we obtain the bound
$$\begin{eqnarray}O(D^{-1/2}x(\log x)^{7}(\log y)^{3})=O(D^{-1/2}x(\log x)^{10}).\end{eqnarray}$$
The Bombieri–Vinogradov range
$R\leqslant x^{4/9}$
is covered by similar arguments, using [Reference Iwaniec and Kowalski9, Theorem 17.4] instead of Lemma 2.3.◻
Deduction of the full Theorem 2.2 from Proposition 2.4.
We let
${\mathcal{K}}$
be the set of powerful numbers, that is for
$k\in {\mathcal{K}}$
if prime
$p$
divides
$k$
then
$p^{2}$
also divides
$k$
. Note that
$|{\mathcal{K}}\cap [1,x]|\ll x^{1/2}$
. Out of every
$n$
counted in the left-hand side of (2.4), we extract the largest powerful divisor
$k$
. Then from the triangle inequality and the bound
$|f(k)|\leqslant 1$
, the left-hand side of (2.4) is at most
$$\begin{eqnarray}\mathop{\sum }_{\substack{ q\leqslant x^{3/5-\unicode[STIX]{x1D700}} \\ (q,a_{1}a_{2})=1}}~\mathop{\sum }_{\substack{ k\in {\mathcal{K}}\cap S(x,y) \\ (k,q)=1}}~\biggl|\mathop{\sum }_{\substack{ n\in S(x/k,y) \\ (n,k)=1}}\unicode[STIX]{x1D707}^{2}(n)f(n)\,\mathfrak{u}_{D}(kna_{2}\overline{a_{1}};q)\biggr|.\end{eqnarray}$$
Let
$K\geqslant 1$
be a parameter. We use the trivial bound (2.2) on the contribution of
$k>K$
, getting
$$\begin{eqnarray}\mathop{\sum }_{q\leqslant x^{3/5-\unicode[STIX]{x1D700}}}~\mathop{\sum }_{\substack{ k\in {\mathcal{K}} \\ k>K}}~\mathop{\sum }_{n\leqslant x/k}\biggl(\mathbf{1}_{ka_{2}n\equiv a_{1}\;\text{mod}\;q}+\frac{D\unicode[STIX]{x1D70F}(q)}{\unicode[STIX]{x1D711}(q)}\biggr)=T_{1}+T_{2},\end{eqnarray}$$
say, where we have separated the contribution of the two summands. Executing the sum over
$q$
first, and separating the case
$kn|a_{1}$
, we find
$$\begin{eqnarray}T_{1}\leqslant \mathop{\sum }_{q\leqslant x^{3/5-\unicode[STIX]{x1D700}}}\unicode[STIX]{x1D70F}(|a_{1}|)^{2}+\mathop{\sum }_{\substack{ k\in {\mathcal{K}} \\ k>K}}~\mathop{\sum }_{n\leqslant x/k}\unicode[STIX]{x1D70F}(|kna_{2}-a_{1}|)\ll x^{4/5}+x^{1+\unicode[STIX]{x1D700}}DK^{-1/2}.\end{eqnarray}$$
It is easy to see that
$T_{2}\ll x^{1+\unicode[STIX]{x1D700}}DK^{-1/2}$
as well. Next, to each
$1\leqslant k\leqslant K$
in (2.7), by hypothesis, we may use Proposition 2.4 with
$x\leftarrow x/k$
,
$a_{2}\leftarrow ka_{2}$
and
$f(n)\leftarrow \mathbf{1}_{(n,k)=1}\unicode[STIX]{x1D707}^{2}(n)f(n)$
, and obtain the existence of
$C,\unicode[STIX]{x1D6FF}_{1}>0$
such that, for
$|a_{1}|,|a_{2}k|\leqslant x^{\unicode[STIX]{x1D6FF}_{1}}$
and
$(\log x)^{C}\leqslant y\leqslant x^{\unicode[STIX]{x1D6FF}_{1}}$
,
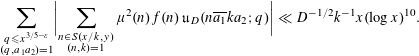$$\begin{eqnarray}\mathop{\sum }_{\substack{ q\leqslant x^{3/5-\unicode[STIX]{x1D700}} \\ (q,a_{1}a_{2})=1}}\biggl|\mathop{\sum }_{\substack{ n\in S(x/k,y) \\ (n,k)=1}}\unicode[STIX]{x1D707}^{2}(n)f(n)\,\mathfrak{u}_{D}(n\overline{a_{1}}ka_{2};q)\biggr|\ll D^{-1/2}k^{-1}x(\log x)^{10}.\end{eqnarray}$$
We take
$\unicode[STIX]{x1D6FF}=\unicode[STIX]{x1D6FF}_{1}/7$
,
$K=x^{\unicode[STIX]{x1D6FF}_{1}/2}$
, and sum over
$k\leqslant K$
, using
$\sum _{k\in {\mathcal{K}}}k^{-1}<\infty$
. By hypothesis
$D\leqslant x^{\unicode[STIX]{x1D6FF}}$
, so that
$x^{4/5}\ll DK^{-1/2}x\ll D^{-1/2}x^{1-\unicode[STIX]{x1D6FF}/2}$
, and we find that (2.7) is at most
$\ll D^{-1/2}x(\log x)^{10}$
as claimed.◻
3 Altering the set of exceptional characters
To prove Theorem 1.2 we need to reduce the set of exceptional characters from
${\mathcal{A}}(D)$
to
$\unicode[STIX]{x1D6EF}$
. We shall set this up in Proposition 3.2.
It is convenient to write
$b=a_{1}/a_{2}$
(which is
$\equiv a_{1}\overline{a_{2}}\;(\text{mod}~q)$
) and to define
$(q,b)$
to mean
$(q,a_{1}a_{2})$
. Thus in Theorem 2.1 we are working with
$$\begin{eqnarray}\mathop{\sum }_{\substack{ q\leqslant Q \\ (q,b)=1}}|\unicode[STIX]{x1D6E5}_{{\mathcal{A}}}(f,x;q,b)|\end{eqnarray}$$
for
$Q=x^{3/5-\unicode[STIX]{x1D700}}$
.
Lemma 3.1. Let
${\mathcal{A}}={\mathcal{A}}(D)$
for some
$D\geqslant 2$
. Suppose that
$\unicode[STIX]{x1D6EF}\subset {\mathcal{A}}$
. If
$(b,q)=1$
then
$$\begin{eqnarray}\displaystyle & & \displaystyle \unicode[STIX]{x1D6E5}_{\unicode[STIX]{x1D6EF}}(f,x;q,b)-\unicode[STIX]{x1D6E5}_{{\mathcal{A}}}(f,x;q,b)\nonumber\\ \displaystyle & & \displaystyle \displaystyle \quad =\frac{1}{\unicode[STIX]{x1D711}(q)}\mathop{\sum }_{\substack{ \ell \geqslant 1 \\ p|\ell \;\Longrightarrow \;p|q}}g(\ell )\mathop{\sum }_{\substack{ d\leqslant D \\ (d,\ell )=1 \\ d|q}}\unicode[STIX]{x1D711}(d)\unicode[STIX]{x1D6E5}_{\unicode[STIX]{x1D6EF}}(f,x/\ell ;d,b\overline{\ell })\mathop{\sum }_{\substack{ n\leqslant D/d \\ n|q/d}}\unicode[STIX]{x1D707}(n),\nonumber\end{eqnarray}$$
where
$g$
is the multiplicative function with
$F(s)G(s)=1$
.
Proof. If
$(b,q)=1$
then
$$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D6E5}_{\unicode[STIX]{x1D6EF}}(f,x;q,b)-\unicode[STIX]{x1D6E5}_{{\mathcal{A}}}(f,x;q,b) & = & \displaystyle \frac{1}{\unicode[STIX]{x1D711}(q)}\mathop{\sum }_{\substack{ \unicode[STIX]{x1D712}\in {\mathcal{A}}_{q} \\ \unicode[STIX]{x1D712}\not \in \unicode[STIX]{x1D6EF}_{q}}}\unicode[STIX]{x1D712}(b)S_{f}(x,\unicode[STIX]{x1D712})\nonumber\\ \displaystyle & = & \displaystyle \frac{1}{\unicode[STIX]{x1D711}(q)}\mathop{\sum }_{\substack{ m\leqslant D \\ m|q}}\mathop{\sum }_{\substack{ \unicode[STIX]{x1D712}\in {\mathcal{P}}(m)_{q} \\ \unicode[STIX]{x1D712}\not \in \unicode[STIX]{x1D6EF}_{q}}}\unicode[STIX]{x1D712}(b)S_{f}(x,\unicode[STIX]{x1D712}),\nonumber\end{eqnarray}$$
where
${\mathcal{P}}(m)$
denotes the set of primitive characters
$(\text{mod}~m)$
, as
${\mathcal{A}}$
is the set of all primitive characters of conductor
${\leqslant}D$
. Let
${\mathcal{C}}(m)$
denote the set of all characters
$(\text{mod}~m)$
. For
$m|q$
we define
$$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D6E5}_{\unicode[STIX]{x1D6EF},q}(f,x;m,b) & := & \displaystyle \mathop{\sum }_{\substack{ n\leqslant x \\ n\equiv a\;(\text{mod}\;m) \\ (n,q)=1}}f(n)-\frac{1}{\unicode[STIX]{x1D711}(m)}\mathop{\sum }_{\substack{ \unicode[STIX]{x1D712}\in {\mathcal{C}}(m)_{q}\cap \unicode[STIX]{x1D6EF}_{q}}}\unicode[STIX]{x1D712}(b)S_{f}(x,\unicode[STIX]{x1D712})\nonumber\\ \displaystyle & = & \displaystyle \frac{1}{\unicode[STIX]{x1D711}(m)}\mathop{\sum }_{\substack{ \unicode[STIX]{x1D712}\in {\mathcal{C}}(m)_{q} \\ \unicode[STIX]{x1D712}\not \in \unicode[STIX]{x1D6EF}_{q}}}\unicode[STIX]{x1D712}(b)S_{f}(x,\unicode[STIX]{x1D712})\nonumber\\ \displaystyle & = & \displaystyle \frac{1}{\unicode[STIX]{x1D711}(m)}\mathop{\sum }_{d|m}\mathop{\sum }_{\substack{ \unicode[STIX]{x1D712}\in {\mathcal{P}}(d)_{q} \\ \unicode[STIX]{x1D712}\not \in \unicode[STIX]{x1D6EF}_{q}}}\unicode[STIX]{x1D712}(b)S_{f}(x,\unicode[STIX]{x1D712}).\nonumber\end{eqnarray}$$
By Möbius inversion we deduce that, for
$m|q$
,
$$\begin{eqnarray}\mathop{\sum }_{\substack{ \unicode[STIX]{x1D712}\in {\mathcal{P}}(m)_{q} \\ \unicode[STIX]{x1D712}\not \in \unicode[STIX]{x1D6EF}_{q}}}\unicode[STIX]{x1D712}(b)S_{f}(x,\unicode[STIX]{x1D712})=\mathop{\sum }_{d|m}\unicode[STIX]{x1D707}(m/d)\unicode[STIX]{x1D711}(d)\unicode[STIX]{x1D6E5}_{\unicode[STIX]{x1D6EF},q}(f,x;d,b).\end{eqnarray}$$
Next we wish to better understand
$\unicode[STIX]{x1D6E5}_{\unicode[STIX]{x1D6EF},q}(f,x;m,a)$
. Let
$f_{q}(p^{k})=f(p^{k})$
if
$p|q,~p\nmid m$
, and
$f_{q}(p^{k})=0$
otherwise. Define
$g_{q}$
from
$g$
in a similar way. Note
$f_{q}$
and
$g_{q}$
are simply
$f$
and
$g$
supported on the integers composed from the prime factors of
$q$
. If
$(a,m)=1$
then
$$\begin{eqnarray}\unicode[STIX]{x1D6E5}_{\unicode[STIX]{x1D6EF}}(f,x;m,a)=\mathop{\sum }_{\substack{ \ell \geqslant 1 \\ (\ell ,m)=1}}f_{q}(\ell )\unicode[STIX]{x1D6E5}_{\unicode[STIX]{x1D6EF},q}(f,x/\ell ;m,a\overline{\ell }),\end{eqnarray}$$
and since
$F_{q}G_{q}=1$
we have
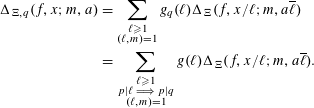$$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D6E5}_{\unicode[STIX]{x1D6EF},q}(f,x;m,a) & = & \displaystyle \mathop{\sum }_{\substack{ \ell \geqslant 1 \\ (\ell ,m)=1}}g_{q}(\ell )\unicode[STIX]{x1D6E5}_{\unicode[STIX]{x1D6EF}}(f,x/\ell ;m,a\overline{\ell })\nonumber\\ \displaystyle & = & \displaystyle \mathop{\sum }_{\substack{ \ell \geqslant 1 \\ p|\ell \;\Longrightarrow \;p|q \\ (\ell ,m)=1}}g(\ell )\unicode[STIX]{x1D6E5}_{\unicode[STIX]{x1D6EF}}(f,x/\ell ;m,a\overline{\ell }).\nonumber\end{eqnarray}$$
Substituting this in above then yields
$$\begin{eqnarray}\mathop{\sum }_{\substack{ \unicode[STIX]{x1D712}\in {\mathcal{P}}(m)_{q} \\ \unicode[STIX]{x1D712}\not \in \unicode[STIX]{x1D6EF}_{q}}}\unicode[STIX]{x1D712}(b)S_{f}(x,\unicode[STIX]{x1D712})=\mathop{\sum }_{d|m}\unicode[STIX]{x1D707}(m/d)\unicode[STIX]{x1D711}(d)\mathop{\sum }_{\substack{ \ell \geqslant 1 \\ p|\ell \;\Longrightarrow \;p|q, \\ (\ell ,d)=1}}g(\ell )\unicode[STIX]{x1D6E5}_{\unicode[STIX]{x1D6EF}}(f,x/\ell ;d,b\overline{\ell }),\end{eqnarray}$$
and the result follows writing
$m=dn$
.◻
Proposition 3.2. Let the notations and assumptions be as in the statement of Theorem 2.1. Suppose that
$\unicode[STIX]{x1D6EF}\subset {\mathcal{A}}$
. Then
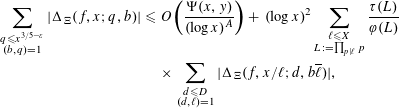$$\begin{eqnarray}\displaystyle \displaystyle \mathop{\sum }_{\substack{ q\leqslant x^{3/5-\unicode[STIX]{x1D700}} \\ (b,q)=1}}|\unicode[STIX]{x1D6E5}_{\unicode[STIX]{x1D6EF}}(f,x;q,b)| & {\leqslant} & \displaystyle O\biggl(\frac{\unicode[STIX]{x1D6F9}(x,y)}{(\log x)^{A}}\biggr)+\,(\log x)^{2}\mathop{\sum }_{\substack{ \ell \leqslant X \\ L:=\mathop{\prod }_{p|\ell }p}}\frac{\unicode[STIX]{x1D70F}(L)}{\unicode[STIX]{x1D711}(L)}\nonumber\\ \displaystyle & & \displaystyle \times \,\displaystyle \mathop{\sum }_{\substack{ d\leqslant D \\ (d,\ell )=1}}|\unicode[STIX]{x1D6E5}_{\unicode[STIX]{x1D6EF}}(f,x/\ell ;d,b\overline{\ell })|,\nonumber\end{eqnarray}$$
where
$X=(1+\unicode[STIX]{x1D6FD})^{2}(\log x)^{2A+6}$
with
$$\begin{eqnarray}\unicode[STIX]{x1D6FD}=\unicode[STIX]{x1D6FD}(\unicode[STIX]{x1D6EF}):=\mathop{\sum }_{\unicode[STIX]{x1D713}\;(\text{mod}\;r_{\unicode[STIX]{x1D713}})\in \unicode[STIX]{x1D6EF}}\frac{1}{r_{\unicode[STIX]{x1D713}}}.\end{eqnarray}$$
Proof. Set
$Q=x^{3/5-\unicode[STIX]{x1D700}}$
. We deduce from Lemma 3.1, as each
$|g(\ell )|\leqslant 1$
since
$f,g\in {\mathcal{C}}$
, that
$$\begin{eqnarray}\displaystyle & & \displaystyle \displaystyle \mathop{\sum }_{\substack{ q\leqslant Q \\ (b,q)=1}}|\unicode[STIX]{x1D6E5}_{\unicode[STIX]{x1D6EF}}(f,x;q,b)|\nonumber\\ \displaystyle & & \displaystyle \quad \leqslant \mathop{\sum }_{\substack{ q\leqslant Q \\ (b,q)=1}}|\unicode[STIX]{x1D6E5}_{{\mathcal{A}}}(f,x;q,b)|+\mathop{\sum }_{\substack{ \ell \geqslant 1 \\ L:=\mathop{\prod }_{p|\ell }p}}\mathop{\sum }_{\substack{ d\leqslant D \\ (d,\ell )=1}}\unicode[STIX]{x1D711}(d)|\unicode[STIX]{x1D6E5}_{\unicode[STIX]{x1D6EF}}(f,x/\ell ;d,b\overline{\ell })|\nonumber\\ \displaystyle & & \displaystyle \displaystyle \qquad \times \,\mathop{\sum }_{\substack{ q\leqslant Q \\ (b,q)=1 \\ dL|q}}\frac{1}{\unicode[STIX]{x1D711}(q)}\biggl|\mathop{\sum }_{\substack{ n\leqslant D/d \\ n|q/d}}\unicode[STIX]{x1D707}(n)\biggr|.\nonumber\end{eqnarray}$$
The first term on the right-hand side is
$\ll _{A}\unicode[STIX]{x1D6F9}(x,y)/(\log x)^{A}$
by Theorem 2.1. For the sum at the end we have an upper bound
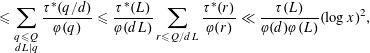$$\begin{eqnarray}{\leqslant}\mathop{\sum }_{\substack{ q\leqslant Q \\ dL|q}}\frac{\unicode[STIX]{x1D70F}^{\ast }(q/d)}{\unicode[STIX]{x1D711}(q)}\leqslant \frac{\unicode[STIX]{x1D70F}^{\ast }(L)}{\unicode[STIX]{x1D711}(dL)}\mathop{\sum }_{\substack{ r\leqslant Q/dL}}\frac{\unicode[STIX]{x1D70F}^{\ast }(r)}{\unicode[STIX]{x1D711}(r)}\ll \frac{\unicode[STIX]{x1D70F}(L)}{\unicode[STIX]{x1D711}(d)\unicode[STIX]{x1D711}(L)}(\log x)^{2},\end{eqnarray}$$
where
$\unicode[STIX]{x1D70F}^{\ast }(m)$
denotes the number of squarefree divisors of
$m$
, writing
$q=dLr$
, as
$L$
is squarefree. Therefore
$$\begin{eqnarray}\displaystyle & & \displaystyle \displaystyle \mathop{\sum }_{\substack{ q\leqslant Q \\ (b,q)=1}}|\unicode[STIX]{x1D6E5}_{\unicode[STIX]{x1D6EF}}(f,x;q,b)|\nonumber\\ \displaystyle & & \displaystyle \quad \leqslant O\biggl(\frac{\unicode[STIX]{x1D6F9}(x,y)}{(\log x)^{A}}\biggr)+(\log x)^{2}\mathop{\sum }_{\substack{ \ell \geqslant 1 \\ L:=\mathop{\prod }_{p|\ell }p}}\frac{\unicode[STIX]{x1D70F}(L)}{\unicode[STIX]{x1D711}(L)}\mathop{\sum }_{\substack{ d\leqslant D \\ (d,\ell )=1}}|\unicode[STIX]{x1D6E5}_{\unicode[STIX]{x1D6EF}}(f,x/\ell ;d,b\overline{\ell })|.\nonumber\end{eqnarray}$$
We will attack this last sum first by employing relatively trivial bounds for the terms with
$\ell$
that are not too small, so that we only have to consider
$\ell d$
that are smallish in further detail. Now [Reference Fouvry and Tenenbaum3, Theorem 1] gives the upper bound
$$\begin{eqnarray}\unicode[STIX]{x1D6F9}_{q}(x,y)\ll \frac{\unicode[STIX]{x1D711}(q)}{q}\unicode[STIX]{x1D6F9}(x,y)\end{eqnarray}$$
provided
$x\geqslant y\geqslant \exp ((\log \log x)^{2})$
and
$q\leqslant x$
. Therefore
$$\begin{eqnarray}|\unicode[STIX]{x1D6E5}_{\unicode[STIX]{x1D6EF}}(f,x;q,a)|\!\leqslant \!\unicode[STIX]{x1D6F9}(x,y;a,q)+\frac{|\unicode[STIX]{x1D6EF}_{q}|}{\unicode[STIX]{x1D711}(q)}\unicode[STIX]{x1D6F9}_{q}(x,y)\!\ll \!\unicode[STIX]{x1D6F9}(x,y;a,q)+\frac{|\unicode[STIX]{x1D6EF}_{q}|}{q}\unicode[STIX]{x1D6F9}(x,y)\end{eqnarray}$$
in this range. Substituting in, the upper bound on the
$\ell$
th term above becomes
$$\begin{eqnarray}\ll (\log x)^{2}\cdot \frac{\unicode[STIX]{x1D70F}(L)}{\unicode[STIX]{x1D711}(L)}\biggl(\mathop{\sum }_{\substack{ d\leqslant D \\ (d,\ell )=1}}\unicode[STIX]{x1D6F9}(x/\ell ,y;d,b\overline{\ell })+\unicode[STIX]{x1D6F9}(x/\ell ,y)\mathop{\sum }_{\substack{ d\leqslant D \\ (d,\ell )=1}}\frac{|\unicode[STIX]{x1D6EF}_{d}|}{d}\biggr).\end{eqnarray}$$
The second sum over
$d$
is therefore
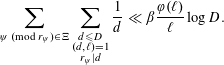$$\begin{eqnarray}\mathop{\sum }_{\unicode[STIX]{x1D713}\;(\text{mod}\;r_{\unicode[STIX]{x1D713}})\in \unicode[STIX]{x1D6EF}}\mathop{\sum }_{\substack{ d\leqslant D \\ (d,\ell )=1 \\ r_{\unicode[STIX]{x1D713}}|d}}\frac{1}{d}\ll \unicode[STIX]{x1D6FD}\frac{\unicode[STIX]{x1D711}(\ell )}{\ell }\log D.\end{eqnarray}$$
For the first term we use [Reference Harper7, Theorem 1] which yields that
$$\begin{eqnarray}\mathop{\sum }_{\substack{ d\leqslant D \\ (d,\ell )=1}}\biggl|\unicode[STIX]{x1D6F9}(x/\ell ,y;d,b\overline{\ell })-\frac{\unicode[STIX]{x1D6F9}_{d}(x/\ell ,y)}{\unicode[STIX]{x1D711}(d)}\biggr|\ll \frac{\unicode[STIX]{x1D6F9}(x/\ell ,y)}{(\log x)^{A}},\end{eqnarray}$$
as
$D\leqslant \sqrt{\unicode[STIX]{x1D6F9}(x,y)}/(\log x)^{B}$
since
$y\geqslant (\log x)^{C}$
. Therefore, expanding the sum and using (3.1), we obtain
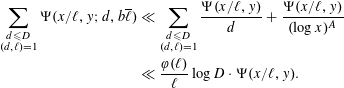$$\begin{eqnarray}\displaystyle \mathop{\sum }_{\substack{ d\leqslant D \\ (d,\ell )=1}}\unicode[STIX]{x1D6F9}(x/\ell ,y;d,b\overline{\ell }) & \ll & \displaystyle \mathop{\sum }_{\substack{ d\leqslant D \\ (d,\ell )=1}}\frac{\unicode[STIX]{x1D6F9}(x/\ell ,y)}{d}+\frac{\unicode[STIX]{x1D6F9}(x/\ell ,y)}{(\log x)^{A}}\nonumber\\ \displaystyle & \ll & \displaystyle \frac{\unicode[STIX]{x1D711}(\ell )}{\ell }\log D\cdot \unicode[STIX]{x1D6F9}(x/\ell ,y).\nonumber\end{eqnarray}$$
By [Reference de la Bretèche and Tenenbaum1, Théorème 2.1] we have
$$\begin{eqnarray}\unicode[STIX]{x1D6F9}(x/\ell ,y)\ll \unicode[STIX]{x1D6F9}(x,y)/\ell ^{\unicode[STIX]{x1D6FC}},\end{eqnarray}$$
where
$\unicode[STIX]{x1D6FC}>3/4$
in our range for
$y$
. Therefore in total the
$\ell$
th term in
$$\begin{eqnarray}\ll \frac{\unicode[STIX]{x1D70F}(L)}{L\ell ^{\unicode[STIX]{x1D6FC}}}\unicode[STIX]{x1D6F9}(x,y)(\log x)^{2}(\log D)\cdot (1+\unicode[STIX]{x1D6FD}).\end{eqnarray}$$
Summing over
$\ell >X$
, we obtain, taking
$\unicode[STIX]{x1D70E}=\unicode[STIX]{x1D6FC}-1/4$
,
$$\begin{eqnarray}\mathop{\sum }_{\substack{ \ell \geqslant X \\ L:=\mathop{\prod }_{p|\ell }p}}\!\!\frac{\unicode[STIX]{x1D70F}(L)}{L\ell ^{\unicode[STIX]{x1D6FC}}}\leqslant \!\!\mathop{\sum }_{\substack{ \ell \\ L:=\mathop{\prod }_{p|\ell }p}}\!\!\frac{\unicode[STIX]{x1D70F}(L)}{L\ell ^{\unicode[STIX]{x1D6FC}}}(\ell /X)^{\unicode[STIX]{x1D70E}}=X^{-\unicode[STIX]{x1D70E}}\mathop{\prod }_{p}\biggl(1+\frac{2}{p(p^{1/4}-1)}\biggr)\ll X^{-1/2}.\end{eqnarray}$$
Taking
$X=(1+\unicode[STIX]{x1D6FD})^{2}(\log x)^{2A+6}$
, the contribution of the
$\ell >X$
is therefore
$\ll \unicode[STIX]{x1D6F9}(x,y)/(\log x)^{A}$
. Combining all of the above then yields the result.◻
4 Putting the pieces together
In order to prove Theorem 1.2 we need Theorem 2.1, Proposition 3.2, Corollary 6.1 (which will be proved in the final two sections), and the following result which is [Reference Granville and Shao6, Proposition 5.1].
Proposition 4.1. Fix
$B\geqslant 0$
and
$0<\unicode[STIX]{x1D702}<\frac{1}{2}$
. Given
$(\log x)^{4B+5}\leqslant y=x^{1/u}\leqslant x^{1/2-\unicode[STIX]{x1D702}}$
let
$$\begin{eqnarray}R=R(x,y):=\min \{y^{\log \log \log x/(3\log u)},x^{\unicode[STIX]{x1D702}/(3\log \log x)}\}~({\leqslant}y^{1/3}).\end{eqnarray}$$
Suppose that
$f\in {\mathcal{C}}$
, and is only supported on
$y$
-smooth numbers. There exists a set,
$\unicode[STIX]{x1D6EF}$
, of primitive characters
$\unicode[STIX]{x1D713}\;(\text{mod}~r)$
with
$r\leqslant R$
, such that if
$q\leqslant R$
and
$(a,q)=1$
then
$$\begin{eqnarray}|\unicode[STIX]{x1D6E5}_{\unicode[STIX]{x1D6EF}}(f,x;q,a)|\ll \frac{1}{\unicode[STIX]{x1D711}(q)}\frac{\unicode[STIX]{x1D6F9}(x,y)}{(\log x)^{B}}.\end{eqnarray}$$
Moreover, one may take
$\unicode[STIX]{x1D6EF}$
to be
$\unicode[STIX]{x1D6EF}=\unicode[STIX]{x1D6EF}(2B+2\frac{1}{3})$
, where
$\unicode[STIX]{x1D6EF}(C)$
is the set of primitive characters
$\unicode[STIX]{x1D713}\;(\text{mod}~r)$
with
$r\leqslant R$
such that there exists
$x^{\unicode[STIX]{x1D702}}<X\leqslant x$
for which
$$\begin{eqnarray}|S_{f}(X,\unicode[STIX]{x1D713})|\geqslant \frac{\unicode[STIX]{x1D6F9}(X,y)}{(u\log u)^{4}(\log x)^{C}}.\end{eqnarray}$$
Proof of Theorem 1.2.
Let
$c>0$
be the small constant from Corollary 6.1. Set
$D=(x/\unicode[STIX]{x1D6F9}(x,y))^{2}(\log x)^{2A+20}$
, and one easily verifies that the hypothesis for
$y$
implies that
$$\begin{eqnarray}D\leqslant \min (R,y^{c},\exp (c\log x/\!\log \log x))\end{eqnarray}$$
from the usual estimate
$\unicode[STIX]{x1D6F9}(x,y)=xu^{-u+o(u)}$
for smooth numbers. We will prove Theorem 1.2 with
$\unicode[STIX]{x1D6EF}=\unicode[STIX]{x1D6EF}(2A+8\frac{1}{3})$
, where
$\unicode[STIX]{x1D6EF}(C)$
is the set of primitive characters
$\unicode[STIX]{x1D713}\;(\text{mod}\;r)$
with
$r\leqslant D$
, such that there exists
$x^{1/4}<X\leqslant x$
for which (4.1) holds. By Proposition 4.1 with
$B=A+3$
and
$\unicode[STIX]{x1D702}=1/4$
, we have the bound
$$\begin{eqnarray}|\unicode[STIX]{x1D6E5}_{\unicode[STIX]{x1D6EF}}(f,x;q,a)|\ll \frac{1}{\unicode[STIX]{x1D711}(q)}\frac{\unicode[STIX]{x1D6F9}(x,y)}{(\log x)^{A+3}}\end{eqnarray}$$
whenever
$q\leqslant D$
and
$(a,q)=1$
. Moreover, we have the same bound with
$x$
replaced by
$x/\ell$
for any
$\ell =x^{o(1)}$
.
The goal of the next two sections will be to prove Corollary 6.1, which implies that
$$\begin{eqnarray}|\unicode[STIX]{x1D6EF}|\ll (\log x)^{6A+38}.\end{eqnarray}$$
This implies that
$\unicode[STIX]{x1D6FD}(\unicode[STIX]{x1D6EF})\ll (\log x)^{3A+19}$
, and so
$X\ll (\log x)^{8A+44}$
in Proposition 3.2. Thus for each
$\ell \leqslant X$
and
$d\leqslant D$
, we have
$$\begin{eqnarray}|\unicode[STIX]{x1D6E5}_{\unicode[STIX]{x1D6EF}}(f,x/\ell ;d,b\overline{\ell })|\ll \frac{1}{\unicode[STIX]{x1D711}(d)}\frac{\unicode[STIX]{x1D6F9}(x/\ell ,y)}{(\log x)^{A+3}}\ll \frac{1}{\unicode[STIX]{x1D711}(d)\ell ^{\unicode[STIX]{x1D6FC}}}\frac{\unicode[STIX]{x1D6F9}(x,y)}{(\log x)^{A+3}},\end{eqnarray}$$
by (3.2). Therefore
$$\begin{eqnarray}\displaystyle & & \displaystyle (\log x)^{2}\mathop{\sum }_{\substack{ \ell \leqslant X \\ L:=\mathop{\prod }_{p|\ell }p}}\frac{\unicode[STIX]{x1D70F}(L)}{\unicode[STIX]{x1D711}(L)}\mathop{\sum }_{\substack{ d\leqslant D \\ (d,\ell )=1}}|\unicode[STIX]{x1D6E5}_{\unicode[STIX]{x1D6EF}}(f,x/\ell ;d,b\overline{\ell })|\nonumber\\ \displaystyle & & \displaystyle \quad \ll \frac{\unicode[STIX]{x1D6F9}(x,y)}{(\log x)^{A+1}}\mathop{\sum }_{\substack{ \ell \leqslant X \\ L:=\mathop{\prod }_{p|\ell }p}}\frac{\unicode[STIX]{x1D70F}(L)}{\unicode[STIX]{x1D711}(L)\ell ^{\unicode[STIX]{x1D6FC}}}\mathop{\sum }_{\substack{ d\leqslant D \\ (d,L)=1}}\frac{1}{\unicode[STIX]{x1D711}(d)}\nonumber\\ \displaystyle & & \displaystyle \quad \ll \frac{\unicode[STIX]{x1D6F9}(x,y)}{(\log x)^{A}}\mathop{\sum }_{\substack{ \ell \leqslant X \\ L:=\mathop{\prod }_{p|\ell }p}}\frac{\unicode[STIX]{x1D70F}(L)}{L\ell ^{\unicode[STIX]{x1D6FC}}}\nonumber\\ \displaystyle & & \displaystyle \quad \leqslant \frac{\unicode[STIX]{x1D6F9}(x,y)}{(\log x)^{A}}\mathop{\prod }_{p\leqslant X}\biggl(1+\frac{2}{p(p^{\unicode[STIX]{x1D6FC}}-1)}\biggr)\ll \frac{\unicode[STIX]{x1D6F9}(x,y)}{(\log x)^{A}}.\nonumber\end{eqnarray}$$
We therefore deduce from Proposition 3.2 that
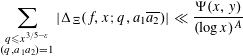$$\begin{eqnarray}\mathop{\sum }_{\substack{ q\leqslant x^{3/5-\unicode[STIX]{x1D700}} \\ (q,a_{1}a_{2})=1}}|\unicode[STIX]{x1D6E5}_{\unicode[STIX]{x1D6EF}}(f,x;q,a_{1}\overline{a_{2}})|\ll \frac{\unicode[STIX]{x1D6F9}(x,y)}{(\log x)^{A}}\end{eqnarray}$$
as desired.
To deduce the second part of Theorem 1.2, about functions
$f$
satisfying the Siegel–Walfisz criterion, we use the following variant of Proposition 3.4 in [Reference Granville and Shao6].
Proposition 4.2. Fix
$\unicode[STIX]{x1D700}>0$
. Let
$(\log x)^{1+\unicode[STIX]{x1D700}}\leqslant y\leqslant x$
be large. Let
$f\in {\mathcal{C}}$
be a multiplicative function supported on
$y$
-smooth integers. Suppose that
$\unicode[STIX]{x1D6EF}$
is a set of primitive characters, containing
$\ll (\log x)^{C}$
elements, such that
$$\begin{eqnarray}\mathop{\sum }_{q\sim Q}|\unicode[STIX]{x1D6E5}_{\unicode[STIX]{x1D6EF}}(f,x;q,a_{q})|\ll \frac{\unicode[STIX]{x1D6F9}(x,y)}{(\log x)^{B}},\end{eqnarray}$$
for
$(a_{q},q)=1$
for all
$q\sim Q$
, where
$Q\leqslant x$
. If the
$D$
-Siegel–Walfisz criterion holds for
$f$
, where
$D\geqslant B+C$
, then
$$\begin{eqnarray}\mathop{\sum }_{q\sim Q}|\unicode[STIX]{x1D6E5}(f,x;q,a_{q})|\ll \frac{\unicode[STIX]{x1D6F9}(x,y)}{(\log x)^{B}}.\end{eqnarray}$$
Proof. By the definition of
$\unicode[STIX]{x1D6E5}_{\unicode[STIX]{x1D6EF}}$
we have
$$\begin{eqnarray}|\unicode[STIX]{x1D6E5}(f,x;q,a_{q})|\leqslant |\unicode[STIX]{x1D6E5}_{\unicode[STIX]{x1D6EF}}(f,x;q,a_{q})|+\frac{1}{\unicode[STIX]{x1D711}(q)}\mathop{\sum }_{\substack{ \unicode[STIX]{x1D712}\;(\text{mod}\;q) \\ \unicode[STIX]{x1D712}\in \unicode[STIX]{x1D6EF}_{q},\unicode[STIX]{x1D712}\neq \unicode[STIX]{x1D712}_{0}}}|S_{f}(x,\unicode[STIX]{x1D712})|.\end{eqnarray}$$
Summing this over
$q\sim Q$
and using the hypothesis, we deduce that
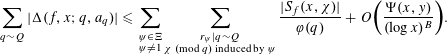$$\begin{eqnarray}\mathop{\sum }_{q\sim Q}|\unicode[STIX]{x1D6E5}(f,x;q,a_{q})|\leqslant \mathop{\sum }_{\substack{ \unicode[STIX]{x1D713}\in \unicode[STIX]{x1D6EF} \\ \unicode[STIX]{x1D713}\neq 1}}\mathop{\sum }_{\substack{ r_{\unicode[STIX]{x1D713}}\mid q\sim Q \\ \unicode[STIX]{x1D712}\;(\text{mod}\;q)\text{ induced by }\unicode[STIX]{x1D713}}}\frac{|S_{f}(x,\unicode[STIX]{x1D712})|}{\unicode[STIX]{x1D711}(q)}+O\biggl(\frac{\unicode[STIX]{x1D6F9}(x,y)}{(\log x)^{B}}\biggr).\end{eqnarray}$$
It suffices to show that, for each fixed
$\unicode[STIX]{x1D713}\;(\text{mod}\;r)\in \unicode[STIX]{x1D6EF}$
with
$r>1$
, we have
$$\begin{eqnarray}\mathop{\sum }_{\substack{ r\mid q\sim Q \\ \unicode[STIX]{x1D712}\;(\text{mod}\;q)\text{ induced by }\unicode[STIX]{x1D713}}}\frac{|S_{f}(x,\unicode[STIX]{x1D712})|}{\unicode[STIX]{x1D711}(q)}\ll \frac{\unicode[STIX]{x1D6F9}(x,y)}{(\log x)^{D}}.\end{eqnarray}$$
The conclusion then follows since
$|\unicode[STIX]{x1D6EF}|\ll (\log x)^{C}$
and
$D\geqslant B+C$
. If
$\unicode[STIX]{x1D712}\;(\text{mod}\;q)$
is induced by
$\unicode[STIX]{x1D713}\;(\text{mod}\;r)$
, then there is a multiplicative function
$h$
supported only on powers of primes which divide
$q$
but not
$r$
, such that
$h\ast f\overline{\unicode[STIX]{x1D713}}=f\overline{\unicode[STIX]{x1D712}}$
. Note that
$h\in {\mathcal{C}}$
since
$f\in {\mathcal{C}}$
, and in particular
$h$
is
$1$
-bounded. It follows that
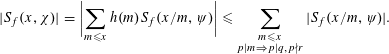$$\begin{eqnarray}|S_{f}(x,\unicode[STIX]{x1D712})|=\biggl|\mathop{\sum }_{m\leqslant x}h(m)S_{f}(x/m,\unicode[STIX]{x1D713})\biggr|\leqslant \mathop{\sum }_{\substack{ m\leqslant x \\ p\mid m\Rightarrow p\mid q,p\nmid r}}|S_{f}(x/m,\unicode[STIX]{x1D713})|.\end{eqnarray}$$
Since
$f$
satisfies the
$D$
-Siegel–Walfisz criterion, we have
$$\begin{eqnarray}\frac{S_{f}(x/m,\unicode[STIX]{x1D713})}{\unicode[STIX]{x1D711}(r)}=\frac{1}{\unicode[STIX]{x1D711}(r)}\mathop{\sum }_{a\;(\text{mod}\;r)}\overline{\unicode[STIX]{x1D713}}(a)\unicode[STIX]{x1D6E5}(f,x/m;r,a)\ll \frac{\unicode[STIX]{x1D6F9}(x/m,y)}{(\log (x/m))^{D}}.\end{eqnarray}$$
Using the bound
$\unicode[STIX]{x1D6F9}(x/m,y)\ll m^{-\unicode[STIX]{x1D6FC}}\unicode[STIX]{x1D6F9}(x,y)$
where
$\unicode[STIX]{x1D6FC}=\unicode[STIX]{x1D6FC}(x,y)\geqslant \unicode[STIX]{x1D700}+o(1)$
, we may bound the left-hand side of (4.3) by
$$\begin{eqnarray}\unicode[STIX]{x1D6F9}(x,y)\mathop{\sum }_{r\mid q\sim Q}\frac{\unicode[STIX]{x1D711}(r)}{\unicode[STIX]{x1D711}(q)}\mathop{\sum }_{\substack{ m\leqslant x \\ p\mid m\Rightarrow p\mid q,p\nmid r}}\frac{1}{m^{\unicode[STIX]{x1D6FC}}(\log (x/m))^{D}}.\end{eqnarray}$$
To analyze the inner sum over
$m$
, we break it into two pieces depending on whether
$m\leqslant x^{1/2}$
or
$m>x^{1/2}$
:
$$\begin{eqnarray}\mathop{\sum }_{\substack{ m\leqslant x \\ p\mid m\Rightarrow p\mid q,p\nmid r}}\frac{1}{m^{\unicode[STIX]{x1D6FC}}(\log (x/m))^{D}}\ll \frac{1}{(\log x)^{D}}\mathop{\sum }_{\substack{ m\leqslant x^{1/2} \\ p\mid m\Rightarrow p\mid q,p\nmid r}}\frac{1}{m^{\unicode[STIX]{x1D6FC}}}+\mathop{\sum }_{\substack{ x^{1/2}<m\leqslant x \\ p\mid m\Rightarrow p\mid q,p\nmid r}}\frac{1}{m^{\unicode[STIX]{x1D6FC}}}.\end{eqnarray}$$
To deal with the sum over
$x^{1/2}<m\leqslant x$
, note that the number of
$m\leqslant x$
with
$p|m\Rightarrow p|q$
is maximized when
$q$
is the product of primes up to
${\sim}\log x$
, in which case the number of such
$m$
is
$x^{o(1)}$
. Thus the sum over
$x^{1/2}<m\leqslant x$
is
$O(x^{-\unicode[STIX]{x1D6FC}/2+o(1)})$
, and their overall contribution to (4.4) is acceptable. To deal with the sum over
$m\leqslant x^{1/2}$
, note that
$$\begin{eqnarray}\mathop{\sum }_{\substack{ m\leqslant x^{1/2} \\ p\mid m\Rightarrow p\mid q,p\nmid r}}\frac{1}{m^{\unicode[STIX]{x1D6FC}}}\leqslant \mathop{\sum }_{\substack{ m\leqslant x^{1/2} \\ m\mid q,(m,r)=1}}\frac{\unicode[STIX]{x1D707}^{2}(m)}{\unicode[STIX]{x1D711}_{\unicode[STIX]{x1D6FC}}(m)},\end{eqnarray}$$
where
$\unicode[STIX]{x1D711}_{\unicode[STIX]{x1D6FC}}(m)=\prod _{p\mid m}(p^{\unicode[STIX]{x1D6FC}}-1)$
. Thus their overall contribution to (4.4) is
$$\begin{eqnarray}\displaystyle & & \displaystyle \ll \frac{\unicode[STIX]{x1D6F9}(x,y)}{(\log x)^{D}}\mathop{\sum }_{(m,r)=1}\frac{\unicode[STIX]{x1D707}^{2}(m)}{\unicode[STIX]{x1D711}_{\unicode[STIX]{x1D6FC}}(m)}\mathop{\sum }_{mr\mid q\sim Q}\frac{\unicode[STIX]{x1D711}(r)}{\unicode[STIX]{x1D711}(q)}\nonumber\\ \displaystyle & & \displaystyle \ll \frac{\unicode[STIX]{x1D6F9}(x,y)}{(\log x)^{D}}\mathop{\sum }_{m}\frac{\unicode[STIX]{x1D707}^{2}(m)}{\unicode[STIX]{x1D711}(m)\unicode[STIX]{x1D711}_{\unicode[STIX]{x1D6FC}}(m)}\nonumber\\ \displaystyle & & \displaystyle \ll \frac{\unicode[STIX]{x1D6F9}(x,y)}{(\log x)^{D}},\nonumber\end{eqnarray}$$
since the infinite sum over
$m$
converges. This establishes (4.3) and completes the proof of the lemma.◻
To deduce the second part of Theorem 1.2, we apply Proposition 4.2 with
$a_{q}\equiv a_{1}\overline{a_{2}}\;(\text{mod}~q)$
for each dyadic interval with
$Q\leqslant x^{3/5-\unicode[STIX]{x1D700}}$
. It is applicable since we assume that the Siegel–Walfisz criterion holds for
$f$
with exponent
$D\geqslant A+(6A+38)$
. Summing up over all dyadic intervals, the second part of the theorem follows (with
$A$
replaced by
$A-1$
).◻
Remark 4.3. The lower bound required for
$y$
in the hypothesis (1.2) comes precisely from (4.2). In fact, one can still deduce Theorem 1.2 even if we just had
$$\begin{eqnarray}D\leqslant \min (R,x^{c})\end{eqnarray}$$
instead. To see this, we follow the arguments above but now use Corollary 6.2 to get
$$\begin{eqnarray}\mathop{\sum }_{\unicode[STIX]{x1D713}\;(\text{mod}\;q)\in \unicode[STIX]{x1D6EF}}\frac{1}{q^{1/2}}\ll (\log x)^{6A+38}.\end{eqnarray}$$
We cannot directly apply Proposition 4.2 now, but if we let
${\mathcal{E}}$
be the set of
$\unicode[STIX]{x1D713}\;(\text{mod}\;r_{\unicode[STIX]{x1D713}})\;\in \unicode[STIX]{x1D6EF}$
with
$r_{\unicode[STIX]{x1D713}}>(\log x)^{14A+78}$
, then removing
${\mathcal{E}}$
from
$\unicode[STIX]{x1D6EF}$
induces an error of at most
$$\begin{eqnarray}\mathop{\sum }_{q\leqslant x}\frac{1}{\unicode[STIX]{x1D711}(q)}\mathop{\sum }_{\unicode[STIX]{x1D712}\in {\mathcal{E}}_{q}}|S_{f}(x,\unicode[STIX]{x1D712})|.\end{eqnarray}$$
As
$|S_{f}(x,\unicode[STIX]{x1D712})|\ll \unicode[STIX]{x1D6F9}_{q}(x,y)\ll (\unicode[STIX]{x1D711}(q)/q)\unicode[STIX]{x1D6F9}(x,y)$
the above is
$$\begin{eqnarray}\ll \unicode[STIX]{x1D6F9}(x,y)\mathop{\sum }_{\unicode[STIX]{x1D713}\in {\mathcal{E}}}\mathop{\sum }_{\substack{ q\leqslant x \\ r_{\unicode[STIX]{x1D713}}|q}}\frac{1}{q}\ll \unicode[STIX]{x1D6F9}(x,y)\log x\mathop{\sum }_{\unicode[STIX]{x1D713}\in {\mathcal{E}}}\frac{1}{r_{\unicode[STIX]{x1D713}}}\ll \frac{\unicode[STIX]{x1D6F9}(x,y)}{(\log x)^{A}},\end{eqnarray}$$
since
$$\begin{eqnarray}\mathop{\sum }_{\unicode[STIX]{x1D713}\in {\mathcal{E}}}\frac{1}{r_{\unicode[STIX]{x1D713}}}\leqslant (\log x)^{-7A-39}\mathop{\sum }_{\unicode[STIX]{x1D713}\in \unicode[STIX]{x1D6EF}}\frac{1}{r_{\unicode[STIX]{x1D713}}^{1/2}}\ll (\log x)^{-A-1}.\end{eqnarray}$$
Thus
$|\unicode[STIX]{x1D6EF}\setminus {\mathcal{E}}|\leqslant (\log x)^{28A+156}$
, and we may apply Proposition 4.2 with
$\unicode[STIX]{x1D6EF}$
replaced by
$\unicode[STIX]{x1D6EF}\setminus {\mathcal{E}}$
to conclude the proof.
Thus if one is able to prove Proposition 4.1 with
$R=x^{c}$
in the full range
$$\begin{eqnarray}x^{\unicode[STIX]{x1D6FF}}>y\geqslant (\log x)^{C},\end{eqnarray}$$
then one can deduce Theorem 1.2 with (1.2) replaced by (4.5), for some
$C$
sufficiently large in terms of
$c$
.
5 A large sieve inequality supported on smooth numbers
In this section we prove a large sieve inequality for sequences supported on smooth numbers, a result which may be of independent interest.
Theorem 5.1 (Large sieve for smooth numbers).
There exists
$C,c>0$
such that the following statement holds. Let
$(\log x)^{C}\leqslant y\leqslant x$
be large, and
$$\begin{eqnarray}Q=\min (y^{c},\exp (c\log x/\!\log \log x)).\end{eqnarray}$$
For any sequence
$\{a_{n}\}$
we have
$$\begin{eqnarray}\mathop{\sum }_{q\leqslant Q}\mathop{\sum }_{\unicode[STIX]{x1D712}\;(\text{mod}\;q)}^{\ast }\biggl|\mathop{\sum }_{\substack{ n\leqslant x \\ P(n)\leqslant y}}a_{n}\unicode[STIX]{x1D712}(n)\biggr|^{2}\ll \unicode[STIX]{x1D6F9}(x,y)\cdot \mathop{\sum }_{\substack{ n\leqslant x \\ P(n)\leqslant y}}|a_{n}|^{2}.\end{eqnarray}$$
The upper bound is sharp up to a constant, as may be seen by taking each
$a_{n}=1$
, so that the
$\unicode[STIX]{x1D712}=1$
term on the left-hand side equals
$\unicode[STIX]{x1D6F9}(x,y)^{2}$
, the size of the right-hand side. This result has the advantage over the traditional large sieve inequality that the sequence
$\{a_{n}\}$
is supported on a sparse set (when
$y=x^{o(1)}$
), but the disadvantage that this inequality holds in a much smaller range for
$q$
than the usual
$q\ll x^{1/2}$
. It may well be that Theorem 5.1 holds with
$Q=\unicode[STIX]{x1D6F9}(x,y)^{1/2}$
.
5.1 Zero-density estimates
To prove Theorem 5.1, we will use the following two consequences of deep zero-density results in the literature. The first is a bound for character sums over smooth numbers assuming a suitable zero-free region for the associated
$L$
-function (see [Reference Harper7, §3]).
Proposition 5.2. There is a small positive constant
$\unicode[STIX]{x1D6FF}>0$
and a large positive constant
$\unicode[STIX]{x1D705}>0$
such that the following statement holds. Let
$(\log x)^{1.1}\leqslant y\leqslant x$
be large. Let
$\unicode[STIX]{x1D712}\;(\text{mod}~q)$
be a non-principal character with
$q\leqslant x$
and conductor
$r:=\operatorname{cond}(\unicode[STIX]{x1D712})\leqslant x^{\unicode[STIX]{x1D6FF}}$
. If
$L(s,\unicode[STIX]{x1D712})$
has no zeros in the region
$$\begin{eqnarray}\text{Re}(s)>1-\unicode[STIX]{x1D700},\qquad |\text{Im}(s)|\leqslant T,\end{eqnarray}$$
where the parameters
$\unicode[STIX]{x1D700},T$
satisfy
$$\begin{eqnarray}\frac{\unicode[STIX]{x1D705}}{\log y}<\unicode[STIX]{x1D700}\leqslant \frac{\unicode[STIX]{x1D6FC}(x,y)}{2},\qquad y^{0.9\unicode[STIX]{x1D700}}(\log x)^{2}\leqslant T\leqslant x^{\unicode[STIX]{x1D6FF}},\end{eqnarray}$$
and moreover
$$\begin{eqnarray}\text{either}~~y\geqslant (\text{Tr})^{\unicode[STIX]{x1D705}}\quad \text{or}\quad \unicode[STIX]{x1D700}\geqslant 40\log \log (qyT)/\!\log y.\end{eqnarray}$$
Then
$$\begin{eqnarray}\biggl|\mathop{\sum }_{\substack{ n\leqslant x \\ P(n)\leqslant y}}\unicode[STIX]{x1D712}(n)\biggr|\ll \unicode[STIX]{x1D6F9}(x,y)\sqrt{(\log x)(\log y)}(x^{-0.3\unicode[STIX]{x1D700}}\log T+T^{-0.02}).\end{eqnarray}$$
We also need the following log-free zero-density estimate by Huxley and Jutila, which can be found in [Reference Harper7, §2].
Proposition 5.3. Let
$\unicode[STIX]{x1D700}\in [0,1/2]$
,
$T\geqslant 1$
and
$Q\geqslant 1$
. Then the function
$G_{Q}(s)=\prod _{q\leqslant Q}\prod _{\unicode[STIX]{x1D712}\;(\text{mod}\;q)}^{\ast }L(s,\unicode[STIX]{x1D712})$
has
$\ll (Q^{2}T)^{(5/2)\unicode[STIX]{x1D700}}$
zeros
$s$
, counted with multiplicity, inside the region (5.1).
5.2 Proof of Theorem 5.1
It suffices to prove its dual form.
Proposition 5.4. There exist
$C,c>0$
such that the following statement holds. Let
$(\log x)^{C}\leqslant y\leqslant x$
be large, and
$$\begin{eqnarray}Q=\min (y^{c},\exp (c\log x/\!\log \log x)).\end{eqnarray}$$
For any sequence
$\{b_{\unicode[STIX]{x1D712}}\}$
we have
$$\begin{eqnarray}\mathop{\sum }_{\substack{ n\leqslant x \\ P(n)\leqslant y}}\biggl|\mathop{\sum }_{q\leqslant Q}\mathop{\sum }_{\unicode[STIX]{x1D712}\;(\text{mod}\;q)}^{\ast }b_{\unicode[STIX]{x1D712}}\unicode[STIX]{x1D712}(n)\biggr|^{2}\ll \unicode[STIX]{x1D6F9}(x,y)\cdot \mathop{\sum }_{q\leqslant Q}\mathop{\sum }_{\unicode[STIX]{x1D712}\;(\text{mod}\;q)}^{\ast }|b_{\unicode[STIX]{x1D712}}|^{2}.\end{eqnarray}$$
Proof. The left-hand side can be bounded by
$$\begin{eqnarray}\mathop{\sum }_{\unicode[STIX]{x1D712}_{1}}\mathop{\sum }_{\unicode[STIX]{x1D712}_{2}}b_{\unicode[STIX]{x1D712}_{1}}\overline{b_{\unicode[STIX]{x1D712}_{2}}}\mathop{\sum }_{\substack{ n\leqslant x \\ P(n)\leqslant y}}(\unicode[STIX]{x1D712}_{1}\overline{\unicode[STIX]{x1D712}_{2}})(n).\end{eqnarray}$$
Thus we need to understand character sums over smooth numbers. The contribution from the diagonal terms with
$\unicode[STIX]{x1D712}_{1}=\unicode[STIX]{x1D712}_{2}$
is clearly acceptable, and thus we focus on non-diagonal terms. For
$\unicode[STIX]{x1D702}\in (0,1/2]$
, define
$\unicode[STIX]{x1D6EF}(\unicode[STIX]{x1D702})$
to be the set of all non-principal characters
$\unicode[STIX]{x1D712}\;(\text{mod}~q)$
with
$q\leqslant Q^{2}$
, such that
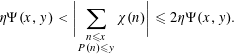$$\begin{eqnarray}\unicode[STIX]{x1D702}\unicode[STIX]{x1D6F9}(x,y)<\biggl|\mathop{\sum }_{\substack{ n\leqslant x \\ P(n)\leqslant y}}\unicode[STIX]{x1D712}(n)\biggr|\leqslant 2\unicode[STIX]{x1D702}\unicode[STIX]{x1D6F9}(x,y).\end{eqnarray}$$
Furthermore, define
$\unicode[STIX]{x1D6EF}^{\ast }(\unicode[STIX]{x1D702})$
to be the set of primitive characters which induce a character in
$\unicode[STIX]{x1D6EF}(\unicode[STIX]{x1D702})$
. The contribution to (5.4) from those
$\unicode[STIX]{x1D712}_{1},\unicode[STIX]{x1D712}_{2}$
with
$\unicode[STIX]{x1D712}_{1}\overline{\unicode[STIX]{x1D712}_{2}}\in \unicode[STIX]{x1D6EF}(\unicode[STIX]{x1D702})$
is
$$\begin{eqnarray}\displaystyle & & \displaystyle \leqslant 2\unicode[STIX]{x1D702}\unicode[STIX]{x1D6F9}(x,y)\mathop{\sum }_{\substack{ \unicode[STIX]{x1D712}_{1},\unicode[STIX]{x1D712}_{2} \\ \unicode[STIX]{x1D712}_{1}\overline{\unicode[STIX]{x1D712}_{2}}\in \unicode[STIX]{x1D6EF}(\unicode[STIX]{x1D702})}}|b_{\unicode[STIX]{x1D712}_{1}}b_{\unicode[STIX]{x1D712}_{2}}|\nonumber\\ \displaystyle & & \displaystyle \leqslant 4\unicode[STIX]{x1D702}\unicode[STIX]{x1D6F9}(x,y)\!\!\mathop{\sum }_{\substack{ \unicode[STIX]{x1D712}_{1},\unicode[STIX]{x1D712}_{2} \\ \unicode[STIX]{x1D712}_{1}\overline{\unicode[STIX]{x1D712}_{2}}\in \unicode[STIX]{x1D6EF}(\unicode[STIX]{x1D702})}}|b_{\unicode[STIX]{x1D712}_{1}}|^{2}\nonumber\\ \displaystyle & & \displaystyle \leqslant 4\unicode[STIX]{x1D702}\unicode[STIX]{x1D6F9}(x,y)\!\!\mathop{\sum }_{\unicode[STIX]{x1D713}\in \unicode[STIX]{x1D6EF}^{\ast }(\unicode[STIX]{x1D702})}\mathop{\sum }_{\unicode[STIX]{x1D712}_{1}}|b_{\unicode[STIX]{x1D712}_{1}}|^{2}\!\!\mathop{\sum }_{\substack{ \unicode[STIX]{x1D712}_{2} \\ \unicode[STIX]{x1D712}_{1}\overline{\unicode[STIX]{x1D712}_{2}}\text{ induced by }\unicode[STIX]{x1D713}}}1.\nonumber\end{eqnarray}$$
We claim that for a given
$\unicode[STIX]{x1D712}_{1}\;(\text{mod}\;q_{1})$
and a given primitive
$\unicode[STIX]{x1D713}\in \unicode[STIX]{x1D6EF}^{\ast }(\unicode[STIX]{x1D702})$
, there is at most one primitive character
$\unicode[STIX]{x1D712}_{2}$
such that
$\unicode[STIX]{x1D712}_{1}\overline{\unicode[STIX]{x1D712}_{2}}$
is induced by
$\unicode[STIX]{x1D713}$
. To see this, suppose that there are two primitive characters
$\unicode[STIX]{x1D712}_{2}\;(\text{mod}\;q_{2})$
and
$\unicode[STIX]{x1D712}_{2}^{\prime }\;(\text{mod}\;q_{2}^{\prime })$
such that both
$\unicode[STIX]{x1D712}_{1}\overline{\unicode[STIX]{x1D712}_{2}}:=\unicode[STIX]{x1D712}$
and
$\unicode[STIX]{x1D712}_{1}\overline{\unicode[STIX]{x1D712}_{2}^{\prime }}:=\unicode[STIX]{x1D712}^{\prime }$
are induced by
$\unicode[STIX]{x1D713}$
. It suffices to show that
$\unicode[STIX]{x1D712}_{2}(n)=\unicode[STIX]{x1D712}_{2}^{\prime }(n)$
whenever
$(n,q_{2}q_{2}^{\prime })=1$
, since this would imply that
$\unicode[STIX]{x1D712}_{2}\unicode[STIX]{x1D712}_{2}^{\prime }$
is the principal character, and thus
$\unicode[STIX]{x1D712}_{2}=\unicode[STIX]{x1D712}_{2}^{\prime }$
as they are both primitive.
If
$(n,q_{2}q_{2}^{\prime })=1$
, then we may find an integer
$k$
such that
$(n+kq_{2}q_{2}^{\prime },q_{1}q_{2}q_{2}^{\prime })=1$
. Thus
$\unicode[STIX]{x1D712}_{1}(n+kq_{2}q_{2}^{\prime })\neq 0$
and
$\unicode[STIX]{x1D712}(n+kq_{2}q_{2}^{\prime })=\unicode[STIX]{x1D712}^{\prime }(n+kq_{2}q_{2}^{\prime })$
. It follows that
$$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D712}_{2}(n) & = & \displaystyle \unicode[STIX]{x1D712}_{2}(n+kq_{2}q_{2}^{\prime })=(\overline{\unicode[STIX]{x1D712}\unicode[STIX]{x1D712}_{1}})(n+kq_{2}q_{2}^{\prime })=(\overline{\unicode[STIX]{x1D712}^{\prime }\unicode[STIX]{x1D712}_{1}})(n+kq_{2}q_{2}^{\prime })\nonumber\\ \displaystyle & = & \displaystyle \unicode[STIX]{x1D712}_{2}^{\prime }(n+kq_{2}q_{2}^{\prime })=\unicode[STIX]{x1D712}_{2}^{\prime }(n).\nonumber\end{eqnarray}$$
This completes the proof of the claim.
It follows that the contribution to (5.4) from those
$\unicode[STIX]{x1D712}_{1},\unicode[STIX]{x1D712}_{2}$
with
$\unicode[STIX]{x1D712}_{1}\overline{\unicode[STIX]{x1D712}_{2}}\in \unicode[STIX]{x1D6EF}(\unicode[STIX]{x1D702})$
is
$$\begin{eqnarray}\ll \unicode[STIX]{x1D702}\unicode[STIX]{x1D6F9}(x,y)|\unicode[STIX]{x1D6EF}^{\ast }(\unicode[STIX]{x1D702})|\mathop{\sum }_{\unicode[STIX]{x1D712}}|b_{\unicode[STIX]{x1D712}}|^{2}.\end{eqnarray}$$
We will show that
$|\unicode[STIX]{x1D6EF}^{\ast }(\unicode[STIX]{x1D702})|\ll \unicode[STIX]{x1D702}^{-1/2}$
so that the result follows by summing over
$\unicode[STIX]{x1D702}$
dyadically. We may assume that
$\unicode[STIX]{x1D702}\geqslant Q^{-8}$
, as the bound follows for smaller
$\unicode[STIX]{x1D702}$
from the trivial bound
$|\unicode[STIX]{x1D6EF}^{\ast }(\unicode[STIX]{x1D702})|\leqslant Q^{4}$
.
We now use Proposition 5.2 to show that if
$\unicode[STIX]{x1D712}\in \unicode[STIX]{x1D6EF}(\unicode[STIX]{x1D702})$
then
$L(s,\unicode[STIX]{x1D712})$
has a zero in the region (5.1) for suitable values of
$\unicode[STIX]{x1D700}$
and
$T$
. This would imply that
$L(s,\unicode[STIX]{x1D713})$
has zero in the region (5.1) for any
$\unicode[STIX]{x1D713}\in \unicode[STIX]{x1D6EF}^{\ast }(\unicode[STIX]{x1D702})$
.
For the purpose of contradiction, let’s assume that
$\unicode[STIX]{x1D712}\in \unicode[STIX]{x1D6EF}(\unicode[STIX]{x1D702})$
and
$L(s,\unicode[STIX]{x1D712})$
has no zero in (5.1) with
$T=Q^{500}$
. We wish to verify the hypotheses in (5.2) and (5.3). The upper bound on
$T$
in (5.2) follows from the definition of
$Q$
. Now
$r\leqslant q\leqslant Q^{2}$
and so the first alternative of (5.3) follows by selecting
$c$
so that
$502c\unicode[STIX]{x1D705}\leqslant 1$
. We define
$$\begin{eqnarray}\unicode[STIX]{x1D700}=\max \biggl(\frac{2\unicode[STIX]{x1D705}}{\log y},\frac{12(\log \unicode[STIX]{x1D702}^{-1}+\log \log x)}{\log x}\biggr).\end{eqnarray}$$
Since
$\log \unicode[STIX]{x1D702}^{-1}\leqslant 8\log Q$
and
$\log \log x\leqslant \log Q$
, we have the upper bound
$$\begin{eqnarray}\unicode[STIX]{x1D700}\leqslant \max \biggl(\frac{2\unicode[STIX]{x1D705}}{\log y},\frac{108\log Q}{\log x}\biggr)\ll \frac{1}{\log \log x},\end{eqnarray}$$
so that
$\unicode[STIX]{x1D700}=o(1)$
and
$y^{\unicode[STIX]{x1D700}}\ll Q^{108}$
. The first hypothesis in (5.2) follows immediately. Finally, by selecting
$C$
so that
$cC\geqslant 2$
we guarantee that
$Q\geqslant (\log x)^{2}$
, so that the lower bound on
$T$
in (5.2) follows easily.
Now
$\unicode[STIX]{x1D700}\geqslant 12(\log \unicode[STIX]{x1D702}^{-1}+\log \log x)/\!\log x$
so that
$x^{-0.3\unicode[STIX]{x1D700}}\leqslant (\unicode[STIX]{x1D702}/\!\log x)^{3.6}$
, and therefore
$$\begin{eqnarray}\sqrt{(\log x)(\log y)}(x^{-0.3\unicode[STIX]{x1D700}}\log T+T^{-0.02})\leqslant \unicode[STIX]{x1D702}^{3.6}(\log x)^{-1.6}+Q^{-10}\log x.\end{eqnarray}$$
Now
$Q^{-10}\log x=o(Q^{-8})=o(\unicode[STIX]{x1D702})$
, as
$Q\geqslant (\log x)^{2}$
. Therefore Proposition 5.2 implies that
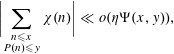$$\begin{eqnarray}\biggl|\mathop{\sum }_{\substack{ n\leqslant x \\ P(n)\leqslant y}}\unicode[STIX]{x1D712}(n)\biggr|\ll o(\unicode[STIX]{x1D702}\unicode[STIX]{x1D6F9}(x,y)),\end{eqnarray}$$
contradicting the definition of
$\unicode[STIX]{x1D6EF}(\unicode[STIX]{x1D702})$
.
By Proposition 5.3 we now deduce (remembering that characters in
$\unicode[STIX]{x1D6EF}^{\ast }(\unicode[STIX]{x1D702})$
have conductors at most
$Q^{2}$
) that
$$\begin{eqnarray}|\unicode[STIX]{x1D6EF}^{\ast }(\unicode[STIX]{x1D702})|\ll (Q^{4}T)^{(5/2)\unicode[STIX]{x1D700}}=Q^{1260\unicode[STIX]{x1D700}}\ll \unicode[STIX]{x1D702}^{-1/2},\end{eqnarray}$$
which completes the proof. ◻
Remark 5.5. Assuming the Riemann hypothesis for Dirichlet
$L$
-functions, by [Reference Harper7, Proposition 1], we have the bound
$\sum _{n\leqslant x,P(n)\leqslant y}\unicode[STIX]{x1D712}(n)=O(x^{1-c})$
uniformly for
$\unicode[STIX]{x1D712}$
non-principal
$\text{mod}\;q$
,
$q\leqslant x^{c}$
,
$(\log x)^{C}\leqslant y\leqslant x^{c}$
, for some absolute constants
$C,c>0$
. This implies an upper bound
$$\begin{eqnarray}\ll (\unicode[STIX]{x1D6F9}(x,y)+Q^{2}x^{1-c})\mathop{\sum }_{\unicode[STIX]{x1D712}}|b_{\unicode[STIX]{x1D712}}|^{2}\end{eqnarray}$$
for (5.4), for all
$Q\leqslant x^{c}$
, and Theorem 5.1 would hold with
$Q=x^{c/3}$
and
$C$
large enough.
5.3 A variant of Theorem 5.1
We may extend the range to
$Q=x^{c}$
in Theorem 5.1 unconditionally if we insert some weights that reduce the effects of characters with large conductor.
Theorem 5.6. There exists
$C,c>0$
such that the following statement holds. Let
$(\log x)^{C}\leqslant y\leqslant x$
be large, and let
$Q=x^{c}$
. For any sequence
$\{a_{n}\}$
we have
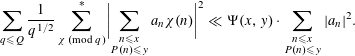$$\begin{eqnarray}\mathop{\sum }_{q\leqslant Q}\frac{1}{q^{1/2}}\mathop{\sum }_{\unicode[STIX]{x1D712}\;(\text{mod}\;q)}^{\ast }\biggl|\mathop{\sum }_{\substack{ n\leqslant x \\ P(n)\leqslant y}}a_{n}\unicode[STIX]{x1D712}(n)\biggr|^{2}\ll \unicode[STIX]{x1D6F9}(x,y)\cdot \mathop{\sum }_{\substack{ n\leqslant x \\ P(n)\leqslant y}}|a_{n}|^{2}.\end{eqnarray}$$
Proof. The proof is similar as the proof of Theorem 5.1. We begin by passing to its dual form, so that we need to prove that
$$\begin{eqnarray}\mathop{\sum }_{\substack{ n\leqslant x \\ P(n)\leqslant y}}\biggl|\mathop{\sum }_{q\leqslant Q}\frac{1}{q^{1/4}}\mathop{\sum }_{\unicode[STIX]{x1D712}\;(\text{mod}\;q)}^{\ast }b_{\unicode[STIX]{x1D712}}\unicode[STIX]{x1D712}(n)\biggr|^{2}\ll \unicode[STIX]{x1D6F9}(x,y)\cdot \mathop{\sum }_{q\leqslant Q}\frac{1}{q^{1/4}}\mathop{\sum }_{\unicode[STIX]{x1D712}\;(\text{mod}\;q)}^{\ast }|b_{\unicode[STIX]{x1D712}}|^{2}\end{eqnarray}$$
for any sequence
$\{b_{\unicode[STIX]{x1D712}}\}$
, where the summation is over all primitive characters
$\unicode[STIX]{x1D712}\;(\text{mod}\;q)$
with
$q\leqslant Q$
. Expanding the square, we can bound the left-hand side above by
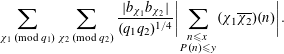$$\begin{eqnarray}\mathop{\sum }_{\unicode[STIX]{x1D712}_{1}\;(\text{mod}\;q_{1})}\mathop{\sum }_{\unicode[STIX]{x1D712}_{2}\;(\text{mod}\;q_{2})}\frac{|b_{\unicode[STIX]{x1D712}_{1}}b_{\unicode[STIX]{x1D712}_{2}}|}{(q_{1}q_{2})^{1/4}}\biggl|\mathop{\sum }_{\substack{ n\leqslant x \\ P(n)\leqslant y}}(\unicode[STIX]{x1D712}_{1}\overline{\unicode[STIX]{x1D712}_{2}})(n)\biggr|.\end{eqnarray}$$
For
$\unicode[STIX]{x1D702}\in (0,1/2]$
, define
$\unicode[STIX]{x1D6EF}(\unicode[STIX]{x1D702})$
and
$\unicode[STIX]{x1D6EF}^{\ast }(\unicode[STIX]{x1D702})$
as in the proof of Theorem 5.1. If
$\unicode[STIX]{x1D712}_{1}\overline{\unicode[STIX]{x1D712}_{2}}\in \unicode[STIX]{x1D6EF}(\unicode[STIX]{x1D702})$
so that it is induced by some
$\unicode[STIX]{x1D713}\;(\text{mod}\;r)\in \unicode[STIX]{x1D6EF}^{\ast }(\unicode[STIX]{x1D702})$
, then
$$\begin{eqnarray}\frac{|b_{\unicode[STIX]{x1D712}_{1}}b_{\unicode[STIX]{x1D712}_{2}}|}{(q_{1}q_{2})^{1/4}}\leqslant \frac{1}{r^{1/8}}\biggl(\frac{|b_{\unicode[STIX]{x1D712}_{1}}|^{2}}{q_{1}^{1/4}}+\frac{|b_{\unicode[STIX]{x1D712}_{2}}|^{2}}{q_{2}^{1/4}}\biggr).\end{eqnarray}$$
Thus the contribution to (5.5) from those
$\unicode[STIX]{x1D712}_{1},\unicode[STIX]{x1D712}_{2}$
with
$\unicode[STIX]{x1D712}_{1}\overline{\unicode[STIX]{x1D712}_{2}}\in \unicode[STIX]{x1D6EF}(\unicode[STIX]{x1D702})$
is
$$\begin{eqnarray}\displaystyle & & \displaystyle \ll \unicode[STIX]{x1D702}\unicode[STIX]{x1D6F9}(x,y)\mathop{\sum }_{\unicode[STIX]{x1D713}\;(\text{mod}\;r)\in \unicode[STIX]{x1D6EF}^{\ast }(\unicode[STIX]{x1D702})}\frac{1}{r^{1/8}}\mathop{\sum }_{\unicode[STIX]{x1D712}_{1}\;(\text{mod}\;q_{1})}\frac{|b_{\unicode[STIX]{x1D712}_{1}}|^{2}}{q_{1}^{1/4}}\mathop{\sum }_{\substack{ \unicode[STIX]{x1D712}_{2} \\ \unicode[STIX]{x1D712}_{1}\overline{\unicode[STIX]{x1D712}_{2}}\text{ induced by }\unicode[STIX]{x1D713}}}1\nonumber\\ \displaystyle & & \displaystyle \ll \unicode[STIX]{x1D702}\unicode[STIX]{x1D6F9}(x,y)\biggl(\mathop{\sum }_{\unicode[STIX]{x1D713}\;(\text{mod}\;r)\in \unicode[STIX]{x1D6EF}^{\ast }(\unicode[STIX]{x1D702})}\frac{1}{r^{1/8}}\biggr)\biggl(\mathop{\sum }_{\unicode[STIX]{x1D712}\;(\text{mod}\;q)}\frac{|b_{\unicode[STIX]{x1D712}}|^{2}}{q^{1/4}}\biggr).\nonumber\end{eqnarray}$$
Hence it suffices to show that
$$\begin{eqnarray}\mathop{\sum }_{\unicode[STIX]{x1D713}\;(\text{mod}\;r)\in \unicode[STIX]{x1D6EF}^{\ast }(\unicode[STIX]{x1D702})}\frac{1}{r^{1/8}}\ll \unicode[STIX]{x1D702}^{-1/2},\end{eqnarray}$$
and then the conclusion follows after dyadically summing over
$\unicode[STIX]{x1D702}$
. For
$1\leqslant R\leqslant Q^{2}$
, let
$\unicode[STIX]{x1D6EF}(\unicode[STIX]{x1D702},R)$
and
$\unicode[STIX]{x1D6EF}^{\ast }(\unicode[STIX]{x1D702},R)$
be the set of characters in
$\unicode[STIX]{x1D6EF}(\unicode[STIX]{x1D702})$
and
$\unicode[STIX]{x1D6EF}^{\ast }(\unicode[STIX]{x1D702})$
with conductors
${\sim}R$
, respectively. Thus it suffices to show that
$$\begin{eqnarray}|\unicode[STIX]{x1D6EF}^{\ast }(\unicode[STIX]{x1D702},R)|\ll \unicode[STIX]{x1D702}^{-1/2}R^{1/9},\end{eqnarray}$$
for each
$\unicode[STIX]{x1D702}\in (0,1/2]$
and
$1\leqslant R\leqslant Q^{2}$
. We may assume that
$\unicode[STIX]{x1D702}\geqslant R^{-4}$
, since otherwise the trivial bound
$|\unicode[STIX]{x1D6EF}^{\ast }(\unicode[STIX]{x1D702},R)|\ll R^{2}$
suffices. From now on fix such
$\unicode[STIX]{x1D702}$
and
$R$
.
We now use Proposition 5.2 to show that if
$\unicode[STIX]{x1D712}\in \unicode[STIX]{x1D6EF}(\unicode[STIX]{x1D702},R)$
then
$L(s,\unicode[STIX]{x1D712})$
has a zero in the region (5.1) for suitable values of
$\unicode[STIX]{x1D700}$
and
$T$
. This would imply that
$L(s,\unicode[STIX]{x1D713})$
has zero in the region (5.1) for any
$\unicode[STIX]{x1D713}\in \unicode[STIX]{x1D6EF}^{\ast }(\unicode[STIX]{x1D702},R)$
.
Set
$T=(\unicode[STIX]{x1D702}^{-1}\log x)^{60}$
. If
$R\leqslant (\log x)^{10}$
(say), then the first alternative of (5.3) holds because
$$\begin{eqnarray}(2TR)^{\unicode[STIX]{x1D705}}\leqslant (\log x)^{2500\unicode[STIX]{x1D705}}\leqslant y,\end{eqnarray}$$
provided that
$C\geqslant 2500\unicode[STIX]{x1D705}$
. In this case we will set
$\unicode[STIX]{x1D700}$
to be exactly the same as before:
$$\begin{eqnarray}\unicode[STIX]{x1D700}:=\max \biggl(\frac{2\unicode[STIX]{x1D705}}{\log y},\frac{12(\log \unicode[STIX]{x1D702}^{-1}+\log \log x)}{\log x}\biggr),\quad \text{if}~R\leqslant (\log x)^{10}.\end{eqnarray}$$
Then (5.2) can be easily verified, and the contrapositive of Proposition 5.2 implies that
$L(s,\unicode[STIX]{x1D712})$
has a zero in the region (5.1) whenever
$\unicode[STIX]{x1D712}\in \unicode[STIX]{x1D6EF}(\unicode[STIX]{x1D702},R)$
. Hence by Proposition 5.3 we have
$$\begin{eqnarray}|\unicode[STIX]{x1D6EF}^{\ast }(\unicode[STIX]{x1D702},R)|\ll (R^{2}T)^{(5/2)\unicode[STIX]{x1D700}}\ll \unicode[STIX]{x1D702}^{-150\unicode[STIX]{x1D700}}R^{5\unicode[STIX]{x1D700}}(\log x)^{150\unicode[STIX]{x1D700}}\ll \unicode[STIX]{x1D702}^{-1/2}R^{1/9},\end{eqnarray}$$
since
$\unicode[STIX]{x1D700}\ll 1/\!\log \log x$
in this case.
It remains to consider the case when
$(\log x)^{10}\leqslant R\leqslant Q^{2}$
. We set
$T$
as above, and we will now set
$$\begin{eqnarray}\unicode[STIX]{x1D700}:=\max \biggl(\frac{2\unicode[STIX]{x1D705}}{\log y},\frac{12(\log \unicode[STIX]{x1D702}^{-1}+\log \log x)}{\log x},\frac{50\log \log x}{\log y}\biggr),\end{eqnarray}$$
so that the second alternative in (5.3) is satisfied. One can still easily verify (5.2), and thus Propositions 5.2 and 5.3 combine to give
$$\begin{eqnarray}|\unicode[STIX]{x1D6EF}^{\ast }(\unicode[STIX]{x1D702},R)|\ll (R^{2}T)^{(5/2)\unicode[STIX]{x1D700}}\ll \unicode[STIX]{x1D702}^{-150\unicode[STIX]{x1D700}}R^{5\unicode[STIX]{x1D700}}(\log x)^{150\unicode[STIX]{x1D700}}\ll \unicode[STIX]{x1D702}^{-1/2}R^{1/9},\end{eqnarray}$$
since
$\unicode[STIX]{x1D700}\leqslant 1/300$
(by choosing
$C$
large enough) and
$\log x\leqslant R^{1/10}$
. This completes the proof.◻
Examining the proof, one easily sees that the weight
$1/q^{1/2}$
can be replaced by
$1/q^{\unicode[STIX]{x1D70E}}$
for any constant
$\unicode[STIX]{x1D70E}>0$
, and the statement remains true provided that
$C$
is large enough in terms of
$\unicode[STIX]{x1D70E}$
. For our purposes, any exponent strictly smaller than
$1$
suffices.
6 Bounding the number of exceptional characters
Corollary 6.1. There exist
$C,c>0$
such that the following statement holds. Let
$(\log x)^{C}\leqslant y\leqslant x^{1/4}$
be large. Let
$\{a_{n}\}$
be an arbitrary
$1$
-bounded sequence. For
$B\geqslant 0$
, let
$\unicode[STIX]{x1D6EF}(B)$
be the set of primitive characters
$\unicode[STIX]{x1D712}\;(\text{mod}\;r)$
with
$r\leqslant Q$
where
$$\begin{eqnarray}Q:=\min (y^{c},\exp (c\log x/\!\log \log x)),\end{eqnarray}$$
such that there exists
$x^{1/4}<X\leqslant x$
for which
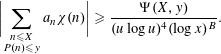$$\begin{eqnarray}\biggl|\mathop{\sum }_{\substack{ n\leqslant X \\ P(n)\leqslant y}}a_{n}\unicode[STIX]{x1D712}(n)\biggr|\geqslant \frac{\unicode[STIX]{x1D6F9}(X,y)}{(u\log u)^{4}(\log x)^{B}}.\end{eqnarray}$$
Then
$|\unicode[STIX]{x1D6EF}(B)|\ll (\log x)^{3B+13}$
.
Proof. Let
$T=(u\log u)^{4}(\log x)^{B}$
. We begin by partitioning the interval
$[x^{1/4},x]$
using a sequence
$x^{1/4}=X_{0}<X_{1}<\cdots <X_{J-1}<X_{J}=x$
with
$J\asymp T\log x$
, such that
$X_{j+1}-X_{j}\asymp \unicode[STIX]{x1D700}X_{j}/T$
, for some fixed small enough
$\unicode[STIX]{x1D700}>0$
, for each
$0\leqslant j<J$
.
For each
$\unicode[STIX]{x1D712}\in \unicode[STIX]{x1D6EF}(B)$
, there exists some
$0\leqslant j<J$
for which
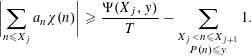$$\begin{eqnarray}\biggl|\mathop{\sum }_{n\leqslant X_{j}}a_{n}\unicode[STIX]{x1D712}(n)\biggr|\geqslant \frac{\unicode[STIX]{x1D6F9}(X_{j},y)}{T}-\mathop{\sum }_{\substack{ X_{j}<n\leqslant X_{j+1} \\ P(n)\leqslant y}}1.\end{eqnarray}$$
Corollary 2 of [Reference Hildebrand8] implies a good upper bound for smooth numbers in short intervals: for any fixed
$\unicode[STIX]{x1D705}>0$
,
$$\begin{eqnarray}\unicode[STIX]{x1D6F9}\biggl(x+\frac{x}{T},y\biggr)-\unicode[STIX]{x1D6F9}(x,y)\ll _{\unicode[STIX]{x1D705}}\frac{\unicode[STIX]{x1D6F9}(x,y)}{T}\quad \text{for }1\leqslant T\leqslant \min \{y^{\unicode[STIX]{x1D705}},x\}.\end{eqnarray}$$
In our case
$u\log u\leqslant \log x$
so that
$T\leqslant (\log x)^{B+4}$
, so the hypothesis here is satisfied, and we therefore have
$$\begin{eqnarray}\mathop{\sum }_{\substack{ X_{j}<n\leqslant X_{j+1} \\ P(n)\leqslant y}}1=\unicode[STIX]{x1D6F9}(X_{j+1},y)-\unicode[STIX]{x1D6F9}(X_{j},y)\ll \unicode[STIX]{x1D700}\frac{\unicode[STIX]{x1D6F9}(X_{j},y)}{T}.\end{eqnarray}$$
By choosing
$\unicode[STIX]{x1D700}$
sufficiently small, we deduce that
$$\begin{eqnarray}\biggl|\mathop{\sum }_{n\leqslant X_{j}}a_{n}\unicode[STIX]{x1D712}(n)\biggr|\geqslant \frac{\unicode[STIX]{x1D6F9}(X_{j},y)}{2T}.\end{eqnarray}$$
We deduce that there exists some
$0\leqslant j<J$
such that (6.2) holds for at least
$|\unicode[STIX]{x1D6EF}(B)|/J$
characters
$\unicode[STIX]{x1D712}\in \unicode[STIX]{x1D6EF}(B)$
. Therefore
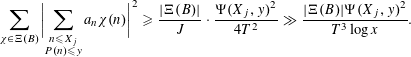$$\begin{eqnarray}\mathop{\sum }_{\unicode[STIX]{x1D712}\in \unicode[STIX]{x1D6EF}(B)}\biggl|\mathop{\sum }_{\substack{ n\leqslant X_{j} \\ P(n)\leqslant y}}a_{n}\unicode[STIX]{x1D712}(n)\biggr|^{2}\geqslant \frac{|\unicode[STIX]{x1D6EF}(B)|}{J}\cdot \frac{\unicode[STIX]{x1D6F9}(X_{j},y)^{2}}{4T^{2}}\gg \frac{|\unicode[STIX]{x1D6EF}(B)|\unicode[STIX]{x1D6F9}(X_{j},y)^{2}}{T^{3}\log x}.\end{eqnarray}$$
On the other hand, Theorem 5.1 implies that
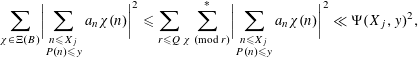$$\begin{eqnarray}\mathop{\sum }_{\unicode[STIX]{x1D712}\in \unicode[STIX]{x1D6EF}(B)}\biggl|\mathop{\sum }_{\substack{ n\leqslant X_{j} \\ P(n)\leqslant y}}a_{n}\unicode[STIX]{x1D712}(n)\biggr|^{2}\leqslant \mathop{\sum }_{r\leqslant Q}\mathop{\sum }_{\unicode[STIX]{x1D712}\;(\text{mod}\;r)}^{\ast }\biggl|\mathop{\sum }_{\substack{ n\leqslant X_{j} \\ P(n)\leqslant y}}a_{n}\unicode[STIX]{x1D712}(n)\biggr|^{2}\ll \unicode[STIX]{x1D6F9}(X_{j},y)^{2},\end{eqnarray}$$
and therefore
$|\unicode[STIX]{x1D6EF}(B)|\ll T^{3}\log x=(u\log u)^{12}(\log x)^{3B+1}\ll (\log x)^{3B+13}$
, as claimed.◻
We also record the following variant which gives a weighted count of exceptional characters, but now with the wider range
$Q=x^{c}$
.
Corollary 6.2. There exist
$C,c>0$
such that the following statement holds. Let
$(\log x)^{C}\leqslant y\leqslant x^{1/4}$
be large. Let
$\{a_{n}\}$
be an arbitrary
$1$
-bounded sequence. For
$B\geqslant 0$
, let
$\unicode[STIX]{x1D6EF}(B)$
be the set of primitive characters
$\unicode[STIX]{x1D712}\;(\text{mod}\;r)$
with
$r\leqslant Q:=x^{c}$
, such that there exists
$x^{1/4}<X\leqslant x$
for which
$$\begin{eqnarray}\biggl|\mathop{\sum }_{\substack{ n\leqslant X \\ P(n)\leqslant y}}a_{n}\unicode[STIX]{x1D712}(n)\biggr|\geqslant \frac{\unicode[STIX]{x1D6F9}(X,y)}{(u\log u)^{4}(\log x)^{B}}.\end{eqnarray}$$
Then
$$\begin{eqnarray}\mathop{\sum }_{\unicode[STIX]{x1D713}\;(\text{mod}\;q)\in \unicode[STIX]{x1D6EF}(B)}\frac{1}{q^{1/2}}\ll (\log x)^{3B+13}.\end{eqnarray}$$
Proof. The proof is the same as above, except that one considers the weighted sum
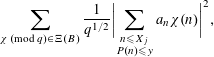$$\begin{eqnarray}\mathop{\sum }_{\unicode[STIX]{x1D712}\;(\text{mod}\;q)\in \unicode[STIX]{x1D6EF}(B)}\frac{1}{q^{1/2}}\biggl|\mathop{\sum }_{\substack{ n\leqslant X_{j} \\ P(n)\leqslant y}}a_{n}\unicode[STIX]{x1D712}(n)\biggr|^{2},\end{eqnarray}$$
and use Theorem 5.6 instead of Theorem 5.1 in the last step. ◻
Acknowledgements
A.G. has received funding from the European Research Council grant agreement no. 670239, and from NSERC Canada under the CRC program. X.S. was supported by a Glasstone Research Fellowship. We would like to thank Adam Harper for a valuable discussion.
