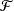1. Introduction
Let  ${\mathbb Z}$
and
${\mathbb Z}$
and  ${\mathbb N}$
be the sets of all integers and nonnegative integers, respectively. Let
${\mathbb N}$
be the sets of all integers and nonnegative integers, respectively. Let  $(\eta_j)_{j\in{\mathbb Z}}$
be a sequence of independent, identically distributed random variables on a probability space
$(\eta_j)_{j\in{\mathbb Z}}$
be a sequence of independent, identically distributed random variables on a probability space  $(\Omega, {\mathcal{A}}, {\mathrm{P}})$
with mean zero and finite second moment
$(\Omega, {\mathcal{A}}, {\mathrm{P}})$
with mean zero and finite second moment  $\sigma^2_\eta={\mathrm{E}}(\eta_1^2)\not =0$
. A sequence
$\sigma^2_\eta={\mathrm{E}}(\eta_1^2)\not =0$
. A sequence  $(X_i)_{i\in{\mathbb Z}}$
of random variables defined by
$(X_i)_{i\in{\mathbb Z}}$
of random variables defined by
 \begin{equation}X_{i}=\sum_{j=0}^\infty \psi_j\eta_{i-j},\qquad i\in{\mathbb Z},\end{equation}
\begin{equation}X_{i}=\sum_{j=0}^\infty \psi_j\eta_{i-j},\qquad i\in{\mathbb Z},\end{equation}
is a linear process provided a sequence of real numbers  $(\psi_j)_{j\in{\mathbb N}}$
is square summable. We say that
$(\psi_j)_{j\in{\mathbb N}}$
is square summable. We say that  $(X_i)_{i\in{\mathbb Z}}$
and its subsequence
$(X_i)_{i\in{\mathbb Z}}$
and its subsequence  $X_1,X_2,\dots$
are short-memory linear processes (with innovations
$X_1,X_2,\dots$
are short-memory linear processes (with innovations  $(\eta_j)$
and summable filter
$(\eta_j)$
and summable filter  $(\psi_j)$
) if, in addition,
$(\psi_j)$
) if, in addition,
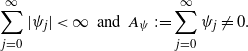 \begin{equation} \sum_{j=0}^\infty |\psi_j|<\infty\ \ \textrm{and}\ \ A_{\psi}\,:\!=\sum_{j=0}^\infty \psi_j\not=0.\end{equation}
\begin{equation} \sum_{j=0}^\infty |\psi_j|<\infty\ \ \textrm{and}\ \ A_{\psi}\,:\!=\sum_{j=0}^\infty \psi_j\not=0.\end{equation}
Given a short-memory linear process  $X_1, X_2,\dots$
, a function
$X_1, X_2,\dots$
, a function  $f\colon[0,1]\to{\mathbb R}$
and a positive integer
$f\colon[0,1]\to{\mathbb R}$
and a positive integer  $n\in{\mathbb N}_{+}$
, let
$n\in{\mathbb N}_{+}$
, let  $\nu_n(\,f)$
be the nth f-weighted sum of linear process defined by
$\nu_n(\,f)$
be the nth f-weighted sum of linear process defined by
 \begin{equation}\nu_n(\,f)\,:\!=\sum_{i=1}^n X_i\,f\Big (\frac{i}{n}\Big ).\end{equation}
\begin{equation}\nu_n(\,f)\,:\!=\sum_{i=1}^n X_i\,f\Big (\frac{i}{n}\Big ).\end{equation}
If  ${\mathcal{F}}$
is a class of real-valued, measurable functions on [0, 1], then
${\mathcal{F}}$
is a class of real-valued, measurable functions on [0, 1], then  $\nu_n=\{\nu_n(\,f)\colon f\in{\mathcal{F}}\}$
is the nth
$\nu_n=\{\nu_n(\,f)\colon f\in{\mathcal{F}}\}$
is the nth  ${\mathcal{F}}$
-weighted sum of linear process, and
${\mathcal{F}}$
-weighted sum of linear process, and  $\nu_n$
,
$\nu_n$
,  $n\in{\mathbb N}_{+}$
, is a sequence of weighted sums of linear process. This type of weighting of random variables has a number of applications in statistics and econometrics (see [Reference Abadir, Distaso, Giraitis and Koul1] and references therein). Some new applications are suggested in the last section of the present paper.
$n\in{\mathbb N}_{+}$
, is a sequence of weighted sums of linear process. This type of weighting of random variables has a number of applications in statistics and econometrics (see [Reference Abadir, Distaso, Giraitis and Koul1] and references therein). Some new applications are suggested in the last section of the present paper.
In this paper we consider classes of functions of bounded q-variation with  $q\in [1,2)$
. Given a class of functions
$q\in [1,2)$
. Given a class of functions  ${\mathcal{F}}$
, let
${\mathcal{F}}$
, let  $\ell^{\infty}({\mathcal{F}})$
be the Banach space of all uniformly bounded, real-valued functions
$\ell^{\infty}({\mathcal{F}})$
be the Banach space of all uniformly bounded, real-valued functions  $\mu$
on
$\mu$
on  ${\mathcal{F}}$
endowed with the uniform norm
${\mathcal{F}}$
endowed with the uniform norm
 \begin{equation}\|\mu\|_{{\mathcal{F}}} \,:\!= \sup\{|\mu(\,f)|\,:\,f \in {\mathcal{F}}\}.\end{equation}
\begin{equation}\|\mu\|_{{\mathcal{F}}} \,:\!= \sup\{|\mu(\,f)|\,:\,f \in {\mathcal{F}}\}.\end{equation}
Each nth  ${\mathcal{F}}$
-weighted sum of linear process
${\mathcal{F}}$
-weighted sum of linear process  $\nu_n$
has sample paths in
$\nu_n$
has sample paths in  $\ell^{\infty}({\mathcal{F}})$
. Whenever
$\ell^{\infty}({\mathcal{F}})$
. Whenever  ${\mathcal{F}}$
is an infinite set the Banach space
${\mathcal{F}}$
is an infinite set the Banach space  $\ell^\infty({\mathcal{F}})$
is non-separable. We show that a normalized sequence of weighted sums of linear process converges in
$\ell^\infty({\mathcal{F}})$
is non-separable. We show that a normalized sequence of weighted sums of linear process converges in  $\ell^{\infty}({\mathcal{F}})$
in outer distribution as defined by J. Hoffmann-Jørgensen (Definition 1 below). Next is the main result of the paper.
$\ell^{\infty}({\mathcal{F}})$
in outer distribution as defined by J. Hoffmann-Jørgensen (Definition 1 below). Next is the main result of the paper.
Theorem 1. Let  $X_1, X_2,\dots$
be a short-memory linear process given by (1), let
$X_1, X_2,\dots$
be a short-memory linear process given by (1), let  $1 \le q < 2$
, and let
$1 \le q < 2$
, and let  ${\mathcal{F}}$
be a bounded set of functions on [0, 1] with bounded q-variation. There exists a version of the isonormal Gaussian process
${\mathcal{F}}$
be a bounded set of functions on [0, 1] with bounded q-variation. There exists a version of the isonormal Gaussian process  $\nu$
restricted to
$\nu$
restricted to  ${\mathcal{F}}$
with values in a separable subset of
${\mathcal{F}}$
with values in a separable subset of  $\ell^{\infty}({\mathcal{F}})$
, it is measurable for the Borel sets on its range, and
$\ell^{\infty}({\mathcal{F}})$
, it is measurable for the Borel sets on its range, and
 \begin{equation}n^{-1/2}\nu_n \xrightarrow{\mathcal{D}^*} \sigma_{\eta}A_{\psi}\nu\quad\mbox{in $\ell^\infty({\mathcal{F}})$ as $n\to\infty$,}\end{equation}
\begin{equation}n^{-1/2}\nu_n \xrightarrow{\mathcal{D}^*} \sigma_{\eta}A_{\psi}\nu\quad\mbox{in $\ell^\infty({\mathcal{F}})$ as $n\to\infty$,}\end{equation}
where  $\sigma_{\eta}$
and
$\sigma_{\eta}$
and  $A_{\psi}$
are parameters describing the short-memory linear process.
$A_{\psi}$
are parameters describing the short-memory linear process.
A weak invariance principle for sample paths of the partial sum process based on a short-memory linear process (Theorem 2) is obtained using the preceding theorem and a duality-type result (Theorem 3).
The paper is organized as follows. Section 2 contains notation and further results. Section 3 contains the proof of convergence of finite-dimensional distributions of the process  $n^{-1/2}\nu_n$
. Asymptotic equicontinuity is discussed in Section 4. The proof of the main result, Theorem 1, is given in Section 5. Further results, Theorems 2 and 3, are proved in Section 6. Finally, Section 7 is devoted to some applications.
$n^{-1/2}\nu_n$
. Asymptotic equicontinuity is discussed in Section 4. The proof of the main result, Theorem 1, is given in Section 5. Further results, Theorems 2 and 3, are proved in Section 6. Finally, Section 7 is devoted to some applications.
2. Notation and results
Since the processes considered in this paper have sample paths in non-separable Banach spaces we use the concept of convergence in outer distribution developed by J. Hoffmann-Jørgensen. Given a probability space  $(\Omega,{\mathcal{A}},{\mathrm{P}})$
, let T be a function from
$(\Omega,{\mathcal{A}},{\mathrm{P}})$
, let T be a function from  $\Omega$
to the extended real line
$\Omega$
to the extended real line  $\bar{\mathbb R}$
. The outer integral of T with respect to
$\bar{\mathbb R}$
. The outer integral of T with respect to  ${\mathrm{P}}$
is defined as
${\mathrm{P}}$
is defined as
 \begin{equation*}{\mathrm{E}}^{\ast}(T)\,:\!=\inf\,\{{\mathrm{E}} (U)\colon\mbox{$U\colon\Omega\to\bar{\mathbb R}$ is measurable, ${\mathrm{E}} (U)$ exists, and $U\geq T$}\}.\end{equation*}
\begin{equation*}{\mathrm{E}}^{\ast}(T)\,:\!=\inf\,\{{\mathrm{E}} (U)\colon\mbox{$U\colon\Omega\to\bar{\mathbb R}$ is measurable, ${\mathrm{E}} (U)$ exists, and $U\geq T$}\}.\end{equation*}
The outer probability of a subset B of  $\Omega$
is
$\Omega$
is  ${\mathrm{P}}^{\ast}(B)\,:\!={\mathrm{E}}^{\ast}(\textbf{1}_B)=\inf\,\{{\mathrm{P}}(A)\colon A\in{\mathcal{A}}, \,A\supset B\}$
; here and elsewhere,
${\mathrm{P}}^{\ast}(B)\,:\!={\mathrm{E}}^{\ast}(\textbf{1}_B)=\inf\,\{{\mathrm{P}}(A)\colon A\in{\mathcal{A}}, \,A\supset B\}$
; here and elsewhere,  $\textbf{1}_B$
is the indicator function of a set B.
$\textbf{1}_B$
is the indicator function of a set B.
Definition 1. Let E be a metric space. For each  $n \in{\mathbb N}$
, let
$n \in{\mathbb N}$
, let  $(\Omega_n, {\mathcal{A}}_n, {\mathrm{P}}_n)$
be a probability space and let
$(\Omega_n, {\mathcal{A}}_n, {\mathrm{P}}_n)$
be a probability space and let  $Z_n$
be a function from
$Z_n$
be a function from  $\Omega_n$
into E. Suppose that
$\Omega_n$
into E. Suppose that  $Z_0$
takes values in some separable subset of E and is measurable for the Borel sets on its range. It is said that the sequence
$Z_0$
takes values in some separable subset of E and is measurable for the Borel sets on its range. It is said that the sequence  $(Z_n)$
converges in outer distribution to
$(Z_n)$
converges in outer distribution to  $Z_0$
, denoted
$Z_0$
, denoted  $Z_n \xrightarrow{\mathcal{D}^*} Z_0$
, if, for every bounded continuous function
$Z_n \xrightarrow{\mathcal{D}^*} Z_0$
, if, for every bounded continuous function  $h\,:\,E \to {\mathbb R}$
,
$h\,:\,E \to {\mathbb R}$
,
 \begin{equation*}\lim_{n\to\infty}{\mathrm{E}}^*(h(Z_n))={\mathrm{E}} (h(Z_0)).\end{equation*}
\begin{equation*}\lim_{n\to\infty}{\mathrm{E}}^*(h(Z_n))={\mathrm{E}} (h(Z_0)).\end{equation*}
Remark 1. If  $Z_n$
,
$Z_n$
,  $n = 0, 1, \dots$
, are random elements taking values in a separable metric space E endowed with the Borel
$n = 0, 1, \dots$
, are random elements taking values in a separable metric space E endowed with the Borel  $\sigma$
-algebra, then the convergence
$\sigma$
-algebra, then the convergence  $Z_n \xrightarrow{\mathcal{D}^*} Z_0$
is equivalent to usual convergence in distribution
$Z_n \xrightarrow{\mathcal{D}^*} Z_0$
is equivalent to usual convergence in distribution  $Z_n \xrightarrow{\mathcal{D}} Z_0$
:
$Z_n \xrightarrow{\mathcal{D}} Z_0$
:
 \begin{equation*}\lim_{n\to\infty}{\mathrm{E}} (h(Z_n))={\mathrm{E}} (h(Z_0))\end{equation*}
\begin{equation*}\lim_{n\to\infty}{\mathrm{E}} (h(Z_n))={\mathrm{E}} (h(Z_0))\end{equation*}
for every bounded continuous function  $h\,:\,E \to {\mathbb R}$
.
$h\,:\,E \to {\mathbb R}$
.
To establish convergence in outer distributions on  $\ell^{\infty}({\mathcal{F}})$
we need a separable subset for a support of a limit distribution. Given a pseudometric d on
$\ell^{\infty}({\mathcal{F}})$
we need a separable subset for a support of a limit distribution. Given a pseudometric d on  ${\mathcal{F}}$
, let
${\mathcal{F}}$
, let  $UC({\mathcal{F}},d)$
be a set of all
$UC({\mathcal{F}},d)$
be a set of all  $\nu\in \ell^\infty({\mathcal{F}})$
which are uniformly d-continuous. The set
$\nu\in \ell^\infty({\mathcal{F}})$
which are uniformly d-continuous. The set  $UC({\mathcal{F}}, d )$
is a separable subspace of
$UC({\mathcal{F}}, d )$
is a separable subspace of  $\ell^{\infty}({\mathcal{F}})$
if and only if
$\ell^{\infty}({\mathcal{F}})$
if and only if  $({\mathcal{F}},d)$
is totally bounded. As usual,
$({\mathcal{F}},d)$
is totally bounded. As usual,  $N(\varepsilon, {\mathcal{F}}, d)$
is the minimal number of open balls of d-radius
$N(\varepsilon, {\mathcal{F}}, d)$
is the minimal number of open balls of d-radius  $\varepsilon$
which are necessary to cover
$\varepsilon$
which are necessary to cover  ${\mathcal{F}}$
. The pseudometric space
${\mathcal{F}}$
. The pseudometric space  $({\mathcal{F}},d)$
is totally bounded if
$({\mathcal{F}},d)$
is totally bounded if  $N(\varepsilon, {\mathcal{F}}, d)$
is finite for every
$N(\varepsilon, {\mathcal{F}}, d)$
is finite for every  $\varepsilon > 0$
. This property always holds under the assumptions imposed below.
$\varepsilon > 0$
. This property always holds under the assumptions imposed below.
Let  ${\mathcal{L}}^2[0,1]={\mathcal{L}}^2([0,1],\lambda)$
be a set of measurable functions which are square-integrable for Lebesgue measure
${\mathcal{L}}^2[0,1]={\mathcal{L}}^2([0,1],\lambda)$
be a set of measurable functions which are square-integrable for Lebesgue measure  $\lambda$
on [0, 1] with a pseudometric
$\lambda$
on [0, 1] with a pseudometric  $\rho_2(\,f, g)=\rho_{2,\lambda}(\,f, g)=(\smallint_{[0,1]}(\,f-g)^2\,d\lambda)^{1/2}$
. Let
$\rho_2(\,f, g)=\rho_{2,\lambda}(\,f, g)=(\smallint_{[0,1]}(\,f-g)^2\,d\lambda)^{1/2}$
. Let  $L^2[0,1]=L^2([0,1],\lambda)$
be the associated Hilbert space endowed with the inner product
$L^2[0,1]=L^2([0,1],\lambda)$
be the associated Hilbert space endowed with the inner product  $\langle\,f, g\rangle =\int_0^1 f(t)g(t)\lambda(\text{d} t)$
. Given a set
$\langle\,f, g\rangle =\int_0^1 f(t)g(t)\lambda(\text{d} t)$
. Given a set  ${\mathcal{F}}\subset {\mathcal{L}}^2[0, 1]$
, let
${\mathcal{F}}\subset {\mathcal{L}}^2[0, 1]$
, let  $\nu=\{\nu(\,f)\colon f\in {\mathcal{F}}\}$
be a centred Gaussian process such that
$\nu=\{\nu(\,f)\colon f\in {\mathcal{F}}\}$
be a centred Gaussian process such that  ${\mathrm{E}}[\nu(\,f)\nu(g)] = \langle\,f, g\rangle$
for all
${\mathrm{E}}[\nu(\,f)\nu(g)] = \langle\,f, g\rangle$
for all  $f, g\in {\mathcal{F}}$
. Such a process exists and provides a linear isometry from
$f, g\in {\mathcal{F}}$
. Such a process exists and provides a linear isometry from  $L^2[0, 1]$
to
$L^2[0, 1]$
to  $L^2(\Omega, {\mathcal{F}}, {\mathrm{P}})$
. By [Reference Dudley7] or [Reference Dudley9, Theorems 2.6.1 and 2.8.6], if
$L^2(\Omega, {\mathcal{F}}, {\mathrm{P}})$
. By [Reference Dudley7] or [Reference Dudley9, Theorems 2.6.1 and 2.8.6], if
 \begin{equation}\int_0^1\sqrt{\log N(x,{\mathcal{F}},\rho_2)}\,\text{d} x<\infty\end{equation}
\begin{equation}\int_0^1\sqrt{\log N(x,{\mathcal{F}},\rho_2)}\,\text{d} x<\infty\end{equation}
then  $\nu=\{\nu(\,f)\colon f\in{\mathcal{F}}\}$
admits a version with almost all sample paths bounded and uniformly continuous on
$\nu=\{\nu(\,f)\colon f\in{\mathcal{F}}\}$
admits a version with almost all sample paths bounded and uniformly continuous on  ${\mathcal{F}}$
with respect to
${\mathcal{F}}$
with respect to  $\rho_2$
. In what follows, we denote a suitable version by the same notation
$\rho_2$
. In what follows, we denote a suitable version by the same notation  $\nu$
, and so
$\nu$
, and so  $\nu$
itself takes values in
$\nu$
itself takes values in  $UC({\mathcal{F}}, \rho_2)$
and is measurable for the Borel sets on its range.
$UC({\mathcal{F}}, \rho_2)$
and is measurable for the Borel sets on its range.
In this paper the condition (6) is applied to sets  ${\mathcal{F}}$
defined as follows. For
${\mathcal{F}}$
defined as follows. For  $-\infty <a<b<\infty$
and
$-\infty <a<b<\infty$
and  $0 < p < \infty$
, the p-variation of a function
$0 < p < \infty$
, the p-variation of a function  $g\colon[a,b]\to{\mathbb R}$
is the supremum
$g\colon[a,b]\to{\mathbb R}$
is the supremum
 \begin{equation*}v_p(g;\ [a, b])\,:\!=\sup\Big\{\sum^m_{i=1}|g(t_i) - g(t_{i-1})|^p\,:\,a=t_0 < t_1 < \cdots
< t_m = b,\ m \in{\mathbb N}_{+}\Big\},\end{equation*}
\begin{equation*}v_p(g;\ [a, b])\,:\!=\sup\Big\{\sum^m_{i=1}|g(t_i) - g(t_{i-1})|^p\,:\,a=t_0 < t_1 < \cdots
< t_m = b,\ m \in{\mathbb N}_{+}\Big\},\end{equation*}
which can be finite or infinite. If  $v_p(g;\ [a, b]) < \infty$
then g is said to have bounded p-variation and the set of all such functions is denoted by
$v_p(g;\ [a, b]) < \infty$
then g is said to have bounded p-variation and the set of all such functions is denoted by  ${\mathcal{W}}_p[a, b]$
. We abbreviate
${\mathcal{W}}_p[a, b]$
. We abbreviate  $v_p(g)\,:\!= v_p(g;\ [0, 1])$
. For each
$v_p(g)\,:\!= v_p(g;\ [0, 1])$
. For each  $g \in {\mathcal{W}}_p[0, 1]$
and
$g \in {\mathcal{W}}_p[0, 1]$
and  $1 \le p < \infty$
, let
$1 \le p < \infty$
, let  $\|g\|_{(p)} \,:\!= v^{1/p}_p(g)$
. Then
$\|g\|_{(p)} \,:\!= v^{1/p}_p(g)$
. Then  $\|g\|_{(p)}$
is a seminorm equal to zero only for constant functions g. The p-variation norm is
$\|g\|_{(p)}$
is a seminorm equal to zero only for constant functions g. The p-variation norm is
 \begin{equation*}\|g\|_{[p]} \,:\!=\|g\|_{\sup} +\|g\|_{(p)} ,\end{equation*}
\begin{equation*}\|g\|_{[p]} \,:\!=\|g\|_{\sup} +\|g\|_{(p)} ,\end{equation*}
where  $\|g\|_{\sup}\,:\!=\sup_{0\le t\le 1}|g(t)|$
. The set
$\|g\|_{\sup}\,:\!=\sup_{0\le t\le 1}|g(t)|$
. The set  ${\mathcal{W}}_p[0, 1]$
is a non-separable Banach space with the norm
${\mathcal{W}}_p[0, 1]$
is a non-separable Banach space with the norm  $\|\cdot\|_{[p]}$
. If
$\|\cdot\|_{[p]}$
. If  ${\mathcal{F}}$
is a bounded subset of
${\mathcal{F}}$
is a bounded subset of  ${\mathcal{W}}_q[0,1]$
with
${\mathcal{W}}_q[0,1]$
with  $1\leq q<2$
, then (6) holds by the proof of Theorem 2.1 in [Reference Dudley8] (see also [Reference Norvaiša and Račkauskas14, Theorem 5]).
$1\leq q<2$
, then (6) holds by the proof of Theorem 2.1 in [Reference Dudley8] (see also [Reference Norvaiša and Račkauskas14, Theorem 5]).
Now we are prepared to formulate further results. Let  $X_1, X_2,\dots$
be a sequence of real-valued random variables. For each positive integer
$X_1, X_2,\dots$
be a sequence of real-valued random variables. For each positive integer  $n\in{\mathbb N}_{+}$
, the nth partial sum process of random variables is defined by
$n\in{\mathbb N}_{+}$
, the nth partial sum process of random variables is defined by
 \begin{equation*}S_n(t)\,:\!=\sum_{i=1}^{\lfloor nt\rfloor}X_i=\sum_{i=1}^nX_i\textbf{1}_{[0,t]}\Big (\frac{i}{n}\Big ),\qquad t\in [0,1].\end{equation*}
\begin{equation*}S_n(t)\,:\!=\sum_{i=1}^{\lfloor nt\rfloor}X_i=\sum_{i=1}^nX_i\textbf{1}_{[0,t]}\Big (\frac{i}{n}\Big ),\qquad t\in [0,1].\end{equation*}
Here, for a real number  $x\geq 0$
,
$x\geq 0$
,  $\lfloor x\rfloor\,:\!=\max\{k\colon k\in{\mathbb N},\,k\leq x\}$
is a value of the floor function. Then the partial sum process is the sequence of nth partial sum processes
$\lfloor x\rfloor\,:\!=\max\{k\colon k\in{\mathbb N},\,k\leq x\}$
is a value of the floor function. Then the partial sum process is the sequence of nth partial sum processes  $S_n=\{S_n(t)\colon t\in [0,1]\}$
,
$S_n=\{S_n(t)\colon t\in [0,1]\}$
,  $n\in{\mathbb N}_{+}$
. Let W be a Wiener process on [0, 1]. In [Reference Norvaiša and Račkauskas14], assuming that the random variables
$n\in{\mathbb N}_{+}$
. Let W be a Wiener process on [0, 1]. In [Reference Norvaiša and Račkauskas14], assuming that the random variables  $X_1, X_2,\dots$
are independent and identically distributed, it is proved that convergence in outer distribution,
$X_1, X_2,\dots$
are independent and identically distributed, it is proved that convergence in outer distribution,
 \begin{equation*} n^{-1/2}S_n \xrightarrow{\mathcal{D}^*} \sigma W\quad\mbox{in ${\mathcal{W}}_p[0,1]$ as $n\to\infty$,}\end{equation*}
\begin{equation*} n^{-1/2}S_n \xrightarrow{\mathcal{D}^*} \sigma W\quad\mbox{in ${\mathcal{W}}_p[0,1]$ as $n\to\infty$,}\end{equation*}
holds if and only if  ${\mathrm{E}} (X_1)=0$
and
${\mathrm{E}} (X_1)=0$
and  $\sigma^2={\mathrm{E}} (X_1^2)<\infty$
. The assumption
$\sigma^2={\mathrm{E}} (X_1^2)<\infty$
. The assumption  $p>2$
cannot be replaced by
$p>2$
cannot be replaced by  $p=2$
since in this case the limiting process W does not belong to
$p=2$
since in this case the limiting process W does not belong to  ${\mathcal{W}}_2[0,1]$
. The next theorem extends this fact to the case where a sequence of random variables
${\mathcal{W}}_2[0,1]$
. The next theorem extends this fact to the case where a sequence of random variables  $X_1, X_2,\dots$
is a short-memory linear process.
$X_1, X_2,\dots$
is a short-memory linear process.
Theorem 2. Let  $X_1, X_2, \dots$
be a short-memory linear process, let
$X_1, X_2, \dots$
be a short-memory linear process, let  $p>2$
, and let W be a Wiener process on [0, 1]. Then
$p>2$
, and let W be a Wiener process on [0, 1]. Then
 \begin{equation*} n^{-1/2}S_n \xrightarrow{\mathcal{D}^*} \sigma_{\eta} A_{\psi}W\quad\mbox{in ${\mathcal{W}}_p[0, 1]$ as $n\to\infty$.}\end{equation*}
\begin{equation*} n^{-1/2}S_n \xrightarrow{\mathcal{D}^*} \sigma_{\eta} A_{\psi}W\quad\mbox{in ${\mathcal{W}}_p[0, 1]$ as $n\to\infty$.}\end{equation*}
For any  $p>0$
, the p-variation of a sample function of the nth partial sum is
$p>0$
, the p-variation of a sample function of the nth partial sum is
 \begin{equation}v_p(S_n)=\max\bigg\{\sum_{j=1}^m \, \bigg |\sum_{i=k_{j-1}+1}^{k_j}\!\!\!\!X_i\bigg |^p\colon 0=k_0<\cdots <k_m=n,\,\,1\leq m\leq n\bigg\}.\end{equation}
\begin{equation}v_p(S_n)=\max\bigg\{\sum_{j=1}^m \, \bigg |\sum_{i=k_{j-1}+1}^{k_j}\!\!\!\!X_i\bigg |^p\colon 0=k_0<\cdots <k_m=n,\,\,1\leq m\leq n\bigg\}.\end{equation}
Theorem 2 and the continuous mapping theorem (e.g. Theorem 1.3.6 in [Reference Van der Vaart and Wellner15]) applied to the p-variation yield the following.
Corollary 1. Under the hypotheses of Theorem 2, we have
 \begin{equation*}n^{-\frac{p}{2}}v_p(S_n) \xrightarrow{\mathcal{D}} \sigma_{\eta}^p A_{\psi}^pv_p(W)\quad\mbox{as $n\to\infty$.}\end{equation*}
\begin{equation*}n^{-\frac{p}{2}}v_p(S_n) \xrightarrow{\mathcal{D}} \sigma_{\eta}^p A_{\psi}^pv_p(W)\quad\mbox{as $n\to\infty$.}\end{equation*}
Suppose that  ${\mathcal{F}}$
contains the family of indicator functions of subintervals of [0, 1]. Then the nth partial sum process of a linear process
${\mathcal{F}}$
contains the family of indicator functions of subintervals of [0, 1]. Then the nth partial sum process of a linear process  $S_n$
and the nth
$S_n$
and the nth  ${\mathcal{F}}$
-weighted sum of linear process
${\mathcal{F}}$
-weighted sum of linear process  $\nu_n$
are related by the equality
$\nu_n$
are related by the equality
 \begin{equation*} S_n(t)=\nu_n(\textbf{1}_{[0,t]})\quad\mbox{ for\ each $t\in [0,1]$.}\end{equation*}
\begin{equation*} S_n(t)=\nu_n(\textbf{1}_{[0,t]})\quad\mbox{ for\ each $t\in [0,1]$.}\end{equation*}
This relation is used in the following theorem to obtain Theorem 2 from a uniform convergence of  $n^{-1/2}\nu_n$
over the set
$n^{-1/2}\nu_n$
over the set  ${\mathcal{F}}_q=\{\,f\in{\mathcal{W}}_q[a,b]\colon \|\,f\|_{[q]}\leq 1\}$
,
${\mathcal{F}}_q=\{\,f\in{\mathcal{W}}_q[a,b]\colon \|\,f\|_{[q]}\leq 1\}$
,  $1\leq q<2$
, which is the unit ball in
$1\leq q<2$
, which is the unit ball in  ${\mathcal{W}}_q[a,b]$
. To this end, the nth
${\mathcal{W}}_q[a,b]$
. To this end, the nth  ${\mathcal{F}}_q$
-weighted sum of linear process
${\mathcal{F}}_q$
-weighted sum of linear process  $\nu_n$
is considered as a bounded linear functional over
$\nu_n$
is considered as a bounded linear functional over  ${\mathcal{W}}_q[a,b]$
.
${\mathcal{W}}_q[a,b]$
.
Theorem 3. Let  $1<p<\infty$
and
$1<p<\infty$
and  $1<q<\infty$
be such that
$1<q<\infty$
be such that  $p^{-1}+q^{-1}=1$
. For a linear bounded functional
$p^{-1}+q^{-1}=1$
. For a linear bounded functional  $L\colon{\mathcal{W}}_q[a,b]\to{\mathbb R}$
, let
$L\colon{\mathcal{W}}_q[a,b]\to{\mathbb R}$
, let  $T(L)(t)\,:\!=L(\textbf{1}_{[a,t]})$
for each
$T(L)(t)\,:\!=L(\textbf{1}_{[a,t]})$
for each  $t\in [a,b]$
. Then T is a linear mapping from the dual space
$t\in [a,b]$
. Then T is a linear mapping from the dual space  ${\mathcal{W}}_q^{\ast}[a,b]$
into
${\mathcal{W}}_q^{\ast}[a,b]$
into  ${\mathcal{W}}_p[a,b]$
, and
${\mathcal{W}}_p[a,b]$
, and
 \begin{equation}\|T(L)\|_{[p]}\leq 5\|L\|_{{\mathcal{F}}_q},\qquad L\in{\mathcal{W}}_q^{\ast}[a,b],\end{equation}
\begin{equation}\|T(L)\|_{[p]}\leq 5\|L\|_{{\mathcal{F}}_q},\qquad L\in{\mathcal{W}}_q^{\ast}[a,b],\end{equation}
where  $\|\cdot\|_{{\mathcal{F}}_q}$
is defined by (4).
$\|\cdot\|_{{\mathcal{F}}_q}$
is defined by (4).
To prove Theorem 1 we use the asymptotic equicontinuity criterion for convergence in law in  $\ell^{\infty}({\mathcal{F}})$
(see, e.g., [Reference Giné and Nickl12, Theorem 3.7.23] or [Reference Van der Vaart and Wellner15, p. 41]). The conclusion of Theorem 1 holds if and only if (i), (ii), and (iii) hold, where
$\ell^{\infty}({\mathcal{F}})$
(see, e.g., [Reference Giné and Nickl12, Theorem 3.7.23] or [Reference Van der Vaart and Wellner15, p. 41]). The conclusion of Theorem 1 holds if and only if (i), (ii), and (iii) hold, where
(i) the finite-dimensional distributions of
 $n^{-1/2}\nu_n$
converge in distribution to the corresponding finite-dimensional distributions of
$n^{-1/2}\nu_n$
converge in distribution to the corresponding finite-dimensional distributions of  $\nu$
;
$\nu$
;(ii)
 $n^{-1/2}\nu_n$
is asymptotically equicontinuous with respect to
$n^{-1/2}\nu_n$
is asymptotically equicontinuous with respect to  $\rho_2$
;
$\rho_2$
;(iii)
 ${\mathcal{F}}$
is totally bounded for
${\mathcal{F}}$
is totally bounded for  $\rho_2$
.
$\rho_2$
.
3. Convergence of finite-dimensional distributions
In this section we establish convergence of finite-dimensional distributions of the processes  $n^{-1/2}\nu_n$
. Recall that
$n^{-1/2}\nu_n$
. Recall that  ${\mathcal{F}}_q=\{\,f\in{\mathcal{W}}_q[0, 1]\colon\|\,f\|_{[q]}\le 1\}$
is endowed with the pseudometric
${\mathcal{F}}_q=\{\,f\in{\mathcal{W}}_q[0, 1]\colon\|\,f\|_{[q]}\le 1\}$
is endowed with the pseudometric  $\rho_2$
. We begin with a one-dimensional case.
$\rho_2$
. We begin with a one-dimensional case.
We have not seen results in the literature which yield the convergence in distribution of real random variables  $n^{-1/2}\nu_n(g)$
when
$n^{-1/2}\nu_n(g)$
when  $g\in{\mathcal{W}}_q[0,1]$
for some
$g\in{\mathcal{W}}_q[0,1]$
for some  $q\in [1,2)$
under the hypotheses of Theorem 4 below. The best available related results are due to K. M. Abadir et al. [Reference Abadir, Distaso, Giraitis and Koul1] and give the desired fact when g has bounded total variation. Next is a more general result for a short-memory linear process with independent, identically distributed inovations and weights given by a function g.
$q\in [1,2)$
under the hypotheses of Theorem 4 below. The best available related results are due to K. M. Abadir et al. [Reference Abadir, Distaso, Giraitis and Koul1] and give the desired fact when g has bounded total variation. Next is a more general result for a short-memory linear process with independent, identically distributed inovations and weights given by a function g.
Theorem 4. Suppose  $(X_i)_{i\in{\mathbb Z}}$
is a linear process defined by (1) and (2), and
$(X_i)_{i\in{\mathbb Z}}$
is a linear process defined by (1) and (2), and  $\nu$
is the isonormal Gaussian processes on
$\nu$
is the isonormal Gaussian processes on  ${\mathcal{L}}_2[0,1]$
. If
${\mathcal{L}}_2[0,1]$
. If  $g\in{\mathcal{W}}_q[0,1]$
for some
$g\in{\mathcal{W}}_q[0,1]$
for some  $1\leq q<2$
, then
$1\leq q<2$
, then
 \begin{equation}n^{-1/2}\nu_n(g) \xrightarrow{\mathcal{D}} \sigma_{\eta}A_{\psi}\nu (g),\quad\mbox{as $n\to\infty$.}\end{equation}
\begin{equation}n^{-1/2}\nu_n(g) \xrightarrow{\mathcal{D}} \sigma_{\eta}A_{\psi}\nu (g),\quad\mbox{as $n\to\infty$.}\end{equation}
Proof. Let  $1\leq q<2$
and
$1\leq q<2$
and  $g\in{\mathcal{W}}_q[0,1]$
. For each
$g\in{\mathcal{W}}_q[0,1]$
. For each  $n\in{\mathbb N}_{+}$
and
$n\in{\mathbb N}_{+}$
and  $k\in{\mathbb N}$
, let
$k\in{\mathbb N}$
, let
 \begin{equation}T_{nk}\,:\!=\sum_{i=1}^n\eta_{i-k}g\Big (\frac{i}{n}\Big ).\end{equation}
\begin{equation}T_{nk}\,:\!=\sum_{i=1}^n\eta_{i-k}g\Big (\frac{i}{n}\Big ).\end{equation}
By (3) and (1) we have the representation
 \begin{align*}\nu_n(g)& = \sum_{i=1}^n\Big (\sum_{k=0}^{\infty}\psi_k\eta_{i-k}\Big )g\Big (\frac{i}{n}\Big )=\sum_{k=0}^{\infty}\psi_kT_{nk}\\
& = \sum_{k=0}^{\infty}\psi_k [T_{nk}-T_{n0}]+ A_{\psi}T_{n0}.\end{align*}
\begin{align*}\nu_n(g)& = \sum_{i=1}^n\Big (\sum_{k=0}^{\infty}\psi_k\eta_{i-k}\Big )g\Big (\frac{i}{n}\Big )=\sum_{k=0}^{\infty}\psi_kT_{nk}\\
& = \sum_{k=0}^{\infty}\psi_k [T_{nk}-T_{n0}]+ A_{\psi}T_{n0}.\end{align*}
Since the function  $g\in{\mathcal{W}}_q[0,1]$
, it is regulated, meaning that it has left limits on (0, 1] and right limits on [0,1) (see, e.g., [Reference Dudley and Norvaiša11, p. 213]). Thus,
$g\in{\mathcal{W}}_q[0,1]$
, it is regulated, meaning that it has left limits on (0, 1] and right limits on [0,1) (see, e.g., [Reference Dudley and Norvaiša11, p. 213]). Thus,  $g^2$
is Riemann integrable, and so
$g^2$
is Riemann integrable, and so
 \begin{equation*}\text{Var}\Big (n^{-1/2}T_{n0}\Big )=\frac{\sigma_{\eta}^2}{n}\sum_{i=1}^ng^2\Big (\frac{i}{n}\Big )\to\sigma_{\eta}^2\int_0^1g^2\,\text{d}\lambda,\quad\mbox{as $n\to\infty$.}\end{equation*}
\begin{equation*}\text{Var}\Big (n^{-1/2}T_{n0}\Big )=\frac{\sigma_{\eta}^2}{n}\sum_{i=1}^ng^2\Big (\frac{i}{n}\Big )\to\sigma_{\eta}^2\int_0^1g^2\,\text{d}\lambda,\quad\mbox{as $n\to\infty$.}\end{equation*}
Since  $\nu$
is the isonormal Gaussian processes on
$\nu$
is the isonormal Gaussian processes on  ${\mathcal{L}}_2[0,1]$
it follows by the Lindeberg central limit theorem that
${\mathcal{L}}_2[0,1]$
it follows by the Lindeberg central limit theorem that
 \begin{equation*}n^{-1/2}T_{n0}=\frac{1}{\sqrt{n}\,}\sum_{i=1}^n\eta_{i}g\Big (\frac{i}{n}\Big )\xrightarrow{\mathcal{D}} \sigma_{\eta}\nu (g),\quad\mbox{as $n\to\infty$.}\end{equation*}
\begin{equation*}n^{-1/2}T_{n0}=\frac{1}{\sqrt{n}\,}\sum_{i=1}^n\eta_{i}g\Big (\frac{i}{n}\Big )\xrightarrow{\mathcal{D}} \sigma_{\eta}\nu (g),\quad\mbox{as $n\to\infty$.}\end{equation*}
Therefore, to prove (9), due to the Slutsky theorem, it is enough to show that
 \begin{equation}R_n\,:\!=\sum_{k=0}^{\infty}\frac{\psi_k}{\sqrt{n}}[T_{nk}-T_{n0}]\to 0\quad\mbox{in probability ${\mathrm{P}}$ as $n\to\infty$.}\end{equation}
\begin{equation}R_n\,:\!=\sum_{k=0}^{\infty}\frac{\psi_k}{\sqrt{n}}[T_{nk}-T_{n0}]\to 0\quad\mbox{in probability ${\mathrm{P}}$ as $n\to\infty$.}\end{equation}
We will show that the following two properties hold true:
 \begin{equation}\sup_{n,k}\frac{1}{n}{\mathrm{E}} (T_{nk}^2)<\infty\end{equation}
\begin{equation}\sup_{n,k}\frac{1}{n}{\mathrm{E}} (T_{nk}^2)<\infty\end{equation}
and
 \begin{equation}\mbox{for each $k\in{\mathbb N}$},\quad\lim_{n\to\infty}\frac{1}{\sqrt{n}\,}|T_{nk}-T_{n0}|= 0\quad\mbox{in probability ${\mathrm{P}}$.}\end{equation}
\begin{equation}\mbox{for each $k\in{\mathbb N}$},\quad\lim_{n\to\infty}\frac{1}{\sqrt{n}\,}|T_{nk}-T_{n0}|= 0\quad\mbox{in probability ${\mathrm{P}}$.}\end{equation}
For the moment, suppose that (12) and (13) hold true. Let  $\epsilon >0$
and
$\epsilon >0$
and  $K\in{\mathbb N}$
. Split the sum
$K\in{\mathbb N}$
. Split the sum  $R_n$
given by (11) into the sum with all
$R_n$
given by (11) into the sum with all  $k\leq K$
and the sum with all
$k\leq K$
and the sum with all  $k>K$
to get the inequality
$k>K$
to get the inequality
 \begin{eqnarray}\lefteqn{{\mathrm{P}}(\{|R_n|>\epsilon\})}\nonumber\\&\leq&{\mathrm{P}}\bigg (\bigg \{ \sum_{k=0}^K\frac{|\psi_k|}{\sqrt{n}}|T_{nk}-T_{n0}|>\frac{\epsilon}{2}\bigg\}\bigg )+{\mathrm{P}}\bigg (\bigg\{\sum_{k>K}\frac{|\psi_k|}{\sqrt{n}}|T_{nk}-T_{n0}|>\frac{\epsilon}{2}\bigg\}\bigg ).\end{eqnarray}
\begin{eqnarray}\lefteqn{{\mathrm{P}}(\{|R_n|>\epsilon\})}\nonumber\\&\leq&{\mathrm{P}}\bigg (\bigg \{ \sum_{k=0}^K\frac{|\psi_k|}{\sqrt{n}}|T_{nk}-T_{n0}|>\frac{\epsilon}{2}\bigg\}\bigg )+{\mathrm{P}}\bigg (\bigg\{\sum_{k>K}\frac{|\psi_k|}{\sqrt{n}}|T_{nk}-T_{n0}|>\frac{\epsilon}{2}\bigg\}\bigg ).\end{eqnarray}
Clearly we have the bound
 \begin{equation*}{\mathrm{P}}\bigg (\bigg\{\sum_{k>K}\frac{|\psi_k|}{\sqrt{n}}|T_{nk}-T_{n0}|>\frac{\epsilon}{2}\bigg\}\bigg )\leq\frac{4}{\epsilon}\sup_{n,k}\bigg (\frac{{\mathrm{E}} (T_{nk}^2)}{n}\bigg )^{1/2}\sum_{k>K}|\psi_k|.\end{equation*}
\begin{equation*}{\mathrm{P}}\bigg (\bigg\{\sum_{k>K}\frac{|\psi_k|}{\sqrt{n}}|T_{nk}-T_{n0}|>\frac{\epsilon}{2}\bigg\}\bigg )\leq\frac{4}{\epsilon}\sup_{n,k}\bigg (\frac{{\mathrm{E}} (T_{nk}^2)}{n}\bigg )^{1/2}\sum_{k>K}|\psi_k|.\end{equation*}
By (12) and (2), taking  $K\in{\mathbb N}$
large enough, one can make the right-hand side of the preceding bound as small as one wishes. Then the first probability on the right-hand side of (14) is as small as one wishes by (13) and taking
$K\in{\mathbb N}$
large enough, one can make the right-hand side of the preceding bound as small as one wishes. Then the first probability on the right-hand side of (14) is as small as one wishes by (13) and taking  $n\in{\mathbb N}_{+}$
large enough. Therefore, (11) holds true and we are left to prove (12) and (13).
$n\in{\mathbb N}_{+}$
large enough. Therefore, (11) holds true and we are left to prove (12) and (13).
Recalling the notation  $T_{nk}$
given by (10), for each
$T_{nk}$
given by (10), for each  $n\in{\mathbb N}_{+}$
and
$n\in{\mathbb N}_{+}$
and  $k\in{\mathbb N}$
, we have
$k\in{\mathbb N}$
, we have
 \begin{equation*}\frac{1}{n}{\mathrm{E}} (T_{nk}^2)=\frac{\sigma_{\eta}^2}{n}\sum_{i=1}^ng^2\Big (\frac{i}{n}\Big )\leq\sigma_{\eta}^2\|g\|_{\sup}^2.\end{equation*}
\begin{equation*}\frac{1}{n}{\mathrm{E}} (T_{nk}^2)=\frac{\sigma_{\eta}^2}{n}\sum_{i=1}^ng^2\Big (\frac{i}{n}\Big )\leq\sigma_{\eta}^2\|g\|_{\sup}^2.\end{equation*}
This proves (12). To prove (13), let  $k\in{\mathbb N}_{+}$
. Changing the index i of summation, it follows that the representation
$k\in{\mathbb N}_{+}$
. Changing the index i of summation, it follows that the representation
 \begin{equation*}T_{nk}-T_{n0}=\sum_{i=1-k}^0\eta_ig\Big (\frac{i+k}{n}\Big )+\sum_{i=1}^{n-k}\eta_i\Big [g\Big (\frac{i+k}{n}\Big ) -g\Big (\frac{i}{n}\Big )\Big ]-\sum_{i=n-k+1}^n\eta_ig\Big (\frac{i}{n}\Big )\end{equation*}
\begin{equation*}T_{nk}-T_{n0}=\sum_{i=1-k}^0\eta_ig\Big (\frac{i+k}{n}\Big )+\sum_{i=1}^{n-k}\eta_i\Big [g\Big (\frac{i+k}{n}\Big ) -g\Big (\frac{i}{n}\Big )\Big ]-\sum_{i=n-k+1}^n\eta_ig\Big (\frac{i}{n}\Big )\end{equation*}
holds for each integer  $n>k$
. Since g is bounded and k is fixed, the first and the third sums on the right-hand side divided by
$n>k$
. Since g is bounded and k is fixed, the first and the third sums on the right-hand side divided by  $\sqrt{n}$
tend to zero in probability
$\sqrt{n}$
tend to zero in probability  ${\mathrm{P}}$
as
${\mathrm{P}}$
as  $n\to\infty$
. For the second sum divided by
$n\to\infty$
. For the second sum divided by  $\sqrt{n}$
we apply the Hölder inequality,
$\sqrt{n}$
we apply the Hölder inequality,
 \begin{equation*}\bigg |\frac{1}{\sqrt{n}\,}\sum_{i=1}^{n-k}\eta_i\Big [g\Big (\frac{i+k}{n}\Big ) -g\Big (\frac{i}{n}\Big )\Big ]\bigg |\leq \bigg (n^{-\frac{p}{2}}\sum_{i=1}^{n-k}|\eta_i|^p\bigg )^{\frac{1}{p}}\bigg (\sum_{i=1}^{n-k}\Big |g\Big (\frac{i+k}{n}\Big ) -g\Big (\frac{i}{n}\Big )\Big |^q\bigg )^{\frac{1}{q}} ,\end{equation*}
\begin{equation*}\bigg |\frac{1}{\sqrt{n}\,}\sum_{i=1}^{n-k}\eta_i\Big [g\Big (\frac{i+k}{n}\Big ) -g\Big (\frac{i}{n}\Big )\Big ]\bigg |\leq \bigg (n^{-\frac{p}{2}}\sum_{i=1}^{n-k}|\eta_i|^p\bigg )^{\frac{1}{p}}\bigg (\sum_{i=1}^{n-k}\Big |g\Big (\frac{i+k}{n}\Big ) -g\Big (\frac{i}{n}\Big )\Big |^q\bigg )^{\frac{1}{q}} ,\end{equation*}
with  $p\in{\mathbb R}$
such that
$p\in{\mathbb R}$
such that  $\frac{1}{p}+\frac{1}{q}\geq 1$
. The telescoping sum representation and repeated application of the Minkowski inequality for sums imply that the inequality
$\frac{1}{p}+\frac{1}{q}\geq 1$
. The telescoping sum representation and repeated application of the Minkowski inequality for sums imply that the inequality
 \begin{equation*}\bigg (\sum_{i=1}^{n-k}\Big |g\Big (\frac{i+k}{n}\Big ) -g\Big (\frac{i}{n}\Big )\Big |^q\bigg )^{\frac{1}{q}}\leq k\|g\|_{(q)}\end{equation*}
\begin{equation*}\bigg (\sum_{i=1}^{n-k}\Big |g\Big (\frac{i+k}{n}\Big ) -g\Big (\frac{i}{n}\Big )\Big |^q\bigg )^{\frac{1}{q}}\leq k\|g\|_{(q)}\end{equation*}
holds for each integer  $n>k$
. Since
$n>k$
. Since  $1\leq q<2$
, then
$1\leq q<2$
, then  $(2/p)<1$
. Also, since k is fixed and
$(2/p)<1$
. Also, since k is fixed and  ${\mathrm{E}}(|\eta_1|^p)^{\frac{2}{p}}=\sigma_{\eta}^2<\infty$
, by the Marcinkiewicz–Zygmund strong law of large numbers we have
${\mathrm{E}}(|\eta_1|^p)^{\frac{2}{p}}=\sigma_{\eta}^2<\infty$
, by the Marcinkiewicz–Zygmund strong law of large numbers we have
 \begin{equation*}\lim_{n\to\infty}n^{-\frac{p}{2}}\sum_{i=1}^{n-k}|\eta_i|^p=0\quad\mbox{with probability 1}.\end{equation*}
\begin{equation*}\lim_{n\to\infty}n^{-\frac{p}{2}}\sum_{i=1}^{n-k}|\eta_i|^p=0\quad\mbox{with probability 1}.\end{equation*}
This completes the proof of (13), and thus Theorem 3 is proved. □
By the definition of the Gaussian process  $\nu$
, for any
$\nu$
, for any  $g_1,\dots,g_d\in {\mathcal{W}}_q$
,
$g_1,\dots,g_d\in {\mathcal{W}}_q$
,  $(\nu (g_1),\dots, \nu (g_d))$
have a jointly normal distribution with covariance given by the inner products
$(\nu (g_1),\dots, \nu (g_d))$
have a jointly normal distribution with covariance given by the inner products  $\int_0^1g_ig_j\,\text{d}\lambda$
,
$\int_0^1g_ig_j\,\text{d}\lambda$
,  $i,j=1, \dots, d$
.
$i,j=1, \dots, d$
.
Proposition 1. Suppose  $(X_i)_{i\in{\mathbb Z}}$
is a short-memory linear process and
$(X_i)_{i\in{\mathbb Z}}$
is a short-memory linear process and  $\nu$
is the isonormal Gaussian processes on
$\nu$
is the isonormal Gaussian processes on  ${\mathcal{L}}_2[0,1]$
. If
${\mathcal{L}}_2[0,1]$
. If  $g_1,\dots,g_d\in{\mathcal{W}}_q[0,1]$
for some
$g_1,\dots,g_d\in{\mathcal{W}}_q[0,1]$
for some  $1\leq q<2$
, then
$1\leq q<2$
, then
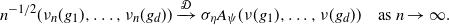 \begin{equation}n^{-1/2}(\nu_n(g_1),\dots,\nu_n(g_d)) \xrightarrow{\mathcal{D}} \sigma_{\eta}A_{\psi}(\nu (g_1),\dots,\nu (g_d))\quad\mbox{as $n\to\infty$.}\end{equation}
\begin{equation}n^{-1/2}(\nu_n(g_1),\dots,\nu_n(g_d)) \xrightarrow{\mathcal{D}} \sigma_{\eta}A_{\psi}(\nu (g_1),\dots,\nu (g_d))\quad\mbox{as $n\to\infty$.}\end{equation}
Proof. Let  $d\in{\mathbb N}_{+}$
, and let
$d\in{\mathbb N}_{+}$
, and let  $g_1,\dots,g_d\in{\mathcal{W}}_q[0,1]$
. To prove (15) we use the Cramér–Wold device. Let
$g_1,\dots,g_d\in{\mathcal{W}}_q[0,1]$
. To prove (15) we use the Cramér–Wold device. Let  $a=(a_1,\dots,a_d)\in{\mathbb R}^d$
. Recalling the definition in (3) of
$a=(a_1,\dots,a_d)\in{\mathbb R}^d$
. Recalling the definition in (3) of  $\nu_n$
, we have
$\nu_n$
, we have
 \begin{equation*}\sum_{h=1}^da_h\nu_n(g_h)=\nu_n\bigg (\sum_{h=1}^da_hg_h\bigg )\end{equation*}
\begin{equation*}\sum_{h=1}^da_h\nu_n(g_h)=\nu_n\bigg (\sum_{h=1}^da_hg_h\bigg )\end{equation*}
for each  $n\in{\mathbb N}_{+}$
. Since
$n\in{\mathbb N}_{+}$
. Since  $\sum_{h=1}^da_hg_h\in{\mathcal{W}}_q[0,1]$
, by Theorem 4 it follows that
$\sum_{h=1}^da_hg_h\in{\mathcal{W}}_q[0,1]$
, by Theorem 4 it follows that
 \begin{equation*}n^{-1/2}\nu_n\bigg (\sum_{h=1}^da_hg_h\bigg ) \xrightarrow{\mathcal{D}} \sigma_{\eta} A_{\psi}\nu\bigg (\sum_{h=1}^da_hg_h\bigg )\quad\mbox{as $n\to\infty$.}\end{equation*}
\begin{equation*}n^{-1/2}\nu_n\bigg (\sum_{h=1}^da_hg_h\bigg ) \xrightarrow{\mathcal{D}} \sigma_{\eta} A_{\psi}\nu\bigg (\sum_{h=1}^da_hg_h\bigg )\quad\mbox{as $n\to\infty$.}\end{equation*}
Due to the linear isometry of  $\nu$
, the convergence
$\nu$
, the convergence
 \begin{equation*}n^{-1/2}a{\cdot}(\nu_n(g_1),\dots,\nu_n(g_d)) \xrightarrow{\mathcal{D}} \sigma_{\eta}A_{\psi}a{\cdot}(\nu (g_1),\dots,\nu (g_d))\quad\mbox{as $n\to\infty$}\end{equation*}
\begin{equation*}n^{-1/2}a{\cdot}(\nu_n(g_1),\dots,\nu_n(g_d)) \xrightarrow{\mathcal{D}} \sigma_{\eta}A_{\psi}a{\cdot}(\nu (g_1),\dots,\nu (g_d))\quad\mbox{as $n\to\infty$}\end{equation*}
holds. Since  $a\in{\mathbb R}^d$
is arbitrary, (15) holds by the Cramér–Wold device. □
$a\in{\mathbb R}^d$
is arbitrary, (15) holds by the Cramér–Wold device. □
4. Asymptotic equicontinuity
Let  $(\mathcal{F},\rho)$
be a pseudometric space. For each
$(\mathcal{F},\rho)$
be a pseudometric space. For each  $n\in{\mathbb N}_{+}=\{1,2,\dots\}$
, let
$n\in{\mathbb N}_{+}=\{1,2,\dots\}$
, let  $Z_{nk}$
,
$Z_{nk}$
,  $k\in{\mathbb Z}$
, be independent stochastic processes indexed by
$k\in{\mathbb Z}$
, be independent stochastic processes indexed by  $f\in \mathcal{F}$
and defined on the product probability space
$f\in \mathcal{F}$
and defined on the product probability space  $(\Omega_n,\mathcal{A}_n,{\mathrm{P}}_n)\,:\!=\bigotimes_{k\in{\mathbb Z}}(\Omega_{nk},\mathcal{A}_{nk},{\mathrm{P}}_{nk})$
so that
$(\Omega_n,\mathcal{A}_n,{\mathrm{P}}_n)\,:\!=\bigotimes_{k\in{\mathbb Z}}(\Omega_{nk},\mathcal{A}_{nk},{\mathrm{P}}_{nk})$
so that  $Z_{nk}(\,f,\omega)=Z_{nk}(\,f,\omega_k)$
for each
$Z_{nk}(\,f,\omega)=Z_{nk}(\,f,\omega_k)$
for each  $\omega=(\omega_k)_{k\in{\mathbb Z}}$
and
$\omega=(\omega_k)_{k\in{\mathbb Z}}$
and  $f\in\mathcal{F}$
. For each
$f\in\mathcal{F}$
. For each  $n\in{\mathbb N}_{+}$
consider a stochastic process defined as the series
$n\in{\mathbb N}_{+}$
consider a stochastic process defined as the series
 \begin{equation*}\sum_{k\in{\mathbb Z}}Z_{nk}(\,f)\,:\!=\lim_{m\to +\infty}\sum_{k=-m}^mZ_{nk}(\,f),\qquad f\in{\mathcal{F}},\end{equation*}
\begin{equation*}\sum_{k\in{\mathbb Z}}Z_{nk}(\,f)\,:\!=\lim_{m\to +\infty}\sum_{k=-m}^mZ_{nk}(\,f),\qquad f\in{\mathcal{F}},\end{equation*}
provided the convergence holds almost surely. We write  $(Z_{nk})\in\mathcal{M} (\Omega_n,\mathcal{A}_n, {\mathrm{P}}_n)$
if every one of the functions
$(Z_{nk})\in\mathcal{M} (\Omega_n,\mathcal{A}_n, {\mathrm{P}}_n)$
if every one of the functions
 \begin{equation}\omega\mapsto\sup\Big\{\Big |\sum_{k\in{\mathbb Z}}e_k[Z_{nk}(\,f,\omega)-Z_{nk}(g,\omega)]\Big | \colon f,g\in\mathcal{F},\,\,\rho (\,f,g)<\delta\Big\} \end{equation}
\begin{equation}\omega\mapsto\sup\Big\{\Big |\sum_{k\in{\mathbb Z}}e_k[Z_{nk}(\,f,\omega)-Z_{nk}(g,\omega)]\Big | \colon f,g\in\mathcal{F},\,\,\rho (\,f,g)<\delta\Big\} \end{equation}
and
 \begin{equation}\omega\mapsto\sup\Big\{\Big |\sum_{k\in{\mathbb Z}}e_k[Z_{nk}(\,f,\omega)-Z_{nk}(g,\omega)]^2\Big | \colon f,g\in\mathcal{F},\,\,\rho (\,f,g)<\delta\Big\} \end{equation}
\begin{equation}\omega\mapsto\sup\Big\{\Big |\sum_{k\in{\mathbb Z}}e_k[Z_{nk}(\,f,\omega)-Z_{nk}(g,\omega)]^2\Big | \colon f,g\in\mathcal{F},\,\,\rho (\,f,g)<\delta\Big\} \end{equation}
is measurable for the completion of the probability space  $(\Omega_n,\mathcal{A}_n,{\mathrm{P}}_n)$
, for every
$(\Omega_n,\mathcal{A}_n,{\mathrm{P}}_n)$
, for every  $\delta >0$
and every tuple
$\delta >0$
and every tuple  $(e_k)_{k\in{\mathbb Z}}$
with
$(e_k)_{k\in{\mathbb Z}}$
with  $e_k\in\{-1,0,1\}$
.
$e_k\in\{-1,0,1\}$
.
The following is Theorem 2.11.1 in [Reference Van der Vaart and Wellner15] adopted to the convergence of sums of linear processes.
Theorem 5. Let  $(\mathcal{F},\rho)$
be a totally bounded pseudometric space. Under the preceding notation, assume that
$(\mathcal{F},\rho)$
be a totally bounded pseudometric space. Under the preceding notation, assume that  $(Z_{nk})\in \mathcal{M}(\Omega_n,\mathcal{A}_n,{\mathrm{P}}_n)$
and there is a subsequence of positive integers
$(Z_{nk})\in \mathcal{M}(\Omega_n,\mathcal{A}_n,{\mathrm{P}}_n)$
and there is a subsequence of positive integers  $(m_n)_{n\in{\mathbb N}_{+}}$
such that
$(m_n)_{n\in{\mathbb N}_{+}}$
such that
 \begin{align}\lim_{n\to\infty}{\mathrm{P}}_n^*\bigg(\bigg\{\bigg\|\sum_{k<-m_n}\!\!\!Z_{nk}+\sum_{k>m_n}\!\!Z_{nk}\bigg\|_{{\mathcal{F}}}>\varepsilon\bigg\}\bigg) & = 0 \quad \mbox{for every $\varepsilon >0$,} \end{align}
\begin{align}\lim_{n\to\infty}{\mathrm{P}}_n^*\bigg(\bigg\{\bigg\|\sum_{k<-m_n}\!\!\!Z_{nk}+\sum_{k>m_n}\!\!Z_{nk}\bigg\|_{{\mathcal{F}}}>\varepsilon\bigg\}\bigg) & = 0 \quad \mbox{for every $\varepsilon >0$,} \end{align}
 \begin{align} \lim_{n\to\infty}\sum_{k=-m_n}^{m_n} \!\!\!{\mathrm{E}}^{\ast}\|Z_{nk}\|_{{{\mathcal{F}}}}^2 \textbf{1}_{\{\| Z_{nk}\|_{{{\mathcal{F}}}}>\epsilon\}} & = 0 \quad \mbox{for every $\epsilon >0$,} \end{align}
\begin{align} \lim_{n\to\infty}\sum_{k=-m_n}^{m_n} \!\!\!{\mathrm{E}}^{\ast}\|Z_{nk}\|_{{{\mathcal{F}}}}^2 \textbf{1}_{\{\| Z_{nk}\|_{{{\mathcal{F}}}}>\epsilon\}} & = 0 \quad \mbox{for every $\epsilon >0$,} \end{align}
 \begin{align} \lim_{n\to\infty}\sup_{\rho (\,f,g)
< \delta_n}\sum_{k=-m_n}^{m_n}\!\!\! {\mathrm{E}}[Z_{nk}(\,f)-Z_{nk}(g)]^2& =0\quad\mbox{for every $\delta_n\downarrow 0$,} \end{align}
\begin{align} \lim_{n\to\infty}\sup_{\rho (\,f,g)
< \delta_n}\sum_{k=-m_n}^{m_n}\!\!\! {\mathrm{E}}[Z_{nk}(\,f)-Z_{nk}(g)]^2& =0\quad\mbox{for every $\delta_n\downarrow 0$,} \end{align}
 \begin{align} \lim_{n\to\infty}\int_0^{\delta_n} \!\!\!\sqrt{\log N(x, \mathcal{F}, d_n)}\,\text{d} x & = 0 \quad \textrm{in}\ {\mathrm{P}}_n^*\ \textrm{for every} \ \delta_n\downarrow 0, \end{align}
\begin{align} \lim_{n\to\infty}\int_0^{\delta_n} \!\!\!\sqrt{\log N(x, \mathcal{F}, d_n)}\,\text{d} x & = 0 \quad \textrm{in}\ {\mathrm{P}}_n^*\ \textrm{for every} \ \delta_n\downarrow 0, \end{align}
where  $d_n$
is a random pseudometric on
$d_n$
is a random pseudometric on  ${\mathcal{F}}$
defined for each
${\mathcal{F}}$
defined for each  $n\in{\mathbb N}_{+}$
and
$n\in{\mathbb N}_{+}$
and  $f,g\in\mathcal{F}$
by
$f,g\in\mathcal{F}$
by
 \begin{equation} d_n(\,f, g)\,:\!=\bigg (\sum_{k=-m_n}^{m_n} [Z_{nk}(\,f)-Z_{nk}(g)]^2 \bigg )^{1/2}.\end{equation}
\begin{equation} d_n(\,f, g)\,:\!=\bigg (\sum_{k=-m_n}^{m_n} [Z_{nk}(\,f)-Z_{nk}(g)]^2 \bigg )^{1/2}.\end{equation}
Then,  $Z_n\,:\!=\sum_{k\in{\mathbb Z}}[Z_{nk}-{\mathrm{E}} (Z_{nk})]$
is asymptotically
$Z_n\,:\!=\sum_{k\in{\mathbb Z}}[Z_{nk}-{\mathrm{E}} (Z_{nk})]$
is asymptotically  $\rho$
-equicontinuous; that is, for every
$\rho$
-equicontinuous; that is, for every  $\varepsilon> 0$
,
$\varepsilon> 0$
,
 \begin{equation*}\lim_{\delta \downarrow 0}\limsup_n{\mathrm{P}}_n^*(\{\sup\{|Z_n(\,f) - Z_n(g)|\colon f,g\in{\mathcal{F}},\,\,\rho(\,f,g)<\delta\}> \varepsilon\})=0.\end{equation*}
\begin{equation*}\lim_{\delta \downarrow 0}\limsup_n{\mathrm{P}}_n^*(\{\sup\{|Z_n(\,f) - Z_n(g)|\colon f,g\in{\mathcal{F}},\,\,\rho(\,f,g)<\delta\}> \varepsilon\})=0.\end{equation*}
Proof. Let  $(m_n)$
be a subsequence of positive integers
$(m_n)$
be a subsequence of positive integers  $(m_n)_{n\in{\mathbb N}_{+}}$
such that (18) holds. Clearly,
$(m_n)_{n\in{\mathbb N}_{+}}$
such that (18) holds. Clearly,  $(Z_{nk})_{-m_n\leq k\leq m_n}\in\mathcal{M} (\Omega_n,\mathcal{A}_n, {\mathrm{P}}_n)$
. Using Theorem 2.11.1 in [Reference Van der Vaart and Wellner15] one can show that
$(Z_{nk})_{-m_n\leq k\leq m_n}\in\mathcal{M} (\Omega_n,\mathcal{A}_n, {\mathrm{P}}_n)$
. Using Theorem 2.11.1 in [Reference Van der Vaart and Wellner15] one can show that
 \begin{equation*}\lim_{\delta \downarrow 0}\limsup_n{\mathrm{P}}_n^*\bigg(\bigg\{\sup\bigg\{\bigg |\sum_{k=-m_n}^{m_n}[Z_{nk}(\,f) - Z_{nk}(g)]\bigg|\colon f,g\in{\mathcal{F}},\,\,\rho(\,f,g)<\delta\bigg\} > \varepsilon\bigg\}\bigg)=0\end{equation*}
\begin{equation*}\lim_{\delta \downarrow 0}\limsup_n{\mathrm{P}}_n^*\bigg(\bigg\{\sup\bigg\{\bigg |\sum_{k=-m_n}^{m_n}[Z_{nk}(\,f) - Z_{nk}(g)]\bigg|\colon f,g\in{\mathcal{F}},\,\,\rho(\,f,g)<\delta\bigg\} > \varepsilon\bigg\}\bigg)=0\end{equation*}
for each  $\varepsilon>0$
. For a given
$\varepsilon>0$
. For a given  $\epsilon >0$
and for each
$\epsilon >0$
and for each  $n\in{\mathbb N}_{+}$
we have
$n\in{\mathbb N}_{+}$
we have
 \begin{multline*} {{\mathrm{P}}_n^*(\{\sup\{|Z_n(\,f)- Z_n(g)|\colon f,g\in{\mathcal{F}},\,\,\rho(\,f,g)<\delta\} > \varepsilon\})} \\\leq{\mathrm{P}}_n^*\bigg(\bigg\{ \sup\bigg\{\bigg |\sum_{k=-m_n}^{m_n}[Z_{nk}(\,f) - Z_{nk}(g)]\bigg|\colon f,g\in{\mathcal{F}},\,\,\rho(\,f,g)<\delta\bigg\}>\frac{\varepsilon}{2}\bigg\}\bigg)\\\quad + {\mathrm{P}}_n^*\bigg(\bigg\{\bigg\|\sum_{k<-m_n}\!\!\!Z_{nk}+\sum_{k>m_n}\!\!Z_{nk}\bigg \|_{{\mathcal{F}}}>\frac{\varepsilon}{4}\bigg\}\bigg ).\end{multline*}
\begin{multline*} {{\mathrm{P}}_n^*(\{\sup\{|Z_n(\,f)- Z_n(g)|\colon f,g\in{\mathcal{F}},\,\,\rho(\,f,g)<\delta\} > \varepsilon\})} \\\leq{\mathrm{P}}_n^*\bigg(\bigg\{ \sup\bigg\{\bigg |\sum_{k=-m_n}^{m_n}[Z_{nk}(\,f) - Z_{nk}(g)]\bigg|\colon f,g\in{\mathcal{F}},\,\,\rho(\,f,g)<\delta\bigg\}>\frac{\varepsilon}{2}\bigg\}\bigg)\\\quad + {\mathrm{P}}_n^*\bigg(\bigg\{\bigg\|\sum_{k<-m_n}\!\!\!Z_{nk}+\sum_{k>m_n}\!\!Z_{nk}\bigg \|_{{\mathcal{F}}}>\frac{\varepsilon}{4}\bigg\}\bigg ).\end{multline*}
By hypothesis (18), the conclusion follows. □
Since the sequence  $X_1, X_2,\dots$
is a short-memory linear process, the sequence of real numbers
$X_1, X_2,\dots$
is a short-memory linear process, the sequence of real numbers  $(\psi_j)_{j\in{\mathbb N}}$
is square summable, and so each series in (1) converges almost surely by Lévy’s equivalence theorem (e.g. [Reference Dudley10, Theorem 9.7.1]). Letting
$(\psi_j)_{j\in{\mathbb N}}$
is square summable, and so each series in (1) converges almost surely by Lévy’s equivalence theorem (e.g. [Reference Dudley10, Theorem 9.7.1]). Letting  $\psi_k\,:\!=0$
for each
$\psi_k\,:\!=0$
for each  $k<0$
, we obtain the representation
$k<0$
, we obtain the representation
 \begin{equation}X_i=\sum_{k=-\infty}^i\psi_{i-k}\eta_k=\sum_{k\in{\mathbb Z}} \psi_{i-k}\eta_k,\qquad i\in{\mathbb Z}.\end{equation}
\begin{equation}X_i=\sum_{k=-\infty}^i\psi_{i-k}\eta_k=\sum_{k\in{\mathbb Z}} \psi_{i-k}\eta_k,\qquad i\in{\mathbb Z}.\end{equation}
Lemma 1. Suppose  $X_1,X_2,\dots$
is a linear process given by (23),
$X_1,X_2,\dots$
is a linear process given by (23),  $f\colon[0,1]\to{\mathbb R}$
, and
$f\colon[0,1]\to{\mathbb R}$
, and  $\nu_n(\,f)$
is the nth f-weighted partial sum given by (3). For each
$\nu_n(\,f)$
is the nth f-weighted partial sum given by (3). For each  $n\in{\mathbb N}_{+}$
and
$n\in{\mathbb N}_{+}$
and  $k\in{\mathbb Z}$
, let
$k\in{\mathbb Z}$
, let
 \begin{equation*}a_{nk}(\,f)=\sum_{i=1}^n\psi_{i-k}\,f\Big (\frac{i}{n}\Big ),\end{equation*}
\begin{equation*}a_{nk}(\,f)=\sum_{i=1}^n\psi_{i-k}\,f\Big (\frac{i}{n}\Big ),\end{equation*}
where  $\psi_{i-k}=0$
if
$\psi_{i-k}=0$
if  $i<k$
. Then, for each
$i<k$
. Then, for each  $n\in {\mathbb N}_{+}$
,
$n\in {\mathbb N}_{+}$
,
 \begin{equation}{\mathrm{E}}[\nu_n^2(\,f)]=\sigma_{\eta}^2\sum_{k\in{\mathbb Z}}a_{nk}^2(\,f)\quad\mbox{and}\quad\nu_n(\,f)=\sum_{k\in{\mathbb Z}}a_{nk}(\,f)\eta_k,\end{equation}
\begin{equation}{\mathrm{E}}[\nu_n^2(\,f)]=\sigma_{\eta}^2\sum_{k\in{\mathbb Z}}a_{nk}^2(\,f)\quad\mbox{and}\quad\nu_n(\,f)=\sum_{k\in{\mathbb Z}}a_{nk}(\,f)\eta_k,\end{equation}
where the random series converges almost surely.
Proof. Let  $n\in{\mathbb N}_{+}$
. For each
$n\in{\mathbb N}_{+}$
. For each  $i,j\in\{1,\dots,n\}$
, since the filter
$i,j\in\{1,\dots,n\}$
, since the filter  $(\psi_k)_{k\in{\mathbb N}}$
is square summable, the series representation
$(\psi_k)_{k\in{\mathbb N}}$
is square summable, the series representation
 \begin{equation*}{\mathrm{E}} (X_iX_j)=\sigma_{\eta}^2\sum_{k\in{\mathbb Z}}\psi_{i-k}\psi_{j-k}\end{equation*}
\begin{equation*}{\mathrm{E}} (X_iX_j)=\sigma_{\eta}^2\sum_{k\in{\mathbb Z}}\psi_{i-k}\psi_{j-k}\end{equation*}
converges absolutely. Thus, we have
 \begin{align*}{\mathrm{E}}[\nu_n^2(\,f)] & = \sum_{i,j=1}^n{\mathrm{E}} (X_iX_j)\,f\Big (\frac{i}{n}\Big )\,f\Big (\frac{j}{n}\Big )\\
& = \sigma_{\eta}^2\sum_{k\in{\mathbb Z}}\sum_{i,j=1}^n\psi_{i-k}\psi_{j-k}f\Big (\frac{i}{n}\Big )f\Big (\frac{j}{n}\Big )=\sigma_{\eta}^2\sum_{k\in{\mathbb Z}}a_{nk}^2(\,f) , \end{align*}
\begin{align*}{\mathrm{E}}[\nu_n^2(\,f)] & = \sum_{i,j=1}^n{\mathrm{E}} (X_iX_j)\,f\Big (\frac{i}{n}\Big )\,f\Big (\frac{j}{n}\Big )\\
& = \sigma_{\eta}^2\sum_{k\in{\mathbb Z}}\sum_{i,j=1}^n\psi_{i-k}\psi_{j-k}f\Big (\frac{i}{n}\Big )f\Big (\frac{j}{n}\Big )=\sigma_{\eta}^2\sum_{k\in{\mathbb Z}}a_{nk}^2(\,f) , \end{align*}
and the series on the right-hand side converges. This proves the first equality in (24). The second one follows next:
 \begin{align*}\nu_n(\,f) & = \sum_{i=1}^n\bigg [\sum_{k\in{\mathbb Z}}\psi_{i-k}\eta_k\bigg ]f\Big (\frac{i}{n}\Big )\\
& = \sum_{k\in{\mathbb Z}}\bigg [\sum_{i=1}^n\psi_{i-k}f\Big (\frac{i}{n}\Big ) \bigg ]\eta_k=\sum_{k\in{\mathbb Z}}a_{nk}(\,f)\eta_k.\end{align*}
\begin{align*}\nu_n(\,f) & = \sum_{i=1}^n\bigg [\sum_{k\in{\mathbb Z}}\psi_{i-k}\eta_k\bigg ]f\Big (\frac{i}{n}\Big )\\
& = \sum_{k\in{\mathbb Z}}\bigg [\sum_{i=1}^n\psi_{i-k}f\Big (\frac{i}{n}\Big ) \bigg ]\eta_k=\sum_{k\in{\mathbb Z}}a_{nk}(\,f)\eta_k.\end{align*}
The series on the right-hand side converges almost surely by Lévy’s equivalence theorem, since  $(a_{nk}(\,f))_{k\in{\mathbb Z}}$
is square summable. □
$(a_{nk}(\,f))_{k\in{\mathbb Z}}$
is square summable. □
5. Proof of Theorem 1
As shown at the end of this section, Theorem 1 is a simple corollary of the next theorem. Following [Reference Giné and Nickl12, p. 267], we say that a set of functions  ${\mathcal{F}}$
satisfies the pointwise countable approximation property provided there exists a countable subset
${\mathcal{F}}$
satisfies the pointwise countable approximation property provided there exists a countable subset  ${\mathcal{F}}_0\subset{\mathcal{F}}$
such that every f in
${\mathcal{F}}_0\subset{\mathcal{F}}$
such that every f in  ${\mathcal{F}}$
is a pointwise limit of functions in
${\mathcal{F}}$
is a pointwise limit of functions in  ${\mathcal{F}}_0$
. Given a probability measure Q on
${\mathcal{F}}_0$
. Given a probability measure Q on  $([0, 1], {\mathcal{B}}_{[0, 1]})$
, let
$([0, 1], {\mathcal{B}}_{[0, 1]})$
, let  $\rho_{2,Q}$
be a pseudometric on
$\rho_{2,Q}$
be a pseudometric on  ${\mathcal{F}}$
with values
${\mathcal{F}}$
with values
 \begin{equation*}\rho_{2,Q}(\,f,g)=\bigg(\int_{[0,1]}(\,f-g)^2\,\text{d} Q\bigg )^{1/2},\qquad f,g\in{\mathcal{F}} .\end{equation*}
\begin{equation*}\rho_{2,Q}(\,f,g)=\bigg(\int_{[0,1]}(\,f-g)^2\,\text{d} Q\bigg )^{1/2},\qquad f,g\in{\mathcal{F}} .\end{equation*}
Theorem 6. Let  $X_1, X_2,\dots$
be a short-memory linear process given by (1) and let
$X_1, X_2,\dots$
be a short-memory linear process given by (1) and let  $1 \le q < 2$
. Suppose that a set of functions
$1 \le q < 2$
. Suppose that a set of functions  ${\mathcal{F}} \subset {\mathcal{W}}_q[0, 1]$
is bounded, satisfies the pointwise countable approximation property, and
${\mathcal{F}} \subset {\mathcal{W}}_q[0, 1]$
is bounded, satisfies the pointwise countable approximation property, and
 \begin{equation}\int^1_0\sup_{Q\in{\mathcal{Q}}}\sqrt{\log N(x,{\mathcal{F}}, \rho_{2,Q})}\, \text{d} x
< \infty,\end{equation}
\begin{equation}\int^1_0\sup_{Q\in{\mathcal{Q}}}\sqrt{\log N(x,{\mathcal{F}}, \rho_{2,Q})}\, \text{d} x
< \infty,\end{equation}
where  ${\mathcal{Q}}$
is the set of all probability measures on
${\mathcal{Q}}$
is the set of all probability measures on  $([0, 1], {\mathcal{B}}_{[0, 1]})$
. There exists a version of the isonormal Gaussian process
$([0, 1], {\mathcal{B}}_{[0, 1]})$
. There exists a version of the isonormal Gaussian process  $\nu$
restricted to
$\nu$
restricted to  ${\mathcal{F}}$
with values in a separable subset of
${\mathcal{F}}$
with values in a separable subset of  $\ell^{\infty}({\mathcal{F}})$
, it is measurable for the Borel sets on its range, and (5) holds.
$\ell^{\infty}({\mathcal{F}})$
, it is measurable for the Borel sets on its range, and (5) holds.
Since  ${\mathcal{F}}\subset{\mathcal{W}}_q[0,1]$
with
${\mathcal{F}}\subset{\mathcal{W}}_q[0,1]$
with  $q\in [1,2)$
, the finite-dimensional distributions of
$q\in [1,2)$
, the finite-dimensional distributions of  $n^{-1/2}\nu_n$
converge in distribution to the corresponding finite-dimensional distributions of
$n^{-1/2}\nu_n$
converge in distribution to the corresponding finite-dimensional distributions of  $\nu$
by Proposition 1. By hypothesis (25),
$\nu$
by Proposition 1. By hypothesis (25),  ${\mathcal{F}}$
is totally bounded with respect to pseudometric
${\mathcal{F}}$
is totally bounded with respect to pseudometric  $\rho_2$
. Therefore, to prove Theorem 6 we have to show that
$\rho_2$
. Therefore, to prove Theorem 6 we have to show that  $n^{-1/2}\nu_n$
is asymptotically equicontinuous with respect to
$n^{-1/2}\nu_n$
is asymptotically equicontinuous with respect to  $\rho_2$
. To this end we use Theorem 5.
$\rho_2$
. To this end we use Theorem 5.
For each  $n\in{\mathbb N}_{+}$
,
$n\in{\mathbb N}_{+}$
,  $k\in{\mathbb Z}$
, and
$k\in{\mathbb Z}$
, and  $f\colon[0,1]\to{\mathbb R}$
, let
$f\colon[0,1]\to{\mathbb R}$
, let
 \begin{equation}u_{nk}(\,f)\,:\!=\frac{1}{\sqrt{n}\,}\sum_{i=1}^n\psi_{i-k}f\Big (\frac{i}{n}\Big )=\frac{a_{nk}(\,f)}{\sqrt{n}},\end{equation}
\begin{equation}u_{nk}(\,f)\,:\!=\frac{1}{\sqrt{n}\,}\sum_{i=1}^n\psi_{i-k}f\Big (\frac{i}{n}\Big )=\frac{a_{nk}(\,f)}{\sqrt{n}},\end{equation}
where  $\psi_{i-k}=0$
if
$\psi_{i-k}=0$
if  $i<k$
. By Lemma 1 we have the useful series representation
$i<k$
. By Lemma 1 we have the useful series representation
 \begin{equation}\frac{\nu_n(\,f)}{\sqrt{n}}=\sum_{k\in{\mathbb Z}}u_{nk}(\,f)\eta_k . \end{equation}
\begin{equation}\frac{\nu_n(\,f)}{\sqrt{n}}=\sum_{k\in{\mathbb Z}}u_{nk}(\,f)\eta_k . \end{equation}
We apply Theorem 5 to the sequence of processes
 \begin{equation}Z_{nk}=\{Z_{nk}(\,f)\,:\!=u_{nk}(\,f)\eta_k\colon f\in {\mathcal{F}}\},\qquad k\in{\mathbb Z},\,\,n\in{\mathbb N}_{+}.\end{equation}
\begin{equation}Z_{nk}=\{Z_{nk}(\,f)\,:\!=u_{nk}(\,f)\eta_k\colon f\in {\mathcal{F}}\},\qquad k\in{\mathbb Z},\,\,n\in{\mathbb N}_{+}.\end{equation}
5.1. Measurability
We can and do assume that  $(\eta_k)_{k\in{\mathbb Z}}$
is defined on the product probability space
$(\eta_k)_{k\in{\mathbb Z}}$
is defined on the product probability space
 \begin{equation*}(\Omega,{\mathcal{A}},{\mathrm{P}})=\bigotimes_{k\in{\mathbb Z}}(\Omega_k,{\mathcal{A}}_k,{\mathrm{P}}_k)\end{equation*}
\begin{equation*}(\Omega,{\mathcal{A}},{\mathrm{P}})=\bigotimes_{k\in{\mathbb Z}}(\Omega_k,{\mathcal{A}}_k,{\mathrm{P}}_k)\end{equation*}
with its joint distribution equal to the product of distributions of  $\eta_k$
. We will show that
$\eta_k$
. We will show that  $(Z_{nk})_{k\in{\mathbb Z}}\in\mathcal{M} (\Omega,{\mathcal{A}},{\mathrm{P}})$
using the fact that
$(Z_{nk})_{k\in{\mathbb Z}}\in\mathcal{M} (\Omega,{\mathcal{A}},{\mathrm{P}})$
using the fact that  ${\mathcal{F}}$
satisfies the pointwise countable approximation property.
${\mathcal{F}}$
satisfies the pointwise countable approximation property.
Given a tuple  $e=(e_k)_{k\in{\mathbb Z}}$
with
$e=(e_k)_{k\in{\mathbb Z}}$
with  $e_k\in\{-1,0,1\}$
, for each
$e_k\in\{-1,0,1\}$
, for each  $i\in\{1,\dots,n\}$
and
$i\in\{1,\dots,n\}$
and  $\omega\in\Omega$
, let
$\omega\in\Omega$
, let
 \begin{equation*}X_i^e(\omega)\,:\!=\sum_{k\in{\mathbb Z}}e_k\psi_{i-k}\eta_k(\omega).\end{equation*}
\begin{equation*}X_i^e(\omega)\,:\!=\sum_{k\in{\mathbb Z}}e_k\psi_{i-k}\eta_k(\omega).\end{equation*}
By (28) and (26), for each pair  $f,g\in{\mathcal{F}}$
,
$f,g\in{\mathcal{F}}$
,  $n\in{\mathbb N}_{+}$
, and
$n\in{\mathbb N}_{+}$
, and  $\omega\in\Omega$
, we have
$\omega\in\Omega$
, we have
 \begin{equation*}\sum_{k\in{\mathbb Z}}e_k[Z_{nk}(\,f,\omega)-Z_{nk}(g,\omega)]=\frac{1}{\sqrt{n}\,}\sum_{i=1}^nX_i^e(\omega)(\,f-g)\Big (\frac{i}{n}\Big )=\!:\,T_n^e(\,f,g,\omega).\end{equation*}
\begin{equation*}\sum_{k\in{\mathbb Z}}e_k[Z_{nk}(\,f,\omega)-Z_{nk}(g,\omega)]=\frac{1}{\sqrt{n}\,}\sum_{i=1}^nX_i^e(\omega)(\,f-g)\Big (\frac{i}{n}\Big )=\!:\,T_n^e(\,f,g,\omega).\end{equation*}
For each  $\delta >0$
, let
$\delta >0$
, let  ${\mathcal{F}}^{\delta}\,:\!=\{(\,f,g)\in{\mathcal{F}}\times{\mathcal{F}}\colon\rho_2(\,f,g)<\delta\}$
. Let
${\mathcal{F}}^{\delta}\,:\!=\{(\,f,g)\in{\mathcal{F}}\times{\mathcal{F}}\colon\rho_2(\,f,g)<\delta\}$
. Let  ${\mathcal{F}}_0\subset{\mathcal{F}}$
be a countable set such that every
${\mathcal{F}}_0\subset{\mathcal{F}}$
be a countable set such that every  $f\in{\mathcal{F}}$
is a pointwise limit of functions in
$f\in{\mathcal{F}}$
is a pointwise limit of functions in  ${\mathcal{F}}_0$
. Then (16) with
${\mathcal{F}}_0$
. Then (16) with  ${\mathcal{F}}_0$
in place of
${\mathcal{F}}_0$
in place of  ${\mathcal{F}}$
is measurable, and
${\mathcal{F}}$
is measurable, and
 \begin{equation*}{\mathrm{P}}^{\ast}\left(\left\{\sup\{|T_n^e(\,f,g,\cdot)|\colon(\,f,g)\in{\mathcal{F}}^{\delta}\}\not =\sup\{|T_n^e(\,f,g,\cdot)|\colon(\,f,g)\in{\mathcal{F}}_0^{\delta}\}\right\}\right)=0\end{equation*}
\begin{equation*}{\mathrm{P}}^{\ast}\left(\left\{\sup\{|T_n^e(\,f,g,\cdot)|\colon(\,f,g)\in{\mathcal{F}}^{\delta}\}\not =\sup\{|T_n^e(\,f,g,\cdot)|\colon(\,f,g)\in{\mathcal{F}}_0^{\delta}\}\right\}\right)=0\end{equation*}
for each  $\delta >0$
, each
$\delta >0$
, each  $e=(e_k)_{k\in{\mathbb Z}}$
, and each
$e=(e_k)_{k\in{\mathbb Z}}$
, and each  $n\in{\mathbb N}_{+}$
. Therefore the function (16) is measurable.
$n\in{\mathbb N}_{+}$
. Therefore the function (16) is measurable.
Measurability of (17) follows similarly once we show that the series
 \begin{equation*}\omega\mapsto\sum_{k\in{\mathbb Z}}[Z_{nk}(\,f,\omega)]^2=\sum_{k\in{\mathbb Z}}u_{nk}^2(\,f)\eta_k^2(\omega)\end{equation*}
\begin{equation*}\omega\mapsto\sum_{k\in{\mathbb Z}}[Z_{nk}(\,f,\omega)]^2=\sum_{k\in{\mathbb Z}}u_{nk}^2(\,f)\eta_k^2(\omega)\end{equation*}
converges for each  $f\in{\mathcal{F}}$
and
$f\in{\mathcal{F}}$
and  $n\in{\mathbb N}_{+}$
. But this is true due to Lemma 1 and to the fact that
$n\in{\mathbb N}_{+}$
. But this is true due to Lemma 1 and to the fact that
 \begin{equation*}{\mathrm{E}}\left [\sum_{k\in{\mathbb Z}}u_{nk}^2(\,f)\eta_k^2\right ] = \frac{\sigma_{\eta}^2}{n}\sum_{k\in{\mathbb Z}}a_{nk}^2(\,f)<\infty.\end{equation*}
\begin{equation*}{\mathrm{E}}\left [\sum_{k\in{\mathbb Z}}u_{nk}^2(\,f)\eta_k^2\right ] = \frac{\sigma_{\eta}^2}{n}\sum_{k\in{\mathbb Z}}a_{nk}^2(\,f)<\infty.\end{equation*}
Therefore,  $(Z_{nk})_{k\in{\mathbb Z}}\in\mathcal{M} (\Omega,{\mathcal{A}},{\mathrm{P}})$
.
$(Z_{nk})_{k\in{\mathbb Z}}\in\mathcal{M} (\Omega,{\mathcal{A}},{\mathrm{P}})$
.
5.2. Hypothesis (18)
By definition, for each  $n\in{\mathbb N}_{+}$
we have
$n\in{\mathbb N}_{+}$
we have  $u_{nk}=0$
for each
$u_{nk}=0$
for each  $k>n$
. Therefore,
$k>n$
. Therefore,  $\sum_{k>n}\|u_{nk}\|_{{\mathcal{F}}}=0$
for each
$\sum_{k>n}\|u_{nk}\|_{{\mathcal{F}}}=0$
for each  $n\in{\mathbb N}_{+}$
. We will choose a subsequence of positive integers
$n\in{\mathbb N}_{+}$
. We will choose a subsequence of positive integers  $(m_n)_{n\in{\mathbb N}_{+}}$
such that
$(m_n)_{n\in{\mathbb N}_{+}}$
such that
 \begin{equation}\lim_{n\to\infty}\sum_{-\infty<k
< -m_n}\|u_{nk}\|_{{\mathcal{F}}}=0.\end{equation}
\begin{equation}\lim_{n\to\infty}\sum_{-\infty<k
< -m_n}\|u_{nk}\|_{{\mathcal{F}}}=0.\end{equation}
Let  ${\mathbb F}_{{\mathcal{F}}}$
be the function on [0, 1] with values
${\mathbb F}_{{\mathcal{F}}}$
be the function on [0, 1] with values
 \begin{equation*}{\mathbb F}_{{\mathcal{F}}}(x)\,:\!= \sup\{|\,f(x)|\,:\,f \in {\mathcal{F}}\},\quad x\in [0, 1].\end{equation*}
\begin{equation*}{\mathbb F}_{{\mathcal{F}}}(x)\,:\!= \sup\{|\,f(x)|\,:\,f \in {\mathcal{F}}\},\quad x\in [0, 1].\end{equation*}
Since  ${\mathcal{F}}$
is bounded in
${\mathcal{F}}$
is bounded in  ${\mathcal{W}}_q[0,1]$
, then
${\mathcal{W}}_q[0,1]$
, then  $\|{\mathbb F}_{{\mathcal{F}}}\|_{\sup}<\infty$
. By (26), for each
$\|{\mathbb F}_{{\mathcal{F}}}\|_{\sup}<\infty$
. By (26), for each  $n\in{\mathbb N}_{+}$
,
$n\in{\mathbb N}_{+}$
,  $k\in{\mathbb Z}$
, and
$k\in{\mathbb Z}$
, and  $f\in{\mathcal{F}}$
we have
$f\in{\mathcal{F}}$
we have
 \begin{equation}|u_{nk}(\,f)|\leq\frac{1}{\sqrt{n}\,}\sum_{i=1}^n|\psi_{i-k}|\Big |f\Big (\frac{i}{n}\Big)\Big |\leq\frac{\|{\mathbb F}_{\mathcal{F}}\|_{\sup}}{\sqrt{n}}\sum_{i=1}^n|\psi_{i-k}|.\end{equation}
\begin{equation}|u_{nk}(\,f)|\leq\frac{1}{\sqrt{n}\,}\sum_{i=1}^n|\psi_{i-k}|\Big |f\Big (\frac{i}{n}\Big)\Big |\leq\frac{\|{\mathbb F}_{\mathcal{F}}\|_{\sup}}{\sqrt{n}}\sum_{i=1}^n|\psi_{i-k}|.\end{equation}
Let  $0\leq m<M$
. Then
$0\leq m<M$
. Then
 \begin{align*}\sum_{-M\leq k\leq -m}\!\!\!\|u_{nk}\|_{{\mathcal{F}}} & \leq \frac{\|{\mathbb F}_{{\mathcal{F}}}\|_{\sup}}{\sqrt{n}}\sum_{-M\leq k\leq -m}\sum_{i=1}^n|\psi_{i-k}|\\
& =\frac{\|{\mathbb F}_{{\mathcal{F}}}\|_{\sup}}{\sqrt{n}}\sum_{i=1}^n\sum_{-M\leq k\leq -m}\!\!\!|\psi_{i-k}|\\
&\leq \frac{\|{\mathbb F}_{{\mathcal{F}}}\|_{\sup}}{\sqrt{n}}\sum_{i=1}^n\sum_{j\geq i+m}\!\!|\psi_j|\leq\frac{\|{\mathbb F}_{{\mathcal{F}}}\|_{\sup}}{\sqrt{n}}n\sum_{j\geq 1+m}\!\!|\psi_j|.\end{align*}
\begin{align*}\sum_{-M\leq k\leq -m}\!\!\!\|u_{nk}\|_{{\mathcal{F}}} & \leq \frac{\|{\mathbb F}_{{\mathcal{F}}}\|_{\sup}}{\sqrt{n}}\sum_{-M\leq k\leq -m}\sum_{i=1}^n|\psi_{i-k}|\\
& =\frac{\|{\mathbb F}_{{\mathcal{F}}}\|_{\sup}}{\sqrt{n}}\sum_{i=1}^n\sum_{-M\leq k\leq -m}\!\!\!|\psi_{i-k}|\\
&\leq \frac{\|{\mathbb F}_{{\mathcal{F}}}\|_{\sup}}{\sqrt{n}}\sum_{i=1}^n\sum_{j\geq i+m}\!\!|\psi_j|\leq\frac{\|{\mathbb F}_{{\mathcal{F}}}\|_{\sup}}{\sqrt{n}}n\sum_{j\geq 1+m}\!\!|\psi_j|.\end{align*}
Now, one can choose a subsequence  $(m_n)_{n\in{\mathbb N}_{+}}$
such that
$(m_n)_{n\in{\mathbb N}_{+}}$
such that  $\sum_{j\geq 1+m_n}|\psi_j|\leq n^{-1}$
for each
$\sum_{j\geq 1+m_n}|\psi_j|\leq n^{-1}$
for each  $n\in{\mathbb N}_{+}$
. Hence,
$n\in{\mathbb N}_{+}$
. Hence,
 \begin{equation*}\sum_{-\infty<k\leq -m_n}\!\!\!\|u_{nk}\|_{{\mathcal{F}}}\leq \frac{\|{\mathbb F}_{{\mathcal{F}}}\|_{\sup}}{\sqrt{n}}\end{equation*}
\begin{equation*}\sum_{-\infty<k\leq -m_n}\!\!\!\|u_{nk}\|_{{\mathcal{F}}}\leq \frac{\|{\mathbb F}_{{\mathcal{F}}}\|_{\sup}}{\sqrt{n}}\end{equation*}
for each  $n\in{\mathbb N}_{+}$
, and so (29) holds. One can assume that
$n\in{\mathbb N}_{+}$
, and so (29) holds. One can assume that  $m_n>n$
for each
$m_n>n$
for each  $n\in{\mathbb N}_{+}$
, and so (18) holds with the subsequence
$n\in{\mathbb N}_{+}$
, and so (18) holds with the subsequence  $(m_n)$
.
$(m_n)$
.
5.3. Hypothesis (19)
To establish hypothesis (19) it is enough to prove that
 \begin{equation}U\,:\!=\sup_{n\ge 1}\bigg (\sum_{k\in{\mathbb Z}}\|u_{nk}\|_{{\mathcal{F}}}^2\bigg )<\infty.\end{equation}
\begin{equation}U\,:\!=\sup_{n\ge 1}\bigg (\sum_{k\in{\mathbb Z}}\|u_{nk}\|_{{\mathcal{F}}}^2\bigg )<\infty.\end{equation}
Indeed, suppose it is true. By (30) and assumption (2) we have
 \begin{equation*}\|u_{nk}\|_{{\mathcal{F}}}\leq\frac{\|{\mathbb F}_{\mathcal{F}}\|_{\sup}}{\sqrt{n}}\sum_{j\in{\mathbb N}}|\psi_{j}|=\!:\,\frac{c}{\sqrt{n}\,}.\end{equation*}
\begin{equation*}\|u_{nk}\|_{{\mathcal{F}}}\leq\frac{\|{\mathbb F}_{\mathcal{F}}\|_{\sup}}{\sqrt{n}}\sum_{j\in{\mathbb N}}|\psi_{j}|=\!:\,\frac{c}{\sqrt{n}\,}.\end{equation*}
By (28), for each  $m,n\in{\mathbb N}_{+}$
and
$m,n\in{\mathbb N}_{+}$
and  $\varepsilon>0$
we have
$\varepsilon>0$
we have
 \begin{align*}\sum_{k=-m}^m{\mathrm{E}}^{\ast}(\|Z_{nk}\|_{{{\mathcal{F}}}}^2) \textbf{1}_{\{\| Z_{nk}\|_{{{\mathcal{F}}}}>\varepsilon\}}& \leq \sum_{k=-m}^m\|u_{nk}\|_{{\mathcal{F}}}^2{\mathrm{E}}(\eta_k^2) \textbf{1}_{\{\| u_{nk}\|_{{{\mathcal{F}}}}|\eta_k|>\varepsilon\}}\\
&\leq U{\mathrm{E}}(\eta_0^2) \textbf{1}_{\{|\eta_0|>c^{-1}\varepsilon\sqrt{n}\}}.\end{align*}
\begin{align*}\sum_{k=-m}^m{\mathrm{E}}^{\ast}(\|Z_{nk}\|_{{{\mathcal{F}}}}^2) \textbf{1}_{\{\| Z_{nk}\|_{{{\mathcal{F}}}}>\varepsilon\}}& \leq \sum_{k=-m}^m\|u_{nk}\|_{{\mathcal{F}}}^2{\mathrm{E}}(\eta_k^2) \textbf{1}_{\{\| u_{nk}\|_{{{\mathcal{F}}}}|\eta_k|>\varepsilon\}}\\
&\leq U{\mathrm{E}}(\eta_0^2) \textbf{1}_{\{|\eta_0|>c^{-1}\varepsilon\sqrt{n}\}}.\end{align*}
This yields (19). We are left to prove (31).
By (30) it is enough to prove that
 \begin{equation}\sup_{n\ge 1}\frac{1}{n}\sum_{k\in {\mathbb Z}}\bigg(\sum_{i=1}^n |\psi_{i-k}|\bigg)^2<\infty.\end{equation}
\begin{equation}\sup_{n\ge 1}\frac{1}{n}\sum_{k\in {\mathbb Z}}\bigg(\sum_{i=1}^n |\psi_{i-k}|\bigg)^2<\infty.\end{equation}
For each  $i\in{\mathbb Z}$
let
$i\in{\mathbb Z}$
let
 \begin{equation*}\widetilde{X}_i=\sum_{k\in{\mathbb N}}|\psi_{k}|\eta_{i-k}.\end{equation*}
\begin{equation*}\widetilde{X}_i=\sum_{k\in{\mathbb N}}|\psi_{k}|\eta_{i-k}.\end{equation*}
Then
 \begin{align*}\sum_{k\in {\mathbb Z}}\bigg(\sum_{i=1}^n |\psi_{i-k}|\bigg)^2&={\mathrm{E}}\bigg(\sum_{k\in {\mathbb Z}}\bigg(\sum_{i=1}^n|\psi_{i-k}|\bigg)\eta_k\bigg)^2\\&={\mathrm{E}}\bigg(\sum_{i=1}^n\sum_{k\in {\mathbb Z}}|\psi_{i-k}|\eta_k\bigg)^2={\mathrm{E}}\bigg(\sum_{i=1}^n \widetilde{X}_i\bigg)^2.\end{align*}
\begin{align*}\sum_{k\in {\mathbb Z}}\bigg(\sum_{i=1}^n |\psi_{i-k}|\bigg)^2&={\mathrm{E}}\bigg(\sum_{k\in {\mathbb Z}}\bigg(\sum_{i=1}^n|\psi_{i-k}|\bigg)\eta_k\bigg)^2\\&={\mathrm{E}}\bigg(\sum_{i=1}^n\sum_{k\in {\mathbb Z}}|\psi_{i-k}|\eta_k\bigg)^2={\mathrm{E}}\bigg(\sum_{i=1}^n \widetilde{X}_i\bigg)^2.\end{align*}
Since the linear process  $(\widetilde{X}_i)$
is covariance stationary, we have
$(\widetilde{X}_i)$
is covariance stationary, we have
 \begin{align*}{\mathrm{E}}\bigg(\sum_{i=1}^n \widetilde{X}_i\bigg)^2&=\sum_{i,j=1}^n {\mathrm{E}}(\widetilde{X}_i\widetilde{X}_j)=n\sum_{j=-(n-1)}^{n-1}\Big (1-\frac{|\,j|}{n}\Big ){\mathrm{E}}(\widetilde{X}_0\widetilde{X}_j)\\
&\le n\sum_{j=0}^n |{\mathrm{E}}(\widetilde{X}_j\widetilde{X}_0)|=n\sigma^2\sum_{j=0}^n\sum_{k=0}^\infty|\psi_{k+j}|\cdot|\psi_k|\\&\le \sigma^2\bigg(\sum_{k=0}^\infty|\psi_k|\bigg)^2 n.\end{align*}
\begin{align*}{\mathrm{E}}\bigg(\sum_{i=1}^n \widetilde{X}_i\bigg)^2&=\sum_{i,j=1}^n {\mathrm{E}}(\widetilde{X}_i\widetilde{X}_j)=n\sum_{j=-(n-1)}^{n-1}\Big (1-\frac{|\,j|}{n}\Big ){\mathrm{E}}(\widetilde{X}_0\widetilde{X}_j)\\
&\le n\sum_{j=0}^n |{\mathrm{E}}(\widetilde{X}_j\widetilde{X}_0)|=n\sigma^2\sum_{j=0}^n\sum_{k=0}^\infty|\psi_{k+j}|\cdot|\psi_k|\\&\le \sigma^2\bigg(\sum_{k=0}^\infty|\psi_k|\bigg)^2 n.\end{align*}
5.4. Hypothesis (20)
To prove hypotheses (20) and (21) we use the following representation of the series (27). For a sequence  $(t_k)_{k\in{\mathbb Z}}$
of real numbers such that
$(t_k)_{k\in{\mathbb Z}}$
of real numbers such that  $\sum_{k\geq 0}\psi_kt_{i-k}$
converges for each
$\sum_{k\geq 0}\psi_kt_{i-k}$
converges for each  $i\in{\mathbb N}_{+}$
, the series
$i\in{\mathbb N}_{+}$
, the series  $\sum_{k\in{\mathbb Z}}\psi_{i-k}t_k$
also converges (here,
$\sum_{k\in{\mathbb Z}}\psi_{i-k}t_k$
also converges (here,  $\psi_k=0$
for
$\psi_k=0$
for  $k<0$
), and for each
$k<0$
), and for each  $n\in{\mathbb N}_{+}$
we have
$n\in{\mathbb N}_{+}$
we have
 \begin{align}\sum_{k\in{\mathbb Z}}\bigg [\sum_{i=1}^n\psi_{i-k}\,f\Big (\frac{i}{n}\Big )\bigg ]t_k&= \sum_{i=1}^n\bigg [\sum_{k\in{\mathbb Z}}\psi_{i-k}t_k\bigg ]\,f\Big (\frac{i}{n}\Big )\nonumber\\
&= \sum_{i=1}^n\bigg [\sum_{k=0}^{\infty}\psi_{k}t_{i-k}\bigg ]\,f\Big (\frac{i}{n}\Big )=\sum_{k=0}^{\infty}\psi_k\bigg [\sum_{i=1}^nt_{i-k}f\Big (\frac{i}{n}\Big )\bigg ].\end{align}
\begin{align}\sum_{k\in{\mathbb Z}}\bigg [\sum_{i=1}^n\psi_{i-k}\,f\Big (\frac{i}{n}\Big )\bigg ]t_k&= \sum_{i=1}^n\bigg [\sum_{k\in{\mathbb Z}}\psi_{i-k}t_k\bigg ]\,f\Big (\frac{i}{n}\Big )\nonumber\\
&= \sum_{i=1}^n\bigg [\sum_{k=0}^{\infty}\psi_{k}t_{i-k}\bigg ]\,f\Big (\frac{i}{n}\Big )=\sum_{k=0}^{\infty}\psi_k\bigg [\sum_{i=1}^nt_{i-k}f\Big (\frac{i}{n}\Big )\bigg ].\end{align}
Now, to establish hypothesis (20), recall [(26) and (28)] that
 \begin{equation*}{\mathrm{E}}[Z_{nk}(\,f)-Z_{nk}(g)]^2={\mathrm{E}}[Z_{nk}(\,f-g)]^2=\frac{\sigma^2}{n}\bigg(\sum_{i=1}^n\psi_{i-k}(\,f-g)\Big(\frac{i}{n}\Big )\bigg)^2 \end{equation*}
\begin{equation*}{\mathrm{E}}[Z_{nk}(\,f)-Z_{nk}(g)]^2={\mathrm{E}}[Z_{nk}(\,f-g)]^2=\frac{\sigma^2}{n}\bigg(\sum_{i=1}^n\psi_{i-k}(\,f-g)\Big(\frac{i}{n}\Big )\bigg)^2 \end{equation*}
for all  $f,g\in {\mathcal{F}}$
,
$f,g\in {\mathcal{F}}$
,  $n\in{\mathbb N}_{+}$
, and
$n\in{\mathbb N}_{+}$
, and  $k\in {\mathbb Z}$
. Let
$k\in {\mathbb Z}$
. Let  $(r_k)_{k\in{\mathbb Z}}$
be a Rademacher sequence,
$(r_k)_{k\in{\mathbb Z}}$
be a Rademacher sequence,  $h\in{\mathcal{F}}$
, and
$h\in{\mathcal{F}}$
, and  $n\in{\mathbb N}_{+}$
. By the Khinchin–Kahane inequality with the constant K, we have
$n\in{\mathbb N}_{+}$
. By the Khinchin–Kahane inequality with the constant K, we have
 \begin{align*}\sum_{k\in{\mathbb Z}}\bigg(\sum_{i=1}^n\psi_{i-k}h\Big(\frac{i}{n}\Big )\bigg)^2 & = {\mathrm{E}}\bigg (\sum_{k\in{\mathbb Z}}\bigg(\sum_{i=1}^n\psi_{i-k}h\Big(\frac{i}{n}\Big )\bigg )r_k\bigg )^2\\
&\leq K^2\bigg ({\mathrm{E}}\bigg |\sum_{k\in{\mathbb Z}}\bigg(\sum_{i=1}^n\psi_{i-k}h\Big(\frac{i}{n}\Big )\bigg )r_k\bigg |\bigg )^2.\end{align*}
\begin{align*}\sum_{k\in{\mathbb Z}}\bigg(\sum_{i=1}^n\psi_{i-k}h\Big(\frac{i}{n}\Big )\bigg)^2 & = {\mathrm{E}}\bigg (\sum_{k\in{\mathbb Z}}\bigg(\sum_{i=1}^n\psi_{i-k}h\Big(\frac{i}{n}\Big )\bigg )r_k\bigg )^2\\
&\leq K^2\bigg ({\mathrm{E}}\bigg |\sum_{k\in{\mathbb Z}}\bigg(\sum_{i=1}^n\psi_{i-k}h\Big(\frac{i}{n}\Big )\bigg )r_k\bigg |\bigg )^2.\end{align*}
The series on the right-hand side converges and has representation (33) with  $t_k=r_k(\omega)$
. Therefore,
$t_k=r_k(\omega)$
. Therefore,
 \begin{align*}{\mathrm{E}}\bigg |\sum_{k\in{\mathbb Z}}\bigg(\sum_{i=1}^n\psi_{i-k}h\Big(\frac{i}{n}\Big )\bigg )r_k\bigg | & = {\mathrm{E}}\bigg |\sum_{k=0}^{\infty}\psi_k\bigg (\sum_{i=1}^nr_{i-k}h\Big(\frac{i}{n}\Big )\bigg )\bigg | \\
&\leq \sum_{k=0}^{\infty}|\psi_k|{\mathrm{E}}\bigg |\sum_{i=1}^nr_{i-k}h\Big(\frac{i}{n}\Big )\bigg | \\&\leq \sum_{k=0}^{\infty}|\psi_k|\bigg (\sum_{i=1}^nh^2\Big(\frac{i}{n}\Big )\bigg )^{1/2}.\end{align*}
\begin{align*}{\mathrm{E}}\bigg |\sum_{k\in{\mathbb Z}}\bigg(\sum_{i=1}^n\psi_{i-k}h\Big(\frac{i}{n}\Big )\bigg )r_k\bigg | & = {\mathrm{E}}\bigg |\sum_{k=0}^{\infty}\psi_k\bigg (\sum_{i=1}^nr_{i-k}h\Big(\frac{i}{n}\Big )\bigg )\bigg | \\
&\leq \sum_{k=0}^{\infty}|\psi_k|{\mathrm{E}}\bigg |\sum_{i=1}^nr_{i-k}h\Big(\frac{i}{n}\Big )\bigg | \\&\leq \sum_{k=0}^{\infty}|\psi_k|\bigg (\sum_{i=1}^nh^2\Big(\frac{i}{n}\Big )\bigg )^{1/2}.\end{align*}
Using the Minkowski inequality for integrals and then the Minkowski inequality for sums, we obtain
 \begin{align}\lefteqn{\bigg(\frac{1}{n}\sum^n_{i=1}h^2\Big(\frac{i}{n} \Big )\bigg)^{1/2}=\bigg(\sum^n_{i=1}\int^{i/n}_{(i-1)/n}\Big[h\Big (\frac{i}{n}\Big )- h(t) + h(t) \Big]^2\text{d} t\bigg)^{1/2}}\nonumber\\&\le \bigg(\sum^n_{i=1}\bigg \{\bigg (\int^{i/n}_{(i-1)/n}\Big[h\Big (\frac{i}{n}\Big )- h(t)\Big ]^2\,\text{d} t\bigg )^{1/2}+\bigg (\int_{(i-1)/n}^{i/n}h^2(t)\,dt\bigg )^{1/2}\bigg \}^2\bigg )^{1/2}\nonumber\\&\le\bigg(\frac{1}{n}\sum^n_{i=1}\sup\bigg\{\Big [h\Big (\frac{i}{n}\Big )-h(t)\Big ]^2\,:\,t \in \Big [\frac{i-1}{n},\frac{i}{n} \Big ]\bigg\}\bigg)^{1/2}+\bigg(\int^1_0 h^2(t) \,\text{d} t\bigg)^{1/2}.\end{align}
\begin{align}\lefteqn{\bigg(\frac{1}{n}\sum^n_{i=1}h^2\Big(\frac{i}{n} \Big )\bigg)^{1/2}=\bigg(\sum^n_{i=1}\int^{i/n}_{(i-1)/n}\Big[h\Big (\frac{i}{n}\Big )- h(t) + h(t) \Big]^2\text{d} t\bigg)^{1/2}}\nonumber\\&\le \bigg(\sum^n_{i=1}\bigg \{\bigg (\int^{i/n}_{(i-1)/n}\Big[h\Big (\frac{i}{n}\Big )- h(t)\Big ]^2\,\text{d} t\bigg )^{1/2}+\bigg (\int_{(i-1)/n}^{i/n}h^2(t)\,dt\bigg )^{1/2}\bigg \}^2\bigg )^{1/2}\nonumber\\&\le\bigg(\frac{1}{n}\sum^n_{i=1}\sup\bigg\{\Big [h\Big (\frac{i}{n}\Big )-h(t)\Big ]^2\,:\,t \in \Big [\frac{i-1}{n},\frac{i}{n} \Big ]\bigg\}\bigg)^{1/2}+\bigg(\int^1_0 h^2(t) \,\text{d} t\bigg)^{1/2}.\end{align}
For each  $i\in\{1,\dots,n\}$
, we have the bound
$i\in\{1,\dots,n\}$
, we have the bound
 \begin{equation*}\sup\bigg\{\Big [h\Big (\frac{i}{n}\Big )-h(t)\Big ]^2\colon\, t \in \Big [\frac{i-1}{n},\frac{i}{n} \Big ]\bigg\}\le v_2\Big(h;\Big [\frac{i-1}{n},\frac{i}{n}\Big ]\Big ).\end{equation*}
\begin{equation*}\sup\bigg\{\Big [h\Big (\frac{i}{n}\Big )-h(t)\Big ]^2\colon\, t \in \Big [\frac{i-1}{n},\frac{i}{n} \Big ]\bigg\}\le v_2\Big(h;\Big [\frac{i-1}{n},\frac{i}{n}\Big ]\Big ).\end{equation*}
Summing the bounds over i, and continuing to bound the right-hand side of (34), it follows that
 \begin{equation*}\bigg(\frac{1}{n}\sum^n_{i=1}h^2\Big(\frac{i}{n} \Big )\bigg)^{1/2}\le n^{-1/2}||h||_{(2)} + \rho_2(h, 0).\end{equation*}
\begin{equation*}\bigg(\frac{1}{n}\sum^n_{i=1}h^2\Big(\frac{i}{n} \Big )\bigg)^{1/2}\le n^{-1/2}||h||_{(2)} + \rho_2(h, 0).\end{equation*}
Summing up the preceding inequalities and replacing h by  $f-g$
, it follows that
$f-g$
, it follows that
 \begin{equation*}\bigg (\sum_{k\in{\mathbb Z}}{\mathrm{E}}[Z_{nk}(\,f)-Z_{nk}(g)]^2\bigg)^{1/2}\le \sigma K\bigg(\sum_{k=0}^{\infty}|\psi_k|\bigg)\bigg [\frac{||f-g||_{(2)}}{\sqrt{n}}+\rho_2(\,f,g)\bigg].\end{equation*}
\begin{equation*}\bigg (\sum_{k\in{\mathbb Z}}{\mathrm{E}}[Z_{nk}(\,f)-Z_{nk}(g)]^2\bigg)^{1/2}\le \sigma K\bigg(\sum_{k=0}^{\infty}|\psi_k|\bigg)\bigg [\frac{||f-g||_{(2)}}{\sqrt{n}}+\rho_2(\,f,g)\bigg].\end{equation*}
Since  ${\mathcal{F}}\subset{\mathcal{W}}_q[0,1]\subset{\mathcal{W}}_2[0,1]$
, this proves hypothesis (20).
${\mathcal{F}}\subset{\mathcal{W}}_q[0,1]\subset{\mathcal{W}}_2[0,1]$
, this proves hypothesis (20).
5.5. Hypothesis (21)
To establish hypothesis (21), recall the random pseudometric  $d_n(\,f,g)$
defined by (22). Since the function
$d_n(\,f,g)$
defined by (22). Since the function  $f\mapsto Z_{nk}(\,f)$
defined by (28) is linear, for simplicity consider instead
$f\mapsto Z_{nk}(\,f)$
defined by (28) is linear, for simplicity consider instead  $p_n(\,f)\,:\!=d_n(\,f,0)$
for each
$p_n(\,f)\,:\!=d_n(\,f,0)$
for each  $f\in{\mathcal{F}}$
. Let
$f\in{\mathcal{F}}$
. Let  $n\in{\mathbb N}_{+}$
,
$n\in{\mathbb N}_{+}$
,  $f\in{\mathcal{F}}$
, and let
$f\in{\mathcal{F}}$
, and let  $(r_k)_{k\in{\mathbb Z}}$
be a Rademacher sequence. By the Khinchin–Kahane inequality with the constant K again, we have
$(r_k)_{k\in{\mathbb Z}}$
be a Rademacher sequence. By the Khinchin–Kahane inequality with the constant K again, we have
 \begin{equation}p_n^2(\,f)=\sum_{k\in{\mathbb Z}}u^2_{nk}(\,f)\eta_k^2={\mathrm{E}}_r\bigg(\sum_{k\in{\mathbb Z}}u_{nk}(\,f)\eta_kr_k\bigg)^2\le K^2\bigg({\mathrm{E}}_r\bigg|\sum_{k\in{\mathbb Z}}u_{nk}(\,f)\eta_kr_k\bigg|\bigg)^2.\end{equation}
\begin{equation}p_n^2(\,f)=\sum_{k\in{\mathbb Z}}u^2_{nk}(\,f)\eta_k^2={\mathrm{E}}_r\bigg(\sum_{k\in{\mathbb Z}}u_{nk}(\,f)\eta_kr_k\bigg)^2\le K^2\bigg({\mathrm{E}}_r\bigg|\sum_{k\in{\mathbb Z}}u_{nk}(\,f)\eta_kr_k\bigg|\bigg)^2.\end{equation}
Now recall the notation in (26) for  $u_{nk}(\,f)$
. The expression in (33) with
$u_{nk}(\,f)$
. The expression in (33) with  $t_k=\eta_k(\omega_1)r_k(\omega_2)$
for the series on the right-hand side gives the equality
$t_k=\eta_k(\omega_1)r_k(\omega_2)$
for the series on the right-hand side gives the equality
 \begin{equation*}\sum_{k\in{\mathbb Z}}u_{nk}(\,f)\eta_kr_k=\frac{1}{\sqrt{n}\,}\sum_{k=0}^{\infty}\psi_k\sum_{i=1}^nf\Big (\frac{i}{n}\Big )\eta_{i-k}r_{i-k}.\end{equation*}
\begin{equation*}\sum_{k\in{\mathbb Z}}u_{nk}(\,f)\eta_kr_k=\frac{1}{\sqrt{n}\,}\sum_{k=0}^{\infty}\psi_k\sum_{i=1}^nf\Big (\frac{i}{n}\Big )\eta_{i-k}r_{i-k}.\end{equation*}
Continuing (35) with this representation, we obtain
 \begin{align}\lefteqn{\frac{\sqrt{n}}{K}p_n(\,f)}\nonumber\\&\le {\mathrm{E}}_r\bigg|\sum_{k=0}^\infty \psi_k\sum_{i=1}^nf\Big (\frac{i}{n}\Big )\eta_{i-k}r_{i-k}\bigg|\le \sum_{k=0}^\infty |\psi_k| {\mathrm{E}}_r\bigg|\sum_{i=1}^n f\Big (\frac{i}{n}\Big )\eta_{i-k}r_{i-k}\bigg|\end{align}
\begin{align}\lefteqn{\frac{\sqrt{n}}{K}p_n(\,f)}\nonumber\\&\le {\mathrm{E}}_r\bigg|\sum_{k=0}^\infty \psi_k\sum_{i=1}^nf\Big (\frac{i}{n}\Big )\eta_{i-k}r_{i-k}\bigg|\le \sum_{k=0}^\infty |\psi_k| {\mathrm{E}}_r\bigg|\sum_{i=1}^n f\Big (\frac{i}{n}\Big )\eta_{i-k}r_{i-k}\bigg|\end{align}
 \begin{align}&\le\sum_{k=0}^{\infty}|\psi_k|\bigg(\sum_{i=1}^nf^2\Big (\frac{i}{n}\Big )\eta_{i-k}^2\bigg)^{1/2}\leq \bigg (\sum_{k=0}^{\infty}|\psi_k|\bigg )^{1/2}\bigg (\sum_{k=0}^{\infty}|\psi_k|\sum_{i=1}^nf^2\Big (\frac{i}{n}\Big )\eta_{i-k}^2\bigg)^{1/2}.\nonumber\end{align}
\begin{align}&\le\sum_{k=0}^{\infty}|\psi_k|\bigg(\sum_{i=1}^nf^2\Big (\frac{i}{n}\Big )\eta_{i-k}^2\bigg)^{1/2}\leq \bigg (\sum_{k=0}^{\infty}|\psi_k|\bigg )^{1/2}\bigg (\sum_{k=0}^{\infty}|\psi_k|\sum_{i=1}^nf^2\Big (\frac{i}{n}\Big )\eta_{i-k}^2\bigg)^{1/2}.\nonumber\end{align}
The last inequality is Hölder’s inequality. On  $([0,1],{\mathcal{B}})$
, define random measures
$([0,1],{\mathcal{B}})$
, define random measures  $\mu_n$
by
$\mu_n$
by
 \begin{equation*}\mu_n(B)\,:\!=\sum_{k=0}^{\infty}|\psi_k|\frac{1}{n}\sum_{i=1}^n\eta_{i-k}^2\delta_{i/n}(B),\qquad B\in{\mathcal{B}},\,\,n\in{\mathbb N}_{+}.\end{equation*}
\begin{equation*}\mu_n(B)\,:\!=\sum_{k=0}^{\infty}|\psi_k|\frac{1}{n}\sum_{i=1}^n\eta_{i-k}^2\delta_{i/n}(B),\qquad B\in{\mathcal{B}},\,\,n\in{\mathbb N}_{+}.\end{equation*}
Since  $\sigma_{\eta}\not =0$
, given
$\sigma_{\eta}\not =0$
, given  $\epsilon >0$
one can find
$\epsilon >0$
one can find  $\Omega_{\epsilon}\subset\Omega$
and
$\Omega_{\epsilon}\subset\Omega$
and  $n_{\epsilon}\in{\mathbb N}$
such that
$n_{\epsilon}\in{\mathbb N}$
such that  ${\mathrm{P}} (\Omega_{\epsilon})<\epsilon$
and
${\mathrm{P}} (\Omega_{\epsilon})<\epsilon$
and  $\mu_n([0,1])>0$
for each
$\mu_n([0,1])>0$
for each  $\omega\not\in\Omega_{\epsilon}$
and
$\omega\not\in\Omega_{\epsilon}$
and  $n\geq n_{\epsilon}$
. Thus, without loss of generality we assume that
$n\geq n_{\epsilon}$
. Thus, without loss of generality we assume that  $\mu_n([0,1])>0$
almost surely. Then
$\mu_n([0,1])>0$
almost surely. Then  $Q_n\,:\!=\mu_n/\mu_n([0,1])$
,
$Q_n\,:\!=\mu_n/\mu_n([0,1])$
,  $n\in{\mathbb N}_{+}$
, are random probability measures on
$n\in{\mathbb N}_{+}$
, are random probability measures on  $([0,1],{\mathcal{B}})$
. For each
$([0,1],{\mathcal{B}})$
. For each  $n\in{\mathbb N}_{+}$
let
$n\in{\mathbb N}_{+}$
let
 \begin{equation*}\xi_n\,:\!=K\bigg (\sum_{k=0}^{\infty}|\psi_k|\bigg )^{1/2}\sqrt{\mu_n([0,1])}=K\bigg (\sum_{k=0}^{\infty}|\psi_k|\bigg)^{1/2}\bigg (\sum_{k=0}^{\infty}|\psi_k|\frac{1}{n}\sum_{i=1}^n\eta_{i-k}^2\bigg )^{1/2}.\end{equation*}
\begin{equation*}\xi_n\,:\!=K\bigg (\sum_{k=0}^{\infty}|\psi_k|\bigg )^{1/2}\sqrt{\mu_n([0,1])}=K\bigg (\sum_{k=0}^{\infty}|\psi_k|\bigg)^{1/2}\bigg (\sum_{k=0}^{\infty}|\psi_k|\frac{1}{n}\sum_{i=1}^n\eta_{i-k}^2\bigg )^{1/2}.\end{equation*}
By (36), it then follows that
 \begin{equation*}d_n(\,f,g)=p_n(\,f-g)\leq\xi_n\rho_{2,Q_n}(\,f,g).\end{equation*}
\begin{equation*}d_n(\,f,g)=p_n(\,f-g)\leq\xi_n\rho_{2,Q_n}(\,f,g).\end{equation*}
By hypothesis (25), the set  ${\mathcal{F}}$
is totally bounded with respect to pseudometric
${\mathcal{F}}$
is totally bounded with respect to pseudometric  $\rho_{2,Q_n}$
. Given
$\rho_{2,Q_n}$
. Given  $x>0$
, since each
$x>0$
, since each  $\rho_{2,Q_n}$
-ball of radius
$\rho_{2,Q_n}$
-ball of radius  $x/\xi_n$
is contained in a
$x/\xi_n$
is contained in a  $d_n$
-ball of radius x, we have
$d_n$
-ball of radius x, we have
 \begin{equation*}N(x,{\mathcal{F}},d_n)\leq N(x/\xi_n,{\mathcal{F}},\rho_{2,Q_n}).\end{equation*}
\begin{equation*}N(x,{\mathcal{F}},d_n)\leq N(x/\xi_n,{\mathcal{F}},\rho_{2,Q_n}).\end{equation*}
Then, by a change of variables it follows that, for each  $\delta > 0$
,
$\delta > 0$
,
 \begin{equation*}I(\delta)\,:\!=\int^\delta_0\sqrt{\log N(x, {\mathcal{F}}, d_n)}\, \text{d} x \leq \xi_n\int^{\delta/\xi_n}_0\sqrt{\log N(x, {\mathcal{F}}, \rho_{2,Q_n})}\, \text{d} x.\end{equation*}
\begin{equation*}I(\delta)\,:\!=\int^\delta_0\sqrt{\log N(x, {\mathcal{F}}, d_n)}\, \text{d} x \leq \xi_n\int^{\delta/\xi_n}_0\sqrt{\log N(x, {\mathcal{F}}, \rho_{2,Q_n})}\, \text{d} x.\end{equation*}
For each  $\delta >0$
, let
$\delta >0$
, let
 \begin{equation*}J(\delta)\,:\!=\int^\delta_0\sup_{Q\in{\mathcal{Q}}}\sqrt{\log N(x, {\mathcal{F}}, \rho_{2,Q})}\, \text{d} x.\end{equation*}
\begin{equation*}J(\delta)\,:\!=\int^\delta_0\sup_{Q\in{\mathcal{Q}}}\sqrt{\log N(x, {\mathcal{F}}, \rho_{2,Q})}\, \text{d} x.\end{equation*}
Let  $\varepsilon>0$
and let
$\varepsilon>0$
and let  $\delta_n \downarrow 0$
. For each
$\delta_n \downarrow 0$
. For each  $0 < m <M < \infty$
and
$0 < m <M < \infty$
and  $n \in {\mathbb N}_{+}$
, we have
$n \in {\mathbb N}_{+}$
, we have
 \begin{equation}{\mathrm{P}}(I(\delta_n) > \varepsilon) \le{\mathrm{P}}(MJ(\delta_n/m) > \varepsilon)+{\mathrm{P}}(\xi_n>M)+{\mathrm{P}}(\xi_n <m).\end{equation}
\begin{equation}{\mathrm{P}}(I(\delta_n) > \varepsilon) \le{\mathrm{P}}(MJ(\delta_n/m) > \varepsilon)+{\mathrm{P}}(\xi_n>M)+{\mathrm{P}}(\xi_n <m).\end{equation}
Taking  $m>0$
small enough, the rightmost probability tends to zero with
$m>0$
small enough, the rightmost probability tends to zero with  $n\to\infty$
since
$n\to\infty$
since  $\liminf_{n\to\infty}\xi_n \geq c\sigma_{\eta}>0$
almost surely. For the next-to-rightmost probability we have
$\liminf_{n\to\infty}\xi_n \geq c\sigma_{\eta}>0$
almost surely. For the next-to-rightmost probability we have
 \begin{equation*}\sup_{n\ge 1}{\mathrm{P}}(\xi_n>M) \le M^{-2}\sup_{n\ge 1} {\mathrm{E}}(\xi_n^2)=\frac{K^2\sigma_{\eta}^2}{M^2}\bigg (\sum_{k=0}^{\infty}|\psi_k|\bigg )^2\to 0\end{equation*}
\begin{equation*}\sup_{n\ge 1}{\mathrm{P}}(\xi_n>M) \le M^{-2}\sup_{n\ge 1} {\mathrm{E}}(\xi_n^2)=\frac{K^2\sigma_{\eta}^2}{M^2}\bigg (\sum_{k=0}^{\infty}|\psi_k|\bigg )^2\to 0\end{equation*}
as  $M \to\infty$
. Since
$M \to\infty$
. Since  $J(\delta_n/m) \to 0$
as
$J(\delta_n/m) \to 0$
as  $n \to\infty$
by condition (25), the first probability on the right-hand side of (37) is zero for sufficiently large n. It then follows that hypothesis (21) holds.
$n \to\infty$
by condition (25), the first probability on the right-hand side of (37) is zero for sufficiently large n. It then follows that hypothesis (21) holds.
Summing up, by Theorem 5,  $n^{-1/2}\nu_n$
is asymptotically equicontinuous with respect to
$n^{-1/2}\nu_n$
is asymptotically equicontinuous with respect to  $\rho_2$
. By Proposition 1, the finite-dimensional distributions of
$\rho_2$
. By Proposition 1, the finite-dimensional distributions of  $n^{-1/2}\nu_n$
converge to finite-dimensional distributions of
$n^{-1/2}\nu_n$
converge to finite-dimensional distributions of  $\sigma_{\eta}A_{\psi}\nu$
. Thus, by Theorem 3.7.23 in [Reference Giné and Nickl12], the conclusion of Theorem 6 is proved.
$\sigma_{\eta}A_{\psi}\nu$
. Thus, by Theorem 3.7.23 in [Reference Giné and Nickl12], the conclusion of Theorem 6 is proved.
5.6. Proof of Theorem 1
The set  ${\mathcal{F}}_{q,M}$
satisfies the pointwise countable approximation property, as proved in Example 3.7.13 of [Reference Giné and Nickl12, p. 235]. Clearly, the pointwise countable approximation property holds for a subset
${\mathcal{F}}_{q,M}$
satisfies the pointwise countable approximation property, as proved in Example 3.7.13 of [Reference Giné and Nickl12, p. 235]. Clearly, the pointwise countable approximation property holds for a subset  ${\mathcal{F}}$
of
${\mathcal{F}}$
of  ${\mathcal{F}}_{q,M}$
. Condition (25) holds by Theorem 5 in [Reference Norvaiša and Račkauskas14]. Therefore, all the hypotheses of Theorem 6 hold true, and its conclusion also holds true. The proof of Theorem 1 is complete.
${\mathcal{F}}_{q,M}$
. Condition (25) holds by Theorem 5 in [Reference Norvaiša and Račkauskas14]. Therefore, all the hypotheses of Theorem 6 hold true, and its conclusion also holds true. The proof of Theorem 1 is complete.
6. Proofs of Theorems 3 and 2
We begin with the proof of Theorem 3. Let  $G\,:\!=T(L)$
,
$G\,:\!=T(L)$
,  $(t_i)_{i=0}^m$
be a partition of [a, b], and let
$(t_i)_{i=0}^m$
be a partition of [a, b], and let  $b=(b_1,\dots,b_m)\in{\mathbb R}^m$
. Then
$b=(b_1,\dots,b_m)\in{\mathbb R}^m$
. Then  $f_b\,:\!=\sum_{i=1}^mb_i\textbf{1}_{(t_{i-1},t_i]}\in{\mathcal{W}}_q[a,b]$
and
$f_b\,:\!=\sum_{i=1}^mb_i\textbf{1}_{(t_{i-1},t_i]}\in{\mathcal{W}}_q[a,b]$
and
 \begin{equation*}\bigg |\sum_{i=1}^mb_i[G(t_i)-G(t_{i-1})]\bigg |=\bigg |L\bigg (\sum_{i=1}^mb_i\textbf{1}_{(t_{i-1},t_i]}\bigg )\bigg |\leq \|L\|_{{\mathcal{F}}_q}\|\,f_b\|_{[q]}.\end{equation*}
\begin{equation*}\bigg |\sum_{i=1}^mb_i[G(t_i)-G(t_{i-1})]\bigg |=\bigg |L\bigg (\sum_{i=1}^mb_i\textbf{1}_{(t_{i-1},t_i]}\bigg )\bigg |\leq \|L\|_{{\mathcal{F}}_q}\|\,f_b\|_{[q]}.\end{equation*}
Let  $\|b\|_q\,:\!=\big(\sum_{i=1}^m|b_i|^q\big)^{1/q}$
. Then
$\|b\|_q\,:\!=\big(\sum_{i=1}^m|b_i|^q\big)^{1/q}$
. Then  $\|\,f_b\|_{\sup}=\max_i|b_i|\leq\|b\|_q$
and
$\|\,f_b\|_{\sup}=\max_i|b_i|\leq\|b\|_q$
and  $\|\,f_b\|_{(q)}\leq 2\|b\|_q$
due to the Minkowski inequality. Using the extremal Hölder equality we obtain the bound
$\|\,f_b\|_{(q)}\leq 2\|b\|_q$
due to the Minkowski inequality. Using the extremal Hölder equality we obtain the bound
 \begin{equation*}\bigg (\sum_{i=1}^m|G(t_i)-G(t_{i-1})|^p\bigg )^{1/p}=\sup\bigg\{\bigg |\sum_{i=1}^mb_i[G(t_i)-G(t_{i-1})]\bigg |\colon\|b\|_q\leq 1\bigg \}\leq 3\|L\|_{{\mathcal{F}}_q}.\end{equation*}
\begin{equation*}\bigg (\sum_{i=1}^m|G(t_i)-G(t_{i-1})|^p\bigg )^{1/p}=\sup\bigg\{\bigg |\sum_{i=1}^mb_i[G(t_i)-G(t_{i-1})]\bigg |\colon\|b\|_q\leq 1\bigg \}\leq 3\|L\|_{{\mathcal{F}}_q}.\end{equation*}
Since the partition  $(t_i)_{i=1}^m$
of [a, b] is arbitrary, it follows that
$(t_i)_{i=1}^m$
of [a, b] is arbitrary, it follows that  $\|G\|_{(q)}\leq 3\|L\|_{{\mathcal{F}}_q}$
. Since
$\|G\|_{(q)}\leq 3\|L\|_{{\mathcal{F}}_q}$
. Since  $\|\textbf{1}_{[a,(\cdot)]}\|_{[q]}=2$
, we have the bound
$\|\textbf{1}_{[a,(\cdot)]}\|_{[q]}=2$
, we have the bound  $\|G\|_{\sup}\leq2\|L\|_{{\mathcal{F}}_q}$
and so (8) holds. The proof of Theorem 3 is complete.
$\|G\|_{\sup}\leq2\|L\|_{{\mathcal{F}}_q}$
and so (8) holds. The proof of Theorem 3 is complete.
To prove Theorem 2, for  $p\in (2,\infty)$
given as the hypothesis, let
$p\in (2,\infty)$
given as the hypothesis, let  $q\,:\!=(p-1)/p$
. Then
$q\,:\!=(p-1)/p$
. Then  $p^{-1}+q^{-1}=1$
and
$p^{-1}+q^{-1}=1$
and  $1<q<2$
. By Theorem 1, the isonormal Gaussian process
$1<q<2$
. By Theorem 1, the isonormal Gaussian process  $\nu$
restricted to
$\nu$
restricted to  ${\mathcal{F}}_q=\{\,f\in{\mathcal{W}}_q[0,1]\colon\|\,f\|_{[q]}\leq 1\}$
takes values in a separable subset of
${\mathcal{F}}_q=\{\,f\in{\mathcal{W}}_q[0,1]\colon\|\,f\|_{[q]}\leq 1\}$
takes values in a separable subset of  $\ell^{\infty}({\mathcal{F}}_q)$
, it is measurable for Borel sets on its range, and
$\ell^{\infty}({\mathcal{F}}_q)$
, it is measurable for Borel sets on its range, and
 \begin{equation}(\sigma_{\eta}|A_{\psi}|\sqrt{n})^{-1}\nu_n {\stackrel{\mathcal{D}} \Longrightarrow} \nu \qquad\mbox{in $\ell^\infty({\mathcal{F}}_q)$.}\end{equation}
\begin{equation}(\sigma_{\eta}|A_{\psi}|\sqrt{n})^{-1}\nu_n {\stackrel{\mathcal{D}} \Longrightarrow} \nu \qquad\mbox{in $\ell^\infty({\mathcal{F}}_q)$.}\end{equation}
By the Skorokhod–Dudley–Wichura representation theorem (Theorem 3.5.1 in [Reference Dudley9]), there exist a probability space  $(S,{\mathcal{S}},Q)$
and perfect measurable functions
$(S,{\mathcal{S}},Q)$
and perfect measurable functions  $g_n\colon\,S\to\Omega$
such that
$g_n\colon\,S\to\Omega$
such that  $Q{\circ}g_n^{-1}={\mathrm{P}}$
on
$Q{\circ}g_n^{-1}={\mathrm{P}}$
on  ${\mathcal{A}}$
for each
${\mathcal{A}}$
for each  $n\in{\mathbb N}$
and
$n\in{\mathbb N}$
and
 \begin{equation}\lim_{n\to\infty}\big\|(\sigma_{\eta}|A_{\psi}|\sqrt{n})^{-1}\nu_n{\circ}g_n-\nu{\circ}g_0\big\|_{{\mathcal{F}}_q}^{\ast}=0\qquad\mbox{almost surely.}\end{equation}
\begin{equation}\lim_{n\to\infty}\big\|(\sigma_{\eta}|A_{\psi}|\sqrt{n})^{-1}\nu_n{\circ}g_n-\nu{\circ}g_0\big\|_{{\mathcal{F}}_q}^{\ast}=0\qquad\mbox{almost surely.}\end{equation}
Here, as for any real-valued function  $\phi$
on a probability space,
$\phi$
on a probability space,  $\phi^{\ast}$
is its measurable cover, which always exists (e.g. Theorem 3.2.1 in [Reference Dudley9]). For each
$\phi^{\ast}$
is its measurable cover, which always exists (e.g. Theorem 3.2.1 in [Reference Dudley9]). For each  $n\in{\mathbb N}_{+}$
and
$n\in{\mathbb N}_{+}$
and  $s\in S$
, let
$s\in S$
, let
 \begin{equation*}\mu_n(\,f,s)\,:\!=\frac{\nu_n(\,f,g_n(s))}{\sigma_{\eta}|A_{\psi}|\sqrt{n}}, \,\,f\in{\mathcal{F}}_q,\quad\mbox{and}\quad W_n(t,s)\,:\!=\mu_n(\textbf{1}_{[0,t]},s),\,\,t\in [0,1].\end{equation*}
\begin{equation*}\mu_n(\,f,s)\,:\!=\frac{\nu_n(\,f,g_n(s))}{\sigma_{\eta}|A_{\psi}|\sqrt{n}}, \,\,f\in{\mathcal{F}}_q,\quad\mbox{and}\quad W_n(t,s)\,:\!=\mu_n(\textbf{1}_{[0,t]},s),\,\,t\in [0,1].\end{equation*}
Also, for each  $n\in{\mathbb N}_{+}$
,
$n\in{\mathbb N}_{+}$
,  $s\in S$
, and
$s\in S$
, and  $f\in{\mathcal{F}}_q$
,
$f\in{\mathcal{F}}_q$
,
 \begin{equation*}|\mu_n(\,f,s)|\leq\frac{\sum_{i=1}^n|X_i(g_n(s))|}{\sigma_{\eta}|A_{\psi}|\sqrt{n}}\|\,f\|_{\sup} .\end{equation*}
\begin{equation*}|\mu_n(\,f,s)|\leq\frac{\sum_{i=1}^n|X_i(g_n(s))|}{\sigma_{\eta}|A_{\psi}|\sqrt{n}}\|\,f\|_{\sup} .\end{equation*}
Hence, for each  $n\in{\mathbb N}_{+}$
and
$n\in{\mathbb N}_{+}$
and  $s\in S$
,
$s\in S$
,  $\mu_n(\cdot,s)$
is a linear bounded functional on
$\mu_n(\cdot,s)$
is a linear bounded functional on  ${\mathcal{W}}_q[0,1]$
. Given
${\mathcal{W}}_q[0,1]$
. Given  $n,m\in{\mathbb N}_{+}$
, let
$n,m\in{\mathbb N}_{+}$
, let  $L\,:\!=\mu_n-\mu_m$
. Then
$L\,:\!=\mu_n-\mu_m$
. Then  $T(L)(t)=L(\textbf{1}_{[0,t]})=W_n(t)-W_m(t)$
for each
$T(L)(t)=L(\textbf{1}_{[0,t]})=W_n(t)-W_m(t)$
for each  $t\in [0,1]$
, and
$t\in [0,1]$
, and
 \begin{equation*}\|W_n-W_m\|_{[p]}\leq 5\|\mu_n-\mu_m\|_{{\mathcal{F}}_q}\end{equation*}
\begin{equation*}\|W_n-W_m\|_{[p]}\leq 5\|\mu_n-\mu_m\|_{{\mathcal{F}}_q}\end{equation*}
for each  $s\in S$
, by Theorem 3. For any functions
$s\in S$
, by Theorem 3. For any functions  $\phi,\xi\colon S\to{\mathbb R}$
, we have
$\phi,\xi\colon S\to{\mathbb R}$
, we have  $(\phi+\xi)^{\ast}\leq\phi^{\ast}+\xi^{\ast}$
almost surely (e.g. Lemma 3.2.2 in [Reference Dudley9]). By (39), it then follows that
$(\phi+\xi)^{\ast}\leq\phi^{\ast}+\xi^{\ast}$
almost surely (e.g. Lemma 3.2.2 in [Reference Dudley9]). By (39), it then follows that
 \begin{equation*}\lim_{m, n\to\infty}\|\mu_n-\mu_m\|_{{\mathcal{F}}_q}^{\ast}=0\qquad\mbox{almost surely.}\end{equation*}
\begin{equation*}\lim_{m, n\to\infty}\|\mu_n-\mu_m\|_{{\mathcal{F}}_q}^{\ast}=0\qquad\mbox{almost surely.}\end{equation*}
Therefore, for each  $s\in S$
,
$s\in S$
,  $(W_n(\cdot,s))$
is a Cauchy sequence in the Banach space
$(W_n(\cdot,s))$
is a Cauchy sequence in the Banach space  ${\mathcal{W}}_p[0,1]$
.
${\mathcal{W}}_p[0,1]$
.
For each  $s\in S$
, let
$s\in S$
, let  $W(s)\,:\!=\{W_t(s)\colon t\in [0,1]\}\in{\mathcal{W}}_p[0,1]$
be a function such that
$W(s)\,:\!=\{W_t(s)\colon t\in [0,1]\}\in{\mathcal{W}}_p[0,1]$
be a function such that  $\|W_n(\cdot,s)-W(s)\|_{[p]}\to 0$
almost surely as
$\|W_n(\cdot,s)-W(s)\|_{[p]}\to 0$
almost surely as  $n\to\infty$
. For each
$n\to\infty$
. For each  $t\in [0,1]$
, since
$t\in [0,1]$
, since  $|W_t-W_n(t)|\leq \|W-W_n\|_{\sup}\to 0$
as
$|W_t-W_n(t)|\leq \|W-W_n\|_{\sup}\to 0$
as  $n\to\infty$
,
$n\to\infty$
,  $W_t$
is measurable, and so W is a stochastic process. For a Borel set
$W_t$
is measurable, and so W is a stochastic process. For a Borel set  $B\in{\mathbb R}^k$
and
$B\in{\mathbb R}^k$
and  $t_1,\dots,t_k\in [0,1]$
, we have
$t_1,\dots,t_k\in [0,1]$
, we have
 \begin{equation*}Q(\{(W_n(t_1),\dots,W_n(t_k))\in B\})={\mathrm{P}}(\{(\sigma_{\eta}|A_{\psi}|\sqrt{n})^{-1}(\nu_n(\textbf{1}_{[0,t_1]}),\dots,\nu_n(\textbf{1}_{[0,t_k]})\in B\} ).\end{equation*}
\begin{equation*}Q(\{(W_n(t_1),\dots,W_n(t_k))\in B\})={\mathrm{P}}(\{(\sigma_{\eta}|A_{\psi}|\sqrt{n})^{-1}(\nu_n(\textbf{1}_{[0,t_1]}),\dots,\nu_n(\textbf{1}_{[0,t_k]})\in B\} ).\end{equation*}
By (38),  $(\sigma_{\eta}|A_{\psi}|\sqrt{n})^{-1}(\nu_n(\textbf{1}_{[0,t_1]}),\dots,\nu_n(\textbf{1}_{[0,t_k]}))$
converge in distribution as
$(\sigma_{\eta}|A_{\psi}|\sqrt{n})^{-1}(\nu_n(\textbf{1}_{[0,t_1]}),\dots,\nu_n(\textbf{1}_{[0,t_k]}))$
converge in distribution as  $n\to\infty$
to
$n\to\infty$
to  $(\nu(\textbf{1}_{[0,t_1]},\dots,\nu (\textbf{1}_{[0,t_k]}))$
for the isonormal Gaussian process
$(\nu(\textbf{1}_{[0,t_1]},\dots,\nu (\textbf{1}_{[0,t_k]}))$
for the isonormal Gaussian process  $\nu$
on
$\nu$
on  ${\mathcal{L}}^2([0,1])$
. Also,
${\mathcal{L}}^2([0,1])$
. Also,  $(W_n(t_1),\dots, W_n(t_k))$
converge in distribution as
$(W_n(t_1),\dots, W_n(t_k))$
converge in distribution as  $n\to\infty$
to
$n\to\infty$
to  $(W_{t_1},\dots,W_{t_k})$
. It then follows that W is a Gaussian process with the covariance of a Wiener process. Since sample paths of
$(W_{t_1},\dots,W_{t_k})$
. It then follows that W is a Gaussian process with the covariance of a Wiener process. Since sample paths of  $\nu$
are uniformly continuous with respect to the pseudometric
$\nu$
are uniformly continuous with respect to the pseudometric  $\rho_2$
, W has almost all sample paths continuous, and so W is a standard Wiener process on [0, 1].
$\rho_2$
, W has almost all sample paths continuous, and so W is a standard Wiener process on [0, 1].
Let  ${\mathcal{C}}{\mathcal{W}}_p^{\ast}[0,1]$
be the set of all
${\mathcal{C}}{\mathcal{W}}_p^{\ast}[0,1]$
be the set of all  $f\in {\mathcal{W}}_p[0,1]$
such that
$f\in {\mathcal{W}}_p[0,1]$
such that
 \begin{equation*}\lim_{\epsilon\downarrow 0}\sup\bigg\{\sum_{k=1}^m|f(t_k)-f(t_{k-1})|^p\colon\,0=t_0<t_1<\cdots<t_m=1,\,\max_k(t_k-t_{k-1})\leq\epsilon\bigg\}=0.\end{equation*}
\begin{equation*}\lim_{\epsilon\downarrow 0}\sup\bigg\{\sum_{k=1}^m|f(t_k)-f(t_{k-1})|^p\colon\,0=t_0<t_1<\cdots<t_m=1,\,\max_k(t_k-t_{k-1})\leq\epsilon\bigg\}=0.\end{equation*}
Then  ${\mathcal{C}}{\mathcal{W}}_p^{\ast}[0,1]$
is a separable, closed subspace of
${\mathcal{C}}{\mathcal{W}}_p^{\ast}[0,1]$
is a separable, closed subspace of  ${\mathcal{W}}_p[0,1]$
([Reference Kisliakov13]). Since for each
${\mathcal{W}}_p[0,1]$
([Reference Kisliakov13]). Since for each  $p'>2$
, almost all sample functions of a Wiener process are of bounded p’-variation on [0, 1], by Lemma 2.14 in [Reference Dudley and Norvaiša11, Part II] it follows that almost all sample functions of W are in
$p'>2$
, almost all sample functions of a Wiener process are of bounded p’-variation on [0, 1], by Lemma 2.14 in [Reference Dudley and Norvaiša11, Part II] it follows that almost all sample functions of W are in  ${\mathcal{C}}{\mathcal{W}}_p^{\ast}[0,1]$
. Therefore,
${\mathcal{C}}{\mathcal{W}}_p^{\ast}[0,1]$
. Therefore,  $W_n$
converges in law to W in
$W_n$
converges in law to W in  ${\mathcal{W}}_p[0,1]$
by Corollary 3.3.5 in [Reference Dudley9]). The proof of Theorem 2 is complete.
${\mathcal{W}}_p[0,1]$
by Corollary 3.3.5 in [Reference Dudley9]). The proof of Theorem 2 is complete.
7. Applications
In this section we apply the preceding results to prove the uniform asymptotic normality of least squares estimators in parametric regression models, and to detect change points in trends of a short-memory linear process. Throughout this section,  $X_1,X_2,\dots$
is again a short-memory linear process given by (1) with innovations
$X_1,X_2,\dots$
is again a short-memory linear process given by (1) with innovations  $(\eta_j)$
and summable filter
$(\eta_j)$
and summable filter  $(\psi_j)$
such that (2) holds.
$(\psi_j)$
such that (2) holds.
7.1. Simple regression model
We start with a simple parametric regression model  $Y_j=\beta Z_{nj}+X_j$
,
$Y_j=\beta Z_{nj}+X_j$
,  $j=1, \dots, n$
, where
$j=1, \dots, n$
, where  $\beta\in {\mathbb R}$
is an unknown parameter and
$\beta\in {\mathbb R}$
is an unknown parameter and  $Z_{nj}$
are explanatory variables for the process
$Z_{nj}$
are explanatory variables for the process  $(Y_j)$
. We assume that
$(Y_j)$
. We assume that  $Z_{nj}=f(j/n)$
for some function f on [0, 1]. Then the least squares estimator of
$Z_{nj}=f(j/n)$
for some function f on [0, 1]. Then the least squares estimator of  $\beta$
is
$\beta$
is
 \begin{equation*}{\widehat{\beta}}_n={\widehat{\beta}}_n(\,f)\,:\!=\bigg(\sum_{j=1}^nf^2\Big (\frac{j}{n}\Big)\bigg)^{-1}\sum_{j=1}^n Y_j\, f\Big(\frac{j}{n}\Big).\end{equation*}
\begin{equation*}{\widehat{\beta}}_n={\widehat{\beta}}_n(\,f)\,:\!=\bigg(\sum_{j=1}^nf^2\Big (\frac{j}{n}\Big)\bigg)^{-1}\sum_{j=1}^n Y_j\, f\Big(\frac{j}{n}\Big).\end{equation*}
As a choice of the function f in the representation of  $Z_{nj}$
is not unique, finding an admissible class of functions becomes an important task. In response to this question we present what follows from our main result.
$Z_{nj}$
is not unique, finding an admissible class of functions becomes an important task. In response to this question we present what follows from our main result.
Note that the equality
 \begin{equation}\sum_{j=1}^n f^2\Big (\frac{j}{n}\Big )[{\widehat{\beta}}_n(\,f)-\beta]=\sum_{j=1}^n X_jf\Big (\frac{j}{n}\Big ) \end{equation}
\begin{equation}\sum_{j=1}^n f^2\Big (\frac{j}{n}\Big )[{\widehat{\beta}}_n(\,f)-\beta]=\sum_{j=1}^n X_jf\Big (\frac{j}{n}\Big ) \end{equation}
holds for each real-valued function f on [0, 1] and each  $n\in{\mathbb N}_{+}$
. By Theorem 4, it then follows that
$n\in{\mathbb N}_{+}$
. By Theorem 4, it then follows that
 \begin{equation*}W_n(\,f)\,:\!=\frac{1}{\sqrt{n}}\sum_{j=1}^n f^2\Big (\frac{j}{n}\Big )[{\widehat{\beta}}_n(\,f)-\beta] \xrightarrow{\mathcal{D}} \sigma_{\eta}A_{\psi}\nu (\,f)\qquad\mbox{as $n\to\infty$,}\end{equation*}
\begin{equation*}W_n(\,f)\,:\!=\frac{1}{\sqrt{n}}\sum_{j=1}^n f^2\Big (\frac{j}{n}\Big )[{\widehat{\beta}}_n(\,f)-\beta] \xrightarrow{\mathcal{D}} \sigma_{\eta}A_{\psi}\nu (\,f)\qquad\mbox{as $n\to\infty$,}\end{equation*}
for each  $f\in{\mathcal{W}}_q[0,1]$
with
$f\in{\mathcal{W}}_q[0,1]$
with  $q\in [1,2)$
, where
$q\in [1,2)$
, where  $\nu$
is the isonormal Gaussian process on
$\nu$
is the isonormal Gaussian process on  ${\mathcal{L}}_2[0,1]$
.
${\mathcal{L}}_2[0,1]$
.
As a straightforward consequence of Theorem 1 and the equality in (40), we obtain a weighted asymptotic normality of the estimator  ${\widehat{\beta}}_n(\,f)$
uniformly over the set of functions
${\widehat{\beta}}_n(\,f)$
uniformly over the set of functions  ${\mathcal{F}}_q=\{\,f\in{\mathcal{W}}_q[0,1]\colon\|\,f\|_{[q]}\leq 1\}$
,
${\mathcal{F}}_q=\{\,f\in{\mathcal{W}}_q[0,1]\colon\|\,f\|_{[q]}\leq 1\}$
,  $1\leq q< 2$
.
$1\leq q< 2$
.
Corollary 2. Let  $1\le q<2$
. There exists a version of the isonormal Gaussian process
$1\le q<2$
. There exists a version of the isonormal Gaussian process  $\nu$
restricted to
$\nu$
restricted to  ${\mathcal{F}}_q$
with values in a separable subset of
${\mathcal{F}}_q$
with values in a separable subset of  $\ell^{\infty}({\mathcal{F}}_q)$
, it is measurable for the Borel sets on its range, and
$\ell^{\infty}({\mathcal{F}}_q)$
, it is measurable for the Borel sets on its range, and
 \begin{equation*}W_n \xrightarrow{\mathcal{D}^*} \sigma_{\eta}A_{\psi}\nu\quad\mbox{in $\ell^{\infty}({\mathcal{F}}_q)$ as $n\to\infty$}.\end{equation*}
\begin{equation*}W_n \xrightarrow{\mathcal{D}^*} \sigma_{\eta}A_{\psi}\nu\quad\mbox{in $\ell^{\infty}({\mathcal{F}}_q)$ as $n\to\infty$}.\end{equation*}
Next, we establish the (unweighted) asymptotic normality of  ${\widehat{\beta}}_n(\,f)$
uniformly over a subset of
${\widehat{\beta}}_n(\,f)$
uniformly over a subset of  ${\mathcal{F}}_q$
. Since each regulated function is a Riemann function, we have
${\mathcal{F}}_q$
. Since each regulated function is a Riemann function, we have
 \begin{equation}I_n(\,f^2)\,:\!=\frac{1}{n}\sum_{j=1}^nf^2\Big (\frac{j}{n}\Big )\to\int_0^1f^2(x)\,\text{d} x=\!:\,I(\,f^2)\qquad\mbox{as $n\to\infty$},\end{equation}
\begin{equation}I_n(\,f^2)\,:\!=\frac{1}{n}\sum_{j=1}^nf^2\Big (\frac{j}{n}\Big )\to\int_0^1f^2(x)\,\text{d} x=\!:\,I(\,f^2)\qquad\mbox{as $n\to\infty$},\end{equation}
for any regulated function f. Each function having bounded p-variation is regulated (see, e.g., [Reference Dudley and Norvaiša11, p. 213]). Therefore, by (40), Theorem 4, and Slutsky’s lemma, if  $f\in{\mathcal{W}}_q[0,1]$
for some
$f\in{\mathcal{W}}_q[0,1]$
for some  $1\leq q<2$
and
$1\leq q<2$
and  $I(\,f^2)\not =0$
, then
$I(\,f^2)\not =0$
, then
 \begin{equation*}n^{1/2}({\widehat{\beta}}_n(\,f)-\beta) \xrightarrow{\mathcal{D}}\sigma_{\eta}A_{\psi}N(0,v^2)\qquad\mbox{as $n\to\infty$},\end{equation*}
\begin{equation*}n^{1/2}({\widehat{\beta}}_n(\,f)-\beta) \xrightarrow{\mathcal{D}}\sigma_{\eta}A_{\psi}N(0,v^2)\qquad\mbox{as $n\to\infty$},\end{equation*}
where  $N(0,v^2)$
is a mean-zero Gaussian random variable with variance
$N(0,v^2)$
is a mean-zero Gaussian random variable with variance  $v^2=(I(\,f^2))^{-1}$
. For each
$v^2=(I(\,f^2))^{-1}$
. For each  $\delta >0$
and
$\delta >0$
and  $q\in [1,2)$
, let
$q\in [1,2)$
, let
 \begin{equation}{\mathcal{F}}_{q,\delta}\,:\!=\{\,f\in{\mathcal{W}}_q[0,1]:\|\,f\|_{[q]}\leq 1,\,\,\,I(\,f^2)>\delta\}.\end{equation}
\begin{equation}{\mathcal{F}}_{q,\delta}\,:\!=\{\,f\in{\mathcal{W}}_q[0,1]:\|\,f\|_{[q]}\leq 1,\,\,\,I(\,f^2)>\delta\}.\end{equation}
Theorem 7. Let  $q\in [1,2)$
and
$q\in [1,2)$
and  $\delta \in (0,1)$
. There exists a version of a Gaussian process
$\delta \in (0,1)$
. There exists a version of a Gaussian process  $\nu_1$
indexed by
$\nu_1$
indexed by  ${\mathcal{F}}_{q,\delta}$
with values in a separable subset of
${\mathcal{F}}_{q,\delta}$
with values in a separable subset of  $\ell^{\infty}({\mathcal{F}}_{q,\delta})$
, it is measurable for the Borel sets on its range, and
$\ell^{\infty}({\mathcal{F}}_{q,\delta})$
, it is measurable for the Borel sets on its range, and
 \begin{equation*}\sqrt{n}({\widehat{\beta}}_n-\beta)\xrightarrow{\mathcal{D}^*} \sigma_{\eta}A_{\psi}\nu_1\quad\mbox{in $\ell^{\infty}({\mathcal{F}}_{q,\delta})$ as $n\to\infty$}.\end{equation*}
\begin{equation*}\sqrt{n}({\widehat{\beta}}_n-\beta)\xrightarrow{\mathcal{D}^*} \sigma_{\eta}A_{\psi}\nu_1\quad\mbox{in $\ell^{\infty}({\mathcal{F}}_{q,\delta})$ as $n\to\infty$}.\end{equation*}
Proof. Let  $\nu$
be the isonormal Gaussian process from Theorem 1. For each
$\nu$
be the isonormal Gaussian process from Theorem 1. For each  $f\in{\mathcal{F}}_{q,\delta}$
, let
$f\in{\mathcal{F}}_{q,\delta}$
, let  $\nu_1(\,f)\,:\!=\nu(\,f)/I(\,f^2)$
. Let
$\nu_1(\,f)\,:\!=\nu(\,f)/I(\,f^2)$
. Let  $z_1,\dots,z_k\in{\mathbb R}$
and let
$z_1,\dots,z_k\in{\mathbb R}$
and let  $f_1,\dots,f_k\in{\mathcal{F}}_{q,\delta}$
. Since
$f_1,\dots,f_k\in{\mathcal{F}}_{q,\delta}$
. Since  $\nu$
is linear, we have
$\nu$
is linear, we have
 \begin{equation*}\sum_{i=1}^k\sum_{j=1}^kz_iz_j{\mathrm{E}}[\nu_1(\,f_i)\nu_1(\,f_j)]={\mathrm{E}}\bigg[\nu^2\bigg (\sum_{i=1}^kz_i\frac{f_i}{I(\,f_i^2)}\bigg )\bigg]=\int_0^1\bigg (\sum_{i=1}^kz_i\frac{f_i}{I(\,f_i^2)}\bigg )^2\text{d}\lambda\geq 0.\end{equation*}
\begin{equation*}\sum_{i=1}^k\sum_{j=1}^kz_iz_j{\mathrm{E}}[\nu_1(\,f_i)\nu_1(\,f_j)]={\mathrm{E}}\bigg[\nu^2\bigg (\sum_{i=1}^kz_i\frac{f_i}{I(\,f_i^2)}\bigg )\bigg]=\int_0^1\bigg (\sum_{i=1}^kz_i\frac{f_i}{I(\,f_i^2)}\bigg )^2\text{d}\lambda\geq 0.\end{equation*}
Therefore,  $\{\nu_1(\,f)\colon f\in{\mathcal{F}}_{q,\delta}\}$
is a Gaussian process with mean zero and variance
$\{\nu_1(\,f)\colon f\in{\mathcal{F}}_{q,\delta}\}$
is a Gaussian process with mean zero and variance  ${\mathrm{E}}[\nu_1^2(\,f)]=(I(\,f^2))^{-1}$
. Since
${\mathrm{E}}[\nu_1^2(\,f)]=(I(\,f^2))^{-1}$
. Since  $\nu$
is linear we can consider
$\nu$
is linear we can consider  $\nu_1$
to be
$\nu_1$
to be  $\nu$
restricted to the set
$\nu$
restricted to the set  $\{\,f/I(\,f^2)\colon f\in{\mathcal{F}}_{q,\delta}\}$
, which is a subset of
$\{\,f/I(\,f^2)\colon f\in{\mathcal{F}}_{q,\delta}\}$
, which is a subset of  $\{\,f\in{\mathcal{W}}_q[0,1]\colon\|\,f\|_{[q]}\leq \delta^{-1}\}$
. Therefore, the Gaussian process
$\{\,f\in{\mathcal{W}}_q[0,1]\colon\|\,f\|_{[q]}\leq \delta^{-1}\}$
. Therefore, the Gaussian process  $\nu_1$
on
$\nu_1$
on  ${\mathcal{F}}_{q,\delta}$
has values in a separable subset of
${\mathcal{F}}_{q,\delta}$
has values in a separable subset of  $\ell^{\infty}({\mathcal{F}}_{q,\delta})$
and it is measurable for the Borel sets on its range.
$\ell^{\infty}({\mathcal{F}}_{q,\delta})$
and it is measurable for the Borel sets on its range.
Using the notation of (15), (3), and the equality in (40), for each  $f\in{\mathcal{F}}_{q,\delta}$
and
$f\in{\mathcal{F}}_{q,\delta}$
and  $n\in{\mathbb N}_{+}$
, we have
$n\in{\mathbb N}_{+}$
, we have
 \begin{equation}\sqrt{n}({\widehat{\beta}}_n(\,f)-\beta)=\bigg (\frac{1}{I_n(\,f^2)}-\frac{1}{I(\,f^2)}\bigg )\frac{\nu_n(\,f)}{\sqrt{n}}+\frac{1}{\sqrt{n}}\nu_n\bigg (\frac{f}{I(\,f^2)}\bigg ).\end{equation}
\begin{equation}\sqrt{n}({\widehat{\beta}}_n(\,f)-\beta)=\bigg (\frac{1}{I_n(\,f^2)}-\frac{1}{I(\,f^2)}\bigg )\frac{\nu_n(\,f)}{\sqrt{n}}+\frac{1}{\sqrt{n}}\nu_n\bigg (\frac{f}{I(\,f^2)}\bigg ).\end{equation}
We show that the second term on the right-hand side converges in outer distribution to  $\sigma_{\eta}A_{\psi}\nu_1$
. Let
$\sigma_{\eta}A_{\psi}\nu_1$
. Let  $C(\,f)\,:\!=1/I(\,f^2)$
for each
$C(\,f)\,:\!=1/I(\,f^2)$
for each  $f\in{\mathcal{F}}_{q,\delta}$
, and let
$f\in{\mathcal{F}}_{q,\delta}$
, and let  $g\colon\ell^{\infty}({\mathcal{F}}_{q,\delta})\to\ell^{\infty}({\mathcal{F}}_{q,\delta})$
be a multiplication function with values
$g\colon\ell^{\infty}({\mathcal{F}}_{q,\delta})\to\ell^{\infty}({\mathcal{F}}_{q,\delta})$
be a multiplication function with values  $g(F)\,:\!=CF$
for each
$g(F)\,:\!=CF$
for each  $F\in\ell^{\infty}({\mathcal{F}}_{q,\delta})$
. One can check that g is bounded and continuous. Let
$F\in\ell^{\infty}({\mathcal{F}}_{q,\delta})$
. One can check that g is bounded and continuous. Let  $h\colon\ell^{\infty}({\mathcal{F}}_{q,\delta})\to{\mathbb R}$
be a bounded and continuous function. Then the composition
$h\colon\ell^{\infty}({\mathcal{F}}_{q,\delta})\to{\mathbb R}$
be a bounded and continuous function. Then the composition  $h{\circ}g$
is also a bounded and continuous function from
$h{\circ}g$
is also a bounded and continuous function from  $\ell^{\infty}({\mathcal{F}}_{q,\delta})$
to
$\ell^{\infty}({\mathcal{F}}_{q,\delta})$
to  ${\mathbb R}$
. Thus, by (5) it follows that
${\mathbb R}$
. Thus, by (5) it follows that
 \begin{equation*}{\mathrm{E}}^{\ast}[h(n^{-1/2}C\nu_n)]={\mathrm{E}}^{\ast}[h{\circ}g(n^{-1/2}\nu_n)]\to{\mathrm{E}} [h{\circ}g(\nu)]={\mathrm{E}}[ h(\sigma_{\eta}A_{\psi}\nu_1)]\end{equation*}
\begin{equation*}{\mathrm{E}}^{\ast}[h(n^{-1/2}C\nu_n)]={\mathrm{E}}^{\ast}[h{\circ}g(n^{-1/2}\nu_n)]\to{\mathrm{E}} [h{\circ}g(\nu)]={\mathrm{E}}[ h(\sigma_{\eta}A_{\psi}\nu_1)]\end{equation*}
as  $n\to\infty$
. Thus, the second term on the right-hand side of (43) converges in outer distribution to
$n\to\infty$
. Thus, the second term on the right-hand side of (43) converges in outer distribution to  $\sigma_{\eta}A_{\psi}\nu_1$
. Finally, we will show that the first term on the right-hand side of (43) converges to zero as
$\sigma_{\eta}A_{\psi}\nu_1$
. Finally, we will show that the first term on the right-hand side of (43) converges to zero as  $n\to\infty$
uniformly in f and in outer probability (Definition 1.9.1 in [Reference Van der Vaart and Wellner15]).
$n\to\infty$
uniformly in f and in outer probability (Definition 1.9.1 in [Reference Van der Vaart and Wellner15]).
Let  $f\in{\mathcal{F}}_{q,\delta}$
and
$f\in{\mathcal{F}}_{q,\delta}$
and  $n\in{\mathbb N}_{+}$
. Then
$n\in{\mathbb N}_{+}$
. Then
 \begin{eqnarray*}\lefteqn{I_n(\,f^2)-I(\,f^2)=\sum_{j=1}^n\int_{(j-1)/n}^{j/n}\!\Big(\,f^2\Big(\frac{j}{n}\Big)-f^2(x)\Big)\text{d} x}\\&=&{}\,2\sum_{j=1}^n\int_{(j-1)/n}^{j/n}\!\!\!f(x)\Big(\,f\Big(\frac{j}{n}\Big )-f(x)\Big)\text{d} x +\sum_{j=1}^n\int_{(j-1)/n}^{j/n}\!\Big(\,f\Big(\frac{j}{n}\Big )-f(x)\Big)^2\text{d} x.\end{eqnarray*}
\begin{eqnarray*}\lefteqn{I_n(\,f^2)-I(\,f^2)=\sum_{j=1}^n\int_{(j-1)/n}^{j/n}\!\Big(\,f^2\Big(\frac{j}{n}\Big)-f^2(x)\Big)\text{d} x}\\&=&{}\,2\sum_{j=1}^n\int_{(j-1)/n}^{j/n}\!\!\!f(x)\Big(\,f\Big(\frac{j}{n}\Big )-f(x)\Big)\text{d} x +\sum_{j=1}^n\int_{(j-1)/n}^{j/n}\!\Big(\,f\Big(\frac{j}{n}\Big )-f(x)\Big)^2\text{d} x.\end{eqnarray*}
Since  $v_2(\,f;\ [a,c])+v_2(\,f;\ [c,b])\leq v_2(\,f;\ [a,b])$
for any
$v_2(\,f;\ [a,c])+v_2(\,f;\ [c,b])\leq v_2(\,f;\ [a,b])$
for any  $0\leq a<c<b\leq 1$
, it follows that
$0\leq a<c<b\leq 1$
, it follows that
 \begin{equation*}\sum_{j=1}^n\int_{(j-1)/n}^{j/n}\!\Big(\,f\Big(\frac{j}{n}\Big )-f(x)\Big)^2\text{d} x\leq\frac{v_2(\,f)}{n}.\end{equation*}
\begin{equation*}\sum_{j=1}^n\int_{(j-1)/n}^{j/n}\!\Big(\,f\Big(\frac{j}{n}\Big )-f(x)\Big)^2\text{d} x\leq\frac{v_2(\,f)}{n}.\end{equation*}
Then, using Hölder’s inequality, we obtain the bound
 \begin{equation*}K_n(\,f)\,:\!=|I_n(\,f^2)-I(\,f^2)|\leq 2(I(\,f^2))^{1/2}\Big (\frac{v_2(\,f)}{n}\Big )^{1/2}+\frac{v_2(\,f)}{n}.\end{equation*}
\begin{equation*}K_n(\,f)\,:\!=|I_n(\,f^2)-I(\,f^2)|\leq 2(I(\,f^2))^{1/2}\Big (\frac{v_2(\,f)}{n}\Big )^{1/2}+\frac{v_2(\,f)}{n}.\end{equation*}
For each  $f\in{\mathcal{F}}_{q,\delta}$
,
$f\in{\mathcal{F}}_{q,\delta}$
,  $I(\,f^2)\leq\|\,f\|_{\sup}^2\leq 1$
and
$I(\,f^2)\leq\|\,f\|_{\sup}^2\leq 1$
and  $v_2(\,f)\leq \|\,f\|_{[q]}^2\leq 1$
since
$v_2(\,f)\leq \|\,f\|_{[q]}^2\leq 1$
since  $q<2$
, and so
$q<2$
, and so  $K_n(\,f)\break <3/\sqrt{n}$
. We observe that, for each
$K_n(\,f)\break <3/\sqrt{n}$
. We observe that, for each  $f\in{\mathcal{F}}_{q,\delta}$
and
$f\in{\mathcal{F}}_{q,\delta}$
and  $n\in{\mathbb N}_{+}$
,
$n\in{\mathbb N}_{+}$
,
 \begin{equation*}D_n(\,f)\,:\!=\bigg |\frac{1}{I_n(\,f^2)}-\frac{1}{I(\,f^2)}\bigg |\leq\frac{K_n(\,f)}{I^2(\,f^2)(1-I^{-1}(\,f^2)K_n(\,f))} ,\end{equation*}
\begin{equation*}D_n(\,f)\,:\!=\bigg |\frac{1}{I_n(\,f^2)}-\frac{1}{I(\,f^2)}\bigg |\leq\frac{K_n(\,f)}{I^2(\,f^2)(1-I^{-1}(\,f^2)K_n(\,f))} ,\end{equation*}
provided  $I^{-1}(\,f^2)K_n(\,f)<1$
. Therefore, for each
$I^{-1}(\,f^2)K_n(\,f)<1$
. Therefore, for each  $n>36/\delta^2$
we have the bound
$n>36/\delta^2$
we have the bound
 \begin{equation}\|D_n\|_{{\mathcal{F}}_{q,\delta}}<\frac{6}{\sqrt{n}\delta^2}.\end{equation}
\begin{equation}\|D_n\|_{{\mathcal{F}}_{q,\delta}}<\frac{6}{\sqrt{n}\delta^2}.\end{equation}
To bound the first term on the right-hand side of (43), note that, for each  $\epsilon >0$
and for each
$\epsilon >0$
and for each  $A\in{\mathbb R}$
,
$A\in{\mathbb R}$
,
 \begin{equation*}{\mathrm{P}}^{\ast}\bigg (\bigg\{\sup_{f\in{\mathcal{F}}_{q,\delta}}\bigg |\frac{1}{I_n(\,f^2)}-\frac{1}{I(\,f^2)}\bigg |\frac{|\nu_n(\,f)|}{\sqrt{n}}>\epsilon\bigg \}\bigg )\leq{\mathrm{P}}^{\ast}(\{\|D_n\|_{{\mathcal{F}}_{q,\delta}}\|\nu_n\|_{{\mathcal{F}}_{q,\delta}}>\epsilon\sqrt{n}\})\end{equation*}
\begin{equation*}{\mathrm{P}}^{\ast}\bigg (\bigg\{\sup_{f\in{\mathcal{F}}_{q,\delta}}\bigg |\frac{1}{I_n(\,f^2)}-\frac{1}{I(\,f^2)}\bigg |\frac{|\nu_n(\,f)|}{\sqrt{n}}>\epsilon\bigg \}\bigg )\leq{\mathrm{P}}^{\ast}(\{\|D_n\|_{{\mathcal{F}}_{q,\delta}}\|\nu_n\|_{{\mathcal{F}}_{q,\delta}}>\epsilon\sqrt{n}\})\end{equation*}
 \begin{equation}\leq{\mathrm{P}}(\{\|D_n\|_{{\mathcal{F}}_{q,\delta}}>\epsilon A\})+{\mathrm{P}}^{\ast}(\{\|\nu_n\|_{{\mathcal{F}}_{q,\delta}}>A\sqrt{n}\}).\end{equation}\vskip-\lastskip\pagebreak
\begin{equation}\leq{\mathrm{P}}(\{\|D_n\|_{{\mathcal{F}}_{q,\delta}}>\epsilon A\})+{\mathrm{P}}^{\ast}(\{\|\nu_n\|_{{\mathcal{F}}_{q,\delta}}>A\sqrt{n}\}).\end{equation}\vskip-\lastskip\pagebreak
By Theorem 1, the isonormal Gaussian process  $\nu$
restricted to
$\nu$
restricted to  ${\mathcal{F}}_{q,\delta}$
has values in separable subset of
${\mathcal{F}}_{q,\delta}$
has values in separable subset of  $\ell^{\infty}({\mathcal{F}}_{q,\delta})$
and is measurable for the Borel sets on its range. Therefore, its law
$\ell^{\infty}({\mathcal{F}}_{q,\delta})$
and is measurable for the Borel sets on its range. Therefore, its law  ${\mathrm{P}}{\circ}\nu^{-1}$
is tight. By Lemma 1.3.8 in [Reference Van der Vaart and Wellner15],
${\mathrm{P}}{\circ}\nu^{-1}$
is tight. By Lemma 1.3.8 in [Reference Van der Vaart and Wellner15],  $n^{-1/2}\nu_n$
is asymptotically tight. It follows that for each
$n^{-1/2}\nu_n$
is asymptotically tight. It follows that for each  $\epsilon >0$
there is
$\epsilon >0$
there is  $A\in{\mathbb R}$
such that
$A\in{\mathbb R}$
such that
 \begin{equation*}\limsup_{n\to\infty}{\mathrm{P}}^{\ast}(\{\|\nu_n\|_{{\mathcal{F}}_{q,\delta}}>A\sqrt{n}\})<\epsilon .\end{equation*}
\begin{equation*}\limsup_{n\to\infty}{\mathrm{P}}^{\ast}(\{\|\nu_n\|_{{\mathcal{F}}_{q,\delta}}>A\sqrt{n}\})<\epsilon .\end{equation*}
By (44), the first probability on the right-hand side of (45) is zero for all sufficiently large n. The first term on the right-hand side of (43) converges to zero as  $n\to\infty$
uniformly in f and in outer probability. Thereforem the right-hand side of (43) converges in outer distribution to
$n\to\infty$
uniformly in f and in outer probability. Thereforem the right-hand side of (43) converges in outer distribution to  $\sigma_{\eta}A_{\psi}\nu_1$
, and so does the left-hand side of (43) by Lemma 1.10.2 in [Reference Van der Vaart and Wellner15]. The proof is complete. □
$\sigma_{\eta}A_{\psi}\nu_1$
, and so does the left-hand side of (43) by Lemma 1.10.2 in [Reference Van der Vaart and Wellner15]. The proof is complete. □
For each real-valued function f on [0, 1] and for each  $n\in{\mathbb N}_{+}$
let
$n\in{\mathbb N}_{+}$
let
 \begin{equation*}Q_n(\,f)\,:\!=\bigg [\sum_{j=1}^n f^2\Big (\frac{j}{n}\Big )\bigg ]^{1/2}[{\widehat{\beta}}_n(\,f)-\beta].\end{equation*}
\begin{equation*}Q_n(\,f)\,:\!=\bigg [\sum_{j=1}^n f^2\Big (\frac{j}{n}\Big )\bigg ]^{1/2}[{\widehat{\beta}}_n(\,f)-\beta].\end{equation*}
Recalling definition (42) of the class of functions  ${\mathcal{F}}_{q,\delta}$
, we have the following result.
${\mathcal{F}}_{q,\delta}$
, we have the following result.
Theorem 8. Let  $q\in [1,2)$
and
$q\in [1,2)$
and  $\delta \in(0,1)$
. There exists a version of a Gaussian process
$\delta \in(0,1)$
. There exists a version of a Gaussian process  $\nu_2$
indexed by
$\nu_2$
indexed by  ${\mathcal{F}}_{q,\delta}$
with values in a separable subset of
${\mathcal{F}}_{q,\delta}$
with values in a separable subset of  $\ell^{\infty}({\mathcal{F}}_{q,\delta})$
, it is measurable for the Borel sets on its range, and
$\ell^{\infty}({\mathcal{F}}_{q,\delta})$
, it is measurable for the Borel sets on its range, and
 \begin{equation*}Q_n \xrightarrow{\mathcal{D}^*} \sigma_{\eta}A_{\psi}\nu_2\quad\mbox{in $\ell^{\infty}({\mathcal{F}}_{q,\delta})$ as $n\to\infty$}.\end{equation*}
\begin{equation*}Q_n \xrightarrow{\mathcal{D}^*} \sigma_{\eta}A_{\psi}\nu_2\quad\mbox{in $\ell^{\infty}({\mathcal{F}}_{q,\delta})$ as $n\to\infty$}.\end{equation*}
Proof. The proof is similar to that of Theorem 7. Indeed, using equality (40), the notation in (41), and (3), we have the representation
 \begin{align*} Q_n(\,f) & = \frac{1}{(I_n(\,f^2))^{1/2}} \frac{\nu_n(\,f)}{\sqrt{n}} \\
& = \left [\frac{1}{(I_n(\,f^2))^{1/2}}-\frac{1}{(I(\,f^2))^{1/2}}\right ]\frac {\nu_n(\,f)}{\sqrt{n}}+\frac{1}{\sqrt{n}\,}\nu_n\bigg (\frac{f}{(I(\,f^2))^{1/2}}\bigg )\end{align*}
\begin{align*} Q_n(\,f) & = \frac{1}{(I_n(\,f^2))^{1/2}} \frac{\nu_n(\,f)}{\sqrt{n}} \\
& = \left [\frac{1}{(I_n(\,f^2))^{1/2}}-\frac{1}{(I(\,f^2))^{1/2}}\right ]\frac {\nu_n(\,f)}{\sqrt{n}}+\frac{1}{\sqrt{n}\,}\nu_n\bigg (\frac{f}{(I(\,f^2))^{1/2}}\bigg )\end{align*}
for each  $f\in{\mathcal{F}}_{q,\delta}$
and each
$f\in{\mathcal{F}}_{q,\delta}$
and each  $n\in{\mathbb N}_{+}$
. Note that
$n\in{\mathbb N}_{+}$
. Note that  $|\sqrt{u}-\sqrt{v}|\leq\sqrt{|u-v|}$
for any
$|\sqrt{u}-\sqrt{v}|\leq\sqrt{|u-v|}$
for any  $u\geq 0$
and
$u\geq 0$
and  $v\geq 0$
. Therefore, the above term in the square brackets approaches zero as
$v\geq 0$
. Therefore, the above term in the square brackets approaches zero as  $n\to\infty$
uniformly for
$n\to\infty$
uniformly for  $f\in{\mathcal{F}}_{q,\delta}$
due to the bound (44) given in the proof of Theorem 7. The conclusion of Theorem 8 then follows as in the preceding proof. □
$f\in{\mathcal{F}}_{q,\delta}$
due to the bound (44) given in the proof of Theorem 7. The conclusion of Theorem 8 then follows as in the preceding proof. □
7.2. Multiple change point model
Consider a time-series model
 \begin{equation*}Y_{nj}=\mu_{nj}+X_j,\qquad j=1, \dots, n, \end{equation*}
\begin{equation*}Y_{nj}=\mu_{nj}+X_j,\qquad j=1, \dots, n, \end{equation*}
which is subject to unknown multiple change points  $(\tau_1^*,\dots,\tau_{d^*-1}^*)$
. We wish to test the null hypothesis
$(\tau_1^*,\dots,\tau_{d^*-1}^*)$
. We wish to test the null hypothesis
 \begin{equation*}H_0:\quad \mu_{n1}=\cdots=\mu_{nn}=0\end{equation*}
\begin{equation*}H_0:\quad \mu_{n1}=\cdots=\mu_{nn}=0\end{equation*}
against the multiple change alternative model
 \begin{equation*} H_{\text{A}}\,:\,\quad \mu_{nj}= \sum_{k=1}^{d^*}\beta_k\textbf{1}_{I^*_k}(j/n), \qquad j=1, \dots, n,\end{equation*}
\begin{equation*} H_{\text{A}}\,:\,\quad \mu_{nj}= \sum_{k=1}^{d^*}\beta_k\textbf{1}_{I^*_k}(j/n), \qquad j=1, \dots, n,\end{equation*}
with  $d^*\in{\mathbb N}_{+}$
,
$d^*\in{\mathbb N}_{+}$
,  $\beta_1,\dots,\beta_{d^*}$
, and
$\beta_1,\dots,\beta_{d^*}$
, and  $I^*_k=(\tau^*_{k-1}, \tau^*_k]$
,
$I^*_k=(\tau^*_{k-1}, \tau^*_k]$
,  $0=\tau^*_0<\tau^*_1<\cdots<\tau^*_d=1$
, being unknown parameters.
$0=\tau^*_0<\tau^*_1<\cdots<\tau^*_d=1$
, being unknown parameters.
There is an enormous amount of literature where change detection problems have been studied. The books by Basseville and Nikiforov [Reference Basseville and Nikiforov2], Csörgo and Horváth [Reference Csörgo and Horváth6], Brodsky and Darkhovskay [Reference Brodsky and Darkhovsky3], and Chen and Gupta [Reference Chen and Gupta5] introduce the basics of various methods. We suggest a testing procedure based on uniform asymptotic normality of the partial sum processes obtained in the present paper.
For each  $d\in{\mathbb N}_{+}$
, let
$d\in{\mathbb N}_{+}$
, let  ${\mathcal T}_d$
be a set of all partitions
${\mathcal T}_d$
be a set of all partitions  $(\tau_k)$
of the interval [0, 1] such that
$(\tau_k)$
of the interval [0, 1] such that  $0=\tau_0<\tau_1<\cdots<\tau_d=1$
. For a partition
$0=\tau_0<\tau_1<\cdots<\tau_d=1$
. For a partition  $\tau=(\tau_k)\in {\mathcal T}_d$
one fits the regression model
$\tau=(\tau_k)\in {\mathcal T}_d$
one fits the regression model
 \begin{equation*} Y_{nj}=\sum_{k=1}^{d}\beta_k\textbf{1}_{I_k}(j/n)+X_j,\qquad j=1, \dots, n,\end{equation*}
\begin{equation*} Y_{nj}=\sum_{k=1}^{d}\beta_k\textbf{1}_{I_k}(j/n)+X_j,\qquad j=1, \dots, n,\end{equation*}
where  $I_k=(\tau_{k-1}, \tau_k]$
. The parameter
$I_k=(\tau_{k-1}, \tau_k]$
. The parameter  $\boldsymbol{\beta}=[\beta_1, \dots, \beta_{d}]'$
is obtained by the least squares estimator
$\boldsymbol{\beta}=[\beta_1, \dots, \beta_{d}]'$
is obtained by the least squares estimator
 \begin{equation*}{\widehat{\boldsymbol{\beta}}}={\widehat{\boldsymbol{\beta}}}(\boldsymbol{\tau})={\textbf{\textit{Q}}}_n^{-1}\bigg[\sum_{j=1}^nY_{nj}\textbf{1}_{I_1}(j/n), \dots, \sum_{j=1}^nY_{nj}\textbf{1}_{I_d}(j/n)\bigg]',\end{equation*}
\begin{equation*}{\widehat{\boldsymbol{\beta}}}={\widehat{\boldsymbol{\beta}}}(\boldsymbol{\tau})={\textbf{\textit{Q}}}_n^{-1}\bigg[\sum_{j=1}^nY_{nj}\textbf{1}_{I_1}(j/n), \dots, \sum_{j=1}^nY_{nj}\textbf{1}_{I_d}(j/n)\bigg]',\end{equation*}
where
 \begin{equation*}{\textbf{\textit{Q}}}_n={\mathrm{diag}}\{[\tau_kn]-[\tau_{k-1}n],\ k=1, \dots, d\}.\end{equation*}
\begin{equation*}{\textbf{\textit{Q}}}_n={\mathrm{diag}}\{[\tau_kn]-[\tau_{k-1}n],\ k=1, \dots, d\}.\end{equation*}
For  $p\geq 1$
let
$p\geq 1$
let  $\|x\|_p$
be the
$\|x\|_p$
be the  $\ell_p$
-norm of a vector
$\ell_p$
-norm of a vector  $x\in{\mathbb R}^d$
. Then
$x\in{\mathbb R}^d$
. Then
 \begin{equation*}\|{\textbf{\textit{Q}}}_n{\widehat{\boldsymbol{\beta}}}\|_p=\bigg(\sum_{k=1}^d\bigg|\sum_{j=1}^nY_{nj}\textbf{1}_{I_k}(j/n)\bigg|^p\bigg)^{1/p}.\end{equation*}
\begin{equation*}\|{\textbf{\textit{Q}}}_n{\widehat{\boldsymbol{\beta}}}\|_p=\bigg(\sum_{k=1}^d\bigg|\sum_{j=1}^nY_{nj}\textbf{1}_{I_k}(j/n)\bigg|^p\bigg)^{1/p}.\end{equation*}
Let
 \begin{equation*}T_n=T_n(Y_{n1}, \dots, Y_{nn})\,:\!=\sup_{d\in{\mathbb N}_{+}}\sup_{(\tau_k)\in {\mathcal T}_d}\|{\textbf{\textit{Q}}}_n{\widehat{\boldsymbol{\beta}}}\|_p.\end{equation*}
\begin{equation*}T_n=T_n(Y_{n1}, \dots, Y_{nn})\,:\!=\sup_{d\in{\mathbb N}_{+}}\sup_{(\tau_k)\in {\mathcal T}_d}\|{\textbf{\textit{Q}}}_n{\widehat{\boldsymbol{\beta}}}\|_p.\end{equation*}
Under the null hypothesis  $H_0$
, by (7), the statistic
$H_0$
, by (7), the statistic  $T_n=\|S_n\|_{(p)}$
, where
$T_n=\|S_n\|_{(p)}$
, where  $S_n$
is the partial sum process of a linear process
$S_n$
is the partial sum process of a linear process  $(X_k)$
. The following fact is based on Corollary 1.
$(X_k)$
. The following fact is based on Corollary 1.
Theorem 9. Let  $p>2$
. Under the null hypothesis
$p>2$
. Under the null hypothesis  $H_0$
we have
$H_0$
we have
 \begin{equation*}n^{-1/2}A_{\psi}^{-1}\sigma_{\eta}^{-1}T_n\xrightarrow{\mathcal{D}} \|W\|_{(p)}\qquad\mbox{as $n\to\infty$}.\end{equation*}
\begin{equation*}n^{-1/2}A_{\psi}^{-1}\sigma_{\eta}^{-1}T_n\xrightarrow{\mathcal{D}} \|W\|_{(p)}\qquad\mbox{as $n\to\infty$}.\end{equation*}
Under the alternative  $H_{\text{A}}$
we have
$H_{\text{A}}$
we have  $n^{-1/2}T_n \xrightarrow[n\to\infty]{\mathrm{P}} \infty$
provided
$n^{-1/2}T_n \xrightarrow[n\to\infty]{\mathrm{P}} \infty$
provided
 \begin{equation*}\sqrt{n}\bigg(\sum_{k=1}^{d^*}(\tau_k^*-\tau^*_{k-1})^p|\beta_k|^p\bigg)^{1/p}\to \infty\qquad\mbox{as $n\to\infty$.}\end{equation*}
\begin{equation*}\sqrt{n}\bigg(\sum_{k=1}^{d^*}(\tau_k^*-\tau^*_{k-1})^p|\beta_k|^p\bigg)^{1/p}\to \infty\qquad\mbox{as $n\to\infty$.}\end{equation*}
Calculations of p-variation of piecewise functions are available in the R environment package under the name pvar developed by Butkus and Norvaiša [Reference Butkus and Norvaiša4]. Simulation analysis of the statistic  $T_n$
is outside the scope of this paper and will appear elsewhere.
$T_n$
is outside the scope of this paper and will appear elsewhere.
Acknowledgement
This research was supported by the Research Council of Lithuania, grant no. S-MIP-17-76. The authors thank the referees of this paper for their useful comments.