1. Introduction
Let X, X 1, …, Xn be independent, identically distributed (i.i.d.) random vectors taking values in ℝd. We assume throughout the paper that the distribution of X, which is denoted by μ, has a density f with respect to Lebesgue measure λ.
Writing ‖⋅‖ for the Euclidean norm on ℝd, set
and let
denote the maximum probability of the nearest-neighbour balls, where S(x, r) := {y ∈ ℝd : ‖y − x‖ ≤ r} stands for the closed ball with centre x and radius r. In this paper we deal with both the finite sample and the asymptotic distribution of
There is a large related literature on the Poisson sample size. Let N be a random variable that is independent of X 1, X 2, … and has a Poisson distribution with 𝔼(N) = n. Then
is a nonhomogeneous Poisson process with intensity function nf. For the nuclei X 1, …, XN,
denotes the Voronoi cell around Xj, and
![]() ${\widehat r_j}$
and
${\widehat r_j}$
and
![]() ${\widehat R_j}$
denote the inscribed and circumscribed radii of
${\widehat R_j}$
denote the inscribed and circumscribed radii of
![]() ${\widetilde A_n}({X_j})$
, respectively, i.e. we have
${\widetilde A_n}({X_j})$
, respectively, i.e. we have
and
If X 1, X 2, … are i.i.d. uniformly distributed on a convex set W ⊂ ℝd with volume 1, then (2a) and (2c) of Theorem 1 of [Reference Calka and Chenavier5] read
and
for y ∈ ℝ. Here αd > 0 is a universal constant, and
denotes the distribution function of the Gumbel extreme value distribution. In the sequel we consider a related problem, namely that of finding the limit distribution of the largest probability content of nearest-neighbour spheres in a nonhomogeneous i.i.d. setting such that the support W can be arbitrary. Such a generality is important for designing and analysing wireless networks; see [Reference Baccelli and Blaszczyszyn1] and [Reference Baccelli and Blaszczyszyn2].
The paper is organized as follows. In Section 2 we study the distribution of nPn − ln n. Theorem 2.1 is on a universal and tight bound on the upper tail of nPn − ln n. Under mild conditions on the density, Theorem 2.2 shows that the number of exceedances of nearest-neighbour ball probabilities over a certain sequence of thresholds has an asymptotic Poisson distribution as n → ∞. As a consequence, the limit distribution of nPn − ln n is the Gumbel extreme value distribution. Theorem 3.1 is the extension of Theorem 2.1 for a Poisson sample size. All proofs are presented in Section 4. The main tool for proving Theorem 2.2 is a novel Poisson limit theorem for sums of indicators of exchangeable events, which is formulated as Proposition 4.1. The final section sheds some light on a technical condition on f that is used in the proof of the main result. We conjecture that our main result holds without any condition on the density f.
Although there is a weak dependence between the probabilities of nearest-neighbour balls, a main message of this paper is that one can neglect this dependence when looking for the limit distribution of the maximum probability.
2. The maximum nearest-neighbour ball
Under the assumption that the density f is sufficiently smooth and bounded away from 0, Henze ([Reference Henze13], [Reference Henze12]) derived the limit distribution of the maximum approximate probability measure max
of nearest-neighbour balls. Here vd = π d/2/Γ(1 + d/2) denotes the volume of the unit ball in ℝd.
In the following, we consider the number of points among X 1, …, Xn for which the probability content of the nearest-neighbour ball exceeds some (large) threshold. To be more specific, we fix y ∈ ℝ and consider the random variable
 $${C_n}:=\sum\limits_{i = 1}^n {\bf 1}\{ n\mu \{ S({X_i},{R_{i,n}})\} \gt y + \ln n\} ,$$
$${C_n}:=\sum\limits_{i = 1}^n {\bf 1}\{ n\mu \{ S({X_i},{R_{i,n}})\} \gt y + \ln n\} ,$$
where 1{⋅} denotes the indicator function. Writing ‘
![]() $\buildrel {\rm{D}} \over \longrightarrow $
’ to denote convergence in distribution, we will show that, under some conditions on the density f,
$\buildrel {\rm{D}} \over \longrightarrow $
’ to denote convergence in distribution, we will show that, under some conditions on the density f,
where Z is a random variable with the Poisson distribution Po(exp (−y)). Now Cn = 0 if and only if nPn − ln n ≤ y, and it follows that lim
Since 1 − G(y) ≤ exp (−y) if y ≥ 0, (2.2) implies that
Our first result is a nonasymptotic upper bound on the upper tail of the distribution of nPn − ln n. This bound holds without any condition on the density and thus entails (2.3) universally.
Theorem 2.1
Without any restriction on the density f, we have
 $${\mathbb P}(n{P_n} - \ln n \ge y) \le \exp ( - {{n - 1} \over n}y + {{\ln n} \over n}){\bf 1}\{ y \le n - \ln n\} ,\quad \quad y \in {\mathbb R}.$$
$${\mathbb P}(n{P_n} - \ln n \ge y) \le \exp ( - {{n - 1} \over n}y + {{\ln n} \over n}){\bf 1}\{ y \le n - \ln n\} ,\quad \quad y \in {\mathbb R}.$$
Theorem 2.1 implies a nonasymptotic upper bound on the mean of nPn − ln n since
 $$\matrix{ {{\mathbb E}[n{P_n} - \ln n]} \hfill & \le \hfill & {{\mathbb E}[(n{P_n} - \ln n{)^ + }]} \hfill \cr {} \hfill & = \hfill & {\int_0^\infty {\mathbb P}(n{P_n} - \ln n \ge y){\rm d}y} \hfill \cr {} \hfill & \le \hfill & {\int_0^\infty \exp ( - {{n - 1} \over n}y + {{\ln n} \over n}){\rm d}y} \hfill \cr {} \hfill & = \hfill & {{n \over {n - 1}}\exp ({{\ln n} \over n}).} \hfill \cr } $$
$$\matrix{ {{\mathbb E}[n{P_n} - \ln n]} \hfill & \le \hfill & {{\mathbb E}[(n{P_n} - \ln n{)^ + }]} \hfill \cr {} \hfill & = \hfill & {\int_0^\infty {\mathbb P}(n{P_n} - \ln n \ge y){\rm d}y} \hfill \cr {} \hfill & \le \hfill & {\int_0^\infty \exp ( - {{n - 1} \over n}y + {{\ln n} \over n}){\rm d}y} \hfill \cr {} \hfill & = \hfill & {{n \over {n - 1}}\exp ({{\ln n} \over n}).} \hfill \cr } $$
Note that this upper bound approaches 1 for large n, and that the mean of the standard Gumbel distribution is the Euler–Mascheroni constant, which is
![]() $ - \int_0^\infty {{\rm e}^{ - y}}\ln y\; {\rm d}y = 0.5772 \ldots $
$ - \int_0^\infty {{\rm e}^{ - y}}\ln y\; {\rm d}y = 0.5772 \ldots $
Recall that the support of μ is defined by
i.e. the support of μ is the smallest closed set in ℝd having μ-measure one.
Theorem 2.2
Assume that β ∈ (0, 1), c max < ∞, and δ > 0 such that, for any r, s > 0 and any x, z ∈ supp(μ) with ‖x − z‖ ≥ max{r, s} and μ(S(x, r)) = μ(S(z, s)) ≤ δ, we have
and
Then
 $$\sum\limits_{i = 1}^n {\bf 1}\{ n\mu \{ S({X_i},{R_{i,n}})\} \gt y + \ln n\}\buildrel {\rm{D}} \over \longrightarrow {\rm{Po}}(\exp ( - y)),\quad \quad y \in {\mathbb R},$$
$$\sum\limits_{i = 1}^n {\bf 1}\{ n\mu \{ S({X_i},{R_{i,n}})\} \gt y + \ln n\}\buildrel {\rm{D}} \over \longrightarrow {\rm{Po}}(\exp ( - y)),\quad \quad y \in {\mathbb R},$$
and, hence,
Remark 2.1
It is easy to see that (2.5) and (2.6) hold if the density is both bounded from above by f max and bounded away from 0 by f min > 0. Indeed, setting
we have
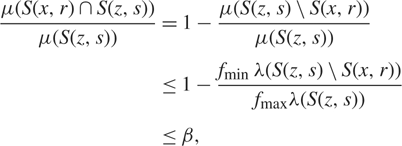 $$\matrix{ {{{\mu (S(x,r) \cap S(z,s))} \over {\mu (S(z,s))}}} \hfill & = \hfill & {1 - {{\mu (S(z,s)\backslash S(x,r))} \over {\mu (S(z,s))}}} \hfill \cr {} \hfill & \le \hfill & {1 - {{{f_{{\rm{min}}}} \lambda (S(z,s)\backslash S(x,r))} \over {{f_{{\rm{max}}}}\lambda (S(z,s))}}} \hfill \cr {} \hfill & \le \hfill & {\beta ,} \hfill \cr } $$
$$\matrix{ {{{\mu (S(x,r) \cap S(z,s))} \over {\mu (S(z,s))}}} \hfill & = \hfill & {1 - {{\mu (S(z,s)\backslash S(x,r))} \over {\mu (S(z,s))}}} \hfill \cr {} \hfill & \le \hfill & {1 - {{{f_{{\rm{min}}}} \lambda (S(z,s)\backslash S(x,r))} \over {{f_{{\rm{max}}}}\lambda (S(z,s))}}} \hfill \cr {} \hfill & \le \hfill & {\beta ,} \hfill \cr } $$
because ‖x − z‖ ≥ max{r, s}. Moreover,
A challenging problem left is to weaken the conditions of Theorem 2.2 or to prove that (2.7) and (2.8) hold without any conditions on the density. We believe that such universal limit results are possible because the summands in (2.7) are identically distributed, and their distribution does not depend on the actual density. Further discussion of condition (2.5) is given in Section 5.
3. The maximum nearest-neighbour ball for a nonhomogeneous Poisson process
In this section we consider the nonhomogeneous Poisson process X 1, …, XN defined by (1.1). Setting
the following result is the Poisson analogue to Theorem 2.1.
Theorem 3.1
Without any restriction on the density f, we have
 $${\mathbb P}(n{\widetilde P_n} - \ln n \ge y) \le {{\rm{e}}^{ - y}}\exp \left({{{{(y + \ln n)}^2}} \over n}\right),\quad \quad y \in {\mathbb R}.$$
$${\mathbb P}(n{\widetilde P_n} - \ln n \ge y) \le {{\rm{e}}^{ - y}}\exp \left({{{{(y + \ln n)}^2}} \over n}\right),\quad \quad y \in {\mathbb R}.$$
4. Proofs
Proof of Theorem 2.1. Since the right-hand side of (2.4) is larger than 1 if y < 0, we take y ≥ 0 in what follows. Moreover, in view of Pn ≤ 1 the left-hand side of (2.4) vanishes if y > n − ln n. We therefore assume without loss of generality that
For a fixed x ∈ ℝd, let
be the distribution function of ‖x − X‖. By the probability integral transform (cf. [Reference Biau and Devroye3, p.8]), the random variable
is uniformly distributed on [0, 1]. We thus have
where
![]() $H_x^{ - 1}(p) = \inf \{ r:{H_x}(r) \ge p\} $
. It follows that
$H_x^{ - 1}(p) = \inf \{ r:{H_x}(r) \ge p\} $
. It follows that
 $$\matrix{ {\mathbb P}{(n{P_n} - \ln n \ge y)} \hfill & = \hfill & {\mathbb P}{(n\mathop {\max }\limits_{1 \le i \le n} \mu \{ S({X_i},{R_{i,n}})\} - \ln n \ge y)} \hfill \cr {} \hfill & \le \hfill & {n{\mathbb P} (n\mu \{ S({X_1},{R_{1,n}})\} - \ln n \ge y)} \hfill \cr {} \hfill & = \hfill & {n{\mathbb P} \left(\mu \{ S({X_1},{R_{1,n}})\} \ge {{y + \ln n} \over n}\right)} \hfill \cr {} \hfill & = \hfill & {n{\mathbb P} \left(\mathop {\min }\limits_{2 \le j \le n} \mu \{ S({X_1},\parallel {X_1} - {X_j}\parallel )\} \ge {{y + \ln n} \over n}\right).} \hfill \cr } $$
$$\matrix{ {\mathbb P}{(n{P_n} - \ln n \ge y)} \hfill & = \hfill & {\mathbb P}{(n\mathop {\max }\limits_{1 \le i \le n} \mu \{ S({X_i},{R_{i,n}})\} - \ln n \ge y)} \hfill \cr {} \hfill & \le \hfill & {n{\mathbb P} (n\mu \{ S({X_1},{R_{1,n}})\} - \ln n \ge y)} \hfill \cr {} \hfill & = \hfill & {n{\mathbb P} \left(\mu \{ S({X_1},{R_{1,n}})\} \ge {{y + \ln n} \over n}\right)} \hfill \cr {} \hfill & = \hfill & {n{\mathbb P} \left(\mathop {\min }\limits_{2 \le j \le n} \mu \{ S({X_1},\parallel {X_1} - {X_j}\parallel )\} \ge {{y + \ln n} \over n}\right).} \hfill \cr } $$
Now (4.1) and (4.3) imply that
 $$\matrix{ {\mathbb P}{(n{P_n} - \ln n \ge y)} \hfill & \le \hfill & {n {\mathbb E}\left[{\mathbb P}\left(\mathop {\min }\limits_{2 \le j \le n} \mu \{ S({X_1},\parallel {X_1} - {X_j}\parallel )\} \ge {{y + \ln n} \over n}|{X_1}\right)\right]} \hfill \cr {} \hfill & = \hfill & {n{{\left(1 - {{y + \ln n} \over n}\right)}^{n - 1}}} \hfill \cr {} \hfill & \le \hfill & {n\exp \left( - {{(y + \ln n)(n - 1)} \over n}\right)} \hfill \cr {} \hfill & = \hfill & {\exp \left( - {{n - 1} \over n}y + {{\ln n} \over n}\right).} \hfill \cr } $$
$$\matrix{ {\mathbb P}{(n{P_n} - \ln n \ge y)} \hfill & \le \hfill & {n {\mathbb E}\left[{\mathbb P}\left(\mathop {\min }\limits_{2 \le j \le n} \mu \{ S({X_1},\parallel {X_1} - {X_j}\parallel )\} \ge {{y + \ln n} \over n}|{X_1}\right)\right]} \hfill \cr {} \hfill & = \hfill & {n{{\left(1 - {{y + \ln n} \over n}\right)}^{n - 1}}} \hfill \cr {} \hfill & \le \hfill & {n\exp \left( - {{(y + \ln n)(n - 1)} \over n}\right)} \hfill \cr {} \hfill & = \hfill & {\exp \left( - {{n - 1} \over n}y + {{\ln n} \over n}\right).} \hfill \cr } $$
Proof of Theorem 3.1. We again assume that (4.1) holds in what follows. By conditioning on N, we have
 $$\matrix{ {\mathbb P}{(n{{\widetilde P}_n} - \ln n \ge y)} \hfill & = \hfill & {\sum\limits_{k = 1}^\infty {\mathbb P}(n{{\widetilde P}_n} - \ln n \ge y|N = k){\mathbb P}(N = k)} \hfill \cr {} \hfill & = \hfill & {\sum\limits_{k = 1}^\infty {\mathbb P}(n{P_k} - \ln n \ge y){\mathbb P}(N = k).} \hfill \cr } $$
$$\matrix{ {\mathbb P}{(n{{\widetilde P}_n} - \ln n \ge y)} \hfill & = \hfill & {\sum\limits_{k = 1}^\infty {\mathbb P}(n{{\widetilde P}_n} - \ln n \ge y|N = k){\mathbb P}(N = k)} \hfill \cr {} \hfill & = \hfill & {\sum\limits_{k = 1}^\infty {\mathbb P}(n{P_k} - \ln n \ge y){\mathbb P}(N = k).} \hfill \cr } $$
Setting yn := (y + ln n)/n, we obtain
and Theorem 2.1 implies that
 $$\matrix{ {\mathbb P} {(k{P_k} - \ln k \ge k{y_n} - \ln k)} \hfill & \le \hfill & {\exp \left( - {{k - 1} \over k}(k{y_n} - \ln k) + {{\ln k} \over k}\right)} \hfill \cr {} \hfill & = \hfill & {\exp \left( - (k - 1){y_n} + \ln k\right).} \hfill \cr } $$
$$\matrix{ {\mathbb P} {(k{P_k} - \ln k \ge k{y_n} - \ln k)} \hfill & \le \hfill & {\exp \left( - {{k - 1} \over k}(k{y_n} - \ln k) + {{\ln k} \over k}\right)} \hfill \cr {} \hfill & = \hfill & {\exp \left( - (k - 1){y_n} + \ln k\right).} \hfill \cr } $$
It follows that
 $$\matrix{ {\mathbb P}{(n{{\widetilde P}_n} - \ln n \ge y)} \hfill & \le \hfill & {\sum\limits_{k = 1}^\infty \exp ( - (k - 1){y_n} + \ln k){\mathbb P}(N = k)} \hfill \cr {} \hfill & = \hfill & {{{\rm e}^{{y_n} - n}}\sum\limits_{k = 1}^\infty k{{({{\rm e}^{ - {y_n}}})}^k}{{{n^k}} \over {k!}}} \hfill \cr {} \hfill & = \hfill & {{{\rm e}^{{y_n} - n}}\sum\limits_{k = 1}^\infty {{{{(n{{\rm e}^{ - {y_n}}})}^k}} \over {(k - 1)!}}} \hfill \cr {} \hfill & = \hfill & {n{{\rm e}^{{y_n} - n - {y_n}}}\exp (n{{\rm e}^{ - {y_n}}})} \hfill \cr {} \hfill & = \hfill & {n\exp ( - n(1 - {{\rm e}^{ - {y_n}}})).} \hfill \cr } $$
$$\matrix{ {\mathbb P}{(n{{\widetilde P}_n} - \ln n \ge y)} \hfill & \le \hfill & {\sum\limits_{k = 1}^\infty \exp ( - (k - 1){y_n} + \ln k){\mathbb P}(N = k)} \hfill \cr {} \hfill & = \hfill & {{{\rm e}^{{y_n} - n}}\sum\limits_{k = 1}^\infty k{{({{\rm e}^{ - {y_n}}})}^k}{{{n^k}} \over {k!}}} \hfill \cr {} \hfill & = \hfill & {{{\rm e}^{{y_n} - n}}\sum\limits_{k = 1}^\infty {{{{(n{{\rm e}^{ - {y_n}}})}^k}} \over {(k - 1)!}}} \hfill \cr {} \hfill & = \hfill & {n{{\rm e}^{{y_n} - n - {y_n}}}\exp (n{{\rm e}^{ - {y_n}}})} \hfill \cr {} \hfill & = \hfill & {n\exp ( - n(1 - {{\rm e}^{ - {y_n}}})).} \hfill \cr } $$
Since z ≥ 0 entails e−z ≤ 1 − z + z 2, we finally obtain
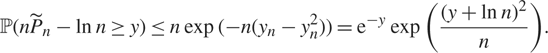 $${\mathbb P}(n{\widetilde P_n} - \ln n \ge y) \le n\exp ( - n({y_n} - y_n^2)) = {{\rm e}^{ - y}}\exp \left({{{{(y + \ln n)}^2}} \over n}\right).$$
$${\mathbb P}(n{\widetilde P_n} - \ln n \ge y) \le n\exp ( - n({y_n} - y_n^2)) = {{\rm e}^{ - y}}\exp \left({{{{(y + \ln n)}^2}} \over n}\right).$$
The main tool in the proof of Theorem 2.2 is the following result. A similar result has been established in the context of random tessellations; see Lemma 4.1 of [Reference Chenavier and Hemsley6].
Proposition 4.1
For each n ≥ 2, let A n,1, …, An,n be exchangeable events, and let
 $${Y_n}:=\sum\limits_{j = 1}^n {\bf 1}\{ {A_{n,j}}\} .$$
$${Y_n}:=\sum\limits_{j = 1}^n {\bf 1}\{ {A_{n,j}}\} .$$
If, for some ν ∈ (0, ∞),
then
Proof. The proof uses the method of moments; see, e.g. [Reference Billingsley4, Section 30]. Setting
and writing Z (k) = Z(Z − 1) ⋅⋅⋅ (Z − k + 1) for the kth descending factorial of a random variable Z, we have
Since A n,1, …, An,n are exchangeable, (4.4) implies that
Now νk = 𝔼[Y (k)], where Y has the Poisson distribution Po(ν). We thus have
Since
 $$Y_n^k = \sum\limits_{j = 0}^k \left\{ \matrix{ k \hfill \cr j \hfill \cr} \right\}Y_n^{(j)},$$
$$Y_n^k = \sum\limits_{j = 0}^k \left\{ \matrix{ k \hfill \cr j \hfill \cr} \right\}Y_n^{(j)},$$
where
![]() $\left\{ \matrix{ k \hfill \cr 0 \hfill \cr} \right\}, \ldots ,\left\{ \matrix{ k \hfill \cr k \hfill \cr} \right\}$
denote Stirling numbers of the second kind (see, e.g. [Reference Graham, Knuth and Patashnik10, p. 262]), (4.5) entails
$\left\{ \matrix{ k \hfill \cr 0 \hfill \cr} \right\}, \ldots ,\left\{ \matrix{ k \hfill \cr k \hfill \cr} \right\}$
denote Stirling numbers of the second kind (see, e.g. [Reference Graham, Knuth and Patashnik10, p. 262]), (4.5) entails
![]() $\mathop {\lim }\nolimits_{n \to \infty } {\mathbb E}[Y_n^k] = {\mathbb E}[{Y^k}]$
for each k ≥ 1. Since the distribution of Y is uniquely determined by the sequence of moments (𝔼[Yk]), k ≥ 1, the assertion follows.
$\mathop {\lim }\nolimits_{n \to \infty } {\mathbb E}[Y_n^k] = {\mathbb E}[{Y^k}]$
for each k ≥ 1. Since the distribution of Y is uniquely determined by the sequence of moments (𝔼[Yk]), k ≥ 1, the assertion follows.
Proof of Theorem 2.2. Fix y ∈ ℝ. In what follows, we will verify (4.4) for
and ν = exp (−y). Throughout the proof, we tacitly assume that
This assumption entails no loss of generality since n tends to ∞. With Hx(⋅) given in (4.2), we set
 $$R_{i,n}^*H_{{X_i}}^{ - 1}\left({{y + \ln n} \over n}\right),\quad \quad i \in \{ 1, \ldots ,n\} .$$
$$R_{i,n}^*H_{{X_i}}^{ - 1}\left({{y + \ln n} \over n}\right),\quad \quad i \in \{ 1, \ldots ,n\} .$$
For the special case k = 1, conditioning on X 1 and (4.3) yield
 $$\matrix{ {n{\mathbb P}({A_{n,1}})} \hfill & = \hfill & {n{\mathbb P}(\mu (S({X_1},{R_{1,n}})) \ge {y_n})} \hfill \cr {} \hfill & = \hfill & {n{\mathbb E}[{\mathbb P}(\mu (S({X_1},{R_{1,n}})) \ge {y_n}|{X_1})]} \hfill \cr {} \hfill & = \hfill & {n{\mathbb E}[(1 - \mu (S({X_1},H_{{X_1}}^{ - 1}({y_n}{{))))}^{n - 1}}]} \hfill \cr {} \hfill & = \hfill & {n{{(1 - {{y + \ln n} \over n})}^{n - 1}}.} \hfill \cr } $$
$$\matrix{ {n{\mathbb P}({A_{n,1}})} \hfill & = \hfill & {n{\mathbb P}(\mu (S({X_1},{R_{1,n}})) \ge {y_n})} \hfill \cr {} \hfill & = \hfill & {n{\mathbb E}[{\mathbb P}(\mu (S({X_1},{R_{1,n}})) \ge {y_n}|{X_1})]} \hfill \cr {} \hfill & = \hfill & {n{\mathbb E}[(1 - \mu (S({X_1},H_{{X_1}}^{ - 1}({y_n}{{))))}^{n - 1}}]} \hfill \cr {} \hfill & = \hfill & {n{{(1 - {{y + \ln n} \over n})}^{n - 1}}.} \hfill \cr } $$
Using the inequalities 1 − 1/t ≤ ln t ≤ t − 1 gives limn→ ∞ n ℙ(A n,1) = e−y. Thus, (4.4) is proved for k = 1, remarkably without any condition on the underlying density f. We now assume that k ≥ 2. The proof of (4.4) for this case is quite technical, but the basic reasoning is clear-cut: the main idea for showing that nkℙ(A n,1 ∩⋅⋅⋅∩ An,n) ≈ (nℙ(A n,1))k ≈ exp (−ky)– which yields the Poisson convergence (2.7) and the Gumbel limit (2.8) – is to prove that the radii have the same behaviour as if they were independent. To this end, we consider two subcases: in the first subcase, which leads to independent events, the balls are sufficiently separated from one another, with the opposite subcase shown to be of asymptotically negligible probability. To proceed, set
Then
![]() ${R_{i,n}} = \min \{ {\widetilde R_{i,k,n}},{r_{i,k}}\} $
. Note that, on a set of probability 1, we have
${R_{i,n}} = \min \{ {\widetilde R_{i,k,n}},{r_{i,k}}\} $
. Note that, on a set of probability 1, we have
![]() ${R_{i,n}} = {\widetilde R_{i,k,n}}$
for each i ∈ {1, …, k} if n is large enough.
${R_{i,n}} = {\widetilde R_{i,k,n}}$
for each i ∈ {1, …, k} if n is large enough.
Conditioning on X 1, …, Xk we have
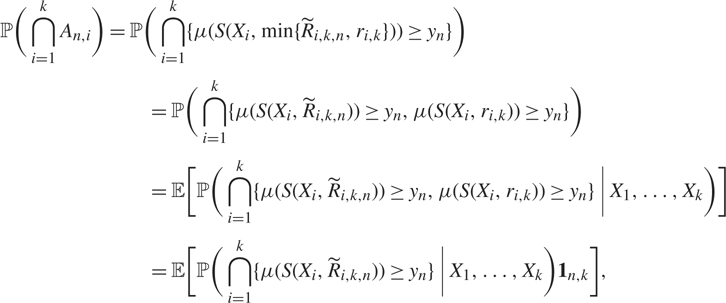 $$\eqalign{{{\mathbb P}\left(\bigcap\limits_{i = 1}^k {A_{n,i}}\right)} & = {{\mathbb P}\left(\bigcap\limits_{i = 1}^k \{ \mu (S({X_i},\min \{ {{\widetilde R}_{i,k,n}},{r_{i,k}}\} )) \ge {y_n}\} \right)} \cr & = {{\mathbb P}\left(\bigcap\limits_{i = 1}^k \{ \mu (S({X_i},{{\widetilde R}_{i,k,n}})) \ge {y_n},\mu (S({X_i},{r_{i,k}})) \ge {y_n}\} \right )} \cr & = {{\mathbb E}\left [{\mathbb P}\left(\bigcap\limits_{i = 1}^k \{ \mu (S({X_i},{{\widetilde R}_{i,k,n}})) \ge {y_n},\mu (S({X_i},{r_{i,k}})) \ge {y_n}\} |{X_1}, \ldots ,{X_k}\right)\right ]} \cr & = {{\mathbb E}\left [{\mathbb P}\left(\bigcap\limits_{i = 1}^k \{ \mu (S({X_i},{{\widetilde R}_{i,k,n}})) \ge {y_n}\} |{X_1}, \ldots ,{X_k}\right){{{\bf 1}}_{n,k}}\right ],}} $$
$$\eqalign{{{\mathbb P}\left(\bigcap\limits_{i = 1}^k {A_{n,i}}\right)} & = {{\mathbb P}\left(\bigcap\limits_{i = 1}^k \{ \mu (S({X_i},\min \{ {{\widetilde R}_{i,k,n}},{r_{i,k}}\} )) \ge {y_n}\} \right)} \cr & = {{\mathbb P}\left(\bigcap\limits_{i = 1}^k \{ \mu (S({X_i},{{\widetilde R}_{i,k,n}})) \ge {y_n},\mu (S({X_i},{r_{i,k}})) \ge {y_n}\} \right )} \cr & = {{\mathbb E}\left [{\mathbb P}\left(\bigcap\limits_{i = 1}^k \{ \mu (S({X_i},{{\widetilde R}_{i,k,n}})) \ge {y_n},\mu (S({X_i},{r_{i,k}})) \ge {y_n}\} |{X_1}, \ldots ,{X_k}\right)\right ]} \cr & = {{\mathbb E}\left [{\mathbb P}\left(\bigcap\limits_{i = 1}^k \{ \mu (S({X_i},{{\widetilde R}_{i,k,n}})) \ge {y_n}\} |{X_1}, \ldots ,{X_k}\right){{{\bf 1}}_{n,k}}\right ],}} $$
where
 $${{\bf 1}_{n,k}}\prod\limits_{i = 1}^k {\bf 1}\{ \mu (S({X_i},{r_{i,k}})) \ge {y_n}\} .$$
$${{\bf 1}_{n,k}}\prod\limits_{i = 1}^k {\bf 1}\{ \mu (S({X_i},{r_{i,k}})) \ge {y_n}\} .$$
Furthermore, we obtain
 $$\eqalign{& {{\mathbb P} \left(\bigcap\limits_{i = 1}^k \{ \mu {(S({X_i},{\widetilde R}_{i,k,n}))} {\ge {y_n}}\} |{X_1}, \ldots ,{X_k}\right)} \cr & \quad = {{\mathbb P}\left(\bigcap\limits_{i = 1}^k \{ {{\widetilde R}_{i,k,n}} \ge H_{{X_i}}^{ - 1}({y_n})\} |{X_1}, \ldots ,{X_k}\right)} \cr & \quad = {{\mathbb P}\left(\bigcap\limits_{i = 1}^k \{ {{\widetilde R}_{i,k,n}} \ge R_{i,n}^*\} |{X_1}, \ldots ,{X_k}\right)} \cr & \quad = {{\mathbb P}\left({X_{k + 1}}, \ldots ,{X_n} \notin \bigcup\limits_{i = 1}^k S({X_i},R_{i,n}^*)|{X_1}, \ldots ,{X_k}\right)} \cr & \quad = {{{\left(1 - \mu \left(\bigcup\limits_{i = 1}^k S({X_i},R_{i,n}^*)\right)\right)}^{n - k}}.}} $$
$$\eqalign{& {{\mathbb P} \left(\bigcap\limits_{i = 1}^k \{ \mu {(S({X_i},{\widetilde R}_{i,k,n}))} {\ge {y_n}}\} |{X_1}, \ldots ,{X_k}\right)} \cr & \quad = {{\mathbb P}\left(\bigcap\limits_{i = 1}^k \{ {{\widetilde R}_{i,k,n}} \ge H_{{X_i}}^{ - 1}({y_n})\} |{X_1}, \ldots ,{X_k}\right)} \cr & \quad = {{\mathbb P}\left(\bigcap\limits_{i = 1}^k \{ {{\widetilde R}_{i,k,n}} \ge R_{i,n}^*\} |{X_1}, \ldots ,{X_k}\right)} \cr & \quad = {{\mathbb P}\left({X_{k + 1}}, \ldots ,{X_n} \notin \bigcup\limits_{i = 1}^k S({X_i},R_{i,n}^*)|{X_1}, \ldots ,{X_k}\right)} \cr & \quad = {{{\left(1 - \mu \left(\bigcup\limits_{i = 1}^k S({X_i},R_{i,n}^*)\right)\right)}^{n - k}}.}} $$
Note that we have the obvious lower bound
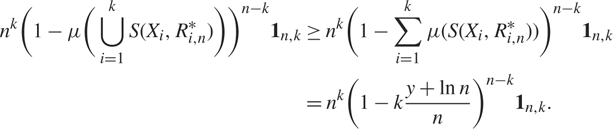 $$\matrix{ {{n^k}{{\left(1 - \mu \left(\bigcup\limits_{i = 1}^k S({X_i},R_{i,n}^*)\right)\right)}^{n - k}}{{\bf 1}_{n,k}}} \hfill & \ge \hfill & {{n^k}{{\left(1 - \sum\limits_{i = 1}^k \mu (S({X_i},R_{i,n}^*))\right)}^{n - k}}{{\bf 1}_{n,k}}} \hfill \cr {} \hfill & = \hfill & {{n^k}{{\left(1 - k{{y + \ln n} \over n}\right)}^{n - k}}{{\bf 1}_{n,k}}.} \hfill \cr } $$
$$\matrix{ {{n^k}{{\left(1 - \mu \left(\bigcup\limits_{i = 1}^k S({X_i},R_{i,n}^*)\right)\right)}^{n - k}}{{\bf 1}_{n,k}}} \hfill & \ge \hfill & {{n^k}{{\left(1 - \sum\limits_{i = 1}^k \mu (S({X_i},R_{i,n}^*))\right)}^{n - k}}{{\bf 1}_{n,k}}} \hfill \cr {} \hfill & = \hfill & {{n^k}{{\left(1 - k{{y + \ln n} \over n}\right)}^{n - k}}{{\bf 1}_{n,k}}.} \hfill \cr } $$
Since the latter converges almost surely to e−ky as n → ∞, Fatou’s lemma implies that
 $$\eqalign{{\mathop {\lim \,{\rm inf}}\limits_{n \to \infty }\; {n^k}{\mathbb P}\left(\bigcap\limits_{i = 1}^k {A_{n,i}}\right)} & = {\mathop {\lim \,{\rm inf}}\limits_{n \to \infty } {\mathbb E}\left[{n^k}{{\left(1 - \mu \left(\bigcup\limits_{i = 1}^k S({X_i},R_{i,n}^*)\right)\right)}^{n - k}}{{\bf 1}_{n,k}}\right]} \cr & \ge {{\mathbb E}\left[\mathop {\lim \,{\rm inf}}\limits_{n \to \infty } {n^k}{{\left(1 - \mu \left(\bigcup\limits_{i = 1}^k S({X_i},R_{i,n}^*)\right)\right)}^{n - k}}{{\bf 1}_{n,k}}\right]} \cr & \ge {{{\rm e}^{ - ky}}.} } $$
$$\eqalign{{\mathop {\lim \,{\rm inf}}\limits_{n \to \infty }\; {n^k}{\mathbb P}\left(\bigcap\limits_{i = 1}^k {A_{n,i}}\right)} & = {\mathop {\lim \,{\rm inf}}\limits_{n \to \infty } {\mathbb E}\left[{n^k}{{\left(1 - \mu \left(\bigcup\limits_{i = 1}^k S({X_i},R_{i,n}^*)\right)\right)}^{n - k}}{{\bf 1}_{n,k}}\right]} \cr & \ge {{\mathbb E}\left[\mathop {\lim \,{\rm inf}}\limits_{n \to \infty } {n^k}{{\left(1 - \mu \left(\bigcup\limits_{i = 1}^k S({X_i},R_{i,n}^*)\right)\right)}^{n - k}}{{\bf 1}_{n,k}}\right]} \cr & \ge {{{\rm e}^{ - ky}}.} } $$
It thus remains to show that
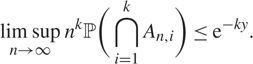 $$\mathop {\lim \,{\rm sup}}\limits_{n \to \infty } \,{n^k}{\mathbb P}\left(\bigcap\limits_{i = 1}^k {A_{n,i}}\right) \le {{\rm e}^{ - ky}}.$$
$$\mathop {\lim \,{\rm sup}}\limits_{n \to \infty } \,{n^k}{\mathbb P}\left(\bigcap\limits_{i = 1}^k {A_{n,i}}\right) \le {{\rm e}^{ - ky}}.$$
Let Dn be the event that the balls
![]() $S({X_i},R_{i,n}^*)$
, i = 1, …, k, are pairwise disjoint. We have
$S({X_i},R_{i,n}^*)$
, i = 1, …, k, are pairwise disjoint. We have
 $$\matrix{ {\mathop {\lim \,{\rm sup}\,}\limits_{n \to \infty } {n^k}{\mathbb P}\left(\bigcap\limits_{i = 1}^k {A_{n,i}}\right)} \hfill \cr { = \mathop {\lim \,{\rm sup}\,}\limits_{n \to \infty } {n^k}{\mathbb E}\left[(1 - \mu (\bigcup\limits_{i = 1}^k S({X_i},R_{i,n}^*{{)))}^{n - k}}{{\bf 1}_{n,k}}\right]} \hfill \cr {\le \mathop {\lim \,{\rm sup}\,}\limits_{n \to \infty } {n^k}{\mathbb E}\left[\exp \left( - (n - k)\mu \left(\bigcup\limits_{i = 1}^k S({X_i},R_{i,n}^*)\right)\right){{\bf 1}_{n,k}}\right]} \hfill \cr {\le \mathop {\lim \,{\rm sup}}\limits_{n \to \infty } \,{n^k}{\mathbb E}\left[\exp \left( - (n - k)k{{y + \ln n} \over n}\right){\bf 1}\{ {D_n}\} \right]} \hfill \cr {\quad + \mathop {\lim \,{\rm sup}\,}\limits_{n \to \infty } {n^k}{\mathbb E}\left[\exp \left( - (n - k)\mu \left(\bigcup\limits_{i = 1}^k S({X_i},R_{i,n}^*)\right)\right){\bf 1}\{ D_n^{\rm{c}}\} {{\bf 1}_{n,k}}\right]} \hfill \cr {\le {{\rm e}^{ - ky}} + \mathop {\lim \,{\rm sup}}\limits_{n \to \infty } \,{n^k}{\mathbb E}\left[\exp \left( - (n - k)\mu \left(\bigcup\limits_{i = 1}^k S({X_i},R_{i,n}^*)\right)\right){\bf 1}\{ D_n^{\rm{c}}\} {{\bf 1}_{n,k}}\right].} \hfill \cr } $$
$$\matrix{ {\mathop {\lim \,{\rm sup}\,}\limits_{n \to \infty } {n^k}{\mathbb P}\left(\bigcap\limits_{i = 1}^k {A_{n,i}}\right)} \hfill \cr { = \mathop {\lim \,{\rm sup}\,}\limits_{n \to \infty } {n^k}{\mathbb E}\left[(1 - \mu (\bigcup\limits_{i = 1}^k S({X_i},R_{i,n}^*{{)))}^{n - k}}{{\bf 1}_{n,k}}\right]} \hfill \cr {\le \mathop {\lim \,{\rm sup}\,}\limits_{n \to \infty } {n^k}{\mathbb E}\left[\exp \left( - (n - k)\mu \left(\bigcup\limits_{i = 1}^k S({X_i},R_{i,n}^*)\right)\right){{\bf 1}_{n,k}}\right]} \hfill \cr {\le \mathop {\lim \,{\rm sup}}\limits_{n \to \infty } \,{n^k}{\mathbb E}\left[\exp \left( - (n - k)k{{y + \ln n} \over n}\right){\bf 1}\{ {D_n}\} \right]} \hfill \cr {\quad + \mathop {\lim \,{\rm sup}\,}\limits_{n \to \infty } {n^k}{\mathbb E}\left[\exp \left( - (n - k)\mu \left(\bigcup\limits_{i = 1}^k S({X_i},R_{i,n}^*)\right)\right){\bf 1}\{ D_n^{\rm{c}}\} {{\bf 1}_{n,k}}\right]} \hfill \cr {\le {{\rm e}^{ - ky}} + \mathop {\lim \,{\rm sup}}\limits_{n \to \infty } \,{n^k}{\mathbb E}\left[\exp \left( - (n - k)\mu \left(\bigcup\limits_{i = 1}^k S({X_i},R_{i,n}^*)\right)\right){\bf 1}\{ D_n^{\rm{c}}\} {{\bf 1}_{n,k}}\right].} \hfill \cr } $$
It thus remains to show that
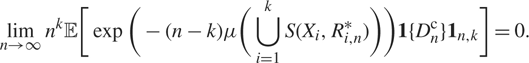 $$\mathop {\lim }\limits_{n \to \infty } {n^k}{\mathbb E}\left[\exp \left( - (n - k)\mu \left(\bigcup\limits_{i = 1}^k S({X_i},R_{i,n}^*)\right)\right){\bf 1}\{ D_n^{\rm{c}}\} {{\bf 1}_{n,k}}\right] = 0.$$
$$\mathop {\lim }\limits_{n \to \infty } {n^k}{\mathbb E}\left[\exp \left( - (n - k)\mu \left(\bigcup\limits_{i = 1}^k S({X_i},R_{i,n}^*)\right)\right){\bf 1}\{ D_n^{\rm{c}}\} {{\bf 1}_{n,k}}\right] = 0.$$
Under some additional smoothness conditions on the density, Henze [Reference Henze13] verified (4.7)for the related problem of finding the limit distribution of the random variable figuring in (2.1). By analogy with his proof technique, we introduce an equivalence relation on the set {1, …, k} as follows. An equivalence class consists of a singleton {i} if
for each j ≠ i. Otherwise, i and j are called equivalent if there is a subset {i 1, …, iℓ } of {1, …, k} such that i = i 1, j = iℓ, and
for each m ∈ {1, …, ℓ − 1}. Let 𝒫 = {Q 1, …, Qq} be a partition of {1, …, k}, and denote by Eu the event that Qu forms an equivalence class. For the event Dn, the partition 𝒫 0 := {{1}, …, {k}} is the trivial partition, while on the complement
![]() $D_n^{\rm{c}}$
any partition 𝒫 is nontrivial, which means that q < k. In order to prove (4.7), we have to show that
$D_n^{\rm{c}}$
any partition 𝒫 is nontrivial, which means that q < k. In order to prove (4.7), we have to show that
 $$\mathop {\lim \,{\rm sup}\,}\limits_{n \to \infty } {n^k}{\mathbb E}\left[\exp \left( - (n - k)\mu \left(\bigcup\limits_{i = 1}^k S({X_i},R_{i,n}^*)\right)\right){{\bf 1}_{n,k}}\prod\limits_{u = 1}^q {\bf 1}\{ {E_u}\} \right] = 0$$
$$\mathop {\lim \,{\rm sup}\,}\limits_{n \to \infty } {n^k}{\mathbb E}\left[\exp \left( - (n - k)\mu \left(\bigcup\limits_{i = 1}^k S({X_i},R_{i,n}^*)\right)\right){{\bf 1}_{n,k}}\prod\limits_{u = 1}^q {\bf 1}\{ {E_u}\} \right] = 0$$
for each nontrivial partition 𝒫. Since balls that belong to different equivalence classes are disjoint, we have
 $$\matrix{ {\mu \left(\bigcup\limits_{i = 1}^k S({X_i},R_{i,n}^*)\right)\prod\limits_{u = 1}^q {\bf 1}\{ {E_u}\} } \hfill & = \hfill & {\mu \left(\bigcup\limits_{u = 1}^q \bigcup\limits_{i \in {Q_u}} S({X_i},R_{i,n}^*)\right)\prod\limits_{u = 1}^q {\bf 1}\{ {E_u}\} } \hfill \cr {} \hfill & = \hfill & {\sum\limits_{u = 1}^q \mu \left(\bigcup\limits_{i \in {Q_u}} S({X_i},R_{i,n}^*)\right)\prod\limits_{u = 1}^q {\bf 1}\{ {E_u}\} .} \hfill \cr } $$
$$\matrix{ {\mu \left(\bigcup\limits_{i = 1}^k S({X_i},R_{i,n}^*)\right)\prod\limits_{u = 1}^q {\bf 1}\{ {E_u}\} } \hfill & = \hfill & {\mu \left(\bigcup\limits_{u = 1}^q \bigcup\limits_{i \in {Q_u}} S({X_i},R_{i,n}^*)\right)\prod\limits_{u = 1}^q {\bf 1}\{ {E_u}\} } \hfill \cr {} \hfill & = \hfill & {\sum\limits_{u = 1}^q \mu \left(\bigcup\limits_{i \in {Q_u}} S({X_i},R_{i,n}^*)\right)\prod\limits_{u = 1}^q {\bf 1}\{ {E_u}\} .} \hfill \cr } $$
Writing |B| for the number of elements of a finite set B, it follows that
 $$\matrix{ {{n^k}\exp \left( - (n - k)\mu \left(\bigcup\limits_{i = 1}^k S({X_i},R_{i,n}^*)\right)\right)\prod\limits_{i = 1}^k {\bf 1}\{ \mu (S({X_i},{r_{i,k}})) \ge {y_n}\} \prod\limits_{u = 1}^q {\bf 1}\{ {E_u}\} } \hfill \cr {\le {{\rm e}^k}\prod\limits_{u = 1}^q {n^{|{Q_u}|}}\prod\limits_{u = 1}^q {{\rm e}^{ - n\mu (\bigcup\limits_{i \in {Q_u}} S({X_i},R_{i,n}^*))}}\prod\limits_{u = 1}^q \prod\limits_{i \in {Q_u}} {\bf 1}\{ \mu (S({X_i},{r_{i,k}})) \ge {y_n}\} \prod\limits_{u = 1}^q {\bf 1}\{ {E_u}\} } \hfill \cr { = {{\rm e}^k}\prod\limits_{u = 1}^q \left({n^{|{Q_u}|}}{{\rm e}^{ - n\mu (\bigcup\limits_{i \in {Q_u}} S({X_i},R_{i,n}^*))}}\prod\limits_{i \in {Q_u}} {\bf 1}\{ \mu (S({X_i},{r_{i,k}})) \ge {y_n}\} {\bf 1}\{ {E_u}\} \right).} \hfill \cr } $$
$$\matrix{ {{n^k}\exp \left( - (n - k)\mu \left(\bigcup\limits_{i = 1}^k S({X_i},R_{i,n}^*)\right)\right)\prod\limits_{i = 1}^k {\bf 1}\{ \mu (S({X_i},{r_{i,k}})) \ge {y_n}\} \prod\limits_{u = 1}^q {\bf 1}\{ {E_u}\} } \hfill \cr {\le {{\rm e}^k}\prod\limits_{u = 1}^q {n^{|{Q_u}|}}\prod\limits_{u = 1}^q {{\rm e}^{ - n\mu (\bigcup\limits_{i \in {Q_u}} S({X_i},R_{i,n}^*))}}\prod\limits_{u = 1}^q \prod\limits_{i \in {Q_u}} {\bf 1}\{ \mu (S({X_i},{r_{i,k}})) \ge {y_n}\} \prod\limits_{u = 1}^q {\bf 1}\{ {E_u}\} } \hfill \cr { = {{\rm e}^k}\prod\limits_{u = 1}^q \left({n^{|{Q_u}|}}{{\rm e}^{ - n\mu (\bigcup\limits_{i \in {Q_u}} S({X_i},R_{i,n}^*))}}\prod\limits_{i \in {Q_u}} {\bf 1}\{ \mu (S({X_i},{r_{i,k}})) \ge {y_n}\} {\bf 1}\{ {E_u}\} \right).} \hfill \cr } $$
Note that the inequality above comes from the trivial inequality
 $$\exp \left(k\mu \left(\bigcup\limits_{i = 1}^k S({X_i},R_{i,n}^*)\right)\right) \le {{\rm e}^k}$$
$$\exp \left(k\mu \left(\bigcup\limits_{i = 1}^k S({X_i},R_{i,n}^*)\right)\right) \le {{\rm e}^k}$$
and the fact that
![]() $k = \sum\nolimits_{u = 1}^q |{Q_u}|$
. Thus, (4.8) is proved if we can show that
$k = \sum\nolimits_{u = 1}^q |{Q_u}|$
. Thus, (4.8) is proved if we can show that
 $$\mathop {\lim }\limits_{n \to \infty }{\mathbb E} \left[{n^{|{Q_u}|}}{{\rm e}^{ - n\mu (\bigcup\limits_{i \in {Q_u}} S({X_i},R_{i,n}^*))}}\prod\limits_{i \in {Q_u}} {\bf 1}\{ \mu (S({X_i},{r_{i,k}})) \ge {y_n}\} {\bf 1}\{ {E_u}\} \right] = 0$$
$$\mathop {\lim }\limits_{n \to \infty }{\mathbb E} \left[{n^{|{Q_u}|}}{{\rm e}^{ - n\mu (\bigcup\limits_{i \in {Q_u}} S({X_i},R_{i,n}^*))}}\prod\limits_{i \in {Q_u}} {\bf 1}\{ \mu (S({X_i},{r_{i,k}})) \ge {y_n}\} {\bf 1}\{ {E_u}\} \right] = 0$$
for each u with 2 ≤ |Qu| < k. Without loss of generality, assume that Qu = {1, …, |Qu|}. Then
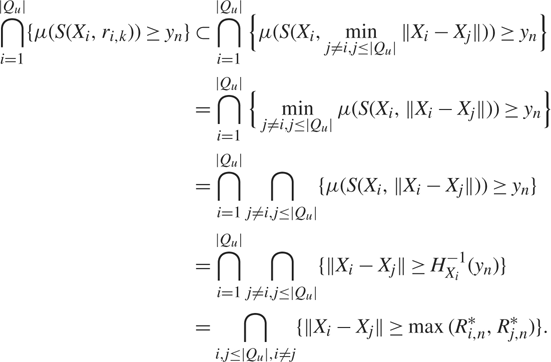 $$\matrix{ {\bigcap\limits_{i = 1}^{|{Q_u}|} \{ \mu (S({X_i},{r_{i,k}})) \ge {y_n}\} \subset } \hfill & = \hfill & {\bigcap\limits_{i = 1}^{|{Q_u}|} \left \{ \mu (S({X_i},\mathop {\min }\limits_{j \ne i,j \le |{Q_u}|} \parallel {X_i} - {X_j}\parallel )) \ge {y_n}\right \} } \hfill \cr {} \hfill & = \hfill & {\bigcap\limits_{i = 1}^{|{Q_u}|} \left \{ \mathop {\min }\limits_{j \ne i,j \le |{Q_u}|} \mu (S({X_i},\parallel {X_i} - {X_j}\parallel )) \ge {y_n}\right \} } \hfill \cr {} \hfill & = \hfill & {\bigcap\limits_{i = 1}^{|{Q_u}|} \bigcap\limits_{j \ne i,j \le |{Q_u}|} \left \{ \mu (S({X_i},\parallel {X_i} - {X_j}\parallel )) \ge {y_n}\right \} } \hfill \cr {} \hfill & = \hfill & {\bigcap\limits_{i = 1}^{|{Q_u}|} \bigcap\limits_{j \ne i,j \le |{Q_u}|} \{ \parallel {X_i} - {X_j}\parallel \ge H_{{X_i}}^{ - 1}({y_n})\} } \hfill \cr {} \hfill & = \hfill & {\bigcap\limits_{i,j \le |{Q_u}|,i \ne j} \{ \parallel {X_i} - {X_j}\parallel \ge \max (R_{i,n}^*,R_{j,n}^*)\} .} \hfill \cr } $$
$$\matrix{ {\bigcap\limits_{i = 1}^{|{Q_u}|} \{ \mu (S({X_i},{r_{i,k}})) \ge {y_n}\} \subset } \hfill & = \hfill & {\bigcap\limits_{i = 1}^{|{Q_u}|} \left \{ \mu (S({X_i},\mathop {\min }\limits_{j \ne i,j \le |{Q_u}|} \parallel {X_i} - {X_j}\parallel )) \ge {y_n}\right \} } \hfill \cr {} \hfill & = \hfill & {\bigcap\limits_{i = 1}^{|{Q_u}|} \left \{ \mathop {\min }\limits_{j \ne i,j \le |{Q_u}|} \mu (S({X_i},\parallel {X_i} - {X_j}\parallel )) \ge {y_n}\right \} } \hfill \cr {} \hfill & = \hfill & {\bigcap\limits_{i = 1}^{|{Q_u}|} \bigcap\limits_{j \ne i,j \le |{Q_u}|} \left \{ \mu (S({X_i},\parallel {X_i} - {X_j}\parallel )) \ge {y_n}\right \} } \hfill \cr {} \hfill & = \hfill & {\bigcap\limits_{i = 1}^{|{Q_u}|} \bigcap\limits_{j \ne i,j \le |{Q_u}|} \{ \parallel {X_i} - {X_j}\parallel \ge H_{{X_i}}^{ - 1}({y_n})\} } \hfill \cr {} \hfill & = \hfill & {\bigcap\limits_{i,j \le |{Q_u}|,i \ne j} \{ \parallel {X_i} - {X_j}\parallel \ge \max (R_{i,n}^*,R_{j,n}^*)\} .} \hfill \cr } $$
Note that the last equality follows from the fact that ∩i,j Ai,j = ∩i,j (Ai,j ∩ Aj,i) for any family of events (Ai,j)i,j. We now obtain
 $$\matrix{ {{n^{|{Q_u}|}}{{\rm e}^{ - n\mu (\bigcup\limits_{i \in {Q_u}} S({X_i},R_{i,n}^*))}}\prod\limits_{i \in {Q_u}} {\bf 1}\{ \mu (S({X_i},{r_{i,k}})) \ge {y_n}\} {\bf 1}\{ {E_u}\} } \hfill \cr {\le {n^{|{Q_u}|}}{{\rm e}^{ - n\mu (\bigcup\limits_{i = 1}^{|{Q_u}|} S({X_i},R_{i,n}^*))}}{\bf 1}\left \{ \bigcap\limits_{i,j \le |{Q_u}|,i \ne j} \{ \parallel {X_i} - {X_j}\parallel \ge \max \{ R_{i,n}^*,R_{j,n}^*\} \} \right \} {\bf 1}\{ {E_u}\} } \hfill \cr {\le {n^{|{Q_u}|}}{{\rm e}^{ - n\mu (\bigcup\limits_{i = 1}^2 S({X_i},R_{i,n}^*))}}1\left \{ \bigcap\limits_{i,j \le |{Q_u}|,i \ne j} \{ \parallel {X_i} - {X_j}\parallel \ge \max \{ R_{i,n}^*,R_{j,n}^*\} \} \right \} {\bf 1}\{ {E_u}\} .} \hfill \cr } $$
$$\matrix{ {{n^{|{Q_u}|}}{{\rm e}^{ - n\mu (\bigcup\limits_{i \in {Q_u}} S({X_i},R_{i,n}^*))}}\prod\limits_{i \in {Q_u}} {\bf 1}\{ \mu (S({X_i},{r_{i,k}})) \ge {y_n}\} {\bf 1}\{ {E_u}\} } \hfill \cr {\le {n^{|{Q_u}|}}{{\rm e}^{ - n\mu (\bigcup\limits_{i = 1}^{|{Q_u}|} S({X_i},R_{i,n}^*))}}{\bf 1}\left \{ \bigcap\limits_{i,j \le |{Q_u}|,i \ne j} \{ \parallel {X_i} - {X_j}\parallel \ge \max \{ R_{i,n}^*,R_{j,n}^*\} \} \right \} {\bf 1}\{ {E_u}\} } \hfill \cr {\le {n^{|{Q_u}|}}{{\rm e}^{ - n\mu (\bigcup\limits_{i = 1}^2 S({X_i},R_{i,n}^*))}}1\left \{ \bigcap\limits_{i,j \le |{Q_u}|,i \ne j} \{ \parallel {X_i} - {X_j}\parallel \ge \max \{ R_{i,n}^*,R_{j,n}^*\} \} \right \} {\bf 1}\{ {E_u}\} .} \hfill \cr } $$
We now use the fact that
![]() $\mu (S({X_i},R_{i,n}^*)) = {y_n}$
for each i. Moreover, on the event
$\mu (S({X_i},R_{i,n}^*)) = {y_n}$
for each i. Moreover, on the event
![]() $\{ \parallel {X_i} - {X_j}\parallel \ge \max \{ R_{i,n}^*,R_{j,n}^*\} \} $
, condition (2.5) implies that
$\{ \parallel {X_i} - {X_j}\parallel \ge \max \{ R_{i,n}^*,R_{j,n}^*\} \} $
, condition (2.5) implies that
 $$\matrix{ {n\mu \left (\bigcup\limits_{i = 1}^2 S({X_i},R_{i,n}^*)\right )} \hfill \cr { = n\mu (S({X_1},R_{1,n}^*)) + n\mu (S({X_2},R_{2,n}^*)) - n\mu (S({X_2},R_{2,n}^*) \cap S({X_1},R_{1,n}^*))} \hfill \cr { = n{{y + \ln n} \over n}\left (2 - {{\mu (S({X_2},R_{2,n}^*) \cap S({X_1},R_{1,n}^*))} \over {\mu (S({X_2},R_{2,n}^*))}}\right)} \hfill \cr {\ge (y + \ln n)(2 - \beta )} \hfill \cr { = :(y + \ln n)(1 + \varepsilon )\quad {\rm{(say)}}{\rm{.}}} \hfill \cr } $$
$$\matrix{ {n\mu \left (\bigcup\limits_{i = 1}^2 S({X_i},R_{i,n}^*)\right )} \hfill \cr { = n\mu (S({X_1},R_{1,n}^*)) + n\mu (S({X_2},R_{2,n}^*)) - n\mu (S({X_2},R_{2,n}^*) \cap S({X_1},R_{1,n}^*))} \hfill \cr { = n{{y + \ln n} \over n}\left (2 - {{\mu (S({X_2},R_{2,n}^*) \cap S({X_1},R_{1,n}^*))} \over {\mu (S({X_2},R_{2,n}^*))}}\right)} \hfill \cr {\ge (y + \ln n)(2 - \beta )} \hfill \cr { = :(y + \ln n)(1 + \varepsilon )\quad {\rm{(say)}}{\rm{.}}} \hfill \cr } $$
Note that ε > 0 since 0 < β < 1. Thus,
 $$\matrix{ {{n^{|{Q_u}|}}{\mathbb E}\left[{{\rm e}^{ - n\mu (\bigcup\limits_{i \in {Q_u}} S({X_i},R_{i,n}^*))}}\prod\limits_{i \in {Q_u}} {\bf 1}\{ \mu (S({X_i},{r_{i,k}})) \ge {y_n}\} {\bf 1}\{ {E_u}\} \right]} \hfill \cr {\le {n^{|{Q_u}|}}{{\rm e}^{ - (y + \ln n)(1 + \varepsilon )}}{\mathbb E}\left[{\bf 1}\left \{ \bigcap\limits_{i,j \le |{Q_u}|,i \ne j} \{ \parallel {X_i} - {X_j}\parallel \ge \max \{ R_{i,n}^*,R_{j,n}^*\} \}\right \} {\bf 1}\{ {E_u}\} \right]} \hfill \cr { = {\rm O}({n^{|{Q_u}| - 1 - \varepsilon }}){\mathbb P}({E_u}).} \hfill \cr } $$
$$\matrix{ {{n^{|{Q_u}|}}{\mathbb E}\left[{{\rm e}^{ - n\mu (\bigcup\limits_{i \in {Q_u}} S({X_i},R_{i,n}^*))}}\prod\limits_{i \in {Q_u}} {\bf 1}\{ \mu (S({X_i},{r_{i,k}})) \ge {y_n}\} {\bf 1}\{ {E_u}\} \right]} \hfill \cr {\le {n^{|{Q_u}|}}{{\rm e}^{ - (y + \ln n)(1 + \varepsilon )}}{\mathbb E}\left[{\bf 1}\left \{ \bigcap\limits_{i,j \le |{Q_u}|,i \ne j} \{ \parallel {X_i} - {X_j}\parallel \ge \max \{ R_{i,n}^*,R_{j,n}^*\} \}\right \} {\bf 1}\{ {E_u}\} \right]} \hfill \cr { = {\rm O}({n^{|{Q_u}| - 1 - \varepsilon }}){\mathbb P}({E_u}).} \hfill \cr } $$
In order to bound ℙ(Eu), we need the following lemma (recall that Qu = {1, …, |Qu|}).
Lemma 4.1. On Eu there is a random integer L ∈ {1, …, |Qu|} depending on
![]() ${X_1}, \ldots ,{X_{|{Q_u}|}}$
such that Qu \ {L} forms an equivalence class.
${X_1}, \ldots ,{X_{|{Q_u}|}}$
such that Qu \ {L} forms an equivalence class.
Proof. Let m := |Qu|. Regard X 1, …, Xm as vertices of a graph in which any two vertices Xi and Xj are connected by a node if
![]() $S({X_i},R_{i,n}^*) \cap S({X_j},R_{j,n}^*) \ne \emptyset $
. Since Qu = {1, …, m} is an equivalence class, this graph is connected. If there is at least one vertex Xj (say) with degree 1, set L := j. Otherwise, the degree of each vertex is at least 2, and we have m ≥ 3. If m = 3, the graph is a triangle, and we can choose L arbitrarily. Now suppose that the lemma holds for any graph having m ≥ 3 vertices, in which each vertex degree is at least 2. If we have an additional (m + 1)th vertex Xm +1, this is connected to at least two other vertices Xi and Xj (say). Of the graph with vertices X 1, …, Xm we can delete one vertex, and the remaining graph is connected. But Xm +1 is then connected to either Xi or Xj, and we may choose L = i or L = j. Note that, for d = 1, the proof is trivial since
$S({X_i},R_{i,n}^*) \cap S({X_j},R_{j,n}^*) \ne \emptyset $
. Since Qu = {1, …, m} is an equivalence class, this graph is connected. If there is at least one vertex Xj (say) with degree 1, set L := j. Otherwise, the degree of each vertex is at least 2, and we have m ≥ 3. If m = 3, the graph is a triangle, and we can choose L arbitrarily. Now suppose that the lemma holds for any graph having m ≥ 3 vertices, in which each vertex degree is at least 2. If we have an additional (m + 1)th vertex Xm +1, this is connected to at least two other vertices Xi and Xj (say). Of the graph with vertices X 1, …, Xm we can delete one vertex, and the remaining graph is connected. But Xm +1 is then connected to either Xi or Xj, and we may choose L = i or L = j. Note that, for d = 1, the proof is trivial since
![]() $\bigcup\nolimits_{i \in {Q_u}} S({X_i},R_{i,n}^*)$
is an interval, and L can be chosen as the index of either the smallest or the largest random variable.
$\bigcup\nolimits_{i \in {Q_u}} S({X_i},R_{i,n}^*)$
is an interval, and L can be chosen as the index of either the smallest or the largest random variable.
By induction, we now show that
 $${\mathbb P}({E_u}) = {\rm O}\left(\left({{\ln n} \over n}\right )^{{|{Q_u}| - 1}}\right)$$
$${\mathbb P}({E_u}) = {\rm O}\left(\left({{\ln n} \over n}\right )^{{|{Q_u}| - 1}}\right)$$
as n → ∞ for each m := |Qu| ∈ {2, …, k − 1}. We start with the base case m = 2. Note that
![]() ${\mathbb P}({E_u}) \le {\mathbb P}(\parallel {X_2} - {X_1}\parallel \le R_{2,n}^* + R_{1,n}^*)$
and
${\mathbb P}({E_u}) \le {\mathbb P}(\parallel {X_2} - {X_1}\parallel \le R_{2,n}^* + R_{1,n}^*)$
and
 $$\matrix{ {{\mathbb P}(\parallel {X_2} - {X_1}\parallel \le R_{2,n}^* + R_{1,n}^*|{X_1})} \hfill \cr { = {\mathbb P}(\parallel {X_2} - {X_1}\parallel \le R_{2,n}^* + R_{1,n}^*,R_{2,n}^* \le R_{1,n}^*|{X_1})} \hfill \cr {\quad + {\mathbb P}(\parallel {X_2} - {X_1}\parallel \le R_{2,n}^* + R_{1,n}^*,R_{2,n}^* \gt R_{1,n}^*|{X_1})} \hfill \cr {\le {\mathbb P}(\parallel {X_2} - {X_1}\parallel \le 2R_{1,n}^*|{X_1}) + {\mathbb P}(\parallel {X_2} - {X_1}\parallel \le 2R_{2,n}^*|{X_1}).} \hfill \cr } $$
$$\matrix{ {{\mathbb P}(\parallel {X_2} - {X_1}\parallel \le R_{2,n}^* + R_{1,n}^*|{X_1})} \hfill \cr { = {\mathbb P}(\parallel {X_2} - {X_1}\parallel \le R_{2,n}^* + R_{1,n}^*,R_{2,n}^* \le R_{1,n}^*|{X_1})} \hfill \cr {\quad + {\mathbb P}(\parallel {X_2} - {X_1}\parallel \le R_{2,n}^* + R_{1,n}^*,R_{2,n}^* \gt R_{1,n}^*|{X_1})} \hfill \cr {\le {\mathbb P}(\parallel {X_2} - {X_1}\parallel \le 2R_{1,n}^*|{X_1}) + {\mathbb P}(\parallel {X_2} - {X_1}\parallel \le 2R_{2,n}^*|{X_1}).} \hfill \cr } $$
Now condition (2.6) entails
 $$\matrix{ {{\mathbb P}(\parallel {X_2} - {X_1}\parallel \le 2R_{1,n}^*|{X_1}) = } \hfill & = \hfill & {\mu (S({X_1},2R_{1,n}^*))} \hfill \cr {} \hfill & \le \hfill & {{c_{{\rm{max}}}}\mu (S({X_1},R_{1,n}^*))} \hfill \cr {} \hfill & = \hfill & {{c_{{\rm{max}}}}{{y + \ln n} \over n}.} \hfill \cr } $$
$$\matrix{ {{\mathbb P}(\parallel {X_2} - {X_1}\parallel \le 2R_{1,n}^*|{X_1}) = } \hfill & = \hfill & {\mu (S({X_1},2R_{1,n}^*))} \hfill \cr {} \hfill & \le \hfill & {{c_{{\rm{max}}}}\mu (S({X_1},R_{1,n}^*))} \hfill \cr {} \hfill & = \hfill & {{c_{{\rm{max}}}}{{y + \ln n} \over n}.} \hfill \cr } $$
Setting
![]() ${\widetilde R_{2,n}}H_{{X_2}}^{ - 1}({c_{{\rm{max}}}}(y + \ln n)/n)$
, a second appeal to (2.6) yields
${\widetilde R_{2,n}}H_{{X_2}}^{ - 1}({c_{{\rm{max}}}}(y + \ln n)/n)$
, a second appeal to (2.6) yields
and, thus,
![]() $2R_{2,n}^* \le {\widetilde R_{2,n}}$
. Consequently,
$2R_{2,n}^* \le {\widetilde R_{2,n}}$
. Consequently,
Let γd be the minimum number of cones of angle π/3 centred at 0 such that their union covers ℝd. Fritz [Reference Fritz9] mentioned that γd is the minimal number of spheres with radius less than
![]() ${\textstyle{1 \over 2}}$
whose union covers the surface of the unit sphere. This constant is roughly 2dd log d, while, according to Lemma 5.5 of [Reference Devroye, Györfi and Lugosi8], we have γd ≤ 4.9d. Further upper and lower bounds on γd are given in [Reference Rogers14]. We refer the reader to Section 20.7 of [Reference Biau and Devroye3] for more information and further bounds. The cone covering lemma (cf. Lemma 10.1 of [Reference Devroye and Györfi7] and Lemma 6.2 of [Reference Györfi, Kohler, KrzyZak and Walk11]) says that, for any 0 ≤ a ≤ 1 and any x 1, we have
${\textstyle{1 \over 2}}$
whose union covers the surface of the unit sphere. This constant is roughly 2dd log d, while, according to Lemma 5.5 of [Reference Devroye, Györfi and Lugosi8], we have γd ≤ 4.9d. Further upper and lower bounds on γd are given in [Reference Rogers14]. We refer the reader to Section 20.7 of [Reference Biau and Devroye3] for more information and further bounds. The cone covering lemma (cf. Lemma 10.1 of [Reference Devroye and Györfi7] and Lemma 6.2 of [Reference Györfi, Kohler, KrzyZak and Walk11]) says that, for any 0 ≤ a ≤ 1 and any x 1, we have
Now (4.10) implies that
whence,
We thus obtain
 $${\mathbb P}(\parallel {X_2} - {X_1}\parallel \le R_{2,n}^* + R_{1,n}^*|{X_1}) = {\rm O}({{\ln n} \over n}),$$
$${\mathbb P}(\parallel {X_2} - {X_1}\parallel \le R_{2,n}^* + R_{1,n}^*|{X_1}) = {\rm O}({{\ln n} \over n}),$$
and so (4.9) is proved for m = 2. For the induction step, assume that (4.9) holds for |Qu|= m ∈ {2, …, k − 2}.If Qu with |Qu|= m + 1 is an equivalence class then, by Lemma 4.1, there are random integers L 1 and L 2 taking values in {1, …, m + 1} such that Qu \{L 1} forms an equivalence class, and
It follows that
 $$\eqalign{{\mathbb P}({E_u}) & \le (m + 1)m{\mathbb P}({E_u} \cap \{ {L_1} = m + 1,{L_2} = 1\} ) \cr & \le k(k - 1){\mathbb P}(\{ {Q_u}\backslash \{ m + 1\} \;{\rm{forms}}\;{\rm{an}}\;{\rm{equivalence}}\;{\rm{class}}\} \cr & \quad \cap \{ \parallel {X_{m + 1}} - {X_1}\parallel \le R_{m + 1,n}^* + R_{1,n}^*\} ) \cr & = k(k - 1){\mathbb E}[{\bf 1}\{ {Q_u}\backslash \{ m + 1\} \;{\rm{forms}}\;{\rm{an}}\;{\rm{equivalence}}\;{\rm{class}}\} \cr & \quad \times {\mathbb P}(\parallel {X_{m + 1}} - {X_1}\parallel \le R_{m + 1,n}^* + R_{1,n}^*|{X_1}, \ldots ,{X_m})] \cr & = k(k - 1){\mathbb E}[{\bf 1}\{ {Q_u}\backslash \{ m + 1\} \;{\rm{forms}}\;{\rm{an}}\;{\rm{equivalence}}\;{\rm{class}}\} \cr & \quad \times {\mathbb P}(\parallel {X_{m + 1}} - {X_1}\parallel \le R_{m + 1,n}^* + R_{1,n}^*|{X_1})] \cr & \le {\rm{O}}\left( {{{\ln n} \over n}} \right){\mathbb P}({Q_u}\backslash \{ m + 1\} \;{\rm{forms}}\;{\rm{an}}\;{\rm{equivalence}}\;{\rm{class}}) \cr & = {\rm{O}}\left( {{{\ln n} \over n}} \right){\rm O}\left( {{{\left( {{{\ln n} \over n}} \right)}^{m - 1}}} \right) \cr & = {\rm{O}}\left( {{{\left( {{{\ln n} \over n}} \right)}^m}} \right)} $$
$$\eqalign{{\mathbb P}({E_u}) & \le (m + 1)m{\mathbb P}({E_u} \cap \{ {L_1} = m + 1,{L_2} = 1\} ) \cr & \le k(k - 1){\mathbb P}(\{ {Q_u}\backslash \{ m + 1\} \;{\rm{forms}}\;{\rm{an}}\;{\rm{equivalence}}\;{\rm{class}}\} \cr & \quad \cap \{ \parallel {X_{m + 1}} - {X_1}\parallel \le R_{m + 1,n}^* + R_{1,n}^*\} ) \cr & = k(k - 1){\mathbb E}[{\bf 1}\{ {Q_u}\backslash \{ m + 1\} \;{\rm{forms}}\;{\rm{an}}\;{\rm{equivalence}}\;{\rm{class}}\} \cr & \quad \times {\mathbb P}(\parallel {X_{m + 1}} - {X_1}\parallel \le R_{m + 1,n}^* + R_{1,n}^*|{X_1}, \ldots ,{X_m})] \cr & = k(k - 1){\mathbb E}[{\bf 1}\{ {Q_u}\backslash \{ m + 1\} \;{\rm{forms}}\;{\rm{an}}\;{\rm{equivalence}}\;{\rm{class}}\} \cr & \quad \times {\mathbb P}(\parallel {X_{m + 1}} - {X_1}\parallel \le R_{m + 1,n}^* + R_{1,n}^*|{X_1})] \cr & \le {\rm{O}}\left( {{{\ln n} \over n}} \right){\mathbb P}({Q_u}\backslash \{ m + 1\} \;{\rm{forms}}\;{\rm{an}}\;{\rm{equivalence}}\;{\rm{class}}) \cr & = {\rm{O}}\left( {{{\ln n} \over n}} \right){\rm O}\left( {{{\left( {{{\ln n} \over n}} \right)}^{m - 1}}} \right) \cr & = {\rm{O}}\left( {{{\left( {{{\ln n} \over n}} \right)}^m}} \right)} $$
Note that the penultimate equation follows from the induction hypothesis, and the last ‘≤’is a consequence of (4.11). Note further that these limit relations imply (4.9); whence,
 $$\eqalign{{n^{|{Q_u}|}} & {\mathbb E} \left[ {{{\rm{e}}^{ - n\mu (\bigcup \limits_{i \in {Q_u}} S ({X_i},R_{i,n}^*))}}\prod\limits_{i \in {Q_u}} {\bf{1}} \{ \mu (S({X_i},{r_{i,k}})) \ge {y_n}\} {\bf{1}}\{ {E_u}\} } \right] \cr & = {\rm{O}}({n^{|{Q_u}| - 1 - \varepsilon }}){\mathbb P}({E_u}) \cr & = {\rm{O}}({n^{|{Q_u}| - 1 - \varepsilon }}){\rm{O}}\left( {{{\left( {{{\ln n} \over n}} \right)}^{|{Q_u}| - 1}}} \right) \cr & = {\rm{O}}({n^{ - \varepsilon }}\ln n).} $$
$$\eqalign{{n^{|{Q_u}|}} & {\mathbb E} \left[ {{{\rm{e}}^{ - n\mu (\bigcup \limits_{i \in {Q_u}} S ({X_i},R_{i,n}^*))}}\prod\limits_{i \in {Q_u}} {\bf{1}} \{ \mu (S({X_i},{r_{i,k}})) \ge {y_n}\} {\bf{1}}\{ {E_u}\} } \right] \cr & = {\rm{O}}({n^{|{Q_u}| - 1 - \varepsilon }}){\mathbb P}({E_u}) \cr & = {\rm{O}}({n^{|{Q_u}| - 1 - \varepsilon }}){\rm{O}}\left( {{{\left( {{{\ln n} \over n}} \right)}^{|{Q_u}| - 1}}} \right) \cr & = {\rm{O}}({n^{ - \varepsilon }}\ln n).} $$
Summarizing, we have shown (4.8) and thus (4.6). Hence, (4.4) is verified with ν = exp (−y), completing the proof of Theorem 2.2.
5. Discussion of condition (2.5)
In this final section we comment on condition (2.5). For d = 1, we verify (2.5) if on S(x, r) ∪ S(z, s) the distribution function F of μ is either convex or concave. If ‖x − z‖ ≥ r + s then S(x, r) and S(z, s) are disjoint; therefore, suppose that r + s ≥ ‖x − z‖ ≥ max (r, s). Assume that F is convex; the proof for concave F is similar. If x < z, the convexity of F and
imply that F(z) − F(z − s) ≤ p/2. Thus,
 $$\matrix{ {\mu (S(x,r) \cap S(z,s))} \hfill & = \hfill & {\mu ([z - s,x + r])} \hfill \cr {} \hfill & \le \hfill & {\min \{ \mu ([z - s,z]),\mu ([x,x + r])\} } \hfill \cr {} \hfill & = \hfill & {\min \{ F(z) - F(z - s),F(x + r) - F(x)\} } \hfill \cr {} \hfill & \le \hfill & {F(z) - F(z - s)} \hfill \cr {} \hfill & \le \hfill & {{1 \over 2}p,} \hfill \cr } $$
$$\matrix{ {\mu (S(x,r) \cap S(z,s))} \hfill & = \hfill & {\mu ([z - s,x + r])} \hfill \cr {} \hfill & \le \hfill & {\min \{ \mu ([z - s,z]),\mu ([x,x + r])\} } \hfill \cr {} \hfill & = \hfill & {\min \{ F(z) - F(z - s),F(x + r) - F(x)\} } \hfill \cr {} \hfill & \le \hfill & {F(z) - F(z - s)} \hfill \cr {} \hfill & \le \hfill & {{1 \over 2}p,} \hfill \cr } $$
and, hence,
Thus, (2.5) is satisfied with
![]() $\beta = {\textstyle{1 \over 2}}$
.
$\beta = {\textstyle{1 \over 2}}$
.
For d > 1, the problem is more involved. Again, suppose that r + s ≥ ‖x − z‖ ≥ max (r, s). Writing ⟨⋅, ⋅⟩ for the inner product in ℝd, introduce the half-spaces
Then
 $$\matrix{ {\mu (S(x,r) \cap S(z,s))} \hfill & = \hfill & {\mu ((S(z,s) \cap {H_2}) \cap (S(x,r) \cap {H_1}))} \hfill \cr {} \hfill & \le \hfill & {{{\mu (S(z,s) \cap {H_2}) + \mu (S(x,r) \cap {H_1})} \over 2}.} \hfill \cr } $$
$$\matrix{ {\mu (S(x,r) \cap S(z,s))} \hfill & = \hfill & {\mu ((S(z,s) \cap {H_2}) \cap (S(x,r) \cap {H_1}))} \hfill \cr {} \hfill & \le \hfill & {{{\mu (S(z,s) \cap {H_2}) + \mu (S(x,r) \cap {H_1})} \over 2}.} \hfill \cr } $$
We introduce another implicit condition as follows. Assume that α ∈ (1, 2) and δ > 0 such that, for any r, s > 0 and any x, z ∈ supp(μ) with r + s ≥ ‖x − z‖ ≥ max (r, s) and μ(S(x, r)) = μ(S(z, s)) ≤ δ, we have either
or
In the case of (5.1), we have
 $$\eqalign{{{\mu (S(z,s) \cap {H_2}) + \mu (S(x,r) \cap {H_1})} \over 2} & \le {{\alpha \mu (S(x,r) \cap H_1^c) + \mu (S(x,r) \cap {H_1})} \over 2} \cr & = {\alpha \over 2}\mu (S(x,r)),}$$
$$\eqalign{{{\mu (S(z,s) \cap {H_2}) + \mu (S(x,r) \cap {H_1})} \over 2} & \le {{\alpha \mu (S(x,r) \cap H_1^c) + \mu (S(x,r) \cap {H_1})} \over 2} \cr & = {\alpha \over 2}\mu (S(x,r)),}$$
and (2.5) is verified with β = α/2. The case of (5.2) is similar.
Acknowledgements
The authors would like to thank a referee and an Associate Editor for many valuable remarks and suggestions.

