1. Introduction
Markov chain Monte Carlo (MCMC) methods are designed to approximate expectations of high-dimensional random vectors; see e.g. [Reference Brooks, Gelman, Jones and Meng8] and [Reference Tierney31]. It is hence important to understand how the efficiency of MCMC algorithms scales with dimension. The optimal scaling literature, initiated by the seminal paper [Reference Roberts, Gelman and Gilks30], indicates that for the high-dimensional algorithms it is the growth of the asymptotic variance with dimension that provides perhaps the most natural measure of efficiency for MCMC (see [Reference Roberts and Rosenthal29, Sections 1.2 and 2.2] and [Reference Roberts and Rosenthal28, Section 3]). For instance, for a product target, the asymptotic variance for the random walk Metropolis (RWM) chain on
![]() ${\mathbb{R}}^d$
is heuristically of order
${\mathbb{R}}^d$
is heuristically of order
![]() ${\mathrm{O}} (d)$
[Reference Roberts and Rosenthal29, Reference Roberts, Gelman and Gilks30]. Moreover, the asymptotic variances of the d-dimensional Metropolis-adjusted Langevin algorithm (MALA), Hamiltonian Monte Carlo, and the fast-MALA are
${\mathrm{O}} (d)$
[Reference Roberts and Rosenthal29, Reference Roberts, Gelman and Gilks30]. Moreover, the asymptotic variances of the d-dimensional Metropolis-adjusted Langevin algorithm (MALA), Hamiltonian Monte Carlo, and the fast-MALA are
![]() ${\mathrm{O}} (d^{1/3})$
[Reference Roberts and Rosenthal28],
${\mathrm{O}} (d^{1/3})$
[Reference Roberts and Rosenthal28],
![]() ${\mathrm{O}} (d^{1/4})$
[Reference Beskos, Pillai, Roberts, Sanz-Serna and Stuart5], and
${\mathrm{O}} (d^{1/4})$
[Reference Beskos, Pillai, Roberts, Sanz-Serna and Stuart5], and
![]() ${\mathrm{O}} (d^{1/5})$
[Reference Durmus, Roberts, Vilmart and Zygalakis12], respectively.
${\mathrm{O}} (d^{1/5})$
[Reference Durmus, Roberts, Vilmart and Zygalakis12], respectively.
This paper constructs a dimension-dependent estimator (see (1.1) below) and proves a bound on its asymptotic variance, suggesting the order
![]() ${\mathrm{O}} (\log(d))$
, for an RWM chain with an independent, identically distributed (i.i.d.) target. The idea is to exploit the following facts: (I) the law of the diffusion scaling limit for the RWM chain (as
${\mathrm{O}} (\log(d))$
, for an RWM chain with an independent, identically distributed (i.i.d.) target. The idea is to exploit the following facts: (I) the law of the diffusion scaling limit for the RWM chain (as
![]() $d\to\infty$
) from [Reference Roberts, Gelman and Gilks30] is close (in the weak sense) to that of the law of the chain itself and (II) the Poisson equation for the limiting Langevin diffusion has an explicit solution. Following ideas from [Reference Mijatović and Vogrinc23], we construct and analyse the estimator using (I) and (II).
$d\to\infty$
) from [Reference Roberts, Gelman and Gilks30] is close (in the weak sense) to that of the law of the chain itself and (II) the Poisson equation for the limiting Langevin diffusion has an explicit solution. Following ideas from [Reference Mijatović and Vogrinc23], we construct and analyse the estimator using (I) and (II).
Specifically, let
![]() $\rho$
be a density on
$\rho$
be a density on
![]() ${\mathbb{R}}$
and let
${\mathbb{R}}$
and let
![]() $\rho_d(\mathbf{x}^d)\,:\!=\prod_{i=1}^d\rho(x^d_i)$
be the corresponding d-dimensional product density, where
$\rho_d(\mathbf{x}^d)\,:\!=\prod_{i=1}^d\rho(x^d_i)$
be the corresponding d-dimensional product density, where
![]() $\mathbf{x}^d=(x_1^d,\ldots,x_d^d)\in{\mathbb{R}}^d$
. Let
$\mathbf{x}^d=(x_1^d,\ldots,x_d^d)\in{\mathbb{R}}^d$
. Let
![]() $\mathbf{X}^d=\{\mathbf{X}^d_n\}_{n\in{\mathbb{N}}}$
be the RWM chain converging to
$\mathbf{X}^d=\{\mathbf{X}^d_n\}_{n\in{\mathbb{N}}}$
be the RWM chain converging to
![]() $\rho_d$
with the normal proposal with variance
$\rho_d$
with the normal proposal with variance
![]() $l^2/d\cdot I_d$
(here
$l^2/d\cdot I_d$
(here
![]() $I_d\mathbf{x}^d=\mathbf{x}^d$
, for all
$I_d\mathbf{x}^d=\mathbf{x}^d$
, for all
![]() $\mathbf{x}^d\in{\mathbb{R}}^d$
, and l a constant), analysed in [Reference Roberts, Gelman and Gilks30]. If
$\mathbf{x}^d\in{\mathbb{R}}^d$
, and l a constant), analysed in [Reference Roberts, Gelman and Gilks30]. If
![]() $f(\mathbf{x}^d)$
depends only on the first coordinate
$f(\mathbf{x}^d)$
depends only on the first coordinate
![]() $x_1^d$
, then
$x_1^d$
, then
Under appropriate conditions, the asymptotic variance
![]() $\sigma^2_{f,d}$
in the central limit theorem (CLT) for the estimator
$\sigma^2_{f,d}$
in the central limit theorem (CLT) for the estimator
![]() $\sum_{i=1}^n f(\mathbf{X}^d_i)/n$
of
$\sum_{i=1}^n f(\mathbf{X}^d_i)/n$
of
![]() $\rho_d(f)$
satisfies
$\rho_d(f)$
satisfies
Here
![]() $\mathrm{Var}_\rho(f)\,:\!=\rho(f^2)-\rho(f)^2$
and
$\mathrm{Var}_\rho(f)\,:\!=\rho(f^2)-\rho(f)^2$
and
![]() $1-\lambda_d$
denotes the spectral gap of the chain
$1-\lambda_d$
denotes the spectral gap of the chain
![]() $\mathbf{X}^d$
. The inequality follows by the spectral representation of
$\mathbf{X}^d$
. The inequality follows by the spectral representation of
![]() $\sigma_{f,d}^2$
in [Reference Geyer14] and [Reference Kipnis and Varadhan18]. The reasoning analogous to that applied to the integrated autocorrelation time in [Reference Roberts and Rosenthal29, Section 2.2] can be used to argue that the spectral gap
$\sigma_{f,d}^2$
in [Reference Geyer14] and [Reference Kipnis and Varadhan18]. The reasoning analogous to that applied to the integrated autocorrelation time in [Reference Roberts and Rosenthal29, Section 2.2] can be used to argue that the spectral gap
![]() $1-\lambda_d$
is of order
$1-\lambda_d$
is of order
![]() ${\mathrm{O}} (1/d)$
. Hence the asymptotic variance
${\mathrm{O}} (1/d)$
. Hence the asymptotic variance
![]() $\sigma_{f,d}^2$
is
$\sigma_{f,d}^2$
is
![]() ${\mathrm{O}} (d)$
.
${\mathrm{O}} (d)$
.
The Poisson equation for the Langevin diffusion arising in the scaling limit of
![]() $\mathbf{X}^d$
in [Reference Roberts, Gelman and Gilks30] is a second-order linear ODE (ordinary differential equation) with solution
$\mathbf{X}^d$
in [Reference Roberts, Gelman and Gilks30] is a second-order linear ODE (ordinary differential equation) with solution
![]() $\skew3\hat f$
given explicitly in terms of f and the density
$\skew3\hat f$
given explicitly in terms of f and the density
![]() $\rho$
; see (2.6) below. For large d, the function
$\rho$
; see (2.6) below. For large d, the function
![]() $\skew3\hat f$
ought to approximate the solution of the Poisson equation for
$\skew3\hat f$
ought to approximate the solution of the Poisson equation for
![]() $\mathbf{X}^d$
. The reasoning in [Reference Mijatović and Vogrinc23] then suggests the form of an estimator for
$\mathbf{X}^d$
. The reasoning in [Reference Mijatović and Vogrinc23] then suggests the form of an estimator for
![]() $\rho_d(f)$
, which, under appropriate technical assumptions, satisfies the following CLT:
$\rho_d(f)$
, which, under appropriate technical assumptions, satisfies the following CLT:
where
![]() $P_d$
is the transition kernel of the chain
$P_d$
is the transition kernel of the chain
![]() $\mathbf{X}^d$
. The main result of this paper (Theorem 2 below) states that for some constant
$\mathbf{X}^d$
. The main result of this paper (Theorem 2 below) states that for some constant
![]() $C>0$
the following inequality holds:
$C>0$
the following inequality holds:
Theorem 2.1 also gives the explicit dependence of the constant C on the function f.
This result suggests that to achieve the same level of accuracy as when estimating
![]() $\rho_d(f)$
by an average over an i.i.d. sample form
$\rho_d(f)$
by an average over an i.i.d. sample form
![]() $\rho_d$
, only
$\rho_d$
, only
![]() ${\mathrm{O}} (\log d)$
times as many RWM samples are needed if the control variate
${\mathrm{O}} (\log d)$
times as many RWM samples are needed if the control variate
![]() $d (P_d\skew3\hat{f}-\skew3\hat{f})$
is added. This should be contrasted with
$d (P_d\skew3\hat{f}-\skew3\hat{f})$
is added. This should be contrasted with
![]() ${\mathrm{O}} (d)$
(resp.
${\mathrm{O}} (d)$
(resp.
![]() ${\mathrm{O}} (d^{1/3})$
,
${\mathrm{O}} (d^{1/3})$
,
![]() ${\mathrm{O}} (d^{1/4})$
,
${\mathrm{O}} (d^{1/4})$
,
![]() ${\mathrm{O}} (d^{1/5})$
) times as many samples for the RWM (resp. MALA, Hamiltonian Monte Carlo, fast-MALA) without the control variate; see [Reference Roberts and Rosenthal29], [Reference Roberts and Rosenthal28], [Reference Beskos, Pillai, Roberts, Sanz-Serna and Stuart5], and [Reference Durmus, Roberts, Vilmart and Zygalakis12].
${\mathrm{O}} (d^{1/5})$
) times as many samples for the RWM (resp. MALA, Hamiltonian Monte Carlo, fast-MALA) without the control variate; see [Reference Roberts and Rosenthal29], [Reference Roberts and Rosenthal28], [Reference Beskos, Pillai, Roberts, Sanz-Serna and Stuart5], and [Reference Durmus, Roberts, Vilmart and Zygalakis12].
The optimal scaling for the proposal variance of a d-dimensional RWM chain is
![]() ${\mathrm{O}} (1/d)$
; see [Reference Roberts and Rosenthal29] for a review and [Reference Beskos, Roberts and Stuart6, Theorem 4] for the proof that other scalings lead to sub-optimal behaviour. To get a non-trivial scaling limit in [Reference Roberts, Gelman and Gilks30], it is necessary to accelerate the chains
${\mathrm{O}} (1/d)$
; see [Reference Roberts and Rosenthal29] for a review and [Reference Beskos, Roberts and Stuart6, Theorem 4] for the proof that other scalings lead to sub-optimal behaviour. To get a non-trivial scaling limit in [Reference Roberts, Gelman and Gilks30], it is necessary to accelerate the chains
![]() $ (\mathbf{X}^d)_{d\in{\mathbb{N}}} $
linearly in dimension. The weak convergence of the accelerated chain to the Langevin diffusion suggests that
$ (\mathbf{X}^d)_{d\in{\mathbb{N}}} $
linearly in dimension. The weak convergence of the accelerated chain to the Langevin diffusion suggests that
![]() $d\skew3\hat{f}$
is close to the solution of the Poisson equation for
$d\skew3\hat{f}$
is close to the solution of the Poisson equation for
![]() $P_d$
and f, making
$P_d$
and f, making
![]() $d (P_d\skew3\hat{f}-\skew3\hat{f})$
a good control variate. Using an approximate solution to the Poisson equation to construct control variates is a common variance reduction technique; see e.g. [Reference Dellaportas and Kontoyiannis9], [Reference Henderson15], [Reference Meyn21], and [Reference Mijatović and Vogrinc23]. In this context, more often than not, an approximate solution used is a solution of a Poisson equation of a simpler related process. For instance, in [Reference Mijatović and Vogrinc23] a sequence of Markov chains on a finite state space, converging weakly to a given RWM chain, is constructed. Then a solution to the Poisson equation of the finite state chain is used to construct a control variate capable of reducing the asymptotic variance of the RWM chain arbitrarily. Here this idea is turned on its head: a solution to the Poisson equation of the limiting diffusion is used to construct a control variate for an RWM chain from a weakly convergent sequence in [Reference Roberts, Gelman and Gilks30]. Since the complexity of the RWM increases arbitrarily as dimension
$d (P_d\skew3\hat{f}-\skew3\hat{f})$
a good control variate. Using an approximate solution to the Poisson equation to construct control variates is a common variance reduction technique; see e.g. [Reference Dellaportas and Kontoyiannis9], [Reference Henderson15], [Reference Meyn21], and [Reference Mijatović and Vogrinc23]. In this context, more often than not, an approximate solution used is a solution of a Poisson equation of a simpler related process. For instance, in [Reference Mijatović and Vogrinc23] a sequence of Markov chains on a finite state space, converging weakly to a given RWM chain, is constructed. Then a solution to the Poisson equation of the finite state chain is used to construct a control variate capable of reducing the asymptotic variance of the RWM chain arbitrarily. Here this idea is turned on its head: a solution to the Poisson equation of the limiting diffusion is used to construct a control variate for an RWM chain from a weakly convergent sequence in [Reference Roberts, Gelman and Gilks30]. Since the complexity of the RWM increases arbitrarily as dimension
![]() $d\to\infty$
, it is infeasible to get an arbitrary variance reduction as in [Reference Mijatović and Vogrinc23]. However, heuristically, the amount of variance reduction measured by the ratio
$d\to\infty$
, it is infeasible to get an arbitrary variance reduction as in [Reference Mijatović and Vogrinc23]. However, heuristically, the amount of variance reduction measured by the ratio
![]() $\sigma_{f,d}^2/\hat \sigma_{f,d}^2$
still tends to infinity at the rate
$\sigma_{f,d}^2/\hat \sigma_{f,d}^2$
still tends to infinity at the rate
![]() $d/\log(d)$
.
$d/\log(d)$
.
If the solution of the Poisson equation for
![]() $\mathbf{X}^d$
and f were available, we could construct an estimator for
$\mathbf{X}^d$
and f were available, we could construct an estimator for
![]() $\rho_d(f)$
with zero variance (see e.g. [Reference Mijatović and Vogrinc23]). Put differently, in this case there would be no need for the chain to explore its state space at all. In our setting, since the jumps of
$\rho_d(f)$
with zero variance (see e.g. [Reference Mijatović and Vogrinc23]). Put differently, in this case there would be no need for the chain to explore its state space at all. In our setting, since the jumps of
![]() $\mathbf{X}^d$
are of size
$\mathbf{X}^d$
are of size
![]() ${\mathrm{O}} (1/\sqrt{d})$
[Reference Roberts, Gelman and Gilks30], after
${\mathrm{O}} (1/\sqrt{d})$
[Reference Roberts, Gelman and Gilks30], after
![]() ${\mathrm{O}} (\log d)$
steps the chain will have explored the distance of
${\mathrm{O}} (\log d)$
steps the chain will have explored the distance of
![]() ${\mathrm{O}} (\log(d)/\sqrt{d})$
. In line with the observation above this distance tends to zero as
${\mathrm{O}} (\log(d)/\sqrt{d})$
. In line with the observation above this distance tends to zero as
![]() $d\to\infty$
since, heuristically,
$d\to\infty$
since, heuristically,
![]() $d\skew3\hat f$
approximates the solution of the Poisson equation for
$d\skew3\hat f$
approximates the solution of the Poisson equation for
![]() $P_d$
and f arbitrarily well.
$P_d$
and f arbitrarily well.
The key technical step in the proof of our result (Theorem 2.2 below) is a type of concentration inequality. It generalizes the limit in [Reference Roberts, Gelman and Gilks30, Lemma 2.6], which essentially states that generators of the accelerated chains
![]() $ (\mathbf{X}^d)_{d\in{\mathbb{N}}} $
converge to the generator of the Langevin limit when applied to a compactly supported and infinitely smooth function, in two ways: (A) it extends the limit to a class of functions of sub-exponential growth and (B) it provides estimates for the rate of convergence. Both of these extensions are key to our main result. (A) allows us to apply Theorem 2.2 to a solution of the Poisson equation, which is not compactly supported. Note that this step in the proof entails identifying the correct space of functions that is closed under the operation of solving the Poisson equation (see Proposition 4.8 below). Estimate (B) allows us to control the asymptotic variance via a classical spectral-gap bound. The proof of Theorem 2.2, outlined in Section 4.1 below, crucially depends on the large deviations theory (Section 5.2), the form of the constant in optimal Young’s inequality (Section 5.3) and Berry–Esseen-type bounds (Section 5.4).
$ (\mathbf{X}^d)_{d\in{\mathbb{N}}} $
converge to the generator of the Langevin limit when applied to a compactly supported and infinitely smooth function, in two ways: (A) it extends the limit to a class of functions of sub-exponential growth and (B) it provides estimates for the rate of convergence. Both of these extensions are key to our main result. (A) allows us to apply Theorem 2.2 to a solution of the Poisson equation, which is not compactly supported. Note that this step in the proof entails identifying the correct space of functions that is closed under the operation of solving the Poisson equation (see Proposition 4.8 below). Estimate (B) allows us to control the asymptotic variance via a classical spectral-gap bound. The proof of Theorem 2.2, outlined in Section 4.1 below, crucially depends on the large deviations theory (Section 5.2), the form of the constant in optimal Young’s inequality (Section 5.3) and Berry–Esseen-type bounds (Section 5.4).
We conclude the introduction with a comment on how the present paper fits into the literature. Since, as discussed above, the asymptotic variance
![]() $\sigma_{f,d}^2$
is approximately equal to the product
$\sigma_{f,d}^2$
is approximately equal to the product
![]() $2\mathrm{Var}_\rho(f)/(1-\lambda_d)$
, two ‘orthogonal’ approaches to speeding up MCMC algorithms are feasible. (a) The MCMC method itself can be modified, with the aim of increasing the spectral gap, leading to many well-known reversible samplers such as MALA and Hamiltonian Monte Carlo [Reference Duane, Kennedy, Pendleton and Roweth10] as well as non-reversible ones [Reference Bierkens and Roberts7, Reference Duncan, Lelièvre and Pavliotis11]. There is a plethora of papers (see [Reference Roberts and Rosenthal28], [Reference Beskos, Pillai, Roberts, Sanz-Serna and Stuart5], [Reference Durmus, Roberts, Vilmart and Zygalakis12], and the references therein) studying the asymptotic properties of such sampling algorithms as dimension increases to infinity. (b) A control variate g, satisfying
$2\mathrm{Var}_\rho(f)/(1-\lambda_d)$
, two ‘orthogonal’ approaches to speeding up MCMC algorithms are feasible. (a) The MCMC method itself can be modified, with the aim of increasing the spectral gap, leading to many well-known reversible samplers such as MALA and Hamiltonian Monte Carlo [Reference Duane, Kennedy, Pendleton and Roweth10] as well as non-reversible ones [Reference Bierkens and Roberts7, Reference Duncan, Lelièvre and Pavliotis11]. There is a plethora of papers (see [Reference Roberts and Rosenthal28], [Reference Beskos, Pillai, Roberts, Sanz-Serna and Stuart5], [Reference Durmus, Roberts, Vilmart and Zygalakis12], and the references therein) studying the asymptotic properties of such sampling algorithms as dimension increases to infinity. (b) A control variate g, satisfying
![]() $\rho(g)=0$
, may be added to f with the aim of reducing
$\rho(g)=0$
, may be added to f with the aim of reducing
![]() $\mathrm{Var}_\rho(f)$
to
$\mathrm{Var}_\rho(f)$
to
![]() $\mathrm{Var}_\rho(f+g)$
without modifying the MCMC algorithm. A number of control variates have been proposed in the MCMC literature [Reference Assaraf and Caffarel1, Reference Dellaportas and Kontoyiannis9, Reference Oates, Girolami and Chopin24, Reference Papamarkou, Mira and Girolami25]. Thematically, the present paper fits under (b) and, to the best of our knowledge, is the first to investigate the growth of the asymptotic variance as the dimension
$\mathrm{Var}_\rho(f+g)$
without modifying the MCMC algorithm. A number of control variates have been proposed in the MCMC literature [Reference Assaraf and Caffarel1, Reference Dellaportas and Kontoyiannis9, Reference Oates, Girolami and Chopin24, Reference Papamarkou, Mira and Girolami25]. Thematically, the present paper fits under (b) and, to the best of our knowledge, is the first to investigate the growth of the asymptotic variance as the dimension
![]() $d\to\infty$
in this context. Moreover, it is feasible that our method could be generalized to some of the algorithms under (a); see Section 3.2 below for a discussion of possible extensions.
$d\to\infty$
in this context. Moreover, it is feasible that our method could be generalized to some of the algorithms under (a); see Section 3.2 below for a discussion of possible extensions.
The remainder of paper is structured as follows. Section 2 gives a detailed description of the assumptions and states the results. Section 3 illustrates algorithms based on our main result with numerical examples and discusses (without proof) potential extensions of our results for other MCMC methods, more general targets, etc. In Section 4 we prove our results. Section 5 develops the tools needed for the proofs of Section 4. Section 5 uses results from probability and analysis but is independent of all that precedes it in the paper.
2. Results
Let
![]() $\mathbf{X}^d=\{\mathbf{X}^d_n\}_{n\in{\mathbb{N}}}$
be an RWM chain in
$\mathbf{X}^d=\{\mathbf{X}^d_n\}_{n\in{\mathbb{N}}}$
be an RWM chain in
![]() ${\mathbb{R}}^d$
with a transition kernel
${\mathbb{R}}^d$
with a transition kernel
![]() $P_df\,:\!=(1/d)\mathcal{G}_df + f$
, where
$P_df\,:\!=(1/d)\mathcal{G}_df + f$
, where
![]() $\mathbf{x}^d\in{\mathbb{R}}^d$
,
$\mathbf{x}^d\in{\mathbb{R}}^d$
,
![]() $\mathbf{Y}^d=(Y_1^d,\ldots,Y_d^d)\sim N(\mathbf{x}^d,l^2/d\cdot I_d)$
and
$\mathbf{Y}^d=(Y_1^d,\ldots,Y_d^d)\sim N(\mathbf{x}^d,l^2/d\cdot I_d)$
and
![]() $x\wedge y\,:\!=\min\{x,y\}$
for all
$x\wedge y\,:\!=\min\{x,y\}$
for all
![]() $x,y\in{\mathbb{R}}$
, started in stationarity
$x,y\in{\mathbb{R}}$
, started in stationarity
![]() $\mathbf{X}^d_1\sim \rho_d$
. Let
$\mathbf{X}^d_1\sim \rho_d$
. Let
![]() $\mathcal{S}^n$
consists of all the functions with their first n derivatives growing more slowly than any exponential function. More precisely, for any
$\mathcal{S}^n$
consists of all the functions with their first n derivatives growing more slowly than any exponential function. More precisely, for any
![]() $n\in{\mathbb{N}}\cup\{0\}$
, define
$n\in{\mathbb{N}}\cup\{0\}$
, define
and
![]() $\mathcal{C}^n({\mathbb{R}})$
(resp.
$\mathcal{C}^n({\mathbb{R}})$
(resp.
![]() $\mathcal{C}^0({\mathbb{R}})$
) denotes n-times continuously differentiable (resp. continuous) functions. Our main result (Theorem 2.1 below) applies to the space
$\mathcal{C}^0({\mathbb{R}})$
) denotes n-times continuously differentiable (resp. continuous) functions. Our main result (Theorem 2.1 below) applies to the space
![]() $\mathcal{S}^1$
, containing functions f for which
$\mathcal{S}^1$
, containing functions f for which
is typically of interest in applications (e.g. polynomials). In addition, spaces in (2.2) are closed for solving Poisson’s equation in (2.5); see Proposition 4.8 below.
Throughout the paper
![]() $\rho$
denotes a strictly positive density on
$\rho$
denotes a strictly positive density on
![]() ${\mathbb{R}}$
with
${\mathbb{R}}$
with
![]() $\log(\rho)\in\mathcal{S}^4$
and
$\log(\rho)\in\mathcal{S}^4$
and
unless otherwise stated. Assumption (2.3) implies that the tails of
![]() $\rho$
decay faster than any exponential, i.e.
$\rho$
decay faster than any exponential, i.e.
![]() $\mathbb{E} [{\mathrm{e}}^{sX}]<\infty$
for any
$\mathbb{E} [{\mathrm{e}}^{sX}]<\infty$
for any
![]() $s\in{\mathbb{R}}$
for
$s\in{\mathbb{R}}$
for
![]() $X\sim\rho$
(see [Reference Jarner and Hansen16, Section 4]). The assumption
$X\sim\rho$
(see [Reference Jarner and Hansen16, Section 4]). The assumption
![]() $\log(\rho)\in\mathcal{S}^4$
prohibits
$\log(\rho)\in\mathcal{S}^4$
prohibits
![]() $\rho$
from decaying too quickly, e.g. proportionally to
$\rho$
from decaying too quickly, e.g. proportionally to
![]() ${\mathrm{e}}^{-{\mathrm{e}}^{|x|}}$
. Both of these assumptions serve brevity and clarity of the proofs and it is feasible that they can be relaxed. Nevertheless, a large class of densities of interest satisfy these assumptions, e.g. mixtures of Gaussian densities or any density proportional to
${\mathrm{e}}^{-{\mathrm{e}}^{|x|}}$
. Both of these assumptions serve brevity and clarity of the proofs and it is feasible that they can be relaxed. Nevertheless, a large class of densities of interest satisfy these assumptions, e.g. mixtures of Gaussian densities or any density proportional to
![]() ${\mathrm{e}}^{-p(x)}$
for a positive polynomial p.
${\mathrm{e}}^{-p(x)}$
for a positive polynomial p.
The scaling limit, introduced in [Reference Roberts, Gelman and Gilks30], of the chain
![]() $\mathbf{X}^d$
as the dimension d tends to infinity is key to all that follows. Consider a continuous-time process
$\mathbf{X}^d$
as the dimension d tends to infinity is key to all that follows. Consider a continuous-time process
![]() $\{U^d_t\}_{t\geq0}$
, given by
$\{U^d_t\}_{t\geq0}$
, given by
![]() $U^d_t\,:\!=X^d_{\lfloor d\cdot t\rfloor,1}$
, where
$U^d_t\,:\!=X^d_{\lfloor d\cdot t\rfloor,1}$
, where
![]() $\lfloor\cdot\rfloor$
is the integer-part function and
$\lfloor\cdot\rfloor$
is the integer-part function and
![]() $X^d_{\cdot,1}$
is the first coordinate of
$X^d_{\cdot,1}$
is the first coordinate of
![]() $\mathbf{X}^d$
(since the proposal distribution for
$\mathbf{X}^d$
(since the proposal distribution for
![]() $X^d_{\cdot,1}$
has variance
$X^d_{\cdot,1}$
has variance
![]() $l^2/d$
, time needs to be accelerated to get a non-trivial limit). As shown in [Reference Roberts, Gelman and Gilks30] (see also [Reference Roberts and Rosenthal29]), the weak convergence
$l^2/d$
, time needs to be accelerated to get a non-trivial limit). As shown in [Reference Roberts, Gelman and Gilks30] (see also [Reference Roberts and Rosenthal29]), the weak convergence
![]() $U^d\Rightarrow U$
holds as
$U^d\Rightarrow U$
holds as
![]() $d\uparrow\infty$
, where U is the Langevin diffusion started in stationarity,
$d\uparrow\infty$
, where U is the Langevin diffusion started in stationarity,
![]() $U_0\sim \rho$
, with generator acting on
$U_0\sim \rho$
, with generator acting on
![]() $f\in\mathcal{C}^2({\mathbb{R}})$
as
$f\in\mathcal{C}^2({\mathbb{R}})$
as
and
![]() $\Phi$
is the distribution of N(0,1). Poisson’s equation for U and a function f takes the form
$\Phi$
is the distribution of N(0,1). Poisson’s equation for U and a function f takes the form
It is immediate that a solution
![]() $\skew3\hat f$
of (2.5) is given by the formula
$\skew3\hat f$
of (2.5) is given by the formula
In the remainder of the paper
![]() $\skew3\hat{f}$
denotes the particular solution in (2.6) of the equation in (2.5).
$\skew3\hat{f}$
denotes the particular solution in (2.6) of the equation in (2.5).
As usual, for
![]() $p\in[1,\infty)$
,
$p\in[1,\infty)$
,
![]() $f\colon {\mathbb{R}}^d\to{\mathbb{R}}$
is in
$f\colon {\mathbb{R}}^d\to{\mathbb{R}}$
is in
![]() $L^p(\rho_d)$
if and only if
$L^p(\rho_d)$
if and only if
![]() $\|\:f\|_p\,:\!=\rho_d(| f|^p)^{1/p}<\infty$
. Finally, note that under our assumptions on
$\|\:f\|_p\,:\!=\rho_d(| f|^p)^{1/p}<\infty$
. Finally, note that under our assumptions on
![]() $\rho$
, the kernel
$\rho$
, the kernel
![]() $P_d$
of the RWM chain
$P_d$
of the RWM chain
![]() $\mathbf{X}^d$
defined above is a self-adjoint bounded operator on the Hilbert space
$\mathbf{X}^d$
defined above is a self-adjoint bounded operator on the Hilbert space
![]() $\{g\in L^2(\rho_d)\colon \rho_d(g)=0\}$
with norm
$\{g\in L^2(\rho_d)\colon \rho_d(g)=0\}$
with norm
![]() $\lambda_d<1$
.
$\lambda_d<1$
.
Theorem 2.1. If
![]() $f\in\mathcal{S}^1$
, then
$f\in\mathcal{S}^1$
, then
![]() $\skew3\hat f\in\mathcal{S}^3$
and CLT (1.1) holds for the function
$\skew3\hat f\in\mathcal{S}^3$
and CLT (1.1) holds for the function
![]() $f+dP_d\skew3\hat{f}-d\skew3\hat{f}$
and the RWM chain
$f+dP_d\skew3\hat{f}-d\skew3\hat{f}$
and the RWM chain
![]() $\mathbf{X}^d$
introduced above. Furthermore, there exists a constant
$\mathbf{X}^d$
introduced above. Furthermore, there exists a constant
![]() $C_1>0$
, such that, for all
$C_1>0$
, such that, for all
![]() $f\in\mathcal{S}^1$
and
$f\in\mathcal{S}^1$
and
![]() $d\in{\mathbb{N}}\setminus\{1\}$
, the asymptotic variance
$d\in{\mathbb{N}}\setminus\{1\}$
, the asymptotic variance
![]() $\hat\sigma^2_{f,d}$
in CLT (1.1) satisfies
$\hat\sigma^2_{f,d}$
in CLT (1.1) satisfies
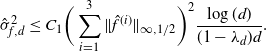 \[\hat\sigma^2_{f,d}\leq C_1 \bigg(\sum_{i=1}^3\|\skew3\hat f^{(i)}\|_{\infty,1/2}\bigg)^2\dfrac{\log(d)}{(1-\lambda_d)d}.\]
\[\hat\sigma^2_{f,d}\leq C_1 \bigg(\sum_{i=1}^3\|\skew3\hat f^{(i)}\|_{\infty,1/2}\bigg)^2\dfrac{\log(d)}{(1-\lambda_d)d}.\]
The proof of Theorem 2.1 is given in Section 4.4 below. It is based on the spectral-gap estimate of the asymptotic variance
![]() $\hat\sigma_{f,d}^2\leq 2\|\mathcal{G}_d\skew3\hat f-\mathcal{G}\skew3\hat f\|^2_2/(1-\lambda_d)$
from [Reference Geyer14] and [Reference Kipnis and Varadhan18], the uniform ergodicity of the chain
$\hat\sigma_{f,d}^2\leq 2\|\mathcal{G}_d\skew3\hat f-\mathcal{G}\skew3\hat f\|^2_2/(1-\lambda_d)$
from [Reference Geyer14] and [Reference Kipnis and Varadhan18], the uniform ergodicity of the chain
![]() $\mathbf{X}^d$
, and the following proposition.
$\mathbf{X}^d$
, and the following proposition.
Proposition 2.1. There exists a constant
![]() $C_2$
such that, for every
$C_2$
such that, for every
![]() $f\in\mathcal{S}^3$
and all
$f\in\mathcal{S}^3$
and all
![]() $d\in{\mathbb{N}}\setminus\{1\}$
, we have
$d\in{\mathbb{N}}\setminus\{1\}$
, we have
 \[
\|\mathcal{G}f-{\mathcal{G}}_df\|_2\leq
C_2 \bigg(\sum_{i=1}^3\|\:f^{(i)}\|_{\infty,1/2}\bigg)\sqrt{\log(d)/d}.
\]
\[
\|\mathcal{G}f-{\mathcal{G}}_df\|_2\leq
C_2 \bigg(\sum_{i=1}^3\|\:f^{(i)}\|_{\infty,1/2}\bigg)\sqrt{\log(d)/d}.
\]
The proof of Proposition 2.1, given in Section 4.3 below, requires pointwise control of the difference
![]() $\mathcal{G}f-{\mathcal{G}}_df$
on a large subset of
$\mathcal{G}f-{\mathcal{G}}_df$
on a large subset of
![]() ${\mathbb{R}}^d$
. To formulate this precisely, we need the following.
${\mathbb{R}}^d$
. To formulate this precisely, we need the following.
Definition 2.1. A positive sequence
![]() $a=\{a_d\}_{d\in{\mathbb{N}}}$
is sluggish if the following holds:
$a=\{a_d\}_{d\in{\mathbb{N}}}$
is sluggish if the following holds:
Theorem 2.2 below is the main technical result of the paper. It generalizes the limit in [Reference Roberts, Gelman and Gilks30, Lemma 2.6] to a class of unbounded functions and provides an error estimate for it. The bound in Theorem 2.2 yields sufficient control of the difference
![]() $\mathcal{G}f-{\mathcal{G}}_df$
to establish Proposition 2.1.
$\mathcal{G}f-{\mathcal{G}}_df$
to establish Proposition 2.1.
Theorem 2.2. Let
![]() $a=\{a_d\}_{d\in{\mathbb{N}}}$
be a sluggish sequence. There exist constants
$a=\{a_d\}_{d\in{\mathbb{N}}}$
be a sluggish sequence. There exist constants
![]() $c_3,C_3>0$
(dependent on a) and measurable sets
$c_3,C_3>0$
(dependent on a) and measurable sets
![]() $\mathcal{A}_d\subset {\mathbb{R}}^d$
, such that, for all
$\mathcal{A}_d\subset {\mathbb{R}}^d$
, such that, for all
![]() $d\in{\mathbb{N}}$
, we have
$d\in{\mathbb{N}}$
, we have
![]() $\rho_d({\mathbb{R}}^d\setminus \mathcal{A}_d)\leq c_3 \,{\mathrm{e}}^{-a_d^2}$
and
$\rho_d({\mathbb{R}}^d\setminus \mathcal{A}_d)\leq c_3 \,{\mathrm{e}}^{-a_d^2}$
and
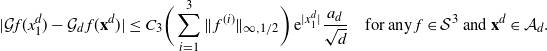 \[ |\mathcal{G}f(x^d_1)-{\mathcal{G}}_df(\mathbf{x}^d)|\leq
C_3\bigg(\sum_{i=1}^3\|\:f^{(i)}\|_{\infty,1/2}\bigg) \,{\mathrm{e}}^{|x^d_1|}
\dfrac{a_d}{\sqrt{d}} \quad\text{for any $f\in\mathcal{S}^3$ and $\mathbf{x}^d\in \mathcal{A}_d$.}\]
\[ |\mathcal{G}f(x^d_1)-{\mathcal{G}}_df(\mathbf{x}^d)|\leq
C_3\bigg(\sum_{i=1}^3\|\:f^{(i)}\|_{\infty,1/2}\bigg) \,{\mathrm{e}}^{|x^d_1|}
\dfrac{a_d}{\sqrt{d}} \quad\text{for any $f\in\mathcal{S}^3$ and $\mathbf{x}^d\in \mathcal{A}_d$.}\]
The proof of Theorem 2.2 is outlined and given in Sections 4.1 and 4.2 below, respectively.
Remark 2.1. The dependence on f in the bound of Theorem 2.2 is not sharp. The factor
![]() $\sum_{i=1}^3\|\:f^{(i)}\|_{\infty,1/2}$
is used because it states concisely that the speed of the convergence of
$\sum_{i=1}^3\|\:f^{(i)}\|_{\infty,1/2}$
is used because it states concisely that the speed of the convergence of
![]() $\mathcal{G}_df$
to
$\mathcal{G}_df$
to
![]() $\mathcal{G}f$
depends linearly on the first three derivatives of f. Moreover, it is not clear if the bound in Theorem 2.1 and Proposition 2.1 is optimal in d. However, if an improvement were possible, the proof would have to be significantly different to that presented here. In particular, better control of the difference
$\mathcal{G}f$
depends linearly on the first three derivatives of f. Moreover, it is not clear if the bound in Theorem 2.1 and Proposition 2.1 is optimal in d. However, if an improvement were possible, the proof would have to be significantly different to that presented here. In particular, better control of the difference
![]() $ |\mathcal{G}f-{\mathcal{G}}_df|$
on
$ |\mathcal{G}f-{\mathcal{G}}_df|$
on
![]() ${\mathbb{R}}^d\setminus \mathcal{A}_d$
would be required.
${\mathbb{R}}^d\setminus \mathcal{A}_d$
would be required.
3. Discussion and numerical examples
3.1. Discussion
In this section we discuss potential extensions of Theorem 2.1 to settings satisfying weaker assumptions or involving related MCMC chains.
3.1.1. Independent and identically distributed target for non-RWM chains in stationarity.
Perhaps the most natural generalization of Theorem 2.1 would be to the MALA and fast-MALA chains (in [Reference Roberts and Rosenthal28] and [Reference Durmus, Roberts, Vilmart and Zygalakis12]) for which it is also possible to obtain non-trivial weak Langevin diffusion limits under appropriate scaling. Since the form of the Poisson equation in (2.5) is preserved, it is possible to define an estimator like that of (1.1), and it seems feasible that a version of Theorem 2.2 can be established in this context using methods analogous to those in this paper.
3.1.2. Independent and identically distributed target in the transient phase for the RWM chain.
Theorem 2.1 is a result only about the stationary behaviour of the chain. As in practice MCMC chains are typically started away from stationarity, it is important to understand the transient behaviour. In [Reference Jourdain, Lelièvre and Miasojedow17] it is shown that the scaling limit described in Section 2 above has mean-field behaviour of the McKean type, that is, the limiting process is a continuous semimartingale with characteristics that at time t depend on the law of the process at t. This suggests that an appropriately chosen time-dependent function
![]() $\skew3\hat f$
in the estimator in (1.1) could further reduce the constant in the bound of Theorem 2.1.
$\skew3\hat f$
in the estimator in (1.1) could further reduce the constant in the bound of Theorem 2.1.
3.1.3. General product target density.
The class of target distributions considered in [Reference Bédard3] and [Reference Bédard and Rosenthal4] preserves the independence (i.e. product) structure but allows for a different, dimension-dependent, scaling of each of the components of the target law. If the proposal variances appropriately reflect the scaling in the target, each component in the infinite-dimensional limit is a Langevin diffusion. Again, as in Section 3.1.1 above, the estimator in (1.1) can be applied directly and an extension of Theorem 2.1 to this setting appears feasible.
3.1.4. Gaussian targets in high dimensions.
Let
![]() $\pi_0$
denote a Gaussian target on
$\pi_0$
denote a Gaussian target on
![]() ${\mathbb{R}}^d$
with mean
${\mathbb{R}}^d$
with mean
![]() $\mu$
and covariance matrix
$\mu$
and covariance matrix
![]() $\operatorname{diag}(\sigma^2_{11},\ldots,\sigma^2_{dd})$
. Inspired by [Reference Roberts and Rosenthal29, Theorem 5] and the proof of Theorem 2.1, a good control variate for the ergodic average estimator for
$\operatorname{diag}(\sigma^2_{11},\ldots,\sigma^2_{dd})$
. Inspired by [Reference Roberts and Rosenthal29, Theorem 5] and the proof of Theorem 2.1, a good control variate for the ergodic average estimator for
![]() $\pi_0(f)$
takes the form
$\pi_0(f)$
takes the form
![]() $d(P_d\skew3\tilde f-\skew3\tilde f)$
, where
$d(P_d\skew3\tilde f-\skew3\tilde f)$
, where
![]() $\skew3\tilde f$
solves the ODE
$\skew3\tilde f$
solves the ODE
with
![]() $h_0(l)\,:\!=2l^2\Phi({-}l\sqrt{J_0}/2)$
and
$h_0(l)\,:\!=2l^2\Phi({-}l\sqrt{J_0}/2)$
and
![]() $J_0\,:\!=1/d\cdot \sum_{j=2}^d1/\sigma^2_{jj}$
. In the case of the mean,
$J_0\,:\!=1/d\cdot \sum_{j=2}^d1/\sigma^2_{jj}$
. In the case of the mean,
![]() $f(x^d_1)=x^d_1$
, we can solve the ODE explicitly:
$f(x^d_1)=x^d_1$
, we can solve the ODE explicitly:
![]() $\skew3\tilde f(x^d_1)=2\sigma^2_{11}/h(l)\cdot x^d_1$
.
$\skew3\tilde f(x^d_1)=2\sigma^2_{11}/h(l)\cdot x^d_1$
.
If
![]() $\pi_0$
has a general non-degenerate covariance matrix
$\pi_0$
has a general non-degenerate covariance matrix
![]() $\Sigma$
, we have an ODE analogous to that above for each eigen-direction of
$\Sigma$
, we have an ODE analogous to that above for each eigen-direction of
![]() $\Sigma$
. The control variate for the mean of the first coordinate,
$\Sigma$
. The control variate for the mean of the first coordinate,
![]() $f(x^d_1)=x^d_1$
, is then a linear combination of the control variates for the means in eigen-directions. Specifically,
$f(x^d_1)=x^d_1$
, is then a linear combination of the control variates for the means in eigen-directions. Specifically,
![]() $\skew3\tilde f \colon {\mathbb{R}}^d\to{\mathbb{R}}$
in the estimator analogous to that of (1.1) (see the numerical example for
$\skew3\tilde f \colon {\mathbb{R}}^d\to{\mathbb{R}}$
in the estimator analogous to that of (1.1) (see the numerical example for
![]() $h=0$
in Section 3.2.2) takes the form
$h=0$
in Section 3.2.2) takes the form
 \begin{equation}
\skew3\tilde f(\mathbf{x}^d)=2/h_0(l) \cdot \sum_{j=1}^dx^d_j\Sigma_{j1},\quad \text{with
} h_0(l)=2l^2\Phi({-}l\sqrt{J_0}/2) \text{ and } J_0=1/d\cdot
\text{Tr}((\Sigma^{-1})_{2:d,2:d}).
\end{equation}
\begin{equation}
\skew3\tilde f(\mathbf{x}^d)=2/h_0(l) \cdot \sum_{j=1}^dx^d_j\Sigma_{j1},\quad \text{with
} h_0(l)=2l^2\Phi({-}l\sqrt{J_0}/2) \text{ and } J_0=1/d\cdot
\text{Tr}((\Sigma^{-1})_{2:d,2:d}).
\end{equation}
Note that
![]() $\skew3\tilde f$
does not depend on the mean of the target, a special feature of the Gaussian setting.
$\skew3\tilde f$
does not depend on the mean of the target, a special feature of the Gaussian setting.
3.1.5. Non-product target density.
A typical non-product target density considered in the literature [6, 20, 26] is a projection of a probability measure
![]() $\Pi$
on a separable real Hilbert space
$\Pi$
on a separable real Hilbert space
![]() $\mathcal{H}$
onto a d-dimensional subspace, where
$\mathcal{H}$
onto a d-dimensional subspace, where
![]() $\Pi$
is given via its Radon–Nikodým derivative
$\Pi$
is given via its Radon–Nikodým derivative
![]() ${{\mathrm{d}} \Pi}/{{\mathrm{d}} \Pi_0}(x)\propto \exp({-}\Psi(x))$
. Here
${{\mathrm{d}} \Pi}/{{\mathrm{d}} \Pi_0}(x)\propto \exp({-}\Psi(x))$
. Here
![]() $\Psi$
is a densely defined positive functional on
$\Psi$
is a densely defined positive functional on
![]() $\mathcal{H}$
and
$\mathcal{H}$
and
![]() $\Pi_0$
is a Gaussian measure on
$\Pi_0$
is a Gaussian measure on
![]() $\mathcal{H}$
specified via a positive trace-class operator on
$\mathcal{H}$
specified via a positive trace-class operator on
![]() $\mathcal{H}$
(see e.g. [Reference Mattingly, Pillai and Stuart20, Section 2.1] for a detailed description and [Reference Beskos, Roberts and Stuart6] for the motivation for this class of measures). A key feature of this framework is that there exists an
$\mathcal{H}$
(see e.g. [Reference Mattingly, Pillai and Stuart20, Section 2.1] for a detailed description and [Reference Beskos, Roberts and Stuart6] for the motivation for this class of measures). A key feature of this framework is that there exists an
![]() $\mathcal{H}$
-valued Langevin diffusion z, driven by a cylindrical Brownian motion on
$\mathcal{H}$
-valued Langevin diffusion z, driven by a cylindrical Brownian motion on
![]() $\mathcal{H}$
(i.e. a solution of a stochastic partial differential equation), that describes the scaling limit of the appropriately accelerated sequence of chains
$\mathcal{H}$
(i.e. a solution of a stochastic partial differential equation), that describes the scaling limit of the appropriately accelerated sequence of chains
![]() $ (\mathbf{X}^d)_{d\in{\mathbb{N}}} $
; see [Reference Mattingly, Pillai and Stuart20] and [Reference Pillai, Stuart and Thiéry26].
$ (\mathbf{X}^d)_{d\in{\mathbb{N}}} $
; see [Reference Mattingly, Pillai and Stuart20] and [Reference Pillai, Stuart and Thiéry26].
An estimator analogous to that of (1.1) would require the solution
![]() $\skew3\hat f$
of the Poisson equation of z. While this might be a feasible strategy theoretically, it would likely be difficult to numerically evaluate the solution
$\skew3\hat f$
of the Poisson equation of z. While this might be a feasible strategy theoretically, it would likely be difficult to numerically evaluate the solution
![]() $\skew3\hat f$
. However, inspired by the Simplified Langevin Algorithm in [Reference Beskos, Roberts and Stuart6], which uses as the proposal chain an Euler scheme for the Langevin diffusion with target
$\skew3\hat f$
. However, inspired by the Simplified Langevin Algorithm in [Reference Beskos, Roberts and Stuart6], which uses as the proposal chain an Euler scheme for the Langevin diffusion with target
![]() $\Pi_0$
(not
$\Pi_0$
(not
![]() $\Pi$
), we suggest constructing the estimator for
$\Pi$
), we suggest constructing the estimator for
![]() $\Pi(f)$
in (1.1), with
$\Pi(f)$
in (1.1), with
![]() $\skew3\hat f$
the solution of the Poisson equation for the Langevin diffusion converging to
$\skew3\hat f$
the solution of the Poisson equation for the Langevin diffusion converging to
![]() $\Pi_0$
(not
$\Pi_0$
(not
![]() $\Pi$
). This strategy is feasible as we are able to produce good control variates for Gaussian product targets in high dimensions in the spirit of Theorem 2.1; see Section 3.1.4 above.
$\Pi$
). This strategy is feasible as we are able to produce good control variates for Gaussian product targets in high dimensions in the spirit of Theorem 2.1; see Section 3.1.4 above.
The main theoretical question in this context is to find suitable assumptions on the functional
![]() $\Psi$
in the Radon–Nikodým derivative above that guarantee the asymptotic variance reduction as
$\Psi$
in the Radon–Nikodým derivative above that guarantee the asymptotic variance reduction as
![]() $d\to\infty$
. Expecting an improvement from polynomial to logarithmic growth is unrealistic as we are solving the Poisson equation for
$d\to\infty$
. Expecting an improvement from polynomial to logarithmic growth is unrealistic as we are solving the Poisson equation for
![]() $\Pi_0$
instead of
$\Pi_0$
instead of
![]() $\Pi$
. However, the numerical example in Section 3.2.2 suggests that this idea may work in practice if
$\Pi$
. However, the numerical example in Section 3.2.2 suggests that this idea may work in practice if
![]() $\Pi$
is close to Gaussian
$\Pi$
is close to Gaussian
![]() $\Pi_0$
. Understanding the settings in which it leads to significant variance reduction is another relevant and important question.
$\Pi_0$
. Understanding the settings in which it leads to significant variance reduction is another relevant and important question.
3.2. Numerical examples
The basic message of the present paper is that the process in the scaling limit of an MCMC algorithm contains useful information that can be utilized to achieve significant savings in high dimensions.
In both examples presented below the problem is to estimate the mean of the first coordinate
![]() $\rho_d(f)$
, where
$\rho_d(f)$
, where
![]() $f(\mathbf{x}^d)\,:\!=x^d_1$
. A run of T steps of a well-tuned RWM algorithm with kernel
$f(\mathbf{x}^d)\,:\!=x^d_1$
. A run of T steps of a well-tuned RWM algorithm with kernel
![]() $P_d$
, defined at the beginning of Section 2, started in stationarity, produces an RWM sample
$P_d$
, defined at the beginning of Section 2, started in stationarity, produces an RWM sample
![]() $\{\mathbf{X}^d_n\}_{n=1,2,\ldots, T}$
and an estimate
$\{\mathbf{X}^d_n\}_{n=1,2,\ldots, T}$
and an estimate
 \[
\hat{\rho}_d(f)\,:\!=\dfrac{1}{T}\sum_{n=1}^{T}f(\mathbf{X}^d_n)
\]
\[
\hat{\rho}_d(f)\,:\!=\dfrac{1}{T}\sum_{n=1}^{T}f(\mathbf{X}^d_n)
\]
of
![]() $\rho_d(f)$
. Take
$\rho_d(f)$
. Take
![]() $\skew3\tilde{f}$
to be the associated solution of the Poisson equation, that we obtain numerically in the first example in Section 3.2.1 and using formula (3.1) in the second example in Section 3.2.2. In both cases we estimate the required unknown quantities (
$\skew3\tilde{f}$
to be the associated solution of the Poisson equation, that we obtain numerically in the first example in Section 3.2.1 and using formula (3.1) in the second example in Section 3.2.2. In both cases we estimate the required unknown quantities (
![]() $\rho_d(\kern1.8ptf)$
and
$\rho_d(\kern1.8ptf)$
and
![]() $\Sigma$
) from the sample
$\Sigma$
) from the sample
![]() $\{\mathbf{X}^d_n\}_{n=1,2,\ldots, T}$
.
$\{\mathbf{X}^d_n\}_{n=1,2,\ldots, T}$
.
Using the same sample, define
 \[
\tilde{\rho}_d(\kern1.8ptf)\,:\!=\dfrac{1}{T}\sum_{n=1}^{T}f(\mathbf{X}^d_n).
\]
\[
\tilde{\rho}_d(\kern1.8ptf)\,:\!=\dfrac{1}{T}\sum_{n=1}^{T}f(\mathbf{X}^d_n).
\]
Since the function
![]() $P_d\skew3\tilde{f}-\skew3\tilde{f}$
is not accessible in closed form, for every
$P_d\skew3\tilde{f}-\skew3\tilde{f}$
is not accessible in closed form, for every
![]() $n\leq T$
we use i.i.d. Monte Carlo to estimate the value
$n\leq T$
we use i.i.d. Monte Carlo to estimate the value
![]() $(P_d\skew3\tilde{f}-\skew3\tilde{f})(\mathbf{X}^d_n)$
as
$(P_d\skew3\tilde{f}-\skew3\tilde{f})(\mathbf{X}^d_n)$
as
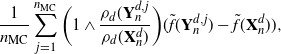 \[
\dfrac{1}{n_{\mathrm{MC}}}\sum_{j=1}^{n_{\mathrm{MC}}} \bigg(1\wedge
\dfrac{\rho_d(\mathbf{Y}^{d,j}_n}{\rho_d(\mathbf{X}^d_n)}\bigg) (\skew3\tilde{f}(\mathbf{Y}^{d,j}_n)-\skew3\tilde{f}(\mathbf{X}^d_n)),\]
\[
\dfrac{1}{n_{\mathrm{MC}}}\sum_{j=1}^{n_{\mathrm{MC}}} \bigg(1\wedge
\dfrac{\rho_d(\mathbf{Y}^{d,j}_n}{\rho_d(\mathbf{X}^d_n)}\bigg) (\skew3\tilde{f}(\mathbf{Y}^{d,j}_n)-\skew3\tilde{f}(\mathbf{X}^d_n)),\]
where
![]() $\mathbf{Y}^{d,1}_n,\ldots,\mathbf{Y}^{d,n_{\mathrm{MC}}}_n$
is an i.i.d. sample of size
$\mathbf{Y}^{d,1}_n,\ldots,\mathbf{Y}^{d,n_{\mathrm{MC}}}_n$
is an i.i.d. sample of size
![]() $n_{\mathrm{MC}}$
from
$n_{\mathrm{MC}}$
from
![]() $N(\mathbf{X}^d_n,l^2/d\cdot I_d)$
. This estimation step can be parallelized (i.e. run on
$N(\mathbf{X}^d_n,l^2/d\cdot I_d)$
. This estimation step can be parallelized (i.e. run on
![]() $n_{\mathrm{MC}}$
cores simultaneously).
$n_{\mathrm{MC}}$
cores simultaneously).
We measure the variance reduction due to the postprocessing above by comparing the mean square errors of
![]() $\hat{\rho}_d(\kern1.8ptf)$
and
$\hat{\rho}_d(\kern1.8ptf)$
and
![]() $\tilde{\rho}_d(\kern1.8ptf)$
as estimators of
$\tilde{\rho}_d(\kern1.8ptf)$
as estimators of
![]() $\rho_d(\kern1.8ptf)$
over
$\rho_d(\kern1.8ptf)$
over
![]() $n_R$
independent runs of the RWM chain,
$n_R$
independent runs of the RWM chain,
where
![]() $ (\hat{\rho}_d(\kern1.8ptf))_k $
and
$ (\hat{\rho}_d(\kern1.8ptf))_k $
and
![]() $ (\tilde{\rho}_d(\kern1.8ptf))_k $
are the averages in the kth run of the chain. Heuristically, this means the estimator
$ (\tilde{\rho}_d(\kern1.8ptf))_k $
are the averages in the kth run of the chain. Heuristically, this means the estimator
![]() $\tilde{\rho}_d(\kern1.8ptf)$
of
$\tilde{\rho}_d(\kern1.8ptf)$
of
![]() $\rho_d(\kern1.8ptf)$
based on T sample points is as good as estimator
$\rho_d(\kern1.8ptf)$
based on T sample points is as good as estimator
![]() $\hat{\rho}_d(\kern1.8ptf)$
based on
$\hat{\rho}_d(\kern1.8ptf)$
based on
![]() $\text{VR}(\rho,f)\cdot T$
sample points.
$\text{VR}(\rho,f)\cdot T$
sample points.
3.2.1. Multi-modal product target.
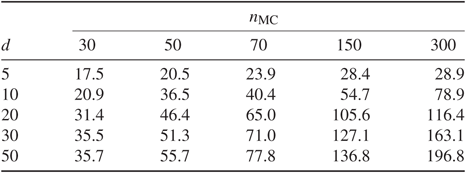
To verify that what theory predicts also happens in practice, we first present an example of an i.i.d. target with each coordinate a bimodal mixture of two Gaussian densities. Given the results in Table 1, we wish to highlight the robustness of the method with respect to numerically estimating
![]() $\skew3\tilde{f}$
and
$\skew3\tilde{f}$
and
![]() $(P_d\skew3\tilde{f}-\skew3\tilde{f})(\mathbf{X}^d_n)$
for each
$(P_d\skew3\tilde{f}-\skew3\tilde{f})(\mathbf{X}^d_n)$
for each
![]() $n\leq T$
.
$n\leq T$
.
Table 1: Variance reduction for different dimensions d and values of ![]() $n_{\mathrm{MC}}$
.
$n_{\mathrm{MC}}$
.
Let
![]() $\rho$
be a mixture of two normal densities
$\rho$
be a mixture of two normal densities
![]() $N(\mu_1,\sigma_1^2)$
and
$N(\mu_1,\sigma_1^2)$
and
![]() $N(\mu_2,\sigma_2^2)$
, with the first arising in the mixture with probability
$N(\mu_2,\sigma_2^2)$
, with the first arising in the mixture with probability
![]() $2/5$
and
$2/5$
and
![]() $\mu_1=-3$
,
$\mu_1=-3$
,
![]() $\mu_2=4$
, and
$\mu_2=4$
, and
![]() $\sigma_1=\sigma_2=7/4$
. The potential of the density
$\sigma_1=\sigma_2=7/4$
. The potential of the density
![]() $\rho$
has two wells and is in a well-known class arising in models of molecular dynamics; see e.g. [Reference Duncan, Lelièvre and Pavliotis11, Section 5.4]. Note that the corresponding density
$\rho$
has two wells and is in a well-known class arising in models of molecular dynamics; see e.g. [Reference Duncan, Lelièvre and Pavliotis11, Section 5.4]. Note that the corresponding density
![]() $\rho_d$
on
$\rho_d$
on
![]() ${\mathbb{R}}^d$
, defined in the introduction, has
${\mathbb{R}}^d$
, defined in the introduction, has
![]() $2^{d}$
modes.
$2^{d}$
modes.
With variance reduction (3.2) we measure how much the estimator
![]() $\tilde{\rho}_d(\kern1.8ptf)$
outperforms the estimator
$\tilde{\rho}_d(\kern1.8ptf)$
outperforms the estimator
![]() $\hat{\rho}_d(\kern1.8ptf)$
of the mean of the first coordinate
$\hat{\rho}_d(\kern1.8ptf)$
of the mean of the first coordinate
![]() $\rho_d(\kern1.8ptf)=6/5$
. The results across a range of dimensions d and values of the parameter
$\rho_d(\kern1.8ptf)=6/5$
. The results across a range of dimensions d and values of the parameter
![]() $n_{\mathrm{MC}}$
(that corresponds to the accuracy of the estimation of
$n_{\mathrm{MC}}$
(that corresponds to the accuracy of the estimation of
![]() $P_d\skew3\tilde{f}-\skew3\tilde{f}$
) are presented in Table 1. All the entries were computed using
$P_d\skew3\tilde{f}-\skew3\tilde{f}$
) are presented in Table 1. All the entries were computed using
![]() $n_R=500$
independent runs of length
$n_R=500$
independent runs of length
![]() $T=2\times 10^5$
.
$T=2\times 10^5$
.
To numerically solve the Poisson equation in (2.5), substitute the derivatives of f and
![]() $\log(\rho)$
with symmetric finite differences and use the estimate
$\log(\rho)$
with symmetric finite differences and use the estimate
![]() $\hat{\rho}(\kern1.8ptf)$
for
$\hat{\rho}(\kern1.8ptf)$
for
![]() $\rho(\kern1.8ptf)$
. Recall that the standard deviation of the proposal in our RWM algorithm is
$\rho(\kern1.8ptf)$
. Recall that the standard deviation of the proposal in our RWM algorithm is
![]() $l/\sqrt{d}$
. The solver uses a grid of hundred points equally spaced in the interval
$l/\sqrt{d}$
. The solver uses a grid of hundred points equally spaced in the interval
where
![]() $\mathbf{X}^d_{n,1}$
is the first coordinate of the nth sample point. We use the Moore–Penrose pseudo-inverse as the linear system is not of full rank. Finally, we take
$\mathbf{X}^d_{n,1}$
is the first coordinate of the nth sample point. We use the Moore–Penrose pseudo-inverse as the linear system is not of full rank. Finally, we take
![]() $\skew3\tilde{f}$
to be the linear interpolation of the solution on the grid. Note that this is a crude approximation of the solution of (2.5), which does not exploit analytical properties of either f or
$\skew3\tilde{f}$
to be the linear interpolation of the solution on the grid. Note that this is a crude approximation of the solution of (2.5), which does not exploit analytical properties of either f or
![]() $\rho$
.
$\rho$
.
The results in Table 1 contain a lot of noise due to numerically solving the ODE, using an approximation
![]() $\hat{\rho}_d(\kern1.8ptf)$
for
$\hat{\rho}_d(\kern1.8ptf)$
for
![]() $\rho_d(\kern1.8ptf)$
and using i.i.d. Monte Carlo to estimate
$\rho_d(\kern1.8ptf)$
and using i.i.d. Monte Carlo to estimate
![]() $\tilde{\rho}_d(\kern1.8ptf)$
. It is interesting to note that despite these additional sources of error, the variance reduction is considerable and behaves as the theoretical results predict. The estimator
$\tilde{\rho}_d(\kern1.8ptf)$
. It is interesting to note that despite these additional sources of error, the variance reduction is considerable and behaves as the theoretical results predict. The estimator
![]() $\tilde{\rho}_d(\kern1.8ptf)$
improves with dimension, and with
$\tilde{\rho}_d(\kern1.8ptf)$
improves with dimension, and with
![]() $n_{\mathrm{MC}}$
. Increasing
$n_{\mathrm{MC}}$
. Increasing
![]() $n_{\mathrm{MC}}$
, however, has a diminishing effect, which is particularly clear in the case
$n_{\mathrm{MC}}$
, however, has a diminishing effect, which is particularly clear in the case
![]() $d=5$
. Due to the asymptotic nature of our result we can only expect limited gain for any fixed d, even if
$d=5$
. Due to the asymptotic nature of our result we can only expect limited gain for any fixed d, even if
![]() $P_d\skew3\tilde{f}-\skew3\tilde{f}$
could be evaluated exactly (corresponding to
$P_d\skew3\tilde{f}-\skew3\tilde{f}$
could be evaluated exactly (corresponding to
![]() $n_{\mathrm{MC}}=\infty$
).
$n_{\mathrm{MC}}=\infty$
).
3.2.2. Bimodal non-product target.
Can the theoretical findings of this paper help us construct control variates in more realistic cases with non-product target densities? It is unreasonable to expect a simple general answer to this question. A more realistic approach for future work seems to be trying to establish specific forms of control variates that work well for classes of targets of a certain type. We briefly explore one such instance in this section. Sections 3.1.4 and 3.1.5 as well as the results in Table 2 suggest that we can construct useful control variates when the target is close to Gaussian.
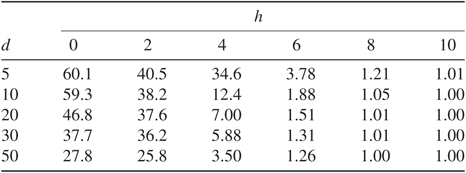
Table 2: Variance reduction for different dimensions d and distances between modes h.
Let
![]() $\mu_{d,h}$
be a d-dimensional vector with entries
$\mu_{d,h}$
be a d-dimensional vector with entries
![]() $(h/2,0,\ldots,0)$
for
$(h/2,0,\ldots,0)$
for
![]() $h\geq 0$
and let
$h\geq 0$
and let
![]() $\Sigma^{(d)}$
be a
$\Sigma^{(d)}$
be a
![]() $d\times d$
covariance matrix with the largest eigenvalue equal to
$d\times d$
covariance matrix with the largest eigenvalue equal to
![]() $\lambda=25$
, with the corresponding eigenvector being
$\lambda=25$
, with the corresponding eigenvector being
![]() $ (1,1,\ldots, 1) $
and all other eigenvalues being equal to one. Take
$ (1,1,\ldots, 1) $
and all other eigenvalues being equal to one. Take
![]() $\Pi_{d,h}$
to be the mixture of two d-dimensional normal densities
$\Pi_{d,h}$
to be the mixture of two d-dimensional normal densities
![]() $N({-}\mu_{d,h},\Sigma^{(d)})$
and
$N({-}\mu_{d,h},\Sigma^{(d)})$
and
![]() $N(\mu_{d,h},\Sigma^{(d)})$
, both arising in the mixture with probability
$N(\mu_{d,h},\Sigma^{(d)})$
, both arising in the mixture with probability
![]() $1/2$
.
$1/2$
.
We wish to estimate the mean of the first coordinate
![]() $\Pi_{d,h}(\kern1.8ptf)=0$
(for
$\Pi_{d,h}(\kern1.8ptf)=0$
(for
![]() $f(\mathbf{x}^d)=x^d_1$
). To produce a control variate we simply pretend we are dealing with a Gaussian target instead of
$f(\mathbf{x}^d)=x^d_1$
). To produce a control variate we simply pretend we are dealing with a Gaussian target instead of
![]() $\Pi_{d,h}$
. Let
$\Pi_{d,h}$
. Let
![]() $\Sigma^{\Pi_{d,h}}$
be the covariance of
$\Sigma^{\Pi_{d,h}}$
be the covariance of
![]() $\Pi_{d,h}$
and let
$\Pi_{d,h}$
and let
![]() $\hat\Sigma^{\Pi_{d,h}}$
be an estimate of
$\hat\Sigma^{\Pi_{d,h}}$
be an estimate of
![]() $\Sigma^{\Pi_{d,h}}$
obtained from the RWM sample
$\Sigma^{\Pi_{d,h}}$
obtained from the RWM sample
![]() $\{\textbf{X}^d_n\}_{n=1,2,\ldots,T}$
. Define
$\{\textbf{X}^d_n\}_{n=1,2,\ldots,T}$
. Define
![]() $\skew3\tilde{f}_{d,h}$
as in (3.1) using
$\skew3\tilde{f}_{d,h}$
as in (3.1) using
![]() $\hat\Sigma^{\Pi_{d,h}}$
. We compare the performance of estimators
$\hat\Sigma^{\Pi_{d,h}}$
. We compare the performance of estimators
![]() $\hat{\Pi}_{d,h}(\kern1.8ptf)$
and
$\hat{\Pi}_{d,h}(\kern1.8ptf)$
and
![]() $\tilde{\Pi}_{d,h}(\kern1.8ptf)$
of
$\tilde{\Pi}_{d,h}(\kern1.8ptf)$
of
![]() $\Pi_{d,h}(\kern1.8ptf)=0$
, respectively defined as
$\Pi_{d,h}(\kern1.8ptf)=0$
, respectively defined as
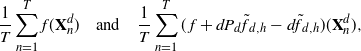 \[
\dfrac{1}{T} \sum_{n=1}^Tf(\textbf{X}^d_n)
\quad\text{and}\quad
\dfrac{1}{T} \sum_{n=1}^T (\kern1.8ptf+dP_d\skew3\tilde{f}_{d,h}-d\skew3\tilde{f}_{d,h})(\textbf{X}^d_n),
\]
\[
\dfrac{1}{T} \sum_{n=1}^Tf(\textbf{X}^d_n)
\quad\text{and}\quad
\dfrac{1}{T} \sum_{n=1}^T (\kern1.8ptf+dP_d\skew3\tilde{f}_{d,h}-d\skew3\tilde{f}_{d,h})(\textbf{X}^d_n),
\]
according to variance reduction (3.2).
Table 2 shows the results across a range of dimensions d and distances between modes h, which measures the ’non-Gaussianity’ of the target. Note that when
![]() $h=0$
the target is Gaussian
$h=0$
the target is Gaussian
![]() $N(0,\Sigma^{(d)})$
, which we include to demonstrate the validity of control variate (3.1) for Gaussian targets. All the entries were calculated using
$N(0,\Sigma^{(d)})$
, which we include to demonstrate the validity of control variate (3.1) for Gaussian targets. All the entries were calculated using
![]() $n_R=500$
independent runs of length
$n_R=500$
independent runs of length
![]() $T=2\times 10^5$
and
$T=2\times 10^5$
and
![]() $n_{\mathrm{MC}}=50$
i.i.d. Monte Carlo steps for computing
$n_{\mathrm{MC}}=50$
i.i.d. Monte Carlo steps for computing
![]() $P_d\skew3\tilde{f}-\skew3\tilde{f}$
at each time step.
$P_d\skew3\tilde{f}-\skew3\tilde{f}$
at each time step.
The quality of results decays with dimension because the proposal is scaled as
![]() $1/d$
in each coordinate. This results in the first coordinate mixing more slowly and for
$1/d$
in each coordinate. This results in the first coordinate mixing more slowly and for
![]() $h\neq 0$
also being less able to cross between modes, hence our estimate
$h\neq 0$
also being less able to cross between modes, hence our estimate
![]() $\hat\Sigma^{\Pi_{d,h}}$
of the covariance becomes worse as we are working with fixed RWM sample length T. When
$\hat\Sigma^{\Pi_{d,h}}$
of the covariance becomes worse as we are working with fixed RWM sample length T. When
![]() $h=10$
(and some cases of
$h=10$
(and some cases of
![]() $h=8$
), it is unlikely that the RWM sample will reach the other mode at all, which results in no gain from the method.
$h=8$
), it is unlikely that the RWM sample will reach the other mode at all, which results in no gain from the method.
If we use the true covariance
![]() $\Sigma^{\Pi_{d,h}}$
of the target in the control variate (3.1), instead of learning it from the sample
$\Sigma^{\Pi_{d,h}}$
of the target in the control variate (3.1), instead of learning it from the sample
![]() $\hat\Sigma^{\Pi_{d,h}}$
, the corresponding results for
$\hat\Sigma^{\Pi_{d,h}}$
, the corresponding results for
![]() $d=50$
are presented in Table 3.
$d=50$
are presented in Table 3.
Table 3: Variance reduction for dimension ![]() $d=50$
and different distances between modes h using the true covariance of the target.
$d=50$
and different distances between modes h using the true covariance of the target.

Unsurprisingly the estimator
![]() $\tilde{\Pi}_{d,h}(\kern1.8ptf)$
does not perform well when the distance between modes h is large. Interestingly, though, the method does offer considerable gain in cases
$\tilde{\Pi}_{d,h}(\kern1.8ptf)$
does not perform well when the distance between modes h is large. Interestingly, though, the method does offer considerable gain in cases
![]() $h\,{=}\,2$
and
$h\,{=}\,2$
and
![]() $h=4$
, and even a noticeable gain in
$h=4$
, and even a noticeable gain in
![]() $h=6$
. For
$h=6$
. For
![]() $h=4$
and
$h=4$
and
![]() $h=6$
the target is already clearly bimodal and different from the Gaussian; the RWM sample stays in the same mode for hundreds, respectively thousands of time steps at a time.
$h=6$
the target is already clearly bimodal and different from the Gaussian; the RWM sample stays in the same mode for hundreds, respectively thousands of time steps at a time.
4. Proofs
Throughout this section we assume the sluggish sequence
![]() $a=\{a_d\}_{d\in{\mathbb{N}}}$
is given and fixed and, as mentioned above, the density
$a=\{a_d\}_{d\in{\mathbb{N}}}$
is given and fixed and, as mentioned above, the density
![]() $\rho$
satisfies
$\rho$
satisfies
![]() $\log(\rho)\in\mathcal{S}^4$
and has sub-exponential tails (2.3). Section 4.1 outlines the proof of Theorem 2.2 by stating the sequence of results needed to establish it. The proofs of these results, given in Section 4.2, rely on the theory developed in Section 5 below. Sections 4.3 and 4.4 establish Proposition 2.1 and Theorem 2.1, respectively.
$\log(\rho)\in\mathcal{S}^4$
and has sub-exponential tails (2.3). Section 4.1 outlines the proof of Theorem 2.2 by stating the sequence of results needed to establish it. The proofs of these results, given in Section 4.2, rely on the theory developed in Section 5 below. Sections 4.3 and 4.4 establish Proposition 2.1 and Theorem 2.1, respectively.
4.1. Outline of the proof of Theorem 2.2
We start by specifying sets
![]() $\mathcal{A}_d\subset {\mathbb{R}}^d$
that have large probability under
$\mathcal{A}_d\subset {\mathbb{R}}^d$
that have large probability under
![]() $\rho_d$
. We need the following fact.
$\rho_d$
. We need the following fact.
Proposition 4.1. There exists a constant
![]() $c_A>0$
such that the following open subset of
$c_A>0$
such that the following open subset of
![]() ${\mathbb{R}}$
satisfies
${\mathbb{R}}$
satisfies
![]() $\rho(A)>0$
:
$\rho(A)>0$
:
Let A satisfy the conclusion of Proposition 4.1 and recall the notation
![]() $\rho(\kern1.8ptf)=\int_{{\mathbb{R}}}f(x)\rho(x) \,{\mathrm{d}} x$
for any appropriate function
$\rho(\kern1.8ptf)=\int_{{\mathbb{R}}}f(x)\rho(x) \,{\mathrm{d}} x$
for any appropriate function
![]() $f \colon {\mathbb{R}}\to{\mathbb{R}}$
. Recall
$f \colon {\mathbb{R}}\to{\mathbb{R}}$
. Recall
![]() $J=\rho(((\log\rho)')^2)=-\rho((\log \rho)'')$
, where the equality follows from assumptions
$J=\rho(((\log\rho)')^2)=-\rho((\log \rho)'')$
, where the equality follows from assumptions
![]() $\log(\rho)\in\mathcal{S}^4$
and (2.3). Define the sets
$\log(\rho)\in\mathcal{S}^4$
and (2.3). Define the sets
![]() $\mathcal{A}_d$
as follows.
$\mathcal{A}_d$
as follows.
Definition 4.1. Any
![]() $\mathbf{x}^d\in{\mathbb{R}}^d$
is in
$\mathbf{x}^d\in{\mathbb{R}}^d$
is in
![]() $\mathcal{A}_d$
if and only if the following four assumptions hold:
$\mathcal{A}_d$
if and only if the following four assumptions hold:
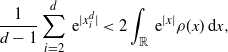 \begin{align}
\dfrac{1}{d-1}\sum_{i=2}^d\,{\mathrm{e}}^{|x^d_i|} & < 2\int_{\mathbb{R}} \,{\mathrm{e}}^{|x|}\rho(x) \,{\mathrm{d}} x,\end{align}
\begin{align}
\dfrac{1}{d-1}\sum_{i=2}^d\,{\mathrm{e}}^{|x^d_i|} & < 2\int_{\mathbb{R}} \,{\mathrm{e}}^{|x|}\rho(x) \,{\mathrm{d}} x,\end{align}
 \begin{align}*
\dfrac{1}{d-1}\sum_{i=2}^d1_{A}(x^d_i) & > \dfrac{\rho(A)}{2},\end{align}
\begin{align}*
\dfrac{1}{d-1}\sum_{i=2}^d1_{A}(x^d_i) & > \dfrac{\rho(A)}{2},\end{align}
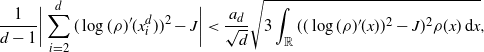 \begin{align}
\dfrac{1}{d-1}\bigg|\sum_{i=2}^d (\log(\rho)'(x^d_i))^2-J\bigg| & <\dfrac{a_d}{\sqrt{d}}
\sqrt{3\int_{{\mathbb{R}}} ( (\log(\rho)'(x))^2-J)^2\rho(x) \,{\mathrm{d}} x},\end{align}
\begin{align}
\dfrac{1}{d-1}\bigg|\sum_{i=2}^d (\log(\rho)'(x^d_i))^2-J\bigg| & <\dfrac{a_d}{\sqrt{d}}
\sqrt{3\int_{{\mathbb{R}}} ( (\log(\rho)'(x))^2-J)^2\rho(x) \,{\mathrm{d}} x},\end{align}
 \begin{align}*
\dfrac{1}{d-1}\bigg|\sum_{i=2}^d \log(\rho)''(x^d_i)+J\bigg| & <\dfrac{a_d}{\sqrt{d}}
\sqrt{3\int_{{\mathbb{R}}} (\log(\rho)''(x)+J)^2\rho(x) \,{\mathrm{d}} x}.
\end{align}
\begin{align}*
\dfrac{1}{d-1}\bigg|\sum_{i=2}^d \log(\rho)''(x^d_i)+J\bigg| & <\dfrac{a_d}{\sqrt{d}}
\sqrt{3\int_{{\mathbb{R}}} (\log(\rho)''(x)+J)^2\rho(x) \,{\mathrm{d}} x}.
\end{align}
Remark 4.1. The precise form of the constants in Definition 4.1 is chosen purely for convenience. It is important that
![]() $\int_{\mathbb{R}} \,{\mathrm{e}}^{|x|}\rho(x) \,{\mathrm{d}} x<\infty$
by (2.3),
$\int_{\mathbb{R}} \,{\mathrm{e}}^{|x|}\rho(x) \,{\mathrm{d}} x<\infty$
by (2.3),
![]() $\rho(A)>0$
by Proposition 4.1 and that the constants in (4.3)–(4.4) are in
$\rho(A)>0$
by Proposition 4.1 and that the constants in (4.3)–(4.4) are in
![]() $ (0,\infty) $
. Moreover, for any
$ (0,\infty) $
. Moreover, for any
![]() $\mathbf{x}^d\in\mathcal{A}_d$
there are no restrictions on its first coordinate
$\mathbf{x}^d\in\mathcal{A}_d$
there are no restrictions on its first coordinate
![]() $x_1^d$
and the sets
$x_1^d$
and the sets
![]() $\mathcal{A}_d$
are typical in the following sense.
$\mathcal{A}_d$
are typical in the following sense.
Proposition 4.2. There exists a constant
![]() $c_1$
such that
$c_1$
such that
![]() $\rho_d({\mathbb{R}}^d\setminus \mathcal{A}_d)\leq c_1 \,{\mathrm{e}}^{-a_d^2}$
for all
$\rho_d({\mathbb{R}}^d\setminus \mathcal{A}_d)\leq c_1 \,{\mathrm{e}}^{-a_d^2}$
for all
![]() $d\in{\mathbb{N}}$
.
$d\in{\mathbb{N}}$
.
Using the theory of large deviations and classical inequalities, the proof of the proposition bounds the probabilities of sets, where each of the above four assumptions in Definition 4.1 fails (see Sections 4.2 and 5.2 below for details).
Pick any
![]() $f\in\mathcal{S}^3$
and express the generator
$f\in\mathcal{S}^3$
and express the generator
![]() $\mathcal{G}_d$
, defined in (2.1), as follows:
$\mathcal{G}_d$
, defined in (2.1), as follows:
where
![]() $\mathbb{E}_{\mathbf{Y}^d-} [\cdot]$
is the expectation with respect to all the coordinates of the proposal
$\mathbb{E}_{\mathbf{Y}^d-} [\cdot]$
is the expectation with respect to all the coordinates of the proposal
![]() $\mathbf{Y}^d$
in
$\mathbf{Y}^d$
in
![]() ${\mathbb{R}}^d$
, except the first one (identify
${\mathbb{R}}^d$
, except the first one (identify
![]() $f\in L^1(\rho)$
with
$f\in L^1(\rho)$
with
![]() $f\in L^1(\rho_d)$
by ignoring the last
$f\in L^1(\rho_d)$
by ignoring the last
![]() $d-1$
coordinates). The strategy of the proof of Theorem 2.2 is to define a sequence of operators, ‘connecting’
$d-1$
coordinates). The strategy of the proof of Theorem 2.2 is to define a sequence of operators, ‘connecting’
![]() $\mathcal{G}_d$
and
$\mathcal{G}_d$
and
![]() $\mathcal{G}$
, such that each approximation can be controlled for
$\mathcal{G}$
, such that each approximation can be controlled for
![]() $f\in\mathcal{S}^3$
and
$f\in\mathcal{S}^3$
and
![]() $\mathbf{x}^d\in\mathcal{A}_d$
.
$\mathbf{x}^d\in\mathcal{A}_d$
.
First, for
![]() $f\in\mathcal{S}^3$
, define
$f\in\mathcal{S}^3$
, define
where, for any
![]() $y\in{\mathbb{R}}$
,
$y\in{\mathbb{R}}$
,
 \begin{equation}
\beta(\mathbf{x}^d, y)\,:\!=\mathbb{E}_{\mathbf{Y}^d-}
\bigg[1\wedge \exp\bigg(\log(\rho)'(x^d_1)( y-x^d_1)+\sum_{i=2}^d K(x^d_i, Y^d_i)\bigg)\bigg],\quad\mathbf{x}^d\in{\mathbb{R}}^d,
\end{equation}
\begin{equation}
\beta(\mathbf{x}^d, y)\,:\!=\mathbb{E}_{\mathbf{Y}^d-}
\bigg[1\wedge \exp\bigg(\log(\rho)'(x^d_1)( y-x^d_1)+\sum_{i=2}^d K(x^d_i, Y^d_i)\bigg)\bigg],\quad\mathbf{x}^d\in{\mathbb{R}}^d,
\end{equation}
and for any
![]() $ (x,y)\in{\mathbb{R}}^2 $
we define
$ (x,y)\in{\mathbb{R}}^2 $
we define
In (4.7), the set A satisfies the conclusion of Proposition 4.1 and the coefficient before
![]() $ ( y\,{-}\,x)^3 $
is chosen so that it is uniformly bounded for all
$ ( y\,{-}\,x)^3 $
is chosen so that it is uniformly bounded for all
![]() $x\in {\mathbb{R}}$
. This property plays an important role in proving that we have uniform control over the supremum norms of certain densities; see Lemmas 4.1 and 4.2 below. We can now prove the following.
$x\in {\mathbb{R}}$
. This property plays an important role in proving that we have uniform control over the supremum norms of certain densities; see Lemmas 4.1 and 4.2 below. We can now prove the following.
Proposition 4.3. There exists a constant C such that, for every
![]() $f\in\mathcal{S}^3$
and all
$f\in\mathcal{S}^3$
and all
![]() $d\in{\mathbb{N}}$
, we have
$d\in{\mathbb{N}}$
, we have
The proof of Proposition 4.3 relies only on the elementary bounds from Section 5.1 below. The idea is to use the Taylor series of
![]() $\log(\rho)(Y_i)$
around
$\log(\rho)(Y_i)$
around
![]() $x^d_i$
for every
$x^d_i$
for every
![]() $i\in\{1,\ldots,d\}$
and then prove that modifying terms of order higher than two if
$i\in\{1,\ldots,d\}$
and then prove that modifying terms of order higher than two if
![]() $i\in\{2,\ldots,d\}$
(resp. one if
$i\in\{2,\ldots,d\}$
(resp. one if
![]() $i=1$
) is inconsequential.
$i=1$
) is inconsequential.
Define the operator
![]() $\hat{\mathcal{G}}_d\kern1.5ptf(\mathbf{x}^d)$
for any
$\hat{\mathcal{G}}_d\kern1.5ptf(\mathbf{x}^d)$
for any
![]() $f\in\mathcal{S}^3$
and
$f\in\mathcal{S}^3$
and
![]() $\mathbf{x}^d\in{\mathbb{R}}^d$
by
$\mathbf{x}^d\in{\mathbb{R}}^d$
by
 \begin{align}
\hat{\mathcal{G}}_d\kern1.5ptf(\mathbf{x}^d)&\,:\!= \dfrac{l^2}{2}f''(x^d_1)\mathbb{E}_{\mathbf{Y}^d-} \Big[1\wedge
{\mathrm{e}}^{\sum_{i=2}^d K(x^d_i, Y^d_i)}\Big] \notag \\
&\quad\, +l^2f'(x^d_1)\log(\rho)'(x^d_1)\mathbb{E}_{\mathbf{Y}^d-} \Big[{\mathrm{e}}^{\sum_{i=2}^d
K(x^d_i, Y^d_i)}1_{\{\sum_{i=2}^d K(x^d_i,
Y^d_i)<0\}}\Big].
\end{align}
\begin{align}
\hat{\mathcal{G}}_d\kern1.5ptf(\mathbf{x}^d)&\,:\!= \dfrac{l^2}{2}f''(x^d_1)\mathbb{E}_{\mathbf{Y}^d-} \Big[1\wedge
{\mathrm{e}}^{\sum_{i=2}^d K(x^d_i, Y^d_i)}\Big] \notag \\
&\quad\, +l^2f'(x^d_1)\log(\rho)'(x^d_1)\mathbb{E}_{\mathbf{Y}^d-} \Big[{\mathrm{e}}^{\sum_{i=2}^d
K(x^d_i, Y^d_i)}1_{\{\sum_{i=2}^d K(x^d_i,
Y^d_i)<0\}}\Big].
\end{align}
We can now prove the following fact.
Proposition 4.4. There exists a constant C such that, for every
![]() $f\in\mathcal{S}^3$
, and all
$f\in\mathcal{S}^3$
, and all
![]() $d\in{\mathbb{N}}$
, we have
$d\in{\mathbb{N}}$
, we have
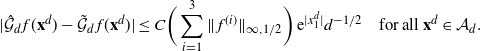 \[ |\hat{\mathcal{G}}_d\kern1.5ptf(\mathbf{x}^d)-\tilde{\mathcal{G}}_d\kern1.5ptf(\mathbf{x}^d)|\leq
C\bigg(\sum_{i=1}^3\|\:f^{(i)}\|_{\infty,1/2}\bigg)\,{\mathrm{e}}^{|x^d_1|}d^{-1/2}\quad \text{{for all} }\mathbf{x}^d\in\mathcal{A}_d.
\]
\[ |\hat{\mathcal{G}}_d\kern1.5ptf(\mathbf{x}^d)-\tilde{\mathcal{G}}_d\kern1.5ptf(\mathbf{x}^d)|\leq
C\bigg(\sum_{i=1}^3\|\:f^{(i)}\|_{\infty,1/2}\bigg)\,{\mathrm{e}}^{|x^d_1|}d^{-1/2}\quad \text{{for all} }\mathbf{x}^d\in\mathcal{A}_d.
\]
Note that if we freeze the coordinates
![]() $x_2^d,\ldots,x_d^d$
in
$x_2^d,\ldots,x_d^d$
in
![]() $\mathbf{x}^d$
, the operator mapping
$\mathbf{x}^d$
, the operator mapping
![]() $f\in\mathcal{S}^3$
to
$f\in\mathcal{S}^3$
to
![]() $x_1^d\mapsto \hat{\mathcal{G}}_d\kern1.5ptf(\mathbf{x}^d)$
generates a one-dimensional diffusion with coefficients of the same functional form as in
$x_1^d\mapsto \hat{\mathcal{G}}_d\kern1.5ptf(\mathbf{x}^d)$
generates a one-dimensional diffusion with coefficients of the same functional form as in
![]() $\mathcal{G}$
, but with slightly modified parameter values. The proof of Proposition 4.4 is based on the third and second degree Taylor’s expansion of
$\mathcal{G}$
, but with slightly modified parameter values. The proof of Proposition 4.4 is based on the third and second degree Taylor’s expansion of
![]() $y\mapsto f( y)$
and
$y\mapsto f( y)$
and
![]() $y\mapsto \beta(\mathbf{x}^d,y)$
(around
$y\mapsto \beta(\mathbf{x}^d,y)$
(around
![]() $x^d_1$
), respectively, applied to the definition of
$x^d_1$
), respectively, applied to the definition of
![]() $\tilde{\mathcal{G}}_d$
in (4.5). The difficult part in proving that the remainder terms can be omitted consists of controlling
$\tilde{\mathcal{G}}_d$
in (4.5). The difficult part in proving that the remainder terms can be omitted consists of controlling
![]() $ {\partial^2}/{\partial y^2}\beta(\mathbf{x}^d,y) $
, as this entails bounding the supremum norm of the density of
$ {\partial^2}/{\partial y^2}\beta(\mathbf{x}^d,y) $
, as this entails bounding the supremum norm of the density of
![]() $\sum_{i=2}^d K(x^d_i, Y^d_i)$
uniformly in d. Condition (4.2), which forces a portion of the coordinates
$\sum_{i=2}^d K(x^d_i, Y^d_i)$
uniformly in d. Condition (4.2), which forces a portion of the coordinates
![]() $x^d_i$
of
$x^d_i$
of
![]() $\mathbf{x}^d$
to be in the set A where the densities of the corresponding summands
$\mathbf{x}^d$
to be in the set A where the densities of the corresponding summands
![]() $K(x^d_i,Y^d_i)$
can be controlled, was introduced for this purpose. The details, explained in Sections 4.2 and 5.3 below, rely crucially on the optimal version of Young’s inequality.
$K(x^d_i,Y^d_i)$
can be controlled, was introduced for this purpose. The details, explained in Sections 4.2 and 5.3 below, rely crucially on the optimal version of Young’s inequality.
Introduce the following normal random variable with mean
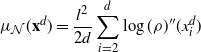 \[
\mu_{\mathcal{N}}(\mathbf{x}^d)=\dfrac{l^2}{2d}\sum_{i=2}^d\log(\rho)''(x^d_i)
\]
\[
\mu_{\mathcal{N}}(\mathbf{x}^d)=\dfrac{l^2}{2d}\sum_{i=2}^d\log(\rho)''(x^d_i)
\]
and variance
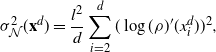 \[
\sigma^2_{\mathcal{N}}(\mathbf{x}^d)=\dfrac{l^2}{d}\sum_{i=2}^d (\log(\rho)'(x^d_i))^2{,} \]
\[
\sigma^2_{\mathcal{N}}(\mathbf{x}^d)=\dfrac{l^2}{d}\sum_{i=2}^d (\log(\rho)'(x^d_i))^2{,} \]
that is,
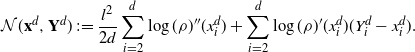 \begin{equation}
\mathcal{N}(\mathbf{x}^d,\mathbf{Y}^d)\,:\!=\dfrac{l^2}{2d}\sum_{i=2}^d\log(\rho)''(x^d_i)+\sum_{i=2}^d\log(\rho)'(x^d_i)(Y^d_i-x^d_i).
\end{equation}
\begin{equation}
\mathcal{N}(\mathbf{x}^d,\mathbf{Y}^d)\,:\!=\dfrac{l^2}{2d}\sum_{i=2}^d\log(\rho)''(x^d_i)+\sum_{i=2}^d\log(\rho)'(x^d_i)(Y^d_i-x^d_i).
\end{equation}
Define the operator
![]() $\breve{\mathcal{G}}_d\kern1.5ptf(\mathbf{x}^d)$
for
$\breve{\mathcal{G}}_d\kern1.5ptf(\mathbf{x}^d)$
for
![]() $f\in\mathcal{S}^3$
and
$f\in\mathcal{S}^3$
and
![]() $\mathbf{x}^d\in{\mathbb{R}}^d$
by
$\mathbf{x}^d\in{\mathbb{R}}^d$
by
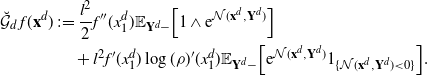 \begin{align*}
\breve{\mathcal{G}}_df(\mathbf{x}^d)&\,:\!= \frac{l^2}{2}f''(x^d_1)\mathbb{E}_{\mathbf{Y}^d-} \Big[1\wedge {\mathrm{e}}^{\mathcal{N}(\mathbf{x}^d,\mathbf{Y}^d)}\Big] \\
& \quad\, + l^2f'(x^d_1)\log(\rho)'(x^d_1)\mathbb{E}_{\mathbf{Y}^d-} \Big[{\mathrm{e}}^{\mathcal{N}(\mathbf{x}^d,\mathbf{Y}^d)}1_{\{\mathcal{N}(\mathbf{x}^d,\mathbf{Y}^d)<0\}}\Big].
\end{align*}
\begin{align*}
\breve{\mathcal{G}}_df(\mathbf{x}^d)&\,:\!= \frac{l^2}{2}f''(x^d_1)\mathbb{E}_{\mathbf{Y}^d-} \Big[1\wedge {\mathrm{e}}^{\mathcal{N}(\mathbf{x}^d,\mathbf{Y}^d)}\Big] \\
& \quad\, + l^2f'(x^d_1)\log(\rho)'(x^d_1)\mathbb{E}_{\mathbf{Y}^d-} \Big[{\mathrm{e}}^{\mathcal{N}(\mathbf{x}^d,\mathbf{Y}^d)}1_{\{\mathcal{N}(\mathbf{x}^d,\mathbf{Y}^d)<0\}}\Big].
\end{align*}
Proposition 4.5. There exists a constant C such that, for every
![]() $f\in\mathcal{S}^3$
and all
$f\in\mathcal{S}^3$
and all
![]() $d\in{\mathbb{N}}$
, we have
$d\in{\mathbb{N}}$
, we have
 \[ |\breve{\mathcal{G}}_df(\mathbf{x}^d)-\hat{\mathcal{G}}_df(\mathbf{x}^d)|\leq C\bigg(\sum_{i=1}^2\|\:f^{(i)}\|_{\infty,1/2}\bigg) \,{\mathrm{e}}^{|x^d_1|}d^{-1/2} \quad\text{{for all} }\mathbf{x}^d\in\mathcal{A}_d. \]
\[ |\breve{\mathcal{G}}_df(\mathbf{x}^d)-\hat{\mathcal{G}}_df(\mathbf{x}^d)|\leq C\bigg(\sum_{i=1}^2\|\:f^{(i)}\|_{\infty,1/2}\bigg) \,{\mathrm{e}}^{|x^d_1|}d^{-1/2} \quad\text{{for all} }\mathbf{x}^d\in\mathcal{A}_d. \]
First we show that
is small (Lemma 4.4 below). Proving that
are close is challenging, as it requires showing that the supremum norm of the difference between the distributions of
![]() $\mathcal{N}(\mathbf{x}^{d},\mathbf{Y}^d)$
and
$\mathcal{N}(\mathbf{x}^{d},\mathbf{Y}^d)$
and
![]() $\sum_{i=2}^{d} K(x^d_i, Y^d_i)$
decays as
$\sum_{i=2}^{d} K(x^d_i, Y^d_i)$
decays as
![]() $d^{-1/2}$
uniformly in its argument. The proof of this fact mimics the proof of the Berry–Esseen theorem and relies on the closeness of the CFs (characteristic functions) of
$d^{-1/2}$
uniformly in its argument. The proof of this fact mimics the proof of the Berry–Esseen theorem and relies on the closeness of the CFs (characteristic functions) of
![]() $\mathcal{N}(\mathbf{x}^d,\mathbf{Y}^d)$
and
$\mathcal{N}(\mathbf{x}^d,\mathbf{Y}^d)$
and
![]() $\sum_{i=2}^d K(x^d_i, Y^d_i)$
. The particular form of K(x,Y) makes it possible to explicitly calculate the CF of K(x,Y), if
$\sum_{i=2}^d K(x^d_i, Y^d_i)$
. The particular form of K(x,Y) makes it possible to explicitly calculate the CF of K(x,Y), if
![]() $x\notin A$
, and bound it appropriately, if
$x\notin A$
, and bound it appropriately, if
![]() $x\in A$
. The details are explained in Sections 4.2 and 5.4 below.
$x\in A$
. The details are explained in Sections 4.2 and 5.4 below.
Since
![]() $\mathcal{N}(\mathbf{x}^d,\mathbf{Y}^d)$
is normal, it is possible to explicitly calculate the expectations
$\mathcal{N}(\mathbf{x}^d,\mathbf{Y}^d)$
is normal, it is possible to explicitly calculate the expectations
(see [Reference Roberts, Gelman and Gilks30, Proposition 2.4]). Using these formulae, Proposition 4.6, which implies Theorem 2.2, can be deduced from assumptions (4.3)–(4.4).
Proposition 4.6. There exists a constant C such that, for every
![]() $f\in\mathcal{S}^3$
and all
$f\in\mathcal{S}^3$
and all
![]() $d\in{\mathbb{N}}$
, we have
$d\in{\mathbb{N}}$
, we have
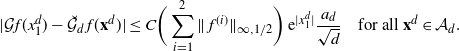 \[ |\mathcal{G}f(x^d_1)-\breve{\mathcal{G}}_df(\mathbf{x}^d)|\leq C\bigg(\sum_{i=1}^2\|\:f^{(i)}\|_{\infty,1/2}\bigg) \,{\mathrm{e}}^{|x^d_1|}\dfrac{a_d}{\sqrt{d}} \quad\text{{for all} }\mathbf{x}^d\in\mathcal{A}_d.\]
\[ |\mathcal{G}f(x^d_1)-\breve{\mathcal{G}}_df(\mathbf{x}^d)|\leq C\bigg(\sum_{i=1}^2\|\:f^{(i)}\|_{\infty,1/2}\bigg) \,{\mathrm{e}}^{|x^d_1|}\dfrac{a_d}{\sqrt{d}} \quad\text{{for all} }\mathbf{x}^d\in\mathcal{A}_d.\]
Remark 4.2. The bounds in Propositions 4.3–4.5 are of order
![]() ${\mathrm{O}} (d^{-1/2})$
. The order
${\mathrm{O}} (d^{-1/2})$
. The order
![]() ${\mathrm{O}} (a_d/\sqrt{d})$
of the bound in Proposition 4.6 gives the order in the bound of Theorem 2.2.
${\mathrm{O}} (a_d/\sqrt{d})$
of the bound in Proposition 4.6 gives the order in the bound of Theorem 2.2.
4.2. Proof of Theorem 2.2
Proof of Proposition 4.1. Let
It suffices to show that the open set
![]() $\tilde A$
is not empty, since
$\tilde A$
is not empty, since
so for some large
![]() $n_0$
the open set
$n_0$
the open set
must have positive Lebesgue measure and we can take
![]() $c_A\,:\!=n_0$
.
$c_A\,:\!=n_0$
.
Assume that
![]() $\skew2\tilde{A}=\emptyset$
, i.e.
$\skew2\tilde{A}=\emptyset$
, i.e.
![]() $|u'|\geq u^2$
on
$|u'|\geq u^2$
on
![]() ${\mathbb{R}}$
, where
${\mathbb{R}}$
, where
![]() $u\,:\!=\log(\rho)'$
. Since
$u\,:\!=\log(\rho)'$
. Since
![]() $\rho$
satisfies (2.3), there exists
$\rho$
satisfies (2.3), there exists
![]() $x_0<0$
and
$x_0<0$
and
![]() $C>0$
such that
$C>0$
such that
![]() $u>C$
on the interval
$u>C$
on the interval
![]() $({-}\infty,x_0)$
. Moreover, since
$({-}\infty,x_0)$
. Moreover, since
![]() $|u'|\geq u^2>C^2>0$
, u’ has no zeros on
$|u'|\geq u^2>C^2>0$
, u’ has no zeros on
![]() $({-}\infty,x_0)$
and satisfies either
$({-}\infty,x_0)$
and satisfies either
![]() $u'\geq u^2$
or
$u'\geq u^2$
or
![]() $-u'\geq u^2$
on the half-infinite interval. Since
$-u'\geq u^2$
on the half-infinite interval. Since
![]() $ (1/u)'=-u'/u^2 $
, integrating the inequalities
$ (1/u)'=-u'/u^2 $
, integrating the inequalities
![]() $-u'/u^2\leq -1$
or
$-u'/u^2\leq -1$
or
![]() $-u'/u^2\geq1$
from any
$-u'/u^2\geq1$
from any
![]() $x\in({-}\infty,x_0)$
to
$x\in({-}\infty,x_0)$
to
![]() $x_0$
, we get
$x_0$
, we get
![]() $1/u(x_0)+x_0-x\leq 1/u(x)$
and
$1/u(x_0)+x_0-x\leq 1/u(x)$
and
![]() $1/u(x_0)+x-x_0\geq 1/u(x)$
. Since by assumption
$1/u(x_0)+x-x_0\geq 1/u(x)$
. Since by assumption
![]() $0<1/u<1/C$
on
$0<1/u<1/C$
on
![]() $ ({-}\infty,x_0) $
, we get a contradiction in both cases.
$ ({-}\infty,x_0) $
, we get a contradiction in both cases.
Proof of Proposition 4.2. Let
![]() $B^d_1$
,
$B^d_1$
,
![]() $B^d_2$
,
$B^d_2$
,
![]() $B^d_3$
, and
$B^d_3$
, and
![]() $B^d_4$
be the subsets of
$B^d_4$
be the subsets of
![]() ${\mathbb{R}}^d$
where assumptions (4.1), (4.2), (4.3), and (4.4) are not satisfied, respectively. Note that
${\mathbb{R}}^d$
where assumptions (4.1), (4.2), (4.3), and (4.4) are not satisfied, respectively. Note that
Recall that by (2.3), L’Hôpital’s rule implies
and hence
![]() $\rho({\mathrm{e}}^{s|x|})<\infty$
for any
$\rho({\mathrm{e}}^{s|x|})<\infty$
for any
![]() $s>0$
. Since
$s>0$
. Since
![]() $\{a_d\}_{d\in{\mathbb{N}}}$
is sluggish, there exists
$\{a_d\}_{d\in{\mathbb{N}}}$
is sluggish, there exists
![]() $n\in{\mathbb{N}}$
such that
$n\in{\mathbb{N}}$
such that
![]() $a_d\leq \sqrt{n\log d}$
for all
$a_d\leq \sqrt{n\log d}$
for all
![]() $d\in{\mathbb{N}}$
. Then, by Proposition 5.4 applied to functions
$d\in{\mathbb{N}}$
. Then, by Proposition 5.4 applied to functions
![]() $x\mapsto ({\mathrm{e}}^{|x|}-\rho({\mathrm{e}}^{|x|}))/\rho({\mathrm{e}}^{|x|})$
and
$x\mapsto ({\mathrm{e}}^{|x|}-\rho({\mathrm{e}}^{|x|}))/\rho({\mathrm{e}}^{|x|})$
and
![]() $x\mapsto 2(\rho(A)-1_A(x))/\rho(A)$
, respectively, there exist constants
$x\mapsto 2(\rho(A)-1_A(x))/\rho(A)$
, respectively, there exist constants
![]() $c_1', c_2'$
such that the inequalities
$c_1', c_2'$
such that the inequalities
![]() $\rho(B^d_1)\leq c_1'd^{-n}\leq c_1'\,{\mathrm{e}}^{-a_d^2}$
and
$\rho(B^d_1)\leq c_1'd^{-n}\leq c_1'\,{\mathrm{e}}^{-a_d^2}$
and
![]() $\rho(B^d_2)\leq c_2'd^{-n}\leq c_2'\,{\mathrm{e}}^{-a_d^2}$
hold for all
$\rho(B^d_2)\leq c_2'd^{-n}\leq c_2'\,{\mathrm{e}}^{-a_d^2}$
hold for all
![]() $d\in{\mathbb{N}}$
.
$d\in{\mathbb{N}}$
.
Likewise, there exist constants
![]() $c_3', c_4'$
such that
$c_3', c_4'$
such that
![]() $\rho(B^d_3)\leq c_3'
\,{\mathrm{e}}^{-a^2_d}$
and
$\rho(B^d_3)\leq c_3'
\,{\mathrm{e}}^{-a^2_d}$
and
![]() $\rho(B^d_4)\leq c_4' \,{\mathrm{e}}^{-a^2_d}$
. This follows by Proposition 5.3, applied to the sequence
$\rho(B^d_4)\leq c_4' \,{\mathrm{e}}^{-a^2_d}$
. This follows by Proposition 5.3, applied to the sequence
![]() $\{a_d\}_{d\in{\mathbb{N}}}$
and functions
$\{a_d\}_{d\in{\mathbb{N}}}$
and functions
(with
![]() $t\,:\!=\sqrt{3\rho(g_3^2)}$
) and
$t\,:\!=\sqrt{3\rho(g_3^2)}$
) and
(with
![]() $t\,:\!=\sqrt{3\rho(g_4^2)}$
), respectively. Hence
$t\,:\!=\sqrt{3\rho(g_4^2)}$
), respectively. Hence
for
![]() $c_1\,:\!=\max\{c_1',c_2',c_3',c_4'\}$
.
$c_1\,:\!=\max\{c_1',c_2',c_3',c_4'\}$
.
Remark 4.3. The proof above shows that the subsets
![]() $B^d_1$
and
$B^d_1$
and
![]() $B^d_2$
are of negligible size in comparison to
$B^d_2$
are of negligible size in comparison to
![]() $B^d_3$
and
$B^d_3$
and
![]() $B^d_4$
, since the
$B^d_4$
, since the
![]() $n\in{\mathbb{N}}$
can be chosen arbitrarily large.
$n\in{\mathbb{N}}$
can be chosen arbitrarily large.
Proof of Proposition 4.3. Pick an arbitrary
![]() $\mathbf{x}^d\in \mathcal{A}_d$
and recall that
$\mathbf{x}^d\in \mathcal{A}_d$
and recall that
![]() $\alpha(\mathbf{x}^d,\mathbf{Y}^d)$
is defined in (2.1). Since
$\alpha(\mathbf{x}^d,\mathbf{Y}^d)$
is defined in (2.1). Since
![]() $|1\wedge {\mathrm{e}}^x-1\wedge {\mathrm{e}}^y|\leq |x-y|$
for all
$|1\wedge {\mathrm{e}}^x-1\wedge {\mathrm{e}}^y|\leq |x-y|$
for all
![]() $x,y\in{\mathbb{R}}$
, for every realization
$x,y\in{\mathbb{R}}$
, for every realization
![]() $Y^d_1$
, Taylor’s theorem implies
$Y^d_1$
, Taylor’s theorem implies
where
![]() $W^d_1$
satisfies
$W^d_1$
satisfies
and
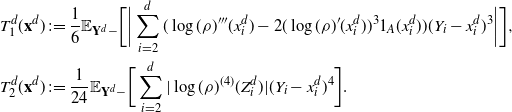 \begin{align*}
T^d_1(\mathbf{x}^d)&\,:\!= \dfrac{1}{6}\mathbb{E}_{\mathbf{Y}^d-}\bigg[\bigg|\sum_{i=2}^d (\log(\rho)'''(x^d_i)-2(\log(\rho)'(x^d_i))^31_{A}(x^d_i))(Y_i-x^d_i)^3\bigg|\bigg], \\
T^d_2(\mathbf{x}^d)&\,:\!= \dfrac{1}{24}\mathbb{E}_{\mathbf{Y}^d-}\bigg[\sum_{i=2}^d|\log(\rho)^{(4)}(Z^d_i)|(Y_i-x^d_i)^4\bigg].
\end{align*}
\begin{align*}
T^d_1(\mathbf{x}^d)&\,:\!= \dfrac{1}{6}\mathbb{E}_{\mathbf{Y}^d-}\bigg[\bigg|\sum_{i=2}^d (\log(\rho)'''(x^d_i)-2(\log(\rho)'(x^d_i))^31_{A}(x^d_i))(Y_i-x^d_i)^3\bigg|\bigg], \\
T^d_2(\mathbf{x}^d)&\,:\!= \dfrac{1}{24}\mathbb{E}_{\mathbf{Y}^d-}\bigg[\sum_{i=2}^d|\log(\rho)^{(4)}(Z^d_i)|(Y_i-x^d_i)^4\bigg].
\end{align*}
Here
![]() $Z^d_i$
satisfies
$Z^d_i$
satisfies
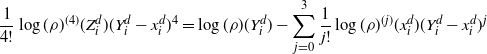 \[
\dfrac{1}{4!}\log(\rho)^{(4)}(Z^d_i)(Y^d_i-x^d_i)^4=\log(\rho)(Y^d_i)-\sum_{j=0}^{3}\dfrac{1}{j!}\log(\rho)^{(j)}(x^d_i)(Y^d_i-x^d_i)^j\]
\[
\dfrac{1}{4!}\log(\rho)^{(4)}(Z^d_i)(Y^d_i-x^d_i)^4=\log(\rho)(Y^d_i)-\sum_{j=0}^{3}\dfrac{1}{j!}\log(\rho)^{(j)}(x^d_i)(Y^d_i-x^d_i)^j\]
for any
![]() $2\leq i\leq d$
. Recall that
$2\leq i\leq d$
. Recall that
![]() $Y^d_i-x^d_i$
is normal
$Y^d_i-x^d_i$
is normal
![]() $N(0,l^2/d)$
, for some constant
$N(0,l^2/d)$
, for some constant
![]() $l>0$
, and
$l>0$
, and
![]() $\log(\rho)\in\mathcal{S}^4$
. Hence we may apply Proposition 5.2 to the function
$\log(\rho)\in\mathcal{S}^4$
. Hence we may apply Proposition 5.2 to the function
to get
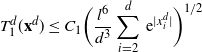 \[
T^d_1(\mathbf{x}^d)\leq C_1 \bigg(\dfrac{l^6}{d^3} \sum_{i=2}^d \,{\mathrm{e}}^{|x^d_i|}\bigg)^{1/2}
\]
\[
T^d_1(\mathbf{x}^d)\leq C_1 \bigg(\dfrac{l^6}{d^3} \sum_{i=2}^d \,{\mathrm{e}}^{|x^d_i|}\bigg)^{1/2}
\]
for some constant
![]() $C_1>0$
, independent of
$C_1>0$
, independent of
![]() $\mathbf{x}^d$
. Since
$\mathbf{x}^d$
. Since
![]() $\mathbf{x}^d\in \mathcal{A}_d$
, the assumption in (4.1) yields
$\mathbf{x}^d\in \mathcal{A}_d$
, the assumption in (4.1) yields
![]() $T^d_1(\mathbf{x}^d)\leq C_1 l^3 (2\rho({\mathrm{e}}^{|x|}))^{1/2}/d$
. Similarly, we apply Proposition 5.1 (with
$T^d_1(\mathbf{x}^d)\leq C_1 l^3 (2\rho({\mathrm{e}}^{|x|}))^{1/2}/d$
. Similarly, we apply Proposition 5.1 (with
![]() $f=\log\rho$
,
$f=\log\rho$
,
![]() $n=k=4$
,
$n=k=4$
,
![]() $m=1$
,
$m=1$
,
![]() $s=1$
and
$s=1$
and
![]() $\sigma^2=l^2/d$
) and assumption (4.1) to get
$\sigma^2=l^2/d$
) and assumption (4.1) to get
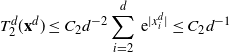 \[
T^d_2(\mathbf{x}^d)\leq C_2 d^{-2}\sum_{i=2}^d\,{\mathrm{e}}^{|x^d_i|}\leq C_2 d^{-1}
\]
\[
T^d_2(\mathbf{x}^d)\leq C_2 d^{-2}\sum_{i=2}^d\,{\mathrm{e}}^{|x^d_i|}\leq C_2 d^{-1}
\]
for some constant
![]() $C_2>0$
and all
$C_2>0$
and all
![]() $\mathbf{x}^d\in \mathcal{A}_d$
.
$\mathbf{x}^d\in \mathcal{A}_d$
.
Recall
![]() $f\in\mathcal{S}^3$
and let
$f\in\mathcal{S}^3$
and let
![]() $\skew2\tilde{W}^d_1$
be as in Proposition 5.1, satisfying
$\skew2\tilde{W}^d_1$
be as in Proposition 5.1, satisfying
Let
![]() $C>0$
be such that
$C>0$
be such that
![]() $T^d_1(\mathbf{x}^d)+T^d_2(\mathbf{x}^d)\leq Cd^{-1}$
for all
$T^d_1(\mathbf{x}^d)+T^d_2(\mathbf{x}^d)\leq Cd^{-1}$
for all
![]() $\mathbf{x}^d\in \mathcal{A}_d$
. The bound in (4.10), Taylor’s theorem applied to f, and Cauchy’s inequality yield
$\mathbf{x}^d\in \mathcal{A}_d$
. The bound in (4.10), Taylor’s theorem applied to f, and Cauchy’s inequality yield
 \begin{align*}
|\mathcal{G}_df(\mathbf{x}^d)-\tilde{\mathcal{G}}_df(\mathbf{x}^d)|
& \leq d \mathbb{E}_{Y^d_1} [ | f(Y^d_1)-f(x^d_1)|
(|\log(\rho)''(W^d_1)|(Y^d_1-x^d_1)^2+Cd^{-1})] \\
& = d \mathbb{E}_{Y^d_1} [ | f'(\skew2\tilde{W}^d_1)\log(\rho)''(W^d_1)(Y^d_1-x^d_1)^3|]+C\mathbb{E}_{Y^d_1} [ | f'(\skew2\tilde{W}^d_1)(Y^d_1-x^d_1)|] \\
& \leq d (\mathbb{E}_{Y^d_1} [ | f'(\skew2\tilde{W}^d_1)^2(Y^d_1-x^d_1)^3|]\mathbb{E}_{Y^d_1} [ | (\log(\rho)'')^2(W^d_1)(Y^d_1-x^d_1)^3|])^{1/2} \\
& \quad\, +C\mathbb{E}_{Y^d_1} [ | f'(\skew2\tilde{W}^d_1)(Y^d_1-x^d_1)|]\\
&\leq
\skew3\bar C d(\|\:f'\|_{\infty,1/2}^2 \,{\mathrm{e}}^{|x_1^d|} d^{-3/2} \cdot {\mathrm{e}}^{|x_1^d|}d^{-3/2})^{1/2} + \skew3\bar C \|\:f'\|_{\infty,1/2}\,{\mathrm{e}}^{|x_1^d|} d^{-1/2}.
\end{align*}
\begin{align*}
|\mathcal{G}_df(\mathbf{x}^d)-\tilde{\mathcal{G}}_df(\mathbf{x}^d)|
& \leq d \mathbb{E}_{Y^d_1} [ | f(Y^d_1)-f(x^d_1)|
(|\log(\rho)''(W^d_1)|(Y^d_1-x^d_1)^2+Cd^{-1})] \\
& = d \mathbb{E}_{Y^d_1} [ | f'(\skew2\tilde{W}^d_1)\log(\rho)''(W^d_1)(Y^d_1-x^d_1)^3|]+C\mathbb{E}_{Y^d_1} [ | f'(\skew2\tilde{W}^d_1)(Y^d_1-x^d_1)|] \\
& \leq d (\mathbb{E}_{Y^d_1} [ | f'(\skew2\tilde{W}^d_1)^2(Y^d_1-x^d_1)^3|]\mathbb{E}_{Y^d_1} [ | (\log(\rho)'')^2(W^d_1)(Y^d_1-x^d_1)^3|])^{1/2} \\
& \quad\, +C\mathbb{E}_{Y^d_1} [ | f'(\skew2\tilde{W}^d_1)(Y^d_1-x^d_1)|]\\
&\leq
\skew3\bar C d(\|\:f'\|_{\infty,1/2}^2 \,{\mathrm{e}}^{|x_1^d|} d^{-3/2} \cdot {\mathrm{e}}^{|x_1^d|}d^{-3/2})^{1/2} + \skew3\bar C \|\:f'\|_{\infty,1/2}\,{\mathrm{e}}^{|x_1^d|} d^{-1/2}.
\end{align*}
The last inequality follows by three applications of Proposition 5.1, where
![]() $\skew3\bar C>0$
is a constant that does not depend on f or
$\skew3\bar C>0$
is a constant that does not depend on f or
![]() $\mathbf{x}^d\in \mathcal{A}_d$
. This concludes the proof of the proposition.
$\mathbf{x}^d\in \mathcal{A}_d$
. This concludes the proof of the proposition.
Before tackling the proof of Proposition 4.4, we need the following three lemmas. Recall that K(x,Y) is defined in (4.7) and the set A satisfies the conclusion of Proposition 4.1.
Lemma 4.1. Pick
![]() $x\in A$
and let
$x\in A$
and let
![]() $Y\sim N(x,l^2/d)$
for some constant
$Y\sim N(x,l^2/d)$
for some constant
![]() $l>0$
. Then K(x, Y) has a density
$l>0$
. Then K(x, Y) has a density
![]() $q_x$
satisfying
$q_x$
satisfying
![]() $\|q_x\|_\infty\leq 4c_A\sqrt{d}/(3l\sqrt{2\pi})$
.
$\|q_x\|_\infty\leq 4c_A\sqrt{d}/(3l\sqrt{2\pi})$
.
Proof. Existence of
![]() $q_x$
follows from (4.7) and Proposition 5.6. By Proposition 4.1 we have
$q_x$
follows from (4.7) and Proposition 5.6. By Proposition 4.1 we have
Consider the polynomial
By (4.7),
![]() $p(Y-x)=K(x,Y)$
. Since
$p(Y-x)=K(x,Y)$
. Since
we have
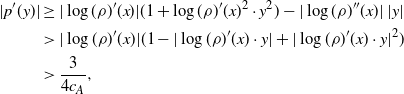 \begin{align*}
|p'( y)|
&\geq |\log(\rho)'(x)|(1+\log(\rho)'(x)^2\cdot y^2) - |\log(\rho)''(x)|\,|y| \\
&> |\log(\rho)'(x)|(1-|\log(\rho)'(x)\cdot y|+|\log(\rho)'(x) \cdot y|^2)\\
&> \dfrac{3}{4c_A},
\end{align*}
\begin{align*}
|p'( y)|
&\geq |\log(\rho)'(x)|(1+\log(\rho)'(x)^2\cdot y^2) - |\log(\rho)''(x)|\,|y| \\
&> |\log(\rho)'(x)|(1-|\log(\rho)'(x)\cdot y|+|\log(\rho)'(x) \cdot y|^2)\\
&> \dfrac{3}{4c_A},
\end{align*}
where the second inequality holds since
![]() $ |\log(\rho)''(x)|< (\log(\rho)'(x))^2$
and the third follows from
$ |\log(\rho)''(x)|< (\log(\rho)'(x))^2$
and the third follows from
![]() $\inf_{z\in{\mathbb{R}}}\{1-|z|+z^2\}=3/4$
and
$\inf_{z\in{\mathbb{R}}}\{1-|z|+z^2\}=3/4$
and
![]() $ |\log(\rho)'(x)|>1/c_A$
. The lemma now follows by Proposition 5.7.
$ |\log(\rho)'(x)|>1/c_A$
. The lemma now follows by Proposition 5.7.
Recall that the proposal is normal
![]() $\mathbf{Y}^d=(Y_1^d,\ldots,Y_d^d)\sim N(\mathbf{x}^d,l^2/d\cdot I_d)$
.
$\mathbf{Y}^d=(Y_1^d,\ldots,Y_d^d)\sim N(\mathbf{x}^d,l^2/d\cdot I_d)$
.
Lemma 4.2. For any
![]() $\mathbf{x}^d\in \mathcal{A}_d$
, the sum
$\mathbf{x}^d\in \mathcal{A}_d$
, the sum
![]() $\sum_{k=2}^dK(x_i^d,Y_i^d)$
possesses a density
$\sum_{k=2}^dK(x_i^d,Y_i^d)$
possesses a density
![]() $\mathbf{q}^d_{\mathbf{x}^d}$
. Moreover, there exists a constant
$\mathbf{q}^d_{\mathbf{x}^d}$
. Moreover, there exists a constant
![]() $C_{K}$
such that
$C_{K}$
such that
![]() $\|\mathbf{q}^d_{\mathbf{x}^d}\|_\infty\leq
C_{K}$
holds for all
$\|\mathbf{q}^d_{\mathbf{x}^d}\|_\infty\leq
C_{K}$
holds for all
![]() $d\in{\mathbb{N}}$
and all
$d\in{\mathbb{N}}$
and all
![]() $\mathbf{x}^d\in \mathcal{A}_d$
.
$\mathbf{x}^d\in \mathcal{A}_d$
.
Proof. Fix
![]() $\mathbf{x}^d\in\mathcal{A}_d$
and, for each i, let
$\mathbf{x}^d\in\mathcal{A}_d$
and, for each i, let
![]() $q_i$
denote the density of
$q_i$
denote the density of
![]() $K(x^d_i,Y^d_i)$
as in the previous lemma. Since the components of
$K(x^d_i,Y^d_i)$
as in the previous lemma. Since the components of
![]() $\mathbf{Y}^d$
are i.i.d., we have
$\mathbf{Y}^d$
are i.i.d., we have
![]() $\mathbf{q}^d_{\mathbf{x}^d}=\mathop{\mbox{\ast}}_{i=2}^d q_i=q_A \mathop{\mbox{\ast}}
q_{{\mathbb{R}}\setminus A}$
, where
$\mathbf{q}^d_{\mathbf{x}^d}=\mathop{\mbox{\ast}}_{i=2}^d q_i=q_A \mathop{\mbox{\ast}}
q_{{\mathbb{R}}\setminus A}$
, where
![]() $q_A\,:\!= \mathop{\mbox{\ast}}_{x^d_i\in A}q_i$
and
$q_A\,:\!= \mathop{\mbox{\ast}}_{x^d_i\in A}q_i$
and
![]() $q_{{\mathbb{R}}\setminus A}\,:\!=\mathop{\mbox{\ast}}_{x^d_i\notin A}q_i$
. By the definition of convolution and the fact that
$q_{{\mathbb{R}}\setminus A}\,:\!=\mathop{\mbox{\ast}}_{x^d_i\notin A}q_i$
. By the definition of convolution and the fact that
![]() $q_{{\mathbb{R}}\setminus A}$
is a density, it follows that
$q_{{\mathbb{R}}\setminus A}$
is a density, it follows that
![]() $\|\mathbf{q}^d_{\mathbf{x}^d}\|_\infty\leq
\|q_A\|_\infty\|q_{{\mathbb{R}}\setminus A}\|_1=\|q_A\|_\infty$
. By Lemma 4.1 there exists
$\|\mathbf{q}^d_{\mathbf{x}^d}\|_\infty\leq
\|q_A\|_\infty\|q_{{\mathbb{R}}\setminus A}\|_1=\|q_A\|_\infty$
. By Lemma 4.1 there exists
![]() $C>0$
such that, for any
$C>0$
such that, for any
![]() $d\in{\mathbb{N}}$
, we have
$d\in{\mathbb{N}}$
, we have
![]() $\|q_i\|_\infty<C\sqrt{d}$
if
$\|q_i\|_\infty<C\sqrt{d}$
if
![]() $x^d_i\in A$
. Condition (4.2) implies there are at least
$x^d_i\in A$
. Condition (4.2) implies there are at least
![]() $ (d-1)\rho(A)/2 $
factors in the convolution
$ (d-1)\rho(A)/2 $
factors in the convolution
![]() $q_A=\mathop{\mbox{\ast}}_{x^d_i\in A}q_i$
. Hence Proposition 5.5 applied to
$q_A=\mathop{\mbox{\ast}}_{x^d_i\in A}q_i$
. Hence Proposition 5.5 applied to
![]() $q_A$
yields
$q_A$
yields
This concludes the proof of the lemma.
Lemma 4.3. Let
![]() $\mathbf{x}^d\in \mathcal{A}_d$
. The function
$\mathbf{x}^d\in \mathcal{A}_d$
. The function
![]() $y\mapsto\beta(\mathbf{x}^d,y)$
, defined in (4.6), is in
$y\mapsto\beta(\mathbf{x}^d,y)$
, defined in (4.6), is in
![]() $\mathcal{C}^2({\mathbb{R}})$
and the following hold:
$\mathcal{C}^2({\mathbb{R}})$
and the following hold:
(i)
![]() $0<\beta(\mathbf{x}^d,y)\leq1$
for all
$0<\beta(\mathbf{x}^d,y)\leq1$
for all
![]() $y\in{\mathbb{R}}$
,
$y\in{\mathbb{R}}$
,
(ii)
![]() $\beta(\mathbf{x}^d,x^d_1)=\mathbb{E}_{\mathbf{Y}^d-} \Big[1\wedge {\mathrm{e}}^{\sum_{i=2}^dK(x^d_i,Y^d_i)}\Big]$
,
$\beta(\mathbf{x}^d,x^d_1)=\mathbb{E}_{\mathbf{Y}^d-} \Big[1\wedge {\mathrm{e}}^{\sum_{i=2}^dK(x^d_i,Y^d_i)}\Big]$
,
(iii)
![]() $ \Big|\dfrac{\partial}{\partial y}\beta(\mathbf{x}^d,y)|\leq |\log(\rho)'(x^d_1)\Big|$
for all
$ \Big|\dfrac{\partial}{\partial y}\beta(\mathbf{x}^d,y)|\leq |\log(\rho)'(x^d_1)\Big|$
for all
![]() $y\in{\mathbb{R}}$
,
$y\in{\mathbb{R}}$
,
(iv)
![]() $\dfrac{\partial}{\partial y}\beta(\mathbf{x}^d,x^d_1)=\log(\rho)'(x^d_1)\mathbb{E}_{\mathbf{Y}^d-} \Big[{\mathrm{e}}^{\sum_{i=2}^dK(x^d_i,Y^d_i)}1_{\{\sum_{i=2}^dK(x^d_i,Y^d_i)<0\}}\Big]$
,
$\dfrac{\partial}{\partial y}\beta(\mathbf{x}^d,x^d_1)=\log(\rho)'(x^d_1)\mathbb{E}_{\mathbf{Y}^d-} \Big[{\mathrm{e}}^{\sum_{i=2}^dK(x^d_i,Y^d_i)}1_{\{\sum_{i=2}^dK(x^d_i,Y^d_i)<0\}}\Big]$
,
(v)
![]() $ \Big|\dfrac{\partial^2}{\partial y^2}\beta(\mathbf{x}^d,y)\Big|\leq |\log(\rho)'(x^d_1)|^2(C_K+1)$
for all
$ \Big|\dfrac{\partial^2}{\partial y^2}\beta(\mathbf{x}^d,y)\Big|\leq |\log(\rho)'(x^d_1)|^2(C_K+1)$
for all
![]() $y\in{\mathbb{R}}$
and constant
$y\in{\mathbb{R}}$
and constant
![]() $C_K$
from Lemma 4.2.
$C_K$
from Lemma 4.2.
Proof. Points (i) and (ii) follow from the definition in (4.6). Since
![]() $x\mapsto 1\wedge {\mathrm{e}}^x$
is Lipschitz (with Lipschitz constant 1) on
$x\mapsto 1\wedge {\mathrm{e}}^x$
is Lipschitz (with Lipschitz constant 1) on
![]() ${\mathbb{R}}$
, the family of functions
${\mathbb{R}}$
, the family of functions
is bounded by one and converges pointwise to
![]() $1_{\{x<0\}}\,{\mathrm{e}}^x$
for all
$1_{\{x<0\}}\,{\mathrm{e}}^x$
for all
![]() $x\in{\mathbb{R}}\setminus\{0\}$
, as
$x\in{\mathbb{R}}\setminus\{0\}$
, as
![]() $h\to0$
. Hence the DCT implies that
$h\to0$
. Hence the DCT implies that
![]() ${\partial}/{\partial y}\beta(\mathbf{x}^d,y)$
exists and can be expressed as
${\partial}/{\partial y}\beta(\mathbf{x}^d,y)$
exists and can be expressed as
implying (iii) and (iv). Let
![]() $\Phi^d_{K}$
denote the distribution of
$\Phi^d_{K}$
denote the distribution of
![]() $\sum_{i=2}^dK(x^d_i,Y^d_i)$
, and recall that by definition we have
$\sum_{i=2}^dK(x^d_i,Y^d_i)$
, and recall that by definition we have
![]() ${\mathrm{e}}^x 1_{\{x<0\}} = 1\wedge {\mathrm{e}}^x - 1_{\{x\geq 0\}}$
for all
${\mathrm{e}}^x 1_{\{x<0\}} = 1\wedge {\mathrm{e}}^x - 1_{\{x\geq 0\}}$
for all
![]() $x\in{\mathbb{R}}$
. Hence, by (4.11), it follows that
$x\in{\mathbb{R}}$
. Hence, by (4.11), it follows that
By Lemma 4.2,
![]() $\Phi_K^d$
is differentiable. Hence, by (4.12),
$\Phi_K^d$
is differentiable. Hence, by (4.12),
![]() ${\partial^2}/{\partial y^2}\beta(\mathbf{x}^d,y)$
also exists and takes the form
${\partial^2}/{\partial y^2}\beta(\mathbf{x}^d,y)$
also exists and takes the form
Part (v) follows from this representation of
![]() ${\partial^2}/{\partial y^2}\beta(\mathbf{x}^d,y)$
and Lemma 4.2.
${\partial^2}/{\partial y^2}\beta(\mathbf{x}^d,y)$
and Lemma 4.2.
Proof of Proposition 4.4. Fix an arbitrary
![]() $\mathbf{x}^d\in\mathcal{A}_d$
. Let
$\mathbf{x}^d\in\mathcal{A}_d$
. Let
![]() $Z_1,W_1$
be random variables, as in Proposition 5.1, that satisfy
$Z_1,W_1$
be random variables, as in Proposition 5.1, that satisfy
 \begin{align*}
f(Y^d_1)-f(x^d_1) & = f'(x^d_1)(Y^d_1-x^d_1)+\frac{f''(x^d_1)}{2}(Y^d_1-x^d_1)^2+\frac{f'''(Z_1)}{6}(Y^d_1-x^d_1)^3, \\
\beta(\mathbf{x}^d,Y^d_1) & = \beta(\mathbf{x}^d,x^d_1)+\frac{\partial}{\partial
y}\beta(\mathbf{x}^d,x^d_1)(Y^d_1-x^d_1)+\frac{{\partial^2}/{\partial
y^2}\beta(\mathbf{x}^d,W_1)}{2}(Y^d_1-x^d_1)^2.
\end{align*}
\begin{align*}
f(Y^d_1)-f(x^d_1) & = f'(x^d_1)(Y^d_1-x^d_1)+\frac{f''(x^d_1)}{2}(Y^d_1-x^d_1)^2+\frac{f'''(Z_1)}{6}(Y^d_1-x^d_1)^3, \\
\beta(\mathbf{x}^d,Y^d_1) & = \beta(\mathbf{x}^d,x^d_1)+\frac{\partial}{\partial
y}\beta(\mathbf{x}^d,x^d_1)(Y^d_1-x^d_1)+\frac{{\partial^2}/{\partial
y^2}\beta(\mathbf{x}^d,W_1)}{2}(Y^d_1-x^d_1)^2.
\end{align*}
Then, by the definition of
![]() $\tilde{\mathcal{G}}_df(\mathbf{x}^d)$
in (4.5) and the fact that
$\tilde{\mathcal{G}}_df(\mathbf{x}^d)$
in (4.5) and the fact that
![]() $Y_1^d-x_1^d\sim N(0,l^2/d)$
, we obtain
$Y_1^d-x_1^d\sim N(0,l^2/d)$
, we obtain
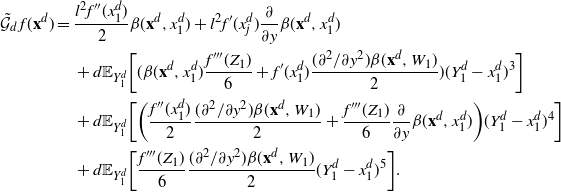 \begin{align*}
\tilde{\mathcal{G}}_df(\mathbf{x}^d)&= \frac{l^2f''(x^d_1)}{2}\beta(\mathbf{x}^d,x^d_1)+l^2f'(x^d_j)\frac{\partial}{\partial y}\beta(\mathbf{x}^d,x^d_1) \\
&\quad\, + d \mathbb{E}_{Y^d_1} \bigg[ (\beta(\mathbf{x}^d,x^d_1)\frac{f'''(Z_1)}{6}+f'(x^d_1)\frac{{\partial^2}/{\partial y^2}\beta(\mathbf{x}^d,W_1)}{2})(Y^d_1-x^d_1)^3\bigg] \\
&\quad\, + d \mathbb{E}_{Y^d_1}\bigg[\bigg(\frac{f''(x^d_1)}{2}\frac{{\partial^2}/{\partial y^2}\beta(\mathbf{x}^d,W_1)}{2}+\frac{f'''(Z_1)}{6}\frac{\partial}{\partial y}\beta(\mathbf{x}^d,x^d_1)\bigg)(Y^d_1-x^d_1)^4\bigg] \\
&\quad\, + d \mathbb{E}_{Y^d_1}\bigg[\frac{f'''(Z_1)}{6}\frac{{\partial^2}/{\partial y^2}\beta(\mathbf{x}^d,W_1)}{2}(Y^d_1-x^d_1)^5\bigg].
\end{align*}
\begin{align*}
\tilde{\mathcal{G}}_df(\mathbf{x}^d)&= \frac{l^2f''(x^d_1)}{2}\beta(\mathbf{x}^d,x^d_1)+l^2f'(x^d_j)\frac{\partial}{\partial y}\beta(\mathbf{x}^d,x^d_1) \\
&\quad\, + d \mathbb{E}_{Y^d_1} \bigg[ (\beta(\mathbf{x}^d,x^d_1)\frac{f'''(Z_1)}{6}+f'(x^d_1)\frac{{\partial^2}/{\partial y^2}\beta(\mathbf{x}^d,W_1)}{2})(Y^d_1-x^d_1)^3\bigg] \\
&\quad\, + d \mathbb{E}_{Y^d_1}\bigg[\bigg(\frac{f''(x^d_1)}{2}\frac{{\partial^2}/{\partial y^2}\beta(\mathbf{x}^d,W_1)}{2}+\frac{f'''(Z_1)}{6}\frac{\partial}{\partial y}\beta(\mathbf{x}^d,x^d_1)\bigg)(Y^d_1-x^d_1)^4\bigg] \\
&\quad\, + d \mathbb{E}_{Y^d_1}\bigg[\frac{f'''(Z_1)}{6}\frac{{\partial^2}/{\partial y^2}\beta(\mathbf{x}^d,W_1)}{2}(Y^d_1-x^d_1)^5\bigg].
\end{align*}
By parts (ii) and (iv) in Lemma 4.3 and the definition of
![]() $\hat{\mathcal{G}}_df(\mathbf{x}^d)$
in (4.8), we have
$\hat{\mathcal{G}}_df(\mathbf{x}^d)$
in (4.8), we have
The three expectations in the display above can each be bounded by a constant times
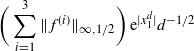 \[
\bigg(\sum_{i=1}^3\|\:f^{(i)}\|_{\infty,1/2}\bigg)\,{\mathrm{e}}^{|x^d_1|}d^{-1/2}
\]
\[
\bigg(\sum_{i=1}^3\|\:f^{(i)}\|_{\infty,1/2}\bigg)\,{\mathrm{e}}^{|x^d_1|}d^{-1/2}
\]
using Proposition 5.1 and Lemma 4.3. For instance, the first expectation can be bounded above using (v) in Lemma 4.3:
Proposition 5.1 yields
for some
![]() $C_0>0$
. Moreover,
$C_0>0$
. Moreover,
as
![]() $\log(\rho)\in\mathcal{S}^4$
and
$\log(\rho)\in\mathcal{S}^4$
and
![]() $f\in\mathcal{S}^3$
. Hence
$f\in\mathcal{S}^3$
. Hence
for some
![]() $C_1>0$
. Similarly, it follows that the second and third expectations above decay as
$C_1>0$
. Similarly, it follows that the second and third expectations above decay as
![]() $d^{-1}$
and
$d^{-1}$
and
![]() $d^{-3/2}$
, respectively. This concludes the proof of the proposition.
$d^{-3/2}$
, respectively. This concludes the proof of the proposition.
Lemma 4.4. Recall that
![]() $\mathcal{N}(\mathbf{x}^d,\mathbf{Y}^d)$
and
$\mathcal{N}(\mathbf{x}^d,\mathbf{Y}^d)$
and
![]() $\sum_{i=2}^dK(x^d_i,Y^d_i)$
are defined in (4.9) and (4.7), respectively. Then there exists a constant C such that, for all
$\sum_{i=2}^dK(x^d_i,Y^d_i)$
are defined in (4.9) and (4.7), respectively. Then there exists a constant C such that, for all
![]() $d\in{\mathbb{N}}$
, we have
$d\in{\mathbb{N}}$
, we have
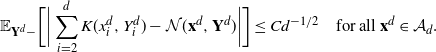 \[\mathbb{E}_{\mathbf{Y}^d-}\bigg[\bigg|\sum_{i=2}^dK(x^d_i,Y^d_i)-\mathcal{N}(\mathbf{x}^d,\mathbf{Y}^d)\bigg|\bigg]\leq
Cd^{-1/2}\quad \text{{for all} }\mathbf{x}^d\in\mathcal{A}_d.\]
\[\mathbb{E}_{\mathbf{Y}^d-}\bigg[\bigg|\sum_{i=2}^dK(x^d_i,Y^d_i)-\mathcal{N}(\mathbf{x}^d,\mathbf{Y}^d)\bigg|\bigg]\leq
Cd^{-1/2}\quad \text{{for all} }\mathbf{x}^d\in\mathcal{A}_d.\]
Proof. The difference in question is smaller than the sum of the following two terms:
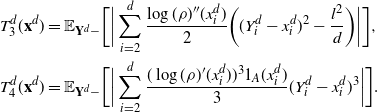 \begin{align*}
T^d_3(\mathbf{x}^d)&= \mathbb{E}_{\mathbf{Y}^d-}\bigg[\bigg|\sum_{i=2}^d\dfrac{\log(\rho)''(x^d_i)}{2}\bigg((Y^d_i-x^d_i)^2-\dfrac{l^2}{d}\bigg)\bigg|\bigg], \\
T^d_4(\mathbf{x}^d)&= \mathbb{E}_{\mathbf{Y}^d-}\bigg[\bigg|\sum_{i=2}^d\dfrac{ (\log(\rho)'(x^d_i))^31_{A}(x^d_i)}{3}(Y^d_i-x^d_i)^3\bigg|\bigg].
\end{align*}
\begin{align*}
T^d_3(\mathbf{x}^d)&= \mathbb{E}_{\mathbf{Y}^d-}\bigg[\bigg|\sum_{i=2}^d\dfrac{\log(\rho)''(x^d_i)}{2}\bigg((Y^d_i-x^d_i)^2-\dfrac{l^2}{d}\bigg)\bigg|\bigg], \\
T^d_4(\mathbf{x}^d)&= \mathbb{E}_{\mathbf{Y}^d-}\bigg[\bigg|\sum_{i=2}^d\dfrac{ (\log(\rho)'(x^d_i))^31_{A}(x^d_i)}{3}(Y^d_i-x^d_i)^3\bigg|\bigg].
\end{align*}
Note that
![]() $X_i\,:\!=(Y^d_i-x^d_i)^2-l^2/d$
,
$X_i\,:\!=(Y^d_i-x^d_i)^2-l^2/d$
,
![]() $2\leq i\leq d$
, are zero mean i.i.d. with
$2\leq i\leq d$
, are zero mean i.i.d. with
![]() $\mathbb{E}[X_i^4] = 2l^4/d^2$
. Hence, as
$\mathbb{E}[X_i^4] = 2l^4/d^2$
. Hence, as
![]() $\log(\rho)\in\mathcal{S}^4$
, we may apply Proposition 5.2 with the function
$\log(\rho)\in\mathcal{S}^4$
, we may apply Proposition 5.2 with the function
![]() $x\mapsto \log(\rho)''(x)$
and
$x\mapsto \log(\rho)''(x)$
and
![]() $X_2$
, for
$X_2$
, for
![]() $2\leq i\leq d$
, to get
$2\leq i\leq d$
, to get
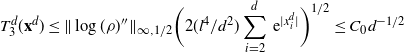 \[
T^d_3(\mathbf{x}^d)\leq \|\log(\rho)''\|_{\infty,1/2} \bigg(2(l^4/d^2)\sum_{i=2}^d \,{\mathrm{e}}^{|x^d_i|}\bigg)^{1/2}\leq C_0 d^{-1/2}
\]
\[
T^d_3(\mathbf{x}^d)\leq \|\log(\rho)''\|_{\infty,1/2} \bigg(2(l^4/d^2)\sum_{i=2}^d \,{\mathrm{e}}^{|x^d_i|}\bigg)^{1/2}\leq C_0 d^{-1/2}
\]
for some constant
![]() $C_0>0$
, where the second inequality follows from (4.1). Similarly, Proposition 5.2 and assumption (4.1), applied to the function
$C_0>0$
, where the second inequality follows from (4.1). Similarly, Proposition 5.2 and assumption (4.1), applied to the function
![]() $x\mapsto (\log(\rho)'(x))^31_{A}(x)$
and random variables
$x\mapsto (\log(\rho)'(x))^31_{A}(x)$
and random variables
![]() $Y^d_i-x^d_i$
, yield
$Y^d_i-x^d_i$
, yield
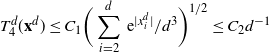 \[
T^d_4(\mathbf{x}^d)\leq C_1 \bigg(\sum_{i=2}^d
\,{\mathrm{e}}^{|x^d_i|}/d^3\bigg)^{1/2}\leq C_2 d^{-1}
\]
\[
T^d_4(\mathbf{x}^d)\leq C_1 \bigg(\sum_{i=2}^d
\,{\mathrm{e}}^{|x^d_i|}/d^3\bigg)^{1/2}\leq C_2 d^{-1}
\]
for some constants
![]() $C_1,C_2>0$
and all
$C_1,C_2>0$
and all
![]() $d\in{\mathbb{N}}$
.
$d\in{\mathbb{N}}$
.
Lemma 4.5. There exist constants
![]() $c_1,c'_1>0$
, such that for any
$c_1,c'_1>0$
, such that for any
![]() $d\in{\mathbb{N}}$
,
$d\in{\mathbb{N}}$
,
![]() $i\in\{2,\ldots,d\}$
,
$i\in\{2,\ldots,d\}$
,
![]() $\mathbf{x}^d\in\mathcal{A}_d$
and
$\mathbf{x}^d\in\mathcal{A}_d$
and
![]() $x^d_i\notin A$
, we have
$x^d_i\notin A$
, we have
where
is the CF of
![]() $K(x^d_i,Y^d_i)$
(see (4.7)).
$K(x^d_i,Y^d_i)$
(see (4.7)).
Remark 4.4. Recall that the set A satisfies the conclusion of Proposition 4.1. The proof of Lemma 4.5 requires control of the functions
![]() $\log(\rho)'$
and
$\log(\rho)'$
and
![]() $\log(\rho)''$
on the complement of A, where they are unbounded. It is hence crucial that their argument
$\log(\rho)''$
on the complement of A, where they are unbounded. It is hence crucial that their argument
![]() $x_i^d$
is the ith coordinate of a point
$x_i^d$
is the ith coordinate of a point
![]() $\mathbf{x}^d\in\mathcal{A}_d$
, since, through assumption (4.1), we have control over the size of
$\mathbf{x}^d\in\mathcal{A}_d$
, since, through assumption (4.1), we have control over the size of
![]() $x_i^d$
in terms of the dimension d of the chain. For an analogous reason we need
$x_i^d$
in terms of the dimension d of the chain. For an analogous reason we need
![]() $i>1$
. These facts play a key role in the proof.
$i>1$
. These facts play a key role in the proof.
Proof. By Lemma 5.3, the following inequality holds for all
![]() $|t|\leq d/(4l^2|\log(\rho)''(x^d_i)|)$
:
$|t|\leq d/(4l^2|\log(\rho)''(x^d_i)|)$
:
 \begin{align}
& \bigg|\log\varphi_i(t)-\bigg(i\dfrac{l^2}{2d}\log(\rho)''(x^d_i)\cdot t-\dfrac{l^2}{2d} (\log(\rho)'(x^d_i))^2\cdot t^2\bigg)\bigg| \notag \\
&\qquad \leq
\dfrac{l^4}{d^2}\bigg(\dfrac{1}{2} (\log(\rho)''(x^d_i))^2\cdot t^2+ (\log(\rho)'(x^d_i))^2 |\log(\rho)''(x^d_i)|\,|t|^3\bigg),
\end{align}
\begin{align}
& \bigg|\log\varphi_i(t)-\bigg(i\dfrac{l^2}{2d}\log(\rho)''(x^d_i)\cdot t-\dfrac{l^2}{2d} (\log(\rho)'(x^d_i))^2\cdot t^2\bigg)\bigg| \notag \\
&\qquad \leq
\dfrac{l^4}{d^2}\bigg(\dfrac{1}{2} (\log(\rho)''(x^d_i))^2\cdot t^2+ (\log(\rho)'(x^d_i))^2 |\log(\rho)''(x^d_i)|\,|t|^3\bigg),
\end{align}
Since
![]() $\mathbf{x}^d\in\mathcal{A}_d$
and
$\mathbf{x}^d\in\mathcal{A}_d$
and
![]() $i>1$
, assumption (4.1) implies that for any
$i>1$
, assumption (4.1) implies that for any
![]() $f\in\mathcal{S}^0$
there exists
$f\in\mathcal{S}^0$
there exists
![]() $C_f>0$
such that
$C_f>0$
such that
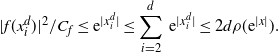 \[
| f(x^d_i)|^2/C_f\leq {\mathrm{e}}^{|x^d_i|}\leq \sum_{i=2}^d\,{\mathrm{e}}^{|x^d_i|}\leq 2d\rho({\mathrm{e}}^{|x|}).
\]
\[
| f(x^d_i)|^2/C_f\leq {\mathrm{e}}^{|x^d_i|}\leq \sum_{i=2}^d\,{\mathrm{e}}^{|x^d_i|}\leq 2d\rho({\mathrm{e}}^{|x|}).
\]
Hence
![]() $| f(x^d_i)|\leq c_f \sqrt{d}$
for all
$| f(x^d_i)|\leq c_f \sqrt{d}$
for all
![]() $d\in{\mathbb{N}}$
and all
$d\in{\mathbb{N}}$
and all
![]() $2\leq i\leq d$
, where
$2\leq i\leq d$
, where
![]() $c_f\,:\!=(2C_f\rho({\mathrm{e}}^{|x|}))^{1/2}$
. Since
$c_f\,:\!=(2C_f\rho({\mathrm{e}}^{|x|}))^{1/2}$
. Since
![]() $\log(\rho)\in\mathcal{S}^4$
, both functions
$\log(\rho)\in\mathcal{S}^4$
, both functions
are in
![]() $\mathcal{S}^0$
. Then (4.13) and the constants
$\mathcal{S}^0$
. Then (4.13) and the constants
![]() $c_1\,:\!=\max\{c_{f_1},c_{f_2}\}$
and
$c_1\,:\!=\max\{c_{f_1},c_{f_2}\}$
and
![]() $c_1'\,:\!=1/(4\sqrt{2c_{f_1}})$
yield the inequalities in the lemma.
$c_1'\,:\!=1/(4\sqrt{2c_{f_1}})$
yield the inequalities in the lemma.
We now deal with the coordinates of
![]() $\mathcal{A}_d$
that are in A. Compared with Lemma 4.5 this is straightforward, as it does not involve the remainder of the coordinates of the point in
$\mathcal{A}_d$
that are in A. Compared with Lemma 4.5 this is straightforward, as it does not involve the remainder of the coordinates of the point in
![]() $\mathcal{A}_d$
.
$\mathcal{A}_d$
.
Lemma 4.6. If
![]() $x\in A$
, then K(x, Y) (see (4.7)), where
$x\in A$
, then K(x, Y) (see (4.7)), where
![]() $Y\sim N(x,l^2/d)$
, satisfies:
$Y\sim N(x,l^2/d)$
, satisfies:
(a)
![]() $\mu_K\,:\!=\mathbb{E}_{Y} [K(x,Y)]\leq \dfrac{l^2c_A^2}{2d}$
, where
$\mu_K\,:\!=\mathbb{E}_{Y} [K(x,Y)]\leq \dfrac{l^2c_A^2}{2d}$
, where
![]() $c_A>0$
is the constant in Proposition 4.1,
$c_A>0$
is the constant in Proposition 4.1,
(b)
![]() $\bigg|\mathbb{E}_{Y}[(K(x,Y)-\mu_K)^2]- (\log(\rho)'(x))^2\dfrac{l^2}{d}\bigg| \leq C_1 d^{-2}$
for some constant
$\bigg|\mathbb{E}_{Y}[(K(x,Y)-\mu_K)^2]- (\log(\rho)'(x))^2\dfrac{l^2}{d}\bigg| \leq C_1 d^{-2}$
for some constant
![]() $C_1>0$
and all
$C_1>0$
and all
![]() $d\in{\mathbb{N}}$
,
$d\in{\mathbb{N}}$
,
(c)
![]() $\mathbb{E}_{Y} [ |K(x,Y)-\mu_K|^3]\leq C_2d^{-3/2}$
for some constant
$\mathbb{E}_{Y} [ |K(x,Y)-\mu_K|^3]\leq C_2d^{-3/2}$
for some constant
![]() $C_2>0$
and all
$C_2>0$
and all
![]() $d\in{\mathbb{N}}$
.
$d\in{\mathbb{N}}$
.
Moreover, constants
![]() $C_1$
and
$C_1$
and
![]() $C_2$
do not depend on the choice of
$C_2$
do not depend on the choice of
![]() $x\in A$
.
$x\in A$
.
Proof. By definition of A in Proposition 4.1 we have
![]() $ |\log(\rho)'(x)|\leq c_A$
and
$ |\log(\rho)'(x)|\leq c_A$
and
![]() $ |\log(\rho)''(x)|\leq
c^2_A$
for
$ |\log(\rho)''(x)|\leq
c^2_A$
for
![]() $x\in A$
. By (4.7),
$x\in A$
. By (4.7),
![]() $\mu_K={l^2}/{(2d)}\log(\rho)''(x)$
and (a) follows. Recall that
$\mu_K={l^2}/{(2d)}\log(\rho)''(x)$
and (a) follows. Recall that
![]() $\mathbb{E}_{Y}[(Y-x)^n]$
is either zero (if n is odd) or of order
$\mathbb{E}_{Y}[(Y-x)^n]$
is either zero (if n is odd) or of order
![]() $d^{-n/2}$
(if n is even) and
$d^{-n/2}$
(if n is even) and
![]() $\mathbb{E}_{Y}[(Y-x)^2]=l^2/d$
. Hence the definition of K in (4.7), the fact
$\mathbb{E}_{Y}[(Y-x)^2]=l^2/d$
. Hence the definition of K in (4.7), the fact
![]() $x\in A$
, and part (a) imply the inequality in part (b). For part (c), note that an analogous argument yields
$x\in A$
, and part (a) imply the inequality in part (b). For part (c), note that an analogous argument yields
![]() $\mathbb{E}_{Y} [(K(x,Y)-\mu_K)^6]\leq C'd^{-3}$
for some constant
$\mathbb{E}_{Y} [(K(x,Y)-\mu_K)^6]\leq C'd^{-3}$
for some constant
![]() $C'\,{>}\,0$
. Cauchy’s inequality concludes the proof of the lemma.
$C'\,{>}\,0$
. Cauchy’s inequality concludes the proof of the lemma.
Lemma 4.7. Let assumptions of Lemma 4.6 hold and let
![]() $\varphi$
denote the characteristic function of K(x, Y). There exist positive constants
$\varphi$
denote the characteristic function of K(x, Y). There exist positive constants
![]() $c_2$
and
$c_2$
and
![]() $c'_2$
such that the following holds for all
$c'_2$
such that the following holds for all
![]() $x\in A$
:
$x\in A$
:
Proof. Let
![]() $\sigma^2_K\,:\!=\mathbb{E}_{Y}[(K(x,Y)-\mu_K)^2]$
and recall
$\sigma^2_K\,:\!=\mathbb{E}_{Y}[(K(x,Y)-\mu_K)^2]$
and recall
![]() $\mu_K={l^2}/{(2d)}\log(\rho)''(x)$
. By Lemma 5.2 we have
$\mu_K={l^2}/{(2d)}\log(\rho)''(x)$
. By Lemma 5.2 we have
By Lemma 4.6(b) we have
![]() $|\sigma^2_K-l^2\log(\rho)'(x)^2/d|\leq C_1d^{-2}$
. Hence
$|\sigma^2_K-l^2\log(\rho)'(x)^2/d|\leq C_1d^{-2}$
. Hence
![]() $\sigma^2_K\leq d^{-1}/\sqrt{c_2'}$
, where
$\sigma^2_K\leq d^{-1}/\sqrt{c_2'}$
, where
![]() $c_2'\,:\!= 1/(l^2c_A^2+ C_1)^2$
, and
$c_2'\,:\!= 1/(l^2c_A^2+ C_1)^2$
, and
![]() $\sigma^4_K\leq C_1'd^{-2}$
for some
$\sigma^4_K\leq C_1'd^{-2}$
for some
![]() $C_1'>0$
. This, together with Lemma 4.6(c), implies that there exists a constant
$C_1'>0$
. This, together with Lemma 4.6(c), implies that there exists a constant
![]() $c_2>0$
, such that the inequality in (4.14) follows from (4.15) for all
$c_2>0$
, such that the inequality in (4.14) follows from (4.15) for all
![]() $|t|\leq c_2' d^{1/2} \leq 1/\sigma_K$
and
$|t|\leq c_2' d^{1/2} \leq 1/\sigma_K$
and
![]() $x\in A$
.
$x\in A$
.
Lemma 4.8. For any
![]() $d\in{\mathbb{N}}$
and
$d\in{\mathbb{N}}$
and
![]() $\mathbf{x}^d\in \mathcal{A}_d$
, let
$\mathbf{x}^d\in \mathcal{A}_d$
, let
![]() $\Phi^d_{K}$
and
$\Phi^d_{K}$
and
![]() $\Phi^d_{\mathcal{N}}$
be the distribution functions of
$\Phi^d_{\mathcal{N}}$
be the distribution functions of
![]() $\sum_{i=2}^dK(x^d_i,Y^d_i)$
and
$\sum_{i=2}^dK(x^d_i,Y^d_i)$
and
![]() $\mathcal{N}(\mathbf{x}^d,\mathbf{Y}^d)$
. Then there exists
$\mathcal{N}(\mathbf{x}^d,\mathbf{Y}^d)$
. Then there exists
![]() $C>0$
such that
$C>0$
such that
Proof. Let
![]() $\varphi_K$
and
$\varphi_K$
and
![]() $\varphi_\mathcal{N}$
be the CFs of
$\varphi_\mathcal{N}$
be the CFs of
![]() $\sum_{i=2}^dK(x^d_i,Y^d_i)$
and
$\sum_{i=2}^dK(x^d_i,Y^d_i)$
and
![]() $\mathcal{N}(\mathbf{x}^d,\mathbf{Y}^d)$
, respectively. We will compare
$\mathcal{N}(\mathbf{x}^d,\mathbf{Y}^d)$
, respectively. We will compare
![]() $\varphi_K$
and
$\varphi_K$
and
![]() $\varphi_\mathcal{N}$
and apply Proposition 5.8 to establish the lemma. Let
$\varphi_\mathcal{N}$
and apply Proposition 5.8 to establish the lemma. Let
![]() $\varphi_i$
be the CF of
$\varphi_i$
be the CF of
![]() $K(x^d_i,Y^d_i)$
and recall, by (4.9),
$K(x^d_i,Y^d_i)$
and recall, by (4.9),
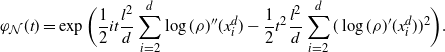 \[
\varphi_\mathcal{N}(t)=\exp \bigg(\dfrac{1}{2}it\dfrac{l^2}{d}\sum_{i=2}^d\log(\rho)''(x^d_i)-\dfrac{1}{2}t^2\dfrac{l^2}{d}\sum_{i=2}^d (\log(\rho)'(x^d_i))^2\bigg).
\]
\[
\varphi_\mathcal{N}(t)=\exp \bigg(\dfrac{1}{2}it\dfrac{l^2}{d}\sum_{i=2}^d\log(\rho)''(x^d_i)-\dfrac{1}{2}t^2\dfrac{l^2}{d}\sum_{i=2}^d (\log(\rho)'(x^d_i))^2\bigg).
\]
Define the positive constants
![]() $c\,:\!=\max\{c_1,c_2\}$
and
$c\,:\!=\max\{c_1,c_2\}$
and
![]() $c'\,:\!=\min\{1,l^2J/(32c),c'_1,c'_2\}$
, where the constants
$c'\,:\!=\min\{1,l^2J/(32c),c'_1,c'_2\}$
, where the constants
![]() $c_1,c_1'$
(resp.
$c_1,c_1'$
(resp.
![]() $c_2,c_2'$
) are given in Lemma 4.5 (resp. Lemma 4.7) and J is as in assumption (4.3). Note that the constants c,c´ do not depend on the choice of
$c_2,c_2'$
) are given in Lemma 4.5 (resp. Lemma 4.7) and J is as in assumption (4.3). Note that the constants c,c´ do not depend on the choice of
![]() $\mathbf{x}^d\in \mathcal{A}_d$
. Lemmas 4.5 and 4.7 imply the following inequality for all
$\mathbf{x}^d\in \mathcal{A}_d$
. Lemmas 4.5 and 4.7 imply the following inequality for all
![]() $d\in{\mathbb{N}}$
and
$d\in{\mathbb{N}}$
and
![]() $\mathbf{x}^d\in \mathcal{A}_d$
:
$\mathbf{x}^d\in \mathcal{A}_d$
:
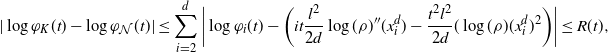 \begin{equation*} |\log\varphi_K(t)-\log\varphi_\mathcal{N}(t)|\leq
\sum_{i=2}^d\bigg|\log\varphi_i(t)-\bigg(i t\dfrac{l^2}{2d}\log(\rho)''(x^d_i)-\dfrac{t^2l^2}{2d} (\log(\rho)(x^d_i)^2\bigg)\bigg| \leq
R(t),
\end{equation*}
\begin{equation*} |\log\varphi_K(t)-\log\varphi_\mathcal{N}(t)|\leq
\sum_{i=2}^d\bigg|\log\varphi_i(t)-\bigg(i t\dfrac{l^2}{2d}\log(\rho)''(x^d_i)-\dfrac{t^2l^2}{2d} (\log(\rho)(x^d_i)^2\bigg)\bigg| \leq
R(t),
\end{equation*}
for all
![]() $|t|\leq r$
, where
$|t|\leq r$
, where
![]() $r\,:\!= c'\sqrt{d}$
and
$r\,:\!= c'\sqrt{d}$
and
![]() $R(t)\,:\!= c(t^2+|t|^3+t^4/\sqrt{d})/\sqrt{d}$
. Since
$R(t)\,:\!= c(t^2+|t|^3+t^4/\sqrt{d})/\sqrt{d}$
. Since
![]() $|t|^3\leq \sqrt{d}c't^2$
and
$|t|^3\leq \sqrt{d}c't^2$
and
![]() $t^4\leq dc'^2t^2$
for
$t^4\leq dc'^2t^2$
for
![]() $|t|\leq r$
, we have
$|t|\leq r$
, we have
By assumption (4.3), there exists
![]() $d_0'\in{\mathbb{N}}$
such that the variance
$d_0'\in{\mathbb{N}}$
such that the variance
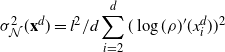 \[
\sigma^2_{\mathcal{N}}(\mathbf{x}^d)=l^2/d\sum_{i=2}^d (\log(\rho)'(x^d_i))^2
\]
\[
\sigma^2_{\mathcal{N}}(\mathbf{x}^d)=l^2/d\sum_{i=2}^d (\log(\rho)'(x^d_i))^2
\]
of
![]() $\mathcal{N}(\mathbf{x}^d,\mathbf{Y}^d)$
satisfies
$\mathcal{N}(\mathbf{x}^d,\mathbf{Y}^d)$
satisfies
![]() $\sigma^2_{\mathcal{N}}(\mathbf{x}^d)\geq l^2J/2$
for all
$\sigma^2_{\mathcal{N}}(\mathbf{x}^d)\geq l^2J/2$
for all
![]() $d\geq d_0'$
and
$d\geq d_0'$
and
![]() $\mathbf{x}^d\in \mathcal{A}_d$
. Let
$\mathbf{x}^d\in \mathcal{A}_d$
. Let
![]() $\gamma\,:\!=1/2$
and pick
$\gamma\,:\!=1/2$
and pick
![]() $d_0\,{\in}\,{\mathbb{N}}$
, greater than
$d_0\,{\in}\,{\mathbb{N}}$
, greater than
![]() $\max\{d_0',(16cl^{-2}/J)^2\}$
. Then, for any
$\max\{d_0',(16cl^{-2}/J)^2\}$
. Then, for any
![]() $d\geq d_0$
, the inequality
$d\geq d_0$
, the inequality
![]() $c/\sqrt{d}\leq \gamma l^2J/8$
holds. Since
$c/\sqrt{d}\leq \gamma l^2J/8$
holds. Since
![]() $c'\leq l^2J/(32c)$
, we have
$c'\leq l^2J/(32c)$
, we have
![]() $2cc'\leq \gamma l^2J/8$
, and the bound in (4.16) implies
$2cc'\leq \gamma l^2J/8$
, and the bound in (4.16) implies
for all
![]() $t\in[-r,r]$
. By Proposition 5.8, for all
$t\in[-r,r]$
. By Proposition 5.8, for all
![]() $d\geq d_0$
,
$d\geq d_0$
,
![]() $\sup_{x\in{\mathbb{R}}} |\Phi^d_{\mathcal{N}}(x)-\Phi^d_{K}(x)|$
is bounded above by
$\sup_{x\in{\mathbb{R}}} |\Phi^d_{\mathcal{N}}(x)-\Phi^d_{K}(x)|$
is bounded above by
where
Since the left-hand side of the inequality in the lemma is bounded above by 1, the inequality holds for all
![]() $d\in{\mathbb{N}}$
if we define
$d\in{\mathbb{N}}$
if we define
![]() $C\,:\!=\max\{C',\sqrt{d_0}\}$
.
$C\,:\!=\max\{C',\sqrt{d_0}\}$
.
Proof of Proposition 4.5. Since
![]() $|1\wedge {\mathrm{e}}^y- 1\wedge {\mathrm{e}}^x|\leq |x-y|$
for all
$|1\wedge {\mathrm{e}}^y- 1\wedge {\mathrm{e}}^x|\leq |x-y|$
for all
![]() $x,y\in{\mathbb{R}}$
, by Lemma 4.4 we have
$x,y\in{\mathbb{R}}$
, by Lemma 4.4 we have
for some constant
![]() $C'>0$
and all
$C'>0$
and all
![]() $d\in{\mathbb{N}}$
. Recall that
$d\in{\mathbb{N}}$
. Recall that
![]() ${\mathrm{e}}^x 1_{\{x<0\}} = 1\wedge {\mathrm{e}}^x - 1 + 1_{\{x\leq 0\}}$
for all
${\mathrm{e}}^x 1_{\{x<0\}} = 1\wedge {\mathrm{e}}^x - 1 + 1_{\{x\leq 0\}}$
for all
![]() $x\in{\mathbb{R}}\setminus\{0\}$
. Hence Lemmas 4.4 and 4.8 yield
$x\in{\mathbb{R}}\setminus\{0\}$
. Hence Lemmas 4.4 and 4.8 yield
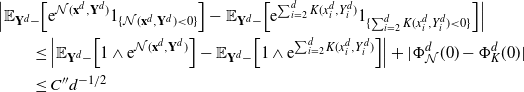 \begin{align*}
& \Big|\mathbb{E}_{\mathbf{Y}^d-} \Big[{\mathrm{e}}^{\mathcal{N}(\mathbf{x}^d,\mathbf{Y}^d)}1_{\{\mathcal{N}(\mathbf{x}^d,\mathbf{Y}^d)<0\}}\Big]-\mathbb{E}_{\mathbf{Y}^d-} \Big[{\mathrm{e}}^{\sum_{i=2}^dK(x^d_i,Y^d_i)}1_{\{\sum_{i=2}^dK(x^d_i,Y^d_i)<0\}}\Big] \Big|\\
&\qquad \leq \Big|\mathbb{E}_{\mathbf{Y}^d-} \Big[1\wedge
{\mathrm{e}}^{\mathcal{N}(\mathbf{x}^d,\mathbf{Y}^d)}\Big]-\mathbb{E}_{\mathbf{Y}^d-} \Big[1\wedge
{\mathrm{e}}^{\sum_{i=2}^dK(x^d_i,Y^d_i)}\Big] \Big|+ |\Phi^d_{\mathcal{N}}(0)-\Phi^d_{K}(0)|\\
& \qquad\leq
C'' d^{-1/2}
\end{align*}
\begin{align*}
& \Big|\mathbb{E}_{\mathbf{Y}^d-} \Big[{\mathrm{e}}^{\mathcal{N}(\mathbf{x}^d,\mathbf{Y}^d)}1_{\{\mathcal{N}(\mathbf{x}^d,\mathbf{Y}^d)<0\}}\Big]-\mathbb{E}_{\mathbf{Y}^d-} \Big[{\mathrm{e}}^{\sum_{i=2}^dK(x^d_i,Y^d_i)}1_{\{\sum_{i=2}^dK(x^d_i,Y^d_i)<0\}}\Big] \Big|\\
&\qquad \leq \Big|\mathbb{E}_{\mathbf{Y}^d-} \Big[1\wedge
{\mathrm{e}}^{\mathcal{N}(\mathbf{x}^d,\mathbf{Y}^d)}\Big]-\mathbb{E}_{\mathbf{Y}^d-} \Big[1\wedge
{\mathrm{e}}^{\sum_{i=2}^dK(x^d_i,Y^d_i)}\Big] \Big|+ |\Phi^d_{\mathcal{N}}(0)-\Phi^d_{K}(0)|\\
& \qquad\leq
C'' d^{-1/2}
\end{align*}
for some
![]() $C''>0$
and all
$C''>0$
and all
![]() $d\in {\mathbb{N}}$
. The proposition follows.
$d\in {\mathbb{N}}$
. The proposition follows.
Proof of Proposition 4.6. For any
![]() $\mathbf{x}^d\in\mathcal{A}_d$
, by [Reference Roberts, Gelman and Gilks30, Proposition 2.4], we have
$\mathbf{x}^d\in\mathcal{A}_d$
, by [Reference Roberts, Gelman and Gilks30, Proposition 2.4], we have
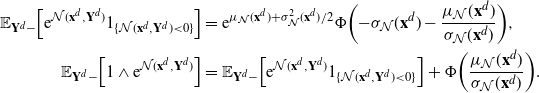 \begin{align*}
\mathbb{E}_{\mathbf{Y}^d-} \Big[{\mathrm{e}}^{\mathcal{N}(\mathbf{x}^d,\mathbf{Y}^d)}1_{\{\mathcal{N}(\mathbf{x}^d,\mathbf{Y}^d)<0\}}\Big] & ={\mathrm{e}}^{\mu_{\mathcal{N}}(\mathbf{x}^d)+{\sigma^2_{\mathcal{N}}(\mathbf{x}^d)}/{2}}\Phi \bigg({-}\sigma_{\mathcal{N}}(\mathbf{x}^d)-\frac{\mu_{\mathcal{N}}(\mathbf{x}^d)}{\sigma_{\mathcal{N}}(\mathbf{x}^d)}\bigg), \\
\mathbb{E}_{\mathbf{Y}^d-} \Big[1\wedge {\mathrm{e}}^{\mathcal{N}(\mathbf{x}^d,\mathbf{Y}^d)}\Big] & =
\mathbb{E}_{\mathbf{Y}^d-} \Big[{\mathrm{e}}^{\mathcal{N}(\mathbf{x}^d,\mathbf{Y}^d)}1_{\{\mathcal{N}(\mathbf{x}^d,\mathbf{Y}^d)<0\}}\Big]
+
\Phi\bigg(\frac{\mu_{\mathcal{N}}(\mathbf{x}^d)}{\sigma_{\mathcal{N}}(\mathbf{x}^d)}\bigg).
\end{align*}
\begin{align*}
\mathbb{E}_{\mathbf{Y}^d-} \Big[{\mathrm{e}}^{\mathcal{N}(\mathbf{x}^d,\mathbf{Y}^d)}1_{\{\mathcal{N}(\mathbf{x}^d,\mathbf{Y}^d)<0\}}\Big] & ={\mathrm{e}}^{\mu_{\mathcal{N}}(\mathbf{x}^d)+{\sigma^2_{\mathcal{N}}(\mathbf{x}^d)}/{2}}\Phi \bigg({-}\sigma_{\mathcal{N}}(\mathbf{x}^d)-\frac{\mu_{\mathcal{N}}(\mathbf{x}^d)}{\sigma_{\mathcal{N}}(\mathbf{x}^d)}\bigg), \\
\mathbb{E}_{\mathbf{Y}^d-} \Big[1\wedge {\mathrm{e}}^{\mathcal{N}(\mathbf{x}^d,\mathbf{Y}^d)}\Big] & =
\mathbb{E}_{\mathbf{Y}^d-} \Big[{\mathrm{e}}^{\mathcal{N}(\mathbf{x}^d,\mathbf{Y}^d)}1_{\{\mathcal{N}(\mathbf{x}^d,\mathbf{Y}^d)<0\}}\Big]
+
\Phi\bigg(\frac{\mu_{\mathcal{N}}(\mathbf{x}^d)}{\sigma_{\mathcal{N}}(\mathbf{x}^d)}\bigg).
\end{align*}
where
![]() $\Phi$
is the distribution of a standard normal random variable. Note first that it is sufficient to prove the inequality in the proposition for all
$\Phi$
is the distribution of a standard normal random variable. Note first that it is sufficient to prove the inequality in the proposition for all
![]() $d> d_0$
for some
$d> d_0$
for some
![]() $d_0\in{\mathbb{N}}$
, since the expectations above are bounded by 1 and we can hence increase the constant C so that the first
$d_0\in{\mathbb{N}}$
, since the expectations above are bounded by 1 and we can hence increase the constant C so that the first
![]() $d_0$
inequalities are also satisfied.
$d_0$
inequalities are also satisfied.
Recall the formulas for
![]() $\mu_{\mathcal{N}}(\mathbf{x}^d)$
and
$\mu_{\mathcal{N}}(\mathbf{x}^d)$
and
![]() $\sigma^2_{\mathcal{N}}(\mathbf{x}^d)$
from (4.9). By assumptions (4.3) and (4.4) it follows that
$\sigma^2_{\mathcal{N}}(\mathbf{x}^d)$
from (4.9). By assumptions (4.3) and (4.4) it follows that
![]() $ |\mu_{\mathcal{N}}(\mathbf{x}^d)+\sigma^2_{\mathcal{N}}(\mathbf{x}^d)/2|\leq c a_d/\sqrt{d}$
for some constant
$ |\mu_{\mathcal{N}}(\mathbf{x}^d)+\sigma^2_{\mathcal{N}}(\mathbf{x}^d)/2|\leq c a_d/\sqrt{d}$
for some constant
![]() $c>0$
and all large d and
$c>0$
and all large d and
![]() $\mathbf{x}^d\in\mathcal{A}_d$
. Note that
$\mathbf{x}^d\in\mathcal{A}_d$
. Note that
![]() $S_a\,:\!=\sup_{d\in{\mathbb{N}}}(a_d/\sqrt{d})<\infty$
since
$S_a\,:\!=\sup_{d\in{\mathbb{N}}}(a_d/\sqrt{d})<\infty$
since
![]() $\{a_d\}_{d\in{\mathbb{N}}}$
is sluggish. The function
$\{a_d\}_{d\in{\mathbb{N}}}$
is sluggish. The function
![]() $x\mapsto {\mathrm{e}}^x$
is Lipschitz on
$x\mapsto {\mathrm{e}}^x$
is Lipschitz on
![]() $[-cS_a,cS_a]$
with constant
$[-cS_a,cS_a]$
with constant
![]() ${\mathrm{e}}^{cS_a}$
. Consequently
${\mathrm{e}}^{cS_a}$
. Consequently
![]() $ |{\mathrm{e}}^{\mu_{\mathcal{N}}(\mathbf{x}^d)+\sigma^2_{\mathcal{N}}(\mathbf{x}^d)/2}-1|\leq {\mathrm{e}}^{cS_a}a_d/\sqrt{d}$
for large d and uniformly in
$ |{\mathrm{e}}^{\mu_{\mathcal{N}}(\mathbf{x}^d)+\sigma^2_{\mathcal{N}}(\mathbf{x}^d)/2}-1|\leq {\mathrm{e}}^{cS_a}a_d/\sqrt{d}$
for large d and uniformly in
![]() $\mathbf{x}^d\in\mathcal{A}_d$
.
$\mathbf{x}^d\in\mathcal{A}_d$
.
By assumption (4.3), for all large
![]() $d\in{\mathbb{N}}$
and all
$d\in{\mathbb{N}}$
and all
![]() $\mathbf{x}^d\in\mathcal{A}_d$
, we have
$\mathbf{x}^d\in\mathcal{A}_d$
, we have
![]() $\sigma_{\mathcal{N}}(\mathbf{x}^d)\geq l\sqrt{J}/\sqrt{2}$
. Hence, since the function
$\sigma_{\mathcal{N}}(\mathbf{x}^d)\geq l\sqrt{J}/\sqrt{2}$
. Hence, since the function
![]() $x\mapsto \sqrt{x}$
is Lipschitz with constant
$x\mapsto \sqrt{x}$
is Lipschitz with constant
![]() $c_1\,:\!=1/(l\sqrt{2J})$
on
$c_1\,:\!=1/(l\sqrt{2J})$
on
![]() $[{l^2J}/{2},\infty)$
, we obtain
$[{l^2J}/{2},\infty)$
, we obtain
where constant
![]() $c_2>0$
exists by (4.3). Moreover,
$c_2>0$
exists by (4.3). Moreover,
for
![]() $c_3>0$
and all large d.
$c_3>0$
and all large d.
Since
the inequalities in the previous paragraph imply that there exists
![]() $c_4>0$
such that
$c_4>0$
such that
for large d and uniformly in
![]() $\mathbf{x}^d\in\mathcal{A}_d$
. Since
$\mathbf{x}^d\in\mathcal{A}_d$
. Since
![]() $\Phi$
is Lipschitz with constant
$\Phi$
is Lipschitz with constant
![]() $1/\sqrt{2\pi}$
, there exists a constant
$1/\sqrt{2\pi}$
, there exists a constant
![]() $C_1'>1$
such that
$C_1'>1$
such that
holds for all large d and all
![]() $\mathbf{x}^d\in\mathcal{A}_d$
. Similarly,
$\mathbf{x}^d\in\mathcal{A}_d$
. Similarly,
for some
![]() $C_2'>0$
all large d and all
$C_2'>0$
all large d and all
![]() $\mathbf{x}^d\in\mathcal{A}_d$
, and the proposition follows.
$\mathbf{x}^d\in\mathcal{A}_d$
, and the proposition follows.
4.3 Proof of Proposition 2.1
We will now prove the following result.
Proposition 4.7. Let
![]() $a=\{a_d\}_{d\in{\mathbb{N}}}$
be a sluggish sequence and
$a=\{a_d\}_{d\in{\mathbb{N}}}$
be a sluggish sequence and
![]() $p\in[1,\infty)$
. There exists a constant
$p\in[1,\infty)$
. There exists a constant
![]() $C_4$
(depending on a and p) such that, for every
$C_4$
(depending on a and p) such that, for every
![]() $f\in\mathcal{S}^3$
and all
$f\in\mathcal{S}^3$
and all
![]() $d\in{\mathbb{N}}$
, we have
$d\in{\mathbb{N}}$
, we have
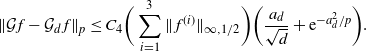 \[\|\mathcal{G}f-{\mathcal{G}}_df\|_p\leq
C_4\bigg(\sum_{i=1}^3\|\:f^{(i)}\|_{\infty,1/2}\bigg) \bigg(\dfrac{a_d}{\sqrt{d}}
+{\mathrm{e}}^{-a_d^2/p}\bigg).\]
\[\|\mathcal{G}f-{\mathcal{G}}_df\|_p\leq
C_4\bigg(\sum_{i=1}^3\|\:f^{(i)}\|_{\infty,1/2}\bigg) \bigg(\dfrac{a_d}{\sqrt{d}}
+{\mathrm{e}}^{-a_d^2/p}\bigg).\]
In the case
![]() $p=2$
, define
$p=2$
, define
![]() $a_d\,:\!=\sqrt{2\log(d)}$
for
$a_d\,:\!=\sqrt{2\log(d)}$
for
![]() $d\in{\mathbb{N}}\setminus\{1\}$
and note that Proposition 2.1 then follows as a special case of Proposition 4.7.
$d\in{\mathbb{N}}\setminus\{1\}$
and note that Proposition 2.1 then follows as a special case of Proposition 4.7.
Lemma 4.9. There exists a constant C such that, for all
![]() $f\in\mathcal{S}^3$
and all
$f\in\mathcal{S}^3$
and all
![]() $d\in{\mathbb{N}}$
, we have
$d\in{\mathbb{N}}$
, we have
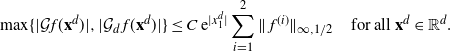 \[\max\{ |\mathcal{G}f(\mathbf{x}^d)|, |\mathcal{G}_df(\mathbf{x}^d)|\}
\leq C
\,{\mathrm{e}}^{|x^d_1|}\sum_{i=1}^2\|\:f^{(i)}\|_{\infty,1/2}\quad\text{{for all} }
\mathbf{x}^d\in{\mathbb{R}}^d.\]
\[\max\{ |\mathcal{G}f(\mathbf{x}^d)|, |\mathcal{G}_df(\mathbf{x}^d)|\}
\leq C
\,{\mathrm{e}}^{|x^d_1|}\sum_{i=1}^2\|\:f^{(i)}\|_{\infty,1/2}\quad\text{{for all} }
\mathbf{x}^d\in{\mathbb{R}}^d.\]
Proof. The triangle inequality, definition (2.4), and
imply the bound in the lemma for
![]() $|\mathcal{G}f(\mathbf{x}^d)|$
. To bound
$|\mathcal{G}f(\mathbf{x}^d)|$
. To bound
![]() $|\mathcal{G}_df(\mathbf{x}^d)|$
, define
$|\mathcal{G}_df(\mathbf{x}^d)|$
, define
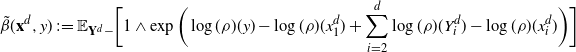 \[\tilde{\beta}(\mathbf{x}^d,y)\,:\!=\mathbb{E}_{\mathbf{Y}^d-}\bigg[1\wedge
\exp\bigg(\log(\rho)( y)-\log(\rho)(x^d_1)+\sum_{i=2}^d\log(\rho)(Y^d_i)-\log(\rho)(x^d_i)\bigg)\bigg]\]
\[\tilde{\beta}(\mathbf{x}^d,y)\,:\!=\mathbb{E}_{\mathbf{Y}^d-}\bigg[1\wedge
\exp\bigg(\log(\rho)( y)-\log(\rho)(x^d_1)+\sum_{i=2}^d\log(\rho)(Y^d_i)-\log(\rho)(x^d_i)\bigg)\bigg]\]
for any
![]() $y\in{\mathbb{R}}$
. Then, if q denotes the density of
$y\in{\mathbb{R}}$
. Then, if q denotes the density of
![]() $Y^d_1-x^d_1\sim N(0,l^2/d)$
, we obtain
$Y^d_1-x^d_1\sim N(0,l^2/d)$
, we obtain
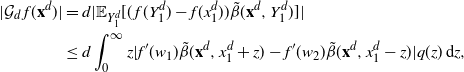 \begin{align}
|\mathcal{G}_df(\mathbf{x}^d)| & =d | \mathbb{E}_{Y^d_1} [ (f(Y^d_1)-f(x^d_1))\tilde{\beta}(\mathbf{x}^d,Y^d_1)]|
\notag \\
& \leq d\int_0^{\infty}z | f'(w_1)\tilde{\beta}(\mathbf{x}^d,x^d_1+z)-f'(w_2)\tilde{\beta}(\mathbf{x}^d,x^d_1-z)|q(z) \,{\mathrm{d}} z,
\end{align}
\begin{align}
|\mathcal{G}_df(\mathbf{x}^d)| & =d | \mathbb{E}_{Y^d_1} [ (f(Y^d_1)-f(x^d_1))\tilde{\beta}(\mathbf{x}^d,Y^d_1)]|
\notag \\
& \leq d\int_0^{\infty}z | f'(w_1)\tilde{\beta}(\mathbf{x}^d,x^d_1+z)-f'(w_2)\tilde{\beta}(\mathbf{x}^d,x^d_1-z)|q(z) \,{\mathrm{d}} z,
\end{align}
where
![]() $w_1\in(x_1^d,x_1^d+z)$
and
$w_1\in(x_1^d,x_1^d+z)$
and
![]() $w_2\in(x_1^d-z,x_1^d)$
satisfy
$w_2\in(x_1^d-z,x_1^d)$
satisfy
respectively. Moreover,
![]() $ | f'(w_1)-f'(w_2)|\leq 2z| f''(w_3)|$
holds for some
$ | f'(w_1)-f'(w_2)|\leq 2z| f''(w_3)|$
holds for some
![]() $w_3$
in the interval
$w_3$
in the interval
![]() ${(x_1^d-z,x_1^d+z)}$
. Since
${(x_1^d-z,x_1^d+z)}$
. Since
![]() $x\mapsto 1\wedge {\mathrm{e}}^x$
is Lipschitz with constant 1, we obtain
$x\mapsto 1\wedge {\mathrm{e}}^x$
is Lipschitz with constant 1, we obtain
for some
![]() $w_4\in (x_1^d-z,x_1^d+z)$
. By adding and subtracting
$w_4\in (x_1^d-z,x_1^d+z)$
. By adding and subtracting
![]() $f'(w_2)\tilde{\beta}(\mathbf{x}^d,x^d_1+z)$
on the right-hand side of (4.17), applying the two bounds we just derived and noting that
$f'(w_2)\tilde{\beta}(\mathbf{x}^d,x^d_1+z)$
on the right-hand side of (4.17), applying the two bounds we just derived and noting that
![]() $\tilde \beta\leq 1$
, we obtain
$\tilde \beta\leq 1$
, we obtain
Note that, since
![]() $\max\{|w_3|,|w_2|,|w_4|\} \leq |x_1^d|+z$
and
$\max\{|w_3|,|w_2|,|w_4|\} \leq |x_1^d|+z$
and
![]() $\|\:f''\|_{\infty,1}\leq \|\:f''\|_{\infty,1/2}$
, we have
$\|\:f''\|_{\infty,1}\leq \|\:f''\|_{\infty,1/2}$
, we have
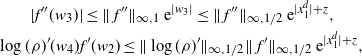 \begin{gather*}
| f''(w_3)| \leq \|\:f''\|_{\infty,1} \,{\mathrm{e}}^{|w_3|} \leq \|\:f''\|_{\infty,1/2} \,{\mathrm{e}}^{|x_1^d|+z},\\
\log(\rho)'(w_4)f'(w_2) \leq \|\log(\rho)'\|_{\infty,1/2}\|\:f'\|_{\infty,1/2}\,{\mathrm{e}}^{|x_1^d|+z},
\end{gather*}
\begin{gather*}
| f''(w_3)| \leq \|\:f''\|_{\infty,1} \,{\mathrm{e}}^{|w_3|} \leq \|\:f''\|_{\infty,1/2} \,{\mathrm{e}}^{|x_1^d|+z},\\
\log(\rho)'(w_4)f'(w_2) \leq \|\log(\rho)'\|_{\infty,1/2}\|\:f'\|_{\infty,1/2}\,{\mathrm{e}}^{|x_1^d|+z},
\end{gather*}
which, together with inequality (4.18), implies the lemma.
Proof of Proposition 4.7. By Theorem 2.2 (on
![]() $\mathcal{A}_d$
) and Lemma 4.9 (on
$\mathcal{A}_d$
) and Lemma 4.9 (on
![]() ${\mathbb{R}}^d\setminus \mathcal{A}_d$
), there exists a constant
${\mathbb{R}}^d\setminus \mathcal{A}_d$
), there exists a constant
![]() $C>0$
such that for any
$C>0$
such that for any
![]() $f\in\mathcal{S}^3$
the following inequality holds:
$f\in\mathcal{S}^3$
the following inequality holds:
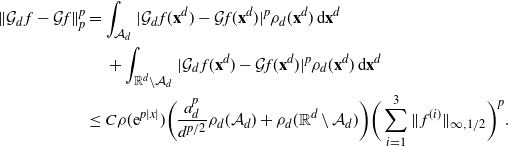 \begin{align*}
\|\mathcal{G}_df-\mathcal{G}f\|^p_p & =
\int_{\mathcal{A}_d} |\mathcal{G}_df(\mathbf{x}^d)-\mathcal{G}f(\mathbf{x}^d)|^p\rho_d(\mathbf{x}^d) \,{\mathrm{d}} \mathbf{x}^d \\
&\quad\, +
\int_{{\mathbb{R}}^d\setminus \mathcal{A}_d} |\mathcal{G}_df(\mathbf{x}^d)-\mathcal{G}f(\mathbf{x}^d)|^p\rho_d(\mathbf{x}^d) \,{\mathrm{d}} \mathbf{x}^d\\
& \leq C\rho({\mathrm{e}}^{p|x|})\bigg(\dfrac{a_d^p}{d^{p/2}}\rho_d(\mathcal{A}_d)+
\rho_d({\mathbb{R}}^d\setminus \mathcal{A}_d)\bigg)\bigg(\sum_{i=1}^3\|\:f^{(i)}\|_{\infty,1/2}\bigg)^p.
\end{align*}
\begin{align*}
\|\mathcal{G}_df-\mathcal{G}f\|^p_p & =
\int_{\mathcal{A}_d} |\mathcal{G}_df(\mathbf{x}^d)-\mathcal{G}f(\mathbf{x}^d)|^p\rho_d(\mathbf{x}^d) \,{\mathrm{d}} \mathbf{x}^d \\
&\quad\, +
\int_{{\mathbb{R}}^d\setminus \mathcal{A}_d} |\mathcal{G}_df(\mathbf{x}^d)-\mathcal{G}f(\mathbf{x}^d)|^p\rho_d(\mathbf{x}^d) \,{\mathrm{d}} \mathbf{x}^d\\
& \leq C\rho({\mathrm{e}}^{p|x|})\bigg(\dfrac{a_d^p}{d^{p/2}}\rho_d(\mathcal{A}_d)+
\rho_d({\mathbb{R}}^d\setminus \mathcal{A}_d)\bigg)\bigg(\sum_{i=1}^3\|\:f^{(i)}\|_{\infty,1/2}\bigg)^p.
\end{align*}
Apply Proposition 4.2 and raise both sides of the inequality to the power
![]() $1/p$
to conclude the proof of the proposition.
$1/p$
to conclude the proof of the proposition.
4.4 Proof of Theorem 2.1
Lemma 4.10. Assume that
![]() $\rho$
is a strictly positive density in
$\rho$
is a strictly positive density in
![]() $\mathcal{C}^1$
and that (2.3) holds. Then, for any
$\mathcal{C}^1$
and that (2.3) holds. Then, for any
![]() $d\in{\mathbb{N}}$
, the RWM chain
$d\in{\mathbb{N}}$
, the RWM chain
![]() $\{\mathbf{X}^d_n\}_{n\in{\mathbb{N}}}$
is V-uniformly ergodic with
$\{\mathbf{X}^d_n\}_{n\in{\mathbb{N}}}$
is V-uniformly ergodic with
![]() $V\,:\!=1/\sqrt{\rho_d}$
.
$V\,:\!=1/\sqrt{\rho_d}$
.
Proof. The lemma follows from [Reference Jarner and Hansen16, Theorem 4.1] if we prove that the target
![]() $\rho_d$
satisfies
$\rho_d$
satisfies
 \begin{gather}
\lim_{|\mathbf{x}^d|\to\infty}\dfrac{\mathbf{x}^d}{|\mathbf{x}^d|}\cdot\nabla\log(\rho_d(\mathbf{x}^d))=
\lim_{|\mathbf{x}^d|\to\infty}\sum_{i=1}^d\dfrac{x^d_i}{|x^d_i|}\log(\rho)'(x^d_i)=-\infty,\end{gather}
\begin{gather}
\lim_{|\mathbf{x}^d|\to\infty}\dfrac{\mathbf{x}^d}{|\mathbf{x}^d|}\cdot\nabla\log(\rho_d(\mathbf{x}^d))=
\lim_{|\mathbf{x}^d|\to\infty}\sum_{i=1}^d\dfrac{x^d_i}{|x^d_i|}\log(\rho)'(x^d_i)=-\infty,\end{gather}
Assumption (2.3) implies that the expression
![]() $x/|x|\cdot \log(\rho)'(x)$
is bounded above and takes arbitrarily large negative values as
$x/|x|\cdot \log(\rho)'(x)$
is bounded above and takes arbitrarily large negative values as
![]() $|x|\to\infty$
. This yields (4.19), since
$|x|\to\infty$
. This yields (4.19), since
![]() $|\mathbf{x}^d|\to\infty$
implies that
$|\mathbf{x}^d|\to\infty$
implies that
![]() $|x^d_i|\to\infty$
holds for at least one
$|x^d_i|\to\infty$
holds for at least one
![]() $i\in\{1,\ldots,d\}$
.
$i\in\{1,\ldots,d\}$
.
Condition (4.20) states that the acceptance probability in the RWM chain is bounded away from zero sufficiently far from the origin. To prove this, recall that
![]() $\mathbf{Y}^d\sim N(\mathbf{x}^d,l^2/d\cdot I_d)$
and define the set
$\mathbf{Y}^d\sim N(\mathbf{x}^d,l^2/d\cdot I_d)$
and define the set
where we interpret
![]() $x^d_i/|x^d_i|\,:\!=1$
if
$x^d_i/|x^d_i|\,:\!=1$
if
![]() $x^d_i=0$
. Clearly
$x^d_i=0$
. Clearly
![]() $\inf_{\mathbf{x}^d\in{\mathbb{R}}^d}\mathbb{P}_{\mathbf{Y}^d} [B(\mathbf{x}^d)
]>0$
. We now prove that if
$\inf_{\mathbf{x}^d\in{\mathbb{R}}^d}\mathbb{P}_{\mathbf{Y}^d} [B(\mathbf{x}^d)
]>0$
. We now prove that if
![]() $|\mathbf{x}^d|$
is sufficiently large, then
$|\mathbf{x}^d|$
is sufficiently large, then
![]() $\rho_d(\mathbf{y}^d)\geq\rho_d(\mathbf{x}^d)$
for all
$\rho_d(\mathbf{y}^d)\geq\rho_d(\mathbf{x}^d)$
for all
![]() $\mathbf{y}^d\in B(\mathbf{x}^d)$
, which implies (4.20).
$\mathbf{y}^d\in B(\mathbf{x}^d)$
, which implies (4.20).
By (2.3), far enough from zero,
![]() $\rho$
is decreasing in a direction away from the origin. Therefore, there exists a compact interval
$\rho$
is decreasing in a direction away from the origin. Therefore, there exists a compact interval
![]() $K\subset {\mathbb{R}}$
such that
$K\subset {\mathbb{R}}$
such that
![]() $ ({-}2l/\sqrt{d},2l/\sqrt{d})\subset K $
and
$ ({-}2l/\sqrt{d},2l/\sqrt{d})\subset K $
and
![]() $\rho( y)\geq \rho(x)$
whenever
$\rho( y)\geq \rho(x)$
whenever
![]() $x\notin K$
and
$x\notin K$
and
![]() $x/|x|\cdot ( y-x)\in ({-}2l/\sqrt{d},-l/\sqrt{d})$
. We claim that for every
$x/|x|\cdot ( y-x)\in ({-}2l/\sqrt{d},-l/\sqrt{d})$
. We claim that for every
![]() $\mathbf{y}^d\in B(\mathbf{x}^d)$
, the inequality
$\mathbf{y}^d\in B(\mathbf{x}^d)$
, the inequality
![]() $\rho( y^d_i)/\rho(x^d_i)\geq (\min_{x\in K}\rho(x))/(\max_{x\in{\mathbb{R}}}\rho(x))\in(0,1)$
holds. If
$\rho( y^d_i)/\rho(x^d_i)\geq (\min_{x\in K}\rho(x))/(\max_{x\in{\mathbb{R}}}\rho(x))\in(0,1)$
holds. If
![]() $x^d_i\in K$
, then
$x^d_i\in K$
, then
![]() $y^d_i\in K$
and the inequality follows trivially. If
$y^d_i\in K$
and the inequality follows trivially. If
![]() $x^d_i\notin K$
, then, by the definition of K, we have
$x^d_i\notin K$
, then, by the definition of K, we have
![]() $\rho( y^d_i)/\rho(x^d_i)\geq 1$
. This proves the claim. Hence, for
$\rho( y^d_i)/\rho(x^d_i)\geq 1$
. This proves the claim. Hence, for
![]() $\mathbf{y}^d\in B(\mathbf{x}^d)$
we have
$\mathbf{y}^d\in B(\mathbf{x}^d)$
we have
We now prove that the ratio
![]() $\rho( y^d_i)/\rho(x^d_i)$
takes arbitrarily large values as
$\rho( y^d_i)/\rho(x^d_i)$
takes arbitrarily large values as
![]() $|x^d_i|\to\infty$
. To show this, pick
$|x^d_i|\to\infty$
. To show this, pick
![]() $\mathbf{y}^d\in B(\mathbf{x}^d)$
and assume the inequality
$\mathbf{y}^d\in B(\mathbf{x}^d)$
and assume the inequality
![]() $y_i^d>x_i^d$
. Then
$y_i^d>x_i^d$
. Then
![]() $x_i^d<0$
and
$x_i^d<0$
and
![]() $y_i^d-x_i^d>l/\sqrt{d}$
.
$y_i^d-x_i^d>l/\sqrt{d}$
.
Moreover, the following holds:
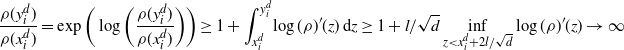 \[\dfrac{\rho( y^d_i)}{\rho(x^d_i)}=\exp\bigg(\log\bigg(\dfrac{\rho( y^d_i)}{\rho(x^d_i)}\bigg)\bigg)\geq
1+\int_{x^d_i}^{y^d_i}\!\log(\rho)'(z) \,{\mathrm{d}} z\geq
1+l/\sqrt{d}\inf_{z<x^d_i+2l/\sqrt{d}}\log(\rho)'(z)\to\infty\]
\[\dfrac{\rho( y^d_i)}{\rho(x^d_i)}=\exp\bigg(\log\bigg(\dfrac{\rho( y^d_i)}{\rho(x^d_i)}\bigg)\bigg)\geq
1+\int_{x^d_i}^{y^d_i}\!\log(\rho)'(z) \,{\mathrm{d}} z\geq
1+l/\sqrt{d}\inf_{z<x^d_i+2l/\sqrt{d}}\log(\rho)'(z)\to\infty\]
as
![]() $x_i^d\to-\infty$
by (2.3). This, together with (4.21), implies (4.20). The case
$x_i^d\to-\infty$
by (2.3). This, together with (4.21), implies (4.20). The case
![]() $y_i^d<x_i^d$
is analogous and the lemma follows.
$y_i^d<x_i^d$
is analogous and the lemma follows.
Proposition 4.8. If a strictly positive
![]() $\rho$
satisfies (2.3) and
$\rho$
satisfies (2.3) and
![]() $\log(\rho)\in\mathcal{S}^{n_\rho}$
and
$\log(\rho)\in\mathcal{S}^{n_\rho}$
and
![]() $f\in\mathcal{S}^{n_f}$
for some integers
$f\in\mathcal{S}^{n_f}$
for some integers
![]() $n_\rho,n_f\in{\mathbb{N}}\cup\{0\}$
, then the function
$n_\rho,n_f\in{\mathbb{N}}\cup\{0\}$
, then the function
![]() $\skew3\hat f$
, defined in (2.6), satisfies
$\skew3\hat f$
, defined in (2.6), satisfies
![]() $\skew3\hat{f}\in\mathcal{S}^{\min(n_f+2,n_\rho+1)}$
.
$\skew3\hat{f}\in\mathcal{S}^{\min(n_f+2,n_\rho+1)}$
.
Proof. Clearly, if
![]() $f\in\mathcal{C}^{n_f}$
and
$f\in\mathcal{C}^{n_f}$
and
![]() $\rho\in\mathcal{C}^{n_\rho}$
and if
$\rho\in\mathcal{C}^{n_\rho}$
and if
![]() $\rho$
is strictly positive, then
$\rho$
is strictly positive, then
![]() $\skew3\hat{f}\in\mathcal{C}^{\min(n_f+2,n_\rho+1)}$
. Pick
$\skew3\hat{f}\in\mathcal{C}^{\min(n_f+2,n_\rho+1)}$
. Pick
![]() $s>0$
. L’Hôpital’s rule implies
$s>0$
. L’Hôpital’s rule implies
The last limit is zero by (2.3). An analogous argument shows
![]() $\lim_{x\to-\infty}\skew3\hat{f}(x)/{\mathrm{e}}^{s|x|}=0$
. Hence
$\lim_{x\to-\infty}\skew3\hat{f}(x)/{\mathrm{e}}^{s|x|}=0$
. Hence
![]() $\|\skew3\hat{f}\|_{\infty,s}<\infty$
holds for all
$\|\skew3\hat{f}\|_{\infty,s}<\infty$
holds for all
![]() $s>0$
. Since
$s>0$
. Since
this argument implies that
![]() $\|\skew3\hat{f}'\|_{\infty,s}<\infty$
holds for all
$\|\skew3\hat{f}'\|_{\infty,s}<\infty$
holds for all
![]() $s>0$
. Hence
$s>0$
. Hence
![]() $\skew3\hat{f}\in \mathcal{S}^{1}$
.
$\skew3\hat{f}\in \mathcal{S}^{1}$
.
Proceed by induction. Assume that for all
![]() $k\leq n$
(where
$k\leq n$
(where
![]() $1\leq
n<\min(n_f+2,n_\rho+1)$
) we have
$1\leq
n<\min(n_f+2,n_\rho+1)$
) we have
![]() $\|\skew3\hat{f}^{(k)}\|_{\infty,s}<\infty$
for any
$\|\skew3\hat{f}^{(k)}\|_{\infty,s}<\infty$
for any
![]() $s>0$
. Pick an arbitrary
$s>0$
. Pick an arbitrary
![]() $u>0$
. By differentiating (2.5) we obtain
$u>0$
. By differentiating (2.5) we obtain
 \[\skew3\hat{f}^{(n+1)}=-\sum_{k=0}^{n-1}\binom{n-1}{k}(\log(\rho))^{(k+1)}\skew3\hat{f}^{(n-k)}+\dfrac{2}{h(l)}(\rho(f)-f)^{(n-1)}.\]
\[\skew3\hat{f}^{(n+1)}=-\sum_{k=0}^{n-1}\binom{n-1}{k}(\log(\rho))^{(k+1)}\skew3\hat{f}^{(n-k)}+\dfrac{2}{h(l)}(\rho(f)-f)^{(n-1)}.\]
Since
![]() $n\leq \min(n_\rho, n_f+1)$
, the induction hypothesis implies
$n\leq \min(n_\rho, n_f+1)$
, the induction hypothesis implies
![]() $\|\skew3\hat{f}^{(k)}\|_{\infty,u/2}<\infty$
for all
$\|\skew3\hat{f}^{(k)}\|_{\infty,u/2}<\infty$
for all
![]() $1\,{\leq}\, k\,{\leq}\,n$
. By assumption we have
$1\,{\leq}\, k\,{\leq}\,n$
. By assumption we have
![]() $\|\:f^{(n-1)}\|_{\infty,u}<\infty$
and
$\|\:f^{(n-1)}\|_{\infty,u}<\infty$
and
![]() $\|(\log(\rho))^{(k)}\|_{\infty,u/2}<\infty$
for all
$\|(\log(\rho))^{(k)}\|_{\infty,u/2}<\infty$
for all
![]() $1\leq k\leq n$
. Hence
$1\leq k\leq n$
. Hence
![]() $\|\skew3\hat{f}^{(n+1)}\|_{\infty,u}<\infty$
holds for an arbitrary
$\|\skew3\hat{f}^{(n+1)}\|_{\infty,u}<\infty$
holds for an arbitrary
![]() $u>0$
and the proposition follows.
$u>0$
and the proposition follows.
Proof of Theorem 2.1. By Lemma 4.10, the RWM chain
![]() $\mathbf{X}^d$
with the transition kernel
$\mathbf{X}^d$
with the transition kernel
![]() $P_d$
is V-uniformly ergodic with
$P_d$
is V-uniformly ergodic with
![]() $V=\rho_d^{-1/2}$
. Moreover, by [Reference Roberts and Rosenthal27, Proposition 2.1 and Theorem 2.1],
$V=\rho_d^{-1/2}$
. Moreover, by [Reference Roberts and Rosenthal27, Proposition 2.1 and Theorem 2.1],
![]() $P_d$
defines a self-adjoint operator on
$P_d$
defines a self-adjoint operator on
![]() $\{g\in L^2(\rho_d)\colon \rho_d(g)=0\}$
with norm
$\{g\in L^2(\rho_d)\colon \rho_d(g)=0\}$
with norm
![]() $\lambda_d<1$
. Proposition 4.4 implies
$\lambda_d<1$
. Proposition 4.4 implies
![]() $\skew3\hat{f}\in\mathcal{S}^3$
, since by assumption we have
$\skew3\hat{f}\in\mathcal{S}^3$
, since by assumption we have
![]() $f\in\mathcal{S}^1$
and
$f\in\mathcal{S}^1$
and
![]() $\log(\rho)\in\mathcal{S}^4$
. By Remark 5.1(c) in Section 5 below we have
$\log(\rho)\in\mathcal{S}^4$
. By Remark 5.1(c) in Section 5 below we have
![]() $\skew3\hat{f}^2\in\mathcal{S}^3$
. Since
$\skew3\hat{f}^2\in\mathcal{S}^3$
. Since
![]() $P_d\skew3\hat f = (1/d)\mathcal{G}_d\skew3\hat f+\skew3\hat f$
, Lemma 4.3 implies that
$P_d\skew3\hat f = (1/d)\mathcal{G}_d\skew3\hat f+\skew3\hat f$
, Lemma 4.3 implies that
![]() $ (P_d\skew3\hat{f})^2(\mathbf{x}^d)\leq C_{\skew3\hat{f}} \,{\mathrm{e}}^{2 |x_1^d|} $
for some positive constant
$ (P_d\skew3\hat{f})^2(\mathbf{x}^d)\leq C_{\skew3\hat{f}} \,{\mathrm{e}}^{2 |x_1^d|} $
for some positive constant
![]() $C_{\skew3\hat{f}}$
and all
$C_{\skew3\hat{f}}$
and all
![]() $\mathbf{x}^d\in{\mathbb{R}}^d$
. Hence (2.3) and the definition of V imply the inequality
$\mathbf{x}^d\in{\mathbb{R}}^d$
. Hence (2.3) and the definition of V imply the inequality
![]() $\max\{\skew3\hat{f}^2,(P_d\skew3\hat{f})^2\}\leq cV$
for some constant
$\max\{\skew3\hat{f}^2,(P_d\skew3\hat{f})^2\}\leq cV$
for some constant
![]() $c>0$
. Consequently, by [Reference Meyn and Tweedie22, Theorem 17.0.1], the CLT for the chain
$c>0$
. Consequently, by [Reference Meyn and Tweedie22, Theorem 17.0.1], the CLT for the chain
![]() $\mathbf{X}^d$
and function
$\mathbf{X}^d$
and function
![]() $f+dP_d\skew3\hat{f}-d\skew3\hat{f}$
holds with some asymptotic variance
$f+dP_d\skew3\hat{f}-d\skew3\hat{f}$
holds with some asymptotic variance
![]() $\hat \sigma^2_{f,d}$
.
$\hat \sigma^2_{f,d}$
.
By [Reference Kipnis and Varadhan18] and [Reference Geyer14] we can represent
![]() $\hat \sigma^2_{f,d}$
in terms of a positive spectral measure
$\hat \sigma^2_{f,d}$
in terms of a positive spectral measure
![]() $E_d( {\mathrm{d}} \lambda)$
associated with the function
$E_d( {\mathrm{d}} \lambda)$
associated with the function
![]() $f-\rho(f)+dP_d\skew3\hat{f}-d\skew3\hat{f}=\mathcal{G}_d\skew3\hat{f}-\mathcal{G}\skew3\hat{f}$
as
$f-\rho(f)+dP_d\skew3\hat{f}-d\skew3\hat{f}=\mathcal{G}_d\skew3\hat{f}-\mathcal{G}\skew3\hat{f}$
as
where
![]() $\Lambda_d\subset[-\lambda_d,\lambda_d]$
denotes the spectrum of the self-adjoint operator
$\Lambda_d\subset[-\lambda_d,\lambda_d]$
denotes the spectrum of the self-adjoint operator
![]() $P_d$
acting on the Hilbert space
$P_d$
acting on the Hilbert space
![]() $\{g\in L^2(\rho_d)\colon \rho_d(g)=0\}$
. By the definition of the spectral measure
$\{g\in L^2(\rho_d)\colon \rho_d(g)=0\}$
. By the definition of the spectral measure
![]() $E_d( {\mathrm{d}} \lambda)$
, we obtain the bound
$E_d( {\mathrm{d}} \lambda)$
, we obtain the bound
Finally, the result follows by Proposition 2.1.
5. Technical results
The results in Section 5 use the ideas of Berry–Esseen theory and large deviations as well as the optimal Young’s inequality, and do not depend on earlier results in this paper.
5.1. Bounds on the expectations of test functions
We start with elementary observations.
Remark 5.1. Recall that
![]() $\mathcal{S}^n$
,
$\mathcal{S}^n$
,
![]() $n\in{\mathbb{N}}\cup\{0\}$
, is defined in (2.2). The following statements hold.
$n\in{\mathbb{N}}\cup\{0\}$
, is defined in (2.2). The following statements hold.
(a) If
![]() $n\leq m$
, then
$n\leq m$
, then
![]() $\mathcal{S}^{m}\subset \mathcal{S}^n$
.
$\mathcal{S}^{m}\subset \mathcal{S}^n$
.
(b) For
![]() $n\in{\mathbb{N}}$
,
$n\in{\mathbb{N}}$
,
![]() $f\in\mathcal{S}^n$
if and only if
$f\in\mathcal{S}^n$
if and only if
![]() $f'\in\mathcal{S}^{n-1}$
.
$f'\in\mathcal{S}^{n-1}$
.
(c) If
![]() $f\in\mathcal{S}^n$
and
$f\in\mathcal{S}^n$
and
![]() $g\in\mathcal{S}^m$
then
$g\in\mathcal{S}^m$
then
![]() $f+g, fg\in\mathcal{S}^{\min(n,m)}$
.
$f+g, fg\in\mathcal{S}^{\min(n,m)}$
.
Proposition 5.1. Pick an arbitrary
![]() $n\in{\mathbb{N}}$
. Assume
$n\in{\mathbb{N}}$
. Assume
![]() $f\in\mathcal{S}^n$
,
$f\in\mathcal{S}^n$
,
![]() $k\leq n$
,
$k\leq n$
,
![]() $x\in{\mathbb{R}}$
and
$x\in{\mathbb{R}}$
and
![]() $Y\sim N(x,\sigma^2)$
. Then there exists measurable Z satisfying
$Y\sim N(x,\sigma^2)$
. Then there exists measurable Z satisfying
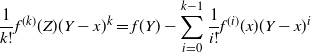 \[
\dfrac{1}{k!}f^{(k)}(Z)(Y-x)^k=f(Y)-\sum_{i=0}^{k-1}\dfrac{1}{i!}f^{(i)}(x)(Y-x)^i
\]
\[
\dfrac{1}{k!}f^{(k)}(Z)(Y-x)^k=f(Y)-\sum_{i=0}^{k-1}\dfrac{1}{i!}f^{(i)}(x)(Y-x)^i
\]
and
![]() $|Z-x|<|Y-x|$
. Furthermore, there exists a constant
$|Z-x|<|Y-x|$
. Furthermore, there exists a constant
![]() $C>0$
(depending on n) such that, for any
$C>0$
(depending on n) such that, for any
![]() $m\in{\mathbb{N}}$
and
$m\in{\mathbb{N}}$
and
![]() $s>0$
, we have
$s>0$
, we have
Proof. A random variable Z, defined via the integral form of the remainder in Taylor’s theorem, lies almost surely between Y and x, implying
![]() $|Z-x|<|Y-x|$
. Cauchy’s inequality yields
$|Z-x|<|Y-x|$
. Cauchy’s inequality yields
Since
![]() $f\in\mathcal{S}^n\subset\mathcal{S}^k$
, we have
$f\in\mathcal{S}^n\subset\mathcal{S}^k$
, we have
As
![]() $Y\sim N(x,\sigma^2)$
, we have the equality
$Y\sim N(x,\sigma^2)$
, we have the equality
where
and
![]() $\Gamma(\cdot)$
is the Euler gamma function. Hence, by (5.1), we obtain
$\Gamma(\cdot)$
is the Euler gamma function. Hence, by (5.1), we obtain
It remains to note that
Proposition 5.2. Let
![]() $f\colon{\mathbb{R}}\to{\mathbb{R}}$
be a measurable (not necessarily continuous) function such that
$f\colon{\mathbb{R}}\to{\mathbb{R}}$
be a measurable (not necessarily continuous) function such that
![]() $\|\:f\|_{\infty,1/2}<\infty$
. Fix
$\|\:f\|_{\infty,1/2}<\infty$
. Fix
![]() $n\in{\mathbb{N}}$
,
$n\in{\mathbb{N}}$
,
![]() $\mathbf{x}^d\in{\mathbb{R}}^d$
and let
$\mathbf{x}^d\in{\mathbb{R}}^d$
and let
![]() $X_1, X_2\ldots, X_d$
be i.i.d. copies of X, satisfying
$X_1, X_2\ldots, X_d$
be i.i.d. copies of X, satisfying
![]() $\mathbb{E} [X^n]=0$
and
$\mathbb{E} [X^n]=0$
and
![]() $\mathbb{E} [X^{2n}]<\infty$
. Then the following inequality holds:
$\mathbb{E} [X^{2n}]<\infty$
. Then the following inequality holds:
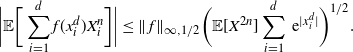 \[\bigg|\mathbb{E}\bigg[\sum_{i=1}^df(x^d_i)X_i^n\bigg]\bigg|\leq
\|\:f\|_{\infty,1/2}
\bigg(\mathbb{E}[X^{2n}]\sum_{i=1}^d\,{\mathrm{e}}^{|x^d_i|}\bigg)^{1/2}.\]
\[\bigg|\mathbb{E}\bigg[\sum_{i=1}^df(x^d_i)X_i^n\bigg]\bigg|\leq
\|\:f\|_{\infty,1/2}
\bigg(\mathbb{E}[X^{2n}]\sum_{i=1}^d\,{\mathrm{e}}^{|x^d_i|}\bigg)^{1/2}.\]
Remark 5.2. Note that the assumptions of Proposition 5.2 imply that, if X is a non-zero random variable, then
![]() $n\in{\mathbb{N}}$
has to be odd.
$n\in{\mathbb{N}}$
has to be odd.
Proof. By Jensen’s inequality, the fact that
![]() $\mathbb{E}[X]=0$
, and the assumption on f, we obtain
$\mathbb{E}[X]=0$
, and the assumption on f, we obtain
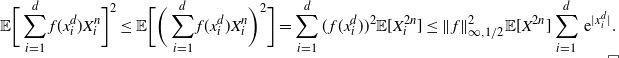 \begin{equation*}
\mathbb{E}\bigg[\sum_{i=1}^df(x^d_i)X_i^n\bigg]^2\leq
\mathbb{E}\bigg[\bigg(\sum_{i=1}^df(x^d_i)X_i^n\bigg)^2\bigg]=
\sum_{i=1}^d (f(x^d_i))^2\mathbb{E} [X_i^{2n}]\leq\|\:f\|^{2}_{\infty,1/2} \mathbb{E}[X^{2n}]\sum_{i=1}^d\,{\mathrm{e}}^{|x^d_i|}.
\end{equation*}
\begin{equation*}
\mathbb{E}\bigg[\sum_{i=1}^df(x^d_i)X_i^n\bigg]^2\leq
\mathbb{E}\bigg[\bigg(\sum_{i=1}^df(x^d_i)X_i^n\bigg)^2\bigg]=
\sum_{i=1}^d (f(x^d_i))^2\mathbb{E} [X_i^{2n}]\leq\|\:f\|^{2}_{\infty,1/2} \mathbb{E}[X^{2n}]\sum_{i=1}^d\,{\mathrm{e}}^{|x^d_i|}.
\end{equation*}
5.2. Deviations of the sums of i.i.d. random variables
Proposition 5.3. Let
![]() $f\in \mathcal{S}^0$
be such that
$f\in \mathcal{S}^0$
be such that
![]() $\rho(f)=0$
and let
$\rho(f)=0$
and let
![]() $a=\{a_d\}_{d\in{\mathbb{N}}}$
be a sluggish sequence. If the random vector
$a=\{a_d\}_{d\in{\mathbb{N}}}$
be a sluggish sequence. If the random vector
![]() $(X_{1,d},\ldots, X_{d,d})$
follows the density
$(X_{1,d},\ldots, X_{d,d})$
follows the density
![]() $\rho_d$
for all
$\rho_d$
for all
![]() $d\in{\mathbb{N}}$
, then for every
$d\in{\mathbb{N}}$
, then for every
![]() $t>0$
the following inequality holds for all but finitely many
$t>0$
the following inequality holds for all but finitely many
![]() $d\in{\mathbb{N}}$
:
$d\in{\mathbb{N}}$
:
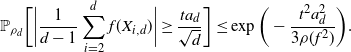 \[ \mathbb{P}_{\rho_d}\bigg[\bigg|\dfrac{1}{d-1}\sum_{i=2}^df(X_{i,d})\bigg|\geq \dfrac{ta_d}{\sqrt{d}}\bigg]\leq \exp\bigg(-\dfrac{t^2a_d^2}{3\rho(f^2)}\bigg).
\]
\[ \mathbb{P}_{\rho_d}\bigg[\bigg|\dfrac{1}{d-1}\sum_{i=2}^df(X_{i,d})\bigg|\geq \dfrac{ta_d}{\sqrt{d}}\bigg]\leq \exp\bigg(-\dfrac{t^2a_d^2}{3\rho(f^2)}\bigg).
\]
Remark 5.3. Proposition 5.3 is an elementary consequence of a deeper underlying result, that the sequence of random variables
 \[
\bigg\{\dfrac{1}{a_d\sqrt{d}}\sum_{i=1}^df(X_{i,d})\bigg\}_{d\in\mathbb{N}}
\]
\[
\bigg\{\dfrac{1}{a_d\sqrt{d}}\sum_{i=1}^df(X_{i,d})\bigg\}_{d\in\mathbb{N}}
\]
satisfies a moderate deviation principle with a good rate function
![]() $t\mapsto t^2/(2\rho(f^2))$
and speed
$t\mapsto t^2/(2\rho(f^2))$
and speed
![]() $a_d^2$
(see [Reference Eichelsbacher and Löwe13] for details). The key inequality needed in the proof of Proposition 5.3 is given in the next lemma.
$a_d^2$
(see [Reference Eichelsbacher and Löwe13] for details). The key inequality needed in the proof of Proposition 5.3 is given in the next lemma.
Lemma 5.1. Let the assumptions of Proposition 5.3 hold. If
![]() $\rho(f^2)>0$
, then for every closed
$\rho(f^2)>0$
, then for every closed
![]() $F\subseteq {\mathbb{R}}$
the following holds:
$F\subseteq {\mathbb{R}}$
the following holds:
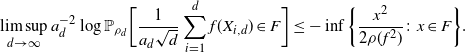 \[\limsup_{d\to\infty}a^{-2}_d\log\mathbb{P}_{\rho_d}\bigg[\dfrac{1}{a_d\sqrt{d}}\sum_{i=1}^df(X_{i,d})\in
F\bigg]\leq -\inf\bigg\{ \dfrac{x^2}{2\rho(f^2)}\colon x\in F\bigg\}.
\]
\[\limsup_{d\to\infty}a^{-2}_d\log\mathbb{P}_{\rho_d}\bigg[\dfrac{1}{a_d\sqrt{d}}\sum_{i=1}^df(X_{i,d})\in
F\bigg]\leq -\inf\bigg\{ \dfrac{x^2}{2\rho(f^2)}\colon x\in F\bigg\}.
\]
Proof. The moderate deviations results [Reference Eichelsbacher and Löwe13, Theorem 2.2, Lemma 2.5, Remark 2.6] yield a sufficient condition for the above inequality. More precisely, for
![]() $X\sim \rho$
, we need to establish
$X\sim \rho$
, we need to establish
Fix an arbitrary
![]() $m\in{\mathbb{N}}$
. Since
$m\in{\mathbb{N}}$
. Since
![]() $f\in\mathcal{S}^0$
, we have
$f\in\mathcal{S}^0$
, we have
![]() $| f(x)|\leq
\|\:f\|_{\infty,1/m} \,{\mathrm{e}}^{|x|/m}$
for every
$| f(x)|\leq
\|\:f\|_{\infty,1/m} \,{\mathrm{e}}^{|x|/m}$
for every
![]() $x\in{\mathbb{R}}$
. Consequently, for all large d, we obtain
$x\in{\mathbb{R}}$
. Consequently, for all large d, we obtain
Since
![]() $\{a_d\}_{d\in{\mathbb{N}}}$
is sluggish, there exists
$\{a_d\}_{d\in{\mathbb{N}}}$
is sluggish, there exists
![]() $ C_0>0$
such that
$ C_0>0$
such that
for all large
![]() $d\in{\mathbb{N}}$
. Hence
$d\in{\mathbb{N}}$
. Hence
for all large
![]() $d\in{\mathbb{N}}$
. Since m was arbitrary, (5.2) follows.
$d\in{\mathbb{N}}$
. Since m was arbitrary, (5.2) follows.
Proof of Proposition 5.3. Note that the proposition holds if
![]() $\rho(f^2)=0$
. Assume
$\rho(f^2)=0$
. Assume
![]() $\rho(f^2)\,{>}\,0$
and fix an arbitrary
$\rho(f^2)\,{>}\,0$
and fix an arbitrary
![]() $t>0$
. Note that since
$t>0$
. Note that since
![]() $\{a_d\}_{d\in{\mathbb{N}}}$
is sluggish, so is
$\{a_d\}_{d\in{\mathbb{N}}}$
is sluggish, so is
![]() $\{a'_d\}_{d\in{\mathbb{N}}}$
,
$\{a'_d\}_{d\in{\mathbb{N}}}$
,
![]() $a'_d\,:\!=a_{d+1}\sqrt{d/(d+1)}$
. Apply Lemma 5.1 to
$a'_d\,:\!=a_{d+1}\sqrt{d/(d+1)}$
. Apply Lemma 5.1 to
![]() $F={\mathbb{R}}\setminus ({-}t,t)$
and
$F={\mathbb{R}}\setminus ({-}t,t)$
and
![]() $\{a'_d\}_{d\in{\mathbb{N}}}$
to get the following inequality:
$\{a'_d\}_{d\in{\mathbb{N}}}$
to get the following inequality:
 \begin{equation}
\mathbb{P}_{\rho_{d-1}}\bigg[\bigg|\dfrac{1}{a'_{d-1}\sqrt{d-1}}\sum_{i=1}^{d-1}f(X_{i,d-1})\bigg|\geq
t\bigg]\leq \exp\bigg(-\dfrac{3(a'_{d-1})^2t^2}{8\rho(f^2)}\bigg)
\end{equation}
\begin{equation}
\mathbb{P}_{\rho_{d-1}}\bigg[\bigg|\dfrac{1}{a'_{d-1}\sqrt{d-1}}\sum_{i=1}^{d-1}f(X_{i,d-1})\bigg|\geq
t\bigg]\leq \exp\bigg(-\dfrac{3(a'_{d-1})^2t^2}{8\rho(f^2)}\bigg)
\end{equation}
for all sufficiently large
![]() $d\in{\mathbb{N}}$
. Since
$d\in{\mathbb{N}}$
. Since
![]() $3(a'_{d-1})^2/4\geq 2a^2_d/3$
for all but finitely many
$3(a'_{d-1})^2/4\geq 2a^2_d/3$
for all but finitely many
![]() $d\in{\mathbb{N}}$
, the right-hand side of (5.3) is bounded above by
$d\in{\mathbb{N}}$
, the right-hand side of (5.3) is bounded above by
![]() $\exp({-}(a_d)^2t^2/(3\rho(f^2)))$
. Recall that
$\exp({-}(a_d)^2t^2/(3\rho(f^2)))$
. Recall that
![]() $\rho_d(\mathbf{x}^d)=\rho_{d-1}(\mathbf{x}^{d-1})\rho(x_d^d)$
and
$\rho_d(\mathbf{x}^d)=\rho_{d-1}(\mathbf{x}^{d-1})\rho(x_d^d)$
and
![]() $a_{d-1}'\sqrt{d-1}=a_d(d-1)/\sqrt{d}$
. Hence the left-hand side of inequality (5.3) equals
$a_{d-1}'\sqrt{d-1}=a_d(d-1)/\sqrt{d}$
. Hence the left-hand side of inequality (5.3) equals
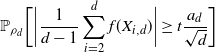 \[
\mathbb{P}_{\rho_d}\bigg[\bigg|\dfrac{1}{d-1}\sum_{i=2}^{d}f(X_{i,d})\bigg|\geq t\dfrac{a_d}{\sqrt{d}}\bigg]
\]
\[
\mathbb{P}_{\rho_d}\bigg[\bigg|\dfrac{1}{d-1}\sum_{i=2}^{d}f(X_{i,d})\bigg|\geq t\dfrac{a_d}{\sqrt{d}}\bigg]
\]
and the proposition follows.
The next result is based on a combinatorial argument. A special case of Proposition 5.4 was used in [Reference Roberts, Gelman and Gilks30].
Proposition 5.4. Let
![]() $n\in{\mathbb{N}}$
and a measurable
$n\in{\mathbb{N}}$
and a measurable
![]() $f\colon{\mathbb{R}}\to{\mathbb{R}}$
satisfy
$f\colon{\mathbb{R}}\to{\mathbb{R}}$
satisfy
![]() $\rho(f)=0$
and
$\rho(f)=0$
and
![]() $\rho(f^{2n})< \infty$
. If the random vector
$\rho(f^{2n})< \infty$
. If the random vector
![]() $(X_{1,d},\ldots,X_{d,d})$
is distributed according to
$(X_{1,d},\ldots,X_{d,d})$
is distributed according to
![]() $\rho_d$
, then there exists a constant C, independent of d, such that
$\rho_d$
, then there exists a constant C, independent of d, such that
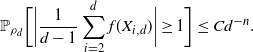 \[
\mathbb{P}_{\rho_d} \bigg[ \bigg|\dfrac{1}{d-1}\sum_{i=2}^df(X_{i,d})\bigg|\geq
1\bigg]\leq C d^{-n}.
\]
\[
\mathbb{P}_{\rho_d} \bigg[ \bigg|\dfrac{1}{d-1}\sum_{i=2}^df(X_{i,d})\bigg|\geq
1\bigg]\leq C d^{-n}.
\]
Remark 5.4. The constant C in Proposition 5.4 may depend on
![]() $n\in{\mathbb{N}}$
and the function f.
$n\in{\mathbb{N}}$
and the function f.
Proof of Proposition 5.4. Fix
![]() $n\in{\mathbb{N}}$
and let
$n\in{\mathbb{N}}$
and let
![]() ${\mathbb{N}}_0\,:\!={\mathbb{N}}\cup\{0\}$
. Markov’s inequality and the multinomial theorem yield
${\mathbb{N}}_0\,:\!={\mathbb{N}}\cup\{0\}$
. Markov’s inequality and the multinomial theorem yield
 \begin{align*}
\mathbb{P}_{\rho_d}\bigg[\bigg|\dfrac{1}{d-1}\sum_{i=2}^df(X_{i,d})\bigg|\geq
1\bigg] & =\mathbb{P}_{\rho_d}\bigg[\bigg|\dfrac{1}{d-1}\sum_{i=2}^d
f(X_{i,d})\bigg|^{2n}\geq 1\bigg] \\
& \leq
\mathbb{E}_{\rho_d}\bigg(\dfrac{1}{d-1}\sum_{i=2}^d
f(X_{i,d})\bigg)^{2n} \\
& =(d-1)^{-2n}\sum_{\substack{k_2+k_3+\cdots
+k_d=2n\\k_2,k_3\ldots,k_d\in{\mathbb{N}}_0\setminus
\{1\}}}\binom{2n}{k_2,k_3,\ldots,k_d}\prod_{i=2}^d\mathbb{E}_{\rho} [ f(X_{i,d})^{k_i}],
\end{align*}
\begin{align*}
\mathbb{P}_{\rho_d}\bigg[\bigg|\dfrac{1}{d-1}\sum_{i=2}^df(X_{i,d})\bigg|\geq
1\bigg] & =\mathbb{P}_{\rho_d}\bigg[\bigg|\dfrac{1}{d-1}\sum_{i=2}^d
f(X_{i,d})\bigg|^{2n}\geq 1\bigg] \\
& \leq
\mathbb{E}_{\rho_d}\bigg(\dfrac{1}{d-1}\sum_{i=2}^d
f(X_{i,d})\bigg)^{2n} \\
& =(d-1)^{-2n}\sum_{\substack{k_2+k_3+\cdots
+k_d=2n\\k_2,k_3\ldots,k_d\in{\mathbb{N}}_0\setminus
\{1\}}}\binom{2n}{k_2,k_3,\ldots,k_d}\prod_{i=2}^d\mathbb{E}_{\rho} [ f(X_{i,d})^{k_i}],
\end{align*}
where the last equality holds since the expectation of any summand of the form
![]() $\prod_{i=2}^{d}f(X_{i,d})^{k_i}$
is zero if any of the indices
$\prod_{i=2}^{d}f(X_{i,d})^{k_i}$
is zero if any of the indices
![]() $k_i=1$
since
$k_i=1$
since
![]() $\rho_d$
has a product structure and
$\rho_d$
has a product structure and
![]() $\rho(f)=0$
. By Jensen’s inequality,
$\rho(f)=0$
. By Jensen’s inequality,
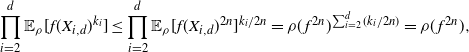 \[
\prod_{i=2}^d\mathbb{E}_{\rho} [ f(X_{i,d})^{k_i}]\leq
\prod_{i=2}^d\mathbb{E}_{\rho} [ f(X_{i,d})^{2n}]^{k_i/2n}=\rho(f^{2n})
^{\sum_{i=2}^{d}{k_i}/{2n}}=\rho(f^{2n}),
\]
\[
\prod_{i=2}^d\mathbb{E}_{\rho} [ f(X_{i,d})^{k_i}]\leq
\prod_{i=2}^d\mathbb{E}_{\rho} [ f(X_{i,d})^{2n}]^{k_i/2n}=\rho(f^{2n})
^{\sum_{i=2}^{d}{k_i}/{2n}}=\rho(f^{2n}),
\]
and hence
 \begin{equation}
\mathbb{P}_{\rho_d}\bigg[\bigg|\dfrac{1}{d-1}\sum_{i=2}^df(X_{i,d})\bigg|\geq
1\bigg]\leq (2n)!\cdot\rho(f^{2n})(d-1)^{-2n}\cdot
|\mathcal{N}_d|,
\end{equation}
\begin{equation}
\mathbb{P}_{\rho_d}\bigg[\bigg|\dfrac{1}{d-1}\sum_{i=2}^df(X_{i,d})\bigg|\geq
1\bigg]\leq (2n)!\cdot\rho(f^{2n})(d-1)^{-2n}\cdot
|\mathcal{N}_d|,
\end{equation}
where
![]() $ |\mathcal{N}_d|$
stands for the cardinality of the set
$ |\mathcal{N}_d|$
stands for the cardinality of the set
 \[\mathcal{N}_d\,:\!=\bigg\{(k_2,k_3,\ldots, k_d)\in{\mathbb{N}}^{d-1}_0\colon \sum_{i=2}^dk_d=2n\text{ and } k_i\neq 1\text{ for all
} 2\leq i\leq d\bigg\}.\]
\[\mathcal{N}_d\,:\!=\bigg\{(k_2,k_3,\ldots, k_d)\in{\mathbb{N}}^{d-1}_0\colon \sum_{i=2}^dk_d=2n\text{ and } k_i\neq 1\text{ for all
} 2\leq i\leq d\bigg\}.\]
Inequality (5.4) and the next claim prove the proposition.
Claim.
![]() $ |\mathcal{N}_d|\leq C' d^n$
for a constant C’ independent of d.
$ |\mathcal{N}_d|\leq C' d^n$
for a constant C’ independent of d.
Proof of the claim. Consider a function
that rounds each entry down to the nearest even number. Every element in the image
![]() $\zeta(\mathcal{N}_d)$
is a
$\zeta(\mathcal{N}_d)$
is a
![]() $(d-1)$
-tuple of non-negative even integers with sum at most 2n. Recall that the number of k-combinations with repetition, chosen from a set of
$(d-1)$
-tuple of non-negative even integers with sum at most 2n. Recall that the number of k-combinations with repetition, chosen from a set of
![]() $d-1$
objects, equals
$d-1$
objects, equals
![]() $\binom{k+d-2}{k}$
. There exists
$\binom{k+d-2}{k}$
. There exists
![]() $C''>0$
, such that
$C''>0$
, such that
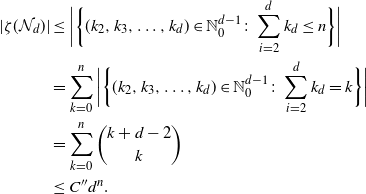 \begin{align*}
|\zeta(\mathcal{N}_d)|&\leq \bigg|\bigg\{(k_2,k_3,\ldots, k_d)\in{\mathbb{N}}^{d-1}_0\colon \sum_{i=2}^dk_d\leq n\bigg\}\bigg| \\
&= \sum_{k=0}^n \bigg|\bigg\{(k_2,k_3,\ldots, k_d)\in{\mathbb{N}}^{d-1}_0\colon \sum_{i=2}^dk_d=k\bigg\}\bigg|\\
& =\sum_{k=0}^n\binom{k+d-2}{k}\\
& \leq C'' d^n.
\end{align*}
\begin{align*}
|\zeta(\mathcal{N}_d)|&\leq \bigg|\bigg\{(k_2,k_3,\ldots, k_d)\in{\mathbb{N}}^{d-1}_0\colon \sum_{i=2}^dk_d\leq n\bigg\}\bigg| \\
&= \sum_{k=0}^n \bigg|\bigg\{(k_2,k_3,\ldots, k_d)\in{\mathbb{N}}^{d-1}_0\colon \sum_{i=2}^dk_d=k\bigg\}\bigg|\\
& =\sum_{k=0}^n\binom{k+d-2}{k}\\
& \leq C'' d^n.
\end{align*}
Note that the pre-image of a singleton under
![]() $\zeta$
contains at most
$\zeta$
contains at most
![]() $2^n$
elements (i.e.
$2^n$
elements (i.e.
![]() $(d-1)$
-tuples) of
$(d-1)$
-tuples) of
![]() $\mathcal{N}_d$
. Indeed, by the definition of
$\mathcal{N}_d$
. Indeed, by the definition of
![]() $\mathcal{N}_d$
, at most n coordinates of an element are not zero and each can either reduce by one or stay the same. Hence, for
$\mathcal{N}_d$
, at most n coordinates of an element are not zero and each can either reduce by one or stay the same. Hence, for
![]() $C'\,:\!=C'' 2^n$
, we have
$C'\,:\!=C'' 2^n$
, we have
![]() $ |\mathcal{N}_d|\leq 2^n\cdot |\zeta(\mathcal{N}_d)|\leq C'd^n$
.
$ |\mathcal{N}_d|\leq 2^n\cdot |\zeta(\mathcal{N}_d)|\leq C'd^n$
.
5.3. Bounds on the densities of certain random variables
The key step in the proof of Proposition 5.5 below is the optimal Young’s inequality: for
![]() $p,q\geq 1$
and
$p,q\geq 1$
and
![]() $r\in[1,\infty]$
, such that
$r\in[1,\infty]$
, such that
![]() $1/p+1/q=1+1/r$
, and functions
$1/p+1/q=1+1/r$
, and functions
![]() $f\in L^p({\mathbb{R}})$
and
$f\in L^p({\mathbb{R}})$
and
![]() $g\in L^q({\mathbb{R}})$
, their convolution
$g\in L^q({\mathbb{R}})$
, their convolution
![]() $f*g$
satisfies the inequality
$f*g$
satisfies the inequality
 \begin{equation}
\|\:f*g\|_r\leq \dfrac{C_pC_q}{C_r}\|\:f\|_p\|g\|_q,\quad\text{where }
C_s\,:\!=\begin{cases}
\sqrt{\dfrac{s^{1/s}}{s'^{1/s'}}}&
\text{if $s\in(1,\infty)$ and $1/s+1/s'=1$,}\\
1& \text{if $s\in\{1,\infty\}$.}
\end{cases}
\end{equation}
\begin{equation}
\|\:f*g\|_r\leq \dfrac{C_pC_q}{C_r}\|\:f\|_p\|g\|_q,\quad\text{where }
C_s\,:\!=\begin{cases}
\sqrt{\dfrac{s^{1/s}}{s'^{1/s'}}}&
\text{if $s\in(1,\infty)$ and $1/s+1/s'=1$,}\\
1& \text{if $s\in\{1,\infty\}$.}
\end{cases}
\end{equation}
For
![]() $s\in[1,\infty)$
,
$s\in[1,\infty)$
,
![]() $\|\cdot\|_s$
is the usual norm on
$\|\cdot\|_s$
is the usual norm on
![]() $L^s({\mathbb{R}})$
and
$L^s({\mathbb{R}})$
and
![]() $\|\cdot\|_\infty$
denotes the essential supremum norm on
$\|\cdot\|_\infty$
denotes the essential supremum norm on
![]() $L^\infty({\mathbb{R}})$
. The proof of (5.5) for
$L^\infty({\mathbb{R}})$
. The proof of (5.5) for
![]() $r<\infty$
is given in [Reference Barthe2, Theorem 1]. In the case
$r<\infty$
is given in [Reference Barthe2, Theorem 1]. In the case
![]() $r=\infty$
, we have
$r=\infty$
, we have
![]() $C_pC_q/C_r=1$
and the inequality in (5.5) follows from the definition of the convolution, translation invariance of the Lebesgue measure and Hölder’s inequality.
$C_pC_q/C_r=1$
and the inequality in (5.5) follows from the definition of the convolution, translation invariance of the Lebesgue measure and Hölder’s inequality.
Proposition 5.5. Let
![]() $X_1,X_2,\ldots, X_d$
be independent random variables, each
$X_1,X_2,\ldots, X_d$
be independent random variables, each
![]() $X_i$
with a bounded density
$X_i$
with a bounded density
![]() $q_i$
. The density
$q_i$
. The density
![]() $Q_d$
of the sum
$Q_d$
of the sum
![]() $\sum_{i=1}^d X_i$
satisfies
$\sum_{i=1}^d X_i$
satisfies
![]() $\|Q_d\|_\infty\leq c \max_{i\leq d}\|q_i\|_\infty/\sqrt{d}$
for some constant
$\|Q_d\|_\infty\leq c \max_{i\leq d}\|q_i\|_\infty/\sqrt{d}$
for some constant
![]() $c>0$
.
$c>0$
.
Remark 5.5. The factor
![]() $d^{-1/2}$
in the inequality of Proposition 5.5 above comes from (5.5) and is crucial for the analysis in this paper. The standard Young’s inequality for convolutions would only yield
$d^{-1/2}$
in the inequality of Proposition 5.5 above comes from (5.5) and is crucial for the analysis in this paper. The standard Young’s inequality for convolutions would only yield
![]() $\|Q_d\|_\infty\leq c \max_{i\leq d}\|q_i\|_\infty$
, which gives insufficient control over
$\|Q_d\|_\infty\leq c \max_{i\leq d}\|q_i\|_\infty$
, which gives insufficient control over
![]() $Q_d$
.
$Q_d$
.
Proof of Proposition 5.5. Since random variables
![]() $X_i$
are independent, the density of their sum is a convolution of the respective densities,
$X_i$
are independent, the density of their sum is a convolution of the respective densities,
![]() $Q_d=\mathop{\mbox{\ast}}_{i=1}^d q_i$
. For all i and each
$Q_d=\mathop{\mbox{\ast}}_{i=1}^d q_i$
. For all i and each
![]() $t>1$
we have
$t>1$
we have
![]() $q_i\in L^{\infty}({\mathbb{R}})\cap L^{1}({\mathbb{R}})\subset L^{t}({\mathbb{R}})$
. Moreover, the following inequality holds for every
$q_i\in L^{\infty}({\mathbb{R}})\cap L^{1}({\mathbb{R}})\subset L^{t}({\mathbb{R}})$
. Moreover, the following inequality holds for every
![]() $k\leq d-1$
:
$k\leq d-1$
:
 \begin{equation}
\|Q_d\|_{\infty}=\bigg\|\mathop{\mbox{\ast}}_{i=1}^d q_i\bigg\|_{\infty}\leq
(C_{{d}/{d-1}})^kC_{{d}/{k}} \bigg(\prod_{i=1}^k\|q_i\|_{{d}{d-1}}\bigg)\bigg\|\mathop{\mbox{\ast}}_{i=k+1}^d
q_i\bigg\|_{{d}/{k}}
\end{equation}
\begin{equation}
\|Q_d\|_{\infty}=\bigg\|\mathop{\mbox{\ast}}_{i=1}^d q_i\bigg\|_{\infty}\leq
(C_{{d}/{d-1}})^kC_{{d}/{k}} \bigg(\prod_{i=1}^k\|q_i\|_{{d}{d-1}}\bigg)\bigg\|\mathop{\mbox{\ast}}_{i=k+1}^d
q_i\bigg\|_{{d}/{k}}
\end{equation}
We prove (5.6) by induction on k. For
![]() $k=1$
, note that d and
$k=1$
, note that d and
![]() ${d}/{d-1}$
are Hölder conjugates, i.e.
${d}/{d-1}$
are Hölder conjugates, i.e.
![]() $1/d +1/(d/(d-1))=1$
. Hence (5.5) for
$1/d +1/(d/(d-1))=1$
. Hence (5.5) for
![]() $r=\infty$
,
$r=\infty$
,
![]() $q=d$
,
$q=d$
,
![]() $p=d/(d-1)$
,
$p=d/(d-1)$
,
![]() $f=q_1$
and
$f=q_1$
and
![]() $g\,{=}\,\mathop{\mbox{\ast}}_{i=2}^d q_i$
implies
$g\,{=}\,\mathop{\mbox{\ast}}_{i=2}^d q_i$
implies
![]() $\|Q_d\|_{\infty}\leq \|q_1\|_{{d}/{d-1}}\|\mathop{\mbox{\ast}}_{i=2}^d q_i\|_{d}$
and
$\|Q_d\|_{\infty}\leq \|q_1\|_{{d}/{d-1}}\|\mathop{\mbox{\ast}}_{i=2}^d q_i\|_{d}$
and
![]() $C_{{d}/{d-1}}=C^{-1}_d$
. Now assume (5.6) holds for some
$C_{{d}/{d-1}}=C^{-1}_d$
. Now assume (5.6) holds for some
![]() $k\leq d-2$
. Since
$k\leq d-2$
. Since
![]() $ (d/(d-1))^{-1}+ (d/(k+1))^{-1}=1+ (d/k)^{-1}$
, the inequality in (5.5) implies
$ (d/(d-1))^{-1}+ (d/(k+1))^{-1}=1+ (d/k)^{-1}$
, the inequality in (5.5) implies
This inequality and the induction hypothesis (i.e. (5.6) for k) implies (5.6) for
![]() $k+1$
.
$k+1$
.
Since
![]() $q_1$
is a density, we have
$q_1$
is a density, we have
![]() $\|q_i\|_1=1$
. Hence we find
$\|q_i\|_1=1$
. Hence we find
for each i, and in particular
![]() $\prod_{i=1}^d\|q_i\|_{{d}/{d-1}}\leq \max_{i\leq d} (\|q_i\|_\infty)$
. By (5.6), for
$\prod_{i=1}^d\|q_i\|_{{d}/{d-1}}\leq \max_{i\leq d} (\|q_i\|_\infty)$
. By (5.6), for
![]() $k=d-1$
we obtain
$k=d-1$
we obtain
 \[\|Q_d\|_{\infty}\leq (C_{{d}/{d-1}})^d\prod_{i=1}^d\|q_i\|_{{d}/{d-1}}\leq
\max_{i\leq d} (\|q_i\|_\infty) (C_{{d}/{d-1}})^d.\]
\[\|Q_d\|_{\infty}\leq (C_{{d}/{d-1}})^d\prod_{i=1}^d\|q_i\|_{{d}/{d-1}}\leq
\max_{i\leq d} (\|q_i\|_\infty) (C_{{d}/{d-1}})^d.\]
Since
![]() $\lim_{d\to\infty}\sqrt{d} (C_{{d}/{d-1}})^d=\sqrt{e}$
, there exists
$\lim_{d\to\infty}\sqrt{d} (C_{{d}/{d-1}})^d=\sqrt{e}$
, there exists
![]() $c>0$
such that
$c>0$
such that
![]() $ (C_{{d}/{d-1}})^d\leq c/ \sqrt{d}$
for all
$ (C_{{d}/{d-1}})^d\leq c/ \sqrt{d}$
for all
![]() $d\in{\mathbb{N}}$
.
$d\in{\mathbb{N}}$
.
Polynomials of continuous random variables play an important role in the proofs of Section 4.
Proposition 5.6. Let X be a continuous random variable and let p be a polynomial. Then the random variable p(X) has a density.
Proof. The set
![]() $B\,:\!=p ((p')^{-1} (\{0\}))$
has finitely many points. Moreover, p is locally invertible on
$B\,:\!=p ((p')^{-1} (\{0\}))$
has finitely many points. Moreover, p is locally invertible on
![]() ${\mathbb{R}}\setminus B$
by the inverse function theorem and the inverses are differentiable. Hence, for any
${\mathbb{R}}\setminus B$
by the inverse function theorem and the inverses are differentiable. Hence, for any
![]() $x\,{\notin}\, B$
, the set
$x\,{\notin}\, B$
, the set
![]() $p^{-1} (({-}\infty,x])$
is a disjoint union of intervals with boundaries that depend smoothly on x. Since
$p^{-1} (({-}\infty,x])$
is a disjoint union of intervals with boundaries that depend smoothly on x. Since
![]() $\mathbb{P}[p(X)\leq x]=\mathbb{P}[X\in p^{-1} (({-}\infty,x])]$
, the proposition follows.
$\mathbb{P}[p(X)\leq x]=\mathbb{P}[X\in p^{-1} (({-}\infty,x])]$
, the proposition follows.
Let
![]() $N=N(\mu,\sigma^2)$
be a normal random variable and let p be a polynomialatisfying
$N=N(\mu,\sigma^2)$
be a normal random variable and let p be a polynomialatisfying
![]() $\inf_{x\in{\mathbb{R}}}|p'(x)|\geq c_p$
for some constant
$\inf_{x\in{\mathbb{R}}}|p'(x)|\geq c_p$
for some constant
![]() $c_p>0$
. Then the random variable p(N) has a probability density function
$c_p>0$
. Then the random variable p(N) has a probability density function
![]() $q_{p(N)}$
, which satisfies
$q_{p(N)}$
, which satisfies
![]() $\|q_{p(N)}\|_\infty\leq (c_p\sigma\sqrt{2\pi})^{-1}$
.
$\|q_{p(N)}\|_\infty\leq (c_p\sigma\sqrt{2\pi})^{-1}$
.
Proof. Obviously, p is strictly monotonic and thus a bijection. Moreover, the distribution
![]() $\Phi_{p(N)}(\cdot)$
of p(N) takes the form
$\Phi_{p(N)}(\cdot)$
of p(N) takes the form
![]() $\mathbb{P} [N\leq p^{-1}(\cdot)]$
or
$\mathbb{P} [N\leq p^{-1}(\cdot)]$
or
![]() $\mathbb{P} [N>p^{-1}(\cdot)]$
. Hence, for any
$\mathbb{P} [N>p^{-1}(\cdot)]$
. Hence, for any
![]() $x\in{\mathbb{R}}$
, the density
$x\in{\mathbb{R}}$
, the density
![]() $q_{p(N)}$
of p(N) satisfies
$q_{p(N)}$
of p(N) satisfies
as the density of N,
![]() $q_N$
, is bounded above by
$q_N$
, is bounded above by
![]() $(\sigma\sqrt{2\pi})^{-1}$
.
$(\sigma\sqrt{2\pi})^{-1}$
.
5.4. CFs and distributions of near-normal random variables
Proposition 5.8. Let N be a normal random variable with mean
![]() $\mu$
and variance
$\mu$
and variance
![]() $\sigma^2$
, and let X be a continuous random variable. Let
$\sigma^2$
, and let X be a continuous random variable. Let
![]() $\varphi_X$
,
$\varphi_X$
,
![]() $\varphi_N$
and
$\varphi_N$
and
![]() $\Phi_X$
,
$\Phi_X$
,
![]() $\Phi_N$
denote the CFs and the distributions of X and N, respectively. Assume there exist constants
$\Phi_N$
denote the CFs and the distributions of X and N, respectively. Assume there exist constants
![]() $r>0$
,
$r>0$
,
![]() $\gamma\in (0,1)$
and a function
$\gamma\in (0,1)$
and a function
![]() $R\colon{\mathbb{R}}\,{\to}\,{\mathbb{R}}$
such that
$R\colon{\mathbb{R}}\,{\to}\,{\mathbb{R}}$
such that
![]() $ |\log\varphi_X(t)-\log\varphi_N(t)|\leq R(t)\leq \gamma\sigma^2
t^2/2$
holds on
$ |\log\varphi_X(t)-\log\varphi_N(t)|\leq R(t)\leq \gamma\sigma^2
t^2/2$
holds on
![]() $|t|\leq r$
. Then
$|t|\leq r$
. Then
Remark 5.6. The result is a direct consequence of the smoothing theorem (see [Reference Kolassa19, Theorem 2.5.2]) commonly used to prove Berry–Esseen-type bounds, that relate CFs and distribution functions of random variables.
Proof of Proposition 5.8. The smoothing theorem implies
Note that, for any
![]() $z\in\mathbb{C}$
, we have
$z\in\mathbb{C}$
, we have
![]() $|{\mathrm{e}}^z-1|\leq |z|\,{\mathrm{e}}^{|z|}$
. For
$|{\mathrm{e}}^z-1|\leq |z|\,{\mathrm{e}}^{|z|}$
. For
![]() $z\,:\!=\log(\varphi_X(t)/\varphi_N(t))$
, this implies
$z\,:\!=\log(\varphi_X(t)/\varphi_N(t))$
, this implies
The result follows from this inequality,
![]() $\sup_{x\in{\mathbb{R}}}|\Phi_N'(x)|=1/(\sigma \sqrt{2\pi})$
, and
$\sup_{x\in{\mathbb{R}}}|\Phi_N'(x)|=1/(\sigma \sqrt{2\pi})$
, and
![]() $|\varphi_N(t)|={\mathrm{e}}^{-\sigma^2t^2/2}$
:
$|\varphi_N(t)|={\mathrm{e}}^{-\sigma^2t^2/2}$
:
Lemma 5.2. Let X be a random variable with finite mean
![]() $\mu$
, variance
$\mu$
, variance
![]() $\sigma^2$
, and absolute third central moment
$\sigma^2$
, and absolute third central moment
![]() $\kappa\,:\!=\mathbb{E} [ |X-\mu|^3]$
. Then the characteristic function
$\kappa\,:\!=\mathbb{E} [ |X-\mu|^3]$
. Then the characteristic function
![]() $\varphi_X$
of X satisfies
$\varphi_X$
of X satisfies
Proof. The result can be established by combining the elementary bound
and the fact that
![]() $z\in\mathbb{C}$
,
$z\in\mathbb{C}$
,
![]() $|z|\leq 1/2$
implies
$|z|\leq 1/2$
implies
![]() $ |(\log(1+z)-z|\leq |z|^2$
(see [Reference Williams32, p. 188] for both).
$ |(\log(1+z)-z|\leq |z|^2$
(see [Reference Williams32, p. 188] for both).
Lemma 5.3. Let
![]() $N=N(0,\sigma^2)$
and let
$N=N(0,\sigma^2)$
and let
![]() $u,v\in{\mathbb{R}}$
. The random variable
$u,v\in{\mathbb{R}}$
. The random variable
![]() $uN+vN^2$
has a characteristic function that satisfies
$uN+vN^2$
has a characteristic function that satisfies
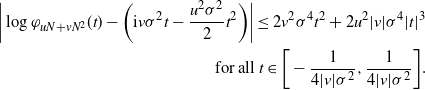 \begin{align*}
\bigg|\log\varphi_{uN+vN^2}(t)-\bigg({\mathrm{i}} v\sigma^2t-\dfrac{u^2\sigma^2}{2}t^2\bigg)\bigg|\leq 2v^2\sigma^4t^2+2u^2|v|\sigma^4|t|^3\\
\text{{for all} } t\in\bigg[-\dfrac{1}{4|v|\sigma^2},\dfrac{1}{4|v|\sigma^2}\bigg].
\end{align*}
\begin{align*}
\bigg|\log\varphi_{uN+vN^2}(t)-\bigg({\mathrm{i}} v\sigma^2t-\dfrac{u^2\sigma^2}{2}t^2\bigg)\bigg|\leq 2v^2\sigma^4t^2+2u^2|v|\sigma^4|t|^3\\
\text{{for all} } t\in\bigg[-\dfrac{1}{4|v|\sigma^2},\dfrac{1}{4|v|\sigma^2}\bigg].
\end{align*}
Proof. The CF
![]() $\varphi_{uN+vN^2}$
can be explicitly computed using standard complex analysis:
$\varphi_{uN+vN^2}$
can be explicitly computed using standard complex analysis:
The rest can then be shown using the elementary inequalities:
![]() $z\in\mathbb{C}$
,
$z\in\mathbb{C}$
,
![]() $|z|\leq 1/2$
implies
$|z|\leq 1/2$
implies
![]() $ |(\log(1+z)-z|\leq |z|^2$
and
$ |(\log(1+z)-z|\leq |z|^2$
and
![]() $ |1/(1-z)-1|\leq 2|z|$
.
$ |1/(1-z)-1|\leq 2|z|$
.
Acknowledgements
We thank Krys Latuszynski for insightful comments. AM is supported in part by the EPSRC grant EP/P003818/1 and the Programme on Data-Centric Engineering funded by Lloyd’s Register Foundation. JV is supported by President’s PhD Scholarship of Imperial College London and by the EPSRC grants EP/P002625/1 and EP/R022100/1.





