We use cookies to distinguish you from other users and to provide you with a better experience on our websites. Close this message to accept cookies or find out how to manage your cookie settings.
We use cookies to distinguish you from other users and to provide you with a better experience on our websites. Close this message to accept cookies or find out how to manage your cookie settings.
In this article, we prove the local-in-time existence of regular solutions to dissipative Aw–Rascle system with the offset equal to gradient of some increasing and regular function of density. It is a mixed degenerate parabolic-hyperbolic hydrodynamic model, and we extend the techniques previously developed for compressible Navier–Stokes equations to show the well-posedness of the system in the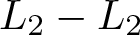 
$L_2-L_2$ setting. We also discuss relevant existence results for offset involving singular or non-local functions of density.
