1. Introduction
In the analysis of multivariate data, a large collection of statistical methods, including principal component analysis, regression analysis, and clustering analysis, require the knowledge of covariance matrices [Reference Cai, Ren and Zhou11]. The advance of data acquisition and storage has led to datasets for which the sample size N and the number of variables M are both large. This high dimensionality cannot be handled using the classical statistical theory.
For applications involving large-dimensional covariance matrices, it is important to understand the local behavior of the the singular values and vectors. Assuming that M is comparable to N, the spectral analysis of the singular values has attracted considerable interest since the seminal work of Marcenko and Pastur [Reference Marčenko and Pastur30]. Since then, numerous researchers have contributed to weakening the conditions on matrix entries as well as extending the class of matrices for which the empirical spectral distributions (ESDs) have nonrandom limits. For a detailed review, we refer the reader to the monograph [Reference Bai and Silverstein2]. Besides the ESDs of the singular values, the limiting distributions of the extreme singular values were analysed in a collection of celebrated papers. The results were first proved for the Wishart matrix (i.e. sample covariance matrices obtained from a data matrix consisting of independent and identically distributed (i.i.d.) centered real or complex Gaussian entries) in [Reference Johnstone23] and [Reference Tracy and Widom38]; they were later proved for matrices with entries satisfying arbitrary subexponential distributions in [Reference Bao, Pan and Zhou5], [Reference Pillai and Yin32], and [Reference Pillai and Yin33]. More recently, the weakest moment condition was given in [Reference Ding and Yang16].
Less is known however for the singular vectors. Therefore, recent research on the limiting behavior of singular vectors has attracted considerable interest among mathematicians and statisticians. Silverstein first derived limit theorems for the eigenvectors of covariance matrices [Reference Silverstein34]; later, the results were proved for a general class of covariance matrices [Reference Bai, Miao and Pan3]. The delocalization property for the eigenvectors were shown in [Reference Bloemendal, Knowles, Yau and Yin8] and [Reference Pillai and Yin33]. The universal properties of the eigenvectors of covariance matrices were analysed in [Reference Bloemendal, Knowles, Yau and Yin8], [Reference Bloemendal9], [Reference Ledoit and Péché27], and [Reference Tao and Vu37]. For a recent survey of the results, we refer the reader to [Reference O’Rourke, Vu and Wang31]. In this paper we prove the universality for the distribution of the singular vectors for a general class of covariance matrices of the form Q = TXX*T*, where T is a deterministic matrix such that T*T is diagonal.
The covariance matrix Q contains a general class of covariance structures and random matrix models [Reference Bloemendal, Knowles, Yau and Yin8, Section 1.2]. The singular values analysis of Q has attracted considerable attention; see, for example, the limiting spectral distribution and Stieltjes transform derived in [Reference Silverstein35], the Tracy–Widom asymptotics of the extreme eigenvalues proved in [Reference Bao, Pan and Zhou5], [Reference El Karoui17], [Reference Knowles and Yin26], and [Reference Lee and Schnelli28], and the anisotropic local law proposed in [Reference Knowles and Yin26]. It is notable that, in general, Q contains the spiked covariance matrices [Reference Baik, Ben Arous and Péché4], [Reference Benaych-Georges and Nadakuditi6], [Reference Benaych-Georges, Guionnet and Maida7], [Reference Bloemendal, Knowles, Yau and Yin8], [Reference Johnstone23]. In such models, the ESD of Q still satisfies the Marcenko–Pastur (MP) law and some of the eigenvalues of will detach from the bulk and become outliers. However, in this paper, we adapt the regularity Assumption 1.2 to rule out the outliers for the purpose of universality discussion. Actually, it was shown in [Reference Capitaine, Donati-Martin and Féral12] and [Reference Knowles and Yin25] that the distributions of the outliers are not universal.
In this paper we study the singular vector distribution of Q. We prove the universality for the components of the edge singular vectors by assuming the matching of the first two moments of the matrix entries. We also prove similar results in the bulk, under the stronger assumption that the first four moments of the two ensembles match. Similar results have been proved for Wigner matrices in [Reference Knowles and Yin24].
1.1. Sample covariance matrices with a general class of populations
We first introduce some notation. Throughout the paper, we will use
Let X = (xij) be an M × N data matrix with centered entries xij = N –1/2q ij, 1 ≤ i ≤ M and 1 ≤ j ≤ N, where q ij are i.i.d. random variables with unit variance and for all p ∈ ℕ, there exists a constant C p such that q 11 satisfies the condition
We consider the sample covariance matrix Q = TXX*T*, where T is a deterministic matrix such that T*T is a positive diagonal matrix. Using the QR factorization [Reference Golub and Van Loan22, Theorem 5.2.1], we find that T = UΣ1/2, where U is an orthogonal matrix and Σ is a positive diagonal matrix. Define Y = Σ1/2X and the singular value decomposition of Y as ![]() \[Y = \sum\nolimits_{k = 1}^{N \wedge M} \sqrt {{\lambda _k}} {\xi _k}\zeta _k^*\], where λ k, k = 1,2, …, N Λ M, are the nontrivial eigenvalues of Q, and
\[Y = \sum\nolimits_{k = 1}^{N \wedge M} \sqrt {{\lambda _k}} {\xi _k}\zeta _k^*\], where λ k, k = 1,2, …, N Λ M, are the nontrivial eigenvalues of Q, and ![]() \[\{ {\xi _k}\} _{k = 1}^M\] and
\[\{ {\xi _k}\} _{k = 1}^M\] and ![]() \[\{ {\zeta _k}\} _{k = 1}^N\] are orthonormal bases of ℝM and ℝN respectively. First, we observe that
\[\{ {\zeta _k}\} _{k = 1}^N\] are orthonormal bases of ℝM and ℝN respectively. First, we observe that
where the columns of Z are ζ1, …,ζN and ΛN is a diagonal matrix with entries λ1, …, λN. As a consequence, U will not influence the right singular vectors of Y. For the left singular vectors, we need to further assume that T is diagonal. Hence, we can make the following assumption on T:
We denote the empirical spectral distribution of Σ by
 \[\pi {\kern 1pt} := \frac{1}{M}\sum\limits_{i = 1}^M {\delta _{{\sigma _i}}}.\](1.4)
\[\pi {\kern 1pt} := \frac{1}{M}\sum\limits_{i = 1}^M {\delta _{{\sigma _i}}}.\](1.4)Suppose that there exists some small positive constant τ such that
For definiteness, in this paper we focus on the real case, i.e. all the entries x ij are real. However, it is clear that our results and proofs can be applied to the complex case after minor modifications if we assume in addition that Re x ij and Im x ij are independent centered random variables with the same variance. To avoid repetition, we summarize the basic assumptions for future reference.
Assumption 1.1. We assume that X is an M × N matrix with centered i.i.d. entries satisfying (1.1) and (1.2). We also assume that T is a deterministic M × M matrix satisfying (1.3) and (1.5).
From now on, we let Y = Σ1/2X and its singular value decomposition ![]() \[Y = \sum\nolimits_{k = 1}^{N \wedge M} \sqrt {{\lambda _k}} {\xi _k}\zeta _k^*\], where λ1 ≥ λ2 ≥ … ≥ λM Λ N.
\[Y = \sum\nolimits_{k = 1}^{N \wedge M} \sqrt {{\lambda _k}} {\xi _k}\zeta _k^*\], where λ1 ≥ λ2 ≥ … ≥ λM Λ N.
1.2 Deformed Marcenko–Pastur law
In this subsection we discuss the empirical spectral distribution of X*T*TX, where we basically follow the discussion of [Reference Knowles and Yin26, Section 2.2]. It is well known that if π is a compactly supported probability measure on ℝ, letting r N > 0, then, for any z ∈ ℂ+, there is a unique m ≡ m N (z) ∈ ℂ+ satisfying
We refer the reader to [Reference Knowles and Yin26, Lemma 2.2] and [Reference Silverstein and Choi36, Section 5] for more details. In this paper we define the deterministic function m ≡ m(z) as the unique solution of (1.6) with π defined in (1.4). We define by ρ the probability measure associated with m (i.e. m is the Stieltjes transform of ρ) and call it the asymptotic density of X*T*TX. Our assumption (1.5) implies that the spectrum of Σ cannot be concentrated at 0; thus, it ensures π is a compactly supported probability measure. Therefore, m and ρ are well defined.
Let z ∈ ℂ+ Then m ≡ m(z) can be characterized as the unique solution of the equation
 \[z = f(m),\quad \quad Im\,m \ge 0,\quad {\rm{where}}\,f(x){\kern 1pt} : = - \frac{1}{x} + \frac{1}{{{r_N}}}\sum\limits_{i = 1}^M \frac{{\pi (\{ {\sigma _i}\} )}}{{x + \sigma _i^{ - 1}}}.\](1.7)
\[z = f(m),\quad \quad Im\,m \ge 0,\quad {\rm{where}}\,f(x){\kern 1pt} : = - \frac{1}{x} + \frac{1}{{{r_N}}}\sum\limits_{i = 1}^M \frac{{\pi (\{ {\sigma _i}\} )}}{{x + \sigma _i^{ - 1}}}.\](1.7)The behavior of ρ can be entirely understood by the analysis of f. We summarize the elementary properties of ρ in the following lemma. It can be found in [Reference Knowles and Yin26, Lemmas 2.4, 2.5, and 2.6].
Lemma 1.1. Define ![]() \[ \overline {\mathbb{R}} = {\mathbb{R}} \cup \{ \infty \} \]. Then f defined in (1.7) is smooth on the M + 1 open intervals of
\[ \overline {\mathbb{R}} = {\mathbb{R}} \cup \{ \infty \} \]. Then f defined in (1.7) is smooth on the M + 1 open intervals of ![]() \[{\overline {\mathbb{R}}}\] defined through
\[{\overline {\mathbb{R}}}\] defined through
We also introduce a multiset ![]() \[{\mathcal{C}} \subset {\overline {\mathbb{R}}}\] containing the critical points of f, using the conventions that a nondegenerate critical point is counted once and a degenerate critical point will be counted twice. In the r N = 1 case, ∞ is a nondegenerate critical point. With the above notation, the following statememts hold.
\[{\mathcal{C}} \subset {\overline {\mathbb{R}}}\] containing the critical points of f, using the conventions that a nondegenerate critical point is counted once and a degenerate critical point will be counted twice. In the r N = 1 case, ∞ is a nondegenerate critical point. With the above notation, the following statememts hold.
We have
 \[|{\mathcal C} \cap {I_0}| = |{\mathcal C} \cap {I_1}| = 1\] and
\[|{\mathcal C} \cap {I_0}| = |{\mathcal C} \cap {I_1}| = 1\] and  \[|{\mathcal C} \cap {I_i}| \in \{ 0,2\} \] for i = 2, …, M. Therefore,
\[|{\mathcal C} \cap {I_i}| \in \{ 0,2\} \] for i = 2, …, M. Therefore,  \[|{\mathcal C}| = 2p\], where, for convenience, we denote by x 1 ≥ x 2 ≥ … ≥ x 2p–1 the 2p – 1 critical points in
\[|{\mathcal C}| = 2p\], where, for convenience, we denote by x 1 ≥ x 2 ≥ … ≥ x 2p–1 the 2p – 1 critical points in  \[{I_1} \cup \ldots \cup {I_M}\] and by x 2p the unique critical point in I 0.
\[{I_1} \cup \ldots \cup {I_M}\] and by x 2p the unique critical point in I 0.Defining ak : = f(xk) we have a 1 ≥ … ≥ a 2p. Moreover, we have xk = m(ak) by assuming that m(0) : = ∞ for rN = 1. Furthermore, for k = 1, …, 2p, there exists a constant C such that 0 ≤ ak ≤ C.
We have
 \[{\rm{supp}}\rho \cap (0,\infty ) = (\bigcup\nolimits_{k = 1}^p [{a_{2k}},{a_{2k - 1}}]) \cap (0,\infty )\].
\[{\rm{supp}}\rho \cap (0,\infty ) = (\bigcup\nolimits_{k = 1}^p [{a_{2k}},{a_{2k - 1}}]) \cap (0,\infty )\].
With the above definitions and properties, we now introduce the key regularity assumption on Σ.
Assumption 1.2. Fix τ > 0. We say that
1. the edges ak, k = 1, …, 2p, are regular if
 \[{a_k} \ge \tau ,\quad \quad \mathop {\min }\limits_{l \ne k} |{a_k} - {a_l}| \ge \tau ,\quad \quad \mathop {\min }\limits_i |{x_k} + \sigma _i^{ - 1}| \ge \tau ;\](1.8)
\[{a_k} \ge \tau ,\quad \quad \mathop {\min }\limits_{l \ne k} |{a_k} - {a_l}| \ge \tau ,\quad \quad \mathop {\min }\limits_i |{x_k} + \sigma _i^{ - 1}| \ge \tau ;\](1.8)2. the bulk components k = 1, …, p are regular if, for any fixed τ′ > 0, there exists a constant c ≡ c τ,τ′ such that the density of ρ in [a 2k + τ′, a 2k – 1 – τ′] is bounded from below by c.
Remark 1.1. The second condition in (1.8) states that the gap in the spectrum of ρ adjacent to a k can be well separated when N is sufficiently large. The third condition ensures a square root behavior of ρ in a small neighborhood of ak. To be specific, consider the right edge of the kth bulk component; by Equation (A.12) of [Reference Knowles and Yin26], there exists some small constant c > 0 such that ρ has the following square root behavior:
As a consequence, it will rule out the outliers. The bulk regularity imposes a lower bound on the density of eigenvalues away from the edges. For examples of matrices Σ verifying the regularity conditions, we refer the reader to [Reference Knowles and Yin26, Examples 2.8 and 2.9].
1.3. Main results
In this subsection we provide the main results of this paper. We first introduce some notation. Recall that the nontrivial classical eigenvalue locations γ 1 ≥ γ 2 ≥ … ≥ γ M Λ N of Q are defined as ![]() \[\int_{{\gamma _i}}^\infty {\kern 1pt} {\rm{d}}\rho = (i - {\textstyle{1 \over 2}})/N\]. By Lemma 1.1, there are p bulk components in the spectrum of ρ. For k = 1, …, p, we define the classical number of eigenvalues of the kth bulk component through
\[\int_{{\gamma _i}}^\infty {\kern 1pt} {\rm{d}}\rho = (i - {\textstyle{1 \over 2}})/N\]. By Lemma 1.1, there are p bulk components in the spectrum of ρ. For k = 1, …, p, we define the classical number of eigenvalues of the kth bulk component through ![]() \[{N_k}{\kern 1pt} : = N\int_{{a_{2k}}}^{{a_{2k - 1}}} {\kern 1pt} {\rm{d}}\rho \]. When p ≥ 1, we relabel λi and γi separately for each bulk component k = 1, …, p by introducing
\[{N_k}{\kern 1pt} : = N\int_{{a_{2k}}}^{{a_{2k - 1}}} {\kern 1pt} {\rm{d}}\rho \]. When p ≥ 1, we relabel λi and γi separately for each bulk component k = 1, …, p by introducing
Equivalently, we can characterize γk,i through
In this paper we will use the following assumption for the technical application of the anisotropic local law.
Assumption 1.3. For k = 1,2, … ,p and i = 1,2, …,N k, γk,i ≥ τ for some constant τ > 0.
We define the index sets ![]() \[{{\mathcal I}_1}{\kern 1pt} : = \{ 1, \ldots ,M\} \] and
\[{{\mathcal I}_1}{\kern 1pt} : = \{ 1, \ldots ,M\} \] and ![]() \[{{\mathcal I}_2}{\kern 1pt} : = \{ M + 1, \ldots ,M + N\} \], with
\[{{\mathcal I}_2}{\kern 1pt} : = \{ M + 1, \ldots ,M + N\} \], with ![]() \[{\mathcal I}{\kern 1pt} : = {{\mathcal I}_1} \cup {{\mathcal I}_2}\]. We will consistently use Latin letters
\[{\mathcal I}{\kern 1pt} : = {{\mathcal I}_1} \cup {{\mathcal I}_2}\]. We will consistently use Latin letters ![]() \[i,j \in {{\mathcal I}_1}\], Greek letters
\[i,j \in {{\mathcal I}_1}\], Greek letters ![]() \[\mu ,\nu \in {{\mathcal I}_2}\], and
\[\mu ,\nu \in {{\mathcal I}_2}\], and ![]() \[s,t \in {\mathcal I}\]. Then we label the indices of the matrix according to
\[s,t \in {\mathcal I}\]. Then we label the indices of the matrix according to ![]() \[X = ({X_{i\mu }}:i \in {{\mathcal I}_1},{\kern 1pt} \mu \in {{\mathcal I}_2})\]. We similarly label the entries of
\[X = ({X_{i\mu }}:i \in {{\mathcal I}_1},{\kern 1pt} \mu \in {{\mathcal I}_2})\]. We similarly label the entries of ![]() \[{\xi_k} \in {{\mathbb{R}}^{{{\mathcal{I}}_1}}}\] and
\[{\xi_k} \in {{\mathbb{R}}^{{{\mathcal{I}}_1}}}\] and ![]() \[{\zeta _k} \in {{\mathbb{R}}^{{{\mathcal{I}}_2}}}.\] In the kth, k = 1,2, …, p, bulk component, we rewrite the index of λ α′ as
\[{\zeta _k} \in {{\mathbb{R}}^{{{\mathcal{I}}_2}}}.\] In the kth, k = 1,2, …, p, bulk component, we rewrite the index of λ α′ as
In this paper we say that l is associated with α′. Note that α′ is the index of λ k,l before the relabeling of (1.10), and the two cases correspond to the right and left edges, respectively. Our main result on the distribution of the components of the singular vectors near the edge is the following theorem. For any positive integers m, k, some function θ : ℝm→ℝ, and x = (x 1,…,x m) ∈ ℝm we define
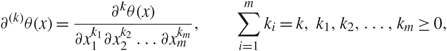 \[{\partial ^{(k)}}\theta (x) = \frac{{{\partial ^k}\theta (x)}}{{\partial x_1^{{k_1}}\partial x_2^{{k_2}} \ldots \partial x_m^{{k_m}}}},\quad \quad \sum\limits_{i = 1}^m {k_i} = k,{\kern 1pt} {k_1},{k_2}, \ldots ,{k_m} \ge 0,\]
\[{\partial ^{(k)}}\theta (x) = \frac{{{\partial ^k}\theta (x)}}{{\partial x_1^{{k_1}}\partial x_2^{{k_2}} \ldots \partial x_m^{{k_m}}}},\quad \quad \sum\limits_{i = 1}^m {k_i} = k,{\kern 1pt} {k_1},{k_2}, \ldots ,{k_m} \ge 0,\]
and ||x||2 to be its l 2 norm. Define ![]() \[{Q_G}{\kern 1pt} : = {\Sigma ^{1/2}}{X_G}X_G^*{\Sigma ^{1/2}}\], where XG is GOE (i.e. a random matrix with entries being i.i.d. real standard Gaussian random variables) and Σ satisfies (1.3) and (1.5).
\[{Q_G}{\kern 1pt} : = {\Sigma ^{1/2}}{X_G}X_G^*{\Sigma ^{1/2}}\], where XG is GOE (i.e. a random matrix with entries being i.i.d. real standard Gaussian random variables) and Σ satisfies (1.3) and (1.5).
Theorem 1.1. Suppose that ![]() \[{Q_V} = {\Sigma ^{1/2}}{X_V}X_V^*{\Sigma ^{1/2}}\] satisfies Assumption 1.1. Let 𝔼G and 𝔼V denote the expectations with respect to XG and XV. Consider the kth, k = 1,2, …, p, bulk component, with l defined in (1.11) or (1.12). Under Assumption 1.2 and 1.3 for any choices of indices
\[{Q_V} = {\Sigma ^{1/2}}{X_V}X_V^*{\Sigma ^{1/2}}\] satisfies Assumption 1.1. Let 𝔼G and 𝔼V denote the expectations with respect to XG and XV. Consider the kth, k = 1,2, …, p, bulk component, with l defined in (1.11) or (1.12). Under Assumption 1.2 and 1.3 for any choices of indices ![]() \[i,j \in {{\mathcal I}_1}\] and
\[i,j \in {{\mathcal I}_1}\] and ![]() \[\mu ,\nu \in {{\mathcal I}_2}\], there exists a δ ∈ (0, 1) such that, when
\[\mu ,\nu \in {{\mathcal I}_2}\], there exists a δ ∈ (0, 1) such that, when ![]() \[l \le N_k^\delta \], we have
\[l \le N_k^\delta \], we have
where θ is a smooth function in ℝ2 that satisfies
Theorem 1.2. Suppose that ![]() \[{Q_V} = {\Sigma ^{1/2}}{X_V}X_V^*{\Sigma ^{1/2}}\] satisfies Assumption 1.1. Consider the k1th, …, k nth, k 1, …, k n} ∈ {1, 2, …, p}, n ≤ p, bulk components for lki defined in (1.11) or (1.12) associated with the k ith, i = 1,2, …, n, bulk component. Under Assumptions 1.2 and 1.3 for any choices of indices
\[{Q_V} = {\Sigma ^{1/2}}{X_V}X_V^*{\Sigma ^{1/2}}\] satisfies Assumption 1.1. Consider the k1th, …, k nth, k 1, …, k n} ∈ {1, 2, …, p}, n ≤ p, bulk components for lki defined in (1.11) or (1.12) associated with the k ith, i = 1,2, …, n, bulk component. Under Assumptions 1.2 and 1.3 for any choices of indices ![]() \[i,j \in {{\mathcal I}_1}\] and
\[i,j \in {{\mathcal I}_1}\] and ![]() \[\mu ,\nu \in {{\mathcal I}_2}\], there exists a δ ∈ (0,1) such that, when
\[\mu ,\nu \in {{\mathcal I}_2}\], there exists a δ ∈ (0,1) such that, when ![]() \[{l_{{k_i}}} \le N_{{k_i}}^\delta \], where
\[{l_{{k_i}}} \le N_{{k_i}}^\delta \], where ![]() \[{l_{{k_i}}}\] is associated with
\[{l_{{k_i}}}\] is associated with ![]() \[\alpha _{{k_i}}^{'}\], i = 1,2, …, n, we have
\[\alpha _{{k_i}}^{'}\], i = 1,2, …, n, we have
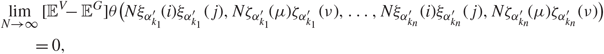 \[\mathop {\lim }\limits_{N \to \infty } [{{\mathbb {E}}^V} - {{\mathbb {E}}^G}]\theta (N{\xi _{\alpha _{{k_1}}^{'}}}(i){\xi _{\alpha _{{k_1}}^{'}}}(j),N{\zeta _{\alpha _{{k_1}}^{'}}}(\mu ){\zeta _{\alpha _{{k_1}}^{'}}}(\nu ), \ldots ,N{\xi _{\alpha _{{k_n}}^{'}}}(i){\xi _{\alpha _{{k_n}}^{'}}}(j),N{\zeta _{\alpha _{{k_n}}^{'}}}(\mu ){\zeta _{\alpha _{{k_n}}^{'}}}(\nu ))\\ \quad \quad = 0,\]
\[\mathop {\lim }\limits_{N \to \infty } [{{\mathbb {E}}^V} - {{\mathbb {E}}^G}]\theta (N{\xi _{\alpha _{{k_1}}^{'}}}(i){\xi _{\alpha _{{k_1}}^{'}}}(j),N{\zeta _{\alpha _{{k_1}}^{'}}}(\mu ){\zeta _{\alpha _{{k_1}}^{'}}}(\nu ), \ldots ,N{\xi _{\alpha _{{k_n}}^{'}}}(i){\xi _{\alpha _{{k_n}}^{'}}}(j),N{\zeta _{\alpha _{{k_n}}^{'}}}(\mu ){\zeta _{\alpha _{{k_n}}^{'}}}(\nu ))\\ \quad \quad = 0,\]where θ is a smooth function in ℝ2n that satisfies
Remark 1.2. The results in Theorems 1.1 and 1.2 can be easily extended to a general form containing more entries of the singular vectors using a general form of the Green function comparison argument. For example, to extend Theorem 1.1, we consider the kth bulk component and choose any positive integer s. Under Assumptions 1.2 and 1.3 for any choices of indices ![]() \[{i_1},{j_1}, \ldots ,{i_s},{j_s} \in {{\mathcal I}_1}\] and
\[{i_1},{j_1}, \ldots ,{i_s},{j_s} \in {{\mathcal I}_1}\] and ![]() \[{\mu _1},{\nu _1}, \ldots ,{\mu _s},{\nu _s} \in {{\mathcal I}_2}\] for the corresponding li, i = 1, 2, …, s, defined in (1.11) or (1.12), there exists some 0 < δ < 1 with
\[{\mu _1},{\nu _1}, \ldots ,{\mu _s},{\nu _s} \in {{\mathcal I}_2}\] for the corresponding li, i = 1, 2, …, s, defined in (1.11) or (1.12), there exists some 0 < δ < 1 with ![]() \[0 \lt \mathop {\max }\nolimits_{1 \le i \le s} \{ {l_i}\} \le N_k^\delta \], such that
\[0 \lt \mathop {\max }\nolimits_{1 \le i \le s} \{ {l_i}\} \le N_k^\delta \], such that
 \[\mathop {\lim }\limits_{N \to \infty } [{{\mathbb {E}}^V} - {{\mathbb {E}}^G}]\theta (N{\xi _{\alpha _1^{'}}}({i_1}){\xi _{\alpha _1^{'}}}({j_1}),N{\zeta _{\alpha _1^{'}}}({\mu _1}){\zeta _{\alpha _1^{'}}}({\nu _1}), \ldots ,N{\xi _{\alpha _s^{'}}}({i_s}){\xi _{\alpha _s^{'}}}({j_s}),N{\zeta _{\alpha _s^{'}}}({\mu _s}){\zeta _{\alpha _s^{'}}}({\nu _s}))\\ \quad \quad = 0,\](1.13)
\[\mathop {\lim }\limits_{N \to \infty } [{{\mathbb {E}}^V} - {{\mathbb {E}}^G}]\theta (N{\xi _{\alpha _1^{'}}}({i_1}){\xi _{\alpha _1^{'}}}({j_1}),N{\zeta _{\alpha _1^{'}}}({\mu _1}){\zeta _{\alpha _1^{'}}}({\nu _1}), \ldots ,N{\xi _{\alpha _s^{'}}}({i_s}){\xi _{\alpha _s^{'}}}({j_s}),N{\zeta _{\alpha _s^{'}}}({\mu _s}){\zeta _{\alpha _s^{'}}}({\nu _s}))\\ \quad \quad = 0,\](1.13)
where ![]() \[\theta \in {{\mathbb {R}}^{2s}}\] is a smooth function satisfying |∂(k) θ (x)| ≤ C(1 + ||x||2)C, k = 1, 2, 3, with some constant C > 0. Similarly, we can extend Theorem 1.2 to contain more entries of singular vectors.
\[\theta \in {{\mathbb {R}}^{2s}}\] is a smooth function satisfying |∂(k) θ (x)| ≤ C(1 + ||x||2)C, k = 1, 2, 3, with some constant C > 0. Similarly, we can extend Theorem 1.2 to contain more entries of singular vectors.
Recall (1.10), and define ϖk : = (|f″(x k)|/2)1/3, k = 1, 2, …, 2p. Then, for any positive integer h, we define
Consider a smooth function θ ∈ ℝ whose third derivative θ (3) satisfies |θ (3)(x)| ≤ C(1 + |x|)C for some constant C > 0. Then, by [Reference Knowles and Yin26, Theorem 3.18], we have
Together with Theorem 1.1, we have the following corollary, which is an analogy of [Reference Knowles and Yin24, Theorem 1.6]. Let t = 2k – 1 if α′ is as given in (1.11) and 2k if α′ is as given in (1.12).
Corollary 1.1. Under the assumptions of Theorem 1.1, for some positive integer h, we have
where θ ∈ ℝ3 satisfies
Corollary 1.1 can be extended to a general form for several bulk components. Let t i = 2k i – 1 if ![]() \[\alpha _{{k_i}}^{'}\] is as given in (1.11) and 2k i if
\[\alpha _{{k_i}}^{'}\] is as given in (1.11) and 2k i if ![]() \[\alpha _{{k_i}}^{'}\] is as given in (1.12).
\[\alpha _{{k_i}}^{'}\] is as given in (1.12).
Corollary 1.2. Under the assumptions of Theorem 1.2, for some positive integer h, we have
 \[\mathop {\lim }\limits_{N \to \infty } [{{\mathbb {E}}^V} - {{\mathbb {E}}^G}]\theta ({{\bf{q}}_{{t_1},h}},N{\xi _{\alpha _{{k_1}}^{'}}}(i){\xi _{\alpha _{{k_1}}^{'}}}(j),N{\zeta _{\alpha _{{k_1}}^{'}}}(\mu ){\zeta _{\alpha _{{k_1}}^{'}}}(\nu ), \ldots ,{{\bf{q}}_{{t_n},h}},N{\xi _{\alpha _{{k_n}}^{'}}}(i){\xi _{\alpha _{{k_n}}^{'}}}(j),\\ \times N{\zeta _{\alpha _{{k_n}}^{'}}}(\mu ){\zeta _{\alpha _{{k_n}}^{'}}}(\nu ))\\ \quad \quad = 0,\]
\[\mathop {\lim }\limits_{N \to \infty } [{{\mathbb {E}}^V} - {{\mathbb {E}}^G}]\theta ({{\bf{q}}_{{t_1},h}},N{\xi _{\alpha _{{k_1}}^{'}}}(i){\xi _{\alpha _{{k_1}}^{'}}}(j),N{\zeta _{\alpha _{{k_1}}^{'}}}(\mu ){\zeta _{\alpha _{{k_1}}^{'}}}(\nu ), \ldots ,{{\bf{q}}_{{t_n},h}},N{\xi _{\alpha _{{k_n}}^{'}}}(i){\xi _{\alpha _{{k_n}}^{'}}}(j),\\ \times N{\zeta _{\alpha _{{k_n}}^{'}}}(\mu ){\zeta _{\alpha _{{k_n}}^{'}}}(\nu ))\\ \quad \quad = 0,\]where θ ∈ ℝ3n is a smooth function that satisfies
Remark 1.3. (i) Similarly to (1.13), the results in Corollaries 1.1 and 1.2 can be easily extended to a general form containing more entries of the singular vectors. For example, to extend Corollary 1.1, we choose any positive integers s and h 1, …, hs. Under Assumptions 1.2 and 1.3 for any choices of indices ![]() \[{i_1},{j_1}, \ldots ,{i_s},{j_s} \in {{\mathcal I}_1}\] and
\[{i_1},{j_1}, \ldots ,{i_s},{j_s} \in {{\mathcal I}_1}\] and ![]() \[{\mu _1},{\nu _1}, \ldots ,{\mu _s},{\nu _s} \in {{\mathcal I}_2}\], for the corresponding li, i = 1, 2, …,s, defined in (1.11) or (1.12), there exists some 0 < δ < 1 with
\[{\mu _1},{\nu _1}, \ldots ,{\mu _s},{\nu _s} \in {{\mathcal I}_2}\], for the corresponding li, i = 1, 2, …,s, defined in (1.11) or (1.12), there exists some 0 < δ < 1 with ![]() \[\mathop {\max }\nolimits_{1 \le i \le s} \{ {l_i}\} \le N_k^\delta \], such that
\[\mathop {\max }\nolimits_{1 \le i \le s} \{ {l_i}\} \le N_k^\delta \], such that
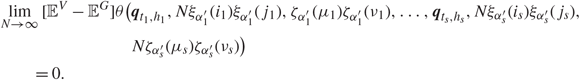 \[
\eqalign{
& \mathop {\lim }\limits_{N \to \infty } [{{\mathbb {E}}^V} - {{\mathbb {E}}^G}]\theta ({q_{{t_1},{h_1}}},N{\xi _{\alpha _1^{'}}}({i_1}){\xi _{\alpha _1^{'}}}({j_1}),{\zeta _{\alpha _1^{'}}}({\mu _1}){\zeta _{\alpha _1^{'}}}({\nu _1}), \ldots ,{q_{{t_s},{h_s}}},N{\xi _{\alpha _s^{'}}}({i_s}){\xi _{\alpha _s^{'}}}({j_s}), \cr
& N{\zeta _{\alpha _s^{'}}}({\mu _s}){\zeta _{\alpha _s^{'}}}({\nu _s})) \cr
& \quad \quad = 0. \cr}
\]
\[
\eqalign{
& \mathop {\lim }\limits_{N \to \infty } [{{\mathbb {E}}^V} - {{\mathbb {E}}^G}]\theta ({q_{{t_1},{h_1}}},N{\xi _{\alpha _1^{'}}}({i_1}){\xi _{\alpha _1^{'}}}({j_1}),{\zeta _{\alpha _1^{'}}}({\mu _1}){\zeta _{\alpha _1^{'}}}({\nu _1}), \ldots ,{q_{{t_s},{h_s}}},N{\xi _{\alpha _s^{'}}}({i_s}){\xi _{\alpha _s^{'}}}({j_s}), \cr
& N{\zeta _{\alpha _s^{'}}}({\mu _s}){\zeta _{\alpha _s^{'}}}({\nu _s})) \cr
& \quad \quad = 0. \cr}
\]where the smooth function θ ∈ ℝ3s satisfies |∂(k)θ (x)| ≤ C(1 + ||x||2)C, k = 1, 2, 3, for some constant C.
(ii) Theorems 1.1 and 1.2, and Corollaries 1.1 and 1.2 still hold for the complex case, where the moment matching condition is replaced by
(iii) All the above theorems and corollaries are stronger than their counterparts from [Reference Knowles and Yin24] because they hold much further into the bulk components. For instance, in the counterpart of Theorem 1.1, which is [Reference Knowles and Yin24, Theorem 1.6], the universality was established under the assumption that l ≤ (log N)C log log N.
In the bulks, similar results hold under the stronger assumption that the first four moments of the matrix entries match those of Gaussian ensembles.
Theorem 1.3. Suppose that ![]() \[{Q_V} = {\Sigma ^{1/2}}{X_V}X_V^*{\Sigma ^{1/2}}\] satisfies Assumption 1.1. Assume that the third and fourth moments of XV agree with those of XG and consider the kth, k = 1, 2, …, p bulk component, with l defined in (1.11) or (1.12). Under Assumptions 1.2 and 1.3 for any choices of indices
\[{Q_V} = {\Sigma ^{1/2}}{X_V}X_V^*{\Sigma ^{1/2}}\] satisfies Assumption 1.1. Assume that the third and fourth moments of XV agree with those of XG and consider the kth, k = 1, 2, …, p bulk component, with l defined in (1.11) or (1.12). Under Assumptions 1.2 and 1.3 for any choices of indices ![]() \[i,j \in {{\mathcal I}_1}\] and
\[i,j \in {{\mathcal I}_1}\] and ![]() \[\mu ,\nu \in {{\mathcal I}_2}\], there exists a small δ ∈ (0,1) such that, when δ Nk ≤ l ≤ (1 – δ)Nk, we have
\[\mu ,\nu \in {{\mathcal I}_2}\], there exists a small δ ∈ (0,1) such that, when δ Nk ≤ l ≤ (1 – δ)Nk, we have
where θ is a smooth function in ℝ2 that satisfies
Theorem 1.4. Suppose that ![]() \[{Q_V} = {\Sigma ^{1/2}}{X_V}X_V^*{\Sigma ^{1/2}}\] satisfies Assumption 1.1. Assume that the third and fourth moments of XV agree with those of XG, and consider the k 1th …, knth, k 1}, …, kn ∈ {1, 2,…, p}, n ≤ p, bulks for l ki defined in (1.11) or (1.12) associated with the kith, i = 1, 2, …, n, bulk component. Under Assumptions 1.2 and 1.3 for any choices of indices
\[{Q_V} = {\Sigma ^{1/2}}{X_V}X_V^*{\Sigma ^{1/2}}\] satisfies Assumption 1.1. Assume that the third and fourth moments of XV agree with those of XG, and consider the k 1th …, knth, k 1}, …, kn ∈ {1, 2,…, p}, n ≤ p, bulks for l ki defined in (1.11) or (1.12) associated with the kith, i = 1, 2, …, n, bulk component. Under Assumptions 1.2 and 1.3 for any choices of indices ![]() \[i,j \in {{\mathcal I}_1}\] and
\[i,j \in {{\mathcal I}_1}\] and ![]() \[\mu ,\nu \in {{\mathcal I}_2}\], there exists a δ ∈ (0, 1) such that, when
\[\mu ,\nu \in {{\mathcal I}_2}\], there exists a δ ∈ (0, 1) such that, when ![]() \[\delta {N_{{k_i}}} \le {l_{{k_i}}} \le (1 - \delta ){N_{{k_i}}}\], i = 1, 2,…, n, we have
\[\delta {N_{{k_i}}} \le {l_{{k_i}}} \le (1 - \delta ){N_{{k_i}}}\], i = 1, 2,…, n, we have
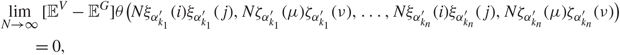 \[\mathop {\lim }\limits_{N \to \infty } [{{\mathbb {E}}^V} - {{\mathbb {E}}^G}]\theta (N{\xi _{{\alpha ^{'}}}}(i){\xi _{{\alpha ^{'}}}}(j),N{\zeta _{{\alpha ^{'}}}}(\mu ){\zeta _{{\alpha ^{'}}}}(\nu )) = 0,\]
\[\mathop {\lim }\limits_{N \to \infty } [{{\mathbb {E}}^V} - {{\mathbb {E}}^G}]\theta (N{\xi _{{\alpha ^{'}}}}(i){\xi _{{\alpha ^{'}}}}(j),N{\zeta _{{\alpha ^{'}}}}(\mu ){\zeta _{{\alpha ^{'}}}}(\nu )) = 0,\]where θ is a smooth function in ℝ2n that satisfies
Remark 1.4. (i) Similarly to Corollaries 1.1 and 1.2 and Remark 1.3(i), we can extend the results to the joint distribution containing singular values. We take the extension of Theorem 1.3 as an example. By Assumption 1.2(ii), in the bulk, we have ![]() \[\int_{{\lambda _{{\alpha ^{'}}}}}^{{\gamma _{{\alpha ^{'}}}}} {\kern 1pt} {\rm{d}}\rho = 1/N + o({N^{ - 1}})\]. Using a similar Dyson Brownian motion argument as in [Reference Pillai and Yin33], combining with Theorem 1.3, we have
\[\int_{{\lambda _{{\alpha ^{'}}}}}^{{\gamma _{{\alpha ^{'}}}}} {\kern 1pt} {\rm{d}}\rho = 1/N + o({N^{ - 1}})\]. Using a similar Dyson Brownian motion argument as in [Reference Pillai and Yin33], combining with Theorem 1.3, we have
where ![]() \[{{\bf {p}}_{{\alpha ^{'}}}}\] is defined as
\[{{\bf {p}}_{{\alpha ^{'}}}}\] is defined as
and θ ∈ ℝ3 satisfies
(ii) Theorems 1.3 and 1.4 still hold for the complex case, where the moment matching condition is replaced by
1.4. Remarks on applications to statistics
In this subsection we give a few remarks on possible applications to statistics and machine learning. First, our results show that, under Assumptions 1.1, 1.2, and 1.3, the distributions of the right singular vectors, i.e. entries of principal components, are independent of the laws of xij. Hence, we can extend the statistical analysis relying on Gaussian or sub-Gaussian assumptions to general distributions. For instance, in the problem of classification, assuming that Y = (yi) and each yi has the same covariance structure but may have different means, i.e. ![]() \[{\mathbb{E}}{y_i} = {\mu _k},{\kern 1pt} i = 1,2, \ldots ,N,k = 1,2, \ldots ,K,\] where K is a fixed constant. We are interested in classifying the samples yi into K clusters. In the classical framework, researchers use the matrix ᴧ V to classify the samples yi, where ᴧ = diag {λ 1, …,λ K} and V = (ζ1, …, ζK) (recall that λi and ζi are the singular values and right singular vectors of Y). Existing statistical analysis needs the sub-Gaussian assumption [Reference Li, Tang, Charon and Priebe29]. In this sense, our result, especially Remark 1.4, can be used to generalize such results.
\[{\mathbb{E}}{y_i} = {\mu _k},{\kern 1pt} i = 1,2, \ldots ,N,k = 1,2, \ldots ,K,\] where K is a fixed constant. We are interested in classifying the samples yi into K clusters. In the classical framework, researchers use the matrix ᴧ V to classify the samples yi, where ᴧ = diag {λ 1, …,λ K} and V = (ζ1, …, ζK) (recall that λi and ζi are the singular values and right singular vectors of Y). Existing statistical analysis needs the sub-Gaussian assumption [Reference Li, Tang, Charon and Priebe29]. In this sense, our result, especially Remark 1.4, can be used to generalize such results.
Next, our results can be used to do statistical inference. It is notable that, in general, the distribution of the singular vectors of the sample covariance matrix Q = TX X*T* is unknown, even for the Gaussian case. However, when T is a scalar matrix (i.e. T = cI, c > 0), Bourgade and Yau [Reference Bourgade and Yau10, Appendix C] showed that the entries of the singular vectors are asymptotically normally distributed. Hence, our universality results imply that, under Assumptions 1.1, 1.2, and 1.3, when T is conformal (i.e. T*T = cI, c > 0), the entries of the right singular vectors are asymptotically normally distributed. Therefore, this can be used to test the null hypothesis:
(H0) T is a conformal matrix.
The statistical testing problem (H0) contains a rich class of hypothesis tests. For instance, when T = I, it reduces to the sphericity test and when c = 1, it reduces to testing whether the covariance matrix of X is orthogonal [Reference Yao, Zheng and Bai40].
To illustrate how our results can be used to test (H0), we assume that c = 1 in the following discussion. Under (H0), denote the QR factorization of T to be T = UI, the right singular vector of TX is the same as X, ζk}, k = 1, 2, …, N. Using [Reference Bourgade and Yau10, Corollary 1.3], we find that, for i, k = 1, 2, …, N,
where ![]() \[{\mathcal N}\] is a standard Gaussian random variable. In detail, we can take the following steps to test whether (H0) holds.
\[{\mathcal N}\] is a standard Gaussian random variable. In detail, we can take the following steps to test whether (H0) holds.
1. Randomly choose two index sets R 1, R 2 ⊂ {1, 2, …, N} with |Ri| = O(1), i = 1, 2.
2. Use the bootstrapping method to sample the columns of Q and obtain a sequence of M × N matrices Q j, j = 1, 2, …, K.
3. Select
 \[\zeta _k^j(i)\], k ∈ R 1, i ∈ R 2, from Q j, j = 1, 2, …, K. Use the classic normality test, for instance, the Shapiro–Wilk test, to check whether (1.16) holds for the above samples. Let A be the number of samples which cannot be rejected by the classic normality test.
\[\zeta _k^j(i)\], k ∈ R 1, i ∈ R 2, from Q j, j = 1, 2, …, K. Use the classic normality test, for instance, the Shapiro–Wilk test, to check whether (1.16) holds for the above samples. Let A be the number of samples which cannot be rejected by the classic normality test.4. Given some pre-chosen significant level α, reject H0 if A/|R 1||R 2| < 1 – α.
Another important piece of information from our result is that the singular vectors are completely delocalized. This property can be applied to the problem of low rank matrix denoising [Reference Ding13], i.e.
where S is a deterministic low rank matrix. Consider that S is of rank one, and assume that the left singular vector u of S is e1 = (1, 0, …, 0) ∈ ℝM. Using the completely delocalized result, it can be shown that ![]() \[{\tilde u_1}\], the first left singular vector of
\[{\tilde u_1}\], the first left singular vector of ![]() \[\hat S\] has the same sparse structure as that of u, i.e.
\[\hat S\] has the same sparse structure as that of u, i.e.
hold with high probability. Thus, to estimate the singular vectors of S, we need only carry out singular value decomposition on a block matrix of ![]() \[\hat S\]. For more details, we refer the reader to [Reference Ding13, Section 2.1].
\[\hat S\]. For more details, we refer the reader to [Reference Ding13, Section 2.1].
Furthermore, delocalization of singular vectors is important in machine learning, especially the perturbation analysis of a singular subspace [Reference Abbe, Fan, Wang and Zhong1], [Reference Ding and Sun15], [Reference Fan, Wang and Zhong21], [Reference Fan and Zhong20], [Reference Zhong and Boumal41]. In these problems, researchers are interested in bounding the difference between the sample singular vectors and those of T. The Davis–Kahan sin θ theorem is often used to bound the l 2 distance. However, in many applications, for instance, the wireless sensor network localization [Reference Fan, Wang and Zhong21] and multidimesional scaling [Reference Ding and Sun15], people are usually interested in bounding the l ∞ distance. Denote the right singular vectors of T by vi and recall that the ζi are the right singular vectors of Y. We aim to bound
To obtain such a bound, an important step is to show the delocalization (i.e. incoherence) of the singular vectors [Reference Abbe, Fan, Wang and Zhong1], [Reference Ding and Sun15], [Reference Zhong and Boumal41]. Hence, our results in this paper can provide the crucial ingredients for such applications.
This paper is organized as follows. In Section 2 we introduce some notation and tools that will be used in the proofs. In Section 3 we prove the singular vector distribution near the edge. In Section 4 we prove the distribution within the bulks. The Green function comparison arguments are mainly discussed in Section 3.2 and Lemma 4.5. The proof of Lemma 3.4 is given in the supplementary material [Reference Ding14] to this paper.
Conventions. We always use C to denote a generic large positive constant, whose value may change from one line to the next. Similarly, we use ε to denote a generic small positive constant. For two quantities aN and bN depending on N, the notation aN = O(bN) means that |aN| ≤ C|bN| for some positive constant C > 0, and aN = o(bN means that |aN| ≤ cN|bN| for some positive constants cN → 0 as N → ∞. We also use the notation aN ∼ bN if aN = O(bN) and bN = O(aN). We write the identity matrix I n × n as 1 or I when there is no confusion about the dimension.
2. Notation and tools
In this section we introduce some notation and tools which will be used in this paper. Throughout the paper, we always use ε 1 to denote a small constant and D 1 to denote a large constant. Recall that the ESD of an N × N symmetric matrix H is defined as
 \[F_H^{(N)}(\lambda ){\kern 1pt} : = \frac{1}{N}\sum\limits_{i = 1}^N {{\bf{1}}_{\{ {\lambda _i}(H) \le \lambda \} }},\]
\[F_H^{(N)}(\lambda ){\kern 1pt} : = \frac{1}{N}\sum\limits_{i = 1}^N {{\bf{1}}_{\{ {\lambda _i}(H) \le \lambda \} }},\]and its Stieltjes transform is defined as
For some small constant τ > 0, we define the typical domain for z = E + iη as
It was shown in [Reference Ding13], [Reference Ding and Yang16], [Reference Knowles and Yin26], and [Reference Xi, Yang and Yin39] that the linearizing block matrix is quite useful in dealing with rectangular matrices.
Definition 2.1. For z ∈ ℂ+, we define the (N + M) × (N + M) self-adjoint matrix
and
By Schur’s complement, it is easy to check that
 \[G = \left( {\begin{array}{*{20}{c}}{{{\mathcal G}_1}(z)} & {{z^{ - 1/2}}{{\mathcal G}_1}(z)Y}\\{{z^{ - 1/2}}{Y^*}{{\mathcal G}_1}(z)} & {{z^{ - 1}}{Y^*}{{\mathcal G}_1}(z)Y - {z^{ - 1}}I}\end{array}} \right)\]\[ = \left( {\begin{array}{*{20}{c}}{{z^{ - 1}}Y{{\mathcal G}_2}(z){Y^*} - {z^{ - 1}}I} & {{z^{ - 1/2}}Y{{\mathcal G}_2}(z)}\\{{z^{ - 1/2}}{{\mathcal G}_2}(z){Y^*}} & {{{\mathcal G}_2}(z)}\end{array}} \right),\](2.4)
\[G = \left( {\begin{array}{*{20}{c}}{{{\mathcal G}_1}(z)} & {{z^{ - 1/2}}{{\mathcal G}_1}(z)Y}\\{{z^{ - 1/2}}{Y^*}{{\mathcal G}_1}(z)} & {{z^{ - 1}}{Y^*}{{\mathcal G}_1}(z)Y - {z^{ - 1}}I}\end{array}} \right)\]\[ = \left( {\begin{array}{*{20}{c}}{{z^{ - 1}}Y{{\mathcal G}_2}(z){Y^*} - {z^{ - 1}}I} & {{z^{ - 1/2}}Y{{\mathcal G}_2}(z)}\\{{z^{ - 1/2}}{{\mathcal G}_2}(z){Y^*}} & {{{\mathcal G}_2}(z)}\end{array}} \right),\](2.4)where
Thus, a control of G directly yields controls of (Y Y* – z)–1 and (Y*Y – z)–1. Moreover, we have
 \[{m_1}(z) = \frac{1}{M}\sum\limits_{i \in {{\mathcal I}_1}} {G_{ii}},\quad \quad {m_2}(z) = \frac{1}{N}\sum\limits_{\mu \in {{\mathcal I}_2}} {G_{\mu \mu }}.\](2.5)
\[{m_1}(z) = \frac{1}{M}\sum\limits_{i \in {{\mathcal I}_1}} {G_{ii}},\quad \quad {m_2}(z) = \frac{1}{N}\sum\limits_{\mu \in {{\mathcal I}_2}} {G_{\mu \mu }}.\](2.5) Recall that ![]() \[Y = \sum\nolimits_{i = 1}^{M \wedge N} \sqrt {{\lambda _k}} {\xi _k}\zeta _k^*,{\kern 1pt} {\xi _k} \in {R^{{I_1}}},\;{\zeta _k} \in {R^{{I_1}}}.\] By (2.4), we have
\[Y = \sum\nolimits_{i = 1}^{M \wedge N} \sqrt {{\lambda _k}} {\xi _k}\zeta _k^*,{\kern 1pt} {\xi _k} \in {R^{{I_1}}},\;{\zeta _k} \in {R^{{I_1}}}.\] By (2.4), we have
 \[G(z) = \sum\limits_{k = 1}^{M \wedge N} \frac{1}{{{\lambda _k} - z}}\left( {\begin{array}{*{20}{c}}{{\xi _k}\xi _k^*} & {{z^{ - 1/2}}{{\sqrt \lambda }_k}{\xi _k}\zeta _k^*}\\{{z^{ - 1/2}}{{\sqrt \lambda }_k}{\zeta _k}\xi _k^*} & {{\zeta _k}\zeta _k^*}\end{array}} \right).\](2.6)
\[G(z) = \sum\limits_{k = 1}^{M \wedge N} \frac{1}{{{\lambda _k} - z}}\left( {\begin{array}{*{20}{c}}{{\xi _k}\xi _k^*} & {{z^{ - 1/2}}{{\sqrt \lambda }_k}{\xi _k}\zeta _k^*}\\{{z^{ - 1/2}}{{\sqrt \lambda }_k}{\zeta _k}\xi _k^*} & {{\zeta _k}\zeta _k^*}\end{array}} \right).\](2.6)Define
 \[\Psi (z){\kern 1pt} : = \sqrt {\frac{{Im\,m(z)}}{{N\eta }}} + \frac{1}{{N\eta }},\quad \quad {\underline \Sigma _o}{\kern 1pt} : = \left( {\begin{array}{*{20}{c}}\Sigma & 0\\0 & I\end{array}} \right),\quad \quad \underline \Sigma {\kern 1pt} : = \left( {\begin{array}{*{20}{c}}{{z^{ - 1/2}}{\Sigma ^{1/2}}} & 0\\0 & I\end{array}} \right).\]\[\](2.7)
\[\Psi (z){\kern 1pt} : = \sqrt {\frac{{Im\,m(z)}}{{N\eta }}} + \frac{1}{{N\eta }},\quad \quad {\underline \Sigma _o}{\kern 1pt} : = \left( {\begin{array}{*{20}{c}}\Sigma & 0\\0 & I\end{array}} \right),\quad \quad \underline \Sigma {\kern 1pt} : = \left( {\begin{array}{*{20}{c}}{{z^{ - 1/2}}{\Sigma ^{1/2}}} & 0\\0 & I\end{array}} \right).\]\[\](2.7)Definition 2.2. For z ∈ ℂ+, we define the ![]() \[{\mathcal I} \times {\mathcal I}\] matrix
\[{\mathcal I} \times {\mathcal I}\] matrix
We will see later from Lemma 2.1 that G(z) converges to Π (z) in probability.
Remark 2.1. In [Reference Knowles and Yin26, Definition 3.2], the linearizing block matrix is defined as
It is easy to check the following relation between (2.2) and (2.9):
In [Reference Knowles and Yin26, Definition 3.3], the deterministic convergent limit of ![]() \[H_o^{ - 1}\] is
\[H_o^{ - 1}\] is
Therefore, by (2.10), we can get a similar relation between (2.8) and (2.11):
Definition 2.3. We introduce the notation X (𝕋) to represent the M × (N–|𝕋|) minor of X by deleting the ith, i ∈ 𝕋, columns of X For convenience, ({i}) will be abbreviated to (i). We will continue to use the matrix indices of X for X (𝕋) that is, ![]() \[X_{ij}^\mathbb {(T)} = {\bf{1}}(j \notin \mathbb T){X_{ij}}.\] Let
\[X_{ij}^\mathbb {(T)} = {\bf{1}}(j \notin \mathbb T){X_{ij}}.\] Let
Consequently, ![]() \[m_1^{({\mathbb{T}})}(z) = {M^{ - 1}}{\rm{Tr}}{\mathcal G}_1^{({\mathbb{T}})}(z)\] and
\[m_1^{({\mathbb{T}})}(z) = {M^{ - 1}}{\rm{Tr}}{\mathcal G}_1^{({\mathbb{T}})}(z)\] and ![]() \[m_2^{({\mathbb{T}})}(z) = {N^{ - 1}}TrG_2^{({\mathbb{T}})}(z).\]
\[m_2^{({\mathbb{T}})}(z) = {N^{ - 1}}TrG_2^{({\mathbb{T}})}(z).\]
Our key ingredient is the anisotropic local law derived by Knowles and Yin [Reference Knowles and Yin26].
Lemma 2.1. Fix τ > 0 Assume that (1.1), (1.2), and (1.5) hold. Moreover, suppose that every edge k = 1,…, 2p satisfies a k ≥ τ and that every bulk component k = 1, …, p is regular in the sense of Assumption 1.2. Then, for all z ∈ D(τ) and any unit vectors u,v ∈ ℝM+N, there exist some small constant ε 1} > 0 and large constant D 1} > 0 such that, when N is large enough, with probability 1 – N –D1, we have
and
Proof. Equation (2.14) was proved in [Reference Knowles and Yin26, Equation (3.11)]. We need only prove (2.13). By (2.10), we have
By [Reference Knowles and Yin26, Theorem 3.6], with probability ![]() \[1 - {N^{ - {D_1}}}\], we have
\[1 - {N^{ - {D_1}}}\], we have
Therefore, by (2.12), (2.15), and (2.16), we conclude our proof. □
It is easy to derive the following corollary from Lemma 2.1.
Corollary 2.1. Under the assumptions of Lemma 2.1, with probability ![]() \[1 - {N^{ - {D_1}}}\], we have
\[1 - {N^{ - {D_1}}}\], we have
where v and u are unit vectors in ℝN and ℝM, respectively.
We use the following Lemma to characterize the rigidity of the eigenvalues within each bulk component, which can be found in [Reference Knowles and Yin26, Theorem 3.12].
Lemma 2.2. Fix τ > 0. Assume that (1.1), (1.2), and (1.5) hold. Moreover, suppose that every edge k = 1, …, 2p satisfies ak ≥ τ and that every bulk component k = 1, …, p is regular in the sense of Assumption 1.2. Recall that Nk is the number of eigenvalues within each bulk. Then, for i = 1, … ,Nk satisfying γ k,i ≥ τ and k = 1, …, p, with probability ![]() \[ 1 - {N^{ - {D_1}}}\], we have
\[ 1 - {N^{ - {D_1}}}\], we have
Within the bulk, we have a stronger result. For small τ′ > 0, define
as the bulk spectral domain. Then [Reference Knowles and Yin26, Theorem 3.15] gives the following result.
Lemma 2.3. Fix τ,τ′ > 0. Assume that (1.1), (1.2), and (1.5) hold and that the bulk component k = 1,…,2p is regular in the sense of Assumption 1.2(ii). Then, for all i=1,…,N k satisfying γ k,I ∈[a 2k+τ′, a 2k–1–τ′] (2.13) and (2.14) hold uniformly for all ![]() \[z \in D_k^b\] and, with probability
\[z \in D_k^b\] and, with probability ![]() \[1 - {N^{ - {D_1}}}\],
\[1 - {N^{ - {D_1}}}\],
As discussed in [Reference Knowles and Yin26, Remark 3.13], Lemmas 2.1 and 2.2 imply complete delocalization of the singular vectors.
Lemma 2.4. Fix τ > 0. Under the assumptions of Lemma 2.1, for any i and μ such that γ i, γ μ ≥ τ, with probability ![]() \[1 - {N^{ - {D_1}}}\], we have
\[1 - {N^{ - {D_1}}}\], we have
Proof. By (2.17), with probability ![]() \[1 - {N^{ - {D_1}}}\], we have max {Im G ii(z), Im G μμ (z)} = O(1). Choosing z 0 = E + i η 0 with η 0 = N – 1 + ε 1 and using the spectral decomposition (2.6) yields
\[1 - {N^{ - {D_1}}}\], we have max {Im G ii(z), Im G μμ (z)} = O(1). Choosing z 0 = E + i η 0 with η 0 = N – 1 + ε 1 and using the spectral decomposition (2.6) yields
 \[\sum\limits_{k = 1}^{N \wedge M} {{{\eta _0}} \over {{{(E - {\lambda _k})}^2} + \eta _0^2}}|{\xi _k}(i{)|^2} = Im{G_{ii}}({z_0}) = O(1),\](2.21)
\[\sum\limits_{k = 1}^{N \wedge M} {{{\eta _0}} \over {{{(E - {\lambda _k})}^2} + \eta _0^2}}|{\xi _k}(i{)|^2} = Im{G_{ii}}({z_0}) = O(1),\](2.21)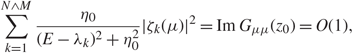 \[\sum\limits_{k = 1}^{N \wedge M} {{{\eta _0}} \over {{{(E - {\lambda _k})}^2} + \eta _0^2}}|{\zeta _k}(\mu {)|^2} = Im{G_{\mu \mu }}({z_0}) = O(1),\](2.22)
\[\sum\limits_{k = 1}^{N \wedge M} {{{\eta _0}} \over {{{(E - {\lambda _k})}^2} + \eta _0^2}}|{\zeta _k}(\mu {)|^2} = Im{G_{\mu \mu }}({z_0}) = O(1),\](2.22)
with probability ![]() \[1 - {N^{ - {D_1}}}\]. Choosing E = λ k in (2.21) and (2.22) completes the proof. □
\[1 - {N^{ - {D_1}}}\]. Choosing E = λ k in (2.21) and (2.22) completes the proof. □
3. Singular vectors near the edges
In this section we prove universality for the distributions of the edge singular vectors of Theorems 1.1 and 1.2, as well as the joint distribution between the singular values and singular vectors of Corollaries 1.1 and 1.2. The main identities on which we will rely are
 \[{\tilde G_{ij}} = \sum\limits_{\beta = 1}^{M \wedge N} {\eta \over {{{(E - {\lambda _\beta })}^2} + {\eta ^2}}}{\xi _\beta }(i){\xi _\beta }(j),\quad \quad {\tilde G_{\mu \nu }} = \sum\limits_{\beta = 1}^{M \wedge N} {\eta \over {{{(E - {\lambda _\beta })}^2} + {\eta ^2}}}{\zeta _\beta }(\mu ){\zeta _\beta }(\nu ),\](3.1)
\[{\tilde G_{ij}} = \sum\limits_{\beta = 1}^{M \wedge N} {\eta \over {{{(E - {\lambda _\beta })}^2} + {\eta ^2}}}{\xi _\beta }(i){\xi _\beta }(j),\quad \quad {\tilde G_{\mu \nu }} = \sum\limits_{\beta = 1}^{M \wedge N} {\eta \over {{{(E - {\lambda _\beta })}^2} + {\eta ^2}}}{\zeta _\beta }(\mu ){\zeta _\beta }(\nu ),\](3.1)
where ![]() \[{\tilde G_{ij}}\] and
\[{\tilde G_{ij}}\] and ![]() \[{\tilde G_{\mu \nu }}\] are defined as
\[{\tilde G_{\mu \nu }}\] are defined as
Owing to similarity, we focus our proofs on the right singular vectors. The proofs rely on three main steps.
1. Writing N ζβ (μ)ζβ η) as an integral of
 \[{\tilde G_{\mu \nu }}\] over a random interval with size O({N ε η), where ε > 0 is a small constant and η = N – 2/3 –ε0, ε 0 > 0, will be chosen later.
\[{\tilde G_{\mu \nu }}\] over a random interval with size O({N ε η), where ε > 0 is a small constant and η = N – 2/3 –ε0, ε 0 > 0, will be chosen later.2. Replacing the sharp characteristic function from step (i) with a smooth cutoff function q in terms of the Green function.
3. Using the Green function comparison argument to compare the distribution of the singular vectors between the ensembles X G and X V.
We will follow the proof strategy of [Reference Knowles and Yin24, Section 3] and slightly modify the details. Specifically, the choices of random interval in step (i) and the smooth function q in step (ii) are different due to the fact that we have more than one bulk component. The Green function comparison argument is also slightly different as we use the linearization matrix (2.6).
We mainly focus on a single bulk component, first proving the singular vector distribution and then extending the results to singular values. The results containing several bulk components will follow after minor modification. We first prove the following result for the right singular vector.
Lemma 3.1. Suppose that ![]() \[{Q_V} = {\Sigma ^{1/2}}{X_V}X_V^*{\Sigma ^{1/2}}\] satisfies Assumption 1.1. Let E G, E V denote the expectations with respect to X G and XV Consider the k th, k = 1, 2, …, p, bulk component, with l defined in (1.11) or (1.12), under Assumptions 1.2 and 1.3 for any choices of indices
\[{Q_V} = {\Sigma ^{1/2}}{X_V}X_V^*{\Sigma ^{1/2}}\] satisfies Assumption 1.1. Let E G, E V denote the expectations with respect to X G and XV Consider the k th, k = 1, 2, …, p, bulk component, with l defined in (1.11) or (1.12), under Assumptions 1.2 and 1.3 for any choices of indices ![]() \[\mu ,\nu \in {{\mathcal{I}}_2}\], there exists a δ ∈ (0, 1) such that, when
\[\mu ,\nu \in {{\mathcal{I}}_2}\], there exists a δ ∈ (0, 1) such that, when ![]() \[l \le N_k^\delta ,\] we have
\[l \le N_k^\delta ,\] we have
where θ is a smooth function in ℝ that satisfies
Near the edges, by (2.18) and (2.20), with probability ![]() \[1 - {N^{ - {D_1}}}\], we have
\[1 - {N^{ - {D_1}}}\], we have
Hence, throughout the proofs of this section, we always use the scale parameter
3.1. Proof of Lemma 3.1
In a first step, we express the singular vector entries as an integral of Green functions over a random interval, which is recorded as the following lemma.
Lemma 3.2. Under the assumptions of Lemma 3.1, there exist some small constants ε, δ > 0 satisfying
for some large constant C > C 1 (recall (3.2) for C 1) such that
where I is defined as
when (1.11) holds
when (1.12) holds. We define
where E ± : = E ± Nε η. The conclusion holds if we replace XV with XG.
Proof. We first observe that
Choose a and b such that
We also observe the elementary inequality (see the equation above Equation (6.10) of [Reference Erdös, Yau and Yin18]), for some constant C > 0,
By (3.3), (3.8), and (3.9), with probability 1 – N –D 1, we have
By (3.2), (3.3), (3.5), (3.10), and mean value theorem, we have
Define ![]() \[\lambda _t^ \pm {\kern 1pt} : = {\lambda _t} \pm {N^\varepsilon }\eta ,{\kern 1pt} t = {\alpha ^{'}},\;{\alpha ^{'}} + 1\], and by (3.8), we have
\[\lambda _t^ \pm {\kern 1pt} : = {\lambda _t} \pm {N^\varepsilon }\eta ,{\kern 1pt} t = {\alpha ^{'}},\;{\alpha ^{'}} + 1\], and by (3.8), we have
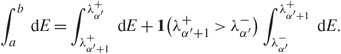 \[\int_a^b {\kern 1pt} {\rm{d}}E = \int_{\lambda _{{\alpha ^{'}} + 1}^ + }^{\lambda _{{\alpha ^{'}}}^ + } {\kern 1pt} {\rm{d}}E + {\bf{1}}(\lambda _{{\alpha ^{'}} + 1}^ + > \lambda _{{\alpha ^{'}}}^ - )\int_{\lambda _{{\alpha ^{'}}}^ - }^{\lambda _{{\alpha ^{'}r} + 1}^ + } {\kern 1pt} {\rm{d}}E.\]
\[\int_a^b {\kern 1pt} {\rm{d}}E = \int_{\lambda _{{\alpha ^{'}} + 1}^ + }^{\lambda _{{\alpha ^{'}}}^ + } {\kern 1pt} {\rm{d}}E + {\bf{1}}(\lambda _{{\alpha ^{'}} + 1}^ + > \lambda _{{\alpha ^{'}}}^ - )\int_{\lambda _{{\alpha ^{'}}}^ - }^{\lambda _{{\alpha ^{'}r} + 1}^ + } {\kern 1pt} {\rm{d}}E.\]By (3.2), (3.3), (3.11), and the mean value theorem, we have
 \[{{\mathbb{E}}^V}\theta (N{\zeta _{{\alpha ^{'}}}}(\mu ){\zeta _{{\alpha ^{'}}}}(\nu )) = {{\mathbb{E}}^V}\theta ({{N\eta } \over \pi }\int_{\lambda _{{\alpha ^{'}} + 1}^ + }^{\lambda _{{\alpha ^{'}}}^ + } {{{\zeta _{{\alpha ^{'}}}}(\mu ){\zeta _{{\alpha ^{'}}}}(\nu )} \over {{{(E - {\lambda _{{\alpha ^{'}}}})}^2} + {\eta ^2}}}{\kern 1pt} {\rm{d}}E) + o(1),\]
\[{{\mathbb{E}}^V}\theta (N{\zeta _{{\alpha ^{'}}}}(\mu ){\zeta _{{\alpha ^{'}}}}(\nu )) = {{\mathbb{E}}^V}\theta ({{N\eta } \over \pi }\int_{\lambda _{{\alpha ^{'}} + 1}^ + }^{\lambda _{{\alpha ^{'}}}^ + } {{{\zeta _{{\alpha ^{'}}}}(\mu ){\zeta _{{\alpha ^{'}}}}(\nu )} \over {{{(E - {\lambda _{{\alpha ^{'}}}})}^2} + {\eta ^2}}}{\kern 1pt} {\rm{d}}E) + o(1),\]
where we used (2.18) and (3.5). Next we can, without loss of generality, consider the case when (1.11) holds. By (3.3) and (3.5), we observe that, with probability ![]() \[1 - {N^{ - {D_1}}}\], we have
\[1 - {N^{ - {D_1}}}\], we have ![]() \[\lambda _{{\alpha ^{'}}}^ + \le {a_{2k - 1}} + {N^{ - 2/3 + \varepsilon }}\] and
\[\lambda _{{\alpha ^{'}}}^ + \le {a_{2k - 1}} + {N^{ - 2/3 + \varepsilon }}\] and ![]() \[\lambda _{{\alpha ^{'}} + 1}^ + \ge {a_{2k - 1}} - {N^{ - 2/3 + \varepsilon }}.\] By (2.18) and the choice of I in (3.6), we have
\[\lambda _{{\alpha ^{'}} + 1}^ + \ge {a_{2k - 1}} - {N^{ - 2/3 + \varepsilon }}.\] By (2.18) and the choice of I in (3.6), we have
Recall (3.1). We can split the summation as
 \[{1 \over \eta }{\tilde G_{\mu \nu }}(z) = \sum\limits_{\beta \ne {\alpha ^{'}}} {{{\zeta _\beta }(\mu ){\zeta _\beta }(\nu )} \over {{{(E - {\lambda _\beta })}^2} + {\eta ^2}}} + {{{\zeta _{{\alpha ^{'}}}}(\mu ){\zeta _{{\alpha ^{'}}}}(\nu )} \over {{{(E - {\lambda _{{\alpha ^{'}}}})}^2} + {\eta ^2}}}.\](3.12)
\[{1 \over \eta }{\tilde G_{\mu \nu }}(z) = \sum\limits_{\beta \ne {\alpha ^{'}}} {{{\zeta _\beta }(\mu ){\zeta _\beta }(\nu )} \over {{{(E - {\lambda _\beta })}^2} + {\eta ^2}}} + {{{\zeta _{{\alpha ^{'}}}}(\mu ){\zeta _{{\alpha ^{'}}}}(\nu )} \over {{{(E - {\lambda _{{\alpha ^{'}}}})}^2} + {\eta ^2}}}.\](3.12) Define ![]() \[{\mathcal A}{\kern 1pt} : = \{ \beta \ne {\alpha ^{'}}:{\lambda _\beta }\] is not in the kth bulk component}. By (3.3), with probability
\[{\mathcal A}{\kern 1pt} : = \{ \beta \ne {\alpha ^{'}}:{\lambda _\beta }\] is not in the kth bulk component}. By (3.3), with probability ![]() \[1 - {N^{ - {D_1}}}\], we have
\[1 - {N^{ - {D_1}}}\], we have
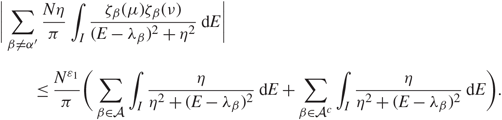 \[|\sum\limits_{\beta \ne {\alpha ^{'}}} {{N\eta } \over \pi }\int_I {{{\zeta _\beta }(\mu ){\zeta _\beta }(\nu )} \over {{{(E - {\lambda _\beta })}^2} + {\eta ^2}}}{\kern 1pt} {\rm{d}}E| \\ \quad \quad \le {{{N^{{\varepsilon _1}}}} \over \pi }(\sum\limits_{\beta \in A} \int_I {\eta \over {{\eta ^2} + {{(E - {\lambda _\beta })}^2}}}{\kern 1pt} {\rm{d}}E + \sum\limits_{\beta \in {A^c}} \int_I {\eta \over {{\eta ^2} + {{(E - {\lambda _\beta })}^2}}}{\kern 1pt} {\rm{d}}E).\](3.13)
\[|\sum\limits_{\beta \ne {\alpha ^{'}}} {{N\eta } \over \pi }\int_I {{{\zeta _\beta }(\mu ){\zeta _\beta }(\nu )} \over {{{(E - {\lambda _\beta })}^2} + {\eta ^2}}}{\kern 1pt} {\rm{d}}E| \\ \quad \quad \le {{{N^{{\varepsilon _1}}}} \over \pi }(\sum\limits_{\beta \in A} \int_I {\eta \over {{\eta ^2} + {{(E - {\lambda _\beta })}^2}}}{\kern 1pt} {\rm{d}}E + \sum\limits_{\beta \in {A^c}} \int_I {\eta \over {{\eta ^2} + {{(E - {\lambda _\beta })}^2}}}{\kern 1pt} {\rm{d}}E).\](3.13) By Assumption 1.2, with probability ![]() \[1 - {N^{{D_1}}}\], we have
\[1 - {N^{{D_1}}}\], we have
 \[{{{N^{{\varepsilon _1}}}} \over \pi }\sum\limits_{\beta \in A} \int_I {\eta \over {{\eta ^2} + {{(E - {\lambda _\beta })}^2}}}{\kern 1pt} {\rm{d}}E \le {N^{{\varepsilon _1}}}\sum\limits_{\beta \in A} {N^{ - 4/3 - {\varepsilon _0} + \varepsilon }}.\](3.14)
\[{{{N^{{\varepsilon _1}}}} \over \pi }\sum\limits_{\beta \in A} \int_I {\eta \over {{\eta ^2} + {{(E - {\lambda _\beta })}^2}}}{\kern 1pt} {\rm{d}}E \le {N^{{\varepsilon _1}}}\sum\limits_{\beta \in A} {N^{ - 4/3 - {\varepsilon _0} + \varepsilon }}.\](3.14)Define
By (3.3), with probability ![]() \[1 - {N^{ - {D_1}}}\], for some small constant 0 < δ < 1, we have
\[1 - {N^{ - {D_1}}}\], for some small constant 0 < δ < 1, we have
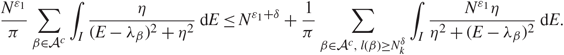 \[{{{N^{{\varepsilon _1}}}} \over \pi }\sum\limits_{\beta \in {A^c}} \int_I {\eta \over {{{(E - {\lambda _\beta })}^2} + {\eta ^2}}}{\kern 1pt} {\rm{d}}E \le {N^{{\varepsilon _1} + \delta }} + {1 \over \pi }\sum\limits_{\beta \in {A^c},{\kern 1pt} l(\beta ) \ge N_k^\delta } \int_I {{{N^{{\varepsilon _1}}}\eta } \over {{\eta ^2} + {{(E - {\lambda _\beta })}^2}}}{\kern 1pt} {\rm{d}}E.\](3.14)
\[{{{N^{{\varepsilon _1}}}} \over \pi }\sum\limits_{\beta \in {A^c}} \int_I {\eta \over {{{(E - {\lambda _\beta })}^2} + {\eta ^2}}}{\kern 1pt} {\rm{d}}E \le {N^{{\varepsilon _1} + \delta }} + {1 \over \pi }\sum\limits_{\beta \in {A^c},{\kern 1pt} l(\beta ) \ge N_k^\delta } \int_I {{{N^{{\varepsilon _1}}}\eta } \over {{\eta ^2} + {{(E - {\lambda _\beta })}^2}}}{\kern 1pt} {\rm{d}}E.\](3.14)By Assumption 1.2, (1.9), (2.18), and the assumption that δ > 2ε, it is easy to check that (see [Reference Knowles and Yin24, Equation (3.12)])
By (3.16), with probability ![]() \[1 - {N^{ - {D_1}}}\], we have
\[1 - {N^{ - {D_1}}}\], we have
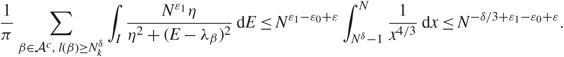 \[\frac{1}{\pi }\sum\limits_{\beta \in {{\mathcal A}^c},{\kern 1pt} l(\beta ) \ge N_k^\delta } \int_I \frac{{{N^{{\varepsilon _1}}}\eta }}{{{\eta ^2} + {{(E - {\lambda _\beta })}^2}}}{\kern 1pt} {\rm{d}}E \le {N^{{\varepsilon _1} - {\varepsilon _0} + \varepsilon }}\int_{{N^\delta } - 1}^N \frac{1}{{{x^{4/3}}}}{\kern 1pt} {\rm{d}}x \le {N^{ - \delta /3 + {\varepsilon _1} - {\varepsilon _0} + \varepsilon }}.\]
\[\frac{1}{\pi }\sum\limits_{\beta \in {{\mathcal A}^c},{\kern 1pt} l(\beta ) \ge N_k^\delta } \int_I \frac{{{N^{{\varepsilon _1}}}\eta }}{{{\eta ^2} + {{(E - {\lambda _\beta })}^2}}}{\kern 1pt} {\rm{d}}E \le {N^{{\varepsilon _1} - {\varepsilon _0} + \varepsilon }}\int_{{N^\delta } - 1}^N \frac{1}{{{x^{4/3}}}}{\kern 1pt} {\rm{d}}x \le {N^{ - \delta /3 + {\varepsilon _1} - {\varepsilon _0} + \varepsilon }}.\] Recall (3.5). We can restrict ε 1 – ε 0 + ε < 0, so that, with probability ![]() \[1 - {N^{ - {D_1}}}\], this yields
\[1 - {N^{ - {D_1}}}\], this yields
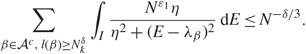 \[\sum\limits_{\beta \in {A^c},{\kern 1pt} l(\beta ) \ge N_k^\delta } \int_I {{{N^{{\varepsilon _1}}}\eta } \over {{\eta ^2} + {{(E - {\lambda _\beta })}^2}}}{\kern 1pt} {\rm{d}}E \le {N^{ - \delta /3}}.\](3.17)
\[\sum\limits_{\beta \in {A^c},{\kern 1pt} l(\beta ) \ge N_k^\delta } \int_I {{{N^{{\varepsilon _1}}}\eta } \over {{\eta ^2} + {{(E - {\lambda _\beta })}^2}}}{\kern 1pt} {\rm{d}}E \le {N^{ - \delta /3}}.\](3.17) By (3.13), (3.14), (3.15), and (3.17), with probability ![]() \[1 - {N^{ - {D_1}}}\], we have
\[1 - {N^{ - {D_1}}}\], we have
 \[|\sum\limits_{\beta \ne {\alpha ^{'}}} {{N\eta } \over \pi }\int_I {{{\zeta _\beta }(\mu ){\zeta _\beta }(\nu )} \over {{{(E - {\lambda _\beta })}^2} + {\eta ^2}}}{\kern 1pt} {\rm{d}}E| \le {N^{\delta + 2{\varepsilon _1}}}.\](3.18)
\[|\sum\limits_{\beta \ne {\alpha ^{'}}} {{N\eta } \over \pi }\int_I {{{\zeta _\beta }(\mu ){\zeta _\beta }(\nu )} \over {{{(E - {\lambda _\beta })}^2} + {\eta ^2}}}{\kern 1pt} {\rm{d}}E| \le {N^{\delta + 2{\varepsilon _1}}}.\](3.18)By (3.2), (3.3), (3.12), (3.18), and the mean value theorem, we have
 \[|{{\mathbb{E}}^V}\theta ({{N\eta } \over \pi }\int_I {{{\zeta _{{\alpha ^{'}}}}(\mu ){\zeta _{{\alpha ^{'}}}}(\nu )} \over {{{(E - {\lambda _{{\alpha ^{'}}}})}^2} + {\eta ^2}}}{\mathcal{X}}(E){\kern 1pt} {\rm{d}}E) - {{\mathbb{E}}^V}\theta ({N \over \pi }\int_I {\tilde G_{\mu \nu }}(E + i\eta ){\mathcal{X}}(E){\kern 1pt} {\rm{d}}E)| \\ \quad \quad \le {N^{{C_1}(\delta + 2{\varepsilon _1})}}{E^V}\sum\limits_{\beta \ne {\alpha ^{'}}} {{N\eta } \over \pi }\int_I {{|{\zeta _\beta }(\mu ){\zeta _\beta }(\nu )|} \over {{{(E - {\lambda _\beta })}^2} + {\eta ^2}}}X(E){\kern 1pt} {\rm{d}}E,\](3.19)
\[|{{\mathbb{E}}^V}\theta ({{N\eta } \over \pi }\int_I {{{\zeta _{{\alpha ^{'}}}}(\mu ){\zeta _{{\alpha ^{'}}}}(\nu )} \over {{{(E - {\lambda _{{\alpha ^{'}}}})}^2} + {\eta ^2}}}{\mathcal{X}}(E){\kern 1pt} {\rm{d}}E) - {{\mathbb{E}}^V}\theta ({N \over \pi }\int_I {\tilde G_{\mu \nu }}(E + i\eta ){\mathcal{X}}(E){\kern 1pt} {\rm{d}}E)| \\ \quad \quad \le {N^{{C_1}(\delta + 2{\varepsilon _1})}}{E^V}\sum\limits_{\beta \ne {\alpha ^{'}}} {{N\eta } \over \pi }\int_I {{|{\zeta _\beta }(\mu ){\zeta _\beta }(\nu )|} \over {{{(E - {\lambda _\beta })}^2} + {\eta ^2}}}X(E){\kern 1pt} {\rm{d}}E,\](3.19)where C 1 is defined in (3.2). To complete the proof, it suffices to estimate the right-hand side of (3.19). Similarly to (3.14), we have
 \[\sum\limits_{\beta \in {\mathcal{A}}} \int_I {\eta \over {{\eta ^2} + {{(E - {\lambda _\beta })}^2}}}{\kern 1pt} {\rm{d}}E \le {N^{ - 1/3 - {\varepsilon _0} + \varepsilon }}.\](3.20)
\[\sum\limits_{\beta \in {\mathcal{A}}} \int_I {\eta \over {{\eta ^2} + {{(E - {\lambda _\beta })}^2}}}{\kern 1pt} {\rm{d}}E \le {N^{ - 1/3 - {\varepsilon _0} + \varepsilon }}.\](3.20)Choose a small constant 0 < δ1 < 1 and repeat the estimation in (3.17) to obtain
 \[\sum\limits_{\beta \in {{\mathcal{A}}^c},{\kern 1pt} l(\beta ) \ge N_k^{{\delta _1}}} \int_I {\eta \over {{\eta ^2} + {{(E - {\lambda _\beta })}^2}}}{\kern 1pt} {\rm{d}}E \le {N^{ - {\delta _1}/3 + \varepsilon - {\varepsilon _0}}}.\](3.21)
\[\sum\limits_{\beta \in {{\mathcal{A}}^c},{\kern 1pt} l(\beta ) \ge N_k^{{\delta _1}}} \int_I {\eta \over {{\eta ^2} + {{(E - {\lambda _\beta })}^2}}}{\kern 1pt} {\rm{d}}E \le {N^{ - {\delta _1}/3 + \varepsilon - {\varepsilon _0}}}.\](3.21)Recall (1.11), (3.3), and (3.9). Using a discussion similar to that above Equation (3.14) of [Reference Knowles and Yin24], we conclude that
 \[\sum\limits_{\beta \in {{\mathcal{A}}^c},{\kern 1pt} l \le l(\beta ) \le N_k^{{\delta _1}}} {{N\eta } \over \pi }{{\mathbb{E}}^V}\int_I {{|{\zeta _\beta }(\mu ){\zeta _\beta }(\nu )|} \over {{{(E - {\lambda _\beta })}^2} + {\eta ^2}}}{\mathcal{X}}(E){\kern 1pt} {\rm{d}}E \\ \quad \quad \le {{\mathbb{E}}^V}\int_{{\lambda _{{\alpha ^{'}} + 1}} + {N^\varepsilon }\eta }^\infty {{{N^{{\varepsilon _1}}}\eta } \over {{{(E - {\lambda _{{\alpha ^{'}} + 1}})}^2} + {\eta ^2}}}{\kern 1pt} {\rm{d}}E \\ \quad \quad \le {N^{ - \varepsilon + {\varepsilon _1}}},\](3.22)
\[\sum\limits_{\beta \in {{\mathcal{A}}^c},{\kern 1pt} l \le l(\beta ) \le N_k^{{\delta _1}}} {{N\eta } \over \pi }{{\mathbb{E}}^V}\int_I {{|{\zeta _\beta }(\mu ){\zeta _\beta }(\nu )|} \over {{{(E - {\lambda _\beta })}^2} + {\eta ^2}}}{\mathcal{X}}(E){\kern 1pt} {\rm{d}}E \\ \quad \quad \le {{\mathbb{E}}^V}\int_{{\lambda _{{\alpha ^{'}} + 1}} + {N^\varepsilon }\eta }^\infty {{{N^{{\varepsilon _1}}}\eta } \over {{{(E - {\lambda _{{\alpha ^{'}} + 1}})}^2} + {\eta ^2}}}{\kern 1pt} {\rm{d}}E \\ \quad \quad \le {N^{ - \varepsilon + {\varepsilon _1}}},\](3.22)
where we have used the fact that ![]() \[\beta \in {{\mathcal{A}}^c}\] and
\[\beta \in {{\mathcal{A}}^c}\] and ![]() \[\;l \lt l(\beta ) \le N_k^{{\delta _1}}\] imply that
\[\;l \lt l(\beta ) \le N_k^{{\delta _1}}\] imply that ![]() \[{\lambda _\beta } \le {\lambda _{{\alpha ^{'}} + 1}}\] It is notable that the above bound is independent of δ. It remains to estimate the summation of the terms when
\[{\lambda _\beta } \le {\lambda _{{\alpha ^{'}} + 1}}\] It is notable that the above bound is independent of δ. It remains to estimate the summation of the terms when ![]() \[\beta \in {{\mathcal{A}}^c}\] and l(β) < l. For a given constant, ε′ satisfies
\[\beta \in {{\mathcal{A}}^c}\] and l(β) < l. For a given constant, ε′ satisfies
We partition ![]() \[I = {I_1} \cup {I_2}\] with
\[I = {I_1} \cup {I_2}\] with ![]() \[{I_1} \cap {I_2} = \emptyset \], where
\[{I_1} \cap {I_2} = \emptyset \], where
By (3.3) and (3.24), using a similar discussion to that used for (3.22), we have
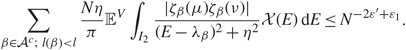 \[\sum\limits_{\beta \in {{\mathcal{A}}^c};\;l(\beta ) \lt l} {{N\eta } \over \pi }{{\mathbb{E}}^V}\int_{{I_2}} {{|{\zeta _\beta }(\mu ){\zeta _\beta }(\nu )|} \over {{{(E - {\lambda _\beta })}^2} + {\eta ^2}}}{\mathcal{X}}(E){\kern 1pt} {\rm{d}}E \le {N^{ - 2{\varepsilon ^{'}} + {\varepsilon _1}}}.\]
\[\sum\limits_{\beta \in {{\mathcal{A}}^c};\;l(\beta ) \lt l} {{N\eta } \over \pi }{{\mathbb{E}}^V}\int_{{I_2}} {{|{\zeta _\beta }(\mu ){\zeta _\beta }(\nu )|} \over {{{(E - {\lambda _\beta })}^2} + {\eta ^2}}}{\mathcal{X}}(E){\kern 1pt} {\rm{d}}E \le {N^{ - 2{\varepsilon ^{'}} + {\varepsilon _1}}}.\] It is easy to check that on I 1 when ![]() \[{\lambda _{{\alpha ^{'}} + 1}} \le {\lambda _{{\alpha ^{'}}}} \lt {\lambda _\beta }\], we have (see (3.15) of [Reference Knowles and Yin24])
\[{\lambda _{{\alpha ^{'}} + 1}} \le {\lambda _{{\alpha ^{'}}}} \lt {\lambda _\beta }\], we have (see (3.15) of [Reference Knowles and Yin24])
By Lemma 2.2, the above equation holds with probability ![]() \[1 - {N^{ - {D_1}}}\]. By (3.3), (3.25), and a discussion similar to that used in [Reference Knowles and Yin24, Equation (3.16)], we have
\[1 - {N^{ - {D_1}}}\]. By (3.3), (3.25), and a discussion similar to that used in [Reference Knowles and Yin24, Equation (3.16)], we have
 \[\sum\limits_{\beta \in {{\mathcal{A}}^c},{\kern 1pt} l(\beta ) \le l} {{N\eta } \over \pi }{{\mathbb{E}}^V}\int_{{I_1}} {{|{\zeta _\beta }(\mu ){\zeta _\beta }(\nu )|} \over {{{(E - {\lambda _\beta })}^2} + {\eta ^2}}}{\mathcal{X}}(E){\kern 1pt} {\rm{d}}E \le {{\mathbb{E}}^V}\int_{{I_1}} {{{N^{{\varepsilon _1} + 2\varepsilon }}{\eta ^2}} \over {{{({\lambda _{{\alpha ^{'}} + 1}} - {\lambda _{{\alpha ^{'}}}})}^2} + {\eta ^2}}}{\kern 1pt} {\rm{d}}E \\ \le {{\mathcal{E}}^V}{\bf{1}}(|{\lambda _{\alpha ' + 1}} - {\lambda _{\alpha '}}| \le {N^{ - 1/3}}{\eta ^{1/2}}) + {N^{ - {D_1} + {\varepsilon _1} + 3\varepsilon }} \\ \le {N^{ - {\varepsilon _0}/2 + 3\varepsilon }}.\](3.26)
\[\sum\limits_{\beta \in {{\mathcal{A}}^c},{\kern 1pt} l(\beta ) \le l} {{N\eta } \over \pi }{{\mathbb{E}}^V}\int_{{I_1}} {{|{\zeta _\beta }(\mu ){\zeta _\beta }(\nu )|} \over {{{(E - {\lambda _\beta })}^2} + {\eta ^2}}}{\mathcal{X}}(E){\kern 1pt} {\rm{d}}E \le {{\mathbb{E}}^V}\int_{{I_1}} {{{N^{{\varepsilon _1} + 2\varepsilon }}{\eta ^2}} \over {{{({\lambda _{{\alpha ^{'}} + 1}} - {\lambda _{{\alpha ^{'}}}})}^2} + {\eta ^2}}}{\kern 1pt} {\rm{d}}E \\ \le {{\mathcal{E}}^V}{\bf{1}}(|{\lambda _{\alpha ' + 1}} - {\lambda _{\alpha '}}| \le {N^{ - 1/3}}{\eta ^{1/2}}) + {N^{ - {D_1} + {\varepsilon _1} + 3\varepsilon }} \\ \le {N^{ - {\varepsilon _0}/2 + 3\varepsilon }}.\](3.26)By (3.20), (3.21), (3.22), (3.23), and (3.26), we conclude the proof of (3.19). It is clear that our proof still applies when we replace X V with X G □
In a second step, we write the sharp indicator function of (3.7) as a some smooth function q of ![]() \[{\tilde G_{\mu \nu }}\]. To be consistent with the proof of Lemma 3.2, we consider the bulk edge a 2k – 1. Define
\[{\tilde G_{\mu \nu }}\]. To be consistent with the proof of Lemma 3.2, we consider the bulk edge a 2k – 1. Define
We define a smooth cutoff function q ≡ q α′: ℝ → ℝ+ as
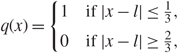 \[q(x) = \left( {\matrix{ 1 & {{\rm{if}}|x - l| \le {\textstyle{1 \over 3}},} \cr 0 & {{\rm{if}}|x - l| \ge {\textstyle{2 \over 3}},} \cr } } \right.\](3.27)
\[q(x) = \left( {\matrix{ 1 & {{\rm{if}}|x - l| \le {\textstyle{1 \over 3}},} \cr 0 & {{\rm{if}}|x - l| \ge {\textstyle{2 \over 3}},} \cr } } \right.\](3.27)where l is defined in (1.11). We also let Q 1=Y*Y
Lemma 3.3. For ε given in (3.5), define
where ![]() \[{E_U} : = {a_{2k - 1}} + 2{N^{ - 2/3 + \varepsilon }}.\], and define
\[{E_U} : = {a_{2k - 1}} + 2{N^{ - 2/3 + \varepsilon }}.\], and define ![]() \[\tilde \eta : = {N^{ - 2/3 - 9{\varepsilon _0}}},\] where ε 0 is defined in (3.4). Then
\[\tilde \eta : = {N^{ - 2/3 - 9{\varepsilon _0}}},\] where ε 0 is defined in (3.4). Then
where I is defined in (3.6) and ‘*’ is the convolution operator.
Proof. For any E 1 < E 2, denote the number of eigenvalues of Q 1 in [E 1, E 2] by
Recall (3.6) and (3.7). It is easy to check that, with probability ![]() \[1 - {N^{ - {D_1}}}\], we have
\[1 - {N^{ - {D_1}}}\], we have
 \[\begin{align} & N\int_I {\tilde G_{\mu \nu }}(z)\mathcal {X}(E) {\rm{d}}E = N\int_I {\tilde G_{\mu \nu }}(z){\bf{1}}(N({E^ - },{E_U}) = l) {\rm{d}}E \\& \quad\quad\quad\quad\quad\quad\quad\quad\quad = N\int_I {\tilde G_{\mu \nu }}(z)q[\rm {Tr}{\mathcal {X}_E}({Q_1})] {\rm{d}}E,\end{align}\](3.30)
\[\begin{align} & N\int_I {\tilde G_{\mu \nu }}(z)\mathcal {X}(E) {\rm{d}}E = N\int_I {\tilde G_{\mu \nu }}(z){\bf{1}}(N({E^ - },{E_U}) = l) {\rm{d}}E \\& \quad\quad\quad\quad\quad\quad\quad\quad\quad = N\int_I {\tilde G_{\mu \nu }}(z)q[\rm {Tr}{\mathcal {X}_E}({Q_1})] {\rm{d}}E,\end{align}\](3.30)
where, for the second equality, we used (2.18) and Assumption 1.2. We use the following Lemma to estimate (3.29) by its delta approximation smoothed on the scale ![]() \[\tilde \eta \]. The proof is given in the supplementary material [Reference Ding14].
\[\tilde \eta \]. The proof is given in the supplementary material [Reference Ding14].
Lemma 3.4
For ![]() \[t = {N^{ - 2/3 - 3{\varepsilon _0}}},\] there exists some constant C, and with probability
\[t = {N^{ - 2/3 - 3{\varepsilon _0}}},\] there exists some constant C, and with probability ![]() \[1 - {N^{ - {D_1}}}\], for any E satisfying
\[1 - {N^{ - {D_1}}}\], for any E satisfying
we have
By Equation (A.7) of [Reference Knowles and Yin26], for any z ∈ D(τ) defined in (2.1), we have
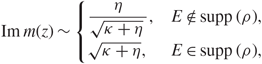 \[{\rm Im} m(z) \sim \left\{ {\matrix{ {{\eta \over {\sqrt {\kappa + \eta } }},} & {E \notin {\rm supp} (\rho ),} \cr {\sqrt {\kappa + \eta } ,} & {E \in {\rm supp} (\rho ),} \cr } } \right.\](3.32)
\[{\rm Im} m(z) \sim \left\{ {\matrix{ {{\eta \over {\sqrt {\kappa + \eta } }},} & {E \notin {\rm supp} (\rho ),} \cr {\sqrt {\kappa + \eta } ,} & {E \in {\rm supp} (\rho ),} \cr } } \right.\](3.32)
where κ := |E – a 2k – 1. When μ = v, with probability ![]() \[1 - {N^{ - {D_1}}}\], we have
\[1 - {N^{ - {D_1}}}\], we have
 \[\begin{align} & \mathop {\sup }\limits_{E \in I} |{\tilde G_{\mu \mu }}(E + {\rm{i}}\eta )| = \mathop {\sup }\limits_{E \in I} |Im{G_{\mu \mu }}(z)| \\ & \quad\quad\quad\quad\quad\quad\quad \le \mathop {\sup }\limits_{E \in I} (Im|{G_{\mu \mu }}(z) - {m_{}}(z)| + |Im{m_{}}(z)|) \\ & \quad\quad\quad\quad\quad\quad\quad \le {N^{ - 1/3 + {\varepsilon _0} + 2\varepsilon }},\end{align}\]
\[\begin{align} & \mathop {\sup }\limits_{E \in I} |{\tilde G_{\mu \mu }}(E + {\rm{i}}\eta )| = \mathop {\sup }\limits_{E \in I} |Im{G_{\mu \mu }}(z)| \\ & \quad\quad\quad\quad\quad\quad\quad \le \mathop {\sup }\limits_{E \in I} (Im|{G_{\mu \mu }}(z) - {m_{}}(z)| + |Im{m_{}}(z)|) \\ & \quad\quad\quad\quad\quad\quad\quad \le {N^{ - 1/3 + {\varepsilon _0} + 2\varepsilon }},\end{align}\]where we have used (2.17) and (3.32). When μ ≠ ν, we use the identity
 \[{\tilde G_{\mu \nu }} = \eta \sum\limits_{k = M + 1}^{M + N} {G_{\mu k}}{\overline G _{\nu k}}.\]
\[{\tilde G_{\mu \nu }} = \eta \sum\limits_{k = M + 1}^{M + N} {G_{\mu k}}{\overline G _{\nu k}}.\] By (2.17) and (3.32), with probability ![]() \[1 - {N^{ - {D_1}}}\], we have
\[1 - {N^{ - {D_1}}}\], we have ![]() \[\mathop {\sup }\nolimits_{E \in I} |{\tilde G_{\mu \nu }}(z)| \le {N^{ - 1/3 + {\varepsilon _0} + 2\varepsilon }}\]. Therefore, for E ∈ I, with probability
\[\mathop {\sup }\nolimits_{E \in I} |{\tilde G_{\mu \nu }}(z)| \le {N^{ - 1/3 + {\varepsilon _0} + 2\varepsilon }}\]. Therefore, for E ∈ I, with probability ![]() \[1 - {N^{ - {D_1}}}\], we have
\[1 - {N^{ - {D_1}}}\], we have
Recall (3.27). By (3.30), (3.31), (3.33), and the smoothness of q, with probability ![]() \[1 - {N^{ - {D_1}}}\], we have
\[1 - {N^{ - {D_1}}}\], we have
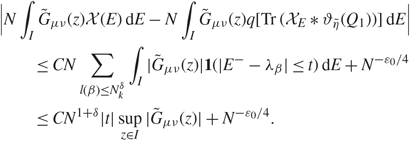 \[\begin{align} & \biggl|N\int_I {\tilde G_{\mu \nu }}(z){\mathcal X}(E) {\rm{d}}E - N\int_I {\tilde G_{\mu \nu }}(z)q[Tr({X_E}*{\vartheta _{\tilde \eta }}({Q_1}))] {\rm{d}}E\biggr| \\ & \quad \le CN\sum\limits_{l(\beta ) \le N_k^\delta } \int_I |{\tilde G_{\mu \nu }}(z)|{\bf{1}}(|{E^ - } - {\lambda _\beta }| \le t) {\rm{d}}E + {N^{ - {\varepsilon _0}/4}} \\ & \quad \le C{N^{1 + \delta }}|t|\mathop {\sup }\limits_{z \in I} |{\tilde G_{\mu \nu }}(z)| + {N^{ - {\varepsilon _0}/4}}.\end{align}\](3.34)
\[\begin{align} & \biggl|N\int_I {\tilde G_{\mu \nu }}(z){\mathcal X}(E) {\rm{d}}E - N\int_I {\tilde G_{\mu \nu }}(z)q[Tr({X_E}*{\vartheta _{\tilde \eta }}({Q_1}))] {\rm{d}}E\biggr| \\ & \quad \le CN\sum\limits_{l(\beta ) \le N_k^\delta } \int_I |{\tilde G_{\mu \nu }}(z)|{\bf{1}}(|{E^ - } - {\lambda _\beta }| \le t) {\rm{d}}E + {N^{ - {\varepsilon _0}/4}} \\ & \quad \le C{N^{1 + \delta }}|t|\mathop {\sup }\limits_{z \in I} |{\tilde G_{\mu \nu }}(z)| + {N^{ - {\varepsilon _0}/4}}.\end{align}\](3.34)Using a discussion similar to that used for (3.13), by (3.2) and (3.5), we complete the proof. □
In the final step, we use the Green function comparison argument to prove the following lemma, whose proof is given in Section 3.2.
Lemma 3.5. Under the assumptions of Lemma 3.3, we have
3.2. The Green function comparsion argument
In this section we prove Lemma 3.5 using the Green function comparison argument. At the end of this section we discuss how we can extend Lemma 3.1 to Theorem 1.1 and Theorem 1.2. By the orthonormal properties of ξ and ζ, and (2.6), we have
 \[{\tilde G_{ij}} = \eta \sum\limits_{k = 1}^M {G_{ik}}{\overline G _{jk}},\quad \quad {\tilde G_{\mu \nu }} = \eta \sum\limits_{k = M + 1}^{M + N} {G_{\mu k}}{\overline G _{\nu k}}.\](3.35)
\[{\tilde G_{ij}} = \eta \sum\limits_{k = 1}^M {G_{ik}}{\overline G _{jk}},\quad \quad {\tilde G_{\mu \nu }} = \eta \sum\limits_{k = M + 1}^{M + N} {G_{\mu k}}{\overline G _{\nu k}}.\](3.35) By (2.17), with probability ![]() \[1 - {N^{ - {D_1}}}\], we have
\[1 - {N^{ - {D_1}}}\], we have
We first drop the all diagonal terms in (3.35).
Lemma 3.6. Recall that E U = a 2k – 1 + 2N – 2/3 + ε and ![]() \[\tilde \eta = {N^{ - 2/3 - 9{\varepsilon _0}}}\]. We have
\[\tilde \eta = {N^{ - 2/3 - 9{\varepsilon _0}}}\]. We have
where
 \[x(E) : = {{N\eta } \over \pi }\sum\limits_{k = M + 1, k \ne \mu ,\nu }^{M + N} {X_{\mu \nu ,k}}(E + {\rm{i}}\eta ),\quad \quad y(E) : = {{\tilde \eta } \over \pi }\int_{{E^ - }}^{{E_U}} \sum\limits_k \sum\limits_{\beta \ne k} {X_{\beta \beta ,k}}(E + {\rm{i}}\tilde \eta ) {\rm{d}}E,\](3.38)
\[x(E) : = {{N\eta } \over \pi }\sum\limits_{k = M + 1, k \ne \mu ,\nu }^{M + N} {X_{\mu \nu ,k}}(E + {\rm{i}}\eta ),\quad \quad y(E) : = {{\tilde \eta } \over \pi }\int_{{E^ - }}^{{E_U}} \sum\limits_k \sum\limits_{\beta \ne k} {X_{\beta \beta ,k}}(E + {\rm{i}}\tilde \eta ) {\rm{d}}E,\](3.38)
and ![]() \[{X_{\mu \nu ,k}} : = {G_{\mu k}}{\overline G _{\nu k}}\]. The conclusion holds if we replace X V with X G.
\[{X_{\mu \nu ,k}} : = {G_{\mu k}}{\overline G _{\nu k}}\]. The conclusion holds if we replace X V with X G.
Proof. We first observe that, by (3.36), with probability ![]() \[1 - {N^{ - {D_1}}}\], we have
\[1 - {N^{ - {D_1}}}\], we have
which implies that
By (3.35) and (3.36), with probability ![]() \[1 - {N^{ - {D_1}}}\], we have
\[1 - {N^{ - {D_1}}}\], we have
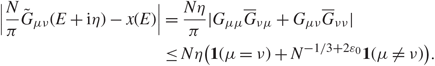 \[|{N \over \pi }{\tilde G_{\mu \nu }}(E + {\rm{i}}\eta ) - x(E)| = {{N\eta } \over \pi }|{G_{\mu \mu }}{\overline G _{\nu \mu }} + {G_{\mu \nu }}{\overline G _{\nu \nu }}| \\ \quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad \le N\eta ({\bf{1}}(\mu = \nu ) + {N^{ - 1/3 + 2{\varepsilon _0}}}{\bf{1}}(\mu \ne \nu )).\](3.41)
\[|{N \over \pi }{\tilde G_{\mu \nu }}(E + {\rm{i}}\eta ) - x(E)| = {{N\eta } \over \pi }|{G_{\mu \mu }}{\overline G _{\nu \mu }} + {G_{\mu \nu }}{\overline G _{\nu \nu }}| \\ \quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad \le N\eta ({\bf{1}}(\mu = \nu ) + {N^{ - 1/3 + 2{\varepsilon _0}}}{\bf{1}}(\mu \ne \nu )).\](3.41)By Equations (5.11) and (6.42) of [Reference Ding and Yang16], we have
 \[{\rm Tr}({{\mathcal X}_E}*{\vartheta _{\tilde \eta }}({Q_1})) = {N \over \pi }\int_{{E^ - }}^{{E_U}} Im\,{m_2}(w + {\rm{i}}\tilde \eta ) {\rm{d}}w,\quad \quad \sum\limits_{\mu \nu } |{G_{\mu \nu }}(w + {\rm{i}}\tilde \eta {)|^2} = {{N\,Im\,{m_2}(w + {\rm{i}}\tilde \eta )} \over {\tilde \eta }}.\](3.42)
\[{\rm Tr}({{\mathcal X}_E}*{\vartheta _{\tilde \eta }}({Q_1})) = {N \over \pi }\int_{{E^ - }}^{{E_U}} Im\,{m_2}(w + {\rm{i}}\tilde \eta ) {\rm{d}}w,\quad \quad \sum\limits_{\mu \nu } |{G_{\mu \nu }}(w + {\rm{i}}\tilde \eta {)|^2} = {{N\,Im\,{m_2}(w + {\rm{i}}\tilde \eta )} \over {\tilde \eta }}.\](3.42)Therefore, we have
 \[{\rm Tr}({{\mathcal X}_E}*{\vartheta _{\tilde \eta }}({Q_1})) - y(E) = {{\tilde \eta } \over \pi }\int_{{E^ - }}^{{E_U}} \sum\limits_{\beta = M + 1}^{M + N} |{G_{\beta \beta }}{|^2} {\rm{d}}w.\](3.43)
\[{\rm Tr}({{\mathcal X}_E}*{\vartheta _{\tilde \eta }}({Q_1})) - y(E) = {{\tilde \eta } \over \pi }\int_{{E^ - }}^{{E_U}} \sum\limits_{\beta = M + 1}^{M + N} |{G_{\beta \beta }}{|^2} {\rm{d}}w.\](3.43)By (3.43), the mean value theorem, and the fact that q is smooth enough, we have
Therefore, by the mean value theorem, (3.2), (3.5), (3.39), (3.40), (3.41), and (3.44), we complete the proof. □
To prove Lemma 3.5, by (3.37), it suffices to prove that
We use the Green function comparison argument to prove (3.45), where we follow the basic approach of [Reference Ding and Yang16, Section 6] and [Reference Knowles and Yin24, Section 3.1]. Define a bijective ordering map Φ on the index set, where
Recall that we relabel ![]() \[{X^V} = (({X_V}{)_{i{\mu _1}}},i \in {{\mathcal{I}}_1}, {\mu _1} \in {{\mathcal{I}}_2})\], and similarly for X G. For any 1 ≤ γ ≤ γmax, we define the matrix
\[{X^V} = (({X_V}{)_{i{\mu _1}}},i \in {{\mathcal{I}}_1}, {\mu _1} \in {{\mathcal{I}}_2})\], and similarly for X G. For any 1 ≤ γ ≤ γmax, we define the matrix ![]() \[{X_\gamma } = \left( {x_{i{\mu _1}}^\gamma } \right)\] such that
\[{X_\gamma } = \left( {x_{i{\mu _1}}^\gamma } \right)\] such that ![]() \[x_{i{\mu _1}}^\gamma = X_{i{\mu _1}}^G\] if Φ (i, μ1) > γ and
\[x_{i{\mu _1}}^\gamma = X_{i{\mu _1}}^G\] if Φ (i, μ1) > γ and ![]() \[x_{i{\mu _1}}^\gamma = X_{i{\mu _1}}^V\] otherwise. Note that X 0 = X G and X γ max = X V. With the above definitions, we have
\[x_{i{\mu _1}}^\gamma = X_{i{\mu _1}}^V\] otherwise. Note that X 0 = X G and X γ max = X V. With the above definitions, we have
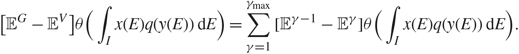 \[[{{\mathbb{E}}^G} - {{\mathbb{E}}^V}]\theta (\int_I x(E)q(y(E)) {\rm{d}}E) = \sum\limits_{\gamma = 1}^{{\gamma _{\max }}} [{{\mathbb{E}}^{\gamma - 1}} - {{\mathbb{E}}^\gamma }]\theta (\int_I x(E)q(y(E)) {\rm{d}}E).\]
\[[{{\mathbb{E}}^G} - {{\mathbb{E}}^V}]\theta (\int_I x(E)q(y(E)) {\rm{d}}E) = \sum\limits_{\gamma = 1}^{{\gamma _{\max }}} [{{\mathbb{E}}^{\gamma - 1}} - {{\mathbb{E}}^\gamma }]\theta (\int_I x(E)q(y(E)) {\rm{d}}E).\]For simplicity, we rewrite the above equation as
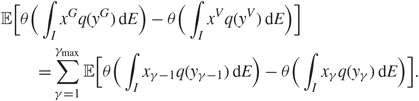 \[{\mathbb{E}}[\theta (\int_I {x^G}q({y^G}) {\rm{d}}E) - \theta (\int_I {x^V}q({y^V}) {\rm{d}}E)] \\ \quad \quad = \sum\limits_{\gamma = 1}^{{\gamma _{\max }}} {\mathbb{E}}[\theta (\int_I {x_{\gamma - 1}}q({y_{\gamma - 1}}) {\rm{d}}E) - \theta (\int_I {x_\gamma }q({y_\gamma }) {\rm{d}}E)].\]
\[{\mathbb{E}}[\theta (\int_I {x^G}q({y^G}) {\rm{d}}E) - \theta (\int_I {x^V}q({y^V}) {\rm{d}}E)] \\ \quad \quad = \sum\limits_{\gamma = 1}^{{\gamma _{\max }}} {\mathbb{E}}[\theta (\int_I {x_{\gamma - 1}}q({y_{\gamma - 1}}) {\rm{d}}E) - \theta (\int_I {x_\gamma }q({y_\gamma }) {\rm{d}}E)].\] The key step of the Green function comparison argument is to use the Lindeberg replacement strategy. We focus on the indices ![]() \[s,t \in {\mathcal{I}}\]; the special case
\[s,t \in {\mathcal{I}}\]; the special case ![]() \[\mu ,\nu \in {{\mathcal{I}}_2}\] follows. Define Y γ := Σ1/2 X γ and
\[\mu ,\nu \in {{\mathcal{I}}_2}\] follows. Define Y γ := Σ1/2 X γ and
 \[{H^\gamma } : = \left( {\matrix{ 0 & {{z^{1/2}}{Y_\gamma }} \cr {{z^{1/2}}Y_\gamma ^*} & 0 \cr } } \right),\quad \quad {G^\gamma } : = {\left( {\matrix{ { - zI} & {{z^{1/2}}{Y_\gamma }} \cr {{z^{1/2}}Y_\gamma ^*} & { - zI} \cr } } \right)^{ - 1}}.\](3.46)
\[{H^\gamma } : = \left( {\matrix{ 0 & {{z^{1/2}}{Y_\gamma }} \cr {{z^{1/2}}Y_\gamma ^*} & 0 \cr } } \right),\quad \quad {G^\gamma } : = {\left( {\matrix{ { - zI} & {{z^{1/2}}{Y_\gamma }} \cr {{z^{1/2}}Y_\gamma ^*} & { - zI} \cr } } \right)^{ - 1}}.\](3.46) As Σ is diagonal, for each fixed γ, H γ and H γ–1 differ only at the (i, μ 1) and (μ 1, i) elements, where Φ (i, μ1) = γ. Then we define the ![]() \[(N + M) \times (N + M)\] matrices V and W by
\[(N + M) \times (N + M)\] matrices V and W by
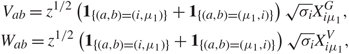 \[{V_{ab}} = {z^{1/2}}\left( {{{\bf{1}}_{\{ (a,b) = (i,{\mu _1})\} }} + {{\bf{1}}_{\{ (a,b) = ({\mu _1},i)\} }}} \right)\sqrt {{\sigma _i}} X_{i{\mu _1}}^G, \\ {W_{ab}} = {z^{1/2}}\left( {{{\bf{1}}_{\{ (a,b) = (i,{\mu _1})\} }} + {{\bf{1}}_{\{ (a,b) = ({\mu _1},i)\} }}} \right)\sqrt {{\sigma _i}} X_{i{\mu _1}}^V,\]
\[{V_{ab}} = {z^{1/2}}\left( {{{\bf{1}}_{\{ (a,b) = (i,{\mu _1})\} }} + {{\bf{1}}_{\{ (a,b) = ({\mu _1},i)\} }}} \right)\sqrt {{\sigma _i}} X_{i{\mu _1}}^G, \\ {W_{ab}} = {z^{1/2}}\left( {{{\bf{1}}_{\{ (a,b) = (i,{\mu _1})\} }} + {{\bf{1}}_{\{ (a,b) = ({\mu _1},i)\} }}} \right)\sqrt {{\sigma _i}} X_{i{\mu _1}}^V,\]so that H γ and H γ–1 can be written as
for some N + M) × (N + M) matrix O satisfying ![]() \[{O_{i{\mu _1}}} = {O_{{\mu _1}i}} = 0,\] with O independent of V and W. Define
\[{O_{i{\mu _1}}} = {O_{{\mu _1}i}} = 0,\] with O independent of V and W. Define
With the above definitions, we can write
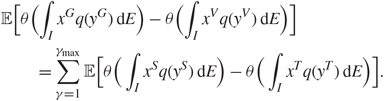 \[{\mathcal{E}}[\theta (\int_I {x^G}q({y^G}) {\rm{d}}E) - \theta (\int_I {x^V}q({y^V}) {\rm{d}}E)] \\ \quad \quad = \sum\limits_{\gamma = 1}^{{\gamma _{\max }}} {\mathcal{E}}[\theta (\int_I {x^S}q({y^S}) {\rm{d}}E) - \theta (\int_I {x^T}q({y^T}) {\rm{d}}E)].\](3.48)
\[{\mathcal{E}}[\theta (\int_I {x^G}q({y^G}) {\rm{d}}E) - \theta (\int_I {x^V}q({y^V}) {\rm{d}}E)] \\ \quad \quad = \sum\limits_{\gamma = 1}^{{\gamma _{\max }}} {\mathcal{E}}[\theta (\int_I {x^S}q({y^S}) {\rm{d}}E) - \theta (\int_I {x^T}q({y^T}) {\rm{d}}E)].\](3.48)The comparison argument is based on the resolvent expansion
For any integer m > 0, by Equation (6.11) of [Reference Ding and Yang16], we have
Define
In [Reference Knowles and Yin24], the discussion relied on a crucial parameter (see [Reference Knowles and Yin24, Equation (3.32)]), which counts the maximum number of diagonal resolvent elements in Δ X μ ν, k. We will follow this strategy using a different counting parameter, and, furthermore, use (3.50) and (3.51) as our key ingredients. Our discussion is slightly easier due to the loss of a free index (i.e. i ≠ μ 1).
Inserting (3.49) into (3.52), by (3.50) and (3.51), we find that there exists a random variable A 1, which depends on the randomness only through O and the first two moments of ![]() \[X_{i{\mu _1}}^G\]. Taking the partial expectation with respect to the (i, μ 1)th entry of X G(recall they are i.i.d.), by (1.2), we have the following result.
\[X_{i{\mu _1}}^G\]. Taking the partial expectation with respect to the (i, μ 1)th entry of X G(recall they are i.i.d.), by (1.2), we have the following result.
Lemma 3.7. Recall (2.7), and let 𝔼γ be the partial expectation with respect to ![]() \[X_{i{\mu _1}}^G\]. Then there exists some constant C > 0, and with probability
\[X_{i{\mu _1}}^G\]. Then there exists some constant C > 0, and with probability ![]() \[1 - {N^{ - {D_1}}}\], we have
\[1 - {N^{ - {D_1}}}\], we have
where s counts the maximum number of resolvent elements in ΔX μ ν, k involving the index μ 1 and is defined as
Proof. Inserting (3.49) into (3.52), the terms in the expansion containing ![]() \[X_{i{\mu _1}}^G\] and
\[X_{i{\mu _1}}^G\] and ![]() \[{(X_{i{\mu _1}}^G)^2}\] will be included in A 1; we consider only the terms containing
\[{(X_{i{\mu _1}}^G)^2}\] will be included in A 1; we consider only the terms containing ![]() \[{(X_{i{\mu _1}}^G)^m}, m \ge 3\]. We consider m = 3 and discuss the terms
\[{(X_{i{\mu _1}}^G)^m}, m \ge 3\]. We consider m = 3 and discuss the terms
By (3.50), we have
In the worst scenario, ![]() \[{R_{{b_1}{a_2}}}\] and
\[{R_{{b_1}{a_2}}}\] and ![]() \[{R_{{b_2}{a_3}}}\] are assumed to be the diagonal entries of R. Similarly, we have
\[{R_{{b_2}{a_3}}}\] are assumed to be the diagonal entries of R. Similarly, we have
and the worst scenario is the case when ![]() \[{R_{{b_1}{a_2}}}\] is a diagonal term. As μ, ν ≠ i always holds and there are only a finite number of terms in the summation, by (1.2) and (3.36), for some constant C, we have
\[{R_{{b_1}{a_2}}}\] is a diagonal term. As μ, ν ≠ i always holds and there are only a finite number of terms in the summation, by (1.2) and (3.36), for some constant C, we have
Similarly, we have
The cases in which 4 ≤ m ≤ 8 can be handled similarly. This completes the proof. □
Lemma 3.5 follows from the following lemma. Recall (3.38), and define
Lemma 3.8. For any fixed μ, ν, and μ, there exists a random variable A, which depends on the randomness only through O and the first two moments of XG, such that
where t := |μ, ν ∩ μ 1|.
The proof of Lemma 3.8 given in the supplementary material [Reference Ding14]. We now show how Lemma 3.8 implies Lemma 3.5.
Proof of Lemma 3.5. It is easy to check that Lemma 3.8 still holds when we replace S with T. Note that in (3.48) there are O(N) terms when t = 1 and O(N 2) terms when t = 0. By (3.54), we have
where we have used the assumption that the first two moments of X V are the same as those of X G. Combine with (3.37) to complete the proof. □
It is clear that our proof can be extended to the left singular vectors. For the proof of Theorem 1.1, the only difference is that we use the mean value theorem in ℝ2 whenever it is needed. Moreover, for the proof of Theorem 1.2, we need to use n intervals defined by
3.3. Extension to singular values
In this section we discuss how the arguments of Section 3.2 can be applied to the general function θ defined in (1.15) containing singular values. We mainly focus on discussing the proof of Corollary 1.1.
On the one hand, similarly to Lemma 3.3, we can write the singular values in terms of an integral of smooth functions of Green functions. Using the comparison argument with θ ∈ ℝ3 and the mean value theorem in ℝ3 completes our proof. Similar discussions and results have been derived in [Reference Erdös, Yau and Yin18, Corollary 6.2 and Theorem 6.3]. For completeness, we basically follow the strategy in [Reference Knowles and Yin24, Section 4] to prove Corollary 1.1. The basic idea is to write the function θ in terms of Green functions by using integration by parts. We mainly look at the right edge of the kth bulk component.
Proof of Corollary 1.1. Let F V be the law of λ α′, and consider a smooth function θ: ℝ→ℝ For δ defined in Lemma 3.2, when ![]() \[l \le N_k^\delta \], by (1.14) and (2.18), it is easy to check that
\[l \le N_k^\delta \], by (1.14) and (2.18), it is easy to check that
where ϖ := ϖ2k – 1 and I is defined in (3.6). Using integration by parts on (3.55), we have
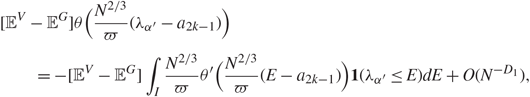 \[[{{\mathcal{E}}^V} - {{\mathcal{E}}^G}]\theta ({{{N^{2/3}}} \over \varpi }({\lambda _{{\alpha ^{'}}}} - {a_{2k - 1}})) \\ \quad \quad = - [{{\mathcal{E}}^V} - {{\mathcal{E}}^G}]\int_I {{{N^{2/3}}} \over \varpi }{\theta ^{'}}({{{N^{2/3}}} \over \varpi }(E - {a_{2k - 1}})){\bf{1}}({\lambda _{{\alpha ^{'}}}} \le E)dE + O({N^{ - {D_1}}}),\]
\[[{{\mathcal{E}}^V} - {{\mathcal{E}}^G}]\theta ({{{N^{2/3}}} \over \varpi }({\lambda _{{\alpha ^{'}}}} - {a_{2k - 1}})) \\ \quad \quad = - [{{\mathcal{E}}^V} - {{\mathcal{E}}^G}]\int_I {{{N^{2/3}}} \over \varpi }{\theta ^{'}}({{{N^{2/3}}} \over \varpi }(E - {a_{2k - 1}})){\bf{1}}({\lambda _{{\alpha ^{'}}}} \le E)dE + O({N^{ - {D_1}}}),\]
where we have used (1.14) and (2.18). Similarly to (3.27), recalling (11), choose a smooth nonincreasing function f l that vanishes on the interval ![]() \[[l + {\textstyle{2 \over 3}},\infty )\] and is equal to 1 on the interval
\[[l + {\textstyle{2 \over 3}},\infty )\] and is equal to 1 on the interval ![]() \[( - \infty ,l + {\textstyle{1 \over 3}}]\]. Recall that E U = a 2k – 1 + 2N – 2/3 + ε and
\[( - \infty ,l + {\textstyle{1 \over 3}}]\]. Recall that E U = a 2k – 1 + 2N – 2/3 + ε and ![]() \[{\mathcal{N}}(E,{E_U})\] denotes the number of eigenvalues of Q 1 located in the interval [E,E U] By (3.56), we have
\[{\mathcal{N}}(E,{E_U})\] denotes the number of eigenvalues of Q 1 located in the interval [E,E U] By (3.56), we have
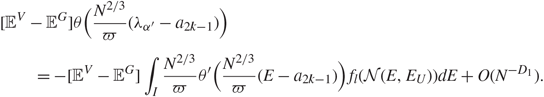 \[[{{\mathbb{E}}^V} - {{\mathbb{E}}^G}]\theta ({{{N^{2/3}}} \over \varpi }({\lambda _{{\alpha ^{'}}}} - {a_{2k - 1}})) \\ \quad \quad = - [{{\mathbb{E}}^V} - {{\mathcal{E}}^G}]\int_I {{{N^{2/3}}} \over \varpi }{\theta ^{'}}({{{N^{2/3}}} \over \varpi }(E - {a_{2k - 1}})){f_l}(N(E,{E_U}))dE + O({N^{ - {D_1}}}).\]
\[[{{\mathbb{E}}^V} - {{\mathbb{E}}^G}]\theta ({{{N^{2/3}}} \over \varpi }({\lambda _{{\alpha ^{'}}}} - {a_{2k - 1}})) \\ \quad \quad = - [{{\mathbb{E}}^V} - {{\mathcal{E}}^G}]\int_I {{{N^{2/3}}} \over \varpi }{\theta ^{'}}({{{N^{2/3}}} \over \varpi }(E - {a_{2k - 1}})){f_l}(N(E,{E_U}))dE + O({N^{ - {D_1}}}).\] Recall that ![]() \[\tilde \eta = {N^{ - 2/3 - 9{\varepsilon _0}}}\]. Similarly to the discussion of (3.31), with probability
\[\tilde \eta = {N^{ - 2/3 - 9{\varepsilon _0}}}\]. Similarly to the discussion of (3.31), with probability ![]() \[1 - {N^{ - {D_1}}}\], we have
\[1 - {N^{ - {D_1}}}\], we have
This yields
 \[[{{\mathbb{E}}^V} - {{\mathbb{E}}^G}]\theta ({{{N^{2/3}}} \over \varpi }({\lambda _{{\alpha ^{'}}}} - {a_{2k - 1}})) \\ \quad = - [{{\mathbb{E}}^V} - {{\mathbb{E}}^G}]\int_I {{{N^{2/3}}} \over \varpi }{\theta ^{'}}({{{N^{2/3}}} \over \varpi }(E - {a_{2k - 1}})){f_l}({\rm Tr}({{\bf{1}}_{[E,{E_U}]}}*{\vartheta _{\tilde \eta }}({Q_1}))){\kern 1pt} {\rm{d}}E + O({N^{ - {D_1}}}).\]
\[[{{\mathbb{E}}^V} - {{\mathbb{E}}^G}]\theta ({{{N^{2/3}}} \over \varpi }({\lambda _{{\alpha ^{'}}}} - {a_{2k - 1}})) \\ \quad = - [{{\mathbb{E}}^V} - {{\mathbb{E}}^G}]\int_I {{{N^{2/3}}} \over \varpi }{\theta ^{'}}({{{N^{2/3}}} \over \varpi }(E - {a_{2k - 1}})){f_l}({\rm Tr}({{\bf{1}}_{[E,{E_U}]}}*{\vartheta _{\tilde \eta }}({Q_1}))){\kern 1pt} {\rm{d}}E + O({N^{ - {D_1}}}).\]Integration by parts yields
 \[[{{\mathbb{E}}^V} - {{\mathbb{E}}^G}]\theta ({{{N^{2/3}}} \over \varpi }({\lambda _{{\alpha ^{'}}}} - {a_{2k - 1}})) \\ \quad \quad = {N \over \pi }[{{\mathbb{E}}^V} - {{\mathcal{E}}^G}]\int_I \theta ({{{N^{2/3}}} \over \varpi }({\lambda _{{\alpha ^{'}}}} - {a_{2k - 1}})) \\ \times f_l^{'}({\rm Tr}({{\bf{1}}_{[E,{E_U}]}}*{\vartheta _{\tilde \eta }}({Q_1})))Im{m_2}(E + {\rm{i}}\tilde \eta ){\kern 1pt} {\rm{d}}E + o(1),\]
\[[{{\mathbb{E}}^V} - {{\mathbb{E}}^G}]\theta ({{{N^{2/3}}} \over \varpi }({\lambda _{{\alpha ^{'}}}} - {a_{2k - 1}})) \\ \quad \quad = {N \over \pi }[{{\mathbb{E}}^V} - {{\mathcal{E}}^G}]\int_I \theta ({{{N^{2/3}}} \over \varpi }({\lambda _{{\alpha ^{'}}}} - {a_{2k - 1}})) \\ \times f_l^{'}({\rm Tr}({{\bf{1}}_{[E,{E_U}]}}*{\vartheta _{\tilde \eta }}({Q_1})))Im{m_2}(E + {\rm{i}}\tilde \eta ){\kern 1pt} {\rm{d}}E + o(1),\]where we have used (3.42). Now we extend θ to the general case defined in (1.15). By Theorem 1.1, it is easy to check that
 \[[{{\mathbb{E}}^V} - {{\mathbb{E}}^G}]\theta ({{{N^{2/3}}} \over \varpi }({\lambda _{{\alpha ^{'}}}} - {a_{2k - 1}}),N{\xi _{{\alpha ^{'}}}}(i){\xi _{{\alpha ^{'}}}}(j),N{\zeta _{{\alpha ^{'}}}}(\mu ){\zeta _{{\alpha ^{'}}}}(\nu )) \\ \quad \quad = {1 \over \pi }[{{\mathbb{E}}^V} - {{\mathbb{E}}^G}]\int_I \theta ({{{N^{2/3}}} \over \varpi }({\lambda _{{\alpha ^{'}}}} - {a_{2k - 1}}),{\phi _{{\alpha ^{'}}}},{\varphi _{{\alpha ^{'}}}}) \\ \times f_l^{'}({\rm Tr}({{\bf{1}}_{[E,{E_U}]}}*{\vartheta _{\tilde \eta }}({Q_1})))NIm{m_2}(E + {\rm{i}}\tilde \eta ){\kern 1pt} {\rm{d}}E + o(1),\](3.57)
\[[{{\mathbb{E}}^V} - {{\mathbb{E}}^G}]\theta ({{{N^{2/3}}} \over \varpi }({\lambda _{{\alpha ^{'}}}} - {a_{2k - 1}}),N{\xi _{{\alpha ^{'}}}}(i){\xi _{{\alpha ^{'}}}}(j),N{\zeta _{{\alpha ^{'}}}}(\mu ){\zeta _{{\alpha ^{'}}}}(\nu )) \\ \quad \quad = {1 \over \pi }[{{\mathbb{E}}^V} - {{\mathbb{E}}^G}]\int_I \theta ({{{N^{2/3}}} \over \varpi }({\lambda _{{\alpha ^{'}}}} - {a_{2k - 1}}),{\phi _{{\alpha ^{'}}}},{\varphi _{{\alpha ^{'}}}}) \\ \times f_l^{'}({\rm Tr}({{\bf{1}}_{[E,{E_U}]}}*{\vartheta _{\tilde \eta }}({Q_1})))NIm{m_2}(E + {\rm{i}}\tilde \eta ){\kern 1pt} {\rm{d}}E + o(1),\](3.57)where
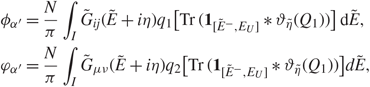 \[{\phi _{{\alpha ^{'}}}} = {N \over \pi }\int_I {\tilde G_{ij}}(\tilde E + i\eta ){q_1}[{\rm Tr}({{\bf{1}}_{[{{\tilde E}^ - },{E_U}]}}*{\vartheta _{\tilde \eta }}({Q_1}))]{\kern 1pt} {\rm{d}}\tilde E, \\ {\varphi _{{\alpha ^{'}}}} = {N \over \pi }\int_I {\tilde G_{\mu \nu }}(\tilde E + i\eta ){q_2}[{\rm Tr}({{\bf{1}}_{[{{\tilde E}^ - },{E_U}]}}*{\vartheta _{\tilde \eta }}({Q_1}))]d\tilde E,\]
\[{\phi _{{\alpha ^{'}}}} = {N \over \pi }\int_I {\tilde G_{ij}}(\tilde E + i\eta ){q_1}[{\rm Tr}({{\bf{1}}_{[{{\tilde E}^ - },{E_U}]}}*{\vartheta _{\tilde \eta }}({Q_1}))]{\kern 1pt} {\rm{d}}\tilde E, \\ {\varphi _{{\alpha ^{'}}}} = {N \over \pi }\int_I {\tilde G_{\mu \nu }}(\tilde E + i\eta ){q_2}[{\rm Tr}({{\bf{1}}_{[{{\tilde E}^ - },{E_U}]}}*{\vartheta _{\tilde \eta }}({Q_1}))]d\tilde E,\]and q 1 and q 2 are the functions defined in (3.27). Therefore, the randomness on the right-hand side of (3.57) is expressed in terms of Green functions. Hence, we can apply the Green function comparison argument to (3.57) as in Section 3.2. The complications are notational and we will not reproduce the details here. □
Finally, the proof of Corollary 1.2 is very similar to that of Corollary 1.1 except that we use n different intervals and a multidimensional integral. We will not reproduce the details here.
4. Singular vectors in the bulks
In this section we prove the bulk universality Theorems 1.3 and 1.4. Our key ingredients, Lemmas 2.1 and 2.4 and Corollary 2.1, are proved for N – 1 + τ ≤ η ≤ τ–1 (recall (2.1)). In the bulks, recalling Lemma 2.3, the eigenvalue spacing is of order N –1. The following Lemma extends the above controls for a small spectral scale all the way down to the real axis. The proof relies on Corollary 2.1 and the details can be found in [Reference Knowles and Yin24, Lemma 5.1].
Lemma 4.1. Recall (2.19). For ![]() $z \in D_k^b$ with 0 < η ≤ τ –1 when N is large enough, with probability
$z \in D_k^b$ with 0 < η ≤ τ –1 when N is large enough, with probability ![]() \[1 - {N^{ - {D_1}}}\], we have
\[1 - {N^{ - {D_1}}}\], we have
Once Lemma 4.1 is established, Lemmas 2.3 and 2.4 will follow. Next we follow the basic proof strategy for Theorem 1.1, but use a different spectral window size. Again, we provide only the proof of Lemma 4.2 below, which establishes the universality for the distribution of ![]() \[{\zeta _{{\alpha ^{'}}}}(\mu ){\zeta _{{\alpha ^{'}}}}(\nu )\] in detail. Throughout this section, we use the scale parameter
\[{\zeta _{{\alpha ^{'}}}}(\mu ){\zeta _{{\alpha ^{'}}}}(\nu )\] in detail. Throughout this section, we use the scale parameter
Therefore, the following bounds hold with probability ![]() \[1 - {N^{ - {D_1}}}\].
\[1 - {N^{ - {D_1}}}\].
The following Lemma states the bulk universality for ![]() \[{\zeta _{{\alpha ^{'}}}}(\mu ){\zeta _{{\alpha ^{'}}}}(\nu )\].
\[{\zeta _{{\alpha ^{'}}}}(\mu ){\zeta _{{\alpha ^{'}}}}(\nu )\].
Lemma 4.2. Suppose that ![]() \[{Q_V} = {\Sigma ^{1/2}}{X_V}X_V^*{\Sigma ^{1/2}}\] satisfies Assumption 1.1. Assume that the third and fourth moments of X V agree with those of X GV, and consider the kth, k = 1, 2, …, p bulk component, with l defined in (1.11) or (1.12). Under Assumptions 1.2 and 1.3, for any choices of indices
\[{Q_V} = {\Sigma ^{1/2}}{X_V}X_V^*{\Sigma ^{1/2}}\] satisfies Assumption 1.1. Assume that the third and fourth moments of X V agree with those of X GV, and consider the kth, k = 1, 2, …, p bulk component, with l defined in (1.11) or (1.12). Under Assumptions 1.2 and 1.3, for any choices of indices ![]() \[\mu ,\nu \in {{\mathcal{I}}_2}\], there exists a small δ ∈ (0, 1) such that, when δ N k} ≤ l ≤ (1 – δ)N k, we have
\[\mu ,\nu \in {{\mathcal{I}}_2}\], there exists a small δ ∈ (0, 1) such that, when δ N k} ≤ l ≤ (1 – δ)N k, we have
where θ is a smooth function in ℝ that satisfies
4.1. Proof of Lemma 4.2
The proof strategy is very similar to that of Lemma 3.1. Our first step is an analogue of Lemma 3.2. The proof is quite similar (actually easier as the window size is much smaller). We omit further details.
Lemma 4.3. Under the assumptions of Lemma 4.2, there exists a 0 < δ < 1 such that
where ![]() \[{\mathcal X}(E)\] is defined in (3.7) and, for ε satisfying (3.5),
\[{\mathcal X}(E)\] is defined in (3.7) and, for ε satisfying (3.5),
Next we express the indicator function in (4.5) using Green functions. Recall (3.28), a key observation is that the size of E –, E U is of order N – 2/3 due to (3.4). As we now use (4.2) and (101) in the bulks, the size here is of order 1. So we cannot use the delta approximation function to estimate ![]() \[{\mathcal X}(E)\]. Instead, we use Helffer–Sjöstrand functional calculus. This has been used many times when the window size η takes the form of (4.2), for example, in the proofs of rigidity of eigenvalues in [Reference Ding and Yang16], [Reference Erdös, Yau and Yin18], and [Reference Pillai and Yin33].
\[{\mathcal X}(E)\]. Instead, we use Helffer–Sjöstrand functional calculus. This has been used many times when the window size η takes the form of (4.2), for example, in the proofs of rigidity of eigenvalues in [Reference Ding and Yang16], [Reference Erdös, Yau and Yin18], and [Reference Pillai and Yin33].
For any 0 < E 1, E 2 ≤ τ– 1, let ![]() \[f(\lambda ) \equiv {f_{{E_1},{E_2},{\eta _d}}}(\lambda )\] be the characteristic function of E 1, E 2 smoothed on the scale
\[f(\lambda ) \equiv {f_{{E_1},{E_2},{\eta _d}}}(\lambda )\] be the characteristic function of E 1, E 2 smoothed on the scale
where f = 1 when λ ∈ E 1, E 2 and f = 0 when λ ∈ ℝ\ [E 1 – ηd, E 2 + ηd], and
for some constant C > 0 By Equation (B.12) of [Reference Erdös, Ramirez, Schlein and Yau19], with ![]() \[{f_E} \equiv {f_{{E^ - },{E_U},{\eta _d}}},\] we have
\[{f_E} \equiv {f_{{E^ - },{E_U},{\eta _d}}},\] we have
where X(γ) is a smooth cutoff function with support [–1, 1] and χ(γ)=1 for ![]() \[|y| \le {1 \over 2}\] with bounded derivatives. Using a similar argument to that used for Lemma 3.3, we have the following result, whose proof is given in the supplementary material [Reference Ding14].
\[|y| \le {1 \over 2}\] with bounded derivatives. Using a similar argument to that used for Lemma 3.3, we have the following result, whose proof is given in the supplementary material [Reference Ding14].
Lemma 4.4. Recall the smooth cutoff function q defined in (3.27). Under the assumptions of Lemma 4.3, there exists a 0 < δ < 1 such that
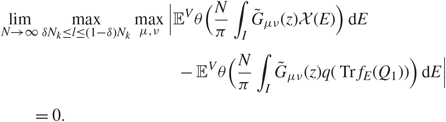 \[\mathop {\lim }\limits_{N \to \infty } \mathop {\max }\limits_{\delta {N_k} \le l \le (1 - \delta ){N_k}} \mathop {\max }\limits_{\mu ,\nu } |{{\mathbb{E}}^V}\theta ({N \over \pi }\int_I {\tilde G_{\mu \nu }}(z){\mathcal X}(E)){\kern 1pt} {\rm{d}}E \\ - {{\mathbb{E}}^V}\theta ({N \over \pi }\int_I {\tilde G_{\mu \nu }}(z)q({\rm Tr}{f_E}({Q_1}))){\kern 1pt} {\rm{d}}E| \\ \quad \quad = 0.\](4.9)
\[\mathop {\lim }\limits_{N \to \infty } \mathop {\max }\limits_{\delta {N_k} \le l \le (1 - \delta ){N_k}} \mathop {\max }\limits_{\mu ,\nu } |{{\mathbb{E}}^V}\theta ({N \over \pi }\int_I {\tilde G_{\mu \nu }}(z){\mathcal X}(E)){\kern 1pt} {\rm{d}}E \\ - {{\mathbb{E}}^V}\theta ({N \over \pi }\int_I {\tilde G_{\mu \nu }}(z)q({\rm Tr}{f_E}({Q_1}))){\kern 1pt} {\rm{d}}E| \\ \quad \quad = 0.\](4.9)Finally, we apply the Green function comparison argument, where we will follow the basic approach of Section 3.2 and [Reference Knowles and Yin24, Section 5]. The key difference is that we will use (4.2) and (4.3).
Lemma 4.5. Under the assumptions of Lemma 4.4, there exists a 0 < δ < 1 such that
Proof. Recall (4.8). By (2.5), we have
Define ![]() \[{\tilde \eta _d}{\kern 1pt} : = {N^{ - 1 - (d + 1){\varepsilon _0}}}\]. We can decompose the right-hand side of (4.11) as
\[{\tilde \eta _d}{\kern 1pt} : = {N^{ - 1 - (d + 1){\varepsilon _0}}}\]. We can decompose the right-hand side of (4.11) as
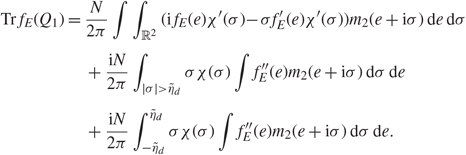 \[{\rm Tr}{f_E}({Q_1}) = {N \over {2\pi }}\int \int_{{{\mathbb{R}}^2}} ({\rm{i}}{f_E}(e){\chi ^{'}}(\sigma ) - \sigma f_E^{'}(e){\chi ^{'}}(\sigma )){m_2}(e + {\rm{i}}\sigma ){\kern 1pt} {\rm{d}}e{\kern 1pt} {\rm{d}}\sigma \\ \quad {\kern 1pt} + {{{\rm{i}}N} \over {2\pi }}\int_{|\sigma | \gt {{\tilde \eta }_d}} \sigma \chi (\sigma )\int f_E^{''}(e){m_2}(e + {\rm{i}}\sigma ){\kern 1pt} {\rm{d}}\sigma {\kern 1pt} {\rm{d}}e \\ \quad {\kern 1pt} + {{{\rm{i}}N} \over {2\pi }}\int_{ - {{\tilde \eta }_d}}^{{{\tilde \eta }_d}} \sigma \chi (\sigma )\int f_E^{''}(e){m_2}(e + {\rm{i}}\sigma ){\kern 1pt} {\rm{d}}\sigma {\kern 1pt} {\rm{d}}e.\]
\[{\rm Tr}{f_E}({Q_1}) = {N \over {2\pi }}\int \int_{{{\mathbb{R}}^2}} ({\rm{i}}{f_E}(e){\chi ^{'}}(\sigma ) - \sigma f_E^{'}(e){\chi ^{'}}(\sigma )){m_2}(e + {\rm{i}}\sigma ){\kern 1pt} {\rm{d}}e{\kern 1pt} {\rm{d}}\sigma \\ \quad {\kern 1pt} + {{{\rm{i}}N} \over {2\pi }}\int_{|\sigma | \gt {{\tilde \eta }_d}} \sigma \chi (\sigma )\int f_E^{''}(e){m_2}(e + {\rm{i}}\sigma ){\kern 1pt} {\rm{d}}\sigma {\kern 1pt} {\rm{d}}e \\ \quad {\kern 1pt} + {{{\rm{i}}N} \over {2\pi }}\int_{ - {{\tilde \eta }_d}}^{{{\tilde \eta }_d}} \sigma \chi (\sigma )\int f_E^{''}(e){m_2}(e + {\rm{i}}\sigma ){\kern 1pt} {\rm{d}}\sigma {\kern 1pt} {\rm{d}}e.\] By (4.3) and (4.7), for some constant C > 0 with probability ![]() \[1 - {N^{ - {D_1}}}\], we have
\[1 - {N^{ - {D_1}}}\], we have
Recall (3.35) and (3.38). Similarly to Lemma 3.6, we first drop the diagonal terms. By (4.1), with probability ![]() \[1 - {N^{ - {D_1}}}\], we have (recall (3.41))
\[1 - {N^{ - {D_1}}}\], we have (recall (3.41))
for some constant C > 0 Hence, by the mean value theorem, we need only prove that
Furthermore, by Taylor’s expansion (4.12), and the definition of χ, it suffices to prove that
where
Next we will use the Green function comparison argument to prove (4.13). In the proof of Lemma 3.5, we used the resolvent expansion until an order of four. However, due to the larger bounds in (4.3), we will use the expansion
Recall (3.47) and (3.48). We have
 \[[{{\mathbb{E}}^V} - {{\mathbb{E}}^G}]\theta (\int_I x(E)q(y(E) + \tilde y(E)){\kern 1pt} {\rm{d}}E) \\ \quad \quad = \sum\limits_{\gamma = 1}^{{\gamma _{\max }}} {\mathbb{E}}\left( {\theta ((\int_I {x^S}q({y^S} + {{\tilde y}^S}))) - \theta ((\int_I {x^T}q({y^T} + {{\tilde y}^T})))} \right).\](4.17)
\[[{{\mathbb{E}}^V} - {{\mathbb{E}}^G}]\theta (\int_I x(E)q(y(E) + \tilde y(E)){\kern 1pt} {\rm{d}}E) \\ \quad \quad = \sum\limits_{\gamma = 1}^{{\gamma _{\max }}} {\mathbb{E}}\left( {\theta ((\int_I {x^S}q({y^S} + {{\tilde y}^S}))) - \theta ((\int_I {x^T}q({y^T} + {{\tilde y}^T})))} \right).\](4.17) We still use the same notation Δ x(E) := xS(E) - xR(E). We basically follow the approach of Section 3.2, where the control (3.36) is replaced by (4.3). We first deal with x(E). Let Δ x (k)(E) denote the summations of the terms in Δ x(E) containing k numbers of ![]() \[X_{i{\mu _1}}^G\]. Similarly to the discussion of Lemma 3.7, recalling (3.52), by (1.2) and (4.3), with probability
\[X_{i{\mu _1}}^G\]. Similarly to the discussion of Lemma 3.7, recalling (3.52), by (1.2) and (4.3), with probability ![]() \[1 - {N^{ - {D_1}}}\], we have
\[1 - {N^{ - {D_1}}}\], we have
This yields
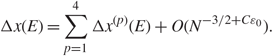 \[\Delta x(E) = \sum\limits_{p = 1}^4 \Delta {x^{(p)}}(E) + O({N^{ - 3/2 + C{\varepsilon _0}}}).\](4.18)
\[\Delta x(E) = \sum\limits_{p = 1}^4 \Delta {x^{(p)}}(E) + O({N^{ - 3/2 + C{\varepsilon _0}}}).\](4.18)Let
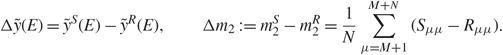 \[\Delta \tilde y(E) = {\tilde y^S}(E) - {\tilde y^R}(E),\quad \quad \Delta {m_2}{\kern 1pt} : = m_2^S - m_2^R = {1 \over N}\sum\limits_{\mu = M + 1}^{M + N} ({S_{\mu \mu }} - {R_{\mu \mu }}).\]
\[\Delta \tilde y(E) = {\tilde y^S}(E) - {\tilde y^R}(E),\quad \quad \Delta {m_2}{\kern 1pt} : = m_2^S - m_2^R = {1 \over N}\sum\limits_{\mu = M + 1}^{M + N} ({S_{\mu \mu }} - {R_{\mu \mu }}).\] We first deal with (4.15). By the definition of χ, we need to restrict ![]() \[{1 \over 2} \le |\sigma | \le 1\]; hence, by (2.17), with probability
\[{1 \over 2} \le |\sigma | \le 1\]; hence, by (2.17), with probability ![]() \[1 - {N^{ - {D_1}}}\], we have
\[1 - {N^{ - {D_1}}}\], we have
By (3.50), (3.51), (4.16), and (4.19), with probability ![]() \[1 - {N^{ - {D_1}}}\], we have
\[1 - {N^{ - {D_1}}}\], we have ![]() \[|\Delta m_2^{(5)}| \le {N^{ - 7/2 + 9{\varepsilon _1}}}\]. This yields the decomposition
\[|\Delta m_2^{(5)}| \le {N^{ - 7/2 + 9{\varepsilon _1}}}\]. This yields the decomposition
 \[\Delta \tilde y(E) = \sum\limits_{p = 1}^4 \Delta {\tilde y^{(p)}}(E) + O({N^{ - 5/2 + C{\varepsilon _0}}}).\](4.20)
\[\Delta \tilde y(E) = \sum\limits_{p = 1}^4 \Delta {\tilde y^{(p)}}(E) + O({N^{ - 5/2 + C{\varepsilon _0}}}).\](4.20) Next we will control (4.14). Define ![]() \[\Delta y(E){\kern 1pt} : = {y^S}(E) - {y^R}(E)\]. By (3.50), (3.51) and (4.1), using a similar discussion to that used for Equation (5.22) of [Reference Knowles and Yin24], with probability
\[\Delta y(E){\kern 1pt} : = {y^S}(E) - {y^R}(E)\]. By (3.50), (3.51) and (4.1), using a similar discussion to that used for Equation (5.22) of [Reference Knowles and Yin24], with probability ![]() \[1 - {N^{ - {D_1}}}\], for
\[1 - {N^{ - {D_1}}}\], for ![]() \[\sigma \ge {\tilde \eta _d},\] we have
\[\sigma \ge {\tilde \eta _d},\] we have
where ![]() \[{\Lambda _\sigma }{\kern 1pt} : = \mathop {\sup }\nolimits_{|e| \le {\tau ^{ - 1}}} \mathop {\max }\nolimits_{\mu \ne \nu } |{G_{\mu \nu }}(e + {\rm{i}}\sigma )|\], recalling that
\[{\Lambda _\sigma }{\kern 1pt} : = \mathop {\sup }\nolimits_{|e| \le {\tau ^{ - 1}}} \mathop {\max }\nolimits_{\mu \ne \nu } |{G_{\mu \nu }}(e + {\rm{i}}\sigma )|\], recalling that ![]() \[\mu ,\nu \in {{\mathcal{I}}_2}\]. In order to estimate Δγ(E), we integrate (4.14) by parts, first in e then in σ. By Equation (5.24) of [Reference Knowles and Yin24], with probability
\[\mu ,\nu \in {{\mathcal{I}}_2}\]. In order to estimate Δγ(E), we integrate (4.14) by parts, first in e then in σ. By Equation (5.24) of [Reference Knowles and Yin24], with probability ![]() \[1 - {N^{ - {D_1}}}\], we have
\[1 - {N^{ - {D_1}}}\], we have
 \[|{N \over {2\pi }}\int_{{{\mathbb{R}}^2}} {\rm{i}}\sigma f_E^{''}(e)\chi (\sigma ){\Delta ^{(5)}}{m_2}(e + {\rm{i}}\sigma ){\bf{1}}(|\sigma | \ge {\tilde \eta _d}){\kern 1pt} {\rm{d}}e{\kern 1pt} {\rm{d}}\sigma | \\ \quad \quad \le CN|\int f_E^{'}(e){\tilde \eta _d}\Delta m_2^{(5)}(e + {\rm{i}}{\tilde \eta _d}){\kern 1pt} {\rm{d}}e| + CN|\int f_E^{'}(e){\kern 1pt} {\rm{d}}e\int_{{{\tilde \eta }_d}}^\infty {\chi ^{'}}(\sigma )\sigma \Delta m_2^{(5)(e + {\rm{i}}\sigma )}{\kern 1pt} {\rm{d}}\sigma | \\ \quad \quad + CN|\int f_E^{'}(e){\kern 1pt} {\rm{d}}e\int_{{{\tilde \eta }_d}}^\infty \chi (\sigma )\Delta m_2^{(5)}(e + {\rm{i}}\sigma ){\kern 1pt} {\rm{d}}\sigma |.\](4.22)
\[|{N \over {2\pi }}\int_{{{\mathbb{R}}^2}} {\rm{i}}\sigma f_E^{''}(e)\chi (\sigma ){\Delta ^{(5)}}{m_2}(e + {\rm{i}}\sigma ){\bf{1}}(|\sigma | \ge {\tilde \eta _d}){\kern 1pt} {\rm{d}}e{\kern 1pt} {\rm{d}}\sigma | \\ \quad \quad \le CN|\int f_E^{'}(e){\tilde \eta _d}\Delta m_2^{(5)}(e + {\rm{i}}{\tilde \eta _d}){\kern 1pt} {\rm{d}}e| + CN|\int f_E^{'}(e){\kern 1pt} {\rm{d}}e\int_{{{\tilde \eta }_d}}^\infty {\chi ^{'}}(\sigma )\sigma \Delta m_2^{(5)(e + {\rm{i}}\sigma )}{\kern 1pt} {\rm{d}}\sigma | \\ \quad \quad + CN|\int f_E^{'}(e){\kern 1pt} {\rm{d}}e\int_{{{\tilde \eta }_d}}^\infty \chi (\sigma )\Delta m_2^{(5)}(e + {\rm{i}}\sigma ){\kern 1pt} {\rm{d}}\sigma |.\](4.22) By (4.21), with probability ![]() \[1 - {N^{ - {D_1}}}\], the first two items of (4.22) can be easily bounded by
\[1 - {N^{ - {D_1}}}\], the first two items of (4.22) can be easily bounded by ![]() \[{N^{ - 5/2 + C{\varepsilon _0}}}\]. For the last item, by (4.21), (4.1), and a similar discussion to the equation below [Reference Knowles and Yin24, Equation (5.24)], it can be bounded by
\[{N^{ - 5/2 + C{\varepsilon _0}}}\]. For the last item, by (4.21), (4.1), and a similar discussion to the equation below [Reference Knowles and Yin24, Equation (5.24)], it can be bounded by
Hence, with probability ![]() \[1 - {N^{ - {D_1}}}\], we have the decomposition
\[1 - {N^{ - {D_1}}}\], we have the decomposition
 \[\Delta y(E) = \sum\limits_{p = 1}^4 \Delta {y^{(p)}}(E) + O({N^{ - 5/2 + C{\varepsilon _0}}}).\](4.23)
\[\Delta y(E) = \sum\limits_{p = 1}^4 \Delta {y^{(p)}}(E) + O({N^{ - 5/2 + C{\varepsilon _0}}}).\](4.23) Similarly to the discussion of (4.18), (4.20), and (4.23), it is easy to check that, with probability ![]() \[1 - {N^{ - {D_1}}}\], we have
\[1 - {N^{ - {D_1}}}\], we have
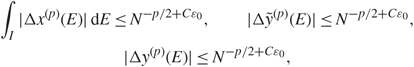 \[\matrix{ {\int_I |\Delta {x^{(p)}}(E)|{\kern 1pt} {\rm{d}}E \le {N^{ - p/2 + C{\varepsilon _0}}},\quad \quad |\Delta {{\tilde y}^{(p)}}(E)| \le {N^{ - p/2 + C{\varepsilon _0}}},} \cr {|\Delta {y^{(p)}}(E)| \le {N^{ - p/2 + C{\varepsilon _0}}},} \cr } \](4.24)
\[\matrix{ {\int_I |\Delta {x^{(p)}}(E)|{\kern 1pt} {\rm{d}}E \le {N^{ - p/2 + C{\varepsilon _0}}},\quad \quad |\Delta {{\tilde y}^{(p)}}(E)| \le {N^{ - p/2 + C{\varepsilon _0}}},} \cr {|\Delta {y^{(p)}}(E)| \le {N^{ - p/2 + C{\varepsilon _0}}},} \cr } \](4.24)
where p = 1, 2, 3, 4 and C > 0 is some constant. Furthermore, by (4.1), with probability ![]() \[1 - {N^{{D_1}}}\], we have
\[1 - {N^{{D_1}}}\], we have
Due to the similarity of (4.20) and (4.23), letting ![]() \[\;\bar y = y + \tilde y,\] we have
\[\;\bar y = y + \tilde y,\] we have
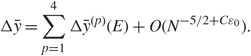 \[\Delta \bar y = \sum\limits_{p = 1}^4 \Delta {\bar y^{(p)}}(E) + O({N^{ - 5/2 + C{\varepsilon _0}}}).\](4.26)
\[\Delta \bar y = \sum\limits_{p = 1}^4 \Delta {\bar y^{(p)}}(E) + O({N^{ - 5/2 + C{\varepsilon _0}}}).\](4.26)By (4.24), (4.26), and Taylor’s expansion, we have
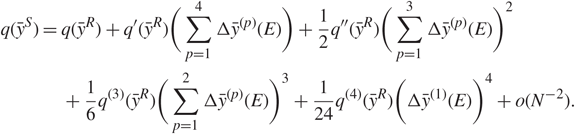 \[q({\bar y^S}) = q({\bar y^R}) + {q^{'}}({\bar y^R})(\sum\limits_{p = 1}^4 \Delta {\bar y^{(p)}}(E)) + {1 \over 2}{q^{''}}({\bar y^R})(\sum\limits_{p = 1}^3 \Delta {\bar y^{(p)}}(E{))^2} \\ \quad {\kern 1pt} + {1 \over 6}{q^{(3)}}({\bar y^R})(\sum\limits_{p = 1}^2 \Delta {\bar y^{(p)}}(E{))^3} + {1 \over {24}}{q^{(4)}}({\bar y^R})(\Delta {\bar y^{(1)}}(E{))^4} + o({N^{ - 2}}).\](4.27)
\[q({\bar y^S}) = q({\bar y^R}) + {q^{'}}({\bar y^R})(\sum\limits_{p = 1}^4 \Delta {\bar y^{(p)}}(E)) + {1 \over 2}{q^{''}}({\bar y^R})(\sum\limits_{p = 1}^3 \Delta {\bar y^{(p)}}(E{))^2} \\ \quad {\kern 1pt} + {1 \over 6}{q^{(3)}}({\bar y^R})(\sum\limits_{p = 1}^2 \Delta {\bar y^{(p)}}(E{))^3} + {1 \over {24}}{q^{(4)}}({\bar y^R})(\Delta {\bar y^{(1)}}(E{))^4} + o({N^{ - 2}}).\](4.27)By (4.4), we have
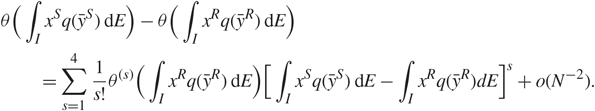 \[\theta (\int_I {x^S}q({\bar y^S}){\kern 1pt} {\rm{d}}E) - \theta (\int_I {x^R}q({\bar y^R}){\kern 1pt} {\rm{d}}E) \\ \quad \quad = \sum\limits_{s = 1}^4 {1 \over {s!}}{\theta ^{(s)}}(\int_I {x^R}q({\bar y^R}){\kern 1pt} {\rm{d}}E)[\int_I {x^S}q({\bar y^S}){\kern 1pt} {\rm{d}}E - \int_I {x^R}q({\bar y^R})dE{]^s} + o({N^{ - 2}}).\](4.28)
\[\theta (\int_I {x^S}q({\bar y^S}){\kern 1pt} {\rm{d}}E) - \theta (\int_I {x^R}q({\bar y^R}){\kern 1pt} {\rm{d}}E) \\ \quad \quad = \sum\limits_{s = 1}^4 {1 \over {s!}}{\theta ^{(s)}}(\int_I {x^R}q({\bar y^R}){\kern 1pt} {\rm{d}}E)[\int_I {x^S}q({\bar y^S}){\kern 1pt} {\rm{d}}E - \int_I {x^R}q({\bar y^R})dE{]^s} + o({N^{ - 2}}).\](4.28) Inserting ![]() \[{x^S} = {x^R} + \sum\nolimits_{p = 1}^4 \Delta {x^{(p)}}\] and (4.27) into (4.28), using the partial expectation argument as in Section 3.2, by (4.4), (4.24), and (4.25), we find that there exists a random variable B that depends on the randomness only through O and the first four moments of
\[{x^S} = {x^R} + \sum\nolimits_{p = 1}^4 \Delta {x^{(p)}}\] and (4.27) into (4.28), using the partial expectation argument as in Section 3.2, by (4.4), (4.24), and (4.25), we find that there exists a random variable B that depends on the randomness only through O and the first four moments of ![]() \[X_{i{\mu _1}}^G\] such that
\[X_{i{\mu _1}}^G\] such that
Hence, together with (4.17), this proves (4.13), which implies (4.10). This completes our proof. □
Acknowledgements
I am very grateful to Jeremy Quastel and Bálint Virág for many valuable insights and helpful suggestions, which have significantly improved the paper. I would like to thank my friend Fan Yang for many useful discussions and pointing out some references, especially [Reference Xi, Yang and Yin39]. I also want to thank two anonymous referees, the Associate Editor, and the Editor for their many helpful comments.


