Hostname: page-component-cb9f654ff-mx8w7 Total loading time: 0 Render date: 2025-07-31T09:40:22.929Z Has data issue: false hasContentIssue false
  • English
  • Français

A multiplicative property of R-sequences and H1-sets

Published online by Cambridge University Press:  24 October 2008

C. P. L. Rhodes
C. P. L. Rhodes
Affiliation:
University College, Cardiff
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Let R be a commutative ring which may not contain a multiplicative identity. A set of elements a1,…,ak in R will be called an H1-set (this notation is explained in section 1) if for each relation r1a1 + … +rkak = 0 (ri ∈ R) there exist elements sij ∈ R such that

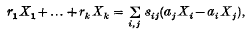
where Xl,…,Xk are indeterminates. Any R-sequence is an H1-set, but there do exist H1-sets which are not R-sequences (see section 1). Throughout this note we consider an H1-set a1,…,ak which we suppose to be partitioned into two non-empty sets bl…, br and cl,…, cs. Our main purpose is to show that the ideals B = Rb1 + … + Rbr and C = Rc1 + … + Rcs satisfy Bm ∩ Cn = BmCn for all positive integers m and n (Corollary 1). This generalizes Lemma 2 of Caruth(2) where the result is proved when a1,…, ak is a permutable R-sequence. Our proof involves more detail than is necessary just for this, and we obtain various other properties of H1-sets. In particular we extend the main results of Corsini(3) concerning the symmetric and Rees algebras of a power of the ideal Ra1 +… + Rak (Corollary 3).

Information

Type
Research Article
Information
Mathematical Proceedings of the Cambridge Philosophical Society , Volume 78 , Issue 1 , July 1975 , pp. 1 - 6
Copyright
Copyright © Cambridge Philosophical Society 1975

References

REFERENCES

(1)Barshay, J.Graded algebras of powers of ideals generated by A-sequences. J. Algebra 25 (1973) 90–99.CrossRefGoogle Scholar
(2)Caruth, A.On powers of ideals generated by R-sequences in a Noetherian local ring. Proc. Cambridge Philos. Soc. 74 (1973), 441–444.CrossRefGoogle Scholar
(3)Corsini, P.Sulle potenze di un ideale generato da una A-successione. Rend. Sem. Mat. Univ. Padova 39 (1967), 190–204.Google Scholar
(4)Davis, E. D.Ideals of the principal class, R-sequences and a certain monoidal transformation. Pacific J. Math. 20 (1967), 197–205.CrossRefGoogle Scholar
(5)Kabele, T.Regularity conditions in non-Noetherian rings. Trans. Amer. Math. Soc. 155 (1971), 363–374.CrossRefGoogle Scholar
(6)Kaplansky, I.Commutative rings (Queen Mary College Mathematics Notes, 1966).Google Scholar
(7)Kirby, D.Isomorphic Koszul complexes. Mathematika 20 (1973), 53–57.CrossRefGoogle Scholar
(8)Micali, A.Sur les algèbres universelles. Ann. Inst. Fourier, Grenoble 14 (1964), 33–87.CrossRefGoogle Scholar
(9)Northcott, D. G.Lessons on rings, modules and multiplicities (Cambridge, 1968).CrossRefGoogle Scholar
(10)Rees, D.The grade of an ideal or module. Proc. Cambridge Philos. Soc. 53 (1957), 28–42.CrossRefGoogle Scholar