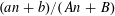1 Introduction
The present paper settles in the affirmative a 30-year-old conjecture of the first author concerning the representation of an arbitrary positive rational by products and quotients of rationals taken from the sequence
$(an+b)/(An+B)$
,
$n=1,2,\ldots \,$
, the fixed coefficient integers
$a$
,
$b$
,
$A$
,
$B$
to satisfy
$a>0$
,
$A>0$
,
$\unicode[STIX]{x1D6E5}=aB-Ab\neq 0$
, cf. [Reference Elliott8, Ch. 23, Unsolved Problems 11, 12].
To appreciate the underlying abstract problem, let
$\mathbb{Q}^{\ast }$
denote the multiplicative group of positive rationals,
$\unicode[STIX]{x1D6E4}$
its subgroup generated by a given sequence of positive rationals
$r_{n}$
,
$n=1,2,\ldots \,$
. The extent to which any further positive rational,
$w$
, has a representation
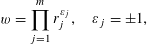$$\begin{eqnarray}w=\mathop{\prod }_{j=1}^{m}r_{j}^{\unicode[STIX]{x1D700}_{j}},\quad \unicode[STIX]{x1D700}_{j}=\pm 1,\end{eqnarray}$$
is encoded in the structure of the quotient group
$G=\mathbb{Q}^{\ast }/\unicode[STIX]{x1D6E4}$
.
We may view
$G$
as free on the positive rational primes, restricted by the relations
$r_{n}=\text{identity}$
,
$n=1,2,\ldots \,$
. It is known that no finite recursive algorithm can be given to determine an arbitrary denumerably infinite abelian group presented in this manner, cf. [Reference Britton2, Reference Elliott8], [Reference Stillwell23, Ch. 23, Exercises 106–108].
However, if
$U$
denotes the complex unit circle and we canonically extend a standard character
$G\rightarrow U$
by
$\mathbb{Q}^{\ast }\rightarrow \mathbb{Q}^{\ast }/\unicode[STIX]{x1D6E4}\rightarrow U$
, then we obtain a complex-valued completely multiplicative function
$g$
on the positive rationals, of absolute value 1, i.e., a character on the group
$\mathbb{Q}^{\ast }$
, that satisfies
$g(r_{n})=1$
on each of the rationals
$r_{n}$
,
$n\geqslant 1$
. We may ask whether the sequence
$r_{n}$
bears enough form to explicitly determine the dual group of
$G$
, hence
$G$
itself.
To this end, following examples of Gauss and Dirichlet, we ask for the asymptotic behaviour of the mean values
$$\begin{eqnarray}x^{-1}\mathop{\sum }_{n\leqslant x}g(r_{n})\end{eqnarray}$$
as
$x$
becomes unbounded.
Viewed within this aesthetic, an implicit early application of harmonic analysis on
$\mathbb{Q}^{\ast }$
is that of Elliott [Reference Elliott4], in which probabilistic number theory is employed to settle affirmatively a 1968 conjecture of Kátai, [Reference Kátai20], that a real-valued additive function vanishing on the shifted primes
$p+1$
vanishes identically.
A more elaborate harmonic treatment of the shifted primes may be found in Elliott [Reference Elliott15], 1995, where the quotient groups
$G_{k}$
corresponding to the subgroups of
$\mathbb{Q}^{\ast }$
generated by the shifted primes
$p+1$
,
$p>k$
, are for all positive
$k$
shown to be of order at most 3.
Moreover, every positive integer
$w$
has infinitely many representations
$$\begin{eqnarray}w^{|G_{k}|}=\mathop{\prod }_{j=1}^{m}(p_{j}+1)^{\unicode[STIX]{x1D700}_{j}},\quad \unicode[STIX]{x1D700}_{j}=\pm 1,\end{eqnarray}$$
with the number of shifted primes necessary for such representations bounded uniformly in
$w$
and
$k$
. Subsequent arguments reduced this bound to
$9$
, cf. Berrizbeitia and Elliott [Reference Berrizbeitia and Elliott1], Elliott [Reference Elliott17].
Note that since they are nested and their orders are uniformly bounded, for all sufficiently large values of
$k$
the groups
$G_{k}$
are isomorphic, cf. Elliott [Reference Elliott, Kanemitsu and Jia18, §6].
Doubtless, in accordance with a century-old conjecture of Dickson, every group
$G_{k}$
is trivial and a single representing ratio
$(p_{1}+1)/(p_{2}+1)$
will suffice.
A mainspring of the upper bound on the orders of the groups
$G_{k}$
is the inequality
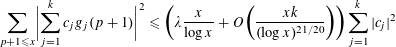$$\begin{eqnarray}\mathop{\sum }_{p+1\leqslant x}\biggl|\mathop{\sum }_{j=1}^{k}c_{\!j}g_{j}(p+1)\biggr|^{2}\leqslant \biggl(\unicode[STIX]{x1D706}\frac{x}{\log x}+O\biggl(\frac{xk}{(\log x)^{21/20}}\biggr)\biggr)\mathop{\sum }_{j=1}^{k}|c_{\!j}|^{2}\end{eqnarray}$$
with
$$\begin{eqnarray}\unicode[STIX]{x1D706}=4+\max _{1\leqslant \ell \leqslant k}\mathop{\sum }_{\substack{ j=1 \\ j\neq \ell }}^{k}\max _{\unicode[STIX]{x1D712}\,(\operatorname{mod}d)}\frac{44d}{\unicode[STIX]{x1D719}(d)^{2}}\biggl|\frac{1}{x}\mathop{\sum }_{n\leqslant x}\overline{g_{\ell }(n)}g_{j}(n)\unicode[STIX]{x1D712}(n)\biggr|,\end{eqnarray}$$
and its variants, cf. Elliott [Reference Elliott15, Theorem 3 and Lemma 15], which hold uniformly for
$x\geqslant 2$
, multiplicative functions
$g_{j}$
with values in the complex unit disc, and complex
$c_{\!j}$
,
$1\leqslant j\leqslant k$
. The inner maximum runs over characters to squarefree moduli.
In particular, the size of the groups
$G_{k}$
is controlled by the size of the partial sums
$$\begin{eqnarray}\mathop{\sum }_{p\leqslant x}p^{-1}(1-\operatorname{Re}g(p)\unicode[STIX]{x1D712}(p)p^{it}),\end{eqnarray}$$
the typical character
$g$
of
$\mathbb{Q}^{\ast }$
braided with a Dirichlet character to an essentially bounded modulus and a standard unitary character on the multiplicative positive reals.
The genesis of the study of products of shifted primes and its connection with illuminating remarks of Wolke [Reference Wolke25], Dress and Volkmann [Reference Dress and Volkmann3], and Meyer [Reference Meyer21], is considered in detail in Chapter 15 of the first author’s 1985 Springer volume, [Reference Elliott8]. An upshot of their results, and which is established in that same chapter, is that the torsion elements of a typical group
$\mathbb{Q}^{\ast }/\unicode[STIX]{x1D6E4}$
are precisely those on which every homomorphism of the group into the additive reals vanishes.
In what follows
$G$
will denote the quotient group
$\mathbb{Q}^{\ast }/\unicode[STIX]{x1D6E4}$
with
$\unicode[STIX]{x1D6E4}$
generated by the rationals
$(an+b)/(An+B)$
,
$n>k$
,
$\unicode[STIX]{x1D6E5}=aB-Ab\neq 0$
,
$k>\max (|a^{-1}b|,|A^{-1}B|)$
. To simplify the exposition it will be further assumed that
$a$
and
$A$
are positive. Replacing
$\mathbb{Q}^{\ast }$
by the multiplicative group of all rationals, simple changes allow that condition to be removed.
It was shown in that same Springer volume that this particular group is finitely generated. A study of the differences
$f(an+b)-f(An+B)$
of a real-valued additive function
$f$
, hence of the homomorphisms of
$G$
into the additive reals, enabled a set of generators for the associated free group and membership of the attached torsion group to be determined.
As its main result the present paper determines the fine structure of the torsion group and establishes the conjecture.
Theorem 1. The dual of the group
$G$
, hence
$G$
itself, may be determined. In particular,
$G$
is finitely generated and its torsion group is an identifiable subgroup of the reduced residue class group
$\,(\operatorname{mod}6(a,A)(aA)^{2}\unicode[STIX]{x1D6E5}^{3})$
, hence its homomorphic image.
In the terminology of [Reference Elliott8, Ch. 22], suitably interpreted
$G$
is arithmic.
The following waystation in the proof is of independent interest.
Theorem 2. Let integers
$a>0$
,
$A>0$
,
$b$
,
$B$
, satisfy
$\unicode[STIX]{x1D6E5}=aB-Ab\neq 0$
. Set
$\unicode[STIX]{x1D6FF}=6(a,A)(aA)^{2}\unicode[STIX]{x1D6E5}^{3}$
.
If a completely multiplicative complex-valued function
$g$
satisfies
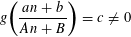$$\begin{eqnarray}g\biggl(\frac{an+b}{An+B}\biggr)=c\neq 0\end{eqnarray}$$
on all but finitely many positive integers,
$n$
, then there is a Dirichlet character
$\,(\operatorname{mod}\unicode[STIX]{x1D6FF})$
with which
$g$
coincides on all primes that do not divide
$\unicode[STIX]{x1D6FF}$
.
Theorem 2 is established in §2. Viewed as a character on
$\mathbb{Q}^{\ast }$
restricted to the integers prime to
$aA\unicode[STIX]{x1D6E5}$
, the function
$g$
is shown to have bounded order, to be essentially a Dirichlet character, then to be exactly a Dirichlet character, and with a modulus that divides
$6(a,A)(aA)^{2}\unicode[STIX]{x1D6E5}^{3}$
.
Attention is drawn to application of a (recent) result of Tao [Reference Tao24], that a sufficiency of large sums
$\sum _{p\leqslant x}p^{-1}(1-\operatorname{Re}g_{1}(p)\unicode[STIX]{x1D712}(p)p^{it})$
,
$\unicode[STIX]{x1D712}$
a Dirichlet character,
$t$
real, forces the logarithmically weighted correlation
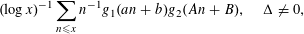$$\begin{eqnarray}(\log x)^{-1}\mathop{\sum }_{n\leqslant x}n^{-1}g_{1}(an+b)g_{2}(An+B),\quad \unicode[STIX]{x1D6E5}\neq 0,\end{eqnarray}$$
of multiplicative functions
$g_{j}$
,
$j=1,2$
with values in the complex unit disc, to be small. This is an important step towards a suitably modified version of the first author’s conjecture, dating from the late 1980s, cf. [Reference Elliott and Goldstein11, Conjecture II], see also [Reference Elliott12], that if for multiplicative functions
$g_{j}$
,
$1\leqslant j\leqslant k$
, with values in the complex unit disc, and integers
$a_{r}>0$
,
$b_{s}$
,
$a_{r}b_{s}-a_{s}b_{r}\neq 0$
,
$1\leqslant r<s\leqslant k$
,
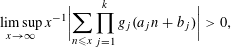$$\begin{eqnarray}\limsup _{x\rightarrow \infty }x^{-1}\biggl|\mathop{\sum }_{n\leqslant x}\mathop{\prod }_{j=1}^{k}g_{j}(a_{j}n+b_{j})\biggr|>0,\end{eqnarray}$$
then there are Dirichlet characters
$\unicode[STIX]{x1D712}_{j}$
and reals
$\unicode[STIX]{x1D70F}_{j}$
, so that the series
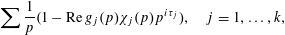$$\begin{eqnarray}\sum \frac{1}{p}(1-\operatorname{Re}g_{j}(p)\unicode[STIX]{x1D712}_{j}(p)p^{i\unicode[STIX]{x1D70F}_{j}}),\quad j=1,\ldots ,k,\end{eqnarray}$$
converge.
That the correlation of two multiplicative functions can be controlled by just one of the functions is already manifest in the first author’s 1994 AMS Memoir in probabilistic number theory, [Reference Elliott14].
Theorem 1 is established in §3. The argument employs Theorem 2 to characterize the group
$G$
theoretically, then reduce its computation to a practicality.
Section 4 contains further practical matters, illustrated by examples. Section 5 considers simultaneous representations and offers variant arguments. Section 6 concludes the paper with a number of historical remarks by the first author concerning the asymptotic estimation of correlations of multiplicative functions.
Here it is convenient to note some constraints.
Constraints. Given integers
$a>0$
,
$A>0$
,
$b$
,
$B$
with
$\unicode[STIX]{x1D6E5}=aB-Ab\neq 0$
, define
$\unicode[STIX]{x1D6FC}=(a,b)$
,
$\unicode[STIX]{x1D6FD}=(A,B)$
,
$a_{1}=a\unicode[STIX]{x1D6FC}^{-1}$
,
$b_{1}=b\unicode[STIX]{x1D6FC}^{-1}$
,
$A_{1}=A\unicode[STIX]{x1D6FD}^{-1}$
,
$B_{1}=B\unicode[STIX]{x1D6FD}^{-1}$
,
$\unicode[STIX]{x1D70C}=\unicode[STIX]{x1D6FC}\unicode[STIX]{x1D6FD}^{-1}$
in lowest terms and
$\unicode[STIX]{x1D6E5}_{1}=a_{1}B_{1}-A_{1}b_{1}$
, so that
$\unicode[STIX]{x1D6E5}=\unicode[STIX]{x1D6FC}\unicode[STIX]{x1D6FD}\unicode[STIX]{x1D6E5}_{1}$
. Define
$\unicode[STIX]{x1D70C}_{0}$
to be that part of
$\unicode[STIX]{x1D70C}$
made up of primes that divide
$(a_{1},A_{1})$
, to be 1 if there are none. This notation is consistent with that of [Reference Elliott8, Ch. 16].
Since there are only two constraints upon
$n$
, we can find a positive
$n$
, and so a complete residue class, for which
$(a_{1}n+b_{1})(A_{1}n+B_{1})$
is not divisible by a given odd prime,
$p$
.
Moreover, either this is possible for
$p=2$
or there is a pair of integers
$n_{1}$
,
$n_{2}$
for which
$2\Vert (a_{1}n_{1}+b_{1})$
,
${\textstyle \frac{1}{2}}(a_{1}n_{1}+b_{1})(A_{1}n_{1}+B_{1})$
is odd, and
$2\Vert (A_{1}n_{2}+B_{1})$
,
$(a_{1}n_{2}+b_{1}){\textstyle \frac{1}{2}}(A_{1}n_{2}+B_{1})$
is odd.
Hence we can either arrange for
$(an+b)/(An+B)=\unicode[STIX]{x1D70C}r$
with
$(r,\unicode[STIX]{x1D6FF})=1$
, or for the pair
$(an_{1}+b)/(An_{1}+B)=2\unicode[STIX]{x1D70C}r_{1}$
,
$(an_{2}+b)/(An_{2}+B)=(\unicode[STIX]{x1D70C}/2)r_{2}$
, with
$(r_{1}r_{2},\unicode[STIX]{x1D6FF})=1$
.
For each prime divisor
$p$
of
$\unicode[STIX]{x1D6FF}$
that does not divide
$(a_{1},A_{1})$
we can arrange a value of
$n$
such that
$p\Vert (a_{1}n+b_{1})/(A_{1}n+B_{1})$
. If
$p^{z}\Vert \unicode[STIX]{x1D6E5}_{1}$
and
$p\nmid a_{1}$
(say), then we choose
$n$
such that
$p^{z+1}\Vert (a_{1}n+b_{1})$
. The identity
$a_{1}(A_{1}n+B_{1})-A_{1}(a_{1}n+b_{1})=\unicode[STIX]{x1D6E5}_{1}$
shows that
$p^{z}\Vert (A_{1}n+B_{1})$
.
2 Proof of Theorem 2
The argument is in four steps, annotated individually. Without loss of generality
$(a,b)=1=(A,B)$
.
Step 1. There is an integer
$m$
for which
$g(p)^{m}=1$
whenever
$(p,aA\unicode[STIX]{x1D6E5})=1$
. Moreover,
$c$
is a root of unity.
For immediacy, in this step only we appeal to results from the first author’s volume on arithmetic functions, [Reference Elliott8], in which
$L^{2}$
additive analogues of correlations are characterized, homomorphisms into the unit circle are replaced by homomorphisms into the additive reals. A merit is that their strong localization lends itself well to computation.
Choose a rational
$r$
for which
$g(r)c=1$
. Then
$g$
has the value
$1$
on all but finitely many of the fractions
$r(an+b)(An+B)^{-1}$
,
$n>0$
. Let
$\unicode[STIX]{x1D6E4}_{0}$
be the subgroup of
$\mathbb{Q}^{\ast }$
that they generate.
We may regard
$g$
as a character on the group
$G_{0}=\mathbb{Q}^{\ast }/\unicode[STIX]{x1D6E4}_{0}$
.
Let
$f$
be a homomorphism of
$G_{0}$
into the additive reals, i.e., a completely additive function that satisfies
$$\begin{eqnarray}f(an+b)-f(An+B)=-f(r),\quad n>n_{0}.\end{eqnarray}$$
According to [Reference Elliott8, Ch. 13], there is a real
$H$
so that
$f(m)=H\log m$
whenever
$(m,aA\unicode[STIX]{x1D6E5})=1$
.
There are two cases. As in Constraints, in the first case there is a residue class for which
$an+b,An+B$
are both prime to
$aA\unicode[STIX]{x1D6E5}$
. In this case
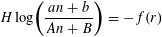$$\begin{eqnarray}H\log \biggl(\frac{an+b}{An+B}\biggr)=-f(r)\end{eqnarray}$$
for infinitely many positive integers, untenable unless
$H=0$
.
Thus
$f(p)=0$
if
$(p,aA\unicode[STIX]{x1D6E5})=1$
, and
$f(r)=0$
.
For each such prime
$p$
there is a positive integer
$v$
, possibly depending upon
$p$
, and a representation
$$\begin{eqnarray}p^{v}=\mathop{\prod }_{j=1}^{k}\biggl(\frac{r(an_{j}+b)}{An_{j}+B}\biggr)^{\unicode[STIX]{x1D700}_{j}},\quad \unicode[STIX]{x1D700}_{j}=\pm 1,n_{j}>n_{0}.\end{eqnarray}$$
As a consequence
$g(p)^{v}=1$
.
Likewise
$g(r)^{w}=1$
for some positive integer, guaranteeing
$c$
to be a root of unity.
If we choose a residue class
$s\,(\operatorname{mod}aA\unicode[STIX]{x1D6E5})$
for which
$((as+b)(As+B),aA\unicode[STIX]{x1D6E5})=1$
, and consider the ratios
$$\begin{eqnarray}(a(aA\unicode[STIX]{x1D6E5}n+s)+b)(A(aA\unicode[STIX]{x1D6E5}n+s)+B)^{-1},\end{eqnarray}$$
then the argument of [Reference Elliott8, Ch. 4], shows that the subgroup of
$G$
generated by the cosets
$p\,(\operatorname{mod}\unicode[STIX]{x1D6E4}_{0})$
,
$(p,aA\unicode[STIX]{x1D6E5})=1$
, is finitely generated, and by similar cosets.
The existence of an integer
$m$
so that the
$g(p)$
are all
$m$
th roots of unity is now clear.
In the second case we can find a residue class for which
$an+b$
is divisible exactly by 2, but by no other prime divisor of
$aA\unicode[STIX]{x1D6E5}$
, whilst
$An+B$
is coprime to
$aA\unicode[STIX]{x1D6E5}$
; also a residue class for which the roles of the parameters
$a$
,
$b$
,
$A$
,
$B$
are reversed.
Once again
$$\begin{eqnarray}f(2)-H\log 2+H\log \biggl(\frac{an+b}{An+B}\biggr)=-f(r),\quad n>n_{1}\end{eqnarray}$$
so that
$H=0$
,
$f(2)=-f(r)$
.
Moreover,
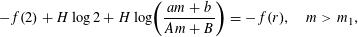$$\begin{eqnarray}-f(2)+H\log 2+H\log \biggl(\frac{am+b}{Am+B}\biggr)=-f(r),\quad m>m_{1},\end{eqnarray}$$
so that
$H=0$
,
$f(2)=f(r)$
.
Hence
$f(2)=0=f(r)$
.
Since we may choose
$r$
to have the form
$2r_{1}$
, where the rational
$r_{1}$
is comprised only of primes not dividing
$aA\unicode[STIX]{x1D6E5}$
,
$c$
itself is again a root of unity.
The inductive argument of [Reference Elliott8, Ch. 4], proceeds, since the class
$2\,(\operatorname{mod}\unicode[STIX]{x1D6E4}_{0})$
has torsion, and for some
$m$
,
$g(p)^{m}=1$
on all primes not dividing
$aA\unicode[STIX]{x1D6E5}$
.
Step 2. There is a Dirichlet character
$\unicode[STIX]{x1D712}\,(\operatorname{mod}D)$
and a set of primes
$q$
with
$\sum q^{-1}$
convergent, such that
$g(p)=\unicode[STIX]{x1D712}(p)$
on all remaining primes.
Remark.
Without loss of generality we may assume
$\unicode[STIX]{x1D712}$
to be primitive.
The following is Tao [Reference Tao24, Theorem 1.3].
Lemma 1. Let the integers
$a>0$
,
$b>0$
,
$c$
,
$d$
, satisfy
$ad-bc\neq 0$
. Let
$\unicode[STIX]{x1D700}>0$
and suppose that
$A_{0}$
is sufficiently large depending upon
$\unicode[STIX]{x1D700}$
,
$a$
,
$b$
,
$c$
,
$d$
. Let
$x\geqslant w\geqslant A_{0}$
and let
$g_{1}$
,
$g_{2}$
be multiplicative functions, with values in the complex unit disc, for which
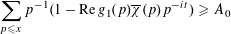$$\begin{eqnarray}\mathop{\sum }_{p\leqslant x}p^{-1}(1-\operatorname{Re}g_{1}(p)\overline{\unicode[STIX]{x1D712}}(p)p^{-it})\geqslant A_{0}\end{eqnarray}$$
for all Dirichlet characters of period at most
$A_{0}$
, and all real numbers
$t$
with
$|t|\leqslant A_{0}x$
.
Then
$$\begin{eqnarray}\biggl|\mathop{\sum }_{x/w<n\leqslant x}n^{-1}g_{1}(an+b)g_{2}(cn+d)\biggr|\leqslant \unicode[STIX]{x1D700}\log w.\end{eqnarray}$$
To implement the result of Tao we apply the following.
Lemma 2. If
$|g(p)|\leqslant 1$
on the primes and
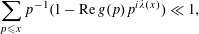$$\begin{eqnarray}\mathop{\sum }_{p\leqslant x}p^{-1}(1-\operatorname{Re}g(p)p^{i\unicode[STIX]{x1D706}(x)})\ll 1,\end{eqnarray}$$
with
$\unicode[STIX]{x1D706}(x)$
real and
$\unicode[STIX]{x1D706}(x)\ll x$
, for
$x\geqslant 2$
, then there is a constant
$\unicode[STIX]{x1D6FC}$
for which
$\unicode[STIX]{x1D706}(x)=\unicode[STIX]{x1D6FC}+O((\log x)^{-1})$
and the series
$\sum p^{-1}(1-\operatorname{Re}g(p)p^{i\unicode[STIX]{x1D6FC}})$
converges.
A somewhat elaborate version of Lemma 2 is employed in the first author’s study of correlations attached to the sums of renormalized shifted additive functions, [Reference Elliott14, §10.3]. The present version may be found as [Reference Elliott19, Lemma 17]. Note that on page 84 line 2 of that account the first sum over the primes contains a surplus factor of
$g(p)$
.
Applying Lemma 1 to
$g(an+b)\overline{g}(An+B)$
guarantees a constant
$A_{0}$
and for each
$x$
sufficiently large a pair
$\unicode[STIX]{x1D712}\,(\operatorname{mod}D_{x})$
,
$t_{x}$
real, with
$\unicode[STIX]{x1D712}$
a Dirichlet character to a modulus
$D_{x}\leqslant A_{0}$
,
$|t_{x}|\leqslant A_{0}x$
, for which the sums
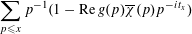$$\begin{eqnarray}\mathop{\sum }_{p\leqslant x}p^{-1}(1-\operatorname{Re}g(p)\overline{\unicode[STIX]{x1D712}}(p)p^{-it_{x}})\end{eqnarray}$$
are uniformly bounded.
The characters belong to a finite set. This provides a positive integer
$k$
for which
$\overline{\unicode[STIX]{x1D712}}(p)^{k}=1$
on all but finitely many primes. The inequality
$1-\operatorname{Re}z^{k}\leqslant k^{2}(1-\operatorname{Re}z)$
, valid in the complex unit disc, shows the sums
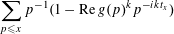$$\begin{eqnarray}\mathop{\sum }_{p\leqslant x}p^{-1}(1-\operatorname{Re}g(p)^{k}p^{-ikt_{x}})\end{eqnarray}$$
to be uniformly bounded.
An application of Lemma 2 guarantees a real
$\unicode[STIX]{x1D6FD}$
for which
$t_{x}=\unicode[STIX]{x1D6FD}+O((\log x)^{-1})$
. Hence
$$\begin{eqnarray}\mathop{\sum }_{p\leqslant x}p^{-1}(1-\operatorname{Re}g(p)\overline{\unicode[STIX]{x1D712}}(p)p^{-it_{x}})\end{eqnarray}$$
differs from a similar sum with
$t_{x}$
replaced by
$\unicode[STIX]{x1D6FD}$
, by
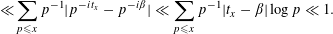$$\begin{eqnarray}\ll \!\mathop{\sum }_{p\leqslant x}p^{-1}|p^{-it_{x}}-p^{-i\unicode[STIX]{x1D6FD}}|\ll \mathop{\sum }_{p\leqslant x}p^{-1}|t_{x}-\unicode[STIX]{x1D6FD}|\log p\ll 1.\end{eqnarray}$$
The sums
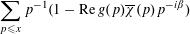$$\begin{eqnarray}\mathop{\sum }_{p\leqslant x}p^{-1}(1-\operatorname{Re}g(p)\overline{\unicode[STIX]{x1D712}}(p)p^{-i\unicode[STIX]{x1D6FD}})\end{eqnarray}$$
are uniformly bounded and, since there are only finitely many possibilities for the character, for some character the corresponding infinite series converges.
Although we shall not need it, it is interesting to note the following.
Lemma 3. If for multiplicative functions
$g_{j}$
,
$j=1,2$
, with values in the complex unit disc,
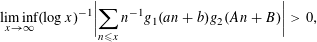$$\begin{eqnarray}\liminf _{x\rightarrow \infty }(\log x)^{-1}\biggl|\mathop{\sum }_{n\leqslant x}n^{-1}g_{1}(an+b)g_{2}(An+B)\biggr|>0,\end{eqnarray}$$
then for some Dirichlet characters
$\unicode[STIX]{x1D712}_{j}$
and reals
$\unicode[STIX]{x1D6FD}_{j}$
the series
$\sum p^{-1}(1-\operatorname{Re}g_{j}(p)\unicode[STIX]{x1D712}_{j}(p)p^{i\unicode[STIX]{x1D6FD}_{j}})$
,
$j=1,2$
, converge.
To complete Step 2 we note that by Step 1,
$g(p)^{m}=1$
on all but finitely many primes. Hence the series
$$\begin{eqnarray}\sum p^{-1}(1-\operatorname{Re}p^{-imk\unicode[STIX]{x1D6FD}})\end{eqnarray}$$
converges; and that is only tenable if
$\unicode[STIX]{x1D6FD}=0$
.
On the primes for which
$g(p)\neq \unicode[STIX]{x1D712}(p)$
,
$g(p)\overline{\unicode[STIX]{x1D712}}(p)$
is a non-trivial
$mk$
th root of unity and the corresponding summands are uniformly bounded from below.
Step 3.
$g(p)=\unicode[STIX]{x1D712}(p)$
provided
$(p,D)=1$
,
$(p,aA\unicode[STIX]{x1D6E5})=1$
.
It is convenient to establish a more general result.
Lemma 4. Let the integers
$a>0$
,
$A>0$
,
$b$
,
$B$
satisfy
$\unicode[STIX]{x1D6E5}=aB-Ab\neq 0$
. Let
$g$
be a completely multiplicative function, with values in the complex unit disc, that satisfies
$$\begin{eqnarray}\limsup _{x\rightarrow \infty }x^{-1}\biggl|\mathop{\sum }_{n\leqslant x}g(an+b)\overline{g}(An+B)\biggr|=1,\end{eqnarray}$$
it being understood that finitely many of the summands may be omitted.
If
$g$
is 1 on all primes that do not belong to a set of primes
$q$
for which
$\sum q^{-1}$
converges, then
$g$
is 1 on all the primes that do not divide
$\unicode[STIX]{x1D6E5}$
.
In the particular case that
$g$
has a non-zero constant value on all but finitely many of the ratios
$(an+b)/(An+B)$
, it is further 1 on the primes that do not divide
$(a/(a,b),A/(A,B))$
.
The next result is a particular case of a theorem of Stepanauskas, [Reference Stepanauskas, Dubrickas, Laurinčikas and Manstavičius22], who was concerned with allowing the parameters
$a_{j}$
,
$b_{j}$
and functions
$g_{j}$
,
$j=1,2$
, to grow with the variable,
$x$
.
Lemma 5. Let
$g_{1}$
,
$g_{2}$
be multiplicative arithmetic functions with values in the complex unit disc. Define the multiplicative functions
$h_{j}$
by
$h_{j}(p^{m})=g_{j}(p^{m})-g_{j}(p^{m-1})$
,
$m=1,2,\ldots \,$
,
$j=1,2$
. Let
$a_{1}$
,
$a_{2}$
,
$b_{1}$
,
$b_{2}$
be integers satisfying
$a_{1}>0$
,
$a_{2}>0$
,
$(a_{j},b_{j})=1$
,
$j=1,2$
,
$\unicode[STIX]{x1D6E5}=a_{1}b_{2}-a_{2}b_{1}\neq 0$
.
Define
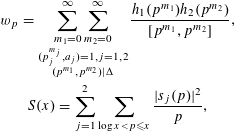$$\begin{eqnarray}\displaystyle & w_{p}=\mathop{\sum }\nolimits_{\substack{ (p_{j}^{m_{j}},a_{j})=1,j=1,2 \\ (p^{m_{1}},p^{m_{2}})\mid \unicode[STIX]{x1D6E5}}}\frac{h_{1}(p^{m_{1}})h_{2}(p^{m_{2}})}{[p^{m_{1}},p^{m_{2}}]}, & \displaystyle \nonumber\\ \displaystyle & S(x)=\mathop{\sum }_{j=1}^{2}\mathop{\sum }_{\log x<p\leqslant x}\frac{|s_{j}(p)|^{2}}{p}, & \displaystyle \nonumber\end{eqnarray}$$
where
$$\begin{eqnarray}s_{j}(p)=\left\{\begin{array}{@{}ll@{}}g_{j}(p)-1\quad & \text{if }p\nmid \unicode[STIX]{x1D6E5}a_{j},\\ g_{1}(p)g_{2}(p)-1\quad & \text{if }p\mid \unicode[STIX]{x1D6E5},p\nmid a_{j},\\ 0\quad & \text{if }p\mid a_{j}.\end{array}\right.\end{eqnarray}$$
Then, uniformly in
$x\geqslant 2$
,
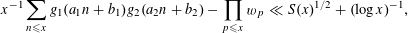$$\begin{eqnarray}x^{-1}\mathop{\sum }_{n\leqslant x}g_{1}(a_{1}n+b_{1})g_{2}(a_{2}n+b_{2})-\mathop{\prod }_{p\leqslant x}w_{p}\ll S(x)^{1/2}+(\log x)^{-1},\end{eqnarray}$$
the implied constant independent of the
$g_{j}$
.
Proof of Lemma 4.
We define the multiplicative function
$h$
by Dirichlet convolution,
$g=1\ast h$
, so that
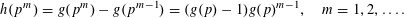$$\begin{eqnarray}h(p^{m})=g(p^{m})-g(p^{m-1})=(g(p)-1)g(p)^{m-1},\quad m=1,2,\ldots .\end{eqnarray}$$
Then by Lemma 5,
$$\begin{eqnarray}\lim _{x\rightarrow \infty }x^{-1}\mathop{\sum }_{n\leqslant x}g(an+b)\overline{g}(An+B)=\mathop{\prod }_{p}w_{p},\end{eqnarray}$$
where, since this result holds for any choices of the
$g(p)$
, we may set all but one
$g(p)=0$
and conclude that
$|w_{p}|\leqslant 1$
. The displayed hypothesis of Lemma 4 then shows that
$|w_{p}|=1$
for each prime
$p$
.
The most interesting case in evaluating the
$w_{p}$
is when
$p\nmid aA$
, but
$p$
may divide
$\unicode[STIX]{x1D6E5}$
. If
$v$
is the highest power of
$p$
to divide
$\unicode[STIX]{x1D6E5}$
, then
$$\begin{eqnarray}w_{p}=2\operatorname{Re}\mathop{\sum }_{k=0}^{v}\overline{h(p^{k})}\mathop{\sum }_{m\geqslant k}\frac{h(p^{m})}{p^{m}}-\mathop{\sum }_{k=0}^{v}\frac{|h(p^{k})|^{2}}{p^{k}}\end{eqnarray}$$
and is real, hence
$\pm 1$
.
The various sums are now geometric progressions and may be readily evaluated.
In our present circumstances
$v=0$
and
$$\begin{eqnarray}\operatorname{Re}\biggl(\frac{1-1/p}{1-g(p)/p}\biggr)=1\text{ or }0\end{eqnarray}$$
is required. As a diagram in the complex plane shows, the left-hand ratio is in absolute value less than 1 unless
$g(p)=1$
, and is certainly not zero.
The cases when
$p$
divides (exactly) one of
$a$
and
$A$
are simpler.
In most applications
$g(p)$
lies on the unit circle and the constraints upon the
$w_{p}$
force
$\operatorname{Re}g(p)$
to satisfy a quadratic equation with real coefficients.
In the narrower context that
$g$
has a fixed non-zero value on all but finitely many of the ratios
$(an+b)/(An+B)$
, let
$p\nmid a$
. If
$p^{s}\Vert \unicode[STIX]{x1D6E5}$
then, with possibly a simple modification in regard to the prime 2, as in Constraints, we can arrange that
$p^{r}\Vert (an+b)$
,
$r>s$
,
$p^{-r}(an+b)$
,
$p^{-s}(An+B)$
free of prime factors of
$\unicode[STIX]{x1D6E5}$
.
Since
$g(p)^{r}$
has a constant value for
$r>s$
,
$g(p)=1$
.
Enhanced by an eratosthenian sieve, this second method will then obviate appeal to Lemma 5, cf. [Reference Elliott8, Ch. 12, particularly Lemma 12.4].
Completion of Step 3 . The argument differs slightly according to the circumstances of the cases considered in Step 1.
In the first case we choose a residue class
$s\,(\operatorname{mod}aA\unicode[STIX]{x1D6E5}D)$
for which
$((as+b)(As+B),aA\unicode[STIX]{x1D6E5}D)=1$
and apply Lemma 4 to the function
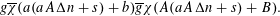$$\begin{eqnarray}g\overline{\unicode[STIX]{x1D712}}(a(aA\unicode[STIX]{x1D6E5}n+s)+b)\overline{g}\unicode[STIX]{x1D712}(A(aA\unicode[STIX]{x1D6E5}n+s)+B).\end{eqnarray}$$
On the primes for which
$(p,aA\unicode[STIX]{x1D6E5}D)=1$
,
$g\overline{\unicode[STIX]{x1D712}}=1$
.
In the second case(s) we adopt the modifications employed in Step 1, noting that
$|g(2)|=1$
.
Step 4.
$D$
divides
$6(a,A)(aA)^{2}\unicode[STIX]{x1D6E5}^{3}$
.
To this end we apply the following result.
Lemma 6. Let the integers
$u_{\!j}>0$
,
$v_{j}$
,
$(u_{\!j},v_{j})=1$
,
$j=1,2$
satisfy
$\unicode[STIX]{x1D6E5}_{1}=u_{1}v_{2}-u_{2}v_{1}\neq 0$
. Assume that the primitive Dirichlet character
$\unicode[STIX]{x1D712}_{D}$
satisfies
$$\begin{eqnarray}\unicode[STIX]{x1D712}_{D}\biggl(\frac{u_{1}k+v_{1}}{u_{2}k+v_{2}}\biggr)=c\neq 0\end{eqnarray}$$
for all
$k$
such that
$(u_{\!j}k+v_{j},D)=1$
,
$j=1,2$
, and that there exists a
$k_{0}$
for which this holds; hence a class
$k_{0}\,(\operatorname{mod}D)$
.
Then
$D\mid 6(u_{1},u_{2})\unicode[STIX]{x1D6E5}_{1}$
.
Proof of Lemma 6.
Define
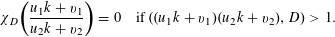$$\begin{eqnarray}\unicode[STIX]{x1D712}_{D}\biggl(\frac{u_{1}k+v_{1}}{u_{2}k+v_{2}}\biggr)=0\quad \text{if }((u_{1}k+v_{1})(u_{2}k+v_{2}),D)>1.\end{eqnarray}$$
If
$D=\prod _{p^{t}\Vert D}p^{t}$
, then there is a decomposition
$\unicode[STIX]{x1D712}_{D}=\prod _{p^{t}\Vert D}\unicode[STIX]{x1D712}_{p^{t}}$
.
Correspondingly
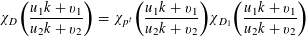$$\begin{eqnarray}\unicode[STIX]{x1D712}_{D}\biggl(\frac{u_{1}k+v_{1}}{u_{2}k+v_{2}}\biggr)=\unicode[STIX]{x1D712}_{p^{t}}\biggl(\frac{u_{1}k+v_{1}}{u_{2}k+v_{2}}\biggr)\unicode[STIX]{x1D712}_{D_{1}}\biggl(\frac{u_{1}k+v_{1}}{u_{2}k+v_{2}}\biggr)\end{eqnarray}$$
where
$D_{1}=p^{-t}D$
.
If we set
$k=\tilde{k}D_{1}+k_{0}$
, then
$(u_{\!j}(\tilde{k}D_{1}+k_{0})+v_{j},D_{1})=1$
,
$j=1,2$
, hence
$$\begin{eqnarray}\unicode[STIX]{x1D712}_{D_{1}}\biggl(\frac{u_{1}(\tilde{k}D_{1}+k_{0})+v_{1}}{u_{2}(\tilde{k}D_{1}+k_{0})+v_{2}}\biggr)=\unicode[STIX]{x1D712}_{D_{1}}\biggl(\frac{u_{1}k_{0}+v_{1}}{u_{2}k_{0}+v_{2}}\biggr)\neq 0.\end{eqnarray}$$
Replacing
$\tilde{k}$
by
$k$
:
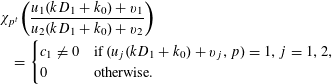$$\begin{eqnarray}\displaystyle & & \displaystyle \unicode[STIX]{x1D712}_{p^{t}}\biggl(\frac{u_{1}(kD_{1}+k_{0})+v_{1}}{u_{2}(kD_{1}+k_{0})+v_{2}}\biggr)\nonumber\\ \displaystyle & & \displaystyle \quad =\left\{\begin{array}{@{}ll@{}}c_{1}\neq 0\quad & \text{if }(u_{\!j}(kD_{1}+k_{0})+v_{j},p)=1,j=1,2,\\ 0\quad & \text{otherwise.}\end{array}\right.\nonumber\end{eqnarray}$$
We have reduced ourselves to the case
$D=p^{t}$
, with
$u_{\!j},v_{j}$
replaced by
$u_{\!j}D_{1}$
,
$k_{0}u_{\!j}+v_{j}$
,
$j=1,2$
.
Note that
$D_{1}u_{1}(k_{0}u_{2}+v_{2})-D_{1}u_{2}(k_{0}u_{1}+v_{1})=D_{1}\unicode[STIX]{x1D6E5}_{1}$
.
For convenience of exposition, write
$w_{j}$
for
$k_{0}u_{\!j}+v_{j}$
,
$j=1,2$
.
Assume that
$p^{s_{j}}\Vert u_{\!j}$
with, without loss of generality,
$s_{2}\leqslant s_{1}$
. Otherwise, consider
$\overline{\unicode[STIX]{x1D712}}_{p^{t}}$
.
If
$s_{2}\geqslant t$
we have
$p^{t}\mid (u_{1},u_{2})$
and we (temporarily) stop. Otherwise, set
$u_{\!j}=p^{s_{j}}m_{j}$
, so that
$p\nmid m_{j}$
,
$j=1,2$
. Then
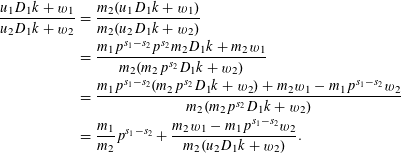$$\begin{eqnarray}\displaystyle \frac{u_{1}D_{1}k+w_{1}}{u_{2}D_{1}k+w_{2}} & = & \displaystyle \frac{m_{2}(u_{1}D_{1}k+w_{1})}{m_{2}(u_{2}D_{1}k+w_{2})}\nonumber\\ \displaystyle & = & \displaystyle \frac{m_{1}p^{s_{1}-s_{2}}p^{s_{2}}m_{2}D_{1}k+m_{2}w_{1}}{m_{2}(m_{2}p^{s_{2}}D_{1}k+w_{2})}\nonumber\\ \displaystyle & = & \displaystyle \frac{m_{1}p^{s_{1}-s_{2}}(m_{2}p^{s_{2}}D_{1}k+w_{2})+m_{2}w_{1}-m_{1}p^{s_{1}-s_{2}}w_{2}}{m_{2}(m_{2}p^{s_{2}}D_{1}k+w_{2})}\nonumber\\ \displaystyle & = & \displaystyle \frac{m_{1}}{m_{2}}p^{s_{1}-s_{2}}+\frac{m_{2}w_{1}-m_{1}p^{s_{1}-s_{2}}w_{2}}{m_{2}(u_{2}D_{1}k+w_{2})}.\nonumber\end{eqnarray}$$
Since
$\unicode[STIX]{x1D712}_{p^{t}}$
is primitive, for an appropriate Gauss sum
$\unicode[STIX]{x1D700}(\unicode[STIX]{x1D712}_{p^{t}})$
with
$|\unicode[STIX]{x1D700}(\unicode[STIX]{x1D712}_{p^{t}})|=p^{t/2}$
,
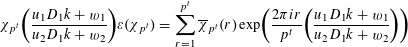$$\begin{eqnarray}\unicode[STIX]{x1D712}_{p^{t}}\biggl(\frac{u_{1}D_{1}k+w_{1}}{u_{2}D_{1}k+w_{2}}\biggr)\unicode[STIX]{x1D700}(\unicode[STIX]{x1D712}_{p^{t}})=\mathop{\sum }_{r=1}^{p^{t}}\overline{\unicode[STIX]{x1D712}}_{p^{t}}(r)\exp \biggl(\frac{2\unicode[STIX]{x1D70B}ir}{p^{t}}\biggl(\frac{u_{1}D_{1}k+w_{1}}{u_{2}D_{1}k+w_{2}}\biggr)\biggr)\end{eqnarray}$$
whenever
$(u_{2}D_{1}k+w_{2},p)=1$
.
In particular,
where
$^{\prime }$
denotes that summation is confined to terms with
$(u_{2}D_{1}k+w_{2},p)=1$
.
The second innersum has the alternative representation
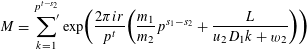
where
$$\begin{eqnarray}L=\overline{m}_{2}(m_{2}w_{1}-m_{1}p^{s_{1}-s_{2}}w_{2}),\qquad m_{2}\overline{m}_{2}\equiv 1\,(\operatorname{mod}p^{t}).\end{eqnarray}$$
Here
$1/(u_{2}D_{1}k+w_{2})$
is likewise interpreted as a group inverse
$\,(\operatorname{mod}p^{t})$
.
For ease of notation we replace
$s_{2}$
by
$s$
.
Assume that
$s\geqslant 1$
. The restriction
$(u_{2}D_{1}k+w_{2},p)=1$
is then automatically satisfied.
For
$1\leqslant k\leqslant p^{t-s}$
, arguing via representations, we map the class
$u_{2}D_{1}k+w_{2}\,(\operatorname{mod}p^{t})$
onto the class
$j_{k}\,(\operatorname{mod}p^{t-s})$
given by
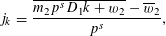$$\begin{eqnarray}j_{k}=\frac{\overline{m_{2}p^{s}D_{1}k+w_{2}}-\overline{w}_{2}}{p^{s}},\end{eqnarray}$$
the inverses taken
$\,(\operatorname{mod}p^{t})$
. Since
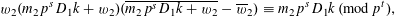$$\begin{eqnarray}w_{2}(m_{2}p^{s}D_{1}k+w_{2})(\overline{m_{2}p^{s}D_{1}k+w_{2}}-\overline{w}_{2})\equiv m_{2}p^{s}D_{1}k\,(\operatorname{mod}p^{t}),\end{eqnarray}$$
$j_{k}$
is well defined. It is the class
$$\begin{eqnarray}(w_{2}(m_{2}p^{s}D_{1}k+w_{2}))^{-1}m_{2}D_{1}k\,(\operatorname{mod}p^{t-s}),\end{eqnarray}$$
the group inverse
$^{-1}$
here taken in the reduced residue class group
$\,(\operatorname{mod}p^{t-s})$
.
Moreover, if
$j_{k_{1}}\equiv j_{k_{2}}\,(\operatorname{mod}p^{t-s})$
,
$1\leqslant k_{1}\leqslant k_{2}\leqslant p^{t-s}$
, then
$$\begin{eqnarray}\overline{m_{2}p^{s}D_{1}k_{1}+w_{2}}-\overline{w}_{2}\equiv \overline{m_{2}p^{s}D_{1}k_{2}+w_{2}}-\overline{w_{2}}\,(\operatorname{mod}p^{t}),\end{eqnarray}$$
from which
$k_{1}\equiv k_{2}\,(\operatorname{mod}p^{t-s})$
rapidly follows. The map is one-to-one and covers every class
$\,(\operatorname{mod}p^{t-s})$
.
In this case
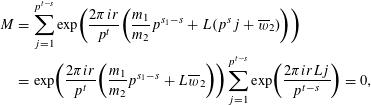$$\begin{eqnarray}\displaystyle M & = & \displaystyle \mathop{\sum }_{j=1}^{p^{t-s}}\exp \biggl(\frac{2\unicode[STIX]{x1D70B}ir}{p^{t}}\biggl(\frac{m_{1}}{m_{2}}p^{s_{1}-s}+L(p^{s}j+\overline{w}_{2})\biggr)\biggr)\nonumber\\ \displaystyle & = & \displaystyle \exp \biggl(\frac{2\unicode[STIX]{x1D70B}ir}{p^{t}}\biggl(\frac{m_{1}}{m_{2}}p^{s_{1}-s}+L\overline{w}_{2}\biggr)\biggr)\mathop{\sum }_{j=1}^{p^{t-s}}\exp \biggl(\frac{2\unicode[STIX]{x1D70B}irLj}{p^{t-s}}\biggr)=0,\nonumber\end{eqnarray}$$
unless
$p^{t-s}\mid L$
. Note that from (1) we may assume that
$(r,p)=1$
.
Hence
$p^{t}\mid p^{s}L$
,
$p^{t}\mid (p^{s}m_{2}w_{1}-p^{s_{1}}m_{1}w_{2})$
, i.e.,
$p^{t}\mid (u_{1}v_{2}-v_{1}u_{2})$
, and once more we (temporarily) stop.
Variant. Suppose now that
$s=s_{2}=0$
, i.e.,
$p\nmid u_{2}$
. In this case
Set
$\unicode[STIX]{x1D6FE}=\exp (2\unicode[STIX]{x1D70B}iru_{1}/p^{t}u_{2})$
. Working within the reduced residue class group
$\,(\operatorname{mod}p^{t})$
, we introduce a new variable
$z=\overline{u_{2}D_{1}k+w_{2}}$
. Since
$z\rightarrow \overline{z}$
permutes the group,
$M$
has a representation
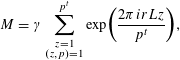$$\begin{eqnarray}M=\unicode[STIX]{x1D6FE}\mathop{\sum }_{\substack{ z=1 \\ (z,p)=1}}^{p^{t}}\exp \biggl(\frac{2\unicode[STIX]{x1D70B}irLz}{p^{t}}\biggr),\end{eqnarray}$$
a Ramanujan sum with an alternative representation in terms of the Möbius function:
$$\begin{eqnarray}M=\unicode[STIX]{x1D6FE}\mathop{\sum }_{d\mid (p^{t},rL)}\unicode[STIX]{x1D707}\biggl(\frac{p^{t}}{d}\biggr)d.\end{eqnarray}$$
If
$p^{t-1}\nmid L$
, then
$d=p^{h}$
with
$h\leqslant t-2$
,
$\unicode[STIX]{x1D707}(p^{t}d^{-1})=0$
and, from (1),
Since the summand with
$k=p^{t}$
is non-zero, this is impossible. Therefore
$p^{t-1}\,\mid \,L$
.
If
$p^{t}\,\mid \,L$
, then we stop, for once again
$p^{t}\,\mid \,\,\overline{m}_{2}(m_{2}w_{1}-m_{1}p^{s_{1}}w_{2})$
,
$p^{t}\,\mid \,(u_{2}w_{1}-u_{1}w_{2})$
, i.e.,
$p^{t}\,\mid \,(u_{1}v_{2}-u_{2}v_{1})$
. Otherwise,
$p^{t-1}\Vert L$
, and the Ramanujan sum has value
$-p^{t-1}$
.
The fundamental relation (1) becomes
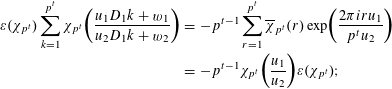$$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D700}(\unicode[STIX]{x1D712}_{p^{t}})\mathop{\sum }_{k=1}^{p^{t}}\unicode[STIX]{x1D712}_{p^{t}}\biggl(\frac{u_{1}D_{1}k+w_{1}}{u_{2}D_{1}k+w_{2}}\biggr) & = & \displaystyle -p^{t-1}\mathop{\sum }_{r=1}^{p^{t}}\overline{\unicode[STIX]{x1D712}}_{p^{t}}(r)\exp \biggl(\frac{2\unicode[STIX]{x1D70B}iru_{1}}{p^{t}u_{2}}\biggr)\nonumber\\ \displaystyle & = & \displaystyle -p^{t-1}\unicode[STIX]{x1D712}_{p^{t}}\biggl(\frac{u_{1}}{u_{2}}\biggr)\unicode[STIX]{x1D700}(\unicode[STIX]{x1D712}_{p^{t}});\nonumber\end{eqnarray}$$
we may cancel the gaussian factors.
Several arguments now present themselves. For example, in absolute value the left-hand sum is at least
$p^{t}-2p^{t-1}$
, guaranteeing that the prime
$p$
is at most 3.
At this stage, our initial hypothesis implies one of:
-
(i)
$p^{t}\,\mid \,(u_{1},u_{2})$
; -
(ii)
$p^{t}\,\mid \,(u_{1}v_{2}-u_{2}v_{1})$
if
$p\geqslant 3$
; -
(iii)
$p^{t-1}\,\mid \,(u_{1}v_{2}-v_{1}u_{2})$
if
$p=2$
or 3.
The conclusion of Lemma 6 is now clear.
Completion of Step 4 . Once again there are small modifications according to the cases of Step 1. In the notation for the first case of Step 3,
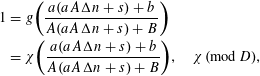$$\begin{eqnarray}\displaystyle 1 & = & \displaystyle g\biggl(\frac{a(aA\unicode[STIX]{x1D6E5}n+s)+b}{A(aA\unicode[STIX]{x1D6E5}n+s)+B}\biggr)\nonumber\\ \displaystyle & = & \displaystyle \unicode[STIX]{x1D712}\biggl(\frac{a(aA\unicode[STIX]{x1D6E5}n+s)+b}{A(aA\unicode[STIX]{x1D6E5}n+s)+B}\biggr),\quad \unicode[STIX]{x1D712}\,(\operatorname{mod}D),\nonumber\end{eqnarray}$$
as long as
$\unicode[STIX]{x1D712}$
is non-zero. By Lemma 6,
$D$
divides
$6(a,A)(aA)^{2}\unicode[STIX]{x1D6E5}^{3}$
.
The remaining cases proceed similarly. Theorem 2 is established.◻
3 Proof of Theorem 1
The argument is in three steps.
We view a standard character on
$G$
as a completely multiplicative function
$g$
with values on the complex unit circle that satisfies
$g((an+b)/(An+B))=1$
for all but finitely many positive integers
$n$
. This enables us to apply Theorem 2 with
$c=1$
and show, in the notation of Constraints, that
$g$
must satisfy the following three conditions:
-
(i) there is a Dirichlet character
$\unicode[STIX]{x1D712}\,(\operatorname{mod}\unicode[STIX]{x1D6FF})$
so that
$g(p)=\unicode[STIX]{x1D712}(p)$
whenever
$(p,\unicode[STIX]{x1D6FF})=1$
, -
(ii)
$g(p)^{2\unicode[STIX]{x1D719}(\unicode[STIX]{x1D6FF})}=1$
if
$p\nmid (a_{1},A_{1})$
;
$g(\unicode[STIX]{x1D70C})^{2\unicode[STIX]{x1D719}(\unicode[STIX]{x1D6FF})}=1$
, -
(iii)
$S(g,\unicode[STIX]{x1D712})=1$
,
where
$$\begin{eqnarray}\displaystyle & S(g,\unicode[STIX]{x1D712})=\displaystyle \sum _{\substack{ d_{j}\,\mid \,\unicode[STIX]{x1D6FF}_{\infty } \\ (d_{1},d_{2})\,\mid \,\unicode[STIX]{x1D6E5}_{1}}}\overline{g}(d_{2})\unicode[STIX]{x1D703}_{d_{1},d_{2}}(\unicode[STIX]{x1D712}), & \displaystyle \nonumber\\ \displaystyle & \unicode[STIX]{x1D703}_{d_{1},d_{2}}(\unicode[STIX]{x1D712})=\frac{1}{\unicode[STIX]{x1D6FF}[d_{1},d_{2}]}\sum ^{\prime }_{n\,(\operatorname{mod}\unicode[STIX]{x1D6FF}[d_{1},d_{2}])}\unicode[STIX]{x1D712}\biggl(\frac{a_{1}n+b_{1}}{d_{1}}\biggr)\overline{\unicode[STIX]{x1D712}}\biggl(\frac{A_{1}n+B_{1}}{d_{2}}\biggr) & \displaystyle \nonumber\end{eqnarray}$$
and
$\unicode[STIX]{x1D6FF}$
is the modulus guaranteed by Theorem 2.
We shall then show that these conditions suffice to determine the dual group of
$G$
, hence
$G$
itself. Moreover, individual groups
$G$
may be determined recursively.
A characterization of
$G$
. Given any character
$g:G\rightarrow \{z\in \mathbb{C},|z|=1\}$
, Theorem 2 provides a Dirichlet character
$\unicode[STIX]{x1D712}\,(\operatorname{mod}\unicode[STIX]{x1D6FF})$
for which condition (i) is satisfied.
The remarks of Constraints, with application of the Chinese Remainder theorem, show condition (ii) to be satisfied.
Moreover,
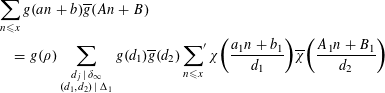$$\begin{eqnarray}\displaystyle & & \displaystyle \mathop{\sum }_{n\leqslant x}g(an+b)\overline{g}(An+B)\nonumber\\ \displaystyle & & \displaystyle =g(\unicode[STIX]{x1D70C})\mathop{\sum }_{\substack{ d_{j}\,\mid \,\unicode[STIX]{x1D6FF}_{\infty } \\ (d_{1},d_{2})\,\mid \,\unicode[STIX]{x1D6E5}_{1}}}g(d_{1})\overline{g}(d_{2})\sum ^{\prime }_{n\leqslant x}\unicode[STIX]{x1D712}\biggl(\frac{a_{1}n+b_{1}}{d_{1}}\biggr)\overline{\unicode[STIX]{x1D712}}\biggl(\frac{A_{1}n+B_{1}}{d_{2}}\biggr)\nonumber\end{eqnarray}$$
where
$d_{j}\,\mid \,\unicode[STIX]{x1D6FF}_{\infty }$
denotes that
$d_{j}$
is comprised of powers of the primes that divide
$\unicode[STIX]{x1D6FF}$
and the innersum is taken over integers
$n$
for which
$a_{1}n+b_{1}$
is divisible by
$d_{1}$
and
$A_{1}n+B_{1}$
by
$d_{2}$
. The value of the innermost summand is determined by the residue class
$\,(\operatorname{mod}\unicode[STIX]{x1D6FF}[d_{1},d_{2}])$
to which
$n$
belongs.
A typical innersum has the uniform bound
$O(x/\max (d_{1},d_{2}))$
, and the asymptotic estimate
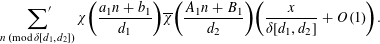$$\begin{eqnarray}\sum ^{\prime }_{n\,(\operatorname{mod}\unicode[STIX]{x1D6FF}[d_{1},d_{2}])}\unicode[STIX]{x1D712}\biggl(\frac{a_{1}n+b_{1}}{d_{1}}\biggr)\overline{\unicode[STIX]{x1D712}}\biggl(\frac{A_{1}n+B_{1}}{d_{2}}\biggr)\biggl(\frac{x}{\unicode[STIX]{x1D6FF}[d_{1},d_{2}]}+O(1)\biggr).\end{eqnarray}$$
In particular, the sum
$\unicode[STIX]{x1D703}_{d_{1},d_{2}}(\unicode[STIX]{x1D712})$
is
$O(\max (d_{1},d_{2})^{-1})$
.
Noting that
$$\begin{eqnarray}\mathop{\sum }_{\substack{ d\leqslant y \\ d\,\mid \,\unicode[STIX]{x1D6FF}_{\infty }}}1\leqslant \mathop{\prod }_{p\,\mid \,\unicode[STIX]{x1D6FF}}\biggl(\biggl[\frac{\log y}{\log p}\biggr]+1\biggr)\ll (\log y)^{\unicode[STIX]{x1D714}}\end{eqnarray}$$
where
$\unicode[STIX]{x1D714}$
denotes the number of distinct prime divisors of
$\unicode[STIX]{x1D6FF}$
, we see that
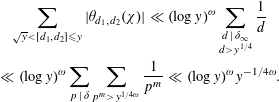$$\begin{eqnarray}\displaystyle & \mathop{\sum }_{\sqrt{y}<[d_{1},d_{2}]\leqslant y}|\unicode[STIX]{x1D703}_{d_{1},d_{2}}(\unicode[STIX]{x1D712})|\ll (\log y)^{\unicode[STIX]{x1D714}}\mathop{\sum }_{\substack{ d\,\mid \,\unicode[STIX]{x1D6FF}_{\infty } \\ d>y^{1/4}}}\frac{1}{d} & \displaystyle \nonumber\\ \displaystyle & \ll (\log y)^{\unicode[STIX]{x1D714}}\mathop{\sum }_{p\,\mid \,\unicode[STIX]{x1D6FF}}\mathop{\sum }_{p^{m}>y^{1/4\unicode[STIX]{x1D714}}}\frac{1}{p^{m}}\ll (\log y)^{\unicode[STIX]{x1D714}}y^{-1/4\unicode[STIX]{x1D714}}. & \displaystyle \nonumber\end{eqnarray}$$
Hence
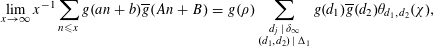$$\begin{eqnarray}\lim _{x\rightarrow \infty }x^{-1}\mathop{\sum }_{n\leqslant x}g(an+b)\overline{g}(An+B)=g(\unicode[STIX]{x1D70C})\mathop{\sum }_{\substack{ d_{j}\,\mid \,\unicode[STIX]{x1D6FF}_{\infty } \\ (d_{1},d_{2})\,\mid \,\unicode[STIX]{x1D6E5}_{1}}}g(d_{1})\overline{g}(d_{2})\unicode[STIX]{x1D703}_{d_{1},d_{2}}(\unicode[STIX]{x1D712}),\end{eqnarray}$$
which sum is
$S(g,\unicode[STIX]{x1D712})$
, and condition (iii) is satisfied.
Conversely, suppose that we choose a
$\unicode[STIX]{x1D712}\,(\operatorname{mod}\unicode[STIX]{x1D6FF})$
, with
$\unicode[STIX]{x1D6FF}=6(a,A)(aA)^{2}\unicode[STIX]{x1D6E5}^{3}$
, and set
$g(p)=\unicode[STIX]{x1D712}(p)$
if
$(p,\unicode[STIX]{x1D6FF})=1$
. If we can, we next choose the
$g(p)$
for
$p$
dividing
$\unicode[STIX]{x1D6FF}$
but not
$(a_{1},A_{1})$
to satisfy
$g(p)^{2\unicode[STIX]{x1D719}(\unicode[STIX]{x1D6FF})}=1$
,
$g(\unicode[STIX]{x1D70C})^{2\unicode[STIX]{x1D719}(\unicode[STIX]{x1D6FF})}=1$
,
$g(\unicode[STIX]{x1D70C})S(g,\unicode[STIX]{x1D712})=1$
. Note that on some of the prime factors of
$\unicode[STIX]{x1D70C}$
, the value of
$g$
may have been chosen in an earlier round.
Then the corresponding completely multiplicative function
$g$
, with values in the complex unit circle, satisfies
$$\begin{eqnarray}\lim _{x\rightarrow \infty }x^{-1}\mathop{\sum }_{n\leqslant x}g(an+b)\overline{g}(An+B)=1.\end{eqnarray}$$
Denoting
$g(an+b)\overline{g}(An+B)$
by
$z_{n}$
for convenience, we note that
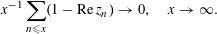$$\begin{eqnarray}x^{-1}\mathop{\sum }_{n\leqslant x}(1-\operatorname{Re}z_{n})\rightarrow 0,\quad x\rightarrow \infty .\end{eqnarray}$$
Here, if
$z_{n}\neq 1$
,
$z_{n}^{2\unicode[STIX]{x1D719}(\unicode[STIX]{x1D6FF})}=1$
guarantees that
$1-\operatorname{Re}z_{n}\geqslant c_{0}>0$
, the value of
$c_{0}$
depending only upon
$\unicode[STIX]{x1D6FF}$
.
In particular, those
$n$
for which
$z_{n}\neq 1$
have asymptotic density zero.
Given an integer
$n_{0}$
for which
$a_{1}n_{0}+b_{1}=w_{1}r_{1}$
with
$w_{1}$
comprised of primes dividing
$\unicode[STIX]{x1D6FF}$
,
$r_{1}$
coprime to
$\unicode[STIX]{x1D6FF}$
, likewise
$A_{1}n_{0}+B_{1}=w_{2}r_{2}$
, then for a sufficiently large
$k$
every integer of the class
$n_{0}\,(\operatorname{mod}\unicode[STIX]{x1D6FF}^{k})$
will give rise to integers
$a_{1}n+b_{1}$
,
$A_{1}n+B_{1}$
of the same form, with identical values of the
$w_{j}$
and with their corresponding
$r_{j}$
belonging to a respective fixed residue class
$\,(\operatorname{mod}\unicode[STIX]{x1D6FF})$
.
Hence
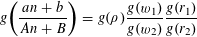$$\begin{eqnarray}g\biggl(\frac{an+b}{An+B}\biggr)=g(\unicode[STIX]{x1D70C})\frac{g(w_{1})}{g(w_{2})}\frac{g(r_{1})}{g(r_{2})}\end{eqnarray}$$
has a constant value on a non-empty residue class.
Such a class has positive asymptotic density, hence contains a representative on which
$g$
has the value 1. Thus
$g$
has the value 1 on the whole class.
In this way every
$g((an+b)/(An+B))=1$
, i.e.
$g$
is a character on
$G$
.
Remarks. The choice of a principal character
$\,(\operatorname{mod}\unicode[STIX]{x1D6FF})$
enables the character
$g$
identically 1 on
$G$
, so the conditions (i)–(iii) are consistent.
For a given character
$\unicode[STIX]{x1D712}\,(\operatorname{mod}\unicode[STIX]{x1D6FF})$
there can be at most one compatible set of values for
$g$
on
$\unicode[STIX]{x1D70C}$
and the remaining torsion primes. The ratio of two compatible values would yield a character on
$G$
that is 1 on the primes not dividing
$\unicode[STIX]{x1D6FF}$
. In view of Lemma 4, it would also be 1 on the primes not dividing
$(a_{1},A_{1})$
, hence on
$\unicode[STIX]{x1D70C}$
.
Not every Dirichlet character
$\,(\operatorname{mod}\unicode[STIX]{x1D6FF})$
need give rise to a character on
$G$
.
This gives a characterization of
$G$
in terms of its dual group.
Consideration of the dual of the exact sequence
$1\rightarrow \unicode[STIX]{x1D6E4}\rightarrow \mathbb{Q}^{\ast }\rightarrow G\rightarrow 1$
shows the dual group of
$\unicode[STIX]{x1D6E4}$
to be isomorphic to the quotient of denumerably many copies of the unit circle, one for each prime, by the dual of
$G$
.
Determination of
$G$
; practical matters. The function
$S(g,\unicode[STIX]{x1D712})$
is given by an infinite series. In this section it will be shown that it factorizes and each of the finitely many factors is a polynomial in its associated variable
$g(p)$
.
Consider a typical sum
$$\begin{eqnarray}\sum ^{\prime }_{n\,(\operatorname{mod}\unicode[STIX]{x1D6FF}[d_{1},d_{2}])}\unicode[STIX]{x1D712}\biggl(\frac{a_{1}n+b_{1}}{d_{1}}\biggr)\overline{\unicode[STIX]{x1D712}}\biggl(\frac{A_{1}n+B_{1}}{d_{2}}\biggr).\end{eqnarray}$$
Let
$\unicode[STIX]{x1D6FF}=\prod _{j\leqslant v}\ell _{j}^{\unicode[STIX]{x1D6FC}_{j}}$
,
$\ell _{j}$
distinct primes,
$d_{1}=\prod _{j\leqslant v}\ell _{j}^{\unicode[STIX]{x1D6FD}_{j}}$
,
$d_{2}=\prod _{j\leqslant v}\ell _{j}^{\unicode[STIX]{x1D6FE}_{j}}$
, where
$\unicode[STIX]{x1D6FD}_{j}=0$
,
$\unicode[STIX]{x1D6FE}_{j}=0$
is possible, but
$\min (\unicode[STIX]{x1D6FD}_{j},\unicode[STIX]{x1D6FE}_{j})$
is bounded by the constraint
$\ell _{j}^{\min (\unicode[STIX]{x1D6FD}_{j},\unicode[STIX]{x1D6FE}_{j})}\,\mid \,\unicode[STIX]{x1D6E5}_{1}$
.
Consider the map
$$\begin{eqnarray}n\,(\operatorname{mod}\unicode[STIX]{x1D6FF}[d_{1},d_{2}])\rightarrow \otimes \,n\,(\operatorname{mod}\ell _{j}^{\unicode[STIX]{x1D6FC}_{j}+\max (\unicode[STIX]{x1D6FD}_{j},\unicode[STIX]{x1D6FE}_{j})})\end{eqnarray}$$
given by
$$\begin{eqnarray}n\rightarrow \mathop{\sum }_{j\leqslant v}u_{\!j}L_{j},\end{eqnarray}$$
where
$L_{j}\equiv 1\,(\operatorname{mod}\ell _{j}^{\unicode[STIX]{x1D6FC}_{j}+\max (\unicode[STIX]{x1D6FD}_{j},\unicode[STIX]{x1D6FE}_{j})})$
,
$L_{j}\equiv 0\,(\operatorname{mod}\ell _{r}^{\unicode[STIX]{x1D6FC}_{r}+\max (\unicode[STIX]{x1D6FD}_{r},\unicode[STIX]{x1D6FE}_{r})})$
if
$1\leqslant r\leqslant v$
,
$r\neq j$
, (Chinese Remainder theorem).
Typically
$a_{1}n+b_{1}\equiv 0\,(\operatorname{mod}d_{1})$
if and only if
$a_{1}n+b_{1}\equiv 0\,(\operatorname{mod}\ell _{j}^{\unicode[STIX]{x1D6FD}_{j}})$
, i.e.
$a_{1}u_{\!j}+b_{1}\equiv 0\,(\operatorname{mod}\ell _{j}^{\unicode[STIX]{x1D6FD}_{j}})$
,
$1\leqslant j\leqslant v$
. Similarly if
$A_{1}n+B_{1}\equiv 0\,(\operatorname{mod}d_{2})$
.
Then
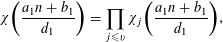$$\begin{eqnarray}\unicode[STIX]{x1D712}\biggl(\frac{a_{1}n+b_{1}}{d_{1}}\biggr)=\mathop{\prod }_{j\leqslant v}\unicode[STIX]{x1D712}_{j}\biggl(\frac{a_{1}n+b_{1}}{d_{1}}\biggr),\end{eqnarray}$$
where
$\unicode[STIX]{x1D712}_{j}$
is a Dirichlet character
$\,(\operatorname{mod}\ell _{j}^{\unicode[STIX]{x1D6FC}_{j}})$
.
In particular,
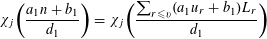$$\begin{eqnarray}\unicode[STIX]{x1D712}_{j}\biggl(\frac{a_{1}n+b_{1}}{d_{1}}\biggr)=\unicode[STIX]{x1D712}_{j}\biggl(\frac{\mathop{\sum }_{r\leqslant v}(a_{1}u_{r}+b_{1})L_{r}}{d_{1}}\biggr)\end{eqnarray}$$
since
$\sum _{r\leqslant v}L_{r}\equiv 1\,(\operatorname{mod}\unicode[STIX]{x1D6FF}[d_{1},d_{2}])$
.
Hence
$$\begin{eqnarray}\unicode[STIX]{x1D712}_{j}\biggl(\frac{a_{1}n+b_{1}}{d_{1}}\biggr)=\unicode[STIX]{x1D712}_{j}\biggl(\frac{a_{1}u_{\!j}+b_{1}}{d_{1}}\biggr)=\unicode[STIX]{x1D712}_{j}\biggl(\frac{a_{1}u_{j}+b_{1}}{\ell _{j}^{\unicode[STIX]{x1D6FD}_{j}}}\biggr)\overline{\unicode[STIX]{x1D712}}_{j}(d_{1j})\end{eqnarray}$$
where
$d_{1j}=\ell _{j}^{-\unicode[STIX]{x1D6FD}_{j}}d_{1}$
,
$1\leqslant j\leqslant v$
; for
$L_{r}/d_{1}$
is divisible by
$\ell _{j}^{\unicode[STIX]{x1D6FC}_{j}}$
if
$r\neq j$
.
Define
$\widehat{\unicode[STIX]{x1D712}}_{j}(\ell _{j}^{\unicode[STIX]{x1D6FD}_{j}})$
to be
$\prod _{1\leqslant r\leqslant v,r\neq j}\overline{\unicode[STIX]{x1D712}}_{r}(\ell _{j}^{\unicode[STIX]{x1D6FD}_{j}})$
,
$1\leqslant j\leqslant v$
, dual analogue of Tate’s lift of a Dirichlet character to a character on the rational idèles.
The sum
$S(g,\unicode[STIX]{x1D712})$
becomes
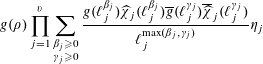$$\begin{eqnarray}g(\unicode[STIX]{x1D70C})\mathop{\prod }_{j=1}^{v}\mathop{\sum }_{\substack{ \unicode[STIX]{x1D6FD}_{j}\geqslant 0 \\ \unicode[STIX]{x1D6FE}_{j}\geqslant 0}}\frac{g(\ell _{j}^{\unicode[STIX]{x1D6FD}_{j}})\widehat{\unicode[STIX]{x1D712}}_{j}(\ell _{j}^{\unicode[STIX]{x1D6FD}_{j}})\overline{g}(\ell _{j}^{\unicode[STIX]{x1D6FE}_{j}})\overline{\widehat{\unicode[STIX]{x1D712}}}_{j}(\ell _{j}^{\unicode[STIX]{x1D6FE}_{j}})}{\ell _{j}^{\max (\unicode[STIX]{x1D6FD}_{j},\unicode[STIX]{x1D6FE}_{j})}}\unicode[STIX]{x1D702}_{j}\end{eqnarray}$$
where
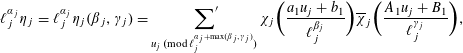$$\begin{eqnarray}\ell _{j}^{\unicode[STIX]{x1D6FC}_{j}}\unicode[STIX]{x1D702}_{j}=\ell _{j}^{\unicode[STIX]{x1D6FC}_{j}}\unicode[STIX]{x1D702}_{j}(\unicode[STIX]{x1D6FD}_{j},\unicode[STIX]{x1D6FE}_{j})=\sum ^{\prime }_{u_{\!j}\,(\operatorname{mod}\ell _{j}^{\unicode[STIX]{x1D6FC}_{j}+\max (\unicode[STIX]{x1D6FD}_{j},\unicode[STIX]{x1D6FE}_{j})})}\unicode[STIX]{x1D712}_{j}\biggl(\frac{a_{1}u_{\!j}+b_{1}}{\ell _{j}^{\unicode[STIX]{x1D6FD}_{j}}}\biggr)\overline{\unicode[STIX]{x1D712}}_{j}\biggl(\frac{A_{1}u_{\!j}+B_{1}}{\ell _{j}^{\unicode[STIX]{x1D6FE}_{j}}}\biggr),\end{eqnarray}$$
it understood that
$a_{1}u_{\!j}+b_{1}\equiv 0\,(\operatorname{mod}\ell _{j}^{\unicode[STIX]{x1D6FD}_{j}})$
,
$A_{1}u_{\!j}+B_{1}\equiv 0\,(\operatorname{mod}\ell _{j}^{\unicode[STIX]{x1D6FE}_{j}})$
, and
$\ell _{j}^{\min (\unicode[STIX]{x1D6FD}_{j},\unicode[STIX]{x1D6FE}_{j})}\,\mid \,\unicode[STIX]{x1D6E5}_{1}$
,
$1\leqslant j\leqslant v$
.
Since
$g(\ell _{j}^{\unicode[STIX]{x1D6FD}})=g(\ell _{j})^{\unicode[STIX]{x1D6FD}}$
,
$\unicode[STIX]{x1D712}^{\unicode[STIX]{x1D6FD}}$
are periodic in
$\unicode[STIX]{x1D6FD}$
, period
$2\unicode[STIX]{x1D719}(\unicode[STIX]{x1D6FF})$
, a typical innersum becomes a polynomial in
$g(\ell _{j})\widehat{\unicode[STIX]{x1D712}}_{j}(\ell _{j})$
, of degree at most
$2\unicode[STIX]{x1D719}(\unicode[STIX]{x1D6FF})-1$
, with coefficients that are linear forms in
$2\unicode[STIX]{x1D719}(\unicode[STIX]{x1D6FF})$
th roots of unity (values of
$\unicode[STIX]{x1D712}$
) that in turn have coefficients that are essentially geometric progressions, indeed rational numbers.
The values of the
$g(p)$
,
$p\nmid (a_{1},A_{1})$
, together with that of
$g(\unicode[STIX]{x1D70C})$
, that fulfill conditions (ii) and (iii) may therefore be ascertained recursively.
Theorem 1 is established.◻
Remark.
For any prime
$\ell$
and integers
$\unicode[STIX]{x1D6FC}\geqslant 1$
,
$\unicode[STIX]{x1D6FD}\geqslant 0$
,
$\unicode[STIX]{x1D6FE}\geqslant 0$
, the sum
$$\begin{eqnarray}\tilde{\unicode[STIX]{x1D702}}(\unicode[STIX]{x1D6FD},\unicode[STIX]{x1D6FE})=\ell ^{-\unicode[STIX]{x1D6FC}}\mathop{\sum }_{\substack{ u\,(\operatorname{mod}\ell ^{\unicode[STIX]{x1D6FC}+\max (\unicode[STIX]{x1D6FD},\unicode[STIX]{x1D6FE})}) \\ \ell ^{\unicode[STIX]{x1D6FD}}\Vert (a_{1}u+b_{1}),\,\ell ^{\unicode[STIX]{x1D6FE}}\Vert (A_{1}u+B_{1})}}1,\end{eqnarray}$$
i.e. a typical
$\unicode[STIX]{x1D702}_{j}$
with
$\unicode[STIX]{x1D712}_{j}$
the principal character
$\,(\operatorname{mod}\ell )$
, represents the asymptotic density of the integers
$n$
for which
$\ell ^{\unicode[STIX]{x1D6FD}}\Vert (a_{1}n+b_{1})$
,
$\ell ^{\unicode[STIX]{x1D6FE}}\Vert (A_{1}n+B_{1})$
. In particular,
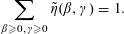$$\begin{eqnarray}\mathop{\sum }_{\unicode[STIX]{x1D6FD}\geqslant 0,\unicode[STIX]{x1D6FE}\geqslant 0}\tilde{\unicode[STIX]{x1D702}}(\unicode[STIX]{x1D6FD},\unicode[STIX]{x1D6FE})=1.\end{eqnarray}$$
In absolute value, each term in the above product representing
$S(g,\unicode[STIX]{x1D712})$
does not exceed 1. In order for
$|S(g,\unicode[STIX]{x1D712})|=1$
to hold it is necessary and sufficient that every term in the product have absolute value 1. In particular, each
$\unicode[STIX]{x1D702}_{j}$
must satisfy
$|\unicode[STIX]{x1D702}_{j}(\unicode[STIX]{x1D6FD}_{j},\unicode[STIX]{x1D6FE}_{j})|=\tilde{\unicode[STIX]{x1D702}}(\unicode[STIX]{x1D6FD}_{j},\unicode[STIX]{x1D6FE}_{j})$
with respect to the appropriate prime
$\ell =\ell _{j}$
.
4 Further practical matters
Let
$k$
be a positive integer. The foregoing argument reduces the determination of the multiplicative group generated by the rationals
$(an+b)/(An+B)$
with
$n\geqslant k$
to a calculation in a polynomial ring over a cyclotomic extension of the rational field.
The following results may accelerate this process.
Example.
The groups
$\mathbb{Q}^{\ast }/\unicode[STIX]{x1D6E4}_{k}$
attached to the ratios
$(3n+1)/(5n+2)$
,
$n\geqslant k$
, introduced in the first author’s volume on arithmetic functions and integer products [Reference Elliott8], were there shown, via homomorphisms into the positive reals, to be finite.
After Theorem 2 each character
$g$
on
$\mathbb{Q}^{\ast }/\unicode[STIX]{x1D6E4}_{k}$
coincides, on the primes
$p$
that do not divide 30, with a product of Dirichlet characters
$\unicode[STIX]{x1D712}_{2}\unicode[STIX]{x1D712}_{3}\unicode[STIX]{x1D712}_{5}$
to moduli 2,
$3^{2}$
and
$5^{2}$
respectively.
For
$\unicode[STIX]{x1D712}=\unicode[STIX]{x1D712}_{3}$
, a typical sum
$$\begin{eqnarray}\unicode[STIX]{x1D702}(\unicode[STIX]{x1D6FD},\unicode[STIX]{x1D6FE})=\sum ^{\prime }_{\substack{ u\,(\operatorname{mod}3^{2+\max (\unicode[STIX]{x1D6FD},\unicode[STIX]{x1D6FE})}) \\ 3^{\unicode[STIX]{x1D6FD}}\Vert (3u+1),\,3^{\unicode[STIX]{x1D6FE}}\Vert (5u+2)}}\unicode[STIX]{x1D712}\biggl(\frac{3u+1}{3^{\unicode[STIX]{x1D6FD}}}\biggr)\overline{\unicode[STIX]{x1D712}}\biggl(\frac{5u+2}{3^{\unicode[STIX]{x1D6FE}}}\biggr)\end{eqnarray}$$
necessarily has
$\unicode[STIX]{x1D6FD}=0$
and, if
$5u_{0}+2\equiv 0\,(\operatorname{mod}3^{\unicode[STIX]{x1D6FE}})$
with
$\unicode[STIX]{x1D6FE}\geqslant 2$
,
$u=u_{0}+3^{\unicode[STIX]{x1D6FE}}k$
, a representation
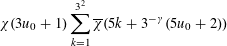$$\begin{eqnarray}\unicode[STIX]{x1D712}(3u_{0}+1)\mathop{\sum }_{k=1}^{3^{2}}\overline{\unicode[STIX]{x1D712}}(5k+3^{-\unicode[STIX]{x1D6FE}}(5u_{0}+2))\end{eqnarray}$$
that vanishes unless the character
$\unicode[STIX]{x1D712}_{3}$
is principal.
The character
$\unicode[STIX]{x1D712}_{5}$
is likewise principal.
The character
$g$
on
$\mathbb{Q}^{\ast }$
is principal on all primes save possibly 2, 3 and 5, and by Lemma 4 on these also.
The groups
$\mathbb{Q}^{\ast }/\unicode[STIX]{x1D6E4}_{k}$
are trivial. Each positive rational
$r$
has infinitely many representations
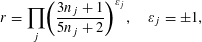$$\begin{eqnarray}r=\mathop{\prod }_{j}\biggl(\frac{3n_{j}+1}{5n_{j}+2}\biggr)^{\unicode[STIX]{x1D700}_{j}},\quad \unicode[STIX]{x1D700}_{j}=\pm 1,\end{eqnarray}$$
with the
$n_{j}$
as large as desired. In the notation of the preface to the volume [Reference Elliott8], we may take
$v=1$
.
Rationalizing the denominators establishes the following.
Multiplicity lemma.
Let the integers
$a_{j}>0$
,
$b_{j}$
,
$j=1,2$
, satisfy
$\unicode[STIX]{x1D6E5}_{0}=a_{1}b_{2}-a_{2}b_{1}\neq 0$
, and the integers
$s$
,
$n$
,
$n^{\prime }$
,
$(s,(a_{2}n+b_{2})(a_{2}n^{\prime }+b_{2}))=1$
.
Then
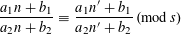$$\begin{eqnarray}\frac{a_{1}n+b_{1}}{a_{2}n+b_{2}}\equiv \frac{a_{1}n^{\prime }+b_{1}}{a_{2}n^{\prime }+b_{2}}\,(\operatorname{mod}s)\end{eqnarray}$$
if and only if
$\unicode[STIX]{x1D6E5}_{0}(n-n^{\prime })\equiv 0\,(\operatorname{mod}s)$
.
Example.
Consider the group
$\mathbb{Q}_{5}^{\ast }/\unicode[STIX]{x1D6E4}$
, where
$\mathbb{Q}_{5}^{\ast }$
denotes the multiplicative positive rationals not divisible by 5 and
$\unicode[STIX]{x1D6E4}$
its subgroup generated by all but finitely many fractions of the form
$(5n+1)/(5n-1)$
. It was established in the first author’s volume [Reference Elliott8] that
$\mathbb{Q}_{5}^{\ast }/\unicode[STIX]{x1D6E4}$
is finite. Reduction
$\,(\operatorname{mod}5)$
shows 2 not to belong to
$\unicode[STIX]{x1D6E4}$
, hence that
$\mathbb{Q}_{5}^{\ast }/\unicode[STIX]{x1D6E4}$
is not trivial.
According to the main result of the present paper, on the primes that do not divide 30 each character
$g$
on
$\mathbb{Q}_{5}^{\ast }/\unicode[STIX]{x1D6E4}$
coincides with a product of Dirichlet characters,
$\unicode[STIX]{x1D712}_{2}\unicode[STIX]{x1D712}_{3}\unicode[STIX]{x1D712}_{5}$
, to moduli
$2^{4}$
, 3 and
$5^{8}$
respectively.
For
$\unicode[STIX]{x1D712}=\unicode[STIX]{x1D712}_{3}$
, a typical sum
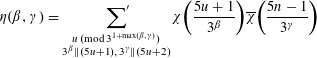$$\begin{eqnarray}\unicode[STIX]{x1D702}(\unicode[STIX]{x1D6FD},\unicode[STIX]{x1D6FE})=\sum ^{\prime }_{\substack{ u\,(\operatorname{mod}3^{1+\max (\unicode[STIX]{x1D6FD},\unicode[STIX]{x1D6FE})}) \\ 3^{\unicode[STIX]{x1D6FD}}\Vert (5u+1),\,3^{\unicode[STIX]{x1D6FE}}\Vert (5u+2)}}\unicode[STIX]{x1D712}\biggl(\frac{5u+1}{3^{\unicode[STIX]{x1D6FD}}}\biggr)\overline{\unicode[STIX]{x1D712}}\biggl(\frac{5n-1}{3^{\unicode[STIX]{x1D6FE}}}\biggr)\end{eqnarray}$$
with
$\unicode[STIX]{x1D6FE}=0$
,
$\unicode[STIX]{x1D6FD}\geqslant 1$
, if
$5u_{0}+1\equiv 0\,(\operatorname{mod}3^{\unicode[STIX]{x1D6FD}})$
, has a representation
$$\begin{eqnarray}\overline{\unicode[STIX]{x1D712}}_{3}(5u_{0}-1)\mathop{\sum }_{k=1}^{3}\unicode[STIX]{x1D712}_{3}(5k+3^{-\unicode[STIX]{x1D6FD}}(5u_{0}+1))\end{eqnarray}$$
that vanishes unless
$\unicode[STIX]{x1D712}_{3}$
is principal.
A similar argument shows that
$\unicode[STIX]{x1D712}_{2}$
is principal.
It follows from the multiplicity lemma that the ratios
$(30n+1)/(30n-1)$
cover
$5^{7}$
distinct residue classes
$\,(\operatorname{mod}5^{8})$
, five times each. From what we have proved so far, if
$\unicode[STIX]{x1D712}=\unicode[STIX]{x1D712}_{5}$
has order
$t$
, then
$5^{7}\leqslant t^{-1}\unicode[STIX]{x1D719}(5^{8})$
;
$t=1,2$
or 4.
Since 3 is a primitive root for all reduced residue class groups
$\,(\operatorname{mod}5^{r})$
,
$r=1,2,\ldots \,$
, and the representative exponents of a given integer
$\,(\operatorname{mod}5)$
and
$\,(\operatorname{mod}5^{8})$
differ by a multiple of 4, we may assume
$\unicode[STIX]{x1D712}$
to be defined
$\,(\operatorname{mod}5)$
. Then
$\unicode[STIX]{x1D712}(3)^{2}=\unicode[STIX]{x1D712}(3^{2})=\unicode[STIX]{x1D712}(-1)=1$
, and
$\unicode[STIX]{x1D712}_{5}$
has order 1 or 2.
An application of Lemma 4 to
$g\overline{\unicode[STIX]{x1D712}}_{5}$
shows that
$g$
coincides with
$\unicode[STIX]{x1D712}_{5}$
on the primes 2 and 3.
The group
$\mathbb{Q}^{\ast }/\unicode[STIX]{x1D6E4}$
generated by the ratios
$(5n+1)/(5n-1)$
has the single free generator,
$5$
, and a torsion group of order 2 determined by its dual through the quadratic Dirichlet character
$\,(\operatorname{mod}5)$
.
There are infinitely many representations
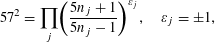$$\begin{eqnarray}57^{2}=\mathop{\prod }_{j}\biggl(\frac{5n_{j}+1}{5n_{j}-1}\biggr)^{\unicode[STIX]{x1D700}_{j}},\quad \unicode[STIX]{x1D700}_{j}=\pm 1,\end{eqnarray}$$
but no such representation is available to 57 itself.
Note that the group
$G=\mathbb{Q}_{5}^{\times }/\unicode[STIX]{x1D6E4}$
, with
$\mathbb{Q}_{5}^{\times }$
the multiplicative rationals prime to 5,
$\unicode[STIX]{x1D6E4}$
its subgroup generated by the ratios
$(5n-1)/(-5n+1)$
,
$n>k$
, has order 4.
In the basic condition (iii)
$S(g,\unicode[STIX]{x1D712})$
is replaced by
$g(-1)S(g,\unicode[STIX]{x1D712})$
where
$g$
is a unitary character on
$\mathbb{Q}_{5}^{\ast }$
extended to
$\mathbb{Q}_{5}^{\times }$
by setting
$g(-1)=1$
or
$-1$
. As a consequence the dual group of
$G$
is generated by a quartic character
$\,(\operatorname{mod}5)$
with
$g(-1)=-1$
.
There is a representation
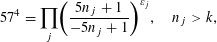$$\begin{eqnarray}57^{4}=\mathop{\prod }_{j}\biggl(\frac{5n_{j}+1}{-5n_{j}+1}\biggr)^{\unicode[STIX]{x1D700}_{j}},\quad n_{j}>k,\end{eqnarray}$$
but no similar representation for
$57^{2}$
.
Remark.
A short elementary proof that a complex-valued multiplicative function constant on all sufficiently large members of a progression
$an+b$
,
$a>0$
, coincides with a Dirichlet character
$\,(\operatorname{mod}a)$
, on the integers prime to
$a$
, may be found as [Reference Elliott8, Lemma 19.3, pp. 334–335].
5 Further results
Two dimensional product representations. Let
$\mathbb{Q}_{2}=\mathbb{Q}^{\ast }\oplus \mathbb{Q}^{\ast }$
be the direct sum of two copies of the multiplicative positive rationals,
$\unicode[STIX]{x1D6E4}_{2}$
its subgroup generated by the pairs
$(an+b)\oplus (An+B)$
,
$n>k$
. Simultaneous representations of the form
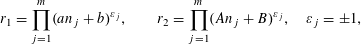$$\begin{eqnarray}r_{1}=\mathop{\prod }_{j=1}^{m}(an_{j}+b)^{\unicode[STIX]{x1D700}_{j}},\qquad r_{2}=\mathop{\prod }_{j=1}^{m}(An_{j}+B)^{\unicode[STIX]{x1D700}_{j}},\quad \unicode[STIX]{x1D700}_{j}=\pm 1,\end{eqnarray}$$
may be studied through the offices of the quotient group
$\mathbb{Q}_{2}/\unicode[STIX]{x1D6E4}_{2}$
. A typical character on that group amounts to a pair of completely multiplicative functions
$g_{1}$
,
$g_{2}$
, with values in the complex unit circle, and that satisfy
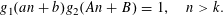$$\begin{eqnarray}g_{1}(an+b)g_{2}(An+B)=1,\quad n>k.\end{eqnarray}$$
We may reduce this two-dimensional problem to a one-dimensional problem by means of the following argument, given in an equivalent form in [Reference Elliott8, Ch. 19]. For ease of notation we shall assume, as we clearly may, that
$b>0$
,
$B>0$
.
Replacing
$n$
by
$bBn$
,
$$\begin{eqnarray}g_{1}(aBn+1)g_{2}(Abn+1)=c_{1}\neq 0.\end{eqnarray}$$
Replacing
$n$
by
$(aB+1)n+1$
,
$$\begin{eqnarray}g_{1}(aBn+1)g_{2}(Ab[(aB+1)n+1]+1)=c_{2}\neq 0.\end{eqnarray}$$
Eliminating between these relations,
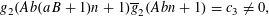$$\begin{eqnarray}g_{2}(Ab(aB+1)n+1)\overline{g}_{2}(Abn+1)=c_{3}\neq 0,\end{eqnarray}$$
to which we can apply Theorem 2. The functions
$g_{2}$
and
$g_{1}$
are essentially Dirichlet characters and we may follow the treatment for a single function.
Variant proof of Theorem 1
. There is an alternative procedure in Steps 2 and 3 that avoids appeal to the results of Step 1 and may more readily generalize to higher dimensional problems. Once Step 2 guarantees the existence of a real
$\unicode[STIX]{x1D6FC}$
for which the series
$\sum p^{-1}(1-\operatorname{Re}g(p)^{k}p^{-i\unicode[STIX]{x1D6FC}})$
converges, Lemma 5 is applied to the completely multiplicative function
$h$
defined by
$p\rightarrow h(p)=g(p)^{k}p^{-i\unicode[STIX]{x1D6FC}}$
. We arrive at an asymptotic estimate
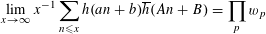$$\begin{eqnarray}\lim _{x\rightarrow \infty }x^{-1}\mathop{\sum }_{n\leqslant x}h(an+b)\overline{h}(An+B)=\mathop{\prod }_{p}w_{p}\end{eqnarray}$$
where the
$w_{p}$
may now depend upon the parameter
$\unicode[STIX]{x1D6FC}$
. Following the argument of Step 3,
$g(p)^{k}=p^{i\unicode[STIX]{x1D6FC}}$
on all but finitely many primes.
Bearing in mind the two cases considered in Constraints, typically, on a suitable residue class
$(g(an+b)\overline{g}(An+B))^{k}$
will coincide with
$((an+b)/(An+B))^{i\unicode[STIX]{x1D6FC}}$
.
A simple analogue of Theorem 2 then suffices to guarantee that
$\unicode[STIX]{x1D6FC}=0$
.
Lemma 7. If integers
$u_{\!j}>0$
,
$v_{j}$
,
$j=1,2$
,
$\unicode[STIX]{x1D6E5}=u_{1}v_{2}-u_{2}v_{1}\neq 0$
, satisfy
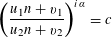$$\begin{eqnarray}\biggl(\frac{u_{1}n+v_{1}}{u_{2}n+v_{2}}\biggr)^{i\unicode[STIX]{x1D6FC}}=c\end{eqnarray}$$
for all
$n$
sufficiently large, then
$\unicode[STIX]{x1D6FC}=0$
and
$c=1$
.
Proof of Lemma 7.
Since
$(u_{\!j}n+v_{j})^{i\unicode[STIX]{x1D6FC}}=(u_{\!j}n)^{i\unicode[STIX]{x1D6FC}}(1+i\unicode[STIX]{x1D6FC}v_{j}(u_{\!j}n)^{-1}+O(n^{-2}))$
,
$j=1,2$
,
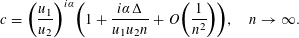$$\begin{eqnarray}c=\biggl(\frac{u_{1}}{u_{2}}\biggr)^{i\unicode[STIX]{x1D6FC}}\biggl(1+\frac{i\unicode[STIX]{x1D6FC}\unicode[STIX]{x1D6E5}}{u_{1}u_{2}n}+O\biggl(\frac{1}{n^{2}}\biggr)\biggr),\quad n\rightarrow \infty .\end{eqnarray}$$
This forces
$(u_{1}/u_{2})^{i\unicode[STIX]{x1D6FC}}=c$
,
$\unicode[STIX]{x1D6FC}=0$
,
$c=1$
in turn.
We may now continue as before until reaching the section on constraints. To once again avoid applying Step 1, choice of an appropriate residue class for
$n$
will, for example, for a given prime
$p$
arrange infinitely many representations
$$\begin{eqnarray}1=g\biggl(\frac{an+b}{An+B}\biggr)=g(p)\unicode[STIX]{x1D712}\biggl(\frac{an+b}{p(An+b)}\biggr)\end{eqnarray}$$
with
$p\Vert (an+b)$
,
$(p^{-1}(an+b)(An+B),\unicode[STIX]{x1D6FF})=1$
, where
$\unicode[STIX]{x1D712}$
is a Dirichlet character
$\,(\operatorname{mod}\unicode[STIX]{x1D6FF})$
.
In particular,
$g(p)$
will be a value of the character
$\unicode[STIX]{x1D712}$
, and
$g(p)^{k}=1$
with
$k$
the order of
$\unicode[STIX]{x1D712}$
.◻
Altogether, this variant argument obviates appeal to the Fourier analysis, involving estimates for Kloosterman sums, that is given in [Reference Elliott8, Chs 2 and 4]. It does not deliver, for the moment at least, the upper bound on the number of terms sufficient to represent group theoretically a typical positive rational,
$r$
, or the underlying recursive argument by which such a bound is obtained there. Moreover, the attendant inequalities on the additive functions in [Reference Elliott8, Ch. 10], are strongly localized.
6 Closing remarks (by the first author)
In anticipation of the validity of an appropriate version of the conjecture that correlations of multiplicative functions with values in the complex unit circle could only satisfy
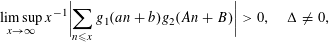$$\begin{eqnarray}\limsup _{x\rightarrow \infty }x^{-1}\biggl|\mathop{\sum }_{n\leqslant x}g_{1}(an+b)g_{2}(An+B)\biggr|>0,\quad \unicode[STIX]{x1D6E5}\neq 0,\end{eqnarray}$$
if there are reals
$\unicode[STIX]{x1D70F}_{j}$
and Dirichlet characters
$\unicode[STIX]{x1D712}_{j}$
so that the series
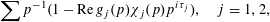$$\begin{eqnarray}\sum p^{-1}(1-\operatorname{Re}g_{j}(p)\unicode[STIX]{x1D712}_{j}(p)p^{i\unicode[STIX]{x1D70F}_{j}}),\quad j=1,2,\end{eqnarray}$$
taken over the prime numbers converge, a particular case of Conjecture II mentioned in the Introduction, Jonathan Kish and I were already in possession of a detailed version of Step 4 in the proof of Theorem 2 by mid 2010—putting the cart before the horse is sometimes helpful.
The conjecture has a root in the probabilistic theory of numbers. In the early 1970s, when studying asymptotic behaviour of additive arithmetic functions with unbounded renormalizations:
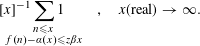$$\begin{eqnarray}\sum _{\substack{ n\leqslant x \\ f(n)-\unicode[STIX]{x1D6FC}(x)\leqslant z\unicode[STIX]{x1D6FD}x}},\quad x\text{(real)}\rightarrow \infty .\end{eqnarray}$$
I felt that the Erdős–Kac realization of an additive function as a sum of independent random variables, in general not valid, might be restored provided a suitable (moving) obstruction were removed from
$f$
.
Where to find such an obstruction? In the event, cf. [Reference Elliott5, Reference Elliott6], perturbation of the underlying probability models, somewhat in the style of the perturbation of planetary orbits within the circle of ideas of the Hamilton–Jacobi equation, led to a satisfactory outcome, the renormalizing functions
$\unicode[STIX]{x1D6FC}(x)$
,
$\unicode[STIX]{x1D6FD}(x)$
classified according to their behaviour under the group of transformations
$x\rightarrow x^{y}$
,
$y>0$
, fixed.
The same point of view could be applied to frequencies involving the sums
$f_{1}(an+b)+f_{2}(An+B)$
of two (or more) possibly distinct additive functions,
$aB-Ab\neq 0$
, cf. [Reference Elliott7].
The respective characteristic functions of the corresponding frequencies have the form
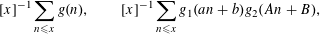$$\begin{eqnarray}[x]^{-1}\mathop{\sum }_{n\leqslant x}g(n),\qquad [x]^{-1}\mathop{\sum }_{n\leqslant x}g_{1}(an+b)g_{2}(An+B),\end{eqnarray}$$
where the functions
$g(n)=\exp (itf(n))$
,
$g_{j}(n)=\exp (itf_{j}(n))$
,
$t$
,
$t_{j}$
real, are multiplicative.
Besides the many experiences in probabilistic number theory, there is the further experience of the Hardy–Ramanujan–Littlewood circle method. One may view that method as resting on the approximation of continuous characters
$\unicode[STIX]{x1D6FC}\rightarrow \exp (2\unicode[STIX]{x1D70B}ik\unicode[STIX]{x1D6FC})$
,
$k=0\pm 1,\pm 2,\ldots \,$
, on the group
$\mathbb{R}/\mathbb{Z}$
dual to the additive group of integers, by the discrete characters
$a/q\rightarrow \exp (2\unicode[STIX]{x1D70B}ika/q)$
, (usually effected with
$(a,q)=1$
) on the additive (reduced) group
$\mathbb{Z}\,(\operatorname{mod}q\mathbb{Z})$
.
For this and other reasons the Dirichlet characters suggested themselves as obstructions in the dual group of the positive rationals under multiplication, the direct product of denumerably many copies of
$\mathbb{R}/\mathbb{Z}$
, and in which, in a certain sense, they are dense, cf. [Reference Elliott16, Ch. 12, Exercise 7]. The role of reduced rationals
$a/q$
is then played by primitive characters.
Whilst the Stone–Weierstrass theorem might offer other approximating functions, the connections between special functions and group representations also suggests the application of associated group characters.
Conjecture III of [Reference Elliott14, p. 65], that there is a positive absolute constant
$c$
such that
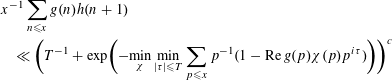$$\begin{eqnarray}\displaystyle & & \displaystyle x^{-1}\mathop{\sum }_{n\leqslant x}g(n)h(n+1)\nonumber\\ \displaystyle & & \displaystyle \quad \ll \biggl(T^{-1}+\exp \biggl(-\!\min _{\unicode[STIX]{x1D712}}\min _{|\unicode[STIX]{x1D70F}|\leqslant T}\mathop{\sum }_{p\leqslant x}p^{-1}(1-\operatorname{Re}g(p)\unicode[STIX]{x1D712}(p)p^{i\unicode[STIX]{x1D70F}})\biggr)\biggr)^{c}\nonumber\end{eqnarray}$$
uniformly for
$x\geqslant 2$
, and multiplicative functions
$g$
,
$h$
with values in the complex unit disc, modified by the requirement that the characters
$\unicode[STIX]{x1D712}$
be to moduli not exceeding
$T$
, as noted in the author’s Cambridge Tract [Reference Elliott16, Ch. 34, p. 315], may well be applied to
$g(an+b)h(An+B)$
,
$aB-Ab\neq 0$
.
It is clear that some restriction must be made upon the size of the defining moduli of the characters
$\unicode[STIX]{x1D712}$
, since the application of Kronecker’s theorem that shows the
$\unicode[STIX]{x1D712}$
to be dense in the dual of
$\mathbb{Q}^{\ast }$
for a given value of
$x$
shows the minimum over
$\unicode[STIX]{x1D712}$
in Conjecture III to be arbitrarily close to zero.
Although the ultimate aim was for a fixed obstruction, experience in Probabilistic Number Theory showed that the variable
$\unicode[STIX]{x1D70F}$
might be allowed to float far past
$x$
in size yet be retrieved, cf. [Reference Elliott10, Reference Elliott19]. Moreover, cf. [Reference Elliott9, Reference Elliott13], I was aware that for considerable ranges of
$\unicode[STIX]{x1D70F}$
and the modulus
$D$
, at most one generalized character
$n\rightarrow \unicode[STIX]{x1D712}(n)n^{i\unicode[STIX]{x1D70F}}$
,
$\unicode[STIX]{x1D712}\,(\operatorname{mod}D)$
, could be near to a given multiplicative function. To this extent the obstruction would be isolated (just as it is in the case of a single renormalized additive function).
Ultimately, one would expect the study of quotient groups of
$\mathbb{Q}^{\ast }$
to embrace integration over appropriate subgroups of the dual group of
$\mathbb{Q}^{\ast }$
.
An extensive survey of problems and results attached to many dimensional product representations of rationals by the values of polynomials on the integers or on the primes, together with a discussion of their attendant groups and
$\mathbb{Q}^{\ast }$
-character sums, may be found in [Reference Elliott, Kanemitsu and Jia18].
Acknowledgements
We thank the referee for a careful reading of the text and have implemented as many of their suggestions as exigencies of publication will allow.
