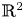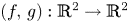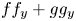1. Introduction
Let $F = (f,\, g): {\mathbb {R}}^{2} \to {\mathbb {R}}^{2}$![]() be a polynomial map whose Jacobian determinant satisfies
be a polynomial map whose Jacobian determinant satisfies
for all $(x,\,y) \in {\mathbb {R}}^{2}$![]() . The map $F$
. The map $F$![]() is locally a diffeomorphism but, after the family of counterexamples found by Pinchuk [Reference Pinchuk15], we know that $F$
is locally a diffeomorphism but, after the family of counterexamples found by Pinchuk [Reference Pinchuk15], we know that $F$![]() is not necessarily globally injective. Pinchuk's counterexamples disprove the real Jacobian conjecture, i.e. the claim that polynomial maps satisfying (1) are injective.
is not necessarily globally injective. Pinchuk's counterexamples disprove the real Jacobian conjecture, i.e. the claim that polynomial maps satisfying (1) are injective.
A natural problem is then to look for additional conditions that guarantee the real Jacobian conjecture. For instance, if the Jacobian determinant of $F$![]() is a constant different from zero, then its injectivity is unknown up to now, and this problem is part of the famous Jacobian conjecture, which is unsolved until these days, see [Reference van den Essen9].
is a constant different from zero, then its injectivity is unknown up to now, and this problem is part of the famous Jacobian conjecture, which is unsolved until these days, see [Reference van den Essen9].
Conditions on the degree of $F$![]() were established in [Reference Braun and dos Santos Filho1,Reference Braun and Oréfice-Okamoto3,Reference Gwoździewicz13]. Conditions on the spectrum of $DF$
were established in [Reference Braun and dos Santos Filho1,Reference Braun and Oréfice-Okamoto3,Reference Gwoździewicz13]. Conditions on the spectrum of $DF$![]() , also valid for non-polynomial maps, can be found in [Reference Cobo, Gutierrez and Llibre7,Reference Fernandes, Gutierrez and Rabanal10]. The aim of this paper is to provide different conditions to the validity of the real Jacobian conjecture. Our main result is Theorem 1, which turns out to be a generalization of the main result of [Reference Braun, Giné and Llibre4]. Theorem 1 is also related to the work [Reference Cima, Gasull and Mañosas6], as explained below. In order to enunciate the theorem, we need some preliminary concepts.
, also valid for non-polynomial maps, can be found in [Reference Cobo, Gutierrez and Llibre7,Reference Fernandes, Gutierrez and Rabanal10]. The aim of this paper is to provide different conditions to the validity of the real Jacobian conjecture. Our main result is Theorem 1, which turns out to be a generalization of the main result of [Reference Braun, Giné and Llibre4]. Theorem 1 is also related to the work [Reference Cima, Gasull and Mañosas6], as explained below. In order to enunciate the theorem, we need some preliminary concepts.
Let $s_1$![]() and $s_2$
and $s_2$![]() be positive integers and set $s = (s_1,\,s_2)$
be positive integers and set $s = (s_1,\,s_2)$![]() . We say that a polynomial function $f \colon {\mathbb {R}}^{2} \to {\mathbb {R}}$
. We say that a polynomial function $f \colon {\mathbb {R}}^{2} \to {\mathbb {R}}$![]() is $s$
is $s$![]() -weight-homogeneous if there is a non-negative integer $d$
-weight-homogeneous if there is a non-negative integer $d$![]() such that
such that
for all $\alpha \in {\mathbb {R}}$![]() , $\alpha > 0$
, $\alpha > 0$![]() , and for all $(x,\,y) \in {\mathbb {R}}^{2}$
, and for all $(x,\,y) \in {\mathbb {R}}^{2}$![]() . In this case, we call $d$
. In this case, we call $d$![]() the weight-degree of $f$
the weight-degree of $f$![]() and $s$
and $s$![]() the weight-exponent of $f$
the weight-exponent of $f$![]() . When $s = (1,\, 1)$
. When $s = (1,\, 1)$![]() we simply say that $f$
we simply say that $f$![]() is homogeneous of degree $d$
is homogeneous of degree $d$![]() . Given a weight-exponent $s$
. Given a weight-exponent $s$![]() and a polynomial $f: {\mathbb {R}}^{2} \to {\mathbb {R}}$
and a polynomial $f: {\mathbb {R}}^{2} \to {\mathbb {R}}$![]() , we can uniquely write $f = f_0 + f_1 + \cdots + f_r$
, we can uniquely write $f = f_0 + f_1 + \cdots + f_r$![]() where $f_{i}$
where $f_{i}$![]() is a $s$
is a $s$![]() -weight-homogeneous polynomial of weight degree $i$
-weight-homogeneous polynomial of weight degree $i$![]() . In this case, when $f_r \neq 0$
. In this case, when $f_r \neq 0$![]() , we say that $f_r$
, we say that $f_r$![]() is the higher $s$
is the higher $s$![]() -weight-homogeneous part of $f$
-weight-homogeneous part of $f$![]() and we also say that $r$
and we also say that $r$![]() is the weight degree of $f$
is the weight degree of $f$![]() . It is straightforward to check the validity of the following Euler formula for a $s$
. It is straightforward to check the validity of the following Euler formula for a $s$![]() -weight-homogeneous polynomial $f$
-weight-homogeneous polynomial $f$![]() with weight degree $d$
with weight degree $d$![]() :
:
Here $f_x$![]() (respectively $f_y$
(respectively $f_y$![]() ) is the partial derivative of $f$
) is the partial derivative of $f$![]() with respect to $x$
with respect to $x$![]() (respectively $y$
(respectively $y$![]() ). It is also clear in this case that $f_x$
). It is also clear in this case that $f_x$![]() (respectively $f_y$
(respectively $f_y$![]() ) is $s$
) is $s$![]() -weight-homogeneous with weight degree $d - s_1$
-weight-homogeneous with weight degree $d - s_1$![]() (respectively $d - s_2$
(respectively $d - s_2$![]() ). Finally, if $p(x,\,y) = (a x + b y)^{k} q(x,\,y)$
). Finally, if $p(x,\,y) = (a x + b y)^{k} q(x,\,y)$![]() , with $p$
, with $p$![]() and $q$
and $q$![]() polynomial functions, $k$
polynomial functions, $k$![]() a positive integer and $a,\, b \in {\mathbb {R}}$
a positive integer and $a,\, b \in {\mathbb {R}}$![]() , then we say that $a x + b y$
, then we say that $a x + b y$![]() is a real linear factor of $f$
is a real linear factor of $f$![]() . We observe that a $s$
. We observe that a $s$![]() -weight-homogeneous polynomial $p$
-weight-homogeneous polynomial $p$![]() , with $s_1 \neq s_2$
, with $s_1 \neq s_2$![]() , can have a real linear factor only in case $a = 0$
, can have a real linear factor only in case $a = 0$![]() or $b = 0$
or $b = 0$![]() . Now we can formulate our main result.
. Now we can formulate our main result.
Theorem 1 Let $F = (f,\,g) \colon {\mathbb {R}}^{2} \to {\mathbb {R}}^{2}$![]() be a polynomial map satisfying (1) and such that there is $z \in {\mathbb {R}}^{2}$
be a polynomial map satisfying (1) and such that there is $z \in {\mathbb {R}}^{2}$![]() with $F(z) = (0,\,0)$
with $F(z) = (0,\,0)$![]() .
.
(a) If either the higher homogeneous terms of the polynomials $f f_x + g g_x$
 and $f f_y + g g_y$
and $f f_y + g g_y$ do not have real linear factors in common, or
do not have real linear factors in common, or(b) if the higher homogeneous term of $f^{2} + g^{2}$
 does not have a factor $(a x + b y)^{2},$
does not have a factor $(a x + b y)^{2},$ with $a b \neq 0,$
with $a b \neq 0,$ and there is a weight-exponent $s$
and there is a weight-exponent $s$ such that the higher $s$
such that the higher $s$ -weight-homogeneous terms of the polynomials $f f_x + g g_x$
-weight-homogeneous terms of the polynomials $f f_x + g g_x$ and $f f_y + g g_y$
and $f f_y + g g_y$ do not have real linear factors in common,
do not have real linear factors in common,
then $F$![]() is injective.
is injective.
The main result of [Reference Braun, Giné and Llibre4] is only statement (a) of Theorem 1, with $z = (0,\,0)$![]() . The following is an example where the injectivity follows from Theorem 1 but not from [Reference Braun, Giné and Llibre4]. Let $F(x,\,y) = (x + y + x^{2},\, y + x^{2})$
. The following is an example where the injectivity follows from Theorem 1 but not from [Reference Braun, Giné and Llibre4]. Let $F(x,\,y) = (x + y + x^{2},\, y + x^{2})$![]() . We have $\det DF = 1$
. We have $\det DF = 1$![]() and
and
The higher homogeneous terms of these polynomials are $4 x^{3}$![]() and $2 x^{2}$
and $2 x^{2}$![]() , respectively, and so the assumptions of [Reference Braun, Giné and Llibre4] are not satisfied. Now the higher homogeneous term of $f^{2} + g^{2}$
, respectively, and so the assumptions of [Reference Braun, Giné and Llibre4] are not satisfied. Now the higher homogeneous term of $f^{2} + g^{2}$![]() is $2 x^{4}$
is $2 x^{4}$![]() and, with weight exponent $s = (1,\, 2)$
and, with weight exponent $s = (1,\, 2)$![]() , the higher $s$
, the higher $s$![]() -weight-homogeneous terms of the above polynomials are $4 x (y + x^{2})$
-weight-homogeneous terms of the above polynomials are $4 x (y + x^{2})$![]() and $2 (y + x^{2})$
and $2 (y + x^{2})$![]() , respectively, that do not have real linear factors in common. So $F$
, respectively, that do not have real linear factors in common. So $F$![]() is injective by Theorem 1.
is injective by Theorem 1.
We point out that the assumptions on Theorem 1 are not necessary for the global injectivity of a polynomial local diffeomorphism, as can be seen by the polynomial diffeomorphism $G(x,\,y) = (x+(x-y)^{2},\, y+(x-y)^{2})$![]() . Here $\det DG = 1$
. Here $\det DG = 1$![]() , the higher homogeneous part of $f^{2}+g^{2}$
, the higher homogeneous part of $f^{2}+g^{2}$![]() is $2 (x-y)^{4}$
is $2 (x-y)^{4}$![]() and the higher homogeneous terms of $f f_x+g g_x$
and the higher homogeneous terms of $f f_x+g g_x$![]() and $f f_y + g g_y$
and $f f_y + g g_y$![]() are $4(x-y)^{3}$
are $4(x-y)^{3}$![]() and $-4(x-y)^{3}$
and $-4(x-y)^{3}$![]() , respectively, and so we can not use Theorem 1.
, respectively, and so we can not use Theorem 1.
It is important to mention here that a standard fact in algebraic geometry is that if a polynomial map $(f,\,g)$![]() satisfying (1) has no points at infinity in $\mathbb {RP}^{2}$
satisfying (1) has no points at infinity in $\mathbb {RP}^{2}$![]() , i.e., the higher homogeneous term of $f^{2}+g^{2}$
, i.e., the higher homogeneous term of $f^{2}+g^{2}$![]() has no real linear factors, then $(f,\,g)$
has no real linear factors, then $(f,\,g)$![]() is a proper map, and so it is a diffeomorphism, according to [Reference Randall16]. A generalization of this to the quasi-homogenous frame is the bidimensional counterpart of [Reference Cima, Gasull and Mañosas6, Theorem A]: polynomial maps $F = (f,\, g)$
is a proper map, and so it is a diffeomorphism, according to [Reference Randall16]. A generalization of this to the quasi-homogenous frame is the bidimensional counterpart of [Reference Cima, Gasull and Mañosas6, Theorem A]: polynomial maps $F = (f,\, g)$![]() satisfying (1) and such that the higher $s$
satisfying (1) and such that the higher $s$![]() -weight-homogeneous parts of $f$
-weight-homogeneous parts of $f$![]() and $g$
and $g$![]() have $(0,\,0)$
have $(0,\,0)$![]() as an isolated common zero, are injective. We observe that in the first example $F$
as an isolated common zero, are injective. We observe that in the first example $F$![]() above, the higher $s$
above, the higher $s$![]() -weight-homogenous parts of $f$
-weight-homogenous parts of $f$![]() and $g$
and $g$![]() are $(y,\, y)$
are $(y,\, y)$![]() , $(y + x^{2},\, y + x^{2})$
, $(y + x^{2},\, y + x^{2})$![]() or $(x^{2},\, x^{2})$
or $(x^{2},\, x^{2})$![]() , depending whether $2 s_1 < s_2$
, depending whether $2 s_1 < s_2$![]() , $2 s_1 = s_2$
, $2 s_1 = s_2$![]() or $2 s_1 > s_2$
or $2 s_1 > s_2$![]() , respectively. None of them have $(0,\,0)$
, respectively. None of them have $(0,\,0)$![]() as an isolated common zero, and hence this example (satisfying the hypotheses of Theorem 1) does not satisfy the assumptions of [Reference Cima, Gasull and Mañosas6, Theorem A]. On the other hand, we do not know if our Theorem 1 implies this result of [Reference Cima, Gasull and Mañosas6], although in case the $s$
as an isolated common zero, and hence this example (satisfying the hypotheses of Theorem 1) does not satisfy the assumptions of [Reference Cima, Gasull and Mañosas6, Theorem A]. On the other hand, we do not know if our Theorem 1 implies this result of [Reference Cima, Gasull and Mañosas6], although in case the $s$![]() -weight degree of $f$
-weight degree of $f$![]() and $g$
and $g$![]() is equal, for some weight $s$
is equal, for some weight $s$![]() , it does, as proven in Lemma 6.
, it does, as proven in Lemma 6.
We emphasize that our proofs rely on qualitative theory of differential equations and uses a characterization of injectivity of $F$![]() via centres of a suitable Hamiltonian vector field associated to $F$
via centres of a suitable Hamiltonian vector field associated to $F$![]() . In our reasoning, we prove a result on polynomial Hamiltonian vector fields in the plane, Proposition 4, which is a generalization of a result of [Reference Cima, Gasull and Mañosas5] that we think is interesting on its own.
. In our reasoning, we prove a result on polynomial Hamiltonian vector fields in the plane, Proposition 4, which is a generalization of a result of [Reference Cima, Gasull and Mañosas5] that we think is interesting on its own.
In § 2, we summarize this and other results needed to the proof of Theorem 1, which is performed in § 3.
After the completion of this work, we took knowledge of the paper [Reference Mello and Xavier14], a partly expository paper with very nice connections between global injectivity and dynamics. The main result of [Reference Mello and Xavier14] is that a polynomial map $(f,\,g)$![]() satisfying (1) is globally injective provided the complexification of the algebraic curve $f=0$
satisfying (1) is globally injective provided the complexification of the algebraic curve $f=0$![]() has one place at infinity (meaning that the curve $f=0$
has one place at infinity (meaning that the curve $f=0$![]() is irreducible and the pre-image of the desingularization map of the curve intersected with the infinity line in $\mathbb {CP}^{2}$
is irreducible and the pre-image of the desingularization map of the curve intersected with the infinity line in $\mathbb {CP}^{2}$![]() has only one point, see the precise definition in [Reference Mello and Xavier14]). This result is different from our Theorem 1 as the polynomial local diffeomorphism $(f,\,g)(x,\,y) = (x+x^{3},\, y+y^{3} )$
has only one point, see the precise definition in [Reference Mello and Xavier14]). This result is different from our Theorem 1 as the polynomial local diffeomorphism $(f,\,g)(x,\,y) = (x+x^{3},\, y+y^{3} )$![]() satisfies the assumption (a) of Theorem 1 but $f$
satisfies the assumption (a) of Theorem 1 but $f$![]() and $g$
and $g$![]() are not irreducible, and so cannot have one place at infinity.
are not irreducible, and so cannot have one place at infinity.
2. Preliminary results and a new condition for degenerate hyperbolic sectors at infinity
We begin this section by explaining the characterization of injectivity of polynomial maps mentioned in the introduction section. By a centre of a vector field $\mathcal {V}$![]() , we mean as usually an equilibrium point $v$
, we mean as usually an equilibrium point $v$![]() of $\mathcal {V}$
of $\mathcal {V}$![]() having a neighbourhood $U$
having a neighbourhood $U$![]() such that $U \setminus \{v\}$
such that $U \setminus \{v\}$![]() is filled with non-constant periodic orbits of $\mathcal {V}$
is filled with non-constant periodic orbits of $\mathcal {V}$![]() . The period annulus of the centre is the maximum neighbourhood of $v$
. The period annulus of the centre is the maximum neighbourhood of $v$![]() with this property. We say that a centre is global if its period annulus is the whole plane.
with this property. We say that a centre is global if its period annulus is the whole plane.
In what follows we assume that $F = (f,\, g)$![]() is a polynomial map satisfying (1). Let the function $H \colon {\mathbb {R}}^{2} \to {\mathbb {R}}$
is a polynomial map satisfying (1). Let the function $H \colon {\mathbb {R}}^{2} \to {\mathbb {R}}$![]() be defined by
be defined by
for $(x,\,y) \in {\mathbb {R}}^{2}$![]() and its associated Hamiltonian vector field $\chi = (P,\,Q)$
and its associated Hamiltonian vector field $\chi = (P,\,Q)$![]() , that is,
, that is,
We observe that $q \in {\mathbb {R}}^{2}$![]() is a singular point of $\chi$
is a singular point of $\chi$![]() if and only if $DF(q)\cdot q = (0,\,0)$
if and only if $DF(q)\cdot q = (0,\,0)$![]() , which is equivalent to $F(q) = (0,\,0)$
, which is equivalent to $F(q) = (0,\,0)$![]() as $\det DF(q) \ne 0$
as $\det DF(q) \ne 0$![]() . Let $U$
. Let $U$![]() be a neighbourhood of $q$
be a neighbourhood of $q$![]() where $F$
where $F$![]() is injective. It follows that $H$
is injective. It follows that $H$![]() is positive in all the points of $U$
is positive in all the points of $U$![]() different from $q$
different from $q$![]() , while $H(q) = 0$
, while $H(q) = 0$![]() , proving that $q$
, proving that $q$![]() is an isolated minimum of $H$
is an isolated minimum of $H$![]() . Then all the orbits of $\chi$
. Then all the orbits of $\chi$![]() in a neighbourhood of $q$
in a neighbourhood of $q$![]() (maybe smaller than $U$
(maybe smaller than $U$![]() ) are closed, proving that $q$
) are closed, proving that $q$![]() is a centre of $X$
is a centre of $X$![]() . We state this result as a lemma for further reference.
. We state this result as a lemma for further reference.
Lemma 2 The singular points of $\chi$![]() are the zeros of $F$
are the zeros of $F$![]() . Each of them corresponds to a centre of $\chi,$
. Each of them corresponds to a centre of $\chi,$![]() and so has index $1$
and so has index $1$![]() .
.
The following is a generalization given in [Reference Braun and Llibre2] of a result from [Reference Sabatini17], see also [Reference Gavrilov11]:
Theorem 3 Let $F: {\mathbb {R}}^{2} \to {\mathbb {R}}^{2}$![]() be a polynomial map satisfying (1). Assume there is $z \in {\mathbb {R}}^{2}$
be a polynomial map satisfying (1). Assume there is $z \in {\mathbb {R}}^{2}$![]() such that $F(z) = (0,\,0)$
such that $F(z) = (0,\,0)$![]() . Then $F$
. Then $F$![]() is injective if and only if the centre $z$
is injective if and only if the centre $z$![]() of $\chi$
of $\chi$![]() is global.
is global.
In what follows we use results and notation on the Poincaré compactification of polynomial vector fields of $ {\mathbb {R}}^{2}$![]() . Particularly, $U_i$
. Particularly, $U_i$![]() , $V_i$
, $V_i$![]() , $i=1,\,2,\,3$
, $i=1,\,2,\,3$![]() , are the canonical local charts of the Poincaré sphere $\mathbb {S}^{2}$
, are the canonical local charts of the Poincaré sphere $\mathbb {S}^{2}$![]() . For details on this technique, we refer the reader to [Reference Dumortier, Llibre and Artés8, Chapter 5] or to [Reference González-Velasco12]. Letting $X$
. For details on this technique, we refer the reader to [Reference Dumortier, Llibre and Artés8, Chapter 5] or to [Reference González-Velasco12]. Letting $X$![]() be a polynomial vector field of $ {\mathbb {R}}^{2}$
be a polynomial vector field of $ {\mathbb {R}}^{2}$![]() , we denote by $p(X)$
, we denote by $p(X)$![]() its compactification. As usual, we say that $q$
its compactification. As usual, we say that $q$![]() is an infinite singular point of $X$
is an infinite singular point of $X$![]() , or of $p(X)$
, or of $p(X)$![]() , if $q$
, if $q$![]() is in the equator of $\mathbb {S}^{2}$
is in the equator of $\mathbb {S}^{2}$![]() . We also say that a hyperbolic sector $h$
. We also say that a hyperbolic sector $h$![]() of $q$
of $q$![]() is degenerate if its two separatrices are contained in the equator of $\mathbb {S}^{2}$
is degenerate if its two separatrices are contained in the equator of $\mathbb {S}^{2}$![]() . Finally, by the Poincaré disc, we mean the projection of the north hemisphere together with the equator of $\mathbb {S}^{2}$
. Finally, by the Poincaré disc, we mean the projection of the north hemisphere together with the equator of $\mathbb {S}^{2}$![]() on the plane $z = 0$
on the plane $z = 0$![]() .
.
Next result studies the infinite singular points of a general polynomial Hamiltonian vector field, giving necessary conditions in order to have a non-degenerate hyperbolic sector. It turns out that the present result generalizes a similar result from [Reference Cima, Gasull and Mañosas5], by considering also weight-homogeneous polynomials. We recall that for a Hamiltonian vector field $X = (-H_y,\, H_x)$![]() , where $H: {\mathbb {R}}^{2} \to {\mathbb {R}}$
, where $H: {\mathbb {R}}^{2} \to {\mathbb {R}}$![]() is a polynomial, the infinite singular points of $p(X)$
is a polynomial, the infinite singular points of $p(X)$![]() in the Poincaré disc are the endpoints of each straight line $a x + b y = 0$
in the Poincaré disc are the endpoints of each straight line $a x + b y = 0$![]() , where $a x + b y$
, where $a x + b y$![]() is a real linear factor of the higher homogeneous part of $H$
is a real linear factor of the higher homogeneous part of $H$![]() .
.
Proposition 4 Let $q$![]() be an infinite singular point of a Hamiltonian system $X = (P,\,Q) = (-H_y,\,H_x)$
be an infinite singular point of a Hamiltonian system $X = (P,\,Q) = (-H_y,\,H_x)$![]() (with $PQ \not \equiv 0$
(with $PQ \not \equiv 0$![]() ), endpoint of the straight line $a x + b y = 0$
), endpoint of the straight line $a x + b y = 0$![]() in the Poincaré disc. If $q$
in the Poincaré disc. If $q$![]() has a non-degenerate hyperbolic sector, then $ax + by$
has a non-degenerate hyperbolic sector, then $ax + by$![]() is a common factor of the higher homogeneous parts of $P$
is a common factor of the higher homogeneous parts of $P$![]() and $Q$
and $Q$![]() . If $a = 0$
. If $a = 0$![]() (respectively $b = 0$
(respectively $b = 0$![]() ), then $y$
), then $y$![]() (respectively $x$
(respectively $x$![]() ) is a common factor of the higher $s$
) is a common factor of the higher $s$![]() -weight-homogeneous parts of $P$
-weight-homogeneous parts of $P$![]() and $Q,$
and $Q,$![]() for each weight-exponent $s = (s_1,\, s_2)$
for each weight-exponent $s = (s_1,\, s_2)$![]() .
.
Proof. We clearly can assume that the degree of $H$![]() is greater than $1$
is greater than $1$![]() and that the higher homogeneous term of $H$
and that the higher homogeneous term of $H$![]() has the form
has the form
where $\tau \geq 1$![]() is an integer and $r(x,\,y)$
is an integer and $r(x,\,y)$![]() is a polynomial that does not have $a x + b y$
is a polynomial that does not have $a x + b y$![]() as a factor.
as a factor.
Clearly if $a b \neq 0$![]() and $\tau \geq 2$
and $\tau \geq 2$![]() , then the higher homogeneous terms of $P$
, then the higher homogeneous terms of $P$![]() and $Q$
and $Q$![]() have both the factor $a x + b y$
have both the factor $a x + b y$![]() , and we are done.
, and we are done.
So it remains to consider the following three cases concerning the higher homogeneous term of $H$![]() : (i) it has the form $r(x,\,y)(a x + b y)$
: (i) it has the form $r(x,\,y)(a x + b y)$![]() with $a b \neq 0$
with $a b \neq 0$![]() , i.e., $\tau = 1$
, i.e., $\tau = 1$![]() ; or (ii) it has the form $r(x,\,y) y^{\tau }$
; or (ii) it has the form $r(x,\,y) y^{\tau }$![]() , i.e., $a = 0$
, i.e., $a = 0$![]() ; or (iii) it has the form $r(x,\,y) x^{\tau }$
; or (iii) it has the form $r(x,\,y) x^{\tau }$![]() , i.e., $b = 0$
, i.e., $b = 0$![]() . By changing $x$
. By changing $x$![]() and $y$
and $y$![]() we do not need to consider case (iii) (observe that with a change like that, a $(s_1,\, s_2)$
we do not need to consider case (iii) (observe that with a change like that, a $(s_1,\, s_2)$![]() -weight-homogeneous polynomial is carried to a $(s_2,\, s_1)$
-weight-homogeneous polynomial is carried to a $(s_2,\, s_1)$![]() -weight-homogeneous polynomial). Also, with a linear change of variable we can transform (i) into (ii) and consider just the later case (because the degree of $H$
-weight-homogeneous polynomial). Also, with a linear change of variable we can transform (i) into (ii) and consider just the later case (because the degree of $H$![]() is greater than $1$
is greater than $1$![]() ). Our conclusion will show that case (ii) with $\tau = 1$
). Our conclusion will show that case (ii) with $\tau = 1$![]() (and so case (i)) cannot happen.
(and so case (i)) cannot happen.
So we assume that case (ii) is in force. Letting $s = (s_1,\, s_2)$![]() be a given weight-exponent, we denote by $m$
be a given weight-exponent, we denote by $m$![]() and $n$
and $n$![]() the weight degrees with respect to $s$
the weight degrees with respect to $s$![]() of $P$
of $P$![]() and $Q$
and $Q$![]() , respectively. In the sequel, we shall use notation on the Poincaré compactification of $X$
, respectively. In the sequel, we shall use notation on the Poincaré compactification of $X$![]() . Observe that $q$
. Observe that $q$![]() is the origin of the local chart $U_1$
is the origin of the local chart $U_1$![]() , that we will treat with the variables $(u,\,v)$
, that we will treat with the variables $(u,\,v)$![]() , with the relation between $(x,\,y)$
, with the relation between $(x,\,y)$![]() and $(u,\,v)$
and $(u,\,v)$![]() given by $(u,\,v) = (y/x,\,1/x)$
given by $(u,\,v) = (y/x,\,1/x)$![]() . The equator of the Poincaré sphere, i.e., the infinite of $ {\mathbb {R}}^{2}$
. The equator of the Poincaré sphere, i.e., the infinite of $ {\mathbb {R}}^{2}$![]() is mapped in the straight line $v = 0$
is mapped in the straight line $v = 0$![]() . Let $r_1$
. Let $r_1$![]() and $r_2$
and $r_2$![]() be the two separatrices of a hyperbolic sector $h$
be the two separatrices of a hyperbolic sector $h$![]() of $(0,\,0)$
of $(0,\,0)$![]() in $U_1$
in $U_1$![]() . Without loss of generality, we assume that the interior of $h$
. Without loss of generality, we assume that the interior of $h$![]() is contained in the region $v > 0$
is contained in the region $v > 0$![]() . Suppose that $r_1$
. Suppose that $r_1$![]() is not contained in the infinite, i.e. in the straight line $v = 0$
is not contained in the infinite, i.e. in the straight line $v = 0$![]() . We claim that $r_2$
. We claim that $r_2$![]() is not contained in the infinite and that $r_1$
is not contained in the infinite and that $r_1$![]() and $r_2$
and $r_2$![]() have the same tangent line at $(0,\,0)$
have the same tangent line at $(0,\,0)$![]() . Indeed, assume on the contrary that there exists a straight half-line $u = \lambda v$
. Indeed, assume on the contrary that there exists a straight half-line $u = \lambda v$![]() , with $v > 0$
, with $v > 0$![]() , between $r_1$
, between $r_1$![]() and $r_2$
and $r_2$![]() . Each obit of $X$
. Each obit of $X$![]() is contained in a level set of $H(x,\,y) = c$
is contained in a level set of $H(x,\,y) = c$![]() of $H$
of $H$![]() . So, by letting
. So, by letting
and $\tilde G(u,\,v) = \tilde H(u,\,v)/v^{d+1}$![]() , points $(u,\,v)$
, points $(u,\,v)$![]() of the compactified orbit will satisfy $\tilde G(u,\,v) = c$
of the compactified orbit will satisfy $\tilde G(u,\,v) = c$![]() . Let $c$
. Let $c$![]() be the value of $\tilde G$
be the value of $\tilde G$![]() in $r_1$
in $r_1$![]() . Since $h$
. Since $h$![]() is an hyperbolic sector, each sequence $\{w_n\}$
is an hyperbolic sector, each sequence $\{w_n\}$![]() in the interior of $h$
in the interior of $h$![]() such that $\lim _{n \to \infty } w_n = (0,\,0)$
such that $\lim _{n \to \infty } w_n = (0,\,0)$![]() will satisfy $\lim _{n \to \infty }\tilde G(w_n) = c$
will satisfy $\lim _{n \to \infty }\tilde G(w_n) = c$![]() . So
. So
Then writing $\tilde H = \sum \nolimits _{i = 0}^{d+1} \tilde H_i$![]() , with $\tilde H_i$
, with $\tilde H_i$![]() being the homogeneous part of degree $i$
being the homogeneous part of degree $i$![]() of $\tilde H$
of $\tilde H$![]() , we get $\tilde H_0(\lambda,\,1) = \cdots = \tilde H_d(\lambda,\, 1) = 0$
, we get $\tilde H_0(\lambda,\,1) = \cdots = \tilde H_d(\lambda,\, 1) = 0$![]() and $\tilde H_{d+1}(\lambda,\, 1) = c$
and $\tilde H_{d+1}(\lambda,\, 1) = c$![]() . Hence
. Hence
meaning that the straight half-line $u = \lambda v$![]() is invariant by the flow, a contradiction. This proves the claim.
is invariant by the flow, a contradiction. This proves the claim.
Clearly $\tilde G(u,\,v)$![]() have the same value $c$
have the same value $c$![]() in $r_1$
in $r_1$![]() and $r_2$
and $r_2$![]() , by the continuity of $\tilde G$
, by the continuity of $\tilde G$![]() in $v > 0$
in $v > 0$![]() . Let $u = \lambda v$
. Let $u = \lambda v$![]() , $v > 0$
, $v > 0$![]() , the common tangent of $r_1$
, the common tangent of $r_1$![]() and $r_2$
and $r_2$![]() at $(0,\,0)$
at $(0,\,0)$![]() . This line is contained in the tangent cone of the algebraic variety $\tilde H(u,\,v) - c v^{d+1} = 0$
. This line is contained in the tangent cone of the algebraic variety $\tilde H(u,\,v) - c v^{d+1} = 0$![]() , with multiplicity at least two, i.e.,
, with multiplicity at least two, i.e.,

with $k \geq 2$![]() and $\tilde {\tilde H}_{k}(u,\,v) = (u - \lambda v)^{2} R(u,\,v)$
and $\tilde {\tilde H}_{k}(u,\,v) = (u - \lambda v)^{2} R(u,\,v)$![]() , where $R(u,\,v)$
, where $R(u,\,v)$![]() is a homogeneous polynomial of degree $k - 2$
is a homogeneous polynomial of degree $k - 2$![]() , and $\tilde { \tilde H}_i$
, and $\tilde { \tilde H}_i$![]() is the homogeneous part of degree $i$
is the homogeneous part of degree $i$![]() of $\tilde H(u,\,v) - c v^{d+1}$
of $\tilde H(u,\,v) - c v^{d+1}$![]() . Therefore, from (3), it follows that
. Therefore, from (3), it follows that

Note that if $k = d+1$![]() then $H(x,\,y) = \tilde H_{d+1}(y)$
then $H(x,\,y) = \tilde H_{d+1}(y)$![]() which is not possible because then $Q \equiv 0$
which is not possible because then $Q \equiv 0$![]() . So, $k < d+1$
. So, $k < d+1$![]() , and $Q$
, and $Q$![]() contains the term $(d + 1 - k) x^{d-k} \tilde {\tilde H}_k(y,\,1)$
contains the term $(d + 1 - k) x^{d-k} \tilde {\tilde H}_k(y,\,1)$![]() . Since $\tilde H_k=(y-\lambda )^{2} \tilde R(y,\,1)$
. Since $\tilde H_k=(y-\lambda )^{2} \tilde R(y,\,1)$![]() we get that $n$
we get that $n$![]() , which is the $s$
, which is the $s$![]() -weight degree of $Q$
-weight degree of $Q$![]() , satisfies
, satisfies
The $s$![]() -weight-homogeneous part of weight degree $n$
-weight-homogeneous part of weight degree $n$![]() of $Q$
of $Q$![]() writes
writes

Since the maximum exponent of $x$![]() in $H$
in $H$![]() is $d + 1 - k$
is $d + 1 - k$![]() , and so the maximum possible exponent of $x$
, and so the maximum possible exponent of $x$![]() in $Q_n$
in $Q_n$![]() is $d - k$
is $d - k$![]() , it follows that if $a_{i j} \neq 0$
, it follows that if $a_{i j} \neq 0$![]() in the above sum, then $(d-k) s_1 + j s_2 \geq n \geq (d-k) s_1 + 2 s_2$
in the above sum, then $(d-k) s_1 + j s_2 \geq n \geq (d-k) s_1 + 2 s_2$![]() , from (4), forcing that $j$
, from (4), forcing that $j$![]() is at least $2$
is at least $2$![]() . This means that
. This means that
where $T(x,\,y)$![]() is a suitable $s$
is a suitable $s$![]() -weight-homogeneous polynomial of weight degree $n - 2 s_2$
-weight-homogeneous polynomial of weight degree $n - 2 s_2$![]() . Since $Q_n = \partial H_{n + s_1}/\partial x$
. Since $Q_n = \partial H_{n + s_1}/\partial x$![]() , where here $H_{n+s_1}$
, where here $H_{n+s_1}$![]() means the $s$
means the $s$![]() -weight-homogeneous term of weight degree $n + s_1$
-weight-homogeneous term of weight degree $n + s_1$![]() of $H$
of $H$![]() (recall that if $H$
(recall that if $H$![]() has $s$
has $s$![]() -weight degree $\ell$
-weight degree $\ell$![]() then $\partial H/\partial x$
then $\partial H/\partial x$![]() , if not zero, has $s$
, if not zero, has $s$![]() -weight degree $\ell - s_1$
-weight degree $\ell - s_1$![]() ), it thus follows that
), it thus follows that
for some polynomial $G(y)$![]() which must be a factor of $y^{2}$
which must be a factor of $y^{2}$![]() , otherwise $H_{n + s_1}$
, otherwise $H_{n + s_1}$![]() is not weight-homogeneous.
is not weight-homogeneous.
Now the higher $s$![]() -weight-homogeneous term, $P_m$
-weight-homogeneous term, $P_m$![]() , of $P = -H_y$
, of $P = -H_y$![]() comes from $H_{m + s_ 2}$
comes from $H_{m + s_ 2}$![]() . Clearly $m + s_2 \geq n + s_1$
. Clearly $m + s_2 \geq n + s_1$![]() by (5). In case $m + s_2 = n + s_1$
by (5). In case $m + s_2 = n + s_1$![]() , then $P_m$
, then $P_m$![]() has a factor $y$
has a factor $y$![]() . On the other hand, if $m + s_2 > n + s_1$
. On the other hand, if $m + s_2 > n + s_1$![]() , it follows that $H_{m + s_2} = s y^{j}$
, it follows that $H_{m + s_2} = s y^{j}$![]() , with $s_2 j = m + s_2$
, with $s_2 j = m + s_2$![]() , otherwise the higher $s$
, otherwise the higher $s$![]() -weight-homogeneous term of $Q$
-weight-homogeneous term of $Q$![]() is not $Q_n$
is not $Q_n$![]() because $m + s_2 - s_1 > n$
because $m + s_2 - s_1 > n$![]() . In particular, $P_m$
. In particular, $P_m$![]() has a factor $y$
has a factor $y$![]() .
.
Observe that our proof shows in particular that the higher $s$![]() -weight-homogeneous term of $H$
-weight-homogeneous term of $H$![]() has the factor $(a x + b y)^{2}$
has the factor $(a x + b y)^{2}$![]() (homogeneous if $a b \neq 0$
(homogeneous if $a b \neq 0$![]() ). In particular, case (i) of the beginning of the proof is not possible.
). In particular, case (i) of the beginning of the proof is not possible.
Corollary 5 Let $H \colon {\mathbb {R}}^{2} \to {\mathbb {R}}$![]() be a polynomial function. Let $q$
be a polynomial function. Let $q$![]() be an infinite singular point of the polynomial Hamiltonian vector field $\chi = (-H_y,\,H_x)$
be an infinite singular point of the polynomial Hamiltonian vector field $\chi = (-H_y,\,H_x)$![]() , endpoint of the straight line $a x + b y = 0$
, endpoint of the straight line $a x + b y = 0$![]() in the Poincaré disc. Assume either that the higher homogeneous terms of $H_x$
in the Poincaré disc. Assume either that the higher homogeneous terms of $H_x$![]() and $H_y$
and $H_y$![]() do not have real linear factors in common, or, if $a = 0,$
do not have real linear factors in common, or, if $a = 0,$![]() (respectively $b = 0$
(respectively $b = 0$![]() ) that $y$
) that $y$![]() (respectively $x$
(respectively $x$![]() ) is not a common factor of the higher $s$
) is not a common factor of the higher $s$![]() -weight-homogeneous parts of $H_x$
-weight-homogeneous parts of $H_x$![]() and $H_y,$
and $H_y,$![]() for some weight-exponent $s = (s_1,\, s_2)$
for some weight-exponent $s = (s_1,\, s_2)$![]() . Then the topological index of $q$
. Then the topological index of $q$![]() is greater than or equal to zero. If this index is zero, then $q$
is greater than or equal to zero. If this index is zero, then $q$![]() is formed by two degenerate hyperbolic sectors.
is formed by two degenerate hyperbolic sectors.
Proof. From Proposition 4, it follows that $q$![]() have no non-degenerate hyperbolic sectors. Thus, the number of hyperbolic sectors of $q$
have no non-degenerate hyperbolic sectors. Thus, the number of hyperbolic sectors of $q$![]() is $h \leq 2$
is $h \leq 2$![]() . By the index formula we conclude that the index of $q$
. By the index formula we conclude that the index of $q$![]() is greater than or equal to the number of elliptic sectors of $q$
is greater than or equal to the number of elliptic sectors of $q$![]() , and so greater than or equal to zero. If the index is zero, it thus clearly follows that there are no elliptic sectors and also that $q$
, and so greater than or equal to zero. If the index is zero, it thus clearly follows that there are no elliptic sectors and also that $q$![]() must have two degenerate hyperbolic sectors.
must have two degenerate hyperbolic sectors.
3. Proof of Theorem 1
We consider the function $H(x,\,y) = (f(x,\,y)^{2} + g(x,\,y)^{2})/2$![]() defined in $ {\mathbb {R}}^{2}$
defined in $ {\mathbb {R}}^{2}$![]() , and the associated Hamiltonian vector field $\chi = (- H_y,\, H_x )$
, and the associated Hamiltonian vector field $\chi = (- H_y,\, H_x )$![]() . Since $F(z) = (0,\,0)$
. Since $F(z) = (0,\,0)$![]() , it follows from Theorem 3 that in order to prove that $F$
, it follows from Theorem 3 that in order to prove that $F$![]() is injective, it is enough to prove that $z$
is injective, it is enough to prove that $z$![]() is a global centre of the vector field $\chi$
is a global centre of the vector field $\chi$![]() .
.
Let $q$![]() be an infinite singular point of $\chi$
be an infinite singular point of $\chi$![]() , endpoint of the straight line $a x + b y = 0$
, endpoint of the straight line $a x + b y = 0$![]() in the Poincaré disc. If we are under assumption (a) of Theorem 1, then we are under the assumptions of Corollary 5. If we assume (b) of the Theorem and $a b \neq 0$
in the Poincaré disc. If we are under assumption (a) of Theorem 1, then we are under the assumptions of Corollary 5. If we assume (b) of the Theorem and $a b \neq 0$![]() , then $a x + b y$
, then $a x + b y$![]() is not a common factor of $H_x$
is not a common factor of $H_x$![]() and $H_y$
and $H_y$![]() (from (2)), and we are again under the assumptions of Corollary 5. On the other hand, if $a b = 0$
(from (2)), and we are again under the assumptions of Corollary 5. On the other hand, if $a b = 0$![]() , assumption (b) guarantees the existence of a weight-exponent $s$
, assumption (b) guarantees the existence of a weight-exponent $s$![]() satisfying the assumptions of Corollary 5. Thus, in any case, it follows from this corollary that the topological index of any infinite singular point of $\chi$
satisfying the assumptions of Corollary 5. Thus, in any case, it follows from this corollary that the topological index of any infinite singular point of $\chi$![]() is greater than or equal to zero.
is greater than or equal to zero.
Also, the index of each finite singular point of $\chi$![]() is one, by Lemma 2. Corresponding to the singular point $z$
is one, by Lemma 2. Corresponding to the singular point $z$![]() of $\chi$
of $\chi$![]() there are two singular points of $p(\chi )$
there are two singular points of $p(\chi )$![]() , the Poincaré compactification of $\chi$
, the Poincaré compactification of $\chi$![]() , one in each hemisphere of the Poincaré sphere, having index $1$
, one in each hemisphere of the Poincaré sphere, having index $1$![]() . Thus the sum of the indices of all the singular points of $p(\chi )$
. Thus the sum of the indices of all the singular points of $p(\chi )$![]() in the Poincaré sphere is at least $2$
in the Poincaré sphere is at least $2$![]() . From the Poincaré–Hopf theorem (see Theorem 6.30 in[Reference Dumortier, Llibre and Artés8]), this sum must be $2$
. From the Poincaré–Hopf theorem (see Theorem 6.30 in[Reference Dumortier, Llibre and Artés8]), this sum must be $2$![]() . So, we conclude that $p(\chi )$
. So, we conclude that $p(\chi )$![]() does not have other finite singular points (other than the two centres corresponding to the centre of $\chi$
does not have other finite singular points (other than the two centres corresponding to the centre of $\chi$![]() ) and $p(\chi )$
) and $p(\chi )$![]() either does not have infinite singular points or each of them has index $0$
either does not have infinite singular points or each of them has index $0$![]() , which again by Corollary 5, must be formed by two degenerate hyperbolic sectors.
, which again by Corollary 5, must be formed by two degenerate hyperbolic sectors.
Looking at the Poincaré disc, we summarize the frame: $\chi$![]() is a polynomial vector field such that its Poincaré compactification $p(\chi )$
is a polynomial vector field such that its Poincaré compactification $p(\chi )$![]() in the Poincaré disc has a centre in its only finite singular point, and $p(\chi )$
in the Poincaré disc has a centre in its only finite singular point, and $p(\chi )$![]() either does not have infinite singular points or they are formed by degenerate hyperbolic sectors. From this, it is not difficult to conclude that $z$
either does not have infinite singular points or they are formed by degenerate hyperbolic sectors. From this, it is not difficult to conclude that $z$![]() must be a global centre of $\chi$
must be a global centre of $\chi$![]() (see, for instance, Corollary 10 and the proof of Theorem 1 in [Reference Braun, Giné and Llibre4]).
(see, for instance, Corollary 10 and the proof of Theorem 1 in [Reference Braun, Giné and Llibre4]).
We end the paper with the following Lemma, that gives a relation between our Theorem and the already mentioned result of [Reference Cima, Gasull and Mañosas6].
Lemma 6 Let $F = (f,\,g) \colon {\mathbb {R}}^{2} \to {\mathbb {R}}^{2}$![]() be a polynomial map and let $s = (s_1,\, s_2)$
be a polynomial map and let $s = (s_1,\, s_2)$![]() be a weight-exponent. Assume that the weight degrees of $f$
be a weight-exponent. Assume that the weight degrees of $f$![]() and $g$
and $g$![]() with respect to $s$
with respect to $s$![]() are equal. If the higher $s$
are equal. If the higher $s$![]() -weight-homogeneous terms of $f$
-weight-homogeneous terms of $f$![]() and $g$
and $g$![]() do not have real linear factors in common, then so do the higher $s$
do not have real linear factors in common, then so do the higher $s$![]() -weight-homogeneous terms of $f f_x + g g_x$
-weight-homogeneous terms of $f f_x + g g_x$![]() and $f f_y + gg_y$
and $f f_y + gg_y$![]() .
.
Proof. We let $m$![]() be the weight degree of $f$
be the weight degree of $f$![]() and $g$
and $g$![]() and write $f = f_0 + \cdots + f_m$
and write $f = f_0 + \cdots + f_m$![]() and $g = g_0 + \cdots + g_m$
and $g = g_0 + \cdots + g_m$![]() the weight decomposition of $f$
the weight decomposition of $f$![]() and $g$
and $g$![]() . We first observe that $(f_m^{2} + g_m^{2})_x \not \equiv 0$
. We first observe that $(f_m^{2} + g_m^{2})_x \not \equiv 0$![]() and $(f_m^{2} + g_m^{2})_y \not \equiv 0$
and $(f_m^{2} + g_m^{2})_y \not \equiv 0$![]() , because if $(f_m^{2} +g_m^{2})_x \equiv 0$
, because if $(f_m^{2} +g_m^{2})_x \equiv 0$![]() , for instance, then (we are dealing with polynomials) $f_m = a_{0\ell } y^{\ell }$
, for instance, then (we are dealing with polynomials) $f_m = a_{0\ell } y^{\ell }$![]() and $g_m = b_{0\ell } y^{\ell }$
and $g_m = b_{0\ell } y^{\ell }$![]() , with $\ell s_2 = m$
, with $\ell s_2 = m$![]() and $a_{0\ell },\, b_{0\ell } \in {\mathbb {R}}$
and $a_{0\ell },\, b_{0\ell } \in {\mathbb {R}}$![]() , a contradiction.
, a contradiction.
Thus, the higher $s$![]() -weigh-homogeneous parts of $f f_x + g g_x$
-weigh-homogeneous parts of $f f_x + g g_x$![]() and $f f_y + g g_y$
and $f f_y + g g_y$![]() are, respectively, $(f_m^{2} + g_m^{2})_x/2$
are, respectively, $(f_m^{2} + g_m^{2})_x/2$![]() and $(f_m^{2} + g_m^{2})_y/2$
and $(f_m^{2} + g_m^{2})_y/2$![]() . If there is a linear factor dividing the last polynomials, it will also divide
. If there is a linear factor dividing the last polynomials, it will also divide
and so this factor will be common to $f_m$![]() and $g_m$
and $g_m$![]() , a contradiction.
, a contradiction.
This lemma is no longer true without the assumption that the weight degrees of $f$![]() and $g$
and $g$![]() are the same, as the map $F(x,\,y) = (x+y^{3},\,y-x^{3})$
are the same, as the map $F(x,\,y) = (x+y^{3},\,y-x^{3})$![]() shows. It satisfies $\det DF = 1+9 x^{2} y^{2}$
shows. It satisfies $\det DF = 1+9 x^{2} y^{2}$![]() and, with $s=(3,\,1)$
and, with $s=(3,\,1)$![]() , the higher homogeneous terms of $f$
, the higher homogeneous terms of $f$![]() and $g$
and $g$![]() are $x+y^{3}$
are $x+y^{3}$![]() and $=x^{3}$
and $=x^{3}$![]() , respectively. But the higher homogeneous terms of $f f_x + g g_x$
, respectively. But the higher homogeneous terms of $f f_x + g g_x$![]() and $f f_y + g g_y$
and $f f_y + g g_y$![]() are $3 x^{5}$
are $3 x^{5}$![]() and $-x^{3}$
and $-x^{3}$![]() , respectively. Here it is worth to mention that with $s = (5,\,3)$
, respectively. Here it is worth to mention that with $s = (5,\,3)$![]() , the higher $s$
, the higher $s$![]() -weight-homogeneous terms of $f f_x +g g_x$
-weight-homogeneous terms of $f f_x +g g_x$![]() and $f f_y + g g_y$
and $f f_y + g g_y$![]() are $3 x^{5}$
are $3 x^{5}$![]() and $-x^{3}+3 y^{5}$
and $-x^{3}+3 y^{5}$![]() , respectively. That is, this map satisfies the assumption of Theorem 1.
, respectively. That is, this map satisfies the assumption of Theorem 1.
Acknowledgements
The first named author was partially supported by the grant $2017$![]() /$00136$
/$00136$![]() -$0$
-$0$![]() , São Paulo Research Foundation (FAPESP). The second named author was partially supported by FCT/Portugal through UID/MAT/$04459$
, São Paulo Research Foundation (FAPESP). The second named author was partially supported by FCT/Portugal through UID/MAT/$04459$![]() /$2013$
/$2013$![]() .
.