1 Introduction
As usual, we define the combinatorial discrepancy of a system
${\mathcal{F}}$
of subsets of some finite set
$P$
as:
$$\begin{eqnarray}\operatorname{disc}{\mathcal{F}}:=\min _{\unicode[STIX]{x1D712}:P\rightarrow \{-1,1\}}\max _{F\in {\mathcal{F}}}\mathop{\sum }_{p\in F}\unicode[STIX]{x1D712}(p).\end{eqnarray}$$
Matoušek [Reference Matoušek26] provides more background on combinatorial and geometric discrepancy. For a large number of applications of combinatorial discrepancy to geometric discrepancy, numerical methods, and computer science, see Chazelle [Reference Chazelle12]. A recent application to private data analysis is described in the author’s PhD Thesis [Reference Nikolov29]. We give more details on applications to geometric discrepancy, numerical integration, data structures, and differential privacy in §2.
Let
${\mathcal{A}}_{d}$
be the family of anchored axis-aligned boxes in
$\mathbb{R}^{d}$
:
${\mathcal{A}}_{d}:=\{A(x):x\in \mathbb{R}^{d}\}$
, where
$A(x):=\{y\in \mathbb{R}^{d}:y_{i}\leqslant x_{i}~\text{for all}~i\in [d]\}$
and
$[d]:=\{1,\ldots ,d\}$
. This is a slight abuse of terminology:
$A(x)$
is not a box, but rather a polyhedral cone. Usually
$A(x)$
is defined to be anchored at 0, i.e. it is defined as the set
$\{y\in \mathbb{R}^{d}:0\leqslant y_{i}\leqslant x_{i}~\text{for all}~i\in [d]\}$
. However, we prefer to “anchor”
$A(x)$
at infinity, since this convention does not affect any of the results in the paper, and allows us to avoid some minor technicalities.
For an
$n$
-point set
$P\subset \mathbb{R}^{d}$
, we denote by
${\mathcal{A}}_{d}(P):=\{A(x)\cap P:x\in \mathbb{R}^{d}\}$
the set system induced by anchored boxes on
$P$
. (Note that this set system is finite, and, in fact, can have at most
$n^{d}$
sets.) Tusnády’s problem asks for tight bounds on the largest possible combinatorial discrepancy of
${\mathcal{A}}_{d}(P)$
over all
$n$
-point sets
$P$
, i.e. for the order of growth of the function
$\operatorname{disc}(n,{\mathcal{A}}_{d}):=\sup \{\operatorname{disc}{\mathcal{A}}_{d}(P):P\subset \mathbb{R}^{d},|P|=n\}$
with
$n$
. The best known upper bound for the Tusnády problem is
$\operatorname{disc}(n,{\mathcal{A}}_{d})=O_{d}(\log ^{d}n)$
, and was recently proved by Bansal and Garg [Reference Bansal and Garg6]. Their result improved on the prior work of Larsen [Reference Larsen22] (see also the proof in [Reference Matoušek, Nikolov and Talwar28]), who showed that
$\operatorname{disc}(n,{\mathcal{A}}_{d})=O_{d}(\log ^{d+1/2}n)$
. Here, and in the rest of this paper, we use the notation
$O_{p}(\cdot ),\unicode[STIX]{x1D6FA}_{p}(\cdot )$
,
$\unicode[STIX]{x1D6E9}_{p}(\cdot )$
to denote the fact that the implicit constant in the asymptotic notation depends on the parameter
$p$
.
In our first result, we improve the upper bounds above.
Theorem 1. For any
$d\geqslant 2$
,
$$\begin{eqnarray}\operatorname{disc}(n,{\mathcal{A}}_{d})=O_{d}(\log ^{d-1/2}n).\end{eqnarray}$$
It was shown in [Reference Matoušek and Nikolov27, Reference Matoušek, Nikolov and Talwar28] that
$\operatorname{disc}(n,{\mathcal{A}}_{d})=\unicode[STIX]{x1D6FA}_{d}(\log ^{d-1}n)$
, so the upper bound above is within a
$O_{d}(\sqrt{\log n})$
factor from the lower bound. This brings us tantalizingly close to a full resolution of Tusnády’s problem.
More generally, let
${\mathcal{F}}$
be a collection of subsets of
$\mathbb{R}^{d}$
, and, for an
$n$
-point set
$P\subset \mathbb{R}^{d}$
, let
${\mathcal{F}}(P)$
be the set system induced by
${\mathcal{F}}$
on
$P$
, i.e.
${\mathcal{F}}(P):=\{F\cap P:F\in {\mathcal{F}}\}$
. We are interested in how the worst-case combinatorial discrepancy of such set systems grows with
$n$
. This is captured by the function
$\operatorname{disc}(n,{\mathcal{F}}):=\sup \{\operatorname{disc}{\mathcal{F}}(P):P\subset \mathbb{R}^{d},|P|=n\}$
.
Let
$K\subseteq \mathbb{R}^{d}$
, and let’s define
${\mathcal{T}}_{K}$
to be the family of images of
$K$
under translations and homothetic transformations:
${\mathcal{T}}_{K}:=\{tK+x:t\in \mathbb{R}_{+},x\in \mathbb{R}^{d}\}$
, where
$\mathbb{R}_{+}$
is the set of positive reals. If we take
$Q:=[0,1]^{d}$
, then it is well known that
$\operatorname{disc}(n,{\mathcal{T}}_{Q})\leqslant 2^{d}\operatorname{disc}(n,{\mathcal{A}}_{d})$
and, therefore, Theorem 1 implies
$\operatorname{disc}(n,{\mathcal{T}}_{Q})=O_{d}(\log ^{d-1/2}n)$
. Our next result shows that this bound holds for any convex polytope
$B$
in
$\mathbb{R}^{d}$
.
Theorem 2. For any
$d\geqslant 2$
, and any closed convex polytope
$B\subset \mathbb{R}^{d}$
,
$$\begin{eqnarray}\operatorname{disc}(n,{\mathcal{T}}_{B})=O_{d,B}(\log ^{d-1/2}n).\end{eqnarray}$$
With essentially the same proof we can establish the stronger fact that
$\operatorname{disc}(n,\text{POL}({\mathcal{H}}))=O_{d,{\mathcal{H}}}(\log ^{d-1/2}n)$
, where
${\mathcal{H}}$
is a family of hyperplanes in
$\mathbb{R}^{d}$
, and
$\text{POL}({\mathcal{H}})$
is the set of all polytopes which can be written as
$\bigcap _{i=1}^{m}H_{i}$
, with each
$H_{i}$
a halfspace whose boundary is parallel to some
$h\in {\mathcal{H}}$
. The best previously known upper bound in this setting is also due to Bansal and Garg [Reference Bansal and Garg6], and is equal to
$O_{d,{\mathcal{H}}}(\log ^{d}n)$
.
Our final result is a nearly matching lower bound for any generic convex polytope
$B$
. (See Definition 2 for the meaning of “generic”.)
Theorem 3. For any generic convex polytope with non-empty interior
$B\subseteq \mathbb{R}^{d}$
,
$$\begin{eqnarray}\operatorname{disc}(n,{\mathcal{T}}_{B})=\unicode[STIX]{x1D6FA}_{d,B}(\log ^{d-1}n).\end{eqnarray}$$
The best previously known lower bound on
$\operatorname{disc}(n,{\mathcal{T}}_{B})$
was
$\unicode[STIX]{x1D6FA}_{d,B}(\log ^{(d-1)/2}n)$
, which follows from a result of Drmota [Reference Drmota13] in geometric discrepancy theory. This lower bound holds for any convex polytope
$B$
, but is quadratically weaker than our lower bound.
We conjecture that the genericity condition in Theorem 3 is not necessary, and, furthermore, that the asymptotic constant in the lower bound need not depend on
$B$
. These conjectures would be implied by certain estimates on the Fourier spectrum of convex polytopes: see §6 for more details. By contrast, the asymptotic constant in the upper bound in Theorem 2 has to depend on
$B$
, because we can approximate the unit Euclidean ball
$D^{d}$
in
$\mathbb{R}^{d}$
arbitrarily well with a convex polytope, and
$\operatorname{disc}(n,{\mathcal{T}}_{D^{d}})=\unicode[STIX]{x1D6FA}_{d}(n^{1/2-1/(2d)})$
[Reference Alexander2].
Our proofs combine the approach to combinatorial discrepancy based on factorization norms, used previously by the author, Matoušek and Talwar [Reference Matoušek, Nikolov and Talwar28, Reference Nikolov, Talwar and Indyk30], with several new ideas. In the proof of Theorem 1 we use a result from Banaszczyk [Reference Banaszczyk4] on balancing series of vectors, and in the proof of Theorem 2 we further use a decomposition of polytopes given by Matoušek [Reference Matoušek25]. The proof of Theorem 3 combines the factorization norms approach with the Fourier analytic method pioneered by Roth [Reference Roth33]. In §3.4 we discuss the techniques in more detail, after we have introduced the relevant background.
Together, these results give nearly tight estimates on the discrepancy function
$\operatorname{disc}(n,{\mathcal{T}}_{B})$
for almost any convex polytope
$B$
. Perhaps surprisingly, they imply that the order of growth of
$\operatorname{disc}(n,{\mathcal{T}}_{B})$
with
$n$
is essentially independent of the particular structure of
$B$
, at least when
$B$
is generic, and, moreover, that order of growth is achieved by the simplest possible example, a cube. In the next section we describe applications of our results to geometric discrepancy, quasi-Monte Carlo methods, data structure lower bounds, and differential privacy.
2 Applications
In this section we outline several applications of our discrepancy upper and lower bounds.
2.1 Geometric discrepancy and numerical integration
Geometric discrepancy measures the irregularity of a distribution of
$n$
points in
$[0,1]^{d}$
with respect to a family of distinguishing sets. In particular, for an
$n$
-point set
$P\subseteq [0,1]^{d}$
and a family of measurable subsets
${\mathcal{F}}$
of
$\mathbb{R}^{d}$
, we define the discrepancy
$$\begin{eqnarray}D(P,{\mathcal{F}}):=\sup _{F\in {\mathcal{F}}}||P\cap F|-\unicode[STIX]{x1D706}_{d}(F\cap [0,1]^{d})|,\end{eqnarray}$$
where
$\unicode[STIX]{x1D706}_{d}$
is the Lebesgue measure on
$\mathbb{R}^{d}$
. The smallest achievable discrepancy over
$n$
-point sets with respect to
${\mathcal{F}}$
is denoted
$D(n,{\mathcal{F}}):=\inf \{D(P,{\mathcal{F}}):$
$P\subset \mathbb{R}^{d},|P|=n\}$
. A famous result from Schmidt [Reference Schmidt34] shows that
$D(n,{\mathcal{A}}_{2})=\unicode[STIX]{x1D6E9}(\log n)$
. The picture is much less clear in higher dimensions. In a seminal paper [Reference Roth32], Roth showed that
$D(n,{\mathcal{A}}_{d})=\unicode[STIX]{x1D6FA}_{d}(\log ^{(d-1)/2}n)$
for any
$d\geqslant 2$
; the best known lower bound in
$d\geqslant 3$
is given by Bilyk, Lacey, and Vagharshakyan [Reference Bilyk, Lacey and Vagharshakyan9] and is
$D(n,{\mathcal{A}}_{d})=\unicode[STIX]{x1D6FA}_{d}(\log ^{(d-1)/2+\unicode[STIX]{x1D702}_{d}}n)$
, where
$\unicode[STIX]{x1D702}_{d}$
is a positive constant depending on
$d$
and going to 0 as
$d$
goes to infinity. On the other hand, the best known upper bound is
$D(n,{\mathcal{A}}_{d})=O_{d}(\log ^{d-1}n)$
and can be achieved in many different ways, one of the simplest being the Halton–Hammersley construction [Reference Halton19, Reference Hammersley20]. Beck and Chen [Reference Beck and Chen8] call the problem of closing this significant gap “the Great Open Problem” (in geometric discrepancy theory). See Matoušek [Reference Matoušek26] for further background on geometric discrepancy.
There is a known connection between combinatorial and geometric discrepancy. Roughly speaking, combinatorial discrepancy is an upper bound on geometric discrepancy. More precisely, we have the following transference lemma, which goes back to the work of Beck on Tusnády’s problem [Reference Beck7] (see [Reference Matoušek26] for a proof).
Lemma 4. Let
${\mathcal{F}}$
be a family of measurable sets in
$\mathbb{R}^{d}$
such that there is some
$F\in {\mathcal{F}}$
which contains
$[0,1]^{d}$
. Assume that
$D(n,{\mathcal{F}})/n$
goes to
$0$
as
$n$
goes to infinity, and that
$\operatorname{disc}(n,{\mathcal{F}})\leqslant f(n)$
for a function
$f$
that satisfies
$f(2n)\leqslant (2-\unicode[STIX]{x1D6FF})f(n)$
for all
$n$
and some fixed
$\unicode[STIX]{x1D6FF}>0$
. Then there exists a constant
$C_{\unicode[STIX]{x1D6FF}}$
that only depends on
$\unicode[STIX]{x1D6FF}$
, for which
$D(n,{\mathcal{F}})\leqslant C_{\unicode[STIX]{x1D6FF}}f(n)$
.
Lemma 4 and Theorem 2 imply that
$D(n,{\mathcal{T}}_{B})=O_{d,B}(\log ^{d-1/2}n)$
for any convex polytope
$B$
in
$\mathbb{R}^{d}$
. This bound gets within an
$O_{d,B}(\sqrt{\log n})$
factor from the best bound known for axis-aligned boxes in
$d$
dimensions. The tightest bound known prior to our work was
$O_{d,B}(\log ^{d}n)$
and was also implied by the best previously known upper bound on combinatorial discrepancy.
Geometric discrepancy can be defined with any Borel probability measure
$\unicode[STIX]{x1D708}$
on
$[0,1]^{d}$
in place of the Lebesgue measure: let’s call the resulting quantities
$D(P,{\mathcal{F}},\unicode[STIX]{x1D708})$
and
$D(n,{\mathcal{F}},\unicode[STIX]{x1D708})$
. It turns out that Lemma 4 holds with
$D(n,{\mathcal{F}})$
replaced by
$D(n,{\mathcal{F}},\unicode[STIX]{x1D708})$
, and, together with Theorem 1 we get that
$D(n,{\mathcal{A}}_{d},\unicode[STIX]{x1D708})=O_{d}(\log ^{d-1/2}n)$
for any Borel probability measure
$\unicode[STIX]{x1D708}$
on
$[0,1]^{d}$
. This bound has an application to the quasi-Monte Carlo method in numerical integration. A version of the Koksma–Hlawka inequality for general measures given by Götz [Reference Götz18] shows that for any real-valued function
$f$
on
$[0,1]^{d}$
of bounded total variation in the sense of Hardy and Krause, we have
$$\begin{eqnarray}\biggl|\int _{[0,1]^{d}}f(x)\,d\unicode[STIX]{x1D708}(x)-\frac{1}{n}\mathop{\sum }_{x\in P}f(x)\biggr|\leqslant \frac{1}{n}V(f)D(P,{\mathcal{A}}_{d},\unicode[STIX]{x1D708}).\end{eqnarray}$$
Here,
$V(f)$
is the Hardy–Krause variation of
$f$
. So, our upper bound implies that for any function
$f$
of constant total variation, and any Borel measure
$\unicode[STIX]{x1D708}$
, we can numerically estimate the integral of
$f$
with respect to
$\unicode[STIX]{x1D708}$
by averaging the values of
$f$
at
$n$
points, and the estimate has error
$O_{d}(n^{-1}\log ^{d-1/2}(n))$
. Contrast this with the
$O_{d}(n^{-1/2})$
error rate achieved by the Monte Carlo method. The error rate we achieve is within
$O_{d}(\sqrt{\log n})$
of the best error rate known for the Lebesgue measure. Integration with respect to measures other than the Lebesgue measure arises often, and a constructive proof of our upper bound could have significant impact in practice. We refer to the note [Reference Aistleitner, Bilyk and Nikolov1] for an exposition of these connections.
2.2 Range searching lower bounds
In the dynamic range searching problem in computer science, we are given a range space
${\mathcal{F}}(P)$
, where
${\mathcal{F}}$
is a collection of subsets of
$\mathbb{R}^{d}$
, and
$P$
is an
$n$
-point set in
$\mathbb{R}^{d}$
; our goal is to design a data structure which keeps a set of weights
$w\in G^{P}$
under updates, where the weights come from a commutative group
$G$
. An update specifies a point
$p$
of
$P$
and an element
$g\in G$
, and asks to change the weight of
$p$
to
$w_{p}+g$
. The data structure should be able to answer range searching queries, where a query is specified by a range
$F\in {\mathcal{F}}(P)$
, and must return the answer
$\sum _{p\in F}w_{p}$
. The main question for this data structure problem is to identify a tight trade-off between the update time and the query time.
Fredman [Reference Fredman17] first observed that many data structures for the dynamic range searching problem can be identified with a matrix factorization
$A=UV$
of the incidence matrix
$A$
of
${\mathcal{F}}(P)$
into two matrices
$U$
and
$V$
with integer entries. Following Larsen [Reference Larsen22], we define an oblivious data structure with multiplicity
$\unicode[STIX]{x1D6E5}$
for the dynamic range searching problem for the range space
${\mathcal{F}}(P)$
as a factorization
$A=UV$
of the incidence matrix of
${\mathcal{F}}(P)$
into matrices
$U$
and
$V$
with integer entries bounded in absolute value by
$\unicode[STIX]{x1D6E5}$
. The update time
$t_{u}$
for such a data structure equals the maximum number of non-zero entries in any column of
$V$
; the query time
$t_{q}$
equals the maximum number of non-zero entries in any row of
$U$
.
Our arguments imply the following result.
Theorem 5. For any generic convex polytope
$B$
in
$\mathbb{R}^{d}$
there exists a family of point sets
$P$
in
$\mathbb{R}^{d}$
so that for any family of oblivious data structures with multiplicity
$\unicode[STIX]{x1D6E5}$
for the dynamic range counting problem with range space
${\mathcal{T}}_{B}(P)$
, we have
$\sqrt{t_{u}t_{q}}=\unicode[STIX]{x1D6FA}_{d,B}(\unicode[STIX]{x1D6E5}^{-1}\log ^{d}n)$
. Conversely, for any convex polytope
$B$
and any
$n$
-point set
$P$
in
$\mathbb{R}^{d}$
there exists an oblivious data structure with multiplicity
$\unicode[STIX]{x1D6E5}=1$
and
$\sqrt{t_{u}t_{q}}=O_{d,B}(\log ^{d}n)$
.
Theorem 5 implies that, as for the discrepancy question, the geometric mean of query and update time grows with
$n$
at the same rate for any (generic) convex polytope
$B$
, and that order of growth is already achieved for orthogonal range searching. Our upper and lower bounds are tight up to constants when the multiplicity is bounded. Our main contributions are the lower bounds, while the upper bounds follow from standard techniques.
2.3 Differential privacy
Range searching and range counting problems also naturally arise in the field of private data analysis. The setting here is that, given the range space
${\mathcal{F}}(P)$
as above, we have as input a database
$D$
which is a multiset of points from
$P$
. The goal is to output the number (with multiplicity) of points in
$D$
that fall in each range
$F\in {\mathcal{F}}(P)$
. However, the database
$D$
could be sensitive because it may, for example, encode the locations of different people. For this reason, we want to approximate the range counts under the constraints of differential privacy [Reference Dwork, Mcsherry, Nissim and Smith14, Reference Dwork and Roth15]. Formally, a randomized algorithm
${\mathcal{M}}$
(“mechanism” in the terminology of differential privacy) is
$(\unicode[STIX]{x1D700},\unicode[STIX]{x1D6FF})$
-differentially private if, for any two databases
$D$
,
$D^{\prime }$
that differ in the location of single point, and all measurable subsets
$S$
of the range of
${\mathcal{M}}$
, we have
$$\begin{eqnarray}\mathbb{P}({\mathcal{M}}(D)\in S)\leqslant \text{e}^{\unicode[STIX]{x1D700}}\mathbb{P}({\mathcal{M}}(D)\in S)+\unicode[STIX]{x1D6FF}.\end{eqnarray}$$
We define the error of a mechanism
${\mathcal{M}}$
as the maximum of
$$\begin{eqnarray}\mathbb{E}\max _{F\in {\mathcal{F}}(P)}|{\mathcal{M}}(D)_{F}-|D\cap F||\end{eqnarray}$$
over databases
$D$
, where the expectation is with respect to the randomness of
${\mathcal{M}}$
, and
${\mathcal{M}}(D)_{F}$
is the output that
${\mathcal{M}}$
gives on input
$D$
for the range
$F$
. Let
$\text{opt}_{\unicode[STIX]{x1D700},\unicode[STIX]{x1D6FF}}({\mathcal{F}}(P))$
be the smallest achievable error of an
$(\unicode[STIX]{x1D700},\unicode[STIX]{x1D6FF})$
-differentially private algorithm on
${\mathcal{F}}(P)$
, and let
$\text{opt}_{\unicode[STIX]{x1D700},\unicode[STIX]{x1D6FF}}(N,{\mathcal{F}})=\sup \text{opt}_{\unicode[STIX]{x1D700},\unicode[STIX]{x1D6FF}}({\mathcal{F}}(P))$
, where the supremum is over all
$N$
-point sets
$P$
in
$\mathbb{R}^{d}$
.
Our techniques imply the following result.
Theorem 6. For any generic convex polytope
$B$
in
$\mathbb{R}^{d}$
, for all small enough
$\unicode[STIX]{x1D700}$
, and all
$\unicode[STIX]{x1D6FF}$
small enough with respect to
$\unicode[STIX]{x1D700}$
, we have
$$\begin{eqnarray}\displaystyle \text{opt}_{\unicode[STIX]{x1D700},\unicode[STIX]{x1D6FF}}(N,{\mathcal{T}}_{B}) & = & \displaystyle \unicode[STIX]{x1D6FA}_{d,B}(\unicode[STIX]{x1D700}^{-1}\log ^{d-1}N),\nonumber\\ \displaystyle \text{opt}_{\unicode[STIX]{x1D700},\unicode[STIX]{x1D6FF}}(N,{\mathcal{T}}_{B}) & = & \displaystyle O_{d,B}(\unicode[STIX]{x1D700}^{-1}\sqrt{\log 1/\unicode[STIX]{x1D6FF}}\log ^{d+1/2}N).\nonumber\end{eqnarray}$$
Moreover, the upper bound holds for any (not necessarily generic) convex polytope
$B$
.
Once again, our result shows that the growth of the best possible error under differential privacy with
$N$
for the range counting problem with ranges induced by a convex polytope
$B$
does not depend strongly on the structure of the particular polytope
$B$
.
3 Preliminaries and techniques
In what follows
$C_{p}$
and
$c_{p}$
are constants that depend only on the parameter
$p$
and may change from one line to the next. All logarithms are assumed to be in base
$e$
(although usually this does not matter). We use
$\langle \cdot ,\cdot \rangle$
for the standard inner product on
$\mathbb{R}^{n}$
, and
$\Vert \cdot \Vert _{2}$
for the corresponding Euclidean norm. We use capital letters to denote matrices, and lower case letters with indexes to denote matrix entries, e.g.
$a_{ij}$
to denote the entry in row
$i$
column
$j$
of the matrix
$A$
. We also use
$\unicode[STIX]{x1D707}_{n}$
for the standard Gaussian measure on
$\mathbb{R}^{n}$
. (We avoid the more standard
$\unicode[STIX]{x1D6FE}_{n}$
to avoid confusion with the
$\unicode[STIX]{x1D6FE}_{2}$
factorization norm.) We use
$\unicode[STIX]{x1D70E}_{d-1}$
for the uniform (rotation invariant, Haussdorff) probability measure on the
$(d-1)$
-dimensional unit Euclidean sphere
$S^{d-1}$
in
$\mathbb{R}^{d}$
. We use
$\unicode[STIX]{x1D703}_{d}$
for the Haar probability measure on the orthogonal group
$\mathbf{O}(d)$
.
3.1 Hereditary discrepancy
Hereditary discrepancy is a robust version of combinatorial discrepancy. For a set system
${\mathcal{F}}$
of subsets of a set
$P$
, the hereditary discrepancy of
${\mathcal{F}}$
is defined by
$\operatorname{herdisc}{\mathcal{F}}=\max _{Q\subseteq P}\operatorname{disc}{\mathcal{F}}(Q)$
. Hereditary discrepancy is often more tractable than discrepancy itself, both analytically, and computationally. For example, while a non-trivial approximation to discrepancy is in general
$\mathsf{N}\mathsf{P}$
-hard [Reference Charikar, Newman, Nikolov and Randall11], hereditary discrepancy can be approximated up to polylogarithmic factors [Reference Matoušek, Nikolov and Talwar28, Reference Nikolov, Talwar and Indyk30]. Importantly for us, this robustness comes at no additional cost: for all collections of sets
${\mathcal{F}}$
that we study, it is easy to see that, for any
$n$
-point set
$P$
in
$\mathbb{R}^{d}$
,
$\operatorname{disc}(n,{\mathcal{F}})\geqslant \operatorname{herdisc}{\mathcal{F}}(P)$
.
3.2 The
$\unicode[STIX]{x1D6FE}_{2}$
factorization norm
The
$\unicode[STIX]{x1D6FE}_{2}$
norm was introduced in functional analysis to study operators that factor through Hilbert space. We say that an operator
$u:X\rightarrow Y$
between Banach spaces
$X$
and
$Y$
factors through a Hilbert space if there exists a Hilbert space
$H$
and bounded operators
$u_{1}:X\rightarrow H$
and
$u_{2}:H\rightarrow Y$
such that
$u=u_{2}u_{1}$
. Then the
$\unicode[STIX]{x1D6FE}_{2}$
norm of
$u$
is
$$\begin{eqnarray}\unicode[STIX]{x1D6FE}_{2}(u):=\inf \Vert u_{1}\Vert \Vert u_{2}\Vert ,\end{eqnarray}$$
where the infimum is taken over all Hilbert spaces
$H$
, and all operators
$u_{1}$
and
$u_{2}$
as above. Here
$\Vert u_{1}\Vert$
and
$\Vert u_{2}\Vert$
are the operator norms of
$u_{1}$
and
$u_{2}$
, respectively. Tomczak-Jaegermann’s book [Reference Tomczak-Jaegermann35] is an excellent reference on factorization norms and their applications in Banach space theory.
In this work we will use the
$\unicode[STIX]{x1D6FE}_{2}$
norm of an
$m\times n$
matrix
$A$
, which is defined as the
$\unicode[STIX]{x1D6FE}_{2}$
norm of the linear operator
$u:\ell _{1}^{n}\rightarrow \ell _{\infty }^{m}$
with matrix
$A$
(in the standard bases of
$\mathbb{R}^{m}$
and
$\mathbb{R}^{n}$
). In the language of matrices, this means that
$$\begin{eqnarray}\unicode[STIX]{x1D6FE}_{2}(A):=\inf \{\Vert U\Vert _{2\rightarrow \infty }\Vert V\Vert _{1\rightarrow 2}:A=UV\},\end{eqnarray}$$
where the infimum is taken over matrices
$U$
and
$V$
,
$\Vert V\Vert _{1\rightarrow 2}$
equals the largest
$\ell _{2}$
norm of a column of
$V$
, and
$\Vert U\Vert _{2\rightarrow \infty }$
equals the largest
$\ell _{2}$
norm of a row of
$U$
. By a standard compactness argument, the infimum is achieved; moreover, we can take
$U\in \mathbb{R}^{m\times r}$
and
$V\in \mathbb{R}^{r\times n}$
, where
$r$
is the rank of
$A$
. Yet another equivalent formulation, which will be convenient for us, is that
$\unicode[STIX]{x1D6FE}_{2}(A)$
is the smallest non-negative real
$t$
for which there exist vectors
$u_{1},\ldots ,u_{m},v_{1},\ldots ,v_{n}\in \mathbb{R}^{r}$
such that for any
$i\in [m],j\in [n]$
,
$a_{ij}=\langle u_{i},v_{j}\rangle$
and
$\Vert u_{i}\Vert _{2}\leqslant t$
,
$\Vert v_{j}\Vert _{2}\leqslant 1$
. For a proof of the not completely trivial fact that
$\unicode[STIX]{x1D6FE}_{2}$
is a norm, see Tomczak-Jaegermann [Reference Tomczak-Jaegermann35]. Given a matrix
$A$
,
$\unicode[STIX]{x1D6FE}_{2}(A)$
can be computed efficiently by solving a semidefinite program [Reference Linial, Mendelson, Schechtman and Shraibman24].
Let us further overload the meaning of
$\unicode[STIX]{x1D6FE}_{2}$
by defining
$\unicode[STIX]{x1D6FE}_{2}({\mathcal{F}})=\unicode[STIX]{x1D6FE}_{2}(A)$
for a set system
${\mathcal{F}}$
with incidence matrix
$A$
. We recall that the incidence matrix of a system
${\mathcal{F}}=\{F_{1},\ldots ,F_{m}\}$
of subsets of a set
$P=\{p_{1},\ldots ,p_{n}\}$
is defined as
$$\begin{eqnarray}a_{ij}:=\left\{\begin{array}{@{}ll@{}}1\quad & p_{j}\in F_{i}\\ 0\quad & p_{j}\not \in F_{i}.\end{array}\right.\end{eqnarray}$$
In other words,
$\unicode[STIX]{x1D6FE}_{2}({\mathcal{F}})$
is the smallest non-negative real
$t$
such that there exist vectors
$u_{1},\ldots ,u_{m},v_{1},\ldots ,v_{n}$
satisfying
$$\begin{eqnarray}\langle u_{i},v_{j}\rangle =\left\{\begin{array}{@{}ll@{}}1\quad & p_{j}\in F_{i}\\ 0\quad & p_{j}\not \in F_{i},\end{array}\right.\end{eqnarray}$$
and
$\Vert u_{i}\Vert _{2}\leqslant t$
,
$\Vert v_{j}\Vert _{2}\leqslant 1$
for all
$i\in [m],j\in [n]$
.
In [Reference Matoušek, Nikolov and Talwar28, Reference Nikolov, Talwar and Indyk30] it was shown that
$\unicode[STIX]{x1D6FE}_{2}({\mathcal{F}})$
is, up to logarithmic factors, equivalent to hereditary discrepancy:
$$\begin{eqnarray}\displaystyle \operatorname{herdisc}{\mathcal{F}} & {\leqslant} & \displaystyle C\sqrt{\log m}\unicode[STIX]{x1D6FE}_{2}({\mathcal{F}}),\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \operatorname{herdisc}{\mathcal{F}} & {\geqslant} & \displaystyle c\frac{\unicode[STIX]{x1D6FE}_{2}({\mathcal{F}})}{\log \operatorname{rank}A},\end{eqnarray}$$
where
$C,c>0$
are absolute constants.
In [Reference Matoušek and Nikolov27, Reference Matoušek, Nikolov and Talwar28] it was also shown that
$\unicode[STIX]{x1D6FE}_{2}$
satisfies a number of nice properties which help in estimating the norm of specific matrices or set systems. Here we only need the following inequality, which holds for a set system
${\mathcal{F}}={\mathcal{F}}_{1}\cup \cdots \cup {\mathcal{F}}_{k}$
, where
${\mathcal{F}}_{1},\ldots ,{\mathcal{F}}_{k}$
are set systems over the same set
$P$
:
$$\begin{eqnarray}\unicode[STIX]{x1D6FE}_{2}({\mathcal{F}})\leqslant \sqrt{\mathop{\sum }_{i=1}^{k}\unicode[STIX]{x1D6FE}_{2}({\mathcal{F}}_{i})^{2}}.\end{eqnarray}$$
We also need the following simple lemma, which follows, e.g. from the results in [Reference Matoušek and Nikolov27, Reference Matoušek, Nikolov and Talwar28], but also appears in a similar form in [Reference Larsen22], and follows from standard dyadic decomposition techniques.
Lemma 7. For any
$d\geqslant 1$
there exists a constant
$C_{d}$
such that for any
$n$
-point set
$P\subset \mathbb{R}^{d}$
,
$\unicode[STIX]{x1D6FE}_{2}({\mathcal{A}}_{d}(P))\leqslant C_{d}(1+\log n)^{d}$
. Moreover, there exists a factorization of the incidence matrix of
${\mathcal{A}}_{d}(P)$
achieving this bound into matrices
$U$
and
$V$
with entries in the set
$\{0,1\}$
.
To prove lower bounds on discrepancy, we use (2) and a dual formula for
$\unicode[STIX]{x1D6FE}_{2}$
:
$$\begin{eqnarray}\unicode[STIX]{x1D6FE}_{2}(A)=\max \{\Vert PAQ\Vert _{\operatorname{tr}}:P,Q\text{ diagonal},\operatorname{tr}P^{2}=\operatorname{tr}Q^{2}=1\},\end{eqnarray}$$
where
$\Vert M\Vert _{\operatorname{tr}}$
is the trace norm of the matrix
$M$
, equal to the sum of singular values. For a proof of this formula, see [Reference Lee, Shraibman and Špalek23, Reference Nikolov, Talwar and Indyk30]. In this paper, we use the easily proved special case derived from (4) by setting
$P=Q=(1/n)I$
:
$$\begin{eqnarray}\unicode[STIX]{x1D6FE}_{2}(A)\geqslant \frac{1}{n}\Vert A\Vert _{\operatorname{tr}}.\end{eqnarray}$$
See [Reference Linial, Mendelson, Schechtman and Shraibman24] for a short direct proof of this inequality.
The
$\unicode[STIX]{x1D6FE}_{2}$
norm is also directly connected to upper and lower bounds for data structures and differentially private mechanisms for range searching and range counting. It follows immediately from the definitions (see §2.2) that the update time
$t_{u}$
and the query time
$t_{q}$
for an oblivious range searching data structure with multiplicity
$\unicode[STIX]{x1D6E5}$
satisfy
$\sqrt{t_{u}t_{q}}\geqslant \unicode[STIX]{x1D6E5}^{-1}\unicode[STIX]{x1D6FE}_{2}({\mathcal{F}}(P))$
; moreover, if
$\unicode[STIX]{x1D6FE}_{2}({\mathcal{F}}(P))$
is achieved by a factorization into matrices with entries in
$\{-\unicode[STIX]{x1D6E5},\ldots ,\unicode[STIX]{x1D6E5}\}$
, then
$\sqrt{t_{u}t_{q}}\leqslant \unicode[STIX]{x1D6FE}_{2}({\mathcal{F}}(P))$
. In differential privacy, we have the following theorem (see §2.3 for the definitions).
Theorem 8. There exists an absolute constant such that the following holds for all small enough
$\unicode[STIX]{x1D700}$
, and
$\unicode[STIX]{x1D6FF}$
small enough with respect to
$\unicode[STIX]{x1D700}$
. Let
${\mathcal{F}}$
be a collection of subsets of
$\mathbb{R}^{d}$
and let
$P$
be an
$N$
-point set in
$\mathbb{R}^{d}$
. Then,
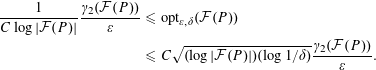$$\begin{eqnarray}\displaystyle \frac{1}{C\log |{\mathcal{F}}(P)|}\frac{\unicode[STIX]{x1D6FE}_{2}({\mathcal{F}}(P))}{\unicode[STIX]{x1D700}} & {\leqslant} & \displaystyle \text{opt}_{\unicode[STIX]{x1D700},\unicode[STIX]{x1D6FF}}({\mathcal{F}}(P))\nonumber\\ \displaystyle & {\leqslant} & \displaystyle C\sqrt{(\log |{\mathcal{F}}(P)|)(\log 1/\unicode[STIX]{x1D6FF})}\frac{\unicode[STIX]{x1D6FE}_{2}({\mathcal{F}}(P))}{\unicode[STIX]{x1D700}}.\nonumber\end{eqnarray}$$
Theorem 8 was essentially proved, although stated differently, in [Reference Nikolov, Talwar and Zhang31]. For a statement equivalent to the one above, and a proof, see [Reference Nikolov29, Theorem 7.1]. Note that [Reference Nikolov29] uses the notation
$\Vert \cdot \Vert _{E_{\infty }}$
in place of the standard
$\unicode[STIX]{x1D6FE}_{2}(\cdot )$
.
3.3 Signed series of vectors
We will use the following result of Banaszczyk.
Lemma 9 [Reference Banaszczyk4].
Let
$v_{1},\ldots ,v_{n}\in \mathbb{R}^{m}$
,
$\forall i:\Vert v_{i}\Vert _{2}\leqslant 1$
, and let
$K\subset \mathbb{R}^{m}$
be a convex body symmetric around the origin. If
$\unicode[STIX]{x1D707}_{m}(K)\geqslant 1-1/(2n)$
, then there exists an assignment of signs
$\unicode[STIX]{x1D712}:[n]\rightarrow \{-1,1\}$
so that
$$\begin{eqnarray}\forall j\in \{1,\ldots ,n\}:\mathop{\sum }_{i=1}^{j}\unicode[STIX]{x1D712}(i)v_{i}\in 5K.\end{eqnarray}$$
This lemma was proved in the context of the well-known Steinitz problem: given vectors
$v_{1},\ldots ,v_{n}$
, each of Euclidean norm at most 1, such that
$v_{1}+\cdots +v_{n}=0$
, find a permutation
$\unicode[STIX]{x1D70B}$
on
$[n]$
such that for all integers
$i$
,
$1\leqslant i\leqslant n$
,
$\Vert v_{\unicode[STIX]{x1D70B}(1)}+\cdots +v_{\unicode[STIX]{x1D70B}(i)}\Vert _{2}\leqslant C\sqrt{m}$
, where
$C$
is an absolute constant independent of
$m$
or
$n$
. Lemma 9 gives the best known partial result in this direction: it can be used to show a bound of
$C(\sqrt{m}+\sqrt{\log n})$
in place of
$C\sqrt{m}$
.
Lemma 9 follows relatively easily from a powerful result Banaszczyk proved in [Reference Banaszczyk3]. Unfortunately, the proof of the latter does not suggest any efficient algorithm to find the signs
$\unicode[STIX]{x1D712}(i)$
, and no such algorithm is yet known, despite some partial progress [Reference Bansal, Dadush, Garg and Dinur5].
3.4 Techniques
Our approach builds on the connection between the
$\unicode[STIX]{x1D6FE}_{2}$
norm and hereditary discrepancy shown in [Reference Matoušek, Nikolov and Talwar28, Reference Nikolov, Talwar and Indyk30]. The new idea which enables the tighter upper bound is the use of Banaszczyk’s signed series result (Lemma 9), in order to get one dimension “for free”. On a very high level, this is similar to the way one dimension comes for free in constructions of point sets with small geometric discrepancy, such as the Halton–Hammersley construction mentioned before. The proof of Theorem 2 combines the ideas in the proof of Theorem 1 with a decomposition given by Matoušek [Reference Matoušek25].
The lower bound for Tusnády’s problem in [Reference Matoušek, Nikolov and Talwar28] relies crucially on the product structure of
${\mathcal{A}}_{d}$
, and does not easily extend to
${\mathcal{T}}_{B}$
when
$B$
is a polytope other than a box. Instead, for the lower bound in this paper, we combine the factorization norm approach with the Fourier method, pioneered in discrepancy theory by Roth [Reference Roth33] and developed further by Beck: see [Reference Beck and Chen8] for an exposition. In order to give a lower bound on
$\unicode[STIX]{x1D6FE}_{2}$
, we use (5), and estimate the trace norm of the incidence matrix
$M$
of a set system related to
${\mathcal{T}}_{B}(P)$
, where
$P$
is a grid in
$[0,1)^{d}$
. We define
$M$
so that it is a convolution matrix (i.e. the matrix of a convolution operator), and its eigenvalues are given by the discrete Fourier transform. While tight estimates are known for the average decay of continuous Fourier coefficients of convex polytopes, we need estimates on discrete Fourier coefficients, about which much less is known. To bridge this gap, we prove a bound on the convergence rate of discrete Fourier coefficients of convex polytopes to the continuous Fourier coefficients. We also use an averaging argument in order to be able to work with bounds on the average decay of the Fourier spectrum, rather than having to estimate specific Fourier coefficients. These techniques are general, and may be more widely applicable to geometric combinatorial discrepancy questions. Our version of the Fourier method has the curious feature that, even though we average over rotations of the polytope
$B$
, in the end the lower bound holds for the set system induced only by translations and dilations of
$B$
.
4 Upper bound for Tusnády’s problem
In this section we give the proof of Theorem 1. Let us fix the
$n$
-point set
$P\subset \mathbb{R}^{d}$
once and for all. Without loss of generality, assume that each
$p\in P$
has a distinct last coordinate, and order the points in
$P$
in increasing order of their last coordinate as
$p_{1},\ldots ,p_{n}$
. Write each
$p_{i}$
as
$p_{i}=(q_{i},r_{i})$
, where
$q_{i}\in \mathbb{R}^{d-1}$
and
$r_{i}\in \mathbb{R}$
. With this notation, and the ordering we assumed, we have that
$r_{i}<r_{j}$
whenever
$i<j$
.
Let
$Q:=\{q_{i}:1\leqslant i\leqslant n\}$
. Notice that this is an
$n$
-point set in
$\mathbb{R}^{d-1}$
. Denote the sets in
${\mathcal{A}}_{d-1}(Q)$
as
$A_{1},\ldots ,A_{m}$
(in no particular order). Using Lemma 7, there exist vectors
$u_{1},\ldots ,u_{m}$
and
$v_{1},\ldots ,v_{n}$
such that
$$\begin{eqnarray}\langle u_{i},v_{j}\rangle =\left\{\begin{array}{@{}ll@{}}1\quad & q_{j}\in A_{i}\\ 0\quad & q_{j}\not \in A_{i},\end{array}\right.\end{eqnarray}$$
and
$\Vert u_{i}\Vert _{2}\leqslant C_{d}(1+\log n)^{(d-1)}$
,
$\Vert v_{j}\Vert _{2}\leqslant 1$
for all
$i$
and
$j$
. Define the symmetric polytope
$$\begin{eqnarray}K:=\{x\in \mathbb{R}^{m}:|\langle u_{i},x\rangle |\leqslant C_{d}^{\prime }(1+\log n)^{d-1/2}~\text{for all}~i\in \{1,\ldots ,m\}\},\end{eqnarray}$$
where
$C_{d}^{\prime }>C_{d}$
is a constant large enough that
$\unicode[STIX]{x1D707}_{m}(K)\geqslant 1-1/(2n)$
. The fact that such a constant exists follows from standard concentration of measure results in Gaussian space. Indeed, using a Bernstein-type inequality for Gaussian measure, we can show that, for
$C_{d}^{\prime }$
big enough,
$\unicode[STIX]{x1D707}_{m}(S_{i})\geqslant 1-1/(2n^{d+1})$
for all
$i\in [m]$
, where
$S_{i}:=\{x:|\langle u_{i},x\rangle |\leqslant C_{d}^{\prime }(1+\log n)^{d-1/2}\}$
. By the union bound, since
$m\leqslant n^{d}$
, this implies
$\unicode[STIX]{x1D707}_{m}(K)=\unicode[STIX]{x1D707}_{m}(\bigcap _{i=1}^{m}S_{i})\geqslant 1-1/2n$
.
The body
$K$
and the vectors
$v_{1},\ldots ,v_{n}$
then satisfy the assumptions of Lemma 9, and, therefore, there exists an assignment of signs
$\unicode[STIX]{x1D712}:[n]\rightarrow \{-1,1\}$
such that, for any
$k$
,
$1\leqslant k\leqslant n$
,
$$\begin{eqnarray}\mathop{\sum }_{j=1}^{k}\unicode[STIX]{x1D712}(j)v_{j}\in 5K.\end{eqnarray}$$
By the definition of
$K$
, this is equivalent to
$$\begin{eqnarray}\forall i\in \{1,\ldots ,m\}:\biggl|\mathop{\sum }_{j=1}^{k}\unicode[STIX]{x1D712}(j)\langle u_{i},v_{j}\rangle \biggr|\leqslant 5C_{d}^{\prime }(1+\log n)^{d-1/2}.\end{eqnarray}$$
For each
$i$
,
$1\leqslant i\leqslant m$
, let us define
$A_{i}^{\prime }=\{p_{j}:q_{j}\in A_{i}\}$
. We claim that for any
$x\in \mathbb{R}^{d}$
, we can write
$A(x)\cap P$
as
$A_{i}^{\prime }\cap \{p_{1},\ldots ,p_{k}\}$
for some
$i$
and
$k$
. (Here we assume that
$A(x)\cap P$
is non-empty: the other case is irrelevant to the proof.) To see this, let
$x=(y,x_{d})$
, where
$y\in \mathbb{R}^{d-1}$
and
$x_{d}\in \mathbb{R}$
. Let
$i$
be such that
$A(y)\cap Q=A_{i}$
, and let
$k$
be the largest integer such that
$r_{k}\leqslant x_{d}$
. Then:
$$\begin{eqnarray}A(x)\cap P=\{p_{j}:q_{j}\in A(y),j\leqslant k\}=A_{i}^{\prime }\cap \{p_{1},\ldots ,p_{k}\}.\end{eqnarray}$$
It follows that
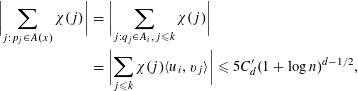$$\begin{eqnarray}\displaystyle \biggl|\mathop{\sum }_{j:p_{j}\in A(x)}\unicode[STIX]{x1D712}(j)\biggr| & = & \displaystyle \biggl|\mathop{\sum }_{j:q_{j}\in A_{i},j\leqslant k}\unicode[STIX]{x1D712}(j)\biggr|\nonumber\\ \displaystyle & = & \displaystyle \biggl|\mathop{\sum }_{j\leqslant k}\unicode[STIX]{x1D712}(j)\langle u_{i},v_{j}\rangle \biggr|\leqslant 5C_{d}^{\prime }(1+\log n)^{d-1/2},\nonumber\end{eqnarray}$$
where the penultimate equality follows from (6), and the final inequality is (7). Since
$x$
was arbitrary, we have shown that
$\operatorname{disc}{\mathcal{A}}_{d}(P)\leqslant 5C_{d}^{\prime }(1+\log n)^{d-1/2}$
, as was required.
5 Upper bound for an arbitrary polytope
The main ingredient in extending Theorem 1 to arbitrary polytopes is a geometric decomposition given by Matoušek. To describe the decomposition we define the admissible
$k$
-composition
$\text{AC}_{k}({\mathcal{F}})$
of sets from a (finite) set system
${\mathcal{F}}$
as follows. For
$k=0$
,
$\text{AC}_{k}({\mathcal{F}})=\emptyset$
; for an integer
$k>0$
, we have
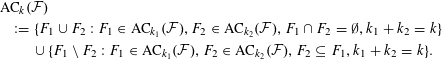$$\begin{eqnarray}\displaystyle & & \displaystyle \text{AC}_{k}({\mathcal{F}})\nonumber\\ \displaystyle & & \displaystyle \quad :=\{F_{1}\cup F_{2}:F_{1}\in \text{AC}_{k_{1}}({\mathcal{F}}),F_{2}\in \text{AC}_{k_{2}}({\mathcal{F}}),F_{1}\cap F_{2}=\emptyset ,k_{1}+k_{2}=k\}\nonumber\\ \displaystyle & & \displaystyle \hspace{25.79993pt}\cup \,\{F_{1}\setminus F_{2}:F_{1}\in \text{AC}_{k_{1}}({\mathcal{F}}),F_{2}\in \text{AC}_{k_{2}}({\mathcal{F}}),F_{2}\subseteq F_{1},k_{1}+k_{2}=k\}.\nonumber\end{eqnarray}$$
By an easy induction on
$k$
, we see that
$$\begin{eqnarray}\displaystyle \operatorname{disc}\text{AC}_{k}({\mathcal{F}}) & {\leqslant} & \displaystyle k\operatorname{disc}{\mathcal{F}},\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D6FE}_{2}(\text{AC}_{k}({\mathcal{F}})) & {\leqslant} & \displaystyle k\unicode[STIX]{x1D6FE}_{2}({\mathcal{F}}).\end{eqnarray}$$
We also extend the notion of anchored boxes to “corners” whose bounding hyperplanes are not necessarily orthogonal. Let
$W=\{w_{1},\ldots ,w_{d}\}$
be a basis of
$\mathbb{R}^{d}$
. Then we define
${\mathcal{A}}_{W}:=\{A_{W}(x):x\in \mathbb{R}^{d}\}$
, where
$A_{W}(x)=\{y\in \mathbb{R}^{d}:\langle w_{i},y\rangle \leqslant \langle w_{i},x\rangle ~\text{for all}~i\in [d]\}$
.
The following lemma gives the decomposition result we need.
Lemma 10 [Reference Matoušek25].
Let
$B\subset \mathbb{R}^{d}$
be a convex polytope. There exists a constant
$k$
depending on
$d$
and
$B$
, and
$k$
bases
$W_{1},\ldots ,W_{k}$
of
$\mathbb{R}^{d}$
such that every
$B^{\prime }\in {\mathcal{T}}_{B}$
belongs to
$\text{AC}_{k}({\mathcal{A}}_{W_{1}}\cup \cdots \cup {\mathcal{A}}_{W_{k}})$
. Moreover,
$e_{1}\in W_{1}\cap W_{2}\cap \cdots \cap W_{k}$
, where
$e_{1}$
is the first standard basis vector of
$\mathbb{R}^{d}$
.
Matoušek does not state the condition after “moreover”; nevertheless, it is easy to verify this condition holds for the recursive decomposition in his proof of Lemma 10.
We will also need a bound on
$\unicode[STIX]{x1D6FE}_{2}({\mathcal{A}}_{W}(P))$
for a basis
$W$
and an
$n$
-point set
$P$
.
Lemma 11. For any
$\ell \geqslant 1$
there exists a constant
$C_{\ell }$
such that the following holds. For any set
$W$
of
$\ell$
linearly independent vectors in
$\mathbb{R}^{d}$
, and any
$n$
-point set
$P$
,
$\unicode[STIX]{x1D6FE}_{2}({\mathcal{A}}_{W}(P))\leqslant C_{\ell }(1+\log n)^{\ell }$
.
Proof. Let
$W=\{w_{1},\ldots ,w_{\ell }\}$
, and let
$u$
be the linear transformation from
$\mathbb{R}^{\ell }$
to
$\mathbb{R}^{d}$
that sends the
$i$
th standard basis vector
$e_{i}$
to
$w_{i}$
for each
$i\in [\ell ]$
. Let
$Q=u^{\ast }(P):=\{u^{\ast }(p):p\in P\}$
, where
$u^{\ast }$
is the adjoint of
$u$
. It is easy to verify that
${\mathcal{A}}_{W}(P)={\mathcal{A}}_{\ell }(Q)$
, and, therefore,
$$\begin{eqnarray}\unicode[STIX]{x1D6FE}_{2}({\mathcal{A}}_{W}(P))=\unicode[STIX]{x1D6FE}_{2}({\mathcal{A}}_{d}(Q))\leqslant C_{\ell }(1+\log n)^{\ell },\end{eqnarray}$$
where the final inequality follows from Lemma 7. ◻
As a warm-up, let us first prove an upper bound on
$\unicode[STIX]{x1D6FE}_{2}({\mathcal{T}}_{B}(P))$
.
Theorem 12. For any
$d\geqslant 1$
and any closed convex polytope
$B\subset \mathbb{R}^{d}$
there exists a constant
$C_{d,B}$
such that for any set
$P$
of
$n$
points in
$\mathbb{R}^{d}$
,
$$\begin{eqnarray}\unicode[STIX]{x1D6FE}_{2}({\mathcal{T}}_{B}(P))\leqslant C_{d,B}(1+\log n)^{d}.\end{eqnarray}$$
Proof. Let
$W_{1},\ldots ,W_{k}$
be as in Lemma 10. Using (3) and Lemma 11,
$$\begin{eqnarray}\unicode[STIX]{x1D6FE}_{2}({\mathcal{A}}_{W_{1}}(P)\cup \cdots \cup {\mathcal{A}}_{W_{k}}(P))\leqslant \sqrt{k}C_{d}(1+\log n)^{d}.\end{eqnarray}$$
Using Lemma 10,
${\mathcal{T}}_{B}(P)\subseteq \text{AC}_{k}({\mathcal{A}}_{W_{1}}(P)\cup \cdots \cup {\mathcal{A}}_{W_{k}}(P))$
. Together with (9) and the trivial fact that
$\unicode[STIX]{x1D6FE}_{2}({\mathcal{F}}^{\prime })\leqslant \unicode[STIX]{x1D6FE}_{2}({\mathcal{F}})$
whenever
${\mathcal{F}}^{\prime }\subseteq {\mathcal{F}}$
, this implies
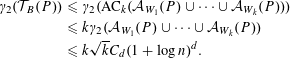$$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D6FE}_{2}({\mathcal{T}}_{B}(P)) & {\leqslant} & \displaystyle \unicode[STIX]{x1D6FE}_{2}(\text{AC}_{k}({\mathcal{A}}_{W_{1}}(P)\cup \cdots \cup {\mathcal{A}}_{W_{k}}(P)))\nonumber\\ \displaystyle & {\leqslant} & \displaystyle k\unicode[STIX]{x1D6FE}_{2}({\mathcal{A}}_{W_{1}}(P)\cup \cdots \cup {\mathcal{A}}_{W_{k}}(P))\nonumber\\ \displaystyle & {\leqslant} & \displaystyle k\sqrt{k}C_{d}(1+\log n)^{d}.\nonumber\end{eqnarray}$$
Since
$k$
depends on
$d$
and
$B$
only, this finishes the proof of the theorem.◻
Proof of Theorem 2.
As in the proof of Theorem 1, we fix the
$n$
-point set
$P\subset \mathbb{R}^{d}$
once and for all, and we order
$P$
as
$p_{1},\ldots ,p_{n}$
in increasing order of the last coordinate. We write each
$p_{i}$
as
$p_{i}=(q_{i},r_{i})$
for
$q_{i}\in \mathbb{R}^{d-1}$
and
$r_{i}\in \mathbb{R}$
, and define
$Q:=\{q_{i}:1\leqslant i\leqslant n\}$
.
Let
$W_{1},\ldots ,W_{k}$
be as in Lemma 10, and let
$W_{i}^{\prime }=W_{i}\setminus \{e_{1}\}$
for each
$i$
,
$1\leqslant i\leqslant k$
. Observe that
$W_{i}^{\prime }$
is a set of
$d-1$
linearly independent vectors, and, using (3) and Lemma 11,
$$\begin{eqnarray}\unicode[STIX]{x1D6FE}_{2}({\mathcal{A}}_{W_{1}^{\prime }}(Q)\cup \cdots \cup {\mathcal{A}}_{W_{k}^{\prime }}(Q))\leqslant \sqrt{k}C_{d}(1+\log n)^{d-1}.\end{eqnarray}$$
With an argument using Lemma 9 analogous to the one used in the proof of Theorem 1, we can then show that there exists a constant
$C_{d,B}^{\prime }$
depending on
$B$
and
$d$
and a coloring
$\unicode[STIX]{x1D712}:[n]\rightarrow \{-1,1\}$
, such that for any integer
$i$
,
$1\leqslant i\leqslant k$
, and any
$x\in \mathbb{R}^{d}$
,
$$\begin{eqnarray}\biggl|\mathop{\sum }_{j:p_{j}\in A_{W_{i}}(x)}\unicode[STIX]{x1D712}(j)\biggr|\leqslant C_{d,B}^{\prime }(1+\log n)^{d-1/2}.\end{eqnarray}$$
Here
$C_{d,B}^{\prime }$
is implicitly assumed to depend on
$k$
as well, which depends on
$B$
and
$d$
. This establishes that
$\operatorname{disc}{\mathcal{F}}\leqslant C_{d,B}^{\prime }(1+\log n)^{d-1/2}$
, where
${\mathcal{F}}={\mathcal{A}}_{W_{1}}(P)\cup \cdots \cup {\mathcal{A}}_{W_{k}}(P)$
. Because, using Lemma 10,
${\mathcal{T}}_{B}(P)\subseteq \text{AC}_{k}({\mathcal{F}})$
, (8) implies
$$\begin{eqnarray}\operatorname{disc}{\mathcal{T}}_{B}(P)\leqslant \operatorname{disc}\text{AC}_{k}({\mathcal{F}})\leqslant k\operatorname{disc}{\mathcal{F}}\leqslant kC_{d,B}^{\prime }(1+\log n)^{d-1/2}.\end{eqnarray}$$
This finishes the proof of the theorem. ◻
The same asymptotic bound with
${\mathcal{T}}_{B}$
replaced by
$\text{POL}({\mathcal{H}})$
for a family of hyperplanes
${\mathcal{H}}$
can be proved by replacing Lemma 10 with an analogous decomposition lemma for
$\text{POL}({\mathcal{H}})$
, also proved in [Reference Matoušek25].
The upper bound on
$\sqrt{t_{u}t_{q}}$
in Theorem 5 follows from Theorem 12 and the observation that the upper bound on
$\unicode[STIX]{x1D6FE}_{2}$
can be achieved by a factorization into matrices with entries in
$\{0,1\}$
, which is equivalent to an oblivious data structure with multiplicity 1. The upper bound on error in Theorem 6 follows from Theorems 8 and 12.
6 Lower bound
In this section we prove lower bounds on
$\operatorname{disc}(n,{\mathcal{T}}_{B})$
matching the known lower bounds on
$\operatorname{disc}(n,{\mathcal{A}}_{d})$
up to constants when
$B$
is a generic convex polytope (“generic” is defined below). In order to use Fourier analytic techniques, it will be convenient to work with a modification of the incidence matrix of
${\mathcal{T}}_{B}(P)$
. To this end, let us call a function
$f:\mathbb{R}^{d}\rightarrow \mathbb{R}$
periodic if for every
$x\in [0,1)^{d}$
and every vector
$y$
in the integer lattice
$\mathbb{Z}^{d}$
we have
$f(x)=f(x+y)$
. Let
$Q_{n}:=\{i/n\}_{i=0}^{n-1}$
. For a periodic function
$f:\mathbb{R}^{d}\rightarrow \mathbb{R}$
, define a real
$n^{d}\times n^{d}$
matrix
$M(f,n)$
indexed by
$Q_{n}^{d}$
:
$$\begin{eqnarray}m_{x,y}(f,n):=f(x-y),\end{eqnarray}$$
where,
$x$
and
$y$
range over
$Q_{n}^{d}$
. Of special interest to us are periodic functions defined by convex polytopes
$B\subseteq [0,1)^{d}$
. Let us define the function
$f_{B}:\mathbb{R}^{d}\rightarrow R$
to be equal to the indicator function
$1_{B}$
of
$B$
on
$[0,1)^{d}$
, extended periodically to the rest of
$\mathbb{R}^{d}$
. For convenience, we use the notation
$M(B,n):=M(f_{B},n)$
.
There are two main observations that motivate studying
$M(B,n)$
. First, each row of
$M(B,n)$
is the indicator vector of the disjoint union of most
$2^{d}$
sets from
${\mathcal{T}}_{-B}(Q_{n}^{d})={\mathcal{T}}_{B}(-Q_{n}^{d})={\mathcal{T}}_{B}(Q_{n}^{d})$
, so any lower bound on the hereditary discrepancy of
$M(B,n)$
implies a lower bound on
$\operatorname{disc}(n,{\mathcal{T}}_{B})$
. Second, because
$M(B,n)$
is the matrix of a convolution operator, it is diagonalized by the (discrete multidimensional) Fourier transform, and we can use known results on the Fourier spectra of convex polytopes to derive bounds on the trace norm of
$M(B,n)$
, and therefore on
$\unicode[STIX]{x1D6FE}_{2}(M(B,n))$
.
Before we continue, let us introduce the standard notation for the Fourier coefficients. For the remainder of this section, we use
$i=\sqrt{-1}$
to denote the imaginary unit. For any
$u\in \mathbb{R}^{d}$
and a periodic function
$f:\mathbb{R}^{d}\rightarrow \mathbb{R}$
integrable on
$[0,1)^{d}$
we define the Fourier coefficient
$$\begin{eqnarray}\hat{f}(\unicode[STIX]{x1D709}):=\int _{[0,1)^{d}}f(x)\text{e}^{-2\unicode[STIX]{x1D70B}\text{i}\langle \unicode[STIX]{x1D709},x\rangle }\,dx.\end{eqnarray}$$
We also define the discrete Fourier coefficients:
$$\begin{eqnarray}\tilde{f}(\unicode[STIX]{x1D709},n):=\frac{1}{n^{d}}\mathop{\sum }_{q\in Q_{n}}f(x)\text{e}^{-2\unicode[STIX]{x1D70B}\text{i}\langle \unicode[STIX]{x1D709},q\rangle }.\end{eqnarray}$$
It is well known, and easy to verify, that the eigenvalues of
$M(B,n)$
are given by
$n^{d}\tilde{f}_{B}(\unicode[STIX]{x1D709},n)$
. There is quite a bit known about the continuous Fourier coefficients
$\hat{f}_{B}(\unicode[STIX]{x1D709})$
, but comparatively less known about the discrete Fourier coefficients. Intuitively, bounds on the Fourier coefficients are easier to prove in the continuous domain because powerful tools like the divergence theorem are available. In order to use the known bounds on
$\hat{f}_{B}(\unicode[STIX]{x1D709})$
, we estimate the rate of convergence of
$\tilde{f}_{B}(\unicode[STIX]{x1D709},n)$
to
$\hat{f}_{B}(\unicode[STIX]{x1D709})$
with
$n$
. We follow an approach similar to that used by Epstein [Reference Epstein16] in the one-dimensional setting. In order to adapt his results to our setting, we need two additional ingredients: a higher-dimensional analog of Jackson’s theorem in approximation theory, and a continuous approximation to the indicator function
$f_{B}$
. Next, we state the higher-dimensional Jackson-type theorem (given by Yudin, also spelled Judin) that we use.
Definition 1. The modulus of continuity of a continuous function
$f:\mathbb{R}^{d}\rightarrow \mathbb{R}$
is defined as
$\unicode[STIX]{x1D714}(f,\unicode[STIX]{x1D6FF}):=\sup \{|f(x+t)-f(x)|:x,t\in \mathbb{R}^{d},\Vert t\Vert _{2}\leqslant \unicode[STIX]{x1D6FF}\}$
.
Theorem 13 [Reference Judin21].
There exists a universal constant
$C$
such that for any function
$f$
and any integer
$n\geqslant 1$
there exists an order
$n$
trigonometric polynomial
$p$
defined by
$$\begin{eqnarray}p(x)=\mathop{\sum }_{\unicode[STIX]{x1D708}\in \mathbb{Z}^{d}:\Vert \unicode[STIX]{x1D708}\Vert _{\infty }\leqslant n}c_{\unicode[STIX]{x1D708}}\text{e}^{2\unicode[STIX]{x1D70B}\text{i}\langle \unicode[STIX]{x1D708},x\rangle }\end{eqnarray}$$
such that
$$\begin{eqnarray}\Vert f-p\Vert _{\infty }:=\sup _{x\in [0,1)^{d}}|f(x)-p(x)|\leqslant 4\unicode[STIX]{x1D714}\biggl(f,\frac{C\sqrt{d}}{n}\biggr).\end{eqnarray}$$
The next lemma is an analogue of [Reference Epstein16, Theorem 3.1].
Lemma 14. There exists a universal constant
$C$
such that the following holds. Let
$f:\mathbb{R}^{d}\rightarrow \mathbb{R}$
be a continuous periodic function with modulus of continuity
$\unicode[STIX]{x1D714}(f,\unicode[STIX]{x1D6FF})$
. Then, for any
$\unicode[STIX]{x1D709}\in \mathbb{Z}^{d}$
such that
$\Vert \unicode[STIX]{x1D709}\Vert _{\infty }\leqslant n$
, we have
$$\begin{eqnarray}|\tilde{f}(\unicode[STIX]{x1D709},2n+1)-\hat{f}(\unicode[STIX]{x1D709})|\leqslant 8\unicode[STIX]{x1D714}\biggl(f,\frac{C\sqrt{d}}{n}\biggr).\end{eqnarray}$$
Proof. Let
$p$
be the trigonometric polynomial of order
$n$
guaranteed by Theorem 13. Using an elementary calculation, for any
$\unicode[STIX]{x1D709}\in \mathbb{Z}^{d}$
such that
$\Vert \unicode[STIX]{x1D709}\Vert _{\infty }\leqslant n$
, we have
$\tilde{p}(\unicode[STIX]{x1D709},2n+1)=\hat{p}(\unicode[STIX]{x1D709})=c_{\unicode[STIX]{x1D709}}$
, where
$c_{\unicode[STIX]{x1D709}}$
is the coefficient of
$\text{e}^{2\unicode[STIX]{x1D70B}\text{i}\langle \unicode[STIX]{x1D709},\cdot \rangle }$
in the expansion of
$p$
. For any
$\unicode[STIX]{x1D709}$
as above, this gives us:
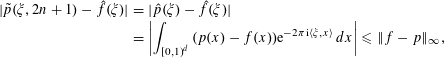$$\begin{eqnarray}\displaystyle |\tilde{p}(\unicode[STIX]{x1D709},2n+1)-\hat{f}(\unicode[STIX]{x1D709})| & = & \displaystyle |\hat{p}(\unicode[STIX]{x1D709})-\hat{f}(\unicode[STIX]{x1D709})|\nonumber\\ \displaystyle & = & \displaystyle \biggl|\int _{[0,1)^{d}}(p(x)-f(x))\text{e}^{-2\unicode[STIX]{x1D70B}\text{i}\langle \unicode[STIX]{x1D709},x\rangle }\,dx\biggr|\leqslant \Vert f-p\Vert _{\infty },\nonumber\end{eqnarray}$$
where we used the trivial case of Hölder’s inequality. Similarly,
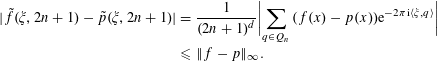$$\begin{eqnarray}\displaystyle |\tilde{f}(\unicode[STIX]{x1D709},2n+1)-\tilde{p}(\unicode[STIX]{x1D709},2n+1)| & = & \displaystyle \frac{1}{(2n+1)^{d}}\biggl|\mathop{\sum }_{q\in Q_{n}}(f(x)-p(x))\text{e}^{-2\unicode[STIX]{x1D70B}\text{i}\langle \unicode[STIX]{x1D709},q\rangle }\biggr|\nonumber\\ \displaystyle & {\leqslant} & \displaystyle \Vert f-p\Vert _{\infty }.\nonumber\end{eqnarray}$$
Combining the two inequalities, and using the bound in Theorem 13, we get
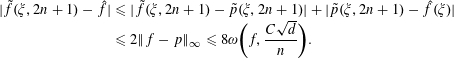$$\begin{eqnarray}\displaystyle |\tilde{f}(\unicode[STIX]{x1D709},2n+1)-\hat{f}| & {\leqslant} & \displaystyle |\tilde{f}(\unicode[STIX]{x1D709},2n+1)-\tilde{p}(\unicode[STIX]{x1D709},2n+1)|+|\tilde{p}(\unicode[STIX]{x1D709},2n+1)-\hat{f}(\unicode[STIX]{x1D709})|\nonumber\\ \displaystyle & {\leqslant} & \displaystyle 2\Vert f-p\Vert _{\infty }\leqslant 8\unicode[STIX]{x1D714}\biggl(f,\frac{C\sqrt{d}}{n}\biggr).\nonumber\end{eqnarray}$$
This completes the proof. ◻
In the next lemma we prove an explicit bound on how fast
$\tilde{f}_{B}(\unicode[STIX]{x1D709},n)$
converges to
$\hat{f}_{B}(\unicode[STIX]{x1D709})$
with
$n$
for a convex polytope
$B$
. The bounds are most likely not tight, but sufficient for our purposes, since we only need that the convergence rate is polynomial in
$1/n$
.
Lemma 15. Let
$B\subseteq [0,1)^{d}$
be a convex polytope with non-empty interior. Then, for any
$\unicode[STIX]{x1D709}\in \mathbb{Z}^{d}$
,
$\Vert \unicode[STIX]{x1D709}\Vert _{\infty }\leqslant n$
, we have
$$\begin{eqnarray}|\tilde{f}_{B}(\unicode[STIX]{x1D709},2n+1)-\hat{f}_{B}(\unicode[STIX]{x1D709})|=O_{d,B}\biggl(\frac{1}{\sqrt{n}}\biggr).\end{eqnarray}$$
Proof. In order to apply Lemma 14, we need a continuous function
$f$
which approximates
$f_{B}$
. We construct this approximation by, roughly, a piecewise linear interpolation along every direction.
Let
$c$
lie in the interior of
$B$
, and pick a real number
$r>0$
such that
$c+rD^{d}\subseteq B$
, where
$D^{d}$
is the unit Euclidean ball in
$\mathbb{R}^{d}$
centered at the origin. Let us define the gauge function
$g$
by
$g(x)=\inf \{t:x\in (1-t)c+tB\}$
on
$[0,1)^{d}$
. Note that
$g(x)\leqslant (1/r)\Vert x-c\Vert _{2}$
, further, that for any
$x,t\in \mathbb{R}^{d}$
,
$g(x+t)\leqslant g(x)+g(t+c)$
. Using these two observations, we get
$$\begin{eqnarray}g(x+t)-g(x)\leqslant g(t+c)\leqslant \frac{1}{r}\Vert t\Vert _{2}.\end{eqnarray}$$
By symmetry, we also get that
$g(x)-g(x+t)\leqslant (1/r)\Vert t\Vert _{2}$
. Therefore,
$\unicode[STIX]{x1D714}(g,\unicode[STIX]{x1D6FF})\leqslant \unicode[STIX]{x1D6FF}/r$
.
We define a periodic function
$f$
on
$[0,1)^{d}$
by
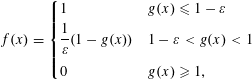$$\begin{eqnarray}f(x)=\left\{\begin{array}{@{}ll@{}}1\quad & g(x)\leqslant 1-\unicode[STIX]{x1D700}\\ \displaystyle \frac{1}{\unicode[STIX]{x1D700}}(1-g(x))\quad & 1-\unicode[STIX]{x1D700}<g(x)<1\\ 0\quad & g(x)\geqslant 1,\end{array}\right.\end{eqnarray}$$
for a parameter
$0<\unicode[STIX]{x1D700}<1$
which depends on
$n$
and will be determined later. We then extend
$f$
periodically to the rest of
$\mathbb{R}^{d}$
. The function
$f$
is defined so that it is continuous and agrees with
$f_{B}$
except for those
$x$
for which
$1-\unicode[STIX]{x1D700}<g(x)<1$
. Moreover, observe that
$$\begin{eqnarray}\unicode[STIX]{x1D714}(f,\unicode[STIX]{x1D6FF})\leqslant \frac{1}{\unicode[STIX]{x1D700}}\unicode[STIX]{x1D714}(g,\unicode[STIX]{x1D6FF})\leqslant \frac{\unicode[STIX]{x1D6FF}}{r\unicode[STIX]{x1D700}}.\end{eqnarray}$$
Then, using Lemma 14, for any
$\unicode[STIX]{x1D709}\in \mathbb{Z}^{d}$
such that
$\Vert \unicode[STIX]{x1D709}\Vert _{\infty }\leqslant n$
, we have
$$\begin{eqnarray}|\tilde{f}(\unicode[STIX]{x1D709},2n+1)-\hat{f}(\unicode[STIX]{x1D709})|\leqslant \frac{8C\sqrt{d}}{r\unicode[STIX]{x1D700}n}.\end{eqnarray}$$
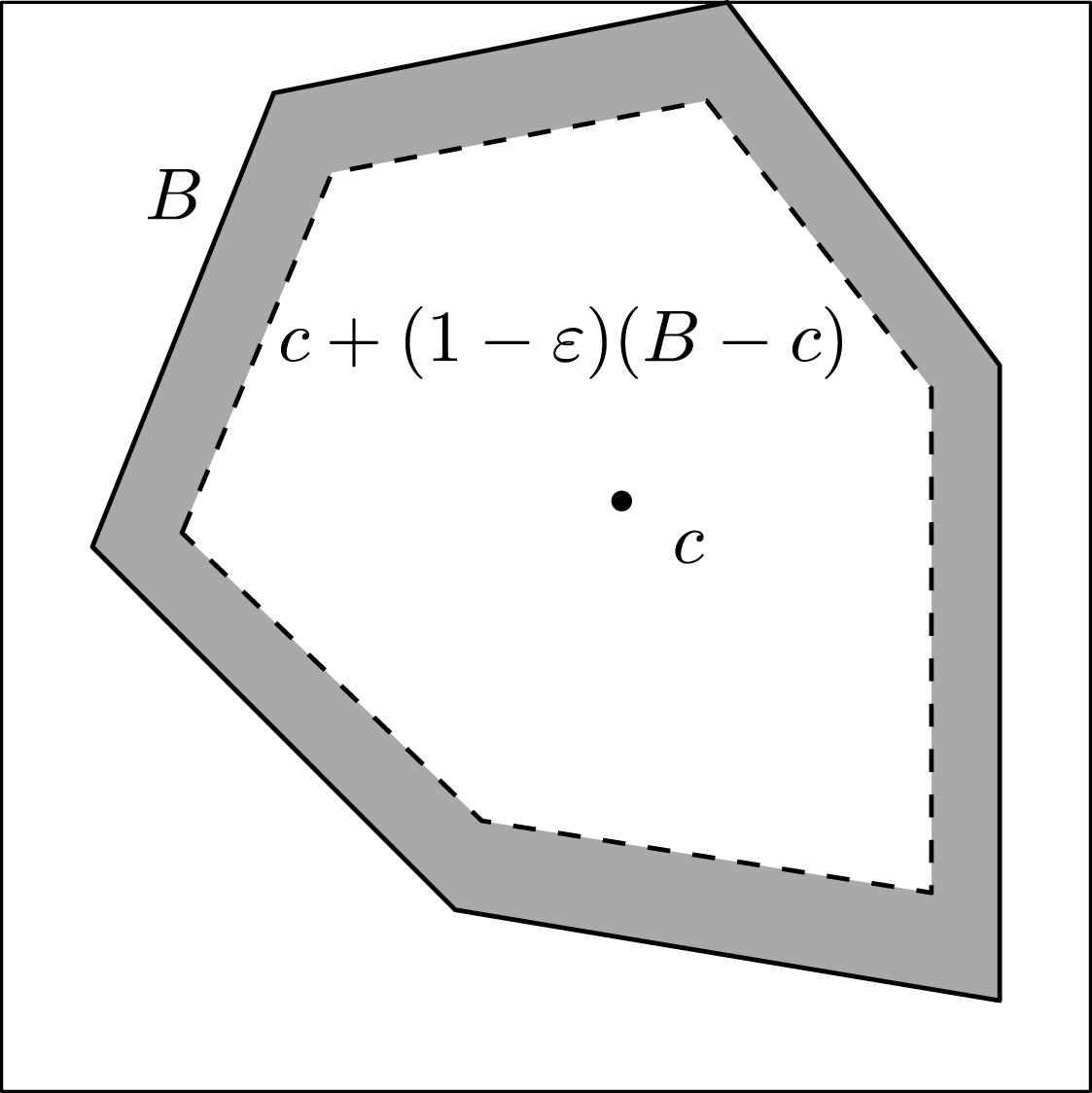
Figure 1 The set
$S$
on which
$f$
and
$f_{B}$
disagree.
It remains to bound
$|\hat{f}_{B}(\unicode[STIX]{x1D709})-\hat{f}(\unicode[STIX]{x1D709})|$
and
$|\tilde{f}_{B}(\unicode[STIX]{x1D709},2n+1)-\tilde{f}(\unicode[STIX]{x1D709},2n+1)|$
. Let
$S=\{x\in [0,1)^{d}:1-\unicode[STIX]{x1D700}<g(x)<1\}$
be the subset of
$[0,1)^{d}$
on which
$f$
and
$f_{B}$
disagree. Notice that the closure of
$S$
is
$B\setminus (\unicode[STIX]{x1D700}c+(1-\unicode[STIX]{x1D700})B)=c+(B-c)\setminus (1-\unicode[STIX]{x1D700})(B-c)$
(see Figure 1), so we have
$$\begin{eqnarray}\unicode[STIX]{x1D706}_{d}(S)=\unicode[STIX]{x1D706}(B\setminus (1-\unicode[STIX]{x1D700})B)=(1-(1-\unicode[STIX]{x1D700})^{d})\unicode[STIX]{x1D706}_{d}(B)\leqslant d\unicode[STIX]{x1D700},\end{eqnarray}$$
where, in the final inequality, we used the assumption
$B\subseteq [0,1)^{d}$
, which implies
$\unicode[STIX]{x1D706}_{d}(B)\leqslant 1$
. (Recall that we use
$\unicode[STIX]{x1D706}_{d}$
for the Lebesgue measure in
$\mathbb{R}^{d}$
.) We can now bound the first of our error terms using Hölder’s inequality: for any
$\unicode[STIX]{x1D709}\in \mathbb{Z}^{d}$
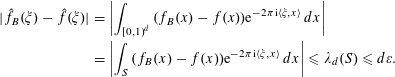$$\begin{eqnarray}\displaystyle |\hat{f}_{B}(\unicode[STIX]{x1D709})-\hat{f}(\unicode[STIX]{x1D709})| & = & \displaystyle \biggl|\int _{[0,1)^{d}}(f_{B}(x)-f(x))\text{e}^{-2\unicode[STIX]{x1D70B}\text{i}\langle \unicode[STIX]{x1D709},x\rangle }\,dx\biggr|\nonumber\\ \displaystyle & = & \displaystyle \biggl|\int _{S}(f_{B}(x)-f(x))\text{e}^{-2\unicode[STIX]{x1D70B}\text{i}\langle \unicode[STIX]{x1D709},x\rangle }\,dx\biggr|\leqslant \unicode[STIX]{x1D706}_{d}(S)\leqslant d\unicode[STIX]{x1D700}.\quad\end{eqnarray}$$
A similar calculation for the discrete Fourier coefficients gives us
$$\begin{eqnarray}\displaystyle |\tilde{f}_{B}(\unicode[STIX]{x1D709},2n+1)-\tilde{f}(\unicode[STIX]{x1D709},2n+1)| & = & \displaystyle \frac{1}{(2n+1)^{d}}\mathop{\sum }_{q\in Q_{n}}(f_{B}-f(x))\text{e}^{-2\unicode[STIX]{x1D70B}\text{i}\langle \unicode[STIX]{x1D709},q\rangle }\nonumber\\ \displaystyle & = & \displaystyle \frac{1}{(2n+1)^{d}}\mathop{\sum }_{q\in Q_{n}\cap S}(f_{B}-f(x))\text{e}^{-2\unicode[STIX]{x1D70B}\text{i}\langle \unicode[STIX]{x1D709},q\rangle }\nonumber\\ \displaystyle & {\leqslant} & \displaystyle \frac{|S\cap Q_{n}|}{(2n+1)^{d}}\nonumber\end{eqnarray}$$
for any
$\unicode[STIX]{x1D709}\in \mathbb{Z}^{d}$
. By a standard volume argument,
$$\begin{eqnarray}|S\cap Q_{n}|\leqslant \frac{\unicode[STIX]{x1D706}_{d}(S+(1/2n)D^{d})}{\unicode[STIX]{x1D706}_{d}((1/2n)D^{d})}=(2n)^{d}\frac{\unicode[STIX]{x1D706}_{d}(S+(1/2n)D^{d})}{\unicode[STIX]{x1D706}_{d}(D^{d})}.\end{eqnarray}$$
Because
$(1/2n)D^{d}\subseteq (1/2rn)(B-c)$
, we have
$S+(1/2n)D^{d}\subseteq c+(1+1/2rn)(B-c)\setminus (1-\unicode[STIX]{x1D700}-1/2rn)(B-c)$
, and, therefore,
$$\begin{eqnarray}\unicode[STIX]{x1D706}_{d}\biggl(S+\frac{1}{2n}D^{d}\biggr)\leqslant \biggl(\biggl(1+\frac{1}{2rn}\biggr)^{d}-\biggl(1-\unicode[STIX]{x1D700}-\frac{1}{2rn}\biggr)^{d}\biggr)\unicode[STIX]{x1D706}_{d}(B)\leqslant \unicode[STIX]{x1D700}d+\frac{3d}{2rn},\end{eqnarray}$$
where the final inequality holds for
$n\geqslant d/2r$
. Putting the estimates together, we have
$$\begin{eqnarray}|\tilde{f}_{B}(\unicode[STIX]{x1D709},2n+1)-\tilde{f}(\unicode[STIX]{x1D709},2n+1)|\leqslant C_{d}\unicode[STIX]{x1D700}+\frac{C_{d}}{rn},\end{eqnarray}$$
for a constant
$C_{d}$
depending on
$d$
and all large enough
$n$
.
Combining (10), (11), and (12), for all large enough
$n$
and any
$\unicode[STIX]{x1D709}\in \mathbb{Z}^{d}$
such that
$\Vert \unicode[STIX]{x1D709}\Vert _{\infty }\leqslant n$
we get
$$\begin{eqnarray}|\tilde{f}_{B}(\unicode[STIX]{x1D709},2n+1)-\hat{f}_{B}(\unicode[STIX]{x1D709},2n+1)|\leqslant \frac{8C\sqrt{d}}{r\unicode[STIX]{x1D700}n}+(C_{d}+d)\unicode[STIX]{x1D700}+\frac{C_{d}}{rn}.\end{eqnarray}$$
By setting
$\unicode[STIX]{x1D700}=n^{-1/2}$
, we get that the right-hand side is in
$O_{d,B}(n^{-1/2})$
, as required.◻
Inspecting the proof of Lemma 15, we see that the only dependence on
$B$
is via the radius
$r$
of the Euclidean ball contained in
$B$
: all other constants depend on the dimension only. By John’s theorem, we can apply an affine transformation to
$B$
so that it is contained in
$[0,1)^{d}$
, and in fact in a Euclidean ball of unit radius, and contains a ball of radius
$1/d$
. However, the estimates we use below on the Fourier coefficients of
$f_{B}$
do depend on
$B$
, so we do not pursue this idea further.
We require a technical definition.
Definition 2. We will say that a polytope
$B$
in
$\mathbb{R}^{d}$
is generic if there exists a sequence of faces
$F_{1}\subseteq F_{3}\subseteq \cdots \subseteq F_{d-1}$
of
$B$
such that
$F_{j}$
is a face of dimension
$j$
, for every
$j\leqslant d-2$
the face
$F_{j}$
is not parallel to any other face of
$F_{j+1}$
, and the facet
$F_{d-1}$
is not parallel to any other facet of
$B$
.
It is easy to see that
$B$
is generic for example if the facets of
$B$
have normal vectors
$u_{1},\ldots ,u_{k}$
that are in general position, in the sense that for every
$J\subseteq [k]$
of size at most
$d$
the set of vectors
$\{u_{j}:j\in J\}$
spans a subspace of dimension
$|J|$
. However, the condition of being generic appears to be much weaker. We use the following estimate on the Fourier coefficients of such a polytope.
Theorem 16 [Reference Brandolini, Colzani and Travaglini10].
Let
$B$
be a generic polytope in
$\mathbb{R}^{d}$
for
$d\geqslant 2$
. There exists a constant
$c_{d,B}$
, possibly depending on
$d$
and
$B$
, such that for any
$\unicode[STIX]{x1D70C}\geqslant 1$
$$\begin{eqnarray}\int _{S^{d-1}}|\hat{f}_{B}(\unicode[STIX]{x1D70C}\unicode[STIX]{x1D709})|\,d\unicode[STIX]{x1D70E}_{d-1}(\unicode[STIX]{x1D709})\geqslant \frac{c_{d,B}\log ^{d-1}(\unicode[STIX]{x1D70C})}{\unicode[STIX]{x1D70C}^{d}},\end{eqnarray}$$
where
$S^{d-1}$
is the unit Euclidean sphere in
$\mathbb{R}^{d}$
and
$\unicode[STIX]{x1D70E}_{d-1}$
is the uniform probability measure on
$S^{d-1}$
.
In [Reference Brandolini, Colzani and Travaglini10] Theorem 16 is stated for a simplex, and after the proof the authors remark that the same proof extends to any polytope which has one face not parallel to any other face. However, in their proof, they induct on lower and lower dimensional faces, and this condition needs to hold for any face they induct on. Our definition of generic appears to be the minimal condition under which their proof goes through. The authors of [Reference Brandolini, Colzani and Travaglini10] note that some genericity-like condition is necessary since Theorem 16 does not hold for all values of
$\unicode[STIX]{x1D70C}$
when
$B$
is a cube. Nevertheless, it is likely that a variant of the theorem in which we average over values of
$\unicode[STIX]{x1D70C}$
in a big enough interval could hold for arbitrary polytopes, and may yield a lower bound with a constant that only depends on
$d$
and not on
$B$
. We leave this extension for future work.
Theorem 16, Lemma 15, and an averaging argument yield the following estimate on discrete Fourier coefficients, which is the final step towards our lower bound.
Lemma 17. Let
$B\subseteq c+D^{d}$
be a generic convex polytope with non-empty interior, where
$D^{d}$
is the Euclidean unit ball in
$\mathbb{R}^{d}$
centered at the origin and
$c$
is the centroid of
$[0,1)^{d}$
. There exists an orthogonal transformation
$u$
such that
$B_{u}:=c+u(B-c)$
satisfies
$$\begin{eqnarray}\mathop{\sum }_{\unicode[STIX]{x1D709}\in \mathbb{Z}^{d}:\Vert \unicode[STIX]{x1D709}\Vert _{\infty }\leqslant n}|\tilde{f}_{B_{u}}(\unicode[STIX]{x1D709},2n+1)|=\unicode[STIX]{x1D6FA}_{d,B}(\log ^{d}(n)).\end{eqnarray}$$
Proof. Recall that we use
$\mathbf{O}(d)$
to denote the group of orthogonal transformations on
$\mathbb{R}^{d}$
, and
$\unicode[STIX]{x1D703}_{d}$
to denote the Haar probability measure on this group. We also use
$\unicode[STIX]{x1D70E}_{d-1}$
for the uniform probability measure on the sphere.
For any
$\unicode[STIX]{x1D709}\in \mathbb{Z}^{d}\setminus \{0\}$
we have
$$\begin{eqnarray}\displaystyle \int _{\mathbf{O}(d)}|\hat{f}_{B_{u}}(\unicode[STIX]{x1D709})|\,d\unicode[STIX]{x1D703}(u) & = & \displaystyle \int _{\mathbf{O}(d)}\biggl|\int _{c+u(B-c)}\text{e}^{-2\unicode[STIX]{x1D70B}\text{i}\langle \unicode[STIX]{x1D709},x\rangle }\,dx\biggr|\,d\unicode[STIX]{x1D703}(u)\nonumber\\ \displaystyle & = & \displaystyle \int _{\mathbf{O}(d)}\biggl|\int _{u(B)}\text{e}^{-2\unicode[STIX]{x1D70B}\text{i}\langle \unicode[STIX]{x1D709},x\rangle }\,dx\biggr|\,d\unicode[STIX]{x1D703}(u)\nonumber\\ \displaystyle & = & \displaystyle \int _{\mathbf{O}(d)}\biggl|\int _{B}\text{e}^{-2\unicode[STIX]{x1D70B}\text{i}\langle \unicode[STIX]{x1D709},u^{\ast }(x)\rangle }\,dx\biggr|\,d\unicode[STIX]{x1D703}(u)\nonumber\\ \displaystyle & = & \displaystyle \int _{\mathbf{O}(d)}\biggl|\int _{B}\text{e}^{-2\unicode[STIX]{x1D70B}\text{i}\langle u(\unicode[STIX]{x1D709}),x\rangle }\,dx\biggr|\,d\unicode[STIX]{x1D703}(u)\nonumber\\ \displaystyle & = & \displaystyle \int _{S^{d-1}}\biggl|\int _{B}\text{e}^{-2\unicode[STIX]{x1D70B}\text{i}\langle \Vert \unicode[STIX]{x1D709}\Vert _{2}\unicode[STIX]{x1D701},x\rangle }\,dx\biggr|\,d\unicode[STIX]{x1D70E}_{d-1}(\unicode[STIX]{x1D701})\nonumber\\ \displaystyle & {\geqslant} & \displaystyle \frac{c\log ^{d-1}(\Vert \unicode[STIX]{x1D709}\Vert _{2})}{\Vert \unicode[STIX]{x1D709}\Vert _{2}^{d}}.\nonumber\end{eqnarray}$$
Above, in the penultimate line we used the fact that for any measurable set
$Y\subseteq S^{d-1}$
, and any
$y\in S^{d-1}$
,
$\unicode[STIX]{x1D70E}_{d-1}(Y)=\unicode[STIX]{x1D703}_{d}(\{u\in \mathbf{O}(d):u(y)\in Y\})$
. The final inequality is implied by Theorem 16 for an appropriate constant
$c$
depending on
$d$
and
$B$
. Therefore,
$$\begin{eqnarray}\int _{\mathbf{O}(d)}\biggl(\mathop{\sum }_{\unicode[STIX]{x1D709}\in \mathbb{Z}^{d}:0<\Vert \unicode[STIX]{x1D709}\Vert _{2}=j}|\hat{f}_{B_{u}}(\unicode[STIX]{x1D709})|\biggr)\,d\unicode[STIX]{x1D703}_{d}(u)\geqslant cm_{j}\frac{\log ^{d-1}(j)}{j^{d/2}},\end{eqnarray}$$
where
$m_{j}=\{\unicode[STIX]{x1D709}\in \mathbb{Z}^{d}:\Vert \unicode[STIX]{x1D709}\Vert _{2}^{2}=j\}$
. By Lemma 15, for all sufficiently large
$n$
and for all
$j$
such that
$j\leqslant (c_{1}n)^{1/d}$
for a sufficiently small constant
$c_{1}$
, we have
$\tilde{f}_{B_{u}}(\unicode[STIX]{x1D709},2n+1)\geqslant \hat{f}_{B_{u}}(\unicode[STIX]{x1D709})-c/2j^{d/2}$
for any
$\unicode[STIX]{x1D709}\in \mathbb{N}_{0}^{d}$
for which
$\Vert \unicode[STIX]{x1D709}\Vert _{2}^{2}=j$
. Therefore,
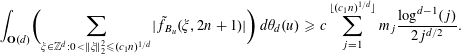$$\begin{eqnarray}\int _{\mathbf{O}(d)}\biggl(\mathop{\sum }_{\unicode[STIX]{x1D709}\in \mathbb{Z}^{d}:0<\Vert \unicode[STIX]{x1D709}\Vert _{2}^{2}\leqslant (c_{1}n)^{1/d}}\!|\tilde{f}_{B_{u}}(\unicode[STIX]{x1D709},2n+1)|\biggr)\,d\unicode[STIX]{x1D703}_{d}(u)\geqslant c\mathop{\sum }_{j=1}^{\lfloor (c_{1}n)^{1/d}\rfloor }m_{j}\frac{\log ^{d-1}(j)}{2j^{d/2}}.\end{eqnarray}$$
There must then exist a choice of
$u\in \mathbf{O}(d)$
such that
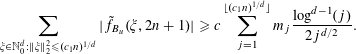$$\begin{eqnarray}\mathop{\sum }_{\unicode[STIX]{x1D709}\in \mathbb{N}_{0}^{d}:\Vert \unicode[STIX]{x1D709}\Vert _{2}^{2}\leqslant (c_{1}n)^{1/d}}|\tilde{f}_{B_{u}}(\unicode[STIX]{x1D709},2n+1)|\geqslant c\mathop{\sum }_{j=1}^{\lfloor (c_{1}n)^{1/d}\rfloor }m_{j}\frac{\log ^{d-1}(j)}{2j^{d/2}}.\end{eqnarray}$$
Let us fix such a
$u$
for the rest of the proof. We proceed to estimate the right-hand side of (13). Define
$\ell =\lfloor (c_{1}n)^{1/d}\rfloor$
to be the upper bound of the summation, and let
$k=\lfloor \sqrt{\ell }\rfloor$
. Let
$m_{{\leqslant}j}=m_{1}+\cdots +m_{j}$
. Using summation by parts, we have
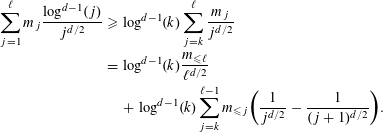$$\begin{eqnarray}\displaystyle \mathop{\sum }_{j=1}^{\ell }m_{j}\frac{\log ^{d-1}(j)}{j^{d/2}} & {\geqslant} & \displaystyle \log ^{d-1}(k)\mathop{\sum }_{j=k}^{\ell }\frac{m_{j}}{j^{d/2}}\nonumber\\ \displaystyle & = & \displaystyle \log ^{d-1}(k)\frac{m_{{\leqslant}\ell }}{\ell ^{d/2}}\nonumber\\ \displaystyle & & \displaystyle +\,\log ^{d-1}(k)\mathop{\sum }_{j=k}^{\ell -1}m_{{\leqslant}j}\biggl(\frac{1}{j^{d/2}}-\frac{1}{(j+1)^{d/2}}\biggr).\nonumber\end{eqnarray}$$
By standard estimates (e.g. Minkowski’s first theorem), there exists a constant
$c_{2}$
depending on the dimension
$d$
such that
$m_{{\leqslant}j}\geqslant c_{2}j^{d/2}$
. By convexity,
$1/j^{d/2}-1/(j+1)^{d/2}\geqslant (d/2)/(j+1)^{(d+2)/2}$
. Plugging these inequalities into the bound above, we get that
$$\begin{eqnarray}\mathop{\sum }_{j=1}^{\ell }m_{j}\frac{\log ^{d-1}(j)}{j^{d/2}}\geqslant c_{2}\log ^{d-1}(k)\mathop{\sum }_{j=k}^{\ell }\frac{j^{d/2}}{(j+1)^{(d+2)/2}}=\unicode[STIX]{x1D6FA}_{d}(\log ^{d}n).\end{eqnarray}$$
Together with (13), this completes the proof of the lemma. ◻
Proof of Theorem 3.
By scaling we can assume that
$B\subseteq c+D^{d}$
, where
$D^{d}$
is the Euclidean unit ball in
$\mathbb{R}^{d}$
centered at the origin and
$c$
is the centroid of
$[0,1)^{d}$
. Let
$u$
be the orthogonal transformation given by Lemma 17, and let
$M:=M(B_{u},2n+1)$
. It is easy to verify that
$M$
is diagonalized by the collection of orthogonal eigenvectors
$\{(\text{e}^{2\unicode[STIX]{x1D70B}\text{i}\langle \unicode[STIX]{x1D709},x\rangle })_{x\in Q_{2n+1}^{d}}:\unicode[STIX]{x1D709}\in \mathbb{Z}^{d},\Vert \unicode[STIX]{x1D709}\Vert _{\infty }\leqslant n\}$
, and the eigenvalue associated with the eigenvector
$(\text{e}^{2\unicode[STIX]{x1D70B}\text{i}\langle \unicode[STIX]{x1D709},x\rangle })_{x\in Q_{2n+1}^{d}}$
is
$(2n+1)^{d}\tilde{f}_{B_{u}}(\unicode[STIX]{x1D709},2n+1)$
. Since
$M$
is a normal matrix, i.e.
$M^{\intercal }M=MM^{\intercal }$
, or, equivalently, since it is diagonalized by a system of orthogonal eigenvectors, its singular values are equal to the absolute values of its eigenvalues. Using Lemma 17 we have the estimate
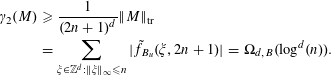$$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D6FE}_{2}(M) & {\geqslant} & \displaystyle \frac{1}{(2n+1)^{d}}\Vert M\Vert _{\operatorname{tr}}\nonumber\\ \displaystyle & = & \displaystyle \mathop{\sum }_{\unicode[STIX]{x1D709}\in \mathbb{Z}^{d}:\Vert \unicode[STIX]{x1D709}\Vert _{\infty }\leqslant n}|\tilde{f}_{B_{u}}(\unicode[STIX]{x1D709},2n+1)|=\unicode[STIX]{x1D6FA}_{d,B}(\log ^{d}(n)).\end{eqnarray}$$
Let
$A$
be the incidence matrix of
${\mathcal{T}}_{B_{u}}(-Q_{2n+1})$
. Notice that every row of
$M$
can be represented as the disjoint sum of at most
$2^{d}$
rows of
$A$
. Therefore, we can write
$M=A_{1}+\cdots +A_{k}$
, where
$k\leqslant 2^{d}$
, and each row of each matrix
$A_{j}$
is also a row of
$A$
. Since duplication and rearrangement of rows preserve
$\unicode[STIX]{x1D6FE}_{2}$
, and dropping rows does not increase it, by the triangle inequality for
$\unicode[STIX]{x1D6FE}_{2}$
we have
$$\begin{eqnarray}\unicode[STIX]{x1D6FE}_{2}(M)\leqslant \mathop{\sum }_{j=1}^{k}\unicode[STIX]{x1D6FE}_{2}(A_{j})\leqslant 2^{d}\unicode[STIX]{x1D6FE}_{2}(A)=2^{d}\unicode[STIX]{x1D6FE}_{2}({\mathcal{T}}_{B_{u}}(-Q_{2n+1})).\end{eqnarray}$$
Define the pointset
$P=\{u^{\ast }(x-c)+c:x\in -Q_{2n+1}\}$
, and notice that
${\mathcal{T}}_{B}(P)={\mathcal{T}}_{B_{u}}(-Q_{2n+1})$
, so, using the inequality above and (14), we have
$$\begin{eqnarray}\unicode[STIX]{x1D6FE}_{2}({\mathcal{T}}_{B}(P))=\unicode[STIX]{x1D6FA}_{d,B}(\log ^{d}n).\end{eqnarray}$$
$$\begin{eqnarray}\operatorname{disc}(n^{d},{\mathcal{T}}_{B})\geqslant \operatorname{herdisc}{\mathcal{T}}_{B}(P)=\unicode[STIX]{x1D6FA}_{d,B}(\log ^{d-1}n).\end{eqnarray}$$
Therefore,
$\operatorname{disc}(n,{\mathcal{T}}_{B})=\unicode[STIX]{x1D6FA}_{d,B}(\log ^{d-1}n)$
, as was to be proved.◻
Equation (15) implies the lower bound on
$\sqrt{t_{u}t_{q}}$
in Theorem 5. The lower bound on error in Theorem 6 follows from equation (15) and Theorem 8.
Acknowledgements
This research was partially supported by NSERC. The author would like to thank the organizers of the 2016 discrepancy theory workshop in Varenna, dedicated to the memory of Klaus Roth and Jiří Matoušek, where some of the initial ideas in this paper were conceived. The author would also like to thank József Beck for suggesting the problem of extending the lower bound for Tusnády’s problem to arbitrary polytopes, and Kunal Talwar for some initial discussions of this problem.
