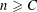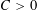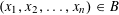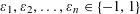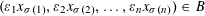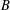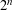1 Introduction
Let
$B$
be a convex body (i.e., a compact convex set with non-empty interior) in
$\mathbb{R}^{n}$
. The well-known problem of Hadwiger [Reference Hadwiger7], independently formulated by Gohberg and Markus, is to find the least number of smaller homothetic copies of
$B$
sufficient to cover
$B$
. An equivalent question is to determine the smallest number
${\mathcal{I}}(B)$
of points in
$\mathbb{R}^{n}\setminus B$
(“light sources”) sufficient to illuminate
$B$
[Reference Hadwiger8]. Here, we say that a collection of points
$\{p_{1},p_{2},\ldots ,p_{m}\}$
illuminates
$B$
if for any point
$x$
on the boundary of
$B$
there is a point
$p_{i}$
such that the line passing through
$p_{i}$
and
$x$
intersects the interior of
$B$
at a point not between
$p_{i}$
and
$x$
. We refer to [Reference Boltyanski, Martini and Soltan6, Ch. VI], [Reference Bezdek1, Ch. 3] and [Reference Bezdek and Khan4] for history of the question.
Following Boltyanski (see, in particular, [Reference Boltyanski, Martini and Soltan6, p. 256]), we say that a boundary point
$x\in B$
is illuminated in a direction
$y\in \mathbb{R}^{n}\setminus \{0\}$
if there is
$\unicode[STIX]{x1D700}>0$
such that the point
$x+\unicode[STIX]{x1D700}y$
belongs to the interior of
$B$
. The entire body
$B$
is illuminated in directions
$\{y^{1},y^{2},\ldots ,y^{m}\}$
if for every boundary point
$x\in B$
there is
$i\leqslant m$
such that
$x$
is illuminated in the direction
$y^{i}$
. The smallest number of directions sufficient to illuminate
$B$
is equal to
${\mathcal{I}}(B)$
(see [Reference Boltyanski, Martini and Soltan6, Theorem 34.3]).
It can be easily checked that the illumination number of an
$n$
-dimensional parallelotope is equal to
$2^{n}$
. The Hadwiger–Gohberg–Markus illumination conjecture asserts that for any
$n$
-dimensional convex body
$B$
different from a parallelotope,
${\mathcal{I}}(B)<2^{n}$
. We refer to [Reference Bezdek1, Ch. 3] and [Reference Bezdek and Khan4] for a list of results, confirming the conjecture in some special cases. Here, let us mention a result of Martini for so-called belt polytopes [Reference Martini10] and their extension to belt bodies due to Boltyanskiĭ [Reference Boltyanskiĭ5]; a paper of Schramm [Reference Schramm13] dealing with bodies of constant width and their generalization to fat spindle bodies by Bezdek [Reference Bezdek2]; and a result of Bezdek and Bisztriczky [Reference Bezdek and Bisztriczky3] for dual cyclic polytopes. For arbitrary convex bodies, the best-known upper bound follows from Rogers’ covering theorem [Reference Rogers12]:
$$\begin{eqnarray}\displaystyle {\mathcal{I}}(B)\leqslant (n\log n+n\log \log n+5n)\frac{\text{Vol}_{n}(B-B)}{\text{Vol}_{n}(B)}, & & \displaystyle\end{eqnarray}$$
where
$B-B$
denotes the Minkowski difference and
$\text{Vol}_{n}(\cdot )$
is the standard Lebesgue volume in
$\mathbb{R}^{n}$
(see, for example, [Reference Bezdek and Khan4, Corollary 2.11] or [Reference Bezdek1, Corollary 3.4.2]).
The aforementioned results of Schramm [Reference Schramm13] and Bezdek [Reference Bezdek2] are based on a probabilistic argument in which directions of illumination are chosen uniformly independently on the sphere
$\text{S}^{n-1}$
(see also [Reference Naszódi11]). Further, in the recent note [Reference Livshyts and Tikhomirov9], it was shown that the general bound (1) can be recovered by illuminating the body
$B$
with independently distributed sources of light. It was suggested in [Reference Livshyts and Tikhomirov9] that randomized models of that type can be helpful and may contribute towards solving the illumination problem.
In this note, we further develop the approach from [Reference Bezdek2, Reference Livshyts and Tikhomirov9, Reference Schramm13] by applying it to convex bodies with many symmetries. Let
$n\geqslant 2$
. We denote by
${\mathcal{C}}_{n}$
the set of all convex bodies
$B$
in
$\mathbb{R}^{n}$
having the following properties:
-
(1)
$(\unicode[STIX]{x1D700}_{1}x_{1},\unicode[STIX]{x1D700}_{2}x_{2},\ldots ,\unicode[STIX]{x1D700}_{n}x_{n})\in B$
for any
$(x_{1},x_{2},\ldots ,x_{n})\in B$
and any choice of signs
$\unicode[STIX]{x1D700}_{i}\in \{-1,1\}$
; and -
(2)
$(x_{\unicode[STIX]{x1D70E}(1)},x_{\unicode[STIX]{x1D70E}(2)},\ldots ,x_{\unicode[STIX]{x1D70E}(n)})\in B$
for any
$(x_{1},x_{2},\ldots ,x_{n})\in B$
and any permutation
$\unicode[STIX]{x1D70E}$
on
$n$
elements.
Note that the Minkowski functionals of convex bodies from
${\mathcal{C}}_{n}$
are
$1$
-symmetric norms in
$\mathbb{R}^{n}$
(with respect to the standard basis) and, conversely, the closed unit ball of any
$1$
-symmetric norm in
$\mathbb{R}^{n}$
belongs to
${\mathcal{C}}_{n}$
. The main result of this note is the following.
Theorem 1. There is a universal constant
$C>0$
with the following property: let
$n\geqslant C$
and let
$B\in {\mathcal{C}}_{n}$
. Assume that
$B$
is not a cube. Then
${\mathcal{I}}(B)<2^{n}$
.
Let us make some remarks. In the paper [Reference Schramm13] of Schramm, it was proved that, given a group
$G$
of orthogonal transformations of
$\mathbb{R}^{n}$
which is generated by reflections through hyperplanes and acts irreducibly on
$\mathbb{R}^{n}$
(i.e., has no non-trivial invariant subspaces) and a strictly convex body
$B$
invariant under the action of
$G$
, we have
${\mathcal{I}}(B)=n+1$
. The group of orthogonal transformations generated by permutations of the standard basis vectors and reflections with respect to coordinate hyperplanes acts irreducibly on
$\mathbb{R}^{n}$
. Hence, the result of Schramm implies that for any strictly convex body
$B\in {\mathcal{C}}_{n}$
, we have
${\mathcal{I}}(B)=n+1$
. However, the theorem of Schramm gives no information about polytopes and, more generally, bodies which are not strictly convex.
The proof of Theorem 1 is split into two parts. In the first part (§3), we illuminate bodies
$B\in {\mathcal{C}}_{n}$
with a small distance to the cube (to be defined below), using purely deterministic arguments. In the second part (§4), we construct a special set of random directions which illuminate any given
$B\in {\mathcal{C}}_{n}$
with a “large” distance to the cube.
2 Preliminaries
Let us start with notation and basic definitions. Given a finite set
$I$
, we denote its cardinality by
$|I|$
. For any natural number
$k$
, we write
$[k]$
instead of
$\{1,2,\ldots ,k\}$
. For a real number
$r$
,
$\lfloor r\rfloor$
denotes the largest integer not exceeding
$r$
and
$\lceil r\rceil$
denotes the smallest integer greater than or equal to
$r$
.
Let
$n$
be a natural number. For a vector
$x=(x_{1},x_{2},\ldots ,x_{n})\in \mathbb{R}^{n}$
, let
$$\begin{eqnarray}I_{0}^{x}:=\{i\leqslant n:x_{i}=0\}.\end{eqnarray}$$
The standard basis vectors in
$\mathbb{R}^{n}$
will be denoted by
$e_{1},e_{2},\ldots ,e_{n}$
and the standard inner product by
$\langle \cdot ,\cdot \rangle$
. The maximum (
$\ell _{\infty }^{n}$
) norm in
$\mathbb{R}^{n}$
will be denoted by
$\Vert \cdot \Vert _{\infty }$
. Given a convex body
$B$
in
$\mathbb{R}^{n}$
, by
$\unicode[STIX]{x2202}B$
we denote its boundary and by
$\text{int}(B)$
its interior. If
$0\in \text{int}(B)$
, then the Minkowski functional
$\Vert \cdot \Vert _{B}$
on
$\mathbb{R}^{n}$
is defined by
$$\begin{eqnarray}\Vert y\Vert _{B}:=\inf \{\unicode[STIX]{x1D706}>0:y\in \unicode[STIX]{x1D706}B\},\quad y\in \mathbb{R}^{n}.\end{eqnarray}$$
Further, for a convex body
$B$
in
$\mathbb{R}^{n}$
and a point
$x\in \unicode[STIX]{x2202}B$
, let the Gauss image
$\unicode[STIX]{x1D708}(B,x)$
be the set of all outer normal unit vectors for supporting hyperplanes at
$x$
. In other words,
$\unicode[STIX]{x1D708}(B,x)$
is the set of all vectors
$v\in \text{S}^{n-1}$
such that
$\langle v,y-x\rangle \leqslant 0$
for all
$y\in B$
. We omit the proof of the next lemma (see, for example, [Reference Schramm13, Lemma 4] for an equivalent statement).
Lemma 2. Given a convex body
$B$
in
$\mathbb{R}^{n}\;(n\geqslant 2)$
, a direction
$y\in \mathbb{R}^{n}\setminus \{0\}$
illuminates
$x\in \unicode[STIX]{x2202}B$
if and only if
$\langle y,v\rangle <0$
for all
$v\in \unicode[STIX]{x1D708}(B,x)$
.
Let
$n\geqslant 2$
and let the class
${\mathcal{C}}_{n}$
be defined as in the Introduction. It is easy to see that, given a body
$B\in {\mathcal{C}}_{n}$
and a vector
$(x_{1},x_{2},\ldots ,x_{n})\in B$
, we have
$(\unicode[STIX]{x1D6FC}_{1}x_{1},\unicode[STIX]{x1D6FC}_{2}x_{2},\ldots ,\unicode[STIX]{x1D6FC}_{n}x_{n})\in B$
for any
$\unicode[STIX]{x1D6FC}_{i}\in [-1,1]$
. Hence, the following holds.
Lemma 3. For any
$B\in {\mathcal{C}}_{n}\;(n\geqslant 2)$
, any
$(x_{1},x_{2},\ldots ,x_{n})\in \unicode[STIX]{x2202}B$
and
$(v_{1},v_{2},\ldots ,v_{n})\in \unicode[STIX]{x1D708}(B,x)$
, we have
$x_{i}v_{i}\geqslant 0$
for all
$i\leqslant n$
.
Again, the proof of Lemma 3 is straightforward, and we omit it.
Lemma 4. Let
$B\in {\mathcal{C}}_{n}\;(n\geqslant 2)$
and let
$x=(x_{1},x_{2},\ldots ,x_{n})\in \unicode[STIX]{x2202}B$
. Then for all
$i,j\leqslant n$
such that
$|x_{i}|>|x_{j}|$
, we have
$|v_{i}|\geqslant |v_{j}|$
for any
$(v_{1},v_{2},\ldots ,v_{n})\in \unicode[STIX]{x1D708}(B,x)$
.
Proof. Assume the opposite: let
$B\in {\mathcal{C}}_{n}$
, a vector
$x=(x_{1},x_{2},\ldots ,x_{n})\in \unicode[STIX]{x2202}B$
and
$v=(v_{1},v_{2},\ldots ,v_{n})\in \unicode[STIX]{x1D708}(B,x)$
be such that for some
$i,j\leqslant n$
we have
$|x_{i}|>|x_{j}|$
and
$|v_{i}|<|v_{j}|$
. Obviously,
$$\begin{eqnarray}H:=\{z\in \mathbb{R}^{n}:\langle z,v\rangle =\langle x,v\rangle \}\end{eqnarray}$$
is a supporting hyperplane for
$B$
. Let
$\unicode[STIX]{x1D700}_{i},\unicode[STIX]{x1D700}_{j}\in \{-1,1\}$
be such that
$\unicode[STIX]{x1D700}_{i}x_{i}v_{j},\unicode[STIX]{x1D700}_{j}x_{j}v_{i}\geqslant 0$
, and denote
$$\begin{eqnarray}y:=\mathop{\sum }_{k\neq i,j}x_{k}e_{k}+\unicode[STIX]{x1D700}_{i}x_{i}e_{j}+\unicode[STIX]{x1D700}_{j}x_{j}e_{i}.\end{eqnarray}$$
Then
$$\begin{eqnarray}\displaystyle \langle y,v\rangle & = & \displaystyle \langle x,v\rangle +|x_{i}v_{j}|+|x_{j}v_{i}|-x_{i}v_{i}-x_{j}v_{j}\nonumber\\ \displaystyle & = & \displaystyle |\langle x,v\rangle |+(|x_{i}|-|x_{j}|)(|v_{j}|-|v_{i}|)\nonumber\\ \displaystyle & {>} & \displaystyle |\langle x,v\rangle |.\nonumber\end{eqnarray}$$
Thus,
$y$
cannot belong to
$B$
, contradicting the definition of the class
${\mathcal{C}}_{n}$
.◻
Given two convex bodies
$B$
and
$\widetilde{B}$
in
${\mathcal{C}}_{n}$
, we define the distance
$\text{d}(B,\widetilde{B})$
between
$B$
and
$\widetilde{B}$
as
$$\begin{eqnarray}\text{d}(B,\widetilde{B})=\inf \{\unicode[STIX]{x1D706}\geqslant 1:B\subset r\widetilde{B}\subset \unicode[STIX]{x1D706}B\text{ for some }r>0\}.\end{eqnarray}$$
In particular,
$\text{d}(B,[-1,1]^{n})$
is equal to the ratio
$\Vert e_{1}+e_{2}+\cdots +e_{n}\Vert _{B}/\Vert e_{1}\Vert _{B}$
. Note that
$\text{d}(B,\widetilde{B})$
is different from the Banach–Mazur distance between convex bodies.
3 Illumination of convex bodies with a small distance to the cube
In this section, we consider the problem of illuminating a set
$B\in {\mathcal{C}}_{n}$
with a small distance to the cube. Here, our construction is purely deterministic. We prove the following.
Proposition 5. Let
$B\in {\mathcal{C}}_{n}$
(
$n\geqslant 2$
) with
$1\neq \text{d}(B,[-1,1]^{n})<2$
. Then at least one of the following is true:
-
(1)
$B$
can be illuminated in directions
$$\begin{eqnarray}\displaystyle & & \displaystyle \{(\unicode[STIX]{x1D700}_{1},\unicode[STIX]{x1D700}_{2},\ldots ,\unicode[STIX]{x1D700}_{n})\in \{-1,1\}^{n}:\exists i\leqslant n-1\text{ with }\unicode[STIX]{x1D700}_{i}=-1\}\nonumber\\ \displaystyle & & \displaystyle \quad \cup \,\{e_{1}+e_{2}+\cdots +e_{n-1}\};\nonumber\end{eqnarray}$$
-
(2)
$B$
can be illuminated in directions
$$\begin{eqnarray}(\{-1,1\}^{n-1}\times \{0\})\cup \{\pm e_{n}\}.\end{eqnarray}$$
Note that the first set in the above statement has cardinality
$2^{n}-1$
and the second
$2^{n-1}+2$
. The proposition is obtained as an easy corollary of Lemmas 7 and 8 given below. But, first, let us prove the following.
Lemma 6. Let
$B\in {\mathcal{C}}_{n}$
(
$n\geqslant 2$
) and let
$x=(x_{1},x_{2},\ldots ,x_{n})\in \unicode[STIX]{x2202}B$
. Further, let
$y\in \{-1,0,1\}^{n}$
be a vector such that (1)
$I_{0}^{y}\subset I_{0}^{x}$
and (2) for any
$i\leqslant n$
such that
$x_{i}\neq 0$
, we have
$y_{i}=-\text{sign}(x_{i})$
. Finally, assume that
$x$
is not illuminated in the direction
$y$
. Then necessarily
$$\begin{eqnarray}\biggl\|\mathop{\sum }_{i\in [n]\setminus I_{0}^{y}}e_{i}\biggr\|_{B}\geqslant \frac{2}{\Vert x\Vert _{\infty }}.\end{eqnarray}$$
Proof. In view of Lemma 2, the fact that
$y=(y_{1},y_{2},\ldots ,y_{n})$
does not illuminate
$x$
means that there is a vector
$v=(v_{1},v_{2},\ldots ,v_{n})\in \unicode[STIX]{x1D708}(B,x)$
such that
$\langle y,v\rangle \geqslant 0$
. By the definition of
$y$
and by Lemma 3, we have
$$\begin{eqnarray}\mathop{\sum }_{i\in [n]\setminus I_{0}^{x}}y_{i}v_{i}=-\mathop{\sum }_{i\in [n]\setminus I_{0}^{x}}|v_{i}|.\end{eqnarray}$$
Thus, the condition
$\langle y,v\rangle \geqslant 0$
implies that
$$\begin{eqnarray}\mathop{\sum }_{i\in I_{0}^{x}\setminus I_{0}^{y}}y_{i}v_{i}\geqslant \mathop{\sum }_{i\in [n]\setminus I_{0}^{x}}|v_{i}|.\end{eqnarray}$$
Clearly,
$$\begin{eqnarray}H:=\{z\in \mathbb{R}^{n}:\langle z,v\rangle =\langle x,v\rangle \}\end{eqnarray}$$
is a supporting hyperplane for
$B$
. On the other hand, we have
$$\begin{eqnarray}\langle \mathop{\sum }_{i\in [n]\setminus I_{0}^{x}}(-y_{i})e_{i}+\mathop{\sum }_{i\in I_{0}^{x}\setminus I_{0}^{y}}y_{i}e_{i},v\rangle \geqslant 2\mathop{\sum }_{i\in [n]\setminus I_{0}^{x}}|v_{i}|\geqslant \frac{2\langle x,v\rangle }{\Vert x\Vert _{\infty }}.\end{eqnarray}$$
Hence, the
$\Vert \cdot \Vert _{B}$
-norm of the vector
$\sum _{i\in [n]\setminus I_{0}^{x}}(-y_{i})e_{i}+\sum _{i\in I_{0}^{x}\setminus I_{0}^{y}}y_{i}e_{i}$
is at least
$2/\Vert x\Vert _{\infty }$
. The result follows.◻
Lemma 7. Let
$B\in {\mathcal{C}}_{n}$
(
$n\geqslant 2$
) be such that
$1\neq \text{d}(B,[-1,1]^{n})<2$
. Then at least one of the following is true:
-
(1)
$B$
can be illuminated in directions
$$\begin{eqnarray}\displaystyle T_{1} & := & \displaystyle \{(\unicode[STIX]{x1D700}_{1},\unicode[STIX]{x1D700}_{2},\ldots ,\unicode[STIX]{x1D700}_{n})\in \{-1,1\}^{n}:\exists i\leqslant n-1\text{ with }\unicode[STIX]{x1D700}_{i}=-1\}\nonumber\\ \displaystyle & & \displaystyle \cup \,\{e_{1}+e_{2}+\cdots +e_{n-1}\};\nonumber\end{eqnarray}$$
-
(2)
$\Vert e_{i}+e_{j}\Vert _{B}>\Vert e_{i}\Vert _{B}$
,
$i\neq j$
.
Proof. Without loss of generality, we can assume that
$\Vert e_{i}\Vert _{B}=1$
(note that this implies that
$B\subset [-1,1]^{n}$
, i.e.,
$\Vert \cdot \Vert _{B}\geqslant \Vert \cdot \Vert _{\infty }$
). Assume that the first condition is not satisfied. Thus, there is a vector
$x\in \unicode[STIX]{x2202}B$
which is not illuminated in directions from
$T_{1}$
. Consider three possibilities:
(a)
$I_{0}^{x}\neq \emptyset$
. Then we can find a vector
$y\in T_{1}$
such that
$I_{0}^{y}\subset I_{0}^{x}$
and
$y_{i}=-\text{sign}(x_{i})$
for all
$i\leqslant n$
with
$x_{i}\neq 0$
. By Lemma 6, we have
$$\begin{eqnarray}\mathop{\biggl\|\mathop{\sum }_{i=1}^{n}e_{i}\biggr\|}\nolimits_{B}\geqslant \frac{2}{\Vert x\Vert _{\infty }}\geqslant 2,\end{eqnarray}$$
contradicting the assumption
$\text{d}(B,[-1,1]^{n})<2$
.
(b)
$I_{0}^{x}=\emptyset$
and
$|x_{n}|\leqslant |x_{i}|$
for all
$i\leqslant n$
. We define
$y=(y_{1},y_{2},\ldots ,y_{n})$
by
$y_{i}:=-\text{sign}(x_{i})$
(
$i\leqslant n-1$
);
$y_{n}:=0$
if
$y_{i}=1$
for all
$i\leqslant n-1$
or
$y_{n}:=-\text{sign}(x_{n})$
, otherwise. It is not difficult to see that
$y\in T_{1}$
. Hence, the direction
$y$
does not illuminate
$x$
and, by Lemma 2, there is
$v=(v_{1},v_{2},\ldots ,v_{n})\in \unicode[STIX]{x1D708}(B,x)$
such that
$\langle y,v\rangle \geqslant 0$
. In view of Lemma 3 and the definition of
$y$
, this implies that
$v_{i}=0$
for all
$i\leqslant n-1$
(and
$v_{n}=\pm 1$
), whence
$$\begin{eqnarray}H:=\{z\in \mathbb{R}^{n}:\langle z,e_{n}\rangle =|x_{n}|\}\end{eqnarray}$$
is a supporting hyperplane of
$B$
. On the other hand,
$e_{n}\in B$
by our assumption, implying that
$|x_{n}|\geqslant 1$
. Thus,
$|x_{1}|,|x_{2}|,\ldots ,|x_{n}|\geqslant 1$
and
$x\in \unicode[STIX]{x2202}B$
. But this contradicts the condition
$B\subset [-1,1]^{n}$
,
$B\neq [-1,1]^{n}$
.
(c)
$I_{0}^{x}=\emptyset$
and there is
$j\leqslant n-1$
such that
$|x_{j}|\leqslant |x_{i}|$
for all
$i\leqslant n$
(clearly,
$j$
does not have to be unique). Define a vector
$y=(y_{1},y_{2},\ldots ,y_{n})$
by
$y_{i}:=-\text{sign}(x_{i})$
(
$i\neq j$
);
$y_{j}:=-1$
. Again,
$y\in T_{1}$
. Hence, there is
$v=(v_{1},v_{2},\ldots ,v_{n})\in \unicode[STIX]{x1D708}(B,x)$
such that
$\langle y,v\rangle \geqslant 0$
. This implies, in view of Lemma 3, that
$$\begin{eqnarray}\displaystyle 0\neq \mathop{\sum }_{i=1}^{n}|v_{i}|\leqslant 2|v_{j}|. & & \displaystyle\end{eqnarray}$$
On the other hand, in view of Lemma 4, we have
$|v_{j}|\leqslant |v_{i}|$
for all
$i\leqslant n$
such that
$|x_{i}|>|x_{j}|$
. The last two conditions can be simultaneously fulfilled only if the set
$$\begin{eqnarray}J:=\{i\leqslant n:|x_{i}|>|x_{j}|\}\end{eqnarray}$$
has cardinality at most
$1$
. The case
$J=\emptyset$
(when all coordinates of
$x$
are equal by absolute value) was covered in part (b). Thus, we only need to consider the situation
$|J|=1$
. Assume that
$k\leqslant n$
is such that
$|x_{k}|>|x_{j}|$
. Then, by (2) and Lemma 4, we have
$|v_{k}|=|v_{j}|$
and
$v_{i}=0$
for all
$i\neq k,j$
. Hence,
$$\begin{eqnarray}H:=\{z=(z_{1},z_{2},\ldots ,z_{n})\in \mathbb{R}^{n}:z_{k}+z_{j}=|x_{k}|+|x_{j}|\}\end{eqnarray}$$
is a supporting hyperplane for
$B$
. At the same time,
$1=\Vert x\Vert _{B}\geqslant \Vert x_{k}e_{k}\Vert _{B}=|x_{k}|>|x_{j}|$
, whence
$|x_{k}|+|x_{j}|<2$
. This implies that
$e_{k}+e_{j}\notin B$
, i.e.,
$\Vert e_{k}+e_{j}\Vert _{B}>1$
.◻
Lemma 8. Let
$B\in {\mathcal{C}}_{n}$
(
$n\geqslant 2$
) and assume that
$\Vert e_{i}+e_{j}\Vert _{B}>\Vert e_{i}\Vert _{B}$
,
$i\neq j$
. Then
$B$
can be illuminated in directions
$$\begin{eqnarray}T_{2}:=(\{-1,1\}^{n-1}\times \{0\})\cup \{\pm e_{n}\}.\end{eqnarray}$$
Proof. We will assume that
$\Vert e_{i}\Vert _{B}=1$
. Let
$x=(x_{1},x_{2},\ldots ,x_{n})\in \unicode[STIX]{x2202}B$
. Consider two cases.
(a)
$|x_{n}|>|x_{i}|$
for all
$i\leqslant n-1$
. In view of Lemmas 3 and 4, for any
$v=(v_{1},v_{2},\ldots ,v_{n})\in \unicode[STIX]{x1D708}(B,x)$
, we have
$v_{n}\neq 0$
and
$\text{sign}(v_{n})=\text{sign}(x_{n})$
. Hence,
$x$
is illuminated by the vector
$-\text{sign}(x_{n})e_{n}\in T_{2}$
.
(b) There is
$j\leqslant n-1$
such that
$|x_{j}|\geqslant |x_{i}|$
for all
$i\leqslant n$
. Define
$y=(y_{1},y_{2},\ldots ,y_{n})$
as
$y_{i}:=-\text{sign}(x_{i})$
for all
$i\leqslant n-1$
, and
$y_{n}:=0$
. Obviously,
$y\in T_{2}$
. If
$y$
illuminates
$x$
, then we are done. Otherwise, by Lemmas 2 and 3, for some
$v=(v_{1},v_{2},\ldots ,v_{n})\in \unicode[STIX]{x1D708}(B,x)$
, we have
$$\begin{eqnarray}0\leqslant \langle y,v\rangle =-\mathop{\sum }_{i=1}^{n-1}|v_{i}|.\end{eqnarray}$$
Hence,
$v=\pm e_{n}$
and the hyperplane
$$\begin{eqnarray}H:=\{z\in \mathbb{R}^{n}:\langle z,e_{n}\rangle =|x_{n}|\}\end{eqnarray}$$
is supporting for
$B$
, whence
$\Vert x_{n}e_{n}\Vert _{B}=1$
. On the other hand, in view of the assumptions of the lemma,
$\Vert x\Vert _{B}\geqslant \Vert x_{j}e_{j}+x_{n}e_{n}\Vert _{B}>\Vert x_{n}e_{n}\Vert _{B}$
. We get that
$\Vert x\Vert _{B}>1$
, contradicting the choice of
$x$
.◻
4 Randomized illumination of convex bodies far from the cube
Assume that
$n\geqslant 2$
. Let
$X$
be an
$n$
-dimensional random vector with independent and identically distributed coordinates taking values
$+1$
and
$-1$
with equal probability
$1/2$
. Further, let
$\{X^{\ell }\}_{\ell =1}^{\infty }$
be copies of
$X$
. Next, for any
$m\leqslant n$
, let
$\text{P}^{(m)}$
be the random coordinate projection in
$\mathbb{R}^{n}$
of rank
$m$
, such that the image of
$\text{P}^{(m)}$
is uniformly distributed on the set of all coordinate subspaces of dimension
$m$
. In other words, for any sequence
$i_{1}<i_{2}<\cdots <i_{m}\leqslant n$
, we have
$\text{Im}\,\text{P}^{(m)}=\text{span}\{e_{i_{1}},e_{i_{2}},\ldots ,e_{i_{m}}\}$
with probability
$\binom{n}{m}^{-1}$
. Let also
$\text{P}_{\ell }^{(m)}$
(
$\ell =1,2,\ldots$
) be copies of
$\text{P}^{(m)}$
. Additionally, we require that all the
$X^{\ell }$
and
$\text{P}_{\ell }^{(m)}$
(
$\ell =1,2,\ldots ;m\leqslant n$
) be jointly independent. Now, for every
$k\leqslant \lceil n/2\rceil$
, we define a random (multi)set of vectors
$$\begin{eqnarray}\displaystyle {\mathcal{S}}_{k}:=\{\text{P}_{\ell }^{(2k-1)}(X^{\ell })\}_{\ell =1}^{\lfloor 2^{n}/n^{2}\rfloor }. & & \displaystyle\end{eqnarray}$$
The cardinality
$\lfloor 2^{n}/n^{2}\rfloor$
has no special meaning; we only need the condition
$$\begin{eqnarray}\biggl|\mathop{\bigcup }_{k=1}^{\lceil n/2\rceil }{\mathcal{S}}_{k}\biggr|<2^{n-1}\end{eqnarray}$$
together with the requirement that the individual sets
${\mathcal{S}}_{k}$
are “sufficiently large”.
Lemma 9. There is a universal constant
$C>0$
such that, given
$n\geqslant C$
and any natural number
$k\leqslant \lceil n/2\rceil$
, the event
$$\begin{eqnarray}\displaystyle {\mathcal{E}}_{k} & := & \displaystyle \{\text{For any }y=(y_{1},y_{2},\ldots ,y_{n})\in \{-1,0,1\}^{n}\text{ with }|I_{0}^{y}|=n-k\text{ there is }\nonumber\\ \displaystyle & & \displaystyle \ell \leqslant 2^{n}/n^{2}\text{ such that }\text{P}_{\ell }^{(2k-1)}(y)=y\text{ and }X_{i}^{\ell }=y_{i}\text{ for all }i\in [n]\setminus I_{0}^{y}\}\nonumber\end{eqnarray}$$
has probability at least
$1-\exp (-2n)$
.
Proof. We shall assume that
$n$
is large. Fix any natural number
$k\leqslant \lceil n/2\rceil$
. Clearly, there are precisely
$\binom{n}{k}2^{k}$
vectors in
$\{-1,0,1\}^{n}$
whose supports have cardinality
$k$
. Hence, it is sufficient to show that for any fixed
$y\in \{-1,0,1\}^{n}$
with
$|I_{0}^{y}|=n-k$
, the probability of the event
$$\begin{eqnarray}\displaystyle {\mathcal{E}}_{y} & := & \displaystyle \{\text{There is }\ell \leqslant 2^{n}/n^{2}\text{ such that }\text{P}_{\ell }^{(2k-1)}(y)=y\text{ and }\nonumber\\ \displaystyle & & \displaystyle X_{i}^{\ell }=y_{i}\text{ for all }i\in [n]\setminus I_{0}^{y}\}\nonumber\end{eqnarray}$$
is at least
$1-2^{-k}\exp (-2n)\binom{n}{k}^{-1}$
.
Take any
$\ell \leqslant 2^{n}/n^{2}$
. Obviously,
$$\begin{eqnarray}\mathbb{P}\{X_{i}^{\ell }=y_{i}\text{ for all }i\in [n]\setminus I_{0}^{y}\}=2^{-k}.\end{eqnarray}$$
Next, in view of the definition of the projection
$\text{P}_{\ell }^{(2k-1)}$
, we have
$$\begin{eqnarray}\mathbb{P}\{\text{P}_{\ell }^{(2k-1)}(y)=y\}=\binom{n-k}{k-1}\binom{n}{2k-1}^{-1}.\end{eqnarray}$$
Using Stirling’s approximation, the last expression can be estimated as follows:
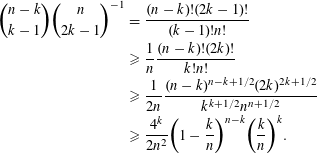$$\begin{eqnarray}\displaystyle \binom{n-k}{k-1}\binom{n}{2k-1}^{-1} & = & \displaystyle \frac{(n-k)!(2k-1)!}{(k-1)!n!}\nonumber\\ \displaystyle & {\geqslant} & \displaystyle \frac{1}{n}\frac{(n-k)!(2k)!}{k!n!}\nonumber\\ \displaystyle & {\geqslant} & \displaystyle \frac{1}{2n}\frac{(n-k)^{n-k+1/2}(2k)^{2k+1/2}}{k^{k+1/2}n^{n+1/2}}\nonumber\\ \displaystyle & {\geqslant} & \displaystyle \frac{4^{k}}{2n^{2}}\biggl(1-\frac{k}{n}\biggr)^{n-k}\biggl(\frac{k}{n}\biggr)^{k}.\nonumber\end{eqnarray}$$
Now, since
$\text{P}_{\ell }^{(2k-1)}$
and
$X^{\ell }$
are independent, we get
$$\begin{eqnarray}\mathbb{P}\{\text{P}_{\ell }^{(2k-1)}(y)=y\text{ and }X_{i}^{\ell }=y_{i}\text{ for all }i\in [n]\setminus I_{0}^{y}\}\geqslant \frac{2^{k}}{2n^{2}}\biggl(1-\frac{k}{n}\biggr)^{n-k}\biggl(\frac{k}{n}\biggr)^{k}.\end{eqnarray}$$
It is not difficult to check that the function
$f(t):=2^{t}(1-t)^{1-t}t^{t}$
, defined for
$t\in [0,1]$
, takes its minimum at
$t=1/3$
. Hence,
$$\begin{eqnarray}\frac{2^{k}}{2n^{2}}\biggl(1-\frac{k}{n}\biggr)^{n-k}\biggl(\frac{k}{n}\biggr)^{k}=\frac{1}{2n^{2}}f(k/n)^{n}\geqslant \frac{1}{2n^{2}}f(1/3)^{n}=\frac{1}{2n^{2}}\biggl(\frac{2}{3}\biggr)^{n}.\end{eqnarray}$$
Finally, we get
$$\begin{eqnarray}\displaystyle 1-\mathbb{P}({\mathcal{E}}_{y}) & = & \displaystyle \mathop{\prod }_{\ell =1}^{\lfloor 2^{n}/n^{2}\rfloor }\mathbb{P}\{\text{P}_{\ell }^{(2k-1)}(y)\neq y\text{ or }X_{i}^{\ell }\neq y_{i}\text{ for some }i\in [n]\setminus I_{0}^{y}\}\nonumber\\ \displaystyle & {\leqslant} & \displaystyle \biggl(1-\frac{1}{2n^{2}}\biggl(\frac{2}{3}\biggr)^{n}\biggr)^{\lfloor 2^{n}/n^{2}\rfloor }\nonumber\\ \displaystyle & \ll & \displaystyle 2^{-k}\exp (-2n)\binom{n}{k}^{-1},\nonumber\end{eqnarray}$$
provided that
$n$
is sufficiently large. The result follows.◻
Now we can prove the following result, which, together with Proposition 5, gives the estimate
${\mathcal{I}}(B)<2^{n}$
for any
$B\in {\mathcal{C}}_{n}$
with
$\text{d}(B,[-1,1]^{n})\neq 1$
.
Proposition 10. There is a universal constant
$C>0$
with the following property: let
$n\geqslant C$
,
$B\in {\mathcal{C}}_{n}$
and assume that
$\text{d}(B,[-1,1]^{n})\geqslant 2$
. Define
$$\begin{eqnarray}T:=\{-1,1\}^{n-1}\times \{0\}.\end{eqnarray}$$
Then, with probability at least
$1-\exp (-n)$
, the set
$B$
can be illuminated in directions
$$\begin{eqnarray}T\cup \mathop{\bigcup }_{k=1}^{\lceil n/2\rceil }{\mathcal{S}}_{k},\end{eqnarray}$$
where the random sets
${\mathcal{S}}_{k}$
are defined by (3).
Proof. Without loss of generality, we may assume that
$\Vert e_{i}\Vert _{B}=1$
. First, we show that any vector
$x\in \unicode[STIX]{x2202}B$
with
$|\{i\leqslant n:|x_{i}|=\Vert x\Vert _{\infty }\}|>\lceil n/2\rceil$
can be illuminated in a direction from
$T$
. Indeed, for any such vector
$x$
, since
$\text{d}(B,[-1,1]^{n})\geqslant 2$
and by the definition of the class
${\mathcal{C}}_{n}$
and Lemma 4, we necessarily have
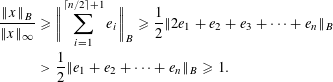$$\begin{eqnarray}\displaystyle \frac{\Vert x\Vert _{B}}{\Vert x\Vert _{\infty }} & {\geqslant} & \displaystyle \mathop{\biggl\|\mathop{\sum }_{i=1}^{\lceil n/2\rceil +1}e_{i}\biggr\|}\nolimits_{B}\geqslant \frac{1}{2}\Vert 2e_{1}+e_{2}+e_{3}+\cdots +e_{n}\Vert _{B}\nonumber\\ \displaystyle & {>} & \displaystyle \frac{1}{2}\Vert e_{1}+e_{2}+\cdots +e_{n}\Vert _{B}\geqslant 1.\nonumber\end{eqnarray}$$
So,
$\Vert x\Vert _{B}>\Vert x\Vert _{\infty }$
, whence for any
$v\in \unicode[STIX]{x1D708}(B,x)$
we have
$|I_{0}^{v}|\leqslant n-2$
and, in particular,
$v\neq \pm e_{n}$
. Now pick a vector
$y=(y_{1},y_{2},\ldots ,y_{n})\in T$
such that
$y_{i}=-\text{sign}(x_{i})$
for all
$i\in [n-1]\setminus I_{0}^{x}$
. For any
$v\in \unicode[STIX]{x1D708}(B,x)$
, we have
$$\begin{eqnarray}\langle y,v\rangle \leqslant -\mathop{\sum }_{i\in [n-1]\setminus I_{0}^{x}}|v_{i}|+\mathop{\sum }_{j\in I_{0}^{x}\setminus \{n\}}|v_{j}|.\end{eqnarray}$$
By Lemma 4, for any
$i\in [n-1]\setminus I_{0}^{x}$
and
$j\in I_{0}^{x}\setminus \{n\}$
, we have
$|v_{i}|\geqslant |v_{j}|$
. Together with the obvious estimate
$|[n-1]\setminus I_{0}^{x}|>|I_{0}^{x}\setminus \{n\}|$
and the condition
$v\neq \pm e_{n}$
, this implies that
$\langle y,v\rangle <0$
, i.e.,
$x$
is illuminated in the direction
$y$
.
Let events
${\mathcal{E}}_{k}$
be defined as in Lemma 9 and denote
$$\begin{eqnarray}{\mathcal{E}}:=\mathop{\bigcap }_{k=1}^{\lceil n/2\rceil }{\mathcal{E}}_{k}.\end{eqnarray}$$
In view of Lemma 9,
$\mathbb{P}({\mathcal{E}})\geqslant 1-\exp (-n)$
, provided that
$n$
is sufficiently large. For the rest of the proof, we fix realizations
$x^{\ell }$
and
$\text{p}_{\ell }^{(2k-1)}$
of vectors
$X^{\ell }$
and projections
$\text{P}_{\ell }^{(2k-1)}$
(
$\ell =1,2,\ldots ;k\leqslant \lceil n/2\rceil$
), respectively, from the event
${\mathcal{E}}$
.
Take any
$x\in \unicode[STIX]{x2202}B$
which is not illuminated in directions from
$T$
. By the above argument, the set
$$\begin{eqnarray}J^{x}:=\{i\leqslant n:|x_{i}|=\Vert x\Vert _{\infty }\}\end{eqnarray}$$
has cardinality at most
$\lceil n/2\rceil$
. Take
$k:=|J^{x}|$
. Then, applying the definition of
${\mathcal{E}}$
to the vector
$y:=-\sum _{i\in J^{x}}\text{sign}(x_{i})e_{i}$
, we get that there is
$\ell \leqslant 2^{n}/n^{2}$
such that
$\langle x^{\ell },e_{i}\rangle =-\text{sign}(x_{i})$
for all
$i\in J_{x}$
and the image of
$\text{p}_{\ell }^{(2k-1)}$
contains
$\text{span}\{e_{i}\}_{i\in J_{x}}$
. Denote
$\widetilde{y}:=\text{p}_{\ell }^{(2k-1)}(x^{\ell })$
. We will show that
$x$
is illuminated in the direction
$\widetilde{y}$
. Indeed, take any
$v=(v_{1},v_{2},\ldots ,v_{n})\in \unicode[STIX]{x1D708}(B,x)$
. Then
$$\begin{eqnarray}\langle \widetilde{y},v\rangle \leqslant -\mathop{\sum }_{i\in J_{x}}|v_{i}|+\mathop{\sum }_{i\in [n]\setminus (J_{x}\cup I_{0}^{\widetilde{y}})}|v_{i}|.\end{eqnarray}$$
Note that by Lemma 4, we have
$|v_{i}|\leqslant |v_{j}|$
for all
$i\in [n]\setminus J_{x}$
and
$j\in J_{x}$
. Further, by the construction of
$\widetilde{y}$
, we have
$|[n]\setminus (J_{x}\cup I_{0}^{\widetilde{y}})|=k-1<|J_{x}|$
. Hence,
$\langle \widetilde{y},v\rangle$
is strictly negative. It remains to apply Lemma 2.
Thus, the convex body
$B$
is illuminated by the union of directions
$T\cup \bigcup _{k=1}^{\lceil n/2\rceil }{\mathcal{S}}_{k}$
with probability at least
$1-\exp (-n)$
, and the proof is complete.◻
Remark 1. For the sake of keeping the presentation transparent, we did not attempt to compute the lower bound for the dimension
$n$
for which the proof starts to work. Neither did we try to decrease the cardinality of the illuminating set. It is natural to ask whether the above argument can be generalized to deal with “
$1$
-unconditional” bodies, i.e., convex bodies symmetric with respect to coordinate hyperplanes. Unfortunately, our proof seems to use the permutation invariance in a crucial way, and some essential new ingredients are needed.
