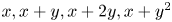1. Introduction
Let $P_1, \ldots , P_{t-1}$![]() be distinct polynomials in $\mathbb {Z}[y]$
be distinct polynomials in $\mathbb {Z}[y]$![]() with zero constant terms. A finite-field version of the polynomial Szemeredi theorem states that for any $\alpha >0$
with zero constant terms. A finite-field version of the polynomial Szemeredi theorem states that for any $\alpha >0$![]() , there exists $p_0=p_0(\alpha )\in \mathbb {N}$
, there exists $p_0=p_0(\alpha )\in \mathbb {N}$![]() with the following property: if $p>p_0$
with the following property: if $p>p_0$![]() is prime and $A\subset \mathbb {F}_p$
is prime and $A\subset \mathbb {F}_p$![]() has size $|A|\geqslant \alpha p$
has size $|A|\geqslant \alpha p$![]() , then $A$
, then $A$![]() contains a polynomial progression
contains a polynomial progression
for some $y\neq 0$![]() . This theorem follows from a multiple recurrence result of Bergelson and Leibman in ergodic theory [Reference Bergelson and Leibman1]. Recently, there have been several attempts at proving a quantitative version of the theorem using ideas from analytic number theory [Reference Bourgain and Chang3], algebraic geometry [Reference Dong, Li and Sawin5] or Fourier analysis [Reference Kuca25, Reference Peluse28, Reference Peluse29], which gave explicit estimates for the quantity $p_0$
. This theorem follows from a multiple recurrence result of Bergelson and Leibman in ergodic theory [Reference Bergelson and Leibman1]. Recently, there have been several attempts at proving a quantitative version of the theorem using ideas from analytic number theory [Reference Bourgain and Chang3], algebraic geometry [Reference Dong, Li and Sawin5] or Fourier analysis [Reference Kuca25, Reference Peluse28, Reference Peluse29], which gave explicit estimates for the quantity $p_0$![]() for certain families of progressions (1). A recurrent idea in these recent approaches is to estimate the number of progressions (1) in an arbitrary subset $A\subset \mathbb {F}_p$
for certain families of progressions (1). A recurrent idea in these recent approaches is to estimate the number of progressions (1) in an arbitrary subset $A\subset \mathbb {F}_p$![]() . In the paper, we prove qualitative estimates for the counts of certain polynomial configurations by relating them to the counts of certain linear forms. Throughout, we let $p$
. In the paper, we prove qualitative estimates for the counts of certain polynomial configurations by relating them to the counts of certain linear forms. Throughout, we let $p$![]() denote a (large) prime.
denote a (large) prime.
Theorem 1.1 Let $A\subseteq \mathbb {F}_p$![]() .
.
(i) The count of $x, x+y, x+y^{2},x+y+y^{2}$
 in $A$
in $A$ is given by
\begin{align*} & |\{(x, x+y, x+y^{2}, x+y+y^{2})\in A^{4}: x,y\in\mathbb{F}_p\}|\\ & \quad = \frac{1}{p}|\{(x,y,u,z)\in A^{4}: x+y=u+z\}| + o(p^{2}). \end{align*}
is given by
\begin{align*} & |\{(x, x+y, x+y^{2}, x+y+y^{2})\in A^{4}: x,y\in\mathbb{F}_p\}|\\ & \quad = \frac{1}{p}|\{(x,y,u,z)\in A^{4}: x+y=u+z\}| + o(p^{2}). \end{align*}
More generally, this estimate holds whenever $x, x+y, x+y^{2}, x+y+y^{2}$
 is replaced by $x, x+Q(y), x+R(y), x+Q(y)+R(y)$
is replaced by $x, x+Q(y), x+R(y), x+Q(y)+R(y)$ for any polynomials $Q,R\in \mathbb {Z}[y]$
for any polynomials $Q,R\in \mathbb {Z}[y]$ with $1\leqslant \deg Q < \deg R$
with $1\leqslant \deg Q < \deg R$ and zero constant terms.
and zero constant terms.(ii) The count of $x, x+y, x+2y, x+y^{3}, x+2y^{3}$
 in $A$
in $A$ is given by
\begin{align*} & |\{(x, x+y, x+2y, x+y^{3}, x+2y^{3})\in A^{5}: x,y\in\mathbb{F}_p\}|\\ & \quad= \frac{1}{p}|\{(x, x+y, x+2y, x+z, x+2z)\in A^{5}: x,y,z\in\mathbb{F}_p\}| + o(p^{2}). \end{align*}More generally, this estimate holds whenever $x, x+y, x+2y, x+y^{3}, x+2y^{3}$
is given by
\begin{align*} & |\{(x, x+y, x+2y, x+y^{3}, x+2y^{3})\in A^{5}: x,y\in\mathbb{F}_p\}|\\ & \quad= \frac{1}{p}|\{(x, x+y, x+2y, x+z, x+2z)\in A^{5}: x,y,z\in\mathbb{F}_p\}| + o(p^{2}). \end{align*}More generally, this estimate holds whenever $x, x+y, x+2y, x+y^{3}, x+2y^{3}$
 is replaced by $x, x+Q(y), x+2Q(y), x+R(y), x+2R(y)$
is replaced by $x, x+Q(y), x+2Q(y), x+R(y), x+2R(y)$ for any polynomials $Q,R\in \mathbb {Z}[y]$
for any polynomials $Q,R\in \mathbb {Z}[y]$ with $1\leqslant \deg Q<(\deg R)/2$
with $1\leqslant \deg Q<(\deg R)/2$ and zero constant terms.
and zero constant terms.
We obtain results like Theorem 1.1 by analysing counting operators of the form
for distinct polynomials $P_1, \ldots , P_{t-1}\in \mathbb {Z}[y]$![]() and functions $f_0, \ldots , f_{t-1}:\mathbb {F}_p\to \mathbb {C}$
and functions $f_0, \ldots , f_{t-1}:\mathbb {F}_p\to \mathbb {C}$![]() that are 1-bounded, i.e. satisfy $\|f_i\|_\infty \leqslant 1$
that are 1-bounded, i.e. satisfy $\|f_i\|_\infty \leqslant 1$![]() . A useful tool to study polynomial progressions is a family of norms on functions $f:\mathbb {F}_p\to \mathbb {C}$
. A useful tool to study polynomial progressions is a family of norms on functions $f:\mathbb {F}_p\to \mathbb {C}$![]() defined by
defined by

where $\mathcal {C}: z\mapsto \overline {z}$![]() is the conjugacy operator and $|w|=w_1+\cdots +w_s$
is the conjugacy operator and $|w|=w_1+\cdots +w_s$![]() . We call $\|f\|_{U^{s}}$
. We call $\|f\|_{U^{s}}$![]() the Gowers norm of $f$
the Gowers norm of $f$![]() of degree $s$
of degree $s$![]() , and we discuss its properties in § 2. It was proved in [Reference Gowers9] that Gowers norms control arithmetic progressions, in the sense that
, and we discuss its properties in § 2. It was proved in [Reference Gowers9] that Gowers norms control arithmetic progressions, in the sense that
for all 1-bounded $f_0, \ldots , f_{s}:\mathbb {F}_p\to \mathbb {C}$![]() . A similar argument has been used to show that Gowers norms control any system of linear forms that are pairwise linearly independent [Reference Green and Tao18, Proposition 7.1]. Finally, Gowers norms are also known to control polynomial progressions of the form (1) for distinct non-zero polynomials $P_1, \ldots , P_{t-1}\in \mathbb {Z}[y]$
. A similar argument has been used to show that Gowers norms control any system of linear forms that are pairwise linearly independent [Reference Green and Tao18, Proposition 7.1]. Finally, Gowers norms are also known to control polynomial progressions of the form (1) for distinct non-zero polynomials $P_1, \ldots , P_{t-1}\in \mathbb {Z}[y]$![]() with zero constant terms [Reference Peluse29, Proposition 2.2], in that there exist $s\in \mathbb {N}_+$
with zero constant terms [Reference Peluse29, Proposition 2.2], in that there exist $s\in \mathbb {N}_+$![]() and $c>0$
and $c>0$![]() depending only on $P_1, \ldots , P_{t-1}$
depending only on $P_1, \ldots , P_{t-1}$![]() such that
such that
for all 1-bounded $f_0, \ldots , f_{t-1}:\mathbb {F}_p\to \mathbb {C}$![]() .
.
In the light of the monotonicity property of Gowers norms
derived e.g. in Section 1 of [Reference Green and Tao16], it is natural to ask what is the smallest-degree Gowers norm controlling a given configuration. The smallest $s$![]() such that $U^{s+1}$
such that $U^{s+1}$![]() controls the configuration is called its true complexity; the precise definition shall be given in § 1.1. The question of determining true complexity has been posed and partially resolved for linear configurations in [Reference Green and Tao17–Reference Green, Tao and Ziegler21], where the authors relate true complexity to algebraic relations between the linear forms in the configuration. It remains largely open for general polynomial progressions (1).
controls the configuration is called its true complexity; the precise definition shall be given in § 1.1. The question of determining true complexity has been posed and partially resolved for linear configurations in [Reference Green and Tao17–Reference Green, Tao and Ziegler21], where the authors relate true complexity to algebraic relations between the linear forms in the configuration. It remains largely open for general polynomial progressions (1).
In the paper, we determine the true complexity of several polynomial progressions. Our main results are the following theorems.
Theorem 1.2 (True complexity of $x, x+y, x+y^{2}, x+y+y^{2}$![]() )
)
For any $\epsilon >0$![]() , there exist $\delta >0$
, there exist $\delta >0$![]() and $p_0\in \mathbb {N}$
and $p_0\in \mathbb {N}$![]() such that for all primes $p>p_0$
such that for all primes $p>p_0$![]() and for all 1-bounded functions $f_0, f_1, f_2, f_3:\mathbb {F}_p\to \mathbb {C}$
and for all 1-bounded functions $f_0, f_1, f_2, f_3:\mathbb {F}_p\to \mathbb {C}$![]() , at least one of which satisfies $\|f_i\|_{U^{2}}\leqslant \delta$
, at least one of which satisfies $\|f_i\|_{U^{2}}\leqslant \delta$![]() , we have
, we have
The $U^{2}$![]() norm is related to Fourier analysis via ${\|\hat {f}\|_{\infty }\leqslant \|f\|_{U^{2}}\leqslant \|\hat {f}\|_\infty ^{{1}/{2}}}$
norm is related to Fourier analysis via ${\|\hat {f}\|_{\infty }\leqslant \|f\|_{U^{2}}\leqslant \|\hat {f}\|_\infty ^{{1}/{2}}}$![]() for 1-bounded functions $f$
for 1-bounded functions $f$![]() , and so Theorem 1.2 can be informally rephrased as follows: if at least one of $f_0, f_1, f_2, f_3$
, and so Theorem 1.2 can be informally rephrased as follows: if at least one of $f_0, f_1, f_2, f_3$![]() has no large Fourier coefficient, then the operator in (5) is small. We can similarly interpret the next three results.
has no large Fourier coefficient, then the operator in (5) is small. We can similarly interpret the next three results.
Theorem 1.3 (True complexity of $x, x+Q(y), x+R(y), x+Q(y)+R(y)$![]() )
)
Let $Q,R\in \mathbb {Z}[y]$![]() be polynomials of zero constant terms satisfying $1\leqslant \deg Q < \deg R$
be polynomials of zero constant terms satisfying $1\leqslant \deg Q < \deg R$![]() . For any $\epsilon >0$
. For any $\epsilon >0$![]() , there exist $\delta >0$
, there exist $\delta >0$![]() and $p_0\in \mathbb {N}$
and $p_0\in \mathbb {N}$![]() such that for all primes $p>p_0$
such that for all primes $p>p_0$![]() and for all 1-bounded functions $f_0, f_1, f_2, f_3:\mathbb {F}_p\to \mathbb {C}$
and for all 1-bounded functions $f_0, f_1, f_2, f_3:\mathbb {F}_p\to \mathbb {C}$![]() , at least one of which satisfies $\|f_i\|_{U^{2}}\leqslant \delta$
, at least one of which satisfies $\|f_i\|_{U^{2}}\leqslant \delta$![]() , we have
, we have
Theorem 1.4 (True complexity of $x, x+y, x+2y, x+y^{3}, x+2y^{3}$![]() )
)
For any $\epsilon >0$![]() , there exist $\delta >0$
, there exist $\delta >0$![]() and $p_0\in \mathbb {N}$
and $p_0\in \mathbb {N}$![]() such that for all primes $p>p_0$
such that for all primes $p>p_0$![]() and for all 1-bounded functions $f_0, f_1, f_2, f_3, f_4:\mathbb {F}_p\to \mathbb {C}$
and for all 1-bounded functions $f_0, f_1, f_2, f_3, f_4:\mathbb {F}_p\to \mathbb {C}$![]() , at least one of which satisfies $\|f_i\|_{U^{2}}\leqslant \delta$
, at least one of which satisfies $\|f_i\|_{U^{2}}\leqslant \delta$![]() , we have
, we have
Theorem 1.5 (True complexity of $x, x+Q(y), x+2Q(y), x+R(y), x+2R(y)$![]() )
)
Let $Q,R\in \mathbb {Z}[y]$![]() be polynomials of zero constant terms satisfying $1\leqslant \deg Q<(\deg R)/2$
be polynomials of zero constant terms satisfying $1\leqslant \deg Q<(\deg R)/2$![]() . For any $\epsilon >0$
. For any $\epsilon >0$![]() , there exist $\delta >0$
, there exist $\delta >0$![]() and $p_0\in \mathbb {N}$
and $p_0\in \mathbb {N}$![]() such that for all primes $p>p_0$
such that for all primes $p>p_0$![]() and for all 1-bounded functions $f_0, f_1, f_2, f_3, f_4:\mathbb {F}_p\to \mathbb {C}$
and for all 1-bounded functions $f_0, f_1, f_2, f_3, f_4:\mathbb {F}_p\to \mathbb {C}$![]() , at least one of which satisfies $\|f_i\|_{U^{2}}\leqslant \delta$
, at least one of which satisfies $\|f_i\|_{U^{2}}\leqslant \delta$![]() , we have
, we have
In the aforementioned configurations, each term can be controlled by the same Gowers norm, the $U^{2}$![]() norm. However, there exist configurations where different Gowers norms control different terms. The following is but one example. The norm $u^{3}$
norm. However, there exist configurations where different Gowers norms control different terms. The following is but one example. The norm $u^{3}$![]() appearing below belongs to a family of norms called polynomial bias norms which satisfy $\|f\|_{u^{s}}\leqslant \|f\|_{U^{s}}$
appearing below belongs to a family of norms called polynomial bias norms which satisfy $\|f\|_{u^{s}}\leqslant \|f\|_{U^{s}}$![]() and will be discussed more broadly in § 2.
and will be discussed more broadly in § 2.
Theorem 1.6 (True complexity of $x, x+y, x+2y, x+y^{2}$![]() )
)
For any $\epsilon >0$![]() , there exist $\delta >0$
, there exist $\delta >0$![]() and $p_0\in \mathbb {N}$
and $p_0\in \mathbb {N}$![]() such that for all primes $p>p_0$
such that for all primes $p>p_0$![]() and for all 1-bounded functions ${f_0, f_1, f_2, f_3:\mathbb {F}_p\to \mathbb {C}}$
and for all 1-bounded functions ${f_0, f_1, f_2, f_3:\mathbb {F}_p\to \mathbb {C}}$![]() , where at least one of $f_0, f_1, f_2$
, where at least one of $f_0, f_1, f_2$![]() satisfies $\|f_i\|_{u^{3}}\leqslant \delta$
satisfies $\|f_i\|_{u^{3}}\leqslant \delta$![]() or $f_3$
or $f_3$![]() satisfies $\|f_3\|_{U^{2}}\leqslant \delta$
satisfies $\|f_3\|_{U^{2}}\leqslant \delta$![]() , we have
, we have
What Theorem 1.6 is saying is that if all Fourier coefficients of $f_3$![]() are small, i.e. if the correlation
are small, i.e. if the correlation
is small for all $\alpha \in \mathbb {F}_p$![]() , or if the correlation
, or if the correlation
is small for all $\alpha , \beta \in \mathbb {Z}$![]() and $i\in \{0,1,2\}$
and $i\in \{0,1,2\}$![]() , then the operator (7) is small as well. The function $e_p$
, then the operator (7) is small as well. The function $e_p$![]() used here is $e_p(x):=e^{{2\pi i x}/{p}}.$
used here is $e_p(x):=e^{{2\pi i x}/{p}}.$![]()
Theorem 1.7 (True complexity of $x, x+y, \ldots , x+(m-1)y, x+y^{d}$![]() )
)
Let $m,d\in \mathbb {N}_+$![]() satisfy $2\leqslant d\leqslant m-1$
satisfy $2\leqslant d\leqslant m-1$![]() . For any $\epsilon >0$
. For any $\epsilon >0$![]() , there exist $\delta >0$
, there exist $\delta >0$![]() and $p_0\in \mathbb {N}$
and $p_0\in \mathbb {N}$![]() such that for all primes $p>p_0$
such that for all primes $p>p_0$![]() and for all 1-bounded functions $f_0, \ldots ,f_{m}:\mathbb {F}_p\to \mathbb {C}$
and for all 1-bounded functions $f_0, \ldots ,f_{m}:\mathbb {F}_p\to \mathbb {C}$![]() , we have
, we have
if $f_m$![]() satisfies $\|f_m\|_{U^{\left \lfloor {\frac {m-1}{d}} \right \rfloor +1}}\leqslant \delta$
satisfies $\|f_m\|_{U^{\left \lfloor {\frac {m-1}{d}} \right \rfloor +1}}\leqslant \delta$![]() or at least one of $f_0, \ldots , f_{m-1}$
or at least one of $f_0, \ldots , f_{m-1}$![]() satisfies $\|f_i\|_{U^{s}}\leqslant \delta$
satisfies $\|f_i\|_{U^{s}}\leqslant \delta$![]() for
for

The main technical innovation used in proving Theorems 1.2–1.5 is the following equidistribution result which should be seen as an extension of (the periodic version of) Theorem 1.2 from [Reference Green and Tao17], which itself generalizes classical equidistribution theorems by Weyl and van der Corput. All the concepts appearing in Theorem 1.8 shall be defined and discussed in § 2 and § 3. Mimicking the notation of [Reference Green and Tao17], we say that an expression $E(A,M)$![]() depending on parameters $A,M>0$
depending on parameters $A,M>0$![]() satisfies $o_{A\to \infty ,M}(1)$
satisfies $o_{A\to \infty ,M}(1)$![]() if $\lim _{A\to \infty }E(A,M)=0$
if $\lim _{A\to \infty }E(A,M)=0$![]() for each fixed $M>0$
for each fixed $M>0$![]() , and similarly for other choices of parameters.
, and similarly for other choices of parameters.
Theorem 1.8 Let $M>0$![]() , and let $\vec {P}\in \mathbb {Z}[x,y]^{t}$
, and let $\vec {P}\in \mathbb {Z}[x,y]^{t}$![]() with $\vec {P}(0,0)=\vec {0}$
with $\vec {P}(0,0)=\vec {0}$![]() take one of the following forms:
take one of the following forms:
(i) $\vec {P}(x,y) = (x, x+Q(y), x+R(y), x+Q(y)+R(y))$
 for $1\leqslant \deg Q<\deg R$
for $1\leqslant \deg Q<\deg R$ ;
;(ii) $\vec {P}(x,y) = (x, x+Q(y), x+2Q(y), x+R(y), x+2R(y))$
 for $1\leqslant \deg Q<(\deg R)/2$
for $1\leqslant \deg Q<(\deg R)/2$ .
.
Given a filtered nilmanifold $G/\varGamma$![]() of complexity $M$
of complexity $M$![]() , there exists a filtered nilmanifold $G^{P}/\varGamma ^{P}\subseteq G^{t}/\varGamma ^{t}$
, there exists a filtered nilmanifold $G^{P}/\varGamma ^{P}\subseteq G^{t}/\varGamma ^{t}$![]() of complexity $O_{M}(1)$
of complexity $O_{M}(1)$![]() such that for any $p$
such that for any $p$![]() -periodic, $A$
-periodic, $A$![]() -irrational sequence $g\in \rm{poly}(\mathbb {Z},G_\bullet )$
-irrational sequence $g\in \rm{poly}(\mathbb {Z},G_\bullet )$![]() satisfying $g(0)=1$
satisfying $g(0)=1$![]() , the sequence $g^{P}\in \rm{poly}(\mathbb {Z}^{2},G^{P}_\bullet )$
, the sequence $g^{P}\in \rm{poly}(\mathbb {Z}^{2},G^{P}_\bullet )$![]() given by
given by
satisfies
uniformly for any $M$![]() -Lipschitz function $F:G^{P}/\varGamma ^{P}\to \mathbb {C}$
-Lipschitz function $F:G^{P}/\varGamma ^{P}\to \mathbb {C}$![]() .
.
What Theorem 1.8 is saying is that if $g$![]() is a ‘highly irrational’ sequence on $G/\varGamma$
is a ‘highly irrational’ sequence on $G/\varGamma$![]() in the sense of Definition 2.11, then the sequence $g^{P}$
in the sense of Definition 2.11, then the sequence $g^{P}$![]() is ‘close to being equidistributed’ on the nilmanifold $G^{P}/\varGamma ^{P}$
is ‘close to being equidistributed’ on the nilmanifold $G^{P}/\varGamma ^{P}$![]() . Combining Theorem 1.8 with Theorem 2.13, a version of the celebrated arithmetic regularity lemma [Reference Green and Tao17, Theorem 1.2], we can then approximate sums of the form (2) by integrals of Lipschitz functions on nilmanifolds.
. Combining Theorem 1.8 with Theorem 2.13, a version of the celebrated arithmetic regularity lemma [Reference Green and Tao17, Theorem 1.2], we can then approximate sums of the form (2) by integrals of Lipschitz functions on nilmanifolds.
Although we only prove Theorem 1.8 for two specific families of polynomial progressions, the construction of the nilmanifold $G^{P}/\varGamma ^{P}$![]() mentioned in the statement of Theorem 1.8 is quite general. This nilmanifold, definable for any polynomial progression, has originally appeared in Section 5 of [Reference Leibman26]. Its versions for linear forms have been used in [Reference Green and Tao17], where the authors call it ‘Leibman nilmanifold’, and we shall stick to this terminology. In § 3, we show that Leibman nilmanifold admits a natural filtration $G^{P}_\bullet$
mentioned in the statement of Theorem 1.8 is quite general. This nilmanifold, definable for any polynomial progression, has originally appeared in Section 5 of [Reference Leibman26]. Its versions for linear forms have been used in [Reference Green and Tao17], where the authors call it ‘Leibman nilmanifold’, and we shall stick to this terminology. In § 3, we show that Leibman nilmanifold admits a natural filtration $G^{P}_\bullet$![]() such that $g^{P}\in {\textrm {poly}}(\mathbb {Z}^{D},G^{P}_\bullet )$
such that $g^{P}\in {\textrm {poly}}(\mathbb {Z}^{D},G^{P}_\bullet )$![]() whenever ${g\in {\textrm {poly}}(\mathbb {Z},G_\bullet )}$
whenever ${g\in {\textrm {poly}}(\mathbb {Z},G_\bullet )}$![]() .
.
Interestingly, there exist progressions for which Theorem 1.8 fails. In Lemma 11.3, we give an example of a torus $G/\varGamma$![]() and a sequence ${g\in {\textrm {poly}}(\mathbb {Z},G_\bullet )}$
and a sequence ${g\in {\textrm {poly}}(\mathbb {Z},G_\bullet )}$![]() that is ‘highly irrational’ on $G/\varGamma$
that is ‘highly irrational’ on $G/\varGamma$![]() , yet the corresponding sequence $g^{P}$
, yet the corresponding sequence $g^{P}$![]() for $\vec {P}(x,y)=(x, x+y, x+2y, x+y^{2})$
for $\vec {P}(x,y)=(x, x+y, x+2y, x+y^{2})$![]() is contained in a ‘low-rank’ subtorus of $G^{P}/\varGamma ^{P}$
is contained in a ‘low-rank’ subtorus of $G^{P}/\varGamma ^{P}$![]() and is ‘far from being equidistributed’ on $G^{P}/\varGamma ^{P}$
and is ‘far from being equidistributed’ on $G^{P}/\varGamma ^{P}$![]() . This seems to be a novel phenomenon, unregistered in the existing literature, and it is essentially connected with the fact that the terms of the progression satisfy an algebraic relation
. This seems to be a novel phenomenon, unregistered in the existing literature, and it is essentially connected with the fact that the terms of the progression satisfy an algebraic relation
that is ‘inhomogeneous’, in the sense that the polynomials in $x, x+y$![]() and $x+2y$
and $x+2y$![]() are quadratic, but the polynomial in $x+y^{2}$
are quadratic, but the polynomial in $x+y^{2}$![]() is linear. This phenomenon does not appear for linear forms, where such inhomogeneous relations are impossible, but it is an important feature of the polynomial world. It also does not show up in the ergodic work on this configuration [Reference Frantzikinakis6] since the author only has to deal with linear sequences $g(n)=a^{n}$
is linear. This phenomenon does not appear for linear forms, where such inhomogeneous relations are impossible, but it is an important feature of the polynomial world. It also does not show up in the ergodic work on this configuration [Reference Frantzikinakis6] since the author only has to deal with linear sequences $g(n)=a^{n}$![]() as opposed to more general polynomial sequences. The natural analogue of Theorem 1.8 cannot therefore be used to prove Theorems 1.6 and 1.7, and we apply a different method to handle these configurations, which essentially comes down to homogenizing the progression $\vec {P}$
as opposed to more general polynomial sequences. The natural analogue of Theorem 1.8 cannot therefore be used to prove Theorems 1.6 and 1.7, and we apply a different method to handle these configurations, which essentially comes down to homogenizing the progression $\vec {P}$![]() using the Cauchy–Schwarz inequality.
using the Cauchy–Schwarz inequality.
We have not been able to extend Theorems 1.2–1.7 to an arbitrary polynomial progression of the form (1) for at least three reasons. First, not all progressions satisfy Theorems 1.8, as evidenced by the aforementioned example of $x, x+y, x+2y, x+y^{2}$![]() . Second, some progressions fail to satisfy ‘filtration condition’ (Definition 3.4), which makes the corresponding nilmanifolds $G^{P}/\varGamma ^{P}$
. Second, some progressions fail to satisfy ‘filtration condition’ (Definition 3.4), which makes the corresponding nilmanifolds $G^{P}/\varGamma ^{P}$![]() harder to analyse. Sections 3 and 10 will explain why this condition is useful; it is unclear at the moment if this is a mere technical annoyance or a genuine obstruction. Third, even though our arguments in the proof of Theorem 1.8 follow the same general strategy for the two families of configurations that the theorem concerns, we have to resort to different tricks in dealing with arising technicalities, which makes it hard to generalize the arguments.
harder to analyse. Sections 3 and 10 will explain why this condition is useful; it is unclear at the moment if this is a mere technical annoyance or a genuine obstruction. Third, even though our arguments in the proof of Theorem 1.8 follow the same general strategy for the two families of configurations that the theorem concerns, we have to resort to different tricks in dealing with arising technicalities, which makes it hard to generalize the arguments.
1.1. True complexity: formal definition, conjecture and known results
Our primary object of study is integral polynomial maps, i.e. configurations of the form $\vec {P}=(P_1, \ldots , P_t)\in \mathbb {Q}[\textbf {x}]^{t}$![]() for integer-valued polynomials $P_1, \ldots , P_t$
for integer-valued polynomials $P_1, \ldots , P_t$![]() with zero constant terms. Following the convention of [Reference Green and Tao17], we use $\vec {v}$
with zero constant terms. Following the convention of [Reference Green and Tao17], we use $\vec {v}$![]() to denote $t$
to denote $t$![]() -dimensional vectors and $\textbf {x}$
-dimensional vectors and $\textbf {x}$![]() to denote $D$
to denote $D$![]() -dimensional vectors. We are now ready to state our main definition.
-dimensional vectors. We are now ready to state our main definition.
Definition 1.9 (True complexity and Gowers controllability) Let $\vec {P}=(P_1, \ldots , P_t)\in \mathbb {Q}[\textbf {x}]^{t}$![]() be an integral polynomial map. We say that $\vec {P}$
be an integral polynomial map. We say that $\vec {P}$![]() has true complexity $s$
has true complexity $s$![]() at an index $1\leqslant i\leqslant t$
at an index $1\leqslant i\leqslant t$![]() if $s$
if $s$![]() is the smallest natural number such that for every $\epsilon >0$
is the smallest natural number such that for every $\epsilon >0$![]() , there exist $\delta >0$
, there exist $\delta >0$![]() and $p_0\in \mathbb {N}$
and $p_0\in \mathbb {N}$![]() such that for all primes $p>p_0$
such that for all primes $p>p_0$![]() and all 1-bounded functions $f_1, \ldots , f_t:\mathbb {F}_p\to \mathbb {C}$
and all 1-bounded functions $f_1, \ldots , f_t:\mathbb {F}_p\to \mathbb {C}$![]() , we have
, we have
whenever $\|f_i\|_{U^{s+1}}<\delta$![]() . If no such $s$
. If no such $s$![]() exists, we say that the true complexity of $\vec {P}$
exists, we say that the true complexity of $\vec {P}$![]() at $i$
at $i$![]() is $\infty$
is $\infty$![]() . We say $\vec {P}$
. We say $\vec {P}$![]() has true complexity $s$
has true complexity $s$![]() if it has true complexity $s$
if it has true complexity $s$![]() at the index $i$
at the index $i$![]() for all $1\leqslant i\leqslant t$
for all $1\leqslant i\leqslant t$![]() . We call $\vec {P}$
. We call $\vec {P}$![]() Gowers controllable if its true complexity at every index is finite.
Gowers controllable if its true complexity at every index is finite.
The true complexity question could also be posed over the integers; however, the problem becomes much harder in this context because each variable would be drawn from an interval of different length depending on the degree of the polynomial map. For instance, when studying the true complexity of $x, x+y, x+y^{2}$![]() , the variable $x$
, the variable $x$![]() would be drawn from an interval of length $N$
would be drawn from an interval of length $N$![]() while $y$
while $y$![]() would be taken from an interval of length only $\Theta (\sqrt {N})$
would be taken from an interval of length only $\Theta (\sqrt {N})$![]() to ensure that the term $x+y^{2}$
to ensure that the term $x+y^{2}$![]() lies inside the interval $\{1, \ldots , N\}$
lies inside the interval $\{1, \ldots , N\}$![]() . As a consequence, not every term of the progression would be globally controlled by a Gowers norm. We refer the reader to [Reference Peluse30–Reference Peluse and Prendiville32] for an in-depth discussion of these issues.
. As a consequence, not every term of the progression would be globally controlled by a Gowers norm. We refer the reader to [Reference Peluse30–Reference Peluse and Prendiville32] for an in-depth discussion of these issues.
Because of the issues highlighted above, we study true complexity over finite fields as opposed to integers. In the language of Definition 1.9, Theorems 1.2–1.7 can be restated as follows.
Theorem 1.10
(i) The configuration $x, x+Q(y), x+R(y), x+Q(y)+R(y)$
 has true complexity 1 for any $Q,R\in \mathbb {Z}[y]$
has true complexity 1 for any $Q,R\in \mathbb {Z}[y]$ of zero constant terms satisfying $1\leqslant \deg Q<\deg R$
of zero constant terms satisfying $1\leqslant \deg Q<\deg R$ .
.(ii) The configuration $x, x+Q(y), x+2Q(y), x+R(y), x+2R(y)$
 has true complexity 1 for any $Q,R\in \mathbb {Z}[y]$
has true complexity 1 for any $Q,R\in \mathbb {Z}[y]$ of zero constant terms satisfying $1\leqslant \deg Q<(\deg R)/2$
of zero constant terms satisfying $1\leqslant \deg Q<(\deg R)/2$ .
.(iii) The configuration $x, x+y, \ldots , x+(m-1)y, x+y^{d}$
 has true complexity $m-1$
has true complexity $m-1$ at $i\in \{0, 1, \ldots ,m-1\}$
at $i\in \{0, 1, \ldots ,m-1\}$ and ${(m-1)}/{d}$
and ${(m-1)}/{d}$ at $i = m$
at $i = m$ whenever $2\leqslant d\leqslant m-1$
whenever $2\leqslant d\leqslant m-1$ and $d|m-1$
and $d|m-1$ .
.(iv) The configuration $x, x+y, \ldots , x+(m-1)y, x+y^{d}$
 has true complexity $m-2$
has true complexity $m-2$ at $i\in \{0, 1, \ldots ,m-1\}$
at $i\in \{0, 1, \ldots ,m-1\}$ and $\left \lfloor {(m-1)}/{d}\right \rfloor$
and $\left \lfloor {(m-1)}/{d}\right \rfloor$ at $i = m$
at $i = m$ whenever $2\leqslant d< m-1$
whenever $2\leqslant d< m-1$ and $d \nmid m-1$
and $d \nmid m-1$ .
.
True complexity turns out to be intimately connected with the algebraic relations between the terms of a polynomial progression. We first state the following definition.
Definition 1.11 (Algebraic independence) Let $\vec {P}=(P_1, \ldots , P_t)\in \mathbb {Q}[\textbf {x}]^{t}$![]() be an integral polynomial map and fix $1 \leqslant i \leqslant t$
be an integral polynomial map and fix $1 \leqslant i \leqslant t$![]() . The progression $\vec {P}$
. The progression $\vec {P}$![]() is algebraically independent of degree $s+1$
is algebraically independent of degree $s+1$![]() at $i$
at $i$![]() if, whenever we have
if, whenever we have
for some $Q_1, \ldots , Q_t\in \mathbb {Z}[y]$![]() , the polynomial $Q_i$
, the polynomial $Q_i$![]() has degree at most $s$
has degree at most $s$![]() . We moreover say that $\vec {P}$
. We moreover say that $\vec {P}$![]() is algebraically independent of degree $s+1$
is algebraically independent of degree $s+1$![]() if it is algebraically independent of degree $s+1$
if it is algebraically independent of degree $s+1$![]() at $i$
at $i$![]() for all $1\leqslant i\leqslant t$
for all $1\leqslant i\leqslant t$![]() .
.
Conjecture 1.12 (Conjecture for true complexity) Let $\vec {P}=(P_1, \ldots , P_t)\in \mathbb {Q}[\textbf {x}]^{t}$![]() be a Gowers controllable integral polynomial map and fix $1 \leqslant i \leqslant t$
be a Gowers controllable integral polynomial map and fix $1 \leqslant i \leqslant t$![]() . The true complexity of $\vec {P}$
. The true complexity of $\vec {P}$![]() at $i$
at $i$![]() is the smallest natural number $s$
is the smallest natural number $s$![]() for which $\vec {P}$
for which $\vec {P}$![]() is algebraically independent of degree $s+1$
is algebraically independent of degree $s+1$![]() at $i$
at $i$![]() .
.
Theorems 1.2–1.7 confirm Conjecture 1.12 in special instances. The terms of $x, x+y, x+y^{2}, x+y+y^{2}$![]() satisfy one linear relation (up to scaling)
satisfy one linear relation (up to scaling)
and so the configuration has complexity 1. Analogously, there is a unique linear relation (up to scaling)
between the terms of $x, x+Q(y), x+R(y), x+Q(y)+R(y)$![]() whenever $Q,R\in \mathbb {Z}[y]$
whenever $Q,R\in \mathbb {Z}[y]$![]() have zero constant terms and satisfy $1\leqslant \deg Q<\deg R$
have zero constant terms and satisfy $1\leqslant \deg Q<\deg R$![]() . For $x, x+y, x+2y, x+y^{3}, x+2y^{3}$
. For $x, x+y, x+2y, x+y^{3}, x+2y^{3}$![]() , there are two linearly independent relations
, there are two linearly independent relations
and similarly for $x, x+Q(y), x+2Q(y), x+R(y), x+2R(y)$![]() whenever $Q,R\in \mathbb {Z}[y]$
whenever $Q,R\in \mathbb {Z}[y]$![]() have zero constant terms and satisfy $1\leqslant \deg Q<(\deg R)/2$
have zero constant terms and satisfy $1\leqslant \deg Q<(\deg R)/2$![]()
One can check by hand that none of these progressions satisfy a higher-order relation. By contrast, the terms of $x, x+y, x+2y, x+y^{2}$![]() satisfy a quadratic relation
satisfy a quadratic relation
in addition to the linear relation $x - 2(x+y) + (x+2y) = 0$![]() , which explains why this configuration has true complexity 2 at $i = 0, 1, 2$
, which explains why this configuration has true complexity 2 at $i = 0, 1, 2$![]() and 1 at $i=3$
and 1 at $i=3$![]() . For $x, x+y, \ldots , x+(m-1)y, x+y^{d}$
. For $x, x+y, \ldots , x+(m-1)y, x+y^{d}$![]() with $2\leqslant d\leqslant m-1$
with $2\leqslant d\leqslant m-1$![]() , there exist polynomials $Q_0, \ldots , Q_{m-1}$
, there exist polynomials $Q_0, \ldots , Q_{m-1}$![]() of degree $d\left \lfloor \frac {m-1}{d}\right \rfloor$
of degree $d\left \lfloor \frac {m-1}{d}\right \rfloor$![]() satisfying
satisfying
in addition to lower-degree relations and an algebraic relation of degree $m-2$![]() between the terms of $x, x+y, \ldots , x+(m-1)y$
between the terms of $x, x+y, \ldots , x+(m-1)y$![]() .
.
The lower bound in Conjecture 1.12 is straightforward to settle. The difficulty lies in proving the upper bound.
Theorem 1.13 (Lower bound for true complexity) Let $\vec {P}=(P_1, \ldots , P_t)\in \mathbb {Q}[\textbf {x}]^{t}$![]() be an integral polynomial map and fix $1 \leqslant i \leqslant t$
be an integral polynomial map and fix $1 \leqslant i \leqslant t$![]() . Suppose that $\vec {P}$
. Suppose that $\vec {P}$![]() is not algebraically independent of degree $s$
is not algebraically independent of degree $s$![]() at index $i$
at index $i$![]() . Then the true complexity of $\vec {P}$
. Then the true complexity of $\vec {P}$![]() at $i$
at $i$![]() is at least $s$
is at least $s$![]() .
.
Proof. By assumption, there exists an algebraic relation
for some $Q_1, \ldots , Q_t\in \mathbb {Z}[y]$![]() , where $Q_i$
, where $Q_i$![]() has degree at least $s$
has degree at least $s$![]() . Let $f_j(x) = e_p(Q_j(x))$
. Let $f_j(x) = e_p(Q_j(x))$![]() for each $1\leqslant j\leqslant t$
for each $1\leqslant j\leqslant t$![]() . The functions $f_j$
. The functions $f_j$![]() are clearly 1-bounded. It follows from the properties of additive characters that
are clearly 1-bounded. It follows from the properties of additive characters that
To prove the theorem, we want to show that $\|f_i\|_{U^{s}}$![]() is small, which will imply that the $U^{s}$
is small, which will imply that the $U^{s}$![]() norm cannot control the $P_i$
norm cannot control the $P_i$![]() term of the configuration. The definition (3) of Gowers norms can be restated as
term of the configuration. The definition (3) of Gowers norms can be restated as
where $\Delta _{h}f({x}):=f({x}+{h})\overline {f({x})}$![]() and $\Delta _{{h}_1,\, \ldots ,{h}_{s}}=\Delta _{{h}_1}\cdots \Delta _{{h}_{s}}$
and $\Delta _{{h}_1,\, \ldots ,{h}_{s}}=\Delta _{{h}_1}\cdots \Delta _{{h}_{s}}$![]() . Since $Q_i$
. Since $Q_i$![]() has degree at least $s$
has degree at least $s$![]() and $e_p(\cdot )$
and $e_p(\cdot )$![]() is an additive character, the function $\Delta _{{h}_1, \ldots ,{h}_{s}}f_i({x})$
is an additive character, the function $\Delta _{{h}_1, \ldots ,{h}_{s}}f_i({x})$![]() is of the form $e_p(Q(x, {h}_1, \ldots , {h}_{s}))$
is of the form $e_p(Q(x, {h}_1, \ldots , {h}_{s}))$![]() for a nonconstant polynomial $Q$
for a nonconstant polynomial $Q$![]() . By properties of exponential sums, the sum in (10) is of size $O_{s}(p^{-c_{s}})$
. By properties of exponential sums, the sum in (10) is of size $O_{s}(p^{-c_{s}})$![]() , and so
, and so
Thus, $U^{s}$![]() norm does not control the $P_i$
norm does not control the $P_i$![]() term of the configuration, implying the theorem.
term of the configuration, implying the theorem.
The constants appearing in the proof of Theorem 1.13, like in all other proofs in the paper, are allowed to depend on the choice of the progression $\vec {P}$![]() . We do not record this dependence so as not to clutter the notation more than necessary.
. We do not record this dependence so as not to clutter the notation more than necessary.
Theorem 1.10 follows from combining Theorems 1.2–1.7 with Theorem 1.13 and remarks above it.
Conjecture 1.12 has so far been proved in a number of special cases. The inequality (4), together with the fact that arithmetic progressions of length $t$![]() satisfy an algebraic relation of degree $t-2$
satisfy an algebraic relation of degree $t-2$![]() , proves it for arithmetic progressions. The work by Green and Tao [Reference Green and Tao17] settles it for all linear configurations satisfying a technical condition called flag conditionFootnote 1, with certain cases having been previously proved by Gowers and Wolf [Reference Green and Tao18–Reference Green, Tao and Ziegler21]. Green and Tao's results are all but ineffective while the work of Gowers and Wolf gives some quantitative bounds. The best bounds, of polynomial type, have been obtained by Manners for linear configurations of length 6 in 3 variables by a skillful use of the Cauchy–Schwarz inequality [Reference Manners27].
, proves it for arithmetic progressions. The work by Green and Tao [Reference Green and Tao17] settles it for all linear configurations satisfying a technical condition called flag conditionFootnote 1, with certain cases having been previously proved by Gowers and Wolf [Reference Green and Tao18–Reference Green, Tao and Ziegler21]. Green and Tao's results are all but ineffective while the work of Gowers and Wolf gives some quantitative bounds. The best bounds, of polynomial type, have been obtained by Manners for linear configurations of length 6 in 3 variables by a skillful use of the Cauchy–Schwarz inequality [Reference Manners27].
As far as non-linear configurations are concerned, the work of Peluse [Reference Peluse29] proves Conjecture 1.12 in a quantitative manner for $x, x+P_1(y), \ldots , x+P_{t-1}(y)$![]() whenever the polynomials $P_1$
whenever the polynomials $P_1$![]() , …, $P_{t-1}$
, …, $P_{t-1}$![]() are linearly independent; it thus settles the complexity 0 case. For configurations of the form
are linearly independent; it thus settles the complexity 0 case. For configurations of the form
where any non-trivial linear combination of $P_m, \ldots , P_{m+k-1}$![]() has degree at least $m$
has degree at least $m$![]() , the conjecture has been settled quantitatively in [Reference Kuca25]; similarly for the systems of linear forms with variables being higher powers.
, the conjecture has been settled quantitatively in [Reference Kuca25]; similarly for the systems of linear forms with variables being higher powers.
In the works on the true complexity of linear forms [Reference Green and Tao17–Reference Green, Tao and Ziegler21], the authors only look at the case $f_1 = \cdots = f_t$![]() and care about the degree $s$
and care about the degree $s$![]() such that $U^{s+1}$
such that $U^{s+1}$![]() controls all the terms of the configuration. For more general polynomial progressions, it, however, makes sense to allow these functions to be different. Since the terms of the progression may have different degrees, the polynomials $Q_1, \ldots , Q_t$
controls all the terms of the configuration. For more general polynomial progressions, it, however, makes sense to allow these functions to be different. Since the terms of the progression may have different degrees, the polynomials $Q_1, \ldots , Q_t$![]() appearing in Conjecture 1.12 may have different degrees as well. As a result, it is reasonable to allow that different terms of the progression be controlled by different Gowers norms.
appearing in Conjecture 1.12 may have different degrees as well. As a result, it is reasonable to allow that different terms of the progression be controlled by different Gowers norms.
Like many other questions surrounding Szemerédi theorem, finding true complexity has a natural analogue in ergodic theory: the problem of determining the smallest characteristic factor. A characteristic factor of a measure-preserving dynamical system $(X, \mathcal {X}, \mu , T)$![]() with respect to (1) is a factor $\mathcal {Y}$
with respect to (1) is a factor $\mathcal {Y}$![]() of $\mathcal {X}$
of $\mathcal {X}$![]() such that if $f_0, \ldots , f_{t-1}\in L^{\infty }(\mu )$
such that if $f_0, \ldots , f_{t-1}\in L^{\infty }(\mu )$![]() and the projection of $f_i\in L^{\infty }(\mu )$
and the projection of $f_i\in L^{\infty }(\mu )$![]() onto $\mathcal {Y}$
onto $\mathcal {Y}$![]() satisfies $\mathbb {E}(f_i|\mathcal {Y})=0$
satisfies $\mathbb {E}(f_i|\mathcal {Y})=0$![]() for some $0\leqslant i\leqslant t-1$
for some $0\leqslant i\leqslant t-1$![]() , then the product
, then the product
converges to 0 in $L^{2}(\mu )$![]() . Host and Kra prove in [Reference Host and Kra23] that there exists a sequence of factors $(\mathcal {Z}_k)_{k\in \mathbb {N}_+}$
. Host and Kra prove in [Reference Host and Kra23] that there exists a sequence of factors $(\mathcal {Z}_k)_{k\in \mathbb {N}_+}$![]() such that $\mathcal {Z}_{t-2}$
such that $\mathcal {Z}_{t-2}$![]() is characteristic for arithmetic progressions of length $t$
is characteristic for arithmetic progressions of length $t$![]() for $t\geqslant 3$
for $t\geqslant 3$![]() . They show furthermore that each $\mathcal {Z}_k$
. They show furthermore that each $\mathcal {Z}_k$![]() is an inverse limit of $k$
is an inverse limit of $k$![]() -step nilsystems; the theory of these factors is fully set up in [Reference Host and Kra24]. In [Reference Host and Kra22], it has been shown that for each progression (1), there exists $k\in \mathbb {N}$
-step nilsystems; the theory of these factors is fully set up in [Reference Host and Kra24]. In [Reference Host and Kra22], it has been shown that for each progression (1), there exists $k\in \mathbb {N}$![]() such that $\mathcal {Z}_k$
such that $\mathcal {Z}_k$![]() is characteristic, which corresponds to the result of Peluse [Reference Peluse29, Proposition 2.2] that (1) is controlled by some Gowers norm. Further works [Reference Frantzikinakis6–Reference Frantzikinakis and Kra8] give the smallest characteristic factors for some specific families of progressions. In particular, Theorems 1.2 and 1.6 are combinatorial, finite-field analogues of the results from [Reference Frantzikinakis6] that the Kronecker factor $\mathcal {K}$
is characteristic, which corresponds to the result of Peluse [Reference Peluse29, Proposition 2.2] that (1) is controlled by some Gowers norm. Further works [Reference Frantzikinakis6–Reference Frantzikinakis and Kra8] give the smallest characteristic factors for some specific families of progressions. In particular, Theorems 1.2 and 1.6 are combinatorial, finite-field analogues of the results from [Reference Frantzikinakis6] that the Kronecker factor $\mathcal {K}$![]() and the affine factor $\mathcal {A}_2$
and the affine factor $\mathcal {A}_2$![]() are characteristic for $x,\; x+y,\; x+y^{2},\; x+y+y^{2}$
are characteristic for $x,\; x+y,\; x+y^{2},\; x+y+y^{2}$![]() and $x,\; x+y,\; x+2y,\; x+y^{2}$
and $x,\; x+y,\; x+2y,\; x+y^{2}$![]() , respectively. Finally, Leibman [Reference Leibman26] has resolved the question of finding the smallest characteristic factor in the case where the underlying dynamical system is a nilsystem.
, respectively. Finally, Leibman [Reference Leibman26] has resolved the question of finding the smallest characteristic factor in the case where the underlying dynamical system is a nilsystem.
1.2. Outline of the paper
We start the paper by presenting necessary definitions and results from higher-order Fourier analysis in the next section. We then proceed in § 3 to define Leibman group for a polynomial progression and describe its properties. In particular, we state a filtration condition on a polynomial progression (Definition 3.4) which makes the corresponding Leibman nilmanifold easier to analyse, and which is satisfied by all the progressions that we are interested in. In § 4, we deduce Theorem 1.8 for the progression $x, x+y, x+y^{2}, x+y+y^{2}$![]() so as to illustrate our arguments with a specific example. In § 5 and § 6, we prove Theorem 1.8 for two general families of progressions for which the theorem is stated. We then show in § 7 how our definition of Leibman group extends the definition of Leibman group for linear forms presented in [Reference Green and Tao17].
so as to illustrate our arguments with a specific example. In § 5 and § 6, we prove Theorem 1.8 for two general families of progressions for which the theorem is stated. We then show in § 7 how our definition of Leibman group extends the definition of Leibman group for linear forms presented in [Reference Green and Tao17].
Having showed that Leibman nilmanifolds are the right thing to look at, we prove in § 8 that Conjecture 1.12 on the connection between true complexity and algebraic relations holds for all progressions that satisfy a variant of Theorem 1.8. In § 9, we deduce Theorem 1.1.
Our method, however, has certain limitations which we outline in the subsequent two sections. In § 10, we give an example of a configuration which does not satisfy the filtration condition. In § 11, we show that our method fails for $x, x+y, x+2y, x+y^{2}$![]() , which does not equidistribute on the corresponding Leibman nilmanifold. To handle this progression, we, therefore, develop a different method in § 12, which proves true complexity for $x, x+y, x+2y, x+y^{2}$
, which does not equidistribute on the corresponding Leibman nilmanifold. To handle this progression, we, therefore, develop a different method in § 12, which proves true complexity for $x, x+y, x+2y, x+y^{2}$![]() as a result of a more general Theorem 1.7.
as a result of a more general Theorem 1.7.
2. Higher-order Fourier analysis
To understand operators of the form
we need to understand how certain polynomial sequences distribute on nilmanifolds. We use this section to define necessary concepts from higher-order Fourier analysis, such as the notions of filtered nilmanifold and polynomial sequence. All of these definitions have appeared in [Reference Candela and Sisask4, Reference Green and Tao16, Reference Green and Tao17, Reference Green and Tao19]. We then state some classical results that we shall need in the paper.
Definition 2.1 (Filtrations) A filtration $G_\bullet =(G_i)_{i=0}^{\infty }$![]() of degree at most $s$
of degree at most $s$![]() on a group $G$
on a group $G$![]() is a sequence of subgroups
is a sequence of subgroups
satisfying $[G_i, G_j]\subseteq G_{i+j}$![]() for all $i,j\geqslant 0$
for all $i,j\geqslant 0$![]() .
.
A standard example of a filtration is the lower central series filtration defined by setting $G_i = [G,G_{i-1}]$![]() for $i\geqslant 2.$
for $i\geqslant 2.$![]()
Definition 2.2 (Filtered nilmanifolds) A filtered nilmanifold $G/\varGamma$![]() of degree $s$
of degree $s$![]() and complexity $M$
and complexity $M$![]() consists of the following data:
consists of the following data:
(i) a quotient $G/\varGamma$
 , where $G$
, where $G$ is a connected, simply connected, nilpotent Lie group of dimension $m\leqslant M$
is a connected, simply connected, nilpotent Lie group of dimension $m\leqslant M$ with identity 1, and $\varGamma \subseteq G$
with identity 1, and $\varGamma \subseteq G$ is a cocompact lattice;
is a cocompact lattice;(ii) a filtration $G_\bullet$
 of degree at most $s\leqslant M$
of degree at most $s\leqslant M$ such that $G_i$
such that $G_i$ are closed and connected subgroups of $G$
are closed and connected subgroups of $G$ and $\varGamma _i:=\varGamma \cap G_i$
and $\varGamma _i:=\varGamma \cap G_i$ is a cocompact lattice in $G_i$
is a cocompact lattice in $G_i$ for each $i\in \mathbb {N}_+$
for each $i\in \mathbb {N}_+$ ;
;(iii) an $M$
 -rational Mal'cev basis $\chi =\{X_1, \ldots , X_m\}$
-rational Mal'cev basis $\chi =\{X_1, \ldots , X_m\}$ adapted to $G_\bullet$
adapted to $G_\bullet$ .
.
Mal'cev basis that appears in Definition 2.2 is a vector space basis for the Lie algebra $\mathfrak {g}$![]() of $G$
of $G$![]() that respects the filtration $G_\bullet$
that respects the filtration $G_\bullet$![]() . Its utility comes from the fact that it provides a natural coordinate system on $G$
. Its utility comes from the fact that it provides a natural coordinate system on $G$![]() . The definition and properties of Mal'cev basis are discussed in details in [Reference Green and Tao19]. The important consequence for us is that it induces a Mal'cev coordinate map, i.e. a diffeomorphism
. The definition and properties of Mal'cev basis are discussed in details in [Reference Green and Tao19]. The important consequence for us is that it induces a Mal'cev coordinate map, i.e. a diffeomorphism
satisfying $\psi (\varGamma )=\mathbb {Z}^{m}$![]() and $\psi (G_i)=\{0\}^{m-m_i}\times \mathbb {R}^{m_i}$
and $\psi (G_i)=\{0\}^{m-m_i}\times \mathbb {R}^{m_i}$![]() for all $1\leqslant i\leqslant s$
for all $1\leqslant i\leqslant s$![]() , where $m_i = \dim G_i$
, where $m_i = \dim G_i$![]() .
.
Nilmanifolds turn out to be a proper framework to define polynomial sequences, which can be thought of as generalizations of polynomials on the torus.
Definition 2.3 (Polynomial sequences) Let $D\in \mathbb {N}_+$![]() . A polynomial sequence on $G$
. A polynomial sequence on $G$![]() adapted to the filtration $G_\bullet$
adapted to the filtration $G_\bullet$![]() is a map $g:\mathbb {Z}^{D}\to G$
is a map $g:\mathbb {Z}^{D}\to G$![]() satisfying $\partial _{{\textbf {h}_1}, \ldots , {\textbf {h}_i}}g\in G_i$
satisfying $\partial _{{\textbf {h}_1}, \ldots , {\textbf {h}_i}}g\in G_i$![]() for each $\textbf {h}_1, \ldots , \textbf {h}_i\in \mathbb {Z}^{D}$
for each $\textbf {h}_1, \ldots , \textbf {h}_i\in \mathbb {Z}^{D}$![]() , where $\partial _{\textbf {h}} g(\textbf {n}):=g(\textbf {n}+\textbf {h})g(\textbf {n})^{-1}$
, where $\partial _{\textbf {h}} g(\textbf {n}):=g(\textbf {n}+\textbf {h})g(\textbf {n})^{-1}$![]() and $\partial _{\textbf {h}_1, \ldots ,\textbf {h}_i}=\partial _{\textbf {h}_1} \cdots \partial _{\textbf {h}_i}$
and $\partial _{\textbf {h}_1, \ldots ,\textbf {h}_i}=\partial _{\textbf {h}_1} \cdots \partial _{\textbf {h}_i}$![]() for $i>1$
for $i>1$![]() . Polynomial sequences adapted to $G_\bullet$
. Polynomial sequences adapted to $G_\bullet$![]() form a group denoted as ${\textrm {poly}}(\mathbb {Z}^{D},G_\bullet )$
form a group denoted as ${\textrm {poly}}(\mathbb {Z}^{D},G_\bullet )$![]() . The degree of $g$
. The degree of $g$![]() is the degree of the filtration $G_\bullet$
is the degree of the filtration $G_\bullet$![]() .
.
In this paper, we shall primarily be interested in the polynomial sequences arising in problems over finite fields. These sequences are periodic in the sense made clear by the following definition.
Definition 2.4 (Periodic sequences) Let $D\in \mathbb {N}_+$![]() . A sequence $g\in {\textrm {poly}}(\mathbb {Z}^{D},G_\bullet )$
. A sequence $g\in {\textrm {poly}}(\mathbb {Z}^{D},G_\bullet )$![]() is $p$
is $p$![]() -periodic if $g(\textbf {n}_1+p \textbf {n}_2)\varGamma =g(\textbf {n}_1)\varGamma$
-periodic if $g(\textbf {n}_1+p \textbf {n}_2)\varGamma =g(\textbf {n}_1)\varGamma$![]() for all $\textbf {n}_1, \textbf {n}_2\in \mathbb {Z}^{D}$
for all $\textbf {n}_1, \textbf {n}_2\in \mathbb {Z}^{D}$![]() . In particular, for a $p$
. In particular, for a $p$![]() -periodic sequence ${g\in {\textrm {poly}}(\mathbb {Z}^{D},G_\bullet )}$
-periodic sequence ${g\in {\textrm {poly}}(\mathbb {Z}^{D},G_\bullet )}$![]() , the map $\textbf {n}\mapsto g(\textbf {n})\varGamma$
, the map $\textbf {n}\mapsto g(\textbf {n})\varGamma$![]() can be viewed as a function from $\mathbb {F}_p^{D}$
can be viewed as a function from $\mathbb {F}_p^{D}$![]() to $G/\varGamma$
to $G/\varGamma$![]() .
.
It turns out that polynomial sequences can be written in a more explicit manner.
Lemma 2.5 (Taylor expansion, Lemma A.1 of [Reference Green and Tao17])
Let $D\in \mathbb {N}_+$![]() . A sequence $g$
. A sequence $g$![]() is in ${\textrm {poly}}(\mathbb {Z}^{D},G_\bullet )$
is in ${\textrm {poly}}(\mathbb {Z}^{D},G_\bullet )$![]() if and only if for each multiindex $\textbf {i}=(i_1, \ldots , i_D)$
if and only if for each multiindex $\textbf {i}=(i_1, \ldots , i_D)$![]() , there exists $g_{\textbf {i}}\in G_{|\textbf {i}|}$
, there exists $g_{\textbf {i}}\in G_{|\textbf {i}|}$![]() satisfying
satisfying
for all $\textbf {n}\in \mathbb {Z}^{D}$![]() . The representation in (11) is unique. The binomial coefficients are defined as
. The representation in (11) is unique. The binomial coefficients are defined as
and the size of the vector $\textbf {i}\in \mathbb {N}^{D}$![]() is $|\textbf {i}|:=i_1+\cdots +i_D$
is $|\textbf {i}|:=i_1+\cdots +i_D$![]() .
.
To examine the distribution of $p$![]() -periodic polynomial sequences on nilmanifolds in a quantitative manner, it is useful to introduce the notion of a nilsequence.
-periodic polynomial sequences on nilmanifolds in a quantitative manner, it is useful to introduce the notion of a nilsequence.
Definition 2.6 (Nilsequences) Suppose $D\in \mathbb {N}_+$![]() . A function $f:\mathbb {Z}^{D}\to \mathbb {C}$
. A function $f:\mathbb {Z}^{D}\to \mathbb {C}$![]() is a nilsequence of degree $s$
is a nilsequence of degree $s$![]() and complexity $M$
and complexity $M$![]() if $f(\textbf {n})=F(g(\textbf {n})\varGamma )$
if $f(\textbf {n})=F(g(\textbf {n})\varGamma )$![]() , where $F$
, where $F$![]() is an $M$
is an $M$![]() -Lipschitz function on a filtered nilmanifold $G/\varGamma$
-Lipschitz function on a filtered nilmanifold $G/\varGamma$![]() of degree $s$
of degree $s$![]() and complexity $M$
and complexity $M$![]() , and $g\in {\textrm {poly}}(\mathbb {Z}^{D},G_\bullet )$
, and $g\in {\textrm {poly}}(\mathbb {Z}^{D},G_\bullet )$![]() . A nilsequence $f$
. A nilsequence $f$![]() is $p$
is $p$![]() -periodic if the underlying polynomial sequence is.
-periodic if the underlying polynomial sequence is.
Definition 2.7 (Equidistribution) Let $D\in \mathbb {N}_+$![]() and $\delta >0$
and $\delta >0$![]() . A $p$
. A $p$![]() -periodic sequence $g\in {\textrm {poly}}(\mathbb {Z}^{D},G)$
-periodic sequence $g\in {\textrm {poly}}(\mathbb {Z}^{D},G)$![]() is $\delta$
is $\delta$![]() -equidistributed on a nilmanifold $G/\varGamma$
-equidistributed on a nilmanifold $G/\varGamma$![]() if
if

for all Lipschitz functions $F:G/\varGamma \to \mathbb {C}$![]() , where the integral is taken with respect to the (left-invariant) Haar measure $\mu$
, where the integral is taken with respect to the (left-invariant) Haar measure $\mu$![]() on $G/\varGamma$
on $G/\varGamma$![]() normalized so that $\mu (G/\varGamma )=1$
normalized so that $\mu (G/\varGamma )=1$![]() .
.
It is natural to ask about obstructions to equidistribution. To state them formally, we need the notion of a horizontal character.
Definition 2.8 (Horizontal characters) A horizontal character on $G$![]() is a continuous group homomorphism $\eta :G\to \mathbb {R}$
is a continuous group homomorphism $\eta :G\to \mathbb {R}$![]() such that $\eta (\varGamma )\in \mathbb {Z}$
such that $\eta (\varGamma )\in \mathbb {Z}$![]() . Each horizontal character can be given in the form $\eta (x) = k\cdot \psi (x)$
. Each horizontal character can be given in the form $\eta (x) = k\cdot \psi (x)$![]() for some $k\in \mathbb {Z}^{m}$
for some $k\in \mathbb {Z}^{m}$![]() , where $\psi :G\to \mathbb {R}^{m}$
, where $\psi :G\to \mathbb {R}^{m}$![]() is the Mal'cev coordinate map. The modulus of $\eta$
is the Mal'cev coordinate map. The modulus of $\eta$![]() is $|\eta |:=|k|=|k_1|+\cdots +|k_m|$
is $|\eta |:=|k|=|k_1|+\cdots +|k_m|$![]() .
.
Horizontal characters in fact annihilate $[G,G]\varGamma$![]() and can be viewed as maps on the quotient $G/[G,G]\varGamma$
and can be viewed as maps on the quotient $G/[G,G]\varGamma$![]() which is isomorphic to $(\mathbb {R}/\mathbb {Z})^{m_{ab}}$
which is isomorphic to $(\mathbb {R}/\mathbb {Z})^{m_{ab}}$![]() for $m_{ab}=\dim G-\dim [G,G]$
for $m_{ab}=\dim G-\dim [G,G]$![]() .
.
In Theorem 1.16 of [Reference Green and Tao19], Green and Tao gave a condition for when a polynomial sequence is close to being equidistributed. We present its periodic version.
Theorem 2.9 (Equidistribution theorem for $p$![]() -periodic sequences)
-periodic sequences)
Let $2< M\leqslant A$![]() and ${D\in \mathbb {N}_+}$
and ${D\in \mathbb {N}_+}$![]() , and let $G/\varGamma$
, and let $G/\varGamma$![]() be a filtered nilmanifold of complexity $M$
be a filtered nilmanifold of complexity $M$![]() . Suppose that the sequence ${g\in {\textrm {poly}}(\mathbb {Z}^{D}, G_\bullet )}$
. Suppose that the sequence ${g\in {\textrm {poly}}(\mathbb {Z}^{D}, G_\bullet )}$![]() is $p$
is $p$![]() -periodic. Then at least one of the following holds:
-periodic. Then at least one of the following holds:
(i) $(g(\textbf {n})\varGamma )_{n\in \mathbb {F}_p^{D}}$
 is $A^{-1}$
is $A^{-1}$ -equidistributed.
-equidistributed.(ii) There exists a non-trivial horizontal character $\eta$
 with $|\eta |\ll _{M,D} A^{C_{M,D}}$
with $|\eta |\ll _{M,D} A^{C_{M,D}}$ such that $\eta \circ g$
such that $\eta \circ g$ is constant mod $\mathbb {Z}$
is constant mod $\mathbb {Z}$ .
.
In the case of a general polynomial sequence, Theorem 1.16 of [Reference Green and Tao19] only guarantees that if $g$![]() is not close to being equidistributed, then the coefficients of the polynomial $\eta \circ g - \eta \circ g(0)$
is not close to being equidistributed, then the coefficients of the polynomial $\eta \circ g - \eta \circ g(0)$![]() are major arc for a non-trivial horizontal character $\eta$
are major arc for a non-trivial horizontal character $\eta$![]() of small modulus. However, the rigidity imposed by the $p$
of small modulus. However, the rigidity imposed by the $p$![]() -periodicity of $g$
-periodicity of $g$![]() allows us to conclude that $\eta \circ g$
allows us to conclude that $\eta \circ g$![]() is in fact constant mod $\mathbb {Z}$
is in fact constant mod $\mathbb {Z}$![]() . More precisely, Theorem 2.9 can be deduced from Theorem 1.16 of [Reference Green and Tao19] as follows: keeping $p$
. More precisely, Theorem 2.9 can be deduced from Theorem 1.16 of [Reference Green and Tao19] as follows: keeping $p$![]() fixed, we set $N = k p$
fixed, we set $N = k p$![]() in Theorem 1.16 of [Reference Green and Tao19] for some $k\in \mathbb {N}_+$
in Theorem 1.16 of [Reference Green and Tao19] for some $k\in \mathbb {N}_+$![]() . If the sequence $g(1), \ldots , g(N)$
. If the sequence $g(1), \ldots , g(N)$![]() is not $A^{-1}$
is not $A^{-1}$![]() -equidistributed, then there exists a non-trivial horizontal character $\eta$
-equidistributed, then there exists a non-trivial horizontal character $\eta$![]() with $|\eta |\ll _{M,D} A^{C_{M,D}}$
with $|\eta |\ll _{M,D} A^{C_{M,D}}$![]() such that the non-zero coefficients of the polynomial $\eta \circ g(\textbf {n}) = \sum \nolimits _{\textbf {i}}a_{\textbf {i}}{{\textbf {n}}\choose {\textbf {i}}}$
such that the non-zero coefficients of the polynomial $\eta \circ g(\textbf {n}) = \sum \nolimits _{\textbf {i}}a_{\textbf {i}}{{\textbf {n}}\choose {\textbf {i}}}$![]() satisfy the bound $\|a_{\textbf {i}}\|_{\mathbb {R}/\mathbb {Z}}\ll A^{-C_{M,D}} N^{-|\textbf {i}|}$
satisfy the bound $\|a_{\textbf {i}}\|_{\mathbb {R}/\mathbb {Z}}\ll A^{-C_{M,D}} N^{-|\textbf {i}|}$![]() . Importantly, the $p$
. Importantly, the $p$![]() -periodicity of $g$
-periodicity of $g$![]() implies that we can take the same $A$
implies that we can take the same $A$![]() for all $k\in \mathbb {N}_+$
for all $k\in \mathbb {N}_+$![]() ; letting $k\to \infty$
; letting $k\to \infty$![]() , we, therefore, deduce that each non-zero coefficient $a_{\textbf {i}}$
, we, therefore, deduce that each non-zero coefficient $a_{\textbf {i}}$![]() is an integer.
is an integer.
We want to define the extent to which a polynomial sequence $g$![]() is irrational. Essentially, irrationality captures how well the sequence $g$
is irrational. Essentially, irrationality captures how well the sequence $g$![]() interacts with objects called $i$
interacts with objects called $i$![]() th level characters, or how close to being in $\varGamma$
th level characters, or how close to being in $\varGamma$![]() its Taylor coefficients $g_{\textbf {i}}$
its Taylor coefficients $g_{\textbf {i}}$![]() are.
are.
Definition 2.10 ($i$![]() th level character)
th level character)
Let $G/\varGamma$![]() be a filtered nilmanifold. An $i$
be a filtered nilmanifold. An $i$![]() th level character on $G/\varGamma$
th level character on $G/\varGamma$![]() is a continuous group homomorphism from $G$
is a continuous group homomorphism from $G$![]() to $\mathbb {R}$
to $\mathbb {R}$![]() that is $\mathbb {Z}$
that is $\mathbb {Z}$![]() -valued on $\varGamma$
-valued on $\varGamma$![]() and vanishes on $G_{i+1}$
and vanishes on $G_{i+1}$![]() and $[G_j, G_{i-j}]$
and $[G_j, G_{i-j}]$![]() for any $0\leqslant j\leqslant i$
for any $0\leqslant j\leqslant i$![]() . It is nontrivial if it is non-zero. Every $i$
. It is nontrivial if it is non-zero. Every $i$![]() th level character can be written in the form $\eta (x)=k\cdot \psi _i(x)$
th level character can be written in the form $\eta (x)=k\cdot \psi _i(x)$![]() for a unique $k\in \mathbb {Z}^{m_i-m_{i+1}}$
for a unique $k\in \mathbb {Z}^{m_i-m_{i+1}}$![]() , where $\psi _i(g_i)$
, where $\psi _i(g_i)$![]() is a tuple consisting of the entries of $g_i$
is a tuple consisting of the entries of $g_i$![]() in $\psi (g_i)$
in $\psi (g_i)$![]() indexed by $m-m_i+1, \ldots ,m- m_{i+1}$
indexed by $m-m_i+1, \ldots ,m- m_{i+1}$![]() . The modulus of $\eta$
. The modulus of $\eta$![]() is defined to be $|\eta |:=|k|=|k_1|+\cdots +|k_{m_i-m_{i+1}}|$
is defined to be $|\eta |:=|k|=|k_1|+\cdots +|k_{m_i-m_{i+1}}|$![]() .
.
Definition 2.11 ($A$![]() -irrationality)
-irrationality)
Let $G/\varGamma$![]() be a filtered nilmanifold of degree $s$
be a filtered nilmanifold of degree $s$![]() . An element $g_i\in G_i$
. An element $g_i\in G_i$![]() is $A$
is $A$![]() -irrational if we have $\eta _i(g_i)\notin \mathbb {Z}$
-irrational if we have $\eta _i(g_i)\notin \mathbb {Z}$![]() for all non-trivial $i$
for all non-trivial $i$![]() th level characters $\eta _i$
th level characters $\eta _i$![]() of complexity $|\eta _i|\leqslant A$
of complexity $|\eta _i|\leqslant A$![]() . A sequence $g\in {\textrm {poly}}(\mathbb {Z}^{D},G)$
. A sequence $g\in {\textrm {poly}}(\mathbb {Z}^{D},G)$![]() is $A$
is $A$![]() -irrational if $g_{\textbf {i}}$
-irrational if $g_{\textbf {i}}$![]() is $A$
is $A$![]() -irrational for each $\textbf {i}\in \mathbb {N}^{D}$
-irrational for each $\textbf {i}\in \mathbb {N}^{D}$![]() with $0<|\textbf {i}|\leqslant s$
with $0<|\textbf {i}|\leqslant s$![]() .
.
Being highly irrational is a stronger property than being close to equidistributed, as implied by the following lemma.
Lemma 2.12 (Irrationality implies equidistribution, Lemma 3.7 of [Reference Green and Tao17])
Let $D\in \mathbb {N}_+$![]() . Let $G/\varGamma$
. Let $G/\varGamma$![]() be a filtered nilmanifold of complexity $M$
be a filtered nilmanifold of complexity $M$![]() , and suppose that $g\in {\textrm {poly}}(\mathbb {Z}^{D}, G_\bullet )$
, and suppose that $g\in {\textrm {poly}}(\mathbb {Z}^{D}, G_\bullet )$![]() is $p$
is $p$![]() -periodic and $A$
-periodic and $A$![]() -irrational. Then $g$
-irrational. Then $g$![]() is $O_{M,D}(A^{-c_{M,D}})$
is $O_{M,D}(A^{-c_{M,D}})$![]() -equidistributed.
-equidistributed.
In our arguments, we shall want to approximate sums like (2) by integrals of Lipschitz functions on nilmanifolds. A key step in doing so is to decompose an arbitrary 1-bounded function into a nilsequence of an appropriate degree and two error terms. We do this via the following lemma, which is a simultaneous and periodic version of the celebrated arithmetic regularity lemma [Reference Green and Tao17, Theorem 1.2].
Lemma 2.13 (Simultaneous periodic irrational arithmetic regularity lemma) Let $s\geqslant 2$![]() and $t\geqslant 1$
and $t\geqslant 1$![]() be integers, $\epsilon >0$
be integers, $\epsilon >0$![]() , and let $\mathcal {F}:\mathbb {R}_+\to \mathbb {R}_+$
, and let $\mathcal {F}:\mathbb {R}_+\to \mathbb {R}_+$![]() be a growth function. There exists $M=O_{s,t,\epsilon ,\mathcal {F}}(1)$
be a growth function. There exists $M=O_{s,t,\epsilon ,\mathcal {F}}(1)$![]() with the property that for all 1-bounded functions $f_1, \ldots , f_t:\mathbb {F}_p\to \mathbb {C}$
with the property that for all 1-bounded functions $f_1, \ldots , f_t:\mathbb {F}_p\to \mathbb {C}$![]() there exist decompositions
there exist decompositions
such that for each $1\leqslant i\leqslant t$![]() , the functions $f_{i, nil}, f_{i,sml}, f_{i,unf}$
, the functions $f_{i, nil}, f_{i,sml}, f_{i,unf}$![]() satisfy the following:
satisfy the following:
(i) $f_{i,nil}(n)=F_i(g(n)\varGamma )$
 for a $M$
for a $M$ -Lipschitz function $F_i: G/\varGamma \to \mathbb {C}$
-Lipschitz function $F_i: G/\varGamma \to \mathbb {C}$ , where $G/\varGamma$
, where $G/\varGamma$ is a filtered nilmanifold of degree $s$
is a filtered nilmanifold of degree $s$ and complexity at most $M$
and complexity at most $M$ , and $g\in {\textrm {poly}}(\mathbb {Z},G_\bullet )$
, and $g\in {\textrm {poly}}(\mathbb {Z},G_\bullet )$ is a $p$
is a $p$ -periodic, $\mathcal {F}(M)$
-periodic, $\mathcal {F}(M)$ -irrational sequence satisfying $g(0)=1$
-irrational sequence satisfying $g(0)=1$ ;
;(ii) $\|f_{i,sml}\|_2\leqslant \epsilon$
 ;
;(iii) $\|f_{i,unf}\|_{U^{s+1}}\leqslant {1}/{\mathcal {F}(M)}$
 ;
;(iv) the functions $f_{i,nil}$
 , $f_{i,sml}$
, $f_{i,sml}$ and $f_{i,unf}$
and $f_{i,unf}$ are 4-bounded.
are 4-bounded.
The important thing about Lemma 2.13 is that we decompose each $f_1, \ldots , f_t$![]() with respect to the same sequence $g$
with respect to the same sequence $g$![]() and the same nilmanifold $G/\varGamma$
and the same nilmanifold $G/\varGamma$![]() . We give its proof in Appendix A.
. We give its proof in Appendix A.
Finally, we shall briefly state the relevant properties of Gowers norms and polynomial bias norms, all of which are discussed more extensively in [Reference Green15, Reference Green and Tao16]. While Gowers norms are the central objects of study in this paper, polynomial bias norms only appear in Theorem 1.6.
Definition 2.14 (Polynomial bias norms) For $s\in \mathbb {N}_+$![]() , the polynomial bias norm of degree $s$
, the polynomial bias norm of degree $s$![]() of a function $f:\mathbb {F}_p\to \mathbb {C}$
of a function $f:\mathbb {F}_p\to \mathbb {C}$![]() is given by
is given by
Gowers norms and polynomial bias norms are seminorms for $s=1$![]() and genuine norms for $s\geqslant 2$
and genuine norms for $s\geqslant 2$![]() . They satisfy the monotonicity property
. They satisfy the monotonicity property
for any $f:\mathbb {F}_p\to \mathbb {C}$![]() . Gowers norms also bound polynomial bias norms in that
. Gowers norms also bound polynomial bias norms in that
For $s=1$![]() , we in fact have $\|f\|_{u^{1}}=\|f\|_{U^{1}}$
, we in fact have $\|f\|_{u^{1}}=\|f\|_{U^{1}}$![]() , and for $s=2$
, and for $s=2$![]() , we have $\|f\|_{u^{2}}\leqslant \|f\|_{U^{2}}\leqslant \|f\|_{u^{2}}^{{1}/{2}}$
, we have $\|f\|_{u^{2}}\leqslant \|f\|_{U^{2}}\leqslant \|f\|_{u^{2}}^{{1}/{2}}$![]() for all 1-bounded $f:\mathbb {F}_p\to \mathbb {C}$
for all 1-bounded $f:\mathbb {F}_p\to \mathbb {C}$![]() , a result known as $U^{2}$
, a result known as $U^{2}$![]() inverse theorem. For $s>2$
inverse theorem. For $s>2$![]() , however, there exist functions that have large $U^{s}$
, however, there exist functions that have large $U^{s}$![]() norms and small $u^{s}$
norms and small $u^{s}$![]() norms. This is due to the fact that having a large $u^{s}$
norms. This is due to the fact that having a large $u^{s}$![]() norm is equivalent to correlating with a polynomial phase of degree $s-1$
norm is equivalent to correlating with a polynomial phase of degree $s-1$![]() , while having a large $U^{s}$
, while having a large $U^{s}$![]() norm corresponds to correlating with a broader category of nilsequences of degree $s-1$
norm corresponds to correlating with a broader category of nilsequences of degree $s-1$![]() . See [Reference Green and Tao16, Reference Green, Tao and Ziegler20, Reference Green, Tao and Ziegler21] for more details on the relationship between Gowers norms and nilsequences.
. See [Reference Green and Tao16, Reference Green, Tao and Ziegler20, Reference Green, Tao and Ziegler21] for more details on the relationship between Gowers norms and nilsequences.
3. Leibman nilmanifold for polynomial progressions
Throughout this section, let $\vec {P}(\textbf {x})=(P_1(\textbf {x}), \ldots ,P_t(\textbf {x}))\in \mathbb {Q}[\textbf {x}]^{t}$![]() be an integral polynomial map of degree $d$
be an integral polynomial map of degree $d$![]() . Suppose that $G/\varGamma$
. Suppose that $G/\varGamma$![]() is a filtered nilmanifold of degree $s$
is a filtered nilmanifold of degree $s$![]() , dimension $m$
, dimension $m$![]() and complexity $M$
and complexity $M$![]() . Given a polynomial sequence $g$
. Given a polynomial sequence $g$![]() adapted to a filtration $G_\bullet$
adapted to a filtration $G_\bullet$![]() on $G/\varGamma$
on $G/\varGamma$![]() , we define
, we define
The main objective of this section is to construct a group $G^{P}$![]() with a filtration $G^{P}_\bullet$
with a filtration $G^{P}_\bullet$![]() such that $g^{P}\in {\textrm {{poly}}}(\mathbb {Z}^{D},G^{P}_\bullet )$
such that $g^{P}\in {\textrm {{poly}}}(\mathbb {Z}^{D},G^{P}_\bullet )$![]() whenever $g\in {\textrm {{poly}}}(\mathbb {Z},G_\bullet )$
whenever $g\in {\textrm {{poly}}}(\mathbb {Z},G_\bullet )$![]() . The group $G^{P}$
. The group $G^{P}$![]() originally appeared in Section 5 of [Reference Leibman26], but we are not aware of the filtration $G^{P}_\bullet$
originally appeared in Section 5 of [Reference Leibman26], but we are not aware of the filtration $G^{P}_\bullet$![]() being defined previously except for the relatively simple case of linear forms in [Reference Green and Tao17].
being defined previously except for the relatively simple case of linear forms in [Reference Green and Tao17].
It is a standard fact that each integral polynomial map $\vec {Q}\in \mathbb {Q}[\textbf {x}]^{t}$![]() can be expressed as
can be expressed as

for some $\vec {b}_{\textbf {i}}\in \mathbb {Z}^{t}$![]() , and we denote its degree- $j$
, and we denote its degree- $j$![]() part by
part by

Thus, for instance, $\mathcal {D}_1(x + y + {{x}\choose {2}}) = x+y$![]() and $\mathcal {D}_2(x + y + {{x}\choose {2}}) = {{x}\choose {2}}$
and $\mathcal {D}_2(x + y + {{x}\choose {2}}) = {{x}\choose {2}}$![]() . To clarify the notation, we denote
. To clarify the notation, we denote
for $D$![]() -dimensional vectors $\textbf {x}$
-dimensional vectors $\textbf {x}$![]() , $\textbf {i}$
, $\textbf {i}$![]() and $t$
and $t$![]() -dimensional vectors $\vec {v}$
-dimensional vectors $\vec {v}$![]() , $\vec {j}$
, $\vec {j}$![]() . If $i$
. If $i$![]() is a scalar, however, we set
is a scalar, however, we set
We endow $\mathbb {R}^{t}$![]() with the structure of a real algebra by letting
with the structure of a real algebra by letting
and setting $\vec {1}=(1, \ldots ,1)$![]() to be the identity vector.
to be the identity vector.
For $i,j\in \mathbb {N}_+$![]() , we define two families of real vector spaces
, we define two families of real vector spaces

We note several facts about these subspaces.
Lemma 3.1 For each $i, i_1, i_2, j, j_1, j_2\in \mathbb {N}_+$![]() , we have the following inclusions:
, we have the following inclusions:
(i) $\mathcal {P}_{i,j}\subseteq \mathcal {P}_{i+1,j}$
 ;
;(ii) $\mathcal {P}_{i,j+1}\subseteq \mathcal {P}_{i,j}$
 ;
;(iii) $\mathcal {P}_{i,j}\subseteq \mathcal {Q}_{i,j}$
 ;
;(iv) $\mathcal {Q}_{i,j}\subseteq \mathcal {Q}_{i+1,j}$
 ;
;(v) $\mathcal {Q}_{i,j+1}\subseteq \mathcal {Q}_{i,j}$
 ;
;(vi) $\mathcal {Q}_{i_1, j_1}\cdot \mathcal {Q}_{i_2,j_2}\subseteq \mathcal {Q}_{i_1+i_2,j_1+j_2}$
 .
.
Proof. Statements (i)–(vi) follow directly from the definitions. Statements (iv) and (v) follow from properties (i)–(iii) by induction.
We define groups $G^{P}_j$![]() for $j\geqslant 1$
for $j\geqslant 1$![]() by setting
by setting
where we let $g^{\vec {v}}:=(g^{{v}_1}, \ldots , g^{{v}_t})$![]() . We moreover set $G^{P}=G^{P}_0=G^{P}_1$
. We moreover set $G^{P}=G^{P}_0=G^{P}_1$![]() and ${\varGamma ^{P}=\varGamma ^{t} \cap G^{P}}$
and ${\varGamma ^{P}=\varGamma ^{t} \cap G^{P}}$![]() . It follows from property $(v)$
. It follows from property $(v)$![]() of Lemma 3.1 that
of Lemma 3.1 that
Each of the groups $G^{P}_j$![]() is normal in $G^{t}$
is normal in $G^{t}$![]() because each $G_i$
because each $G_i$![]() is normal in $G$
is normal in $G$![]() .
.
For instance, if $G_\bullet$![]() is a filtration of degree 2 and $\vec {P}(x,y) = (x, x+y, x+2y)$
is a filtration of degree 2 and $\vec {P}(x,y) = (x, x+y, x+2y)$![]() is the 3-term arithmetic progression, then $\mathcal {P}_{1,1} = \mathcal {Q}_{1,1} = {\textrm {{Span}}}\{(1,1,1), (0,1,2)\}$
is the 3-term arithmetic progression, then $\mathcal {P}_{1,1} = \mathcal {Q}_{1,1} = {\textrm {{Span}}}\{(1,1,1), (0,1,2)\}$![]() , $\mathcal {P}_{2,1}=\mathcal {P}_{2,2}=\mathcal {Q}_{2,1}=\mathcal {Q}_{2,2} = \mathbb {R}^{3}$
, $\mathcal {P}_{2,1}=\mathcal {P}_{2,2}=\mathcal {Q}_{2,1}=\mathcal {Q}_{2,2} = \mathbb {R}^{3}$![]() and $\mathcal {Q}_{1,2} = \mathcal {Q}_{2,3} = \{\vec {0}\}$
and $\mathcal {Q}_{1,2} = \mathcal {Q}_{2,3} = \{\vec {0}\}$![]() ; thus $G^{P}_\bullet$
; thus $G^{P}_\bullet$![]() is given by
is given by

Lemma 3.2 The chain of subgroups $(G^{P}_j)_{j=0}^{\infty }$![]() defines a filtration on $G^{P}$
defines a filtration on $G^{P}$![]() of degree $sd$
of degree $sd$![]() .
.
Proof. Take generators $g_{1}^{\vec {v}_{1}}\in G^{P}_{j_1}$![]() and $g_{2}^{\vec {v}_{2}}\in G^{P}_{j_2}$
and $g_{2}^{\vec {v}_{2}}\in G^{P}_{j_2}$![]() for some elements $g_1\in G_1$
for some elements $g_1\in G_1$![]() and $g_2\in G_2$
and $g_2\in G_2$![]() as well as vectors $\vec {v}_{1} \in \mathcal {Q}_{i_1, j_1}$
as well as vectors $\vec {v}_{1} \in \mathcal {Q}_{i_1, j_1}$![]() and $\vec {v}_{2} \in \mathcal {Q}_{i_2, j_2}$
and $\vec {v}_{2} \in \mathcal {Q}_{i_2, j_2}$![]() . We want to show that their commutator is in $G^{P}_{j_1+j_2}$
. We want to show that their commutator is in $G^{P}_{j_1+j_2}$![]() . If this is true for the generators, then by Lemma 7.3 of [Reference Green and Tao19] it holds for arbitrary two elements of $G_{j_1}$
. If this is true for the generators, then by Lemma 7.3 of [Reference Green and Tao19] it holds for arbitrary two elements of $G_{j_1}$![]() and $G_{j_2}$
and $G_{j_2}$![]() , proving the lemma.
, proving the lemma.
By (41), we have
where each $g_\alpha$![]() is a commutator of $k_1$
is a commutator of $k_1$![]() copies of $g_1$
copies of $g_1$![]() and $k_2$
and $k_2$![]() copies of $g_2$
copies of $g_2$![]() for some ${k_1, k_2\geqslant 1}$
for some ${k_1, k_2\geqslant 1}$![]() satisfying $k_1+k_2\geqslant 3$
satisfying $k_1+k_2\geqslant 3$![]() , and
, and
for some polynomial $Q_\alpha (x_1, x_2)$![]() that has degree at most $k_1$
that has degree at most $k_1$![]() in $x_1$
in $x_1$![]() and at most $k_2$
and at most $k_2$![]() in $x_2$
in $x_2$![]() , and vanishes when $x_1 = 0$
, and vanishes when $x_1 = 0$![]() or $x_2 = 0$
or $x_2 = 0$![]() .
.
By the filtration property of $G$![]() , the commutator $[g_1, g_2]$
, the commutator $[g_1, g_2]$![]() is in $G_{i_1+i_2}$
is in $G_{i_1+i_2}$![]() . We moreover have that
. We moreover have that
by part (vi) of Lemma 3.1. Consequently, the element $[g_1, g_2]^{\vec {v}_1 \cdot \vec {v}_2}$![]() is contained in $G^{P}_{j_1+j_2}$
is contained in $G^{P}_{j_1+j_2}$![]() .
.
We handle the terms $g_\alpha ^{Q_\alpha (\vec {v}_1, \vec {v}_2)}$![]() in a similar manner. If $g_\alpha$
in a similar manner. If $g_\alpha$![]() is a commutator of $k_1$
is a commutator of $k_1$![]() copies of $g_1$
copies of $g_1$![]() and $k_2$
and $k_2$![]() copies of $g_2$
copies of $g_2$![]() , then $g_\alpha \in G_{k_1 i_1 + k_2 i_2}$
, then $g_\alpha \in G_{k_1 i_1 + k_2 i_2}$![]() by the filtration property of $G$
by the filtration property of $G$![]() . The polynomial $Q_\alpha$
. The polynomial $Q_\alpha$![]() can then be written as $Q_\alpha (x_1, x_2) = \sum \nolimits _{ \substack {1\leqslant l_1\leqslant k_1,\\ 1\leqslant l_2\leqslant k_2}}\beta _{l_1, l_2}x_1^{l_1} x_2^{l_2}$
can then be written as $Q_\alpha (x_1, x_2) = \sum \nolimits _{ \substack {1\leqslant l_1\leqslant k_1,\\ 1\leqslant l_2\leqslant k_2}}\beta _{l_1, l_2}x_1^{l_1} x_2^{l_2}$![]() , and so
, and so

by Lemma 3.1. Thus, $g_\alpha ^{Q_\alpha (\vec {v}_1, \vec {v}_2)}$![]() is contained in $G^{P}_{j_1+ j_2}$
is contained in $G^{P}_{j_1+ j_2}$![]() for each $\alpha$
for each $\alpha$![]() which implies that $[g_{1}^{\vec {v}_{1}}, g_{2}^{\vec {v}_{2}}]\in G^{P}_{j_1+j_2}$
which implies that $[g_{1}^{\vec {v}_{1}}, g_{2}^{\vec {v}_{2}}]\in G^{P}_{j_1+j_2}$![]() .
.
We now aim to prove the topological properties of $G^{P}$![]() and $G^{P}_j$
and $G^{P}_j$![]() , and we do this by following the arguments presented in [Reference Green and Tao17] after Lemma 3.5. Our first goal is to show that $G^{P}$
, and we do this by following the arguments presented in [Reference Green and Tao17] after Lemma 3.5. Our first goal is to show that $G^{P}$![]() is a connected, simply connected Lie group. By Lemma 3.1, we have a chain of subspaces
is a connected, simply connected Lie group. By Lemma 3.1, we have a chain of subspaces
that can be defined over $\mathbb {Q}$![]() . Letting $t_i = \dim \mathcal {Q}_{i,1}$
. Letting $t_i = \dim \mathcal {Q}_{i,1}$![]() , we can find a basis $\vec {v}_1, \ldots , \vec {v}_{t_s}$
, we can find a basis $\vec {v}_1, \ldots , \vec {v}_{t_s}$![]() for $\mathcal {Q}_{s,1}$
for $\mathcal {Q}_{s,1}$![]() satisfying the following properties:
satisfying the following properties:
(i) (Integrality) $\vec {v}_1, \ldots , \vec {v}_{t_s}$
 are all integer-valued,
are all integer-valued,(ii) (Partial span) $\vec {v}_1, \ldots , \vec {v}_{t_i}$
 span $\mathcal {Q}_{i,1}$
span $\mathcal {Q}_{i,1}$ for each $1\leqslant i\leqslant s$
for each $1\leqslant i\leqslant s$ ,
,(iii) (Row echelon form) For each $1\leqslant k\leqslant t_s$
 there exists an index $1\leqslant r_k\leqslant t$
there exists an index $1\leqslant r_k\leqslant t$ such that $\vec {v}_k(r_k)\neq 0$
such that $\vec {v}_k(r_k)\neq 0$ but $\vec {v}_l(r_k) = 0$
but $\vec {v}_l(r_k) = 0$ for all $k < l\leqslant t_s$
for all $k < l\leqslant t_s$ .
.
Fixing such a basis, we let $\deg (\vec {v}_k)$![]() to be the smallest $i$
to be the smallest $i$![]() such that $\vec {v}_k$
such that $\vec {v}_k$![]() is in $\mathcal {Q}_{i,1}$
is in $\mathcal {Q}_{i,1}$![]() . We can express each element of $G^{P}$
. We can express each element of $G^{P}$![]() as a finite product of $g_k^{\vec {v}_k}$
as a finite product of $g_k^{\vec {v}_k}$![]() where $g_k\in G_{\deg (\vec {v}_k)}$
where $g_k\in G_{\deg (\vec {v}_k)}$![]() and $1\leqslant k\leqslant t_s$
and $1\leqslant k\leqslant t_s$![]() . By applying the corollaries (40) and (41) to the Baker–Campbell–Hausdorff formula many times, we can then rewrite an arbitrary element of $G^{P}$
. By applying the corollaries (40) and (41) to the Baker–Campbell–Hausdorff formula many times, we can then rewrite an arbitrary element of $G^{P}$![]() as
as

where $g_k\in G_{\deg \vec {v}_k}$![]() for all $1\leqslant k\leqslant t_s$
for all $1\leqslant k\leqslant t_s$![]() . This representation is unique, implying that $G^{P}$
. This representation is unique, implying that $G^{P}$![]() is indeed a connected, simply connected Lie subgroup. From the fact that each $\vec {v}_k$
is indeed a connected, simply connected Lie subgroup. From the fact that each $\vec {v}_k$![]() has integer entries, it can be further deduced that $\varGamma ^{P}$
has integer entries, it can be further deduced that $\varGamma ^{P}$![]() is cocompact in $G^{P}$
is cocompact in $G^{P}$![]() . Similar arguments, where we replace $\mathcal {Q}_{i,1}$
. Similar arguments, where we replace $\mathcal {Q}_{i,1}$![]() in (12) by $\mathcal {Q}_{i,j}$
in (12) by $\mathcal {Q}_{i,j}$![]() , show that each $G^{P}_j$
, show that each $G^{P}_j$![]() is a closed connected subgroup of $G^{P}$
is a closed connected subgroup of $G^{P}$![]() and $\varGamma ^{P}_j = \varGamma ^{t}\cap G^{P}_j$
and $\varGamma ^{P}_j = \varGamma ^{t}\cap G^{P}_j$![]() is cocompact in $G^{P}_j$
is cocompact in $G^{P}_j$![]() . This implies that $G^{P}/\varGamma ^{P}$
. This implies that $G^{P}/\varGamma ^{P}$![]() is a filtered nilmanifold. Finally, the same argument combined with the fact that $\mathcal {P}_{i,j}=\mathcal {Q}_{i,j}=0$
is a filtered nilmanifold. Finally, the same argument combined with the fact that $\mathcal {P}_{i,j}=\mathcal {Q}_{i,j}=0$![]() whenever $j>i d$
whenever $j>i d$![]() shows that $G^{P}$
shows that $G^{P}$![]() is a subnilmanifold of $G^{t}$
is a subnilmanifold of $G^{t}$![]() when we endow $G^{t}$
when we endow $G^{t}$![]() with the filtration $(G^{t})'_j = (G_{\lceil \frac {j}{d}\rceil })^{t}$
with the filtration $(G^{t})'_j = (G_{\lceil \frac {j}{d}\rceil })^{t}$![]() .
.
The next lemma explains why we have imposed this particular filtration on $G^{P}$![]() .
.
Lemma 3.3 If $g\in {\textrm {poly}}(\mathbb {Z},G_\bullet )$![]() , then $g^{P}\in {\textrm {poly}}(\mathbb {Z}^{D},G^{P}_\bullet )$
, then $g^{P}\in {\textrm {poly}}(\mathbb {Z}^{D},G^{P}_\bullet )$![]() .
.
Proof. We first decompose

and note that $\vec {v}_{i,\textbf {j}}\in \mathcal {P}_{i, |\textbf {j}|}$![]() . Therefore, $g_i^{\vec {v}_{i,\textbf {j}}}\in G^{P}_{|\textbf {j}|}$
. Therefore, $g_i^{\vec {v}_{i,\textbf {j}}}\in G^{P}_{|\textbf {j}|}$![]() by definition of $G_{|\textbf {j}|}^{P}$
by definition of $G_{|\textbf {j}|}^{P}$![]() . Using (40) and (41), we regroup the terms of
. Using (40) and (41), we regroup the terms of

to bring all the elements involving the same monomial ${{\textbf {x}}\choose {\textbf {j}}}$![]() together. Thus, the Taylor coefficient of ${{\textbf {x}}\choose {\textbf {j}}}$
together. Thus, the Taylor coefficient of ${{\textbf {x}}\choose {\textbf {j}}}$![]() is of the form
is of the form

where the terms $g_\alpha ^{\vec {v}_{\alpha }}$![]() come from applying (40) and (41). For each label $\alpha$
come from applying (40) and (41). For each label $\alpha$![]() , the element $g_\alpha$
, the element $g_\alpha$![]() is a commutator consisting of $k_r$
is a commutator consisting of $k_r$![]() copies of $g_{i_r}$
copies of $g_{i_r}$![]() for $1\leqslant r\leqslant n$
for $1\leqslant r\leqslant n$![]() , and so $g_\alpha \in G_{i_1 k_1 + \cdots + i_n k_n}$
, and so $g_\alpha \in G_{i_1 k_1 + \cdots + i_n k_n}$![]() by the filtration property of $G$
by the filtration property of $G$![]() . The vector $\vec {v}_\alpha$
. The vector $\vec {v}_\alpha$![]() is a rational multiple of ${\vec {v}_{i_1, |\textbf {j}_1|}^{l_1}} \cdots {\vec {v}_{i_n, |\textbf {j}_n|}^{l_n}}$
is a rational multiple of ${\vec {v}_{i_1, |\textbf {j}_1|}^{l_1}} \cdots {\vec {v}_{i_n, |\textbf {j}_n|}^{l_n}}$![]() for some $1\leqslant l_1\leqslant k_1$
for some $1\leqslant l_1\leqslant k_1$![]() , …, $1\leqslant l_n\leqslant k_n$
, …, $1\leqslant l_n\leqslant k_n$![]() and $|\textbf {j}_1|+ \cdots + |\textbf {j}_n|\geqslant |\textbf {j}|$
and $|\textbf {j}_1|+ \cdots + |\textbf {j}_n|\geqslant |\textbf {j}|$![]() . Therefore, $\vec {v}_\alpha \in \mathcal {Q}_{i_1 l_1 + \cdots + i_n l_n, |\textbf {j}_1|+ \cdots + |\textbf {j}_n|}$
. Therefore, $\vec {v}_\alpha \in \mathcal {Q}_{i_1 l_1 + \cdots + i_n l_n, |\textbf {j}_1|+ \cdots + |\textbf {j}_n|}$![]() by part (vi) of Lemma 3.1. It follows from parts (iv) and (v) of the same lemma that
by part (vi) of Lemma 3.1. It follows from parts (iv) and (v) of the same lemma that
implying that $g_\alpha ^{\vec {v}_\alpha }\in G^{P}_{|\textbf {j}|}$![]() for each $\alpha$
for each $\alpha$![]() . Thus, the coefficient (14) is in $G^{P}_{|\textbf {j}|}$
. Thus, the coefficient (14) is in $G^{P}_{|\textbf {j}|}$![]() , as claimed.
, as claimed.
Even though the definition of $\mathcal {Q}_{i,j}$![]() guarantees that $G^{P}$
guarantees that $G^{P}$![]() is filtration, it is not very handy to work with because of the terms $\mathcal {Q}_{i_1,j_1}\cdot \mathcal {Q}_{i_2,j_2}$
is filtration, it is not very handy to work with because of the terms $\mathcal {Q}_{i_1,j_1}\cdot \mathcal {Q}_{i_2,j_2}$![]() that appear there. However, many of the configurations that we look at satisfy a condition that allows us to work with $\mathcal {P}_{i,j}$
that appear there. However, many of the configurations that we look at satisfy a condition that allows us to work with $\mathcal {P}_{i,j}$![]() instead.
instead.
Definition 3.4 (Filtration condition) We say that an integral polynomial ${\vec {P}\in \mathbb {Q}[\textbf {x}]^{t}}$![]() satisfies the filtration condition if $\mathcal {P}_{i_1, j_1}\cdot \mathcal {P}_{i_2, j_2}\subseteq \mathcal {P}_{i_1+i_2, j_1 + j_2}$
satisfies the filtration condition if $\mathcal {P}_{i_1, j_1}\cdot \mathcal {P}_{i_2, j_2}\subseteq \mathcal {P}_{i_1+i_2, j_1 + j_2}$![]() for all $i_1, i_2, j_1, j_2\geqslant 1$
for all $i_1, i_2, j_1, j_2\geqslant 1$![]() .
.
Lemma 3.5 Suppose an integral polynomial ${\vec {P}\in \mathbb {Q}[\textbf {x}]^{t}}$![]() satisfies the filtration condition. Then $\mathcal {P}_{i,j}=\mathcal {Q}_{i,j}$
satisfies the filtration condition. Then $\mathcal {P}_{i,j}=\mathcal {Q}_{i,j}$![]() for all $i,j\in \mathbb {N}_+$
for all $i,j\in \mathbb {N}_+$![]() .
.
Proof. Whenever $i=1$![]() or $j=1$
or $j=1$![]() , the lemma follows by definition. Other cases follow by induction on $(i,j)$
, the lemma follows by definition. Other cases follow by induction on $(i,j)$![]() .
.
For progressions satisfying the filtration condition, we can relate the group $G^{P}_j$![]() to $G^{P}_{j+1}$
to $G^{P}_{j+1}$![]() in a handy manner.
in a handy manner.
Lemma 3.6 Let $j\in \mathbb {N}_+$![]() , and suppose $\vec {P}$
, and suppose $\vec {P}$![]() satisfies the filtration condition. For any $i\in \mathbb {N}_+$
satisfies the filtration condition. For any $i\in \mathbb {N}_+$![]() , let $X_{i,j+1}=\{\vec {v}_1, \ldots , \vec {v}_{l_i}\}\subseteq \mathbb {Z}^{t}$
, let $X_{i,j+1}=\{\vec {v}_1, \ldots , \vec {v}_{l_i}\}\subseteq \mathbb {Z}^{t}$![]() be a basis for $\mathcal {P}_{i,j+1}$
be a basis for $\mathcal {P}_{i,j+1}$![]() that extends to a basis $X_{i,j}=\{\vec {v}_1, \ldots , \vec {v}_{l_i}, \ldots , \vec {v}_{l_i+k_i}\}\subseteq \mathbb {Z}^{t}$
that extends to a basis $X_{i,j}=\{\vec {v}_1, \ldots , \vec {v}_{l_i}, \ldots , \vec {v}_{l_i+k_i}\}\subseteq \mathbb {Z}^{t}$![]() for $\mathcal {P}_{i,j}$
for $\mathcal {P}_{i,j}$![]() . Then
. Then
Proof. Since $\vec {P}$![]() satisfies the filtration condition, we have by Lemma 3.5 that $\mathcal {P}_{i,j}=\mathcal {Q}_{i,j}$
satisfies the filtration condition, we have by Lemma 3.5 that $\mathcal {P}_{i,j}=\mathcal {Q}_{i,j}$![]() . By definition of $G^{P}_j$
. By definition of $G^{P}_j$![]() , the group is generated by elements of the form $g^{\vec {v}}$
, the group is generated by elements of the form $g^{\vec {v}}$![]() for $i\in \mathbb {N}_+$
for $i\in \mathbb {N}_+$![]() , $g\in G_i$
, $g\in G_i$![]() , $\vec {v}=\sum \nolimits _{r=1}^{l_i+k_i}a_r\vec {v}_r$
, $\vec {v}=\sum \nolimits _{r=1}^{l_i+k_i}a_r\vec {v}_r$![]() and $a_r\in \mathbb {R}$
and $a_r\in \mathbb {R}$![]() . Letting $\vec {w}=\sum \nolimits _{r=1}^{l_i}a_r\vec {v}_r$
. Letting $\vec {w}=\sum \nolimits _{r=1}^{l_i}a_r\vec {v}_r$![]() , we observe that $g^{\vec {w}}\in G^{P}_{j+1}$
, we observe that $g^{\vec {w}}\in G^{P}_{j+1}$![]() , and so
, and so
Thus each generator $g^{\vec {v}}$![]() in $G^{P}_{j}$
in $G^{P}_{j}$![]() is a product of an element from $G^{P}_{j+1}$
is a product of an element from $G^{P}_{j+1}$![]() and $h_r^{\vec {v}_r}$
and $h_r^{\vec {v}_r}$![]() for $l_i+1 \leqslant r\leqslant l_i+k_i$
for $l_i+1 \leqslant r\leqslant l_i+k_i$![]() and $h_r=g^{a_r}\in G_i$
and $h_r=g^{a_r}\in G_i$![]() .
.
3.1. Progressions of a special form
The technical results presented so far in this section work for arbitrary integral polynomial maps. However, we shall mostly work with polynomial maps of the form
For configurations of this type, we can relate the coefficients of ${{\vec {P}(x,y)}\choose {i}}$![]() to the coefficients of ${{\vec {P}(x,y)}\choose {i-k}}$
to the coefficients of ${{\vec {P}(x,y)}\choose {i-k}}$![]() for $k>0$
for $k>0$![]() in a way that will prove useful in future sections.
in a way that will prove useful in future sections.
Lemma 3.7 Let $i, k,l\in \mathbb {N}$![]() satisfy $i>0$
satisfy $i>0$![]() , $k\leqslant i$
, $k\leqslant i$![]() and $l\leqslant (i-k)d$
and $l\leqslant (i-k)d$![]() . Suppose $\vec {P}$
. Suppose $\vec {P}$![]() is an integral polynomial map of the form (15). Then the coefficient of ${{x}\choose {k}}{{y}\choose {l}}$
is an integral polynomial map of the form (15). Then the coefficient of ${{x}\choose {k}}{{y}\choose {l}}$![]() in ${{\vec {P}(x,y)}\choose {i}}$
in ${{\vec {P}(x,y)}\choose {i}}$![]() is the same as the coefficient of ${{y}\choose {l}}$
is the same as the coefficient of ${{y}\choose {l}}$![]() in ${{\vec {P}(x,y)}\choose {i-k}}$
in ${{\vec {P}(x,y)}\choose {i-k}}$![]() .
.
Proof. If $\vec {P}$![]() is of the form (15), then $\vec {P}(x,y)=\vec {1}x + \vec {P}(0,y)$
is of the form (15), then $\vec {P}(x,y)=\vec {1}x + \vec {P}(0,y)$![]() . Using the property
. Using the property

which can be proved by looking at two ways in which one picks $i$![]() elements from a union of disjoint sets of size $a_1$
elements from a union of disjoint sets of size $a_1$![]() , …, $a_l$
, …, $a_l$![]() , respectively, we can rewrite
, respectively, we can rewrite

for some $\vec {v}_{l,n}\in \mathbb {Z}^{t}$![]() . Replacing $i$
. Replacing $i$![]() by $i-k$
by $i-k$![]() , we obtain
, we obtain

The lemma follows by taking $n=i-k$![]() in both cases and fixing $1\leqslant l\leqslant (i-k)d$
in both cases and fixing $1\leqslant l\leqslant (i-k)d$![]() .
.
Lemma 3.8 Suppose $\vec {P}$![]() is an integral polynomial map of the form (15). Then $\mathcal {P}_{i,j}\subseteq \mathcal {P}_{i+1,j+1}$
is an integral polynomial map of the form (15). Then $\mathcal {P}_{i,j}\subseteq \mathcal {P}_{i+1,j+1}$![]() for all $i,j\in \mathbb {N}_+$
for all $i,j\in \mathbb {N}_+$![]() .
.
Proof. By Lemma 3.7, the coefficient $\vec {v}$![]() of ${{x}\choose {k}}{{y}\choose {l}}$
of ${{x}\choose {k}}{{y}\choose {l}}$![]() in ${{\vec {P}(x,y)}\choose {i}}$
in ${{\vec {P}(x,y)}\choose {i}}$![]() is the same as the coefficient of ${{x}\choose {k+1}}{{y}\choose {l}}$
is the same as the coefficient of ${{x}\choose {k+1}}{{y}\choose {l}}$![]() in ${{\vec {P}(x,y)}\choose {i+1}}$
in ${{\vec {P}(x,y)}\choose {i+1}}$![]() whenever $l\leqslant (i-k)d$
whenever $l\leqslant (i-k)d$![]() . If $k+l\geqslant j$
. If $k+l\geqslant j$![]() , then $k+1+l\geqslant j+1$
, then $k+1+l\geqslant j+1$![]() , and so if $\vec {v}\in \mathcal {P}_{i,j}$
, and so if $\vec {v}\in \mathcal {P}_{i,j}$![]() , then $\vec {v}\in \mathcal {P}_{i+1,j+1}$
, then $\vec {v}\in \mathcal {P}_{i+1,j+1}$![]() .
.
We remark that the property $\mathcal {P}_{i,j}\subset \mathcal {P}_{i+1,j+1}$![]() for all $i,j\in \mathbb {N}_+$
for all $i,j\in \mathbb {N}_+$![]() also holds for an arbitrary integral polynomial map $\vec {P}$
also holds for an arbitrary integral polynomial map $\vec {P}$![]() that satisfies the filtration condition and $\vec {1}\in \mathcal {P}_{1,1}$
that satisfies the filtration condition and $\vec {1}\in \mathcal {P}_{1,1}$![]() . However, the advantage of assuming (15) comes from the fact that we do not need $\vec {P}$
. However, the advantage of assuming (15) comes from the fact that we do not need $\vec {P}$![]() to satisfy the filtration condition in this case.
to satisfy the filtration condition in this case.
Lemma 3.8 has one important corollary that we shall use several times.
Corollary 3.9 Let $\vec {P}$![]() be of the form (15), $i,j\in \mathbb {N}_+$
be of the form (15), $i,j\in \mathbb {N}_+$![]() , $\vec {v}\in \mathcal {P}_{i,j}\cap \mathbb {Z}^{t}$
, $\vec {v}\in \mathcal {P}_{i,j}\cap \mathbb {Z}^{t}$![]() , and let $\eta : G^{P}\to \mathbb {R}$
, and let $\eta : G^{P}\to \mathbb {R}$![]() be a horizontal character that vanishes on $G_{j+1}^{P}$
be a horizontal character that vanishes on $G_{j+1}^{P}$![]() . Then the map
. Then the map
is an $i$![]() th level character.
th level character.
Proof. It is straightforward to see that $\xi$![]() is a group homomorphism. Since $\vec {v}$
is a group homomorphism. Since $\vec {v}$![]() has integer entries, the element $g^{\vec {v}}\in \varGamma ^{P}$
has integer entries, the element $g^{\vec {v}}\in \varGamma ^{P}$![]() for any $g\in \varGamma _i$
for any $g\in \varGamma _i$![]() , and so $\xi (\varGamma _i)\in \mathbb {Z}$
, and so $\xi (\varGamma _i)\in \mathbb {Z}$![]() . It vanishes on $[G,G]\cap G_i$
. It vanishes on $[G,G]\cap G_i$![]() because its codomain is abelian, and to show that it is an $i$
because its codomain is abelian, and to show that it is an $i$![]() th level character, it remains to show that $\xi |_{G_{i+1}}=0$
th level character, it remains to show that $\xi |_{G_{i+1}}=0$![]() . Suppose $g\in G_{i+1}$
. Suppose $g\in G_{i+1}$![]() . From Lemma 3.8, we have that $\vec {v}\in \mathcal {P}_{i+1,j+1}$
. From Lemma 3.8, we have that $\vec {v}\in \mathcal {P}_{i+1,j+1}$![]() , and so $g^{\vec {v}}\in G_{j+1}^{P}$
, and so $g^{\vec {v}}\in G_{j+1}^{P}$![]() . It follows that $\xi (g^{\vec {v}})=0$
. It follows that $\xi (g^{\vec {v}})=0$![]() from the fact that $\eta$
from the fact that $\eta$![]() vanishes on $G_{j+1}^{P}$
vanishes on $G_{j+1}^{P}$![]() .
.
4. An equidistribution result for $x, x+y, x+y^{2}, x+y+y^{2}$
The goal of the next few sections is to prove Theorem 1.8 for various configurations for which the theorem holds. We give them a name, so that it is easier to refer to them in later sections.
Definition 4.1 (Equidistributing progressions) Let $\vec {P}=(P_1, \ldots , P_t)\in \mathbb {Q}[\textbf {x}]^{t}$![]() be an integral polynomial map. We say that $\vec {P}$
be an integral polynomial map. We say that $\vec {P}$![]() equidistributes if for each ${s, D\in \mathbb {N}_+}$
equidistributes if for each ${s, D\in \mathbb {N}_+}$![]() , $M>0$
, $M>0$![]() , a filtered nilmanifold $G/\varGamma$
, a filtered nilmanifold $G/\varGamma$![]() of degree $s$
of degree $s$![]() and complexity $M$
and complexity $M$![]() , and a $p$
, and a $p$![]() -periodic, $A$
-periodic, $A$![]() -irrational sequence $g\in {\textrm {poly}}(\mathbb {Z},G_\bullet )$
-irrational sequence $g\in {\textrm {poly}}(\mathbb {Z},G_\bullet )$![]() satisfying $g(0)=1$
satisfying $g(0)=1$![]() , the sequence $g^{P}\in {\textrm {poly}}(\mathbb {Z}^{D},G^{P}_\bullet )$
, the sequence $g^{P}\in {\textrm {poly}}(\mathbb {Z}^{D},G^{P}_\bullet )$![]() is $o_{A\to \infty , M}(1)$
is $o_{A\to \infty , M}(1)$![]() -equidistributed on $G^{P}/\varGamma ^{P}$
-equidistributed on $G^{P}/\varGamma ^{P}$![]() .
.
We start with a seemingly simple example

It is a special case of the progression discussed in § 5. However, we analyse it separately to give a concrete example of how our general argument works.
We start by obtaining the formulas for $\mathcal {P}_{i,j}$![]() for various values of $i,j\in \mathbb {N}_+$
for various values of $i,j\in \mathbb {N}_+$![]() . From (17), we deduce that
. From (17), we deduce that

where
Our next goal is to deduce expressions for $\mathcal {P}_{i,j}$![]() whenever $i>1$
whenever $i>1$![]() .
.
Lemma 4.2 For $i>1$![]() , the following holds:
, the following holds:

Proof. The case $j>2i$![]() follows from the fact that the polynomial map ${{\vec {P}(x,y)}\choose {i}}$
follows from the fact that the polynomial map ${{\vec {P}(x,y)}\choose {i}}$![]() has degree $2i$
has degree $2i$![]() . For the case $j=2i$
. For the case $j=2i$![]() , note that the only monomial of ${{\vec {P}(x,y)}\choose {i}}$
, note that the only monomial of ${{\vec {P}(x,y)}\choose {i}}$![]() of degree $2i$
of degree $2i$![]() is ${{y}\choose {2i}}$
is ${{y}\choose {2i}}$![]() , which comes from the term $y^{2}$
, which comes from the term $y^{2}$![]() in $\vec {P}(x,y)$
in $\vec {P}(x,y)$![]() , and one can verify directly that the coefficient of ${{y}\choose {2i}}$
, and one can verify directly that the coefficient of ${{y}\choose {2i}}$![]() in ${{\vec {P}(x,y)}\choose {i}}$
in ${{\vec {P}(x,y)}\choose {i}}$![]() is $(0,0,{(2i)!}/{i!}, {(2i)!}/{i!})$
is $(0,0,{(2i)!}/{i!}, {(2i)!}/{i!})$![]() . Consequently, $\mathcal {P}_{i,2i}={\textrm {Span}}\{\vec {v}_3\}$
. Consequently, $\mathcal {P}_{i,2i}={\textrm {Span}}\{\vec {v}_3\}$![]() .
.
In the case $i+1\leqslant j\leqslant 2i-1$![]() , we have
, we have
because the polynomials ${{x}\choose {i}}$![]() and ${{x+y}\choose {i}}$
and ${{x+y}\choose {i}}$![]() both have degree $i$
both have degree $i$![]() , and we claim that (18) is an equality. Since $\mathcal {P}_{i,2i}\subseteq \mathcal {P}_{i,j}$
, and we claim that (18) is an equality. Since $\mathcal {P}_{i,2i}\subseteq \mathcal {P}_{i,j}$![]() , we know that $\mathcal {P}_{i,j}$
, we know that $\mathcal {P}_{i,j}$![]() contains $\vec {v}_3$
contains $\vec {v}_3$![]() , and it remains to show that $\mathcal {P}_{i,j}$
, and it remains to show that $\mathcal {P}_{i,j}$![]() contains a vector of the form $(0,0,a,b)$
contains a vector of the form $(0,0,a,b)$![]() for some $a \neq b$
for some $a \neq b$![]() . To this goal, we look at the coefficient of ${{y}\choose {2i-1}}$
. To this goal, we look at the coefficient of ${{y}\choose {2i-1}}$![]() in ${{\vec {P}(x,y)}\choose {i}}$
in ${{\vec {P}(x,y)}\choose {i}}$![]() . Note that
. Note that
where $R(y)$![]() has degree $2i-2$
has degree $2i-2$![]() . In particular, the polynomial $y{{y^{2}}\choose {i-1}}$
. In particular, the polynomial $y{{y^{2}}\choose {i-1}}$![]() has degree $2i-1$
has degree $2i-1$![]() , and so has a non-zero coefficient at ${{y}\choose {2i-1}}$
, and so has a non-zero coefficient at ${{y}\choose {2i-1}}$![]() . Therefore, the coefficient of ${{y}\choose {2i-1}}$
. Therefore, the coefficient of ${{y}\choose {2i-1}}$![]() in ${{\vec {P}(x,y)}\choose {i}}$
in ${{\vec {P}(x,y)}\choose {i}}$![]() is of the form $(0,0,a,b)$
is of the form $(0,0,a,b)$![]() for distinct integers $a\neq b$
for distinct integers $a\neq b$![]() , implying that $\mathcal {P}_{i,j}=\{0\}\times \{0\}\times \mathbb {R}\times \mathbb {R}$
, implying that $\mathcal {P}_{i,j}=\{0\}\times \{0\}\times \mathbb {R}\times \mathbb {R}$![]() , as claimed.
, as claimed.
To handle the case $1\leqslant j\leqslant i$![]() , we look at $\mathcal {P}_{i,i}$
, we look at $\mathcal {P}_{i,i}$![]() and note that $\mathcal {P}_{i,j}\supseteq \mathcal {P}_{i,i}$
and note that $\mathcal {P}_{i,j}\supseteq \mathcal {P}_{i,i}$![]() for these values of $j$
for these values of $j$![]() by Lemma 3.1. By the previous case, we already know that $\mathcal {P}_{i,j}\supseteq \{0\}\times \{0\}\times \mathbb {R} \times \mathbb {R}$
by Lemma 3.1. By the previous case, we already know that $\mathcal {P}_{i,j}\supseteq \{0\}\times \{0\}\times \mathbb {R} \times \mathbb {R}$![]() . The space $\mathcal {P}_{i,i}$
. The space $\mathcal {P}_{i,i}$![]() moreover contains $\vec {v}_1$
moreover contains $\vec {v}_1$![]() , which is the coefficient of ${{x}\choose {i}}$
, which is the coefficient of ${{x}\choose {i}}$![]() in ${{\vec {P}(x,y)}\choose {i}}$
in ${{\vec {P}(x,y)}\choose {i}}$![]() , and $\vec {v}_2$
, and $\vec {v}_2$![]() , which is the coefficient of ${{x}\choose {i-1}}y$
, which is the coefficient of ${{x}\choose {i-1}}y$![]() by Lemma 3.7 and (17). Thus, $\mathcal {P}_{i,i}$
by Lemma 3.7 and (17). Thus, $\mathcal {P}_{i,i}$![]() is all of $\mathbb {R}^{4}$
is all of $\mathbb {R}^{4}$![]() .
.
Having established the structure of $\mathcal {P}_{i,j}$![]() , it is straightforward to establish the following lemma.
, it is straightforward to establish the following lemma.
Corollary 4.3 The polynomial map $\vec {P}$![]() satisfies the filtration condition.
satisfies the filtration condition.
Proof. The proof proceeds by verifying that $\mathcal {P}_{i_1,j_1}\cdot \mathcal {P}_{i_2,j_2}\subseteq \mathcal {P}_{i_1+i_2, j_1+j_2}$![]() for all ${i_1,i_2,j_1,j_2\geqslant 1}$
for all ${i_1,i_2,j_1,j_2\geqslant 1}$![]() on a case-by-case basis using Lemma 4.2. The details are rather tedious and unsophisticated; therefore, we leave them to the reader.
on a case-by-case basis using Lemma 4.2. The details are rather tedious and unsophisticated; therefore, we leave them to the reader.
Using Lemma 4.2, we get an explicit presentation for $G^{P}_j$![]() which tells us how this subgroup distinguishes from $G^{P}_{j+1}$
which tells us how this subgroup distinguishes from $G^{P}_{j+1}$![]() .
.
Lemma 4.4 For $j=1$![]() , we have
, we have
If $j\geqslant 1$![]() is even, then
is even, then
If $j\geqslant 3$![]() is odd, then
is odd, then
Proof. The lemma follows from combining Lemmas 4.3 and 3.6 with the structural information on $\mathcal {P}_{i,j}$![]() that we obtain from Lemma 4.2.
that we obtain from Lemma 4.2.
Having established the structure of the subgroups $G^{P}_j$![]() , we are ready to prove that $\vec {P}$
, we are ready to prove that $\vec {P}$![]() equidistributes.
equidistributes.
Theorem 4.5 $x, x+y, x+y^{2}, x+y+y^{2}$![]() equidistributes
equidistributes
Let $G/\varGamma$![]() be a filtered nilmanifold of degree $s$
be a filtered nilmanifold of degree $s$![]() and complexity $M$
and complexity $M$![]() . Suppose $g\in {\textrm {poly}}(\mathbb {Z},G_\bullet )$
. Suppose $g\in {\textrm {poly}}(\mathbb {Z},G_\bullet )$![]() is $p$
is $p$![]() -periodic, $A$
-periodic, $A$![]() -irrational, and satisfies $g(0)=1$
-irrational, and satisfies $g(0)=1$![]() . Then the sequence $g^{P}\in {\textrm {poly}}(\mathbb {Z}^{2},G^{P}_\bullet )$
. Then the sequence $g^{P}\in {\textrm {poly}}(\mathbb {Z}^{2},G^{P}_\bullet )$![]() is $O_{M}(A^{-c_M})$
is $O_{M}(A^{-c_M})$![]() -equidistributed on $G^{P}/\varGamma ^{P}$
-equidistributed on $G^{P}/\varGamma ^{P}$![]() for some $c_M>0$
for some $c_M>0$![]() .
.
In the proof of Theorem 4.5, we shall use the following useful lemma.
Lemma 4.6 (Integer multiples do not matter) Let $j\geqslant 1$![]() , and suppose that $\eta : G \to \mathbb {R}$
, and suppose that $\eta : G \to \mathbb {R}$![]() is a horizontal character such that $\eta \circ g^{P}$
is a horizontal character such that $\eta \circ g^{P}$![]() is $\mathbb {Z}$
is $\mathbb {Z}$![]() -valued and $\eta |_{G_{j+1}^{P}}=0$
-valued and $\eta |_{G_{j+1}^{P}}=0$![]() . Suppose moreover that for some $\vec {v}\in \mathcal {P}_{i,j}\cap \mathbb {Z}^{4}$
. Suppose moreover that for some $\vec {v}\in \mathcal {P}_{i,j}\cap \mathbb {Z}^{4}$![]() there exists a non-zero integer $a$
there exists a non-zero integer $a$![]() such that $\eta (g_i^{a\vec {v}})\in \mathbb {Z}$
such that $\eta (g_i^{a\vec {v}})\in \mathbb {Z}$![]() . Then $\eta (g_i^{\vec {v}})\in \mathbb {Z}$
. Then $\eta (g_i^{\vec {v}})\in \mathbb {Z}$![]() assuming that $p$
assuming that $p$![]() is sufficiently large with respect to $a$
is sufficiently large with respect to $a$![]() .
.
There is nothing special about our particular progression here – Lemma 4.6 works for any polynomial progression; therefore, we shall also use it for progressions examined in the next sections.
Proof. By Lemma C.1, $g_i^{p^{i}}\in \varGamma _i$![]() mod $G_{i+1}$
mod $G_{i+1}$![]() , and so $g_i^{\vec {v}} = (\gamma _i h)^{\vec {v}}$
, and so $g_i^{\vec {v}} = (\gamma _i h)^{\vec {v}}$![]() for some $\gamma _i\in \varGamma _i$
for some $\gamma _i\in \varGamma _i$![]() and $h\in G_{i+1}$
and $h\in G_{i+1}$![]() . Using (40), Lemmas 3.1 and 3.8, we note that $h^{\vec {v}}\in G_{j+1}^{P}$
. Using (40), Lemmas 3.1 and 3.8, we note that $h^{\vec {v}}\in G_{j+1}^{P}$![]() , and similarly for commutators emerging from applying (40). We, therefore, have $g_i^{p^{i}\vec {v}}\in \varGamma _j^{P}\mod G^{P}_{j+1}$
, and similarly for commutators emerging from applying (40). We, therefore, have $g_i^{p^{i}\vec {v}}\in \varGamma _j^{P}\mod G^{P}_{j+1}$![]() , from which we deduce that $p^{i}\eta (g_i^{\vec {v}})\in \mathbb {Z}$
, from which we deduce that $p^{i}\eta (g_i^{\vec {v}})\in \mathbb {Z}$![]() . The assumption that ${\eta (g_i^{a\vec {v}})\in \mathbb {Z}}$
. The assumption that ${\eta (g_i^{a\vec {v}})\in \mathbb {Z}}$![]() for some non-zero integer $a$
for some non-zero integer $a$![]() further implies that $\gcd (a, p^{i})\eta (g_i^{\vec {v}})\in \mathbb {Z}$
further implies that $\gcd (a, p^{i})\eta (g_i^{\vec {v}})\in \mathbb {Z}$![]() . Taking $p$
. Taking $p$![]() sufficiently large guarantees that $\gcd (a, p^{i})=1$
sufficiently large guarantees that $\gcd (a, p^{i})=1$![]() , and so $\eta (g_i^{\vec {v}})\in \mathbb {Z}$
, and so $\eta (g_i^{\vec {v}})\in \mathbb {Z}$![]() .
.
The general strategy of our proof of Theorem 4.5, as well as Theorems 5.3, 6.3 and 12.6, follows the methods used in [Reference Green and Tao17] to prove Theorem 1.11, the counting lemma. However, the technical details are quite different due to the fact that progressions dealt with in these theorems are no longer homogeneous. The main difficulty comes from the fact that the coefficients of polynomial maps of the form $\eta \circ g^{P}(x,y)$![]() for some horizontal character $\eta$
for some horizontal character $\eta$![]() have contributions coming from ${{\vec {P}(x,y)}\choose {i}}$
have contributions coming from ${{\vec {P}(x,y)}\choose {i}}$![]() for several values of $i$
for several values of $i$![]() . This difficulty is not present when $\vec {P}$
. This difficulty is not present when $\vec {P}$![]() is a linear form in several variables, as then each power ${{\vec {P}}\choose {i}}$
is a linear form in several variables, as then each power ${{\vec {P}}\choose {i}}$![]() is a homogeneous polynomial map of a different degree.
is a homogeneous polynomial map of a different degree.
Proof of Theorem 4.5. Suppose that the sequence $g^{P}\in {\textrm {poly}}(\mathbb {Z}^{2},G^{P}_\bullet )$![]() is not $O_{M}(A^{-c_M})$
is not $O_{M}(A^{-c_M})$![]() -equidistributed. By Theorem 2.9, there exists a non-trivial horizontal character $\eta :G^{P}\to \mathbb {R}$
-equidistributed. By Theorem 2.9, there exists a non-trivial horizontal character $\eta :G^{P}\to \mathbb {R}$![]() of complexity at most $cA$
of complexity at most $cA$![]() for an appropriately chosen $c>0$
for an appropriately chosen $c>0$![]() , for which the polynomial $\eta \circ g^{P}$
, for which the polynomial $\eta \circ g^{P}$![]() is $\mathbb {Z}$
is $\mathbb {Z}$![]() -valued. Let $j$
-valued. Let $j$![]() be the largest natural number such that $\eta |_{G^{P}_j}\neq 0$
be the largest natural number such that $\eta |_{G^{P}_j}\neq 0$![]() . By assumption, $\eta$
. By assumption, $\eta$![]() annihilates ${G^{P}_{j+1}}$
annihilates ${G^{P}_{j+1}}$![]() .
.
We use the maximality of $j$![]() , the properties of $\eta$
, the properties of $\eta$![]() , and the structural information on $G^{P}$
, and the structural information on $G^{P}$![]() contained in Lemma 4.4 to contradict the $A$
contained in Lemma 4.4 to contradict the $A$![]() -irrationality of $g$
-irrationality of $g$![]() . We do this by inspecting the coefficients of $\eta \circ g^{P}$
. We do this by inspecting the coefficients of $\eta \circ g^{P}$![]() .
.
We first do the model case $j=1$![]() ; it is different from and less complicated than the case $j>1$
; it is different from and less complicated than the case $j>1$![]() , and it can be used to illustrate the argument for the latter. Assuming $j=1$
, and it can be used to illustrate the argument for the latter. Assuming $j=1$![]() , we have
, we have
as all the other terms are annihilated by $\eta$![]() . Using the fact that $\eta \circ g^{P}(x,y)\in \mathbb {Z}$
. Using the fact that $\eta \circ g^{P}(x,y)\in \mathbb {Z}$![]() for all $x,y\in \mathbb {F}_p$
for all $x,y\in \mathbb {F}_p$![]() , we deduce that $\eta (g_1^{\vec {v}_1})$
, we deduce that $\eta (g_1^{\vec {v}_1})$![]() and $\eta (g_1^{\vec {v}_2})$
and $\eta (g_1^{\vec {v}_2})$![]() are both in $\mathbb {Z}$
are both in $\mathbb {Z}$![]() .
.
We define
for each $i = 1,2$![]() and $h\in G_1$
and $h\in G_1$![]() . By Corollary 3.9, the functions $\xi _i$
. By Corollary 3.9, the functions $\xi _i$![]() are 1-st level characters that annihilate $g_1$
are 1-st level characters that annihilate $g_1$![]() . By Lemma 4.4, if both of them are trivial, then so is $\eta$
. By Lemma 4.4, if both of them are trivial, then so is $\eta$![]() ; therefore, at least one of them is non-trivial. The bound on the modulus of $\eta$
; therefore, at least one of them is non-trivial. The bound on the modulus of $\eta$![]() and the fact that the vectors $\vec {v}_1$
and the fact that the vectors $\vec {v}_1$![]() have entries of size $O(1)$
have entries of size $O(1)$![]() imply that $|\xi _{i}|\leqslant A$
imply that $|\xi _{i}|\leqslant A$![]() , provided that the constant $c$
, provided that the constant $c$![]() is appropriately chosen. This contradicts the $A$
is appropriately chosen. This contradicts the $A$![]() -irrationality of $g$
-irrationality of $g$![]() , implying that $g^{P}$
, implying that $g^{P}$![]() is $O_{M}(A^{-c_M})$
is $O_{M}(A^{-c_M})$![]() -equidistributed.
-equidistributed.
For the rest of the proof, we assume that $j>1$![]() . We split into two cases based on the parity of $j$
. We split into two cases based on the parity of $j$![]() . We shall only give the proof when $j$
. We shall only give the proof when $j$![]() is even, as the other case follows similarly. First, the assumption that $\eta \circ g^{P}$
is even, as the other case follows similarly. First, the assumption that $\eta \circ g^{P}$![]() is $\mathbb {Z}$
is $\mathbb {Z}$![]() -valued implies that $\eta (g_j^{\vec {v}_1})\in \mathbb {Z}$
-valued implies that $\eta (g_j^{\vec {v}_1})\in \mathbb {Z}$![]() , since this is the coefficient of ${{x}\choose {j}}$
, since this is the coefficient of ${{x}\choose {j}}$![]() . Second, we have $\eta (g_j^{\vec {v}_2})\in \mathbb {Z}$
. Second, we have $\eta (g_j^{\vec {v}_2})\in \mathbb {Z}$![]() , as this is the coefficient of ${{x}\choose {j-1}}y$
, as this is the coefficient of ${{x}\choose {j-1}}y$![]() by Lemma 3.7 and (17). By Lemma 4.2, we have $g_j^{\vec {v}_3}, g_j^{\vec {v}_4}\in G^{P}_{j+1}$
by Lemma 3.7 and (17). By Lemma 4.2, we have $g_j^{\vec {v}_3}, g_j^{\vec {v}_4}\in G^{P}_{j+1}$![]() , implying $\eta (g_j^{\vec {v}_3})= \eta (g_j^{\vec {v}_4})=0$
, implying $\eta (g_j^{\vec {v}_3})= \eta (g_j^{\vec {v}_4})=0$![]() . Using the fact that each vector in $\mathbb {Z}^{4}$
. Using the fact that each vector in $\mathbb {Z}^{4}$![]() is an integral linear combination of $\vec {v}_1, \vec {v}_2, \vec {v}_3, \vec {v}_4$
is an integral linear combination of $\vec {v}_1, \vec {v}_2, \vec {v}_3, \vec {v}_4$![]() , we obtain that
, we obtain that
for any $\vec {v}\in \mathbb {Z}^{4}$![]() .
.
Our goal now is to show that $\eta (g_{{j}/{2}}^{\vec {v}_3})\in \mathbb {Z}$![]() . To this end, we look at the coefficient of ${{y}\choose {j}}$
. To this end, we look at the coefficient of ${{y}\choose {j}}$![]() in $\eta \circ g^{P}(x,y)$
in $\eta \circ g^{P}(x,y)$![]() , which is of the form
, which is of the form

for some $\vec {w}_i\in \mathcal {P}_{i,j}$![]() . Note that there is no contribution coming from $g_i$
. Note that there is no contribution coming from $g_i$![]() for $i<{j}/{2}$
for $i<{j}/{2}$![]() because $\deg ({{P(x,y)}\choose {i}})< j$
because $\deg ({{P(x,y)}\choose {i}})< j$![]() for these values of $i$
for these values of $i$![]() . If $i\neq j$
. If $i\neq j$![]() and $i\geqslant {j}/{2}+1$
and $i\geqslant {j}/{2}+1$![]() , then $\vec {w}_i\in {\textrm {Span}}\{\vec {v}_3,\vec {v}_4\}$
, then $\vec {w}_i\in {\textrm {Span}}\{\vec {v}_3,\vec {v}_4\}$![]() because ${{x}\choose {i}}$
because ${{x}\choose {i}}$![]() and ${{x+y}\choose {i}}$
and ${{x+y}\choose {i}}$![]() are homogeneous polynomials of degree $i$
are homogeneous polynomials of degree $i$![]() , and so $g_i^{\vec {w}_i}\in G_{j+1}^{P}$
, and so $g_i^{\vec {w}_i}\in G_{j+1}^{P}$![]() by Lemma 4.2. Therefore, $\eta (g_i^{\vec {w}_i})=0$
by Lemma 4.2. Therefore, $\eta (g_i^{\vec {w}_i})=0$![]() by the property of $j$
by the property of $j$![]() th level characters. If $i = j$
th level characters. If $i = j$![]() , then $\vec {w}_i\in \mathbb {Z}^{4}$
, then $\vec {w}_i\in \mathbb {Z}^{4}$![]() , but we know from (19) that $\eta (g_j^{\vec {w}})\in \mathbb {Z}$
, but we know from (19) that $\eta (g_j^{\vec {w}})\in \mathbb {Z}$![]() for any $\vec {w}\in \mathbb {Z}^{4}$
for any $\vec {w}\in \mathbb {Z}^{4}$![]() . Thus, the entire contribution of $\sum \nolimits _{i={j}/{2}+1}^{s}\eta (g_i^{\vec {w}_i})$
. Thus, the entire contribution of $\sum \nolimits _{i={j}/{2}+1}^{s}\eta (g_i^{\vec {w}_i})$![]() is in $\mathbb {Z}$
is in $\mathbb {Z}$![]() . Using Lemma 4.6, we deduce that $\eta (g_{{j}/{2}}^{\vec {v}_3})\in \mathbb {Z}$
. Using Lemma 4.6, we deduce that $\eta (g_{{j}/{2}}^{\vec {v}_3})\in \mathbb {Z}$![]() for sufficiently large $p$
for sufficiently large $p$![]() .
.
We define
for $i=1,2$![]() on $G_{{j}/{2}}$
on $G_{{j}/{2}}$![]() and $G_j$
and $G_j$![]() , respectively. By Lemma 3.9, the functions $\tau$
, respectively. By Lemma 3.9, the functions $\tau$![]() and $\xi$
and $\xi$![]() are ${j}/{2}$
are ${j}/{2}$![]() th and $j$
th and $j$![]() th level characters which send $g_{{j}/{2}}$
th level characters which send $g_{{j}/{2}}$![]() and $g_j$
and $g_j$![]() to $\mathbb {Z}$
to $\mathbb {Z}$![]() , respectively. By Lemma 4.4, if all of them are trivial, then so is $\eta$
, respectively. By Lemma 4.4, if all of them are trivial, then so is $\eta$![]() , and therefore, at least one of $\tau , \xi _i$
, and therefore, at least one of $\tau , \xi _i$![]() is non-trivial and of complexity at most $O(|\eta |)\leqslant A$
is non-trivial and of complexity at most $O(|\eta |)\leqslant A$![]() upon taking $c>0$
upon taking $c>0$![]() sufficiently small. This contradicts the $A$
sufficiently small. This contradicts the $A$![]() -irrationality of $g$
-irrationality of $g$![]() , implying that $g^{P}$
, implying that $g^{P}$![]() is $O_{M}(A^{-c_M})$
is $O_{M}(A^{-c_M})$![]() -equidistributed.
-equidistributed.
5. An equidistribution result for $x, x+Q(y), x+R(y), x+Q(y)+R(y)$
We now generalize the result of the previous section by considering the configuration
for integral polynomials $Q,R$![]() of degrees $1\leqslant d_1 < d_2$
of degrees $1\leqslant d_1 < d_2$![]() , respectively. From (21), we can deduce that
, respectively. From (21), we can deduce that

where
Our next goal is to deduce expressions for $\mathcal {P}_{i,j}$![]() for $i>1$
for $i>1$![]() .
.
Lemma 5.1 For $i>1$![]() , the following holds:
, the following holds:

Proof. The case $j>id_2$![]() follows trivially from the fact that the polynomial ${{\vec {P}(x,y)}\choose {i}}$
follows trivially from the fact that the polynomial ${{\vec {P}(x,y)}\choose {i}}$![]() has degree $id_2$
has degree $id_2$![]() .
.
In the process of deducing the other cases, we shall use the fact that
and (16). Combining (22) and (16), we rewrite ${{\vec {P}(x,y)}\choose {i}}$![]() as
as

We can further rewrite the last vector in the sum as

From (23) and (24), we see that the only monomials in ${{\vec {P}(x,y)}\choose {i}}$![]() of degree greater than $(i-1)d_2+d_1$
of degree greater than $(i-1)d_2+d_1$![]() in ${{\vec {P}(x,y)}\choose {i}}$
in ${{\vec {P}(x,y)}\choose {i}}$![]() have coefficients of the form $a\vec {v}_3$
have coefficients of the form $a\vec {v}_3$![]() for some $a\in \mathbb {Z}$
for some $a\in \mathbb {Z}$![]() . In particular, the value $a$
. In particular, the value $a$![]() will be non-zero for the coefficient of ${{y}\choose {i d_2}}$
will be non-zero for the coefficient of ${{y}\choose {i d_2}}$![]() , implying the case $(i-1)d_2+d_1+1 \leqslant j \leqslant id_2$
, implying the case $(i-1)d_2+d_1+1 \leqslant j \leqslant id_2$![]() by Lemma 4.6.
by Lemma 4.6.
To deduce the case $i d_1+1\leqslant j\leqslant (i-1)d_2+d_1$![]() , we note that the projection of ${{\vec {P}(x,y)}\choose {i}}$
, we note that the projection of ${{\vec {P}(x,y)}\choose {i}}$![]() onto the first coordinate has degree $i$
onto the first coordinate has degree $i$![]() , while its projection onto the second coordinate has degree $id_1$
, while its projection onto the second coordinate has degree $id_1$![]() , and so
, and so
for these values of $j$![]() . We claim this is an equality. We already know that ${\vec {v}_3\in \mathcal {P}_{i,j}}$
. We claim this is an equality. We already know that ${\vec {v}_3\in \mathcal {P}_{i,j}}$![]() since its multiple is the coefficient of ${{y}\choose {i d_2}}$
since its multiple is the coefficient of ${{y}\choose {i d_2}}$![]() . We claim that the coefficient of the monomial ${{y}\choose {(i-1)d_2+d_1}}$
. We claim that the coefficient of the monomial ${{y}\choose {(i-1)d_2+d_1}}$![]() is of the form $a\vec {v}_3+b\vec {v}_4$
is of the form $a\vec {v}_3+b\vec {v}_4$![]() for integers $a,b$
for integers $a,b$![]() such that $b\neq 0$
such that $b\neq 0$![]() , which will imply this case. This follows from (24), the assumption $d_1< d_2$
, which will imply this case. This follows from (24), the assumption $d_1< d_2$![]() , and the observation that the polynomial ${Q(y)}{{R(y)}\choose {i-1}}$
, and the observation that the polynomial ${Q(y)}{{R(y)}\choose {i-1}}$![]() has degree $(i-1)d_2+d_1$
has degree $(i-1)d_2+d_1$![]() , thus contributing to the coefficient of ${{y}\choose {(i-1)d_2+d_1}}$
, thus contributing to the coefficient of ${{y}\choose {(i-1)d_2+d_1}}$![]() .
.
The next case, $i+1\leqslant j\leqslant id_1$![]() , only happens if $d_1>1$
, only happens if $d_1>1$![]() , and so we make this assumption. Since the projection of ${{\vec {P}(x,y)}\choose {i}}$
, and so we make this assumption. Since the projection of ${{\vec {P}(x,y)}\choose {i}}$![]() onto the first coordinate has degree $i$
onto the first coordinate has degree $i$![]() , we deduce that
, we deduce that
To prove that this is an equality, it remains to show in the light of the previous cases that a vector of the form $a\vec {v}_2+b\vec {v}_3+c\vec {v}_3$![]() is in $\mathcal {P}_{i,j}$
is in $\mathcal {P}_{i,j}$![]() for some $a\neq 0$
for some $a\neq 0$![]() . Since the projection of ${{\vec {P}(x,y)}\choose {i}}$
. Since the projection of ${{\vec {P}(x,y)}\choose {i}}$![]() onto the second coordinate has degree $i d_1$
onto the second coordinate has degree $i d_1$![]() , the coefficient of ${{y}\choose {i d_1}}$
, the coefficient of ${{y}\choose {i d_1}}$![]() is of this form, implying this case.
is of this form, implying this case.
If $d_1 =1$![]() , then the same argument implies that $\vec {v}_2\in \mathcal {P}_{i,i}$
, then the same argument implies that $\vec {v}_2\in \mathcal {P}_{i,i}$![]() .
.
Finally, the case $1\leqslant j\leqslant i$![]() follows from combining the previous case, Lemma 3.1 and the observation that $\vec {v}_1$
follows from combining the previous case, Lemma 3.1 and the observation that $\vec {v}_1$![]() is the coefficient of ${{x}\choose {i}}$
is the coefficient of ${{x}\choose {i}}$![]() .
.
Having established the structure of $\mathcal {P}_{i,j}$![]() , it is straightforward to deduce the following lemma.
, it is straightforward to deduce the following lemma.
Corollary 5.2 The polynomial map $P$![]() satisfies the filtration condition.
satisfies the filtration condition.
We come to the main result of this section, which is case (i) of Theorem 1.8.
Theorem 5.3 $x, x+Q(y), x+R(y), x+Q(y)+R(y)$![]() equidistributes
equidistributes
Let $G/\varGamma$![]() be a filtered nilmanifold of degree $s$
be a filtered nilmanifold of degree $s$![]() and complexity $M$
and complexity $M$![]() . Suppose $g\in {\textrm {poly}}(\mathbb {Z},G_\bullet )$
. Suppose $g\in {\textrm {poly}}(\mathbb {Z},G_\bullet )$![]() is $p$
is $p$![]() -periodic, $A$
-periodic, $A$![]() -irrational, and satisfies $g(0)=1$
-irrational, and satisfies $g(0)=1$![]() . Then the sequence $g^{P}\in {\textrm {poly}}(\mathbb {Z}^{2},G^{P}_\bullet )$
. Then the sequence $g^{P}\in {\textrm {poly}}(\mathbb {Z}^{2},G^{P}_\bullet )$![]() is $O_{M}(A^{-c_M})$
is $O_{M}(A^{-c_M})$![]() -equidistributed on $G^{P}/\varGamma ^{P}$
-equidistributed on $G^{P}/\varGamma ^{P}$![]() for some $c_M>0$
for some $c_M>0$![]() .
.
Proof. Suppose that the sequence $g^{P}\in {\textrm {poly}}(\mathbb {Z}^{2},G^{P}_\bullet )$![]() is not $O_{M}(A^{-c_M})$
is not $O_{M}(A^{-c_M})$![]() - equidistributed. By Theorem 2.9, there exists a non-trivial horizontal character $\eta :G^{P}\to \mathbb {R}$
- equidistributed. By Theorem 2.9, there exists a non-trivial horizontal character $\eta :G^{P}\to \mathbb {R}$![]() of complexity at most $cA$
of complexity at most $cA$![]() for some $c>0$
for some $c>0$![]() to be chosen later, such that $\eta \circ g^{P}\in \mathbb {Z}$
to be chosen later, such that $\eta \circ g^{P}\in \mathbb {Z}$![]() . Let $j$
. Let $j$![]() be the largest natural number such that $\eta |_{G^{P}_j}\neq 0$
be the largest natural number such that $\eta |_{G^{P}_j}\neq 0$![]() . By assumption, $\eta$
. By assumption, $\eta$![]() annihilates ${G^{P}_{j+1}}$
annihilates ${G^{P}_{j+1}}$![]() .
.
If $j=1$![]() , we proceed exactly as in Theorem 4.5, and so we assume that $j>1$
, we proceed exactly as in Theorem 4.5, and so we assume that $j>1$![]() . For any $i\geqslant 1$
. For any $i\geqslant 1$![]() , we define
, we define
for $h\in G_i$![]() and each $k\in \{1,2,3,4\}$
and each $k\in \{1,2,3,4\}$![]() such that $\vec {v}_k\in \mathcal {P}_{i,j}$
such that $\vec {v}_k\in \mathcal {P}_{i,j}$![]() but $\vec {v}_k\notin \mathcal {P}_{i,j+1}$
but $\vec {v}_k\notin \mathcal {P}_{i,j+1}$![]() . The maps $\xi _{i,k}$
. The maps $\xi _{i,k}$![]() define $i$
define $i$![]() th level characters on $G$
th level characters on $G$![]() by Corollary 3.9. By Lemma 3.6, if all of $\xi _{i,k}$
by Corollary 3.9. By Lemma 3.6, if all of $\xi _{i,k}$![]() were trivial, so would be $\eta$
were trivial, so would be $\eta$![]() , implying that at least one of $\xi _{i,k}$
, implying that at least one of $\xi _{i,k}$![]() is non-trivial. The bound on the modulus of $\eta$
is non-trivial. The bound on the modulus of $\eta$![]() and the fact that the vectors $\vec {v}_k$
and the fact that the vectors $\vec {v}_k$![]() have entries of size $O(1)$
have entries of size $O(1)$![]() imply that $|\xi _{i,k}|\leqslant A$
imply that $|\xi _{i,k}|\leqslant A$![]() , provided that the constant $c$
, provided that the constant $c$![]() is appropriately chosen.
is appropriately chosen.
Our goal is to show that for all pairs $(i,k)$![]() as above, we have $\xi _{i,k}(g_i)\in \mathbb {Z}$
as above, we have $\xi _{i,k}(g_i)\in \mathbb {Z}$![]() . Since at least one of these $\xi _{i,k}$
. Since at least one of these $\xi _{i,k}$![]() is non-trivial and of modulus at most $A$
is non-trivial and of modulus at most $A$![]() , we obtain a contradiction of the $A$
, we obtain a contradiction of the $A$![]() -irrationality of $g$
-irrationality of $g$![]() , implying that $g^{P}$
, implying that $g^{P}$![]() is $O_{M}(A^{-c_M})$
is $O_{M}(A^{-c_M})$![]() -equidistributed. By enumerating all such pairs $(i,k)$
-equidistributed. By enumerating all such pairs $(i,k)$![]() , we observe that all we have to show is that $\eta$
, we observe that all we have to show is that $\eta$![]() sends the following elements to $\mathbb {Z}$
sends the following elements to $\mathbb {Z}$![]() :
:
(i) $g_j^{\vec {v}_1}$
 ;
;(ii) $g_{{j}/{d_1}}^{\vec {v}_2}$
 , if $d_1|j$
, if $d_1|j$ ;
;(iii) $g_{{(j+d_2-d_1)}/{d_2}}^{\vec {v}_4}$
 , if $d_2| (j-d_1)$
, if $d_2| (j-d_1)$ ;
;(iv) $g_{{j}/{d_2}}^{\vec {v}_3}$
 , if $d_2|j$
, if $d_2|j$ .
.
That $\eta (g_j^{\vec {v}_1})\in \mathbb {Z}$![]() follows from observing that this is precisely the coefficient of ${{x}\choose {j}}$
follows from observing that this is precisely the coefficient of ${{x}\choose {j}}$![]() is $\eta (g_j^{\vec {v}_1})$
is $\eta (g_j^{\vec {v}_1})$![]() ; showing that other elements are sent to $\mathbb {Z}$
; showing that other elements are sent to $\mathbb {Z}$![]() is a bit more involved.
is a bit more involved.
We assume $d_1|j$![]() , and we claim that $\eta (g_{{j}/{d_1}}^{\vec {v}_2})\in \mathbb {Z}$
, and we claim that $\eta (g_{{j}/{d_1}}^{\vec {v}_2})\in \mathbb {Z}$![]() . From Lemma 3.7 we know that the coefficient of ${{x}\choose {{j}/{d_1}-1}}{{y}\choose {d_1}}$
. From Lemma 3.7 we know that the coefficient of ${{x}\choose {{j}/{d_1}-1}}{{y}\choose {d_1}}$![]() is of the form
is of the form

for some integers $a,b$![]() such that $a\neq 0$
such that $a\neq 0$![]() , and some integer vectors $\vec {w}_i\in {\textrm {Span}}\{\vec {v}_2, \vec {v}_3, \vec {v}_4\}$
, and some integer vectors $\vec {w}_i\in {\textrm {Span}}\{\vec {v}_2, \vec {v}_3, \vec {v}_4\}$![]() . If $i\geqslant {j}/{d_1}+1$
. If $i\geqslant {j}/{d_1}+1$![]() , then $j\leqslant id_1 - d_1$
, then $j\leqslant id_1 - d_1$![]() , and so $j+1\leqslant id_1$
, and so $j+1\leqslant id_1$![]() . It follows from this that $\vec {w}_i\in \mathcal {P}_{i,j+1}$
. It follows from this that $\vec {w}_i\in \mathcal {P}_{i,j+1}$![]() , therefore $\eta (g_i^{\vec {w}_i})=0$
, therefore $\eta (g_i^{\vec {w}_i})=0$![]() . We moreover have that $\vec {v}_3\in \mathcal {P}_{{j}/{d_1},j+1}$
. We moreover have that $\vec {v}_3\in \mathcal {P}_{{j}/{d_1},j+1}$![]() , and so $\eta (g_{{j}/{d_1}}^{\vec {v}_3})=0$
, and so $\eta (g_{{j}/{d_1}}^{\vec {v}_3})=0$![]() as well. From this, Lemma 4.6 and the vanishing of the coefficient of ${{x}\choose {{j}/{d_1}-1}}{{y}\choose {d_1}}$
as well. From this, Lemma 4.6 and the vanishing of the coefficient of ${{x}\choose {{j}/{d_1}-1}}{{y}\choose {d_1}}$![]() mod $\mathbb {Z}$
mod $\mathbb {Z}$![]() , we conclude that $\eta (g_{{j}/{d_1}}^{\vec {v}_2})\in \mathbb {Z}$
, we conclude that $\eta (g_{{j}/{d_1}}^{\vec {v}_2})\in \mathbb {Z}$![]() .
.
We are left with showing that the elements in (iii) and (iv) are sent to $\mathbb {Z}$![]() by $\eta$
by $\eta$![]() . Note that since $1\leqslant d_1< d_2$
. Note that since $1\leqslant d_1< d_2$![]() , the number $d_2$
, the number $d_2$![]() cannot simultaneously divide $j-d_1$
cannot simultaneously divide $j-d_1$![]() and $j$
and $j$![]() ; therefore, only one of these cases at a time is available. We assume that $d_2$
; therefore, only one of these cases at a time is available. We assume that $d_2$![]() divides $j$
divides $j$![]() , and the other case will follow similarly. To show that $\eta (g_\frac {j}{d_2}^{\vec {v}_3})\in \mathbb {Z}$
, and the other case will follow similarly. To show that $\eta (g_\frac {j}{d_2}^{\vec {v}_3})\in \mathbb {Z}$![]() , we look at the coefficient of ${{y}\choose {d_2}}$
, we look at the coefficient of ${{y}\choose {d_2}}$![]() , which is of the form
, which is of the form

for some non-zero integer $a$![]() and vectors $w_i\in {\textrm {Span}}\{\vec {v}_2, \vec {v}_3, \vec {v}_4\}\cap \mathcal {P}_{i,j}\cap \mathbb {Z}^{4}$
and vectors $w_i\in {\textrm {Span}}\{\vec {v}_2, \vec {v}_3, \vec {v}_4\}\cap \mathcal {P}_{i,j}\cap \mathbb {Z}^{4}$![]() . By Lemma 5.1, we have $w_i\in \mathcal {P}_{i,j+1}$
. By Lemma 5.1, we have $w_i\in \mathcal {P}_{i,j+1}$![]() unless $j = id_1$
unless $j = id_1$![]() or $j=(i-1)d_2+d_1$
or $j=(i-1)d_2+d_1$![]() . If $d_1$
. If $d_1$![]() divides $j$
divides $j$![]() , then we have already shown that $\eta (g_{{j}/{d_1}}^{\vec {v}_2})\in \mathbb {Z}$
, then we have already shown that $\eta (g_{{j}/{d_1}}^{\vec {v}_2})\in \mathbb {Z}$![]() , and we moreover have $\eta (g_{{j}/{d_1}}^{\vec {v}_3})=0$
, and we moreover have $\eta (g_{{j}/{d_1}}^{\vec {v}_3})=0$![]() and $\eta (g_{{j}/{d_1}}^{\vec {v}_4})=0$
and $\eta (g_{{j}/{d_1}}^{\vec {v}_4})=0$![]() since $\vec {v}_3, \vec {v}_4\in \mathcal {P}_{{j}/{d_1}, j+1}$
since $\vec {v}_3, \vec {v}_4\in \mathcal {P}_{{j}/{d_1}, j+1}$![]() . Therefore, $\eta (g_{{j}/{d_1}}^{\vec {w}})\in \mathbb {Z}$
. Therefore, $\eta (g_{{j}/{d_1}}^{\vec {w}})\in \mathbb {Z}$![]() for any $w\in {\textrm {Span}}\{\vec {v}_2, \vec {v}_3, \vec {v}_4\}\cap \mathcal {P}_{i,j}\cap \mathbb {Z}^{4}$
for any $w\in {\textrm {Span}}\{\vec {v}_2, \vec {v}_3, \vec {v}_4\}\cap \mathcal {P}_{i,j}\cap \mathbb {Z}^{4}$![]() . The case $j=(i-1)d_2+d_1$
. The case $j=(i-1)d_2+d_1$![]() does not happen by our assumption that $d_2$
does not happen by our assumption that $d_2$![]() does not divide $j-d_1$
does not divide $j-d_1$![]() . Thus the sum in (25) vanishes mod $\mathbb {Z}$
. Thus the sum in (25) vanishes mod $\mathbb {Z}$![]() , implying that $a\eta (g_{{j}/{d_2}}^{\vec {v}_3})\in \mathbb {Z}$
, implying that $a\eta (g_{{j}/{d_2}}^{\vec {v}_3})\in \mathbb {Z}$![]() . That $\eta (g_{{j}/{d_2}}^{\vec {v}_3})\in \mathbb {Z}$
. That $\eta (g_{{j}/{d_2}}^{\vec {v}_3})\in \mathbb {Z}$![]() follows by Lemma 4.6.
follows by Lemma 4.6.
6. An equidistribution result for $x, x+Q(y), x+2Q(y), x+R(y), x+2R(y)$
We now turn our attention to the configuration
for polynomials $Q, R\in \mathbb {Z}[y]$![]() with zero constant terms of degrees $d_1, d_2$
with zero constant terms of degrees $d_1, d_2$![]() , respectively, that moreover satisfy $1\leqslant d_1 < d_2 / 2$
, respectively, that moreover satisfy $1\leqslant d_1 < d_2 / 2$![]() . Letting
. Letting
we observe that

and we prove the following lemma giving the structure of the spaces $\mathcal {P}_{i,j}$![]() for $i>1$
for $i>1$![]()
Lemma 6.1 Let $i>1$![]() . Then
. Then

where $\vec {v}^{k} = (\vec {v}(1)^{k}, \vec {v}(2)^{k}, \vec {v}(3)^{k}, \vec {v}(4)^{k}, \vec {v}(5)^{k})$![]() for any $k\in \mathbb {R}\setminus {\{0\}}$
for any $k\in \mathbb {R}\setminus {\{0\}}$![]() and $\vec {v}\in \mathbb {R}^{5}$
and $\vec {v}\in \mathbb {R}^{5}$![]() .
.
Proof. The statement is trivial for $j>id_2$![]() . To obtain the expressions for $\mathcal {P}_{i,j}$
. To obtain the expressions for $\mathcal {P}_{i,j}$![]() for other values of $j$
for other values of $j$![]() , we make two observations. First, we note from Lemma 3.7 that for $0\leqslant k\leqslant i-1$
, we make two observations. First, we note from Lemma 3.7 that for $0\leqslant k\leqslant i-1$![]() , the coefficient of ${{x}\choose {k}}{{y}\choose {l}}$
, the coefficient of ${{x}\choose {k}}{{y}\choose {l}}$![]()
for some integers $a_{k,l}$![]() which satisfy $a_{k,l}=0$
which satisfy $a_{k,l}=0$![]() if $l>(i-k)d_1$
if $l>(i-k)d_1$![]() and $b_{k,l}=0$
and $b_{k,l}=0$![]() if $l>(i-k)d_2$
if $l>(i-k)d_2$![]() . Moreover, the numbers $a_{k,(i-k)d_1}$
. Moreover, the numbers $a_{k,(i-k)d_1}$![]() and $b_{k, (i-k)d_2}$
and $b_{k, (i-k)d_2}$![]() are non-zero since $Q$
are non-zero since $Q$![]() and $R$
and $R$![]() have degrees $d_1$
have degrees $d_1$![]() , $d_2$
, $d_2$![]() , respectively. By substituting $k=0,1$
, respectively. By substituting $k=0,1$![]() and using $d_1< d_2$
and using $d_1< d_2$![]() , we deduce that
, we deduce that
but
Second, we observe that for $k>1$![]() , we have $\vec {v}_2^{i-k}\in {\textrm {Span}}\{\vec {v}_2^{i}, \vec {v}_2^{i-1}\}$
, we have $\vec {v}_2^{i-k}\in {\textrm {Span}}\{\vec {v}_2^{i}, \vec {v}_2^{i-1}\}$![]() and $\vec {v}_3^{i-k}\in {\textrm {Span}}\{\vec {v}_3^{i}, \vec {v}_3^{i-1}\}$
and $\vec {v}_3^{i-k}\in {\textrm {Span}}\{\vec {v}_3^{i}, \vec {v}_3^{i-1}\}$![]() , and moreover $(i-k')d_r+k'\leqslant (i-k)d_r + k$
, and moreover $(i-k')d_r+k'\leqslant (i-k)d_r + k$![]() for any $k'< k$
for any $k'< k$![]() and $r\in \{1, 2\}$
and $r\in \{1, 2\}$![]() . From this, we see that to specify a basis for $\mathcal {P}_{i,j}$
. From this, we see that to specify a basis for $\mathcal {P}_{i,j}$![]() , it is sufficient to look at whether $\vec {v}_2^{i-1}$
, it is sufficient to look at whether $\vec {v}_2^{i-1}$![]() , $\vec {v}_2^{i}$
, $\vec {v}_2^{i}$![]() , $\vec {v}_3^{i-1}$
, $\vec {v}_3^{i-1}$![]() and $\vec {v}_3^{i}$
and $\vec {v}_3^{i}$![]() are in $\mathcal {P}_{i,j}$
are in $\mathcal {P}_{i,j}$![]() or not. The statements for $j>i$
or not. The statements for $j>i$![]() follow by combining these observations.
follow by combining these observations.
Lastly, we note that $\vec {v}_1$![]() is the coefficient of ${{x}\choose {i}}$
is the coefficient of ${{x}\choose {i}}$![]() , which together with $\mathcal {P}_{i,j}\supseteq \mathcal {P}_{i,j+1}$
, which together with $\mathcal {P}_{i,j}\supseteq \mathcal {P}_{i,j+1}$![]() implies the case $1\leqslant j\leqslant i$
implies the case $1\leqslant j\leqslant i$![]() .
.
Corollary 6.2 The polynomial map $P$![]() satisfies the filtration condition.
satisfies the filtration condition.
We are now ready to show that if $g$![]() is irrational on $G/\varGamma$
is irrational on $G/\varGamma$![]() , then $g^{P}$
, then $g^{P}$![]() equidistributes on $G^{P}/\varGamma ^{P}$
equidistributes on $G^{P}/\varGamma ^{P}$![]() . The proof follows the same logic as the proofs of Theorem 4.5, 5.3 and 6.3; however, the technical details are different, as we are working with a different configuration
. The proof follows the same logic as the proofs of Theorem 4.5, 5.3 and 6.3; however, the technical details are different, as we are working with a different configuration
Theorem 6.3 $x, x+Q(y), x+2Q(y), x+R(y), x+2R(y)$![]() equidistributes
equidistributes
Let $G/\varGamma$![]() be a filtered nilmanifold of degree $s$
be a filtered nilmanifold of degree $s$![]() and complexity $M$
and complexity $M$![]() . Suppose $g\in {\textrm {poly}}(\mathbb {Z},G_\bullet )$
. Suppose $g\in {\textrm {poly}}(\mathbb {Z},G_\bullet )$![]() is $p$
is $p$![]() -periodic, $A$
-periodic, $A$![]() -irrational, and satisfies $g(0)=1$
-irrational, and satisfies $g(0)=1$![]() . Then the sequence $g^{P}\in {\textrm {poly}}(\mathbb {Z}^{2},G^{P}_\bullet )$
. Then the sequence $g^{P}\in {\textrm {poly}}(\mathbb {Z}^{2},G^{P}_\bullet )$![]() is $O_{M}(A^{-c_M})$
is $O_{M}(A^{-c_M})$![]() -equidistributed on $G^{P}/\varGamma ^{P}$
-equidistributed on $G^{P}/\varGamma ^{P}$![]() for some $c_M>0$
for some $c_M>0$![]() .
.
Proof. Suppose that the sequence $g^{P}\in {\textrm {poly}}(\mathbb {Z}^{2},G^{P}_\bullet )$![]() is not $O_{M}(A^{-c_M})$
is not $O_{M}(A^{-c_M})$![]() - equidistributed. By Theorem 2.9, there exists a non-trivial horizontal character $\eta :G^{P}\to \mathbb {R}$
- equidistributed. By Theorem 2.9, there exists a non-trivial horizontal character $\eta :G^{P}\to \mathbb {R}$![]() of complexity at most $cA$
of complexity at most $cA$![]() for an appropriately chosen $c>0$
for an appropriately chosen $c>0$![]() , such that $\eta \circ g^{P}\in \mathbb {Z}$
, such that $\eta \circ g^{P}\in \mathbb {Z}$![]() . Let $j$
. Let $j$![]() be the largest natural number such that $\eta |_{G^{P}_j}\neq 0$
be the largest natural number such that $\eta |_{G^{P}_j}\neq 0$![]() . By assumption, $\eta$
. By assumption, $\eta$![]() annihilates ${G^{P}_{j+1}}$
annihilates ${G^{P}_{j+1}}$![]() .
.
Like in Theorems 4.5 and 5.3, we use the properties of $\eta$![]() and the structural information on $G^{P}$
and the structural information on $G^{P}$![]() contained in Lemma 6.1 to contradict the $A$
contained in Lemma 6.1 to contradict the $A$![]() -irrationality of $g$
-irrationality of $g$![]() . We do this by inspecting the coefficients of $\eta \circ g^{P}$
. We do this by inspecting the coefficients of $\eta \circ g^{P}$![]() . For any $i\geqslant 1$
. For any $i\geqslant 1$![]() , we define
, we define
for $h\in G_i$![]() and each $k\in \{1,2,3\}$
and each $k\in \{1,2,3\}$![]() , $l\in \{i-1,i\}$
, $l\in \{i-1,i\}$![]() such that $\vec {v}_k^{l}\in \mathcal {P}_{i,j}$
such that $\vec {v}_k^{l}\in \mathcal {P}_{i,j}$![]() but $\vec {v}_k^{l}\notin \mathcal {P}_{i,j+1}$
but $\vec {v}_k^{l}\notin \mathcal {P}_{i,j+1}$![]() . The maps $\xi _{i,k,l}$
. The maps $\xi _{i,k,l}$![]() define $i$
define $i$![]() th level characters on $G$
th level characters on $G$![]() by Corollary 3.9. By definition of $G^{P}_{j}$
by Corollary 3.9. By definition of $G^{P}_{j}$![]() , the group is generated precisely by $G^{P}_{j+1}$
, the group is generated precisely by $G^{P}_{j+1}$![]() and the elements of the form $h^{\vec {v}_k^{l}}$
and the elements of the form $h^{\vec {v}_k^{l}}$![]() for $h\in G_i$
for $h\in G_i$![]() , $\vec {v}_k^{l}\in \mathcal {P}_{i,j}\setminus {\mathcal {P}_{i,j+1}}$
, $\vec {v}_k^{l}\in \mathcal {P}_{i,j}\setminus {\mathcal {P}_{i,j+1}}$![]() and $i\geqslant 1$
and $i\geqslant 1$![]() . Therefore, if all of $\xi _{i,k,l}$
. Therefore, if all of $\xi _{i,k,l}$![]() were trivial, so would be $\eta$
were trivial, so would be $\eta$![]() , implying that at least one of $\xi _{i,k,l}$
, implying that at least one of $\xi _{i,k,l}$![]() is non-trivial. The bound on the modulus of $\eta$
is non-trivial. The bound on the modulus of $\eta$![]() and the fact that the vectors $\vec {v}_k^{l}$
and the fact that the vectors $\vec {v}_k^{l}$![]() have entries of size $O(1)$
have entries of size $O(1)$![]() imply that $|\xi _{i,k,l}|\leqslant A$
imply that $|\xi _{i,k,l}|\leqslant A$![]() , provided that the constant $c$
, provided that the constant $c$![]() is appropriately chosen.
is appropriately chosen.
Our goal is to show that for all triples $(i,k,l)$![]() as above, we have $\xi _{i,k,l}(g_i)\in \mathbb {Z}$
as above, we have $\xi _{i,k,l}(g_i)\in \mathbb {Z}$![]() . Since at least one of these $\xi _{i,k,l}$
. Since at least one of these $\xi _{i,k,l}$![]() is non-trivial and of modulus at most $A$
is non-trivial and of modulus at most $A$![]() , we obtain a contradiction of the $A$
, we obtain a contradiction of the $A$![]() -irrationality of $g$
-irrationality of $g$![]() , implying that $g^{P}$
, implying that $g^{P}$![]() is $O_{M}(A^{-c_M})$
is $O_{M}(A^{-c_M})$![]() -equidistributed. We are thus left to show that $\eta$
-equidistributed. We are thus left to show that $\eta$![]() sends the following elements to $\mathbb {Z}$
sends the following elements to $\mathbb {Z}$![]() :
:
(i) $g_j^{\vec {v}_1}$
 ,
,(ii) $g_{{(j-1)}/{d_1}+1}^{\vec {v}_2^{{(j-1)}/{d_1}}}$
 , if $d_1|(j-1)$
, if $d_1|(j-1)$ and $j>1$
and $j>1$ ,
,(iii) $g_{{j}/{d_1}}^{\vec {v}_2^{{j}/{d_1}}}$
 , if $d_1|j$
, if $d_1|j$ ,
,(iv) $g_{{(j-1)}/{d_2}+1}^{\vec {v}_3^{{(j-1)}/{d_2}}}$
 , if $d_2|(j-1)$
, if $d_2|(j-1)$ and $j>1$
and $j>1$ ,
,(v) $g_{{j}/{d_2}}^{\vec {v}_3^{{j}/{d_2}}}$
 , if $d_2|j$
, if $d_2|j$ .
.
We first look at the model case $j=1$![]() , and then move on to the case $j>1$
, and then move on to the case $j>1$![]() . Assuming $j=1$
. Assuming $j=1$![]() , we have to show that $\eta (g_j^{\vec {v}_1})\in \mathbb {Z}$
, we have to show that $\eta (g_j^{\vec {v}_1})\in \mathbb {Z}$![]() , and also $\eta (g_1^{\vec {v}_2})$
, and also $\eta (g_1^{\vec {v}_2})$![]() if $d_1 = 1$
if $d_1 = 1$![]() . The first statement follows from inspecting the coefficient of $x$
. The first statement follows from inspecting the coefficient of $x$![]() . For the second statement, we assume $d_1 = 1$
. For the second statement, we assume $d_1 = 1$![]() ; then $Q(y)=ay$
; then $Q(y)=ay$![]() for some $a\in \mathbb {Z}$
for some $a\in \mathbb {Z}$![]() , and so the coefficient of $y$
, and so the coefficient of $y$![]() is of the form $a\eta (g_1^{\vec {v}_2})$
is of the form $a\eta (g_1^{\vec {v}_2})$![]() plus terms that vanish by assumption that $\eta |_{G^{P}_2}=0$
plus terms that vanish by assumption that $\eta |_{G^{P}_2}=0$![]() . Lemma 4.6 thus implies that $\eta (g_1^{\vec {v}_2})\in \mathbb {Z}$
. Lemma 4.6 thus implies that $\eta (g_1^{\vec {v}_2})\in \mathbb {Z}$![]() , which finishes this case.
, which finishes this case.
We assume from now on that $j>1$![]() . The number $\eta (g_j^{\vec {v}_1})$
. The number $\eta (g_j^{\vec {v}_1})$![]() vanishes mod $\mathbb {Z}$
vanishes mod $\mathbb {Z}$![]() because it is the coefficient of ${{x}\choose {j}}$
because it is the coefficient of ${{x}\choose {j}}$![]() . We now proceed to show that the elements in (iii) and (v) are in $\mathbb {Z}$
. We now proceed to show that the elements in (iii) and (v) are in $\mathbb {Z}$![]() . To this end, we look at the coefficient of ${{y}\choose {j}}$
. To this end, we look at the coefficient of ${{y}\choose {j}}$![]() and assume that at least one of $d_1$
and assume that at least one of $d_1$![]() , $d_2$
, $d_2$![]() divides $j$
divides $j$![]() . By evaluating the contributions coming from $\eta (g_i^{{\vec {P}(x,y)}\choose {i}})$
. By evaluating the contributions coming from $\eta (g_i^{{\vec {P}(x,y)}\choose {i}})$![]() for each $i\geqslant 1$
for each $i\geqslant 1$![]() , we observe that the coefficient of ${{y}\choose {j}}$
, we observe that the coefficient of ${{y}\choose {j}}$![]() is of the form
is of the form

for integers $a_i, b_i\in \mathbb {Z}$![]() . If $i>{j}/{d_1}$
. If $i>{j}/{d_1}$![]() , then $j+1\leqslant i d_1$
, then $j+1\leqslant i d_1$![]() , and so $\vec {v}_2^{i}\in \mathcal {P}_{i,j+1}$
, and so $\vec {v}_2^{i}\in \mathcal {P}_{i,j+1}$![]() by Lemma 6.1. Similarly, we have $\vec {v}_3^{i}\in \mathcal {P}_{i,j+1}$
by Lemma 6.1. Similarly, we have $\vec {v}_3^{i}\in \mathcal {P}_{i,j+1}$![]() whenever $i>{j}/{d_2}$
whenever $i>{j}/{d_2}$![]() . Therefore, the coefficient of ${{y}\choose {j}}$
. Therefore, the coefficient of ${{y}\choose {j}}$![]() reduces to the rather unfortunate looking
reduces to the rather unfortunate looking
for some integers $a$![]() and $b$
and $b$![]() .
.
We pause for a moment to analyse what happens if $j$![]() is not divisible by one of $d_1$
is not divisible by one of $d_1$![]() , $d_2$
, $d_2$![]() . If $d_1$
. If $d_1$![]() does not divide $j$
does not divide $j$![]() , then $\left \lceil {j}/{d_1}\right \rceil > {j}/{d_1}$
, then $\left \lceil {j}/{d_1}\right \rceil > {j}/{d_1}$![]() , implying that $\vec {v}_2^{\left \lceil {j}/{d_1}\right \rceil }$
, implying that $\vec {v}_2^{\left \lceil {j}/{d_1}\right \rceil }$![]() by the argument in the previous paragraph. Then the coefficient of ${{y}\choose {j}}$
by the argument in the previous paragraph. Then the coefficient of ${{y}\choose {j}}$![]() is an integer multiple of $\eta (g_{{j}/{d_2}}^{\vec {v}_3^{{j}/{d_2}}})$
is an integer multiple of $\eta (g_{{j}/{d_2}}^{\vec {v}_3^{{j}/{d_2}}})$![]() , and so $\eta (g_{{j}/{d_2}}^{\vec {v}_3^{{j}/{d_2}}})\in \mathbb {Z}$
, and so $\eta (g_{{j}/{d_2}}^{\vec {v}_3^{{j}/{d_2}}})\in \mathbb {Z}$![]() by Lemma 4.6. We similarly have $\eta (g_{{j}/{d_1}}^{\vec {v}_2^{{j}/{d_1}}})\in \mathbb {Z}$
by Lemma 4.6. We similarly have $\eta (g_{{j}/{d_1}}^{\vec {v}_2^{{j}/{d_1}}})\in \mathbb {Z}$![]() if $d_2$
if $d_2$![]() does not divide $j$
does not divide $j$![]() .
.
The interesting case is when both $d_1$![]() and $d_2$
and $d_2$![]() divide $j$
divide $j$![]() , which we assume from now on. In this case, both $a$
, which we assume from now on. In this case, both $a$![]() and $b$
and $b$![]() are non-zero due to the fact that $Q$
are non-zero due to the fact that $Q$![]() has degree $d_1$
has degree $d_1$![]() and $R$
and $R$![]() has degree $d_2$
has degree $d_2$![]() . The strategy now is this: by looking at the coefficients of $x{{y}\choose {j-d_1}}$
. The strategy now is this: by looking at the coefficients of $x{{y}\choose {j-d_1}}$![]() , ${{x}\choose {2}}{{y}\choose {j-2d_1}}$
, ${{x}\choose {2}}{{y}\choose {j-2d_1}}$![]() and ${{x}\choose {2}}{{y}\choose {j-d_1}}$
and ${{x}\choose {2}}{{y}\choose {j-d_1}}$![]() , we shall show that $\eta (g_{{j}/{d_1}}^{\vec {v}_2^{{j}/{d_1}-1}})$
, we shall show that $\eta (g_{{j}/{d_1}}^{\vec {v}_2^{{j}/{d_1}-1}})$![]() and $\eta (g_{{j}/{d_1}}^{\vec {v}_2^{{j}/{d_1}-2}})$
and $\eta (g_{{j}/{d_1}}^{\vec {v}_2^{{j}/{d_1}-2}})$![]() are both in $\mathbb {Z}$
are both in $\mathbb {Z}$![]() . Since the vector $\vec {v}_2^{{j}/{d_1}}$
. Since the vector $\vec {v}_2^{{j}/{d_1}}$![]() is an integer linear combination of $\vec {v}_2^{{j}/{d_1}-1}$
is an integer linear combination of $\vec {v}_2^{{j}/{d_1}-1}$![]() and $\vec {v}_2^{{j}/{d_1}-2}$
and $\vec {v}_2^{{j}/{d_1}-2}$![]() , we deduce that $\eta (g_{{j}/{d_2}}^{\vec {v}_3^{{j}/{d_2}}})$
, we deduce that $\eta (g_{{j}/{d_2}}^{\vec {v}_3^{{j}/{d_2}}})$![]() is in $\mathbb {Z}$
is in $\mathbb {Z}$![]() . By Lemma 4.6 and the fact that the coefficient of ${{y}\choose {d_1}}$
. By Lemma 4.6 and the fact that the coefficient of ${{y}\choose {d_1}}$![]() takes the form (27), it follows that $\eta (g_{{j}/{d_2}}^{\vec {v}_3^{{j}/{d_2}}})\in \mathbb {Z}$
takes the form (27), it follows that $\eta (g_{{j}/{d_2}}^{\vec {v}_3^{{j}/{d_2}}})\in \mathbb {Z}$![]() as well.
as well.
We start by analysing the coefficient of $x{{y}\choose {y-d_1}}$![]() , which is
, which is

for $a_i, b_i\in \mathbb {Z}$![]() . The lower bounds in the range for $i$
. The lower bounds in the range for $i$![]() come from $d_1< d_2$
come from $d_1< d_2$![]() and the observation that terms with smaller $i$
and the observation that terms with smaller $i$![]() do not contribute to this monomial. By rearranging the inequality $i\geqslant {j}/{d_1}+1$
do not contribute to this monomial. By rearranging the inequality $i\geqslant {j}/{d_1}+1$![]() and Lemma 6.1, we infer that $\vec {v}_2^{i-1}\in \mathcal {P}_{i,j+1}$
and Lemma 6.1, we infer that $\vec {v}_2^{i-1}\in \mathcal {P}_{i,j+1}$![]() whenever $i\geqslant {j}/{d_1}+1$
whenever $i\geqslant {j}/{d_1}+1$![]() . Similarly, $\vec {v}_3^{i-1}\in \mathcal {P}_{i,j+1}$
. Similarly, $\vec {v}_3^{i-1}\in \mathcal {P}_{i,j+1}$![]() whenever $i\geqslant {j}/{d_2}+1$
whenever $i\geqslant {j}/{d_2}+1$![]() . Since $\eta$
. Since $\eta$![]() vanishes on $G^{P}_{j+1}$
vanishes on $G^{P}_{j+1}$![]() , we deduce that the coefficient of $x{{y}\choose {y-d_1}}$
, we deduce that the coefficient of $x{{y}\choose {y-d_1}}$![]() is an integer multiple of $\eta (g_{{j}/{d_1}}^{\vec {v}_2^{{j}/{d_1}-1}})$
is an integer multiple of $\eta (g_{{j}/{d_1}}^{\vec {v}_2^{{j}/{d_1}-1}})$![]() , implying that $\eta (g_{{j}/{d_1}}^{\vec {v}_2^{{j}/{d_1}-1}})\in \mathbb {Z}$
, implying that $\eta (g_{{j}/{d_1}}^{\vec {v}_2^{{j}/{d_1}-1}})\in \mathbb {Z}$![]() by Lemma 4.6.
by Lemma 4.6.
We move on to the coefficient of ${{x}\choose {2}}{{y}\choose {j-2d_1}}$![]() , which takes the form
, which takes the form

for some $a_i, b_i\in \mathbb {Z}$![]() . An important point here is that the second sum starts at $i={j}/{d_2}+2$
. An important point here is that the second sum starts at $i={j}/{d_2}+2$![]() ; this results from the observation that by the assumption $d_2 > 2d_1$
; this results from the observation that by the assumption $d_2 > 2d_1$![]() , all monomials of ${{x}\choose {2}}{{R(y)}\choose {{j}/{d_2}-1}}$
, all monomials of ${{x}\choose {2}}{{R(y)}\choose {{j}/{d_2}-1}}$![]() have degree at most $j-d_2 < j-2d_1$
have degree at most $j-d_2 < j-2d_1$![]() in $y$
in $y$![]() ; therefore, they do not contribute to ${{x}\choose {2}}{{y}\choose {j-2d_1}}$
; therefore, they do not contribute to ${{x}\choose {2}}{{y}\choose {j-2d_1}}$![]() (this is the only point where we are using the assumption). Performing a similar analysis as above, we deduce that all the terms involving $\vec {v}_2$
(this is the only point where we are using the assumption). Performing a similar analysis as above, we deduce that all the terms involving $\vec {v}_2$![]() and $\vec {v}_3$
and $\vec {v}_3$![]() with $i\geqslant {j}/{d_1}+2$
with $i\geqslant {j}/{d_1}+2$![]() and $i\geqslant {j}/{d_2}+2$
and $i\geqslant {j}/{d_2}+2$![]() , respectively, vanish mod $\mathbb {Z}$
, respectively, vanish mod $\mathbb {Z}$![]() . This leaves us with a coefficient of the form
. This leaves us with a coefficient of the form
for some integers $a,b$![]() with $a\neq 0$
with $a\neq 0$![]() . This is not exactly what we wanted; however, analysing the coefficient of ${{x}\choose {2}}{{y}\choose {j-d_1}}$
. This is not exactly what we wanted; however, analysing the coefficient of ${{x}\choose {2}}{{y}\choose {j-d_1}}$![]() and using Lemma 4.6 allows us to conclude that $\eta (g_{{j}/{d_1}+1}^{\vec {v}_2^{{j}/{d_1}-1}})\in \mathbb {Z}$
and using Lemma 4.6 allows us to conclude that $\eta (g_{{j}/{d_1}+1}^{\vec {v}_2^{{j}/{d_1}-1}})\in \mathbb {Z}$![]() . We leave the details on how this is done to the reader; they are no less tedious and no more informative than our analysis of the coefficients of $x{{y}\choose {y-d_1}}$
. We leave the details on how this is done to the reader; they are no less tedious and no more informative than our analysis of the coefficients of $x{{y}\choose {y-d_1}}$![]() and ${{x}\choose {2}}{{y}\choose {j-2d_1}}$
and ${{x}\choose {2}}{{y}\choose {j-2d_1}}$![]() . As a consequence, we deduce that $\eta (g_{{j}/{d_1}}^{\vec {v}_2^{{j}/{d_1}-2}})\in \mathbb {Z}$
. As a consequence, we deduce that $\eta (g_{{j}/{d_1}}^{\vec {v}_2^{{j}/{d_1}-2}})\in \mathbb {Z}$![]() .
.
This is the last missing step needed to show that $\eta (g_{{j}/{d_1}}^{\vec {v}_2^{{j}/{d_1}}}), \eta (g_{{j}/{d_2}}^{\vec {v}_3^{{j}/{d_2}}})\in \mathbb {Z}$![]() . We have thus showed that the elements in (iii) and (v) in the statement of the proof are sent to integers by $\eta$
. We have thus showed that the elements in (iii) and (v) in the statement of the proof are sent to integers by $\eta$![]() . The argument showing that $\eta$
. The argument showing that $\eta$![]() sends the elements in (ii) and (iv) to $\mathbb {Z}$
sends the elements in (ii) and (iv) to $\mathbb {Z}$![]() is very similar: instead of analysing the coefficients of ${{y}\choose {j}}$
is very similar: instead of analysing the coefficients of ${{y}\choose {j}}$![]() , $x{{y}\choose {j-d_1}}$
, $x{{y}\choose {j-d_1}}$![]() , ${{x}\choose {2}}{{y}\choose {j-2d_1}}$
, ${{x}\choose {2}}{{y}\choose {j-2d_1}}$![]() and ${{x}\choose {2}}{{y}\choose {j-d_1}}$
and ${{x}\choose {2}}{{y}\choose {j-d_1}}$![]() , we would look at the coefficients of $x{{y}\choose {j-1}}$
, we would look at the coefficients of $x{{y}\choose {j-1}}$![]() , ${{x}\choose {2}}{{y}\choose {j-1-d_1}}$
, ${{x}\choose {2}}{{y}\choose {j-1-d_1}}$![]() , ${{x}\choose {3}}{{y}\choose {j-1-2d_1}}$
, ${{x}\choose {3}}{{y}\choose {j-1-2d_1}}$![]() and ${{x}\choose {3}}{{y}\choose {j-1-d_1}}$
and ${{x}\choose {3}}{{y}\choose {j-1-d_1}}$![]() . We leave the details to an interested reader.
. We leave the details to an interested reader.
7. The connection with the Leibman group for a system of linear forms
As remarked in the introduction, the construction of the group $G^{P}$![]() generalizes the construction of Leibman group $G^{\varPsi }$
generalizes the construction of Leibman group $G^{\varPsi }$![]() for a system of linear forms given in Definition 1.10 of [Reference Green and Tao17]. In this section, we illustrate how the definition of $G^{\varPsi }$
for a system of linear forms given in Definition 1.10 of [Reference Green and Tao17]. In this section, we illustrate how the definition of $G^{\varPsi }$![]() fits into this framework. Let $\vec {\varPsi }=(\varPsi _1, \ldots , \varPsi _t)$
fits into this framework. Let $\vec {\varPsi }=(\varPsi _1, \ldots , \varPsi _t)$![]() be a tuple of $t$
be a tuple of $t$![]() linear forms in variable ${\textbf {x}=(x_1, \ldots , x_D)}$
linear forms in variable ${\textbf {x}=(x_1, \ldots , x_D)}$![]() . We observe that
. We observe that

In [Reference Green and Tao17], Green and Tao labelled the space in (21) as $\varPsi ^{[i]}$![]() . Green and Tao also defined
. Green and Tao also defined
for $j\geqslant 1$![]() , calling $G^{\varPsi } = G^{\varPsi }_0:=G^{\varPsi }_1$
, calling $G^{\varPsi } = G^{\varPsi }_0:=G^{\varPsi }_1$![]() the Leibman group for $\vec {\varPsi }$
the Leibman group for $\vec {\varPsi }$![]() . The property $\mathcal {P}_{i,j}=0$
. The property $\mathcal {P}_{i,j}=0$![]() for $i< j$
for $i< j$![]() implies that $G^{\varPsi }_j = G^{P}_j$
implies that $G^{\varPsi }_j = G^{P}_j$![]() , and so Leibman group for $\vec {\varPsi }$
, and so Leibman group for $\vec {\varPsi }$![]() is a special instance of our construction.
is a special instance of our construction.
The system $\vec {\varPsi }$![]() satisfies flag condition if $\varPsi ^{[i]}\subseteq \varPsi ^{[i+1]}$
satisfies flag condition if $\varPsi ^{[i]}\subseteq \varPsi ^{[i+1]}$![]() , or equivalently if $\mathcal {P}_{i,i}\subseteq \mathcal {P}_{i+1,i+1}$
, or equivalently if $\mathcal {P}_{i,i}\subseteq \mathcal {P}_{i+1,i+1}$![]() , for any $i\in \mathbb {N}_+$
, for any $i\in \mathbb {N}_+$![]() . If $\vec {\varPsi }$
. If $\vec {\varPsi }$![]() satisfies the flag condition, then $\vec {\varPsi }$
satisfies the flag condition, then $\vec {\varPsi }$![]() equidistributes by the periodic version of Theorem 1.11 of [Reference Green and Tao17], which has been stated as Theorem 4.1 in [Reference Candela and Sisask4]Footnote 2 .
equidistributes by the periodic version of Theorem 1.11 of [Reference Green and Tao17], which has been stated as Theorem 4.1 in [Reference Candela and Sisask4]Footnote 2 .
The reader might want to know whether the flag condition is related in any way to the filtration condition that we have defined in Definition 3.4. It turns out that any $\vec {\varPsi }$![]() satisfies the filtration condition, and so these two conditions are unrelated. We prove this in the next two lemmas.
satisfies the filtration condition, and so these two conditions are unrelated. We prove this in the next two lemmas.
Lemma 7.1 For any $\vec {\varPsi }$![]() , we have
, we have
Proof. Let $a_0, \ldots , a_i$![]() be rational numbers such that ${{n}\choose {i}} = a_i n^{i} + \cdots + a_0$
be rational numbers such that ${{n}\choose {i}} = a_i n^{i} + \cdots + a_0$![]() . Then
. Then
Since $\vec {\varPsi }$![]() is a linear form, each $\vec {\varPsi }^{l}$
is a linear form, each $\vec {\varPsi }^{l}$![]() is a homogeneous polynomial of degree $l$
is a homogeneous polynomial of degree $l$![]() . It, therefore, follows that
. It, therefore, follows that

The lemma follows from the observation that since the polynomials $\mathcal {D}_l{{\vec {\varPsi }(\textbf {x})}\choose {i}}$![]() are homogeneous of distinct degrees, we have
are homogeneous of distinct degrees, we have

Corollary 7.2 Any $\vec {\varPsi }$![]() satisfies the filtration condition.
satisfies the filtration condition.
Proof. Let $i_1, i_2, j_1, j_2\in \mathbb {N}_+$![]() . If $i_1 < j_i$
. If $i_1 < j_i$![]() then $\mathcal {P}_{i_1, j_1} = \{0\}$
then $\mathcal {P}_{i_1, j_1} = \{0\}$![]() , and so $\mathcal {P}_{i_1, j_1}\cdot \mathcal {P}_{i_2,j_2}\subseteq \mathcal {P}_{i_1+i_2, j_1 +j_2}$
, and so $\mathcal {P}_{i_1, j_1}\cdot \mathcal {P}_{i_2,j_2}\subseteq \mathcal {P}_{i_1+i_2, j_1 +j_2}$![]() trivially. The same happens if $i_2 < j_2$
trivially. The same happens if $i_2 < j_2$![]() . We can therefore assume that $i_1\geqslant j_1$
. We can therefore assume that $i_1\geqslant j_1$![]() and $i_2\geqslant j_2$
and $i_2\geqslant j_2$![]() . From Lemma 7.1 and Corollary 3.4 of [Reference Green and Tao17], it follows that
. From Lemma 7.1 and Corollary 3.4 of [Reference Green and Tao17], it follows that

We also record a corollary which describes the spaces $\mathcal {P}_{i,j}$![]() for systems satisfying the flag condition.
for systems satisfying the flag condition.
Corollary 7.3 Suppose that $\vec {\varPsi }$![]() satisfies the flag condition. Then
satisfies the flag condition. Then
for any $i\in \mathbb {N}_+$![]() .
.
Proof. By the flag condition, $\varPsi ^{[l]}\subseteq \varPsi ^{[i]} =\mathcal {P}_{i,i}$![]() for every $1\leqslant l\leqslant i$
for every $1\leqslant l\leqslant i$![]() . Therefore,
. Therefore,
for any $1\leqslant j\leqslant i$![]() .
.
8. True complexity of equidistributing progressions
We have shown in previous sections that many progressions, including $x, x+y, x+y^{2}, x+y+y^{2}$![]() or $x, x+y, x+2y, x+y^{3}, x+2y^{3}$
or $x, x+y, x+2y, x+y^{3}, x+2y^{3}$![]() , equidistribute, i.e. if $g$
, equidistribute, i.e. if $g$![]() is highly irrational on $G$
is highly irrational on $G$![]() , then the corresponding sequence $g^{P}$
, then the corresponding sequence $g^{P}$![]() is close to being equidistributed on $G^{P}$
is close to being equidistributed on $G^{P}$![]() . In this section, we shall prove Conjecture 1.12 for all equidistributing progressions.
. In this section, we shall prove Conjecture 1.12 for all equidistributing progressions.
Theorem 8.1 Let $t\in \mathbb {N}_+$![]() , and fix $1\leqslant l\leqslant t$
, and fix $1\leqslant l\leqslant t$![]() . Let $\vec {P}=(P_1, \ldots , P_t)\in \mathbb {Q}[\textbf {x}]^{t}$
. Let $\vec {P}=(P_1, \ldots , P_t)\in \mathbb {Q}[\textbf {x}]^{t}$![]() be a Gowers controllable integral polynomial map that equidistributes and is algebraically independent of degree $s+1$
be a Gowers controllable integral polynomial map that equidistributes and is algebraically independent of degree $s+1$![]() at $l$
at $l$![]() . Then the true complexity of $\vec {P}$
. Then the true complexity of $\vec {P}$![]() at $l$
at $l$![]() is at most $s$
is at most $s$![]() .
.
The logic of the proof is very similar to the proof of Theorem 7.1 in [Reference Green and Tao17], with small modifications that allow us to get a control of weights on different terms of the progression by different Gowers norms.
Proof. We let all implied constants in this proof depend on $\vec {P}$![]() , $s$
, $s$![]() and $t$
and $t$![]() without mentioning the dependence explicitly.
without mentioning the dependence explicitly.
Fix $\epsilon >0$![]() . Since $\vec {P}$
. Since $\vec {P}$![]() is Gowers controllable, there exists an integer $s_0\geqslant 1$
is Gowers controllable, there exists an integer $s_0\geqslant 1$![]() , a threshold $p_0\in \mathbb {N}$
, a threshold $p_0\in \mathbb {N}$![]() , and a real number $\delta >0$
, and a real number $\delta >0$![]() such that for all primes $p>p_0$
such that for all primes $p>p_0$![]() ,
,
for all 1-bounded functions $f_1, \ldots , f_t:\mathbb {F}_p\to \mathbb {C}$![]() , at least one of which satisfies $\|f_{i}\|_{U^{s_0+1}}\leqslant \delta$
, at least one of which satisfies $\|f_{i}\|_{U^{s_0+1}}\leqslant \delta$![]() . We let $\mathcal {F}:\mathbb {R}_+\to \mathbb {R}_+$
. We let $\mathcal {F}:\mathbb {R}_+\to \mathbb {R}_+$![]() be a growth function depending on $\epsilon$
be a growth function depending on $\epsilon$![]() to be fixed later. If $s\geqslant s_0$
to be fixed later. If $s\geqslant s_0$![]() , then we are done, so suppose $s< s_0$
, then we are done, so suppose $s< s_0$![]() .
.
Suppose that $f_1, \ldots , f_t:\mathbb {F}_p\to \mathbb {C}$![]() are 1-bounded functions, and suppose moreover that $\|f_{l}\|_{U^{s+1}}\leqslant \delta$
are 1-bounded functions, and suppose moreover that $\|f_{l}\|_{U^{s+1}}\leqslant \delta$![]() . We use Lemma 2.13 to find $M=O_{\epsilon , \mathcal {F}}(1)$
. We use Lemma 2.13 to find $M=O_{\epsilon , \mathcal {F}}(1)$![]() , a filtered nilmanifold $G/\varGamma$
, a filtered nilmanifold $G/\varGamma$![]() of degree $s_0$
of degree $s_0$![]() and complexity $M$
and complexity $M$![]() , a $p$
, a $p$![]() -periodic, $\mathcal {F}(M)$
-periodic, $\mathcal {F}(M)$![]() -irrational sequence $g\in {\textrm {poly}}(\mathbb {Z},G_\bullet )$
-irrational sequence $g\in {\textrm {poly}}(\mathbb {Z},G_\bullet )$![]() with $g(0)=1$
with $g(0)=1$![]() , and decompositions
, and decompositions
satisfying the conditions of Lemma 2.13. Decomposing each of $f_i$![]() this way, we get $3^{t}$
this way, we get $3^{t}$![]() terms. All the terms involving $f_{i,{sml}}$
terms. All the terms involving $f_{i,{sml}}$![]() can be bounded by $O(\epsilon )$
can be bounded by $O(\epsilon )$![]() . By choosing $\mathcal {F}$
. By choosing $\mathcal {F}$![]() growing sufficiently fast depending on $\delta$
growing sufficiently fast depending on $\delta$![]() , we can assume that $\|f_{i,{unf}}\|_{s_0+1}\leqslant {1}/{\mathcal {F}(M)}\leqslant {\delta }/{4}$
, we can assume that $\|f_{i,{unf}}\|_{s_0+1}\leqslant {1}/{\mathcal {F}(M)}\leqslant {\delta }/{4}$![]() , which together with 4-boundedness of $f_{i,{unf}}$
, which together with 4-boundedness of $f_{i,{unf}}$![]() implies that terms involving $f_{i,{unf}}$
implies that terms involving $f_{i,{unf}}$![]() contribute at most $O(\epsilon )$
contribute at most $O(\epsilon )$![]() . This leaves us with
. This leaves us with

where $F((u_1, \ldots , u_t)\varGamma ^{P})=F_1(u_1\varGamma )\cdots F_t(u_t\varGamma )$![]() . Since $\vec {P}$
. Since $\vec {P}$![]() equidistributes, we have
equidistributes, we have
By the assumption of algebraic independence, the polynomial ${{P_l}\choose {s+1}}$![]() is not a linear combination of ${{P_1}\choose {s+1}}, \ldots , {{P_{l-1}}\choose {s+1}}, {{P_{l+1}}\choose {s+1}}, \ldots , {{P_t}\choose {s+1}}$
is not a linear combination of ${{P_1}\choose {s+1}}, \ldots , {{P_{l-1}}\choose {s+1}}, {{P_{l+1}}\choose {s+1}}, \ldots , {{P_t}\choose {s+1}}$![]() . Consequently, the space $\mathcal {Q}_{s+1,1}$
. Consequently, the space $\mathcal {Q}_{s+1,1}$![]() contains the vector $\vec {e}_l$
contains the vector $\vec {e}_l$![]() that has 1 in the $l$
that has 1 in the $l$![]() th coordinate and 0 elsewhere. This implies that the group
th coordinate and 0 elsewhere. This implies that the group
is contained in $G^{P}$![]() . In fact, $H$
. In fact, $H$![]() is a normal subgroup of $G^{P}$
is a normal subgroup of $G^{P}$![]() due to the normality of $G_{s+1}$
due to the normality of $G_{s+1}$![]() in $G$
in $G$![]() . Therefore,
. Therefore,
where $F_{\leqslant s}\left ((u_1, \ldots , u_t)\varGamma ^{P}\right )=\left (\prod _{\substack {1\leqslant i \leqslant t, \\ i\neq l}} F_i(u_i\varGamma )\right )F_{l,\leqslant s}(u_l\varGamma )$![]() and $F_{l,\leqslant s}$
and $F_{l,\leqslant s}$![]() is the average of $F_l$
is the average of $F_l$![]() over cosets of $G_{s+1}$
over cosets of $G_{s+1}$![]() :
:
It is straightforward to see that $F_{l, \leqslant s}$![]() is 1-bounded and $M$
is 1-bounded and $M$![]() -Lipschitz. We moreover have the bound
-Lipschitz. We moreover have the bound
which implies that

The function $F_{l, \leqslant s}$![]() is invariant on $G_{s+1}$
is invariant on $G_{s+1}$![]() -cosets by construction while $F_{l}-F_{l, \leqslant s}$
-cosets by construction while $F_{l}-F_{l, \leqslant s}$![]() vanishes on each coset. As a consequence, the two functions are orthogonal, implying
vanishes on each coset. As a consequence, the two functions are orthogonal, implying
By the $\mathcal {F}(M)$![]() -irrationality of $g$
-irrationality of $g$![]() , we have
, we have
We let $\psi (n)=\overline {F_{l,\leqslant s}}(g(n)\varGamma )$![]() . By the $G_{s+1}$
. By the $G_{s+1}$![]() -invariance of $F_{\leqslant s}$
-invariance of $F_{\leqslant s}$![]() , this is a nilsequence of degree $\leqslant s$
, this is a nilsequence of degree $\leqslant s$![]() and complexity $M$
and complexity $M$![]() . By (29), we have
. By (29), we have
We then split $\mathbb {E}_{n\in \mathbb {F}_p} F_{l}(g(n)\varGamma )\psi (n)$![]() into three terms. Using the Cauchy–Schwarz inequality, the term involving $f_{l,sml}$
into three terms. Using the Cauchy–Schwarz inequality, the term involving $f_{l,sml}$![]() can be bounded as
can be bounded as
To evaluate the contribution coming from $f_{l}$![]() , we use $\|f_{l}\|_{U^{s+1}}\leqslant \delta$
, we use $\|f_{l}\|_{U^{s+1}}\leqslant \delta$![]() and the converse to the inverse theorem for Gowers norms (Proposition 1.4 of Appendix G of [Reference Green, Tao and Ziegler20]) to conclude that
and the converse to the inverse theorem for Gowers norms (Proposition 1.4 of Appendix G of [Reference Green, Tao and Ziegler20]) to conclude that
Similarly, we use $\|f_{l,unf}\|_{U^{s_0+1}}\leqslant \delta$![]() and $s_0\geqslant s$
and $s_0\geqslant s$![]() to conclude that
to conclude that
Combining all these estimates, we have
By choosing $\mathcal {F}$![]() growing sufficiently fast and $\delta$
growing sufficiently fast and $\delta$![]() sufficiently small depending on $\epsilon$
sufficiently small depending on $\epsilon$![]() , we obtain
, we obtain
which proves the theorem.
9. An asymptotic for the count of progressions of complexity 1
One of the applications of true complexity is that we can obtain an asymptotic for the count of polynomial progressions of complexity 1 like those in Theorem 1.1. We rewrite the integral polynomial map $\vec {P}\in \mathbb {Q}[\textbf {x}]^{t}$![]() in the form
in the form

for some $\vec {v}_1, \ldots , \vec {v}_r\in \mathbb {Z}^{t}$![]() and integer-valued $Q_1, \ldots , Q_r\in \mathbb {Q}[\textbf {x}]$
and integer-valued $Q_1, \ldots , Q_r\in \mathbb {Q}[\textbf {x}]$![]() . Given such a polynomial map, we define the corresponding linear map
. Given such a polynomial map, we define the corresponding linear map

The relationship between the two progressions is given by
and we aim to understand the relationship between the appropriate counts

and

where $P_k$![]() and $\psi _k$
and $\psi _k$![]() denote the $k$
denote the $k$![]() th coordinates of $\vec {P}$
th coordinates of $\vec {P}$![]() and $\vec {\varPsi }$
and $\vec {\varPsi }$![]() respectively.
respectively.
Theorem 9.1 Let $\vec {P}$![]() and $\vec {\varPsi }$
and $\vec {\varPsi }$![]() be given as above. Suppose moreover that $\vec {P}$
be given as above. Suppose moreover that $\vec {P}$![]() is Gowers controllable, equidistributes and is algebraically independent of degree 2. Then
is Gowers controllable, equidistributes and is algebraically independent of degree 2. Then
for an error term $o(1)$![]() that depends on $\vec {P}$
that depends on $\vec {P}$![]() but not on the choice of 1-bounded functions ${f_1, \ldots , f_{t}:\mathbb {F}_p\to \mathbb {C}}$
but not on the choice of 1-bounded functions ${f_1, \ldots , f_{t}:\mathbb {F}_p\to \mathbb {C}}$![]() .
.
Corollary 9.2 Let $\vec {P}$![]() and $\vec {\varPsi }$
and $\vec {\varPsi }$![]() be given as above, and suppose that $\vec {P}$
be given as above, and suppose that $\vec {P}$![]() is Gowers controllable, equidistributes and is algebraically independent of degree 2. For any $A\subseteq \mathbb {F}_p$
is Gowers controllable, equidistributes and is algebraically independent of degree 2. For any $A\subseteq \mathbb {F}_p$![]() , we have
, we have
and the error term is uniform in all subsets $A$![]() .
.
What Theorem 9.1 is indicating is that for configurations satisfying only linear relations and of true complexity 1, each polynomial $Q_i$![]() can be thought of as a separate variable. Therefore, the counts of $\vec {P}$
can be thought of as a separate variable. Therefore, the counts of $\vec {P}$![]() and $\vec {\varPsi }$
and $\vec {\varPsi }$![]() are so strongly related.
are so strongly related.
We specialize Corollary 9.2 to two families of polynomial progressions that we have explicitly looked at.
Corollary 9.3 Let $Q,R\in \mathbb {Z}[y]$![]() be non-zero polynomials that have zero constant terms and satisfy $1\leqslant \deg Q<\deg R$
be non-zero polynomials that have zero constant terms and satisfy $1\leqslant \deg Q<\deg R$![]() . For any 1-bounded functions $f_0, f_1, f_2, f_3:\mathbb {F}_p\to \mathbb {C}$
. For any 1-bounded functions $f_0, f_1, f_2, f_3:\mathbb {F}_p\to \mathbb {C}$![]() , we have
, we have
where the error term is independent of the choice of $f_0, f_1, f_2, f_3$![]() . Moreover, for any $A\subseteq \mathbb {F}_p$
. Moreover, for any $A\subseteq \mathbb {F}_p$![]() , we have
, we have

uniformly in the choice of $A$![]() .
.
We have thus related the number of progressions $x, x+Q(y), x+R(y), x+Q(y)+R(y)$![]() in an arbitrary subset $A\subseteq \mathbb {F}_p$
in an arbitrary subset $A\subseteq \mathbb {F}_p$![]() to the number of solutions to the Sidon equation $x+y=u+z$
to the number of solutions to the Sidon equation $x+y=u+z$![]() , which is a well-studied quantity known as additive energy. To learn more about Sidon equation or additive energy, consult e.g. [Reference Tao and Vu34].
, which is a well-studied quantity known as additive energy. To learn more about Sidon equation or additive energy, consult e.g. [Reference Tao and Vu34].
Proof. The first part of Corollary 9.3 is a straightforward application of Theorem 9.1. The second part follows by observing that two-dimensional cubes $x, x+y, x+z, x+y+z$![]() parametrize solutions to the Sidon equation.
parametrize solutions to the Sidon equation.
Corollary 9.4 Let $Q,R\in \mathbb {Z}[y]$![]() be non-zero polynomials that have zero constant terms and satisfy $1\leqslant \deg Q<(\deg R)/2$
be non-zero polynomials that have zero constant terms and satisfy $1\leqslant \deg Q<(\deg R)/2$![]() . For any 1-bounded functions $f_0, f_1, f_2, f_3, f_4:\mathbb {F}_p\to \mathbb {C}$
. For any 1-bounded functions $f_0, f_1, f_2, f_3, f_4:\mathbb {F}_p\to \mathbb {C}$![]() , we have
, we have
and the error term is independent of the choice of $f_0, f_1, f_2, f_3, f_4$![]() . Moreover, for any $A\subseteq \mathbb {F}_p$
. Moreover, for any $A\subseteq \mathbb {F}_p$![]() , we have
, we have

uniformly in the choice of $A$![]() .
.
Corollaries 9.3 and 9.4 together imply Theorem 1.1.
Proof of Theorem 9.1. We adopt the notation from [Reference Green and Tao17] to set
to be the analogue of $\mathcal {P}_{i,j}$![]() for the progression $\vec {\varPsi }$
for the progression $\vec {\varPsi }$![]() for $1\leqslant j \leqslant i$
for $1\leqslant j \leqslant i$![]() . We also let $G^{\varPsi }$
. We also let $G^{\varPsi }$![]() denote the Leibman group for $\vec {\varPsi }$
denote the Leibman group for $\vec {\varPsi }$![]() .
.
By assumption, the squares $P_1(\textbf {x})^{2}, \ldots , P_t(\textbf {x})^{2}$![]() are linearly independent, implying that $\mathcal {P}_{2,1}=\mathbb {R}^{t}$
are linearly independent, implying that $\mathcal {P}_{2,1}=\mathbb {R}^{t}$![]() . From (30), it follows that $\mathcal {P}_{1,1}=\varPsi ^{[1]}$
. From (30), it follows that $\mathcal {P}_{1,1}=\varPsi ^{[1]}$![]() and $\mathcal {P}_{i,1}\subseteq \varPsi ^{[i]}$
and $\mathcal {P}_{i,1}\subseteq \varPsi ^{[i]}$![]() for $i>1$
for $i>1$![]() . Together with the fact that $\mathcal {P}_{2,1} = \mathbb {R}^{t}$
. Together with the fact that $\mathcal {P}_{2,1} = \mathbb {R}^{t}$![]() , this implies that $\varPsi ^{[2]}=\mathcal {P}_{2,1}$
, this implies that $\varPsi ^{[2]}=\mathcal {P}_{2,1}$![]() , and so the groups $G^{P}=G^{\varPsi }$
, and so the groups $G^{P}=G^{\varPsi }$![]() are in fact the same for any group $G$
are in fact the same for any group $G$![]() .
.
Given $\epsilon >0$![]() , we take $\delta >0$
, we take $\delta >0$![]() and $p_0\in \mathbb {N}$
and $p_0\in \mathbb {N}$![]() that works as in Theorem 8.1 for both $\vec {P}$
that works as in Theorem 8.1 for both $\vec {P}$![]() and $\vec {\Phi }$
and $\vec {\Phi }$![]() , and we let $\mathcal {F}:\mathbb {R}_+\to \mathbb {R}_+$
, and we let $\mathcal {F}:\mathbb {R}_+\to \mathbb {R}_+$![]() be a growth function to be fixed later. We moreover assume from now on that $p>p_0$
be a growth function to be fixed later. We moreover assume from now on that $p>p_0$![]() . By Lemma 2.13, there exist $M=O_{\epsilon , t,\mathcal {F}}(1)$
. By Lemma 2.13, there exist $M=O_{\epsilon , t,\mathcal {F}}(1)$![]() , a filtered nilmanifold $G/\varGamma$
, a filtered nilmanifold $G/\varGamma$![]() of degree $1$
of degree $1$![]() and complexity $M$
and complexity $M$![]() , and a $p$
, and a $p$![]() -periodic, $\mathcal {F}(M)$
-periodic, $\mathcal {F}(M)$![]() -irrational sequence $g\in {\textrm {poly}}(\mathbb {Z},G_\bullet )$
-irrational sequence $g\in {\textrm {poly}}(\mathbb {Z},G_\bullet )$![]() with $g(0)=1$
with $g(0)=1$![]() such that there exist decompositions
such that there exist decompositions
of functions $f_1, \ldots , f_{t}:\mathbb {F}_p\to \mathbb {C}$![]() satisfying the conditions of Lemma 2.13. By taking $\mathcal {F}$
satisfying the conditions of Lemma 2.13. By taking $\mathcal {F}$![]() growing fast enough with respect to $\delta$
growing fast enough with respect to $\delta$![]() , we can assume that $\|f_{i,unf}\|_{U^{2}}\leqslant {1}/{\mathcal {F}(M)}\leqslant \delta /4$
, we can assume that $\|f_{i,unf}\|_{U^{2}}\leqslant {1}/{\mathcal {F}(M)}\leqslant \delta /4$![]() for each $i$
for each $i$![]() .
.
By applying the aforementioned decomposition to $f_1, \ldots , f_{t}$![]() , each of the operators $\varLambda _P(f_1, \ldots , f_{t})$
, each of the operators $\varLambda _P(f_1, \ldots , f_{t})$![]() and $\varLambda _\varPsi (f_1, \ldots , f_{t})$
and $\varLambda _\varPsi (f_1, \ldots , f_{t})$![]() splits into $3^{t}$
splits into $3^{t}$![]() terms. The expressions involving at least one $f_{i, sml}$
terms. The expressions involving at least one $f_{i, sml}$![]() can be bounded crudely by $O(\epsilon )$
can be bounded crudely by $O(\epsilon )$![]() . Using Theorem 8.1, the expressions involving at least one $f_{i, unf}$
. Using Theorem 8.1, the expressions involving at least one $f_{i, unf}$![]() can be bounded by $O(\epsilon )$
can be bounded by $O(\epsilon )$![]() as well. We thus have
as well. We thus have
and similarly for $\varLambda _\varPsi (f_1, \ldots , f_{t})$![]() . Since both $\vec {P}$
. Since both $\vec {P}$![]() and $\vec {\varPsi }$
and $\vec {\varPsi }$![]() equidistribute, we have
equidistribute, we have
where $F((u_1, \ldots , u_{t})\varGamma ^{P})=F_1(u_1\varGamma )\cdots F_{t}(u_{t}\varGamma )$![]() . Likewise, we have
. Likewise, we have
Using the fact that $G^{P}=G^{\varPsi }$![]() and combining all the estimates so far, we obtain that
and combining all the estimates so far, we obtain that
The theorem follows by letting $\mathcal {F}$![]() grow sufficiently fast with respect to $\epsilon$
grow sufficiently fast with respect to $\epsilon$![]() , and by taking $\epsilon \to 0$
, and by taking $\epsilon \to 0$![]() as $p\to \infty$
as $p\to \infty$![]() .
.
Note that the only two facts that we use in the proof of Theorem 9.1 is that the progressions $\vec {P}$![]() and $\vec {\varPsi }$
and $\vec {\varPsi }$![]() are controlled by some Gowers norm (so that we can apply regularity lemma) and that the Leibman groups $G^{P}$
are controlled by some Gowers norm (so that we can apply regularity lemma) and that the Leibman groups $G^{P}$![]() and $G^{\varPsi }$
and $G^{\varPsi }$![]() are the same. It is the latter fact that follows from the algebraic independence of degree 2 of $\vec {P}$
are the same. It is the latter fact that follows from the algebraic independence of degree 2 of $\vec {P}$![]() . We do not strictly require the information that $\vec {P}$
. We do not strictly require the information that $\vec {P}$![]() and $\vec {\varPsi }$
and $\vec {\varPsi }$![]() are controlled by the $U^{2}$
are controlled by the $U^{2}$![]() norm.
norm.
10. A progression not satisfying filtration condition
While many naturally defined polynomial progressions satisfy filtration condition, one can also find a configuration for which the condition fails. We present one such example in this section. Let

It is straightforward to deduce that

We claim that $\mathcal {P}_{1,1}\cdot \mathcal {P}_{1,3}\notin \mathcal {P}_{2,4}$![]() . To obtain $\mathcal {P}_{2,4}$
. To obtain $\mathcal {P}_{2,4}$![]() , we write
, we write

From the fact that

we deduce that
From the description of $\mathcal {P}_{1,j}$![]() above, we have that $\vec {v}=(0,1,0,0,0)\in \mathcal {P}_{1,1}$
above, we have that $\vec {v}=(0,1,0,0,0)\in \mathcal {P}_{1,1}$![]() and $\vec {w}=(0,1,2,3,4)\in \mathcal {P}_{1,3}$
and $\vec {w}=(0,1,2,3,4)\in \mathcal {P}_{1,3}$![]() ; however, the product $\vec {v}\cdot \vec {w}=(0,1,0,0,0)$
; however, the product $\vec {v}\cdot \vec {w}=(0,1,0,0,0)$![]() is not contained in $\mathcal {P}_{2,4}$
is not contained in $\mathcal {P}_{2,4}$![]() . Therefore, the progression $\vec {P}$
. Therefore, the progression $\vec {P}$![]() does not satisfy the filtration condition.
does not satisfy the filtration condition.
11. Failure of equidistribution for $x, x+y, x+2y, x+y^{2}$
Failure to satisfy filtration condition is one reason why it may be hard to work with Leibman group for more general polynomial progressions. Perhaps more interestingly, we can find progressions that satisfy filtration condition, yet they do not equidistribute on the Leibman nilmanifold. In particular, these arguments break for the configuration
For this progression, we have

and we can moreover prove the following.
Lemma 11.1 For $i\geqslant 2$![]() , we have
, we have

Proof. The case $j> 2i$![]() follows from the fact that $\deg ({{\vec {P}(x,y)}\choose {i}})=2i$
follows from the fact that $\deg ({{\vec {P}(x,y)}\choose {i}})=2i$![]() . For $i+1 \leqslant j\leqslant 2i$
. For $i+1 \leqslant j\leqslant 2i$![]() , we note that ${{x}\choose {i}}$
, we note that ${{x}\choose {i}}$![]() , ${{x+y}\choose {i}}$
, ${{x+y}\choose {i}}$![]() and ${{x+2y}\choose {i}}$
and ${{x+2y}\choose {i}}$![]() all have degree $i$
all have degree $i$![]() , and so $\mathcal {P}_{i,j}\subseteq 0\times 0 \times 0 \times \mathbb {R}$
, and so $\mathcal {P}_{i,j}\subseteq 0\times 0 \times 0 \times \mathbb {R}$![]() . That this is equality follows from the fact that the coefficient of ${{y}\choose {2}}$
. That this is equality follows from the fact that the coefficient of ${{y}\choose {2}}$![]() is a non-zero multiple of the vector $(0,0,0,1)$
is a non-zero multiple of the vector $(0,0,0,1)$![]() . The case $1\leqslant j\leqslant i$
. The case $1\leqslant j\leqslant i$![]() follows from the fact that
follows from the fact that

and $\mathcal {P}_{i,j}\supseteq \mathcal {P}_{2,j}$![]() for $i\geqslant 2$
for $i\geqslant 2$![]() by Lemma 3.1.
by Lemma 3.1.
Corollary 11.2 The polynomial map $\vec {P}$![]() satisfies the filtration condition.
satisfies the filtration condition.
To prove that progressions in § 4–§ 6 equidistribute, we showed that if a polynomial sequence $g$![]() is highly irrational on a nilmanifold $G/\varGamma$
is highly irrational on a nilmanifold $G/\varGamma$![]() , then $g^{{P}}$
, then $g^{{P}}$![]() is close to being equidistributed on the nilmanifold $G^{P}/\varGamma ^{P}$
is close to being equidistributed on the nilmanifold $G^{P}/\varGamma ^{P}$![]() . More precisely, we proved the contrapositive: if there exists a non-trivial horizontal character on $G^{P}/\varGamma ^{P}$
. More precisely, we proved the contrapositive: if there exists a non-trivial horizontal character on $G^{P}/\varGamma ^{P}$![]() of small modulus that annihilates $g^{{P}}$
of small modulus that annihilates $g^{{P}}$![]() , then for some $j\geqslant 1$
, then for some $j\geqslant 1$![]() there must exist a $j$
there must exist a $j$![]() th level character on $G/\varGamma$
th level character on $G/\varGamma$![]() of small modulus that annihilates the $j$
of small modulus that annihilates the $j$![]() th Taylor coefficient $g_j$
th Taylor coefficient $g_j$![]() of $g$
of $g$![]() . It turns out this is not the case for $x, x+y, x+2y, x+y^{2}$
. It turns out this is not the case for $x, x+y, x+2y, x+y^{2}$![]() : we can find a highly irrational sequence $g$
: we can find a highly irrational sequence $g$![]() on a nilmanifold $G/\varGamma$
on a nilmanifold $G/\varGamma$![]() such that $g^{{P}}$
such that $g^{{P}}$![]() is annihilated by a horizontal character of a small modulus.
is annihilated by a horizontal character of a small modulus.
That our arguments from previous sections would not work here is already clear from Lemma 11.1. If $\vec {P}$![]() equidistributed, then the fact that $\mathcal {P}_{2,1}$
equidistributed, then the fact that $\mathcal {P}_{2,1}$![]() is all of $\mathbb {R}^{4}$
is all of $\mathbb {R}^{4}$![]() would imply that the sequence $(x,y)\mapsto g^{P}(x,y)G_2^{4}$
would imply that the sequence $(x,y)\mapsto g^{P}(x,y)G_2^{4}$![]() would be close to being equidistributed on the 1-step nilmanifold $G/G_2\varGamma$
would be close to being equidistributed on the 1-step nilmanifold $G/G_2\varGamma$![]() for any highly irrational $p$
for any highly irrational $p$![]() -periodic sequence $g$
-periodic sequence $g$![]() , and so we would expect $\vec {P}$
, and so we would expect $\vec {P}$![]() to be of complexity 1. We know by Theorem 1.13 that this cannot possibly happen because of the quadratic relation (9). In the ergodic theoretic language, this instantiates the fact that the Vandermonde complexity and the Weyl complexity of the progression are differentFootnote 3.
to be of complexity 1. We know by Theorem 1.13 that this cannot possibly happen because of the quadratic relation (9). In the ergodic theoretic language, this instantiates the fact that the Vandermonde complexity and the Weyl complexity of the progression are differentFootnote 3.
Lemma 11.3 There exists a degree-2 filtered nilmanifold $G/\varGamma$![]() of complexity $O(1)$
of complexity $O(1)$![]() , a $p^{{1}/{2}}$
, a $p^{{1}/{2}}$![]() -irrational sequence $g\in {\textrm {poly}}(\mathbb {Z}, G_\bullet )$
-irrational sequence $g\in {\textrm {poly}}(\mathbb {Z}, G_\bullet )$![]() , and a horizontal character $\eta :G^{P}\to \mathbb {R}$
, and a horizontal character $\eta :G^{P}\to \mathbb {R}$![]() of modulus $O(1)$
of modulus $O(1)$![]() such that $\eta \circ g^{P} = 0$
such that $\eta \circ g^{P} = 0$![]() .
.
Proof. We take $G=\mathbb {R} \times \mathbb {R}$![]() and $\varGamma =\mathbb {Z}\times \mathbb {Z}$
and $\varGamma =\mathbb {Z}\times \mathbb {Z}$![]() with the degree-2 filtration given by
with the degree-2 filtration given by
Let $\alpha = \lfloor \sqrt {p}\rfloor /p$![]() . We define a sequence $g\in {\textrm {poly}}(\mathbb {Z}, G_\bullet )$
. We define a sequence $g\in {\textrm {poly}}(\mathbb {Z}, G_\bullet )$![]() by setting $g_1=(\alpha , 0)$
by setting $g_1=(\alpha , 0)$![]() , $g_2 = (0, \alpha )$
, $g_2 = (0, \alpha )$![]() , so that $g(n) = (\alpha n, \alpha {{n}\choose {2}})$
, so that $g(n) = (\alpha n, \alpha {{n}\choose {2}})$![]() . It is straightforward to see that $g$
. It is straightforward to see that $g$![]() is indeed $p^{{1}/{2}}$
is indeed $p^{{1}/{2}}$![]() -irrational.
-irrational.
Having established irrationality of $g$![]() , we shall construct a horizontal character on $G^{P}$
, we shall construct a horizontal character on $G^{P}$![]() of bounded modulus that annihilates $g^{P}$
of bounded modulus that annihilates $g^{P}$![]() . Let $(x,y,u,z)$
. Let $(x,y,u,z)$![]() denote an arbitrary element of $G^{4}$
denote an arbitrary element of $G^{4}$![]() , where $x=(x_1, x_2)$
, where $x=(x_1, x_2)$![]() and similarly for $y,u,z$
and similarly for $y,u,z$![]() . We define $\eta : G^{4}\to \mathbb {R}$
. We define $\eta : G^{4}\to \mathbb {R}$![]() by setting
by setting
The function $\eta$![]() defines a horizontal character on $G^{4}$
defines a horizontal character on $G^{4}$![]() , and by abuse of notation we use $\eta$
, and by abuse of notation we use $\eta$![]() to denote its restriction to $G^{P}$
to denote its restriction to $G^{P}$![]() . It is clear that $|\eta |\ll 1$
. It is clear that $|\eta |\ll 1$![]() . We claim that $\eta$
. We claim that $\eta$![]() annihilates $g^{P}$
annihilates $g^{P}$![]() . Expanding $\eta \circ g^{P}$
. Expanding $\eta \circ g^{P}$![]() , we obtain
, we obtain

Because of the way we defined $\eta$![]() , we see that it annihilates $g_1^{(1,1,1,1)}$
, we see that it annihilates $g_1^{(1,1,1,1)}$![]() because
because
Other terms of the polynomial $\eta \circ g^{P}$![]() are annihilated for similar reasons, with one interesting exception: the coefficient of ${{y}\choose {2}}$
are annihilated for similar reasons, with one interesting exception: the coefficient of ${{y}\choose {2}}$![]() . The function $\eta$
. The function $\eta$![]() annihilates neither $g_1^{(0,0,0,2)}$
annihilates neither $g_1^{(0,0,0,2)}$![]() nor $g_2^{(0,1,4,6)}$
nor $g_2^{(0,1,4,6)}$![]() , but it does annihilate their product, and from this it follows that $\eta \circ g^{P} =0$
, but it does annihilate their product, and from this it follows that $\eta \circ g^{P} =0$![]() . This is the point where the argument from Theorems 4.5, 5.3 and 6.3 breaks; we can no longer conclude that non-triviality of $\eta$
. This is the point where the argument from Theorems 4.5, 5.3 and 6.3 breaks; we can no longer conclude that non-triviality of $\eta$![]() implies irrationality of a Taylor coefficient of $g$
implies irrationality of a Taylor coefficient of $g$![]() , which was a crucial step in obtaining contradictions in Theorems 4.5, 5.3 and 6.3.
, which was a crucial step in obtaining contradictions in Theorems 4.5, 5.3 and 6.3.
This example illustrates that irrationality of $g$![]() is in general not sufficient to guarantee equidistribution of $g^{P}$
is in general not sufficient to guarantee equidistribution of $g^{P}$![]() on $G^{P}/\varGamma ^{P}$
on $G^{P}/\varGamma ^{P}$![]() . The main obstruction in our example is that the sequence $g$
. The main obstruction in our example is that the sequence $g$![]() is irrational but not jointly irrational; that is, there exist a 1-horizontal character $\eta _1$
is irrational but not jointly irrational; that is, there exist a 1-horizontal character $\eta _1$![]() and a 2-horizontal character $\eta _2$
and a 2-horizontal character $\eta _2$![]() satisfying $|\eta _1|, |\eta _2|\ll 1$
satisfying $|\eta _1|, |\eta _2|\ll 1$![]() such that $\eta _1(g_1) + \eta _2(g_2)\in \mathbb {Z}$
such that $\eta _1(g_1) + \eta _2(g_2)\in \mathbb {Z}$![]() but $\eta _1(g_1), \eta _2(g_2)\notin \mathbb {Z}$
but $\eta _1(g_1), \eta _2(g_2)\notin \mathbb {Z}$![]() . This type of obstruction does not appear if one works with linear forms since each power of a linear form is a homogeneous polynomial of different degree. In the case of general polynomial maps, however, one may get the same monomial coming from different powers of the same polynomial, like ${{y}\choose {2}}$
. This type of obstruction does not appear if one works with linear forms since each power of a linear form is a homogeneous polynomial of different degree. In the case of general polynomial maps, however, one may get the same monomial coming from different powers of the same polynomial, like ${{y}\choose {2}}$![]() in Lemma 11.3. Therefore, some sort of ‘joint irrationality’ is necessary.
in Lemma 11.3. Therefore, some sort of ‘joint irrationality’ is necessary.
12. True complexity of $x, x+y, \ldots , x+(m-1)y, x+y^{d}$
The reasoning presented in § 11 shows that the arguments used to tackle $x, x+y, x+y^{2}, x+y+y^{2}$![]() or $x, x+y, x+2y, x+y^{3}, x+2y^{3}$
or $x, x+y, x+2y, x+y^{3}, x+2y^{3}$![]() cannot be used for $x, x+y, x+2y, x+y^{2}$
cannot be used for $x, x+y, x+2y, x+y^{2}$![]() . However, we can circumvent the difficulties and determine true complexity for this and related configurations via a different method. This method comes down to making the progression more homogeneous by replacing it with a longer progressions involving higher number of variables using several applications of the Cauchy–Schwarz inequality.
. However, we can circumvent the difficulties and determine true complexity for this and related configurations via a different method. This method comes down to making the progression more homogeneous by replacing it with a longer progressions involving higher number of variables using several applications of the Cauchy–Schwarz inequality.
In this section, we prove Conjecture 1.12 for
whenever $2\leqslant d\leqslant m-1$![]() , the case $d\geqslant m$
, the case $d\geqslant m$![]() being handled quantitatively in [Reference Kuca25]. We start by proving true complexity for the non-linear term at index $m$
being handled quantitatively in [Reference Kuca25]. We start by proving true complexity for the non-linear term at index $m$![]() .
.
Proposition 12.1 Let $m, d\in \mathbb {N}_+$![]() satisfy $m\geqslant 3$
satisfy $m\geqslant 3$![]() and $d\geqslant 2$
and $d\geqslant 2$![]() . Given $\epsilon >0$
. Given $\epsilon >0$![]() , there exists $\delta >0$
, there exists $\delta >0$![]() and $p_0\in \mathbb {N}$
and $p_0\in \mathbb {N}$![]() s.t. for all $p>p_0$
s.t. for all $p>p_0$![]() , we have
, we have
uniformly for all 1-bounded functions $f_0, \ldots , f_m:\mathbb {F}_p\to \mathbb {C}$![]() satisfying $\|f_m\|_{U^{\left \lceil {m}/{d}\right \rceil }}\leqslant \delta$
satisfying $\|f_m\|_{U^{\left \lceil {m}/{d}\right \rceil }}\leqslant \delta$![]() .
.
We note that one cannot get a control by a lower-degree Gowers norm here; this follows from
and the fact that the space of polynomials in $x$![]() and $y$
and $y$![]() of degree at most $m-1$
of degree at most $m-1$![]() is spanned by polynomials in $x$
is spanned by polynomials in $x$![]() , $x+y$
, $x+y$![]() , …, $x+(m-1)y$
, …, $x+(m-1)y$![]() of degree at most $m-1$
of degree at most $m-1$![]() , so, in particular, it contains the $\left \lfloor {(m-1)}/{d}\right \rfloor$
, so, in particular, it contains the $\left \lfloor {(m-1)}/{d}\right \rfloor$![]() th power of $x+y^{d}$
th power of $x+y^{d}$![]() .
.
Proof. We let all the constants depend on $m$![]() and $d$
and $d$![]() without mentioning the dependence explicitly. We only prove the case $2\leqslant d\leqslant m-1$
without mentioning the dependence explicitly. We only prove the case $2\leqslant d\leqslant m-1$![]() , as the case $d\geqslant m$
, as the case $d\geqslant m$![]() has been handled in [Reference Kuca25].
has been handled in [Reference Kuca25].
By Proposition 2.2 of [Reference Peluse29], we have
for some $c>0$![]() and $s\in \mathbb {N}$
and $s\in \mathbb {N}$![]() independent of the choice of 1-bounded functions $f_0, \ldots , f_m:\mathbb {F}_p\to \mathbb {C}$
independent of the choice of 1-bounded functions $f_0, \ldots , f_m:\mathbb {F}_p\to \mathbb {C}$![]() .
.
Let $\mathcal {F}:\mathbb {R}_+\to \mathbb {R}_+$![]() be a growth function to be fixed later. By Lemma 2.13, there exist $M=O_{\epsilon ,\mathcal {F}}(1)$
be a growth function to be fixed later. By Lemma 2.13, there exist $M=O_{\epsilon ,\mathcal {F}}(1)$![]() , a filtered manifold $G/\varGamma$
, a filtered manifold $G/\varGamma$![]() of degree $s$
of degree $s$![]() and complexity at most $M$
and complexity at most $M$![]() , and a $p$
, and a $p$![]() -periodic, $\mathcal {F}(M)$
-periodic, $\mathcal {F}(M)$![]() -irrational sequence $g\in {\textrm {poly}}(\mathbb {Z},G_\bullet )$
-irrational sequence $g\in {\textrm {poly}}(\mathbb {Z},G_\bullet )$![]() with $g(0)=1$
with $g(0)=1$![]() , for which there exists a decomposition
, for which there exists a decomposition
such that $f_{nil}(n)=F(g(n)\varGamma )$![]() for an $M$
for an $M$![]() -Lipschitz function $F: G/\varGamma \to \mathbb {C}$
-Lipschitz function $F: G/\varGamma \to \mathbb {C}$![]() , ${\|f_{sml}\|_2\leqslant \epsilon }$
, ${\|f_{sml}\|_2\leqslant \epsilon }$![]() and $\|f_{unf}\|_{U^{s+1}}\leqslant {1}/{\mathcal {F}(M)}$
and $\|f_{unf}\|_{U^{s+1}}\leqslant {1}/{\mathcal {F}(M)}$![]() . By picking $\mathcal {F}$
. By picking $\mathcal {F}$![]() to be growing sufficiently fast, we can assume that $\|f_{unf}\|_{U^{s+1}}\leqslant \epsilon ^{{1}/{c}}$
to be growing sufficiently fast, we can assume that $\|f_{unf}\|_{U^{s+1}}\leqslant \epsilon ^{{1}/{c}}$![]() . Assuming that $p$
. Assuming that $p$![]() is large enough with respect to $\epsilon$
is large enough with respect to $\epsilon$![]() , we thus have
, we thus have

By applying the triangle inequality and translating $x\mapsto x-y$![]() exactly $m$
exactly $m$![]() times to remove $f_0, f_1, \ldots , f_{m-1}$
times to remove $f_0, f_1, \ldots , f_{m-1}$![]() , we have
, we have

where

for each $w\in \{0,1\}^{m}$![]() . Given $w\in \{0,1\}^{m}$
. Given $w\in \{0,1\}^{m}$![]() , we let $\vec {e}_w$
, we let $\vec {e}_w$![]() denote the basis vector in $\mathbb {R}^{\{0,1\}^{m}}$
denote the basis vector in $\mathbb {R}^{\{0,1\}^{m}}$![]() of the form
of the form

Let
and $G^{P}$![]() be the corresponding Leibman group. The next lemma gives the structure of the polynomial spaces $\mathcal {P}_{i,j}$
be the corresponding Leibman group. The next lemma gives the structure of the polynomial spaces $\mathcal {P}_{i,j}$![]() .
.
Lemma 12.2 For each $i\in \mathbb {N}_+$![]() and $1\leqslant j\leqslant id$
and $1\leqslant j\leqslant id$![]() , the space $\mathcal {P}_{i,j}$
, the space $\mathcal {P}_{i,j}$![]() is spanned by the vectors
is spanned by the vectors
for all $k_1, \ldots , k_{id}\in \{1, \ldots , m\}$![]() . For $j>id$
. For $j>id$![]() , we have $\mathcal {P}_{i,j}=0$
, we have $\mathcal {P}_{i,j}=0$![]() .
.
Proof. The case $j>id$![]() is easy to see from the fact that ${{\vec {P}(x,y)}\choose {i}}$
is easy to see from the fact that ${{\vec {P}(x,y)}\choose {i}}$![]() has degree $id$
has degree $id$![]() , and so we proceed to the other case. The vector $\sum \nolimits _{w}(-1)^{|w|}\vec {e}_w$
, and so we proceed to the other case. The vector $\sum \nolimits _{w}(-1)^{|w|}\vec {e}_w$![]() is in $\mathcal {P}_{i,id}$
is in $\mathcal {P}_{i,id}$![]() because its integer multiple is the coefficient of ${{y}\choose {id}}$
because its integer multiple is the coefficient of ${{y}\choose {id}}$![]() . To see that each vector of the form $\sum \nolimits _{\substack {w: \\ w_{k_1} = \cdots = w_{k_n}=1}}(-1)^{|w|}\vec {e}_w$
. To see that each vector of the form $\sum \nolimits _{\substack {w: \\ w_{k_1} = \cdots = w_{k_n}=1}}(-1)^{|w|}\vec {e}_w$![]() is in $\mathcal {P}_{i,id}$
is in $\mathcal {P}_{i,id}$![]() for $1\leqslant n\leqslant id$
for $1\leqslant n\leqslant id$![]() and $k_1, \ldots , k_n\in \{1, \ldots , m\}$
and $k_1, \ldots , k_n\in \{1, \ldots , m\}$![]() , we observe that the coefficient of
, we observe that the coefficient of
is a non-zero integer multiple of $\sum \nolimits _{\substack {w: \\ w_{k_1} = \cdots = w_{k_n}=1}}(-1)^{|w|}\vec {e}_w$![]() and use Lemma 4.6. To show the converse, we note that the coefficient of a monomial of ${{\vec {P}(x,y)}\choose {i}}$
and use Lemma 4.6. To show the converse, we note that the coefficient of a monomial of ${{\vec {P}(x,y)}\choose {i}}$![]() is an integer multiple of $\sum \nolimits _{\substack {w: w_{k_1} = \cdots = w_{k_n}=1}}(-1)^{|w|}\vec {e}_w$
is an integer multiple of $\sum \nolimits _{\substack {w: w_{k_1} = \cdots = w_{k_n}=1}}(-1)^{|w|}\vec {e}_w$![]() for $0\leqslant n\leqslant id$
for $0\leqslant n\leqslant id$![]() if and only if the monomial contains the variables $h_{k_1}, \ldots , h_{k_l}$
if and only if the monomial contains the variables $h_{k_1}, \ldots , h_{k_l}$![]() but does not contain $h_k$
but does not contain $h_k$![]() for $k\in \{1, \ldots , m\}\setminus {\{k_1, \ldots , k_n\}}$
for $k\in \{1, \ldots , m\}\setminus {\{k_1, \ldots , k_n\}}$![]() .
.
Corollary 12.3 The progression $\vec {P}$![]() satisfies the filtration condition.
satisfies the filtration condition.
Proof. This follows from Lemma 12.2 and the observation that

for any $k_1, \ldots , k_{n_1}, k'_1, \ldots , k'_{n_2}\in \{1, \ldots , m\}$![]() .
.
Corollary 12.4 If $i\geqslant {m}/{d}$![]() , then $\mathcal {P}_{i,1}=\cdots =\mathcal {P}_{i,id}=\mathbb {R}^{\{0,1\}^{m}}$
, then $\mathcal {P}_{i,1}=\cdots =\mathcal {P}_{i,id}=\mathbb {R}^{\{0,1\}^{m}}$![]() .
.
Proof. We first observe that the set

spans $\mathcal {P}_{i,1}=\cdots =\mathcal {P}_{i,id}$![]() and consists of linearly independent vectors as long as $id\leqslant m$
and consists of linearly independent vectors as long as $id\leqslant m$![]() . If $id\geqslant m$
. If $id\geqslant m$![]() , then $X$
, then $X$![]() has $2^{m}$
has $2^{m}$![]() elements, implying that $\mathcal {P}_{i,1}=\cdots =\mathcal {P}_{i,id}=\mathbb {R}^{\{0,1\}^{m}}$
elements, implying that $\mathcal {P}_{i,1}=\cdots =\mathcal {P}_{i,id}=\mathbb {R}^{\{0,1\}^{m}}$![]() , as required.
, as required.
This leads to the following important corollary which we shall need to prove that the sequence $g^{P}$![]() is close to being equidistributed on $G^{P}$
is close to being equidistributed on $G^{P}$![]() .
.
Corollary 12.5 Let $i=\left \lceil {m}/{d}\right \rceil$![]() . Then $G_i^{\{0,1\}^{m}}\subseteq G^{P}$
. Then $G_i^{\{0,1\}^{m}}\subseteq G^{P}$![]() .
.
Theorem 12.6 The sequence $g^{P}\in {\textrm {poly}}(\mathbb {Z}^{m+2},G^{P}_\bullet )$![]() is $O_{M}(\mathcal {F}(M)^{-c_M})$
is $O_{M}(\mathcal {F}(M)^{-c_M})$![]() - equidistributed.
- equidistributed.
Proof. Suppose that $g^{P}\in {\textrm {poly}}(\mathbb {Z}^{m+2},G^{P}_\bullet )$![]() is not $O_{M}(\mathcal {F}(M)^{-c_M})$
is not $O_{M}(\mathcal {F}(M)^{-c_M})$![]() -equidistributed. By Theorem 2.9, there exists a non-trivial horizontal character $\eta :G^{P}\to \mathbb {R}$
-equidistributed. By Theorem 2.9, there exists a non-trivial horizontal character $\eta :G^{P}\to \mathbb {R}$![]() of complexity at most $c\mathcal {F}(M)$
of complexity at most $c\mathcal {F}(M)$![]() for some $c>0$
for some $c>0$![]() to be chosen later, such that $\eta \circ g^{P}\in \mathbb {Z}$
to be chosen later, such that $\eta \circ g^{P}\in \mathbb {Z}$![]() . Let $j$
. Let $j$![]() be the largest natural number such that $\eta |_{G^{P}_j}\neq 0$
be the largest natural number such that $\eta |_{G^{P}_j}\neq 0$![]() . By assumption, $\eta$
. By assumption, $\eta$![]() annihilates ${G^{P}_{j+1}}$
annihilates ${G^{P}_{j+1}}$![]() .
.
When $j$![]() is not divisible by $d$
is not divisible by $d$![]() , we have $\mathcal {P}_{i,j}=\mathcal {P}_{i,j+1}$
, we have $\mathcal {P}_{i,j}=\mathcal {P}_{i,j+1}$![]() for all $i\geqslant 1$
for all $i\geqslant 1$![]() , implying that any $j$
, implying that any $j$![]() th level character is trivial. We can, therefore, assume without loss of generality that $d$
th level character is trivial. We can, therefore, assume without loss of generality that $d$![]() divides $j$
divides $j$![]() . Moreover, the only $i$
. Moreover, the only $i$![]() such that $\mathcal {P}_{i,j}\neq \mathcal {P}_{i,j+1}$
such that $\mathcal {P}_{i,j}\neq \mathcal {P}_{i,j+1}$![]() is $i={j}/{d}$
is $i={j}/{d}$![]() , in which case we have $\mathcal {P}_{i,j+1}=0$
, in which case we have $\mathcal {P}_{i,j+1}=0$![]() . We, therefore, fix $i={j}/{d}$
. We, therefore, fix $i={j}/{d}$![]() . Given $\vec {v}\in X_i$
. Given $\vec {v}\in X_i$![]() , where $X_i$
, where $X_i$![]() is defined as in (34), we let
is defined as in (34), we let
for $h\in G_i$![]() . The map $\xi _{\vec {v}}$
. The map $\xi _{\vec {v}}$![]() defines an $i$
defines an $i$![]() th level character on $G$
th level character on $G$![]() by a straightforward generalization of Corollary 3.9. By Lemma 12.2, the non-triviality of $\eta$
by a straightforward generalization of Corollary 3.9. By Lemma 12.2, the non-triviality of $\eta$![]() implies that $\xi _{\vec {v}}$
implies that $\xi _{\vec {v}}$![]() is non-trivial for at least one $\vec {v}\in X_i$
is non-trivial for at least one $\vec {v}\in X_i$![]() . The bound on the modulus of $\eta$
. The bound on the modulus of $\eta$![]() and the fact that the vectors $\vec {v}_k$
and the fact that the vectors $\vec {v}_k$![]() have entries of size $O(1)$
have entries of size $O(1)$![]() imply that $|\xi _{\vec {v}}|\leqslant A$
imply that $|\xi _{\vec {v}}|\leqslant A$![]() , provided that the constant $c$
, provided that the constant $c$![]() is appropriately chosen.
is appropriately chosen.
We claim that $\xi _{\vec {v}}(g_i)\in \mathbb {Z}$![]() for each $\vec {v}\in X_i$
for each $\vec {v}\in X_i$![]() . This follows from inspecting the coefficients of ${{y}\choose {id}}$
. This follows from inspecting the coefficients of ${{y}\choose {id}}$![]() and ${{h_{k_1}}\choose {id+1-n}}h_{k_2}\cdots h_{k_n}$
and ${{h_{k_1}}\choose {id+1-n}}h_{k_2}\cdots h_{k_n}$![]() for all $k_1, \ldots , k_n\in \{1, \ldots , m\}$
for all $k_1, \ldots , k_n\in \{1, \ldots , m\}$![]() . They are integer multiples of the vectors $\sum \nolimits _{w}(-1)^{|w|}\vec {e}_w$
. They are integer multiples of the vectors $\sum \nolimits _{w}(-1)^{|w|}\vec {e}_w$![]() and $\sum \nolimits _{w: w_{k_1}=\cdots =w_{k_n}=1}(-1)^{|w|}\vec {e}_w$
and $\sum \nolimits _{w: w_{k_1}=\cdots =w_{k_n}=1}(-1)^{|w|}\vec {e}_w$![]() respectively, and so the claim follows by Lemma 4.6. Together with the argument from the previous paragraph, this contradicts the $\mathcal {F}(M)$
respectively, and so the claim follows by Lemma 4.6. Together with the argument from the previous paragraph, this contradicts the $\mathcal {F}(M)$![]() -irrationality of $g$
-irrationality of $g$![]() , implying that $g^{P}$
, implying that $g^{P}$![]() is $O_{M}(\mathcal {F}(M)^{-c_M})$
is $O_{M}(\mathcal {F}(M)^{-c_M})$![]() -equidistributed.
-equidistributed.
Combining (33) with Theorem 12.6, we see that

The rest of the proof follows the logic of the proofs of Theorem 8.1 and Theorem 7.1 from [Reference Green and Tao17]. We let
to be the average of $F$![]() over the coset of $G_{\left \lceil {m}/{d}\right \rceil }/\varGamma _{\left \lceil {m}/{d}\right \rceil }$
over the coset of $G_{\left \lceil {m}/{d}\right \rceil }/\varGamma _{\left \lceil {m}/{d}\right \rceil }$![]() containing $x\varGamma$
containing $x\varGamma$![]() . Using the fact that $G_{\left \lceil {m}/{d}\right \rceil }^{\{0,1\}^{m}}\subseteq G^{P}$
. Using the fact that $G_{\left \lceil {m}/{d}\right \rceil }^{\{0,1\}^{m}}\subseteq G^{P}$![]() and the crude bound
and the crude bound

we obtain

By the $\mathcal {F}(M)$![]() -irrationality of $g$
-irrationality of $g$![]() , we have
, we have
We let $\psi (n)=\overline {F_{\leqslant {\left \lceil {m}/{d}\right \rceil }-1}}(g(n)\varGamma )$![]() . By the $G_{{\left \lceil {m}/{d}\right \rceil }}$
. By the $G_{{\left \lceil {m}/{d}\right \rceil }}$![]() -invariance of $F_{\leqslant {\left \lceil {m}/{d}\right \rceil }-1}$
-invariance of $F_{\leqslant {\left \lceil {m}/{d}\right \rceil }-1}$![]() , this is a nilsequence of degree $\leqslant {\left \lceil {m}/{d}\right \rceil }-1$
, this is a nilsequence of degree $\leqslant {\left \lceil {m}/{d}\right \rceil }-1$![]() and complexity $M$
and complexity $M$![]() . By (29), we have
. By (29), we have
We then split the average on the right-hand side of (36) into three terms. By Cauchy–Schwarz inequality, we have
To evaluate the contribution coming from $f_m$![]() , we use $\|f_{m}\|_{U^{{\left \lceil {m}/{d}\right \rceil }}}\leqslant \delta$
, we use $\|f_{m}\|_{U^{{\left \lceil {m}/{d}\right \rceil }}}\leqslant \delta$![]() and the converse to the inverse theorem for Gowers norms (Proposition 1.4 of Appendix G of [Reference Green, Tao and Ziegler20]) to conclude that
and the converse to the inverse theorem for Gowers norms (Proposition 1.4 of Appendix G of [Reference Green, Tao and Ziegler20]) to conclude that
Similarly, we use $\|f_{unf}\|_{U^{s+1}}\leqslant {1}/{\mathcal {F}(M)}$![]() and monotonicity of Gowers norms to conclude that
and monotonicity of Gowers norms to conclude that
Combining all these estimates, we have

By choosing $\mathcal {F}$![]() growing sufficiently fast and $\delta$
growing sufficiently fast and $\delta$![]() sufficiently small depending on $\epsilon$
sufficiently small depending on $\epsilon$![]() , we obtain
, we obtain
which proves Proposition 12.1.
The control by a low-degree Gowers norm of the non-linear term $x+y^{d}$![]() is useful in that when combined with the regularity lemma (Lemma 2.13), it allows us to replace the function $f_m$
is useful in that when combined with the regularity lemma (Lemma 2.13), it allows us to replace the function $f_m$![]() by a low-degree nilsequence $\psi$
by a low-degree nilsequence $\psi$![]() . Lemma 12.7 shows how we can deal with $\psi$
. Lemma 12.7 shows how we can deal with $\psi$![]() if it has sufficiently low degree.
if it has sufficiently low degree.
Lemma 12.7 (Twisted generalized von Neumann's lemma) Let $2\leqslant m\leqslant M$![]() . There exists $c_M>0$
. There exists $c_M>0$![]() such that for any $\delta _1, \delta _2>0$
such that for any $\delta _1, \delta _2>0$![]() and any 1-bounded functions $f_0, \ldots , f_{m-1}:\mathbb {F}_p\to \mathbb {C}$
and any 1-bounded functions $f_0, \ldots , f_{m-1}:\mathbb {F}_p\to \mathbb {C}$![]() satisfying
satisfying
the following holds:
(i) if $\psi (x,y)=F(g(x,y)\varGamma )$
 is a $p$
is a $p$ -periodic nilsequence of complexity $M$
-periodic nilsequence of complexity $M$ and degree $m-2$
and degree $m-2$ , then
\begin{align*} \mathbb{E}_{x,y\in\mathbb{F}_p}f_0(x)\cdots f_{m-1}(x+(m-1)y)\psi(x,y)\ll_M \delta_1^{c_M}; \end{align*}
, then
\begin{align*} \mathbb{E}_{x,y\in\mathbb{F}_p}f_0(x)\cdots f_{m-1}(x+(m-1)y)\psi(x,y)\ll_M \delta_1^{c_M}; \end{align*}
(ii) if $\psi (x,y)=F(g(x,y)\varGamma )$
 is a $p$
is a $p$ -periodic nilsequence of complexity $M$
-periodic nilsequence of complexity $M$ and degree $m-1$
and degree $m-1$ , then
\begin{align*} \mathbb{E}_{x,y\in\mathbb{F}_p}f_0(x)\cdots f_{m-1}(x+(m-1)y)\psi(x,y)\ll_M \delta_2^{c_M}. \end{align*}
, then
\begin{align*} \mathbb{E}_{x,y\in\mathbb{F}_p}f_0(x)\cdots f_{m-1}(x+(m-1)y)\psi(x,y)\ll_M \delta_2^{c_M}. \end{align*}
Proof. Lemma 12.7 is a variation of Lemma 4.2 of [Reference Green and Tao17], and our proof follows very closely the proof of Lemma 4.2 of [Reference Green and Tao17]. We proceed by induction on $m$![]() . For $m=2$
. For $m=2$![]() , the statement $(i)$
, the statement $(i)$![]() is trivial since $\psi$
is trivial since $\psi$![]() , being a 0-step nilsequence, is just a constant.
, being a 0-step nilsequence, is just a constant.
To prove $(ii)$![]() for $m=2$
for $m=2$![]() , we let $\delta >0$
, we let $\delta >0$![]() be a parameter to be fixed later. Since $\psi$
be a parameter to be fixed later. Since $\psi$![]() is of the form $\psi (x,y)=F(\alpha x+\beta y)$
is of the form $\psi (x,y)=F(\alpha x+\beta y)$![]() for some 1-bounded, $M$
for some 1-bounded, $M$![]() -Lipschitz function $F:\mathbb {R}^{M}/\mathbb {Z}^{M}\to \mathbb {C}$
-Lipschitz function $F:\mathbb {R}^{M}/\mathbb {Z}^{M}\to \mathbb {C}$![]() and $\alpha ,\beta \in ({1}/{p})\mathbb {Z}/\mathbb {Z})^{M}$
and $\alpha ,\beta \in ({1}/{p})\mathbb {Z}/\mathbb {Z})^{M}$![]() , we can convolve $F$
, we can convolve $F$![]() with Fejér kernel to find a 1-bounded trigonometric polynomial $F_1:\mathbb {R}^{M}/\mathbb {Z}^{M}\to \mathbb {C}$
with Fejér kernel to find a 1-bounded trigonometric polynomial $F_1:\mathbb {R}^{M}/\mathbb {Z}^{M}\to \mathbb {C}$![]() of degree $O_M(\delta ^{-C_M})$
of degree $O_M(\delta ^{-C_M})$![]() satisfying $\|F-F_1\|_\infty \leqslant \delta$
satisfying $\|F-F_1\|_\infty \leqslant \delta$![]() . Details of how this can be done may be found in the proof of Proposition 3.1 of [Reference Green and Tao19], for instance. It then follows from the pigeonhole principle that
. Details of how this can be done may be found in the proof of Proposition 3.1 of [Reference Green and Tao19], for instance. It then follows from the pigeonhole principle that
for some $a,b\in \mathbb {Z}$![]() . Incorporating $e_p(ax)$
. Incorporating $e_p(ax)$![]() into $f_0$
into $f_0$![]() and applying Cauchy–Schwarz inequality twice to remove $f_0(x)$
and applying Cauchy–Schwarz inequality twice to remove $f_0(x)$![]() and $e_p(by)$
and $e_p(by)$![]() , respectively, allows us to bound
, respectively, allows us to bound
from above by $\|f_1\|_{U^{2}}$![]() , and similar maneuvers also give a bound by $\|f_0\|_{U^{2}}$
, and similar maneuvers also give a bound by $\|f_0\|_{U^{2}}$![]() ; thus
; thus
Letting $\delta =\delta _2^{c_M}$![]() for a sufficiently small $0< c_M<1$
for a sufficiently small $0< c_M<1$![]() , we obtain the claim.
, we obtain the claim.
We now assume $m>2$![]() , and we let $\psi (x,y)=F(g(x,y)\varGamma )$
, and we let $\psi (x,y)=F(g(x,y)\varGamma )$![]() be a nilsequence of complexity $M$
be a nilsequence of complexity $M$![]() and degree $s\in \{m-2,m-1\}$
and degree $s\in \{m-2,m-1\}$![]() . Let $\delta >0$
. Let $\delta >0$![]() . Using the vertical decomposition of $F$
. Using the vertical decomposition of $F$![]() [Reference Green and Tao19, Section 3], we can find a 1-bounded function $F_1:G/\varGamma \to \mathbb {C}$
[Reference Green and Tao19, Section 3], we can find a 1-bounded function $F_1:G/\varGamma \to \mathbb {C}$![]() that is a linear combination of $O_{M}(\delta ^{-C_M})$
that is a linear combination of $O_{M}(\delta ^{-C_M})$![]() functions with vertical characters, i.e. functions $f:G/\varGamma \to \mathbb {C}$
functions with vertical characters, i.e. functions $f:G/\varGamma \to \mathbb {C}$![]() for which there exists a continuous homomorphism $\xi :G_s/\varGamma _s\to \mathbb {R}/\mathbb {Z}$
for which there exists a continuous homomorphism $\xi :G_s/\varGamma _s\to \mathbb {R}/\mathbb {Z}$![]() satisfying $f(g_s u)=e(\xi (g_s))f(u)$
satisfying $f(g_s u)=e(\xi (g_s))f(u)$![]() for any $g_s\in G_s$
for any $g_s\in G_s$![]() . Using pigeonhole principle, we can thus find a 1-bounded, $M$
. Using pigeonhole principle, we can thus find a 1-bounded, $M$![]() -Lipschitz function $F_2:G/\varGamma \to \mathbb {C}$
-Lipschitz function $F_2:G/\varGamma \to \mathbb {C}$![]() with a vertical character $\xi : G_s/\varGamma _s\to \mathbb {C}$
with a vertical character $\xi : G_s/\varGamma _s\to \mathbb {C}$![]() satisfying
satisfying

where $\psi _2(x,y)=F_2(g(x,y)\varGamma )$![]() .
.
By the Cauchy–Schwarz inequality and change of variables, we have

where we recall that $\Delta _h f(x):= f(x+h)\overline {f(x)}$![]() . A straightforward adaptation of the arguments from Section 7 of [Reference Green and Tao19] shows that the function $\tilde {\psi }_h(x,y)=\psi _2(x,y+h)\overline {\psi _2(x,y)}$
. A straightforward adaptation of the arguments from Section 7 of [Reference Green and Tao19] shows that the function $\tilde {\psi }_h(x,y)=\psi _2(x,y+h)\overline {\psi _2(x,y)}$![]() is a nilsequence of complexity $O_M(1)$
is a nilsequence of complexity $O_M(1)$![]() and degree $s-1$
and degree $s-1$![]() . Picking $\delta =\delta _2^{c_M}$
. Picking $\delta =\delta _2^{c_M}$![]() for an appropriate value of $0< c_M<1$
for an appropriate value of $0< c_M<1$![]() and applying inductive hypothesis, we obtain
and applying inductive hypothesis, we obtain
An application of the Hölder inequality and the recursive definition of Gowers norms give
for some $0< c'_M<1$![]() . A slight modification of the argument gives the same bound in terms of $\|f_0\|_{U^{s}}$
. A slight modification of the argument gives the same bound in terms of $\|f_0\|_{U^{s}}$![]() , completing the proof of the lemma.
, completing the proof of the lemma.
Knowing thanks to Lemma 12.7 how to proceed in the special case of $f_m$![]() being a nilsequence, we now prove the general case. Proposition 12.1 and Proposition 12.8 together prove Theorem 1.7.
being a nilsequence, we now prove the general case. Proposition 12.1 and Proposition 12.8 together prove Theorem 1.7.
Proposition 12.8 Let $m,d\in \mathbb {N}_+$![]() satisfy $2\leqslant d\leqslant m-1$
satisfy $2\leqslant d\leqslant m-1$![]() . Given any $\epsilon >0$
. Given any $\epsilon >0$![]() , there exists $\delta >0$
, there exists $\delta >0$![]() and $p_0\in \mathbb {N}$
and $p_0\in \mathbb {N}$![]() s.t. for all $p>p_0$
s.t. for all $p>p_0$![]() , we have
, we have
uniformly for all 1-bounded functions $f_0, \ldots ,f_m:\mathbb {F}_p\to \mathbb {C}$![]() such that $\|f_i\|_{U^{s}}\leqslant \delta$
such that $\|f_i\|_{U^{s}}\leqslant \delta$![]() for some $i\in \{0,\ldots , m-1\}$
for some $i\in \{0,\ldots , m-1\}$![]() , where
, where

Proof. We fix $\epsilon >0$![]() , and we let $\delta >0$
, and we let $\delta >0$![]() , $p_0\in \mathbb {N}_+$
, $p_0\in \mathbb {N}_+$![]() and a growth function $\mathcal {F}:\mathbb {R}_+\to \mathbb {R}_+$
and a growth function $\mathcal {F}:\mathbb {R}_+\to \mathbb {R}_+$![]() be chosen later. Suppose that $\min _{0\leqslant i\leqslant m-1}\|f_i\|_{U^{s}}\leqslant \delta$
be chosen later. Suppose that $\min _{0\leqslant i\leqslant m-1}\|f_i\|_{U^{s}}\leqslant \delta$![]() . By Lemma 2.13, there exist $M=O_{\epsilon ,\mathcal {F}}(1)$
. By Lemma 2.13, there exist $M=O_{\epsilon ,\mathcal {F}}(1)$![]() , a filtered manifold $G/\varGamma$
, a filtered manifold $G/\varGamma$![]() of degree $s_0=\left \lceil {m}/{d}\right \rceil - 1$
of degree $s_0=\left \lceil {m}/{d}\right \rceil - 1$![]() and complexity at most $M$
and complexity at most $M$![]() , and a $p$
, and a $p$![]() -periodic sequence $g\in {\textrm {poly}}(\mathbb {Z},G_\bullet )$
-periodic sequence $g\in {\textrm {poly}}(\mathbb {Z},G_\bullet )$![]() with $g(0)=1$
with $g(0)=1$![]() , for which there exists a decomposition
, for which there exists a decomposition
such that $f_{nil}(n)=F(g(n)\varGamma )$![]() for an $M$
for an $M$![]() -Lipschitz function $F: G/\varGamma \to \mathbb {C}$
-Lipschitz function $F: G/\varGamma \to \mathbb {C}$![]() , ${\|f_{sml}\|_2\leqslant \epsilon }$
, ${\|f_{sml}\|_2\leqslant \epsilon }$![]() and $\|f_{unf}\|_{U^{s_0+1}}\leqslant \frac {1}{\mathcal {F}(M)}$
and $\|f_{unf}\|_{U^{s_0+1}}\leqslant \frac {1}{\mathcal {F}(M)}$![]() . Using the bound on $f_{sml}$
. Using the bound on $f_{sml}$![]() , we crudely evaluate its contribution by
, we crudely evaluate its contribution by
To bound the contribution of $f_{unf}$![]() , we choose $\delta '>0$
, we choose $\delta '>0$![]() and $p_0$
and $p_0$![]() that work for $\epsilon$
that work for $\epsilon$![]() as in Proposition 12.1. We then pick $\mathcal {F}$
as in Proposition 12.1. We then pick $\mathcal {F}$![]() to be growing sufficiently fast so that $\|f_{unf}\|_{U^{s_0+1}}\leqslant \delta '$
to be growing sufficiently fast so that $\|f_{unf}\|_{U^{s_0+1}}\leqslant \delta '$![]() . Assuming that $p>p_0$
. Assuming that $p>p_0$![]() and applying Proposition 12.1, we have
and applying Proposition 12.1, we have
Finally, we observe that $f_{nil}(x+y^{d})$![]() is a $p$
is a $p$![]() -periodic nilsequence of complexity $M$
-periodic nilsequence of complexity $M$![]() and degree $d\left \lfloor \frac {m-1}{d}\right \rfloor \leqslant s-1$
and degree $d\left \lfloor \frac {m-1}{d}\right \rfloor \leqslant s-1$![]() . Using Lemma 12.7, we choose $\delta >0$
. Using Lemma 12.7, we choose $\delta >0$![]() in such a way as to guarantee that
in such a way as to guarantee that
In the case of $x, x+y, x+2y, x+y^{2}$![]() , Proposition 12.8 gives us control of the first three terms by the $U^{3}$
, Proposition 12.8 gives us control of the first three terms by the $U^{3}$![]() norm. It turns out, however, that for this specific example, we can get control by the $u^{3}$
norm. It turns out, however, that for this specific example, we can get control by the $u^{3}$![]() norm instead.
norm instead.
Proposition 12.9 Given any $\epsilon >0$![]() , there exists $\delta >0$
, there exists $\delta >0$![]() and $p_0\in \mathbb {N}$
and $p_0\in \mathbb {N}$![]() s.t. for all $p>p_0$
s.t. for all $p>p_0$![]() , we have
, we have
uniformly for all 1-bounded functions $f_0, f_1, f_2, f_3:\mathbb {F}_p\to \mathbb {C}$![]() satisfying $\|f_i\|_{u^{3}}\leqslant \delta$
satisfying $\|f_i\|_{u^{3}}\leqslant \delta$![]() for some $i\in \{0, 1,2\}$
for some $i\in \{0, 1,2\}$![]() .
.
Propositions 12.1 and 12.9 together prove Theorem 1.6.
Proof. Fix $\epsilon >0$![]() , and let $\epsilon '>0$
, and let $\epsilon '>0$![]() be chosen later. Given $\epsilon '>0$
be chosen later. Given $\epsilon '>0$![]() , we choose $\delta '>0$
, we choose $\delta '>0$![]() and $p_0$
and $p_0$![]() given by Proposition 12.1. Suppose that for at least one of $f_0, f_1, f_2$
given by Proposition 12.1. Suppose that for at least one of $f_0, f_1, f_2$![]() , we have $\|f_i\|_{u^{3}}\leqslant \delta$
, we have $\|f_i\|_{u^{3}}\leqslant \delta$![]() for $\delta >0$
for $\delta >0$![]() to be chosen later. Without loss of generality, suppose this holds for $f_0$
to be chosen later. Without loss of generality, suppose this holds for $f_0$![]() .
.
We apply the following decomposition based on the Hahn–Banach theorem, a variant of which was used in [Reference Gowers10, Reference Green and Tao18–Reference Green, Tao and Ziegler21, Reference Kuca25, Reference Peluse29, Reference Peluse and Prendiville31].
Lemma 12.10 (Hahn–Banach decomposition) Let $f:\mathbb {F}_p\to \mathbb {C}$![]() and $\|\cdot \|$
and $\|\cdot \|$![]() be a norm on the space of $\mathbb {C}$
be a norm on the space of $\mathbb {C}$![]() -valued functions from $\mathbb {F}_p$
-valued functions from $\mathbb {F}_p$![]() . Suppose $\|f\|_{L^{2}}\leqslant 1$
. Suppose $\|f\|_{L^{2}}\leqslant 1$![]() and $\eta >0$
and $\eta >0$![]() . Then there exists a decomposition
. Then there exists a decomposition
with $\|f_a\|^{*}\leqslant \delta '^{-2}\epsilon '^{-{1}/{2}}$![]() , $\|f_b\|_{1}\leqslant \epsilon '^{{1}/{4}}$
, $\|f_b\|_{1}\leqslant \epsilon '^{{1}/{4}}$![]() , $\|f_c\|_{\infty }\leqslant \epsilon '^{-{1}/{2}}$
, $\|f_c\|_{\infty }\leqslant \epsilon '^{-{1}/{2}}$![]() , $\|f_c\|\leqslant \delta '\epsilon '^{{1}/{2}}$
, $\|f_c\|\leqslant \delta '\epsilon '^{{1}/{2}}$![]() provided $0<\delta ', \epsilon '<{1}/{10}$
provided $0<\delta ', \epsilon '<{1}/{10}$![]() .
.
We use Lemma 12.10 to split $f_3$![]() with respect to the $U^{2}$
with respect to the $U^{2}$![]() norm. The contribution of the term $f_b$
norm. The contribution of the term $f_b$![]() to the counting operator is given by
to the counting operator is given by
Using Proposition 12.1, the contribution of $f_c$![]() is
is

Finally, the contribution coming from $f_a$![]() can be evaluated using $U^{2}$
can be evaluated using $U^{2}$![]() inverse theorem as
inverse theorem as

Since there exist quadratic polynomials $Q_0, Q_1, Q_2$![]() satisfying
satisfying
we can bound

Bringing all the bounds together, we have
Upon setting $\epsilon '=\epsilon ^{4}$![]() and $\delta = \epsilon ^{3}\delta '^{2}$
and $\delta = \epsilon ^{3}\delta '^{2}$![]() , and using $\|f_0\|_{U^{s}}\leqslant \delta$
, and using $\|f_0\|_{U^{s}}\leqslant \delta$![]() , we obtain
, we obtain
as required.
Acknowledgements
The author would like to thank Sean Prendiville for suggesting the problem, directing to relevant literature and help with editing the paper. The author is also indebted to Tuomas Sahlsten for comments on an earlier version of the paper, and to the anonymous referee for helpful suggestions.
Appendix A. Proof of Lemma 2.13
In this section, we give the proof of Lemma 2.13, which is the simultaneous and periodic version of arithmetic regularity lemma.
Proof of Lemma 2.13. Fix $\epsilon >0$![]() and a growth function $\mathcal {F}:\mathbb {R}_+\to \mathbb {R}_+$
and a growth function $\mathcal {F}:\mathbb {R}_+\to \mathbb {R}_+$![]() . We pick another growth function $\mathcal {F}_0$
. We pick another growth function $\mathcal {F}_0$![]() that grows sufficiently slowly with respect to $\mathcal {F}$
that grows sufficiently slowly with respect to $\mathcal {F}$![]() . By Theorem 3.4 of [Reference Candela and Sisask4], there exists $0< M_0=O_{ s,\epsilon , \mathcal {F}_0}(1)$
. By Theorem 3.4 of [Reference Candela and Sisask4], there exists $0< M_0=O_{ s,\epsilon , \mathcal {F}_0}(1)$![]() such that for each $i$
such that for each $i$![]() there is a filtered nilmanifold $G_i/\varGamma _i$
there is a filtered nilmanifold $G_i/\varGamma _i$![]() of complexity $M_0$
of complexity $M_0$![]() and degree $s$
and degree $s$![]() , a $p$
, a $p$![]() -periodic sequence $g_i\in {\textrm {poly}}(\mathbb {Z},(G_i)_\bullet )$
-periodic sequence $g_i\in {\textrm {poly}}(\mathbb {Z},(G_i)_\bullet )$![]() , and an $M_0$
, and an $M_0$![]() -Lipschitz function $F'_i:G_i/\varGamma _i\to \mathbb {C}$
-Lipschitz function $F'_i:G_i/\varGamma _i\to \mathbb {C}$![]() for which $f_i$
for which $f_i$![]() decomposes into
decomposes into
where the properties (ii), (iii), (iv) in Lemma 2.13 hold with $M_0$![]() in place of $M$
in place of $M$![]() and $\mathcal {F}_0$
and $\mathcal {F}_0$![]() in place of $\mathcal {F}$
in place of $\mathcal {F}$![]() , and moreover $f_{i,nil}(n)=F'_i(g_i(n)\varGamma _i)$
, and moreover $f_{i,nil}(n)=F'_i(g_i(n)\varGamma _i)$![]() . By redefining $F'_i$
. By redefining $F'_i$![]() and increasing its Lipschitz norm by a factor $O_{M_0}(1)$
and increasing its Lipschitz norm by a factor $O_{M_0}(1)$![]() if necessary, we can also assume that $g_i'(0)=1$
if necessary, we can also assume that $g_i'(0)=1$![]() for all $1\leqslant i\leqslant t$
for all $1\leqslant i\leqslant t$![]() .
.
We let
and we define $F_i(x_1\varGamma _1, \ldots , x_t\varGamma _t) := F'_i(x_i\varGamma _i)$![]() . With this definition, we can realize each $f_{i,nil}$
. With this definition, we can realize each $f_{i,nil}$![]() as a $p$
as a $p$![]() -periodic nilsequence $f_{i,nil}(n)=F_i(g(n)\varGamma )$
-periodic nilsequence $f_{i,nil}(n)=F_i(g(n)\varGamma )$![]() of degree $s$
of degree $s$![]() and complexity $M_0 t$
and complexity $M_0 t$![]() on the same nilmanifold $G/\varGamma$
on the same nilmanifold $G/\varGamma$![]() using the same $p$
using the same $p$![]() -periodic sequence $g$
-periodic sequence $g$![]() for all $1\leqslant i\leqslant t$
for all $1\leqslant i\leqslant t$![]() .
.
The next step is to obtain irrationality on the nilsequences $f_{1,nil}$![]() , …, $f_{t, nil}$
, …, $f_{t, nil}$![]() . In doing so, we apply the proof of Theorem 5.1 of [Reference Candela and Sisask4], which we rerun here for completeness. Given a growth function $\mathcal {F}_1$
. In doing so, we apply the proof of Theorem 5.1 of [Reference Candela and Sisask4], which we rerun here for completeness. Given a growth function $\mathcal {F}_1$![]() to be chosen later, we use Proposition 5.2 of [Reference Candela and Sisask4] to obtain $M_1\in [M_0, O_{M_0, t, \mathcal {F}_1}(1)]$
to be chosen later, we use Proposition 5.2 of [Reference Candela and Sisask4] to obtain $M_1\in [M_0, O_{M_0, t, \mathcal {F}_1}(1)]$![]() and a $p$
and a $p$![]() -periodic polynomial $g'\in {\textrm {poly}}(\mathbb {Z},G'_\bullet )$
-periodic polynomial $g'\in {\textrm {poly}}(\mathbb {Z},G'_\bullet )$![]() on some nilmanifold $G'/\varGamma '$
on some nilmanifold $G'/\varGamma '$![]() of complexity $O_{M_1}(1)$
of complexity $O_{M_1}(1)$![]() satisfying $g'(n)\varGamma = g(n)\varGamma$
satisfying $g'(n)\varGamma = g(n)\varGamma$![]() . By abuse of notation, we let $F_i$
. By abuse of notation, we let $F_i$![]() denote now its restriction to $G'/\varGamma '$
denote now its restriction to $G'/\varGamma '$![]() for each $1\leqslant i\leqslant t$
for each $1\leqslant i\leqslant t$![]() . It is $O_{M_1}(1)$
. It is $O_{M_1}(1)$![]() -Lipschitz on $G'/\varGamma '$
-Lipschitz on $G'/\varGamma '$![]() . Therefore, the nilsequence $f_{i, nil}$
. Therefore, the nilsequence $f_{i, nil}$![]() has complexity $M\leqslant \mathcal {F}_2(M_1)$
has complexity $M\leqslant \mathcal {F}_2(M_1)$![]() for some function $\mathcal {F}_2$
for some function $\mathcal {F}_2$![]() . Letting $\mathcal {F}_1(x)=\mathcal {F}(\mathcal {F}_2(x))$
. Letting $\mathcal {F}_1(x)=\mathcal {F}(\mathcal {F}_2(x))$![]() thus guarantees that $g'$
thus guarantees that $g'$![]() is $\mathcal {F}(M)$
is $\mathcal {F}(M)$![]() -irrational. To guarantee $\|f_{i,nil}\|_{U^{s}}\leqslant {1}/{\mathcal {F}(M)}$
-irrational. To guarantee $\|f_{i,nil}\|_{U^{s}}\leqslant {1}/{\mathcal {F}(M)}$![]() , we pick $\mathcal {F}_0$
, we pick $\mathcal {F}_0$![]() so that $\mathcal {F}_0(M_0)\geqslant \mathcal {F}(M)$
so that $\mathcal {F}_0(M_0)\geqslant \mathcal {F}(M)$![]() using $M = O_{M_1}(1)=O_{M_0,t,\mathcal {F}}(1)$
using $M = O_{M_1}(1)=O_{M_0,t,\mathcal {F}}(1)$![]() . Combining all the bounds, we have $M=O_{s,t,\epsilon , \mathcal {F}}(1)$
. Combining all the bounds, we have $M=O_{s,t,\epsilon , \mathcal {F}}(1)$![]() , as desired.
, as desired.
In their statement of Theorem 3.4 of [Reference Candela and Sisask4], the authors only considered functions from $\mathbb {F}_p$![]() to $[0,1]$
to $[0,1]$![]() . However, the statement works for arbitrary 1-bounded functions from $\mathbb {F}_p$
. However, the statement works for arbitrary 1-bounded functions from $\mathbb {F}_p$![]() to $\mathbb {C}$
to $\mathbb {C}$![]() by splitting them into the real and imaginary part, and the positive and negative part. This way, we split a 1-bounded function from $\mathbb {F}_p$
by splitting them into the real and imaginary part, and the positive and negative part. This way, we split a 1-bounded function from $\mathbb {F}_p$![]() to $\mathbb {C}$
to $\mathbb {C}$![]() into four 1-bounded functions from $\mathbb {F}_p$
into four 1-bounded functions from $\mathbb {F}_p$![]() to $[0,1]$
to $[0,1]$![]() , implying the 4-boundedness of $f_{i,nil}$
, implying the 4-boundedness of $f_{i,nil}$![]() , $f_{i,sml}$
, $f_{i,sml}$![]() and $f_{i,unf}$
and $f_{i,unf}$![]() .
.
Appendix B. Baker–Campbell–Hausdorff formula
This section describes some useful consequences of Baker–Campbell–Hausdorff formula and contains the same material as Appendix C in [Reference Green and Tao17], which we restate here for completeness.
Let $G$![]() be a $s$
be a $s$![]() -step nilpotent, connected, simply connected Lie group with Lie algebra $\mathfrak {g}$
-step nilpotent, connected, simply connected Lie group with Lie algebra $\mathfrak {g}$![]() and the exponential map $\exp :\mathfrak {g}\to G$
and the exponential map $\exp :\mathfrak {g}\to G$![]() . For any $X_1, X_2\in \mathfrak {g}$
. For any $X_1, X_2\in \mathfrak {g}$![]() , we have
, we have

where $c_\alpha ={c_{1,\alpha }}/{c_{2,\alpha }}\in \mathbb {Q}$![]() for integers $c_{1,\alpha }, c_{2,\alpha }\ll _s 1$
for integers $c_{1,\alpha }, c_{2,\alpha }\ll _s 1$![]() , and $X_\alpha$
, and $X_\alpha$![]() is a Lie bracket of $k_1=k_{1,\alpha }$
is a Lie bracket of $k_1=k_{1,\alpha }$![]() copies of $X_1$
copies of $X_1$![]() and $k_2=k_{2,\alpha }$
and $k_2=k_{2,\alpha }$![]() copies of $X_2$
copies of $X_2$![]() for some $k_1, k_2\geqslant 1$
for some $k_1, k_2\geqslant 1$![]() and $k_1+k_2\geqslant 3$
and $k_1+k_2\geqslant 3$![]() .
.
In particular, for any $g_1, g_2\in G$![]() and $x\in \mathbb {R}$
and $x\in \mathbb {R}$![]() , we have
, we have
where $g_\alpha$![]() is an iterated commutator of $k_1=k_{1,\alpha }$
is an iterated commutator of $k_1=k_{1,\alpha }$![]() copies of $g_1$
copies of $g_1$![]() and $k_2 = k_{2,\alpha }$
and $k_2 = k_{2,\alpha }$![]() copies of $g_2$
copies of $g_2$![]() for $k_1, k_2\geqslant 1$
for $k_1, k_2\geqslant 1$![]() , and $Q_\alpha :\mathbb {R}\to \mathbb {R}$
, and $Q_\alpha :\mathbb {R}\to \mathbb {R}$![]() is a polynomial of degree at most $k_1+k_2$
is a polynomial of degree at most $k_1+k_2$![]() satisfying $Q_\alpha (0)=0$
satisfying $Q_\alpha (0)=0$![]() .
.
Moreover, for any $g_1, g_2\in G$![]() and $x_1, x_2\in \mathbb {R}$
and $x_1, x_2\in \mathbb {R}$![]() , we have
, we have
where $g_\alpha$![]() is an iterated commutator of $k_1=k_{1,\alpha }$
is an iterated commutator of $k_1=k_{1,\alpha }$![]() copies of $g_1$
copies of $g_1$![]() and $k_2 = k_{2,\alpha }$
and $k_2 = k_{2,\alpha }$![]() copies of $g_2$
copies of $g_2$![]() for $k_1, k_2\geqslant 1$
for $k_1, k_2\geqslant 1$![]() , $k_1+k_2\geqslant 3$
, $k_1+k_2\geqslant 3$![]() whereas $Q_\alpha :\mathbb {R}\times \mathbb {R}\to \mathbb {R}$
whereas $Q_\alpha :\mathbb {R}\times \mathbb {R}\to \mathbb {R}$![]() is a polynomial of degree at most $k_1$
is a polynomial of degree at most $k_1$![]() in $x_1$
in $x_1$![]() and $k_2$
and $k_2$![]() in $x_2$
in $x_2$![]() , which moreover satisfies $Q_\alpha (x_1,0)=Q_\alpha (0,x_2)=0$
, which moreover satisfies $Q_\alpha (x_1,0)=Q_\alpha (0,x_2)=0$![]() .
.
Appendix C. Scaling a polynomial sequence
The following lemma is a stronger version of Lemma 5.3 in [Reference Candela and Sisask4], which itself specializes Lemma A.8 of [Reference Green and Tao17].
Lemma C.1 Let $G/\varGamma$![]() be a filtered nilmanifold of degree $s$
be a filtered nilmanifold of degree $s$![]() and $g\in {\textrm {poly}}(\mathbb {Z},G_\bullet )$
and $g\in {\textrm {poly}}(\mathbb {Z},G_\bullet )$![]() be given by $g(n)=\prod _{i=0}^{s} g_i^{{n}\choose {i}}$
be given by $g(n)=\prod _{i=0}^{s} g_i^{{n}\choose {i}}$![]() . Define $h(n)=g(pn)=\prod _{i=0}^{s} h_i^{{n}\choose {i}}$
. Define $h(n)=g(pn)=\prod _{i=0}^{s} h_i^{{n}\choose {i}}$![]() . Then
. Then
for any $i\in \mathbb {N}_+$![]() .
.
Proof. We fix $i\in \mathbb {N}_+$![]() . Since we only care about the value of $h_i$
. Since we only care about the value of $h_i$![]() mod $G_{i+1}$
mod $G_{i+1}$![]() , we can quotient out $G$
, we can quotient out $G$![]() by $G_{i+1}$
by $G_{i+1}$![]() , so that
, so that

By observing that ${{pn}\choose {k}}=p^{k}{{n}\choose {k}}+\sum \nolimits _{l=1}^{k-1}a_{k,l}{{n}\choose {l}}$![]() for some ${a_{k,l}\in \mathbb {Z}}$
for some ${a_{k,l}\in \mathbb {Z}}$![]() , we rewrite
, we rewrite

After rearranging the terms of $g(n)$![]() using (40) and (41), we obtain
using (40) and (41), we obtain

for some $h_k \in G_k$![]() and some commutators $g_\alpha$
and some commutators $g_\alpha$![]() .
.
The important observation here is that each commutator $g_\alpha$![]() is obtained iteratively from (40) or (41) applied to elements $\tilde {g}_{i_1}^{{n}\choose {l_1}}$
is obtained iteratively from (40) or (41) applied to elements $\tilde {g}_{i_1}^{{n}\choose {l_1}}$![]() , $\tilde {g}_{i_2}^{{n}\choose {l_2}}$
, $\tilde {g}_{i_2}^{{n}\choose {l_2}}$![]() belonging to $G_{i_1}$
belonging to $G_{i_1}$![]() and $G_{i_2}$
and $G_{i_2}$![]() respectively, where $1\leqslant l_1\leqslant i_1$
respectively, where $1\leqslant l_1\leqslant i_1$![]() and $1\leqslant l_2 \leqslant i_2$
and $1\leqslant l_2 \leqslant i_2$![]() . However, we do not have $l_1 = i_1$
. However, we do not have $l_1 = i_1$![]() and $l_2 = i_2$
and $l_2 = i_2$![]() simultaneously because we never commute the elements $g_{i_1}^{p^{i_1}{{n}\choose {i_1}}}$
simultaneously because we never commute the elements $g_{i_1}^{p^{i_1}{{n}\choose {i_1}}}$![]() and $g_{i_2}^{p^{i_2}{{n}\choose {i_2}}}$
and $g_{i_2}^{p^{i_2}{{n}\choose {i_2}}}$![]() with each other. Without loss of generality, assume then that $l_2< i_2$
with each other. Without loss of generality, assume then that $l_2< i_2$![]() . If $g_\alpha$
. If $g_\alpha$![]() therefore is a $(k_1+k_2)$
therefore is a $(k_1+k_2)$![]() -fold commutator consisting of $k_1$
-fold commutator consisting of $k_1$![]() copies of $\tilde {g}_{i_1}$
copies of $\tilde {g}_{i_1}$![]() and $k_2$
and $k_2$![]() copies of $\tilde {g}_{i_2}$
copies of $\tilde {g}_{i_2}$![]() , then $g_\alpha \in G_{i_1 k_1+i_2 k_2}$
, then $g_\alpha \in G_{i_1 k_1+i_2 k_2}$![]() while $Q_\alpha$
while $Q_\alpha$![]() is a polynomial of degree at most
is a polynomial of degree at most
If $g_\alpha ^{Q_\alpha (n)}$![]() thus contributes to the Taylor coefficient of ${{n}\choose {i}}$
thus contributes to the Taylor coefficient of ${{n}\choose {i}}$![]() in $h$
in $h$![]() , then $k_1 l_1 + k_2 l_2\geqslant i$
, then $k_1 l_1 + k_2 l_2\geqslant i$![]() , implying that $k_1 i_1 + k_2 i_2 \geqslant i+1$
, implying that $k_1 i_1 + k_2 i_2 \geqslant i+1$![]() . Hence $g_\alpha \in G_{i+1}$
. Hence $g_\alpha \in G_{i+1}$![]() , as claimed.
, as claimed.