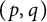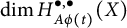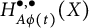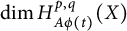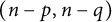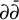Refine search
Actions for selected content:
1 results
Deformed Aeppli cohomology: canonical deformations and jumping formulas
- Part of
-
- Journal:
- Canadian Journal of Mathematics , First View
- Published online by Cambridge University Press:
- 21 July 2025, pp. 1-34
-
- Article
- Export citation
-
Given a complex analytic family of complex manifolds, we consider canonical Aeppli deformations of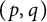
$(p,q)$-forms and study its relations to the varying of dimension of the deformed Aeppli cohomology 
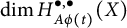$\dim H^{\bullet ,\bullet }_{A\phi (t)}(X)$. In particular, we prove the jumping formula for the deformed Aeppli cohomology 
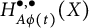$H^{\bullet ,\bullet }_{A\phi (t)}(X)$. As a direct consequence, 
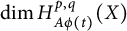$\dim H^{p,q}_{A\phi (t)}(X)$ remains constant iff the Bott–Chern deformations of 
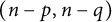$(n-p,n-q)$-forms and the Aeppli deformations of 
$(n-p-1,n-q-1)$-forms are canonically unobstructed. Furthermore, the Bott–Chern/Aeppli deformations are shown to be unobstructed if some weak forms of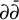 
${ \partial }{ \bar {\partial } }$-lemma is satisfied.
